初中数学一题多解题
【中考复习】初中数学典型一题多解试题汇编(含解析)

初中数学一题多解(试题)1、若()16x 3-m 2x 2++ 是关于x 的完全平方公式(或完全平方数),则m=2、4的平方根为 ,16的平方根为 3、若2a =时, a 为 。
在数轴上,到原点的距离为3个单位的数有 。
4、若64x 1x 2=⎪⎭⎫ ⎝⎛+ ,则代数式=+x 1x 5、若关于x 的方程16-x 3m 4x m 4-x 12+=++无解,则m 的值为 6、在平面直角坐标系xoy 中,已知点A (3,4),点P 在x 轴上,若△AOP 为等腰三角形,则点P 的坐标是7、在一个等腰三角形中,有一个角为70°,则另两个角分别为8、已知直角三角形的两边长分别为5和12,那么以这个直角三角形的斜边为边长的正方形的面积为9、 在△ABC 中,AB=15,AC=13,BC 边上的高为12,求BC 边的边长为10、在平行四边形ABCD 中,∠A 的角平分线把BC 边分为3和4的两条线段,则此平行四边形ABCD 的周长为11、若⊙O 的半径为5cm ,某个点A 到圆上的距离为2cm ,则圆心到点A 的距离为12、 若⊙O 中的某条弦AB 所对的圆心角为120°,则弦AB 所对的圆周角为13、已知x满足62x1x22=+,则x1x+的值是14、当-2≤x≤1时,二次函数()1mm-x-y22++=有最大值4,则实数m 的值为15、在平面直角坐标系中有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标为16、若某条线段AB长为2,则该线段AB的黄金分割点离A点的距离为17、若△OAB与△OCD是以坐标原点O为位似中心的位似图形,相似比为3:4,∠OCD=90°,∠AOB=60°,若点B的坐标为(6,0),则点A的对应点C的坐标为18、如下图在△ABC中,AB=5,AC=4,点Q从点A出发向点B以2个单位/s的速度出发,点P从点C向点A以1个单位/s的速度出发,若要使△ABC 与△AQP相似,则运动的时间为s。
人教版数学八年级上册代数经典集锦---一题多解(含答案)

2019--2020人教版数学八年级代数经典集锦---一题多解在初中几何的证明和求解中,需要培养学生严密推理论证能力、灵动转化变换思维等方面素养,而在初中代数的计算过程中,需要培养学生多角度、多维度思考问题,掌握整体与局部、特例分析等全方位能力,从而寻求结果,下面以一道经典例题的不同解法,展开思维训练。
1、已知:x y = - 2,则x 2-2xy-3y 2x 2-6xy-7y 2 = .解法一:令x=2,y=-1,则x 2-2xy-3y 2=22-2*2*(-1)-3*(-1)2=4+4-3=5,X 2-6xy-7y 2=22-6*2*(-1)-7*(-1)2=4+12-7=9,所以,原式=59 .李老师点评:本解法是最简单却学生最不容易想到的解法。
原式看起来很复杂,x,y 只给出了比例关系,没有给出具体数值,那么取特例也是满足题设要求的,所以,当没有寻找到更好的解决办法时,可以取特殊值进行计算。
解法二:由已知比例x y = - 2变形有:x=-2y ┅┅①将①带入原式有:x 2-2xy-3y 2=(-2y)2-2*(-2y)*y-3y 2=5y 2,X 2-6xy-7y 2=(-2y)2-6*(-2y)*y-7y 2=9y 2,x 2-2xy-3y 2x 2-6xy-7y 2 =59 .李老师点评:本解法使用了带入消元法进行解题,带入消元法是解决含有未知数类求值问题最基本的解题方法之一。
解法三:∵x y = - 2,∴x ≠0,y ≠0则将原式分子和分母同时除以y 2得到:x 2-2xy-3y 2x 2-6xy-7y 2 = = 59=李老师点评:本解法是一种技巧型解法,首先通过观察x,y 的取值情况以及原式中分子分母所含式子,我们会发现:x,y 都不等于0,同时分子分母其实每一项都是二次项(将x,y 都看作未知数),所以分子分母同时除以y2,便可以轻松的将原式化成已知条件中的样子,从而得解。
初中中考数学一题多解详细讲解一题

题目:如图1,△ABC中,∠C=90°,AC=8cm,AB=10cm,点P由点C出发以每秒2cm 的速度沿着线段CA向点A运动(不运动至A点),⊙O的圆心在BP上,且⊙O分别与AB、AC相切,当点P运动2秒钟时,⊙O的半径是( )A、cmB、cmC、cmD、2cm一、相似三角形与面积解法一:在Rt△ABC中,∵AB=10cm,AC=8cm,∴BC=6cm。
∵PC=4cm,∴PA=4cm。
设OD=x,⊙O的半径为r,∵OD∥AC,∴。
∴x=4-r。
∵S△ABC=S△AOC+ S△BOC+ S△AOB∴×10r+×8r+×6r=×6×8。
∴5r+4r+3(4-r)=24,∴r=(图1) (图2)解法二:如图2,在Rt△ABC中,∵AB=10cm,AC=8cm,∴BC=6cm∵P是AC的中点,∴S△ABP=×S△ABC=12∴AB×PH=24,PH=∵OE∥BC,OF∥PH,∴由①+②得∴r=(图3) (图4)二、相似三角形与勾股定理解法三:如图3,设OD=x,⊙O的半径为r,∵OD∥AC,∴。
∴x=4-r ①∵AE=AF=8-x,∴BF=2+x∴OD2+BD2=OF2+BF2,∴x2+(6-x)2=r2+(2+x)2,∴x=8-3r ②由①、②得4-r=8-3r,解得r=.三、三角函数与勾股定理解法四:如图4,设PE=x,⊙O的半径为r∵tg∠CDB=,∴x=r,由勾股定理得:PO=r,∴BO=2,解得r=四、三角形内角平分线性质解法五:如右图,∵AE、AF是⊙O的切线,∴∠1=∠2,∴,∴∵OE∥BC,∴,∴r=。
初中数学几何:一题多解

A D C P B初中数学培优专题:一题多解一题多解是数学学科的奇妙所在,尤其体现在几何的学习过程之中. 很多学生会从喜欢上几何从而喜欢上数学的原因,就在于几何图形的变换中,对“多解”的追求给他们带来思维创造的快乐. 数学教师在解题教学中也会通过“多解”的呈现和对比来调动学生思维的积极性、激发学生思维的灵活性. 笔者在教学过程中,通过对几何的“多解”探索,使笔者又有了新的认识.1 题目呈现如图1,在等腰直角三角形ABC 中,点P 为斜边AB 上一个动点(不与A 、B 两点重合),以CP 为斜边在直线CP 的左侧作等腰直角 CDP ∆,判断ADP ∆的形状并证明.图12 教学过程简录方法一:如图2,过C 点作AB CQ ⊥,连接DQ .易证DQ 平分CQA ∠,∴ 45=∠=∠DQA CQD∴CQD ∆≌AQD ∆(SAS ),∴CD AD =,又∵PD CD =∴DP AD =∴ADP ∆是等腰三角形 图2方法二:如图3,过C 点作AB CQ ⊥,连接DQ .易证CDQ ∆∽CPB ∆,∴ 45=∠=∠B DQC∴CQD ∆≌AQD ∆(SAS )以下同方法一.图3方法三:如图4,过C 点作CP CQ ⊥交PD 的延长线于点Q ,连接AQ . 易证CQA ∆≌CPB ∆∴PB AQ =, 45=∠=∠CBP CAQ∴ 90=∠QAP . 在等腰直角CPQ ∆中,D 点是PQ 的中点, 图4 ∴在PAQ Rt ∆中,PQ AD 21=,∴DP AD =∴ADP ∆是等腰三角形 . 方法四:如图5,过点C 作CD CM ⊥,过P 点作PD PM ⊥ 交CM 于点M ,过C 点作AB CQ ⊥交AB 于点Q ,连接QM ,BM . 易证四边形CDPM 为正方形,QM 平分CQP ∠,∴ 45=∠=∠PQM CQM , 图5∴CQM ∆≌BQM ∆(SAS )∴CM BM =,又∵PD CM =∴PD BM =易证CMB ∆≌CDA ∆,∴AD BM =,∴DP AD =∴ADP ∆是等腰三角形 .方法五:如图6,过点C 作CD CQ ⊥,过P 点作PD PQ ⊥交CQ 于点Q ,过点D 作AB DM ⊥交AB 于点M ,过点Q 作AB QN ⊥交AB 于点N .易证PDM ∆≌QPN ∆,CQB ∆≌CDA ∆. 图6∴PD PQ =,AD QB =,CQB CDA ∠=∠, 90=∠+∠PDM PQN . 又∵ADC CMB ADC ADP ∠-=∠-∠-=∠27036090-∠=∠-∠=∠CQB CQP CQB PQB∴ 180=∠+∠PQB ADP ,∴ 90=∠+∠ADM BQN ,∴DAM BQN ∠=∠,易证ADM ∆≌QBN ∆,∴QM AD =,∴DP AD =∴ADP ∆是等腰三角形 .3 对解法的再认识该图形简单又漂亮,更重要的是我们在初二几何里学的常见的辅助线的构造都可以在该图形中呈现.比如方法一,看到等腰三角形想“三线合一”,故过C 点作AB CQ ⊥交AB 于点Q ,由于CDP ∆是等腰直角三角形,则得到了常见的基本图形,如图7:如果CDP ∆为等腰三角形,QP CQ ⊥,那么连接直角三角形的直角顶点DQ ,则DQ 是CQP ∆的外角平分线,即45=∠=∠DQA CQD ,我们平时称该图形为“钻石三角形”. 再由CQD ∆和AQD ∆对称全等,得结果.与方法一类似,还可以构造“钻石三角形”的内角平分线,如图5. 由等腰 图7 直角CDP ∆想到构造正方形CDPM ,那么在图形CQPM 中,如图8:因为CMP ∆是等腰直角三角形,QP CQ ⊥,所以连接QM ,则QM 平分CQP ∠.(“钻石三角形”内角平分线),其它见方法四.在原题中,如图1,仔细观察该图形,是一个等腰三角形的顶点对另一个等腰三角形的底角的形式(简称“两个等腰三角形的顶对底”),我们还可以想到“加倍或减半”进行构造. 图8“加倍”如图4,就得到了共顶点的两个等腰直角三角形CPQ ∆和CBA ∆,构造“手拉手”基本模型,得全等,即CDP ∆≌CQA ∆.其实图5当中构造正方形也是另外一种形式的“加倍”,同样可构造“手拉手”基本模型.“减半”即把CAB ∆减半 ,如图3. 减半之后就得到了两个底角对底角的等腰直角三角形,CDP ∆和CQB ∆.那么通过“边对边、底对低”可得三角形相似,即CDQ ∆和CPB ∆相似,既而得到 45=∠=∠B DQC ,具体思路见方法二.或者看到等腰直角三角形,想到构造“三垂直”,如图6. 但这种方法要比其它方法复杂一点,就是要看到ADP ∠和PQB ∠互补,证明方法见方法五. 不过该方法也有它特别的一面,就是再往后研究,我们可以发现ADP ∆和BQP ∆不仅都是等腰三角形,而且面积也相等.综上以上五种方法可用一句话总结:过C 点通过旋转或翻折构造全等或相似.几何图形很神秘、很美妙、很漂亮,经常会有让人看它一眼就再也无法忘记的特别存在. 我们就是这样被它吸引着,不知不觉中发现了它们各自的独特美又发现了它们美的通性,而自己的思维与想象也在不断的发生着变化,从量变到质变,眼界与能力同时也得到了升华.。
最新初中数学一题多变、一题多解
CBAS 2S 3S 1CBAS 3S 2S 1S 3S 2S 1CBA一题多解、一题多变原题条件或结论的变化所谓条件或结论的变化,就是对某一问题的条件或结论进行变化探讨,并针对问题的内涵与外延进行深入与拓展,从而得到一类变式题组。
通过对问题的分析解决,使我们掌握某类问题的题型结构,深入认识问题的本质,提高解题能力。
例1 求证:顺次连接平行四边形各边中点所得的四边形是平行四边形。
变式1 求证:顺次连接矩形各边中点所得的四边形是菱形。
变式2 求证:顺次连接菱形各边中点所得的四边形是矩形。
变式3 求证:顺次连接正方形各边中点所得的四边形是正方形。
变式4 顺次连接什么四边形各边中点可以得到平行四边形? 变式5 顺次连接什么四边形各边中点可以得到矩形? 变式6 顺次连接什么四边形各边中点可以得到菱形? ……通过这样一系列变式训练,使学生充分掌握了四边形这一章节所有基础知识和基本概念,强化沟通了常见特殊四边形的性质定理、判定定理、三角形中位线定理等,极大地拓展了学生的解题思路,活跃了思维,激发了兴趣。
一、几何图形形状的变化如图1,分别以Rt ABC 的三边为边向外作三个正方形,其面积分别为321S S S 、、,则321S S S 、、之间的关系是图1 图2 图3E S 3S 2S 1DCBAS 3S 2S 1ABCDABCD S 3S 2S 1变式1:如图2,如果以Rt ∆ABC 的三边为直径向外作三个半圆,其面积分别为321S S S 、、,则321S S S 、、之间的关系是变式2:如图3,如果以Rt ∆ABC 的三边为边向外作三个正三角形,其面积分别为321S S S 、、,则321S S S 、、之间的关系是变式3:如果以Rt ∆ABC 的三边为边向外作三个一般三角形,其面积分别为321S S S 、、,为使321S S S 、、之间仍具有上述这种关系,所作三角形应满足什么条件?证明你的结论。
初中数学一题多变一题多解(六)

一题多解,一题多变(六)中考几何母题的一题多解(多变)一、三角形一题多解如图:已知AB=AC,E是AC延长线上一点,且有BF=CE,连接FE交BC于D。
求证:FD=DE。
证法一证明:过E点作EM ∥AB交DC延长线于M点,则∠M=∠B,又因为∠ACB=∠B∠ACB=∠ECM=∠M,所以CE=EM,又EC=BF 从而EM=BF,∠BFD=∠DEM则△DBF≌△DME,故FD=DE;证法二证明:过E点作EM ∥AB交DC延长线于M点,则∠M=∠B,又因为∠ACB=∠B∠ACB=∠ECM=∠M,所以CE=EM,又EC=BF 从而EM=BF,∠BFD=∠DEM则△DBF≌△DME,故 FD=DE;证法二证明:过F点作FM∥AE,交BD于点M,则∠1=∠2 = ∠B 所以BF=FM,又∠4=∠3 ∠5=∠E所以△DMF≌△DCE,故 FD=DE。
二、平行四边形一题多解如图4,平行四边形ABCD中AD=2AB,E、F在直线AB上,且AE=BF=AB,求证:DF⊥CE.证法一、易知ΔADF、ΔBCE为等腰三角形,故∠1=∠F, ∠2=∠E,又CD∥AB,故∠3=∠F, ∠4=∠E,从而∠1=∠3,∠2=∠4,而∠1+∠2+∠3+∠4=1800,故∠3+∠4=900,表明∠COD=900,所以DF⊥CE。
证法二、如图5,连接MN,则CD=BF,且CD∥BF,故BFCD为平行四边形,则CN=BN=AB,同理,DM=MA=AB,故CN=DM且CN∥DM,得平行四边形CDMN,易见CD=DM,故CDMN也是菱形,根据菱形的对角线互相垂直,结论成立。
证法三、如图6,连接BM、AN, 可证ΔAFN中,BN=BF=BA,则ΔAFN为直角三角形,即DF⊥AN,利用中位线定理可知AN∥CE,故DF⊥CE。
证法四、如图7,作DG∥CE交AE延长线于G,则EG=CD=AB=AE,故AD=AG=AF,从而DF⊥DG,而DGCE,故DF⊥CE四\一题多解、多变《四边形面积》1.如图所示,一个长为a,宽为b的矩形,两个阴影都是长为c的矩形与平行四边形,则阴影部分面积是多少。
初中数学竞赛试卷一题多解

一题多解:解法一:构造辅助线,利用平行四边形的性质证明。
步骤:1. 过点E作EG垂直于AD,交AD于点G。
2. 由于AE=3,AD=4,所以EG=√(AE²-AD²)=√(3²-4²)=√7。
3. 因为EF平行于AD,所以∠EAF=∠ADF=45°,∠EAG=∠ADF=45°。
4. 由于∠EAG=∠ADF,且∠EAF=∠ADF,所以三角形EAG与三角形ADF相似。
5. 根据相似三角形的性质,得到AE/AD=EG/DF,即3/4=√7/DF。
6. 解得DF=√74/3。
7. 由于BE=BC-BE=4-3=1,所以BE=DF。
8. 由于AE=AF=3,所以四边形BEFD是菱形。
解法二:利用向量方法证明。
步骤:1. 以点A为原点,建立直角坐标系,设点B(4,0),点C(4,4),点D(0,4)。
2. 点E在BC边上,设点E(4,y),其中0≤y≤4。
3. 点F在AB边上,设点F(x,0),其中0≤x≤4。
4. 由于AE=3,所以3²=(4-x)²+y²,即x²-8x+16+y²=9。
5. 由于EF平行于AD,所以向量EF=向量AD,即(4-x, -y)=(0, 4)。
6. 解得x=4,y=4。
7. 所以点E(4,4),点F(4,0)。
8. 由于BE=BC-BE=4-4=0,所以BE=DF。
9. 由于AE=AF=3,所以四边形BEFD是菱形。
解法三:利用勾股定理证明。
步骤:1. 在直角三角形ABE中,AE=3,AB=4,所以BE=√(AB²-AE²)=√(4²-3²)=√7。
2. 在直角三角形ADF中,AF=3,AD=4,所以DF=√(AD²-AF²)=√(4²-3²)=√7。
3. 由于BE=DF,所以BE=DF=√7。
河南初三初中数学专题试卷带答案解析

河南初三初中数学专题试卷班级:___________ 姓名:___________ 分数:___________一、填空题1.、在Rt△ABC中,∠C=90°,BC=12cm,BC边上的中线AD=10cm则sinB=2.如图,某建筑物BC直立于水平地面,∠BAC=30°,AC=9m,需建造阶梯AB,使每阶高不超过20cm,则此阶梯最少要建阶。
(取1.732)3.如图,当矩形ABCD变成边长不变的BCEF时,面积变为原来是的一半,则∠FBG= 。
4.、如图,在△ABC中,∠ACB=90°,AC=2,斜边AB在x轴上,点C在y轴的正半轴上,点A的坐标为(2,0),则直角边BC所在直线的解析式为。
5.某商品进货单价为30元,按40元一个销售,能卖40个,若销售单价每涨一元,销售量就减少一个,则为了获得最大利润,此商品的最佳售价应为 _____元。
6.x人去旅游共需支出y元,若x,y之间满足关系式y="2x2" - 20x + 1050,则当人数为_____时总支出最少。
7.已知一直角三角形两条直角边的和是6cm,则以这个直角三角形的斜边为边长的正方形的面积的最小值是______.8.周长为16cm的矩形的最大面积为____,此时矩形边长为____,实际上此时矩形是______.9.某厂的年利润为50万元,年增长率为x, 第三年的利润为y万元,则y与x之间的函数关系式为____________.10.已知等腰三角形的面积s与底边x有如下关系:s=-5x2+10x+14,要使s有最大值,则x=_____.11.把4m的木料锯成六段,制成如图所示的窗户,若用Xm表示横料AB的长,Ym2表示窗户的面积,则Y与X 之间的函数关系式为________,当X=____时窗户面积最大。
12.周长为8米的铝合金条制成如图形状的窗框,使窗户的透光面积最大,则最大透光面积是____.二、解答题1.计算。
(完整)初中数学一题多解题

初中数学一题多解题例题一、两个连续奇数的积是323,求出这两个数方法一、设较小的奇数为x,另外一个就是x+2x(x+2)=323解方程得:x1=17,x2=-19所以,这两个奇数分别是:17、19,或者-17,-19方法二、设较大的奇数x,则较小的奇数为323/x则有:x-323/x=2解方程得:x1=19,x2=-17同样可以得出这两个奇数分别是:17、19,或者-17,-19方法三、设x为任意整数,则这两个连续奇数分别为:2x-1,2x+1(2x-1)(2x+1)=323即4x^2-1=323x^2=81x1=9,x2=-92x1-1=17,2x1+1=192x2-1=-19,2x2+1=-17所以,这两个奇数分别是:17、19,或者-17,-19方法四、设两个连续奇数为x-1,x+1则有x^2-1=323x^2=324=4*81x1=18,x2=-18x1-1=17,x1+1=19x2-1=-19,x2+1=-17所以,这两个奇数分别是:17、19,或者-17,-19例题二、某人买13个鸡蛋、5个鸭蛋、9个鹌鹑蛋,共用去9.25元;如果买2个鸡蛋,4个鸭蛋,3个鹌鹑蛋,则共用去3.20元,试问只买鸡蛋、鸭蛋、鹌鹑蛋各一个,共需多少钱?解:设鸡、鸭、鹌鹑三种蛋的单价分别为x 、y 、z 元,则根据题意,得135992512433202x y z x y z ++=<>++=<>⎧⎨⎩.. 分析:此方程组是三元一次方程组,由于只有两个三元一次方程,因而要分别求出x 、y 、z 的值是不可能的,但注意到所求的是x y z ++的代数和,因此,我们可通过变形变换得到多种解法。
1. 凑整法解1:<>+<>123,得5344153x y z ++=<>.<>+<>23,得7735().x y z ++=∴++=x y z 105. 答:只买鸡蛋、鸭蛋、鹌鹑蛋各一个,共需1.05元(下面解法后的答均省略) 解2:原方程组可变形为134292522320()().()().x y z y z x y z y z ++-+=++++=⎧⎨⎩ 解之得:x y z ++=105.2. 主元法解3:视x 、y 为主元,视z 为常数,解<1>、<2>得x z =-0505..,y z =-05505.. ∴++=+-+=x y z z z 05505105...解4:视y 、z 为主元,视x 为常数,解<1>、<2>得y x z x =+=-00512.,∴++=+-+=x y z x x x 1052105..解5:视z 、x 为主元,视y 为常数,解<1>、<2>得x y z y =-=-005112.., ∴++=-++-=x y z y y y 005112105...3. “消元”法解6:令x =0,则原方程组可化为5992543320051y z y z y z +=+=⎧⎨⎩⇒==⎧⎨⎩... ∴++=x y z 105.解7:令y =0,则原方程组可化为1399252332000511x z x z x z +=+=⎧⎨⎩⇒=-=⎧⎨⎩.... ∴++=x y z 105.解8:令z =0,则原方程组可化为1359252432005055x y x y x y +=+=⎧⎨⎩⇒==⎧⎨⎩.... ∴++=x y z 105.4. 参数法解9:设x y z k ++=,则1359925124332023x y z x y z x y z k ++=<>++=<>++=<>⎧⎨⎪⎩⎪..∴<>-<>⨯123,得x y -=-<>0054.<>⨯-<>332,得x y k -=-<>3325.∴由<4>、<5>得332005k -=-..∴=k 105.即x y z ++=105.5. 待定系数法解10. 设x y z a x y z b x y z a b x a b y a b z ++=+++++=+++++<>()()()()()135924313254931则比较两边对应项系数,得1321541931121421a b a b a b a b +=+=+=⎧⎨⎪⎩⎪⇒==⎧⎨⎪⎪⎩⎪⎪ 将其代入<1>中,得x y z ++=⨯+⨯=⨯=121925421321212205105....附练习题1. 有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨;5辆大车与6辆小车一次可以运货35吨。
中考数学模型巧构辅圆解难题一题多解
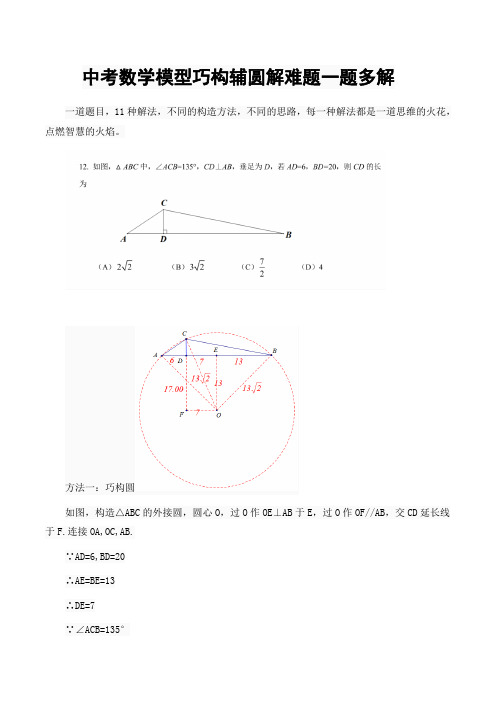
中考数学模型巧构辅圆解难题一题多解一道题目,11种解法,不同的构造方法,不同的思路,每一种解法都是一道思维的火花,点燃智慧的火焰。
方法一:巧构圆如图,构造△ABC的外接圆,圆心O,过O作OE⊥AB于E,过O作OF//AB,交CD延长线于F.连接OA,OC,AB.∵AD=6,BD=20∴AE=BE=13∴DE=7∵∠ACB=135°∴∠AOB=90°∴OE=13,AO=BO=CO=13√2由辅助线易得,四边形OEDF是矩形.∴OF=7由勾股定理可得,CF=17∴CD=4方法二:勾股定理如图,延长AC,过点B作BE⊥AC延长线于E设,BE=x,因为∠ACB=135°,所以∠BCE=45°,则CE=x,BC=√2x,则勾股定理可得其余线段的长度如上图。
由题很容易得到△ADC∽△AEB,则则CD=4或9√10(多出来一个解,有谁知道为什么吗?).备注:上面的方程很难解!所以虽然这个方法可以解出来,但是不推荐。
如果数字小一点,可以使用。
向另外一边作垂线一样可以求出,如下图:评述:第一种方法,根据135度圆周角所对圆心角是90度,巧妙的构造圆,然后巧妙转化,解决问题。
第二种方法,从135度的邻补角是45度入手,构造直角三角形。
通过勾股定理来解决。
第一种方法辅助线多,构思巧妙,不容易想到,第二种方法容易想到,但是数字比较大,方程难解。
从普通的条件入手,开拓思路,张引路老师的方法还是很巧妙的解法三:面积法如上图,过A作AE//BC,BE//AC交于E点.过E作EF⊥BC于F.因为∠ACB=135°,所以∠CBE=45°∴∴∴解得 x=4简评:这个方法同样存在方程难题的问题,如果数字比较小可以用。
解法三变式三角形的面积公式可以表示为直接用三角形面积公式,不过初中没有学过这个公式,还有一个就是sin135°的问题,好的学生可以补充,老师参考一下,拓宽一下思路。
初中数学一题多解题选编

初中数学一题多解题选编(Ⅰ)1、已知抛物线y=ax 2经过点(2,-8),若点A 为抛物线y=ax 2上一点,直线AB 垂直于x 轴,线段AB=5,沿y 轴平移抛物线y=ax 2,使之过点B ,求平移后所得抛物线的函数表达式.(y=-2x 2+5或y=-2x 2-5)2、已知抛物线y=-x 2+ax-4的顶点在坐标轴上,求a 的值.(0,4,-4)3、若一抛物线形状与y=-5x 2+2相同,顶点坐标是(4,-2),则其对应的函数表达式是________________________.(y=-5(x-4)2-2或y=5(x-4)2-2)4、已知函数y=(m+2)42-+m m x +8x-1是关于x 的二次函数,则m=_________.(-3或2)5、若抛物线y=2x 2-mx-m 2与x 轴有两个不同的交点A 、B ,且点A (1,0),求点B 的坐标.( (-2,0)或(-21,0) ) 6、已知函数y=mx 2-6x+1(m 是常数)(1)求证:不论m 为何值,该函数的图象都经过y 轴上的一个定点;(2)若该函数的图象与x 轴只有一个交点,求m 的值.(0或9)7、如图,矩形ABCD 的对角线BD 经过坐标原点,矩形的边分别平行于坐标轴,点C 在反比例函数xk k y 122++=的图象上,若点A 的坐标为(-2,-2),则k 的值为( D )A 、1B 、-3C 、4D 、1或-38、二次函数y=x 2-6x+c 的图象的顶点与原点的距离为5,则c=_________.(5或13)9、已知a 、b 、c 、d 是成比例线段,其中a=3cm ,b=2cm ,c=6cm ,则d=________cm . (4,1或9)10、已知三个数1,2,3,请你再添上一个数,使它们能构成一个比例式,这个数可以是________.(32,23或6) 11、已知a=4,c=9,若b 是a 、c 的比例中项,求b 的值。
初中数学专题复习一题多解

一题多解探究数学问题解决的新思路,对于学生发散性思维和创造性思维的培养是十分有利的。
下面一道例题,是从多维度角度出发来探究解题新思路的: 例:如图(1)在梯形ABCD 中,AB ∥CD ,四边形ACED 是平行四边形,延长DC 交BE 于F. 求证:EF=FB分析:这个题目本身不难,求证也容易,但通过对题设和结论的深入挖掘与探索,我们可以得出许多好的证法,总结如下:I E FBCA证明一:如图所示,作BQ∥AD,交DF 延长线于Q 点,则四边形ABQD 是平行四边形,从而BQ=AD ,再由题设可证△CEF≌△QBF, 得证EF=FB.Q IEF BCA证明二:如左图所示:作FM∥DA 交AB 于M ,则四边形ADFM 是平行四边形,从而FM=DA.再证△CEF≌△MFB,从而结论可得证.MIEFBCA证明三:作CN∥EB 交AB 于N ,则四边形CNBF 是□,从而CN=FB. 再证:△ANC≌△DFE,可得CN=EF ,即EF=FB.NIEFBCA证明四:作DP ∥FB 交AB 于P ,证明△ADP ≌△CEF ,从而得出结论.PIEF BCA证明五:延长EC 交AB 于G ,则四边形ADCG 是□,∴CE=AD=GC ,即C 是EG 中点.又CF ∥GB ,∴F 是EB 中点,结论得证.GIEF BCA证明六:连结AE 交CD 于O 点,则O 是AE 中点,又OF ∥AB , ∴F 是AB 中点,得证.IEF BCA证明七:延长ED 交BA 延长线于H 点,则HACD 是□ ,∴CA=DH=ED ∴D 是EH 中点.又DF ∥HB ∴F 是EB 中点,得证.HIEF BCA证明八:作ES ∥CD 交AD 延长线于S ,则CDSE 是□ ∴DS=CE=AD, ∴D 是AS 中点.又SE ∥CD ∥AB ∴F 是EB 中点,得证.S IE F BCA证明九:在证明一作的辅助线基础上,连结EQ ,则可得ECBQ 是□,从而F 是□ECBQ 对角线EB 的中点。
初中数学一题多解

初中数学一题多解【一】圆的多解题型1、平面上一点到圆的最大距离、最小距离分别是6和2,求圆的直径。
〔分点在圆内和圆外两种情况,直径是6+2或6-2〕2、圆的两条弦长6和8,半径5,求两条弦的距离。
〔分弦在圆心的同旁和两旁两种情况,距离是4+3或4-3〕3、半径是4的圆中,长是4的弦所对的圆周角是多少度?〔分弦所对的优弧和劣弧对的圆周角两种情况,度数是30或150〕4、相切两圆半径分别是4和6,求圆心距。
〔分内切、外切两种情况,圆心距是6-4或6+4〕5、相交两圆半径分别是25和39,公共弦长30,求圆心距。
〔分两圆心在公共弦的同旁和两旁两种情况,是36-20或36+20〕6、三角形ABC的外接圆半径是4,BC=4,求角A的度数。
〔分圆心在三角形内部和外部两种情况,是30度或150度)【二】数的多解题型1、a的相反数是本身,b的倒数是本身,那么a-b的值是多少?〔倒数是本身的数有1和-1,结果是-1或1〕2、平方是本身的数是_____(是0或1〕3、a的立方根是2,a的平方根是几?〔正数的平方根都有两个,是正负2根号2〕4、a、b的平方相等,a+2=3,b-2的差是几?〔平方相等的数要么相等要么互为相反数,b是1或-1,差是-1或-3〕5、绝对值是5的数与平方根是3的数的和是几?〔绝对值是正数的数有两个,和是8或-2〕6、数轴上,与表示2的点距离等于6的点表示的数,是倒数等于1.5的数的多少倍?〔距离是6的点表示的数是原数加上6或减去6,结果是-6倍或12倍〕【三】三角形的多解题型1、等腰三角形一腰上的高等于腰长的一半,求顶角。
〔分锐角三角形和钝角三角形两种情况,顶角30°或150°〕2、等腰三角形两边长5和6,求周长。
〔两边分别是腰和底两种情况,得周长16或17〕3、直角三角形两边长3和4,求第三边。
〔第三部边是斜边、直角边两种情况,是5或根号7〕4、三角形的一个30°角对的边为5,一条邻边是8,求面积。
初中数学 一题多解

一题多解题1.已知a、b为实数,且ab≠0=.2.小明等五名同学四月份参加某次数学测验(满分为120)的成绩如下:100、100、x、x、80.已知这组数据的中位数和平均数相等,那么整数x的值为.3.“五一”期间,某超市推出如下购物优惠方案:(1)一次性购物在100元(不含100元)以内时,不享受优惠;(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时一律享受九折的优惠;(3)一次购物在300元(含300元)以上时,一律享受八折的优惠.在此期间某顾客一次性购物付款252元,那么该顾客比平时购买总价相同的商品(没有优惠的时候)优惠了元.4.已知,如图1:在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A、C的坐标分别为A(10,0)、C(0,4),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为.5.线段AB的两端点的坐标为A(-1,0),B(0,-2)现请你在坐标轴上找一点P,使得以P、A、B为顶点的三角形是直角三角形,则满足条件的P点的坐标是6.如图2,在直角坐标系中,已知A(1,0)、B(-1,-2)、C(2,-2)三点坐标,若以A、B、C、D为顶点的四边形是平行四边形,那么点D的坐标可以是7.已知矩形的长为3,宽为1,现将四个这样的矩形用不同的方式拼成一个面积为12的大矩形,那么这个大矩形的周长是8.如图4,在边长为1的正方形网格中画有一个圆心为O的半圆,请在网格中以O为圆心,画一个与已知半圆的半径不同,且面积相等的扇形.9. 题a:如图5,AB=AC,AD⊥BC于点D,请你在△ABC内部,仅用圆规确定E、F两点,使∠BEC=∠BFC=90°.题b:如图6,四边形ABCD是一个等腰梯形,请直接在图中仅用直尺,准确..画出它的对称轴.10.把一个等边三角形分成四个等腰三角形,要求:1.除图a外再画出三种互不相同的分法,2.像图a一样,注明每个等腰顶角的度数.11..如图8是由三个小正方形组成的图形,现再给你一个同样的小正方形拼接在原图上,使原图形变为一个轴对称图形,请你分别在图a、b、c中画出不同的拼接方案,并画出对称轴.12.甲同学用如图9所示方法作出了C点,在△OA B中,∠OAB=90°,OA=2,AB=3,且点O、A、C在同一数轴上,OB=OC.(1)C点所表示的数是;(2)仿照甲同学的做法,在如下所给数轴上描出表示-29的点C.13.如图10,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;(1)先作△ABC关于直线l成轴对称的图形,再向上平移1个单位,得到△A1B1C1;(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.14.甲、乙两同学对关于y 、x 的抛物线f: 22222y x mx m m =-++进行探讨交流时,各得出一个结论.甲同学:当抛物线f 经过原点时,顶点在第三象限平分线所在的直线上;乙同学:不论m 取什么实数值,抛物线f 顶点一定不在第四象限.(1)请你求出抛物线f 经过原点时m 的值及顶点坐标,并说明甲同学的结论是否正确?(2)乙同学的结论正确吗?若你认为正确,请求出当实数m 变化时,抛物线f 顶点的纵横坐标之间的函数关系式,并说明顶点不在第四象限的理由;若你认为不正确,求出抛物线f 顶点在第四象限时,m 的取值范围.15.已知抛物线2141y x x =++的图象向上平移m 个单位(0m >)得到的新抛物线过点(1,8).(1)求m 的值,并将平移后的抛物线解析式写成22()y a x h k =-+的形式;(2)将平移后的抛物线在x 轴下方的部分沿x 轴翻折到x 轴上方,与平移后的抛物线没有变化的部分构成一个新的图象.请写出这个图象对应的函数y 的解析式,在所给的平面直角坐标系中直接画出简图,并直接写出y 与1y 之间关系式.16. 已知抛物线m 、n 的解析式分别是关于y 与x 的关系式:2222m y x mx =--22222m y x mx +=--与. (1)对上述两个抛物线说法正确的序号是 ;①两条抛物线与y 轴的交点一定不在x 轴的上方②在抛物线m、n中,可以将其中一条抛物线经过向上或向下平移得到另一条抛物线③在抛物线m、n中,可以将其中一条抛物线经过向左或向右平移得到另一条抛物线④两条抛物线的顶点之间的距离为1(2)若这两条抛物线中,只有一条与x轴交于A、B(A点在左)两个不同的点,问是哪条抛物线经过A、B两点?为什么?并求出A、B两点的坐标.17. 某校七年级学生准备去购买《英汉词典》一书,此书的标价为20元,现A,B两书店都有此书出售,A店按如下方法促销:若只购1本则按标价销售,若一次性购买多于1本,但不多于20本时,每多购1本,每本售价在标价的基础上优惠2%(例如买两本,每本价优惠2%;买3本每本价优惠4%,依此类推),若多于20本时,每本售价为12元;B书店一律按标价的7折销售.(1)试分别写出在两书店购此书总价y,B y与购书本数x之间的函数关系式;A(2)若某班一次性购买多于20本时,那么去哪家书店购买更合算,为什么?若要一次性购买不多于20本时,先写出y(y=y-B y)与购书本数x之间的函数式,画出其函数图象,再利用函数图象分析去哪家书店买更合算.。
初中数学一题多变一题多解(二)

一题多解一题多变(二)1、一题多解,培养思维的发散性一题多解实际上是解题或证明定理、公式的变式,因为它的实质是以不同的论证方式反映条件和结论问的同一必然的本质联系,运用这种变式教学,可以引导学生对同一材料,从不同角度、从不同方位、用各种途径、多种方法思考问题,探求不同的解答方案,这样,既可暴露学生解题的思维过程,增加教学透明度,又能够拓广学生思路,使学生熟练掌握知识的内在联系,使思维向多方向发展,培养思维的发散性。
这方面的例子很多,尤其是几何证明题。
已知:点O是等边△ABC内一点,OA=4,OB=5,OC=3求∠AOC的度数。
练习:把此题适当变式:变式在△ABC中,AB=AC,∠BAC=90°OA=4,OB=6,OC=2求∠AOC的度数。
变式2:如图,点O是等边△ABC内一点,∠AOB=110°, ∠BOC=135°试问:(1)以OA、OB、OC为边能否构成一个三角形?若能,请求出三角形各内角的度数;若不能,请说明理由.(2)如果∠AOB的大小保持不变,那么当∠BOC等于多少度时, 以OA、OB、OC为边的三角形是一个直角三角形?2、一题多变,培养思维的灵活性一题多变是题目结构的变式,是指变换题目的条件或结论,或者变换题目的形式,而题目的实质不变,以便从不同角度,不同方面揭示题目的本质,用这种方式进行教学,能使学生随时根据变化了的情况积极思索,设法想出解决的办法,从而防止和消除呆板和僵化,培养思维的灵活性。
一题多变可以改变条件,保留结论;也可以保留条件,改变结论;或者同时改变条件和结论;也可以将某项条件与结论对换等等。
例如:已知:C 为AB 上一点,△ACM 和△CBN 为等边三角形(如图所示)求证:AN=BM(分析:如对此题多做一些引申,既可以培养学生的探索能力,又可培养学生的创新素质)探索一:设CM 、CN 分别交AN 、BM 于P 、Q ,AN 、BM 交于点R 。
初中数学一题多解习题

初中数学一题多解习题练习一、思维定势干扰例 1.直角三角形的两条边长分别为6和8,那么这个三角形的外接圆半径等于。
例2.已知实数a、b满足a2+ 2a = 2,b2 + 2b = 2,求1 + 1的值。
a b二、审题草率例3. 一组数据5,7,7,x的中位数与平均数相等,则x的值为例4. 一次函数y=kx+b的自变量的取值范围是- 3< x < 6,相应函数值的取值范围是-5 < y <-2,则这个函数的解析式为。
三、忽视了数学的一些规定例5.当a 取什么数时,关于未知数x 的方程ax 2 + 4x -1 = 0只有正实数根?四、忽视图形的位置或形状例6.若圆O 的直径AB 为2,弦AC 为五,弦AD 为也,则S 扇形0co (其中 2s 扇形OCD < S 圆。
)为 ---------------------- 。
例7.为美化环境,计划在某小区内用30m 2的草皮铺设一块边长为10m 的等 腰三角形绿地,请你求出这个等腰三角形绿地的另两边长。
五、忽视了比例线段之间的不同对应关系例8.(江西)如图6所示,已知4ABC内接于圆O, AE切圆O于点A, BC//AE。
(1)求证:△ ABC是等腰三角形;(2)设AB=10cm,BC=8cm,点P是射线AE上的点,若以A、P、C为顶点的三角形与4ABC相似,求AP的长。
一、圆的多解题型1、平面上一点到圆的最大距离、最小距离分别感和2,求圆的直径。
2、圆的两条弦长6和8,半径5,求两条弦的距离。
3、半径是4的圆中,长是4的弦所对的圆周角是多少度?4、相切两圆半径分别是4和6,求圆心距。
5、相交两圆半径分别是25和39,公共弦长30,求圆心距。
6、三角形ABC的外接圆半径是4, BC=4,求角A的度数。
二、数的多解题型1、a的相反数是本身,b的倒数是本身,则a-b的值是多少?2、平方是本身的数是____3、a的立方根是2, a的平方根是几?4、a、b的平方相等,a+2=3, b-2的差是几?5、绝对值是5的数与平方根是3的数的和是几?6、数轴上,与表示2的点距离等于6的点表示的数,是倒数等于1.5的数的多少倍?三、三角形的多解题型1、等腰三角形一腰上的高等于腰长的一半,求顶角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学一题多解题例题一、两个连续奇数的积是323,求出这两个数方法一、设较小的奇数为x,另外一个就是x+2x(x+2)=323解方程得:x1=17,x2=-19所以,这两个奇数分别是:17、19,或者-17,-19方法二、设较大的奇数x,则较小的奇数为323/x则有:x-323/x=2解方程得:x1=19,x2=-17同样可以得出这两个奇数分别是:17、19,或者-17,-19方法三、设x为任意整数,则这两个连续奇数分别为:2x-1,2x+1(2x-1)(2x+1)=323即4x^2-1=323x^2=81x1=9,x2=-92x1-1=17,2x1+1=192x2-1=-19,2x2+1=-17所以,这两个奇数分别是:17、19,或者-17,-19方法四、设两个连续奇数为x-1,x+1则有x^2-1=323x^2=324=4*81x1=18,x2=-18x1-1=17,x1+1=19x2-1=-19,x2+1=-17所以,这两个奇数分别是:17、19,或者-17,-19例题二、某人买13个鸡蛋、5个鸭蛋、9个鹌鹑蛋,共用去9.25元;如果买2个鸡蛋,4个鸭蛋,3个鹌鹑蛋,则共用去3.20元,试问只买鸡蛋、鸭蛋、鹌鹑蛋各一个,共需多少钱?解:设鸡、鸭、鹌鹑三种蛋的单价分别为x 、y 、z 元,则根据题意,得135992512433202x y z x y z ++=<>++=<>⎧⎨⎩.. 分析:此方程组是三元一次方程组,由于只有两个三元一次方程,因而要分别求出x 、y 、z 的值是不可能的,但注意到所求的是x y z ++的代数和,因此,我们可通过变形变换得到多种解法。
1. 凑整法解1:<>+<>123,得5344153x y z ++=<>.<>+<>23,得7735().x y z ++=∴++=x y z 105.答:只买鸡蛋、鸭蛋、鹌鹑蛋各一个,共需1.05元(下面解法后的答均省略) 解2:原方程组可变形为134292522320()().()().x y z y z x y z y z ++-+=++++=⎧⎨⎩解之得:x y z ++=105.2. 主元法解3:视x 、y 为主元,视z 为常数,解<1>、<2>得x z =-0505..,y z =-05505..∴++=+-+=x y z z z 05505105...解4:视y 、z 为主元,视x 为常数,解<1>、<2>得y x z x =+=-00512.,∴++=+-+=x y z x x x 1052105..解5:视z 、x 为主元,视y 为常数,解<1>、<2>得x y z y =-=-005112..,∴++=-++-=x y z y y y 005112105...3. “消元”法解6:令x =0,则原方程组可化为5992543320051y z y z y z +=+=⎧⎨⎩⇒==⎧⎨⎩...∴++=x y z 105.解7:令y =0,则原方程组可化为1399252332000511x z x z x z +=+=⎧⎨⎩⇒=-=⎧⎨⎩....∴++=x y z 105.解8:令z =0,则原方程组可化为1359252432005055x y x y x y +=+=⎧⎨⎩⇒==⎧⎨⎩.... ∴++=x y z 105.4. 参数法解9:设x y z k ++=,则1359925124332023x y z x y z x y z k ++=<>++=<>++=<>⎧⎨⎪⎩⎪..∴<>-<>⨯123,得x y -=-<>0054.<>⨯-<>332,得x y k -=-<>3325.∴由<4>、<5>得332005k -=-..∴=k 105.即x y z ++=105.5. 待定系数法解10. 设x y z a x y z b x y z a b x a b y a b z ++=+++++=+++++<>()()()()()135924313254931则比较两边对应项系数,得1321541931121421a b a b a b a b +=+=+=⎧⎨⎪⎩⎪⇒==⎧⎨⎪⎪⎩⎪⎪ 将其代入<1>中,得x y z ++=⨯+⨯=⨯=121925421321212205105....附练习题1. 有大小两种货车,2辆大车与3辆小车一次可以运货15.5吨;5辆大车与6辆小车一次可以运货35吨。
求3辆大车与5辆小车一次可以运货多少吨?(答案:24.5吨)2. 有甲、乙、丙三种货物,若购甲3件、乙7件、丙1件共需3.15元;若购甲4件、乙10件、丙1件共需4.20元。
问若购甲、乙、丙各1件共需多少元?(答案:1.05元)平面几何在完成一个数学题的解答时,有必要对该题的内容、形式、条件、结论,做进一步的探讨,以真正掌握该题所反映的问题的实质。
如果能对一个普通的数学题进行一题多变,从变中总结解题方法;从变中发现解题规律,从变中发现“不变”,必将使人受益匪浅。
“一题多变”的常用方法有:1、变换命题的条件与结论;2、保留条件,深化结论;3、减弱条件,加强结论;4、探讨命题的推广;5、考查命题的特例;6、生根伸枝,图形变换;7、接力赛,一变再变;8、解法的多变等。
19、(增加题1的条件)AE平分∠BAC交BC于E,求证:CE:EB=CD:CB20、(增加题1的条件)CE平分∠BCD,AF平分∠BAC交BC于F求证:(1)BF·CE= BE·DF(2)AE⊥CF(3)设AE与CD交于Q,则FQ‖BC21、已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,以CD为直径的圆交AC、BC于E、F,求证:CE:BC=CF:AC(注意本题和16题有无联系)22、已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,以AD为直径的圆交AC于E,以BD为直径的圆交BC于F,求证:EF是⊙O1和⊙O2的一条外公切线23、已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,作以AC为直径的圆O1,和以CD为弦的圆O2,求证:点A到圆O2的切线长和AC相等(AT=AC)24、已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,E为ACD的中点,连ED并延长交CB的延长线于F,求证:DF:CF=BC:AC25、如图,⊙O1与⊙O2外切与点D,内公切线DO交外公切线EF于点O,求证:OD是两圆半径的比例中项。
题14解答:因为CD^2=AD·DBAC^2=AD·ABBC^2=BD·AB所以1/AC^2+1/BC^2=1/(AD·AB)+1/(BD·AB)=(AD+DB)/(AD·BD·AB)=AB/AD·BD·AB=1/AD·BD=1/CD^215题解答:因为M为AB的中点,所以AM=MB,AD-DB=AM+DM-(MB-DM)=2DMAC^2-BC^2=AD*AB-DB*AB=(AD-DB)AB=2DM*AB26、(在19题基础上增加一条平行线)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,AE平分∠BAC交BC于E、交CD于F,FG‖AB交BC于点G,求证:CE=BG27、(在19题基础上增加一条平行线)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,AE平分∠BAC交BC于E、交CD于F,FG‖BC交AB于点G,连结EG,求证:四边形CEGF是菱形28、(对19题增加一个结论)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,AE平分∠BAC交BC于E、交CD于F,求证:CE=CF29、(在23题中去掉一个圆)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,作以AC为直径的圆O1,求证:过点D的圆O1的切线平分BC30、(在19题中增加一个圆)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,AE平分∠BAC交BC于E,交CD于F,求证:⊙CED平分线段AF31、(在题1中增加一个条件)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,∠A=30度,求证:BD=AB/4(沪科版八年级数学第117页第3题)32、(在18题基础上增加一条直线)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,作∠BCE=∠BCDP为AC上任意一点,直线PQ交CD于Q,交CB于M,交CE于N求证:PQ/PN=QM/MN32题证明:作NS‖CD交直线AC与点S,则PQ/PN=CQ/SN又∠BCE=∠BCD∴QM/MN=CQ/CN(三角形内角平分线性质定理)∠BCE+∠NCS=∠BCD +∠ACDNS‖CD,∴∠NSC=∠ACD∴∠NSC=∠NCS∴SN=CN∴PQ/PN=QM/MN题33在“题一中”,延长CB到E,使EB=CB,连结AE、DE,求证:DE·AB= AE·BE题33证明CB^2= BD·AB因EB=CB∴EB^2= BD·AB∴EB:BD=AB:BE又∠EBD=∠ABE∴△EBD∽△ABE∴EB:AB=DE:AE∴DE·AB= AE·BE题34(在19题基础上增加一条垂线)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,AE平分CD于F,EG⊥AB交AB于点G,求证:EG^2= BE·EC证明:延长AC、GE,设交点为H,∴△EBG∽△EHC∴EB:EH=EG:EC∴EH·EG= BE·EC又HG‖CD,CF=FD∴EH=EG∴EG^2= BE·EC题35(在题19中增加点F)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,AE平分∠BCA交BC于点E,交CD于F,求证:2CF·FD = AF·EF题36、(在题16中,减弱条件,删除∠ACB=90度这个条件)已知,△ABC中,CD⊥AB,D为垂足,DE⊥AC于E,DF⊥BC于F,求证:CE/BC=CF/AC题37(在题17中,删除∠ACB=90度和CD⊥AB,D为垂足这两个条件,增加D是AB上一点,满足∠ACD=∠ABC)已知,△ABC中,D是AB上一点,满足∠ACD=∠ABC,又CE平分∠BCD求证:AE^2= AD·AB题38已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,PC为⊙ABC的切线求证:P A/AD=PB/BD题39(在题19中点E“该为E为BC上任意一点”)已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足,E为BC上任意一点,连结AE,CF⊥AE,F为垂足,连结DF,求证:△ADF∽△AEB题40:已知,△ABC中,∠ACB=90度,CD⊥AB,D为垂足求证:S⊙ADC:S⊙BDC=AD:DB题41已知,如图,△ABC中,CD⊥AB,D为垂足,且AD/CD=CD/BD,求∠ACB的度数。
