平行四边形知识点
平行四边形的判定知识点小结

平行四边形的判定知识点小结一、平行四边形的判定方法。
1. 定义判定。
- 两组对边分别平行的四边形是平行四边形。
- 用符号语言表示:如果AB∥CD,AD∥BC,那么四边形ABCD是平行四边形。
这是平行四边形最基本的判定方法,它是从平行四边形的定义直接得出的。
2. 边的判定。
- 两组对边分别相等的四边形是平行四边形。
- 符号语言:若AB = CD,AD = BC,则四边形ABCD是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
- 符号语言:若AB∥CD且AB = CD(或者AD∥BC且AD = BC),则四边形ABCD 是平行四边形。
3. 角的判定。
- 两组对角分别相等的四边形是平行四边形。
- 符号语言:若∠A = ∠C,∠B = ∠D,则四边形ABCD是平行四边形。
4. 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
- 符号语言:若OA = OC,OB = OD(其中O为对角线AC、BD的交点),则四边形ABCD是平行四边形。
二、平行四边形判定方法的证明思路。
1. 定义法证明。
- 一般通过已知条件中的平行关系,如角相等推出直线平行(同位角、内错角相等,两直线平行)等方法来证明两组对边分别平行。
- 例如:已知∠1 = ∠2,∠3 = ∠4,可推出AD∥BC,AB∥CD,从而证明四边形ABCD是平行四边形。
2. 边的判定证明。
- 对于两组对边分别相等的判定方法,通常利用三角形全等的知识来证明。
- 例如:连接AC,在△ABC和△CDA中,已知AB = CD,BC = DA,AC = CA(公共边),通过SSS(边 - 边 - 边)全等判定定理证明△ABC≌△CDA,进而得出∠1 = ∠2,∠3 = ∠4,所以AD∥BC,AB∥CD,四边形ABCD是平行四边形。
- 对于一组对边平行且相等的判定方法,可通过平移线段构造平行四边形或者利用三角形全等和平行线的判定来证明。
- 例如:已知AB∥CD且AB = CD,延长AB到E,使BE = CD,连接CE,可证明四边形BECD是平行四边形,从而得出BD∥CE,再结合已知条件证明四边形ABCD是平行四边形。
平行四边形和多边形知识点

平行四边形和多边形知识点一、平行四边形知识点。
1. 平行四边形的定义。
- 两组对边分别平行的四边形叫做平行四边形。
用符号“▱”表示,如平行四边形ABCD记作“▱ABCD”。
2. 平行四边形的性质。
- 边的性质。
- 平行四边形的对边平行且相等。
即AB = CD,AD = BC;AB∥CD,AD∥BC。
- 角的性质。
- 平行四边形的对角相等,邻角互补。
即∠A = ∠C,∠B = ∠D;∠A+∠B = 180°,∠B + ∠C=180°等。
- 对角线的性质。
- 平行四边形的对角线互相平分。
即AO = CO,BO = DO(设AC、BD相交于点O)。
3. 平行四边形的判定。
- 边的判定。
- 两组对边分别平行的四边形是平行四边形(定义判定)。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
- 角的判定。
- 两组对角分别相等的四边形是平行四边形。
- 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
4. 平行四边形的面积。
- 平行四边形的面积 = 底×高,即S = ah(a为底,h为这条底边上的高)。
二、多边形知识点。
1. 多边形的定义。
- 在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形。
- 如果一个多边形由n条线段组成,那么这个多边形叫做n边形。
2. 多边形的内角和。
- n边形的内角和公式为(n - 2)×180^∘(n≥3且n为整数)。
- 例如三角形(n = 3)内角和为(3 - 2)×180^∘=180^∘;四边形(n = 4)内角和为(4 - 2)×180^∘=360^∘。
3. 多边形的外角和。
- 多边形的外角和等于360°,与边数无关。
4. 正多边形。
- 定义:各个角都相等,各条边都相等的多边形叫做正多边形。
- 正n边形的每个内角为frac{(n - 2)×180^∘}{n},每个外角为frac{360^∘}{n}。
数学平行四边形重要知识点

数学平行四边形重要知识点
平行四边形(Parallelogram),是在同一个二维平面内,由两组平行线段组成的闭合图形。
下面是店铺整理的数学平行四边形重要知识点,欢迎阅览。
1、平行四边形的概念
两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
2、平行四边形的性质
(1)平行四边形的邻角互补,对角相等。
(2)平行四边形的对边平行且相等。
推论:夹在两条平行线间的平行线段相等。
(3)平行四边形的对角线互相平分。
(4)若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的'交点为中点,并且这两条直线二等分此平行四边形的面积。
3、平行四边形的判定
(1)定义:两组对边分别平行的四边形是平行四边形
(2)定理1:两组对角分别相等的四边形是平行四边形
(3)定理2:两组对边分别相等的四边形是平行四边形
(4)定理3:对角线互相平分的四边形是平行四边形
(5)定理4:一组对边平行且相等的四边形是平行四边形
4、两条平行线的距离
两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线的距离。
平行线间的距离处处相等。
5、平行四边形的面积
S平行四边形=底边长×高=ah
【数学平行四边形重要知识点】。
平行四边形专题详解

平行四边形专题详解18.1 平行四边形知识框架{基础知识点{ 平行四边形的定义平行四边形的性质平行四边形的判定定理三角形中位线定理典型题型{利用平行线的性质求角度平行线间距离的运用平行四边形的证明难点题型{平行四边形间距离的应用平行四边形有关的计算平行四边形的有关证明一、基础知识点知识点1 平行四边形的定义1)平行四边形的定义:两组对边分别平行的四边形。
平行四边形用“▱”表示,平行四边形ABCD 表示为“▱ABCD ”,读作“平行四边形ABCD ”注:只要满足对边平行的四边形都是平行四边形。
矩形、菱形、正方形都是特殊的平行四边形 2)平行四边形的高:一条边上任取一点作另一边的垂线,该垂线的长度称作平行四边形在该边上的高。
3)两条平行线之间的距离:一条直线上任一点到另一直线的距离。
平行线间距离处处相等。
例1.如图,AB ∥EG ,EF ∥BC ,AC ∥FG ,A ,B ,C 分别在EF ,EG 上,则图中有 个平行四边形,可分别记作 。
例2.如图,▱ABCD 中,DE ⊥AB ,BF ⊥CD ,垂足分别为E ,F .求证:BE=DF 。
例3.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法错误的是()A.AB=CDB.CE=FGC.直线a,b之间的距离是线段AB的长D.直线a,b之间的距离是线段CE的长知识点2 平行四边形的性质平行四边形的性质,主要讨论:边、角、对角线,有时还会涉及对称性。
如下图,四边形ABCD是平行四边形:1)性质1(边):①对边相等;②,即:AB=CD,AD=BC;AB∥CD,AD∥BC2)性质2(角):对角相等,即:∠BAD=∠BCD,∠ABC=∠ADC3)性质3(对角线):对角线相互平分,即:AO=OC,BO=OD注:①平行四边形仅对角线相互平分,对角线不相等,即AC≠BD(矩形的对角线才相等);②平行四边形对角相等,但对角线不平分角,即∠DAO≠∠BAO(菱形对角线才平分角)4)性质4(对称性):平行四边形不是轴对称图形,是中心对称图形。
平行四边形初中知识点

平行四边形初中知识点
一、平行四边形的定义。
1. 两组对边分别平行的四边形叫做平行四边形。
- 用符号“▱”表示平行四边形,例如平行四边形ABCD记作“▱ABCD”。
二、平行四边形的性质。
1. 边的性质。
- 平行四边形的对边平行且相等。
- 即若▱ABCD,则AB = CD,AD = BC;AB∥CD,AD∥BC。
2. 角的性质。
- 平行四边形的对角相等,邻角互补。
- 在▱ABCD中,∠A = ∠C,∠B = ∠D;∠A+∠B = 180°,∠B + ∠C=180°等。
3. 对角线的性质。
- 平行四边形的对角线互相平分。
- 若▱ABCD,对角线AC、BD相交于点O,则AO = CO,BO = DO。
三、平行四边形的判定。
1. 边的判定。
- 两组对边分别平行的四边形是平行四边形(定义判定)。
- 两组对边分别相等的四边形是平行四边形。
- 一组对边平行且相等的四边形是平行四边形。
2. 角的判定。
- 两组对角分别相等的四边形是平行四边形。
3. 对角线的判定。
- 对角线互相平分的四边形是平行四边形。
四、平行四边形的面积。
1. 平行四边形的面积等于底乘以高。
- 若平行四边形的底为a,这条底边上的高为h,则面积S = ah。
- 同底(等底)等高的平行四边形面积相等。
平行四边形知识点
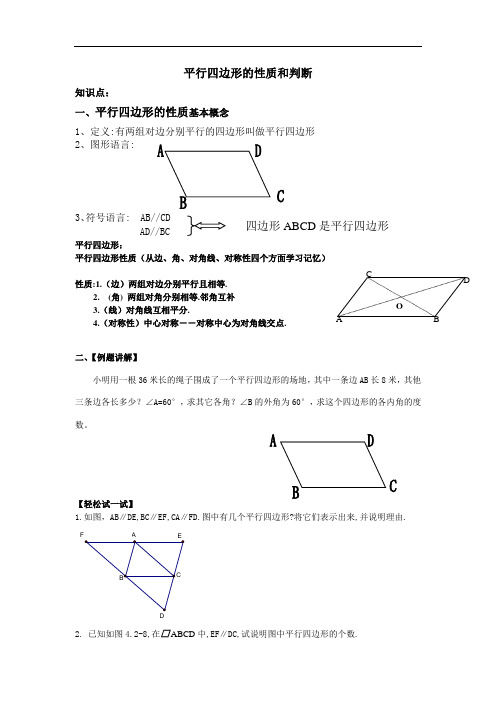
A BC DO 平行四边形的性质和判断知识点:一、平行四边形的性质基本概念1、定义:有两组对边分别平行的四边形叫做平行四边形2、图形语言:3、符号语言平行四边形:平行四边形性质(从边、角、对角线、对称性四个方面学习记忆) 性质:1.(边)两组对边分别平行且相等.2. (角) 两组对角分别相等.邻角互补3.(线)对角线互相平分.4.(对称性)中心对称--对称中心为对角线交点.二、【例题讲解】小明用一根36米长的绳子围成了一个平行四边形的场地,其中一条边AB 长8米,其他三条边各长多少?∠A=60°,求其它各角?∠B 的外角为60°,求这个四边形的各内角的度数。
【轻松试一试】1.如图,AB ∥DE,BC ∥EF,CA ∥FD.图中有几个平行四边形?将它们表示出来,并说明理由.AFD2. 已知如图4.2-8,中,EF ∥DC,试说明图中平行四边形的个数.NMH G F E D CBA图4.2-8角的计算:1、中, BC=2AB, CA ⊥AB,则∠B=______度,∠CAD=______度.DCB A2中,∠A : ∠B=3:2,则∠C=___ 度,∠D=______度.边及周长的计算1、如图,平行四边形的对角线相交于点O ,BC=7㎝,BD=10㎝,AC=6㎝。
求△AOD 的周长。
2平行四边形的周长是100cm, AB:BC=4:1,则AB 的长是_______。
3.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长是______________.4.用20米长的一铁丝围成一个平行四边形,使长边与短边的比为3:2,则它的边长为________短边长为__________.平行四边形的判断平行四边形的四个(或五个)判定方法,这些判定的方法是: 从边看: ①两组对边分别平行的四边形是平行四边形; ②两组对边分别相等的四边形是平行四边形; ③一组对边平行且相等的四边形是平行四边形.从对角线看:对角线互相平分的四边形是平行四边形.(从角看:两组对角分别相等的四边形是平行四边形.)【例题讲解】已知:如图,ABCD 中,E 、F 分别是AD 、BC 的中点,求证:BE=DF .分析:证明BE=DF ,可以证明两个三角形全等,也可以证明四边形BEDF 是平行四边形,比较方法,可以看出第二种方法简单. 证明:∵ 四边形ABCD 是平行四边形, ∴ AD ∥CB ,AD=CD . ∵ E 、F 分别是AD 、BC 的中点, ∴ DE ∥BF ,且DE=21AD ,BF=21BC .∴ DE=BF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形). ∴ BE=DF .例2、已知:如图,ABCD 中,E 、F 分别是AC 上两点,且BE ⊥AC 于E ,DF ⊥AC 于F .求证:四边形BEDF 是平行四边形.分析:因为BE ⊥AC 于E ,DF ⊥AC 于F ,所以BE ∥DF .需再证明BE=DF ,这需要证明△ABE 与△CDF 全等,由角角边即可.证明:∵ 四边形ABCD 是平行四边形, ∴ AB=CD ,且AB ∥CD . ∴ ∠BAE=∠DCF .∵ BE ⊥AC 于E ,DF ⊥AC 于F ,∴ BE ∥DF ,且∠BEA=∠DFC=90°. ∴ △ABE ≌△CDF (AAS ). ∴ BE=DF .∴ 四边形BEDF 是平行四边形(一组对边平行且相等的四边形平行四边形)例3、 已知:如图3,E 、F 是平行四边形ABCD 对角线AC 上两点,且AE =CF 。
初中数学知识点总结:平行四边形

初中数学知识点总结:平行四边形
知识点总结
1.定义:两组对边分别平行的四边形叫平行四边形
2.平行四边形的性质
〔1〕平行四边形的对边平行且相等;
〔2〕平行四边形的邻角互补,对角相等;
〔3〕平行四边形的对角线互相平分;
3.平行四边形的判定
平行四边形是几何中一个重要内容,如何根据平行四边形的性质,判定一个四边形是平行四边形是个重点,下面就对平行四边形的五种判定方法,进行划分:
第一类:与四边形的对边有关
〔1〕两组对边分别平行的四边形是平行四边形;
〔2〕两组对边分别相等的四边形是平行四边形;
〔3〕一组对边平行且相等的四边形是平行四边形;
第二类:与四边形的对角有关
〔4〕两组对角分别相等的四边形是平行四边形;
第三类:与四边形的对角线有关
〔5〕对角线互相平分的四边形是平行四边形
常见考法
〔1〕利用平行四边形的性质,求角度、线段长、周长;〔2〕求平行四边形某边的取值范围;〔3〕考查一些综合计算问题;〔4〕
利用平行四边形性质证明角相等、线段相等和直线平行;〔5〕利用判定定理证明四边形是平行四边形。
误区提醒
〔1〕平行四边形的性质较多,易把对角线互相平分,错记成对角线相等;〔2〕〝一组对边平行且相等的四边形是平行四边形〞错记成〝一组对边平行,一组对边相等的四边形是平行四边形〞后者不是平行四边形的判定定理,它只是个等腰梯形。
平行四边形知识点总结

平行四边形知识点总结
平行四边形是初中数学中一个重要的几何概念。
在学习平行四边形时,我们需要了解它的定义、性质、判定方法、面积计算及其应用等知识点。
一、定义
平行四边形是由两组平行线段围成的四边形。
它的对边相等且平行,相邻两边互相垂直。
二、性质
1. 对边相等且平行,相邻两边互相垂直;
2. 对角线互相平分;
3. 对角线相交处的角相互补;
4. 有一个角是直角,则它是矩形。
三、判定方法
1. 两组对边分别相等;
2. 一组对边相等且平行,另一组对边互相垂直;
3. 一组对边平行,且有一对角是直角。
四、面积计算
平行四边形的面积可以通过以下公式求得:
S = 底边× 高
其中,底边为平行四边形的一条边,高为从该边所在的顶点到另一条平行边的距离。
五、应用
平行四边形在实际生活中有着广泛的应用。
例如,在建筑设计中,常常需要考虑平行四边形的形状和面积,来确定建筑物的结构和装修方案。
在工程设计中,平行四边形的面积计算可以帮助我们计算出材料的用量,从而控制成本。
学习平行四边形的知识还有助于我们锻炼几何思维和推理能力,提高数学素养和解决实际问题的能力。
平行四边形是初中数学中一个重要的几何概念,我们需要掌握它的定义、性质、判定方法、面积计算及其应用等知识点,以便在实际生活和学习中得到应用和提高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形中位线定理
(1)三角形中位线定理:
三角形的中位线平行于第三边,并且等于第三边的一半.
(2)几何语言:
如图,∵点D、E分别是AB、AC的中点
∴DE∥BC,DE=BC.
平行四边形的性质
(1)平行四边形的概念:有两组对边分别平行的四边形叫做平行四边形.(2)平行四边形的性质:
①边:平行四边形的对边相等.
②角:平行四边形的对角相等.
③对角线:平行四边形的对角线互相平分.
(3)平行线间的距离处处相等.
(4)平行四边形的面积:
①平行四边形的面积等于它的底和这个底上的高的积.
②同底(等底)同高(等高)的平行四边形面积相等.
平行四边形的判定
(1)两组对边分别平行的四边形是平行四边形.符号语言:∵AB∥DC,AD∥BC ∴四边行ABCD是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.符号语言:∵AB=DC,AD=BC∴四边行ABCD是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
符号语言:∵AB∥DC,AB=DC∴四边行ABCD是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
符号语言:∵∠ABC=∠ADC,∠DAB=∠DCB∴四边行ABCD是平行四边形.(5)对角线互相平分的四边形是平行四边形.符号语言:∵OA=OC,OB=OD∴四
边行ABCD是平行四边形.
平行四边形的判定与性质
平行四边形的判定与性质的作用
平行四边形对应边相等,对应角相等,对角线互相平分及它的判定,是我们证明直线的平行、线段相等、角相等的重要方法,若要证明两直线平行和两线段相等、两角相等,可考虑将要证的直线、线段、角、分别置于一个四边形的对边或对角的位置上,通过证明四边形是平行四边形达到上述目的.
运用定义,也可以判定某个图形是平行四边形,这是常用的方法,不要忘记平行四边形的定义,有时用定义判定比用其他判定定理还简单.
凡是可以用平行四边形知识证明的问题,不要再回到用三角形全等证明,应直接运用平行四边形的性质和判定去解决问题.
菱形的性质
(1)菱形的定义:有一组邻边相等的平行四边形叫做菱形.
(2)菱形的性质
①菱形具有平行四边形的一切性质;
②菱形的四条边都相等;
③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.
(3)菱形的面积计算
①利用平行四边形的面积公式.
②菱形面积=ab.(a、b是两条对角线的长度)
菱形的判定
①菱形定义:一组邻边相等的平行四边形是菱形(平行四边形+一组邻边相等=菱
形);
②四条边都相等的四边形是菱形.
几何语言:∵AB=BC=CD=DA∴四边形ABCD是菱形;
③对角线互相垂直的平行四边形是菱形(或“对角线互相垂直平分的四边形是菱
形”).
几何语言:∵AC⊥BD,四边形ABCD是平行四边形∴平行四边形ABCD是菱形
矩形的性质
(1)矩形的定义:有一个角是直角的平行四边形是矩形.
(2)矩形的性质
①平行四边形的性质矩形都具有;
②角:矩形的四个角都是直角;
③边:邻边垂直;
④对角线:矩形的对角线相等;
⑤矩形是轴对称图形,又是中心对称图形.它有2条对称轴,分别是每组对边中
点连线所在的直线;对称中心是两条对角线的交点.
(3)由矩形的性质,可以得到直角三角形的一个重要性质,直角三角形斜边上的中线等于斜边的一半.
矩形的判定
(1)矩形的判定:
①矩形的定义:有一个角是直角的平行四边形是矩形;
②有三个角是直角的四边形是矩形;
③对角线相等的平行四边形是矩形(或“对角线互相平分且相等的四边形是矩形”)(2)①证明一个四边形是矩形,若题设条件与这个四边形的对角线有关,通常
证这个四边形的对角线相等.
②题设中出现多个直角或垂直时,常采用“三个角是直角的四边形是矩形”来判定
矩形.
正方形的判定
正方形的判定方法:
①先判定四边形是矩形,再判定这个矩形有一组邻边相等;
②先判定四边形是菱形,再判定这个菱形有一个角为直角.
③还可以先判定四边形是平行四边形,再用1或2进行判定.
梯形
(1)梯形的定义:一组对边平行,另一组对边不平行的四边形叫做梯形.
梯形中平行的两边叫梯形的底,其中较短的底叫上底,不平行的两边叫梯形的腰,两底的距离叫梯形的高.
(2)等腰梯形:两腰相等的梯形叫做等腰梯形.
(3)直角梯形:有一个角是直角的梯形叫做直角梯形.
直角梯形
直角梯形:有一个角是直角的梯形叫做直角梯形.
边:有一条腰与底边垂直,另一条腰不垂直.
角:有两个内角是直角.
过不是直角的一个顶点作梯形的高,则把直角梯形分割成一个矩形和直角三角形.这是常用的一种作辅助线的方法.
等腰梯形的性质
(1)性质:
①等腰梯形是轴对称图形,它的对称轴是经过上下底的中点的直线;
②等腰梯形同一底上的两个角相等;
③等腰梯形的两条对角线相等.
(2)由等腰梯形的性质可知,如果过上底的两个顶点分别作下底的两条高,可把等腰梯形分成矩形和两个全等的直角三角形,因此可知等腰梯形是轴对称图形,而一般的梯形不具备这个性质.
等腰梯形的判定
(1)利用定义:两腰相等的梯形叫做等腰梯形;
(2)定理:同一底上两个角相等的梯形是等腰梯形.
(3)对角线:对角线相等的梯形是等腰梯形.
判定一个梯形是否为等腰梯形,主要判断梯形的同一底上的两个角是否相等,可以通过添加辅助线把梯形底上的两个角平移到同一个三角形中,利用三角形来证明角的关系.
注意:对角线相等的梯形是等腰梯形这个判定方法不可以直接应用.。
