任意角的三角比
任意角的三角比

任意角的三角比一、基础知识熟练记忆1、任意角的三角比——对于任意角的三角比,我们利用平面直角坐标系来进行研究。
(1)设α是一个任意角,在α的终边上任取(异于原点的)一点P (x,y ) 则点P 与原点的距离02222>+=+=y x y x r(2)比值r y叫做α的正弦 记作: r y =αsin 比值r x叫做α的余弦 记作: r x =αcos 比值x y叫做α的正切 记作: xy =αtan 比值y x叫做α的余切 记作: yx =αcot 比值x r叫做α的正割 记作: x r =αsec 比值y r叫做α的余割 记作: yr =αcsc 根据相似三角形的知识,对于终边不在坐标轴上确定的角α, 上述六个比值都不会随P 点在α的终边上的位置的改变而改变。
当角α的终边在纵轴上时,即Z)(2∈+=k k ππα时,终边上任意一点P 的横坐标x 都为0,所以tan α、sec α无意义;当角α的终边在横轴上时,即α=kπ(k∈Z )时, 终边上任意一点P 的纵坐标y都为0,所以cot α、csc α无意义。
几个需要注意的问题:① 凡是终边相同的角的三角函数值相等。
sin(2k π+α)=sin α cos(2k π+α)=cos α tan(2k π+α)=tan α cot(2k π+α)=cot α② 0>r 而x,y 的正负是随象限的变化而不同,故三角函数的符号应由象限确定。
第一象限:0,0.>>y x∴sin α>0,cos α>0,tan α>0,cot α>0 第二象限:0,0.><y x∴sin α>0,cos α<0,tan α<0,cot α<0O A M P Txyα的终边 x yO A M T yOAM xyOAM TPα的终边第三象限:0,0.<<y x∴sin α<0,cos α<0,tan α>0,cot α>0 第四象限:0,0.<>y x∴sin α<0,cos α>0,tan α<0,cot α<0记忆法则:第一象限全为正,二正三切四余弦。
任意角的三角比

视频1:在直角坐标系中角的终边上任意一点的坐标来定义任意角的三角比。
设(),P x y 是角α终边上的任意一点(不重合于角的顶点),则P 点到坐标原点O 的距离为r OP ==,定义:①正弦:sin α=;②余弦:cos α=;③正切:tan α=; ④余割:csc α=;⑤正割:sec α=;⑥余切:cot α=;Note :①任意角的三角比仅与角的终边位置有关,而与终边上所取点P 的位置 。
②当角α的终边落在y 轴时,(),P x y 是角α终边上的任意一点(不重合于角的顶点),此时x =,则cos α=,且tan α与sec α ;③当角α的终边落在x 轴时,(),P x y 是角α终边上的任意一点(不重合于角的顶点),此时y =,则sin α=,且 与 无意义;④角α的终边无论落在什么位置,(),P x y 是角α终边上的任意一点(不重合于角的顶点),此时0r =>,故sin α与cos α总是存在的。
⑤22sin cos αα+=练习:已知角α的终边上一点()12,5P -,求角α的六个三角比的值。
6分钟视频2:正弦函数在第一象限为 ,第二象限为 ,第三象限为 ,第四象限为 ; 余弦函数在第一象限为 ,第二象限为 ,第三象限为 ,第四象限为 ; 正切函数在第一象限为 ,第二象限为 ,第三象限为 ,第四象限为 。
练习:确定下列三角函数值的符号。
①cos 250︒;②sin 4π⎛⎫-⎪⎝⎭;③()tan 672︒-;④tan 3π 5分钟视频3:练习:根据下列条件确定角θ属于哪个象限: ①sin cos 0θθ>;②sin 0θ<且tan 0θ> 2分钟视频4:从开始--------05:27结束(将开头删掉)。
设α是一个任意角,它的终边与单位圆交于点(),P x y ,那么 ①正弦:sin α=;②余弦:cos α=;③正切:tan α=; ④余割:csc α=;⑤正割:sec α=;⑥余切:cot α=;Note1:常见的三角函数的定义域与值域①正弦函数sin y x =,定义域为 ,值域为 。
第十五讲 任意角的三角比

第十五讲 任意角的三角比⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎪⎪⎪⎪⎩正角概念负角零角角度制表示法任意角弧度制—扇形的弧长、面积象限角与轴线角终边相同的角与终边有关的角1. 角概念的推广 (1)任意角的形成角能够看成是由一条射线绕着它的端点旋转而成的,射线的端点叫做角的顶点,旋转开始时的射线叫做角的始边,终止时的射线叫做角的终边。
(2)正角、负角和零角按逆时针方向旋转所形成的角叫做正角;按顺时针方向旋转所形成的角叫做负角;当射线没有任何旋转时,形成的角叫做零角。
2.表示法:角度制与弧度制 (1)1弧度的角等于半径长的圆弧所对的圆心角叫做1弧度的角。
弧度制的建立,使任意角与实数之间建立了一一对应关系.0↔⎧⎪↔⎨⎪↔⎩正角正数负角负数零角 (2)角度与弧度的换算:π弧度(rad )=180 (3)扇形的弧长与面积公式:||l r α=;211||22S lr r α== 练习1 已知一个扇形OAB 的面积是42cm ,它的周长是10cm ,求它的圆心角和弦AB 的长. 答案:12α=,18sin 4AB =.变式:已知一个扇形的周长为2(0)a a >,问这个扇形半径为何值时,才能使这个扇形面积最大?最大面积为多少?并求此时扇形的圆心角.答案:2ar =时,扇形面积最大,最大值为24a ,此时圆心角为2.3.象限角与轴线角角的顶点与坐标原点重合,角的始边与x 轴的正半轴重合,角的终边落在第几象限,就称这个角为第几象限的角;角的终边在坐标轴上,就认为这个角不属于任何象限,即称为轴线角.第Ⅰ象限角:{|22,}2x k x k k Z πππ<<+∈; 第Ⅱ象限角:{|22,}2x k x k k Z ππππ+<<+∈;第Ⅲ象限角:3{|22,}2x k x k k Z ππππ+<<+∈;第Ⅳ象限角:{|22,}2x k x k k Z πππ-<<∈; 终边落在x 轴正半轴上的角的集合:{|2,}x x k k Z π=∈; 终边落在x 轴负半轴上的角的集合:{|2,}x x k k Z ππ=+∈ 终边落在x 轴上的角的集合:{|,}x x k k Z π=∈ 终边落在y 轴正半轴上的角的集合:{|2,}2x x k k Z ππ=+∈ 终边落在y 轴负半轴上的角的集合:{|2,}2x x k k Z ππ=-∈终边落在y 轴上的角的集合:{|,}2x x k k Z ππ=+∈ 终边落在坐标轴上的角的集合:{|,}2x x k k Z π=⋅∈练习2 若tan 0,cot cos 0sin αααα<⋅>,则角α,2α分别是第几象限的角? 答案:α是第二象限角,2α是第一、三象限的角。
01任意角三角比

例5 已知角α的顶点与坐标原点重合,始边与 x轴的正方向重合, α的终边上一点P (5a,-12a),(a<0)。 求Sinα,cosα ,tgα的值。 分析: 根据三角比的定义,应先求出r,注 意隐含条件r>0 。
解:
∵ α<0,
∴r=(5a)2+(-12a)2=13|a|=-13a
∴sinα= cosα= tgα=
(2k
第二象限 (k· 3600+900, k· 3600+1800)
2
, 2 k )
第三象限 (k· 3600+1800, k· 3600+2700)
第四象限 (k· 3600+2700, k· 3600+3600)
3 (2k , 2k ) 2
3 (2k , 2k 2 ) 2
例8:已知角α的终边经过点P(2,-3), 求α的六个三角函数值.
例9(1)将112°30′化成弧度制。
9 (3)10 °约等于多少弧度(保留四个 有效数字)。
(4)3弧度约等于多少度(精确到整 数度)。
4 (2)将 4π化成角度制。 9
解:
(1) 112030’=
0 225 = 2
225 55π × = 弧度 2 180 8
(1)另解:
∵-546°=-720°+174°=-2×360°+174°
(2)1998°=5 × 360°+198°, α=198° ∴1998°属于第三象限。
(3)-21.3 π=-22 π+0.7 π =-11 ×2 π+ (7π)/ 10 ∴ α=(7π)/10,-21.3 π属于第二象限
(4)∵1弧度≈57.3 °, ∴-5弧度≈-5 × 57.3=-286.5 ° ∴-5弧度≈-1 × 360 °+73.5 ° ∴ α ≈73.5 °, -5属于第一象限角。
沪教版高中一年级数学第二学期:任意角的三角比

(1) sin 2370
(2) cos( ) tan 4
5
7
6.根据下列条件,判断 是第几象限角?
(1) sin < 0, tan 0 (2)csc tan < 0
1.会求任意角的六个三角比,注意有些角的三 角比是不存在的。
2.知道任意角的六个三角比在各个象限内的符 号,能确定某个角的三角比的符号。
3、(1)求 5 的 六 个 三 角 比 的 值
6
针对训练:
练习 : 求 sin( 23 )
3、( 2 )求 0和
3
6
的 正 弦, 余 弦 和 正 切 的 值
2
4.已知角的终边上有一点p到原点的距离为 1,0 且tan = -1(0< < ),求点P的坐标。 3
(二)三角比的符号
Q:若确定了角α终边所在的象限,则角α的六个三角比 的正负能否确定?
结论:任意三角比的符号在各个象限都是确定的!
y
1
0y
++
-+
0
0 -1
1
0
x
--
- 0+ x
y
不存在
-+
0
0
+0 - x
sin- 1
0
cos
不存在
tan
Q:若角α的终边在坐标轴上,这三个三角比是什么 呢?
针对训练
5.判别下列各式的符号:
3.写出三角比公式,并将三角比三要素(x, y, r)代入运算;
注意:求任意角的六个三角比关键是 求三个三角比:正弦、余弦和正切
针对训练:
2. 已知角 的终边经过点 P(6a,8a)
(a 0) ,求 sin cos 。
任意角的三角比

第一组诱导公式:
Q 2kπ + α (k ∈ Z )与α有相同的终边,而三角比值仅与终边的位置有关
∴ sin( 2kπ + α ) = sin α cos(2kπ + α ) = cos α tan(2kπ + α ) = tan α cot(2kπ + α ) = cot α 其中k ∈ Z
练习:计算下列个三角比 25π sin 3 5π cot(− ) 4 31π tan 6
例2 : 求 和- 的正弦,余弦正切和余切 2 2 π 解:在角 的终边,即y轴的正半轴上取一点(0,1)
π
π
∴ x = 0, y = 1 π y 得,sin = = 1 2 r π tg tan 不存在 2
π
2
∴ r = x2 + y2 = 1
x cos = = 0 2 r π π x ctg cot = = 0 2 2 y
π
在角- 的终边,即y轴的负半轴上取一点(0,-1) 2 ∴ r = x2 + y2 = 1 ∴ x = 0, y = −1
π x y 得,sin(− ) = = −1 cos(− ) = = 0 2 r 2 r ππ ππ x tan( − ) 不 存 在 cot(ctg ) = = 0 − tg 22 22 y
y
r
P ( x,
y)
y
α
o
x
Q
x
可见,锐角的三角比可以用该角终边上任意一点的坐标来定义 可见 锐角的三角比可以用该角终边上任意一点的坐标来定义. 锐角的三角比可以用该角终边上任意一点的坐标来定义 我们可以仿照锐角的三角比的定义来定义任意角的三角比
设P是角 终边上任意一点,(点P不能是角的顶点) 是角α终边上任意一点,(点 不能是角的顶点) 是角 终边上任意一点,( 不能是角的顶点 它的坐标为( ) 它的坐标为(x,y), op = r = x 2 + y 2
任意角的三角比教案

任意角的三角比教案
三角比是指三角形中各边的比值,通常包括正弦、余弦和正切。
在教学这个概念时,可以从以下几个角度进行教案设计:
1. 概念介绍,首先,要介绍三角形的基本概念,包括顶点、边、角度等,并引入三角比的概念。
可以通过图示和实际示例来让学生
直观理解三角比的含义和作用。
2. 正弦、余弦和正切的定义,分别介绍正弦、余弦和正切的定义,以及它们在直角三角形和任意角三角形中的计算方法。
可以通
过几何图形和实际问题来说明三角比的定义和计算方法。
3. 三角比的性质,介绍三角比的基本性质,如正弦、余弦和正
切的周期性、奇偶性等,以及它们之间的关系。
通过数学推导和实
例演示来让学生理解三角比的性质。
4. 三角比的应用,介绍三角比在实际生活和工程中的应用,如
测量高度、距离、角度等。
可以通过实际案例和问题让学生体会三
角比在实际中的重要性和作用。
5. 综合练习,设计一些综合性的练习题,包括计算三角比、证明三角比的性质、解决实际问题等,以帮助学生巩固所学的知识和技能。
在教学过程中,可以结合多媒体教学、小组讨论、实验演示等多种教学方法,让学生在实践中感受三角比的奥妙,提高他们的学习兴趣和能力。
同时,教师应该注重引导学生思考,培养他们的数学思维和解决问题的能力,使他们能够灵活运用三角比解决实际问题。
任意角的三角比
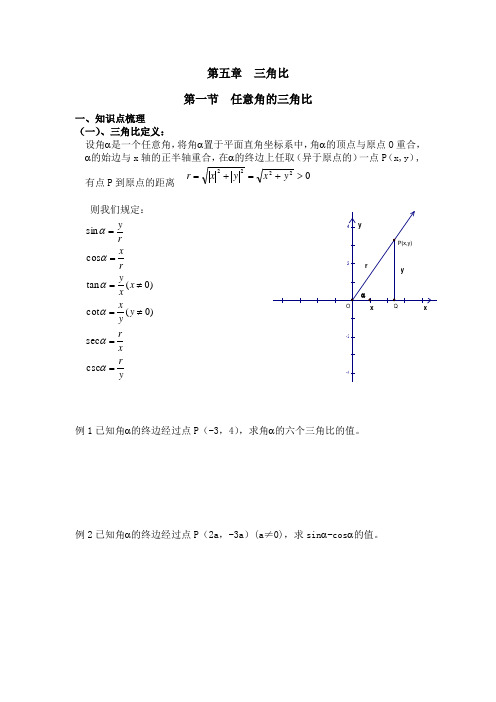
第五章 三角比 第一节 任意角的三角比一、知识点梳理 (一)、三角比定义: 设角α是一个任意角,将角α置于平面直角坐标系中,角α的顶点与原点O 重合,α的始边与x 轴的正半轴重合,在α的终边上任取(异于原点的)一点P (x,y ), 有点P 到原点的距离 02222>+=+=y x y x r则我们规定:y rx ry y xx x yr xr y ==≠=≠===ααααααcsc sec )0(cot )0(tan cos sin例1已知角α的终边经过点P (-3,4),求角α的六个三角比的值。
例2已知角α的终边经过点P (2a ,-3a )(a ≠0),求sin α-cos α的值。
例3求65π的六个三角比的值。
例4应用三角比的定义证明: (1)平方关系222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+= (2)倒数关系sin αcsc α=1,cos αsec α=1,tan αcot α=1, (3)商数关系sin cos tan ,cot cos sin αααααα==专题训练1、分别求0、2π、π、23π、π的三角比值。
2、分别求6π、4π、3π、65π、43π、32π的三角比值。
3、已知角α的终边与函数y=-3x 的图形重合,求角α的各三角比的值。
4、已知角α的终边与x轴重合,求cosα得值。
评注:三角比的定义是三角知识的源头,务必充分理解,灵活应用,熟练掌握。
(二)、三角函数线:1、正弦线:无论α是第几象限角,过α的终边与单位圆的交点P作x轴的垂线,交x轴于M,有向线段MP的符号与点P的纵坐标y的符号一致,长度等于|y|.所以有→MP=y=sinα.我们把有向线段→MP叫做角α的正弦线,正弦线是角α的正弦值的几何形式.2、余弦线:有向线段→OM叫做α的余弦线。
3、正切线:过A(1,0)点作单位圆的切线(x轴的垂线),设α的终边或其反向延长线与这条切线交于T点,那么有向线段→AT叫做角α的正切线。
任意角的三角比教案

任意角的三角比教案
一、教学目标
1. 理解正弦、余弦和正切的概念。
2. 掌握如何计算任意角的正弦、余弦和正切值。
3. 能够运用三角函数解决相关实际问题。
二、教学重点和难点
1. 重点:正弦、余弦和正切的概念及计算方法。
2. 难点:任意角的三角比的应用。
三、教学内容
1. 正弦、余弦和正切的定义:在直角三角形中,对于任意角A,定义如下:
正弦(sinA)= 对边/斜边,余弦(cosA)= 邻边/斜边,正切(tanA)= 对边/邻边。
2. 任意角的三角比的计算:
对于任意角A,可以通过相关公式计算其正弦、余弦和正切值。
sinA = b/c, cosA = a/c, tanA = b/a,其中a、b、c分别为直角三角形的边长。
四、教学过程
1. 引入:
通过实际问题引入正弦、余弦和正切的概念,比如航海、建筑等领域中的应用。
2. 讲解:
讲解正弦、余弦和正切的定义,并介绍如何计算任意角的三角比。
3. 示例分析:
给出一些具体的例子,让学生通过三角函数的计算,解决相关实际问题。
4. 练习:
让学生做一些相关练习,巩固所学知识。
五、教学小结
通过本节课的学习,学生能够理解正弦、余弦和正切的概念,掌握计算任意角的三角比的方法,并能够运用到实际问题中。
六、作业布置
布置相关的练习题,鼓励学生在课后复习所学知识,并思考如何应用到生活中。
七、教学反思
回顾本节课的教学过程,总结学生的学习情况,思考如何更好地教学。
高一数学上《任意角的三角比》教案_

芯衣州星海市涌泉学校任意角三角比一、任意角三角比教学内容分析任意角的三角比分为4个课时。
第一课时学习与角有关的概念,如正角、负角、零角、象限角、终边一样的角,并且能按要求正确表示。
第二课时通过比较角度制与弧度制,体会弧度制在解决问题中的优点;能正确进展弧度与角度的换算;会利用弧长公式和扇形面积公式解决实际问题。
第三课时通过任意三角比的学习进展求值、化简和证明。
第四课时领会象限角的三角比的符号及坐标角的三角比值,并在此根底上进展计算、判断和求值等。
二、教学目的设计1、知识与技能领会与角有关的概念,如正角、负角、零角、象限角、终边一样的角,并且能按要求正确表示;通过比较角度制与弧度制,体会弧度制在解决问题中的优点;能正确进展弧度与角度的换算;会利用弧长公式和扇形面积公式解决实际问题;学会使用单位圆中的有向线段表示三角比;通过任意三角比的学习进展求值、化简和证明;领会象限角的三角比的符号,及坐标角的三角比值。
2、过程与方法通过生活中的实例感悟角度概念推广的必要性,体会“旋转成角〞的概念;通过回忆锐角三角比,感悟任意三角比的定义及相关要点;通过三角比的建立,是学生初步领会用代数方法解决几何问题的数形结合思想。
3、情感态度与价值观在整个教学过程中用运动变化的观点审视事物,用对立统一的规律提醒生活中的空间形式和数量关系。
培养学生的辩证唯物主义观点。
三、教学重点及难点重点:理解任意角的相关概念,掌握弧度制与角度制的关系和运用,掌握任意角三角比的值与符号,并能进展应用。
难点:弧度制的应用,任意角三角比的值与符号形成与认识。
四、教学流程设计第一课时:任意角及其度量〔1〕 华东师范大学附属东昌中学杨雪教学目的:1、 通过生活中的实例感悟角度概念推广的必要性,体会“旋转成角〞的概念。
2、 领会与角有关的概念,如正角、负角、零角、象限角、终边一样的角,并且能按要求正确表示。
3、 树立辩证唯物主义的世界观。
教学用具: 多媒体。
任意角的三角比

2π 4. 确定符号: cos 315° ; (2) sin − (1) 3 13π ' (3) tan( −588°12 ) ; (4) cot . 4
;
解: + (1)
(2) −
θ
(3) −
(1) S△OBC < S扇OBC < S△OCD
B
D
1 1 1 2 ⇒ ⋅1⋅ sin α < α ⋅1 < ⋅1 ⋅ tan α 2 2 2
O
A
C
∴ sin α < α < tan α
(2) sin α + cos α = AB + OA > OB = 1
4 3 4 sin α = , cos α = − , tan α = − , 5 5 3
3 5 5 cot α = − , sec α = − , csc α = . 4 3 4
2. 角 β 终边上一点 M 到原点的距离为 10,且 4 cos β = − (0 < β < π ),求 M 的坐标。 5
(2) tan(−3250°) = tan 350° < 0
4.(1) 设 tan α ⋅ cos α > 0,且 cot α ⋅ sin α < 0,则α 在第几象限? (2) 已知 cos α < 0,且 tan α ≥ 0,确定角α 终边的位置。
解: tan α ⋅ cos α > 0 ⇒ α ∈ (1) Ⅰ或Ⅱ
4. 各三角比在各个象限的符号:
+
+
-
+ +
5.2(1)任意角三角比

五、课堂小结
1、掌握任意角的三角比的定义与符号. 2、会求任意角的三角比. 3、熟记特殊角的三角比值.
.
1.三角比的值与角 规定正割 sec 和余割 csc 终边上的点P的位 r sec ( k , k Z ) 置是否有关?
y
x 2 r ( k , k Z ) csc y
2.任何角的三角比 都存在吗?
例 1、已知角的终边经过点 P(2, 1),求角的 六个三角比的值.
例4、已知角的终边经过点 P(3a,4a)(a 0), 求: 2 sin cos.
解: x 3a, y 4a r (3a) (4a) 5 a
2 2
(1)当a 0时,r 5a,则:
(2)当a 0时,r 5a,则:
y x 4a 3a 2 sin cos 2 2 1 r r 5a 5a
一、锐角三角比的定义
对边 sin 斜边 邻边 cos 斜边 对边 tan 邻边 邻边 cot 对边 a c b c a b b a
B c A a
b
C
y
r
O
.
y x
P(x,y)
x
二、任意角三角比的定义
在任意角终边上任取一点P( x,y), (除原点外) 2 2 设OP r x y (r 0) y y x P(x,y) sin cos r r y O x tan ( k , k Z ) x 2 x 提问: ( k , k Z ) cot
y x 4a 3a 1 2 sin cos 2 2 r r 5a 5a
练习: 1. 已知角 的终边过点 P 4,3,求 的六个三角比;
任意角的三角比

PT
O
M A x
交角 的终边与点 T
MP sin , OM cos , AT tan
思考 这些结论是否对于任意角都成立?
一、正弦值、余弦值和正切值的几何表示
y
T
y
1
P P
1
规定:有向线段
A
MP, OM , AT
x
O
M A x T
M O
y
T
与坐标轴同向时, 其数量为正值.
例3.判断角 所在象限: (1) sin( ) 0, tan(4 ) 0 (2) sin(2 ) cos(2 ) 0 解: (1) sin 0, tan 0
属于第三象限;
cos(2 ) cos
(2) sin(2 ) sin
y
T P
(2)
P
y
1
1
A
O
M A x
M O
T
x
例1.作出下列各角的正弦线、余弦线、正切线: 5 2 13 (1) (2) (3) (4) 3 6 3 6 解:正弦线 MP ,余弦线 OM ,正切线 AT (3)
y
T
(4)
y
1
1
M
O
M A A x
O
P
P
T
x
例2.已知 (0, ) ,利用三角函数线证明: 2 y T (1) sin cos 1
第II组诱导公式
P
M
O
A
y
1
T'
sin( ) sin cos( ) cos
tan( ) tan
3.2任意角的三角比

=|cos(70°+360°)|
=cos70°
练习
1. 已知cosɑ=35,0<ɑ<2,求sinɑ和tanɑ的值.
解:∵cosɑ=35
3
4
∵cosɑ=
,sinɑ=
9
5
5
∴cos2ɑ=25
ɑ 4 5
4
∴tanɑ=
=
×
=
ɑ 5 3
3
∵sin2ɑ+cos2ɑ=1
9
16
∴sin2ɑ=1-cos2ɑ=1-25
25
∴tanɑ=
=×()=
ɑ
5
3
3
∵sin2ɑ+cos2ɑ=1
25−16
9
∴cos2ɑ=1-sin2ɑ=1-16
=
=
25
25
25
∴cosɑ=±
9
25
=±35
∵ɑ是第三象限角
∴x<0
∵cosɑ=,r>0
∴cosɑ<0
∴cosɑ=-35
3.化简下列三角式:
ɑcosɑ
(1)cosɑtanɑ;(2) 1− ɑ ;(3) 1 − 2130°.
2
解:(1)cosɑtanɑ
ɑ
=cosɑ·ɑ
=sinɑ
ɑcosɑ
2
1− ɑ
ɑɑ
2ɑ
(2)
=
=tanɑ
(3) 1 − 2130°
=-cos130°
a的算数平方根记为
,a 的 平 方 根 记 为
± .
1
2
4.已知sinx-cosx= ,求(sinx+cosx)2的值.
任意角的三角比

三角比在各象限旳符号
sin y csc 全+ tan o cos x cot sec
例1、求下列各角旳六个三角比值:
(1) 5
6
(2) 7
6
根据计算成果,你能发觉这两个 角之间有什么关系吗? 从而,你能推断出什么结论吗?
终边相同旳角旳同名三角比相等。
sin(2k ) sin cos(2k ) cos tan(2k ) tan cot(2k ) cot
R
y
正割
sec r
x
|
k
+
2
,
k
Z
, 1
1,
余割 csc r y
| k , k Z
, 1 1,
y
正割 sec r
x
余切 cot x
y
y 角α旳终边
r P(x,y)
o
x
试说出上述六个三角比中: (1) 角α旳取值范围; (2) 六个三角比旳取值范围。
三角比 角α旳取值范围 三角比旳范围
正弦 sin y
r
R
1,1
余弦 cos x
R
正切
r
tan y
x
|
k
+
2
,
k
Z
1,1
R
余切 cot x | k , k Z
kZ
这组公式旳作用: 能够将任意角旳三角比转化为[0,2π)内 旳角旳三角比。
练习:求值
1、cos 9
4
4、cot( 31 )
4
2、sin 1470 5、sec(1050 )
3、tan( 11 )
3
6、csc 19
任意角的三角比

任意角的三角比(一)、引入复习锐角三角比:初中是怎样定义锐角三角比的?(二)、新课 一、锐角三角比的定义出发,能否对任意角定义三角比呢?使锐角三角比是它的特殊情况。
二、任意角三角比的定义: 1.用坐标法定义三角比:(1)设α是一个任意角,以α的顶点为原点,以它的始边作为x 轴的非负半轴; (2)在角α的终边上任取一点P ; (3)设P (x ,y ),计算|OP|=r (r>0).;sin ,sin ,)1(r yr y =ααα即记作的正弦叫做比值 ;cos ,cos ,)2(r xr x =ααα即记作的余弦叫做比值 ;tan ,tan ,)3(x yx y =ααα即记作的正切叫做比值;cot ,cot ,)4(y xy x =ααα即记作的余切叫做比值 ;sec ,sec ,)5(x rx r =ααα即记作的正割叫做比值 .csc ,csc ,)6(y ry r =ααα即记作的余割叫做比值A B Ca b c(x P)y2三、典型例题(3个,基础的或中等难度)例1、已知角α的终边经过点P(2,-3),求α角的六个三角比值。
例2.求下列各角的六个三角比值: (1)0 (2)π (3)23π例3:已知角α的终边上有一点P(4,y)(y ≠0)且sin α=5y,求角α六个三角比。
四、课堂练习(2个,基础的或中等难度)1、已知角α终边过点P(-1,2),则cos α=________。
2、若点P(-3,y )是角α终边上一点,且sin α=-21,则y 的值是________。
3、化简psin2π+qcos 2π=__________。
五、拓展探究(2个)1、已知角α终边经过点P(3a ,-4a )(a ≠0),求2sin α+cos α的值。
2、已知tan α=-31,且α是第四象限角。
(1)若P 为角α终边上的一点,写出符合条件的一个P 点坐标; (2)求sin α,cos α的值3、三角函数线:(1)单位圆:圆心在原点,半径等于单位长度的圆叫单位圆。
任意角的三角比,正弦,余弦,正切,三角函数线

任意角的三角比1.设α是一个任意大小的角,α的终边上任意一点P 的坐标是(),x y,它与原点的距离是()0r r =>,则α的六个三角比为:其中第二行的三角比分别为第一行三角比的倒数。
2.三角比在各象限的符号:(1)正弦值(r ya =sin )的正负看角终边的纵坐标; (2)余弦值(r xa =cos )的正负看角终边的横坐标;(3)正切值(xya =tan )的正负看角终边的横、纵坐标之商;(1)平方关系:; (2)倒数关系:sin αcsc α=1,cos αsec α=1,tan αcot α=1; (3)商数关系:sin cos tan ,cot cos sin αααααα==; 注意:已知一个角任意一个三角比,就可以求出它的其他五个三角比的值。
5.三角函数线:在单位圆中(r=1),正弦y r y a ===sin ;余弦x rxa ===cos ; 正切OAx y a ===tan ;我们把、OM 、AT 三条有向线段叫做三角函数线。
注意:(1)三角函数线的字母顺序不能调换,它是有方向的,其方向的正负性代表了三角比的正负性:与坐标轴的正方向相同表示三角比的值是正值;与坐标轴的正方向相反表示三角比的值是负值。
(2)角的正切线的方向为由A 点指向T 点。
T 点为过A 点垂直于x 轴的直线与角的终边(角的终边在一、四象限时)或终边延长线(角的终边在二、三象限时)的交点。
222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+=三角函数线第二象限第一象限第三象限第四象限6.三角函数线可以用来求三角函数的定义域、求解和证明三角不等式、比较大小等。
例1.解答下列问题:(1)若θ在第四象限,试判断sin(cos θ)·cos(sin θ)的正负性;(2)若tan(cos θ)·tan(sin θ)>0,试指出θ所在象限,并用图形表示出θ2所取的范围。
高一年级第二讲任意角的三角比

课题 任意角的三角比一、主要知识1、 任意角的三角比的定义 设施一个任意角,的终边上任意一点P (除端点外)的坐标是(x ,y ),它与原点的距离是r (r=>0),那么: 比值叫做α的正弦,记作sin,即sin =(∈R ); 比值叫做α的余弦,记作cos ,即cos =(∈R );比值叫做α的正切,记作tan ,即tan =(≠kπ+,k ∈Z ); 比值叫做α的余切,记作cot ,即cot =(≠kπ,k ∈Z ); 比值叫做α的正割,记作sec ,即sec =(≠kπ+,k ∈Z ); 比值叫做α的余割,记作csc ,即csc =(≠kπ,k ∈Z );2、 单位圆中的三角函数线设任意角α的终边与单位圆相交于点P (x ,y ),那么,sin α=r y =y ,cos α=rx = x ,如上右图,单位圆中的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线,即sin α=MP ,cos α=OM ,tan α=A T 。
二、例题分析例1、已知角α的终边上有一点P (3t ,4t )(t≠0),求角α的六种三角函数值。
II 、任意三角比的第一组诱导公式及各三角比在每个象限的符号1、 第一组诱导公式终边相同的角的同一三角函数值相等,即:sin (α+k·360°)=sin αcos (α+k·360°)=cos αtan (α+k·360°)=tan α2. 一些特殊角的三角函数值3. 各三角比在每个象限的符号sin(csc) cos(sec) tan(cot) 例2、根据下列条件,确定α是第几象限的角。
(1) sin α>0,tan α<0;(2) cos α·tan α>0; (3) sin2α>0,cos α<0。
三、巩固练习1、 已知α∈(0,2π),求证:sin α<α<tan α。
任意角的三角比

一、任意角的三角比定义 锐角三角比
y r P(x,y) P y x
sinα = cosα = tanα =
角的对边 MP y 角的斜边 OP r
α
O
x 角的邻边 OM 角的斜边 OP r
x M
y 角的对边 MP x 角的邻边 OM
x 角的邻边 OM y 角的对边 MP
例14、 (1) 求满足cosθ=0.5的角θ 的值;
2k , k Z
3
(2) 求满足cosθ<0.5的角θ 的取值范围;
(3) 解不等式tanx 1;
5 2k 2k , k Z 3 3 k
(4) 已知 sin 3m 1 ,求m的取值范围. 1 4m 2 m 3 or m
并加以研究.
四、第一组诱导公式
sin(2k ) sin cos(2k ) cos tan(2k ) tan cot(2k ) cot
注:
其中kR
1)一个角加上或者减去2的整数倍时,角的三角比不变;
2)任意角的三角比都可转化为属于[0,2)的角的三角比.
r x y
2
2
cotα =
一、任意角的三角比定义 锐角三角比
y r P(x,y) P y x
sinα = cosα = tanα =
角的对边 MP y 角的斜边 OP r 角的邻边 OM x 角的斜边 OP r 角的对边 MP y 角的邻边 OM x 角的邻边 OM x 角的对边 MP y
例9、求下列各三角比的值:
(1) (2)
(3)
1 sin 30 sin1470 2 15 2 cos( ) cos 4 2 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总结:3
4
(1)直接法:求出 的范围,分类讨论.
ⅣⅠ Ⅰ O Ⅳx
n
ⅡⅢ
(2)几何法:把各象限均分n等份,从x轴的正向的上方起,
依次将各区域标上Ⅰ、Ⅱ、Ⅲ、Ⅳ,并循环一周,则α原
来是第几象限的符号所表示的区域即为 (n∈N*)的终边
所在的区域.
n
第17讲 §5.1-1任意角的三角比(1) Ⅱ.基本方法 3.扇形弧长、弦长、面积的求法:
例8一扇形的周长为c(c>0),当扇形的圆心角α等于多少 弧度时,这个扇形的面积最大?最大面积是多少?
③终边在x轴上:
④终边在y轴正半轴上:
⑤终边在y轴负半轴上:
k k k
180O (k Z ) 360O +90O (k Z ) 360O +270O (k Z
)
k (k Z)
2k (k 2k 2 (k
Z Z
) )
⑥终边在y轴上: k 180O ⑦终边在坐标轴上: k
90O(k Z )
第17讲 §5.1-1任意角的三角比(1) Ⅰ.基础知识
一、角的概念的推广
1.角的定义:平面内由一条射线绕着其端点从初始位置旋
转到终止位置所形成的图形.
B
始边:射线的初始位置OA.
终边:射线的终止位置OB.
顶点:射线的端点O 2.角的分类:
O•
A
C
(1)正角:一条射线绕端点按逆时针方向旋转所形成的角.
Ⅱ.基本方法
1.同终边角的求法: 8 例1.若边θ与角 的的终终边边与相同5的的角终为边_相_同_,_则_在[0,2π]上终
总结:先写4 出同终边的角,然后按条件求出角.
2.已知角α的范围,,;3 则n是2是第第____象象限限角角. ; Ⅲy Ⅱ
再用定义求值.
第17讲 §5.1-1任意角的三角比(1) Ⅲ.常用公式
1.同终边角的公式: 2k (k Z) k 360O (k Z )
2.三角比公式:1.sin
y ;2.cos
x ;3.tan
y ; 4.cot
x ;
r
r
x
5.sec
r x ;6.csc
r; y
y
3.角度与弧度互换公式: 1O = 0.01745329(弧度)
半轴重合,此时角的终边在第几象限,就说这个角是第几
象限的角,或者说这个角属于第几象限.(当角的终边落
在坐标轴上,则此角不属于任何一个象限)
5.轴线角:终边落在坐标轴上的角.
①终边在x轴正半轴上: k 360O (k Z ) 2k (k Z)
②终边在x轴负半轴上: k 360O +180O (k Z) (2k 1) (k Z)
5.sec r ;正割 6.csc r ;余割
OP r x2 y2 0
x
y
2.三角比的符号:
第1象限 第2象限 第3象限 第4象限
siny csc
sin
O x
cos
cosy sec y O x
tan cot
sec
tanO cotx
csc
第17讲 §5.1-1任意角的三角比(1)
例3 一个扇形 AOB 的面积是1cm2,它的周长是4cm,则中 心角为___弧度,弦长|AB|=___.
总结: 弧长、弦长、面积的求法:
画出图形,利用条件和弧长公式、扇形面积公式,解 三角形求解.
练习:两弧度的圆心角所对弦长为2,这个圆心角所夹的 扇形的面积为___.
4.三角比的求法: 在角的终边上取一点P(x,y),求出r,判定角的范围,
(2)负角:一条射线绕端点按顺时针方向旋转所形成的角. (3)零角:一条射线没有旋转时所形成的角.
第17讲 §5.1-1任意角的三角比(1) Ⅰ.基础知识 一、角的概念的推广 3.同终边的角:{ | k 360O (k Z )} { | 2k (k Z)}
4.象限角:把角的顶点置于坐标原点,角的始边与x轴的正
90O
(k
Z
)
k
2
(k
Z)
k
2
2
(k
Z)
第17讲 Ⅰ.基础知识 二、角的度量
§5.1-1任意角的三角比(1)
1.角度制:把周角分成360等分,每一份叫做1度的角.
用“度”作为单位来度量角的单位制叫做角度 2.弧度制制. :把弧长等于半径的弧对的圆周角叫做1弧度的
角.用符号rad表示,读作弧度.
(1)定义:用“弧度”作为单位来度量角的单位制叫做弧度
例5若角α是第二象限角,则角2α的终边落在__________.
例6如图,α、β分别为终边落在OM、ON位置上的两个角, 且α=30O,β=300O. (1)求终边落在阴影部分(含边界)时所有角的集合; (2)求终边落在阴影部分,且在[0,2π]内所有角的集合.
例7一扇形的周长为20cm,当扇形的圆心角α等于多少弧度 时,这个扇形的面积最大?最大面积是多少?
B
三、任意角的三角比 1. sin a ; 2. cos b ;
c
a
1.三角比的定义: ①锐角的三角比:
3.
tan
a; b
c
4. cot
b. a
c
Ay
α
b
C
②任意角的三角比:
1.sin
y ;2.cos
x ;3.tan
y ; 4.cot
x ;
r
•P(x, y)
y
正弦 r 余弦 r 正切 x 余切 y O x M x
180
4.圆心角公式:| | l
r
1弧度= 180O 57.30O 57O18
5.弧长公式: l | | r l n r
180
6.扇形面积公式:S 1 lr 1 | | r2
22
n r 2
S 360
第17讲 §5.1-1任意角的三角比(1) Ⅳ.例题讲解 例4已知角α=45O,找出 -720O~0O内所有与α同终边的角.
(2)公式:制| .| l
360O 2 弧度
(3)角度与弧度r的互换: 1O 2 = = 0.01745329(弧度)
360 180
1弧度 360O = 180O 57.30O 57O18
2
角度数 30O 45O 60O 90O 180O 270O 360O
弧度数 6
4
3
2
3
2
2
第17讲 §5.1-1任意角的三角比(1)
