吉林省长春市第五中学高一数学任意角的三角比课件
5.2.1_任意角的三角比2017.2.20

r x r 余割 csc 正割 sec 余切 cot y y x
例1.已知角 的终边经过点 P(2,1) ,求角 的六个 三角比值. 解:x 2, y 1 因此 r (2) 2 12 5 r y 1 5 csc 5 sin y r 5 5 x 2 r 2 5 5 cos sec r x 5 2 5 x 1 y 1 cot 2 tan y 2 x 2
二、 角的度量(弧度制与角度制)
1、弧度的角与弧度制; 1 2、 角度制与弧度制的换算;
如:y 轴上角的集合{ | k , k Z} 2 第二象限角 { | 2k 2k , k Z} 2
与角 终边关于x 轴对称的角的集合 { | 2k , k Z}
(1)如果 sin 0, 且 tan 0, 试确定 是第几象限角. 试确定 是第几象限角.
(2)如果 sin cos 0,
1
0
tanα
3 2 3 3
0
1
3 不存在
0 1 0 1 1 0 0 不存在 0
3 2
2
二、三角比有意义的条件
设 P( x, y) 为角 终边上一点 OP r (r 0) r y k , k Z csc sin R y r r x k , k Z sec cos R 2 x r x y tan k , k Z cot k , k Z y 2 x
r x y 0
2 2
5 例2.求角 的正弦、余弦和正切值. 3 5 解:在直角坐标系中作角 AOB 3 OP 1 在终边上取点 P 且满足: 1 3 POM P( , ) 3 2 2 1 3 即 x , y ,r 1 2 2 5 5 1 5 3 sin cos tan 3 3 3 2 3 2
最新0127高一第1讲任意角的三角比

第1讲 任意角的三角比一、知识梳理: Ⅰ、三角比定义:设角α是一个任意角,将角α置于平面直角坐标系中,角α的顶点与原点O 重合,α的始边与x 轴的正半轴重合, 在α的终边上任取(异于原点的)一点P (x,y ), 有点P 到原点的距离 02222>+=+=y x yx r则我们规定:y rx ry y xx x yr xr y ==≠=≠===ααααααcsc sec )0(cot )0(tan cos sin例1已知角α的终边经过点P (-3,4),求角α的六个三角比的值。
例2已知角α的终边经过点P (2a ,-3a )(a≠0),求sin α-cos α的值。
例3求65π的六个三角比的值。
例4应用三角比的定义证明: (1)平方关系222222sin cos 1,1tan sec ,1cot csc αααααα+=+=+=(2)倒数关系sin αcsc α=1,cos αsec α=1,tan αcot α=1, (3)商数关系sin cos tan ,cot cos sin αααααα==针对性练习: 1、分别求0、2π、π、23π、π的三角比值。
2、分别求6π、4π、3π、65π、43π、32π的三角比值。
3、已知角α的终边与函数y=-3x 的图形重合,求角α的各三角比的值。
4、已知角α的终边与x 轴重合,求cos α得值。
Ⅱ、三角函数线: 1、正弦线:无论α是第几象限角,过α的终边与单位圆的交点P 作x 轴的垂线,交x 轴于M ,有向线段MP 的符号与点P 的纵坐标y 的符号一致,长度等于|y |.所以有→MP =y=sinα.我们把有向线段→MP 叫做角α的正弦线,正弦线是角α的正弦值的几何形式.2、余弦线:有向线段→OM 叫做α的余弦线。
3、正切线:过A (1,0)点作单位圆的切线(x 轴的垂线),设α的终边 或其反向延长线与这条切线交于T 点,那么有向线段→AT 叫做 角α的正切线。
任意角的三角比PPT课件

解:x2,y–3, r 22 (3)2 13
cssctioaensstncryxyrrxyxy1231212332333132311313133
7
二、单位圆与三角函数线
在平面直角坐标系中,称以原点O为圆心、 以1为半径的圆为单位圆(unit circle).
10
三角函数线
y
Y’
N
PT
α
o
M Ax
y
Y’
y
T α终边在第一象限
y
Y’
P
N
α
A
Mo
x
Y’
T
α终边在第二象限
Mo
PNΒιβλιοθήκη Axα终边在第三象限
o
MA x
N
P
T α终边在第四象限 11
例2、 求角7 的正弦、 余弦和正切的值.
4
解:如图 AOB 7
4
则BOA
4
y
在终边OB上取一点P,使OP=1
x2 y2
x y
1 3
10
x
y
13或xy
1 3
又 2 y 0
P(1, 3)
13
例4、填表:
α
点P的 坐标
OP
sinα
cosα tanα
cotα
secα cscα
0 (1,0) 1
0
1
0 不存在 1 不存在
思考1:如图,已知角的终边 与单位圆的交点为P,如何求点 P坐标?
单位圆上点P的坐标为 (cos,sin)
y P(x, y)
30、任意角的三角比(包括弧度制)
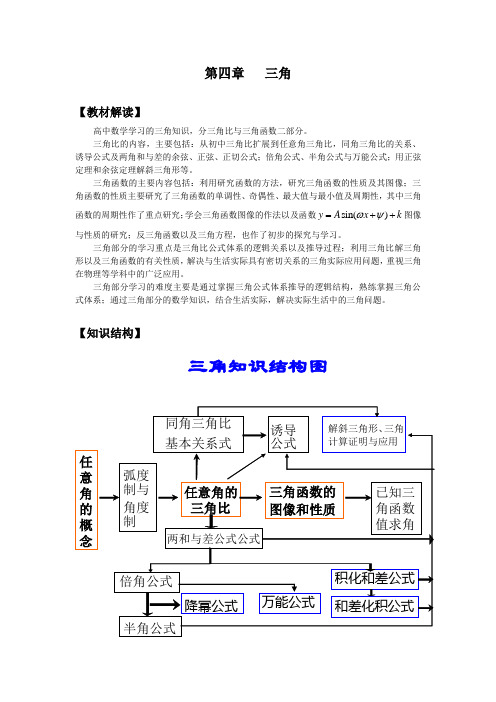
第四章 三角【教材解读】高中数学学习的三角知识,分三角比与三角函数二部分。
三角比的内容,主要包括:从初中三角比扩展到任意角三角比,同角三角比的关系、诱导公式及两角和与差的余弦、正弦、正切公式;倍角公式、半角公式与万能公式;用正弦定理和余弦定理解斜三角形等。
三角函数的主要内容包括:利用研究函数的方法,研究三角函数的性质及其图像;三角函数的性质主要研究了三角函数的单调性、奇偶性、最大值与最小值及周期性,其中三角函数的周期性作了重点研究;学会三角函数图像的作法以及函数sin()y A x k ωψ=++图像与性质的研究;反三角函数以及三角方程,也作了初步的探究与学习。
三角部分的学习重点是三角比公式体系的逻辑关系以及推导过程;利用三角比解三角形以及三角函数的有关性质,解决与生活实际具有密切关系的三角实际应用问题,重视三角在物理等学科中的广泛应用。
三角部分学习的难度主要是通过掌握三角公式体系推导的逻辑结构,熟练掌握三角公式体系;通过三角部分的数学知识,结合生活实际,解决实际生活中的三角问题。
【知识结构】三角知识结构图任 意 角 的 概 念31.任意角的三角比(包括弧度制)【教学目标】1.通过任意角的三角比的复习,进一步理解引出任意角、建立弧度制、角与实数之间一一对应关系的意义;2.掌握任意角、象限角、终边相同的角、弧度的概念;会角度与弧度之间互化; 3.熟练掌握任意角的三角比的定义; 4.借助单位圆理解任意角三角比的意义.【教学重点】理解任意角的推广以及任意角三角比的定义。
【教学难点】弧度制的概念的建立,任意角的定义.【知识整理】1.角的概念的推广一条射线绕端点按逆时针方向旋转所形成的角为正角,其度量值为正的;按顺时针方向旋转所形成的角为负角,其度量值为负的;没有旋转时,形成的角称为零角.象限角:角的顶点与原点重合,角的始边与x 轴正半轴重合,终边在第几象限的角就称为第几象限角;终边在坐标轴上的角不属于任何一个象限。
讲义15:任意角的三角比

精锐教育学科教师辅导讲义讲义编号_学员编号:年级:高一课时数:3 学员姓名:辅导科目:数学学科教师:课题任意角的三角比授课日期及时段教学目的掌握角的概念的推广、正角、负角、象限角,终边相同的角的表示;掌握弧度制、弧度与角度的转化关系,扇形面积及弧长公式;根据任意角的正弦、余弦、正切、余切、正割、余割的定义,掌握这些三角比的值在各象限的符号;并能根据角α的某种三角比值的符号,反馈出α可能存在的象限。
教学内容一、知识梳理及例题分析任意角1、角的概念的推广角可以看成平面内一条射线绕着端点从初始位置旋转到终止位置所形成的图形。
规定:按逆时针方向旋转所形成的角叫正角(positive angle),按顺时针方向旋转所形成的角叫负角(negativeangle)。
如果一条射线没有旋转时,我们称它形成了一个零角(zero angle),记作0。
提问:始边与终边重合的角是零角?[说明]确定一个角的大小不仅要看始边、终边的位置,更要看角形成的过程。
象限角:角的顶点与原点重合,角的始边与x轴的正半轴重合,此时角的终边在第几象限,我们就说这个角是第几象限的角,或者说这个角属于第几象限。
特别规定:如果角的终边在坐标轴上,就认为这个角不属于任何一个象限。
特别地:若α与β的终边相同,则它们的数量关系可以表示为。
若α与β的终边关于x轴对称,则它们的数量关系可以表示为。
若α与β的终边关于y轴对称,则它们的数量关系可以表示为。
若α与β的终边关于原点对称,则它们的数量关系可以表示为。
第一象限角表示为。
第二象限角表示为。
第三象限角表示为。
第四象限角表示为。
2、角的度量角度制:将圆周分为360份,每一份所对的圆心角叫1度的角。
弧度制的概念:把弧长等于半径的弧所对的圆心角叫做1弧度的角。
用弧度制来度量角,实际上是在角的集合与实数集R 之间建立这样的一一对应关系。
角度制与弧度制的互化:8157)180(1)(180'≈== ππ弧度弧度 π23600=(弧度) 弧度弧度017453.0)(18010≈=π 弧长公式:r l ⋅=α 扇形面积公式:22121r lr S α== 说明:① 用弧度制表示终边重合的角的方法2()k k Z βπα=+∈;② 把一角化为2k πα+形式,其中,[0,2)k Z απ∈∈,从而可判断角所在的象限;③ 在同一问题求解过程中,两种单位不能混用,如{|2k ααπ=+ 30,}k Z ∈写法不妥。
《任意角的三角比》高中数学

课后练习
3、已知角的终边在直线y 2 x上,求角的sin ,cos , tan 的值.
解: 1当角的终边在第一象限时,
在角的终边上取点1, 2 ,则r= 12 22 5
sin 2 2 5 1 5 2 ,cos , tan 2 5 5 1 5 5
任意角 的三角函数值仅与 有关,而与点 P 在角的 终边上的位置无关.
巩固
求
提高
练习 1、已知角
的终边过点
P 12,5 ,
的三个三角比的值.
解:由已知可得:
r x y
2 2
12
2
52 13
y 5 于是,sin r 13 y 5 tan x 12
2当角的终边在第三象限时,
在角的终边上取点 1, 2,则r
1 2
2
2
5
sin
2 2 5 1 5 2 ,cos , tan 2 5 5 1 5 5
归纳
总结
1. 内容总结: 三角比的概念. 2 .解题方法总结: 运用了定义法、数形结合法、分类讨论法解题. 3 .体现的数学思想: 数形结合的思想 、分类讨论的思想
单位圆中定义任意角
实例
例1
剖析
求 5 的正弦、余弦和正切值. 3 5 ,易知 AOB 解:在直角坐标系中,作 AOB 的终边与单位圆的交点坐标为
,
3
,
5 3 所以 sin 3 2 y
5 3
o
﹒
A
x
﹒B
5 tan 3 3 7 5 思考:若把角 改为 呢? 3 6 7 1 sin , 6 2 7 3 cos , 6 2
高一年级第二讲任意角的三角比

课题 任意角的三角比一、主要知识1、 任意角的三角比的定义 设施一个任意角,的终边上任意一点P (除端点外)的坐标是(x ,y ),它与原点的距离是r (r=>0),那么: 比值叫做α的正弦,记作sin,即sin =(∈R ); 比值叫做α的余弦,记作cos ,即cos =(∈R );比值叫做α的正切,记作tan ,即tan =(≠kπ+,k ∈Z ); 比值叫做α的余切,记作cot ,即cot =(≠kπ,k ∈Z ); 比值叫做α的正割,记作sec ,即sec =(≠kπ+,k ∈Z ); 比值叫做α的余割,记作csc ,即csc =(≠kπ,k ∈Z );2、 单位圆中的三角函数线设任意角α的终边与单位圆相交于点P (x ,y ),那么,sin α=r y =y ,cos α=rx = x ,如上右图,单位圆中的有向线段MP 、OM 、AT 分别叫做角α的正弦线、余弦线、正切线,即sin α=MP ,cos α=OM ,tan α=A T 。
二、例题分析例1、已知角α的终边上有一点P (3t ,4t )(t≠0),求角α的六种三角函数值。
II 、任意三角比的第一组诱导公式及各三角比在每个象限的符号1、 第一组诱导公式终边相同的角的同一三角函数值相等,即:sin (α+k·360°)=sin αcos (α+k·360°)=cos αtan (α+k·360°)=tan α2. 一些特殊角的三角函数值3. 各三角比在每个象限的符号sin(csc) cos(sec) tan(cot) 例2、根据下列条件,确定α是第几象限的角。
(1) sin α>0,tan α<0;(2) cos α·tan α>0; (3) sin2α>0,cos α<0。
三、巩固练习1、 已知α∈(0,2π),求证:sin α<α<tan α。
高三复习第15讲——任意角的三角比

第十五讲 任意角的三角比一、任意角⎧⎧⎪⎪⎨⎪⎪⎪⎩⎪⎪⎧⎪⎨⎨⎩⎪⎪⎪⎪⎪⎪⎩正角概念负角零角角度制表示法任意角弧度制—扇形的弧长、面积象限角与轴线角终边相同的角与终边有关的角1. 角概念的推广 (1)任意角的形成角可以看成是由一条射线绕着它的端点旋转而成的,射线的端点叫做角的顶点,旋转开始时的射线叫做角的始边,终止时的射线叫做角的终边。
(2)正角、负角和零角按逆时针方向旋转所形成的角叫做正角;按顺时针方向旋转所形成的角叫做负角;当射线没有任何旋转时,形成的角叫做零角。
2.表示法:角度制与弧度制 (1)1弧度的角等于半径长的圆弧所对的圆心角叫做1弧度的角。
弧度制的建立,使任意角与实数之间建立了一一对应关系.0↔⎧⎪↔⎨⎪↔⎩正角正数负角负数零角 (2)角度与弧度的换算:π弧度(rad )=180 (3)扇形的弧长与面积公式:||l r α=;211||22S lr r α== 练习1 已知一个扇形OAB 的面积是42cm ,它的周长是10cm ,求它的圆心角和弦AB 的长. 答案:12α=,18sin 4AB =.变式:已知一个扇形的周长为2(0)a a >,问这个扇形半径为何值时,才能使这个扇形面积最大?最大面积为多少?并求此时扇形的圆心角.答案:2ar =时,扇形面积最大,最大值为24a ,此时圆心角为2.3.象限角与轴线角角的顶点与坐标原点重合,角的始边与x 轴的正半轴重合,角的终边落在第几象限,就称这个角为第几象限的角;角的终边在坐标轴上,就认为这个角不属于任何象限,即称为轴线角.第Ⅰ象限角:{|22,}2x k x k k Z πππ<<+∈; 第Ⅱ象限角:{|22,}2x k x k k Z ππππ+<<+∈;第Ⅲ象限角:3{|22,}2x k x k k Z ππππ+<<+∈;第Ⅳ象限角:{|22,}2x k x k k Z πππ-<<∈; 终边落在x 轴正半轴上的角的集合:{|2,}x x k k Z π=∈; 终边落在x 轴负半轴上的角的集合:{|2,}x x k k Z ππ=+∈ 终边落在x 轴上的角的集合:{|,}x x k k Z π=∈ 终边落在y 轴正半轴上的角的集合:{|2,}2x x k k Z ππ=+∈ 终边落在y 轴负半轴上的角的集合:{|2,}2x x k k Z ππ=-∈终边落在y 轴上的角的集合:{|,}2x x k k Z ππ=+∈ 终边落在坐标轴上的角的集合:{|,}2x x k k Z π=⋅∈练习2 若tan 0,cot cos 0sin αααα<⋅>,则角α,2α分别是第几象限的角? 答案:α是第二象限角,2α是第一、三象限的角。
高一数学任意角的三角比2.doc

任意角三角比一、任意角三角比教学内容分析任意角的三角比分为4个课时。
第一课时学习与角有关的概念,如正角、负角、零角、象限角、终边相同的角,并且能按要求正确表示。
第二课时通过比较角度制与弧度制,体会弧度制在解决问题中的优点;能正确进行弧度与角度的换算;会利用弧长公式和扇形面积公式解决实际问题。
第三课时通过任意三角比的学习进行求值、化简和证明。
第四课时领会象限角的三角比的符号及坐标角的三角比值,并在此基础上进行计算、判断和求值等。
二、教学目标设计1、知识与技能领会与角有关的概念,如正角、负角、零角、象限角、终边相同的角,并且能按要求正确表示;通过比较角度制与弧度制,体会弧度制在解决问题中的优点;能正确进行弧度与角度的换算;会利用弧长公式和扇形面积公式解决实际问题;学会使用单位圆中的有向线段表示三角比;通过任意三角比的学习进行求值、化简和证明;领会象限角的三角比的符号,及坐标角的三角比值。
2、过程与方法通过生活中的实例感悟角度概念推广的必要性,体会“旋转成角”的概念;通过回忆锐角三角比,感悟任意三角比的定义及相关要点;通过三角比的建立,是学生初步领会用代数方法解决几何问题的数形结合思想。
3、情感态度与价值观在整个教学过程中用运动变化的观点审视事物,用对立统一的规律揭示生活中的空间形式和数量关系。
培养学生的辩证唯物主义观点。
三、教学重点及难点重点:理解任意角的相关概念,掌握弧度制与角度制的关系和运用,掌握任意角三角比的值与符号,并能进行应用。
难点:弧度制的应用,任意角三角比的值与符号形成与认识。
四、教学流程设计五、教学过程设计第一课时:任意角及其度量(1)华东师范大学附属东昌中学杨雪教学目标:1、通过生活中的实例感悟角度概念推广的必要性,体会“旋转成角”的概念。
2、领会与角有关的概念,如正角、负角、零角、象限角、终边相同的角,并且能按要求正确表示。
3、树立辩证唯物主义的世界观。
教学用具:多媒体。
教学方法:讲授法。
