工程力学课后习题答案第十二章-组合变形
大学《工程力学》课后习题解答-精品
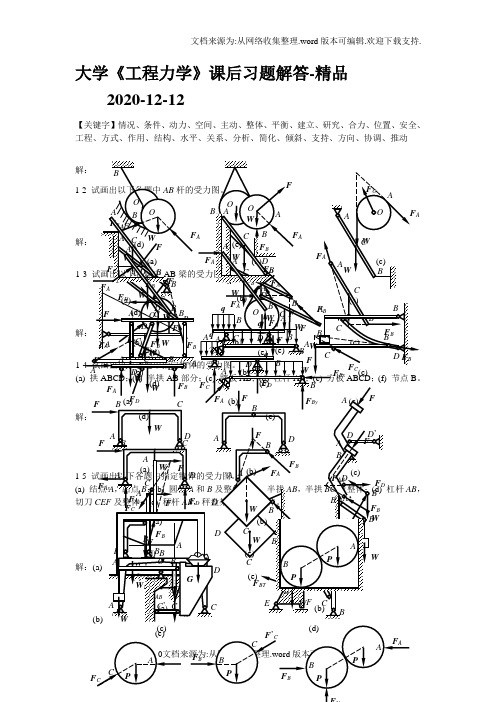
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接,另一端均与墙面铰接,如图所示,F 1和F 2作用在销钉C 上,F 1=445 N ,F 2=535 N ,不计杆重,试求两杆所受的力。
解:(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。
解:(1) 取整体(2) 2-4 在简支梁,力的大小等于20KN ,如图所示。
若解:(1)(2)求出约束反力:2-6 如图所示结构由两弯杆ABC 和DE 构成。
构件重量不计,图中的长度单位为cm 。
已知F =200 N ,试求支座A 和E 的约束力。
解:(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解:(1)取铰链B (2) 取铰链C 由前二式可得:F FF ADF2-9 三根不计重量的杆AB,AC,AD在A点用铰链连接,各杆与水平面的夹角分别为450,,450和600,如图所示。
试求在与O D平行的力F作用下,各杆所受的力。
已知F=0.6 kN。
解:(1)间汇交力系;(2)解得:AB、AC3-1 已知梁AB 上作用一力偶,力偶矩为M ,梁长为l ,梁重不计。
求在图a ,b ,c 三种情况下,支座A 和B 的约束力解:(a) (b) (c) 3-2 M ,试求A 和C解:(1) 取 (2) 取 3-3 Nm ,M 2解:(1)(2) 3-5 大小为AB 。
各杆 解:(1)(2)可知:(3) 研究OA 杆,受力分析,画受力图:列平衡方程:AB A3-7 O1和O2圆盘与水平轴AB固连,O1盘垂直z轴,O2盘垂直x轴,盘面上分别作用力偶(F1,F’1),(F2,F’2)如题图所示。
12黄向明工程力学(材料力学组合变形)

A 2 150 50 15000 m m2
A 15000 mm2 z0 75mm z1 125mm
立柱横截面的内力 FN F
M F 350 75103 425F 103 N.m
t . max
Mz 0 FN Iy A
I y 5.31107 mm4 (3)立柱横截面的最大应力
1、拉(压)弯组合变形 a、轴向力与横向力同时作用 b、偏心拉(压)载荷的作用 2、弯扭组合变形
§12 - 2
一、 受力特点
拉伸(压缩)与弯曲
作用在杆件上的 外力既有轴向拉 ( 压 ) 力,还有横向力, 杆将发生拉伸 (压缩 ) 与弯曲组合
y
Py
P
Px
x
§12 - 2
拉伸(压缩)与弯曲
y z
二、 拉(压)与弯曲内力分析 一般地,杆件横截面上产生弯矩 MZ 或 My (或二者皆有) 、轴力 N 、以及剪力。 对于实心截面,剪力引起的剪应力较小, 故一般不考虑。 三、 应力分析 横截面上任意一点 ( z, y) 处的正应力计算公式为
例题1
铸铁压力机框架,立柱横截面尺寸如图所示,材料的许用 拉应力[t]=30MPa,许用压应力[c]=120MPa。试按立柱 的强度计算许可载荷F。 解:
F F
350
F
350
(1)立柱横截面的内力
M
FN F
y1
z0
y
FN
z1
M F 350 z0 103 N.m
(2)立柱横截面的几何性 质
§ 12 - 3 偏心拉伸(压缩)
定义:作用在直杆上的外力,当其作用线与杆的轴线平行
但不重合时,将同时引起轴向拉伸(压缩)和平面
《工程力学》课后习题解答
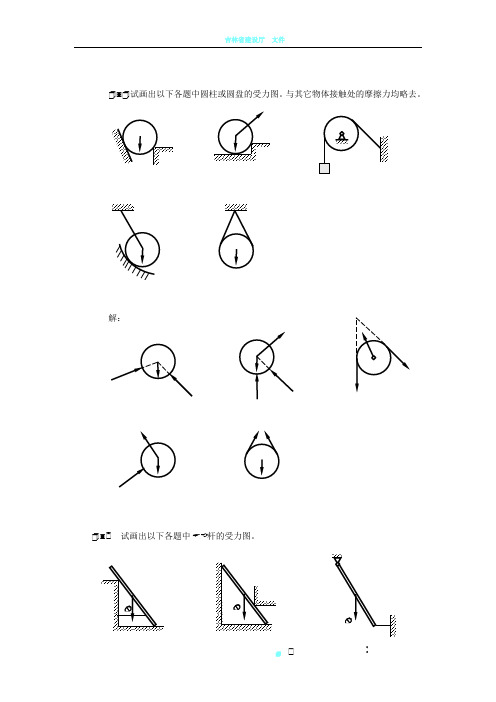
试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解: 试画出以下各题中✌杆的受力图。
✌☎☞☎☎☎✌☎☞☎☞☎☞☎☞☎✌☎☞解: 试画出以下各题中✌梁的受力图。
☎☎☞ ☞☎☞☎☞☞☎☞☎☎☞☎ 试画出以下各题中指定物体的受力图。
☎♋✆ 拱✌;☎♌✆ 半拱✌部分;☎♍✆ 踏板✌;☎♎✆ 杠杆✌;☎♏✆ 方板✌;☎♐✆ 节点 。
解:☎☞☎☎☎☎☞ ⌧☎☎☎☎☎☎ 试画出以下各题中指定物体的受力图。
☎♋✆ 结点✌,结点 ;☎♌✆ 圆柱✌和 及整体;☎♍✆ 半拱✌,半拱 及整体;☎♎✆ 杠杆✌,切刀 ☜☞及整体;☎♏✆ 秤杆✌,秤盘架 及整体。
☎☞☎☎☞☞ ☎☎☎✌☎解:☎♋✆☎♌✆☎♍✆☎♏✆✌✌❆☞ ✌☞❼ 杆✌、 在 处铰接,另一端均与墙面铰接,如图所示,☞ 和☞ 作用在销钉上,☞ ☠,☞ ☠,不计杆重,试求两杆所受的力。
解:☎✆ 取节点 为研究对象,画受力图,注意✌、 都为二力杆,☎✆ 列平衡方程:12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ ✌与 两杆均受拉。
水平力☞作用在刚架的 点,如图所示。
如不计刚架重量,试求支座✌和 处的约束力。
解:☎✆ 取整体✌为研究对象,受力分析如图,画封闭的力三角形:☞☞⌧☞☞ ☞✌☞☎✆ 由力三角形得211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴=== 在简支梁✌的中点 作用一个倾斜 ☐的力☞,力的大小等于 ☠,如图所示。
若梁的自重不计,试求两支座的约束力。
解:☎✆ 研究✌,受力分析并画受力图:☎✆ 画封闭的力三角形:相似关系:B A F F FCDE cde CD CE ED∆≈∆∴== 几何尺寸:11 22CE BD CD ED =====求出约束反力:☞☞☞♎♍♏☞12010 22010.4 45arctan 18.4B A o oCE F F kNCDED F F kN CDCECD α=⨯=⨯==⨯===-= 如图所示结构由两弯杆✌和 ☜构成。
材料力学第2版 课后习题答案 第12章 变形能法
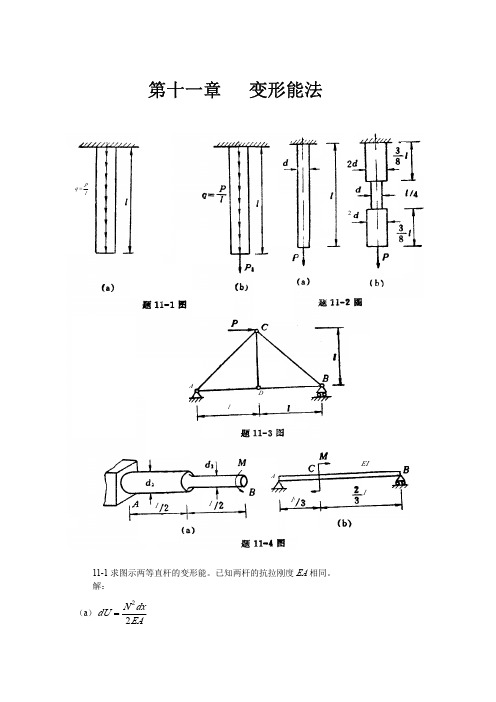
3 d1 ; 2
(b) 梁的抗弯刚度EI,略去剪切变形的影响。 解: (a) M n1 = m
M n2 = m U2 = J P2 =
9.6m 2 l Gπd14
U1 = J P1 =
m 2l 4GJ P1 π 4 d1 32
m 2l 4GJ P2 π 4 5.06π 4 d2 = d1 32 32
故
U a 16 = Ub 7
11-3 图示桁架各杆材料相同,截面面积相等,试求在 P 力作用下,桁架的变形能。 解:
支反力
R Ax = P R Ay = R B =
各杆的轴力和变形能如表所示 杆号 1 内力 Ni 杆长 各杆的变形能 Ui
P 2
2P 2
2l
2 P 2 l (4 EA)
2
− 2P 2
求 θA
M 0 ( x1 ) = −1 M 0 ( x 2 ) = −1
θA =
1 EJ
⎡ ⎛L ⎤ 1 ⎞ − P⎜ + x2 ⎟(− 1)⎥ dx 2 ∫0 (− Px1 )(− 1)dx1 + 2EJ ∫0 2 ⎢ ⎠ ⎣ ⎝2 ⎦
2
L
L
1 L2 1 = ⋅P⋅ + EJ 8 2 EJ =
求 δB
0
2l
l l l
2 P 2 l (4 EA)
0
3 4 5ຫໍສະໝຸດ P 2 P 2P 2 l (8EA) P 2l (8 EA)
故珩架的变形能为
5
U = ∑ Ui =
i =1
2 2 + 1 P 2l P 2l = 0.957 4 EA EA
11-4 试计算图示各杆的变形能。 (a) 轴材料的剪切弹性模量为G, d 2 =
《工程力学》课后习题答案全集

(mm/s)
故 =100(mm/s)
又有: ,因
故:
即:
第四章 刚体的平面运动
思考题
1.×;2.√; 3.√;4.√;5.×.
习题四
1.图示自行车的车速 m/s,此瞬时后轮角速度 rad/s,车轮接触点A打滑,试求点A的速度。
解:如图示,车轮在A点打滑, m/s, =rad/s,车轮作平面运动,以O为基点。
解:设该力系主矢为 ,其在两坐标轴上的投影分别为 、 。由合力投影定理有:
=-1.5kN
kN
kN
;
由合力矩定理可求出主矩:
合力大小为: kN,方向
位置: m cm,位于O点的右侧。
2.火箭沿与水平面成 角的方向作匀速直线运动,如图所示。火箭的推力 kN与运动方向成 角。如火箭重 kN,求空气动力 和它与飞行方向的交角 。
解: 是四杆机构。速度分析如图。点P是AB杆和轮Ⅱ的速度瞬心,故:
杆 的角速度为: rad/s
两轮齿合点M的速度和轮Ⅰ的角速度分别为:
, rad/s
6.在图所示星齿轮结构中,齿轮半径均为 cm。试求当杆OA的角速度 rad/s、角加速度 时,齿轮Ⅰ上B和C两点的加速度。
解:(1)B为轮Ⅰ的速度瞬心,
即
以轮为研究对象列方程
⑦
;
将①和③代入②得
由于轮做纯滚动
8.如图所示两等长杆AB与BC在点B用铰链连接,又在杆的D、E两点连一弹簧。弹簧的刚度系数为k,当距离AC等于a时,弹簧内拉力为零,不计各构件自重与各处摩擦。如在点C作用一水平力F,杆系处于平衡,求距离AC之值。
解:(图)
弹簧力如图:为
各力作用点横向坐标及其变分为
解:火箭在空中飞行时,若只研究它的运行轨道问题,可将火箭作为质点处理。这时画出其受力和坐标轴 、 如下图所示,可列出平衡方程。
工程力学-组合变形

10 组合变形1、斜弯曲,弯扭,拉(压)弯,偏心拉伸(压缩)等组合变形的概念;2、危险截面和危险点的确定,中性轴的确定;如双向偏心拉伸, 中性轴方程为p po o22y zz y1z y0i i++⋅=3、危险点的应力计算,强度计算,变形计算、。
4、截面核心。
10.1、定性分析图10.1 示结构中各构件将发生哪些基本变形?图10.1解题范例[解](a)AD杆时压缩、弯曲组合变形,BC杆是压缩、弯曲组合变形;AC杆不发生变形。
(b)AB杆是压弯组合变形,BC杆是弯曲变形。
(c)AB是压缩弯曲组合变形,BC是压弯组合变形。
(d)CD是弯曲变形,BD发生压缩变形,AB发生弯伸变形,BC发生拉弯组合变形。
10.2分析图10.2中各杆的受力和变形情况。
图10.2[解] (a)力可分解成水平和竖直方向的分力,为压弯变形。
(b)所受外力偶矩作用,产生弯曲变形。
(c)该杆受竖向集中荷载,产生弯曲变形.(d)该杆受水平集中荷载,偏心受压,产生压缩和弯曲变形。
(e)AB段:受弯,弯曲变形,BC段:弯曲。
(f)AB段:受弯,弯曲变形,BC段:压弯组合。
(g)AB段:斜弯曲,BC段:弯纽扭合。
10.3分析图10.3 示构件中(AB、BC和CD) 各段将发生哪些变形?图10.3[解] AB段发生弯曲变形,BC段发生弯曲、扭转变形;CD段发生拉伸、双向弯曲变形。
10.4一悬臂滑车架如图10.4 所示,杆AB为18号工字钢(截面面积30.6cm2,Wz=185cm3),其长度为l=2.6m。
试求当荷载F=25kN作用在AB的中点处时,杆内的最大正应力。
设工字钢的自重可略去不计。
Bl/2F20kN300CDAl图10.4[解]取AB为研究对象,对A点取矩可得NBCYF12.5kN=则3225==NBCXNABFF分别作出AB 的轴力图和弯矩图:kNll /232254FlkN.m轴力作用时截面正应力均匀分布,AF N=σ(压) 弯矩作用时截面正应力三角形分布,WzM=σ(下拉上压) 可知D 截面处上边缘压应力最大,叠加可得最大正应力94.9MPa (压10.5如图 10.5 所示,截面为 16a 号槽钢的简支梁,跨长 L=4.2m, 受集度为 q 的均布荷载作用 ,q=2KN/m 。
清华出版社工程力学答案-第12章 简单的静不定问题

①
②
③ l
(a)
A a FP A
B a
C
FN1
FN2 B a
FN3 C
(b) a
FP A1 (c) A Δl1 A′
习题 12-4 图
B1 B B′
Δl2
C′ Δl3 C
即
Δl1 − Δl3 = 2Δl2
3. 物理方程
(b)
Δl1 =
FN1l , EA 5FP , 6
Δl2 =
FN 2l , EA
Δl3 =
FP 铜,Ec=105GPa 铝,Ea=70GPa
300
25 60
FP
习题 12-2 图
ε=
0.24 = 8 × 10 − 4 300
轴向载荷等于二者受力之和:
FP = σ cu Acu + σ al Aal = Ecu εAcu + Eal εAal
π π = 105 × 109 × 8 × 10−4 × × 252 × 10 −6 +70 × 109 × 8 × 10−4 × ( 602 − 252 ) × 10−6 4 4 = 172.1 kN
4. 联立求解 将(a) 、 (b) 、 (c)三式联立,求得:
F1 =
(16 + 2 ) l
2 Eδ
2 EAδ
, F2 =
1
(16 + 2 ) l
4 EAδ
1
据此求得二杆横截面上的正应力分别为:
F1杆 = F2杆 =
(16 + 2 ) l
4 Eδ
=
2 × 200 ×109 × 1. 5 × 10−3
7
FA =
7F 4
建筑力学 第十二章 组合变形

图12.1
二、组合变形的分析方法及计算原理 处理组合变形问题的方法: 1.将构件的组合变形分解为基本变形; 2.计算构件在每一种基本变形情况下的应力; 3.将同一点的应力叠加起来,便可得到构 件在组合变形情况下的应力。 叠加原理是解决组合变形计算的基本原理 叠加原理应用条件:即在材料服从胡克定 律,构件产生小变形,所求力学量定荷载 的一次函数的情况下,
对于不同的截面形状, Wz/Wy 的比值 可按下述范围选取: 矩形截面: Wz/Wy = h/b=1.2~2; 工字形截面:Wz/Wy =8~10; 槽形截面: Wz/Wy =6~8。
【例12.1】跨度l=4m的吊车梁,用32a号工字钢制成, 材料为A3钢,许用应力[σ]=160MPa。作用在梁上的 集中力P=30kN,其作用线与横截面铅垂对称轴的夹角 φ=15°,如图12.3所示。试校核吊车梁的强度。 【解】(1) 荷载分解图11.9
(2) 计算横梁的内力 横梁在Ry、P和Ny的作用下产生平面弯曲,横梁中 点截面D的弯矩最大,其值为 Mmax= Pl/4 = 15.5×3.4/4 kN· m=13.18kN· m 横梁在Rx和Nx作用下产生轴向压缩,各截面的轴 力都相等,其值为 N=Rx=17.57kN (3) 选择工字钢型号 由式(12.7),有 σymax=|- N/A - Mmax/Wz|≤[σ]
§12.2 斜弯曲
• 对于横截面具有对称轴的梁,当横 向力作用在梁的纵向对称面内时,梁变 形后的轴线仍位于外力所在的平面内, 这种变形称为平面弯曲。 • 如果外力的作用平面虽然通过梁轴 线,但是不与梁的纵向对称面重合时, 梁变形后的轴线就不再位于外力所在的 平面内,这种弯曲称为斜弯曲。
变形后,杆件的轴线弯成一空间曲线称为斜弯 曲。斜弯曲可分解为两个平面弯曲。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章 组合变形习 题12.1 矩形截面杆受力如图所示。
已知kN 8.01=F ,kN 65.12=F ,mm 90=b ,mm 180=h ,材料的许用应力[]MPa 10=σ,试校核此梁的强度。
Oxyz1F 2F 1m 1mbh题12.1图解:危险点在固定端max yz z yM M W W σ=+max 6.69[]10MPa MPa σσ=<=12.2 受集度为q 的均布载荷作用的矩形截面简支梁,其载荷作用面与梁的纵向对称面间的夹角为030=α,如图所示。
已知该梁材料的弹性模量GPa 10=E ;梁的尺寸为m 4=l ,mm 160=h ,mm 120=b ;许用应力[]M Pa 12=σ;许可挠度[]150lw =。
试校核梁的强度和刚度。
题12.2图22zmax 11cos3088y M q l q l ==⋅解:22ymax 11sin 3088z M q l q l ==⋅22ymaxzmax 2211cos30sin 308866z yq l q l M M bh bh W W σ⋅⋅=+=+26cos30sin 30()8ql bh h b=+32616210422 ()8120160100.1600.120-⨯⨯⨯=+⨯⨯⨯ []6 11.971012.0,Pa MPa σ=⨯==强度安全 44z 35512sin 30384384z y q l q l W EI Ehb ⨯==4435512cos30384384y y z q l q l W EI Ehb ⨯==22maxcos30sin 30)()W ==+ =[]40.0202150m w m =<=刚度安全。
12.3 简支于屋架上的檩条承受均布载荷kN/m 14=q ,30=ϕ,如图所示。
檩条跨长m 4=l ,采用工字钢制造,其许用应力[]M Pa 160=σ,试选择工字钢型号。
14 kN/mq =题12.3图解:cos ,sin y z q q q q ϕϕ==22max max,88y z z y q l q l M M ==max max max[]y z z yM M W W σσ=+≤对工字钢,zyW W 大约在6~10之间,现设为8,由上式得 max 6max max16010/8y z z z M M Pa W W σ=+≤⨯330.85110z W m -≥⨯查40C 号钢,有,331190,99.6z y W cm W cm ==验算max maxmax 6616111901099.610y z M M MPa σ--=+=⨯⨯ 最大应力略大于许用应力,但不超过许用应力的5%,工程上允许,故可选40C 号钢12.4 图示构架的立柱AB 用25号工字钢制成,已知kN 20=F ,[]M Pa 160=σ,试校核立柱的强度。
F45BCCD题12.4图解: 由图可知,,BC CD A F F F F F ===由受力图可知D 截面为危险截面,其上的轴力和弯矩分别为20,360N F F KN M F KN ====max zF MA W σ=+ 25号钢3402z W cm =,248.541A cm =33max4620106010153.37[]48.5411040210MPa σσ--⨯⨯=+=≤⨯⨯12.5 图示一混凝土挡水墙,浇筑于牢固的基础上。
墙高为m 2,墙厚为m 5.0,试求:(1)当水位达到墙顶时,墙底处的最大拉应力和最大压应力(混凝土重力密度3kN/m 24=γ)。
(2)如果要求混凝土中不出现拉应力,试求最大允许水深h 为多少?题12.5图解:以单位宽度的水坝计算水压30 1.0109.8219.6/q gh kN m ρ==⨯⨯⨯=混凝土对墙底的压力3241020.524/F ghb kN m ρ==⨯⨯⨯=墙坝的弯曲截面系数230.0836bh W m ==墙坝的截面面积21A bh m ==墙底处的最大拉应力0,max1230.1328t h q h F MPa W A σ⋅⋅=-= 最大压应力0,max1230.1908c h q h F MPa W A σ⋅⋅=+= 如果混凝土中不出现拉应力,即0,max1230t h q h F W Aσ⋅⋅=-=0123h q h F W bh ⋅⋅= 1.063h m =12.6图示一楼梯木斜梁的长度为m 4=l ,截面为m 1.0m 2.0⨯的矩形,受均布载荷作用,m /kN 2=q 。
试作梁的轴力图和弯矩图,并求横截面上的最大拉应力和最大压应力。
题12.6图--4kNF N-3.464kN-F +M+3.464kN·mF F 30°F BA Bqy cos30 2B A q lF F ⋅==解: 3242 3.4642kN ==1sin 302442Ax F q l kN =⋅=⨯⨯=()22N lF kN =杆为弯压组合变形,最大压应力和最大拉应力分别发生在跨中截面上边缘和下边缘处:max ,max()2N c l F M W Aσ=+ 3323.46410210 5.290.10.20.10.26MPa ⨯⨯=+=⨯⨯ ,max 5.190.1 5.09t MPa MPa MPa σ=-=11.7 图示一悬臂滑车架,杆AB 为18号工字钢,其长度为m 6.2=l 。
试求当载荷kN 25=F 作用在AB 的中点D 处时,杆内的最大正应力。
设工字钢的自重可略去不计。
题12.7图解: 取AB 杆为隔离体, 由∑=0AM ,即 030sin 2=⋅︒+⋅-l F l F B ∴ FB =F由B 点平衡可知 F F F B NAB 2330cos -=︒-= 杆AB 在D 点的弯矩 Fl W W 41max ==故杆AB 在D 点截面有最大压应力,查18号工字钢,得A =30.6cm 2,Wz=185cm 3∴ 6343max 1018546.21025106.30210253423--⨯⨯⨯⨯+⨯⨯⨯⨯=+=+=z z NAB W Fl A F W M A F σ =94.9 MPa12.8 若图示边长为a 的正方形截面短柱,受到轴向压力F 作用,若在中间开一切槽,其面积为原面积的一半,试问最大压应力是不开槽的几倍?1-1截面题12.8图切槽前,柱的变形为轴向压缩,柱内各点压应力为 ()2242a F a F==σ切槽后,柱的切槽部分为偏心压缩,其最大压应力为23max22121222a Fa a a Fa a a F =⨯⨯⨯+⨯='σ ∴ 8max='σσ,即切槽后柱内的最大压应力是原来的8倍12.9 承受偏心拉力的矩形截面杆如图所示。
实验测得杆两侧的纵向应变为1ε和2ε,试证明:62121he ⋅+-=εεεε。
题12.9图解:如图偏心受拉构件11E σε=22E σε=126F Fe bh bh σ=+ 226F Fe bh bhσ=-1212212()FeE bh σσεε-==- 12122()FE bhσσεε+==+12126e h εεεε-=+ 62121he ⋅+-=εεεε12.10 图示短柱受载荷如图,试求固定端截面上角点A 、B 、C 、D 的正应力,并确定其中性轴的位置。
题12.10图解:这是一个偏心压缩问题,截面ABCD 上的内分量如图所示。
125N F F kN ==310.025(25100.025)625y M F N m N m =⨯=⨯⨯⋅=⋅320.6(5100.6)30000z M F N m N m =⨯=⨯⨯⋅=⋅ 25Sy F F kN ==A 、B 、C 、D 各点的正应力分别为y N zA y zM F M A W W σ=-++3222510662563000() 0.150.10.150.10.10.15Pa ⨯⨯⨯=-++⨯⨯⨯8.83MPa =y N zB y z M F M A W W σ=--+3222510662563000() 0.150.10.150.10.10.15Pa ⨯⨯⨯=--+⨯⨯⨯3.83MPa =y N zC y z M F M A W W σ=---3222510662563000() 0.150.10.150.10.10.15Pa ⨯⨯⨯=---⨯⨯⨯12.2MPa =-y N z D y zM F MA W W σ=-+-3222510662563000() 0.150.10.150.10.10.15Pa ⨯⨯⨯=-+-⨯⨯⨯ 7.17MPa =-设0y 、0z 为中性轴上任意一点的坐标,则在该轴上的任一点的应力均为零,即0000(,)0y N z y zM z F M y y z A I I σ=-++= 3003325106251230001200.10.150.150.10.10.15z y ⨯⨯⨯-++=⨯⨯⨯ 由上式得中性轴方程 0029.963.910z y +-=若令00z =,得 115.663.9y a m mm == 若令00y =,得 133.429.9z a m mm ==y a 、 z a 分别是中性轴与y 、z 轴的截距。
12.11 图示电动机的功率为kW 9,转速715 r /min ,皮带轮直径mm 250=D ,主轴外伸部分长mm 120=l ,主轴直径mm 40=d ,若[]M Pa 60=σ,试用第三强度理论校核轴的强度。
题12.11图解:这是一个弯扭组合变形问题。
显然危险截面在主轴根部。
该处的内力分量分别为99549(9549).715P T N m n ==⨯扭矩 根据平衡条件 222D DF F T ⨯-⨯=得 221209600.25T F N N D ⨯===弯矩 3(39600.12)M Fl N m ==⨯⨯⋅ 应用第三强度理论 2222max 33120346(4010)32M T Pa W σπ-++==⨯⨯ []58.360MPa MPa σ=<=最大工作应力小于许用应力,满足强度要求,故安全。
12.12铁道路标圆信号板,装在外径mm 60=D 的空心圆柱上,所受的最大风载2m /kN 2=p ,[]M Pa 60=σ。
试按第三强度理论选定空心柱的厚度。
题12.12图解:忽略风载对空心柱的分布压力,只计风载对信号板的压力,则信号板受风力 2230.50.51039344F p N ππ⨯⨯⨯===空心柱固定端处为危险截面,其弯矩:0.8314M F N =⨯=扭矩:0.6236T F N =⨯=[]3r wσσ=≤34{}1()32D d D σπ≤⎡⎤-⎢⎥⎣⎦[]443(1d D D πσ≤-6010d D -≤=⨯354.71054.7m mm -=⨯=6054.7 2.6522D d mm δ--≥== 12.13 在图示的轴 AB 上装有两个轮子,作用在轮子上的力kN 3=F 和Q ,设此二力处于平衡状态,轴的许用应力[]M Pa 60=σ,试用最大切应力理论选择轴的直径d 。
