强度理论典型习题解析
强度理论典型习题解析

强度理论典型习题解析1 已知铸铁的拉伸许用应力MPa 30][t =σ,压缩许用应力MPa 90][c =σ,30.0=µ,试对铸铁零件进行强度校核,危险点的主应力为:(1) MPa 301=σ,MPa 202=σ,MPa 153=σ; (2) MPa 201−=σ,MPa 302−=σ,MPa 403−=σ; (3) MPa 101=σ,MPa 202−=σ,MPa 303−=σ。
解题分析:选用强度理论时,不但要考虑材料是脆性或是塑性,还要考虑危险点处的应力状态。
解:(1) MPa 301=σ,MPa 202=σ,MPa 153=σ,危险点处于三向拉应力状态,不论材料本身是塑性材料或是脆性材料,均采用第一强度理论,即:][0MPa 3t 1r1σσσ===,安全(2) MPa 201−=σ,MPa 302−=σ,MPa 403−=σ,危险点处于三向压应力状态,即使是脆性材料,也应采用第三或第四强度理论,即:][MPa 20)MPa 40(MPa 20t 31r3σσσσ<=−−−=−=,安全 ])MPa 20MPa 40()MPa 40MPa 30()MPa 30MPa 20[(21222r4+−++−++−=σ, ][MPa 3.17t σ<=,安全。
(3) MPa 101=σ,MPa 202−=σ,MPa 303−=σ,脆性材料的危险点处于以压应力为主的应力状态,且许用拉应力与许用压应力不等,宜采用莫尔强度理论,即:][MPa 02MPa)30(MPa90MPa30MPa 10][][t 3c t 1rM σσσσσσ<=−−=⋅−=,安全 2 图示实心圆轴受轴向外力F 和外力偶M 作用。
已知圆轴直径d =10 mm ,M =Fd /10。
(1)材料为钢时,许用应力MPa 160][=σ;材料为铸铁时,许用应力MPa 30][t =σ。
试分别计算圆轴的许可载荷;(2)材料为铸铁,且F =2 kN 、E =100 GPa 、][F 25.0=µ,计算圆轴表面上与轴线成30°方位上的正应变。
08第八章 材料力学习题解答(应力状态分析和强度理论)
σ x +σ y
2 +
+
σ x −σ y
2
cos 2α − τ xy sin 2α
80 + σ y
80 − σ y
2 2 ∴σ y = 40 MPa
(3) 主应力
cos(120o ) − 0
σ 1 = σ x = 80 MPa
8.6. 图示矩形截面梁某截面上的弯矩和剪力分别为 M=10 kN.m, Q=120 kN。 试绘出截面上 1、 2、3、4 各点的应力状态单元体,并求其主应力。
y 50 1 2 100 z 3 4 50
M
25
x
Q 解:(1) 截面上 1 点的应力:
σ (1) = −
M 1 2 bh 6
=−
10 × 103 1 × 0.05 × 0.12 6
27MPa 60MPa
4
2 σ max ⎫ 60 ⎧70.4 MPa ⎛ 60 ⎞ ± ⎜ ⎟ + 27 2 = ⎨ ⎬= σ min ⎭ 2 ⎝ 2 ⎠ ⎩ −10.4 MPa σ 1 = 70.4 MPa σ 2 = 0 σ 3 = −10.4 MPa
(4) 截面上 4 点的应力:
σ (4) = −σ (1) = 120 MPa
δ
T P 解:(1) A 点的应力状态 T
30 A
o
d
P
τxy σx
属二向应力状态,应力分量是
P 20000 = = 63.7 × 106 Pa = 63.7 MPa A π × 50 × 2 × 10−6 σy =0
σx =
τ xy = −
T 600 =− = −70.6 × 106 Pa = −70.6 MPa 2 2π r t 2π × 262 × 2 × 10−9
材料力学第2版 课后习题答案 第10章 强度理论

解: t ≥
pD =
2[σ ]
3×106 ×1 2 × 300×106
= 0.01m = 1.0cm
2
9-8 铸铁圆柱形容器外直径D = 20 cm,壁厚t=2cm,受内压强p=4MPa,并在容器两端
受轴向压力P=200 kN作用,设 µ = 0.25 ,
许用拉应力[σ +]=25 MPa,(1)用第二强
论作强度校核。 解:
σ
4 xd
=
σ 2 + 3τ 2
σ
= 1202 + 3× 402 = 138MPa < [σ ]
τ
σ τ
题 9-3 图
所以安全。
9-4 某梁在平面弯曲下,已知危险截面上作用有弯矩M=50.9 kN ⋅ m ,剪力FS=134.6 kN,截面为No. 22b工字钢,[σ ]=160 MPa,试根据第三强度理对梁作主应力校核。
σ
m xd
=
σ
1
−
σ σ
+ b − b
σ3
= 1.027 −
256 × (−101.027)
625
=
42.4MPa
9-12 内径为d,壁厚为t的圆筒容器,内部盛有比重为γ ,高度为H的液体,竖直吊装如
图示。试按第三强度理论沿容器器壁的母线绘制圆筒的相当应力σ
3 xd
图(不计端部影响)。
解:
σ
y
=
πd2 4
应力校核。
70
(+)
(−) 30
( Q −图)
(−) 20
(−) 30
24.44 (+)
(M −图)
(−) 20
Wz
机械设计强度篇章典型试题剖析

一. 是非题:正确的在()中写“√”,错误的在()中写“×”1、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,将会降低该零件的冲击强度。
( )2、在不改变零件静强度的条件下,加大在一定载荷下零件的弹性变形量,可提高耐冲击强度。
( )3、设计零件时,安全系数应尽可能选大些,使该零件工作更可靠与安全。
( )4、某转轴采用40钢(σS MPa =335),经校核其扭转刚度不够,可改选高强度合金结构钢40Cr ()σS MPa =785,以提高刚度。
( )5、设计某普通碳钢零件时,校核后刚度不足,采用高强度合金钢时,对提高其刚度是不起作用的。
( )6、在变应力作用下,零件的主要失效形式将是疲劳断裂,而在静应力作用下,其失效形式将是塑性变形或断裂。
( )7、只要材料的平均极限应力σlim 大于零件的平均工作应力σm ,则安全系数S 就大于1,工作是可靠的。
( )8、若材料的平均极限应力σlim 大于零件的平均工作应力σm ,则零件的安全系数不一定总是大于1。
( )9、渐开线圆柱直齿轮传动空载运转时,可以认为是处于齿面线接触状态。
( )10、渐开线圆柱直齿轮传动工作时,齿面载荷的传递是通过真实的线接触进行的。
( )11、两圆柱体相接触,其轴线互相平行,在受法向压力作用下,则两零件的接触应力不等,直径大的零件所受接触应力小。
( )12、两圆柱体相接触,其轴线互相平行,受法向压力,则两零件的接触应力相等。
( )二、选择题:把正确的选项代号填入()中1、在受轴向变载荷的紧螺栓联接中,采用柔性螺栓,是为了_____________。
A.增大变载荷下的剩余预紧力,提高联接可靠性;B.改善变载荷下的螺母支承面接触状态;C.降低应力幅σa;D.可减轻螺栓重量,节省材料。
2、已知某转轴在复合应力状态下工作,其弯矩作用与扭矩作用下的安全系数分别为Sσ=6.1,Sτ=18.5,则该转轴的实际安全系数大小为_____________________。
第十章 强度理论(习题解答)
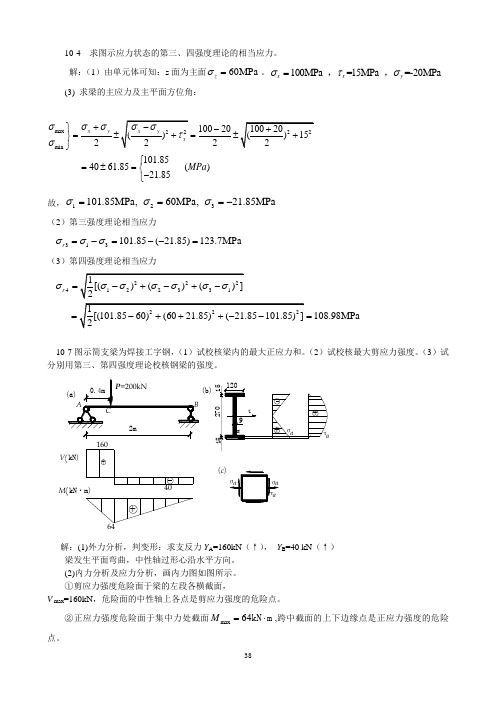
10-4 求图示应力状态的第三、四强度理论的相当应力。
解:(1)由单元体可知:z 面为主面60MPa z σ=。
100MPa =15MPa =-20MPa x x y στσ=,, (3) 求梁的主应力及主平面方位角:max min 1002022101.854061.85()21.85x y MPa σσσσ+⎫-=±=±⎬⎭⎧=±=⎨-⎩故,123101.85MPa,60MPa,21.85MPa σσσ===-(2)第三强度理论相当应力313101.85(21.85)123.7MPa r σσσ=-=--=(3)第四强度理论相当应力4108.98MPa r σ===10-7图示简支梁为焊接工字钢,(1)试校核梁内的最大正应力和。
(2)试校核最大剪应力强度。
(3)试分别用第三、第四强度理论校核钢梁的强度。
M kN ·m)64+V kN)(c )(b)解:(1)外力分析,判变形:求支反力Y A =160kN (↑), Y B =40 kN (↑)梁发生平面弯曲,中性轴过形心沿水平方向。
(2)内力分析及应力分析,画内力图如图所示。
①剪应力强度危险面于梁的左段各横截面,V max =160kN ,危险面的中性轴上各点是剪应力强度的危险点。
②正应力强度危险面于集中力处截面max 64M =⋅kN m ,跨中截面的上下边缘点是正应力强度的危险点。
③按第三、四强度理论,集中力处C 的左截面也可能是危险面,C 的左截面腹板和翼板的交界处为强度理论的危险点。
(3)求截面的几何性质:336512030055.5270287.9108.79101212z I -⨯⨯=-⨯=⨯=⨯44mm m4,30012015(7.5)256500 2.565102z a S *-=⨯⨯-==⨯33mm m 4,30013512015(7.5)1359338512.5 3.3851022z S *-=⨯⨯-+⨯⨯==⨯半33mm m m mm 135.0135==a y(4)对梁进行正应力校核[]3max max 564100.150109.21608.7910b zM y I σσ-⨯=⋅=⨯==⨯Pa MPa <MPa故,满足正应力强度。
工程力学 第12章 强度理论 习题及解析

工程力学(工程静力学与材料力学)习题与解答第12章 强度理论12-1 对于建立材料在一般应力状态下的失效判据与设计准则,试选择如下合适的论述。
(A )逐一进行试验,确定极限应力;(B )无需进行试验,只需关于失效原因的假说;(C )需要进行某些试验,无需关于失效原因的假说; (D )假设失效的共同原因,根据简单试验结果。
知识点:建立强度理论的主要思路 难度:一般 解答:正确答案是 D 。
12-2 对于图示的应力状态(y x σσ>)若为脆性材料,试分析失效可能发生在: (A )平行于x 轴的平面; (B )平行于z 轴的平面;(C )平行于Oyz 坐标面的平面; (D )平行于Oxy 坐标面的平面。
知识点:脆性材料、脆性断裂、断裂原因 难度:难 解答:正确答案是 C 。
12-3 对于图示的应力状态,若x y σσ=,且为韧性材料,试根据最大切应力准则,失效可能发生在: (A )平行于y 轴、其法线与x 轴的夹角为45°的平面,或平行于x 轴、其法线与y 轴的夹角为45°的平面内;(B )仅为平行于y 轴、法线与z 轴的夹角为45°的平面; (C )仅为平行于z 轴、其法线与x 轴的夹角为45°的平面; (D )仅为平行于x 轴、其法线与y 轴的夹角为45°的平面。
知识点:韧性材料、塑性屈服、屈服原因 难度:难 解答:正确答案是 A 。
12-4 铸铁处于图示应力状态下,试分析最容易失效的是: (A )仅图c ; (B )图a 和图b ; (C )图a 、b 和图c ; (D )图a 、b 、c 和图d 。
知识点:脆性材料、脆性断裂、断裂准则 难度:一般 解答:正确答案是 C 。
12-5低碳钢处于图示应力状态下,若根据最大切应力准则, 试分析最容易失效的是: (A )仅图d ; (B )仅图c ; (C )图c 和图d ; (D )图a 、b 和图d 。
强度理论(习题)

8
7.5 10
3
4 .93 MPa
r 4 x 3 2 xy 138 2 4 .93 2 138.3 MPa
§9–3
莫尔强度理论
莫尔准则(Mohr Criterion)
本世纪初,德国工程师莫尔考虑到某些材料拉伸与压缩 强度不等的情况,将最大剪应力理论加以推广,提出了 莫尔强度理论.
E a
C左: F SC 40 kN , M C 40 kNm E左(右): FSE 8 kN , M E 48kNm
②弯曲正应力强度条件:
max
ME W
(kN) FS
+
8 8
_
40
W 300cm 3
选22a号工字截面:
W 309cm 3 , I z 3400cm 4 Iz 18.9cm S max
④校核危险截面E处F点强度 (即校核梁的主应力)
x
M E yF 48 10 3 110 12.3 10 3 3400 10
8
12.3
F
Iz
110
138MPa
yx
x
xy
FSE S * z b Iz
xy yx
xy
x 8 10 3 110 12.3 116.15 10 9
8
40 10 3 110 12.3 116.15 10 9 7.5 10
3
25 MPa
2 2 r 4 x 3 xy 1152 3 252 121MPa
7.5
E左(右): FSE 8 kN , M E 48kNm
材料力学 第8章强度理论

同的材料,式(8.8)可演化成式(8.6)。
8.4 各种强度理论的适用范围
8.4.1 强度理论的选用原则 1. 强度理论的选用原则 (1) 脆性材料:当最小主应力大于等于 0 时,使用第一理论;当最小主应力小于 0 而
·176·
第 8 章 强度理论
·177·
最大主应力大于 0 时,使用莫尔理论。当最大主应力小于等于 0 时,使用第三或第四强度 理论。
强度条件:
相当应力表达式:
σ1
−
[σ [σ
+ −
] ]
σ
3
≤
[σ
]
(8.8)
σ rm
= σ1
−
[σ [σ
+ −
] ]
σ
3
≤ [σ
]
(8.9)
分析:莫尔强度理论考虑了材料抗拉和抗压能力不等的情况,这符合脆性材料(如岩石
混凝土等)的破坏特点,但未考虑中间主应力σ 2 的影响是其不足之处。对于 [σ + ] 和 [σ − ] 相
综合分析材料破坏的现象,认为构件由于强度不足将引发两种失效形式: (1) 脆性断裂:材料无明显的塑性变形即发生断裂,断面较粗糙,且多发生在垂直于 最大正应力的截面上,如铸铁受拉、扭,低温脆断等。关于断裂的强度理论为:最大拉应 力理论和最大伸长线应变理论。 (2) 塑性屈服(流动):材料破坏前发生显著的塑性变形,破坏断面粒子较光滑,且多发 生在最大切应力面上,例如低碳钢拉、扭,铸铁压。关于屈服的强度理论为最大切应力理 论和形状改变比能理论。 为此,对强度破坏提出了各种不同的假说。各种假说尽管各有差异,但它们都认为: 材料之所以按某种方式破坏(屈服或断裂),是由于应力、应变和应变能等诸因素中的某一 因素引起的。按照这类假说,无论单向应力状态还是复杂应力状态,造成破坏原因是相同 的,即引起破坏的因素是相同的。强度理论就是关于材料破坏现象主要原因的假设。即认 为不论是简单应力状态还是复杂应力状态,材料某一类型的破坏是由于某一种因素引起 的。据此,可以利用简单应力状态的实验结果,来建立复杂应力状态的强度条件。我们称 其为强度理论(strength theories)。
材料力学强度理论

2
2
2
u f 6E
σ1 σ 2 σ 2 σ3 σ3 σ1
将 σ1 σ s , σ 2 σ3 0 代入上式,可得材料的极限值
u fu
1 ν
6E
2
2 s
强度条件为:
1
2
2
2
2 1 2 2 3 3 1
2
2
2
2
2
设 ,则
2 2
1 2 3
由第四强度理论的计算应力 状态 (a )
r4 2 3 2
状态 (b ) r4 2 3 2
两种情况下的危险程度相等。
基本观点
构件受外力作用而发生破坏时,不论破坏的 表面现象如何复杂,其破坏形式总不外乎几种类型, 而同一类型的破坏则可能是某一个共同因素所引起的。
材料破坏的两种类型(常温、静载荷)
1. 脆断破坏: 无明显的变形下突然断裂。 2. 屈服失效: 材料出现显著的塑性变形而丧
失其正常的工作能力。
引起破坏的某一共同因素
1 3
70 2
30
2 50 MPa
70
2
30 2
402
94.72
50 20 5
MPa
5.28
r 3 89.44MPa , r 4 77.5MPa
例题 2 两种应力状态分别如图所示,试按第四强度理论, 比较两者的危险程度。
(a)
120MPa
(2)对于图 b 所示的单元体,
应力状态分析和强度理论(例题)

50 x 100 x 100 cos 600 0
300
2
2
100MPa x
(3)求主应力:因为τxy = 0,所以有
1 100 MPa 2 0 3 100 MPa
(4)求最大剪应力:
100 100 100MPa
max
例题
例7-4 薄壁锅炉的平均直径D=1060 mm,壁厚t=25 mm,蒸气压力p=2.5 MPa,材料许用应力
[σ]=40 MP;按最大剪应力理论校核锅炉的强度。
σ’ p
σ’
p
σ’’
σ’’
强度不够,重新设计 pD
r3
1
3
2t
t
pD
2
0.033m
(5)用最大形状改变比能理论计算
210 109
3.11104
τα
σα
300
τxy
p.5
例题
例题
例7-4 薄壁锅炉的平均直径D=1060 mm,壁厚t=25 mm,蒸气压力p=2.5 MPa,材料许用应力
[σ]=40 MP;按最大剪应力理论校核锅炉的强度。
σ’ p
σ’
p
σ’’
σ’’
解:(1)由横截面分离体的平衡条件
' Dt p 1 D2 4
例题
(d) (1)应力分量 (2)用解析法求斜截面上的应力
(3)应力圆
p.9
例题
例题
例7-6. 已知应力状态如图所示,图中的应力单位为MPa。试求:
(1)主应力大小,主平面位置;(2)在单元体上给出主平面位置及主应力方向;(3)最大剪应力。
应力状态分析和强度理论 - 例题

3. 求斜截面上的应力
τ
三维投影成二维
x y
2
σ
x y
2
TSINGHUA UNIVERSITY
cos2 xysin2
τ σ
x y
2
sin2 xy cos2
σx=63.7 MPa,σy=0,
τxy=一76.4 MPa,α =120º 。
120
x y
2
sin2 xy cos2
63.7MPa 0 = sin 2 120 76.4MPa cos 2 120 2 = 10.7MPa
3.确定主应力与最大剪应力
τ σ
=
TSINGHUA UNIVERSITY
x y
y
试求(1) 斜面上的应力;
xy
(2)主应力、主平面;
(3)绘出主应力单元体。
x
(1) 斜面上的应力
α =-30
x 60MPa,
y 40MPa,
xy 30MPa,
30。
y
xy
x y x y cos 2 xy sin 2 2 2
63.7MPa 02 4 76.4MPa 2
=0
确定主应力与最大剪应力
1 = 114.6MPa
2 =0
TSINGHUA UNIVERSITY
3 = 50.9MPa
114.6MPa--50.9MPa = =82.75MPa 2
1.确定主应力
应用平面应力状态主应力公式
第九章强度理论

第九章 强度理论1.图示应力状态,用第三强度理论校核时,其相当应力为:(A )213τσγ=; (B )=3γστ;(C )=3γστ213; (D )=3γσ2τ;正确答案是 。
2和许用拉应力的关系为:(A )[τ] = [σ]; (B )[τ] =[σ] / 2 ;(C )[τ] = [σ] / 213; (D )[τ] = [σ] / 3 ;正确答案是 。
3.塑性材料的下列应力状态中,那一种最易发生剪切破坏:45.第三强度理论和第四强度理论的相当应力分别为3γσ 及4γσ ,对于纯剪应力状态,恒有3γσ / 4γσ= 。
6.按第三强度理论计算图示单元体的相当应力3γσ= 。
7.图示①、②、③为三个平面应力状态的应力圆,试画出各应力圆所对应的主平面微元体上的应力。
8.图示为承受气体压力p 的封闭薄壁圆筒,平均直径为D ,壁厚t ,气体压强p 均为已知,用第三强度理论校核筒壁强度的相当应力3γσ= 。
9.单元体如图,已知αττσ42−==xy y 。
证明:2/3/=y x σσ ;6/7/=x σσα。
τx10.证明线弹性材料的泊松比μ满足关系式:0<μ<0.511.图(a )、(b )表示同一材料的两个单元体。
材料的屈服极限s σ= 275 MPa 。
试根据第三强度理论求两个单元体同时进入屈服极限时拉应力σ 与剪应力τ的值。
若σ> τ。
(a) (b)12.图示受扭圆轴的d = 30 mm ,材料的弹性模量 ,v =0.3 ,屈服极限MPa E 5101.2×=S σ= 240MPa ,实验测得a b 方向的应变为 0002.0=ε 。
试按第三强度理论确定设计该轴时采用的安全系数。
13.从低碳钢零件中某点处取出一单元体,其应力状态如图所示,试按第三、四强度理论计算单元体的相当应力。
单元体上的应力为60=ασ,80−=βσ,(°+=90αβ),40−=ατ (单位:MPa 。
德州学院,材料力学,期末试题7章习题讲解

德州学院,材料⼒学,期末试题7章习题讲解第七章⼒和应变分析强度理论 §7.1应⼒状态概述1.过受⼒构件内⼀点,取截⾯的不同⽅位,这⼀点在各个⾯上的(D ). (A )正应⼒相同,切应⼒不同;(B )正应⼒不同,切应⼒相同;(C )正应⼒和切应⼒都相同;(D )正应⼒和切应⼒都不同。
2.关于单元体的描述,下列正确的是A(A )单元体的三维尺⼨必须是微⼩的;(B )单元体是平⾏六⾯体;(C )单元体必须是正⽅体;。
(D )单元体必须有⼀对横截⾯。
3.对于图⽰承受轴向拉伸的锥形杆上的A 点,哪⼀种应⼒状态是正确的Dxτxx4.在单元体的主平⾯上()。
(A )正应⼒⼀定最⼤;(B )正应⼒⼀定为零;(C)切应⼒⼀定最⼩;(D )切应⼒⼀定为零。
§7.2⼆向应⼒状态实例1. Q235钢制成的薄壁圆筒形蒸汽锅炉,壁厚δ,内径D ,蒸汽压⼒p ,试计算锅炉壁内任意⼀点处的三个主应⼒。
注:薄壁圆筒受⼒均匀,因此,任意点的应⼒状态均相同。
1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz 薄壁圆筒与纸⾯垂直⽅向上的σz 为零.总结:薄壁圆筒的三个主应⼒为:薄壁圆筒为两向应⼒状态注意事项:1.注意单位配套使⽤;2. 纵向截⾯上正应⼒是横截⾯正应⼒的两倍;3.按规定排列正应⼒。
课本215页例7.1如下由Q235钢制成的蒸汽锅炉,壁厚δ=10mm,内径D=1m,蒸汽压⼒p=3MPa,试计算锅炉壁内任意⼀点处的三个主应⼒。
经分析,薄壁圆筒为两向应⼒状态2. 圆球形容器的壁厚为δ,内径为D,内压为p,求容器内任意⼀点的应⼒。
注:薄壁圆球受⼒均匀,因此,任意点的应⼒状态均相同。
1.求⽔平⽅向上的正应⼒σx2.求竖直⽅向上的正应⼒σy3.求垂直于纸⾯⽅向上的正应⼒σz薄壁圆筒与纸⾯垂直⽅向上的σz为零.球形薄壁容器的三个主应⼒为:受内压的球形薄壁容器为⼆向应⼒状态§7.3 ⼆向应⼒状态分析——解析法⼆向应⼒状态下,单元体各⾯上应⼒分量皆为已知,如下图所⽰:求垂直于xy平⾯的任意斜截⾯ef上的应⼒及主应⼒和主平⾯⼀.符号规定1.正应⼒正负号规定2.切应⼒正负号规定使微元或其局部顺时针⽅向转动为正;反之为负。
材料力学B试题7应力状态-强度理论

材料力学B试题7应力状态-强度理论LT应力状态 强度理论1. 图示单元体,试求(1) 指定斜截面上的应力;(2) 主应力大小及主平面位置,并将主平面标在单元体上。
解:(1)MPa6.762sin 2cos 22=--++=ατασσσσσαx yx yxMPa 7.322cos 2sin 2-=+-=ατασσταx yx(2)22min max )2(2xy y x y x τσσσσσσ+-±+=98.12198.81-=MPa 98.811=σMPa ,02=σ,98.1213-=σ35.3940200arctan 21)2arctan(210==--=yx xyσστα2.解:取合适坐标轴令25=x σ MPa ,9.129-=xτ由02cos 2sin 2120=+-=ατασστxy yx得125-=yσMPa所以22min max )2(2xy y x y x τσσσσσσ+-±+=20010015050)9.129(755022-=±-=-+±-= MPa1001=σMPa ,02=σ,2003-=σ MPa3. 一点处两个互成 45平面上的应力如图所示,其中σ未知,求该点主应力。
解:150=yσMPa ,120-=x τ MPaMPa由 ατασστ2cos 2sin 245xy yx +-=802150-=-=x σ得10-=x σ MPa所以22min max )2(2xyy x y x τσσσσσσ+-±+=22.7422.214-= MPa22.2141=σ MPa ,02=σ,22.743-=σ4. 图示封闭薄壁圆筒,内径100=d mm ,壁厚2=t mm ,承受内压4=p MPa ,外力偶矩192.0=e MkN ·m 。
求靠圆筒内壁任一点处的主应力。
解:75.505.032)1.0104.0(π10192.0443=⨯-⨯=x τ MPa504==t pd x σ MPa1002==tpd y σ MPa35.497.100)2(222min max =+-±+=xy y x y xτσσσσσσ MPa7.1001=σ MPa ,35.492=σ MPa ,43-=σ MPa5. 受力体某点平面上的应力如图示,求其主应力大小。
《材料力学》第7章-应力状态和强度理论-习题解

(↑); (↓)
K截面的弯矩与剪力:
;
K点的正应力与切应力:
;
故坐标面应力为:X( ,0),Y(0,— )
(最大正应力 的方向与 正向的夹角),故
[习题7—22]一直径为 的实心钢球承受静水压力,压强为 。设钢球的 , .试问其体积减小多少?
解:体积应变
=
[习题7-23]已知图示单元体材料的弹性常数 , 。试求该单元体的形状改变能密度。
解:坐标面应力X(70,21),Y(14,—21)
所画的圆变成椭圆,其中
(长轴)
(短轴)
[习题7—14]已知一受力构件表面上某点处的 , , ,单元体的三个面上都没有切应力.试求该点处的最大正应力和最大切应力。
解:最大正应力为 。最小正应力是 。
最大切应力是
[习题7—15]单元体各面上的应力如图所示。试用应力圆的几何关系求主应力及最大切应力。
解:左支座为A,右支座为B,左集中力作用点为C,右集中力作用点为D。
支座反力: (↑)
=
(1)梁内最大正应力发生在跨中截面的上、下边缘
超过 的5。3%,在工程上是允许的。
(2)梁内最大剪应力发生在支承截面的中性轴处
(3)在集中力作用处偏外侧横截面上校核点a的强度
超过 的3.53%,在工程上是允许的。
点,则C为应力圆的圆心。设圆心坐标为C( )
则根据垂直平线上任一点到线段段两端的距离相等
性质,可列以下方程:
解以上方程得: 。即圆心坐标为C(86,0)
应力圆的半径:
主应力为:
(2)主方向角
(上斜面A与中间主应力平面之间的夹角)
(上斜面A与最大主应力平面之间的夹角)
(3)两截面间夹角:
材料力学习题解答9

l 200 mm
l
木噱头的最大 拉应力为:
l M
F F
bs
F
b
c a c
t
F M [ t ] bc Wz F 6 F (a c) / 2 4 3a b[ t ] [ t ] 2 2 bc c c F bc 4 60 2 3 10 2 c 147 mm c 147 mm c c 木噱头的最大压应力为: F M F 6 F (a c) / 2 c [ c ] [ c ] 2 bc Wz bc bc 3 3a b[ c ] 2 显然:c 147 mm 故取:c 147 mm c c F
7. 如图所示结构,立柱直径 d 50 mm , F 3 kN q 2 kN/m 。材料的许用应力 [ ] 160MPa 。试用第 四强度理论校核立柱的强度。 解: 结构危险截面在固定端A截面。
H 300
q
B
D
F
M 1 qa
ad 0.4 0.05 2 0.4 0.18 kNm 2 2 M 2 FH 3 0.3 0.9 kNm
解: 危险截面为固定端截面。
3a 1 M qa qa 2 2qa 2 2 2 FN qa sin qa sin 2qa sin
b
q
q
A
a
B
C
a
sin
b a2 b2
300 400 2 300 2
300 0.6 500
max
FN M 4 FN 32M 8qa sin 64qa 2 2 2 A Wz d d 3 d d 3
强度理论例题
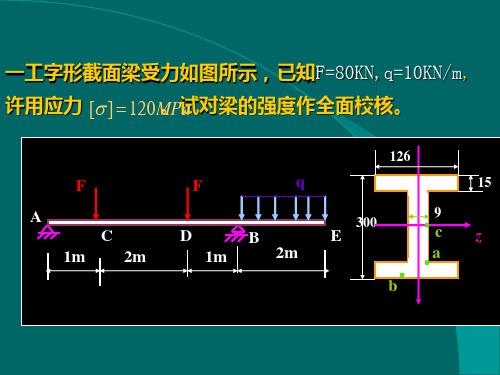
按第三和第四强度理论校核: 按第三和第四强度理论校核:
a
σr3 −[σ] < 5% [σ]
σr4
所以C截面强度足够。 所以 截面强度足够。 截面强度足够
(5)对D截面强度校核
FsD右 = Fs,max = 85KN, MD = 65KN ⋅ m;
最大正应力在b点 最大正应力在 点: MD 65×103 σmax = = Pa WZ 0.611×10−3 =106M <[σ] 对于a 点: 对于
300 9
15
σr4
b 对于c 点: 对于
c a y
z
FsD ⋅ (Sz )max 85×103 ×3.51×10−4 ∴τ = = = 36.2M Pa IZ b 91.6×10−6 ×9×10−3
*
∴σ1 =τ,σ2 = 0,σ3 = −τ
按第三和第四强度理论校核: 按第三和第四强度理论校核:
所以D截面强度足够。 所以 截面强度足够。 截面强度足够
126 15 300 9
b
σ
单向应力状态) (单向应力状态)
c a b y
z a
(平面应力状态) 平面应力状态)
τ
全面校核
c
纯剪应力状态) (纯剪应力状态)
F A C 1m (+)
(-)
F D 2m 75 20 (+) 5
Fs图 kN (-) ( )
q B E 2m
解: (1)求支座反 力并作内力图 作剪力图、弯矩图。 作剪力图、弯矩图。 (2)确定危险截面
300
126 15 9
z a b y
MD ⋅ ya 65×103 ×135×10−3 σ= = 95.8M Pa = −6 IZ 91.6×10
应力状态分析及强度理论习题讲解

2
50 80
F
G
30 60 30
O
B E C
1
A
(b)
= GE AE tan 30 (80 50) tan 30
=10 3 =17.3MPa 10 3 r 20MPa sin 60 3/2 = OB OA AB 80 2r 40MPa 所以 1 80MPa , 2 40MPa , 3 0
3)求主应力 15 1 2 2 1, 15 4 15 3 2 2 (-9.27)MPa 0 铸铁为脆性材料,抗拉与抗压强度不等,又 1 3 , 主应力中压力占优。 选第二强度理论
r 2 , 0.5
1 t
t
3)对中碳钢,虽为塑性材料,但比低碳钢塑性要差, 可选用第三强度理论。 1 2 2 2 r4 1 2 2 3 3 1 2 3 2 * 而强度条件 * 式在平面应力状态下(即应力分量 、 在同一平面内,见图(b))分别选用第三、四理论推 得的结果。
(a)
2
解:求主应力(可用应力圆法或解析法)
1 2 , 2 , 3
)对低碳钢,选第三理论或第四理论
r 1 3 3 , 0.333
3
1 2 2 2 r4 2 3 7 , 2 0.378 2)对铸铁,拉应力占优,选第一理论
答案:
D
四、计算
1.已知应力状态如图(a)所示,要求:1)用截面法求指定 截面上应力;2)用斜截面上应力公式校核;3)用应力圆 法校核。
40MPa
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xy平面支反力 FCy=12.5 kN,
FDy=4.5 kN
xz平面支反力 FCz=9.1 kN,FDz=2.1 kN
2、画内力图,确定危险截面
3
轴 AB 段的扭矩为 T = 1.5 kN ⋅ m (图 c),弯矩 M y 和 M z 如图 d、e 所示。从内力图
看出,危险截面是 C 或 B 截面。分别计算 C、B 两截面的总弯矩:
σ r3 = σ1 − σ 3 = −20MPa − (−40)MPa = 20MPa < [σ t ] ,安全
σ r4 =
1 2
[(−20
MPa
+
30
MPa) 2
+
(−30MPa
+
40
MPa) 2
+
(−40
MPa
+
20
MPa) 2
]
,
= 17.3 MPa < [σ t ] ,安全。
(3) σ1 = 10MPa , σ 2 = −20MPa , σ 3 = −30MPa ,脆性材料的危险点处于以压应力为主
态如图 c 所示,σ = 44.4 MPa ,τ = τ 2 = 35.6 MPa 。g 点处应力状态与 e 点处类似,只 是正应力为压应力。 f 点处为纯剪切应力状态,切应力大小为
τ = τ1 +τ 2 = 1.67 MPa + 35.6 MPa = 37.3 MPa
5
h 点处应力状态也为纯剪切,切应力大小为 τ = τ 2 −τ1 = 35.6 MPa -1.67 MPa = 33.93 MPa 。
态。
解:(1) σ1 = 30MPa , σ 2 = 20MPa , σ 3 = 15MPa ,危险点处于三向拉应力状态,不论材 料本身是塑性材料或是脆性材料,均采用第一强度理论,即:
σ r1 = σ1 = 30MPa = [σ t ] ,安全 (2) σ1 = −20MPa ,σ 2 = −30MPa ,σ 3 = −40MPa ,危险点处于三向压应力状态,即使是 脆性材料,也应采用第三或第四强度理论,即:
2、计算 B 截面的内力
剪力 FS = F = 1000N
弯矩 M = FR = 1000N × 0.2m = 200N ⋅ m
扭矩 T = FR = 1000N × 0.2m = 200N ⋅ m
3、确定 B 截面的危险点及危险点处的应力状态(图 b)
截面上弯矩引起的最大正应力发生在截面顶边 ab 和底边 cd 各点,顶边受拉应力,底
材料为钢时,许用应力 [σ ] = 160 MPa ;材料为铸铁时,许用应力 [σ t ] = 30 MPa 。试分别计算
圆轴的许可载荷 [F] ;(2)材料为铸铁,且 F=2 kN、E=100 GPa、 µ = 0.25 ,计算圆轴表面
上与轴线成 30°方位上的正应变。
1
F 30o
M
题2图 解题分析:本题中,轴为拉伸和扭转组合变形。轴的各个横截面上的扭矩、轴力均相同,所 以可以任取一截面作为危险截面。在危险截面上,轴力引起的拉伸正应力处处相等,扭矩引 起的切应力在靠近轴外表面的各点处最大,所以危险点为靠近轴表面的各点。危险点处的应 力状态如图示。 解:1、计算危险点的主应力
σ 2 + 4τ 2 =
4τ
2 max
= 2τ max
= 2 × 72.9MPa = 145.8MPa
5 图示薄壁容器承受内压 p。在容器外表面沿平行于轴向贴电阻应变片 A,测得 ε A = 100 ×10-6 ,在垂直于轴向贴电阻应变片 B,测得 ε B = 350 ×10-6 。已知制成容器材料的 弹性模量 E=200 GPa, µ = 0.25 ,试计算筒壁内轴向及周向应力,并确定内压 p。
2
根据广义胡克定律公式,要计算与轴线成 30°方位上的正应变,必须知道该方向的 正应力和与该方向垂直的方向上的正应力。设要计算的方位为-30°,则与其垂直的方 位为 60°,首先计算-30°、60°两方位上的正应力。
与轴线平行方向上的正应力、切应力分别为
σ = 1.27 ×104 m−2F = 1.27 ×104 m−2 × 2 ×103 N = 25.4 MPa
边受压应力,大小为
σ
=
M W
=
200N ⋅ m 4500 ×10 −9 m3
= 44.4 ×106 Pa
= 44.4 MPa
ቤተ መጻሕፍቲ ባይዱ
最大弯曲切应力发生在截面中性轴 h f 线上各点,方向向下,大小为
τ1
=
3 2
FS A
=
3 2
×
1000N 900 ×10−6
m
2
= 1.67 ×106 Pa
= 1.67MPa
2
2
σ 60D
=σ 2
+σ 2
cos(2 × 60D ) −τ sin(2 × 60D )
= 25.4 MPa + 25.4 MPa cos(2 × 60D ) −10.18 MPa sin(2 × 60D ) = −2.47 MPa
2
2
由广义胡克定律,轴表面与轴线成 30°方位上的正应变为
ε −30D
强度理论
典型习题解析
1 已知铸铁的拉伸许用应力 [σ t ] = 30MPa ,压缩许用应力 [σ c ] = 90 MPa , µ = 0.30 ,试对铸 铁零件进行强度校核,危险点的主应力为:
(1) σ1 = 30MPa , σ 2 = 20MPa , σ 3 = 15MPa ; (2) σ1 = −20MPa , σ 2 = −30MPa , σ 3 = −40MPa ; (3) σ1 = 10MPa , σ 2 = −20MPa , σ 3 = −30MPa 。 解题分析:选用强度理论时,不但要考虑材料是脆性或是塑性,还要考虑危险点处的应力状
)2
+
(0.509 ×104 m −2 F ) 2
2
于是主应力为 σ1 = 1.45 ×104 m−2F , σ 2 = 0 , σ 3 = −0.179 ×104 m −2 F 2、材料为钢材时,确定轴的许用载荷
根据第三强度理论,有
σ r3 = σ 1 − σ 3 = 1.45×10 4 m −2 F + 0.179 ×10 4 m −2 F = 1.63×10 4 m −2 F ≤ [σ ] = 160 MPa
解题分析:本题轮轴为弯扭组合变形。首先要将所有外力向轴线上简化,并绘制内力图,以
便寻找危险截面。找到危险截面和危险点后,即可按强度条件设计轴直径。
解: 1、计算轴上的载荷
取如图示坐标系,则外力偶矩
M eA
=
M eB
=
(5 - 2)
kN
D 2
= (5 - 2) kN × 1m = 1.5 kN ⋅ m 2
按第三强度理论设计轴的直径。直接采用
(a) A
y
MeA
(b) z
5kN C
2kN
300
5kN
500
FCz 7kN
B
2kN
500
MeB FC5y kN
12kN
D
FDz
x
FDy
圆轴弯扭组合情况下的强度条件,得
σ r3 =
M 2 + T 2 ≤ [σ ] W
(c) T
2.1 kN·m
1.5 kN·m
3
d ≥ 32 M 2 + T 2 π[σ ]
(d) My
1.05 kN·m 2.25kN·m
3
=
32
(2.58×103 N ⋅ m)2 + (1.5×103 N ⋅ m)2 π × 80 ×106 Pa
= 7(e2).4 ×1M0z−3 m = 72.4 mm
1.5 kN·m
如果按第四强度理论设计轴的直径,则
σ r4 =
M 2 + 0.75T 2 ≤ [σ ] W
比较四点处的应力状态,可知 e 点为 B 截面的危险点。按第三强度理论计算其相当应 力为
σ r3 = σ 2 + 4τ 2 = (44.4 MPa) 2 + 4 × (35.6 MPa) 2 = 83.9 MPa 4、计算 C 截面上内力和应力
剪力 FS = F = 1000N 弯矩 M=0 扭矩 T = 2FR = 2 ×1000N × 0.2m = 400N ⋅ m 5、计算 C 截面危险点的应力(图 d) C 截面各点处均为纯剪切应力状态,最大切应力发生在 C 截面轴内侧中点,即图 d 中 f 点处,其值为
得
[
F
]
=
160 MPa 1.63×104 m
−2
= 9820
N
= 9.82 kN
该轴用钢材制造时,许可载荷[F ] = 9.82 kN
3、材料为铸铁时,确定轴的许可载荷
按第一强度理论,有
σ r1 = σ1 = 1.45 ×104 m−2F ≤ [σ t ] = 30 MPa
得许可载荷 [F ] = 2 kN 4、计算铸铁轴表面与轴线成 30°方位上的正应变
τ max
=
3 2
FS A
+T Wp
=
3 2
F+ A
2FR βb2
=
F b2
(3 + 2
2R βb
)
=
1000N (30 ×10−3 m)2
(3 2
+
2 × 200 ×10−3 m 0.208 × 30 ×10−3 m )
=
72.9 ×106 Pa
=
72.9MPa
按第三强度理论计算相当应力
