(完整版)概率论第八讲二维离散随机变量的概率分布
合集下载
32二维离散型随机变量的分布律及性质
P { X x , Y y }p i j ij P { X x Y y } ,i 1 , 2 , (2.4) i j P { Y y } p j j
易知，上述条件概率满足概率分布的性质
(1) P { X x y } 0 , i 1 , 2 , iY j
(2)
p 1 j p 1 i j p p i 1 p 1 j j i j
p i j
P { X x } 0 同理，设 p ，则可得到在 X xi i i 时随机变量 Y的条件概率分布为：
P { X x , Y y } p i j i j P { Y y X x } ,j 1 , 2 ,( 2 . 5 ) j i P { X x } p i i
{ X x , Y y } P { X x } P { Y y } 即P (2.7) i j i j
例4
X ,Y
相互独立，填如下表3-8空白处的值
解：
例5 设 X 表示把硬币掷三次时头两次掷出正面的 Y 表示这三次投掷中出现正面的总次数那么， 次数， 二维随机变量 ( X ,Y ) 概率分布如表3-9所示.问随机 变量 X与Y 是不是相互独立？
且
(1) P { Y y x } 0 ,j 1 , 2 , jX i
(2)
p 1 i p 1 ij p p i i i i j 1p 1 p ij
i 1 , 2 , ,
例3 设二维离散形随机变量 ( X ,Y ) 的概率分布如表3-7, 1时关于 X 的条件概率分布及 X 0 时关于 Y 的 求 Y 条件概率分布。
解：
四、 独立性
易知，上述条件概率满足概率分布的性质
(1) P { X x y } 0 , i 1 , 2 , iY j
(2)
p 1 j p 1 i j p p i 1 p 1 j j i j
p i j
P { X x } 0 同理，设 p ，则可得到在 X xi i i 时随机变量 Y的条件概率分布为：
P { X x , Y y } p i j i j P { Y y X x } ,j 1 , 2 ,( 2 . 5 ) j i P { X x } p i i
{ X x , Y y } P { X x } P { Y y } 即P (2.7) i j i j
例4
X ,Y
相互独立，填如下表3-8空白处的值
解：
例5 设 X 表示把硬币掷三次时头两次掷出正面的 Y 表示这三次投掷中出现正面的总次数那么， 次数， 二维随机变量 ( X ,Y ) 概率分布如表3-9所示.问随机 变量 X与Y 是不是相互独立？
且
(1) P { Y y x } 0 ,j 1 , 2 , jX i
(2)
p 1 i p 1 ij p p i i i i j 1p 1 p ij
i 1 , 2 , ,
例3 设二维离散形随机变量 ( X ,Y ) 的概率分布如表3-7, 1时关于 X 的条件概率分布及 X 0 时关于 Y 的 求 Y 条件概率分布。
解：
四、 独立性
§2 二维离散型随机变量及其分布
P{X xi , Y y j } pij ， i 1, 2,, j 1, 2, ，
就称上式为二维离散型随机变量 ( X , Y ) 的分布律或 X 和 Y 的 联合分布律，
1
二维离散型随机变量的分布律也记列表为
X
Y
x1
p11 p12 p1 j
x2
xi
y1 y2 yj
§2
二维离散型随机变量及其分布
一、二维离散型随机变量及其分布律的概念
定义 2.1 如果二维随机变量 ( X , Y ) 的所有可能取值为有限对 或可列对，就称 ( X , Y ) 为 二维离散型随机变量．
定义 2.2 设 ( X , Y ) 为二维离散型随机变量，其所有可能的取 值为 ( xi , y j ) ，其中 i 1, 2,, j 1, 2, ，且
p21
pi1
p22 pi 2 p2 j pi j
2
例 2.1
设同一品种的五个产品中，有两个次品，每次从中取一
个检验，连续两次．设 X 表示第一次取到的次品个数； Y 表示 第二次取到的次品个数．试分别就⑴不放回；⑵有放回两种情 况，求出 ( X , Y ) 的概率分布．
pij ，其中 D 为任一平面区域．
( X , Y ) 的分布函数为
F ( x, y ) P X x, Y y
xi x y j y
p
ij
，
x , y ．
6
例 2.2
已知二维随机变量 ( X , Y ) 的分布律为
X Y 0 1
i j
ij
所以 b 0.2 ． 1知，0.7 a b 1 ，
2.2 概率论——二维离散型随机变量及其分布
1,
x 0或y 0, 0 x 1, y 0或0 y 1, x 0 x 1, y 1
P(X1=1, X2=1) = P(|Y|<1, |Y|<2)= P(|Y|<1) = 0.6826
列表为：
X1 X2 0 1
0
0.0455 0
1
0.2719 0.6826
例5：设二维d.r.v.(X,Y)服从二元两点分布：
Y X
0
1
0
q
0
1
0
p
试求（X，Y）的分布函数。
0, F ( x, y) q,
2.2 二维d.r.v.及其分布
定义 如果随机向量 ( X,Y ) 的全部取值 (向量或点 ) 为有限多个或至多可列个，则称 ( X,Y )为离散型随机向量。
( X,Y )为离散型随机向量
X与Y均为离散型随机变量
记( X ,Y )的取值集合为 E {( xi , y j ), i, j 1,2, } P{ X xi ,Y y j } pij , i, j 1,2,
(1) 确定随机变量 (X, Y) 的所有取值数对. (2) 计算取每个数值对的概率. (3) 列出表格.
对任意的A E
P{( X ,Y ) A} pij
ij
( xi , y j ) A
( X ,Y )的联合分布函数
F(x, y) P{X x,Y y}
pij
xi x y j y
解 (1) X 可能的取值为 1，2，3，Y 可能的取值为2，3，4,
但 ( X ,Y )的取值为(1,2),(1,3),(1,4),(2,3)，(2,4),(3,4)。
由古典概型公式
P{ X
1,Y
2}
x 0或y 0, 0 x 1, y 0或0 y 1, x 0 x 1, y 1
P(X1=1, X2=1) = P(|Y|<1, |Y|<2)= P(|Y|<1) = 0.6826
列表为：
X1 X2 0 1
0
0.0455 0
1
0.2719 0.6826
例5：设二维d.r.v.(X,Y)服从二元两点分布：
Y X
0
1
0
q
0
1
0
p
试求（X，Y）的分布函数。
0, F ( x, y) q,
2.2 二维d.r.v.及其分布
定义 如果随机向量 ( X,Y ) 的全部取值 (向量或点 ) 为有限多个或至多可列个，则称 ( X,Y )为离散型随机向量。
( X,Y )为离散型随机向量
X与Y均为离散型随机变量
记( X ,Y )的取值集合为 E {( xi , y j ), i, j 1,2, } P{ X xi ,Y y j } pij , i, j 1,2,
(1) 确定随机变量 (X, Y) 的所有取值数对. (2) 计算取每个数值对的概率. (3) 列出表格.
对任意的A E
P{( X ,Y ) A} pij
ij
( xi , y j ) A
( X ,Y )的联合分布函数
F(x, y) P{X x,Y y}
pij
xi x y j y
解 (1) X 可能的取值为 1，2，3，Y 可能的取值为2，3，4,
但 ( X ,Y )的取值为(1,2),(1,3),(1,4),(2,3)，(2,4),(3,4)。
由古典概型公式
P{ X
1,Y
2}
概率论和数理统计-二维离散随机变量及分布27页PPT
1
0
、
倚
南
窗
以
寄
傲
，
审
容
膝
之
易
安
。
谢谢
11、越是没有本领的就越加自命不凡。——邓拓 12、越是无能的人，越喜欢挑剔别人的错儿。——爱尔兰 13、知人者智，自知者明。胜人者有力，自胜者强。——老子 14、意志坚强的人能把世界放在手中像泥块一样任意揉捏。——歌德 15、最具挑战性的挑战莫过于提升自我。——迈克尔·F·斯特利
概率论和数理统计-二维离散随机变量 及分布
6
、
露
凝
无
游
氛
，
天
高
风
景
澈
。
7、翩翩新 来燕，双双入我庐 ，先巢故尚在，相 将还旧居。
8
、
吁Байду номын сангаас
嗟
身
后
名
，
于
我
若
浮
烟
。
9、 陶渊 明（ 约 365年 —427年 ），字 元亮， （又 一说名 潜，字 渊明 ）号五 柳先生 ，私 谥“靖 节”， 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
文 家 。汉 族 ，东 晋 浔阳 柴桑 人 （今 江西 九江 ） 。曾 做过 几 年小 官， 后辞 官 回家 ，从 此 隐居 ，田 园生 活 是陶 渊明 诗 的主 要题 材， 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
二维随机变量函数的概率分布.ppt
0 x 1, 其 它.
fY
y
e y 0,
,
y 0, y 0.
设随机变量Z=X+Y的密度函数fZ(z),则有
fZ z f X x fY z xdx 0 x 1, z x 0
随机变量函数的分布
f Z z f X x fY z xdx, z
不可能事件的0概率x等于10,. z x 0 1
随机变量函数的分布
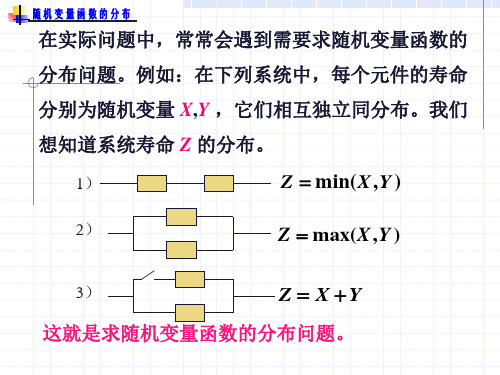
在实际问题中，常常会遇到需要求随机变量函数的
分布问题。例如：在下列系统中，每个元件的寿命
分别为随机变量 X,Y ，它们相互独立同分布。我们 想知道系统寿命 Z 的分布。
1）
Z min(X ,Y )
2）
Z max(X ,Y )
3）
Z X Y
这就是求随机变量函数的分布问题。
离散型随机变量、
x
FZ z PZ z PX Y z
O
f x， ydxdy
x yzz ຫໍສະໝຸດ zxdddxxu fffx，xx，，uuyxdxdyudx
作变换：y u x,
随机变量函数的分布
z
F (z) du f x， u xdx
利用分布函数与密度函数的关系,对FZ(z)求导, 得Z=X+Y的密度函数:
1 4
0
82
1 8
5 8
由此得 Z=X+Y的分布律
Z123 P 1/4 1/8 5/8
随机变量函数的分布
2.连续型随机变量和的分布
设(X,Y)是二维连续型随机变量，其联合概率密度
函数为f (x , y), 令：Z=X+Y.试求随机变量Z的密度函
数fZ(z).
y
1.计算随机变量Z=X+Y的分布函数FZ(z).
概率论 第八讲 二维离散随机变量的概率分布
第八讲 二维离散随机变量的概率 分布
教学目的： 教学目的 1.讲解二维离散随机变量的概率分布 （联合、边缘）； 2. 讲解二维随机变量的分布函数 (联合、边缘；离散→连续） ; 3. 讲解随机变量的独立性. 教学内容：§ 2.9 ～ 2.11(与书上不 教学内容 同)
多 维 分 布
在实际问题中, 在实际问题中 试验结果有时需要同 来描述. 时用两个或两个以上的 r.v.来描述 来描述 用温度和风力来描述天气情况. 例如 用温度和风力来描述天气情况 通过对含碳、含硫、 通过对含碳、含硫、含磷量的测定来研究 钢的成分. 之间的联系, 钢的成分 要研究这些 r.v.之间的联系 就 之间的联系 及其取值规律—多维分布 需考虑多维 r.v.及其取值规律 多维分布 及其取值规律 多维分布.
其中A , B , C 为常数. (1) 确定A , B , C ； (2) 求X 和Y 的边缘分布函数； (3) 求P (X > 2)
B + π C + π = 1 解 (1) F (+∞,+∞) = A 2 2 B − π C + π = 0 F (−∞,+∞) = A 2 2 B + π C − π = 0 F (+∞,−∞) = A 2 2
联合分布律
设( X ,Y )的所有可能的取值为 则称
( xi , y j ),
i, j = 1,2,⋯
i, j = 1,2,⋯
P( X = xi , Y = y j ) = pij ,
为二维 r.v.( X ,Y ) 的联合概率分布 也简称 概率分布 或 分布律 解析表示法 性质: pij ≥ 0, i, j = 1,2,⋯
教学目的： 教学目的 1.讲解二维离散随机变量的概率分布 （联合、边缘）； 2. 讲解二维随机变量的分布函数 (联合、边缘；离散→连续） ; 3. 讲解随机变量的独立性. 教学内容：§ 2.9 ～ 2.11(与书上不 教学内容 同)
多 维 分 布
在实际问题中, 在实际问题中 试验结果有时需要同 来描述. 时用两个或两个以上的 r.v.来描述 来描述 用温度和风力来描述天气情况. 例如 用温度和风力来描述天气情况 通过对含碳、含硫、 通过对含碳、含硫、含磷量的测定来研究 钢的成分. 之间的联系, 钢的成分 要研究这些 r.v.之间的联系 就 之间的联系 及其取值规律—多维分布 需考虑多维 r.v.及其取值规律 多维分布 及其取值规律 多维分布.
其中A , B , C 为常数. (1) 确定A , B , C ； (2) 求X 和Y 的边缘分布函数； (3) 求P (X > 2)
B + π C + π = 1 解 (1) F (+∞,+∞) = A 2 2 B − π C + π = 0 F (−∞,+∞) = A 2 2 B + π C − π = 0 F (+∞,−∞) = A 2 2
联合分布律
设( X ,Y )的所有可能的取值为 则称
( xi , y j ),
i, j = 1,2,⋯
i, j = 1,2,⋯
P( X = xi , Y = y j ) = pij ,
为二维 r.v.( X ,Y ) 的联合概率分布 也简称 概率分布 或 分布律 解析表示法 性质: pij ≥ 0, i, j = 1,2,⋯
2 二维离散型随机变量的分布律及性质
解：
6
二、 二维离散型随机变量的边缘概率分布
二维随机变量 ( X , Y ) 作为一个整体，具有分 布函数 F ( x, y ) ,而 X和 Y 都是随机变量，也分别具 FY ( y) ．依次称为二维 有分布函数，记之为 F ( x) ， 随机变量 ( X , Y ) 关于 X 和 Y 的边缘分布函数．边 缘分布函数可以由 ( X , Y )的分布函数 F ( x, y ) 所确定， FX ( x) P{X x} P{X x, Y } F ( x, ) 事实上 FX ( x) F ( x, ) 即 （2.2） FY ( y) F (, y) 同理 （2.3） 对离散型随机变量，由（2.1）和（2.2） 可得： F ( x) F ( x,) p
pij
pi
,
j 1, 2,
(2.5)
且
(1) P{Y y j X xi } 0,
j 1,2,
(2)
j 1
pij
1 pi p i
i 1
pij
pi 1 pi
i 1,2,,
14
例3 设二维离散形随机变量 ( X , Y ) 的概率分布如表3-7, 求 Y 1 时关于 X 的条件概率分布及 X 0 时关于 Y 的 条件概率分布。
F ( x, y )
xi x y j y
P{ X x , Y y } p
i j xi x y j y
ij
(2.1)
5
例 1 一口袋中有三个球，它们依次标有数字1、2、2.从这 袋中任取一球后，不放回袋中，再从袋中任取一球. X 设每次取球时，袋中各个球被取到的可能性相同．以 、 Y 分别记第一次、第二次取得球上标有的数字，求 ( X , Y )的概率分布．
6
二、 二维离散型随机变量的边缘概率分布
二维随机变量 ( X , Y ) 作为一个整体，具有分 布函数 F ( x, y ) ,而 X和 Y 都是随机变量，也分别具 FY ( y) ．依次称为二维 有分布函数，记之为 F ( x) ， 随机变量 ( X , Y ) 关于 X 和 Y 的边缘分布函数．边 缘分布函数可以由 ( X , Y )的分布函数 F ( x, y ) 所确定， FX ( x) P{X x} P{X x, Y } F ( x, ) 事实上 FX ( x) F ( x, ) 即 （2.2） FY ( y) F (, y) 同理 （2.3） 对离散型随机变量，由（2.1）和（2.2） 可得： F ( x) F ( x,) p
pij
pi
,
j 1, 2,
(2.5)
且
(1) P{Y y j X xi } 0,
j 1,2,
(2)
j 1
pij
1 pi p i
i 1
pij
pi 1 pi
i 1,2,,
14
例3 设二维离散形随机变量 ( X , Y ) 的概率分布如表3-7, 求 Y 1 时关于 X 的条件概率分布及 X 0 时关于 Y 的 条件概率分布。
F ( x, y )
xi x y j y
P{ X x , Y y } p
i j xi x y j y
ij
(2.1)
5
例 1 一口袋中有三个球，它们依次标有数字1、2、2.从这 袋中任取一球后，不放回袋中，再从袋中任取一球. X 设每次取球时，袋中各个球被取到的可能性相同．以 、 Y 分别记第一次、第二次取得球上标有的数字，求 ( X , Y )的概率分布．
2.2 二维离散型随机变量及其分布
P{ X xi , Y y j } pij , i , j 1,2,
上式称为X与Y的联合概率分布，或( X , Y )的概率分布。
联合概率分布可用下面 的概率分布表表示：
X Y
x1 x2 xi
y1
y2
yjቤተ መጻሕፍቲ ባይዱ
p11 p12 p1 j p21 p22 p2 j .......... .......... .......... .......... ..
2， 3， 4 例2 从分别标有号码 1， 2， 3，的 6 个球中任取三球， X , Y分别表示其中的最小号 码与最大号码， 求： (1)( X , Y )的联合概率分布； ( 2) P { X Y 5}及联合分布函数值F (1,3)。
解 (1) X 可能的取值为 1， 3，Y 可能的取值为 2， 4, 2， 3，
(1)不放回抽取
( 2)有放回抽取
1
X1
0
1
X2
0
X1
0
1
X2
0
1
1 3 4 15
4 15 2 15
9 25 6 25
6 25 4 25
( 2)有放回抽取 事件“X 1 i”与“X 2 j”相互独立, 则有 P{ X1 0, X 2 0} P{ X1 0} P{ X 2 0} 6 6 9 10 10 25 类似可得其余三个联合 概率(见上表)。
P{ X 1, Y 2} P{ X 1, Y 3}
0 .3
2 例3 设随机变量 U在区间 [2，]上服从均匀分布， 随机
变量
1 , U 1 X 1 , U 1
1 Y 1
上式称为X与Y的联合概率分布，或( X , Y )的概率分布。
联合概率分布可用下面 的概率分布表表示：
X Y
x1 x2 xi
y1
y2
yjቤተ መጻሕፍቲ ባይዱ
p11 p12 p1 j p21 p22 p2 j .......... .......... .......... .......... ..
2， 3， 4 例2 从分别标有号码 1， 2， 3，的 6 个球中任取三球， X , Y分别表示其中的最小号 码与最大号码， 求： (1)( X , Y )的联合概率分布； ( 2) P { X Y 5}及联合分布函数值F (1,3)。
解 (1) X 可能的取值为 1， 3，Y 可能的取值为 2， 4, 2， 3，
(1)不放回抽取
( 2)有放回抽取
1
X1
0
1
X2
0
X1
0
1
X2
0
1
1 3 4 15
4 15 2 15
9 25 6 25
6 25 4 25
( 2)有放回抽取 事件“X 1 i”与“X 2 j”相互独立, 则有 P{ X1 0, X 2 0} P{ X1 0} P{ X 2 0} 6 6 9 10 10 25 类似可得其余三个联合 概率(见上表)。
P{ X 1, Y 2} P{ X 1, Y 3}
0 .3
2 例3 设随机变量 U在区间 [2，]上服从均匀分布， 随机
变量
1 , U 1 X 1 , U 1
1 Y 1
概率论二维随机变量
联合概率密度函数法
对于连续型随机变量，可以通过联合概率密度函数积分计算边缘分布的概率密 度函数。
边缘分布的应用场景
统计推断
在统计分析中，常常需要利用边缘分布来推断另 一个随机变量的统计性质，如均值、方差等。
概率模型简化
在复杂概率模型中，可以通过计算边缘分布来简 化模型，便于分析和计算。
数据处理
在处理多维数据时，可以利用边缘分布来提取单 维数据，进行进一步的分析和处理。
条件概率与条件期望
条件概率
在概率论中，条件概率是指在某个条件下的概率。对于二维随机变量，条件概率是指在给定某个变量的条件下， 另一个变量的概率分布。
条件期望
条件期望是指在给定某个变量的条件下，另一个变量的期望值。在二维随机变量中，条件期望是指在给定某个变 量的条件下，另一个变量的加权平均值。
05
例如温度和压力的联合分布。
02
二维随机变量的定义与性质
二维随机变量的定义
1 2
定义
二维随机变量是两个随机变量的组合，通常表示 为 (X, Y)，其中 X 和 Y 都是随机变量。
定义域
二维随机变量的定义域是 X 和 Y 的取值范围的 组合，通常表示为 D，D 是实数域 R 的子集。
3
概率空间
二维随机变量是概率空间的一个元素，概率空间 由样本空间、事件域和概率函数组成。
联合概率分布满足概率的基本性质，即非 负性、归一性和可加性。
03
二维随机变量的期望与方差
二维随机变量的期望
01
02
03
定义
二维随机变量的期望是所 有可能取值的概率加权和。
计算公式
E(X,Y)=∫−∞∞∫−∞∞(x,y )f(x,y)dxdy，其中f(x,y)是 联合概率密度函数。
对于连续型随机变量，可以通过联合概率密度函数积分计算边缘分布的概率密 度函数。
边缘分布的应用场景
统计推断
在统计分析中，常常需要利用边缘分布来推断另 一个随机变量的统计性质，如均值、方差等。
概率模型简化
在复杂概率模型中，可以通过计算边缘分布来简 化模型，便于分析和计算。
数据处理
在处理多维数据时，可以利用边缘分布来提取单 维数据，进行进一步的分析和处理。
条件概率与条件期望
条件概率
在概率论中，条件概率是指在某个条件下的概率。对于二维随机变量，条件概率是指在给定某个变量的条件下， 另一个变量的概率分布。
条件期望
条件期望是指在给定某个变量的条件下，另一个变量的期望值。在二维随机变量中，条件期望是指在给定某个变 量的条件下，另一个变量的加权平均值。
05
例如温度和压力的联合分布。
02
二维随机变量的定义与性质
二维随机变量的定义
1 2
定义
二维随机变量是两个随机变量的组合，通常表示 为 (X, Y)，其中 X 和 Y 都是随机变量。
定义域
二维随机变量的定义域是 X 和 Y 的取值范围的 组合，通常表示为 D，D 是实数域 R 的子集。
3
概率空间
二维随机变量是概率空间的一个元素，概率空间 由样本空间、事件域和概率函数组成。
联合概率分布满足概率的基本性质，即非 负性、归一性和可加性。
03
二维随机变量的期望与方差
二维随机变量的期望
01
02
03
定义
二维随机变量的期望是所 有可能取值的概率加权和。
计算公式
E(X,Y)=∫−∞∞∫−∞∞(x,y )f(x,y)dxdy，其中f(x,y)是 联合概率密度函数。
二维离散型随机变量
ρ(X,Y)=Cov(X,Y)σ(X)σ(Y)
相关系数具有对称性，即 ρ(X,Y)=ρ(Y,X)。
05 二维离散型随机变量的函 数变换
线性变换
线性变换的定义
线性变换是指对二维离散型随机变量进行加、减、缩放等线性运算，得到新的二维离散型 随机变量。
线性变换的性质
线性变换保持了概率分布的平移、旋转和伸缩不变性，即变换后的随机变量的概率分布与 原随机变量的概率分布相同。
协方差与相关系数
协方差
计算公式
相关系数
计算公式
性质
二维离散型随机变量的 协方差是每个取值的横 坐标与期望值之差的乘 积和每个取值的纵坐标 与期望值之差的乘积的 期望值之和。
Cov(X,Y)=∑[(x−E(X))*(y −E(Y))]p(x,y)dxdy
协方差除以两个随机变 量的标准差的乘积，用 于衡量两个随机变量的 线性相关程度。
意义
联合概率分布函数提供了两个随机变量之间 关系的完整描述，包括它们同时发生的概率 。
性质
非负性
联合概率分布函数 F(x, y) 的值总是非负的。
01
归一化
联合概率分布函数满足条件，即所有可 能取值的概率之和为1。
02
03
独立性
如果两个随机变量是独立的，则它们 的联合概率分布函数可以表示为两个 边缘概率分布函数的乘积。
性质
可数性
二维离散型随机变量的取值可以 一一对应到自然数集上，即其取 值是可数的。
有限性
二维离散型随机变量的取值集合 通常是有限的，即其取值个数是 有限的。
独立性
在某些情况下，二维离散型随机 变量可能具有独立性，即两个随 机事件的发生与否相互独立。
联合概率分布
二维离散型随机变量及其分布律
Ｙ Ｘ １
２
１
２
０
1/3
1/3
1/3
2.边缘分布律
1). 通过联合分布律,求各个分量的分布律.
定义2.5 ( X ,Y ) 关于分量X的边缘分布律 pi· =P{Xxi}= pij (i1,2, ); j1 ( X ,Y ) 关于分量Y的边缘分布律 p· j=P{Yyj}= pij (j1,2, ). i1
p 21
。。。...
p i1
y2。。。Biblioteka p 12。。。...
p 22
。。。...
... 。。。
p i2
。。。... ... 。。。
yj
p1j
p2j
。。。
...
p ij
... 。。。
... 。。。 。。。... 。。。...
...
... 。。。 ... 。。。 ... 。。。 ... 。。。 ... 。。。
定义24表格形式常见形式表格形式常见形式例210看书一个口袋中有三个球依次标有数字122从中任取一个不放回袋中再任取一个设每次取球时各球被取到的可能性相等
第三节 二维离散型随机变量及其分布律
一、联合分布律与边缘分布律 1.定义.设X,Y为定义在同一样本空间Ω上的随机 变量，则称向量(X,Y )为Ω上的一个二维随机变 量。 二维随机变量(X,Y )的取值可看作平面上的点
A （x，y）
二维离散型随机变量:若二维随机变量(X,Y )的所 有可能取值只有限对或可列对，则称(X,Y )为二 维离散型随机变量。
2.联合分布律 1).定义2.4 pij P{xi,yj}P{Xxi,Yyj}
(i1,2, ;j1,2, )
表格形式（常见形式）
概率论与数理统计 二维随机变量及其分布 课件
即得 X 和 Y 的联合分布律为
P { X m , Y n} p q
2 n2
( n 2)个
,
其中q 1 p, n 2,3,; m 1,2,, n 1. 现在求条件分布律。
P { X m Y n }, P {Y n X m },
由于
P{ X m }
8 3 , 2 14 8 1 , 2 28 8 9 , 2 28 8 3 . 2 28
故所求分布律为
X
0 1 2
Y
0
3 28
9 28
3 281 23 14Fra bibliotek1 28
3 14
0
0
0
3.2.2 边缘分布律与条件分布律
4 7
3 7
注意
联合分布
边缘分布
2. 条件分布律
二维离散型随机变量中一个随机变量取值 受另一个随机变量影响的概率分布规律称为条 件分布律。 如果p· j>0,考虑条件概率
P{ X xi Y y j } P { X xi ,Y y j } P {Y y j } p ij p j
设(X,Y)的密度函数为f(x,y)，那么对任意 实数a,b(a<b)，总有
P {a X b} P {a X b , Y }
[
a
b
f ( x , y ) d y]d x ,
且
f ( x, y)d y 0
， f ( x , y ) d y 1,
P {Y y j }
i
p i j p j , j 1, 2 ,
概率论与数理统计 二维离散随机变量及其分布
概率论与数理统计
3 P{ X = 1, Y = 1} = C C C C = , 14 1 0 2 0 2 P{ X = 0, Y = 2} = C3 C2 C3 C8 = , 28 9 1 0 1 2 P{ X = 1, Y = 0} = C3C2 C3 / C8 = , 28 3 2 0 0 2 P{ X = 2, Y = 0} = C3 C2 C3 / C8 = . 28
Y X x1 x2 . . . xi . . . 概率论与数理统计 y1 p11 p21 . . . pi1 . . . y2 p12 p22 . . . pi2 . . . … … … . . . … . . . yj p1j p2j . . . pij . . .
P(X= xj ) = pj
pj ≥ 0; ∑ p = 1. j j
… … … . . . … . . .
X
a1 a2 ⋮ ai ⋮
Y
b1
b2
⋯
bj
⋯
p 11
p 21
⋯
p i1
⋯
p12 ⋮
p i1 ⋮
∞ j =1
p22 ⋯ ⋮
pi2 ⋮ ⋯
∞
pi 2 ⋯ ⋮
p ij ⋮
i =1
⋯
P{ X = ai } = ∑ pij , i = 1, 2,⋯. P{ X = b j } = ∑ pij , j = 1, 2, ⋯ ;
1 3 1 2 0 3 2 8
概率论与数理统计
故所求分布律为
Y
X
0 1 2
0
3 28
9 28
3 28
1 2
3 14
1 28
3 14
0
0
3 P{ X = 1, Y = 1} = C C C C = , 14 1 0 2 0 2 P{ X = 0, Y = 2} = C3 C2 C3 C8 = , 28 9 1 0 1 2 P{ X = 1, Y = 0} = C3C2 C3 / C8 = , 28 3 2 0 0 2 P{ X = 2, Y = 0} = C3 C2 C3 / C8 = . 28
Y X x1 x2 . . . xi . . . 概率论与数理统计 y1 p11 p21 . . . pi1 . . . y2 p12 p22 . . . pi2 . . . … … … . . . … . . . yj p1j p2j . . . pij . . .
P(X= xj ) = pj
pj ≥ 0; ∑ p = 1. j j
… … … . . . … . . .
X
a1 a2 ⋮ ai ⋮
Y
b1
b2
⋯
bj
⋯
p 11
p 21
⋯
p i1
⋯
p12 ⋮
p i1 ⋮
∞ j =1
p22 ⋯ ⋮
pi2 ⋮ ⋯
∞
pi 2 ⋯ ⋮
p ij ⋮
i =1
⋯
P{ X = ai } = ∑ pij , i = 1, 2,⋯. P{ X = b j } = ∑ pij , j = 1, 2, ⋯ ;
1 3 1 2 0 3 2 8
概率论与数理统计
故所求分布律为
Y
X
0 1 2
0
3 28
9 28
3 28
1 2
3 14
1 28
3 14
0
0
二维离散型随机变量的条件分布
•设是二维连续型随机变量，因为对任意的有，所以不能直接用条件概率公式得到条件分布。
下面我们用极限的方法导出条件分布函数。
),(Y X y x ,0}{==x X P 0}{==y Y P 二维连续型随机变量的条件分布例2已知( X, Y ) 的联合p.d.f.为⎩⎨⎧<<<<=其他,010,10,4),(1y x xy y x f (1)⎩⎨⎧<<<<=其他,010,0,8),(2y y x xy y x f (2)讨论X ,Y 是否独立？方法将与Y 有关的事件转化成X 的事件求随机因变量Y = g ( X )的密度函数或分布律)(y f Y 问题已知r.v.X 的p.d.f.)(x f X 或分布律.随机变量的函数的分布也是一个随机变量．则Y ()x g y Y x X =取值时，取值当设r.v. X 的分布律为,2,1,)(===k p x X P k k 由已知函数g ( x )可求出r.v. Y 的所有可能取值，则Y 的概率分布为,2,1,)()(:===∑=i p y Y P ik y x g k k i 离散型r.v.的函数的分布等价的X 的不等式.这样做是为了利用已知的X 的分布，从而求出相应Y的概率。
从上述例中可以看到，键的一步是设法从{}y X g ≤)(中解出X ,从而得到与}y X g ≤)(在求P (Y ≤y ) 的过程中，随机变量函数分布——小结很多重要的分布，往往都是通过研究函数的二、连续型随机变量和的分布定理设(X ,Y )概率密度为 f (x ,y ),则随机变量Z=X+Y 的概率密度为()()()()Z Z f z f z y y dy f z f x z x dx+∞-∞+∞-∞=-=-⎰⎰，，,,X Y 特别如果随机变量与相互独立则有()()(),X Y f x y f x f y =()()()Z X Y f z f x f z x dx +∞-∞⇒=-⎰()()()Z X Y f z f z y f y dy+∞-∞=-⎰例1解)1,0(,服从区间相互独立与设随机变量X Y X 由题意，可知()⎩⎨⎧<<=其它0101x x f X ()⎩⎨⎧≤>=-00y y ey f yY ()，则有的密度函数为设随机变量z f Y X Z Z +=()()()+∞-=dxx z f x fz f，令的指数分布服从上的均匀分布Y X Z Y +==,1,λ的概率密度。
4.1_1二维离散型随机变量及其分布
计算可得:
P X 1,Y 1 P X 1 P Y 1 X 1
100 4
P X 2,Y 1 P X 2 P Y 1 X 2
21 1 43 6
类似可得所有点上的概率值, 因此联合概率函数为
X \Y 1 2 3
1
0
11 6 12
2 111 666
3 110 12 6
0.8
解⑶ 由边缘概率函数定义计算可得
X 01 Pr. 4 1
55
Y 01 Pr. 4 1
55
在上题中, 若作有放回抽样, 求问题⑴, ⑶. 解 ⑴同样由乘法公式可得联合概率函数如下:
X \ Y 0 1 pi 0 0.64 0.16 0.8 1 0.16 0.04 0.2 p j 0.8 0.2
试求: ⑴ X ,Y 的联合概率函数; ⑵概率值 P X Y ;
⑶分别求 X与Y 的边缘概率函数.
解⑴ 同例1, 利用乘法公式
P X i,Y j P X i P Y j X i
可以求得:
X \Y 0 1 0 0.6 0.2 1 0.2 0
解⑵ P X Y
P X ,Y 1,1,1,0,0,0
Pr . 1 2 1 6 36
又 P X1X2 0 1, 求 P X1 X2 .
解 由 P X1X 2 0 1, 知 P X1X 2 0 0 , 即有
P X1, X2 1, 1,1,1,1, 1,1,1 0
故随机变量 X1, X 2 的联合概率函数即有下列形式:
X1 \ X 2 1 0 1 pi
1
1 0 p12 0 6
0
p21
p22
p23
2 310 Nhomakorabeap32
二维随机变量及其概率分布
类比条件概率定义条件分布函数→
定义 : 设对固定的实数即任意y 0, 有Py y Y y, 如果 y
X x y y Y y lim PX x , y y Y y lim P
y 0 y 0
P y y Y y
第三章
二维随机变量及其概率分布
从本讲起，我们开始第三章的学习. 它是第二章内容的推广. 一维随机变量及其分布
多维随机变量及其分布 由于从二维推广到多维一般无实质性的 困难，故我们重点讨论二维随机变量 ，3.6节 的n维随机变量留待大家自习。
有些随机现象只用一个随机变量来描述是不够 的，需要用几个随机变量同时来描述。例如：
1. 某人的体检数据——血压(X)和心律(Y)；
2. 某炉钢的基本指标——含碳量(X)、含硫 量(Y)与硬度(Z)； 3. 导弹在空中的位置——坐标(X, Y, Z);
4. 在打靶时,命中点的位置——坐标(X,Y).
一般地，我们称n个随机变量的整体 X=(X1, X2, …，Xn)为n维随机变量或随 机向量. 以下重点讨论二维随机变量.
F x, y f x, y xy
2
二、边缘分布 设 X ,Y 的联合概率密度为f x, y ，由于X的分布函数
F x F x , f u, v dv du
x X
被积函数
F x , 故由f x f X x f x , y dy x
p
P y P X , Y y p p Y
j xi ij i
j
ij
分布律及边缘分布的表格形式 →
Y X x x x p
定义 : 设对固定的实数即任意y 0, 有Py y Y y, 如果 y
X x y y Y y lim PX x , y y Y y lim P
y 0 y 0
P y y Y y
第三章
二维随机变量及其概率分布
从本讲起，我们开始第三章的学习. 它是第二章内容的推广. 一维随机变量及其分布
多维随机变量及其分布 由于从二维推广到多维一般无实质性的 困难，故我们重点讨论二维随机变量 ，3.6节 的n维随机变量留待大家自习。
有些随机现象只用一个随机变量来描述是不够 的，需要用几个随机变量同时来描述。例如：
1. 某人的体检数据——血压(X)和心律(Y)；
2. 某炉钢的基本指标——含碳量(X)、含硫 量(Y)与硬度(Z)； 3. 导弹在空中的位置——坐标(X, Y, Z);
4. 在打靶时,命中点的位置——坐标(X,Y).
一般地，我们称n个随机变量的整体 X=(X1, X2, …，Xn)为n维随机变量或随 机向量. 以下重点讨论二维随机变量.
F x, y f x, y xy
2
二、边缘分布 设 X ,Y 的联合概率密度为f x, y ，由于X的分布函数
F x F x , f u, v dv du
x X
被积函数
F x , 故由f x f X x f x , y dy x
p
P y P X , Y y p p Y
j xi ij i
j
ij
分布律及边缘分布的表格形式 →
Y X x x x p
二维离散型随机变量及其分布
Two-dimension Discrete Random Variable and Distribution
[例3] 见例1，判断X,Y是否相互独立？
Two-dimension Discrete Random Variable and Distribution
例4 已知随机变量(X,Y)的分布律为
在实际问题中，有一些实验的结果需要同时 用两个或两个以上的随机变量来描述。 例如，炮弹击中点的位置要用其横坐标X 与纵坐标Y来确定。
(X,Y)
Two-dimension Discrete Random Variable and Distribution
在模特比赛中，要同时考虑到模特身高、胸 围、腰围、臀围等多个变量。
Two-dimension Discrete Random Variable and Distribution
1.联合分布函数：F ( x, y) P( X x, Y y)
FX ( x) P{ X x} lim F ( x, y) 2.边缘分布函数： y
FY ( y ) P{Y y} lim F ( x, y )
P{ X xi } P{ X xi , } P{ X xi , (Y y j )}
j 1
P{ ( X xi , Y y j )} P{ X xi , Y y j } pij
j 1 j 1 j 1
Two-dimension Discrete Random Variable and Distribution
x1 p11 p21 … … pi1 …
p12 … p1j …
p22 … … pi2 … … … … … … p2j … … … … … pij … … …
2.3.1 二维离散型随机变量的分布律及常用分布
pij 1.
ij
*
第二章
2
第三二节维离散型随机变量的分布律及常用分布
市场现状分析
例1 口袋中有三个球，依次标有数字1,2,2,从中任取一个, 不放回袋中,再任取一个, 以 , 分别记第一次和第二次取 到的球上标有的数字,求 , 的联合分布.
X \Y 1
2
1 0 12 2 2 1 32 21
第三二节维离散型随机变量的分布律及常用分布 1、二维离散型随机变量的分布律
市场现状分析
若二维离散型随机变量 , 所取的值用 , 表示， 1,2, ⋯ , ⋯ , , 1,2, ⋯ , , ⋯
则等式
,
或表格
,
,
,
⋯
,
⋯
⋯
⋯
*
第二章
1
第三二节维离散型随机变量的分布律及常用分布
或矩形表
y1 y2 y j
x1 p11 p12 p1 j x2 p21 p22 p2 j
xi pi1 pi2 pij
称为( X ,Y )的联合分布律或分布律。
市场现状分析
二维离散型随机变量 ( X ,Y )的分布律有性质：
1) 0 pi j 1， 2)
2. 二维离散型随机变量常用的分布
(1) 超几何分布： , ~ , , ,
,
.
0,1, ⋯ , ， 0,1, ⋯ , ，
(2) 三项分布： , ~
, ( , 0,1, ⋯ , 0 , 1，
,,
1 ， 1
市场现状分析
第二章
，
*
6
, 的分布律。(1)无放回 (2)有放回
解(1) , 可能取的数值只有(0,3), (0,2), (0,1), (1,2), (1,1) 以及(1,0),(2,1),(2,0).
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例1 某校新选出的学生会 6 名女委员, 文、 理、工科各占1/6、1/3、1/2，现从中随机 指定 2 人为学生会主席候选人. 令X , Y 分 别为候选人中来自文、理科的人数.
求(X, Y) 的联合分布律和边缘分布律.
解 X 与Y 的可能取值分别为0 , 1与0 , 1 , 2. 由乘法公式
P(X 0,Y 0) P(x 0)P(Y 0 X 0)
C
2 5
C
2 6
C C
2 3
2 5
3/15,
或由古典概型
P( X
0,Y
0)
C
2 3
/
C
2 6
3/15,
相仿有
P(X
0,Y
1)
C12C13
/
C
2 6
6 /15,
P(X
0,Y
2)
C
2 2
/
C
2 6
1/ 15;
P(X
1,Y
0)
C11C13
/
C
2 6
3/15,
P(X 1,Y 1) C11C12 / C62 2 /15,
联合分布律
设( X ,Y )的所有可能的取值为
则称 (xi , y j ), i, j 1,2,
P( X xi ,Y y j ) pij , i, j 1,2,
为二维 r.v.( X ,Y ) 的联合概率分布
也简称 概率分布 或 分布律 解析表示法
性质: pij 0, i, j 1,2,
F(x, y)
pij , x , y .
第八讲 二维离散随机变量的概率
分布
教学目的： 1.讲解二维离散随机变量的概率分布 （联合、边缘）； 2. 讲解二维随机变量的分布函数 (联合、边缘；离散→连续） ; 3. 讲解随机变量的独立性.
教学内容：§ 2.9 ～ 2.11(与书上不 同)
多 维 分 布
在实际问题中, 试验结果有时需要同 时用两个或两个以上的 r.v.来描述.
讨论： 二维r.v.作为一个整体的概率特性 其中每一个r.v.的概率特性与整体 的概率特性之间的关系
二维离散型 r.v.及其概率特性
定义 若二维 r.v.(X ,Y )所有可能的取值
为有限多个或无穷可列多个, 则称 (X ,Y ) 为二维离散型 r.v.
要描述二维离散型 r.v.的概率特性及 其与每个 r.v.之间的关系常用其联合 概率分布和边缘概率分布
y (x, y)
x
(, )
联合分布函数的性质
y
① 0 F(x, y) 1
F(, ) 1
y
F(, ) 0
(,)
(,)
x
(x, y)
x
F(x, ) 0
F(, y) 0
y
x
y
x
② 对每个变量单调不减 固定 x , 对任意的 y1< y2 , F (x, y1) F (x, y2) 固定 y , 对任意的 x1< x2 , F (x1,y) F (x2, y)
3 P(X 0,Y 1) 0
(X, Y) 的联合分布律及边缘分布为pij X Y0 Nhomakorabea1
p• j
-1
0
1
1
3
0
0
pi•
1 3
1
1
3
3
1
0
3
1
1
3
3
2
3
二维随机变量的联合分布函数
定义 设( X , Y ) 为二维 r.v. 对任何一对 实数( x , y ), 事件
(X x) (Y y) (记为X x,Y y )
的概率 PX x,Y y 定义了一个二元
实函数 F ( x , y )，称为二维 r.v.( X ,Y ) 的分布函数，即
F(x, y) PX x,Y y
分布函数的几何意义
如果用平面上的点 (x, y) 表示二维r.v. (X , Y )的一组可能的取值，则 F (x, y) 表示 (X , Y ) 的取值落入图所示角形区域的概率.
联合分布律 及边缘分布律
Y X x1 xi
p• j
y1
p11 pi1
p•1
yj
p1 j pij
p•
j
pi•
p1• pi
1
•
pij P(X xi , Y y j ) 的求法
⑴ 利用古典概型直接求； ⑵ 利用乘法公式
pij P(X xi)P(Y yj X xi) .
③ 对每个变量右连续 F (x0 , y0) = F (x0+ 0 , y0 )
F (x0 , y0) = F (x0 , y0 + 0 )
④ 对于任意 a < b , c < d
F (b,d) – F (b,c) – F (a,d) + F (a,c) 0
事实上
d
F (b,d) – F (b,c)
P(X 1,Y 2) 0.
故联合分布律与边缘分布律为
XY 0 1
p•
j
01
2
pi
•
3/15 6/15 1/15 2/3
3/15 2/15 0 1/3
6/15 8/15 1/15 1
例2 二元两点分布
pij X
1
Y
1
p
0
p• j
0p
0
0
pi•
p
q1
p + q = 1 ，0 < p < 1
例3 设 X的分布为
c
– F (a,d) + F (a,c)
Pa
X
b, c
Y
d
a
0
b
注意 对于二维 r.v.
PX a,Y c 1 F(a,c)
PX a,Y c
(a,+) (+,+)
P(a X ,c Y ) y
1 F(,c)
c (a,c) (+,c)
F(a,) F(a,c)
a
x
二维离散 r.v.的联合分布函数
pij 1
i1 j1
( X ,Y ) 的联合分布律表
X Y
y1
x1
p11
xi
pi1
yj
p1 j
pij
二维离散 r.v.的边缘分布律
记作
P(X xi ) pij pi•, i 1,2,
j1
记作
P(Y y j ) pij p•j , j 1,2,
i1
由联合分布可确定边缘分布,其逆不真.
P(X 1) P(X 0) P(X 1) 1 3
Y X 2, 求(X, Y) 的联合分布律及边缘分布.
P(X 1,Y 0) P(X 1)P(Y 0 X 1) 0 P(X 1,Y 1) P(X 1)P(Y 1 X 1) 1 P(X 0,Y 0) P(X 0)P(Y 0 X 0) 1 3
例如 用温度和风力来描述天气情况. 通过对含碳、含硫、含磷量的测定来研究 钢的成分. 要研究这些 r.v.之间的联系, 就 需考虑多维 r.v.及其取值规律—多维分布.
二维随机变量及其分布
定义 设为随机试验的样本空间，
一定法则 X (),Y () R2
则称( X , Y )为二维r.v.或二维随机向量