概率论与数理统计二维随机变量
合集下载
概率论与数理统计3.1.2 二维离散型随机变量及其联合分布律
表示方法:(1)公式法;(2)列表法。
2.表格形式下二维离散型随机变量的分布律的表示:
3.联合分布律的性质
二、典型例题
例1袋中有2只白球,3只黑球,现摸球两次,定义
,
求(1)有放回取球下(X,Y)的分布律。
(2)不放回取球下(X,Y)的分布律。
(3)不放回下
解:(1)
(2)
(3)
注:
补充说明
二维一定要在一维的基础上展开,讲解二维离散型随机变量分布律的定义与求法时,一定要与一维对比讲解。这样就有很好的过渡过程,不仅可以加深学生对概念的理解,还有助于复习前面的知识。
例1应细致讲解,通过例题可让学生回忆概率求解的方法,更能让学生掌握求二维随机变量联合分布律的方法。
授课对象
机械设计制造及自动化、材料科学与工程专业等
教学目标
掌握二维离散型随机变量定义及其联合分布律的求法,并能熟练运用到实际问题中。
教学方式
启发式
教学内容
二维离散型随机变量定义及其联合分布律的求法。
教学重点
二维离散型随机变量定义及其联合分布律的求法
教学难点
实际问题中求解联合分布律
教学方法和策略
采用多媒体课件辅助,对比一ห้องสมุดไป่ตู้离散型随机变量分布律的求法深入讲解二维离散型随机变量定义及其联合分布律的求法,举例说明其用法;注意师生互动,以学生为教学主体,共同完成教学目标。
教学重点二维离散型随机变量定义及其联合分布律的求法教学难点实际问题中求解联合分布律教学方法和策略采用多媒体课件辅助对比一维离散型随机变量分布律的求法深入讲解二维离散型随机变量定义及其联合分布律的求法举例说明其用法
讲稿
课程名称
《概率论与数理统计》
2.表格形式下二维离散型随机变量的分布律的表示:
3.联合分布律的性质
二、典型例题
例1袋中有2只白球,3只黑球,现摸球两次,定义
,
求(1)有放回取球下(X,Y)的分布律。
(2)不放回取球下(X,Y)的分布律。
(3)不放回下
解:(1)
(2)
(3)
注:
补充说明
二维一定要在一维的基础上展开,讲解二维离散型随机变量分布律的定义与求法时,一定要与一维对比讲解。这样就有很好的过渡过程,不仅可以加深学生对概念的理解,还有助于复习前面的知识。
例1应细致讲解,通过例题可让学生回忆概率求解的方法,更能让学生掌握求二维随机变量联合分布律的方法。
授课对象
机械设计制造及自动化、材料科学与工程专业等
教学目标
掌握二维离散型随机变量定义及其联合分布律的求法,并能熟练运用到实际问题中。
教学方式
启发式
教学内容
二维离散型随机变量定义及其联合分布律的求法。
教学重点
二维离散型随机变量定义及其联合分布律的求法
教学难点
实际问题中求解联合分布律
教学方法和策略
采用多媒体课件辅助,对比一ห้องสมุดไป่ตู้离散型随机变量分布律的求法深入讲解二维离散型随机变量定义及其联合分布律的求法,举例说明其用法;注意师生互动,以学生为教学主体,共同完成教学目标。
教学重点二维离散型随机变量定义及其联合分布律的求法教学难点实际问题中求解联合分布律教学方法和策略采用多媒体课件辅助对比一维离散型随机变量分布律的求法深入讲解二维离散型随机变量定义及其联合分布律的求法举例说明其用法
讲稿
课程名称
《概率论与数理统计》
概率论与数理统计第四章二维随机变量及其分布

(4)
fX Y (x
y)
f (x, y) fY ( y)
= ex
fY X ( y
x)
f (x, y) fX (x)
= ey
(5)
f (x, y) exy fX (x) fY ( y)
因此X ,Y相互独立。
二、二维连续型随机变量函数的分布
1.Z=X+Y的分布 设(X,Y)的联合密度函数为f(x,y),则由分布函数的定义知, Z=X+Y的分布函数为:
3. F (x , y) 为连续函数,且在f(x,y)的连续点处,
2F(x, y) f (x, y) xy
一、二维连续型随机变量概念
定义8 称
f X (x)
f (x, y)dy
( x )
为X的边缘密度函数。
称
fY ( y)
f (x , y)dx
( y )
为Y的边缘密度函数。一、二维连ຫໍສະໝຸດ 型随机变量概念定义9称
fX Y (x
y)
f (x, y) fY ( y)
为在Y=y条件下X的条件概率密
度,称
f (x, y) fY X ( y x) fX (x)
为在X=x条件下Y的条件概率密度.
定理2 设(X,Y)为二维连续型随机变量,则X与Y相互独 立等价于 f (x, y) fX (x) fY ( y)
y)
一、二维随机变量的概念
联合分布函数F(x,y)有如下的性质:
1. 0 F(x , y) 1
2. F(x , y) 关于x、关于y单调不减;
3. F(x , y) 关于x、关于y右连续
4.
lim F(x , y) 0 , lim F(x , y) 1
概率论与数理统计313 二维连续型随机变量及其联合概率密度

数f(x)的性质
概率密度函数f(x, y)的性质
(4) 在f(x)的连续点处有: f (x) F'(x)
(4)若f (x, y)在(x, y)连续,
则有 2F(x, y) f (x, y). xy
用来求概率密度f(x)的方法
用来求概率密度 f(x,y)的方法
例2 设随机变量(X ,Y )的联合分布函数为
解: 由规范性
f (x, y)dxdy 1
Ae(2x y)dxdy 1 A 2 00
二、联合概率密度函数的性质:
(3)设D是xOy平面上的任意一个平面区域,点(X ,Y ) 落在D内的概率为
P{(X ,Y) D} f (x, y) d x d y.
D
z
z f (x, y)
求:(1)常数A;(2) F ( x, y ) ;(3) P{Y X};
(4) P{1 X 1,1 Y 1}.
解: P{1 X 1,1 Y 1}.
f (x, y) d x d y
D
1 2e 1 (2x y) d y d x 01 01
1
2 e1 2x dx 1ey)(1 e1).
y
1
O
D 1
x
1
(x,y)
求(X ,Y )的联合密度函数.
例3 设
Ae(2x y) , x 0, y 0
(X ,Y ) ~ f (x, y)
0, 其它
求:(1)常数A;(2) F ( x, y ) ;(3) P{Y X};
(4) P{1 X 1,1 Y 1}.
解:
(1)由规范性
f (x, y)dxdy 1
y
o
D x
(3) 对于任意平面区域D R2,
《概率论与数理统计》课件3-2 二维离散型随机变量

++
(2)规范性
pij = 1
i =1 j =1
边缘分布律
+
P X = xi } = P X = xi ,Y < + } = P{X = xi , Y = yj }
j= 1
+
= pij = pi •
j= 1
(i = 1,2, )
+
} } P Y = yj = P X < + ,Y = yj = P{X = xi , Y = yj } i= 1
+
}=
j=1 P{X = xi , Y = yj } =
pij = pi • (i = 1,2,)
j= 1
+
+
P Y = yi } = P X + ,Y = yi } =
P{X = xi , Y = yj }=
pij =
p •j
(j
=
1,2, )
i =1
i =1
3.2- P63— 1 2 3
A
C
B
D
提交
P
XY
( X, Y)X xi }=P{X xi Y
},
j1
pj
pij P{Y yj } P{X
i1
i 1, 2, ,
j 1, 2, ,
Y yi },
pi p j (X,Y)
X
Y
.
Y X
y1
y2
yj
x1
p 11 p 12
x2
p 21 p 22
p1j
p2 j
xi
pp
i1
且满足P{X1X2 = 0} = 1,则 P X1 = X2 } = ( )。
概率论与数理统计第3章第一节-二维随机变量3-1解析

X, Y X e, Y e e S
看作一个整体,因为 X 与Y 之间是有联系的;
⑶ 在几何上,二维随机变量 ( X ,Y ) 可看 作平面上的随机点. 二维随机变量(X,Y)的性质不仅与X及Y有关,而且 还依赖于这两个随机变量的相互关系,因此,逐个 地研究X及Y的性质是不够的,还需将(X,Y)作为 一个整体来研究.和一维的情况类似,我们也借 助“分布函数”来研究二维随机变量
时 F x1, y F x2, y ;
对任意固定的 x R 及 y1 , y2 R , 当 y1 y2
时 F x, y1 F x, y2 ;
x1, y y
x2, y
x1 O
x2 x
X ,Y
X ,Y
3 . 0 F x, y 1, 且
对任意固定的 y R , F , y 0 ,
得
1
F
,
A
B
2
C
2
0 F x, A B arctan x C
2 2
0 F , y A B C arctan y
2
3
由 以 上 三 式 可 得A,
1,
2
B
,
2
C
2
.
n 维随机变量
设 E 是一个随机试验,S是其样本空间,
Xi Xi e e S i 1, 2, , n
我们称此函数为n维随机变量的分布函数.
二、二维离散型随机变量
1.定义:
若二维随机向量(X,Y)的可能取值只有有限个或可 列个,则称(X,Y)是离散型二维随机向量.
若二维离散型随机向量(X,Y)的所有可能取值为
(xi,yj),i,j=1,2,…
记P{X=xi,Y=yj}=pij, i, j=1,2,…
看作一个整体,因为 X 与Y 之间是有联系的;
⑶ 在几何上,二维随机变量 ( X ,Y ) 可看 作平面上的随机点. 二维随机变量(X,Y)的性质不仅与X及Y有关,而且 还依赖于这两个随机变量的相互关系,因此,逐个 地研究X及Y的性质是不够的,还需将(X,Y)作为 一个整体来研究.和一维的情况类似,我们也借 助“分布函数”来研究二维随机变量
时 F x1, y F x2, y ;
对任意固定的 x R 及 y1 , y2 R , 当 y1 y2
时 F x, y1 F x, y2 ;
x1, y y
x2, y
x1 O
x2 x
X ,Y
X ,Y
3 . 0 F x, y 1, 且
对任意固定的 y R , F , y 0 ,
得
1
F
,
A
B
2
C
2
0 F x, A B arctan x C
2 2
0 F , y A B C arctan y
2
3
由 以 上 三 式 可 得A,
1,
2
B
,
2
C
2
.
n 维随机变量
设 E 是一个随机试验,S是其样本空间,
Xi Xi e e S i 1, 2, , n
我们称此函数为n维随机变量的分布函数.
二、二维离散型随机变量
1.定义:
若二维随机向量(X,Y)的可能取值只有有限个或可 列个,则称(X,Y)是离散型二维随机向量.
若二维离散型随机向量(X,Y)的所有可能取值为
(xi,yj),i,j=1,2,…
记P{X=xi,Y=yj}=pij, i, j=1,2,…
《概率论与数理统计》第3章 二维随机变量及其分布

23 April 2012
第三章 多维随机变量及其分布
注意点
第32页
(1) X 与Y是独立的其本质是: 任对实数a, b, c, d,有
Pa X b, c Y d Pa X b Pc Y d
(2) X 与Y 是独立的,则g(X)与h(Y)也是独立的.
23 April 2012
0
=A/6
所以, A=6
23 April 2012
第三章 多维随机变量及其分布
第22页
例3.3.2
若
(X,
Y)
~
p( x,
y)
6e(2x3y) , 0,
x 0, y 0 其它
试求 P{ X< 2, Y< 1}.
23 April 2012
第三章 多维随机变量及其分布
第23页
y
解: P{ X<2, Y<1} p(x, y)dxdy
3.1.2 联合分布函数
定义3.1.2 (以下仅讨论两维随机变量)
任对实数 x 和 y, 称 F(x, y) = P( X x, Y y)
为(X, Y) 的联合分布函数.
注意:
F(x, y)为(X, Y)落在点(x, y)的左下区域的概率.
23 April 2012
第三章 多维随机变量及其分布
x1 x2 … xi …
23 April 2012
y1 y2 … yj …
p11 p12 … p1j … p21 p22 … p2j … … … ……… pi1 pi2 … pi j … … … ………
第三章 多维随机变量及其分布
第9页
联合分布列的基本性质
(1) pij 0, i, j = 1, 2,… (非负性)
概率论与数理统计(第3-5章)

2y1
y 2
y 1时 ,
F(x,y) 4dxdy 4S三角形1
三角形
整理课件
所以,所求的分布函数为
0,
(x 1 或y 0) 2
2
y
2
x
y 2
1
,
( 1 x 0, 0 y 2 x 1) 2
F
(x,
y)
4
x
1 2
2
,
( 1 x 0,2x 1 y) 2
2
y
f(x,y) 1 8(6xy), 0x2,2y4
0,
其 他
求概率 PXY4X1
解答 PXY4X1
4
PXY4,X1
2
PX1
2
dx
4x 1 (6 x y)dy
1 2 8
7 48 7
2
dx
1
4 1 (6 x 28
y)整d理y课件
38
18
12
二维均匀分布
设二维随机变量 ( X , Y ) 的概率密度为
D
1
dx
31(6xy)dy
0 28
0 11 8(6yxy1 2y2)3 2dx8 3
2 12
整理课件
续解 ……….
PXY3f(x,y)dxdy
D
1
dx
3x1(6xy)dy
0 28
011 8(6yxy1 2y2)3 2xdx
5 24
整理课件
x+y=3
思考 已知二维随机变量(X,Y)的分布密度为
x2
+F(x1,y1)
P(x1 X x2,y1 Y y2) = F(x2,y2)- F(x2,y1)- F(x1,y2) + F(x1,y1)
概率论与数理统计(二维随机变量函数的分布)

将上述x与z的关系描绘在xOz平面上便是图中的阴 影部分.
3.5.2
二维连续型随机变量函数的分布
e y , y 0 , 1 , 0 x 1 , fY ( y ) fX ( x) 0 , 其它 , 0 , 其它,
fZ ( z )
f X ( x ) fY ( z x )dx
定理3.1(正态分布的重要性质)若X1,X2 ,…,Xn 为相互独立的随机变量,且 X i ~ N (i , i 2 ), i 1,2,...,n C1,C2,…,Cn为n个任意常数,则
C X
i 1 i
n
i
~ N ( C i i , C i i )
2 2 i 1 i 1
i 1 n
3.5.2
二维连续型随机变量函数的分布
(2) 将Xi共同的分布函数F(x)代入(1)的结果中, 得 n
FY ( y) [F ( y)] FZ ( z ) 1 [1 F ( z )]n
(3) Y和Z的分布函数仍为上述两式,概率密度可 由上述两式分别对y和z求导得到
fY ( y) n[F ( y)]n1 f ( y) fZ ( z ) n[1 F ( z )]n1 f ( z )
二维连续型随机变量函数的分布
【例3.22】(和的分布)设(X,Y)的概率密度为
f(x,y),求Z = X + Y的概率密度.
解:事件X + Y Z所占有的区域如图,
由 FZ ( z ) P{ X Y z }
x y z
f ( x, y)dxdy
f ( x, y)dx]dy
t 2
概率论与数理统计 二维连续性随机变量及其分布

计算公式: 计算公式 cov(X,Y) =E(XY)-E(X)E(Y).
概率论与数理统计
例5 (X,Y)分布律如下,求cov(X,Y) X,Y)
−1 0 2 P +∞ 0.3 0.45 0.25 P 0.55 0.25 0.2 E( X ) = ∑xi pi = 0×0.3+1×0.45 + 2×0.25 = 0.95,
E ( X ) = ∫−∞ xf ( x)dx
+∞
概率论与数理统计
3.随机变量函数的数学期望 (1)X为随机变量,Y=g(X), 离散型: 离散型: E (Y ) = E[ g ( X )] = ∑ g ( xi ) pi
i =1 ∞
连续型: 连续型:E (Y ) = E[ g ( X )] =
∫
]
E{[ X − E ( X )][Y − E (Y )]} D ( X ) D(Y ) Cov( X , Y )
D ( X ) D(Y )
概率论与数理统计
若D (X ) > 0, D (Y ) > 0 ,称
( X − E( X ))(Y − E(Y) cov( X ,Y) E = D( X ) D(Y) D( X ) D(Y)
−∞ −∞
概率论与数理统计
j =1 i =1
解 X 型区域D : 0 ≤ y ≤ x, 0 ≤ x ≤ 1;
y
D
O
x
概率论与数理统计
X 型区域D : 0 ≤ y ≤ x, 0 ≤ x ≤ 1;
概率论与数理统计
1.E (C ) = C 2. E (aX ) = a E (X ) 3.E (X + Y ) = E (X ) + E (Y )
概率论与数理统计
例5 (X,Y)分布律如下,求cov(X,Y) X,Y)
−1 0 2 P +∞ 0.3 0.45 0.25 P 0.55 0.25 0.2 E( X ) = ∑xi pi = 0×0.3+1×0.45 + 2×0.25 = 0.95,
E ( X ) = ∫−∞ xf ( x)dx
+∞
概率论与数理统计
3.随机变量函数的数学期望 (1)X为随机变量,Y=g(X), 离散型: 离散型: E (Y ) = E[ g ( X )] = ∑ g ( xi ) pi
i =1 ∞
连续型: 连续型:E (Y ) = E[ g ( X )] =
∫
]
E{[ X − E ( X )][Y − E (Y )]} D ( X ) D(Y ) Cov( X , Y )
D ( X ) D(Y )
概率论与数理统计
若D (X ) > 0, D (Y ) > 0 ,称
( X − E( X ))(Y − E(Y) cov( X ,Y) E = D( X ) D(Y) D( X ) D(Y)
−∞ −∞
概率论与数理统计
j =1 i =1
解 X 型区域D : 0 ≤ y ≤ x, 0 ≤ x ≤ 1;
y
D
O
x
概率论与数理统计
X 型区域D : 0 ≤ y ≤ x, 0 ≤ x ≤ 1;
概率论与数理统计
1.E (C ) = C 2. E (aX ) = a E (X ) 3.E (X + Y ) = E (X ) + E (Y )
《概率论与数理统计》第一节二维随机变量及其分布

( x,y)
Ae (2 x3 y) ,
0,
x 0, 其它.
y
ห้องสมุดไป่ตู้
0,
求:(1)常数A;(2) (X, Y)的分布函数F(x, y); (3) (X, Y)落在三角形区域D:x0, y0, 2x+3y6内的概率.
解:(1)
f ( x, y)dxdy
Ae (2 x3 y)dxdy
00
A
e2 xdx
0
e3 ydy
0
A 3
e2xdx
0
A 3
(
1 2
e
2
x
)
0
A, 6
A 6
1,
A
6.
(2) ( X ,Y )的分布函数为:
F(x, y)
x
y
f
(u,
v
)dudv
x y 6e(2u3v)dudv,
00
0,
x 0, y 0, 其它.
(1
e2 0,
x
)(1
e3
注: P{x1 X x2 , y1 Y y2 } F( x2,y2 ) F( x1,y2 ) F( x2,y1 ) F( x1,y1 ).
3. 分布函数F(x, y)的性质:
(1)非负规范: 对任意(x, y) R2 , 0 F(x, y) 1, 且
F (, ) lim F ( x, y) 1,F (, ) lim F ( x, y) 0,
XY 0 1
0 0.3 0.3
1 0.3 0.1 若把不放回改为有放回的摸球,则( X ,Y )的分布律为:
XY 0 1
0 0.36 0.24
1 0.24 0.16
概率论与数理统计—二维随机变量

解 ( X, Y ) 的可能取值为 (1,2), (2,1), (2,2).
P{ X 1,Y 2} 1 2 1 , P{ X 2,Y 1} 2 1 1 ,
32 3
32 3
P{X 2,Y 2} 2 1 1 . 32 3
p11 0,
p12
p21
p22
1, 3
故 ( X , Y ) 的分布律为
P{ X xi , Y y j } pij , i, j 1, 2,, 称此为二维离散型随机变量 ( X ,Y ) 的分布律, 或随机变量 X 和Y 的联合分布律.
其中 pij 0,
pij 1.
i1 j1
二维随机变量 ( X,Y ) 的分布律也可表示为
X Y
y1 y2
yj
x1
x2 xi
机变量 X 和 Y 的联合概率密度.
2.性质
(1) f ( x, y) 0.
(2)
f ( x, y) d x d y F (,) 1.
(3) 设 G 是 xoy 平面上的一个区域, 点 ( X ,Y ) 落在
G 内的概率为
P{(X ,Y ) G} f ( x, y) d x d y.
,
(x, y) D,
0, 其他.
则称 ( X , Y ) 在 D 上服从 均匀分布.
例3 已知随机变量 ( X , Y ) 在 D上服从均匀分布, 试求( X , Y )的分布密度,其中D为x 轴, y 轴及直线 y = x+1 所围成的三角形区域 .
解
由
f
( x,
y)
1 S
0,
,
(x, y) D, 其他.
G
(4)若 f ( x, y)在( x, y)连续,则有2F ( x, y) f ( x, y). xy
P{ X 1,Y 2} 1 2 1 , P{ X 2,Y 1} 2 1 1 ,
32 3
32 3
P{X 2,Y 2} 2 1 1 . 32 3
p11 0,
p12
p21
p22
1, 3
故 ( X , Y ) 的分布律为
P{ X xi , Y y j } pij , i, j 1, 2,, 称此为二维离散型随机变量 ( X ,Y ) 的分布律, 或随机变量 X 和Y 的联合分布律.
其中 pij 0,
pij 1.
i1 j1
二维随机变量 ( X,Y ) 的分布律也可表示为
X Y
y1 y2
yj
x1
x2 xi
机变量 X 和 Y 的联合概率密度.
2.性质
(1) f ( x, y) 0.
(2)
f ( x, y) d x d y F (,) 1.
(3) 设 G 是 xoy 平面上的一个区域, 点 ( X ,Y ) 落在
G 内的概率为
P{(X ,Y ) G} f ( x, y) d x d y.
,
(x, y) D,
0, 其他.
则称 ( X , Y ) 在 D 上服从 均匀分布.
例3 已知随机变量 ( X , Y ) 在 D上服从均匀分布, 试求( X , Y )的分布密度,其中D为x 轴, y 轴及直线 y = x+1 所围成的三角形区域 .
解
由
f
( x,
y)
1 S
0,
,
(x, y) D, 其他.
G
(4)若 f ( x, y)在( x, y)连续,则有2F ( x, y) f ( x, y). xy
东华大学《概率论与数理统计》课件 第三章 二维随机变量
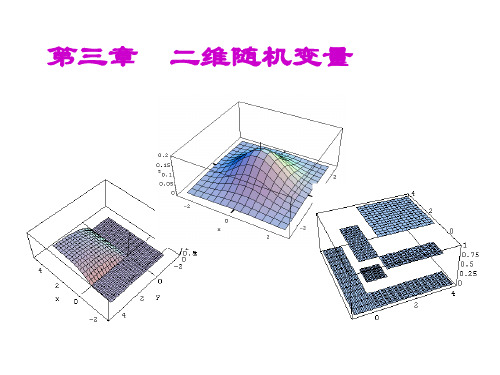
Y
X
y1
y2
yn
x1
p11
p12
p1 n
x2
p21
p22
p2n
n
pi• =
pij
j =1
p1•
p2•
xm
pm1
pm2
pmn
m
p• j =
pij
p•1
p•2
p• n
i =1
其中, pij = P( X = xi ,Y = y j ) ,
pm•
n
m
p• j = pi• = 1
j −1
( x,
y)
=
1 s
,
0,
(x, y) S (x, y) S
3.体积为v的空间区域V上
(
x,
y,
z)
=
1 v
,
0,
(x, y, z) V (x, y, z) V
基本概念:随机向量、联合分布函数。 离散型随机变量:联合概率分布、阶梯型分布函
数。 连续型随机变量:概率密度函数、连续型分布函
数。
即
FY
(
y)
=
F
(+,
y)
=
lim
x→+
F
(
x,
y)
F ( x) = F ( x,+)
1 = F(+,+)
0 = F(−, y) O
二维随机变量 (X ,Y) 的分布函数: F(x, y) = P(X x,Y y)
y
y
(x,y)
0
x
x
二维分布函数 F(x,y) 的性质: (1)(非降性) F(x, y) 是 x 或 y 的单调非降函数.
概率论与数理统计3.1.3 二维连续型随机变量及其联合概率密度

§3.1.3 二维连续型随机变量 及其联合概率密度
一、二维连续型随机变量的定义及联合概率密度 二、联合概率密度函数的性质
一、 二维连续型随机变量的定义及联合概率密度函数
一维连续型随机变量X F(x)为随机变量X的分布
函数,若存在非负可积函数 f(x),使得
F(x) P{X x}
x
f (t)dt ( x )
(4) 在f(x)的连续点处有: f (x) F'(x)
(4)若f (x, y)在(x, y)连续,
则有 2F (x, y) f (x, y). xy
用来求概率密度f(x)的方法
用来求概率密度 f(x,y)的方法
例2 设随机变量(X ,Y )的联合分布函数为
(x,y)
用来求待定常数的方法
y
曲线下x轴上
所围面积为1
连续型随机变量(X,Y)联合 概率密度函数f(x, y)的性质
(1) 非负性: f (x, y) 0;
(2) 规范性:
f (x, y)dxdy 1
F(, ).
f (x, y)
用来求待定 常数的方法
曲面下xoy平 面上所围体积
o
(x, y)
X
x
x
X
y
Y
(x, y)
推断:设D是xOy平面上的 一个区域,点( X ,Y )落在D内 的概率为
P{(X ,Y ) D}
f (x, y) d x d y.
D
二、联合概率密度函数的性质:
连续型随机变量X的概率密度函 数f(x)的性质
(1) f(x)≥0; (2) f(x)dx 1 F().
一、二维连续型随机变量的定义及联合概率密度 二、联合概率密度函数的性质
一、 二维连续型随机变量的定义及联合概率密度函数
一维连续型随机变量X F(x)为随机变量X的分布
函数,若存在非负可积函数 f(x),使得
F(x) P{X x}
x
f (t)dt ( x )
(4) 在f(x)的连续点处有: f (x) F'(x)
(4)若f (x, y)在(x, y)连续,
则有 2F (x, y) f (x, y). xy
用来求概率密度f(x)的方法
用来求概率密度 f(x,y)的方法
例2 设随机变量(X ,Y )的联合分布函数为
(x,y)
用来求待定常数的方法
y
曲线下x轴上
所围面积为1
连续型随机变量(X,Y)联合 概率密度函数f(x, y)的性质
(1) 非负性: f (x, y) 0;
(2) 规范性:
f (x, y)dxdy 1
F(, ).
f (x, y)
用来求待定 常数的方法
曲面下xoy平 面上所围体积
o
(x, y)
X
x
x
X
y
Y
(x, y)
推断:设D是xOy平面上的 一个区域,点( X ,Y )落在D内 的概率为
P{(X ,Y ) D}
f (x, y) d x d y.
D
二、联合概率密度函数的性质:
连续型随机变量X的概率密度函 数f(x)的性质
(1) f(x)≥0; (2) f(x)dx 1 F().
概率论与数理统计(二维随机变量的边缘分布)

其中 x1, x2 ,, xn 为任意实数.
(2) n维随机变量的概率密度函数
若存在非负函数 f ( x1, x2 ,, xn ), 使对于任意 实数 x1, x2 ,, xn 有
F ( x1, x2,, xn )
xn
xn1
x1
f ( x1, x2,, xn ) d x1 d x2 d xn,
f ( x, y)dx 为(X,Y)关于Y的边缘
概率密度.
3.2.3 二维连续型随机变量的边缘概率密度
【例3.10】设二维随机变量(X,Y)的联合概率密度
为
f
(
x,
y)
1, 0,
0 x 1,| y | x 其它
求边缘概率密如图:
x
6 d y,
x2
0d
y,
0 x1 其他
y (1,1)
y x
6( x x2 ), 0 x 1
0,
其他
O
y x2
x
由于
6( x x2 ),
fX (x)
0,
x
FX ( x) fX ( x)dx
x
0dx,
2 1
所以
fX (x)
f ( x, y)dy
1
e
(
x 1
2
2 1
)2
exp{
1
( y 2 x 1 )2}dy
2 1 2 1 2
2(1 2 ) 2
1
令t 1 ( y 2 x 1 ),则有
(2) n维随机变量的概率密度函数
若存在非负函数 f ( x1, x2 ,, xn ), 使对于任意 实数 x1, x2 ,, xn 有
F ( x1, x2,, xn )
xn
xn1
x1
f ( x1, x2,, xn ) d x1 d x2 d xn,
f ( x, y)dx 为(X,Y)关于Y的边缘
概率密度.
3.2.3 二维连续型随机变量的边缘概率密度
【例3.10】设二维随机变量(X,Y)的联合概率密度
为
f
(
x,
y)
1, 0,
0 x 1,| y | x 其它
求边缘概率密如图:
x
6 d y,
x2
0d
y,
0 x1 其他
y (1,1)
y x
6( x x2 ), 0 x 1
0,
其他
O
y x2
x
由于
6( x x2 ),
fX (x)
0,
x
FX ( x) fX ( x)dx
x
0dx,
2 1
所以
fX (x)
f ( x, y)dy
1
e
(
x 1
2
2 1
)2
exp{
1
( y 2 x 1 )2}dy
2 1 2 1 2
2(1 2 ) 2
1
令t 1 ( y 2 x 1 ),则有
二维随机变量的边缘分布

概率论与数理统计
❖ 3.边缘概率密度 1.概念
➢由连续型随机变量的定义知,X是一个连续型随机变
量,且其概率密度为
fX ( x)
f ( x, y)dy
同样,Y也是一个连续型随机变量,其概率密度为
fY ( y) f ( x, y)dx
➢分别称
fX ( x) f ( x, y)dy 和 fY ( y) f ( x, y)dx
➢ 例3.4.1 设(X,Y)的分布函数为
1
F ( x,
y)
2
(arctan x
)(arctany 2
), 2x,y求关于X和Y的边缘分布函数FX(x)、FY(y).
➢ 解:由定义知
1
FX (x)
lim F( x,
y
y)
lim [
y
2
(arctan x
)(arctany 2
)] 2
1
(arctanx )
❖ 2.边缘分布律 1.概念
➢ 例3.4.2 袋中有2只白球3只黑球,现从中摸两次,每次摸一球,分
别采用有无放回两种摸球方式,令
1, 第一次摸出白球,
1, 第二次摸出白球,
X 0, 第一次摸出黑球, Y 0, 第二次摸出黑球.
求 X 和 Y 的联合分布律与边缘分布律.
➢ 解 利用古典概型的方法求其分布律.
概率密度为 f(x, y),因为X的分布函数为
x
FX ( x) F ( x, )
(
f ( x, y)dy)dx
➢由连续型随机变量的定义知, X 是一个连续型随机变量,
且其概率密度为
fX ( x)
f ( x, y)dy
同样, Y 也是一个连续型随机变量,其概率密度为
《概率论与数理统计》第三章

§1 二维随机变量
定义:设E是一个随机试验,样本空间S={e}; 设X=X(e)和Y=Y(e)是定义
y
X e,Y e
在S上的随机变量,由它们构成的
向量(X,Y)叫做二维随机向量 或二维随机变量。
e S
x
定义:设(X,Y)是二维随机变量对于任意实数x,y,
二元函数
ቤተ መጻሕፍቲ ባይዱ
y
F(x, y) P(X x) (Y y)
1 4
1 i
,
ji
0, j i
(X,Y)的联合分布律为:
YX
1
1
1/4
23 4 1/8 1/12 1/16
2
0 1/8 1/12 1/16
3
0
0 1/12 1/16
4
0
0 0 1/16
例3:设有10件产品,其中7件正品,3件次品。现从中
任取一件产品,取后不放回,令
1 X 0
第一次取到的产品是次品 1
z f (x, y)为顶面的柱体体积。
所以 X,Y 落在面积为零的区域的概率为零。
例3:设二维随机变量(X,Y)具有概率密度:
2e(2x y) , x 0,y 0
y f (x, y) 0,
其他
1 求分布函数F(x, y);2求P{X 2,Y 3};
3求P(Y X )的概率
解: (1)当x>0,y>0时
f (x, y)xy
————————
概率微分
(4) f ( x, y)的作用 : 求二维随机变量(X,Y)取值
落在区域G内的事件的概率
P((X ,Y ) G) f ( x, y)dxdy
G
G
注:1在几何上,z f (x, y)表示空间一个曲面,
概率论与数理统计课件 2.6 二维随机变量的边缘分布

xi
pi1
pi 2
pij
pi
p j
p1
p2
p j
1
例2 设随机变量 X 在数1,2,3,4中等可能取值,另一个随机变量 Y
在1至 X 之间等可能取值,试求二维随机变量 (X ,Y )的联合
分布律与边缘分布律.
1
解
P(X i,Y j) P(X i)P(Y j | X i) ,
§2.6 二维随机变量的边缘分布
一、二维随机变量的边缘分布函数
FX (x) P(X x) P(X x,Y ) F(x, )
二、二维离散型随机变量的边缘分布律
pi P( X xi ) pij , i 1, 2, 3, . j 1
三、二维连续型随机变量的边缘密度函数
若二维随机变量 (X ,Y ) 的联合分布函数为 F(x, y) ,则 (X ,Y )
中随机变量 X 的分布函数称为 (X ,Y )关于 X 的边缘分布函数,
记为
FX (x) P(X x) P(X x,Y ) F(x, )
二维随机变量 (X ,Y )关于随机变量 Y 的边缘分布函数
fY
( y)
f
(x,
y)dx
3(1 0,
y ),
0 y 1, 其它.
均匀分布的边缘分布不一定是均匀分布
若 D 是矩形区域, 则 (X ,Y) 的边缘分布仍为均匀分布
解 (X ,Y ) 的联合分布律为
关于X 的边缘分布
关于 Y 的边缘分布
几何分布
帕斯卡分布.
例4 已知随机变量 X 和 Y 的分布律分别为
概率论与数理统计3.3二维随机变量函数的分布ppt课件

解:
1 x2 y2
f (x, y) e 2 , ( x , y )
2
FZ (z) P(Z z) P( X 2 Y 2 z)
当z<0,显然FZ(z)=0,
当z≥0,
FFFFZZZZ((((zzzz))))xx2xx222yy2yy222zz2zz22222122111eeeexx2xx22222y22y2yy2d22dddxxxxddddyyyy
( x z )2 2
e dx 22 2
2
2 e 令x z t e2 e e edt dx 2 e 2
zzz44222
e2 dx e2 4
z
2
4
(( xx
t
2
zz 22
))22
(x
z 2
)2
z2 4
1
z2
e4
2
X~ N(μ1 , σ12) Y~ N(μ2 , σ22) X与Y相互独立
二维离散型随机变量函数的分布
设(X,Y)为离散型随机变量,
P(X xi ,Y y j ) pij, i, j 1,2,...
Z=g(X,Y)为一维离散型随机变量.若对于 不同的(xi,yj),g (xi,yj)的值互不相同,则Z的 分布律为
P(Z g(xi , y j )) pij i, j 1,2,...
k
p(i)q(k i) i0
离散型 卷积公式
例3:设X,Y相互独立,且X~P(λ1), Y~P(λ2) 证明:Z=X+Y~P(λ1+λ2)
证: P( X k) 1k e1 , k0,1,2,,
k!
P(Y k) k2 e2 , k0,1,2,,
k!
P(Z k) P( X Y k) Pik0( X i,Y k i)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i 3 j
1 3! 27 i! j!(3 i j )!
0≤i+j≤3 ,0≤i,j≤3
首页 上页 返回 下页 结束 铃
当i+j>3或i+j<0时 pij=0 其对应的概率分布表为
Y X 0 1 2 3
首页
0
1 27 1 9 1 9 1 27
上页
1
2
3
1 9 2 9 1 9 0
返回
1 9 1 9 0 0
下页
结束
铃
二元概率密度函数f(x,y)从图形上看是在xoy平面上方 的一个曲面, 包围着下方的体积为1.
首页
上页
2)
f(x, y)dxdy F (,) 1
(8)
2 F (x,y ) f (x,y ) xy
下页 结束 铃
3) 若f(x,y)在点(x,y)连续,则有
首页 上页 返回
4)设G是xoy平面上的一个区域,点(X,Y)落在G内的概率为
P{( X , Y ) G} f ( x, y )dxdy
2)0≤F(x,y)≤1,且 固定y,F(-∞,y)=0 y∈(-∞,+∞), 固定x,F(x,-∞)=0 x∈(-∞, +∞), F(-∞, -∞)=0,F(+∞, +∞)=1
(4)
3)右连续性:F(x,y)关于x右连续,即F(x+0,y) = F(x,y) , F(x,y)关于y右连续,即F(x,y+0) = F(x,y) 4)对于任意(x1,y1),(x2,y2),x1<x2,y1<y2, 则F(x2,y2)-F(x2,y1)-F(x1,y2)+F(x1,y1)≥0
. . .
p1j … p2j … . . . pij … ∶ .
结束 铃
例1 把三个相同的球等可能地放入编号为1,2,3的三个 盒子中,记落入第1号盒子中的球的个数为X,落入第2号盒 子中球的个数为Y,求(X,Y)的分布律。
解:pij=P{X=i,Y=j} =P{X=i|Y=j}P{Y=j},
0≤i+j≤3
2) p pij 1 (6)
i, j ij i1 j 1
首页
上页
返回
下页
结束
铃
有时我们也用表格来表示其联合分布。
Y X
y1
y2
…
yj …
x1 x2 . . . xi ∶ .
首页
p11 p21 . . . pi1 ∶ .
上页
p12 p22 . . . pi2 ∶ .
返回 下页
首页
上页
返回
下页
结束
铃
同理可知(X,Y)落在(x1<X≤x2,y1<Y≤y2)的概率 P{ x1<X≤x2,y1<Y≤y2} =F(x2,y2)-F(x2,y1) -F(x1,y2) +F(x1,y1) (3)
y2
y1
x1
首页 上页
x2
返回 下页 结束 铃
性质: 1)F(x,y)是变量x和y的单调不减函数: 对于任意x1<x2,有F(x1,y)≤ F(x2,y)(y固定,y∈(-∞, ∞));对 于任意y1<y2,有F(x,y1)≤ F(x,y2)(x固定, x ∈(-∞, +∞))。
P{ X x,Y y }
-∞<x,y<+∞ (1)
为(X,Y)的分布函数或联合分布函数。
首页
上页
返回
下页
结束
铃
推广:n维随机变量的联合分布函数 F(x1,x2,…,xn)= P{ X1≤x 1,X2≤x 2,…,Xn≤x n} (2) 若将(X,Y)看成是平面上随机 点的坐标,则F(x,y)在(x,y)处的 函数值就是随机点(X,Y)落在右 图阴影中的概率
下页 结束
1 27 0 0 0
铃
例2 将一试验在同一条件下重复进行,直到成功两次为止. 设每次试验成功的概率为p,令X为第一次成功之前失败的次数, Y为两次成功之间的失败次数,求X和Y的联合分布律.
解: 由题意,X,Y均服从几何分布,且事件{X=xi},{Y=yj}相互独 立,其概率分别为
P{X=i}=pqi, P{Y=j}=pqj, 则 Pij=P{X=i,Y=j}=P{X=i}P{Y=j} =pqi pqj = p2qi+j 即为X和Y的联合分布律.
0≤j≤3
P{Y j}
C 3(
j
P{X i | Y j}
1 1 C ( ) ( ) 2 2
i 3 j
3 j j
1 2 )( ) 3 3
j
3 j
i
3 j i
C 3 j (
3 j
i
1 ) 2
3 j
0≤i+j≤3
p
ij
2 1 i 1 C ( ) C 3( ) ( ) 3 3 2
首页 上页 返回 下页 结束 铃
二、离散型二维随机变量
定义3 如果随机变量(X,Y)可能取的值只有有限对或可列 无限对,则称(X,Y)为二维离散型随机变量,其取值的概率: P{X=xi,Y=yj}=pij , i,j=1,2,… (5) 称为二维随机变量(X,Y)的概率分布或分布律,或X和Y的联合 分布律 注:由分布函数的性质知 1)pij≥0
首页 上页 返回 下页 结束 铃
i=0,1,2,… j=0,1,2Biblioteka …i , j=0,1,2,…
三、二维连续型随机变量
定义4 对二维随机变量(X,Y),如果存在非负函数f(x,y),使 对于任意x,y有
F ( x, y)
x
y
f (u, )dud
(7)
则称(X,Y)为连续型的二维随机变量,称f(x,y)为(X,Y)的概率密 度或随机变量X和Y的联合概率密度。 概率密度的性质: 1) f(x,y)≥0
显然, 对任意实数a<b及c<d, 有
G
(9)
P{a b, c d } f ( x, y)dxdy
由此得,(X,Y)的分布函数F(x,y) 可由下式求出:
F ( x, y )
a c
x y
b d
(10)
f (u, v)dudv
(11)
首页
上页
返回
一、二维随机变量及其分布函数
定义 1 设 E 是一个随机试验,其样本空间为 S={e} ,设 X=X(e) 和 Y=Y(e) 是定义在 S 上的两个随机变量,由它们构成 的二维向量(X,Y)称为二维随机向量或二维随机变量。 推广:S上的n个随机变量X1,X2,…,Xn构成的向量 (X1,X2,…,Xn)称为n维随机变量。 定义2 设(X,Y)是二维随机变量,称函数 F(x,y)=P{(X≤x)∩(Y≤y)}
1 3! 27 i! j!(3 i j )!
0≤i+j≤3 ,0≤i,j≤3
首页 上页 返回 下页 结束 铃
当i+j>3或i+j<0时 pij=0 其对应的概率分布表为
Y X 0 1 2 3
首页
0
1 27 1 9 1 9 1 27
上页
1
2
3
1 9 2 9 1 9 0
返回
1 9 1 9 0 0
下页
结束
铃
二元概率密度函数f(x,y)从图形上看是在xoy平面上方 的一个曲面, 包围着下方的体积为1.
首页
上页
2)
f(x, y)dxdy F (,) 1
(8)
2 F (x,y ) f (x,y ) xy
下页 结束 铃
3) 若f(x,y)在点(x,y)连续,则有
首页 上页 返回
4)设G是xoy平面上的一个区域,点(X,Y)落在G内的概率为
P{( X , Y ) G} f ( x, y )dxdy
2)0≤F(x,y)≤1,且 固定y,F(-∞,y)=0 y∈(-∞,+∞), 固定x,F(x,-∞)=0 x∈(-∞, +∞), F(-∞, -∞)=0,F(+∞, +∞)=1
(4)
3)右连续性:F(x,y)关于x右连续,即F(x+0,y) = F(x,y) , F(x,y)关于y右连续,即F(x,y+0) = F(x,y) 4)对于任意(x1,y1),(x2,y2),x1<x2,y1<y2, 则F(x2,y2)-F(x2,y1)-F(x1,y2)+F(x1,y1)≥0
. . .
p1j … p2j … . . . pij … ∶ .
结束 铃
例1 把三个相同的球等可能地放入编号为1,2,3的三个 盒子中,记落入第1号盒子中的球的个数为X,落入第2号盒 子中球的个数为Y,求(X,Y)的分布律。
解:pij=P{X=i,Y=j} =P{X=i|Y=j}P{Y=j},
0≤i+j≤3
2) p pij 1 (6)
i, j ij i1 j 1
首页
上页
返回
下页
结束
铃
有时我们也用表格来表示其联合分布。
Y X
y1
y2
…
yj …
x1 x2 . . . xi ∶ .
首页
p11 p21 . . . pi1 ∶ .
上页
p12 p22 . . . pi2 ∶ .
返回 下页
首页
上页
返回
下页
结束
铃
同理可知(X,Y)落在(x1<X≤x2,y1<Y≤y2)的概率 P{ x1<X≤x2,y1<Y≤y2} =F(x2,y2)-F(x2,y1) -F(x1,y2) +F(x1,y1) (3)
y2
y1
x1
首页 上页
x2
返回 下页 结束 铃
性质: 1)F(x,y)是变量x和y的单调不减函数: 对于任意x1<x2,有F(x1,y)≤ F(x2,y)(y固定,y∈(-∞, ∞));对 于任意y1<y2,有F(x,y1)≤ F(x,y2)(x固定, x ∈(-∞, +∞))。
P{ X x,Y y }
-∞<x,y<+∞ (1)
为(X,Y)的分布函数或联合分布函数。
首页
上页
返回
下页
结束
铃
推广:n维随机变量的联合分布函数 F(x1,x2,…,xn)= P{ X1≤x 1,X2≤x 2,…,Xn≤x n} (2) 若将(X,Y)看成是平面上随机 点的坐标,则F(x,y)在(x,y)处的 函数值就是随机点(X,Y)落在右 图阴影中的概率
下页 结束
1 27 0 0 0
铃
例2 将一试验在同一条件下重复进行,直到成功两次为止. 设每次试验成功的概率为p,令X为第一次成功之前失败的次数, Y为两次成功之间的失败次数,求X和Y的联合分布律.
解: 由题意,X,Y均服从几何分布,且事件{X=xi},{Y=yj}相互独 立,其概率分别为
P{X=i}=pqi, P{Y=j}=pqj, 则 Pij=P{X=i,Y=j}=P{X=i}P{Y=j} =pqi pqj = p2qi+j 即为X和Y的联合分布律.
0≤j≤3
P{Y j}
C 3(
j
P{X i | Y j}
1 1 C ( ) ( ) 2 2
i 3 j
3 j j
1 2 )( ) 3 3
j
3 j
i
3 j i
C 3 j (
3 j
i
1 ) 2
3 j
0≤i+j≤3
p
ij
2 1 i 1 C ( ) C 3( ) ( ) 3 3 2
首页 上页 返回 下页 结束 铃
二、离散型二维随机变量
定义3 如果随机变量(X,Y)可能取的值只有有限对或可列 无限对,则称(X,Y)为二维离散型随机变量,其取值的概率: P{X=xi,Y=yj}=pij , i,j=1,2,… (5) 称为二维随机变量(X,Y)的概率分布或分布律,或X和Y的联合 分布律 注:由分布函数的性质知 1)pij≥0
首页 上页 返回 下页 结束 铃
i=0,1,2,… j=0,1,2Biblioteka …i , j=0,1,2,…
三、二维连续型随机变量
定义4 对二维随机变量(X,Y),如果存在非负函数f(x,y),使 对于任意x,y有
F ( x, y)
x
y
f (u, )dud
(7)
则称(X,Y)为连续型的二维随机变量,称f(x,y)为(X,Y)的概率密 度或随机变量X和Y的联合概率密度。 概率密度的性质: 1) f(x,y)≥0
显然, 对任意实数a<b及c<d, 有
G
(9)
P{a b, c d } f ( x, y)dxdy
由此得,(X,Y)的分布函数F(x,y) 可由下式求出:
F ( x, y )
a c
x y
b d
(10)
f (u, v)dudv
(11)
首页
上页
返回
一、二维随机变量及其分布函数
定义 1 设 E 是一个随机试验,其样本空间为 S={e} ,设 X=X(e) 和 Y=Y(e) 是定义在 S 上的两个随机变量,由它们构成 的二维向量(X,Y)称为二维随机向量或二维随机变量。 推广:S上的n个随机变量X1,X2,…,Xn构成的向量 (X1,X2,…,Xn)称为n维随机变量。 定义2 设(X,Y)是二维随机变量,称函数 F(x,y)=P{(X≤x)∩(Y≤y)}
