【免费下载】概率论与数理统计 第三章 二维随机变量及其概率分布 例题
概率统计第三章

第三章二维随机变量及其分布练习题 3.1一、判断题1(X,Y)的分布可确定 X 与 Y 的边缘分布。
()、由2、设、是两个随机变量,则是二维随机变量。
3、设二维随机变量 (,)的联合分布函数为 F (x, y) ,则 F ( x, y)P{x,y} 1 P{x,y} 。
() 4、设二维随机变量(,) 的联合分布函数为 F (x, y) 则,P{ x1x2 , y1y2 } F (x2 , y2 ) F ( x1 , y1 )()5、由( X,Y)的两个边缘分布可确定 ( X ,Y )的联合分布()6、若(X,Y)为离散型二维随机变量,则P{ X a,Y b}P{ x a, y b} (其中 a,b 为常数)() 7、设( , )的概率分布为0133 1010131 1010则, U的概率分布为U012343。
( )P1010 10二、填空题1.设二维随机变量 ( , ) 的联合概率分布为01200.10.2010.30.10.120.100.1则 P0 =____。
2.设二维随机变量 ( , ) 的概率密度e y0 x yx, y0其他而的边缘密度为y ,则 2 =________。
3.设二维随机变量 ( , ) 的概率密度为1 0 x 1,0 y1x, y0其他则概率 P0.5,0.6 =________。
4.设二维随机变量 ( , ) 的概率密度为4xy0 x1,0y1x, y0其他则 P 01 , 12 41=___________,P{} =_________,P{} =_________。
5.(X ,Y)是二维连续型随机变量,用(X ,Y)的联合分布函数 F ( x, y)表示下列概率(1)p( a X b, Y c)__________ __________;(2)p( X a, Y b)____________________ ;(3) p(0 Y a ) __________ __________;(4) p( X a, Y b) ____________________ .练习题 3.2一、选择题1、设,为随机变量,则事件1,1的逆事件为 ().A1, 1 ;B1, 1 ;C1, 1 ;D1 1 .2、p ij P{x i ,y j }( i, j1,2,) 是离散型二维随机变量( ,) 的()。
概率论与数理统计3.1.2 二维离散型随机变量及其联合分布律

pk
xi
pi1 pi2 ... pij ...
分布律的性质 (1)非负性:pk 0 , k 1, 2, ;
(2)规范性: pk 1. k 1
3.联合分布律的性质
(1) 非负性: pij 0,i, j 1, 2, ;
(2) 规范性: pij 1 i1 j1
p{(X 0,Y 0)} P{(X 1,Y 0)} P{(X 1,Y 1)}
0.3 0.3 0.1 0.7
注 P{(X ,Y ) D}
p{X xi ,Y y j}
pij
:
( xi , y j )D
( xi , y j )D
P{X 0,Y 0} P{X 0}p{Y 0}
33 9 5 5 25
Y X
0
1
P{X 0,Y 1} 3 2 6
5 5 25
P{X 1,Y 0} 2 3 6 5 5 25
P{X 1,Y 1} 2 2 4
0 1
9
6
25
25
625
例1 袋中有2只白球,3只黑球,现摸球两次,定义
1 X 0
第一次摸到白球,求 (1) 有放回取球下(X,Y)的分布律。 第一次摸到黑球 (2) 不放回取球下(X,Y)的分布律。
Y
1 0
第二次摸到白球 第二次摸到黑球
(3)不放回下 P{X Y}.
例1 袋中有2只白球,3只黑球,现摸球两次,定义
1 X 0
第一次摸到白球,求 (1) 有放回取球下(X,Y)的分布律。 第一次摸到黑球 (2) 不放回取球下(X,Y)的分布律。
第三章 二维随机变量及其分布《概率论与数理统计》西南交大峨眉校区

X
0 1
pX ( xi )
3 2 5 5
9 6
25 25
5
6 4
25 25
5
pY ( y j )
3
2
1
(2)不放回取球
Y
X
0 1
0
1
pX ( xi )
3 2 5 5
6 6
20 20
5
6 2
20 20
5
pY ( y j )
3
2
1
三、二维离散型随机变量的独立性
定义 5:对二维离散型随机变量 ( X , Y ) 的任意一对可能取值 ( xi , y j ) , 若满足:
例如,研究某一社区儿童的生长发育状况,常需要将身高和体重作为一个整 体来研究,才能合理地对生长发育状况做出评价。 故:样本空间 该社区的全体儿童 , 身 高 H ( ) 和 体 重 W ( ) 是 定 义 在 样本 空 间 上 的 两个 随 机变 量 , 则
( H ( ),W ( )) 是二维随机变量。
( X xi , Y y2 )
( X xi , Y yn ) ,
按照互不相容事件的概率加法定理,可得:
pX ( xi ) = P( X xi , Y y1 ) P( X xi , Y y2 )
P( X xi , Y yn )
P( X xi , Y y j ) p( xi , y j )
Y
X
0 1
0
1
9 6
25 25
6 4
25 25
二维离散型随机变量的联合概率函数的性质
① 非负性: pij 0 ; ② 归一性:
概率论与数理统计第三章习题及答案

概率论与数理统计习题 第三章 多维随机变量及其分布习题3-1 盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球.以X 表示取到黑球的只数,以Y 表示取到红球的只数,求X 和Y 的联合分布律.(X ,Y )的可能取值为(i , j ),i =0,1,2,3, j =0,12,i + j ≥2,联合分布律为 P {X=0, Y=2 }=351472222=C C C P {X=1, Y=1 }=35647221213=C C C C P {X=1, Y=2 }=35647122213=C C C C P {X=2, Y=0 }=353472223=C C C P {X=2, Y=1 }=351247121223=C C C C P {X=2, Y=2 }=353472223=C C C P {X=3, Y=0 }=352471233=C C C P {X=3, Y=1 }=352471233=C C C P {X=3, Y=2 }=0习题3-2 设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其它,0,42,20),6(),(y x y x k y x f(1) 确定常数k ; (2) 求{}3,1<<Y X P (3) 求{}5.1<X P ; (4) 求{}4≤+Y X P . 分析:利用P {(X , Y)∈G}=⎰⎰⎰⎰⋂=oD G Gdy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)83)6(81)3,1(321⎰⎰=--=<<dy y x dxY X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)32)6(81)4(4020=--=≤+⎰⎰-dy y x dxY X P x习题3-3 将一枚硬币掷3次,以X 表示前2次出现H 的次数,以Y 表示3次中出现H 的次数,求Y X ,的联合分布律以及),(Y X 的边缘分布律。
概率论与数理统计(理工类,第四版)吴赣昌主编课后习题答案第三章

第三章多维随机变量及其分布3.1 二维随机变量及其分布习题1设(X,Y)的分布律为X\Y12311/61/91/1821/3a1/9求a.分析:dsfsd1f6d54654646解答:由分布律性质∑i⋅jPij=1,可知1/6+1/9+1/18+1/3+a+1/9=1,解得a=2/9.习题2(1)2.设(X,Y)的分布函数为F(x,y),试用F(x,y)表示:(1)P{a<X≤b,Y≤c};解答:P{a<X≤b,Y≤c}=F(b,c)-F(a,c).习题2(2)2.设(X,Y)的分布函数为F(x,y),试用F(x,y)表示:(2)P{0<Y≤b};解答:P{0<Y≤b}=F(+∞,b)-F(+∞,0).习题2(3)2.设(X,Y)的分布函数为F(x,y),试用F(x,y)表示:(3)P{X>a,Y≤b}.解答:P{X>a,Y≤b}=F(+∞,b)-F(a,b).习题3(1)3.设二维离散型随机变量的联合分布如下表:试求:(1)P{12<X<32,0<Y<4;解答:P{12<X<23,0<Y<4P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=P{X=1,Y=1}+P{X=1,Y=2}+P{X=1,Y=3}=14+0+0=14.习题3(2)3.设二维离散型随机变量的联合分布如下表:试求:(2)P{1≤X≤2,3≤Y≤4};解答:P{1≤X≤2,3≤Y≤4}=P{X=1,Y=3}+P{X=1,Y=4}+P{X=2,Y=3}+P{X=2,Y=4}=0+116+0+14=516.习题3(3)3.设二维离散型随机变量的联合分布如下表:试求:(3)F(2,3).解答:F(2,3)=P(1,1)+P(1,2)+P(1,3)+P(2,1)+P(2,2)+P(2,3)=14+0+0+116+14+0=916.习题4设X,Y为随机变量,且P{X≥0,Y≥0}=37,P{X≥0}=P{Y≥0}=47,求P{max{X,Y}≥0}.解答:P{max{X,Y}≥0}=P{X,Y至少一个大于等于0}=P{X≥0}+P{Y≥0}-P{X≥0,Y≥0}=47+47-37=57.习题5(X,Y)只取下列数值中的值:(0,0),(-1,1),(-1,13),(2,0)且相应概率依次为16,13,112,512,请列出(X,Y)的概率分布表,并写出关于Y的边缘分布.解答:(1)因为所给的一组概率实数显然均大于零,且有16+13+112+512=1,故所给的一组实数必是某二维随机变量(X,Y)的联合概率分布. 因(X,Y)只取上述四组可能值,故事件:{X=-1,Y=0},{X=0,Y=13,{X=0,Y=1},{X=2,Y=13,{X=2,Y=1}均为不可能事件,其概率必为零. 因而得到下表:Y01/31pk7/121/121/3习题6设随机向量(X,Y)服从二维正态分布N(0,0,102,102,0),其概率密度为f(x,y)=1200πex2+y2200,求P{X≤Y}.解答:由于P{X≤Y}+P{X>Y}=1,且由正态分布图形的对称性,知P{X≤Y}=P{X>Y},故P{X≤Y}=12.习题7设随机变量(X,Y)的概率密度为f(x,y)={k(6-x-y),0<x<2,2<y<40,其它, (1)确定常数k;(2)求P{X<1,Y<3};(3)求P{X<1.5};(4)求P{X+Y≤4}.解答:如图所示(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数k.∫02∫24k(6-x-y)dydx=k∫02(6-2x)dx=8k=1,所以k=18.(2)P{X<1,Y<3}=∫01dx∫2318(6-x-y)dy=38.(3)P{X<1.5}=∫01.5dx∫2418(6-x-y)dy=2732.(4)P{X+Y≤4}=∫02dx∫24-x18(6-x-y)dy=23.习题8已知X和Y的联合密度为f(x,y)={cxy,0≤x≤1,0≤y≤10,其它,试求:(1)常数c;(2)X和Y的联合分布函数F(x,y).解答:(1)由于1=∫-∞+∞∫-∞+∞f(x,y)dxdy=c∫01∫01xydxdy=c4,c=4.(2)当x≤0或y≤0时,显然F(x,y)=0;当x≥1,y≥1时,显然F(x,y)=1;设0≤x≤1,0≤y≤1,有F(x,y)=∫-∞x∫-∞yf(u,v)dudv=4∫0xudu∫0yvdv=x2y2.设0≤x≤1,y>1,有F(x,y)=P{X≤1,Y≤y}=4∫0xudu∫01ydy=x2.最后,设x>1,0≤y≤1,有F(x,y)=P{X≤1,Y≤y}=4∫01xdx∫0yvdv=y2.函数F(x,y)在平面各区域的表达式F(x,y)={0,x≤0或y≤0x2,0≤x≤1,y>1x2y2,0≤x≤1,0≤y≤1.y2,x>习题9设二维随机变量(X,Y)的概率密度为f(x,y)={4.8y(2-x),0≤x≤1,x≤y≤10,其它,求边缘概率密度fY(y).解答:fX(x)=∫-∞+∞f(x,y)dy={∫0x4.8y(2-x)dy,0≤x≤10,其它={2.4x2(2-x),0≤x≤10,其它.fY(y)=∫-∞+∞f(x,y)dx={∫0y4.8y(2-x)dx,0≤y≤10,其它={2.4y(4y-y2),0≤y≤10,其它.习题10设(X,Y)在曲线y=x2,y=x所围成的区域G里服从均匀分布,求联合分布密度和边缘分布密度. 解答:区域G的面积A=∫01(x-x2)dx=16,由题设知(X,Y)的联合分布密度为f(x,y)={6,0≤x≤1,x2≤y≤x0,其它,从而fX(x)=∫-∞+∞f(x,y)dy=6∫x2xdy=6(x-x2),0≤x≤1,即fX(x)={6(x-x2),0≤x≤10,其它,fY(y)=∫-∞+∞f(x,y)dx=6∫yydx=6(y-y),0≤y≤1,即fY(y)={6(y-y),0≤y≤10,其它.3.2 条件分布与随机变量的独立性习题1二维随机变量(X,Y)的分布律为从而(X,Y)的联合概率分布为P{X≤a,∣X∣≤a}=P{X≤a}⋅P{∣X∣≤a},而事件{∣X∣≤a}⊂{X≤a},故由上式有P{∣X∣≤a}==P{X≤a}⋅P{∣X∣≤a},⇒P{∣X∣≤a}(1-P{X≤a})=0⇒P{∣X≤a∣}=0或1=P{X≤a}⋅(∀a>0)但当a>0时,两者均不成立,出现矛盾,故X与∣X∣不独立.习题9设X和Y是两个相互独立的随机变量,X在(0,1)上服从均匀分布,Y的概率密度为fY(y)={12e-y2,y>00,y≤0,(1)求X与Y的联合概率密度;(2)设有a的二次方程a2+2Xa+Y=0,求它有实根的概率.解答:(1)由题设易知fX(x)={1,0<x<10,其它,又X,Y相互独立,故X与Y的联合概率密度为f(x,y)=fX(x)⋅fY(y)={12e-y2,0<x<1,y>00,其它;(2)因{a有实根}={判别式Δ2=4X2-4Y≥0}={X2≥Y},故如图所示得到:P{a有实根}=P{X2≥Y}=∫∫x2>yf(x,y)dxdy=∫01dx∫0x212e-y2dy=-∫01e-x22dx=1-[∫-∞1e-x22dx-∫-∞0e-x22dx]=1-2π[12π∫-∞1e-x22dx-12π∫-∞0e-x22dx]=1-2π[Φ(1)-Φ(0),又Φ(1)=0.8413,Φ(0)=0.5,于是Φ(1)-Φ(0)=0.3413,所以P{a有实根}=1-2π[Φ(1)-Φ(0)]≈1-2.51×0.3413=0.1433.3.3 二维随机变量函数的分布习题1设随机变量X和Y相互独立,且都等可能地取1,2,3为值,求随机变量U=max{X,Y}和V=min{X,Y}的联合分布.解答:由于U≥V,可见P{U=i,V=j}=0(i<j).此外,有P{U=V=i}=P{X=Y=i}=1/9(i=1,2,3),P{U=i,V=j}=P{X=i,Y=j}+P{X=j,Y=i}=2/9(i>j),于是,随机变量U和V的联合概率分布为=∫01dy∫y2y12dx=14,P{U=1,V=1}=1-P{U=0,V=0}-P{U=0,V=1}-P{U=1,V=0}=1/2,即U\V01011/401/41/2习题4设(X,Y)的联合分布密度为f(x,y)=12πe-x2+y22,Z=X2+Y2,求Z的分布密度.解答:FZ(z)=P{Z≤z}=P{X2+Y2≤z}.当z<0时,FZ(z)=P(∅)=0;当z≥0时,FZ(z)=P{X2+Y2≤z2}=∫∫x2+y2≤z2f(x,y)dxdy=12π∫∫x2+y2≤z2e-x2+y22dxdy=12π∫02πdθ∫0ze-ρ22ρdρ=∫0ze-ρ22ρdρ=1-e-z22.故Z的分布函数为FZ(z)={1-e-z22,z≥00,z<0.Z的分布密度为fZ(z)={ze-z22,z>00,z≤0.习题5设随机变量(X,Y)的概率密度为f(x,y)={12(x+y)e-(x+y),x>0,y>00,其它,(1)问X和Y是否相互独立?(2)求Z=X+Y的概率密度.解答:(1)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞12(x+y)e-(x+y)dy,x>00,x≤0\under2line令x+y=t{∫x+∞12te-tdt=12(x+1)e-x,x>00,x≤0,由对称性知fY(y)={12(y+1)e-y,y>00,y≤0,显然f(x,y)≠fX(x)fY(y),x>0,y>0,所以X与Y不独立.(2)用卷积公式求fZ(z)=∫-∞+∞f(x,z-x)dx.当{x>0z-x>0即{x>0x<z时,f(x,z-x)≠0,所以当z≤0时,fZ(z)=0;当z>0时,fZ(z)=∫0z12xe-xdx=12z2e-z.于是,Z=X+Y的概率密度为fZ(z)={12z2e-z,z>00,z≤0.习题6设随机变量X,Y相互独立,若X服从(0,1)上的均匀分布,Y服从参数1的指数分布,求随机变量Z=X+Y的概率密度.解答:据题意,X,Y的概率密度分布为fX(x)={1,0<x<10,其它,fY(y)={e-y,y≥00,y<0,由卷积公式得Z=X+Y的概率密度为fZ(z)=∫-∞+∞fX(x)fY(z-x)dx=∫-∞+∞fX(z-y)fY(y)dy=∫0+∞fX(z-y)e-ydy.由0<z-y<1得z-1<y<z,可见:当z≤0时,有fX(z-y)=0,故fZ(z)=∫0+∞0⋅e-ydy=0;当z>0时,fZ(z)=∫0+∞fX(z-y)e-ydy=∫max(0,z-1)ze-ydy=e-max(0,z-1)-e-z,即fZ(z)={0,z≤01-e-z,0<z≤1e1-z-e-z,z>1.习题7设随机变量(X,Y)的概率密度为f(x,y)={be-(x+y),0<x<1,0<y<+∞,0,其它.(1)试确定常数b;(2)求边缘概率密度fX(x),fY(y);(3)求函数U=max{X,Y}的分布函数.解答:(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1,确定常数b.∫01dx∫0+∞be-xe-ydy=b(1-e-1)=1,所以b=11-e-1,从而f(x,y)={11-e-1e-(x+y),0<x<1,0<y<+∞,0,其它.(2)由边缘概率密度的定义得fX(x)={∫0+∞11-e-1e-(x+y)dy=e-x1-e-x,0<x<1,0,其它,fY(x)={∫0111-e-1e-(x+y)dx=e-y,0<y<+∞,0,其它(3)因为f(x,y)=fX(x)fY(y),所以X与Y独立,故FU(u)=P{max{X,Y}≤u}=P{X≤u,Y≤u}=FX(u)F Y(u),其中FX(x)=∫0xe-t1-e-1dt=1-e-x1-e-1,0<x<1,所以FX(x)={0,x≤0,1-e-x1-e-1,0<x<1,1,x≥1.同理FY(y)={∫0ye-tdt=1-e-y,0<y<+∞,0,y≤0,因此FU(u)={0,u<0,(1-e-u)21-e-1,0≤u<1,1-e-u,u≥1.习题8设系统L是由两个相互独立的子系统L1和L2以串联方式联接而成,L1和L2的寿命分别为X与Y,其概率密度分别为ϕ1(x)={αe-αx,x>00,x≤0,ϕ2(y)={βe-βy,y>00,y≤0,其中α>0,β>0,α≠β,试求系统L的寿命Z的概率密度.解答:设Z=min{X,Y},则F(z)=P{Z≥z}=P{min(X,Y)≤z}=1-P{min(X,Y)>z}=1-P{X≥z,Y≥z}=1-[1P{X<z}][1-P{Y<z}]=1-[1-F1{z}][1-F2{z}]由于F1(z)={∫0zαe-αxdx=1-e-αz,z≥00,z<0,F2(z)={1-e-βz,z≥00,z<0,故F(z)={1-e-(α+β)z,z≥00,z<0,从而ϕ(z)={(α+β)e-(α+β)z,z>00,z≤0.习题9设随机变量X,Y相互独立,且服从同一分布,试证明:P{a<min{X,Y}≤b}=[P{X>a}]2-[P{X>b}]2.解答:设min{X,Y}=Z,则P{a<min{X,Y}≤b}=FZ(b)-FZ(a),FZ(z)=P{min{X,Y}≤z}=1-P{min{X,Y}>z}=1-P{X>z,Y>z}=1-P{X>z}P{Y>z}=1-[P{X>z}]2,代入得P{a<min{X,Y}≤b}=1-[P{X>b}]2-(1-[P{X>a}]2)=[P{X>a}]2-[P{X>b}]2.证毕.复习总结与总习题解答习题1在一箱子中装有12只开关,其中2只是次品,在其中取两次,每次任取一只,考虑两种试验:(1)放回抽样;(2)不放回抽样.我们定义随机变量X,Y如下:X={0,若第一次取出的是正品1,若第一次取出的是次品, Y={0,若第二次取出的是正品1,若第二次取出的是次品,试分别就(1),(2)两种情况,写出X和Y的联合分布律.解答:(1)有放回抽样,(X,Y)分布律如下:P{X=0,Y=0}=10×1012×12=2536; P{X=1,Y=0}=2×1012×12=536,P{X=0,Y=1}=10×212×12=536, P{X=1,Y=1}=2×212×12=136,(2)不放回抽样,(X,Y)的分布律如下:P{X=0,Y=0}=10×912×11=4566, P{X=0,Y=1}=10×212×11=1066,P{X=1,Y=1}=2×112×11=166,习题2假设随机变量Y服从参数为1的指数分布,随机变量Xk={0,若Y≤k1,若Y>k(k=1,2),求(X1,X2)的联合分布率与边缘分布率.解答:因为Y服从参数为1的指数分布,X1={0,若Y≤11,若Y>1, 所以有P{X1=1}=P{Y>1}=∫1+∞e-ydy=e-1,P{X1=0}=1-e-1,同理P{X2=1}=P{Y>2}=∫2+∞e-ydy=e-2,P{X2=0}=1-e-2,因为P{X1=1,X2=1}=P{Y>2}=e-2,P{X1=1,X2=0}=P{X1=1}-P{X1=1,X2=1}=e-1-e-2,P{X1=0,X2=0}=P{Y≤1}=1-e-1,P{X1=0,X2=1}=P{X1=0}-P{X1=0,X2=0}=0,故(X1,X2)联合分布率与边缘分布率如下表所示:习题3在元旦茶话会上,每人发给一袋水果,内装3只橘子,2只苹果,3只香蕉. 今从袋中随机抽出4只,以X记橘子数,Y记苹果数,求(X,Y)的联合分布.解答:X可取值为0,1,2,3,Y可取值0,1,2.P{X=0,Y=0}=P{∅}=0,P{X=0,Y=1}=C30C21C33/C84=2/70,P{X=0,Y=2}=C30C22C32/C84=3/70,P{X=1,Y=0}=C31C20C33/C84=3/70,P{X=1,Y=1}=C31C21C32/C84=18/70,P{X=1,Y=2}=C31C22C31/C84=9/70,P{X=2,Y=0}=C32C20C32/C84=9/70,P{X=2,Y=1}=C32C21C31/C84=18/70,P{X=2,Y=2}=C32C22C30/C84=3/70,P{X=3,Y=0}=C33C20C31/C84=3/70,P{X=3,Y=1}=C33C21C30/C84=2/70,P{X=3,Y=2}=P{∅}=0,所以,(X,Y)的联合分布如下:习题4设随机变量X与Y相互独立,下表列出了二维随机变量(X,Y)的联合分布律及关于X与Y解答:由题设X与Y相互独立,即有pij=pi⋅p⋅j(i=1,2;j=1,2,3), p⋅1-p21=p11=16-18=124,又由独立性,有p11=p1⋅p⋅1=p1⋅16故p1⋅=14.从而p13=14-124-18, 又由p12=p1⋅p⋅2, 即18=14⋅p⋅2.从而p⋅2=12. 类似的有p⋅3=13,p13=14,p2⋅=34.将上述数值填入表中有习题5设随机变量(X,Y)的联合分布如下表:求:(1)a值;(2)(X,Y)的联合分布函数F(x,y);(3)(X,Y)关于X,Y的边缘分布函数FX(x)与FY(y).解答:(1)\because由分布律的性质可知∑i⋅jPij=1, 故14+14+16+a=1,∴a=13.(2)因F(x,y)=P{X≤x,Y≤y}①当x<1或y<-1时,F(x,y)=0;②当1≤x<2,-1≤y<0时,F(x,y)=P{X=1,Y=-1}=1/4;③当x≥2,-1≤y<0时,F(x,y)=P{X=1,Y=-1}+P{X=2,Y=-1}=5/12;④当1≤x<2,y>0时,F(x,y)=P{X=1,Y=-1}+P{X=1,Y=0}=1/2;⑤当x≥2,y≥0时,F(x,y)=P{X=1,Y=-1}+P{X=2,Y=-1}+P{X=1,Y=0}+P{X=2,Y=0}=1;综上所述,得(X,Y)联合分布函数为F(x,y)={0,x<1或y<-11/4,1≤x<2,-1≤y<05/12,x≥2,-1≤y<01/2,1≤x<2,y≥01,x≥2,y≥0.(3)由FX(x)=P{X≤x,Y<+∞}=∑xi<x∑j=1+∞pij, 得(X,Y)关于X的边缘分布函数为:FX(x)={0,x<114+14,1≤x<214+14+16+13,x≥2={0,x<11/2,1≤x<21,x≥2,同理,由FY(y)=P{X<+∞,Y≤y}=∑yi≤y∑i=1+∞Pij, 得(X,Y)关于Y的边缘分布函数为FY(y)={0,y<-12/12,-1≤y<01,y≥0.习题6设随机变量(X,Y)的联合概率密度为f(x,y)={c(R-x2+y2),x2+y2<R0,x2+y2≥R,求:(1)常数c; (2)P{X2+Y2≤r2}(r<R).解答:(1)因为1=∫-∞+∞∫-∞+∞f(x,y)dydx=∫∫x2+y2<Rc(R-x2+y)dxdy=∫02π∫0Rc(R-ρ)ρdρdθ=cπR33,所以有c=3πR3.(2)P{X2+Y2≤r2}=∫∫x2+y2<r23πR3[R-x2+y2]dxdy=∫02π∫0r3πR3(R-ρ)ρdρdθ=3r2R2(1-2r3R).习题7设f(x,y)={1,0≤x≤2,max(0,x-1)≤y≤min(1,x)0,其它,求fX(x)和fY(y).解答:max(0,x-1)={0,x<1x-1,x≥1, min(1,x)={x,x<11,x≥1,所以,f(x,y)有意义的区域(如图)可分为{0≤x≤1,0≤y≤x},{1≤x≤2,1-x≤y≤1},即f(x,y)={1,0≤x≤1,0≤y≤x1,1≤x≤2,x-1≤y≤1,0,其它所以fX(x)={∫0xdy=x,0≤x<1∫x-11dy=2-x,1≤x≤20,其它,fY(y)={∫yy+1dx=1,0≤y≤10,其它.习题8若(X,Y)的分布律为则α,β应满足的条件是¯, 若X与Y独立,则α=¯,β=¯.解答:应填α+β=13;29;19.由分布律的性质可知∑i⋅jpij=1, 故16+19+118+13+α+β=1,即α+β=13.又因X与Y相互独立,故P{X=i,Y=j}=P{X=i}P{Y=j}, 从而α=P{X=2,Y=2}=P{X=i}P{Y=j},=(19+α)(14+α+β)=(19+α)(13+13)=29,β=P{X=3,Y=2}=P{X=3}P{Y=2}=(118+β)(13+α+β)=(118+β)(13+13),∴β=19.习题9设二维随机变量(X,Y)的概率密度函数为f(x,y)={ce-(2x+y),x>0,y>00,其它,(1)确定常数c; (2)求X,Y的边缘概率密度函数;(3)求联合分布函数F(x,y); (4)求P{Y≤X};(5)求条件概率密度函数fX∣Y(x∣y); (6)求P{X<2∣Y<1}.解答:(1)由∫-∞+∞∫-∞+∞f(x,y)dxdy=1求常数c.∫0+∞∫0+∞ce-(2x+y)dxdy=c⋅(-12e-2x)\vline0+∞⋅(-e-y)∣0+∞=c2=1,所以c=2.(2)fX(x)=∫-∞+∞f(x,y)dy={∫0+∞2e-2xe-ydy,x>00,x≤0={2e-2x,x>00,x≤0,fY(y)=∫-∞+∞f(x,y)dx={∫0+∞2e-2xe-ydx,y>00,其它={e-y,y>00,y≤0.(3)F(x,y)=∫-∞x∫-∞yf(u,v)dvdu={∫0x∫0y2e-2ue-vdvdu,x>0,y>00,其它={(1-e-2x)(1-e-y),x>0,y>00,其它.(4)P{Y≤X}=∫0+∞dx∫0x2e-2xe-ydy=∫0+∞2e-2x(1-e-x)dx=13.(5)当y>0时,fX∣Y(x∣y)=f(x,y)fY(y)={2e-2xe-ye-y,x>00,x≤0={2e-2x,x>00,x≤0.(6)P{X<2∣Y<1}=P{X<2,Y<1}P{Y<1}=F(2,1)∫01e-ydy=(1-e-1)(1-e-4)1-e-1=1-e-4.习题10设随机变量X以概率1取值为0, 而Y是任意的随机变量,证明X与Y相互独立.解答:因为X的分布函数为F(x)={0,当x<0时1,当x≥0时, 设Y的分布函数为FY(y),(X,Y)的分布函数为F(x,y),则当x<0时,对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{∅∩(Y≤y)}=P{∅}=0=FX(x)FY(y);当x≥0时,对任意y, 有F(x,y)=P{X≤x,Y≤y}=P{(X≤x)∩(Y≤y)}=P{S∩(Y≤y)}=P{Y≤y}=Fy(y)=FX(x)FY(y),依定义,由F(x,y)=FX(x)FY(y)知,X与Y独立.习题11设连续型随机变量(X,Y)的两个分量X和Y相互独立,且服从同一分布,试证P{X≤Y}=1/2. 解答:因为X,Y独立,所以f(x,y)=fX(x)fY(y).P{X≤Y}=∫∫x≤yf(x,y)dxdy=∫∫x≤yfX(x)fY(y)dxdy=∫-∞+∞[fY(y)∫-∞yfX(x)dx]dy=∫-∞+∞[fY(y)FY(y)]dy=∫-∞+∞FY(y)dFY(y)=F2(y)2∣-∞+∞=12,也可以利用对称性来证,因为X,Y独立同分布,所以有P{X≤Y}=P{Y≤X},而P{X≤Y}+P{X≥Y}=1, 故P{X≤Y}=1/12.习题12设二维随机变量(X,Y)的联合分布律为若X与Y相互独立,求参数a,b,c的值.解答:关于X的边缘分布为由于X与Y独立,则有p22=p2⋅p⋅2 得b=(b+19)(b+49) ①p12=p1⋅p⋅2 得19=(a+19)(b+49) ②由式①得b=29, 代入式②得a=118. 由分布律的性质,有a+b+c+19+19+13=1,代入a=118,b=29, 得c=16.易验证,所求a,b,c的值,对任意的i和j均满足pij=pi⋅×p⋅j.因此,所求a,b,c的值为a=118,b=29,c=16.习题13已知随机变量X1和X2的概率分布为且P{X1X2=0}=1.(1)求X1和X2的联合分布律;(2)问X1和X2是否独立?解答:(1)本题是已知了X1与X2的边缘分布律,再根据条件P{X1X2=0}=1, 求出联合分布. 列表如下:P{X1=1,X2=1}=0,P{X1=-1,X2=1}=0.再由p⋅1=p-11+p11+p01, 得p01=12, p-10=p-1⋅=p-11=14,p10=p1⋅-p11=14,从而得p00=0.(2)由于p-10=14≠p-1⋅⋅p⋅0=14⋅12=18, 所以知X1与X2不独立.习题14设(X,Y)的联合密度函数为f(x,y)={1πR2,x2+y2≤R20,其它,(1)求X与Y的边缘概率密度;(2)求条件概率密度,并问X与Y是否独立?解答:(1)当x<-R或x>R时,fX(x)=∫-∞+∞f(x,y)dy=∫-∞+∞0dy=0;当-R≤x≤R时,fX(x)=∫-∞+∞f(x,y)dy=1πR2∫-R2-x2R2-x2dy=2πR2R2-x2.于是fX(x)={2R2-x2πR2,-R≤x≤R0,其它.由于X和Y的地位平等,同法可得Y的边缘概率密度是:fY(y)={2R2-y2πR2,-R≤y≤R0,其它.(2)fX∣Y(x∣y)=f(x,y)fY(y)注意在y处x值位于∣x∣≤R2-y2这个范围内,f(x,y)才有非零值,故在此范围内,有fX∣Y(x∣y)=1πR22πR2⋅R2-y2=12R2-y2,即Y=y时X的条件概率密度为fX∣Y(x∣y)={12R2-y2,∣x∣≤R2-y20,其它.同法可得X=x时Y的条件概率密度为fY∣X(y∣x)={12R2-x2,∣y∣≤R2-x20,其它.由于条件概率密度与边缘概率密度不相等,所以X与Y不独立.习题15设(X,Y)的分布律如下表所示X\Y -112-12 1/102/103/102/101/101/10求:(1)Z=X+Y; (2)Z=max{X,Y}的分布律.解答:与一维离散型随机变量函数的分布律的计算类似,本质上是利用事件及其概率的运算法则. 注意,Z的相同值的概率要合并.概率(X,Y)X+YXYX/Ymax{X,Y}1/102/103/102/101/101/10(-1,-1)(-1,1)(-1,2)(2,-1)(2,1)(2,2)-2011341-1-2-2241-1-1/2-221-112222于是(1)习题16设(X,Y)的概率密度为f(x,y)={1,0<x<1,0<y<2(1-x)0,其他,求Z=X+Y的概率密度.解答:先求Z的分布函数Fz(z),再求概率密度fz(z)=dFz(z)dz.如右图所示.当z<0时,Fz(z)=P{X+Y≤z}=0;当0≤z<1时,Fz(z)=P{X+Y≤z}=∫∫x+y≤zf(x,y)dxdy=∫0zdx∫0z-x1dy=∫0z(z-x)dx=z2-12x2∣0z=12z2;当1≤z<2时,Fz(z)=∫02-zdx∫0z-xdy+∫2-z1dx∫02(1-x)dy=z(2-z)-12(2-z)2+(z-1)2;当z≥2时,∫∫Df(x,y)dxdy=∫01dx∫02(1-x)dy=1.综上所述Fz(z)={0,z<012z2,0≤z<1z(2-z)-12(2-z)2+(z-1)2,1≤z<21,z≥2,故fz(z)={z,0≤z<12-z,1≤z<20,其它.习题17设二维随机变量(X,Y)的概率密度为f(x,y)={2e-(x+2y),x>0,y>00,其它,求随机变量Z=X+2Y的分布函数.解答:按定义FZ(Z)=P{x+2y≤z},当z≤0时,FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫∫x+2y≤z0dxdy=0.当z>0时,FZ(Z)=∫∫x+2y≤zf(x,y)dxdy=∫0zdx∫0(z-x)/22e-(x+2y)dy=∫0ze-x⋅(1-ex-z)dx=∫0z(e-x-e-z)dx=[-e-x]∣0z-ze-z=1-e-z-ze-z,故分布函数为FZ(Z)={0,z≤01-e-z-ze-z,z>0.习题18设随机变量X与Y相互独立,其概率密度函数分别为fX(x)={1,0≤x≤10,其它, fY(y)={Ae-y,y>00,y≤0,求:(1)常数A; (2)随机变量Z=2X+Y的概率密度函数.解答:(1)1=∫-∞+∞fY(y)dy=∫0+∞A⋅e-ydy=A.(2)因X与Y相互独立,故(X,Y)的联合概率密度为f(x,y)={e-y,0≤x≤1,y>00,其它.于是当z<0时,有F(z)=P{Z≤z}=P{2X+Y≤z}=0;当0≤z≤2时,有F(z)=P{2X+Y≤z}=∫0z/2dx∫0z-2xe-ydy=∫0z/2(1-e2x-z)dx;当z>2时,有F(z)=P{2X+Y≤2}=∫01dx∫0z-2xe-ydy=∫01(1-e2x-z)dx.利用分布函数法求得Z=2X+Y的概率密度函数为fZ(z)={0,z<0(1-e-z)/2,0≤z<2(e2-1)e-z/2,z≥2.习题19设随机变量X,Y相互独立,若X与Y分别服从区间(0,1)与(0,2)上的均匀分布,求U=max{X,Y}与V=min{X,Y}的概率密度.解答:由题设知,X与Y的概率密度分别为fX(x)={1,0<x<10,其它, fY(y)={1/2,0<y<20,其它,于是,①X与Y的分布函数分别为FX(x)={0,x≤0x,0≤x<11,x≥1, FY(y)={0,y<0y/2,0≤y<21,y≥2,从而U=max{X,Y}的分布函数为FU(u)=FX(u)FY(u)={0,u<0u2/2,0≤u<1u/2,1≤u<21,u≥2,故U=max{X,Y}的概率密度为fU(u)={u,0<u<11/2,1≤u<20,其它.②同理,由FV(v)=1-[1-FX(v)][1-FY)]=FX(v)+FY(v)-FX(v)FY(v)=FX(v)+FY(v)-FU(v),得V=min{X,Y}的分布函数为FV(v)={0,v<0v2(3-v),0≤v<11,v≥1,故V=min{X,Y}的概率密度为fV(v)={32-v,0<v<10,其它.注:(1)用卷积公式,主要的困难在于X与Y的概率密度为分段函数,故卷积需要分段计算;(2)先分别求出X,Y的分布函数FX(x)与FY(y), 然后求出FU(u),再求导得fU(u); 同理先求出FV(v), 求导即得fV(v).。
《概率论与数理统计》习题三答案-设二维随机变量(x,y)
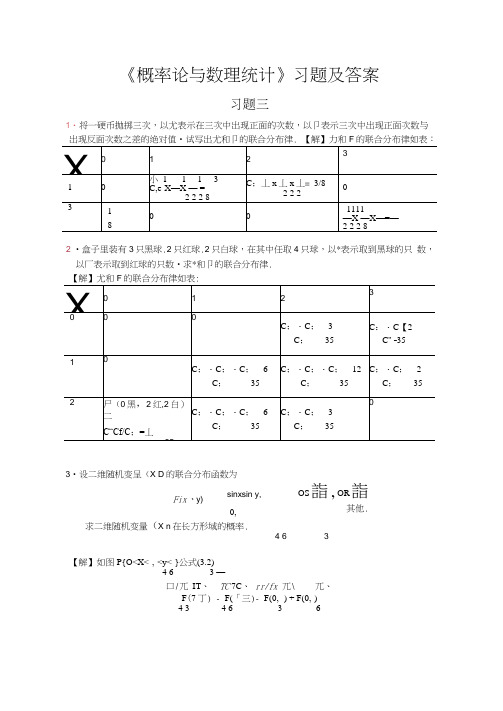
《概率论与数理统计》习题及答案习题三1・将一硬币抛掷三次,以尤表示在三次中出现正面的次数,以卩表示三次中出现正面次数与2 •盒子里装有3只黑球.2只红球.2只白球,在其中任取4只球,以*表示取到黑球的只 数,以厂表示取到红球的只数•求*和卩的联合分布律.3•设二维随机变呈(X D 的联合分布函数为求二维随机变量(X n 在长方形域的概率.4 63【解】如图P{O<X<-,-<y<-}公式(3.2)4 6 3 —口/兀 IT 、 TC 7C 、 rr/fx 兀\ 兀、F (7 丁) - F(「三)- F(0, -) + F(0,-) 4 3 4 6 3 6Fix 、y)sinxsin y,0,OS詣,OR 詣其他.=sin —>sin — 一 sin —•sin — 一 sin O ・sin — + sin 0>sin= ^(73-1).4说明:也可先求出密度函数,再求概率。
4•设随机变量(匕D 的分布密度Ae H3r+4v \ x>0,y>0, 0, 其他.£' £' 12e _(3M+4v,di/dv _J(l-e _3x )(1-e -4-) y > 0,x > 0,0° ° =| o,其他(3) P{0<X<l,0<y<2)= p{o<x<i,o<y<2}=fj : 12e _<3t *4v,d.vdy = (l-e-3 )(l-e _8)« 0.9499.5.设随机变量(X D 的概率密度为k(6 一兀一 y), 0 < x < 2, 2 <f (儿 y)=<0,(1) 确定常数k; (2) 求 P{X<\. K3}; (3) 求 HK1.5}; (4)求 PUHW4}.【解】(1)由性质有fix. y)=<求:(1)(2) (3) 常数川随机变量(x n 的分布函数;P{owg 0WK2}・【解】(1)由匚匚 fg y)dxdy =门「Ae 「'i &dy =£ = 1得(2)J=12由定义,有j* J f(x, y)dvdy = J ( J k(6 - x - y)dydx =8k = 1,故 R = -8(2) P{X v 1, Y v 3} = J :/(x,y)dydx一 曲•皿 €⑶ P{ X v 1.5} = JJ /(x, y)dAdy如图a [J/(x, y)d.vdyATP 曲 i —y)dy = ||.⑷ P{X+r<4}= JJ /(x,y)dxdy 如图y)dxdyX+YS4Dy6•设尤和F 是两个相互独立的随机变量,尤在(0, 0.2)上服从均匀分布,卩的密度函数为—r求:(1) X 与卩的联合分布密度;(2) P{Y^X\.【解】(1)因尤在(0, 0.2)上服从均匀分布,所以X 的密度函数为0, 其他.x<1.5fx(x )= 0 210<x<0.2,所以f(^y)X.Y 独立办(x)M(y)(2) P (y<X)= JJ fg y)dvdy 如图[f25e"5v dvdyy<x D=£'2 dxj : 25e® dy = J (「(一5e 亠 + 5)<Lv =e _l a 0.3679・7•设二维随机变疑(x n 的联合分布函数为求(上D 的联合分布密度.&设二维随机变呈(儿力的概率密度为求边缘概率密度. 【解】办(X )=匚/'(X,刃dy「4・8y(2-x)dy \lAx 2(l-x)y 0 <x< h o. 1°, 其他f Y (y) =匚/(兀刃 dxJ 4.8y(2 -x)dx _ J2.4y(3 -4y + y 2), 0 < y < 1, o =|o, 其他,y > o. 其他.0,25e _5v ,0,0<x<0.2且y >0, 其他.F5刃屮十*严)0.x > 0, y > 0,其他【解】oxdy0、 x >0,y> 0,其他.4.8y(2-A 0,0<x<l,0<y<x,其他y)=<求边缘概率密度.【解】办(尤)=匚f(x,y)dyI e~v dy=Jx ・=<0, ・A(y) = JJ/GvoOdx10.设二维随机变量(X D的概率密度为cFy, X2 < y < 1,0, 其他匚匚 /(也y )^2如图|7 fg y)dxdy1)=f dvj1, ex2 ydy = * c = 1.21c = —•4fx W =匚/a,y)dyy)=<fix、e0,0<x< ”其他(1)(2)试确定常数c;求边缘概率密度.x> 0,其他.0,f S e'v cLv=< Jo0,y>0, a 其他.yiw o Xf (x、y)=<【解】(1)题10图【解】办(兀)=匚/(血刃⑪f ldy = 2x.= J-x 0.ildv = 1 + y,一1 vy <0,所以丄,I y l< x < 1,2x 0, 其他J ;pyd ),0,—x~(l — %4), —lSxSl,8 0,其他.0,7 ?0<y<t 厶0,其他.11 •设随机变量(上D 的概率密度为 1, 0,f (%, y)=<|y| < x, 0 < x < 1,其他求条件概率密度fnx (y I X ),A (y) =匚/(""nf ldx = 1 -y, 0,0<y<h 其他.0< x< 1, 其他.AirCviy) =/g)A(y)1o,-y < A: <1,其他.345P{X=x t} 11 _ 1 c[ = To2 _ 2 c[ = io3 _ 3 c[ = lo610201 _ 1 cf ~io2 _ 2 c[_lo310 3001 _ 1 c[= 10110P{y = y i}1To3 To61012•袋中有五个1, 2. 3, 4, 5,从中任取三个,记这三个中最小的为兀最大的为X (1)求X与『的联合概率分布;(2)X与卩是否相互独立?【解】(1)尤与卩的联合分布律如下表⑵因吩=啊一3}=劭存侖工存吟+ = 3}故尤与卩不独立(2)尤与卩是否相互独立?(2)因P{X= 2}.P{Y = 0.4} = 0.2x0.8 = 0.160.15 = P(X = 2,K = 0.4),1)上服从均匀分布,F 的概率密度为y > 0,其他.(1) 求尤和卩的联合概率密度;(2)设含有日的二次方程为才+2炉扫0,试求臼有实根的概率.(2)方程a 2+2Xa + Y = 0有实根的条件是△ = (2X)2-43 0故斤2 K,从而方程有实根的概率为:P{X 2>r )= JJ /(x,y)drdyA 2>V= I -V^[①⑴-①(0)]= 0.1445.15 •设才和F 分别表示两个不同电子器件的寿命(以小时计),并设X 和卩相互独立,且服从同一分布,其概率密度为[1000f 3 ==〔0,求Z^X/Y 的概率密度.故尤与卩不独立.【解】(1) 14•设*和卩是两个相互独立的随机变量,*在(0,0,x > 1000, 其他fi (y)=【解】如图,z 的分布函数巧⑵= P{Z<z} = P[—<z}当O 〈z<l 时,(这时当尸1000时,尸型2)(如图a ) 106Fz ⑵=”詈"dy =打dy 打毎dx〉•注(1) 当zWO 时,巧(z )= o2zz> 1, /z ⑵£2y0,0<z<l, 其他.ZT 5 Z ' I , 2z—,0 < z < h 2 0, 其他.16 •设某种型号的电子管的寿命(以小时计)近似地服从M160,20‘)分布•随机地选取4 求其中没有一只寿命小于180的概率.【解】设这四只寿命为上(住123,4),则尤二2(160 , 202),只,(2)当时,(这时当尸10’时,尸102)(如图b )传⑵=JI 詈dg ,=叵呱;詈"103 106 12z从而P{minCX,, X 2, X 3, X 4) > 180)X.之间独AtPfX, > 180}<P{X 2 > 180}P{X 3>180)eP{X 4>180)=[1 一P{XV80}]・[1 一P{X? v 180}]41-P{X 3<180}J41-P{X 4<180}]= [1-0(1)]4=(O 」58『 =0・00063・17•设匕F 是相互独立的随机变量,其分布律分别为P{X-k} =p (&), A=0, L 2,…,P{JM=g (r), r=0, U 2,….证明随机变疑卅卩的分布律为PC}二工 p (k)q(i -灯,,二0, 1> 2, •••・【证明】因X 和卩所有可能值都是非负整数,所以^Z = i} = {X + Y = i]= {X=0,Y = i}U{X = l" = i — l}U ・・・U{X=/』= 0}于是P{Z = i} = y P{X =k,Y = i-k}X.Y 相互独立 y P{X = k}.P{Y = i-k}R.O'女.0= ±P(k)q(i -k)£■(>1&设兀卩是相互独立的随机变量,它们都服从参数为”,p 的二项分布.证明Z=X+Y 服从参 数为2m, p 的二项分布•【证明】方法一:贰F 可能取值为0, 1, 2,…,2n.kP {X +Y = R } =工p{xf-0= [1-P{X 1 <180)]4=180-160H20 jjk= ^P(X =i^P{Y = k-i}J-0方法二:设“】,“2,・「"n ; “J , P2 ,…,"J 均服从两点分布(参数为P ),则 於 “l+“2+・・・+〃m U +"/ +•••+“/ •於片 “|+〃2+・・・+“/"「+"/ +•••+“/ ,所以,卅F 服从参数为(2/7.P )的二项分布.X0 1 2 3 4 5 0 0 0.01 0. 03 0. 05 0. 07 0. 09 1 0.01 0. 02 0. 04 0. 05 0. 06 0. 08 2 0.01 0. 03 0. 05 0. 05 0. 05 0. 06 30.010. 020. 040. 060. 060. 05(1)求 刊后2 I 比2}, P{K=3 I 后0}(2) 求J^max (X JO 的分布律; (3) 求itmin (X JO 的分布律; (4)求炉卅卩的分布律.【解】⑴吩—J ;/二「P{X=2,Y = 2} j^P{X=i,Y = 2} J-0P{X=0V = 3} £p{X=0,UI(2) P{V=i} = P{max(X.Y) = i} = P{X=i,Y<i} + P{X <i.Y = i]r-li=》P{X =i,Y = £} +》P{X =«Y = f},7 = 0,1,2,3,4.5 JO10P F2n-k(2n\J >0.05 ~ 0^25P{Y = 3IX =0}=P{Y = 3,X =0) P{X=0}0.01 _ 1 0^03~3p"q 21所以J/的分布律为J^max (Z Y)0 1 2 3 4 5p0. 040. 160. 28 0. 240. 28(3) P{U=i} = P{min(X,Y) = i}= P{X =i.Y>i} + P{X >i,Y = i]35= ^P{X=i y Y = k}+ Z P{X=k,Y = i} k7(4) 类似上述过程,有1 2 3 4 56780?020?06 6773671902467196712 676520•雷达的圆形屛幕半径为乩设目标出现点(上力在屏幕上服从均匀分布. (1)求 P{J>0 I (2)设 JhnaxU ; y\9【解】因(上力的联合概率密度为Jj/(’y)dby>0 y>x ___________jj/(A-,y)do-i = 0J,2,3,于是V0. 280. 30 0. 25 0. 17/(儿 y)= < 1TI R 20, X 1 + y 2 <R\其他.(1) P{Y>0\Y>X} =P{Y>0”>X}P{Y>X}y>x3/8 _ 3172 "4(2) P{M>Q] = P{max(X.y )>0} = l-P{max(X,Y)<0}= l-P{X<0,r<0} = l-JJ f(x. y)db.r<0 y<021 •设平面区域〃由曲线y-\/x 及直线尸0, A=l,x=e 2所围成,二维随机变量(上力 在区域〃上服从均匀分布,求(尤D 关于尤的边缘概率密度在齐2处的值为多少?r c 2 1【解】区域〃的面枳为S o = | -cLv = lnx f =2. (XK)的联合密度函数为 J1 V1 <x<e 2,0< y < —,x 其他.(X D 关于才的边缘密度函数为所以人⑵冷22•设随机变量尤和卩相互独立,下表列出了二维随机变量(儿 力联合分布律及关于/和 卩的边/3P{F 对二P :X\ Xz1/8 1/8"{y=y.} =P >1/61【解】因P{Y = y j } = P j =XP{X=x i ,Y = y j },(-1故 P{Y = y }} = P{X=x r Y = y {} + P{X=x 2.Y = yi }.从而 P{X=x v Y = y,}丄1 _ 1 "6^8" 24* 而才与卩独立,故 P{X =x i ]^P{Y = yj} = P{X =x p y = y.). 从而 P{X=x l }x- = P{X=x }>Y = y }] = —.624即:P{X 十眾 又 P{X=x }} = P{X=x }.Y = y }} + P{X=x^Y = y 2} + P{X=x {.Y = y 3}.£/(x,y)= 20,1 <x<e 2, 其他.即丄=-L + l + P{X=xr = yJ,4 24 8 i••狎从而P{X=x r Y = y3} = ^. 丄乙13同理P{Y = y2} = -. P{X=x2.Y = y2} = -2o3 1 1 1 又工卩{丫=儿} = 1・故川丫=儿} =1_7_3 = ?3同理P{X=x2} = -.从而P{X=x2,Y = y i} = P{Y = y i}-P{X=x r Y = y.} = L-^ = L 故23•设某班车起点站上客人数才服从参数为人(/1>0)的泊松分布,每位乘客在中途下车的概率为p(o<p<l),且中途下车与否相互独立,以F表示在中途下车的人数,求:(1)在发车时有”个乘客的条件下,中途有刃人下车的概率;(2)二维随机变量(尤,力的概率分布. 【解】仃)P{Y = m\X=n} = C;;p m(1 -p)n'm,0</n</?,H = 0J,2,• • •.(2) P{X=mY = m} = P{X=n}>P{Y = m\X= n}A 1', n < m <n,n = 0,1,2,・・・・1 2 )24•设随机变量*和卩独立,其中才的概率分布为FL 而卩的概率密度为fg(0.3 0.7;求随机变量決於F 的概率密度g(u).【解】设尸(刃 是F 的分布函数,则由全概率公式,知作於卩的分布函数为G(u) = P{X +Y <u} = 0.3P{X +Y <u \ X = \} + 0.7P{X + Y <u \ X = 2}= 0・3P{mX=l} + 0・7P{YS — 2IX=2} 由于才和卩独立,可见G(w) = 0・3P{ y<z/-l} + 0.7P{y<M-2} = 0・3F (M —l) + 0・7F(" — 2)・由此,得〃的概率密度为g(“)= G f(u) = 0.3F\u -1) + 0.7F (“ 一 2)=0・3/(" — 1) + 0・7/(“一2)・25. 25.设随机变量*与F 相互独立,且均服从区间[0.3]上的均匀分布,求/^{max(X H W1}.解:因为随即变量服从[0, 3]上的均匀分布,于是有因为兀卩相互独立,所以0<x<3,0<y<3,x<0, y<0,x>3, y>3.推得 P{max{X,y}<l)=l.26.设二维随机变量(尢力的概率分布为10 1 1 a0.2 0 0. 1 b0.210. 1c其中a 、b 、c 为常数,且X 的数学期望Eg 0.2/{卩冬0|辰0}二0・5,记Z-X^Y.求://!£fM = <30<x<3,(X x<0,x>3;£/(>') = * 30,0<y<3, y < 0,y > 3.fg y)=1-9(1) a 、b 、c 的值;(2) Z 的概率分布;(3) P{X^ ・解 (1)由概率分布的性质知,0“心0・6=1由 E (X ) = -0.2,可得-a + c = -OA.得a +b = 0.3.解以上关于血b 9 c 的三个方程得a = 0・2,b = 0・l,c = 0.1.(2) Z 的可能取值为2, L 0, h 2,P{Z = _2} = P{X =_1,丫 = _1} = 0.2,P{Z = —1} = P{X=—1" = O} + P{X=O,Y = —1}=O ・1,P{Z = O} = P{X=—1,Y = 1} + P{X=OV = O} + P{X=1V = —1} = O ・3,P{Z = 1} = P{X =1V = O} + P{X=OV = 1} = O ・3,P{Z = 2} = P{X=l" = l} = 0.1,即z 的概率分布为P{X=Z} = P{Y = 0}=0」+b + 0・2 = 0・l + 0・l + 0・2 = 0・4.即 a+b+c = 0. 4.再由p{r<o|x<o ( =p{x<o,r<o )P{X<0}= 0.5a +b + 0.5。
概率论与数理统计作业(第三章)

院(系) 班 姓名 学号第三章 随机向量练习3.1 二维随机向量及其分布一、填空1.设二维随机变量),(Y X 的概率密度为, 510,49,(,)0, C x y f x y其它 ,则C ;2. 设二维随机变量),(Y X 的概率密度为(2)2, 0,0,(,)0, x y e x y f x y 其它,则{1}P X Y ;3.设二维随机变量),(Y X 的分布函数为1, 0,0,(,)0, x y x y e e e x y F x y 其它,则二维随机变量),(Y X 的概率密度为 ; 4. 设二维随机变量),(Y X 的概率密度为22220(,)(16)(25)f x y x y,则二维随机变量),(Y X 的分布函数为 ;5.用),(Y X 的联合分布函数),(y x F 表示下述概率:(1) },{c Y b X a P ; (2) },{b Y a X P ; (3) }0{a Y P ; (4) },{b Y a X P . 二、选择题1、设随机变量101,1,2111424i X i,且满足条件12{+=0}=1P X X ,则12{}P X X ( )A.0B.14 C. 12D.1 2.已知随机变量),(Y X 在区域{(,)|11,11}D x y x y 上服从均匀分布,则下列概率等于14的是( ) A. {0}P X Y B. {0}P X YC. {(,)0}P MAX X YD. {(,)0}P Min X Y三.掷二枚硬币,以X 表示第一枚硬币出现正面的次数,Y 表示第二枚硬币出现正面的次数,试求二维随机变量),(Y X 的联合分布。
四、设二维随机变量),(Y X 的概率密度2, 01,02,(,)30, xyx x y f x y 其它 ,试求{1}P X Y 。
五、设二维随机变量),(Y X的概率密度222222( ,(,)0, C R x y R f x y x y R,求:(1) 系数C ; (2) ),(Y X 落在222()x y r r R 内的概率。
概率论与数理统计:c3_1 二维随机变量及其分布

例3.1.8
命题 3 .1 .1 若 X , Y ~ N 1 , 1 2 ; 2 , 2 2 ; 则
X
~
N
1
,
2 1
Y
~
N
2
,
2 2
2021/3/5
16
例:炮弹发射试验
炮弹在地面的命中点位置要由两个随 机变量( X , Y )来确定。
飞机在空中飞行的位置由三个随机变 量( X , Y, Z )来确定。
3 若f x , y在x , y处 连续 。 则
2Fx, y
f x, y
xy
2021/3/5
11
二维随机变量及其分布
4 若G R2 , 有
p X ,Y G f x, y dxdy
5
x
,
y的
边
缘
概
率
G
密
度
为
fX x
f x , ydy
fY y
f x , ydx
证:FX x F x ,
定义:对任意实数对 ( x , y ) ∈R2 记
{ X ≤ x , Y ≤ y } = { X ≤ x } ∩{ Y ≤ y }
称二元函数
F(x,y)=P{X≤x,Y≤y}
为( X , Y ) 的联合分布函数.
一维随机变量 X、Y 的分布函数FX(x)与 FY(y)称
为( X, Y ) 的边缘分布函数。
X
2021/3/5
23
解:
fY
y
f
x,
y
dx
0 y0
1
1 y
2
x
2
dx y
0 y1
1
y
2
概率论与数理统计第3章:二维随机变量及其分布总复习题

第3章总复习题()()1.15 选择题:小题,每小题4分,共20分.下列每小题给出的4个选项中,只有一个是符合题目要求的.()()()()(){}()1,,1,1.X Y X Y F x y F x F y P X Y >>=设随机变量的联合分布函数为,其边缘分布函数为和,其概率()()11,1.A F -()()()111.X YB F F --()()()()1,1111.X Y C F F F --+()()()()1,111 1.X Y D F F F ++-()1.C 答案为()(){}()222011.X Y P X Y +≤=设随机变量和相互独立,且都服从区间,上的均匀分布,则()1.4A ()12B ().8C π().4D π()2.D 答案为()()(){}()31,1min ,2.X Y E P X Y <<设相互独立的两个随机变量与均服从指数分布则的值为()12.A e e ---()11.B e --()21.C e --()24.D e e ---()3.D 答案为()()()()40111.X Y X N Y N 设随机变量与相互独立,且,,,,则(){}10.2A P X Y +≤=(){}11.2B P X Y +≤=(){}102C P X Y -≤=(){}11.2D P X Y -≤=()4.B 答案为(){}()151.2X Y B P X Y ⎛⎫== ⎪⎝⎭设随机变量和相互独立,它们的概率分布均为,,则()0.A ()1.4B ()1.4C ()1.D ()5.C 答案为()()2.610.填空题小题,每题4分,共20分()6.X Y Z X Y λ=+已知随机变量和相互独立,且均服从参数为的泊松分布,则服从的分布为()()62.Z P λ 答案:()()(){}7,0,1,0,2,.X Y X U Y U P X Y <=已知随机变量和相互独立则(){}()37,.4x yP XY f x y dxdy <<==⎰⎰答案:()()()()()21,20418,01,20,,1,4.x X f x x F x y X X F ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩-,设随机变量的概率密度为,记为二维随机变其它。
概率习题答案

k
55
P{X=k∣Y=51} 6/287/285/285/285/28
习题 3 已知(X,Y)的分布律如下表所示,试求:
(1)在 Y=1 的条件下,X 的条件分布律;
(2)在 X=2 的条件下,Y 的条件分布律.
X\Y
012
012 1/41/8001/301/601/8 解答: 由联合分布律得关于 X,Y 的两个边缘分布律为
解答: P{max{X,Y}≥0}=P{X,Y 至少一个大于等于 0}
=P{X≥0}+P{Y≥0}-P{X≥0,Y≥0} =47+47-37=57.
习题 5 (X,Y)只取下列数值中的值:
且相应概率依次为 16,13,112,512, 的边缘分布.
(0,0),(-1,1),(-1,13),(2,0) 请列出(X,Y)的概率分布表,并写出关于 Y
当 x≥1,y≥1 时,显然 F(x,y)=1; 设 0≤x≤1,0≤y≤1, 有
2y2.
F(x,y)=∫-∞x∫-∞yf(u,v)dudv=4∫0xudu∫0yvdv=x
设 0≤x≤1,y>1, 有 F(x,y)=P{X≤1,Y≤y}=4∫0xudu∫01ydy=x2.
最后,设 x>1,0≤y≤1, 有
=14+0+0=14.
习题 3(2) 3.设二维离散型随机变量的联合分布如下表: 试求:
(2)P{1≤X≤2,3≤Y≤4}; 解答: P{1≤X≤2,3≤Y≤4}
=P{X=1,Y=3}+P{X=1,Y=4}+P{X=2,Y=3}+P{X=2,Y=4} =0+116+0+14=516.
习题 3(3) 3.设二维离散型随机变量的联合分布如下表: 试求:
概率论与数理统计 第三章 二维随机变量及其概率分布 例题

1.甲乙两人独立地进行两次射击,命中率分别为0.2、0.5,把X、Y分别表示甲乙命中的次数,求(X,Y)联合分布律。
2.袋中有两只白球,两只红球,从中任取两只以X、Y表示其中黑球、白球的数目,求(X,Y)联合分布律。
3.设,且P{}=1,求(,)的联合分布律,并指出,是否独立。
4.设随机变量X的分布律为Y=,求(X,Y)联合分布律。
5.设(X,Y)的概率分布为且事件{X=0}与{X+Y=1}独立求a,b。
6. 设某班车起点上车人数X服从参数λ(λ>0)的泊松分布,每位乘客中途下车的概率为P (0<P<1)相互独立。
以Y表示中途下车的人数。
(1)求在发车时有n个人的情况下,中途m个人下车的概率;(2)求(X,Y)联合分布律。
7. 设二维随机变量(X,Y)联合分布函数F(x.y)=A(B+arctan) (C+arctan)。
(1)A、B、C (2)(X,Y)的联合密度f(x,y) (3)(X,Y)的边缘密度,概率论与数理统计第三章二维随机变量及其概率分布例题8.设f(x,y)=为二维随机变量(X,Y)的联合密度函数,求:其它(1)C的值(2), (3)P{X+Y1}并判别X与Y是否独立。
为(X,Y)的密度函数,求:9.设f(x,y)=其它(3)P{X>1/2|Y>0}为(X,Y)的密度函数,求10. 设f(x,y)=其它11. 设f(x,y)=为(X,Y)的密度函数,求()的联合分布其它函数。
12.设X,Y独立,均服从(0,1)上的均匀分布,Z的密度函数。
13. 设f(x,y)=()为(X,Y)的密度函数,Z=X+Y,求的密度函其它数。
概率论与数理统计第三章二维随机变量及其概率分布例题14.设X,Y独立,X~N(μ,),Y~V(-π,π),Z=X+Y,求,结果用Φ( x)表示。
15.设(X,Y)的联合密度函数为f(x,y)=,Z=X+Y,求Z的概率密度。
为(X,Y)的密度函数,Z=X+2Y,求的密度函数。
概率论与数理统计(二维随机变量函数的分布)

将上述x与z的关系描绘在xOz平面上便是图中的阴 影部分.
3.5.2
二维连续型随机变量函数的分布
e y , y 0 , 1 , 0 x 1 , fY ( y ) fX ( x) 0 , 其它 , 0 , 其它,
fZ ( z )
f X ( x ) fY ( z x )dx
定理3.1(正态分布的重要性质)若X1,X2 ,…,Xn 为相互独立的随机变量,且 X i ~ N (i , i 2 ), i 1,2,...,n C1,C2,…,Cn为n个任意常数,则
C X
i 1 i
n
i
~ N ( C i i , C i i )
2 2 i 1 i 1
i 1 n
3.5.2
二维连续型随机变量函数的分布
(2) 将Xi共同的分布函数F(x)代入(1)的结果中, 得 n
FY ( y) [F ( y)] FZ ( z ) 1 [1 F ( z )]n
(3) Y和Z的分布函数仍为上述两式,概率密度可 由上述两式分别对y和z求导得到
fY ( y) n[F ( y)]n1 f ( y) fZ ( z ) n[1 F ( z )]n1 f ( z )
二维连续型随机变量函数的分布
【例3.22】(和的分布)设(X,Y)的概率密度为
f(x,y),求Z = X + Y的概率密度.
解:事件X + Y Z所占有的区域如图,
由 FZ ( z ) P{ X Y z }
x y z
f ( x, y)dxdy
f ( x, y)dx]dy
t 2
概率论与数理统计(茆诗松)第二版第三章课后习题3.2-3.3(部分)参考答案

习题3.21. 设二维离散随机变量(X , Y ) 的可能值为(0, 0),(−1, 1),(−1, 2),(1, 0),且取这些值的概率依次为1/6, 1/3, 1/12, 5/12,试求X 与Y 各自的边际分布列. 解:因X 的全部可能值为−1, 0, 1,且12512131}1{=+=−=X P , 61}0{==X P , 125}1{==X P , 故X 的边际分布列为12561125101PX − 因Y 的全部可能值为0, 1, 2,且12712561}0{=+==X P , 31}1{==X P , 121}2{==X P , 故Y 的边际分布列为12131127210PY2. 设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧>>−−−=−−−−−.,0,0,0,e e e 1),(},max{122121其他y x y x F y x y x y x λλλλλ 试求X 与Y 各自的边际分布函数.解:当x ≤ 0时,F (x , y ) = 0,有F X (x ) = F (x , + ∞) = 0,当x > 0时,⎩⎨⎧≤>−−−=−−−−−.0,0,0,e e e 1),(},max{122121y y y x F y x y x y x λλλλλ 有 x y x y x y x y X x F x F 1122121e 1]e e e 1[lim ),()(},max{λλλλλλ−−−−−−+∞→−=−−−=∞+=,故⎩⎨⎧≤>−=−.0,0,0,e 1)(1x x x F x X λ 当y ≤ 0时,F (x , y ) = 0,有F Y ( y ) = F (+ ∞, y ) = 0,当y > 0时,⎩⎨⎧≤>−−−=−−−−−.0,0,0,e e e 1),(},max{122121x x y x F y x y x y x λλλλλ 有 y y x y x y x x Y y F y F 2122121e 1]e e e 1[lim ),()(},max{λλλλλλ−−−−−−+∞→−=−−−=+∞=,故⎩⎨⎧≤>−=−.0,0,0,e 1)(2y y y F y Y λ 3. 试求以下二维均匀分布的边际分布:⎪⎩⎪⎨⎧≤+=.,0,1,π1),(22其他y x y x p解:当x < −1或x > 1时,p X (x ) = 0,当−1 ≤ x ≤ 1时,2111π2π1),()(22x dy dy y x p x p x x X −===∫∫−−−∞+∞−, 故⎪⎩⎪⎨⎧≤≤−−=.,0,11,1π2)(2其他x x x p X当y < −1或y > 1时,p Y ( y ) = 0,当−1 ≤ y ≤ 1时,2111π2π1),()(22y dx dx y x p y p y y Y −===∫∫−−−∞+∞−, 故⎪⎩⎪⎨⎧≤≤−−=.,0,11,1π2)(2其他y y y p Y4. 设平面区域D 由曲线y = 1/ x 及直线y = 0,x = 1,x = e 2所围成,二维随机变量(X , Y ) 在区域D 上服从均匀分布,试求X 的边际密度函数.解:因平面区域D 的面积为2ln 122e 1e 1===∫x dx xS D , 则(X , Y ) 的联合密度函数为⎪⎩⎪⎨⎧∉∈=.),(,0,),(,21),(D y x D y x y x p 当x < 1或x > e 2时,p X (x ) = 0,当1 ≤ x ≤ e 2时,xdy dy y x p x p x X 2121),()(10===∫∫∞+∞−, 故⎪⎩⎪⎨⎧≤≤=.,0,e 1,21)(2其他x x x p X5. 求以下给出的(X , Y ) 的联合密度函数的边际密度函数p x (x ) 和p y ( y ):(1)⎩⎨⎧<<=−.,0;0,e ),(1其他y x y x p y (2)⎪⎩⎪⎨⎧−<<+=.,0;10),(45),(222其他x y y x y x p(3)⎪⎩⎪⎨⎧<<<=.,0;10,1),(3其他x y x y x p解:(1)当x ≤ 0时,p X (x ) = 0,当x > 0时,x xyxy X dy dy y x p x p −+∞−+∞−+∞∞−=−===∫∫e e e ),()(1,故⎩⎨⎧≤>=−.0,0;0,e )(x x x p x X 当y ≤ 0时,p Y ( y ) = 0, 当y > 0时,y yy Y y dx dx y x p y p −−+∞∞−===∫∫e e ),()(01,故⎩⎨⎧≤>=−.0,0;0,e )(y y y y p y Y (2)当x ≤ −1或x ≥ 1时,p X (x ) = 0,当−1 < x < 1时,)1(85)21(45)(45),()(41022102222x y y x dy y x dy y x p x p x x X −=+=+==−−+∞∞−∫∫,故⎪⎩⎪⎨⎧<<−−=.,0;11),1(85)(4其他x x x p X当y ≤ 0或y ≥ 1时,p Y ( y ) = 0,当0 < y < 1时,y y xy x dx y x dx y x p y p y y yyY −+=+=+==−−−−−−+∞∞−∫∫1)21(65)31(45)(45),()(113112, 故⎪⎩⎪⎨⎧<<−+=.,0;10,1)21(65)(其他y y y y p Y (3)当x ≤ 0或x ≥ 1时,p X (x ) = 0,当0 < x < 1时,111),()(03=⋅===∫∫+∞∞−xx dy x dy y x p x p xX , 故⎩⎨⎧<<=.,0;10,1)(其他x x p X当y ≤ 0或y ≥ 1时,p Y ( y ) = 0, 当0 < y < 1时,y y x dx xdx y x p y p y y Y ln ln 1ln ln 1),()(1−=−====∫∫+∞∞−, 故⎩⎨⎧<<−=.,0;10,ln )(其他y y y p Y6. 设二维随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,10,6),(2其他x y x y x p 试求边际密度函数p x (x ) 和p y ( y ). 解:当x ≤ 0或x ≥ 1时,p X (x ) = 0,当0 < x < 1时,)(66),()(22x x dy dy y x p x p xxX −===∫∫+∞∞−,故⎩⎨⎧<<−=.,0,10),(6)(2其他x x x x p X 当y ≤ 0或y ≥ 1时,p Y ( y ) = 0, 当0 < y < 1时,)(66),()(y y dx dx y x p y p yyY −===∫∫+∞∞−,故⎪⎩⎪⎨⎧<<−=.,0,10),(6)(其他y y y y p Y7. 试验证:以下给出的两个不同的联合密度函数,它们有相同的边际密度函数.⎩⎨⎧≤≤≤≤+=.,0,10,10,),(其他y x y x y x p ⎩⎨⎧≤≤≤≤++=.,0,10,10),5.0)(5.0(),(其他y x y x y x g 证:当x < 0或x > 1时,p X (x ) = 0,当0 ≤ x ≤ 1时,5.0)21()(),()(1021+=+=+==∫∫+∞∞−x y xy dy y x dy y x p x p X ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他x x x p X 当y < 0或y > 1时,p Y ( y ) = 0, 当0 ≤ y ≤ 1时,5.0)21()(),()(10210+=+=+==∫∫+∞∞−y xy x dx y x dx y x p y p Y ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他y y y p Y 并且当x < 0或x > 1时,g X (x ) = 0,当0 ≤ x ≤ 1时,5.0)5.0(21)5.0()5.0)(5.0(),()(1021+=+⋅+=++==∫∫+∞∞−x y x dy y x dy y x g x g X ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他x x x g X 当y < 0或y > 1时,g Y ( y ) = 0,当0 ≤ y ≤ 1时,5.0)5.0()5.0(21)5.0)(5.0(),()(1021+=+⋅+=++==∫∫+∞∞−y y x dx y x dx y x g y g Y ,则⎩⎨⎧≤≤+=.,0,10,5.0)(其他y y y g Y 故它们有相同的边际密度函数.8. 设随机变量X 和Y 独立同分布,且P {X = −1} = P {Y = −1} = P {X = 1} = P {Y = 1} = 1/2,试求P {X = Y }.解:因X 和Y 独立同分布,且P {X = −1} = P {Y = −1} = P {X = 1} = P {Y = 1} = 1/2,则(X , Y ) 的联合概率分布21212141411214141111ji p p X Y ⋅⋅−− 故P {X = Y } = P {X = −1, Y = −1} + P {X = 1, Y = 1} = 1/2.9. 甲、乙两人独立地各进行两次射击,假设甲的命中率为0.2,乙的命中率为0.5,以X 和Y 分别表示甲和乙的命中次数,试求P {X ≤ Y }. 解:因X 的全部可能取值为0, 1, 2,且P {X = 0} = 0.8 2 = 0.64,32.08.02.012}1{=××⎟⎟⎠⎞⎜⎜⎝⎛==X P ,P {X = 2} = 0.2 2= 0.04, 又因Y 的全部可能取值为0, 1, 2,且P {Y = 0} = 0.5 2 = 0.25,5.05.05.012}1{=××⎟⎟⎠⎞⎜⎜⎝⎛==Y P ,P {Y = 2} = 0.5 2= 0.25,则(X , Y ) 的联合概率分布25.05.025.004.001.002.001.0232.008.016.008.0164.016.032.016.00210ji p p X Y ⋅⋅故P {X ≤ Y } = 1 − P {X > Y } = 1 − P {X = 1, Y = 0} − P {X = 2, Y = 0} − P {X = 2, Y = 1} = 0.89. 10.设随机变量X 和Y 相互独立,其联合分布列为3/19/19/121321b x c a x y y y X Y试求联合分布列中的a , b , c .解:因c a p ++=⋅911,9431912+=++=⋅b b p ,911+=⋅a p ,b p +=⋅912,c p +=⋅313, 根据独立性,知81495919422222++=⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=⋅==⋅⋅b b b b p p b p , 可得0814942=+−b b ,即0922=⎟⎠⎞⎜⎝⎛−b , 故92=b ; 再根据独立性,知⎟⎠⎞⎜⎝⎛+=⎟⎠⎞⎜⎝⎛+⎟⎠⎞⎜⎝⎛+=⋅==⋅⋅91969194911221a a b p p p ,可得6191=+a ,故181=a ; 由正则性,知1953191912131=+++=+++++=∑∑==c b a b c a p i j ij ,可得94=++c b a ,故6118394==−−=b ac . 11.设X 和Y 是两个相互独立的随机变量,X ~ U (0, 1),Y ~ Exp (1).试求(1)X 与Y 的联合密度函数;(2)P {Y ≤ X };(3)P {X + Y ≤ 1}.解:(1)因X 与Y 相互独立,且边际密度函数分别为⎩⎨⎧<<=.,0,10,1)(其他x x p X ⎩⎨⎧<≥=−.0,0,0,e )(y y y p y Y故X 与Y 的联合密度函数为⎩⎨⎧≥<<==−.,0,0,10,e )()(),(其他y x y p x p y x p y Y X (2)1111101e 1e 1)e ()e 1()e (e }{−−−−−−=−+=+=−=−⋅==≤∫∫∫∫x x x y xy x dx dx dy dx X Y P ;(3)11110110101010e )e ()e 1()e (e }1{−−−−−−−=−=−=−⋅==≤+∫∫∫∫x x x y xy x dx dx dy dx Y X P .12.设随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<<=.,0,0,10,3),(其他x y x x y x p 试求(1)边际密度函数p x (x ) 和p y ( y );(2)X 与Y 是否独立.解:(1)当x ≤ 0或x ≥ 1时,p X (x ) = 0,当0 < x < 1时,2033),()(x xdy dy y x p x p xX ===∫∫+∞∞−,故⎩⎨⎧<<=.,0,10,3)(2其他x x x p X 当y ≤ 0或y ≥ 1时,p Y ( y ) = 0, 当0 < y < 1时,)1(23233),()(2121y x xdx dx y x p y p yyY −====∫∫+∞∞−, 故⎪⎩⎪⎨⎧<<−=.,0,10),1(23)(2其他y y y p Y (2)因⎪⎩⎪⎨⎧<<<<−=.,0,10,10),1(29)()(22其他y x y x y p x p Y X 即p x (x ) p y ( y ) ≠ p (x , y ),故X 与Y 不独立.13.设随机变量(X , Y ) 的联合密度函数为⎩⎨⎧<<<=.,0,10,||,1),(其他y y x y x p 试求(1)边际密度函数p x (x ) 和p y ( y );(2)X 与Y 是否独立.解:(1)当x ≤ −1或x ≥ 1时,p X (x ) = 0,当−1 < x < 0时,x dy dy y x p x p xX +===∫∫−+∞∞−11),()(1,当0 ≤ x < 1时,x dy dy y x p x p xX −===∫∫+∞∞−11),()(1,故⎪⎩⎪⎨⎧<≤−<<−+=.,0,10,1,01,1)(其他x x x x x p X当y ≤ 0或y ≥ 1时,p Y ( y ) = 0,当0 < y < 1时,y dx dx y x p y p yyY 21),()(===∫∫−+∞∞−,故⎩⎨⎧<<=.,0,10,2)(其他y y y p Y(2)因⎪⎩⎪⎨⎧<<<≤−<<<<−+=.,0,10,10),1(2,10,01),1(2)()(其他y x x y y x x y y p x p Y X 即p x (x ) p y ( y ) ≠ p (x , y ),故X 与Y 不独立.14.设二维随机变量(X , Y ) 的联合密度函数如下,试问X 与Y 是否相互独立?(1)⎩⎨⎧>>=+−.,0;0,0,e ),()(其他y x x y x p y x (2)+∞<<∞−++=y x y x y x p ,,)1)(1(π1),(222;(3)⎩⎨⎧<<<=.,0;10,2),(其他y x y x p (4)⎩⎨⎧<+<<<<<=.,0;10,10,10,24),(其他y x y x xy y x p(5)⎩⎨⎧<<<<−=.,0;10,10),1(12),(其他y x x xy y x p(6)⎪⎩⎪⎨⎧<<=.,0;1,421),(22其他y x y x y x p解:(1)因x e − (x + y ) = x e −x ⋅ e −y 可分离变量,x > 0, y > 0是广义矩形区域,故X 与Y 相互独立;(2)因)1π(1)1π(1)1)(1(π122222y x y x +⋅+=++可分离变量,−∞ < x , y < +∞是广义矩形区域, 故X 与Y 相互独立;(3)因0 < x < y < 1不是矩形区域,故X 与Y 不独立;(4)因0 < x < 1, 0 < y < 1, 0 < x + y < 1不是矩形区域,故X 与Y 不独立;(5)因12xy (1 − x ) = 12x (1 − x ) ⋅ y 可分离变量,0 < x < 1, 0 < y < 1是矩形区域,故X 与Y 相互独立; (6)因x 2 < y < 1不是矩形区域,故X 与Y 不独立.15.在长为a 的线段的中点的两边随机地各取一点,求两点间的距离小于a / 3的概率.解:设X 和Y 分别表示这两个点与线段中点的距离,有X 和Y 相互独立且都服从[0, a / 2]的均匀分布,则(X , Y ) 的联合密度函数为 ⎪⎩⎪⎨⎧<<<<=.,0,20,20,4),(2其他a y a x a y x pa a故所求概率为922321}3{22=⎟⎠⎞⎜⎝⎛⎟⎠⎞⎜⎝⎛×==<+a a S S aY X P DG . 16.设二维随机变量(X , Y ) 服从区域D = {(x , y ): a ≤ x ≤ b , c ≤ y ≤ d }上的均匀分布,试证X 与Y 相互独立. 证:因(X , Y ) 的联合密度函数为⎪⎩⎪⎨⎧≤≤≤≤−−=.,0;,,))((1),(其他d y c b x a c d a b y x p当x < a 或x > b 时,p X (x ) = 0,当a ≤ x ≤ b 时,a b dy c d a b dy y x p x p d c X −=−−==∫∫+∞∞−1))((1),()(, 则⎪⎩⎪⎨⎧≤≤−=.,0;,1)(其他b x a a b x p X当y < c 或y > d 时,p Y ( y ) = 0,当c ≤ y ≤ d 时,cd dx c d a b dx y x p y p b aY −=−−==∫∫+∞∞−1))((1),()(, 则⎪⎩⎪⎨⎧≤≤−=.,0;,1)(其他d y c c d y p Y因p x (x ) p y ( y ) = p (x , y ), 故X 与Y 相互独立.17.设X 1, X 2, …, X n 是独立同分布的正值随机变量.证明n k n k X X X X E n k ≤=⎟⎟⎠⎞⎜⎜⎝⎛++++,11L L .证:因X 1, X 2, …, X n 是独立同分布的正值随机变量,则由对称性知),,2,1(1n i X X X niL L =++同分布,且满足101<++<niX X X L ,可得⎟⎟⎠⎞⎜⎜⎝⎛++n i X X X E L 1存在,且⎟⎟⎠⎞⎜⎜⎝⎛++==⎟⎟⎠⎞⎜⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++n n n n X X X E X X X E X X X E L L L L 11211,因11111211=⎟⎟⎠⎞⎜⎜⎝⎛++++=⎟⎟⎠⎞⎜⎜⎝⎛++++⎟⎟⎠⎞⎜⎜⎝⎛+++⎟⎟⎠⎞⎜⎜⎝⎛++n n n n n n X X X X E X X X E X X X E X X X E L L L L L L , 则n X X X E X X X E X X X E n n n n 111211=⎟⎟⎠⎞⎜⎜⎝⎛++==⎟⎟⎠⎞⎜⎜⎝⎛++=⎟⎟⎠⎞⎜⎜⎝⎛++L L L L , 故n k n k XX X X E n k≤=⎟⎟⎠⎞⎜⎜⎝⎛++++,11L L .习题3.31. 设二维随机变量(X , Y ) 的联合分布列为09.007.004.0222.011.007.0120.015.005.00321X Y 试分布求U = max{X , Y } 和V = min{X , Y } 的分布列.解:因P {U = 1} = P {X = 0, Y = 1} + P {X = 1, Y = 1} = 0.05 + 0.07 = 0.12;P {U = 2} = P {X = 0, Y = 2} + P {X = 1, Y = 2} + P {X = 2, Y = 2} + P {X = 2, Y = 1}= 0.15 + 0.11 + 0.07 + 0.04 = 0.37;P {U = 3} = P {X = 0, Y = 3} + P {X = 1, Y = 3} + P {X = 2, Y = 3} = 0.20 + 0.22 + 0.09 = 0.51; 故U 的分布列为51.037.012.0321P U因P {V = 0} = P {X = 0, Y = 1} + P {X = 0, Y = 2} + P {X = 0, Y = 3} = 0.05 + 0.15 + 0.20 = 0.40; P {V = 1} = P {X = 1, Y = 1} + P {X = 1, Y = 2} + P {X = 1, Y = 3} + P {X = 2, Y = 1}= 0.07 + 0.11 + 0.22 + 0.04 = 0.44;P {V = 2} = P {X = 2, Y = 2} + P {X = 2, Y = 3} = 0.07 + 0.09 = 0.16; 故V 的分布列为16.044.040.0210P V2. 设X 和Y 是相互独立的随机变量,且X ~ Exp (λ ),Y ~ Exp (µ ).如果定义随机变量Z 如下⎩⎨⎧>≤=.,0,,1Y X Y X Z 当当 求Z 的分布列.解:因(X , Y ) 的联合密度函数为⎩⎨⎧>>==+−.,0,0,0,e )()(),()(其他y x y p x p y x p y x Y X µλλµ 则∫∫∫+∞+∞+−+∞+∞+−−⋅==≤==0)(0)(e )(e }{}1{xy x xy x dx dy dx Y X P Z P µλµλλλµµλλµλλλµλµλ+=+−==+∞+−+∞+−∫0)(0)(e e xx dx ,µλµ+==−==}1{1}0{Z P Z P ,故Z 的分布列为µλλµλµ++PZ 13. 设随机变量X 和Y 的分布列分别为4/12/14/1101P X − 2/12/110P Y已知P {XY = 0} = 1,试求Z = max{X , Y }的分布列.解:因P {X 1 X 2 = 0} = 1,有P {X 1 X 2 ≠ 0} = 0,即P {X 1 = −1, X 2 = 1} = P {X 1 = 1, X 2 = 1} = 0,可得 (X , Y ) 的联合分布列为因{Z P {Z P 故Z 4.(1)X (2)X 解:(1)(X , 因P {Z = 0} = P {X = 0, Y = 0} = 0.25;P {Z = 1} = 1 − P {Z = 0} = 0.75; 故Z 的分布列为75.025.010P Z(2)因P {Z = k } = P {X = k , Y ≤ k } + P {X < k , Y = k } = P {X = k } P {Y ≤ k } + P {X < k } P {Y = k }p p p p p p p p k k i i kj j k 1111111)1()1()1()1(−−=−=−−−⋅−+−⋅−=∑∑p p p p p p p p p p k k k k 111)1()1(1)1(1)1(1)1(1)1(−−−−⋅−−−−+−−−−⋅−= = (1 − p ) k − 1 p ⋅ [2 − (1 − p ) k − 1 − (1 − p ) k ]故Z = max{X , Y }的概率函数为p z (k ) = (1 − p ) k − 1 p ⋅ [2 − (1 − p ) k − 1 − (1 − p ) k ],k = 1, 2, ….5. 设X 和Y 为两个随机变量,且73}0,0{=≥≥Y X P ,74}0{}0{=≥=≥Y P X P , 试求P {max{X , Y } ≥ 0}.解:设A 表示事件“X ≥ 0”,B 表示事件“Y ≥ 0”,有73)(=AB P ,74)()(==B P A P , 故75737474)()()()(}0},{max{=−+=−+==≥AB P B P A P B A P Y X P U .6. 设X 与Y 的联合密度函数为⎩⎨⎧>>=+−.,0,0,0,e ),()(其他y x y x p y x 试求以下随机变量的密度函数(1)Z = (X + Y )/2;(2)Z = Y − X .解:方法一:分布函数法(1)作曲线簇z yx =+2,得z 的分段点为0,当z ≤ 0时,F Z (z ) = 0,当z > 0时,∫∫∫−+−−+−−⋅==z x z y x zx z y x Z dx dy dx z F 2020)(2020)(]e [e )(z z x z z x z z x dx 2202202e )12(1)e e ()e e (−−−−−+−=−−=+−=∫,因分布函数F Z (z ) 连续,有Z = (X + Y )/2为连续随机变量, 故Z = (X + Y )/2的密度函数为⎩⎨⎧≤>=′=−.0,0,0,e 4)()(2z z z z F z p z Z Z (2)作曲线簇y − x = z ,得z 的分段点为0,当z ≤ 0时,∫∫∫∫+∞−−+−+∞−++−+∞−++−−=−⋅==zx z x zz x y x zzx y x Z dx dy dx z F e []e [e )()2(0)(0)(z z z z x z x e 21e e 21e e 21)2(=⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−=+∞−−+−, 当z > 0时,∫∫∫∫+∞−+−+∞++−+∞++−+−=−⋅==0)2(0)(0)(]e e []e [e )(dx dx dy dx z F x z x z x y x zx y x Zz z x z x −−+∞−+−−=⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−=e 2111e 21e e 210)2(,因分布函数F Z (z )连续,有Z = Y − X 为连续随机变量,故Z = Y − X 的密度函数为⎪⎩⎪⎨⎧>≤=′=−.0,e 21,0,e 21)()(z z z F z p zzZ Z 方法二:增补变量法 (1)函数2yx z +=对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎪⎩⎪⎨⎧=+=,,2y v y x z 有反函数⎩⎨⎧=−=,,2v y v z x 且21012=−=′′′′=vz vzy y x x J , 则∫∫+∞∞−+∞∞−−=⋅−=dv v v z p dv v v z p z p Z ),2(22),2()(,作曲线簇z yx =+2,得z 的分段点为0, 当z ≤ 0时,p Z (z ) = 0,当z > 0时,z z z Z z dv z p 2202e 4e 2)(−−==∫, 故Z = (X + Y )/2的密度函数为⎩⎨⎧≤>=−.0,0,0,e 4)(2z z z z p z Z(2)函数z = y − x 对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎩⎨⎧=−=,,y v x y z 有反函数⎩⎨⎧=−=,,v y z v x 且11011−=−=′′′′=v z vzy y x x J , 则∫+∞∞−−=dv v z v p z p Z ),()(,作曲线簇y − x = z ,得z 的分段点为0, 当z ≤ 0时,zz v z v Z dv z p e 21e 21e )(0202=−==+∞+−+∞+−∫, 当z > 0时,z zzv z z v Z dv z p −+∞+−+∞+−=−==∫e 21e 21e )(22, 故Z = Y − X 的密度函数为⎪⎩⎪⎨⎧>≤=−.0,e 21,0,e 21)(z z z p zzZ 7. 设X 与Y 的联合密度函数为⎩⎨⎧<<<<=.,0,0,10,3),(其他x y x x y x p 试求Z = X − Y 的密度函数.解:方法一:分布函数法作曲线簇x − y = z ,得z 的分段点为0, 1, 当z < 0时,F Z (z ) = 0,当0 ≤ z < 1时,31203102102123233333)(z z z x x xzdx dx x xdy dx xdy dx z F z z zz z xzx z x Z −=+=+=+=∫∫∫∫∫∫−,当z ≥ 1时,F Z (z ) = 1,因分布函数F Z (z ) 连续,有Z = X − Y 为连续随机变量, 故Z = X − Y 的密度函数为⎪⎩⎪⎨⎧<<−=′=.,0,10),1(23)()(2其他z z z F z p Z Z方法二:增补变量法函数z = x − y 对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎩⎨⎧=−=,,y v y x z 有反函数⎩⎨⎧=+=,,v y v z x 且11011==′′′′=vz vzy y x x J , 则∫+∞∞−+=dv v v z p z p Z ),()(,作曲线簇x − y = z ,得z 的分段点为0, 1,当z ≤ 0或z ≥ 1时,p Z (z ) = 0, 当0 < z < 1时,)1(23)(23)(3)(210210z v z dv v z z p z z Z −=+=+=−−∫, 故Z = X − Y 的密度函数为⎪⎩⎪⎨⎧<<−=.,0,10),1(23)(2其他z z z p Z 8. 某种商品一周的需要量是一个随机变量,其密度函数为⎩⎨⎧≤>=−.0,0,0,e )(1t t t t p t设各周的需要量是相互独立的,试求(1)两周需要量的密度函数p 2 (x );(2)三周需要量的密度函数p 3 (x ). 解:方法一:根据独立伽玛变量之和仍为伽玛变量设T i 表示“该种商品第i 周的需要量”,因T i 的密度函数为⎪⎩⎪⎨⎧≤>Γ=−−.0,0,0,e )2(1)(121t t t t p t可知T i 服从伽玛分布Ga (2, 1),(1)两周需要量为T 1 + T 2,因T 1与T 2相互独立且都服从伽玛分布Ga (2, 1),故T 1 + T 2服从伽玛分布Ga (4, 1),密度函数为 ⎪⎩⎪⎨⎧≤>=⎪⎩⎪⎨⎧≤>Γ=−−−.0,0,0,e 61.0,0,0,e )4(1)(3142x x x x x x x p x x (2)三周需要量为T 1 + T 2 + T 3,因T 1, T 2, T 3相互独立且都服从伽玛分布Ga (2, 1),故T 1 + T 2 + T 3服从伽玛分布Ga (6, 1),密度函数为 ⎪⎩⎪⎨⎧≤>=⎪⎩⎪⎨⎧≤>Γ=−−−.0,0,0,e 1201.0,0,0,e )6(1)(5163x x x x x x x p xx 方法二:分布函数法(1)两周需要量为X 2 = T 1 + T 2,作曲线簇t 1 + t 2 = x ,得x 的分段点为0,当x ≤ 0时,F 2 (x ) = 0,当x > 0时,∫∫∫−−−−−−−−−⋅=⋅=xt x t t t xt x t t t t dt dt t t dt x F 02110221121221121)e e (e e e )( ∫−−+−−=xt x dt t t xt t 0111121]e e )[(1xt t x t t x t t 0121213111e e e 212131⎥⎦⎤⎢⎣⎡−−⎟⎠⎞⎜⎝⎛−−=−−−11)1(e e e 212131233−−−−⎟⎠⎞⎜⎝⎛−−=−−−x x x x x x xxx x x x x x −−−−−−−−=e 61e 21e e 132, 因分布函数F 2 (x )连续,有X 2 = T 1 + T 2为连续随机变量, 故X 2 = T 1 + T 2的密度函数为⎪⎩⎪⎨⎧≤>=′=−.0,0,0,e 61)()(322x x x x F x p x(2)三周需要量为X 3 = T 1 + T 2 + T 3 = X 2 + T 3,作曲线簇x 2 + t 3 = x ,得x 的分段点为0,当x ≤ 0时,F 3 (x ) = 0,当x > 0时,∫∫∫−−−−−−−−−⋅=⋅=x x x t t x x x x t x t x dx dt t x dx x F 003322003332232332232)e e (e 61e e 61)(∫−−+−−=x x x dx x x x x x 0232323242]e e )[(6`12 xx x x x x x x x x x x x 0222324242522222e 6e 6e 3e e 41415161⎥⎦⎤⎢⎣⎡−−−−⎟⎠⎞⎜⎝⎛−−=−−−−− )1(e e e 21e 61e 4141516123455−−−−−−⎟⎠⎞⎜⎝⎛−−=−−−−−x x x x x x x x x x x xx x x x x x x x x x −−−−−−−−−−−−=e 1201e 241e 61e 21e e 15432, 因分布函数F 3 (x ) 连续,有X 3 = T 1 + T 2 + T 3为连续随机变量, 故X 3 = T 1 + T 2 + T 3的密度函数为⎪⎩⎪⎨⎧≤>=′=−.0,0,0,e 1201)()(533x x x x F x p x 方法三:卷积公式(增补变量法)(1)两周需要量为X 2 = T 1 + T 2,卷积公式∫+∞∞−−=2222)()()(21dt t p t x p x p T T ,作曲线簇t 1 + t 2 = x ,得x 的分段点为0, 当x ≤ 0时,p 2 (x ) = 0, 当x > 0时,xxx xxxt t x x t x t dt t xt dt t t x x p −−−−−−=⎟⎠⎞⎜⎝⎛−=−=⋅−=∫∫e 61e3121e )(e e )()(30322202222022)(2222, 故X 2 = T 1 + T 2的密度函数为⎪⎩⎪⎨⎧≤>=−.0,0,0,e 61)(32x x x x p x(2)三周需要量为X 3 = T 1 + T 2 + T 3 = X 2 + T 3,卷积公式∫+∞∞−−=3333)()()(32dt t p t x p x p T X ,作曲线簇x 2 + t 3 = x ,得x 的分段点为0,当x ≤ 0时,p 3 (x ) = 0,21当x > 0时,∫∫−−−−−+−=−=x x xt t x dt t xt t x t x dt t t x x p 03433323233033)(333e )33(61e e )(61)(33 x xx x t x t x t x t −−=⎟⎠⎞⎜⎝⎛−+−=e 1201e 51432161505343233323, 故X 3 = T 1 + T 2 + T 3的密度函数为⎪⎩⎪⎨⎧≤>=−.0,0,0,e 1201)(53x x x x p x9. 设随机变量X 与Y 相互独立,试在以下情况下求Z = X + Y 的密度函数:(1)X ~ U (0, 1),Y ~ U (0, 1); (2)X ~ U (0, 1),Y ~ Exp (1). 解:方法一:分布函数法(1)作曲线簇x + y = z ,得z 的分段点为0, 1, 2,当z < 0时,F Z (z ) = 0,当0 ≤ z < 1时,2020002121)(1)(z x zx dx x z dy dx z F zz zxz Z =⎟⎠⎞⎜⎝⎛−=−==∫∫∫−,当1 ≤ z < 2时,1121110110110)(211)(111)(−−−−−−−−−=−+=+=∫∫∫∫∫∫z z z z xz z Zx z z dx x z dx dy dx dy dx z F121221)1(21122−−=+−−−=z z z z , 当z ≥ 2时,F Z (z ) = 1,因分布函数F Z (z ) 连续,有Z = X + Y 为连续随机变量, 故Z = X + Y 的密度函数为⎪⎩⎪⎨⎧<≤−<≤=′=.,0,21,2,10,)()(其他z z z z z F z p Z Z(2)作曲线簇x + y = z ,得z 的分段点为0, 1,当z < 0时,F Z (z ) = 0, 当0 ≤ z < 1时,z z x z zx z zx z y z xz y Z z x dx dx dy dx z F −+−+−−−−−+−=−=−=−⋅==∫∫∫∫e 1)e ()e 1()e (e )(0000,当z ≥ 1时,z z x z x z x z y xz y Z x dx dx dy dx z F −−+−+−−−−−+−=−=−=−⋅==∫∫∫∫e e 1)e ()e 1()e (e )(111110,因分布函数F Z (z ) 连续,有Z = X + Y 为连续随机变量, 故Z = X + Y 的密度函数为⎪⎩⎪⎨⎧<≥−<≤−=′=−−.0,0,1,e )1(e ,10,e 1)()(z z z z F z p z z Z Z方法二:卷积公式(增补变量法) 卷积公式∫+∞∞−−=dy y p y z p z p Y X Z )()()(,(1)作曲线簇x + y = z ,得z 的分段点为0, 1, 2,2当z ≤ 0或z ≥ 2时,p Z (z ) = 0, 当0 < z < 1时,z dy z p zZ ==∫01)(,当1 ≤ z < 2时,z dy z p z Z −==∫−21)(11,故Z = X + Y 的密度函数为⎪⎩⎪⎨⎧<≤−<≤=.,0,21,2,10,)(其他z z z z z p Z(2)作曲线簇x + y = z ,得z 的分段点为0, 1,当z ≤ 0时,p Z (z ) = 0,当0 < z < 1时,z zy z y Z dy z p −−−−=−==∫e 1)e (e )(0,当z ≥ 1时,zz z z z yzz yZ dy z p −+−−−−−−−=+−=−==∫e )1(e ee )e (e)(111,故Z = X + Y 的密度函数为⎪⎩⎪⎨⎧<≥−<≤−=−−.0,0,1,e )1(e ,10,e 1)(z z z z p z z Z10.设随机变量X 与Y 相互独立,试在以下情况下求Z = X /Y 的密度函数:(1)X ~ U (0, 1),Y ~ Exp (1); (2)X ~ Exp (λ1),Y ~ Exp (λ2). 解:方法一:分布函数法(1)作曲线簇z yx=,即直线簇z x y =,得z 的分段点为0,当z ≤ 0时,F Z (z ) = 0, 当z > 0时,)e 1(e)(e)e (e)(111011zz x zx zx yz x yZ z z dx dx dy dx z F −−−∞+−∞+−−=−==−⋅==∫∫∫∫,因分布函数F Z (z ) 连续,有Z = X /Y 为连续随机变量, 故Z = X /Y 的密度函数为⎪⎩⎪⎨⎧≤>−−=′=−−.0,0;0,e 1e 1)()(11z z z z F z p z z Z Z(2)作曲线簇z yx =,即直线簇z xy =,得z 的分段点为0,当z ≤ 0时,F Z (z ) = 0,当z > 0时,∫∫∫∫∞+−−∞+∞+−−∞+∞+−−⋅=−⋅⋅=⋅=0101021212121ee)e(eee)(dx dx dy dx z F zx xzx yxzx yxZ λλλλλλλλλλ2110)(2110)(12121eeλλλλλλλλλλλ+=+−==+∞+−∞++−∫z z zdx xzxz,因分布函数F Z (z ) 连续,有Z = X /Y 为连续随机变量,zz故Z = X /Y 的密度函数为⎪⎩⎪⎨⎧≤>+=′=.0,0;0,)()()(22121z z z z F z p Z Z λλλλ方法二:增补变量法(1)函数z = x / y 对任意固定的y 关于x 严格单调增加,增补变量v = y ,可得⎩⎨⎧==,,/y v y x z 有反函数⎩⎨⎧==,,v y zv x 且v z v y y x x J vz vz==′′′′=10, 则∫+∞∞−⋅=dv v v zv p z p Z ||),()(,作曲线簇x / y = z ,得z 的分段点为0,当z ≤ 0时,p Z (z ) = 0,当z > 0时,z z z z v z vZ z z v vdv z p 1111010e 1e 11e 11e )1(e )(−−−−−−−=+⎟⎠⎞⎜⎝⎛+−=+−=⋅=∫,故Z = X /Y 的密度函数为⎪⎩⎪⎨⎧≤>−−=−−.0,0;0,e 1e 1)(11z z z z p z z Z(2)作曲线簇x / y = z ,得z 的分段点为0,当z ≤ 0时,p Z (z ) = 0,当z > 0时,+∞+−∞+−−⎥⎦⎤⎢⎣⎡+++−=⋅⋅=∫)(22121210212121e )(1e e )(v z v zv Z z z v vdv z p λλλλλλλλλλλλ 22121)(λλλλ+=z , 故Z = X /Y 的密度函数为⎪⎩⎪⎨⎧≤>+=.0,0;0,)()(22121z z z z p Z λλλλ 11.设X 1 , X 2 , X 3为相互独立的随机变量,且都服从(0, 1)上的均匀分布,求三者中最大者大于其他两者之和的概率.解:设A i 分别表示X i 大于其他两者之和,i = 1, 2, 3,显然A 1 , A 2 , A 3两两互不相容,且P (A 1) = P (A 2) = P (A 3), 则P (A 1∪A 2∪A 3) = P (A 1) + P (A 2) + P (A 3) = 3P (A 3) = 3P {X 3 > X 1 + X 2} 因X 1 , X 2 , X 3相互独立且都服从(0, 1)上的均匀分布,则由几何概型知61121131}{213=××=+>X X X P , 故21}{3)(213321=+>=X X X P A A A P U U . 12.设随机变量X 1与X 2相互独立同分布,其密度函数为⎩⎨⎧<<=.,0;10,2)(其他x x x p1试求Z = max {X 1, X 2} − min {X 1, X 2}的分布. 解:分布函数法,二维随机变量(X 1, X 2) 的联合密度函数为⎩⎨⎧<<<<=.,0;10,10,4),(212121其他x x x x x x p 因Z = max {X 1, X 2} − min {X 1, X 2} = | X 1 − X 2 |,作曲线簇 | x 1 − x 2 | = z ,得z 的分段点为0, 1, 当z < 0时,F Z (z ) = 0, 当0 ≤ z < 1时,∫∫∫∫+−−=⋅−=−=−−111221311221112211)2(41221421)(11zzz x zzx Z dx x z zx x x x dx dx x x dx z F323823244232414123244142444212123141z z z z z z z z x z zx x z +−=⎟⎟⎠⎞⎜⎜⎝⎛+−+⎟⎟⎠⎞⎜⎜⎝⎛+−−=⎟⎟⎠⎞⎜⎜⎝⎛+−−=,当z ≥ 1时,F Z (z ) = 1,因分布函数F Z (z ) 连续,有Z = max {X 1, X 2} − min {X 1, X 2}为连续随机变量, 故Z = max {X 1, X 2} − min {X 1, X 2}的密度函数为⎪⎩⎪⎨⎧<<+−=′=.,0;10,34438)()(3其他z z z z F z p Z Z13.设某一个设备装有3个同类的电器元件,元件工作相互独立,且工作时间都服从参数为λ 的指数分布.当3个元件都正常工作时,设备才正常工作.试求设备正常工作时间T 的概率分布. 解:设T i 表示“第i 个元件正常工作”,有T i 服从指数分布Exp (λ),分布函数为3,2,1.0,0,0,e 1)(=⎩⎨⎧≤>−=−i t t t F t i λ,则设备正常工作时间T = min {T 1, T 2, T 3},分布函数为F (t ) = P {T = min {T 1, T 2, T 3} ≤ t } = 1 − P {min {T 1, T 2, T 3} > t } = 1 − P {T 1 > t }P {T 2 > t }P {T 3 > t }= 1 − [1 − F 1 (t )][1 − F 2 (t )][1 − F 3 (t )]当t ≤ 0时,F (t ) = 0,当t > 0时,F (t ) = 1 − (e − λ t )3 = 1 − e − 3λ t ,故设备正常工作时间T 服从参数为3λ 的指数分布Exp (3λ),密度函数为⎩⎨⎧≤>=′=−.0,0,0,e 3)()(3t t t F t p t λλ14.设二维随机变量(X , Y ) 在矩形G = {(x , y ) | 0 ≤ x ≤ 2, 0 ≤ y ≤ 1}上服从均匀分布,试求边长分别为X 和Y的矩形面积Z 的密度函数.解:二维随机变量(X , Y ) 的联合密度函数为⎪⎩⎪⎨⎧≤≤≤≤=.,0,10,20,21),(其他y x y x p 方法一:分布函数法矩形面积Z = XY ,作曲线族xy = z ,得z 的分段点为0, 2, 当z ≤ 0时,F Z (z ) = 0,1当0 < z < 2时,∫∫∫∫∫∫+=+=20020102212121)(z z z z Z dx x z dx dy dx dy dx z F x z)ln 2(ln 22ln 222z z z x z z z −+=+=, 当z ≥ 2时,F Z (z ) = 1,因分布函数F Z (z ) 连续,有Z = XY 为连续随机变量, 故矩形面积Z = XY 的密度函数为⎪⎩⎪⎨⎧<<−=′=.,0,20),ln 2(ln 21)()(其它z z z F z p Z Z 方法二:增补变量法矩形面积Z = XY ,函数z = xy 对任意固定的y ≠ 0关于x 严格单调增加,增补变量v = y , 可得⎩⎨⎧==,,y v xy z 有反函数⎪⎩⎪⎨⎧==,,v y v z x 且v vzv y y x x J vz vz1112=−=′′′′=, 则∫+∞∞−⋅⎟⎠⎞⎜⎝⎛=dv vv v z p z p Z 1,)(, 作曲线族xy = z ,得z 的分段点为0, 2, 当z ≤ 0或z ≥ 2时,p Z (z ) = 0, 当0 < z < 2时,)ln 2(ln 212ln 210ln 2121)(1212z z v dy v z p z zZ −=−===∫, 故矩形面积Z = XY 的密度函数为⎪⎩⎪⎨⎧<<−=.,0,20),ln 2(ln 21)(其它z z z p Zz。
第三专题 二维随机变量

一、选择题1、设f (x)为连续函数,⎰⎰=tty dx x f dy t F 1)()(,则)2(F '等于(A) 2f (2). (B) f (2). (C) –f (2). (D) 0.2、设二维随机变量(X,Y) 的概率分布为X Y 0 1 0 0.4 a 1 b 0.1 已知随机事件}0{=X 与}1{=+Y X 相互独立,则(A) a=0.2, b=0.3 (B) a=0.4, b=0.1(C) a=0.3, b=0.2 (D) a=0.1, b=0.4 3、设随即变量服从二维正态分布,且与不相关,,分别表示的概率密度,则在的条件下,的条件概率密度为(A) (B)(C)(D)4、设随机变量独立同分布且分布函数为,则分布函数为(A)(B) (C)(D)5、设随机变量与相互独立,且服从标准正态分布,的概率分布为,记为随机变量的分布函数,则函数的间断点个数为(A)0(B)1(C)2 (D)36、设随机变量x 与y 相互独立,且分别服从参数为1与参数为4的指数分布,则{}=<y x p ()1124()() () ()5355A B C D(,)X Y X Y ()X f x ()Y f y ,X Y Y y =X |(|)X Y f x y ()X f x ()Y f y ()X f x ()Y f y ()()X Y f x f y ,X Y X ()F x {}max ,Z X Y =()2Fx ()()F x F y ()211F x --⎡⎤⎣⎦()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦X Y X ()0,1N Y {}{}1012P Y P Y ====()Z F z Z XY =()Z F z7、设随机变量X 与Y 相互独立,且都服从区间(0.1)上的均匀分布,则{}221P X Y +≤= ( )(A)14 (B) 12 (C) 8π (D)4π 8、设随机变量X 和Y 相互独立,则X 和Y 的概率分布分别为,则{2}P X Y +== ( )(A )112 (B )18 (C )16 (D )12二、填空题1、从数1,2,3,4中任取一个数,记为X, 再从中任取一个数,记为Y , 则=2、设随机变量相互独立,且均服从区间上的均匀分布,则.3、设二维随机变量(,)x y 服从正态分布(1,0;1,1,0)N ,则{0}__.P XY Y -<=4、设随机变量X 与Y 相互独立,且11~(1,),~(2,),32X B Y B 则{}P X Y == ( )5、已知随机变量X 与Y 相互独立,X 服从参数为λ的指数分布, P {Y =−1}=14, P {Y =1}=34, 则概率 P{XY≤2} = .X ,,2,1 }2{=Y P X Y 与[]0,3{}{}max ,1P X Y ≤=三、计算题1、设随机变量X 与Y 独立,其中X 的概率分布为 ,而Y 的概率密度为f (y ),求随机变量U =X +Y 的概率密度g (u ). 2、设A,B 为随机事件,且111432P(A),P(B A),P(A B )===,令 ;,,0,1不发生发生A A X ⎩⎨⎧=.,,0,1不发生发生B B Y ⎩⎨⎧= 求:(I )二维随机变量(X ,Y )的概率分布;(II )X 和Y 的相关系数.XY ρ 3、设二维随机变量(X,Y)的概率密度为.,20,10,0,1),(其他x y x y x f <<<<⎩⎨⎧=求:(I ) (X,Y)的边缘概率密度)(),(y f x f Y X ; (II )Y X Z -=2的概率密度).(z f Z ( III ) (数三) 4、设随机变量的概率密度为,令为二维随机变量的分布函数.(Ⅰ) 求的概率密度;(Ⅱ) ;(Ⅲ) . 5、设二维随机变量的概率密度为⎪⎪⎭⎫ ⎝⎛7.03.021~X }.2121{≤≤X Y P X ()1,1021,0240,X x f x x ⎧-<<⎪⎪⎪=≤<⎨⎪⎪⎪⎩ 其他()2,,Y X F x y =(,)X Y Y ()Y f y Cov(,)X Y 1,42F ⎛⎫- ⎪⎝⎭(,)X Y 2,01,0 1.(,)0,x y x y f x y --<<<<⎧=⎨⎩其他(Ⅰ)求;(Ⅱ)求的概率密度. 6、设随机变量与相互独立,的概率分布为,的概率密度为,记,(1)求.(2)求的概率密度.7、袋中有1个红色球,2个黑色球与3个白球,现有回放地从袋中取两次,每次取一球,以分别表示两次取球所取得的红球、黑球与白球的个数.(1) 求. (2)求二维随机变量概率分布8、设二维随机变量的概率密度为(Ⅰ)求条件概率密度(Ⅱ)求条件概率 9、设二维随机变量的概率密度为求常数及条件概率密度10、设随机变量X 与Y 的概率分布分别为且{}221P X Y ==.(I) 求二维随机变量(,)X Y 的概率分布;(II) 求Z XY =的概率分布; (III) 求X 与Y 的相关系数XY ρ.11、设二维随机变量(,)X Y 服从区域G 上的均匀分布,其中G 是由0,2x y x y -=+=与0y =所围成的三角形区域.(I) 求X 的概率密度()X f x ;(II) 求条件概率密度|(|)X Y f x y .{}2P X Y >Z X Y =+()Z f z X Y X {}()11,0,13P X i i ===-Y ()1010Y y f y ≤≤⎧=⎨⎩其它Z X Y =+102P Z X ⎧⎫≤=⎨⎬⎩⎭Z ,,X Y Z {}10p X Z ==(),X Y (,)X Y 0(,)0xe y xf x y -⎧<<=⎨⎩其他()Y X f y x 11P X Y =⎡≤≤⎤⎣⎦()X Y +2222(,)e ,,,x xy y f x y A x y -+-=-∞<<∞-∞<<∞A |(|).Y X f y x(Ⅰ)求{}2P X Y =;(Ⅱ)求Cov(,)X Y Y -.13、设随机变量X 与Y 相互独立,且服从参数为1的指数分布. 记{}max ,U X Y =,{}min ,V X Y =(Ⅰ)求V 的概率密度()V f v ;(Ⅱ)求()E U V +.14、设随机变量X 的分布为2121====)()(X P X P ,在给定i X =的条件下,随机变量Y 服从均匀分布210,),,(=i i U . (1) 求Y 的分布函数; (2) 求期望).(Y E15、设随机变量X 与Y 的概率分布相同,X 的概率分布为12{0},{1},33P X P X ====且X 与Y 的相关系数12XY ρ=(1) 求(X ,Y )的概率分布(2) 求P{X+Y ≤1}16、设二维随机变量(,)X Y 在区域(){2,01,D x y x x y =<<<<上服从均匀分布,令1,0,X YU X Y≤⎧=⎨>⎩(I )写出(,)X Y 的概率密度;(II )问U 与X 是否相互独立?并说明理由; (III )求Z U X =+的分布函数()F z .17、设随机变量,X Y 相互独立,且X 的概率分布为{}10{2}2P X P X ====,Y 的概率密度为2,01()0,y y f y <<⎧=⎨⎩其他.(1)求概率P Y EY ≤(); (2)求Z X Y =+的概率密度.18、已知随机变量,X Y 相互独立,且1(1)(1)2p X p X ===-=,Y 服从参数为λ的泊松分布,Z XY =(I )求(,)COV X Z ;(II )求Z 的分布律.19、在区间(0,2)上随机取一点,将该区间分成两段,较短一段的长度为X ,较长一段的长度记为 Y .令 Z =YX .(Ⅰ)求X 的概率密度;(Ⅱ)求Z 的概率密度; (Ⅲ)求 E (XY).20、设二维随机变量(X ,Y )的概率密度为 ()()222221,0x y ,x y ,f x y ,.π⎧++≤⎪=⎨⎪⎩其他(1)求X 与Y 的协方差; (2)X 与Y 是否相互独立? (3)求Z 22X Y =+的概率密度.。
概率论与数理统计第三章课后习题及参考答案

概率论与数理统计第三章课后习题及参考答案1.设二维随机变量),(Y X 只能取下列数组中的值:)0,0(,)1,1(-,31,1(-及)0,2(,且取这几组值的概率依次为61,31,121和125,求二维随机变量),(Y X 的联合分布律.解:由二维离散型随机变量分布律的定义知,),(Y X 的联合分布律为2.某高校学生会有8名委员,其中来自理科的2名,来自工科和文科的各3名.现从8名委员中随机地指定3名担任学生会主席.设X ,Y 分别为主席来自理科、工科的人数,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:(1)由题意,X 的可能取值为0,1,2,Y 的可能取值为0,1,2,3,则561)0,0(3833====C C Y X P ,569)1,0(381323====C C C Y X P ,569)2,0(382313====C C C Y X P ,561)3,0(3833====C C Y X P ,283)0,1(382312====C C C Y X P ,289)1,1(38131312====C C C C Y X P ,283)2,1(382312====C C C Y X P ,0)3,1(===Y X P ,563)0,2(381322====C C C Y X P ,563)1,2(381322====C C C Y X P ,0)2,2(===Y X P ,0)3,2(===Y X P .),(Y X 的联合分布律为:(2)X 的边缘分布律为X 012P1452815283Y 的边缘分布律为Y 0123P285281528155613.设随机变量),(Y X 的概率密度为⎩⎨⎧<<<<--=其他.,0,42,20),6(),(y x y x k y x f 求:(1)常数k ;(2))3,1(<<Y X P ;(3))5.1(<Y P ;(4))4(≤+Y X P .解:方法1:(1)⎰⎰⎰⎰--==+∞∞-+∞∞-422d d )6(d d ),(1yx y x k y x y x f ⎰--=42202d |)216(y yx x x k k y y k 8d )210(42=-=⎰,∴81=k .(2)⎰⎰∞-∞-=<<31d d ),()3,1(y x y x f Y X P ⎰⎰--=32102d d )216(yx yx x x ⎰--=32102d |)216(81y yx x x 83|)21211(81322=-=y y .(3)),5.1()5.1(+∞<<=<Y X P X P ⎰⎰+∞∞-∞---=5.1d d )6(81yx y x ⎰⎰--=425.10d d )6(81y x y x y yx x x d )216(81422⎰--=3227|)43863(81422=-=y y .(4)⎰⎰≤+=≤+4d d ),()4(y x y x y x f Y X P ⎰⎰---=2042d )6(d 81x y y x x ⎰+-⋅=202d )812(2181x x x 32|)31412(1612032=+-=x x x .方法2:(1)同方法1.(2)20<<x ,42<<y 时,⎰⎰∞-∞-=yxv u v u f y x F d d ),(),(⎰⎰--=y xv u v u 20d d )6(81⎰--=y xv uv u u 202d |)216(81⎰--=y v xv x x 22d )216(81y xv v x xv 222|)21216(81--=)1021216(81222x xy y x xy +---=,其他,0),,(=y x F ,∴⎪⎩⎪⎨⎧<<<<+---=其他.,0,42,20),1021216(81),(222y x x x xy y x xy y x F 83)3,1()3,1(==<<F Y X P .(3))42,5.1(),5.1()5.1(<<<=+∞<<=<Y X P Y X P X P )2,5.1()4,5.1(<<-<<=Y X P Y X P 3227)2,5.1()4,5.1(=-=F F .(4)同方法1.4.设随机变量),(Y X 的概率密度为⎩⎨⎧>>=--其他.,0,0,0,e ),(2y x A y x f y x 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)⎰⎰⎰⎰+∞+∞--+∞∞-+∞∞-==02d d e d d ),(1yx A y x y x f y x ⎰⎰+∞+∞--=002d e d e y x A y x2|)e 21(|)e (020A A y x =-⋅-=∞+-∞+-,∴2=A .(2)0>x ,0>y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰--=yxv u vu 02d d e 2yv x u 020|)e 21(|)e (2---⋅-=)e 1)(e 1(2y x ----=,其他,0),(=y x F ,∴⎩⎨⎧>>--=--其他.,0,0,0),e 1)(e 1(),(2y x y x F y x .5.设随机变量),(Y X 的概率密度为⎩⎨⎧≤≤≤≤=其他.,0,10,10,),(y x Axy y x f 求:(1)常数A ;(2)),(Y X 的联合分布函数.解:(1)2121d d d d ),(11010⋅⋅===⎰⎰⎰⎰+∞∞-+∞∞-A y y x x A y x y x f ,∴4=A .(2)10≤≤x ,10≤≤y 时,⎰⎰∞-∞-=y xv u v u f y x F d d ),(),(⎰⎰=yxv u uv 0d d 4220202||y x v u yx =⋅=,10≤≤x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4xv u uv 210202||x v u x =⋅=,10≤≤y ,1>x 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=100d d 4yu v uv 202102||y v u y =⋅=,1>x ,1>y 时,⎰⎰∞-∞-=yx v u v u f y x F d d ),(),(⎰⎰=101d d 4v u uv 1||102102=⋅=v u,其他,0),(=y x F ,∴⎪⎪⎪⎩⎪⎪⎪⎨⎧>>≤≤>>≤≤≤≤≤≤=其他.,0,1,1,1,10,1,,1,10,,10,10,),(2222y x y x y y x x y x y x y x F .6.把一枚均匀硬币掷3次,设X 为3次抛掷中正面出现的次数,Y 表示3次抛掷中正面出现次数与反面出现次数之差的绝对值,求:(1)),(Y X 的联合分布律;(2)X 和Y 的边缘分布律.解:由题意知,X 的可能取值为0,1,2,3;Y 的可能取值为1,3.易知0)1,0(===Y X P ,81)3,0(===Y X P ,83)1,1(===Y X P ,0)3,1(===Y X P 83)1,2(===Y X P ,0)3,2(===Y X P ,0)1,3(===Y X P ,81)3,3(===Y X P 故),(Y X 得联合分布律和边缘分布律为:7.在汽车厂,一辆汽车有两道工序是由机器人完成的:一是紧固3只螺栓;二是焊接2处焊点,以X 表示由机器人紧固的螺栓紧固得不牢的数目,以Y 表示由机器人焊接的不良焊点的数目,且),(Y X 具有联合分布律如下表:求:(1)在1=Y 的条件下,X 的条件分布律;(2)在2=X 的条件下,Y 的条件分布律.解:(1)因为)3,3()1,2()1,1()1,0()1(==+==+==+====Y X P Y X P Y X P Y X P Y P 08.0002.0008.001.006.0=+++=,所以43)1()1,0()1|0(=======Y P Y X P Y X P ,81)1()1,1()1|1(=======Y P Y X P Y X P ,101)1()1,2()1|2(=======Y P Y X P Y X P ,401)1()1,3()1|3(=======Y P Y X P Y X P ,故在1=Y 的条件下,X 的条件分布律为X 0123P4381101401(2)因为)2,2()1,2()0,2()2(==+==+====Y X P Y X P Y X P X P 032.0004.0008.002.0=++=,所以85)2()0,2()2,0(=======X P Y X P X Y P ,4)2()1,2()2,1(=======X P Y X P X Y P ,81)2()2,2()2,2(=======X P Y X P X Y P ,故在2=X 的条件下,Y 的分布律为:Y 012P8541818.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧>>=+-其他.,0,0,0,e ),()2(y x c y x f y x 求:(1)常数c ;(2)X 的边缘概率密度函数;(3))2(<+Y X P ;(4)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)⎰⎰⎰⎰+∞+∞+-+∞∞-+∞∞-==0)2(d d e d d ),(1yx c y x y x f y x⎰⎰+∞+∞--=002d e d ey x c y x2|)e (|)e 21(002c c y x =-⋅-=∞+-∞+-,∴2=c .(2)0>x 时,⎰+∞∞-=y y x f x f X d ),()(⎰+∞+-=0)2(d e 2y y x x y x 202e 2|)e (e 2-+∞--=-=,0≤x 时,0)(=x f X ,∴⎩⎨⎧≤>=-.0,0,0,e 2)(2x x x f x X ,同理⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)⎰⎰<+=<+2d d ),()2(y x y x y x f Y X P ⎰⎰---=2202d d e 2xy x yx 422202e e 21d e d e 2-----+-==⎰⎰xy x y x .(4)由条件概率密度公式,得,当0>y 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e 2,0,0,e e 2)(),()|(22|x x y f y x f y x f xy y x Y Y X ,0≤y 时,0)|(|=y x f Y X ,所以⎩⎨⎧>>=-其他.,0,0,0,e 2)|(2|y x y x f x Y X ;同理,当0>x 时,有⎩⎨⎧>=⎪⎩⎪⎨⎧>==----其他.其他.,0,0,e ,0,0,2e e 2)(),()|(22|y y x f y x f x y f yx y x X X Y 0≤x 时,0)|(|=x y f X Y ,所以⎩⎨⎧>>=-其他.,0,0,0,e )|(|y x x y f y X Y .9.设二维随机变量),(Y X 的概率密度函数为⎩⎨⎧<<<<=其他.,0,0,10,3),(x y x x y x f求:(1)关于X 、Y 的边缘概率密度函数;(2)条件概率密度函数)|(|y x f Y X ,)|(|x y f X Y .解:(1)10<<x 时,⎰+∞∞-=y y x f x f X d ),()(203d 3x y x x==⎰,其他,0)(=x f X ,∴⎩⎨⎧<<=其他.,0,10,3)(2x x x f X ,密度函数的非零区域为}1,10|),{(}0,10|),{(<<<<=<<<<x y y y x x y x y x ,∴10<<y 时,⎰+∞∞-=x y x f y f Y d ),()()1(23d 321y x x y-==⎰,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<-=其他.,0,10),1(23)(2y y y f Y .(2)当10<<y 时,有⎪⎩⎪⎨⎧<<-=⎪⎪⎩⎪⎪⎨⎧<<-==其他.其他.,0,1,12,0,1,)1(233)(),()|(22|x y y x x y y xy f y x f y x f Y Y X ,其他,0)|(|=y x f Y X ,故⎪⎩⎪⎨⎧<<<<-=其他.,0,10,1,12)|(2|y x y y xy x f Y X .当10<<x 时,有⎪⎩⎪⎨⎧<<=⎪⎩⎪⎨⎧<<==其他.其他.,0,0,1,0,0,33)(),()|(2|x y x x y x x x f y x f x y f X X Y ,其他,0)|(|=x y f X Y ,故⎪⎩⎪⎨⎧<<<<=其他.,0,10,0,1)|(|x x y x x y f X Y .10.设条件密度函数为⎪⎩⎪⎨⎧<<<=其他.,0,10,3)|(32|y x yx y x f Y X Y 的概率密度函数为⎩⎨⎧<<=其他.,0,10,5)(4y y y f Y 求21(>X P .解:⎩⎨⎧<<<==其他.,0,10,15)|()(),(2|y x y x y x f y f y x f Y X Y ,则6447d )(215d d 15d d ),(21(121421211221=-===>⎰⎰⎰⎰⎰>x x x x y y x y x y x f X P xx .11.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧<<<<+=其他.,0,20,10,3),(2y x xyx y x f 求:(1)),(Y X 的边缘概率密度;(2)X 与Y 是否独立;(3))),((D Y X P ∈,其中D 为曲线22x y =与x y 2=所围区域.解:(1)10<<x 时,x x y xy x y y x f x f X 322d )3(d ),()(222+=+==⎰⎰+∞∞-,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<+=其他.,0,10,322)(2x x x x f X ,20<<y 时,⎰+∞∞-=x y x f y f Y d ),()(316)d 3(12+=+=⎰y x xy x ,其他,0)(=y f Y ,∴⎪⎩⎪⎨⎧<<+=其他.,0,20,316)(y y y f Y .(2)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(3)}22,10|),{(2x y x x y x D ≤≤<<=,∴⎰⎰+=∈102222d d )3()),((x xx y xy x D Y X P 457d )32238(10543=--=⎰x x x x .12.设二维随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=-其他.,0,0,0,e )1(),(2y x y x y x f x试讨论X ,Y 的独立性.解:当0>x 时,xx x X x yx y y x y y x f x f -∞+-∞+-∞+∞-=+-=+==⎰⎰e |11e d )1(e d ),()(002,当0≤x 时,0)(=x f X ,故⎩⎨⎧≤>=-.0,0,0,e )(x x x x f x X ,同理,可得⎪⎩⎪⎨⎧≤>+=.0,0,0,)1(1)(2y y y y f Y ,因为)()(),(y f x f y x f Y X =,所以X 与Y 相互独立.13.设随机变量),(Y X 在区域}|),{(a y x y x g ≤+=上服从均匀分布,求X 与Y 的边缘概率密度,并判断X 与Y 是否相互独立.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤+=其他.,0,,21),(2a y x a y x f ,当0<<-x a 时,有)(1d 21d ),()(2)(2x a ay a y y x f x f xa x a X +===⎰⎰++-+∞∞-,当a x <≤0时,有)(1d 21d ),()(2)(2x a a y a y y x f x f x a x a X -===⎰⎰---+∞∞-,当a x ≥时,0d ),()(==⎰+∞∞-y y x f x f X ,故⎪⎩⎪⎨⎧≥<-=.a x a x x a a x f X ,0,),(1)(2,同理,由轮换对称性,可得⎪⎩⎪⎨⎧≥<-=.a y a y y a a y f Y ,0,),(1)(2,显然)()(),(y f x f y x f Y X ≠,所以X 与Y 不相互独立.14.设X 和Y 时两个相互独立的随机变量,X 在)1,0(上服从均匀分布,Y 的概率密度为⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2y y y f yY (1)求X 和Y 的联合概率密度;(2)设含有a 的二次方程为022=++Y aX a ,试求a 有实根的概率.解:(1)由题可知X 的概率密度函数为⎩⎨⎧<<=其他.,0,10,1)(x x f X ,因为X 与Y 相互独立,所以),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧><<==-其他.,0,0,10,e 21)()(),(2y x y f x f y x f yY X ,(2)题设方程有实根等价于}|),{(2X Y Y X ≤,记为D ,即}|),{(2X Y Y X D ≤=,设=A {a 有实根},则⎰⎰=∈=Dy x y x f D Y X P A P d d ),()),(()(⎰⎰⎰---==1021002d )e 1(d d e 2122xx y x x y⎰--=102d e12x x ⎰--=12e 21212x x ππππ23413.01)]0()1([21-=Φ-Φ-=.15.设i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,求行列式4321X X X X X =的分布律.解:由i X ~)4.0,1(b ,4,3,2,1=i ,且1X ,2X ,3X ,4X 相互独立,易知41X X ~)84.0,16.0(b ,32X X ~)84.0,16.0(b .因为1X ,2X ,3X ,4X 相互独立,所以41X X 与32X X 也相互独立,又32414321X X X X X X X X X -==,则X 的所有可能取值为1-,0,1,有)1()0()1,0()1(32413241======-=X X P X X P X X X X P X P 1344.016.084.0=⨯=,)1,1()0,0()0(32413241==+====X X X X P X X X X P X P )1()1()0()0(32413241==+===X X P X X P X X P X X P 7312.016.016.084.084.0=⨯+⨯=,)0()1()0,1()1(32413241=======X X P X X P X X X X P X P 1344.084.016.0=⨯=,故X 的分布律为X 1-01P1344.07312.01344.016.设二维随机变量),(Y X 的概率密度为⎩⎨⎧>>=+-其他.,0,0,0,e 2),()2(y x y x f y x 求Y X Z 2+=的分布函数及概率密度函数.解:0≤z 时,若0≤x ,则0),(=y x f ;若0>x ,则0<-=x z y ,也有0),(=y x f ,即0≤z 时,0),(=y x f ,此时,0d d ),()2()()(2==≤+=≤=⎰⎰≤+zy x Z y x y x f z Y X P z Z P z F .0>z 时,若0≤x ,则0),(=y x f ;只有当z x ≤<0且02>-=xz y 时,0),(≠y x f ,此时,⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 2d d ),()2()()(⎰⎰-+-=zx z y x y x 020)2(d e 2d z z z ----=e e 1.综上⎩⎨⎧≤>--=--.0,0,0,e e 1)(z z z z F z z Z ,所以⎩⎨⎧≤<='=-.0,0,0,e )()(z z z z F z f z Z Z .17.设X ,Y 是相互独立的随机变量,其概率密度分别为⎩⎨⎧≤≤=其他.,0,10,1)(x x f X ,⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y 求Y X Z +=的概率密度.解:0<z 时,若0<x ,则0)(=x f X ;若0≥x ,则0<-=x z y ,0)(=-x z f Y ,即0<z 时,0)()(=-x z f x f Y X ,此时,0d )()()(=-=⎰+∞∞-x x z f x f z f Y X Z .10≤≤z 时,若0<x ,则0)(=x f X ;只有当z x ≤≤0且0>-=x z y 时0)()(≠-x z f x f Y X ,此时,z zx z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e 1d e d )()()(0)(.1>z 时,若0<x ,0)(=x f X ;若1>x ,0)(=x f X ;若10≤≤x ,则0>-=x z y ,此时,0)()(≠-x z f x f Y X ,z x z Y X Z x x x z f x f z f ---+∞∞--==-=⎰⎰e )1e (d e d )()()(1)(.综上,⎪⎩⎪⎨⎧<>-≤≤-=--.0,0,1,e )1e (,10,e 1)(z z z z f z z Z .18.设随机变量),(Y X 的概率密度为⎪⎩⎪⎨⎧>>+=+-其他.,0,0,0,e)(21),()(y x y x y x f y x (1)X 和Y 是否相互独立?(2)求Y X Z +=的概率密度.解:(1)),()()(y x f y f x f Y X ≠,∴X 与Y 不独立.(2)0≤z 时,若0≤x ,则0)(=x f X ;若0>x ,则0<-=x z y ,0),(=y x f ,此时,0d ),()(=-=⎰+∞∞-x x z x f z f Z .0≥z 时,若0≤x ,则0)(=x f X ;只有当z x <<0且0>-=x z y 时0),(≠y x f ,此时,⎰+∞∞--=x x z x f z f Z d ),()(⎰+-+=zy x x y x 0)(d e )(21⎰-=z z x z 0d e 21z z -=e 212,所以⎪⎩⎪⎨⎧≤>=-.0,0,0,e 21)(2z z z z f zZ .19.设X 和Y 时相互独立的随机变量,它们都服从正态分布),0(2σN .证明:随机变量22Y X Z +=具有概率密度函数⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.解:因为X 与Y 相互独立,均服从正态分布),0(2σN ,所以其联合密度函数为2222)(2e 121),(σσπy x y xf +-⋅=,(+∞<<∞-y x ,)当0≥z 时,有⎰⎰≤+=≤+=≤=zy x Z yx y x f z Y X P z Z P z F 22d d ),()()()(22⎰⎰≤++-⋅=zy x y x y x 22222d e 1212)(2σσπ⎰⎰-⋅=πσθσπ2022d ed 12122zr r r ⎰-=zr r r 022d e122σσ,此时,2222e)(σσz Z z z f -=;当0<z 时,=≤+}{22z Y X ∅,所以0)()()(22=≤+=≤=z Y X P z Z P z F Z ,此时,0)(=z f Z ,综上,⎪⎩⎪⎨⎧<≥=-.0,0,0,e )(2222z z z z f z Z σσ.20.设),(Y X 在矩形区域}10,10|),{(≤≤≤≤=y x Y X G 上服从均匀分布,求},min{Y X Z =的概率密度.解:由题可知),(Y X 的联合概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其他.,0,20,10,21),(y x y x f ,易证,X ~]1,0[U ,Y ~]2,0[U ,且X 与Y 相互独立,⎪⎩⎪⎨⎧≥<≤<=.1,1,10,,0,0)(x x x x x F X ,⎪⎪⎩⎪⎪⎨⎧≥<≤<=.2,1,20,2,0,0)(y y yy y F Y ,可得)](1)][(1[1)(z F z F z F Y X Z ---=)()()()(z F z F z F z F Y X Y X -+=⎪⎪⎩⎪⎪⎨⎧≥<≤-<=.1,1,10,223,0,02z z z z z ,求导,得⎪⎩⎪⎨⎧<<-=其他.,0,10,23)(z z z f Z .21.设随机变量),(Y X 的概率密度为⎩⎨⎧+∞<<<<=+-其他.,0,0,10,e ),()(y x b y x f y x (1)试确定常数b ;(2)求边缘概率密度)(x f X 及)(y f Y ;(3)求函数},max{Y X U =的分布函数.解:(1)⎰⎰⎰⎰+∞+-+∞∞-+∞∞-==01)(d d e d d ),(1yx b y x y x f y x ⎰⎰+∞--=10d e d e y x b y x)e 1(|)e(|)e (10102-+∞---=-⋅=b b y x ,∴1e11--=b .(2)10<<x 时,1)(1e1e d e e 11d ),()(--∞++--∞+∞--=-==⎰⎰x y x X y y y x f x f ,其他,0)(=x f X ,∴⎪⎩⎪⎨⎧<<-=--其他.,0,10,e 1e )(1x x f xX ,0>y 时,⎰+∞∞-=x y x f y f Y d ),()(yy x x -+--=-=⎰e d e e 1110)(1,0≤y 时,0)(=y f Y ,∴⎩⎨⎧≤>=-.0,0,0,e )(y y y f y Y .(3)0≤x 时,0)(=x F X ,10<<x 时,101e1e 1d e 1e d )()(----∞---=-==⎰⎰xxt xX X t t t f x F ,1≥x 时,1)(=x F X ,∴⎪⎪⎩⎪⎪⎨⎧≥<<--≤=--.1,1,10,e 1e1,0,0)(1x x x x F x X ;0≤y 时,0)(=y F Y ,0>y 时,y yv y Y Y v v v f y F --∞--===⎰⎰e 1d e d )()(0,∴⎩⎨⎧≤>-=-.0,0,0,e 1)(y y y F y Y ,故有)()()(y F x F u F Y X U =⎪⎪⎩⎪⎪⎨⎧≥-<≤--<=---.1,e 1,10,e 1e1,0,01u u u uu .。
概率论与数理统计第3章题库

第3章 多维随机向量及其分布填空题1. 二维随机向量(,)X Y 的联合分布律如下表所示已知随机事件}0{=X 与}1{=+Y X 相互独立,则a = _______ , b =________. 答案:0.4,0.1知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 1提示一: 二维离散型随机向量的联合分布律的性质 提示二: 事件的独立性 提示三:无 提示四(同题解) 题型:填空题题解:{0}0.4P X a ==+,{1}0.5P X Y a b +==+= {0,1}{0,1}P X X Y P X Y a =+=====由独立性知,(0.4)0.5a a =+⨯,0.4a =,0.1b =. 2. 设二维随机变量(,)X Y 的概率密度为6,01(,)0,x x y f x y ≤≤≤⎧=⎨⎩其他则=≤+}1{Y X P __________ . 答案:41知识点: 二维连续型随机向量的联合概率密度参考页: P63 学习目标: 2 难度系数: 1提示一: 利用联合概率密度计算二维连续型随机向量取值的概率 提示二:无 提示三:无 提示四(同题解) 题型:填空题题解:由题设,有 =≤+}1{Y X P ⎰⎰⎰⎰≤+-=121016),(y x xxxdy dx dxdy y x f=.41)126(2102=-⎰dx x x 3.设(,)X Y 的联合分布函数为230,0(1)(1),(,)0,x y x y e e F x y --≥≥⎧--=⎨⎩其他,则(,)X Y 的联合概率密度为___________.答案:230,06,(,)0,x y x y e e f x y --≥≥⎧=⎨⎩其他知识点: 二维连续型随机向量的联合概率密度 参考页: P63 学习目标: 2 难度系数: 1提示一: 二维连续型随机向量的联合概率密度与联合分布函数之间的关系 提示二:无 提示三:无 提示四(同题解) 题型:填空题题解:230,06,(,)(,)0,x y x y e e F x y f x y x y --≥≥⎧∂==⎨∂∂⎩其他.4. 设平面区域D 由曲线1y x=及直线20,1,y x x e ===所围成,二维随机变量(,)X Y 在区域D上服从均匀分布,则(,)X Y 关于X 的边缘概率密度在2x =处的值为.答案:230,06,(,)0,x y x y e e f x y --≥≥⎧=⎨⎩其他知识点: 二维均匀分布, 二维连续型随机向量的边缘概率密度 参考页: P65,P66 学习目标: 4,2 难度系数: 2提示一: 二维均匀分布的定义提示二: 二维连续型随机向量的边缘概率密度的定义 提示三:无 提示四(同题解) 题型:填空题题解:2112e D S dx x ==⎰,211, 1,0(,)20, x e y f x y x ⎧≤≤≤≤⎪=⎨⎪⎩其他21,x e ≤≤111()22xX f x dy x ==⎰,1(2)4X f = 5. 随机变量,X Y 相互独立且服从同一分布,1{}{}3k P X k P Y k +====,1,0=k ,则{}P X Y ==答案:59知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 离散型随机变量的独立性 提示二:无 提示三:无 提示四(同题解) 题型:填空题题解:{}{0,0}{1,1}P X Y P X Y P X Y ====+=={0}{0}{1}{1}P X P Y P X P Y ===+==1122533339=⋅+⋅=6. 若Y X 、的分布律为:设Y X 、相互独立,则β= . 答案:19知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 离散型随机变量的独立性 提示二:无 提示三:无 提示四(同题解) 题型:填空题 题解:1{1}=3P Y =,所以2{2}=3P Y =,又1{3}=18P X β=+ 由Y X 、相互独立知{3,2}{3}{2}P X Y P X P Y =====, 即12()183ββ=+⨯,所以19β= 7.设随机变量X 与Y 相互独立,且均服从区间[]0,3上的均匀分布,则{}{}max ,2P X Y ≤= _________ .答案:49知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 连续型随机变量的独立性 提示二: 均匀分布 提示三:无 提示四(同题解) 题型:填空题题解:{}{}max ,1P X Y ≤={1,1}{1}{1}P X Y P X P Y ≤≤=≤≤4=9. 8.设,,X Y Z 相互独立,且都服从参数为λ的指数分布,则随机向量(,,)X Y Z 的联合概率密度为___________.答案: 3(),0,0,0(,,)0,x y z e x y z f x y z λλ-++⎧>>>=⎨⎩其他知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 连续型随机变量的独立性 提示二: 指数分布 提示三:无 提示四(同题解) 题型:填空题题解:, 0() 0, 0x e x f x x λλ-⎧>=⎨≤⎩,3(),0,0,0(,,)0,x y z e x y z f x y z λλ-++⎧>>>=⎨⎩其他.9.设,X Y 为随机变量,已知{}20,05P X Y ≥≥=, 3{0}{0}5P X P Y ≥=≥=, 则 {}{}max ,0P X Y ≥= ______ ; {}{}min ,0P X Y <= ______ .答案:45,35知识点: 离散型随机变量函数的分布 参考页: P76 学习目标: 5 难度系数: 2提示一:随机变量函数的取值的概率 提示二: 事件运算的性质 提示三:无 提示四(同题解) 题型:填空题题解:设{0},{0}A X B Y =≥=≥, 依题意有32()(),()55P A P B P AB === {}{}{}{}max ,01max ,0P X Y P X Y ≥=-<{}10,0P X Y =-<<1()1()()()()()P AB P A B P A B P A P B P AB =-=-+=+=+-45={}{}min ,0P X Y <={}{}1min ,01{0,0}P X Y P X Y -≥=-≥≥35=.选择题1.已知二维随机变量(,)X Y 的联合分布表如左表所示,且已知{0}0.6P X ==,则b a ,分别为( )(A) 4.0,1.0==b a ; (B) 1.0,4.0==b a ; (C)3.0,2.0==b a ; (D) 0.1,0.3a b ==.答案:(C )知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 1提示一: 二维离散型随机向量的联合分布律的性质 提示二:无 提示三:无 提示四(同题解) 题型:选择题题解:{0}0.4P X a ==+,即0.40.6a += ,所以0.2a =由分布律的性质{1}0.5P X Y a b +==+=,所以0.3b =. 故选(C ). 2.设随机变量i X (1,2i =)的概率分布为且12{0}1P X X ==,则12{}P X X ==( ) (A )0; (B )14; (C )12; (D )1.答案:(A )知识点: 二维离散型随机向量的联合分布律, 二维离散型随机向量的边缘分布律 参考页: P60,P61 学习目标: 2 难度系数: 1提示一: 二维离散型随机向量的联合分布律的性质提示二: 二维离散型随机向量的边缘分布律与联合分布律的关系 提示三:无 提示四(同题解) 题型:选择题题解:由12{0}1P X X ==可求得12(X X ,)的联合分布律12{}P X X ==121212{1,1}{0,0}{1,1}0P X X P X X P X X =-=-+==+===故选(A ).3. 设二维随机变量(,)X Y 服从G 上的均匀分布,区域G 由曲线2x y =与x y =所围,则(,)X Y 的联合概率密度为( ).(A )⎩⎨⎧∈=他其,0),(,6),(G y x y x f ; (B )⎩⎨⎧∈=他其,0),(,6/1),(G y x y x f ;(C )⎩⎨⎧∈=他其,0),(,2),(G y x y x f ; (D )⎩⎨⎧∈=他其,0),(,2/1),(Gy x y x f .答案:(A )知识点: 二维均匀分布 参考页: P65 学习目标: 4 难度系数: 1提示一: 二维均匀分布的定义 提示二:无 提示三:无 提示四(同题解) 题型:选择题题解:1201()6G S x x dx =-=⎰,所以联合概率密度为⎩⎨⎧∈=他其,0),(,6),(G y x y x f ,故选(A ).4. 设随机变量,X Y 相互独立,,X Y 的概率分布分别为则 {}2P X Y +==( ). (A)112; (B) 18; (C) 16; (D) 12. 答案:(C )知识点: 随机变量的独立性 参考页: P67 学习目标:3 难度系数: 1提示一: 离散型随机变量的独立性 提示二:无提示三:无 提示四(同题解) 题型:选择题题解:{}2{1,1}{2,0}{3,1}P X Y P X Y P X Y P X Y +====+==+==- {1}{1}{2}{0}{3}{1}P X P Y P X P Y P X P Y ===+==+==- 11111114383836=⋅+⋅+⋅=, 选(C). 5. 设随机变量X Y 、相互独立且同分布,则下列等式成立的是( )(A ) X Y =-; (B ) {}0P X Y ==; (C ) 1{}2P X Y == ; (D ) {}1P X Y ==. 答案:(C )知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 离散型随机变量的独立性 提示二:无 提示三:无 提示四(同题解) 题型:选择题题解:{}{1,1}{1,1}P X Y P X Y P X Y ===-=-+==1{1}{1}{1}{1}2P X P Y P X P Y ==-=-+===. 故选(C ).6. 设随机变量X 和Y 相互独立且同分布,1{1}{1},2P X P Y =-==-={1}P X ==1{1}2P Y ==,则下列各式中成立的是( ).(A ) 1{}2P X Y ==; (B ) 1{0}4P X Y +==;(C ) {}1P X Y ==; (D ) 1{1}4P XY ==.答案:(A )知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 离散型随机变量的独立性 提示二:无 提示三:无 提示四(同题解) 题型:选择题题解:{}{1,1}{1,1}P X Y P X Y P X Y ===-=-+==1{1}{1}{1}{1}2P X P Y P X P Y ==-=-+===,选(A ).7. 设随机变量X 与Y 相互独立,且都服从区间()0,1上的均匀分布,则{}221P X Y +≤( ) (A )14; (B )12; (C )8π; (D )4π. 答案:(D )知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 连续型随机变量的独立性 提示二: 二维均匀分布的定义 提示三:无 提示四(同题解) 题型:选择题题解:(),X Y 的联合概率密度为1, 01,01(,) x y f x y <<<<⎧=⎨⎩0,其他则{}224114P X Y ππ+≤==,选(D ).8. 设随机变量,X Y 相互独立,且分别服从参数为1与参数为4的指数分布,则{}P X Y <=( ) (A )15; (B )13; (C )25; (D )45. 答案:(A )知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 1提示一: 连续型随机变量的独立性 提示二: 指数分布提示三: 利用联合概率密度计算二维连续型随机向量取值的概率 提示四(同题解) 题型:选择题题解:(),X Y 的联合概率密度为44, 0,0(,) x y e x y f x y --⎧>>=⎨⎩0,其他则440{}44y x y y xyP X Y dy e dx e e dy +∞+∞----≤==-⎰⎰⎰45014()5y y e e dy +∞--=-=⎰,选(A ). 9. 设随机变量X 与Y 相互独立,已知X 服从区间[]0,1上的均匀分布,Y 的分布律如下表所示,则{}1max ,2P X Y ⎧⎫≥⎨⎬⎩⎭为( ) . (A )1; (B )1 ; (C )1; (D )23. 答案:(D )知识点: 随机变量的独立性 参考页: P67 学习目标: 3 难度系数: 2提示一: 连续型随机变量的独立性提示二: 均匀分布 提示三:无 提示四(同题解) 题型:选择题题解:{}{}11max ,1max ,22P X Y P X Y ⎧⎫⎧⎫≥=-<⎨⎬⎨⎬⎩⎭⎩⎭ 11111,12222P X Y P X P Y ⎧⎫⎧⎫⎧⎫=-<<=-<<⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭1221233=-⋅=,选(D ).10. 如果),(Y X 的概率密度,21),(22)1(2)1(-+--=y x e y x f π则X 与Y ( )(A )均服从(0,1)N ; (B )一定相互独立; (C )不一定相互独立; (D )一定不相互独立. 答案:(B )知识点: 二维正态分布 参考页: P74 学习目标: 4 难度系数: 1提示一: 二维正态分布的定义提示二: 二维正态分布的随机变量X 与Y 不相关的充要条件是X 与Y 独立 提示三:无 提示四(同题解) 题型:选择题题解:二维正态分布的定义知,随机变量X 与Y 不相关,所以X 与Y 相互独立. 选(B ). 11.设随机变量,X Y 独立同分布,且X 的分布律是 则min{,}Z X Y =的分布律是( ). (A ) (B )(C ) (D )答案:(B )知识点: 离散型随机变量函数的分布 参考页: P76 学习目标: 5 难度系数: 2提示一: 离散型随机变量函数的分布 提示二: 二维随机变量的独立性 提示三:无 提示四(同题解) 题型:选择题题解:Z 的取值是0,1. {1}{min{,}1}P Z P X Y ==={1,1}P X Y ==={1}{1}P X P Y ===224339=⨯= 5{0}1{1}9P Z P Z ==-==. 故选(B ). 12. 设随机变量,X Y 相互独立,)1,0(~N X ,)1,1(~N Y ,则正确的选项是( ).(A )1{0}2P X Y +≤=; (B )1{1}2P X Y +≤=; (C )1{0}2P X Y -≤=; (D )1{1}2P X Y -≤=.答案:(B )知识点: 连续型随机变量函数的分布 参考页: P78 学习目标: 5 难度系数: 1提示一: 连续型随机变量函数的分布 提示二: 正态分布的性质提示四(同题解) 题型:选择题题解: )1,0(~N X ,)1,1(~N Y ,又,X Y 相互独立,所以~(1,2)X Y N + 由正态分布的性质1{1}2P X Y +≤=. 故选(B ). 13. 设随机变量X Y 、相互独立且均服从正态分布2~(,)X N μσ,则{}1P X Y -<( )(A) 随μ的增加而增加; (B) 随μ的增加而减少; (C) 随σ的增加而增加; (D) 随σ的增加而减少. 答案:(D )知识点: 连续型随机变量函数的分布 参考页: P78 学习目标: 5 难度系数: 2提示一: 连续型随机变量函数的分布提示二: 用标准正态分布函数计算正态变量取值概率 提示三: 分布函数的性质 提示四(同题解) 题型:选择题题解: X Y 、相互独立且均服从正态分布2~(,)X N μσ,所以2~(0,2)X Y N σ- {}1P X Y P -<=<=Φ,选(D )14. 设随机变量,,X Y Z 相互独立, ~(1,2)X N ,~ (22)Y N ,,~ (3,7)Z N , 记{}{},a P X Y b P Y Z =<=<, 则( ).(A) a b <; (B) a b >;(C) a b =; (D) a b ,大小关系不确定. 答案:(B )知识点: 连续型随机变量函数的分布 参考页: P78难度系数: 2提示一: 连续型随机变量函数的分布提示二: 用标准正态分布函数计算正态变量取值概率 提示三: 分布函数的性质 提示四(同题解) 题型:选择题题解: ,,X Y Z 相互独立, ~(1,2)X N ,~ (22)Y N ,,~ (3,7)Z N所以~(1,4), ~(1,9)X Y N Y Z N ---- {}{}10110()222X Y a P X Y P X Y P -++⎧⎫=<=-<=<=Φ⎨⎬⎩⎭ {}{}10110()333Y Z b P Y Z P Y Z P -++⎧⎫=<=-<=<=Φ⎨⎬⎩⎭11()()23Φ>Φ, 由()x Φ单调不减知a b >,故选(B ).15. 随机变量,X Y 独立同分布且X 分布函数为()F x ,则{}max ,Z X Y =分布函数为( )(A) ()2F x ;(B) ()()F x F y ;(C) ()211F x --⎡⎤⎣⎦;(D) ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦.答案:(A )知识点: 连续型随机变量函数的分布 参考页: P78 学习目标: 5 难度系数: 2提示一: 连续型随机变量函数的分布 提示二: 随机变量的独立性 提示三: 分布函数的定义 提示四(同题解) 题型:选择题题解: 2(){max{,}}{,}()Z F z P X Y z P X z Y z F z =≤=≤≤=,选(A ).16. 随机变量,X Y 独立同分布且X 的分布函数为()F x ,则{}min ,Z X Y =的分布函数为( ).(A) ()2F x ;(B) ()()F x F y ;(C) ()211F x --⎡⎤⎣⎦;(D) ()()11F x F y --⎡⎤⎡⎤⎣⎦⎣⎦.答案:(C )知识点: 连续型随机变量函数的分布 参考页: P78 学习目标: 5 难度系数: 2提示一: 连续型随机变量函数的分布 提示二: 随机变量的独立性 提示三: 分布函数的定义 提示四(同题解) 题型:选择题题解:(){min{,}}1{min{,}}Z F z P X Y z P X Y z =≤=->21{,}1[1()]P X z Y z F z =->>=--,选(C ).17.设随机变量X 与Y 相互独立,且X 服从标准正态分布(0,1)N , Y 的分布律为1{0}{1}2P Y P Y ====,记()z F z 为随机变量Z XY =的分布函数,则函数()z F z 的间断点个数为( ). (A )0 ;(B )1 ;(C )2 ;(D )3 .答案:(B )知识点: 连续型随机变量函数的分布 参考页: P78 学习目标: 5 难度系数: 3提示一: 连续型随机变量函数的分布 提示二: 随机变量的独立性提示三: 用标准正态分布函数计算正态变量取值概率 提示四 分布函数的性质 题型:选择题题解:}(}){{P Z z P X z z Y F =≤=≤{0}{0/0}{1}{/1}P Y P z Y P Y P X z Y ==≤=+=≤= 1(), 021[1()], 02XX z z z z ⎧Φ<⎪⎪=⎨⎪+Φ≥⎪⎩ 011lim ()lim ()24z z z F z z --→→=Φ=,0013lim ()lim [1()]24zz z F z z ++→→=+Φ=,选(B ).计算题1. 一电子仪器由两个部件组成,以X 和Y 分别表示两个部件的寿命(单位:千小时)已知,X Y 的联合分布函数为:0.50.50.5()1,0,0(,)0,.xy x y ee e x y F x y ---+⎧--+≥≥⎪=⎨⎪⎩其他(1)问,X Y 是否独立为什么(2)求两个部件的寿命都超过100小时的概率. 答案:(1) ,X Y 独立;(2)0.1e-知识点: 二维随机向量的边缘分布函数 参考页: P59 学习目标: 1 难度系数: 1提示一: 由二维随机向量的联合分布函数确定边缘分布函数 提示二: 随机变量的独立性 提示三:无 提示四(同题解) 题型:计算题题解:(1)先求边缘分布函数:0.51,0,()lim (,)0,0.x X y e x F x F x y x -→+∞⎧-≥==⎨<⎩0.51,0,()lim (,)0,0.y Y x e y F y F x y y -→+∞⎧-≥==⎨<⎩因为(,)()()X Y F x y F x F y =⋅,所以,X Y 独立.(2){0.1,0.1}{0.1}{0.1}[1{0.1}][1{0.1}]P X Y P X P Y P X P Y ≥≥=≥≥=-≤-≤ 0.050.050.1ee e ---=⋅=.2.设随机变量(,)X Y 的联合分布律如下表,求X 和Y 的边缘分布律,并验证X 和Y 的独立性. 答案:,X Y 不独立知识点: 二维离散型随机向量的边缘分布律 参考页: P61 学习目标: 2 难度系数: 1提示一: 由二维离散型随机向量的联合分布律确定边缘分布律 提示二: 随机变量的独立性 提示三:无 提示四(同题解) 题型:计算题题解:先求边缘分布律1{1}={1,1}+{1,2}{1,3}9P X P X Y P X Y P X Y =====+===213{2}={2,1}+{2,2}{2,3}999P X P X Y P X Y P X Y =====+===+=2215{3}={3,1}+{3,2}{3,3}9999P X P X Y P X Y P X Y =====+===++=1225{1}={1,1}+{2,1}{3,1}9999P Y P X Y P X Y P X Y =====+===++=213{2}={1,2}+{2,2}{3,2}999P Y P X Y P X Y P X Y =====+===+=1{3}={1,3}+{2,3}{3,3}9P Y P X Y P X Y P X Y =====+===由于1155{1,1}{1}{1}99981P X Y P X P Y ===≠===⨯=,故X 和Y 不独立. 3. 箱内装有12件产品,其中2件为次品,从箱中随机地取两次产品,每次1件,定义随机变量,X Y 如下:0,1,X ⎧=⎨⎩第一次取出的是正品第一次取出的是次品 0,1,Y ⎧=⎨⎩第二次取出的是正品第二次取出的是次品(1)在有放回抽样情形下求(,)X Y 的联合分布律与边缘分布律; (2)在不放回抽样情形下求(,)X Y 的联合分布律与边缘分布律; (3)问在上述两种情形下X 与Y 是否相互独立 答案:(1)(2)(3)有放回抽样时,X 与Y 相互独立;不放回抽样时,X 与Y 不独立.知识点: 二维离散型随机向量的联合分布律, 二维离散型随机向量的边缘分布律 参考页: P60, P61 学习目标: 2 难度系数: 1提示一: 二维离散型随机向量的联合分布律提示二: 由二维离散型随机向量的联合分布律确定边缘分布律 提示三: 随机变量的独立性 提示四(同题解) 题型:计算题 题解:(1)有放回抽样{}1010250,0121236P X Y ===⋅=(正正) ,{}10250,1121236P X Y ===⋅=(正反) {}21051,0121236P X Y ===⋅=(反正), {}2211,1121236P X Y ===⋅=(反反) (,)X Y 的联合分布律与边缘分布律为(2)不放回抽样{}109150,0121122P X Y ===⋅=(正正) ,{}10250,1121133P X Y ===⋅=(正反) {}21051,0121133P X Y ===⋅=(反正), {}2111,1121166P X Y ===⋅=(反反)(,)X Y 的联合分布律与边缘分布律为(3) 显然,有放回抽样时,X 与Y 相互独立;不放回抽样时,X 与Y 不独立.4.袋中有5个球,分别标有数字1,1,2,2,3,从袋中任取一球后不放回,再取第二次,分别以,X Y 为第一次、第二次取得球上标有的数字,求:(1)(,)X Y 的联合分布律与,X Y 的边缘分布律;(2),X Y 是否独立 答案:(1)(2),X Y 不独立知识点: 二维离散型随机向量的联合分布律, 二维离散型随机向量的边缘分布律 参考页: P60, P61 学习目标: 2 难度系数: 1提示一: 二维离散型随机向量的联合分布律提示二: 由二维离散型随机向量的联合分布律确定边缘分布律 提示三: 随机变量的独立性 提示四(同题解) 题型:计算题题解:(1) {}2111,15410P X Y ===⋅=,{}2211,2545P X Y ===⋅= {}2111,35410P X Y ===⋅=,{}2212,1545P X Y ===⋅={}2112,25410P X Y ===⋅=,{}2112,35410P X Y ===⋅={}1213,15410P X Y ===⋅=,{}1213,25410P X Y ===⋅=(,)X Y 的联合分布律与,X Y 的边缘分布律为(2)因为,,,j i j p p p ⋅⋅⋅≠⨯,所以,X Y 不独立.5. 将一枚硬币连掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值,试写出(,)X Y 的联合分布律及边缘分布律. 答案:知识点: 二维离散型随机向量的联合分布律, 二维离散型随机向量的边缘分布律 参考页: P60, P61 学习目标: 2 难度系数: 1提示一: 二维离散型随机向量的联合分布律提示二: 由二维离散型随机向量的联合分布律确定边缘分布律 提示三:无 提示四(同题解) 题型:计算题题解:一枚硬币连掷三次相当于3重伯努利试验,故1~(3,).2X B 331{}(),0,1,2,32k P X k C k ===,{0,1}{0}{1|0}0P X Y P X P Y X =======,03311{0,3}{0}{3|0}()128P X Y P X P Y X C =======⨯=,13313{1,1}{1}{1|1}()128P X Y P X P Y X C =======⨯=, {1,3}{1}{3|1}0P X Y P X P Y X =======, 23313{2,1}{2}{1|2}()128P X Y P X P Y X C =======⨯=, {2,3}{2}{3|2}0P X Y P X P Y X =======,{3,1}{3}{1|3}0P X Y P X P Y X =======,33311{3,3}{3}{3|3}()128P X Y P X P Y X C =======⨯=,于是(,)X Y 的联合分布律和边缘分布律为6. 袋中有1 个红球,2 个黑球与3 个白球,现有放回地从袋中取两次,每次取一个球.以,,X Y Z 分别表示两次取球所取得的红球、黑球与白球的个数. (1)求{}1/0P X Z ==;(2)求二维随机变量(,)X Y 的联合分布律. 答案: (1)49(2)知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 2 提示一: 条件概率 提示二: 古典概型提示三: 二维离散型随机向量的联合分布律 提示四(同题解) 题型:计算题题解:(1){}1/0P X Z ==11122222{1,0}463{0}96C C P X Z P Z ======. (2),X Y 的可能取值均为0,1,2, 且{}22310,064P X Y ====,{}11232210,163C C P X Y ====, {}22210,269P X Y ====,{}132211,066C P X Y ====,{}122211,169C P X Y ====,{}1,20P X Y ===,{}2112,0636P X Y ====,{}{}2,12,20P X Y P X Y ======. 所以二维随机变量(,)X Y 的联合分布律为7. 箱内有6个球,其中红球,白球,黑球个数分别为1,2,3. 现从箱中随机地取两个球,以,X Y 分别表示取得的红球与白球的个数. 求随机变量(,)X Y 的联合分布律. 答案:知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 2 提示一: 古典概型提示二: 二维离散型随机向量的联合分布律 提示三: 无 提示四(同题解) 题型:计算题题解:X 的可能取值为0,1, Y 的可能取值为0,1,2, 于是{}232610,05C P X Y C ====,{}11232620,15C C P X Y C ====,{}222610,215C P X Y C ====,{}11132611,05C C P X Y C ====,{}11122621,115C C P X Y C ====,{}1,20P X Y ===.所以随机变量(,)X Y 的联合分布律为8. 已知随机变量,X Y 以及XY 的分布律如下表所示,求{2}P X Y =. 答案:14知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 2提示一: 二维离散型随机向量的联合分布律与边缘分布律的关系 提示二: 利用联合分布律计算二维离散型随机向量取值的概率 提示三: 无 提示四(同题解) 题型:计算题题解:1{4}{2,2}12P XY P X Y =====; {2}{2,1}{1,2}0P XY P X Y P X Y ====+===;1{1}{1,1}3P XY P X Y =====; 由已知,X Y 的分布律可确定(,)X Y 取其他值时的概率,(,)X Y 的联合分布律为故{2}{0,0}{2,1}044P X Y P X Y P X Y ====+===+=. 9. 设随机变量X 的概率分布为2Y X =,求二维随机变量(,)X Y 的联合分布律.答案:知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 2提示一: 二维离散型随机向量的联合分布律与边缘分布律的关系 提示二: 二维离散型随机向量的联合分布律 提示三: 无 提示四(同题解) 题型:计算题 题解:{1,0}0P X Y =-==,1{1,1}{1}4P X Y P X =-===-=1{0,0}{0}2P X Y P X =====,{0,1}0P X Y === {1,0}0P X Y ===,1{1,1}{1}4P X Y P X =====10. 设随机变量X 与Y 独立同分布,其中X 的概率分布为记max{,}U X Y =,min{,}V X Y =. 求(,)U V 的联合分布律. 答案:知识点: 二维离散型随机向量的联合分布律 参考页: P60 学习目标: 2 难度系数: 2提示一: 二维离散型随机向量的联合分布律与边缘分布律的关系 提示二: 二维离散型随机向量的联合分布律 提示三: 无 提示四(同题解) 题型:计算题题解:4{1,1}{1,1}9P U V P X Y ======4{2,1}{1,2}{2,1}9P U V P X Y P X Y =====+=== 1{2,2}{2,2}9P U V P X Y ======. (,)U V 的联合概率分布律为11.设随机变量Z 服从[2,2]-上的均匀分布,令随机变量1,11,1Z X Z ⎧-≤-⎪=⎨⎪>-⎩若若,1,11,1Z Y Z ⎧-≤⎪=⎨⎪>⎩若若,试求:(1)(,)X Y 的联合分布律;(2)关于X 和关于Y 的边缘分布律; (3)判断X 与Y 是否独立 答案:(1)(2)(3)X 与Y 不独立.知识点: 二维离散型随机向量的联合分布律, 二维离散型随机向量的边缘分布律 参考页: P60, P61 学习目标: 2 难度系数: 2提示一: 二维离散型随机向量的联合分布律 提示二: 均匀分布提示三: 由二维离散型随机向量的联合分布律确定边缘分布律 提示四: 随机变量的独立性 题型:计算题题解:(1)(,)X Y 的可能取值为(-1,-1),(-1,1),(1,-1),(1,1),且1211{1,1}{1,1}{1}44P X Y P Z Z P Z dx --=-=-=≤-≤=≤-==⎰{1,1}{1,1}0P X Y P Z Z =-==≤->=1111{1,1}{1,1}{11}42P X Y P Z Z P Z dx -==-=>-≤=-<≤==⎰2111{1,1}{1,1}{1}44P X Y P Z Z P Z dx ===>->=>==⎰故(,)X Y 的联合分布律为(2)X 与Y 的边缘分布律为(3)因为有1{1,1}{1}{1}4P X Y P X P Y =-=-=≠=-=-, 故X 与Y 不相互独立.12. 设随机变量X 服从参数1λ=的指数分布,令0, ln 21, ln 2X U X <⎧=⎨≥⎩,0, ln31, ln3X V X <⎧=⎨≥⎩ (1)求(,)U V 的联合分布律; (2)判断U 与V 是否相互独立 答案:(1)(2)U 与V 不独立.知识点: 二维离散型随机向量的联合分布律, 二维离散型随机向量的边缘分布律 参考页: P60, P61 学习目标: 2 难度系数: 2提示一: 二维离散型随机向量的联合分布律 提示二: 指数分布提示三: 由二维离散型随机向量的联合分布律确定边缘分布律 提示四: 随机变量的独立性 题型:计算题题解:(1){0,0}{ln2,ln3}{ln2}P U V P X X P X ===<<=<ln 211122x e dx -==-=⎰{0,1}{ln 2,ln3}0P U V P X X ===<>={1,0}{ln2,ln3}{ln2ln3}P U V P X X P X ===≥<=≤<ln 3ln 2111236x e dx -==-=⎰{1,1}{ln2,ln3}{ln3}P U V P X X P X ===≥≥=≥ln 313x e dx +∞-==⎰(,)U V 的联合分布律为(2) 由于{0,0}{0}{0}P U V P U P V ==≠==,所以U 与V 不独立. 13. 设(,)X Y 的联合概率密度为1(6),02,24(,)80,x y x y f x y ⎧--<<<<⎪=⎨⎪⎩其他又(1){(,)|1,3}D x y x y =<<;(2){(,)|3}D x y x y =+<. 求{(,)}P X Y D ∈ 答案:(1)38 (2) 524知识点: 二维连续型随机向量的联合概率密度 参考页: P63 学习目标: 2 难度系数: 1提示一: 利用联合概率密度计算二维连续型随机向量取值的概率 提示二:无 提示三:无 提示四(同题解) 题型:计算题题解:(1)13021{(,)}(6)8P x y D x y dxdxy ∈=--⎰⎰1194368228-⎡⎤=--=⎢⎥⎣⎦; (2)13021{(,)}(6)8x P X Y D x y dxdy -∈=--⎰⎰11200113(1)[(3)4]82x x dx x dx ⎧⎫=-----⎨⎬⎩⎭⎰⎰524=.14.设(,)X Y 的联合概率密度为6(1),01(,)0,y x y f x y -<<<⎧=⎨⎩其他(1) 求}5.0,5.0{>>Y X P ; (2) 求}5.0{<X P 和}5.0{<Y P ; (3) 求}1{<+Y X P . 答案:(1)18 (2) 78,12 (3) 34知识点: 二维连续型随机向量的联合概率密度 参考页: P63 学习目标: 2难度系数: 1提示一: 利用联合概率密度计算二维连续型随机向量取值的概率 提示二:无 提示三:无 提示四(同题解) 题型:计算题题解: (1) }5.0,5.0{>>Y X P 11120.50.516(1)6(1)2x y dydx x dx =-=-⎰⎰⎰18=; (2) }5.0{<X P 0.510.520016(1)6(1)2x y dydx x dx =-=-⎰⎰⎰78=,}5.0{<Y P 0.50.50.5200116(1)6[(1)]24x y dydx x dx =-=--⎰⎰⎰12=;(3) }1{<+Y X P 0.510.5220016(1)6[(1)]2x x y dydx x x dx -=-=--⎰⎰⎰34=.15. 设二维随机向量(,)X Y 的联合概率密度为(1),0,0,1(,)0,Ay x y x y x y f x y -->>+<⎧=⎨⎩其他 (1) 求常数A ;(2) 求{}P Y X <.答案:(1) 24 (2)14知识点: 二维连续型随机向量的联合概率密度 参考页: P63 学习目标: 2 难度系数: 1提示一: 二维连续型随机向量联合概率密度的性质提示二: 利用联合概率密度计算二维连续型随机向量取值的概率 提示三:无 提示四(同题解) 题型:计算题题解:(1) 由联合概率密度的正则性,有1101(,)(1)xf x y dxdy Ay x y dydx +∞+∞--∞-∞==--⎰⎰⎰⎰3310(1)(1)[]23x x A dx --=-⎰24A=, 所以24A =.(2)1112221{}24(1)12(12)4y yP Y X dy y x y dx y y dy -<=--=-=⎰⎰⎰. 16. 设 随机变量),(Y X 的分布函数为),(y x F = )23)(22(ππ++y arctg x arctgA ,试求(1)A ;(2)),(Y X 的联合概率密度(,)f x y ;(3)求X 与Y 的边缘概率密度)(x f X ,)(y f Y ;(4)X 与Y 是否独立 答案:(1)21π (2)2226(4)(9)x y π++ (3) 22()(4)X f x x π=+,23()(9)Yf y y π=+ (4),X Y 独立知识点: 二维随机向量的联合分布函数 二维连续型随机向量的联合概率密度, 二维连续型随机向量的边缘概率密度 参考页: P59, P63,P66 学习目标: 1,2 难度系数: 2提示一: 二维随机向量的联合分布函数的性质提示二: 二维连续型随机向量联合分布函数与联合概率密度的关系 提示三: 利用二维连续型随机向量的联合概率密度计算边缘概率密度 提示四: 随机变量的独立性 题型:计算题题解:(1) (,)[][]12222F A ππππ+∞+∞=++=,21A π= (2)2226(,)(,)(4)(9)XY f x y F x y x y π''==++(3)22()(,)(4)X f x f x y dy x π+∞-∞==+⎰)9(3),()(2y dx y x f y f Y +==⎰+∞∞=π (4)(,)()(),X Y f x y f x f y x y ∴=⋅-∞<<+∞,X Y 相互独立.17. 设(,)X Y 的联合概率密度为(34)0,0,(,)0,x y x y ke f x y -+>>⎧=⎨⎩其他(1) 求常数k ;(2) 求(,)X Y 的联合分布函数(,)F x y ; (3) 求{}01,02P X Y <≤<≤;(4) 求{}(,)P X Y D ∈,区域{}343,0,0),(<+>>=y x y x y x D .答案:(1) 12 (2) 340,0(1)(1),(,)0,x y x y e e F x y -->>⎧--=⎨⎩其他 (3) 38(1)(1)e e ---- (4)314e --知识点: 二维随机向量的联合分布函数 二维连续型随机向量的联合概率密度 参考页: P59, P63 学习目标: 1,2 难度系数: 2提示一: 二维连续型随机向量联合概率密度的性质提示二: 二维连续型随机向量联合分布函数与联合概率密度的关系 提示三: 利用联合概率密度计算二维连续型随机向量取值的概率 提示四:(同题解) 题型:计算题 题解:(1) (34)01(,)x y f x y dxdy k e dxdy +∞+∞+∞+∞-+-∞-∞==⎰⎰⎰⎰34340()()1212x y xyk kke dx e dy e e +∞+∞---+∞-+∞===⎰⎰, 12k =; (2) 0,0x y >>(34)0(,)(,)12xyxyu v F x y f u v dudv e dudv -+-∞-∞==⎰⎰⎰⎰34343400034()()(1)(1)xy u v u x v yx y e du e dv e e e e ------=⋅==--⎰⎰340,0(1)(1),(,) 0,x y x y e e F x y -->>⎧--=⎨⎩其他;(3) {}01,02(0,0)(1,2)(0,2)(1,0)(1,2)P X Y F F F F F <≤<≤=+--=38(1)(1)e e --=--; (4) {}331(34)4(,)(,)12x x y DP X Y D f x y dxdy e dxdy --+∈==⎰⎰⎰⎰133-3303(1)14x x e e dx e --=--=-⎰.18.设随机变量,X Y 相互独立,且都服从(,)b b -上的均匀分布,求方程20t tX Y ++=有实根的概率.答案:4b ≤时,1242b +;4b >时,1-知识点: 二维连续型随机向量的联合概率密度 参考页: P63 学习目标: 2 难度系数: 3提示一: 利用联合概率密度计算二维连续型随机向量取值的概率 提示二: 均匀分布 提示三:无 提示四(同题解) 题型:计算题题解: 设A ={方程有实根},则A 发生240X Y ⇔-≥ 即 224()(4)(,)x yP A P X Y f x y dxdy ≥=≥=⎰⎰2242211()444x bb bbb x dxdy b dx b b ---==+⎰⎰⎰ 32211[2]46242b b b b =+=+, 4b ≤.2221(4)1()44x P X Y b dx b -≥=--⎰33222111[4(88)]412b b b =-+1=19.已知随机变量X 和Y 的联合概率密度为4,01,01(,)0,xy x y f x y ≤≤≤≤⎧=⎨⎩其他求X 和Y 的联合分布函数.答案:22220,00,,01,01(,),01,1,,1,01,1,1, 1.x y x y x y F x y x x y y x y x y ⎧<<⎪≤≤≤≤⎪⎪=≤≤>⎨⎪>≤≤⎪⎪>>⎩或 知识点: 二维随机向量的联合分布函数 二维连续型随机向量的联合概率密度 参考页: P59, P63 学习目标: 1,2 难度系数: 2提示一: 二维连续型随机向量联合分布函数与联合概率密度的关系 提示二:无 提示三:无 提示四:无 题型:计算题题解1:设(,)X Y 的分布函数为(,)F x y ,由联合概率密度定义有(,)(,)x y F x y f u v dudv -∞+∞=⎰⎰001001000,00,4,01,01,4,01,1,4,1,01,1,1, 1.x y x y x y uvdudv x y uydudy x y xvdxdv x y x y ⎧<<⎪⎪≤≤≤≤⎪⎪⎪=≤≤>⎨⎪⎪>≤≤⎪⎪>>⎪⎩⎰⎰⎰⎰⎰⎰或22220,00,,01,01,,01,1,,1,01,1,1, 1.x y x y x y x x y y x y x y ⎧<<⎪≤≤≤≤⎪⎪=≤≤>⎨⎪>≤≤⎪⎪>>⎩或题解2:由联合概率密度得边缘概率密度分别为2,01,()0,;X x x f x ≤≤⎧=⎨⎩其他 2,01()0,Y y y f y ≤≤⎧=⎨⎩其他,所以,X Y 独立.,X Y 边缘分布函数分别为(),()X Y F x F y ,20,0,()(),01,1, 1.x X X x F x f u du x x x -∞<⎧⎪==≤≤⎨⎪>⎩⎰20,0,()(),01,1, 1.y Y X y F y f v dv y y y -∞<⎧⎪==≤≤⎨⎪>⎩⎰设(,)X Y 的分布函数为(,)F x y ,则22220,00,,01,01(,)()(),01,1,,1,01,1,1, 1.X Y x y x y x y F x y F x F y x x y y x y x y ⎧<<⎪≤≤≤≤⎪⎪=⋅=≤≤>⎨⎪>≤≤⎪⎪>>⎩或20. 设随机变量(,)X Y 在区域D 上服从均匀分布,求(,)X Y 的联合分布函数. 其中D 是由x 轴、y 轴及直线21y x =+所围三角形区域.答案:22210 02142 002121(,)441 02122 >00<11 >01x y xy y y x y x F x y x x x y x y y x y x y ⎧≤-≤⎪⎪⎪+--<≤<≤+⎪⎪⎪=++-<≤>+⎨⎪⎪-≤⎪>⎪⎪⎪⎩,或,且,且,且,且 知识点: 二维随机向量的联合分布函数 二维连续型随机向量的联合概率密度 参考页: P59, P63 学习目标: 1,2难度系数: 3提示一: 二维均匀分布提示二: 二维连续型随机向量联合分布函数与联合概率密度的关系 提示三:无 提示四:无 题型:计算题 题解:图3-1 图3-2区域D 如图3-1所示.由二维均匀分布的定义知,(,)X Y 的联合概率密度为4, (,)(,)0, x y Dx y ϕ∈⎧=⎨⎩其他将区域分为五块区域,如图3-2 ① 当12x ≤-或0y ≤时 因为(,)0x y ϕ=,所以(,)0F x y =; ② 当102x -<≤且021y x <≤+时,因为(,)4x y ϕ= 所以(,)(,)x y F x y u v dudv ϕ-∞-∞=⎰⎰1(1)24yx y dudv -=⎰⎰242xy y y =+-;③ 当102x -<≤且21y x >+时 (,)(,)x yF x y u v dudv ϕ-∞-∞=⎰⎰211 024xx dvdu +-=⎰⎰2441x x =++;④ 当0x >且0<1y ≤时,)(,)x y F x y u v dudv ϕ-∞-∞=⎰⎰(01(1)24y y dudv -=⎰⎰22y y =-;⑤ 当0x >且1y >时0211 02(,)4x F x y dvdu +-=⎰⎰1=.综上所述,(,)X Y 的联合分布函数为22210 02142 002121(,)441 02122 >00<11 >01x y xy y y x y x F x y x x x y x y y x y x y ⎧≤-≤⎪⎪⎪+--<≤<≤+⎪⎪⎪=++-<≤>+⎨⎪⎪-≤⎪>⎪⎪⎪⎩,或,且,且,且,且. 21. 设(,)X Y 在区域G 上服从均匀分布,其中G 是由0x y -=,2x y +=与0y =所围成的三角形区域, 求X 和Y 的边缘概率密度()X f x 和()Y f y .答案:,01()2,120, X x x f x x x ≤≤⎧⎪=-<≤⎨⎪⎩其他,2(1),01()0,Y y y f x -≤≤⎧=⎨⎩其他知识点: 二维连续型随机向量的边缘概率密度 参考页: P66 学习目标: 2 难度系数: 2提示一: 利用二维连续型随机向量的联合概率密度计算边缘概率密度 提示二:无 提示三:无 提示四:无 题型:计算题 题解: 1,01,2(,)0,y y x yf x y <<<<-⎧=⎨⎩其他当10≤≤x 时, 0()(,)1xX f x f x y dy dy x +∞-∞===⎰⎰当12x <≤时, 20()(,)12xX f x f x y dy dy x +∞--∞===-⎰⎰,01()2,120, X x x f x x x ≤≤⎧⎪=-<≤⎨⎪⎩其他.当10≤≤y 时,2()(,)122y Y yf y f x y dx dx y +∞--∞===-⎰⎰2(1),01()0,Y y y f x -≤≤⎧=⎨⎩其他. 22. 设二维随机变量),Y X (的联合概率密度为, 01, 01(,)0, A x y f x y <<<<⎧=⎨⎩其他 求:(1) 参数A ;(2)X 和Y 的边缘概率密度并判断X 和Y 是否独立;答案:(1) 1 (2) 1,01()0,X x f x <<⎧=⎨⎩其他 1,01()0,Y y f y <<⎧=⎨⎩其他,X Y 独立知识点: 二维连续型随机向量的联合概率密度, 二维连续型随机向量的边缘概率密度 参考页: P63,P66 学习目标: 2 难度系数: 1提示一: 二维连续型随机向量的联合概率密度性质提示二: 利用二维连续型随机向量的联合概率密度计算边缘概率密度 提示三: 随机变量的独立性 提示四: (同题解) 题型:计算题 题解:(1)(,)1f x y dydx +∞+∞-∞-∞=⎰⎰,1A ⇒=(2)当10<<x 时,10()(,)11X f x f x y dy dy +∞-∞===⎰⎰当10<<y 时,10()(,)11Y f y f x y dx dx +∞-∞===⎰⎰()()(,)X Y f x f y f x y ⋅=,所以X 和Y 独立.23. 设(,)X Y 的联合概率密度为212,(,)0xy x y f x y ⎧≤≤⎪=⎨⎪⎩, 其他(1) 求,X Y 的边缘概率密度()X f x 和()Y f y ; (2) 问X 与Y 是否独立答案:(1) 256(),01()0,X x x x f x ⎧-≤≤=⎨⎩其他, 256(),01()0,Y y y y f y ⎧-≤≤=⎨⎩其他(2) ,X Y 不独立知识点: 二维连续型随机向量的边缘概率密度 参考页: P66 学习目标: 2 难度系数: 2提示一: 利用二维连续型随机向量的联合概率密度计算边缘概率密度 提示二: 随机变量的独立性 提示三: 无 提示四: (同题解) 题型:计算题题解:(1)当10≤≤x 时, 225()(,)6()X xf x f x y dy xydy x x +∞-∞===-⎰其他, 0)(=x f X当10≤≤y 时,225()(,)6()Y yf y f x y dx xydx y y +∞-∞===-⎰其他, 0)(=y f Y即256(),01()0,X x x x f x ⎧-≤≤=⎨⎩其他, 256(),01()0,Y y y y f y ⎧-≤≤=⎨⎩其他(2)因为)()(),(y f x f y x f Y X ≠,所以X 和Y 不独立.24. 设二维随机变量(,)X Y 的联合概率密度为215,01(,)0,xy y x f x y ⎧≤≤≤=⎨⎩其他,求关于,X Y 的边缘概率密度()X f x , ()Y f y ,并判别X 与Y 的独立性.答案:(1) 45, 01()0, X x x f x ⎧≤≤=⎨⎩其他, ()22151, 01()20, Y y y y f y ⎧-≤≤⎪=⎨⎪⎩其他(2) ,X Y 不独立知识点: 二维连续型随机向量的边缘概率密度 参考页: P66 学习目标: 2 难度系数: 2提示一: 利用二维连续型随机向量的联合概率密度计算边缘概率密度 提示二: 随机变量的独立性 提示三: 无 提示四: (同题解) 题型:计算题 题解:(1)()()24015, 015, 01,0, 0, xX xy dy x x x f x f x y dy +∞-∞⎧⎧≤≤≤≤⎪===⎨⎨⎩⎪⎩⎰⎰其他其他()()()12221515, 011, 01,20, 0, y Y xy dy y y y y f y f x y dx +∞-∞⎧⎧≤≤-≤≤⎪⎪===⎨⎨⎪⎪⎩⎩⎰⎰其他其他 (2)因为()()(),X Y f x y f x f y ≠,所以,X 与Y 不独立. 25. 设随机变量(,)X Y 的概率密度为6, 01(,)0, y y x f x y <<<⎧=⎨⎩其他(1)试求关于X 与Y 的边缘概率密度;(2)判断X 与Y 是否相互独立,并说明理由.答案:(1) 23,01()0,X x x f x ⎧<<=⎨⎩其他, 6(1),01()0,Y y y y f y -<<⎧=⎨⎩其他(2) ,X Y 不独立知识点: 二维连续型随机向量的边缘概率密度 参考页: P66 学习目标: 2 难度系数: 2提示一: 利用二维连续型随机向量的联合概率密度计算边缘概率密度。
概率论与数理统计习题及答案第3章习题详解

习题三1.将一硬币抛掷三次,以X 表示在三次中出现正面的次数,以Y 表示三次中出现正面次数与出现反面次数之差的绝对值.试写出X 和Y 的联合分布律. 111222⨯⨯111222⨯⨯=2.盒子里装有3只黑球、2只红球、2只白球,在其中任取4只球,以X 表示取到黑球的只数,以Y 表示取到红球的只数.求X 和Y 的联合分布律. 【解】X 和Y 的联合分布律如表: 23247C 3C 35= 13247C 2C 35= 1232247C C 6C 35= 1132247C C 12C 35= 13247C 2C 35= 2427C /C =2132247C C 6C 35= 23247C 3C 35=3.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎪⎩⎪⎨⎧≤≤≤≤.,020,20,sin sin 其他ππy x y x求二维随机变量(X ,Y )在长方形域⎭⎬⎫⎩⎨⎧≤<≤<36,40πππy x 内的概率. 【解】如图πππ{0,}(3.2)463P X Y <≤<≤公式 ππππππ(,)(,)(0,)(0,)434636F F F F --+ππππππsin sin sin sin sin 0sin sin 0sin 4346362(31).4=--+=-题3图说明:也可先求出密度函数,再求概率。
4.设随机变量(X ,Y )的分布密度f (x ,y )=⎩⎨⎧>>+-.,0,0,0,)43(其他y x A y x e求:(1) 常数A ;(2) 随机变量(X ,Y )的分布函数; (3) P {0≤X <1,0≤Y <2}. 【解】(1) 由-(34)0(,)d d e d d 112x y Af x y x y A x y +∞+∞+∞+∞+-∞-∞===⎰⎰⎰⎰得 A =12 (2) 由定义,有 (,)(,)d d y xF x y f u v u v -∞-∞=⎰⎰(34)340012ed d (1e )(1e )0,0,0,0,y yu v x y u v y x -+--⎧⎧-->>⎪==⎨⎨⎩⎪⎩⎰⎰其他(3) {01,02}P X Y ≤<≤<12(34)3800{01,02}12e d d (1e )(1e )0.9499.x y P X Y x y -+--=<≤<≤==--≈⎰⎰5.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<<--.,0,42,20),6(其他y x y x k(1) 确定常数k ;(2) 求P {X <1,Y <3}; (3) 求P {X <1.5}; (4) 求P {X +Y ≤4}. 【解】(1) 由性质有242(,)d d (6)d d 81,f x y x y k x y y x k +∞+∞-∞-∞=--==⎰⎰⎰⎰故 18R =(2) 13{1,3}(,)d d P X Y f x y y x -∞-∞<<=⎰⎰130213(6)d d 88k x y y x =--=⎰⎰ (3) 11.5{ 1.5}(,)d d a (,)d d x D P X f x y x y f x y x y <<=⎰⎰⎰⎰如图1.542127d (6)d .832x x y y =--=⎰⎰(4) 24{4}(,)d d (,)d d X Y D P X Y f x y x y f x y x y +≤+≤=⎰⎰⎰⎰如图b240212d (6)d .83xx x y y -=--=⎰⎰题5图6.设X 和Y 是两个相互独立的随机变量,X 在(0,0.2)上服从均匀分布,Y 的密度函数为f Y (y )=⎩⎨⎧>-.,0,0,55其他y y e求:(1) X 与Y 的联合分布密度;(2) P {Y ≤X }.题6图【解】(1) 因X 在(0,0.2)上服从均匀分布,所以X 的密度函数为1,00.2,()0.20,.X x f x ⎧<<⎪=⎨⎪⎩其他 而55e ,0,()0,.y Y y f y -⎧>=⎨⎩其他所以(,),()()X Y f x y X Y f x f y 独立5515e25e ,00.20,0.20,0,yy x y --⎧⎧⨯<<>⎪==⎨⎨⎩⎪⎩且其他. (2) 5()(,)d d 25e d d y y xDP Y X f x y x y x y -≤≤=⎰⎰⎰⎰如图0.20.2-550-1d 25e d (5e 5)d =e 0.3679.xyx x y x-==-+≈⎰⎰⎰7.设二维随机变量(X ,Y )的联合分布函数为F (x ,y )=⎩⎨⎧>>----.,0,0,0),1)(1(24其他y x y x e e求(X ,Y )的联合分布密度.【解】(42)28e ,0,0,(,)(,)0,x y x y F x y f x y x y -+⎧>>∂==⎨∂∂⎩其他. 8.设二维随机变量(X ,Y )的概率密度为f (x ,y )= 4.8(2),01,0,0,.y x x y x -≤≤≤≤⎧⎨⎩其他求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰x204.8(2)d 2.4(2),01,=0,.0,y x y x x x ⎧⎧--≤≤⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰12y 4.8(2)d 2.4(34),01,=0,.0,y x x y y y y ⎧-⎧-+≤≤⎪=⎨⎨⎩⎪⎩⎰其他题8图 题9图9.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<-.,0,0,其他e y x y求边缘概率密度. 【解】()(,)d X f x f x y y +∞-∞=⎰e d e ,0,=0,.0,y x x y x +∞--⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰0e d e ,0,=0,.0,yy x x y y --⎧⎧>⎪=⎨⎨⎩⎪⎩⎰其他题10图10.设二维随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧≤≤.,0,1,22其他y x y cx(1) 试确定常数c ;(2) 求边缘概率密度. 【解】(1)(,)d d (,)d d Df x y x y f x y x y +∞+∞-∞-∞⎰⎰⎰⎰如图2112-14=d d 1.21xx cx y y c ==⎰⎰ 得214c =. (2) ()(,)d X f x f x y y +∞-∞=⎰212422121(1),11,d 840,0,.x x x x x y y ⎧⎧--≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他 ()(,)d Y f y f x y x +∞-∞=⎰522217d ,01,420,0, .y y x y x y y -⎧⎧≤≤⎪⎪==⎨⎨⎪⎪⎩⎩⎰其他 11.设随机变量(X ,Y )的概率密度为f (x ,y )=⎩⎨⎧<<<.,0,10,,1其他x x y求条件概率密度f Y |X (y |x ),f X |Y (x |y ).题11图【解】()(,)d X f x f x y y +∞-∞=⎰1d 2,01,0,.x x y x x -⎧=<<⎪=⎨⎪⎩⎰其他111d 1,10,()(,)d 1d 1,01,0,.y Y y x y y f y f x y x x y y -+∞-∞⎧=+-<<⎪⎪⎪===-≤<⎨⎪⎪⎪⎩⎰⎰⎰其他所以|1,||1,(,)(|)2()0,.Y X X y x f x y f y x xf x ⎧<<⎪==⎨⎪⎩其他|1, 1,1(,)1(|),1,()10,.X Y Y y x y f x y f x y y x f y y⎧<<⎪-⎪⎪==-<<⎨+⎪⎪⎪⎩其他12.袋中有五个号码1,2,3,4,5,从中任取三个,记这三个号码中最小的号码为X ,最大的号码为Y .(1) 求X 与Y 的联合概率分布; (2) X 与Y 是否相互独立? 【解】(1) X 与Y 的联合分布律如下表3 4 5{}i P X x =13511C 10= 3522C 10= 3533C 10= 610 23511C 10=3522C 10=310 3 02511C 10= 110{}i P Y y =110 310610(2) 因6161{1}{3}{1,3},101010010P X P Y P X Y ===⨯=≠=== 故X 与Y 不独立13.设二维随机变量(X ,Y )的联合分布律为 2 5 80.4 0.80.15 0.30 0.35 0.05 0.12 0.03(1)求关于X 和关于Y 的边缘分布; (2) X 与Y 是否相互独立? 【解】(1)X 和Y 的边缘分布如下表2 5 8 P {Y=y i } 0.4 0.15 0.30 0.35 0.8 0.80.05 0.12 0.03 0.2{}i P X x =0.20.420.38YXXYXY(2) 因{2}{0.4}0.20.8P X P Y ===⨯0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独立.14.设X 和Y 是两个相互独立的随机变量,X 在(0,1)上服从均匀分布,Y 的概率密度为f Y (y )=⎪⎩⎪⎨⎧>-.,0,0,212/其他y y e (1)求X 和Y 的联合概率密度;(2) 设含有a 的二次方程为a 2+2Xa +Y =0,试求a 有实根的概率.【解】(1) 因1,01,()0,X x f x <<⎧==⎨⎩其他; 21e ,1,()20,yY y f y -⎧>⎪==⎨⎪⎩其他.故/21e01,0,(,),()()20,.y X Y x y f x y X Y f x f y -⎧<<>⎪=⎨⎪⎩独立其他题14图(2) 方程220a Xa Y ++=有实根的条件是2(2)40X Y ∆=-≥故 X 2≥Y ,从而方程有实根的概率为:22{}(,)d d x yP X Y f x y x y ≥≥=⎰⎰21/2001d e d 212[(1)(0)]0.1445.x y x yπ-==-Φ-Φ=⎰⎰15.设X 和Y 分别表示两个不同电子器件的寿命(以小时计),并设X 和Y 相互独立,且服从同一分布,其概率密度为f (x )=⎪⎩⎪⎨⎧>.,0,1000,10002其他x x求Z =X /Y 的概率密度.【解】如图,Z 的分布函数(){}{}Z XF z P Z z P z Y=≤=≤ (1) 当z ≤0时,()0Z F z =(2) 当0<z <1时,(这时当x =1000时,y =1000z)(如图a) 3366102222101010()d d d d yz Z zx y zF z x y y x x y x y +∞≥==⎰⎰⎰⎰ 33610231010=d 2z zy yzy +∞⎛⎫-= ⎪⎝⎭⎰题15图(3) 当z ≥1时,(这时当y =103时,x =103z )(如图b )3366222210101010()d d d d zy Z xy zF z x y y x x yx y +∞≥==⎰⎰⎰⎰ 336231010101=d 12y y zy z +∞⎛⎫-=- ⎪⎝⎭⎰即 11,1,2(),01,20,.Z z z zf z z ⎧-≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 故 21,1,21(),01,20,.Z z z f z z ⎧≥⎪⎪⎪=<<⎨⎪⎪⎪⎩其他 16.设某种型号的电子管的寿命(以小时计)近似地服从N (160,202)分布.随机地选取4 只,求其中没有一只寿命小于180的概率.【解】设这四只寿命为X i (i =1,2,3,4),则X i ~N (160,202),从而123412{min(,,,)180}{180}{180}i P X X X X X P X P X ≥≥≥之间独立34{180}{180}P X P X ≥≥ 1234[1{180}][1{180}][1{180}][1{180}]P X P X P X P X =-<-<-<-<44144180160[1{180}]120[1(1)](0.158)0.00063.P X ⎡-⎤⎛⎫=-<=-Φ ⎪⎢⎥⎝⎭⎣⎦=-Φ== 17.设X ,Y 是相互独立的随机变量,其分布律分别为P {X =k }=p (k ),k =0,1,2,…, P {Y =r }=q (r ),r =0,1,2,….证明随机变量Z =X +Y 的分布律为P {Z =i }=∑=-ik k i q k p 0)()(,i =0,1,2,….【证明】因X 和Y 所有可能值都是非负整数,所以 {}{}Z i X Y i ==+={0,}{1,1}{,0}X Y i X Y i X i Y =====-==于是0{}{,},i k P Z i P X k Y i k X Y =====-∑相互独立0{}{}ik P X k P Y i k ===-∑()()ik p k q i k ==-∑18.设X ,Y 是相互独立的随机变量,它们都服从参数为n ,p 的二项分布.证明Z =X +Y 服从参数为2n ,p 的二项分布.【证明】方法一:X +Y 可能取值为0,1,2,…,2n .{}{,}ki P X Y k P X i Y k i =+====-∑00202(){}2ki ki n i k i n k ii k k n k i k n k P X i P Y k i n n p q p q i k i n n p qi k i n p q k =---+=-=-===-⎛⎫⎛⎫= ⎪ ⎪-⎝⎭⎝⎭⎛⎫⎛⎫= ⎪⎪-⎝⎭⎝⎭⎛⎫= ⎪⎝⎭∑∑∑方法二:设μ1,μ2,…,μn ;μ1′,μ2′,…,μn ′均服从两点分布(参数为p ),则X =μ1+μ2+…+μn ,Y =μ1′+μ2′+…+μn ′, X +Y =μ1+μ2+…+μn +μ1′+μ2′+…+μn ′,所以,X +Y 服从参数为(2n ,p )的二项分布.(1) 求P {X =2|Y =2},P {Y =3|X =0}; (2) 求V =max (X ,Y )的分布律; (3) 求U =min (X ,Y )的分布律; (4) 求W =X +Y 的分布律. 【解】(1){2,2}{2|2}{2}P X Y P X Y P Y ======5{2,2}0.051,0.252{,2}i P X Y P X i Y ========∑ {3,0}{3|0}{0}P Y X P Y X P X ======3{0,3}0.011;0.033{0,}j P X Y P X Y j ========∑ (2){}{max(,)}{,}{,}P V i P X Y i P X i Y i P X i Y i ====<+≤=10{,}{,},i ik k P X i Y k P X k Y i -=====+==∑∑ 0,1,2,3,4,5i =所以V 的分布律为 V =max(X ,Y ) 0 1 2 3 4 5 P 00.040.160.280.240.28(3) {}{min(,)}P U i P X Y i ===351{,}{,}{,}{,}k ik i P X i Y i P X i Y i P X i Y k P X k Y i ==+==≥+>====+==∑∑0,1,2,3,i =于是 U =min(X ,Y ) 0 1 2 3 P0.280.300.250.17(4)类似上述过程,有W =X +Y 0 1 2 3 4 5 6 7 8 P0.020.060.130.190.240.190.120.0520.雷达的圆形屏幕半径为R ,设目标出现点(X ,Y )在屏幕上服从均匀分布. (1) 求P {Y >0|Y >X };(2) 设M =max{X ,Y },求P {M >0}.题20图【解】因(X ,Y )的联合概率密度为22221,,(,)π0,.x y R f x y R⎧+≤⎪=⎨⎪⎩其他 (1){0,}{0|}{}P Y Y X P Y Y X P Y X >>>>=>0(,)d (,)d y y xy xf x y f x y σσ>>>=⎰⎰⎰⎰π2π/405π42π/401d d π1d d πRR r rR r rR θθ=⎰⎰⎰⎰3/83;1/24== (2) {0}{max(,)0}1{max(,)0}P M P X Y P X Y >=>=-≤00131{0,0}1(,)d 1.44x y P X Y f x y σ≤≤=-≤≤=-=-=⎰⎰21.设平面区域D 由曲线y =1/x 及直线y =0,x =1,x=e 2所围成,二维随机变量(X ,Y )在区域D 上服从均匀分布,求(X ,Y )关于X 的边缘概率密度在x =2处的值为多少?题21图【解】区域D 的面积为 22e e 0111d ln 2.S x x x===⎰(X ,Y )的联合密度函数为211,1e ,0,(,)20,.x y f x y x ⎧≤≤<≤⎪=⎨⎪⎩其他(X ,Y )关于X 的边缘密度函数为1/2011d ,1e ,()220,.x X y x f x x⎧=≤≤⎪=⎨⎪⎩⎰其他 所以1(2).4X f =22.设随机变量X 和Y 相互独立,下表列出了二维随机变量(X ,Y )联合分布律及关于X 和y 1 y 2 y 3P {X =x i }=p ix 1 x 21/81/8P {Y =y j }=p j 1/61【解】因21{}{,}j j iji P Y y P P X x Y y ======∑,故11121{}{,}{,},P Y y P X x Y y P X x Y y ====+== 从而11111{,}.6824P X x Y y ===-= YX而X 与Y 独立,故{}{}{,}i j i i P X x P Y y P X x Y y =====,从而11111{}{,}.624P X x P X x Y y =⨯==== 即:1111{}/.2464P X x === 又1111213{}{,}{,}{,},P X x P X x Y y P X x Y y P X x Y y ====+==+==即1,3111{},4248P X x Y y =++== 从而131{,}.12P X x Y y === 同理21{},2P Y y == 223{,}8P X x Y y ===又31{}1jj P Y y ===∑,故3111{}1623P Y y ==--=. 同理23{}.4P X x == 从而23313111{,}{}{,}.3124P X x Y y P Y y P X x Y y ====-===-=故23.设某班车起点站上客人数X 服从参数为λ(λ>0)的泊松分布,每位乘客在中途下车的概率为p (0<p <1),且中途下车与否相互独立,以Y 表示在中途下车的人数,求:(1)在发车时有n 个乘客的条件下,中途有m 人下车的概率;(2)二维随机变量(X ,Y )的概率分布.【解】(1) {|}C (1),0,0,1,2,m m n mn P Y m X n p p m n n -===-≤≤=.(2) {,}{}{|}P X n Y m P X n P Y m X n ======e C (1),,0,1,2,.!m m n mnnp p n m n n n λλ--=-≤≤=24.设随机变量X 和Y 独立,其中X 的概率分布为X ~⎪⎪⎭⎫⎝⎛7.03.021,而Y 的概率密度为f (y ),求随机变量U =X +Y 的概率密度g (u ).【解】设F (y )是Y 的分布函数,则由全概率公式,知U =X +Y 的分布函数为(){}0.3{|1}0.7{|2}G u P X Y u P X Y u X P X Y u X =+≤=+≤=++≤=0.3{1|1}0.7{2|2}P Y u X P Y u X =≤-=+≤-=由于X 和Y 独立,可见()0.3{1}0.7{2}G u P Y u P Y u =≤-+≤-0.3(1)0.7(2).F u F u =-+-由此,得U 的概率密度为()()0.3(1)0.7(2)g u G u F u F u '''==-+-0.3(1)0.7(2).f u f u =-+-25. 25. 设随机变量X 与Y 相互独立,且均服从区间[0,3]上的均匀分布,求P {max{X ,Y }≤1}.解:因为随即变量服从[0,3]上的均匀分布,于是有1, 03,()30, 0,3;x f x x x ⎧≤≤⎪=⎨⎪<>⎩ 1, 03,()30, 0, 3.y f y y y ⎧≤≤⎪=⎨⎪<>⎩ 因为X ,Y 相互独立,所以1, 03,03,(,)90, 0,0,3, 3.x y f x y x y x y ⎧≤≤≤≤⎪=⎨⎪<<>>⎩ 推得 1{max{,}1}9P X Y ≤=. 26. 设二维随机变量(X ,Y )的概率分布为其中a ,b ,c 为常数,且X 的数学期望E (X )= -0.2,P {Y ≤0|X ≤0}=0.5,记Z =X +Y .求:(1) a ,b ,c 的值; (2) Z 的概率分布; (3) P {X =Z }.解 (1) 由概率分布的性质知,a+b+c +0.6=1 即 a+b+c = 0.4. 由()0.2E X =-,可得0.1a c -+=-.再由 {0,0}0.1{00}0.5{0}0.5P X Y a b P Y X P X a b ≤≤++≤≤===≤++,得 0.3a b +=.解以上关于a ,b ,c 的三个方程得0.2,0.1,0.1a b c ===.(2) Z 的可能取值为-2,-1,0,1,2,{2}{1,1}0.2P Z P X Y =-==-=-=,{1}{1,0}{0,1}0.1P Z P X Y P X Y =-==-=+==-=,{0}{1,1}{0,0}{1,1}0.3P Z P X Y P X Y P X Y ===-=+==+==-=,{1}{1,0}{0,1}0.3P Z P X Y P X Y ====+===,{2}{1,1}0.1P Z P X Y =====,即Z(3) {}{0}0.10.20.10.10.20.4P X Z P Y b ====++=++=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
概率论与数理统计 第三章 二维随机变量及其概率分布 例题1.甲乙两人独立地进行两次射击,命中率分别为0.2、0.5,把X 、Y 分别表示甲乙命中的次数,求(X,Y )联合分布律。
2.袋中有两只白球,两只红球,从中任取两只以X 、Y 表示其中黑球、白球的数目,求(X,Y )联合分布律。
3.设,且P{}=1,求()的X 1=(‒1011/41/21/4)
X 2=(011/21/2)X 1X 2=0X 1,X 2联合分布律,并指出是否独立。
X 1,X 24.设随机变量X 的分布律为Y=,求(X,Y )联合分布律。
X 2X Y 01
概率论与数理统计 第三章 二维随机变量及其概率分布 例题
5.设(X,Y )的概率分布为 且事件{X=0}与{X+Y=1}独立求a ,b 。
6. 设某班车起点上车人数X 服从参数λ(λ>0)的泊松分布,每位乘客中途下车的概率为P (0<P<1)相互独立。
以Y 表示中途下车的人数。
(1)求在发车时有n 个人的情况下,中途m 个人下车的概率;(2)求(X,Y )联合分布律。
7. 设二维随机变量(X,Y )联合分布函数F(x.y)=A(B+arctan ) (C+arctan )。
x 2y
3(1)A 、B 、C (2)(X,Y)的联合密度f(x,y) (3)(X,Y )的边缘密度,f z (x)f Y (y)8.设f(x,y)= 为二维随机变量(X,Y )的联合密度函数,求:{C(x +y)00≤y ≤x ≤1其它01/3B 1
a 1/4
概率论与数理统计 第三章 二维随机变量及其概率分布 例题(1)C 的值 (2), (3)P{X+Y ≤1}并判别X 与Y 是否独立。
f z (x)f Y (y)9.设f(x,y)= 为(X,Y )的密度函数,求{10 |y |<x,0<x <1其它:(1) f X (x ), f Y (y ) (3)P{X>1/2|Y>0}(2) f Y|X (y|x ), f X|Y (x|y )10. 设f(x,y)= 为(X,Y )的密度函数,求 {12x 2y 0 1x ≤y ≤x,x ≥1 其它 f X|Y (x|y )11. 设f(x,y)= 为(X,Y )的密度函数,求的联合分布
{4xy 0 0≤x ≤1,0≤y ≤1 其它 (X,Y )
概率论与数理统计 第三章 二维随机变量及其概率分布 例题
函数。
12.设X,Y 独立,均服从(0,1)上的均匀分布,Z 的密度函数f Z (Z )。
13. 设f(x,y)= 为(X,Y )的密度函数,Z=X+Y,求的密度函{2(x +y )0 0≤x ≤y ≤1 其它 Z 数。
f Z (Z )14.设X,Y 独立,X~N(μ,),Y~V(-π,π),Z=X+Y,求,结果用Φ(x)表示。
σ2
f Z (Z )
15.设(X,Y )的联合密度函数为f(x,y)=,Z=X+Y,求Z 的概率密度。
12πδ12δ22e ‒12(x 2δ12+y 2δ22
)16.
设f(x,y)= 为(X,Y )的密度函数,Z=X+2Y,求的密度函数
{2e ‒x ‒2y 0 x >0,y >0 其它 Z 。
f Z (Z )17. 设X,Y 独立,均服从N (0,1),Z==, 求的密度函数。
X 2+Y 2 Z f Z (Z )
18. 设X,Y 独立,均服从U (-1,1),Z==, 求的密度函数。
XY Z f Z (Z )19. 设X,Y 独立,均服从U (0,1),Z==, 求的密度函数。
X Y Z f Z (Z )20. 设X,Y 独立,其分布函数分别为,分别求max{X,Y},min{X,Y}的分布函数。
f Z (x )f Y (y )。
