衢州二中高三第一学期期中考试试卷
4.2 指数函数(精讲)(原卷版附答案).docx
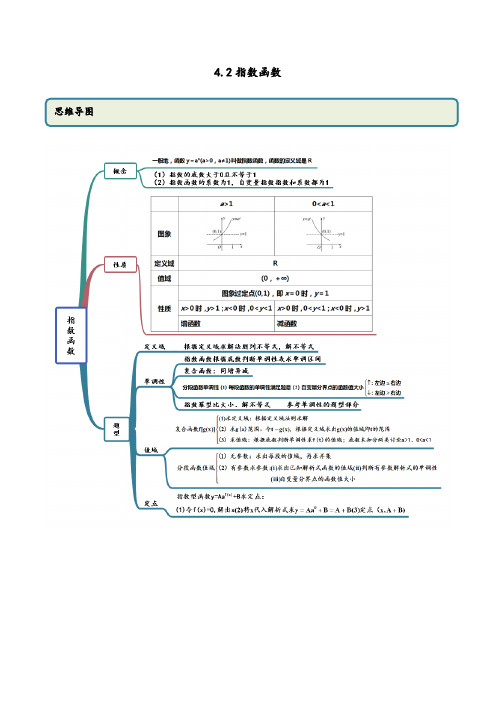
4.2指数函数考点一 指数函数的判断【例1-1】(2019·河北桥西.邢台一中高一月考)下列函数中指数函数的个数是( )①23x y =⋅ ②13x y += ③3xy = ④()21xy a =-(a 为常数,12a >,1a ≠) ⑤3y x = ⑥4xy =- ⑦()4xy =-A .1B .2C .3D .4【例1-2】(2019·河南中原.郑州一中高一开学考试)函数f (x )=(a 2﹣3a +3)a x 是指数函数,则a 的值为( ) A .1 B .3 C .2 D .1或3【一隅三反】1.(2019·山东高三学业考试)函数()2xy a a =-是指数函数,则( )A .1a =或3a =B .1a =C .3a =D .0a >且1a ≠2.(2019·呼和浩特开来中学高一期中)若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为( )A .2B .-2C .-D .3.(2019·辽宁葫芦岛.高一月考)下列函数不是指数函数的是( ) A .12x y +=B .3x y -=C .4x y =D .32x y =考点二 定义域和值域【例2-1】(2020·全国高一课时练习)求下列函数的定义域和值域:(1)142x y -=;(2)23y ⎛= ⎪⎝⎭(3)22312x x y --⎛⎫=⎪⎝⎭.【例2-2】(2018·湖南开福.长沙一中高一月考)若函数y =的值域为[0,+∞),则实数a 的取值范围是_____.【一隅三反】1.(2020·全国高一课时练习)求下列函数的定义域和值域; (1)12x y +=;(2)y =(3)y =2.(2020·全国高一课时练习)求下列函数的定义域与值域.(1)y =(2)1(0,1x x a y a a -=>+且1)a ≠(3)110.3;x y -=(4)y =3.(2020·河北新华.石家庄二中高二期末)若函数()1,121,14xxx f x a x ⎧⎛⎫<⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+≥ ⎪⎪⎝⎭⎩的值域为(),+∞a ,则a 的取值范围为( )A .1,4⎡⎫+∞⎪⎢⎣⎭B .11,42⎡⎤⎢⎥⎣⎦C .1,12⎡⎤⎢⎥⎣⎦D .1,14⎛⎤⎥⎝⎦4.(2020·云南五华.昆明一中高三其他(理))设函数y =A ,函数12x y -=的值域为B ,则AB =( )A .()0,1B .(]0,1C .()1,1-D .[]1,1-5.(2019·湖南高一期中)若函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,则实数a 的值为( )A .2-B .1-C .1D .2考点三 指数函数性质【例3】(1)(2020·贵溪市实验中学高二期末(文))若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A .9,34⎛⎫⎪⎝⎭B .9,34⎡⎫⎪⎢⎣⎭C .()1,3D .()2,3(2)(2019·湖南岳阳楼.岳阳一中高一期中)已知函数1()2xf x ⎛⎫= ⎪⎝⎭,则不等式()24(3)f a f a ->的解集为( ) A .(4,1)-B .(1,4)-C .(1,4)D .(0,4)(3)(2019·湖北襄阳)如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,那么( )A .a b a a a b <<B .a a b a b a <<C .b a a a a b <<D .b a a a b a <<【一隅三反】1.(2019·浙江南湖.嘉兴一中高一月考)函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是( )A .[)1,-+∞B .(],1-∞-C .[)1,+∞D .(],1-∞2.(2019·浙江柯城.衢州二中高三一模)已知定义在R 上的函数()||32x m f x -+=+m 为实数)为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )A .c b a <<B .c a b <<C .a c b <<D .a b c <<3.(2020·浙江高一课时练习)设0.914y =,0.4828y =, 1.5312y -⎛⎫= ⎪⎝⎭,则( )A .312y y y >>B .213y y y >>C .123y y y >>D .132y y y >>1.指数函数性质记忆口诀指数增减要看清,抓住底数不放松; 反正底数大于0,不等于1已表明; 底数若是大于1,图象从下往上增; 底数0到1之间,图象从上往下减; 无论函数增和减,图象都过(0,1)点. 2.比较幂值大小的三种类型及处理方法4.(2020·永安市第三中学高二月考)若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是( )A .(,8][0,)-∞-+∞B .(),4-∞-C .[8,4)--D .(,8]-∞-5(2020·上海高一课时练习)已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭,则该函数的单调递增区间是__________.6.(2020·上海普陀.曹杨二中高一期末)函数12x y =-的单调递增区间为________7.(2020·全国高一课时练习)比较下列各题中的两个值的大小. (1)0.10.8-,0.21.25;(2)1ππ-⎛⎫ ⎪⎝⎭,1;(3)30.2-,()0.23-.考点四 定点【例4】(2020·浙江高一课时练习)函数()-1=4+x f x a (0a >,且1a ≠)的图象过定点P ,则P 点的坐标为( ) A .(1,5) B .(1,4) C .(0,5)D .(0,4)【一隅三反】1.(2019·涡阳县第九中学高二期末)函数()10,1xy a a a =+>≠的图象必经过点( )A .(0,1)B .(1,1)C .()0,2D .(2,2)2.(2019·贵州省织金县第二中学高一期中)函数21()x f x a-=(0a >且1)a ≠过定点( ) A .(1,1) B .1(,0)2C .(1,0)D .1(,1)23.(2020·宁夏贺兰县景博中学高一月考)函数y=a x ﹣1+2(a >0且a≠1)图象一定过点( )A .(1,1)B .(1,3)C .(2,0)D .(4,0)考点五 图像【例5-1】(2020·广东顺德一中高一期中)函数1(0,1)xy a a a a=->≠的图像可能是( ). A . B .C .D .【例5-2】(2020·浙江高一课时练习)若函数(01,1)xy a a a m =>-≠+的图像在第一、三、四象限内,则( ) A .1a >B .1a >,且0m <C .01a <<,且0m >D .01a <<【一隅三反】1.(2019·浙江高一期中)函数y x a =+与xy a =,其中0a >,且1a ≠,它们的大致图象在同一直角坐标系中有可能是 ( )A .B .C .D .2.(2020·全国高一课时练习)在如图所示的图象中,二次函数2y ax bx c =++与函数xb y a ⎛⎫= ⎪⎝⎭的图象可能是( )A .B .C .D .3.(2020·上海高一课时练习)若函数2xy m =+的图像不经过第二象限,则m 的取值范围是( )A .m 1≥B .1m <C .1m >-D .1m ≤-4.(2020·内蒙古集宁一中高二期末(理))若直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点,则a的取值范围是___________4.2指数函数考点一 指数函数的判断【例1-1】(2019·河北桥西.邢台一中高一月考)下列函数中指数函数的个数是( )①23x y =⋅ ②13x y += ③3xy = ④()21xy a =-(a 为常数,12a >,1a ≠) ⑤3y x = ⑥4xy =- ⑦()4xy =-A .1B .2C .3D .4【参考答案】B【解析】对①:指数式的系数为2,不是1,故不是指数函数;对②:其指数为1x +,不是x ,故不是指数函数; 对③④:满足指数函数的定义,故都是指数函数; 对⑤:是幂函数,不是指数函数;对⑥:指数式的系数为-1,不是1,故不是指数函数;对⑦:指数的底数为-4,不满足底数大于零且不为1的要求,故不是; 综上,是指数函数的只有③④,故选:B.【例1-2】(2019·河南中原.郑州一中高一开学考试)函数f (x )=(a 2﹣3a +3)a x 是指数函数,则a 的值为( ) A .1B .3C .2D .1或3【参考答案】C【解析】因为函数f (x )=(a 2﹣3a +3)a x 是指数函数,故可得2331a a -+=解得1a =或2a =, 当1a =时,不是指数函数,舍去.故选:C.【一隅三反】1.(2019·山东高三学业考试)函数()2xy a a =-是指数函数,则( )A .1a =或3a =B .1a =C .3a =D .0a >且1a ≠【参考答案】C【解析】因为函数()2xy a a =-是指数函数所以21a -=,0a >且1a ≠,解得3a =.故选:C.2.(2019·呼和浩特开来中学高一期中)若函数1()(3)2xf x a a =-⋅是指数函数,则1()2f 的值为( )A .2B .-2C.-D.【参考答案】D【解析】∵函数f (x )=(12a ﹣3)•a x 是指数函数,∴12a ﹣3=1,a >0,a ≠1,解得a =8, ∴f (x )=8x ,∴f (12)==,故选:D . 3.(2019·辽宁葫芦岛.高一月考)下列函数不是指数函数的是( ) A .12x y += B .3x y -= C .4x y = D .32x y =【参考答案】A【解析】指数函数是形如xy a =(0a >且1a ≠)的函数. 对于A :1222x x y +==⨯,系数不是1,所以不是指数函数;对于B :133xx y -⎛⎫== ⎪⎝⎭,符合指数函数的定义,所以是指数函数;对于C :4xy =,符合指数函数的定义,所以是指数函数;对于D :382x xy ==,符合指数函数的定义,所以是指数函数.故选:A.考点二 定义域和值域【例2-1】(2020·全国高一课时练习)求下列函数的定义域和值域: (1)142x y -=;(2)23y ⎛= ⎪⎝⎭(3)22312x x y --⎛⎫=⎪⎝⎭.【参考答案】(1)定义域{|4}x x ≠,值域为{|0y y >且1}y ≠; (2)定义域{|0}x x =,值域{|1}y y =;(3)定义域R ,值域(]0,16【解析】(1)要使函数式有意义,则40x -≠,解得4x ≠.所以函数142x y -=的定义域为{|4}x x ≠.因为104x ≠-,所以1421x -≠,即函数142x y -=的值域为{|01}y y y >≠,且. (2)要使函数式有意义,则||0x -,解得0x =,所以函数23y ⎛= ⎪⎝⎭{|0}x x =.因为0x =,所以022133⎛⎛⎫== ⎪ ⎪⎝⎭⎝⎭,即函数23y ⎛= ⎪⎝⎭{|1}y y =.(3)函数的定义域为R .因为2223(1)44x x x --=--≥-,所以2234111622x x ---⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭. 又223102x x --⎛⎫>⎪⎝⎭,所以函数22312x x y --⎛⎫= ⎪⎝⎭的值域为(]0,16.【例2-2】(2018·湖南开福.长沙一中高一月考)若函数y =的值域为[0,+∞),则实数a 的取值范围是_____. 【参考答案】(﹣∞,﹣2]【解析】设()421x x g x a =+⋅+,若函数y =的值域为[0,)+∞,则等价于[0,)+∞是()g x 值域的子集,2()421(2)21x x x x g x a a =+⋅+=+⋅+,设2x t =,则0t >,则2()1y h t t at ==++,(0)10h =>,∴当对称轴02at =-,即0a 时,不满足条件. 当02at =->,即0a <时,则判别式△240a =-,即022a a a <⎧⎨-⎩或,则2a -, 即实数a 的取值范围是(-∞,2]-.故参考答案为:(-∞,2]-【一隅三反】1.(2020·全国高一课时练习)求下列函数的定义域和值域; (1)12x y +=;(2)y =(3)y =【参考答案】(1)定义域为R ,值域为(0,)+∞;(2)(,0]-∞,[0,1);(3)[0,)+∞,[1,)+∞.【解析】(1)12x y +=的定义域为R ,值域为(0,)+∞.(2)由120x -≥知0x ,故y =(,0]-∞;由0121x -<知0121x -<,故y =[0,1).(3)y =[0,)+∞0x 知1x,故y =[1,)+∞.2.(2020·全国高一课时练习)求下列函数的定义域与值域.(1)y =(2)1(0,1x x a y a a -=>+且1)a ≠(3)110.3;x y -=(4)y =【参考答案】(1)定义域为[0,)+∞;值域为[0,1);(2)定义域为R ;值域为(-1,1);(3)定义域为{1}xx ≠∣;值域为{0y y >∣且1}y ≠;(4)定义域为15xx ⎧⎫≥⎨⎬⎩⎭∣;值域为{1}yy ≥∣. 【解析】(1)1102x⎛⎫-≥ ⎪⎝⎭,解得:0x ≥, ∴原函数的定义域为[0,)+∞,令11(0)2xt x ⎛⎫=-≥ ⎪⎝⎭,则01,01t ≤<∴≤∴原函数的值域为[0,1) (2)原函数的定义域为R.设x a t =,则(0,)t ∈+∞,11221111t t y t t t -+-===-+++, 0,11t t >∴+>,1201,2011t t -∴<<∴-<<++,21111t ∴-<-<+,即原函数的值域为(1,1)-. (3)由10x -≠得1x ≠,所以函数定义域为{|1}x x ≠,由101x ≠-得1y ≠, 所以函数值域为{|0y y >且1}y ≠.(4)由510x -≥得15x ≥,所以函数定义域为15x x ⎧⎫≥⎨⎬⎩⎭∣,0≥得1y ≥,所以函数值域为{1}yy ≥∣. 3.(2020·河北新华.石家庄二中高二期末)若函数()1,121,14xxx f x a x ⎧⎛⎫<⎪ ⎪⎪⎝⎭=⎨⎛⎫⎪+≥⎪⎪⎝⎭⎩的值域为(),+∞a ,则a 的取值范围为( )A .1,4⎡⎫+∞⎪⎢⎣⎭B .11,42⎡⎤⎢⎥⎣⎦C .1,12⎡⎤⎢⎥⎣⎦D .1,14⎛⎤ ⎥⎝⎦【参考答案】B【解析】当1x <时,()1,212xf x ⎛⎫∈+∞⎛ ⎪⎝⎫= ⎪⎭⎭⎝ 当1≥x 时,()114,4xf x a a a ⎛⎤∈+⎛⎫=+ ⎪⎝⎭ ⎥⎝⎦ 函数()f x 的值域为(),+∞a 114212a a ⎧+≥⎪⎪∴⎨⎪≤⎪⎩,即11,42a ⎡⎤∈⎢⎥⎣⎦故选:B 4.(2020·云南五华.昆明一中高三其他(理))设函数y =A ,函数12x y -=的值域为B ,则AB =( )A .()0,1B .(]0,1C .()1,1-D .[]1,1-【参考答案】A【解析】函数定义域满足:210x ->,即11x -<<,所以{}11A x x =-<<,函数12x y -=的值域{}0B y y =>,所以()0,1AB =,故选:A.5.(2019·湖南高一期中)若函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,则实数a 的值为( )A .2-B .1-C .1D .2【参考答案】D【解析】由于函数2411()3ax x f x -+⎛⎫= ⎪⎝⎭有最大值3,所以0a >,且当422x a a-=-=时,()f x 取得最大值为2224411412113333a a a aaf a ⎛⎫⋅-⋅+-+ ⎪-⎝⎭⎛⎫⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故4411,2,2a a a-===.故选:D 考点三 指数函数性质【例3】(1)(2020·贵溪市实验中学高二期末(文))若函数6(3)3,7(),7x a x x f x a x ---≤⎧=⎨>⎩单调递增,则实数a 的取值范围是( )A .9,34⎛⎫⎪⎝⎭B .9,34⎡⎫⎪⎢⎣⎭C .()1,3D .()2,3(2)(2019·湖南岳阳楼.岳阳一中高一期中)已知函数1()2xf x ⎛⎫= ⎪⎝⎭,则不等式()24(3)f a f a ->的解集为( ) A .(4,1)-B .(1,4)-C .(1,4)D .(0,4)(3)(2019·湖北襄阳)如果1111222b a⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,那么( )A .a b a a a b <<B .a a b a b a <<C .b a a a a b <<D .b a a a b a <<【参考答案】(1)B (2)B(3)C【解析】(1)函数6(3)3,7(),7x a x x f x a x ---⎧=⎨>⎩单调递增,()301373a a a a⎧->⎪∴>⎨⎪-⨯-≤⎩解得934a ≤<所以实数a 的取值范围是9,34⎡⎫⎪⎢⎣⎭.故选:B .(2)可知函数()f x 为减函数,由2(4)(3)f a f a ->,可得243a a-<,整理得2340a a --<,解得14a -<<,所以不等式的解集为(1,4)-.故选B.(3) 根据函数()1()2x f x =在R 是减函数,且1111222ba⎛⎫⎛⎫<<< ⎪ ⎪⎝⎭⎝⎭,所以10b a >>>,所以a a b a b a <<,故选C.【一隅三反】1.(2019·浙江南湖.嘉兴一中高一月考)函数2213x xy -+⎛⎫= ⎪⎝⎭为增函数的区间是( )A .[)1,-+∞B .(],1-∞-C .[)1,+∞D .(],1-∞【参考答案】C【解析】∵13uy ⎛⎫= ⎪⎝⎭是减函数,222(1)1u x x x =-+=--+在(,1]-∞上递增,在[1,)+∞上递减,∴函数2213x xy -+⎛⎫= ⎪⎝⎭的增区间是[1,)+∞.故选:C .2.(2019·浙江柯城.衢州二中高三一模)已知定义在R 上的函数()||32x m f x -+=+m 为实数)为偶函数,记()0.2log 3a f =,()5log b f e =,()c f m π=+,则( )11.指数函数性质记忆口诀指数增减要看清,抓住底数不放松; 反正底数大于0,不等于1已表明; 底数若是大于1,图象从下往上增; 底数0到1之间,图象从上往下减; 无论函数增和减,图象都过(0,1)点. 2.比较幂值大小的三种类型及处理方法A .c b a <<B .c a b <<C .a c b <<D .a b c <<【参考答案】B【解析】()f x 为偶函数,()()f x f x ∴-=,||||3232x m x m --+-+∴+=+,||||x m x m ∴-+=+;0m ∴=;||()32x f x -∴=+;()f x ∴在[0,)+∞上单调递减,并且0.25(|log 3|)(log 3)a f f ==,5(log )b f e =,()()c f m f ππ=+=550log log 3e π<<<c a b ∴<<.故选:B .3.(2020·浙江高一课时练习)设0.914y =,0.4828y =, 1.5312y -⎛⎫= ⎪⎝⎭,则( )A .312y y y >>B .213y y y >>C .123y y y >>D .132y y y >>【参考答案】D【解析】 1.50.920.9 1.80.4830.481.44 1.35121422,22282,y y y -⨯⨯⎛⎫======⎝== ⎪⎭,因为函数2xy =在定义域上为单调递增函数,所以132y y y >>.故选:D .4.(2020·永安市第三中学高二月考)若关于x 的方程()94340xxa ++⋅+=有解,则实数a 的取值范围是( )A .(,8][0,)-∞-+∞B .(),4-∞-C .[8,4)--D .(,8]-∞-【参考答案】D【解析】由9(4)340x xa ++⋅+=,得443(4)0,(4)3433xxx x a a +++=∴-+=+≥(当且仅当32x =时等号成立),解得8a ≤-故选D5(2020·上海高一课时练习)已知函数2221()2x x f x ++⎛⎫= ⎪⎝⎭,则该函数的单调递增区间是__________.【参考答案】(,1]-∞-【解析】由题得函数的定义域为R . 设2122,()2uu x x v =++=,函数222,u x x =++在∞(-,-1]单调递减,在[1,)-+∞单调递增,函数1()2uv =在其定义域内单调递减,所以2221()2x x f x ++⎛⎫= ⎪⎝⎭在∞(-,-1]单调递增,在[1,)-+∞单调递减.故参考答案为:(,1]-∞-.6.(2020·上海普陀.曹杨二中高一期末)函数12x y =-的单调递增区间为________【参考答案】(,0]-∞【解析】函数12,010221,1x xxy x x ⎧->⎪=⎨⎛⎫-≤⎪ ⎪⎝⎭=⎩-, 根据指数函数单调性可得,函数在(,0]-∞单调递增,在0,单调递减,所以函数12xy =-的单调递增区间为(,0]-∞.故参考答案为:(,0]-∞ 7.(2020·全国高一课时练习)比较下列各题中的两个值的大小. (1)0.10.8-,0.21.25;(2)1ππ-⎛⎫ ⎪⎝⎭,1;(3)30.2-,()0.23-.【参考答案】(1)0.10.20.81.25-<(2)11ππ-⎛⎫> ⎪⎝⎭(3)()0.230.23->-【解析】(1)因为0.10.10.1450.854--⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭, 0.20.251.254⎛⎫= ⎪⎝⎭, 又指数函数54xy ⎛⎫= ⎪⎝⎭为增函数,且0.10.2<,所以0.10.25544⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭,即0.10.20.8 1.25-<. (2)1ππ-⎛⎫ ⎪⎝⎭01πππ=>=,(3)30.2-00.21>=,()()10.25330-=-=<,所以()0.230.23->-.考点四 定点【例4】(2020·浙江高一课时练习)函数()-1=4+x f x a (0a >,且1a ≠)的图象过定点P ,则P 点的坐标为( ) A .(1,5) B .(1,4) C .(0,5)D .(0,4)【参考答案】A【解析】因为xy a =的图象恒过(0,1)点,则1x y a-=的图象恒过(1,1)点,所以()-1=4+x f x a恒过定点()1,5P .故选A .【一隅三反】1.(2019·涡阳县第九中学高二期末)函数()10,1xy a a a =+>≠的图象必经过点( )A .(0,1)B .(1,1)C .()0,2D .(2,2)【参考答案】C【解析】函数x y a =的图象过点(0,1),而函数1x y a =+的图象是把函数x y a =的图象向上平移1个单位,∴函数1x y a =+的图象必经过的点(0,2).故选:C .2.(2019·贵州省织金县第二中学高一期中)函数21()x f x a-=(0a >且1)a ≠过定点( ) A .(1,1) B .1(,0)2C .(1,0)D .1(,1)2【参考答案】D【解析】令12102x x -=⇒=,所以函数21()x f x a -=(0a >且1)a ≠过定点1(,1)2. 3.(2020·宁夏贺兰县景博中学高一月考)函数y=a x ﹣1+2(a >0且a≠1)图象一定过点( )A .(1,1)B .(1,3)C .(2,0)D .(4,0)【参考答案】B 由x ﹣1=0,解得x=1,此时y=1+2=3,即函数的图象过定点(1,3),故选B考点五 图像【例5-1】(2020·广东顺德一中高一期中)函数1(0,1)xy a a a a=->≠的图像可能是( ). A . B .C .D .【参考答案】D 【解析】∵0a >,∴10a>,∴函数x y a =需向下平移1a 个单位,不过(0,1)点,所以排除A,当1a >时,∴101a <<,所以排除B,当01a <<时,∴11a>,所以排除C,故选D. 【例5-2】(2020·浙江高一课时练习)若函数(01,1)xy a a a m =>-≠+的图像在第一、三、四象限内,则( ) A .1a >B .1a >,且0m <C .01a <<,且0m >D .01a <<【参考答案】B【解析】因为函数xy a =的图像在第一、二象限内,所以欲使其图像在第三、四象限内,必须将xy a =向下移动,因为当01a <<时,图像向下移动,只能经过第一、二、四象限或第二、三、四象限, 所以只有当1a >时,图像向下移动才可能经过第一、三、四象限,故1a >,因为图像向下移动小于一个单位时,图像经过第一、二、三象限,而向下移动一个单位时,图像恰好经过原点和第一、三象限,所以欲使图像经过第一、三、四象限,则必须向下平移超过一个单位, 故11m -<-,0m <,故选:B.【一隅三反】1.(2019·浙江高一期中)函数y x a =+与xy a =,其中0a >,且1a ≠,它们的大致图象在同一直角坐标系中有可能是 ( )A .B .C .D .【参考答案】D【解析】因为函数y x a =+单调递增,所以排除AC 选项;当1a >时,y x a =+与y 轴交点纵坐标大于1,函数xy a =单调递增,B 选项错误;当01a <<时,y x a =+与y 轴交点纵坐标大于0小于1,函数xy a =单调递减;D 选项正确.故选:D2.(2020·全国高一课时练习)在如图所示的图象中,二次函数2y ax bx c =++与函数xb y a ⎛⎫= ⎪⎝⎭的图象可能是( )A .B .C .D .【参考答案】A【解析】根据选项中二次函数图象,可知0c ,根据选项中指数函数的图象,可知01b a <<,所以1022b a-<-<, 所以二次函数2y ax bx c =++的对称轴在y 轴左侧,且1,022b x a ⎛⎫=-∈- ⎪⎝⎭, 所以可排除B 、C 、D,只有A 符合题意.故选:A.3.(2020·上海高一课时练习)若函数2xy m =+的图像不经过第二象限,则m 的取值范围是( )A .m 1≥B .1m <C .1m >-D .1m ≤-【参考答案】D【解析】指数函数2x y =过点0,1,则函数2xy m =+过点()0,1m +,若图像不经过第二象限,则10m +≤,即1m ≤-,故选:D4.(2020·内蒙古集宁一中高二期末(理))若直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点,则a 的取值范围是___________【参考答案】102⎛⎫ ⎪⎝⎭,【解析】当01,1a a <<>时,做出|1|xy a =-图象,如下图所示,直线2y a =与函数|1|(0,1)x y a a a =->≠的图象有两个大众点时,1021,02a a <<<<. 故参考答案为:102⎛⎫ ⎪⎝⎭,知识改变命运。
高考关键词、点评、广告词、对联的写法

2014学年第一学期十校联合体高三期中联考 欣赏丰子恺先生的漫画《取苹果》,ห้องสมุดไป่ตู้一段文字, 表现画面的旨趣。(4分) 要求:①配合画面情景;②运用一种修辞,使表 达鲜明生动;③字数不超过40字。
【参考答案】没有什么能难住一个孩子!桌 子上的苹果啊,你怎会想到那拉开的抽屉就 是到达你的天梯? (内容完整准确,2分;突出童趣,运用修辞 、表达生动,2分,字数超过1—3个扣1分,4 个及以上扣2分。)
:Z&xx&]
第一类: ③④ ⑥命名:岗位职责; 第二类: ①②⑤命名:任职要求。
3、(14山东卷) 用下面的短语组成两副有 关春节和端午的对联。要求:上下联各为7字 ,语言连贯,符合节日和对联特点,不得重 复使用短语。(4分) 门上桃符 碧波竞舟 江边柳线 青艾驱 瘴 迎春绿 十里欢 耀眼红 千家乐 【试题答案】示例: 春 节:江边柳线迎春绿 门上桃符耀眼红 端午节:青艾驱瘴千家乐 碧波竞舟十里欢
(14湖南卷)中国美术馆和台湾长流美术馆共同举办的 “江山万里——张大千艺术展”今日与观众见面。走进中 国美术馆五层展厅,迎面的青绿山水画《谷口人家》前站 满了凝神观看的人。这青绿泼彩渲染的画面,墨色浑厚华 滋,层次分明;章法疏密相间,错落有致;勾皴笔法遒劲 雄健,开阖有度,令人叹为观止。在展厅右侧,一幅《江 山万里图》静静地面对着来来往往的人流。 “ ”开阔的画面及其意境,向人们展示着笔墨 点染间的艺术功力,也仿佛在诉说着画家眷恋故土的情怀 。 3.下列选项中的“人家”与语段中加点词“人家”意 义相同的一项是 A.人家在何许?云外一声鸡 B.小女子已许配了人家 C.你走了,教人家怎么办呢 D.诗书门第,勤俭人 家
4、14天津)阅读下面示例,按要求作答〈5分) “丢手绢”是几代人童年时的游戏,多少小朋友 学会洗的第一件衣物就是自己的小手绢。现在的你 还有手绢吗?今天的小朋友可能已经不知道手绢为 何物,纸巾的泛滥几乎让“手绢”成了只存在于词 典中的一个词,“美丽天津· 重拾手绢行动”倡导 大家:少用纸巾,多用手绢。 活动主题:把丢掉的手绢捡起来 宣传语:捡起的是童年记忆 ,留下的是绿树蓝天 生活中还有什么有趣的、美好的或是有价值的东 西正在离我们远去?为了留住它,请你策划一个 小活动,拟出活动主题和宣传语。
浙江省衢州二中2025届高三第二次调研数学试卷含解析

浙江省衢州二中2025届高三第二次调研数学试卷考生须知:1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知,都是偶函数,且在上单调递增,设函数,若,则( )A .且B .且C .且D .且2.复数2(1)41i z i -+=+的虚部为( )A .—1B .—3C .1D .23.将函数()sin 2f x x =的图象向左平移02πϕϕ⎛⎫≤≤ ⎪⎝⎭个单位长度,得到的函数为偶函数,则ϕ的值为( ) A .12π B .6π C .3π D .4π 4.下列不等式正确的是( ) A .3sin130sin 40log 4>> B .tan 226ln 0.4tan 48<< C .()cos 20sin 65lg11-<<D .5tan 410sin 80log 2>>5.已知函数()()sin 06f x A x a a A ωπ⎛⎫=+-<< ⎪⎝⎭在区间70,3ωπ⎡⎤⎢⎥⎣⎦有三个零点1x ,2x ,3x ,且123x x x <<,若123523x x x π++=,则()f x 的最小正周期为( ) A .2πB .23πC .πD .43π 6.已知数列满足,且,则数列的通项公式为( ) A .B .C .D .7.设函数()()ln 1f x x =-的定义域为D ,命题p :x D ∀∈,()f x x ≤的否定是( ) A .x D ∀∈,()f x x >B .0x D ∃∈,()00f x x ≤C .xD ∀∉,()f x x > D .0x D ∃∈,()00f x x >8. “纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样.为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷200个点,己知恰有80个点落在阴影部分据此可估计阴影部分的面积是( )A .165B .325C .10D .1859.已知定义在R 上的奇函数()f x 和偶函数()g x 满足()()2x xf xg x a a -+=-+(0a >且1a ≠),若(2)g a =,则函数()22f x x +的单调递增区间为( ) A .(1,1)-B .(,1)-∞C .(1,)+∞D .(1,)-+∞10.如果实数x y 、满足条件10{1010x y y x y -+≥+≥++≤,那么2x y -的最大值为( )A .2B .1C .2-D .3-11.20世纪产生了著名的“31x +”猜想:任给一个正整数x ,如果x 是偶数,就将它减半;如果x 是奇数,则将它乘3加1,不断重复这样的运算,经过有限步后,一定可以得到1.如图是验证“31x +”猜想的一个程序框图,若输入正整数m 的值为40,则输出的n 的值是( )A .8B .9C .10D .1112.,,a b αβαβ//////,则a 与b 位置关系是 ( ) A .平行 B .异面C .相交D .平行或异面或相交二、填空题:本题共4小题,每小题5分,共20分。
2024-2025学年高中上学期高二物理期中模拟卷(全解全析)(浙江专用)

2024-2025学年高二物理上学期期中模拟卷(考试时间:90分钟,分值:100分)注意事项:1.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.测试范围:第9~12章,人教版2019必修第三册。
4.难度系数:0.70。
第Ⅰ卷一、选择题Ⅰ(本题共13小题,每小题3分,共39分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)1.下列物理量是比值法定义且为矢量的是()A .加速度F a m =B .电场强度F E q =C .电势p E q ϕ=D .电容r 4S C kd επ=【答案】B【详解】A .F a m =是加速度的决定式,v a t ∆=∆是加速度的定义式,加速度a 是矢量,故A 错误B .F E q=是电场强度的定义式,电场强度E 与F 、Q 无关,E 是矢量,故B 正确;C .p E qϕ=是电势的定义式,电势ϕ与p E 、q 均无关,但电势ϕ是标量,故C 错误;D .r 4S C kdεπ=是电容的决定式,Q C U =是电容的定义式,故D 错误。
故选B 。
2.在电磁学发展过程中,许多科学家做出了贡献,下列说法正确的是()A .法拉第最先引入“场”的概念,并最早发现了电流的磁效应现象B .库仑发现了点电荷的相互作用规律,并通过油滴实验测定了元电荷的数值C .安培在研究磁场与通电导线的相互作用方面做出了杰出的贡献,并提出分子电流假说D .奥斯特发现了磁场对电流的作用规律【答案】C【详解】A.法拉第最先引入“场”的概念,奥斯特最早发现了电流的磁效应现象,选项A错误;B.库仑发现了点电荷的相互作用规律,密立根通过油滴实验测定了元电荷的数值,选项B错误;C.安培在研究磁场与通电导线的相互作用方面做出了杰出的贡献,并提出分子电流假说,选项C正确;D.奥斯特发现了电流的磁效应,安培发现了磁场对电流的作用规律,选项D错误。
浙江省部分市2023-2024学年高三上学期11月英语汇编:应用文写作(含解析)

Li Hua
浙江省杭州市2023-2024学年高三上学期11月期中教学质量检测英语试题
第一节(满分15分)
假定你是李华。为迎接爱尔兰姐妹学校来访,你校英语俱乐部将举行学生活动图片展,现正向全校学生征集照片。你打算参与,请你写一封邮件,说明相关信息,内容包括:
1.描述照片内容;
2.选择该照片的理由;
3.另约时间。
注意:1.写作词数应为80左右;
2.请按如下格式在答题卡的相应位置作答。
Dear Philip,
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Thank you for considering my opinion. I’m confident that the course will benefit students in their future endeavors.
Yours,
Li Hua
【解析】
【导语】本篇是应用文写作。要求写一封信给你的外国朋友Albert,向他介绍中国高中生对于是否需要开设学生职业生涯规划课程的想法。
Yours sincerely,
Li Hua
浙江省湖州丽水衢州三市2023-2024学年高三上学期11月期中教学质量检测考试英语试题
第二章 直线和圆的方程 专题测试(原卷版+解析版) (人教A版)高二数学选择性必修一

第二章 直线和圆的方程专题测试注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、单选题(每题只有一个选项为正确答案,每题5分,共40分)1.(2020·福建高二学业考试)已知直线1l :2y x =-,2l :y kx =,若12//l l ,则实数k =( ) A .-2B .-1C .0D .12.(2020·洮南市第一中学高一月考)直线()()1:2140l a x a y -+++=与()2:190l a x ay ++-=互相垂直,则a 的值是( ). A .-0.25B .1C .-1D .1或-13.(2020·江苏省海头高级中学高一月考)直线:l (1)230m x my m ---+=(m R ∈)过定点A ,则点A 的坐标为( ) A .(3,1)-B .(3,1)C .(3,1)-D .(3,1)--4.(2020·广东高二期末)设a R ∈,则“a =1”是“直线ax+y -1=0与直线x+ay+1=0平行”的 A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件,5.(2020·黑龙江高一期末)若曲线y 与直线y =k (x ﹣2)+4有两个交点,则实数k 的取值范围是( ) A .3,14⎛⎤⎥⎝⎦B .3,4⎛⎫+∞⎪⎝⎭C .(1,+∞)D .(1,3]6.(2020·浙江柯城。
衢州二中高三其他)已知直线x y t +=与圆()2222x y t tt R +=-∈有公共点,则()4t t -的最大值为( )A .4B .289C .329D .3277.(2020·广东高一期末)若两平行直线20,(0)x y m m ++=>与30x ny --=则m +n =( ) A .0B .1C .1-D .2-8.(2020·北京市第五中学高三其他)过直线y =x 上的一点作圆22(5)(1)2x y -+-=的两条切线l 1,l 2,当直线l 1,l 2关于y =x 对称时,它们之间的夹角为( ) A .30°B .45°C .60°D .90°二、多选题(每题不止有一个选项为正确答案,每题5分,共20分)9.(2020·江苏省苏州第十中学校高一期中)圆221:20x y x O +-=和圆222:240O x y x y ++-=的交点为A ,B ,则有( )A .公共弦AB 所在直线方程为0x y -= B .线段AB 中垂线方程为10x y +-=C .公共弦ABD .P 为圆1O 上一动点,则P 到直线AB 距离的最大值为12+ 10.(2020·江苏徐州.高一期末)已知直线12:10,:(2)330l x my l m x y +-=-++=,则下列说法正确的是( )A .若12l l //,则m =-1或m =3B .若12l l //,则m =3C .若12l l ⊥,则12m =-D .若12l l ⊥,则12m =11.(2020·江苏扬州.高一期末)已知直线l 与圆22:240C x y x y a ++-+=相交于,A B 两点,弦AB 的中点为()0,1M ,则实数a 的取值可为( ) A .1B .2C .3D .412.(2020·江苏省江阴高级中学高一期中)下列说法正确的是( ) A .直线32()y ax a a R =-+∈必过定点(3,2) B .直线32y x =-在y 轴上的截距为2-C 10y ++=的倾斜角为60°D .过点(1,2)-且垂直于直线230x y -+=的直线方程为20x y +=第II 卷(非选择题)三、填空题(每题5分,共20分)13.(2020·湖南张家界。
浙江省2023-2024学年高二上学期语文期中试卷(含答案)

浙江省2023-2024学年高二上学期语文期中试卷姓名:__________ 班级:__________考号:__________阅读下面的文字,完成问题。
材料一:在许多文明的历史中,早期记忆与当代记忆之间出现了“浮动缺口”,在艺术史上表现为经典艺术史因排除民间艺术而形成的历史书写缺口。
在中国艺术发展进程中也可以看到这种文化记忆缺口的存在。
先秦的诗乐舞等艺术虽有雅郑之分,但都具有仪式性、民间性的群落文化性质。
体现精英文化创造性的经典艺术从汉代开始发展,经历唐宋元诸朝代的繁荣,在明代达到经典化的高峰。
明代中期文学批评中乃至唐宋派等诸流派的繁荣与纷争,都是以秦汉唐宋的艺术经典为标准和指归而展开的,民间文艺似乎在精英文化的发展繁荣中没落了。
然而就在这种经典艺术观达到繁荣顶峰的明代后期,个人和民间艺术趣味却又以推崇“性灵”的方式出现,形成了“复古派”与“性灵派”之争。
这种论争呈现出中国艺术发展史中的“浮动缺口”现象--民间艺术在经典艺术及其观念发展的过程中消隐了,而在性灵派的艺术主张和趣味中又浮现了出来。
复古派的代表人物之一李梦阳在晚年也看到了这个“缺口”的历史意义,他惊叹“今真诗乃在民间”,意味着一直被文人视为粗鄙不文的民间艺术并非已经消亡,在经典繁荣的“今”日以其“真”而仍然具有生命力。
历史缺口的发现意味着不同于经典的另外一种艺术史--作为“天地自然之音”的民间艺术史的显现。
近代学者王国维在研究中国艺术思想史的同时注意到了经典艺术和民间艺术两类不同文化传统的美学特征。
他在《人间词话》中研究的是“词”这类经典的文人创作,在元曲研究中则深入探讨了具有典型民间艺术特征的元杂剧。
可以说,他的研究视野沟通了中国艺术史的“缺口”。
他在谈到元杂剧时,毫不客气地批评“关目之拙劣,所不问也;思想之卑陋,所不讳也;人物之矛盾,所不顾也”,显然视之为稚拙朴陋的民间作品;然而同时又誉其为“一代之绝作”“中国最自然之文学”。
浙江省湖州丽水衢州三市2023-2024学年高三上学期11月期中教学质量检测考试英语试题

浙江省湖州丽水衢州三市2023-2024学年高三上学期11月期中教学质量检测考试英语试题学校:___________姓名:___________班级:___________考号:___________一、阅读理解Four Books about Curious CreaturesIn these brilliant books find out about fleas, foxes and some unexpected friendships. Animal Sidekicksby Macken Murphy.Illustrated by Dragan KordicThis illustrated book explores the idea of symbiosis-animals that form amazing relationships to help each other. You'll learn about clownfish living peacefully with poisonous sea anemone, the frog that lives with a tarantula, and lots more.The Secret Life of Foxesby Chloe Petrylak.Have you ever spotted a fox on the streets of your town at night or even in your back garden? Wildlife enthusiasts will love finding out more about the mysterious lives of foxes. As well as lots of interesting information, this book includes great ideas for ways to help foxes near you.Please Don't Bite Meby Nazzy Pakpour.Illustrated by Owen DaveyDid you know that wasps can build nests as much as five metres wide? Or that fleas can jump 150 times their own height? How do mosquitoes track you down? This interesting illustrated book digs out the surprising lives of some of the buzzing, biting and stinging insects that are all around.Stone age beastsby BenLerwill.Illustrated by Grahame Baker-SmithTravel back in time to meet incredible creatures in this beautiful book. It features many of the prehistoric animals that our human ancestors would have met face-to-face in the Stone Age. Learn about the woolly mammoth, the sabre-toothed cat, and the six-metre snake thatonce slithered along the forest floor.1.In which book can you find the fish that help clean sharks' teeth?A.Animal Sidekicks.B.The Secret Life of Foxes.C.Please Don't Bite Me.D.Stone Age Beasts.2.How is the book The Secret Life of Foxes different from others?A.It deals with a curious creature.B.It has no illustrations in the book.C.It only attracts wildlife enthusiasts.D.It doesn't mention relationships ofcreatures.3.What kind of creatures are mentioned in the book Stone Age Beasts?A.Amazing and giant ocean life.B.Mysterious and fascinating birds.C.Interesting and surprising insects.D.Unbelievable and ancient animals.From the time he was a young boy, Jim Haskins always had a book in his hand. While other kids were outside playing ball, Jim was usually reading. He could be found in one of his favorite places: curled up underneath the kitchen table or up in the tree that grew in his front yard.Jim was born in Demopolis, Alabama, during the time of segregation (隔离). Because Jim was Black, he was not allowed to check out a single book at the public library. Libraries were for whites only. The laws of segregation separated Jim from all the books he longed to read. But Jim was determined. He convinced a teacher at school to lend him books of her own. He even managed to get some public library books through a white woman whom his mom worked for doing laundry.When Jim was a teenager, Black Americans’ struggle for equal rights was becoming the civil rights movement. Many brave people were taking risks by refusing to follow unfair segregation laws. Jim went to Montgomery, Alabama, and joined a civil rights group. The group was headed by Dr. Martin Luther King, Jr. Jim believed in King’s nonviolent approach to change. Once, during a peaceful march, Jim was arrested. Because of that, his college expelled him.He did graduate from another college. Afterward, he went on to teach school in Harlem, a part of New York City. As a teacher, he had trouble finding books that interested his Black students. So he decided to write his own books about successful Black Americans. Through his writing, he met and interviewed many of the people he admired, including Rosa Parks.Today, libraries have more than one hundred books written by Jim Haskins, the boy who loved to read, and today, children of all races can walk through the doors of any public library and find interesting books that inform, entertain, and inspire them.4.What can we learn from the description in paragraph 1?A.Jim Haskins studied harder than other kids.B.Jim Haskins had no interest in playing ball.C.Jim Haskins was enthusiastic about reading.D.Jim Haskins preferred to read under the table.5.What does the underlined word “expelled” in paragraph 3 mean?A.Dismissed.B.Promoted.C.Praised.D.Monitored. 6.Why was Jim Haskins determined to write his own books?A.To rise to be a famous writer.B.To put an end to segregation.C.To appeal to Black students.D.To introduce the people he admired. 7.What can be a suitable title for the text?A.Pathways into the Library B.Anxiety for KnowledgeC.Struggle for Equal Rights D.Protest against SegregationSome talk of building settlements on the moon or mars to help make sure humanity survives long into the future. Others have their sights set closer to home: on future cities under the ocean.“Technologically speaking, it is absolutely possible to colonize the bottom of the sea,” says Fabien Cousteau, a well-known ocean explorer who once spent 31 days living in what is now the world’s only functioning undersea habitat, Aquarius. It’s about the size of a school bus and located 62 feet below the ocean surface off the Florida Keys.Just as astronauts test what it would be like to live in space, aquanauts try out undersea living with an eye on the future. Escaping from disasters such as climate change, wars, or pandemics is one reason to live under the sea. Others include studying, exploring, or appreciating the ocean. It’s costly and expensive to constantly keep up an ocean habitat which must pump in or make its own air, electricity, and fresh water. Inhabitants have to deal with high pressure. And infections can develop rapidly due to high humidity.Despite the challenges, several new ocean habitats and cities are under construction. A series of space station-like undersea living quarters for aquanauts called Proteus arescheduled to be completed by 2025 off Curacao, an island north of Venezuela in South America. An undersea colony called Ven Base Alpha will be built near a hydrothermal vent, which would supply it with energy. Meanwhile, an undersea city called Ocean Spiral in Japan would link its surface to the deep sea, using the difference in pressure to generate energy and produce fresh water. This sounds amazing, but it would be extremely expensive and remains just a design.Not everyone agrees that building homes in the ocean is a good idea. This type of development could place even more strain on ecosystems that are already struggling with pollution and climate change. It’s important to make sure that any construction is done carefully, says Susanne Menden-Deuer, an oceanographer at the University of Rhode Island. Wild undersea habitats should be treated as “the precious, irreplaceable resource that they are,” she says.8.What do we know about Aquarius?A.It is still under construction.B.It functions as an undersea school bus.C.It is the only ocean habitat in operation.D.It only allows a person to live there for 31 days.9.What is paragraph 3 mainly about?A.The present and future of living under the sea.B.The reasons and challenges of living under the sea.C.The purpose and cost of building undersea settlements.D.The problems and findings of building undersea settlements.10.What would be the result of building homes in the ocean according to the text?A.Rapid development of undersea habitats.B.Protection of irreplaceable ocean resource.C.Negative impacts on undersea ecosystems.D.Struggles with pollution and climate change.11.Where is the text most probably taken from?A.A textbook.B.An exam paper.C.An academic article.D.A science magazine.Far, far below your feet lies a source of nearly endless energy. Earth's core is about as hot as the surface of the Sun, so hot that it melts the rocky layers above it into magma, or liquid rock. Wouldn't it be great if we could tap into all that energy? In some places, we do!The Geysers is an area north of San Francisco in California where magma's heat turns a reservoir of underground water into steam. This region is home to 18 geothermal power plants. The steam rises up through spaces between the rocks underground, a bit like how steam pours from a teakettle boiling on a stove. The power plant has pipelines that send the steam into the turbines (涡轮机) where electricity flow is generated. Once the steam leaves the turbine, it goes into a cooling tower where it turns back into liquid. Then it's piped back into the reservoir to be reheated again. Other kinds of geothermal power plants pump hot groundwater into the power plant. Then the pressure is reduced, causing the liquid to flash into steam that turns the turbine and generates electricity flow. Once the steam cools and turns back into liquid, it's pumped back down into the reservoir to begin the cycle again.So why don't we all heat our homes with free steam from the earth? First, the heat has to be close enough to the surface for us to reach it. Next, there has to be plenty of underground water to be heated. Finally, there has to be a layer of rock that water or steam can flow through. So in places where all three of those things come together, geothermal energy can be a powerful renewable energy source. Besides, when a geothermal plant returns water back into the hot rocks of a reservoir, it makes the rock crack a bit, which can cause small earthquakes. There's another danger that comes with drilling near magma-pipes and other equipment might melt if they hit a pocket of magma or are caught in an eruption. One geothermal plant in Hawaii was partially buried by lava in 2018. But engineers are hopeful that the repaired plant will generate even more power. Geothermal energy isn't the answer for everywhere, but it's a piece of the puzzle to help slow climate change.12.In which part of power plants is the electricity made?A.The turbine.B.The reservoir.C.The pipeline.D.The tower. 13.What prevents free steam from being widely developed according to paragraph 3?A.Hard surface and possible earthquakes.B.Changeable climate and unqualified equipment.C.Limited underground water and thin layers of rock.D.Unsuitable geological conditions and potential dangers.14.Why is the buried geothermal plant in Hawaii mentioned?A.To demonstrate the great effort that engineers made.B.To show the power that the repaired plant can generate.C.To illustrate the danger caused by drilling near magma.D.To praise the engineers who repaired the generate plant.15.What is the author's attitude towards geothermal energy?A.Unconcerned.B.Unclear.C.Doubtful.D.Approving.二、七选五Tips for Foreign Students in ChinaChina is a very popular destination for foreign students today. 16 At this point, the most popular choices for study are management and technical courses, though the interest in other disciplines is growing every minute. Here is a short list of some great tips for you if you want to study in China.Learn the cultureChina has a history of over five thousand years. Depending on where you come from, you might find it hard to fit in. This is the rule that applies to any transfer you make in the world. 17 The more you learn, the sooner you’ll make friends.Learn the languageEven when travelling for a short time, it’s always wise to learn the basic phrases of the language people speak in your target country. 18 This will help you connect better with the people and show that you’ve made an effort.Know your budgeWherever you go, you need to set your budget before you depart. This is extremely important if you plan to live on a budget for a certain period of time. Before you leave for China to study, check the costs in your selected city or area and plan your budget accordingly.19Don’t limit yourselfMoving across the world to study in a place you don’t know with people you have never seen can seem daunting. 20 Don’t limit yourself. Go all in.A.Get a Chinese phrasebook and learn the must-knows.B.Then, make sure to keep track of it and follow your plan.C.Once you choose the program, arrange the rest of the details.D.If you’re moving to a place with a different culture, learn a bit before you go.E.The colleges and universities are known for their excellence and high standards.F.Studying abroad is a big step, but also one of the best experiences students get to live today.G.However, students who have gone to China to study always regret not spending more time there.三、完形填空27.A.painful B.stressful C.meaningful D.peaceful 28.A.commented on B.escaped from C.thought about D.brought back 29.A.hire B.pick C.interview D.appoint 30.A.frequently B.encouragingly C.likely D.importantly 31.A.dream B.relax C.enjoy D.survive 32.A.difficult B.interesting C.normal D.unusual 33.A.forget B.realize C.promise D.regret 34.A.challenges B.activities C.responsibilities D.jobs 35.A.overcome B.advertised C.highlighted D.imagined四、用单词的适当形式完成短文阅读下面材料,在空白处填入适当的内容(1个单词)或括号内单词的正确形式。
浙江省新高考2023-2024学年高二上学期期中联考语文试卷(含答案)

浙江省新高考2023-2024学年高二上学期期中联考语文试卷学校:___________姓名:___________班级:___________考号:___________一、现代文阅读阅读下面文字,完成各题。
材料一:一部好小说应该具有哪些特性?它的主题应该能引起广泛的兴趣,即不仅能使一群人——不管是批评家、教授、有高度文化修养的人,还是公共汽车售票员或者酒吧侍者——感兴趣,而且具有较普遍的人性,对普通男女都有感染力。
主题还应该能引起持久的兴趣,一个选择只有一时兴趣的题材进行创作的小说家,是个浅薄的小说家,因为一旦人们对这样的题材失去兴趣,他的小说也就像上星期的报纸一样不值一读了。
作者讲述的故事应该合情合理而且有条有理,故事应该有开端、中间和结尾,结尾必须是开端的自然结局。
情节要具有可能性,不仅仅要有利于主题发展,还应该是由故事自然产生的。
小说中的人物要有个性,他们的行为应该缘于他们的性格,决不能让读者议论说:“某某人是决不会干那种事的。
”相反,要读者不得不承认:“某某人那样做,完全是情理之中的事。
”要是人物又很有趣,那就更好。
福楼拜的《感情教育》虽然受到许多著名批评家的高度称赞,但是他选择的主人公却是个没有个性、没有生气,也没有任何特点的人,以致他的所作所为以及在他身上所发生的一切,都无法使人产生兴趣。
结果,虽然小说中有许多出色之处,但整部小说还是难以卒读。
为什么我认为人物必须具有个性。
因为要求小说家创造出完全新型的人物,是强人所难,小说家使用的材料是人性,虽然在各种不同的环境中人性千变万化,但也不是无限的,人们创作小说、故事、戏剧、史诗已有几千年历史,一个小说家能够创造出一种新型人物的机会,可说微乎其微,回顾整个小说史,我所能想到的唯一具有独创性的人物就是堂·吉诃德。
然而,即便是他,我还是毫不惊讶地听说,有个知识渊博的批评家已为他找到一个古老的祖先。
因此,只要一个小说家能通过个性来观察他的人物,只要他的人物个性鲜明,而且鲜明到足以让人错以为他是一种独创的人物,那么这个小说家就已经是很成功了。
2024学年第一学期浙江省9+1高中联盟高三年级期中考试数学试卷及答案

绝密★考试结束前
2024学年第一学期浙江省9+1高中联盟高三年级期中考试
命题:衢州二中李萌浩 审题:慈溪中学施斌义乌中学楼萍数学
萍
考生须知:
1.本卷满分150分,考试时间120分钟;
2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息;
3.所有答案必须写在答题卷上,写在试卷上无效,考试结束后,只需上交答题卷:
4.参加联批学校的学生可关注“启望教育”公众号查询个人成绩分析。
一、单项选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合
题目要求的.
1.已知集合A={0,-1},B={0,1,2-a}且A∈B,则a等于(
▲)A . 1C .-3
D . 3B .-12.设复数=,=在复平面内对应的点关于实轴对称,==2-i,则
A .8.c .0.
3.若命题“3x∈R,x²+2x+a<0成立”是真命题,则实数a的取值范围是(▲)
A .a ≤1
B . a <1 c. a ≥1D .a >1
4.在△ABC中,D是BC上一点,满足BD=2DC,M是AD的中点,若BM=ABA+μBC,则A+μ=(▲)c .a .0.
8.,
5.已知圆锥的侧面展开图是一个面积为π的半圆,则该圆锥的高为( ▲ )
c。
与其交于A,B两点,若
6.函数y=sin(2ox+9)(o>0)的部分图象如图所示,直线
则o =(▲ )第6题图
A .4
B .3
C . 2
D . 1
高三数学试题第1页(共4页)。
超实用高考英语复习:阅读理解——词义猜测题 ----测 (解析版)

专题15 阅读理解:词意猜测题备考高考英语二轮复习名校最新模拟试题词义猜测(共20小题)1. (云南省昆明市云南师范大学附属中学2022-2023学年高三上学期适应性月考)Although it can be found in natural vanilla bean extract, vanillin also can be made synthetically using chemicals coming from petrol. To create it from plastic, instead, researchers genetically modified a strain of E. coli bacteria so that it can make vanillin from a raw material used in the production of plastic bottles.33. Which of the following words has the closest meaning to the underlined word “synthetically” in paragraph 3?A. NaturallyB. ArtificiallyC. BiologicallyD. Industrially【答案】B【解析】词句猜测题。
由第三段“Although it can be found in natural vanilla bean extract, vanillin also can be made synthetically using chemicals coming from petrol. To create it from plastic, instead, researchers genetically modified a strain of E. coli bacteria so that it can make vanillin from a raw material used in the production of plastic bottles. (虽然香草香精可以在天然香子兰豆提取物中找到,但也可以使用来自汽油的化学物质synthetically香草香精。
浙江省衢州第二中学2014届高三上学期期中考试地理试题(教师版)

衢州二中二〇一四学年第一学期期中考试高三地理命题:高三地理备课组 审核:舒春霞提示:卷Ⅰ共30道单选题,60分;卷II 共3道综合题,40分;全卷满分100分。
卷I北京时间11月3日19:05,本世纪第二次日全环食上演,回答下列1-3题。
1.本次日食过程中,内罗毕(东三区)人们看见月影扫过太阳表面方向可能是A B C D2.月影在地表的移动速度大大超过地球自转速度,日食时间持续时间往往很短。
法国曾有天文学家乘坐超音速飞机追赶地表月影,使当时他的观测时间延长到了74分钟。
采用此法延长日食观测时间时,飞机的飞行方向一般应是A .偏东B .偏西C .偏南D .偏北3.这一天,太阳直射点在地表的移动路径是A B C D4.中国第30次南极科学考察队于2013年11月7日从上海启程,选择这个时间出发的原因主要是A .出发地上海秋高气爽,便于出行B .便于在极昼期对南极进行考察C .便于研究体验南极之“寒极”特点D .11月南极臭氧层臭氧密度较高 读全球昼长纬度分布示意图,①②③④线条代表日期,回答5-6题。
5.①②③④线条中不可能存在的是A .①B .②C .③6.衢州昼短夜长且昼渐长的时间段可能为A .①至③B .④至①C 7.下列对该日描述正确的是A .E 日落地方时比C 晚2个小时B .北京时间而言,B 与C 同时迎来日出C .B 日出地方时为8时 E E E ED .北京时间而言,A 与C 同时迎来日落8.此时刻,下列地点组合中太阳高度相同的一组是A .(66.5°N ,150°E)、(66.5°S ,150°E)B .(43.5°N,150°E)、(3.5°S,150°E)C .(0°,30°E)、(0°,90°W )D .(0°,0°)、 (0°,180°)9.几小时后,E 处平原的人们将看见太阳位于地平线上(x ≥0且为整数)A .3+xB .3+6xC .2+12xD .2+24x2012年6月21日为夏至日,这天我国白昼时长排前三名的省会依次是:哈尔滨(3:44日出,19:27日落)、长春(3:56日出,19:25日落)、乌鲁木齐。
德州期中考试试卷高三

德州期中考试试卷高三一、试卷基本信息1. 试卷名称:德州期中考试试卷高三2. 考试科目:语文3. 考试时间:120分钟4. 满分:150分5. 考试日期:2024年4月15日6. 考试地点:德州高级中学二、试卷结构1. 选择题:共20题,每题3分,满分60分。
2. 填空题:共10题,每题4分,满分40分。
3. 阅读理解:共2篇,每篇5题,每题5分,满分50分。
4. 作文题:1题,满分50分。
三、试卷排版及格式要求1. 试卷纸张:A4纸,单面打印。
2. 字体要求:宋体,小四号。
3. 行距:1.5倍行距。
4. 页边距:上下左右均为2.5厘米。
5. 标题居中,加粗,字号为小二号。
6. 题号右对齐,与题目内容之间空两个字符。
7. 题目内容左对齐,首行缩进两个字符。
8. 选择题选项用圆圈表示,如A)、B)、C)、D)。
9. 填空题空格用下划线表示,如:_ _ _ _。
10. 阅读理解题目与文章之间空一行。
11. 作文题要求在题目下方用粗体字标出。
12. 试卷底部注明试卷编号、考生姓名、准考证号、座位号。
四、试卷内容示例1. 选择题1) 以下哪部作品是鲁迅的代表作?A) 《红楼梦》B) 《呐喊》C) 《西游记》D) 《水浒传》2) “春眠不觉晓,处处闻啼鸟”出自唐代哪位诗人之手?A) 李白B) 杜甫C) 王维D) 白居易2. 填空题1) “明月几时有,把酒问青天”是宋代诗人______的名句。
2) 《滕王阁序》是唐代文学家______的代表作。
3. 阅读理解文章一阅读以下文章,回答后面的问题。
...(文章内容)1) 文章中提到的“孤帆远影碧空尽”是什么意思?2) 作者在文中表达了怎样的情感?...(其他问题)4. 作文题请以“我眼中的春天”为题,写一篇不少于800字的作文。
五、注意事项1. 考生必须在规定时间内完成试卷。
2. 考生必须在指定的答题卡上作答。
3. 考生不得在试卷上做任何标记。
4. 考试结束后,考生必须将试卷和答题卡一并交回。
浙江省9+1高中联盟2023-2024学年高三上学期期中考试语文试题及答案

浙江省9+1高中联盟2023-2024学年高三上学期期中考试语文试题考生须知:1.本卷满分150分,考试时间150分钟;2.答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息;3.所有答案必须写在答题卷上,写在试卷上无效,考试结束后,只需上交答题卷;4.参加联批学校的学生可关注“启望教育”公众号查询个人成绩分析。
一、现代文阅读(35分)(一)现代文阅读Ⅰ(本题共5小题,19分)阅读下面的文字,完成1-5题。
暑期档《长安三万里》热映,不仅展现了唐朝诗人李白、高适和杜甫的风采,还精心描画出唐代街巷坊肆的日常景象。
时光荏苒,长安已是“西安”,城市布局与唐代相比有了很多变化。
近代以降,这座城市的唐风并不浓郁,直至2010年大明宫国家遗址公园建成,西安因地制宜,走出一条复现古都风貌的独特路径:长安西市遗址上修建的大唐西市博物馆于原址“就地展示”,对汉唐城市遗址修葺则“修旧如旧”。
6个仿唐街区复现“丹柱素壁”的建筑外表,商铺林立,游客熙攘,一派浓郁烟火气,一如今人对古代长安繁华街市的想象。
严格说来,历史文化名城难以真正“复原”。
城市不是西伯利亚荒原上偶然发现的猛犸象遗体,能在冰冻岁月中保持原貌。
一座城市的社会生活如流水般奔腾不息,后人很难分辨汉代长安、唐代长安与宋元“长安”之间的区别。
同时,即便古代城市规划设计明确,现有证据仍不足以完整复原整座城市。
比如,初至京城便明白“长安居不易”的白居易,年近五旬终于在长安新昌坊有了住宅。
对此,诗人并未吝惜笔墨,但我们仅能从诗中依稀得知他住在新昌坊东边,“最近东头是白家”,且宅前有松,“但有双松当砌下”,更多信息则无从知晓。
那么,如何在历史信息的汪洋大海中复现一座古代城市呢?理论上,我们可以立足此时此地,从现状倒推出一座城市最初的样貌。
以西安为例,在时光长河中逆流而上,观察明清西安府城墙的营建,欣赏元初马可·波罗赞美的“城甚壮丽”,了解北宋吕大忠始建碑林的动机,感受盛唐帝都的万千气象,直到见证隋文帝营造大兴城的那一刻。
标点符号的使用--逗号

们虽然罪行是无可争辩的,但是对于犯罪者是无法简单判定的。而在这部小说的后
两部分,[乙]我们接触到最多的词汇,是“麻木”二字:审判者是麻木的;旁听者是麻
木的;甚至证人——集中营的幸存者也是麻木的。[丙]反倒只有汉娜——这个站在
被告席上的人表现出丰富的性格:时而倔强,时而骄傲,甚至有些天真——尤其是她
反问法官(只有职业表情的人)“换了您,会怎么做呢?”这无疑是对那些自认为无罪
• 2.(2018衢州二中高三一模,3)阅读下面的文字,回答问题。 • 与当下“模西建筑热”同样饱受诟病的,还有“仿古建筑热”。如果前者是对西
式风格的盲目崇拜,后者则是复古思维的畸形生长。[甲]无论是抄袭还是效颦,建 筑设计与规划的盲从背后,是对文化根底不自知、对文化传统不自信。我们的文 化与历史,已经给建筑留下了丰富的馈赠。[乙]“求木之长者,必固其根本”,立 足文化本体,深挖地域特色,根深方能叶茂。[丙]缺了非物质文化的滋养,建筑再 雄伟也缺少一条脊梁,而有了乡愁和人文的淬火,哪怕穿越千年,安身之所也能成 为精神家园。 • 文段中画线的甲、乙、丙句,标点有误的一项是 ( ) • A.甲 B.乙 C.丙
二、逗号误用
⑴燕子去了,有再来的时候,杨柳枯了,有再青的时候,桃 花谢了,有再开的时候。
⑵ 我要开花,是因为我知道自己有美丽的花,我要开花,是 为了完成作为一株花的庄严使命,我要开花,是由于自己喜 欢以花来证明自己的存在。
桃花开了,红得像火;梨花开了,白得像雪;郁金香也 开了,黄色、紫色交相辉映,好一派万紫千红的灿烂春光。
注意但意义丰富的细节。 • C.当年我们的祖先,在山洞边点燃篝火、看月亮初升、星汉灿烂,也许他
们欣赏的才是美景。 • D.难以相信这就是天空中“展翅三千里,扶摇上九霄”的勇者。是什么力
江苏省扬州市2023-2024学年高三上学期期中考试语文答案

2023-2024学年度第一学期期中检测试题高三语文参考答案2023.111.C(坚持收玉米,主要不是来自外力,而是来源于内在的朴素自觉)2.C(“提倡老百姓的工作和生活都应该超越功利性”的说法过于绝对)3.A(材料和A项都可以用来论证乡土社会中人们的道德自觉)4.(1)丰富论据,共同论证了中国乡土文化中存在的相同的文化基因:为人做事依据良知,超越功利;(2)表明这一文化基因自古有之,不曾断绝,为提倡更好地挖掘和延续这一文化基因、重拾乡土文化的主张提供依据;(3)故事中李贤祖父的行为对李贤有积极影响,从而肯定了李贤祖父的“盛德”,作者借此也间接肯定了六爸行为的重要意义。
(每点2分,答对两点即可)5.(1)前一个例子语言古典雅致,如“次日,大雨至,十数日不断,村庄田地遂为水淹,无法收割”等有文言特色;(2)后一个例子语言质朴直白,如“我们村玉米地全被水淹了,玉米泡在积水里,无法收获……”等用白话表达,直白自然;(3)亦文亦白的语言,契合文本内容,使行文自然,让文章更显摇曳之美。
(每点2分)6.D(文章中心思想并不是赞美匠人们对手艺的钟情和追求,文章叙述手艺人的生活和他们的手艺,借此表达对“手艺”与“尊严”以及乡村“真相”的思考,流露出深沉、真挚的情感)7.C(“也表现了他们讨生活的不易”理解错误,文章写他们说喜话,没有表现他们生活不易之意)8.(1)生存的尊严:依靠手艺生活,养活自己;(2)匠人的尊严:苦学大本领,成为大师傅,受人敬重;(3)手艺的尊严:享受手艺的“滋味”,追求技艺的价值认同。
(每点2分,答出两点即可)9.示例:甲组:(1)文章用大量说明性文字介绍相关常识,如木匠的种类、搘锅的讲究等,实录了村庄生活与风俗文化的真实存在;(2)文章通过记叙、描写生动展现了手艺匠人及其技艺,呈现了村庄手艺人的真实生存状态;(3)文章首尾用议论方式,思考“手艺”与“尊严”等内容,揭示了村庄的内在精神本质。
浙江省2023-2024学年高一上学期语文期中考试试卷(含答案)

浙江省2023-2024学年高一上学期语文期中试卷姓名:__________ 班级:__________考号:__________现代文阅读Ⅰ材料一:打开各大互联网视频平台,很容易就能在视频播放页面找到“倍速播放”选项。
倍速播放指在不改变原视频基本制式的基础上,由用户自行选择加速或者减速的播放行为。
调查显示,在18—40岁年龄段的受访者中,使用倍速观看视频的网友接近七成,倍速播放已经成为年轻观众网络追剧的“标配”。
这一收视行为不仅体现当下年轻观众的审美需求和文艺接受特点,也折射出媒介发展对艺术创新的技术驱动。
不过,观众对影视作品进行倍速播放是有选择的。
“为什么年轻人看剧用倍速”话题曾经登上微博热搜。
倍速播放不仅能够让观众在有限时间里快速了解热门影视剧,而且对白和音乐的轻微“变形”也会营造出陌生感和新鲜感,让观众觉得更加有趣。
不过,当面对品质好剧时,观众不但不会选择“加速”,反而会再次或多次观看。
作品中那些意蕴丰富的视听语言、饱含深情的台词、直击人心的表演以及精心设计的细节交相辉映,形成强烈的感染力,让观众一再品味。
可以说,倍速播放显示出观众艺术欣赏的个性化需求,而流媒体技术为这种个性化提供了调试和选择的可能。
在新媒体终端尚未普及时,录像机、VCD机或DVD机播放已经具备了快进或快退的功能,但彼时的倍速播放操作并不便利,观赏效果也不甚理想,很难形成潮流。
随着互联网技术的不断发展,传输速度不断提高,上网看剧越来越便捷,倍速播放的实现也越来越容易。
人们在视频网站观看文艺作品时,什么作品常被“倍速”、哪些环节容易被“倍速”等信息,都会被精准捕捉并反馈给播放平台,成为内容分析、产品定位的参考数据。
在这个意义上说,倍速播放还能反哺艺术创作,促进艺术品质的提升和艺术表现的优化,激发艺术形式的调整升级。
为了适配当下人们的收看习惯,一些视频网站和制作团队不断进行尝试,探索适应新媒介的艺术表现形式,比如有的播放平台将时长两三个小时的故事切割成若干短小精悍的单元,对剧作结构进行不同于传统影视长片的重新剪辑,让观众可以一览剧作精华。
江浙皖高中(县中)发展共同体2024-2025学年高三上学期10月联考地理试题(浙江卷)

江浙皖高中(县中)发展共同体2024-2025学年高三上学期10月联考(浙江卷)地理试题命题:衢州二中审题:桐乡市高级中学舟山中学考生须知:1. 本卷满分 100分, 考试时间90分钟;2. 答题前,在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息;3. 所有答案必须写在答题卷上,写在试卷上无效,考试结束后,只需上交答题卷;4. 参加联批学校的学生可关注“启望教育”公众号查询个人成绩分析。
一、选择题(本大题共25题,每小题2分,共50分。
每小题列出的四个备选项中只有一个是符合题目要求的,不选、多选、错选均不得分)东北平原土壤肥沃,但近年来,土地退化严重。
政府部门利用遥感与物联网等多种设备和手段对黑土进行多维监测,加强对黑土的精准保护。
据此完成1、2题。
1. 影响黑土有机质含量高的主要因素是A. 岩石生物B. 气候生物C. 地形气候D. 时间地形2. 利用遥感技术可A. 测算土壤有机碳含量B. 开具精准施肥处方C. 监测农作物生长趋势D. 优化作物种植结构东印度洋——西太平洋海区是全球重要的热量和水汽源区。
与南赤道太平洋水体相比,北赤道太平洋水体温度较低。
晚中新世以来,受周边地区强烈构造运动的影响,该海区的洋流系统发生了明显的变化。
下图为构造运动前后该海区及洋流模式示意图。
读图,完成3、4题。
3. 造成海区洋流系统发生明显变化的构造运动主要是A. 板块挤压碰撞B. 板块张裂分离C. 海浪沉积加强D. 海面快速下降4. 由于构造运动导致印尼海道关闭后,东印度洋海区的表层海水A. 密度变大,盐度升高B. 密度变大,盐度降低C. 温度升高,密度减小D. 温度升高,盐度升高在多年冻土区,由于地下冰融化,会积水形成热融湖塘 (如图)。
热融湖会提升周边地温,加速释放土壤中的碳元素。
读图,完成5、6题。
5. 下列区域中,有热融湖塘发育的是A. 云贵高原B. 青藏高原C. 德干高原D. 南非高原6. 热融湖塘不断发育对自然地理环境的影响有A. 减少区域下渗水量B. 加剧全球气候变暖C. 改善当地生态环境D. 缓解冻土融化速度陕西省洋县被誉为“地球上同纬度生态最好的地区”之一,上世纪洋县的农业发展一度陷入“绿色贫困”的困局。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
衢州二中高三第一学期期中考试试卷理科数学命题人:余建新 审核人:郑志坚一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合要求的.(1)若集合{}{}2||,0A x x x B x x x ===+≥,则A B =I ( ) A .[1,0]- B .[0,)+∞ C . [1,)+∞ D .(,1]-∞-(2)设1:-<x p 或 2:,1-<>x q x 或1>x ,则p ⌝是q ⌝的 ( ) A.充分但不必要条件 B.必要但不充分条件 C.充要条件 D.既不充分也不必要条件 (3)函数()()111x f x x x -=>+的反函数为 ( ) A .()1,0,1x y x x +=∈+∞- B .()1,1,1xy x x +=∈+∞-C .()1,0,11x y x x +=∈-D .()1,0,11x y x x +=∈-(4)在等差数列{}n a 中,若24681080a a a a a ++++=,则7812a a -的值为 ( )A .4B .6C .8D .10(5)设,21cos sin ,0=+<<ααπα则α2cos 的值为 ( )A .47B .47-C .47±D .41-(6) 已知奇函数)(x f 在)0,(-∞为减函数,且0)2(=f ,则不等式0)1()1(>--x f x 的解集为( )A .{}13-<<-x x B .{}213>-<<-x x x 或C .{}303><<-x x x 或D .{}3111<<<<-x x x 或(7)数列}{n a 中,若),2(11,2111N n n a a a n n ∈≥-==-,则2007a 的值为 ( ) A .-1 B .21C .1D .2(8)定义行列式运算:.32414231a a a a a a a a -=将函数xxx f cos sin 13)(----=的图象向左平移m 个单位)0(>m ,所得图象对应的函数为偶函数,则m 的最小值是 ( ) A.8π B.3πC. 32πD. 65π(9)称||),(b a b a d -=为两个向量a 、b 间的“距离”.若向量a 、b 满足:①1||=b ;②b a ≠;③对任意的R t ∈,恒有),(),(b a d b t a d ≥则 ( ) A.b a ⊥ B.)(b a a -⊥ C. )()(b a b a -⊥+ D. )(b a b -⊥ (10)已知函数]2,2[)()(-==在和x g y x f y 的图象如下所示给出下列四个命题:(1)方程0)]([=x g f 有且仅有6个根 (2)方程0)]([=x f g 有且仅有3个根 (3)方程0)]([=x f f 有且仅有5个根 (4)方程0)]([=x g g 有且仅有4个根 其中正确的命题个数是A .4个 B .3个 C .2个 D .1个 ( )二.填空题:本大题共7小题,每小题4分,共28分. (11)2(12)(32)1i i i+-++= . (12)1lim →x 54222-+-+x x x x =.(13)若关于x 的不等式02>+-x ax 的解集为),,3()2,(+∞--∞Y 则实数=a . (14)函数)1()1(613842->+++=x x x x y 的最小值是 . (15)设P 为ABC ∆内一点,且AC AB AP 5152+=.则=∆∆ABC ABP S S .(16)设)(x f 是以2为周期的奇函数,且.3)52(=-f 若,55sin =α则)4cos 4(αf 的值是.(17)某个QQ 群中有n 名同学在玩一个数字哈哈镜游戏,这些同学依次编号为1,2,…,n 。
在哈哈镜中,每个同学看到的像用数对))(,(q p q p <表示,规则如下:若编号为k 的同学看到像为),(q p ,则编号为1+k 的同学看到像为),(r q ,且k p q =-),,(*N r q p ∈。
已知编号为1的同学看到的像为(5,6).则编号为n 的同学看到的像是 .衢州二中高三第一学期期中考试试卷理科数学答题卷二.填空题)47(⨯11. 12. 13. 14.15. 16. 17.三.解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤. (18)(本题14分)已知函数2()2cos 2f x x x ωω=(其中01ω<<),若直线3x π=为其一条对称轴,(Ⅰ)试求ω的值;(Ⅱ)先列表再作出函数()f x 在区间[],ππ-上的图象.(19) (本题14分)已知,,a b c R ∈,2()f x ax bx c =++.⑴若0a ≠,且(2)(2)f x f x +=-,且方程()0f x =两实根的平方和为10,函数()y f x =的图象过点(0,3),求函数()y f x =的解析式.⑵若函数2()f x ax bx c =++的图象过点)0,1(-,是否存在常数c b a ,,,使不等式)1(21)(2x x f x +≤≤对一切实数x 都成立?(20)(本题14分)设数列}{n a 是首项为0的递增数列,(N n ∈),,)(1sin)(n n a x nx f -=,[n a x ∈]1+n a 满足:对于任意的b x f b n =∈)(),1,0[总有两个不同的根. (Ⅰ)试写出)(1x f y =,并求出2a ; (Ⅱ)求n n a a -+1,并求出}{n a 的通项公式; (Ⅲ)设n n n a a a a a S 14321)1(--++-+-=Λ,求n S .(21) (本题14分)已知函数()ln f x x =, a a x x g (21)(2+=为常数),直线l 与函数)(x f 、)(x g 的图象都相切,且l 与函数)(x f 图象的切点的横坐标为1. (Ⅰ)求直线l 的方程及a 的值;(Ⅱ)若)()1()(x g x f x h '-+=(注: x g (')是)(x g 的导函数),求函数)(x h 的单调递增区间;(Ⅲ)当R k ∈时,试讨论方程k x g x f =-+)()1(2的解的个数.(22)(本题14分)已知数列{}n a 满足411=a ,()),2(2111N n n a a a n n n n ∈≥--=--. (Ⅰ)试判断数列()⎭⎬⎫⎩⎨⎧-+n n a 11是否为等比数列,并说明理由; (Ⅱ)设21nn a b =,求数列{}n b 的前n 项和n S ; (Ⅲ)设2)12(sin π-=n a c n n ,数列{}n c 的前n 项和为n T .求证:对任意的*∈N n ,74<n T .衢州二中高三第一学期期中考试理科数学答案1. B2.A3.C4.C5.B6.D7.A8.D9.D 10. B11.i 38+, 12.21, 13.3, 14.2 , 15.51, 16.3- 17.)210,210(22+++-n n n n (18)解:(1)化简可得:()1cos 2212sin(2)6f x x x x πωωω=+=++Q 以直线3xπ=为对称,∴2sin()136ωππ+=±,∴2()362k k Z ωππππ+=+∈ 3122k ω∴=+,111010332k k ωω<<∴-<<∴=∴=Q(2)()12sin(6f x x π=++图略.19.解 ⑴∵(2)(2)f x f x +=-,∴函数()f x 的对称轴为22bx a=-=,……① ∵函数图象过点(0,3),所以3c =, ……② 设方程()0f x =的两根为12,x x ,则222121212()2x x x x x x +=+-=2()210b c a a--= …③由①②③得1,4,3a b c ==-=,∴函数()f x 的解析式为2()43f x x x =-+⑵由0,a c +=得c a =-,2()f x ax bx a ∴=+-,假设0a =或2b a≥. ①由0a =,得()f x bx =,依题设可知0b ≠,因而函数()f x 在[]1,1-上是单调函数,,()f x 的最大值为b ,最小值为b -,于是252b b ⎧=⎪⎨-=-⎪⎩,由此得到矛盾,故0a ≠.②.41,21,41===c b a20.(1)∵01=a ,当1=n 时,|sin ||)sin(|)(11x a x x f =-=,],0[2a x ∈, 又∵对任意的)1,0[∈b ,b x f =)(1总有两个不同的根,∴π=2a∴],0[,sin )(1π∈=x x x f , π=2a(1) 由(1),],[|,2cos ||)(21sin ||)(21sin|)(322a x xx a x x f ππ∈=-=-= ∵对任意的)1,0[∈b ,b x f =)(1总有两个不同的根, ∴π33=a],3[|,31sin ||)3(31sin ||)(31sin |)(433a x x a x x f πππ∈=-=-=∵对任意的)1,0[∈b ,b x f =)(1总有两个不同的根, ∴π64=a由此可得πn a a n n =-+1, 2)1(π-=n n a n当Z k k n ∈=,2,k k k a a a a a a S 21243212-++-+-=-ΛΛππππππ4])12(53[)()()[(221223412n k k a a a a a a k k -=-=-++++-=-++-+--=-ΛΛ∴π42n S n -= 当Z k k n ∈+=,12,πππ4)1)(1(22)12(212212+-=++-=+=++n n k k k a S S k k k∴π4)1)(1(+-=n n S n21、解:(Ⅰ)1()1,x f x ='=故直线l 的斜率为1,切点为(1,f(1)),即(1,0) ∴直线l 的方程为: 1y x =- 直线l 与()y g x =图象相切,等价于方程组2112y x y x a =-⎧⎪⎨=+⎪⎩只有一解, 即方程0)1(212=++-a x x 有两个相等实根,∴△=1-4·0)1(21=+a 。
∴12a =-.(Ⅱ)∵x x x x h ()1ln()(-+=>-1),由,1111)(+-=-+='x xx x h)(x h '>0,11+x <0, ∴-1<x <0。
