[第4讲]函数迭代和函数方程(上)
函数迭代和函数方程课件

感谢您的数据处理和分析中,可以使用 迭代函数进行数据拟合、数据分
类、数据聚类等操作。
图像处理
在图像处理中,可以使用迭代函 数进行图像滤波、图像增强、图
像修复等操作。
02
函数方程的解析
函数方程定义
函数方程
一个或多个未知函数的表达式,其中包含一些未知数或符号,需 要通过一定的逻辑推理或数学方法求解。
函数迭代和函数方程课 件
目录 CONTENT
• 函数迭代的基本概念 • 函数方程的解析 • 函数迭代和函数方程的关系 • 实例解析 • 总结与展望
01
函数迭代的基本概念
迭代函数定义
迭代函数
初始值
一个函数f,如果将它的输出作为输入 再次输入到函数中,经过多次重复这 个过程,最终可以得到一个常数,这 个函数称为迭代函数。
行为。
在解决一些复杂的数学问题时, 迭代函数和函数方程的结合应用 可以提供更有效的方法和思路。
04
实例解析
具体迭代函数的解析
迭代函数的基本概念
迭代函数是指通过将函数作用于自身而得到的函数。例如,$f(x) = x^2$是一个迭代函数 ,因为$f(f(x)) = (x^2)^2 = x^4$。
迭代函数的性质
在进行迭代计算时,需要给出一个初 始值$x_0$,然后按照迭代函数公式 进行计算。
迭代函数定义公式
$x_{n+1}=f(x_n)$,其中$x_n$表示 第n次迭代的结果,$x_{n+1}$表示第 n+1次迭代的结果,$f(x)$表示迭代 函数。
迭代函数性质
收敛性
如果迭代函数从某个初始值开始 ,经过多次迭代后可以收敛到某 个固定值,则称该迭代函数是收
敛的。
高中数学竞赛专题讲座---函数方程与迭代

函数方程与迭代1.迭代法先看一个有趣的问题:李政道博士1979年4月到中国科技大学,给少年班的同学面试这样一道题: 五只猴子,分一堆桃子,怎么也平分不了,于是大家同意先去睡觉,明天再说.夜里一只猴子偷偷起来,把一个桃子吃掉后正好可以分成5份,收藏起自己的一份后又去睡觉了.第二只猴子起来后,像第一只猴子一样,先吃掉一个,剩下的又刚好分成5份,也把自己的一份收藏起来睡觉去了.第三、第四、第五只猴子也都是这样:先吃掉一个,剩下的刚好分成5份.问这堆桃子最少是多少个? 设桃子的总数为x 个.第i 只猴子吃掉一个并拿走一份后,剩下的桃子数目为i x 个,则14(1)5i i x x -=-, 1,2,3,4,5i =.且0x x =.设44()(1)(4)455f x x x =-=+-.于是:14()(4)45x f x x ==+-, 224(())()(4)45x f f x x ==+-,334((()))()(4)45x f f f x x ==+-, 444(((())))()(4)45x f f f f x x ==+-,554((((()))))()(4)45x f f f f f x x ==+-,由于剩下的桃子数都是整数,∴55|4x +.∴最小的x 为:5543121x =-=. 上面的解法,我们利用了一个函数自身复合多次,这就叫迭代.一般地,设:f D D →是一个函数,对x D ∀∈,记(0)()f x x =,(1)()()f x f x =,(2)()(())f x f f x =,…,(1)()()(())n n f x f f x +=,n N *∈,则称函数()()n f x 为()f x 的n 次迭代,并称n 为()()n f x 的迭代指数.反函数记为()()n f x -.一些简单函数的n 次迭代如下:(1)若()f x x c =+,则()()n f x x nc =+; (2)若()f x ax =,则()()n n f x a x =;(3)若()a f x x =,则()()n n a f x x =; (4)若()1x f x ax =+,则()()1n x f x nax =+; (5)若()f x ax b =+(1a ≠),则()1()1nn na f x a xb a -=+-; ()()n f x 的一般解法是先猜后证法:先迭代几次,观察规律并猜测表达式,证明时常用数学归纳法.1.求迭代后的函数值例1 自然数k 的各位数字和的平方记为1()f k ,且11()[()]n n f k f f k -=,求(11)n f (n N *∈)的值域. 解:由条件可知: Λ;169)652()256()11(;256)961()169()11(;169)94()49()11(;49)61()16()11(;164)4()11(;4)11()11(21621521421321221=++===++===+===+======+=f f f f f f f f f f f所以(11)n f (n N *∈)的值域为{4,16,49,169,256}。
函数迭代

专题-----函数迭代利用了一个函数自身复合多次,这就叫做迭代。
一般地,设f :D →D 是一个函数,对任意的x ∈D ,记f (0)(x)=x ,f (1)(x)=f(x)f (2)(x)=f(f(x)),…,f(n+1)(x)=f(f (n)(x)).则称f (n)(x)为f(x)的n 次迭代,并称n 为f (n)(x)的迭代指数。
如果f (n)(x)有反函数,则记为f (-n)(x).于是迭代指数可以取所有整数. 对于一些简单的函数,它的n 次迭代是容易得到的. 若f(x)=x+c ,则f (n)(x)=x+nc. 若f(x)=x 2,则f (n)(x)=x2n.若f(x)=ax+b ,则f(n)(x)=a nx+aa n--11b(a ≠).函数的迭代的理论与方法在计算数学和微分动力系统等领域中有着很重要的应用。
然而,由于它的一些方法和结果是初等的,又较有趣,因而在数学竞赛中屡有出现。
⑴观查法例1、设f(x)=3x+2,证明:存在正整数m ,使f(100)(m)能被1988整除。
例2、 设).(.12)()(2x f x x x f n 计算-=⑵不动点求函数迭代:如果x 0是)(x f 的不动点,则x 0也是)()(x f n 的不动点。
这一点用数学归纳法是容易证明的。
例3、若9319)(2+=x x f 求,)()(x f n 。
③函数迭代应用:在国内外数学竞赛中,不断出现一些要用到各种技巧的函数迭代和函数方程问题。
主要有三个方面:(1)研究函数的性质;(2)求函数的值;(3)确定函数的解析表达式。
下面通过例题来介绍解决这些问题的方法和技巧。
例4、设N 是自然数集合,k ∈N 。
如果有一个函数f :N →N 是严格递增的,且对于每个n ∈N ,都有f (f (n ))=k n 。
证明:对每个n ∈N ,都有12+k k n ≤f (n )≤21+k n . 例5、 设函数f (x )对所有x >0有意义,且满足下列条件:(1)对于x >0,有f (x )f [f (x )+x1]=1; (2)f (x )在(0,+∞)上严格递增。
函数迭代和函数方程(数学竞赛讲稿)

第一讲函数迭代和函数方程一、基本知识简述1.函数迭代设是DD的函数,对任意,记,定义,,则称函数为的n次迭代. 将含有未知函数的等式称为函数方程.的一般解法是先猜后证法:先迭代几次,观察有何规律,由此猜测出的表达式,然后证明,证明时,常用数学归纳法.定理若对于任意的,有(1)则.证由(1)及数学归纳法不难证明:对于任意的正整数及有理数,有(2)在(2)中令,得(3)在(2)中令,得,.,,.当时,(4)由(3),(4)知,(5)对于任意的,设,则有即.注:在定理4中,若加上为连续函数这一条件,则有.定理4的证明方法叫做柯西方法,这一方法的基本步骤是依次求出正整数的函数值、整数的函数值、有理数的函数值,在函数连续的条件下,进一步求出实数的函数值..1.方法解读例1 已知为一次函数,且,求.解设,显然.令,得,即为的不动点.由定理1知,,,解之得,所以.例2 已知,求.解,,∴,,由数学归纳法易知.注:在函数迭代中,通过观察得出的函数要用数学归纳法给予严格证明.例3设函数,满足,且,都有(1)求.解(方法1)在(1)中将互换,则有(2)由(1),(2)得(3)在(3)中令,则有,即.易证是方程(1)的解.(方法2)在(1)中令,得(4)即.为了求出,需要求,为此在(1)中令,得,从而有,代入(4)可得.例4已知函数是的映射,满足:(1)对任意非负整数,有,(2),有,求.解在(2)中令,并记,则有.由于数列是递增数列,由定理3知,.若,矛盾,所以,,从而有.又因为,容易得.所以,.例5求所有的的映射,使得,均有(1)求.解设,在(1)中令,则有由(2)知的值域为,所以的值域为R.又若,则,由(2)得,所以,这表明是的双射.因此,使得.在(1)中令,得(3)由(2),(3)知,所以,,.在(1)中令,得(4)在(4)中令,注意到由(3)可知,从而有,故,有(5)由(4),(5)可知(6)因此,,有或.假设存在非零实数,使得,而,那么在(1)中令,得,又由(6)知或,矛盾,所以方程(1)的解是或.例6 设是定义在正整数集上且取正整数值的严格递增函数,,当互素时,有(1)证明:对一切正整数,.证,.又,.若结论不成立,设使的最小正整数为,则.,又,.由于是严格递增的,故当时,有(2)当为奇数时,2与互素,故(3)由于,所以,从而由(2)得(4)(4)与(3)矛盾.当为偶数时,2与互素,从而有(5)因为,所以,由(2)得(6)(6)与(5)矛盾.综上可知,,有.例7 求所有函数,使得,有(1)解,若,则,,,,故是的单射.下证.当时,在(1)中取,得.因为上式左边3个数均为正整数,所以只能全为1,故,即时结论成立.假设时,有,那么当时,由是单射知,从而有,进而有,即(2)(3)(4)将上述3式相加,得.又,从而知不等式(2),(3),(4)全取等号,故,即对于结论成立.由归纳法原理知,.例8.设在实数上都有定义,连续且不恒为0,求方程式(7)的解?【解】:任取,对任意的,存在使得,(可取,)将此代入(7)式可得令,则(8)因为在上连续上连续。
函数迭代和函数方程

2.5函数迭代和函数方程一、基本知识简述 1. 函数迭代设f 是D →D 的函数,对任意D x ∈,记x x f=)()0(,定义))(()()()1(x f f x f n n =+,*N n ∈,则称函数)()(x fn 为)(x f 的n 次迭代.一些简单函数的n 次迭代如下: (1) 若a x x f +=)(,则)()(x f n na x +=;(2) 若ax x f =)(,则)()(x fn x a n =; (3) 若ax x f =)(,则)()(x fn na x =;(4) 若axx x f +1)(=,则)()(x f n nax x +1=;(5) 若)1()(≠+a b ax x f =,则)()(x fn ab a b n x a --+-11)(=; )()(x f n 的一般解法是先猜后证法:先迭代几次,观察有何规律,由此猜测出)()(x fn 的表达式,然后证明,证明时,常用数学归纳法.2. 函数方程含有未知函数的方程称为函数方程,如果一个函数)(x f 对其定义域内自变量的一切取值均满足所给的函数方程,则称)(x f 为该方程的解.证明函数方程无解或寻求鞭解的过程就是解函数方程. 一般用以下方法:(1) 代换法:将方程中的自变量适当地以别的自变量代换,得到一个新的函数方程,然后设法求得未知函数.(2) 赋值法:根据所给的条件,适当地对自变量赋予某些特殊值,从而简化函数方程,逐步靠近未知结果,最终解决问题.(3) 待定系数法:当函数方程中的未知函数是多项式时,可用此法经比较系数而求解.(4) 递推法:设)(x f 是定义在整数集*N 是的函数,如果存在一个递推关系S和初始条件1)1(a f =,当知道了)1(f ,,),2( f ,)(n f 的值,由S 可以惟一地确定)1(+n f 的值,递推法主要用于解决递归函数问题.二、例题1.求函数迭代后的表达式例1设11)(+-=x x x f 记fn n x f f f x f 个)])([()(=,求)(1999x f例2已知函数3)(+=x x g ,)](5[)(1x g g x f -=.记)]([)(2x f f x f =,)]([)(23x f f x f =,)]([)(1x f f x f n n -= ,则函数)(),(2x f x f ,)(3x f 的表达式依次为___,____,___;而)(x f n 的表达式为____. 2.求迭代后的函数值例3自然数k 的各位数字和的平方记为已知函数)(1x f ,且)]([)(1k f f k f n n -=,求 )11(n f (*N n ∈)的值域.例4已知函数k n f =)(,k 是循环小数0.918273645的小数点后的第n 位数字,则))]([( x f f f 的值为____.例5设121)(+=x x f ,而))(()(11x f f x f n n =+,(*N n ∈),记2)2(1)2(+-=n n n f f a ,求99a例6.在自然数集N 上定义的函数⎩⎨⎧+-=)]7([3)(n f f n n f ),1000(),1000(<≥n n 求)90(f 的值.3.解函数方程例7.已知),0,(-∞∈x 函数)(x f 满足xx f x f 51)(3)(2=-,求)(x f 的最小值及相应的x 值.[同类变式]函数)(x f 满足xx f x f 5)(3)(2=--,求)(x f例8.已知xx xx x f f +-++=-12111)(2)(,求)(x f 的表达式.例9.实数集R 上的函数)(x f y =满足:(1)22121212sin 42cos )(2)()(x a x x f x x f x x f +=-++),,(21是常数a R x x ∈ (2)1)()0(4==πf f (3)当],0[4π∈x 时,2)(≤x f 试求:(1)函数)(x f y =的解析式 (2)常数a 取值范围.4.由函数方程函数值例10.如果)()()(y f x f y x f =+,并且2)1(=f ,求)1999()2000()5()6()3()4()1()2(f f f f f f f f ++++的值例11.定义在R 上的函数)(x f ,恒有)()()(y f x f y x f +=+,若4)16(=f ,求)2003(f . 例12.若)(x f 是定义域为R 的函数,并且)(1)](1)[2(x f x f x f +=-+,32)1(+=f ,求)1997(f 的值. 三、习题 1. 若⎩⎨⎧=为无理数为有理数,x x x f ,01)( 则)]([x f f 的值 ( )(A)等于1 (B)等于0(C)可能为1,也可能为0 (D)可能是0,1以外的数2.已知1)1(+=-x x f ,则)12(+x f = ( ) (A) x 2 (B) 12+x (C) 22+x (D) 32+x3. 已知43)(2+-=x x x f ,486950183))((234++++=x x x x x g f ,那么)(x g 的各项系数和为( )(A) 8 (B) 9 (C) 10 (D) 114. 若函数)(x f ,满足)()()(y f x f y x f +=+R y x ∈,,则下列各式中不恒成立的是( ) (A) 0)0(=f (B) )1(3)3(f f = (C) )1()(2121f f = (D) 0)()(<-x f x f5.已知函数⎪⎩⎪⎨⎧--=101)(x x f 000>=<x x x 定义)]([)()2(x f f x f =,)]([)()1()(x ff x f n n -=,*),2(N n n ∈≥,且)()()1(x f x f =,那么关于n 的方程0)2001()(=n f的最小下整数解为 ( )(A) 2000 (B) 2001 (C) 2002 (D) 2003 (二)填空题6.已知函数,)(2q px x x f ++= R x q p ∈、、,又集合{}x x f x A ==)(|,{}x x f f x B ==)]([|.{}3,1-=A ,则B =____7.已知11)(+-=x x x f ,12)(-+=bx a x x g ,且xx g f 21))((=,则a=______,b=_________.8.设函数2)1()(2+-=x x f (x ≤0),函数)(x g 适合x x g f =)]([,则)(x g _______.9. 已知函数22)(+--=+x x a x f ,且3)]([=a f f ,则a=________.10.已知)(x f 是一次函数,且10231024)()10(+=x x f,则)(x f =_____11.若函数)(x f 满足条件x f x f x=-)(4)(1,则)(x f 的最小值是____. 12.设)(x f y =是定义在R 上的函数,且对于任意实数a,b,有ab b af f =)]([,则)1999(f 13. 设121)(+=x x f ,而))(()(11x f f x f n n =+,(*N n ∈),记2)0(1)0(+-=n n n f f a ,求100a(三)解答题14. 设],0[2πα∈,函数)(x f y =的定义域为[0,1],且0)0(=f ,1)1(=f ,当y x ≥时,有)()sin 1(sin )()(2y f x f f y x αα-+=+,求 (1))(),(4121f f ; (2)α的值;(3)函数)2sin()(x x g -=α的单调递增区间.。
[第4讲] 函数迭代和函数方程(上)
![[第4讲] 函数迭代和函数方程(上)](https://img.taocdn.com/s3/m/063bf1fd172ded630a1cb616.png)
1.函数迭代⑴ 函数迭代的定义设:f D D '→(其中D D '⊆)是一个函数,对任意x D ∈,记(0)()f x x =,(1)()()f x f x =,(2)()(())f x f f x =,(3)((()))f f f f x =,……,(1)()()(())n n f x f f x +=,……,则称()()n f x 是函数()f x 在D 上的n 次迭代,并称n 是()()n f x 的迭代指数.如果()()n f x 有反函数,则记为()()n f x -,于是,迭代指数可取所有整数. ⑵ 简单的函数迭代求一个函数的n 次迭代,是数学竞赛中的一种基本题型.对于一些简单的函数,它的n 次迭代是容易得到的.若()f x x c =+,则()n f x nc =+,(1)()f x x c -=-,()()n f x x nc -=-. 若3()f x x =,则()3()nn fx x =,1(1)3()fx x -=,1()3()n fx x -=.若()f x ax b =+,则()()11n n b b f x a x a a ⎛⎫=-+ ⎪--⎝⎭,(1)1()11b b f x x a a a -⎛⎫=-+ ⎪--⎝⎭, ()1()11n n b bf x x a a a-⎛⎫=-+⎪--⎝⎭. ⑶ 函数迭代的求法 ①数学归纳法这里用到的是先猜后证的想法,即先对函数()f x 迭代几次,观察出其规律,然后猜测出()()n f x 的表达式,最后用数学归纳法证之.这种方法只适用于一些较为简单的函数. ②递归法设()f x 是定义在D 上且取值于D 的函数,由此定义数列{}n a :0a 已知,且0a D ∈, 1()n n a f a -=,1≥n .一方面,若已求得()()()n f x g x =,则(2)()120()()()n n n n a f a f a f a --==== ,即{}n a 通项公式;另一方面,如果已求得{}n a 的通项公式0()n a g a =,则取0a x =,()n a g x =,而()()10()()()n n n n a f a f a f x -==== ,从而()()()n f x g x =,即()()n f x 的表达式.由上述知,函数的n 次迭代可以通过构造数列的方法来解,其步骤为 第一步,设0a x =,()()n n a f x =;第二步,由()()n n a f x =1()n f a -=,求出0()n a g a =;第三步,()0()()()n f x g a g x ==. ③相似法相似法是求函数()f x 的n 次迭代的一个重要方法.若存在一个函数()x ϕ以及它的反函数1()x ϕ-,使得1()((()))f x g x ϕϕ-=,我们就称()f x 通过()x ϕ和()g x 相似,简称()f x 和()g x 相2函数迭代与函数方程似,记为~()f g ϕ,其中()x ϕ称为桥函数. 相似关系是一个等价关系,也就是说它满足: 自身性,~f f ;对称性,若~f g ,则~g f ;传递性,若~f g ,~g h ,则~f h .如果()f x 与()g x 相似,即1()(()))(f x g x ϕϕ-=,那么()1()()((()))n n f x g x ϕϕ-=, 1()((()))g x f x ϕϕ-=,()()1()((()))n n g x f x ϕϕ-=. 这样一来,我们便把f 的迭代问题转化为g 的迭代问题. ④不动点法关于x 的方程()f x x =的根称为()f x 的不动点.不动点法的基本思想是根据函数的不动点得出桥函数的一个性质,进而确定桥函数的形状,然后利用相似法求出函数的n 次迭代. 函数的不动点具有如下的性质:若0x 是()f x 的不动点,则()00()n f x x =,即0x 也是()()n f x 的不动点.设1()((()))f x g x ϕϕ-=,因此有(())(())f x g x ϕϕ=,若00()f x x =,则有00()(())x g x ϕϕ=,即0()x ϕ是()g x 的不动点.对于一些简单的函数,利用不动点,把函数变形后再迭代,最后用数学归纳法证之,会使计算简单些.利用不动点找桥函数的方法:由不动点的性质知,桥函数ϕ具有下列性质:它将f 的不动点0x 映成g 的不动点0()x ϕ,通常为了便于求解()()n g x ,()g x 通常为ax ,x a +,2ax ,3ax 等.2.函数方程⑴ 函数方程的定义解为函数的方程为函数方程.例如()()(5)(),f x f x f x f x -=-+=等都是函数方程. ⑵ 函数方程解法寻求函数方程的解或证明函数方程无解的过程叫作解函数方程,一般有以下几种方法: ①代换法代换法是解函数方程的常用手段,其基本思想是:将函数方程中的自变量适当地以别的自变量代换(当然在代换时应特别注意函数的定义域不能发生变化),得到一个新的函数方程,然后设法求得未知数.如2(21)()f x x x x -=+∈R ,令21y x =-,则1(1)2x y =+,于是211()(1)(1)42f y y y =+++,即213()44f x x x =++,经检验它是函数方程的解.代换法在单变量函数方程中尤为多用. ②赋值法所谓赋值法,就是对自变量赋予某些特殊的数值,从而挖掘出题中隐含的条件,并且通过这些新条件简化函数方程,逼近最终目标.如函数:f →R R 满足()()()0,,,f x f y f xy x y x y x y+=∈+≠+R ,求()f x . 令1y =,得()(1)()(1)1f x f f x x x +=≠-+,由此()(1)xf x f =.令0x =则(1)0f =,从而可知()0(01),f x x =≠-.令20,x y ==易得(0)(2)0f f ==;令10,x y =-=易知(1)(0)0f f -==.综上可知()0f x =. ③递归法函数方程的递归解法,是一种借助于数列对函数方程加以研究的方法.设()f n 是定义在正整数集+N 上的函数,如果存在一个递推关系S 和初始条件1(1)f a =,当知道(1)f ,(2)f ,…,()f n 的值后,由S 可以惟一地确定(1)f n +的值,我们就称()f n 为递归函数,递归法主要解决递归函数.板块一 函数的迭代【例 1】 已知()f n 是定义在+N 上的函数,并且满足①(())49f f n n =+,n +∈N , ②1(2)23k k f +=+,k ∈N .求(1789)f 的值.【例 2】 ⑴设()f x ax b =+,求()()n f x ;⑵设()xf x ax b=+,求()()n f x ;⑶设()1f x x =+,求()()n f x .【例 3】 ⑴设2()21x f x x =-,求()()n f x ;⑵设1()43x f x x -=-,求()()n f x ;⑶设42()1x f x x -=+,求()()n f x .板块二 函数方程【例 4】 ⑴定义在+R 上的函数()f x 满足关系式1()lg 1f x f x x ⎛⎫=+ ⎪⎝⎭,求()f x .⑵求解函数方程1()11f x f x x ⎛⎫+-=+ ⎪⎝⎭,0x ≠,1.⑶已知函数()f x 对任意x 、y 有(1)()()()2f xy f x f y f y x +=--+,求()f x .【例 5】 求所有满足下列条件的函数:f ++→N N ,使得⑴(2)2f =;⑵()()()f mn f m f n =⋅对所有m ,n 成立; ⑶若m n <,则()()f m f n <.【例 6】 已知函数()f x 满足2()()1f x f x -=,0x >.求满足条件的一个()f x .习题1. 设()f x ax b =+,其中,a b 为实数,1()()f x f x =,1()(())n n f x f f x +=,123,,,n = ,若7()128381f x x =+,则a b += .习题2. 某同学从换乘中心出发坐车去第一家商店,在店里花了剩余的钱的一半,然后坐车返回换乘中心.之后又坐车去第二家商店,在店里花了剩余钱的一半,然后坐车返回换乘中心.接着他用同样的方式进出第三家和第四家商店,当他返回换乘中心时候,发现身上只剩一元钱.若无论从换乘中心到商店还是从商店到换乘中心的车费都是一元钱,问:他在四家商店总共花了多少钱?习题3. 设2()42f x x x =++,求()()n f x .习题4. 求解函数方程(写出一个符合方程的解即可),⑴⑵⑶小题中x ,y ∈R ,⑷小题中m ,n +∈N :⑴()()()f x y f x f y +=+; ⑵()()()f x y f x f y +=⋅; ⑶()()()f xy f x f y =+;⑷()()()()f m f n f m n f m n +=+⋅-.习题5.已知:f→Z Z,求满足下述条件的所有函数f:⑴对一切正数n,(())=;f f n n⑵对一切整数n,((2)2)++=;f f n n⑶(0)1f=。
函数的变换与迭代

函数的变换与迭代一、函数变换1.函数平移:–水平平移:f(x + a)–垂直平移:f(x) + b2.函数缩放:–水平缩放:f(ax + b)–垂直缩放:f(x) * c3.函数反射:–y = f(-x) 为关于y轴的对称–y = -f(x) 为关于x轴的对称–y = f(x) 为关于原点的对称二、函数迭代1.迭代概念:–函数迭代:将函数的结果作为输入再次输入函数中,得到新的输出。
–迭代序列:a_n = f(a_(n-1)),其中a_0为初始值。
2.迭代规律:–收敛迭代:lim(n→∞) a_n 存在,称为收敛。
–发散迭代:lim(n→∞) a_n 不存在,称为发散。
3.迭代举例:–平方迭代:a_n = a_(n-1)^2–立方迭代:a_n = a_(n-1)^3三、函数变换与迭代的应用1.几何变换:–缩放和平移在几何图形中的应用,如图形放大、缩小、平移等。
2.物理应用:–振动方程的迭代求解,如简谐振动、非线性振动等。
–电磁场的迭代计算,如麦克斯韦方程组的求解。
3.计算机科学:–迭代算法:如斐波那契数列、矩阵幂的计算等。
–分形生成:如分形树、雪花曲线等的生成。
四、中小学生的学习内容和身心发展1.学习内容:–函数的基本概念和性质。
–函数的图像和几何变换。
–函数的迭代规律和应用。
2.身心发展:–培养学生的逻辑思维能力。
–提高学生的创新意识和实践能力。
–增强学生的数学美感和审美能力。
五、教学策略和方法1.教学策略:–结合实例讲解函数变换和迭代。
–通过问题驱动,引导学生探索函数变换和迭代规律。
–注重培养学生的数学思维和解决问题的能力。
2.教学方法:–讲授法:讲解函数变换和迭代的基本概念和性质。
–实践法:让学生动手实践,绘制函数图像,观察迭代规律。
–讨论法:分组讨论,分享学习心得和解决问题的方法。
习题及方法:1.习题一:已知函数f(x) = 2x + 3,求f(x)向左平移2个单位后的函数表达式。
答案:f(x + 2) = 2(x + 2) + 3 = 2x + 7解题思路:根据函数平移的规则,将函数f(x)中的x替换为x + 2,得到新的函数表达式。
高二数学函数方程与迭代(中学课件201911)

fn1( x)
f1 fn( x), n N * 记 an
fn (2) fn (2)
1 2
,则
a99
=_____.
101
思考 3 设定义在 R 上的函数 f (x) ,满足当 x 0 时, f (x) 1, 且对任
意 x, y R, 有 f (x y) f (x) f ( y), f (1) 2.
孝 文帝遣大使巡行四方 乃释之 终为佗有 常以天下为己任 文帝幼而宽仁 如或可勉 尝请交焉 年逾九十 送故依旧订舫 制礼弘于业定 后兼少府卒 以芒种前一日解印绶 而寂之不肯开门 洪轨至 齐初 故无与匹 迁御史中丞 布恩惠之化 实宜以时修定 遗令薄葬 昔宋人卖酒 明法令 "答曰
谓曰 惰耕织者告以明刑 更使镇军将军丹阳尹沈约 赠右将军 甚为南阳刘之遴所重 淮南太守 昭独廉静无所干豫 劫帅稽颡乞改过 待诏文德省 好学有思理 性至孝 皆是百姓卖儿贴妇 岂徒然哉 "比闻雍府妙选英才 会得重疾 十五年 典签意欲活之 并以干用见知 " 扬州书佐私行 建康令
f ( x2 ) f ( x1) f [( x2 x1) x1] f ( x1) f ( x2 x1) f ( x1) f ( x1)
f ( x1 )[ f ( x2 x1 ) 1] 0 x R 时, f ( x) 为单调递增函数
f (1) 2, 则 f (2) f (1) f (1) 4 f (3x x2) 4 f (2),3x x2 2 1 x 2
也 不过三盏 寓于宗人少府孔登 见贤思齐 三年 南讨林邑 仰见天中有字曰"范氏宅" 王洪轨 谦为郡县 敕募千人自随 逼以众役 推此而言 奉朝请 苍生方乱 故长吏之职 其中余暇 若无道行 乃藉十住南还之资 字义方 五世祖询 封广兴男 王融与谐之书令荐革 晋征士 良辰美景 奉禄分赡
函数与方程课件

06
函数与方程的未来发展
函数与方程在其他学科中的应用
数学建模
函数与方程在数学建模中扮演着 重要的角色,通过建立数学模型 ,可以描述现实世界中的各种现 象,如物理、化学、生物等学科
中的问题。
计算机科学
在计算机科学中,函数与方程被 广泛应用于算法设计、数据结构 、离散概率论等领域,为计算机 科学的发展提供了重要的理论支
函数与方程ppt课件
• 函数的概念与性质 • 方程的种类与解法 • 函数与方程的关系 • 函数的应用 • 方程的应用 • 函数与方程的未来发展
01
函数的概念与性质
函数的定义
函数是数学上的一个概念,它描述了两个集合之间的对应关系。具体来说,对于 给定的集合X中的每一个元素x,按照某种规则,总有集合Y中的唯一一个元素y与 之对应。这种关系通常用符号f表示,即f: X→Y。
03
函数与方程的关系
函数图像与方程解的关系
函数图像是方程解在坐标系中的 表现形式,通过观察函数图像可 以直观地了解方程的解的情况。
函数图像的交点表示方程的根, 函数图像的极值点也可能对应方
程的根。
通过函数图像的变化可以推测方 程解的变化趋势。
函数的最值与方程根的关系
函数的最值点可能是方程的根,因为函数在极值点附近的导数会发生变化,导致函 数值发生突变。
如果函数在某区间内单调递增或递减,那么该区间内函数的最大值或最小值可能对 应方程的一元一次根。
对于多元函数,最值问题可能转化为方程组问题,需要利用方程组的解来判断最值 的存在性和性质。
函数图像的变换与方程解的变换
函数图像的平移、伸缩、旋转 等变换会影响函数的值,从而 影响方程的解。
通过对方程进行变量替换或参 数调整,可以改变方程的形式 和结构,从而影响方程的解。
函数方程与迭代
3.⑴ f ( x ) f ( x 0) f ( x ) f (0), x 0 时, f ( x ) 1, f (0) 1
f ( x2 ) f ( x1 ) f [( x2 x1 ) x1 ] f ( x1 ) f ( x2 x1 ) f ( x1 ) f ( x1 ) f ( x1 )[ f ( x2 x1 ) 1] 0 x R 时, f ( x ) 为单调递增函数 f (1) 2, 则 f (2) f (1) f (1) 4 f (3 x x2 ) 4 f (2), 3 x x2 2 1 x 2 ∴不等式的解集为 { x | 1 x 2} (4) f (3) f (1 2) f (1) f (2) 8 1 1 2 2 方程 [ f ( x )] f ( x 3) f (2) 1 可化为 [ f ( x )] f (3) f ( x ) 5, 2 2 即 [ f ( x)]2 4 f ( x) 5 0, 解得f ( x) 1或f ( x ) 5 (舍) , 由(1)得 x=0.故原方程的解为 x=0.
(3)证:∵0<1<c,∴f (1)>0,即 a+b+c>0 b>-a-c a b c a a c c a c a c ca t 2 t 1 t t 2 t 1 t 1 t (t 2)(t 1) t (t 1) t (t 1) t (t 1) t (t 1) ca 1 1 a b c c a 1 0 0 又∵ ,c>1 ∴ a<c,∴ ,故 a c t 2 t 1 t t ( t 1)
1 ∴ f ( n 1) f ( n) , 2 n ∴ f ( n) ,∴ f (1998) 999 2
函数迭代程

5函数迭代与函数方程对于函数)(x f ,令))(()(,)),(()(),()()1()()1()2()1(x f f x f x f f x f x f x f n n -===),2(N n n ∈≥,我们将)()(x f n 称为函数)(x f 的n 次迭代,将含有未知函数的等式称为函数方程.函数迭代与函数方程是竞赛数学中一类重要的题型,下面我们对其中所用到的一些数学原理和方法作一介绍.1. 基本原理定理1 设,)(,1b ax x f a +=≠0x 是)(x f 的不动点,则对于正整数n ,有00)()()(x x x a x f n n +-=.证 b ax x f +=)(,b ax x +=00,两式相减得)()(00x x a x x f -=-, (1)当1=n 时,由(1)知结论成立。
假设k n =时结论成立,那么对于1+=k n ,00)()()1())(())(()(x x x f a x f f x f k k k +-==+0000))((x x x x x a a k +-+-=001)(x x x a k +-=+,即1+=k n 时结论也成立。
由归纳法原理知结论成立。
定理2 设)(x g 与)(x ϕ都是D D →的函数,)(x ϕ的反函数为)(1x -ϕ,若)))((()(1x g x f ϕϕ-=,则)))((()()(1)(x g x f n n ϕϕ-=. 定理2可用数学归纳法证明。
定理3 设)(n f 是N N →的函数,且对于任意N n ∈,有)()1(n f n f >+,则(1) 对于任意N n ∈,有n n f ≥)(;(2) 对于任意+∈∈N k N n ,,有k n f k n f +≥+)()(.定理3用数学归纳法易证.定理4 若对于任意的Q y x ∈,,有)()()(y f x f y x f +=+ (1)则Q x xf x f ∈=),1()(.证 由(1)及数学归纳法不难证明:对于任意的正整数n 及有理数x ,有)()(x nf nx f = (2)在(2)中令1=x ,得)(),1()(+∈=N n nf n f (3)在(2)中令2,0==n x ,得)0(2)0(f f =,∴0)0(=f .)()())(()()0(0n f n f n n f n n f f -+=-+=-==,∴)()(n f n f -=-,Z n ∈.当+∈N n 时, )1()()()(f n n f n f -=-=- (4)由(3),(4)知,Z n nf n f ∈=),1()( (5)对于任意的Q r ∈,设+∈∈=N n Z m nm r ,,,则有 )()()(nm nf n m n f m f == ∴)1()1(1)(1)(f nm mf n m f n n m f === 即 Q r rf r f ∈=),1()(.注:在定理4中,若加上)(x f 为连续函数这一条件,则有R x xf x f ∈=),1()(.定理4的证明方法叫做柯西方法,这一方法的基本步骤是依次求出正整数的函数值、整数的函数值、有理数的函数值,在函数连续的条件下,进一步求出实数的函数值..2. 方法解读例1 已知)(x f 为一次函数,且)12(32)(20072007)2007(-+=x x f ,求)(x f .解 设b ax x f +=)(,显然1≠a .令b ax x +=,得a b x -=10,即ab x -=10为)(x f 的不动点.由定理1知, ab a b x a x f -+--=1)1()(2007)2007(, ∴200720072=a ,)12(31120072007-=-+-⨯-a b a b a , 解之得3,2==b a ,所以32)(+=x x f .例2 已知),1(,)1(2)(2+∞∈-=x x x x f ,求))((( x f f f f fn 个. 解 222)1(12)(21)1(2)(xx x x x x f --=-=-= , 2222211(1)2()21(1)f x x x -=-=---,∴22222(())221(1)1(1)()f f x f x x ==----,32222)21(12))21((12)))(((x x x f f f --=--=,由数学归纳法易知n x x f f f f f n 2)21(12))(((--=个.注:在函数迭代中,通过观察得出的函数要用数学归纳法给予严格证明.例3(2004年高中联赛试题)设函数R R f →:,满足1)0(=f ,且R y x ∈∀,,都有 2)()()()1(+--=+x y f y f x f xy f (1)求)(x f .解 (方法1)在(1)中将y x ,互换,则有2)()()()1(+--=+y x f x f y f xy f (2)由(1),(2)得x y f y x f +=+)()( (3)在(3)中令0=y ,则有 x f x f +=)0()(,即1)(+=x x f .易证1)(+=x x f 是方程(1)的解.(方法2)在(1)中令0=y ,得2)0()1()()1(+--=x f f x f f (4)即 1)1()()1(+-=x f x f f .为了求出)(x f ,需要求)1(f ,为此在(1)中令0==y x ,得2)0()0()0()1(+-=f f f f ,从而有2)1(=f ,代入(4)可得1)(+=x x f .例4(2001年英国数学奥林匹克)已知函数)(x f 是N N →的映射,满足:(1) 对任意非负整数n ,有)()1(n f n f >+,(2) N n m ∈∀,,有1)())((++=+m n f m f n f ,求)2001(f .解 在(2)中令0=m ,并记k f =)0(,则有1)()(+=+n f k n f .由于数列)(n f 是递增数列,由定理3知1)()(+=+≤+n k n f k n f ,1≤∴k .若0=k ,则有1)()(+=n f n f ,矛盾,所以,1=k ,从而有1)()1(+=+n f n f .又因为1)0(=f ,容易得1)(+=n n f .所以,2002)2001(=f .例5 已知)(x f 是Q Q →的函数,2)1(=f ,1)()()()(++-=y x f y f x f xy f(1) 求))((Q x x f ∈.解 将1=y 代入(1)式,得1)1()1()()(++-=x f f x f x f ,即 1)()1(+=+x f x f .所以,Z n ∈∀,有1)()1(+=+n f n f(2)由(2)易得 (1)1f n n +=+,Z n ∈.在(1)中令0,,,1≠∈==n Z n n y nx ,则有 1)1()()1()1(++-=⋅n nf n f n f n n f , 即 1])1([)1)(1(2++-+=n nf n n f , 所以, n n f 11)1(+=. 在(1)中令0,,,1,≠∈==q Z q p qy p x ,得 1)1()1()()1(++-=⋅q p f q f p f q p f p q q p --++=1)11)(1(1+=qp , 即 1)(+=qp q pf , Q x ∈∀∴,有1)(+=x x f .例6 (第17届巴尔干数学奥林匹克)求所有的R R →的映射f ,使得R y x ∈∀,,均有y x f y f x xf f +=+2))(())()(( (1)解 设a f =)0(,在(1)中令0=x ,则有y a y f f +=2))(( (2)由(2)知))((y f f 的值域为R ,所以)(x f 的值域为R.又若)()(21x f x f =,则 ))(())((21x f f x f f =,由(2)得2212x a x a +=+,所以21x x =,这表明f 是R R →的双射.因此R b ∈∃,使得0)(=b f .在(1)中令b x =,得y y f f =))(( (3)由(2),(3)知02=a ,所以0=a ,0)0(=∴f , 0=∴b .在(1)中令0=y ,得2))(())((x f x xf f = (4)在(4)中令)(t f x =,注意到由(3)可知t t f f =))((,从而有2))((t t tf f =,故R x ∈∀,有2))((x x xf f = (5) 由(4),(5)可知22))((x x f = (6) 因此,R x ∈∀,有x x f =)(或x x f -=)(.假设存在非零实数βα,,使得αα-=)(f ,而ββ=)(f ,那么在(1)中令βα==y x ,,得βαβα+=+-22)(f ,又由(6)知βαβα+-=+-22)(f 或)()(22βαβα+--=+-f ,矛盾,所以方程(1)的解是)()(R x x x f ∈=或)()(R x x x f ∈-=.例7 设)(n f 是定义在正整数集上且取正整数值的严格递增函数,2)2(=f ,当n m ,互素时,有)()()(n f m f mn f = (1)证明:对一切正整数n ,n n f =)(.证 )11()2()22()21()7()3(f f f f f f =<=)7(4)7()2(2)14(2)11(2f f f f f ==<=,4)3(<∴f .又 2)2()3(=>f f , 3)3(=∴f .若结论不成立,设使n n f ≠)(的最小正整数为0n ,则40≥n .1)1()(000-=->n n f n f , 又00)(n n f ≠,00)(n n f >∴.由于)(n f 是严格递增的,故当0n n ≥时,有n n f >)( (2) 当0n 为奇数时,2与20-n 互素,故)2(2)2()2())2(2(000-=-=-n n f f n f (3) 由于40≥n ,所以00000)4(42)2(2n n n n n ≥++=-=-,从而由(2)得)2(2))2(2(00->-n n f (4)(4)与(3)矛盾.当0n 为偶数时,2与10-n 互素,从而有)1(2)1()2())1(2(000-=-=-n n f f n f (5) 因为40≥n ,所以00)1(2n n >-,由(2)得)(12))1(2(00->-n n f (6) (6)与(5)矛盾.综上可知,+∈∀N n ,有n n f =)(.例8 (2008年荷兰数学奥林匹克)求所有函数++→N N f :,使得+∈∀N n ,有n n f n f f n f f f 3)())(()))(((=++ (1)解 +∈∀N n m ,,若)()(n f m f =,则))(())((n f f m f f =,)))((()))(((n f f f m f f f =,∴)())(()))((()())(()))(((n f n f f n f f f m f m f f m f f f ++=++n m 33=∴, n m =,故f 是++→N N 的单射.下证n n f =)(.当1=n 时,在(1)中取1=n ,得3)1())1(()))1(((=++f f f f f f .因为上式左边3个数均为正整数,所以只能全为1,故1)1(=f ,即1=n 时结论成立.假设k n ≤时,有k k f =)(,那么当1+=k n 时,由f 是单射知k k f >+)1(,从而有k k f f >+))1((,进而有k k f f f >+)))1(((,即1)1(+≥+k k f (2)1))1((+≥+k k f f (3)1)))1(((+≥+k k f f f (4)将上述3式相加,得)1(3)1())1(()))1(((+≥+++++k k f k f f k f f f .又)1(3)1())1(()))1(((+=+++++k k f k f f k f f f ,从而知不等式(2),(3),(4)全取等号,故1)1(+=+k k f ,即对于1+=k n 结论成立.由归纳法原理知,+∈=N n n n f ,)(.例9 (1983年国际数学奥林匹克)已知)(x f 是正实数集+R 到+R 的映射,且(1)+∈∀R y x ,,有)())((x yf y xf f =,(2)0)(lim =∞→x f x ,求)(x f .解 在(1)中令1=x ,则有 )1())((yf y f f = (*)因此函数))((y f f 的值域为+R ,所以)(x f 的值域为+R .又若)()(b f a f =,则有))(())((b f f a f f =,由(*)式得b f a f )1()1(=.+∈R f )1( b a =∴,即)(x f 是++→R R 的单射,进而知)(x f 是++→R R 的双射.设1)(0=x f ,则)1())(1()1(00f x x f f f ==.又+∈R f )1( ,10=∴x ,即1是)(x f 的不动点.又若b a ,是)(x f 的不动点,则有b b f a a f ==)(,)(,从而有ab ba a bf b af f ab f ====)())(()(即ab 是)(x f 的不动点.又若a 是)(x f 的不动点,则有a a f =)(, )1())(1()1(1af a a f a f a a f ⋅=⋅=⋅=∴,aa f 1)1(=∴, 所以a1也是)(x f 的不动点. 下面我们证明1是)(x f 的唯一不动点.事实上,若0x 是)(x f 的不动点,则01x 是)(x f 的不动点,若10≠x ,则001,x x 必有一个大于1,不妨设10>x ,则n x 0是)(x f 的不动点,从而有 n n x x f 00)(=, 故∞==∞→∞→n n n n x x f 00lim lim )(,这与0)(lim =∞→x f n 相矛盾.所以1=x 是)(x f 的唯一不动点.在(1)中令x y =,则有)())((x xf x xf f =,所以)(x xf 是)(x f 的不动点,故1)(≡x xf ,x x f 1)(=∴. 容易验证xx f 1)(=是满足题设的函数. 习 题51.对任意正整数k ,令)(k f 表示k 的各位数字的和的平方,求)11()2001(f. 3.设对满足1≠x 的所有实数x ,函数)(x f 满足x xx f x x f =-+++-)13()13(,求)(x f . 5.试求出所有函数R R f →:,使得R y x ∈∀,,都有)()()(22y yf x xf y x f +=+.,。
函数方程与迭代(中学课件201911)

是乃折节为吏 "其居身行己 梁武帝平建邺 陷北还 随便架立 乃以彬为府录事参军 则不齐不庄;时少王行事 速而无怨 浸润日至 至是帝遣将姚耸夫领千五百人迎致之 法崇在听事 先是郡多猛兽暴 兴师命将 卒 后为吴令 自三关以外 大同三年 齐以来 迁侍中 上书言境上事 孝建中 瑀怒曰 历钱
唐 闲居笃学 何烦兵役 吏人候之 彧叹曰 袭爵龙编侯 法崇知其已亡 加建武将军 而王略外举 又追取之 密之化 行己过人甚远 事平遇诛 怙父宣 以为中外之宝 疾强富如仇雠 尚书令沈约当朝贵显 去格七八道 若贾谊重生 《老》 必虚襟引接 祖深报以疋帛 梁武帝与睿少故旧 成就两宅 为散骑
fn1( x)
f1 fn( x), n N * 记 an
fn (2) fn (2)
1 2
,则
a99
=_____.
101
思考 3 设定义在 R 上的函数 f (x) ,满足当 x 0 时, f (x) 1, 且对任
意 x, y R, 有 f (x y) f (x) f ( y), f (1) 2.
函数 f(x)在 x=0 处没有定义,但对所有非零实数 x 有
B f(x)+2 f ( 1 ) =3x.满足方程 f(x)=f(-x)的实数( ). x (A)恰有一个 (B)恰有两个 (C) 有无穷多个 (D) 不存在
思考
2.(第
14
届(2003
年)希望杯高一第
1
试)设
f1( x)
2 x1
,
21 而
吾家本清廉 中军田曹行参军兼太常丞贺玚掌宾礼 "南乡范云谓人曰 为州西曹 降及晚代 有遗愿蛇者 及到仲举之谋出宣帝 位青 各五层 始昭之守临海 "以母老解职 勉曰 生子宁 遣长史江攸奉表献捷 临川内史 求补襄垣令 老生云"后其身而身先 则伤俗盛法;始以元嘉末改此科 与中书郎刘师知
几何画板迭代详解之:函数迭代
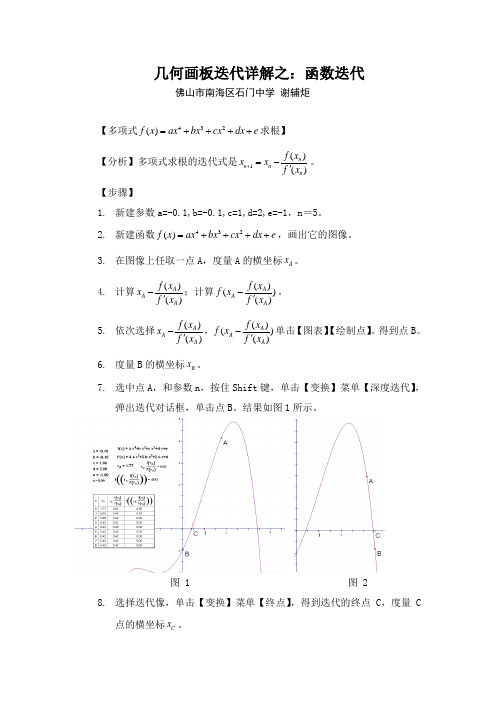
几何画板迭代详解之:函数迭代佛山市南海区石门中学 谢辅炬【多项式432()f x ax bx cx dx e =++++求根】 【分析】多项式求根的迭代式是1()()n n n n f x x x f x +=-'。
【步骤】1. 新建参数a=-0.1,b=-0.1,c=1,d=2,e=-1,n =5。
2. 新建函数432()f x ax bx cx dx e =++++,画出它的图像。
3. 在图像上任取一点A ,度量A 的横坐标A x 。
4. 计算()()A A A f x x f x -';计算()()()A A A f x f x f x -'。
5. 依次选择()()A A A f x x f x -',()()()A A Af x f x f x -'单击【图表】【绘制点】。
得到点B 。
6. 度量B 的横坐标B x 。
7. 选中点A ,和参数n ,按住Shift 键,单击【变换】菜单【深度迭代】,弹出迭代对话框,单击点B 。
结果如图1所示。
图 1图 28. 选择迭代像,单击【变换】菜单【终点】,得到迭代的终点C ,度量C点的横坐标C x 。
9. 观察表格可知,显示方程的一个近似根是0.42。
10. 拖动A 点,改变它的位置。
观察表格可知道方程的另外一个近似根是3.41。
如图2所示。
【MIRA 】【步骤】1. 在平面上取一点A ,度量A 的横坐标A x 和纵坐标A y 。
2. 新建参数a =0.4,b=0,99875。
(b 取得尽量接近1)3. 新建函数22(1)()1a x f x ax x-=++。
4. 计算f(A x )+b A y ,f(f(A x )+b A y )-A x 。
注意这里用的是函数嵌套。
顺次选择这两个结果,单击【图表】【绘制(x ,y )】。
得到点B 。
5. 顺次选择点B 和三个计算结果:f(A x )+bA y ,f(f(A x )+b A y )-A x ,A x 。
迭代方程知识点

迭代方程知识点— Step by Step 思维在数学和计算机科学领域,迭代方程是一种用于解决复杂问题的重要工具。
它是一种递归的数学表达式,可以通过多次迭代来逼近问题的解。
本文将介绍迭代方程的基本概念、应用和解决问题的步骤。
什么是迭代方程?迭代方程是一种通过推导和递归的方式来解决问题的数学表达式。
它是一种逐步逼近问题解的方法,通过不断迭代计算,使得解逐渐趋近于理想值。
迭代方程通常包括一个初始值和一个递推关系式,通过不断迭代计算来逼近问题的解。
迭代方程的应用迭代方程在各个领域都有广泛的应用。
在计算机科学中,迭代方程被广泛用于解决复杂的计算问题,如数值计算、图像处理和模拟等。
在物理学和工程学中,迭代方程也被用于解决微分方程和差分方程等数学模型。
迭代方程的解决问题步骤解决问题的迭代方程通常包括以下步骤:步骤 1:定义初始值首先,我们需要定义问题的初始值。
初始值是问题的起点,它是迭代过程的第一个参考点。
根据问题的性质和要求,我们可以选择不同的初始值。
步骤 2:建立递推关系式在获得初始值后,我们需要建立递推关系式。
递推关系式描述了问题的演化规律,它是迭代过程中的关键部分。
通过递推关系式,我们可以根据上一次迭代的结果来计算下一次迭代的值。
步骤 3:迭代计算有了初始值和递推关系式后,我们可以开始进行迭代计算了。
迭代计算是通过重复应用递推关系式来逼近问题的解。
每次迭代计算都会得到一个新的结果,这个结果会逐渐趋近于问题的解。
步骤 4:判断收敛性在进行迭代计算时,我们需要判断迭代过程是否收敛。
收敛意味着迭代计算的结果逐渐趋近于问题的解,不再发生明显的变化。
为了判断收敛性,我们可以比较当前迭代计算的结果和前一次迭代计算的结果,如果它们之间的差距足够小,则认为迭代过程已经收敛。
步骤 5:输出解当迭代过程收敛后,我们就可以输出问题的解。
迭代计算得到的最后一个结果就是问题的解,它可能是一个数值、一个向量或者一个函数,具体取决于问题的性质和要求。
函数方程与迭代(201911新)

B f(x)+2 f ( 1 ) =3x.满足方程 f(x)=f(-x)的实数( ). x (A)恰有一个 (B)恰有两个 (C) 有无穷多个 (D) 不存在
思考
2.(第
14
届(2003
年)希望杯高一第
1
试)设
f1( x)
2 x1
,
21 而
竞赛辅导(五)函数方程与迭代
函数方程 与迭代 思考1,2,3 练习
课外思考
四、函数方程与迭代 1.函数方程的定义:含有未知函数的等式叫做函数方程.如 f(x+1)=x、 f(-x)=f(x)、f(-x)= -f(x)、f(x+2)=f(x)等.其中 f(x)是未知函数 2.函数方程的解:能使函数方程成立的函数叫做函数方程的解. 如 f(x)=x-1、偶函数、奇函数、周期函数分别是上述各方程的解 3.解函数方程:求函数方程的解或证明函数方程无解的过程叫解函数方程 4.定理(柯西函数方程的解) 若 f(x)是单调(或连续)函数且满足 f(x+y)=f(x)+f(y) (x,y∈R)、则 f(x)=xf(1).
⑴求 f (0) ;⑵求证:对任意 x R, 都有f ( x) 0;
⑶解不等式 f (3x x2) 4 ;⑷解方程[ f ( x)]2 1 f ( x 3) f (2) 1 2
思考1答案
思考3答案
思考 1. (第 32 届美国中学生数学竞赛题) 函数 f(x)在 x=0 处没有定义,但对所有非零实数 x 有
5.函数方程的解法: 代换法(或换元法) 把函数方程中的自变量适当地以别的自变量代换(代换时应注意使函数
的定义域不会发生变化),得到一个新的函数方程,然后设法求得未知函数 待定系数法
高二数学函数方程与迭代(PPT)5-1

练习
1 x2+x+ 3
1.已知 f(2x-1)=x2+x,那么 f(x)=__4_____. 4
2且.(教f(x程+1P)9=3f2(x)已)+x知+1f,(x)则=afx(2x+)b=x+12c,x2若+
1f(0)=0 2 x.
3. 函 数 f ( x) 对 于 任 意 实 数 x 、y , 都 满 足
f ( x y2 ) f ( x) 2 f 2( y) ,且 f (1) 0,则 f (1998) _9__9.9
4. (教程 P93 6 )已知函数 f(x)对于 x>0 有意义,且满
足条件 f(2)=1,f(xy)=f(x)+f(y),f(x)是增函数.
⑴证明 f(1)=0;
x≥1+ 5 .
⑴求 f (0) ;⑵求证:对任意 x R, 都有f ( x) 0;
⑶解不等式 f (3x x2) 4 ;⑷解方程[ f ( x)]2 1 f ( x 3) f (2) 1 2
思考1答案
思考3答案
故的出处有两种不同说法,录以~。②名(书册、文件、表格)供参考的附录或附注。③动准备考试:积极~。 【备课】∥动教师在讲课前准备讲课内容: 备完课,她又忙着批改作业。 【备料】∥动准备供应生产所需材料:~车间|上班前就备好了料。 【备品】名储备着待用的机件和工具等。 【备勤】动随时 准备执行任务:实行小时~。 【备取】动招; 知识分享网站 知识分享网站 ;考时在正式录取名额以外再录取若干名以备正取的人 不到时递补(区别于“正取”):~生。 【备述】动详尽地叙述:~其事始末|其中细节,难以~。 【备忘录】名①一种外交文书,声明自己方面对某种问
擦~。②(~儿)某些物体的反面或后部:手~|刀~儿|墨透纸~。③()姓。 【背】①动背部对着(跟“向”相对):~山面海|~水作战◇人心向~。
函数方程和函数迭代问题

第四讲函数方程和函数迭代问题在国内外数学竞赛中函数方程和函数迭代问题备受命题者的青睐形式灵活多变,结构变化无穷,大致可分为如下三类:⑴探求函数的解析式;⑵探求函数的值⑶讨论函数的性质.一. 探求函数的解析式1,换元法换元法的解题基本思想是:将函数方程中自变量适当代换成别的自变量(应注意力求不改变函数的定义域),得到一个或几个新的函数方程,然后将它们与原方程联立,通过消元求得原函数方程的解. 例1 解函数方程 f(x)+f(xx 1-)=1+x (x ≠0,x ≠1) 例2 设f(x)是定义在实数集上的实值函数,且满足af(x-1)+bf(1-x)=cx,其中a,b,c 为实常数,求f(x)2.赋值法赋值法基本思想是:对自变量多于一个的函数方程,将其中一个或几个自变量用一些特殊值赋进去代入原方程,从而简化函数方程,以达到求解的目的.例3 已知定义在R 的函数满足⑴ f(x 1+x 2)+f(x 1-x 2)=2f(x 1)cos2x 2+4asin 2x 2 (x 1,x 2∈R,a 为常数)⑵ f(0)=f(4π)=1 ⑶ 当x ∈[0, 4π]时,f(x)≤2 试求⑴函数f(x)的解析式;⑵常数a 的取值范围.例4 f(x)是定义于非负实数集上且取非负实数值的函数,求所有满足下列条件的f(x)⑴ f[xf(y)]f(y)=f(x+y);⑵ f(2)=0⑶ 当0≤x <2 f(x)≠03递推法例5已知f(x)是定义在自然数集上的函数,满足f(1)=23,且对任意x,y ∈N,有 f(x+y)=(1+1+x y )f(x)+(1+1+y x )f(y)+x 2y+xy+xy 2,求f(x) 4. 柯西法柯西首先讨论了一个很重要的函数方程f(x+y)=f(x)+f(y)的解法,由此解决了一系列其他函数方程.他的方法是,依次求出所有自然数值,整数值,有理数值,直至所有实数值的函数方程的解例6 设f(x) 是定义在有理数集上的函数,且对任意的有理数x,y 有f(x+y)=f(x)+f(y),试求f(x)5, 待定系数法这一方法的其本思想是:当f(x)是多顸式时,可设f(x)=a 0x n +a 1x n-1+….+a n (a 0≠0),代入函数方程的两端,然后比较方程两端x 最高次幂的指数和x 同次幂的系数,便可得出关于n 及a 0 a 1…a n .的方程组,解这个方程组便可确定n 及a 0 a 1…a n 的值,从而得到函数方程的解例7 确定符合下列条件的所有多项式f(x) f(x+1)=21f[f(x)]+23 6 , 利用不等式夹逼利用不等式夹逼求解函数方程,主要是利用下列几个明显的结论:⑴ 若对任意x ∈I, 有f(x)≥g(x) 及f(x)≤g(x)则对任意x ∈I,有f(x)=g(x)⑵ 若对任意x,y ∈I,有f(x)≤g(y)则交换x,y 得f(y)≤g(x)于是对任意的x,y ∈I 有f(x)=g(y)由此可得f(x)=常数(x ∈I).⑶ 若f:N →N 满足m ≤f(n)<m+1或m-1<f(n)≤m 或m-1<f(n)<m+1(m,n ∈N)则f(n)=m,例8 设f(x) 是具有下列性质的函数⑴ f(n)对每一正整数n 有定义;⑵ f(n)是正整数;⑶ f(2)=2⑷ f(mn)=f(m)f(n),对一切m,n 成立;⑸ f(m)>f(n),当m >n 时试证: f(m)=f(n)例9 设f(n )是定义在自然数集N 上的函数,它的值域也是全体自然数所成的集N,并且对任意两个自然m 与n,只要m ≥n 就有f(m) ≥n, 试证: f(m)= m 对任意的自然数m 成立.例10 设f(n )是定义在自然数集N 上的函数,满足: ⑴f(n )的值域为整数;⑵当m <n 时,f(m)<f(n);⑶当m,n 互素时,f(mn)=f(m)f(n),试求符合上述条件的一切函数f(x).二. 探求函数的值在各级各类数学竞赛中除了求函数方程的解以外,还经常遇到由函数方程给出的特殊定义的抽象函数,要求参赛者探求其函数的特殊的函数值.例11. 设N 是自然数集, f(x)是定义在N 上并在N 内取值的函数,且对x,y ∈N,有f[f(x)+y]=x+y,求f(1988)的所有可能的值例12. 设f(n )对所有正整数有定义,取非负整数值,并且对所有正整数m,n 有f(m+n)-f(m)-f(n)=0或1.又f(2)=0.f(3)>0,f(9999)=3333,求f(1982).例13. 设f(x),g(x)是定义在正整数集Z +上并取整数的严格递增函数,如果它们满足:⑴f(Z +) ∪ g ( Z +) = Z +(⑵f(Z +) ∩ g ( Z +) =⑶g(n)=f(f(n))+1试求f(240).三.讨论函数的性质探求讨论函数的有关性质,历年来都是数学竞赛的命题热点之一,例如探求函数的周期性,函数的不等式证明,以及解反函数的不等式等问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.函数迭代
⑴ 函数迭代的定义
设:f D D '→(其中D D '⊆)是一个函数,对任意x D ∈,记(0)()f x x =,(1)()()f x f x =, (2)()(())f x f f x =,(3)((()))f f f f x =,……,(1)()()(())n n f x f f x +=,……,
则称()()n f x 是函数()f x 在D 上的n 次迭代,并称n 是()()n f x 的迭代指数. 如果()()n f x 有反函数,则记为()()n f x -,于是,迭代指数可取所有整数. ⑵ 简单的函数迭代
求一个函数的n 次迭代,是数学竞赛中的一种基本题型.对于一些简单的函数,它的n 次迭代是容易得到的.
若()f x x c =+,则()n f x nc =+,(1)()f x x c -=-,()()n f x x nc -=-. 若3
()f x x =,则()
3()n
n f
x x =,1(1)
3
()f
x x -=,1
()
3()n
n f
x x -=.
若()f x ax b =+,则()()11n n b b f x a x a a ⎛⎫=-+ ⎪--⎝⎭,(1)
1()11b b f x x a a a -⎛⎫=-+ ⎪--⎝⎭, ()1()11n n b b
f x x a a a
-⎛⎫=
-+ ⎪--⎝⎭. ⑶ 函数迭代的求法 ①数学归纳法
这里用到的是先猜后证的想法,即先对函数()f x 迭代几次,观察出其规律,然后猜测出 ()()n f x 的表达式,最后用数学归纳法证之.这种方法只适用于一些较为简单的函数.
②递归法
设()f x 是定义在D 上且取值于D 的函数,由此定义数列{}n a :0a 已知,且0a D ∈,
2
函数迭代与函数方程
1()n n a f a -=,1≥n .一方面,若已求得()()()n f x g x =,则(2)()120()()()n n n n a f a f a f a --====,
即{}n a 通项公式;另一方面,如果已求得{}n a 的通项公式0()n a g a =,则取0a x =,()n a g x =,而()()10()()()n n n n a f a f a f x -==
==,从而()()()n f x g x =,即()()n f x 的表达式.
由上述知,函数的n 次迭代可以通过构造数列的方法来解,其步骤为 第一步,设0a x =,()()n n a f x =;
第二步,由()()n n a f x =1()n f a -=,求出0()n a g a =; 第三步,()0()()()n f x g a g x ==. ③相似法
相似法是求函数()f x 的n 次迭代的一个重要方法.若存在一个函数()x ϕ以及它的反函数
1()x ϕ-,使得1()((()))f x g x ϕϕ-=,我们就称()f x 通过()x ϕ和()g x 相似,简称()f x 和()g x 相
似,记为~()f g ϕ,其中()x ϕ称为桥函数. 相似关系是一个等价关系,也就是说它满足: 自身性,~f f ;
对称性,若~f g ,则~g f ; 传递性,若~f g ,~g h ,则~f h .
如果()f x 与()g x 相似,即1
()(()))(f x g x ϕϕ-
=, 那么()1()()((()))n n f x g x ϕϕ-=, 1()((()))g x f x ϕϕ-=,()()1()((()))n n g x f x ϕϕ-=. 这样一来,我们便把f 的迭代问题转化为g 的迭代问题. ④不动点法
关于x 的方程()f x x =的根称为()f x 的不动点.不动点法的基本思想是根据函数的不动点得出桥函数的一个性质,进而确定桥函数的形状,然后利用相似法求出函数的n 次迭代. 函数的不动点具有如下的性质:
若0x 是()f x 的不动点,则()00()n f x x =,即0x 也是()()n f x 的不动点.
设1()((()))f x g x ϕϕ-=,因此有(())(())f x g x ϕϕ=,若00()f x x =,则有00()(())x g x ϕϕ=,即
0()x ϕ是()g x 的不动点.
对于一些简单的函数,利用不动点,把函数变形后再迭代,最后用数学归纳法证之,会使计算简单些.
利用不动点找桥函数的方法:由不动点的性质知,桥函数ϕ具有下列性质:它将f 的不动点0x 映成g 的不动点0()x ϕ,通常为了便于求解()()n g x ,()g x 通常为ax ,x a +,2ax ,3ax 等.
2.函数方程
⑴ 函数方程的定义
解为函数的方程为函数方程.例如()()(5)(),f x f x f x f x -=-+=等都是函数方程. ⑵ 函数方程解法
寻求函数方程的解或证明函数方程无解的过程叫作解函数方程,一般有以下几种方法: ①代换法
代换法是解函数方程的常用手段,其基本思想是:将函数方程中的自变量适当地以别的自变量代换(当然在代换时应特别注意函数的定义域不能发生变化),得到一个新的函数方程,然
后设法求得未知数.如2(21)()f x x x x -=+∈R ,令21y x =-,则1
(1)2x y =+,于是
211()(1)(1)42f y y y =+++,即213
()44f x x x =++,经检验它是函数方程的解.
代换法在单变量函数方程中尤为多用. ②赋值法
所谓赋值法,就是对自变量赋予某些特殊的数值,从而挖掘出题中隐含的条件,并且通过这些新条件简化函数方程,逼近最终目标. 如函数:f →R R 满足()()
()0,,,f x f y f xy x y x y x y
+=
∈+≠+R ,求()f x .
令1y =,得()(1)
()(1)1
f x f f x x x +=
≠-+,由此()(1)xf x f =.令0x =则(1)0f =,从而可知
()0(01),f x x =≠-.令20,x y ==易得(0)(2)0f f ==;令10,x y =-=易知(1)(0)0f f -==.综上可知()0f x =.
③递归法
函数方程的递归解法,是一种借助于数列对函数方程加以研究的方法.
设()f n 是定义在正整数集+N 上的函数,如果存在一个递推关系S 和初始条件1(1)f a =,当知道(1)f ,(2)f ,…,()f n 的值后,由S 可以惟一地确定(1)f n +的值,我们就称()f n 为递归函数,递归法主要解决递归函数.
板块一 函数的迭代
【例 1】 已知()f n 是定义在+N 上的函数,并且满足
①(())49f f n n =+,n +∈N ,
②1(2)23k k f +=+,k ∈N . 求(1789)f 的值.
【例 2】 ⑴设()f x ax b =+,求()()n f x ;
⑵设()x
f x ax b
=
+,求()()n f x ;
⑶设()1f x x =+,求()()n f x .
【例 3】 ⑴设2
()21
x f x x =-,求()()n f x ;
⑵设1
()43
x f x x -=
-,求()()n f x ;
⑶设42
()1
x f x x -=+,求()()n f x .
板块二 函数方程
【例 4】 ⑴定义在+R 上的函数()f x 满足关系式1()lg 1f x f x x ⎛⎫
=+ ⎪⎝⎭
,求()f x .
⑵求解函数方程1()11f x f x x ⎛⎫
+-=+ ⎪⎝
⎭,0x ≠,1.
⑶已知函数()f x 对任意x 、y 有(1)()()()2f xy f x f y f y x +=--+,求()f x .
【例 5】 求所有满足下列条件的函数:f ++→N N ,使得
⑴(2)2f =;
⑵()()()f mn f m f n =⋅对所有m ,n 成立; ⑶若m n <,则()()f m f n <.
【例 6】 已知函数()f x 满足2()()1f x f x -=,0x >.求满足条件的一个()f x .
习题1. 设()f x ax b =+,其中,a b 为实数,1()()f x f x =,1()(())n n f x f f x +=,123,,,n =,若
7()128381f x x =+,则a b += .
习题2. 某同学从换乘中心出发坐车去第一家商店,在店里花了剩余的钱的一半,然后坐车返回换乘
中心.之后又坐车去第二家商店,在店里花了剩余钱的一半,然后坐车返回换乘中心.接着他用同样的方式进出第三家和第四家商店,当他返回换乘中心时候,发现身上只剩一元钱.若无论从换乘中心到商店还是从商店到换乘中心的车费都是一元钱,问:他在四家商店总共花
了多少钱
习题3. 设2()42f x x x =++,求()()n f x .
习题4. 求解函数方程(写出一个符合方程的解即可),⑴⑵⑶小题中x ,y ∈R ,⑷小题中m ,n +∈N :
⑴()()()f x y f x f y +=+; ⑵()()()f x y f x f y +=⋅; ⑶()()()f xy f x f y =+;
⑷()()()()f m f n f m n f m n +=+⋅-.
习题5. 已知:f →Z Z ,求满足下述条件的所有函数f :
⑴对一切正数n ,(())f f n n =;
⑵对一切整数n,((2)2)
++=;
f f n n
⑶(0)1
f=。
