工程力学材料力学知识点及典型例题
材料力学(资料例题)

材料力学(一)轴向拉伸与压缩【内容提要】材料力学主要研究构件在外力作用下的变形、受力与破坏、失效的规律。
为设计既安全可靠又经济合理的构件,提供有关强度、刚度与稳定性分析的基本理论与方法。
【重点、难点】重点考察基本概念,掌握截面法求轴力、作轴力图的方法,截面上应力的计算。
【内容讲解】一、基本概念强度——构件在外力作用下,抵抗破坏的能力,以保证在规定的使用条件下,不会发生意外的断裂或显著塑性变形。
刚度——构件在外力作用下,抵抗变形的能力,以保证在规定的使用条件下不会产生过分的变形。
稳定性——构件在外力作用下,保持原有平衡形式的能力,以保证在规定的使用条件下,不会产生失稳现象。
杆件——一个方向的尺寸远大于其它两个方向的尺寸的构件,称为杆件或简称杆。
根据轴线与横截面的特征,杆件可分为直杆与曲杆,等截面杆与变截面杆。
二、材料力学的基本假设工程实际中的构件所用的材料多种多样,为便于理论分析,根据它们的主要性质对其作如下假设。
(一)连续性假设——假设在构件所占有的空间内均毫无空隙地充满了物质,即认为是密实的。
这样,构件内的一些几何量,力学量(如应力、位移)均可用坐标的连续函数表示,并可采用无限小的数学分析方法。
(二)均匀性假设——很设材料的力学性能与其在构件中的位置无关。
按此假设通过试样所测得的材料性能,可用于构件内的任何部位(包括单元体)。
(三)各向同性假设——沿各个方向均具有相同力学性能。
具有该性质的材料,称为各向同性材料。
综上所述,在材料力学中,一般将实际材料构件,看作是连续、均匀和各向同性的可变形固体。
三、外力内力与截面法(一)外力对于所研究的对象来说,其它构件和物体作用于其上的力均为外力,例如载荷与约束力。
外力可分为:表面力与体积力;分布力与集中力;静载荷与动载荷等。
当构件(杆件)承受一般载荷作用时,可将载荷向三个坐标平面(三个平面均通过杆的轴线,其中两个平面为形心主惯性平面)内分解,使之变为两个平面载荷和一个扭转力偶作用情况。
工程力学精彩试题库-材料力学

⼯程⼒学精彩试题库-材料⼒学材料⼒学基本知识复习要点1.材料⼒学的任务材料⼒学的主要任务就是在满⾜刚度、强度和稳定性的基础上,以最经济的代价,为构件确定合理的截⾯形状和尺⼨,选择合适的材料,为合理设计构件提供必要的理论基础和计算⽅法。
2.变形固体及其基本假设连续性假设:认为组成物体的物质密实地充满物体所在的空间,毫⽆空隙。
均匀性假设:认为物体内各处的⼒学性能完全相同。
各向同性假设:认为组成物体的材料沿各⽅向的⼒学性质完全相同。
⼩变形假设:认为构件在荷载作⽤下的变形与构件原始尺⼨相⽐⾮常⼩。
3.外⼒与内⼒的概念外⼒:施加在结构上的外部荷载及⽀座反⼒。
内⼒:在外⼒作⽤下,构件内部各质点间相互作⽤⼒的改变量,即附加相互作⽤⼒。
内⼒成对出现,等值、反向,分别作⽤在构件的两部分上。
4.应⼒、正应⼒与切应⼒应⼒:截⾯上任⼀点内⼒的集度。
正应⼒:垂直于截⾯的应⼒分量。
切应⼒:和截⾯相切的应⼒分量。
5.截⾯法分⼆留⼀,内⼒代替。
可概括为四个字:截、弃、代、平。
即:欲求某点处内⼒,假想⽤截⾯把构件截开为两部分,保留其中⼀部分,舍弃另⼀部分,⽤内⼒代替弃去部分对保留部分的作⽤⼒,并进⾏受⼒平衡分析,求出内⼒。
6.变形与线应变切应变变形:变形固体形状的改变。
线应变:单位长度的伸缩量。
练习题⼀.单选题1、⼯程构件要正常安全的⼯作,必须满⾜⼀定的条件。
下列除()项,其他各项是必须满⾜的条件。
A、强度条件B、刚度条件C、稳定性条件D、硬度条件2、物体受⼒作⽤⽽发⽣变形,当外⼒去掉后⼜能恢复原来形状和尺⼨的性质称为()A.弹性B.塑性C.刚性D.稳定性3、结构的超静定次数等于()。
A.未知⼒的数⽬B.未知⼒数⽬与独⽴平衡⽅程数⽬的差数C.⽀座反⼒的数⽬D.⽀座反⼒数⽬与独⽴平衡⽅程数⽬的差数4、各向同性假设认为,材料内部各点的()是相同的。
A.⼒学性质B.外⼒C.变形D.位移5、根据⼩变形条件,可以认为()A.构件不变形B.结构不变形C.构件仅发⽣弹性变形D.构件变形远⼩于其原始尺⼨6、构件的强度、刚度和稳定性()A.只与材料的⼒学性质有关B.只与构件的形状尺⼨有关C.与⼆者都有关D.与⼆者都⽆关7、在下列各⼯程材料中,()不可应⽤各向同性假设。
材料力学练习-知识归纳整理
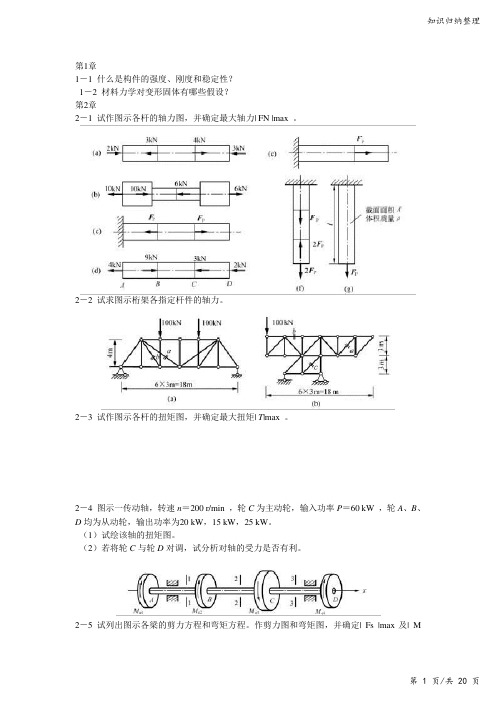
知识归纳整理第1章1-1 什么是构件的强度、刚度和稳定性?1-2 材料力学对变形固体有哪些假设?第2章2-1 试作图示各杆的轴力图,并确定最大轴力| FN |max 。
2-2 试求图示桁架各指定杆件的轴力。
2-3 试作图示各杆的扭矩图,并确定最大扭矩| T|max 。
2-4 图示一传动轴,转速n=200 r/min ,轮C为主动轮,输入功率P=60 kW ,轮A、B、D均为从动轮,输出功率为20 kW,15 kW,25 kW。
(1)试绘该轴的扭矩图。
(2)若将轮C与轮D 对调,试分析对轴的受力是否有利。
2-5 试列出图示各梁的剪力方程和弯矩方程。
作剪力图和弯矩图,并确定| Fs |max及| M求知若饥,虚心若愚。
|max 值。
2-6 试用简易法作图示各梁的剪力图和弯矩图,并确定| F s |max及| M|max值,并用微分关系对图形举行校核。
2-7 图示起重机横梁AB承受的最大吊重F P=12kN,试绘出横梁A B 的内力图。
2-8 图示处于水平位置的控制手柄,在自由端C处受到一铅垂向下的集中力F p作用。
试画出AB段的内力图。
千里之行,始于足下。
第3章3-1图示圆截面阶梯杆,承受轴向荷载F1=50kN与F2的作用,AB与BC段的直径分别为d1=20mm与d2=30mm,如欲使AB与BC段横截面上的正应力相同,试求荷载F2之值。
3-2变截面直杆如图所示。
已知A1=8cm2,A2=4cm2,E=200GPa 。
求杆的总伸长量。
3-3 在图示结构中,AB为刚性杆,CD为钢斜拉杆。
已知F P1=5kN ,F P2=10kN ,l=1m ,杆CD的截面积A=100mm2 ,钢的弹性模量E=200GPa 。
试求杆CD的轴向变形和刚性杆AB在端点B 的铅垂位移。
3-4 一木柱受力如图所示。
柱的横截面为边长200mm的正方形,材料可以为符合胡克定律,其弹性模量E=10GPa。
如不计柱的自重,试求:求知若饥,虚心若愚。
材料力学总复习

一、基本变形
外力
拉伸与压缩
扭转
弯曲
内力
FN F
应力 强度条件
变形
FN
A
max [ ]
l FNl EA
刚度条件
T Me
T
IP
max [ ]
Mnl
GI P
FS 外力
M 外力对形心之矩
My
,
FS
S
* z
Iz
bI z
, max [ ] max [ ]
1、积分法
2、叠加法
∑Fix= 0, FN1 cos30°+FN2=0 (1)
(2)画节点A的位移图(见图c) (3)建立变形方程
△L1=△L2cos30°
(4)建立补充方程
△L1=△LN1+△LT,
即杆①的伸长△l1由两部份组成,△l N1表示由轴力FN1引起的变形, △lT表示温度升高引起的变形,因为△T 升温,故△lT 是正值。
因为AB 杆受的是拉力,所以沿AB 延
长线量取BB1等于△L1;同理,CB 杆受
的也是拉力,所以沿杆CB 的延长线量取
BB2 等于△L。
分别在点B1 和B2 处作BB1 和BB2 的垂
线,两垂线的交点B′为结构变形后节点
B应有的新位置。即结构变形后成为
ABˊC 的形状。图c称为结构的变形图。
为了求节点B的位置,也可以单独作出节点B的位移图。位移图的作 法和结构变形图的作法相似,如图d所示。
C1 5、求应力并校核强度:
A1
1
FN 1 A
66 .7 MPa ,
2
FN 2 A
133 .2MPa ,
剪切
F AB A1
F BC A2
工程力学---材料力学第七章-梁弯曲时位移计算与刚度设计经典例题及详解

P
B C
l 2 l 2
A
x
P 解:AC段:M ( x ) x 2 y P EIy x 2 A P 2 EIy x C x 4 l 2 P 3 EIy x Cx D 12
P
B C
l 2
x
由边界条件: x 0时,y 0
l 由对称条件: x 时,y 0 2
梁的转角方程和挠曲线方程分别为:
最大转角和最大挠度分别为:
11qa max A 1 x1 0 6 EI 19qa 4 ymax y2 x2 2 a 8EI
3
例5:图示变截面梁悬臂梁,试用积分法
求A端的挠度 P
I
2I
l
fA 解: AC段 0 x l
B
P 3 2 EIy x C2 x D2 6
由边界条件: x l时,y=0, =0
得:
C2
1 1 Pl 2 , D2 Pl 3 2 3
l x 时,yC左 =yC右 , C左 = C右 由连续条件: 2
5 3 2 C1 Pl , D1 Pl 3 16 16
由连续条件: x1 x2 a时, y1 y2 , y1 y2
由边界条件: x1 0时, y1 0
0 x 2 a 时 , y 由对称条件: 2 2
得 D1 0
C1 C2 得 D1 D2
11 3 得 C2 qa 6
qa 1 (11a 2 3 x12 ) 0 x1 a 6 EI q 2 [3ax2 2 ( x2 a)3 11a 3 a x2 2a 6 EI qa y1 (11a 2 x1 x13 ) 0 x1 a 6 EI q y2 [4ax23 ( x2 a) 4 44a 3 x2 ] a x2 2a 24 EI
工程力学材料力学篇复习资料

工程力学材料力学篇学习资料声明一:材料力学篇书上有好多经典的例题,需要你认真琢磨~考试比重来讲静力学也就占20分,而材料力学则占80分,所以要认真复习哦~声明二:本资料列出的都是考试重点,可能不会包含程老师上课讲的所有内容,彻底掌握本资料上的所有内容考试就ok啦~声明三:由于本人比较笨,有些图片不会用电脑生成,只能用相机照下来再插进去,可能效果不太好,望见谅声明四:本资料在编辑过程中难免会出现一些错误,本人也会尽最大努力保证资料的准确性,避免严重性的错误,如发现错误,还望见谅并告诉笔者,笔者会第一时间进行修正。
声明五:本资料会先说知识点后讲题,基本都是课后练习题(我们那届留的作业~但可能会跟你们的有些出入)声明六:本资料的所有解释与注释都是本人原创,全世界独一无二~如有盗版,追究到底!PS:吐血整理B Y吴奂……下面进入正题第七章:绪论本章概况:本章会引入几个新的概念,了解并且掌握就可以了重点一:何谓应力?答:应力有点类似我们初中学的压强一样,如图所示,在界面m-m上任意一点k的周围取一微笑面积△A,并设作用在该面积上的内力为△F,则△A与△F的比值,称为△A内的平均应力,用p表示,即p=△F/△A,当△A趋近于0时,p称为k点处的应力或总应力。
重点二:何谓正应力与切应力?答:如图可知,应力p的方向与F的方向是一致的,为了分析方便,通常将应力p延截面法向与切线方向分解为两个分量,延截面法向的应力分量称为正应力,用σ表示;延截面切向的应力分量称为切应力,用τ表示;很显然p²=σ²+τ²。
重点三:单位换算力与面积的基本单位分别为N与m²,应力的单位是Pa,名为帕斯卡,1Pa=1N/m²,应力的常用单位是MPa,1MPa=10³x10³Pa(没有找到10的6次方这个符号,囧==!)PS:正应变与切应变考试不考,划重点的时候应该不会画,如果画了看看书120页就会了,本章没有课后练习题。
工程力学--材料力学(第五、六章)经典例题及讲解
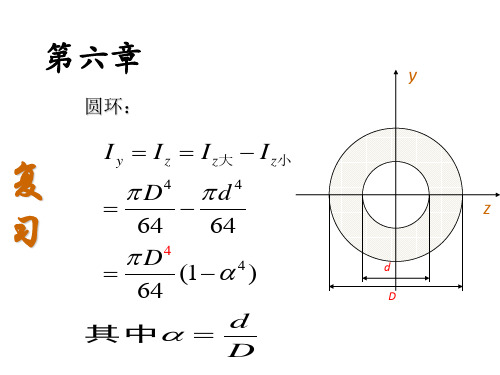
P
A
0.5 m
C D
0.4 m 1m
B
20
40
解:C点的应力 σ C = E ε = 200 × 10 3 × 6 × 10 − 4
= 120M Pa
C截面的弯矩
M C = σ C W z = 640 N ⋅ m
由 M C = 0.5 R A = 0.5 × 0.4 P = 0.2 P = 640 N ⋅ m 得 P = 3.2kN
度减小一半时,从正应力强度条件考虑, 该梁的承载能力将是原来的多少倍? 解: 由公式
σ max
M max M max = = 2 Wz bh 6
可以看出:该梁的承载能力将是原来的2 可以看出:该梁的承载能力将是原来的2倍。
例4:主梁AB,跨度为l,采用加副梁CD AB,跨度为l 采用加副梁CD
的方法提高承载能力, 的方法提高承载能力,若主梁和副梁材料 相同,截面尺寸相同, 相同,截面尺寸相同,则副梁的最佳长度 a为多少? 为多少?
2 2
2
bh b( d − b ) Wz = = 6 6
2 2 2
∂ Wz d 2 b 2 = − =0 ∂b 6 2
d 由此得 b = 3
d
2 2
h
h = d −b =
h = 2 ≈3:2 b
2 d 3
b
例12:跨长l =2m的铸铁梁受力如图示,已知材料许用拉、 12:跨长l =2m的铸铁梁受力如图示 已知材料许用拉、 的铸铁梁受力如图示,
10 kN / m
200 2m 4m 100
10 kN / m
200
2m
Fs( kN ) 25 Fs(
45 kN
4m
100
工程力学材料力学-知识点-及典型例题
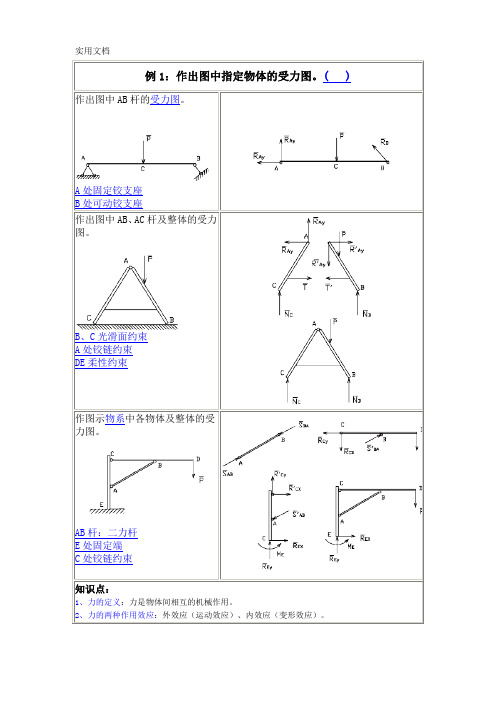
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆:二力杆E处固定端C处铰链约束(1)运动效应:力使物体的机械运动状态发生变化的效应。
(2)变形效应:力使物体的形状发生和尺寸改变的效应。
3、力的三要素:力的大小、方向、作用点。
4、力的表示方法:(1)力是矢量,在图示力时,常用一带箭头的线段来表示力;(注意表明力的方向和力的作用点!)(2)在书写力时,力矢量用加黑的字母或大写字母上打一横线表示,如F、G、F1等等。
5、约束的概念:对物体的运动起限制作用的装置。
6、约束力(约束反力):约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点,在约束与被约束物体的接处7、主动力:使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束:如绳索、链条、胶带等。
(1)约束的特点:只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点:约束反力沿柔索的中心线作用,离开被约束物体。
()9、光滑接触面:物体放置在光滑的地面或搁置在光滑的槽体内。
(1)约束的特点:两物体的接触表面上的摩擦力忽略不计,视为光滑接触面约束。
被约束的物体可以沿接触面滑动,但不能沿接触面的公法线方向压入接触面。
(2)约束反力的特点:光滑接触面的约束反力沿接触面的公法线,通过接触点,指向被约束物体。
()10、铰链约束:两个带有圆孔的物体,用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力;一般用一对正交的力来表示,指向假定。
()11、固定铰支座(1)约束的构造特点:把中间铰约束中的某一个构件换成支座,并与基础固定在一起,则构成了固定铰支座约束。
(2)约束反力的特点:固定铰支座的约束反力同中间铰的一样,也是方向未定的一个力;用一对正交的力来表示,指向假定。
()12、可动铰支座(1)约束的构造特点把固定铰支座的底部安放若干滚子,并与支撑连接则构成活动铰链支座约束,又称锟轴支座。
材料力学典型例题与详解(经典题目)
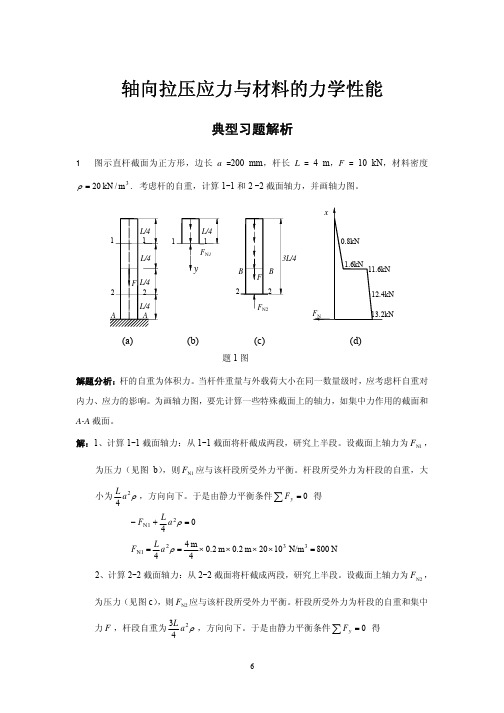
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
工程力学材料力学部分课后习题详解
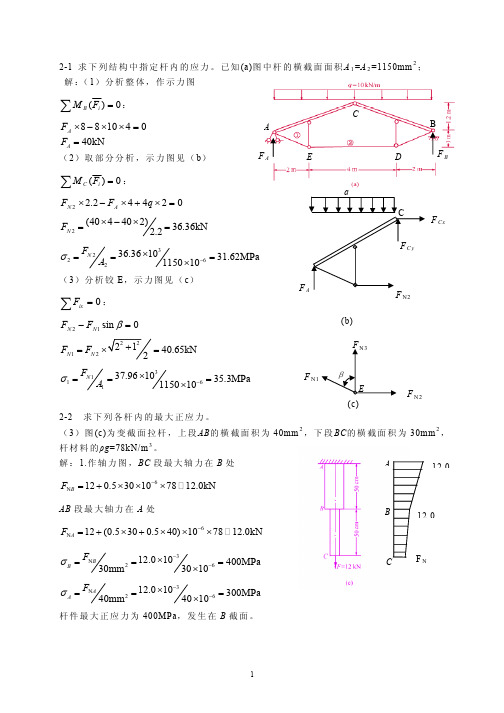
2-1 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:CB 041088=××−×A F AF N1F N2(c)40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=×+×−×q F F A N2(404402)36.36kN 2.2N F ×−×==3262236.361031.62MPa 115010N F A σ−×===×(3)分析铰E ,示力图见(c )∑=0ix F :0sin 12=−βN N F F1240.65kN N N F F == 3161137.961035.3MPa 115010N F A σ−×===×2-2 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F −=+×××AB 段最大轴力在A 处6N 12(0.5300.540)107812.0kN A F −=+×+×××3N 2612.010400MPa 30mm3010B B F σ−−×===× 3N 2612.010300MPa 40mm 4010AA F σ−−×===×杆件最大正应力为400MPa ,发生在B 截面。
EDF BF AF CxF N2(b)A120B120F NC2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比µ。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第3章 力系的平衡
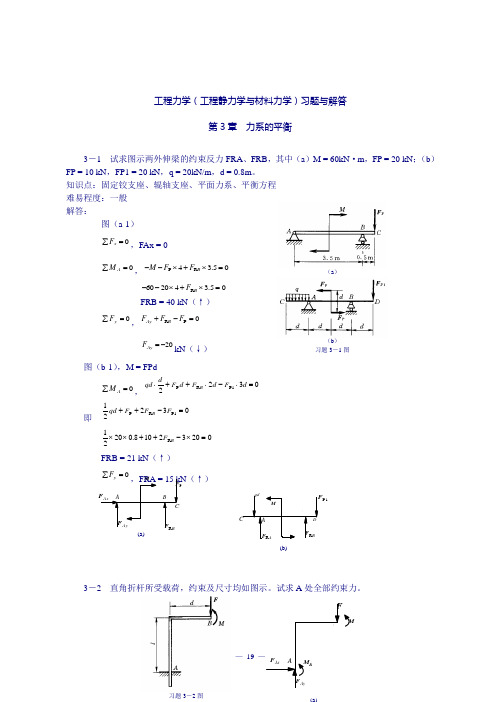
工程力学(工程静力学与材料力学)习题与解答第3章 力系的平衡3-1 试求图示两外伸梁的约束反力FRA 、FRB ,其中(a )M = 60kN ·m ,FP = 20 kN ;(b )FP = 10 kN ,FP1 = 20 kN ,q = 20kN/m ,d = 0.8m 。
知识点:固定铰支座、辊轴支座、平面力系、平衡方程 难易程度:一般 解答:图(a-1) 0=∑x F ,FAx = 00=∑A M ,05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN (↑)=∑y F ,0P R =-+F F F B Ay20-=Ay F kN (↓)图(b-1),M = FPd 0=∑A M ,03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN (↑)=∑y F ,FRA = 15 kN (↑)3-2 直角折杆所受载荷,约束及尺寸均如图示。
试求A 处全部约束力。
A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)(a )(b ) 习题3-1图FMB习题3-3图sF W A F ABF BF AN F(a)知识点:固定端约束、平面力系、平衡方程 难易程度:一般 解答: 图(a ): 0=∑x F ,0=Ax F=∑y F ,=Ay F (↑)0=∑A M ,0=-+Fd M M AM Fd M A -=3-3 图示拖车重W = 20kN ,汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时,车轮A 、B 对地面的正压力。
知识点:固定端约束、平面力系、平衡方程 难易程度:一般解答: 图(a ):0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ,4.6NA =F kN3-4 图示起重机ABC 具有铅垂转动轴AB ,起重机重W = 3.5kN ,重心在D 。
工程力学A(1)材料力学概念题

第一章是非判断题1-1材料力学是研究构件承载能力的一门学科。
( )1-2材料力学的任务是尽可能使构件安全地工作。
( )1-3材料力学主要研究弹性范围内的小变形情况。
( )1-4因为构件是变形固体,在研究构件的平衡时,应按变形后的尺寸进行计算。
( )1-5外力就是构件所承受的载荷。
( )1-6材料力学研究的内力是构件各部分间的相互作用力。
( )1-7用截面法求内力时,可以保留截开后构件的任一部分进行平衡计算。
( )1-8压强是构件表面的正应力。
( )1-9应力是横截面上的平均内力。
( )1-10材料力学只研究因构件变形引起的位移。
( )1-11线应变是构件中单位长度的变形量。
( )1-12构件内一点处各方向线应变均相等。
( )1-13切应变是变形后构件中任意两根微线段夹角角度的变化量。
( )1-14材料力学只限于研究等截面直杆。
( )1-15杆件的基本变形只是拉(压)、剪、扭和弯四种,如果还有另一种变形,必定是这四种变形的某种组合。
( )答案:1-1 √1-2 ×1-3 √1-4 ×1-5 ×1-6 ×1-7 √1-8 ×1-9 ×1-10 √1-11 ×1-12 ×1-13 ×1-14 ×1-15 √第二章1 是非判断题2-1使杆件产生轴向拉压变形的外力必须是一对沿杆轴线的集中力。
( )2-2拉杆伸长后,横向会缩短,这是因为杆有横向应力存在。
( )2-3虎克定律适用于弹性变形范围内。
( )2-4材料的延伸率与试件的尺寸有关。
( )2-5 只有超静定结构才可能有装配应力和温度应力。
( )2填空题2-6承受轴向拉压的杆件,只有在( )长度范围内变形才是均匀的。
2-7根据强度条σ≤[σ]可以进行( )三个方面的强度计算。
2-8低碳钢材料由于冷作硬化,会使( )提高,而使( )降低。
2-9铸铁试件的压缩破坏和( )应力有关。
材料力学(答案)-知识归纳整理
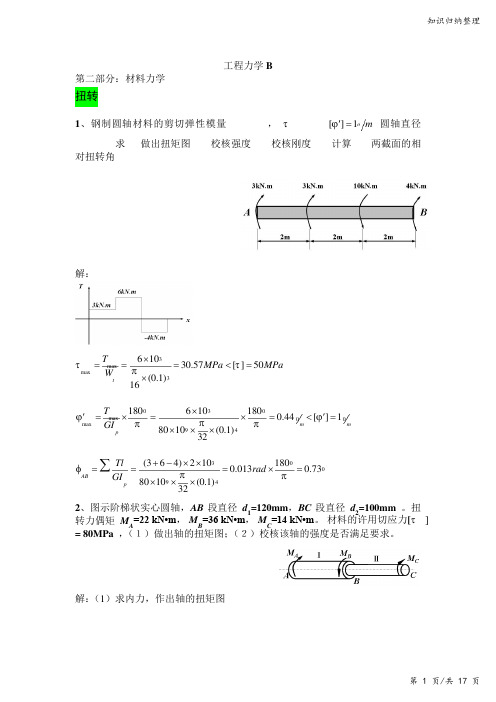
工程力学 B第二部分:材料力学扭转1、钢制圆轴材料的剪切弹性模量G=80Gpa ,[τ]=50Mpa,m o 1][='ϕ,圆轴直径d=100mm;求(1)做出扭矩图;(2)校核强度;(3)校核刚度;(4)计算A,B 两截面的相对扭转角.解:3max max361030.57[]50(0.1)16tT MPa MPa W ττπ⨯===<=⨯030max 00max941806101800.44[]18010(0.1)32m m pT GI ϕϕπππ⨯''=⨯=⨯=<=⨯⨯⨯30094(364)2101800.0130.738010(0.1)32ABpTl rad GI φππ+-⨯⨯===⨯=⨯⨯⨯∑2、图示阶梯状实心圆轴,AB 段直径 d 1=120mm ,BC 段直径 d 2=100mm 。
扭转力偶矩 M A =22 kN•m ,M B =36 kN•m , M C =14 kN•m 。
材料的许用切应力[τ ] = 80MPa ,(1)做出轴的扭矩图;(2)校核该轴的强度是否满足要求。
解:(1)求内力,作出轴的扭矩图知识归纳整理(2)计算轴横截面上的最大切应力并校核强度 AB 段:11,max1t T W τ=()333221064.8MPa π1201016-⨯==⨯⨯[]80MPa τ<= BC 段:()322,max332141071.3MPa π1001016t T Wτ-⨯===⨯⨯[]80MPa τ<=综上,该轴满足强度条件。
3、传动轴的转速为n =500r/min ,主动轮A 输入功率P 1=400kW ,从动轮B ,C 分别输出功率P 2=160kW ,P 3=240kW 。
已知材料的许用切应力[τ]=70MP a ,单位长度的许可扭转角[ϕ, ]=1º/m ,剪切弹性模量G =80GP a 。
(1)画出扭矩图。
(完整版)材料力学必备知识点

材料力学必备知识点1、 材料力学的任务:满足强度、刚度和稳定性要求的前提下,为设计既经济又安全的构件,提供必要的理论基础和计算方法。
2、 变形固体的基本假设:连续性假设、均匀性假设、各向同性假设。
3、 杆件变形的基本形式:拉伸或压缩、剪切、扭转、弯曲。
4、 低碳钢:含碳量在0.3%以下的碳素钢。
5、 低碳钢拉伸时的力学性能:弹性阶段、屈服阶段、强化阶段、局部变形阶段 极限:比例极限、弹性极限、屈服极限、强化极限6、 名义(条件)屈服极限:将产生0.2%塑性应变时的应力作为屈服指标7、 延伸率δ是衡量材料的塑性指标塑性材料 随外力解除而消失的变形叫弹性变形;外力解除后不能消失的变形叫塑性变形。
>5%的材料称为塑性材料: <5%的材料称为脆性材料8、 失效:断裂和出现塑性变形统称为失效9、 应变能:弹性固体在外力作用下,因变形而储存的能量10、应力集中:因杆件外形突然变化而引起的局部应力急剧增大的现象11、扭转变形:在杆件的两端各作用一个力偶,其力偶矩大小相等、转向相反且作用平面垂直于杆件轴线,致使杆件的任意两个横截面都发生绕轴线的相对转动。
12、翘曲:变形后杆的横截面已不再保持为平面;自由扭转:等直杆两端受扭转力偶作用且翘曲不受任何限制;约束扭转:横截面上除切应力外还有正应力13、三种形式的梁:简支梁、外伸梁、悬臂梁14、组合变形:由两种或两种以上基本变形组合的变形15、截面核心:对每一个截面,环绕形心都有一个封闭区域,当压力作用于这一封闭区域内时,截面上只有压应力。
16、根据强度条件 可以进行(强度校核、设计截面、确定许可载荷)三方面的强度计算。
17、低碳钢材料由于冷作硬化,会使(比例极限)提高,而使(塑性)降低。
18、积分法求梁的挠曲线方程时,通常用到边界条件和连续性条件;因杆件外形突然变化引起的局部应力急剧增大的现象称为应力集中;轴向受压直杆丧失其直线平衡形态的现象称为失稳19、圆杆扭转时,根据(切应力互等定理),其纵向截面上也存在切应力。
工程力学材料力学第一章

直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。
直杆轴向拉伸或压缩时斜截面上的应力 k
设有一等直杆受拉力P作用。 P 求:斜截面k-k上的应力。 解:采用截面法 由平衡方程:Pα=P P P k P
α α
k Pα k
Pα 则: pα = Aα
Aα:斜截面面积;Pα:斜截面上内力。
A 由几何关系: α = cos Aα
σ 0 ( 45°斜截面上剪应力达到最大 ) |τ 当α = ± 45°时, α |max =
目 录
公式的应用条件: 公式的应用条件: 直杆、杆的截面无突变、 的距离。 直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。 圣维南( 原理: 圣维南 Saint-Venant)原理: 原理 离开载荷作用处一定距离, 离开载荷作用处一定距离,应力分布与大小不受外载荷作 用方式的影响。 用方式的影响。 应力集中( 应力集中(Stress Concentration): ): 在截面尺寸突变处,应力急剧变大。 在截面尺寸突变处,应力急剧变大。
工程构件,大多数情形下,内力并非均匀分布,集度的定 义不仅准确而且重要,因为“破坏”或“失效”往往从内力集 度最大处开始。 2. 应力的表示: 应力的表示: ① 平均应力: 平均应力: ∆P M ∆A
ΔP pM = ΔA
全应力(总应力): ② 全应力(总应力):
p = lim
∆A → 0
∆P dP = ∆ A dA
目 录
目 录
目 录
例题
图示结构,已知斜杆AB长2m,横截面面积为 图示结构,已知斜杆AB长2m,横截面面积为 AB 水平杆AC的横截面面积为250mm AC的横截面面积为 200mm2。水平杆AC的横截面面积为250mm2。材料的 弹性摸量E=200GPa 载荷F=10kN 试求节点A E=200GPa。 F=10kN。 弹性摸量E=200GPa。载荷F=10kN。试求节点A的位 移。 计算各杆件的轴力。(设斜杆为1 。(设斜杆为 解:1、计算各杆件的轴力。(设斜杆为1杆,水 平杆为2 用截面法取节点A 平杆为2杆)用截面法取节点A为研究对象
工程力学-材料力学部分

A 代入上式,得: Aa cos a
pa s cos a 斜截面上总应力:
斜截面上总应力: pa s cos a 分解: pa
k
F F
sa pa cosa s cos a
2
k
F
a
k
a
sa
Pa
t a pa sin a s cos a sin a
s
2
sin 2a
a
工程力学材料力学部分:
主要研究作用在物体上的力及变形规律。研究构件在相应 承载能力的条件下,以最经济的代价为构件确定合理的形状和 尺寸,选择适当的材料,为构件的设计提供必要的理论基础和 计算方法。
主要内容:
1、内力、应力的概念; 2、轴向拉伸与压缩; 3、剪切和挤压; 4、圆轴扭转; 5、梁的弯曲。
截面面积A成反比,这一比例关系称为胡克定律。即
FN l l = EA
E 为材料的弹性模量,取值与材料有关,由实验测定, 单位常用GPa。 胡克定律的另一表达式:
s E
32
胡克定律表明:当 FN 和 l 不变时, EA 值越大,绝对 变形量越小。说明EA是杆件抵抗拉压变形能力的度量。
例5.3
并求与横截面夹角30°的斜截面上的正应力和切应力。 解:拉压杆斜截面上的应力,直接由公式求之:
s0
F 4 10000 127 .4MPa 2 A 3.14 10
τ max σ 0 /2 127.4/2 63.7MPa
3 s a s 0 cos a 127 .4 95.5MPa 4
m
F F
m
(a)
以作用力FN替代弃去部分对研究对象的作用。
材料力学第四版重点。典型例题及详解

材料力学小结(2010.4)一、轴向拉伸和压缩1.内力、截面法、轴力及轴力图2.应力、拉(压)杆内的应力3.拉(压)杆的变形、胡克定律4.力学性能试验5.安全因素、许用应力、强度条件二、扭转1.薄壁圆筒的扭转2.传动轴的外力偶矩、扭矩及扭矩图3.等直圆杆扭转时的应力、强度条件4.等直圆杆扭转时的变形、刚度条件三、弯曲内力和应力1.对称弯曲的概念及梁的计算简图2.梁的剪力和弯矩、剪力图和弯矩图3.平面刚架和曲杆的内力图4.梁横截面上的正应力、正应力强度条件5.梁横截面上的切应力、切应力强度条件6.梁的合理设计四、 梁弯曲时的位移 1. 梁的变形参数2. 挠曲线近似微分方程及其积分3. 叠加原理计算梁的位移4. 梁的刚度校核、提高梁的刚度的措施五、 简单的超静定问题 1. 超静定问题及其解法 2. 拉压超静定问题 3. 扭转超静定问题 4. 简单超静定梁1、两根材料、长度l 都相同的等直柱子,一根的横截面面积为A 1,另一根为A 2,且A 2>A 1。
如图所示。
两杆都受自重作用。
这两杆的最大压应力相等,最大压缩量也相等。
( )2、图示在拉力P 作用下的螺栓,已知材料的剪切许(b)(a)用应力[τ]是拉伸许用应力[σ]的0.6倍,则螺栓直径d 和螺栓头高度h 的合理比值为__________。
3、 如图所示,象矿山升降机钢缆这类很长的拉杆,应考虑其自重的影响。
设材料单位体积的质量为ρ,许用应力为[]σ。
若钢缆下端所受拉力为P 。
钢缆截面不变,求钢缆的允许长度及其总伸长。
图2.4dx (a )(x )ρgxA(b )[解] 钢缆任意横截面上的轴力为()gxA P x N ρ+=。
如图2.4(b )所示。
设钢缆在自重和拉力P 作用下,不被拉断的极限长度L ,则危险截是钢缆的上端面。
该端面上的轴力为gLA P x N ρ+=)(根据强度要求,应有[]σρσ≤+==AgLAP A N即[]gA P A L ρσ-≤从而知钢缆允许的最大长度为[]gAPA L ρσ-=钢缆的伸长量由虎克定律确定,即()[]⎰⎰-=+==∆LLg EA P A dx EA gxA P dx EA x N l 022222ρσρ4、 图示螺栓,拧紧时产生mm l 10.0=∆得轴向变形,试求预紧力P ,并校核螺栓强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作出图中AB杆的受力图。
A处固定铰支座B处可动铰支座作出图中AB、AC杆及整体的受力图。
B、C光滑面约束A处铰链约束DE柔性约束作图示物系中各物体及整体的受力图。
AB杆:二力杆E处固定端C处铰链约束(1)运动效应:力使物体的机械运动状态发生变化的效应。
(2)变形效应:力使物体的形状发生和尺寸改变的效应。
3、力的三要素:力的大小、方向、作用点。
4、力的表示方法:(1)力是矢量,在图示力时,常用一带箭头的线段来表示力;(注意表明力的方向和力的作用点!)(2)在书写力时,力矢量用加黑的字母或大写字母上打一横线表示,如F、G、F1等等。
5、约束的概念:对物体的运动起限制作用的装置。
6、约束力(约束反力):约束作用于被约束物体上的力。
约束力的方向总是与约束所能限制的运动方向相反。
约束力的作用点,在约束与被约束物体的接处7、主动力:使物体产生运动或运动趋势的力。
作用于被约束物体上的除约束力以外的其它力。
8、柔性约束:如绳索、链条、胶带等。
(1)约束的特点:只能限制物体原柔索伸长方向的运动。
(2)约束反力的特点:约束反力沿柔索的中心线作用,离开被约束物体。
()9、光滑接触面:物体放置在光滑的地面或搁置在光滑的槽体内。
(1)约束的特点:两物体的接触表面上的摩擦力忽略不计,视为光滑接触面约束。
被约束的物体可以沿接触面滑动,但不能沿接触面的公法线方向压入接触面。
(2)约束反力的特点:光滑接触面的约束反力沿接触面的公法线,通过接触点,指向被约束物体。
()10、铰链约束:两个带有圆孔的物体,用光滑的圆柱型销钉相连接。
约束反力的特点:是方向未定的一个力;一般用一对正交的力来表示,指向假定。
()11、固定铰支座(1)约束的构造特点:把中间铰约束中的某一个构件换成支座,并与基础固定在一起,则构成了固定铰支座约束。
(2)约束反力的特点:固定铰支座的约束反力同中间铰的一样,也是方向未定的一个力;用一对正交的力来表示,指向假定。
()12、可动铰支座(1)约束的构造特点把固定铰支座的底部安放若干滚子,并与支撑连接则构成活动铰链支座约束,又称锟轴支座。
(2)约束反力的特点:垂直于支承面的一个力,指向假定。
()13、二力杆约束(1)约束的构造特点:杆件的自重不计,杆件的两端均用铰链(或固定铰支座)与周围的其它物体相连接。
两铰链之间不受任何力作用。
杆件可以是直杆或曲杆。
二力杆约束又称链杆约束,约束中的杆件又称之为二力杆。
(2)约束的约束特:性限制了物体沿杆件两端铰链连线方向的运动。
但不能阻止物体沿铰链的转动。
()(3)约束反力特点:根据二力平衡公理,二力杆约束的约束反力的方向必沿杆件两端铰链中心的连线,指向不定的一个力。
(二力平衡公理:一个刚体受两个力作用处于平衡的必要和充分条件:两个力等值、反向、共线)13、固定端约束:(1)约束的构造特点把杆件的端部与周围物体进行刚性连接。
两连接物体不能绕连接点有任何的相对转动。
(2)约束反力的特点:用一对正交的力和一个反力偶(用M表示)来表示。
()14、受力图:反映物体受力情况的图形。
15、画受力图的步骤:(1)确定研究对象,取脱离体。
(只画研究对象本身,不能画与它相连接的周围其它物体!)(2)画主动力。
(只画研究对象直接受到的主动力)(3)画约束反力。
(只画研究对象以外的其它物体对研究对象的约束反力,按每种约束的反力特点画)()16、物系:由两个及两个以上的物体构成的物体系统。
17、作用与反作用公理:两物体之间的相互作用力总是大小相等、方向相反、作用在同一直线上。
知识点:1、平衡:物体相对于地面处于静止或作匀速直线运动。
(物体受到的力的合力等于零)2、力在坐标轴上的投影:通过力的起点和终点分别作坐标轴的垂线,两垂线与坐标轴的交点之间的线段就是力在坐标轴上的投影。
(如图中的Fx和Fy)力的投影有正负,力的箭头指向与座标的正向一致为正;反之为负。
若力与正向夹角为α,则:Fx=FcosαFy=-Fcosα合力投影定理:力系的合力在任意轴上的投影等于各分力在同一轴上投影的代数和。
R X=F1X+F2X+...F nX=∑F XR Y=F1Y+F2Y+...F nY=∑F Y3、力矩:力矩是力对物体绕某一点转动其转动效果大小的度量。
它等于力的大小(F)乘以该点到力的距离(力臂d)。
并规定,力使物体绕该点顺转为负,逆转为正。
力矩的计算公式:M O(F)=±F×d4、合力矩定理:合力对某一点之矩等于各分力对同一点之矩的代数和。
M O(F R)=M O(F1)+M O(F2)+...M O(F n)=∑M O(F)分布力对某点之矩等于分布力的合力对该点之矩。
均匀分布的分布力的合力作用点在分布段的中点。
5、力偶:力偶是等值、反向、相互平行的一对特殊的力。
力偶对物体只起转动效果。
力偶矩的计算公式:M O(F)=±F×d [其中:d---力偶臂(两平行力之间的距离)]规定逆时针转向的力偶其力偶矩取正(+),顺时针转向的力偶其力偶矩取负号(-)。
力偶的基本性质:试求图示组合平面图形的形心坐标。
(单位:mm)解:1、将图示组合平面图形分成如右图所示的矩形I和矩形II组合后再减去圆III(认为其面积为负的)2、I、II、III的面积和形心坐标分别为:A 1=(100-20)×20=1600mm2 X1=10mm Y1=20+40=60mmA2=80×20=1600mm2 X2=40mm Y2=10mmA3=-πR2=3.14×52=-78.5mm2X3=10mm Y3=90mm3、利用形心坐标公式计算形心坐标知识点:1、重心:物体的重力的合力作用点称为物体的重心。
(与组成该物体的物质有关)2、形心:物体的几何中心。
(只与物体的几何形状和尺寸有关,与组成该物体的物质无关)一般情况下重心和形心是不重合的,只有物体是由同一种均质材料构成时,重心和形心才重合。
3、平面图形的形心坐标公式:(1)、分割法:工程中的零部件往往是由几个简单基本图形组合而成的,在计算它们的形心时,可先将其分割为几个基本图形,利用查表法查出每个基本图形的形心位置与面积,然后利用形心计算公式求出整体的形心位置。
此法称为分割法。
(2)、负面积法:仍然用分割法的公式,只不过去掉部分的面积用负值。
上式中的A i是每一个基本图形的面积;X i、Y i分别是每一个基本图形的形心的X、Y坐标。
上述两种方法可以分别使用,也可以同时使用。
如图所示的轴向拉压杆,已知材料的许用应力[σ]=10MPa,若截面为圆形,试设计其直径d。
解:1、用截面法求杆件上各段的轴力分别假想地用截面沿(a)图的1-1、2-2、3-3截面处将杆切开,取左段或右段为研究对象,画出其受力图如图(b)、(c)、(d)。
(图中的轴力最好都假设为拉力)由(b)图列平衡方程得:2+N1=0 N1=-2kN(压力)由(c)图列平衡方程得:2-3+N2=0 N2=1kN(拉力)由(d)图列平衡方程得:-N3-4=0 N3=-4kN(压力)2、作杆件的轴力图如图(e)由轴力图可得:|N|max=4kN(杆件的危险截面)3、根据强度条件设计截面尺寸知识点:1、变形:物体形状和尺寸的改变。
2、强度:强度是构件承受外力时抵抗破坏的能力。
3、刚度:刚度是构件承受外力时抵抗变形的能力。
4、稳定性:稳定性是构件承受外力时保持原有平衡状态的能力。
5、杆件的基本变形形式:轴向拉伸和压缩、剪切、扭转、弯曲。
6、轴向拉伸和压缩的受力特点:杆件受到的力(或合力)与其轴线重合。
7、轴力:与杆件的轴线重合的内力(用F N或N表示)(拉为正,压为负)。
8、截面法:用一假想的截面从要求内力处将杆件切开分成两段,取其中的任意一段为研究对象,画出其受力图,利用平衡方程,求出内力。
其步骤可归结为下列四步:切、取、代、平9、轴力图:将杆件的轴力随截面位置变化的关系用一个图形来表示。
10、应力:应力是分布内力的集度。
垂直于截面上的应力叫正应力,用σ表示。
切于截面的应力叫切应力(剪应力),用τ表示。
11、轴向拉压杆横截面上正应力的计算公式:12、极限应力(σu):材料失效时的应力。
塑性材料的极限应力是屈服极限(σs);脆性材料的极限应力是强度极限(σb)。
13、许用应力[σ]:保证构件安全工作,材料许可承担的最大应力。
其中:n---安全系数14、安全系数:为保证构件具有一定安全贮备而选取的一个大于1的系数。
安全系数越大构件越安全,但越不经济。
15、轴向拉压杆的强度条件:16、三类强度计算(1)、强度校核校核是否成立。
成立则强度够,不成立则强度不够。
(2)、截面设计计算出杆件的横截面面积,从而根据截面形状设计尺寸。
(3)、确定许可荷载计算出杆件的轴力,从而根据轴力与荷载的关系确定许可荷载的大小。
如图所示的铆钉联接,已知铆钉的许用剪应力[τ]=80MPa,铆钉和钢板的许用挤压应力[σjbs]=200MPa,钢板的许用正应力[σ]=160MPa,铆钉直径d=20mm,钢板厚度t=8mm,钢板宽度b=60mm,P=10kN,试校核此联接的强度。
知识点:1、剪切的受力特点:构件受到一对大小相等、方向相反、作用线相隔很近的平行力作用。
2、剪切的变形特点:沿平行两力作用线之间的面发生相对错动。
发生相对错动的面称为剪切面。
剪切变形是工程实际中常见的一种基本变形。
常出现于联接件中,如:铆钉联接、螺栓联接、销钉联接、键联接、榫头联接等等。
3、挤压:剪切变形中传递力的接触面发生的局部受压现象。
传递力的接触面称为挤压面(d图中的阴影部分a图的挤压面计算面积)。
4、剪应力计算公式:(工程实用计算中假设剪应力是均匀分布在剪切面上的)其中:τ---剪应力 FS---剪切面上的剪力 A---剪切面面积 [τ]---许用剪应力5、剪切的强度条件:6、挤压的应力计算公式:(工程实用计算中假设挤压应力是均匀分布在挤压面的计算面积上的)其中:Fbs---挤压力σbs---挤压应力 Ajbs---挤压面计算面积(是其最大正投影面面积)7、挤压的强度条件:由上述两个强度条件可进行三个方面的强度计算:(1)、强度校核(2)、截面设计(3)、确定许可荷载8、轴向拉压杆的强度条件:图示圆轴AB所受的外力偶矩M e1=800N·m,M e2=1200N·m,M e3=400N·m,G=80GPa,l2=2l1=600mm [τ]=50MPa,[φ/]=0.25(º)/m。
试设计轴的直径。
知识点:1、扭转:杆件的两端受到大小相等、转向相反且作用平面直垂于杆轴线的力偶的作用,致使杆件各横截面都绕杆轴线发生相对转动,杆件表面的纵向线将变成螺旋线。
