高等数学试题五(附答案)
高等数学练习题(附答案)

《高等数学》专业年级学号姓名一、判断题.将√或×填入相应的括号内.(每题2分,共20分)()1.收敛的数列必有界.()2.无穷大量与有界量之积是无穷大量.()3.闭区间上的间断函数必无界.()4.单调函数的导函数也是单调函数.()5.若f (x )在x 0点可导,则f (x )也在x 0点可导.()6.若连续函数y =f (x )在x 0点不可导,则曲线y =f (x )在(x 0,f (x 0))点没有切线.()7.若f (x )在[a ,b ]上可积,则f (x )在[a ,b ]上连续.()8.若z =f (x ,y )在(x 0,y 0)处的两个一阶偏导数存在,则函数z =f (x ,y )在(x 0,y 0)处可微.()9.微分方程的含有任意常数的解是该微分方程的通解.()10.设偶函数f (x )在区间(-1,1)内具有二阶导数,且f ''(0)=f '(0)+1,则f (0)为f (x )的一个极小值.二、填空题.(每题2分,共20分)1.设f (x -1)=x ,则f (x +1)=.22.若f (x )=2-12+11x1x,则lim +=.x →03.设单调可微函数f (x )的反函数为g (x ),f (1)=3,f '(1)=2,f ''(3)=6则---------------------------------------------------------------------------------------------------------------------------------g '(3)=.4.设u =xy +2x,则du =.y35.曲线x =6y -y 在(-2,2)点切线的斜率为.6.设f (x )为可导函数,f '(1)=1,F (x )=f ()+f (x ),则F '(1)=.7.若1x2⎰f (x )0t 2dt =x 2(1+x ),则f (2)=.8.f (x )=x +2x 在[0,4]上的最大值为.9.广义积分⎰+∞0e -2x dx =.2210.设D 为圆形区域x +y ≤1,⎰⎰y D1+x 5dxdy =.三、计算题(每题5分,共40分)111+Λ+).1.计算lim(2+22n →∞n (n +1)(2n )2.求y =(x +1)(x +2)(x +3)ΛΛ(x +10)在(0,+∞)内的导数.23103.求不定积分⎰1x (1-x )dx .4.计算定积分⎰πsin 3x -sin 5xdx .3225.求函数f (x ,y )=x -4x +2xy -y 的极值.6.设平面区域D 是由y =x ,y =x 围成,计算⎰⎰Dsin ydxdy .y7.计算由曲线xy =1,xy =2,y =x ,y =3x 围成的平面图形在第一象限的面积.---------------------------------------------------------------------------------------------------------------------------------8.求微分方程y '=y -2x的通解.y四、证明题(每题10分,共20分)1.证明:arc tan x=arcsinx 1+x 2(-∞<x <+∞).2.设f (x )在闭区间[a ,b ]上连续,且f (x )>0,F (x )=⎰f (t )dt +⎰x xb1dt f (t )证明:方程F (x )=0在区间(a ,b )内有且仅有一个实根.《高等数学》参考答案一、判断题.将√或×填入相应的括号内(每题2分,共20分)1.√;2.×;3.×;4.×;5.×;6.×;7.×;8.×;9.√;10.√.二、填空题.(每题2分,共20分)21.x +4x +4; 2.1; 3.1/2;4.(y +1/y )dx +(x -x /y )dy ;25.2/3;6. 1;7.336;8.8;9.1/2;10.0.三、计算题(每题5分,共40分)n +1111n +1<++L +<1.解:因为(2n )2n 2(n +1)2(2n )2n 2且lim 由迫敛性定理知:lim(n →∞n +1n +1=0lim ,=0n →∞(2n )2n →∞n 2111++Λ+)=0222n (n +1)(2n )2.解:先求对数ln y =ln(x +1)+2ln(x +2)Λ+10ln(x +10)---------------------------------------------------------------------------------------------------------------------------------∴11210y '=++Λ+y x +1x +2x +10∴y '=(x +1)Λ(x +10)(3.解:原式=21210++Λ+)x +1x +2x +10⎰11-xd x =2⎰11-(x )2d x=2arcsin4.解:原式=x +c⎰πsin 3x cos 2xdxπ32=⎰π2020cos x sin xdx -⎰cos x sin xdx232ππ32=⎰sin xd sin x -⎰ππ2sin xd sin x32222-[sin 2x ]π=[sin 2x ]0π552=4/525.解:f x'=3x -8x -2y =0f y'=2x -2y =05π5故⎨⎧x =0⎧x =2或⎨⎩y =0⎩y =2当⎨⎧x =0''(0,0)=-2,f xy ''(0,0)=2''(0,0)=-8,f yy 时f xx⎩y =0---------------------------------------------------------------------------------------------------------------------------------Θ∆=(-8)⨯(-2)-22>0且A=-8<0∴(0,0)为极大值点且f (0,0)=0当⎨⎧x =2''(2,2)=-2,f xy ''(2,2)=2''(2,2)=4,f yy 时f xxy =2⎩Θ∆=4⨯(-2)-22<0∴无法判断6.解:D=(x ,y )0≤y ≤1,y 2≤x ≤y{}∴⎰⎰D1y sin y 1sin y sin y dxdy =⎰dy ⎰2dx =⎰[x ]y dyy 20y 0y y y =⎰(sin y -y sin y )dy1=[-cos y ]+10⎰1yd cos y 1=1-cos1+[y cos y ]0-⎰cos ydy 01=1-sin17.解:令u =xy ,v =y;则1≤u ≤2,1≤v ≤3x1x uJ =yuxv =2uv y vv-u 2v v =12v u2u v231dv =ln 3∴A =⎰⎰d σ=⎰du ⎰112v D8.解:令y =u ,知(u )'=2u -4x由微分公式知:u =y =e ⎰22dx 2(⎰-4xe ⎰-2dx dx +c )---------------------------------------------------------------------------------------------------------------------------------=e 2x (⎰-4xe -2x dx +c )=e 2x (2xe -2x +e -2x +c )四.证明题(每题10分,共20分)1.解:设f (x )=arctan x -arcsinx 1+x 221Θf '(x )=-21+x 1x 1-1+x 221+x -⋅1+x 2x 21+x 2=0∴f (x )=c-∞<x <+∞令x =0Θf (0)=0-0=0∴c =0即:原式成立。
高等数学复旦大学出版社习题答案五
在总利润最大的基础上再多生产100台时,利润的增量为
ΔL(x)= .
即此时总利润减少1万元.
21.某企业投资800万元,年利率5%,按连续复利计算,求投资后20年中企业均匀收入率为200万元/年的收入总现值及该投资的投资回收期.
解:投资20年中总收入的现值为
在(3,0)处的切线是y=2x+6
两切线交点是( ,3).故所求面积为
(7)
(8)摆线x=a(tsint),y=a(1cost)的一拱(0t2)与x轴;
解:当t=0时,x=0,当t=2时,x=2a.
所以
(8)
(9)极坐标曲线ρ=asin3φ;
解:
.
(9)
(10)ρ=2acosφ;
解:
.
(10)
2.求下列各曲线所围成图形的公共部分的面积:
1.求下列各曲线所围图形的面积:
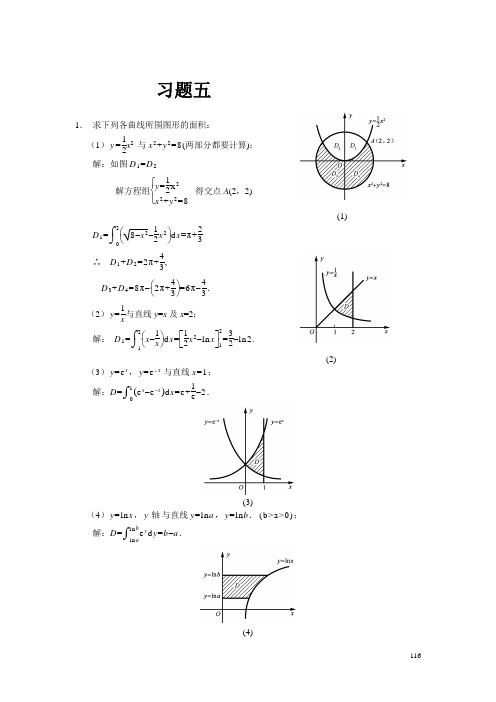
(1) 与x2+y2=8(两部分都要计算);
解:如图D1=D2
解方程组 得交点A(2,2)
(1)
∴ ,
.
(2) 与直线y=x及x=2;
解: .
(2)
(3)y=ex,y=ex与直线x=1;
解: .
(3)
(4)y=lnx,y轴与直线y=lna,y=lnb.(b>a>0);
≈0.385386万元=3853.86元.
yt′=3asin2tcost
xt′2+yt′2=9a2sin2tcos2t,利用曲线的对称性,
.
9.求对数螺线 相应θ=0到θ=φ的一段弧长.
解:
.
10.求半径为R,高为h的球冠的表面积.
高数习题5 3答案

高数习题5 3答案高数习题5-3答案高等数学是大学数学的一门重要课程,对于理工科学生来说尤为重要。
学习高等数学不仅需要掌握理论知识,还需要通过大量的习题来巩固和提高自己的能力。
本文将为大家提供高数习题5-3的答案,希望能够帮助到大家。
习题5-3是一道关于极限的题目。
在这道题目中,我们需要求出函数f(x) =(x^2 - 1) / (x - 1) 在x趋近于1时的极限。
首先,我们可以将函数进行化简,得到 f(x) = x + 1。
因此,当x趋近于1时,f(x)也会趋近于2。
所以,答案是2。
在解答这道题目的过程中,我们需要运用到一些数学的基本概念和技巧。
首先,我们需要了解极限的概念,即当自变量趋近于某个特定的值时,函数的取值会趋近于一个确定的值。
在这道题目中,我们需要求出当x趋近于1时,函数f(x)的极限。
其次,我们需要运用到函数的化简技巧,将给定的函数进行简化,以便更好地求解极限。
最后,我们需要运用到极限的性质,即当两个函数的极限存在且相等时,它们的极限值也相等。
通过解答这道题目,我们不仅能够巩固自己对于极限概念的理解,还能够提高自己的运算能力和思维能力。
在学习高等数学的过程中,通过大量的习题练习,我们能够更好地掌握和应用数学知识,提高自己的解决问题的能力。
除了解答这道具体的习题,我们还可以通过类似的题目来拓展自己的思维。
比如,我们可以考虑当x趋近于其他值时,函数的极限会有什么变化。
我们还可以思考,如果给定的函数无法通过化简来求解极限,我们应该如何处理。
通过这样的思考和探索,我们能够更好地理解和应用极限的概念。
总之,高等数学是一门重要的课程,通过大量的习题练习,我们能够更好地掌握和应用数学知识。
本文提供了高数习题5-3的答案,并对解答过程进行了简要的分析。
希望这篇文章能够帮助到大家,提高大家的数学能力。
同时,也希望大家在学习数学的过程中保持积极的态度,勇于挑战和探索,不断提升自己的数学水平。
高等数学试题(含答案)

高等数学试题(含答案)高等数学试题(含答案)一、选择题1.已知函数f(x)=x^2+3x+2,下列哪个选项是f(x)的导数?A. 2x+3B. 2x+2C. x^2+3D. 3x+22.若函数f(x)=e^x,那么f'(x)等于:A. e^-xB. e^xC. ln(x)D. e^x+13.设函数y=f(x)在点x=2处可导,且f'(2)=3,则曲线y=f(x)在点(2,f(2))处的切线斜率为:A. 2B. 3C. 1D. 6二、计算题1.计算极限lim(x→1) [(x-1)/(x^2-1)]答案:1/22.计算积分∫(0 to 1) (2x+1) dx答案:3/23.设曲线C的方程为y=x^3,计算曲线C的弧长。
答案:∫(0 to 1) √(1+9x^4) dx三、证明题证明:若函数f(x)在区间[a,b]上连续,且在(a,b)可导,那么必然存在c∈(a,b),使得 f'(c) = [f(b)-f(a)] / (b-a)。
证明过程:由于f(x)在区间[a,b]上连续,根据连续函数的介值定理,f(x)在[a,b]上会取到最大值M和最小值m。
设在点x=c处取得最大值M(即f(c)=M)。
根据费马定理,如果f(x)在点x=c处可导,并且f'(c)存在,那么f'(c)=0。
由于f(x)在(a,b)可导,故f'(c)存在。
那么,根据导数的定义,f'(c)=[f(c)-f(a)]/(c-a)。
又因为f(c)=M,将其代入上式得到f'(c)=(M-f(a))/(c-a)。
同理,根据费马定理,如果f(x)在点x=d处取得最小值m(即f(d)=m),那么f'(d)也等于0。
将f(d)=m代入上式得到f'(d)=(m-f(a))/(d-a)。
由于f(x)是连续函数,故在区间[a,b]上必然存在一个点c∈(a,b),使得它处于最大值M和最小值m之间,即m<f(c)<M。
高等数学考试题目及答案

高等数学考试题目及答案一、单项选择题(每题3分,共30分)1. 函数f(x)=x^2+2x+1的导数是:A. 2x+2B. x^2+2C. 2xD. 2x+1答案:A2. 曲线y=x^3在点(1,1)处的切线斜率是:A. 0B. 1C. 3D. -3答案:C3. 极限lim(x→0) (sin(x)/x)的值是:A. 0B. 1C. πD. -1答案:B4. 不定积分∫x^2 dx等于:A. (x^3)/3 + CB. x^3 + CC. (x^2)/2 + CD. 2x^3 + C答案:A5. 函数y=e^x的原函数是:A. e^x + CB. e^x - CC. e^(-x) + CD. -e^x + C答案:A6. 函数y=ln(x)的二阶导数是:A. 1/x^2B. 1/xC. -1/x^2D. -1/x答案:A7. 曲线y=x^2+2x+1与x轴的交点个数是:A. 0B. 1C. 2D. 3答案:A8. 函数y=x^3-3x的拐点是:A. (0,0)B. (1,-2)C. (-1,2)D. (2,2)答案:C9. 函数y=x^2-4x+4的极值点是:A. (2,0)B. (0,4)C. (4,0)D. (-2,0)答案:A10. 函数y=sin(x)的周期是:A. 2πB. πC. 1D. 0答案:A二、填空题(每题4分,共20分)11. 函数f(x)=x^3的导数是_________。
答案:3x^212. 曲线y=cos(x)在点(π/2,0)处的切线斜率是_________。
答案:013. 极限lim(x→∞) (1/x)的值是_________。
答案:014. 不定积分∫1/x dx等于_________。
答案:ln|x| + C15. 函数y=e^(-x)的原函数是_________。
答案:-e^(-x) + C三、解答题(每题10分,共50分)16. 求函数f(x)=x^2-4x+4在区间[1,3]上的最大值和最小值。
高等数学考试题及答案

高等数学考试题及答案一、选择题(每题2分,共20分)1. 函数f(x) = x^2 - 3x + 2在区间[1, 4]上的最大值是:A. 0B. 3C. 5D. 62. 级数∑(1/n^2)从n=1到∞的和是:A. π^2/6B. eC. 1D. 23. 微分方程dy/dx + y = x^2的通解是:A. y = x^2 - x + CB. y = x^2 + CC. y = x^2 + x + CD. y = x^2 - 2x + C4. 曲线y = x^3 - 2x^2 + 3x在点(1, 2)处的切线斜率是:A. -1B. 0C. 1D. 25. 函数f(x) = sin(x) + cos(x)的周期是:A. πB. 2πC. π/2D. 16. 曲线y = x^2与直线y = 4x在第一象限的交点坐标是:A. (2, 8)B. (0, 0)C. (1, 4)D. (4, 16)7. 极限lim(x→∞) (1 + 1/x)^x的值是:A. eB. 1C. 0D. ∞8. 函数f(x) = x^3 - 6x^2 + 11x - 6的零点个数是:A. 0B. 1C. 2D. 39. 已知函数f(x) = x^2 + 2x + 1,求f'(x):A. 2x + 2B. 2x + 1C. 2x - 1D. x^2 + 210. 函数y = ln(x)的导数是:A. 1/xB. xC. ln(x)D. 1二、填空题(每题2分,共20分)11. 函数f(x) = x^3 - 3x^2 + 2的极值点是________。
12. 函数f(x) = sin(x)的反函数是________。
13. 曲线y = x^2 - 4x + 4在x轴上的截距是________。
14. 曲线y = 1/x在点(1, 1)处的切线斜率是________。
15. 函数f(x) = x^2 - 4的根是________。
高等数学试题及及答案

高等数学试题及及答案高等数学试题及答案一、选择题(每题4分,共20分)1. 函数f(x)=x^2-2x+1的最小值是()。
A. 0B. 1C. -1D. 22. 极限lim(x→0) (sin(x)/x)的值是()。
A. 0B. 1C. -1D. 23. 函数y=e^x的导数是()。
A. e^xB. -e^xC. 1/e^xD. 04. 曲线y=x^3-3x+2在x=1处的切线斜率是()。
A. 0B. 1C. -1D. 25. 积分∫(0 to 1) (x^2 dx)的值是()。
A. 1/3B. 1/2C. 1D. 2二、填空题(每题4分,共20分)6. 函数f(x)=3x^2-6x+5的顶点坐标是()。
7. 函数y=ln(x)的定义域是()。
8. 函数y=x^3的二阶导数是()。
9. 曲线y=e^x与直线y=x相切的切点坐标是()。
10. 积分∫(0 to 1) (x dx)的值是()。
三、解答题(每题15分,共60分)11. 求函数f(x)=x^3-3x+2在区间[-1, 2]上的定积分,并画出积分图。
12. 求极限lim(x→∞) ((x^2+1)/(x^3+x))。
13. 求函数y=x^2-4x+3的极值点,并说明极值点的性质。
14. 求曲线y=x^2+2x-3在点(1, -2)处的切线方程。
四、附加题(10分)15. 证明:对于任意正整数n,有1/n^2 < 1/(n^2-1) + 1/(n^2+1)。
答案:一、选择题1. B2. B3. A4. C5. A二、填空题6. (1, 2)7. (0, +∞)8. 6x9. (1, e)10. 1/2三、解答题11. ∫(-1 to 2) (x^3-3x+2 dx) = (1/4x^4 - 3/2x^2 + 2x) | (-1 to 2) = 17/4积分图略。
12. 原式=lim(x→∞) (x^2+1)/(x^3+x) = lim(x→∞) (1/x + 1/x^3) = 013. y'=2x-4,令y'=0,得x=2,此时y=3,为极小值点。
高数试题及答案 五套

高学试题及答案一、单项选择题(本大题共5小题,每小题2分,共10分)1.设f(x)=lnx ,且函数ϕ(x)的反函数1ϕ-2(x+1)(x)=x-1,则[]ϕ=f (x)( ) ....A B C D x-2x+22-x x+2 ln ln ln ln x+2x-2x+22-x2.()02lim1cos t t xx e e dtx-→+-=-⎰( )A .0B .1C .-1D .∞3.设00()()y f x x f x ∆=+∆-且函数()f x 在0x x =处可导,则必有( ).lim 0.0.0.x A y B y C dy D y dy ∆→∆=∆==∆= 4.设函数,131,1x x x ⎧≤⎨->⎩22x f(x)=,则f(x)在点x=1处( )A.不连续B.连续但左、右导数不存在C.连续但不可导D. 可导5.设C +⎰2-x xf(x)dx=e,则f(x)=( )2222-x -x -x -x A.xe B.-xe C.2e D.-2e二、填空题(本大题共10小题,每空3分,共30分) 请在每小题的空格中填上正确答案。
错填、不填均无分。
6.设函数f(x)在区间[0,1]上有定义,则函数f(x+14)+f(x-14)的定义域是__________. 7.()()2lim 1_________n n a aq aq aq q →∞++++<=8.arctan lim _________x x x→∞=9.已知某产品产量为g 时,总成本是2g C(g)=9+800,则生产100件产品时的边际成本100__g ==MC10.函数3()2f x x x =+在区间[0,1]上满足拉格朗日中值定理的点ξ是_________.11.函数3229129y x x x =-+-的单调减少区间是___________.12.微分方程3'1xy y x -=+的通解是___________. 13.设2ln 2,6aa π==⎰则___________.14.设2cos xz y=则dz= _______.15.设{}2(,)01,01y DD x y x y xe dxdy -=≤≤≤≤=⎰⎰,则_____________. 三、计算题(一)(本大题共5小题,每小题5分,共25分)16.设1xy x ⎛⎫= ⎪⎝⎭,求dy.17.求极限0ln cot lim ln x x x +→18.求不定积分.19.计算定积分I=.⎰20.设方程2z x 2e 1y xz -+=确定隐函数z=z(x,y),求','x y z z 。
高等数学复习题五答案

高等数学复习题五答案一、选择题1. 极限的定义中,ε-δ定义描述的是函数值与极限值之间的距离,当这个距离小于任意给定的正数ε时,存在一个正数δ,使得当自变量x满足0<|x-x₀|<δ时,函数值f(x)与极限值A之间的距离小于ε。
以下哪个选项正确描述了ε-δ定义?A. 当|f(x) - A| < ε时,存在一个δ,使得0 < |x - x₀| < δB. 当0 < |x - x₀| < δ时,|f(x) - A| < εC. 当|f(x) - A| ≥ ε时,不存在δ,使得0 < |x - x₀| < δD. 当0 < |x - x₀| < δ时,|f(x) - A| ≥ ε答案:B2. 函数f(x) = x^2在x=0处的导数是:A. 0B. 1C. 2D. -1答案:B3. 以下哪个级数是收敛的?A. 1 + 1/2 + 1/4 + 1/8 + ...B. 1 - 1/2 + 1/3 - 1/4 + ...C. 1 + 2 + 3 + 4 + ...D. 1 - 1/2 + 1/4 - 1/8 + ...答案:A二、填空题4. 函数f(x) = ln(x)的导数是________。
答案:1/x5. 利用洛必达法则计算极限lim (x→0) (sin(x)/x),结果是________。
答案:16. 函数f(x) = x^3 - 3x^2 + 2的极值点是________。
答案:x = 1, x = 2三、简答题7. 简述泰勒公式的定义及其在数学分析中的应用。
答案:泰勒公式是将一个具有n阶可导的函数f(x)在x=a处展开成多项式的形式,即f(x) = f(a) + f'(a)(x-a) + f''(a)(x-a)^2/2!+ ... + f^(n)(a)(x-a)^n/n! + R_n(x),其中R_n(x)是余项。
高等数学试题(含答案)

《高等数学》试题库一、选择题 (一)函数1、下列集合中( )是空集。
{}{}4,3,02,1,0. a {}{}7,6,53,2,1. b (){}x y x y y x c 2,.==且 {}01.≥〈x x x d 且2、下列各组函数中是相同的函数有( )。
()()()2,.x x g x x f a == ()()2,.x x g x x f b ==()()x x x g x f c 22cos sin ,1.+== ()()23,.x x g xx x f d ==3、函数()5lg 1-=x x f 的定义域是( )。
()()+∞∞-,55,. a ()()+∞∞-,66,. b()()+∞∞-,44,. c ()()()()+∞∞-,66,55,44,. d4、设函数()⎪⎩⎪⎨⎧-+2222x x x〈+∞≤〈≤〈∞〈-x x x 2200 则下列等式中,不成立的是( )。
()()10.f f a = ()()10.-=f f b ()()22.f f c =- ()()31.f f d =-5、下列函数中,( )是奇函数。
x xa . x xb sin .211.+-x x a a c 21010.x x d -- 6、下列函数中,有界的是( )。
arctgx y a =. t g xy b =. xy c 1.= xy d 2.= 7、若()()11-=-x x x f ,则()=x f ( )。
()1.+x x a ()()21.--x x b ()1.-x x c .d 不存在8、函数x y sin =的周期是( )。
π4.a π2.b π.c 2.πd 9、下列函数不是复合函数的有( )。
xy a ⎪⎭⎫ ⎝⎛=21. ()21.x y b --= x y c s i n lg .= x ey d s i n1.+=10、下列函数是初等函数的有( )。
11.2--=x x y a ⎩⎨⎧+=21.xx y b 00≤〉x x x y c c o s 2.--=()()2121lg 1sin .⎪⎪⎭⎫ ⎝⎛+-=x e y d x11、区间[,)a +∞, 表示不等式( ).(A )a x <<+∞ (B )+∞<≤x a (C )a x < (D )a x ≥12、若ϕ3()1t t =+,则 ϕ3(1)t +=( ).(A )31t + (B )61t + (C )62t + (D )963332t t t +++13、函数log (a yx =+ 是( ).(A )偶函数 (B )奇函数 (C )非奇非偶函数 (D )既是奇函数又是偶函数 14、函数()yf x =与其反函数1()y f x -=的图形对称于直线( ). (A )0y = (B )0x = (C )y x = (D )y x =-15、函数1102x y-=-的反函数是( ).(A )1xlg22y x =- (B )log 2x y = (C )21log y x= (D )1lg(2)y x =++ 16、函数sin cos yx x =+是周期函数,它的最小正周期是( ).(A )2π (B )π (C )2π (D )4π 17、设1)(+=x x f ,则)1)((+x f f =( ). A . x B .x + 1 C .x + 2 D .x + 3 18、下列函数中,( )不是基本初等函数. A . x y )e1(= B . 2ln x y = C . xx y cos sin =D . 35x y = 19、若函数f(e x)=x+1,则f(x)=( )A. e x+1 B. x+1 C. ln(x+1) D. lnx+120、若函数f(x+1)=x 2,则f(x)=( )A.x 2B.(x+1) 2C. (x-1) 2D. x 2-1 21、若函数f(x)=lnx ,g(x)=x+1,则函数f(g(x))的定义域是( ) A.x>0 B.x ≥0 C.x ≥1 D. x>-1 22、若函数f(x)的定义域为(0,1)则函数f(lnx+1)的定义域是( )A.(0,1)B.(-1,0)C.(e -1,1)D. (e -1,e) 23、函数f(x)=|x-1|是( )A.偶函数B.有界函数C.单调函数D.连续函数 24、下列函数中为奇函数的是( )A.y=cos(1-x)B.⎪⎭⎫ ⎝⎛++=21ln x x y C.e x D.sinx 2 25、若函数f(x)是定义在(-∞,+∞)内的任意函数,则下列函数中( )是偶函数。
高等数学最难试题及答案

高等数学最难试题及答案一、单项选择题(每题5分,共20分)1. 函数f(x) = x^3 - 6x^2 + 11x - 6的导数是()。
A. 3x^2 - 12x + 11B. 3x^2 - 12x + 10C. 3x^2 - 6x + 11D. 3x^2 - 6x + 10答案:A2. 极限lim(x→0) (sin x)/x的值是()。
A. 0B. 1C. 2D. 3答案:B3. 曲线y = x^2 + 2x + 1在点(1, 4)处的切线斜率是()。
A. 2B. 3C. 4D. 5答案:B4. 函数y = sin(x) + cos(x)的不定积分是()。
A. -cos(x) + sin(x) + CB. cos(x) + sin(x) + CC. -cos(x) - sin(x) + CD. cos(x) - sin(x) + C答案:A二、填空题(每题5分,共20分)1. 已知函数f(x) = e^x,求f'(0)的值为______。
答案:12. 函数y = ln(x)的导数为______。
答案:1/x3. 曲线y = x^3 - 3x^2 + 2在点(2, 2)处的切线方程为______。
答案:y = 2x - 24. 求定积分∫(0 to 1) x^2 dx的值为______。
答案:1/3三、解答题(每题15分,共40分)1. 求函数f(x) = x^3 - 3x^2 + 2的极值点。
解:首先求导数f'(x) = 3x^2 - 6x = 3x(x - 2)。
令f'(x) = 0,解得x = 0 或 x = 2。
通过二阶导数测试,f''(x) = 6x - 6,当x = 0时,f''(0) = -6 < 0,所以x = 0是极大值点;当x = 2时,f''(2) = 6 > 0,所以x = 2是极小值点。
(完整)高等数学考试题库(附答案)

高等数学考试题库(附答案)一、选择题1. 设函数 $ f(x) = x^3 3x + 2 $,则 $ f'(0) $ 的值为多少?A. 0B. 1C. 1D. 3答案:A2. 设 $ f(x) = e^x $,则 $ f''(x) $ 等于多少?A. $ e^x $B. $ e^x + x $C. $ e^x x $D. $ e^x + 2 $答案:A3. 设 $ y = \ln(x + 1) $,则 $ y' $ 等于多少?A. $ \frac{1}{x + 1} $B. $ \frac{1}{x} $C. $ \frac{1}{x 1} $D. $ \frac{1}{x + 2} $答案:A4. 设 $ y = x^2 $,则 $ y'' $ 等于多少?A. 2B. 4D. 1答案:B5. 设 $ y = \sin(x) $,则 $ y' $ 等于多少?A. $ \cos(x) $B. $ \cos(x) $C. $ \tan(x) $D. $ \tan(x) $答案:A二、填空题1. 设函数 $ f(x) = x^4 2x^3 + x^2 $,则 $ f'(x) $ 的表达式为______。
答案:$ 4x^3 6x^2 + 2x $2. 设 $ y = \ln(x) $,则 $ y' $ 的表达式为______。
答案:$ \frac{1}{x} $3. 设 $ y = e^x $,则 $ y'' $ 的表达式为______。
答案:$ e^x $4. 设 $ y = \cos(x) $,则 $ y' $ 的表达式为______。
答案:$ \sin(x) $5. 设 $ y = \sqrt{x} $,则 $ y' $ 的表达式为______。
答案:$ \frac{1}{2\sqrt{x}} $三、解答题1. 求函数 $ f(x) = x^3 3x + 2 $ 在点 $ x = 1 $ 处的切线方程。
(完整)高等数学考试题库(附答案)

高等数学考试题库(附答案)1. 解析:求函数 f(x) = x^2 在区间 [0, 2] 上的定积分。
2. 解析:求函数 f(x) = e^x 在区间 [1, 1] 上的定积分。
3. 解析:求函数 f(x) = sin(x) 在区间[0, π] 上的定积分。
4. 解析:求函数 f(x) = cos(x) 在区间[0, π/2] 上的定积分。
5. 解析:求函数 f(x) = ln(x) 在区间 [1, e] 上的定积分。
6. 解析:求函数 f(x) = x^3 在区间 [1, 1] 上的定积分。
7. 解析:求函数f(x) = √x 在区间 [0, 4] 上的定积分。
8. 解析:求函数 f(x) = 1/x 在区间 [1, 2] 上的定积分。
9. 解析:求函数 f(x) = tan(x) 在区间[0, π/4] 上的定积分。
10. 解析:求函数 f(x) = 1/(1 + x^2) 在区间 [0, 1] 上的定积分。
11. 解析:求函数 f(x) = x^2 + 1 在区间 [0, 1] 上的定积分。
12. 解析:求函数 f(x) = e^(x) 在区间 [0, 2] 上的定积分。
13. 解析:求函数 f(x) = sin^2(x) 在区间[0, π] 上的定积分。
14. 解析:求函数 f(x) = cos^2(x) 在区间[0, π/2] 上的定积分。
15. 解析:求函数 f(x) = 1/(1 + x^2) 在区间 [1, 1] 上的定积分。
16. 解析:求函数f(x) = √(1 x^2) 在区间 [1, 1] 上的定积分。
17. 解析:求函数 f(x) = x^3 3x^2 + 2x 在区间 [0, 2] 上的定积分。
18. 解析:求函数 f(x) = e^(2x) 在区间 [1, 1] 上的定积分。
19. 解析:求函数 f(x) = ln(x) 在区间 [1, e^2] 上的定积分。
20. 解析:求函数 f(x) = sin(x)cos(x) 在区间[0, π/2] 上的定积分。
高数D综合测试题5参考答案

高数D 综合测试题5参考答案一、填空题(每题3分,共30分) 1.函数(,)f x y =的定义域是22{(,):1}x y x y +<.2. 若23()(2519),f x x x =-+ 则(7)()f x =0 . (解:函数为6次多项式,求7阶导数,值为零)3. 若分段函数1(1),0,()5,0,x x x f x a x ⎧+≠⎪=⎨⎪=⎩是连续函数,则a =15e .(解:15115500lim(1)lim(1)55x x x x x xe ⋅→→+=+=) 4. 图形21x y x =+的垂直渐近线为1x =- .(解:21lim 1x x x →-=∞+)5. 若(),x z xyf y =()f u 可导,则z z x y x y ∂∂+=∂∂2()xxyf y .(解:21[()()][()()]2()z z x x x x x xxy x yf xyf y xf xyf xyf x y y y y y y y y∂∂-''+=+⋅++⋅=∂∂) 6. 函数233y x x =-的拐点为(1,2) .(解: 263,66,y x x y x '''=-=-令0y ''=可得1x =,由于60,y '''=-≠故拐点为(1,2)) 7. 反常积分131dx x π+∞=⎰2π.(解: 213211122dx xx πππ+∞+∞=-=⎰)8. 设22ln()z x y =+,则全微分dz =222222x ydx dy x y x y+++. 9. 已知函数arcsin()z x xy =+,则(0,1)zy ∂=∂0. (解:arcsin()()dz dx d xy dx xy dx =+=+=+故(0,1)0z y∂==∂)10.设22:4D x y +≤,则22()Df x y dxdy +⎰⎰写成极坐标系下的二次积分形式为2220()f r rdrd πθ⎰⎰.二、单项选择题(每题2分,共10分)1.若()sin ,f x x '=则()f x 的原函数之一是(D ) A.1sin x + B.1sin x - C.1cos x + D.1cos x -2.0x =是函数1sin y x x=的(A )型间断点.A. 可去B. 跳跃C.无穷D.震荡 3.变量11xy e =-在(C )的过程中是无穷小量. A.0x +→ B.0x -→ C.x →∞D.1x →(解:由于1111100lim ,lim 0,lim 1,lim ,xxxxx x xx e e e e e +-→∞→→→=∞===故选择C.) 4.若(,)z f x y =在点000(,)P x y 处的两个偏导数存在,则函数在该点(D ) A. 有极限 B. 连续 C. 可微 D. 有切线5.若函数,0,(),0,x e x f x a bx x ⎧<=⎨+≥⎩在点0x =处可导,则有( B )A.0,0a b ==B.1,1a b ==C.0,1a b ==D.1,0a b ==(解:0lim ()lim()(0),lim ()lim 11,xx x x x f x a bx a f f x e a ++--→→→→=+====⇒=而 0000()(0)11()(0)1lim lim ,lim lim 1100x x x x x f x f bx f x f e b b x x x x++--→→→→-+---====⇒=--.)三、计算及证明题(每题6分,共48分)1.求极限111lim[].1335(21)(21)n n n →∞+++⋅⋅-+解:原式111111111lim (1)lim (1).233521212212n n n n n →∞→∞=-+-++-=-=-++ 2.求极限ln(1)lim .x x e x →+∞+解:ln(1)lim x x e x →+∞+11lim lim 1.1101x x x x x e e e -→+∞→+∞====+++ 3.求不定积分3).x e dx +⎰解:3)x e dx +⎰arcsin 3.x x e C =+++4.求定积分31ln .xdx ⎰解:31ln xdx ⎰333111[ln ]13ln3[]3ln3 2.x x dx x =-=-=-⎰5.方程1y y xe =-确定隐函数()y y x =,求.y '解:方程两边关于x 求导,得yyy e xe y ''=--,从而得到.1yye y xe'=-+ 6.用二重积分计算抛物线22y x =-与直线21y x =+所围成图形的面积. 解:抛物线与直线的交点为(1,1)--和(3,7),213, 221x x y x -≤≤-≤≤+,所围成图形面积为232132121()(23)x x Dd dy dx x x dx σ+---==-+⎰⎰⎰⎰⎰2331132[3].33x x x -=-+=7.证明方程531x x -=在1与2之间至少存在一个实根.解:令5()31F x x x =--,则()F x 在闭区间[1,2]连续,且(1)30F =-<,(2)250F =>,由零点定理,至少存在一点(1,2)ξ∈,使得()0F ξ=,即方程531x x -=在1与2之间至少存在一个实根.8.求微分方程222x y xy xe -'+=的通解. 解:(法一)利用通解公式:()()[()]P x dxP x dx y e Q x e dx C -⎰⎰=+⎰可知22222222[(2)][(2)]().xdx xdxx x x x x y e xe e dx C e xe e dx C e x C -----⎰⎰=+=+=+⎰⎰(法二)两边乘以2x e ,得2()2x ye x '=,即,2()2x d ye xdx =,两边关于x 积分,得22x ye x C =+,解得 22()x y x C e -=+,其中C 为任意常数.四、(10分)求抛物线243y x x =-+-及其在点(0,3)-和(3,0)处的切线所围成的图形的面积.解:24y x '=-+,过点(0,3)-的切线方程:43y x =-,与x 轴交点3(,0)4过点(3,0)的切线方程:26y x =-+,两条直线方程的交点:3(,3)2.所围图形为两个X 型区域:233, 434342x x x y x ≤≤-+-≤≤-,233, 43262x x x y x ≤≤-+-≤≤-+. 所围图形面积:22343326233434324()()x x x x x x dy dx dy dx --+-+--+-+⎰⎰⎰⎰33322333223333244211135(3)[][(3)].3364x dx x dx x x =+-=+-=⎰⎰ 五、(6分)求函数2332y x x =-的单调区间与极值.解:定义域为(,)-∞+∞,131y x-'=-=,令0y '=,解得驻点:1x =. 奇点:0x =,可知单调递增区间为(,0],[1)-∞+∞,单调递减区间为[0,1],极大值(0)0y =,极小值1(1)2y =-.六、(6分)设()f x 在[0,1]上连续,在(0,1)内可导,且1233()(0),f x dx f =⎰证明在(0,1)内存在一点ξ使得()0.f ξ'=证明:由积分中值定理可得1211312()(),[,1]33f x dx f ξξ=∈⎰即1213()3()(0),f f x dx f ξ==⎰在1[0,]ξ上用罗尔定理,可知1(0,)(0,1)ξξ∃∈⊂使得()0.f ξ'=。
高等数学综合试卷(五至七章 )

二、单选题
综合试题1
三、计算题
1. 设 量矩阵是
是三维欧氏空间V的一组基,这组基的度
(1)求内积
(2)求 (3)求V的一组标准正交基.
综合试题1
四、证明题
1.设V是n维欧氏空间,证有对任意的n阶正定矩阵A,在V中总
存在基
,使这组基的度量矩阵为A,又问,这样的基
是不是唯一的?
答案 返回目录
下一套试卷
也是正定矩阵. 7. 如果与n阶矩阵A相似的矩阵只有A自身,则A为单位矩阵
8. 设n阶可逆矩阵A与B相似,则A与B有相同的特征向量
二、单选题
1. 在下列R3的变换中是线性变换的为
综合试题4
2. 设A,B,C是线性空间V的线性变换,O是V的零变换,则
(A)A≠O ,AB = O则B = O (B)AB = O则A = O或 B =O
一、判断题
综合试题1答案
1. × 2. √ 3.√ 4. √ 5. √ 6. √ 7. × 8. × 9. ×
二、单选题
1.C 2.A 3.A 4.C 5.D
三、计算题
1.(1)0;0;3 (2)1 (3)标准正交基
返回试题 返回目录 下一套试卷
一、判断题
综 合 试 题2
二、单选题
综合试题2
三、计算题
4. 任何方阵与它的转置矩阵有相同的特征值. 5. 若 是矩阵A的特征向量,则 也是矩阵(A+E)2的特征向量
7. 设A是线性空间V的可逆线性变换, 是A的一个特征值,则 是 的一个特征值。
二、单选题
综合试题3
三、计算题 1. 设A是欧氏空间V的线性变换,A在V的一组基
下的矩阵为
求V的另一组基
高数同济版第五章答案

习题5-11. 利用定积分定义计算由抛物线y =x 2+1, 两直线x =a 、x =b (b >a )及横轴所围成的图形的面积.解 第一步: 在区间[a , b ]内插入n -1个分点i nab a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 把区间[a , b ]分成n 个长度相等的小区间, 各个小区间的长度为: nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 第二步: 在第i 个小区间[x i -1, x i ] (i =1, 2, ⋅ ⋅ ⋅, n )上取右端点i nab a x i i -+==ξ, 作和 nab i n a b a x f S ni i i ni n -⋅+-+=∆=∑∑==]1)[()(211ξ ∑=+-+-+-=n i i na b i n a b a a n a b 12222]1)()(2[]6)12)(1()(2)1()(2[)(222n n n n n a b n n n a b a na n a b +++⋅-++⋅-+-= ]16)12)(1()()1)(()[(222+++-++-+-=n n n a b n n a b a a a b . 第三步: 令λ=max{∆x 1, ∆x 2, ⋅ ⋅ ⋅ , ∆x n }nab -=, 取极限得所求面积 ∑⎰=→∆==ni i i ba x f dx x f S 10)(lim )(ξλ]16)12)(1()()1)(()[(lim 222+++-++-+-=∞→n n n a b n n a b a a a b n a b a b a b a b a a a b -+-=+-+-+-=)(31]1)(31)()[(3322.2. 利用定积分定义计算下列积分: (1)xdx b a ⎰(a <b ); (2)dx e x ⎰10. 解 (1)取分点为i n a b a x i -+=(i =1, 2, ⋅ ⋅ ⋅, n -1), 则nab x i -=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点i nab a x i i -+==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是∑∑⎰=∞→=∞→-⋅-+=∆=ni n ni i i n ba nab i n a b a x xdx 11)(lim lim ξ )(21]2)1()()([lim )(22222a b n n n a b a b a a b n -=+-+--=∞→.(2)取分点为ni x i =(i =1, 2, ⋅ ⋅ ⋅, n -1), 则n x i 1=∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间上取右端点nix i i ==ξ (i =1, 2, ⋅ ⋅ ⋅, n ). 于是) (1lim 1lim 21110n n n n n n i n i n xe e e nn e dx e +⋅⋅⋅++==∞→=∞→∑⎰1)1(]1[lim1])(1[1lim 11111-=--=--⋅=∞→∞→e e n e e e e e nn n n n n n .3. 利用定积分的几何意义, 说明下列等式: (1)1210=⎰xdx ; (2)4112π=-⎰dx x ;(3)⎰-=ππ0sin xdx ; (4)⎰⎰=-2022cos 2cos πππxdx xdx .解 (1)⎰102xdx 表示由直线y =2x 、x 轴及直线x =1所围成的面积, 显然面积为1.(2)⎰-1021dx x 表示由曲线21x y -=、x 轴及y 轴所围成的四分之一圆的面积, 即圆x 2+y 2=1的面积的41:41411212ππ=⋅⋅=-⎰dx x .(3)由于y =sin x 为奇函数, 在关于原点的对称区间[-π, π]上与x 轴所夹的面积的代数和为零, 即 ⎰-=ππ0sin xdx .(4)⎰-22cos ππxdx 表示由曲线y =cos x 与x 轴上]2 ,2[ππ-一段所围成的图形的面积. 因为cos x为偶函数, 所以此图形关于y 轴对称. 因此图形面积的一半为⎰20cos πxdx , 即⎰⎰=-2022cos 2cos πππxdx xdx .4. 水利工程中要计算拦水闸门所受的水压力, 已知闸门上水的压强p (单位面积上的压力大小)是水深h 的函数, 且有p =9⋅8h (kN/m 2). 若闸门高H =3m, 宽L =2m, 求水面与闸门顶相齐时闸门所受的水压力P .解 建立坐标系如图. 用分点i nHx i =(i =1, 2, ⋅ ⋅ ⋅, n -1)将区间[0, H ]分为n 分个小区间, 各小区间的长为nHx i =∆(i =1, 2, ⋅ ⋅ ⋅, n ). 在第i 个小区间[x i -1, x i ]上, 闸门相应部分所受的水压力近似为 ∆P i =9.8x i l ⋅∆x i . 闸门所受的水压力为22118.42)1(lim8.9lim 8.98.9lim H L n n n H L n Hi n H L x L x P n n i n n i i i n ⋅=+⋅=⋅=∆⋅⋅=∞→=∞→=∞→∑∑. 将L =2, H =3代入上式得P =88.2(千牛).5. 证明定积分性质:(1)⎰⎰=b a b a dx x f k dx x kf )()(; (2)a b dx dx ba b a -==⋅⎰⎰1. 证明 (1)⎰∑∑⎰=∆=∆==→=→ba ni i i ni i i ba dx x f k x f k x kf dx x kf )()(lim )(lim )(1010ξξλλ.(2)a b a b x x dx ni i ni i ba -=-=∆=∆⋅=⋅→=→=→∑∑⎰)(lim lim 1lim 101010λλλ.6. 估计下列各积分的值: (1)⎰+412)1(dx x ; (2)⎰+ππ4542)sin 1(dx x ;(3)⎰331arctan xdx x ; (4)⎰-022dx e xx.解 (1)因为当1≤x ≤4时, 2≤x 2+1≤17, 所以 )14(17)1()14(2412-⋅≤+≤-⋅⎰dx x , 即 51)1(6412≤+≤⎰dx x . (2)因为当ππ454≤≤x 时, 1≤1+sin 2x ≤2, 所以 )445(2)sin 1()445(14542ππππππ-⋅≤+≤-⋅⎰dx x ,即 ππππ2)sin 1(4542≤+≤⎰dx x .(3)先求函数f (x )=x arctan x 在区间]3 ,31[上的最大值M 与最小值m .21a r c t a n )(xx x x f ++='. 因为当331≤≤x 时, f '(x )>0, 所以函数f (x )=x arctan x 在区间]3 ,31[上单调增加. 于是3631arctan31)31(π===f m , 33arctan 3)3(π===f M .因此)313(3arctan )313(36331-≤≤-⎰ππxdx x ,即32arctan 9331ππ≤≤⎰xdx x . (4)先求函数xx e x f -=2)(在区间[0, 2]上的最大值M 与最小值m .)12()(2-='-x e x f xx, 驻点为21=x .比较f (0)=1, f (2)=e 2, 1)21(-=e f ,得1-=e m , M =e 2. 于是)02()02(220412-⋅≤≤-⎰--e dx e e xx,即 1022222---≤≤-⎰e dx dx e e xx .7. 设f (x )及g (x )在[a , b ]上连续, 证明:(1)若在[a , b ]上, f (x )≥0, 且0)(=⎰ba dx x f , 则在[a ,b ]上f (x )≡0; (2)若在[a , b ]上, f (x )≥0, 且f (x )≢0, 则0)(>⎰ba dx x f ;(3)若在[a , b ]上, f (x )≤g (x ), 且⎰⎰=b a ba dx x g dx x f )()(, 则在[a ,b ]上f (x )≡g (x ).证明 (1)假如f (x )≢0, 则必有f (x )>0. 根据f (x )在[a , b ]上的连续性, 在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是0)(2)()()()()()(0>-≥≥++=⎰⎰⎰⎰⎰c d x f dx x f dx x f dx x f dx x f dx x f dc bd dc ca ba . 这与条件0)(=⎰ba dx x f 相矛盾. 因此在[a ,b ]上f (x )≡0.(2)证法一 因为f (x )在[a , b ]上连续, 所以在[a , b ]上存在一点x 0, 使f (x 0)>0, 且f (x 0)为f (x )在[a , b ]上的最大值.再由连续性, 存在[c , d ]⊂[a , b ], 且x 0∈[c , d ], 使当x ∈[c , d ]时, 2)()(0x f x f >. 于是⎰⎰>-≥≥badcc d x f dx x f dx x f 0)(2)()()(0.证法二 因为f (x )≥0, 所以0)(≥⎰ba dx x f . 假如0)(>⎰ba dx x f 不成立. 则只有0)(=⎰ba dx x f , 根据结论(1), f (x )≡0, 矛盾. 因此0)(>⎰ba dx x f . (3)令F (x )=g (x )-f (x ), 则在[a ,b ]上F (x )≥0且0)()()]()([)(=-=-=⎰⎰⎰⎰ba b a b a b a dx x f dx x g dx x f x g dx x F ,由结论(1), 在[a , b ]上F (x )≡0, 即f (x )≡g (x ).4. 根据定积分的性质及第7题的结论, 说明下列积分哪一个的值较大: (1)⎰102dx x 还是⎰103dx x ? (2)⎰212dx x 还是⎰213dx x ? (3)⎰21ln xdx 还是⎰212)(ln dx x ? (4)⎰10xdx 还是⎰+10)1ln(dx x ? (5)⎰10dx e x 还是⎰+10)1(dx x ?解 (1)因为当0≤x ≤1时, x 2≥x 3, 所以⎰⎰≥103102dx x dx x . 又当0<x <1时, x 2>x 3, 所以⎰⎰>103102dx x dx x . (2)因为当1≤x ≤2时, x 2≤x 3, 所以⎰⎰≤213212dx x dx x . 又因为当1<x ≤2时, x 2<x 3, 所以⎰⎰<213212dx x dx x .(3)因为当1≤x ≤2时, 0≤ln x <1, ln x ≥(ln x )2, 所以⎰⎰≥21221)(ln ln dx x xdx . 又因为当1<x ≤2时, 0<ln x <1, ln x >(ln x )2, 所以⎰⎰>21221)(ln ln dx x xdx . (4)因为当0≤x ≤1时, x ≥ln(1+x ), 所以⎰⎰+≥1010)1ln(dx x xdx . 又因为当0<x ≤1时, x >ln(1+x ), 所以⎰⎰+>1010)1ln(dx x xdx .(5)设f (x )=e x -1-x , 则当0≤x ≤1时f '(x ) =e x -1>0, f (x )=e x -1-x 是单调增加的. 因此当0≤x ≤1时, f (x )≥f (0)=0, 即e x ≥1+x , 所以⎰⎰+≥1010)1(dx x dx e x . 又因为当0<x ≤1时, e x >1+x , 所以⎰⎰+>1010)1(dx x dx e x . 习题5-21. 试求函数⎰=xtdt y 0sin 当x =0及4π=x 时的导数.解 x tdt dx d y x sin sin 0=='⎰, 当x =0时, y '=sin0=0; 当4π=x 时, 224sin =='πy . 2. 求由参数表示式⎰=tudu x 0sin , ⎰=tudu y 0cos 所给定的函数y 对x 的导数. 解 x '(t )=sin t , y '(t )=cos t ,t t x t y dx dy cos )()(=''=. 3. 求由⎰⎰=+xyt tdt dt e 000cos 所决定的隐函数y 对x 的导数dxdy. 解 方程两对x 求导得 e y y ' +cos x =0,于是 y exdx dy cos -=.4. 当x 为何值时, 函数⎰-=xt dt te x I 02)(有极值?解 2)(x xe x I -=', 令I '(x )=0, 得x =0. 因为当x <0时, I '(x )<0; 当x >0时, I '(x )>0, 所以x =0是函数I (x )的极小值点. 5. 计算下列各导数:(1)⎰+2021x dt t dx d ;(2)⎰+32411x x dt tdx d ;(3)⎰x xdt t dx d cos sin 2)cos(π. 解 (1)42022021221112x x x u dxdu dt t du d u x dt t dx d u x +=⋅+=⋅+=+⎰⎰令. (2)⎰⎰⎰+++=+323204044111111x x x x dt t dx d dt t dx d dt t dx d ⎰⎰+++-=3204041111x x dt tdx d dt t dx d )()(11)()(11343242'⋅++'⋅+-=x x x x12281312xx xx +++-=.(3)⎰⎰⎰+-=x x x x dt t dx d dt t dx d dt t dx d cos 02sin 02cos sin 2)cos()cos()cos(πππ =-cos(πsin 2x )(sin x )'+ cos(πcos 2x )( cos x )'=-cos x ⋅cos(πsin 2x )-sin x ⋅cos(πcos 2x ) =-cos x ⋅cos(πsin 2x )- sin x ⋅cos(π-πsin 2x ) =-cos x ⋅cos(πsin 2x )+ sin x ⋅cos(πsin 2x ) =(sin x -cos x )cos(πsin 2x ).6. 计算下列各定积分: (1)⎰+-adx x x 02)13(;解a a a x x x dx x xaa+-=+-=+-⎰230230221|)21()13(.(2)⎰+2142)1(dx x x ;解 852)11(31)22(31|)3131()1(333321332142=---=-=+---⎰x x dx x x . (3)⎰+94)1(dx x x ; 解6145)421432()921932(|)2132()()1(22322394223942194=+-+=+=+=+⎰⎰x x dx x x dx x x .(4)⎰+33121xdx;解66331arctan3arctan arctan 13313312πππ=-=-==+⎰xxdx . (5)⎰--212121xdx ;解3)6(6)21arcsin(21arcsin arcsin 121121212πππ=--=--==---⎰xx dx .(6)⎰+axa dx3022;解aa a a xax a dxa a 30arctan 13arctan 1arctan1303022π=-==+⎰. (7)⎰-124xdx ;解60arcsin 21arcsin 2arcsin41012π=-==-⎰xx dx . (8)dx x x x ⎰-+++012241133; 解 41)1arctan()1(|)arctan ()113(11333013012201224π+=----=+=++=+++---⎰⎰x x dx x x dx x x x . (9)⎰---+211e xdx;解1ln 1ln ||1|ln 12121-=-=+=+------⎰e x x dx e e .(10)⎰402tan πθθd ; 解4144tan)(tan )1(sec tan 40402402πππθθθθθθπππ-=-=-=-=⎰⎰d d .(11)dx x ⎰π20|sin |; 解⎰⎰⎰-=ππππ2020sin sin |sin |xdx xdx dx x =-cos x |π0+cos x |ππ2=-cos π +cos0+cos2π-cos π=4.(12)⎰20)(dx x f , 其中⎪⎩⎪⎨⎧>≤+=1 211 1)(2x x x x x f .解38|)61(|)21(21)1()(2131022121020=++=++=⎰⎰⎰x x x dx x dx x dx x f . 7. 设k 为正整数. 试证下列各题: (1)⎰-=ππ0cos kxdx ; (2)⎰-=ππ0sin kxdx ; (3)⎰-=πππkxdx 2cos ; (4)⎰-=πππkxdx 2sin .证明 (1)⎰--=-=--==ππππππ000)(sin 1sin 1|sin 1cos k kk k kx k kxdx . (2)⎰--=+-=-+-=-=ππππππππ0cos 1cos 1)(cos 1cos 1|cos 1sin k kk k k k k k kx k kxdx . (3)πππππππππ=+=+=+=---⎰⎰22|)2sin 21(21)2cos 1(21cos 2kx k x dx kx kxdx . (4)πππππππππ=+=-=-=---⎰⎰22|)2sin 21(21)2cos 1(21sin 2kx k x dx kx kxdx . 8. 设k 及l 为正整数, 且k ≠l . 试证下列各题: (1)⎰-=ππ0sin cos lxdx kx ; (2)⎰-=ππ0cos cos lxdx kx ; (3)⎰-=ππ0sin sin lxdx kx .证明 (1)⎰⎰----+=ππππdx x l k x l k lxdx kx ])sin()[sin(21sin cos 0])cos()(21[])cos()(21[=----++-=--ππππx l k l k x l k l k . (2)⎰⎰---++=ππππdx x l k x l k lxdx kx ])cos()[cos(21cos cos 0])sin()(21[])sin()(21[=--+++=--ππππx l k l k x l k l k . (3)⎰⎰----+-=ππππdx x l k x l k lxdx kx ])cos()[cos(21sin sin .0])sin()(21[])sin()(21[=--+++-=--ππππx l k l k x l k l k . 9. 求下列极限:(1)xdtt xx ⎰→02cos lim;(2)⎰⎰→xt xt x dttedt e 0220022)(lim.解 (1)11cos lim cos lim20020==→→⎰x xdtt x xx . (2)2222222222002002000022002lim2lim)(2lim)(limx xt x x xxt x x xt xt x xt xt x xedt e xee dt e xedt e dt e dttedt e ⎰⎰⎰⎰⎰⎰→→→→=⋅='⋅=2212lim 22lim2020222=+=+=→→x e x e e x xx xx . 10. 设⎩⎨⎧∈∈=]2 ,1[ ]1 ,0[ )(2x x x x x f . 求⎰=xdt t f x 0)()(ϕ在[0, 2]上的表达式, 并讨论ϕ(x )在(0, 2)内的连续性.解 当0≤x ≤1时, 302031)()(x dt t dt t f x x x ===⎰⎰ϕ;当1<x ≤2时, 6121212131)()(2211020-=-+=+==⎰⎰⎰x x tdt dt t dt t f x x x ϕ.因此 ⎪⎩⎪⎨⎧≤<-≤≤=21 612110 31)(23x x x x x ϕ.因为31)1(=ϕ, 3131lim )(lim 30101==-→-→x x x x ϕ, 316121)6121(lim )(lim 20101=-=-=+→+→x x x x ϕ,所以ϕ(x )在x =1处连续, 从而在(0, 2)内连续.11. 设⎪⎩⎪⎨⎧><≤≤=ππx x x x x f 或0 00 sin 21)(. 求⎰=x dt t f x 0)()(ϕ在(-∞, +∞)内的表达式.解 当x <0时, 00)()(00===⎰⎰xx dt dt t f x ϕ;当0≤x ≤π时, 21cos 21|cos 21sin 21)()(000+-=-===⎰⎰x t tdt dt t f x xx x ϕ; 当x >π时, 10cos 21cos 21|cos 210sin 21)()(000=+-=-=+==⎰⎰⎰πϕπππt dt tdt dt t f x x x . 因此 ⎪⎪⎩⎪⎪⎨⎧≥≤≤-<=ππϕx x x x x 10 )cos 1(210 0)(.12. 设f (x )在[a , b ]上连续, 在(a , b )内可导且f '(x )≤0,⎰-=xadt t f a x x F )(1)(. 证明在(a , b )内有F '(x )≤0. 证明 根据积分中值定理, 存在ξ∈[a , x ], 使))(()(a x f dt t f xa -=⎰ξ. 于是有 ))(()(1)(1)(1)()(1)(22a x f a x x f a x x f a x dt t f a x x F xa----=-+--='⎰ξ)]()([1ξf x f ax --=. 由f '(x )≤0可知f (x )在[a , b ]上是单调减少的, 而a ≤ξ≤x , 所以f (x )-f (ξ)≤0. 又在(a , b )内, x -a >0, 所以在(a , b )内 0)]()([1)(≤--='ξf x f ax x F . 习题5-31. 计算下列定积分:(1)⎰+πππ)3sin(dx x ;解 0212132cos 34cos)3cos()3sin(2=-=+-=+-=+⎰ππππππππx dx x . (2)⎰-+123)511(x dx;解51251110116101)511(2151)511(22122123=⋅+⋅-=+-⋅=+-----⎰x x dx. (3)⎰203cos sin πϕϕϕd ;解 410cos 412cos 41cos 41sin cos cos sin 33203203203=+-=-=-=⎰⎰πϕϕϕϕϕϕπππd s d . (4)⎰-πθθ03)sin 1(d ;解⎰⎰⎰⎰-+=+=-πππππθθθθθθθθ02002003cos )cos 1(cos sin )sin 1(d d d d34)cos 31(cos 03-=-+=πθθππ.(5)⎰22cos ππudu ;解222222sin 4121)2cos 1(21cos ππππππππu u du u udu +=+=⎰⎰836)3sin (sin 41)62(21-=-+-=πππππ.(6)dx x ⎰-2022;解dt t tdt t t x dx x ⎰⎰⎰+=⋅=-02022)2cos 1(cos 2cos 2sin 22ππ令2)2sin 21(20ππ=+=t t .(7)dy y ⎰--22228; 解⎰⎰⎰---⋅=-=-44222222cos 2cos 22sin 24228ππxdx x xy dy y dy y 令)2(2)2sin 21(22)2cos 1(224444+=+=+=--⎰πππππy x dx x .(8)⎰-121221dx xx ;解41)cot ()1sin 1(cos sin cos sin 122212122πππππππ-=--=-=⋅=-⎰⎰⎰t t dt t tdt t t t x dx x x 令.(9)⎰-adx x a x 0222; 解⎰⎰⎰=⋅⋅=-2024202202222sin4cos cos sin sin ππtdt a tdt a t a t a t a x dx x a xa令164sin 328)4cos 1(84204204204ππππa t a t a dt t a =-=-=⎰.(10)⎰+31221xxdx ;解⎰⎰⋅⋅=+223122secsec tan 1tan 1ππtdt t t tx xxdx 令3322sin 1sin cos 34342-=-==⎰ππππt dt tt. (11)⎰--1145xxdx ;解61)315(81)5(81454513133211=--=-=--⎰⎰-u u du u u x x xdx 令. (12)⎰+411xdx ;解)32ln 1(2|)1|ln (2)111(2211121212141+=+-=+-=⋅+=+⎰⎰⎰u u du u udu u u x x dx 令.(13)⎰--14311x dx ;解2ln 21|)1|ln (2)111(2)2(11111210210021143-=-+=-+=-⋅-=---⎰⎰⎰u u du u du u u ux x dx 令.(14)⎰-axa xdx 20223;解)13(3)3(3121320202222222022-=--=---=-⎰⎰a x a x a d x a xa xdx a a a.(15)dt te t ⎰-1022;解110102221021)2(222-----=-=--=⎰⎰e etd e dt tet t t .(16)⎰+21ln 1e x x dx; 解)13(2ln 12ln ln 11ln 1222111-=+=+=+⎰⎰e e e xx d xxx dx .(17)⎰-++02222x x dx;解 2)1arctan(1arctan )1arctan()1(112202022022π=--=+=++=++---⎰⎰x dx x x x dx .(18)⎰-22cos cos ππxdx x ;解32)sin 32(sin sin )sin 21(2cos cos 23222=-=-=---⎰⎰ππππππx x x d x xdx x . (19)⎰--223cos cos ππdx x x ;解⎰⎰---=-2223cos 1cos cos cos ππππdx x x dx x x34cos 32cos 32sin cos )sin (cos 20230223202=-=+-=--⎰⎰ππππx xxdx x dx x x (20)⎰+π02cos 1dx x . 解22cos 2sin 22cos 1000=-==+⎰⎰πππxxdx dx x .2. 利用函数的奇偶性计算下列积分: (1)⎰-ππxdx x sin 4;解 因为x 4sin x 在区间[-π, π]上是奇函数, 所以0sin 4=⎰-ππxdx x . (2)⎰-24cos 4ππθθd ;解⎰⎰⎰+==-0244)22cos 1(8cos 42cos 4ππππθθθθθd x d d ⎰⎰++=++=20202)4cos 212cos 223(2)2cos 2cos 21(2ππθθd x x d x x23)4sin 412sin 23(20πθπ=++=x x .(3)⎰--2121221)(arcsin dx xx ;解⎰⎰⎰=-=--1021022212122)(arcsin )(arcsin 21)(arcsin 21)(arcsin x d x dx x x dx x x324)(arcsin 3232103π==x .(4)⎰-++55242312sin dx x x xx . 解 因为函数12sin 2423++x x x x 是奇函数, 所以012sin 552423=++⎰-dx x x x x .3. 证明:⎰⎰-=aa adx x dx x 022)(2)(ϕϕ, 其中ϕ(u )为连续函数.证明 因为被积函数ϕ(x 2)是x 的偶函数, 且积分区间[-a , a ]关于原点对称, 所以有⎰⎰-=aa adx x dx x 022)(2)(ϕϕ.4. 设f (x )在[-b , b ]上连续, 证明⎰⎰---=bb bb dx x f dx x f )()(. 证明 令x =-t , 则dx =-dt , 当x =-b 时t =b , 当x =b 时t =-b , 于是 ⎰⎰⎰----=--=b b bb bbdt t f dt t f dx x f )()1)(()(,而 ⎰⎰---=-bb bb dx x f dt t f )()(, 所以⎰⎰---=bb bb dx x f dx x f )()(.5. 设f (x )在[a , b ]上连续., 证明⎰⎰-+=ba ba dx xb a f dx x f )()(. 证明 令x =a +b -t , 则dx =d t , 当x =a 时t =b , 当x =b 时t =a , 于是 ⎰⎰⎰-+=--+=b a ba ab dt t b a f dt t b a f dx x f )()1)(()(, 而 ⎰⎰-+=-+ba badx x b a f dt t b a f )()(,所以⎰⎰-+=ba ba dx xb a f dx x f )()(.6. 证明:⎰⎰>+=+11122)0(11x x x dx x dx.证明 令t x 1=, 则dt tdx 21-=, 当x =x 时x t 1=, 当x =1时t =1, 于是⎰⎰⎰+=-⋅+=+1112112211)1(1111x x xdt t dt t t x dx , 而⎰⎰+=+xx dx x dt t 1121121111,所以 ⎰⎰+=+1112211x x x dx x dx.7. 证明:⎰⎰-=-1010)1()1(dx x x dx x x m n n m .证明 令1-x =t , 则⎰⎰⎰⎰-=-=--=-10100110)1()1()1()1(dx x x dt t t dt t t dx x x m n n m n m n m , 即⎰⎰-=-1010)1()1(dx x x dx x x m n n m . 8. 证明: ⎰⎰=ππ00sin 2sin xdx xdx nn .证明 ⎰⎰⎰+=ππππ2020sin sin sin xdx xdx xdx nn n ,而 ⎰⎰⎰⎰==---=20200sin sin ))((sin sinπππππππxdx tdt dt t t x xdx n n n n 令,所以⎰⎰=ππ020sin 2sinxdx xdx n n.9. 设f (x )是以l 为周期的连续函数, 证明⎰+1)(a a dx x f 的值与a 无关.证明 已知f (x +l )=f (x ). ⎰⎰⎰⎰⎰⎰⎰-+=++=+++ala ll la ll a a adx x f dx x f dx x f dx x f dx x f dx x f dx x f 00001)()()()()()()(,而 ⎰⎰⎰⎰=+=++=+a a ala ldx x f dx l x f dt l t f l t x dx x f 000)()()()(令,所以 ⎰⎰=+la adx x f dx x f 01)()(.因此⎰+1)(a adx x f 的值与a 无关.10. 若f (t )是连续函数且为奇函数, 证明⎰xdt t f 0)(是偶函数; 若f (t )是连续函数且为偶函数, 证明⎰xdt t f 0)(是奇函数.证明 设⎰=xdt t f x F 0)()(.若f (t )是连续函数且为奇函数, 则f (-t )=-f (t ), 从而)()()()1)(()()(0000x F dx x f dx u f du u f u t dt t f x F x x xx ===---==-⎰⎰⎰⎰-令,即⎰=xdt t f x F 0)()(是偶函数.若f (t )是连续函数且为偶函数, 则f (-t )=f (t ), 从而)()()()1)(()()(0000x F dx x f dx u f du u f u t dt t f x F x x x x -=-=-=---==-⎰⎰⎰⎰-令,即⎰=xdt t f x F 0)()(是奇函数.11. 计算下列定积分: (1)⎰-10dx xe x ; 解11011010101021--------=--=+-=-=⎰⎰⎰e e e dx e xe xde dx xe xx x x x .(2)⎰e xdx x 1ln ; 解)1(414121121ln 21ln 21ln 21220212121+=-=⋅-==⎰⎰⎰e x e dx x x x x xdx xdx x ee e e e. (3)⎰ωπω20sin tdt t (ω为常数); 解⎰⎰⎰+-=-=ωπωπωπωπωωωωωωω20202020cos 1cos 1cos 1sin tdt tt t td tdt t 220222sin 12ωπωωωπωπ-=+-=t.(4)⎰342sin ππdx xx ;解344344342sin ln 4313cot cot cot sin ππππππππππππx xdx xx x xd dx x x++⋅-=+-=-=⎰⎰⎰23ln 21)9341(+-=π.(5)⎰41ln dx xx;解⎰⎰⎰⋅-==4141414112ln 2ln 2ln dx xx xx x xd dx xx)12ln 2(442ln 8122ln 84141-=-=-=⎰x dx x.(6)⎰10arctan xdx x ;解x d xx x x xdx xdx x ⎰⎰⎰+⋅-==1022102102101121arctan 21arctan 21arctan 214)41(218)arctan (218)111(21810102-=--=--=+--=⎰πππππx x x d x .(7)⎰202cos πxdx e x ; 解⎰⎰⎰-==202202202202sin 2sin sin cos ππππxdx e xe x d e xdx e x x x x⎰⎰⎰-+=-+=+=202202202202cos 42cos 4cos 2cos 2πππππππxdx e e xdx e xe e x d e e x x xx所以)2(51cos 02-=⎰ππe xdx e x ,于是(8)⎰212log xdx x ; 解⎰⎰⎰⋅-==212212221222122ln 121log 21log 21log dx x x x x xdx xdx x 2ln 432212ln 212212-=⋅-=x . (9)⎰π02)sin (dx x x ; 解⎰⎰⎰-=-=ππππ02302022sin 4161)2cos 1(21)sin (x d x x dx x x dx x x πππππππ03000332cos 41622sin 412sin 416⎰⎰-=⋅+-=xxd xdx x x x 462sin 81462cos 412cos 416303003ππππππππ-=+-=+-=⎰x xdx x x .(10)⎰edx x 1)sin(ln ; 解法一 ⎰⎰⋅=101sin ln )sin(ln dt e t t x dx x te令.因为⎰⎰⎰-==⋅10101010cos sin sin sin tdt e te tde dt e t t tt t⎰⎰--⋅=-⋅=101010sin cos 1sin cos 1sin tdt e t e e tde e t t t⎰-+⋅-⋅=10sin 11cos 1sin tdt e e e t , 所以 )11cos 1sin (21sin 10+⋅-⋅=⎰e e tdt et.因此)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e. 解法二⎰⎰⎰-⋅=⋅⋅-⋅=e e eedx x e dx x x x x x dx x 1111)cos(ln 1sin 1)cos(ln )sin(ln )sin(ln ⎰⋅⋅-⋅-⋅=e edx x x x x x e 111)sin(ln )cos(ln 1sin ⎰-+⋅-⋅=edx x e e 0)sin(ln 11cos 1sin , 故)11cos 1sin (21)sin(ln 1+⋅-⋅=⎰e e dx x e . (11)dx x e e⎰1|ln |; 解⎰⎰⎰⎰⎰-++-=+-=eee eee e e dx dx xx x x dx x dx x dx x 1111111111ln ln ln ln |ln |)11(2)1()11(1e e e e e -=---++-=.(12)⎰-1022)1(dx x m (m 为自然数); 解⎰⎰+=-2011022cos sin )1(πtdt t x dx xm m 令.根据递推公式⎰⎰--=20220cos 1cos ππxdx n n xdx n n ,⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅+⋅⋅⋅⋅⋅⋅--⋅--⋅+=-⎰为偶数为奇数m m m m m m m m m m m m m m dx x m325476 34121 2214365 34121)1(102π. (13)⎰=π0sin xdx x J m m (m 为自然数). 解 因为⎰⎰⎰⎰-=----=ππππππππ0000sin sin )1)((sin )(sintdt t tdt dt t t t x xdx x mm m m令,所以 ⎰⎰⎰⎰=⋅===202000sin sin 22sin 2sin πππππππxdx xdx xdx xdx x J m m m m m (用第8题结果). 根据递推公式⎰⎰--=20220sin 1sin ππxdx n n xdx n n , ⎪⎩⎪⎨⎧⋅⋅⋅⋅⋅--⋅--⋅-⋅⋅⋅⋅⋅⋅--⋅--⋅-=为奇数为偶数m m m m m m m m m m m m m m J m 325476 45231 2214365 452312ππ.习题5-71. 判别下列各反常积分的收敛性, 如果收敛, 计算反常积分的值:(1)⎰+∞14xdx; 解 因为3131)31(lim 3131314=+-=-=-+∞→+∞-+∞⎰x x x dx x , 所以反常积分⎰+∞14x dx收敛, 且3114=⎰∞+x dx . (2)⎰+∞1xdx ;解 因为+∞=-==+∞→+∞∞+⎰22lim 211x xxdx x , 所以反常积分⎰+∞1xdx 发散.(3)dx e ax ⎰+∞-0(a >0); 解 因为aa e a e adx e ax x ax ax 11)1(lim 100=+-=-=-+∞→+∞-+∞-⎰, 所以反常积分dx e ax ⎰+∞-0收敛, 且adx e ax 10=⎰+∞-.(4)⎰+∞-0ch tdt e pt (p >1); 解 因为1]1111[21][21ch 20)1()1(0)1()1(0-=+--=+=+∞+--∞++--∞+-⎰⎰p p e pe p dt e e tdt e tp t p t p tp pt ,所以反常积分⎰+∞-0ch tdt e pt 收敛, 且1ch 20-=⎰∞+-p p tdt e pt .(5)⎰+∞-0sin tdt e pt ω(p >0, ω>0); 解⎰⎰+∞-+∞--=0cos 1sin t d e tdt ept ptωω⎰⎰+∞-+∞-+∞--=-⋅+-=020sin 1)(cos 1cos 1t d e pdt pe t te pt pt pt ωωωωωωω⎰+∞-+∞--⋅+-=0202)(sin sin 1dt pe t pte p ptpt ωωωωω⎰+∞--=022sin 1tdt e p pt ωωω,所以 22sin w p tdt e pt +=⎰+∞-ωω.(6)⎰+∞∞-++222x x dx;解 πππ=--=+=++=++⎰⎰+∞∞-+∞∞-+∞∞-)2(2)1arctan()1(12222x x dxx x dx .(7)dx xx ⎰-121;解 这是无界函数的反常积分, x =1是被积函数的瑕点.11)1(lim 112110212=+--=--=--→⎰x x dx x x x . (8)⎰-22)1(x dx;解 这是无界函数的反常积分, x =1是被积函数的瑕点. 因为⎰⎰⎰-+-=-212102202)1()1()1(x dxx dx x dx , 而 +∞=--=-=--→⎰111lim 11)1(110102x x x dx x , 所以反常积分⎰-202)1(x dx发散.(9)⎰-211x xdx ;解 这是无界函数的反常积分, x =1是被积函数的瑕点.21232121]12)1(32[)111(1-+-=-+-=-⎰⎰x x dx x x x xdx322]12)1(32[lim 38231=-+--=+→x x x . (10)⎰-ex x dx 12)(ln 1.解 这是无界函数的反常积分, x =e 是被积函数的瑕点.2)arcsin(ln lim )arcsin(ln ln )(ln 11)(ln 111212π===-=--→⎰⎰x x x d x x x dx ex e ee.2. 当k 为何值时, 反常积分⎰+∞)(ln kx x dx收敛? 当k 为何值时, 这反常积分发散? 又当k 为何值时, 这反常积分取得最小值?解 当k <1时, +∞=-==+∞+-+∞+∞⎰⎰2122)(ln 11ln )(ln 1)(ln k kk x k x d x x x dx ; 当k =1时, +∞===+∞+∞+∞⎰⎰222)ln(ln ln ln 1)(ln x x d x x x dxk ; 当k >1时, kk k k k x k x d x x x dx -+∞+-+∞+∞-=-==⎰⎰12122)2(ln 11)(ln 11ln )(ln 1)(ln . 因此当k >1时, 反常积分⎰+∞0)(ln kx x dx 收敛; 当k ≤1时, 反常积分⎰+∞0)(ln k x x dx发散.当k >1时, 令k kk x x dx k f -∞+-==⎰10)2(ln 11)(ln )(, 则 )2ln ln 11()1(2ln ln )2(ln 2ln ln )2(ln 11)2(ln )1(1)(21112+---=----='---k k k k k f k kk. 令f '(k )=0得唯一驻点2ln ln 11-=k . 因为当2ln ln 111-<<k 时f '(k )<0, 当2ln ln 11->k 时f '(k )>0, 所以2ln ln 11-=k 为极小值点, 同时也是最小值点, 即当2ln ln 11-=k 时, 这反常积分取得最小值 3. 利用递推公式计算反常积分⎰+∞-=0dx e x I x n n . 解 因为101000-+∞--+∞-+∞-+∞-=+-=-==⎰⎰⎰n x n x n x n x n n nI dx e x n e x de x dx e x I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1. 又因为 1000001=-=+-=-==+∞-+∞-+∞-+∞-+∞-⎰⎰⎰xx xx x e dx e xe xde dx xe I ,所以 I n = n ⋅(n -1)⋅(n -2)⋅ ⋅ ⋅2⋅I 1=n !. 总习题五1. 填空:(1)函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的______条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积______的条件;解 函数f (x )在[a , b ]上(常义)有界是f (x )在[a , b ]上可积的___必要___条件, 而f (x )在[a , b ]上连续是f (x )在[a , b ]上可积___充分___的条件;(2)对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的______条件;解 对[a , +∞)上非负、连续的函数f (x ), 它的变上限积分⎰xa dx x f )(在[a , +∞)上有界是反常积分⎰+∞a dx x f )(收敛的___充分___条件;(3)绝对收敛的反常积分⎰+∞a dx x f )(一定______; 解 绝对收敛的反常积分⎰+∞a dx x f )(一定___收敛___;(4)函数f (x )在[a , b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰ba dx x f )(______存在. 解 函数f (x )在[a ,b ]上有定义且|f (x )|在[a , b ]上可积, 此时积分⎰b a dx x f )(___不一定___存在.2. 计算下列极限: (1)∑=∞→+n i n nin 111lim ;解 )122(32)1(32111lim 103101-=+=+=+⎰∑=∞→x dx x n i n n i n . (2)121lim+∞→+⋅⋅⋅++p pp p n nn (p >0);解 11111])( )2()1[(lim 21lim101101+=+==⋅⋅⋅⋅++=+⋅⋅⋅+++∞→+∞→⎰p x p dx x n n n n n nn p p p p p n p p p p n . (3)nn nn !lnlim ∞→; 解 ]ln 1)ln 2ln 1(ln 1[lim !lnlim n n nn n n n n nn ⋅-+⋅⋅⋅++=∞→∞→nn n n n n 1)]ln (ln )ln 2(ln )ln 1[(ln lim ⋅-+⋅⋅⋅+-+-=∞→⎰=⋅+⋅⋅⋅++=∞→1ln 1)ln 2ln 1(ln lim xdx n n n n n n1)ln ()ln (10101010-=-=-=⎰x x x dx x x .(4)⎰-→xaa x dt t f a x x )(lim, 其中f (x )连续; 解法一 )()(lim )(lima af xf dt t f ax x axa ax ==-→→⎰ξξ (用的是积分中值定理). 解法二 )(1)()(lim)(lim )(lima af x xf dt t f ax dt t f x dt t f a x x xa ax xa ax xa a x =+=-=-⎰⎰⎰→→→ (用的是洛必达法则).(5)1)(arctan lim 22+⎰+∞→x dtt xx .解4)(arctan 1lim 1)(arctan lim 1)(arctan lim22222202π=+=+=+∞→+∞→+∞→⎰x x x x x x x dtt x x xx . 3. 下列计算是否正确, 试说明理由:(1)⎰⎰----=-=+-=+111111222)1arctan ()1(1)1(1πx x x d x dx ;解 计算不正确, 因为x 1在[-1, 1]上不连续. (2)因为⎰⎰--++-=++111122111t t dt tx x x dx , 所以⎰-=++11201x x dx .解 计算不正确, 因为t1在[-1, 1]上不连续.(3)01lim 122=+=+⎰⎰-∞→+∞∞-A A A dx x xdx x x . 解 不正确, 因为⎰⎰⎰⎰-+∞→+∞→+∞∞--∞→+≠+++=+A A A b b a a dx xxdx x x dx x x dx x x 2020221lim 1lim 1lim 1. 4. 设p >0, 证明⎰<+<+10111p x dx p p. 证明 p pp p p p px x x x x x x ->+-=+-+=+>11111111. 因为⎰⎰⎰<+<-1010101)1(dx x dxdx x pp,而 110=⎰dx , pp p x x dx x p p+=+-=-+⎰1)1()1(10110, 所以⎰<+<+10111pxdx p p. 5. 设f (x )、g (x )在区间[a , b ]上均连续, 证明: (1)⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222;证明 因为[f (x )-λg (x )]2≥0, 所以λ2g 2(x )-2λ f (x )g (x )+f 2(x )≥0, 从而 0)()()(2)(222≥+-⎰⎰⎰ba ba ba dx x f dx x g x f dx x g λλ.上式的左端可视为关于λ的二次三项式, 因为此二次三项式大于等于0, 所以其判别式小于等于0, 即0)()(4])()([4222≤⋅-⎰⎰⎰ba ba ba dx x g dx x f dx x g x f ,亦即 ⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222. (2)()()()212212212)()()]()([⎰⎰⎰+≤+b ab a b a dx x g dx x f dx x g x f , 证明⎰⎰⎰⎰++=+ba b a b a ba dx x g x f dx x g dx x f dx x g x f )()(2)()()]()([222212222])()([2)()(⎰⎰⎰⎰⋅++≤ba ba ba ba dx x g dx x f dx x g dx x f ,又()2212212212222])([])([])()([2)()(⎰⎰⎰⎰⎰⎰+=⋅++ba ba b a ba b a badx x g dx x f dx x g dx x f dx x g dx x f ,所以()()()212212212)()()]()([⎰⎰⎰+≤+b ab a b a dx x g dx x f dx x g x f . 6. 设f (x )在区间[a , b ]上连续, 且f (x )>0. 证明⎰⎰-≥⋅ba baa b x f dxdx x f 2)()()(. 证明 已知有不等式⎰⎰⎰⋅≤ba ba ba dx x g dx x f dx x g x f )()(])()([222, 在此不等式中, 取)(1)(x f x f =, )()(x f x g =, 则有⎰⎰⎰⋅≥⋅⋅ba ba ba dx x f x f dx x f dx x f 222])(1)([])(1[])([,即⎰⎰-≥⋅b a baa b x f dxdx x f 2)()()(.。
高中数学五测试题及答案

高中数学五测试题及答案一、选择题(每题3分,共30分)1. 下列函数中,哪一个是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^2 - 1D. f(x) = x^3 - 3x答案:B2. 计算下列极限:\[\lim_{x \to 0} \frac{\sin x}{x}\]A. 0B. 1C. 2D. 不存在答案:B3. 已知等差数列的前三项为3, 7, 11,求该数列的通项公式。
A. a_n = 4n - 1B. a_n = 4n + 1C. a_n = 2n + 1D. a_n = 2n - 1答案:A4. 函数f(x) = 2x^2 - 3x + 1的顶点坐标是:A. (-1/4, 7/8)B. (1/2, 7/4)C. (1/4, 7/8)D. (-1/2, 7/4)答案:A5. 集合A = {1, 2, 3},集合B = {2, 3, 4},求A∩B。
A. {1, 2, 3}B. {2, 3}C. {1, 2}D. {3, 4}答案:B6. 已知圆的方程为x^2 + y^2 - 6x + 8y - 24 = 0,求圆心坐标。
A. (3, -4)B. (-3, 4)C. (3, 4)D. (-3, -4)答案:A7. 计算定积分:\[\int_{0}^{1} x^2 dx\]A. 1/3B. 1/2C. 2/3D. 1答案:B8. 函数f(x) = |x - 2|的图像关于:A. x轴对称B. y轴对称C. 直线x = 2对称D. 原点对称答案:C9. 已知直线y = 2x + 3与x轴的交点坐标是:A. (-3/2, 0)B. (3/2, 0)C. (0, 3)D. (0, -3)答案:B10. 计算复数z = 2 + 3i的模。
A. √7B. √13C. √17D. √21答案:A二、填空题(每题4分,共20分)11. 函数f(x) = x^4 - 4x^2 + 4的最小值为______。
5高数五答案

浙江师范大学《高等数学五(下) 》试卷参考答案及评分标准 2005.6.5一、选择题(每小题2分,共14分)1、 A2、D3、C4、B5、B6、A7、D二、填空题(每小题2分,共16分)① 2()xy x x y e −++ ② ③ 26x y z ++−=022d (,)d x f x y y −∫④ 4 ⑤23⑥ 02n n n x ∞=∑ ⑦ 212e e x C C x −−+ ⑧ π ab 三、计算题(每小题8分,共48分) 1. 求函数的一阶偏导数和全微分.y z x =解 的全微分为, (4分)y z x =1d d ln y y z y x x x x y −=⋅+d x y z x =的一阶偏导数为, (8分) 1y x z y x −=⋅ln y y z x =2. 设函数,(,)z f xy x y =+f 具有二阶连续偏导数,求z x ∂∂,2z x y∂∂∂. 解 1z yf f x∂′=+∂2′, (4分) 2z x y ∂∂∂12()yf f y∂′′=+∂111221221xyf yf xf f f ′′′′′′′′′=++++ (8分) 3. 计算22d D x y σ∫∫,其中由曲线D 1,,1,y y x x x x 2====所围成. 解 222121d d x x Dx x 2d x y y y σ=∫∫∫∫ (4分) 2211()d x xx x y =−∫231()d x x x =−∫.49=(8分) 4.交换累次积分的次序400d (,)d (aI x f x y y a =>∫∫0).解 04,:0x a D y ≤≤⎧⎪⎨≤≤⎪⎩ (3分) 2240d (,)a ay a d I y f x y =∫∫x 4 (8分) 5. 计算22(2)d ()d L I x xy x x y y =+++∫,其中为由点到点的 L )0,0(O )1,1(A 曲线πsin 2y x =. 解 x xy x yy P 2)2(2=+∂∂=∂∂, x y x xx Q 2)(42=+∂∂=∂∂, 即,xQ y P ∂∂=∂∂ (4分) 1124d 00d (1)x x y =++∫∫故原式y .1523= (8分)6. 求幂级数11(1)nn n x n ∞−=−∑的收敛区间. 解 收敛半径为1lim lim 11n n n n a n R a n +→∞→∞==+=, (2分) 而当1x =时,原级数收敛,当时,原级数发散, (5分)1x =−故幂级数11(1)n n n x n ∞−=−∑的收敛区间为(]1,1− (8分) 四、应用题(每小题8分,共16分)1. 已知某曲线的切线在纵轴上的截距等于切点的横坐标,且曲线经过点(1,1), 求它的方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学》
专业 学号 姓名
一、判断(每小题 2 分,共 20 分)
1. f(x)在点x 0处有定义是f(x)在点x 0处连续的必要条件. ( )
2. 无穷小量与有界变量之积为无穷小量. ( )
3. y=f(x)在x 0处可导,则y=|f(x)|在x 0处也可导. ( )
4. 初等函数在其定义域内必连续. ( )
5. 可导函数f(x)的极值点一定是f(x) 的驻点. ( )
6. 对任意常数k,有⎰dx x kf )(=k ⎰dx x f )(. ( )
7. 若f(x)在[a,b]上可积,则f(x)在[a,b]上有界. ( )
8. 若f(x,y)在区域D 上连续且区域D 关于y 轴对称,则当f(x,y) 为关于x 的奇函数时,⎰⎰D
dxdy y x f ),(=0. ( )
9. )(y '2=-2x -e x 的通解中含有两个独立任意常数. ( )
10. 若z=f(x,y)在P o 的两个偏导数都存在,则z=f(x,y)在P 0连续. ( )
二、填空(每空 2 分,共20 分)
1.∞
→x lim [xsin
x
1+
x
1sinx+(
x
x +2)x ]= .
2. 函数f(x)=x x -3在[0,3]上满足罗尔定理的条件,定理中的数值ξ= .
3. 设f(x)=⎩⎨
⎧≥+<0
0x x
a x e x
当a= 时,f(x)在x=0处连续.
4. 设z=e
y
x 22
+ ,则dz | (0,0)= .
5. 函数f(x)=e x
-x -1在 内单调增加;在 内单调减少.
6. 函数32y ax bx cx d =+++满足条件 时, 这函数没有极值.
7.
dx
d ⎰
b a
x 2
sin dx = 其中a,b 为常数.
8. f '(x)=1且(0)0f =,则⎰dx x f )(= . 9.若I=⎰⎰
1
02
),(x x
y x f dx dxdy 交换积分次序后得 .
三、计算(每小题 5 分,共 40 分)
1. 求0
lim →x (
2
1x
-
xtgx
1) ; 2.
dt t
t x
e ⎰
1
ln +dt t y
)3(cos 1
⎰+=2,求dy ;
3. 求dx x x ⎰
+)
1(1; 4. 求dx x ⎰--1
4
3
1
11 ; 5. 求dx xe
x
⎰
∞+-0
2;
6. 设z=ln(x 2
+y 2
) 求
x
z ∂∂,
y
x z ∂∂∂2
;
7. 计算 I=⎰⎰D
xdxdy .其中D 是由圆x 2+y 2=4围成的区域;
8. 求微分方程-ydx+(x+y 3)dy=0的通解.
四、应用题(每题7分,共14分)
1. 某车间靠墙壁要盖一间长方形小屋,现有存砖只够砌20米长的墙壁,问应围成的长方形的长,宽各为多少才能使这间小屋面积最大.
2. 求由y=
x
1,x=1,x=2与x 轴所围成的图形的面积及该图绕x 轴旋转一周的旋转体的体积.
五、证明(本题6分)
证明:当x >0时,不等式1+
x x +>
121成立.
高等数学参考答案
一、判断正误(每题2分,共20分)
1 √ ;
2 √ ;
3 ╳ ;
4 ╳ ;
5 √ ; 6╳ ; 7 √ ; 8 √ ; 9 ╳ ; 10 ╳.
二、填空题(每题4分,共20分)
1. 21e +;
2. 2 ;
3. 1 ;
4. 2dx ;
5.[0)∞,+,,0]∞(- ;
6. 2
30b ac -<;
7.0; 8.
2
12
x c + ;
9. 10
(,)y
dy f x y dx ⎰⎰
.
三、计算题与证明题(共计60分)
1. 2011lim tan x x x x →⎛⎫- ⎪⎝⎭=20tan lim tan x x x x x →-⎛⎫ ⎪⎝⎭=3
0tan lim x x x x →-⎛⎫
⎪⎝⎭
=20sec 1lim 3x x x →-⎛⎫
= ⎪⎝⎭202sec tan 1lim 63
x x x x →⎛⎫= ⎪⎝⎭ 2. 方程两边同时对x 求导得:
则
ln (cos 3)0x
x
x e e y y e
'++=
(cos 3)0x y ++=
cos 3
x y y '=-
+
cos 3
x dy dx y =-
+
3. ⎰
=
2
1d
x +⎰
=1
2⎰
=2arctan c
4、 令
2
12t x t
dx tdt ==-=-
当 34
x =
时12
t =;当1x =时0t =
原式=
112
21
t dt t --⎰
=11
220
12211
1
t dt dt t t =+
--⎰
⎰
=1
20
2[ln 112ln 2t t +-=-
5.⎰
⎰
∞
+-∞
+-'-
=
20
2)2
1(dx e
x dx xe
x
x
⎰
∞
+-+∞
--
-
-
=0
20
2)2
1()
2
1(dx e
e
x x
x
4
14
10
2=
-
=+∞
-x
e
6.
2
22
2
2
2
2)(1y
x x
y x y
x x z +=
'++=
∂∂
2
2
2
2
2
2
2
)
(42)
(2y x xy y y x x y
x z +-
=+-
=∂∂∂
7.令 ⎩
⎨⎧==θθ
sin cos r y r x ,
⎰
⎰⋅=
π
θθ20
2
cos rdr r d I
0]3
1[][sin cos 2032020
2
2=⋅==
⎰
⎰
r dr r d π
π
θθ
θ
8.解:
2
1y x y
dy
dx =-
)(1
2
1
c dy e
y e
x dy
y dy y +⎰⎰⎰=-
)21(2
c y y +=
∴ 原方程的通解为:)2
1(2
c y y x +=
四、(每题7分,共14分)
1.解:设长方形的长和宽分别为x 和y ,面积为s ,则202=+y x 即 y x 220-= 2
220y y xy s -== )0(>y
0420=-='y s ,得5=y
04<-=''s
∴当长10=x M ;宽5=y M 时,面积最大。
五、(本题6分)
令x x x f +-
+
=12
11)( 01212
1)(>+-
=
'x
x f
∴
0)0()(=>f x f 即x x +>
+1211。
