(专题精选)初中数学三角形难题汇编及答案
三角形难点题型提高精选题(含答案)

三角形难点题型精选题一.选择题(共17小题)1.如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需()个五边形.A.6 B.7 C.8 D.92.如图,在Rt△ADB中,∠D=90°,C为AD上一点,∠ACB=6x,则x值可以是()A.10°B.20°C.30°D.40°3.现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是()A.1个 B.2个 C.3个 D.4个4.如图三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是()A.∠γ=∠α+∠βB.2∠γ=∠α+∠βC.3∠γ=2∠α+∠βD.3∠γ=2(∠α+∠β)5.如图,∠ACB=90°,CD⊥AB,则∠1与∠B的关系是()A.互余B.互补C.相等D.不确定6.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为()A.5 B.6 C.7 D.107.如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=()A.15°B.20°C.25°D.30°8.一个多边形截取一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是()A.10 B.11 C.12 D.以上都有可能9.如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=()A.30°B.40°C.80°D.不存在10.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为()A.6米 B.8米 C.12米D.不能确定11.已知△ABC的三边a,b,c满足a2+b+|﹣2|=10a+2,则△ABC 为()A.等腰三角形B.正三角形C.直角三角形D.等腰直角三角形12.已知正六边形的半径为2,则这个正六边形的面积是()A.6 B.12 C.D.13.如果正n边形的一个内角等于一个外角的2倍,那么n的值是()A.4 B.5 C.6 D.714.把一副三角尺按如图所示叠放在一起,则下图中∠α=()A.75°B.60°C.65°D.55°15.如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP 为直角三角形,则满足这样条件的点P共有()A.2个 B.4个 C.6个 D.7个16.如图,多边形的相邻两边均互相垂直,则这个多边形的周长为()A.21 B.26 C.37 D.4217.若一个多边形的内角和为外角和的3倍,则这个多边形为()A.八边形B.九边形C.十边形D.十二边形二.填空题(共8小题)18.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度.19.如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2=度.20.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有个三角形出现.21.△ABC中,∠B的外角平分线的与∠C外角平分线相交于点P,且∠BPC=80°,则∠BAP的度数为.22.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于度.23.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数为.24.如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2008BC的平分线与∠A2008CD的平分线交于点A2009,得∠A2009,则∠A2009=.25.如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).三.解答题(共1小题)26.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:.三角形难点题型精选题参考答案与试题解析一.选择题(共17小题)1.如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环还需()个五边形.A.6 B.7 C.8 D.9【解答】解:五边形的内角和为(5﹣2)•180°=540°,所以正五边形的每一个内角为540°÷5=108°,如图,延长正五边形的两边相交于点O,则∠1=360°﹣108°×3=360°﹣324°=36°,360°÷36°=10,∵已经有3个五边形,∴10﹣3=7,即完成这一圆环还需7个五边形.故选B.2.如图,在Rt△ADB中,∠D=90°,C为AD上一点,∠ACB=6x,则x值可以是()A.10°B.20°C.30°D.40°【解答】解:根据三角形的外角性质,∠ACB=6x>90°,解得x>15°,∵∠ACB是钝角,∴6x<180°,∴x<30°,∴15°<x<30°,纵观各选项,只有20°符合.故选B.3.现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是()A.1个 B.2个 C.3个 D.4个【解答】解:四条木棒的所有组合:3,4,7和3,4,9和3,7,9和4,7,9;只有3,7,9和4,7,9能组成三角形.故选:B.4.如图三角形的顶点落在折叠后的四边形内部,则∠γ与∠α+∠β之间的关系是()A.∠γ=∠α+∠βB.2∠γ=∠α+∠βC.3∠γ=2∠α+∠βD.3∠γ=2(∠α+∠β)【解答】解:如图,∠1+∠2=180°﹣∠γ,∵三角形的顶点落在折叠后的四边形内部,∴∠α+2∠1+∠β+2∠2=180°×2,即∠α+∠β+2(∠1+∠2)=360°,∴∠α+∠β+360°﹣2∠γ=360°,∴2∠γ=∠α+∠β.故选B.5.如图,∠ACB=90°,CD⊥AB,则∠1与∠B的关系是()A.互余B.互补C.相等D.不确定【解答】解:∵∠ACB=90°,∴∠1+∠BCD=90°,∵CD⊥AB,∴∠B+∠BCD=90°,∴∠1=∠B.故选C.6.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为()A.5 B.6 C.7 D.10【解答】解:已知4条木棍的四边长为2、3、4、6;①选2+3、4、6作为三角形,则三边长为5、4、6;5﹣4<6<5+4,能构成三角形,此时两个螺丝间的最长距离为6;②选3+4、6、2作为三角形,则三边长为2、7、6;6﹣2<7<6+2,能构成三角形,此时两个螺丝间的最大距离为7;③选4+6、2、3作为三角形,则三边长为10、2、3;2+3<10,不能构成三角形,此种情况不成立;④选6+2、3、4作为三角形,则三边长为8、3、4;而3+4<8,不能构成三角形,此种情况不成立;综上所述,任两螺丝的距离之最大值为7.故选:C.7.如图,在△ABC中,∠ABC的平分线与∠ACB的外角平分线相交于D点,∠A=50°,则∠D=()A.15°B.20°C.25°D.30°【解答】解:∵∠ABC的平分线与∠ACB的外角平分线相交于D点,∴∠1=∠ACE,∠2=∠ABC,又∠D=∠1﹣∠2,∠A=∠ACE﹣∠ABC,∴∠D=∠A=25°.故选C.8.一个多边形截取一个角后,形成另一个多边形的内角和是1620°,则原来多边形的边数是()A.10 B.11 C.12 D.以上都有可能【解答】解:∵内角和是1620°的多边形是边形,又∵多边形截去一个角有三种情况.一种是从两个角的顶点截取,这样就少了一条边,即原多边形为12边形;另一种是从两个边的任意位置截,那样就多了一条边,即原多边形为10边形;还有一种就是从一个边的任意位置和一个角顶点截,那样原多边形边数不变,还是11边形.综上原来多边形的边数可能为10、11、12边形,故选D.9.如图,小林从P点向西直走12米后,向左转,转动的角度为α,再走12米,如此重复,小林共走了108米回到点P,则α=()A.30°B.40°C.80°D.不存在【解答】解:∵108÷12=9,∴小林从P点出发又回到点P正好走了一个9边形,∴α=360°÷9=40°.故选B.10.科技馆为某机器人编制一段程序,如果机器人在平地上按照图中所示的步骤行走,那么该机器人所走的总路程为()A.6米 B.8米 C.12米D.不能确定【解答】解:∵机器人从点A出发再回到点A时正好走了一个正多边形,∴多边形的边数为360°÷30=12,∴他第一次回到出发点O时一共走了12×1=12米.故选C.11.已知△ABC的三边a,b,c满足a2+b+|﹣2|=10a+2,则△ABC 为()A.等腰三角形B.正三角形C.直角三角形D.等腰直角三角形【解答】解:∵a2+b+|﹣2|=10a+2,∴a2﹣10a+25+b﹣4﹣2+1+|﹣2|=0即(a﹣5)2+(﹣1)2+|﹣2|=0根据几个非负数的和为0,则这几个非负数同时为0,得a=5,b=5,c=5.故该三角形是等边三角形,即正三角形.故选B.12.已知正六边形的半径为2,则这个正六边形的面积是()A.6 B.12 C.D.【解答】解:根据题意,正六边形的半径为2,而正六边形可以分解为六个全等的三角形,如图且每个三角形的边长都为2,易得每个三角形的面积为,故这个正六边形的面积是6.故选C.13.如果正n边形的一个内角等于一个外角的2倍,那么n的值是()A.4 B.5 C.6 D.7【解答】解:设外角是x度,则内角是2x度,根据题意得x+2x=180,解得x=60度,所以n=360÷60=6.故选C.14.把一副三角尺按如图所示叠放在一起,则下图中∠α=()A.75°B.60°C.65°D.55°【解答】解:已知,∠ADE=45°,∠F=60°,∴∠α=180°﹣60°﹣45°=75°.故选A.15.如图,已知点A(﹣1,0)和点B(1,2),在坐标轴上确定点P,使得△ABP 为直角三角形,则满足这样条件的点P共有()A.2个 B.4个 C.6个 D.7个【解答】解:①以A为直角顶点,可过A作直线垂直于AB,与坐标轴交于一点,这一点符合点P的要求;②以B为直角顶点,可过B作直线垂直于AB,与坐标轴交于两点,这两点也符合P点的要求;③以P为直角顶点,可以AB为直径画圆,与坐标轴共有3个交点.所以满足条件的点P共有6个.故选C.16.如图,多边形的相邻两边均互相垂直,则这个多边形的周长为()A.21 B.26 C.37 D.42【解答】解:多边形的周长=16×2+5×2=42.故选D.17.若一个多边形的内角和为外角和的3倍,则这个多边形为()A.八边形B.九边形C.十边形D.十二边形【解答】解:设这个多边形是n边形,根据题意,得(n﹣2)•180°=3×360°,解得:n=8,即这个多边形为八边形.故选A.二.填空题(共8小题)18.一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为85度.【解答】解:∵∠ADF=100°,∠EDF=30°,∴∠MDB=180°﹣∠ADF﹣∠EDF=180°﹣100°﹣30°=50°,∴∠BMD=180°﹣∠B﹣∠MDB=180°﹣45°﹣50°=85°.故答案为:85.19.如图,四边形ABCD中,若去掉一个60°的角得到一个五边形,则∠1+∠2= 240度.【解答】解:∵四边形的内角和为(4﹣2)×180°=360°,∴∠B+∠C+∠D=360°﹣60°=300°,∵五边形的内角和为(5﹣2)×180°=540°,∴∠1+∠2=540°﹣300°=240°,故答案为:240.20.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有0或3或4或8个三角形出现.【解答】解:∵①当四个点共线时,不能作出三角形;②当三个点共线,第四个点不在这条直线上时,能够画出3个三角形;③若4个点能构成凹四边形,则能画出4个三角形;④当任意的三个点不共线时,则能够画出8个三角形.∴0或3或4或8.21.△ABC中,∠B的外角平分线的与∠C外角平分线相交于点P,且∠BPC=80°,则∠BAP的度数为10°.【解答】解:如图,BP、CP为△ABC两外角∠ABC、∠ACB的平分线,∴∠BCP=(∠A+∠ABC)、∠PBC=(∠A+∠ACB),由三角形内角和定理得,∠BPC=180°﹣∠BCP﹣∠PBC,=180°﹣[∠A+(∠A+∠ABC+∠ACB)],=180°﹣(∠A+180°),=90°﹣∠A;∵∠BPC=80°,∴∠CAB=20°,∴∠BAP=10°;故答案为:10°22.如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于270度.【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°,∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.故答案为:270°.23.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数为7.【解答】解:设这个多边形的边数是n,根据题意得,(n﹣2)•180°=2×360°+180°,n=7.故答案为:7.24.如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1得∠A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2008BC的平分线与∠A2008CD的平分线交于点A2009,得∠A2009,则∠A2009=.【解答】解:∵∠ACA1=∠A1CD=∠ACD=(∠A+∠ABC),又∵∠ABA1=∠A1BD=∠ABD,∠A1CD=∠A1BD+∠A1,∴∠A1=∠A=α.同理∠A2=∠A1,…即每次作图后,角度变为原来的.故∠A2009=.25.如图,学校有一块三角形空地(即△ABC),现准备将它分成面积相等的两块地,栽种不同的花草,请你把它分出来.(作图题要求:尺规作图,保留作图痕迹,不写作法,不要求证明).【解答】解:作图如下:.三.解答题(共1小题)26.认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+,理由如下:∵BO和CO分别是∠ABC和∠ACB的角平分线∴∴又∵∠ABC+∠ACB=180°﹣∠A∴∴∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣∠A)=探究2:如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)结论:∠BOC=90°﹣∠A.【解答】解:(1)探究2结论:∠BOC=∠A,理由如下:∵BO和CO分别是∠ABC和∠ACD的角平分线,∴∠1=∠ABC,∠2=∠ACD,又∵∠ACD是△ABC的一外角,∴∠ACD=∠A+∠ABC,∴∠2=(∠A+∠ABC)=∠A+∠1,∵∠2是△BOC的一外角,∴∠BOC=∠2﹣∠1=∠A+∠1﹣∠1=∠A;(2)探究3:∠OBC=(∠A+∠ACB),∠OCB=(∠A+∠ABC),∠BOC=180°﹣∠0BC﹣∠OCB,=180°﹣(∠A+∠ACB)﹣(∠A+∠ABC),=180°﹣∠A﹣(∠A+∠ABC+∠ACB),结论∠BOC=90°﹣∠A.。
人教版初中数学三角形难题汇编附答案

人教版初中数学三角形难题汇编附答案一、选择题1.如图,在ABC ∆中,AB 的垂直平分线交BC 于D ,AC 的中垂线交BC 于E ,20DAE ∠=o ,则BAC ∠的度数为( )A .70oB .80oC .90oD .100o【答案】D【解析】【分析】 根据线段垂直平分线的性质得到DA=DB,EA=EC,在由等边对等角,根据三角形内角和定理求解.【详解】如图所示:∵DM 是线段AB 的垂直平分线,∴DA=DB,B DAB ∠=∠ ,同理可得:C EAC ∠=∠ ,∵ 20DAE ∠=o ,180B DAB C EAC DAE ︒∠+∠+∠+∠+∠=,∴80DAB EAC ︒∠+∠=∴100BAC ︒∠=故选:D【点睛】本题考查了线段的垂直平分线和三角形的内角和定理,解题的关键是掌握线段垂直平分线上的点到线段两端的距离相等.2.如图,在平行四边形ABCD 中,用直尺和圆规作∠BAD 的平分线AG 交BC 于点E ,若BF=6,AB=5,则AE 的长为( )A .4B .8C .6D .10【答案】B【解析】【分析】【详解】 解:设AG 与BF 交点为O ,∵AB=AF ,AG 平分∠BAD ,AO=AO ,∴可证△ABO ≌△AFO ,∴BO=FO=3,∠AOB=∠AOF=90º,AB=5,∴AO=4,∵AF ∥BE ,∴可证△AOF ≌△EOB ,AO=EO ,∴AE=2AO=8,故选B .【点睛】本题考查角平分线的作图原理和平行四边形的性质.3.如图,OA =OB ,OC =OD ,∠O =50°,∠D =35°,则∠OAC 等于( )A .65°B .95°C .45°D .85°【答案】B【解析】【分析】 根据OA =OB ,OC =OD 证明△ODB ≌△OCA ,得到∠OAC=∠OBD ,再根据∠O =50°,∠D =35°即可得答案.【详解】解:OA =OB ,OC =OD ,在△ODB 和△OCA 中,OB OA BOD AOC OD OC =⎧⎪∠=∠⎨⎪=⎩∴△ODB ≌△OCA (SAS ),∠OAC=∠OBD=180°-50°-35°=95°,故B 为答案.【点睛】本题考查了全等三角形的判定、全等三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.4.AD 是△ABC 中∠BAC 的平分线,DE ⊥AB 于点E ,DF ⊥AC 交AC 于点F .S △ABC =7,DE=2,AB=4,则AC 长是( )A .4B .3C .6D .2【答案】B【解析】【分析】 首先由角平分线的性质可知DF=DE=2,然后由S △ABC =S △ABD +S △ACD 及三角形的面积公式得出结果.【详解】解:AD 是△ABC 中∠BAC 的平分线,∠EAD=∠FADDE ⊥AB 于点E ,DF ⊥AC 交AC 于点F ,∴DF=DE ,又∵S △ABC =S △ABD +S △ACD ,DE=2,AB=4, 11742222AC ∴=⨯⨯+⨯⨯ ∴AC=3. 故答案为:B【点睛】本题主要考查了角平分线的性质,熟练掌握角平分线的性质、灵活运用所学知识是解题的关键.5.如图,在矩形ABCD 中, 3,4,AB BC ==将其折叠使AB 落在对角线AC 上,得到折痕,AE 那么BE 的长度为( )A .1B .2C .32D .85【答案】C【解析】【分析】由勾股定理求出AC 的长度,由折叠的性质,AF=AB=3,则CF=2,设BE=EF=x ,则CE=4x -,利用勾股定理,即可求出x 的值,得到BE 的长度.【详解】解:在矩形ABCD 中,3,4AB BC ==,∴∠B=90°,∴5AC ==,由折叠的性质,得AF=AB=3,BE=EF ,∴CF=5-3=2,在Rt △CEF 中,设BE=EF=x ,则CE=4x -,由勾股定理,得:2222(4)x x +=-, 解得:32x =; ∴32BE =. 故选:C .【点睛】本题考查了矩形的折叠问题,矩形的性质,折叠的性质,以及勾股定理的应用,解题的关键是熟练掌握所学的性质,利用勾股定理正确求出BE 的长度.6.△ABC 中,∠A :∠B :∠C =1:2:3,最小边BC =4cm ,则最长边AB 的长为( )cmA .6B .8CD .5【答案】B【解析】【分析】根据已知条件结合三角形的内角和定理求出三角形中角的度数,然后根据含30度角的直角三角形的性质进行求解即可.【详解】设∠A =x ,则∠B =2x ,∠C =3x ,由三角形内角和定理得∠A+∠B+∠C =x+2x+3x =180°,解得x =30°,即∠A =30°,∠C =3×30°=90°,此三角形为直角三角形,故AB =2BC =2×4=8cm ,故选B .【点睛】本题考查了三角形内角和定理,含30度角的直角三角形的性质,熟练掌握“直角三角形中30°的角所对的直角边等于斜边的一半”是解题的关键.7.下列长度的三条线段能组成三角形的是()A.2, 2,5B.1,3,3C.3,4,8D.4,5,6【答案】D【解析】【分析】三角形的任何一边大于其他两边之差,小于两边之和,满足此关系的可组成三角形,其实只要最小两边的和大于最大边就可判断前面的三边关系成立.【详解】根据三角形三边关系可知,三角形两边之和大于第三边.A、2+2=4<5,此选项错误;B、1+3<3,此选项错误;C、3+4<8,此选项错误;D、4+5=9>6,能组成三角形,此选项正确.故选:D.【点睛】此题考查三角形三边关系,解题关键在于掌握三角形两边之和大于第三边.即:两条较短的边的和小于最长的边,只要满足这一条就是满足三边关系.8.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是()A.12 B.10 C.8 D.6【答案】C【解析】【分析】由折叠的性质可知;DC=DE,∠DEA=∠C=90°,在Rt△BED中,∠B=30°,故此BD=2ED,从而得到BC=3BC,于是可求得DE=8.【详解】解:由折叠的性质可知;DC=DE,∠DEA=∠C=90°,∵∠BED+∠DEA=180°,∴∠BED=90°.又∵∠B=30°,∴BD=2DE.∴BC=3ED=24.∴DE=8.故答案为8.【点睛】本题考查的是翻折的性质、含30°锐角的直角三角形的性质,根据题意得出BC=3DE是解题的关键.9.如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3 B.4 C.5 D.6【答案】C【解析】【分析】先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF 的最小值,再根据菱形的性质求出E′F的长度即可.【详解】解:如图∵四边形ABCD是菱形,对角线AC=6,BD=8,∴2234,作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,∵AC是∠DAB的平分线,E是AB的中点,∴E′在AD上,且E′是AD的中点,∵AD=AB,∴AE=AE′,∵F是BC的中点,∴E′F=AB=5.故选C.10.如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是()A.n B.2n-1 C.(1)2n nD.3(n+1)【答案】C【解析】【分析】根据条件可得图1中△ABD≌△ACD有1对三角形全等;图2中可证出△ABD≌△ACD,△BDE≌△CDE,△ABE≌△ACE有3对全等三角形;图3中有6对全等三角形,根据数据可分析出第n个图形中全等三角形的对数.【详解】∵AD是∠BAC的平分线,∴∠BAD=∠CAD.在△ABD与△ACD中,AB=AC,∠BAD=∠CAD,AD=AD,∴△ABD≌△ACD.∴图1中有1对三角形全等;同理图2中,△ABE≌△ACE,∴BE=EC,∵△ABD≌△ACD.∴BD=CD,又DE=DE,∴△BDE≌△CDE,∴图2中有3对三角形全等;同理:图3中有6对三角形全等;由此发现:第n 个图形中全等三角形的对数是()12n n +.故选C.【点睛】考查全等三角形的判定,找出数字的变化规律是解题的关键.11.满足下列条件的两个三角形不一定全等的是( )A .有一边相等的两个等边三角形B .有一腰和底边对应相等的两个等腰三角形C .周长相等的两个三角形D .斜边和一条直角边对应相等的两个等腰直角三角形【答案】C【解析】A.根据全等三角形的判定,可知有一边相等的两个等边三角形全等,故选项A 不符合;B.根据全等三角形的判定,可知有一腰和底边对应相等的两个等腰三角形全等,故选项B 不符合;C.根据全等三角形的判定,可知周长相等的两个三角形不一定全等,故选项C 符合;D.根据全等三角形的判定,可知斜边和直角边对应相等的两个等腰直角三角形全等,故选项B 不符合.故本题应选C.12.如图,直线a b ∥,点A 、B 分别在直线a 、b 上,145∠︒=,若点C 在直线b 上,105BAC ∠︒=,且直线a 和b 的距离为3,则线段AC 的长度为( )A .32B .33C .3D .6【答案】D【解析】【分析】 过C 作CD ⊥直线a ,根据30°角所对直角边等于斜边的一半即可得到结论.【详解】过C 作CD ⊥直线a ,∴∠ADC =90°.∵∠1=45°,∠BAC =105°,∴∠DAC =30°.∵CD =3,∴AC =2CD =6.故选D .【点睛】本题考查了平行线间的距离,含30°角的直角三角形的性质,正确的理解题意是解题的关键.13.如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为()A.23B.13C.4 D.32【答案】B【解析】【分析】如下图,作AD⊥BC,设半径为r,则在Rt△OBD中,OD=3-1,OB=r,BD=3,利用勾股定理可求得r.【详解】如图,过A作AD⊥BC,由题意可知AD必过点O,连接OB;∵△BAC是等腰直角三角形,AD⊥BC,∴BD=CD=AD=3;∴OD=AD-OA=2;Rt△OBD中,根据勾股定理,得:22+BD OD13故答案为:B.【点睛】本题考查了等腰直角三角形的性质和勾股定理的应用,解题关键是利用等腰直角三角形ABC判定点O在AD上.14.将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则 h 的取值范围是()A .h≤15cmB .h≥8cmC .8cm≤h≤17cmD .7cm≤h≤16cm【答案】C【解析】【分析】 筷子浸没在水中的最短距离为水杯高度,最长距离如下图,是筷子斜卧于杯中时,利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时,筷子浸没水中距离最短,为杯高=8cmAD 是筷子,AB 长是杯子直径,BC 是杯子高,当筷子如下图斜卧于杯中时,浸没在水中的距离最长由题意得:AB=15cm ,BC=8cm ,△ABC 是直角三角形∴在Rt △ABC 中,根据勾股定理,AC=17cm∴8cm ≤h ≤17cm故选:C【点睛】本题考查勾股定理在实际生活中的应用,解题关键是将题干中生活实例抽象成数学模型,然后再利用相关知识求解.15.如图,四边形ABCD 和EFGH 都是正方形,点E H ,在ADCD ,边上,点F G ,在对角线AC 上,若6AB ,则EFGH 的面积是( )A .6B .8C .9D .12【答案】B【解析】【分析】 根据正方形的性质得到∠DAC =∠ACD =45°,由四边形EFGH 是正方形,推出△AEF 与△DFH是等腰直角三角形,于是得到DE =2EH =2EF ,EF =2AE ,即可得到结论. 【详解】解:∵在正方形ABCD 中,∠D =90°,AD =CD =AB ,∴∠DAC =∠DCA =45°,∵四边形EFGH 为正方形,∴EH =EF ,∠AFE =∠FEH =90°,∴∠AEF =∠DEH =45°,∴AF =EF ,DE =DH ,∵在Rt △AEF 中,AF 2+EF 2=AE 2,∴AF =EF =2AE ,同理可得:DH =DE EH 又∵EH =EF ,∴DE =2EF =2×2AE =12AE , ∵AD =AB =6,∴DE =2,AE =4,∴EH DE =,∴EFGH 的面积为EH 2=()2=8,故选:B .【点睛】本题考查了正方形的性质,等腰直角三角形的判定及性质以及勾股定理的应用,熟练掌握图形的性质及勾股定理是解决本题的关键.16.如图,在ABC ∆中,AB AC =,分别是以点A ,点B 为圆心,以大于12AB 长为半径画弧,两弧交点的连线交AC 于点D ,交AB 于点E ,连接BD ,若40A ∠=︒,则DBC ∠=( )A .40︒B .30︒C .20︒D .10︒【答案】B【解析】【分析】 根据题意,DE 是AB 的垂直平分线,则AD=BD ,40ABD A ==︒∠∠,又AB=AC ,则∠ABC=70°,即可求出DBC ∠.【详解】解:根据题意可知,DE 是线段AB 的垂直平分线,∴AD=BD ,∴40ABD A ==︒∠∠,∵AB AC =, ∴1(18040)702ABC ∠=⨯︒-︒=︒, ∴704030DBC ∠=︒-︒=︒;故选:B.【点睛】 本题考查了垂直平分线的性质,等腰三角形的性质,以及三角形的内角和,解题的关键是熟练掌握所学的性质,正确求出DBC ∠的度数.17.满足下列条件的是直角三角形的是( )A .4BC =,5AC =,6AB =B .13BC =,14AC =,15AB = C .::3:4:5BC AC AB =D .::3:4:5A B C ∠∠∠= 【答案】C【解析】【分析】要判断一个角是不是直角,先要知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【详解】A .若BC=4,AC=5,AB=6,则BC 2+AC 2≠AB 2,故△ABC 不是直角三角形;B.若13BC =,14AC =,15AB =,则AC 2+AB 2≠CB 2,故△ABC 不是直角三角形; C .若BC :AC :AB=3:4:5,则BC 2+AC 2=AB 2,故△ABC 是直角三角形;D .若∠A :∠B :∠C=3:4:5,则∠C <90°,故△ABC 不是直角三角形;故答案为:C .【点睛】 本题主要考查了勾股定理的逆定理,如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2,那么这个三角形就是直角三角形.18.下列几组线段中,能组成直角三角形的是( )A .2,3,4B .3,4,6C .5,12,13D .2,5,5【答案】C【解析】【分析】要验证是否可以组成直角三角形,根据勾股定理的逆定理,只要验证三边的关系是否满足两边平方是否等于第三边的平方即可,分别验证四个选项即可得到答案.【详解】A .222234+≠,故不能组成直角三角形;B. 222346+≠,故不能组成直角三角形;C .22251213+=,故可以组成直角三角形;D .222255+≠,故不能组成直角三角形;故选C .【点睛】本题主要考查了勾股定理的逆定理(如果三角形两边的平方等于第三边的平方,那么这个三角形是直角三角形),掌握勾股定理的逆定理是解题的关键.19.如图,已知AC=FE,BC=DE,点A,D,B,F 在一条直线上,要利用“SSS”证明△ABC ≌△FDE,还可以添加的一个条件是( )A .AD=FBB .DE=BDC .BF=DBD .以上都不对【答案】A【解析】∵AC=FE ,BC=DE , ∴要利用“SSS”证明△ABC ≌△FDE ,需添加条件“AB=DF”或“AD=BF”.故选A.20.下列长度的三根小木棒能构成三角形的是()A.2cm,3cm,5cm B.7cm,4cm,2cm C.3cm,4cm,8cm D.3cm,3cm,4cm 【答案】D【解析】【详解】A.因为2+3=5,所以不能构成三角形,故A错误;B.因为2+4<6,所以不能构成三角形,故B错误;C.因为3+4<8,所以不能构成三角形,故C错误;D.因为3+3>4,所以能构成三角形,故D正确.故选D.。
(易错题精选)初中数学三角形真题汇编附答案

(易错题精选)初中数学三角形真题汇编附答案一、选择题1.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A.4 B.5 C.6 D.7【答案】B【解析】试题解析:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.此时DP+CP=DP+PC′=DC′的值最小.∵DC=1,BC=4,∴BD=3,连接BC′,由对称性可知∠C′BE=∠CBE=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=4,根据勾股定理可得DC′=22'+=22BC BD+=5.故选B.342.如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠OAC等于()A.65°B.95°C.45°D.85°【答案】B【解析】【分析】根据OA=OB,OC=OD证明△ODB≌△OCA,得到∠OAC=∠OBD,再根据∠O=50°,∠D=35°即可得答案.【详解】解:OA =OB ,OC =OD ,在△ODB 和△OCA 中,OB OA BOD AOC OD OC =⎧⎪∠=∠⎨⎪=⎩∴△ODB ≌△OCA (SAS ),∠OAC=∠OBD=180°-50°-35°=95°,故B 为答案.【点睛】本题考查了全等三角形的判定、全等三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.3.如图,在△ABC 中,AC =BC ,D 、E 分别是AB 、AC 上一点,且AD =AE ,连接DE 并延长交BC 的延长线于点F ,若DF =BD ,则∠A 的度数为( )A .30B .36C .45D .72【答案】B【解析】【分析】 由CA=CB ,可以设∠A=∠B=x .想办法构建方程即可解决问题;【详解】解:∵CA=CB ,∴∠A=∠B ,设∠A=∠B=x .∵DF=DB ,∴∠B=∠F=x ,∵AD=AE ,∴∠ADE=∠AED=∠B+∠F=2x ,∴x+2x+2x=180°,∴x=36°,故选B .【点睛】本题考查等腰三角形的性质、三角形的内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.4.如图,ABCD Y 的对角线AC 与BD 相交于点O ,AD BD ⊥,30ABD ∠=︒,若23AD =.则OC 的长为( )A .3B .3C 21D .6【答案】C【解析】【分析】 先根据勾股定理解Rt ABD △求得6BD =,再根据平行四边形的性质求得3OD =,然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得21OC OA ==【详解】解:∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中,30ABD ∠=︒,23AD =∴243AB AD ==∴226BD AB AD =-=∵四边形ABCD 是平行四边形∴132OB OD BD ===,12OA OC AC == ∴在Rt AOD △中,23AD =3OD = ∴2221OA AD OD += ∴21OC OA ==故选:C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.5.下列长度的三根小木棒能构成三角形的是( )A .2cm ,3cm ,5cmB .7cm ,4cm ,2cmC .3cm ,4cm ,8cmD .3cm ,3cm ,4cm【答案】D【解析】【详解】A .因为2+3=5,所以不能构成三角形,故A 错误;B .因为2+4<6,所以不能构成三角形,故B 错误;C .因为3+4<8,所以不能构成三角形,故C 错误;D .因为3+3>4,所以能构成三角形,故D 正确.故选D .6.如图,11∥l 2,∠1=100°,∠2=135°,则∠3的度数为( )A .50°B .55°C .65°D .70°【答案】B【解析】【分析】 如图,延长l 2,交∠1的边于一点,由平行线的性质,求得∠4的度数,再根据三角形外角性质,即可求得∠3的度数.【详解】如图,延长l 2,交∠1的边于一点,∵11∥l 2,∴∠4=180°﹣∠1=180°﹣100°=80°,由三角形外角性质,可得∠2=∠3+∠4,∴∠3=∠2﹣∠4=135°﹣80°=55°,故选B .【点睛】本题考查了平行线的性质及三角形外角的性质,熟练运用平行线的性质是解决问题的关键.7.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA x ⊥轴,点C 在函数()0k y x x=>的图象上,若1AB =,则k 的值为( )A .1B .22C .2D .2【答案】A【解析】【分析】 根据题意可以求得 OA 和 AC 的长,从而可以求得点 C 的坐标,进而求得 k 的值,本题得以解决.【详解】Q 等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA ⊥x 轴,1AB =,45BAC BAO ︒∴∠=∠=,2OA OB ∴==,2AC =, ∴点C 的坐标为2,22⎛⎫ ⎪ ⎪⎝,Q 点C 在函数()0k y x x=>的图象上, 2212k ∴=⨯=, 故选:A .【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键 是明确题意,利用数形结合的思想解答.8.图中的三角形被木板遮住了一部分,这个三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .以上都有可能【答案】D【解析】 从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,故选D .9.如图,已知△ABC 是等腰直角三角形,∠A =90°,BD 是∠ABC 的平分线,DE ⊥BC 于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm【答案】B【解析】【分析】根据“AAS”证明ΔABD≌ΔEBD .得到AD=DE,AB=BE,根据等腰直角三角形的边的关系,求其周长.【详解】∵BD是∠ABC的平分线,∴∠ABD=∠EBD.又∵∠A=∠DEB=90°,BD是公共边,∴△ABD≌△EBD (AAS),∴AD=ED,AB=BE,∴△DEC的周长是DE+EC+DC=AD+DC+EC=AC+EC=AB+EC=BE+EC=BC=10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质,角平分线的定义,全等三角形的判定与性质. 掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.4,1, 点D的坐标为10.如图,在菱形ABCD中,点A在x轴上,点B的坐标轴为()()0,1,则菱形ABCD的周长等于()A .5B .43C .45D .20【答案】C【解析】【分析】 如下图,先求得点A 的坐标,然后根据点A 、D 的坐标刻碟AD 的长,进而得出菱形ABCD 的周长.【详解】如下图,连接AC 、BD ,交于点E∵四边形ABCD 是菱形,∴DB ⊥AC ,且DE=EB又∵B ()4,1,D ()0,1∴E(2,1)∴A(2,0)∴AD=()()2220015-+-=∴菱形ABCD 的周长为:45故选:C【点睛】本题在直角坐标系中考查菱形的性质,解题关键是利用菱形的性质得出点A 的坐标,从而求得菱形周长.11.如图,在△ABC 和△DEF 中,∠B =∠DEF ,AB =DE ,若添加下列一个条件后,仍然不能证明△ABC ≌△DEF ,则这个条件是( )A .∠A =∠DB .BC =EF C .∠ACB =∠FD .AC =DF【答案】D【解析】 解:∵∠B =∠DEF ,AB =DE ,∴添加∠A =∠D ,利用ASA 可得△ABC ≌△DEF ;∴添加BC =EF ,利用SAS 可得△ABC ≌△DEF ;∴添加∠ACB =∠F ,利用AAS 可得△ABC ≌△DEF ;故选D .点睛:本题考查了全等三角形的判定,掌握全等三角形的判定方法:SSS 、ASA 、SAS 、AAS 和HL 是解题的关键.12.如图,在菱形ABCD 中,60BCD ∠=︒,BC 的垂直平分线交对角线AC 于点F ,垂足为E ,连接BF 、DF ,则DFC ∠的度数是( )A .130︒B .120︒C .110︒D .100︒【答案】A【解析】【分析】 首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB 即可解决问题;【详解】∵四边形ABCD 是菱形,∴∠ACD =∠ACB =12∠BCD=25°, ∵EF 垂直平分线段BC ,∴FB=FC ,∴∠FBC=∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故选:A .【点睛】此题考查菱形的性质、线段的垂直平分线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.如图,在△ABC 中,点D 为BC 的中点,连接AD ,过点C 作CE ∥AB 交AD 的延长线于点E ,下列说法错误的是( )A .△ABD ≌△ECDB .连接BE ,四边形ABEC 为平行四边形C .DA =DED .CE =CD【答案】D【解析】【分析】 根据平行线的性质得出∠B=∠DCE ,∠BAD=∠E ,然后根据AAS 证得△ABD ≌△ECD ,得出AD=DE ,根据对角线互相平分得到四边形ABEC 为平行四边形,CE=AB ,即可解答.【详解】∵CE ∥AB ,∴∠B=∠DCE ,∠BAD=∠E ,在△ABD 和△ECD 中,===B DCE BAD E BD CD ∠∠⎧⎪∠∠⎨⎪⎩∴△ABD ≌△ECD (AAS ),∴DA=DE ,AB=CE ,∵AD=DE ,BD=CD ,∴四边形ABEC 为平行四边形,故选:D .【点睛】此题考查平行线的性质,三角形全等的判定和性质以及平行四边形的性判定,解题的关键是证明△ABD ≌△ECD .14.满足下列条件的是直角三角形的是( )A .4BC =,5AC =,6AB =B .13BC =,14AC =,15AB = C .::3:4:5BC AC AB =D .::3:4:5A B C ∠∠∠= 【答案】C【解析】【分析】要判断一个角是不是直角,先要知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【详解】A .若BC=4,AC=5,AB=6,则BC 2+AC 2≠AB 2,故△ABC 不是直角三角形; B.若13BC =,14AC =,15AB =,则AC 2+AB 2≠CB 2,故△ABC 不是直角三角形; C .若BC :AC :AB=3:4:5,则BC 2+AC 2=AB 2,故△ABC 是直角三角形;D .若∠A :∠B :∠C=3:4:5,则∠C <90°,故△ABC 不是直角三角形;故答案为:C .【点睛】本题主要考查了勾股定理的逆定理,如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2,那么这个三角形就是直角三角形.15.如图:AD AB ⊥,AE AC ⊥,AD AB =,AE AC =,连接BE 与DC 交于M ,则:①DAC BAE ∠=∠;②DAC BAE ∆∆≌;③DC BE ⊥;正确的有( )个A .0B .1C .2D .3【答案】D【解析】【分析】 利用垂直的定义得到90DAB EAC ∠=∠=︒,则ADC BAE ∠=∠,于是可对①进行判断;利用“SAS ”可证明DAC BAE ∆≅∆,于是可对②进行判断;利用全等的性质得到ADC ABE ∠=∠,则根据三角形内角和和对顶角相等得到90DMB DAB ∠=∠=︒,于是可对③进行判断.【详解】解:AD AB ⊥Q ,AE AC ⊥,90DAB ∴∠=︒,90EAC ∠=︒,DAB BAC EAC BAC ∴∠+=∠+∠,即ADC BAE ∠=∠,所以①正确;在DAC ∆和BAE ∆中,DA AB DAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩,()DAC BAE SAS ∴∆≅∆,所以②正确;ADC ABE ∴∠=∠,∵∠AFD=∠MFB ,90DMB DAB ∴∠=∠=︒,DC BE ∴⊥,所以③正确.故选:D .【点睛】本题考查了全等三角形的判定:熟练掌握全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件.16.如图,经过直线AB外一点C作这条直线的垂线,作法如下:(1)任意取一点K,使点K和点C在AB的两旁.(2)以点C为圆心,CK长为半径作弧,交AB于点D和E.(3)分别以点D和点E为圆心,大于12DE的长为半径作弧,两弧相交于点F.(4)作直线CF.则直线CF就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定...是等腰三角形的为()A.△CDF B.△CDK C.△CDE D.△DEF【答案】A【解析】【分析】根据作图过程和等腰三角形的定义进行分析即可.【详解】由作图过程可得:CD=CD,DF=EF,CD=CK所以,是等腰三角形的有△CDK,△CDE,△DEF;△CDF不一定是等腰三角形.故选:A【点睛】考核知识点:等腰三角形.理解等腰三角形的定义是关键.17.如果把直角三角形的两条直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的()A.1倍B.2倍C.3倍D.4倍【答案】B【解析】设原直角三角形的三边长分别是,且,则扩大后的三角形的斜边长为,即斜边长扩大到原来的2倍,故选B.18.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有()A.1个B.2个C.3个D.4个【答案】C【解析】【分析】【详解】要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P2,P4三个,故选C.19.如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A的度数为( )A.30°B.45°C.36°D.72°【答案】A【解析】∵AB=AC,BD=BC=AD,∴∠ABC=∠C=∠BDC,∠A=∠ABD,又∵∠BDC=∠A+∠ABD,∴∠BDC=∠C=∠ABC=2∠A,∵∠A+∠ABC+∠C=180°,∴∠A+2∠A+2∠A=180°,即5∠A=180°,∴∠A=36°.故选A.20.如图,四边形ABCD 和EFGH 都是正方形,点E H ,在ADCD ,边上,点F G ,在对角线AC 上,若6AB ,则EFGH 的面积是( )A .6B .8C .9D .12【答案】B【解析】【分析】 根据正方形的性质得到∠DAC =∠ACD =45°,由四边形EFGH 是正方形,推出△AEF 与△DFH 是等腰直角三角形,于是得到DE =22EH =22EF ,EF =22AE ,即可得到结论. 【详解】解:∵在正方形ABCD 中,∠D =90°,AD =CD =AB ,∴∠DAC =∠DCA =45°,∵四边形EFGH 为正方形,∴EH =EF ,∠AFE =∠FEH =90°,∴∠AEF =∠DEH =45°,∴AF =EF ,DE =DH ,∵在Rt △AEF 中,AF 2+EF 2=AE 2,∴AF =EF =22AE , 同理可得:DH =DE =22EH 又∵EH =EF ,∴DE =2EF =2×2AE =12AE , ∵AD =AB =6,∴DE =2,AE =4,∴EH DE =,∴EFGH 的面积为EH 2=()2=8,故选:B .【点睛】本题考查了正方形的性质,等腰直角三角形的判定及性质以及勾股定理的应用,熟练掌握图形的性质及勾股定理是解决本题的关键.。
(专题精选)初中数学三角形难题汇编及答案解析

∴∠BAE=∠EAD=60°
∴△ABE是等边三角形,
∴AE=AB=BE,∠AEB=60°,
∵AB= BC,
∴AE=BE= BC,
∴AE=CE,故①正确;
∴∠EAC=∠ACE=30°
∴∠BAC=90°,
∴S△ABC= AB•AC,故②错误;
∵BE=EC,
∴E为BC中点,O为AC中点,
(专题精选)初中数学三角形难题汇编及答案解析
一、选择题
1.如图,已知 ,若 , , ,下列结论:① ;② ;③ ;④ 与 互补;⑤ ,其中正确的有()
A.2个B.3个C.4个D.5个
【答案】C
【解析】
【分析】
根据平行线的判定得出AC∥DE,根据垂直定义得出∠ACB=∠CDB=∠CDA=90°,再根据三角形内角和定理求出即可.
∴S△ABE=S△ACE=2S△AOE,故③正确;
∵四边形ABCD是平行四边形,
∴AC=CO,
∵AE=CE,
∴EO⊥AC,
∵∠ACE=30°,
∴EO= EC,
∵EC= AB,
∴OE= BC,故④正确;
故正确的个数为3个,
故选:C.
【点睛】
此题考查平行四边形的性质,等边三角形的判定与性质.注意证得△ABE是等边三角形是解题关键.
15.如图,四边形 和 都是正方形,点 在 边上,点 在对角线 上,若 ,则 的面积是()
A.6B.8C.9D.12【答Βιβλιοθήκη 】B【解析】【分析】
根据正方形的性质得到∠DAC=∠ACD=45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是得到DE= EH= EF,EF= AE,即可得到结论.
初中数学三角形难题汇编附答案

∴∠ACB=∠CDB=90°,
∴∠A+∠B=90°,∠3+∠B=90°,
∴∠A=∠3,故②正确;
∵AC∥DE,AC⊥BC,
∴DE⊥BC,
∴∠DEC=∠CDB=90°,
∴∠3+∠2=90°(∠2和∠3互余),∠2+∠EDB=90°,
∴∠3=∠EDB,故③正确,④错误;
∵AC⊥BC,CD⊥AB,
∴∠AEC=180°﹣∠DEC=180°﹣107°=73°,
∴∠ቤተ መጻሕፍቲ ባይዱ'EA=∠D'EC﹣∠AEC=107°﹣73°=34°.
故选:B.
【点睛】
本题考查了平行四边形的性质、折叠的性质、三角形的内角和定理等知识,属于常考题型,熟练掌握上述基本知识是解题关键.
6.如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是()
∴∠AOP=∠COP=30°,
∵CP∥OA,
∴∠AOP=∠CPO,
∴∠COP=∠CPO,
∴OC=CP=2,
∵∠PCE=∠AOB=60°,PE⊥OB,
∴∠CPE=30°,
∴CE= CP=1,
∴PE= ,
∴OP=2PE=2 ,
∵PD⊥OA,点M是OP的中点,
∴DM= OP= .
故选C.
考点:角平分线的性质;含30度角的直角三角形;直角三角形斜边上的中线;勾股定理.
A.BC = EFB.AC//DFC.∠C =∠FD.∠BAC =∠EDF
【答案】C
【解析】
【分析】
根据全等三角形的判定方法逐项判断即可.
(专题精选)初中数学三角形难题汇编含答案

(专题精选)初中数学三角形难题汇编含答案一、选择题1.如图所示,将含有30°角的三角板(∠A=30°)的直角顶点放在相互平行的两条直线其中一条上,若∠1=38°,则∠2的度数()A.28°B.22°C.32°D.38°【答案】B【解析】【分析】延长AB交CF于E,求出∠ABC,根据三角形外角性质求出∠AEC,根据平行线性质得出∠2=∠AEC,代入求出即可.【详解】解:如图,延长AB交CF于E,∵∠ACB=90°,∠A=30°,∠ABC=60°,∵∠1=38°,∴∠AEC=∠ABC-∠1=22°,∵GH∥EF,∴∠2=∠AEC=22°,故选B.【点睛】本题考查了三角形的内角和定理,三角形外角性质,平行线性质的应用,主要考查学生的推理能力.2.如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A .8cmB .10cmC .12cmD .14cm【答案】B【解析】【分析】 根据“AAS”证明 ΔABD ≌ΔEBD .得到AD =DE ,AB =BE ,根据等腰直角三角形的边的关系,求其周长.【详解】∵ BD 是∠ABC 的平分线,∴ ∠ABD =∠EBD .又∵ ∠A =∠DEB =90°,BD 是公共边,∴ △ABD ≌△EBD (AAS),∴ AD =ED ,AB =BE ,∴ △DEC 的周长是DE +EC +DC=AD +DC +EC=AC +EC =AB +EC=BE +EC =BC=10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质,角平分线的定义,全等三角形的判定与性质. 掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.3.如图,ABCD 的对角线AC 与BD 相交于点O ,AD BD ⊥,30ABD ∠=︒,若23AD =.则OC 的长为( )A .3B .3C 21D .6【答案】C【解析】【分析】 先根据勾股定理解Rt ABD △求得6BD =,再根据平行四边形的性质求得3OD =,然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得OC OA ==【详解】解:∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中,30ABD ∠=︒,AD =∴2AB AD ==∴6BD ==∵四边形ABCD 是平行四边形 ∴132OB OD BD ===,12OA OC AC ==∴在Rt AOD △中,AD =3OD =∴OA =∴OC OA ==故选:C【点睛】本题考查了含30角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.4.下列长度的三条线段能组成三角形的是( )A .2, 2,5B .C .3,4,8D .4,5,6【答案】D【解析】【分析】三角形的任何一边大于其他两边之差,小于两边之和,满足此关系的可组成三角形,其实只要最小两边的和大于最大边就可判断前面的三边关系成立.【详解】根据三角形三边关系可知,三角形两边之和大于第三边.A 、2+2=4<5,此选项错误;B 、<3,此选项错误;C 、3+4<8,此选项错误;D 、4+5=9>6,能组成三角形,此选项正确.故选:D .【点睛】此题考查三角形三边关系,解题关键在于掌握三角形两边之和大于第三边.即:两条较短的边的和小于最长的边,只要满足这一条就是满足三边关系.5.如图,已知AB ∥CD ,直线AB ,CD 被BC 所截,E 点在BC 上,若∠1=45°,∠2=35°,则∠3=( )A .65°B .70°C .75°D .80°【答案】D【解析】【分析】 由平行线的性质可求得∠C ,在△CDE 中利用三角形外的性质可求得∠3.【详解】解:∵AB ∥CD ,∴∠C =∠1=45°,∵∠3是△CDE 的一个外角,∴∠3=∠C+∠2=45°+35°=80°,故选:D .【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a ∥b ,b ∥c ⇒a ∥c .6.将一个边长为4的正方形ABCD 分割成如图所示的9部分,其中ABE △,BCF ,CDG ,DAH 全等,AEH △,BEF ,CFG △,DGH 也全等,中间小正方形EFGH 的面积与ABE △面积相等,且ABE △是以AB 为底的等腰三角形,则AEH △的面积为( )A .2B .169C .32D 2【答案】C【解析】【分析】【详解】 解:如图,连结EG 并向两端延长分别交AB 、CD 于点M 、N ,连结HF ,∵四边形EFGH 为正方形,∴EG FH =,∵ABE △是以AB 为底的等腰三角形,∴AE BE =,则点E 在AB 的垂直平分线上,∵ABE △≌CDG ,∴CDG 为等腰三角形,∴CG DG =,则点G 在CD 的垂直平分线上,∵四边形ABCD 为正方形,∴AB 的垂直平分线与CD 的垂直平分线重合,∴MN 即为AB 或CD 的垂直平分线,则,EM AB GN CD ,EM GN ,∵正方形ABCD 的边长为4,即4AB CDAD BC , ∴4MN =, 设EM GN x ,则42EG FH x , ∵正方形EFGH 的面积与ABE △面积相等, 即2114(42)22x x ,解得:121,4x x ==,∵4x =不符合题意,故舍去,∴1x =,则S 正方形EFGH 14122==⨯⨯=ABE S , ∵ABE △,BCF ,CDG ,DAH 全等, ∴2====ABE BCF CDG DAHS S S S , ∵正方形ABCD 的面积4416=⨯=,AEH △,BEF ,CFG △,DGH 也全等, ∴1(4=AEH S S 正方形ABCD − S 正方形EFGH 134)(16242)42-=⨯--⨯=ABE S , 故选:C .【点睛】本题考查了正方形的性质、全等三角形的性质和等腰三角形的性质,解题的关键是求得ABE △的面积.7.图中的三角形被木板遮住了一部分,这个三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .以上都有可能【答案】D【解析】 从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,故选D .8.如图,直线a b ∥,点A 、B 分别在直线a 、b 上,145∠︒=,若点C 在直线b 上,105BAC ∠︒=,且直线a 和b 的距离为3,则线段AC 的长度为( )A .32B .33C .3D .6【答案】D【解析】【分析】 过C 作CD ⊥直线a ,根据30°角所对直角边等于斜边的一半即可得到结论.【详解】过C 作CD ⊥直线a ,∴∠ADC =90°.∵∠1=45°,∠BAC =105°,∴∠DAC =30°.∵CD =3,∴AC =2CD =6.故选D .【点睛】本题考查了平行线间的距离,含30°角的直角三角形的性质,正确的理解题意是解题的关键.9.如图,在菱形ABCD 中,对角线AC =8,BD =6,点E ,F 分别是边AB ,BC 的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3 B.4 C.5 D.6【答案】C【解析】【分析】先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF 的最小值,再根据菱形的性质求出E′F的长度即可.【详解】解:如图∵四边形ABCD是菱形,对角线AC=6,BD=8,∴22,34作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,∵AC是∠DAB的平分线,E是AB的中点,∴E′在AD上,且E′是AD的中点,∵AD=AB,∴AE=AE′,∵F是BC的中点,∴E′F=AB=5.故选C.10.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=12∠CGE.其中正确的结论是( )A.②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案.【详解】①∵EG∥BC,∴∠CEG=∠ACB,又∵CD是△ABC的角平分线,∴∠CEG=∠ACB=2∠DCB,故正确;②∵∠A=90°,∴∠ADC+∠ACD=90°,∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC+∠BCD=90°.∵EG∥BC,且CG⊥EG,∴∠GCB=90°,即∠GCD+∠BCD=90°,∴∠ADC=∠GCD,故正确;③条件不足,无法证明CA平分∠BCG,故错误;④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,∴∠AEB+∠ADC=90°+12(∠ABC+∠ACB)=135°,∴∠DFE=360°-135°-90°=135°,∴∠DFB=45°=12∠CGE,,正确.故选B.【点睛】本题主要考查了角平分线的定义,平行线的性质,三角形内角和定理及多边形内角和,三角形外角的性质,熟知直角三角形的两锐角互余是解答此题的关键.11.如图,△ABC ≌△A E D ,∠C =40°,∠E AC =30°,∠B =30°,则∠E AD =( );A .30°B .70°C .40°D .110°【答案】D【解析】【分析】【详解】∵△ABC ≌△AED , ∴∠D=∠C=40°,∠C=∠B=30°,∴∠E AD=180°-∠D -∠E =110°,故选D.12.如图,在菱形ABCD 中,60BCD ∠=︒,BC 的垂直平分线交对角线AC 于点F ,垂足为E ,连接BF 、DF ,则DFC ∠的度数是( )A .130︒B .120︒C .110︒D .100︒【答案】A【解析】【分析】 首先求出∠CFB=130°,再根据对称性可知∠CFD=∠CFB 即可解决问题;【详解】∵四边形ABCD 是菱形,∴∠ACD =∠ACB =12∠BCD=25°, ∵EF 垂直平分线段BC ,∴FB=FC ,∴∠FBC=∠FCB=25°,∴∠CFB=180°-25°-25°=130°,根据对称性可知:∠CFD=∠CFB=130°,故选:A .【点睛】此题考查菱形的性质、线段的垂直平分线的性质,解题的关键是熟练掌握基本知识,属于中考常考题型.13.如图,在平面直角坐标系中,已知点A (﹣2,0),B (0,3),以点A 为圆心,AB 长为半径画弧,交x 轴的正半轴于点C ,则点C 的横坐标介于( )A .0和1之间B .1和2之间C .2和3之间D .3和4之间【答案】B【解析】【分析】 先根据点A ,B 的坐标求出OA ,OB 的长度,再根据勾股定理求出AB 的长,即可得出OC 的长,再比较无理数的大小确定点C 的横坐标介于哪个区间.【详解】∵点A ,B 的坐标分别为(﹣2,0),(0,3),∴OA =2,OB =3,在Rt △AOB 中,由勾股定理得:AB 222+313=∴AC =AB 13,∴OC 132,∴点C 132,0), ∵3134<< , ∴11322<< ,即点C 的横坐标介于1和2之间,故选:B .【点睛】本题考查了弧与x 轴的交点问题,掌握勾股定理、无理数大小比较的方法是解题的关键.14.满足下列条件的是直角三角形的是( )A .4BC =,5AC =,6AB =B .13BC =,14AC =,15AB = C .::3:4:5BC AC AB =D .::3:4:5A B C ∠∠∠= 【答案】C【解析】【分析】要判断一个角是不是直角,先要知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【详解】A.若BC=4,AC=5,AB=6,则BC2+AC2≠AB2,故△ABC不是直角三角形;B.若13BC=,14AC=,15AB=,则AC2+AB2≠CB2,故△ABC不是直角三角形;C.若BC:AC:AB=3:4:5,则BC2+AC2=AB2,故△ABC是直角三角形;D.若∠A:∠B:∠C=3:4:5,则∠C<90°,故△ABC不是直角三角形;故答案为:C.【点睛】本题主要考查了勾股定理的逆定理,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.15.等腰三角形的一个角比另一个角的2倍少20度,则等腰三角形顶角的度数是()A.140B.20或80C.44或80D.140或44或80【答案】D【解析】【分析】设另一个角是x,表示出一个角是2x-20°,然后分①x是顶角,2x-20°是底角,②x是底角,2x-20°是顶角,③x与2x-20°都是底角根据三角形的内角和等于180°与等腰三角形两底角相等列出方程求解即可.【详解】设另一个角是x,表示出一个角是2x-20°,①x是顶角,2x-20°是底角时,x+2(2x-20°)=180°,解得x=44°,∴顶角是44°;②x是底角,2x-20°是顶角时,2x+(2x-20°)=180°,解得x=50°,∴顶角是2×50°-20°=80°;③x与2x-20°都是底角时,x=2x-20°,解得x=20°,∴顶角是180°-20°×2=140°;综上所述,这个等腰三角形的顶角度数是44°或80°或140°.故答案为:D.【点睛】本题考查了等腰三角形两底角相等的性质,三角形的内角和定理,难点在于分情况讨论,特别是这两个角都是底角的情况容易漏掉而导致出错.16.如图,90ACB ∠=︒,AC CD =,过D 作AB 的垂线,交AB 的延长线于E ,若2AB DE =,则BAC ∠的度数为( )A .45°B .30°C .22.5°D .15°【答案】C【解析】【分析】 连接AD ,延长AC 、DE 交于M ,求出∠CAB=∠CDM ,根据全等三角形的判定得出△ACB ≌△DCM ,求出AB=DM ,求出AD=AM ,根据等腰三角形的性质得出即可.【详解】解:连接AD ,延长AC 、DE 交于M ,∵∠ACB=90°,AC=CD ,∴∠DAC=∠ADC=45°,∵∠ACB=90°,DE ⊥AB ,∴∠DEB=90°=∠ACB=∠DCM ,∵∠ABC=∠DBE ,∴∠CAB=∠CDM ,在△ACB 和△DCM 中CAB CDM AC CDACB DCM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACB ≌△DCM (ASA ),∴AB=DM ,∵AB=2DE ,∴DM=2DE ,∴DE=EM ,∵DE ⊥AB ,∴AD=AM ,114522.522BAC DAE DAC ︒︒∴∠=∠=∠=⨯= 故选:C .【点睛】 本题考查了全等三角形的性质和判定,等腰直角三角形,等腰三角形的性质和判定等知识点,能根据全等求出AB=DM 是解此题的关键.17.如图为一个66⨯的网格,在ABC ∆,A B C '''∆和A B C ''''''∆中,直角三角形有( )个A .0B .1C .2D .3【答案】C【解析】【分析】 根据题中的网格,先运用勾股定理计算出各个三角形的边长,再根据勾股定理的逆定理判断是否为直角三角形即可.【详解】设网格的小正方形的边长是1,由勾股定理(两直角边的平方等于斜边的平方)可知,ABC ∆的三边分别是:10,5,5; 由于2225510+=, 根据勾股定理的逆定理得:ABC ∆是直角三角形; '''A B C ∆的三边分别是:''A B 10, ''B C 5 ,''AC 13 由于22210513,根据勾股定理的逆定理得:'''A B C ∆不是直角三角形;A B C ''''''∆的三边分别是:A B ''''18B C ''''8 ,A C ''''26;由于22218826, 根据勾股定理的逆定理得:A B C ''''''∆是直角三角形;因此有两个直角等三角形;故选C .【点睛】本题主要考查了勾股定理和勾股定理的逆定理,能灵活运用所学知识是解题的关键.18.如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,3),点C的坐标为(12,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )A.132B.312C.3+192D.2 7【答案】B【解析】如图,作点A关于OB的对称点点D,连接CD交OB于点P,此时PA+PC最小,作DN⊥x 轴交于点N,∵B(33OA=3,AB3OB3BOA=30°,∵在Rt△AMO中,∠MOA=30°,AO=3,∴AM=1.5,∠OAM=60°,∴∠ADN=30°,∵在Rt△AND中,∠ADN=30°,AD=2AM=3,∴AN=1.5,DN 33 2∴CN=3-12-1.5=1,∴CD2=CN2+DN2=12+3322=314,∴CD=312.故选B.点睛:本题关键在于先借助轴对称的性质确定出P点的位置,然后结合特殊角30°以及勾股定理计算.19.如图,Rt△ABC中,∠C =90°,∠ABC的平分线BD交AC于D,若AD =5cm,CD=3cm,则点D到AB的距离DE是()A .5cmB .4cmC .3cmD .2cm【答案】C【解析】 ∵点D 到AB 的距离是DE ,∴DE ⊥AB ,∵BD 平分∠ABC ,∠C =90°,∴把Rt △BDC 沿BD 翻折后,点C 在线段AB 上的点E 处,∴DE=CD ,∵CD =3cm ,∴DE=3cm.故选:C.20.如图,在ABC 中,90C ∠=︒,60CAB ∠=︒,按以下步骤作图:①分别以A ,B 为圆心,以大于12AB 的长为半径画弧,两弧分别相交于点P 和Q . ②作直线PQ 交AB 于点D ,交BC 于点E ,连接AE .若4CE =,则AE 的值为( ) A .6B .2C .43D .8 【答案】D【解析】【分析】根据垂直平分线的作法得出PQ 是AB 的垂直平分线,进而得出∠EAB =∠CAE =30°,即可得出AE 的长.【详解】由题意可得出:PQ 是AB 的垂直平分线,∴AE =BE ,∵在△ABC中,∠C=90°,∠CAB=60°,∴∠CBA=30°,∴∠EAB=∠CAE=30°,∴CE=12AE=4,∴AE=8.故选D.【点睛】此题主要考查了垂直平分线的性质以及直角三角形中,30°所对直角边等于斜边的一半,根据已知得出∠EAB=∠CAE=30°是解题关键.。
初中数学三角形难题汇编附答案

初中数学三角形难题汇编附答案一、选择题1.如图,4aBC的角平分线CD、8E相交于F, ZA=90°f EG//BC,且CG_LEG于G,下列结论:®ZCEG=2ZDCB- Q)ZADC=ZGCD-③CA 平分N8CG;®ZDFB=-Z2 CGE.其中正确的结论是()A.②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案. 【详解】©VEG/7BC,AZCEG=ZACB,又「CD是AABC的角平分线,AZCEG=ZACB=2ZDCB,故正确;(2)VZA=90°,:.ZADC+ZACD=90°,:CD 平分NACB,,ZACD=ZBCD,:.ZADC+ZBCD=90°.•••EG〃BC,且CGJ_EG,AZGCB=90°, BPZGCD+ZBCD=90°,AZADC=ZGCD,故正确;③条件不足,无法证明CA平分NBCG,故错误;④ 「ZEBC+ZACB=ZAEB, NDCB+NABONADC,A ZAEB+ZADC=90°+- (ZABC+ZACB) =135%2,ZDFE=360o-135°-90o=135°,AZDFB=45°=-ZCGE,,正确.2故选B.【点睛】本题主要考查了角平分线的定义,平行线的性质,三角形内角和定理及多边形内角和,三角形外角的性质,熟知直角三角形的两锐角互余是解答此题的关键.2.把一副三角板如图甲放置,其中NACB=NDEC=90。
,NA-45。
,ZD=30°,斜边AB=6, DC=7,把三角板DCE绕着点C顺时针旋转15。
得到A D I CE I(如图乙),此时AB与CD1交于点0,则线段AD1的长度为()D.而【答案】B【解析】【分析】【详解】由题意易知:NCAB=45。
新初中数学三角形难题汇编及答案解析

新初中数学三角形难题汇编及答案解析一、选择题1.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A.4 B.5 C.6 D.7【答案】B【解析】试题解析:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.此时DP+CP=DP+PC′=DC′的值最小.∵DC=1,BC=4,∴BD=3,连接BC′,由对称性可知∠C′BE=∠CBE=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=4,根据勾股定理可得DC′=22'+=22BC BD+=5.故选B.342.如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm【答案】B【解析】【分析】根据“AAS”证明ΔABD≌ΔEBD .得到AD=DE,AB=BE,根据等腰直角三角形的边的关系,求其周长.【详解】∵ BD 是∠ABC 的平分线,∴ ∠ABD =∠EBD .又∵ ∠A =∠DEB =90°,BD 是公共边,∴ △ABD ≌△EBD (AAS),∴ AD =ED ,AB =BE ,∴ △DEC 的周长是DE +EC +DC=AD +DC +EC=AC +EC =AB +EC=BE +EC =BC=10 cm.故选B.【点睛】本题考查了等腰直角三角形的性质,角平分线的定义,全等三角形的判定与性质. 掌握全等三角形的判定方法(即SSS 、SAS 、ASA 、AAS 和HL )和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.3.如图,OA =OB ,OC =OD ,∠O =50°,∠D =35°,则∠OAC 等于( )A .65°B .95°C .45°D .85°【答案】B【解析】【分析】 根据OA =OB ,OC =OD 证明△ODB ≌△OCA ,得到∠OAC=∠OBD ,再根据∠O =50°,∠D =35°即可得答案.【详解】解:OA =OB ,OC =OD ,在△ODB 和△OCA 中,OB OA BOD AOC OD OC =⎧⎪∠=∠⎨⎪=⎩∴△ODB ≌△OCA (SAS ),∠OAC=∠OBD=180°-50°-35°=95°,故B 为答案.【点睛】本题考查了全等三角形的判定、全等三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.4.下列长度的三条线段能组成三角形的是()A.2, 2,5B.1,3,3C.3,4,8D.4,5,6【答案】D【解析】【分析】三角形的任何一边大于其他两边之差,小于两边之和,满足此关系的可组成三角形,其实只要最小两边的和大于最大边就可判断前面的三边关系成立.【详解】根据三角形三边关系可知,三角形两边之和大于第三边.A、2+2=4<5,此选项错误;B、1+3<3,此选项错误;C、3+4<8,此选项错误;D、4+5=9>6,能组成三角形,此选项正确.故选:D.【点睛】此题考查三角形三边关系,解题关键在于掌握三角形两边之和大于第三边.即:两条较短的边的和小于最长的边,只要满足这一条就是满足三边关系.5.把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为()A.115°B.120°C.145°D.135°【答案】D【解析】【分析】由三角形的内角和等于180°,即可求得∠3的度数,又由邻补角定义,求得∠4的度数,然后由两直线平行,同位角相等,即可求得∠2的度数.【详解】在Rt△ABC中,∠A=90°,∵∠1=45°(已知),∴∠3=90°-∠1=45°(三角形的内角和定理),∴∠4=180°-∠3=135°(平角定义),∵EF∥MN(已知),∴∠2=∠4=135°(两直线平行,同位角相等).故选D.【点睛】此题考查了三角形的内角和定理与平行线的性质.注意两直线平行,同位角相等与数形结合思想的应用.6.下列命题是假命题的是()A.三角形的外心到三角形的三个顶点的距离相等B.如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16C.将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限D.若关于x的一元一次不等式组213x mx-≤⎧⎨+>⎩无解,则m的取值范围是1m£【答案】B【解析】【分析】利用三角形外心的性质、等腰三角形的性质和三角形三边关系定理、一次函数图象的平移规律、解一元一次不等式组分别判断后即可确定正确的选项.【详解】A. 三角形的外心到三角形的三个顶点的距离相等,正确,是真命题;B. 如果等腰三角形的两边长分别是5和6,那么这个等腰三角形的周长为16或17,错误,是假命题;C. 将一次函数y=3x-1的图象向上平移3个单位,所得直线不经过第四象限,正确,是真命题;D. 若关于x的一元一次不等式组213x mx-≤⎧⎨+>⎩无解,则m的取值范围是1m£,正确,是真命题;故答案为:B【点睛】本题考查了命题与定理的知识,解题的关键是了解三角形外心的性质、等腰三角形的性质和三角形三边关系定理、一次函数图象的平移规律、解一元一次不等式组.7.如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于12MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()A .BP 是∠ABC 的平分线B .AD=BDC .:1:3CBD ABD S S V V D .CD=12BD 【答案】C【解析】【分析】 A 、由作法得BD 是∠ABC 的平分线,即可判定;B 、先根据三角形内角和定理求出∠ABC 的度数,再由BP 是∠ABC 的平分线得出∠ABD =30°=∠A,即可判定;C ,D 、根据含30°的直角三角形,30°所对直角边等于斜边的一半,即可判定.【详解】解:由作法得BD 平分∠ABC ,所以A 选项的结论正确;∵∠C =90°,∠A =30°,∴∠ABC =60°,∴∠ABD =30°=∠A ,∴AD =BD ,所以B 选项的结论正确;∵∠CBD =12∠ABC =30°, ∴BD =2CD ,所以D 选项的结论正确;∴AD =2CD ,∴S △ABD =2S △CBD ,所以C 选项的结论错误.故选:C .【点睛】此题考查含30°角的直角三角形的性质,尺规作图(作角平分线),解题关键在于利用三角形内角和进行计算.8.如图11-3-1,在四边形ABCD 中,∠A=∠B=∠C ,点E 在边AB 上,∠AED=60°,则一定有()A.∠ADE=20°B.∠ADE=30°C.∠ADE=12∠ADC D.∠ADE=13∠ADC【答案】D【解析】【分析】【详解】设∠ADE=x,∠ADC=y,由题意可得,∠ADE+∠AED+∠A=180°,∠A+∠B+∠C+∠ADC=360°,即x+60+∠A=180①,3∠A+y=360②,由①×3-②可得3x-y=0,所以13x y,即∠ADE=13∠ADC.故答案选D.考点:三角形的内角和定理;四边形内角和定理.9.如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是()A.3 B.4 C.5 D.6【答案】C【解析】【分析】先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF 的最小值,再根据菱形的性质求出E′F的长度即可.【详解】解:如图∵四边形ABCD是菱形,对角线AC=6,BD=8,∴2234,作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,∵AC是∠DAB的平分线,E是AB的中点,∴E′在AD上,且E′是AD的中点,∵AD=AB,∴AE=AE′,∵F是BC的中点,∴E′F=AB=5.故选C.10.将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则 h 的取值范围是()A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm【答案】C【解析】【分析】筷子浸没在水中的最短距离为水杯高度,最长距离如下图,是筷子斜卧于杯中时,利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时,筷子浸没水中距离最短,为杯高=8cmAD是筷子,AB长是杯子直径,BC是杯子高,当筷子如下图斜卧于杯中时,浸没在水中的距离最长由题意得:AB=15cm ,BC=8cm ,△ABC 是直角三角形∴在Rt △ABC 中,根据勾股定理,AC=17cm∴8cm ≤h ≤17cm故选:C【点睛】本题考查勾股定理在实际生活中的应用,解题关键是将题干中生活实例抽象成数学模型,然后再利用相关知识求解.11.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC ≌△AED 的是( )A .BC=EDB .∠BAD=∠EAC C .∠B=∠ED .∠BAC=∠EAD【答案】C【解析】 解:A .∵AB =AE ,AC =AD ,BC =ED ,∴△ABC ≌△AED (SSS ),故A 不符合题意; B . ∵∠BAD =∠EAC ,∴∠BAC =∠EAD .∵AB =AE ,∠BAC =∠EAD ,AC =AD , ∴△ABC ≌△AED (SAS ),故B 不符合题意;C .不能判定△ABC ≌△AED ,故C 符合题意.D .∵AB =AE , ∠BAC =∠EAD ,AC =AD ,∴△ABC ≌△AED (SAS ),故D 不符合题意. 故选C .12.如图,ABC V 中,5AB AC ==,AE 平分BAC ∠交BC 于点E ,点D 为AB 的中点,连接DE ,则DE 的长为( )A .2B .2.5C .3D .5【答案】B【解析】【分析】 根据等腰三角形三线合一可得AE ⊥BC ,再根据直角三角形斜边上的中线是斜边的一半即可求得DE 的长度.【详解】解:∵5AB AC ==,AE 平分BAC ∠,∴AE ⊥BC ,又∵点D 为AB 的中点,∴1 2.52DE AB ==, 故选:B .【点睛】 本题考查等腰三角形三线合一和直角三角形斜边上的中线.熟练掌握相关定理,并能正确识图,得出线段之间的关系是解题关键.13.如图,AB 是⊙O 的直径,AC 是⊙O 的切线,连接OC 交⊙O 于点D ,连接BD ,∠C=40°.则∠ABD 的度数是( )A .30°B .25°C .20°D .15°【答案】B【解析】试题分析:∵AC为切线∴∠OAC=90°∵∠C=40°∴∠AOC=50°∵OB=OD ∴∠ABD=∠ODB ∵∠ABD+∠ODB=∠AOC=50°∴∠ABD=∠ODB=25°.考点:圆的基本性质.14.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1,P2,P3,P4四个点中找出符合条件的点P,则点P有()A.1个B.2个C.3个D.4个【答案】C【解析】【分析】【详解】要使△ABP与△ABC全等,必须使点P到AB的距离等于点C到AB的距离,即3个单位长度,所以点P的位置可以是P1,P2,P4三个,故选C.15.如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是()A.AD=FB B.DE=BD C.BF=DB D.以上都不对【答案】A【解析】∵AC=FE,BC=DE,∴要利用“SSS”证明△ABC≌△FDE,需添加条件“AB=DF”或“AD=BF”.故选A.16.△ABC中,AB=AC,∠A=36°,∠ABC和∠ACB的平分线BE、CD交于点F,则共有等腰三角形( )A.7个B.8个C.9个D.10个【答案】B【解析】∵等腰三角形有两个角相等,∴只要能判断出有两个角相等就行了,将原图各角标上后显示如左下:因此,所有三角形都是等腰三角形,只要判断出有哪几个三角形就可以了.如右上图,三角形有如下几个:①,②,③;①+②,③+②,①+④,③+④;①+②+③+④;共计8个.故选:B.点睛:本题考查了等腰三角形的判定与性质、三角形内角和定理以及三角形外角的性质,此题难度不大,解题的关键是求得各角的度数,掌握等角对等边与等边对等角定理的应用.17.一个等腰三角形的顶角为钝角,则底角a的范围是()A.0°<a<9 B.30°<a<90° C.0°<a<45° D.45°<a<90°【答案】C【解析】:∵等腰三角形顶角为钝角∴顶角大于90°小于180°∴两个底角之和大于0°小于90°∴每个底角大于0°小于45°故选:C18.如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,若添加下列一个条件后,仍然不能证明△ABC≌△DEF,则这个条件是()A.∠A=∠D B.BC=EF C.∠ACB=∠F D.AC=DF【答案】D【解析】解:∵∠B=∠DEF,AB=DE,∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;∴添加BC=EF,利用SAS可得△ABC≌△DEF;∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;故选D.点睛:本题考查了全等三角形的判定,掌握全等三角形的判定方法:SSS、ASA、SAS、AAS 和HL是解题的关键.19.如图,AA',BB'表示两根长度相同的木条,若O是AA',BB'的中点,经测量AB=9 cm,则容器的内径A'B'为()A.8 cm B.9 cm C.10 cm D.11 cm【答案】B【解析】解:由题意知:OA=OA′,∠AOB=∠A′OB′,OB=OB′,∴△AOB≌△A′OB′,∴A′B′=AB=9cm.故选B.点睛:本题考查了全等三角形的判定及性质的应用;解答本题的关键是设计三角形全等,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.20.如图,AB是⊙O的直径,弦CD⊥AB于点M,若CD=8 cm,MB=2 cm,则直径AB的长为()A.9 cm B.10 cm C.11 cm D.12 cm【答案】B【解析】【分析】由CD⊥AB,可得DM=4.设半径OD=Rcm,则可求得OM的长,连接OD,在直角三角形DMO中,由勾股定理可求得OD的长,继而求得答案.【详解】解:连接OD,设⊙O半径OD为R,∵AB是⊙O的直径,弦CD⊥AB于点M,∴DM=12CD=4cm,OM=R-2,在RT△OMD中,OD²=DM²+OM²即R²=4²+(R-2)²,解得:R=5,∴直径AB的长为:2×5=10cm.故选B.【点睛】本题考查了垂径定理以及勾股定理.注意掌握辅助线的作法及数形结合思想的应用.。
初中数学三角形难题汇编及答案

A.3B.2 C.2 D.6
【答案】D
【解析】
【分析】
根据题意画出图形,利用勾股定理解答即可.
【详解】
设AC=b,BC=a,分别在直角△ACE与直角△BCD中,根据勾股定理得到:
两式相加得:
根据勾股定理得到斜边
故选:D.
故答案为:B
【点睛】
本题考查了命题与定理的知识,解题的关键是了解三角形外心的性质、等腰三角形的性质和三角形三边关系定理、一次函数图象的平移规律、解一元一次不等式组.
6.如图,在菱形ABCD中,AB=10,两条对角线相交于点O,若OB=6,则菱形面积是( )
A.60B.48C.24D.96
【答案】D
【解析】
∴AF=DF,BF=EF;
可得③⑤正确,
故选:B.
【点睛】
此题考查平行四边形的性质、全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.
13.下列几组线段中,能组成直角三角形的是()
A. , , B. , , C. , , D. , ,
【答案】C
【解析】
【分析】
【答案】B
【解析】
【分析】
由AAS证明△ABF≌△DEF,得出对应边相等AF=DF,BF=EF,即可得出结论,对于①②④不一定正确.
【详解】
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,即AB∥CE,
∴∠ABF=∠E,
∵DE=CD,
∴AB=DE,
在△ABF和△DEF中,
∵ ,
∴△ABF≌△DEF(AAS),
∵ , ,
初中数学三角形难题汇编含答案

A. B. C. D.
【答案】D
【解析】
【分析】
三角形的任何一边大于其他两边之差,小于两边之和,满足此关系的可组成三角形,其实只要最小两边的和大于最大边就可判断前面的三边关系成立.
【详解】
根据三角形三边关系可知,三角形两边之和大于第三边.
A、2+2=4<5,此选项错误;
Rt△OBD中,根据勾股定理,得:
OB=
故答案为:B.
【点睛】
本题考查了等腰直角三角形的性质和勾股定理的应用,解题关键是利用等腰直角三角形ABC判定点O在AD上.
9.如图,△ABC中,AB=AC=10,BC=12,D是BC的中点,DE⊥AB于点E,则DE的长为( )
A. B. C. D.
【答案】D
【解析】
A.∠A=∠DB.BC=EFC.∠ACB=∠FD.AC=DF
【答案】D
【解析】
解:∵∠B=∠DEF,AB=DE,∴添加∠A=∠D,利用ASA可得△ABC≌△DEF;
∴添加BC=EF,利用SAS可得△ABC≌△DEF;
∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF;
故选D.
点睛:本题考查了全等三角形的判定,掌握全等三角形的判定方法:SSS、ASA、SAS、AAS和HL是解题的关键.
(3)分别以点D和点E为圆心,大于 的长为半径作弧,两弧相交于点F.
(4)作直线CF.
则直线CF就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为()
A.△CDFB.△CDKC.△CDED.△DEF
【答案】A
本题考查了菱形的性质,勾股定理,掌握菱形的对角线互相垂直平分是本题的关键.
三角形难题(有规范标准答案)

三角形难题(有规范标准答案)三角形难题三角形是几何学中非常重要且基础的图形之一,我们经常会面对各种与三角形相关的难题。
本文将针对一些常见的三角形难题进行探讨,并给出规范的标准答案。
一、边长关系的难题在三角形中,其边长的关系是一个常见的问题。
假设有一个三角形ABC,已知边长AB为5cm,BC为8cm,AC为7cm,我们要求出三角形ABC的面积。
解答:根据海伦公式,我们可以计算出三角形ABC的面积。
海伦公式为:面积= √[s(s-a)(s-b)(s-c)]其中,s为三角形的半周长,即s = (a + b + c)/2。
代入已知边长,有s = (5 + 8 + 7)/2 = 10cm。
将已知边长代入公式,面积= √[10(10-5)(10-8)(10-7)] = √[10*5*2*3] = 10√3 cm²。
因此,三角形ABC的面积为10√3平方厘米。
二、角度关系的难题在三角形中,角度关系也是一个常见的问题。
假设有一个三角形DEF,已知∠D = 40°,∠E = 60°,要求求出∠F的度数。
解答:三角形的内角和为180°,因此可以得到∠F = 180° - ∠D - ∠E = 180° - 40° - 60° = 80°。
所以,∠F的度数为80°。
三、相似三角形的难题相似三角形也是三角形难题中的一个重要内容。
假设有两个相似的三角形ABC和DEF,已知AC = 10cm,DF = 15cm,BC = 6cm,要求求出EF的长度。
解答:由于三角形ABC与DEF相似,我们可以得知它们的对应边长之比相等。
即AC/DF = BC/EF。
将已知边长代入上述等式,有10/15 = 6/EF。
通过交叉相乘法则,我们可以得到10*EF = 15*6,即10EF = 90。
解得EF = 9cm。
所以,EF的长度为9厘米。
四、三角形的中线问题在三角形中,中线也是一个重要的概念。
(易错题精选)初中数学三角形难题汇编及答案

【答案】B
【解析】
【分析】
【详解】
由题意易知:∠CAB=45°,∠ACD=30°,
若旋转角度为15°,则∠ACO=30°+15°=45°.
∴∠AOC=180°-∠ACO-∠CAO=90°.
在等腰Rt△ABC中,AB=6,则AC=BC= .
同理可求得:AO=OC=3.
在Rt△AOD1中,OA=3,OD1=CD1-OC=4,
6.把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( )
A.115°B.120°
C.145°D.135°
【答案】D
【解析】
【分析】
由三角形的内角和等于180°,即可求得∠3的度数,又由邻补角定义,求得∠4的度数,然后由两直线平行,同位角相等,即可求得∠2的度数.
【详解】
在Rt△ABC中,∠A=90°,
【详解】
A中,三个角之比为1:2:3,则这三个角分别为:30°、60°、90°,是直角三角形;
D中,三个角之比为1:1:2,则这三个角分别为:45°、45°、90°,是直角三角形;
B中,三边之比为3:4:5,设这三条边长为:3x、4x、5x,满足: ,是直角三角形;
C中,三边之比为8:16:17,设这三条边长为:8x、16x、17x, ,不满足勾股定理逆定理,不是直角三角形
A.△ABD≌△ECDB.连接BE,四边形ABEC为平行四边形
C.DA=DED.CE=CD
【答案】D
【解析】
【分析】
根据平行线的性质得出∠B=∠DCE,∠BAD=∠E,然后根据AAS证得△ABD≌△ECD,得出AD=DE,根据对角线互相平分得到四边形ABEC为平行四边形,CE=AB,即可解答.
最新初中数学三角形难题汇编附答案解析(1)
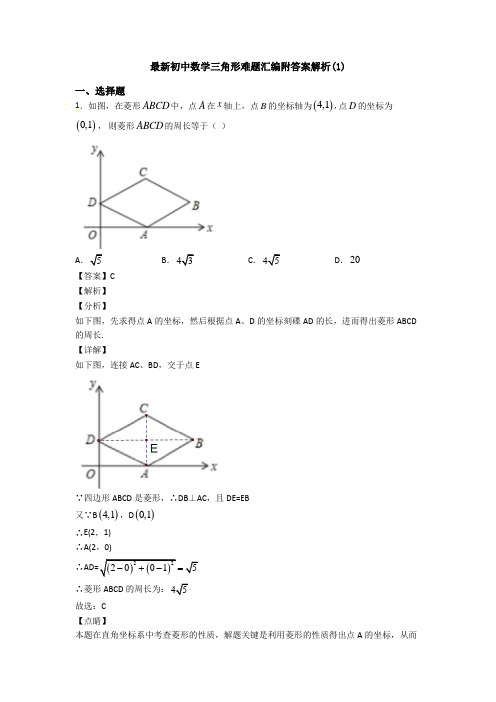
最新初中数学三角形难题汇编附答案解析(1)一、选择题1.如图,在菱形ABCD 中,点A 在x 轴上,点B 的坐标轴为()4,1, 点D 的坐标为()0,1, 则菱形ABCD 的周长等于( )A .5B .43C .45D .20【答案】C【解析】【分析】 如下图,先求得点A 的坐标,然后根据点A 、D 的坐标刻碟AD 的长,进而得出菱形ABCD 的周长.【详解】如下图,连接AC 、BD ,交于点E∵四边形ABCD 是菱形,∴DB ⊥AC ,且DE=EB 又∵B ()4,1,D ()0,1∴E(2,1)∴A(2,0)∴()()2220015-+-=∴菱形ABCD 的周长为:5故选:C【点睛】本题在直角坐标系中考查菱形的性质,解题关键是利用菱形的性质得出点A 的坐标,从而求得菱形周长.2.如图,OA =OB ,OC =OD ,∠O =50°,∠D =35°,则∠OAC 等于( )A .65°B .95°C .45°D .85°【答案】B【解析】【分析】 根据OA =OB ,OC =OD 证明△ODB ≌△OCA ,得到∠OAC=∠OBD ,再根据∠O =50°,∠D =35°即可得答案.【详解】解:OA =OB ,OC =OD ,在△ODB 和△OCA 中,OB OA BOD AOC OD OC =⎧⎪∠=∠⎨⎪=⎩∴△ODB ≌△OCA (SAS ),∠OAC=∠OBD=180°-50°-35°=95°,故B 为答案.【点睛】本题考查了全等三角形的判定、全等三角形的性质,熟练掌握全等三角形的判定与性质是解题的关键.3.AD 是△ABC 中∠BAC 的平分线,DE ⊥AB 于点E ,DF ⊥AC 交AC 于点F .S △ABC =7,DE=2,AB=4,则AC 长是( )A .4B .3C .6D .2【答案】B【解析】【分析】 首先由角平分线的性质可知DF=DE=2,然后由S △ABC =S △ABD +S △ACD 及三角形的面积公式得出结果.【详解】解:AD 是△ABC 中∠BAC 的平分线,∠EAD=∠FADDE ⊥AB 于点E ,DF ⊥AC 交AC 于点F ,∴DF=DE ,又∵S △ABC =S △ABD +S △ACD ,DE=2,AB=4, 11742222AC ∴=⨯⨯+⨯⨯ ∴AC=3.故答案为:B【点睛】本题主要考查了角平分线的性质,熟练掌握角平分线的性质、灵活运用所学知识是解题的关键.4.如图,△ABC 中,AB =AC =10,BC =12,D 是BC 的中点,DE ⊥AB 于点E ,则DE 的长为( )A .65B .85C .125D .245【答案】D【解析】【分析】连接AD ,根据已知等腰三角形的性质得出AD ⊥BC 和BD=6,根据勾股定理求出AD ,根据三角形的面积公式求出即可.【详解】解:连接AD∵AB=AC ,D 为BC 的中点,BC=12,∴AD ⊥BC ,BD=DC=6,在Rt △ADB 中,由勾股定理得:22221068AB BD =+=,∵S△ADB=12×AD×BD=12×AB×DE,∴DE=8624105 AD BDAB⨯⨯==,故选D.【点睛】本题考查了等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)、勾股定理和三角形的面积,能求出AD的长是解此题的关键.5.下列长度的三根小木棒能构成三角形的是()A.2cm,3cm,5cm B.7cm,4cm,2cm C.3cm,4cm,8cm D.3cm,3cm,4cm 【答案】D【解析】【详解】A.因为2+3=5,所以不能构成三角形,故A错误;B.因为2+4<6,所以不能构成三角形,故B错误;C.因为3+4<8,所以不能构成三角形,故C错误;D.因为3+3>4,所以能构成三角形,故D正确.故选D.6.如图,11∥l2,∠1=100°,∠2=135°,则∠3的度数为()A.50°B.55°C.65°D.70°【答案】B【解析】【分析】如图,延长l2,交∠1的边于一点,由平行线的性质,求得∠4的度数,再根据三角形外角性质,即可求得∠3的度数.【详解】如图,延长l2,交∠1的边于一点,∵11∥l2,∴∠4=180°﹣∠1=180°﹣100°=80°,由三角形外角性质,可得∠2=∠3+∠4,∴∠3=∠2﹣∠4=135°﹣80°=55°,故选B .【点睛】本题考查了平行线的性质及三角形外角的性质,熟练运用平行线的性质是解决问题的关键.7.如图,在ABC ∆中,33B ∠=︒,将ABC ∆沿直线m 翻折,点B 落在点D 的位置,则12∠-∠的度数是( )A .33︒B .56︒C .65︒D .66︒【答案】D【解析】【分析】 由折叠的性质得到∠D=∠B ,再利用外角性质即可求出所求角的度数.【详解】解:如图,由折叠的性质得:∠D=∠B=33°,根据外角性质得:∠1=∠3+∠B ,∠3=∠2+∠D ,∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+66°,∴∠1-∠2=66°.故选:D .【点睛】此题考查了翻折变换以及三角形外角性质的运用,熟练掌握折叠的性质是解本题的关键.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.8.如图11-3-1,在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有()A.∠ADE=20°B.∠ADE=30°C.∠ADE=12∠ADC D.∠ADE=13∠ADC【答案】D【解析】【分析】【详解】设∠ADE=x,∠ADC=y,由题意可得,∠ADE+∠AED+∠A=180°,∠A+∠B+∠C+∠ADC=360°,即x+60+∠A=180①,3∠A+y=360②,由①×3-②可得3x-y=0,所以13x y,即∠ADE=13∠ADC.故答案选D.考点:三角形的内角和定理;四边形内角和定理.9.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A-45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕着点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长度为()A.32B.5 C.4 D.31【答案】B【解析】【分析】【详解】由题意易知:∠CAB=45°,∠ACD=30°,若旋转角度为15°,则∠ACO=30°+15°=45°.∴∠AOC=180°-∠ACO-∠CAO=90°.在等腰Rt△ABC中,AB=6,则AC=BC=32.同理可求得:AO=OC=3.在Rt△AOD1中,OA=3,OD1=CD1-OC=4,由勾股定理得:AD1=5.故选B.10.如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,∠BAF=600,那么∠DAE等于()A.45°B.30 °C.15°D.60°【答案】C【解析】【分析】先根据矩形的性质得到∠DAF=30°,再根据折叠的性质即可得到结果.【详解】解:∵ABCD是长方形,∴∠BAD=90°,∵∠BAF=60°,∴∠DAF=30°,∵长方形ABCD沿AE折叠,∴△ADE≌△AFE,∴∠DAE=∠EAF=12∠DAF=15°.故选C.【点睛】图形的折叠实际上相当于把折叠部分沿着折痕所在直线作轴对称,所以折叠前后的两个图形是全等三角形,重合的部分就是对应量.11.对于图形的全等,下列叙述不正确的是()A.一个图形经过旋转后得到的图形,与原来的图形全等B.一个图形经过中心对称后得到的图形,与原来的图形全等C.一个图形放大后得到的图形,与原来的图形全等D.一个图形经过轴对称后得到的图形,与原来的图形全等【答案】C【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意,故选C.【点睛】本题考查了对全等图形的认识,解题的关键是要明确通过旋转、轴对称、平移等都可以得到与原图形全等的图形,而通过放大或缩小只能得到与原图形形状一样的图形,得不到全等图形.12.如图,在□ABCD中,延长CD到E,使DE=CD,连接BE交AD于点F,交AC于点G.下列结论中:①DE=DF;②AG=GF;③AF=DF;④BG=GC;⑤BF=EF,其中正确的有()A.1个B.2个C.3个D.4个【答案】B【解析】【分析】由AAS证明△ABF≌△DEF,得出对应边相等AF=DF,BF=EF,即可得出结论,对于①②④不一定正确.【详解】解:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,即AB∥CE,∴∠ABF=∠E,∵DE=CD,∴AB=DE,在△ABF和△DEF中,∵===ABF EAFB DFE AB DE∠∠⎧⎪∠∠⎨⎪⎩,∴△ABF ≌△DEF (AAS ),∴AF=DF ,BF=EF ;可得③⑤正确,故选:B .【点睛】此题考查平行四边形的性质、全等三角形的判定与性质、平行线的性质;熟练掌握平行四边形的性质,证明三角形全等是解题的关键.13.满足下列条件的是直角三角形的是( )A .4BC =,5AC =,6AB =B .13BC =,14AC =,15AB = C .::3:4:5BC AC AB =D .::3:4:5A B C ∠∠∠= 【答案】C【解析】【分析】要判断一个角是不是直角,先要知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.【详解】A .若BC=4,AC=5,AB=6,则BC 2+AC 2≠AB 2,故△ABC 不是直角三角形; B.若13BC =,14AC =,15AB =,则AC 2+AB 2≠CB 2,故△ABC 不是直角三角形; C .若BC :AC :AB=3:4:5,则BC 2+AC 2=AB 2,故△ABC 是直角三角形;D .若∠A :∠B :∠C=3:4:5,则∠C <90°,故△ABC 不是直角三角形;故答案为:C .【点睛】 本题主要考查了勾股定理的逆定理,如果三角形的三边长a ,b ,c 满足a 2+b 2=c 2,那么这个三角形就是直角三角形.14.如图,在ABC ∆,90C =o ∠,以A 为圆心,任意长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以M ,N ,为圆心,大于12MN 长为半径画弧,两弧交于点O ,作弧线AO ,交BC 于点E .已知3CE =,5BE =,则AC 的长为( )A .8B .7C .6D .5【答案】C【解析】【分析】直接利用基本作图方法得出AE 是∠CAB 的平分线,进而结合全等三角形的判定与性质得出AC=AD ,再利用勾股定理得出AC 的长.【详解】过点E 作ED ⊥AB 于点D ,由作图方法可得出AE 是∠CAB 的平分线,∵EC ⊥AC ,ED ⊥AB ,∴EC=ED=3,在Rt △ACE 和Rt △ADE 中,AE AE EC ED ⎧⎨⎩==, ∴Rt △ACE ≌Rt △ADE (HL ),∴AC=AD ,∵在Rt △EDB 中,DE=3,BE=5,∴BD=4,设AC=x ,则AB=4+x ,故在Rt △ACB 中,AC 2+BC 2=AB 2,即x 2+82=(x+4)2,解得:x=6,即AC 的长为:6.故答案为:C .【点睛】此题主要考查了基本作图以及全等三角形的判定与性质、勾股定理等知识,正确得出BD 的长是解题关键.15.如图,AD ∥BC ,∠C =30°, ∠ADB:∠BDC= 1:2,则∠DBC 的度数是( )A .30°B .36°C .45°D .50° 【答案】D【解析】【分析】直接利用平行线的性质得出∠ADC=150°,∠ADB=∠DBC,进而得出∠ADB的度数,即可得出答案.【详解】∵AD∥BC,∠C=30°∴∠ADC=150°,∠ADB=∠DBC∵∠ADB:∠DBC=1:2∴∠ADB=13×150°=50°,故选D.【点睛】熟练掌握平行线的性质是本题解题的关键.16.如图,已知AE=AD,AB=AC,EC=DB,下列结论:①∠C=∠B;②∠D=∠E;③∠EAD=∠BAC;④∠B=∠E;其中错误的是()A.①②B.②③C.③④D.只有④【答案】D【解析】【分析】【详解】解:因为AE=AD,AB=AC,EC=DB;所以△ABD≌△ACE(SSS);所以∠C=∠B,∠D=∠E,∠EAC=∠DAB;所以∠EAC-∠DAC=∠DAB-∠DAC;得∠EAD=∠CAB.所以错误的结论是④,故选D.【点睛】此题考查了全等三角形的判定方法,根据已知条件利用SSS证明两个三角形全等,还考查了全等三角形的性质:全等三角形的对应角相等,全等三角形的对应边相等.17.王师傅用4根木条钉成一个四边形木架,如图.要使这个木架不变形,他至少还要再钉上几根木条?().A.0根B.1根C.2根D.3根【答案】B【解析】三角形具有稳定性,连接一条对角线,即可得到两个三角形,故选B18.满足下列条件的两个三角形不一定全等的是()A.有一边相等的两个等边三角形B.有一腰和底边对应相等的两个等腰三角形C.周长相等的两个三角形D.斜边和一条直角边对应相等的两个等腰直角三角形【答案】C【解析】A.根据全等三角形的判定,可知有一边相等的两个等边三角形全等,故选项A不符合;B.根据全等三角形的判定,可知有一腰和底边对应相等的两个等腰三角形全等,故选项B 不符合;C.根据全等三角形的判定,可知周长相等的两个三角形不一定全等,故选项C符合;D.根据全等三角形的判定,可知斜边和直角边对应相等的两个等腰直角三角形全等,故选项B不符合.故本题应选C.19.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是()A.BC=ED B.∠BAD=∠EACC.∠B=∠E D.∠BAC=∠EAD【答案】C【解析】解:A.∵AB=AE,AC=AD,BC=ED,∴△ABC≌△AED(SSS),故A不符合题意;B.∵∠BAD=∠EAC,∴∠BAC=∠EAD.∵AB=AE,∠BAC=∠EAD ,AC=AD,∴△ABC≌△AED(SAS),故B不符合题意;C.不能判定△ABC≌△AED,故C符合题意.D.∵AB=AE,∠BAC=∠EAD,AC=AD,∴△ABC≌△AED(SAS),故D不符合题意.故选C.20.如图,在ABC ∆中,90C =o ∠,30B ∠=o ,以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ,再分别以M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连结AP 并延长交BC 于点D ,则下列说法中正确的个数是( ) ①AD 是BAC ∠的平分线;②ADC 60∠=o ;③点D 在AB 的垂直平分线上;④:1:3DAC ABC S S ∆∆=A .1B .2C .3D .4【答案】D【解析】【分析】 根据题干作图方式,可判断AD 是∠CAB 的角平分线,再结合∠B=30°,可推导得到△ABD 是等腰三角形,根据这2个判定可推导题干中的结论.【详解】题干中作图方法是构造角平分线,①正确;∵∠B=30°,∠C=90°,AD 是∠CAB 的角平分线 ∴∠CAD=∠DAB=30°∴∠ADC=60°,②正确∵∠DAB=∠B=30°∴△ADB 是等腰三角形∴点D 在AB 的垂直平分线上,③正确在Rt △CDA 中,设CD=a ,则AD=2a在△ADB 中,DB=AD=2a∵1122DAC S CD AC a CD ∆=⨯⨯=⨯,13(CD+DB)22BAC S AC a CD ∆=⨯⨯=⨯ ∴:1:3DAC ABC S S ∆∆=,④正确故选:D【点睛】本题考查角平分线的画法及性质、等腰三角形的性质,解题关键是熟练角平分线的绘制方法.。
2020-2021初中数学三角形难题汇编附答案解析

2020-2021初中数学三角形难题汇编附答案解析一、选择题1.将一根 24cm 的筷子,置于底面直径为 15cm,高 8cm 的装满水的无盖圆柱形水杯中,设筷子浸没在杯子里面的长度为hcm,则 h 的取值范围是()A.h≤15cm B.h≥8cm C.8cm≤h≤17cm D.7cm≤h≤16cm【答案】C【解析】【分析】筷子浸没在水中的最短距离为水杯高度,最长距离如下图,是筷子斜卧于杯中时,利用勾股定理可求得.【详解】当筷子笔直竖立在杯中时,筷子浸没水中距离最短,为杯高=8cmAD是筷子,AB长是杯子直径,BC是杯子高,当筷子如下图斜卧于杯中时,浸没在水中的距离最长由题意得:AB=15cm,BC=8cm,△ABC是直角三角形∴在Rt△ABC中,根据勾股定理,AC=17cm∴8cm≤h≤17cm故选:C【点睛】本题考查勾股定理在实际生活中的应用,解题关键是将题干中生活实例抽象成数学模型,然后再利用相关知识求解.2.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为()A.4 B.8 C.6 D.10【答案】B【解析】【分析】【详解】解:设AG 与BF 交点为O ,∵AB=AF ,AG 平分∠BAD ,AO=AO ,∴可证△ABO ≌△AFO ,∴BO=FO=3,∠AOB=∠AOF=90º,AB=5,∴AO=4,∵AF ∥BE ,∴可证△AOF ≌△EOB ,AO=EO ,∴AE=2AO=8,故选B .【点睛】本题考查角平分线的作图原理和平行四边形的性质.3.如图,在△ABC 中,AC =BC ,D 、E 分别是AB 、AC 上一点,且AD =AE ,连接DE 并延长交BC 的延长线于点F ,若DF =BD ,则∠A 的度数为( )A .30B .36C .45D .72【答案】B【解析】【分析】 由CA=CB ,可以设∠A=∠B=x .想办法构建方程即可解决问题;【详解】解:∵CA=CB ,∴∠A=∠B ,设∠A=∠B=x .∵DF=DB ,∴∠B=∠F=x ,∵AD=AE ,∴∠ADE=∠AED=∠B+∠F=2x ,∴x+2x+2x=180°,∴x=36°,故选B .【点睛】本题考查等腰三角形的性质、三角形的内角和定理等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.4.如图,ABCD Y 的对角线AC 与BD 相交于点O ,AD BD ⊥,30ABD ∠=︒,若23AD =OC 的长为( )A .3B .3C 21D .6【答案】C【解析】【分析】 先根据勾股定理解Rt ABD △求得6BD =,再根据平行四边形的性质求得3OD =,然后根据勾股定理解Rt AOD △、平行四边形的性质即可求得21OC OA ==【详解】解:∵AD BD ⊥∴90ADB ∠=︒∵在Rt ABD △中,30ABD ∠=︒,23AD =∴243AB AD == ∴226BD AB AD =-=∵四边形ABCD 是平行四边形 ∴132OB OD BD ===,12OA OC AC == ∴在Rt AOD △中,23AD =3OD = ∴2221OA AD OD += ∴21OC OA ==故选:C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.5.下列长度的三条线段能组成三角形的是( )A .2, 2,5B .3,3C .3,4,8D .4,5,6【答案】D【解析】【分析】三角形的任何一边大于其他两边之差,小于两边之和,满足此关系的可组成三角形,其实只要最小两边的和大于最大边就可判断前面的三边关系成立.【详解】根据三角形三边关系可知,三角形两边之和大于第三边.A 、2+2=4<5,此选项错误;B 、1+3<3,此选项错误;C 、3+4<8,此选项错误;D 、4+5=9>6,能组成三角形,此选项正确.故选:D .【点睛】此题考查三角形三边关系,解题关键在于掌握三角形两边之和大于第三边.即:两条较短的边的和小于最长的边,只要满足这一条就是满足三边关系.6.把一块直尺与一块三角板如图放置,若∠1=45°,则∠2的度数为( )A .115°B .120°C .145°D .135°【答案】D【解析】【分析】由三角形的内角和等于180°,即可求得∠3的度数,又由邻补角定义,求得∠4的度数,然后由两直线平行,同位角相等,即可求得∠2的度数.【详解】在Rt △ABC 中,∠A=90°,∵∠1=45°(已知),∴∠3=90°-∠1=45°(三角形的内角和定理),∴∠4=180°-∠3=135°(平角定义),∵EF ∥MN (已知),∴∠2=∠4=135°(两直线平行,同位角相等).故选D .【点睛】此题考查了三角形的内角和定理与平行线的性质.注意两直线平行,同位角相等与数形结合思想的应用.7.如图,在Rt ABC ∆中,90BCA ∠=︒,CD 是高,BE 平分∠ABC 交CD 于点E ,EF ∥AC 交AB 于点F ,交BC 于点G .在结论:(1) EFD ∠=BCD ∠;(2) AD CD =;(3)CG EG =;(4) BF BC =中,一定成立的有( )A .1个B .2个C .3个D .4个【答案】B【解析】【分析】 根据两直线平行,同旁内角互补求出∠CGE=∠BCA=90°,然后根据等角的余角相等即可求出∠EFD=∠BCD ;只有△ABC 是等腰直角三角形时AD=CD ,CG=EG ;利用“角角边”证明△BCE 和△BFE 全等,然后根据全等三角形对应边相等可得BF=BC .【详解】∵EF ∥AC ,∠BCA=90°,∴∠CGE=∠BCA=90°,∴∠BCD+∠CEG=90°,又∵CD 是高,∴∠EFD+∠FED=90°,∵∠CEG=∠FED (对顶角相等),∴∠EFD=∠BCD ,故(1)正确;只有∠A=45°,即△ABC 是等腰直角三角形时,AD=CD ,CG=EG 而立,故(2)(3)不一定成立,错误;∵BE 平分∠ABC ,∴∠EBC=∠EBF ,在△BCE 和△BFE 中,EFD BCD EBC EBF BE BE ∠∠∠∠⎧⎪⎨⎪⎩===,∴△BCE ≌△BFE (AAS ),∴BF=BC ,故(4)正确,综上所述,正确的有(1)(4)共2个.故选:B .【点睛】本题主要考查了角平分线的性质,全等三角形的判定与性质,直角三角形的性质,等腰直角三角形的性质,综合题,但难度不大,熟记性质是解题的关键.8.如图,在平面直角坐标系中,等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA x ⊥轴,点C 在函数()0k y x x=>的图象上,若1AB =,则k 的值为( )A .1B .22C 2D .2【答案】A【解析】【分析】 根据题意可以求得 OA 和 AC 的长,从而可以求得点 C 的坐标,进而求得 k 的值,本题得以解决.【详解】Q 等腰直角三角形ABC 的顶点A 、B 分别在x 轴、y 轴的正半轴上,90ABC ∠=︒,CA ⊥x 轴,1AB =,45BAC BAO ︒∴∠=∠=,22OA OB ∴==,2AC =, ∴点C 的坐标为22⎝, Q 点C 在函数()0k y x x=>的图象上, 2212k ∴==, 故选:A .【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形,解答本题的关键 是明确题意,利用数形结合的思想解答.9.如图,在菱形ABCD 中,对角线AC =8,BD =6,点E ,F 分别是边AB ,BC 的中点,点P 在AC 上运动,在运动过程中,存在PE +PF 的最小值,则这个最小值是( )A.3 B.4 C.5 D.6【答案】C【解析】【分析】先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF 的最小值,再根据菱形的性质求出E′F的长度即可.【详解】解:如图∵四边形ABCD是菱形,对角线AC=6,BD=8,∴22,34作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,∵AC是∠DAB的平分线,E是AB的中点,∴E′在AD上,且E′是AD的中点,∵AD=AB,∴AE=AE′,∵F是BC的中点,∴E′F=AB=5.故选C.10.图中的三角形被木板遮住了一部分,这个三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .以上都有可能【答案】D【解析】 从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角,故选D .11.如果把直角三角形的两条直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的( )A .1倍B .2倍C .3倍D .4倍【答案】B【解析】 设原直角三角形的三边长分别是,且,则扩大后的三角形的斜边长为,即斜边长扩大到原来的2倍,故选B.12.下列说法不能得到直角三角形的( )A .三个角度之比为 1:2:3 的三角形B .三个边长之比为 3:4:5 的三角形C .三个边长之比为 8:16:17 的三角形D .三个角度之比为 1:1:2 的三角形【答案】C【解析】【分析】三角形内角和180°,根据比例判断A 、D 选项中是否有90°的角,根据勾股定理的逆定理判断B 、C 选项中边长是否符合直角三角形的关系.【详解】A 中,三个角之比为1:2:3,则这三个角分别为:30°、60°、90°,是直角三角形; D 中,三个角之比为1:1:2,则这三个角分别为:45°、45°、90°,是直角三角形;B 中,三边之比为3:4:5,设这三条边长为:3x 、4x 、5x ,满足:()()()222345x x x +=,是直角三角形;C 中,三边之比为8:16:17,设这三条边长为:8x 、16x 、17x ,()()()22281617x x x +≠,不满足勾股定理逆定理,不是直角三角形故选:C【点睛】本题考查直角三角形的判定,常见方法有2种;(1)有一个角是直角的三角形;(2)三边长满足勾股定理逆定理.13.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=12∠CGE.其中正确的结论是( )A.②③B.①②④C.①③④D.①②③④【答案】B【解析】【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案.【详解】①∵EG∥BC,∴∠CEG=∠ACB,又∵CD是△ABC的角平分线,∴∠CEG=∠ACB=2∠DCB,故正确;②∵∠A=90°,∴∠ADC+∠ACD=90°,∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠ADC+∠BCD=90°.∵EG∥BC,且CG⊥EG,∴∠GCB=90°,即∠GCD+∠BCD=90°,∴∠ADC=∠GCD,故正确;③条件不足,无法证明CA平分∠BCG,故错误;④∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,∴∠AEB+∠ADC=90°+12(∠ABC+∠ACB)=135°,∴∠DFE=360°-135°-90°=135°,∴∠DFB=45°=12∠CGE,,正确.故选B .【点睛】本题主要考查了角平分线的定义,平行线的性质,三角形内角和定理及多边形内角和,三角形外角的性质,熟知直角三角形的两锐角互余是解答此题的关键.14.如图,在菱形ABCD 中,点A 在x 轴上,点B 的坐标轴为()4,1, 点D 的坐标为()0,1, 则菱形ABCD 的周长等于( )A .5B .43C .45D .20【答案】C【解析】【分析】 如下图,先求得点A 的坐标,然后根据点A 、D 的坐标刻碟AD 的长,进而得出菱形ABCD 的周长.【详解】如下图,连接AC 、BD ,交于点E∵四边形ABCD 是菱形,∴DB ⊥AC ,且DE=EB 又∵B ()4,1,D ()0,1∴E(2,1)∴A(2,0)∴()()2220015-+-=∴菱形ABCD 的周长为:5故选:C【点睛】本题在直角坐标系中考查菱形的性质,解题关键是利用菱形的性质得出点A的坐标,从而求得菱形周长.15.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为()A.4 B.5 C.6 D.7【答案】B【解析】试题解析:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.此时DP+CP=DP+PC′=DC′的值最小.∵DC=1,BC=4,∴BD=3,连接BC′,由对称性可知∠C′BE=∠CBE=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=4,根据勾股定理可得DC22'+22BC BD+.故选B.3416.下列条件中,不能判断一个三角形是直角三角形的是()A.三条边的比为2∶3∶4 B.三条边满足关系a2=b2﹣c2C.三条边的比为1∶12D.三个角满足关系∠B+∠C=∠A【答案】A【解析】【分析】根据直角三角形的判定方法,对选项进行一一分析,排除错误答案.【详解】A、三条边的比为2:3:4,22+32≠42,故不能判断一个三角形是直角三角形;B、三条边满足关系a2=b2-c2,即a2+c2=b2,故能判断一个三角形是直角三角形;C 、三条边的比为1:1:2,12+12=(2)2,故能判断一个三角形是直角三角形; D 、三个角满足关系∠B+∠C=∠A ,则∠A 为90°,故能判断一个三角形是直角三角形. 故选:A .【点睛】此题考查勾股定理的逆定理的应用.解题关键在于掌握判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可;若已知角,只要求得一个角为90°即可.17.如图,90ACB ∠=︒,AC CD =,过D 作AB 的垂线,交AB 的延长线于E ,若2AB DE =,则BAC ∠的度数为( )A .45°B .30°C .22.5°D .15°【答案】C【解析】【分析】 连接AD ,延长AC 、DE 交于M ,求出∠CAB=∠CDM ,根据全等三角形的判定得出△ACB ≌△DCM ,求出AB=DM ,求出AD=AM ,根据等腰三角形的性质得出即可.【详解】解:连接AD ,延长AC 、DE 交于M ,∵∠ACB=90°,AC=CD ,∴∠DAC=∠ADC=45°,∵∠ACB=90°,DE ⊥AB ,∴∠DEB=90°=∠ACB=∠DCM ,∵∠ABC=∠DBE ,∴∠CAB=∠CDM ,在△ACB 和△DCM 中CAB CDM AC CDACB DCM ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACB ≌△DCM (ASA ),∴AB=DM ,∵AB=2DE ,∴DM=2DE ,∴DE=EM ,∵DE ⊥AB ,∴AD=AM , 114522.522BAC DAE DAC ︒︒∴∠=∠=∠=⨯= 故选:C . 【点睛】 本题考查了全等三角形的性质和判定,等腰直角三角形,等腰三角形的性质和判定等知识点,能根据全等求出AB=DM 是解此题的关键.18.在直角三角形中,自锐角顶点引的两条中线为10和35,则这个直角三角形的斜边长是( )A .3B .23C .25D .6 【答案】D【解析】【分析】根据题意画出图形,利用勾股定理解答即可.【详解】设AC =b ,BC =a ,分别在直角△ACE 与直角△BCD 中,根据勾股定理得到:2222 10235,2a b b a ⎧⎛⎫+=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩两式相加得:2236a b +=,根据勾股定理得到斜边36 6.==故选:D.【点睛】考查勾股定理,画出图形,根据勾股定理列出方程是解题的关键.19.如图,ABC V 中,5AB AC ==,AE 平分BAC ∠交BC 于点E ,点D 为AB 的中点,连接DE ,则DE 的长为( )A .2B .2.5C .3D 5【答案】B【解析】【分析】 根据等腰三角形三线合一可得AE ⊥BC ,再根据直角三角形斜边上的中线是斜边的一半即可求得DE 的长度.【详解】解:∵5AB AC ==,AE 平分BAC ∠,∴AE ⊥BC ,又∵点D 为AB 的中点, ∴1 2.52DE AB ==, 故选:B .【点睛】 本题考查等腰三角形三线合一和直角三角形斜边上的中线.熟练掌握相关定理,并能正确识图,得出线段之间的关系是解题关键.20.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点M ,若CD =8 cm ,MB =2 cm ,则直径AB 的长为( )A.9 cm B.10 cm C.11 cm D.12 cm【答案】B【解析】【分析】由CD⊥AB,可得DM=4.设半径OD=Rcm,则可求得OM的长,连接OD,在直角三角形DMO中,由勾股定理可求得OD的长,继而求得答案.【详解】解:连接OD,设⊙O半径OD为R,∵AB是⊙O的直径,弦CD⊥AB于点M,∴DM=12CD=4cm,OM=R-2,在RT△OMD中,OD²=DM²+OM²即R²=4²+(R-2)²,解得:R=5,∴直径AB的长为:2×5=10cm.故选B.【点睛】本题考查了垂径定理以及勾股定理.注意掌握辅助线的作法及数形结合思想的应用.。
2020-2021初中数学三角形难题汇编含答案解析

2020-2021初中数学三角形难题汇编含答案解析一、选择题1.如图,□ABCD的对角线AC、BD交于点O,AE平分BAD交BC于点E,且∠ADC=60°,AB=12BC,连接OE.下列结论:①AE=CE;②S△ABC=AB•AC;③S△ABE=2S△AOE;④OE=14BC,成立的个数有()A.1个B.2个C.3个D.4【答案】C【解析】【分析】利用平行四边形的性质可得∠ABC=∠ADC=60°,∠BAD=120°,利用角平分线的性质证明△ABE是等边三角形,然后推出AE=BE=12BC,再结合等腰三角形的性质:等边对等角、三线合一进行推理即可.【详解】∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,∴AE=AB=BE,∠AEB=60°,∵AB=12 BC,∴AE=BE=12 BC,∴AE=CE,故①正确;∴∠EAC=∠ACE=30°∴∠BAC=90°,∴S△ABC=12AB•AC,故②错误;∵BE=EC,∴E为BC中点,O为AC中点,∴S△ABE=S△ACE=2 S△AOE,故③正确;∵四边形ABCD是平行四边形,∴AC=CO,∵AE=CE,∴EO⊥AC,∵∠ACE=30°,∴EO=12 EC,∵EC=12 AB,∴OE=14BC,故④正确;故正确的个数为3个,故选:C.【点睛】此题考查平行四边形的性质,等边三角形的判定与性质.注意证得△ABE是等边三角形是解题关键.2.△ABC中,∠A:∠B:∠C=1:2:3,最小边BC=4cm,则最长边AB的长为()cmA.6 B.8 C D.5【答案】B【解析】【分析】根据已知条件结合三角形的内角和定理求出三角形中角的度数,然后根据含30度角的直角三角形的性质进行求解即可.【详解】设∠A=x,则∠B=2x,∠C=3x,由三角形内角和定理得∠A+∠B+∠C=x+2x+3x=180°,解得x=30°,即∠A=30°,∠C=3×30°=90°,此三角形为直角三角形,故AB=2BC=2×4=8cm,故选B.【点睛】本题考查了三角形内角和定理,含30度角的直角三角形的性质,熟练掌握“直角三角形中30°的角所对的直角边等于斜边的一半”是解题的关键.3.如图,在▱ABCD中,E为边AD上的一点,将△DEC沿CE折叠至△D′EC处,若∠B=48°,∠ECD=25°,则∠D′EA的度数为()A.33°B.34°C.35°D.36°【答案】B【解析】【分析】由平行四边形的性质可得∠D=∠B,由折叠的性质可得∠D'=∠D,根据三角形的内角和定理可得∠DEC,即为∠D'EC,而∠AEC易求,进而可得∠D'EA的度数.【详解】解:∵四边形ABCD是平行四边形,∴∠D=∠B=48°,由折叠的性质得:∠D'=∠D=48°,∠D'EC=∠DEC=180°﹣∠D﹣∠ECD=107°,∴∠AEC=180°﹣∠DEC=180°﹣107°=73°,∴∠D'EA=∠D'EC﹣∠AEC=107°﹣73°=34°.故选:B.【点睛】本题考查了平行四边形的性质、折叠的性质、三角形的内角和定理等知识,属于常考题型,熟练掌握上述基本知识是解题关键.4.如图,折叠直角三角形纸片的直角,使点C落在AB上的点E处,已知BC=24,∠B=30°,则DE的长是()A.12 B.10 C.8 D.6【答案】C【解析】【分析】由折叠的性质可知;DC=DE,∠DEA=∠C=90°,在Rt△BED中,∠B=30°,故此BD=2ED,从而得到BC=3BC,于是可求得DE=8.【详解】解:由折叠的性质可知;DC=DE,∠DEA=∠C=90°,∵∠BED+∠DEA=180°,∴∠BED=90°.又∵∠B=30°,∴BD=2DE.∴BC=3ED=24.∴DE=8.故答案为8.【点睛】本题考查的是翻折的性质、含30°锐角的直角三角形的性质,根据题意得出BC=3DE是解题的关键.5.如图,已知AB∥CD,直线AB,CD被BC所截,E点在BC上,若∠1=45°,∠2=35°,则∠3=()A.65°B.70°C.75°D.80°【答案】D【解析】【分析】由平行线的性质可求得∠C,在△CDE中利用三角形外的性质可求得∠3.【详解】解:∵AB∥CD,∴∠C=∠1=45°,∵∠3是△CDE的一个外角,∴∠3=∠C+∠2=45°+35°=80°,故选:D.【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a∥b,b ∥c⇒a∥c.6.如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA ,BC 于点M 、N ;再分别以点M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,作射线BP 交AC 于点D ,则下列说法中不正确的是()A .BP 是∠ABC 的平分线B .AD=BDC .:1:3CBD ABD S S V V D .CD=12BD 【答案】C【解析】【分析】 A 、由作法得BD 是∠ABC 的平分线,即可判定;B 、先根据三角形内角和定理求出∠ABC 的度数,再由BP 是∠ABC 的平分线得出∠ABD =30°=∠A,即可判定;C ,D 、根据含30°的直角三角形,30°所对直角边等于斜边的一半,即可判定.【详解】解:由作法得BD 平分∠ABC ,所以A 选项的结论正确;∵∠C =90°,∠A =30°,∴∠ABC =60°,∴∠ABD =30°=∠A ,∴AD =BD ,所以B 选项的结论正确;∵∠CBD =12∠ABC =30°, ∴BD =2CD ,所以D 选项的结论正确;∴AD =2CD ,∴S △ABD =2S △CBD ,所以C 选项的结论错误.故选:C .【点睛】此题考查含30°角的直角三角形的性质,尺规作图(作角平分线),解题关键在于利用三角形内角和进行计算.7.将一个边长为4的正方形ABCD 分割成如图所示的9部分,其中ABE △,BCF V ,CDG V ,DAH V 全等,AEH △,BEF V ,CFG △,DGH V 也全等,中间小正方形EFGH 的面积与ABE △面积相等,且ABE △是以AB 为底的等腰三角形,则AEH △的面积为( )A .2B .169C .32D .2【答案】C【解析】【分析】【详解】 解:如图,连结EG 并向两端延长分别交AB 、CD 于点M 、N ,连结HF ,∵四边形EFGH 为正方形,∴EG FH =,∵ABE △是以AB 为底的等腰三角形,∴AE BE =,则点E 在AB 的垂直平分线上,∵ABE △≌CDG V ,∴CDG V 为等腰三角形,∴CG DG =,则点G 在CD 的垂直平分线上,∵四边形ABCD 为正方形,∴AB 的垂直平分线与CD 的垂直平分线重合,∴MN 即为AB 或CD 的垂直平分线,则,EM AB GN CD ^^,EM GN =,∵正方形ABCD 的边长为4,即4AB CD AD BC ====,∴4MN =,设EM GN x ==,则42EG FH x ==-,∵正方形EFGH 的面积与ABE △面积相等, 即2114(42)22x x ?-,解得:121,4x x ==, ∵4x =不符合题意,故舍去,∴1x =,则S 正方形EFGH 14122==⨯⨯=V ABE S , ∵ABE △,BCF V ,CDG V ,DAH V 全等,∴2====V V V V ABE BCF CDG DAH S S S S ,∵正方形ABCD 的面积4416=⨯=,AEH △,BEF V ,CFG △,DGH V 也全等, ∴1(4=V AEH S S 正方形ABCD − S 正方形EFGH 134)(16242)42-=⨯--⨯=V ABE S , 故选:C .【点睛】本题考查了正方形的性质、全等三角形的性质和等腰三角形的性质,解题的关键是求得ABE △的面积.8.如图,在ABC V 中,AB AC =,点E 在AC 上,ED BC ⊥于点D ,DE 的延长线交BA 的延长线于点F ,则下列结论中错误的是( )A .AE CE =B .12DEC BAC ∠=∠ C .AF AE =D .1902B BAC ∠+∠=︒ 【答案】A【解析】【分析】 由题意中点E 的位置即可对A 项进行判断;过点A 作AG ⊥BC 于点G ,如图,由等腰三角形的性质可得∠1=∠2=12BAC ∠,易得ED ∥AG ,然后根据平行线的性质即可判断B 项;根据平行线的性质和等腰三角形的判定即可判断C 项;由直角三角形的性质并结合∠1=12BAC ∠的结论即可判断D 项,进而可得答案. 【详解】 解:A 、由于点E 在AC 上,点E 不一定是AC 中点,所以,AE CE 不一定相等,所以本选项结论错误,符合题意;B 、过点A 作AG ⊥BC 于点G ,如图,∵AB =AC ,∴∠1=∠2=12BAC ∠, ∵ED BC ⊥,∴ED ∥AG ,∴122DEC BAC ∠=∠=∠,所以本选项结论正确,不符合题意;C 、∵ED ∥AG ,∴∠1=∠F ,∠2=∠AEF ,∵∠1=∠2,∴∠F =∠AEF ,∴AF AE =,所以本选项结论正确,不符合题意;D 、∵AG ⊥BC ,∴∠1+∠B =90°,即1902B BAC ∠+∠=︒,所以本选项结论正确,不符合题意.故选:A .【点睛】本题考查了等腰三角形的判定和性质、平行线的判定和性质以及直角三角形的性质等知识,属于基本题型,熟练掌握等腰三角形的判定和性质是解题的关键.9.长度分别为2,7,x 的三条线段能组成一个三角形,的值可以是( )A .4B .5C .6D .9【答案】C【解析】【分析】根据三角形的三边关系可判断x 的取值范围,进而可得答案.【详解】解:由三角形三边关系定理得7-2<x<7+2,即5<x<9.因此,本题的第三边应满足5<x<9,把各项代入不等式符合的即为答案.4,5,9都不符合不等式5<x<9,只有6符合不等式,故选C.【点睛】本题考查的是三角形的三边关系,属于基础题型,掌握三角形的三边关系是解题的关键.10.如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD 于F,交AB于G,连接EF,则线段EF的长为()A.1 B.34C.23D.12【答案】D【解析】【分析】由等腰三角形的判定方法可知△AGC是等腰三角形,所以F为GC中点,再由已知条件可得EF为△CBG的中位线,利用中位线的性质即可求出线段EF的长.【详解】∵AD是△ABC角平分线,CG⊥AD于F,∴△AGC是等腰三角形,∴AG=AC=3,GF=CF,∵AB=4,AC=3,∴BG=1,∵AE是△ABC中线,∴BE=CE,∴EF为△CBG的中位线,∴EF=12BG=12,故选:D.【点睛】此题考查等腰三角形的判定和性质、三角形的中位线性质定理,解题关键在于掌握三角形的中位线平行于第三边,并且等于第三边的一半.11.对于图形的全等,下列叙述不正确的是()A .一个图形经过旋转后得到的图形,与原来的图形全等B .一个图形经过中心对称后得到的图形,与原来的图形全等C .一个图形放大后得到的图形,与原来的图形全等D .一个图形经过轴对称后得到的图形,与原来的图形全等【答案】C【解析】A. 一个图形经过旋转后得到的图形,与原来的图形全等,正确,不符合题意;B. 一个图形经过中心对称后得到的图形,与原来的图形全等,正确,不符合题意;C. 一个图形放大后得到的图形,与原来的图形不全等,故错误,符合题意;D. 一个图形经过轴对称后得到的图形,与原来的图形全等,正确,不符合题意, 故选C.【点睛】本题考查了对全等图形的认识,解题的关键是要明确通过旋转、轴对称、平移等都可以得到与原图形全等的图形,而通过放大或缩小只能得到与原图形形状一样的图形,得不到全等图形.12.如图,在ABC ∆中,90C =o ∠,30B ∠=o ,以A 为圆心,任意长为半径画弧分别交AB 、AC 于点M 和N ,再分别以M 、N 为圆心,大于12MN 的长为半径画弧,两弧交于点P ,连结AP 并延长交BC 于点D ,则下列说法中正确的个数是( ) ①AD 是BAC ∠的平分线;②ADC 60∠=o ;③点D 在AB 的垂直平分线上;④:1:3DAC ABC S S ∆∆=A .1B .2C .3D .4【答案】D【解析】【分析】 根据题干作图方式,可判断AD 是∠CAB 的角平分线,再结合∠B=30°,可推导得到△ABD 是等腰三角形,根据这2个判定可推导题干中的结论.【详解】题干中作图方法是构造角平分线,①正确;∵∠B=30°,∠C=90°,AD 是∠CAB 的角平分线∴∠CAD=∠DAB=30°∴∠ADC=60°,②正确∵∠DAB=∠B=30°∴△ADB 是等腰三角形∴点D 在AB 的垂直平分线上,③正确在Rt △CDA 中,设CD=a ,则AD=2a在△ADB 中,DB=AD=2a ∵1122DAC S CD AC a CD ∆=⨯⨯=⨯,13(CD+DB)22BAC S AC a CD ∆=⨯⨯=⨯ ∴:1:3DAC ABC S S ∆∆=,④正确故选:D【点睛】本题考查角平分线的画法及性质、等腰三角形的性质,解题关键是熟练角平分线的绘制方法.13.如图,正方体的棱长为6cm ,A 是正方体的一个顶点,B 是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A 爬到点B 的最短路径是( )A .9B .310C .326+D .12【答案】B【解析】【分析】 将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.【详解】解:如图,AB=22(36)3310++= .故选:B .【点睛】此题求最短路径,我们将平面展开,组成一个直角三角形,利用勾股定理求出斜边就可以了.14.如图,在ABC ∆中,AB AC =,分别是以点A ,点B 为圆心,以大于12AB 长为半径画弧,两弧交点的连线交AC 于点D ,交AB 于点E ,连接BD ,若40A ∠=︒,则DBC ∠=( )A .40︒B .30︒C .20︒D .10︒【答案】B【解析】【分析】 根据题意,DE 是AB 的垂直平分线,则AD=BD ,40ABD A ==︒∠∠,又AB=AC ,则∠ABC=70°,即可求出DBC ∠.【详解】解:根据题意可知,DE 是线段AB 的垂直平分线,∴AD=BD ,∴40ABD A ==︒∠∠,∵AB AC =,∴1(18040)702ABC ∠=⨯︒-︒=︒, ∴704030DBC ∠=︒-︒=︒;故选:B.【点睛】 本题考查了垂直平分线的性质,等腰三角形的性质,以及三角形的内角和,解题的关键是熟练掌握所学的性质,正确求出DBC ∠的度数.15.如图,D 、E 分别是ABC V 边AB 、BC 上的点,2AD BD =,点E 为BC 中点,设ADF V 的面积为1S ,CEF △的面积为2S ,若ABC S =V 9,则12S S -=( )A .12B .1C .32D .2【答案】C【解析】【分析】根据12S S -=ABE BCD S S -V V ,根据三角形中线的性质及面积求解方法得到ABE S V ,BCD S △,故可求解.【详解】∵点E 为BC 中点∴ABE S V =12ABC S =V 4.5 ∵2AD BD = ∴BCD S △=13ABC S =V 3 ∵ABE BCD S S -V V =()()ADF CEF BEFD BEFD S S S S +-+V V 四边形四边形=ADF CEF S S -V V∴12S S -=4.5-3=32故选C .【点睛】此题主要考查三角形的面积求解,解题的关键是熟知中线的性质.16.如图,在ABC ∆,90C =o ∠,以A 为圆心,任意长为半径画弧,分别交AC ,AB 于点M ,N ,再分别以M ,N ,为圆心,大于12MN 长为半径画弧,两弧交于点O ,作弧线AO ,交BC 于点E .已知3CE =,5BE =,则AC 的长为( )A .8B .7C .6D .5【答案】C【解析】【分析】直接利用基本作图方法得出AE 是∠CAB 的平分线,进而结合全等三角形的判定与性质得出AC=AD ,再利用勾股定理得出AC 的长.【详解】过点E 作ED ⊥AB 于点D ,由作图方法可得出AE 是∠CAB 的平分线,∵EC ⊥AC ,ED ⊥AB ,∴EC=ED=3,在Rt △ACE 和Rt △ADE 中,AE AE EC ED ⎧⎨⎩==, ∴Rt △ACE ≌Rt △ADE (HL ),∴AC=AD ,∵在Rt △EDB 中,DE=3,BE=5,∴BD=4,设AC=x ,则AB=4+x ,故在Rt △ACB 中,AC 2+BC 2=AB 2,即x 2+82=(x+4)2,解得:x=6,即AC 的长为:6.故答案为:C .【点睛】此题主要考查了基本作图以及全等三角形的判定与性质、勾股定理等知识,正确得出BD 的长是解题关键.17.如图,已知A ,D,B,E 在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC ≌△DEF 的是( )A .BC = EFB .AC//DFC .∠C = ∠FD .∠BAC = ∠EDF【答案】C【解析】根据全等三角形的判定方法逐项判断即可.【详解】∵BE=CF,∴BE+EC=EC+CF,即BC=EF,且AC = DF,∴当BC = EF时,满足SSS,可以判定△ABC≌△DEF;当AC//DF时,∠A=∠EDF,满足SAS,可以判定△ABC≌△DEF;当∠C = ∠F时,为SSA,不能判定△ABC≌△DEF;当∠BAC = ∠EDF时,满足SAS,可以判定△ABC≌△DEF,故选C.【点睛】本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.18.如果把直角三角形的两条直角边长同时扩大到原来的2倍,那么斜边长扩大到原来的()A.1倍B.2倍C.3倍D.4倍【答案】B【解析】设原直角三角形的三边长分别是,且,则扩大后的三角形的斜边长为,即斜边长扩大到原来的2倍,故选B.19.如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是()A.BC=ED B.∠BAD=∠EACC.∠B=∠E D.∠BAC=∠EAD【答案】C【解析】解:A.∵AB=AE,AC=AD,BC=ED,∴△ABC≌△AED(SSS),故A不符合题意;B.∵∠BAD=∠EAC,∴∠BAC=∠EAD.∵AB=AE,∠BAC=∠EAD ,AC=AD,∴△ABC≌△AED(SAS),故B不符合题意;C.不能判定△ABC≌△AED,故C符合题意.D.∵AB=AE,∠BAC=∠EAD,AC=AD,∴△ABC≌△AED(SAS),故D不符合题意.20.如图11-3-1,在四边形ABCD中,∠A=∠B=∠C,点E在边AB上,∠AED=60°,则一定有()A.∠ADE=20°B.∠ADE=30°C.∠ADE=12∠ADC D.∠ADE=13∠ADC【答案】D【解析】【分析】【详解】设∠ADE=x,∠ADC=y,由题意可得,∠ADE+∠AED+∠A=180°,∠A+∠B+∠C+∠ADC=360°,即x+60+∠A=180①,3∠A+y=360②,由①×3-②可得3x-y=0,所以13x y,即∠ADE=13∠ADC.故答案选D.考点:三角形的内角和定理;四边形内角和定理.。
解三角形难题及答案

解三角形难题及答案(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--解三角形难题及答案1、在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,若B b A a sin cos =,则=+B A A 2cos cos sin ___D______A 、21- B 、21 C 、-1 D 、1 2、在ABC ∆的三个内角满足13:11:5sin :sin :sin =C B A ,则ABC ∆=_C____A 、一定是锐角三角形B 、一定是直角三角形C 、一定是钝角三角形D 、可能是锐角三角形,也可能是钝角三角形 3、ABC ∆的三内角A 、B 、C 的对边边长分别为a 、b 、c ,若b a 25=,B A 2=,则=B cos ( B )A 、35B 、45C 、55D 、65 4、在ABC ∆中,D 为BC 边上的一点,BC=3BD ,2=AD , 135=∠ADB ,若AC=AB 2,则BD=_52+_______5、在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,若C a A c b cos cos )3(=-,则=A cos ___33___ 6、设A 、B 、C 为三角形的三内角,且方程0)sin (sin )sin (sin )sin (sin 2=-+-+-B C x C A x A B 有等根,那么B ∠=___B_____A 、︒〉60B B 、︒≥60BC 、︒〈60BD 、︒≤60B 解析:0)(42222=+---+-ab ac b bc c ac a04)(4)(22=++-+b c a b c a0)2(=-+b c aac b c a 22≥=+123cos 2-=acb B1cos 21≤≤B 7、在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若C=120°,a c 2=,则()A 、b a 〉B 、b a 〈C 、a=bD 、a 与b 的大小关系不能确定5、满足A=45°,6=c ,a=2的△ABC 的个数记为m ,则m a 的值为( A )A 、4B 、2C 、1D 、不定3、在三角形ABC中,a=5,b=4,3231)cos(=-B A ,则=cos _81_____4、在△ABC 中,︒=60B ,ac b =2,则三角形的形状为____等边三角形_________1、已知△ABC三内角A、B 、C 满足B C A 2=+,B C A cos 2cos 1cos 1-=+,求2cos C A -的值。
(专题精选)初中数学三角形真题汇编及答案

(专题优选)初中数学三角形真题汇编及答案一、选择题1.如图,在V ABC中,AB AC ,A 30,直线 a ∥ b ,极点 C 在直线 b 上,直线a 交AB 于点D,交AC与点E,若1 145,则 2 的度数是()A.30°B. 35°C. 40°D. 45°【答案】 C【分析】【剖析】先依据等腰三角形的性质和三角形内角和可得ACB 度数,由三角形外角的性质可得AED 的度数,再依据平行线的性质得同位角相等,即可求得 2 .【详解】∵ AB AC,且 A 30,∴18030ACB75 ,2在ADE 中,∵1A AED145∴AED 145 A 14530115∵a// b ,,,∴AED2ACB ,即 2 1157540 ,应选: C.【点睛】本题考察综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容.等腰三角形的性质定理:等腰三角形两底角相等;三角形内角和定理:三角形三个内角的和等于180 ;三角形外角的性质:三角形的外角等于与它不相邻的两个内角之和;两直线平行,同位角相等.2.把一副三角板如图(1)搁置,此中∠ACB=∠ DEC=90°,∠ A= 45°,∠ D= 30°,斜边AB= 4, CD= 5.把三角板DCE绕着点 C 顺时针旋转15°获得△D CE(如图 2),此时 AB 与11CD 交于点 O,则线段 AD 的长度为()11A.13B.5C.22D.4【答案】 A【分析】试题剖析:由题意易知:∠CAB=45°,∠ ACD=30°.若旋转角度为15°,则∠ ACO=30°+15°=45°.∴∠ AOC=180°-∠ ACO-∠CAO=90°.在等腰 Rt△ABC中, AB=4,则 AO=OC=2.在 Rt△AOD1中, OD1=CD1-OC=3,由勾股定理得: AD1= 13.应选 A.考点 : 1.旋转; 2.勾股定理 .3.长度分别为2, 7 ,x的三条线段能构成一个三角形,的值能够是()A.4B.5C.6D.9【答案】 C【分析】【剖析】依据三角形的三边关系可判断x 的取值范围,从而可得答案.【详解】解:由三角形三边关系定理得7- 2< x< 7+2,即 5< x< 9.所以,本题的第三边应知足5<x< 9,把各项代入不等式切合的即为答案.4,5, 9 都不切合不等式5< x< 9,只有 6 切合不等式,应选 C.【点睛】本题考察的是三角形的三边关系,属于基础题型,掌握三角形的三边关系是解题的重点. 4.如图, OA= OB, OC= OD,∠ O= 50°,∠ D= 35°,则∠ OAC 等于 ()A.65°B. 95°C. 45°D. 85°【答案】 B【分析】【剖析】依据 OA= OB, OC=OD 证明△ODB≌△ OCA,获得∠ OAC=∠ OBD,再依据∠ O= 50°,∠ D=35°即可得答案 .【详解】解: OA= OB, OC=OD,在△ODB 和△OCA中,OB OABOD AOCOD OC∴△ ODB≌△ OCA( SAS) ,∠OAC=∠ OBD=180°-50 °-35 °=95°,故 B为答案.【点睛】本题考察了全等三角形的判断、全等三角形的性质,娴熟掌握全等三角形的判断与性质是解题的重点 .△ABC=7,5.AD 是△ABC中∠ BAC的均分线, DE⊥ AB 于点 E,DF⊥ AC 交 AC 于点 F. SDE=2, AB=4,则 AC长是()A.4B.3C.6D.2【答案】 B【分析】【剖析】第一由角均分线的性质可知DF=DE=2,而后由 S△ABC=S△ABD+S△ACD及三角形的面积公式得出结果.【详解】解: AD 是△ABC中∠ BAC的均分线,∠E AD=∠FADDE⊥AB 于点 E,DF⊥AC 交 AC 于点 F ,∴D F=DE,又∵ S△ABC=S△ABD+S△ACD, DE=2, AB=4,117 4 2AC 222∴A C=3.故答案为: B【点睛】本题主要考察了角均分线的性质,娴熟掌握角均分线的性质、灵巧运用所学知识是解题的重点 .6.如图,在△ABC 中, AC= BC, D、 E 分别是 AB、 AC 上一点,且AD= AE,连结 DE并延伸交 BC的延伸线于点F,若 DF= BD,则∠ A 的度数为()A.30B. 36C. 45D. 72【答案】 B【分析】【剖析】由 CA=CB,能够设∠ A=∠B=x.想方法建立方程即可解决问题;【详解】解:∵ CA=CB,∴∠ A=∠ B,设∠ A=∠B=x.∵DF=DB,∴∠B=∠F=x,∵AD=AE,∴∠ ADE=∠ AED=∠B+∠ F=2x,∴x+2x+2x=180°,∴x=36°,应选B.【点睛】本题考察等腰三角形的性质、三角形的内角和定理等知识,解题的重点是娴熟掌握基本知识,属于中考常考题型.7.如图,Y ABCD 的对角线AC 与 BD订交于点 O ,AD BD ,ABD30 ,若AD 23.则 OC 的长为()A .3B .4 3C . 21D . 6【答案】 C 【分析】 【剖析】先依据勾股定理解 Rt △ABD 求得 BD 6 ,再依据平行四边形的性质求得 OD3,而后依据勾股定理解 Rt △ AOD 、平行四边形的性质即可求得 OC OA21.【详解】解:∵AD BD∴ADB 90∵在 Rt △ABD 中, ABD 30 , AD2 3∴ AB 2AD 43∴BDAB 2 AD 26∵四边形 ABCD 是平行四边形∴ OB1 BD 3,OA OC1ODAC22∴在 Rt △ AOD 中, AD 2 3,OD3∴OAAD 2 OD 221∴OC OA 21.应选: C 【点睛】本题考察了含 30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,娴熟掌握有关知识点是解决问题的重点.8.等腰三角形两边长分别是5cm 和 11cm ,则这个三角形的周长为()A .16cmB . 21cm 或27cmC . 21cmD . 27cm【答案】 D【分析】【剖析】分两种状况议论:当5 是腰时或当 11 是腰时,利用三角形的三边关系进行剖析求解即可.【详解】解:当 5 是腰时,则 5+5<11,不可以构成三角形,应舍去;当 11 是腰时, 5+11> 11,能构成三角形,则三角形的周长是5+11×2=27cm .应选D .【点睛】本题主要考察了等腰三角形的性质, 三角形三边关系,掌握等腰三角形的性质, 三角形三边关系是解题的重点.9.如图,已知于点 E.假如点OP 均分∠ AOB,∠ AOB= 60°,CP= 2,CP∥ OA, PD⊥OA 于点M 是 OP 的中点,则DM 的长是 ()D, PE⊥ OBA.2B.2C.3D.23【答案】 C【分析】【剖析】由 OP 均分∠ AOB,∠ AOB=60°, CP=2, CP∥ OA,易得△OCP是等腰三角形,∠ COP=30°,又由含 30°角的直角三角形的性质,即可求得PE的值,既而求得 OP的长,而后由直角三角形斜边上的中线等于斜边的一半,即可求得DM 的长.【详解】解:∵ OP 均分∠ AOB,∠ AOB=60°,∴∠ AOP=∠ COP=30°,∵CP∥ OA,∴∠ AOP=∠ CPO,∴∠ COP=∠ CPO,∴OC=CP=2,∵∠ PCE=∠ AOB=60°, PE⊥OB,∴∠ CPE=30°,∴CE=1CP=1 2,∴PE=CP2CE2 3 ,∴O P=2PE=2 3,∵PD⊥ OA,点 M 是 OP 的中点,∴DM= 1OP= 3.2应选 C.考点:角均分线的性质;含30 度角的直角三角形;直角三角形斜边上的中线;勾股定理.10.如图,点O是ABC的心里,M、 N 是 AC 上的点,且 CM CB , AN AB ,若 ABC 100 ,则MON(). 60.70. 80. 100A B C D【答案】 C【分析】【剖析】BOCMOC ,AOBAON ,即∠依据题意,连结,,,从而求得CBO= OA OB OC∠CMO,∠ OBA=∠ONA,依据三角形内角和定理即可获得∠MON 的度数 .【详解】如图,连结OA,OB, OC,∵点 O是ABC 的心里,∴BCO MCO ,∵CM=CB,OC=OC,∴ BOC MOC ( SAS) ,∴CBO CMO ,同理可得:AOB AON ,∴ABO ANO ,∵CBA CBO ABO100 ,∴CMO ANO100 ,∴MON180 (CMO ANO) 80 ,应选: C.【点睛】本题主要考察了三角形全等的性质及判断,三角形的内角和定理及角度的变换,娴熟掌握有关协助线的画法及三角形全等的判断是解决本题的重点.11.如图,在V ABC中,分别以点 A 和点 B 为圆心,以同样的长(大于1 AB )为半径作2弧,两弧订交于点M 和点N,作直线MN交AB 于点D,交AC 于点E,连结CD.已知△CDE 的面积比△CDB的面积小4,则VADE 的面积为()A.4B.3C.2D.1【答案】 A【分析】【剖析】由作图步骤可知直线MN 为线段 AB 的垂直均分线,依据三角形中线的性质可得S△CDA=S△CDB,依据△CDE的面积比△CDB的面积小 4 即可得答案.【详解】由作图步骤可知直线MN 为线段 AB 的垂直均分线,∴CD 为 AB 边中线,∴S△CDA=S△CDB,∵△ CDE的面积比△CDB的面积小4,∴S△ADE=S△CDA-S△CDE=S△CDB-S△CDE=4.应选: A.【点睛】本题考察尺规作图——垂直均分线的画法及三角形中线的性质,三角形的中线,把三角形分红两个面积相等的三角形;娴熟掌握三角形中线的性质是解题重点.12.如图,11∥ l2,∠ 1= 100 °,∠ 2=135 °,则∠ 3 的度数为()A.50°B. 55°C. 65°D. 70°【答案】B【分析】【剖析】如图,延伸l 2,交∠ 1的边于一点,由平行线的性质,求得∠ 4 的度数,再依据三角形外角性质,即可求得∠ 3 的度数.【详解】如图,延伸l 2,交∠ 1 的边于一点,∵11∥ l2,∴∠ 4= 180°﹣∠ 1=180°﹣100°=80°,由三角形外角性质,可得∠2=∠ 3+∠ 4,∴∠ 3=∠ 2﹣∠ 4= 135°﹣ 80°= 55°,应选 B.【点睛】本题考察了平行线的性质及三角形外角的性质,娴熟运用平行线的性质是解决问题的重点.13.如图,在Rt ABC中,BCA 90, CD是高, BE均分∠A BC交 CD 于点 E,EF∥ AC 交 AB 于点 F,交 BC 于点 G.在结论: (1)EFD BCD ;(2)AD CD ;(3) CG = EG; (4) BF BC中,必定建立的有 ()A.1 个B.2 个C.3 个D.4 个【答案】 B【分析】【剖析】依据两直线平行,同旁内角互补求出∠CGE=∠ BCA=90°,而后依据等角的余角相等即可求出∠ EFD=∠BCD;只有△ABC 是等腰直角三角形时AD=CD, CG=EG;利用“角角边”证明△BCE 和△BFE全等,而后依据全等三角形对应边相等可得BF=BC.【详解】∵EF∥ AC,∠ BCA=90°,∴∠ CGE=∠ BCA=90°,∴∠ BCD+∠CEG=90°,又∵ CD是高,∴∠ EFD+∠FED=90°,∵∠ CEG=∠ FED(对顶角相等),∴∠ EFD=∠BCD,故( 1)正确;只有∠ A=45°,即△ABC是等腰直角三角形时,AD=CD, CG=EG而立,故( 2)( 3)不必定建立,错误;∵BE 均分∠ ABC,∴∠ EBC=∠EBF,在△BCE和△BFE中,EFD=BCDEBC=EBF ,BE=BE∴△ BCE≌△ BFE( AAS),∴BF=BC,故( 4)正确,综上所述,正确的有(1)( 4)共 2 个.应选: B.【点睛】本题主要考察了角均分线的性质,全等三角形的判断与性质,直角三角形的性质,等腰直角三角形的性质,综合题,但难度不大,熟记性质是解题的重点.14.如图,在平面直角坐标系中,等腰直角三角形ABC 的极点A 、B分别在x轴、 y 轴的正半轴上, ABC90 ,CA x 轴,点 C 在函数y k x0 的图象上,若xAB 1,则 k 的值为()A.1B.22D. 2C.2【答案】 A【分析】【剖析】依据题意能够求得OA 和 AC的长,从而能够求得点 C 的坐标,从而求得k 的值,本题得以解决.【详解】Q 等腰直角三角形ABC 的极点 A 、B分别在x轴、 y 轴的正半轴上,ABC 90 ,CA ⊥x 轴,AB1,BAC BAO 45 ,OA OB2,AC 2,2点 C 的坐标为 2 ,2,2Q 点C在函数 y k x0的图象上,xk21 ,22应选: A.【点睛】本题考察反比率函数图象上点的坐标特点、等腰直角三角形,解答本题的重点是明确题意,利用数形联合的思想解答.15.如图 11-3-1,在四边形 ABCD中,∠ A=∠ B=∠ C,点 E 在边 AB 上,∠ AED=60°,则必定有()AADE=20°BADE=30°1∠ADC D ADE=1∠ADCCADE=.∠.∠.∠.∠32【答案】 D【分析】【剖析】【详解】设∠ ADE=x,∠ ADC=y,由题意可得,∠ADE+∠AED+∠ A=180°,∠ A+∠ B+∠C+∠ADC=360°,即 x+60+∠ A=180①, 3∠ A+y=360②,由①×3-②可得 3x-y=0,所以 x1y ,即∠ADE=1∠ ADC.33故答案选D.考点:三角形的内角和定理;四边形内角和定理.16.如图,⊙ O 过点 B、 C,圆心 O 在等腰直角△ABC的内部,∠ BAC=90°, OA= 1, BC=6,则⊙ O 的半径为()A.23B.13C.4D.32【答案】 B【分析】【剖析】以以下图,作 AD⊥ BC,设半径为 r,则在 Rt△OBD中, OD=3- 1, OB=r, BD=3,利用勾股定理可求得 r.【详解】如图,过 A 作 AD⊥ BC,由题意可知AD 必过点 O,连结 OB;∵△ BAC是等腰直角三角形,AD⊥ BC,∴B D=CD=AD=3;∴O D=AD-OA=2;Rt△OBD 中,依据勾股定理,得:OB=BD2OD213故答案为: B.【点睛】本题考察了等腰直角三角形的性质和勾股定理的应用,解题重点是利用等腰直角三角形ABC判断点 O 在 AD 上.17.如图,四边形ABCD 和EFGH都是正方形,点E,H在AD, CD 边上,点F, G 在对角线AC 上,若AB 6 ,则EFGH的面积是()A.6B.8C.9D.12【答案】 B【分析】【剖析】依据正方形的性质获得∠DAC=∠ ACD= 45°,由四边形EFGH是正方形,推出△AEF与△DFH是等腰直角三角形,于是获得DE=2EH=2EF, EF=2AE,即可获得结论.222【详解】解:∵在正方形ABCD中,∠ D=90°,AD= CD= AB,∴∠ DAC=∠ DCA= 45°,∵四边形EFGH为正方形,∴EH= EF,∠ AFE=∠ FEH= 90°,∴∠ AEF=∠ DEH=45°,∴A F= EF, DE= DH,∵在 Rt△AEF中, AF2+EF2=AE2,∴AF= EF=2AE,2同理可得: DH= DE=2EH 2又∵ EH=EF,∴DE=2EF= 2 × 21AE= AE,2222∵AD= AB=6,∴DE=2, AE= 4,∴EH= 2 DE=2 2 ,∴EFGH 的面积为EH2=(22)2=8,应选: B.本题考察了正方形的性质,等腰直角三角形的判断及性质以及勾股定理的应用,娴熟掌握图形的性质及勾股定理是解决本题的重点.18.以下条件中,不可以判断一个三角形是直角三角形的是()A.三条边的比为 2∶ 3∶4B.三条边知足关系 a2= b2﹣ c2C.三条边的比为 1∶ 1∶2D.三个角知足关系∠ B+∠ C=∠ A 【答案】 A【分析】【剖析】依据直角三角形的判断方法,对选项进行一一剖析,清除错误答案.【详解】2 2 2,故不可以判断一个三角形是直角三角形;A、三条边的比为 2: 3:4, 2 +3 ≠4B、三条边知足关系a2=b2-c2,即 a2 +c2=b2,故能判断一个三角形是直角三角形;C、三条边的比为1: 1: 2 ,12+12=(2)2,故能判断一个三角形是直角三角形;D、三个角知足关系∠B+∠C=∠A,则∠ A 为 90°,故能判断一个三角形是直角三角形.应选: A.【点睛】本题考察勾股定理的逆定理的应用.解题重点在于掌握判断三角形能否为直角三角形,已知三角形三边的长,只需利用勾股定理的逆定理加以判断即可;若已知角,只需求得一个角为 90°即可.19.如图,经过直线AB 外一点 C 作这条直线的垂线,作法以下:(1)随意取一点 K,使点 K 和点 C 在 AB 的两旁.(2)以点 C 为圆心, CK长为半径作弧,交 AB 于点 D 和 E.1 DE 的长为半径作弧,两弧订交于点F.(3)分别以点 D 和点 E 为圆心,大于2(4)作直线CF.则直线 CF就是所求作的垂线.依据以上尺规作图过程,若将这些点作为三角形的极点,其中不必定是等腰三角形的为()...A.△CDF B.△CDK C.△CDE D.△DEF【答案】 A【剖析】依据作图过程和等腰三角形的定义进行剖析即可.【详解】由作图过程可得:CD=CD,DF=EF,CD=CK所以,是等腰三角形的有△CDK,△CDE,△DEF;△CDF不必定是等腰三角形.应选: A【点睛】查核知识点:等腰三角形.理解等腰三角形的定义是重点.20.以下长度的三根小木棒能构成三角形的是()A.2cm ,3cm ,5cm B. 7cm, 4cm, 2cm C. 3cm, 4cm ,8cm D. 3cm, 3cm ,4cm 【答案】D【分析】【详解】A.由于2+3=5,所以不可以构成三角形,A 错误;故B 错误;B.由于2+4< 6,所以不可以构成三角形,故C.由于3+4< 8,所以不可以构成三角形,C 错误;故D.由于3+3> 4,所以能构成三角形,故 D 正确.应选D.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴E′在AD上,且E′是AD的中点,
∵AD=AB,
∴AE=AE′,
∵F是BC的中点,
∴E′F=AB=5.
故选C.
10.如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )
A.4B.5C.6D.7
【答案】C
【解析】
【分析】
先根据菱形的性质求出其边长,再作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,再根据菱形的性质求出E′F的长度即可.
【详解】
解:如图
∵四边形ABCD是菱形,对角线AC=6,BD=8,
∴AB= =5,
作E关于AC的对称点E′,连接E′F,则E′F即为PE+PF的最小值,
A. B.1C. D.2
【答案】C
【解析】
【分析】
根据 ,根据三角形中线的性质及面积求解方法得到 , ,故可求解.
【详解】
∵点 为 中点
∴ = 4.5
∵
∴ =睛】
此题主要考查三角形的面积求解,解题的关键是熟知中线的性质.
13.下列几组线段中,能组成直角三角形的是()
6.如图,在 中, ,将 沿直线 翻折,点 落在点 的位置,则 的度数是()
A. B. C. D.
【答案】D
【解析】
【分析】
由折叠的性质得到∠D=∠B,再利用外角性质即可求出所求角的度数.
【详解】
解:如图,由折叠的性质得:∠D=∠B=33°,
根据外角性质得:∠1=∠3+∠B,∠3=∠2+∠D,
∴∠1=∠2+∠D+∠B=∠2+2∠B=∠2+66°,
A.4B.8C.6D.10
【答案】B
【解析】
【分析】
【详解】
解:设AG与BF交点为O,∵AB=AF,AG平分∠BAD,AO=AO,∴可证△ABO≌△AFO,∴BO=FO=3,∠AOB=∠AOF=90º,AB=5,∴AO=4,∵AF∥BE,∴可证△AOF≌△EOB,AO=EO,∴AE=2AO=8,故选B.
(专题精选)初中数学三角形难题汇编及答案
一、选择题
1.如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD,则∠CAD的度数是( )
A.20°B.30°C.45°D.60°
【答案】B
【解析】
【分析】
根据内角和定理求得∠BAC=60°,由中垂线性质知DA=DB,即∠DAB=∠B=30°,从而得出答案.
∴DE= ,
故选D.
【点睛】
本题考查了等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)、勾股定理和三角形的面积,能求出AD的长是解此题的关键.
5.如图,在 中, 的垂直平分线交 于 , 的中垂线交 于 , ,则 的度数为( )
A. B. C. D.
【答案】D
【解析】
【分析】
17.如图,已知AC=FE,BC=DE,点A,D,B,F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是()
A.AD=FBB.DE=BDC.BF=DBD.以上都不对
【答案】A
【解析】
∵AC=FE,BC=DE,
∴要利用“SSS”证明△ABC≌△FDE,需添加条件“AB=DF”或“AD=BF”.
∴∠1-∠2=66°.
故选:D.
【点睛】
此题考查了翻折变换以及三角形外角性质的运用,熟练掌握折叠的性质是解本题的关键.折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
7.如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为( )
【解析】
【分析】
根据题意画出图形,利用勾股定理解答即可.
【详解】
设AC=b,BC=a,分别在直角△ACE与直角△BCD中,根据勾股定理得到:
两式相加得:
根据勾股定理得到斜边
故选:D.
【点睛】
考查勾股定理,画出图形,根据勾股定理列出方程是解题的关键.
15.如图,AD∥BC,∠C =30°,∠ADB:∠BDC= 1:2,则∠DBC的度数是( )
A. B. C. D.
【答案】D
【解析】
【分析】
连接AD,根据已知等腰三角形的性质得出AD⊥BC和BD=6,根据勾股定理求出AD,根据三角形的面积公式求出即可.
【详解】
解:连接AD
∵AB=AC,D为BC的中点,BC=12,
∴AD⊥BC,BD=DC=6,
在Rt△ADB中,由勾股定理得:AD= ,
∵S△ADB= ×AD×BD= ×AB×DE,
【详解】
在△ABC中,∵∠B=30°,∠C=90°,
∴∠BAC=180°-∠B-∠C=60°,
由作图可知MN为AB的中垂线,
∴DA=DB,
∴∠DAB=∠B=30°,
∴∠CAD=∠BAC-∠DAB=30°,
故选B.
【点睛】
本题主要考查作图-基本作图,熟练掌握中垂线的作图和性质是解题的关键.
2.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为()
【答案】B
【解析】
试题解析:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC,连接DC′,交AB于P,连接CP.
此时DP+CP=DP+PC′=DC′的值最小.∵DC=1,BC=4,∴BD=3,连接BC′,由对称性可知∠C′BE=∠CBE=45°,∴∠CBC′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=4,根据勾股定理可得DC′= = =5.故选B.
根据线段垂直平分线的性质得到DA=DB,EA=EC,在由等边对等角,根据三角形内角和定理求解.
【详解】
如图所示:
∵DM是线段AB的垂直平分线,
∴DA=DB, ,
同理可得: ,
∵ , ,
∴
∴
故选:D
【点睛】
本题考查了线段的垂直平分线和三角形的内角和定理,解题的关键是掌握线段垂直平分线上的点到线段两端的距离相等.
故选:C
【点睛】
本题考查直角三角形的判定,常见方法有2种;
(1)有一个角是直角的三角形;
(2)三边长满足勾股定理逆定理.
9.如图,在菱形ABCD中,对角线AC=8,BD=6,点E,F分别是边AB,BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
A.3B.4C.5D.6
A.三个角度之比为1:2:3的三角形B.三个边长之比为3:4:5的三角形
C.三个边长之比为8:16:17的三角形D.三个角度之比为1:1:2的三角形
【答案】C
【解析】
【分析】
三角形内角和180°,根据比例判断A、D选项中是否有90°的角,根据勾股定理的逆定理判断B、C选项中边长是否符合直角三角形的关系.
D. ,故不能组成直角三角形;
故选C.
【点睛】
本题主要考查了勾股定理的逆定理(如果三角形两边的平方等于第三边的平方,那么这个三角形是直角三角形),掌握勾股定理的逆定理是解题的关键.
14.在直角三角形中,自锐角顶点引的两条中线为 和 ,则这个直角三角形的斜边长是( )
A.3B.2 C.2 D.6
【答案】D
【详解】
A中,三个角之比为1:2:3,则这三个角分别为:30°、60°、90°,是直角三角形;
D中,三个角之比为1:1:2,则这三个角分别为:45°、45°、90°,是直角三角形;
B中,三边之比为3:4:5,设这三条边长为:3x、4x、5x,满足: ,是直角三角形;
C中,三边之比为8:16:17,设这三条边长为:8x、16x、17x, ,不满足勾股定理逆定理,不是直角三角形
A.1B.2C.3D.4
【答案】C
【解析】
【分析】
由题意可知:中间小正方形的边长为a﹣b,根据勾股定理以及题目给出的已知数据即可求出小正方形的边长.
【详解】
解:由题意可知:中间小正方形的边长为:a﹣b,
∵每一个直角三角形的面积为: ab= ×8=4,
故选A.
18.如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D,若AD=5cm,CD=3cm,则点D到AB的距离DE是()
A.5cmB.4cmC.3cmD.2cm
【答案】C
【解析】
∵点D到AB的距离是DE,
∴DE⊥AB,
∵BD平分∠ABC,∠C =90°,
∴把Rt△BDC沿BD翻折后,点C在线段AB上的点E处,
∴∠1=∠2,∠3=∠4,
∠ACE=∠A+∠ABC,
即∠1+∠2=∠3+∠4+∠A,
∴2∠1=2∠3+∠A,
∵∠1=∠3+∠D,
∴∠D= ∠A= ×30°=15°.
故选A.
【点睛】
点评:本题考查了三角形内角和定理,关键是根据三角形内角和是180°和三角形外角性质进行分析.
8.下列说法不能得到直角三角形的()
A.30°B.36°C.45°D.50°
【答案】D
【解析】
【分析】
直接利用平行线的性质得出∠ADC=150°,∠ADB=∠DBC,进而得出∠ADB的度数,即可得出答案.
【详解】
∵AD∥BC,∠C=30°
∴∠ADC=150°,∠ADB=∠DBC
∵∠ADB:∠DBC=1:2
∴∠ADB= ×150°=50°,故选D.
