《花边有多宽》PPT课件
合集下载
九年级数学上册2.1《花边有多宽》课件 北师大版

(A)0<x<1
(B)1<x<2
(C)2<x<3
(D)3<x<4
【解析】选B.∵当x=1时,x2-x-1=-1<0,
当x=2时x2-x-1=1>0,
∴方程x2-x-1=0的正数根的范围是1<x<2.
3.根据关于x的一元二次方程x2+px+q=0,可列表如下:
则方程x2+px+q=0的正数解满足( ) (A)解的整数部分是0,十分位是5 (B)解的整数部分是0,十分位是8 (C)解的整数部分是1,十分位是1 (D)解的整数部分是1,十分位是2
列表计算
所以1<x<2.进一步列表计算
所以1.5<x<1.6.进一步列表计算
所以x可取近似值1.57. 所以会议室四周留空宽度约为1.57 m.
8.(8分)已知m是方程x2-2 010x+1=0的一个根,求m2-
2 010m+ 2 010m 的值.
m2 1
【解析】∵m是方程x2-2 010x+1=0的一个根,
(1)到3月3日一共贴了多少枚? (2)当此同学在某一天贴了144枚时,是3月几日? (3)若3月1日、3月2日像图④⑤那样贴,当贴的总数是483 枚时,是3月几日? 【解析】(1)25枚 (2)设是3月n日,根据规律,得8(n-1)=144,n=19,所以 是3月19日. (3)设是3月n日,根据规律,得(2n-1)(2n+1)=483, 即:4n2-1=483,∴4n2=484,n2=121, 显然n=11.所以是3月11日.
(D)x2-65x-350=0
【解析】选B.∵金色纸边的宽为x cm, ∴整个挂图的长为(80+2x)cm, 宽为(50+2x)cm, 由题意得(80+2x)(50+2x)=5 400, 整理得x2+65x-350=0.
花边有多宽 PPT课件 5 北师大版

•
52、思想如钻子,必须集中在一点钻下去才有力量。
•
53、年少时,梦想在心中激扬迸进,势不可挡,只是我们还没学会去战斗。经过一番努力,我们终于学会了战斗,却已没有了拼搏的勇气。因此,我们转向自身,攻击自己,成为自己最大的敌人。
•
54、最伟大的思想和行动往往需要最微不足道的开始。
•
55、不积小流无以成江海,不积跬步无以至千里。
•
25、世上最累人的事,莫过於虚伪的过日子。
•
26、事不三思终有悔,人能百忍自无忧。
•
27、智者,一切求自己;愚者,一切求他人。
•
28、有时候,生活不免走向低谷,才能迎接你的下一个高点。
•
29、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。
•
30、经验是由痛苦中粹取出来的。
•
31、绳锯木断,水滴石穿。
如果设花边的宽为xm,那么地毯中央长方 形图
案的长为 据题
m,宽为
m,根
意,可列方程:
实例1图解
可变为
5cm
5cm
8cm
8cm
实例2
观察下面等式:
102+112+122=132+142
如果设五个连续整数的第一个数为x,那么后
面的四个数依次为 ,。
,
,
根据题意,可得方程:
实例3
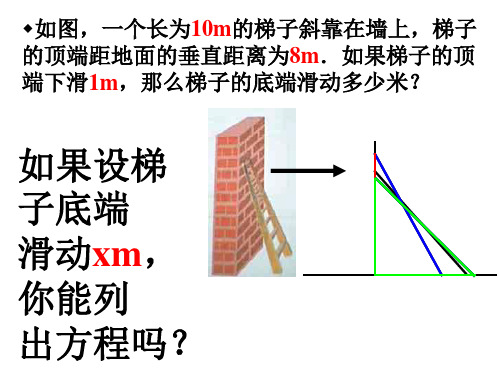
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距 地面的垂直距离为8m.如果梯子的顶端下滑1m,那 么梯子的底端滑动多少米?
五、归纳小结,反思提高
理解了一元二次方程的概念,记住一元二次 方程成立的条件,根据概念能够判断一元 二次方程。
能够准确找出一元二次方程的二次项、一次 项、常数项,以及二次项、一次项的系数。
(1)2.1花边有多宽14精品PPT课件

Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
。
合作学习4 思考2′交流2′展示2′ 1分
自学P48页的议一议,思考: 1、观察:(8 2x)(5 2x) 18;(x 6)2 72 102;
x2 (x 1)2 (x 2)2 (x 3)2 (x 4)2, 这三个方程有什么特点?
提示:从未知数、方程左右两边的式子、整理后的形
式三方面说。
一般形式ax2+bx+c=0(a,b,c为常数,
a≠0)和有关概念,如二次项、一次项、常 数项、二次项系数、一次项系数.
• 2.会用一元二次方程表示实际生活中的数 量关系
• 你准备如何去求方程中的未知数呢?
提问与解答环节
Questions And Answers
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
2、什么叫一元二次方程?
3、一元二次方程的一般形式表示为:
,
二次项, 一次项, 常数项, 分别
称为二次项系数和一次项系数。
特点: 1、只含有一个未知数。 2、方程左右两边都是整式。 3、化简后含有未知数的最高指数为2次。
一元二次方程:只含有一个未知数 x 的整式方程,并
且都可以化成 ax2 bx c 0(a、b、c为常数的a 0)
第二章 一元二次方程
花边有多宽
三峡初中:张宗兰
学习目标
1、通过实例,体会到一元二次方程是刻画现实世界 中数量关系的有效数学模型。
2、理解一元二次方程的概念,并能正确的判断一个 方程是不是一元二次方程。
。
合作学习4 思考2′交流2′展示2′ 1分
自学P48页的议一议,思考: 1、观察:(8 2x)(5 2x) 18;(x 6)2 72 102;
x2 (x 1)2 (x 2)2 (x 3)2 (x 4)2, 这三个方程有什么特点?
提示:从未知数、方程左右两边的式子、整理后的形
式三方面说。
一般形式ax2+bx+c=0(a,b,c为常数,
a≠0)和有关概念,如二次项、一次项、常 数项、二次项系数、一次项系数.
• 2.会用一元二次方程表示实际生活中的数 量关系
• 你准备如何去求方程中的未知数呢?
提问与解答环节
Questions And Answers
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
2、什么叫一元二次方程?
3、一元二次方程的一般形式表示为:
,
二次项, 一次项, 常数项, 分别
称为二次项系数和一次项系数。
特点: 1、只含有一个未知数。 2、方程左右两边都是整式。 3、化简后含有未知数的最高指数为2次。
一元二次方程:只含有一个未知数 x 的整式方程,并
且都可以化成 ax2 bx c 0(a、b、c为常数的a 0)
第二章 一元二次方程
花边有多宽
三峡初中:张宗兰
学习目标
1、通过实例,体会到一元二次方程是刻画现实世界 中数量关系的有效数学模型。
2、理解一元二次方程的概念,并能正确的判断一个 方程是不是一元二次方程。
花边有多宽(1)课件(北师大版年级上) 公开课获奖课件
高考总分:711分 毕业学校:北京八中 语文139分 数学140分 英语141分 理综291分 报考高校:
北京大学光华管理学院
北京市理科状元杨蕙心
班主任 孙烨:杨蕙心是一个目标高远 的学生,而且具有很好的学习品质。学 习效率高是杨蕙心的一大特点,一般同 学两三个小时才能完成的作业,她一个 小时就能完成。杨蕙心分析问题的能力 很强,这一点在平常的考试中可以体现。 每当杨蕙心在某科考试中出现了问题, 她能很快找到问题的原因,并马上拿出 解决办法。
解:如果设花边的宽为xm ,那么地毯中央长方 (8-2x) 形图案的长为 m,宽为(5-2x)m,根据题 (8 - 2x) (5 - 2x) = 18. 意,可得方程: 8
数学化
x
x
(8-2x)
x
18m2
5
x
你能化简这个方程吗?
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的 垂直距离为8m.如果梯子的顶端下滑1m,那么梯子的底端滑 动多少米? 解:由勾股定理可知, 滑动前梯子底端距墙 m. 6 如果设梯子底端滑动 X m,那么滑动后梯子 底端距墙 x+6 m; 根据题意,可得方程: 数学化 1m 8m
“用好课堂40分钟最重要。我的经验是,哪怕 是再简单的内容,仔细听和不上心,效果肯 定是不一样的。对于课堂上老师讲解的内容, 有的同学觉得很简单,听讲就不会很认真, 但老师讲解往往是由浅入深的,开始不认真, 后来就很难听懂了;即使能听懂,中间也可 能出现一些知识盲区。高考试题考的大多是 基础知识,正就是很多同学眼里很简单的内 容。”常方舟告诉记者,其实自己对竞赛试 题类偏难的题目并不擅长,高考出色的原因 正在于试题多为基础题,对上了自己的“口 味”。
曹杨二中高三(14)班学生 班级职务:学习委员 高考志愿:北京 大学中文系 高考成绩:语文121分数学146分 英语146分历史134分 综合28分总分 575分 (另有附加分10 分)
花边有多宽 北师大版(PPT)2-2
•
•
今日本色在此癫,无人过眼无人厌。 我笑他人伤醉酒,何不学我来发癫。 一笑无人回我语,二笑我心已癫狂。 今夜寒风呼啸,北国风雪飘飘。 顿时举国上下,美梦睡中突醒。 风呼啸,鸡飞狗跳。 一曲清幽,一夜无眠。 万里山水,数亿生灵,尽皆殆灭。 一夜癫狂后清醒,人生能得几回癫。 今朝痛楚随疯去,明日依旧笑人生。 三笑放下心中事,四笑心静如止水。 天降倾盆大雨,地落涛涛江水。 我独一人望月 雨嚎嚎,乱水成荒。 天初晓,鸡鸣不在;日初升,生机不存。 此世独我存!心孤寥,人已亡。
如图,一个长为10m的梯子斜靠在墙上,梯子 的顶端距地面的垂直距离为8m.如果梯子的顶 端下滑1m,那么梯子的底端滑动多少米?
如果设梯 子底端 滑动xm, 你能列 出方程吗?
你能找到五个连续 整数,使前三个数 的平方和等股票入门基础知识 股票入门基础知识
•
北师大版数学花边有多宽课件 优质课件

个解.
0 ≤ x ≤2.5
x
01 2
2x2 –13x+11
11 0 -7
当x=1时,2x2 –13x+11=0 ,
所以方程的解为x=1
若在x许可的范围内取整数值, 没有一个数能够使方程的左边等于0怎么办?
练习1
(x+6)²+7 ²=10²
7m
10m
一化简: x²+12x-15 =0
X+6 二:X的大致范围 是1 < x <2 ,整数部分是1 三:保留整数部分不变,从0.1取到0.9找十分位
教学目标: 1会根据题意列一元二次方程。 2会探索一元二次方程的解或近似解。
教学重点: 1正确的列出一元二次方程 2探索一元二次方程的解或近似解。
1一元二次方程的定义
经过变形后,只含有一个未知数,并且未知数的次数 是二次,这样的整式方程叫一元二次方程
2一元二次方程的一般形式:
ax2+bx+c=0 (a≠0 ,a,b,c 为常数 )
x(15 -x)=54
(2) x表示长方形的实际宽,不可能小于0 (3)不可能,因为长与宽的和是15, x可能大于15.
一个长方形的周长为30厘米,面积为54厘米,设长为x厘米 (1)根据题意列方程。 (2)x可能小于0吗?说出理由. (3)x可能大于15吗?说出理 (4)能否想一个办法求得长方形的长x?
化成一般形式为: x2 -3x+2=0
根据题意得x的范围是:0 < x ≤ 6
x
x2 -3x+2
12 3 456
0 0 2 6 12 20
x =1 或 x=2 当x =1 时这个两位数是15
花边有多宽(一)演示文稿16页PPT

42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
花边有多宽(一)演示文稿
46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法பைடு நூலகம்兹
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
花边有多宽(一)演示文稿
46、法律有权打破平静。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法பைடு நூலகம்兹
北师大数学九上花边有多宽课件

(3)关于x的方程(k-3)x2 + 2x-1=0,当k ≠3 时,是一元二次方程。 ___
(4)关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,当k ≠±1 时,是一元二次方程, 当k =-1 时,是一元一次方程。
生活中的数学
如图,一个长为10m的梯子斜靠在墙上,梯子的 顶端距地面的垂直距离为8m.如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米? 解:由勾股定理可知, 滑动前梯子底端距墙 6 m. 如果设梯子底端滑动x m,那么滑动后梯子 底端距墙 x+6 m; 根据题意,可得方程:
设花边的宽为xm,那么地 毯中央长方形图案的长为 (8-2x) ,宽为______m (5-2x) , ______m 依题意得 (8-2x)(5-2x)=18 _____________
俄罗斯一位著名的画家威尔 斯特有一幅名画,画名叫“难 题”。在画面上画着一块黑板, 上面有一道难题:口算:
10 11 12 13 14 =2 365
义务教育课程标准实验教科书(北师大版)
花边有多宽
讲授:谭杰中 单位:中国工程与物理研究院科学城一中 (国家级示范高中)
本周末,举办 什么活动好呢?
开个舞会吧!
用彩灯装扮一个长为16米,宽为10米的长 方形舞池,在舞池四周做上相同宽度的彩灯花边, 若要使得舞池中央长方形空地的面积为112平方 米,那么花边的宽度该如何确定呢?
x2 + (x+1)2 + (x+ 2)2 = (x+3)2 + (x+4)2
合作探究 知识整合 课后实践
从前有一天,一个醉汉拿着竹竿进屋,横拿 竖拿都进不去,横着比门框宽4尺,竖着比门框 高2尺,另一个醉汉教他沿着门的两个对角斜着 拿竿,这个醉汉一试,不多不少刚好进去了.你 知道竹竿有多长吗?请根据这一问题列出方程.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. 2
B. 3
C. 4
D. 5
精选课件ppt
10
2、下列方程哪些是一元二次方程?
(1) x 2 9
2 (2) x2 x 5
(3)2 x 2 5xy 6 y 2 0
(4) y 2 0 (5)x2 2 x 3 1 x2 2
(6) 2x x2 1 0
精选课件ppt
11
合作交流
由勾股定理得,滑动前梯子底端距墙 6 m,
设底端滑动x m,那么滑动后底端距墙 (x 6) m,
根据题意,得方程:(x 6)2 (8 1)2 102.
精选课件ppt
6
将下列三个方程进行变形:
(8 2x)(5 2x) 18 2x2 13x 11 0 x2 (x 1)2 (x 2)2 (x 3)2 (x 4)2 x2 8x 11 0 (x 6)2 (8 1)2 102 x2 12x 15 0
(2)三个连续整数两两相乘,再求和,结果为 242,这三个数分别是多少?
精选课件ppt
18
巩固练习
4、从前有一个醉汉拿着竹竿进屋,横拿竖拿都 进不去,横着比门框宽4尺,竖着比门框高2尺。 另一个醉汉教他沿着门的两个对角斜着拿杆,这 个醉汉一试,不多不少刚好进去了。你知道竹竿 有多长吗?
精选课件ppt
ax2是二次项, a为二次项系数; bx是一次项, b为一次项数; c是常数项。
精选课件ppt
13
1、关于x的方程(k-3)x2 + 2x-1=0,当k _≠_3_ 时,是一元二次方程.
2、关于x的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k ≠±1 时,是一元二次方程.,当k =-1 时,
2.1 花边有多宽(1)
精选课件ppt
1
1、什么是方程?举例说明。
2、方程3x+7=9是什么方程?
3、你学过哪些方程?
4、方程3x2+7x=9与上面的方程相
同吗?
精选课件ppt
2
一长方形图案的面积为18m2, 求花边有多宽?
ⅲ、观察下列三个方程:
2x2 13x 11 0
x2 8x 11 0
ax2 bx c 0
x2 12x 15 0
一元二次方程的一般式
精选课件ppt
12
新知归纳
一元二次方程的相关概念: (1)一元二次方程的一般式:
ax2+bx+c=0 (a、b、c为常数,a≠0) (2)一元二次方程的组成:
只含有一个未知数x的整式方程,并且都可 以化成ax2+bx+c=0(a、b、c为常数,a≠0)的形式, 这样的方程叫做一元二次方程。
精选课件ppt
9
巩固练习
1、下列方程中,一元二次方程有( )个
(1)x2 3 (2)5x2 3(x 1)
(3) 1 x x
(4) 1 x x2 5 (5)5x2 2x 5(x 2)(x 1) 4
19
选做题: ①已知关于x的方程
(k2-1)x2+2(k-1)x+2k+2=0
当k_______时,它是一元二次方程, 此时各项系数分别为
__________________ 当k_______时,它是一元一次方程。
精选课件ppt
20
课堂小结
1、一元二次方程的定义: 只含有一个未知数x的整式方程,并且都可
精选课件ppt
21
常数项
3x2 5x1
(x2)x(1)6
47x2 0
精选课件ppt
16
范例讲解
例2、根据题意列出方程:已知直角三角形的三 边长为连续整数,求它的三边长。
精选课件ppt
17
巩固练习 3、根据题意,列出方程:
(1)有一面积为54m2的长方形,将它的一边剪短 5m,另一边剪短2m,恰好变成一个正方形,这 个正方形的边长是多少?
是一元一次方程.
精选课件ppt
14
范例讲解
例1、把方程 (3x2)24(x3)2化成一元二次方
程的一般形式,并写出它的二次项系数、一次项 系数和常数项。
精选课件ppt
15
巩固练习
2、把下列方程化成一元二次方程的一般形式, 并写出它的二次项系数、一次项系数和常数项:
方程
一般形 式
二次项 系数
一次项 系数
精选课件ppt
3
设花边的宽为x m ,那么地毯中央长方 形图案的长为 (8-2x)m,宽为 (5-2x)m, 根据题意,可得方程:(8 - 2x) (5 - 2x) = 18.
(8-2x)
(5-2x) 18m2
精选课件ppt
4
观察下面等式:
102 112 122 132 142
你还能找到其他的五个连续整数,使前三个 数的平方和等于后两个数的平方和吗?
精选课件ppt
7
观察下列三个方程:
2x2 13x 11 0 x2 8x 11 0 x2 12x 15 0
它们有什么共同特点? 1、只含有一个未知数; 2、都是整式方程;
3、都可以化成 ax2 bx c 0的形式;
a、b、精c选为课件常ppt 数,a≠0
8
新知归纳
一元二次方程的定义:
设五个连续整数中第一个为x ,那么后四个
数为 (x 1) 、(x 2)、(x 3)、(x 4),根据题意,
得方程:x2 (x 1)2 (x 2)2 (x 3)2 (x 4)2.
精选课件ppt
5
一个长为10m的梯子些靠在墙上,梯子的顶 端距底面的垂直距离为8m。如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
以化成ax2+bx+c=0(a、b、c为常数,a≠0)的形式, 这样的方程叫做一元二次方程。
2、一元二次方程的相关概念:
(1)一元二次方程的一般式: ax2+bx+c=0(a、b、c为常数,a≠0)
(2)一元二次方程的组成:
ax2是二次项, a为二次项系数;
bx是一次项, b为一次项系数;
c是常数项。
