4时间序列参数估计
简述时间序列预测的步骤

简述时间序列预测的步骤
时间序列预测的步骤通常包括以下几个方面:
1. 数据收集与预处理:收集时间序列数据,并进行预处理,如处理缺失值、异常值、平滑数据等。
2. 可视化与探索性分析:对时间序列数据进行可视化,包括绘制时间序列图、自相关图、偏自相关图等,以便了解数据的趋势、季节性、周期性等特征。
3. 模型选择和参数估计:根据数据的特点选择合适的时间序列模型,如ARIMA、ARMA、AR、MA等模型,并通过最大似然估计、最小二乘估计等方法估计模型的参数。
4. 模型诊断与改进:对所选模型进行诊断,包括检验模型的残差序列是否为白噪声、检验模型的拟合优度等。
如果模型不符合要求,则需要改进模型或选择其他合适的模型。
5. 模型评估与验证:使用历史数据来评估模型的性能,可以计算平均绝对误差(MAE)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)等指标。
还可以使用交叉验证等方法来验证模型的泛化能力。
6. 预测与评估:使用训练好的模型对未来一段时间的数据进行预测,同时计算预测误差,并评估预测的准确性和可靠性。
7. 模型应用和监控:根据预测结果制定相应的策略和决策,同
时对模型的性能进行监控,及时更新模型或调整参数以适应数据的变化。
时间序列预测的常用方法及优缺点分析

时间序列预测的常用方法及优缺点分析一、常用方法1. 移动平均法(Moving Average)移动平均法是一种通过计算一系列连续数据的平均值来预测未来数据的方法。
这个平均值可以是简单移动平均(SMA)或指数移动平均(EMA)。
SMA是通过取一定时间窗口内数据的平均值来预测未来数据,而EMA则对旧数据赋予较小的权重,新数据赋予较大的权重。
移动平均法的优点是简单易懂,适用于稳定的时间序列数据预测;缺点是对于非稳定的时间序列数据效果较差。
2. 指数平滑法(Exponential Smoothing)指数平滑法是一种通过赋予过去观测值不同权重的方法来进行预测。
它假设未来时刻的数据是过去时刻的线性组合。
指数平滑法可以根据数据的特性选择简单指数平滑法、二次指数平滑法或霍尔特线性指数平滑法。
指数平滑法的优点是计算简单,对于较稳定的时间序列数据效果较好;缺点是对于大幅度波动的时间序列数据预测效果较差。
3. 季节分解法(Seasonal Decomposition)季节分解法是一种将周期性、趋势性和随机性分开处理的方法。
它假设时间序列数据可以被分解为这三个不同的分量,并独立预测各分量。
最后将这三个分量合并得到最终的预测结果。
季节分解法的优点是可以更准确地预测具有强烈季节性的时间序列数据;缺点是需要根据具体情况选择合适的模型,并且较复杂。
4. 自回归移动平均模型(ARMA)自回归移动平均模型是一种统计模型,通过考虑当前时刻与过去时刻的相关性来进行预测。
ARMA模型考虑了数据的自相关性和滞后相关性,能够对较复杂的时间序列数据进行预测。
ARMA模型的优点是可以更准确地预测非稳定的时间序列数据;缺点是模型参数的选择和估计比较困难。
5. 长短期记忆网络(LSTM)长短期记忆网络是一种深度学习模型,通过引入记忆单元来记住时间序列数据中的长期依赖关系。
LSTM模型可以有效地捕捉时间序列数据中的非线性模式,具有很好的预测性能。
LSTM模型的优点是适用于各种类型的时间序列数据,可以提供较准确的预测结果;缺点是对于数据量较小的情况,LSTM模型容易过拟合。
时间序列分析基础

时间序列分析基础时间序列分析是一种重要的统计分析方法,用于研究时间序列数据的规律性、趋势性和周期性。
时间序列数据是按照时间顺序排列的一系列数据点,例如股票价格、气温变化、销售额等。
通过时间序列分析,我们可以揭示数据中的模式、趋势和周期性,从而进行预测和决策。
本文将介绍时间序列分析的基础知识,包括时间序列数据的特点、常见的时间序列模型以及时间序列分析的步骤。
一、时间序列数据的特点时间序列数据具有以下几个特点:1. 趋势性:时间序列数据通常会呈现出长期的趋势,即数据随着时间的推移呈现出逐渐增长或逐渐减小的规律。
2. 季节性:时间序列数据可能会呈现出周期性的波动,这种波动通常是由季节因素引起的,例如节假日、季节变化等。
3. 周期性:除了季节性波动外,时间序列数据还可能存在其他周期性的波动,这种波动的周期可能不固定。
4. 随机性:时间序列数据中通常还包含一定程度的随机波动,这些波动是由各种随机因素引起的,难以预测。
二、常见的时间序列模型在时间序列分析中,常用的时间序列模型包括:1. 移动平均模型(MA):移动平均模型是一种利用过去若干期数据的加权平均来预测未来数据的模型,通常用MA(q)表示,其中q为移动平均阶数。
2. 自回归模型(AR):自回归模型是一种利用过去若干期数据的线性组合来预测未来数据的模型,通常用AR(p)表示,其中p为自回归阶数。
3. 自回归移动平均模型(ARMA):自回归移动平均模型是自回归模型和移动平均模型的结合,用于处理同时具有自相关和滞后相关的时间序列数据。
4. 差分自回归移动平均模型(ARIMA):差分自回归移动平均模型是对非平稳时间序列数据进行差分处理后应用ARMA模型的一种方法,用于处理非平稳时间序列数据。
5. 季节性自回归移动平均模型(SARIMA):季节性自回归移动平均模型是对具有季节性波动的时间序列数据应用ARIMA模型的一种方法,用于处理具有季节性的时间序列数据。
三、时间序列分析的步骤进行时间序列分析时,通常需要按照以下步骤进行:1. 数据收集:首先需要收集时间序列数据,确保数据的完整性和准确性。
第六章 时间序列分析-参数估计

例:求MA(1)模型系数的矩估计
MA(1)模型 方程 xt t 1 t 1
0 (1 12 ) 2 1 1 1 2 矩估计 0 1 12 1 1
ˆ 1 1 4 12 ˆ1 ˆ 2 1
f X1 , X 2 , X3 x1 , x2 , x3 ; , 2 f X1 , X 2 x1 , x2 ; , 2 f X3 X 2 , X1 x3 x2 , x1 ; , 2
24
极大似然估计
一般地,样本中第 t 个 X t 在前 t-1 个已知的条件下,由于模 型的特点,实际上前 t-1 个 X t 1 ,, X1 只有 X t 1 作用于 X t ,因此 有
ˆ 其中 k y
ˆˆ ˆ
i 0 j 0 i
p
p
j i j k
, k 0,1,, q
13
对矩估计的评价
优点
估计思想简单直观 不需要假设总体分布 计算量小(低阶模型场合)
缺点
信息浪费严重 只用到了p+q个样本自相关系数信息,其他信息都被忽
15
极大似然估计
本节将要讨论的是根据极大似然原理,给出模型参数 1 ,, p ,
1 ,,q 和白噪声方差 2 的极大似然估计。为此,首先需要给定样本
x1,, xT 的联合分布,
F x1,, xT ; θ
θ 1 , , p , 1 , , q , 2 。 其中
3. ARMA模型的矩估计 第一步,先给出AR部分的参数 估计。
1 ,, p
的矩
q1 q 12 q p 1 p q 1 q 1 1 q 2 q p 2 p q 2 q p 11 q p 22 q p q p
时间序列分析教程(四)AR与MA模型详细分析(公式推导慎入)

时间序列分析教程(四)AR与MA模型详细分析(公式推导慎入)时间序列分析中,AR模型(Autoregressive Model)和MA模型(Moving Average Model)是两种常用的模型类型。
本教程将详细介绍AR和MA模型的公式推导,让读者更好地理解其原理和应用。
首先,我们先来解释AR和MA模型的概念。
AR模型是一种基于时间序列过去的值来预测未来值的模型。
AR模型的基本思想是当前值与过去若干个时间点的值相关,即当前值是过去值的加权和。
AR模型的表示形式为AR(p),其中p表示过去时间点的数量。
MA模型是一种基于时间序列过去的误差项来预测未来值的模型。
MA 模型的基本思想是当前值与过去若干个时间点的误差项相关,即当前值是过去误差的加权和。
MA模型的表示形式为MA(q),其中q表示过去误差的数量。
下面我们将对AR和MA模型的公式进行推导。
一、AR模型的公式推导假设我们有一个时间序列{Y_t},其中Y_t表示时间点t的值。
AR(p)模型的一般形式为:Y_t=c+ϕ₁Y_(t-1)+ϕ₂Y_(t-2)+...+ϕ_pY_(t-p)+ε_t其中c是常数项,ϕ₁、ϕ₂、..、ϕ_p是过去时间点的权重系数,ε_t 是一个白噪声误差项。
为了方便推导,我们将AR(p)模型简化为AR(1)模型,即只考虑过去一个时间点的值。
即:Y_t=c+ϕY_(t-1)+ε_t我们首先假设时间序列{Y_t}是平稳的,即均值和方差不随时间变化。
然后,我们将AR(1)模型代入Y_(t-1)的表达式中,得到:Y_t=c+ϕ(c+ϕY_(t-2)+ε_(t-1))+ε_t展开后整理得:Y_t=c(1+ϕ)+ϕ²Y_(t-2)+ϕε_(t-1)+ε_t再次代入Y_(t-2)的表达式中,得到:Y_t=c(1+ϕ+ϕ²)+ϕ³Y_(t-3)+ϕ²ε_(t-2)+ϕε_(t-1)+ε_t以此类推,我们可以得到AR(1)模型的一般表达式:Y_t=c(1+ϕ+ϕ²+...+ϕ^p-1)+ϕ^pY_(t-p)+ϕ^(p-1)ε_(t-p+1)+...+ϕ²ε_(t-2)+ϕε_(t-1)+ε_t其中,c(1+ϕ+ϕ²+...+ϕ^p-1)是常数项,ϕ^pY_(t-p)是过去p个时间点的加权和,ϕ^(p-1)ε_(t-p+1)、..、ϕ²ε_(t-2)、ϕε_(t-1)和ε_t是误差项。
应用时间序列分析第4章答案
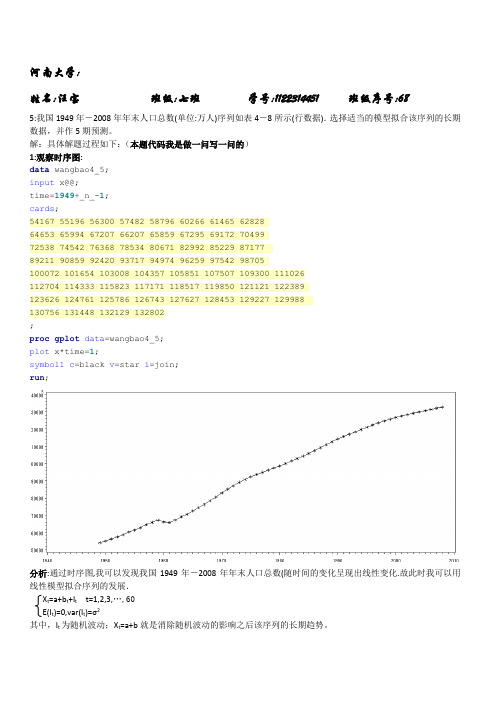
河南大学:姓名:汪宝班级:七班学号:1122314451 班级序号:685:我国1949年-2008年年末人口总数(单位:万人)序列如表4-8所示(行数据).选择适当的模型拟合该序列的长期数据,并作5期预测。
解:具体解题过程如下:(本题代码我是做一问写一问的)1:观察时序图:data wangbao4_5;input x@@;time=1949+_n_-1;cards;54167 55196 56300 57482 58796 60266 61465 6282864653 65994 67207 66207 65859 67295 69172 7049972538 74542 76368 78534 80671 82992 85229 8717789211 90859 92420 93717 94974 96259 97542 98705100072 101654 103008 104357 105851 107507 109300 111026112704 114333 115823 117171 118517 119850 121121 122389123626 124761 125786 126743 127627 128453 129227 129988130756 131448 132129 132802;proc gplot data=wangbao4_5;plot x*time=1;symbol1c=black v=star i=join;run;分析:通过时序图,我可以发现我国1949年-2008年年末人口总数(随时间的变化呈现出线性变化.故此时我可以用线性模型拟合序列的发展.X t=a+b t+I t t=1,2,3,…,60E(I t)=0,var(I t)=σ2其中,I t为随机波动;X t=a+b就是消除随机波动的影响之后该序列的长期趋势。
2:进行线性模型拟合:proc autoreg data=wangbao4_5;model x=time;output out=out p=wangbao4_5_cup;run;proc gplot data=out;plot x*time=1 wangbao4_5_cup*time=2/overlay ;symbol2c=red v=none i=join w=2l=3;run;分析:由上面输出结果可知:两个参数的p值明显小于0.05,即这两个参数都是具有显著非零,4:模型检验又因为Regress R-square=total R-square=0.9931,即拟合度达到99.31%所以用这个模型拟合的非常好。
如何使用隐马尔科夫模型进行时间序列预测(四)

隐马尔科夫模型(Hidden Markov Model,HMM)是一种常用于时间序列分析和预测的统计模型。
它能够对观测序列进行建模,并根据隐藏的状态推断未来的观测值。
本文将以时间序列预测为主题,介绍如何使用隐马尔科夫模型进行预测,并讨论其应用和局限性。
一、隐马尔科夫模型简介隐马尔科夫模型由隐藏的马尔科夫链和可观察的输出组成。
隐藏的马尔科夫链是一个随机过程,其状态在不同时间点转移,并产生可观察的输出。
在预测问题中,隐藏的状态通常是未知的,而可观察的输出是已知的时间序列数据。
隐马尔科夫模型的目标是根据观测数据推断隐藏的状态,并基于隐藏的状态进行预测。
二、隐马尔科夫模型的参数估计在使用隐马尔科夫模型进行时间序列预测时,首先需要进行模型的参数估计。
一般来说,隐马尔科夫模型有三类参数:初始状态概率、状态转移概率和观测概率。
这些参数可以通过最大似然估计或期望最大化算法进行估计。
通过对观测数据进行学习,可以得到模型的参数估计值,从而建立起模型。
三、隐马尔科夫模型的预测一旦建立了隐马尔科夫模型,就可以利用该模型进行时间序列预测。
在预测过程中,首先需要对观测序列进行解码,推断隐藏的状态序列。
然后,基于隐藏的状态序列,利用模型的状态转移概率和观测概率进行未来观测值的预测。
隐马尔科夫模型在预测过程中考虑了隐藏的状态转移,因此能够较为准确地对时间序列进行预测。
四、隐马尔科夫模型的应用隐马尔科夫模型在时间序列预测中有着广泛的应用。
例如,在金融领域,可以利用隐马尔科夫模型对股票价格进行预测,以辅助投资决策。
在气象领域,隐马尔科夫模型可以用于气象数据的预测和分析。
此外,隐马尔科夫模型还被应用于语音识别、自然语言处理等领域。
由于其模型结构的灵活性和可解释性,隐马尔科夫模型在时间序列预测中具有较强的优势。
五、隐马尔科夫模型的局限性尽管隐马尔科夫模型在时间序列预测中具有一定的优势,但也存在一些局限性。
首先,隐马尔科夫模型假设隐藏的状态是马尔科夫链,这在某些实际场景下可能并不成立。
SAS学习系列39.时间序列分析Ⅲ—ARIMA模型

39. 时间序列分析Ⅱ—-ARIMA 模型随着对时间序列分析方法的深入研究,人们发现非平稳序列的确定性因素分解方法(如季节模型、趋势模型、移动平均、指数平滑等)只能提取显著的确定性信息,对随机性信息浪费严重,同时也无法对确定性因素之间的关系进行分析。
而非平稳序列随机分析的发展就是为了弥补确定性因素分解方法的不足。
时间序列数据分析的第一步都是要通过有效手段提取序列中所蕴藏的确定性信息。
Box 和Jenkins 使用大量的案例分析证明差分方法是一种非常简便有效的确定性信息的提取方法。
而Gramer 分解定理则在理论上保证了适当阶数的差分一定可以充分提取确定性信息。
(一)ARMA 模型即自回归移动平均移动模型,是最常用的拟合平稳时间序列的模型,分为三类:AR 模型、MA 模型和ARMA 模型。
一、AR(p )模型——p 阶自回归模型 1。
模型:011t t p t p t x x x φφφε--=+++其中,0p φ≠,随机干扰序列εt 为0均值、2εσ方差的白噪声序列(()0t s E εε=, t ≠s ),且当期的干扰与过去的序列值无关,即E (x t εt )=0.由于是平稳序列,可推得均值011pφμφφ=---. 若00φ=,称为中心化的AR (p )模型,对于非中心化的平稳时间序列,可以令01(1)p φμφφ=---,*t t x x μ=-转化为中心化。
记B 为延迟算子,1()p p p B I B B φφΦ=---称为p 阶自回归多项式,则AR (p )模型可表示为:()p t t B x εΦ=.2. 格林函数用来描述系统记忆扰动程度的函数,反映了影响效应衰减的快慢程度(回到平衡位置的速度),G j 表示扰动εt —j 对系统现在行为影响的权数。
例如,AR(1)模型(一阶非齐次差分方程),1, 0,1,2,j j G j φ==模型解为0t j t j j x G ε∞-==∑.3。
时间序列的预处理与分析

时间序列的预处理与分析一、时间序列的预处理步骤1. 数据清洗:首先,我们需要对时间序列数据进行清洗,去除可能存在的异常值、缺失值和异常数据。
异常值可以通过异常检测方法识别和处理,缺失值可以通过插值方法填补。
2. 数据转换:有时候,时间序列数据在原始尺度上的波动很大,难以进行分析。
这时,我们需要进行数据转换,常见的方法有对数变换、差分变换和平滑变换等,以使数据更平稳或更趋于正态分布。
3. 数据平滑:平滑是一种常用的数据预处理方法,可以消除噪声和随机波动,揭示时间序列的长期趋势。
常用的平滑方法包括移动平均法和指数平滑法。
4. 季节性调整:如果时间序列数据存在季节性变化,那么我们需要进行季节性调整。
常见的方法有季节差分法、季节指数法和回归模型法等,以便更好地分析和预测数据。
5. 数据分解:有时候,时间序列数据可能包含趋势、季节性和残差三个成分,我们需要将其分解出来,分别进行分析和建模。
分解方法有经典分解法和小波分解法等。
二、时间序列的分析方法1. 描述统计分析:描述统计分析是时间序列分析的基础,可以通过计算均值、方差、相关系数和自相关系数等指标,揭示数据的基本特征和变化规律。
2. 自相关分析:自相关分析是一种常用的时间序列分析方法,可以识别和度量数据内部存在的自相关关系。
自相关系数图和自相关函数图可以帮助我们判断数据是否存在自相关性,并确定合适的滞后阶数。
3. 谱分析:谱分析是一种用于分析时间序列数据频率特征的方法,可以揭示时间序列数据随时间变化的周期和频率成分。
常见的谱分析方法有周期图、功率谱图和谱密度图等。
4. ARIMA模型:ARIMA模型是一种常用的时间序列建模方法,包括自回归(AR)、差分(I)和移动平均(MA)三个部分。
通过对时间序列数据进行模型识别、参数估计和模型检验,可以进行预测和预测误差分析。
5. 指数平滑模型:指数平滑模型是一种简单且有效的时间序列预测方法,常用于对平稳或趋势性变化的数据进行预测。
第六章 时间序列分析-参数估计

ˆ0 y
112 L
2 q
2M
ˆk y k k 1 1 L qqk 2 , k 1, 2,L q
pp
其中 ˆk y
ˆiˆjˆi jk , k 0,1,K , q
i0 j0
13
对矩估计的评价
▪ 优点
➢ 估计思想简单直观 ➢ 不需要假设总体分布 ➢ 计算量小(低阶模型场合)032源自条件极大似然估计ˆ
T t2
xt xt1
T
x2 t 1 t2
T
ˆ 2 1
T 1 t2
xt
ˆxt1
2
为参数 θ 的条件极大似然估计。
33
对极大似然估计的评价
▪ 优点
➢ 极大似然估计充分应用了每一个观察值所提供 的信息,因而它的估计精度高
➢ 同时还具有估计的一致性、渐近正态性和渐近 有效性等许多优良的统计性质
▪ 残差平方和方程
n
n
t
Q(%)
2 t
[xt
i xt1]2
▪ 解法
i 1
i 1
i 1
➢ 迭代法
36
对最小二乘估计的评价
▪ 优点
➢ 最小二乘估计充分应用了每一个观察值所提供 的信息,因而它的估计精度高
➢ 条件最小二乘估计方法使用率最高
▪ 缺点
➢ 需要假定总体分布
37
例2.5续
▪ 确定1950年——1998年北京市城乡居民定 期储蓄比例序列拟合模型的口径
▪ 缺点
➢ 信息浪费严重
只用到了p+q个样本自相关系数信息,其他信息都被忽 略
➢ 估计精度差
▪ 通常矩估计方法被用作极大似然估计和最小二乘 估计迭代计算的初始值
利用分位数回归进行时间序列模型的参数估计

利用分位数回归进行时间序列模型的参数估计下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!随着经济发展的不断加快,时间序列模型的应用在经济研究中发挥着越来越重要的作用。
时间序列参数估计

时间序列参数估计在时间序列分析中,有几种常用的方法用于参数估计,包括最小二乘法、最大似然估计和贝叶斯估计。
首先,最小二乘法是一种常用的参数估计方法,通过最小化观测数据与模型预测值之间的差异,来估计模型的参数。
最小二乘法的基本思想是选择使得预测值与观测值之差的平方和最小化的参数。
对于线性模型,可以使用最小二乘法来估计线性回归模型的参数。
对于非线性模型,可以使用非线性最小二乘法来估计参数。
其次,最大似然估计是一种常用的参数估计方法,它基于观测数据出现的概率来选择最有可能产生观测数据的参数。
最大似然估计的核心思想是找到使得观测数据出现的概率最大化的参数。
通过最大似然估计,可以估计出模型的参数,并用于预测未来数据。
最大似然估计在时间序列分析中广泛应用,尤其适用于正态分布的时间序列模型。
最后,贝叶斯估计是一种基于贝叶斯理论的参数估计方法,它通过将先验信息和观测数据结合起来,来推断模型参数的后验分布。
贝叶斯估计的核心思想是基于观测数据和先验知识来更新参数的概率分布。
通过贝叶斯估计,可以得到参数的概率分布,并用于预测未来数据。
贝叶斯估计在时间序列分析中具有很大的灵活性,在参数估计问题中常常是最优的方法。
在时间序列参数估计中,一个重要的问题是选择适当的模型来描述数据。
常用的时间序列模型包括自回归移动平均模型(ARMA)、自回归集成移动平均模型(ARIMA)、季节性自回归移动平均模型(SARMA)等。
根据数据的特点和假设的条件,可以选择适当的模型进行参数估计。
对于时间序列参数估计,还有一些要考虑的问题。
首先,数据的平稳性是进行时间序列分析的前提条件之一,因此在进行参数估计之前要对数据进行平稳性检验。
其次,模型的阶数选择是一个重要的问题,需要通过模型诊断和信息准则来选择最佳的模型阶数。
此外,对于多变量的时间序列,可以使用向量自回归模型(VAR)来进行参数估计。
总的来说,时间序列参数估计是一种重要的数据分析方法,通过对历史数据进行建模和估计,可以预测未来的数据。
时间序列分析实验报告

时间序列分析实验报告一、实验目的时间序列分析是一种用于处理和分析随时间变化的数据的统计方法。
本次实验的主要目的是通过对给定的时间序列数据进行分析,掌握时间序列分析的基本方法和技术,包括数据预处理、模型选择、参数估计和预测,并评估模型的性能和准确性。
二、实验数据本次实验使用了一组某商品的月销售量数据,数据涵盖了过去两年的时间范围,共 24 个观测值。
数据的具体形式为一个时间序列,其中每个观测值表示该商品在相应月份的销售量。
三、实验方法1、数据预处理首先,对数据进行了可视化,绘制了时间序列图,以便直观地观察数据的趋势、季节性和随机性。
然后,对数据进行了平稳性检验。
采用了 ADF(Augmented DickeyFuller)检验来判断数据是否平稳。
如果数据不平稳,则需要进行差分处理,使其达到平稳状态。
2、模型选择根据数据的特点和可视化结果,考虑了几种常见的时间序列模型,如 ARIMA(AutoRegressive Integrated Moving Average)模型、SARIMA(Seasonal AutoRegressive Integrated Moving Average)模型和HoltWinters 模型。
通过对不同模型的参数进行估计,并比较它们在训练数据上的拟合效果和预测误差,选择了最适合的模型。
3、参数估计对于选定的模型,使用最大似然估计或最小二乘法等方法来估计模型的参数。
通过对参数的估计值进行分析,判断模型的合理性和稳定性。
4、预测使用估计得到的模型参数,对未来一段时间内的销售量进行预测。
为了评估预测的准确性,采用了均方根误差(RMSE)、平均绝对误差(MAE)等指标来衡量预测值与实际值之间的差异。
四、实验过程1、数据可视化通过绘制时间序列图,发现数据呈现出明显的季节性和上升趋势。
同时,数据的波动范围也较大,存在一定的随机性。
2、平稳性检验对原始数据进行 ADF 检验,结果表明数据是非平稳的。
No.11-第4章-时间序列模型的参数估计与检验

所示,拟合AR(2)模型 t对 X t3 和 t对 t1 的散点图如图2、3所示。图1
有微弱的负相关趋势,说明AR(1)不是适应模型,而图2、3看不出有相关 趋势,说明AR(2)是适应模型。
图1
图2
图3
(2)估计相关系数法
1 j m
检验统计量
T
nm
ˆ j j a jj Q(~)
~ t(n m)
取检验水平 ,可得检验的拒绝域为
t t1 2 n m
小结:时间序列模型的检验
当我们对模型进行识别并估计出模型参数之后,所得到的时间序列模型 是否可用,还需要进行检验。
模型是否适用,可以检验残差序列是否为白噪声序列。 参数是否合适,可以构造统计量做假设检验,以使模型结构更为精简、 有效。 检验通过之后就可以利用所得到的模型进行预测和预报了。
(*)
令
Xt Xt ˆ1Xt1 ˆ2 Xt2 ˆp Xtp
于是(*)可以写成:
X~t t 1t1 2t2 qtq
构成一个MA模型。按照估计MA模型参数的方法,可以得到 1,2, ,q
以及
2
的估计值。
需要说明的是,在上述模型的平稳性、识别与估计的讨论中, ARMA(p,q)模型中均未包含常数项。
然后利用Yule Walker方程组,求解模型参数的估计值 ˆ1,ˆ2,...,ˆp
ˆ1 ˆ0 ˆ1
ˆ2
ˆ1
ˆ0
ˆ
p
ˆ
p 1
ˆ p2
ˆ p1 1 ˆ1
ˆ
p
时间序列预测区间估计方法

时间序列预测区间估计方法
时间序列预测区间估计是指一种评估分析预测区间时以预测结果范围为基础的,一般
通过根据以往相关历史数据和模型,对未来某一时间段中预测参数所属范围进行区间估计,
以给出置信度较高的结果。
时间序列预测区间估计的常用方法有:1、普通的统计学方法,如极大似然概率估计、方差分析、回归分析等。
这些方法广泛应用于统计软件,可以利用样本上的观测数据来估
计参数的未知取值范围。
2、模糊理论,模糊理论可以结合时间序列波动特性,将系统模
型中的参数有效地表达出来,并实现参数的区间估计。
3、小波分析。
小波分析可以建立
特定数据序列的多项式重构式,然后使用矩阵分解技术对参数进行区间估计,从而得到较
为准确的结果。
4、神经网络分析方法,神经网络通过训练,根据输入和输出变量的概率
关系,可以进行参数区间估计.
以上是时间序列预测区间估计的几种常见方法,它们各有优点和缺点。
例如,普通统
计学方法极其容易推导出结果,但是容易受数据噪声的影响;模糊理论能够很好地表达非
线性关系,但是编码过程复杂;小波分析具有鲁棒性强和时间效率高的优点,但是其算法
复杂度较高;神经网络具有较高的预测精度,但是模型复杂度较高,需要调整大量参数。
总之,时间序列预测区间估计是一种用于计算置信度较高预测参数估计值范围的方法。
由于它具有较高的稳定性,被广泛应用于时间序列数据的精确预测。
时间序列_实验报告

一、实验目的1. 了解时间序列分析的基本原理和方法;2. 掌握时间序列数据的平稳性检验、模型识别和参数估计等基本操作;3. 通过实例,学习使用ARIMA模型进行时间序列预测。
二、实验环境1. 操作系统:Windows 102. 软件环境:EViews 9.0、R3.6.1三、实验数据1. 数据来源:某城市1980年1月至2020年12月每月的GDP数据;2. 数据格式:Excel表格。
四、实验步骤1. 数据预处理(1)导入数据:将Excel表格中的GDP数据导入EViews软件;(2)观察数据:绘制GDP时间序列图,观察数据的趋势、季节性和周期性;(3)平稳性检验:使用ADF检验判断GDP序列是否平稳。
2. 模型识别(1)自相关函数(ACF)和偏自相关函数(PACF)图:观察ACF和PACF图,初步确定ARIMA模型的阶数;(2)模型选择:根据ACF和PACF图,选择合适的ARIMA模型。
3. 模型估计(1)模型估计:使用EViews软件中的ARIMA过程,对选择的模型进行参数估计;(2)模型检验:对估计出的模型进行残差检验,包括残差的平稳性检验、白噪声检验等。
4. 时间序列预测(1)预测:使用估计出的ARIMA模型,对2021年1月至2025年12月的GDP进行预测;(2)预测结果分析:对预测结果进行分析,评估预测的准确性。
五、实验结果与分析1. 数据预处理(1)导入数据:将Excel表格中的GDP数据导入EViews软件;(2)观察数据:绘制GDP时间序列图,发现GDP序列存在明显的上升趋势和季节性;(3)平稳性检验:使用ADF检验,发现GDP序列在5%的显著性水平下拒绝原假设,序列是平稳的。
2. 模型识别(1)自相关函数(ACF)和偏自相关函数(PACF)图:根据ACF和PACF图,初步确定ARIMA模型的阶数为(1,1,1);(2)模型选择:根据ACF和PACF图,选择ARIMA(1,1,1)模型。
概率与数理统计第4章时间序列分析

概率与数理统计第4章时间序列分析第4章时间序列分析[引例]某酿酒公司⽣产⼀种红葡萄酒,这种红葡萄酒颇受市场欢迎,其销售量稳步上升(表4-1),对公司盈利起到重要作⽤。
表4-1 某酿酒公司红葡萄酒销售量单位:件——资料来源:国际通⽤MBA教材配套案例《管理统计案例》机械⼯业出版社1999.3 本章⼩结1.时间序列是把同⼀现象在不同时间上的观察数据按时间先后顺序排列起来所形成的数列,它是动态分析的基础。
时间序列的分析有指标分析和构成因素分析两类。
时间序列的影响因素可归结为长期趋势、季节变动、循环变动和不规则变动等四种,常以乘法模型为基础来进⾏时间序列的分解和组合。
2.⽔平分析指标主要有平均发展⽔平、增减量(逐期、累计)和平均增减量。
不同类型的时间序列计算平均发展⽔平的⽅法有所不同。
累计增减量等于相应逐期增减量之和。
平均增减量是观察期内各个逐期增减量的平均数。
速度分析指标有发展速度、增减速度、平均发展速度和平均增减速度。
定基发展速度也即发展总速度,它等于相应时期内各环⽐发展速度的连乘积。
增减速度等于发展速度减1。
平均发展速度是环⽐发展速度的平均数,其计算⽅法通常采⽤⼏何平均法。
平均增减速度等于平均发展速度减1。
3. 长期趋势的分析⽅法主要有平滑法(移动平均、指数平滑法)和⽅程拟合法。
移动平均关键在于选择平均项数;能消除序列中的季节影响(平均项数与季节周期长度必须⼀致)。
指数平滑法是关键在于确定平滑系数。
⽅程拟合法通常采⽤最⼩⼆乘法来估计趋势⽅程中的参数。
4. 季节⽐率的测定⽅法:原资料平均法和趋势剔除法。
原资料平均法适⽤于⽔平趋势的季节序列;趋势剔除法适⽤于有明显上升(或下降)趋势的季节序列。
当没有季节因素影响时,季节⽐率为1或100%。
序列的季节调整即以原始数据除以对应季节的季节⽐率,⽬的是从时间序列中去掉季节影响,便于分析其它成分。
5.利⽤分析⼯具库中的“移动平均”、“指数平滑法”、“回归”或图表中的添加趋势线功能,可以测定时间序列的长期趋势。
管理统计学4 第四章 时间序列

星蓝海学习网
4.2序时平均数和平均发展速度
4.2.2相对数的序时平均数和平均数的序时平均数
库存周转速度属于相对数,该相对数的分母为时点数。从年度上看,年周转速度应等 于年销售量与年平均库存量的比值。因此,先平均后对比是计算相对数序时平均的基 本方法。 平均数序时平均数的计算与相对数的序时平均数的计算方法相同,也是先平均后对比。
管理统计学 [第四版]
星蓝海学习网
第四章 时间序列分析
星蓝海学习网
案例导入
近年来,中国房地产发展繁荣,房价更是水涨船高。下表是国家统计局对十 年来广东省商品房年销售价格的统计数。
年份 2005 2006 2007 2008 2009 2010 2011 2012 2013 2014 售价 4443 4853 5914 5953 6513 7486 7879 8112 9090 9083
4.1 发展水平和发展速度分析
4.1.2 发展水平和增长量
发展水平 发展水平是指时间数列上指标的具体数值。 发展水平的指标形式可以是绝对数,也可以是相对数或平均数。 增长量 为了分析上方便,就把作为研究对象的发展水平称为报告期水平,把要对比的基础水 平则称为基期水平。 用报告期水平减去基期水平,就等于增长量。其中,当基期水平为上期水平时,就称 为逐期增长量;当基期水平为某个时期的固定发展水平(X0)时,就称为累计增长量。 逐期增长量:X1-X0、X2-X1、X3-X2、…Xn-Xn-1 。 累计增长量:X1-X0、X2-X0、X3-X0、…Xn-X0。 二者的关系:(Xn-X0)= (X1 -X0)+(X2-X1)+(X3-X2)+…(Xn-Xn-1)。
时间序列模型评估常用方法

时间序列模型评估常用方法时间序列模型是一种用于分析时间序列数据的统计模型,广泛应用于经济学、金融学、气象学、销售预测等领域。
评估时间序列模型的常用方法包括模型拟合度评估、预测准确度评估和模型稳定性评估。
一、模型拟合度评估模型拟合度评估是衡量时间序列模型对观测数据的拟合程度的指标。
常用的评估方法包括残差分析、拟合优度和信息准则。
1. 残差分析:通过对模型的残差进行统计检验,来评估模型是否能够拟合数据的特征。
常用的残差分析方法包括检验残差序列的自相关性、白噪声检验、残差的正态性检验等。
2. 拟合优度:拟合优度是指模型对观测数据的拟合程度。
常用的拟合优度指标包括均方误差(MSE)、平均绝对误差(MAE)、均方根误差(RMSE)等。
这些指标可以用于比较不同模型的拟合程度,越小表示模型拟合得越好。
3. 信息准则:信息准则是用于选择模型的指标,常用的有赤池信息准则(AIC)、贝叶斯信息准则(BIC)等。
这些准则考虑了模型的拟合度和复杂度,能够在拟合度与过拟合之间找到平衡。
二、预测准确度评估预测准确度评估是衡量时间序列模型预测结果与实际观测值的差异程度的指标。
常用的评估方法包括平均绝对百分比误差(MAPE)、均方误差(MSE)、均方根误差(RMSE)等。
1. 平均绝对百分比误差(MAPE):MAPE用于衡量预测值与实际值之间的相对误差程度,可以消除量纲的影响。
MAPE越小表示模型的预测准确度越高。
2. 均方误差(MSE):MSE用于衡量预测值与实际值之间的平方误差,可以消除正负误差的抵消效应。
MSE越小表示模型的预测准确度越高。
3. 均方根误差(RMSE):RMSE是MSE的平方根,用于衡量预测值与实际值之间的平均误差。
RMSE越小表示模型的预测准确度越高。
三、模型稳定性评估模型稳定性评估是衡量时间序列模型参数估计的稳定性和可靠性的指标。
常用的评估方法包括参数估计的稳定性检验、模型的稳定性检验等。
1. 参数估计的稳定性检验:通过对模型参数进行统计检验,来评估参数估计的稳定性和可靠性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间序列模型参数估计1理论基础1.1矩估计1.1.1AR模型矩估计法参数估计的思路:即从样本中依次求中r k然后求其对应的参数Φk值方差:1.1.2MA模型对于MA模型采用矩估计是比较不精确的,所以这里不予讨论1.1.3ARMA(1,1)矩估计法参数估计的思路:方差:1.2最小二乘估计1.2.1AR模型最小二乘参数估计的思路:对于AR(P)而言也可以得到类似矩估计得到的方程,即最小二乘与矩估计得到的估计量相同。
1.2.2MA模型最小二乘参数估计的思路:1.2.3ARMA模型最小二乘参数估计的思路:1.3极大似然估计与无条件最小二乘估计2R中如何实现时间序列参数估计2.1对于AR模型ar(x, aic = TRUE, order.max = NULL,method=c("yule-walker", "burg", "ols", "mle", "yw"),na.action, series, ...)> ar(ar1.s,order.max=1,AIC=F,method='yw')#即矩估计Call:ar(x = ar1.s, order.max = 1, method = "yw", AIC = F)Coefficients:10.8314Order selected 1 sigma^2 estimated as 1.382> ar(ar1.s,order.max=1,AIC=F,method='ols')#最小二乘估计Call:ar(x = ar1.s, order.max = 1, method = "ols", AIC = F)Coefficients:10.857Intercept: 0.02499 (0.1308)Order selected 1 sigma^2 estimated as 1.008> ar(ar1.s,order.max=1,AIC=F,method='mle')#极大似然估计Call:ar(x = ar1.s, order.max = 1, method = "mle", AIC = F)Coefficients:10.8924Order selected 1 sigma^2 estimated as 1.041采用自编函数总结三个不同的估计值> Myar(ar2.s,order.max=3)最小二乘估计矩估计极大似然估计1 1.5137146 1.4694476 1.50613692 -0.8049905 -0.7646034 -0.79644532.2对于ARMA模型arima(x, order = c(0, 0, 0), seasonal = list(order = c(0, 0, 0), period = NA), xreg = NULL, include.mean = TRUE, transform.pars = TRUE, fixed = NULL,init = NULL, method = c("CSS-ML", "ML", "CSS"), n.cond, optim.control = list(), kappa = 1e+06, io = NULL, xtransf, transfer = NULL)order的三个参数分别代表AR,差分MA的阶数> arima(arma11.s,order=c(1,0,1),method='CSS')Call:arima(x = arma11.s, order = c(1, 0, 1), method = "CSS")Coefficients:ar1 ma1 intercept0.5586 0.3669 0.3928s.e. 0.1219 0.1564 0.3380sigma^2 estimated as 1.199: part log likelihood = -150.98> arima(arma11.s,order=c(1,0,1),method='ML')Call:arima(x = arma11.s, order = c(1, 0, 1), method = "ML")Coefficients:ar1 ma1 intercept0.5647 0.3557 0.3216s.e. 0.1205 0.1585 0.3358sigma^2 estimated as 1.197: log likelihood = -151.33, aic = 308.65 采用自编函数总结三个不同的估计值> Myarima(arma11.s,order=c(1,0,1))$coef条件SS估计极大似然估计条件似然估计ar1 0.5585828 0.5647477 0.5647498ma1 0.3668814 0.3556965 0.3556973intercept 0.3927654 0.3216166 0.3216152$log条件SS估计极大似然估计条件似然估计[1,] -150.984 -151.3268 -151.3268$sigma2条件SS估计极大似然估计条件似然估计[1,] 1.199378 1.196984 1.196984$aic条件SS估计极大似然估计条件似然估计[1,] NA 308.6537 308.65372.3采用自助法arima.boot()此函数估计的是参数的取值置信区间,而不是指具体的某个值,与arima是不同的。
> res=arima(sqrt(hare),order=c(3,0,0),include.mean=T)> set.seed(12345)> # Method I以最初三个观测为条件,并假设误差服从正态分布,得到95%的置信区间quantile用于计算置信区间值,signif类似于四舍五入函数,保留有效数值。
>coefm.cond.norm=arima.boot(res,cond.boot=T,is.normal=T,B=1000,init=sqrt(ha re))> signif(apply(coefm.cond.norm,2,function(x){quantile(x,c(.025,.975),na.rm=T)}),3) ar1 ar2 ar3 intercept noise var2.5% 0.593 -0.667 -0.6740 5.12 0.54897.5% 1.280 0.244 -0.0135 6.38 1.540>> # Method II假设误差并不服从正态分布,而是需要从样本抽样中得到coefm.cond.replace=arima.boot(res,cond.boot=T,is.normal=F,B=1000,init=sqrt( hare))>signif(apply(coefm.cond.replace,2,function(x){quantile(x,c(.025,.975),na.rm=T)}),3) ar1 ar2 ar3 intercept noise var2.5% 0.611 -0.700 -0.6720 4.98 0.51697.5% 1.300 0.241 -0.0417 6.32 1.500> # Method III基于平稳自助法的置信区间,且误差服从正态分布>coefm.norm=arima.boot(res,cond.boot=F,is.normal=T,ntrans=100,B=1000,init=s qrt(hare))> signif(apply(coefm.norm,2,function(x){quantile(x,c(.025,.975),na.rm=T)}),3) ar1 ar2 ar3 intercept noise var2.5% 0.687 -0.747 -0.6600 4.99 0.50897.5% 1.380 0.192 -0.0168 6.33 1.500>> # Method IV基于平稳自助法的置信区间,且误差不服从正态分布coefm.replace=arima.boot(res,cond.boot=F,is.normal=F,ntrans=100,B=1000,init =sqrt(hare))> signif(apply(coefm.replace,2,function(x){quantile(x,c(.025,.975),na.rm=T)}),3) ar1 ar2 ar3 intercept noise var2.5% 0.70 -0.715 -0.6620 4.98 0.4797.5% 1.36 0.183 -0.0187 6.30 1.503附自编函数3.1Myar#用于自回归模型的参数估计,整合矩估计,最小二乘估计,以及极大似然估计#该函数用于对时间序列中心化数据(因此截距项一定为0)估计AR模型的参数,AIC为真时,滞后项根据AIC准则确定,为假时则根据设置的order.max设定Myar=function(tsdata, order.max = 1,AIC = F){library(TSA)ols<-ar(tsdata,order=order.max,AIC=AIC,method='ols')yw<-ar(tsdata,order=order.max,AIC=AIC,method='yw')mle<-ar(tsdata,order=order.max,AIC=AIC,method='mle')olscoef<-ols[[2]]ywcoef<-yw[[2]]mlecoef<-mle[[2]]result=data.frame(olscoef,ywcoef,mlecoef)colnames(result)=c('最小二乘估计','矩估计','极大似然估计')return(result)}3.2Myarima#用于自回归模型的参数估计,整合矩估计,最小二乘估计,以及极大似然估计#该函数用于对时间序列中心化数据(因此截距项一定为0)估计AR模型的参数,AIC为真时,滞后项根据AIC准则确定,为假时则根据设置的order.max设定Myarima=function(tsdata, order=c(0,0,0)){library(TSA)result=NULLcss<-arima(tsdata,order=order,method='CSS')ml<-arima(tsdata,order=order,method='ML')cssml<-arima(tsdata,order=order)result$coef=cbind(css$coef,ml$coef,cssml$coef)result$log=cbind(css$log,ml$log,cssml$log)result$sigma2=cbind(css$sigma2,ml$sigma2,cssml$sigma2)result$aic=cbind(NA,ml$aic,cssml$aic)colnames(result$coef)=c('条件SS估计','极大似然估计','条件似然估计') colnames(result$log)=c('条件SS估计','极大似然估计','条件似然估计') colnames(result$aic)=c('条件SS估计','极大似然估计','条件似然估计') colnames(result$sigma2)=c('条件SS估计','极大似然估计','条件似然估计') return(result)}。
