常微分方程的初等解法
常微分方程的解

常微分方程的解是千儿的首篇笔记啦(^_−)☆这一系列笔记大概是来梳理一下各种常微分方程的解法。
证明部分暂时不会作为重点。
这篇笔记将梳理常微分方程的基本解法。
笔记主要采用的教材是丁同仁老师的《常微分方程教程》。
〇、一些名词1、常微分方程凡是联系自变量 x ,这个自变量的未知函数 y = y(x)及其直到 n 阶导数在内的函数方程f(x,y,y',y'',...,y^{(n)}) = 0 叫做常微分方程,并称 n为常微分方程的阶。
如果在上式中, f 对 y,y',...,y^{(n)} 而言都是一次的,那么我们称该方程为线性常微分方程,否则称其为非线性的。
如果未知函数是多元的,那么称之为偏微分方程。
在学习常微分方程的过程中,需要辩证地看待常微分方程和偏微分方程的关系,并及时进行转换。
这样就可以灵活地求解常微分方程。
2、解和通解若函数 y = \varphi (x) 在区间 j 内连续,且存在直到n 阶的导数。
若把 \varphi (x) 及其对应的各阶导数代入原方程,得到关于 x 的恒等式,那么我们称 y = \varphi(x)是原方程在区间 j 上的一个解。
如果解 y = \varphi(x, c_1,c_2,...,c_n) 中包含 n 个独立的任意常数c_1,c_2,...,c_n ,那么我们称其为通解。
若解中不包含任意常数,那么我们称其为特解。
3、初等积分法初等积分法是用一些初等函数或它们的积分来表示微分方程的解的方法。
这也是我们在本节中讨论的方法。
一、恰当方程对于形如 p(x,y)\text dx + q(x,y)\text dy = 0 的方程,如果存在一个可微函数 \phi (x,y) 使得 \text d \phi (x,y) = p(x,y)\text dx = q(x,y) \text dy,那么我们称其为一个恰当方程,或全微分方程。
恰当方程有解的充要条件是 \frac {\partial p(x,y)} {\partial y} = \frac{ \partial q(x,y)}{\partial x} 。
常微分方程的常见解法

# 定义网格密度
arrows=LINE,
# 定义线段类型
axes=NORMAL);
# 定义坐标系类型
在MATLAB的向量场命令为 quiver(x,y,px,py)
回车后Maple就在1 1 的网格点上画出了向量场
44
的图形,并给出了过点(-2, 2) (-2 ,1) (-2,2) 的三
条积分曲线,见下图
M (x,y)co x s2xye , y
N (x,y)co x s2xye x
M(x,y)N(x,y)
y
x
所以方程为全微分方程。
由公式F (x ,y ) 0M (s ,y )d s 0N (0 ,s )d s
x(yc o ss 2 se y)d sy2 d s
0
0
ysinxx2ey2y
或
x
y
F (x ,y )x 0M (s ,y ) d s y 0N (x 0 ,s ) d
s
例:验证方程
( y c o s x 2 x e y ) d x ( s i n x x 2 e y 2 ) d y 0
是全微分方程,并求它的通解。 解:由于 M (x ,y ) y c o sx 2 x e yN (x ,y ) s in x x 2 e y 2
dx
令 zy1n,则 dz(1n)yndy
dx
dx
d z (1 n )P (x )z (1 n )Q (x )
d x
求出此方程通解后, 换回原变量即得伯努利方程的通解。
例 湖泊的污染
设一个化工厂每立方米的废水中含有3.08kg盐酸, 这些废水流入一个湖泊中,废水流入的速率20 立方米每小时. 开始湖中有水400000立方米. 河水 中流入不含盐酸的水是1000立方米每小时, 湖泊 中混合均匀的水的流出的速率是1000立方米每小 时,求该厂排污1年时, 湖泊水中盐酸的含量。 解: 设t时刻湖泊中所含盐酸的数量为 x ( t )
常微分方程小结

常微分方程小结姓名:邱俊铭学号:2010104506姓名:李林学号:2010104404姓名:曾治云学号: 2010104509初等积分法:变量分离形式一、一阶微分程:dy/dx=h(x)g(y) ,其中函数h(x)在区间(a,b)上连续,g(y)在区间(c,d)上连续且不等于0.经过分离变量得: dy/g(y)=h(x)dx 两端积分得:G(y)=H(x)+c ,其中c任意的常数且G(y)= ∧dy/g(y),H(x)= ∧h(x)®x,所以G’(y)=1/g(y)不为0,故G存在逆函数,从而得到:y= (H(x)+c).例1. dy /dx=2xy解:当y ≠0时,分离变量后得:dy/ y =2xdx ,两边积分得:ln|y|=x^2+c1 ,此外y=0也是方程的解,从而方程的解为y=Ce^(x^2),g(y)=0,则y=是方程的解,其中C为任意的常数。
初值问题的解,即y取任意一个数得到的结果,代入通解中,求出具体y 值。
例2.y(1+x^2)dy=x(1+y^2)dx,y(0)=1;解:这是变量分离的方程,分离变量后得:y/(1+y^2)dy=x/(1+x^2),两边积分得其通解为:1+y^2=C(1+x^2),其中C为任意常数,代入初值条件得:C=2.。
故所给的初值问题的解为y=.二、常数变易法一阶非线性方程:dy/dx=a(x)y+f(x).(1)当f(x)=0时,方程为齐次线性方程,解法和上述的一样,通解为y=C ,C为任意的常数。
现在求齐次线性方程的通解,常数C换成x的函数c(x),得到:y= c(x),对x 求导,然后代入(1)中化简,两端积分,得:y=C +f x e ..例3. dy/dx-2xy=x.解:dy/dx=2xy+x ,这里a(x)=2x,f(x).从而可求出原方程的通解为: Y=exp(2 ∧x ®x)(c+ ∧xexp(-2∧x ®x)®x)=-1/2+ce^(x^2),即-1/2+ce^(x^2),其中c 为任意的常数。
二阶常系数常微分方程的初等解法求解技巧(K12教育文档)

二阶常系数常微分方程的初等解法求解技巧(word版可编辑修改)二阶常系数常微分方程的初等解法求解技巧(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(二阶常系数常微分方程的初等解法求解技巧(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为二阶常系数常微分方程的初等解法求解技巧(word版可编辑修改)的全部内容。
二阶常系数常微分方程的初等解法求解技巧(word版可编辑修改)二阶常系数常微分方程的初等解法求解技巧郑燕,王俊霞太原师范学院数学系,山西晋中,030619摘要:本文总结介绍了三类二阶常系数常微分方程的初等解法求解技巧,分别是:特征根法;常数变易法;比较系数法.同时结合例题进行具体讲解.虽然当今社会关于二阶常微分方程初等解法求解技巧的研究已经获得了很大的成就,但它的已有理论仍然得不到求知者的满足,需要大家进一步发展,使之更加完善。
关键词:二阶常系数齐次线性微分方程;特征根法;常数变易法;比较系数法;二阶常系数非齐次线性微分方程.1。
预备知识(1.1)其中以及f(t)都是连续函数并且区间是a t b。
如果,则方程(1)就变成了(1.2)我们形如方程(1.2)的方程叫做二阶齐次线性微分方程,把方程(1。
1)叫做二阶非齐次线性微分方程.并且把方程(1.1)叫做方程(1.2)对应的齐次线性微分方程。
2.求解方法技巧2.1常数变易法常数变易法是将常数看作是的待定函数,然后求出非齐次线性方程的通解。
求解过程如下:设,是方程(1.2)的基本解组,则(2.1.1)是方程(1。
2)的通解。
将常数看作是t的待定函数,那么方程(2。
常微分方程的初等解法与求解技巧

山西师范大学本科毕业论文(设计)常微分方程的初等解法与求解技巧姓名张娟院系数学与计算机科学学院专业信息与计算科学班级12510201学号1251020126指导教师王晓锋答辩日期成绩常微分方程的初等解法与求解技巧内容摘要常微分方程在数学中发挥着举足轻重的作用,同时它的应用在日常生活里随处可见,因此掌握常微分方程的初等解法与求解技巧是非常必要的.本论文主要论述了其发展、初等解法与求解技巧,前者主要有变量分离、积分因子、一阶隐式微分方程的参数表示,通过举例从中总结出其求解技巧,目的是掌握其求解技巧.【关键词】变量分离一阶隐式微分方程积分因子求解技巧Elementary Solution and Solving Skills of OrdinaryDifferential EquationAbstractOrdinary differential equations take up significant position in mathematics, and at the same time, the application of it can be seen everywhere in our daily life, therefore, it’s necessary to grasp the elementary solution of ordinary differential equations and solving skills. This paper mainly introduced the definition of ordinary differential equations, elementary solution method and solving skills, the former mainly included the separation of variables, integral factor, a parameter-order differential equations implicit representation, by way of examples to sum up their solving skills, the purpose is to master the skills to solve.【Key Words】the separation of variables the first order implicit differential equation integrating factor solution techniques目录1.引论 ............................................................................................................................. 1 2.变量分离方程与变量变换 .. (1)2.1变量分离方程的解法 .............................................................................................. 1 2.2变量分离方程的举例 .............................................................................................. 2 2.3变量分离方程的几种类型 .. (2)3.线性微分方程和常数变易法 (6)3.1线性微分方程与常数变易法 ................................................................................. 6 3.2伯努利微分方程 .. (8)4.恰当微分方程与积分因子 (9)4.1恰当微分方程 ......................................................................................................... 9 4.2积分因子 (11)5.一阶隐式微分方程与参数表示 (13)5.1一阶隐式微分方程的主要类型 (13)6.常微分方程的若干求解技巧 (18)6.1将一阶微分方程dx dy变为dydx 的形式 ................................................................... 18 6.2分项组合 (19)6.3积分因子的选择 (20)7.总结 ........................................................................................................................... 21 参考文献 ........................................................................................ 错误!未定义书签。
常微分方程初等积分法解法研究(二)伯努利方程

例题: 求解方程:
方程两端同除以 :令有:ຫໍສະໝຸດ 利用常数变易法求出其通解为:
代换
得原方程通解为:
例题:
解以下微分方程:
两边除以 ,得:
利用分离变量法,可得:
他可以用积分因子方法求解:
两边乘以
,得:
等式的左边是
的导数,两边积分
于是:
伯努利微分方程
伯努利微分方程是形如 的常微分 方程。其中 、 为 的连续函数, 为常数 且 0,1。
求解方法:变量替换法
利用变量替换法可将伯努利方程化为线性方程。
步骤如下: ⑴ 方程两端同除以 ,得:
⑵令
即可化为一阶线性微分方程:
⑶ 通过常数变易法求得一阶线性非齐次方程 的通解。
⑷ 最后经变量代换得原方程的通解:
常微分方程第二章 一阶微分方程的初等解法
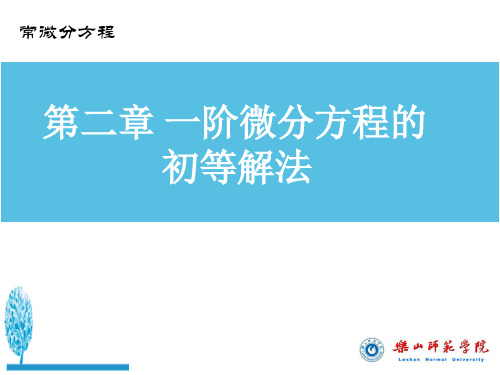
du dx 1u2 x
两边积分得: ln u 1 u2 ln x ln c
整理后得 u 1 u2 cx
变量还原得 y 1 ( y )2 cx
x
x
du dx 1u2 x
最后由初始条件 y(1) 0,可定出c 1.
故初值问题的解为 y 1 (x2 1) 2
可2、化d为y 变a量1x 分b1 y离 方c1 法
由对数的定义有
y e p( x)dxc1
y e p( x)dxc1
即
y ec1e p(x)dx ce p(x)dx.
此外y 0也是方程的解,若在上式中充许c 0, 即知y 0也包括在上式中,
故方程的通解为
y ce p(x)dx , c为任常数.
例4
求初值问题
dy dx
y2
c os x的特解.
例:
y y sin x 0
并求满足条件的 y( ) 2 特解。
2
线性微分方程
例:
1、cos x dy y sin x cos2 x dx
二 伯努利(Bernoulli )方程
形如 dy p(x) y Q(x) yn dx
的方程,称为伯努利方程. 这里P(x), Q(x)为x的连续函数 。
故对应齐次方程通解为 y c(x 1)n
y
ce p(x)dx
ce
n dx x 1
c(x
1)n
其次应用常数变易法求非齐线性方程的通解,
令y c(x)( x 1)n为原方程的通解 , 代入得
dc(x) (x 1)n nc(x)(x 1)n1 nc(x)(x 1)n1 ex (x 1)n dx
解的步骤:
10
解方程组aa21xx
一阶常微分方程初等解法

dy 例6 求方程 x 1 ny e x 1 的通解, dx 这里n为常数. dy n y e x 1 . 解 将方程改写为 dx x 1 dy n y 0 的通解, 首先,求其次线性微分方程 dx x 1 为 y c x 1 .
容易验证,原方程的通解就是
u x, y c,
( c 是任意常数).
2 2 3
例7
3x 6 xy dx 6 x y 4 y dy 0 的通解.
2
解 这里 M 3x 6 xy , N 6 x y 4 y , 这时 M N 12 xy, 12 xy, 因此方程是恰当微分方程. y x 现在求 u, 是它同时满足如下两个方程: u u 3x 6 xy , 6 x y 4 y . x y 前一个式子,对 x 积分,得到 u x 3x y y ,
在上一张我们已经了解了微分方程的一些基本特点, 下面我们来看一个题来回忆一下微分方程:
dx x 例 求解方程 dy y .
解 可以变化为:ydy xdx , y x c 两边积分,即得 2 2 2 ,
2 2
因而,通解为 x y c .
2 2
1.1变量分离方程
形如
2 2 2 3
2
2
2
3
3
2
2
将得到的方程对 y 求导,并使它满足上一个方程,即得 u d y 6x y 6x y 4 y , 于是 y dy d y 4 y , 积分后可得 y y , dy
2 2 3
4
3
u x 3x y y .
3 2 2 4
因此,方程的通解为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常微分方程的初等解法1.常微分方程的基本概况1.1.定义:自变量﹑未知函数及函数的导数(或微分)组成的关系式,得到的便是微分方程,通过求解微分方程求出未知函数,自变量只有一个的微分方程称为常微分方程。
1.2.研究对象:常微分方程是研究自然科学和社会科学中的事物、物体和现象运动﹑演化和变化规律的最为基本的数学理论和方法。
物理﹑化学﹑生物﹑工程﹑航空﹑航天﹑医学﹑经济和金融领域中的许多原理和规律都可以描述成适当的常微分方程。
如牛顿运动规律、万有引力﹑能量守恒﹑人口发展规律﹑生态总群竞争﹑疾病传染﹑遗传基因变异﹑股票的涨伏趋势﹑利率的浮动﹑市场均衡价格的变化等。
对这些规律的描述﹑认识和分析就归结为对相应的常微分方程的理论和方法不仅广泛应用于自然科学,而且越来越多的应用于社会科学各个领域。
1.3.特点:常微分方程的概念、解法、和其它理论很多,比如,方程和方程组的种类及解法、解的存在性和唯一性、奇解、定性理论等等。
下面就方程解的有关几点简述一下,以了解常微分方程的特点。
求通解在历史上曾作为微分方程的主要目标,一旦求出通解的表达式,就容易从中得到问题所需要的特解。
也可以由通解的表达式,了解对某些参数的依赖情况,便于参数取值适宜,使它对应的解具有所需要的性能,还有助于进行关于解的其他研究。
1.4.应用:现在,常微分方程在很多学科领域内有着重要的应用,自动控制、各种电子学装置的设计、弹道的计算、飞机和导弹飞行的稳定性的研究、化学反应过程稳定性的研究等。
这些问题都可以化为求常微分方程的解,或者化为研究解的性质的问题。
应该说,应用常微分方程理论已经取得了很大的成就,但是,它的现有理论也还远远不能满足需要,还有待于进一步的发展,使这门学科的理论更加完善。
2.一阶的常微分方程的初等解法一阶常微分的初等解法包括变量分离方程与变量变换﹑可以化为变量分离方程的类型﹑线性微分方程与常数变易法﹑恰当微分方程与积分因子,下面我们就具体分析一阶常微分方程的初等解法。
2.1、变量分离方程法 形如)()(y x f dxdy ϕ=,(2.1)的方程,称为变量分离方程,这里的)(x f ,)(y ϕ分别是x ,y 的连续函数。
如果0)(≠y ϕ,我们可将(2.1)改写成dx x f y dy )()(=ϕ,这样变量就“分离”开来了。
两边积分得到⎰⎰+c dx x f y dy )()(ϕ,(2.2)。
例1:方程yx dx dy -=就可以用变量分离法求解方程 解: 变量分离,得到 xdx ydy -=,两边积分,即得 22222c x y +-=, 因而,通解为 c y x =+22,(c 为任意常数)2.2、可化为变量分离方程的类型(1) 形如)(xy g dx dy =,(2.3)的方程,称为齐次微分方程,这里)(u g 是u 的连续函数。
作变量变换x y u =,(2.4)即ux y =,于是u dxdu x dx dy +=,(2.5).将(2.4),(2.5)代入(2.3),则原方程变为)(u g u dx du x =+,整理后,得到xu u g dx du -=)(,(2.6).方程(2.6)是一个变量分离方程,这就所为的可以化为变量分离的方程。
例2方程xy x y dx dy tan += 就是一个可以化为变量分离的方程。
解 这是齐次微分方程,以u x y = 及u dx du x dx dy +=代入,则原方程变为u u u dx du x tan +=+。
即xu dx du tan =。
将上式分离变量,既有 x dx udu =cot , 两边积分,得到 c x u +=ln sin ln ,(c 为任意常数)整理,得到 x e u c •±=sin , 令c e c =±,得到 cx u =sin将x y u =代入上式,得到方程的通解为 cx xy =sin (2)形如222111c y b x a c y b x a dx dy ++++=,(2.7)的方程也可以经变量变换化为变量分离方程,1a ,2a ,1b ,2b ,1c ,2c 均为常数。
我们分三种情况来讨论:①k c c b b a a ===212121(常数)情形。
这时方程化为k dx dy =,有通解c kx y +=,其中c 为任意常数。
②212121c c k b b a a ≠==情形。
令y b x a u 22+=,这时有212222c u c ku b a dx dy b a dx du +++=+=是变量分离方程。
③2121b b a a ≠情形。
如果方程(2.7)中1c ,2c 不全为零,方程右端分子﹑分母都是x ,y 的一次多项式,因此⎩⎨⎧=++=++﹐0﹐0222111c y b x a c y b x a (2.8).代表Oxy 平面上两条相交的直线,设交点为)﹐(βα。
若令⎩⎨⎧-=-=﹐﹐βαy Y x X (2.9)。
则(2.8)化为⎩⎨⎧=+=+﹐0﹐02211Y b X a Y b X a 从而(2.7)变为)(2211YX g Y b X a Y b X a dX dY =++=,(2.10)。
因此,求解上述变量分离方程,最后代回原变量即可得原方程(2.7)的解。
如果方程(2.7)中021==c c ,可不必求解(2.8),直接取变换xy u =即可。
上述解题的方法和步骤也适用于比方程(2.7)更一般的方程类型)(222111c y b x a c y b x a f dx dy ++++=。
例3 方程31-++-=y x y x dx dy 就可以用上述方法来求解。
解 解方程组 ⎩⎨⎧=-+=+-﹐03﹐01y x y x 得x=1,y=2.令 ⎩⎨⎧+=+=﹐2﹐1Y y X x 代入原方程,则有YX Y X dX dY +-=, 再令X Y u =,即uX Y =,则上式化为du u u u X dX 2211--+=, 两边积分,得 c u u X +-+-=12ln ln 22,因此 c e u u X ±=-+)12(22,记1c e c =±,并代回原变量,得1222c X XY Y =-+,把⎩⎨⎧-=-=21y Y x X 代入上式 得122)1()2)(1(2)2(c x y x y =----+-整理,得c x y x xy y =---+26222 (c 为任意常数)2.3、线性微分方程与常数变易法 一阶线性微分方程)()(x Q y x P dxdy +=,(2.9)。
其中P (x ),Q (x )在考虑的区间上是x 的连续函数。
若Q (x )=0,(2.9)变为y x P dy dx )(=,(2.10),(2.10)称为一阶其次线性微分方程。
若0)(≠x Q ,(2.9)称为一阶非其次线性微分方程。
(2.10)是变量分离方程它的解为⎰=dx x p ce y )(,(2.11)这里的c 为任意常数。
现在讨论非奇次线性微分方程(2.9)通解的求法。
不难看出,(2.10)是(2.9)的特殊情形,可以设想(2.11)中将常数c 变易为x 的待定函数c(x).令⎰=dx x p e x c y )()(,( 2.12)微分之,得到⎰+⎰=dx x p dx x p e x p x c e dxx dc dx dy )()()()()(,(2.13).将(2.12),(2.13)代入(2.9),得到)()()()()()()()()(x Q e x c x P e x P x c e dxx dc dx x p dx x p dx x p +⎰=⎰+⎰。
即⎰=-dx x p e x Q dx x dc )()()(,积分后得到⎰+⎰=-c dx e x Q x c dx x p )()()(,这里的c 是任意常数。
将上式代入(2.12),得到方程(2.9)的通解⎰+⎰⎰=-))(()()(c dx e x Q e y dx x p dx x p ,(2.14)。
这种将常数变易为待定函数的方法,我们通称为常数变易法。
常数变易法实际上也是一种变量变换的方法,通过变换(2.12)可将方程(2.9)化为变量分离方程。
若方程不能化为(2.9)形式,可将x 看作y 的函数,再看是否为(2.9)形式。
例4 方程1)1()1(++=-+n x x e ny dxdy x (n 为常数)就可以用常数变易法求解。
解 将方程改写为 n x x e y x n dx dy )1(1+=+-,① 首先,求齐次线性微分方程01=+-y x n dx dy 的通解从 dx x n y dy 1+=,得到齐次线性微分方程的通解n x c y )1(+= 其次,应用常数变易法求非齐次线性微分方程的通解。
为此,在上式中把c 看成为x 的待定函数c (x ),即n x x c y )1)((+=,②微分之,得到 )()1()1()(1x c x n x dxx dc dx dy n n ++++=,③ 把②,③代入①,得到 x e dxx dc =)(, 积分之,求得 c e x c x +=)(因此,以所求的c (x )代入②,即得原方程的通解 )()1(c e x y x n ++=, (c 为任意常数)2.4、恰当微分方程与积分因子2.4.1恰当微分方程如果方程0﹐y)dy (﹐y)dx (=+x N x M ,的左端恰好是某个二元函数﹐y)(x u 的全微分,即﹐y)dx (x M +﹐y)dy (x N =dy yu dx x du ∂∂+∂∂=x u ﹐y)(则称原式为恰当微分方程。
容易验证恰当微分方程的通解就是c ﹐y)(=x u ,这里的c 为任意常数。
如果方程是恰当微分方程时,函数﹐y)﹐N (x ﹐y)(x M 应该具有以下性质。
M xu =∂∂和N y u =∂∂分别对y ,x 求偏导,得到y M x y u ∂∂=∂∂∂2,x M y x u ∂∂=∂∂∂2,由x N ﹐∂∂∂∂y M 得连续性,可得y x u x y u ∂∂∂=∂∂∂22,故xN y M ∂∂=∂∂,这就是恰当微分方程的必要条件。
如果是恰当微分方程我们可以利用“分项组合”的办法来求解。
利用公式⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧+-=--=+=-=+==+﹐)(ln 21﹐)(arctan x xdy -ydx ﹐)(ln ﹐)(xdy ydx -﹐)(xdy -ydx ﹐)(222222y x y x d y x xdy ydx y x d y y x d xy xdy ydx x y d x y x d y xy d xdy ydx (2.15) 例5 方程0)46()63(3222=+++dy y y x dx xy x 就可以用“分项组合” 方法来求解。
