上海交大819十年真题
上海交大819复试笔试题-仅含通信方向

图1 7.鉴频器的组成框图如图 2 所示,则 u01 为 频)波,方框 A 为 。 8.
图2 (调幅0 cos(2π × 10 6 t + 10 cos 2000πt) (V) ,则此信号在单位电 W
阻上的功率为
9. 已知载波 v0=V0cosω0t,调制信号 vΩ=VΩsinΩt,,则 PM 波的表达式为: 。 10. 皮尔斯晶体振荡器中,石英晶体等效为 。
1
上海交大高频电子线路复试试卷
学号: 姓名:
2009.3
(注意:在答题纸上答题,不必重新抄题,只写题号即可,共计 50 分)
一、单项选择题(10 分,每小题 3 分) 1、 二极管大信号峰值包络检波器, 原电路正常工作。 若放电时间常数 RLC 加倍, 会引起( ) 。 A.底部切割失真(负峰切割失真) B. 惰性失真(对角线切割失真) C. 惰性和底部切割失真 2、在调制信号频率相同的条件下,调频波比调幅波所占频带宽度( A、宽 B、窄 C、相等 3、若要求功率放大器输出功率最大,功放应工作于( A. 欠压 B、临界 C、弱过压 D、过压 4、下列正弦波振荡器类型中,哪一种频率稳定度最高( A 克拉泼振荡器 B 西勒振荡器 C 石英晶体振荡器 5、 自身带有限幅功能的鉴频器是( ) A 电感耦合相位鉴频器 B 电容耦合相位鉴频器 )状态 )
学号: 姓名:
2009.3
(注意:在答题纸上答题,不必重新抄题,只写题号即可,共计 50 分)
一 填空题 1.四元离散信源的四个符号出现的概率分别为 1/4、 1/2、 1/8、 1/8, 其信源熵为 。理论上,四元信源的最大熵为 ,条件是 。 2.在四进制系统中每秒钟传输 1000 个四进制符号,则此系统的码速率 RB 为 ,信息速率 Rb 为 。 3.码组(01001)的码重为 ,它与码组(10011)之间的码距 是 。 4.线性分组码(n,k),若要求它能纠正 2 个随机错误,则其最小码 距为 ;若要求它能纠正 2 个随机错误且能检测到 4 个随机错误,则 其最小码距为 。 5.模拟通信系统中,已调信号带宽与有效性之间的定性关系为 , 接收机输出信噪比与可靠性之间的定性关系为 。 6.某调频信号的时域表达式为 10cos[2π×10 t+5sin2π×10 t],此信 号的带宽为 ,当调频灵敏度为 5kHZ/V 时,基带信号的时域表达式为 。 7.在 AM、 SSB、 FM 系统中, 有效性最好的是 , 可靠性最好的是 。 8.对某模拟信号进行线性 PCM 编码,设抽样频率为 8kHZ,编码位数为 7,则此 PCM 信号的信息速率为 ;当抽样频率不变而编码位数由 7 增 大到 12 时,量化信噪比提高 dB。 9.设信息速率为 2.048Mbit/s,则 2DPSK 信号带宽为 ,QPSK 信号 的带宽为 。 10.格雷码的特点是 ,四进制符号-3,-1,+1,+3 对应的格雷码 分别为 。
上海交通大学819信号与系统

—————————————————————————————————————————————————————————— 中国绝对第一的专业课辅导平台 专业课钻石卡高级辅导——成功率趋近 100% 考研专业课频道 咨询专 线: 010-62682299 2
圆圆工作室 内部版本:仅供学习,禁止传播!
通信原理:《通信原理》曹志刚,清华大学;《通信原理》樊昌信,华中科技大学 高频电子电路:《高频电子电路》张肃文,高等教育出版社。 模拟电路:《电子技术基础(模拟部分) 》 (第五版), 康华光, 高等教育出版社 数字电路: 《 数字电子技术基础(第五版) 》, 阎石, 高等教育出版社 3 复试复习建议(从准备时间、准备内容及其注意事项去阐述) 准备时间 考完就应该开始 准备内容 梳理脉络,熟练习题 注意事项
第二部分
专业与就业解析
2.1 上海交大专业综合介绍
081000 信息与通信工程 01 通信与信息系统 光纤通信与区域通信网;无线通信、移动通信与个人通信;图象处理与图 象通信、数字电视;网络攻防与安全评估; 02 信号与信息处理 多媒体信号处理及数字通信;数字信号处理系统设计与应用;数字电视专 用芯片设计;协同信号处理技术 1.可以跨学科报考的专业:计算机科学与技术专业,电子科学与技术专业。 2.复试时需进行笔试,内容包括通信基本电路、通信原理等基础知识和技 能。 080900 电子科学与技术 01 电路与系统 研究内容: 模拟和数字集成电路设计;语音信号处理;自动测试系统;嵌入式系统设 计与应用;多媒体交互技术 1.可以跨学科报考的专业:控制科学与工程,信息与通信工程,计算机科 学与应用专业;2、复试时需进行笔试,内容包括模拟电子技术、数字电子 技术等基础知识和技能。
第四部分
上海交通大学信号与系统819考研教材习题参考答案 (5)-慧易升考研

(b)证明略
(c) α = sin[(θ p − ω p ) / 2] sin[(θ p + ω p ) / 2]
(d) 2π / 3,π / 2,π / 4
(e)
Z −1
=
−
z−1 + 1 + αz
α
−1
,α
=
−
cos[(θ p cos[(θ p
− ω p ) / 2] + ω p ) / 2]
(f) π / 3,π / 2
扩充题 7.42 (a)证明略
(b) yc (nT ) − yc (nT − T ) ≅ TAxc (nT ) − Tcyc (nT )
(c) H (z) =
A
c + 1 − 1 z−1
TT
(d) 证明略
(e) 稳定,模拟虚轴映射到以 1/2 为圆心 1/2 为半径的圆上,T 小时逼近好
(f) s = z −1 ,模拟虚轴映射到 Re{z}=1 线上,不一定稳定,T 小时逼近好
Td 2j
cot(ω
/
2),Td
=π
/ 4 (令红圆点的值相等)时,低频良好逼近
H c ( jΩ)
研 考
H (e jω )
统
系
-π -π/2
与 π/2 π
Ω
-π -π/2
π/2 π
ω
号
819信 (d)
G(z)
=
2 Td
⎜⎜⎝⎛
1 1
− +
z −1 z −1
⎟⎟⎠⎞,|
z
|> 1 , g[n] =
2 Td
3 2
(d) I 型,4L+1
上海交通大学 通信信号819考研之经验

经典文章推荐:##交通大学通信信号819考研之经验暑假快到了,现在发表自己对于考研的一点看法是因为我觉得考研从暑假开始足矣,只要你努力并且心无旁骛。
〔我是从9月底开始复习的,没有任何炫耀的意思,只是想说明情况〕先说一下我自己的情况:我是考819的,电子系信号与信息处理1、很多人会问这样的问题:辅导班要不要上?我的意见是:辅导班不用去上,只要把那些辅导班资料看一下就可以了〔资料的选取我一会儿会说〕当然这也取决于个人的学习习惯。
我觉得上辅导班的效果不一定好,尤其是对于像我这样不太会听课的,所以我什么班都没报,当然这个因人而异。
而且辅导班上教师都是对着讲义讲的,同学也只有记笔记的份,效果有多好,自己心里明白,没必要花好几百块钱,心理作用而已。
2、至于复习,总是听人说什么要到哪里哪里去自习。
这种过于苛求细节的做法其实不可取。
考研心态也很重要,我就是抱着随遇而安的心情每天随便找一间教室坐下看书就行了,成天奔到图书馆去占座不代表学得有多认真,最多说明你在自习教室这个问题上比拟执着。
还有就是住不住到学校外面去的问题,这个问题其实根本就不是问题。
如果你的心态好,住哪都一样。
〔当初我们寝室另外三个睡得都很晚,也不是特别安静,但只要你心态好就行〕3、复习时要注重效率:有时候明显自己看不进书就出去走走又何妨?收拾一下心情看书会更好4、复习要不连续考研其实就是考谁能够反复不断地看书学习保持考试状态,说得极端点就是比谁更有耐力所有的课都要不停的滚,不停的做题。
否那么半个月不练某一方面的东西就几乎全忘了,这对心理的打击是比拟大的下面来说一下具体的课程:1、政治这没什么说的,做做题,考前看看大题就OK了〔政治只要过就行,别指望政治拉什么差距〕2、英语考前一个月把新题型和作文看一下,平时主要练阅读。
很多人说完形难,其实我觉得根阅读差不多,没必要把这个当成洪水猛兽3、数学我考数学一高数里面最烦的是重积分、曲面、线积分。
建议把800题的相关章节认真看一下,区分清楚各个定理的使用情况。
上海交通大学 通信信号819考研之经验word精品文档9页

经典文章推荐:上海交通大学通信信号819考研之经验暑假快到了,现在发表自己对于考研的一点看法是因为我觉得考研从暑假开始足矣,只要你努力并且心无旁骛。
(我是从9月底开始复习的,没有任何炫耀的意思,只是想说明情况)先说一下我自己的情况:我是考819的,电子系信号与信息处理1、很多人会问这样的问题:辅导班要不要上?我的意见是:辅导班不用去上,只要把那些辅导班资料看一下就可以了(资料的选取我一会儿会说)当然这也取决于个人的学习习惯。
我觉得上辅导班的效果不一定好,尤其是对于像我这样不太会听课的,所以我什么班都没报,当然这个因人而异。
而且辅导班上老师都是对着讲义讲的,同学也只有记笔记的份,效果有多好,自己心里明白,没必要花好几百块钱,心理作用而已。
2、至于复习,总是听人说什么要到哪里哪里去自习。
这种过于苛求细节的做法其实不可取。
考研心态也很重要,我就是抱着随遇而安的心情每天随便找一间教室坐下看书就行了,成天奔到图书馆去占座不代表学得有多认真,最多说明你在自习教室这个问题上比较执着。
还有就是住不住到学校外面去的问题,这个问题其实根本就不是问题。
如果你的心态好,住哪都一样。
(当初我们寝室另外三个睡得都很晚,也不是特别安静,但只要你心态好就行)3、复习时要注重效率:有时候明显自己看不进书就出去走走又何妨?收拾一下心情看书会更好4、复习要不间断考研其实就是考谁能够反复不断地看书学习保持考试状态,说得极端点就是比谁更有耐力所有的课都要不停的滚,不停的做题。
否则半个月不练某一方面的东西就几乎全忘了,这对心理的打击是比较大的下面来说一下具体的课程:1、政治这没什么说的,做做题,考前看看大题就OK了(政治只要过就行,别指望政治拉什么差距)2、英语考前一个月把新题型和作文看一下,平时主要练阅读。
很多人说完形难,其实我觉得根阅读差不多,没必要把这个当成洪水猛兽3、数学我考数学一高数里面最烦的是重积分、曲面、线积分。
建议把800题的相关章节认真看一下,区分清楚各个定理的使用情况。
上海交通大学信号与系统819考研教材习题参考答案 (4)-慧易升考研
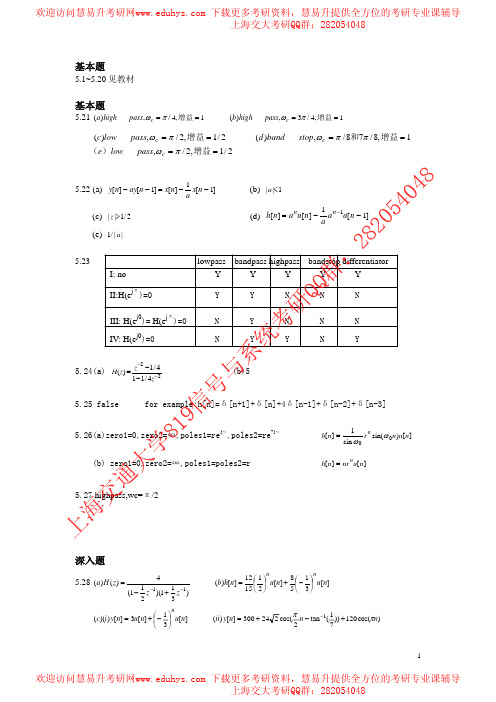
考 研
sin[( n − α )π ] ( n − α )π
I,
II
]
5.42 (a)A(ej )=1,Φ(ω)=-αω
ω
|ω|<π
群
: 28
稳定逆系统 Y Y Y N
20
54 04 8
欢迎访问慧易升考研网 下载更多考研资料,慧易升提供全方位的考研专业课辅导 上海交大考研QQ群:282054048
: 28
2
欢迎访问慧易升考研网 下载更多考研资料,慧易升提供全方位的考研专业课辅导 上海交大考研QQ群:282054048
20
54 04 8
欢迎访问慧易升考研网 下载更多考研资料,慧易升提供全方位的考研专业课辅导 上海交大考研QQ群:282054048
jπ
1 x[n − 1] a
(b) | a |< 1
n (d) h[ n ] = a u[ n ] −
Y
jπ
Y Y Y
N N
n
群
N N N
lowpass Y
bandpass highpass Y Y
bandstop differentiator Y Y N N Y
III: H(e )= H(e )=0 IV: H(e )=0
(b) G ( z ) = z −( M −1) / 2 − 1 / 4 z − M / 2 = H ( z1 / 2 )
M:even
5.31 (a) y[n] = ⎜ ⎟ u[n] − (3)n u[−n − 1] − u[n]
7 3 (c )hi [ n] = δ [n + 2] − δ [n + 1] + δ [n] 2 2
2014 上海交通大学819真题 回忆

1 信号部分:拉氏变换题型:给出流图要求推倒H(S) ,流图连接形式和小白皮书193页6.27很像,具体支路不一样,且题目中反馈支路带a、b两个未知数。
稳定性的判断:a/b范围为何时,该系统稳定给定a/b值求H(s);然后就是给一些特定输入信号求其响应、稳态响应2 信号部分:Z变换考得比较基础,Z变换那一章计算题型基本都涉及到,包括作图画幅度响应(好像Z变换,今年考了2个大题,另一个实在想不起来了)4 信号部分:采样模型基于连续时间采样系统框图讨论是否可以恢复出原信号问的是采样后的表达式;频率满足什么关系可以恢复成原信号(但是我对这题有疑问,框图中给的重构滤波器是时域门函数,频域就是Sa(w*t)函数,幅度非线性相乘,怎么恢复出原信号?)4 DSP部分:奥本第五章给两个H1(Z)、H2(Z),设计H(Z)达到一定设计要求,要求涉及相位补偿、全通分解、逆系统、最小相位系统(奥书可参考例5.45 5.46 5.64)有4小问都是要求写出H(Z)表达式剩下的DSP 部分,写的比较顺所以印象不深刻,但涉及的考点列出来了1 线性卷积与循环卷积的关系:给了两个序列并判断哪处线性卷积与循环卷积是一致的2 FFT的推导:时抽的FFT 即奥书(9.10到9.14)及4点到8点的流图3 N/2点FFT实现N点的计算8 DSP:滤波器设计题目文字挺多的,大体意思给出连续域滤波器的要求,设计数字滤波器并给出设计的过程。
题目给了类似7.20式的式子文字太多,有些不理解的地方,所以我只写了第一步推导类似双线性变换法的推导过程:奥书(7.20式经过7.26/27 得到7.28/29 式)记得不是很清楚,所以欢迎就需补充和指正学长只能帮你到这了~~~~~。
(2021年整理)上海交大819信号系统与信号处理考研大合集

上海交大819信号系统与信号处理考研大合集编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(上海交大819信号系统与信号处理考研大合集)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为上海交大819信号系统与信号处理考研大合集的全部内容。
ee 的经——sjtu819信号系统与信号处理考研大合集复试终于结束了,一切都算是顺利,虽然找导师还没搞定,但是总算是半只脚进入了交大的大门,对我的两年考研之路有了个不错的交代,对所有支持我关心我的朋友们有了一个交代。
现在和很多学弟学妹接触,有不少的感触,下面我想谈一谈我的一些想法,我的文笔是出奇的烂,请大家多多包涵。
第一,关于考研的选择每次经常在819群里看到学弟学妹们在讨论关于交大各个方向的报录比啊,保研人数之类的问题,还有很多人问我“交大电院难不难考?"、“我现在准备是不是太晚了?”、“我考不上能调剂工程硕士嘛?"这样的问题,对这样的问题有种说不出的感觉,当然关注一下考研难度,做出自己的选择这是很必要的。
但是如果把过多的精力都在用来纠结这些问题,就太不应该了。
如果你决定考交大电院,难道我说电院很难考,你准备的有点晚,你就放弃了么?如果是这么容易就动摇的话还是趁早选择一个简单一点的学校,或者干脆不要考研了,因为你这么不坚定,考研大半年的日子你肯定会受到各种事情的影响,肯定会受到外界的各种干扰。
选择很重要,但是一旦自己做出了自己的决定,我建议大家就好好的静下心来,排除外界各种干扰,开始努力学习,即便从暑假开始,6个月的时间,如果你能好好把握住,相信你会取得不错的成绩。
即便像我一样,第一年没考上,这段考研历程也绝对你是人生中的一笔财富。
上海交大2013年819真题

(1)n h2 [n], n 0,1,....11 (5), h4 [n] , h4 [n] 是否为高通滤波器?无需证明,简述理由. 0, else
七, 两个 6 点的序列 x1[n], x2 [n] 如图所示, X 1[k ], X 2 [k ] 为其 6 点 DFT. (1),用 A(k )e
五, h[n], g[n] 分别是截止频率为 / 2 的低通和高通滤波器. 画出 v0 [n], v1[n], w0 [n], w1[ n] 的频谱图(只需画一个周期) :
六,已知 H d (e )
jw
e j 5.5 w ,| w | 0.3 , 0.3 | w | 0
2
y[n] x1[n] x 2 [n] , 用 x[n] 的傅里叶变换表示 y[n] 的 DFS.( 还有一个表示 x[n] 的 DFS
的……)
x1[n]
x2 [ n ]
Apcyu, 2013/1/7
HFቤተ መጻሕፍቲ ባይዱ
3
八,基 2 时域 FFT (1),推导基 2 时域第一步(分裂一次). (2),在下图填空 (3),用 FFT 处理 N 点序列需要多少次复数乘法和复数加法.
Apcyu, 2013/1/7
HF
2
jw (1),求 H d (e ) 的群延时以及 hd [ n ] ;
n (2),若 h1[n] (1) hd [ n] ; h2 [n]
sin (n 5.5) hd [n]. .. h1[n], h2 [n] 是否为高通滤波器,写 (n 5.5)
jw jw 出 H1 (e ), H 2 (e ) . jw (3), x[n] cos(0.6 n) [n 3] 5 ,通过 H d (e ) ,求输出( x[n] 是对的,通过什么系统记不
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H� (k )/N 1−zk z−1
,其中
zk = ej(2Nπ)k , k = 0,1,2,3 … … N − 1
试求: 1. 用系统函数为(1-z-N)的 FIR 系统与一节 IIR 系统的并联组合进行组合进行级联来实现该
采样滤波器,画出这种信号的信号流图。 2. 求采样滤波器的单位样值响应。
3. 证明常数H�(k)就是系统频率响应在等间隔频率ωk = �2Nπ� k , (k = 0,1,2 … … N − 1)上 的样本。
并写出相应的步骤。
二、N 阶 FIR 数字滤波器的单位样值响应为 h(n),N 为奇数,且又有 h(n)=-h(N-1-n)。试证 明该滤波器不可能是低通或者高通滤波器。
三、已知 y(n)=x1(n)+jx2(n),x1(n)和 x2(n)均为具有长度为 N 的实序列。设 y(n)的离散傅里叶
变换
Y(k)
X(s)
2.判断该系统的稳定性。若不稳定则该选择什么样的 h(t)才能使系统稳定?
3.若因果系统的输入
x(t)的拉氏变换X(s)
=
1 1+e−s
,
Re(s)
>
0,求该系统的零状态响应。
4.当系统稳定时候,若输入为 cost,求系统的稳态响应。
九、下图为某 LSI 系统的模拟框图,k 为待定系数。试求:
2. 用双线性法求 Ha(jΩ)。
3. 试画出用以上两种方法得到的 Ha(jΩ)的幅频响应,并比较哪一个没有失真。
八、图中λ1和λ2为状态变量,输入和输出分别 x(t)和 y(t),试求:
X(t)
Y(t)
D
c
b
D a
1. 写出状态方程和输出方程。
2. 如果输入 x(t)=u(t)作用下,其状态方程为零状态,解为
八、假定关于某个 LTI 系统的已知下列信息:1)系统是因果的, 2)系统函数是有理的,且 仅有两个极点在 S=-2 和 s=4,3)对于任意时间 t,当系统输入为 e(t)=1 时,系统的输出为 r(t)=0, 4)系统的单位冲激响应的初值为 4,试求:
1.系统的电压传输系数 H(s)=Y(s)及单位冲激函数 h(t),写出描述该系统的微分方程。
二、某离散时间 LSI 因果系统。当输入为 x(n)=2nu(n),完全响应为
2 3
(−1)n
− (−2)n
+
1 3
(2)n
,n>0,当
x(n)=u(n)时候,y(n)
=
1 2
(−1)n
−
2 3
(−2)n
+1
6
。
试求:
1. H(Z),h(n) 以及系统的差分方程。 2. 用直接Ⅱ型画出本系统的信号流图。
2.如果 T 和 X(jw)不变,试分别求出∫−∞∞ x(t)dt 和 ∑∞n=−∞ x(n)。
3.如果 x(t)是频率受限的信号,X(jw)=0,|ω| ≥ W,欲使等式T ∑∞n=−∞ x(n) = ∫−∞∞ x(t) dt
成立,试求采样周期 T 和信号带宽 W 的关系。
x(t)
∑ Xp(t)
脉冲序列
=
x(n)
+ x(−n) 2
,
xo
=
x(n)
− x(−n) 2
已知
x(n)离散傅里叶变换
XR(ejw)=
1−acosw 1−2acosw +a2
。其中|a| < 1为实数。试求:
1. x(n),X(ejw),x(z)。 2. 设 X(ejw)=XR(ejw)+jX1(ejw),试导出 XR(ejw)与 X1(ejw)之间的关系。
3.
当y(−1)
=
0,
y(−2)
=
1 2
,
x(n)
=
n
∗
(−2)n u(n)
时候,求系统的完全响应。
三、如下图所示,假设
Sc(t)是带限的,Sc(jΩ)=0,|Ω|
≥
π,对
T
xc(t)进行采样,采样周期是
T,
得到序列 x(n)=xc(nT)。试求: 1. xc(t)的傅里叶变换和 x(n)的离散傅里叶变换。 2.如下离散时间系统仿真图,试选择该离散时间系统函数 H(ejw),当输入 s(n)=sc(nT)时候, 输出为 y(n)=xc(nT)。
真题由 ee 提供,功整理,有任何疑问发送 gong819@
三,如下图 a 所示系统,x(t)为如图 b 所示的周期对称方波。周期 T=2π(s),系统 H1(w) 和 H2(w)分别如图 c 和 d 所示,试求系统的输出 y(t)。
x(t)
s(t)
f(t)
H1(w)
∑
y(t) H2(w)
七、设某已经被调制的窄带实带通信号 s(t),它的等效低通表示形式为 s(t)=Re�s1(t)ejωct�, 式中复信号 s1(t)为 s(t)的等效低通,wc 为调制信号的载波频率。试求:
1.如果 s1(t)的频谱为 S1(w),求 s(t)的频谱 S(w)。 2.用 x(t)=Re�Am g(t)ejωct�, 0 ≤ t ≤ T,表示幅度调制信号,Am 为调制幅度,g(t)为实信号脉 冲,其频谱 G(w)如下图所示,试画出 x(t)的频谱 X(w)。
GSc((wt))
-wm
wm
wt
3.如果y(t) = Re�Am [g(t) + jg�(t)]ejωct�, 0 ≤ t ≤ T, g�(t)为上一问中的 g(t)的希尔伯特变换。 求 y(t)的频谱 Y(w)。
4.比较 X(w)和 Y(w),你能得出什么结论?
真题由 ee 提供,功整理,有任何疑问发送 gong819@
x(n)
P(t) 图a
X(jw)
-2000π
1 2000π w
图b
五、一个线性非因果离散时间系统具有系统函数为
H(z)=
(1−0.5z −1 )(1+4z −2 ) (1−0.64z−2) ,
1. 求 一 个 最 小 相 位 系 统 H1(z) 和 一 个 全 通 系 统 Hap(z) 的 表 示 式 , 使 满 足
1 1−e −j ω
=
1 2
−
j 2
cot
ω 2
。
真题由 ee 提供,功整理,有任何疑问发送 gong819@
六、令 x(k)表示 N 点序列,x(n)的 N 点 DFT,试证明: 1.若 x(n)满足 x(n)=-x(N-1-n),则 X(0)=0。
2.当 N 为偶数时候,x(n)=x(N-1-n),则 x(N)=0。
图a
X(t) 1
T
T
−4
4
图b H1(w)
t H2(w)
π 4
-4 -2
2 4W
π
-3
3
W
图c
图d
真题由 ee 提供,功整理,有任何疑问发送 gong819@
四、如下图 a 所示系统,p(t)=∑∞k=−∞ δ(t − kT),T 为采样周期,x(t),xp(t)和 x(n)的 傅里叶变换分别为用 X(jw),Xp(jw)和 X(ejΩ)表示。 1.如果 T=0.5X10-3(s),X(jw)如图 b 所示,试分别画出 Xp(jw)和 X(ejΩ)。
2
X(z)
z-1
z-1
Y(z)
2k 1
2 1. 根据给定的系统模拟框图,画出对应的信号流图。
2. 求系统的传输函数H(z) = Y(z)及描述该系统的差分方程。
X(z)
3. 能够使因果系统稳定的系数 K 的取值范围。
4.
当k = 13
16
时,对于 H(z)的所有可能收敛域,求相应的单位样值响应 h(n)。
H1(w)
Y(t) H2(w)
Cos2t
1.
x(t)
=
sin 2t t
时,求输出 y(t)。
2. x(t)=Sa(t)cos4t 时,求输出 y(t)。
3. 当 x(t)为如下波形时,再求 y(t)。
2
-2
2
-2
五、实序列 x(n)与其偶部及其奇部之间满足如下关系:
x(n)
=
xe (n)
+
xo(n). xe
真题由 ee 提供,功整理,有任何疑问发送 gong819@
五、假设信号 x(n)的频谱在
π 4
≤ |ω| ≤ π
范围内为 0,另一信号 s(n)与 x(n)之间的关系表示
为s(n) = x(n) ∑∞m=−∞ δ(n − 1 − 4k),试设计一个低通滤波器的频率响应 H(ejw),使之当该滤 波器的输入为 s(n)时输出为 x(n)。
2004 年上海交通大学《信号与系统》试题
一、某因果系统其系统函数是 H(S)有理的,且仅有两个极点:S1=-2,S2=-4。有且仅有 两个零点:Z1=2,Z2=4。系统阶跃稳态响应的最大值是 1。试求: 1.系统函数 H(S),且画出零极图,判断系统的稳定性。 2.当输入为 e(t)=e-4u(t)时候,求系统的零状态响应。 3.当输入为 e(t)=sin(2t)u(t)时候,求稳态响应。 4.画出幅频特性图,并采用 RLC 图来实现系统,标出元件值。
H(z)=H1(z)*Hap(z),画出 H1(z)和 Hap(z)的零极点图。
A
(s−B)2+C,其中
(s +B )2 +C
A,B,C
均为实待定系数,
试求: 1. 当系统的阶跃响应中包含有包络 e-t,角频率为ω0 = 40π(rad/s)的衰减震荡信号
时,确定系统函数 H(s)中的待定系数 B 和 C,画出系统的零极图。 2. 如果系统的阶跃响应的初值 g(0+)=1,确定系统函数 H(s)中的待定系数 A,并求
