《大学物理习题集》上)习题解答

合集下载

大学物理习题及解答(运动学、动量及能量)

1-1.质点在Oxy 平面内运动，其运动方程为j t i t r )219(22-+=。

求：（1）质点的轨迹方程；（2）s .t 01=时的速度及切向和法向加速度。

1-2.一质点具有恒定加速度j i a 46+=，在0=t 时，其速度为零，位置矢量i r 100=。

求：（1）在任意时刻的速度和位置矢量；（2）质点在oxy 平面上的轨迹方程，并画出轨迹的示意图。

1-3. 一质点在半径为m .r 100=的圆周上运动，其角位置为342t +=θ。

（1）求在s .t 02=时质点的法向加速度和切向加速度。

（2）当切向加速度的大小恰等于总加速度大小的一半时，θ值为多少？（3）t 为多少时，法向加速度和切向加速度的值相等？题3解： (1)由于342t +=θ，则角速度212t dt d ==θω，在t = 2 s 时，法向加速度和切向加速度的数值分别为 222s 2t n s m 1030.2-=⋅⨯==ωr a22s t t s m 80.4d d -=⋅==t r a ω(2)当2t 2n t 212a a a a +==时，有2n 2t 3a a=，即 22212)24(3)r t (tr = s 29.0s 321==t此时刻的角位置为 rad.t 153423=+=θ (3)要使t n a a =，则有2212)24()t (r tr =s .t 550=3-1如图所示，在水平地面上，有一横截面2m 20.0=S 的直角弯管，管中有流速为1s m 0.3-⋅=v 的水通过，求弯管所受力的大小和方向。

解：在t ∆时间内，从管一端流入（或流出）水的质量为t vS m ∆=∆ρ,弯曲部分AB 的水的动量的增量则为()()A B A B v v t vS v v m p -∆=-∆=∆ρ依据动量定理p I ∆=，得到管壁对这部分水的平均冲力()A B v v I F -=∆=Sv t ρ从而可得水流对管壁作用力的大小为N 105.2232⨯-=-=-='Sv F F ρ作用力的方向则沿直角平分线指向弯管外侧。

大学物理和习题答案

向走动时，则此平台相对地面旋转的角速度和旋转方向分别为
[A ]
（A） mR2 （ V ），顺时针。 JR
（B） mR2 （ V ），逆时针。 JR
——————3——————
大学物理习题集（上）
（C） mR 2 （ V ），顺时针。（D） mR 2 （ V ），逆时针。
J mR 2 R
J mR 2 R
F
l 2
1 12
ml 2
A
Fl
1 3
ml 2
B
由上两式可解得 A
6F ml
,B
3F ml
,可见 A
B
所以应选（B）。
9．质量为 m 的小孩站在半径为 R 的水平平台边缘上，平台可以绕通过其中心的竖直光滑固定轴自由转动，
转动惯量为 J，平台和小孩开始时均静止，当小孩突然以相对于地面为 v 的速率在平台边缘沿逆时针转
。
2
解答以圆盘和橡皮沁组成一系统，则系统所受重力对铅直轴 O 的力矩为零，所以系统的角动量守
——————6——————
大学物理习题集（上）
恒，圆盘的角动量为
J0
，橡皮泥（视为质点）对
O
轴的转动惯量为
m
R 2
2
，则有
1 2
MR20
1 2
MR2
m
R 2
2
解得
1 2
MR
20
2M 0
1 2
（D）只取决于转轴的位置，与刚体的质量和质量的空间分布无关。
2. 均匀细棒 OA 可绕通过某一端 O 而与棒垂直的水平固定光滑轴转动，今使棒从水平位置由静止开始自
由下降，在棒摆到竖直位置的过程中，下述说法哪一种是正确的？

大学物理课后习题答案(上册)

解：假设墙壁对小球的压力为N1，木板对小球的压力为N2。
由受力分析图可知：
所以当所以增大，小球对木板的压力为N2将减小；
同时：
所以增大，小球对墙壁的压力也减小。
2-2. 质量分别为m1和m2的两滑块A和B通过一轻弹簧水平连结后置于水平桌面上，滑块与桌面间的摩擦系数均为μ，系统在水平拉力F作用下匀速运动，如图所示．如突然撤消拉力，则刚撤消后瞬间，二者的加速度aA和aB分别为多少？
解：（1）轨道方程为
这是一条空间螺旋线。
在O 平面上的投影为圆心在原点，半径为R的圆，螺距为h
（2）
（3）
思考题1
1-1. 质点作曲线运动，其瞬时速度为，瞬时速率为，平均速度为，平均速率为，则它们之间的下列四种关系中哪一种是正确的?
（1）；（2）；（3）；（4）
答：（3）
1-2. 质点的关系如图，图中，，三条线表示三个速度不同的运动．问它们属于什么类型的运动?哪一个速度大？哪一个速度小？
解：在绳子中距离转轴为r处取一小段绳子，假设其质量为dm，可知：，分析这dm的绳子的受力情况，因为它做的是圆周运动，所以我们可列出：。
距转轴为r处绳中的张力T(r)将提供的是r以外的绳子转动的向心力，所以两边积分：
2-3. 已知一质量为的质点在轴上运动，质点只受到指向原点的引力作用，引力大小与质点离原点的距离的平方成反比，即，是比例常数．设质点在时的速度为零，求质点在处的速度的大小。
解：由题意和牛顿第二定律可得：
再采取分离变量法可得：，
两边同时取积分，则：
所以：
2-4. 一质量为的质点，在平面上运动，受到外力 (SI)的作用，时，它的初速度为 (SI)，求时质点的速度及受到的法向力 .

大学物理习题参考解答上静电场环路定理_电势能_电势和电势差

02. 如图所示， CDEF 是一矩形，边长分别为 l 和 2l 。在 DC 延长线上 CA l 处的 A 点有点电荷 q ，在 CF 的中点 B 点有点电荷 q ，若使单位正电荷从 C 点沿 CDEF 路径运动到 F 点，则电场
力所作的功等于：
【D】
(A)
q 4ol
5 1； 5l
(B)
q 4ol
三判断题
09. 静电场中某点电势值的正负取决于电势零点的选取。
【对】
10. 在已知静电场分布的条件下，任意两点 P1 和 P2 之间的电势差决定于 P1 和 P2 两点的位置。【对】
11. 正电荷在电势高的地方，电势能也一定高。 12. 电场强度的方向总是指向电势降落最快的方向。
【对】【对】
1 4 0
4 r12 r1
1 4 0
4 r22 r2
0

——
r1 ' r2 0
XCH
第3页
20XX-3-24
大学物理教程_上_习题集参考解答
r1 r2
—— 外球面带负电
外球面应放掉电荷： Q Q Q Q 4 r22 4 r22
Q
(1
r1 r2
)
4
r22
将 r1 10 cm and r2 20 cm ， 8.85 109C / m2 代入上式得到：
13. 静电场的保守性体现在电场强度的环流等于零。
【对】
四计算题
14. 如图所示， AB 2L ， OCD 是以 B 为中心 L 为半径的半圆， A 和 B 两处分别有正负电荷 q 和 q ，试问：
1) 把单位正电荷从 O 沿 OCD 移动到 D ，电场力对它作了多少功？
XCH

大学物理练习册(上册)答案

练习一（第一章质点运动学）一、选择题 1、（D ）2、（C ）3、（D ）4、（B ）5、（D ）二、填空题1、（1）A （2）1.186s(或4133-s) （3）0.67s （或32s ） 2、8m 10m3、（1）t e t t A βωβωωωβ-+-]sin 2cos )[(22 （2）ωπωπk +2（ ,2,1,0=k ） 4、3/30Ct v + 400121Ct t v x ++ 5、（1）5m/s (2) 17m/s 三、计算题1、解：dxdvv dt dx dx dv x dt dv a ==+==262分离变数积分⎰⎰+=xvdx x vdv 020)62(得 )1(422x x v +=质点在任意位置处的速度为 )1(22x x v +=（由初始时刻的加速度大于零，可知速度的大小为非负）。

2、解：（1）第二秒内的位移为 m x x x 5.0)1()2(-=-=∆ 第二秒内的平均速度为s m txv /5.0-=∆∆= （2）t 时刻的速度为 269t t dtdxv -==第二秒末的瞬时速度为 s m s m s m v /6/26/292-=⨯-⨯=（3）令0692=-==t t dtdxv ，解得s t 5.1= 第二秒内的路程为 m x x x x s 25.2)5.1()2()1()5.1(=-+-=。

3、解：（1）由几何关系θθsin cos r y r x ==质点作匀速率圆周运动故dtd θω=，代入初始条件0=t 时0=θ，得 t 时刻t ωθ=，所以j y i x r+=)sin (cos j t i t rωω+=（2）速度为)cos sin (j t i t r dtrd v ωωω+-==加速度为)sin (cos 2j t i t r dt vd a ωωω+-==（3）r j t i t r dtv d a 22)sin (cos ωωωω-=+-==由此知加速度的方向与径矢的方向相反，即加速度的方向指向圆心。

大学物理学上册习题解答完整版

大学物理学上册习题解答HUA system office room 【HUA16H-TTMS2A-HUAS8Q8-HUAH1688】大学物理学习题答案习题一答案习题一1.1 简要回答下列问题：(1)位移和路程有何区别在什么情况下二者的量值相等在什么情况下二者的量值不相等(2) 平均速度和平均速率有何区别在什么情况下二者的量值相等(3) 瞬时速度和平均速度的关系和区别是什么瞬时速率和平均速率的关系和区别又是什么(4)质点的位矢方向不变，它是否一定做直线运动质点做直线运动，其位矢的方向是否一定保持不变(5) (6)r ∆和r ∆有区别吗？v ∆和v ∆有区别吗？0dv dt =和0d v dt=各代表什么运动？ (7)设质点的运动方程为：()x x t =，()y y t =，在计算质点的速度和加速度时，有人先求出r =dr v dt= 及 22d r a dt =而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即v = 及 a = 你认为两种方法哪一种正确两者区别何在(7) 如果一质点的加速度与时间的关系是线性的，那么，该质点的速度和位矢与时间的关系是否也是线性的？(8)“物体做曲线运动时，速度方向一定在运动轨道的切线方向，法向分速度恒为零，因此其法向加速度也一定为零.”这种说法正确吗？(9)(9) 任意平面曲线运动的加速度的方向总指向曲线凹进那一侧，为什么？(10) 质点沿圆周运动，且速率随时间均匀增大，n a 、t a 、a 三者的大小是否随时间改变？(11) 一个人在以恒定速度运动的火车上竖直向上抛出一石子，此石子能否落回他的手中如果石子抛出后，火车以恒定加速度前进，结果又如何1.2 一质点沿x 轴运动，坐标与时间的变化关系为224t t x -=，式中t x ,分别以m 、s 为单位，试计算：(1)在最初s 2内的位移、平均速度和s 2末的瞬时速度；(2)s 1末到s 3末的平均加速度；(3)s 3末的瞬时加速度。

大学物理教程 (上)课后习题答案

物理部分课后习题答案（标有红色记号的为老师让看的题）27页 1-2 1-4 1-121-2 质点的运动方程为22,(1)x t y t ==-，,x y 都以米为单位，t 以秒为单位，求：（1）质点的运动轨迹；（2）从1t s =到2t s =质点的位移的大小；（3） 2t s =时，质点的速度和加速度。

解：（1）由运动方程消去时间t 可得轨迹方程，将t =代入，有21)y =或1=（2）将1t s =和2t s =代入，有11r i = ， 241r i j =+213r r r i j =-=-位移的大小 r ==（3） 2x dxv t dt== 2(1)y dy v t dt ==-22(1)v ti t j =+-2xx dv a dt ==， 2y y dv a dt==22a i j =+当2t s =时，速度和加速度分别为42/v i j m s =+22a i j =+m/s 21-4 设质点的运动方程为cos sin ()r R ti R t j SI ωω=+，式中的R 、ω均为常量。

求（1）质点的速度；（2）速率的变化率。

解（1）质点的速度为sin cos dr v R ti R t j dtωωωω==-+（2）质点的速率为v R ω==速率的变化率为0dv dt= 1-12 质点沿半径为R 的圆周运动，其运动规律为232()t SI θ=+。

求质点在t 时刻的法向加速度n a 的大小和角加速度β的大小。

解由于 4d t dtθω== 质点在t 时刻的法向加速度n a 的大小为2216n a R Rt ω==角加速度β的大小为 24/d rad s dtωβ==77页2-15, 2-30， 2-34，2-15 设作用于质量1m kg =的物体上的力63()F t SI =+，如果物体在这一力作用下，由静止开始沿直线运动，求在0到2.0s 的时间内力F 对物体的冲量。

大学物理学(第三版上) 课后习题6答案详解

习题66.1选择题(1)一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到最大位移处的过程中：(A)它的动能转化为势能. (B)它的势能转化为动能.(C)它从相邻的一段质元获得能量其能量逐渐增大.(D)它把自己的能量传给相邻的一段质元，其能量逐渐减小.[答案：D ](2) 某时刻驻波波形曲线如图所示，则a,b 两点位相差是(A)π (B)π/2 (C)5π/4 (D)0[答案：A](3) 设声波在媒质中的传播速度为ｕ，声源的频率为v s ．若声源Ｓ不动，而接收器Ｒ相对于媒质以速度V B 沿着Ｓ、Ｒ连线向着声源Ｓ运动，则位于Ｓ、Ｒ连线中点的质点Ｐ的振动频率为 (A)s v (B)s Bv uV u + (C)s B v V u u + (D) s Bv V u u-[答案：A]6.2填空题(1)频率为100Hz ，传播速度为300m/s 的平面简谐波，波线上两点振动的相位差为π/3，则此两点相距____m 。

[答案：0.5m ](2)一横波的波动方程是))(4.0100(2sin 02.0SI x t y -=π，则振幅是____，波长是____，频率是____，波的传播速度是____。

[答案：0.02;2.5;100;250/m m Hz m s ](3) 设入射波的表达式为])(2cos[1πλνπ++=xt A y ，波在x ＝0处反射，反射点为一固定端，则反射波的表达式为________________，驻波的表达式为____________________，入射波和反射波合成的驻波的波腹所在处的坐标为____________________。

[答案：)(2cos 2λνπxt A y -= ；2cos(2)cos(2)22x A t ππππνλ++ (21)4x k λ=-]6.3产生机械波的条件是什么？两列波叠加产生干涉现象必须满足什么条件？满足什么条件的两列波才能叠加后形成驻波？在什么情况下会出现半波损失？答：产生机械波必须具备两个条件：有作机械振动的物体即波源；有连续的介质。

大学物理习题集(上,含解答)

大学物理习题集（上册，含解答）第一章质点运动学1．1 一质点沿直线运动，运动方程为x (t ) = 6t 2 - 2t 3．试求：（1）第2s 内的位移和平均速度；（2）1s 末及2s 末的瞬时速度，第2s 内的路程；（3）1s 末的瞬时加速度和第2s 内的平均加速度．[解答]（1）质点在第1s 末的位置为：x (1) = 6×12 - 2×13 = 4(m)．在第2s 末的位置为：x (2) = 6×22 - 2×23 = 8(m)．在第2s 内的位移大小为：Δx = x (2) – x (1) = 4(m)，经过的时间为Δt = 1s ，所以平均速度大小为：v =Δx /Δt = 4(m·s -1)．（2）质点的瞬时速度大小为：v (t ) = d x /d t = 12t - 6t 2，因此v (1) = 12×1 - 6×12 = 6(m·s -1)，v (2) = 12×2 - 6×22 = 0质点在第2s 内的路程等于其位移的大小，即Δs = Δx = 4m ．（3）质点的瞬时加速度大小为：a (t ) = d v /d t = 12 - 12t ，因此1s 末的瞬时加速度为：a (1) = 12 - 12×1 = 0，第2s 内的平均加速度为：a = [v (2) - v (1)]/Δt = [0 – 6]/1 = -6(m·s -2)．[注意] 第几秒内的平均速度和平均加速度的时间间隔都是1秒．1．2 一质点作匀加速直线运动，在t = 10s 内走过路程s = 30m ，而其速度增为n = 5倍．试证加速度为22(1)(1)n sa n t-=+，并由上述数据求出量值． [证明]依题意得v t = nv o ，根据速度公式v t = v o + at ，得a = (n – 1)v o /t ， (1)根据速度与位移的关系式v t 2 = v o 2 + 2as ，得 a = (n 2 – 1)v o 2/2s ，(2) （1）平方之后除以（2）式证得：22(1)(1)n sa n t-=+．计算得加速度为：22(51)30(51)10a -=+= 0.4(m·s -2)．1．3 一人乘摩托车跳越一个大矿坑，他以与水平成22.5°的夹角的初速度65m·s -1从西边起跳，准确地落在坑的东边．已知东边比西边低70m ，忽略空气阻力，且取g = 10m·s -2．问：（1）矿坑有多宽？他飞越的时间多长？（2）他在东边落地时的速度？速度与水平面的夹角？ [解答]方法一：分步法．（1）夹角用θ表示，人和车（人）在竖直方向首先做竖直上抛运动，初速度的大小为v y 0 = v 0sin θ = 24.87(m·s -1)．取向上的方向为正，根据匀变速直线运动的速度公式v t - v 0 = at ，这里的v 0就是v y 0，a = -g ；当人达到最高点时，v t = 0，所以上升到最高点的时间为t 1 = v y 0/g = 2.49(s)．再根据匀变速直线运动的速度和位移的关系式：v t 2 - v 02 = 2a s ，可得上升的最大高度为：h 1 = v y 02/2g = 30.94(m)．人从最高点开始再做自由落体运动，下落的高度为;h 2 = h 1 + h = 100.94(m)．根据自由落体运动公式s = gt 2/2，得下落的时间为:2t =．图1.3因此人飞越的时间为：t = t 1 + t 2 = 6.98(s)．人飞越的水平速度为;v x 0 = v 0cos θ = 60.05(m·s -1)，所以矿坑的宽度为：x = v x 0t = 419.19(m)．（2）根据自由落体速度公式可得人落地的竖直速度大小为：v y = gt = 69.8(m·s -1)，落地速度为：v = (v x 2 + v y 2)1/2 = 92.08(m·s -1)，与水平方向的夹角为：φ = arctan(v y /v x ) = 49.30º，方向斜向下．方法二：一步法．取向上为正，人在竖直方向的位移为y = v y 0t - gt 2/2，移项得时间的一元二次方程201sin 02gt v t y θ-+=，解得：0(sin t v g θ=．这里y = -70m ，根号项就是人落地时在竖直方向的速度大小，由于时间应该取正值，所以公式取正根，计算时间为：t = 6.98(s)．由此可以求解其他问题．1．4 一个正在沿直线行驶的汽船，关闭发动机后，由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度，即d v /d t = -kv 2，k 为常数．（1）试证在关闭发动机后，船在t 时刻的速度大小为011kt v v =+；（2）试证在时间t 内，船行驶的距离为01ln(1)x v kt k =+． [证明]（1）分离变量得2d d vk t v =-，故 020d d v t v v k t v =-⎰⎰，可得：011kt v v =+．（2）公式可化为001v v v kt=+，由于v = d x/d t ，所以：00001d d d(1)1(1)v x t v kt v kt k v kt ==+++ 积分00001d d(1)(1)x tx v kt k v kt =++⎰⎰．因此 01ln(1)x v kt k=+．证毕．[讨论]当力是速度的函数时，即f = f (v )，根据牛顿第二定律得f = ma ．由于a = d 2x /d t 2，而 d x /d t = v ， a = d v /d t ，分离变量得方程：d d ()m vt f v =，解方程即可求解．在本题中，k 已经包括了质点的质量．如果阻力与速度反向、大小与船速的n 次方成正比，则 d v /d t = -kv n ．（1）如果n = 1，则得d d vk t v=-，积分得ln v = -kt + C ．当t = 0时，v = v 0，所以C = ln v 0，因此ln v/v 0 = -kt ，得速度为：v = v 0e -kt ．而d v = v 0e -kt d t ，积分得：0e `ktv x C k-=+-．当t = 0时，x = 0，所以C` = v 0/k ，因此0(1-e )kt vx k -=．（2）如果n ≠1，则得d d n vk t v=-，积分得11n v kt C n -=-+-．当t = 0时，v = v 0，所以101n v C n-=-，因此11011(1)n n n kt v v --=+-．如果n = 2，就是本题的结果．如果n ≠2，可得1(2)/(1)020{[1(1)]1}(2)n n n n n v kt x n v k----+--=-，读者不妨自证．1．5 一质点沿半径为0.10m 的圆周运动，其角位置（以弧度表示）可用公式表示：θ = 2 + 4t 3．求：（1）t = 2s 时，它的法向加速度和切向加速度；（2）当切向加速度恰为总加速度大小的一半时，θ为何值？（3）在哪一时刻，切向加速度和法向加速度恰有相等的值？ [解答]（1）角速度为ω = d θ/d t = 12t 2 = 48(rad·s -1)，法向加速度为 a n = rω2 = 230.4(m·s -2)；角加速度为 β = d ω/d t = 24t = 48(rad·s -2)，切向加速度为 a t = rβ = 4.8(m·s -2)．（2）总加速度为a = (a t 2 + a n 2)1/2，当a t = a /2时，有4a t 2 = a t 2 + a n 2，即n a a =由此得2r r ω=22(12)24t =解得36t =．所以3242(13)t θ=+=+=3.154(rad)．（3）当a t = a n 时，可得rβ = rω2，即： 24t = (12t 2)2，解得： t = (1/6)1/3 = 0.55(s)．1．6 一飞机在铅直面内飞行，某时刻飞机的速度为v = 300m·s -1，方向与水平线夹角为30°而斜向下，此后飞机的加速度为am·s -2，方向与水平前进方向夹角为30°而斜向上，问多长时间后，飞机又回到原来的高度？在此期间飞机在水平方向飞行的距离为多少？[解答]建立水平和垂直坐标系，飞机的初速度的大小为v 0x = v 0cos θ， v 0y = v 0sin θ．加速度的大小为a x = a cos α， a y = a sin α．运动方程为2012x x x v t a t =+， 2012y y y v t a t =-+．即 201cos cos 2x v t a t θα=⋅+⋅， 201sin sin 2y v t a t θα=-⋅+⋅．令y = 0，解得飞机回到原来高度时的时间为：t = 0（舍去）；02sin sin v t a θα==．将t 代入x 的方程求得x = 9000m ．[注意]选择不同的坐标系，如x 方向沿着a 的方向或者沿着v 0的方向，也能求出相同的结果．1．7 一个半径为R = 1.0m 的轻圆盘，可以绕一水平轴自由转动．一根轻绳绕在盘子的边缘，其自v 图1.7由端拴一物体A ．在重力作用下，物体A 从静止开始匀加速地下降，在Δt = 2.0s 内下降的距离h = 0.4m ．求物体开始下降后3s 末，圆盘边缘上任一点的切向加速度与法向加速度．[解答]圆盘边缘的切向加速度大小等于物体A 下落加速度．由于212t h a t =∆，所以a t = 2h /Δt 2 = 0.2(m·s -2)．物体下降3s 末的速度为v = a t t = 0.6(m·s -1)，这也是边缘的线速度，因此法向加速度为2n v a R== 0.36(m·s -2)．1．8 一升降机以加速度1.22m·s -2上升，当上升速度为2.44m·s -1时，有一螺帽自升降机的天花板上松落，天花板与升降机的底面相距2.74m ．计算：（1）螺帽从天花板落到底面所需的时间；（2）螺帽相对于升降机外固定柱子的下降距离．[解答]在螺帽从天花板落到底面时，升降机上升的高度为21012h v t at =+；螺帽做竖直上抛运动，位移为22012h v t gt =-．由题意得h = h 1 - h 2，所以21()2h a g t =+，解得时间为t ．算得h 2 = -0.716m ，即螺帽相对于升降机外固定柱子的下降距离为0.716m ．[注意]以升降机为参考系，钉子下落时相对加速度为a + g ，而初速度为零，可列方程h = (a + g )t 2/2，由此可计算钉子落下的时间，进而计算下降距离．1．9 有一架飞机从A 处向东飞到B 处，然后又向西飞回到A 处．已知气流相对于地面的速度为u ，AB 之间的距离为l ，飞机相对于空气的速率v 保持不变．（1）如果u = 0（空气静止），试证来回飞行的时间为02l t v =；（2）如果气流的速度向东，证明来回飞行的总时间为01221/t t u v =-；（3）如果气流的速度向北，证明来回飞行的总时间为2t =．[证明]（1）飞机飞行来回的速率为v ，路程为2l ，所以飞行时间为t 0 = 2l /v ．（2）飞机向东飞行顺风的速率为v + u ，向西飞行逆风的速率为v - u ，所以飞行时间为1222l l vl t v u v u v u =+=+-- 022222/1/1/t l v u v u v==--．（3）飞机相对地的速度等于相对风的速度加风相对地的速度．为了使飞机沿着AB 之间的直线飞行，就要使其相对地的速度偏向北方，可作矢量三角形，其中沿AB方向的速度大小为V =，所以飞行时间为22l t V ==== 证毕．1．10 如图所示，一汽车在雨中沿直线行驶，其速度为v 1，下落雨的速度方向与铅直方向的夹角为θ，偏向于汽车前进方向，速度为v 2．今在车后放一长方形物体，问车速v 1为多大时此物体刚好不会被雨水淋湿？AB AB vv + uv - uABvuuvv[解答]雨对地的速度2v 等于雨对车的速度3v 加车对地的速度1v ，由此可作矢量三角形．根据题意得tan α = l/h ．方法一：利用直角三角形．根据直角三角形得v 1 = v 2sin θ + v 3sin α，其中v 3 = v ⊥/cos α，而v ⊥ = v 2cos θ，因此v 1 = v 2sin θ + v 2cos θsin α/cos α，即 12(sin cos )lv v hθθ=+．证毕．方法二：利用正弦定理．根据正弦定理可得12sin()sin(90)v v θαα=+︒-，所以：12sin()cos v v θαα+=2sin cos cos sin cos v θαθαα+=2(sin cos tan )v θθα=+，即 12(sin cos )lv v hθθ=+．方法三：利用位移关系．将雨滴的速度分解为竖直和水平两个分量，在t 时间内，雨滴的位移为 l = (v 1 – v 2sin θ)t ， h = v 2cos θ∙t ．两式消去时间t 即得所求．证毕．第二章运动定律与力学中的守恒定律(一) 牛顿运动定律2．1 一个重量为P 的质点，在光滑的固定斜面（倾角为α）上以初速度0v 运动，0v 的方向与斜面底边的水平约AB 平行，如图所示，求这质点的运动轨道．[解答]质点在斜上运动的加速度为a = g sin α，方向与初速度方向垂直．其运动方程为 x = v 0t ，2211sin 22y at g t α==⋅．将t = x/v 0，代入后一方程得质点的轨道方程为22sin g y x v α=，这是抛物线方程．2．2 桌上有一质量M = 1kg 的平板，板上放一质量m = 2kg 的另一物体，设物体与板、板与桌面之间的滑动摩擦因素均为μk = 0.25，静摩擦因素为μs = 0.30．求：（1）今以水平力F 拉板，使两者一起以a = 1m·s -2的加速度运动，试计算物体与板、与桌面间的相互作用力；（2）要将板从物体下面抽出，至少需要多大的力？[解答]（1）物体与板之间有正压力和摩擦力的作用．板对物体的支持大小等于物体的重力：N m = mg = 19.6(N)，这也是板受物体的压力的大小，但压力方向相反．物体受板摩擦力做加速运动，摩擦力的大小为：f m = ma = 2(N)，这也是板受到的摩擦力的大小，摩擦力方向也相反．板受桌子的支持力大小等于其重力：N M = (m + M )g = 29.4(N)，图1.101h lα图2.1这也是桌子受板的压力的大小，但方向相反．板在桌子上滑动，所受摩擦力的大小为：f M = μk N M = 7.35(N)．这也是桌子受到的摩擦力的大小，方向也相反．（2）设物体在最大静摩擦力作用下和板一起做加速度为a`的运动，物体的运动方程为 f =μs mg = ma`，可得 a` =μs g ．板的运动方程为F – f – μk (m + M )g = Ma`，即 F = f + Ma` + μk (m + M )g= (μs + μk )(m + M )g ，算得 F = 16.17(N)．因此要将板从物体下面抽出，至少需要16.17N 的力．2．3 如图所示：已知F = 4N ，m 1 = 0.3kg ，m 2 = 0.2kg ，两物体与水平面的的摩擦因素匀为0.2．求质量为m 2的物体的加速度及绳子对它的拉力．（绳子和滑轮质量均不计）[解答]利用几何关系得两物体的加速度之间的关系为a 2 = 2a 1，而力的关系为T 1 = 2T 2．对两物体列运动方程得T 2 - μm 2g = m 2a 2， F – T 1 – μm 1g = m 1a 1．可以解得m 2的加速度为 12212(2)/22F m m g a m m μ-+=+= 4.78(m·s -2)，绳对它的拉力为2112(/2)/22m T F m g m m μ=-+= 1.35(N)．2．4 两根弹簧的倔强系数分别为k 1和k 2．求证：（1）它们串联起来时，总倔强系数k 与k 1和k 2．满足关系关系式12111k k k =+；（2）它们并联起来时，总倔强系数k = k 1 + k 2．[解答]当力F 将弹簧共拉长x 时，有F = kx ，其中k 为总倔强系数．两个弹簧分别拉长x 1和x 2，产生的弹力分别为 F 1 = k 1x 1，F 2 = k 2x 2．（1）由于弹簧串联，所以F = F 1 = F 2，x = x 1 + x 2，因此 1212F F F kk k =+，即：12111k k k =+．（2）由于弹簧并联，所以F = F 1 + F 2，x = x 1 = x 2，因此 kx = k 1x 1 + k 2x 2，即：k = k 1 + k 2．2．5 如图所示，质量为m 的摆悬于架上，架固定于小车上，在下述各种情况中，求摆线的方向（即摆线与竖直线的夹角θ）及线中的张力T ．（1）小车沿水平线作匀速运动；（2）小车以加速度1a 沿水平方向运动；（3）小车自由地从倾斜平面上滑下，斜面与水平面成φ角；（4）用与斜面平行的加速度1b 把小车沿斜面往上推（设b 1 = b ）；（5）以同样大小的加速度2b （b 2 = b ），将小车从斜面上推下来．[解答]（1）小车沿水平方向做匀速直线运动时，摆在水平方向没有受到力12图2.32 图2.4的作用，摆线偏角为零，线中张力为T = mg ．（2）小车在水平方向做加速运动时，重力和拉力的合力就是合外力．由于tan θ = ma/mg ，所以 θ = arctan(a/g )；绳子张力等于摆所受的拉力：T ==（3）小车沿斜面自由滑下时，摆仍然受到重力和拉力，合力沿斜面向下，所以θ = φ； T = mg cos φ．（4）根据题意作力的矢量图，将竖直虚线延长，与水平辅助线相交，可得一直角三角形，θ角的对边是mb cos φ，邻边是mg + mb sin φ，由此可得：cos tan sin mb mg mb ϕθϕ=+，因此角度为cos arctansin b g b ϕθϕ=+；而张力为T=．（5）与上一问相比，加速度的方向反向，只要将上一结果中的b 改为-b 就行了．2．6 如图所示：质量为m =0.10kg 的小球，拴在长度l =0.5m 的轻绳子的一端，构成一个摆．摆动时，与竖直线的最大夹角为60°．求：（1）小球通过竖直位置时的速度为多少？此时绳的张力多大？（2）在θ < 60°的任一位置时，求小球速度v 与θ的关系式．这时小球的加速度为多大？绳中的张力多大？（3）在θ = 60°时，小球的加速度多大？绳的张力有多大？[解答]（1）小球在运动中受到重力和绳子的拉力，由于小球沿圆弧运动，所以合力方向沿着圆弧的切线方向，即F = -mg sin θ，负号表示角度θ增加的方向为正方向．小球的运动方程为 22d d s F ma m t ==，其中s 表示弧长．由于s = Rθ = lθ，所以速度为d d d d s v l t t θ==，因此d d d d d d d d v v m v F mm v t t l θθθ===，即 v d v = -gl sin θd θ，（1）取积分60d sin d Bv v v gl θθ︒=-⎰⎰，（2）图2.6得2601cos 2B v gl θ︒=，解得：B v =s -1)．由于：22B BB v v T mg m m mgR l -===，所以T B = 2mg = 1.96(N)．（2）由（1）式积分得21cos 2C v gl C θ=+，当 θ = 60º时，v C = 0，所以C = -lg /2，因此速度为C v =切向加速度为a t = g sin θ；法向加速度为2(2cos 1)Cn v a g R θ==-．由于T C – mg cos θ = ma n ，所以张力为T C = mg cos θ + ma n = mg (3cos θ – 1)．（3）当 θ = 60º时，切向加速度为2t a g== 8.49(m·s -2)，法向加速度为 a n = 0，绳子的拉力T = mg /2 = 0.49(N)．[注意]在学过机械能守恒定律之后，求解速率更方便．2．7 小石块沿一弯曲光滑轨道上由静止滑下h 高度时，它的速率多大？（要求用牛顿第二定律积分求解）[解答]小石块在运动中受到重力和轨道的支持力，合力方向沿着曲线方向．设切线与竖直方向的夹角为θ，则F = mg cos θ．小球的运动方程为22d d sF ma m t ==，s 表示弧长．由于d d s v t =，所以 22d d d d d d d ()d d d d d d d s s v v s v v t t t t s t s ====，因此 v d v = g cos θd s = g d h ，h 表示石下落的高度．积分得 212v gh C =+，当h = 0时，v = 0，所以C = 0，因此速率为v =2．8 质量为m 的物体，最初静止于x 0，在力2kf x =-(k 为常数)作用下沿直线运动．证明物体在x处的速度大小v = [2k (1/x – 1/x 0)/m ]1/2．[证明]当物体在直线上运动时，根据牛顿第二定律得方程图2.7222d d k x f ma m x t =-==利用v = d x/d t ，可得22d d d d d d d d d d x v x v v v t t t x x ===，因此方程变为2d d k xmv v x =-，积分得212k mv C x =+．利用初始条件，当x = x 0时，v = 0，所以C = -k /x 0，因此2012k k mv x x =-，即v =证毕．[讨论]此题中，力是位置的函数：f = f (x )，利用变换可得方程：mv d v = f (x )d x ，积分即可求解．如果f (x ) = -k/x n ，则得21d 2nx mv k x =-⎰．（1）当n = 1时，可得21ln 2mv k x C =-+利用初始条件x = x 0时，v = 0，所以C = ln x 0，因此 21ln 2x mv k x =，即v =（2）如果n ≠1，可得21121n k mv x C n -=-+-．利用初始条件x = x 0时，v = 0，所以101n k C x n -=--，因此 2110111()21n n k mv n x x --=--，即v =当n = 2时，即证明了本题的结果．2．9 一质量为m 的小球以速率v 0从地面开始竖直向上运动．在运动过程中，小球所受空气阻力大小与速率成正比，比例系数为k ．求：（1）小球速率随时间的变化关系v (t )；（2）小球上升到最大高度所花的时间T ．[解答]（1）小球竖直上升时受到重力和空气阻力，两者方向向下，取向上的方向为下，根据牛顿第二定律得方程d d vf mg kv mt =--=，分离变量得d d()d v m mg kv t m mg kv k mg kv +=-=-++，积分得ln ()mt mg kv C k =-++．当t = 0时，v = v 0，所以0ln ()mC mg kv k =+，因此00/ln ln/m mg kv m mg k v t k mg kv k mg k v ++=-=-++，小球速率随时间的变化关系为0()exp()mg kt mgv v k m k =+--．（2）当小球运动到最高点时v = 0，所需要的时间为00/ln ln(1)/mg k v kv m m T k mg k k mg +==+．[讨论]（1）如果还要求位置与时间的关系，可用如下步骤：由于v = d x/d t ，所以0d [()exp()]d mg kt mg x v t k m k =+--，即0(/)d d exp()d m v mg k kt mgx tk m k +=---，积分得0(/)exp()`m v mg k kt mgx t C k m k +=---+，当t = 0时，x = 0，所以0(/)`m v mg k C k +=，因此0(/)[1exp()]m v mg k kt mg x tk m k +=---．（2）如果小球以v 0的初速度向下做直线运动，取向下的方向为正，则微分方程变为d d vf mg kv mt =-=，用同样的步骤可以解得小球速率随时间的变化关系为0()exp()mg mg ktv v k k m =---．这个公式可将上面公式中的g 改为-g 得出．由此可见：不论小球初速度如何，其最终速率趋于常数v m =mg/k ．2．10 如图所示：光滑的水平桌面上放置一固定的圆环带，半径为R ．一物体帖着环带内侧运动，物体与环带间的滑动摩擦因数为μk ．设物体在某时刻经A 点时速率为v 0，求此后时刻t 物体的速率以及从A 点开始所经过的路程．[解答]物体做圆周运动的向心力是由圆环带对物体的压力，即 N = mv 2/R ．物体所受的摩擦力为f = -μk N ，负号表示力的方向与速度的方向相反．根据牛顿第二定律得2d d k v v f m m R t μ=-=，即： 2d d k vt R v μ=-．积分得：1k t C R v μ=+．当t = 0时，v = v 0，所以01C v =-，因此 011kt Rv v μ=-．解得 001/k v v v t R μ=+．由于0000d d(1/)d 1/1/k k k k v t v t R R x v t R v t R μμμμ+==++，积分得0ln (1)`k kv tR x C Rμμ=++，当t = 0时，x = x 0，所以C = 0，因此0ln (1)k kv tRx Rμμ=+．2．11 如图所示，一半径为R 的金属光滑圆环可绕其竖直直径转动．在环上套有一珠子．今逐渐增大圆环的转动角速度ω，试求在不同转动速度下珠子能静止在环上的位置．以珠子所停处的半径与竖直直径的夹角θ表示．[解答]珠子受到重力和环的压力，其合力指向竖直直径，作为珠子做圆周运动的向心力，其大小为：F = mg tg θ．珠子做圆周运动的半径为r = R sin θ．根据向心力公式得F = mg tg θ = mω2R sin θ，可得2cos mgR ωθ=，解得2arccosg R θω=±．(二)力学中的守恒定律2．12 如图所示，一小球在弹簧的弹力作用下振动．弹力F = -kx ，而位移x = A cos ωt ，其中k ，A 和ω都是常数．求在t = 0到t = π/2ω的时间间隔内弹力予小球的冲量．[解答]方法一：利用冲量公式．根据冲量的定义得d I = F d t = -kA cos ωt d t ，积分得冲量为 /20(cos )d I kA t tωω=-⎰π，/20sin kAkAtωωωω=-=-π方法二：利用动量定理．小球的速度为v = d x/d t = -ωA sin ωt ，设小球的质量为m ，其初动量为p 1 = mv 1 = 0，末动量为p 2 = mv 2 = -mωA ，mg图2.11小球获得的冲量为I = p 2 – p 1 = -mωA ，可以证明k =mω2，因此I = -kA /ω．2．13一个质量m = 50g ，以速率的v = 20m·s -1作匀速圆周运动的小球，在1/4周期内向心力给予小球的冲量等于多少？[解答]小球动量的大小为p = mv ，但是末动量与初动量互相垂直，根据动量的增量的定义21p p p ∆=- 得：21p p p =+∆，由此可作矢量三角形，可得：p ∆==．因此向心力给予小球的的冲量大小为I p =∆= 1.41(N·s)．[注意]质点向心力大小为F = mv 2/R ，方向是指向圆心的，其方向在不断地发生改变，所以不能直接用下式计算冲量24v TI Ft mR ==2/42R T T mv mvR ππ==．假设小球被轻绳拉着以角速度ω = v/R 运动，拉力的大小就是向心力F = mv 2/R = mωv ，其分量大小分别为 F x = F cos θ = F cos ωt ，F y = F sin θ = F sin ωt ，给小球的冲量大小为 d I x = F x d t = F cos ωt d t ，d I y = F y d t = F sin ωt d t ，积分得 /4/4cos d sin T T x FI F t t tωωω==⎰Fmvω==，/4/4sin d cos T T y FI F t t tωωω==-⎰Fmvω==，合冲量为I ==，与前面计算结果相同，但过程要复杂一些．2．14 用棒打击质量0.3kg ，速率等于20m·s -1的水平飞来的球，球飞到竖直上方10m 的高度．求棒给予球的冲量多大？设球与棒的接触时间为0.02s ，求球受到的平均冲力？[解答]球上升初速度为y v =s -1)，其速度的增量为v ∆== 24.4(m·s -1)．棒给球冲量为I = m Δv = 7.3(N·s)，对球的作用力为（不计重力）：F = I/t = 366.2(N)．v xΔvv y2．15 如图所示，三个物体A 、B 、C ，每个质量都为M ，B 和C 靠在一起，放在光滑水平桌面上，两者连有一段长度为0.4m 的细绳，首先放松．B 的另一侧则连有另一细绳跨过桌边的定滑轮而与A 相连．已知滑轮轴上的摩擦也可忽略，绳子长度一定．问A 和B 起动后，经多长时间C 也开始运动？C 开始运动时的速度是多少？（取g = 10m·s -2）[解答]物体A 受到重力和细绳的拉力，可列方程Mg – T = Ma ，物体B 在没有拉物体C 之前在拉力T 作用下做加速运动，加速度大小为a ，可列方程：T = Ma ，联立方程可得：a = g/2 = 5(m·s -2)．根据运动学公式：s = v 0t + at 2/2，可得B 拉C之前的运动时间；t =．此时B 的速度大小为：v = at = 2(m·s -1)．物体A 跨过动滑轮向下运动，如同以相同的加速度和速度向右运动．A 和B 拉动C 运动是一个碰撞过程，它们的动量守恒，可得：2Mv = 3Mv`，因此C 开始运动的速度为：v` = 2v /3 = 1.33(m·s -1)．2．16 一炮弹以速率v 0沿仰角θ的方向发射出去后，在轨道的最高点爆炸为质量相等的两块，一块沿此45°仰角上飞，一块沿45°俯角下冲，求刚爆炸的这两块碎片的速率各为多少？[解答] 炮弹在最高点的速度大小为v = v 0cos θ，方向沿水平方向．根据动量守恒定律，可知碎片的总动量等于炮弹爆炸前的总动量，可作矢量三角形，列方程得 /2`cos 452mmv v =︒，所以 v` = v /cos45°= 0cos θ．2．17 如图所示，一匹马拉着雪撬沿着冰雪覆盖的弧形路面极缓慢地匀速移动，这圆弧路面的半径为R ．设马对雪橇的拉力总是平行于路面．雪橇的质量为m ，它与路面的滑动摩擦因数为μk ．当把雪橇由底端拉上45°圆弧时，马对雪橇做了多少功？重力和摩擦力各做了多少功？[解答]取弧长增加的方向为正方向，弧位移d s 的大小为d s = R d θ．重力G 的大小为：G = mg ，方向竖直向下，与位移元的夹角为π + θ，所做的功元为1d d cos(/2)d W G s G s θ=⋅=+π sin d mgR θθ=-，积分得重力所做的功为454510(sin )d cos W mgR mgR θθθ︒︒=-=⎰(1mgR =-．摩擦力f 的大小为：f = μk N = μk mg cos θ，方向与弧位移的方向相反，所做的功元为2d d cos d W f s f s =⋅=πcos d k u mg R θθ=-，积分得摩擦力所做的功为图2.174520(cos )d k W mgR μθθ︒=-⎰450sin k k mgR mgR μθ︒=-=．要使雪橇缓慢地匀速移动，雪橇受的重力G 、摩擦力f 和马的拉力F 就是平衡力，即0F G f ++=，或者 ()F G f =-+．拉力的功元为：d d (d d )W F s G s f s =⋅=-⋅+⋅12(d d )W W =-+，拉力所做的功为12()W W W =-+(1)k mgR μ=．由此可见，重力和摩擦力都做负功，拉力做正功．2．18 一质量为m 的质点拴在细绳的一端，绳的另一端固定，此质点在粗糙水平面上作半径为r 的圆周运动．设质点最初的速率是v 0，当它运动1周时，其速率变为v 0/2，求：（1）摩擦力所做的功；（2）滑动摩擦因数；（3）在静止以前质点运动了多少圈？[解答] （1）质点的初动能为：E 1 = mv 02/2，末动能为：E 2 = mv 2/2 = mv 02/8，动能的增量为：ΔE k = E 2 – E 1 = -3mv 02/8，这就是摩擦力所做的功W ．（2）由于d W = -f d s = -μk N d s = -μk mgr d θ，积分得：20()d 2k k W mgr mgrπμθπμ=-=-⎰．由于W = ΔE ，可得滑动摩擦因数为20316k v gr μ=π．（3）在自然坐标中，质点的切向加速度为：a t = f/m = -μk g ，根据公式v t 2 – v o 2 = 2a t s ，可得质点运动的弧长为22008223k v v r s a g πμ===，圈数为 n = s/2πr = 4/3．[注意]根据用动能定理，摩擦力所做的功等于质点动能的增量：-fs = ΔE k ，可得 s = -ΔE k /f ，由此也能计算弧长和圈数。

大学物理(上)课后习题答案解析

第1章质点运动学 P211.8一质点在xOy 平面上运动,运动方程为：x =3t +5, y =21t 2+3t -4. 式中t 以 s 计,x ,y 以m 计。

⑴以时间t 为变量,写出质点位置矢量的表示式；⑵求出t =1 s 时刻和t ＝2s 时刻的位置矢量,计算这1秒内质点的位移；⑶计算t＝0 s 时刻到t ＝4s 时刻内的平均速度；⑷求出质点速度矢量表示式,计算t ＝4 s 时质点的速度；<5>计算t ＝0s 到t ＝4s 内质点的平均加速度；<6>求出质点加速度矢量的表示式,计算t ＝4s 时质点的加速度<请把位置矢量、位移、平均速度、瞬时速度、平均加速度、瞬时加速度都表示成直角坐标系中的矢量式>。

解：〔1j t t i t r)4321()53(2-+++=m⑵1=t s,2=t s 时,j i r5.081-=m ；2114r i j =+m∴213 4.5r r r i j ∆=-=+m⑶0t =s 时,054r i j =-；4t =s 时,41716r i j =+∴140122035m s 404r r r i j i j t --∆+====+⋅∆-v ⑷1d 3(3)m s d ri t j t-==++⋅v ,则：437i j =+v 1s m -⋅ <5> 0t =s 时,033i j =+v ；4t =s 时,437i j =+v<6> 2d 1 m s d a j t-==⋅v这说明该点只有y 方向的加速度,且为恒量。

1.9质点沿x 轴运动,其加速度和位置的关系为226a x =+,a 的单位为m/s 2,x 的单位为m 。

质点在x =0处,速度为10m/s,试求质点在任何坐标处的速度值。

解：由d d d d d d d d x a t x t x===v v v v得：2d d (26)d a x x x ==+v v 两边积分210d (26)d xx x =+⎰⎰vv v 得：2322250x x =++v∴ 31225 m s x x -=++⋅v1.11一质点沿半径为1 m 的圆周运动,运动方程为θ=2+33t ,式中θ以弧度计,t 以秒计,求：⑴t ＝2 s 时,质点的切向和法向加速度；⑵当加速度的方向和半径成45°角时,其角位移是多少?解： t tt t 18d d ,9d d 2====ωβθω ⑴s 2=t 时,2s m 362181-⋅=⨯⨯==βτR a⑵当加速度方向与半径成ο45角时,有：tan 451n a a τ︒== 即：βωR R =2,亦即t t 18)9(22=,解得：923=t 则角位移为：322323 2.67rad 9t θ=+=+⨯= 1.13 一质点在半径为0.4m 的圆形轨道上自静止开始作匀角加速度转动,其角加速度为α=0.2 rad/s 2,求t ＝2s 时边缘上各点的速度、法向加速度、切向加速度和合加速度。

大学物理习题集答案

一、选择题1. 对一个作简谐振动的物体，下面哪种说法是正确的？ [ C ](A) 物体处在运动正方向的端点时，速度和加速度都达到最大值； (B) 物体位于平衡位置且向负方向运动时，速度和加速度都为零； (C) 物体位于平衡位置且向正方向运动时，速度最大，加速度为零；(D) 物体处在负方向的端点时，速度最大，加速度为零。

2. 一沿X 轴作简谐振动的弹簧振子，振幅为A ，周期为T ，振动方程用余弦函数表示，如果该振子的初相为43π，则t=0时，质点的位置在： [ D ](A) 过1x A 2=处，向负方向运动； (B) 过1x A 2=处，向正方向运动；(C) 过1x A 2=-处，向负方向运动；(D) 过1x A 2=-处，向正方向运动。

3. 一质点作简谐振动，振幅为A ，在起始时刻质点的位移为/2A ，且向x 轴的正方向运动，代表此简谐振动的旋转矢量图为 [ B ]x o A ϖ x ω(A) A/2 ω (B) (C)(D)o ooxxxA ϖ x ω ωA ϖA ϖxA/2 -A/2 -A/2 (3)题4. 图(a)、(b)、(c)为三个不同的谐振动系统，组成各系统的各弹簧的倔强系数及重物质量如图所示，(a)、(b)、(c)三个振动系统的 (为固有圆频率)值之比为：[ B ](A) 2：1：1； (B) 1：2：4； (C) 4：2：1； (D) 1：1：25. 一弹簧振子，当把它水平放置时，它可以作简谐振动，若把它竖直放置或放在固定的光滑斜面上如图，试判断下面哪种情况是正确的： [ C ](A) 竖直放置可作简谐振动，放在光滑斜面上不能作简谐振动；(B) 竖直放置不能作简谐振动，放在光滑斜面上可作简谐振动； (C) 两种情况都可作简谐振动； (D) 两种情况都不能作简谐振动。

6. 一谐振子作振幅为A 的谐振动，它的动能与势能相等时，它的相位和坐标分别为： [ C ]2153(A),or ;A;(B),;332663223(C),or ;(D),;4433ππ±±π±±±π±ππ±±π±±±π±7. 一质点沿x 轴作简谐振动，振动方程为 10.04cos(2)3x t ππ=+（SI ），从t = 0时刻起，到质点位置在x = m 处，且向x 轴正方向运动的最短时间间隔为 [ D ](A)s 81； (B) s 61； (C) s 41； (D) s 218. 图中所画的是两个简谐振动的振动曲线，这两个简谐振动叠加后合成的余弦振动的初相为[ C ]xtOx 1x 2(8)题(A) π23； (B) π； (C) π21 ； (D) 0二、填空题9. 一简谐振动用余弦函数表示，振动曲线如图所示，则此简谐振动的三个特征量为： A=10cm ,/6rad /s =ωπ， /3=φπ10. 用40N 的力拉一轻弹簧，可使其伸长20 cm 。

大学物理习题集马文蔚,第四版,上册

第二十单元热力学第二定律[课本内容] 马文蔚，第四版，上册 [6]-[40]练习二十一、选择题：20-1．关于可逆过程和不可逆过程有以下几种说法： (1) 可逆过程一定是平衡过程． (2) 平衡过程一定是可逆过程．(3) 不可逆过程发生后一定找不到另一过程使系统和外界同时复原． (4) 非平衡过程一定是不可逆过程．以上说法，正确的是：［］ (A) (1)、(2)、(3). (B) (2)、(3)、(4).(C) (1)、(3)、(4). (D) (1)、(2)、(3) 、(4). 提示：无摩擦的平衡过程是可逆的，选C20-2．根据热力学第二定律可知： (A) 功可以全部转换为热，但热不能全部转换为功．(B) 热可以从高温物体传到低温物体，但不能从低温物体传到高温物体 (C) 不可逆过程就是不能向相反方向进行的过程．(D) 一切自发过程都是不可逆的．［］提示：（A ）应为：但热在不引起其它变化的条件下，不能全部转换为功（B ）应为：但在不引起其它变化是不能从低温物体传到高温物体（C ）应为：在不引起其它变化的条件下不可能向反方向进行的过程选D20-3．一绝热容器被隔板分成两半，一半是真空，另一半是理想气体．若把隔板抽出，气体将进行自由膨胀，达到平衡后 (A) 温度不变，熵增加． (B) 温度升高，熵增加．(C) 温度降低，熵增加． (D) 温度不变，熵不变．［］提示：0,0Q A ==0,E ∴∆=温度不变又这是一个不可逆的绝热过程 ∴ 熵增加。

选A20-4．关于热功转换和热量传递过程，有下面一些叙述： (1) 功可以完全变为热量，而热量不能完全变为功； (2) 一切热机的效率都只能够小于1； (3) 热量不能从低温物体向高温物体传递； (4) 热量从高温物体向低温物体传递是不可逆的．以上这些叙述［］ (A) 只有(2)、(4)正确． (B) 只有(2)、(3) 、(4)正确． (C) 只有(1)、(3) 、(4)正确． (D) 全部正确．提示：（1）功可以完全变为热量而热量在不引起其它变化时不能完全变为功（3）在不引起其它变化时，热量不能从低温物体向高温物体传递 ∴选 A20-5．热力学第二定律表明： (A) 不可能从单一热源吸收热量使之全部变为有用的功． (B) 在一个可逆过程中，工作物质净吸热等于对外作的功．(C) 摩擦生热的过程是不可逆的．(D) 热量不可能从温度低的物体传到温度高的物体．［］提示：（A ）应为：不可能从单一热源吸收热量使之全部变为有用的功而不引起其它变化（B ）应为：在一个可逆过程中，工作物质净吸热等于对外作的功和不对外放出热量（D ）应为：热量不可能从温度低的物体传到温度高的物体而不引起其它变化所以选C二、选择题20-6．一个作可逆卡诺循环的热机，其效率为η，它逆向运转时便成为一台致冷机.该致冷机的致冷系数212T T T w -=，则 η与w 的关系为__________．提示：221111T T T T ηη=-⇒=-1W ηη-∴=20-7．可逆卡诺热机可以逆向运转．逆向循环时, 从低温热源吸热,向高温热源放热,而且吸的热量和放出的热量等于它正循环时向低温热源放出的热量和从高温热源吸的热量.设高温热源的温度为T 1 =450 K , 低温热源的温度为T 2 =300 K, 卡诺热机逆向循环时从低温热源吸热 Q 2 =400 J ，则该卡诺热机逆向循环一次外界必须作功W ＝_________．提示：212112003200T W W W T W Q W η=-=⇒=⇒=++20-8．热力学第二定律的开尔文表述和克劳修斯表述是等价的，表明在自然界中与热现象有关的实际宏观过程都是不可逆的，开尔文表述指出了_______________________________的过程是不可逆的，而克劳修斯表述指出了________________的过程是不可逆的．提示：热功转换，热传导20-9．从统计的意义来解释, 不可逆过程实质上是一个____ _____________________ ____________________的转变过程, 一切实际过程都向着____________的方向进行．提示：从几率小的宏观状态到几率大的宏观态；几率增大20-10．在一个孤立系统内，一切实际过程都向着______________的方向进行．这就是热力学第二定律的统计意义．从宏观上说，一切与热现象有关的实际的过程都是____________．提示：熵增加；不可逆的20-11．熵是______________________________________的定量量度．若一定量的理想气体经历一个等温膨胀过程，它的熵将________________________．(填入:增加，减少，不变．)提示：分子热运动的无序性或混乱性；增加第十九单元绝热过程循环过程[课本内容] 马文蔚，第四版，上册 [6]-[40] [典型例题]例19-1．一定量的理想气体，分别经历如图（a ）所示的abc 过程，（图中虚线ac 为等温线），和图（b ）所示的def 过程（图中虚线df 为绝热线），这两种过程是吸热还是放热。

安徽理工大学大学物理上习题集讲解------ 第三单元牛顿定律动量和冲量

第三单元牛顿定律动量和冲量[课本内容] 马文蔚，第四版，上册 [30]-[50]，[58]-[65] [典型例题]例3-1．桌面上有一块质量为M 的木板，木板上放一个质量为的物体。

物体和木板之间、木板与桌面之间的滑动摩擦系数为，静止摩擦系数为。

现在要使木板从物体F至少多大？解：例3-2．质量分别为m 和M 的滑块A 和B ，叠放在光滑水平面上，如图．A 、B 间的静摩擦系数为μS ，滑动摩擦系数为μk ,系统原先处于静止状态．今将水平力F 作用于B 上，要使A 、B 间不发生相对滑动，应有。

(ans .)例3-3．图中所示的装置中，略去一切摩擦力以及滑轮和绳的质量，且绳不可伸长，则质量为m 1的物体的加速度a 1= __________.解：对m 1：T 1=m 1a 1对m 2： m 2g －T 2=m 2a 2又 T 2=2T 1， a 1=2a 2 ………例3-4．质量为m 的平板A ，用竖立的弹簧支持而处在水平位置，如图．从平台上投掷一个质量也是m 的球B ，球的初速为v ，沿水平方向．球由于重力作用下落，与平板发生完全弹性碰撞。

假定平板是光滑的．则与平板碰撞后球的运动方向应为(A) A 0方向． (B) A 1方向．(C) A 2方向． (D) A 3方向．［］提示：竖直方向上动量守恒，m B v By =m A v A 。

B 与A 碰后只有A 2方向速度。

所以选A 。

例3-5．三个物体A 、B 、C 每个质量都是M 。

B 、C 靠在一起，放在光滑水平桌面上，两者间连有一段长为0. 4m 的细绳，原先放松着B 的另一侧用一跨过桌边的定滑轮的细绳与A 相连(如图)。

滑轮和绳子的质量及轮轴上的摩擦不计，绳子不可伸长。

问：(1) A 、B 起动后，经多长时间C 也开始运动?(2) C 开始运动时速度的大小是多少? (取g=10m ·s -2)解：（1）设绳中张力为T ，分别对A 、B 列动力学方程解得设B 、C 之间绳长为，在时间t 内B 物体作匀加速运动，有m k μS μg M m F Ma g M m mg F mamg k s k s s ))(()(++=⇒⎩⎨⎧=+--≥μμμμμmg M M m F s)(+≤μa M T g M A A =-a M T B =)/(B A A M M g M a +=M M M B A == g a 21=∴l 4/2221gt at l ==12 3（2）B 和C 之间绳子刚拉紧时，A 和B 所达到的速度为令B 、C 间拉紧后，C 开始运动时A 、B 、C 三者的速度大小均为V ，由动量定理（T AB 为AB 间绳中张力，T BC 为BC 间绳中张力）得例3-6．如图，用传送带A 输送煤粉，料斗口在A 上方高h=0.5m 处，煤粉自料斗口自由落在A 上，设料斗口连续卸煤的流量为q m =40kg/s ，A 以v=2.0m/s 的水平速度匀速向右移动。

大学物理习题参考解答上电磁场理论_电磁感应习题课

的感应电动势，并判断感应电流的方向。
选取逆时针为回路绕行正方向，长圆柱外的磁场为零。
穿过回路 abcd 的磁通量为穿过图中面积 S 的磁通量：
B
(
1 2
R2
)
B
(
1 2
ab
Oa
cos
1 2
)
B
(
1 2
R2
)
1 2
B
(Oa 2
sin
)
6
R2B
3 Oa2B 4
根据法拉第电磁感应定律： Ei
d dt
计算题_18 图示
填空题_09 图示
10. 如图所示为一充电后的平行板电容器， A 板带正电， B 板带负电，当将开关 K 合上时， AB 板之间的电场方向为 x 轴的正方向，位移电流的方向为 x 轴的负方向。 (按图所标 x 轴正方向来回答)
填空题_10 图示
填空题_11 图示
11. 如图所示， (1) 中是充电后切断电源的平行板电容器； (2) 中是一直与电源相接的电容器，当两
极板间距离相互靠近或分离时，试判断两种情况的极板间有无位移电流，并说明原因。
(1) 中：无位移电流，因为极板上的电荷分布不变，电场不随时间变化； (2) 中：在两极板间距离相互靠近或分离时，均有位移电流。因为在保持极板两端的电压不变
的前提下，极板距离的变化引起电容的变化和极板上电荷的变化，因此极板间的电场发生变化。位
S
D
dS
V
dV
，
L
E
dl
S
B t
dS
，
S
B
dS
0
，
J
D t
)
dS
四计算题

大学物理上册课后练习答案解析

初速度大小为dt1-2 一石子从空中由静止下落，由于空气阻力，石子并非作自由落体运动。

现测得其加速度 a = A-B V ，式中A 、1-1 已知质点的运动方程为：x 10t30t 2 ,y 15t 20t 2。

式中x 、y 的单位为m , t 的单位为s 。

试求: (1)初速度的大小和方向；(2)加速度的大小和方向。

分析由运动方程的分量式可分别求出速度、加速度分析本题亦属于运动学第二类问题，与上题不同之处在于加速度是速度 V 的函数，因此需将式d V = a (V )d t 分离变量为-d ^ dt 后再两边积分.a(v)的分量再由运动合成算出速度和加速度的大小和方向. 解选取石子下落方向为y 轴正向,下落起点为坐标原点.vdv dv v 0A Bv(3)船在行驶距离 x 时的速率为v=v 0e kx 。

一 dv［证明］(1)分离变数得 — kdt ,v第一章质点的运动B 为正恒量，求石子下落的速度和运动方程。

解(1)速度的分量式为Vv y当 t = 0 时,V o x = -10 m sdx10 60tdt dy15 40t dt-1, V o y = 15 m-1(1)由题dvadt 用分离变量法把式 A Bv(1)改写为dvA Bv将式(2)两边积分并考虑初始条件，有(1)dt ⑵V 0 V 0x V 0y 18.0m得石子速度 V -(1 e Bt)B 设V o 与x 轴的夹角为a 则tanV 0y V ox由此可知当,t is 时,v A为一常量，通常称为极限速度Ba= 123 °1(2)加速度的分量式为a x dV x dt 60a ydV y dt40或收尾速度.(2)再由v—y —(1 e 氏)并考虑初始条件有dt BytABtdy -(1 e )dt 0 0 BA A得石子运动方程y t 2 (e Bt 1)B B 2则加速度的大小为 a .. a x 2a y 272.1 ms 2a y2 设a 与x 轴的夹角为B,则tan B -a x3B= -33 °1 '(或326 °9 )1-3 一个正在沿直线行驶的汽船，关闭发动机后，由于阻力得到一个与速度反向、大小与船速平方成正比例的加速度，即a = - kv 2, k 为常数。

PART_ONE_05_角动量和角动量守恒定律_刚体力学习题课

刚体绕定轴转动的角速度： ω = ω0 + α t ， α = 转过的角度： θ = ω0t + 转过的圈数： N =
ω − ω0
t
，α = −
ω0
t
， α = −3π rad / s
2
1 2 α t ， θ = 600π rad 2
θ = 300 2π
当 t = 10 s ， ω = ω0 + α t ， ω0 = 60π / s ， ω = 30π rad / s 线速度： v = ωR = 3π m / s 切向加速度： aτ =
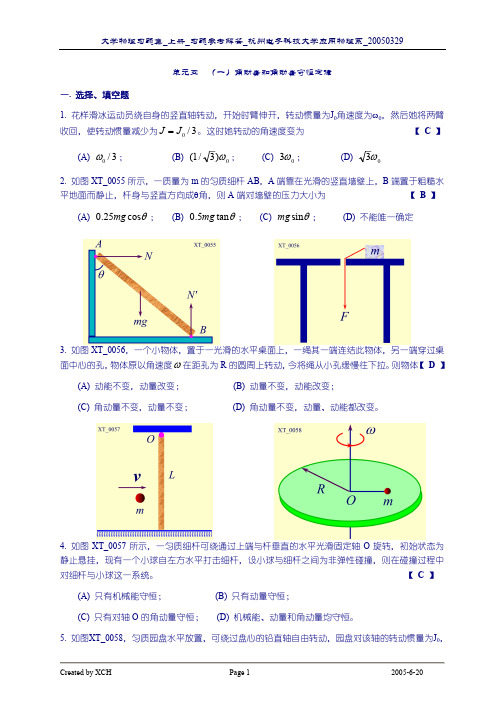
5. 如图XT_0058，匀质园盘水平放置，可绕过盘心的铅直轴自由转动，园盘对该轴的转动惯量为J0，
Created by XCH
Page 1
2005-6-20
大学物理习题集_上册_习题参考解答_杭州电子科技大学应用物理系_20050329 当转动角速度为ω0时，有一质量为m的质点落到园盘上，并粘在距轴R/2 处(R为园盘半径)，则它们的角速度 ω =
1 1 MR 2ω1 + mr 2ω1 = MR 2ω + mR 2ω 2 2
当人走到台边时，转台和人一起转动的角速度：
ω=
MR 2 + 2mr 2 ω1 , ω = 0.95 rad / s MR 2 + 2mR 2
*5. 如图XT_0063 所示，均匀细麦杆长为L，可绕通过中心O的固定水平轴在铅垂面内自由转动。开落下后立始时麦杆静止于水平位置。一质量与麦杆相同的甲虫以速度v0垂直落到麦杆的 1/4 长度处，即向端点爬行。试问：1) 为使麦杆以均匀的角速度转动，甲虫沿麦杆的爬行速度应是多少？ 2) 为使甲虫在麦杆转到铅直位置前能爬到端点，甲虫下落速度v0最大是多少？研究系统为甲虫和麦杆，碰撞为完全非弹性碰撞，系统对转轴的角动量守恒：

陕师大《大学物理学》(上册_)习题解答

大学物理学(上册)习题解答陕西师范大学物理学与信息技术学院基础物理教学组2006-6-26第2章运动学2－1 一质点作直线运动，其运动方程为222t t x -+= , x 以m 计，t 以s 计。

试求：（1）质点从t = 0到t = 3 s 时间内的位移；（2）质点在t = 0到t = 3 s 时间内所通过的路程解（1）t = 0时，x 0 = 2 ；t =3时，x 3 = －1；所以， m 3)0()3(-==-==t x t x x ∆ （2）本题需注意在题设时间内运动方向发生了变化。

对x 求极值，并令022d d =-=t tx可得t = 1s ,即质点在t = 0到t = 1s 内沿x 正向运动，然后反向运动。

分段计算m 1011=-===t t x x x ∆， m 4)1()3(2-==-==t x t x x ∆路程为 m 521=+=x x s ∆∆2－2 已知质点沿x 轴作直线运动，其运动方程为32262t t x -+=。

试求：（1）质点在最初4s 内位移；（2）质点在最初4s 时间内所通过的路程解（1）t = 0时，x 0 = 2 ；t = 4时，x 4 = －30 所以，质点在最初4s 内位移的大小 m 3204-=-=∆x x x（2）由0612d d 2=-=t t tx可求得在运动中质点改变运动方向的时刻为 t 1 = 2 s , t 2 = 0 (舍去) 则 m 0.8021=-=∆x x x ，m 40242-=-=∆x x x所以，质点在最初4 s 时间间隔内的路程为 m 4821=∆+∆=x x s2－3 在星际空间飞行的一枚火箭，当它以恒定速率燃烧它的燃料时，其运动方程可表示为 )1ln(1bt t b u ut x -⎪⎭⎫⎝⎛-+=，其中m/s 100.33⨯=u 是喷出气流相对于火箭体的喷射速度， s /105.73-⨯=b 是与燃烧速率成正比的一个常量。

《大学物理习题集》(上)习题解答

)2(选择题(5)选择题(7)选择题单元一质点运动学（一）一、选择题1. 下列两句话是否正确：(1) 质点作直线运动，位置矢量的方向一定不变；【 ⨯ 】(2) 质点作园周运动位置矢量大小一定不变。

【 ⨯ 】 2. 一物体在1秒内沿半径R=1m 的圆周上从A 点运动到B 点，如图所示，则物体的平均速度是：【 A 】 (A) 大小为2m/s ，方向由A 指向B ； (B) 大小为2m/s ，方向由B 指向A ； (C) 大小为3.14m/s ，方向为A 点切线方向； (D) 大小为3.14m/s ，方向为B 点切线方向。

3. 某质点的运动方程为x=3t-5t 3+6(SI)，则该质点作【 D 】(A) 匀加速直线运动，加速度沿X 轴正方向； (B) 匀加速直线运动，加速度沿X 轴负方向;(C) 变加速直线运动，加速度沿X 轴正方向; (D)变加速直线运动，加速度沿X 轴负方向 4. 一质点作直线运动，某时刻的瞬时速度v=2 m/s ，瞬时加速率a=2 m/s 2则一秒钟后质点的速度:【 D 】(A) 等于零(B) 等于-2m/s (C) 等于2m/s (D) 不能确定。

5. 如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向边运动。

设该人以匀速度V 0收绳，绳不伸长、湖水静止，则小船的运动是【 C 】(A)匀加速运动; (B) 匀减速运动; (C) 变加速运动; (D) 变减速运动; (E) 匀速直线运动。

6. 一质点沿x 轴作直线运动，其v-t 曲线如图所示，如t=0时，质点位于坐标原点，则t=4.5s 时，质点在x 轴上的位置为【 C 】(A) 0； (B) 5m ； (C) 2m ； (D) -2m ； (E) -5m*7. 某物体的运动规律为t kv dtdv2-=，式中的k 为大于零的常数。

当t=0时，初速为v 0，则速度v 与时间t 的函数关系是【 C 】(A) 02v kt 21v += (B) 02v kt 21v +-=(C) 02v 1kt 21v 1+=(D) 02v 1kt 21v 1+-=二、填空题1. )t t (r )t (r ∆+ϖϖ与为某质点在不同时刻的位置矢量，)t (v ϖ和)t t (v ∆+ϖ为不同时刻的速度矢量，试在两个图中分别画出s ,r ,r ∆∆∆ϖ和v ,v ∆∆ϖ。

大学物理习题参考解答物理习题参考解答刚体基本运动_转动定律_动能定理

选择题_03图示单元四刚体基本运动转动动能 1一选择题01. 一刚体以每分钟60转绕z 轴做匀速转动(ω沿转轴正方向)。

设某时刻刚体上点P 的位置矢量为345r i j k =++，单位210m -，以210/m s -为速度单位，则该时刻P 点的速度为：【 B 】(A) 94.2125.6157.0v i j k =++；(B) 25.118.8v i j =-+；(C) 25.118.8v i j =--；(D) 31.4v k =。

02. 轮圈半径为R ，其质量M 均匀布在轮缘上，长为R ，质量为m 的均质辐条固定在轮心和轮缘间，辐条共有2N 根。

今若将辐条数减少N 根但保持轮对通过轮心，垂直于轮平面轴的转动惯量保持不变，则轮圈的质量为【 D 】(A)12N m M +； (B) 6N m M +； (C) 23N m M +； (D) 3Nm M +。

03. 如图所示，一质量为m 的均质杆长为l ，绕铅直轴OO '成θ角转动，其转动惯量为【 C 】(A)2112ml ；(B) 221sin 4ml θ；(C) 221sin 3ml θ； (D) 213ml 。

04. 关于刚体对轴的转动惯量，下列说法中正确的是【 C 】 (A) 只取决于刚体的质量,与质量的空间分布和轴的位置无关； (B) 取决于刚体的质量和质量的空间分布，与轴的位置无关； (C) 取决于刚体的质量、质量的空间分布和轴的位置；(D) 只取决于转轴的位置，与刚体的质量和质量的空间分布无关。

05. 两个匀质圆盘A 和B 的密度分别为A ρ和B ρ，若A B ρρ>，但两圆盘的质量与厚度相同，如两盘对通过盘心垂直于盘面轴的转动惯量各为A J 和B J ，则【 B 】(A) A B J J >； (B) B A J J >；(C) A B J J =； (D) A J 和B J 哪个大，不能确定。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

)2(选择题(5)选择题单元一质点运动学（一）一、选择题1. 下列两句话是否正确：(1) 质点作直线运动，位置矢量的方向一定不变；【 ⨯ 】(2) 质点作园周运动位置矢量大小一定不变。

5. 如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向边运动。

6. 一质点沿x 轴作直线运动，其v-t 曲线如图所示，如t=0时，质点位于坐标原点，则t=4.5s 时，(7)选择题质点在x 轴上的位置为【 C 】(A) 0； (B) 5m ； (C) 2m ； (D) -2m ； (E) -5m*7. 某物体的运动规律为t kv dtdv2-=，式中的k 为大于零的常数。

当t=0时，初速为v 0，则速度v 与时间t 的函数关系是【 C 】(A) 02v kt 21v += (B) 02v kt 21v +-= (C)2v 1kt 21v 1+= (D)2v 1kt 21v 1+-=二、填空题1. )t t (r )t (r ∆+ϖϖ与为某质点在不同时刻的位置矢量，)t (v ϖ和)t t (v ∆+ϖ为不同时刻的速度矢量，试在两个图中分别画出s ,r ,r ∆∆∆ϖ和v ,v ∆∆ϖ。

2. 一质点从P 点出发以匀速率1cm/s 作顺时针转向的圆周运动，圆半径为1m ，如图当它走过2/3圆周时，走过的路程是m 34π；这段时间平均速度大小为：s /m 40033π；方向是与X 正方向夹角3πα=3. 一质点作直线运动，其坐标x 与时间t 的函数曲线如图所示，则该质点在第3秒瞬时速度为零；在第3秒至第6秒间速度与加速度同方向。

(1)填空题(2)填空题(3)填空题)3(计算题三、计算题1. 已知一质点的运动方程为t ,r ,j )t 2(i t 2r 2ϖϖϖϖ-+=分别以m 和s 为单位，求:(1) 质点的轨迹方程，并作图； (2) t=0s 和t=2s 时刻的位置矢量；(3) t=0s 到t=2s 质点的位移?v ,?r ==ϖϖ∆(1)轨迹方程：08y 4x 2=-+； (2) j 2r 0ϖϖ=，j 2i 4r 2ϖϖϖ-=(3) j 4i 4r r r 02ϖϖϖϖϖ-=-=∆，j 2i 2tr v ϖϖϖϖ-==∆∆2. 一质点沿x 轴作直线运动，其运动方程为x=3+5t+6t 2-t 3 (SI)，求 (1) 质点在t=0时刻的速度； (2) 加速度为零时，该质点的速度。

任一时刻的速度：2t 3t 125dt dx v -+==，任一时刻的加速度：t 612dtdv a -== s 0t =时的速度：s /m 5v =；当加速度为零：s 2t =，速度：s /m 17v =*3. 湖中一小船，岸边有人用绳子跨过高出水面h 的滑轮拉船，如图所示。

如用速度V 0收绳，计算船行至离岸边x 处时的速度和加速度。

选取如图所示的坐标，任一时刻小船满足：222h x l +=，两边对时间微分dt dx x dt dl l=，dt dl V 0-=，dtdxV =022V xh x V +-=方向沿着X 轴的负方向。

方程两边对时间微分：xa V V 220+=，xV V a 220-=3220xh V a -=，方向沿着X 轴的负方向。

4. 质点沿X 轴运动，其速度与时间的关系为v=4+t 2 m/s ，当t=3s 时质点位于x=9m 处，求质点的运动方程。

当t=2s 时，质点的位置在哪里?质点的位置满足： )dt t 4(vdt x 2+==⎰⎰，C t 31t 4x 3++=由初始条件：t=3s 时质点位于x=9m ，得到c=-12，12t 31t 4x 3-+= 当t=2s 时，质点的位置：m 3412388x -=-+= *5. 质点沿X 轴运动，其加速度和位置的关系是)SI (x 62a 2+=。

如质点在x=0处的速度为1s m 10-⋅，求质点在任意坐标x 处的速度。

由速度和加速度的关系式：dt dv a =，dxdv v dt dx dx dv a == vdv adx =，vdv dx )x 62(2=+，两边积分，并利用初始条件：0x =，10s m 10v -⋅=vdv dx )x 62(v102x⎰⎰=+，得到质点在任意坐标x 处的速度：25x x 2v 3++=单元一质点运动学（二）一、选择题1. 一质点在平面上运动，已知质点的位置矢量为j bt i at r ϖϖϖ22+= (a ，b 为常数)则质点作: 【 B 】 (A) 匀速直线运动； (B) 变速直线运动； (C) 抛物线运动；(D) 一般曲线运动。

2. 质点作曲线运动，r ϖ表示位置矢量，S 表示路程，a t 表示切向加速度，下列表达式中，【 D 】(1) a dt dV =； (2) V dt dr =； (3) V dtds=； (4)t a dt V d =ρ。

(A) 只有(1)、(2)是对的； (B) 只有(2)、（4）是对的； (C) 只有(2)是对的； (D) 只有(3)是对的。

3. 某人骑自行车以速率v 向正西方向行驶，遇到由北向南刮的风 (风速大小也为v ) 则他感到风是从【 C 】(A) 东北方向吹来；(B) 东南方向吹来； (C) 西北方向吹来；(D) 西南方向吹来。

4. 在相对地面静止的坐标系内，A 、B 两船都以1s m 2-⋅的速率匀速行驶，A 船沿X 轴正向，B 船沿y 轴正向，今在A 船上设置与静止坐标系方向相同的坐标系(x ，y 方向单位矢量ϖϖi j ,表示)，那么从A船看B船它相对A 船的速度(以1sm -⋅为单位)为【 B 】；j 2i 2)D (,j 2i 2)C (,j 2i 2)B (,j 2i 2)A (ϖϖϖϖϖϖϖϖ---+-+5. 一条河设置A ， B 两个码头，相距1 km ，甲，乙两人需要从码头A 到码头B ，再由B 返回，甲划船前去，船相对河水的速度4 km/h ；而乙沿岸步行，步行速度也为4 km/h ，如河水流速为2km/h ，方向从A 到B 下述结论中哪个正确?【 A 】(A) 甲比乙晚10分钟回到A ； (B) 甲和乙同时回到A ； (C) 甲比乙早10分钟回到A ；(D) 甲比乙早2分钟回到A二、填空题1. 在x ，y 面内有一运动质点其运动方程为 )SI (jt 5sin 10i t 5cos 10r ϖϖϖ+=，则t 时刻其速度j t 5cos 50i t 5sin 50v ϖϖϖ+-=；其切向加速度0a =τ；该质点运动轨迹是100y x 22=+。

2. 一质点作如图所示的抛体运动，忽略空气阻力。

回答:(A) 标量值dv dt 是否变化：变化；矢量值dtvd ϖ是否变化：不变；a n 是否变化：变化(B) 轨道最高点A 的曲率半径g )cos v (20A θρ=，落地点B 的曲率半径θρcos g v 2B =。

3. 试说明质点作何种运动时，将出现下述各种情况0v ≠ (1) 0a ,0a n t ≠≠：变速曲线运动(2) 0a ,0a n t =≠：变速直线运动， a a t n ,分别表示切向加速度和法向加速度。

4. 如图所示，小球沿固定的光滑的1/4圆弧从A 点由静止开始下滑，圆弧半径为R ，则小球在A 点处的切向加速度g a t =，小球在B 点处的法向加速度g 2a n =。

5. 在一个转动的齿轮上，一个齿尖P 做半径为R 的圆周运动，其路程S 随时间的变化规律为020v ,bt 21t v S 其中+=和b 都是正的常量，则t 时刻齿尖P 的速度大小为：bt v 0+，加速度大小)2(填空题)4(填空题)9(填空题为：2402R)bt v (b a ++=。

6. 一物体在某瞬时，以初速度ϖv 0从某点开始运动，在∆t 时间内，经一长度为S 的曲线路径后，又回到出发点，此时速度为-ϖv 0，则在这段时间内:(1) 物体的平均速率是tS∆； (2) 物体的平均加速度是t v 20∆ϖ-。

7. 一质点沿半径为R 的圆周运动，路程随时间的变化规律为),SI (ct 21bt S 2-=式中b ，c 为大于零的常数，且21c R c b ⎪⎭⎫ ⎝⎛>。

(1) 质点运动的切向加速度：c a -=τ；法向加速度：R)ct b (a 2n -=；(2) 质点经过cR c b t ±=时，n t a a =。

8. 质点沿半径R 作圆周运动，运动方程为)SI (t 232+=θ，则t 时刻质点法向加速度大小2n Rt 16a =，角加速度4=β，切向加速度大小R 4a =τ。

9. 楔形物体A 的斜面倾角为α，可沿水平方向运动，在斜面上物体B 沿斜面以ϖv t 相对斜面下滑时，物体A 的速度为ϖv ，如图，在固接于地面坐标oxy 中，B 的速度是矢量式 j )sin v (i )v cos v (v t t B ρϖϖαα-+-=地分量式 v cos v v t x -=α，αsin v v t y -=三、计算题1. 如图，一质点作半径R=1m 的圆周运动， t=0时质点位于A 点，然后顺时针方向运动，运动方程)SI (t t s 2ππ+=求： (1) 质点绕行一周所经历的路程、位移、平均速度和平均速率；(2) 质点在1秒末的速度和加速度的大小。

(1) 质点绕行一周所需时间：R 2t t 2πππ=+，s 1t =质点绕行一周所经历的路程：)m (2R 2s ππ==)1(计算题位移：0r =ϖ∆；平均速度：0tr v ==∆∆ϖϖ平均速率：s /m 2tsv π∆==(2) 质点在任一时刻的速度大小：ππ+==t 2dtdsv 加速度大小：22222n )dtdv ()R v (a a a +=+=τϖ 质点在1秒末速度的大小： )s /m (3v π=加速度的大小：222)2()9(a ππ+=ϖ，)s /m (96.88a 2=ϖ2. 如图，飞机绕半径r=1km 的圆弧在竖直平面内飞行，飞行路程服从)m (t 50)t (s 3+=的规律，飞机飞过最低点A 时的速率1A s m 192v -⋅=，求飞机飞过最低点A 时的切向加速度a t ，法向加速度n a 和总加速度ϖa 。