偏摩尔量.ppt
合集下载
2010-4-1偏摩尔量
第四章 多组分系统热力学
1
引
言
实际系统绝大多数为多组分系统或变组成系统, 必 须掌握处理多组分系统的热力学方法. 混合物 气态混合物 液态混合物 l1 + l2 + … 固态混合物(相平衡章) 液态溶液 l + (l , s, g) 理想液态混合物
多 各 组 分 组 等同对待 分 均 相 溶 液 系 统 区分溶剂
和 溶 质
真实液态混合物
理想稀溶液 真实溶液
固态溶液(相平衡章)
电解质溶液在电化学章讨论.
2
补充：
(1) ① ② ③
混合物的组成标度和溶液中溶质B的组成标度
混合物常用的组成标度
B的分子浓度 CB B的质量浓度 B的质量分数
def
def def
N B /V
mB / V mB / mA
A
(1) (2) (3)
偏摩尔内能 偏摩尔焓
V VB n B
U UB n B
T , p,nC nB
T , p,nC nB
H HB n B T , p,nC nB S SB n B T , p,nC nB
17
§4.2 化 学 势
化学势的定义式
B
def G GB n B T , p ,nC nB
1. 多组分单相系统的热力学公式 对多组分组成可变的单相系统 G＝f (T, p, nB, nC , ……) G G G dG dT dp dnB p n T p,nC T ,n B T , p ,n n B
C2H5OH *(l)
1
引
言
实际系统绝大多数为多组分系统或变组成系统, 必 须掌握处理多组分系统的热力学方法. 混合物 气态混合物 液态混合物 l1 + l2 + … 固态混合物(相平衡章) 液态溶液 l + (l , s, g) 理想液态混合物
多 各 组 分 组 等同对待 分 均 相 溶 液 系 统 区分溶剂
和 溶 质
真实液态混合物
理想稀溶液 真实溶液
固态溶液(相平衡章)
电解质溶液在电化学章讨论.
2
补充：
(1) ① ② ③
混合物的组成标度和溶液中溶质B的组成标度
混合物常用的组成标度
B的分子浓度 CB B的质量浓度 B的质量分数
def
def def
N B /V
mB / V mB / mA
A
(1) (2) (3)
偏摩尔内能 偏摩尔焓
V VB n B
U UB n B
T , p,nC nB
T , p,nC nB
H HB n B T , p,nC nB S SB n B T , p,nC nB
17
§4.2 化 学 势
化学势的定义式
B
def G GB n B T , p ,nC nB
1. 多组分单相系统的热力学公式 对多组分组成可变的单相系统 G＝f (T, p, nB, nC , ……) G G G dG dT dp dnB p n T p,nC T ,n B T , p ,n n B
C2H5OH *(l)
3.1~3.2化学势和偏摩尔量
物理意义——在温度、压力和其他组分的含量恒定 的条件下，增加1mol组分i引起的体系总吉布斯自由 能的改变量。
考试题：下列各式中，哪个是化学势的定义式： D
A、 U ( ni )T,P,n j
B、 S
( ni
)T,P,n j
C、
(
H ni
)T
,P,n
j
D、
G
( ni
)T,P,n j
相转移到 相，
dn dn
dn dn
dG BdnB
dG dn dn dn dn
dGT ,P,W ' 0 ( )dn
(1) 若 μβ < μα 则 dG < 0 物质从α→β相的转移 是自发过程;
(2) 若 μβ > μα 则 dG > 0 物质从β→α相的转移 是自发过程;
V nB
T ,P,n j
3、对于纯物质的均相系统，偏摩尔量即为
该物质的摩尔量
VB,m
( V n
)T
,P
Vm
二. 集合公式
在一定的温度, 压力和浓度的条件下,多组分体系处于 一定的状态, 体系的某一广度性质可用下式计算
Z nBZB,m
B
V nBVB,m
B
S nB SB,m
1、单一组分的过冷液体的化学势比其固体的化学势 A
A、高
B、低
C、相等
D、不可比较
2、0℃，Pθ时，水的化学势比冰的化学势如何 C
A、高
B、低
C、相等
D、不可比较
3、从多孔硅胶的强烈吸水性能说明自由水分子与吸附在硅 胶表面的水分子比较，化学势如何 A
2.13偏摩尔量和化学势讲解
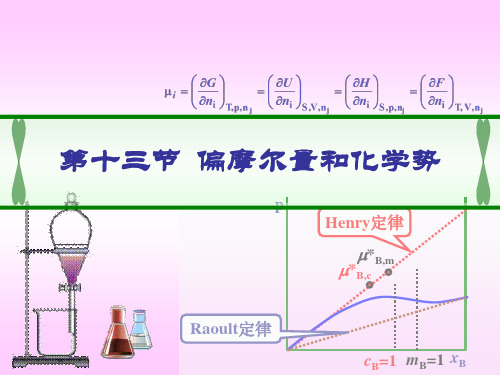
X X dX dT dp X B ,m dnB T p ,ni B p T ,ni
一、偏摩尔量
2. 多组分系统的偏摩尔量
VB ,m V n B T , p , n j B U B ,m U H H B ,m n n B T , p , n j B B T , p , n j B GB , m G n B T , p , n j B
二、化学势
(2) 化学势广义定义
U H 广义定义： B nB S ,V ,n j B nB S , p ,n j B F G nB T ,V ,n j B nB T , p ,n j B
G f(T , p, n1 , n2 ,..........)
-SdT
Vdp
B
B
dnB
dG SdT Vdp ( B dnB )
B
二、化学势
(2) 化学势广义定义 dU = TdS - pdV
U f( S ,V , n1 , n2 ,....)
U U U dU dS dV dnB S V ,ni V S ,ni B nB S ,V , n jB
一、偏摩尔量
3. 偏摩尔量的集合公式 因为偏摩尔量是强度性质，所以只要多组分系统中各物质的 比例（组成）不变，则某个物质的偏摩尔量也不变。
dX
T,p
X B ,m dnB
B
在保持偏摩尔量不变的情况下对上式积分
X X 1,m dn1 X 2,m dn2 X i ,m dni
偏摩尔量和化学势
ni表示所有的物质, nj表示除了某一物质之外的所有物质
一、偏摩尔量
2. 多组分系统的偏摩尔量 等温等压下
X dX dnB B nB T , P , n j B
X B ,m X nB T , P ,n j B
定义：偏摩尔量
指的是多组分系统中B物质的某种广度性质的偏摩尔量（换 句话说，就是某种组分的物质的量对某个系统性质的贡献 的大小） 那么对于多组分系统的某个广度性质则存在
B
dH TdS Vdp BdnB
B
dA sdT pdV BdnB
X f(T , p, n1 , n2 ,...........ni )
当系统状态发生微小变化时，用全微分表示
X X X dX dT dn1 T P ,ni p T ,ni n1 T , P ,n j1 X dn2 ......... n2 T , P ,n j2
X X dX dT dp X B ,m dnB T p ,ni B p T ,ni
一、偏摩尔量
2. 多组分系统的偏摩尔量
VB ,m V n B T , p , n j B U B ,m U H H B ,m n n B T , p , n j B B T , p , n j B GB , m G n B T , p , n j B
G dG SdT VdP dnB n B T , P , n j B
U dU TdS pdV dnB nB V , S ,n j B
F dF SdT pdV dnB n B T ,V ,n jB
一、偏摩尔量
2. 多组分系统的偏摩尔量 等温等压下
X dX dnB B nB T , P , n j B
X B ,m X nB T , P ,n j B
定义：偏摩尔量
指的是多组分系统中B物质的某种广度性质的偏摩尔量（换 句话说，就是某种组分的物质的量对某个系统性质的贡献 的大小） 那么对于多组分系统的某个广度性质则存在
B
dH TdS Vdp BdnB
B
dA sdT pdV BdnB
X f(T , p, n1 , n2 ,...........ni )
当系统状态发生微小变化时，用全微分表示
X X X dX dT dn1 T P ,ni p T ,ni n1 T , P ,n j1 X dn2 ......... n2 T , P ,n j2
X X dX dT dp X B ,m dnB T p ,ni B p T ,ni
一、偏摩尔量
2. 多组分系统的偏摩尔量
VB ,m V n B T , p , n j B U B ,m U H H B ,m n n B T , p , n j B B T , p , n j B GB , m G n B T , p , n j B
G dG SdT VdP dnB n B T , P , n j B
U dU TdS pdV dnB nB V , S ,n j B
F dF SdT pdV dnB n B T ,V ,n jB
3-8偏摩尔量
12
3、相平衡条件
5、化学势与T、p的关系
G p
T
V
G S T p
一般
B
p
T
VB
>0
一般
B
T
p
SB
<0
dG = -SdT + Vdp 对于组成恒定的系统：
恒温时 p μB
恒压时 T μB
注意：化学势不是某种形式的能量！
例题：
化学势是一个状态函数，没有确切的物理意义。 化学势是一个表示变化方向的指标。
V GB p T ,nC
Bp
G nB
T
,
p
,nAB
T
,nA
nB
G p
T
,nA
V
nB
T , p ,nAB
T , p ,nAB
VB
10
4. 偏摩尔量之间 的函数关系
二、 化学势
1、化学势的定义
B
def
GB
G nB
T ,P ,n(C,CB)
G＝f (T，p，nA，nB……)
对多组分系统 X＝ f (T, p, nB, nC, …)
全微分为
dX
X T
dT
p,nB;nC
X p
dp
T ,nB;nC
X nB
T ,
dnB
p,nC;nD
X nC
T
,
dnC
p,nB ;nD
定义
X
B
def
X nB
T
,
p,nC
XB 偏摩尔量
该式表示在恒温恒压和除B 组分以外其它组分的含量都 不变的条件下, 任一广延性质X 随B组分物质的量的变化率, 相当于每单位量引起的X 的增量( 折合值, 对应于一定状态)4.
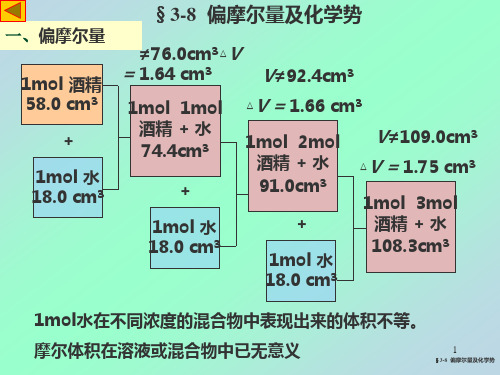
3、相平衡条件
5、化学势与T、p的关系
G p
T
V
G S T p
一般
B
p
T
VB
>0
一般
B
T
p
SB
<0
dG = -SdT + Vdp 对于组成恒定的系统：
恒温时 p μB
恒压时 T μB
注意：化学势不是某种形式的能量！
例题：
化学势是一个状态函数，没有确切的物理意义。 化学势是一个表示变化方向的指标。
V GB p T ,nC
Bp
G nB
T
,
p
,nAB
T
,nA
nB
G p
T
,nA
V
nB
T , p ,nAB
T , p ,nAB
VB
10
4. 偏摩尔量之间 的函数关系
二、 化学势
1、化学势的定义
B
def
GB
G nB
T ,P ,n(C,CB)
G＝f (T，p，nA，nB……)
对多组分系统 X＝ f (T, p, nB, nC, …)
全微分为
dX
X T
dT
p,nB;nC
X p
dp
T ,nB;nC
X nB
T ,
dnB
p,nC;nD
X nC
T
,
dnC
p,nB ;nD
定义
X
B
def
X nB
T
,
p,nC
XB 偏摩尔量
该式表示在恒温恒压和除B 组分以外其它组分的含量都 不变的条件下, 任一广延性质X 随B组分物质的量的变化率, 相当于每单位量引起的X 的增量( 折合值, 对应于一定状态)4.
3.1 偏摩尔量
偏摩尔量与摩尔量的区别
V xAV x V
id m * A
* B B
偏摩尔量与摩尔量的区别
V xAV x V
id m * A
表 3–1 101325Pa，20℃
xB
id Vm cm3 mol 1
* B B
混合时的体积变化
V id / cm 3 V / cm 3 ( nA 10 mol )( nA 10mol)
T , p ,n ji
X dX T
X K dT p dp i 1 X i dni p ,n j T ,n j
X X i n i
def
T , p ,n ji
解：当nB 1.000m ol时 ，
3 VB (51.832 0.2788 1.000)cm m ol1
o
52.111cm 3 m ol1 VA (18.0681 0.00251 1.0002 )cm3 m ol1 18.0656 cm 3 m ol1
i 1
K
S ni S i
i 1
K
A ni Ai
i 1
G ni Gi
i 1
K
例：25 C、101325Pa时，HAc(B)溶于1kgH2O(A) 中所成溶液的体积 V 与物质的量 nB (nB = 0.16 ~ 2.5mol 时）的关系如下： V=[1002.935+51.832(nB/mol)+0.1394(nB/mol)2]cm3 试将HAc和H2O的偏摩尔体积表示为nB的函数，并 求nB=1.000mol 时HAc和H2O的偏摩尔体积。 解：
偏摩尔量与化学势ppt课件
S B,m
S nB
T ,P,nC (C B)
注意
• 对偏摩尔量的定义都是指等温等压条件下， 若非此条件，如
H nB
T ,V ,nC (C B)
H B,m
• 这个偏微商就不是偏摩尔量，当然也就不
能用
H nB
T ,V ,nC (C B)
来求算H。
二、化学势
• 1.定义
• 当某均相体系含有不止一种物质时，它的 任何热力学性质都应是P、V、T等热力学函 数中任取两个独立变量再加上各物质物质 的量的函数，如吉布斯自由能：
Z Z (T , P, n1, n2 , n3...... nk )
• 等温等压下，有
•令
dZ
B
Z nB
dnB
T ,P,nC (C B)
Z nB
T ,P,nC (C B)
Z B,m
•则
k
dZ Z B,m dnB B 1
• ZB,m即为物质B的某种容量性质Z的偏摩尔 量（Partial molar quantity）。
• 正如温度T决定相间是否存在热平衡、压力P决定
相间是否存在力学平衡一样，状态函数化学势 B
决定相间是否存在物质平衡。
b.化学势在反应平衡中的应用
• 化学反应中的平衡条件：
B B 0
B
• 应用于达到反应平衡，只做P-V功的封闭体 系。
• 式中 B 是反应中各物种B的化学势， B 是各物质的化学计量系数，对生成物取正 值，对反应物取负值。
二、亨利定律
• 针对挥发性溶质在溶液中的溶解度，亨利定律规 定：
在一定温度和平衡状态下，气体在溶液中的
溶解度（物质的量分数）与该气体的平衡分压成
2.14偏摩尔量
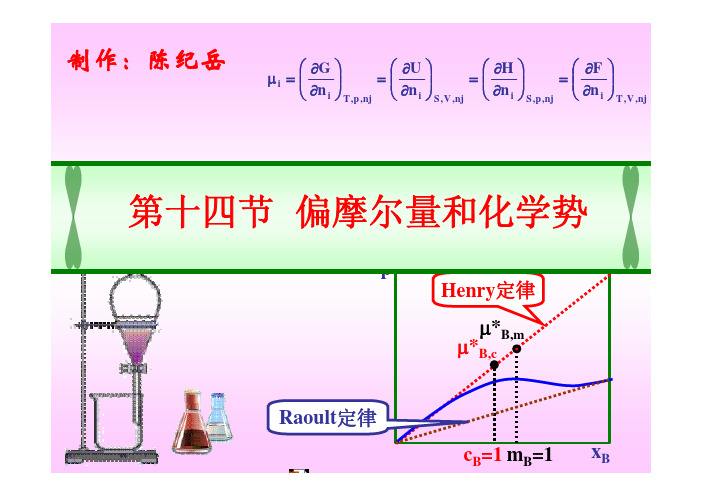
pnj,V,Tinj,p,Sinj,V,Sinj,p,Tii nFnHnUnG⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂=μ制作：陈纪岳第十四节偏摩尔量和化学势返回=？mL 由于分子间的作用力，总体积减少。
减少的量与两者的比例有关。
100105110115120125130020406080100乙醇浓度％总体积（mL）50 mL 水＋50 mL 乙醇≠100 mL混合前总体积混合后总体积20601008040因此V = f ( T, p , n 水, n 乙醇)混合返回""""23n ,1n ,p ,T 213n ,2n ,p ,T 1dn n V dn n V dV ⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂== V 1, m dn 1+ V 2, m dn 2+ ……= ΣV i, m dn i式中"3n ,2n ,p ,T 1m,1n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质1 的偏摩尔体积"3n ,1n ,p ,T 2m,2n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质2 的偏摩尔体积若在恒温恒压下，多种物质混合，V = f ( n 1, n 2, ……)1. 偏摩尔量体积返回式中"3n ,2n ,p ,T 1m,1n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质1 的偏摩尔体积"3n ,1n ,p ,T 2m ,2n V V ⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质2 的偏摩尔体积通式()i j nj ,p ,T i m ,i n V V ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=称为物质i 的偏摩尔体积其意义为恒温恒压和其它物质不变时，i 物质的改变引起的总体积的改变率。
返回偏摩尔内能，()i j nj ,p ,T i m,i n U U ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔焓，()i j nj ,p ,T i m ,i n H H ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔熵，()i j nj ,p ,T i m ,i n S S ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔亥姆霍滋能，()i j nj ,p ,T im,i n F F ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔吉布斯能，()i j nj ,p ,T i m ,i n G G ≠⎟⎟⎠⎞⎜⎜⎝⎛∂∂=偏摩尔量特点：（1）只有容量性质的热力学函数才有偏摩尔量（2）T ，p 恒定，n j 不变2．偏摩尔量恒温恒压和其它物质不变时，某物质的改变引起的热力学函数的改变率返回3. 偏摩尔量集合公式如果两种物质混合，总体积不变（分子间作用力相同）V = n 1V 1+ n 2V 2( V 1，V 2为摩尔体积)如总体积改变，V = n 1V 1,m + n 2V 2,m ( V 1,m ，V 2,m 为偏摩尔体积)一般地，容量性质X = Σn i X i,m称为偏摩尔量集合公式返回4. 吉布斯－杜亥姆公式二组分体系dX=X 1,m dn 1+ X 2,m dn 2按集合公式X = n 1X 1,m + n 2X 2,m全微分dX = X 1,m dn 1 + n 1 dX 1,m +X 2,m dn 2+ n 2dX 2,m 吉-杜公式n 1 dX 1,m + n 2dX 2,m = 0 多组分通式Σn i dX i,m =0意义：等温等压时，由浓度变化引起偏摩尔量变化时受到制约的条件返回对于多组分体系，应考虑组分对热力学函数的影响，如G = f ( T ，p ，n 1，n 2…)∑⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂=i nj,p ,T i ni ,T ni ,p dn n G dp p G dT T G dG ∑⎟⎟⎠⎞⎜⎜⎝⎛∂∂++−=i nj,p ,T i dn n G Vdp SdT 同理，还有∑⎟⎟⎠⎞⎜⎜⎝⎛∂∂+−=i nj,V ,S i dn n U pdV TdS dU 1. 化学势定义返回⎞⎛∂G 以上四式中加和号内的偏导式是相等的。
偏摩尔量
由于偏摩尔量只决定于组成，与总量无关；当我们按 比例加入n1, n2,...nB…时, XB偏 (简写为 XB) 不变
由dXT,p=X1dn1+ X2dn2+...+ XBdnB+... dXT,p= X1dn1+ X2dn2+...+ XBdnB+... XT,p = X1n1 + X2n2+...+ XBnB+...
确定系统状态的独立变量数多于三个
V f (T, p, n1, n2,)
2019/11/20
物理化学II
5
溶液体系热力学
偏摩尔量
（一）偏摩尔量的定义
对一个处于热平衡和力平衡的均相系统，其任一广 度性质除取决于温度和压力外，还取决于组成该系统 的某组分的量（nB）
以体积为例:
V f (T , p, n1, n2,)
dV (V T ) p,n1,n2 ,dT (V p)T ,n1,n2 ,dp (V n1)T , p,n2 ,dn1 (V n2 )T , p,n1,dn2
2019/11/20
物理化学II
6
溶液体系热力学
偏摩尔量
定义 VB (V n )B T , p,nc,
偏摩尔体积
同理:
偏摩尔内能 偏摩尔焓 偏摩尔熵
U B (U nB )T , p,nc , H B (H nB )T , p,nc ,
SB (S nB )T , p,nc ,
偏摩尔量并不等于 B 组分本身的性质，还取决于体系 内其他组分的存在。
2019/11/20
物理化学II
(G/p)T, x= V
(Gm/p)T, x= Vm (GB/p)T, x = VB
4-1 偏摩尔量
第四章 多组分系统热力学
多组分多相系统 混合物 多组分单相系统
气态混合物 √ 液态混合物 √ 固态混合物
(第六章)
固态溶液 溶液 液态溶液
按处理方法的不同划分： 按处理方法的不同划分： 混合物：各组分选用相同的标准态和相同的方法研究 各组分选用相同的标准态和相同的方法研究； 混合物 各组分选用相同的标准态和相同的方法研究； 溶液：区分为溶质、溶剂，选用不同的标准态和研究方法。 溶液：区分为溶质、溶剂，选用不同的标准态和研究方法。 ——为研究方便人为划分 无本质区别。 为研究方便人为划分， ——为研究方便人为划分，无本质区别。 按聚集状态划分： 、 、 按聚集状态划分：g、l、s 按规律性划分：理想混合物、理想稀溶液； 按规律性划分：理想混合物、理想稀溶液；真实混合物及溶液
均存在同样的结果: 对所有广度量 X 均存在同样的结果
X ¹
å
* n BX B
B
原因： 原因： 水分子之间、 ① 水分子之间、乙醇分子之间和水分子与乙醇分子之间的 分子间相互作用不同； 分子间相互作用不同； 水分子与乙醇分子体积及形状不同。 ② 水分子与乙醇分子体积及形状不同。 2. 偏摩尔量 定义： ① 定义： 系统广度量 X 为温度 T、压力 p 及系统各组分物质的量 nB、 、 nC、nD、…等的函数： 等的函数： 等的函数
X = f (T , P, nB , nC , nD ,⋯)
当系统发生微变时： 当系统发生微变时：
∂X ∂X dX = ( ) p ,nB ,nc dT + ( )T ,nB ,nc dp ∂p ∂T ∂X ∂X +( )T , p ,nc ,nD dnB + ( )T , p ,nB ,nD dnC + ⋯ ∂nB ∂nC
多组分多相系统 混合物 多组分单相系统
气态混合物 √ 液态混合物 √ 固态混合物
(第六章)
固态溶液 溶液 液态溶液
按处理方法的不同划分： 按处理方法的不同划分： 混合物：各组分选用相同的标准态和相同的方法研究 各组分选用相同的标准态和相同的方法研究； 混合物 各组分选用相同的标准态和相同的方法研究； 溶液：区分为溶质、溶剂，选用不同的标准态和研究方法。 溶液：区分为溶质、溶剂，选用不同的标准态和研究方法。 ——为研究方便人为划分 无本质区别。 为研究方便人为划分， ——为研究方便人为划分，无本质区别。 按聚集状态划分： 、 、 按聚集状态划分：g、l、s 按规律性划分：理想混合物、理想稀溶液； 按规律性划分：理想混合物、理想稀溶液；真实混合物及溶液
均存在同样的结果: 对所有广度量 X 均存在同样的结果
X ¹
å
* n BX B
B
原因： 原因： 水分子之间、 ① 水分子之间、乙醇分子之间和水分子与乙醇分子之间的 分子间相互作用不同； 分子间相互作用不同； 水分子与乙醇分子体积及形状不同。 ② 水分子与乙醇分子体积及形状不同。 2. 偏摩尔量 定义： ① 定义： 系统广度量 X 为温度 T、压力 p 及系统各组分物质的量 nB、 、 nC、nD、…等的函数： 等的函数： 等的函数
X = f (T , P, nB , nC , nD ,⋯)
当系统发生微变时： 当系统发生微变时：
∂X ∂X dX = ( ) p ,nB ,nc dT + ( )T ,nB ,nc dp ∂p ∂T ∂X ∂X +( )T , p ,nc ,nD dnB + ( )T , p ,nB ,nD dnC + ⋯ ∂nB ∂nC
《物理化学第4版》第四章4-2 偏摩尔量ppt课件
def
V nB
T
,
p,n
CB
VB 的物理意义可理解为:在等温、等 压以及除B 物质的量 nB 之外其它组分物 质的量保持不变条件下，V 随 nB的变化 率.
4
也可以理解为：在T、p条件下， 向一个包含物 质的量无比巨大的系 统中加入 1mol 物质B 引起的系统体 积 V 的变化。
例如: 25℃和p, 向一大池某浓度的乙 醇水溶液中加入1mol的水(18.0cm3), 而整池溶液的体积增大了17.3cm3 ,则此 时水的偏摩尔体积为17.3 cm3mol-1。
V2/cm3mol-1=(V/n2)T,p,n1 =234.69[(b/b) -0.07]
b2=0.05 molkg-1时， V2/cm3mol-1= -1.39
20
V=n1V1+n2V2 V1/cm3mol-1= (V-n2V2) /n1 1000g水中, n2=b21kg=0.05mol; n1=1000g/18.02 gmol-1=55.49mol，
例如乙醇水溶液的体积为： V=n乙醇V乙醇+n水V水
12
单组分系统中，体积对物质的摩尔体 积具有加和性，
多组分系统的体积对物质的摩尔体积
不具有加和性，V混合 nB V*m,B, 对偏摩
尔体积具有加和性。
13
集合公式同样适用于任一广延性质。如： U = nB UB ； H = nB HB ； S = nB SB ； A= nB AB ； G = nB GB ；
偏摩尔量在少数情况下可能为负值。 例如当质量摩尔浓度小于0.07 molkg-1 时，向MgSO4稀溶液中继续加入 MgSO4，系统的体积不增大却减小， 对应MgSO4的偏摩尔体积小于零。
《偏摩尔量》PPT课件
y
1 x z
y
z z w x y w y x y
x
z y
x
y
y
z x
y
x
2021/4/25
13
1.22 混合物及溶液
1. 概念
含一个以上组分的系统称多组分系统 多组分均相系统又可以区分为混合物或溶液
溶液中的各组分区分为溶剂及溶质，并选用不 同的标准态加以研究
H2O，18.07cm3 + C2H5OH，5.74cm3
定温、定压混合
混合物， 23.30cm3
298K,101.325kPa
23.30cm3≠23.81cm3
2021/4/25
17
说明什么?
18.07cm3 (T，p) 水单独存在或在大量水中体积贡献都是
18.07 cm3； 但同样量的水对乙醇水混合物的体积贡献不是 18.07cm3
滴加2
• 定温、定压、n1不变条件下，滴加2
• 测定n2和V
n2
……
V
……
组分 1，2
• 利用实验数据绘制 V—n2 曲线
2021/4/25
20
• 利用实验数据绘制 V—n2 曲线
如何从V—n2图得到浓度是
V V'
x2'=n2 ' /（n1+n2 ' ）的V2=？
.. ..
n2 ' n2
V n2
T，p，n1
公式
2021/4/25
33
2. 再谈热力学基本方程
已学过组成一定，量一定的均相系统的热力学基本方程
利用化学势，热力学基本方程可扩展到 多组分组成可变的均相系统 多组分组成可变的多相系统
§4.3 偏摩尔量
, nk
Z dT p T ,n1 ,n2 ,n3 , dn2
, nk
Z dp n 1 T , p ,n2 ,n3 , dnk
, nk-1
dn1
, nk
Z n 2 T , p ,n1 ,n3 ,
, nk
Z n k T , p ,n1 ,n2 ,n3 ,
Gibbs-Duhem公式
n1dZ1 n2dZ2 nk dZk 0
即
n dZ
B B=1
k
B
0
Байду номын сангаас
这就称为Gibbs-Duhem公式，说明偏摩尔量之 间是具有一定联系的。某一偏摩尔量的变化可从其它 偏摩尔量的变化中求得。
例4例5
这个公式在多组分系统中很有用
12
Z BdnB
B=1 k
5
常见的偏摩尔量定义式有：
VB
def
V nB T , p ,nC(C B) H nB T , p ,nC(C B) A nB T , p ,nC(C B)
UB
def
U nB T , p ,nC(C B) S nB T , p ,nC(C B) G nB T , p ,nC(C B)
§4.3 偏摩尔量
偏摩尔量的定义
偏摩尔量的加和公式
Gibbs-Duhem公式—— 系统中偏摩尔量之间的关系
1
多组分系统与单组分系统的差别 单组分系统的广度性质具有加和性 若1 mol单组分B物质的体积为 则2 mol单组分B物质的体积为
* Vm,B * 2 Vm,B
最新第4章偏摩尔性质、逸度和活度ppt课件
3.45
60.24
110.92 106.93
3.99
50.20
113.55 109.43
4.12
40.16
116.18 112.22
3.96
36.12
118.81 115.25
3.56
20.08
121.44 118.56
2.88
10.04
124.07 122.25
1.82
结论
1. 真实混合物的广度性质不能用纯物质的摩尔性质 加和来简单地表示，并且其广度性质和T，p，组 成均有关系。即：
(Fugacity and Fugacity Coefficient)
➢ 逸度和逸度系数的定义及物理意义 ➢ 纯气体逸度的计算 ➢ 纯液体逸度的计算 ➢ 混合物中组元逸度的计算
逸度和逸度系数的定义及物理意义
1. 定义
1 mol 纯物质 i： diG V id pSidT （T 恒定）
Ideal gas
4.2.1偏摩尔性质概念的引入
对于理想混合物，例如体积符合Amagat分体积 定律
V t nV niV i
i
但对于真实混合物而言，不能用加和的方法来 处理，因为事实上真实混合物的焓、Gibbs自由 能、体积等广度性质并不等于纯物质的性质加 和。
V t nV niV i
i
乙醇含量（质 量%） 10 20 30 40 50 60 70 80 90
T,p,nji
ln fˆ i xi
是（nlnf）的偏摩尔量
lnxfˆ11lnfx2ddln2xf
lnxfˆ2 2lnf1x2ddln 2fx
dM
M M12M Mx12dxx22ddM x2
lnˆi nn ln iT,p,nji
化学势 偏 摩 尔 量PPT学习教案
3.理想溶液的特点:
p
mixV = 0
即
Vi
=
V
m,i
p
mixH = 0
Hi
=
H
m,i
A
4. 理想溶液的蒸气压:
pB
pA p
pB = pB* xB
B
pA = pA* xA
0
xB
p = pA + pB
1
xA
0
第29页/共82页
30
例3 苯(A)和甲苯(B)的混合物可看作理想溶液 20℃时它们的饱和蒸气压分别为9.96kPa和2.97kPa。 试计算(1)xA=0.200时，溶液中苯和甲苯的分压和蒸气 总压；(2)当蒸气的yA=0.200时，液相的xA和蒸气总压 。 解: (1)应用拉乌尔定律
(T )
RT
ln
pi p
]
ni [i
(T )
RT
ln
pi p
]
mix G
RT nA
ln
pA pA
nB
ln
pB pB
V d pA
p*A A
p
V dp pB
p*B B
TmixS
其中pi分别为混合后i 气体的分压
第16页/共82页
17
二、实际气体的化学势，逸度 fugacity
令逸度 f = p
第30页/共82页
31
四、理想稀溶液
在稀溶液范围内, 溶剂遵守R.L, 溶质遵守H.L 即：p1 = p1 x1 ；p2 = kxx2 p2x2
溶质的蒸气压(见图)
p2
kx
kx> p2 ，对R.L正偏差
p2
kx< p2，对R.L负偏差
第1节 偏摩尔量
偏摩尔量XB的定义为：
XB
def
X n B
T , p , nC
XB称为物质B的某种容量性质X的偏摩尔量。
X X dX dp X BdnB dT T p , nB B p T , nB
第三章 化学势
§3.1 偏摩尔量 §3.2 化学势
§3.3 气体物质的化学势
§3.4 理想液态混合物中物质的化学势
§3.5 理想稀溶液中物质的化学势
§3.6 不挥发性溶质理想稀溶液的依数性
§3.7 非理想多组分系统中物质的化学势
§3.1 偏摩尔量
一、偏摩尔量 (Partial Molar Quantity) 1、问题的提出
96% 56%
14.61 17.11
58.01 56.58
解：(1) 首先求算10.0 m3的含乙醇96%的酒中水和
乙醇的物质的量。
n乙 M 乙 0.96 n乙 M 乙 n水 M 水
n乙 4610 kg mol n水 1810 kg mol
n乙 46103 kg mol1
* n V H2O m (H2O) V (H2O) * n V CH 3CH 2OH m (CH3CH2OH) V (CH3CH2OH)
?
n
* H2O m
V (H2O) n
* CH 3CH 2OH m
V (CH3CH2OH) V ?
2、偏摩尔体积(定义)
V VB n B T , p ,nC
在恒温恒压下：
dX X BdnB
B
使用偏摩尔量时应注意：
1.偏摩尔量的含义是：在等温、等压、保持B物质 以外的所有组分的物质的量不变的条件下，改变 dnB所引起广度性质X的变化值，或在等温、等压条
4-1 偏摩尔量
均存在同样的结果: 对所有广度量 X 均存在同样的结果
X ¹
å
* n BX B
B
原因： 原因： 水分子之间、 ① 水分子之间、乙醇分子之间和水分子与乙醇分子之间的 分子间相互作用不同； 分子间相互作用不同； 水分子与乙醇分子体积及形状不同。 ② 水分子与乙醇分子体积及形状不同。 2. 偏摩尔量 定义： ① 定义： 系统广度量 X 为温度 T、压力 p 及系统各组分物质的量 nB、 、 nC、nD、…等的函数： 等的函数： 等的函数
理想实际多组分单相系统混合物气态混合物液态混合物固态混合物溶液固态溶液液态溶液非电解质溶液电解质溶液第七章第六章多组分多相系统40组成表示法kgmol质量摩尔浓度溶液1kg溶剂a所含溶质b的物质的量dmmol体积摩尔浓度溶液1m的溶液中所含溶质b的物质的量对于二元系ab几种不同组成表示之间可用以下式子相互换算
非电解质溶液 √ 电解质溶液( (第七章) )
研究方法： 研究方法：理想 → 实际
§4.0 组成表示法
摩尔分数——混合物，溶液 混合物， ⒈ 摩尔分数 混合物
nB xB = ∑ nB
B
nB yB = ∑ nB
B
∑x
B
B
=1
⒉ 质量分数 质量分数——混合物，溶液 混合物， 混合物
mB wB = ∑ mB
X = ∑nB XB
B B
dX = ∑nBdXB + ∑XBdnB
B
dX = ∑ X B dnB
B
——微分形式 微分形式
B
∑n dX
B B B B
=0 =0
Gibbs-Duhem
对上式除以系统总量， 对上式除以系统总量，则
∑x dX
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dT
X p
T ,nj
dp
K i 1
X
i
dni
X i def
X ni
T , p,nji
Vi
V ni
T , p,nji
Ui
U ni
T , p,nji
Hi
H ni
T , p,nji
Si
S ni
T , p,nji
Ai
A ni
T , p,nji
Gi
G ni
T , p,nji
nB A mA
量纲为一 mol kg1
组成表示法：
(5)物质B的浓度（物质的量浓度）
cB
B
def
nB V
mol m3
换算关系（二元系A—B)：
xB
M A wB MBwA MAwB
VA* B VB* A VA*B
M AbB
M AcB
M AbB 1 M AcB MBcB
3.2 偏摩尔量
Xi 是在系统恒定T，p 和其它物质的量时，改变 1mol i 物质引起的系统广延性质X的变化.
X i def
X ni
T , p,nji
只有广延量才有偏摩尔量，强度量是不存在偏 摩尔量的。
X ni
T , p,nji
U ni
S ,V ,n ji
H ni
S , p,nji
Xi 是状态函数，强度性质
表 3–1 101325Pa，20℃
xB
Vmid
Vm
cm3 mol1 cm3 mol1
与 C2H5OH(B) H2O(A) 混合时的体积变化
Vm
nB / mol
V id / cm3 V / cm3
cm3 mol1 (nA 10mol) (nA 10mol) (nA 10mol)
0.0416 19.76 19.54 –0.22 0.4345 206.23 203.85
1.偏摩尔量的定义与物理意义
设广延性质 X， 状态函数的基本假定
X X (T , p, n1, n2 , , nK )
dX
X T
p,nj
dT
X p
dp T ,nj
K i 1
X ni
dni
T , p,nji
偏摩尔量
X i def
X ni
T , p,nji
dX
X T
p,nj
0.1435 23.87 23.11 –0.76 1.6759 278.69 269.81
0.2068 26.42 25.47 –0.95 2.6070 333.04 321.06
0.2811 29.41 28.34 –1.07 3.9105 409.12 394.27
0.3697 32.98 31.86 –1.12 5.8657 523.24 505.41
Xi 是在系统恒定T，p 和其它物质的量时，改变1mol i 物质引起的系统广延性质X的变化.
2.集合公式
T , p, xi
X i X i (T , p, x1 , x2 , , xK 1 )
2.集合公式
dX
X T
p,nj
dT
X p
T ,nj
dp
K i 1
X
idni
K i 1
第3章 多组分系统的热力学， 逸度和活度
3.1 引 言
气态混合物（如空气）
混合物
多组分 单相系统
溶液 （稀溶液）
液态混合物（如煤油、酒）
固态混合物（如金铜合金）
气态溶液（如萘溶解于高 压二氧化碳中）
液态溶液（如氮溶解于水 中、糖水、盐水）
固态溶液（如单体溶解于 聚合物中）
组成表示法：
(1)物质B的摩尔分数
X
i dni
X
X
dX
0
n1 0
X 1dn1
1.偏摩尔量的定义与物理意义 有关状态函数的基本假定:
对于一个均相系统，如果不考虑除压力以外的 其它广义力，为了确定平衡态，除了系统中每一种 物质的数量外，还需确定两个独立的状态函数。
设有一个均相系统是由组分1，2，3，…,K所组成 的含有K个组分的多组分系统，系统的任一广延性 质用X表示。
X X (T , p, n1, n2 , , nK )
0.0891 21.67 21.18 –0.49 0.9776 237.93 232.48
0.1435 23.87 23.11 –0.76 1.6759 278.69 269.81
0.2068 26.42 25.47 –0.95 2.6070 333.04 321.06
0.2811 29.41 28.34 –1.07 3.9105 409.12 394.27
X i X i (T , p, n1 , n2 , , nK )
X i X i (T , p, x1 , x2 , , xK 1 )
对纯组分系统 Xi 即 Xi*
偏摩尔量与摩尔量的区别
Vmid xAVA* xBVB*
表 3–1 101325Pa，20℃ C2H5OH(B) 与 H2O(A) 混合时的体积变化
0.3697 32.98 31.86 –1.12 5.8657 523.24 505.41
0.4771 37.31 36.19 –1.12 9.1247 713.47 692.07
0.6100 42.66 41.65 –1.01
0.7787 49.46 48.73 –0.73
偏摩尔量与摩尔量的区别 Vmid xAVA* xBVB*
量纲为一
xB
(
yB
) def
nB n
，n
B nB nB1 nB2 nBK
B xB 1
(2)物质B的质量分数
量纲为一
wdef B
mB B mB
B wB 1
组成表示法：
(3)物质B的体积分数
B def
xBVB* B xBVB*
BB 1
(4)物质B的质量摩尔浓度
def
bB mB
xB
Vmid
Vm
Vm
nB / mol
V id / cm3 V / cm3
cm3 mol1 cm3 mol1 cm3 mol1 (nA 10mol) (nA 10mol) (nA 10mol)
0.0416 19.76 19.54 –0.22 0.4345 206.23 203.85
0.0891 21.67 21.18 –0.49 0.9776 237.93 232.48
0.4771 37.31 36.19 –1.12 9.1247 713.47 692.07
0.6100 42.66 41.65 –1.01
0.7787 49.46 48.73 –0.73
偏摩尔量与摩尔量的区别 Vmid xAVA* xBVB*
偏摩尔量与摩尔Βιβλιοθήκη 的区别Vmid xAVA* xBVB*