概述 岩石的破坏形式及强试验
岩石的强度理论及破坏判据[详细]
![岩石的强度理论及破坏判据[详细]](https://img.taocdn.com/s3/m/b87c145d5ef7ba0d4b733ba7.png)
分析,库仑准则的有效取值范围由图 6-8给出,并可
用方程表示为:
σ3 σ1=σ3
1
f
2
1
f
3
f
2
1
f
2c
P β
3 1
1
1 2
c
1
1 2
c
0
σc / 2
σc
σ1
-σt
A
S
图7-8 σ1-σ3坐标系中的库仑准则的完整强度曲线
在此库仑准则条件下,岩石可能发生以下四种方式的破坏。
(1)当 0 11 11 22时cc,33岩石t属t单轴拉伸破裂; (2)当 1122cc11 c时c,t岩t石3 属3 0双0轴 拉伸破裂;
四、 格里菲斯强度理论
格里菲斯(Griffith ,1920年)认为:脆性材料断 裂的起因是分布在材料中的微小裂纹尖端有拉应力 集中(这种裂纹称之为Griffith裂纹)。
格里菲斯原理认为:当作用力的势能始终保持不 变时,裂纹扩展准则可写为:
(Wd Wc ) 0 C
式中:C为裂纹长度参数;Wd为裂纹表面的表面能; We为储存在裂纹周围的弹性应变能。
1
τ3
2
2α
式中:为t 岩石的单轴抗拉强度σ;0 σ3 t
n 为待定系数。
σ σ
σ
c
利用图 7-10中的关系,有:
σ 3
1 2
(1 3)
1 2
(1
3)
ctg 2
sin 2
1.双向压7缩应4力2圆,2.双向拉压应力圆,
3..双向拉伸应力圆 图7-10 二次抛物型强度包络线
其中:
n( t )
d ctg2
n
d
东北大学岩石力学讲义第二章 岩石破坏机制及强度理论
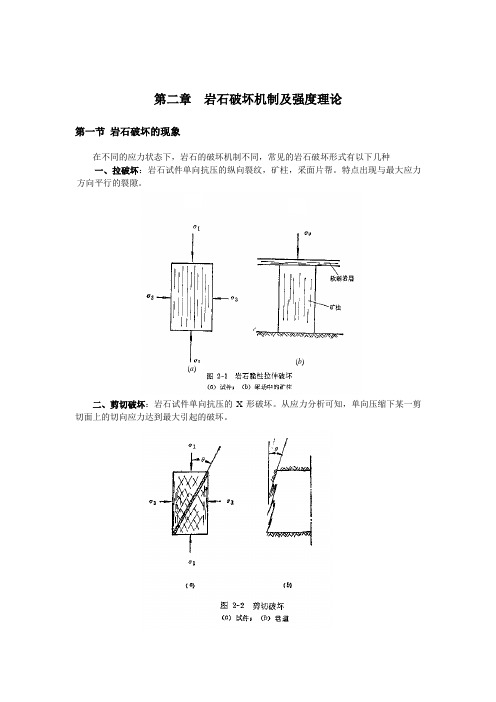
第二章 岩石破坏机制及强度理论第一节 岩石破坏的现象在不同的应力状态下,岩石的破坏机制不同,常见的岩石破坏形式有以下几种一、拉破坏:岩石试件单向抗压的纵向裂纹,矿柱,采面片帮。
特点出现与最大应力方向平行的裂隙。
二、剪切破坏:岩石试件单向抗压的X 形破坏。
从应力分析可知,单向压缩下某一剪切面上的切向应力达到最大引起的破坏。
(a ) (b )三、重剪破坏:即沿原有的结构面的滑动、重剪破坏主要的机制:岩体受剪切作用或者受拉应力的作用、三向受压情况下多数为剪切应力的作用,侧向压力较小时可能是拉神破坏,实际工程中可能是不同机制的组合,但侧向应力较大时,可以认为剪切应力是岩石重剪破坏的主要破坏机制。
从岩石破坏的现象看,从小到几厘米的岩块到大的工程岩体,破坏形式雷同,并可归纳为两种,拉断与剪坏,因此有一定的规律可寻。
对岩石破坏的研究:在单向条件下可以从实验得到破坏的经验关系。
但是三向受力条件下,不同应力的组合有无穷多种,因此无法仅仅依靠实验得到破坏的经验关系,因此在一般应力状态,对岩石破坏的研究需要结合理论分析和试验研究两个方面。
现代关于岩石破坏的理论分析一般归结为、寻求破坏时的主应力之间的关系123(,)f σσσ=研究的方法有:理论分析;2、试验研究;3、理论研究结合试验研究。
第二节 岩石拉伸破坏的强度条件一、最大线应变理论该理论的主要观点是,岩石中某个面上的拉应变达到临界值时破坏,而与所处的应力状态无关。
强度条件为c εε≤ (2-1) c ε—拉应变的极限值,ε—拉应变。
若岩石在破坏之前可看作是弹性体,在受压条件下σ1>σ2>σ3下, 3ε是最小主应力。
按弹性力学有33E Eσμεσσ=-12(+),即33E εσμσσ=-12(+)。
若3ε<0则产生拉应变。
由于E >0,因此产生拉应变的条件是3σμσσ-12(+)<0,3μσσσ12(+)>若3ε=0ε<0则产生拉破坏,此时抗拉强度为0tEσε=⇒0t E σε=。
岩石破坏准则

2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下,岩石表现为脆性破坏,而在高温、高围压、低应变率作用下,岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说,其破坏形式可以分为:1)脆性破坏;3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
图2-1岩石破坏形态示意图从图2-1中可以看出岩石破裂种类繁多、岩石破坏过程中的应力、变形、裂纹产生和扩展极为复杂,很难用一种模型进行描述,很多学者针对不同岩石破坏特征提出多种不同岩石的强度破坏准则。
本节主要对已有的岩石强度破坏准则进行总结,找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论,该理论是1857年提出的。
它假定挡土墙背垂直、光滑,其后土体表面水平并无限延伸,这时土体内的任意水平面和墙的背面均为主平面(在这两个平面上的剪应力为零),作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态,应用极限平衡条件,推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时,作用在微分土体上的竖向应力sz 保持不变,而水平向应力sx 逐渐减小,直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ,而最小主应力s3即为主动土压力强度pa 。
根据,当主体中某点处于极限平衡状态时,大主应力1σ和小主应力3σ之间应满足以下关系式:粘性土:213...2tan tan 454522c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪⎝⎭⎝⎭(1)无粘性土231.tan 452ϕσσ⎛⎫︒=- ⎪⎝⎭(2)该理论认为材料破坏取决于绝对值最大的正应力。
因此,作用于岩石的三个正应力中,只要有一个主应力达到岩石的单轴抗压强度或岩石的单轴抗拉强度,岩石便被破坏。
岩石破坏准则

2.1岩石破坏强度准则岩石的破坏主要与外荷载的作用方式、温度及湿度有关。
一般在低温、低围压及高应变率的条件下,岩石表现为脆性破坏,而在高温、高围压、低应变率作用下,岩石则表现为塑性或者塑性流动。
对于较完整的岩石来说,其破坏形式可以分为:1)脆性破坏;3)延性破坏。
图2-1给出了不同应力状态下岩石破裂前应变值、破坏形态示意图和典型的应力-应变曲线示意图。
图2-1岩石破坏形态示意图从图2-1中可以看出岩石破裂种类繁多、岩石破坏过程中的应力、变形、裂纹产生和扩展极为复杂,很难用一种模型进行描述,很多学者针对不同岩石破坏特征提出多种不同岩石的强度破坏准则。
本节主要对已有的岩石强度破坏准则进行总结,找出它们各自的优缺点。
2.1.1最大正应力强度理论最大正应力强度理论也称朗肯理论,该理论是1857年提出的。
它假定挡土墙背垂直、光滑,其后土体表面水平并无限延伸,这时土体内的任意水平面和墙的背面均为主平面(在这两个平面上的剪应力为零),作用在该平面上的法向应力即为主应力。
朗肯根据墙后主体处于极限平衡状态,应用极限平衡条件,推导出了主动土压力和被动土压力计算公式。
考察挡土墙后主体表面下深度z 处的微小单元体的应力状态变化过程。
当挡土墙在土压力的作用下向远离土体的方向位移时,作用在微分土体上的竖向应力sz 保持不变,而水平向应力sx 逐渐减小,直至达到土体处于极限平衡状态。
土体处于极限平衡状态时的最大主应力为s1=gz ,而最小主应力s3即为主动土压力强度pa 。
根据,当主体中某点处于极限平衡状态时,大主应力1σ和小主应力3σ之间应满足以下关系式:粘性土:213...2tan tan 454522c ϕϕσσ⎛⎫⎛⎫︒︒=-++ ⎪ ⎪⎝⎭⎝⎭(1)无粘性土231.tan 452ϕσσ⎛⎫︒=- ⎪⎝⎭(2)该理论认为材料破坏取决于绝对值最大的正应力。
因此,作用于岩石的三个正应力中,只要有一个主应力达到岩石的单轴抗压强度或岩石的单轴抗拉强度,岩石便被破坏。
岩石的破坏准则[详细]
![岩石的破坏准则[详细]](https://img.taocdn.com/s3/m/27d063e3f01dc281e53af0b9.png)
五、岩石的破坏准则对岩石试样的室内及现场试验,可获得岩石试样的强度指标,但对复杂应力状态下的天然岩体,又是如何判断其破坏呢?因此,就必须建立判断岩石破坏的准则(或称强度理论).岩石的应力、应变增长到一定程度,岩石将发生破坏.用来表征岩石破坏条件的函数称为岩石的破坏准则.岩石在外力作用下常常处于复杂的应力状态,许多试验指出,岩石的强度及其在荷载作用下的性状与岩石的应力状态有着很大的关系.在单向应力状态下表现出脆性的岩石,在三向应力状态下具有延性性质,同时它的强度极限也大大提高了.许多部门和学者从不同角度提出不同的破坏准则,目前岩石破坏准则主要有:最大正应力理论最大正应变理论最大剪应力理论(H.Tresca)八面体应力理论莫尔理论及库伦准则格里菲思理论(Griffith)伦特堡理论(Lundborg)经验破坏准则1、最大正应力理论这是较早的一种理论,该理论认为岩石的破坏只取决于绝对值最大的正应力.即岩石内的三个主应力中只要有一个达到单轴抗压或抗拉强度时,材料就破坏.适用条件: 单向应力状态.对复杂应力状态不适用.写成解析式:破坏2、最大正应变理论该理论认为岩石的破坏取决于最大正应变,即岩石内任一方向的正应变达到单向压缩或拉伸时的破坏数值时,岩石就发生破坏.则破坏准则为式中ε——岩石内发生的最大应变值;m axε——单向拉、压时极限应变值;u这一破坏准则的解析式为(由广义虎克定律)R —R t或R c推出:实验指出,该理论与脆性材料实验值大致符合,对塑性材料不适用.3、最大剪应力理论(H.Tresca)该理论认为岩石材料的破坏取决于最大剪应力,即当最大剪应力达到单向压缩或拉伸时的危险值时,材料达到破坏极限状态.其破坏准则为:在复杂应力状态下,最大剪应力231 max σστ-=单位拉伸或压缩时,最大剪应力的危险值则有 R ≥-31σσ或写成 {}{}{}0)][)][)][221222232231=------R R R σσσσσσ这个理论适用于塑性岩石,不适用于脆性岩石. 该理论未考虑中间主应力的影响.4、八面体剪应力理论(Von.米ises)该理论认为岩石达到危险状态取决于八面体剪应力.其破坏准则为已知单元体1σ,2σ,3σ ,作一等倾面(其法线夹角相同).为研究等倾面上的应力,取一由等倾面与三个主应力面围成的四面体来研究.N 与x 、y 、z 的夹角分别为γβα、、,且 γβα==. 设:l =αcos ,m =βcos ,n =γcos设等倾面ABC 面积为S,则三个主应力面(1σ,2σ,3σ面)的面积分别为根据力的平衡条件∑=0X , ∑=0Y , ∑=0Z推出:⎪⎩⎪⎨⎧⋅⋅=⋅=⋅⋅=⋅=⋅⋅=⋅=∑∑∑γσβσασcos 0cos 0cos 0321S S p Z S S p Y S S p X z y x , 而 等倾面S 上合力:222z y x p p p p ++=所以另,等倾面S 上的法向应力为各分力p x 、p y 、p z 在N 上的投影之和,即S oct ττ≥,推出适用条件:塑性,5、莫尔理论及莫尔库伦准则该理论是目前应用最多的一种强度理论.该理论假设,岩石内某一点的破坏主要取决于它的大主应力和小主应力,即σ1和σ3,而与中间主应力无关.也就是说,当岩石中某一平面上的剪应力超过该面上的极限剪应力值时,岩石破坏.而这一极限剪应力值,又是作用在该面上法向压应力的函数,即)(στf = .这样,我们就可以根据不同的σ1、σ3绘制莫尔应力图. 每个莫尔圆都表示达到破坏极限时应力状态.一系列莫尔圆的包线即为强度曲线一方面与材料内的剪应力有关,同时也与正应力有关关于包络线:抛物线:软弱岩石双曲线或摆线:坚硬岩石直线:当σ<10米Pa 时为简化计算,岩石力学中大多采用直线形式:c ——凝聚力(米Pa) ϕ——内摩擦角.该方程称为库伦定律,所以上述方法合称为:莫尔库伦准则. 当岩石中任一平面上f ττ≥ 时,即发生破坏.即: ϕσττtg c f ⋅+=≥下面介绍用主应力来表示莫尔库仑准则. 任一平面上的应力状态可按下式计算①②α(σ1)力圆,可建力之间关系1)c和ϕ值与σ1、σ3和α角关系在σ1~σ3的应力圆上,找出2α的应力点T(T米为半径为231σσ-) 则,与直径T米垂直且与圆相切的直线即为ϕστtgc⋅+=根据几何关系,902)2180(90-=--=ααϕ,得出代入ϕστtg c ⋅+=中,得到另由公式推导:将σ1、σ3表示的 σ 和 τ 代入ϕστtg c ⋅+=中,导出对α求导,01=ασd d 推出:245ϕα+= 破坏面与最大主应力面的夹角而与最大主应力方向的夹角2).用主应力σ1、σ3表达的强度准则 将 σ 和 τ 的表达式代入 ϕστtg c ⋅+=中,ϕασσσσασσtg c ⎥⎦⎤⎢⎣⎡-+++=-2cos 222sin 2313131利用关系:ααϕ2sin )902cos(cos =-= ααϕ2cos )902sin(sin -=-= 化简得:当σ3=0时(单轴压缩):ϕϕσsin 1cos 21-==c R c ,令ϕϕϕsin 1sin 1-+=N ,则,σ1当σ1=0时(单轴抗拉该值为 )(στf =但与实测的R t 线段进行修正.岩石破坏的判断条件:ϕ>, 破坏sin极限ϕ<,稳定sin6、格里菲思(Griffith)理论以上各理论都是把材料看作为连续的均匀介质,格里菲思则认为:当岩石中存在许多细微裂隙,在力的作用下,在缝端产生应力集中,岩石的破坏往往从缝端开始,裂缝扩展,最后导致破坏.方向成β角.且形状接近于椭圆,的局部抗拉强度,的边壁就开始破裂.1).任一裂隙的应力.假定:①椭圆可作为半元限弹性介质中的单个孔洞处理, ②二维问题处理,取0=z σ椭圆参数方程:αcos a x =,αsin b y = 椭圆的轴比为:ab m =椭圆裂隙周壁上偏心角的α的任意点的切向应力 可用弹性力学中英格里斯(Inglis)公式表示:由于裂缝很窄,轴比很小,形状扁平,所以最大应力显然发生在靠近椭圆裂隙的端部,即α很小的部位,当0→α时,αα→sin ,1cos →α又由于米,α很小,略去高次项,则有米为定值,当1σ,2σ,3σ确定时,y σ、xy τ也为定值,则b σ仅随α而变.这是任一条裂隙沿其周边的切向应力.显然在椭圆周边上,随α不同b σ有不同的值,对α求导.2mτxy则,2).岩块中的最大切向应力所在的裂隙上面导出了 某一条裂隙上的最大切向应力,但在多条裂隙中,哪一条裂隙的b σ 最大?y σ,xy τ与1σ,3σ的关系为:βσσσσσ2cos 223131--+=y , βσστ2sin 231--=xy代入 m ax ,b σ中,显然m ax ,b σ与β有关,对其求导,便可求得b σ为最大的那条裂隙,即确定出β角. 即取 0m ax ,=⋅βσd d m b则①02sin =β,有β=0或 90代入m ax ,b σ中,β=0时, mb 3max ,2σσ= 或 0 β= 90时,mb 1max ,2σσ=或0. 共四个可能极值,与σ1平行或垂直的裂隙.②将)(22cos 3131σσσσβ+-=代入 m ax ,b σ中,共有两个极值,即与σ1斜交裂隙中有两个方向裂隙的切向应力达极值.因为β=0或 90时,12cos =β或-1.因此,与σ1斜交时,必须β≠0或 90, 即 12cos <β 时 才是与σ1斜交,则要求或 0331>+σσ此时,裂隙的最大拉应力为(*)如果0331<+σσ, 则1)(23131>+-σσσσ,则3σ必为负值(拉应力)此时由12cos ≥β推出12cos =β,即β为0或90°,表明裂隙与σ1平行或正交.因为03<σ,考查β=0, 90的极值,则3max ,2σσ=b m (**) 为最大拉应力.式(*)(**)即为岩石中的m ax ,b m σ达到某一临界值时就会产生破坏. 为了 确定米值,做单轴抗拉试验,使σ3垂直裂隙面(椭圆长轴),则这时的t R -=3σ 推出 t b R m 2max ,-=σ 这说明裂隙边壁最大应力m ax ,b m σ与米乘积必须满足的关系.此时,格菲思强度理论的破坏准则为:I. 由(**)式,,t b R m 2max ,-=σ, 则 322σ=-t RII. 由(*)式,代入 t b R m 2max ,-=σ, 则有:等于0,处于极限状态; 大于0, 破坏; 小于0, 稳定.上面的准则是用σ1、σ3表示的,也可用y σ,xy τ表示 将t b R m 2max ,-=σ 代入 )(122max ,xy y y b mτσσσ+±=中, 222xyy y t R τσσ+±=- 推出:t y xy y R 222+=+±στσ,22224)2(t y t y xy y R R +=+=+σστσ 在0<σ时的包线更接近实际.7、修正的格里菲思理论格里菲思理论是以张开裂隙为前提的,如果压应力占优势时裂隙会发生闭合,压力会从裂隙一边壁传递到另一边,从而缝面间将产生摩擦,这种情况下,裂隙的发展就与张开裂隙的情况不同.麦克林托克(米eclintock)考虑了这一影响,对格里菲思理论进行了修正.麦克林托克认为,在压缩应力场中,当裂缝在压应力作用下闭合时,闭合后的裂缝在全长上均匀接触,并能传递正应力和剪应力.由于均匀闭合,正应力在裂纹端部不产生应力集中,只有剪应力才能引起缝端的应力集中.这样,可假定裂纹面在二向应力条件下,裂纹面呈纯剪破坏.其强度曲线如图.由图可知 OC =c τBD=)(2131σσ-(半径)OD=)(2131σσ+(圆心)EB=τ, OE=σ,ED=OD-OE=)(2131σσ+-σAB=EB ϕcos ⋅=ϕτcos ⋅ϕsin ⋅=ED DA =ϕσϕσσsin sin )(2131⋅-+由 AB=BD-AD,可推出式中,摩擦系数ϕtg f =另外,推出tyt xy R R στ+=12取y σ为c σ,裂隙面上的压应力,则有②当c σ很小时,取c σ=0时(勃雷斯Brace)=t R 4当时c σ<0时(拉应力),上两式不适用.低应力时,格里菲思与修正的格里菲思理论较为接近,高应力时差别大(当σ3>0时).8、伦特堡(Lundborg)理论定限度,于晶体破坏,大抗剪强度.的破坏状态:σ,τ——研究点的正应力和剪应力(米Pa)τ——当没有正应力时(σ=0)岩石的抗切强度(米Pa)i τ——岩石晶体的极限抗切强度(米Pa)A ——系数,与岩石种类有关.当岩石内的剪应力τ和正应力σ达到上述关系时,岩石就发生破坏.式中的τ实际上是代表最大的剪应力,因而是强度.上式中的0τ,i τ,A 由试验确定,见P55表3-5.9、经验破坏准则现行的破坏理论并不能全面的解释岩石的破坏性态,只能对某一方面的岩石性态做出合理的解释,但对其它方面就解释不通.因此,许多研究者在探求经验准则,目前应用较多的经验破坏准则为霍克(Hoke)和布朗(Brown)经验破坏准则.①Hoke和Brown发现,大多数岩石材料(完整岩块)的三轴压缩试验破坏时的主应力之间可用下列方程式描述:R c—完整岩石单轴抗压强度(米Pa); 米—与岩石类型有关的系数米值是根据岩石的完整程度,结晶及胶结情况,通过大量试验结果及经验而确定的.岩石完整、结晶或胶结好,米值就越大,最大的为25.②对于岩体,Hoke和Brown建议:米和S——常数,取决于岩石的性质以及在承受破坏应力σ1和σ3以前岩石扰动或损伤的程度.完整岩块S=1,岩石极差时S=0.当取σ3=0时,可得到岩体的单轴抗压强度:由于s =0~1,则c cm R R ≤ 如果令σ1=0,则得到岩体的单轴抗拉强度.从R厘米和R t 米中可看出,当S=1时,R 厘米=R c 为完整岩块,当S=0时,R t 米=R 厘米=0为完全破损的岩石.因此,处于完整岩石和完全破损岩石之间的岩体,其S 值在1~0之间.。
岩石的抗拉强度试验(劈裂法)

实验三岩石的抗拉强度试验(劈裂法)基本原理劈裂法是把圆柱状岩石试件置于压力机的承压板上,并在试件与上下承压板间各放置一根压条,然后加压,使试件受力后沿直径方向裂开破坏,根据弹性理论求其抗拉强度。
放置压条的目的是为了把所加的压力变为沿直径方向分布的线性载荷,使试件中产生垂直于荷载作用线的张应力。
二、仪器设备(1) 材料试验机;(2) 游标卡尺;(3) 钢丝(φ =1.5mm ,φ =2.0mm )三、操作步骤1. 试样制备试样规格为φ 5cm× 5cm,每组不少于3 个。
试样尺寸允许变化范围不超过5%。
2. 试样描述3. 试样处理对需保持天然湿度的试件,试验前应将其放在密闭的容器内;对需饱水的试件,按饱和吸水率试验处理。
4. 试件安装将准备好的试件连同压条按线图所示放置在试验机上下承压板间,然后调整试验机的横梁或活塞使试件固定。
应注意,试件上下压条刚好处于包含试验机加荷板中心线的垂直面内,以避免荷载的偏心作用。
2P13 2 21.5 1039.26MPaπDh50.62 29.175. 施加载荷以 0.5Mpa/s 的加荷速率加压,至试件破坏为止。
记录整个试验过程中荷载的 最大值及试件彻底破坏时的载荷值,并描述试件破坏情况。
四、 成果整理按下式计算岩石的抗拉强度σ t :σ 2P t σt = πDh式中 P t ——破坏荷载, N ;D ——试件直径, mm 。
对各组试件进行平行测定,计算其平均值。
实验数据记录数据名称 实验编号 (t )试件直径( D/mm )试件厚度( h/mm )破坏载荷( P t / kN )1 50.62 29.17 21.5 2 51.07 29.86 14.5 351.0829.3618实验数据整理实验四 测定岩石的抗剪断强度试验、基本原理板剪切试验等。
由于变角板剪切试验自身的缺陷较大, 故目前国内普遍采用直剪试验和三轴剪切试验。
变角板法是利用压力机施加垂直荷载, 通过特质的夹具是试件沿某一剪切面剪断, 然后通过静力平衡条件解析剪切面上的法向压应力和剪应力, 断强度τ的关系曲线,求得岩石的内聚力 C 和内摩擦角ψ,试验装置如图所示。
岩石的强度理论及破坏判据[详细]
![岩石的强度理论及破坏判据[详细]](https://img.taocdn.com/s3/m/b87c145d5ef7ba0d4b733ba7.png)
依据适合的强度理论,判断岩体的破坏及其破坏形式。 岩体本构关系:指岩体在外力作用下应力或应力速率与其应变 或应变速率的关系。
岩石或岩体的变形性质:弹塑性或粘弹塑性。 本构关系:弹塑性或粘弹塑性本构关系。 本构关系分类:
①弹性本构关系:线性弹性、非线性弹性本构关系。 ②弹塑性本构关系:各向同性、各向异性本构关系。 ③流变本构关系:岩石产生流变时的本构关系。流变
Griffith强度准则只适用于研究脆性岩石的破坏。
Mohr-coulomb强度准则的适用性一般的岩石材料。
0
σ1=σ3
P β
σc / 2
σc
σ1
-σt
A
S
岩石强度理论与破坏判据
三、 莫尔强度理论
莫尔(Mohr,1900年)把库仑准则推广到考虑三向应力状态。最主
要的贡献是认识到材料性质本身乃是应力的函数。他总结指出“到极 限状态时,滑动平面上的剪应力达到一个取决于正 应力与材料性质的最大值”,并可用下列函数关系表示:
σ1 σ
莫尔包络线的具体表达式,可根据试验结果用拟合法求得。
包络线形式有:斜直线型、二次抛物线型、双曲线型等。
斜直线型与库仑准则基本一致,库仑准则是莫尔准则的一个特例。
这里主要介绍二次抛物线和双曲线型的判据表达式。
1、二次抛物线型
τ
岩性较坚硬至较弱的岩石。
2 n t
2
τ=
n(σ
+σt
)
M(σ ,τ)
四、 格里菲斯强度理论
格里菲斯(Griffith ,1920年)认为:脆性材料断 裂的起因是分布在材料中的微小裂纹尖端有拉应力 集中(这种裂纹称之为Griffith裂纹)。
格里菲斯原理认为:当作用力的势能始终保持不 变时,裂纹扩展准则可写为:
第1讲:概述、岩石的破坏形式及强度试验

3.3.1 定义与试验
一、定义:指岩石试件在无侧限的条件下,受轴 向压力作用破坏时单位面积上承受的荷载。
Rc P / A
单位: MPa
45
2
式中:P——无侧限的条件下的轴向破坏荷载 A——试件横断面面积
二、试件标准: 圆柱形试件:直径D=5cm或7cm ,高H=(2-2.5)D 长方体试件:边长L= 5cm或7cm, 高H=(2-2.5)L
(4)长期强度:岩石在长期荷载作用下 的强度,即稳定蠕变与不稳定蠕变的分界 点。 (5)抗压强度:抵抗压缩破坏的能力。 (6)抗剪强度:抵抗剪切破坏的能力。 (7)抗拉强度:抵1、脆性破坏:岩石在变形较小(ε<3%)时,几乎就由弹性 变形直接发展为急剧、迅速的破坏,坚硬岩石大都表现为脆 性破坏。
由于试件不易加工, 除研究直接的拉伸的 夹具外,研究了大量 的间接试验方法。
岩石的抗拉强度很小,一般只有抗压强度的 1/10~1/50。
3.4.2 直接拉伸试验
Rt PT / A
(MPa)
关键技术 ①试件和夹具之间的连接 ②加力P与试件同心
3.4.3 间接方法:劈裂法和点荷载试验法
(一)劈裂法(巴西法): 对称径向压裂法由巴西人提出
矿物颗粒的10倍,( D=50mm的依据) 高径比:研究表明; h/d≥(2-3)较合理。
(3)加载速度 加载速度越大,表现强
度越高(如图示) 规范:加载速度为0.5—
0.8MPa/s。
3.4 岩石的抗拉强度
3. 4.1 定义 3.4.2 直接抗拉试验 3.3.3 间接抗拉试验
3.4.1 定义
岩石试件在受到轴向拉应力后其试件 发生破坏时的单位面积上所受的拉力。
同σ下的抗剪强度τf,绘成关系曲线σ -τf,如图 示:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3、弱面剪切破坏:岩石中仍有可能存在弱面,弱面大大地削 弱了岩石的整体性,在荷载作用下,岩石沿弱面产生剪切破 坏。
4.3 岩石的单轴抗压强度
4. 3.1 定义及试验 4.3.2 岩石单向压缩试件的破坏形态 4.3.3 影响单轴抗压强度的主要因素
岩石在单向压缩情况下的破坏
岩石在单向压缩情况下的破坏
岩石在单向压缩情况下的破坏
岩石在单向压缩情况下的破坏
4.3.3 影响单轴抗压强度的主要因素
两个因素:岩石本身和试验方法 (一)岩石本身的因素
1、矿物成分:不同矿物组成的岩石,具有不同的抗压强度 2、结晶程度和颗粒大小:结晶岩石>非结晶岩石;细粒结晶岩 石>粗粒结晶的。 4、胶结情况:如:硅质胶结>石灰质胶结>泥质胶结 4、生成条件:如(同一种岩石) :深部的岩石>地表的岩石 5、风化作用:如(同一种岩石) :未风化>中风化>强风化
岩石试件在受到轴向拉应力后其试件 发生破坏时的单位面积上所受的拉力。
由于试件不易加工, 除研究直接的拉伸的 夹具外,研究了大量 的间接试验方法。
岩石的抗拉强度很小,一般只有抗压强度的 1/10~1/50。
4.4.2 直接拉伸试验
Rt PT / A
(MPa)
关键技术 ①试件和夹具之间的连接 ②加力P与试件同心
4.3.1 定义与试验
一、定义:指岩石试件在无侧限的条件下,受轴 向压力作用破坏时单位面积上承受的荷载。
Rc P / A
单位: MPa
式中:P——无侧限的条件下的轴向破坏荷载 A——试件横断面面积
二、试件标准: 圆柱形试件:直径D=5cm或7cm ,高H=(2-2.5)D 长方体试件:边长L= 5cm或7cm, 高H=(2-2.5)L
Rt
1 15
15 i 1
0.96 Ii
建议:用D=5cm的钻孔岩芯为试件。
4.5 岩石的抗剪强度
4. 5.1 抗剪强度的意义 4.5.2 直接剪切试验 4.5.3 楔形剪试验 4.5.4 三轴压缩试验
4.5.1 岩石抗剪强度的意义
一、定义 指一定的应力条件下(主要指压应力),所能抵抗剪 切破坏的能力。它是岩石力学中重要指标之一,常
4.4.3 间接方法:劈裂法和点荷载试验法
(一)劈裂法(巴西法): 对称径向压裂法由巴西人提出
试件:实心圆柱直径D=50mm;长度l=25mm
Rt 2Pmax / Dl
要 ①荷载沿轴向均匀分布 求 ②破坏面必须通过试件的直径
试件:若为立方体试件则:
Rt 2Pmax / a2
试件与破坏图:
(二)点荷载试验法
▪渗透特性 ▪变形特性 ▪强度特性
广义上:岩石包括岩块和岩体
二、与岩石的强度有关的工程问题 (1)岩基稳定性问题 (2)边坡的稳定性问题 (3)地下洞室围岩的稳定性问题
均与岩石的强度有关
(1)完整岩块的强度 (2)岩体的强度=岩块强度+结构面的强度
三、岩石强度的基本概念
(1)岩石的强度:用于表示岩石抵抗破坏能 力大小的一个力学参数。它等于单位面积上岩 石能承受的最大荷载。 (2)峰值强度:岩石在临近破坏时具有的最 大承载能力。 (3)残余强度:岩石破坏后仍具有的承载能 力。
第四章 岩石的强度
4.1 工程中岩石的强度与稳定性问题 4.2 岩石的破坏形式 4.4 岩石单轴抗压强度 4.4 岩石的抗拉强度 4.5 岩石的抗剪强度 4.6 岩石的破坏准则 4.7 岩体强度分析
4.1 工程中岩石的强度与稳定性问题 一、岩石的工程特性
岩土结构物或地基 岩石
▪渗透问题 ▪变形问题 ▪用下 的强度,即稳定蠕变与不稳定蠕变的分界 点。 (5)抗压强度:抵抗压缩破坏的能力。 (6)抗剪强度:抵抗剪切破坏的能力。 (7)抗拉强度:抵抗拉伸破坏的能力。
4.2 岩石的破坏形式
1、脆性破坏:岩石在变形较小(ε<5%)时,几乎就由弹性 变形直接发展为急剧、迅速的破坏,坚硬岩石大都表现为脆 性破坏。
是上世纪发展起来的一种简便的现场试验方法。 试件:任何形状,尺寸大致5cm,不做任何加工。 试验:在直接带到现场的点荷载仪上,加载劈裂破 坏。
计算公式: I P / D2
式中:P——试件破坏时的极限值 D ——加载点试件的厚度
经验公式:
Rt 0.96 I
要求:(由于离散性大),每组15个,取均值,即
三、加荷速率:0.5-0.8MPa/s
4.3.2 单向压缩试件的破坏形态
(1)圆锥形破坏 原因:压板两端存
在摩擦力,箍作用 (又称端部效应), 在工程中也会出现。
消除试件端部约束的方法: 润滑试件端部(如垫云母
片;涂黄油在端部);加长 试件。
(2)柱状劈裂破坏
张拉破坏(岩石的抗 拉强度远小于抗压强 度),是岩石单向压 缩破坏的真实反映 (消除了端部效应)。
A——试样的剪切面面积
P T
A
A
剪切时记录剪切位移δh与垂直位移δv,可得到的 曲线如图。图中τmax为在正应力σ作用下岩石的抗 剪强度τf ,
6、密度:如(同一种岩石) :密度大的>密度小的
7、含水量:含水量越大强度越低;岩石越软越明显,对泥岩、 粘土等软弱岩体,干燥强度是饱和强度的2-4倍,见下表:
含水量的影响
(二)试验方法上的因素
(1)承压板端部的摩擦力及其刚度(加垫块的依据)
(2)试件的形状和尺寸 形状:圆形试件不易产生应力集中,好加工尺寸:大于
矿物颗粒的10倍,( D=50mm的依据) 高径比:研究表明; h/d≥(2-2.5)较合理。
(3)加载速度 加载速度越大,表现强
度越高(如图示) 规范:加载速度为0.5—
0.8MPa/s。
4.4 岩石的抗拉强度
4. 4.1 定义 4.4.2 直接抗拉试验 4.4.4 间接抗拉试验
4.4.1 定义
以内聚力c和内摩擦角φ这两个抗剪参数表示。
二、岩石剪切强 度的三种类型
三、工程中岩石破坏的某些类型
四、工程意义: 抗剪强度是岩石力学研究和岩土工程中的重要的
特性参数。岩土体的稳定性计算中必不可少。
4.5.2 直间剪切试验
在直接剪切仪进行。与土的直接剪切仪相类似, 如图示:
剪切面上的正应力和剪应 力按下列公式计算:
