高速公路超高缓和段的超高旋转与计算
公路工程高程计算公式
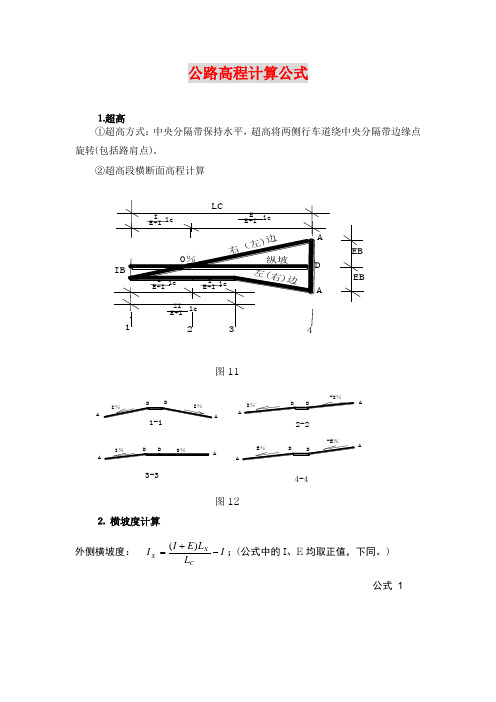
公路高程计算公式⒈超高①超高方式:中央分隔带保持水平,超高将两侧行车道绕中央分隔带边缘点旋转(包括路肩点)。
②超高段横断面高程计算图11AA AAAAAA2-23-34-4图12⒉横坡度计算外侧横坡度:ILLEIICXX-+=)(;(公式中的I、E均取正值,下同。
)公式1EBEB内侧横坡度: I L IE I L L I E IL I E I CC CX X +*+-*+--=22)((。
公式 2式中:2 I/(E+I)* L C —在L C 段内横坡等于I %的长度,m 。
X 在区间0~2 I/(E+I)*LC 时,横坡度为I ; 在区间2 I/(E+I)* L C ~L C 段内时,横坡度为I ~E 。
I —横坡度设计值, E —超高设计值, L C —缓和曲线长,m 。
⒊ 竖曲线计算公式:W=I 1-I 2; 当w >0时,为凸曲线;当w <0时,为凹曲线。
L=R*W ; E=T 2/2R ; H=l 2/2r ;T=TA=TB=L/2=R*W/2。
式中:H —切线上任一点至竖曲线上的垂直距离;M . l —曲线上相应于H 的P 点至切点A 或B 点的距离,M .R—二次抛物线的参数。
(原点处的曲率半径)通常称竖曲率半径,M.I1、I2—切线的斜率,即纵坡度,%.纵坡度(%),从左向右上坡取“+”,下坡取“-”值.当α很小时,tanα1≈α1=I1, tan α2≈α2=I2。
T—切线长(M),ZH路线平面图L—竖曲线的曲线长(M)。
双车道公路超高缓和段长度按式(7.5.4)计算:(7.5.4)式中 Lc --超高缓和段长度(m);B --旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);Δi --超高坡度与路拱坡度代数差(%):p --超高渐变率,即旋转轴线与行车道(设路缘带时为路缘带)外侧边缘线之间的相对坡度,其值如表7.5.4。
缓和曲线超高计算

公路缓和曲线知识与计算公式未知2010-04-04 17:34:42 本站一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的 0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , l h=s 则 l h=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,a s= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在 3°—— 29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路缓和曲线原理及缓和曲线计算公式

一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车4)与圆曲线配合得当,增加线形美观2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A2/ρ(A:与汽车有关的参数)ρ=C/sC=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R,l h=s 则 l h=A2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ρ,a s=Δa/t≤0.62)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s)3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
发布日期:2012-01-31 作者:李秋生浏览次数:1494)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
高速公路线路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式

高速公正路路(缓和曲线、竖曲线、圆曲线、匝道)坐标计算公式未知2021-12-27 21:40:34 本站高速公路的一些线路坐标、高程计算公式(缓和曲线、竖曲线、圆曲线、匝道)一、缓和曲线上的点坐标计算:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反x Z,y Z为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:x Z,y Z计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,那么:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反x Z,y Z为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度〔或缓曲上任意点到缓曲起点的长度〕l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算:①第一坡度:i1(上坡为“+〞,下坡为“-〞)②第二坡度:i2(上坡为“+〞,下坡为“-〞)③变坡点桩号:S Z④变坡点高程:H Z⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点〔过渡段终点〕的间隔:x求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-〞,右转为“+〞)⑦曲线终点处曲率:P1(左转为“-〞,右转为“+〞) 求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
(完整版)道路超高公式

内
缘
过
渡
段
外
缘
中
线
内
缘
B——行车道宽度(m);
bJ——路肩宽度(m);
bw——圆曲线的加宽值(m);
bx——x距离处的路基加宽值(m);
——超高横坡度;
——路拱横坡度;
——路肩横坡度;
x0——与路拱同坡度的单向超高点至超高缓和段起点的距离(m);
x——超高缓和段中任意一点至超高缓和段起点的距离(m);
绕内边线旋转超高值计算公式
超高位置
计算公式
备注
圆曲线
外缘
1.计算结果均为与设计高之高差
2.临界断面距超高缓和段起点:
3.Hale Waihona Puke 宽值 按加宽计算公式计算。中线
内缘
过
渡
段
外缘
中线
内缘
绕中线旋转超高值计算公式
超高
位置
计算公式
备注
圆曲线
外缘
1.计算结果均为与设计高之高差
2.临界断面距超高缓和段起点:
3.加宽值 按加宽计算公式计算。
超高缓和段长度计算公式

超高缓和段长度计算公式超高缓和段长度的计算可是道路工程中的一个重要知识点呢。
咱们先来说说啥是超高缓和段。
简单来讲,它就是从直线段的双向横坡渐变到圆曲线段单向横坡的这一段过渡路段。
为啥要有超高缓和段呢?就好比你骑自行车,突然要拐个急弯,如果路面还是平平的,那可容易失去平衡摔跟头。
有了超高缓和段,就能让车辆在拐弯时更平稳、更安全。
那超高缓和段长度咋算呢?这就得用到一个公式啦。
公式看起来有点复杂,不过别担心,咱们慢慢拆解。
假设超高缓和段长度用 Lc 表示,旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度用 b 表示,超高坡度与路拱坡度的代数差用Δi 表示,超高渐变率用P 表示。
那么超高缓和段长度的计算公式就是:Lc = b × Δi / P 。
举个例子吧,有一条公路,旋转轴至行车道外侧边缘的宽度是5 米,超高坡度与路拱坡度的代数差是 0.04,超高渐变率规定是 1/150 。
那按照公式算一下,超高缓和段长度 Lc 就是 5×0.04×150 = 30 米。
这计算过程说起来简单,实际操作中可得考虑好多因素。
我记得有一次去一个新修的公路施工现场,工程师们正在为超高缓和段长度的计算争论不休。
有人觉得按照标准公式算出来的长度不太够,因为这段路弯道特别急,车辆速度又快,需要更长的超高缓和段来保证安全。
另一些人则觉得如果太长了,会影响道路的整体布局和美观。
大家各抒己见,最后经过反复的实地勘察和计算,综合考虑了各种因素,才确定了最合适的超高缓和段长度。
在实际工程中,不能仅仅依赖公式,还得结合具体的地形、车速、交通流量等因素来灵活调整。
毕竟,道路的安全和顺畅才是最重要的。
总之,超高缓和段长度的计算公式是基础,但具体应用时要多思考、多观察,这样才能设计出既安全又实用的道路。
希望大家以后在遇到相关问题时,都能准确计算出超高缓和段的长度,为咱们的出行保驾护航!。
【高速公路】第四章-4-5曲线上的超高与加宽解析
<3240 <1940 <1710 <1550 <1240 <1130 <810 <720 <1710 <1550 <810 <720 <1210 <1130 <390 <360 <780 <720 <230 <210 <390 <360 <105 <95
3
~ 2160 ~ 1290 ~ 1220 ~ 1050 ~ 830 ~ 750 ~ 570 ~ 460 ~ 1220 ~ 1050 ~ 570 ~ 460 ~ 840 ~ 750 ~ 270 ~ 230 ~ 530 ~ 460 ~ 150 ~ 130 ~ 270 ~ 230 ~ 70 ~ 60
<1620 <970 <950 <760 <620 <520 <430 <300 <950 <760 <430 <300 <630 <520 <200 <150 <390 <300 <110 <80 <200 <150 <55 <40
5
~ 1300 ~ 780 ~ 770 ~ 550 ~ 500 ~ 360 ~ 340 ~ 190 ~ 770 ~ 550 ~ 340 ~ 190 ~ 500 ~ 360 ~ 150 ~ 90 ~ 300 ~ 190 ~ 80 ~ 50 ~ 150 ~ 90 40 ~ 25
4-5 弯道的超高与加宽
一、超高 1.定义
为抵消车辆在曲线路段 上行驶时所产生的离心 力,在该路段横断面上 设置的外侧高于内侧的 单向横坡,称之为超高。 当汽车行驶在设有超高 的弯道上时,汽车自重 分力将抵消一部分离心 力,从而提高行车的安 全性和舒适性。超高的 布置如图所示。
高速公路超高缓和段的超高旋转与计算

高速公路超高缓和段的超高旋转与计算摘要:本文介绍了缓和曲线的超高缓和段的超高方式的旋转与计算, 有些对在旋转过程中的表述与以前不太一样, 计算公式简捷、准确。
关键词: 缓和曲线超高旋转计算为使车辆在曲线段上安全行使, 依据设计超高横坡, 分析、理解超高在旋转过程中的动态情况, 准确计算超高值至关重要, 现在分别介绍超高缓和段的超高方式和计算。
1.超高方式1. 1 绕路面内侧边缘旋转( 简称边轴旋转)它是使旋转轴在路面内侧边缘保留在水平位置( 不考虑路线纵坡) 。
首先在超高缓和段起点之时, 迅速将外侧路肩横坡变为路拱横坡度。
然后逐渐抬高外侧路面与路肩, 使之达到与内侧路拱坡度一致的单向横坡。
继续旋转使整个断面达到超高横坡度为止。
( 见图一)1. 2 绕路中线旋转( 简称中轴旋转)它是使旋转轴在路面中线保留在水平位置( 不考虑路线纵坡) 。
首先在超高缓和段起点之时, 迅速将外侧路肩横坡度变为路拱横坡度。
然后逐渐抬高外侧路面与路肩, 使之达到与内侧路拱坡度一致的单向横坡。
继续旋转使整个断面达到超高横坡度为止。
( 见图二)2.超高值计算2.1 计算X 0它是与路拱同坡度的单向超高点至超高缓和段起点距离的计算, 无论超高方式如何它都是由路拱坡度变为与路拱坡度一致的单向坡度。
2.2 计算超高值( 见附表)在计算超高缓和段超高值时,分三种情况考虑:a. 当i c<i g时在旋转过程中, 由外侧路拱-i g( 相对内侧) 逐渐抬高至i g, 变化率为2 i g, 这时超高横坡未起作用, 无论边轴旋转、中轴旋转, 计算h cx公式统为b. 当i c>i g时这时超高旋转已进入超高横坡, 计算h cx公式为c. 当i c=i g时上述计算h cx公式都可采用.例:江西省昌万公路某里程的缓和曲线为边轴旋转,已知:L c=85 ,b=9,a=1.5,i g=2% ,i j=3%,i c=5%, 求x=x0处的单向横坡的外侧边缘超高值h cx。
高速公路边轴旋转超高方式横坡计算
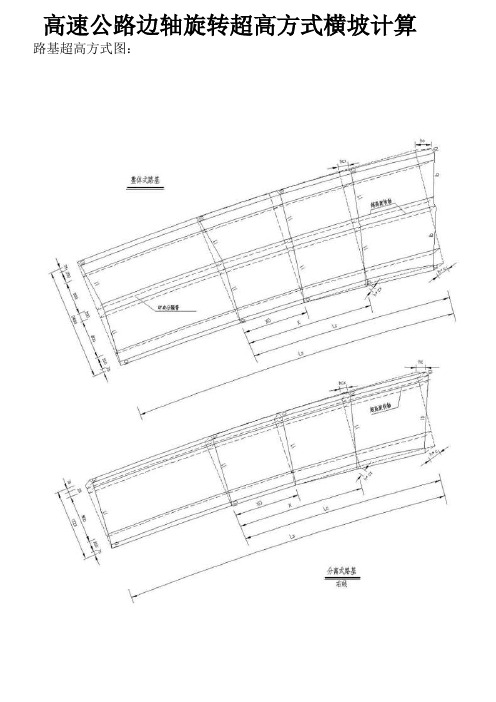
高速公路边轴旋转超高方式横坡计算路基超高方式图:说明∶1.路基超高采用边轴旋转,整体式路基旋转轴为中央分隔带边缘线;分离式路基为行车道前进方向左侧路基边缘内侧1.0米处。
2.行车道和硬路肩超高,土路肩不超高。
3.图中所示符号∶Ls--缓和曲线长,Lc--超高过渡段长;X0--与路拱同坡的单向超高点至超高过渡段起点的距离,I1--路拱横坡度;X--过渡段上任意点至超高过渡段起点的距离,I0--路肩横坡度;Ib--弯道超高横坡度,hc--路基外缘最大抬高值,h″c--路基内缘最大降低值;h″cx--x点路基内缘降低值,hcx--x点路基外缘抬高值.4.超高方式:圆曲线为全超高路段,超高过渡段长度(LC)从缓圆点(HY)往直缓点(ZH)或从圆缓点(YH)往缓直点(HZ)点计算。
先按超高渐变率p=1/330算出超高过渡段长度Lc,若Lc<Ls,则超高渐变率p=1/330。
若算出的Lc>Ls,则取Lc=Ls,超高过渡段长度等于缓和曲线长度。
5.图中尺寸均以厘米为单位,适用于设计时速V=80Km/h。
备注:正常路拱横坡(即直线段)为-2%;横坡计算按硬路肩比路缘带低为负。
一、整体式路基:图上为一左转直线到圆曲线的超高方式图。
半径为800m,缓和曲线长250m。
读图可得:R=800m,所以Ib弯道超高横坡度=4%;左转曲线,则黑线表示右幅,红线表示左幅;红点为直缓点;黑点为右幅超高起点;黄点为左幅超高起点;蓝点为缓圆点。
R=800,那么Lc=205<Ls=250.则:红点与黑点距离为:Ls-Lc=45m;黄点到蓝点距离为TX:(lb-|i左|)/(lb+|i右|)*Lc=(4-2)/(4+2)*205=68.333m; 黑点到黄点距离(与路拱同坡的单向超高点至超高过渡段起点):X0=Lc-68.333=136.667m 。
由此可得:1.直线段左右幅横坡都为-2%;2.圆曲线上分2种情况:曲线左转则:左幅横坡为-lb;右幅横坡为lb;曲线右转则:左幅横坡为lb;右幅横坡为-lb;3缓和曲线分为4种情况设桩号K:曲线左转:第一缓和曲线上则:左幅横坡= -2% -(K - (HY - TX)) / TX * (lb - 2%)右幅横坡= -2% +(K - (HY - Lc)) / lc * (lb + 2%)第二缓和曲线上则:左幅横坡= -lb + (K - YH) / TX * (lb - 2%)右幅横坡= lb - (K - YH) / lc * (lb + 2%)曲线右转:第一缓和曲线上则:左幅横坡= -2% +(K - (HY - Lc)) / Lc * (lb +2%)右幅横坡= -2% -(K - (HY - TX)) / TX * (lb -2%)第二缓和曲线上则:左幅横坡= lb - (K - YH) / Lc * (lb + 2%)右幅横坡=-lb + (K - YH) / TX * (lb - 2%)将缓和曲线公式汇总:设转向ZX,左转为-1,右转为1;设路幅A,左幅为-1,右幅为1;设与路拱同坡的过渡长TX,左转左幅或右转右幅Lc=TX,,即当ZX*A=1时,Lc=TX;公式为:第一缓和曲线:HP = -2% - ZX * A * (K - (HY - lc)) / lc * (lb - A * ZX * lz)第二缓和曲线:HP = -ZX * A * lb + ZX * A * (K - YH) / lc * (lb - ZX * A * lz)附:整体式路基excel VBA公式宏。
缓和曲线竖曲线超高过渡段计算

一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K(1或-1)⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度(或缓曲上任意点到缓曲起点的长度)l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1(上坡为“+”,下坡为“-”)②第二坡度:i2(上坡为“+”,下坡为“-”)③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点(过渡段终点)的距离:x 求:待求处的横坡:i解:d=x/Li=(i2-i1)(1-3d2+2d3)+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0(左转为“-”,右转为“+”)⑦曲线终点处曲率:P1(左转为“-”,右转为“+”)求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgn(x)函数是取符号函数,当x<0时sgn(x)=-1,当x>0时sgn(x)=1,当x=0时sgn(x)=0。
高速公路线路缓和曲线竖曲线圆曲线匝道坐标计算公式

高速公路线路缓和曲线、竖曲线、圆曲线、匝道坐标计算公式_★★高速公路的一些线路坐标、高程计算公式缓和曲线、竖曲线、圆曲线、匝道一、缓和曲线上的点坐标计算已知:①缓和曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K1或-1⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当计算第二缓和曲线上的点坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与计算第一缓和曲线时相反xZ,yZ为点HZ的坐标切线角计算公式:二、圆曲线上的点坐标计算已知:①圆曲线上任一点离ZH点的长度:l②圆曲线的半径:R③缓和曲线的长度:l0④转向角系数:K1或-1⑤过ZH点的切线方位角:α⑥点ZH的坐标:xZ,yZ计算过程:说明:当曲线为左转向时,K=1,为右转向时,K=-1,公式中n的取值如下:当只知道HZ点的坐标时,则:l为到点HZ的长度α为过点HZ的切线方位角再加上180°K值与知道ZH点坐标时相反xZ,yZ为点HZ的坐标三、曲线要素计算公式公式中各符号说明:l——任意点到起点的曲线长度或缓曲上任意点到缓曲起点的长度l1——第一缓和曲线长度l2——第二缓和曲线长度l0——对应的缓和曲线长度R——圆曲线半径R1——曲线起点处的半径R2——曲线终点处的半径P1——曲线起点处的曲率P2——曲线终点处的曲率α——曲线转角值四、竖曲线上高程计算已知:①第一坡度:i1上坡为“+”,下坡为“-”②第二坡度:i2上坡为“+”,下坡为“-”③变坡点桩号:SZ④变坡点高程:HZ⑤竖曲线的切线长度:T⑥待求点桩号:S计算过程:五、超高缓和过渡段的横坡计算已知:如图,第一横坡:i1第二横坡:i2过渡段长度:L待求处离第二横坡点过渡段终点的距离:x求:待求处的横坡:i解:d=x/Li=i2-i11-3d2+2d3+i1六、匝道坐标计算已知:①待求点桩号:K②曲线起点桩号:K0③曲线终点桩号:K1④曲线起点坐标:x0,y0⑤曲线起点切线方位角:α0⑥曲线起点处曲率:P0左转为“-”,右转为“+”⑦曲线终点处曲率:P1左转为“-”,右转为“+”求:①线路匝道上点的坐标:x,y②待求点的切线方位角:αT计算过程:注:sgnx函数是取符号函数,当x<0时sgnx=-1,当x>0时sgnx=1,当x=0时sgnx=0;在计算器中若无此函数可编一个小子程序代替;转载自:。
超高讲解与程序

1.超高方式3种①绕路面内边缘旋转(常用)②绕路面中心线旋转(多用于旧路改建,以便控制中线标高)③绕路面外边缘旋转(路基很高或从路容考虑时才可能采用)2.超高缓和段长度Lc=B*▵i÷P(B为旋转轴到外侧路边缘距离,▵i为超高度与旋转轴外侧路拱度之代数差,P为超高渐变率,一般来说Lc采用缓和曲线长度L1)3.超高值的计算⑴第一种方式(内副路面坡度保持不变,外副路面绕路中心线旋转,旋转至和内副路面同坡度时,全副路面绕内边缘旋转到超高度。
)①正常断面h中=a*i2+b/2*i1 h内=h外=0②提肩断面(距缓和段起点1-2m内完成提肩。
即路肩坡度和路面坡度一致)h中=a*i2+b/2*i1 h内=h外=a(i2-i1)③双坡断面h内=a*i2-(a+e x)*i1 (e x=x/Lc*e) (e为加宽值,x为缓和段内任意计算点到缓和起点的距离。
)h中=a*i2+b/2*i1h外=h1*x/L1+a(i2-i1) ( L1=i1/ib*Lc h1=(b+2a)*i1 )④旋转断面(X≥L1)h内=a*i2-(a+e x)*i x (i x=x/Lc*i b;i b为超高)h中=a*i2+b/2*i xh外=a*i2+(a+b)*i x⑤全超高断面h内=a*i2-(a+e x)*i bh中=a*i2+b/2*i bh外=a*i2+(a+b)*i b⑵第二种方式(内副路面坡度保持不变,外副路面绕路中心线旋转,旋转至和内副路面同坡度时,全副路面绕路中心线旋转到超高度。
)①正常断面h中=a*i2+b/2*i1 h内=h外=0②提肩断面(距缓和段起点1-2m内完成提肩。
即路肩坡度和路面坡度一致)h中=a*i2+b/2*i1 h内=h外=a(i2-i1)③双坡断面h内=a*i2-(a+e x)*i1 (e x=x/Lc*e)h中=a*i2+b/2*i1h外=h1*x/L1+a(i2-i1) ( L1=2*i1/(i b+i1)*Lc h1=(b+2a)*i1 ) ④旋转断面(X≥L1)h内=a*i2+b/2*i1-(a+e x+b/2)i x ( i x=x/Lc*i b-(Lc-x)/Lc*i1 ) h中=a*i2+b/2*i1h外=a*i2+b/2*i1+(a+b/2)i x⑤全超高断面h内=a*i2+b/2*i1-(a+e+b/2)*i bh中=a*i2+b/2*i1h外=a*i2+b/2*i1+(a+b/2)*i bFx-5800平曲线超高、加宽计算程序(已测试)CG --- JKLbI 0:CIs:“ZH”?C:“HZ”?E:“LBK”?A:“I1”?B:“IC”?P:“Z-1,Y+1”?Z:“LS1”? G:“LS2”? N:“JK”?X←LbI 1 :CIs:DO:“CD,<0=>Return”?S: “SJBG=”?Y:If S<0 Or S>E:Then Goto 0:If End ←G=0=>Goto5 ←N=0=>Goto5 ←S<C=>Goto5 ←S>E=>Goto5 ←S>C+G=>Goto2 ←0.04G÷(P+B)+C→H:(S-C)÷G→L:L(P+B)-B→I: LX+A→J←If S<H:Then -BJ→D:AI→F:EIse -IJ→D:AI→F:If End ←Goto4←LbI 2 :S>E-N=>Goto3 ←X+A→J:-P(A+X)→D:AP→F:Goto4 ←LbI 3 :E-0.04N÷(P+B)→K:(E-S)÷N→L:LX+A→J:L(P+B)-B→I←If S<K:Then -IJ→D:AI→F:EIse -BJ→D:AI→F:If End ←Goto4←LbI 4:If Z<0:Then J→H:A→K:D→L:F→M:Goto6:If End ←If Z≥0:Then A→H:J→K:F→L:D→M:Goto6:If End ←LbI 5 :A→H:A→K:-BA→L:-BA→M:Goto6←LbI 6:CIs←“ZK=”:Locate 4,1,H◢“YK=”:Locate 4,2,k◢“Z-H=”:Locate 5,3,L◢“Y-H=”:Locate 5,4,M◢“HL=”:Y+L◢“HP=”:Y◢“HR=”:Y+M÷K*L◢“IZ(%)=”:L÷H*100◢“IY(%)=”:M÷K*100◢Goto1←说明:该程序适用于绕中轴旋转的一、二级公路,三、四级公路设计I 类加宽可用,II 类加宽需将LbI 3 =(4L^3-3L^4)X+A→J改为LX+A→J 即可。
缓和曲线 长度计算方法

缓和曲线段长度的计算分析——上海市政工程设计研究总院中原分院 郭建光在道路线形设计的过程中,缓和曲线占据着非常重要的角色,如何科学合理的设置其长度是很多路线设计者一个很关心的问题。
本文中将讲述计算缓和曲线长度的具体方法。
关键词:超高 缓和曲线 长度 1 从满足超高缓和段的角度分析 给出超高缓和段长度计算公式 'B t Lc q∆=B'——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度,m ;t ∆—— 超高坡度与路拱坡度的代数差,%; q —— 超高渐变率。
根据y i i i ∆=- 2127y V i Rμ=-这两个公式可知,只要确定了μ,就可以在设计速度V 和半径R 一定的情况下计算出超高缓和段的长度了。
为了保证汽车行驶的横向稳定性,有Y μψ<(具体推导过程在这里不再详述,如有兴趣参见裴玉龙著道路勘测设计),Yψ为横向摩擦系数。
根据实验和经验,一般采用0.6~0.7Y ψψψ=,ψ为路面的摩擦系数。
一般正常干燥情况下的沥青路面摩擦系数为0.6,水泥混凝土路面在干燥情况下与沥青路面相差不大。
所以取0.6ψ=。
经过计算给出以下条件下的超高和超高缓和段长度。
条件:高速公路四车道路基宽度28m,路拱横坡2%,绕中线旋转2从满足规范的角度考虑(1)须大于回旋线最小长度。
(2)大于R/9小于R。
(3)和圆曲线长度的比例为1:1。
从以上条件可得出设计速度为120km/h,路基宽度28m,路拱横坡2%,绕中线旋转的高速公路的缓和曲线长度推荐值为:当R<=1800时,缓和曲线段长度l>=Lc。
当R>1800时,缓和曲线段长度l>R/9。
其他条件下的缓和曲线段长度参照以上方法计算即可。
高等级公路路线设计中超高缓和段设置的分析

高等级公路路线设计中超高缓和段设置的分析1 高等级公路缓和段设计规范高速公路的超高部分应设计有缓和段,此种设计包括了两个方面的内容,一则是超高缓和段长度的设计;二则是超高缓和段在缓和曲线长度的设计。
为了满足此种要求,超高缓和度长度的设计应当符合国家的相关规范,如:公路路线设计规范,其中规定最小的超高缓和段长度来设计。
第二个方面则需要按照规范的标准,当圆曲线半径小于不设超高最小圆曲线半径的时候,圆曲线与直线相接的缓和曲线,即利用回旋设计来计算。
利用公式计算当圆曲线半径和缓和曲线的参数为定值的时候,缓和曲线的长度也就固定,而缓和曲线上的任何一点的曲率半径则在一个范围内。
2 最大、最小超高的合成坡度按照超高横坡的计算公式分析,可以计算获得一个曲线的超高横坡值,按照前面所述的规范规定,超高横坡度的计算是按照形成速度、半径、路面材料、自然条件、车辆构成等情况进行综合确定。
当超高横坡度的计算小于路拱坡度值的时候,应设置等于路拱横坡的超高;高速公路、一级公路的超高横向坡度影响小于10%,其他公路则小于8%,而存在积雪的路面应小于6%。
同时在规范中规定对个等级公路不同半径下的公路规定了超高的横坡值,但是标准中关于超高的规定和附录中的说明可以看出,超高的设置在特殊的情况下是应因地制宜的,如在特定的环境下,一条平原丘陵区中的三级公路,路面为中级路面,路拱横坡按照各方面的因素综合设定为4%,如果一平曲线半径的范围是750m~1 500m之间则根据规范其超高横坡则是2%,但是因为其路拱为4%,因此范围内半径所选择的超高横坡为4%。
同时设置超高横坡的时候,还应对合成坡度的大小进行综合考虑,从而提高路面降水可以即使的排除,从而提高路面的通行能力。
3 全超高段高横坡设计按照以往的设计方式,全超高横坡为单向的路拱横坡,资料显示与计算公式仍然是此种思路,但是规范中却在硬路肩坡度规定对其超高横坡有明确的规定,而在规范中没有相应的体现,所以一些设计仍然将全超高路段的超高横坡设计为单向路拱横坡,这与规范的硬路肩超高横坡是矛盾的,规范规定硬路肩大于或者等于2.25m,应设置外倾斜横坡,当横坡值大于8%的时候,曲线外侧应设置相内倾斜的横坡,其参考值为行车道的横坡相等;当硬路肩小于2.25m时候,曲线外侧路肩横坡方向和其坡度参数应与行车道一致、因此在设计全超高路段的横坡时,以路肩参数和横坡值为标准。
缓和段曲线参数及超高、加宽计算

第三节 缓和段一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形,是道路平面线形要素之一。
1.缓和曲线的作用 1)便于驾驶员操纵方向盘2)乘客的舒适与稳定,减小离心力变化3)满足超高、加宽缓和段的过渡,利于平稳行车 4)与圆曲线配合得当,增加线形美观 2.缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的0°均匀地增加到圆曲线上。
S=A 2/ρ(A :与汽车有关的参数)ρ=C/s C=A 2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3.回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R ,l h =s 则 l h =A 2/R4.缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1)根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a 1=0,a 2=v 2/ρ,a s =Δa/t ≤0.6 RVl h 3035.0≥2)依驾驶员操纵方向盘所需时间求缓和曲线长度(t=3s) 2.16.3V t V vt l h ===3)根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
ph l c h ≥4)从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在3°——29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5.直角坐标及要素计算 1)回旋线切线角(1)缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
缓和曲线超高计算

公路缓和曲线知识与计算公式未知2010-04-04 17:34:42 本站一、缓和曲线缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间,由较大圆曲线向较小圆曲线过渡的线形 , 是道路平面线形要素之一。
1 .缓和曲线的作用1 )便于驾驶员操纵方向盘2 )乘客的舒适与稳定,减小离心力变化3 )满足超高、加宽缓和段的过渡,利于平稳行车4 )与圆曲线配合得当,增加线形美观2 .缓和曲线的性质为简便可作两个假定:一是汽车作匀速行驶;二是驾驶员操作方向盘作匀角速转动,即汽车的前轮转向角从直线上的 0 °均匀地增加到圆曲线上。
S=A2/ρ( A :与汽车有关的参数)ρ=C/s C=A2由上式可以看出,汽车行驶轨迹半径随其行驶距离递减,即轨迹线上任一点的半径与其离开轨迹线起点的距离成反比,此方程即回旋线方程。
3 .回旋线基本方程即用回旋线作为缓和曲线的数学模型。
令:ρ=R , l h=s 则 l h=A2/R4 .缓和曲线最小长度缓和曲线越长,其缓和效果就越好;但太长的缓和曲线也是没有必要的,因此这会给测设和施工带来不便。
缓和曲线的最小长度应按发挥其作用的要求来确定:1 )根据离心加速度变化率求缓和曲线最小长度为了保证乘客的舒适性,就需控制离心力的变化率。
a1=0,a2=v2/ ρ ,a s= Δ a/t ≤ 0.62 )依驾驶员操纵方向盘所需时间求缓和曲线长度 (t=3s)3 )根据超高附加纵坡不宜过陡来确定缓和曲线最小长度超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后,因路基外侧由双向横坡逐渐变成单向超高横坡,所产生的附加纵坡。
4 )从视觉上应有平顺感的要求计算缓和曲线最小长度缓和曲线的起点和终点的切线角β最好在 3°—— 29°之间,视觉效果好。
《公路工程技术标准》规定:按行车速度来求缓和曲线最小长度,同时考虑行车时间和附加纵坡的要求。
5 .直角坐标及要素计算1 )回旋线切线角( 1 )缓和曲线上任意点的切线角缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。
公路超高缓和段长度的计算公式
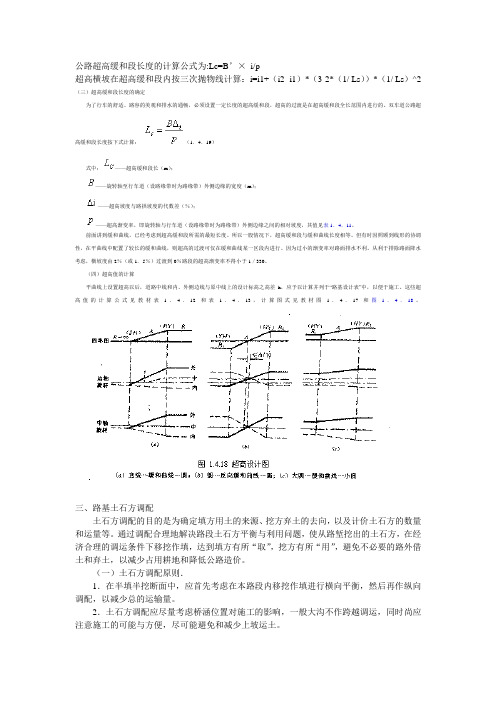
公路超高缓和段长度的计算公式为:Lc=B’×i/p超高横坡在超高缓和段内按三次抛物线计算:i=i1+(i2 -i1)*(3-2*(1/ Ls))*(1/ Ls)^2 (三)超高缓和段长度的确定为了行车的舒适、路容的美观和排水的通畅,必须设置一定长度的超高缓和段,超高的过渡是在超高缓和段全长范围内进行的。
双车道公路超高缓和段长度按下式计算:(1.4.19)式中:——超高缓和段长(m);——旋转轴至行车道(设路缘带时为路缘带)外侧边缘的宽度(m);——超高坡度与路拱坡度的代数差(%);——超高渐变率,即旋转轴与行车道(设路缘带时为路缘带)外侧边缘之间的相对坡度,其值见表1.4.11。
前面讲到缓和曲线,已经考虑到超高缓和段所需的最短长度。
所以一股情况下,超高缓和段与缓和曲线长度相等。
但有时因照顾到线形的协调性,在平曲线中配置了较长的缓和曲线,则超高的过渡可仅在缓和曲线某一区段内进行。
因为过小的渐变率对路面排水不利。
从利于排除路面降水考虑,横坡度由2%(或1.5%)过渡到0%路段的超高渐变率不得小于1/330。
(四)超高值的计算平曲线上设置超高以后,道路中线和内、外侧边线与原中线上的设计标高之高差h,应予以计算并列于“路基设计表”中,以便于施工。
这些超高值的计算公式见教材表1.4.12和表1.4.13,计算图式见教材图1.4.17和图1.4.18。
三、路基土石方调配土石方调配的目的是为确定填方用土的来源、挖方弃土的去向,以及计价土石方的数量和运量等。
通过调配合理地解决路段土石方平衡与利用问题,使从路堑挖出的土石方,在经济合理的调运条件下移挖作填,达到填方有所“取”,挖方有所“用”,避免不必要的路外借土和弃土,以减少占用耕地和降低公路造价。
(一)土石方调配原则.1.在半填半挖断面中,应首先考虑在本路段内移挖作填进行横向平衡,然后再作纵向调配,以减少总的运输量。
2.土石方调配应尽量考虑桥涵位置对施工的影响,一般大沟不作跨越调运,同时尚应注意施工的可能与方便,尽可能避免和减少上坡运土。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高速公路超高缓和段的超高旋转与计算
摘要:本文介绍了缓和曲线的超高缓和段的超高方式的旋转与计算 , 有些对在旋转过程中的表述与以前不太一样 , 计算公式简捷、准确。
关键词: 缓和曲线超高旋转计算
为使车辆在曲线段上安全行使 , 依据设计超高横坡 , 分析、理解超高在旋转过程中的动态情况 , 准确计算超高值至关重要 , 现在分别介绍超高缓和段的超高方式和计算。
1. 超高方式
1. 1 绕路面内侧边缘旋转 ( 简称边轴旋转 )
它是使旋转轴在路面内侧边缘保留在水平位置 ( 不考虑路线纵坡 ) 。
首先在超高缓和段起点之时 , 迅速将外侧路肩横坡变为路拱横坡度。
然后逐渐抬高外侧路面与路肩 , 使之达到与内侧路拱坡度一致的单向横坡。
继续旋转使整个断面达到超高横坡度为止。
( 见图一 )
1. 2 绕路中线旋转 ( 简称中轴旋转 )
它是使旋转轴在路面中线保留在水平位置 ( 不考虑路线纵坡 ) 。
首先在超高缓和段起点之时 , 迅速将外侧路肩横坡度变为路拱横坡度。
然后逐渐抬高外侧路面与路肩 , 使之达到与内侧路拱坡度一致的单向横坡。
继续旋转使整个断面达到超高横坡度为止。
( 见图二 )
2. 超高值计算
2.1 计算 X
它是与路拱同坡度的单向超高点至超高缓和段起点距离的计算 , 无论超高方式如何它都是由路拱坡度变为与路拱坡度一致的单向坡度。
2.2 计算超高值 ( 见附表 )
在计算超高缓和段超高值时,分三种情况考虑:
a. 当 i c <i g 时
在旋转过程中 , 由外侧路拱 -i g ( 相对内侧 ) 逐渐抬高至 i g , 变化率为 2 i g , 这时超高横坡未起作用 , 无论边轴旋转、中轴旋转 , 计算 h cx 公式统为
b. 当 i c >i g 时
这 时超高旋转已进入超高横坡 , 计算 h cx 公式为
c. 当 i c =i g 时
上 述计算 h cx 公式都可采用 .
例:江西省昌万公路某里程的缓和曲线为边轴旋转,已知: L c =85 ,
b=9,a=1.5,i g =2% , i j =3%,i c =5%, 求 x=x 0 处的单向横坡的外侧边缘超高值 h cx 。
X
L c
原计算公式: h cx =a(i j -i g )+[ai j +(a+b)i c ]
=0.243
现计算公式:
根据两者计算公式和结果可知,只有在 Hy 处的 h c 相等外,其他任何处的 h cx 都有误差。
式图中: b-- 路面宽度 ( m );
a-- 路肩宽度 ( m );
-- 路拱横坡 ;
i
g
i
-- 路肩横坡 ;
j
—超高横坡;
i
c
-- 超高缓和段长度 ( 或缓和曲线长度 )( m );
L
c
-- 与路拱同坡度单向超高点至超高缓和起点距离 ( m );
X
X -- 超高缓和段上任一点至起点的距离 ( m );
-- 路基外缘最大超高值 (m);
h
c
-- 路中线最大超高值 ( m) ;
h ˊ
c
h ˊˊ
-- 路基内缘最大降低值 (m);
c
-- x 距离处路基外缘抬高值 (m);
h
cx
h ˊ
-- x 距离处路中线抬高值 (m);
cx
-- x 距离处路基内缘降低值 (m);
h ˊˊ
cx
ZH-- 第一缓和曲线起点(直缓);
HY-- 第一缓和曲线终点(缓圆);
-- 路基加宽值 (m);
B
j
--x 距离处路基加宽值 (m).
B
jx
3. 结束语
正确分析、理解超高在旋转过程中的动态情况 , 精确计算超高缓和段的超高值,是确保行车安全的关键。
本文介绍了超高的旋转过程及超高值的计算公式。
如有欠妥之处 , 请读者指正。
