正四面体内切球和外接球(好用)
立体几何中球的内切和外接问题完美版

S
A.
B.
C.1
D.
答案:D.
O
,即
.
C
A
M
B
7
若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
例 9、已知三棱锥的四个顶点都在球 的球面上,
且
,,
解:
且
,
,
因为 所以
所以知 所以可得图形为:
,
,
,
,求球 的体积。
P
在
中斜边为
在
中斜边为
B
取斜边的中点 , 在
中
在
中
所以在几何体中
则这个球的表面积是( )
A.16π
B.20π
C.24π
D.32π
4
举一反三-突破提升
2.正六棱柱的底面边长为 4,高为 6,则它的外接球的表面积为
A. 20 B. 25 C. 100 D. 200
4
举一反三-突破提升
已知正三棱锥 P-ABC 的主视图和俯视图如图所 示,
则此三棱锥的外接球的表面积为 ( )
B、体积为 3
D、外接球的表面积为 16
3
1正视图
1
3 1 侧视图
俯视图
点 A、B、C、D 均在同一球面上,其中
是正三角形,
AD 平面 ABC,AD=2AB=6,则该球的体积为 ( )
(A)
(B)
(C)
(D)
平面四边形 ABCD中, AB AD CD1, BD 2, BD CD ,
将其沿对角线 BD 折成四面体 A'BCD,使平面 A' BD 平面 BCD,
∴S 表=S 侧+S 底=9
探求正四面体外接球、内切球半径求法知识讲解

探求正四面体外接球、内切球半径求法探求正四面体外接球、内切球半径正四面体是特殊的正三棱锥,所有的棱长都相等,四个面是全等的等边三角形,有外接球、内切球,且球心重合.已知正四面体ABCD 棱长为a ,设外接球半径为R ,内切球半径为r ,球心为O ,则正四面体的高h a a 即34R h =;内切球a 即14r h =. 外接球半径是内切球半径的3倍. 下面从不同角度、用不同方法进行探求:方法一:(勾股定理)作 平面于点,则点H 是的中心,AH BCD H BCD ⊥V高3h AH a ==,设O 为球心,则.O AH ∈ 连结,.BH BO 在Rt BOH V 中,222BO BH OH =+,即222()()33R a a R =+-,,.R a r h R a a a ∴==-=-= 方法二:(三角正切倍角公式)作 平面于点,则点H 是的中心,AH BCD H BCD ⊥V高3h AH a ==,设O 为球心,则.O AH ∈ 连结,.BH BO = ,2.AO BO ABO BAO BOH θθ=∴∠=∠∠=Q在Rt ABHV中,tan,23aBHAHθ===在Rt OBHV中,3tan2,3aBHOH r rθ===23r⨯∴==,.r a R h r a a a∴==-=-=方法三:(分割等体积)作平面于点,则点H是的中心,AH BCD H BCD⊥V高3h AH a==,设O为球心,则.O AH∈连结,,,BO CO DO得到四个以O为顶点的小棱锥,它们的底面是正四面体的一个面,高是内切球的半径r,设正四面体每个面的面积为S,则4,O BCD A BCDV V--=即114,33S r S AH⨯=g g11,4412.3124r AH h aR h r a a a∴====-=-=方法四:(侧棱、高相似或三角)作平面于点,则点H是的中心,AH BCD H BCD⊥V22tantan2,1tanθθθ=-Q高3h AH a ==,设O 为球心,则.O AH ∈ 设M 是AB 的中点,连结,,,OM OB BHAO BO OM AB =∴⊥QAMO AHB Rt ∴∠=∠=∠,又MAO HAB ∠=∠,AMO AHB ∴V :V , AM AO AH AB∴=, 即,aR a =,.R a r h R a a a ∴==-=-= 或:设BAH MAO θ∠=∠=,则在Rt ABH V中,3cos a AH AB aθ==, 在Rt AMO V 中,2cos .aAM AO Rθ==32a aa R∴= , 以下同上. 方法五:(斜高、高相似或三角)作 平面于点,则点H 是的中心,AH BCD H BCD ⊥V高h AH a ==,设O 为球心,则.O AH ∈ 设E 为BC 中点,连结,AE EH ,作ON AE ⊥于N 点,则N 是ABC V 中心,N 是AE 的三等分点,平面,ON 是内切圆半径r,ON ABC ⊥且 ,Rt ANO Rt AEH V :VAN AO AH AE ∴=,32a R = ,,.43412R a r h R a a a ∴==-=-= 或:设EAH NAO θ∠=∠=,则在Rt AEH V中,cos 2a AH AEθ==, 在Rt ANO V中,3cos .a AN AO Rθ==3aa R∴=, 以下同上. 方法六:(斜高、侧棱相似或三角)作 平面于点,则点H 是的中心,AH BCD H BCD ⊥V高h AH a ==,设O 为球心,则.O AH ∈ 设E 为BC 中点,连结,,AE DE DO ,延长DO 交AE 于N ,则N 是AE 的三等分点,.H DE ∈ 且DN ⊥平面.ABC则,Rt ODH Rt DNE V :V OH OD NE DE∴= 即 OH OD = NE DE 13=, 13r R ∴=, 3.R r ∴=又,R r AH h a +===13,.41244r h a R h a ∴==== 或:在Rt DNE V 中,1sin ,3NE NDE DE ∠== 在Rt DOH V 中,sin sin ,OH NDE ODH OD∠=∠= 13OH OD ∴=, 即13r R =, 3.R r ∴=又,3R r AH h a +===13,.41244r h a R h a ∴==== 方法七:(构造正方体)正四面体的四个顶点是正方体的顶点,此时正四面体的外接球也是正方体的外接球,正四面体的棱长为a的棱长为.2a 正方体的体对角线等于外接球直径,有22a R ⨯=,,.43412R a r h R a a a ∴==-=-= 方法八:(相交弦定理)设外接球球心为O ,半径为R ,过A 点作球的直径,交底面BCD V 于H ,则H 为BCD V 的外心,求得,,33AH a BH a == 由相交弦定理得2(2)).333a R a a -=g解得.4R a =.r h R a a a ∴=-=-= 以上从不同角度针对正四面体的外接球半径、内切球半径作了讨论,从而从不同方面对思维作了训练,不仅对正四面体的外接球半径、内切球半径有了透彻的认识,同时对解题能力的提高是有帮助的.。
立体几何中球的内切和外接问题(完美版)
2 3 A. 3
B. 3 3
3 3 C. 2
正方体 ABCD A1 B1C1 D1 的棱长为 2 , MN 是它的内切球的一条弦 (我们把球面上任意两点之间的线段称为球的弦) , P 为正方体表面上 的动点,当弦 MN 的长度最大时, PM PN 的取值范围是 .
,∴ , ,∴
,
, .
∴外接球的半径为
,∴球的表面积等于
解析:球内接多面体,利用圆内接多边形的性质求出小 圆半径,通常用到余弦定理求余弦值,通过余弦值再利 c 用正弦定理得到小圆半径 sin C 2r ,从而解决问题。
5
A.
正棱锥的外接球的球心是在其高上
,侧棱 PA 与底面 )
例 5 在三棱锥 P-ABC 中,PA=PB=PC=
测棱相等的锥体顶点的投影在底面外接圆心
例 7、.若三棱锥 S-ABC 的底面是以 AB 为斜边的等腰直角三角形,AB=2, SA=SB=SC=2,则该三棱锥的外接球的球心到平面 ABC 的距离为( )
B.
C.1
D.
S
O
,即 .
C M B
A
7
,
解: 因为 所以 在 且
若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
D
1 r S全 3 2 2 3 r 3
E
r
6 2 S球 85 2 6
1 1 V多面体 S 全 r V S全 内切球 多 面 体3
3
r内 切 球
变式训练:一个正方体内接于一个球,过球心作一截面,如图所示,则截 面的可能图形是( )
考点三 4
组合体的表面积与体积
正四面体的性质及应用

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载正四面体的性质及应用地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容正四面体的性质及应用正四面体是立体几何中的基本几何体,它蕴涵着极为丰富的线面的位置、数量关系.在近年来各类考试中,正四面体倍受命题者青睐,命题者常以正四面体中的线面问题为载体,借以考察学生的数学思维能力和思维品质.因此,一线师生在教学过程中,应对这个几何体引起足够的重视.笔者在长期的教学中对正四面体进行了深入研究、潜心挖掘,得出了一些优美、简洁的结论.下面给出正四面体的相关结论,并利用这些结论解决问题,以期能对同学们学习立体几何有所启示.一、理顺正四面体性质——固本清源不妨设正四面体ABCD的棱长为a,则存在着以下定理:定理1.正四面体的3对异面棱均互相垂直,任意一对异面棱之间的距离均为;定理2.正四面体的高为;定理3.正四面体的内切球半径为,外接球半径为,且有;略证:如图1,易知正四面体的外接球心与内切球心重合为点O,并且位于正四面体的高AH上,连结BO、CO、DO,易知,且,从而AO、BO、CO、DO两两所确定的平面将正四面体分割成四个形状相同的正三棱锥:,,且每一个小正三棱锥的高都是内切球的半径,于是有,即,亦即有,所以,.故定理4.正四面体的全面积为,体积为;定理5.正四面体底面内任一点O到三个侧面的距离的之和;正四面体内任意一点到四个侧面的距离之和(仿定理3利用体积分割法易证).定理6.正四面体的侧棱与其底面所成的线面角大小为;定理7.正四面体相邻侧面所成的二面角的大小为;略证:设相邻两个侧面所成的角为,由于四个侧面的面积均相等,所以由射影面积公式知.定理8.设正四面体的侧棱与底面所成的角为,相邻两个侧面所成的二面角记为,则有略证:如图1所示,易知,,由H为的中心,易知,从而.定理9.正四面体的外接球的球心与内切球的球心O重合且为正四面体的中心;中心与各个顶点的四条连线中两两夹角相等,其大小为,此角即为化学中甲烷分子结构式中的键位角.略证:如图1,在三角形AOB中,,,由余弦定理可求得,于是.同理可得.定理10.正四面体内接于一正方体,且它们共同内接于同一个球,球的直径等于正方体的对角线.二、运用正四面体性质——化繁为易1.巧算空间距离例1.一个球与正四面体的6条棱都相切,若正四面体的棱长为a,则求此球的体积.分析一:由定理10知,将正四面体嵌于正方体的内部,然后再利用正四面体的棱与球相切,则该半径与正方体的内切半径相等进行求解.解法一.如图2所示,将正四面体补成正方体,易知与正四面体的各棱相切的球即为正方体的内切球.∵ 正四面体的棱长为a,∴ 正方体的棱长为.∴ 正方体的内切球半径.∴ .分析二:根据正四面体的对称性,结合定理1可知,该球的球心应位于正四面体的中心,其直径即为正四面体相对棱之间的距离.解法二.∵ 正四面体的棱长为a,∴ 由定理1可知,相对棱间的距离为.即该球的半径为.∴ .例2.在棱长为2的正四面体木块ABCD的棱AB上有一点P(),过P点要锯出与棱AB垂直的截面,当锯到某个位置时因故停止,这时量得在面ABD上锯痕,在面ABC上的锯缝,求锯缝MN的值.解:如图3,取AB的中点E,连结CE,DE,则为正四面体相邻两面的二面角的平面角,由条件知∠MPN也是正四体相邻两面的二面角的平面角,即∠NPM=∠CED,由定理7可知,于是,在中,由余弦定理得,∴2.妙求空间角例3.设P为空间一点,PA、PB、PC、PD是四条射线,若PA、PB、PC、PD两两所成的角相等,则这些角的余弦值为.解:如图4,构造正四面体ABCD,设P为四面体的中心,则PA、PB、PC、PD两两所成的角相等,设,由正四面体的性质,可知余弦值为例4.如图5,在正四面体ABCD中,E、F分别为棱AD、BC的中点,连结AF、CE.⑴求异面直线直线AF和CE所成的角;⑵求CE与面BCD所成的角.解:⑴连结FD,在平面AFD内,过点E作EG∥AF交DF于点G.则是异面直线AF与CE所成的角(或其补角).设正四面体ABCD的棱长为a,可得,,.由余弦定理可求得.故异面直线AF与CE所成的角为.⑵由已知易知平面AFD⊥平面BCD,在平面AFD内,过点E作EH⊥FD于点H,连结CH,则∠ECH为CE与平面BCD所成的角.∵ EH为正四面体高的一半,由正四面体性质的定理2知.∴ .∴ CE 与底面BCD所成的角为.例5.如图6,正四面体ABCD的四个顶点在同一个球面上,CC1和DD1是该球的直径,求面ABC与面AC1D1所成角的正弦值.解:由正四面体性质定理10知正四面体内接于一球,该正方体也内接于此球,且正方体的对角线为此球的直径,如图所示,即CC1、DD1为该球的直径.连结C1D1,交AB于点M,连结MC.∵ MC⊥AB,MD1⊥AB,∴ ∠CMD1为平面ABC与平面AC1D1所成的角.设正方体棱长为a,在中,.∴ 平面ABC与平面ACD所成的角的正弦值为.归纳反思:正四面体是立体几何中一个重要的数学问题载体,在平时的学习过程中若能有意识地研究它、利用它,就能较好地培养我们数学思维的“方向感”和思路的“归属感”,有助于促进自己数学思维空间的拓展、数学品质的提升.1.在正四面体中,、、分别是、、的中点,下面四个结论中不成立的是②.①面;②面面;③面;④面面.2.正四面体中,与平面所成角的余弦值为.3.如图,正四面体的棱长为2,点,分别为棱,的中点,则的值为A.4 B.C.D.2选:.44.以下说法①三个数,,之间的大小关系是;②已知:指数函数过点,则;③已知正四面体的边长为,则其外接球的体积为;④已知函数的值域是,,则的值域是,;⑤已知直线平面,直线在内,则与平行.其中正确的序号是①③.555555555.在正四面体中,为的中点,则直线与所成角的余弦值为A.B.C.D.选:.6.在正四面体中,、分别为棱、的中点,连接、,则异面直线和所成角的正弦值为A.B.C.D.选:.【点评】本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.本题易错点在于要看清是求异面直线和所成角的正弦值,而不是余弦值,不要错选答案.7.如图所示,在正四面体中,是棱的中点,是棱上一动点,的最小值为,则该正四面体的外接球的体积是A.B.C.D.选:.8.棱长为1的正四面体中,为棱上一点(不含,两点),点到平面和平面的距离分别为,,则的最小值为.【考点】:基本不等式及其应用【专题】31:数形结合;35:转化思想;:空间位置关系与距离;:不等式【分析】设点是正三角形的中心,连接,作,垂足为点.交于点,则点为的中点.设.,,.由,可得.同理可得:.代入利用基本不等式的性质即可得出.【解答】解:如图所示,设点是正三角形的中心,连接,作,垂足为点.交于点,则点为的中点.设.,.,.同理可得:.,当且仅当时取等号.故答案为:.9.已知是正四面体棱的中点,是棱上异于端点,的任一点,则下列结论中,正确的个数有(1);(2)若为中点,则与所成角为;(3)平面平面;(4)存在点,使得过的平面与垂直.A.1个B.2个C.3个D.4个【考点】:异面直线及其所成的角;:空间中直线与直线之间的位置关系;:直线与平面垂直;:平面与平面垂直【专题】14:证明题【分析】连接、,可证明出平面,从而,得(1)正确;取中点,连接、,利用三角形中位线定理证明出、所成的直角或锐角,就是异面直线、所成的角,再通过余弦定理,可以求出与所成角为,故(2)正确;根据(1)的正确结论:,结合平面与平面垂直的判定定理,得到(3)正确;对于(4),若存在点,使得过的平面与垂直,说明存在的一个位置,使.因此证明出“不论在线段上的何处,都不可能有”,从而说明不存在点,使得过的平面与垂直.【解答】解:(1)连接、正中,为的中点同理,结合平面,而平面,故(1)是正确的;(2)取中点,连接、中,、分别是、的中点,.、所成的直角或锐角,就是异面直线、所成的角设正四面体棱长为,在中,则中在中,,即异面直线、所成的角是,故(2)正确;(3)由(1)的证明知:平面平面平面平面,故(3)正确;(4)若有,根据(1)的结论,因为、相交于点,所以平面中,,可得是锐角,说明点在线段上从到运动过程中,的最大值是锐角,不可能是直角,因为平面,与不能垂直,以上结论与平面矛盾,故不论在线段上的何处,都不可能有.因此不存在点,使得过的平面与垂直.综上所述,正确的命题为(1)(2)(3)故选:.10.棱长为的正四面体中,给出下列命题:①正四面体的体积为;②正四面体的表面积为;③内切球与外接球的表面积的比为;④正四面体内的任意一点到四个面的距离之和均为定值.上述命题中真命题的序号为②③④.【考点】:棱柱、棱锥、棱台的侧面积和表面积;:棱柱、棱锥、棱台的体积【专题】31:数形结合;35:转化思想;49:综合法;:空间位置关系与距离【分析】①正四面体的高,体积为,计算即可判断出正误;②正四面体的表面积为,即可判断出正误;③分别设内切球与外接球的半径为,,则,解得;,解得,即可判断出正误;④正四面体内的任意一点到四个面的距离之和为,则,化简即可判断出正误.【解答】解:①正四面体的高,体积为,因此不正确;②正四面体的表面积为,正确;③分别设内切球与外接球的半径为,,则,解得;,解得.,因此表面积的比为,正确;④正四面体内的任意一点到四个面的距离之和为,则,化简可得:,即为正四面体的高,均为定值,正确.上述命题中真命题的序号为②③④.。
高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题

高中数学解题指导八个无敌模型全搞定空间几何的外接球和内切球问题八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型墙角模型是指三条线段两两垂直的几何体,通过公式(2R) = a + b + c,即2R = a^2 + b^2 + c^2,可以求出其外接球半径R。
例1:1)已知顶点都在同一球面上的正四棱柱的高为4,体积为16,求该球的表面积。
解:由V = ah = 16,得a = 2,4R = a + a + h = 4 + 4 + 16 = 24,S = 24π,答案为C。
2)若三棱锥的三个侧面两两垂直,且侧棱长均为3,求其外接球的表面积。
解:由2R = a + b + c = 3 + 3 + 3 = 9,得R = 9/4,S =4πR^2 = 9π。
3)在正三棱锥S-ABC中,M、N分别是棱SC、BC的中点,且AM⊥MN,若侧棱SA = 23,求正三棱锥S-ABC外接球的表面积。
解:由墙角模型的特点可知,正三棱锥的对棱互垂直。
连接AB、BC的中点D、E,连接AE、CD,交于H,则H是底面正三角形ABC的中心。
由AM⊥MN,SB//MN,可得AM⊥SB,AC⊥SB,故SB⊥平面SAC,SB⊥SA,SB⊥SC,即SB⊥SA,BC⊥SA,故SA⊥平面SBC,SA⊥SC。
因此,三棱锥S-ABC的三棱条侧棱两两互相垂直,由2R^2 = 23^2 + 23^2 + 23^2 = 36,得R^2 = 9,S = 36π。
类型二、棱台模型棱台模型是指上底面和下底面都是正多边形,且两底面中心连线与侧棱垂直的几何体。
通过勾股定理和相似三角形,可以求出其外接球半径R和内切球半径r。
例2:1)已知棱台的上底面和下底面都是正三角形,上底边长为3,下底边长为6,侧棱长为5,求其外接球半径R和内切球半径r。
解:由勾股定理可得棱台的高为4√3.设外接球半径为R,内切球半径为r,则有R/r = (a + b + c)/(a + b - c) = (3 + 6 +5)/(3 + 6 - 5) = 7,解得R = 7r。
正四面体中的几个性质

正四面体中的几个性质作者:祁绍锋来源:《中学生数理化·学研版》2014年第01期在立体几何中,正四面体是一种特殊的正三棱锥,它有一些很重要的几何性质.回顾近几年的高考试题,我们可以发现有关正四面体的问题是考查的一个热点.命题者往往以正四面体为载体出题,考查立体几何中有关角和距离的知识点,因此我们很有必要系统地整理出它的几何性质,这样有关正四面体的几何问题就能迎刃而解.我们不妨以棱长是的正四面体为例.如右图1,O为底面BCD的中心,AO⊥底面BCD,AO为正四面A-BCD的高,∠ABO是棱AB与底面BCD所成的角,连结BO延长交CD于点E,则E为CD中点且BE⊥CD,,连结AE,则AE⊥CD,AE为正四面体的斜高,∠AEO 为侧面ACD与底面BCD所成的二面角的平面角.一、垂直问题(1)对棱互相垂直(如图1中AB⊥CD)简证:因为O是△ABC的中心,所以BE⊥CD,BE是AB在平面BCD内的射影,由三垂线定理可知AB⊥CD.(2)设O1为AO的中点,则BO1、CO1、DO1两两垂直简证:如图2中CO1=DO1= ,而CD= , CO12+DO12=CD2,故∠CO1D=90°,即CO1⊥DO1,同理可证CO1⊥BO1 ,BO1⊥DO1.所以BO1、CO1、DO1两两垂直.应用举例:如右图,正四面体ABCD的棱长为1,G是底面△ABC的重心,点M在线段DG上,且使得∠AMB=90°,则DM的长为 .略解:由上可知当M为DG的中点时,满足∠AMB=90°,所以DM= .二、距离问题(1)顶点A到底面BCD的距离(正四面体顶点到底面的距离)如图1中AO⊥底面BCD,所以AO为顶点A到底面BCD的距离,AO= = = .应用举例:把半径为1的四个球垒成两层放在桌面上,下层放三个,上层放一个,两两相切,求上层小球最高点离桌面的高度.分析:四个球的球心构成一个正四面体顶点.解:四个球两两相切,球心组成一个正四面体的顶点,正四面体的棱长为2,此正四面体的高为,所以上层小球最高点离桌面的高度 +2.(2)棱AB与棱CD的距离(正四面体中对棱的距离)如图3中E、F分别为AB与CD的中点,易证EF为AB与CD的公垂线,EF= = = .应用举例:某同学为加强体育组环境管理,订做了半径为2R圆柱形铁筐(既有上盖也有下底),用来盛放半径为R的篮球,则该筐最多可放篮球的个数为()A 22B 24C 26D 28略解:当如右图所示两球两球交替上叠,相邻四个篮球两两相切,任意相邻四个篮球球心的连线刚好组成一个正四面体,这样能装得最多,若记同一高度的两个篮球为一层,则上层两球心的连线与下层两球心的连线刚好是棱长为2R的正四面体的一组对棱,距离为,假设最多可以叠放n层.那么20R-2R≥ ×(n-1)(n∈N*),n≤9 +1≈13.728;所以最多可放13层,共26个篮球.所以选C.评注:球与球相组合的问题,直观图比较难画,一般可考虑通过画球心代替球,组成一个多面体来解决相关问题.三、空间角问题(1)对棱所成的角(异面直线所成的角)为90°略解:方法一:如右图中G为AC中点,连结FG与EG,则FG=EG= ,又因为EF= ,所以EG2+FG2=EF2,即EG⊥FG, AD与BC所成的角是90°.方法二:∵AD与BC异面垂直,∴AD与BC所成的角是90°.(2)侧棱与底面所成的角(直线与平面所成的角)为 .略解:如图1中∠ABO为棱AB与底面BCD所成的角,∵BO= ×BE= × = ,AB= ,AO⊥BO,∴ = = , = .(3)两侧面所成的角或侧面与底面所成的角(面与面所成的角)为略解:∵BE⊥CD,AE⊥CD,方法一:如图1中∠AEO为侧面ACD与底面BCD所成的二面角的平面角,在Rt△AEO 中,EO= BE= AE, = ,所以 = .方法二:如图1中∠AEB为侧面ACD与底面BCD所成的二面角的平面角,在△ABE 中,AE=BE= ,AB= , = = ,所以 = .评注:在正四面体中求直线所成角、二面角的时候,通常转化到斜高、斜高在底面的射影与高线或侧棱、侧棱在底面的射影与高线所组成的直角三角形中,将空间图形转化为平面图形,这样求解将会变得比较方便.四、内切球与外接球问题(1)内切球半径 =略解:设一个面的面积为S,内切球球心O1,连结A O1、CO1、DO1,则 = + + +即 =4× S×,因此 = .评注:用等体积法求几何体中内切球半径是一种学生比较容易掌握的方法.(2)外接球半径R=略解:棱长为的正四面体可以补出一个与它有相同外接球的正方体,正四面体的六条棱刚好是正方体六个面的六条面对线,而正方体的外接球半径等于正方体对角线长的一半,设此正方体的棱长为x,则外接球的半径R= x,由图可知 = ,所以R= .应用举例:甲烷分子由一个碳原子和四个氢原子组成,其空结构为一个各条棱都相等的四面体,四个氢原子分别位于该四面体的四个顶点上,碳原子位于该四面体的中心,它与每个氢原子的距离都是 .若将碳原子和氢原子均视为一个点,则任意两个氢原子之间的距离为()A B C D略解:先补出以四个氢原子为顶点的正四面体的外接正方体,它们有相同的外接球半径,由题意可知此外接球半径为,任意两个氢原子之间的距离 = = .所以选C.评注:正四面体中与外接球半径有关的问题,我们可以将正四面体补形为正方体,这样解题可以避免复杂的作图过程.。
正四面体的外接球与内切球PPT讲稿

解题小结:
(1) V1:V2=R13:R23; S1:S2=R12:R22.
(2) 注意扩大与扩大到的区别.
(3) 解这类问题的关键:找到变化前 后半径的大小关系.
例3. 长方体的三个相邻面的面积分别为2,3, 6,这个长方体的顶点都在同一个球面上,求这个 球的表面积。
例4.在球心同侧有相距9cm的两个平行截面,它们的面 积分别为49πcm²和400πcm²,求球的表面积。
若将“球心同侧”这个条件去掉,又如何?
O₂
A
O₁
B
O
题组二:
1、一个四面体的所有2的棱都
一球为面上,,则四此个球顶的点表在面同积
( ) A 3л
B 4л C
3 3
D 6л
2、若正四体的棱长都为6,内有一 切球。与求四球个的面表都面相积。
1、一个四面体的所有的2 棱都
一球为面上,,则四此个球顶的点表在A面同积
的外接球,此时球的直径
为 3,
D
S球 =4 (
3 )2 2
3 ,
选A
A
C1 B1
C B
2、若正四体的棱长都为6,内有一
切球,与求四球个的面表都面相积。
解:作出过一条侧棱PC和高PO的截面,则截面三
角形PDC的边PD是斜高,DC是斜高的射影,球被截
P
成的大圆与DP、DC相切,连结EO,设球半径为r,
R2 2 ( 3
2 R)2,解得R 3
3 2
, 所以S球
4
R2
3 .
1、一个四面体的所有的2 棱都 一 (A为球3л面)上,B则四4л 此个C 球顶的点表在3 面同3 积 D 6л
解法2 构造棱长为1的正 方体,如图。则A1、C1、B、D
玩转外接球、内切球、棱切球经典问题--高一数学微专题(十四大题型)(解析版)

玩转外接球、内切球、棱切球经典问题【题型归纳目录】题型一:正方体、长方体模型题型二:正四面体模型题型三:对棱相等模型题型四:直棱柱模型题型五:直棱锥模型题型六:正棱锥与侧棱相等模型题型七:侧棱为外接球直径模型题型八:共斜边拼接模型题型九:垂面模型题型十:最值模型题型十一:二面角模型题型十二:圆锥圆柱圆台模型题型十三:锥体内切球题型十四:棱切球【方法技巧与总结】技巧总结一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.2.长方体的外接球的球心为其体对角线的中点,半径为体对角线长的一半.3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直,则可将其放入某个长方体内,如图1所示.(2)若三棱锥的四个面均是直角三角形,则此时可构造长方体,如图2所示.(3)正四面体P -ABC 可以补形为正方体且正方体的棱长a =PA2,如图3所示.(4)若三棱锥的对棱两两相等,则可将其放入某个长方体内,如图4所示图1图2图3图4技巧总结二:正四面体外接球如图,设正四面体ABCD 的的棱长为a ,将其放入正方体中,则正方体的棱长为22a ,显然正四面体和正方体有相同的外接球.正方体外接球半径为R =22a ⋅32=64a ,即正四面体外接球半径为R =64a .技巧总结三:对棱相等的三棱锥外接球四面体ABCD中,AB=CD=m,AC=BD=n,AD=BC=t,这种四面体叫做对棱相等四面体,可以通过构造长方体来解决这类问题.如图,设长方体的长、宽、高分别为a,b,c,则b2+c2=m2a2+c2=n2a2+b2=t2,三式相加可得a2+b2+c2=m2+n2+t22,而显然四面体和长方体有相同的外接球,设外接球半径为R,则a2+b2+c2=4R2,所以R=m2+n2+t28.技巧总结四:直棱柱外接球如图1,图2,图3,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形)图1图2图3第一步:确定球心O的位置,O1是ΔABC的外心,则OO1⊥平面ABC;第二步:算出小圆O1的半径AO1=r,OO1=12AA1=12h(AA1=h也是圆柱的高);第三步:勾股定理:OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2,解出R技巧总结五:直棱锥外接球如图,PA⊥平面ABC,求外接球半径.解题步骤:第一步:将ΔABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O ;第二步:O 1为ΔABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理,得a sin A =b sin B =c sin C =2r ),OO 1=12PA ;第三步:利用勾股定理求三棱锥的外接球半径:①(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;②R 2=r 2+OO 12⇔R =r 2+OO 12.技巧总结六:正棱锥与侧棱相等模型1.正棱锥外接球半径:R =r 2+h 22h.2.侧棱相等模型:如图,P 的射影是ΔABC 的外心⇔三棱锥P -ABC 的三条侧棱相等⇔三棱锥P -ABC 的底面ΔABC 在圆锥的底上,顶点P 点也是圆锥的顶点.解题步骤:第一步:确定球心O 的位置,取ΔABC 的外心O1,则P ,O ,O 1三点共线;第二步:先算出小圆O1的半径AO1=r,再算出棱锥的高PO1=h(也是圆锥的高);第三步:勾股定理:OA2=O1A2+O1O2⇒R2=(h-R)2+r2,解出R=r2+h2 2h.技巧总结七:侧棱为外接球直径模型方法:找球心,然后作底面的垂线,构造直角三角形.技巧总结八:共斜边拼接模型如图,在四面体ABCD中,AB⊥AD,CB⊥CD,此四面体可以看成是由两个共斜边的直角三角形拼接而形成的,BD为公共的斜边,故以“共斜边拼接模型”命名之.设点O为公共斜边BD的中点,根据直角三角形斜边中线等于斜边的一半的结论可知,OA=OC=OB=OD,即点O到A,B,C,D四点的距离相等,故点O就是四面体ABCD外接球的球心,公共的斜边BD就是外接球的一条直径.技巧总结九:垂面模型如图1所示为四面体P-ABC,已知平面PAB⊥平面ABC,其外接球问题的步骤如下:(1)找出△PAB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面PAB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.图1图2技巧总结十:最值模型这类问题是综合性问题,方法较多,常见方法有:导数法,基本不等式法,观察法等技巧总结十一:二面角模型如图1所示为四面体P-ABC,已知二面角P-AB-C大小为α,其外接球问题的步骤如下:(1)找出△PAB和△ABC的外接圆圆心,分别记为O1和O2.(2)分别过O1和O2作平面PAB和平面ABC的垂线,其交点为球心,记为O.(3)过O1作AB的垂线,垂足记为D,连接O2D,则O2D⊥AB.(4)在四棱锥A-DO1OO2中,AD垂直于平面DO1OO2,如图2所示,底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径.技巧总结十二:圆锥圆柱圆台模型1.球内接圆锥如图1,设圆锥的高为h,底面圆半径为r,球的半径为R.通常在△OCB中,由勾股定理建立方程来计算R.如图2,当PC>CB时,球心在圆锥内部;如图3,当PC<CB时,球心在圆锥外部.和本专题前面的内接正四棱锥问题情形相同,图2和图3两种情况建立的方程是一样的,故无需提前判断.由图2、图3可知,OC=h-R或R-h,故(h-R)2+r2=R2,所以R=h2+r2 2h.2.球内接圆柱如图,圆柱的底面圆半径为r,高为h,其外接球的半径为R,三者之间满足h2+r2=R2.3.球内接圆台R 2=r 22+r 22-r 21-h 22h 2,其中r 1,r 2,h 分别为圆台的上底面、下底面、高.技巧总结十三:锥体内切球方法:等体积法,即R =3V 体积S 表面积技巧总结十四:棱切球方法:找切点,找球心,构造直角三角形【典型例题】题型一:正方体、长方体模型1(2024·天津市第一中学滨海学校高一阶段练习)正方体外接球的体积是323π,那么外接球的直径为,正方体的表面积为.【答案】 4 32【解析】解:正方体外接球的体积是323π,设外接球的半径为R ,则43πR 3=323π,解得R =2,则外接球的直径2R =4,即正方体的体对角线的长为4,设正方体的棱长为a ,则a 2+a 2+a 2=4,解得a =433或a =-433(舍去);所以正方体的表面积S =6a 2=6×4332=32;故答案为:4;32.2(2024·辽宁·东港市第二中学高一阶段练习)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BC =CC 1=1;点E ,F 分别为AB 、CD 中点;那么长方体ABCD -A 1B 1C 1D 1外接球表面积为;三棱锥的D 1-BEF外接球的体积为.【答案】 6π11116π【解析】长方体对角线长为l =22+12+12=6,所以长方体外接球半径为R =l 2=62,表面积为S =4π×62 2=6π;如图,G ,H ,I ,J 分别是A 1D 1,AD ,BC ,B 1C 1中点,则GHIJ 是矩形,平面GHIJ ⎳平面CDD 1C 1,E ,F 分别是AB ,CD 中点,则EF ⎳AD ,而AD ⊥平面CDD 1C 1,所以EF ⊥平面CDD 1C 1,所以EF ⊥平面GHIJ ,而EF ⊂平面D 1EF ,EF ⊂平面BEF ,所以平面D 1EF ⊥平面GHIJ ,平面BEF ⊥平面GHIJ ,由EF ⊥平面CDD 1C 1,D 1F ⊂平面CDD 1C 1,得EF ⊥D 1F ,而EF ⊥EB ,设平面GHIJ 与D 1E ,BF ,EF 的交点分别为N ,M ,Q ,则N ,M ,Q 分别是D 1E ,BF ,EF 的中点,所以N ,M 分别是△D 1EF 和△EFB 的外心,在平面GHIJ 内过N 作PN ⊥NQ ,过M 作PM ⊥QM 交PN 于点P ,由EF ⊥平面CDD 1C 1,得EF ⊥PN ,EF ⊥PM ,而NQ ∩EF =Q ,NQ ,EF ⊂平面D 1EF ,所以PN ⊥平面D 1EF ,同理PM ⊥平面BEF ,所以P 是三棱锥D 1-BEF 的外接球球心.四边形PMQN 是圆内接四边形,由长方体性质知∠NQH =∠D 1FD =π4,所以∠NQM =3π4,NQ =12D 1F =22,MQ =12,MN =12+14-2×22×12×cos 3π4=52,由PM ⊥平面BEF ,BM ⊂平面BEF ,得PM ⊥BM ,PQ =MNsin ∠NQM=52sin 3π4=102,PM =PQ 2-QM 2=32,BM =12BF =22,所以PB =PM 2+BM 2=112,所以三棱锥的D 1-BEF 外接球的体积为V =4π3×1123=11116π.故答案为:6π;11116π.3(2024·湖南·高一阶段练习)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵;将底面为矩形,一侧棱垂直于底面的四棱锥称为阳马;将四个面均为直角三角形的四面体称为鳖臑.如图,在堑堵ABC -A 1B 1C 1中,AC ⊥BC ,AA 1=6,AB =8,则鳖臑A 1CBC 1外接球的表面积为,阳马A 1-BCC 1B 1体积的最大值为.【答案】 100π 64【解析】鳖臑A 1CBC 1外接球即为堑堵ABC -A 1B 1C 1的外接球,可将堑堵ABC -A 1B 1C 1补成长方体,则外接球直径为A 1B =62+82=10,∴其表面积为S =100π.∵64=AC 2+BC 2≥2AC ⋅BC ,当且仅当AC =BC =42时取等号,所以AC ⋅BC ≤32,∴阳马A 1-BCC 1B 1的体积为13BC ⋅BB 1⋅A 1C 1=13AC ⋅BC ⋅AA 1≤64.故答案为:100π,64题型二:正四面体模型1(江苏省镇江市2023-2024学年高一学期期末数学试题)一个正四面体的四个顶点都在一个表面积为24π的球面上,则该四面体的体积为.【答案】1623【解析】设正四面体的棱长为a ,外接球半径为R ,如图正四面体ABCD 中,E 为CD 的中点,M 为△BCD 的中心,连接AM ,则AM ⊥平面BCD ,O 为正四面体ABCD 外接球的球心,连接OB ,则BM =23BE =23×32a =33a ,所以AM =AB 2-BM 2=a 2-39a 2=63a ,因为正面体外接球的表面积为24π,所以4πR 2=24π,得R =6,所以AO =OB =6,所以OM =AM -OA =63a -6,在Rt △OBM 中,OM 2+BM 2=OB 2,则63a -6 2+33a 2=6 2,解得a =4或a =0(舍去),所以该四面体的体积为13S △BCD ⋅AM =13×34×42×63×4=1632,故答案为:16232(2024·天津南开·高二学业考试)表面积为43的正四面体外接球的体积为.【答案】6π【解析】设正四面体的边长为a ,△ABC 的外接圆圆心为D ,正四面体外接球的球心为O ,半径为R ,如图所示:因为4×12a2×32=43,解得a=2.因为2sin60°=2CD,所以CD=233,SD=22-2332=236.在RT△COD中,236-R2+233 2=R2解得R=62.正四面体外接球的体积V=43π×623=6π.故答案为:6π3(2024·辽宁鞍山·二模)已知正四面体ABCD的表面积为23,且A,B,C,D四点都在球O的球面上,则球O的体积为.【答案】3 2π【解析】正四面体各面都是全等的等边三角形,设正四面体的棱长为a,所以该正四面体的表面积为S=4×12×a×a2-a2 2=3a2,所以a=2,又正方体的面对角线可构成正四面体,若正四面体棱长为2,可得正方体的棱长为1,所以正方体的外接球即为该正四面体的外接球,所以外接球的直径为3,半径为3 2,所以球O的体积为32π.故答案为:3 2π题型三:对棱相等模型1如图,在三棱锥P-ABC中,PA=BC=3,PB=AC=2,PC=AB=5,则三棱锥P-ABC外接球的体积为()A.2πB.3πC.6πD.6π【解析】解:由题意,PA=BC=3,PB=AC=2,PC=AB=5,将三棱锥P-ABC放到长方体中,可得长方体的三条对角线分别为3,2,5,即a2+b2=3,a2+c2=2,c2+b2=5,解得:a=1,b=2,c=3.外接球的半径R=12×a2+b2+c2=62.∴三棱锥P-ABC外接球的体积V=43πR3=6π.故选:C.2(2024•永安市校级期中)在三棱锥P-ABC中,PA=BC=4,PB=AC=5,PC=AB=11,则三棱锥P-ABC的外接球的表面积为()A.26πB.12πC.8πD.24π【解析】解:∵三棱锥P-ABC中,PA=BC=4,PB=AC=5,PC=AB=11,∴构造长方体,使得面上的对角线长分别为4,5,11,则长方体的对角线长等于三棱锥P-ABC外接球的直径.设长方体的棱长分别为x,y,z,则x2+y2=16,y2+z2=25,x2+z2=11,∴x2+y2+z2=26,∴三棱锥P-ABC外接球的直径为26,∴三棱锥P-ABC外接球的表面积为4π2622=26π.故选:A.3(2024•五华区校级期中)如图,蹴鞠,又名“蹋鞠”、“蹴球”、“蹴圆”、“筑球”、“踢圆”等,“跳”有用脚蹴、蹋、踢的含义,“鞠”最早系皮革外包、内实米糠的球.因而“蹴鞠”就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家级非物质文化遗产名录.若将“鞠”的表面视为光滑的球面,已知某“鞠”表面上的四个点A,B,C,D满足AB=CD =13cm,BD=AC=25cm,AD=BC=5cm,则该“鞠”的表面积为()A.20πcm2B.24πcm2C.27πcm2D.29πcm2【解析】解:因为鞠表面上的四个点A,B,C,D满足AB=CD=13cm,BD=AC=25cm,AD=BC=5cm,所以可以把A,B,C,D四点放到长方体的四个顶点上,则该长方体的体对角线就是鞠的直径,设该长方体的长、宽、高分别为x,y,z,鞠的半径为R,则(2R)2=x2+y2+z2,由题意得x2+y2=20,x2+z2=13,y2+z2=25,所以(2R)2=x2+y2+z2=29,即4R2=29,所以该鞠的表面积为4πR2=29πcm2,故选:D.题型四:直棱柱模型1(2024·辽宁·昌图县第一高级中学高一阶段练习)已知直三棱柱ABC-A1B1C1的6个顶点都在球O 的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的表面积为()A.36πB.144πC.169πD.256π【答案】C【解析】如图,取B1C1,BC的中点分别为O1,O2,根据题意,它们分别是△A1B1C1,△ABC的外心,因为B1O1⎳BO1,B1O1=BO2,所以四边形BO2O1B1是平行四边形,所以B1B⎳O1O2,B1B=O1O2,而B1B⊥底面ABC,所以O1O2⊥底面ABC,取O1O1的中点O,于是点O为该直三棱柱外接球的球心.连接OB,容易求得OO2=6,BO2=12AC=1232+42=52,则外接球半径OB=OO22+BO22=36+254,于是外接球的表面积为4π×36+25 4=169π.故选:C.2(2024·广西桂林·高二期末)直三棱柱ABC-A1B1C1的各个顶点都在同一个球面上,若AB=AC= AA1=2,∠BAC=120°则此球的表面积为()A.20πB.200πC.10πD.30π【答案】A【解析】由题意,棱柱底面三角形中BC=23,底面外接圆半径r=BC2sin∠BAC=2,又ABC-A1B1C1为直三棱柱且AA1=2,所以其外接球半径R=r2+AA122=5,故球体表面积为4πR2=20π.故选:A3(2024·河北·张北县第一中学高一阶段练习)已知正三棱柱ABC-A1B1C1所有棱长都为6,则此三棱柱外接球的表面积为()A.48π B.64πC.84πD.144π【答案】C【解析】如图,D 为棱BC 的中点,G 为正△ABC 的中心,O 为外接球的球心根据直棱柱外接球的性质可知OG ∥AA 1,OG =12AA 1=3,外接球半径R =OC ,∵正△ABC 的边长为6,则CG =23∴R 2=OC 2=OG 2+CG 2=21外接球的表面积S =4πR 2=84π故选:C .题型五:直棱锥模型1(2024·全国·高三专题练习)在四棱锥P -ABCD 中,已知底面ABCD 为矩形,PA ⊥底面ABCD ,PA =6,AB =1,AD =3,则四棱锥P -ABCD 的外接球O 的表面积是()A.80π B.160π C.60πD.40π【答案】D【解析】由题意底面矩形的外接圆半径r =121+3=1,则原四棱锥外接球半径R =r 2+h 22=10,S =4πR 2=40π故选:D2(2024·河南·濮阳一高高一期中)已知三棱锥D -ABC 中,AD ⊥底面ABC ,AD =2,BC =1,∠BAC =30°,则此几何体外接球的体积为()A.43π B.4πC.82π3D.8π【答案】C【解析】解:设底面△ABC 外接圆的半径为r ,则2r =BC sin ∠BAC=112=2,设外接球的半径为R ,则2R 2=2r 2+AD 2,即2R 2=22+22=8,所以R =2,所以外接球的体积V =4πR 33=4π2 33=82π3;故选:C3(2024·黑龙江·勃利县高级中学高一期中)据《九章算术》记载,“鳖臑”为四个面都是直角三角形的三棱锥.如图所示,现有一个“鳖臑”,PA⊥底面ABC,AB⊥BC,且PA=AB=BC=2,三棱锥外接球表面积为()A.10πB.12πC.14πD.16π【答案】B【解析】如图,将三棱锥补形为正方体,则外接球半径R=PC2=AP2+AB2+BC22=4+4+42=3.所以三棱锥外接球表面积S=4πR2=4π×3=12π.故选:B.题型六:正棱锥与侧棱相等模型1(2024·江苏南通·高三期末)已知正四棱锥P-ABCD的底面边长为22,侧棱PA与底面ABCD所成的角为45°,顶点P,A,B,C,D在球O的球面上,则球O的体积是()A.16πB.323π C.8π D.823π【答案】B【解析】在正四棱锥P-ABCD中,连接AC,BD,AC∩BD=O ,连PO ,如图,则有PO ⊥平面ABCD ,∠PAO 为侧棱PA 与底面ABCD 所成的角,即∠PAO =45°,于是得O P =O A =O B =O C =O D =22AB =2,因此,顶点P ,A ,B ,C ,D 在以O 为球心,2为半径的球面上,即点O 与O 重合,所以球O 的体积是V =43π×23=323π.故选:B2(2024·江苏·扬中市第二高级中学高二阶段练习)已知正三棱锥P -ABC 的四个顶点都在半径为R 的球面上,且AB =2,若三棱锥P -ABC 体积为32R ,则该球的表面积为()A.32π9B.64π9C.64π27D.16π9【答案】B【解析】如图,PG 为正三棱锥P -ABC 的高,则其外接球的球心O 在PG 上,且OA =OP ,延长AG 交BC 于D ,则AD =32AB =3,所以AG =23AD =233,因为三棱锥P -ABC 体积为32R ,所以13S △ABC ⋅PG =13×34×22⋅PG =32R ,得PG =32R ,在直角△AOG 中,AG 2+OG 2=OA 2,所以233 2+32R -R 2=R 2,解得R 2=169,所以该球的表面积为4πR 2=4π⋅169=64π9,故选:B3(2024·重庆市实验中学高一阶段练习)三棱锥P -ABC 体积为36,且PA =PB =PC ,AB =AC =1,BC =3,则三棱锥外接球的表面积为.【答案】254π【解析】三棱锥P -ABC 中,取BC 中点D ,连PD ,连AD 并延长至O 1,使DO 1=AD ,连接BO 1,CO 1,PO 1,如图:于是得四边形ABO 1C 为平行四边形,而AB =AC =1,▱ABO 1C 是菱形,在△ABC 中,BC =3,由余弦定理有cos ∠BAC =AB 2+AC 2-BC 22AB ⋅AC=-12,即∠BAC =120°,则∠ABO 1=60°,△ABO 1是正三角形,O 1A =O 1B =O 1C =1,于是得O 1是△ABC 外接圆圆心,因PA =PB =PC ,D 为BC 中点,则PD ⊥BC ,又AO 1⊥BC ,PD ∩AO 1=D ,PD ,AO 1⊂平面PAO 1,从而有BC ⊥平面PAO 1,PO 1⊥BC ,同理PO 1⊥AC ,而AC ∩BC =C ,从而得PO 1⊥平面ABC ,由球的截面小圆性质知,三棱锥P -ABC 外接球球心O 在直线PO 1上,又S △ABC =12AB ⋅AC sin120°=34,则V P -ABC =13PO 1⋅S △ABC =36,解得PO 1=2,设球O 的半径为R ,则OB =OP =R ,OO 1=|R -2|,Rt △OO 1B 中,O 1B 2+O 1O 2=OB 2,即1+(R -2)2=R 2,解得R =54,则球O 的表面积为S =4πR 2=25π4,所以三棱锥外接球的表面积为254π.故答案为:254π题型七:侧棱为外接球直径模型1(2024•本溪月考)已知三棱锥S -ABC 的所有顶点都在球O 的球面上,ΔABC 是边长为1的正三角形,SC 为球O 的直径,且SC =2;则棱锥V O -ABC :V O -SAB =()A.1:1B.1:2C.2:1D.1:3【解析】解:根据题意作出图形:设球心为O ,过ABC 三点的小圆的圆心为O 1,则OO 1⊥平面ABC ,延长CO 1交球于点D ,则SD ⊥平面ABC .∵CO 1=23×32=33,∴OO1=12-33 2=63,∴高SD=2OO1=263,∵ΔABC是边长为1的正三角形,∴SΔABC=34,∴V S-ABC=13×34×263=26.V O-ABC=13×34×63=212,∴V O-SAB=V S-ABC-V O-ABC=26-212=212,∴棱锥V O-ABC:V O-SAB=1:1.故选:A.2(2024•云南校级月考)已知三棱锥S-ABC的所有顶点都在球O的球面上,ΔABC是边长为2的正三角形,SC为球O的直径,且SC=4,则此棱锥的体积为()A.423B.433C.823D.42【解析】解:因为ΔABC是边长为2的正三角形,所以ΔABC外接圆的半径r=23 3,所以点O到平面ABC的距离d=R2-r2=26 3,SC为球O的直径,点S到平面ABC的距离为2d=463,此棱锥的体积为V=13SΔABC×2d=13×3×463=423,故选:A.3(2024•防城港模拟)体积为26的三棱锥S-ABC的所有顶点都在球O的球面上,已知ΔABC是边长为1的正三角形,SC为球O的直径,则球O的表面积为()A.πB.2πC.4πD.6π【解析】解:根据题意作出图形:设球心为O,球的半径r.过ABC三点的小圆的圆心为O1,则OO1⊥平面ABC,延长CO1交球于点D,则SD⊥平面ABC.∵CO1=23×32=33,∴OO1=r2-13,∴高SD=2OO1=2r2-13,∵ΔABC是边长为1的正三角形,∴SΔABC=34,∴V三棱锥S-ABC =13×34×2r2-13=26,∴r=1.则球O的表面积为4π故选:C.题型八:共斜边拼接模型1(2024·安徽·芜湖一中高二期中)已知三棱锥P-ABC中,PA=1,PB=3,PC=5,AB=22,CA=CB=2,则此三棱锥的外接球的表面积为()A.14π3B.28π3C.9πD.12π【答案】C【解析】因为PA=1,AB=22,PB=3,则PB2=PA2+AB2,所以PA⊥AB,又因为AB=22,BC=2,AC=2,则AB2=BC2+AC2,所以AC⊥BC,由PA=1,AC=2,PC=5,则PC2=PA2+AC2,所以PA⊥AC,又由PC=5,BC=2,PB=3,则PB2=PC2+BC2,所以PC⊥BC,可得PB为三棱锥P-ABC的外接球的直径,又由PC2=PA2+AC2+BC2=1+4+4=9,所以此三棱锥的外接球半径为R=4+4+12=32,所以球的表面积为S=4πR2=9π.故选:C.2(2024·江西赣州·高二期中)在三棱锥A -SBC 中,AB =10,∠ASC =∠BSC =π4,AC =AS ,BC =BS 若该三棱锥的体积为153,则三棱锥A -SBC 外球的体积为()A.πB.π3C.5πD.43π【答案】D【解析】如图所示:设SC 的中点为O ,AB 的中点为D ,连接OA 、OB 、OD ,因为∠ASC =∠BSC =π4,AC =AS ,BC =BS ,所以∠SAC =∠SBC =π2,则OA =OB =OC =OS ,所以O 为其外接球的球心,设球的半径为R ,因为OD ⊥AB ,AB =10,所以AD =DB =102,OD =R 2-102 2,所以S △AOB =12⋅AB ⋅OD =1210R 2-25,因为SC ⊥OA ,SC ⊥OB ,OA ∩OB =O ,所以SC ⊥平面AOB ,所以V A -SBC =13⋅S AOB ⋅SC =13⋅1210R 2-25⋅2R =153,解得R =3,所以其外接球的体积为V =43⋅π⋅R 3=43π,故选:D3(2024·全国·高三专题练习)三棱锥D-ABC中,AB=DC=3,AC=DB=2,AC⊥CD,AB⊥DB.则三棱锥D-ABC外接球的表面积是( ).A.9πB.13πC.36πD.52π【答案】B【解析】取AD的中点为O,连接OC,OB,因为AC⊥CD,AB⊥DB∴OC=OA=OD=OB即O为棱锥D-ABC外接球的球心,又AB=DC=3,AC=DB=2,∴AD=22+32=13,∴三棱锥D-ABC外接球的表面积为13π.故选:B.题型九:垂面模型1(2024·全国·高三专题练习)四棱锥P-ABCD的底面ABCD是矩形,侧面PAD⊥平面ABCD,∠APD=120°,AB=PA=PD=2,则该四棱锥P-ABCD外接球的体积为()A.32π3B.205π3C.86πD.36π【答案】B【解析】取AD的中点E,连接PE,△PAD中,∠APD=120°,PA=PD=2∴PE=1,AD=23,设ABCD的中心为O ,球心为O,则O B=12BD=2,设O到平面ABCD的距离为d,则R2=d2+22=22+(2-d)2,∴d=1,R=5,∴四棱锥P-ABCD的外接球的体积为43πR3=2053π.故选:B.2(2024·山西·祁县中学高三阶段练习(文))已知四棱锥P-ABCD的底面为矩形,平面PBC⊥平面ABCD,PE⊥BC于E,EC=1,AB=26,BC=3,PE=2,则四棱锥P-ABCD外接球的表面积为()A.36πB.39πC.42πD.66π【答案】A【解析】如图,设ΔPBC外接圆圆心为O1,半径为r,因为BC=3,EC=1,所以BE=2,又PE⊥BC,PE=2,所以∠PBE=45°,由正弦定理可得:PCsin∠PBC =2r,即2r=PCsin∠PBE=PE2+EC2sin45°=522=10,所以r=10 2,因为底面ABCD为矩形,则四棱锥P-ABCD外接球的球心到平面PBC的距离与到AD的距离相等,设四棱锥P-ABCD外接球的球心为O,半径为R,则易知:OO1=12AB=262,所以有R2=r2+OO12=1022+262 2=9,所以外接球表面积为S=4πR2=36π.故选:A3(2024·福建·厦门一中高三阶段练习(理))三棱锥P-ABC中,PA=PB=22,AB=4,BC=3,AC=5,若平面PAB⊥平面ABC,则三棱锥P-ABC外接球的表面积为.【答案】25π【解析】由AB=4,BC=3,AC=5,可知△ABC是角B为直角的直角三角形.即BC⊥AB.取AC中点F,则F是△ABC的外心.取AB中点E,连接PE,EF,则PE⊥AB.在Rt△PAE,PA=22,AE=2,所以PE=2.又平面PAB⊥平面ABC,∴PE⊥平面ABC.又PE⊂平面ABC所以PE⊥EF.由E,F分别为AB,AC的中点,则EF⎳BC.则EF=3 2,所以在直角△PEF中,PF=EF2+PE2=322+22=52又在直角三角形△ABC中,F是AC中点.所以AF=AC=BF=12AC=52所以AF=AC=BF=PF=5 2所以三棱锥P-ABC外接球的球心为点F,半径为5 2所以三棱锥P-ABC外接球的表面积为S=4π×522=25π故答案为:25π题型十:最值模型1(2024·贵州遵义·高三开学考试)已知三棱锥S-ABC的四个顶点均在体积为323π的球面上,AB=BC=1,AC=3,则三棱锥S-ABC的体积的最大值为()A.23+312B.3+14C.23+34D.3+112【答案】A【解析】若球体半径为R,则43πR3=323π,可得R=2,而底面ABC中AB=BC=1,AC=3,易得:cos B=AB2+BC2-AC22AB⋅BC=-12,又0<B<π,故B=120°,则底面外接圆半径为r=AC2sin B=1,要使三棱锥S-ABC的体积的最大,只需S在球面上离面ABC最远,而R2-r2=3,所以S在球面上离面ABC最远距离为3+2,故最大体积V S -ABC =13×(3+2)×12×1×1×sin120°=3+2312.故选:A2(2024·全国·三模)已知三棱锥S -ABC 的体积为2833,其外接球的体积为5003π,若AB =AC =4,∠BAC =120°,则线段SA 的长度的最小值为()A.8 B.52C.6D.42【答案】B【解析】如图,O 1是△ABC 所在截面圆圆心,O 是球心,OO 1⊥平面ABC ,SH ⊥平面ABC ,H 为垂足,连接HA ,HO 1,则SH ⊥AH ,SH ⊥O 1H ,则OO 1⎳SH ,AB =AC =4,∠BAC =120°,则BC =2AB sin60°=43,2O 1A =BC sin ∠BAC ,O 1A =432sin120°=4,S △ABC =12×4×4×sin120°=43,由V S -ABC =13S △ABC⋅SH 得SH =7,由球体积V =43πR 3得43πR 3=5003π,R =5,即OS =OA =5,OO 1=OA 2-O 1A 2=52-42=3,在直角梯形SOO 1H 中,O 1H =OO 12-(SH -OH )2=3,即H 在以O 1为圆心,3为半径的圆上,AH min =AO 1-O 1H =4-3=1,所以SA min =72+12=52.故选:B .3(2024·辽宁抚顺·一模)已知三棱柱ABC -A 1B 1C 1的顶点都在球O 的表面上,且AC =BC ,∠ACB =2π3,若三棱柱ABC -A 1B 1C 1的侧面积为12+63,则球O 的表面积的最小值是()A.8πB.12πC.24πD.32π【答案】C【解析】依题意可知三棱柱ABC -A 1B 1C 1是直三棱柱,设其高为h ,设AB =c ,AC =BC =a ,则a +a +c ×h =12+63,h =12+632a +c,h 24=14×12+632a +c 2=6+332a +c 2=63+3634a 2+c 2+4ac,由余弦定理得c2=a2+a2-2a2cos 2π3,即c2=3a2,c=3a,设三角形ABC的外接圆半径为r,则csin2π3=2r,r=c3,所以球O的半径R2=r2+h22=c23+h24=c23+63+363 4a2+c2+4ac=a2+63+3637+43a2=a2+9a2≥2a2⋅9a2=6,当且仅当a4=9,a2=3,a=3时等号成立.所以球O的表面积的最小值为4π×6=24π.故选:C题型十一:二面角模型1(2024·全国·高三专题练习)在三棱锥P-ABC中,△ABC为等腰直角三角形,AB=AC=2,△PAC为正三角形,且二面角P-AC-B的平面角为π6,则三棱锥P-ABC的外接球表面积为()A.529π B.49π C.283π D.329π【答案】C【解析】如图所示,△ABC为直角三角形,又AB=AC=2,所以BC=22,因为△PAC为正三角形,所以PA=PC=AC=2,连接PD,DE,D为AC的中点,E为BC中点,则PD⊥AC,DE⊥AC,所以∠PDE为二面角P-AC-B的平面角所以∠PDE=30°.因为△ABC为直角三角形,E为BC中点,所以点E为△ABC的外接圆的圆心,设G为△PAC的中心,则G为△PAC的外接圆圆心.过E作面ABC的垂线,过G作面PAC的垂线,设两垂线交于O.则O即为三棱锥P-ABC的外接球球心.设GO与DE交于点H,GD =13PD =33,DH =DG cos30°=33×23=23,所以HE =DE -DH =13,OE =HE ×tan60°=33,∴R 2=CO 2=CE 2+EO 2=2+13=73.所以S =4πR 2=283π,故选:C .2(2024·江苏·南京市金陵中学河西分校高三阶段练习)在三棱锥A -BCD 中,△BCD 是边长为3的正三角形,且AD =3,AB =23,二面角A -BD -C 的大小为π3,则此三棱锥外接球的体积为.【答案】1313π6【解析】根据题意,AD 2+BD 2=AB 2,所以AD ⊥BD ,取BD 中点为E ,AB 中点M ,则ME ⎳AD ,ME =12AD =32,ME ⊥DB ,△BCD 是正三角形,CE ⊥DB ,∠MEC 是二面角A -BD -C 的平面角,∠MEC =60°,∠ADB =90°,M 是△ADB 的外心,设N 是△DBC 的外心,设过M 与平面ABD 垂直的直线与过N 垂直于平面BCD 的直线交于点O ,则O 是三棱锥A -DBC 外接球球心,CN =BN =33×3=3,EN =32,又EM =32,由于平面MNO 与MEO 同时垂直于BD ,所以M 、E 、N 、O 共面,在四边形MENO 中,由∠MEC =60°,EN =32,ME =32,∠OME =∠ONE =900,可得:ON =12,外接球半径为r =OB =BN 2+ON 2=3+14=132,体积为V =43π×132 3=13136π.故答案为:13136π3(2024·全国·高三专题练习)四边形ABDC 是菱形,∠BAC =60°,AB =3,沿对角线BC 翻折后,二面角A -BD -C 的余弦值为-13,则三棱锥D -ABC 的外接球的体积为.【答案】6π【解析】如图,取BC 的中点为M ,连接AM ,DM ,则AM ⊥BC ,DM ⊥BC ,则二面角A -BC -D 的平面角为∠AMD ,AB =3,由四边形ABDC 是菱形,∠BAC =60°可知△ABC ,△DBC 为正三角形,设球心O 在平面ABC 内的射影为O 1,在平面BCD 内的射影为O 2,则O 1,O 2为△ABC ,△DBC 的中心,所以DM =32,DO 2=1,O 2M =12,由于二面角A -BD -C 的余弦值为-13,故设∠AMD =2θ,θ∈π4,π2 ,则cos2θ=2cos 2θ-1=-13,cos 2θ=13,故sin 2θ=23,则tan θ=2,∴OO 2=O 2M tan θ=22,球O 的半径R =DO 22+OO 22=62,所求外接球的体积为V =43π623=6π,题型十二:圆锥圆柱圆台模型1(2024·全国·高三专题练习)如图,半径为4的球O 中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与圆柱的表面积之差为()A.64πB.48πC.32πD.16π【答案】D 【解析】如图.设圆柱底面半径为r ,球的半径与圆柱底面夹角为∠OMN =α,则MN =r =R ⋅cos α=4cos α,ON =R ⋅sin α=4sin α,∴圆柱的高h =8sin α,∴圆柱的侧面积为S =2π⋅r ⋅h =32π⋅sin2α,当且仅当α=π4时,sin2α=1,圆柱的侧面积最大,为32π,球的表面积与圆柱的表面积之差为4πR 2-2πrh -2×π(22)2=64π-32π-16π=16π.故选:D .2(2024·云南昆明·高三开学考试)“云南十八怪”描述的是由云南独特的地理位置、民风民俗所产生的一些特有的现象或生活方式,是云南多元民族文化的写照.“云南十八怪”中有一怪“摘下草帽当锅盖”所指的锅盖是用秸秆或山茅草编织成的,因其形状酷似草帽而传为佳话.一种草帽锅盖呈圆锥形,其母线长为6dm ,侧面积为183πdm 2,若此圆锥的顶点和底面圆都在同一个球面上,则该球体的表面积等于dm 2.【答案】144π【解析】设圆锥的底面半径为r ,由πr ×6=183π,解得r =33πdm ,如图AB =33πdm ,设外接球的球心为O 半径为R ,由PB ⊥圆B 得AB 2+PB 2=AP 2,即27+PB 2=36,解得PB =3,由AB 2+R -PB 2=R 2得R =6,所以该球体的表面积等于4π×62=144πdm 2 .3(2024·全国·高三专题练习)已知圆台上底半径为1,下底半径为3,高为2,则此圆台的外接球的表面积为.【答案】40π【解析】如图所示,设外接球半径为r ,球心到上底的距离为h ,则球心到下底的距离为|h -2|则有r 2=1+h 2,r 2=9+(2-h )2,解得h =3,r =10.所以外接球的表面积为4πr 2=40π.故答案为:40π题型十三:锥体内切球1(2024·全国·高三专题练习)已知三棱锥A -BCD 中,AB =CD =2,AD =AC =BC =BD =3,则该三棱锥内切球的表面积为.【答案】7π8【解析】如图,在长方体AHDG -EBFC 中,设EC =c ,EB =b ,EA =a ,则a 2+b 2=4,c 2+b 2=9,a 2+c 2=9,所以a =b =2,c =7,故四面体ABCD 的体积V =abc -4×13×12abc =273,四面体ABCD 的表面积S =4S △ABC =4×12×2×32-12=82,设三棱锥内切球的半径为r ,由等体积可得273=13×82r ,解得r =742,所以三棱锥内切球的表面积为4π×7422=7π8.故答案为:7π8.2(2024·全国·高三专题练习)已知△ABC 中,AB =4,BC =3,AC =5,以AC 为轴旋转一周得到一个旋转体,则该旋转体的内切球的表面积为()A.4936π B.57649π C.57625π D.34525π【答案】B【解析】旋转体的轴截面如图所示,其中O 为内切球的球心,过O 作AB ,BC 的垂线,垂足分别为E ,F ,则OE =OF =r (r 为内切球的半径),故AO =r sin ∠BAC =53r ,CO =r sin ∠BCA =54r ,故5=AO +OC =53r +54r ,故5=AO +OC =53r +54r ,故r =127,故旋转体的内切球的表面积为4π×127 2=57649π,故选:B3(2024·甘肃酒泉·模拟预测)三棱锥A -BCD 中,AB ⊥平面BCD ,BC ⊥CD ,且AB =CD =4,BC =3,则该三棱锥内切球的表面积为()A.916π B.94π C.169π D.43π【答案】B 【解析】由AB⊥平面BCD,CD⊂平面BCD,得AB⊥CD.又BC⊥CD,且AB,BC⊂平面ABC,AB∩BC= B,所以CD⊥平面ABC,又AC⊂平面ABC,所以CD⊥AC.由AB=CD=4,BC=3,得AC=BD=5,所以三棱锥A-BCD的表面积S=2×12×3×4+2×12×4×5=32,三棱锥A-BCD的体积V=13×12×3×4×4=8.设三棱锥内切球球心为O,半径为r,由V=V O-ABC+V O-ABD+V O-ACD+V O-BCD=13Sr,得r=3VS=34,所以该三棱锥内切球的表面积S球=4πr2=4π×916=94π.故选:B.题型十四:棱切球1(2024·江西·进贤县第一中学高二期中)球与棱长为32的正四面体各条棱都相切,则该球的表面积为()A.6πB.18πC.9πD.10π【答案】C【解析】将正四面体补形为一个正方体如图所示(红色线条表示正四面体),则正四面体的棱为正方体的面对角线,因为球与正四面体的各条棱都相切,所以球与正方体的各个面都相切,所以所求的球为正方体的内切球,又因为正方体的棱长为322=3,所以球的半径R=32,所以球的表面积为:4π⋅322=9π,故选:C.。
高中数学关于球的内切外接问题

处理球的“内切”“外接”问题与球有关的组合体问题,一种是内切,一种是外接。
作为这种特殊的位置关系在高考中也是考查的重点,但同学们又因缺乏较强的空间想象能力而感到模糊。
解决这类题目时要认真分析图形,明确切点和接点的位置及球心的位置,画好截面图是关键,可使这类问题迎刃而解。
一、棱锥的内切、外接球问题例1.正四面体的外接球和内切球的半径是多少? 分析:运用正四面体的二心合一性质,作出截面图,通过点、线、面关系解之。
解:如图1所示,设点O 是内切球的球心,正四面体棱长为a .由图形的对称性知,点O 也是外接球的球心.设内切球半径为r ,外接球半径为R .正四面体的表面积223434a a S =⨯=表. 正四面体的体积22221234331BE AB a AE a V BCD A -=⨯⨯=- BCD A V r S -=⋅表31Θ,a aaS V r BCD A 12631223323=⨯==∴-表在BEO Rt ∆中,222EO BE BO +=,即22233r a R +⎪⎪⎭⎫ ⎝⎛=,得a R 46=,得r R 3= 【点评】由于正四面体本身的对称性可知,内切球和外接球的两个球心是重合的,为正四面体高的四等分点,即内切球的半径为4h ( h 为正四面体的高),且外接球的半径43h,从而可以通过截面图中OBE Rt ∆建立棱长与半径之间的关系。
图1例2.设棱锥ABCD M -的底面是正方形,且MD MA =,AB MA ⊥,如果AMD ∆的面积为1,试求能够放入这个棱锥的最大球的半径.解:?⊥∴⊥⊥AB MA AB AD AB ,,Θ平面MAD , 由此,面⊥MAD 面AC .记E 是AD 的中点, 从而AD ME ⊥.⊥∴ME 平面AC ,EF ME ⊥设球O 是与平面MAD 、平面AC 、平面MBC 都相切的球.如图2,得截面图MEF ∆及内切圆O不妨设∈O 平面MEF ,于是O 是MEF ∆的内心. 设球O 的半径为r ,则MFEM EF S r MEF++=∆2,设a EF AD ==,1=∆AMD S Θ.222,2⎪⎭⎫⎝⎛+==∴a a MF a EM ,12222222222-=+≤⎪⎭⎫⎝⎛+++=a a a a r当且仅当aa 2=,即2=a 时,等号成立. ∴当2==ME AD 时,满足条件的球最大半径为12-.练习:一个正四面体内切球的表面积为π3,求正四面体的棱长。
立体几何中的“内切”与“外接”问题的探究(完美版)

立体几何中的“内切”与“外接”问题的探究一、由球心的定义确定球心在空间,如果一个定点与一个简单多面体的所有顶点的距离都相等,那么这个定点就是该简单多面体的外接球球心。
二、由上述性质可以得出以下多面体外接球的结论:结论1:正方体或长方体的外接球的球心是其体对角线的中点。
结论2:正棱柱的外接球的球心是上下底面中心的连线的中点。
结论3:直三棱柱的外接球的球心是上下底面三角形外心的连线的中点。
结论4:正棱锥的外接球的球心是在其高上,具体位置可通过计算得到。
结论5:若棱锥的顶点可构成共斜边的直角三角形,则共斜边的中点就是其外接球的球心。
一、定义法例1、 在矩形ABCD 中,4,3AB BC ==,沿AC 将矩形ABCD 折成一个直二面角B AC D --,则四面体ABCD 的外接球的体积为A.12512πB.1259πC.1256πD.1253π 解 设矩形对角线的交点为O ,则由矩形对角线互相平分,可知OA OB OC OD ===.∴点O 到四面体的四个顶点A B C D 、、、的距离相等,即点O 为四面体的外接球的球心,如图2所示.∴外接球的半径52R OA ==.故3412536V R ππ==球.选C.二、求正方体、长方体的外接球的有关问题结论1:正方体或长方体的外接球的球心是其体对角线的中点。
①出现“墙角”结构利用构造法(补形法),联系长方体。
【原理】:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为222c b a l ++=,几何体的外接球直径R 2为体对角线长l 即2222c b a R ++=例1、若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 . 解 据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三棱锥可以补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球.设其外接球的半径为R ,则有()()()()222223339R =++=.∴294R =. 故其外接球的表面积249S R ππ==.小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2222R a b c =++.②出现正四面体外接球时利用构造法(补形法),联系正方体。
高考数学中的内切球和外接球问题---专题复习

高考数学中的内切球和外接球问题---专题复习高考数学:内切球和外接球问题多面体的顶点都在同一球面上时,称该多面体为球的内接多面体,该球为多面体的外接球。
多面体外接球问题是立体几何的重点,也是高考的热点,考查学生的空间想象能力和化归能力。
解决该问题需要运用多面体和球的知识,并特别注意多面体的几何元素与球的半径之间的关系。
多面体外接球半径的求法在解题中往往起到至关重要的作用。
一、直接法(公式法)1、求正方体的外接球的有关问题例1:若正方体的棱长为3且顶点都在同一球面上,求该球的表面积。
解析:要求球的表面积,只需知道球的半径。
由于正方体内接于球,所以它的体对角线正好为球的直径,因此求球的半径可转化为先求正方体的体对角线长,再计算半径。
故表面积为27π。
例2:一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为多少?解析:要求球的体积,还需先求出球的半径。
由正方体表面积可求出棱长,从而求出正方体的体对角线长为3√3.因此,该球的半径为3,故该球的体积为36π。
2、求长方体的外接球的有关问题例1:一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1、2、3,则该球的表面积为多少?解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。
长方体体对角线长为√14,故球的表面积为14π。
例2:已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则该球的表面积为多少?解析:正四棱柱也是长方体。
由长方体的体积16及高4可以求出长方体的底面边长为2,因此,长方体的长、宽、高分别为2、2、4.故该球的表面积为24π。
3、求多面体的外接球的有关问题例:一个底面为正六边形的六棱柱,侧棱垂直于底面,已知该六棱柱的顶点都在同一球面上,且该六棱柱的体积为8,底面周长为3,则该球的体积为多少?解析:设正六棱柱的底面边长为x,高为h。
由底面周长可得x=3/6=1/2,由体积可得h=4/3.因此,正六棱柱的底面圆的半径为√3/2,外接球的半径为√13/2.故该球的体积为(52/3)π。
正四面体内切球和外接球(好用).ppt.ppt
[题组冲关] 3.假如某爱国实业家在20世纪初需要了解全国各地商业信
息,可采用的最快捷的方式是
(
)
A.乘坐飞机赴各地了解 B.通过无线电报输送讯息 C.通过互联网 D.乘坐火车赴各地了解
解析:本题考查中国近代物质生活的变迁。注意题干信 息“20世纪初”“最快捷的方式”,因此应选B,火车速度
远不及电报快。20世纪30年代民航飞机才在中国出现,
1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A.打破了外商对中国航运业的垄断 B.阻止了外国对中国的经济侵略 C.标志着中国近代化的起步 ( )
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵
(2)1924年国民党“一大”召开,标志着第 一
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)20世纪初,孙中山提出“民族、民权、 民生”三民主义,成为以后辛亥革命 的
指导思想。 (2)三民主义没有明确提出反帝要求,也 没 有提出废除封建土地制度,是一个 不彻 底的资产阶级革命纲领。
报先后发明。
(3)近代以来,交通、通讯工具的进步,推 动了经济与社会的发展。
关键词——交通和通讯不断进步、辛亥革命和国民大革命顺应 时 代潮流 图说历史 主旨句归纳 (1)1911年,革命党人发动武昌起义,辛亥
革命
爆发,随后建立了中华民国,颁布了《中 华
民国临时约法》;辛亥革命是中国近代化
高中数学立体几何之外接球与内切球问题常见模型归纳(完整版)
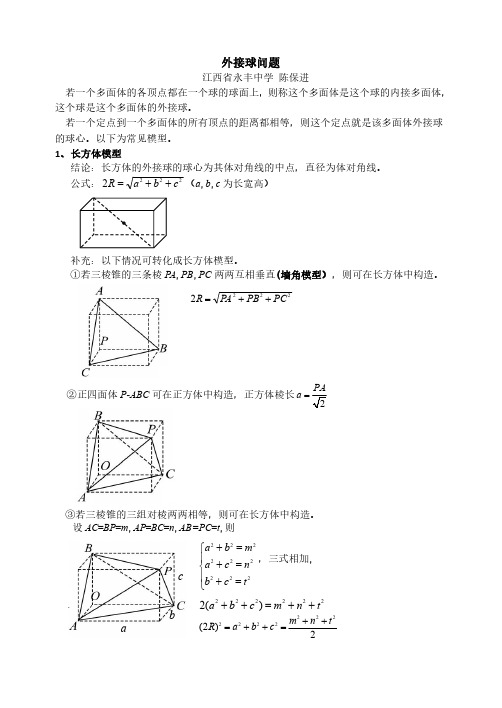
外接球问题江西省永丰中学陈保进若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。
若一个定点到一个多面体的所有顶点的距离都相等,则这个定点就是该多面体外接球的球心。
以下为常见模型。
1、长方体模型结论:长方体的外接球的球心为其体对角线的中点,直径为体对角线。
公式:2222c b a R ++=(a ,b ,c 为长宽高)补充:以下情况可转化成长方体模型。
①若三棱锥的三条棱PA ,PB ,PC 两两互相垂直(墙角模型),则可在长方体中构造。
2222PC PB P A R ++=②正四面体P -ABC 可在正方体中构造,正方体棱长2=PA a ③若三棱锥的三组对棱两两相等,则可在长方体中构造。
设AC =BP =m ,AP =BC =n ,AB=PC =t ,则⎪⎩⎪⎨⎧=+=+=+222222222t c b n c a m b a ,三式相加,222222)(2t n m c b a ++=++2)2(2222222t n m c b a R ++=++=abc2、直三棱柱模型结论:直三棱柱外接球的球心是上、下底面外心连线的中点,222()2hR r =+r 为底面三角形外接圆的半径,可用正弦定理求,h 为直三棱柱的高。
补充:有一条侧棱垂直底面的三棱锥可补成直三棱柱,如图P -ABC 中,PA ⊥平面ABC ,则可补成直三棱柱PB 1C 1-ABC ,外接球半径公式同上。
提醒:底面具有外接圆的直棱柱才有外接球,比如正棱柱,且球心在上、下底面外心连线的中点,底面无外接圆的直棱柱,以及所有斜棱柱均无外接球。
3、共斜边模型四面体D-ABC 中,DC AD ⊥,BC AB ⊥,AC 为公共的斜边,O 为AC 的中点,则O 为四面体D-ABC 外接球的球心。
4、正棱锥模型外接球的球心在正棱锥的高所在直线上,如图正三棱锥A-BCD 中,作AO 1⊥平面BCD ,则易得BO 1=CO 1=DO 1,所以O 1为△BCD 的外心,设O 为其外接球球心,半径为R ,则BO =AO =R ,设AO 1=h ,BO 1=r ,则由BO 2=BO 12+OO 12,得R 2=r 2+(h-R )2。
专题讲解 立体几何中的外接球与内切球问题(学生版)
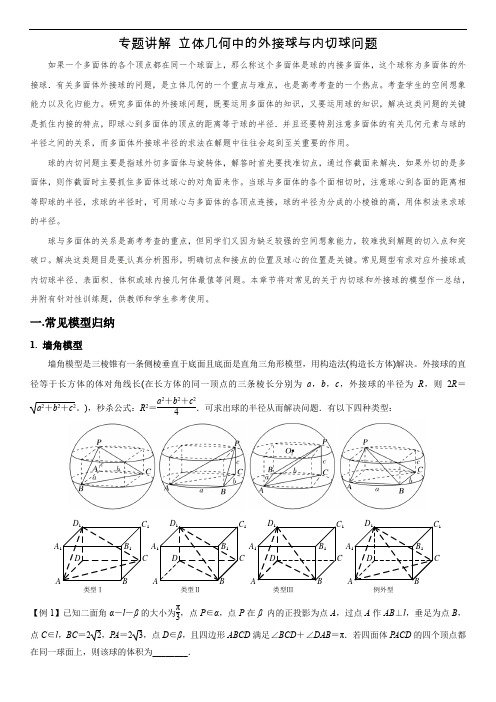
专题讲解立体几何中的外接球与内切球问题如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点与难点,也是高考考查的一个热点。
考查学生的空间想象能力以及化归能力。
研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,解决这类问题的关键是抓住内接的特点,即球心到多面体的顶点的距离等于球的半径.并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用。
球的内切问题主要是指球外切多面体与旋转体,解答时首先要找准切点,通过作截面来解决.如果外切的是多面体,则作截面时主要抓住多面体过球心的对角面来作。
当球与多面体的各个面相切时,注意球心到各面的距离相等即球的半径,求球的半径时,可用球心与多面体的各顶点连接,球的半径为分成的小棱锥的高,用体积法来求球的半径。
球与多面体的关系是高考考查的重点,但同学们又因为缺乏较强的空间想象能力,较难找到解题的切入点和突破口。
解决这类题目是要认真分析图形,明确切点和接点的位置及球心的位置是关键。
常见题型有求对应外接球或内切球半径、表面积、体积或球内接几何体最值等问题。
本章节将对常见的关于内切球和外接球的模型作一总结,并附有针对性训练题,供教师和学生参考使用。
一.常见模型归纳1. 墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决。
外接球的直径等于长方体的体对角线长(在长方体的同一顶点的三条棱长分别为a,b,c,外接球的半径为R,则2R=a 2+b2+c2。
),秒杀公式:R2=a2+b2+c24.可求出球的半径从而解决问题.有以下四种类型:【例1】已知二面角α-l-β的大小为π3,点P∈α,点P在β内的正投影为点A,过点A作AB⊥l,垂足为点B,点C∈l,BC=22,P A=23,点D∈β,且四边形ABCD满足∠BCD+∠DAB=π.若四面体P ACD的四个顶点都在同一球面上,则该球的体积为________.A BCDA1B1C1D1类型ⅠA BCDA1B1C1D1类型ⅡA BCDA1B1C1D1类型ⅢA BCDA1B1C1D1例外型【例2】已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( ).A .68πB .64πC .62πD .6π【变式练习1】在空间直角坐标系Oxyz 中,四面体ABCD 各顶点的坐标分别为A (2,2,1),B (2,2,-1),C (0,2, 1),D (0,0,1),则该四面体外接球的表面积是( )A .16πB .12πC .43πD .6π【变式练习2】在长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为32的正方形,AA 1=3,E 是线段A 1B 1上一点, 若二面角A -BD -E 的正切值为3,则三棱锥A -A 1D 1E 外接球的表面积为________.2. 对棱相等模型对棱相等模型是三棱锥的三组对棱长分别相等模型,用构造法(构造长方体)解决。
等面四面体的内切球与外接球

等面四面体的内切球与外接球引理2 任意四面体都有内切球及外接球。
引理 3 任意四面体的内切球在四个面上的切点与各面顶点连线给出切点处的周角的一个相同划分。
证明 如图3—8,四面体ABCD 的内切球在各面上的切点分别为O 1、O 2、O 3、O 4.由于球外一点向球引的切线长相等,可得AO 2=AO 3=AO 4,BO 1=BO 3=BO 4,…. 于是△O 1BC ≌△O 4BC , △O 2CD ≌△O 1CD ,….可设∠CO 1D=∠CO 2D=α,∠DO 1B=∠DO 3B=β, ∠CO 1B=∠CO 4B=γ,∠AO 3B=∠AO 4B=x ,∠AO 2C=∠AO 4C=y ,∠AO 2D=∠AO 3D=z . 由周角360°,图3—8 得︒=++360γβα ①︒=++360γy x ② ︒=++360αz y ③ ︒=++360βx z ④ 四式相加,除以2,得︒=+++++720z y x γβα ⑤ ⑤式减①式,得︒=++360z y x ⑥ ⑥式分别与②、③、④式联立,可解得γβα===z y x引理3得证。
定理5 等面四面体的各顶点到内切球的切线长相等。
此定理的另一种叙述方式是:等面四面体内切球在各面上的切点是该面的外接圆圆心。
证明 如图3—8,由于△ABC ≌△DCB ,可移动并翻转△ABC ,使其与△DCB 重合(A 、B 、C 分别与D 、C 、B 重合). 现考察O 4与O 1的位置关系.假设O 4与O 1不重合,则O 4在△BO 1D 、△BO 1C 、△CO 1D 中的某一个内部或边上。
不失一般性,不妨设O 4点在△BO 1内或在BO 1上,则∠BO 4D>∠BO 1D,∠BO 4D 即是原△ABC 中的∠CO 4A 。
由引理3,得∠CO 4A=∠BO 1D ,存在矛盾,因此O 4必与O 1重合。
于是O 1B=O 4C=O 1C ,同理O 1D=O 1C ,即O 1是△BCD 的外心。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
M
●
D
C
3、若正四体的棱长都为a,内有一球与四个面都相
切,求球的半径.
解法1:球被截成的大圆与DP、DC 相切,连结EO,设球半径为r,
由 Rt PEO ∽ Rt PO1D
E
P
6 r a 12
A D B
O C
O1
3、若正四体的棱长都为a,内有一球与四个面都相切, 求球的半径
解法2:连结OA、OB、OC、 OP,那么
正方体的内切球
正方体的外接球
几个切点?切点在什么位置?
求棱长为a的正四面体的高.
P
6 PO a 3
A D B
C O
典例精析
1、若球O有一棱长为a
的内接正四面体,则球 的半径为__________.
4 3
A
球 的 组 合 体DLeabharlann C法一:B
法二、
6 R a 4
B ●
A●
R ● O1
● ●
O
·
D
6 R a 4
O
A B
H
C
6 r a 12
典例精析
1、在一个倒置的正三棱锥容器内放入一个钢球,
钢球恰与棱锥的四个面都接触,过棱锥的一条
侧棱和高作截面,正确的截面图形是( B )
A
B
C
D
考点练习 3、自球面上一点P作球的两两垂直的三条弦PA,PB, PC,球的半径为R,则PA2+PB2+PC2=( ) A、4 R 2 B、3R 2 C、2 R 2 D、 R2 2
P
VP ABC VOPAB VO PBC VO PCA VO ABC 4VO ABC
VO ABC
因VP ABC
1 S ABC OO1 , 3
1 S ABC PO1 , 3
A D
E
O C
O1 B
所以PO1 4r
6 r a 12
求棱长为a的正四面体的外接球 和它的内切球的体积之比
