工程力学A单辉祖第13章应力状态分析.ppt
合集下载
工程力学第十三章

2 2 2
3.单元体与应力圆的对应关系 点面对应;转向相同,转角二倍。 点面对应;转向相同,转角二倍。
证明: 证明:
应力状态分析
§13-3 极值应力与主应力 13正应力的极值——主应力、主平面的确定 主应力、 一、正应力的极值 主应力 dσ α =0 得 根据式(13- ),由求极值条件 由求极值条件, 根据式(13-1),由求极值条件, dα
n
xy x yx y
∑F
τ α dA (τ xy dA cos α )cos α (σ x dA cos α ) sin α
+ (σ y dA sin α )cos α + (τ yx dA sin α ) sin α = 0
t
=0
考虑切应力互等和三角变换, 考虑切应力互等和三角变换,得:
σα =
正应力取极值的面(也是切应力为零的面) 主平面, 正应力取极值的面(也是切应力为零的面)为主平面, 主方向, 主平面的外法线方向称主方向 正应力的极值称主应力 主平面的外法线方向称主方向,正应力的极值称主应力 对平面一般应力状态通常有两个非零主应力: ,对平面一般应力状态通常有两个非零主应力σ 、σ :
σx
τzx B
τxz
C
τ xy
主平面、主单元体、 六、主平面、主单元体、主应力
σ σyy
y
y
主平面( 1.主平面(Principal Plane): ) 切应力为零的截面。 切应力为零的截面。 主单元体(主平面微体) 2.主单元体(主平面微体):各侧 面上切应力均为零的单元体。 面上切应力均为零的单元体。 主平面上的正应力。 主平面上的正应力。 区分: 区分:正应力和主应力 4.主应力排列规定:按代数值大小 主应力排列规定: 代数值大小
3.单元体与应力圆的对应关系 点面对应;转向相同,转角二倍。 点面对应;转向相同,转角二倍。
证明: 证明:
应力状态分析
§13-3 极值应力与主应力 13正应力的极值——主应力、主平面的确定 主应力、 一、正应力的极值 主应力 dσ α =0 得 根据式(13- ),由求极值条件 由求极值条件, 根据式(13-1),由求极值条件, dα
n
xy x yx y
∑F
τ α dA (τ xy dA cos α )cos α (σ x dA cos α ) sin α
+ (σ y dA sin α )cos α + (τ yx dA sin α ) sin α = 0
t
=0
考虑切应力互等和三角变换, 考虑切应力互等和三角变换,得:
σα =
正应力取极值的面(也是切应力为零的面) 主平面, 正应力取极值的面(也是切应力为零的面)为主平面, 主方向, 主平面的外法线方向称主方向 正应力的极值称主应力 主平面的外法线方向称主方向,正应力的极值称主应力 对平面一般应力状态通常有两个非零主应力: ,对平面一般应力状态通常有两个非零主应力σ 、σ :
σx
τzx B
τxz
C
τ xy
主平面、主单元体、 六、主平面、主单元体、主应力
σ σyy
y
y
主平面( 1.主平面(Principal Plane): ) 切应力为零的截面。 切应力为零的截面。 主单元体(主平面微体) 2.主单元体(主平面微体):各侧 面上切应力均为零的单元体。 面上切应力均为零的单元体。 主平面上的正应力。 主平面上的正应力。 区分: 区分:正应力和主应力 4.主应力排列规定:按代数值大小 主应力排列规定: 代数值大小
工程力学13应力状态分析.ppt

t
sx
s y
2
sin 2
tx
cos 2
n
Ox
t
图2
§13–3 平面应力状态分析——图解法
sy
一、应力圆( Stress Circle)
sx
s
sx
s y
2
sx
s y
2
cos 2
t x
sin 2
y
tx
t
sx
s y
2
sin 2
tx
cos 2
Ox
sx
主平面上的正应力。
s1
主应力排列规定:按代数值大小,
s 1s 2 s 3
三向应力状态( Three—Dimensional State of Stress): 三个主应力都不为零的应力状态。
二向应力状态(Plane State of Stress): 一个主应力为零的应力状态。
单向应力状态(Unidirectional State of Stress): 一个主应力不为零的应力状态。
第十三章 应力状态分析
§13–1 应力状态的概念 §13–2 平面应力状态分析——解析法 §13–3 平面应力状态分析——图解法 §13–4 三向应力状态简介 §13–5 复杂应力状态下的应力--应变关系(广义虎克定律)
§13–1 应力状态的概念
一、引言
1、铸铁与低碳钢的拉、压、扭试验现象是怎样产生的?
P1
P2
q
1
2 3 4
5
sx ty tx
解:由梁弯曲应力公式:
s
x
My Iz
tx
QS
工程力学应力状态分析

H
x y 2
x y 2
cos2
s
x
i
n
2
同理:
H
五、应力圆的应用
§13-2 平面应力状态应力分析
H
H (, )
• 利用应力圆明晰的几何关
系推导并记忆一些基本公
式,避免死记硬背;
o
D H
C 220x
y
F
• 在应用过程中,应当将应 力圆作为思考、分析问题 的工具,而不是计算工具;
y E
(
x
2
y
)2
2
(
x
2
y
)2
x2
—坐标系下的圆方程
圆心坐标:
( x y , 0) 2
o
R
半径:
R
(
x 2
y
)2
2 x
(x+ y)/2
结论:平面应力状态下各方向的应力轨迹为一个圆
——应力圆
三、应力圆的绘制
绘制方法1:
§13-2 平面应力状态应力分析
以 ( x y , 0) 为圆心,
0
当
d d
0
时,正应力有极值。
2
x
y 2
sin2
c
x
o
s
2
0
最大正应力方位角α0:
tan2
0
2 x x
y
max x y
•
3、Patience is bitter, but its fruit is sweet. (Jean Jacques Rousseau , French thinker)忍耐是痛苦的,但它的果实是甜蜜的。08:305.26.202108:305.26.202108:3008:30:575.26.202108:305.26.2021
工程力学:第19课_第13章_应力状态分析(1)

x
F
y
x+y)/2 x-y)/2 x
设x面和y面的应力分别为 D( x , x ), E ( y , y ),
由于 x
y ,
故DE中点坐标
C(
x
2
y
,
0)
为圆心,DE为直径。
29
第十三章 应力状态分析
y
y y
n
x
x x
D
C x
o
y
F
绘图:以ED为直径,C为圆心作圆
y
面应力: 考察D点逆时针转动2α
2
60 cos60
=8.35MPa
还可取何值 150; 30 (x轴向左)
N 180 不改变 25
第十三章 应力状态分析
二、应力圆
一、应力圆
应力转轴公式
x
2
y
x
2
y
cos2
xsin2
x
2
y
sin2
xcos2
在 平面上, , 的轨迹?
应力转轴公式形式变换
x
2
推论:微体互垂截面,对应应力圆同一直径两端 微体平行对边, 对应应力圆同一点
32
第十三章 应力状态分析
几种简单受力状态的应力圆
单向受力状态
x
x
纯剪切受力状态 y
x
E 0,0
o
R=x/2
C
D x ,0
D 0,
R=x
o
双向等拉
C
o
x/2
D 0,
45º方向面上既有正应力又有 45º方向面上只有正应力无剪 剪应力,但正应力不是最大 应力,且正应力最大。 值,剪应力却最大。
工程力学第13章应力状态分析

解:⑴ 求C 点所在截面的剪力、弯矩 F
FS 2 50kN MFl 25kNm
8 ⑵ 求C 点在横截面上的正应力、切应力
M y 2 5 1 0 3 6 0 0 1 0 3/4
CIz 2 0 0 6 0 0 3 1 0 1 2/1 21 .0 4 M P a
C 3 2 F b h S(14 h y 2 2)2 2 3 0 0 5 0 6 0 0 1 0 3 1 0 6(14 6 0 1 0 5 2 0 2 1 0 1 0 6 6)
63.7sin240o( 76.4)cos240o 2
10.7MPa
x 63.7MPa y 0 x76.4MPa
⑶ 求D 点的主应力和主方向及最大切应力
m m a in x x 2y (x 2y)2x 2
63.7 2
(63.7)2(76.4)2 2
114.6M P a
50.9M
Pa
1 1 1 4 . 6 M P a2 03 5 0 . 9 M P a
D63.7MPa D76.4MPa
⑵ 作出D点的应力状态图
x 63.7MPa y 0 x76.4MPa
120o
x 2 y x 2 yc o s2 xsin 2
6 3 .7 6 3 .7 c o s2 4 0 o ( 7 6 .4 ) sin 2 4 0 o 22
50.3M Pa
x 2ysin2xcos2
同理:平行于主应力σ2和σ3方向的任意斜面 II 和 III 上的正 应力和切应力分别与σ2和σ3无关,可分别由应力圆 II 和 III 表
示。
三向应力状态中空间任 意方向面上的正应力和切 应力对应于应力圆I、II、 III所围阴影区域内某一点 的坐标值。
FS 2 50kN MFl 25kNm
8 ⑵ 求C 点在横截面上的正应力、切应力
M y 2 5 1 0 3 6 0 0 1 0 3/4
CIz 2 0 0 6 0 0 3 1 0 1 2/1 21 .0 4 M P a
C 3 2 F b h S(14 h y 2 2)2 2 3 0 0 5 0 6 0 0 1 0 3 1 0 6(14 6 0 1 0 5 2 0 2 1 0 1 0 6 6)
63.7sin240o( 76.4)cos240o 2
10.7MPa
x 63.7MPa y 0 x76.4MPa
⑶ 求D 点的主应力和主方向及最大切应力
m m a in x x 2y (x 2y)2x 2
63.7 2
(63.7)2(76.4)2 2
114.6M P a
50.9M
Pa
1 1 1 4 . 6 M P a2 03 5 0 . 9 M P a
D63.7MPa D76.4MPa
⑵ 作出D点的应力状态图
x 63.7MPa y 0 x76.4MPa
120o
x 2 y x 2 yc o s2 xsin 2
6 3 .7 6 3 .7 c o s2 4 0 o ( 7 6 .4 ) sin 2 4 0 o 22
50.3M Pa
x 2ysin2xcos2
同理:平行于主应力σ2和σ3方向的任意斜面 II 和 III 上的正 应力和切应力分别与σ2和σ3无关,可分别由应力圆 II 和 III 表
示。
三向应力状态中空间任 意方向面上的正应力和切 应力对应于应力圆I、II、 III所围阴影区域内某一点 的坐标值。
工程力学-应力状态

σ 30 100 50 2 100 50 2
sy
n
例1 已知 sx= –100MPa、sy =50MPa 、tx = – 60MPa,a = –30º
cos[2 ( 30)] ( 60)sin[2 ( 30)]
114.5MPa
τ 30
上海应用技术学院
τ T WP
此时不适用基本变形下的强度条件,应同时考虑s 、t 的影响。 又如:受内压容器筒壁
上海应用技术学院
sy
A 筒壁某点A处应力: sx 、sy,为双向受拉状态。 又如:火车车轮与铁轨接触处表层
4
sx
s s
A
s
A点应力:为三向受压状态。 此外:在通过A点不同斜截面上的应力是不同的,将影响到构 件的破坏形式。
s
OC CFcos2 α DFsin2 α σx σy σx σy cos2 α τ x sin2 α σ α 2 2
上海应用技术学院
证明: H点横坐标: OM 纵坐标: MH CD与s 轴夹角为2a0
OM σx σy 2 σx σy 2 cos2 α τ x sin2 α σ α
ty
e
cos2 α τ x sin2 α
b
sy
切线方向上: Σ F 0 τ
τ α d A (σ x d A cos α )sin α ( τ x d A cos α )cos α (σ y d A sin α )cos α ( τ y d A sin α )sin α 0
∴ τ α σ x sin α cos α σ y sin α cos α τ x cos2 α τ y sin 2 α
上海应用技术学院
sy
n
例1 已知 sx= –100MPa、sy =50MPa 、tx = – 60MPa,a = –30º
cos[2 ( 30)] ( 60)sin[2 ( 30)]
114.5MPa
τ 30
上海应用技术学院
τ T WP
此时不适用基本变形下的强度条件,应同时考虑s 、t 的影响。 又如:受内压容器筒壁
上海应用技术学院
sy
A 筒壁某点A处应力: sx 、sy,为双向受拉状态。 又如:火车车轮与铁轨接触处表层
4
sx
s s
A
s
A点应力:为三向受压状态。 此外:在通过A点不同斜截面上的应力是不同的,将影响到构 件的破坏形式。
s
OC CFcos2 α DFsin2 α σx σy σx σy cos2 α τ x sin2 α σ α 2 2
上海应用技术学院
证明: H点横坐标: OM 纵坐标: MH CD与s 轴夹角为2a0
OM σx σy 2 σx σy 2 cos2 α τ x sin2 α σ α
ty
e
cos2 α τ x sin2 α
b
sy
切线方向上: Σ F 0 τ
τ α d A (σ x d A cos α )sin α ( τ x d A cos α )cos α (σ y d A sin α )cos α ( τ y d A sin α )sin α 0
∴ τ α σ x sin α cos α σ y sin α cos α τ x cos2 α τ y sin 2 α
上海应用技术学院
工程力学第十三章课件
z
zx xz
x
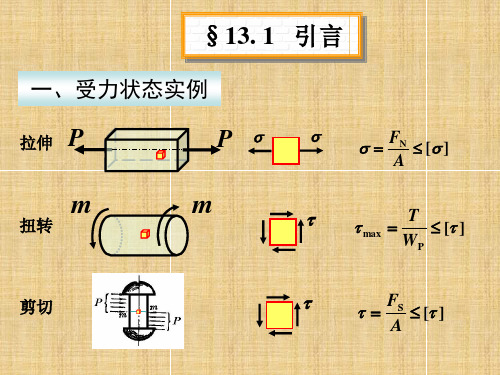
微体上任意方向面上
的应力均匀分布。
z
当一个微体的三个坐标平面上的应力为已知时, 总可以用截面法(平衡条件)求出任意方向面上的 应力,于是当微体三个坐标平面的应力已确定时, 就称该微体的应力状态已确定。
2、主平面、主应力、主方向、主平面微体 定义:微体中
切应力为零的平面称为主平面;主平面上的正应 力称为主应力;主平面的法线方向称为主方向;
微体上角相同的转向
量取圆弧 Dx D ,使 其所对应的圆心角
DxCD 2
F o
Dy
(y,y)
D点的横坐标 OM D点的纵坐标 MD
D (, ) Dx(x,x)
2
x
CM K
n
y
x
y
x
x
y
例题 如图所示微体中已知x=40MPa,x= –30MPa,y= 60MPa,y=30MPa,试用应力 圆求=45,=90+ 两截面上的应力。
0
0
0
0
两向均压
x
2
y
x
y
2
cos 2
x
s in 2
x
y
2
s in 2
x
cos 2
q q
q q
思考:
图示拉扳,试画出A点应力状态的应力圆。
作业:
:拉应力为正,压应力为负。
:顺时针为正,逆时针为负。
y n n
x
y
t
y
:从 x 轴正向逆时针转到截面外法
线方向为正,反之为负。
y
此处任意斜截面的意义,平行
于z轴的任意斜面,该面外法线方向
x
n 与x轴夹角为 ,称为面。
工程力学 (静力学)单辉祖主编PPT课件

y
F
y F
O
x
O
x
(a)
(b)
1-1-2 力的性质
例3:用图解法求合力
(a)
1-1-2 力的性质
例4:用图解法求Fx,Fy,Fz的合力
z Fz
FxxO源自Fyy1-1-2 力的性质
例4:已知系统平衡,画出B、C两点的受力方向
1-1-2 力的性质
例5:已知构件处于平衡状态,求Fc的方向
Fc
(a) (b)
➢ 固体力学研究在外力作用下,可变形固体内部各质点所产生的 位移、运动、应力、应变及破坏等的规律。属于固体力学范畴 的有材料力学、结构力学、弹性力学和塑性力学、复合材料力 学、断裂力学等。
➢ 流体力学的研究对象是气体和液体。研究在力的作用下,流体 本身的静止状态、运动状态及流体和固体间有相对运动时的相 互作用和流动规律等。属于流体力学的有水力学、空气动力学、 环境流体力学等。
据自己的爱好和特长,进一步广泛深入地研究工程力 学相关的其它问题
学习方法与要求
学习要求:
➢ 不可迟到、早退、旷课 ➢ 上课不允许睡觉、做与本课程无关的事、说与上课无关的话 ➢ 积极参与教学过程,认真完成课堂练习 ➢ 按教师要求及时、独立完成课后作业 ➢ 上课带教材、课堂笔记本、练习本、画图工具、计算器
M x M i xM y M i yM z M i z
M= ﹝(∑Mix)2+(Miy)2+(Miz)2 ﹞ ½
n
平面力偶系的简M化:Mi Mi i1
力偶系的平衡条件:
n
M Mi 0
或
i 1
M x M i x 0 M y M i y 0 M z M i z 0
平面力偶系的平衡条件:
《应力状态分析》课件

意义
揭示了物体在受力状态下 内部应力的分布规律,为 分析强度、刚度和稳定性 问题提供依据。
空间应力状态的分类
单向应力状态
物体只承受单向正应力作 用,即一维应力状态。
二向应力状态
物体承受两个正交方向的 正应力作用,即平面应力 状态。
三向应力状态
物体承受三个正交方向的 的正应力作用,即空间应 力状态。
02 平面应力状态分析
平面应力状态的概念
平面应力状态
在二维平面上,各应力分量均平行于平面,且均沿z轴方向变化的 应力状态。
平面应力状态的特点
各应力分量均平行于平面,且均沿z轴方向变化。
平面应力状态的应用
在工程中,许多问题可以简化为平面应力状态进行分析,如薄板、 薄壳等结构的应力分析。
平面应力状态的分类
数值法
通过有限元、有限差分等方法求解平面应力状态 的应力和应变。
3
实验法
通过实验测试和测量平面应力状态的应力和应变 。
03 空间应力状态分析
空间应力状态的概念
01
02
03
空间应状态
描述物体内部各点应力矢 量在空间位置和方向上的 分布情况。
定义
空间中任意一点处的应力 状态由三个正交的主应力 及相应的主方向组成。
将物体离散化为有限个小的单元,对 每个单元进行受力分析,再通过单元 的集合得到整体的平衡方程,求解得 到各点的应力分量。适用于复杂几何 形状和边界条件的物体。
通过实验测试得到物体的应力应变关 系,从而反推出物体的应力状态。适 用于无法通过理论分析求解的复杂问 题。
05 应变与应力的关系
应变的概念
复杂应力状态的分类
按主应力大小分类
分为三向主应力状态和二向主应力状态。
第章应力状态分析-PPT课件

1
2
1
单辉祖:材料力学教程
x1
2
2
x2
3
t3
13
取单元体示例二
l
y
1
S 截面
S截面
FP
a
4
z
2
3
单辉祖:材料力学教程
x
14
忽略弯曲切应力
y
1
FQy
M 1 W
x p
1 4
z
x1
Mz Wz
Mz
x
3
Mx 3 Wp
Mz Wz
2 3
Mx
x
3
4
单辉祖:材料力学教程
3
单辉祖:材料力学教程 19
二、 应力圆
应力圆原理
x y x y
2 2
2
x y sin2 cos2 x
cos2 sin2 x
x y x y
2
0
x y
§7 复合材料应力应变关系简介
单辉祖:材料力学教程 2
§1 引 言
实例 应力与应变状态 平面与空间应力状态
单辉祖:材料力学教程
3
应力状态的概念
1、问题的提出 问题1:同一点处不同方位截面上的应力不相同;
轴向拉伸杆件
F 横截面应力: A
F F F
4
n
F
斜截面应力:
x p
cos sin ( )sin cos ( )sin cos cos sin
2 2 x y x y
第十三章应力状态分析PPT课件

应力的三个重要概念
m 应力的点的概念; m 应力的面的概念; m 应力状态的概念.
FN M z
FQ
横截面上正应力分析和切应力分析 的结果表明:同一面上不同点的应力各
不相同,此即应力的点的概念。
y
x
y
单元体平衡分析结果表明:即使 同一点不同方向面上的应力也是各不相
同的,此即应力的面的概念。
应力
300
600
x
y
40MPa
在二向应力状态下,任意两个垂直面上,其σ的和为一常数。
分析轴向拉伸杆件的最大切应力的作用面,说明低碳钢 拉伸时发生屈服的主要原因。
低碳钢拉伸时,其上任意一点都是单向应力状态。
450
x y 2
x y cos2
2
x sin2
x
x
2
y
2
co2s
x y sin2 xco2s
弯曲变形
τ
σ
τσ
σy τ y
σx
τx σx
σ
τσ
x
MZy Iz
F
s
S
* z
IZb
y σy
x
y
y z
x
三
平
向
面
应
应
力 状
特例
力 状
态
态
单向应力状态 纯剪应力状态
§13-2 平面(二向)应力状态应力分析
一、斜截面应力:
a
n Fn 0 F 0
a
x
y
x
yc
x
x
b
y
c
y
co2s1co2s
a
3 20MPa
c
30MPa
13应力状态分析ppt课件

第 13 章 应力状态分析
本章主要研究:
应力状态应力分析基本理论 应力、应变间的一般关系 复合材料应力应变关系简介
单辉祖:工程力学
精品课件
1
§1 引言 §2 平面应力状态应力分析 §3 极值应力与主应力 §4 复杂应力状态的最大应力 §5 广义胡克定律 §6 复合材料应力应变关系简介
单辉祖:工程力学
空间应力状态一般形式
单辉祖:工程力学
精品课件
8
§2 平面应力状态应力分析
应力分析的解析法 应力圆 例题
单辉祖:工程力学
精品课件
9
应力分析的解析法
问题
斜截面:// z 轴;方位用 a 表示;应力为 sa , ta
符号规定:
切应力 t - 以企图使微体沿 旋转者为正 方位角 a - 以 x 轴为始边、 者为正
单辉祖:工程力学 sm11M 5精品P 课件atm35MPa
19
§3 极值应力与主应力
平面应力状态的极值应力 主平面与主应力 纯剪切与扭转破坏 例题
单辉祖:工程力学
精品课件
20
平面应力状态的极值应力
极值应力数值
ssm mainxOCCAsx 2sy sx 2sy2tx2
ttmmainx CK
精品课件
2
§1 引 言
实例 应力状态概念 平面与空间应力状态
单辉祖:工程力学
精品课件
3
实例
微体A
单辉祖:工程力学
精品课件
4
微体abcd
单辉祖:工程力学
精品课件
5
微体A
单辉祖:工程力学
精品课件
6
应力状态概念
应力状态 过构件内一点所作各微截面的应力状况,称为该点 处的应力状态
本章主要研究:
应力状态应力分析基本理论 应力、应变间的一般关系 复合材料应力应变关系简介
单辉祖:工程力学
精品课件
1
§1 引言 §2 平面应力状态应力分析 §3 极值应力与主应力 §4 复杂应力状态的最大应力 §5 广义胡克定律 §6 复合材料应力应变关系简介
单辉祖:工程力学
空间应力状态一般形式
单辉祖:工程力学
精品课件
8
§2 平面应力状态应力分析
应力分析的解析法 应力圆 例题
单辉祖:工程力学
精品课件
9
应力分析的解析法
问题
斜截面:// z 轴;方位用 a 表示;应力为 sa , ta
符号规定:
切应力 t - 以企图使微体沿 旋转者为正 方位角 a - 以 x 轴为始边、 者为正
单辉祖:工程力学 sm11M 5精品P 课件atm35MPa
19
§3 极值应力与主应力
平面应力状态的极值应力 主平面与主应力 纯剪切与扭转破坏 例题
单辉祖:工程力学
精品课件
20
平面应力状态的极值应力
极值应力数值
ssm mainxOCCAsx 2sy sx 2sy2tx2
ttmmainx CK
精品课件
2
§1 引 言
实例 应力状态概念 平面与空间应力状态
单辉祖:工程力学
精品课件
3
实例
微体A
单辉祖:工程力学
精品课件
4
微体abcd
单辉祖:工程力学
精品课件
5
微体A
单辉祖:工程力学
精品课件
6
应力状态概念
应力状态 过构件内一点所作各微截面的应力状况,称为该点 处的应力状态
工程力学:第20课_第13章 应力状态分析(2)
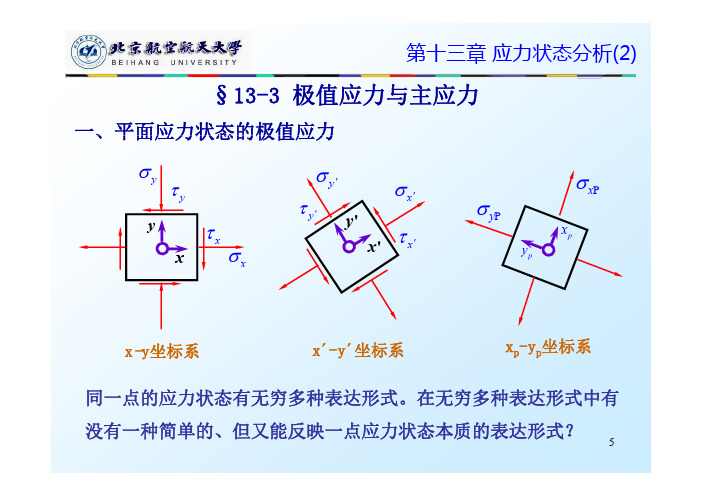
解析法:构造如图所示微体
B
B
15
x
x
2 15
2
x 15 cos
2
sin 2(90 )
2(90 ) 15sin 2(90 ) 15cos 2(90 ) 20MPa
40MPa
两个未知数, 两个方程,求解得:
y
x
47MPa 35.5
故:
max
x
y
2
(
x
y )2
2
2 x
52.9MPa
max min 18
第十三章 应力状态分析(2)
例:纯剪应力状态下不同的断裂机理: 低碳钢圆轴扭转时滑移与剪断发生在max的作用面:
铸铁圆轴扭转时断裂发生在max 的作用面:
A
B
思考:1. 如何扭才能造成上图所示的断裂面?A 还是B?
2. 如果两端再加上一些拉力,则断裂面的角度大于
还是小于45?
图解法501051965051961030105196505196两点联结de以de为直径作应力圆2量ab两点坐标bd的方位角得两点联结de以de为直径作应力圆22max第十三章应力状态分析2一三向应力圆134复杂应力状态的最大应力三向应力状态应力圆第十三章应力状态分析2二其它任意斜截面上的应力任意斜截面的应力值位于三向应力圆的阴影区内coscoscoscoscoscoscoscoscosbcdobcadcoscosbocabccoscosabcboc分离体平衡
py2
pz2
2 1
cos2
2 2
cos2
2 3
cos2
正应 力: 切应 力:
n px cos py cos pz cos 1 cos2 2 cos2 3 cos2
工程力学之应力状态分析和强度计算PPT(50张)

3
2 主应变:主应力方向上的应变
1 1 2 3 1 2 3 1 2 3
工
1 单独作用 2 单独作用 3 单独作用
程 力
1
1
2
3
E
E
E
学
2
1
E
2
E
3
E
3
1
E
2
E
3
E
同时作用
1
1
E
( 2 ) ( 3
E
E
)
13
§10.应力状态分析和强度理论—— 广义胡克定律
Fn 0
A x Ax cos y Ay sin x Ax sin y Ay cos 0
F 0
A x Ax sin y Ay cos x Ax cos y Ay sin 0
x
2
y
x
y
2
cos 2
x
sin
2
x
2
y
sin
2
x
cos 2 7
§10.应力状态分析和强度理论——平面应力状态分析
=0
tg2o
2 x x y
9
§10.应力状态分析和强度理论——平面应力状态分析
x 2y(x 2y)2(x)2sin 2 ()
工 程
(x 2y)2(x)2cos2 ()
力
学 ● 最大和最小剪应力
21 0
or
max min
(
x
2平面与主平面的夹角为45°: 1 0 45
(2)相互平行的平面上,应力大小和性质完全相同。 (3) 相邻垂直面上的切应力根据切应力互等定理确定.
4
§10.应力状态分析和强度理论——概 述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本章主要研究:
应力状态应力分析的基本理论 应力、应变间的一般关系
一、强度条件回顾
§13-1 引言
强度条件:保证结构或构件不致因强度不够而破坏的条件。
• 拉压杆强度条件:
m
a
=
x
FN A
max
单向应力状态
• 圆轴强度条件:
max
T W p
max
纯剪切应力状态
•
梁的强度条件: max
a
max
O
max
b 1 1
c
t ,max
b
b
1
1
d
C ,max
c
c t ,max
y
y
a 点处: 纯剪切; c , d 点处: 单向应力;
b 点处: , 联合作用
复杂应力状态下(一般情况下),如何建立强度条件 ?
分别满足 ? 做实验找破坏时的组合形式?工作量与难度 ?
建立复杂应力状态强度条件的研究思路:
§13-2 平面应力状态应力分析
y y y
x
x x
• 证明分析
C
o y
D ( x , x )
x
F
y E ( y , y )
(x+y)/2 (x-y)/2
x
C
(
x
y
,
0)
2
R
(
x 2
y
)2
2 x
§13-2 平面应力状态应力分析 四、应力圆与微体对应关系 • 点面对应:
微体截面上的正应力和切应力与应力圆点的坐标值一一对应。
§13-2 平面应力状态应力分析
二、应力圆(图解法)
斜截面上的应力公式
x
y
2
x
2
y co s 2
x s in 2
x
y sin 2
2
x co s2
x
2
y
x
2
y
co s2
x sin 2
0
x
2
y
s i n 2
x co s2
(
x
2
y
)2
2
(
x
2
y
)2
2 x
§13-2 平面应力状态应力分析
E(y ,x)
§13-2 平面应力状态应力分析
五、应力圆的应用
H
H (, )
计算斜截面上的应力
y
y y
n
x
x x
D H
C 220x
o y
F
y E
(x+y)/2 (x-y)/2
x
x
y
y x
x
平
三
面
向
单向应力状态
应
应
纯剪应力状态
力
特例
状 态
特例
力 状 态
§13-2 平面应力状态应力分析
y
y
• 平面应力状态
y yy x
x xx
微体有一对平行表面不受力的应力状态。
➢ 微体仅有四个面作用有应力;
x
x ➢ 应力作用线均平行于不受力表面;
z
y
y
y y
α x α x
• 平面应力状态的应力分析
y y
xx
H( , )
O
c
E(y ,x)
D(x ,x)
§13-2 平面应力状态应力分析 四、应力圆与微体对应关系
• 夹角2倍、转向一致:
• 夹角2倍:应力圆半径转过的角度是微体截面法线旋转角度的两倍。 • 转向一致:应力圆半径旋转方向与微体截面法线旋转方向一致。
y y
xx
H( , )
2
O
c
D(x ,x)
已知x , y, x , y 求任意平行于z轴的斜截面上的应力 x
z
§13-2 平面应力状态应力分析
一、平面应力状态斜截面应力
正负号规定
:拉为正;压为负
τx = − τy
τ:使微元体顺时针转动为正(与剪力Fs规定相同)
α:从坐标轴x正向逆时针旋转至斜截面法线方向为正
§13-2 平面应力状态应力分析
材料物质点应力状态· 应力微体 材料失效机理
强度条件
• 应力状态
A
构件受力后,通过其内一点在不同方向面上应力的集合, 称之为该点的应力状态。
• 微(元)体、单元体 围绕所研究点取无限小微六面体
(1)微体的尺寸无限小,边长为1; (2)每个面上应力均匀分布; (3)对面上应力相等。
选取原则:面上应力已知或可求
(
x
2
y
)2
2
(
x
2
y
)2
x2
—坐标系下的圆方程
圆心坐标:
( x y , 2
0)
o
R
半径:
R
(
x 2
y )2
x2
(x+ y)/2
结论:平面应力状态下各方向的应力轨迹为一个圆
——应力圆
三、应力圆的绘制
绘制方法1:
§13-2 平面应力状态应力分析
以 ( x y , 0) 为圆心,
平面应力状态下任意斜截面上应力表达式
x
y
2
x
y
2
cos 2
x
sin 2
x
y
2
sin 2
x
cos 2
§13-2 平面应力状态应力分析
斜截面上的应力公式
解析法
x
2
y
x
2
y cos2
x sin 2
x
2
y
s i n 2
xcos2
上述关系式是建立在静力学基础上,与材料性质无关。 换句话说,它既适用于各向同性与线弹性情况,也适 用于各向异性、非线弹性与非弹性问题。
R
2
o
R
(
x 2
y
)2
2 x
为半径作圆
(x+ y)/2
缺点:
• 需用解析法计算圆心坐标和半径
• 没有反映应力圆上的点与微体截面方位的对应关系
三、应力圆的绘制
§13-2 平面应力状态应力分析
绘制方法2(重点)
y
y
B
O
x
x
c
E(y ,x)
D(x ,x)
建立坐标系
σ−τ
找两点
确定圆心和半径
D( x , x )、E( y , y )
y
y
y
x
x x
x
z
y
微元体
§13-1 引言
三向(空间)应力状态
x x
z
z
zx zy
xz yz
xy
yx
y y
平面(二向)应力状态
y
y
y
x
x x
x
y
§13-1 引言
单向应力状态 y
( One Dimensional
State of Stresses )
纯剪应力状态
( Shearing State of Stresses )
M Wz
max
[ ]
max
F SS z ,max I z
max
[ ]
单向应力状态
纯剪切应力状态
建立强度条件的依据? 危险点处的应力状态!
螺旋桨轴:
§13-1 引言
A
F
F
T
微体A
采用拉伸强度条件、扭转强度条件,还是其它强度条件?
工字梁
d
d C ,max
1
a maxLeabharlann C az工程力学A
Engineering Mechanics A
主讲教师:李荣涛
建筑工程学院
College of Civil Engineering and Architecture
第十三章 应力状态分析
§13-1 引言 §13-2 平面应力状态应力分析 §13-3 极值应力与主应力 §13-4 复杂应力状态的最大应力 §13-5 广义胡克定律
Fn 0 : F 0 :
dA ( xdAcos )sin ( xdAcos )cos ( ydAsin )cos ( ydAsin )sin 0
dA ( xdAcos )cos ( xdAcos )sin ( ydAsin )cos ( xdAsin )sin 0
§13-2 平面应力状态应力分析
