2018初三一模24题汇编

合集下载

2018年上海各区中考化学一模试题分类汇编-物质分类(word答案版)

2018年上海各区中考化学一模试题分类汇编-物质分类【2018年上海宝山区一模】30. 属于纯净物的是（） A. 矿泉水 B. 冰水C. 自来水D. 汽水【答案】B【2018年上海宝山区一模】34. 不属于同素异形体的一组物质是（） A. 红磷和白磷 B. 干冰和冰C. 氧气和臭氧D. 金刚石和石墨【答案】B【2018年上海奉贤区一模】29. 属于氧化物的是（） A. 2OB. 22H OC. NaClD. 24H SO【答案】B【2018年上海奉贤区一模】31. 互为同素异形的一组物质是（） A. 氧气与臭氧 B. 冰与干冰 C. 银与水银 D. 水与双氧水【答案】A【2018年上海奉贤区一模】41. 分类是研究物质的常用方法。

右图是纯净物、单质、化合物、氧化物之间关系的形象表示，若整个大圆圈表示纯净物，则属于X 范围的物质是（）A. 红磷B. 干冰C. 氯酸钾D. 食盐水【答案】A【2018年上海虹口区一模】30. 属于氧化物的是（） A. Na 2CO 3 B. O 2 C. Al 2O 3 D. KOH【答案】C【2018年上海虹口区一模】33. 属于同素异形体的是（） A. CO 和CO 2 B. 石墨和C 60 C. 氧气和液氧 D. 水和双氧水【答案】B【2018年上海虹口区一模】34. 属于纯净物的是（） A. 蒸馏水B. 白醋C. 芝麻油D. 牛奶【答案】A【2018年上海虹口区一模】40. 有关物质的用途正确的是（）A. 氧气：植物光合作用的原料B. 氦气：保护气C. 冰：人工降雨D. 金刚石：电极【答案】B【2018年上海嘉定区一模】29.属于纯净物的是（）A. 洁净空气B. 可乐C. 大理石D. 蒸馏水【答案】D【2018年上海嘉定区一模】31.不属于碳元素的同素异形体的是（）A. 金刚石B. 石墨C. 二氧化碳D. C60【答案】C【2018年上海嘉定区一模】41.关于物质用途的描述正确的是（）A. CO具有还原性，可用于冶炼金属B. N2的密度比空气小，可用作灯泡保护气C. O2具有可燃性，可用作气体燃料D. 活性炭有吸附性，可用于杀菌消毒【答案】A【2018年上海静安区一模】6. 物质的用途错误的是（）A. 稀有气体制作电光源B. 二氧化碳制作碳酸饮料C. 氧气作燃料D. 氧化钙作干燥剂【答案】C【2018年上海静安区一模】11. 下列属于纯净物的是（）A. 糖水B. 大理石C. 加碘食盐D. 五氧化二磷【答案】D【2018年上海静安区一模】12. 造成温室效应的主要气体是（）A. 二氧化硫B. 一氧化碳C. 二氧化碳D. 氧气【答案】C【2018年上海静安区一模】18. 既含游离态氧元素又含化合态氧元素的物质是（）A. 氧气 B. 空气 C. 二氧化碳 D. 水【答案】B【2018年上海静安区一模】23. 下列物质的俗名错误的是（）A. 固体二氧化碳干冰B. 硫酸铜胆矾C. 氢氧化钙熟石灰D. 氧化钙生石灰【答案】B【2018年上海静安区一模】27. 石墨烯是从石墨中分离出来的单原子层石墨，它具有超强导电、导热的性能。

2018年初三一诊考试数学试卷及答案

2018年初三一诊考试数学试题答案及解析一、选择题（本大题共8小题，每小题3分，共24分）1．（3分）﹣的相反数是（）A．5B．C．﹣D．﹣52．（3分）已知空气的单位体积质量是0.001239g/cm3，则用科学记数法表示该数为（）A．1.239×10﹣3g/cm3B．1.239×10﹣2g/cm3C．0.1239×10﹣2g/cm3D．12.39×10﹣4g/cm33．（3分）如图，立体图形的俯视图是（）A．B．C．D．4．（3分）如图，AB为⊙O的直径，点C在⊙O上，若∠OCA=50°，AB=4，则的长为（）A．πB．πC．πD．π5．（3分）如图，在平行四边形ABCD中，E是边CD上一点，将△ADE沿AE折叠至△AD′E处，AD′与CE交于点F，若∠B=52°，∠DAE=20°，则∠FED′的度数为（）A．40°B．36°C．50°D．45°（6．（3分）如图，四边形ABCD是菱形，AC=8，DB=6，DH⊥AB于H，则DH等于（）A．B．C．5D．47．3分）使得关于x的不等式组有解，且使分式方程有非负整数解的所有的m的和是（）A．﹣1B．2C．﹣7D．08．（3分）如图，正方形ABCD的边长为4，点P、Q分别是CD、AD的中点，动点E从点A向点B运动，到点B时停止运动；同时，动点F从点P出发，沿P→D→Q运动，点E、F的运动速度相同．设点E的运动路程为△x，AEF的面积为y，能大致刻画y与x的函数关系的图象是（）A．B．C．D．二、填空题（本大题共8小题，每小题3分，共24分）9．（3分）因式分解：9a3b﹣ab=．10．（3分）如图，直线a∥b，∠P=75°，∠2=30°，则∠1=．11．（3分）已知一组数据：3，3，4，5，5，则它的方差为．12．（3分）今年“五一”节，A、B两人到商场购物，A购3件甲商品和2件乙商F （品共支付 16 元，B 购 5 件甲商品和 3 件乙商品共支付 25 元，求一件甲商品和一件乙商品各售多少元．设甲商品售价 x 元/件，乙商品售价 y 元/件，则可列出方程组．13．（3 分）如图，在 Rt △ABC 中，∠A=30°，BC=2 ，以直角边 AC 为直径作⊙O 交 AB 于点 D ，则图中阴影部分的面积是．14．（3 分）已知 x 1，x 2 是关于 x 的方程 x 2+ax ﹣2b=0 的两实数根，且 x 1+x 2=﹣2， x 1•x 2=1，则 b a 的值是．15．（3 分）对于实数 a ，b ，我们定义符号 max {a ，b }的意义为：当 a ≥b 时， max {a ，b }=a ；当 a ＜b 时，max {a ，b ]=b ；如：max {4，﹣2}=4，max {3，3}=3，若关于 x 的函数为 y=max {x +3，﹣x +1}，则该函数的最小值是．16．（3 分）如图，在正方形 ABCD 中，AC 为对角线，E 为 AB 上一点，过点 E 作EF ∥AD ，与 AC 、DC 分别交于点 G ，，H 为 CG 的中点，连接 DE ，EH ，DH ，FH ．下列结论：①EG=DF ；②∠AEH +∠ADH=180°；③△EHF ≌△DHC ；④若，其中结论正确的有．△DHC= ，则 3S △EDH =13S三、解答题（本大题共 8 个题，共 72 分）17．（10 分）（1）计算：|﹣2|﹣（π﹣2015）0+（）﹣2﹣2sin60°+；（2）先化简，再求值：÷（2+ ），其中 a=．18． 6 分）如图，分别过点C 、B 作△ABC 的 BC 边上的中线 AD 及其延长线的垂线，垂足分别为 E 、F ．求证：BF=CE ．（19．8分）“热爱劳动，勤俭节约”是中华民族的光荣传统，某小学校为了解本校3至6年级的3000名学生帮助父母做家务的情况，以便做好引导和教育工作，随机抽取了200名学生进行调查，按年级人数和做家务程度，分别绘制了条形统计图（图1）和扇形统计图（图2）．（1）四个年级被调查人数的中位数是多少？（2）如果把“天天做”、“经常做”、“偶尔做”都统计成帮助父母做家务，那么该校3至6年级学生帮助父母做家务的人数大约是多少？（3）在这次调查中，六年级共有甲、乙、丙、丁四人“天天帮助父母做家务”，现准备从四人中随机抽取两人进行座谈，请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率．20．（8分）某商城销售A，B两种自行车．A型自行车售价为2100元/辆，B型自行车售价为1750元/辆，每辆A型自行车的进价比每辆B型自行车的进价多400元，商城用80000元购进A型自行车的数量与用64000元购进B型自行车的数量相等．（1）求每辆A，B两种自行车的进价分别是多少？（2）现在商城准备一次购进这两种自行车共100辆，设购进A型自行车m辆，这100辆自行车的销售总利润为y元，要求购进B型自行车数量不超过A型自行车数量的2倍，总利润不低于13000元，求获利最大的方案以及最大利润．21．（8分）如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼DE，在小楼的顶端D处测得障碍物边缘点C的俯角为30°，测得大楼顶端A的仰角为45°（点B，C，E在同一水平直线上）．已知AB=80m，DE=10m，求障碍物B，C两点间的距离．（结果保留根号）22．（10分）如图，在平面直角坐标xOy中，正比例函数y=kx的图象与反比例函数y=的图象都经过点A（2，﹣2）．（1）分别求这两个函数的表达式；（2）将直线OA向上平移3个单位长度后与y轴交于点B，与反比例函数图象在第四象限内的交点为C，连接AB，AC，求点C的坐标及△ABC的面积．23．（10分）如图，PB与⊙O相切于点B，过点B作OP的垂线BA，垂足为C，交⊙O于点A，连结PA，AO，AO的延长线交⊙O于点E，与PB的延长线交于点D．（1）求证：PA是⊙O的切线；（2）若tan∠BAD=，且OC=4，求BD的长．24．（12分）如图，已知抛物线y=+bx+c经过△ABC的三个顶点，其中点A （0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的一个动点．（1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q 为顶点的三角形与△ABC相似？若存在，求出点Q的坐标；若不存在，请说明理由．2参考答案一、选择题（本大题共 8 小题，每小题 3 分，共 24 分）1-8．B A C B B A CA二、填空题（本大题共 8 小题，每小题 3 分，共 24 分）9． ab （3a +1）（3a ﹣1）．10. 45° ．11．12．13．14．．．﹣ π ．．15． 2 ．16． ①②③④ ．三、解答题（本大题共 8 个题，共 72 分）17．（1）|﹣2|﹣（π﹣2015）0+（）﹣﹣2sin60°+=2﹣1+4﹣2×+2=2﹣1+4﹣+2=5+ ；（2）==÷（2+ ）=，当 a=时，原式= = ﹣1．（（18．证明：根据题意，知 CE ⊥AF ，BF ⊥AF ，∴∠CED=∠BFD=90°，又∵AD 是边 BC 上的中线，∴BD=DC ；在 Rt △BDF 和 Rt △CDE 中，∠BDF=∠CDE （对顶角相等），BD=CD ，∠CED=∠BFD ，∴△BDF ≌△CDE （AAS ），∴BF=CE （全等三角形的对应边相等）．19．解：（1）四个年级被抽出的人数由小到大排列为 30，45，55，70，∴中位数为 50；（2）根据题意得：3000×（1﹣25%）=2250 人，则该校帮助父母做家务的学生大约有 2250 人；（3）画树状图，如图所示：所有等可能的情况有 12 种，其中恰好是甲与乙的情况有 2 种，则 P== ．20、解：1）设每辆 B 型自行车的进价为 x 元，则每辆 A 型自行车的进价为（x +400）元，根据题意，得= ，解得 x=1600，经检验，x=1600 是原方程的解，x +400=1 600+400=2 000，答：每辆 A 型自行车的进价为 2 000 元，每辆 B 型自行车的进价为 1 600 元；（2）由题意，得 y=（2100﹣2000）m +（1750﹣1600） 100﹣m ）=﹣50m +15000，根据题意，得，解得：33≤m≤40，∵m为正整数，∴m=34，35，36，37，38，39，40．∵y=﹣50m+15000，k=﹣50＜0，∴y随x的增大而减小，∴当m=34时，y有最大值，最大值为：﹣50×34+15000=13300（元）．答：当购进A型自行车34辆，B型自行车66辆时获利最大，最大利润为13300元．21．解：过点D作DF⊥AB于点F，过点C作CH⊥DF于点H．则DE=BF=CH=10m，在Rt△ADF中，AF=AB﹣BF=70m，∠ADF=45°，∴DF=AF=70m．在Rt△CDE中，DE=10m，∠DCE=30°，∴CE===10（m），∴BC=BE﹣CE=（70﹣10）m．答：障碍物B，C两点间的距离为（70﹣10）m．22．解：（1）根据题意，将点A（2，﹣2）代入y=kx，得：﹣2=2k，解得：k=﹣1，∴正比例函数的解析式为：y=﹣x，将点A（2，﹣2）代入y=，得：﹣2=，解得：m=﹣4；∴反比例函数的解析式为：y=﹣；（2）直线OA：y=﹣x向上平移3个单位后解析式为：y=﹣x+3，则点B的坐标为（0，3），联立两函数解析式，解得：或，∴第四象限内的交点C的坐标为（4，﹣1），∵OA∥BC，∴S△ABC=S △OBC=×BO×xC=×3×4=6．23．解：（1）连结OB，则OA=OB．如图1，∵OP⊥AB，∴AC=BC，∴OP是AB的垂直平分线，∴PA=PB．在△PAO和△PBO中，∵，∴△PAO≌△PBO（SSS），∴∠PBO=∠PAO．∵PB为⊙O的切线，B为切点，∴∠PBO=90°，∴∠PAO=90°，即PA⊥OA，∴PA是⊙O的切线；（2）连结BE．如图2，∵在Rt△AOC中，tan∠BAD=tan∠CAO==，且OC=4，∴AC=6，则 BC=6．在 Rt △APO 中，∵AC ⊥OP ，∴△PAC ∽△AOC ，∴AC 2=OC•PC ，解得 PC=9，∴OP=PC +OC=13．在 Rt △ PBC 中，由勾股定理，得PB==3，∵AC=BC ，OA=OE ，即 OC 为△ABE 的中位线．∴OC= BE ，OC ∥BE ，∴BE=2OC=8．∵BE ∥OP ，∴△DBE ∽△DPO ，∴=，即=，解得 BD=．24．解：（1）将 A （0，1），B （﹣ 9，10）代入函数解析式，得，解得，抛物线的解析式 y=+2x +1；（2 分）（2）∵AC ∥x 轴，A （0，1），∴ x 2+2x +1=1，解得 x 1=﹣6，x 2=0（舍），即 C 点坐标为（﹣6，1），∵点 A （ 0，1），点 B （﹣9，10），∴直线 AB 的解析式为 y=﹣x +1，设 P （m ，m 2+2m +1），∴E （m ，﹣m +1），∴PE=﹣m +1﹣（ m 2+2m +1）=﹣ m 2﹣3m ，∵AC⊥PE，AC=6，（4分）∴S四边形AECP =S△AEC+S△APC=AC•EF+AC•PF，=AC•（EF+PF）=AC•EP=×6（﹣m2﹣3m）=﹣m2﹣9m=﹣（m+）2+，∵﹣6＜m＜0，∴当m=﹣时，四边形AECP的面积最大值是，此时P（﹣，﹣）；（6分）（3）∵y=x2+2x+1=（x+3）2﹣2，∴顶点P（﹣3，﹣2）．∴PF=2+1=3，CF=6﹣3=3，∴PF=CF，PC=3，∴∠PCF=45°，同理可得∠EAF=45°，∴∠PCF=∠EAF，∵A（0，1），B（﹣9，10），∴AB==9，∴在直线AC上存在满足条件得点Q，设Q（t，1），∵以C，P，Q为顶点的三角形与△ABC相似，①当△CPQ∽△ABC时，，CQ=2，（7分）∴Q（﹣4，1）；（8分）②当△CPQ∽△ACB时，则=，，∴=，CQ=9，（9分）∴Q（3，1）；综上所述：当点P为抛物线的顶点时，在直线AC上存在点Q，使得以C、P、Q 为顶点的三角形与△ABC相似，Q点的坐标为（﹣4，1）或（3，1）．（10分）11/11。

2018年九年级一模数学试题及答案

2017-2018学年九年级一模数学试卷一、选择题（每题3分，共30分） 1.4的值为A.2B.±2C.-2D.16 2.要使分式1x 2+有意义，则x 的取值应满足 A. x=2 B. x 2≠- C. x 2>- D. x 2<-3.计算2)2+x （，正确的是 A ．42+x B ．22+x C ．442++x x D ．2x +4 4.掷一枚质地均匀的骰子，下列事件是不可能事件是A. 向上一面点数是奇数.B. 向上一面点数是偶数 .C. 向上一面点数是大于6.D. 向上一面点数是小于7. 5.下列整式运式计算的是结果为6a 是A ．a 3+a 3B ．（a 2）3C ．a 12÷a 2D ．（a 2）46．已知，线段CD 是由线段AB 平移得到的，点A （﹣1，4）的对应点为C （4，7），则点B （﹣4，﹣1）的对应点D 的坐标为A ．(1，2)B ．(2,9)C ．(5,3)D ．(-9,-4) 7.如图是由几个大小相同的小正方体搭成的几何体的俯视图，小正方体中的数字表示该位置小正方体的个数，则该几何体的左视图是A. B . C . D.8.某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是A ．中位数是4，平均数是3.75B ．众数是4，平均数是3.75C ．中位数是4，平均数是3.8D ．众数是2，平均数是3.8 9.一个整数的所有正约数之和可以按如下方法求得，如：6=2×3，则6的所有正约数之和（1+3）+（2+6）=（1+2）×（1+3）=12；12=22×3，则12的所有正约数之和（1+3）+（2+6）+（4+12）=（1+2+22）×（1+3）=28；36=22×32，则36的所有正约数之和（1+3+9）+（2+6+18）+（4+12+36）=（1+2+22）×（1+3+32）=91．参照上述方法，那么200的所有正约数之和为A ．420B ．434C ．450D ．46510.如图,等边△ABC 是⊙O 的内接三角形，D 是弧BC 上一点，当PB =3PC 时，则△ABC 与四边形ABPC 的面积比是 A.1613 B. 1310 C. 119 D. 97二、填空题（每题3分，共18分） 11.计算（﹣3）+（﹣9）的结果是_________. 12.化简aaa ---111的结果是_________. 13.若同时抛掷两枚质地均匀的骰子，则事件“两枚骰子朝上的点数互不相同”的概率是． 14.如图，将平行四边形ABCD 沿对角线AC 折叠，使点B 落在点B ’处.若∠1=∠2=44°，则∠D = 度．15.“如果二次函数y ＝ax 2＋bx ＋c 的图象与一次函数y=kx ＋b 有两个公共点，那么一元二次方程ax 2＋bx ＋c=kx ＋b 有两个不相等的实数根.”请根据你对这句话的理解，解决下面问题：若方程a x x =+-142有四个解，则a 的取值范围是 .16.如图，面积为6的平行四边形纸片ABCD 中，AB =3，∠BAD =45°，按下列步骤进行裁剪和拼图．第一步：如图①，将平行四边形纸片沿对角线BD 剪开，得到△ABD 和△BCD 纸片，再将△ABD 纸片沿AE 剪开（E 为BD 上任意一点），得到△ABE 和△ADE 纸片；第二步：如图②，将△ABE 纸片平移至△DCF 处，将△ADE 纸片平移至△BCG 处；第三步：如图③，将△DCF 纸片翻转过来使其背面朝上置于△PQM 处（边PQ 与DC 重合，△PQM 和△DCF 在DC 同侧），将△BCG 纸片翻转过来使其背面朝上置于△PRN 处，（边PR 与BC 重合，△PRN 和△BCG 在BC 同侧）．则由纸片拼成的五边形PMQRN 中，对角线MN 长度的最小值为．三、解答题（共8小题，共72分）17.（本题满分8分）解方程：5x ＋2＝3(x ＋2) ． 18.（本题满分8分）如图，点,B ，E ，F ，C 在一条直线上，AB =DE ，AC =DF ，BE =CF .求证A B ∥DE.19.（本题满分8分）“保护环境，人人有责”，为了了解某市的空气质量情况，某校环保兴趣小组，随机抽取了2016年内该市若干天的空气质量情况作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）.请你根据图中提供的信息，解答下列问题：（1）补全条形统计图；（2）估计该市这一年（365天）空气质量达到“优”和“良”的总天数；（3）计算随机选取这一年内的某一天，空气质量是“优”的概率.20.（本题满分8分）某汽车专卖店销售A ，B 两种型号的新能源汽车．上周售出1辆A 型车和3辆B 型车，销售额为96万元；本周已售出2辆A 型车和1辆B 型车，销售额为62万元．（1）求每辆A 型车和B 型车的售价各为多少元；（2）甲公司拟向该店购买A ，B 两种型号的新能源汽车共6辆，购车费不少于130万元，且不超过140万元．则有哪几种购车方案？21．（本题满分8分）如图，已知AB 是⊙O 的直径，直线CD 与⊙O 相切于点C ，AD ⊥CD 于点D .(1) 求证： AC 平分∠DAB ；(2) 若点E 为⌒AB 的中点，AD =532，AC =8，求CE 的长.22（本题满分10分）如图，已知一次函数32+-=x y 的图象与x 轴交于点A ，与反比例函数xy 5-=的图象交于B ，C 两点．点P 是线段AB 上的一个动点．（1）当x 取何值时，反比例函数的值小于一次函数的值；（2）过点P 作x 轴的平行线与反比例函数xy 5-=的图象相交于点D ,求△PAD 的面积的最大值；（3）在反比例函数xy 5-=的图象上找点E ，使∠BCE 为直角，直接写出点E 的坐标.23.（本题满分10分）(1)如图1，△ABC 中，∠C =90º,AB 的垂直平分线交AC 于点D ,连接BD .若AC =2，BC =1，则△BCD 的周长为；(2)O 是正方形ABCD 的中心，E 为CD 边上一点，F 为AD 边上一点，且△EDF 的周长等于AD 的长.①在图2中作出△EDF ，有适当的文字说明，并求出∠EOF 的度数； ②若322=OE OF ,求CEAF的值.24．（本题满分12分）抛物线y =c bx x ++231经过A （-4,0），B （2,0）两点，与y 轴交于点C ,顶点为D ，对称轴与x 轴交于点H ，过点H 的直线m 交抛物线于P ，Q 两点，其中点P 位于第二象限,点Q 在y 轴的右侧．（1）求D 点坐标；（2)若∠PBA=21∠OBC,求P 点坐标；（3）设PQ 的中点为M ，点N 在抛物线上，则以DP 为对角线的四边形DMPN 能否为菱形？若能，求出点N 的坐标；若不能，请说明理由．2017-2018学年九年级一模数学参考答案一、选择题（30分）二、填空题（18分）11.-12 12.1 13.6514.114 15. 0<a <3 16. 5106 ．三、解题题（共8小题，共72分）17.解：去括号得5x ＋2＝3x ＋6，---------------3分移项合并得2x ＝4，---------------6分 ∴x ＝2．---------------8分 18.证明：∵BE =CF ，∴BC =EF在△ABC 和△DEF 中，∵⎪⎩⎪⎨⎧===.,,EF BC DF AC DE AB∴△ABC ≌△DEF (SSS), ---------------5分 ∴∠B =∠DEF, ∴AB ∥DE.---------------8分 19.（1）补全条形统计图如下图---------------3分（2）由(1)知样本容量是60∴该市2015年空气质量达到“优”的天数约为：（天）.该市2015年（365天）空气质量达到“良”的天数约为：（天）.∴该市2015年（365天）空气质量达到“优”、“良”的总天数约为：73+219=292（天）.- --------------6分（3）随机选取2015年内某一天，空气质量是“优”的概率为： --------------8分20.（1）每辆A 型车和B 型车的售价分别是x 万元、y 万元．则，解得．答：每辆A 型车的售价为18万元，每辆B 型车的售价为26万元； --------------4分（2）设购买A 型车a 辆，则购买B 型车（6﹣a ）辆，则依题意得，解得 2≤a ≤3．∵a 是正整数，∴a=2或a=3． ∴共有两种方案：方案一：购买2辆A 型车和4辆B 型车；方案二：购买3辆A 型车和3辆B 型车． --------------8分 21．(1)证明：连结OC ．∵直线CD 与⊙O 相切于点C ， ∴OC ⊥CD ．∵AD ⊥CD ， ∴OC ∥AD ． ∴∠DAC =∠ACO ． ∵OA =OC ∴∠OAC =∠ACO ．∴∠DAC =∠CAO ．即AC 平分∠DAB ． ---------------3分 (2)解：连接BC ，∵AB 是⊙O 的直径，∴∠ACB =90°=∠ADC ． ∵∠DAC =∠CAO ，∴△ADC ∽△ACB ．∴ABACAC AD =． ∵325AD =，AC =8， ∴AB =10. ----------------------------------------5分 ∵点E 为⌒AB 的中点，∴∠ACE =45°．过点A 作CE 的垂线，垂足为F ，∴CF =AE =AC sin45°=8在Rt △ACB 中，6BC ==， ∴84tan tan =63E B ==．在Rt △AEF 中，4tan =3AF E = ，∴3=4EF ⨯∴CE =． ------------------------------8分22.(1)求出B )5,1(-、C )2,25(-两点坐标，当x ＜-1或0＜x ＜25，反比例函数的值小于一次函数的值； -------------2分 (2)可求得A （，0），点P （m ，n ）在直线AB 上，∴32+-=m n ．而231<<-m ，所以0＜n ＜5． ∴点P （，n ），PD ∥x 轴，则D 、P 的纵坐标都是n ，此时D 点坐标是（﹣，n ），则PD=+，由S=•n •PD ，可求△PAD 的面积表达式为S=•n •PD=（+）×n=﹣（n ﹣）2+，∴当n=，即P （，）时，S 的最大值是． --------------5分(3)(4,45-) --------------8分23.(1)3; --------------3分 (2)①作法：在AD 上取点G,使AG=DE;再连接EG,然后作EF 的垂直平分线交AD 于点F.点F 就是所求的点.连接OA,OG,OF,OE.可证△AOG ≌△DOE,∴∠AOG=∠DOE,∴∠EOG=∠DOA=90º, 又证△EOF ≌△GOF ，∴∠EOF=∠GOF=45º. --------------7分 (3)连接OC,∵∠ECO=∠EOF=∠OAF=45º,∠EOC=∠AFO∴△COE ∽△AFO∴CE OAOE OF CO AF ==∴=⋅CE OA CO AF ⋅OE OF OEOF∴=CE AF22)322()(=OE OF =98. --------------10分24．(1)y=（x+1）2﹣3，D(-1,-3) --------------3分(2)作∠OBC 的角平分线BE 角y 轴于点E,过点E 作EF ⊥BC,垂足为点C,设OE=t,EF=t,由△CEF ∽△CBO ，求出t=1,直线BE 的解析式为121-=x y 若BP 满足条件，则BE 的解析式为121-+=x y ，与抛物线的解析式联立方程组解得 P(415,211-) --------------7分（3）设P （x 1，y 1）、Q （x 2，y 2）且过点H （﹣1，0）的直线PQ 的解析式为y=kx+b ， ∴﹣k+b=0，∴b=k ，∴y=kx+k ．由，∴+（﹣k ）x ﹣﹣k=0，∴x 1+x 2=﹣2+3k ，y 1+y 2=kx 1+k+kx 2+k=3k 2，∵点M 是线段PQ 的中点，∴由中点坐标公式的点M （k ﹣1， k 2）． --------------8分假设存在这样的N 点如图，直线DN ∥PQ ，设直线DN 的解析式为y=kx+k ﹣3由，解得：x 1=﹣1，x 2=3k ﹣1，∴N （3k ﹣1，3k 2﹣3） --------------9分当DN=DM 时，（3k ）2+（3k 2）2=（）2+（）2，整理得：3k 4﹣k 2﹣4=0，∵k 2+1＞0，∴3k 2﹣4=0，解得k=±，∵k ＜0，∴k=﹣， --------------10分∴P （﹣3﹣1，6），M （﹣﹣1，2），N （﹣2﹣1，1）∴PM=DN=2，∵PM ∥DN ，∴四边形DMPN 是平行四边形， ∵DM=DN ，∴四边形DMPN 为菱形，∴以DP 为对角线的四边形DMPN 能成为菱形，此时点N 的坐标为（﹣2﹣1，1）．--------------12分。

2018一模试卷正式版

轴的垂线，图中所构成的阴影部分面积从左到右依次为 S1，S2，S3，已知点 A，B 的横
坐标分别为 2，3，S1=2S2，S2+S3= 14 ，则 k 的值为 ▲ ． 3
16.如图，在△ABC 中，AB=BC=13，AC=10，将它分成“1”，“2”，“3”，“4”四块，点 D，E 分别是 AB，BC 的中点，将其中“1”，“2”，“3”三块进行平移或旋转，与第 4 块构成了正方形 MNOP. 则 LM 的长为 ▲ ．
l D
的表达式为 y=x+b，交 y 轴于点 E，若 2EB=BD，则菱形 ABCD 的面积为（ ▲ ）
A． 4√2
B． 8.
C． 8√2
D． 16
B
E
C
O
x
（第 9 题）
九年级数学试卷第 1 页共 4 页
10. 小发明点亮生活，如图 1 小宴设计的“机巧螺旋”可轻松让相框保持水平.其设计原理如图 2 所示，将半径为 1 的圆周 12 等分，过各等分点作圆的切线，在第一条切线上量
取 A1P1= C ，C 为圆的周长,在第二条切线上量取 A2P2= 2C ，在第三条切线上量取 A3P3=
12
12
3C ，在第四条切线上量取 A4P4= 4C ，依此类推，将 P1,P2…P11 用光滑的曲线连结.调
12
12
节模型至相框上边缘 MN 水平，若此时 A6P6⊥NQ 于 P6,A9P9⊥MN 于 P9，A11P11 所在
于点 E，AC 平分∠BCE. （1）求证：AD=CD.
A
B
E
（2）若 AB=2，CD=6，求 BC 的长.
D
C
（第 18 题）
19.（本题 8 分）为强健学生体质，某校积极开展“快乐运动”活动，共开设排球、足球、

2018年初三物理一模试题及答案

2018年初三物理一模试题及答案一、单项选择题：下列各小题均有四个选项，其中只有一个选项符合题意(每小题2分，共24分)1.在国际单位中压强的单位是A.焦耳B.帕斯卡C.瓦特D.牛顿2.图1所示的四种现象中，属于光的反射现象的是3.下列用品中，通常情况下属于导体的是A.玻璃棒B.塑料尺C. 陶瓷碗D. 铜线4.图2所示的四个实例中，目的是为了减小压强的是5.图3所示的四种现象中属于熔化的是6.图4所示的用具中，属于费力杠杆的是7.图5所示的四种用电器中，利用电流热效应工作的是8.图6所示的四种情景中，人对物体做功的是9.下列的估测，最接近实际的是A.普通课桌的高度约为80cmB.一个鸡蛋的质量约为500gC.一位普通中学生步行时的速度约为10m/sD.一个苹果在地球上受到的重力约为50N10.下列做法中，为了减小摩擦的是A.拔河比赛中，运动员握紧赛绳B.自行车刹车时，用力捏车闸C.旅行箱安装小轮子D.汽车轮胎上制有花纹11.图7所示电路，电源两端电压保持不变。

开关S由闭合到断开，下列判断正确的是A.电压表的示数不变B.电流表的示数增大C.电压表与电流表的比值不变D.灯泡的亮度不变12.在图8中，底面积为S=100cm2的圆柱形容器中装有密度为的某种液体。

图8甲中，液体的深度是20cm，此时手对细线的拉力是8 N，物体A对容器底部的压力是F1;图8乙中，手对细线的拉力是15N;图8丙中，物体A露出液面的体积是总体积的五分之二，液体对物体A表面的压力是F2，液体的深度是16cm，手对细线的拉力是19.8N，，液体对容器底部的压强为p (g取10N/kg)以下说法正确的是A.F1 =6NB.= 1.0103kg/m3 ,C.P=2.4103 PaD. F2 = 12N二、多项选择题(下列各小题均有四个选项，其中符合题意的选项均多于一个。

本大题共12分，每小题3分。

每小题选项全选对的得3分，选对但不全的得2分，错选不得分)13.关于一些物理概念和规律，下列说法正确的是A.甲物体对乙物体施加力的同时，甲物体也一定受到了力的作用B.如果两个力三要素相等，这两个力一定是平衡力C.做匀速直线运动的汽车受到的合力一定为零D.跳远时助跑是为了增大身体的惯性14.关于电磁现象，下列说法中正确的是A.电动机是根据磁场对导体有力的作用制成的B.小磁针N极在磁场中受力方向就是磁场方向C.通电螺线管能够产生磁场D.导体在磁场中做切割磁感线运动时，导体中就会产生感应电流15. 下列说法中正确的是A.一桶水的比热容比一杯水的比热容大B.晶体在熔化过程中，吸收热量温度保持不变C.物体温度升高一定是吸收了热量D.高压锅是利用提高锅内的气压，从而提高锅内水的沸点工作的16.下列说法中不正确的是A.使用滑轮组做功时，通过增加动滑轮个数来增加承受拉力的绳的段数，是为了提高机械效率B.骑自行车上坡前紧蹬几下，是为了增大自行车的动能C.自行车的轮胎刻有凹凸不平的花纹，是为了减小摩擦D.使用动滑轮一定可以省力三、填空题(每空2分，共14分)17.光在真空中的传播速度是__________m/s。

2018年中考第1次模拟考试数学试卷(含答案)

2018年初三第一次模拟考试数学试题一、选择题（本大题共16题，1-8小题，9-16小题，每题3分，共40分） 1.如图，数轴上表示－2的相反数的点是（） A.点P B.点Q C.点M D.点N 2.下列运算正确的是（） A.9=±3B. 532)(m m =C. 532a a a =⋅D.222)(y x y x +=+3.如图，AD 与BC 相交于点O,AB//CD,如果∠B ＝20°，∠D ＝40° ，那么∠BOD 为（） A. 40° B.50° C.60° D.70°4.估计18-的值在（）A. 0到1之间B. 1到2之间C.2到3之间D. 3至4之间 5.用配方法解一元二次方程0542=-+x x ，此方程可变形（） A. 9)2(2=+xB. 9)2(2=-xC. 1)2(2=+xD. 1)2(2=-x6.下列各因式分解正确的是（） A.22)1(12-=-+x x xB.)2)(2()2(22+-=-+-x x xC.)2)(2(43-+=-x x x x xD.22)1(22++=+x x x7.若a>b,则下列式子一定成立的是（）A.0>+b aB. 0>-b aC.0>abD.0>ba8.△ABC 中，已知AB=8，∠C=90°，∠A=30°，DE 是中位线，则DE 的长是（） A. 4B. 5C.32D. 29.若关于x 的一元一次不等式组⎩⎨⎧>-<-001a x x 无解，则a 的取值范围是（）A.1≥aB.1>aC. 1≤aD.1-<a 10.已知点A ),(11y x ，B ),(22y x 是反比例函数xy 2=图像上的点，若210x x >>，则一定成立的是（） A.021>>y yB.210y y >>C.210y y >>D.120y y >>11.如图是王老师去公园锻炼及原路返回家的距离y （千米）与时间t （分钟）之间的函数图像，根据图像信息，下列说法正确的是（） A. 王老师去时所用时间少于回家的时间 B. B. 王老师在公园锻炼了40分钟C. 王老师去时走上坡路，回家时走下坡路D. D.王老师去时速度比回家时的速度慢12.如图，CD 是Rt △ABC 斜边AB 边上的高，将△BCD 沿CD 折叠，B 点恰好落在AB 的中点E 处，则∠A 等于（） A. 60° B.45° C. 30° D.25° 13.如图，在Rt △ABC 中，∠C ＝90°，AC=4cm ，BC=6cm ，动点P 从点C 沿CA,以1cm/s 的速度向点A 运动，同时动点O 从点C 沿CB,以2cm/s 的速度向点B 运动，其中一个动点运动到终点时，另一个动点也停止运动。

上海-初三数学一模-2018年-24题-分题合集

上海-初三数学一模-2018年-24题-分题合集1.如图，在平面直角坐标系xOy中，已知抛物线y=38 2+bx+c与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，﹣3），经过点A的射线AM与y 轴相交于点E，与抛物线的另一个交点为F，且 =13．（1）求这条抛物线的表达式，并写出它的对称轴；（2）求∠FAB的余切值；（3）点D是点C关于抛物线对称轴的对称点，点P是y轴上一点，且∠AFP＝∠DAB，求点P的坐标．2.（2018•虹口区一模）如图，在平面直角坐标系x O y中，抛物线与x轴相交于点A（﹣2，0）、B（4，0），与y轴交于点C（0，﹣4），BC与抛物线的对称轴相交于点D．（1）求该抛物线的表达式，并直接写出点D的坐标；（2）过点A作AE⊥AC交抛物线于点E，求点E的坐标．3.（2018•金山区一模）平面直角坐标系x O y中（如图），已知抛物线y=ax2+bx+3与y轴相交于点C，与x轴正半轴相交于点A，OA=OC，与x轴的另一个交点为B，对称轴是直线x=1，顶点为P．（1）求这条抛物线的表达式和顶点P的坐标；（2）抛物线的对称轴与x轴相交于点M，求∠PMC的正切值；（3）点Q在y轴上，且△BCQ与△CMP相似，求点Q的坐标．4.（2018•黄浦区一模）在平面直角坐标系x O y中，对称轴为直线x=1的抛物线y=ax2+bx+8过点（﹣2，0）．（1）求抛物线的表达式，并写出其顶点坐标；（2）现将此抛物线沿y轴方向平移若干个单位，所得抛物线的顶点为D，与y轴的交点为B，与x轴负半轴交于点A，过B作x轴的平行线交所得抛物线于点C，若AC∥BD，试求平移后所得抛物线的表达式．5.（2018•深圳模拟）抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（32，0），且与y轴相交于点C．（1）求这条抛物线的表达式；（2）求∠ACB的度数；（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．6.（2018•深圳模拟）在直角坐标平面内，直线y=12x+2分别与x轴、y轴交于点A、C．抛物线y=﹣12 2+bx+c经过点A与点C，且与x轴的另一个交点为点B．点D在该抛物线上，且位于直线AC的上方．（1）求上述抛物线的表达式；（2）联结BC、BD，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4：5，求∠DBA的余切值；（3）过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．7.（2018•松江区一模）如图，在平面直角坐标系x O y中，抛物线y=x2+bx+c的对称轴为直线x=1，抛物线与x轴交于A、B两点（点A在点B的左侧），且AB=4，又P是抛物线上位于第一象限的点，直线AP与y轴交于点D，与对称轴交于点E，设点P的横坐标为t．（1）求点A的坐标和抛物线的表达式；（2）当AE：EP=1：2时，求点E的坐标；（3）记抛物线的顶点为M，与y轴的交点为C，当四边形CDEM是等腰梯形时，求t的值．8.（2018•嘉定区一模）已知在平面直角坐标系x O y（如图）中，已知抛物线y=23 2+bx+c点经过A（1，0）、B（0，2）．（1）求该抛物线的表达式；（2）设该抛物线的对称轴与x轴的交点为C，第四象限内的点D在该抛物线的对称轴上，如果以点A、C、D所组成的三角形与△AOB相似，求点D 的坐标；（3）设点E在该抛物线的对称轴上，它的纵坐标是1，联结AE、BE，求sin∠ABE．9.（2018•宝山区一模）设a，b是任意两个不等实数，我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当m≤x≤n时，有m≤y≤n，我们就称此函数是闭区间[m，n]上的“闭函数”．如函数y=﹣x+4，当x=1时，y=3；当x=3时，y=1，即当1≤x≤3时，恒有1≤y≤3，所以说函数y=﹣x+4是闭区间[1，3]上的“闭函数”，同理函数y=x也是闭区间[1，3]上的“闭函数”．（1）反比例函数y=2018 是闭区间[1，2018]上的“闭函数”吗？请判断并说明理由；（2）如果已知二次函数y=x2﹣4x+k是闭区间[2，t]上的“闭函数”，求k 和t的值；（3）如果（2）所述的二次函数的图象交y轴于C点，A为此二次函数图象的顶点，B为直线x=1上的一点，当△ABC为直角三角形时，写出点B的坐标．10.（2018•马边县模拟）如图，抛物线y=﹣43 2+bx+c过点A（3，0），B（0，2）．M（m，0）为线段OA上一个动点（点M与点A不重合），过点M作垂直于x 轴的直线与直线AB和抛物线分别交于点P、N．（1）求直线AB的解析式和抛物线的解析式；（2）如果点P是MN的中点，那么求此时点N的坐标；（3）如果以B，P，N为顶点的三角形与△APM相似，求点M的坐标．11.（2018•徐汇区一模）如图，在平面直角坐标系x O y中，直线y=kx（k≠0）沿着y轴向上平移3个单位长度后，与x轴交于点B（3，0），与y轴交于点C，抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A．（1）求直线BC及该抛物线的表达式；（2）设该抛物线的顶点为D，求△DBC的面积；（3）如果点F在y轴上，且∠CDF=45°，求点F的坐标．12.（2018•长春模拟）如图，在平面直角坐标系x O y中，抛物线y=ax2+bx+c（a＞0）与x轴相交于点A（﹣1，0）和点B，与y轴交于点C，对称轴为直线x=1．（1）求点C的坐标（用含a的代数式表示）；（2）联结AC、BC，若△ABC的面积为6，求此抛物线的表达式；（3）在第（2）小题的条件下，点Q为x轴正半轴上一点，点G与点C，点F与点A关于点Q成中心对称，当△CGF为直角三角形时，求点Q的坐标．13.（2018•杨浦区一模）在平面直角坐标系x O y中，抛物线y=﹣x2+2mx﹣m2﹣m+1交y轴于点为A，顶点为D，对称轴与x轴交于点H．（1）求顶点D的坐标（用含m的代数式表示）；（2）当抛物线过点（1，﹣2），且不经过第一象限时，平移此抛物线到抛物线y=﹣x2+2x的位置，求平移的方向和距离；（3）当抛物线顶点D在第二象限时，如果∠ADH=∠AHO，求m的值．14.（2018•静安区一模）在平面直角坐标系x O y中（如图），已知抛物线y=ax2+bx ﹣53，经过点A（﹣1，0）、B（5，0）．（1）求此抛物线顶点C的坐标；（2）联结AC交y轴于点D，联结BD、BC，过点C作CH⊥BD，垂足为点H，抛物线对称轴交x轴于G，联结HG，求HG的长．15.（2018•浦东新区一模）已知抛物线y=ax2+bx+5与x轴交于点A（1，0）和点B（5，0），顶点为M．点C在x轴的负半轴上，且AC=AB，点D的坐标为（0，3），直线l经过点C、D．（1）求抛物线的表达式；（2）点P是直线l在第三象限上的点，联结AP，且线段CP是线段CA、CB的比例中项，求tan∠CPA的值；（3）在（2）的条件下，联结AM、BM，在直线PM上是否存在点E，使得∠AEM=∠AMB？若存在，求出点E的坐标；若不存在，请说明理由．16.（12分）（2018•普陀区一模）如图，已知在平面直角坐标系中，已知抛物线y＝ax2+2ax+c（其中a、c为常数，且a＜0）与x轴交于点A，它的坐标是（﹣3，0），与y轴交于点B，此抛物线顶点C到x轴的距离为4（1）求抛物线的表达式；（2）求∠CAB的正切值；（3）如果点P是抛物线上的一点，且∠ABP＝∠CAO，试直接写出点P 的坐标．。

2018上海初三数学一模压轴题汇总(各区23~25题)

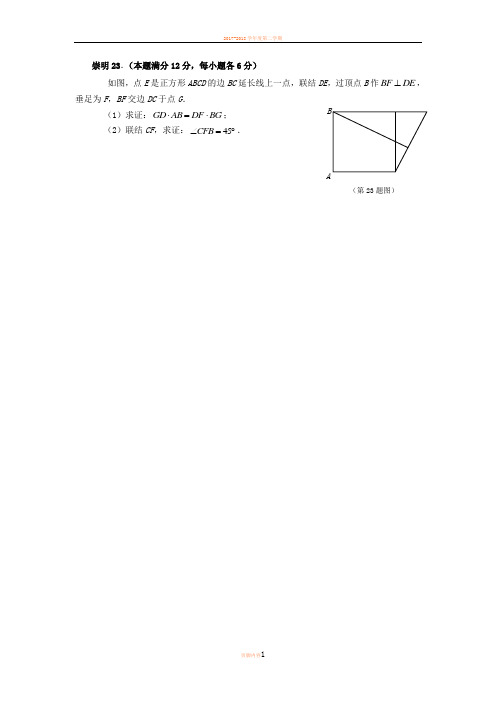
崇明23．（本题满分12分，每小题各6分）如图，点E 是正方形ABCD 的边BC 延长线上一点，联结DE ，过顶点B 作BF DE ⊥，垂足为F ，BF 交边DC 于点G ．（1）求证：GD AB DF BG ⋅=⋅；（2）联结CF ，求证：45CFB ∠=︒．（第23题图）ABDECGF崇明24．（本题满分12分，每小题各4分）如图，抛物线24yx bx c =-++过点(3,0)A ，(0,2)B ．(,0)M m 为线段OA 上一个x P 、N ．（（第24题图）xx（备用图）崇明25．（本题满分14分，第(1)小题4分，第(2)小题5分，第(3)小题5分）如图，已知ABC △中，90ACB ∠=︒，8AC =，4cos 5A =，D 是AB 边的中点，E 是AC 边上一点，联结DE ，过点D 作DF DE ⊥交BC 边于点F ，联结EF ．（1）如图1，当DE AC ⊥时，求EF 的长；（2）如图2，当点E 在AC 边上移动时，DFE ∠的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出DFE ∠的正切值；（3）如图3，联结CD 交EF 于点Q ，当CQF △是等腰三角形时，请直接写出．．．．BF 的长．（第25题图1）ABCDFEBDFECA（第25题图2）BDFECA（第25题图3）金山23. （本题满分12分，每小题6分）如图，已知在Rt△ABC中，∠ACB=90°，AC＞BC，CD是Rt△ABC的高，E是AC的中点，ED的延长线与CB的延长线相交于点F．（1）求证：DF是BF和CF的比例中项；（2）在AB上取一点G，如果AE：AC=AG：AD，求证：EG：CF=ED：DF．金山24. （本题满分12分，每小题4分）y ax bx与y轴相交于点C，与平面直角坐标系xOy中（如图），已知抛物线23x轴正半轴相交于点A，OA OC，与x轴的另一个交点为B，对称轴是直线1x，顶点为P．（1）求这条抛物线的表达式和顶点P的坐标；（2）抛物线的对称轴与x轴相交于点M，求∠PMC的正切值；（3）点Q在y轴上，且△BCQ与△CMP相似，求点Q的坐标．金山25. （本题满分14分，第（1）小题3分，第（2）小题5分，第（3）小题6分）如图，已知在△ABC中，4 5,cos5AB AC B，P是边AB一点，以P为圆心，PB 为半径的P与边BC的另一个交点为D，联结PD、AD．（1）求△ABC的面积；（2）设PB =x，△APD的面积为y，求y关于x的函数关系式，并写出定义域；（3）如果△APD是直角三角形，求PB的长．青浦23．（本题满分12分，第（1）小题4分，第（2）小题8分）如图8，已知点D、E分别在△ABC的边AC、BC上，线段BD与AE交于点F，且CD CA CE CB⋅=⋅．（1）求证：∠CAE＝∠CBD；（2）若BE ABEC AC=，求证：AB AD AF AE⋅=⋅．AB CDEF图青浦24．（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图9，在平面直角坐标系xOy 中，抛物线()20y axbx c a =++>与x 轴相交于点A （-1，0）和点B ，与y 轴交于点C ，对称轴为直线1x =．（1）求点C 的坐标（用含a 的代数式表示）；（2）联结AC 、BC ，若△ABC 的面积为6，求此抛物线的表达式；（3）在第（2）小题的条件下，点Q 为x 轴正半轴上一点，点G 与点C ，点F 与点A 关于点Q 成中心对称，当△CGF 为直角三角形时，求点Q 的坐标．图青浦25．（本题满分14分，第（1）小题5分，第（2）小题5分，第（3）小题4分）如图10，在边长为2的正方形ABCD 中，点P 是边AD 上的动点（点P 不与点A 、点 D 重合），点Q 是边CD 上一点，联结PB 、PQ ，且∠PBC ＝∠BPQ ．（1）当QD ＝QC 时，求∠ABP 的正切值；（2）设AP =x ，CQ =y ，求y 关于x 的函数解析式；（3）联结BQ ，在△PBQ 中是否存在度数不变的角，若存在，指出这个角，并求出它的度数；若不存在，请说明理由．图QP D C BA 备用图A B CD黄浦23、（本题满分12分）如图，BD 是ABC △的角平分线，点E 位于边BC 上，已知BD 是BA 与BE 的比例中项.（1）求证：12CDE ABC ∠=∠（2）求证：AD CD AB CE ⋅=⋅ED CBA黄浦24、（本题满分12分）在平面直角坐标系xOy 中，对称轴为直线1x =的抛物线28y ax bx =++过点()2,0-. （1）求抛物线的表达式，并写出其顶点坐标；（2）现将此抛物线沿y 方向平移若干个单位，所得抛物线的顶点为D ，与y 轴的交点为B ,与x 轴负半轴交于点A ，过点B 作x 轴的平行线交所得抛物线于点C ，若AC BD ∥，试求平移后所得抛物线的表达式.黄浦25、（本题满分14分）如图，线段5AB =，4AD =，90A ∠=︒，DP AB ∥，点C 为射线DP 上一点，BE 平分ABC ∠交线段AD 于点E （不与端点A 、D 重合）.（1）当ABC ∠为锐角，且tan 2ABC ∠=时，求四边形ABCD 的面积；（2）当ABE △与BCE △相似时，求线段CD 的长；（3）设DC x =，DE y =，求y 关于x 的函数关系式，并写出定义域.PDBA P EDC BA松江23．（本题满分12分，每小题6分）已知四边形ABCD中，∠BAD=∠BDC=90°，2=⋅．BD AD BC（1）求证：AD∥BC；（2）过点A作AE∥CD交BC于点E．请完善图形并求证：2=⋅．CD BE BC松江24．（本题满分12分，每小题4分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++的对称轴为直线x =1，抛物线与x 轴交于A 、B 两点（点A 在点B 的左侧），且AB =4，又P 是抛物线上位于第一象限的点，直线AP 与y 轴交于点D ，与对称轴交于点E ，设点P 的横坐标为t ．（1）求点A 的坐标和抛物线的表达式；（2）当AE :EP =1:2时，求点E 的坐标；（3）记抛物线的顶点为M ，与y 轴的交点为C ，当四边形CDEM 是等腰梯形时，求t 的值．松江25．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，已知△ABC中，∠ACB=90°，AC=1，BC=2，CD平分∠ACB交边AB与点D,P是射线CD上一点，联结AP．（1）求线段CD的长；（2）当点P在CD的延长线上，且∠PAB=45°时，求CP的长；（3）记点M为边AB的中点，联结CM、PM，若△CMP是等腰三角形，求CP的长．闵行23．（本题共2小题，每小题6分，满分12分）如图，已知在△ABC 中，∠BAC =2∠B ，AD 平分∠BAC ，DF //BE ，点E 在线段BA 的延长线上，联结DE ，交AC 于点G ，且∠E =∠C ．（1）求证：2AD AF AB =⋅；（2）求证：AD BE DE AB ⋅=⋅．（第23题ABDCEFG闵行24．（本题共3题，每小题4分，满分12分）抛物线23(0)y ax bx a=++≠经过点A（1-，0），B（3 2且与y轴相交于点C．（1）求这条抛物线的表达式；（2）求∠ACB的度数；（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．（第24题x闵行25．（共3小题，第（1）小题4分，第（2）小题6分，第（3）小题4分，满分14分）如图，在Rt △ABC 中，∠ACB =90°，AC =4，BC =3，CD 是斜边上中线，点E 在边AC 上，点F 在边BC 上，且∠EDA =∠FDB ，联结EF 、DC 交于点G ．（1）当∠EDF =90°时，求AE 的长；（2）CE = x ，CF = y ，求y 关于x 的函数关系式，并指出x 的取值范围；（3）如果△CFG 是等腰三角形，求CF 与CE 的比值．（备用图）ABDC（第25题ABEFG浦东23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图，已知，在锐角△ABC 中，CE ⊥AB 于点E ，点D 在边AC 上，联结BD 交CE 于点F ，且DF FB FC EF ⋅=⋅. （1）求证：BD ⊥AC ；（2）联结AF ，求证：AF BE BC EF ⋅=⋅.A （第23题DEFBC浦东24．（本题满分12分，每小题4分）已知抛物线y＝ax2＋bx＋5与x轴交于点A(1，0)和点B(5，0)，顶点为M．点C在x轴的负半轴上，且AC＝AB，点D的坐标为(0，3)，直线l经过点C、D．（1）求抛物线的表达式；（2）点P是直线l在第三象限上的点，联结AP，且线段CP是线段CA、CB的比例中项，求tan∠CPA的值；（3）在（2）的条件下，联结AM、BM，在直线PM上是否存在点E，使得∠AEM=∠AMB.若存在，求出点Ex（第24题图）浦东25．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，已知在△ABC中，∠ACB=90°，BC=2，AC=4，点D在射线BC上，以点D为圆心，BD为半径画弧交边AB于点E，过点E作EF⊥AB交边AC于点F，射线ED交射线AC于点G．（1）求证：△EFG∽△AEG；（2）设FG=x，△EFG的面积为y，求y关于x的函数解析式并写出定义域；（3）联结DF，当△EFD是等腰三角形时，请直接．．写出FG的长度．（第25题备用图）AB C（第25题备用图）AB C虹口23．（本题满分12分，第（1）题满分6分，第（2）题满分6分）如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，DE 、BC 的延长线相交于点F ，且EF DF BF CF ⋅=⋅．（1）求证AD AB AE AC ⋅=⋅；（2）当AB =12，AC =9，AE =8时，求BD 的长与△△ADEECFS S 的值．虹口24．（本题满分12分，第（1）小题满分4分，第（2）小题满分4分，第（3）小题满分4分）如图，在平面直角坐标系xOy中，抛物线与x轴相交于点A（-2,0）、B（4,0），与y轴交于点C（0，-4），BC与抛物线的对称轴相交于点D．（1）求该抛物线的表达式，并直接写出点D的坐标；（2）过点A作AE⊥AC交抛物线于点E，求点E的坐标；（3）在（2）的条件下，点F在射线AE上，若△ADF∽△ABC，求点F的坐标．虹口25．（本题满分14分，第（1）小题满分5分，第（2）小题满分5分，第（3）小题满分4分）已知AB=5，AD=4，AD∥BM，3cos5B=（如图），点C、E分别为射线BM上的动点（点C、E都不与点B重合），联结AC、AE，使得∠DAE=∠BAC，射线EA交射线CD于点F．设BC=x，AFyAC=．（1）如图1，当x=4时，求AF的长；（2）当点E在点C的右侧时，求y关于x的函数关系式，并写出函数的定义域；（3）联结BD交AE于点P，若△ADP是等腰三角形，直接写出x的值．普陀23. （本题满分12分）已知：如图9，四边形ABCD 的对角线AC 和BD 相交于点E ，2,AD DC DC DE DB ==⋅．求证：（1）BCE ADE ∽；（2）··AB BC BD BE =．图9A Bx普陀24．（本题满分12分，每小题满分各4分）如图10，在平面直角坐标系中，已知抛物线22y ax ax c +=+（其中a c 、为常数，且0a <）与x 轴交于点A ，它的坐标是()3, 0-，与y 轴交于点B ，此抛物线顶点C 到x 轴的距离为4．（1）求该抛物线的表达式；（2）求CAB ∠的正切值；（3）如果点P 是抛物线上的一点，且ABP CAO ∠=∠，试直接写出点P 的坐标．普陀25．（本题满分14分，第（1）小题满分3分，第（1）小题满分5分，第（1）小题满分6分）如图11，BAC ∠的余切值为2，AB =D 是线段AB 上的一动点（点D 不与点A B 、重合），以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上，且点F 在点E 的右侧．联结BG ，并延长BG ，交射线EC 于点P ．（1）点D 在运动时，下列的线段和角中，______是始终保持不变的量（填序号）； ①AF ； ②FP ； ③BP ； ④BDG ∠； ⑤GAC ∠； ⑥BPA ∠；（2）设正方形的边长为x ，线段AP 的长为y ，求y 与x 之间的函数关系式，并写出定义域；（3）如果PFG 与AFG 相似，但面积不相等，求此时正方形的边长．备用图图11BPACCE F嘉定23．（本题满分12分，每小题6分）如图6，已知梯形ABCD 中，AD ∥BC ，CD AB =，点E 在对角线AC 上，且满足BAC ADE ∠=∠.（1）求证：BC DE AE CD ⋅=⋅；（2）以点A 为圆心，AB 长为半径画弧交边BC 于点F ，联结求证：CA CE AF ⋅=2.C图嘉定24．（本题满分12分，每小题4分）已知在平面直角坐标系xOy （如图7）中，已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B .（1）求该抛物线的表达式；（2）设该抛物线的对称轴与x 轴的交点为C ，第四象限内的点D 在该抛物线的对称轴上，如果以点A 、C 、D 所组成的三角形与△AOB 相似，求点D 的坐标；（3）设点E 在该抛物线的对称轴上，它的纵坐标是1，联结AE 、BE ，求ABE ∠sin .嘉定25．（满分14分，第（1）小题4分，第（2）、（3）小题各5分）在正方形ABCD 中，8=AB ，点P 在边CD 上，43tan =∠PBC ，点Q 是在射线BP 上的一个动点，过点Q 作AB 的平行线交射线AD 于点M ，点R 在射线AD 上，使RQ 始终与直线BP 垂直．（1）如图8，当点R 与点D 重合时，求PQ 的长；（2）如图9，试探索：MQRM的比值是否随点Q 的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；（3）如图10，若点Q 在线段BP 上，设x PQ =，y RM =，求y 关于x 的函数关系式，并写出它的定义域．QM 图8M 图9图10静安23. （本题满分12分，其中第1小题6分，第2小题6分）已知：如图，梯形ABCD 中，//,,DC AB AD BD AD DB =⊥，点E 是腰AD 上一点，作45EBC ∠=，联结CE ，交DB 于点F ．（1）求证：ABE ∽DBC ；（2）如果56BC BD =，求BCE BDAS S 的值．静安24. （本题满分12分，第1小题4分，第2小题8分）在平面直角坐标系xOy中（如图），已知抛物线25 3y ax bx=+-经过点(1,0)A-、(5,0)B．（1）求此抛物线顶点C的坐标；（2）联结AC交y轴于点D，联结BD、BC，过点C作CH BD⊥，垂足为点H，抛物线对称轴交x轴于点G，联结HG，求HG的长．静安25. （本题满分14分，第1小题4分，第2小题6分，第3小题4分）已知：如图，四边形ABCD 中，090,,,BAD AD DC AB BC AC <∠≤==平分BAD ∠．（1）求证：四边形ABCD 是菱形；（2）如果点E 在对角线AC 上，联结BE 并延长，交边DC 于点G ，交线段AD 的延长线于点F （点F 可与点D 重合），AFB ACB ∠=∠，设AB 长度是a （a 实常数，且0a >），,AC x AF y ==，求y 关于x 的函数解析式，并写出定义域；（3）在第（2）小题的条件下，当CGE 是等腰三角形时，求AC 的长．（计算结果用含a 的代数式表示）长宁23．（本题满分12分，第（1）小题6分，第（2）小题6分）如图，在∆ABC 中，点D 在边BC 上，联结AD ，∠ADB=∠CDE ，DE 交边AC 于点E ，DE 交BA 延长线于点F ，且DF DE AD ⋅=2．（1）求证：BFD ∆∽CAD ∆；（2）求证：AD AB DE BF ⋅=⋅．F EDA第23题长宁24．（本题满分12分，每小题4分）在直角坐标平面内，直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ，且与x 轴的另一个交点为点B . 点D 在该抛物线上，且位于直线AC 的上方．（1）求上述抛物线的表达式；（2）联结BC 、BD ，且BD 交AC 于点E ，如果∆ABE 的面积与∆ABC 的面积之比为4:5，求∠DBA 的余切值；（3）过点D 作DF ⊥AC ，垂足为点F ，联结CD . 若∆CFD 与∆AOC 相似，求点D 的坐标．备用图第24题长宁25．（本题满分14分，第（1）小题3分，第（2）小题6分，第（3）小题5分）已知在矩形ABCD 中，AB =2，AD =4. P 是对角线BD 上的一个动点（点P 不与点B 、D 重合），过点P 作PF ⊥BD ，交射线BC 于点F . 联结AP ，画∠FPE =∠BAP ，PE 交BF 于点E .设PD=x ，EF =y ．（1）当点A 、P 、F 在一条直线上时，求 ABF 的面积；（2）如图1，当点F 在边BC 上时，求y 关于x 的函数解析式，并写出函数定义域；（3）联结PC ，若∠FPC =∠BPE ，请直接写出PD 的长．备用图备用图图1DCBA DCBA F EP D CB A 第25题图徐汇23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图在△ABC中，AB=AC，点D、E、F分别在边BC、AB、AC上，且∠ADE=∠B，∠ADF=∠C，线段EF交线段AD于点G．（1）求证：AE=AF；（2）若DF CFDE AE,求证：四边形EBDF是平行四边形．徐汇24．（本题满分12分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分5分）如图，在平面直角坐标系xOy 中，直线y =kx （k ≠0）沿着y 轴向上平移3个单位长度后，与x 轴交于点B （3,0），与y 轴交于点C ，抛物线2y x bx c =++过点B 、C 且与x 轴的另一个交点为A ．（1）求直线BC 及该抛物线的表达式；（2）设该抛物线的顶点为D ，求△DBC 的面积；（3）如果点F 在y 轴上，且∠CDF =45°，求点F 的坐标．徐汇25．（本题满分14分，第（1）小题3分，第（2）小题7分，第（3）小题4分）已知，在梯形ABCD中，AD∥BC，∠A=90°，AD=2，AB=4，BC=5，在射线BC任取一点M，联结DM，作∠MDN=∠BDC，∠MDN的另一边DN交直线BC于点N（点N在点M的左侧）．（1）当BM的长为10时，求证：BD⊥DM；（2）如图（1），当点N在线段BC上时，设BN=x，BM=y，求y关于x的函数关系式，并写出它的定义域；（3）如果△DMN是等腰三角形，求BN的长．杨浦23．（本题满分12分，第（1）小题5分，第（2）小题7分）已知：梯形ABCD 中，AD //BC ，AD =AB ，对角线AC 、BD 交于点E ，点F 在边BC 上，且∠BEF =∠BAC .（1）求证：△AED ∽△CFE ；（2）当EF //DC 时，求证：AE =DE .（第23题C杨浦24．（本题满分12分，第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，抛物线2221y x mx m m =-+--+交 y 轴于点为A ，顶点为D ，对称轴与x 轴交于点H .（1）求顶点D 的坐标（用含m 的代数式表示）；（2）当抛物线过点（1，-2），且不经过第一象限时，平移此抛物线到抛物线22y x x =-+的位置，求平移的方向和距离；（3）当抛物线顶点D 在第二象限时，如果∠ADH =∠AHO ，求m 的值.x（第24题图）杨浦25．（本题满分14分，第（1）、（2）小题各6分，第（3）小题2分）已知：矩形ABCD 中，AB =4，BC =3，点M 、N 分别在边AB 、CD 上，直线MN 交矩形对角线AC 于点E ，将△AME 沿直线MN 翻折，点A 落在点P 处，且点P 在射线CB 上.（1）如图1，当EP ⊥BC 时，求CN 的长；（2）如图2，当EP ⊥AC 时，求AM 的长；（3）请写出线段CP 的长的取值范围，及当CP 的长最大时MN 的长.（备用（图1）A B C D NP ME（图2） A B C D N P M E （第25题A B CD奉贤23．（本题满分 12 分，每小题满分各 6 分）已知：如图 8，四边形90ABCD DCB ∠=︒，，对角线 BD ⊥AD ，点 E 是边 AB 的中点，CE 与 BD 相交于点 F ，2·BD AB BC =．（1）求证：BD 平分∠ABC ；（2）求证：··BE CF BC EF ＝．奉贤24. （本题满分 12 分，每小题满分各 4 分）如图9，在平面直角坐标系xOy 中，抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ，与y 轴相交于点(0,3)C -，经过点A 的射线AM 与y 轴相交于点E ，与抛物线的另一个交点为点F ，且13AE EF =．（1）求这条抛物线的表达式，并写出它的对称轴；（2）求FAB ∠的余切值；（3）点D 是点C 关于抛物线对称轴的对称点，点 P 是 y 轴上一点，且AFP DAB ∠=∠，求点 P 的坐标．奉贤25．（本题满分 14 分，第（1）小题满分 3 分，第（1）小题满分 5 分，第（1）小题满分 6 分）已知：如图10，在梯形ABCD 中，//,90,2AB CD D AD CD ∠===，点E 在边AD 上（不与点A 、D 重合），45,CEB EB ∠=与对角线AC 相交于点F ，设DE x =．（1）用含x 的代数式表示线段CF 的长；（2）如果把CAE 的周长记作CAE C，BAF 的周长记作BAF C，设CAE BAFCy C=，求y关于x 的函数关系式，并写出它的定义域；（3）当ABE ∠的正切值是35时，求AB 的长．宝山23、（满分12分，每小题各6分）如图，ABC 中，AB AC =，过点C 作//CF AB 交ABC 的中位线DE 的延长线于F ，联结BF ，交AC 于点G .（1）求证：AE EGAC CG=；（2）若AH 平分BAC ∠，交BF 于H ，求证：BH 是HG 和HF 的比例中项.宝山24、（满分12分，每小题各4分）设,a b 是任意两个不等实数，我们规定：满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间，表示为[],a b ，对于一个函数，如果它的自变量x 与函数值y 满足：当m x n ≤≤时，有m y n ≤≤，我们就此称此函数是闭区间[],m n 上的“闭函数”。

2018中考真题汇编浮力一

2018中考真题汇编浮力一一．选择题（共24小题）1. （2018•江西）如图所示，在乙调好的天平的两个托盘上放上两个一模一样装满水的桶，其中右桶上飘着一小木块。

关于天平会向哪边倾斜的说法中正确的是（）A.天平不倾斜B.向左盘倾斜C.向右盘倾斜D.无法判断2. （2018•桂林）小关与同学们去游觉桂林两江四湖，登上游船后，船会下沉一些，那么（）A.船的重力将减小B.水对船的浮力将减小C.水对船的浮力将增大D.水对船的浮力将保持不变3. （2018•海南）如图所示，两只相同的气球，分别充入氢气和空气，充气后体积相同，放飞气球时只有氢气气球升上空中。

若它们在空气中受到的浮力分别为F 氢和F 空，则下列说法中正确的是（）C F 氢＜F 空D.条件不足，无法比较4. （2018•荆门）水上救援往往需要打捞沉没的货物，我们将该情景简化为如图所示的物理过程，假设物体浸没在水深h=0.5m 的容器底部（非密合），现利用弹簧测力计将物体从水中匀速提出，当物体有一半体积露出水面时，弹簧测力计示数为3N,当物体全部离开水面后，弹簧测力计示数为5N,已知水的密度p 水=1.0X103kg/m 3.取g=10N/kg 。

则（）A.物体在水面下上升的过程中所受浮力逐渐减小B.物体在容器底部时，受到的浮力为2NC.物体在容器底部时，水对其底部的压强为5X104PaD.物体的密度为1.25X 103kg/m3A. F >F 氢空B. F 氢*5.（2018•湖州）圆柱体先后放入密度为p 1和p 2的2种液体中，均处于漂浮状态，如图所示。

圆柱体在两液体中所受浮力依次是F1和「，则（）A. p 1>p 2F 1>F 2B. p 1<p 2F 1<F 2C. p 1<p 2F 1=F 2D. p 1>p 2 F 1=F6. （2018•东营）三个相同容器内分别盛满不同的液体，现将三个完全相同的小球轻轻放入容器中，小球静止后的状A.液体的密度关系是p 甲＞「丙＞「乙B.液体对容器底部的压强关系是P 乙＞p 甲＞p 丙C.容器对桌面的压强关系是p'甲＞p ：＞p'丙D.小球受到的浮力大小关系是F 广F 丙＞F 甲7. （2018•眉山）如图所示，放在水平桌面上的三个完全相同的容器内，装有适量的水，将A 、B 、C 三个体积相同正方体分别放入容器内，待正方体静止后，三个容器内水面高度相同。

2018年河南省郑州九年级一模模拟测试数学试题及答案精品

郑州2018年九年级一模模拟测试数学试题一选择题(每小题3分，共24分,下列各小题均有四个答案，其中只有一个是正确)1.－5的绝对值是（）A. 15- B. 15C. 5-D. 52.下列四个交通标志中，轴对称图形是（）3.不等式组： 2011x x +≥⎧⎨-<⎩的解集在数轴上表示正确的是( )4.某校有21名学生参加某比赛，预赛成绩各不同，要取前11名参加决赛，小颖已经知道了自己的成绩，她想知道自己能否进入决赛，只需要再知道这21名同学成绩的（） A ．最高分 B 。

平均分 C.极差 D.中位数5.一个几何体的三视图如图所示，则这个几何体摆放的位置是（）主视图左视图C6.三角形两边的长是3和4，第三边的长是方程212350x x-+=的根，则该三角形的周长为（）A. 14B. 12C. 14 或12D.以上都不对7.如图，线段AB是⊙O的直径，弦CD⊥AB，∠CAB =20°，则∠AOD等于（）A. 160°B. 150°C. 140°D．120°8.如图，在正方形ABCD中，AB=3cm，动点M自A点出发沿AB 方向以每秒1cm的速度运动，同时动点N从A点出发沿折线AD →DC→CB以每秒３cm的速度运动，到达B时运动同时停止，设△AMN的面积为y（cm2），运动时间为x(秒)，则下列图象中能大致反映y与x之间的函数关系的是二、填空题（每小题3分，共21分）9.1)=______________10.一副三角板叠在一起如图放置，最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上，BC与DE交于点M，如果∠ADF ＝100°,那么∠BMD为_____________度11.如图，A、B两点在双曲线4y=上，分别经过A、B两点向坐x标轴作垂线，已知S 阴影=1，则12S S +=__________________ 12.如图，经过点B （－2，0）的直线y kx b =+与直线42y x =+相交于点A （－1，－2），则不等式4x+2<kx+b<0的解集为__________________13.三辆车按1，2，3编号，舟舟和嘉嘉两人可任意选坐一辆车，则两人同坐3号车的概率是______14.如图，在Rt △ABC 中，∠ABC=90°，AB=3，AC=5，点E 在BC 上，将△ABC 沿AE 折叠，使点B 落在AC 边上的点B ′处，则BE 的长为___________15.如图，正方形ABCD 的边长为3cm ，E 为CD 边上一点，∠DAE=30°，M 为AE 的中点，过点M 、BC 相交于点P 、Q ，若PQ=AE ，则AP 等于第15题EB ′ABCE 第14题三、解答题（本题共8个小题，共75分） 16.（8分）请你化简 22236911211x x x x x x x +++÷+--++，再取恰当x 的值代入求值。

2018年北京市中考数学一模分类24题统计题

2018年北京市中考数学一模分类——24题统计题东24．随着高铁的建设，春运期间动车组发送旅客量越来越大.相关部门为了进一步了解春运期间动车组发送旅客量的变化情况，针对2014年至2018年春运期间铁路发送旅客量情况进行了调查，具体过程如下.()收集、整理数据请将表格补充完整：（）描述数据为了更直观地显示春运期间动车组发送旅客量占比的变化趋势，需要用 ___________(填“折线图”或“扇形图”)进行描述；（）分析数据、做出推测预计2019年春运期间动车组发送旅客量占比约为___________，你的预估理由是 _________________________________________ .西23. 某同学所在年级的500名学生参加“志愿北京”活动，现有以下5个志愿服务项目：A．纪念馆志愿讲解员；B．书香社区图书整理；C．学编中国结及义卖；D．家风讲解员；E．校内志愿服务.每位同学都从中选择一个项目参加.为了解同学们选择这5个项目的情况，该同学随机对年级中的40名同学选择的志愿服务项目进行了调查，过程如下．收集数据设计调查问卷，收集到如下的数据（志愿服务项目的编号，用字母代号表示）B，E，B，A，E，C，C，C，B，B，A，C，E，D，B，A，B，E，C，A，D，D，B，B，C，C，A，A，E，B，C，B，D，C，A，C，C，A，C，E.整理、描述数据划记、整理、描述样本数据、绘制统计图如下.请补全统计表和统计图．选择各志愿服务项目的人数统计表分析数据、推断结论a.抽样的40个样本数据（志愿服务项目的编号）的众数是（填A-E的字母代号）b. 请你任选A-E中的两个志愿服务项目，根据该同学的样本数据估计全年级大约有多少名同学选择这两个志愿服务项目．海24．某校九年级八个班共有280名学生，男女生人数大致相同，调查小组为调查学生的体质健康水平，开展了一次调查研究，请将下面的过程补全.收集数据调查小组计划选取40名学生的体质健康测试成绩作为样本，下面的取样方法中，合理的是___________（填字母）；A．抽取九年级1班、2班各20名学生的体质健康测试成绩组成样本B．抽取各班体育成绩较好的学生共40名学生的体质健康测试成绩组成样本C．从年级中按学号随机选取男女生各20名学生学生的体质健康测试成绩组成样本整理、描述数据抽样方法确定后，调查小组获得了40名学生的体质健康测试成绩如下：77 83 80 64 86 90 75 92 838185 86 88 62 65 86 97 96 827386 84 89 86 92 73 57 77 878291 81 86 71 53 72 90 76 6878整理数据，如下表所示：2018年九年级部分学生学生的体质健康测试成绩统计表分析数据、得出结论调查小组将统计后的数据与去年同期九年级的学生的体质健康测试成绩（直方图）进行了对比，你能从中得到的结论是_____________，你的理由是________________________________.体育老师计划根据2018年的统计数据安排75分以下的同学参加体质加强训练项目，则全年级约有________名同学参加此项目.朝24. 水果基地为了选出适应市场需求的小西红柿秧苗，在条件基本相同的情况下，把两个品种的小西红柿秧苗各300株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性，进行了抽样调查，过程如下，请补充完整．收集数据从甲、乙两个大棚各收集了25株秧苗上的小西红柿的个数：甲26 32 40 51 44 74 44 63 73 74 81 54 6241 33 54 43 34 51 63 64 73 64 54 33乙48576675474671整理、描述数据按如下分组整理、描述这两组样本数据个数株数x大棚25≤x<3535≤x<4545≤x<55 55≤x<6565≤x<7575≤x<85甲 5 5 5 5 4 1乙 2 4 6 2（说明：45个以下为产量不合格，45个及以上为产量合格，其中45~65个为产量良好，65~85个为产量优秀）分析数据两组样本数据的平均数、众数和方差如下表所示：大棚平均数众数方差甲53 54 3047得出结论a．估计乙大棚产量优秀的秧苗数为株；b．可以推断出大棚的小西红柿秧苗品种更适应市场需求，理由为．（至少从两个不同的角度说明推断的合理性）丰24．第二十四届冬季奥林匹克运动会将于2022年2月4日至2月20日在北京举行，北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市．某区举办了一次冬奥知识网上答题竞赛，甲、乙两校各有400名学生参加活动，为了解这两所学校的成绩情况，进行了抽样调查，过程如下，请补充完整．【收集数据】从甲、乙两校各随机抽取20名学生，在这次竞赛中他们的成绩如下：甲 30 60 6070608030901006060100 80 60 7060 6090 60 60乙 8090 40 60 8080 90 4080 5080 70 70 70 7060805080 80成【整理、描述数据】按如下分数段整理、描述这两组样本数据：（说明：优秀成绩为80＜x≤100，良好成绩为50＜x≤80，合格成绩为30≤x≤50．）【分析数据】两组样本数据的平均分、中位数、众数如下表所示：其中a=__________.【得出结论】（1）小明同学说：“这次竞赛我得了70分，在我们学校排名属中游略偏上！”由表中数据可知小明是________校的学生；（填“甲”或“乙”）（2）张老师从乙校随机抽取一名学生的竞赛成绩，试估计这名学生的竞赛成绩为优秀的概率为________；（3）根据以上数据推断一所你认为竞赛成绩较好的学校，并说明理由．（至少从两个不同的角度说明推断的合理性）石24．某校诗词知识竞赛培训活动中，在相同条件下对甲、乙两名学生进行了10次测验，他们的10次成绩如下（单位：分）：整理、分析过程如下，请补充完整．（1）按如下分数段整理、描述这两组数据：（2）两组数据的极差、平均数、中位数、众数、方差如下表所示：（3）若从甲、乙两人中选择一人参加知识竞赛，你会选（填“甲”或“乙），理由为．门24.地球环境问题已经成为我们日益关注的问题.学校为了普及生态环保知识，提高学生生态坏境保护意识，举办了“我参与，我环保”的知识竞赛.以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析，成绩如下：初一： 76 88 93 65 78 94 89 68 95 5089 88 89 89 77 94 87 88 92 91初二： 74 97 96 89 98 74 69 76 72 7899 72 97 76 99 74 99 73 98 74（1）根据上表中的数据，将下列表格补充完整；整理、描述数据：（说明：成绩分及以上为优秀，~分为良好，~分为合格，分以下为不合格）分析数据：（2）得出结论：你认为哪个年级掌握生态环保知识水平较好并说明理由.（至少从两个不同的角度说明推断的合理性）.顺23．中华文明，源远流长，中华汉字，寓意深广，为了传承优秀传统文化，某校九年级组织600名学生参加了一次“汉字听写”大赛．赛后发现所有参赛学生的成绩均不低于60分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩作为样本，成绩如下：90，92，81，82，78，95，86，88，72，66， 62，68，89，86，93，97，100，73，76，80， 77，81，86，89，82，85，71，68，74，98， 90，97，100，84，87，73，65，92，96，60.对上述成绩（成绩x取整数，总分100分）进行了整理，得到下列不完整的统计图表：请根据所给信息，解答下列问题：（1）a = ，b = ，c = ，d = ；（2）请补全频数分布直方图；（3）若成绩在90分以上（包括90分）的为“优”等，请你估计参加这次比赛的600名学生中成绩“优”等的约有多少人？通怀24.某校初三体育考试选择项目中，选择篮球项目和排球项目的学生比较多.为了解学生掌握篮球技巧和排球技巧的水平情况，进行了抽样调查，过程如下，请补充完整.收集数据从选择篮球和排球的学生中各随机抽取16人，进行了体育测试，测试成绩（十分制）如下：排球 109.59.510899.5971045.5 10 9.5 9.5 10篮球 9.5 9 8.5 8.510 9.5 10 86 9.5 10 9.5 9 8.5 9.5 6整理、描述数据按如下分数段整理、描述这两组样本数据：（说明：成绩8.5分及以上为优秀，6分及以上为合格，6分以下为不合格.）分析数据两组样本数据的平均数、中位数、众数如下表所示：得出结论(1)如果全校有160人选择篮球项目，达到优秀的人数约为人；(2)初二年级的小明和小军看到上面数据后，小明说：排球项目整体水平较高.小军说：篮球项目整体水平较高.你同意的看法，理由为.（至少从两个不同的角度说明推断的合理性）房24. 某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每个营业员在某月的销售额（单位：万元），数据如下，请补充完整．收集数据 17 18 16 12 24 1527 2518 1922 17 16 19 31 29 16 14 15 2515 3123 17 15 15 27 2716 19整理、描述数据分析数据样本数据的平均数、众数、中位数如下表所示：得出结论⑴如果想让一半左右的营业员都能达到销售目标，你认为月销售额应定为万元．⑵如果想确定一个较高的销售目标，这个目标可以定为每月万元，理由为．大24.甲乙两组各有10名学生，进行电脑汉字输入速度比赛，现将他们的成绩进行统计，过程如下：收集数据各组参赛学生每分钟输入汉字个数统计如下表：分析数据两组数据的众数、中位数、平均数、方差如下表所示：得出结论(1)若每分钟输入汉字个数136及以上为优秀，则从优秀人数的角度评价甲、乙两组哪个成绩更好一些？(2)请你根据所学的统计知识，从不同角度评价甲、乙两组学生的比赛成绩（至少从两个角度进行评价）.平23．为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整.收集数据随机抽取甲乙两所学校的20名学生的数学成绩进行分析：整理、描述数据按如下数据段整理、描述这两组数据分析数据两组数据的平均数、中位数、众数、方差如下表：经统计，表格中m的值是．得出结论a 若甲学校有400名初二学生，估计这次考试成绩80分以上人数为.b可以推断出学校学生的数学水平较高，理由为. （至少从两个不同的角度说明推断的合理性）延24．从北京市环保局证实，为满足2022年冬奥会对环境质量的要求，北京延庆正在对其周边的环境污染进行综合治理，率先在部分村镇进行“煤改电”改造．在治理的过程中，环保部门随机选取了永宁镇和千家店镇进行空气质量监测．过程如下，请补充完整.收集数据:从2016年12月初开始，连续一年对两镇的空气质量进行监测（将30天的空气污染指数（简称：API）的平均值作为每个月的空气污染指数，12个月的空气污染指数如下：千家店镇：120 115 100 100 95 85 80 70 50 50 50 45永宁镇：110 90 105 80 90 85 90 60 90 45 70 60整理、描述数据：空气质量按如下表整理、描述这两镇空气污染指数的数据：（说明：空气污染指数≤50时，空气质量为优；50＜空气污染指数≤100时，空气质量为良；100＜空气污染指数≤150时，空气质量为轻微污染．）分析数据：两镇的空气污染指数的平均数、中位数、众数如下表所示；请将以上两个表格补充完整；得出结论：可以推断出______镇这一年中环境状况比较好，理由为_____________.（至少从两个不同的角度说明推断的合理性）。

2018届九年级数学第一次模拟考试试题扫描版

∴CE=AF=3，EF= ，……5分
∵AE2+EF2=7+2=9,AF2=9，即AE2+EF2=AF2∴△AEF为直角三角形，……7分
∴∠BEF=90∘∴∠AED=∠AEF+DEF=90∘+45∘=135∘；……8分
(3)∵M是AB中点，∴MA= AB= AD，
∵AB∥CD，∴ ，……9分
在Rt△DAM中,DM=
∴DO= ，∵OF= ，∴DF= ，……10分
∵∠DFN=∠DCO=45∘，∠FDN=∠CDO，∴△DFN∽△DCO，……11分
……12分
27.(1)∵C(0,4)，∴OC=4.
∵OA=OC=4OB，∴OA=4，OB=1，
∴A(4,0),B(−1,0)，
设抛物线解析式：y=a(x+1)(x−4)，
∴4=−4a，∴a=−1.∴y=−x2+3x+4.……3分
=1- …………3分
(2)原式=a2-6+2a-a2………2分,
=2a-6………3分
20.（1）解得：x＜4………1分
解得：x ………2分
所以原不等式组的解集是2 x＜4………3分
(2)由x2-4x+3=0得（x-1）(x-3)=0………1分
∴x-1=0或x-3=0………2分
∴x1=1,x2=3………3分
(3)Q(0,0),(-4,0), .……12分
(3)以BC为底，则BC边上的高AE为3+2=5，∴S△ABC= ×2×5=5.……10分
26.(1)CE=AF；……1分
证明：在正方形ABCD,等腰直角三角形CEF中,FD=DE,CD=CA,∠ADC=∠EDF=90∘
∴∠ADF=∠CDE，∴△ADF≌△CDE，∴CE=AF.……4分

2018市中一模和答案

2018年初三数学模拟考试试题一、选择题：(每题4分，共计48分) 1．﹣3的倒数是（） A.31-B.31C.-3D.3解：A2．如下图所示的一个几何体，它的主视图是（）A. B. C. D.解：B3．2017年按照济南市政府“拆违拆临，建绿透绿”决策部署，济南市各个部门通力协作，年内共拆除违法建设约32900000平方米，拆违拆临工作取得重大历史性突破，数字32900000用科学计数法表示为（） A. 329×105 B. 3.29×105 C. 3.29×106 D. 3.29×107 解：D4．下列各式计算正确的是（）A ．a 2•a 3=a 6B ．（a 2）3=a 6C ．a 2+a 2=a 3D ．a 6÷a 2=a 3解：B ．5.下列所示的图形中既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ．解:B6.如果一组数据2，4，x ，3，5的众数是4，那么该组数据的平均数是（） A. 5.2 B. 4.6 C. 4 D. 3.6 解：D7.如果一元二次方程x 2﹣2x+p=0总有实数根，那么p 应满足的条件是（） A ．p ＞1 B ．p=1 C ．p ＜1 D ．p ≤1 解：D8.已知A 、B 两地之间铁路长为450千米，动车比火车每小时多行驶50千米，从A 市到B 市乘动车比乘火车少用40分钟，设动车速度为每小时x 千米，则可列方程为（） A ．4045050450=--x x B ．4050450450=--x x C ．3250450450=+-x x D ．3245050450=--x x 选：D ．9.如图是一副三角尺ABC 和与DEF 拼成的图案，若将三角尺DEF 绕点M 按顺时针方向旋转，则边DE 与边AB 第一次平行时，旋转角的度数是（）P OFEDCBAA ．75°B ．60°C ．45°D ．30°选C ．10. 如图所示，圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上．已知铁片的圆心为O ，三角尺的直角顶点C 落在直尺的10cm 处，铁片与直尺的唯一公共点A 落在直尺的14cm 处，铁片与三角尺的唯一公共点为B ，下列说法错误的是（）A.圆形铁片的半径是4cmB. 四边形AOBC 为正方形C.弧AB 的长度为4πcmD. 扇形OAB 的面积是4πcm 2解：C11. 如图，菱形ABCD 的对角线AC 与BD 交于点O ，AC=6，BD=8．动点E 从点B 出发，沿着B ﹣A ﹣D 在菱形ABCD 的边上运动，运动到点D 停止．点F 是点E 关于BD 的对称点，EF 交BD 于点P ，若BP=x ，△OEF 的面积为y ，则y 与x 之间的函数图象大致为（）A ．B． C ． D.解:∵四边形ABCD 是菱形， ∴AB=BC=CD=DA ，OA=21AC=3，OB=21BD=4，AC ⊥BD ， ① 当0＜BP ＜4时，∵点E 与点F 关于BD 对称，∴EF ⊥BD ，∴EF ∥AC ，∴△BEF ∽△BAC ，∴BO BP AC EF =，即：46xEF =， ∴x EF 23=，∵x OP -=4， ∴OEF ∆的面积=x x x x EF OP 34323)4(21212+-=⋅-=⋅⋅. ∴y 与x 之间的函数图象是抛物线，开口向下，对称轴x=2.②当BP =4时，OEF ∆不存在. ② 当4＜BP ＜8时，OEF ∆的面积=3)643-823)4(21212+--=⋅-=⋅⋅x x x EF OP （）（. y 与x 之间的函数图象是抛物线，开口向下，对称轴时x=6综上所述，选D12. 二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，下列四个结论中：①4ac ﹣b 2＜0；②4a+c ＜2b ；③3b+2c ＜0；④m （am+b ）+b ＜a （m ≠﹣1），其中正确结论的个数是（）A ．4个B ．3个C ．2个D ．1个解：∵抛物线和x 轴有两个交点，∴b 2﹣4ac ＞0，∴4ac ﹣b 2＜0，∴①正确；∵对称轴是直线x=﹣1，和x 轴的一个交点在点（0，0）和点（1，0）之间， ∴抛物线和x 轴的另一个交点在（﹣3，0）和（﹣2，0）之间，∴把（﹣2，0）代入抛物线得：y=4a ﹣2b+c ＞0，∴4a+c ＞2b ，∴②错误； ∵把（1，0）代入抛物线得：y=a+b+c ＜0， ∴2a+2b+2c ＜0，∵b=2a ，∴3b+2c ＜0，∴③正确；∵抛物线的对称轴是直线x=﹣1，∴y=a ﹣b+c 的值最大，即把（m ，0）（m ≠0）代入得：y=am 2+bm+c ＜a ﹣b+c ，∴am 2+bm+b ＜a ，即m （am+b ）+b ＜a ，∴④正确；即正确的有3个，故选B ．二、填空题（每题4分，共24分）13．分解因式：x 3﹣2x 2y+xy 2= ．解：2)(y x x -14.如果实数x ，y 满足方程组，那么x 2﹣y 2的值为．解：45-15．已知点P （1，2）关于x 轴的对称点为P′，且P′在直线y=kx +3上，把直线y=kx +3的图象向上平移2个单位后，所得的直线解析式为．解：55+-=x y16.如图，在Rt△ABC 中，∠ACB=90°，点D ，E ，F 分别为AB ，AC ，BC 的中点．若CD=5，则EF 的长为．解：516题图 17题图 18题图17．已知菱形A1B1C1D1的边长为2，且∠A1B1C1=60°，对角线A1C1，B1D1相较于点O，以点O为坐标原点，分别以OA1，OB1所在直线为x轴、y轴，建立如图所示的直角坐标系，以B1D1为对角线作菱形B1C2D1A2 ，使得∠B1A2D1=60°；再以A2C2为对角线作菱形A2B2C2D2，使得∠A2B2C2=60°；再以B2D2为对角线作菱形B2C3D2A3，使得∠B2A3D2=60°…，按此规律继续作下去，在x轴的正半轴上得到点A1，A2，A3，…，A n，则点A2018的坐标为．解：∵菱形A1B1C1D1的边长为2，∠A1B1C1=60°，∴OA1=A1B1•sin30°=2×=1，OB1=A1B1•cos30°=2×=，∴A1（1，0）．∵B1C2D1A2与菱形A1B1C1D1都含有60°的角。

2018-2019学年上海中考数学各区一模汇编提升题(18、23、24、25题

目录Ⅰ第18题（填空小压轴） (3)【2019届一模徐汇】 (3)【2019届一模浦东】 (3)【2019届一模杨浦】 (3)【2019届一模普陀】 (4)【2019届一模奉贤】 (4)【2019届一模松江】 (4)【2019届一模嘉定】 (5)【2019届一模青浦】 (5)【2019届一模青浦】 (5)【2019届一模静安】 (6)【2019届一模宝山】 (6)【2019届一模长宁】 (6)【2019届一模金山】 (7)【2019届一模闵行】 (7)【2019届一模虹口】 (7)Ⅱ第23题（几何证明题） (8)【2019届一模徐汇】 (8)【2019届一模浦东】 (8)【2019届一模杨浦】 (9)【2019届一模普陀】 (9)【2019届一模奉贤】 (10)【2019届一模松江】 (10)【2019届一模嘉定】 (11)【2019届一模青浦】 (11)【2019届一模静安】 (12)【2019届一模宝山】 (12)【2019届一模长宁】 (13)【2019届一模金山】 (13)【2019届一模闵行】 (14)【2019届一模虹口】 (14)Ⅲ第24题（二次函数综合） (15)【2019届一模徐汇】 (15)【2019届一模浦东】 (16)【2019届一模普陀】 (18)【2019届一模奉贤】 (19)【2019届一模松江】 (20)【2019届一模嘉定】 (21)【2019届一模青浦】 (22)【2019届一模静安】 (23)【2019届一模宝山】 (24)【2019届一模长宁】 (25)【2019届一模金山】 (26)【2019届一模闵行】 (27)【2019届一模虹口】 (28)Ⅳ第25题（压轴题） (29)【2019届一模徐汇】 (29)【2019届一模浦东】 (30)【2019届一模杨浦】 (31)【2019届一模普陀】 (32)【2019届一模奉贤】 (33)【2019届一模松江】 (34)【2019届一模嘉定】 (35)【2019届一模青浦】 (36)【2019届一模静安】 (37)【2019届一模宝山】 (38)【2019届一模长宁】 (39)【2019届一模金山】 (40)【2019届一模闵行】 (41)【2019届一模虹口】 (42)Ⅰ第18题（填空小压轴）【2019届一模徐汇】18．在梯形ABCD 中，AB ∥DC ，∠B =90°，BC=6，CD =2，3tan 4A =．点E 为BC 上一点，过点E 作EF ∥AD 交边AB 于点F ．将△BEF 沿直线EF 翻折得到△GEF ，当EG 过点D 时，BE 的长为 ▲ ．【2019届一模浦东】18. 将矩形纸片ABCD 沿直线AP 折叠，使点D 落在原矩形ABCD 的边BC 上的点E 处，如果∠AED 的余弦值为35，那么ABBC =__________.【2019届一模杨浦】18．Rt △ABC 中，∠C =90°，AC =3，BC =2，将此三角形绕点A 旋转，当点B 落在直线BC 上的点D 处时，点C 落在点E 处，此时点E 到直线BC 的距离为 ▲ .GEABC DF （第18题图）ACB（第18题图）18．如图5，△ABC 中，8AB AC ==，3cos 4B =，点D 在边BC 上，将△ABD 沿直线AD 翻折得到△AED ，点B 的对应点为点E ，AE 与边BC 相交于点F ，如果2BD =，那么EF = ▲ ．【2019届一模奉贤】18．如图5，在△ABC 中，AB =AC =5，3sin =5C ，将△ABC 绕点A 逆时针旋转得到△ADE ,点B 、C 分别与点D 、E 对应，AD 与边BC 交于点F ．如果AE //BC ，那么BF 的长是 ▲ ．【2019届一模松江】18．如图，在直角坐标平面xoy 中，点A 坐标为（3，2），∠AOB ＝90°，∠OAB ＝30°，AB 与x 轴交于点C ，那么AC :BC 的值为______．图5ABCD图5AB C（第18题图）xyC BOA18．在△ABC 中，︒=∠90ACB ，点D 、E 分别在边BC 、AC 上，AE AC 3=，︒=∠45CDE (如图3)，△DCE 沿直线DE 翻折，翻折后的点C 落在△ABC 内部的点F ，直线AF 与边BC 相交于点G ，如果AE BG =，那么=B tan ▲ ．【2019届一模青浦】17．如图，在Rt △ABC 中，∠ACB=90°，AC=1，tan ∠CAB=2，将△ABC 绕点A 旋转后，点B 落在AC 的延长线上的点D ，点C 落在点E ，DE 与直线BC 相交于点F ，那么CF= ▲ ．【2019届一模青浦】18．对于封闭的平面图形，如果图形上或图形内的点S 到图形上的任意一点P 之间的线段都在图形内或图形上，那么这样的点S 称为“亮点”．如图，对于封闭图形ABCDE ，S 1是 “亮点”，S 2不是“亮点”，如果AB ∥DE ，AE ∥DC ， AB=2，AE=1，∠B=∠C= 60°，那么该图形中所有“亮点” 组成的图形的面积为 ▲ ．EDCBAS 2S 1（第18题图）18．如图6，将矩形ABCD 沿对角线BD 所在直线翻折后，点A 与点E 重合，且ED 交BC 于点F ，联结AE ．如果2tan 3DFC ∠=，那么BDAE的值是 ▲ ．【2019届一模宝山】18．如图4，Rt △ABC 中，∠ACB =90°，AC =4，BC =5，点P 为AC 上一点，将△BCP 沿直线BP 翻折，点C落在C ’处，连接AC ’，若AC ’∥BC ，则CP 的长为 ▲ ．【2019届一模长宁】18．如图，点P 在平行四边形ABCD 的边BC 上，将ABP ∆沿直线AP 翻折，点B 恰好落在边AD 的垂直平分线上，如果5=AB ，8=AD ，34tan =B ，那么BP 的长为 ▲ ．AC（图4）B图6F BACDEBACD第18题图18．如图，在ABC Rt ∆中，o90=∠C ，8=AC ，6=BC ．在边AB 上取一点O ，使BC BO =，以点O 为旋转中心，把ABC ∆逆时针旋转90，得到C B A '''∆（点A 、B 、C 的对应点分别是点A '、B '、C '），那么ABC ∆与C B A '''∆的重叠部分的面积是 ▲ ．【2019届一模闵行】18．如图，在Rt △ABC 中，∠ACB = 90°，BC = 3，AC = 4，点D 为边AB 上一点．将△BCD 沿直线CD 翻折，点B 落在点E 处，联结AE ．如果AE // CD ，那么BE = ▲ ．【2019届一模虹口】18．如图，正方形ABCD 的边长为4，点O 为对角线AC 、BD 的交点，点E 为边AB 的中点，△BED 绕着点B 旋转至△BD 1E 1，如果点D 、E 、D 1在同一直线上，那么EE 1的长为 ▲ ．ABC第18题OABC （第18题图）C第18题图A BDE OⅡ第23题（几何证明题）【2019届一模徐汇】23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图，已知菱形ABCD ，点E 是AB 的中点，AF BC ⊥于点F ，联结EF 、ED 、DF ，DE 交AF 于点G ，且2AE EG ED =⋅．(1) 求证：DE EF ⊥； (2) 求证：22BC DF BF =⋅．【2019届一模浦东】23. （本题满分12分，其中每小题各6分）已知：如图8，在平行四边形ABCD 中，M 是边BC 的中点，E 是边BA 延长线上的一点，联结EM ，分别交线段AD 于点F 、AC 于点G .（1）求证：GF EFGM EM=; （2）当22BC BA BE =⋅时，求证：∠EMB =∠ACD .G DEF BCA（第23题图）（图8）DCM BAF GE23．（本题满分12分，每小题各6分）已知：如图，在△ABC 中，点D 在边AB 上，点E 在线段CD 上，且∠ACD =∠B =∠BAE. （1）求证：AD DEBC AC=；（2）当点E 为CD 中点时，求证：22AE ABCE AD=.【2019届一模普陀】23．（本题满分12分）已知：如图9，△ADE 的顶点E 在△ABC 的边BC 上，DE 与AB 相交于点F ，AE AF AB =⋅2，DAF EAC ∠=∠．（1）求证：△ADE ∽△ACB ；（2）求证：DF CE DE CB=．（第23题图）EABCDF图9ABCDE23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）已知：如图9，在△ABC 中，点D 在边AC 上，BD 的垂直平分线交CA 的延长线于点E ，交BD 于点F ，联结BE ，EC EA ED •=2．（1）求证：∠EBA =∠C ；（2）如果BD =CD ，求证：AC AD AB •=2．【2019届一模松江】23.（本题满分12分，第（1）小题5分，第（2）小题7分）已知：如图，在梯形ABCD 中，AD ∥BC ，AB=DC ，E 是对角线AC 上一点，且AC ·CE=AD ·BC . （1）求证：∠DCA=∠EBC ；（2）延长BE 交AD 于F ，求证：AB 2=AF ·AD .ABCDEF图9（第23题图）EDCBAF（第23题图）EDCBA23．（本题满分12分，每小题6分）如图6，已知点D 在△ABC 的外部，AD //BC ，点E 在边AB 上，AE BC AD AB ⋅=⋅．（1）求证：AED BAC ∠=∠；（2）在边AC 取一点F ，如果D AFE ∠=∠，求证：ACAFBC AD =．【2019届一模青浦】23．（本题满分12分，第（1）小题7分，第（2）小题5分）已知：如图，在△ABC 中，点D 、E 分别在边BC 、AC 上，点F 在DE 的延长线上，AD=AF ，AE CE DE EF ⋅=⋅．（1）求证：△ADE ∽△ACD ；（2）如果AE BD EF AF ⋅=⋅，求证：AB=AC ．图6BCDAE FABCDEF（第23题图）23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）已知：如图9，在ABC ∆中，点D 、E 分别在边BC 和AB 上，且AD AC =，EB ED =，分别延长ED 、AC 交于点F ．（1）求证：ABD ∆∽FDC ∆；（2）求证：2AE BE EF =⋅．【2019届一模宝山】23．（本题满分12分）地铁10号线某站点出口横截面平面图如图8所示，电梯AB 的两端分别距顶部9.9米和2.4米，在距电梯起点A 端6米的P 处，用1.5米的测角仪测得电梯终端B 处的仰角为14°，求电梯AB 的坡度与长度．参考数据：24.014sin ≈︒，25.014tan ≈︒，97.014cos ≈︒.Q 9.9米B出口顶部1.5米（图8）AP6米2.4米︒14图9 AC BDEF23．（本题满分12分，第（1）小题5分，第（2）小题7分）如图，点D 、E 分别在ABC ∆的边AC 、AB 上，延长DE 、CB 交于点F ，且AC AD AB AE ⋅=⋅．（1）求证：C FEB ∠=∠；（2）联结AF ，若FD CD AB FB =，求证：FB AC AB EF ⋅=⋅．【2019届一模金山】23．如图，M 是平行四边形ABCD 的对角线上的一点，射线AM 与BC 交于点F ，与DC 的延长线交于点H ．（1）求证：MH MF AM ⋅=2．（2）若DM BD BC ⋅=2，求证：ADC AMB ∠=∠．第23题图CEDABF ABCD HF M第23题23．（本题共2小题，每小题6分，满分12分）如图，在△ABC 中，点D 为边BC 上一点，且AD = AB ，AE ⊥BC ，垂足为点E ．过点D 作DF // AB ，交边AC 于点F ，联结EF ，212EF BD EC =⋅．（1）求证：△EDF ∽△EFC ；（2）如果14EDF ADC S S =V V ，求证：AB = BD ．【2019届一模虹口】23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图，在△ABC 中，AB=AC ，D 是边BC 的中点，DE ⊥AC ，垂足为点E ．（1）求证：DE CD AD CE ⋅=⋅；（2）设F 为DE 的中点，联结AF 、BE ，求证：=AF BC AD BE ⋅⋅．ABCDE F（第23题图）D 第23题图AECBⅢ第24题（二次函数综合）【2019届一模徐汇】24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xoy 中，顶点为M 的抛物线C 1:2(0)y ax bx a =+<经过点A 和x 轴上的点B ，AO =OB =2，120AOB ∠=o ．（1）求该抛物线的表达式；（2）联结AM ，求AOM S V ；（3）将抛物线C 1向上平移得到抛物线C 2，抛物线C 2与x 轴分别交于点E 、F （点E 在点F 的左侧），如果△MBF 与△AOM 相似，求所有符合条件的抛物线C 2的表达式．（第24题图）【2019届一模浦东】24.（本题满分12分，其中每小题各4分）已知：如图9，在平面直角坐标系xOy中，直线12y x b=-+与x轴相交于点A，与y轴相交于点B. 抛物线244y ax ax=-+经过点A和点B，并与x轴相交于另一点C，对称轴与x轴相交于点D.（1）求抛物线的表达式;（2）求证: △BOD∽△AOB;（3）如果点P在线段AB上，且∠BCP=∠DBO，求点P的坐标.（图9）xBO Ay【2019届一模杨浦】24．（本题满分12分，每小题各4分）在平面直角坐标系xOy 中，抛物线2(0)y ax bx c a =++?与y 轴交于点C （0,2），它的顶点为D （1,m ），且1tan 3COD ?. （1）求m 的值及抛物线的表达式；（2）将此抛物线向上平移后与x 轴正半轴交于点A ，与y 轴交于点B ，且OA =OB .若点A 是由原抛物线上的点E 平移所得，求点E 的坐标；（3）在（2）的条件下，点P 是抛物线对称轴上的一点（位于x 轴上方），且∠APB =45°.求P 点的坐标.O xy 1 2 3 4 1 2 3 45-1-2 -3 -1 -2 -3 （第24题图）24．（本题满分12分）如图10，在平面直角坐标系xOy 中，抛物线23y ax bx =+-(0)a ≠与x 轴交于点A ()1,0-和点B ，且3OB OA =，与y 轴交于点C ，此抛物线顶点为点D ．（1）求抛物线的表达式及点D 的坐标；（2）如果点E 是y 轴上的一点（点E 与点C 不重合），当BE DE ⊥时，求点E 的坐标；（3）如果点F 是抛物线上的一点，且135FBD ∠=，求点F 的坐标．图10C BAOyx24．（本题满分12分，每小题满分6分）如图10，在平面直角坐标系xOy 中，直线AB 与抛物线2y ax bx =+交于点A (6，0)和点B (1，－5)．（1）求这条抛物线的表达式和直线AB 的表达式；（2）如果点C 在直线AB 上，且∠BOC 的正切值是32，求点C 的坐标．图10 ABxyo24.（本题满分12分，第（1）小题3分，第（2）小题4分，第（3）小题5分）如图，抛物线c bx x y ++-=221经过点A （﹣2，0），点B （0，4）. （1）求这条抛物线的表达式；（2）P 是抛物线对称轴上的点，联结AB 、PB ，如果∠PBO=∠BAO ，求点P 的坐标；（3）将抛物线沿y 轴向下平移m 个单位，所得新抛物线与y 轴交于点D ，过点D 作DE ∥x 轴交新抛物线于点E ，射线EO 交新抛物线于点F ，如果EO =2OF ，求m 的值.(第24题图)y xOBA24．（本题满分12分，每小题4分）在平面直角坐标系xOy （如图7）中，抛物线22++=bx ax y 经过点)0,4(A 、)2,2(B ，与y 轴的交点为C ．（1）试求这个抛物线的表达式；（2）如果这个抛物线的顶点为M ，求△AMC 的面积；（3）如果这个抛物线的对称轴与直线BC 交于点D ，点E 在线段AB 上，且︒=∠45DOE ，求点E 的坐标．图7O 11 xy--24．（本题满分12分，其中第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，将抛物线2y x =-平移后经过点A （-1，0）、B （4，0），且平移后的抛物线与y 轴交于点C （如图）．（1）求平移后的抛物线的表达式；（2）如果点D 在线段CB 上，且CD =2，求∠CAD 的正弦值；（3）点E 在y 轴上且位于点C 的上方，点P 在直线BC 上，点Q 在平移后的抛物线上，如果四边形ECPQ 是菱形，求点Q 的坐标．CB A xyOCB A xyO（第24题图）（备用图）24．（本题满分12分，其中第（1）小题4分，第（2）小题3分，第（3）小题5分）在平面直角坐标系xOy 中（如图10），已知抛物线2(0)y ax bx c a =++≠的图像经过点(40)B ，、(53)D ，，设它与x 轴的另一个交点为A （点A 在点B 的左侧），且ABD ∆的面积是3．（1）求该抛物线的表达式；（2）求ADB ∠的正切值；（3）若抛物线与y 轴交于点C ，直线CD 交x 轴于点E ，点P 在射线AD 上，当APE ∆与 ABD ∆相似时，求点P 的坐标．BD O图10xy﹒﹒24．（本题满分12分，第(1)小题满分6分，第(2)小题满分6分）如图9，已知：二次函数2y x bx =+的图像交x 轴正半轴于点A ，顶点为P ,一次函数132y x =-的图像交x 轴于点B ，交y 轴于点C , ∠OCA 的正切值为23． (1)求二次函数的解析式与顶点P 坐标；(2)将二次函数图像向下平移m 个单位,设平移后抛物线顶点为P ’,若，求m 的值．A B C O yx（图9）24．（本题满分12分，每小题4分）如图，在直角坐标平面内，抛物线经过原点O 、点)3,1(B ，又与x 轴正半轴相交于点A ，︒=∠45BAO ，点P 是线段AB 上的一点，过点P 作OB PM //，与抛物线交于点M ，且点M 在第一象限内．（1）求抛物线的表达式；（2）若AOB BMP ∠=∠，求点P 的坐标；（3）过点M 作x MC ⊥轴，分别交直线AB 、x 轴于点N 、C ，若ANC ∆的面积等于PMN ∆的面积的2倍，求NC MN 的值．第24题图 xO A By备用图xO A By24．已知抛物线c bx x y ++=2经过点()6,0A ，点()3,1B ，直线1l ：()0≠=k kx y ，直线2l ：2--=x y ，直线1l 经过抛物线c bx x y ++=2的顶点P ，且1l 与2l 相交于点C ，直线2l 与x 轴、y 轴分别交于点D 、E .若把抛物线上下平移，使抛物线的顶点在直线2l 上（此时抛物线的顶点记为M ），再把抛物线左右平移，使抛物线的顶点在直线1l 上（此时抛物线的顶点记为N ）．（1）求抛物线c bx x y ++=2的解析式．（2）判断以点N 为圆心，半径长为4的圆与直线2l 的位置关系，并说明理由．（3）设点F 、H 在直线1l 上（点H 在点F 的下方），当MHF ∆与OAB ∆相似时，求点F 、H 的坐标（直接写出结果）．第24题yxO24．（本题共3小题，每小题4分，满分12分）已知：在平面直角坐标系xOy 中，抛物线2y a x b x =+经过点A （5，0）、B （-3，4），抛物线的对称轴与x 轴相交于点D ．（1）求抛物线的表达式；（2）联结OB 、BD ．求∠BDO 的余切值；（3）如果点P 在线段BO 的延长线上，且∠P AO =∠BAO ，求点P 的坐标．xy O （第24题图）24．（本题满分12分，第（1）小题满分4分，第（2）小题满分4分，第（3）小题满分4分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴相交于原点O 和点B （4，0），点A （3，m ）在抛物线上．（1）求抛物线的表达式，并写出它的对称轴；（2）求tan ∠OAB 的值；（3）点D 在抛物线的对称轴上，如果∠BAD =45°，求点D 的坐标．OAy 第24题图xBF EA CB DF E A CB DⅣ第25题（压轴题）【2019届一模徐汇】25. （本题满分14分，第（1）小题4分，第（2）小题4分，第（3）小题6分）已知：在梯形ABCD 中，AD //BC ，AC ＝BC ＝10，54cos =∠ACB ，点E 在对角线AC 上(不与点A 、C 重合)，EDC ACB ∠=∠，DE 的延长线与射线CB 交于点F ，设AD 的长为x ．（1）如图1，当DF BC ⊥时，求AD 的长；（2）设EC 的长为y ，求y 关于x 的函数解析式，并直接写出定义域；（3）当△DFC 是等腰三角形时，求AD 的长．（第25题图1）（第25题图）【2019届一模浦东】25. （本题满分14分，其中第（1）小题3分，第（2）小题5分，第（3）小题6分）将大小两把含30°角的直角三角尺按如图10-1位置摆放，即大小直角三角尺的直角顶点C 重合，小三角尺的顶点D 、E 分别在大三角尺的直角边AC 、BC 上，此时小三角尺的斜边DE 恰好经过大三角尺的重心G . 已知∠A =∠CDE =30°，AB =12. （1）求小三角尺的直角边CD 的长;（2）将小三角尺绕点C 逆时针旋转，当点D 第一次落在大三角尺的边AB 上时（如图10-2），求点B 、E 之间的距离;（3）在小三角尺绕点C 旋转的过程中，当直线DE 经过点A 时，求∠BAE 的正弦值.G（图10-1）（图10-2）E DCABDCBAE25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）已知：梯形ABCD 中，AD //BC ，AB ⊥BC ，AD =3，AB =6，DF ⊥DC 分别交射线AB 、射线CB 于点E 、F .（1）当点E 为边AB 的中点时（如图1），求BC 的长；（2）当点E 在边AB 上时（如图2），联结CE ，试问：∠DCE 的大小是否确定？若确定，请求出∠DCE 的正切值；若不确定，则设AE =x ，∠DCE 的正切值为y ，请求出y 关于x 的函数解析式，并写出定义域；（3）当△AEF 的面积为3时，求△DCE 的面积.A BC D EF （图1）（第25题图） A B C D E F （图2）25．（本题满分14分）如图11，点O 在线段AB 上，22AO OB a ==，60BOP ∠=︒，点C 是射线OP 上的一个动点．（1）如图11①，当90ACB ∠=︒，2OC =，求a 的值；（2）如图11②，当AC =AB 时，求OC 的长（用含a 的代数式表示）；（3）在第（2）题的条件下，过点A 作AQ ∥BC ，并使∠QOC=∠B ，求:AQ OQ 的值．A BCPOABCPO图11①图11②25．（本题满分14分，第(1)小题满分4分，第(2)小题满分5分，第(3)小题满分5分）如图11，已知梯形ABCD 中，AB ∥CD ，∠DAB =90°，AD =4，26AB CD ==，E 是边BC 上一点，过点D 、E 分别作BC 、CD 的平行线交于点F ，联结AF 并延长，与射线DC 交于点G ．（1）当点G 与点C 重合时，求:CE BE 的值；（2）当点G 在边CD 上时，设CE m =，求△DFG 的面积；（用含m 的代数式表示）（3）当AFD ∆∽ADG ∆时，求∠DAG 的余弦值．图11ABC D F E G 备用图ABC D25．（本题满分14分，第（1）小题4分，第（2）、（3）小题各5分）如图，已知△ABC 中，∠ACB =90°，D 是边AB 的中点，P 是边AC 上一动点，BP 与CD 相交于点E ．（1）如果BC =6，AC =8，且P 为AC 的中点，求线段BE 的长；（2）联结PD ，如果PD ⊥AB ，且CE =2，ED =3，求cosA 的值；（3）联结PD ，如果222BP CD ，且CE =2，ED =3，求线段PD 的长．（备用图2）ABCD（备用图1）ABCD（第25题图）ABPC D E25．（满分14分，第（1）小题4分，第（2）、（3）小题各5分）在矩形ABCD 中，6=AB ，8=AD ，点E 是边AD 上一点，EC EM ⊥交AB 于点M ，点N 在射线MB 上，且AE 是AM 和AN 的比例中项. （1）如图8，求证：DCE ANE ∠=∠；（2）如图9，当点N 在线段MB 之间，联结AC ，且AC 与NE 互相垂直，求MN 的长；（3）联结AC ，如果△AEC 与以点E 、M 、N 为顶点所组成的三角形相似，求DE 的长．A备用图BD CA 图8B M E DC N A 备用图 BD C ME N A 图9 B D C25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在梯形ABCD 中，AD//BC ，BC =18，DB =DC =15，点E 、F 分别在线段BD 、CD 上，DE =DF =5． AE 的延长线交边BC 于点G ， AF 交BD 于点N 、其延长线交BC 的延长线于点H ．（1）求证：BG =CH ；（2）设AD =x ，△ADN 的面积为y ，求y 关于x 的函数解析式，并写出它的定义域；（3）联结FG ，当△HFG 与△ADN 相似时，求AD 的长．NHGFEDC AB （第25题图）图11ABCPQM25．（本题满分14分，其中第（1）小题4分，第（2）小题5分，第（3）小题5分）已知：如图11，在ABC ∆中，6AB =，9AC =，tan 22ABC ∠=．过点B 作BM //AC ，动点P 在射线BM 上（点P 不与点B 重合），联结PA 并延长到点Q ，使AQC ABP ∠=∠．（1）求ABC ∆的面积；（2）设BP x =，AQ y =，求y 关于x 的函数解析式，并写出x 的取值范围；（3）联结PC ，如果PQC ∆是直角三角形，求BP 的长．25．（本题满分14分，第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分4分）如图10，已知：梯形ABCD 中，∠ABC =90°，∠A =45°，AB ∥DC ，DC =3，AB =5，点 P 在AB 边上，以点A 为圆心AP 为半径作弧交边DC 于点E ，射线EP 与射线CB 交于点F ．（1）若13AP ，求DE 的长；（2）联结CP ，若CP=EP ，求AP 的长；（3）线段CF 上是否存在点G ，使得△ADE 与△FGE 相似，若相似，求FG 的值；若不相似，请说明理由．备用图A BCD PEABCDF（图10）25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）已知锐角MBN ∠的余弦值为53，点C 在射线BN 上，25=BC ，点A 在MBN ∠的内部，且︒=∠90BAC ，MBN BCA ∠=∠．过点A 的直线DE 分别交射线BM 、射线BN 于点D 、E ．点F 在线段BE 上（点F 不与点B 重合），且MBN EAF ∠=∠．（1）如图1，当BN AF ⊥时，求EF 的长；（2）如图2，当点E 在线段BC 上时，设x BF =，y BD =，求y 关于x 的函数解析式并写出函数定义域；（3）联结DF ，当ADF ∆与ACE ∆相似时，请直接写出BD 的长．第25题图图2 BFE C N DA MB FC E N AD M图1备用图BC NAM25．已知多边形ABCDEF 是⊙O 的内接正六边形，联结AC 、FD ，点H 是射线AF 上的一个动点，联结CH ,直线CH 交射线DF 于点G ，作CH MH ⊥交CD 的延长线于点M ，设⊙O 的半径为()0>r r ．（1）求证：四边形ACDF 是矩形．（2）当CH 经过点E 时，⊙M 与⊙O 外切，求⊙M 的半径（用r 的代数式表示）．（3）设()900<<=∠ααHCD ，求点C 、M 、H 、F 构成的四边形的面积（用r 及含α的三角比的式子表示）．A B C D EF G O HM第25题图第25题备用图 ABCD E FO25．（本题满分14分，其中第（1）小题4分、第（2）、（3）小题各5分）如图，在梯形ABCD 中，AD // BC ，AB = CD ，AD = 5，BC = 15，5cos 13ABC ∠=．E 为射线CD 上任意一点，过点A 作AF // BE ，与射线CD 相交于点F ．联结BF ，与直线AD 相交于点G ．设CE = x ，AG y DG=．（1）求AB 的长；（2）当点G 在线段AD 上时，求y 关于x 的函数解析式，并写出函数的定义域；（3）如果23ABEFABCDS S =四边形四边形，求线段CE 的长．AB CDEFG （第25题图）A B C D （备用图）25．（本题满分14分，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分4分）如图，在四边形ABCD 中，AD ∥BC ，∠A =90°，AB =6，BC =10，点E 为边AD 上一点，将△ABE 沿BE 翻折，点A 落在对角线BD 上的点G 处，联结EG 并延长交射线BC 于点F ．（1）如果cos ∠DBC =23，求EF 的长；（2）当点F 在边BC 上时，联结AG ，设AD=x ，ABG BEFS y S ∆∆= ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结CG ，如果△FCG 是等腰三角形，求AD 的长．第25题备用图 A B C 第25题图 E A B C F D G。

【中小学资料】吉林省2018届九年级数学第一次模拟考试试题

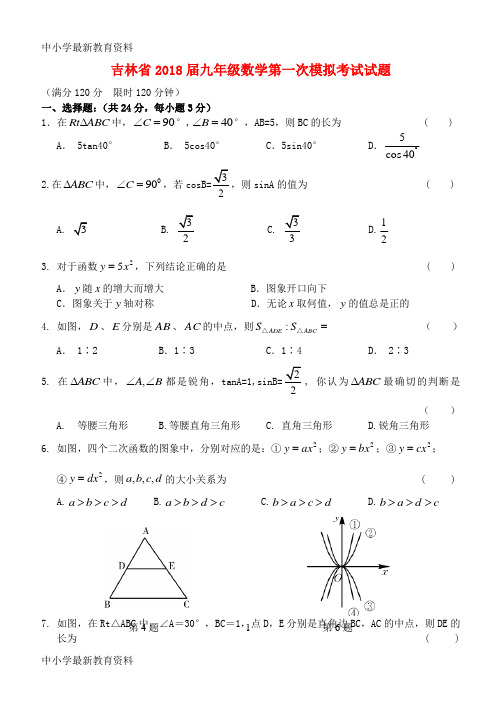
吉林省2018届九年级数学第一次模拟考试试题（满分120分限时120分钟）一、选择题：（共24分，每小题3分）1．在Rt ABC ∆中，90C ∠=°,40B ∠=°，AB=5，则BC 的长为 ( )A ． 5tan40°B ． 5cos40°C ．5sin40°D ．°5cos 402.在ABC ∆中，090C ∠=，若，则sinA 的值为 ( )B.2C. 3D.12 3. 对于函数25y x =，下列结论正确的是 ( )A ．y 随x 的增大而增大B ．图象开口向下C ．图象关于y 轴对称D ．无论x 取何值，y 的值总是正的4. 如图，D 、E 分别是AB 、AC 的中点，则:ADE ABC S S =△△ （）A ． 1∶2B ．1∶3C ．1∶4D ． 2∶35. 在ABC ∆中，,A B ∠∠都是锐角，tanA=1,sinB=2, 你认为ABC ∆最确切的判断是（）A. 等腰三角形B.等腰直角三角形C. 直角三角形D.锐角三角形6. 如图，四个二次函数的图象中，分别对应的是：①2y ax =；②2y bx =；③2y cx =；④2y dx =，则,,,a b c d 的大小关系为 ( )A.a b c d >>>B.a b d c >>>C.b a c d >>>D.b a d c >>>7. DE 的长为 )A ．1B ．2 C. 3 D ．1＋ 38. 如图，菱形ABCD 的周长为20cm ，DE ⊥AB ，垂足为E ，4cos 5A =，则下列结论中： ①DE=3cm ； ②EB=1cm ； ③215S cm =菱形ABCD ．正确的个数为（）A ．0个B ．1个C ．2个D ．3个第7题第8题第12题二、填空：（共18分，每小题3分）9. 若22(2)32m y m x x -=++-是二次函数，则m 的值是 ________.10. 已知点A(－3，1y )，B(－1，2y )，C(2，3y )在抛物线223y x =上，则1y ，2y ，3y 的大小关系是 ________________.（用“<”连接）11. ABC △中，90C ∠=，4tan 3A =，则sin cos A A += _________. 12. 如图，四边形ABCD 中，点P 是对角线BD 的中点，点E ，F 分别是AB ，CD 的中点，AD ＝BC ，∠PEF ＝35°，则∠PFE 的度数是 _________°.13. 如果某人沿坡度i =4：3的斜坡前进50米后，•他所在的位置比原来的位置升高了_______米．14. 已知在ABC ∆中，BC=6，AC=∠A=30°，则AB 的长是________________.三、解答题：（共78分）15. 计算：（8分）（1）()2cos602009πtan 45--+ （2）2sin 603tan 302sin 452-+-.16.（6分）如图，在边长均为1的小正方形网格纸中，△OAB 的顶点O ，A ，B 均在格点上，且O 是直角坐标系的原点，点A 在x 轴上．(1)以O 为位似中心，将△OAB 放大，使得放大后的△OA 1B 1与△OAB 对应线段的比为2∶1，画出△OA 1B 1(所画△OA 1B 1与△OAB 在原点两侧)；(2)直接写出点A 1、B 1的坐标______________________.（3）直接写出11tan OA B ∠=____________.17.（6分）如图,一段河坝的断面为梯形ABCD,试根据图中数据,求出坡角α和坝底宽AD.（结果保留根号）18.（7分）如图，M 是△ABC 的边BC 的中点，AN 平分∠BAC ，BN ⊥AN 于点N ，延长BN 交AC于点D ，已知AB ＝10，BC ＝15，MN ＝3.(1)求证：BN ＝DN ；(2)直接写出△ABC 的周长是______________.19.（7分）如图，直线2y x =-+过x 轴上的点A(2，0)，且与抛物线2y ax =交于B ，C 两点，点B 坐标为(1，1)．(1)求抛物线的函数表达式；(2)连结OC ，求出AOC ∆的面积.20.（8分）如图，在矩形ABCD 中，DE ⊥AC 于E ，3cos 5ADE ∠=，AB ＝3，（1）求AD 的值.（2）直接写出DEC S ∆的值是_____________.21. （8分）如图，在∆ABC 中，AD 是BC 边上的高，tan cos B DAC =∠。