机械制图直角三角形法 课件
合集下载
机械制图求作实长、实形的方法
实长
d'
C1
Y坐标差
图a
c' X
e
c
Y坐标差
O
d
例1： 试利用Y坐标差求一般位置线段CD的实长。 在图a中作线段ED∥c' d',形成直角三角形CED，其斜边CD为线段的实长。
d'
Y坐标差
图a
c'
X
D1
e
实长 c
O
d
Y坐标差
例2 已知△ABC的两面投影，试求△ABC的实形。
B
AC边实长
b'
X
B
#39; X
b1
b'
O
a
b
逆时针旋转求实长
例2：求斜切圆锥表面上任一素线的实长。
截掉素线的实长
s'
余下素线的实长
a1' a'
b1' b'
第九章 钣金展开图
一、直角三角形法
过点A作AC∥ab,则在空间构成一个直角三角形ABC，其斜边AB是线段 的实长。
作图方法一
Z坐标差
b' Z坐标差
求线段实长的直观图。
a'
c'
X
O
b
a
实长
B1
投影图。
一、直角三角形法
过点A作AC∥ab,则在空间构成一个直角三角形ABC，其斜边AB是线段
的实长。
B1
作图方法二
Z坐标差
b' B1
Z坐标差
实长
a'
c'
A1
X
O
作
b
1）以线段某一投影（如水平投影）的长度为一直角边。
d'
C1
Y坐标差
图a
c' X
e
c
Y坐标差
O
d
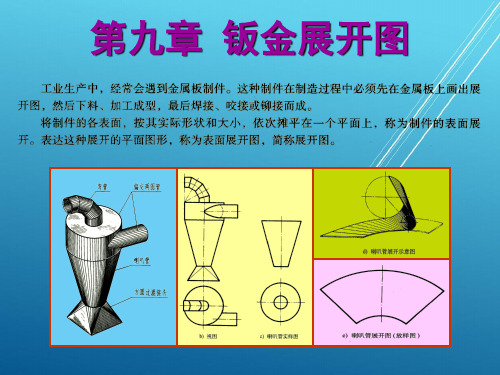
例1： 试利用Y坐标差求一般位置线段CD的实长。 在图a中作线段ED∥c' d',形成直角三角形CED，其斜边CD为线段的实长。
d'
Y坐标差
图a
c'
X
D1
e
实长 c
O
d
Y坐标差
例2 已知△ABC的两面投影，试求△ABC的实形。
B
AC边实长
b'
X
B
#39; X
b1
b'
O
a
b
逆时针旋转求实长
例2：求斜切圆锥表面上任一素线的实长。
截掉素线的实长
s'
余下素线的实长
a1' a'
b1' b'
第九章 钣金展开图
一、直角三角形法
过点A作AC∥ab,则在空间构成一个直角三角形ABC，其斜边AB是线段 的实长。
作图方法一
Z坐标差
b' Z坐标差
求线段实长的直观图。
a'
c'
X
O
b
a
实长
B1
投影图。
一、直角三角形法
过点A作AC∥ab,则在空间构成一个直角三角形ABC，其斜边AB是线段
的实长。
B1
作图方法二
Z坐标差
b' B1
Z坐标差
实长
a'
c'
A1
X
O
作
b
1）以线段某一投影（如水平投影）的长度为一直角边。
机械制图直角三角形法
机械制图：直角三角形法机械制图是机械工程中非常重要的一部分，是用于表达和传递机械工程设计信息的工具。
在机械制图中，直角三角形法是常用的一种绘制方法之一。
本文将对直角三角形法的相关知识进行详细解析。
什么是直角三角形法？在机械制图中，直角三角形法是一种绘制直线的方法。
所谓直角三角形法，就是利用直角三角形的性质，在平面上绘制出一条直线的方法。
直角三角形法的基本原理直角三角形法的基本原理是勾股定理，即直角三角形斜边的平方等于两条直角边的平方和。
在机械制图中，我们将一条已知直线和一个已知的与该直线垂直的直线相交，然后再根据勾股定理来确定需要绘制的直线的长度。
直角三角形法的具体步骤利用直角三角形法绘制一条直线的具体步骤如下：1.画出一条已知的直线和一个垂直于这条直线的线段（一般起点都是已知直线的端点），标出直角。
2.在这个直角三角形中，设直角边的长度为a，另一直角边的长度为b，斜边的长度为c。
3.根据勾股定理得到：c^2 = a^2 + b^2。
4.求出需要绘制的直线在这个直角三角形中对应的边的长度。
5.根据已知直线和垂直线段的位置，利用尺子在图纸上测量出需要绘制的直线的位置和长度。
直角三角形法的应用直角三角形法在机械制图中有着广泛的应用，比如绘制直线、绘制平行线、绘制角度等等。
在绘制机械零件的图纸时，它是非常常用的一种绘制方法。
注意事项在使用直角三角形法时，需要注意以下几点：1.按照要求绘制直角。
2.已知的直线和垂直线段必须准确无误地画在图纸上，否则会影响到绘制的直线的准确性。
3.在使用尺子测量需要绘制的直线的长度时，要确保尺子与图纸垂直，并且尺子上的刻度要准确无误。
直角三角形法是机械制图中非常常用的一种绘制方法。
在绘制机械零件的图纸时，掌握这种方法非常重要。
在使用直角三角形法绘制直线时，需要注意要按照要求绘制直角，并且已知的直线和垂直线段必须准确无误地画在图纸上，否则会影响到绘制的直线的准确性。
《直角三角形》PPT课件
直角三角形
学习目标
• 1.掌握直角三角形的性质定理和判定 定理
• 2.掌握含30º角的直角三角形的性质
学习重点和难点
• 重点：
• 直角三角形的性质定理和判定定理
• •
难点： PPT模板：素材： PPT背景：图表： PPT下载：教程： 资料下载：范文下载： 试卷下载：教案下载： PPT论坛：课件： 语文课件：数学课件： 英语课件：美术课件： 科学课件：物理课件： 化学课件：生物课件：
3、直你得角到三了角什形么斜结边论上？ 的中线等于斜边的一半．
命题：直角三角形斜边上的中线等于斜边的一半
已 知 ： 在 Rt△ABC 中 ， ACB=90° ， CD 是
斜边AB上的中线。求证：CD= 1AB 2
A
E
证明：延长CD到点E,使
DE=DC，连接AE.
D
C
B
已知：在Rt△ABC中，ACB=90°，CD是
2 AB,那
由此可得出结论：
在直角三角形中，如果一条直角边等于斜边的一半，那么 这条直角边所对的角等于30°
例2
在A岛周围20海里（1海里=1852 m）水域内有暗礁，
一轮船由西向东航行到O处时，发现A到在北偏东60°
的方向，且与轮船相距 30 3 海里，如图所示。该船 如果保持航向不变，有触礁的危险吗？
斜边AB上的中线。
求证：CD=
1 2
AB
证明：延长CD到C’,使C’D＝CD，连接AC’
在△ADC’与△BDC中
｛AD=BD
（已知）
ADC’= BDC（对顶角相等）
C’D=CD
（已作）
∴ △ADC’ ≌ △BDC (SAS)
A
C’
学习目标
• 1.掌握直角三角形的性质定理和判定 定理
• 2.掌握含30º角的直角三角形的性质
学习重点和难点
• 重点：
• 直角三角形的性质定理和判定定理
• •
难点： PPT模板：素材： PPT背景：图表： PPT下载：教程： 资料下载：范文下载： 试卷下载：教案下载： PPT论坛：课件： 语文课件：数学课件： 英语课件：美术课件： 科学课件：物理课件： 化学课件：生物课件：
3、直你得角到三了角什形么斜结边论上？ 的中线等于斜边的一半．
命题：直角三角形斜边上的中线等于斜边的一半
已 知 ： 在 Rt△ABC 中 ， ACB=90° ， CD 是
斜边AB上的中线。求证：CD= 1AB 2
A
E
证明：延长CD到点E,使
DE=DC，连接AE.
D
C
B
已知：在Rt△ABC中，ACB=90°，CD是
2 AB,那
由此可得出结论：
在直角三角形中，如果一条直角边等于斜边的一半，那么 这条直角边所对的角等于30°
例2
在A岛周围20海里（1海里=1852 m）水域内有暗礁，
一轮船由西向东航行到O处时，发现A到在北偏东60°
的方向，且与轮船相距 30 3 海里，如图所示。该船 如果保持航向不变，有触礁的危险吗？
斜边AB上的中线。
求证：CD=
1 2
AB
证明：延长CD到C’,使C’D＝CD，连接AC’
在△ADC’与△BDC中
｛AD=BD
（已知）
ADC’= BDC（对顶角相等）
C’D=CD
（已作）
∴ △ADC’ ≌ △BDC (SAS)
A
C’
机械工程制图(几何)PPT课件
本课程的学习方法
理论与实践结合
第一章 制图的基本知识
第一节 制图国家标准的规定
• 一．图纸幅面和格式（GB/T14689-1993）
1．幅面
2．图框格式
留有装订边：
• 不留装订边：
• 对中符号和方向符号：
3．标题栏
• 学生用标题栏
二.比例（GB/T14690-1993 ）
绘制图样时，应在表中选择适当的比例，并优先 选择第一系列。
A
三．斜度与锥度
1.斜度Rake
一直线（或平面）对另一直线 （或平面）的倾斜程度称斜度。
tgα=H/L=1:n
画法及标注 2 0
1:3 α L
60
H
三．斜度与锥度
2.锥度Taper
正圆锥的底圆直径与锥高
之比称锥度。 锥度=D/H=(D-d)/h=1:n
画法及标注如图示
2 0
D d
α h
H
1:4
55
值为依据，与图形的大小以及绘图的准确度无 关。
• (2) 每一尺寸，只标注一次。 • (3) 图样中所注的尺寸规定以毫米为单位。 • (4) 图样中的尺寸为机件的最后完工尺寸。
• 2． 尺寸的组成 • (1) 尺寸界线 • (2) 尺寸线 • (3) 尺寸线终端 • (4) 尺寸数
• 线性尺寸数字方向
画出连接线段R20
14 50
170
28
?35 R34 R90
R10
R87
?70
R86
R89 R70 5
平面图形尺寸标注
标注平面图形尺寸的要求是： 1) 正确 尺寸要符合国家标准规定标注，尺寸数字不能写错。 2）完整 尺寸标注要齐全，既不遗漏又无多余尺寸。 3）清晰 尺寸标注在图形的明显处，布局整齐，标注清楚。
理论与实践结合
第一章 制图的基本知识
第一节 制图国家标准的规定
• 一．图纸幅面和格式（GB/T14689-1993）
1．幅面
2．图框格式
留有装订边：
• 不留装订边：
• 对中符号和方向符号：
3．标题栏
• 学生用标题栏
二.比例（GB/T14690-1993 ）
绘制图样时，应在表中选择适当的比例，并优先 选择第一系列。
A
三．斜度与锥度
1.斜度Rake
一直线（或平面）对另一直线 （或平面）的倾斜程度称斜度。
tgα=H/L=1:n
画法及标注 2 0
1:3 α L
60
H
三．斜度与锥度
2.锥度Taper
正圆锥的底圆直径与锥高
之比称锥度。 锥度=D/H=(D-d)/h=1:n
画法及标注如图示
2 0
D d
α h
H
1:4
55
值为依据，与图形的大小以及绘图的准确度无 关。
• (2) 每一尺寸，只标注一次。 • (3) 图样中所注的尺寸规定以毫米为单位。 • (4) 图样中的尺寸为机件的最后完工尺寸。
• 2． 尺寸的组成 • (1) 尺寸界线 • (2) 尺寸线 • (3) 尺寸线终端 • (4) 尺寸数
• 线性尺寸数字方向
画出连接线段R20
14 50
170
28
?35 R34 R90
R10
R87
?70
R86
R89 R70 5
平面图形尺寸标注
标注平面图形尺寸的要求是： 1) 正确 尺寸要符合国家标准规定标注，尺寸数字不能写错。 2）完整 尺寸标注要齐全，既不遗漏又无多余尺寸。 3）清晰 尺寸标注在图形的明显处，布局整齐，标注清楚。
解直角三角形完整版PPT课件
余弦或正切函数计算得出。
已知一边和一角求另一边
02
在直角三角形中，已知一边长和一个锐角大小可以求出另一边
长，通过正弦、余弦或正切函数计算得出。
解直角三角形的实际应用
03
例如测量建筑物高度、计算航海距离等。
三角函数在实际问题中应用
测量问题
在测量问题中，可以利用三角函数计算高度、距离等未知量。例如，利用正切函数可以计算 山的高度或者河的宽度。
直角三角形重要定理
勾股定理
如上所述，勾股定理描述了直角三角 形三边之间的数量关系。
射影定理
相似三角形判定定理
若两个直角三角形的对应角相等，则 这两个直角三角形相似。根据此定理， 可以推导出一些重要的直角三角形性 质和定理。
射影定理涉及直角三角形中斜边上的 高与斜边及两直角边之间的数量关系。
02
三角函数在解直角三角形中应用
• 性质：正弦、余弦函数值域为[-1,1]，正切函数值域为R；正弦、余弦函 数在第一象限为正，第二象限正弦为正、余弦为负，第三象限正弦、余 弦都为负，第四象限余弦为正、正弦为负；正切函数在第一、三象限为 正，第二、四象限为负。
利用三角函数求边长和角度
已知两边求角度
01
在直角三角形中，已知两边长可以求出锐角的大小，通过正弦、
注意单位换算和精确度
在求解过程中，要注意单位换算和精确度的控制，避免因单位或精 度问题导致答案错误。
拓展延伸：非直角三角形解法简介
锐角三角形和钝角三角形的解法
对于非直角三角形，可以通过作高线或利用三角函数等方法将其转化为直角三角形进行 求解。
三角形的边角关系和面积公式
了解三角形的边角关系和面积公式，有助于更好地理解和解决非直角三角形问题。
机械制图系列课件-11机械识图总结
补齐下列剖视图中的缺线
补齐下列剖视图中的缺线
主视图改成全剖视，左视图改 为半剖视，标注剖切符号
作出全剖左视图
表面粗糙度
• 粗糙度符号的含义 • 如何标注要掌握，合理性不要求 • 粗糙度符号应从材料外指向材料内，注 意符号中尾部短线的方向 • 粗糙度上Ra值的标注方向
粗糙度改错，把正确的注法注写 在右面的视图中。
两解
例8 已知定点A及正平线CD。试过点A作直线与已知直 线CD 垂直相交。
例12 已知菱形对角线AC的两面投影及b’,求该菱形的投影 空间分析：
中点N 等分对角线 AC⊥BD 对边平行且相等
3-25 一等腰直角△ABC，AC 为斜边，顶点B 在直线NC 上，完成其 两面投影。 空间分析：
I
II
改错
螺纹联接
• 功用：联接螺纹和传动螺纹 • 联接螺纹：普通螺纹中有粗牙和细牙之 分，代号为M；管螺纹代号为G • 传动螺纹：锯齿螺纹（B），梯形螺纹 （Tr）、方形螺纹（非标准螺纹） • 了解标注中各符号的含义。
键联接
作用：周向固定，传递扭矩
A A-A
A
B
A
A
B
A-A
技术要求 1、铸件不得有砂眼，气孔； 2、未注明圆角均为R2.
主视图采用 局部剖 表达方法。 在俯视图中找出两个定位尺寸和 两个定形尺寸 41，68 14，24
补注出零件图中所缺的定位尺寸。
填空
• 零件左端螺纹标注G1/2是表示 管 螺 纹，大径为 20.955。 • 36H8(+0.039 )的基本尺寸是 36 ，公差 0 等级 8 ，基本偏差代号是 H ，最大、 最小极限尺寸分别是 36.039，36 。 • 图中C2表示 倒角，距离为2 。 • 画出B-B剖视图。
解直角三角形的应用(19张ppt)课件
选择合适的解法
根据实际情况选择合适的解法，如近似计算、 精确计算等。
注意单位统一
在实际应用中，要注意单位统一，避免计算 错误。
考虑多解情况
在某些情况下，解直角三角形可能存在多个 解，需要全面考虑。
06
练习与巩固
基础练习题
总结词
掌握基本概念和公式
直角三角形中的角度和边长关系
理解直角三角形中锐角、直角和钝角之间 的关系，以及边长与角度之间的勾股定理 。
利用三角函数定义求解
总结词
通过已知角度和邻边长度，求对边或 斜边长度。
详细描述
根据三角函数定义，已知一个锐角和它 所对的边，可以通过三角函数求出其他 两边。例如，已知∠A=30°和a=1，可 以通过三角函数sin(30°)求出对边b。
利用勾股定理求解
总结词
通过已知两边的长度，求第三边长度。
详细描述
向。
确定建筑物的角度
在建筑设计中，通过解直角三角形， 可以确定建筑物的角度和方向。
确定建筑物的长度
在建筑设计中，通过解直角三角形， 可以确定建筑物的长度和方向。
物理问题中的运用
确定物体的运动轨迹
在物理问题中，通过解直角三角形，可以确定物体的运动轨 迹和方向。
确定物体的受力情况
在物理问题中，通过解直角三角形，可以确定物体的受力情 况和方向。
04
实际应用案例
测高问题
01
02
03
测量山的高度
通过测量山脚和山顶的仰 角，利用解直角三角形的 知识，可以计算出山的高 度。
测量楼的高度
利用解直角三角形的知识， 通过测量楼底和楼顶的仰 角，可以计算出楼的高度。
测量树的高度
通过测量树底部和树顶部 的仰角，利用解直角三角 形的知识，可以计算出树 的高度。
《直角三角形》PPT课件
证明：∵∠ACB=90°， ∴∠A+∠B=90°， ∵∠ACD=∠B， ∴∠A+∠ACD=90°， ∴△ACD是直角三角形.
课堂小结
直角三角形的两个锐角互余
性 质 定 理 直角三角形斜边上的中线等于斜边的一半
直角三 角形
在直角三角形中，30°角所对的直角边等于 斜边的一半
判定定理
如果一个三角形的两个角互余， 那么这个三角形是直角三角形
★ 练一练
1、如图，公路AC、BC互相垂直，公路AB的中点M与点C被湖隔开 ，若测得AM的长为1.2km，则M、C两点间的距离为( D )
A.0.5km B.0.6km C.0.9km D.1.2km
2、在直角三角形中，斜边及其中线之和为6，那么
该三角形的斜边长为___4_____．
知识讲解
含30°角的直角三角形的性质
你还有其 他证法吗？
试一试
C
又∵DE⊥AC，DF⊥BC，
∴DE为AC的垂直平分线，
CFB
A D
B
DF为BC的垂直平分线.
∴AD=CD=BD(线段垂直平分线的性质定理).
E 提示：延长CD，使得CD=DE,连结BE，
CD=
1 2
AB.
先证△ACD≌ △BED，然后证△ACB≌ △EBC .
直角三角形斜边上的中线等于斜边的一半.
我们已经知道，如果一个三角形是直角三角形，那么这个三角形有两 个角互余.反过来，有两个角互余的三角形是直角三角形吗？ A
在△ABC中，因为 ∠A +∠B+∠C=180°， 又∠A +∠B=90°， 所以∠C=90°. 于是可知△ABC是直角三角形.
直角三角形的判定定理：
B
课堂小结
直角三角形的两个锐角互余
性 质 定 理 直角三角形斜边上的中线等于斜边的一半
直角三 角形
在直角三角形中，30°角所对的直角边等于 斜边的一半
判定定理
如果一个三角形的两个角互余， 那么这个三角形是直角三角形
★ 练一练
1、如图，公路AC、BC互相垂直，公路AB的中点M与点C被湖隔开 ，若测得AM的长为1.2km，则M、C两点间的距离为( D )
A.0.5km B.0.6km C.0.9km D.1.2km
2、在直角三角形中，斜边及其中线之和为6，那么
该三角形的斜边长为___4_____．
知识讲解
含30°角的直角三角形的性质
你还有其 他证法吗？
试一试
C
又∵DE⊥AC，DF⊥BC，
∴DE为AC的垂直平分线，
CFB
A D
B
DF为BC的垂直平分线.
∴AD=CD=BD(线段垂直平分线的性质定理).
E 提示：延长CD，使得CD=DE,连结BE，
CD=
1 2
AB.
先证△ACD≌ △BED，然后证△ACB≌ △EBC .
直角三角形斜边上的中线等于斜边的一半.
我们已经知道，如果一个三角形是直角三角形，那么这个三角形有两 个角互余.反过来，有两个角互余的三角形是直角三角形吗？ A
在△ABC中，因为 ∠A +∠B+∠C=180°， 又∠A +∠B=90°， 所以∠C=90°. 于是可知△ABC是直角三角形.
直角三角形的判定定理：
B
画法几何及机械制图 3-3
H 投影面的倾 角α。
§3-3 求一般位置线段的实长
一、直角三角形法
1.原理分析2
△AAOB 为直角三角形
结论：
AOB=a’b’ V
a'
X
Ao
AA0=Ya-Yb
b'
Z
已知线段的 两个投影，可
B实
β
长
O
利用直角三角 形法，求出线 段的实长及对
V 投影面的倾
A
b
角β 。
a
Y
Ya-Yb
§3-3 求一般位置线段的实长
§3-3 求一般位置线段的实长
一、直角三角形法 二、换面法
§3-3 求一般位置线段的实长
一、直角三角形法
1.原理分析1
实V 长
△ABB0 为直角三角形
b’
Zb’Z- Za’
B BB0=Zb’-Za’
a’ X
α B0 O
A
b
a
AB0 =ab
Y
结论：
已知线段的 两个投影，可 利用直角三角 形法，求出线 段的实长及对
一、直角三角形法
例1 求线段AB 的实长及α。
V
b'
Z
B
a'
Zb’-Za’
a’
b’
实长
Zb’-Za’
α
X
α B0 O
X
A
b
o
b
a
方法2
Y
aα
1.以Zb’- Za’ 为一直角边； 2.取ab 为另一直角边;
实长
所得直角三角形的斜边即实长AB 。AB 与ab 的夹角为α。
§3-3 求一般位置线段的实长
a’1
实长
§3-3 求一般位置线段的实长
一、直角三角形法
1.原理分析2
△AAOB 为直角三角形
结论：
AOB=a’b’ V
a'
X
Ao
AA0=Ya-Yb
b'
Z
已知线段的 两个投影，可
B实
β
长
O
利用直角三角 形法，求出线 段的实长及对
V 投影面的倾
A
b
角β 。
a
Y
Ya-Yb
§3-3 求一般位置线段的实长
§3-3 求一般位置线段的实长
一、直角三角形法 二、换面法
§3-3 求一般位置线段的实长
一、直角三角形法
1.原理分析1
实V 长
△ABB0 为直角三角形
b’
Zb’Z- Za’
B BB0=Zb’-Za’
a’ X
α B0 O
A
b
a
AB0 =ab
Y
结论：
已知线段的 两个投影，可 利用直角三角 形法，求出线 段的实长及对
一、直角三角形法
例1 求线段AB 的实长及α。
V
b'
Z
B
a'
Zb’-Za’
a’
b’
实长
Zb’-Za’
α
X
α B0 O
X
A
b
o
b
a
方法2
Y
aα
1.以Zb’- Za’ 为一直角边； 2.取ab 为另一直角边;
实长
所得直角三角形的斜边即实长AB 。AB 与ab 的夹角为α。
§3-3 求一般位置线段的实长
a’1
实长
机械制图第二章3ppt课件
d' a'
1'
2'
c'
b'
c
a（b）
2
1
d
.
4
end
五、直角投影定理
例：已知矩形ABCD的顶点C在EF直线上，补全此矩形的投影。
e' c'
d'
b'
f'
a'
a
b
f
d
c
e
.
5
end
六、直角三角形法
V
b'
b'
AB实长
B a'
β BB1=Bb-Aa
a'
B1
b
Aα
b
AB1=ab
a
a
H
用直角三角形法求线段实长及倾角的作图方法是：以直线的一个投
.
9
end
五、直角投影定理
当互相垂直的两直线都不平行于投影面时，其投影不反映直角。
当互相垂直的两直线同时平行于某个投影面时，它们在该投影 面上的投影反映直角。
直角投影定理 当成直角的两直线，其中有一条直线平行于某 一投影面时，则两直线在该投影面上的投影也成直角。
已知：相交两直线AB⊥AC，
A
且AB∥H面。
B
求证： ∠bac=90°
影作为利底用边一，般以位直置线线的段两的端投点影到图该，投通影过面作的直距角离三差角为形另求一得直线角段边，
所的得实直长角和三对角投形影的面斜夹边角即的为方直法线，的.称实为长直，角斜三边角与形底法边。的夹角就是直6
线对这个投影面的倾角。
end
六、直角三角形法
例：求线段AB的实长及倾角α、β 。
机械制图直角三角形法2021推选
一、直角三角形法
例1 求线段AB 的实长及α。
V
b'
Z
b'
实长
B
a'
zb’-za’
a'
zb’-za’
α
X
α B0 O
X
A
b
o b
a
方法2
Y
aα
1.以zb’- za’ 为一直角边； 2.取ab 为另一直角边;
实长
所得直角三角形的斜边即实长AB 。AB 与ab 的夹角为α。
§3-3 求一般位置线段的实长
例3 EF =30 ，试完成e’f’ 。
方法2
以R30 为半径画弧，在另一直角边上截得e’f’ ;
y -y 1.以 为一直角边； e f 取ab 为另一直角边;
例3 EF =30 ，试完成e’f’ 。
△A A0B 为直角三角形
2.以R30 为半径画弧， 以ya – yb 为一直角边；
例2 求线段AB 的实长及β。 例3 EF =30 ，试完成e’f’ 。
e’f’ e'
在另一直角边上截得 例1 求线段AB 的实长及α。
在f f ’ 投影连线上定f ’ 点，完成 e’f’ 。
e’f’ ; 例1 求线段AB 的实长及α。
以zb’- za’ 为一直角边；
X
1)实长、坐标差、投影长、倾角为直角三角形的四要素。
e’f’ 3.以 为半径画弧, AB 与a’b’ 的夹角为β。
一、直角三角形法
例2 求线段AB 的实长及β。
V
b'
Z
AB b'
β
a' A0
X
方法1
β
A a