求平面直角坐标系中三角形的面积

人教版初一数学下册平面直角坐标系中求三角形的面积

在直角坐标系中求图形的面积图形的面积可以利用相应的面积公式求得，但是在平面直角坐标系内的求面积问题，往往不直接给出边或高之类的条件，而是给出一些点的坐标。

我们常常会遇到在平面直角坐标系中求三角形面积和一些不规则图形面积的问题，解题时我们要注意其中的解题方法和解题技巧。

现对这类题目的解法举例说明如下：一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y 轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C （-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD ×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.。

三角形面积公式在坐标中表示方法

三角形面积公式在坐标中表示方法
坐标系中三角形面积公式：
S=(1/2)*(x1y2+x2y3+x3y1-x1y3-x2y1-x3y2)。

坐标系，是理科常用辅助方法。

常见有直线坐标系，平面直角坐标系。

为了说明质点的位置、运动的快慢、方向等，必须选取其坐标系。

在参照系中，为确定空间一点的位置，按规定方法选取的有次序的一组数据，这就叫做“坐标”。

三角形是由同一平面内不在同一直线上的三条线段首尾顺次连接所组成的封闭图形，在数学、建筑学有应用。

常见的三角形按边分有普通三角形（三条边都不相等），等腰三角（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）。

在平面直角坐标系中三角形面积的求法

在平面直角坐标系中三角形面积的求法在平面直角坐标系中，三角形面积的求法是一种基本的几何计算方法。

本文将介绍两种常用的计算三角形面积的方法：海伦公式和向量法。

一、海伦公式海伦公式是一种通过三角形的三条边长来计算其面积的方法。

假设三角形的三条边长分别为a、b、c，则三角形的面积S可以通过以下公式来计算：S = √(s(s-a)(s-b)(s-c))其中，s为三角形的半周长，可以通过以下公式求得：s = (a + b + c) / 2通过海伦公式，我们可以很方便地计算任意三角形的面积。

下面通过一个具体的例子来演示海伦公式的应用。

例：已知三角形的三个顶点坐标分别为A(1, 1)，B(2, 3)，C(4, 1)，求该三角形的面积。

计算三条边的长度：AB = √((2-1)^2 + (3-1)^2) = √5BC = √((4-2)^2 + (1-3)^2) = 2√2AC = √((4-1)^2 + (1-1)^2) = 3然后，计算半周长s：s = (AB + BC + AC) / 2 = (√5 + 2√2 + 3) / 2代入海伦公式求得三角形的面积：S = √(s(s-AB)(s-BC)(s-AC))将计算得到的数值代入公式，即可得到三角形的面积。

二、向量法向量法是另一种计算三角形面积的常用方法。

我们知道，三角形的面积可以通过任意两边的向量叉乘来计算。

假设三角形的两条边的向量分别为a和b，则三角形的面积S可以通过以下公式来计算：S = 1/2 * |a × b|其中，|a × b|表示向量a和向量b的叉乘的模。

通过向量法，我们可以将三角形的面积转化为向量的计算问题，进而简化计算过程。

下面通过一个具体的例子来演示向量法的应用。

例：已知三角形的三个顶点坐标分别为A(1, 1)，B(2, 3)，C(4, 1)，求该三角形的面积。

计算两条边的向量：AB = (2-1, 3-1) = (1, 2)AC = (4-1, 1-1) = (3, 0)然后，计算向量的叉乘：a ×b = AB × AC = (1 * 0 - 3 * 2) = -6代入向量法公式求得三角形的面积：S = 1/2 * |a × b| = 1/2 * |-6| = 3通过以上计算，我们可以得到三角形的面积为3。

如何求平面直角坐标系中三角形的面积

如何求平面直角坐标系中三角形的面积平面直角坐标系中的三角形，根据其位置的不同，我们可以将其分为两大类：第一类，三角形有边在坐标轴上或与一条坐标轴平行；第二类，三角形中没有边在坐标轴上或与一条坐标轴平行。

下面，我们就这两种情况来分析平面直角坐标系中三角形面积求法。

先看第一种情况：①三角形有边在坐标轴上如图，△ABC 三个顶点坐标分别为A(-2,0),B(4,0),C(3,4),求△ABC 的面积。

很明显，可以直接利用三角形面积公式求解：S △ABC =h AB ••21=4621⨯⨯=12②三角形的一边与一条坐标轴平行如图，△ABC 三个顶点坐标分别为A(-1,2),B(-1,-1),C(2,4),求△ABC 的面积。

这种情形，与①相比，只需利用顶点坐标求出底边AB 长及AB 边上的高h 的值，再代入三角形面积公式求解即可：S △ABC =h AB ••21=293321=⨯⨯以上①与②是坐标系中求三角形面积问题的基础。

位置无此特殊性的三角形可转化为该情况后再求解。

再看第二种情况：三角形中没有边在坐标轴上或与一条坐标轴平行。

例1：已知△ABC 三个顶点的坐标分别为：A(1,2)，B(4,6)，C(2,21)，求这个三角形的面积。

分析：如果用三角形面积公式进行求解，知道点的坐标，容易求得线段的长度，底的问题解决了，但底边上的高呢？有点麻烦。

我们不妨试试下面的方法。

分别过点A 、B 、C 作x 轴、y 轴的平行线，则所求三角形的面积S △ABC =S 矩形BDEF -S △ADB -S △AEC -S △BCF =4172112212312143212113=⨯⨯-⨯⨯-⨯⨯-⨯过点C 作y 轴的平行线交AB 边于点M ，将原三角形化作有边与一条坐标轴平行的问题来解决。

易知所求三角形面积S △ABC =S △AMC +S △BMC =)(2121212121h h MC h MC h MC +••=••+••=PQ MC ••21 其中，线段PQ 的长度可由A 、B 两点的横坐标求得，线段MC 的长度需知道点M 与点C 的纵坐标，所以，接下来主要是求得点M 的坐标的问题。

平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，二、有一边与坐标轴平行例2 如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y 轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x 轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.平面直角坐标系中的面积问题（提高篇）“割补法”的应用一、已知点的坐标，求图形的面积。

平面直角坐标系中三角形面积的计算

平面直角坐标系中三角形面积的计算设直角坐标系中的三角形的三个顶点分别为A(x1,y1)，B(x2,y2)，C(x3,y3)。

我们可以利用向量的性质和行列式的方法求出三角形的面积。

首先，我们计算向量AB和向量AC的坐标分量分别为(u,v)和(w,z)。

则有：u=x2-x1v=y2-y1w=x3-x1z=y3-y1然后，根据向量的性质，可以计算向量AB与向量AC的叉积的大小，即面积的两倍：2*面积=，u*z-v*w最后，我们可以通过取绝对值并除以2来得到三角形的面积，即：面积=，u*z-v*w，/2这就是通过向量的方法计算三角形面积的基本公式。

下面我们通过一个具体的例子来演示一下计算三角形面积的过程。

设直角坐标系中的三角形的三个顶点分别为A(2,3)，B(5,6)，C(8,1)。

我们将依次计算向量AB和向量AC的坐标分量：u=5-2=3v=6-3=3w=8-2=6z=1-3=-2然后，根据公式面积=，u*z-v*w，/2，我们计算：面积=，3*(-2)-3*6，/2=，-6-18，/2=24/2=12所以，三角形ABC的面积为12平方单位。

除了向量方法，我们还可以使用行列式的方式来计算三角形的面积。

具体步骤如下：1.将三个顶点的坐标按照行列式的顺序排列，构成一个3×3的矩阵：x1y1x2y2x3y32.计算矩阵的行列式的值。

3.取行列式的绝对值并除以2，即为三角形的面积。

以上就是使用行列式方法计算三角形面积的基本步骤。

总结起来，平面直角坐标系中三角形的面积可以通过向量或行列式的方法进行计算。

这些方法都是基于向量叉积的性质和行列式的性质进行推导和计算的。

无论是哪一种方法，核心思想都是通过计算向量叉积的大小来获得三角形的面积。

如何求平面直角坐标系中三角形的面积

如何求平面直角坐标系中三角形的面积在平面直角坐标系中，求解三角形的面积是几何学中的基本问题之一。

下面将介绍两种求解平面直角坐标系中三角形面积的方法。

方法一：行列式法行列式法是一种常用的求解三角形面积的方法。

设三角形的顶点为A(x1, y1)，B(x2, y2)，C(x3, y3)。

首先将三个顶点的坐标依次排列成行：A(x1, y1) B(x2, y2) C(x3, y3)然后将A点的坐标复制到下方形成两行：A(x1, y1) B(x2, y2) C(x3, y3)A(x1, y1) B(x2, y2) C(x3, y3)接下来按照主对角线往右上方的方向连线，并将相乘的结果写在对应的线上：A(x1, y1) B(x2, y2) C(x3, y3)A(x1, y1) B(x2, y2) C(x3, y3)计算两条斜线上的乘积之和，再减去两条副对角线上的乘积之和，最后除以2即可得到三角形的面积。

行列式法的计算较为繁琐，但是适用于所有类型的三角形。

方法二：海伦公式海伦公式是通过三角形的边长来求解三角形面积的一种方法。

假设三角形的三边长度分别为a、b、c，半周长为p。

首先计算半周长p：p = (a + b + c) / 2然后套用海伦公式进行计算：面积S = √(p * (p - a) * (p - b) * (p - c))海伦公式较为简单，适用于已知三边长度的情况。

根据不同的题目要求和数据提供的形式，可以选择适合的方法进行计算。

总之，无论使用哪种方法，都可以准确求解平面直角坐标系中三角形的面积。

三角形的面积计算在实际生活中有着广泛的应用。

例如，在建筑工程中，需要计算地基的面积以确定施工方案；在地理测量学中，需要求解地理图形的面积和边长，以准确描述地理实体特征。

因此，掌握求解三角形面积的方法是十分重要的。

总结起来，通过行列式法和海伦公式，我们可以准确求解平面直角坐标系中的三角形面积。

无论是使用繁琐的行列式法，还是简便的海伦公式，都能满足求解三角形面积的需求。

平面直角坐标系中三角形面积的求法

平面直角坐标系中三角形面积的求法嘿，伙计们！今天我们来聊聊一个很有趣的话题——平面直角坐标系中三角形面积的求法。

你们知道吗，三角形可是我们生活中无处不在的东西，从房子到衣服再到冰淇淋，都离不开三角形。

而我们要学的就是如何计算这些三角形的面积。

别着急，我会用最简单的语言和你们分享这个知识点，让我们一起来看看吧！我们要知道什么是三角形。

三角形是由三条线段相互连接而成的图形，这三条线段叫做三角形的边。

我们可以用三个顶点来表示一个三角形，这三个顶点分别是A、B和C。

现在我们要用平面直角坐标系来表示这个三角形。

在平面直角坐标系中，每个点都有一个坐标。

比如说，A点的坐标是(x1, y1),B点的坐标是(x2, y2),C点的坐标是(x3, y3)。

我们就可以用这三个坐标来表示这个三角形了。

我们要做的就是计算这个三角形的面积。

说到计算三角形的面积，我们首先要知道一个概念——底和高。

底是指三角形的一条边，而高是指从这条边的对顶点垂直于这条边的线段。

有了底和高，我们就可以用一个公式来计算三角形的面积了。

这个公式叫做“海伦公式”，它的名字来源于古希腊数学家海伦。

海伦公式是这样的：面积 = sqrt(p * (p a) * (p b) * (p c)),其中a、b、c分别是三角形的三条边的长度，p是半周长，即(a + b + c) / 2。

有了这个公式，我们就可以轻松地计算出任何一个三角形的面积了。

我们现在就来试试看吧！假设我们要计算一个三角形的面积，它的三条边的长度分别是3、4和5。

我们要计算半周长p:p = (3 + 4 + 5) / 2 = 6。

我们把这个值代入海伦公式：面积 = sqrt(6 * (6 3) * (6 4) * (6 5)) = sqrt(6 * 3 * 2 * 1) = 6。

这个三角形的面积就是6平方单位。

我们在实际生活中遇到的三角形可能会更复杂一些，但是只要我们掌握了海伦公式，就可以轻松地计算出它们的面积。

三角形的面积公式及其推导

三角形的面积公式及其推导
三角形是几何中常见的形状之一，具有广泛的应用。

在计算三角形
面积时，我们可以使用面积公式，并通过推导来理解其原理。

面积公式：对于已知底和高的三角形，其面积可以通过底乘以高的
一半来计算。

即：
面积 = （底 ×高）/ 2
推导过程如下：
假设三角形的底为b，高为h。

首先，将三角形放置在一个平面直角坐标系中，使得底边与x轴平行。

此时，可以将顶点坐标表示为（0，0），底边的两个顶点坐标分
别表示为（b，0）和（c，h）。

现在，我们可以将底所在的直线表示为y = 0，而高所在的直线表示为x = h。

由此可知，高线与底线围成的区域正好是三角形的面积。

接下来，我们需要计算高线与底线之间的面积。

因为这个区域是一
个矩形，其面积可以通过计算矩形的高和宽的乘积来获得。

在这种情
况下，矩形的宽为b，高为h。

所以，这个矩形的面积为bh。

然而，这个矩形的面积并不等于三角形的面积，因为矩形的高线超
出了三角形的顶点（c，h）。

因此，我们需要计算矩形的面积的一半，即（bh）/ 2。

最后，我们得到三角形的面积公式：
面积 = （底 ×高）/ 2 = （b × h）/ 2
这就是三角形面积公式的推导过程。

总结：
三角形的面积公式是通过底和高的关系推导得出的，可以很方便地计算任意三角形的面积。

在实际应用中，通过该公式可以快速求解三角形的面积，从而实现各种几何计算和设计。

掌握三角形面积公式的推导过程，可以帮助我们更好地理解几何学中的相关概念。

三角形在平面直角坐标系中的面积公式

三角形在平面直角坐标系中的面积公式1. 三角形的魅力说到三角形，大家可能会想，这小东西有什么好说的？但其实，三角形在我们生活中可真是随处可见，像一块披萨，一片蛋糕，甚至是你最爱的屋顶形状。

想象一下，坐在家里的阳台，喝着冰镇饮料，看着三角形的屋顶，心里是不是美滋滋的？可别小看这几条边，它们可是数学的超级明星。

今天我们就来聊聊三角形在平面直角坐标系中的面积公式，绝对让你感叹“原来如此”！2. 面积公式的来历2.1 从基础开始首先，大家得知道，三角形的面积公式其实是个简单的公式：( S = frac{1{2 times 底 times 高 )。

这个公式就像煮方便面一样简单，底和高的乘积，再除以二，哎呀，方便得很！不过，想要在坐标系中找到这两个值，那可得动动脑筋。

2.2 坐标系中的三角形在平面直角坐标系中，三角形的三个顶点可以是任意的坐标，比如说 A(x1, y1)，B(x2, y2)，C(x3, y3)。

为了计算面积，我们得想办法找到底和高。

底可以是任意两点之间的距离，而高则是从第三个点到底边的垂直距离。

听起来复杂，其实就是在玩一场拼图游戏，找对了位置，面积自然就出来了。

3. 用公式计算面积3.1 计算过程来，咱们用一个公式吧，面积 S 的计算可以用如下公式来表达：。

S = frac{1{2 | x_1(y_2 y_3) + x_2(y_3 y_1) + x_3(y_1 y_2) | 。

看，数学的魅力在于它的简洁和优雅！你只需要把点的坐标代进去，算一算，就能得到最终的面积。

感觉就像是在做一场魔术，把数据变成美丽的数字。

3.2 举个例子假如我们有三角形的顶点 A(1, 2)，B(4, 6)，C(5, 1)，让我们来计算一下面积。

把这些坐标代入上面的公式，算一算：。

S = frac{1{2 | 1(6 1) + 4(1 2) + 5(2 6) | 。

经过一番计算，我们就能知道这个三角形的面积是多少，简直就像是找到了隐藏在沙滩里的贝壳，特别有成就感！4. 实际应用4.1 生活中的应用那么，三角形的面积公式到底有什么用呢？实际上，它在建筑、设计、甚至在我们的日常生活中都大有用处。

【初一方法归纳专题】平面直角坐标系中图形面积的求法

1.面积公式：（1）三角形的面积：S三角形＝1/2×底×高（2）梯形的面积：S梯形＝1/2×（上底+下底）×高2.两点间的距离：（1）当两点横坐标相同时，两点间的距离为这两点纵坐标差的绝对值（2）当两点纵坐标相同时，两点间的距离为这两点横坐标差的绝对值基础篇——三角形面积的求法题型1 三角形有一边在坐标轴上【例1】如图，平面直角坐标系中，已知三角形ABC的三个顶点的坐标分别是A（2，3），B（-4，0），C（4，0），求三角形ABC的面积.温馨提示：【思路及解答】请观看视频【方法归纳】当三角边有一边在坐标轴上时，将此边作为底边，那么高便垂直于坐标轴，底和高就能通过两点间的距离很快求出.题型2 三角形有一边与坐标轴平行【例2】如图，平面直角坐标系中，已知三角形ABC的三个顶点的坐标分别是A（-1，-4），B（2，0），C（-4，-4），求三角形ABC 的面积.温馨提示：【思路及解答】请观看视频【方法归纳】当三角边有一边与坐标轴平行时，将此边作为底边，那么高便垂直于坐标轴，底和高就能通过两点间的距离很快求出.根据图形特殊，我们通常把平行于坐标轴的一边作为底边.题型3 三角形三边均不与坐标轴平行【例3】在如图所示的正方形网格中，每个小正方形的单位长度均为1，三角形ABC的三个顶点恰好是正方形网格的格点.（1）写出图中所示各顶点的坐标；（2）求三角形ABC的面积.温馨提示：【思路及解答】请观看视频【方法归纳】当三角边的三边均不与坐标轴平行时：（1）将原三角形围在一个梯形或长方形中，用长方形或梯形的面积，减去长方形或梯形边缘的直角三角形的面积，即可求得原三角形的面积，这种方法叫做补形法；（2）若三角形内一割线长度已知，并且它平行于坐标轴，那么可将其作为底边，把原三角形拆分为两个三角形，则两高的长度可得，面积即可求得，这种方法叫做分割法.以上两种方法就是数学几何图形运算中常用的割补法.例题讲授视频三角形面积的求法同学们，例题看明白了吗？方法掌握了吧！快来试试下面的变式训练吧！变式训练【变式训练1】如图，在平面直角坐标系中，三角形ABC的顶点坐标分别为A(－3，0)，B(0，3)，C(0，－1)，则三角形ABC的面积为．。

平面坐标内的三角形面积公式

平面坐标内的三角形面积公式一、已知三角形三个顶点坐标的通用公式。

1. 公式内容。

- 设三角形三个顶点的坐标分别为A(x_1,y_1)，B(x_2,y_2)，C(x_3,y_3)，则三角形ABC的面积S=(1)/(2)<=ft| x_1(y_2 - y_3)+x_2(y_3 - y_1)+x_3(y_1 - y_2)right|。

2. 推导过程（简单理解）- 我们可以把三角形ABC看作是由三个梯形组合（或拆分）而成的。

- 以x轴为基准，比如过A、B两点向x轴作垂线，过C点向AB所在直线作垂线。

- 通过计算三个梯形（可以是两个正的和一个负的，或者其他组合方式）的面积之和（或差），经过化简就可以得到上述公式。

二、特殊情况。

1. 直角三角形（已知直角顶点坐标及两直角边所在直线方程）- 如果在平面直角坐标系中，已知直角三角形ABC，∠ C = 90^∘，C(x_0,y_0)，直线AC的方程为y = k_1(x - x_0)+y_0，直线BC的方程为y=k_2(x -x_0)+y_0（这里k_1k_2=- 1）。

- 先求出A、B两点的坐标（通过联立直线方程与坐标轴方程求解）。

假设A(x_1,y_1)，B(x_2,y_2)，那么三角形ABC的面积S=(1)/(2)<=ft|(x_1 - x_0)(y_2 -y_0)right|。

- 这是因为直角三角形的面积等于两直角边乘积的一半，| x_1 - x_0|和| y_2 - y_0|分别是两直角边的长度（在坐标中的表示）。

2. 三角形有一边平行于坐标轴（以平行于x轴为例）- 设三角形ABC，AB平行于x轴，A(x_1,y_0)，B(x_2,y_0)，C(x_3,y_3)。

- 此时三角形ABC的面积S=(1)/(2)| x_1 - x_2|| y_3 - y_0|。

- 这是因为| x_1 - x_2|是AB的长度（平行于x轴），| y_3 - y_0|是C点到AB 边的距离（也就是高），根据三角形面积公式S=(1)/(2)×底×高得到此公式。

求平面直角坐标系中三角形的面积

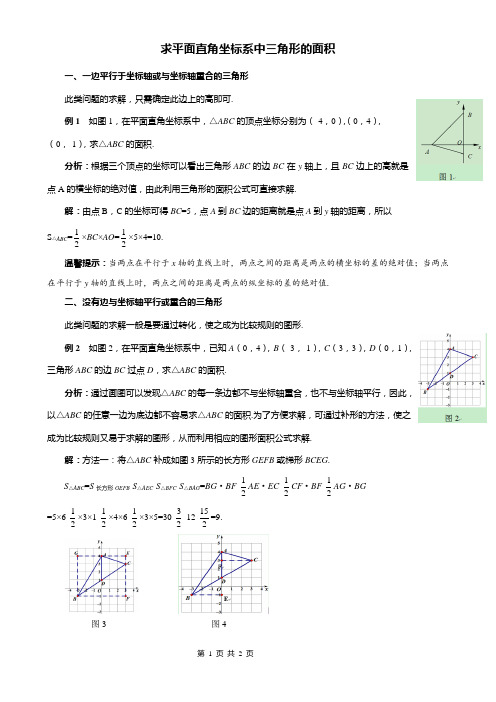
求平面直角坐标系中三角形的面积一、一边平行于坐标轴或与坐标轴重合的三角形此类问题的求解，只需确定此边上的高即可.例1 如图1，在平面直角坐标系中，△ABC的顶点坐标分别为（-4，0），（0，4），（0，-1），求△ABC的面积.分析：根据三个顶点的坐标可以看出三角形ABC的边BC在y轴上，且BC边上的高就是点A的横坐标的绝对值，由此利用三角形的面积公式可直接求解.解：由点B，C的坐标可得BC=5，点A到BC边的距离就是点A到y轴的距离，所以S△ABC=12×BC×AO=12×5×4=10.温馨提示：当两点在平行于x轴的直线上时，两点之间的距离是两点的横坐标的差的绝对值；当两点在平行于y轴的直线上时，两点之间的距离是两点的纵坐标的差的绝对值.二、没有边与坐标轴平行或重合的三角形此类问题的求解一般是要通过转化，使之成为比较规则的图形.例2 如图2，在平面直角坐标系中，已知A（0，4），B（-3，-1），C（3，3），D（0，1），三角形ABC的边BC过点D，求△ABC的面积.分析：通过画图可以发现△ABC的每一条边都不与坐标轴重合，也不与坐标轴平行，因此，以△ABC的任意一边为底边都不容易求△ABC的面积.为了方便求解，可通过补形的方法，使之成为比较规则又易于求解的图形，从而利用相应的图形面积公式求解.解：方法一：将△ABC补成如图3所示的长方形GEFB或梯形BCEG.S△ABC=S长方形GEFB-S△AEC-S△BFC-S△BAG=BG·BF-12AE·EC-12CF·BF-12AG·BG=5×6-12×3×1-12×4×6-12×3×5=30-32-12-152=9.图3 图4方法二：如图4，分割成两个三角形，根据铅垂线与水平线求三角形的面积.S△ABC= S△ABD+ S△ACD=12AD·BE+12AD·CF=12×3×3+12×3×3=92+92=9.牛刀小试：如图5，在平面直角坐标系中，△ABC的顶点坐标分别为A（2，0），B（0，4），C（-3，2），求△ABC的面积.图5答案：如图6，过点C作CD⊥x轴于点D，则S△A BC=S梯形O BC D+S△O A B-S△A C D=12×（2+4）×3+12×2×4-12×5×2=8.图6。

平面直角坐标系中三角形面积的计算

（）１求此抛物线的解析式；（）点作线段Ａ２过Ｂ的垂线交抛物线于点Ｄ，果如
（）２分别过ＡＢ作轴的垂线，，垂足分别是Ｄ，，Ｅ则
ＤＥ＝６
・
‘ ．
ｃ是直线ＡＢ与Ｙ轴的交点，
当：０时，
・．．．．Fra bibliotek：２－－ＤＥ ×ＯＣ：１
×６×２：６
如ｓ＝ａ，ｌａｓＣ海伦公式．是这些方法在直ｈＳ＝ｂｉｎ但
，
２在二次函数中的应用
ｙＩＩ
角坐标系中往往很难应用，文介绍一种简单的方法并本举例说明它的应用．
如图ｌ图２过ＡＡＣ的三个顶点分别作出与水平，，Ｂ
Ｃ莽Ｉ
Ａ｜ｏ
线垂直的三条直线，外侧两条直线之间的距离叫ＡＡＣＢ的“ 水平宽 ” ０，（）中间的这条直线在ＡＢＡＣ内部线段的长度叫ＡＡＣ的“ Ｂ铅垂高（）．们可得出一种计算三ｈ ”我
又因为抛物线经过点Ａ（，）将其坐标代人上式，３０，
得０＝Ⅱ ３—１＋４，得ｎ＝一１（）解．
‘
标为（一１ｍ，３ｍ＋）
．
。
．
该抛物线的表达式为）＝一（，一１十，）４即
Ｙ一。＋２＋３
．
以点ｃ为圆心的圆与直线ＢＤ相切，判断抛物线的对请
称轴ＺＯＣ有怎样的位置关系，与并给出证明；

三角形面积平面直角坐标系

三角形面积平面直角坐标系好嘞，今天咱们聊聊三角形的面积，顺便在这个平面直角坐标系里游玩一番。

哎呀，说到三角形，谁能不想起那种咱们小时候画的简单图形呢？就是那种三个角，三条边，像个小披萨一样，啧啧，想得我都饿了！不过，这三角形可不只是用来画画的，面积这个概念可真是让人又爱又恨。

先说说三角形的面积怎么算吧，简单得很，就像吃西瓜。

咱们用公式，面积等于底乘以高再除以二。

就这么简单，听起来是不是有点像在唱歌？要是你在坐标系里找三角形，那就更有意思了。

想象一下，你在平面上找到了三个点，咱们给它们起个名字，比如说A、B、C。

它们的坐标分别是A(x1, y1)，B(x2, y2)，C(x3, y3)。

这个时候，你就能用一些简单的数学运算，轻松搞定它的面积。

说到这里，你可能会问，哎，三角形到底有多重要呢？这不就是一些线条和点吗？可别小看它们。

三角形在建筑、工程、设计等各个领域可都是大明星。

要是没有三角形，咱们的房子能不能建得稳当？哈哈，估计得一阵摇摇晃晃。

试想一下，房顶上没有三角形，风一吹，整座楼都可能跟着摇摆，简直就是“东倒西歪”！所以，三角形这玩意儿在生活中无处不在，连你吃的汉堡，都是三角形的故事。

好啦，咱们继续说面积的计算。

说真的，坐标系里的三角形面积计算，可是个有趣的过程。

你得找出这三点的坐标，你就用公式算啦。

具体的公式是这样的：面积等于1/2乘以（x1(y2y3) + x2(y3y1) + x3(y1y2)）。

看着这些数字，有没有觉得自己像个数学家？当然了，别紧张，别怕搞错，偶尔来点“小失误”也是常有的事。

说到这里，我又想起了小时候的趣事。

有一次，老师教我们怎么计算三角形的面积，结果我心急火燎，居然把底和高搞反了。

最后出来的结果简直是让人捧腹大笑，旁边的小伙伴们都笑得前仰后合。

哎，虽然那时候有点丢脸，但现在想想，真的很可爱呀。

这种搞笑的事，正是生活的调味品。

三角形的美不止于此。

你想想，正三角形、直角三角形、等腰三角形，各有各的魅力。

三角形面积公式平面直角坐标系

三角形面积公式平面直角坐标系好的，以下是为您生成的文章：咱今儿就来唠唠三角形面积公式和平面直角坐标系这俩玩意儿。

先说说三角形面积公式吧。

这可是数学里挺重要的一块知识呢！你看哈，三角形面积公式 S = 1/2 ×底 ×高。

这就好比咱盖房子，底就是房子的地基长度，高就是房子的高度，面积就是房子能占多大地方。

我想起之前给学生讲这部分知识的时候，有个小家伙特别逗。

那天上课，我在黑板上画了个三角形，问大家怎么求它的面积。

这小家伙把手举得高高的，我就让他回答。

他站起来特别自信地说：“老师，我觉得三角形面积就是三条边加起来除以 3！”全班同学哄堂大笑。

我就耐心地给他解释，还带着他一起做了几道题，最后他可算是搞明白了。

再来讲讲平面直角坐标系。

这东西就像是给每个点都安了个“家”，有了坐标，就能准确找到它们的位置。

比如说（3，5）这个坐标，就表示在横轴上走 3 个单位，纵轴上走 5 个单位的那个点。

有一次，我带学生们做了个小游戏。

我在教室里的地上画了一个超大的平面直角坐标系，然后给每个同学发一个小卡片，上面写着一个坐标。

让他们根据自己的坐标找到在坐标系中的位置。

同学们可积极了，到处跑着找自己的“地盘”，那场面热闹极了。

三角形面积公式和平直坐标系在生活中的用处也不少。

比如说，咱要给家里铺个三角形的地毯，就得用面积公式算算需要多少布料。

还有导航里的定位，不就是靠平面直角坐标系的原理嘛。

学数学呀，可别觉得枯燥，其实这里面的乐趣多着呢。

就像三角形面积公式和平直坐标系，看似简单的知识，却能解决好多实际问题。

只要咱认真学，多琢磨，就能发现数学的美。

反正我觉得，不管是三角形面积公式还是平面直角坐标系，都是咱数学世界里的宝贝。

掌握好了它们，就像手里有了厉害的工具，能解决好多难题，让咱在数学的海洋里畅游得更畅快！所以同学们，加油学吧，未来还有更多有趣的数学知识等着咱去探索呢！。