倒立摆PD控制
单级移动倒立摆建模及串联PID控制器设

题 目: 单级移动倒立摆建模及串联PID 控制器设计 初始条件:要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求)(1) 研究该装置的非线性数学模型,并提出合理的线性化方法,建立该装置的线性数学模型-传递函数(以u 为输入,θ为输出);(2) 要求系统输出动态性能满足,5.1%,3.4%s t s ≤≤σ试设计串联PID 校正装置。
(3) 用Matlab 对校正后的系统进行仿真分析,比较校正装置加在线性化前的模型上和线性化后的模型上的时域响应有何区别,并说明原因。
(4) 对上述任务写出完整的课程设计说明书,说明书中必须进行原理分析,写清楚分析计算的过程及其比较分析的结果,并包含Matlab 源程序或Simulink 仿真模型,说明书的格式按照教务处标准书写。
时间安排:任务时间(天)指导老师下达任务书,审题、查阅相关资料2 分析、计算 2 编写程序 1 撰写报告 2 论文答辩1指导教师签名: 年 月 日 系主任(或责任教师)签名: 年 月 日图示为一个倒立摆装置,该装置包含一个小车和一个安装在小车上的倒立摆杆。
由于小车在水平方向可适当移动,因此,控制小车的移动可使摆杆维持直立不倒。
2/10,5.0,2.0,1s m g m l kg m kg M ====目录摘要 (I)1 单级移动倒立摆系统建模 (1)1.1 倒立摆系统建模 (1)1.2 倒立摆系统的传递函数 (2)2 系统校正前性能分析 (3)2.1 未校正移动倒立摆系统时域响应 (3)2.2 绘制bode图 (3)2.3 绘制根轨迹图 (4)2.4 系统校正前的阶跃响应及性能分析 (5)3 PID控制器设计 (6)3.1 PID控制器参数选择 (6)3.2 校正后系统性能指标 (8)3.3 系统校正前后性能比较 (9)4 小结体会 (10)参考文献............................................................................................................................... 错误!未定义书签。
倒立摆PID调节模糊控制

倒立摆系统的简介倒立摆系统发展倒立摆系统的研究意义倒立摆系统的简介倒立摆系统是日常生活中所见到的任何重心在上,支点在下的控制问题的抽象。
例如杂技顶杆表演,人们常为演员的精湛技艺叹服,然而其机理更引发了人们的深思。
它深刻的揭示了自然界的一种基本规律.即一个自然不稳定的被控对象,通过控制手段可使之具有良好的稳定性。
不难看出杂技演员顶杆的物理机制可简化为一个倒置的倒立摆,也就是人们常称之为倒立摆或一级倒立摆系统。
一级倒立摆系统是一个复杂的非线性系统,小车可以自由地在限定的轨道上左右移动,小车上的倒立摆一端被铰链链接在小车顶部,另一端可以在小车轨道所在的垂直平面上自由转动。
系统的控制目的是通过电机带动小车运动,使倒立摆平衡并保持小车不与轨道两端相撞。
倒立摆已经由原来的直线倒立摆扩大很多种类,典型的有直线倒立摆,环形倒立摆,平面倒立摆等,倒立摆系统是运动模块上装有倒立摆装置,由于在相同的运动模块上可以装载不同的倒立摆装置,倒立摆的种类由此而丰富很多倒立摆的控制方法倒立摆作为一个典型的被控对象,适合用多种理论和方法进行控制。
当前,倒立摆的控制规律有: (1)PID 控制,通过对倒立摆物理模型的分析,建立倒立摆的动力学模型,然后使用状态空间理论推导出其非线性模型,再在平衡点处进行线性化得到倒立摆系统的状态方程和输出方程,于是就可设计出PID 控制器实现其控制;(2) 状态反馈H ∞控制,通过对倒立摆物理模型的分析,建立倒立摆的动力学模型,然后使用状态空间理论推导出状态方程和输出方程,于是就可应用H ∞状态反馈和Kalman 滤波相结合的方法,实现对倒立摆的控制; (3) 利用云模型实现对倒立摆的控制,用云模型构成语言值,用语言值构成规则,形成一种定性的推理机制。
这种拟人控制不要求给出被控对象精确的数学模型,仅仅依据人的经验、感受和逻辑判断,将人用自然语言表达的控制经验,通过语言原子和云模型转换到语言控制规则器中,就能解决非线性问题和不确定性问题; (4) 神经网络控制,业已证明,神经网络(Neural Network ,NN) 能够任意充分地逼近复杂的非线性关系,NN 能够学习与适应严重不确定性系统的动态特性,所有定量或定性的信息都等势分布贮存于网络内的各种神经元,故有很强的鲁棒性和容错性;也可将Q 学习算法和BP 神经网络有效结合,实现状态未离散化的倒立摆的无模型学习控制; (5) 遗传算法( Genetic Algorithms , GA) ,高晓智在Michine 的倒立摆控制Boxes 方案的基础上,利用GA 对每个BOX 中的控制作用进行了寻优,结果表明GA 可以有效地解决倒立摆的平衡问题; (6) 自适应控制,主要是为倒立摆设计出自适应控制器; (7) 模糊控制,主要是确定模糊规则,设计出模糊控制器实现对倒立摆的控制; (8) 使用几种智能控制算法相结合实现倒立摆的控制,比如模糊自适应控制,分散鲁棒自适应控制等等; (9) 采用GA 与NN 相结合的算法,这也是我们采用的方法,首先建立倒立摆系统的数学模型,然后为其设计出神经网络控制器,再利用改进的贵传算法训练神经网络的权值,从而实现对倒立摆的控制,采用GA 学习的NN 控制器兼有NN 的广泛映射能力和GA 快速收敛以及增强式学习等性能。
单级倒立摆稳定控制

单级倒立摆稳定控制摘要单级倒立摆是一种受控系统,在工业控制和机器人技术中有着广泛的应用。
这篇文档将介绍单级倒立摆的结构、原理和控制方法,特别是借助PID控制系统来实现单级倒立摆的稳定控制。
单级倒立摆是一种类人形机器人,它通常由一个水平旋转的轮子和一个通过电机传动的滑移杆组成,最后再由摆杆上的陀螺控制实现倒立。
这种结构使得单级倒立摆成为了机器人应用领域中的一个挑战问题。
为了实现单级倒立摆的稳定控制,需要在控制系统中引入一个合适的控制机制。
PID控制算法是一种最为通用的控制算法之一,常被用于像单级倒立摆这样的机器人平衡控制。
PID控制PID控制是一种基于反馈的控制系统,在工业和机器人技术中得到了广泛的应用。
PID控制通过比较实际的输出值与期望的输入值之间的差异,来作出对输出值的控制。
PID控制可以对输出值的稳定性、可靠性和精度进行控制,适用于不同类型的工业和机器人控制系统。
PID控制通常由三个部分组成:比例(P)、积分(I)和微分(D)控制。
比例控制反馈调整输出值,使得实际输出值逼近期望输入值。
积分控制记录过去所有误差,并将这些误差相乘来调整输出值。
微分控制通过记录过去的误差变化率,来防止输出值的快速变化。
在单级倒立摆稳定控制中,采用PID控制可以较好地解决因摩擦力、惯性、重心偏移等因素导致的系统不稳定问题,进而实现系统的平衡控制。
单级倒立摆的稳定控制实现单级倒立摆的稳定控制需要进行以下步骤:步骤1:系统建模将单级倒立摆系统建模,根据运动学和动力学原理,得到系统的运动方程。
步骤2:PID参数调节通过对PID控制算法中比例、积分、微分三个部分的参数进行调整,得到较好的控制效果。
步骤3:PID控制实现将PID控制器与单级倒立摆系统进行连接,实现单级倒立摆的稳定控制。
本文档介绍了单级倒立摆的结构、原理和控制方法,分析了PID控制算法在单级倒立摆稳定控制中的应用。
通过对步骤进行深入的解析,得到了单级倒立摆的稳定控制方法。
倒立摆pd控制 matlab

倒立摆pd控制 matlab倒立摆是一种经典的控制系统问题,它的应用广泛,常常用于教学和研究。
在本文中,我们将探讨倒立摆的 PD 控制方法,并使用MATLAB 实现该算法。
首先,让我们简要介绍一下倒立摆问题。
倒立摆是一种由单摆和质点组成的系统,其目标是将摆杆竖直并保持平衡。
在这个问题中,我们需要设计一个控制器来控制摆杆的位置和角度,以保持系统的稳定运行。
因此,控制器的设计对于倒立摆的运行非常重要。
在倒立摆的控制中,PD 控制是一种广泛使用的方法。
PD 控制器根据当前系统状态的误差和其变化率来计算控制输入。
因此,它可以更好地应对一些不稳定的系统,并具有更快的响应速度和更小的稳态误差。
接下来,我们将步骤如下:1.模型建立首先,我们需要建立倒立摆的数学模型。
该模型可以用一组偏微分方程来表示,但通常我们使用更简单的状态空间模型来描述系统。
在这种模型中,我们将系统状态表示为一组变量,通常包括摆角度和摆杆角速度等。
2.控制器设计接下来,我们将使用 PD 控制器来计算控制输入。
PD 控制器的输出等于当前误差和误差变化率乘以控制器的比例和微分增益。
这两个增益参数的选择是控制器设计中最重要的部分之一,通常需要通过试验和优化来确定。
3.仿真验证为了验证 PD 控制器的性能,我们将使用 MATLAB 对倒立摆进行仿真。
在仿真中,我们将输入控制信号并观察系统响应。
通过改变比例和微分增益,我们可以评估控制器的性能,并选择最优的参数。
4.实际应用最后,我们可以将 PD 控制器应用于实际倒立摆系统中。
在这种情况下,我们将需要将控制器代码嵌入到实际控制器硬件中,并进行实际运行测试。
通过不断调整比例和微分增益,我们可以优化控制器的性能,并实现更好的稳定性和控制效果。
总之,倒立摆 PD 控制是一种广泛使用的控制方法,可以应用于许多不同的控制系统。
通过 MATLAB 仿真,可以有效地评估控制器性能并选择最佳参数。
在将控制器应用于实际系统之前,我们需要进行充分的测试和优化,以确保其稳定性和控制效果。
基于RBF神经网络补偿的不确定性倒立摆PD控制

基于RBF神经网络补偿的不确定性倒立摆PD控制作者:姜峰蔡伯峰郝建春刘振兴来源:《硅谷》2014年第01期摘要针对带有参数不确定性的非线性倒立摆的跟踪控制问题,提出一种RBF神经网络补偿的PD控制方法。
该方法采用RBF神经网络逼近系统不确定非线性函数,结合常规的PD控制方法设计控制器,实现倒立摆的跟踪控制。
仿真结果表明,该方法能有效实现倒立摆的快速跟踪,并保证了对不确定参数的不敏感性。
关键词不确定性;跟踪控制;RBF神经网络中图分类号:TP273 文献标识码:A 文章编号:1671-7597(2014)01-0040-02倒立摆本身是一种复杂非线性系统,具有多变量、耦合性强、稳定性差且极不稳定的特点,很多典型的实验研究都基于此展开,跟踪控制就是其中之一。
目前已有很多文献使用不同的控制方法针对倒立摆进行跟踪控制的研究,比如使用滑模变结构控制方法、鲁棒控制等。
文中使用RBF神经网络对带有参数不确定性的非线性部分进行逼近,结合常规的PD控制方法设计控制器,对非线性的倒立摆进行跟踪控制研究。
1 问题描述考虑如下一类二阶非线性系统:(1)式(1)中,为未知函数部分,为已知函数部分,和分别为系统的输入和输出。
式(1)还可以写为:设位置指令为,令,选择,使多项式的所有根部都在复平面左半平面上。
取控制律为(2)将(2)代入式(1),得到闭环控制系统的方程:由于的选取,可得时,,即系统的输出及其导数渐进地收敛于理想输出及其导数。
文中提到的一类非线性系统中,如果是确定的,则可以选择来消除其非线性的属性,再由线性控制理论设计控制器;假如不能确定且系统含有其他不确定性因素,控制律(2)则很难实现;而RBF神经网络具有万能逼近的特性,若采用RBF网络对不确定项进行自适应逼近,即采用神经网络系统代替,可实现自适应神经网络的补偿,同时可以测试控制器对不确定性因素的不敏感性。
2 控制器设计20世纪80年代末J.Moody和C.Darken提出了径向基函数(RBF-Radial Basis Function)神经网络,它是具有单隐层的三层前馈网络。
细说倒立摆与pid

一、总体原则PID调试一般原则a.在输出不振荡时,增大比例增益P。
b.在输出不振荡时,减小积分时间常数Ti。
c.在输出不振荡时,增大微分时间常数Td。
二、各环节作用[P]比例调节作用:是按比例反应系统的偏差,系统一旦出现了偏差,比例调节立即产生调节作用用以减少偏差。
比例作用大,可以加快调节,减少误差,但是过大的比例,使系统的稳定性下降,甚至造成系统的不稳定。
反之,过小,更不上系统需求。
[I]积分调节作用:是使系统消除稳态误差,提高无差度。
因为有误差,积分调节就进行,直至无差,积分调节停止,积分调节输出一常值。
积分作用的强弱取决与积分时间常数Ti,Ti越小,积分作用就越强。
反之Ti大则积分作用弱,加入积分调节可使系统稳定性下降,动态响应变慢。
一般情况是将时间常数设置很小。
积分作用常与另两种调节规律结合,组成PI调节器或PID调节器。
[D]微分调节作用:微分作用反映系统偏差信号的变化率,具有预见性,能预见偏差变化的趋势,因此能产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除。
因此,可以改善系统的动态性能。
在微分时间选择合适情况下,可以减少超调,减少调节时间。
微分作用对噪声干扰有放大作用,因此过强的加微分调节,对系统抗干扰不利。
此外,微分反应的是变化率,而当输入没有变化时,微分作用输出为零。
微分作用不能单独使用,需要与另外两种调节规律相结合,组成PD或PID控制器。
三、细说[分为PID、PI、PD]1、确定比例增益P确定比例增益P 时,首先去掉PID的积分项和微分项,一般是令Ti=0、Td=0(具体见PID的参数设定说明),使PID为纯比例调节。
输入设定为系统允许的最大值的60%~70%,由0逐渐加大比例增益P,直至系统出现振荡;再反过来,从此时的比例增益P逐渐减小,直至系统振荡消失,记录此时的比例增益P,设定PID的比例增益P为当前值的60%~70%。
比例增益P调试完成。
【解说】我们知道P是调节与预设值(即输入值)的偏差的作用的,因此P很大时,当反馈值很小时也会造成很大的波动,最终是震荡状态,这个可以试出来的,这时的P是Pmax。
一阶直线倒立摆双闭环PID控制仿真报告

目录摘要 (2)一、一阶倒立摆系统建模 (3)1、对象模型 (3)2、电动机、驱动器及机械传动装置的模型 (4)二、双闭环PID控制器设计 (5)1、仿真验证 (6)2、内环控制器的设计 (9)3、系统外环控制器设计 (12)三、仿真实验 (15)1、绘图子程序 (15)2、仿真结果 (16)四、结论 (18)摘要本报告旨在借助Matlab 仿真软件,设计基于双闭环PID 控制的一阶倒立摆控制系统。
在如图0.1所示的“一阶倒立摆控制系统”中,通过检测小车的位置与摆杆的摆动角,来适当控制驱动电动机拖动力的大小,控制器由一台工业控制计算机(IPC )完成。
图0.1 一阶倒立摆控制系统分析工作原理,可以得出一阶倒立摆系统原理方框图:图0.2 一阶倒立摆控制系统动态结构图本报告将借助于“Simulink 封装技术——子系统”,在模型验证的基础上,采用双闭环PID 控制方案,实现倒立摆位置伺服控制的数字仿真实验。
一、一阶倒立摆系统建模1、对象模型如图1.1所示,设小车的质量为m 0,倒立摆均匀杆的质量为m ,摆长为2l ,摆的偏角为θ,小车的位移为x ,作用在小车上的水平方向的力为F ,O 1为摆角质心。
θxyOFF xF x F yF yllxO 1图1.1 一阶倒立摆的物理模型根据刚体绕定轴转动的动力学微分方程,转动惯量与角加速度乘积等于作用于刚体主动力对该轴力矩的代数和,则 1)摆杆绕其中心的转动方程为θθθcos sin y l F l F J x-= (1-1) 2)摆杆重心的水平运动可描述为)sin (22x θl x dtd m F += (1-2)3)摆杆重心在垂直方向上的运动可描述为)cos (22y θl dtd m mg F =- (1-3)4)小车水平方向上的运动可描述为220dtxd m F F x =- (1-4)由式(1-2)和式(1-4)得F ml x m m =⋅-⋅++)sin (cos )(20θθθθ (1-5) 由式(1-1)、(式1-2)和式(1-3)得θθθsin g cos 2ml x ml ml J =⋅++ )( (1-6) 整理式(1-5)和式(1-6),得⎪⎪⎩⎪⎪⎨⎧++-+-⋅+⋅=-++-⋅+++=))((cos sin )(cos sin cos cos ))((cos sin sin )()(x 2022202222220222222m l J m m l m m l m m l m F m l l m m m m l J g l m m l J lm F m l J θθθθθθθθθθθθ(1-7) 以上式1-7为一阶倒立摆精确模型。
基于PID的倒立摆控制系统设计

基于PID的倒立摆控制系统设计摘要:倒立摆(Inverted Pendulum)控制系统设计是控制理论教学中的一种典型的实验对象,具有很高的教学和科研价值。
本文基于PID控制算法,设计一个倒立摆控制系统,对倒立摆进行控制。
首先介绍了倒立摆系统模型和其动力学方程,然后详细介绍PID控制算法的原理和设计方法,并将其应用于倒立摆系统中,进行控制器的设计。
最后,通过MATLAB/Simulink软件进行系统仿真,并对仿真结果进行分析和讨论。
研究结果表明,PID控制算法能够有效地控制倒立摆系统,并且具有良好的控制性能和稳定性。
一、引言倒立摆控制系统是一种实验教学中常见的控制对象,其模型简单、控制复杂度适中,具有很高的教学和科研价值。
倒立摆系统被广泛应用于控制理论教学、控制算法研究以及控制系统设计等领域。
PID控制是一种常用的控制算法,具有简单、易实现、稳定性好等特点。
因此,本文将基于PID控制算法设计一个倒立摆控制系统,对倒立摆进行控制。
二、倒立摆系统模型和动力学方程倒立摆系统由一个竖直放置的杆和一个可沿杆轴线做直线运动的摆组成。
根据杆的位置和速度,可以得到倒立摆的状态变量,进而得到系统的动力学方程。
本文采用小角度近似,假设杆的运动范围很小,可以将其近似为线性系统,动力学方程可以表示为:$$(M+m)l\ddot{\theta}-ml\ddot{x}\cos(\theta)+m\sin(\theta)g=0$$$$\ddot{x}-\ddot{\theta}l=0$$其中,M为杆的质量,m为摆的质量,l为杆的长度,g为重力加速度,x为摆的位置,$\theta$为杆的倾斜角度。
三、PID控制算法原理和设计方法PID控制算法是一种基于误差信号的反馈控制算法,由比例控制、积分控制和微分控制三部分组成。
比例控制根据当前误差的大小进行控制;积分控制用于消除系统的稳态误差;微分控制用于预测误差的变化趋势,提高系统的响应速度和稳定性。
倒立摆的PID控制

S= -2.3635+20.43961 -2.3635-20.43961 -0.0001 -0.0001 系统的脉冲响应曲线如图(2)所示:
(2)
系统闭环极点均位于S平面左半部,系统稳定。系统 稳定时间约为2s,满足要求。由于此时稳态误差 为0,所以不需要改变积分环节(可以改变积分系 数,观察系统响应如何变化),系统响应的超调 亮比较大,威力较小超调,增加微分系数Kp,取 Kp=20,响应曲线如图(3)所示
• • • • • • • • •
M m b L I F x Φ θ
小车的质量 摆杆质量 小车摩擦系数 摆杆转动轴心到杆质心的长度 摆杆惯量 加在小车上的力 小车位置 摆杆与垂直向上的夹角 摆杆与垂直向下方向的夹角
矢量方向定义
应用Newton方法来建立系统的动力学方程过程如下。 .. .. (1)分析小车水平方向所受的合力,可以得到以下方 程如下。 Mx=F-bx-N (2) 由摆摊水平方向的受力进行分析可以得到下面等 式 N=md^2/(dt^2)*(x+l*sinθ)
G2(s)=(X(s)/U(s)=(I+m*l^2)/q*(s^2)-m*g*l/q)/ (S^4+b*(I+m*l^2)/q*(s^3)(M+m)*m*g*l/q*(s^2 )-b*m*g*l/q*s) 可以看出,den1=den2=den,小车的算式可以 简化成: X(s)=((num2)*(denPID)/(denPID)*(den)+k*(num PID)*(num1))*F(s)
由于输入信号r(s)=0,所以可以把结果图转换成如图2所示
(2)变换后的控制图
其中,反馈环代表我哦们面前设计的摆杆的控制器。 从此框图我们可以看出此处支队摆杆角度进行了控制, 并没有对小车位置进行控制。小车位置输出为
倒立摆pid参数

倒立摆系统的PID参数整定是关键,对于系统的稳定和响应速度有着重要影响。
在位置环中,PID控制器的参数一般设定为:比例增益(KP)、积分增益(KI)和微分增益(KD)。
具体数值需要根据实际情况进行调试,例如,在某些模型中,位置环的比例增益(KP_Pos)可能设定为8.3,而积分增益(KD_Pos)可能设定为6.8。
然而,这些参数并非一劳永逸,可能需要根据系统的实际运行情况进行动态调整。
此外,还需要注意的是,位置环是正反馈系统,如果屏蔽掉直立环,推着倒立摆转,它会朝那个方向越转越快,所以位置环会削弱直立环的作用。
在调节过程中,你可以通过仿真软件进行辅助,例如Matlab里的simscape就提供了很好的工具。
总的来说,倒立摆PID参数的整定是一个反复试验的过程,需要耐心和细致。
倒立摆的PID控制

(b)当L=0.5时
(2)再整定积分系数KI,首先置积分时间常数为一个较大的值,并适当调整第一步确定的Kp,然后减小积分时间常数,并使系统在保持良好的动态响应的情况下,消除静差。这种调整可以根据动态响应,反复改变Kp和KI以期望得到满意的控制过程。
(3)为得到良好的动态过程,再加入微分环节。在第二步整定的基础上,逐步增大KD,同时相应改变KP和KI,逐步试凑以获得满意的调节效果。
二、数学模型的建立
运用拉格朗日方法建立倒立摆系统的数学模型。拉格朗日方程为:
(2-1)
其中L为拉格朗日算子,q为系统的广义坐标,T为系统的动能,V为系统的势能。
(2-2)
其中i=1,2,3……n,fi为系统在第i个广义坐标上的外力。
基于拉格朗日定理分析倒立摆模型如下:
1、计算系统的动能
(1)小车的动能: (2-3)
>>dt=0.02;
>>sys=c2d(sysl,dt,'zoh');
>> [a,b,c,d]=ssdata(sys)
得:
a =
2.0118 -1.0000
1.0000 0
b =
0.2500
0
c =
-0.0706 -0.0706
d =
-3
所以可知离散系统状态空间表达式为:
(2)当L=0.5时
>>clear
(4)由仿真可得当摆杆长L=0.25时,Kp=0.3,KI=60,KD=0.27时可得到良好的响应曲线,如图4(a)所示;当摆杆长L=0.5时,Kp=0.56,KI=80,KD=0.11时可得到良好的响应曲线,如图4(b)所示。(仿真程序见附录)
柔性倒立摆的PD实时控制

并 通 过 弹簧带 动从动 小 车运动 , 以保持 摆杆 平衡 。 在 忽 略 各种 磨 擦 、 气 阻 力 后 , 将 直 线 一 级 空 可
1 系 统 建 模
直 线一 级柔 性倒 立 摆 系统 是 由计 算 机 、 动 控 运
柔性倒立摆系统抽象成 由弹簧 、 匀质 摆杆 、 车和 小 质量 块组 成 的系统 , 图 2所示 。 如
建立 了系统的数学模型 , 并利 用极点 配置方法整定控制 器参数进行仿 真实验 , 将所设计 的控 制 器在 实际
的 实验 设备 上 进 行 实 时控 制 实验 。 实际 控 制 结 果验 证 了方 案 的 有 效 性 和 正 确 性 。
关 键 词 : 线 一级 柔性 倒 立摆 ; D控 制 器 ; 时控 制 直 P 实 中 图分 类 号 :P 7 T23 文 献 标 志 码 : A
还 比较少 。柔 性 倒 立 摆 系 统 是 一 种 新 型 的更 加 复
Fg 1Ln a - a ef xbejit i. ier1s g eil on t l
i e t d- ndu um y t m nv r e pe l sse
直线 一级 柔性 倒立 摆 系统 的工 作 原 理 是 : 电 光 码盘 1 光 电码 盘 2分 别 将 主 动 小 车 和 从 动 小 车 的 、 位移 和速 度信 号反 馈 给伺 服 驱 动 器 和 运 动 控 制 卡 ;
倒立 摆 是 一 个 非 线 性 、 耦 合 、 稳 定 的 控 制 强 不
成 的闭 环系统 。系统框 图如 图 1所示 。
对象 , 常被作 为 典 型 的实 验 控 制对 象 来 验 证 各 种 通 先进 的控 制算 法 。近 几 年 来 , 内外 学 者 已经 运 用 国 各种 控制 方法 对直 线 型 多 级倒 立 摆 、 面 型 倒 立 摆 平
一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真

一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真倒立摆PID控制及其Matlab仿真学生姓名:学院:电气信息工程学院专业班级:专业课程:控制系统的MATLAB仿真与设计任课教师:2014 年 6 月 5 日倒立摆PID控制及其Matlab仿真Inverted Pendulum PID Control and ItsMatlab Simulation摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,对倒立摆的控制研究无论在理论上和方法上都有深远的意义。
本论文以实验室原有的直线一级倒立摆实验装置为平台,重点研究其PID 控制方法,设计出相应的PID控制器,并将控制过程在MATLAB上加以仿真。
本文主要研究内容是:首先概述自动控制的发展和倒立摆系统研究的现状;介绍倒立摆系统硬件组成,对单级倒立摆模型进行建模,并分析其稳定性;研究倒立摆系统的几种控制策略,分别设计了相应的控制器,以MATLAB为基础,做了大量的仿真研究,比较了各种控制方法的效果;借助固高科技MATLAB实时控制软件实验平台;利用设计的控制方法对单级倒立摆系统进行实时控制,通过在线调整参数和突加干扰等,研究其实时性和抗千扰等性能;对本论文进行总结,对下一步研究作一些展望。
关键词:倒立摆;PID控制器;MATLAB仿真设计报告正文1.简述一级倒立摆系统的工作原理;倒立摆是一个数字式的闭环控制系统,其工作原理为:角度、位移信号检测电路获取后,由微分电路获取相应的微分信号。
这些信号经A/D转换器送入计算机,经过计算及内部的控制算法解算后得到相应的控制信号,该信号经过D/A变换、再经功率放大由执行电机带动皮带卷拖动小车在轨道上做往复运动,从而实现小车位移和倒立摆角位移的控制。
2.依据相关物理定理,列写倒立摆系统的运动方程;2lO1小车质量为M ,倒立摆的质量为m ,摆长为2l ,小车的位置为x ,摆的角度为θ,作用在小车水平方向上的力为F ,1O 为摆杆的质心。
(完整版)倒立摆实验报告(PID控制)

专业实验报告3. 实验装置直线单级倒立摆控制系统硬件结构框图如图1所示,包括计算机、I/O设备、伺服系统、倒立摆本体和光电码盘反馈测量元件等几大部分,组成了一个闭环系统。
图1 一级倒立摆实验硬件结构图对于倒立摆本体而言,可以根据光电码盘的反馈通过换算获得小车的位移,小车的速度信号可以通过差分法得到。
摆杆的角度由光电码盘检测并直接反馈到I/O设备,速度信号可以通过差分法得到。
计算机从I/O设备中实时读取数据,确定控制策略(实际上是电机的输出力矩),并发送给I/O设备,I/O设备产生相应的控制量,交与伺服驱动器处理,然后使电机转动,带动小车运动,保持摆杆平衡。
图2是一个典型的倒立摆装置。
铝制小车由6V的直流电机通过齿轮和齿条机构来驱动。
小车可以沿不锈钢导轨做往复运动。
小车位移通过一个额外的与电机齿轮啮合的齿轮测得。
小车上面通过轴关节安装一个摆杆,摆杆可以绕轴做旋转运动。
系统的参数可以改变以使用户能够研究运动特性变化的影响,同时结合系统详尽的参数说明和建模过程,我们能够方便地设计自己的控制系统。
图2 一级倒立摆实验装置图上面的倒立摆控制系统的主体包括摆杆、小车、便携支架、导轨、直流伺服电机等。
主图7 直线一级倒立摆PD控制仿真结果图从上图可以看出,系统在1.5秒后达到平衡,但是存在一定的稳态误差。
为消除稳态误差,我们增加积分参数Ki,令Kp=40,Ki=60,Kd=2,得到以下仿真结果:图8 直线一级倒立摆PID控制仿真结果图从上面仿真结果可以看出,系统可以较好的稳定,但由于积分因素的影响,稳定时间明显增大。
双击“Scope1”,得到小车的位置输出曲线为:图9 施加PID控制器后小车位置输出曲线图由于PID 控制器为单输入单输出系统,所以只能控制摆杆的角度,并不能控制小车的位置,所以小车会往一个方向运动,PID控制分析中的最后一段,若是想控制电机的位置,使得倒立摆系统稳定在固定位置附近,那么还需要设计位置PID闭环。
PID控制的一阶倒立摆
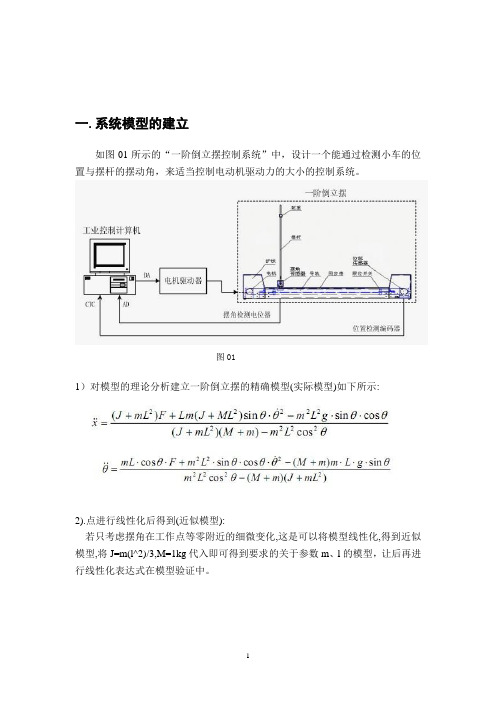
一.系统模型的建立如图01所示的“一阶倒立摆控制系统”中,设计一个能通过检测小车的位置与摆杆的摆动角,来适当控制电动机驱动力的大小的控制系统。
图011)对模型的理论分析建立一阶倒立摆的精确模型(实际模型)如下所示:2).点进行线性化后得到(近似模型):若只考虑摆角在工作点等零附近的细微变化,这是可以将模型线性化,得到近似模型,将J=m(l^2)/3,M=1kg代入即可得到要求的关于参数m、l的模型,让后再进行线性化表达式在模型验证中。
二.模型验证1)子系统的建立实际模型图1Fcn:(((4*m*(l^2))/3)*u[1]+l*m*((4*m*(l^2))/3)*sin(u[3])*(u[2]^2)-10*(m^2)*(l^2)*sin(u[3])*co s(u[3]))/(((4*m*(l^2))/3)*(1+m)-(m^2)*(l^2)*power(cos(u[3]),2))Fcn1:(m*l*cos(u[3])*u[1]+(m^2)*(l^2)*sin(u[3])*cos(u[3])*(u[2]^2)-10*(1+m)*m*l*sin(u[3]))/(( m^2)*(l^2)*power(cos(u[3]),2)-(1+m)*(4*m*(l^2))/3)线性模型图2Fcn2:(30*(1+m*u[2]-3*u[1])/(l*(4+m)Fcn3:(5*u[1]-30*m*u[2])/(4+m)做完以上之后点击鼠标左键不放对图形进行选定,接着右击creat subsystem如下图所示:图32)模型的封装:倒立摆的振子质量m和倒摆长度L作为子系统的参数:图4双击函数模块:图5欲改变其中的任一个参数只要点击其中二者之一的函数方块就行,在其中的m,l改就行了。
有两种实现的方法:一种是利用示波器观察如下图所示,另一种是采用绘图程序实现。
1)示波器实现如图6:图6示波器显示结果如图7所示图72)用程序实现:%Inerted pendulum%Model test in open loop%Signals recuperation%将导入到xy.mat中的仿真试验数据读出load xy.matt=signals(1,: ); %读取时间信号f=signals(2,: ); %读取作用力F信号x=signals(3,: ); %读取精确模型中的小车位置信号q=signals(4,: ); %读取精确模型中的倒摆摆角信号xx=signals(5,: ); %读取简化模型中的小车位置信号qq=signals(6,: ); %读取简化模型中的倒立摆摆角信号%Drawing control and x(t) response signals%画出在控制力的作用下的系统响应曲线%定义曲线的纵坐标、标题、坐标范围和曲线的颜色等特征figure(1) %定义第一个图形hf=line(t,f (:)); %连接时间-作用力曲线grid on;xlabel('Time (s)') %定义横坐标ylabel('Force (N)') %定义纵坐标axis([0 1 0 0.12]) %定义坐标范围axet=axes('Position',get (gca,'Position'),...'XAxisLocation','bottom',...'YAxisLocation','right','Color','None',...'XColor','k','YClor','k'); %定义曲线属性ht=line(t,x,'color','r','parent',axet); %连接时间-小车位置曲线ht=line(t,xx,'color','r','parent',axet); %连接时间-小车速度曲线ylabel('Evolution of the x position (m)') %定义坐标名称axis([0 1 0 0.1]) %定义坐标范围title('Response x and x'' in meter to a f (t)pulse of 0.1 N')%定义曲线标题名称gtext ( '\leftarrow f (t)'),gext('x (t) \rightarrow'),gtext ( '\leftarrow x''(t)')%drawing control and theta (t)response singalsfigure (2)hf=line (t, f (:));grid onxlabel('Time')ylabel('Force in N')axet=axes('Position',get (gca,'Position'),...'XAxisLocation','bottom',...'YAxisLocation','right','Color','None',...'XColor','k','YClor','k');ht=line(t,q,'color','r','parent',axet);ht=line(t,qq,'color','r','parent',axet);ylabel('Angle evolution (rad)')axis([0 1 -0.3 0])title('Response\theta (t) and \theta'' (t)in rad to a f (t)pulse of 0.1 N')gtext ( '\leftarrow f (t)'),gext('\theta (t) \rightarrow'),gtext ( '\leftarrow\theta ''(t)')在·m文件里写入如上程序,在运行该程序之前,先运行系统。
一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真

一级倒立摆课程设计--倒立摆PID控制及其Matlab仿真倒立摆PID控制及其Matlab仿真学生姓名:学院:电气信息工程学院专业班级:专业课程:控制系统的MATLAB仿真与设计任课教师:2014 年 6 月 5 日倒立摆PID控制及其Matlab仿真Inverted Pendulum PID Control and ItsMatlab Simulation摘要倒立摆系统是一个典型的快速、多变量、非线性、不稳定系统,对倒立摆的控制研究无论在理论上和方法上都有深远的意义。
本论文以实验室原有的直线一级倒立摆实验装置为平台,重点研究其PID 控制方法,设计出相应的PID控制器,并将控制过程在MATLAB上加以仿真。
本文主要研究内容是:首先概述自动控制的发展和倒立摆系统研究的现状;介绍倒立摆系统硬件组成,对单级倒立摆模型进行建模,并分析其稳定性;研究倒立摆系统的几种控制策略,分别设计了相应的控制器,以MATLAB为基础,做了大量的仿真研究,比较了各种控制方法的效果;借助固高科技MATLAB实时控制软件实验平台;利用设计的控制方法对单级倒立摆系统进行实时控制,通过在线调整参数和突加干扰等,研究其实时性和抗千扰等性能;对本论文进行总结,对下一步研究作一些展望。
关键词:倒立摆;PID控制器;MATLAB仿真设计报告正文1.简述一级倒立摆系统的工作原理;倒立摆是一个数字式的闭环控制系统,其工作原理为:角度、位移信号检测电路获取后,由微分电路获取相应的微分信号。
这些信号经A/D转换器送入计算机,经过计算及内部的控制算法解算后得到相应的控制信号,该信号经过D/A变换、再经功率放大由执行电机带动皮带卷拖动小车在轨道上做往复运动,从而实现小车位移和倒立摆角位移的控制。
2.依据相关物理定理,列写倒立摆系统的运动方程;2lO1小车质量为M ,倒立摆的质量为m ,摆长为2l ,小车的位置为x ,摆的角度为θ,作用在小车水平方向上的力为F ,1O 为摆杆的质心。
倒立摆PD控制解读

倒立摆PD控制解读倒立摆PD控制摘要:倒立摆系统是一个比较复杂的不稳定、多变量、带有非线性和强耦合特性的高阶机械系统,它的稳定控制是控制理论应用的一个典型范例[1]。
倒立摆系统存在严重的不确定性,一方面是系统的参数的不确定性,一方面是系统的受到不确定因素的干扰。
通过对它的研究不仅可以解决控制中的理论问题,还将控制理论涉及的相关主要学科:机械、力学、数学、电学和计算机等综合应用。
在多种控制理论与方法的研究和应用中,特别是在工程中,存在一种可行性的实验问题,将其理论和方法得到有效的验证,倒立摆系统可以此提供一个从控制理论通过实践的桥梁。
有很多种倒立摆的研究方法,本文采用的是一种基于精确模型极点配制的PD控制器设计方法。
关键词:倒立摆、PD控制Abstract: Inverted pendulum system is a complex of instability, multivariable, nonlinear and strong coupling features advanced mechanical system, its stability control is a typical example of control theory in [1]. Inverted pendulum system exists serious uncertainty, on the one hand is the uncertainty of the parameters of the system, on the one hand is the uncertainty of disturbance of the system.Through the study of it can not only solve the problem of control in theory, will also control theory involving major courses: mechanical, mechanics, mathematics, electrical and computer integrated application. In a variety of control theory and method of research and application, especially in engineering, there is a kind of feasible experiment, it effectively validation of the theory and method, an inverted pendulum system can be provided from the control theory, through the practice of the bridge. There are many kinds ofresearch methods of inverted pendulum, this paper USES is a PD controller design method based on the precise model of pole configuration.一、倒立摆的分类:倒立摆系统诞生之初为单级直线形式,即仅有的一级摆杆一端自由,另一端铰接于可以在直线导轨上自由滑动的小车上。
柔性倒立摆的PD实时控制

4c2 ! x 2 - 4 m lsin ! 2 m + 4 M2 + 3 m sin
∀
= f 3 ( x 1, x 2, x 2, , ) =
为:
3g (m + M ) sin + 3k ( x 1 - x 2 ) cos 2 l(m + 3 m sin + 4 M2) 3c2 co s ! x 2 - 3 lm cos sin ! 2 l(m + 3 m sin + 4 M2) 系统方程为 : x1 x2 q
- 2 207. 5 - 0 . 176 6 0 0
- 6 622. 5 - 0 . 529 8
图 3 PD 控制器结构图 F ig . 3 PD con troller struc tural d iagram
0 0 . 909 1 B = 0 0 0 0 0 D = 0 0 C = 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0
图 3中 , r 1, r 2, r3 分别是主动小车位移、 从动小 车位移和摆杆角度的参考位置。 由图 3 可知直线一级柔性连接倒立摆的控制规 律为: u = u 1 + u2 + u 3. 三个 PD 控制器需要整定的 6 个参数和状态变 量是一一对应的 , 而且其结构与状态反馈控制系统 是一样的, 所以可以利用状态反馈控制系统的极点 配置方法确定 PD 控制器的 6 个参数 极点配置步骤: ( 1) 检验系统的可控性条件 根据系统的状态空 间表达式计算出 可控性矩 阵 [ B A B A B A B A B A B ] 的秩为 6 , 可以 看出系统的状态完全可控性矩阵的秩等 于系统的 状态变量维数, 所以系统是可控的。 ( 2) 由矩阵 A 的特征多项式 [ sI - A ] = s + a1 s + a 2 s + a3 s + a4 s + a 5 s + a6 确定 a 1、 a2、 a3、 a 4、 a5、 a6 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倒立摆PD控制摘要:倒立摆系统是一个比较复杂的不稳定、多变量、带有非线性和强耦合特性的高阶机械系统,它的稳定控制是控制理论应用的一个典型范例[1]。
倒立摆系统存在严重的不确定性,一方面是系统的参数的不确定性,一方面是系统的受到不确定因素的干扰。
通过对它的研究不仅可以解决控制中的理论问题,还将控制理论涉及的相关主要学科:机械、力学、数学、电学和计算机等综合应用。
在多种控制理论与方法的研究和应用中,特别是在工程中,存在一种可行性的实验问题,将其理论和方法得到有效的验证,倒立摆系统可以此提供一个从控制理论通过实践的桥梁。
有很多种倒立摆的研究方法,本文采用的是一种基于精确模型极点配制的PD控制器设计方法。
关键词:倒立摆、PD控制Abstract: Inverted pendulum system is a complex of instability, multivariable, nonlinear and strong coupling features advanced mechanical system, its stability control is a typical example of control theory in [1]. Inverted pendulum system exists serious uncertainty, on the one hand is the uncertainty of the parameters of the system, on the one hand is the uncertainty of disturbance of the system.Through the study of it can not only solve the problem of control in theory, will also control theory involving major courses: mechanical, mechanics, mathematics, electrical and computer integrated application. In a variety of control theory and method of research and application, especially in engineering, there is a kind of feasible experiment, it effectively validation of the theory and method, an inverted pendulum system can be provided from the control theory, through the practice of the bridge. There are many kinds of research methods of inverted pendulum, this paper USES is a PD controller design method based on the precise model of pole configuration.一、倒立摆的分类:倒立摆系统诞生之初为单级直线形式,即仅有的一级摆杆一端自由,另一端铰接于可以在直线导轨上自由滑动的小车上。
在此基础上,人们又进行拓展,产生了多种形式的倒立摆。
按照基座的运动形式,主要分为三大类:直线倒立摆、环形倒立摆和平面倒立摆,每种形式的倒立摆再按照摆杆数量的不同可进一步分为一级、二级、三级及多级倒立摆等[4]。
摆杆的级数越多,控制难度越大,而摆杆的长度也可能是变化的。
多级摆的摆杆之间属于自有连接(即无电动机或其他驱动设备)。
目前,直线型倒立摆作为一种实验仪器以其结构相对简单、形象直观、构件参数易于改变和价格低廉等优点,已经广泛运用于教学[5]。
关于直线倒立摆的控制技术已经基本趋于成熟,在该领域所出的成果也相当丰富。
尽管环形倒立摆的基座运动形式与直线倒立摆有所差异,但二者相同之处是基座仅有一个自由度,可以借鉴比较成熟的直线倒立摆的研究经验,所以近几年来也产生了大量的理论成果。
平面倒立摆是倒摆系统中最复杂的一类,这是因为平面倒立摆的基座可以在平面内自由运动,并且摆杆可以沿平面内的任一轴线转动,使系统的非线性、耦合性、多变量等特性更加突出,从而增加了控制的难度,而且机械和电子器件发展遇到瓶颈性的困难,给平面倒立摆的工程实现也带来了一定的难度。
按摆杆的材质不同,倒立摆系统分为刚体摆杆倒立摆系统和柔性倒立摆系统。
在柔性倒立摆系统中,摆杆本身己经变成了非线性分布参数系统。
根据研究的目的和方法不同,倒立摆系统又分为悬挂式倒立摆、球平衡系统和平行式倒立摆。
其中,研究比较多的是悬挂式倒立摆。
这种倒立摆开始工作时,摆杆处于自由下垂状态。
控制开始时,首先使摆杆按自由振荡频率摆动,随着摆杆振荡幅度的加大,当摆杆接近于倒立摆竖直倒立位置时,自动转换控制方法,使其稳定于倒置状态。
根据导轨的形状小同,倒立摆的运动轨道可以是水平的,也可以是倾斜的。
倾斜倒立摆对实际机器人的步行稳定控制研究非常有意义。
尽管倒立摆系统的结构形式多种多样,但是无论属于哪一种结构,就其本身而言,都是一个非线性、多变量、强耦合、绝对不稳定性系统[6]二、倒立摆的控制方法:倒立摆系统的输入为小车的位移(即位置)和摆杆的倾斜角度期望值,计算机在每一个采样周期中采集来自传感器的小车与摆杆的实际位置信号,与期望值进行比较后,通过控制算法得到控制量,再经数模转换驱动电机实现倒立摆的实时控制。
电机通过皮带带动小车在固定的轨道上运动,摆杆的一端安装在小车上,能以此点为轴心使摆杆能在垂直的平面上自由地摆动。
作用力平行于轨道的方向作用于小车,使杆绕小车上的轴在竖直平面内旋转,小车沿着水平导轨运动。
当没有作用力时,摆杆处于垂直的稳定的平衡位置(竖直向下)。
为了使摆杆摆动或者达到竖直向上的稳定,需要给小车一个控制力,使其在轨道上被往前或朝后拉动。
因此,倒立摆系统的控制原理可简述如下:用一种强有力的控制方法对小车的速度作适当的控制,从而使摆杆倒置稳定于小车正上方。
倒立摆刚开始工作时,首先使小车按摆杆的自由振荡频率摆动,摆杆随之大幅度摆动。
经过几次摆动后,摆杆能自动直立起来。
这种被控量既有角度,又有位置,且它们之问又有关联,具有非线性、时变、多变量耦合的性质。
四:单级倒立摆建模:1.直线一级倒立摆系统的硬件组成以及工作原理倒立摆系统包含倒立摆本体、电控箱及出计算机和运动控制卡组成的控制平台三大部分,组成了一个闭环系统。
其结构件图如图2.1所示:图2.1 一级倒立摆系统结构简图其中电控箱内主要有以下部件:(1)交流伺服驱动器;(2)I/O接口板;(3)开关电源。
控制平台主要部分组成:(1)与IBM PC/AI机兼容的PC机,带PCI/SCI总线插槽;(2)GT400一SV—PCI运动控制卡;(3)GT400.SV—PCI运动控制卡用户接口软件。
电机通过同步带驱动小车在滑杆上来回运动,以保持摆杆平衡。
直线一级倒立摆系统的工作原理如图2.2所示:图2.2 倒立摆系统工作原理框图电机编码器和角码器向运动控制卡反馈小车和摆杆位置,小车的位移可以根据光Ffl码盘l的反馈通过换算获得,速度信号可以通过对位移的差分得到,并同时反馈给伺服驱动器和运动控制卡;摆杆的角度由光电码盘2测量得到,而角速度信号可以通过对角度的差分得到,并同时反馈给控制卡和伺服驱动器。
计算机从运动控制卡中读取实时数据,确定控制决策(小车向哪个方向移动,移动速度,加速度等),并由运动控制卡来实现控制决策,产生相应的控制量,使电机转动,带动小车运动,保持摆杆平衡。
下面来介绍一级倒立摆系统的一些硬件组成:(1)伺服电机伺服电机又称为执行电动机,在自动控制系统中作为执行元件,它将输入的电压信号变换成转轴的角位移或者角速度输出。
输入的电压信号又称为控制信号或者控制电压。
改变控制电压可以变更伺服电机的转速和转向。
自动控制系统对伺服电机的基本要求如下:1)宽广的调速范围伺服电机的转速随着控制电压的改变能在宽广的范围内实现连续调节。
2)机械特性和调节特性均为线性伺服电机的机械特性是指控制电压一定时转速随转距的变化关系;调节特性是指电机转矩一定时,转速随控制电压的变化关系。
线性的机械特性和调节特性有利于提高自动控制系统的动态精度。
3)无“自转”现象伺服电机在控制电压为零时,能够自行停转。
4)快速响应电机的机电常数要小,相应的伺服电机要有较大的堵转转矩和较小的转动惯量。
这样,电机的转速便能随着控制电压的改变而迅速变化。
(2) 编码器编码器作为检测转速、线速度、角速度、线位移、角位移的一种传感器,是利用码盘将这些信号转换成亮、暗光信号,再用各种光电器件的光电效应将信号转换成电信号输出。
可以说是一种最简单的数字式传感器,精度高且可靠,应用非常广泛。
编码器有两种形式:增量式编码器和绝对编码器。
(3)限位开关限位开关又称行程开关,可以安装在相对静止的物体(如固定架、门框等,简称静物)上或者运动的物体(如行车、门等,简称动物)上。
当动物接近静物时,开关的连杆驱动开关的接点引起闭合的接点分断或者断开的接点闭合。
由开关接点开、合状态的改变去控制电路和机构的动作。
限位开关也可分为旋转限位开关及直行限位开关。
(4)运动控制器3.2建立单级倒立摆的数学模型数学模型是分析、设计、预报和控制系统的基础。
建立系统数学模型有两种方法:一种是从基本物理定律,即利用各个专门学科领域提出来的物质和能量的守恒性、连续性原理,以及系统的结构数据推导出模型。
这种方法得出的数学模型称为机理模型或解析模型,这种建立模型的方法称为解析法。
另一种是系统运行和实验数据建立系统的模型(模型结构和参数),这种方法称为系统辨识。
倒立摆的形状较为规则,而且是一个不稳定系统,无法通过测量频率特性方法获取其数学模型,故适合用数学工具进行理论推导[16]。
直线倒立摆系统是一个机电一体化系统,由小车和摆杆组成。
小车可以沿水平方向上的导轨运动,导轨的一端固定有位置传感器,可以测量小车的位移;摆杆通过转轴固定在小车上,小车和摆杆的连接处固定有共轴角度传感器,用以测量摆杆的角度。
直流永磁力矩电机和位置传感器固定在同一侧,直流电机通过传送带驱动小车沿导轨运动。
导轨的两端装有行程开关,限制小车的左右位置。
为了在数学上推导和处理问题的方便,可作出如下假设:(1)摆杆在运动中是不变形的刚体;(2)齿型带与轮之间无相对滑动,齿型带无拉长现象;(3)小车在运动过程中,摩擦系数一定;(4)忽略空气阻力;基于以上几点,可将直线一级倒立摆系统抽象成小车和匀质杆组成的系统(图2.3)图2.3 一级倒立摆小车摆杆位置图首先,对小车进行受力分析,小车的受力分析如图2.4所示。
