河南省许昌市高一下学期数学期末考试试卷
河南省许昌市高级中学2024届高一数学第二学期期末考试试题含解析

河南省许昌市高级中学2024届高一数学第二学期期末考试试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.设变量,x y 满足约束条件203603x y x y y --≤⎧⎪+-≥⎨⎪≤⎩,则目标函数21z x y =-++的最小值为( ) A .7-B .6-C .1-D .22.在等比数列{}n a中,若357a a a =-28a a =( ) A .3BC .9D .133.截一个几何体,各个截面都是圆面,则这个几何体一定是( ) A .圆柱B .圆锥C .球D .圆台4.在区间[1,4]-内随机取一个实数a ,使得关于x 的方程2420x x a ++=有实数根的概率为( ) A .25B .13C .35D .235.以下给出了4个命题:(1)两个长度相等的向量一定相等; (2)相等的向量起点必相同;(3)若a b a c ⋅=⋅,且0a ≠,则b c =; (4)若向量a 的模小于b 的模,则a b <. 其中正确命题的个数共有( ) A .3 个B .2 个C .1 个D .0个6.已知圆C 的圆心与点(1,0)关于直线y x =对称,直线4320x y --=与圆C 相交于A ,B 两点,且6AB =,则圆C 的半径长为( )A .10B .22C .3D .137.已知一个几何体是由半径为2的球挖去一个三棱锥得到(三棱锥的顶点均在球面上).若该几何体的三视图如图所示(侧视图中的四边形为菱形),则该三棱锥的体积为( )A .23B .43C .83D .1638.若关于x 的一元二次不等式的解集为R ,则实数a 的取值范围是( ) A .B .C .D .9.sin 45sin 75sin 45sin15+=( )A .0B .12C .32D .110.在数列{}n a 中,若12a =,()*121nn n a a n a +=∈+N ,则5a =( ) A .417B .317 C .217D .517二、填空题:本大题共6小题,每小题5分,共30分。
河南省许昌市高一下学期数学期末考试试卷

河南省许昌市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (201920高三上·长宁期末) 已知,则“ ”是“ ”的()A . 充分非必要条件B . 必要非充分条件C . 充要条件D . 既非充分又非必要条件2. (2分)已知命题p:在△ABC中,“C>B”是“sinC>sinB”的充分不必要条件;命题q:“a>b”是“ac2>bc2”的充分不必要条件,则下列选项中正确的是()A . p真q假B . p假q真C . “”为假D . “”为真3. (2分)把红、黄、蓝、白4张纸牌随机地分发给甲、乙、丙、丁4个人,事件“甲分得红牌”与“乙分得蓝牌”是()A . 对立事件B . 不可能事件C . 互斥但不对立事件D . 对立不互斥事件4. (2分) (2016高一下·汕头期末) 如图程序运行的结果是()A . 515B . 23C . 21D . 195. (2分)某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。
现用分层抽样的方法在这70名学生中抽样,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为()A . 6B . 10C . 8D . 96. (2分) (2018高二上·牡丹江期中) 若椭圆的离心率为,则双曲线的离心率为()A .B .C .D .7. (2分) (2018高二上·嘉兴期末) 中心在坐标原点的椭圆,焦点在轴上,焦距为,离心率为,则该椭圆的方程为()A .B .C .D .8. (2分) (2019高二上·钦州期末) 如图,圆内切于扇形,,若在扇形内任取一点,则该点不在圆内的概率为()A .B .C .D .9. (2分) (2019高二上·双流期中) 已知实数x , y满足方程x2+y2-8x+15=0.则x2+y2最大值为()A . 3B . 5C . 9D . 2510. (2分) (2016高二下·宜春期末) 已知F1和F2分别是双曲线的左、右焦点,P 是双曲线左支的一点,,,则该双曲线的离心率为()A .B .C .D .11. (2分) (2019高二上·尚志月考) 椭圆的离心率是()A .B .C .D .12. (2分)已知椭圆的面积为.现有一个椭圆,其中心在坐标原点,一个焦点坐标为(4,0),且长轴长与短轴长的差为2,则该椭圆的面积为()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2017高二上·阜宁月考) 已知椭圆的焦点分别为,离心率为,过的直线交椭圆于A、B两点,则的周长为________.14. (1分) (2018高一下·西华期末) 用秦九韶算法计算多项式时的值时,的值为________.15. (1分) (2018高二上·南阳月考) 已知为椭圆上的点,O 为原点,则的取值范围是________.16. (1分) (2020高二上·遂宁期末) 如图,这是某校高一年级一名学生七次数学测试成绩(满分100分)的茎叶图. 去掉一个最高分和一个最低分后,所剩数据的方差是 ________三、解答题 (共6题;共50分)17. (5分)(2020·长春模拟) 在平面直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,圆的极坐标方程为 .(Ⅰ)求直线的普通方程和圆的直角坐标方程;(Ⅱ)直线与圆交于两点,点,求的值.18. (20分)有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:摄氏温度/ -504712151923273136热饮杯数15615013212813011610489937654(1)画出散点图;(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;(3)求回归方程;(4)如果某天的气温是,预测这天卖出的热饮杯数.19. (5分) (2017高二上·太原月考) 已知:,:,若是的充分不必要条件,求正实数的取值范围.20. (5分)(2017·青岛模拟) 已知椭圆C: =1(a>b>0)的左、右顶点分别为A1、A2 ,上、下顶点分别为B2、B1 , O为坐标原点,四边形A1B1A2B2的面积为4,且该四边形内切圆的方程为x2+y2= .(Ⅰ)求椭圆C的方程;(Ⅱ)若M、N是椭圆C上的两个不同的动点,直线OM、ON的斜率之积等于﹣,试探求△OMN的面积是否为定值,并说明理由.21. (10分) (2018高一下·平顶山期末) 某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)参加书法社团未参加书法社团参加演讲社团85未参加书法社团230(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学 ,3名女同学 .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求被选中且未被选中的概率.22. (5分) (2016高二上·黑龙江期中) 设椭圆C: =1(a>b>0)的左焦点为F,离心率为,过点F且与x轴垂直的直线被椭圆截得的线段长为,求椭圆的标准方程.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、答案:略三、解答题 (共6题;共50分)17-1、18-1、答案:略18-2、18-3、答案:略18-4、答案:略19-1、20-1、答案:略21-1、答案:略21-2、答案:略22-1、。
河南省许昌市实验中学高一数学理下学期期末试卷含解析

河南省许昌市实验中学高一数学理下学期期末试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 函数的零点所在的大致区间是A. B. C. D.参考答案:D2. 且<0,则的取值范围是()A. B. C. D.参考答案:A3. 等比数列{a n}的各项均为正数,且,则()A. 7B. 8C. 9D. 10参考答案:B【分析】根据题意,由对数的运算性质可得,又由对数的运算性质可得,计算可得答案.【详解】根据题意,等比数列的各项均为正数,且,则有,则;故选:.【点睛】本题考查等比数列的性质以及对数的运算,属于基础题.4. 等差数列{a n}和{b n},它们的前n项之和分别为S n和T n,若=,则的值是()A.B.C.D.参考答案:C【考点】8F:等差数列的性质.【分析】由等差数列{a n}与{b n}的性质和前n项和公式可得:,代入若=求值.【解答】解:由等差数列{a n}与{b n}的性质和前n项和公式可得:===,∵,∴===,故选:C.【点评】本题考查等差数列的前n项和公式、等差数列的性质的灵活应用,解题的关键是熟练掌握公式.5. 函数的定义域为()A B C DA6. 如图所示,当时,函数的图象是 ( )参考答案:D7. 直线与圆交于A,B两点,且,过点A,B分别作l的垂线与y轴交于点M,N,则等于()A. B. 8 C. D.参考答案:C根据题中的条件可知圆的半径等于3,所以直径等于6,所以直线过圆心,即直线过坐标原点,从而可以求得,结合图形的特征,.8. 若,则的值为()(A)(B)(C) (D)C略9. 已知ABCD为平行四边形,若向量,则向量为( )A.B.C.D.参考答案:C10. 函数f(x)=|lgx|﹣sinx的零点个数为()A.1个B.2个C.3个D.4个参考答案:D【考点】函数零点的判定定理.【专题】计算题;函数思想;数形结合法;函数的性质及应用.【分析】本题即求函数y=|lgx|的图象和函数y=sinx的图象的交点个数,数形结合可得结论.【解答】解:函数f(x)=|lgx|﹣sinx的零点的个数,即函数y=lgx的图象和函数y=sinx的图象的交点个数,如图所示:显然,函数y=|lgx|的图象和函数y=sinx的图象的交点个数为4,故选:D.【点评】本题主要考查函数的两点个数的判断方法,体现了转化以及数形结合的数学思想,属于中档题.二、填空题:本大题共7小题,每小题4分,共28分11. 给出下列五个命题:①函数f(x)=2a2x-1-1的图象过定点(,-1);②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.③若log a>1,则a的取值范围是(,1);④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;⑤对于函数f(x)=ln x,其定义域内任意x1≠x2都满足f()≥其中所有正确命题的序号是______.参考答案:③④⑤【分析】由指数函数的图象的特点解方程可判断①;由奇函数的定义,解方程可判断②;由对数不等式的解法可判断③;由函数的对称性可判断④;由对数函数的运算性质可判断⑤.【详解】解:①函数,则,故①错误;②因为当时,,且,所以由函数f(x)是定义在R上的奇函数得,故②错误;③若,可得,故③正确;④因为,则f(x)图象关于直线x=2对称,故④正确;⑤对于函数当且仅当取得等号,其定义域内任意都满足,故⑤正确.故答案为:③④⑤.【点睛】本题考查函数的单调性、奇偶性和对称性、凹凸性,以及函数图象,考查运算能力和推理能力,属于中档题.12. 已知幂函数为实常数)的图象过点(2,),则= ▲.参考答案:4略13. 若函数y=log a(2﹣ax)在区间(0,1)上单调递减,则a的取值范围为_____.参考答案:【分析】确定函数单调递减,再根据复合函数单调性和定义域得到答案.【详解】,故函数单调递减,函数y=log a(2﹣ax)在区间(0,1)上单调递.故,且满足,故.故答案为:.【点睛】本题考查了根据函数的单调性求参数,忽略掉定义域的情况是容易发生的错误.14. 下列命题中,正确的是①平面向量与的夹角为,,,则;②已知,是平面内两个非零向量,则平面内任一向量都可表示为,其中;③已知,,其中,则;④是所在平面上一定点,动点P满足:,,则直线一定通过的内心。
2022-2023学年河南省许昌市高一(下)期末数学试卷【答案版】

2022-2023学年河南省许昌市高一(下)期末数学试卷一、单项选择题:本题共8小题,每小题5分,共40分。
在每个小题给出的四个选项中,只有一项符合题目要求。
1.已知复数z 满足(1﹣i )2z =2﹣4i ,其中i 为虚数单位,则复数z 的虚部为( ) A .2B .1C .﹣2D .i2.甲、乙两名射击运动员进行射击比赛,甲的中靶概率为0.8,乙的中靶概率为0.9,则两人都中靶的概率为( ) A .0.26B .0.98C .0.72D .0.93.已知向量a →=(1,1),b →=(1,﹣1).若(a →+λb →)⊥(a →+μb →),则( ) A .λ+μ=1B .λ+μ=﹣1C .λμ=1D .λμ=﹣14.设m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题中正确的为( ) A .若m ⊥n ,m ⊂α,n ⊂β,则α∥βB .若α∥β,m ⊂α,n ⊂β,则m ∥nC .若m ∥n ,n ⊂α,α∥β,则m ∥βD .若m ⊥α,n ⊥β,α∥β,则m ∥n5.中国古代四大名楼鹳雀楼,位于山西省运城市永济市蒲州镇,因唐代诗人王之涣的诗作《登鹳雀楼》而流芳后世.如图,某同学为测量鹳雀楼的高度MN ,在鹳雀楼的正东方向找到一座建筑物AB ,高约为37m ,在地面上点C 处(B ,C ,N 三点共线)测得建筑物顶部A ,鹳雀楼顶部M 的仰角分别为30°和45°,在A 处测得楼顶部M 的仰角为15°,则鹳雀楼的高度约为( )A .91mB .74mC .64mD .52m6.平行四边形ABCD 中,点M 在边AB 上,AM =3MB ,记CA →=a →,CM →=b →,则AD →=( )A .43a →−73b → B .23b →−43a → C .73b →−43a → D .13a →−43b →7.四名同学各掷骰子5次,分别记录每次骰子出现的点数.根据四名同学的统计结果,可以判断出一定没有出现点数6的是( )A .平均数为3,中位数为2B .中位数为3,众数为2C .平均数为2,方差为2.5D .中位数为3,方差为2.88.正四棱锥S ﹣ABCD 中,底面边长AB =2,侧棱SA =√5,在该四棱锥的内部有一个小球,则小球表面积的最大值为( ) A .4πB .16πC .8π3D .4π3二、多项选择题:本题共4小题,每小题5分,共20分。
河南省许昌市高一下学期期末数学试卷

河南省许昌市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共14分)1. (1分) (2020高三上·静安期末) 若直线和直线的倾斜角分别为和则与的夹角为________.2. (1分) (2019高三上·柳州月考) 曲线在处的切线的倾斜角为 ________.3. (1分) (2016高一下·徐州期末) 函数f(x)=(sinx﹣cosx)2的最小正周期为________.4. (1分) (2016高一下·徐州期末) 某工厂生产A,B,C三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样方法抽出一个容量为n的样本,若样本中A种型号产品有12件,那么样本的容量n=________.5. (1分) (2016高一下·徐州期末) 同时掷两枚质地均匀的骰子,所得点数之和大于10的概率为________.6. (1分) (2016高一下·徐州期末) 根据如图所示的伪代码,可知输出的结果S为________.7. (1分) (2016高一下·徐州期末) 某校举行元旦汇演,七位评委为某班的小品打出的分数如茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差是________.8. (1分) (2016高一下·徐州期末) 若数列{an}满足an+1﹣2an=0(n∈N*),a1=2,则{an}的前6项和等于________.9. (1分) (2016高一下·徐州期末) 已知变量x,y满足,则目标函数z=2x+y的最大值是________.10. (1分) (2016高一下·徐州期末) 欧阳修《卖油翁》中写到:(翁)乃取一葫芦置于地,以钱覆其口,徐以杓酌油沥之,自钱孔人,而钱不湿.可见“行行出状元”,卖油翁的技艺让人叹为观止.若铜钱是直径为3cm 的圆,中间有边长为1cm的正方形孔,若随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落人孔中的概率是________.11. (1分) (2016高一下·徐州期末) 在△ABC中,若acosB=bcosA,则△ABC的形状为________.12. (1分) (2016高一下·徐州期末) 已知直线l1:ax+2y+6=0与l2:x+(a﹣1)y+a2﹣1=0平行,则实数a的取值是________.13. (1分) (2016高一下·徐州期末) 已知等差数列{an}中,首项为a1(a1≠0),公差为d,前n项和为Sn ,且满足a1S5+15=0,则实数d的取值范围是________.14. (1分) (2016高一下·徐州期末) 已知正实数x,y满足,则xy的取值范围为________.二、解答题 (共6题;共60分)15. (5分)正方形中心为G(﹣1,0),一边所在直线的斜率为3,且此正方形的面积为14.4,求此正方形各边所在的直线方程.16. (10分) (2019高二下·深圳期中) 已知的三个内角所对的边分别为,是锐角,且 .(1)求;(2)若,的面积为,求的值.17. (10分) (2017高一下·孝感期末) 已知函数f(x)= ,其中 =(2cosx, sin2x), =(cosx,1),x∈R(1)求函数y=f(x)的最小正周期和单调递增区间:(2)在△ABC中,角A,B,C所对的边分别为a,b,c,f(A)=2,a= 且sinB=2sinC,求△ABC的面积.18. (10分)设,求解下列问题:(1)求的单调区间;(2)在锐角△ AB C 中,角∠ A , B , C ,的对边分别为 a , b , c ,若 = 0 , a = 1 ,求△ A B C 面积的最大值.(1)求的单调区间;(2)在锐角中,角,的对边分别为,若,求面积的最大值.19. (10分) (2016高三下·娄底期中) 已知向量 =(1,3cosα), =(1,4tanα),,且 =5.(1)求| + |;(2)设向量与的夹角为β,求tan(α+β)的值.20. (15分) (2016高一下·徐州期末) 已知数列{an}满足an+1+an=4n﹣3,n∈N*(1)若数列{an}是等差数列,求a1的值;(2)当a1=﹣3时,求数列{an}的前n项和Sn;(3)若对任意的n∈N* ,都有≥5成立,求a1的取值范围.参考答案一、填空题 (共14题;共14分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共60分)15-1、16-1、16-2、17-1、17-2、18-1、18-2、19-1、19-2、20-1、20-2、20-3、。
河南省许昌市高一下学期期末数学试卷

河南省许昌市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)若A=a2+3ab,B=4ab﹣b2 ,则A、B的大小关系是()A . A≤BB . A≥BC . A<B或A>BD . A>B2. (2分) (2016高二上·桃江期中) 已知向量 =(3,﹣2), =(x,y﹣1)且∥ ,若x,y均为正数,则 + 的最小值是()A . 24B . 8C .D .3. (2分) (2017高一下·河口期末) 在中,角对边分别为,且,则()A . 或B .C .D . 或4. (2分)已知公比为的等比数列的前项和为,则下列结论中:(1)成等比数列;(2);(3)正确的结论为()A . (1)(2).B . (1)(3).C . (2)(3).D . (1)(2)(3).5. (2分) (2016高二上·澄城期中) 若等差数列{an}满足a7+a8+a9>0,a7+a10<0,则当{an}的前n项和最大时n的值为()A . 7B . 8C . 9D . 106. (2分)读右侧程序框图,该程序运行后输出的A值为()A .B .C .D .7. (2分) (2017高二下·淄川开学考) 若对于任意的x>0,不等式≤a恒成立,则实数a的取值范围为()A . a≥B . a>C . a<D . a≤8. (2分)已知两座灯塔A和B与海洋观察站C的距离都等于a km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与B的距离为()A . a kmB . a kmC . a kmD . 2a km9. (2分)设变量x,y满足约束条件则目标函数z=3x-y的最大值为()A .B .C .D . 410. (2分) (2016高一下·内江期末) 数列{an}为等差数列,满足a2+a4+…+a20=10,则数列{an}前21项的和等于()A .B . 21C . 42D . 84二、填空题 (共5题;共5分)11. (1分)不等式|2x﹣1|+1<0的解集为________.12. (1分)(2014·辽宁理) 对于c>0,当非零实数a,b满足4a2﹣2ab+4b2﹣c=0且使|2a+b|最大时,﹣ + 的最小值为________.13. (1分) (2019高三上·广州月考) 已知数列为等比数列,为其前n项和,,且,,则 ________.14. (1分) (2015高三上·包头期末) 已知a,b,c分别为△ABC的三个内角A,B,C的对边,a=2且(2+b)(sinA﹣sinB)=(c﹣b)sinC,则△ABC面积的最大值为________.15. (1分) (2015高二上·滨州期末) 已知两个具有线性相关关系的变量x与y的几组数据如下表x3456y m4根据上表数据所得线性回归直线方程为 = x+ ,则m=________.三、解答题 (共4题;共40分)16. (15分) (2016高二上·船营期中) 已知数列{an}满足3(n+1)an=nan+1(n∈N*),且a1=3,(1)求数列{an}的通项公式;(2)求数列{an}的前n项和Sn;(3)若 = ,求证:≤ + +…+ <1.17. (5分)(2018·南充模拟) 在中,内角的对边分别为,已知 .(Ⅰ)若,,求边;(Ⅱ)若,求角 .18. (10分) (2016高一下·宝坻期末) 已知关于x的不等式ax2﹣(a+2)x+2<0.(1)当a=﹣1时,解不等式;(2)当a∈R时,解不等式.19. (10分) (2016高一下·孝感期中) 已知关于x的不等式(m﹣1)x2+(m﹣1)x+2>0(1)若m=0,求该不等式的解集(2)若该不等式的解集是R,求m的取值范围.参考答案一、选择题 (共10题;共20分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、二、填空题 (共5题;共5分)11-1、12-1、13-1、14-1、15-1、三、解答题 (共4题;共40分) 16-1、16-2、16-3、17-1、18-1、18-2、19-1、19-2、。
河南省许昌市2021-2022学年高一下学期期末考试数学试卷(文科)(解析版)

河南省许昌市2021-2022学年高一下学期期末考试数学试题(文科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一项是符合题目要求的.1.已知i 为虚数单位,复数z 满足(1)2i z i +=-,则复数z 在复平面所对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限〖解 析〗(1)2i z i +=-,∴2(2)(1)131(1)(1)22i i i z i i i i ---===-++-, ∴复数z 在复平面所对应的点13(,)22-在第四象限.〖答 案〗D2.已知平面向量(3,1)a =,(,2)b x =-,且a b ⊥,则(x = ) A .1B .1-C .23D .23-〖解 析〗(3,1)a =,(,2)b x =-,a b ⊥,∴320a b x ⋅=-=,∴23x =. 〖答 案〗C3.某学校计划从3名男生和4名女生中任选4名参加七一征文比赛,记事件M 为“至少3名女生参加”,则下列事件与事件M 对立的是( ) A .恰有1名女生参加 B .至多有2名男生参加C .至少有2名男生参加D .恰有2名女生参加〖解 析〗至少3名女生的对立面是至多两名女生,总共选4名,也即为至少2名男生. 〖答 案〗C4.已知向量a ,b ,且||9a =,||12b =,a 与b 的夹角为4π,则(a b ⋅= )A .36B .C .54D .〖解 析〗因为||9a =,||12b =,a 与b 的夹角为4π,所以||||cos ,912cos 4a b a b a b π⋅=<>=⨯⨯=〖答 案〗D5.已知P 在ABC ∆所在平面内,满足||||||PA PB PC ==,则P 是ABC ∆的( ) A .外心B .内心C .垂心D .重心〖解 析〗||||||PA PB PC ==表示P 到A ,B ,C 三点距离相等,P 为外心. 〖答 案〗A6.正方体的棱长扩大到原来的6倍,则其表面积扩大到原来的( ) A .2倍B .12倍C .18倍D .36倍〖解 析〗设正方体棱长为a ,则其表面积为26a ,故正方体的棱长扩大到原来的6倍,则其表面积为2636a ⨯,扩大到原来的36倍. 〖答 案〗D7.下列四个命题中不正确的是( ) A .平行线段在直观图中仍然平行 B .相等的角在直观图中仍然相等C .直线与平面相交有且只有一个公共点D .垂直于同一个平面的两条直线平行 〖解 析〗逐一考查所给的选项:A .平行线段在直观图中仍然平行,A 说法正确;B .相等的角在直观图中不一定相等,B 说法错误;C .直线与平面相交有且只有一个公共点,C 说法正确;D .由面面垂直的性质可知垂直于同一个平面的两条直线平行,D 说法正确.〖答 案〗B8.某校开展“正心立德,劳动树人”主题教育活动,对参赛的100名学生的劳动作品的得分情况进行统计,并绘制了如图所示的频率分布直方图,图中信息,下列结论错误的 是( )A .图中的x 值为0.020B .得分在80分及以上的人数为40C .这组数据平均数的估计值为77D .这组数据第80百分位数的估计值为85〖解 析〗由频率之和为1得:10(0.0050.0350.0300.010)1x ++++=, 解得:0.020x =,A 说法正确;得分在80分及以上的人数为(0.0300.010)1010040+⨯⨯=,B 说法正确;因为10(550.005650.020750.035850.030950.010)77⨯⨯+⨯+⨯+⨯+⨯=,C 说法正确;0.005100.020100.035100.60.8⨯+⨯+⨯=<,0.005100.020100.035100.030100.90.8⨯+⨯+⨯+⨯=>,所以这组数据第80百分位数的估计值落在区间[80,90)内,0.80.626080100.90.63-+⨯=-,故这组数据第80百分位数的估计值不为85,D 说法错误. 〖答 案〗D9.已知a ,b 是两个不共线向量,向量b ta -,1322a b -共线,则实数(t = )A .13-B .13C .34-D .34〖解 析〗由向量b ta -与1322a b -共线,得11322t -=-,解得:13t =.〖答 案〗B10.在ABC ∆中,60B ∠=︒,2AB =,M 是BC 的中点,AM =(AC =) A .B .4C .D .〖解 析〗因为60B ∠=︒,2AB =,M 是BC 的中点,AM =, 所以在ABM ∆中,由余弦定理2222cos AM AB BM AB BM B =+-⋅⋅, 可得21124222BM BM =+-⨯⨯⨯,整理可得2280BM BM --=, 解得4BM =,或2-(舍去),所以28BC BM ==,所以由余弦定理可得AC ==.〖答 案〗A11.已知a ,b 是两条不同的直线,α,β,γ是三个不同的平面.给出下列命题: ①若αβ⊥,a αβ=,a b ⊥,则b α⊥或b β⊥;②若//αβ,a αγ=,b βγ=,则//a b ;③若a αβ=,b αγ=,//a b ,则//βγ;④“若αγ⊥,βγ⊥,则αβ⊥”是随机事件;⑤若a ,b 是异面直线,则存在平面α过直线a 且垂直于直线b . 其中正确的命题是( ) A .①③B .②⑤C .③④D .②④〖解 析〗若αβ⊥,a αβ=,a b ⊥,b 与α,β可能垂直也可能不垂直,①错;由面面平行的性质定理知②正确;三棱柱的两个侧面与第三个侧面的交线相互平行,但这两个侧面相交,③错;若αγ⊥,βγ⊥,则α与β可能垂直也可能不垂直,“若αγ⊥,βγ⊥,则αβ⊥”是随机事件,④正确;若存在平面α过直线a 且垂直于直线b ,则a b ⊥,但已知中a ,b 不一定垂直,⑤错误. 〖答 案〗D12.已知对任意平面向量(,)AB x y =,把AB 绕其起点沿逆时针方向旋转θ角得到向量(cos sin ,sin cos )AP x y x y θθθθ=-+,叫做把点B 绕点A 沿逆时针方向旋转θ角得到点P .已知平面内点(1,2)A ,点(2,3)B ,把点B 绕点A 沿顺时针方向旋转116π得到点P ,则点P 的坐标为( )A .33(22--+B .11(22-+C .15(22--D .15(22+〖解 析〗平面内点(1,2)A ,点(2,3)B ,所以(1,1)AB =, 把点B 绕点A 顺时针旋转116π后得到点P , 即把点B 绕点A 沿逆时针方向旋转6π得到点P ,则(cos sin AP x y θθ=-,sin cos )(cos sin66x y ππθθ+=-,1sincos )662ππ+=-,12,设(,)P a b ,则(1AP a =-,2)(b -=12,12,解得12a =+,52b =+. 所以点P的坐标为12+,52+. 〖答 案〗D二、填空题:本大题共4小题,每小题5分,共20分. 13.2(23)(23)(1)i i i +-+= .〖解 析〗2(23)(23)(1)(49)(2)26i i i i i +-+=+⨯=. 〖答 案〗26i14.已知向量(2,5)a =,(,4)b λ=,且//a b ,则λ= . 〖解 析〗因为(2,5)a =,(,4)b λ=,且//a b , 所以245λ⨯=,则85λ=. 〖答 案〗8515.在ABC ∆中,已知6b =,45A =︒,75C =︒,则a = . 〖解 析〗因为6b =,45A =︒,75C =︒,所以18060B A C =︒--=︒,由正弦定理sin sin a bA B=,可得6sin sin b A a B ⋅=== 〖答案〗16.19世纪,美国天文学家西蒙⋅纽康在翻阅对数表时,偶然发现表中以1开头的数出现的频率更高.约半个世纪后,物理学家本福特又重新发现这个现象,从实际生活得出的大量数据中,以1开头的数出现的频率约为总数的三成,接近期望值19的3倍,并提出本福特定律,即在大量b 进制随机数据中,以n 开头的数出现的概率为1()log ()b b n P n n+=,如斐波那契数、阶乘数、素数等都比较符合该定律.后来常有数学爱好者用此定律来检验某些经济数据、选举数据等大数据的真实性.根据本福特定律,若1012()3ni P i =∑,则n 的最大值为 .〖解 析〗由1()log ()b b n P n n +=可得,10101()log ()(1)i P i lg i lgi i+==+-, 所以101()(1)ni P i lg n ==+∑,又1012()3ni P i =∑,所以,2(1)3lg n +,即3(1)100n +, 所以,1n =,2,3, 则n 的最大值为3. 〖答 案〗3三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)求证:夹在两个平行平面间的平行线段相等. (1)画图,并用图中字母写出已知、求证; (2)写出证明过程.(1)解:已知:如图,//αβ,且//AB CD , 且A α∈,C α∈,B β∈,D β∈. 求证:AB CD =.(2)证明:过平行直线AB ,CD 作平面γ,与平面α和β分别相交于AC 和BD .//αβ,//BD AC ∴.又//A CD ∴,∴四边形ABDC 是平行四边形.AB CD ∴=.18.(12分)某项密码破译工作需甲、乙、丙、丁四人完成,已知每人独立译出密码的概率为13,若二人合为一组,则该组破译的概率为34,若三人合为一组,则该组破译的概率为45. (1)若四人独立翻译,求破译出密码的概率;(2)若将四人分成两组,两组独立破译密码,求破译出密码的概率. 解:由题意可知,(1)四人均没有成功破译密码的概率为4116(1)381-=.所以密码能被译出的概率为166518181-=. (2)①若每组两人,两组独立翻译,由二人合为一组,该组破译的概率为34, 则密码能被译出的概率为:23151(1)416--=.②若一组三人、一组一人, 三人合为一组,该组破译的概率为45, 则密码能被译出的概率为:41131(1)(1)5315---=.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD ∆为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =.(1)求证:PA ⊥平面PCD ;(2)求直线AD 与平面PAC 所成角的正弦值. (1)证明:取棱PC 的中点N ,连接DN ,由题意可知,DN PC ⊥,又因为平面PAC ⊥平面PCD ,平面PAC ⋂平面PCD PC =, 所以DN ⊥平面PAC ,又PA ⊂平面PAC , 故DN PA ⊥,又PA CD ⊥,CD DN D =,CD ,DN ⊂平面PCD ,则PA ⊥平面PCD ;(2)解:连接AN ,由(2)可知,DN ⊥平面PAC , 则DAN ∠为直线AD 与平面PAC 所成的角,因为PCD ∆为等边三角形,2CD =且N 为PC 的中点,所以DN ,又DN AN ⊥,在Rt AND ∆中,sin DN DAN AD ∠==故直线AD与平面PAC.20.(12分)鱼塘中养了某种鱼,到了收获季节,鱼塘主人为了了解鱼塘中鱼的情况,通过随机撒网的方式捕了200条鱼,逐个称重,发现重量(单位:克)都在[500,1000]之间,这些鱼的重量按照[500,600),[600,700),[700,800),[800,900),[900,1000]分组得到如下频率分布直方图.(Ⅰ)求这200条鱼中,重量不小于700克的鱼的条数;(Ⅱ)求鱼塘中所有鱼重量的平均数的估计值;(Ⅲ)根据这种鱼的市场情况,现有两种销售方案,方案一:不论鱼的大小,统一定价为每100克10元;方案二:重量小于700克的鱼,每100克8元,重量在[700,800)(克)之间的鱼,每100克12元,重量不小于800克的鱼,每100克10元.方案二需要付分拣费:每100条鱼50元请根据收入的估计值,帮该鱼塘主人选择合适的销售方案.注:频率分布直方图中每组数据取区间中点值为代表.解:(Ⅰ)根据频率分布直方图,重量不小于700克的鱼的条数为:200(0.0030.00250.0015)100140⨯++⨯=.(Ⅱ)鱼塘中所有鱼重量的平均数的估计值为:5500.16500.27500.38500.259500.15765⨯+⨯+⨯+⨯+⨯=.(Ⅲ)以这200条鱼的销售收入为参考.若选方案一:销售收入的估计值为7651020015300 100⨯⨯=.若选方案二:由题意,200条鱼中重量在各区间的条数依次为20,40,60,50,30.销售收入减去分拣费的估计值为:55065075085095082084012601050103010015360 100100100100100⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯-=.因为1536015300>,所以应该选方案二.21.(12分)已知a,b,c分别为ABC∆三个内角A,B,C的对边,cos sin0a C Cb c+--=(1)求A;(2)若2a =,ABC ∆b ,c .解:(1)由正弦定理得:cos sin 0a C C b c --=,即sin cos sin sin sin A C A C B C =+sin cos sin sin()sin A C A C A C C ∴=++,cos 1A A -=,1sin(30)2A ∴-︒=.3030A ∴-︒=︒60A ∴=︒;(2)若2a =,ABC ∆的面积1sin 2bc A =4bc ∴=.①再利用余弦定理可得:2222cos a b c bc A =+-⋅22()2()344b c bc bc b c =+--=+-⨯=,4b c ∴+=.② 结合①②求得2b c ==.22.(12分)如图1,在边长为4的正方形ABCD 中,点P 、Q 分别是边AB 、BC 的中点,将APD ∆、CDQ ∆分别沿DP 、DQ 折叠,使A 、C 两点重合于点M ,连BM 、PQ ,得到图2所示几何体.(1)求证:PM DQ ⊥;(2)在线段MD 上是否存在一点F ,使//BM 平面PQF ,如果存在,求FMFD的值,如果不存在,说明理由.(1)证明:由图1可得2MP MQ ==,PQ =,222MP MQ PQ ∴+=,MP MQ ∴⊥,MP MD ⊥,MD MQ M =,MD 、MQ ⊂平面MDQ ,MP ∴⊥平面MDQ ,DQ ⊂平面MDQ ,MP MQ ∴⊥;(2)解:当13MF MD =时,//BM 平面PQF , 理由如下:连BD 交PQ 于点O ,连OF ,由图1可得OB ,BD =,即14BO BD =,因为13MF MD =,所以14FD MD =,所以OD FD BD MD =,所以//BM OF , 因为BM ⊂/平面PQF ,OF ⊂平面PQF ,所以//BM 平面PQF .河南省许昌市2021-2022学年高一下学期期末考试数学试题(文科)一、选择题:本题共12小题,每小题5分,共60分.在每小题给的四个选项中,只有一项是符合题目要求的.1.已知i 为虚数单位,复数z 满足(1)2i z i +=-,则复数z 在复平面所对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限〖解 析〗(1)2i z i +=-,∴2(2)(1)131(1)(1)22i i i z i i i i ---===-++-, ∴复数z 在复平面所对应的点13(,)22-在第四象限.〖答 案〗D2.已知平面向量(3,1)a =,(,2)b x =-,且a b ⊥,则(x = ) A .1B .1-C .23D .23-〖解 析〗(3,1)a =,(,2)b x =-,a b ⊥,∴320a b x ⋅=-=,∴23x =. 〖答 案〗C3.某学校计划从3名男生和4名女生中任选4名参加七一征文比赛,记事件M 为“至少3名女生参加”,则下列事件与事件M 对立的是( ) A .恰有1名女生参加 B .至多有2名男生参加C .至少有2名男生参加D .恰有2名女生参加〖解 析〗至少3名女生的对立面是至多两名女生,总共选4名,也即为至少2名男生.〖答 案〗C4.已知向量a ,b ,且||9a =,||12b =,a 与b 的夹角为4π,则(a b ⋅= )A .36B .C .54D .〖解 析〗因为||9a =,||12b =,a 与b 的夹角为4π,所以||||cos ,912cos 4a b a b a b π⋅=<>=⨯⨯=〖答 案〗D5.已知P 在ABC ∆所在平面内,满足||||||PA PB PC ==,则P 是ABC ∆的( ) A .外心B .内心C .垂心D .重心〖解 析〗||||||PA PB PC ==表示P 到A ,B ,C 三点距离相等,P 为外心. 〖答 案〗A6.正方体的棱长扩大到原来的6倍,则其表面积扩大到原来的( ) A .2倍B .12倍C .18倍D .36倍〖解 析〗设正方体棱长为a ,则其表面积为26a ,故正方体的棱长扩大到原来的6倍,则其表面积为2636a ⨯,扩大到原来的36倍. 〖答 案〗D7.下列四个命题中不正确的是( ) A .平行线段在直观图中仍然平行 B .相等的角在直观图中仍然相等C .直线与平面相交有且只有一个公共点D .垂直于同一个平面的两条直线平行 〖解 析〗逐一考查所给的选项:A .平行线段在直观图中仍然平行,A 说法正确;B .相等的角在直观图中不一定相等,B 说法错误;C .直线与平面相交有且只有一个公共点,C 说法正确;D .由面面垂直的性质可知垂直于同一个平面的两条直线平行,D 说法正确.〖答 案〗B8.某校开展“正心立德,劳动树人”主题教育活动,对参赛的100名学生的劳动作品的得分情况进行统计,并绘制了如图所示的频率分布直方图,图中信息,下列结论错误的是( )A .图中的x 值为0.020B .得分在80分及以上的人数为40C .这组数据平均数的估计值为77D .这组数据第80百分位数的估计值为85〖解 析〗由频率之和为1得:10(0.0050.0350.0300.010)1x ++++=, 解得:0.020x =,A 说法正确;得分在80分及以上的人数为(0.0300.010)1010040+⨯⨯=,B 说法正确;因为10(550.005650.020750.035850.030950.010)77⨯⨯+⨯+⨯+⨯+⨯=,C 说法正确;0.005100.020100.035100.60.8⨯+⨯+⨯=<,0.005100.020100.035100.030100.90.8⨯+⨯+⨯+⨯=>,所以这组数据第80百分位数的估计值落在区间[80,90)内,0.80.626080100.90.63-+⨯=-,故这组数据第80百分位数的估计值不为85,D 说法错误. 〖答 案〗D9.已知a ,b 是两个不共线向量,向量b ta -,1322a b -共线,则实数(t = )A .13-B .13C .34-D .34〖解 析〗由向量b ta -与1322a b -共线,得11322t -=-,解得:13t =.〖答 案〗B10.在ABC ∆中,60B ∠=︒,2AB =,M 是BC 的中点,AM =(AC =) A .B .4C .D .〖解 析〗因为60B ∠=︒,2AB =,M 是BC 的中点,AM =, 所以在ABM ∆中,由余弦定理2222cos AM AB BM AB BM B=+-⋅⋅,可得21124222BM BM =+-⨯⨯⨯,整理可得2280BM BM --=, 解得4BM =,或2-(舍去),所以28BC BM ==,所以由余弦定理可得AC ==.〖答 案〗A11.已知a ,b 是两条不同的直线,α,β,γ是三个不同的平面.给出下列命题: ①若αβ⊥,a αβ=,a b ⊥,则b α⊥或b β⊥;②若//αβ,a αγ=,b βγ=,则//a b ;③若a αβ=,b αγ=,//a b ,则//βγ;④“若αγ⊥,βγ⊥,则αβ⊥”是随机事件;⑤若a ,b 是异面直线,则存在平面α过直线a 且垂直于直线b . 其中正确的命题是( ) A .①③B .②⑤C .③④D .②④〖解 析〗若αβ⊥,a αβ=,a b ⊥,b 与α,β可能垂直也可能不垂直,①错;由面面平行的性质定理知②正确;三棱柱的两个侧面与第三个侧面的交线相互平行,但这两个侧面相交,③错;若αγ⊥,βγ⊥,则α与β可能垂直也可能不垂直,“若αγ⊥,βγ⊥,则αβ⊥”是随机事件,④正确;若存在平面α过直线a 且垂直于直线b ,则a b ⊥,但已知中a ,b 不一定垂直,⑤错误. 〖答 案〗D12.已知对任意平面向量(,)AB x y =,把AB 绕其起点沿逆时针方向旋转θ角得到向量(cos sin ,sin cos )AP x y x y θθθθ=-+,叫做把点B 绕点A 沿逆时针方向旋转θ角得到点P .已知平面内点(1,2)A ,点(2,3)B ,把点B 绕点A 沿顺时针方向旋转116π得到点P ,则点P 的坐标为( )A.33(22--+B.11(22-+C.15(22--D.15(22+〖解 析〗平面内点(1,2)A ,点(2,3)B ,所以(1,1)AB =, 把点B 绕点A 顺时针旋转116π后得到点P , 即把点B 绕点A 沿逆时针方向旋转6π得到点P , 则(cos sin AP x y θθ=-,sin cos )(cos sin66x y ππθθ+=-,1sincos )662ππ+=-,12,设(,)P a b ,则(1AP a =-,2)(b -=12,12,解得12a =+,52b =+. 所以点P的坐标为12+,52+. 〖答 案〗D二、填空题:本大题共4小题,每小题5分,共20分. 13.2(23)(23)(1)i i i +-+= .〖解 析〗2(23)(23)(1)(49)(2)26i i i i i +-+=+⨯=. 〖答 案〗26i14.已知向量(2,5)a =,(,4)b λ=,且//a b ,则λ= . 〖解 析〗因为(2,5)a =,(,4)b λ=,且//a b , 所以245λ⨯=,则85λ=. 〖答 案〗8515.在ABC ∆中,已知6b =,45A =︒,75C =︒,则a = . 〖解 析〗因为6b =,45A =︒,75C =︒,所以18060B A C =︒--=︒,由正弦定理sin sin a bA B=,可得6sin sin b A a B ⋅=== 〖答案〗16.19世纪,美国天文学家西蒙⋅纽康在翻阅对数表时,偶然发现表中以1开头的数出现的频率更高.约半个世纪后,物理学家本福特又重新发现这个现象,从实际生活得出的大量数据中,以1开头的数出现的频率约为总数的三成,接近期望值19的3倍,并提出本福特定律,即在大量b 进制随机数据中,以n 开头的数出现的概率为1()log ()b b n P n n+=,如斐波那契数、阶乘数、素数等都比较符合该定律.后来常有数学爱好者用此定律来检验某些经济数据、选举数据等大数据的真实性.根据本福特定律,若1012()3ni P i =∑,则n 的最大值为 . 〖解 析〗由1()log ()b b n P n n +=可得,10101()log ()(1)i P i lg i lgi i+==+-, 所以101()(1)ni P i lg n ==+∑,又1012()3ni P i =∑,所以,2(1)3lg n +,即3(1)100n +, 所以,1n =,2,3, 则n 的最大值为3. 〖答 案〗3三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤. 17.(10分)求证:夹在两个平行平面间的平行线段相等. (1)画图,并用图中字母写出已知、求证; (2)写出证明过程.(1)解:已知:如图,//αβ,且//AB CD , 且A α∈,C α∈,B β∈,D β∈. 求证:AB CD =.(2)证明:过平行直线AB ,CD 作平面γ,与平面α和β分别相交于AC 和BD .//αβ,//BD AC ∴.又//A CD ∴,∴四边形ABDC 是平行四边形.AB CD ∴=.18.(12分)某项密码破译工作需甲、乙、丙、丁四人完成,已知每人独立译出密码的概率为13,若二人合为一组,则该组破译的概率为34,若三人合为一组,则该组破译的概率为45. (1)若四人独立翻译,求破译出密码的概率;(2)若将四人分成两组,两组独立破译密码,求破译出密码的概率. 解:由题意可知,(1)四人均没有成功破译密码的概率为4116(1)381-=.所以密码能被译出的概率为166518181-=. (2)①若每组两人,两组独立翻译, 由二人合为一组,该组破译的概率为34, 则密码能被译出的概率为:23151(1)416--=.②若一组三人、一组一人, 三人合为一组,该组破译的概率为45, 则密码能被译出的概率为:41131(1)(1)5315---=.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,PCD ∆为等边三角形,平面PAC ⊥平面PCD ,PA CD ⊥,2CD =,3AD =.(1)求证:PA ⊥平面PCD ;(2)求直线AD 与平面PAC 所成角的正弦值. (1)证明:取棱PC 的中点N ,连接DN ,由题意可知,DN PC ⊥,又因为平面PAC ⊥平面PCD ,平面PAC ⋂平面PCD PC =, 所以DN ⊥平面PAC ,又PA ⊂平面PAC , 故DN PA ⊥,又PA CD ⊥,CD DN D =,CD ,DN ⊂平面PCD ,则PA ⊥平面PCD ;(2)解:连接AN ,由(2)可知,DN ⊥平面PAC , 则DAN ∠为直线AD 与平面PAC 所成的角,因为PCD ∆为等边三角形,2CD =且N 为PC 的中点,所以DN ,又DN AN ⊥,在Rt AND ∆中,sin DN DAN AD ∠==故直线AD 与平面PAC . 20.(12分)鱼塘中养了某种鱼,到了收获季节,鱼塘主人为了了解鱼塘中鱼的情况,通过随机撒网的方式捕了200条鱼,逐个称重,发现重量(单位:克)都在[500,1000]之间,这些鱼的重量按照[500,600),[600,700),[700,800),[800,900),[900,1000]分组得到如下频率分布直方图.(Ⅰ)求这200条鱼中,重量不小于700克的鱼的条数; (Ⅱ)求鱼塘中所有鱼重量的平均数的估计值;(Ⅲ)根据这种鱼的市场情况,现有两种销售方案,方案一:不论鱼的大小,统一定价为每100克10元;方案二:重量小于700克的鱼,每100克8元,重量在[700,800)(克)之间的鱼,每100克12元,重量不小于800克的鱼,每100克10元.方案二需要付分拣费:每100条鱼50元请根据收入的估计值,帮该鱼塘主人选择合适的销售方案. 注:频率分布直方图中每组数据取区间中点值为代表.解:(Ⅰ)根据频率分布直方图,重量不小于700克的鱼的条数为: 200(0.0030.00250.0015)100140⨯++⨯=.(Ⅱ)鱼塘中所有鱼重量的平均数的估计值为:5500.16500.27500.38500.259500.15765⨯+⨯+⨯+⨯+⨯=.(Ⅲ)以这200条鱼的销售收入为参考. 若选方案一:销售收入的估计值为7651020015300100⨯⨯=. 若选方案二:由题意,200条鱼中重量在各区间的条数依次为20,40,60,50,30. 销售收入减去分拣费的估计值为:55065075085095082084012601050103010015360100100100100100⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯-=. 因为1536015300>,所以应该选方案二.21.(12分)已知a ,b ,c 分别为ABC ∆三个内角A ,B ,C 的对边,cos sin 0a C C b c +--=(1)求A ;(2)若2a =,ABC ∆b ,c .解:(1)由正弦定理得:cos sin 0a C C b c --=,即sin cos sin sin sin A C A C B C =+sin cos sin sin()sin A C A C A C C ∴=++,cos 1A A -=,1sin(30)2A ∴-︒=.3030A ∴-︒=︒60A ∴=︒;(2)若2a =,ABC ∆的面积1sin 2bc A =4bc ∴=.①再利用余弦定理可得:2222cos a b c bc A =+-⋅22()2()344b c bc bc b c =+--=+-⨯=,4b c ∴+=.② 结合①②求得2b c ==.22.(12分)如图1,在边长为4的正方形ABCD 中,点P 、Q 分别是边AB 、BC 的中点,将APD ∆、CDQ ∆分别沿DP 、DQ 折叠,使A 、C 两点重合于点M ,连BM 、PQ ,得到图2所示几何体.(1)求证:PM DQ ⊥;(2)在线段MD 上是否存在一点F ,使//BM 平面PQF ,如果存在,求FMFD的值,如果不存在,说明理由.(1)证明:由图1可得2MP MQ ==,PQ =,222MP MQ PQ ∴+=,MP MQ ∴⊥,MP MD ⊥,MDMQ M =,MD 、MQ ⊂平面MDQ ,MP ∴⊥平面MDQ ,DQ⊂平面MDQ,MP MQ∴⊥;(2)解:当13MFMD=时,//BM平面PQF,理由如下:连BD交PQ于点O,连OF,由图1可得OB,BD=,即14BO BD=,因为13MFMD=,所以14FDMD=,所以OD FDBD MD=,所以//BM OF,因为BM⊂/平面PQF,OF⊂平面PQF,所以//BM平面PQF.。
河南省许昌市高一下学期数学期末考试试卷
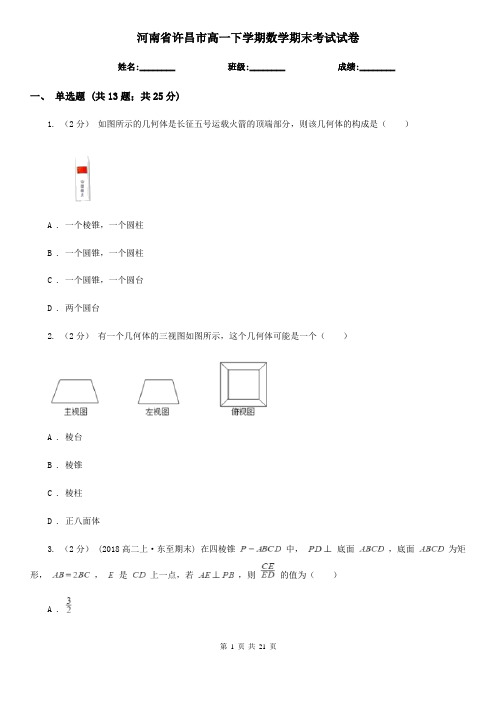
河南省许昌市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共13题;共25分)1. (2分)如图所示的几何体是长征五号运载火箭的顶端部分,则该几何体的构成是()A . 一个棱锥,一个圆柱B . 一个圆锥,一个圆柱C . 一个圆锥,一个圆台D . 两个圆台2. (2分)有一个几何体的三视图如图所示,这个几何体可能是一个()A . 棱台B . 棱锥C . 棱柱D . 正八面体3. (2分) (2018高二上·东至期末) 在四棱锥中,底面,底面为矩形,,是上一点,若,则的值为()A .B .C .D . 44. (2分)对于使成立的所有常数M中,我们把M的最小值1叫做-x2+2x的上确界,若,且a+b=1,则的上确界为()A .B .C .D . -45. (2分)已知M={x|x2-2x-3>0},N={x|x2+ax+b≤0},若M∪N=R,M∩N=(3,4],则a+b=()A . 7B . -1C . 1D . -76. (2分)(2019·云南模拟) 在等比数列中,若,,成等差数列,则数列的公比为()A . 0或1或-2B . 1或2C . 1或-2D . -27. (2分) (2019高一下·永安月考) 如图,是水平放置的的直观图,则的面积为()A . 6B .C .D . 128. (2分)如图是某几何体的三视图,其中正视图是腰长为2的等腰三角形,俯视图是半径为1的半圆,则该几何体的体积是()A .B .C .D .9. (2分) (2018高二上·万州期中) 棱长分别为2、、的长方体的外接球的表面积为()A .B .C .D .10. (2分) (2019高二上·宜昌月考) 如图,在四面体ABCD中,已知那么D在面ABC 内的射影H必在()A . 直线AB上B . 直线BC上C . 直线AC上D . 内部11. (2分)已知点E,F,G分别是正方体ABCD-A1B1C1D1的棱AA1 , CC1 , DD1的中点,点M,N,Q,P 分别在线段DF,AG,BE,C1B1上.以M,N,Q,P为顶点的三棱锥P-MNQ的俯视图不可能是()A .B .C .D .12. (2分) (2018高一下·鹤岗期末) 三棱锥的四个顶点都在体积为的球的表面上,平面所在的小圆面积为,则该三棱锥的高的最大值是()A . 7B . 7.5C . 8D . 913. (1分)(2020·吉林模拟) 如图,在五面体ABCDEF中, // ,,,四边形为平行四边形,平面,,则直线AB到平面EFCD距离为________.二、填空题 (共3题;共3分)14. (1分) (2020高三上·青浦期末) 直线和直线的夹角大小是________15. (1分) (2019高一下·淮安期末) 一个长方体的三个面的面积分别是,,,则这个长方体的体积为________.16. (1分) (2019高三上·大庆期中) 如图,AB为圆O的直径,点C在圆周上异于点A, ,直线PA垂直于圆O所在的平面,点M是线段PB的中点有以下四个命题:① ∥平面;② ∥平面;③ 平面;④平面平面.其中正确的命题的序号是________.三、解答题 (共6题;共55分)17. (10分) (2019高一下·宁波期末) 如图,在正方体中,M是的中点,在上,且 .(1)求证:平面;(2)在线段上存在一点,,若平面,求实数的值.18. (10分) (2018高三上·广东月考) 已知是一个公差大于的等差数列, 且满足.(1)求数列的通项公式;(2)若数列和数列满足等式 ,求数列的前项和 .19. (10分) (2016高二下·温州期中) 已知数列{an}是公差不为零的等差数列,a1=1,且a2 , a4 , a8成等比数列.(1)求数列{an}的通项公式;(2)设数列{bn}满足:a1b1+a2b2+a3b3+…+anbn=2n+1 ,n∈N* ,令cn= ,n∈N* ,求数列{cncn+1}的前n项和Sn .20. (5分) (2017高二上·安平期末) 如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= .(Ⅰ)证明:AC⊥平面BCDE;(Ⅱ)求直线AE与平面ABC所成的角的正切值.21. (10分)(2017·蔡甸模拟) 如图,四棱锥P﹣ABCD中,平面PAC⊥底面ABCD,BC=CD= AC=2,∠ACB=∠ACD=.(1)证明:AP⊥BD;(2)若AP= ,AP与BC所成角的余弦值为,求二面角A﹣BP﹣C的余弦值.22. (10分)(2020·泰州模拟) 如图,在三棱锥中,平面,,点D、E、F分別是、、的中点.(1)求证:平面;(2)求证:平面平面.参考答案一、单选题 (共13题;共25分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:答案:13-1、考点:解析:二、填空题 (共3题;共3分)答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:三、解答题 (共6题;共55分)答案:17-1、答案:17-2、考点:解析:答案:18-1、答案:18-2、考点:解析:答案:19-1、答案:19-2、考点:解析:答案:20-1、考点:解析:答案:21-1、答案:21-2、考点:。
河南省许昌市高一下学期数学期末考试试卷

河南省许昌市高一下学期数学期末考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)如图,平行四边形ABCD中,,点M在AB边上,且,则等于()A .B .C . -1D . 12. (2分)等于()A .B .C .D .3. (2分) (2018高二上·遂宁期末) 从孝感地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是()A . 简单的随机抽样B . 按性别分层抽样C . 按学段分层抽样D . 系统抽样4. (2分)具有A、B、C三种性质的总体,其容量为63,将A、B、C三种性质的个体按1∶2∶4的比例进行分层抽样调查,如果抽取的样本容量为21,则A、B、C三种元素分别抽取的个数是()A . 12、6、3B . 12、3、6C . 3、6、12D . 3、12、65. (2分)已知,则()A . M<NB . M>NC . M=ND . 以上都有可能6. (2分)(2016·河北模拟) 如图是一个程序框图,则输出的S的值是()A . 0B . 1C . 2D . 47. (2分)(2018·全国Ⅲ卷文) 若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为()A . 0.3B . 0.4C . 0.6D . 0.78. (2分) (2016高一下·三原期中) ABCD为长方形,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为()A .B .C .D .9. (2分)已知变量与正相关,且由观测数据算得样本平均数,则由该观测数据算得的线性回归方程可能是()A .B .C .D .10. (2分)某厂对一批元件进行抽样检测.经统计,这批元件的长度数据 (单位:mm)全部介于93至105之间.将长度数据以2为组距分成以下6组:[93,95),[95,97),[97,99),[99,101),[101,103),[103,105),得到如图所示的频率分布直方图.若长度在内的元件为合格品,根据频率分布直方图,估计这批产品的合格率是()A . 80%B . 90%C . 20%D . 85.5%11. (2分)已知﹣<α<0,sinα+cosα= ,则的值为()A .B .C .D .12. (2分) (2016高一下·福建期中) 函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数的解析式可以是()A . f(x)=2cos(3x+ )B . f(x)=2sin()C . f(x)=2sin(3x﹣)D . f(x)=2sin(3x﹣)或f(x)=2sin()二、填空题 (共4题;共4分)13. (1分) (2016高二下·大庆期末) 已知平面向量,且,则=________.14. (1分)(2013·新课标Ⅱ卷理) 从n个正整数1,2,…,n中任意取出两个不同的数,若取出的两数之和等于5的概率为,则n=________.15. (1分)若,则 =________.16. (1分) (2019高一下·上海月考) 已知,则 ________.三、解答题 (共6题;共55分)17. (10分) (2016高一下·郑州期末) 已知:、、是同一平面内的三个向量,其中 =(1,2)(1)若| |=2 ,且∥ ,求的坐标;(2)若| |= ,且 +2 与2 ﹣垂直,求与的夹角θ.18. (5分)已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)的图象经过点(0,1),且其相邻两对称轴之间的距离为π.(1)求函数f(x)的解析式;(2)设若sinα+f(α)=,α∈(0,π),求的值.19. (10分) (2017高二下·都匀开学考) 某种商品价格与该商品日需求量之间的几组对照数据如表:价格x(元/kg)1015202530日需求量y(kg)1110865参考公式:线性回归方程,其中.(1)求y关于x的线性回归方程;(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?20. (15分) (2018高一下·临沂期末) 某车间将名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的茎叶图如图,已知两组技工在单位时间内加工的合格零件的平均数都为 .(1)求,的值;(2)求甲、乙两组技工在单位时间内加工的合格零件的方差和,并由此分析两组技工的加工水平;(3)质检部门从该车间甲、乙两组技工中各随机抽取一名,对其加工的零件进行检测,若两人加工的合格零件个数之和大于,则称该车间“质量合格”,求该车间“质量合格”的概率.附:方差,其中为数据的平均数21. (10分) (2016高一下·珠海期末) 在区间[﹣1,1]上任取两个数a,b,在下列条件时,分别求不等式x2+2a x+b2≥0恒成立时的概率:(1)当a,b均为整数时;(2)当a,b均为实数时.22. (5分)某地农业监测部门统计发现:该地区近几年的生猪收购价格每四个月会重复出现,但生猪养殖成本逐月递增.下表是今年前四个月的统计情况:现打算从以下两个函数模型:①y=Asin(ωx+φ)+B,(A>0,ω>0,﹣π<φ<π),②y=log2(x+a)+b中选择适当的函数模型,分别来拟合今年生猪收购价格(元/斤)与相应月份之间的函数关系、养殖成本(元/斤)与相应月份之间的函数关系.(1)请你选择适当的函数模型,分别求出这两个函数解析式;(2)按照你选定的函数模型,帮助该部门分析一下,今年该地区生猪养殖户在接下来的月份里有没有可能亏损?参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分) 17-1、17-2、18-1、19-1、19-2、20-1、20-2、20-3、21、答案:略22-1、。
2010-2023历年河南省许昌市六校联考高一下学期期末考试数学卷

2010-2023历年河南省许昌市六校联考高一下学期期末考试数学卷第1卷一.参考题库(共10题)1.已知函数求:(1)函数的定义域和单调区间;(2)判断函数的奇偶性;(3)判断函数的周期性,如果是周期函数,求出它的最小正周期。
2.下面给出的赋值语句中正确的是()A.3="A"B.M=-MC.B="A=2"D.3.计算;4.当时,如果直线的倾斜角满足关系式,则此直线方程的斜率为;5.设(1)写出函数的最小正周期;(2)试用“五点法”画出函数在一个周期内的简图;(3)若时,函数的最小值为2,试求出函数的最大值。
6.若函数,则= ;7.已知Cos,则Cos的值为()A.B.C.D.8.已知函数的最大值是1,其图象经过点。
(1)求函数的解析式;(2)已知的值。
9.下列命题中正确的是()A.若;B.若,;C.对于任意向量;D.对于任意向量10.若正方形ABCD的边长为1等于()A.0B.C.D.3第1卷参考答案一.参考题库1.参考答案:(1)依题意得所以函数的定义域为;由复合函数的单调性知,函数的单调增区间为单调减区间为 (6)(2)因为函数的定义域不关于原点对称所以函数既不是奇函数,也不是偶函数; (8)(3) (11)函数的最小正周期。
(12)2.参考答案:B3.参考答案:4.参考答案:5.参考答案:依题意得(1)所以最小正周期为 (5)(2)图略 (8)(3)由(1)得 (12)6.参考答案:27.参考答案:D8.参考答案:依题意得A=1(1)所以将点代入得又所以 (6)(2)由(1)得。
(12)9.参考答案:D10.参考答案:C。
河南省许昌市高一下学期数学期末考试试卷

河南省许昌市高一下学期数学期末考试试卷姓名:________班级:________成绩:________一、 单选题 (共 12 题;共 24 分)1. (2 分) (2017·泰安模拟) 已知集合 A={x|x2+2x﹣3<0},B={x|0<x<3},则 A∩B=( )A . (0,1)B . (0,3)C . (﹣1,1)D . (﹣1,3)2. (2 分) sin(﹣ )=( )A. B.C.D.3. (2 分) (2016·连江模拟) 设 A.0 B.1 C.2 D.3 4. (2 分) 函数 A.则值为( )的单调增区间为( )第 1 页 共 12 页B.C.D.5. (2 分) 已知,则等于( )A. B.7C. D . -76. (2 分) (2018 高三上·西安模拟) 在平行四边形中,,且,若将其沿 折起使平面平面,则三棱锥的外接球的表面积为( )A.B.C.D.7. (2 分) (2019 高二上·上海期中) 已知两个不相等的非零向量 与 ,两组向量 , , , , 和 , , , , 均有 2 个 和 3 个 按照某种顺序排成一列所构成,记,且表示 所有可能取值中的最小值,有以下结论:①有 5 个不同的值;②若,则与 无关;③ 若 ∥ ,则与 无关;④ 若,则;⑤若,且,则 与 的夹角为 ;正确的结论的序号是( )A . ①②④B . ②④第 2 页 共 12 页C . ②③D . ①⑤8. (2 分) 在△ABC 中,若 2cosBsinA=sinC,则△ABC 的形状一定是( )A . 等腰直角三角形B . 直角三角形C . 等腰三角形D . 等边三角形9. (2 分) (2017 高二下·深圳月考) 已知,,且,则 的最小值为( )A. B.C. D.10. (2 分) .已知 M 是△ABC 内的一点,且面积分别,则的最小值是A.9B . 18C . 16D . 20, (), 若△MBC, △MCA 和△MAB 的11. (2 分) (2018 高二上·海口期中) 与向量平行的一个向量的坐标是( )A.第 3 页 共 12 页B.C.D.12. (2 分) 如果, 那么A.2B.3C.4D.5二、 填空题 (共 4 题;共 4 分)的最小值是( )13. (1 分) (2017·深圳模拟)=________.14. (1 分) (2017 高一下·宿州期末) 如果实数 x,y 满足约束条件 的最小值为________.,那么目标函数 z=2x﹣y15. (1 分)(2019 高三上·宁德月考) 在边长为 2 的菱形中,,以折起,使点 到达点 的位置,且点 在面内的正投影为的重心 ,则的球心 到点 的距离为________.为折痕将 的外接球16. (1 分) 若锐角△ABC 的面积为 10 , 且 AB=5,AC=8,则 BC 等于________三、 解答题 (共 6 题;共 55 分)17. (10 分) (2019 高一下·绵阳月考)中,分别是角所对的边且.(1) 求 (2) 若的值; ,当角 最大时,求的面积.第 4 页 共 12 页18. (5 分) (2017·自贡模拟) 在△ABC 中,A,B,C 的对边分别为 a、b、c,为.(Ⅰ)求 c 的值;(Ⅱ)求 cos(B﹣C)的值.19. (10 分) (2017 高二上·汕头月考) 已知数列 的前 项和,.(1) 求 的通项公式;,△ABC 的面积(2) 设,数列 的前 项和为 .20. (5 分) 已知 A、B、C、D 是函数 y=sin(ωx+φ)(ω>0,0<φ< )一个周期内的图象上的四个点, 如图所示,A(﹣ , 0),B 为 y 轴的点,C 为图象上的最低点,E 为该函数图象的一个对称中心,B 与 D 关于点 E 对称, 在 x 轴方向上的投影为 .求函数 f(x)的解析式及单调递减区间;21. (10 分) (2018·吉林模拟) 四棱锥 等边三角形中,底面为菱形,,为(1) 求证:;第 5 页 共 12 页(2) 若,求二面角的余弦值.22. (15 分) (2019 高二下·常州期中) 已知 (1) 求实数 的值;是奇函数.(2) 求函数在上的值域;(3) 令,求不等式的解集.第 6 页 共 12 页一、 单选题 (共 12 题;共 24 分)1-1、 2-1、 3-1、 4-1、 5-1、 6-1、 7-1、 8-1、 9-1、 10-1、 11-1、 12-1、二、 填空题 (共 4 题;共 4 分)13-1、 14-1、参考答案15-1、第 7 页 共 12 页16-1、三、 解答题 (共 6 题;共 55 分)17-1、17-2、18-1、第 8 页 共 12 页19-1、19-2、20-1、第 9 页 共 12 页21-1、第 10 页 共 12 页21-2、22-1、22-2、22-3、。
河南省许昌市高一下学期期末数学试卷

河南省许昌市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共17分)1. (1分) (2019高一上·儋州期中) 函数的定义域为________.2. (1分)长方形ABCD中,AB=2,BC=1,O为AB的中点,在长方形ABCD内随机取一点,取到的点到O的距离大于1的概率为________3. (1分) (2016高三上·六合期中) 执行如图所示的伪代码,输出的结果是________.4. (2分)某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为________,众数为________.5. (2分)已知=(sinx,m+cosx),=(cosx,-m+cosx),且f(x)=•,当x[-,]时,f(x)的最小值是﹣4,求此时函数f(x)的最大值________ ,此时x=________6. (1分) (2016高一下·滑县期末) 在1,3,5,7,9中任取2个不同的数,则这2个数的和大于9的概率为________.7. (1分) (2016高三上·辽宁期中) 已知α、β是三次函数f(x)= x3+ ax2+2bx(a,b∈R)的两个极值点,且α∈(0,1),β∈(1,2),则的取值范围是________.8. (1分)已知函数f(x)=asinx﹣(a∈R),若函数f(x)在(0,π)的零点个数为2个,则当x∈[0, ],f(x)的最大值为________.9. (1分) (2016高二上·上海期中) 数列{an}中,a3=2,a7=1,又数列{ }是等差数列,则a1=________10. (1分) (2016高二上·黄骅期中) 已知抛物线C:x2=4y的焦点为F,过点F且斜率为1的直线与抛物线相交于M、N两点,设直线l是抛物线C的切线,且l∥MN,P为l上一点,则的最小值为________.11. (2分)函数f(x)=sin(x+)+cos(x﹣),x∈[0,π],当x=________ 时,f(x)取到最大值为________12. (1分)(2017·南开模拟) 若a>0,b>0,且2a+b=1,则2 ﹣4a2﹣b2的最大值是________.13. (1分)(2017·莱芜模拟) 若定义域为R的偶函数y=f(x)满足f(x+2)=﹣f(x),且当x∈[0,2]时,f(x)=2﹣x2 ,则方程f(x)=sin|x|在[﹣3π,3π]内根的个数是________.14. (1分) (2017高一下·安平期末) 若数列{an}满足,则a2017=________.二、解答题 (共6题;共55分)15. (10分) (2016高一上·菏泽期中) 已知集合A={x|﹣4≤x﹣6≤0},集合B={x|2x﹣6≥3﹣x}.(1)求∁R(A∩B);(2)若C={x|x≤a},且A∩C=A,求实数a的取值范围.16. (10分) (2017高三上·唐山期末) 在中,角、、所对的边分别为、、 .已知 .(1)求;(2)若,求 .17. (5分)已知数列{an},{bn}(bn≠0,n∈N*)满足bn+1=,且a1=b1=1.(1)令cn=,求数列{cn}的通项公式;(2)若数列{bn}为各项均为正数的等比数列,且b32=9b2b6 ,求数列{an}的前n项和.18. (5分)(2017高一下·瓦房店期末) 的内角的对边分别为,已知.(Ⅰ)求角的大小;(Ⅱ)若,求的最大值.19. (10分) (2017高一下·徐州期末) 某单位拟建一个扇环形状的花坛(如图所示),按设计要求扇环的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).(1)求θ关于x的函数关系式;(2)已知对花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用之比为y,求y关于x的函数关系式,并求出y的最大值.20. (15分) (2017高一下·彭州期中) 已知数列{an}的首项a1= ,an+1= ,n=1,2,…(1)求证:{ ﹣1}是等比数列,并求出{an}的通项公式;(2)证明:对任意的x>0,an≥ ﹣(﹣x),n=1,2,…(3)证明:n﹣≥a1+a2+…+an>.参考答案一、填空题 (共14题;共17分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共55分)15-1、15-2、16-1、16-2、17-1、18-1、19-1、19-2、20-1、20-2、20-3、。
河南省许昌市2023-2024学年高一下学期7月期末教学质量检测数学试题(含答案)

许昌市2023-2024学年高一下学期7月期末教学质量检测数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、单项选择题:本题共8小题,每小题5分,共40分.在每个小题给出的四个选项中,只有一项符合题目要求.1.复数52i-+的共轭复数是( )A .2i +B .2i -+C .2i --D .2i -2.在ABC △中,AB c = ,AC b = ,若点D 满足2BD DC = ,以b ,c 作为基底,则AD 等于()A .2133b c + B .5233c b - C .2133b c - D .1233b c + 3.有一组样本数据如下:56,62,63,63,65,67,68,69,71,74,76,76,77,78,79,79,80,85,87,88,95,98,则其25%分位数与75%分位数的和为( )A .144B .145C .146D .1474.设l ,m 是两条不同的直线,α,β是两个不同的平面,则下面命题中正确的是()A .若l m ⊥,m α∥,则l α⊥B .若l α∥,m αβ= ,⊂,则l m ∥C .若l m ⊥,m α⊂,则l α⊥D .若l β⊥,m β⊥,m α⊥,则l α⊥5.若样本11x +,21x +,31x +,1n x +的平均数为10,方差为2,则对于样本122x +,222x +,32x +,…,22n x +,下列结论正确的是( )A .平均数为20,方差为4B .平均数为11,方差为4C .平均数为20,方差为8D .平均数为21,方差为86.小明与小华两人玩游戏,则下列游戏不公平的是()A .抛掷一枚骰子,向上的点数为奇数,小明获胜,向上的点数为偶数,小华获胜B .同时抛掷两枚硬币,恰有一枚正面向上,小明获胜,两枚都正面向上,小华获胜C .从一副不含大小王的扑克牌中抽一张,扑克牌是红色,小明获胜,扑克牌是黑色,小华获胜D .小明、小华两人各写一个数字6或8,如果两人写的数字相同,小明获胜,否则小华获胜7.农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角泰”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.小明在和家人一起包粽子时,想将一丸子(近似为球)包入其中,如图,将粽叶展开后得到由六个边长为9的等边三角形所构成的平行四边形,将粽叶沿虚线折起来,可以得到如图所示的粽子形状的六面体,则放入丸子的体积最大值为( ).A .B .C .D .8.有6个相同的球,分别标有数字1,2,3,4,5,6,从中有放回地随机取两次,每次取1个球.甲表示事件“第一次取出的球的数字是1”,乙表示事件“第二次取出的球的数字是2”,丙表示事件“两次取出的球的数字之和是8”,丁表示事件“两次取出的球的数字之和是7”,则()A .甲与丙相互独立B .乙与丙相互独立C .甲与丁相互独立D .丙与丁相互独立二、多项选择题:本题共3小题,每小题6分,共18分.在每个小题给出的四个选项中,有多项符合题目要求.全部选对得6分,部分选对得部分分,有选错的得0分.9.下列命题中错误的是( )A .若x 是实数,则x 可能不是复数B .若z 是虚数,则z 不是实数C .一个复数为纯虚数的充要条件是这个复数的实部等于零D .1-没有平方根10.已知向量)a =,()cos ,sin b αα= ,π0,2α⎡⎫∈⎪⎢⎣⎭,则下列结论正确的有( )A .1b = B .若a b ∥,则π3α=C .a b ⋅ 的最大值为2D .a b - 的最小值为211.已知正方体1111ABCD A B C D -的棱长为2,P 为底面ABCD 内(包括边界)的动点,则下列结论正确的是( )A .三棱锥111BCD P -的体积为定值B .存在点P ,使得1D P ∥平面11A BCC .若11D P B P ⊥,则P 点在正方形底面ABCD 内的运动轨迹长为D .若点P 是AB 的中点,点Q 是AB 的中点,经过1D ,P ,Q 三点的正方体的截面周长为+三、填空题:本题共3小题,每小题5分,共15分.12.正四棱台上、下底面的边长分别为2,4,且侧面积等于两底面面积之和,则该棱台的体积是______.13.已知()1,2a = ,()2,2b =- ,则a 在b 方向上的投影向量坐标为______.14.在三棱锥P ABC -中,若AB BC ⊥,3AB =,6BC =,且PB =,PA =,PC =,Q 为底面ABC △内部及边界上的动点,则PQ 与底面ABC 所成角的正弦值的取值范围为______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知4a = ,8b = ,a 与b 的夹角是120︒.(1)求a b ⋅ 的值及2a b - 的值;(2)当k 为何值时,()()2a b ka b +⊥- ?16.(15分)在一个文艺比赛中,10名专业人士和10名观众代表各组成一个评委小组,给参赛选手打分,下面是两组评委对同一名选手的打分:小组A 45 48 46 52 47 49 55 42 51 45小组B 55 36 70 66 75 49 68 42 62 47(1)如果选择方差度量每一组评委打分相似性的量,计算每组评委打分的方差;(2)你能据此判断小组A 和小组B 中哪一个更像是由专业人士组成的吗?17.(15分)已知a ,b ,c 分别为ABC △三个内角A ,B ,C 的对边,且cos sin 0a C C b c +--=.(1)求A ;(2)若2a =,求ABC △面积的取值范围.18.(17分)某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在[]100,150,[]150,200,[]200,250,[]250,300,[]300,350,[]350,400(单位:克)中,经统计得频率分布直方图如图所示.(1)根据频率分布直方图估计这组数据的中位数;(2)现按分层随机抽样的方法从质量在[]250,300,[]300,350内的芒果中随机抽取6个,再从这6个中随机抽取3个,求这3个芒果中质量至少有一个在[]300,350内的概率;(3)若该种植园中还未摘下的芒果大约有10000个,以各组数据的中间数代表这组数据的平均值,用样本估计总体.某经销商来收购未摘芒果,提出如下两种收购方案:A :所有芒果以10元/千克收购;B :对质量低于250克的芒果以2元/个收购,高于或等于250克的芒果以3元/个收购.通过计算确定该种植园选择哪种方案获利更多?19.(17分)如图,三棱柱111ABC A B C -中,ABC △是正三角形,1A C BC ⊥,1A C BC =,平面11AA C C ⊥平面ABC ,E 、F 分别为11A C ,11B C 的中点.(1)证明:1A C ⊥平面ABC ;(2)若P 为底面ABC 内(包括边界)动点,1A P ∥平面EFC ,且P 的轨迹长度为l ,求三棱柱111ABC A B C -的体积;(3)在(2)的条件下,求二面角1A AB C --的正切值.高一数学(答案与解析)一、单选:1-4.BADD 5-8.CBAC二、多选:9.ACD 10.AC 11.ABC三、填空题:12.1129;13.11,22⎛⎫- ⎪⎝⎭;14.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)【解】(1)1cos ,48162a b a b a b ⎛⎫⋅=⋅=⨯⨯-=- ⎪⎝⎭,2a b -==== ;(2)因为()()2a b ka b +⊥- ,所以()()()2222210a b ka b ka b k a b +⋅-=-+-⋅= ,整理得()()1612821160k k -+--=,解得7k =-.即当7k =-时,()()2a b ka b +⊥- .16.(15分)【解】(1)454846524749554251454810A x +++++++++== ,553670667549684262475710B x +++++++++== ,()()()()222221454848484648454813.410A S ⎡⎤=-+-+-++-=⎣⎦ ,()()()()2222215557365770574757155.410B S ⎡⎤=-+-+-++-=⎣⎦ ;(2)由于专业人士给分更符合专业规则,相似程度更高由(1)可知213.4A S =,2155.4B S =,因而13.4155.4<,根据方差越大数据波动越大,因此A 组更像是由专业人士组成的.17.(15分)【解】(1)由cos sin 0a C C b c --=及正弦定理得:sin cos sin sin sin 0A C A C B C +--=,即()sin cos sin sin sin 0A C A C A C C +-+-=,sin cos sin sin cos cos sin sin 0A C A C A C A C C ---=,sin cos sin sin 0A C A C C --=,因为()0,πC ∈,因此sin 0C >,cos 1A A -=,即π1sin 62A ⎛⎫-= ⎪⎝⎭,得π2π3A k =+或()π2π,A k k Z =+∈,又因为()0,πA ∈,所以π3A =.(2)由正弦定理得:2πsin sin sin sin 3a b c A B C ====所以b B =,c C =,所以1πsin sin sin 23ABC S bc A B C B B ⎛⎫====+ ⎪⎝⎭△π1sin 262B ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦,因为π3A =,所以2π0,3B ⎛⎫∈ ⎪⎝⎭,因此ππ7π2666B -<-<,1πsin 2126B ⎛⎫-<-≤ ⎪⎝⎭,所以(ABC S ∈△.因此:ABC △面积的取值范围是:(.18.(17分)【解】设中位数为x ,由频率分布直方图可得:()0.352500.0080.5x +-⨯=,解得:268.75x =.这组数据的中位数是268.75.(2)抽取的6个芒果中,质量在[)250,300和[)300,350内的分别有4个和2个.设质量在[)250,300内的4个芒果分别为A ,B ,C ,D ,质量在[)300,350内的2个芒果分别为a ,b .从这6个芒果中选出3个,样本空间为:()()()()()()()()(){(),,,,,,,,,,,,,,,,,,,,,,,,,,,,,,A B C A B D A B a A B b A C D A C a A C b A D a A D b A a b Ω=()()()()()()()()()()},,,,,,,,,,,,,,,,,,,,,,,,,,,,,B C D B C a B C b B D a B D b B a b C D a C D b C a b D a b ,()Ω20n =,设“至少有一个在[)300,350内”为事件M ,则()()()()()()()()(){,,,,,,,,,,,,,,,,,,,,,,,,,,,M A B a A B b A C a A C b A D a A D b B C a B C b B D a =()()()()()()()},,,,,,,,,,,,,,,,,,,,B D b C D a C D b A a b B a b C a b D a b ,()16n M =,因此()()()164205n P M n M Ω===,所以从6个芒果中随机抽取3个,至少有一个在[)300,350内的概率为45.(3)A 方案可获利:()1250.0021750.0022250.0032750.0083250.0043750.001⨯+⨯+⨯+⨯+⨯+⨯5010000100.00125750⨯⨯⨯⨯=(元).B 方案可获利:()()0.0020.0020.003501000020.0080.0040.0015010000326500++⨯⨯⨯+++⨯⨯⨯=(元)由于2575026500<,因此该种植园选择B 方案获利更多.19.(17分)【解】(1)取AC 的中点D ,连接BD .因为ABC △是等边三角形,所以BD AC ⊥.又平面11AA C C ⊥平面ABC ,且平面11AA C C 平面ABC AC =,BD 在面ABC 内,所以BD ⊥平面11AA C C .因为1A C ⊂平面11AA C C ,所以1BD A C ⊥.因为1A C BC ⊥,BD BC B = ,,BD BC ⊂平面ABC ,所以1A C ⊥平面ABC .(2)取BC 的中点M ,连接DM ,1A D ,1A M ,因为E ,F 分别为11A C ,11B C 的中点,11EF A B ∴∥,D 、M 分别为AC ,BC 的中点,DM AB ∴∥,因为三棱柱111ABC A B C -,∴侧面11A B BA 为平行四边形,11A B BA ∴∥,DM EF ∴∥,EF ⊂ 平面EFC ,DM ⊄平面EFC ,DM ∴∥平面EFC ,因为三棱柱111ABC A B C -,∴侧面11A C CA 为平行四边形,D ,E 分别为AC ,11A C 的中点,1A E DC ∴∥且1A E DC =,∴四边形1A EDC 是平行四边形,1A D EC ∴∥,EC ⊂ 平面EFC ,1A D ⊄平面EFC ,1A D ∴∥平面EFC ,又EF EC E = ,,EF EC ⊂平面EFC ,所以平面1A DM ∥平面EFC .P 为底面ABC 内(包括边界)的动点,当P DM ∈时,1A P ⊂平面1A DM ,1A P ∴∥平面CEF ,P ∴的轨迹为DM ,DM l ∴=,2AB l ∴=,又因为ABC △是正三角形,2122ABC S l ∴=⋅=△由(1)知:三棱柱111ABC A B C -的高为1A C ,12A C BC l ∴==,∴三棱柱111ABC A B C -的体积2312ABC V S A C l =⨯=⋅=△.(3)取AB 的中点H ,连接CH ,1A H ,ABC △是正三角形,H 为AB 的中点,CH AB ∴⊥,1A C ⊥ 平面ABC ,AB ⊂平面ABC ,1A C AB ∴⊥,又1CH A C C = ,1,CH A C ⊂平面1A CH ,AB ⊥ 平面1A CH ,又1A H ⊂平面1A CH ,1AB A H ∴⊥,∴二面角1A AB C --的平面角为1A HC ∠,在1Rt A HC △中,12A C l =,CH =,1tan A HC ∠==.∴二面角1A AB C --。
河南省许昌市高一下学期期末数学试卷

河南省许昌市高一下学期期末数学试卷姓名:________ 班级:________ 成绩:________一、填空题 (共14题;共15分)1. (1分) (2016高一下·南沙期末) 不等式﹣x2﹣2x+3>0的解集为________;(用区间表示)2. (1分) G(x)表示函数y=2cosx+3的导数,在区间上,随机取值a,G(a)<1的概率为________3. (1分)(2020·贵州模拟) 如图所示的茎叶图记录了甲乙两位射箭运动员的5次比赛成绩(单位:环),若两位运动员平均成绩相同,则成绩较为稳定(方差较小)的那位运动员成绩的方差为________.4. (1分)运行如图所示的伪代码,当输入a=4时,其结果为________.5. (1分) (2017高一上·上海期中) 已知a2>a1>0,b2>b1>0,且a1+a2=b1+b2=1,记A=a1b1+a2b2 ,B=a1b2+a2b1 , C= ,则按A、B、C从小到大的顺序排列是________.6. (1分) (2019高一下·广州期中) 已知数列的前项和为,则数列的通项公式为________.7. (1分) (2019高二上·郑州月考) 在中,角,,的对边分别是,,,,,,则的面积为________.8. (1分)(2019·西城模拟) 能说明“在数列中,若对于任意的,,则为递增数列”为假命题的一个等差数列是________.(写出数列的通项公式)9. (1分)(2019·吉林模拟) 西周初数学家商高在公元前1000年发现勾股定理的一个特例:勾三,股四,弦五.此发现早于毕达哥拉斯定理五百到六百年.我们把可以构成一个直角三角形三边的一组正整数称为勾股数.现从,,,,,,,这8组勾股数中中随机抽取1组,则被抽出的这组勾股数刚好构成等差数列的概率为________.10. (1分)(2017·汉中模拟) 已知各项均为正数的数列{an}的前n项和为Sn ,且Sn满足n(n+1)Sn2+(n2+n﹣1)Sn﹣1=0(n∈N*),则S1+S2+…+S2017=________.11. (1分)(2020·广西模拟) 实数满足不等式组,则的最大值是________12. (1分) (2019高一下·双鸭山月考) 如图,一栋建筑物的高为 m ,在该建筑物的正东方向有一个通信塔,在它们之间的地面点(三点共线)处测得楼顶,塔顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则通信塔的高为________13. (2分) (2020高二下·宁波期中) 已知函数则的最小值为________,最大值为________.14. (1分) (2015高二上·天水期末) 设Sn是数列{an}的前n项和,且a1=﹣2,Sn=2an+2,则an=________.二、解答题 (共6题;共50分)15. (5分) (2016高二上·郑州开学考) 某校从参加高三模拟考试的学生中随机抽取60名学生,按其数学成绩(均为整数)分成六组[90,100),[100,110),…,[140,150]后得到如下部分频率分布直方图,观察图中的信息,回答下列问题:(Ⅰ)补全频率分布直方图;(Ⅱ)估计本次考试的数学平均成绩(同一组中的数据用该组区间的中点值作代表);(Ⅲ)用分层抽样的方法在分数段为[110,130)的学生成绩中抽取一个容量为6的样本,再从这6个样本中任取2人成绩,求至多有1人成绩在分数段[120,130)内的概率.16. (10分) (2017高二下·红桥期末) 已知函数f(x)=m•6x﹣4x ,m∈R.(1)当m= 时,求满足f(x+1)>f(x)的实数x的范围;(2)若f(x)≤9x对任意的x∈R恒成立,求实数m的范围.17. (10分) (2020高一下·金华期末) 在锐角中,,D为边上一点,且.(1)已知,,求的面积;(2)已知:,,求 .18. (5分) (2016高二上·衡阳期中) 某工厂修建一个长方体形无盖蓄水池,其容积为4800立方米,深度为3米.池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底长方形长为x米.(Ⅰ)求底面积并用含x的表达式表示池壁面积;(Ⅱ)怎样设计水池能使总造价最低?最低造价是多少?19. (10分)已知函数f(x)=5+lnx,g(x)= (k∈R).(1)若函数f(x)在点(1,f(1))处的切线与函数y=g(x)的图象相切,求k的值;(2)若k∈N* ,且x∈(1,+∞)时,恒有f(x)>g(x),求k的最大值.(参考数据:ln5≈1.61,ln6≈1.7918,ln( +1)=0.8814)20. (10分) (2019高三上·海南月考) 已知是数列的前项和,且.(1)求;(2)求数列的前项和为.参考答案一、填空题 (共14题;共15分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、13-1、14-1、二、解答题 (共6题;共50分)15-1、16-1、16-2、17-1、17-2、18-1、19-1、19-2、20-1、20-2、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省许昌市高一下学期数学期末考试试卷
姓名:________ 班级:________ 成绩:________
一、填空题 (共12题;共13分)
1. (1分) (2016高一下·盐城期末) 直线y=x﹣3的倾斜角为________.
2. (1分) (2018高一上·广东期末) 直线与直线平行,则
________.
3. (1分) (2019高一下·贺州期末) 不论k为何实数,直线通过一个定点,这个定点的坐标是________.
4. (1分)已知,且,则的最小值为________.
5. (1分)(2017·黑龙江模拟) 过动点P作圆:(x﹣3)2+(y﹣4)2=1的切线PQ,其中Q为切点,若|PQ|=|PO|(O为坐标原点),则|PQ|的最小值是________.
6. (2分)若如图为某直三棱柱(侧棱与底面垂直)被削去一部分后的直观图与三视图中的侧视图、俯视图,则其正视图的面积为________ ,三棱锥D﹣BCE的体积为________
7. (1分) (2012·新课标卷理) 设x,y满足约束条件:;则z=x﹣2y的取值范围为________
8. (1分)设点A(﹣3,5)和B(2,15),在直线l:3x﹣4y+4=0上找一点P,使|PA|+|PB|为最小,则这个最小值为________ .
9. (1分) Sn是数列{an}的前n项和,若Sn=3n﹣1,则a12+a22+a32+…+an2=________.
10. (1分)在正方体ABCD﹣A1B1C1D1中,与AA1平行的棱有________条.
11. (1分) (2020高一下·萍乡期末) 已知锐角的角的对边分别为,且,三角形的面积,则的取值范围为________.
12. (1分) (2018高一下·苏州期末) 已知函数,若关于的不等式
恒成立,则实数的取值范围是________.
二、解答题 (共8题;共80分)
13. (10分) (2016高三上·湖州期末) 在锐角△ABC中,内角A,B,C所对的边分别为a,b,c,已知sin2
+cos2A= .
(1)求A的值;
(2)若a= ,求bc的最大值.
14. (15分) (2020高一下·响水期中) 已知直线且 .圆C与直线相切于点A,且点A的纵坐标为,圆心C在直线上.
(1)求直线之间的距离;
(2)求圆C的标准方程;
(3)若直线经过点且与圆C交于两点,当△CPQ的面积最大时,求直线的方程.
15. (5分)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=, AF=1,M是线段EF的中点.
(1)求证AM∥平面BDE;
(2)试在线段AC上确定一点P,使得PF与CD所成的角是60°.
16. (10分)已知数列的前n项和为,且对任意正整数n都有 .
(1)求证:为等比数列.
(2)若,求数列的前n项和 .
17. (10分) (2017高一上·平遥期中) 二次函数f(x)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
18. (10分) (2016高一下·蓟县期中) 某货轮在A处看灯塔B在货轮北偏东75°,距离为海里;在A处看灯塔C在货轮的北偏西30°,距离为海里.货轮由A处向正北航行到D处时,再看灯塔B在北偏东120°,求:
(1) A处与D处之间的距离;
(2)灯塔C与D处之间的距离.
19. (10分) (2017高一上·长春期末) 已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
(1)设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
(2)设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
20. (10分) (2019高一下·佛山月考) 设等差数列前项和为满足,且,,
成公比大于的等比数列.
(1)求数列的通项公式.
(2)设,求数列的前项和 .
参考答案一、填空题 (共12题;共13分)
1-1、
2-1、
3-1、
4-1、
5-1、
6-1、
7-1、
8-1、
9-1、
10-1、
11-1、
12-1、
二、解答题 (共8题;共80分)
13-1、13-2、14-1、14-2、
14-3、15-1、
16-1、16-2、17-1、17-2、18-1、18-2、
19-1、19-2、
20-1、20-2、。
