第六章时序逻辑电路作业题解
阎石《数字电子技术基础》(第6版)考研真题精选-第6章 时序逻辑电路【圣才出品】

第6章时序逻辑电路一、选择题1.下列逻辑电路中哪个是时序逻辑电路:()。
[江苏大学2016研]A.二进制译码器B.二进制加法器C.移位寄存器D.数据选择器【答案】C【解析】ABD三项都属于组合逻辑电路,C项移位寄存器是由触发器组成的,具有存储功能,它属于时序逻辑电路。
2.同步时序电路和异步时序电路比较,其差异在于后者()。
[重庆大学2015研] A.没有触发器B.没有统一的时钟控制C.没有稳定状态D.输出只与内部状态有关【答案】B【解析】A项是组合逻辑电路和时序逻辑电路的区别;C项是无稳态电路与稳态电路的区别;D项是米勒型电路和摩尔型电路的区别。
3.对于状态表6-1,下列说法正确的是:()。
[北京邮电大学2015研]表6-1A.状态A和B肯定等价B.状态D和E肯定等价C.状态A和C肯定等价D.状态B和F肯定等价【答案】B【解析】根据状态表6-1可知,状态D和E在输入0后,次态都为自身且输出Z=0,而在输入1后,次态都变为C且输出Z=0。
所以,可以视为两者状态等价,同样的分析方法用于A、C、D三项,可以发现这三个选项是错误的。
二、填空题1.时序电路中“等价状态”是______,在实际应用中起______作用。
[重庆大学2014研]【答案】相同的输入下,输出相同且次态也相同;化简【解析】状态等价是指在相同的输入变量条件下,次态相同且输出也相同,等价的状态主要用于化简状态转换表,也就是减少电路的状态数量,可以优化构成相应电路的硬件结构。
2.一个模值为6的计数器,状态转移图如图6-1所示,若初始状态为000,则经过100个CP脉冲后,其状态为______。
[北京邮电大学2015研]图6-1【答案】110【解析】每经过一个CP脉冲,计数器的状态按照顺序变化一次,100/6=16···4,所以经过了100CP脉冲后,计数器循环了16个完整计数周期,然后又进行了4次状态变化,所以此时状态为110。
数字逻辑设计第6章 时序逻辑电路习题与解答
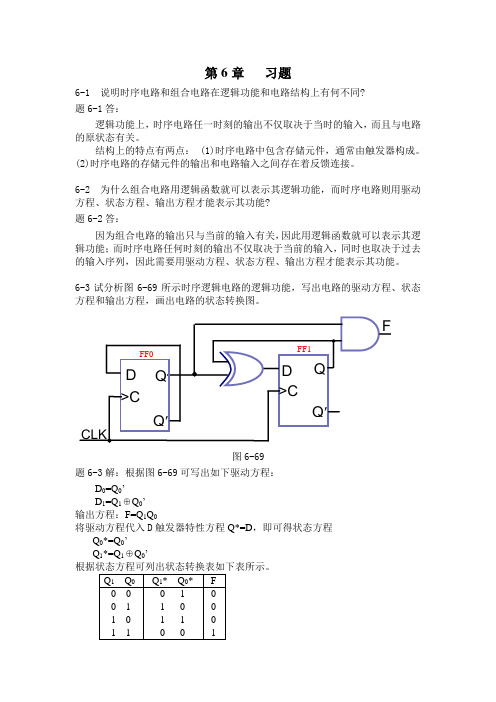
将方程代入 D 触发器的状态方程 Q*=D,得状态方程:
Q0*= Q0’,CLK 下降沿触发 Q1*=Q1’,Q0 上升沿触发 Q2*=Q2’, Q1 上升沿触发 根据状态方程可以画出 Q0、Q1、Q2 的波形图如下图所示,由图可见,该电路为 3 位异步二进制减法器。
6-14 用 74HCl61 构成的电路如图 6-77 所示,试分析其逻辑功能。
图 6-77 题 6-14 解:
由图可见,两个十六进制计数器 74HC161 形成级联方式,其中,161(1)的装
入值为 1100,进位输出 CO 接 161(2)的使能端 P 和 T,所以 161(1)为低 4 位,161(2) 为高 4 位,低 4 位计数达到 1111 时,进位输出 CO 有效,使下一时钟 CLK 上升沿 到达时,161(2)开始计数,而 161(2)计数达到 1111 时,其 CO 经反向形成装入 信号,高 4 位的装入值为 0011,所以在反复计数时,161(2)的计范围是从 0011 至 1111,而低 4 位的计数范围是从 1100 至 1111,整个 8 位从 00111100 到 11111111,其计数范围是从 60 到 255,共 196 个状态,所以该电路两片之间是 196 进制计数器。 6-15 试用 74HCl61 构成十一进制计数器。 题 6-15 解:
Q0*= Q0’ Q1*= Q0’Q1’+ Q0Q1 Q2*= Q0’Q1’Q2’+(Q0’Q1’)’Q2 根据状态方程可列出状态转换表如下:
C=1
C=0
Q2 Q1 Q0 000
Q2*Q1*Q0* 001
时序逻辑电路课后习题答案

第9章习题解答9.1 题9.1图所示电路由D 触发器构成的计数器,试说明其功能,并画出与CP 脉冲对应的各输出端波形。
Q CP题9.1图解:(1)写方程时钟方程:0CP CP =;10CPQ =;21CP Q = 驱动方程:00n D Q =;11n D Q =;22n D Q =状态方程:0100n n Q D Q CP +==↑;11110n n Q D Q Q +==↑;21221n nQ D Q Q +==↑(2)列状态转换表 (3)画状态转换图111210210n n n n n n CP Q Q Q Q Q Q +++0 0 0 0 1 1 11 1 1 1 1 1 02 1 1 0 1 0 13 1 0 1 1 0 04 1 0 0 0 1 15 0 1 1 0 1 06 0 1 0 0 0 17 0 0 1 0 0 0(4)画波形图CP 2Q 1Q 0Q(5)分析功能该电路为异步三位二进制减法计数器。
9.6 已知题9.6图电路中时钟脉冲CP 的频率为1MHz 。
假设触发器初状态均为0,试分析电路的逻辑功能,画出Q 1、Q 2、Q 3的波形图,输出端Z 波形的频率是多少?CP题9.6图解:(1)写方程时钟方程:123CP CP CP CP ===驱动方程:113n n D Q Q =;212n n D Q Q =⊕;312n n D Q Q =状态方程:11113n n n Q D Q Q CP +==↑;12212n n n Q D Q Q CP +==⊕↑;13312n n n Q D Q Q CP +==↑ 输出方程:3n Z Q =(2)列状态转换表 (3)画状态转换图111321321n n n n n n CP Q Q Q QQ Q Z+++0 0 0 0 0 0 1 01 0 0 1 0 1 0 02 0 1 0 0 1 1 03 0 1 1 1 0 0 04 1 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 0 0 1 0 1 1 1 0 0 1 0 1(4)画波形图(5)分析功能该电路为能够自启动的同步5进制加法计数器。
第06章时序逻辑电路习题解

[题6.20]分析图P 6.20给出的电路,说明这是多少进制的计数器,两片之间是多少进制。 74LSl61的功能表见表6.3.4。
解:这是采用整体置数法接成的计数器。 在出现LD'=0信号以前,两片74LSl61均按十六进制计数。即第(1)片到第(2) 片为十六进制。当第(1)片计为2,第(2)片计为5时产生LD'=0信号,待下一个 CLK信号到达后两片74LSl61同时被置零,总的进制为 5 X 16+2+1=83 故为八十三进制计数器。
图A 6.12
[题6.13]试分析图P 6.13的计数器在M=1和M=0时各为几进制。
解:图P6.13电路是采用同步置数法用74160接成的可变进制计数器。在M=1的 状态下,当电路进入Q3Q2Q1Q0=1001(九)以后,LD'=0。下一个CLK到达时将 D3D2D1D0=0100(四)置入电路中,使Q3Q2Q1Q0=0100,再从0100继续作加 法计数。因此,电路在0100到1001这六个状态间循环,构成六进制计数器。同 理,在M=0的情况下,电路计到1001后置入0010(二),故形成八进制计数器。
[题6.6]分析图P 6.6给出的时序电路,画出电路的状态转换图,检查电路能否自启动,说 明电路实现的功能。A为输入变量。
解:由电路图写出驱动方程为 J1=K1=1 J2=K2=A Q1 将上述驱动方程代入JK触发器的特性方程,得到状态方程 Q1*=Q1' Q2*=A Q1 Q2 输出方程为 Y=AQ1Q2+A'Q1'Q2' 根据状态方程和输出方程画出的状态转换图如图A 6.6所示。因为不存在无效 状态,所以电路不存在自启动与否的问题。 当A=0时电路对CLK脉冲作二进制加法计数,A=1时作二进制减法计数。
数字逻辑 第六章习题答案
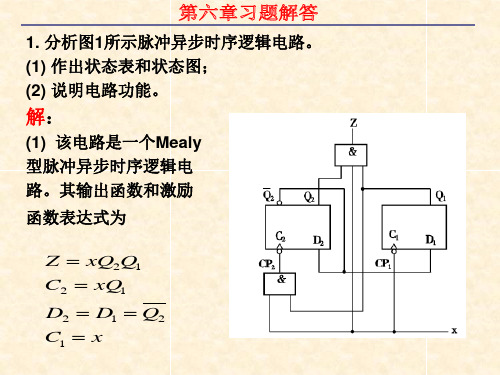
根据真值表画出激励函数和输出函数卡诺图(略),化简后可 得:
(5) 画出逻辑电路图 根据激励函数和输出函数表达式,可画出实现给定功能的逻 辑电路如图11所示。该电路存在无效状态10,但不会产生挂 起现象,即具有自启动功能。
7 试用与非门构成的基本R-S触发器设计一个 脉冲异步模4加1计数器。 解(1) 设电路输入脉冲为x,状态变量为 y1y0,其状态表如表9所示。
(2)该电路的状态图、状态表
(3)该电路是一个“x1—x2—x3”序列检测器。
4 分析图7所示脉冲异步时序电路,作出时间 图并说明该电路逻辑功能。
解:(1) 该电路是一个 Moore型脉冲异步时序逻辑 电路,其输出即电路状态。激 励函数表达式为
(2)电路次态真值表
(3)时间图
(4)该电路是一个模4计数器。
(4) 确定激励函数和输出函数 确定激励函数和输出函数时注意: ● 对于多余状态y2y1=10和不允许输入x2x1=11,可作为无关条 件处理; ● 当输入x2x1=00时,电路状态保持不变; ● 由于触发器时钟信号作为激励函数处理,所以,可假定次态 与现态相同时,触发器时钟信号为0,T端为d。 据此,可列出激励函数和输出函数真值表如表8所示。
(2) 根据状态表和RS触发器的功能表,可列出激 励函数真值表如表10所示。
Байду номын сангаас
(3)化简后,可得激 励函数最简表达式为:
(4)根据激励函数表达式,可画出逻辑电路 图如图12所示。
5 用D触发器作为存储元件,设计一个脉冲异 步时序电路。该电路在输入端x的脉冲作用 下,实现3位二进制减1计数的功能,当电 路状态为“000”时,在输入脉冲作用下输 出端Z产生一个借位脉冲,平时Z输出0。
第6章-时序逻辑电路
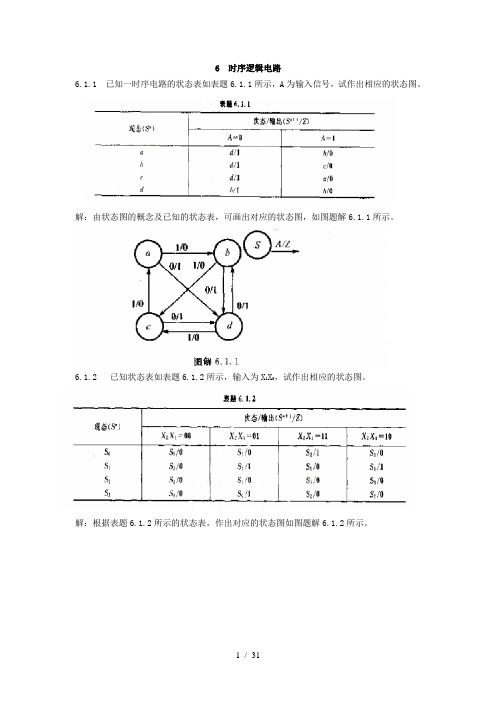
6 时序逻辑电路6.1.1 已知一时序电路的状态表如表题6.1.1所示,A为输入信号,试作出相应的状态图。
解:由状态图的概念及已知的状态表,可画出对应的状态图,如图题解6.1.1所示。
6.1.2已知状态表如表题6.1.2所示,输入为X1X0,试作出相应的状态图。
解:根据表题6.1.2所示的状态表,作出对应的状态图如图题解6.1.2所示。
6.1.3已知状态图如图题6.1.3所示,试列出它的状态表。
解:按图题6.1.3列出的状态表如表题解6.1.3所示。
6.1.5 图题6.1.5所示是某时序电路的状态图,设电路的初始状态为01,当序列A=100110(自左至右输入)时,求该电路输出Z的序列。
解:由图题6.1.5所示的状态图可知,当初态为01,输入信号的序列A=100110时,该时序电路将按图题解6.1.5所示的顺序改变状态,因而对应的输出序列为Z=011010。
6.1.6已知某时序电路的状态表如表题6.1.6所示,输入A,试画出它的状态图。
如果电路的初始状态在b,输入信号A一次是0、1、0、1、1、1、1,试求出其相应的输出。
解:根据表题6.1.6所示的状态表,可直接画出与其对应的状态图,如图题解6.1.6(a)当从初态b开始,依次输入0、1、0、1、1、1、1信号时,该时序电路将按图题解6.1.6(b)所示的顺序改变状态,因而其对应的输出为1、0、1、0、1、0、1。
6.2 同步时序逻辑电路的分析6.2.1 试分析图题6.2.1(a)所示时序电路,画出其状态表和状态图。
设电路的初始状态为0,试画出6.2.1(b)所示波形作用下,Q和Z的波形图。
解:由所给电路图可写出该电路的状态方程和输出方程,分别为1n nQ A QZAQ+=⊕=其状态表如表题解6.2.1所示,状态图如图题解6.2.1(a)所示,Q和Z的波形图如图题解6.2.1(b)所示。
6.2.2 试分析图题6.2.2(a)所示时序电路,画出其状态表和状态图。
第06章时序逻辑电路习题解

课件主编:徐 梁
习题解
第1题
第8题
第15题
数
字
第2题
第9题
第16题
电
第3题
第10题
第17题
子 技
第4题
第11题
第18题
时序电路分析 时序电路设计 计数器分析设计
术
第5题
第12题
基 础
第6题
第13题
序列信号发生器 VHDL设计
第7题
第14题
★★
A组★ B组★
[题6.1]分析图P 6.1时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图和时序图。
图A 6.4
[题6.5]试分析图P 6.5时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图。A为输入逻辑变量。
解:首先从电路图写出它的驱动方程 D1=AQ2' D2=A(Q1'Q2')'=A(Q1+Q2) 将上式代入D触发器的特性方程后得到电路的状态方程 Q1*=AQ2' Q2*=A(Q1+Q2) 电路的输出方程为 Y=AQ1'Q2 根据状态方程和输出方程画出的状态转换图如图A 6.5所示。
[题6.2]分析图P6.2时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画 出电路的状态转换图,并说明该电路能否自启动。
解:由给定的电路图写出驱动方程为 D1=Q3' D2=Q1 D3=Q1Q2 将驱动方程代入D触发器的特性方程Q*=D,得到电路的状态方程 Q1*=Q3' Q2*=Q1 Q3*=Q1Q2 电路的输出方程为 Y=(Q1'Q3)'=Q1+Q3' 电路的状态转换图如图A 6.2所示,电路能够自启动。
第6章 时序逻辑电路-习题答案
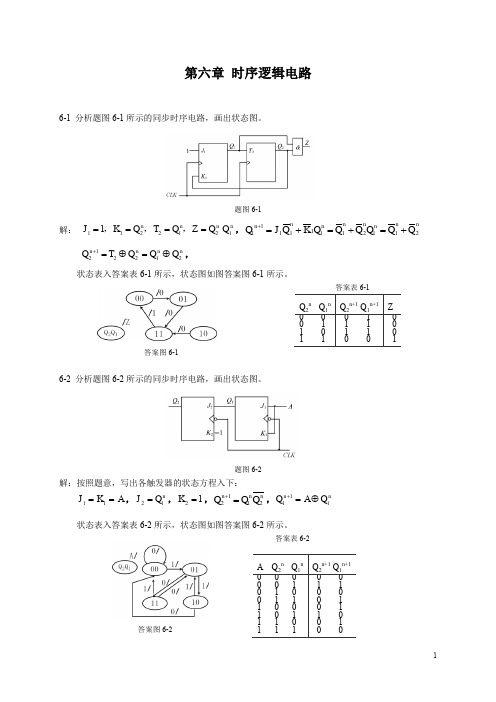
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路,画出状态图。
题图6-1解: 11221211n n n n J K Q T Q Z Q Q ====,,,,11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕,状态表入答案表6-1所示,状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路,画出状态图。
题图6-2 解:按照题意,写出各触发器的状态方程入下:11J K A ==,21n J Q =,21K =,1212n n nQ Q Q +=,111n n Q A Q +=⊕状态表入答案表6-2所示,状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路,画出状态图。
题图6-3解:按照题意,写出各触发器的状态方程入下:1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1,,, 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中,已知寄存器的初始状态Q 1Q 2Q 3=111。
时序逻辑电路习题解答
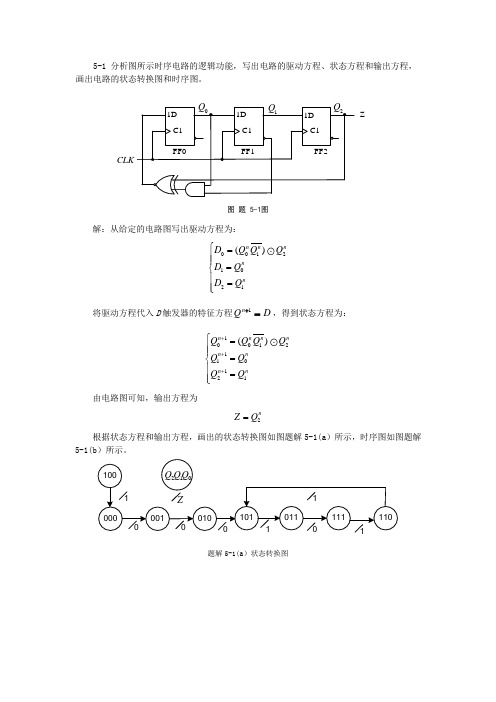
5-1 分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图。
CLKZ图 题 5-1图解:从给定的电路图写出驱动方程为:00121021()n n nn n D Q Q Q D Q D Q ⎧=⎪⎪=⎨⎪=⎪⎩将驱动方程代入D 触发器的特征方程D Qn =+1,得到状态方程为:10012110121()n n n n n n n n Q Q Q Q Q Q Q Q +++⎧=⎪⎪=⎨⎪=⎪⎩由电路图可知,输出方程为2nZ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-1(a )所示,时序图如图题解5-1(b )所示。
题解5-1(a )状态转换图1Q 2/Q ZQ题解5-1(b )时序图综上分析可知,该电路是一个四进制计数器。
5-2 分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
YA图 题 5-2图解:首先从电路图写出驱动方程为:()0110101()n n n n nD AQ D A Q Q A Q Q ⎧=⎪⎨==+⎪⎩将上式代入触发器的特征方程后得到状态方程()101110101()n n n n n n nQ AQ Q A Q Q A Q Q ++⎧=⎪⎨==+⎪⎩电路的输出方程为:01n nY AQ Q =根据状态方程和输出方程,画出的状态转换图如图题解5-2所示YA题解5-2 状态转换图综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态“00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3 已知同步时序电路如图(a)所示,其输入波形如图 (b)所示。
试写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
X(a) 电路图1234CLK5678X(b)输入波形 图 题 5-3图解:电路的驱动方程、状态方程和输出方程分别为:00101100011011011, ,n n n n n n n n n nJ X K X J XQ K XQ X Q XQ XQ XQ Q XQ XQ XQ Y XQ ++⎧==⎪⎨==⎪⎩⎧=+=⎪⎨⎪=+=+⎩= 根据状态方程和输出方程,可分别做出1110,n n Q Q ++和Y 的卡诺图,如表5-1所示。
时序逻辑电路作业题解

并码转换电路。
解:因为需要实现周期性自动转换的控制码“0”, 故一共需要9位数码存储器,74194有8位以及DFF 有1位正好满足设计要求。
首先使用RD复位脉冲将74194和DFF异步清零; 清零之后,2号74194的Q3端的0通过非门产生1,送 到两片74194的M1端形成并行送数工作模式; 等到CP↑到来时,将两片74194的并行输入端的 数据01111111存入,同时串行端的第一位数据D0'
附:异步二进制加法计数器的设计(Q端输出); 异步二进制加法计数器的基本结构为 a.采用T′FF
b.CP1=CP,CPi = Qi-1 (上升沿触发) ( i=2,3,…,n )
2023年11月25日星期六
章目录
第六章 时序逻辑电路 19
异步加法器电路如下图所示。
Q4
Q3
Q2
Q1
1D
1D
1D
1D
C1
1 D4
D3 74151
Z
0 D2
1
D1
0 D0
A2 A1 A0
计数器状态转移表
Q3 Q2 Q1 Q0 Z
0000 0 0 0 0 1 CP⊕1
0010 0
CR Q3 Q2 Q1 Q0
LD
74161
P1
0 0 1 1 CP⊕1
CP
D3 D2 D1 D0
T1
0100 1
章目录
5.25 (1)用DFF设计移存型序列信号发生器,要 求产生的序列信号为11110000…
③各触发器的次态方程
④电路的输出方程 无输出信号Z (3)作状态转移表、状态转移图(下一页) (4)电路的逻辑功能描述
第6章-时序逻辑电路-课后答案

第六章 时序逻辑电路【题 6.3】 分析图P6.3时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.3【解】驱动方程:11323131233J =K =Q J =K =Q J =Q Q ;K =Q ⎧⎪⎨⎪⎩ 输出方程:3YQ =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+11313131n 12121221n+13321Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q +⎧=+=⎪=+=⊕⎨⎪=⎩ 电路能自启动。
状态转换图如图A6.3【题 6.5】 分析图P6.5时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入逻辑变量。
图A6.3Y图P6.5【解】驱动方程: 1221212()D AQ D AQ Q A Q Q ⎧=⎪⎨==+⎪⎩输出方程: 21Y AQ Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+112n+1212()Q AQ QA Q Q ⎧=⎪⎨=+⎪⎩ 电路的状态转换图如图A6.51图A6.5【题 6.6】 分析图P6.6时序电路的逻辑功能,画出电路的状态转换图,检查电路能否自启动,说明电路能否自启动。
说明电路实现的功能。
A 为输入变量。
AY图P6.6【解】驱动方程: 112211J K J K A Q ==⎧⎨==⊕⎩输出方程: 1212Y AQ Q AQ Q =+将驱动方程带入JK 触发器的特性方程后得到状态方程为:n+111n+1212QQ Q A Q Q ⎧=⎪⎨=⊕⊕⎪⎩ 电路状态转换图如图A6.6。
A =0时作二进制加法计数,A =1时作二进制减法计数。
01图A6.6【题 6.7】 分析图P6.7时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
Y图P6.7【解】驱动方程: 001023102032013012301;;;J K J Q Q Q K Q J Q Q K Q Q J Q Q Q K Q==⎧⎪=∙=⎪⎨==⎪⎪==⎩ 输出方程: 0123Y Q Q Q Q =将驱动方程带入JK 触发器的特性方程后得到状态方程为:*00*1012301*2023012*3012303()Q ()Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q Q⎧=⎪=++⎪⎨=++⎪⎪=+⎩ 设初态Q 1Q 3Q 2Q 1 Q 0=0000,由状态方程可得:状态转换图如图A6.7。
时序逻辑电路思考题与习题题解

思考题与习题题解5-1 填空题(1)组合逻辑电路任何时刻的输出信号,与该时刻的输入信号有关;与电路原来所处的状态无关;时序逻辑电路任何时刻的输出信号,与该时刻的输入信号有关;与信号作用前电路原来所处的状态有关。
(2)构成一异步n2进制加法计数器需要n 个触发器,一般将每个触发器接成计数或T’型触发器。
计数脉冲输入端相连,高位触发器的CP 端与邻低位Q端相连。
(3)一个4位移位寄存器,经过 4 个时钟脉冲CP后,4位串行输入数码全部存入寄存器;再经过 4 个时钟脉冲CP后可串行输出4位数码。
(4)要组成模15计数器,至少需要采用 4 个触发器。
5-2 判断题(1)异步时序电路的各级触发器类型不同。
(×)(2)把一个5进制计数器与一个10进制计数器串联可得到15进制计数器。
(×)(3)具有N 个独立的状态,计满N 个计数脉冲后,状态能进入循环的时序电路,称之模N计数器。
(√)(4)计数器的模是指构成计数器的触发器的个数。
(×)5-3 单项选择题(1)下列电路中,不属于组合逻辑电路的是(D)。
A.编码器B.译码器C. 数据选择器D. 计数器(2)同步时序电路和异步时序电路比较,其差异在于后者( B )。
A.没有触发器B.没有统一的时钟脉冲控制C.没有稳定状态D.输出只与内部状态有关(3)在下列逻辑电路中,不是组合逻辑电路的有( D)。
A.译码器B.编码器C.全加器D.寄存器(4)某移位寄存器的时钟脉冲频率为100KHz,欲将存放在该寄存器中的数左移8位,完成该操作需要(B)时间。
μS μS μS(5)用二进制异步计数器从0做加法,计到十进制数178,则最少需要( C )个触发器。
(6)某数字钟需要一个分频器将32768Hz的脉冲转换为1HZ的脉冲,欲构成此分频器至少需要(B)个触发器。
(7)一位8421BCD码计数器至少需要(B)个触发器。
5-4 已知图5-62所示单向移位寄存器的CP 及输入波形如图所示,试画出0Q 、1Q 、2Q 、3Q 波形(设各触发初态均为0)。
时序逻辑电路例题及解析过程

时序逻辑电路例题及解析过程下面以一个简单的时序逻辑电路例题来进行解析:题目:设计一个时序逻辑电路,该电路具有两个输入信号A和B,一个输出信号Y。
当输入信号A的值为1持续1个时钟周期,并且在此期间B的值为0时,输出信号Y才为1,否则输出信号Y为0。
解析过程如下:1.首先,我们了解到输入信号A需要保持1个时钟周期,因此需要一个时钟信号作为输入。
2.我们需要一个计数器来计算时钟的周期数。
假设我们使用一个4位计数器,可以计数0到153.由于题目要求输入信号A的值需为1持续1个时钟周期,因此我们可以使用计数器的其中一位(假设为最高位)作为输入A。
当最高位为1时,表示1个时钟周期已经过去。
4.同时,我们需要判断输入信号B的值是否为0。
我们可以使用一个2输入与门来实现。
将A和B连接到与门的输入端,当A为1且B为0时,与门的输出为15.最后,我们需要将与门的输出作为输出信号Y。
如果与门的输出为1,则表示满足题目要求,Y为1;否则Y为0。
综上所述,这个时序逻辑电路可以由一个时钟信号、一个计数器、一个输入与门和一个输出门组成。
值得注意的是,以上只是一个简单的例题,实际设计中可能还需要考虑到多个输入信号的组合和时序要求的复杂度。
此外,时序逻辑电路中的存储器也可以根据需要进行选择和设计。
总结起来,时序逻辑电路是一种根据时序要求对输入信号进行处理和存储的电路。
在实际设计中,需要根据具体要求选择合适的计数器、逻辑门和存储器等组件来完成设计。
通过理解电路的工作原理和特点,我们可以更好地进行时序逻辑电路的设计和应用。
《数字电子技术》康华光习题解答第6章时序逻辑电路

第六章时序逻辑电路(选择、判断共30题)一、选择题1.同步计数器和异步计数器比较,同步计数器的显著优点是。
A.工作速度高B.触发器利用率高C.电路简单D.不受时钟C P控制。
2.把一个五进制计数器与一个四进制计数器串联可得到进制计数器。
A.4B.5C.9D.203.下列逻辑电路中为时序逻辑电路的是。
A.变量译码器B.加法器C.数码寄存器D.数据选择器4.N个触发器可以构成最大计数长度(进制数)为的计数器。
A.NB.2NC.N2D.2N5.N个触发器可以构成能寄存位二进制数码的寄存器。
A.N-1B.NC.N+1D.2N6.五个D触发器构成环形计数器,其计数长度为。
A.5B.10C.25D.327.同步时序电路和异步时序电路比较,其差异在于后者。
A.没有触发器B.没有统一的时钟脉冲控制C.没有稳定状态D.输出只与内部状态有关8.一位8421B C D码计数器至少需要个触发器。
A.3B.4C.5D.109.欲设计0,1,2,3,4,5,6,7这几个数的计数器,如果设计合理,采用同步二进制计数器,最少应使用级触发器。
A.2B.3C.4D.810.8位移位寄存器,串行输入时经个脉冲后,8位数码全部移入寄存器中。
A.1B.2C.4D.811.用二进制异步计数器从0做加法,计到十进制数178,则最少需要个触发器。
A.2B.6C.7D.8E.1012.某电视机水平-垂直扫描发生器需要一个分频器将31500H Z的脉冲转换为60H Z的脉冲,欲构成此分频器至少需要个触发器。
A.10B.60C.525D.3150013.某移位寄存器的时钟脉冲频率为100K H Z ,欲将存放在该寄存器中的数左移8位,完成该操作需要时间。
A.10μSB.80μSC.100μSD.800m s 14.若用J K 触发器来实现特性方程为,则J K 端的方程为 。
AB Q A Q n 1n +=+A.J =A B ,K = B.J =A B ,K = C.J =,K =A B D.J =,K =A B B A +B A B A +B A 15.要产生10个顺序脉冲,若用四位双向移位寄存器CT74LS194来实现,需要 片。
时序逻辑电路习题解答

5-1分析图所示时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程, 画出电路的状态转换图和时序图。
解:从给定的电路图写出驱动方程为:D o (Q 0Q i n)e Q 2D i Q 01D 2 Q i nQ 01 1(Q 0Q n)eQ ;Q i n 1Q 0Q 21Q ;由电路图可知,输出方程为Z Q ;CLK将驱动方程代入D 触发器的特征方程Q n 1D ,得到状态方程为:5-1(a )所示,时序图如图题解Z图题5-1图根据状态方程和输出方程,画出的状态转换图如图题解题解5-1(a )状态转换图综上分析可知,该电路是一个四进制计数器。
5-2分析图所示电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图。
A 为输入变量。
解:首先从电路图写出驱动方程为:D o A& D i A Qg :A (Q : Q i n)将上式代入触发器的特征方程后得到状态方程Q 0 1AQ :Q :1 AQ 0Q :A (Q nQ :)电路的输出方程为:CLKQ i12345——-A1 11 t----------- 1------------ 1|| 1 » 1 1 1----------- 1 ---------- 1 --------------►CLK0 Q 2/Z 仝题解5-1(b )时序图0 Q o 胃AY图题5-2图丫AQoQ;根据状态方程和输出方程,画出的状态转换图如图题解5-2 所示综上分析可知该电路的逻辑功能为:当输入为0时,无论电路初态为何,次态均为状态" 00”,即均复位;当输入为1时,无论电路初态为何,在若干CLK 的作用下,电路最终回到状态“10”。
5-3已知同步时序电路如图(a )所示,其输入波形如图 (b )所示。
试写出电路的驱动方 程、状态方程和输出方程,画出电路的状态转换图和时序图,并说明该电路的功能。
CLK 1 2345678(b )输入波形 图题5-3图解:电路的驱动方程、状态方程和输出方程分别为:J 。
时序逻辑电路习题解答
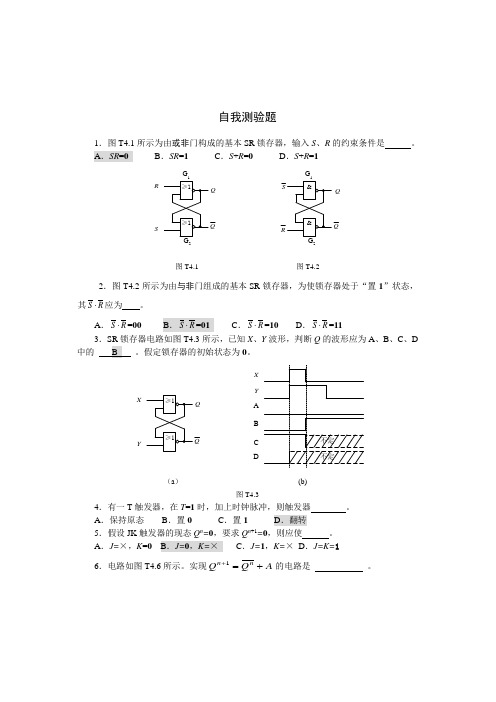
自我测验题1.图T4.1所示为由或非门构成的基本SR锁存器,输入S、R的约束条件是。
A.SR=0B.SR=1C.S+R=0D.S+R=1QG22QRS图T4.1 图T4.22.图T4.2所示为由与非门组成的基本SR锁存器,为使锁存器处于“置1”状态,其RS⋅应为。
A.RS⋅=00C.RS⋅=10D.RS⋅=113.SR锁存器电路如图T4.3所示,已知X、Y波形,判断Q的波形应为A、B、C、D 中的。
假定锁存器的初始状态为0。
XYXYABCD不定不定(a)(b)图T4.34.有一T触发器,在T=1时,加上时钟脉冲,则触发器。
A.保持原态B.置0C.置1D.翻转5.假设JK触发器的现态Q n=0,要求Q n+1=0,则应使。
A.J=×,K=0B.J=0,K=×C.J=1,K=×D.J=K=16.电路如图T4.6所示。
实现AQQ nn+=+1的电路是。
A AA AA .B .C .D .图T4.67.电路如图T4.7所示。
实现n n Q Q =+1的电路是 。
CPCPCPA .B .C .D .图T4.78.电路如图T4.8所示。
输出端Q 所得波形的频率为CP 信号二分频的电路为 。
1A . B . C .D .图T4.89.将D 触发器改造成T 所示电路中的虚线框内应是 。
TQ图T4.9A .或非门B .与非门C .异或门D .同或门 10.触发器异步输入端的作用是 。
A .清0 B .置1 C .接收时钟脉冲 D .清0或置1 11.米里型时序逻辑电路的输出是 。
A .只与输入有关B .只与电路当前状态有关C .与输入和电路当前状态均有关D .与输入和电路当前状态均无关12.摩尔型时序逻辑电路的输出是 。
A .只与输入有关 B .只与电路当前状态有关C .与输入和电路当前状态均有关D .与输入和电路当前状态均无关13.用n 只触发器组成计数器,其最大计数模为 。
A .nB .2nC .n 2D .2 n14.一个5位的二进制加计数器,由00000状态开始,经过75个时钟脉冲后,此计数B .01100C .01010D .00111图T4.1516.电路如图T4.16所示,假设电路中各触发器的当前状态Q 2 Q 1 Q 0为100,请问在时钟作用下,触发器下一状态Q 2 Q 1 Q 0为 。
第六章时序逻辑电路典型例题分析

第六章时序逻辑电路典型例题分析第一部分:例题剖析触发器分析例1在教材图6.1所示的基本RS触发器电路中,若⎺R、⎺S 的波形如图P6.1(a)和(b),试分别画出对应的Q和⎺Q端的波形。
解:基本RS触发器,当⎺R、⎺S同时为0时,输出端Q、⎺Q均为1,当⎺R=0、⎺S=1时,输出端Q为0、⎺Q为1,当⎺R=⎺S=1时,输出保持原态不变,当⎺R=1、⎺S=0时,输出端Q为1、⎺Q为0,根据给定的输入波形,输出端对应波形分别见答图P6.1(a)和(b)。
需要注意的是,图(a)中,当⎺R、⎺S同时由0(见图中t1)变为1时,输出端的状态分析时不好确定(见图中t2),图中用虚线表示。
例2 在教材图6.2.3(a)所示的门控RS触发器电路中,若输入S 、R和E的波形如图P6.2(a)和(b),试分别画出对应的输出Q和⎺Q端的波形。
解:门控RS触发器,当E=1时,实现基本RS触发器功能,即:R=0(⎺R=1)、S=1(⎺S=0),输出端Q为1、⎺Q为0;R=1(⎺R=0)、S=0(⎺S=1)输出端Q为0、⎺Q为1;当E=0时,输出保持原态不变。
输出端波形见答图P6.2。
例3在教材图6.2.5所示的D锁存器电路中,若输入D、E的波形如图P6.3(a)和(b)所示,试分别对应地画出输出Q和Q端的波形。
解:D锁存器,当E=1时,实现D锁存器功能,即:Q n+1=D,当E=0时,输出保持原态不变。
输出端波形见答图P6.3。
例4在图P6.4(a)所示的四个边沿触发器中,若已知CP、A、B的波形如图(b)所示,试对应画出其输出Q端的波形。
设触发器的初始状态均为0。
解:图中各电路为具有异步控制信号的边沿触发器。
图(a)为边沿D触发器,CP上升沿触发,Q1n+1= A,异步控制端S D接信号C(R D=0),当C=1时,触发器被异步置位,输出Q n+1=1 ;图(b)为边沿JK触发器,CP上升沿触发,Q2n+1= A⎺Q2n +⎺BQ2n,异步控制端⎺R D接信号C(⎺S D =1),当C=0时,触发器被异步复位,输出Q n+1=0;图(c)为边沿D触发器,CP下降沿触发,Q3n+1= A,异步控制端⎺S D接信号C(⎺R D =1),当C=0时,触发器被异步置位,输出Q n+1=1;图(d)为边沿JK触发器,CP下降沿触发,Q4n+1= A⎺Q4n +⎺BQ4n,异步控制端R D接信号C(S D =0),当C=1时,触发器被异步复位,输出Q n+1=0。
《时序逻辑电路》练习题及答案
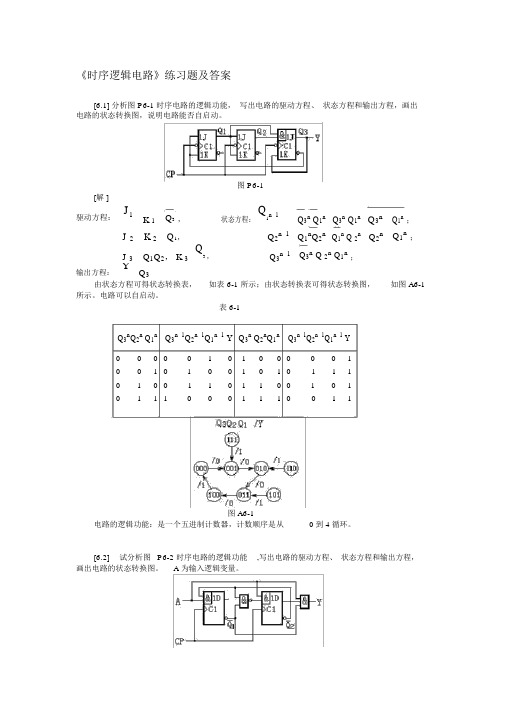
《时序逻辑电路》练习题及答案[6.1] 分析图 P6-1 时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,说明电路能否自启动。
图 P6-1[解 ]驱动方程:J1K 1Q3,状态方程:Q1n 1Q3n Q1n Q3n Q1n Q3n Q1n;J 2K 2Q1,Q2n 1Q1n Q2n Q1n Q 2n Q2n Q1n;J 3Q1Q2, K 3Q3 ,Q3n 1Q3n Q 2n Q1n;输出方程:YQ3由状态方程可得状态转换表,如表 6-1 所示;由状态转换表可得状态转换图,如图 A6-1所示。
电路可以自启动。
表 6-1Q3n Q2n Q1n Q3n 1Q2n 1Q1n 1 Y Q3n Q2n Q1n Q3n 1Q2n 1Q1n 1 Y00000101000001001010010101110100110110010101110001110011图 A6-1电路的逻辑功能:是一个五进制计数器,计数顺序是从0到 4循环。
[6.2]试分析图P6-2 时序电路的逻辑功能画出电路的状态转换图。
A 为输入逻辑变量。
,写出电路的驱动方程、状态方程和输出方程,图 P6-2 [解 ]驱动方程:D1AQ2 ,D2 AQ1Q 2状态方程: Q1n 1AQ2n,Q2n 1AQ1n Q2n A(Q2n Q1n )输出方程:YAQ1 Q2表 6-2由状态方程可得状态转换表,如表6-2 所示;由状态转换表AQ2n Q1n Q2n 1Q1n 1Y可得状态转换图,如图 A6-2所示。
电路的逻辑功能是:判断 A 是否连续输入四个和四个以上“1”000010信号,是则 Y=1 ,否则 Y=0 。
001100010110011001100111111100110010图 A6-2101000[6.3] 试分析图 P6-3 时序电路的逻辑功能,写出电路的驱动方程、状态方程和输出方程,画出电路的状态转换图,检查电路能否自启动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4
5
1
1
1
0
0
0
Q3 n
Q2 n
Q1 n
Q3n+1
Q2n+1
Q1n+1
J3
K3
J2
K2
J1
K1
0
0
0
0
1
0
0
Φ
1
Φ
0
Φ
0
1
0
0
1
1
0
Φ Φ
Φ Φ
0
1 Φ Φ
Φ
0
1
1
1
0
1
1 Φ
1 Φ
0
1
0
1
1
1
0
0
1
1
1
1
0
1
0
0
Φ Φ
0
Φ
1 Φ
0
Φ Φ
1
0
0
0
0
0
1
0
0
偏 离 态
0
0
1
0
0
0
0 Φ
Φ
0 Φ
Φ
该电路具有自启动性。
图 6.3.1 题 6.6 的状态转移图
22
6.5 八位并行→串行转换
启动 启 动
&
&
在下图基础上增加芯片2 的Q2输出线到与非门,另 外在串行输出端增加两个 DFF和一个或门及与门
0
0
0
0
0
0
0
串输 行出 串行输出
M0
1 CR CP
Q0 Q1 Q2 Q3
Q0 Q1 Q2 Q3 M0 CR CP D SR 1
1
1 1 0 0 0 0 1 1
1
1 0 0 0 0 1 1 1
1
0 0 0 0 1 1 1 1
0
M=8 √
0 0 0 1 1 1 1
标题区
节目录
18
④求激励函数D1 Q2Q1 Q4Q3
00 01 11 10 1 1 Ø 00 1
01 Ø Ø 1 Ø
11 0
10 0
Ø 0
0
Ø Ø Ø
D1 D1 = Q4
n Q3
n Q2
]· CP
Qn 1
+
n Q 2 ]· CP
④电路的输出方程
(3)作状态转移表、状态转移图 (4)电路的逻辑功能描述 模M=5的异步计数器,具备自启动性。
标题区
节目录
6
图P6.8的状态转移表
Q3 Q2 Q1 0 0 0 1 1 0 0 0 1 1 1 1 0 1 0 1 0 0 1 0 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 1 CP1(CP)↓CP2(CP)↓CP3(Q1)↓ 0 1 1 1 1 1 0 1 0 1 0 1
( i=2,3,…,n )
标题区
节目录
14
电路如下图所示。
Q4 Q3 Q2 Q1
1D C1
1D C1
1D C1
1D C1
CP
题6.12电路图 (省略了初始置0电路)
标题区
节目录
15
6.35 用DFF设计移存型序列信号发生器,要求 产生的序列信号为 (1)11110000…;
解:① 求触发器的级数
74161 ( 1 ) D3 D2 D1 D0
D2 D2 D1 D0
1
CP
31
• 6.22 试分析图P6.22(a)(b)2个计数器的分 频比为多少? • 解:(a)74195是四位可并入的右移寄存器。 根据图示,该电路工作于并入右移状态, 注意第一级Q0的状态是由Q0和J\K决定。 J=Q3 K=Q3
标题区
0 1 1 1 1 1 0 1 0 1 0 1
节目录
0 0 0 1 0 1 0 0 0 0 0 0
右列 中“1” 表示 有↓
红 色 为 偏 离 态
7
Q3Q2Q1
000 101 100
011
有效循环
001
110 010
偏离状态
111
图P6.8的状态转移图
标题区
节目录
8
6.4 试画出用MSI移存器74194构成8位串行—并
6.1解:这是包含一个JKFF的同步时序电路
J X1 X 2 K X1 X 2 (激励方程) (次态方程)
Q n1 ( X 1 X 2 Q n X 1 X 2Q n )CP X1 X 2 Qn
Z X 1 X 2Q n X 1 X 2 Q n X 1 X 2 Q n X 1 X 2Q n (输出方程)
1
0
CP
题6.4 图3
标题区 节目录
13
1
74194 (2) M 1
D SL
6.12 用四个D触发器设计以下电路:
(1)异步二进制加法计数器(Q端输出);
解:异步二进制加法计数器的基本结构为
a.采用T′FF (注意:同步加减法器不能使用T′FF)
b.CP1=CP, i = Qi-1 (上升沿触发) CP
Φ Φ
1
1
1
1
1
1
0
0
0
1
27
J3K3J2K2J1K1分别是关于现态Q的六个函数, 用卡诺图分别予以化简,得
J 3 Q2Q1 J 2 Q3 Q1 J1 Q 3Q2
K 3 Q 2 Q1 K 2 Q3 Q1 K1 Q 2 Q3
按照以上连接关系即得题意设计
28
6.19 试用74161设计循环顺序为0、1、2、 3、4、5、10、11、12、13、14、15、0、 1…..的模长为12的计数电路。
Q '0 Q '1 Q '2 Q '3 Q0 Q1 Q2 Q3 CR CP D SR M0 1
74194 (1) M 1
D SL D 0 D1 D 2 D 3 0
1 1
串 入 串入
Q '4 Q ' 5 Q ' 6 Q '7 RD CR CP D SR Q0 Q1 Q2 Q3 1 M0
1
Q '8 Q ' 9 Q ' 1 0 Q '1 1 Q0 Q1 Q2 Q3 CR CP D SR M0 1
32
Q0
0 1
Q1
0 0
Q2
0ቤተ መጻሕፍቲ ባይዱ0
Q3
0 0
J
1 1
K
0 0
0
1 0 0
1
0 1 0
0
1 0 1
0
0 1 0
1
1 0 1
0
0 1 0
33
Q0 1 1 0 1 1 1
Q1 0 1 1 0 1 1
Q2 0 0 1 1 0 1
Q3 1 0 0 1 1 0
J 0 1 1 0 0 1
K 1 0 0 1 1 0
74194 (1) M 1
D SL D 0 D1 D 2 D 3
74194 (2) M 1
D SL D 0 D1 D 2 D 3
1
0
CP
题6.4 图2
标题区 节目录
12
用两片74194和一个D触发器(Q’8)构成。
串入 串 入
D' D' D' D' D' D' D' D' 7 6 5 4 3 2 1 0
M=8,由 log 2 M n log 2 M 1 得n=3。 ②列状态转移表
标题区
节目录
16
Q3 1
Q2 1
Q1 1
状态转移路线
模数
M=1
1 1 1
×
③取n=4,列状态转移表及相应D1的值。
标题区
节目录
17
Q4 Q3 Q2 Q1 状态转移路线
模数
D1
1
1 1 1 0 0 0 0 1
①时钟方程 CP1 = CP2 = CP;CP3 = Q1
②各触发器的激励方程 J3 = 1 ;
n Q3 ; J2 =
K3 =
n Q2
J1 = 1 ;
K2 = 1 n Q2 K1 =
③各触发器的次态方程
标题区 节目录
5
Q
n 1 3
(Q Q Q )Q1
n 3 n 2 n 3
Qn+1=[ 2 Qn+1=[ 1
串入 串 入
D' 7 D' 6 D' 5 D' 4 D' 3 D' 2 D' 1 D' 0 1D C1
Q '0
R
Q '1 Q ' 2 Q ' 3 Q '4 RD CR CP D SR Q0 Q1 Q2 Q3 1 M0
1
Q '5 Q ' 6 Q ' 7 Q '8 Q0 Q1 Q2 Q3 CR CP D SR M0 1
标题区
节目录
19
⑤画电路图
Q4 Q3 Q2 Q1
1D S C1
1D S C1
1D S C1
1D S C1
CP
题 6.35 图
标题区
节目录
20
解:激励方程:J1 =K1 =1; J2 =Q1n Q3 n ,K2 =Q1 n J3 =Q1n Q2 n ,K3 =Q1 n 状态方程:Q1n+1 =Q1 n· CP Q2n+1 =[Q1n Q3 n Q2n +Q1 n Q2n ]· CP Q3n+1 =[Q1n Q2 n Q3n +Q1 n Q3 n ]· CP 状态转移表 6.3.7:
