立体几何专题复习

合集下载

高考数学立体几何专题复习(含答案)

9、如图，在四棱锥 P ABCD 中，底面 ABCD 是正方形，侧棱 PD 底面 ABCD ， PD DC 2 ， E 是 PC
的中点.
（Ⅰ）证明： PA / / 平面 EDB ；（Ⅱ）求三棱锥 A BDP 的体积.
试卷第 2 页，总 2 页
参考答案
1、【答案】(1)详见解析;(2) . 试题分析（：1）过 B 作 CD 的垂线交 CD 于 F，则
6、如图所示，在直三棱柱 ABC－A1B1C1 中，AC＝3，BC＝4，AB＝5，AA1＝4，点 D 是 AB 的中点． (1)求证：AC1∥平面 CDB1； (2)求异面直线 AC1 与 B1C 所成角的余弦值．
7、如图所示，在三棱锥 A BOC 中，OA 底面 BOC ，OAB OAC 300 ， AB AC 2 ， BC 2 ，
高考数学—立体几何专题复习
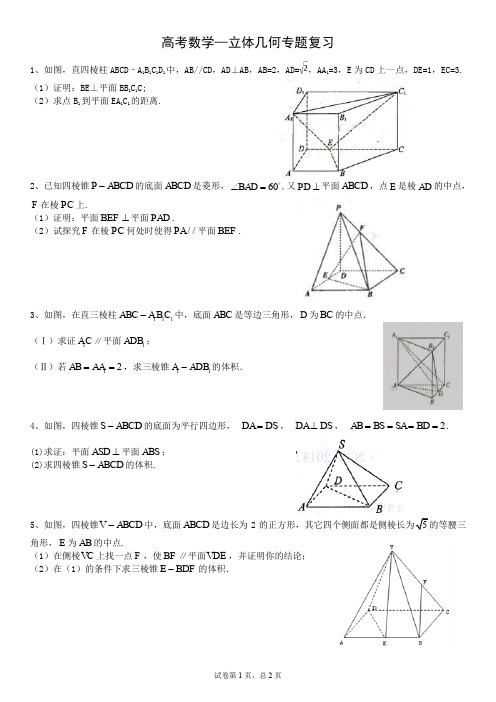
1、如图，直四棱柱 ABCD–A1B1C1D1 中，AB//CD，AD⊥AB，AB=2，AD= ，AA1=3，E 为 CD 上一点，DE=1，EC=3. （1）证明：BE⊥平面 BB1C1C; （2）求点 B1 到平面 EA1C1 的距离.
2、已知四棱锥 P ABCD 的底面 ABCD 是菱形， BAD 60 ,又 PD 平面 ABCD ，点 E 是棱 AD 的中点， F 在棱 PC 上. （1）证明：平面 BEF 平面 PAD . （2）试探究 F 在棱 PC 何处时使得 PA / / 平面 BEF .
答案第 1 页，总 6 页
试题解析：
（1）证明：
PD EB

平面ABCD 平面ABCD

PD

EB
,
又底面 ABCD 是 A 60 的菱形，且点 E 是棱 AD 的中点，所以 EB AD ，

立体几何综合复习——空间角(完整版)

立体几何专题复习-----空间角的求法（一）异面直线所成的角：定义：已知两条异面直线,a b ，经过空间任一点O 作直线//,//a a b b ''，,a b ''所成的角的大小与点O 的选择无关，把,a b ''所成的锐角（或直角）叫异面直线,a b 所成的角（或夹角）．为了简便，点O 通常取在异面直线的一条上理解说明：（1）平移法：即根据定义，以“运动”的观点，用“平移转化”的方法，使之成为相交直线所成的角。

（2）异面直线所成的角的范围：]2,0(π（3）异面直线垂直：如果两条异面直线所成的角是直角，则叫两条异面直线垂直．两条异面直线,a b 垂直，记作a b ⊥．（4）求异面直线所成的角的方法：法1：通过平移，在一条直线上找一点，过该点做另一直线的平行线；法2;找出与一条直线平行且与另一条相交的直线，那么这两条相交直线所成的角即为所求(5).向量法： CDAB CD AB →→=.cos θ（二）直线和平面所成的角1．线面角的定义：平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角2、记作：θ；3、范围：[0，2π]；当一条直线垂直于平面时，所成的角θ＝2π，即直线与平面垂直；1.二面角的平面角：（1）过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线,OA OB ，则AOB ∠叫做二面角lαβ--的平面角（2）一个平面垂直于二面角l αβ--的棱l ，且与两半平面交线分别为,,OA OB O 为垂足，则AOB ∠也是l αβ--的平面角说明：（1）二面角的平面角范围是[0,180]；（2）二面角的平面角为直角时，则称为直二面角，组成直二面角的两个平面互相垂直（3）二面角的平面角的特点：1）角的顶点在棱上；2）角的两边分别在两个面内；3）角的边都要垂直于二面角的棱。

2、作二面角的平面角的常用方法：①、点P 在棱上——作垂直于棱的直线（如图1）；②、点P 在一个半平面——三垂线定理法；（如图2） ③、点P 在二面角内——垂面法。

高考立体几何专题复习公开课获奖课件

（7）假如一种平面与另一种平面垂线平行，则这两个平面互相垂直
第20页
面面垂直鉴定
假如一种平面通过另一种平面一条垂线，则这两个平面互相垂直
推论:假如一种平面与另一种平面垂线平行，则这两个平面互相垂直
第21页
面面垂直性质
假如两个平面垂直，则在一种平面内垂直于它们交线直线垂直于另一种平面
推论:假如两个相交平面都与另一种平面垂直，则这两个平面交线 l 垂直于另一种平面
（3）推论：
假如一种平面内两条相交直线与另一种平面两条相交直线分别平行，那么这两个平面平行。
第10页
（4）运用线面垂直：
假如两个平面分别垂直于同一条直线，那么这两个平面平行。
（5）运用面面平行：
假如两个平面都平行于第三个平面，那么这两个平面平行。
（6）运用距离：
假如一种平面上所有点到另一种平面距离相等，那么这两个平面平行。
α
a
直线与平面所成角
βA Pm
αB
二面角
00<θ≤900
00≤ θ≤900
00≤θ ≤1800
空间角计算环节：一作、二证、三算
第34页
空间中角解法小结
1、异面直线所成角措施（1）平移法（2）补形法
2、直线与平面所成角措施
关键：抓垂足、斜足，找斜线在平面内射影。
3、二面角
找二面角棱,进而找棱两条垂线
第6页
（4）运用垂直
假如一条直线和一种平面分别与另一种平面垂直，且直线不在这个平面内，则这条直线和这个平面平行。
（5）运用平行假如一条直线与两个平行平面中一种平行且不在另一种平面内，则这条直线与另一种平面平行。
（6）运用距离

高考数学(文)《立体几何》专题复习

(2)两个平面垂直的判定和性质
✓ 考法5 线面垂直的判定与性质
1.证明直线与平面垂直的方法
2.线面垂直的性质与线线垂直
（1）判定定理（常用方法）：一条直线与一个平面内的两条相交直线都垂直,则该直线
与此平面垂直.判定定理中的两条相交直线必须保证“在平面内相交”这一条件. （2）性质： ①应用面面垂直的性质（常用方法）：若两平面垂直,则在一个平面内垂直于交线的直线必垂直于另一个平面，是证明线面垂直的主要方法； ②（客观题常用）若两条平行直线中的一条垂直于一个平面, 则另一条也垂直于这个平面.
64
65
✓ 考法4 面面平行的判定与性质
1.证明平面与平面平行的常用方法 2.空间平行关系之间的转化
66
✓ 考法3 面面平行的判定与性质
1.证明平面与平面平行的常用方法
这是立体几何中证明平行关系常用的思路,三种平行关系的转化可结合下图记忆
2.空间平行关系之间的转化
67
68
600分基础考点&考法
定义判定方法
2.等角定理
判定定理反证法两条异面直线所成的角
✓ 考法2 异面直线所成的角
常考形式
直接求求其三角函数值
常用方法
作角
正弦值余弦值正切值
证明求值取舍
55
56
57
58
600分基础考点&考法
➢ 考点46 线面、面面平行的判定与性质 ✓ 考法3 线面平行的判定与性质 ✓ 考法4 面面平行的判定与性质
1.计算有关线段的长
2.外接球、内切球的计算问题
观察几何体的特征利用一些常用定理与公式 (如正弦定理、余弦定理、勾股定理、三角函数公式等) 结合题目的已知条件求解

新高中数学立体几何多选题专题复习及答案

新高中数学立体几何多选题专题复习及答案一、立体几何多选题1．如图，正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2，则下列说法正确的是（）A ．异面直线1AB 与1AD 所成的角是3πB ．1BD ⊥平面11AC DC ．平面1ACB 截正四面体11A BDC -所得截面面积为3D ．正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ，利用正方体的结构特征找到异面直线所成的角；选项B ，根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证；选项C ，由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一；选项D ，分别求出正方体的体对角线长和正四面体11A BDC -的高，然后判断数量关系即可得解. 【详解】A ：正方体1111ABCD ABCD -中，易知11//AD BC ，异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角，即11A BC ∠，11A BC 为等边三角形，113A BC π∠=，正确；B ：连接11B D ，1B B ⊥平面1111DC B A ，11A C ⊂平面1111D C B A ，即111AC B B ⊥，又1111AC B D ⊥，1111B B B D B ⋂=，有11A C ⊥平面11BDD B ，1BD ⊂平面11BDD B ，所以111BD AC ⊥，同理可证：11BD A D ⊥，1111AC A D A ⋂=，所以1BD ⊥平面11AC D ，正确；C ：易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=，错误；D ：易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -的高为22222262213⎛⎫--⨯= ⎪⎝⎭，故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23，正确. 故选：ABD. 【点睛】关键点点睛：利用正方体的性质，找异面直线所成角的平面角求其大小，根据线面垂直的判定证明1BD ⊥平面11AC D ，由正四面体的性质，结合几何图形确定截面的面积，并求高，即可判断C 、D 的正误.2．一副三角板由一块有一个内角为60°的直角三角形和一块等腰直角三角形组成，如图所示，090B F ∠=∠=，060,45,A D BC DE ∠=∠==，现将两块三角形板拼接在一起，得三棱锥F CAB -，取BC 中点O 与AC 中点M ，则下列判断中正确的是（）A ．BC FM ⊥B ．AC 与平面MOF 所成的角的余弦值为32C ．平面MOF 与平面AFB 所成的二面角的平面角为45°D ．设平面ABF 平面MOF l =，则有//l AB【答案】AD 【分析】证明BC ⊥面FOM 可判断A ；根据AC 与平面MOF 所成的角为060CMO ∠=判断B ；利用特殊位置判断C ；先证明//AB 面MOF ，由线面平行的性质定理可判断D ；【详解】由三角形中位线定理以及等腰三角形的性质可得,,BC OF BC OM OM OF O ⊥⊥=，所以BC ⊥面FOM BC FM ⇒⊥，故A 正确；因为BC ⊥面FOM ，所以AC 与平面MOF 所成的角为060CMO ∠=，所以余弦值为12，故B 错误；对于C 选项可以考虑特殊位置法，由BC ⊥面FOM 得面ABC ⊥面FOM ，所以点F 在平面ABC 内的射影在直线OM 上，不妨设点F 平面ABC 内的射影为M ，过点M 作//BC MN ，连结NF .易证AB ⊥面MNF ，则l ⊥面MNF ，所以MFN ∠为平面MOF与平面AFB 所成的二面角的平面角，不妨设2AB =，因为060A，所以23BC =，则13,12OF BC OM ===，显然MFN ∠不等于45°，故C 错误. 设面MOF 与平面ABF 的交线为l ，又因为//,AB OM AB ⊄面MOF ，OM ⊂面MOF ，所以//AB 面MOF ，由线面平行的性质定理可得：//l AB ，故D 正确；故选：AD.【点睛】方法点睛：求直线与平面所成的角有两种方法：一是传统法，证明线面垂直找到直线与平面所成的角，利用平面几何知识解答；二是利用空间向量，求出直线的方向向量以及平面的方向向量，利用空间向量夹角余弦公式求解即可.3．在长方体1111ABCD A B C D -中，4AB BC ==，18AA =，点P 在线段11A C 上，M 为AB 的中点，则（） A ．BD ⊥平面PACB ．当P 为11AC 的中点时，四棱锥P ABCD -外接球半径为72C ．三棱锥A PCD -体积为定值D ．过点M 作长方体1111ABCD A B C D -的外接球截面，所得截面圆的面积的最小值为4π 【答案】ACD 【分析】利用线面垂直的判定定理可判断A 选项的正误；判断出四棱锥P ABCD -为正四棱锥，求出该四棱锥的外接球半径，可判断B 选项的正误；利用等体积法可判断C 选项的正误；计算出截面圆半径的最小值，求出截面圆面积的最小值，可判断D 选项的正误. 【详解】对于A 选项，因为AB BC =，所以，矩形ABCD 为正方形，所以，BD AC ⊥，在长方体1111ABCD A B C D -中，1AA ⊥底面ABCD ，BD ⊂平面ABCD ，1BD AA ∴⊥，1AC AA A ⋂=，AC 、1AA ⊂平面PAC ，所以，BD ⊥平面PAC ，A 选项正确；对于B 选项，当点P 为11A C 的中点时，()22221182262PA AA PA =+=+=同理可得PB PC PD ===因为四边形ABCD 为正方形，所以，四棱锥P ABCD -为正四棱锥，取AC 的中点N ，则PN 平面ABCD ，且四棱锥P ABCD -的外接球球心在直线PN上，设该四棱锥的外接球半径为R ，由几何关系可得222PN R AN R -+=，即2288R R -+=，解得92R =，B 选项错误；对于C 选项，2114822ACDSAD CD =⋅=⨯=，三棱锥P ACD -的高为18AA =，因此，116433A PCD P ACD ACD V V S AA --==⋅=△，C 选项正确；对于D 选项，设长方体1111ABCD A B C D -的外接球球心为E ，则E 为1BD 的中点，连接EN 、MN ，则1142EN DD ==，122MN AD ==， E 、N 分别为1BD 、BD 的中点，则1//EN DD ， 1DD ⊥平面ABCD ，EN ∴⊥平面ABCD ，MN ⊂平面ABCD ，EN MN ∴⊥，EM ∴==过点M 作长方体1111ABCD A B C D -的外接球截面为平面α，点E 到平面α的距离为d ，直线EM 与平面α所成的角为θ，则sin d EM θθ==≤ 当且仅当2πθ=时，等号成立，长方体1111ABCD A B C D -的外接球半径为R '==，所以，截面圆的半径2r =≥=，因此，截面圆面积的最小值为4π，D 选项正确.故选：ACD. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.4．如图，已知正方体1ABCD ABC D -的棱长为a ，E 是棱CD 上的动点.则下列结论中正确的有（）A ．11EB AD ⊥B ．二面角11E A B A --的大小为4π C ．三棱锥11A B D E -体积的最小值为313a D ．1//D E 平面11A B BA 【答案】ABD 【分析】连接1A D 、1B C ，则易证1AD ⊥平面11A DCB ，1EB ⊂平面11A DCB ，则由线面垂直的性质定理可以判断选项A 正确；二面角11E A B A --的平面角为1DA A ∠，易知14DA A π∠=，则可判断选项B 正确；用等体积法，将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积，当点E 与D 重合时，三棱锥11E AB D -的体积最小，此时的值为316a ，则选项C 错误；易知平面11//D DCC 平面11A B BA ，而1D E ⊂平面11D DCC ，则根据面面平行的性质定理可得1//D E 平面11A B BA ，可判断选项D 正确. 【详解】选项A ，连接1A D 、1B C ，则由正方体1ABCD ABC D -可知，11A D AD ⊥，111A B AD ⊥，1111A DA B A =，则1AD ⊥平面11A DCB ，又因为1EB ⊂平面11A DCB ，所以11EB AD ⊥，选项A 正确；选项B ，因为11//DE A B ，则二面角11E A B A --即为二面角11D A B A --，由正方体1ABCD ABC D -可知，11A B ⊥平面1DA A ，则1DA A ∠为二面角11D A B A --的平面角，且14DA A π∠=，所以选项B 正确；选项C ，设点E 到平面11AB D 的距离为d ，则11111113A B D E E AB D AB D V V S d --==⋅，连接1C D 、1C B ，易证平面1//BDC 平面11AB D ，则在棱CD 上，点D 到平面11AB D 的距离最短，即点E 与D 重合时，三棱锥11A B D E -的体积最小，由正方体1ABCD ABC D -知11A B ⊥平面1ADD ，所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=，则选项C 错误；选项D ，由正方体1ABCD ABC D -知，平面11//CC D D 平面11A B BA ，且1D E ⊂平面11CC D D ，则由面面平行的性质定理可知1//D E 平面11A B BA ，则选项D 正确. 故选：ABD. 【点睛】关键点点睛：本题对于选项C 的判断中，利用等体积法求三棱锥的体积是解题的关键.5．已知四面体ABCD 的所有棱长均为2，则下列结论正确的是（） A ．异面直线AC 与BD 所成角为60︒B ．点A 到平面BCDC ．四面体ABCDD ．动点P 在平面BCD 上，且AP 与AC 所成角为60︒，则点P 的轨迹是椭圆【答案】BC 【分析】在正四面体中通过线面垂直可证得AC ⊥BD ，通过计算可验证BC,通过轨迹法可求得P 的轨迹为双曲线方程即可得D 错误. 【详解】取BD 中点E ,连接,AE CE ,可得BD ⊥面ACE ,则AC ⊥BD ,故A 错误；在四面体ABCD 中，过点A 作AF ⊥面BCD 于点F ,则F 为为底面正三角形BCD 的重心，因为所有棱长均为2,AF ==即点A 到平面BCD 的距离为3,故B 正确；设O 为正四面体的中心则OF 为内切球的半径，OA 我外接球的半径，因为11433A BCD BCD BCD V S AF S OF -=⋅=⨯⋅△△，所以4AF OF =，即2=6OF AO =,所以四面体ABCD 的外接球体积334433V R OA ππ===,故C 正确；建系如图：26230,0,,0,,0A C ⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,设(,,0)P x y ，则262326,,0,,333AP x y AC →→⎛⎫⎛⎫=-=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，因为cos 60AP AC AP AC →→→→⋅=，所以22232481224193972y x y +=++⨯+⨯，即222388=33y x y +++，平方化简可得：2232340039y x y ----，可知点P 的轨迹为双曲线,故D 错误. 故选：BC ．【点睛】方法点睛：立体几何中动点轨迹的求解问题，解决此类问题可采用空间向量法，利用空间向量法表示出已知的角度或距离的等量关系，从而得到轨迹方程.6．（多选题）如图所示，正方体1111ABCD A B C D -中，1AB =，点P 在侧面11BCC B 及其边界上运动，并且总是保持1AP BD ⊥，则以下四个结论正确的是（）A ．113P AA D V -=B ．点P 必在线段1BC 上C ．1AP BC ⊥D ．AP ∥平面11AC D【答案】BD 【分析】对于A ，1111111113326P AA D AA DV S CD -=⋅=⨯⨯⨯⨯=，对于B,C,D ，如图以D 为坐标原点可建立空间直角坐标系，利用空间向量判即可. 【详解】对于A ，因为点P 在平面11BCC B ，平面11BCC B ∥平面1AA D ，所以点P 到平面1AA D 即为C 到平面1AA D 的距离，即为正方体棱长，所以1111111113326P AA D AA DV S CD -=⋅=⨯⨯⨯⨯=，A 错误；对于B ，以D 为坐标原点可建立如下图所示的空间直角坐标系：则11(1,0,0),(,1,),(1,1,0),(0,0,1),(1,1,1),(0,1,0)A P x z B D B C 所以11(1,1,),(1,1,1),(1,0,1)AP x z BD BC =-=--=--, 因为1AP BD ⊥，所以1110AP BD x z ⋅=--+=，所以x z =，即(,1,)P x x ，所以(,0,)CP x x =,所以1CP xBC =-，即1,,B C P 三点共线，所以点P 必在线段1B C 上，B 正确；对于C ，因为1(1,1,),(1,0,1)AP x x BC =-=-，所以111AP BC x x ⋅=-+=，所以1AP BC ⊥不成立，C 错误；对于D ，因为11(1,0,1),(0,1,1),(0,0,0)A C D , 所以11(1,0,1),(0,1,1)DA DC ==, 设平面11AC D 的法向量为(,,)n x y z =，则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，令1x =，则1,1z y =-=，所以(1,1,1)n =-，所以110AP n x x ⋅=-+-=，所以AP n ⊥，所以AP ∥平面11AC D ，D 正确，故选：BD【点睛】此题考查了空间线线垂直的判定，线面平行的判定，三棱锥的体积，考查空间想象能力，考查计算能力，属于较难题.7．（多选题）在四面体P ABC -中，以上说法正确的有（）A ．若1233AD AC AB =+，则可知3BC BD = B ．若Q 为△ABC 的重心，则111333PQ PA PB PC =++ C ．若0PA BC =，0PC AB =，则0PB AC =D ．若四面体P ABC -各棱长都为2，M N ，分别为,PA BC 的中点，则1MN =【答案】ABC【分析】作出四面体P ABC -直观图，在每个三角形中利用向量的线性运算可得.【详解】对于A ，1233AD AC AB =+，32AD AC AB ∴=+，22AD AB AC AD ∴-=- ， 2BD DC ∴=，3BD BD DC BC ∴=+=即3BD BC ∴=，故A 正确；对于B ，Q 为△ABC 的重心，则0QA QB QC ++=，33PQ QA QB QC PQ ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++= 即111333PQ PA PB PC ∴=++，故B 正确；对于C ，若0PA BC =，0PC AB =，则0PA BC PC AB +=，()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+=0CA BC PC AC ∴+=,0AC CB PC AC ∴+=()0AC PC CB ∴+=，0AC PB ∴=，故C 正确；对于D ，111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+22211122222222222222222=++-⨯⨯⨯-⨯⨯⨯+⨯⨯⨯= 2MN ∴=，故D 错误.故选：ABC【点睛】用已知向量表示某一向量的三个关键点(1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量．(3)在立体几何中三角形法则、平行四边形法则仍然成立．8．如图，线段AB 为圆O 的直径，点E ，F 在圆O 上，//EF AB ，矩形ABCD 所在平面和圆O 所在平面垂直，且2AB =，1EF AD ==，则下述正确的是（）A ．//OF 平面BCEB ．BF ⊥平面ADFC ．点A 到平面CDFE 的距离为7D ．三棱锥C BEF -【答案】ABC【分析】由1EF OB ==，//EF OB ，易证//OF 平面BCE ，A 正确；B ，由所矩形ABCD 所在平面和圆O 所在平面垂直，易证AD ⊥平面ABEF ，所以AD BF ⊥，由线段AB 为圆O 的直径，所以BF FA ⊥，易证故B 正确.C ，由C DAF A CDF V V --=可求点A 到平面CDFE ，C 正确.D ，确定线段DB 的中点M 是三棱锥C BEF -外接球心，进一步可求其体积，可判断D 错误.【详解】解：1EF OB ==，//EF OB ，四边形OFEB 为平行四边形，所以//OF BE ， OF ⊄平面BCE ，BE ⊂平面BCE ，所以//OF 平面BCE ，故A 正确.线段AB 为圆O 的直径，所以BF FA ⊥，矩形ABCD 所在平面和圆O 所在平面垂直，平面ABCD平面ABEF AB =，AD ⊂平面 ABCD ，所以AD ⊥平面ABEF ，BF ⊂平面ABEF ，所以AD BF ⊥AD ⊂平面ADF ，AF ⊂平面ADF ，AD AF A =，所以BF ⊥平面ADF ，故B 正确.1OF OE EF ===，OFE △是正三角形，所以1EF BE AF ===，//DA BC ，所以BC ⊥平面ABEF ，BC BF ⊥，BF =2CF ==，DF ===2AB CD ==，CDF 是等腰三角形，CDF 的边DF 上的高2==，122CDF S =⨯=△ //DA BC ，AD ⊂平面ADF ，BC ⊄平面ADF ，//BC 平面ADF ，点C 到平面ADF 的距离为BF =111122DAF S =⨯⨯=△，C DAF A CDF V V --=，设点A 到平面CDFE 的距离为h ，1133ADF CFD S FB S h ⨯⨯=⨯⨯△△，111733232h ⨯⨯=⨯⨯，所以21h =，故C 正确. 取DB 的中点M ，则//MO AD ，12MO =，所以MO ⊥平面CDFE ，所以215122ME MF MB MC ⎛⎫====+= ⎪⎝⎭所以M 是三棱锥C BEF -5，三棱锥C BEF -外接球的体积为33445553326V r ππ⎛==⨯= ⎝⎭，故D 错误，故选：ABC.【点睛】综合考查线面平行与垂直的判断，求点面距离以及三棱锥的外接球的体积求法，难题.9．在边长为2的等边三角形ABC 中，点,D E 分别是边,AC AB 上的点，满足//DE BC 且ADAC λ=，（()01λ∈，），将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中，下列结论不成立的是（）A ．在边A E '上存在点F ，使得在翻折过程中，满足//BF 平面A CD 'B ．存在102λ∈⎛⎫ ⎪⎝⎭,，使得在翻折过程中的某个位置，满足平面A BC '⊥平面BCDE C ．若12λ=，当二面角A DE B '--为直二面角时，||10A B '= D ．在翻折过程中，四棱锥A BCDE '-体积的最大值记为()fλ，()f λ23【答案】ABC【分析】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，即可判断出结论.对于B ，102λ∈⎛⎫ ⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，即可判断出结论.对于C ，12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，可得AM ⊥平面BCDE .可得22A B AM BM '=+，结合余弦定理即可得出.对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-，()01λ∈，，利用导数研究函数的单调性即可得出. 【详解】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，如图所示，则可得FN 平行且等于BG ，即四边形BGNF 为平行四边形，∴//NG BE ，而GN 始终与平面ACD 相交，因此在边A E '上不存在点F ，使得在翻折过程中，满足//BF 平面A CD '，A 不正确.对于B ，102λ∈⎛⎫ ⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，因此不满足平面A BC '⊥平面BCDE ，因此B 不正确.对于C.12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，如图所示：可得AM ⊥平面BCDE ，则22223111010()1()21cos120222A B AM BM '=+=++-⨯⨯⨯︒=≠，因此C 不正确；对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅⋅=-，()01λ∈，，()213f λλ'=-，可得33λ=时，函数()f λ取得最大值()312313f λ⎛⎫=-= ⎪⎝⎭，因此D 正确. 综上所述，不成立的为ABC.故选：ABC.【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值，考查了推理能力空间想象能力与计算能力，属于难题.10．如图，1111ABCD A B C D -为正方体，下列结论中正确的是（）A ．11A C ⊥平面11BB D DB ．1BD ⊥平面1ACBC ．1BD 与底面11BCC B 2D ．过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD【分析】由直线与平面垂直的判定判断A 与B ；求解1BD 与底面11BCC B 所成角的正切值判断C ；利用空间向量法可判断D ．【详解】对于A 选项，如图，在正方体1111ABCD A B C D -中，1BB ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111BB A C ⊥，由于四边形1111D C B A 为正方形，则1111AC B D ⊥，1111BB B D B =，因此，11A C ⊥平面11BB D D ，故A 正确；对于B 选项，在正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ，1AC DD ∴⊥，因为四边形ABCD 为正方形，所以，AC BD ⊥，1D DD BD =，AC ∴⊥平面11BB D D ，1BD ⊂平面11BB D D ，1AC BD ∴⊥，同理可得11BD B C ⊥， 1ACB C C =，1BD ∴⊥平面1ACB ，故B 正确；对于C 选项，由11C D ⊥平面11BCC B ，得11C BD ∠为1BD 与平面11BCC B 所成角，且111112tan 2C D C BD BC ∠==，故C 错误；对于D 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，设正方体的棱长为1，则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ，()1,0,0DA =，()11,0,1CB =，设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =，则221cos ,21DA mDA m DA m y z ⋅<>===⋅++， 1122111cos ,221CB m z CB m CB m y z ⋅+<>===⋅⋅++，整理可得2222341y z y z z ⎧+=⎨=++⎩，消去y 并整理得2210z z +-=，解得12z =-12z =-由已知可得3z ≤，所以，12z =-+22y =±因此，过点1A 与异面直线AD 与1CB 成60角的直线有2条，D 选项正确.故选：ABD.【点睛】方法点睛：证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．。

立几专题(三视图)

立体几何专题复习(三视图)知识梳理1.三视图：正俯视图长对正、正侧视图高平齐、俯侧视图宽相等.2.直观图:已知图形中平行于x 轴和z 轴的线段,在直观图中保持长度不变,平行于y 轴的线段平行性不变,但在直观图中其长度为原来的一半.3.体积与表面积公式:(1)柱体的体积公式:V =柱Sh ;锥体的体积公式: V =锥13Sh ; 台体的体积公式: V =棱台1()3h S S '+;球的体积公式: V =球343r π. (2)球的表面积公式: 24S R π=球.4.有关球与正方体、长方体、圆柱、圆锥、圆台的结合体问题，要抓住球的直径与这些几何体的有关元素的关系.典例分析考点一三视图及其还原例1．【2102福建文4】一个几何体的三视图形状都相同，大小均等，则几何体不可以是（） A 球 B 三棱锥 C 正方体 D 圆柱变式1.一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为．．．．( ) ．． ①长方形；②正方形；③圆；④椭圆.其中正确的是 A ．①② B ． ②③ C ．③④ D ． ①④变式2.【2012.．可能．．是( )变式 3.（2011年高考江西卷文科9)将长方体截去一个四棱锥，得到的几何体如右图所示，则该几何体的左视图为（）考点二直观图(斜二测法)例2．已知矩形如图所示,请利用斜二测法作出其直观图.变式练习. 如下图所示，直观图///B A O 是有一个角为045的三角形，则其原平面图形的面积为________.考点三表面积与体积例3.【2012高考安徽文】某几何体的三视图如图所示，则该几何体的体积等于______。

变式练习1.【2012高考辽宁文】一个几何体的三视图如图所示，则该几何体的体积为_______________.变式练习2.(2008广东文数)已知某几何体的俯视图是如图5所示的矩形，正视图(或称主视图)是一个底边长为8、高为4的等腰三角形，侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形．(1)求该几何体的体积V ； (2)求该几何体的侧面积S ．考点四几何组合体的面积与体积问题例4. 右图是底面半径为1，母线长均为2的圆锥和圆柱的组合体，则该组合体的侧视图的面积为（）A ．B ．C ．D ．变式练习.如下图为一个几何体的三视图，尺寸如图所示，则该几何体的表面积为（不考虑接触点）( ) A. 6+3+πB. 18+3+π4 C. 18+23+π D. 32+π课堂检测1.【2012高考上海文5】一个高为2的圆柱，底面周长为2π，该圆柱的表面积为2. —个几何体的三视图及其尺寸如下(左)，则该几何体的表面积( ) A.B.C.D.3.右上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是_________4．如图是某几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是．8π6π42正视图侧视图俯视图正视图俯视图侧视图5.若某几何体的三视图（单位：），如图所示，则此几何体的体积是．6.平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为 ( )（A ）6π （B ）43π （C ）46π （D ）63π7.【2012高考湖北文】已知某几何体的三视图如图所示，则该几何体的体积为____________.8.(2010广东)某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P －EFGH,下半部分是长方体ABCD －EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图. （1）请画出该安全标识墩的侧(左)视图;（2）求该安全标识墩的体积cm 3cm。

立体几何复习专题及答案-高中数学

立体几何复习专题姓名：班级：考点一、空间中的平行关系1．如图，在三棱锥P ABC -中，02,3,90PA PB AB BC ABC ====∠=,平面PAB ⊥平面ABC ，D 、E 分别为AB 、AC 的中点． (1)求证：DE //平面PBC ； (2)求证：AB PE ⊥；(3)求三棱锥B PEC -的体积．2．如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形，PCD △为等边三角形，平面PAC ⊥平面PCD ，PA CD ⊥，2CD =，3AD =，（Ⅰ）设G H ，分别为PB AC ，的中点，求证：GH ∥平面PAD ；（Ⅱ）求证：PA ⊥平面PCD ；3．如图，七面体ABCDEF 的底面是凸四边形ABCD ，其中2AB AD ==，120BAD ∠=︒，AC ，BD 垂直相交于点O ，2OC OA =，棱AE ，CF 均垂直于底面ABCD .（1）证明：直线DE 与平面BCF 不．平行；4.（2014新课标Ⅱ）如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点．（Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D AE C --为60°，AP =1，AD =3，求三棱锥E ACD -的体积．考点二、空间中的垂直关系5．如图，在四面体ABCD 中，E ，F 分别是线段AD ，BD 的中点，90ABD BCD ∠=∠=，2EC =，2AB BD ==，直线EC 与平面ABC 所成的角等于30．（1）证明：平面EFC ⊥平面BCD ；6．已知某几何体的直观图和三视图如下图所示，其中正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．（1）求证：BN ⊥平面11C B N ；（2）设M 为AB 中点，在C B 边上求一点P ，使//MP 平面1C NB ，求CBPP 的值．7．（2016全国I ）如图，在以A ，B ，C ，D ，E ，F 为顶点的五面体中，面ABEF为正方形，2AF FD =，90AFD ∠=，且二面角D AF E --与二面角C BE F --都是60．（I ）证明：平面ABEF⊥平面EFDC ；（II ）求二面角E BC A --的余弦值．考点三、折叠问题和探究性问题中的位置关系8．如图 1，在直角梯形ABCD 中， //,AB CD AB AD ⊥，且112AB AD CD ===．现以AD 为一边向外作正方形ADEF ，然后沿边AD 将正方形ADEF 翻折，使ADEF 平面与平面ABCD 垂直， M 为ED 的中点，如图 2．（1）求证： //AM 平面BEC ；（2）求证： BC ⊥平面BDE ； .9．如图，在边长为4的正方形ABCD 中，点E,F 分别是AB,BC 的中点，点M 在AD 上，且14AM AD =，将AED,DCF 分别沿DE,DF 折叠，使A,C 点重合于点P ，如图所示2.()1试判断PB 与平面MEF的位置关系，并给出证明；()2求二面角M EF D --的余弦值.10．如图所示，直角梯形ABCD 中，//AD BC ，AD AB ⊥，22AB BC AD ===，四边形EDCF 为矩形，3CF =，平面EDCF ⊥平面ABCD ． (1)求证：DF //平面ABE ；(2)求平面ABE 与平面EFB 所成锐二面角的余弦值． (3)在线段DF 上是否存在点P ，使得直线BP 与平面ABE 所成角的正弦值为34，若存在，求出线段BP 的长，若不存在，请说明理由．11．如图1，在边长为4的正方形ABCD中，E是AD的中点，F是CD的中点，现-.将三角形DEF沿EF翻折成如图2所示的五棱锥P ABCFE（1）求证：AC//平面PEF；（2）若平面PEF⊥平面ABCFE，求直线PB与平面PAE所成角的正弦值.12．（2011•浙江）如图，在三棱锥P﹣ABC中，AB=AC，D为BC的中点，PO⊥平面ABC，垂足O落在线段AD上，已知BC=8，PO=4，AO=3，OD=2（1）证明：AP⊥BC；（2）在线段AP上是否存在点M，使得二面角A﹣MC﹣β为直二面角？若存在，求出AM的长；若不存在，请说明理由．13．如图，在直三棱柱111ABC A B C -中，底面ABC 为等边三角形，122CC AC ==.（Ⅰ）求三棱锥11C CB A -的体积；（Ⅱ）在线段1BB 上寻找一点F ，使得1CF AC ⊥，请说明作法和理由.考点四、知空间角求空间角问题14．（2014天津）如图四棱锥P ABCD -的底面ABCD 是平行四边形，2BA BD ==2AD =,5PA PD ==E ,F 分别是棱AD ,PC 的中点．（Ⅰ）证明: EF ∥平面PAB ；（Ⅱ）若二面角P AD B --为60°，（ⅰ）证明：平面PBC ⊥平面ABCD（ⅱ）求直线EF 与平面PBC 所成角的正弦值． PCDBF15．四棱锥P ABCD -中，底面ABCD 为矩形，PA ABCD ⊥平面，E 为PD 的中点．(1)证明：//E PB A C 平面；(2)设13AP AD ==，，三棱锥P ABD -的体积34V =，求二面角D -AE -C 的大小16．如图，四棱锥P ABCD -中， PA ⊥底面ABCD ，底面ABCD 是直角梯形，90ADC ∠=︒， //AD BC ， AB AC ⊥， 2AB AC ==，点E 在AD 上，且2AE ED =．（Ⅰ）已知点F 在BC 上，且2=CF FB ，求证：平面PEF ⊥平面PAC ；（Ⅱ）当二面角--A PB E 的余弦值为多少时，直线PC 与平面PAB 所成的角为45︒？立体几何专题参考答案1． (1)证明：∵在△ABC 中，D 、E 分别为AB 、AC 的中点，∴DE ∥BC . ∵DE ⊄平面PBC 且BC ⊂平面PBC ，∴DE ∥平面PBC . (2)证明：连接PD .∵PA ＝PB ，D 为AB 的中点，∴PD ⊥AB .∵DE ∥BC ，BC ⊥AB ，∴DE ⊥AB .又∵PD 、DE 是平面PDE 内的相交直线， ∴AB ⊥平面PDE .∵PE ⊂平面PDE ，∴AB ⊥PE .(3)解：∵PD ⊥AB ，平面PAB ⊥平面ABC ，平面PAB ∩平面ABC ＝AB ，∴PD ⊥平面ABC ，可得PD 是三棱锥P －BEC 的高．又∵33,2BECPD S==，1332B PEC P BEC BEC V V S PD --∆∴==⨯=. 2．（I ）见解析；（II ）见解析；（III ）33. （I ）证明：连接BD ，易知AC BD H ⋂=，BH DH =，又由BG PG =，故GHPD ，又因为GH ⊄平面PAD ，PD ⊂平面PAD ，所以GH ∥平面PAD .（II ）证明：取棱PC 的中点N ，连接DN ，依题意，得DN PC ⊥，又因为平面PAC ⊥平面PCD ，平面PAC平面PCD PC =，所以DN ⊥平面PAC ，又PA ⊂平面PAC ，故DN PA ⊥，又已知PA CD ⊥，CD DN D =，所以PA ⊥平面PCD . 3．（1）见解析；（2）23535本卷由系统自动生成，请仔细校对后使用，答案仅供参考。

福建省永春县第一中学高中数学立体几何多选题专题复习含解析

福建省永春县第一中学高中数学立体几何多选题专题复习含解析一、立体几何多选题1．在棱长为1的正方体1111ABCD A B C D -中，P 为底面ABCD 内（含边界）一点．（） A ．若13A P =，则满足条件的P 点有且只有一个 B ．若12A P =，则点P 的轨迹是一段圆弧 C ．若1//A P 平面11B D C ，则1A P 长的最小值为2D ．若12A P =且1//A P 平面11B DC ，则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ，B 可利用球的截面小圆的半径来判断；由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD 上，1A P 长的最大值为2；结合以上条件点P 与B 或D 重合，利用12sin 60A P r =︒，求出63r =，进而求出面积. 【详解】对A 选项，如下图：由13A P =，知点P 在以1A 为球心，半径为3的球上，又因为P 在底面ABCD 内（含边界），底面截球可得一个小圆，由1A A ⊥底面ABCD ，知点P 的轨迹是在底面上以A 为圆心的小圆圆弧，半径为22112r A P A A =-=，则只有唯一一点C满足，故A 正确；对B 选项，同理可得点P 在以A 为圆心，半径为22111r A P A A =-=的小圆圆弧上，在底面ABCD 内（含边界）中，可得点P 轨迹为四分之一圆弧BD .故B 正确；对C 选项，移动点P 可得两相交的动直线与平面11B D C 平行，则点P 必在过1A 且与平面11B D C 平行的平面内，由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD上，则1A P 长的最大值为12A B =，则C 不正确；对选项D ，由以上推理可知，点P 既在以A 为圆心，半径为1的小圆圆弧上，又在线段BD 上，即与B 或D 重合，不妨取点B ，则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆，利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选：ABD 【点睛】（1）平面截球所得截面为圆面，且满足222=R r d +（其中R 为球半径，r 为小圆半径，d 为球心到小圆距离）；（2）过定点A 的动直线平行一平面α，则这些动直线都在过A 且与α平行的平面内.2．如图，在棱长为2的正方体1111ABCD A B C D -，中，E 为棱1CC 上的中点，F 为棱1AA 上的点，且满足1:1:2A F FA =，点F ，B ，E ，G ，H 为过三点B ，E ，F 的平面BMN 与正方体1111ABCD A B C D -的棱的交点，则下列说法正确的是（）A ．//HF BEB ．三棱锥的体积14B BMN V -=C ．直线MN 与平面11A B BA 所成的角为45︒D ．11:1:3D G GC = 【答案】ABD 【分析】面面平行性质定理可得出A 正确；等体积法求得B 正确；直线MN 与平面11A B BA 所成的角为1B MN ∠，求其正切值不等于1即可得出C 错误；利用面面平行性质定理和中位线求出11,D G GC 长度即可得出D 正确. 【详解】解：对于A.在正方体1111ABCD A B C D -中平面11//ADA D 平面11BCB C ，又平面11ADA D 平面BMN HF =，平面11BCB C ⋂平面BMN BE =，有平面与平面平行的性质定理可得//HF BE ，故正确；对于B.因为1:1:2A F FA =，所以111332B M A B ==，又E 为棱1CC 上的中点，所以14B N =, 所以1111234432B BMN N B BM V V --⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭，故正确；对于C.由题意及图形可判定直线MN 与平面11A B BA 所成的角为1B MN ∠，结合B 选项可得1114tan 13B N B MN B M ∠==≠，故错误；对于D.同A 选项证明方法一样可证的11//GC B M ，因为E 为棱1CC 上的中点，1C 为棱1B N 上的中点，所以1113=22GC B M = 所以11G=2D ，所以11:1:3D G GC =，故正确. 故选：ABD 【点睛】求体积的常用方法：（1）直接法：对于规则的几何体，利用相关公式直接计算；（2）等体积法：选择合适的底面来求几何体体积，常用于求三棱锥的体积，即利用三棱锥的任一个面可作为三棱锥的底面进行等体积变换；（3）割补法：首先把不规则的几何体分割成规则的几何体，然后进行体积计算；或者把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体，便于计算.3．在长方体1111ABCD A B C D -中，AB =12AD AA ==，P 、Q 、R 分别是AB 、1BB 、1A C 上的动点，下列结论正确的是（）A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥C ．当1AR A C ⊥时，1ARD R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系，再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示，建立空间直角坐标系，设(2,,0)P a，0a ⎡∈⎣，(2,)Q b ，[]0,2b ∈，设11A R AC λ=，得到(22,,22)R λλ--，[]0,1λ∈. 1(2,,2)D P a =-，(2,0,)CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；1(22,2)D R λλ=--，12(22)2D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确；1AR A C ⊥，则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=，解得：15λ=，此时12282()()05555AR D R ---⋅=⋅=，1AR D R ⊥，C 正确；113AC A R =，则44(,)333R，142(,)333D R =-，设平面1BDC 的法向量为(,,)n x y z =，则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,n =-，故10n D R ⋅=，故1//D R 平面1BDC ，D 正确.故选：ABCD.【点睛】本题考查了空间向量在立体几何中的应用，是偏难题.4．（多选题）如图所示，正方体1111ABCD A B C D -中，1AB =，点P 在侧面11BCC B 及其边界上运动，并且总是保持1AP BD ⊥，则以下四个结论正确的是（）A ．113P AA D V -=B ．点P 必在线段1BC 上 C ．1AP BC ⊥D ．AP ∥平面11AC D【答案】BD 【分析】对于A ，1111111113326P AA D AA DV S CD -=⋅=⨯⨯⨯⨯=，对于B,C,D ，如图以D 为坐标原点可建立空间直角坐标系，利用空间向量判即可. 【详解】对于A ，因为点P 在平面11BCC B ，平面11BCC B ∥平面1AA D ，所以点P 到平面1AA D 即为C 到平面1AA D 的距离，即为正方体棱长，所以1111111113326P AA D AA DV S CD -=⋅=⨯⨯⨯⨯=，A 错误；对于B ，以D 为坐标原点可建立如下图所示的空间直角坐标系：则11(1,0,0),(,1,),(1,1,0),(0,0,1),(1,1,1),(0,1,0)A P x z B D B C 所以11(1,1,),(1,1,1),(1,0,1)AP x z BD BC =-=--=--, 因为1AP BD ⊥，所以1110AP BD x z ⋅=--+=，所以x z =，即(,1,)P x x ，所以(,0,)CP x x =,所以1CP xBC =-，即1,,B C P 三点共线，所以点P 必在线段1B C 上，B 正确；对于C ，因为1(1,1,),(1,0,1)AP x x BC =-=-，所以111AP BC x x ⋅=-+=，所以1AP BC ⊥不成立，C 错误；对于D ，因为11(1,0,1),(0,1,1),(0,0,0)A C D , 所以11(1,0,1),(0,1,1)DA DC ==, 设平面11AC D 的法向量为(,,)n x y z =，则1100n DA x z n DC y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩，令1x =，则1,1z y =-=，所以(1,1,1)n =-，所以110AP n x x ⋅=-+-=，所以AP n ⊥，所以AP ∥平面11AC D ，D 正确，故选：BD 【点睛】此题考查了空间线线垂直的判定，线面平行的判定，三棱锥的体积，考查空间想象能力，考查计算能力，属于较难题.5．如图，正方体1111ABCD A B C D -的棱长为1，线段11B D 上有两个动点E ，F ，且22EF =.则下列结论正确的是（）A ．三棱锥A BEF -的体积为定值B ．当E 向1D 运动时，二面角A EF B --逐渐变小C ．EF 在平面11ABB A 内的射影长为12D ．当E 与1D 重合时，异面直线AE 与BF 所成的角为π4【答案】AC 【分析】对选项分别作图，研究计算可得. 【详解】选项A:连接BD ,由正方体性质知11BDD B 是矩形，1112212224BEF S EF BB ∆∴=⋅=⨯=连接AO 交BD 于点O由正方体性质知AO ⊥平面11BDD B ,所以，AO 是点A 到平面11BDD B 的距离，即22AO =112213312A BEF BEF V S AO -∆∴=⨯==A BEF V -∴是定值.选项B:连接11A C 与11B D 交于点M ，连接11,AD AB ，由正方体性质知11AD AB =,M 是11B D 中点，AM EF ∴⊥ ,又1BB EF ⊥,11//BB AAA EFB ∴--的大小即为AM 与1AA 所成的角，在直角三角形1AA M 中，12tan 2MAA ∠=为定值. 选项C:如图，作1111,,,FH A B EG A B ET EG ⊥⊥⊥ 在直角三角形EFT 中，221cos 452FT EF =⨯=⨯=12HG FT ∴== 选项D:当E 与1D 重合时，F 与M 重合，连接AC 与BD 交于点R ，连接1D R ,1//D R BM 异面直线AE 与BF 所成的角,即为异面直线1AD 与1D R 所成的角, 在三角形1AD R 中，22111132,2AD D R MB BB M B ===+=2AR =由余弦定理得1cos AD R ∠= 故选：AC 【点睛】本题考查空间几何体性质问题.求解思路：关键是弄清(1)点的变化，点与点的重合及点的位置变化；(2)线的变化，应注意其位置关系的变化；(3)长度、角度等几何度量的变化．求空间几何体体积的思路：若所给定的几何体是柱体、锥体或台体等规则几何体，则可直接利用公式进行求解．其中，求三棱锥的体积常用等体积转换法；若所给定的几何体是不规则几何体，则将不规则的几何体通过分割或补形转化为规则几何体，再利用公式求解.6．在边长为2的等边三角形ABC 中，点,D E 分别是边,AC AB 上的点，满足//DE BC 且AD ACλ=，（()01λ∈，），将ADE 沿直线DE 折到A DE '△的位置.在翻折过程中，下列结论不成立的是（）A ．在边A E '上存在点F ，使得在翻折过程中，满足//BF 平面A CD 'B ．存在102λ∈⎛⎫⎪⎝⎭,，使得在翻折过程中的某个位置，满足平面A BC '⊥平面BCDEC ．若12λ=，当二面角A DE B '--为直二面角时，||A B '=D ．在翻折过程中，四棱锥A BCDE '-体积的最大值记为()f λ，()f λ【答案】ABC 【分析】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，即可判断出结论.对于B ，102λ∈⎛⎫ ⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，即可判断出结论. 对于C ，12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，可得AM ⊥平面BCDE .可得A B '=.对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()313BCDE f S λλλ=⋅=-，()01λ∈，，利用导数研究函数的单调性即可得出.【详解】对于A.在边A E '上点F ，在A D '上取一点N ，使得//FN ED ，在ED 上取一点H ，使得//NH EF ，作//HG BE 交BC 于点G ，如图所示，则可得FN 平行且等于BG ，即四边形BGNF 为平行四边形， ∴//NG BE ，而GN 始终与平面ACD 相交，因此在边A E '上不存在点F ，使得在翻折过程中，满足//BF 平面A CD '，A 不正确.对于B ，102λ∈⎛⎫⎪⎝⎭,，在翻折过程中，点A '在底面BCDE 的射影不可能在交线BC 上，因此不满足平面A BC '⊥平面BCDE ，因此B 不正确. 对于C.12λ=，当二面角A DE B '--为直二面角时，取ED 的中点M ，如图所示：可得AM ⊥平面BCDE ，则22223111010()1()21cos120222A B AM BM '=+=++-⨯⨯⨯︒=≠，因此C 不正确；对于D.在翻折过程中，取平面AED ⊥平面BCDE ，四棱锥A BCDE '-体积()3133BCDE f S λλλλ=⋅=-，()01λ∈，，()213f λλ'=-，可得3λ=()f λ取得最大值()31231339f λ⎛⎫=-=⎪⎝⎭，因此D 正确. 综上所述，不成立的为ABC. 故选：ABC. 【点睛】本题考查了利用运动的观点理解空间线面面面位置关系、四棱锥的体积计算公式、余弦定理、利用导数研究函数的单调性极值与最值，考查了推理能力空间想象能力与计算能力，属于难题.7．如图所示，在长方体1111ABCD A B C D -中，11,2,AB BC AA P ===是1A B 上的一动点，则下列选项正确的是( )A ．DP 35B ．DP 5C ．1AP PC +6D ．1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值，即求1DA B △底边1A B 上的高即可；旋转11A BC 所在平面到平面11ABB A ，1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值，即求1DA B △底边1A B 上的高，易知115,2A B A D BD ===，所以1A B 边上的高为355h =111,AC BC ，得11A BC ，以1A B 所在直线为轴，将11A BC 所在平面旋转到平面11ABB A ，设点1C 的新位置为C '，连接AC '，则AC '即为所求的最小值，易知11122,2,cos 10AA AC AAC ''==∠=-，所以217042222()105AC '=+-⨯⨯⨯-=.故选：AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否， (1)点的变化，点与点的重合及点的位置变化；(2)线的变化，翻折、旋转前后应注意其位置关系的变化；(3)长度、角度等几何度量的变化．8．在正方体1111ABCD A B C D -中，如图，,M N 分别是正方形ABCD ，11BCC B 的中心.则下列结论正确的是（）A ．平面1D MN 与11BC 的交点是11B C 的中点 B ．平面1D MN 与BC 的交点是BC 的三点分点 C ．平面1D MN 与AD 的交点是AD 的三等分点 D ．平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ，延长DE ，1D N ，并交于点F ，连FM 并延长分别交,BC AD 于,P Q ，连1,D Q PN 并延长交11B C 与H ，平面四边形1D HPQ 为所求的截面，进而求出,,P Q H 在各边的位置，利用割补法求出多面体11QPHD C CD 的体积，即可求出结论.【详解】如图，取BC 的中点E ，延长DE ，1D N ，并交于点F ，连接FM 并延长，设FM BC P ⋂=，FM AD Q ⋂=，连接PN 并延长交11B C 于点H .连接1D Q ，1D H ，则平面四边形1D HPQ 就是平面1D MN 与正方体的截面，如图所示.111111////,22NE CC DD NE CC DD ==，NE ∴为1DD F ∆的中位线，E ∴为DF 中点，连BF ， ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒， ,,A B F ∴三点共线，取AB 中点S ，连MS ，则12//,,23BP FB MS BP MS BC MS FS =∴==， 22111,33236BP MS BC BC PE BC ∴==⨯=∴=，E 为DF 中点，11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心，11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点，点Q 是线段AD 靠近点D 的三等分点，点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P '，做出线段11A D 靠近1D 的三等分点G ，连接QP '，HP '，QG ，GH ，1H QPP Q GHD V V '--=，所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积，确定出平面与正方体的交线是解题的关键，考查直观想象、逻辑推理能力，属于较难题.9．如图所示，在棱长为1的正方体1111ABCD A B C D -中，过对角线1BD 的一个平面交棱1AA 于点E ，交棱1CC 于点F ，得四边形1BFD E ，在以下结论中，正确的是（）A ．四边形1BFD E 有可能是梯形B ．四边形1BFD E 在底面ABCD 内的投影一定是正方形C ．四边形1BFDE 有可能垂直于平面11BB D DD ．四边形1BFDE 面积的最小值为6 【答案】BCD 【分析】四边形1BFD E 有两组对边分别平行知是一个平行四边形四边形；1BFD E 在底面ABCD 内的投影是四边形ABCD ；当与两条棱上的交点是中点时，四边形1BFD E 垂直于面11BB D D ；当E ，F 分别是两条棱的中点时，四边形1BFD E 的面积最小为62.【详解】过1BD 作平面与正方体1111ABCD A B C D -的截面为四边形1BFD E ，如图所示，因为平面11//ABB A 平面11DCC D ，且平面1BFD E 平面11ABB A BE =.平面1BFD E平面1111,//DCC D D F BE D F =，因此，同理1//D E BF ，故四边形1BFD E 为平行四边形，因此A 错误；对于选项B ，四边形1BFD E 在底面ABCD 内的投影一定是正方形ABCD ，因此B 正确；对于选项C ，当点E F 、分别为11,AA CC 的中点时，EF ⊥平面11BB D D ，又EF ⊂平面1BFD E ，则平面1BFD E ⊥平面11BB D D ，因此C 正确；对于选项D ，当F 点到线段1BD 的距离最小时，此时平行四边形1BFD E 的面积最小，此时点E F 、分别为11,AA CC 的中点，此时最小值为16232⨯⨯=，因此D 正确. 故选：BCD【点睛】关键点睛：解题的关键是理解想象出要画的平面是怎么样的平面，有哪些特殊的性质，考虑全面即可正确解题.10．如图，正四棱锥S －BCDE 底面边长与侧棱长均为a ，正三棱锥A －SBE 底面边长与侧棱长均为a ，则下列说法正确的是（）A ．AS ⊥CDB ．正四棱锥S －BCDE 的外接球半径为2a C ．正四棱锥S －BCDE 的内切球半径为212a ⎛⎫- ⎪ ⎪⎝⎭ D ．由正四棱锥S －BCDE 与正三棱锥A －SBE 拼成的多面体是一个三棱柱【答案】ABD 【分析】取BE 中点H ，证明BE ⊥平面SAH 即可证AS CD ⊥；设底面中心为1O ，有1122O B O S a ==，可求得球半径为22a ；用等体积法求内切球半径即可判断；由////SA DE BC 且==SA DE BC 可知多面体是一个三棱柱.【详解】如图所示：A 选项：取BE 中点H 连接,AH SH ，正三棱锥A SBE -中，,AH BE SH BE ⊥⊥ 又AHSH H =，所以BE ⊥平面SAH ，则BE AS ⊥，又//BE CD 所以AS CD ⊥ ，故A 正确；B 选项：设底面中心为1O ，球心为O 半径为R ，因为正四棱锥S －BCDE 外接球球心在1O S 上，所以OS OB R ==，因为，正四棱锥S －BCDE 底面边长与侧棱长均为a所以112O B O S ==，由()22211OB O B O S OS =+-得22222R a R ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭解得2R =，故B 正确； C 选项：设内切球半径为r，易求得侧面面积为221sin 23S a π=⋅=，由等体积法得222111432334a a a r a r ⋅=⋅+⋅⋅⋅解得4a r = ，故C 错；D 选项：取SE 中点F ，连结AF ，DF ，BF ，则BFD ∠和BFA ∠分别是D SE B --和A SE B --的二面角的平面角，由)22222221cos 2322BF DF BD BFD BF DF a ⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===-⋅⎛⎫⎪⎝⎭22222221cos 232a AF BF BA AFD AF BF ⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===⋅⎫⎪⎝⎭，故BFD ∠与BFA ∠互补，所以ASDE 共面，又因为AS AE ED SD ===，则ASDE 为平行四边形，故////AS ED BC 故正四棱锥S －BCDE 与正三棱锥A －SBE 拼成的多面体是一个三棱柱，所以D 正确故选：ABD 【点睛】求外接球半径的常用方法：（1）补形法：侧面为直角三角形或正四面体或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；（2）利用球的性质：几何体在不同面均对直角的棱必然是球的直径；（3）定义法：到各个顶点距离均相等的点为球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.。

立体几何专题复习(自己精心整理)

专题一证明平行垂直问题题型一证明平行关系(1）如图所示,在正方体ABCD－A1B1C1D1中，M，N分别是C1C，B1C1的中点．求证：MN∥平面A1BD。

（2）在正方体AC1中,M，N，E，F分别是A1B1，A1D1,B1C1，C1D1的中点，求证：平面AMN∥平面EFDB.思考题1（1）如图所示，平面PAD⊥平面ABCD，ABCD为正方形，△PAD是直角三角形，且PA＝AD＝2，E,F,G分别是线段PA,PD,CD的中点，求证：平面EFG∥平面PBC.（2)如图,在四面体A－BCD中，AD⊥平面BCD，BC⊥CD，AD＝2,BD＝22，M是AD的中点，P是BM的中点，点Q在线段AC上，且AQ＝3QC.求证：PQ∥平面BCD。

题型二证明垂直关系(微专题)微专题1:证明线线垂直(1）已知空间四边形OABC中，M为BC中点，N为AC中点，P为OA中点，Q为OB中点，若AB＝OC。

求证：PM⊥QN.（2)(2019·山西太原检测）如图,直三棱柱ABC－A1B1C1中，AA1＝AB＝AC＝1，E，F分别是CC1,BC的中点，AE⊥A1B1，D为棱A1B1上的点，求证:DF⊥AE。

微专题2：证明线面垂直（3）在正方体ABCD－A1B1C1D1中,求证:BD1⊥平面ACB1.(4)（2019·河南六市一模）在如图所示的几何体中，ABC－A1B1C1为三棱柱，且AA1⊥平面ABC，四边形ABCD为平行四边形，AD＝2CD，∠ADC＝60°.若AA1＝AC，求证：AC1⊥平面A1B1CD。

微专题3：证明面面垂直（5)已知正方体ABCD－A1B1C1D1中，E，F分别是BB1，CD的中点,求证:平面DEA⊥平面A1FD1.（6)如图，四边形ABCD为正方形,PD⊥平面ABCD，PD∥QA，QA＝AB＝错误!PD，求证:平面PQC⊥平面DCQ。

思考题2(1)(2019·北京东城区模拟)如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD,PD＝DC，E是PC的中点,作EF⊥BP交BP于点F，求证：PB⊥平面EFD。

立体几何平行垂直问题专题复习

立体几何平行垂直问题专题复习一、平面平行问题1. 平行线基础定义平行线是在同一平面内不相交的两条直线。

两条平行线之间的距离是它们之间所有直线段中最短的。

平行线符号为“||”。

2. 垂直平分线垂直平分线是将一条线段分成两个相等的部分，并且垂直于线段的线。

3. 平行四边形平行四边形是指两组相互平行的边构成的四边形，它的对边长度相等，对边平等，对角线互相平分。

4. 平行线判定定理对于两条直线l, m以及平面内的任意一条直线n，若n与l平行，则n与m 平行；若n与l垂直，则n与m垂直。

5. 平行线和对角线的关系平行线所构成的平行四边形的对角线互相平分。

二、垂直问题1. 垂线基础定义垂线是指与一条直线或平面呈直角的线段。

2. 垂线距离垂线距离是垂线所代表的点到直线的最短距离。

3. 垂心垂心是指在三角形的一个顶点下，作该点到对边的垂线并与对边相交的点。

4. 直角三角形直角三角形是指三角形中有一角为90度的。

5. 正方体中垂直面的距离正方体中两个垂直面的距离为边长。

三、立体几何应用问题1. 立方体立方体的六个面都是正方形。

每个面都有相同的面积，边长相等。

2. 长方体长方体是指六个面中有一个面是长方形，其余五个面都是正方形。

3. 圆柱体圆柱体是指由一个矩形和两个相等的圆所组成的立体，其中矩形是圆柱体的腰，两个圆为圆柱体的顶底面。

4. 圆锥体圆锥体是由一个圆和一个尖端共同组成的立体，圆锥体的侧面是一条射线和圆的切线。

圆锥体中心角为360度。

5. 球体球体是由一个半径相等的圆旋转所得到的立体，其表面上所有点到球心的距离都是相等的。

以上就是关于立体几何中的平行垂直问题专题复习的内容，包括了平面平行问题、垂直问题、立体几何应用问题，希望对大家在学习立体几何时有所帮助。

高中数学《立体几何》专题复习 (3)

高中数学《立体几何》专题复习三1．(2017·唐山模拟)正三棱锥的高和底面边长都等于6，则其外接球的表面积为( ) A ．64π B ．32π C ．16π D ．8π答案 A解析如图，作PM ⊥平面ABC 于点M ，则球心O 在PM 上，PM ＝6，连接AM ，AO ，则OP ＝OA ＝R(R 为外接球半径)，在Rt △OAM 中，OM ＝6－R ，OA ＝R ，又AB ＝6，且△ABC 为等边三角形，故AM ＝2362－32＝23，则R 2－(6－R)2＝(23)2，则R ＝4，所以球的表面积S ＝4πR 2＝64π.2．已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积是( ) A ．16π B ．20π C ．24π D ．32π答案 C解析由V ＝Sh ，得S ＝4，得正四棱柱底面边长为2.画出球的轴截面可得，该正四棱柱的对角线即为球的直径，所以球的半径为R ＝1222＋22＋42＝ 6.所以球的表面积为S ＝4πR 2＝24π.故选C.3．若一个正方体的体积是8，则这个正方体的内切球的表面积是( ) A ．8π B ．6π C ．4π D ．π答案 C解析设正方体的棱长为a ，则a 3＝8.因此内切球直径为2，∴S 表＝4πr 2＝4π.4．(2017·课标全国Ⅲ)已知圆柱的高为1，它的两个底面的圆周在直径长为2的同一个球的球面上，则该圆柱的体积为( ) A ．π B.3π4 C.π2 D.π4 答案 B解析根据已知球的半径长是1，圆柱的高是1，如图，所以圆柱的底面半径r ＝22－122＝32，所以圆柱的体积V ＝πr 2h ＝π×(32)2×1＝34π.故选B. 5．(2018·安徽合肥模拟)已知球的直径SC ＝6，A ，B 是该球球面上的两点，且AB ＝SA ＝SB ＝3，则三棱锥S －ABC 的体积为( ) A.324B.924 C.322 D.922答案 D解析设该球球心为O ，因为球的直径SC ＝6，A ，B 是该球球面上的两点，且AB ＝SA ＝SB ＝3，所以三棱锥S －OAB 是棱长为3的正四面体，其体积V S －OAB ＝13×12×3×332×6＝924，同理V O －ABC ＝924，故三棱锥S －ABC 的体积V S －ABC ＝V S －OAB ＋V O －ABC ＝922，故选D.6．已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的球面上，若AB ＝3，AC ＝4，AB ⊥AC ，AA 1＝12，则球O 的半径为( ) A.3172B ．210 C.132 D ．310 答案 C解析如图，由球心作平面ABC 的垂线，则垂足为BC 的中点M. 又AM ＝12BC ＝52，OM ＝12AA 1＝6，所以球O 的半径R ＝OA ＝（52）2＋62＝132. 7．(2018·广东惠州一模)已知一个水平放置的各棱长均为4的三棱锥形容器内有一小球O(质量忽略不计)，现从该三棱锥形容器的顶端向内注水，小球慢慢上浮，当注入的水的体积是该三棱锥体积的78时，小球与该三棱锥各侧面均相切(与水面也相切)，则小球的表面积等于( ) A.76π B.43πC.23π D.12π 答案 C解析由题知，没有水的部分的体积是三棱锥形容器的体积的18，三棱锥形容器的体积为13·34·42·63·4＝1623，所以没有水的部分的体积为223.设其棱长为a ，则其体积为13×34a 2×63a ＝223，∴a ＝2，设小球的半径为r ，则4×13×3×r ＝223，解得r ＝66，∴球的表面积为4π×16＝23π，故选C.8.如图，ABCD －A 1B 1C 1D 1是棱长为1的正方体，S －ABCD 是高为1的正四棱锥，若点S ，A 1，B 1，C 1，D 1在同一个球面上，则该球的体积为( ) A.25π16 B.49π16 C.81π16 D.243π128答案 C解析如图所示，O 为球心，设OG 1＝x ，则OB 1＝SO ＝2－x ，同时由正方体的性质可知B 1G 1＝22，则在Rt △OB 1G 1中，OB 12＝G 1B 12＋OG 12，即(2－x)2＝x 2＋(22)2，解得x ＝78，所以球的半径R ＝OB 1＝98，所以球的表面积S ＝4πR 2＝81π16，故选C. 9．(2018·郑州质检)四棱锥P －ABCD 的五个顶点都在一个球面上，该四棱锥的三视图如图所示，E ，F 分别是棱AB ，CD 的中点，直线EF 被球面所截得的线段长为22，则该球的表面积为( )A ．9πB ．3πC ．22πD ．12π答案 D解析该几何体的直观图如图所示，该几何体可看作由正方体截得，则正方体外接球的直径即为PC.由直线EF 被球面所截得的线段长为22，可知正方形ABCD 对角线AC 的长为22，可得正方形ABCD 的边长a ＝2，在△PAC 中，PC ＝22＋（22）2＝23，球的半径R ＝3，∴S 表＝4πR 2＝4π×(3)2＝12π.10．(2014·湖南)一块石材表示的几何体的三视图如图所示．将该石材切削、打磨，加工成球，则能得到的最大球的半径等于( )A ．1B ．2C ．3D ．4答案 B解析此几何体为一直三棱柱，底面是边长为6，8，10的直角三角形，侧棱为12，故其最大球的半径为底面直角三角形内切圆的半径，故其半径为r ＝12×(6＋8－10)＝2，故选B.11．(2017·天津)已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为________．答案 92π解析设正方体的棱长为a ，则6a 2＝18，得a ＝3，设该正方体外接球的半径为R ，则2R ＝3a ＝3，得R ＝32，所以该球的体积为43πR 3＝43π(32)3＝92π.12．若一个正四面体的表面积为S 1，其内切球的表面积为S 2，则S 1S 2＝________．答案63π解析设正四面体的棱长为a ，则正四面体的表面积为S 1＝4·34·a 2＝3a 2，其内切球半径为正四面体高的14，即r ＝14·63a ＝612a ，因此内切球表面积为S 2＝4πr 2＝πa 26，则S 1S 2＝3a 2π6a 2＝63π. 13．已知一圆柱内接于球O ，且圆柱的底面圆的直径与母线长均为2，则球O 的表面积为________．答案 8π解析圆柱的底面圆的直径与母线长均为2，所以球的直径为22＋22＝8＝22，即球半径为2，所以球的表面积为4π×(2)2＝8π.14．(2017·衡水中学调研卷)已知正三棱锥P －ABC ，点P ，A ，B ，C 都在半径为3的球面上，若PA ，PB ，PC 两两相互垂直，则球心到截面ABC 的距离为________．答案33解析方法一：先在一个正方体中找一个满足条件的正三棱锥，再利用正方体的性质解题．如图，满足题意的正三棱锥P －ABC 可以是正方体的一部分，其外接球的直径是正方体的体对角线，且面ABC 与体对角线的交点是体对角线的一个三等分点，所以球心到平面ABC 的距离等于体对角线长的16，故球心到截面ABC 的距离为16×23＝33.方法二：用等体积法：V P －ABC ＝V A －PBC 求解)．15．(2018·四川成都诊断)已知一个多面体的三视图如图所示，其中正视图与侧视图都是直角边长为1的等腰直角三角形，俯视图是边长为1的正方形，若该多面体的顶点都在同一个球面上，则该球的表面积为________．答案3π解析由三视图知几何体为四棱锥，且四棱锥的一条侧棱垂直于底面，高等于1，其底面是边长为1的正方形，∴四棱锥的外接球即是边长为1的正方体的外接球，∴外接球的直径为3，∴外接球的表面积S＝4π×(32)2＝3π.16．(2018·河北唐山模拟)已知矩形ABEF所在的平面与矩形ABCD所在平面互相垂直，AD＝2，AB＝3，AF＝332，M为EF的中点，则多面体M－ABCD的外接球的表面积为________．答案16π解析记多面体M－ABCD的外接球的球心为O，如图，过点O分别作平面ABCD和平面ABEF的垂线，垂足分别为Q，H，连接MH并延长，交AB于点N，连接OM，NQ，AQ，设球O的半径为R，球心到平面ABCD的距离为d，即OQ＝d，∵矩形ABEF所在的平面与矩形ABCD所在的平面互相垂直，AF＝332，M为EF的中点，∴MN＝332，∴AN＝NB＝32，NQ＝1，∴R2＝(4＋92)2＋d2＝12＋(332－d)2，∴d＝32，R2＝4，∴多面体M－ABCD的外接球的表面积为4πR2＝16π.1．(2017·课标全国Ⅱ，文)长方体的长，宽，高分别为3，2，1，其顶点都在球O的球面上，则球O的表面积为________．答案14π解析依题意得，长方体的体对角线长为32＋22＋12＝14，记长方体的外接球的半径为R，则有2R＝14，R＝142，因此球O的表面积等于4πR2＝14π.2．(2018·湖南长沙一中模拟)如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为()A ．8π B.25π2C ．12π D.41π4答案 D解析根据三视图得出，几何体是正方体中的一个四棱锥O －ABCD ，正方体的棱长为2，A ，D 为所在棱的中点．根据几何体可以判断，球心应该在过A ，D 的平行于正方体底面的中截面上，设球心到平面BCO的距离为x ，则到AD 的距离为2－x ，所以R 2＝x 2＋(2)2，R 2＝12＋(2－x)2，解得x ＝34，R＝414，该多面体外接球的表面积为4πR 2＝414π，故选D. 3．(2014·陕西，理)已知底面边长为1，侧棱长为2的正四棱柱的各顶点均在同一个球面上，则该球的体积为( ) A.32π3B ．4πC ．2π D.4π3答案 D解析因为该正四棱柱的外接球的半径是四棱柱体对角线的一半，所以半径r ＝1212＋12＋（2）2＝1，所以V 球＝4π3×13＝4π3.故选D.4．(2018·洛阳统一考试)如图是某几何体的三视图，则该几何体的外接球的表面积为( )A ．200πB ．150πC ．100πD ．50π答案 D解析由三视图知，该几何体可以由一个长方体截去3个角后得到，该长方体的长、宽、高分别为5、4、3，所以其外接球半径R 满足2R ＝42＋32＋52＝52，所以该几何体的外接球的表面积为S ＝4πR 2＝4π×(522)2＝50π，故选D.5．(2018·广东清远三中月考)某一简单几何体的三视图如图所示，则该几何体的外接球的表面积是( )A ．13πB ．16πC ．25πD ．27π答案 C解析由三视图可知该几何体是底面为正方形的长方体，底面对角线为4，高为3，设外接球半径为r ，则2r ＝（22）2＋（22）2＋32＝5，∴r ＝52，∴长方体外接球的表面积S ＝4πr 2＝25π.6．(2018·福建厦门模拟)已知球O 的半径为R ，A ，B ，C 三点在球O 的球面上，球心O 到平面ABC 的距离为32R ，AB ＝AC ＝BC ＝23，则球O 的表面积为( ) A.163π B ．16π C.643π D ．64π答案 D解析因为AB ＝AC ＝BC ＝23，所以△ABC 为正三角形，其外接圆的半径r ＝232sin60°＝2，设△ABC 外接圆的圆心为O 1，则OO 1⊥平面ABC ，所以OA 2＝OO 12＋r 2，所以R 2＝(32R)2＋22，解得R 2＝16，所以球O 的表面积为4πR 2＝64π，故选D.7．(2018·四川广元模拟)如图，边长为2的正方形ABCD 中，点E ，F 分别是AB ，BC 的中点，将△ADE ，△EBF ，△FCD 分别沿DE ，EF ，FD 折起，使得A ，B ，C 三点重合于点A ′，若四面体A ′EFD 的四个顶点在同一个球面上，则该球的半径为________．答案62解析由题意可知△A ′EF 是等腰直角三角形，且A ′D ⊥平面A ′EF.由于△A ′EF 可以补全为边长为1的正方形，则该四面体必能补全为长、宽、高分别为1，1，2的正四棱柱，三棱锥的外接球与正四棱柱的外接球是同一个球，易知正四棱柱的外接球的直径为12＋12＋22＝ 6.故球的半径为62. 8．(2017·德州模拟)一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，该几何体的体积是________；若该几何体的所有顶点在同一球面上，则球的表面积是________．答案 133π解析由三视图知该几何体是底面为1的正方形，高为1的四棱锥，故体积V ＝13×1×1×1＝13，该几何体与棱长为1的正方体具有相同的外接球，外接球直径为3，该球表面积S ＝4π×(32)2＝3π，正方体、长方体的体对角线即为外接球的直径．。

立体几何复习专题---- 线线夹角

立体几何复习专题--空间角之线线角一、基础知识1.定义：直线a 、b 是异面直线，经过空间一交o ，分别a ΄//a ，b ΄//b ，相交直线a ΄b ΄所成的锐角（或直角）叫做异面直线夹角。

2.范围： ⎥⎦⎤⎝⎛∈2,0πθ3.方法：平移法、（1）平移法：在图中选一个恰当的点（通常是线段端点或中点）作a 、b 的平行线，构造一个三角形，并解三角形求角。

步骤：①根据定义，通过平移，找到异面直线所成的角θ；②解含有θ的三角形，求出角θ的大小.(常用到余弦定理)余弦定理： abcb a 2cos 222-+=θ (计算结果可能是其补角)（2）补形法：把空间图形补成正方体、平行六面体、长方体等几何体,以便发现异面直线间的关系（3）三线角公式用于求线面角和线线角.斜线和平面内的直线与斜线的射影所成角的余弦之积等于斜线和平面内的直线所成角的余弦即：θθθc o s c o s c o s 21=若 OA 为平面的一条斜线，O 为斜足，OB 为OA 在面α内的射影，OC 为面α内的一条直线，其中θ为OA 与OC 所成的角，θ1为OA 与OB 所成的角，即线面角，θ2为OB 与OC 所成的角，那么 cos θ=cos θ1·cos θ2 （同学们可自己证明），它揭示了斜线和平面所成的角是这条斜线和这个平面内的直线所成的一切角中最小的角（常称为最小角定理）【典型例题】【例1】在正方体1111ABCD A BC D -中，下列几种说法正确的是（） A 、11AC AD ⊥ B 、11D C AB ⊥ C 、1AC 与DC 成45角 D 、11AC 与θcba B αOAC1BC 成60角答案：D 。

解析：A 1C 1与AD 成45°，D 1C 1与AB 平行，AC 1与DC 所成角的正切为22。

【例2】（1）如图，在正方体1111ABCD A B C D -中，E,FG,H 分别为1AA ，AB ，1BB ，11B C 的中点，则异面直线EF 与GH 所成的角等于（2）如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为(3) 如图，在直三棱柱ABC －A 1B 1C 1中，∠BCA= 90，点D 1、F 1分别是A 1B 1和A 1C 1的中点，若BC=CA=CC 1，求BD 1与AF 1所成的角的余弦值_________。

高中数学《立体几何》专题复习 (1)

高中数学《立体几何》专题复习一1．(2018·安徽东至二中段测)将一个等腰梯形绕着它的较长的底边所在直线旋转一周，所得的几何体包括()A．一个圆台、两个圆锥B．两个圆台、一个圆柱C．两个圆台、一个圆锥D．一个圆柱、两个圆锥答案 D解析把等腰梯形分割成两个直角三角形和一个矩形，由旋转体的定义可知所得几何体包括一个圆柱、两个圆锥．故选D.2．以下关于几何体的三视图的论述中，正确的是()A．正方体的三视图是三个全等的正方形B．球的三视图是三个全等的圆C．水平放置的正四面体的三视图都是正三角形D．水平放置的圆台的俯视图是一个圆答案 B解析画几何体的三视图要考虑视角，但对于球无论选择怎样的视角，其三视图总是三个全等的圆．3．如图所示，几何体的正视图与侧视图都正确的是()答案 B解析侧视时，看到一个矩形且不能有实对角线，故A，D排除．而正视时，有半个平面是没有的，所以应该有一条实对角线，且其对角线位置应为B中所示，故选B.4．一个几何体的三视图如图，则组成该几何体的简单几何体为()A．圆柱和圆锥B．正方体和圆锥C．四棱柱和圆锥D．正方体和球答案 C5．(2018·沧州七校联考)三棱锥S－ABC及其三视图中的正视图和侧视图如图所示，则棱SB 的长为()A．16 3 B.38C．4 2 D．211答案 C解析由已知中的三视图可得SC⊥平面ABC，且底面△ABC为等腰三角形．在△ABC中，AC＝4，AC边上的高为23，所以BC＝4.在Rt△SBC中，由SC＝4，可得SB＝4 2. 6．(2017·衡水中学调研卷)已知一个四棱锥的高为3，其底面用斜二侧画法所画的水平放置的直观图是一个边长为1的正方形，则此四棱锥的体积为()A．2 2 B．6 2C．1 D. 2答案 A解析因为底面用斜二侧画法所画的水平放置的直观图是一个边长为1的正方形，所以在直角坐标系中，底面是边长为1和3的平行四边形，且平行四边形的一条对角线垂直于平行四边形的短边，此对角线的长为22，所以该四棱锥的体积为V＝13×22×1×3＝2 2.7.(2018·四川泸州模拟)一个正四棱锥的所有棱长均为2，其俯视图如图所示，则该正四棱锥的正视图的面积为()A. 2B. 3C．2 D．4答案 A解析由题意知，正视图是底边长为2，腰长为3的等腰三角形，其面积为12×2×（3）2－1＝ 2.8．(2018·湖南郴州模拟)一只蚂蚁从正方体ABCD－A1B1C1D1的顶点A出发，经正方体的表面，按最短路线爬行到顶点C1的位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图的是()A．①②B．③④C．①③D．②④答案 D解析由点A经正方体的表面，按最短路线爬行到达顶点C1的位置，共有6种路线(对应6种不同的展开方式)，若把平面ABB1A1和平面BCC1B1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过BB1的中点，此时对应的正视图为②；若把平面ABCD和平面CDD1C1展到同一个平面内，连接AC1，则AC1是最短路线，且AC1会经过CD的中点，此时对应的正视图为④.而其他几种展开方式对应的正视图在题中没有出现．故选D.9．某几何体的正视图和侧视图均如图所示，则该几何体的俯视图不可能是()答案 D解析依题意，此几何体为组合体，若上、下两个几何体均为圆柱，则俯视图为A；若上边的几何体为正四棱柱，下边几何体为圆柱，则俯视图为B；若上边的几何体为底面为等腰直角三角形的直三棱柱，下边的几何体为正四棱柱时，俯视图为C；若俯视图为D，则正视图中还有一条虚线，故该几何体的俯视图不可能是D，故选D.10．(2018·江西上馓质检)点M，N分别是正方体ABCD－A1B1C1D1的棱A1B1，A1D1的中点，用过平面AMN和平面DNC1的两个截面截去正方体的两个角后得到的几何体如图，则该几何体的正(主)视图，侧(左)视图、俯视图依次为()A．①②③B．②③④C．①③④D．②④③答案 B解析由直视图可知，该几何体的正(主)视图、侧(左)视图、俯视图依次为②③④，故选B. 11．(2018·四川宜宾期中)某几何体的三视图如图所示，则该几何体最长棱的长度为()A．4 B．3 2C．2 2 D．2 3答案 D解析由三视图可知，该几何体为如图所示的四棱锥P－ABCD，由图可知其中最长棱为PC，因为PB2＝PA2＋AB2＝22＋22＝8，所以PC2＝PB2＋BC2＝8＋22＝12，则PC＝23，故选D.12．(2018·北京东城区期末)在空间直角坐标系O－xyz中，一个四面体的顶点坐标分别为(0，0，2)，(2，2，0)，(0，2，0)，(2，2，2)．画该四面体三视图中的正视图时，以xOz平面为投影面，则得到的正视图可以为()答案 A解析设S(2，2，2)，A(2，2，0)，B(0，2，0)，C(0，0，2)，则此四面体S－ABC如图①所示，在xOz平面的投影如图②所示．其中S′是S在xOz平面的投影，A′是A在xOz平面的投影，O是B在xOz平面的投影，SB 在xOz平面的投影是S′O，并且是实线，CA在xOz平面的投影是CA′，且是虚线，如图③. 13．(2018·江西宜春模拟)某四面体的三视图如图所示，正视图、俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大为()A．2 2 B．4C．2 3 D．2 6答案 C解析由三视图知该几何体为棱锥S－ABD，其中SC⊥平面ABCD，将其放在正方体中，如图所示．四面体S－ABD的四个面中△SBD的面积最大，三角形SBD是边长为22的等边三角形，所以此四面体的四个面中面积最大为34×8＝2 3.故选C.14．(2018·江苏张家港一模)若将一个圆锥侧面沿一条母线剪开，其展开图是半径为2 cm的半圆，则该圆锥的高为________cm.答案 3解析设圆锥的底面圆半径为r cm，则2πr＝2π，解得r＝1 cm，∴h＝22－1＝ 3 cm. 15．(2018·成都二诊)已知正四面体的俯视图如图所示，其中四边形ABCD是边长为2的正方形，则这个四面体的正视图的面积为________．答案2 2解析由俯视图可得，原正四面体AMNC可视作是如图所示的正方体的一内接几何体，则该正方体的棱长为2，正四面体的正视图为三角形，其面积为12×2×22＝2 2.16.(2018·上海长宁区、嘉定区质检)如图，已知正三棱柱的底面边长为2，高为5，一质点自A点出发，沿着三棱柱的侧面绕行两周到达A1点的最短路线的长为________．答案13解析将正三棱柱ABC－A1B1C1沿侧棱AA1展开，再拼接一次，如图所示，在展开图中，最短距离是六个矩形形成的大矩形对角线的长度，也即为三棱柱的侧面上所求距离的最小值．由已知求得矩形的长等于6×2＝12，宽等于5，由勾股定理得d＝122＋52＝13.17．某几何体的正(主)视图和侧(左)视图如图1，它的俯视图的直观图是矩形O1A1B1C1如图2，其中O1A1＝6，O1C1＝2，则该几何体的侧面积为________．答案96解析由俯视图的直观图可得y轴与C1B1交于D1点，O1D1＝22，故OD＝42，俯视图是边长为6的菱形，则该几何体是直四棱柱，侧棱长为4，则侧面积为6×4×4＝96. 1．(课本习题改编)如图为一个几何体的三视图，则该几何体是()A．四棱柱B．三棱柱C．长方体D．三棱锥答案 B解析由几何体的三视图可知，该几何体的直观图如图所示，即为一个平放的三棱柱．2．(2018·山东泰安模拟)某三棱锥的三视图如图所示，其侧视图为直角三角形，则该三棱锥最长的棱长等于()A．4 2 B.34C.41 D．5 2答案 C解析根据几何体的三视图，得该几何体是底面为直角三角形，有两个侧面垂直于底面，高为5的三棱锥，最长的棱长等于25＋16＝41，故选C.3．(2018·安徽毛坦厂中学月考)已知一个几何体的三视图如图所示，则这个几何体的直观图是()答案 C解析A项中的几何体，正视图不符，侧视图也不符，俯视图中没有虚线；B项中的几何体，俯视图中不出现虚线；C项中的几何体符合三个视图；D项中的几何体，正视图不符．故选C.4．(2017·山东德州质检)如图是正方体截去阴影部分所得的几何体，则该几何体的侧视图是()答案 C解析此几何体的侧视图是从左边往右边看，故其侧视图应选C.5.(2017·广东汕头中学摸底)如图是一正方体被过棱的中点M，N，顶点A及过N，顶点D，C1的两个截面截去两角后所得的几何体，该几何体的正视图是()答案 B6．(2017·贵州七校联考)如图所示，四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形，起辅助作用)，则四面体ABCD的三视图是(用①②③④⑤⑥代表图形)()A．①②⑥B．①②③C．④⑤⑥D．③④⑤答案 B解析正视图应该是边长为3和4的矩形，其对角线左下到右上是实线，左上到右下是虚线，因此正视图是①；侧视图应该是边长为5和4的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此侧视图是②；俯视图应该是边长为3和5的矩形，其对角线左上到右下是实线，左下到右上是虚线，因此俯视图是③，故选B.7．(2014·课标全国Ⅰ)如图，网格纸的各小格都是正方形，粗实线画出的是一个几何体的三视图，则这个几何体是()A．三棱锥B．三棱柱C．四棱锥D．四棱柱答案 B解析由题知，该几何体的三视图为一个三角形，两个四边形，经分析可知该几何体为三棱柱，故选B.8.用一个平行于水平面的平面去截球，得到如图所示的几何体，则它的俯视图是()答案 B解析D项为主视图或者侧视图，俯视图中显然应有一个被遮挡的圆，所以内圆是虚线，故选B.9．底面水平放置的正三棱柱的所有棱长均为2，当其正(主)视图有最大面积时，其侧(左)视图的面积为()A．2 3 B．3C. 3 D．4答案 A解析当正视图面积最大时，侧视图是一个矩形，一个边长为2，另一边长是三棱柱底面三角形的高为3，故侧视图面积为2 3.10．(2015·北京，文)某四棱锥的三视图如图所示，该四棱锥最长棱的棱长为()A．1 B. 2C. 3 D．2答案 C解析将三视图还原成几何体的直观图，如图，由三视图可知，底面ABCD是边长为1的正方形，SB⊥底面ABCD，SB＝AB＝1，由勾股定理可得SA＝SC＝2，SD＝SB2＋DB2＝1＋2＝3，故四棱锥中最长棱的棱长为 3.故选C. 11．(2017·南昌模拟)若一几何体的正视图与侧视图均为边长为1的正方形，则下列图形一定不是该几何体的俯视图的是()答案 D解析若该几何体的俯视图为选项D ，则其正视图为长方形，不符合题意，故选D. 12．某几何体的正视图与侧视图如图所示，若该几何体的体积为13，则该几何体的俯视图可以是( )答案 D解析通过分析正视图和侧视图，结合该几何体的体积为13，可知该几何体的底面积应为1，因为符合底面积为1的选项仅有D 选项，故该几何体为一个四棱锥，其俯视图为D. 13．(2018·兰州诊断考试)某几何体的三视图如图所示，且该几何体的体积是3，则正视图中x 的值是( )A ．2 B.92 C.32 D ．3答案 D解析由三视图知，该几何体是四棱锥，底面是一个直角梯形，底面积S ＝12×(1＋2)×2＝3，高h ＝x ，所以其体积V ＝13Sh ＝13×3x ＝3，解得x ＝3，故选D.14．某几何体的三视图如图所示，则该几何体中，最大侧面的面积为( )A.12B.22C.52D.62答案 C解析由三视图知，该几何体的直观图如图所示．平面AED ⊥平面BCDE ，四棱锥A －BCDE 的高为1.四边形BCDE 是边长为1的正方形，则S △AED ＝12×1×1＝12，S △ABC ＝S △ABE ＝12×1×2＝22，S △ACD ＝12×1×5＝52，故选C.15.(2017·山东师大附中月考)如图是各棱长均为2的正三棱柱ABC －A 1B 1C 1的直观图，则此三棱柱侧视图的面积为________．答案 2 3解析依题意，得此三棱柱的侧视图是边长分别为2，3的矩形BB 1D 1D ，故其面积是2 3.16.(2017·北京西城区期末)已知一个正三棱柱的所有棱长均相等，其侧(左)视图如图所示，那么此三棱柱正(主)视图的面积为________．答案 2 3解析由正三棱柱三视图还原直观图可得正(主)视图是一个矩形，其中一边的长是侧(左)视图中三角形的高，另一边是棱长．因为侧(左)视图中三角形的边长为2，所以高为3，所以正视图的面积为2 3.17．用小立方块搭一个几何体，使它的正视图和俯视图如图所示，则它最多需要______个小立方块．答案14解析本题考查了三视图的有关知识．需要小立方块最多则：第一层最多6个，第二层最多5个，第三层最多3个，故最多用14个．18．(2017·湖南株洲质检)已知底面为正方形的四棱锥，其一条侧棱垂直于底面，那么该四棱锥的三视图可能是下列各图中的()答案 C解析通过对以下四个四棱锥的三视图对照可知，只有选项C是符合要求．。

专题五立体几何专题复习

专题五、立体几何1、线面平行的证法：面∥线面线面线线∥线⇒⎪⎭⎪⎬⎫⊄⊂①关键是在平面内找（用直尺平移到平面内）一条直线与已知直线平行②在证线线平行时，常用到三角形中位线定理或平行四边形对边平行2、线面垂直的证法：αα面线面线线线线线线线⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂⊥⊥l b a b a b l al ,关键是在平面内找两条相交直线与已知直线垂直 3、面面垂直的证法βαβα面面面线面线⊥⇒⎭⎬⎫⊂⊥l l4、面面垂直的作用（证明线面垂直）αββαβα面线线线面线线面面面面⊥⇒⎪⎪⎭⎪⎪⎬⎫⊥⊂=⊥l m l l m注：在条件中寻找线线垂直时，常用结论有①勾股定理逆定理 ②等腰三角形三线合一 ③直径所对圆周角是直角一、考点分析：（理科）考点一：三视图与表面积、体积的结合三视图的识别，多以考查组合体为主，大部分是已知部分（或全部）三视图，进而考查立体图形直观图的还原及计算问题。

几何体的表面积和体积的综合，往往以球为载体，结合棱柱、棱锥。

近三年高考题2011年（6）在一个几何体的三视图中，正视图和俯视图如右图所示，则相应的侧视图可以为（15）已知矩形ABCD 的顶点都在半径为4的球O 的球面上，且6,23AB BC ==,则棱锥O ABCD -的体积为。

2012年（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A ）6 （B ）9 （C ）12 （D ）18（11）已知三棱锥S ABC -的所有顶点都在球O 的球面上，ABC ∆是边长为1的正三角形，SC 为球O 的直径，且2SC =，则此棱锥的体积为（A ）26 （B ）36 （C ）23 （D ）222013年（7）一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分别是（1，0，1），（1，1，0），（0，1，1），（0，0，0），画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到正视图可以为考点二：空间线面关系的判断该部分的基础是平面的性质、空间直线与直线的位置关系，重点是空间线面平行和垂直关系的判定和性质，面面平行和垂直关系的判定和性质．在复习中要牢牢掌握四个公理和八个定理及其应用，重点掌握好平行关系和垂直关系的证明方法．考点三：求空间角考查空间角的计算为主，解决这类问题往往有两种方法：传统几何法和向量法，这两种方法各有所长，传统几何法的主要思想是把立体问题转化为平面问题，难点在逻辑推理、空间想象能力；向量法在建立空间坐标系后把问题转化成坐标运算，其难点在代数运算。

高三《立体几何》专题复习

高三《立体几何》专题复习一、常用知识点回顾1、三视图。

正侧一样高，正俯一样长，侧府一样宽，看不到的线画虚线。

2、常用公式与结论。

（1）圆柱、圆锥、圆台的侧面展开图及侧面积公式；（2）空间几何体的表面积与体积公式；（3）全品高考复习方案（听课手册）105页的常用结论3、两条异面直线所成的角；直线与平面所成的角。

4、证明两条直线平行的常用方法；直线与平面平行的判定与性质；面面平行的判定与性质。

5、证明两条直线垂直的常用方法；直线与平面垂直的判定与性质；两个平面垂直的判定与性质。

二、题型训练题型一：三视图的运用，求几何体的体积、表面积例1、如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（）（A）18+（B）54+（C）90（D）81【练习1】某圆柱的高为2,底面周长为16,其三视图如右图.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为（）C.3D.2【练习2】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为（）A.90πB.63πC.42πD.36π【练习3】如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）（A ）20π（B ）24π（C ）28π（D ）32π例2、在封闭的直三棱柱ABC －A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ，AB =6，BC =8，AA 1=3，则V 的最大值是（）（A ）4π （B ）9π2 （C ）6π （D ）32π3变式1：在封闭的直三棱柱ABC－A1B1C1内有一个体积为V的球.若AB⊥BC，AB=6，BC=8，AA1=5，则V的最大值是变式2：在封闭的长方体ABCD－A1B1C1D1内有一个体积为V的球.若AB=BC=6，AA1=3，则V的最大值是变式3：（1）长方体的长、宽、高分别为3,2,1，其顶点都在球O的球面上，则球O的表面积为（2）体积为8的正方体的顶点都在同一球面上，则该球面的表面积为变式4：【练习1】已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为（）A. B.12π C. D.10π【练习3】已知圆锥的顶点为S，母线SA，SB互相垂直，SA与圆锥底面所成角为30°，若SAB的面积为8，则该圆锥的体积为_______题型二：平行问题例1、如图，四棱锥P-ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.（I）证明MN∥平面PAB; （II）求四面体N-BCM的体积.【练习1】如图，四棱锥P-ABCD中，侧面PADAD,为等边三角形且垂直于底面ABCD，AB=BC=12∠BAD=∠ABC=90°。

高中数学立体几何专题复习

图2侧视图俯视图正视图4x33x4DCBA侧视图正视图立体几何专题(一)一、三视图考点透视：①能想象空间几何体的三视图，并判断（选择题） ②通过三视图计算空间几何体的体积或表面积③解答题中也可能以三视图为载体考查证明题和计算题④旋转体（圆柱、圆锥、圆台或其组合体）的三视图有两个视图一样。

⑤基本几何体的画法，如：三棱柱（侧视图）、挡住的注意画虚线。

1. 一空间几何体的三视图如图2所示, 该几何体的体积为85123π+，则正视图中x 的值为 A. 5 B . 4 C. 3 D . 22. 一个正方体截去两个角后所得几何体的正视图（又称主视图）、侧视图（又称左视图）如右图所示，则其俯视图为c3．如图4，已知一个锥体的正视图（也称主视图），左视图（也称侧视图）和俯视图均为直角三角形，且面积分别为3，4，6，则该锥体的体积是 4 ．4. 如图1－3，某几何体的正视图（主视图）是平行四边形，侧视图（左视图）和俯视图都是矩形，则该几何体的体积为A ．63B ．93C ．123D ．1835、已知某几何体的直观图(图1)与它的三视图(图2)，其中俯视图为正三角形，其它两个视图是矩形.已知D 是正视图左视图俯视图图4_3 _3 这个几何体的棱11C A 上的中点。

（Ⅰ）求出该几何体的体积；（Ⅱ）求证：直线11//BC AB D 平面； (Ⅲ)求证:直线11B D AA D ⊥平面.二、直观图掌握直观图的斜二测画法：①平行于两坐标轴的平行关系保持不变；②平行于y 轴的长度为原来的一半，x 轴不变；③新坐标轴夹角为45°。

6、如图，梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图(斜二测)，若A 1D 1∥O 1y 1，A 1B 1∥C 1D 1，A 1B 1＝2，C 1D 1＝3，A 1D 1＝1，则梯形ABCD 的面积是( ) A ．10 B ．5 C ．5 2D ．102三、表面积和体积不要求记忆，但要会使用公式。

高三立体几何专题复习

高考立体几何专题复习一．考试要求：〔1〕掌握平面的根本性质，会用斜二测的画法画水平放置的平面图形的直观图，能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。

〔2〕了解空两条直线的位置关系，掌握两条直线平行与垂直的判定定理和性质定理，掌握两条直线所成的角和距离的概念〔对于异面直线的距离，只要求会计算已给出公垂线时的距离〕。

〔3〕了解空间直线和平面的位置关系，掌握直线和平面平行的判定定理和性质定理，理解直线和平面垂直的判定定理和性质定理，掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念，了解三垂线定理及其逆定理。

〔4〕了解平面与平面的位置关系，掌握两个平面平行的判定定理和性质定理。

掌握二面角、二面角的平面角、两个平面间的距离的概念，掌握两个平面垂直的判定定理和性质定理。

〔5〕会用反证法证明简单的问题。

〔6〕了解多面体的概念，了解凸多面体的概念。

〔7〕了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图。

〔8〕了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图。

〔9〕了解正多面体的概念，了解多面体的欧拉公式。

〔10〕了解球的概念，掌握球的性质，掌握球的外表积、体积公式。

二．复习目标：1．在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的根底上，研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用；在有关问题的解决过程中，进一步了解和掌握相关公理、定理的容和功能，并探索立体几何中论证问题的规律；在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用．2．在掌握空间角(两条异面直线所成的角，平面的斜线与平面所成的角及二面角)概念的根底上，掌握它们的求法(其根本方法是分别作出这些角，并将它们置于*个三角形通过计算求出它们的大小)；在解决有关空间角的问题的过程中，进一步稳固关于直线和平面的平行垂直的性质与判定的应用，掌握作平行线(面)和垂直线(面)的技能；通过有关空间角的问题的解决，进一步提高学生的空间想象能力、逻辑推理能力及运算能力．3．通过复习，使学生更好地掌握多面体与旋转体的有关概念、性质，并能够灵活运用到解题过程中．通过教学使学生掌握根本的立体几何解题方法和常用解题技巧，开掘不同问题之间的在联系，提高解题能力．4．在学生解答问题的过程中，注意培养他们的语言表述能力和"说话要有根据〞的逻辑思维的习惯、提高思维品质．使学生掌握化归思想，特别是将立体几何问题转化为平面几何问题的思想意识和方法，并提高空间想象能力、推理能力和计算能力．5．使学生更好地理解多面体与旋转体的体积及其计算方法，能够熟练地使用分割与补形求体积，提高空间想象能力、推理能力和计算能力．三．教学过程：〔Ⅰ〕根底知识详析高考立体几何试题一般共有4道(选择、填空题1--2道, 解答题1道), 共计总分20分左右,考察的知识点在20个以. 选择填空题考核立几中的计算型问题, 而解答题着重考察立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着"多一点思考,少一点计算〞的开展.从历年的考题变化看, 以多面体和旋转体为载体的线面位置关系的论证,角与距离的探常考常新的热门话题.1．有关平行与垂直(线线、线面及面面)的问题，是在解决立体几何问题的过程中，大量的、反复遇到的，而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的容，因此在主体几何的总复习中，首先应从解决"平行与垂直〞的有关问题着手，通过较为根本问题，熟悉公理、定理的容和功能，通过对问题的分析与概括，掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想，以提高逻辑思维能力和空间想象能力．2．判定两个平面平行的方法：〔1〕根据定义——证明两平面没有公共点；〔2〕判定定理——证明一个平面的两条相交直线都平行于另一个平面；〔3〕证明两平面同垂直于一条直线。

立体几何专题复习

立体几何专题复习例1：如图1，在棱长均为4的三棱柱ABC－A1B1C1中，若平面ABC⊥平面BCC1B1，∠B1BC＝60°，求三棱锥B1－ABC的体积．【解答】设BC的中点为D，连结AD.则在△ABC中∵AB＝AC且D为BC的中点∴AD⊥BC∵平面ABC⊥平面B1C1CB，其交线为BC，AD⊂平面ABC，∴AD⊥平面B1C1CB在△ABC中，由AB＝AC＝BC＝4得AD＝2 3.在△B1BC中，∵B1B＝BC＝4，∠B1BC＝60°图1∴△B1BC是等边三角形∴S△B1BC＝34×42＝43，而三棱锥B1－ABC的体积等于三棱锥A－B1BC的体积，即VB1－ABC＝VA－B1BC＝13×S△B1BC·AD＝13×43×23＝8.【点评】锥体的体积求解的关键是求高,本题利用面面垂直的性质定理，通过作交线的垂线，得到线面垂直,从而找到高所在直线．例2：如图2,在边长为6 cm的正方形ABCD中，E、F分别为BC、CD的中点，M、N分别为AB、CF的中点，现沿AE、AF、EF折叠，使B、C、D三点重合，构成一个三棱锥．求多面体E－AFNM的体积．图2【解答】 ∵⎭⎬⎫AB ⊥BE AB ⊥BF ⇒AB ⊥平面BEF 且AB ＝6，BE ＝BF ＝3∴V A －BEF ＝9，又V E －AFNM V E －ABF ＝S 四边形AFNM S △ABF＝34∴V E －AFNM ＝274. 【点评】本题中求多面体E －AFNM 的体积，采取的是比例法，由于E 点到平面ABF 的高不易求出，故采取等体积转化，先求出整个三棱锥的体积，再通过同高可以将体积转化为面积之比．如图3，四棱锥P －ABCD 中，PA ⊥平面ABCD ，底面ABCD 为直角梯形且AB ∥CD ，∠BAD ＝90°，PA＝AD ＝DC ＝2，AB ＝4.(1)求证：BC ⊥PC ；(2)四面体A －PBC 的体积．【解答】 (1)证明：作CE ⊥AB 于点E ，则AE ＝EB ＝CE ＝2，BC ＝22，连结AC ，则AC ＝22，故∠ACB ＝90°，即AC ⊥CB .又PA ⊥平面ABCD ，故PA ⊥BC∴BC ⊥平面PAC 又PC ⊂面PAC ，因此BC ⊥PC . 图3(2)过A 作AM ⊥PC ，由(1)易得BC ⊥平面PAC ，故BC ⊥AM ，所以AM ⊥PBC ，因此线段AM 的长为点A 到平面PBC 的距离．在Rt △PAC 中，PC ＝23，AM ＝263，即点A 到平面PBC 的距离为263. 在△PBC 中，PC ＝23，BC ＝22，PB ＝25，由余弦定理得cos ∠PBC ＝PB 2＋BC 2－PC 22PB ·BC ＝105，∴sin∠PBC＝155，∴S△PBC＝12PB·BC·sin∠PBC＝26，∴V A－PBC＝13S△PBC·AM＝83.即AC⊥CB.又PA⊥平面ABCD，故PA⊥BC，∴BC⊥平面PAC又PC⊂面PAC，因此BC⊥PC.(2)过A作AM⊥PC，由(1)易得BC⊥平面PAC，故BC⊥AM，所以AM⊥PBC，因此线段AM的长为点A到平面PBC的距离．在Rt△PAC中，PC＝23，AM＝263，即点A到平面PBC的距离为263.在△PBC中，PC＝23，BC＝22，PB＝25，由余弦定理得cos∠PBC＝PB2＋BC2－PC22PB·BC＝105，∴sin∠PBC＝155，∴S△PBC＝12PB·BC·sin∠PBC＝26，∴V A－PBC＝13S△PBC·AM＝83.规律总结1：1.空间几何体的表面积和体积的研究策略研究空间几何体的结构→计算相关边长→代入公式计算．2．空间几何体的结构的研究策略运用转化的思想，将空间几何体的问题转化为平面问题，如几何体的外接球或内切球问题；转化为多边形与圆的外接或内切问题．3．组合体体积的求解组合体的体积求解无论是分割还是补形，关键是有利于求出几何体的高，即找到线面垂直．例3：已知m，n，l是直线，α、β是平面，下列命题中，正确命题的序号是________．①若l垂直于α内两条直线，则l⊥α；②若l平行于α，则α内有无数条直线与l平行；③若m∥β，m⊂α，n⊂β，则m∥n；④若m⊥α，m⊥β，则α∥β.【答案】②④【解析】①中只有当两条直线相交时l⊥α才恒成立，故①不正确；若l ∥α，则过l任作平面β与α相交，则交线必与l平行，由于β的任意性，故②正确；③中只有当n是α与β的交线时结论才恒成立，故③不正确，④正确。

立体几何专题复习

高考数学立体几何专题复习(含答案)

立体几何综合复习——空间角(完整版)

高考立体几何专题复习公开课获奖课件

高考数学(文)《立体几何》专题复习

新高中数学立体几何多选题专题复习及答案

立几专题(三视图)

立体几何复习专题及答案-高中数学

福建省永春县第一中学高中数学立体几何多选题专题复习含解析

立体几何专题复习(自己精心整理)

立体几何平行垂直问题专题复习

高中数学《立体几何》专题复习 (3)

立体几何复习专题---- 线线夹角

高中数学《立体几何》专题复习 (1)

专题五 立体几何专题复习

高三《立体几何》专题复习

高中数学 立体几何专题复习

高三立体几何专题复习

立体几何专题复习

专题五立体几何专题复习

高中数学立体几何专题复习