沪教版七年级数学下册 第十四章 全等三角形 练习题(无答案)
2022年强化训练沪教版七年级数学第二学期第十四章三角形专项测评试卷(含答案详解)

沪教版七年级数学第二学期第十四章三角形专项测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、在下列长度的四根木棒中,能与3cm ,9cm 的两根木棒首尾顺次相接钉成一个三角形的是( )A .3cmB .6cmC .10cmD .12cm2、下列叙述正确的是( )A .三角形的外角大于它的内角B .三角形的外角都比锐角大C .三角形的内角没有小于60°的D .三角形中可以有三个内角都是锐角3、如图,在ABC 中,5AB =,8BC =,60B ︒∠=,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,CD 的长为( )A .3B .4C .5D .64、如图,在ABC ∆中,BD 、CD 分别平分ABC ∠、ACB ∠,过点D 作直线平行于BC ,分别交AB 、AC 于点E 、F ,当A ∠大小变化时,线段EF 和BE CF +的大小关系是( )A .EF BE CF >+B .EF BE CF <+C .EF BE CF =+D .不能确定5、三根小木棒摆成一个三角形,其中两根木棒的长度分别是8cm 和5cm ,那么第三根小木棒的长度不可能是( )A .5cmB .8cmC .10cmD .13cm6、如图,△ ABC ≌△CDA ,∠BAC =80°,∠ABC =65°,则∠CAD 的度数为( )A .35°B .65°C .55°D .40°7、如图,90A D ∠=∠=︒,AC ,BD 相交于点O .添加一个条件,不一定能使ABC ≌DCB 的是( )A .AB DC =B .OB OC = C .ABO DCO ∠=∠D .ABC DCB ∠=∠8、如图,在△ABC 和△DEF 中,∠A =∠D ,AF =DC ,添加下列条件中的一个仍无法证明△ABC ≌△DEF 的是( )A .BC =EFB .AB =DEC .∠B =∠ED .∠ACB =∠DFE9、如果三角形一边上的中线等于这条边的一半,那么这个三角形一定是( ).A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形10、如图,ABC 和DEF 全等,且A D ∠=∠,AC 对应DE .若6AC =,5BC =,4AB =,则DF 的长为( )A .4B .5C .6D .无法确定第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,已知30MON ∠=︒,点1A ,2A ,3A ,⋅⋅⋅在射线ON 上,点1B ,2B ,3B ,⋅⋅⋅在射线OM 上,112A B A △,223A B A △,334A B A △,⋅⋅⋅均为等边三角形,若1OA a =,则223A B A △的边长为______.1n n n A B A +△的边长为______.2、如图,点F ,A ,D ,C 在同一条直线上,ABC DEF △≌△,3AD =,CF 10=,则AC 等于_____.3、如图,在△ABC 中,∠ACB =90°,点D 在AB 上,将△ABC 沿CD 折叠,点A 落在BC 边上的点A '处,若∠B =35°,则BDA '∠的度数为___________.4、如图,在ABC 中,AB AC =,40A ∠=︒,E 为BC 延长线上一点,ABC ∠与ACE ∠的平分线相交于点D ,则∠D 的度数为______.5、如图,在三角形ABC 中,40BAC ∠=︒,点D 为射线CB 上一点,过点D 作DE AC ∥交直线AB 于点E ,DF AB ∥交直线AC 于点F ,CG 平分ACB ∠交DF 于点G .若:3:4FDC EDC ∠∠=,则DGC ∠=______°.三、解答题(10小题,每小题5分,共计50分)1、如图,在等边ABC 中,D 为BC 边上一点,连接AD ,将ACD △沿AD 翻折得到AED ,连接BE 并延长交AD 的延长线于点F ,连接CF .(1)若20CAD ∠=︒,求CBF ∠的度数;(2)若a CAD ∠=,求CBF ∠的大小;(3)猜想CF ,BF ,AF 之间的数量关系,并证明.2、如图,在△ABC 中,AB =AC ,M ,N 分别是AB ,AC 边上的点,并且MN ∥BC .(1)△AMN 是否是等腰三角形?说明理由;(2)点P 是MN 上的一点,并且BP 平分∠ABC ,CP 平分∠ACB .①求证:△BPM 是等腰三角形;②若△ABC 的周长为a ,BC =b (a >2b ),求△AMN 的周长(用含a ,b 的式子表示).3、数学课上,王老师布置如下任务:如图,已知∠MAN<45°,点B是射线AM上的一个定点,在射线AN上求作点C,使∠ACB=2∠A.下面是小路设计的尺规作图过程.作法:①作线段AB的垂直平分线l,直线l交射线AN于点D;②以点B为圆心,BD长为半径作弧,交射线AN于另一点C,则点C即为所求.根据小路设计的尺规作图过程,(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明:证明:连接BD,BC,∵直线l为线段AB的垂直平分线,∴DA=,( )(填推理的依据)∴∠A =∠ABD ,∴∠BDC =∠A +∠ABD =2∠A .∵BC =BD ,∴∠ACB =∠ ,( )(填推理的依据)∴∠ACB =2∠A .4、如图,已知点B ,F ,C ,E 在同一直线上,AB ∥DE ,BF =CE ,AB =ED ,求证:∠A =∠D .5、如图,ABC 是等边三角形,∥DE BC ,分别交AB ,AC 于点D ,E .(1)求证:ADE 是等边三角形;(2)点F 在线段DE 上,点G 在ABC 外,BF CG =,ABF ACG ∠=∠,求证:AF FG =.6、如图,AD 是ABC 的中线,分别过点C 、B 作AD 及其延长线的垂线,垂足分别为F 、E .(1)求证:CFD BED △△;(2)若ACF 的面积为8,CFD △的面积为6,求ABE △的面积.7、如图,将一副直角三角板的直角顶点C 叠放在一起.(1)如图(1),若∠DCE =33°,则∠BCD = ,∠ACB = .(2)如图(1),猜想∠ACB 与∠DCE 的大小有何特殊关系?并说明理由.(3)如图(2),若是两个同样的直角三角板60°锐角的顶点A 重合在一起,则∠DAB 与∠CAE 的数量关系为 .8、阅读填空,将三角尺(△MPN ,∠MPN =90°)放置在△ABC 上(点P 在△ABC 内),如图①所示,三角尺的两边PM 、PN 恰好经过点B 和点C ,我们来研究∠ABP 与∠ACP 是否存在某种数量关系.(1)特例探索:若∠A =50°,则∠PBC +∠PCB = 度,∠ABP +∠ACP = 度.(2)类比探索:∠ABP、∠ACP、∠A 的关系是 .(3)变式探索:如图②所示,改变三角尺的位置,使点P 在△ABC 外,三角尺的两边PM 、PN 仍恰好经过点B 和点C ,则∠ABP、∠ACP、∠A 的关系是 .9、如图,在等边三角形ABC 中,点P 为△ABC 内一点,连接AP ,BP ,CP ,将线段AP 绕点A 顺时针旋转60°得到'AP ,连接PP BP '', .(1)用等式表示BP ' 与CP 的数量关系,并证明;(2)当∠BPC =120°时,①直接写出P BP '∠ 的度数为 ;②若M 为BC 的中点,连接PM ,请用等式表示PM 与AP 的数量关系,并证明.10、如图,ADC AEB ∠=∠,AD AE =,求证:OB OC =.-参考答案-一、单选题1、C【分析】设第三根木棒的长度为x cm ,再确定三角形第三边的范围,再逐一分析各选项即可得到答案.【详解】解:设第三根木棒的长度为x cm ,则9393,x612,x所以A ,B ,D 不符合题意,C 符合题意,故选C【点睛】本题考查的是三角形的三边的关系,掌握“利用三角形的三边关系确定第三边的范围”是解本题的关键.2、D【分析】结合直角三角形,钝角三角形,锐角三角形的内角与外角的含义与大小逐一分析即可.【详解】解:三角形的外角不一定大于它的内角,锐角三角形的任何一个外角都大于内角,故A 不符合题意; 三角形的外角可以是锐角,不一定比锐角大,故B 不符合题意;三角形的内角可以小于60°,一个三角形的三个角可以为:20,70,90, 故C 不符合题意; 三角形中可以有三个内角都是锐角,这是个锐角三角形,故D 符合题意;故选D【点睛】本题考查的是三角形的的内角与外角的含义与大小,掌握“直角三角形,钝角三角形,锐角三角形的内角与外角”是解本题的关键.3、A【分析】先根据旋转的性质可得AB AD =,再根据等边三角形的判定与性质可得5BD AB ==,然后根据线段的和差即可得.【详解】由旋转的性质得:5AB AD ==,60B ∠=︒,ABD ∴是等边三角形,5BD AB ∴==,8BC =,853CD BC BD ∴=-=-=.故选:A .【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点,熟练掌握旋转的性质是解题关键.4、C【分析】由平行线的性质和角平分线的定义可得EBD EDB ∠=∠,则ED BE =,同理可得DF FC =,则EF BE CF =+,可得答案.【详解】解://EF BC ,EDB DBC ∴∠=∠, BD 平分ABC ∠,EBD DBC ∴∠=∠,EDB EBD ∴∠=∠,ED BE ∴=,同理DF FC =,ED DF BE FC∴+=+,=+.即EF BE CF故选:C【点睛】本题主要考查了等腰三角形的判定,平行线的性质,角平分线的定义,熟练掌握等腰三角形的判定定理,平行线的性质定理,角平分线的定义是解题的关键.5、D【分析】设第三根木棒长为x厘米,根据三角形的三边关系可得8﹣5<x<8+5,确定x的范围即可得到答案.【详解】解:设第三根木棒长为x厘米,由题意得:8﹣5<x<8+5,即3<x<13,故选:D.【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和>第三边,任意两边之差<第三边.6、A【分析】先根据三角形内角和定理求出∠ACB=35°,再根据全等三角形性质即可求出∠CAD=35°.【详解】解:∵∠BAC=80°,∠ABC=65°,∴∠ACB=180°-∠BAC-∠ABC=35°,∵△ABC ≌△CDA ,∴∠CAD =∠ACB =35°.故选:A【点睛】本题考查了三角形的内角和定理,全等三角形的性质,熟知两个定理是解题关键.7、C【分析】直接利用直角三角形全等的判定定理(HL 定理)即可判断选项A ;先根据等腰三角形的性质可得ACB DBC ∠=∠,再根据三角形全等的判定定理(AAS 定理)即可判断选项B ;直接利用三角形全等的判定定理(AAS 定理)即可判断选项D ,由此即可得出答案.【详解】解:当添加条件是AB DC =时,在Rt ABC 和Rt DCB △中,AB DC BC CB=⎧⎨=⎩, ()Rt ABC Rt DCB HL ∴≅,则选项A 不符题意;当添加条件是OB OC =时,ACB DBC ∴∠=∠,在ABC 和DCB 中,90A D ACB DBC BC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()DCB A AA BC S ∴≅,则选项B 不符题意;当添加条件是ABC DCB ∠=∠时,在ABC 和DCB 中,90A D ABC DCB BC CB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩, ()DCB A AA BC S ∴≅,则选项D 不符题意;当添加条件是ABO DCO ∠=∠时,不一定能使ABC DCB ≅,则选项C 符合题意;故选:C .【点睛】本题考查了三角形全等的判定、等腰三角形的性质,熟练掌握三角形全等的判定方法是解题关键.8、A【分析】根据AF =DC 求出AC =DF ,再根据全等三角形的判定定理逐个判断即可.【详解】解:∵AF =DC ,∴AF +FC =DC +FC ,即AC =DF ,A 、BC =EF ,AC =DF ,∠A =∠D ,不符合全等三角形的判定定理,不能推出△ABC ≌△DEF ,故本选项符合题意;B 、AB =DE ,∠A =∠D ,AC =DF ,符合全等三角形的判定定理SAS ,能推出△ABC ≌△DEF ,故本选项不符合题意;C .∠B =∠E ,∠A =∠D ,AC =DF ,符合全等三角形的判定定理AAS ,能推出△ABC ≌△DEF ,故本选项不符合题意;D .∠ACB =∠DFE ,AC =DF ,∠A =∠D ,符合全等三角形的判定定理ASA ,能推出△ABC ≌△DEF ,故本选项不符合题意;故选:A .【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.9、B【分析】根据题意画出图形,利用等腰三角形的性质及三角形内角和定理即可得到答案.【详解】如图,在△ABC中,CD是边AB上的中线∵AD=CD=BD∴∠A=∠DCA,∠B=∠DCB∵∠A+∠ACB+∠B=180°∴ ∠A+∠DCA+∠DCB+∠B=180即2∠A+2∠B=180°∴∠A+∠B=90°∴∠ACB=90°∴△ABC是直角三角形故选:B【点睛】本题考查了等腰三角形的性质及三角形内角和定理,熟练运用这两个知识是关键.10、A【分析】全等三角形对应边相等,对应角相等,根据题中信息得出对应关系即可.【详解】∵ABC和DEF全等,A D∠=∠,AC对应DE≅∴ABC DFE∴AB=DF=4故选:A.【点睛】本题考查了全等三角形的概念及性质,应注意①对应边、对应角是对两个三角形而言的,指两条边、两个角的关系,而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等,对应角的平分线相等,对应边上的中线相等,周长及面积相等③全等三角形有传递性.二、填空题1、2a 2n﹣1a【分析】利用等边三角形的性质得到∠A1OB1=∠A1B1O=30°,OA1=A1B1=A2B1=a,利用同样的方法得到A2O=A2B2=2a=21a,A3B3=A3O=2A2O=4=22a,利用此规律即可得到A n B n=2n﹣1a.【详解】解:∵△A1B1A2为等边三角形,∠MON=30°,∴∠A1OB1=∠A1B1O=30°,OA1=A1B1=A2B1=a,同理:A2O=A2B2=2=21a,A3B3=A3O=2A2O=4a=22a,…….以此类推可得△A n B n A n+1的边长为A n B n=2n﹣1a.故答案为:2a;2n﹣1a.【点睛】本题考查规律型:图形的变化类,等边三角形的性质,解题关键是掌握三角形边长的变化规律.2、6.5【分析】AD=,求出由全等三角形的性质可得到AC=DF,从而推出AF=CD,再由10=++=,3CF AF AD CD=+=.==,则 6.5AC AD CD3.5AF CD【详解】解:∵△ABC≌△DEF,∴AC=DF,即AF+AD=CD+AD,∴AF=CD,AD=,∵10CF AF AD CD=++=,3∴7AF CD+=,∴ 3.5==,AF CD∴ 6.5=+=,AC AD CD故答案为:6.5.【点睛】本题主要考查了全等三角形的性质,线段的和差,解题的关键在于能够熟练掌握全等三角形的性质.3、20°度【分析】先根据三角形内角和求出∠A ,利用翻折不变性得出55CA D A ∠'=∠=︒,再根据三角形外角的性质即可解决问题.【详解】解:90ACB ∠=︒,∠B =35°,180180903555A ACB B ∴∠=︒-∠-∠=︒-︒-︒=︒,CDA '△是由CDA 翻折得到,55CA D A ∴∠'=∠=︒,20CA D B BDA B ∠'=∠+∠'=∠+︒,553520BDA CA D B ''∴∠=∠-∠=︒-︒=︒.故答案为:20°.【点睛】本题考查三角形内角和定理和三角形外角的性质,翻折变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.4、20°度【分析】 根据角平分线的性质得到1,122DBC ABC DCE ACE ∠=∠∠=∠,再利用三角形外角的性质计算. 【详解】解:∵ABC ∠与ACE ∠的平分线相交于点D ,∴1,122DBC ABC DCE ACE ∠=∠∠=∠, ∵∠ACE=∠A+∠ABC ,∠DCE=∠D +∠DBC ,∴∠D=∠DCE-∠DBC =11()2022ACE ABC A ∠-∠=∠=︒,故答案为:20°.【点睛】此题考查了三角形的外角性质及角平分线的性质,熟记三角形外角的性质定理是解题的关键. 5、80【分析】先求解40,DFC 再求解140,60,80,40,EDF FDC FCD FCG 再利用三角形的外角的性质可得答案.【详解】 解: 40BAC ∠=︒,DF AB ∥,40,DFC BAC DE AC ∥,180140,EDF DFC:3:4FDC EDC ∠∠=,140,EDC FDC314060,7FDC 180406080,FCD CG 平分ACB ∠, 140,2FCGFCD 404080.DGC FCG DFC故答案为:80【点睛】本题考查的是角平分线的定义,平行线的性质,三角形的内角和定理,三角形的外角的性质,熟练的运用平行线的性质探究角之间的关系是解本题的关键.三、解答题1、(1)20°;(2)CBF α∠=;(3)AF = CF +BF ,理由见解析【分析】(1)由△ABC 是等边三角形,得到AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,∠EAD =∠CAD =20°,AC =AE ,则∠BAE =∠BAC -∠EAD -∠CAD =20°,AB =AE ,()1180=802ABE AEB BAE ==︒-︒∠∠∠,∠CBF =∠ABE -∠ABC =20°; (2)同(1)求解即可;(3)如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,先证明△AEF ≌△ACF 得到∠AFE =∠AFC ,然后证明∠AFE =∠AFC =60°,得到∠BFC =120°,即可证明F 、C 、G 三点共线,得到△AFG 是等边三角形,则AF =GF =CF +CG =CF +BF .【详解】解:(1)∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,∠EAD =∠CAD =20°,AC =AE ,∴∠BAE =∠BAC -∠EAD -∠CAD =20°,AB =AE , ∴()1180=802ABE AEB BAE ==︒-︒∠∠∠, ∴∠CBF =∠ABE -∠ABC =20°;(2)∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,EAD CAD α∠=∠=,AC =AE ,∴602BAE BAC EAD CAD α∠=∠-∠-∠=︒- ,AB =AE , ∴()1180=602ABE AEB BAE α==︒-︒+∠∠∠, ∴CBF ABE ABC α∠=∠-∠=;(3)AF = CF +BF ,理由如下:如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,∴AF =AG ,∠FAG =60°,∠ACG =∠ABF ,BF =CG在△AEF 和△ACF 中,=AE AC EAF CAF AF AF =⎧⎪∠∠⎨⎪=⎩, ∴△AEF ≌△ACF (SAS ),∴∠AFE =∠AFC ,∵∠CBF +∠BCF +∠BFD +∠CFD =180°,∠CAF +∠CFA +∠ACD +∠CFD =180°,∴∠BFD =∠ACD =60°,∴∠AFE =∠AFC =60°,∴∠BFC =120°,∴∠BAC +∠BFC =180°,∴∠ABF +∠ACF =180°,∴∠ACG +∠ACF =180°,∴F 、C 、G 三点共线,∴△AFG 是等边三角形,∴AF=GF=CF+CG=CF+BF.【点睛】本题主要考查了等边三角形的性质与判定,旋转的性质,折叠的性质,全等三角形的性质与判定,三角形内角和定理,熟知相关知识是解题的关键.2、(1)△AMN是是等腰三角形;理由见解析;(2)①证明见解析;②a﹣b.【分析】(1)由等腰三角形的性质得到∠ABC=∠ACB,由平行线的性质得到∠AMN=∠ABC,∠ANM=∠ACB,于是得到∠AMN=∠ANM,根据等角对等边即可证得结论;(2)①由角平分线的定义得到∠PBM=∠PBC,由平行线的性质得到∠MPB=∠PBC,于是得到∠PBM=∠MPB,根据等角对等边即可证得结论;②由①知MB=MP,同理可得:NC=NP,故△AMN的周长=AB+AC,再根据已知条件即可求出结果.(1)解:△AMN是是等腰三角形,理由如下:∵AB=AC,∴∠ABC=∠ACB,∵MN∥BC,∴∠AMN=∠ABC,∠ANM=∠ACB,∴∠AMN=∠ANM,∴AM=AN,∴△AMN是等腰三角形;(2)①证明:∵BP平分∠ABC,∴∠PBM=∠PBC,∵MN∥BC,∴∠MPB=∠PBC∴∠PBM=∠MPB,∴MB=MP,∴△BPM是等腰三角形;②由①知MB=MP,同理可得:NC=NP,∴△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC,∵△ABC的周长为a,BC=b,∴AB+AC+b=a,∴AB+AC=a﹣b∴△AMN的周长=a﹣b.【点睛】本题考查了等腰三角形的性质和判定,平行线的性质,列代数式,能够灵活应用这些性质是解决问题的关键.3、(1)见解析;(2)DB;线段垂直平分线上的点到线段两端的距离相等;BDC;等边对等角.【分析】(1)根据题目中的小路的尺规作图过程,直接作图即可.(2)根据垂直平分线的性质以及等边对等角进行解答即可.【详解】解:(1) 根据题目中的小路的设计步骤,补全的图形如图所示;(2)解:证明:连接BD,BC,∵直线l为线段AB的垂直平分线,∴DA=DB,(线段垂直平分线上的点到线段两端的距离相等)(填推理的依据)∴∠A=∠ABD,∴∠BDC=∠A+∠ABD=2∠A.∵BC=BD,∴∠ACB=∠BDC ,(等边对等角)(填推理的依据)∴∠ACB=2∠A.【点睛】本题主要是考查了尺规作图能力以及垂直平分线和等边对等角的性质,熟练掌握垂直平分线和等边对等角的性质,是解决该题的关键.4、见解析根据平行线的性质得出∠B =∠E ,进而利用SAS 证明ABC DEF ≅,利用全等三角形的性质解答即可.【详解】证明:FB CE =,FB CF CE CF ∴+=+,即BC EF =.//AB DE ,B E ∴∠=∠.在ABC 和DEF 中,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩, ()ABC DEF SAS ∴≅△△A D ∴∠=∠.【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证ABC DEF ≅是解题的关键.5、(1)见详解;(2)见详解【分析】(1)由题意易得60ABC ACB BAC ∠=∠=∠=︒,然后根据平行线的性质可得60ADE AED ∠=∠=︒,进而问题可求证;(2)连接AG ,由题意易得AB =AC ,然后可知△ABF ≌△ACG ,则有AF =AG ,进而可得∠FAG =60°,最后问题可求证.证明:(1)∵ABC 是等边三角形,∴60ABC ACB BAC ∠=∠=∠=︒,∵DE ∥BC ,∴60,60ADE ABC AED ACB ∠=∠=︒∠=∠=︒,∴60ADE AED ∠=∠=︒,∴ADE 是等边三角形;(2)连接AG ,如图所示:∵ABC 是等边三角形,∴60BAC ∠=︒,AB =AC ,∵BF CG =,ABF ACG ∠=∠,∴△ABF ≌△ACG (SAS ),∴,AF AG BAF CAG =∠=∠,∵60BAF FAC BAC ∠+∠=∠=︒,∴60CAG FAC FAG ∠+∠=∠=︒,∴AFG 是等边三角形,∴AF FG =.【点睛】本题主要考查全等三角形及等边三角形的性质与判定,熟练掌握全等三角形及等边三角形的性质与判定是解题的关键.6、(1)见解析(2)ABE △的面积为20.【分析】(1)根据已知条件得到E CFD ∠=∠、BD CD =,然后利用全等三角形的判定,进行证明即可.(2)分别根据ACF 和CFD △的面积,用CF 表示AF 、D F ,通过CFD BED ≅△△,得到BE CF =,DE DF =,用CF 表示出AE 的长,最后利用面积公式求解即可.(1)(1)解:由题意可知:90E CFD ∠=∠=︒AD 是ABC 的中线BD CD ∴=在CFD ∆与BED ∆中CDF BDE C CFD E D BD ∠=∠=∠=∠⎧⎪⎨⎪⎩∴∆∆()CFD BED AAS ≌.(2) 解:ACF 的面积为8,CFD △的面积为6.182AF CF ∴⋅=,即16AF CF =162DF CF ⋅=,即12DF CF = 由(1)可知:CFD BED ∆∆≌BE CF ∴=,12DE DF CF== 40AE AF DF DE CF ∴=++= 1202ABE S AE BE ∆∴=⋅=. 【点睛】本题主要是考查了全等三角形的判定和性质,熟练根据条件证明三角形全等,利用其性质,证明对应边相等,这是解决本题的关键.7、(1)57°,147°;(2)∠ACB =180°-∠DCE ,理由见解析;(3)∠DAB+∠CAE =120°【分析】(1)根据角的和差定义计算即可.(2)利用角的和差定义计算即可.(3)利用特殊三角板的性质,角的和差定义即可解决问题.【详解】解:(1)由题意,903357BCD ∠=︒-︒=︒;9057147ACB ∠=︒+︒=︒;故答案为:57°,147°.(2)∠ACB =180°-∠DCE ,理由如下:∵ ∠ACE =90°-∠DCE ,∠BCD =90°-∠DCE ,∴ ∠ACB=∠ACE+∠DCE+∠BCD=90°-∠DCE+∠DCE+90°-∠DCE=180°-∠DCE.(3)结论:∠DAB+∠CAE=120°.理由如下:∵∠DAB+∠CAE=∠DAE+∠CAE+∠BAC+∠CAE=∠DAC+∠EAB,又∵∠DAC=∠EAB=60°,∴∠DAB+∠CAE=60°+60°=120°.故答案为:∠DAB+∠CAE=120°.【点睛】本题考查三角形的内角和定理,角的和差定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.8、(1)90,40 ;(2)∠ABP+∠ACP+∠A=90°;(3)∠A+∠ACP-∠ABP=90°.【分析】△和ABC中的角的关系即可.(1)由三角形内角和为180°计算BPC(2)由(1)所得即可得出∠ABP、∠ACP、∠A的关系为∠ABP+∠ACP+∠A=90°.(3)由三角形外角的性质即可推出∠A+∠ACP-∠ABP=90°.【详解】△中(1)在BPC∵∠MPN=90°∴∠PBC+∠PCB=180°-∠MPN=180°-90°=90°在ABC中∵∠A+∠ABC+∠ACB=180°又∵∠ABC =∠PBC +∠ABP,∠ACB =∠ACP +∠BCP∴∠A +∠PBC +∠ABP +∠ACP +∠BCP =180°∵∠PBC +∠PCB =90°,∠A =50°∴∠ABP +∠ACP =180°-90°-50°=40°(2)由(1)问可知∠A +∠PBC +∠ABP +∠ACP +∠BCP =180°又∵∠PBC +∠PCB =90°∴∠A +∠ABP +∠ACP =180°-(∠PBC +∠PCB )=180°-90°=90°(3)如图所示,设PN 与AB 交于点H∵∠A +∠ACP =∠AHP又∵∠ABP +∠MPN =∠AHP∴∠A +∠ACP =∠ABP +∠MPN又∵∠MPN =90°∴∠A +∠ACP =90°+∠ABP∴∠A +∠ACP -∠ABP =90°.【点睛】本题考查了三角形的性质以及三角尺的角度计算问题,三角板的角度分别为90°,45°,45°;90°,60°,30°两种直角三角尺,三角形内角和是180°,三角形的一个外角等于与它不相邻的两个内角的和.9、(1)BP CP '=,理由见解析;(2)①60°;②PM =12AP ,见解析【分析】(1)根据等边三角形的性质,可得AB =AC ,∠BAC =60°,再由由旋转可知:60AP AP PAP ''=∠=︒,,从而得到BAP CAP '∠=∠,可证得ABP ACP '≌,即可求解 ;(2)①由∠BPC =120°,可得∠PBC +∠PCB =60°.根据等边三角形的性质,可得∠BAC =60°,从而得到∠ABC +∠ACB =120°,进而得到∠ABP +∠ACP =60°.再由ABP ACP '≌,可得ABP ACP '∠=∠ ,即可求解;②延长PM 到N ,使得NM =PM ,连接BN .可先证得△PCM ≌△NBM .从而得到CP =BN ,∠PCM =∠NBM .进而得到BN BP '= .根据①可得60P BP '∠︒=,可证得PNB PP B '≌,从而得到PN PP '= .再由PAP ' 为等边三角形,可得P P AP '= .从而得到PN AP = ,即可求解.【详解】解:(1)BP CP '= .理由如下:在等边三角形ABC 中,AB =AC ,∠BAC =60°,由旋转可知:60AP AP PAP ''=∠=︒,,∴PAP BAP BAC BAP '∠-∠=∠-∠即BAP CAP '∠=∠在ABP '△和△ACP 中AB AC BAP CAP AP AP =⎧⎪∠=''=∠⎨⎪⎩∴ABP ACP SAS '≌() .∴BP CP '= .(2)①∵∠BPC =120°,∴∠PBC +∠PCB =60°.∵在等边三角形ABC 中,∠BAC =60°,∴∠ABC +∠ACB =120°,∴∠ABP +∠ACP =60°.∵ABP ACP '≌ .∴ABP ACP '∠=∠ ,∴∠ABP +∠ABP '=60°.即60P BP '∠︒= ;②PM =12AP .理由如下:如图,延长PM 到N ,使得NM =PM ,连接BN .∵M 为BC 的中点,∴BM =CM .在△PCM 和△NBM 中PM NM PMC NMB CM BM =⎧⎪∠=∠⎨⎪=⎩∴△PCM ≌△NBM (SAS ).∴CP =BN ,∠PCM =∠NBM .∴BN BP '= .∵∠BPC =120°,∴∠PBC +∠PCB =60°.∴∠PBC +∠NBM =60°.即∠NBP =60°.∵∠ABC +∠ACB =120°,∴∠ABP +∠ACP =60°.∴∠ABP +∠ABP '=60°.即60P BP '∠︒= .∴P BP NBP '∠∠= .在△PNB 和P B P ' 中BN BP NBP P BP BP BP ''=⎧⎪∠=∠⎨⎪=⎩∴PNB PP B '≌ (SAS ).∴PN PP '= .∵60AP AP PAP ''=∠=︒,,∴PAP ' 为等边三角形,∴P P AP '= .∴PN AP = ,∴PM =12AP .【点睛】本题主要考查了等边三角形判定和性质,全等三角形的判定和性质,图形的旋转,熟练掌握等边三角形判定和性质定理,全等三角形的判定和性质定理,图形的旋转的性质是解题的关键.10、证明过程见解析【分析】先证明AEB ADC ≅,得到DB EC =,B C ∠=∠,再证明DOB EOC ≅△△,即可得解;【详解】由题可得,在AEB △和ADC 中,A A AE AD AEB ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴AEB ADC ≅,∴AB AC =,B C ∠=∠,又∵AD AE =,∴DB EC =,在DOB 和EOC △中,B C DOB EOC DB EC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴DOB EOC ≅△△,∴OB OC =.【点睛】本题主要考查了全等三角形的判定与性质,准确分析证明是解题的关键.。
沪教版数学七年级下 第十四章三角形 14.4 全等三角形的判定练习一和参考答案
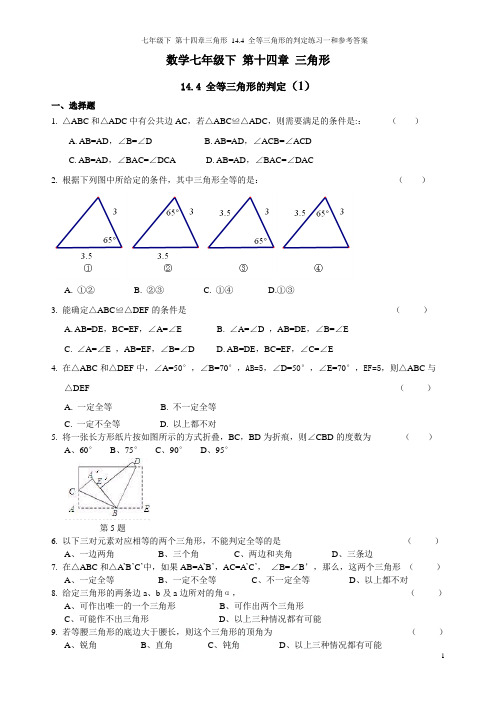
数学七年级下第十四章三角形14.4 全等三角形的判定(1)一、选择题1. △ABC和△ADC中有公共边AC,若△ABC≌△ADC,则需要满足的条件是::()A. AB=AD,∠B=∠DB. AB=AD,∠ACB=∠ACDC. AB=AD,∠BAC=∠DCAD. AB=AD,∠BAC=∠DAC2. 根据下列图中所给定的条件,其中三角形全等的是:()A. ①②B. ②③C. ①④D.①③3. 能确定△ABC≌△DEF的条件是()A. AB=DE,BC=EF,∠A=∠EB. ∠A=∠D ,AB=DE,∠B=∠EC. ∠A=∠E ,AB=EF,∠B=∠DD. AB=DE,BC=EF,∠C=∠E4. 在△ABC和△DEF中,∠A=50°,∠B=70°,AB=5,∠D=50°,∠E=70°,EF=5,则△ABC与△DEF ()A. 一定全等B. 不一定全等C. 一定不全等D. 以上都不对5. 将一张长方形纸片按如图所示的方式折叠,BC,BD为折痕,则∠CBD的度数为()A、60°B、75°C、90°D、95°第5题6. 以下三对元素对应相等的两个三角形,不能判定全等的是()A、一边两角B、三个角C、两边和夹角D、三条边7. 在△ABC和△A’B’C’中,如果AB=A’B’,AC=A’C’,∠B=∠B’,那么,这两个三角形()A、一定全等B、一定不全等C、不一定全等D、以上都不对8. 给定三角形的两条边a、b及a边所对的角α,()A、可作出唯一的一个三角形B、可作出两个三角形C、可能作不出三角形D、以上三种情况都有可能9. 若等腰三角形的底边大于腰长,则这个三角形的顶角为()10. 在△ABC和△DEF中,如果AB=DE,∠B=∠E,要使△ABC≌△DEF,则下列补充条件中错误的是()A、AC=DFB、BC=EFC、∠A=∠DD、∠C=∠F二、填空题11、如图,AB=DC,∠ABC=∠DCB,则△ABC≌△DCB,依据是_____________;若AC=DB,∠ACB=∠DBC,则△_________≌△________。
难点详解沪教版七年级数学第二学期第十四章三角形难点解析试题(含解析)
沪教版七年级数学第二学期第十四章三角形难点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,在Rt△ABC中,∠ACB=90°,∠BAC=40°,直线a∥b,若BC在直线b上,则∠1的度数为()A.40°B.45°C.50°D.60°2、BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=()A .30°B .40°C .50°D .60°3、如图:将一张长为40cm 的长方形纸条按如图所示折叠,若AB =3BC ,则纸条的宽为( )A .12B .14C .16D .184、满足下列条件的两个三角形不一定全等的是( ) A .周长相等的两个三角形 B .有一腰和底边对应相等的两个等腰三角形 C .三边都对应相等的两个三角形D .两条直角边对应相等的两个直角三角形5、已知三角形的两边长分别为2cm 和3cm ,则第三边长可能是( ) A .6cmB .5cmC .3cmD .1cm6、如图,钝角ABC 中,2∠为钝角,AD 为BC 边上的高,AE 为BAC ∠的平分线,则DAE ∠与1∠、2∠之间有一种等量关系始终不变,下面有一个规律可以表示这种关系,你发现的是( )A .21DAE ∠=∠-∠B .212DAE ∠-∠∠=C .212DAE ∠∠=-∠ D .122DAE ∠+∠∠=7、如图,ABC 和DEF 全等,且A D ∠=∠,AC 对应DE .若6AC =,5BC =,4AB =,则DF 的长为( )A .4B .5C .6D .无法确定8、定理:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠ACD 是△ABC 的外角.求证:∠ACD =∠A +∠B .下列说法正确的是( )A.证法1用特殊到一般法证明了该定理B.证法1只要测量够100个三角形进行验证,就能证明该定理C.证法2还需证明其他形状的三角形,该定理的证明才完整D.证法2用严谨的推理证明了该定理9、△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC =5,则五边形DECHF的周长为()A.8 B.10 C.11 D.1210、已知等腰三角形有一个角为50°,则这个等腰三角形的底角度数是().A.65°B.65°或80°C.50°或80°D.50°或65°第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、若一个立体图形从正面看和从左面看都是等腰三角形,从上面看是带有圆心的圆,则这个立体图形是_____.2、如图,在△ABC中,∠C=62°,△ABC两个外角的角平分线相交于G,则∠G的度数为_____.3、已知:如图,AB = DB .只需添加一个条件即可证明ABC DBC ≌△△.这个条件可以是______.(写出一个即可).4、如图,在ABC 中,90ACB ∠=︒,DE AB ⊥交BC 的延长线于点E ,若AD DE =,点C 是BE 中点,则B ∠=______°.5、如图,在△ABC 中,已知点D E F 、、分别为BC AD CE 、、的中点,若△ABC 的面积为24m ,则阴影部分的面积为 _________ 2cm三、解答题(10小题,每小题5分,共计50分)1、如图,在ABC 中,AB AC =,AD 是角平分线,E 是AB 边上一点,连接ED ,CB 是ACF ∠的平分线,ED 的延长线与CF 交于点F .(1)求证:BE CF =;(2)若46CDF ∠=︒,AD DF =,则ACF ∠=______度.2、如图,在等腰△ABC 和等腰△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE 且C 、E 、D 三点共线,作AM ⊥CD 于M .若BD =5,DE =4,求CM .3、如图,在四边形ABCD中,点E在BC上,连接DE、AC相交于点F,∠BAE=∠CAD,AB=AE,AD=AC.(1)求证:∠DEC=∠BAE;(2)如图2,当∠BAE=∠CAD=30°,AD⊥AB时,延长DE、AB交于点G,请直接写出图中除△ABE、△ADC以外的等腰三角形.4、下面是“作一个角的平分线”的尺规作图过程.已知:如图,钝角AOB∠.求作:射线OC,使AOC BOC∠=∠.作法:如图,①在射线OA 上任取一点D ;②以点О为圆心,OD 长为半径作弧,交OB 于点E ;③分别以点D ,E 为圆心,大于12DE 长为半径作弧,在AOB ∠内,两弧相交于点C ; ④作射线OC .则OC 为所求作的射线. 完成下面的证明. 证明:连接CD ,CE由作图步骤②可知OD =______. 由作图步骤③可知CD =______. ∵OC OC =, ∴OCD OCE ≌△△. ∴AOC BOC ∠=∠(________)(填推理的依据).5、 “三等分角”是被称为几何三大难题的三个古希腊作图难题之一.如图1所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒PA ,PB 组成,两根棒在P 点相连并可绕点P 旋转,C 点是棒PA 上的一个固定点,点A ,O 可在棒PA ,PB 内的槽中滑动,且始终保持OA =OC =PC .∠AOB 为要三等分的任意角.则利用“三等分角仪”可以得到∠APB =13∠AOB .我们把“三等分角仪”抽象成如图2所示的图形,完成下面的证明. 已知:如图2,点O ,C 分别在∠APB 的边PB ,PA 上,且OA =OC =PC .求证:∠APB=13∠AOB.6、已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.(1)如图1,求证:AB∥CD;(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=17∠CDB,求∠GMH的度数.7、如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段AB的端点都在格点上.要求以AB为边画一个等腰ABC,且使得点C为格点.请在下面的网格图中画出3种不同的等腰ABC.8、如图,ABC 为等边三角形,D 是BC 中点,60ADE ∠=︒,CE 是ABC 的外角ACF ∠的平分线. 求证:AD DE =.9、如图所示,四边形ABCD 的对角线AC 、BD 相交于点O ,已知OAB OBA ∠=∠,CBA DAB ∠=∠.求证:(1)ABC BAD ≌; (2)OC OD =.10、(1)我们把两个面积相等但不全等的三角形叫做“偏等积三角形”,如图1,ABC 中,7,9,10===AC BC AB ,P 为AC 上一点,当AP =_______时,ABP △与CBP 是偏等积三角形;(2)如图2,四边形ABED 是一片绿色花园,ACB △、DCE 是等腰直角三角形,()90090∠=∠=︒<∠<︒ACB DCB BCE .①ACD △与BCE 是偏等积三角形吗?请说明理由;②已知60m,=BE ACD 的面积为22100m .如图3,计划修建一条经过点C 的笔直的小路CF ,F 在BE 边上,FC 的延长线经过AD 中点G .若小路每米造价600元,请计算修建小路的总造价.-参考答案-一、单选题1、C【分析】根据三角形内角和定理确定50ABC ∠=︒,然后利用平行线的性质求解即可.【详解】解:∵40BAC ∠=︒,90ACB ∠=︒,∴50ABC ∠=︒,∵a b ∥,∴150ABC ∠=∠=︒,故选:C .【点睛】题目主要考查平行线的性质,三角形内角和定理等,熟练掌握运用平行线的性质是解题关键.2、A【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠P 的度数.【详解】∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,∵∠PCM是△BCP的外角,∴∠P=∠PCM−∠CBP=50°−20°=30°,故选:A.【点睛】本题考查三角形外角性质以及角平分线的定义,解题时注意:一个三角形的外角等于与它不相邻的两个内角的和.3、B【分析】如图,延长NO交AD的延长线于点P,设BC=x,则AB=3x,利用折叠的性质和等腰直角三角形的性质可表示出纸条的宽MO,NO的长,从而可表示出纸条的长2PN的长,然后根据长方形纸条的长为40,可得到关于x的方程,解方程求出x的值,即可求出纸条的宽.【详解】解:如图,延长NO交AD的延长线于点P,设BC=x,则AB=3x,∵折叠,∴AB=BM=CO=CD=PO=3x,∴纸条的宽为:MO=NO=3x+3x+x=7x,∴纸条的长为:2PN=2(7x+3x)=20x=40解得:x=2,∴纸条的宽NO=7×2=14.故答案为:B.【点睛】此题考查了折叠的性质,等腰直角三角形的性质,一元一次方程应用题,解题的关键是正确分析题目中的等量关系列出方程求解.4、A【分析】根据全等三角形的判定方法求解即可.判定三角形全等的方法有:SSS,SAS对各选项进行一一判断即可.【详解】解:A、周长相等的两个三角形不一定全等,符合题意;B、有一腰和底边对应相等的两个等腰三角形根据三边对应相等判定定理可判定全等,不符合题意;C、三边都对应相等的两个三角形根据三边对应相等判定定理可判定全等,不符合题意;D、两条直角边对应相等的两个直角三角形根据SAS判定定理可判定全等,不符合题意.故选:A.【点睛】此题考查了全等三角形的判定方法,解题的关键是熟练掌握全等三角形的判定方法.判定三角形全等的方法有:SSS,SAS,AAS,ASA,HL(直角三角形).5、C【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.【详解】解:设第三边长为x cm,根据三角形的三边关系可得:3-2<x<3+2,解得:1<x<5,只有C选项在范围内.故选:C.【点睛】本题考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.6、B【分析】根据三角形内角和定理、角平分线的性质、三角形外角的性质依次推理即可得出结论.【详解】解:由三角形内角和知∠BAC=180°-∠2-∠1,∵AE为∠BAC的平分线,∴∠BAE=12∠BAC=12(180°-∠2-∠1).∵AD为BC边上的高,∴∠ADC=90°=∠DAB+∠ABD.又∵∠ABD=180°-∠2,∴∠DAB=90°-(180°-∠2)=∠2-90°,∴∠EAD=∠DAB+∠BAE=∠2-90°+12(180°-∠2-∠1)=12(∠2-∠1).故选:B 【点睛】本题主要考查了三角形的内角和定理,角平分线的定义、三角形外角性质及三角形的高的定义,解答的关键是找到已知角和所求角之间的联系.7、A【分析】全等三角形对应边相等,对应角相等,根据题中信息得出对应关系即可.【详解】∵ABC和DEF全等,A D∠=∠,AC对应DE≅∴ABC DFE∴AB=DF=4故选:A.【点睛】本题考查了全等三角形的概念及性质,应注意①对应边、对应角是对两个三角形而言的,指两条边、两个角的关系,而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等,对应角的平分线相等,对应边上的中线相等,周长及面积相等③全等三角形有传递性.8、D【分析】利用测量的方法只能是验证,用定理,定义,性质结合严密的逻辑推理推导新的结论才是证明,再逐一分析各选项即可得到答案.【详解】解:证法一只是利用特殊值验证三角形的一个外角等于与它不相邻的两个内角的和,证法2才是用严谨的推理证明了该定理,故A不符合题意,C不符合题意,D符合题意,证法1测量够100个三角形进行验证,也只是验证,不能证明该定理,故B不符合题意;故选D【点睛】本题考查的是三角形的外角的性质的验证与证明,理解验证与证明的含义及证明的方法是解本题的关键.9、B【分析】证明△AFH ≌△CHG (AAS ),得出AF =CH .由题意可知BE =FH ,则得出五边形DECHF 的周长=AB +BC ,则可得出答案.【详解】解:∵△GFH 为等边三角形,∴FH =GH ,∠FHG =60°,∴∠AHF +∠GHC =120°,∵△ABC 为等边三角形,∴AB =BC =AC =5,∠ACB =∠A =60°,∵∠AHF =180°-∠FHG -∠GHC =120°-∠GHC ,∠HGC =180°-∠C -∠GHC =120°-∠GHC ,∴∠AHF =∠HGC ,在△AFH 和△CHG 中A C AHF HGC FH GH ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AFH ≌△CHG (AAS ),∴AF =CH .∵△BDE 和△FGH 是两个全等的等边三角形,∴五边形DECHF的周长=DE+CE+CH+FH+DF=BD+CE+AF+BE+DF,=(BD+DF+AF)+(CE+BE),=AB+BC=10.故选:B.【点睛】本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.10、D【分析】50︒可以是底角,也可以是顶角,分情况讨论即可.【详解】当50︒角为底角时,底角就是50︒,︒-︒÷=︒,当50︒角为等腰三角形的顶角时,底角为(18050)265因此这个等腰三角形的底角为50︒或65︒.故选:D.【点睛】本题考查了等腰三角形的性质;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.二、填空题1、圆锥【分析】根据立体图形视图、等腰三角形的性质分析,即可得到答案.根据题意,这个立体图形是圆锥故答案为:圆锥.【点睛】本题考查了等腰三角形、圆锥、立体图形视图的知识;解题的关键是熟练掌握立体图形视图的性质,从而完成求解.2、59°【分析】先利用三角形内角和定理求出∠CAB +∠CBA =180°-∠C =118°,从而利用三角形外角的性质求出∠DAB +∠EBA =2∠C +∠CAB +∠CBA =242°,再由角平分线的定义求出11==12122GAB GBA DAB EBA ++︒∠∠∠∠,由此求解即可. 【详解】解:∵∠C =62°,∴∠CAB +∠CBA =180°-∠C =118°,∵∠DAB =∠C +∠CBA ,∠EBA =∠C +∠CAB ,∴∠DAB +∠EBA =2∠C +∠CAB +∠CBA =242°,∵△ABC 两个外角的角平分线相交于G , ∴1=2GAB DAB ∠∠,12GBA EBA ∠=∠, ∴11==12122GAB GBA DAB EBA ++︒∠∠∠∠, ∴∠G =180°-∠GAB -∠GBA =59°,故答案为:59°.【点睛】本题主要考查了三角形内角和定理,三角形外角的性质,角平分线的定义,熟知相关知识是解题的关键.3、AC =DC【分析】由题意可得,BC 为公共边,AB =DB ,即添加一组边对应相等,可证△ABC 与△DBC 全等.【详解】解:∵AB =DB ,BC =BC ,添加AC =DC ,∴在△ABC 与△DBC 中,AB DB BC BC AC DC =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△DBC (SSS ),故答案为:AC =DC .【点睛】本题考查了全等三角形的判定,灵活运用全等三角形的判定是本题的关键.4、67.5°【分析】连接AE,先得出∠BAC=12∠BAE,再根据AD DE=,得出∠BAC=22.5°,最后得出结果.【详解】解:连接AE,∵点C是BE中点,∴BC=CE,∵∠ACB=90°,∴AC⊥BE,∴AB=AE,∴∠BAC=12∠BAE,∵DE⊥AB,∴∠ADE=90°,∵AD DE=,∴∠AED=∠DAE=45°,∴∠BAC=12∠BAE=22.5°,∴∠B=90°-∠BAC=67.5°.故答案为:67.5°.【点睛】本题考查了线段垂直平分线的性质,等腰三角形的性质及直角三角形的性质,正确作出辅助线是解题的关键.5、1【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.【详解】解:∵点E是AD的中点,∴S△ABE=12S△ABD,S△ACE=12S△ADC,∴S△ABE+S△ACE=12S△ABC=12×4=2cm2,∴S△BCE=12S△ABC=12×4=2cm2,∵点F是CE的中点,∴S△BEF=12S△BCE=12×2=1cm2.故答案为:1.【点睛】本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.三、解答题1、(1)见解析,(2)46【分析】(1)根据等腰三角形的性质和角平分线得到∠B=∠ACB=∠BCF,由AD是角平分线,得到BD=CD,证△BDE≌△CDF即可;(2)根据全等三角形的性质得到DE=DF=DA,根据46∠=︒求得∠DAB,进而求出∠B的度数即CDF可.【详解】=,(1)证明:∵AB AC∴∠B=∠ACB,∠的平分线,∵CB是ACF∴∠ACB=∠BCF,∴∠B=∠BCF,∵AD是角平分线,AB=AC,∴BD=CD,∵∠BDE=∠CDF,∴△BDE≌△CDF(AAS);=;∴BE CF(2)∵△BDE≌△CDF;∴ED=FD,∵AD DF=,∵46CDF ADE ∠=∠=︒, ∴180672ADE BAD ︒-∠∠==︒, ∴2134BAC BAD ∠=∠=︒,∴∠B =∠ACB =∠BCF =23°,∴246ACF BCF ∠=∠=︒,故答案为:46.【点睛】本题考查了等腰三角形的性质和全等三角形的判定与性质,解题关键是熟练运用相关知识进行推理证明和计算.2、CM =7.【分析】根据题意由“SAS ”可证△AEC ≌△ADB ,可得BD =CE ,由等腰三角形的性质可得DM =ME =2进行分析计算即可得出答案.【详解】解:∵∠BAC =∠DAE ,∴∠BAC ﹣∠BAE =∠DAE ﹣∠BAE ,∴∠BAD =∠CAE ,在△AEC 和△ADB 中,AE AD BAD CAE AC AB =⎧⎪∠=∠⎨⎪=⎩, ∴△AEC ≌△ADB (SAS ),∴CE =BD =5,∵AD =AE ,AM ⊥CD ,DE =4, ∴114222ME DE ==⨯=, ∴CM =CE +EM =5+2=7.【点睛】本题考查全等三角形的判定和性质以及等腰三角形的性质,熟练掌握全等三角形的判定定理是解答本题的关键.3、(1)见解析;(2)△AEF 、△ADG 、△DCF 、△ECD【分析】(1)根据已知条件得到∠BAE =∠CAD ,根据全等三角形的性质得到∠AED =∠ABC ,根据等腰三角形的性质得到∠ABC =∠AEB ,于是得到结论;(2)根据等腰三角形的判定定理即可得到结论.【详解】证明:(1)如图1,∵∠BAE =∠CAD ,∴∠BAE +∠CAE =∠CAD +∠CAE ,即∠BAC =∠EAD ,在△AED 与△ABC 中,AB AE BAC EAD AD AC ⎧⎪∠∠⎨⎪⎩=== ∴△AED ≌△ABC ,∴∠AED =∠ABC ,∵∠BAE+∠ABC+∠AEB=180°,∠CED+∠AED+∠AEB=180°,∵AB=AE,∴∠ABC=∠AEB,∴∠BAE+2∠AEB=180°,∠CED+2∠AEB=180°,∴∠DEC=∠BAE;(2)解:如图2,①∵∠BAE=∠CAD=30°,∴∠ABC=∠AEB=∠ACD=∠ADC=75°,由(1)得:∠AED=∠ABC=75°,∠DEC=∠BAE=30°,∵AD⊥AB,∴∠BAD=90°,∴∠CAE=30°,∴∠AFE=180°−30°−75°=75°,∴∠AEF=∠AFE,∴△AEF是等腰三角形,②∵∠BEG=∠DEC=30°,∠ABC=75°,∴∠G=45°,在Rt△AGD中,∠ADG=45°,∴△ADG是等腰直角三角形,③∠CDF =75°−45°=30°,∴∠DCF =∠DFC =75°,∴△DCF 是等腰直角三角形;④∵∠CED =∠EDC =30°,∴△ECD 是等腰三角形.【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的判定,等腰三角形的判定和性质,熟练掌握全等三角形的判定与性质是解题的关键.4、OE ; CE ;全等三角形的对应角相等【分析】根据圆的半径相等可得OD =OE ,CD =CE ,再利用SSS 可证明OCD OCE ≌△△,从而根据全等三角形的性质可得结论.【详解】证明:连接CD ,CE由作图步骤②可知OD =___OE ___.由作图步骤③可知CD =__CE ___.∵OC OC =,∴OCD OCE ≌△△. ∴AOC BOC ∠=∠(__全等三角形对应角相等__)故答案为:OE ; CE ;全等三角形的对应角相等【点睛】本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了全等三角形的判定和性质.5、见解析【分析】由OA OC PC ==,得出,POC AOC 为等腰三角形,由外角的性质及等量代换得2CAO APB ∠=∠,再次利用外角的性质及等量代换得3AOB APB ∠=∠,即可证明.【详解】解:OA OC PC ==,,POC AOC ∴为等腰三角形,,APB COP ACO CAO ∴∠=∠∠=∠,由外角的性质得:2ACO APB COP APB ∠=∠+∠=∠,2CAO APB ∠=∠,再由外角的性质得:AOB APB CAO ∠=∠+∠,3AOB APB ∴∠=∠,13APB AOB ∴∠=∠. 【点睛】本题考查了等腰三角形、外角的性质、解题的关键是掌握外角的性质及等量代换的思想进行求解.6、(1)见详解;(2)∠MEB =40°,(3)∠GMH =80°【分析】(1)根据等角的补角性质得出∠ABD =∠CDV ,根据同位角相等两直线平行可得AB ∥CD ;(2)根据AB ∥CD ;利用内错角相等得出∠ABD =∠RDB ,根据BE ∥DF ,得出∠EBD =∠FDB ,利用等量减等量差相等得出∠ABE =∠FDR ,根据∠FDR =35°,可得∠ABE =∠FDR =35°即可;(3)设ME 交AB 于S ,根据MG ∥EN ,得出∠NES =∠GMS =∠GES ,设∠NES =y °,可得∠NEG =∠NES +∠GES=2∠NES =2y °,根据∠EBD =2∠NEG ,得出∠EBD =4∠NES =4y °,根据∠EDC =17∠CDB ,设∠EDC =x °,得出∠CDB =7x °,根据AB ∥CD ,得出∠GBE +∠EBD +∠CDB =180°,可得35+4y +7x =180根据三角形内角和∠BDE =∠BDC -∠EDC =7x -x =6x ,∠BED =180°-∠EBD -∠EDB =180°-4y °-6x °,利用EB 平分∠DEN ,得出y °+40°=180°-4y °-6x °,解方程组7414565140x y x y +=⎧⎨+=⎩,解得1510x y =⎧⎨=⎩,可证ME ∥UV ,根据MH ⊥UV ,可求∠SMH =90°,∠SMG =∠NES =10°即可. 【详解】(1)证明:∵∠ABU +∠ABD =180°,∠ABU +∠CDV =180°.∴∠ABU =180°-∠ABD ,∠CDV =180°-∠ABU ,∴∠ABD =∠CDV ,∴AB ∥CD ;(2)解:∵AB ∥CD ;∴∠ABD =∠RDB ,∴∠ABE +∠EBD =∠FDB +∠FDR ,∵BE ∥DF ,∴∠EBD =∠FDB ,∴∠ABE =∠FDR ,∵∠FDR =35°,∴∠ABE =∠FDR =35°,∴∠MEB =∠ABE +5°=35°+5°=40°,(3)解:设ME 交AB 于S ,∵MG ∥EN ,∴∠NES =∠GMS =∠GES ,设∠NES =y °,∵∠EBD=2∠NEG∴∠NEG=∠NES+∠GES=2∠NES=2y°,∴∠EBD=4∠NES=4y°,∵∠EDC=17∠CDB,设∠EDC=x°∴∠CDB=7x°,∵AB∥CD,∴∠ABD+∠CDB=180°,即∠GBE+∠EBD+∠CDB=180°,∴35+4y+7x=180,∵∠BDE=∠BDC-∠EDC=7x-x=6x,∴∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,∵EB平分∠DEN,∴∠NEB=∠BED,∵∠NEB=∠NES+∠SEB=y°+40°,∴y°+40°=180°-4y°-6x°,∴74145 65140x yx y+=⎧⎨+=⎩,解得1510xy=⎧⎨=⎩,∴∠EBD=4y°=40°=∠MEB,∴ME∥UV,∵MH⊥UV,∴MH⊥ME,∴∠SMH=90°,,∵∠SMG=∠NES=10°,∴∠GMH=90°-∠SMG=90°-10°=80°.【点睛】本题考查平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组,掌握平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组是解题关键.7、答案见解析【分析】AB为4个等边三角形组成的平行四边形的对角线,因此只要找到另一腰也4个等边三角形组成的平行四边形的对角线即可【详解】解:如图,……[答案不唯一]【点睛】本题考查等腰三角形的绘图,掌握等边三角形和等腰三角形性质即可.8、证明见解析.【分析】过D作DG∥AC交AB于G,由等边三角形的性质和平行线的性质得到∠BDG=∠BGD=60°,于是得到△BDG是等边三角形,再证明△AGD≌△DCE即可得到结论.【详解】证明:过D作DG∥AC交AB于G,∵△ABC是等边三角形,∴AB=AC,∠B=∠ACB=∠BAC=60°,又∵DG∥AC,∴∠BDG=∠BGD=60°,∴△BDG是等边三角形,∠AGD=180°−∠BGD=120°,∴DG=BD,∵点D为BC的中点,∴BD=CD,∴DG=CD,∵EC是△ABC外角的平分线,∴∠ACE =12(180°−∠ACB )=60°,∴∠BCE =∠ACB +∠ACE =120°=∠AGD ,∵AB =AC ,点D 为BC 的中点,∴∠ADB =∠ADC =90°,又∵∠BDG =60°,∠ADE =60°,∴∠ADG =∠EDC =30°,在△AGD 和△ECD 中,AGD ECD GD CDADG EDC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AGD ≌△ECD (ASA ).∴AD =DE .【点睛】本题是三角形综合题,主要考查了平行线的性质,全等三角形的性质与判定,等边三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.9、(1)证明见解析;(2)证明见解析.【分析】(1)根据全等三角形的判定定理可直接证明;(2)根据(1)中结论可得AC BD =,再由等角对等边得出OA OB =,运用等式的性质进行计算即可证明.(1)解:在ABC 与BAD 中,CAB DBA AB BACBA DAB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABC BAD ≅;(2)由(1)可得:ABC BAD ≅,∴AC BD =,∵OAB OBA ∠=∠,∴OA OB =,∴AC OA BD OB -=-,即OC OD =.【点睛】题目主要考查全等三角形的判定和性质,等角对等边的性质,理解题意,综合运用这些知识点是解题关键.10、(1)72;(2)①ACD △与BCE 是偏等积三角形,理由见详解;②修建小路的总造价为42000元【分析】(1)当AP CP =时,则72AP =,证ABP CBP S S ∆∆=,再证ABP ∆与CBP ∆不全等,即可得出结论;(2)①过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,证()ACM BCN AAS ∆∆≌,得AM BN =,则ACD BCE S S ∆∆=,再证ACD ∆与BCE ∆不全等,即可得出结论;②过点A 作//AN CD ,交CG 的延长线于N ,证得()AGN DGC AAS ∆∆≌,得到AN CD =,再证()ACN CBE SAS ∆∆≌,得ACN CBE ∠=∠,由余角的性质可证CF BE ⊥,然后由三角形面积和偏等积三角形的定义得12BCE S BE CF ∆=⋅,2100BCEACD S S ∆∆==,求出70()CF m =,即可求解. 【详解】解:(1)当72AP CP ==时,ABP ∆与CBP ∆是偏等积三角形,理由如下:设点B 到AC 的距离为h ,则12ABP S AP h ∆=⋅,12CBP S CP h ∆=⋅,ABP CBP S S ∆∆∴=,10AB =,7BC =,AB BC ∴≠,AP CP =、PB PB =,ABP ∴∆与CBP ∆不全等,ABP ∴∆与CBP ∆是偏等积三角形, 故答案为:72;(3)①ACD ∆与BCE ∆是偏等积三角形,理由如下:过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,如图3所示:则90AMC BNC ∠=∠=︒,ACB ∆、DCE ∆是等腰直角三角形,90ACB DCE ∴∠=∠=︒,AC BC =,CD CE =,3603609090180BCN ACD ACB DCE ∴∠+∠=︒-∠-∠=︒-︒-︒=︒,180ACM ACD ∠+∠=︒,ACM BCN ∴∠=∠,在∆ACM 和BCN ∆中,AMC BNC ACM BCN AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ACM BCN AAS ∴∆∆≌,AM BN ∴=,12ACD S CD AM ∆=⋅,12BCE S CE BN ∆=⋅, ACD BCE S S ∆∆∴=,180BCE ACD ∠+∠=︒,090BCE ︒<∠<︒,ACD BCE ∴∠≠∠,CD CE =,AC BC =,ACD ∴∆与BCE ∆不全等,ACD ∴∆与BCE ∆是偏等积三角形;②如图4,过点A 作//AN CD ,交CG 的延长线于N ,则N GCD ∠=∠, G 点为AD 的中点,AG GD ∴=,在AGN ∆和DGC ∆中,N GCD AGN DGC AG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AGN DGC AAS ∴∆∆≌,AN CD ∴=,CD CE =,AN CE ∴=,//AN CD ,180CAN ACD ∴∠+∠=︒,90ACB DCE ∠=∠=︒,3609090180ACD BCE ∴∠+∠=︒-︒-︒=︒,BCE CAN ∴∠=∠,在ACN ∆和CBE ∆中,AN CE CAN BCE AC CB =⎧⎪∠=∠⎨⎪=⎩, ()ACN CBE SAS ∴∆∆≌,ACN CBE ∴∠=∠,1809090ACN BCF ∠+∠=︒-︒=︒,90CBE BCF ∴∠+∠=︒,90BFC ∴∠=︒,CF BE ∴⊥.由①得:ACD ∆与BCE ∆是偏等积三角形,12BCE S BE CF ∆∴=⋅,2100BCE ACD S S ∆∆==, 22210070()60BCE S CF m BE ∆⨯∴===, ∴修建小路CF 的总造价为:6007042000⨯=(元).【点睛】本题是四边形综合题目,考查了新定义“偏等积三角形”的定义、全等三角形的判定与性质、等腰直角三角形的性质、三角形面积等知识;本题综合性强,熟练掌握“偏等积三角形”的定义,证明ACM BCN ∆∆≌和ACN CBE ∆∆≌是解题的关键,属于中考常考题型.。
2021-2022学年基础强化沪教版七年级数学第二学期第十四章三角形章节练习试题(含答案及详细解析)

沪教版七年级数学第二学期第十四章三角形章节练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,AB=AC,点D、E分别在AB、AC上,补充一个条件后,仍不能判定△ABE≌△ACD的是()A.∠B=∠C B.AD=AE C.BE=CD D.∠AEB=∠ADC2、如图,ABC的面积为18,AD平分∠BAC,且AD⊥BD于点D,则ADC的面积是()A.8 B.10 C.9 D.163、如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是()A .两点确定一条直线B .两点之间,线段最短C .三角形具有稳定性D .三角形的任意两边之和大于第三边4、在下列长度的四根木棒中,能与3cm ,9cm 的两根木棒首尾顺次相接钉成一个三角形的是( )A .3cmB .6cmC .10cmD .12cm5、如图,ABC 中,∠ABC =45°,CD ⊥AB 于D ,BE 平分∠ABC ,且BE ⊥AC 于E ,与CD 相交于点F ,DH ⊥BC 于H ,交BE 于G ,下列结论中正确的是( ) ①BCD 为等腰三角形;②BF =AC ;③CE =12BF ;④BH =CE .A .①②B .①③C .①②③D .①②③④6、下列长度的三条线段能组成三角形的是( )A .3 4 8B .4 4 10C .5 6 10D .5 6 117、如图,钝角ABC 中,2∠为钝角,AD 为BC 边上的高,AE 为BAC ∠的平分线,则DAE ∠与1∠、2∠之间有一种等量关系始终不变,下面有一个规律可以表示这种关系,你发现的是( )A.21DAE∠=∠-∠B.212 DAE∠-∠∠=C.212DAE∠∠=-∠D.122DAE∠+∠∠=8、有两边相等的三角形的两边长为4cm,5cm,则它的周长为()A.8cm B.14cm C.13cm D.14cm或13cm9、下列四个命题是真命题的有()①同位角相等;②相等的角是对顶角;③直角三角形两个锐角互余;④三个内角相等的三角形是等边三角形.A.1个B.2个C.3个D.4个10、我们称网格线的交点为格点.如图,在4×4的长方形网格中有两个格点A、B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,则满足条件的格点C的个数是()A .3B .4C .5D .6第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、等腰三角形的两边长分别是4和9,则它的周长为________.2、如图,方格纸中是9个完全相同的正方形,则∠1+∠2的值为 _____.3、如图,在ABC 中,AB AC =,40A ∠=︒,E 为BC 延长线上一点,ABC ∠与ACE ∠的平分线相交于点D ,则∠D 的度数为______.4、如图,在ABC 中,AB =AC ,∠A =36°,点D 在AC 上,且BD =BC ,则∠BDC =_______.5、如图,两根旗杆CA ,DB 相距20米,且CA ⊥AB ,DB ⊥AB ,某人从旗杆DB 的底部B 点沿BA 走向旗杆CA 底部A 点.一段时间后到达点M ,此时他分别仰望旗杆的顶点C 和D ,两次视线的夹角∠CMD =90°,且CM =DM .已知旗杆BD 的高为12米,该人的运动速度为每秒2米,则这个人从点B 到点M 所用时间是 _____秒.三、解答题(10小题,每小题5分,共计50分)1、如图,ABC 是等边三角形,∥DE BC ,分别交AB ,AC 于点D ,E .(1)求证:ADE 是等边三角形;(2)点F 在线段DE 上,点G 在ABC 外,BF CG =,ABF ACG ∠=∠,求证:AF FG =.2、直线l 经过点A ,ABC 在直线l 上方,AB AC =.(1)如图1,90BAC ∠=︒,过点B ,C 作直线l 的垂线,垂足分别为D 、E .求证:ABD CAE ≌(2)如图2,D ,A ,E 三点在直线l 上,若BAC BDA AEC α∠=∠=∠=(α为任意锐角或钝角),猜想线段DE 、BD 、CE 有何数量关系?并给出证明.(3)如图3,90BAC ∠=︒过点B 作直线l 上的垂线,垂足为F ,点D 是BF 延长线上的一个动点,连结AD ,作90DAE ∠=︒,使得AE AD =,连结DE ,CE .直线l 与CE 交于点G .求证:G 是CE 的中点.3、如图,点D ,E 在△ABC 的边BC 上,AB =AC ,AD =AE ,求证:BD =CE .4、如图,在ABC 中,AB BC =,120ABC ∠=︒,点D 在边AC 上,且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,点F 是ED 与AB 的交点.(1)求证:AE CD =;(2)若40∠=︒DBC ,求BFE ∠的度数.5、如图,等边△ABC 中,点D 在BC 上,CE =CD ,∠BCE =60°,连接AD 、BE .(1)如图1,求证:AD=BE;(2)如图2,延长AD交BE于点F,连接DE、CF,在不添加任何辅助线和其它字母的情况下,请直接写出等于120°的角.6、如图,△ABC中,AB=AC,D为BC边的中点,AF⊥AD,垂足为A.求证:∠1=∠27、“三等分角”是被称为几何三大难题的三个古希腊作图难题之一.如图1所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒PA,PB组成,两根棒在P点相连并可绕点P 旋转,C点是棒PA上的一个固定点,点A,O可在棒PA,PB内的槽中滑动,且始终保持OA=OC=PC.∠AOB为要三等分的任意角.则利用“三等分角仪”可以得到∠APB=13∠AOB.我们把“三等分角仪”抽象成如图2所示的图形,完成下面的证明.已知:如图2,点O,C分别在∠APB的边PB,PA上,且OA=OC=PC.求证:∠APB=13∠AOB.8、如图,在Rt ACB △中,90ACB ∠=︒,CA CB =,点D 是ACB △内一点,连接CD ,过点C 作CE CD ⊥且CE CD =,连接AD ,BE .求证:AD BE =.9、如图,点A ,B ,C ,D 在一条直线上,AB CD =,AE CF ∥,E F ∠=∠.求证:BE DF =.10、如图,AD 是ABC 的中线,分别过点C 、B 作AD 及其延长线的垂线,垂足分别为F 、E .(1)求证:CFD BED ≅△△;(2)若ACF 的面积为8,CFD △的面积为6,求ABE △的面积.-参考答案-一、单选题1、C【分析】根据全等三角形的判定定理进行判断即可.【详解】解:根据题意可知:AB =AC ,A A ∠=∠,若B C ∠=∠,则根据()ASA 可以证明△ABE ≌△ACD ,故A 不符合题意;若AD =AE ,则根据(SAS)可以证明△ABE ≌△ACD ,故B 不符合题意;若BE =CD ,则根据()SSA 不可以证明△ABE ≌△ACD ,故C 符合题意;若∠AEB =∠ADC ,则根据()AAS 可以证明△ABE ≌△ACD ,故D 不符合题意;故选:C .【点睛】本题考查了全等三角形的判定,熟练掌握全等三角形的判定定理是解本题的关键.2、C【分析】延长BD 交AC 于点E ,根据角平分线及垂直的性质可得:BAD EAD ∠=∠,ADB ADE ∠=∠,依据全等三角形的判定定理及性质可得:ABD AED ≌,BD DE =,再根据三角形的面积公式可得:S SSSS =S SSSS ,S SSSS =S SSSS ,得出S SSSS =12S SSSS ,求解即可.【详解】解:如图,延长BD 交AC 于点E ,∵AD 平分BAE ∠,AD BD ⊥,∴BAD EAD ∠=∠,ADB ADE ∠=∠,在ABD 和AED 中,BAD EAD AD ADADB ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABD AED ≌,∴BD DE =,∴S SSSS =S SSSS ,S SSSS =S SSSS ,∴S SSSS =12S SSSS =12×18=9,故选:C .【点睛】题目主要考查全等三角形的判定和性质,角平分线的定义等,熟练掌握基础知识,进行逻辑推理是解题关键.3、C【分析】根据三角形具有稳定性进行求解即可.【详解】解:工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是三角形具有稳定性,故选C.【点睛】本题主要考查了三角形的稳定性,熟知三角形具有稳定性是解题的关键.4、C【分析】设第三根木棒的长度为x cm,再确定三角形第三边的范围,再逐一分析各选项即可得到答案.【详解】解:设第三根木棒的长度为x cm,则9393,x612,x所以A,B,D不符合题意,C符合题意,故选C【点睛】本题考查的是三角形的三边的关系,掌握“利用三角形的三边关系确定第三边的范围”是解本题的关键.5、C【分析】根据∠ABC=45°,CD⊥AB可得出BD=CD;利用AAS判定Rt△DFB≌Rt△DAC,从而得出BF=AC;再利用AAS判定Rt△BEA≌Rt△BEC,即可得到CE=12BF;由CE=12BF,BH=12BC,在三角形BCF中,比较BF、BC的长度即可得到CE<BH.【详解】解:∵CD⊥AB,∠ABC=45°,∴△BCD是等腰直角三角形.∴BD=CD,故①正确;在Rt△DFB和Rt△DAC中,∵∠DBF=90°﹣∠BFD,∠DCA=90°﹣∠EFC,且∠BFD=∠EFC,∴∠DBF=∠DCA.又∵∠BDF=∠CDA=90°,BD=CD,∴△DFB≌△DAC.∴BF=AC,故②正确;在Rt△BEA和Rt△BEC中∵BE平分∠ABC,∴∠ABE=∠CBE.又∵BE=BE,∠BEA=∠BEC=90°,∴Rt△BEA≌Rt△BEC.∴CE=12AC=12BF,故③正确;∵CE=12AC=12BF,BH=12BC,在△BCF中,∠CBE=12∠ABC=22.5°,∠DCB=∠ABC=45°,∴∠BFC=112.5°,∴BF<BC,∴CE<BH,故④错误;故选:C.【点睛】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、SSA、HL.在复杂的图形中有45°的角,有垂直,往往要用到等腰直角三角形,要注意掌握并应用此点.6、C【分析】根据三角形的任意两边之和大于第三边对各选项分析判断求解即可.【详解】解:A.∵3+4<8,∴不能组成三角形,故本选项不符合题意;B.∵4+4<10,∴不能组成三角形,故本选项不符合题意;C.∵5+6>10,∴能组成三角形,故本选项符合题意;D.∵5+6=11,∴不能组成三角形,故本选项不符合题意;故选:C.【点睛】本题考查了三角形的三边关系,熟记三角形的任意两边之和大于第三边是解决问题的关键.7、B【分析】根据三角形内角和定理、角平分线的性质、三角形外角的性质依次推理即可得出结论.【详解】解:由三角形内角和知∠BAC=180°-∠2-∠1,∵AE为∠BAC的平分线,∴∠BAE=12∠BAC=12(180°-∠2-∠1).∵AD为BC边上的高,∴∠ADC=90°=∠DAB+∠ABD.又∵∠ABD=180°-∠2,∴∠DAB=90°-(180°-∠2)=∠2-90°,∴∠EAD=∠DAB+∠BAE=∠2-90°+12(180°-∠2-∠1)=12(∠2-∠1).故选:B【点睛】本题主要考查了三角形的内角和定理,角平分线的定义、三角形外角性质及三角形的高的定义,解答的关键是找到已知角和所求角之间的联系.8、D【分析】有两边相等的三角形,是等腰三角形,两边分别为5cm和4cm,但没有明确哪是底边,哪是腰,所以有两种情况,需要分类讨论.【详解】解:当4为底时,其它两边都为5,4、5、5可以构成三角形,周长为14cm;当4为腰时,其它两边为4和5,4、4、5可以构成三角形,周长为13cm.综上所述,该等腰三角形的周长是13cm或14cm.故选:D.【点睛】本题考查了等腰三角形的性质和三角形的三边关系,解题的关键是对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.9、B【分析】利用平行线的性质、对顶角的定义、直角三角形的性质及等边三角形的性质分别判断后即可确定正确的选项.【详解】①两直线平行,同位角相等,故错误,是假命题;②相等的角是对顶角,错误,是假命题;③直角三角形两个锐角互余,正确,是真命题;④三个内角相等的三角形是等边三角形,正确,是真命题,综上所述真命题有2个,故选:B.【点睛】本题考查了命题真假的判断,要说明一个命题是正确的,需要根据命题的题设和已学的有关公理、定理进行说明、推理、证明,正确的命题叫做真命题,错误的命题叫做假命题.10、A【分析】根据题意,结合图形,分两种情况讨论:①AB为等腰直角△ABC底边;②AB为等腰直角△ABC其中的一条腰.【详解】解:如图:分情况讨论:①AB为等腰直角△ABC底边时,符合条件的格点C点有0个;②AB为等腰直角△ABC其中的一条腰时,符合条件的格点C点有3个.故共有3个点,故选:A.【点睛】本题考查了等腰三角形的性质和判定;解答本题关键是根据题意,画出符合实际条件的图形,数形结合的思想是数学解题中很重要的解题思想.二、填空题1、22【分析】分两种情况讨论:当腰长为4时,当腰长为9时,再结合三角形的三边关系,从而可得答案.【详解】解:等腰三角形的两边长分别是4和9,当腰长为4时,此时4+49,不符合题意,舍去,当腰长为9时,此时4+99,符合题意,所以三角形的周长为:4+9+9=22,故答案为:22【点睛】本题考查的是等腰三角形的定义,三角形的三边关系,掌握“等腰三角形的两腰相等,再分情况讨论”是解本题的关键.2、90︒【分析】如图(见解析),先根据三角形全等的判定定理证出ABC ADE ≅,再根据全等三角形的性质可得23∠∠=,由此即可得出答案.【详解】解:如图,在ABC 和ADE 中,AC AE A A AB AD =⎧⎪∠=∠⎨⎪=⎩, ()ABC ADE SAS ∴≅,23∴∠=∠,121390∴∠+∠=∠+∠=︒,故答案为:90︒.【点睛】本题考查了三角形全等的判定定理与性质等知识点,正确找出两个全等三角形是解题关键. 3、20°度【分析】 根据角平分线的性质得到1,122DBC ABC DCE ACE ∠=∠∠=∠,再利用三角形外角的性质计算.【详解】解:∵ABC ∠与ACE ∠的平分线相交于点D , ∴1,122DBC ABC DCE ACE ∠=∠∠=∠, ∵∠ACE=∠A+∠ABC ,∠DCE=∠D +∠DBC ,∴∠D=∠DCE-∠DBC =11()2022ACE ABC A ∠-∠=∠=︒,故答案为:20°.【点睛】此题考查了三角形的外角性质及角平分线的性质,熟记三角形外角的性质定理是解题的关键. 4、72°72度【分析】根据AB =AC 求出∠ACB ,利用BD =BC ,求出∠BDC 的度数.【详解】解:∵AB =AC ,∠A =36°, ∴1(180)722ABC ACB A ∠=∠=︒-∠=︒,∵BD =BC ,∴∠BDC =∠ACB =72°,故答案为:72°.【点睛】此题考查了等腰三角形的性质:等边对等角,熟记性质是解题的关键.5、4【分析】先说明C DMB ∠=∠,再利用AAS 证明ACM BMD ≌,然后根据全等三角形的性质可得12AM BD ==米,再根据线段的和差求得BM 的长,最后利用时间=路程÷速度计算即可.【详解】解:∵90CMD ∠=︒,∴90CMA DMB +=︒∠∠,又∵90CAM ∠=︒,∴90CMA C ︒∠+∠=,∴C DMB ∠=∠,在Rt ACM 和Rt BMD △中,A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()Rt ACM Rt BMD AAS ≌,∴12AM BD ==米,20128BM =-=(米),∵该人的运动速度2m/s ,他到达点M 时,运动时间为824÷=s .故答案为:4.【点睛】本题主要考查了全等三角形的判定与性质,根据题意证得Rt ACM Rt BMD ≌是解答本题的关键.三、解答题1、(1)见详解;(2)见详解【分析】(1)由题意易得60ABC ACB BAC ∠=∠=∠=︒,然后根据平行线的性质可得60ADE AED ∠=∠=︒,进而问题可求证;(2)连接AG ,由题意易得AB =AC ,然后可知△ABF ≌△ACG ,则有AF =AG ,进而可得∠FAG =60°,最后问题可求证.【详解】证明:(1)∵ABC 是等边三角形,∴60ABC ACB BAC ∠=∠=∠=︒,∵DE ∥BC ,∴60,60ADE ABC AED ACB ∠=∠=︒∠=∠=︒,∴60ADE AED ∠=∠=︒,∴ADE 是等边三角形;(2)连接AG ,如图所示:∵ABC 是等边三角形,∴60BAC ∠=︒,AB =AC ,∵BF CG =,ABF ACG ∠=∠,∴△ABF ≌△ACG (SAS ),∴,AF AG BAF CAG =∠=∠,∵60BAF FAC BAC ∠+∠=∠=︒,∴60CAG FAC FAG ∠+∠=∠=︒,∴AFG 是等边三角形,∴AF FG =.【点睛】本题主要考查全等三角形及等边三角形的性质与判定,熟练掌握全等三角形及等边三角形的性质与判定是解题的关键.2、(1)见解析;(2)猜想:DE BD CE =+,见解析;(3)见解析【分析】(1)先证明BDA AEC ∠=∠和ABD CAE ∠=∠,再根据AAS 证明ABD CAE ≌即可;(2)根据AAS 证明ABD CAE ≌得BD AE =,DA EC =,进一步可得出结论;(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,得出CM =EN ,证明CMG ENG ≌得CG EG =,从而可得结论.【详解】解:(1)证明:∵BD l ⊥,CE l ⊥,∴90BDA AEC ∠=∠=︒,∴90ABD DAB ∠+∠=︒∵90BAC ∠=︒,∴90CAE DAB ∠+∠=︒∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,(2)猜想:DE BD CE =+,∵BDA BAC α∠=∠=∴180180ABD DAB BDA α∠+∠=︒-∠=︒-,180180CAE DAB BAC α∠+∠=︒-∠=︒-∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABD CAE AAS ≌,∴BD AE =,DA EC =,∴DE AE DA BD CE =+=+(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,∴AF CM =,AF EN =∴CM EN =,∵CM l ⊥,EN l ⊥,∴90CMG ENG ∠=∠=︒在CMG 与ENG 中CMG ENG CGM EGN CM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩=,∴CG EG∴G为CE的中点.【点睛】本题考查了全等三角形的判定与性质、垂线的定义、角的互余关系,证得△ABD≌△CAE是解决问题的关键.3、见解析【分析】过A作AF⊥BC于F,根据等腰三角形的性质得出BF=CF,DF=EF,即可求出答案.【详解】证明:如图,过A作AF⊥BC于F,∵AB =AC ,AD =AE ,∴BF =CF ,DF =EF ,∴BF -DF =CF -EF ,∴BD =CE .【点睛】本题考查了等腰三角形的性质的应用,注意:等腰三角形的底边上的高,底边上的中线,顶角的平分线互相重合.4、(1)见解析;(2)110︒【分析】(1)由旋转的性质可得BD BE =,120EBD ∠=︒,再证明DBC ABE ∠=∠,结合,AB BC = 从而可得结论;(2)由ABE △≌CBD 可得40DBC ABE ∠==∠︒,再利用等腰三角形的性质求解30BED BDE ∠=∠=︒,再利用三角形的内角和定理可得答案.【详解】证明:(1)∵线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,∴BD BE =,120EBD ∠=︒,∵AB BC =,120ABC ∠=︒,∴120ABD DBC ABD ABE ∠+∠=∠+∠=︒,∴DBC ABE ∠=∠,∴ABE △≌CBD (S A S ),∴AE CD =.(2)解:由(1)知ABE △≌CBD∴ 40DBC ABE ∠==∠︒,BD BE =,120EBD ∠=︒, ∴()1180120302BED BDE ∠=∠=︒-︒=︒, ∴1801803040110BFE BED ABE ∠=︒-∠-∠=︒-︒-︒=︒.【点睛】本题考查的是全等三角形的判定与性质,旋转的性质,等腰三角形的性质,掌握“旋转前后的对应边相等,对应角相等”是解本题的关键.5、(1)见解析;(2)等于120°的角有∠BFC 、∠BDE 、∠DFE =120°.【分析】(1)利用SAS 证明△ADC ≌△BEC ,即可证明AD =BE ;(2)证明△CDE 为等边三角形,可求得∠BDE =120°;利用全等三角形的性质可求得∠BFD =∠BCA =60°,推出∠DFE =120°;同理可推出∠BFC =∠AFC +∠BFD =120°.【详解】(1)证明:等边△ABC 中,CA =CB ,∠ACB =60°,∵CE =CD ,∠BCE =60°,∴△ADC ≌△BEC (SAS ),∴AD =BE ;(2)等于120°的角有∠BFC 、∠BDE 、∠DFE =120°.∵CE =CD ,∠BCE =60°,∴△CDE为等边三角形,∴∠CDE=60°,∴∠BDE=120°;∵△ADC≌△BEC,∴∠DAC=∠EBC,又∠BDF=∠ADC,∴∠BFD=∠BCA=60°,∴∠DFE=120°;同理可求得∠AFC=∠ABC=60°,∴∠BFC=∠AFC+∠BFD=120°;综上,等于120°的角有∠BFC、∠BDE、∠DFE=120°.【点睛】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,熟记各图形的性质并准确识图是解题的关键.6、见详解.【分析】根据等腰三角形三合一性质以及等边对等角性质得出AD⊥BC,∠B=∠C,根据AF⊥AD,利用在同一平面内垂直同一直线的两直线平行得出AF∥BC,利用平行线性质得出∠1=∠B,∠2=∠C即可.【详解】证明:∵△ABC 中,AB =AC ,D 为BC 边的中点,∴AD ⊥BC ,∠B =∠C ,∵AF ⊥AD ,∴AF∥BC ,∴∠1=∠B ,∠2=∠C ,∴∠1=∠2.【点睛】本题考查等腰三角形性质,平行线的判定与性质,掌握等腰三角形性质,平行线的判定与性质是解题关键.7、见解析【分析】由OA OC PC ==,得出,POC AOC 为等腰三角形,由外角的性质及等量代换得2CAO APB ∠=∠,再次利用外角的性质及等量代换得3AOB APB ∠=∠,即可证明.【详解】解:OA OC PC ==,,POC AOC ∴为等腰三角形,,APB COP ACO CAO ∴∠=∠∠=∠,由外角的性质得:2ACO APB COP APB ∠=∠+∠=∠,2CAO APB ∠=∠,再由外角的性质得:AOB APB CAO ∠=∠+∠,3AOB APB ∴∠=∠,13APB AOB ∴∠=∠. 【点睛】本题考查了等腰三角形、外角的性质、解题的关键是掌握外角的性质及等量代换的思想进行求解.8、证明见解析.【分析】先根据角的和差可得ACD BCE ∠=∠,再根据三角形全等的判定定理证出ACD BCE ≅△△,然后根据全等三角形的性质即可得证.【详解】证明:90ACB ∠=︒,90ACD BCD ∴∠+∠=︒,CE CD ⊥,90BCE BCD ∠∴∠+=︒,ACD BCE ∠∠∴=,在ACD △和BCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ()ACD BCE SAS ∴≅,AD BE ∴=.【点睛】本题考查了三角形全等的判定定理与性质等知识点,熟练掌握三角形全等的判定方法是解题关键.9、见解析【分析】根据平行线的性质得出A FCD ∠=∠,运用“角角边”证明△AEB ≌△CFD 即可.【详解】证明:∵AE CF ∥,∴A FCD ∠=∠,在△AEB 和△CFD 中,E F A FCD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AEB ≌△CFD ,∴BE DF =.【点睛】本题考查了全等三角形的判定与性质,解题关键是熟练运用全等三角形的判定定理进行证明. 10、(1)见解析(2)ABE △的面积为20.【分析】(1)根据已知条件得到E CFD ∠=∠、BD CD =,然后利用全等三角形的判定,进行证明即可.(2)分别根据ACF 和CFD △的面积,用CF 表示AF 、D F ,通过CFD BED ≅△△,得到BE CF =,DE DF =,用CF 表示出AE 的长,最后利用面积公式求解即可.(1)(1)解:由题意可知:90E CFD ∠=∠=︒AD 是ABC 的中线BD CD ∴=在CFD ∆与BED ∆中CDF BDE C CFD E D BD ∠=∠=∠=∠⎧⎪⎨⎪⎩∴∆∆()CFD BED AAS ≌.(2) 解:ACF 的面积为8,CFD △的面积为6.182AF CF ∴⋅=,即16AF CF = 162DF CF ⋅=,即12DF CF = 由(1)可知:CFD BED ∆∆≌BE CF ∴=,12DE DF CF== 40AE AF DF DE CF ∴=++= 1202ABE S AE BE ∆∴=⋅=. 【点睛】本题主要是考查了全等三角形的判定和性质,熟练根据条件证明三角形全等,利用其性质,证明对应边相等,这是解决本题的关键.。
2022年最新沪教版七年级数学第二学期第十四章三角形定向测评试题(含答案解析)

沪教版七年级数学第二学期第十四章三角形定向测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC =5,则五边形DECHF的周长为()A.8 B.10 C.11 D.122、如图,点F,C在BE上,AC=DF,BF=EC,AB=DE,AC与DF相交于点G,则与2∠DFE相等的是()A.∠A+∠D B.3∠B C.180°﹣∠FGC D.∠ACE+∠B3、已知三角形的两边长分别是3cm 和7cm ,则下列长度的线段中能作为第三边的是( )A .3cmB .4cmC .7cmD .10cm4、如图,在ABC 中,AD 、AE 分别是边BC 上的中线与高,4AE =,CD 的长为5,则ABC 的面积为( )A .8B .10C .20D .405、如图,ABC ≌DEF ,点B 、E 、C 、F 在同一直线上,若BC =7,EC =4,则CF 的长是()A .2B .3C .4D .76、在△ABC 中,∠A =50°,∠B 、∠C 的平分线交于O 点,则∠BOC 等于( )A .65°B .80°C .115°D .50°7、如图,ABC DEC ≌△△,点E 在线段AB 上,75B ∠=︒,则ACD ∠的度数为( )A .20°B .25°C .30°D .40°8、已知三角形的两边长分别为4cm 和10cm ,则下列长度的四条线段中能作为第三边的是( )A .15cmB .6cmC .7cmD .5cm9、下列长度的三条线段能组成三角形的是( )A .3,4,7B .3,4,8C .3,4,5D .3,3,710、下列三角形与下图全等的三角形是( )A .B .C .D .第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、在平面直角坐标系xOy 中,()2,0A ,()0,4C -,AB AC =,90BAC ∠=︒,则点B 的坐标为__________.2、如图,在△ABC 中,已知点D E F 、、分别为BC AD CE 、、的中点,若△ABC 的面积为24m ,则阴影部分的面积为 _________ 2cm3、如图,上午9时,一艘船从小岛A 处出发,以12海里/时的速度向正北方向航行,10时40分到达小岛B 处,若从灯塔C 处分别测得小岛A 、B 在南偏东34°、68°方向,则小岛B 处到灯塔C 的距离是______海里.4、已知a ,b ,c 是ABC 的三边长,满足()2720a b -+-=,c 为奇数,则c =______.5、如图,ABC 是等腰直角三角形,AB 是斜边,以BC 为一边在右侧作等边三角形BCD ,连接AD 与BC 交于点E ,则BED ∠的度数为______度.三、解答题(10小题,每小题5分,共计50分)1、△ABC 中,AB =AC ,BD 平分∠ABC 交AC 于点D ,从点A 作AE ∥BC 交BD 的延长线于点E .(1)若∠BAC =40°,求∠E 的度数;(2)点F 是BE 上一点,且FE =BD .取DF 的中点H ,请问AH ⊥BE 吗?试说明理由.2、命题:如图,已知,AC EF AC FE =∥,A D B F ,,,共线,(1),那么ABC FDE ∆≅∆.(1)从①AB FD =和②BC DE =两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);(2)根据你选择的条件,判定ABC FDE ∆≅∆的方法是________;(3)根据你选择的条件,完成ABC FDE ∆≅∆的证明.3、如图,点A ,B ,C ,D 在一条直线上,AE DF ∥,AE DF =,AB CD =.(1)求证:AEC DFB ≅.(2)若40A ∠=︒,145ECD ∠=︒,求∠F 的度数.4、如图,在△ABC 中,AB =AC ,CD ⊥AB 于点D ,∠A =50°,求∠BCD 的度数.5、在ABC 中,AC BC =,90ACB ∠=︒,点D 是直线AC 上一动点,连接BD 并延长至点E ,使ED BD =.过点E 作EF AC ⊥于点F .(1)如图1,当点D 在线段AC 上(点D 不与点A 和点C 重合)时,此时DF 与DC 的数量关系是______.(2)如图2,当点D 在线段AC 的延长线上时,依题意补全图形,并证明:2AD AF EF =+.(3)当点D 在线段CA 的延长线上时,直接用等式表示线段AD ,AF ,EF 之间的数量关系是______.6、如图,Rt△ACB 中,∠ACB =90°,AC =BC ,E 点为射线CB 上一动点,连结AE ,作AF ⊥AE 且AF =AE .(1)如图1,过F 点作FD ⊥AC 交AC 于D 点,求证:FD =BC ;(2)如图2,连结BF 交AC 于G 点,若AG =3,CG =1,求证:E 点为BC 中点.(3)当E 点在射线CB 上,连结BF 与直线AC 交子G 点,若BC =4,BE =3,则AG CG= .(直接写出结果)7、如图,点D 在AC 上,BC ,DE 交于点F ,BA BD =,BC BE =,ABD CBE ∠=∠.(1)求证:ABC DBE ≌;(2)若20ABD ∠=︒,求∠CDE 的度数.8、如图,点C 是线段AB 上一点,ACF 与BCE 都是等边三角形,连接AE ,BF .(1)求证:AE BF =;(2)若点M ,N 分别是AE ,BF 的中点,连接CM ,MN ,NC .①依题意补全图形;②判断CMN △的形状,并证明你的结论.9、如图,在ABC 中,8AB cm =,6BC cm =,5AC cm =,BD 是ABC 的角平分线,点E 在AB 边上,2AE cm =.求AED 的周长.10、如图,在ABC 中,AD 是BC 边上的高,CE 平分ACB ∠,若20CAD ∠=︒,50B ∠=︒,求AEC ∠的度数.-参考答案-一、单选题1、B【分析】证明△AFH ≌△CHG (AAS ),得出AF =CH .由题意可知BE =FH ,则得出五边形DECHF 的周长=AB +BC ,则可得出答案.【详解】解:∵△GFH 为等边三角形,∴FH =GH ,∠FHG =60°,∴∠AHF +∠GHC =120°,∵△ABC 为等边三角形,∴AB =BC =AC =5,∠ACB =∠A =60°,∵∠AHF =180°-∠FHG -∠GHC =120°-∠GHC ,∠HGC =180°-∠C -∠GHC =120°-∠GHC ,∴∠AHF =∠HGC ,在△AFH 和△CHG 中A C AHF HGC FH GH ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AFH ≌△CHG (AAS ),∴AF =CH .∵△BDE 和△FGH 是两个全等的等边三角形,∴BE =FH ,∴五边形DECHF 的周长=DE +CE +CH +FH +DF =BD +CE +AF +BE +DF ,=(BD +DF +AF )+(CE +BE ),=AB +BC =10.故选:B .【点睛】本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.2、C【详解】由题意根据等式的性质得出BC =EF ,进而利用SSS 证明△ABC 与△DEF 全等,利用全等三角形的性质得出∠ACB =∠DFE ,最后利用三角形内角和进行分析解答.【分析】解:∵BF =EC ,∴BF +FC =EC +FC ,∴BC =EF ,在△ABC 与△DEF 中,AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△DEF (SSS ),∴∠ACB =∠DFE ,∴2∠DFE =180°﹣∠FGC ,故选:C .【点睛】本题考查全等三角形的判定与性质,其中全等三角形的判定方法有:SSS ;SAS ;ASA ;AAS ;以及HL(直角三角形的判定方法).3、C【分析】设三角形第三边的长为x cm,再根据三角形的三边关系求出x的取值范围,找出符合条件的x的值即可.【详解】解:设三角形的第三边是xcm.则7-3<x<7+3.即4<x<10,四个选项中,只有选项C符合题意,故选:C.【点睛】本题主要考查了三角形三边关系的应用.此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.4、C【分析】根据三角形中线的性质得出CB的长为10,再用三角形面积公式计算即可.【详解】解:∵AD是边BC上的中线,CD的长为5,∴CB=2CD=10,ABC的面积为1110420 22BC AE⨯=⨯⨯=,故选:C.【点睛】本题考查了三角形中线的性质和面积公式,解题关键是明确中线的性质求出底边长.5、B【分析】根据全等三角形的性质可得BC EF =,根据CF EF EC =-即可求得答案.【详解】 解:ABC ≌DEF ,∴BC EF =点B 、E 、C 、F 在同一直线上,BC =7,EC =4,∴CF EF EC =-743BC EC -=-=故选B【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.6、C【分析】根据题意画出图形,求出∠ABC +∠ACB =130°,根据角平分线的定义得到∠CBD =12∠ABC ,∠ECB =12∠ACB ,再根据三角形内角和定理和角的代换即可求解.【详解】解:如图,∵∠A =50°,∴∠ABC +∠ACB =180°-∠A =130°,∵BD 、CE 分别是∠ABC 、∠ACB 的平分线,∴∠CBD =12∠ABC ,∠ECB =12∠ACB ,∴∠BOC =180°-∠CBD -∠ECB =180°-(∠CBD +∠ECB )=180°- 12(∠ABC +∠ACB )=180°- 12×130°=115°.故选:C【点睛】本题考查了三角形内角和定理,角平分线的定义,熟知三角形内角和定理,并能根据角平分线的定义进行角的代换是解题关键.7、C【分析】根据全等三角形的性质可证得BC=CE ,∠ACB =∠DCE 即∠ACD =∠BCE ,根据等腰三角形的性质和三角形的内角和定理求解∠B =∠BEC 和∠BCE 即可.【详解】解:∵ABC DEC ≌△△,∴BC=CE ,∠ACB =∠DCE ,∴∠B =∠BEC ,∠ACD =∠BCE ,∵75B ∠=︒,∴∠ACD =∠BCE=180°-2×75°=30°,故选:C .【点睛】本题考查全等三角形的性质、等腰三角形的性质、三角形的内角和定理,熟练掌握全等三角形的性质和等腰三角形的性质是解答的关键.8、C【分析】根据三角形的三边关系可得104104x -<<+,再解不等式可得答案.【详解】解:设三角形的第三边为xcm ,由题意可得:104104x -<<+,即614x <<,故选:C .【点睛】本题主要考查了三角形的三边关系,解题的关键是掌握三角形两边之和大于第三边;三角形的两边差小于第三边.9、C【分析】根据组成三角形的三边关系依次判断即可.【详解】A 、 3,4,7中3+4=7,故不能组成三角形,与题意不符,选项错误.B 、 3,4,8中3+4<8,故不能组成三角形,与题意不符,选项错误.C 、 3,4,5中任意两边之和都大于第三边,任意两边之差都小于第三边,故能组成三角形,符合题意,选项正确.D 、 3,3,7中3+3<7,故不能组成三角形,与题意不符,选项错误.故选:C .【点睛】本题考查了三角形的三边关系,在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边.10、C【分析】根据已知的三角形求第三个内角的度数,由全等三角形的判定定理即可得出答案.【详解】由题可知,第三个内角的度数为180514980︒-︒-︒=︒,A.只有两边,故不能判断三角形全等,故此选项错误;B.两边夹的角度数不相等,故两三角形不全等,故此选项错误;C.两边相等且夹角相等,故能判断两三角形全等,故此选项正确;D. 两边夹的角度数不相等,故两三角形不全等,故此选项错误.故选:C .【点睛】本题考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.二、填空题1、(6),-2【分析】按照在x 轴的上下方,分成两类情况讨论,如解析中的图像所示,分别利用边和角证明1Rt OAC Rt EB A ∆∆≌和2Rt OAC DB A ∆∆≌成立,然后根据对应边相等,即可求出两种情况对应的点B 的坐标.【详解】解:如下图所示:由()2,0A ,()0,4C -可知:2OA =,4OC =.当B 点在x 轴下方时,过点B 1向x 轴作垂线,垂足为E .90BAC ∠=︒,190OAC EAB ∴∠+∠=︒90OAC OCA ∠+∠=︒1OCA EAB ∴∠=∠在Rt OAC ∆与1Rt EB A ∆中:111AOC B EA OCA EAB AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩1()Rt OAC Rt EB A AAS ∴∆∆≌12EB OA ∴==,4EA OC ==6OE OA EA ∴=+=1B ∴点坐标为(6),-2当B 点在x 轴上方时,过点B 2向x 轴作垂线,垂足为D .由题意可知:2290B AC B AD OAC ∠=∠+∠=︒90OAC OCA ∠+∠=︒2B AD OAC ∴∠=∠在Rt OAC ∆与2Rt DB A ∆中222OAC B AD AOC B DA AC AB ∠=∠⎧⎪∠=∠⎨⎪=⎩2()Rt OAC DB A AAS ∴∆∆≌22DB OA ∴==,4AD OC ==2OD AD OA ∴=-=∴点2B 坐标为(22)-,故答案为:(6),-2或(22)-,. 【点睛】本题主要是考查了全等三角形的判定和性质以及坐标点的求解,熟练利用全等三角形证明边相等,进而利用边长求解点的坐标,这是解决该题的关键.2、1【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.【详解】解:∵点E 是AD 的中点,∴S △ABE =12S △ABD ,S △ACE =12S △ADC ,∴S △ABE +S △ACE =12S △ABC =12×4=2cm 2,∴S△BCE=12S△ABC=12×4=2cm2,∵点F是CE的中点,∴S△BEF=12S△BCE=12×2=1cm2.故答案为:1.【点睛】本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.3、20【分析】根据所给的角的度数,容易证得BCA∆是等腰三角形,而AB的长易求,所以根据等腰三角形的性质,BC的值也可以求出.【详解】解:据题意得,34A∠=︒,68DBC∠=︒,DBC A C∠=∠+∠,34A C∴∠=∠=︒,AB BC∴=,512203AB=⨯=,20BC∴=(海里).故答案是:20.【点睛】本题考查了等腰三角形的性质及方向角的问题,解题的关键是由已知得到三角形是等腰三角形,要学会把实际问题转化为数学问题,用数学知识进行解决实际问题的方法.4、7【分析】绝对值与平方的取值均≥0,可知70a -=,20b -=,可得a 、b 的值,根据三角形三边关系a b c a b c+>⎧⎨-<⎩求出c 的取值范围,进而得到c 的值.【详解】 解:()2720a b -+-= 70a ∴-=,20b -=72a b ∴==,由三角形三边关系a b c a b c +>⎧⎨-<⎩可得95c c >⎧⎨<⎩ 59c ∴<<c 为奇数7c ∴=故答案为:7.【点睛】本题考查了绝对值、平方的非负性,三角形的三边关系等知识点.解题的关键是确定所求边长的取值范围.5、75【分析】由题意,ACD △是等腰三角形,然后求出CAE ∠的度数,再根据三角形的外角性质,即可求出BED ∠的度数.【详解】解:∵ABC 是等腰直角三角形,∴AC =BC ,∠ABC =∠BAC =45°,∠ACB =90°,∵△BCD 是等边三角形,∴BC =CD ,∠BCD =60°,∴AC =CD ,∠ACD =90°+60°=150°,∴ACD △是等腰三角形, ∴1(180150)152CAE CDE ∠=∠=⨯︒-︒=︒,∴451530BAE ∠=︒-︒=︒,∴304575BED BAE ABE ∠=∠+∠=︒+︒=︒;故答案为:75.【点睛】本题考查了等边三角形的性质,等腰直角三角形的性质,三角形的外角性质,三角形的内角和定理,解题的关键是掌握所学的知识,正确的求出15CAE CDE ∠=∠=︒.三、解答题1、(1)∠E =35°;(2)AH ⊥BE .理由见解析.【分析】(1)根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD 的度数,最后根据两直线平行,内错角相等求出;(2)由“SAS ”可证△ABD ≌△AEF ,可得AD =AF ,由等腰三角形的性质可求解.【详解】解:(1)∵AB =AC ,∴∠ABC =∠ACB ,∵∠BAC =40°,∴∠ABC =12(180°-∠BAC )=70°,∵BD 平分∠ABC ,∴∠CBD =12∠ABC =35°,∵AE ∥BC ,∴∠E =∠CBD =35°;(2)∵BD 平分∠ABC ,∠E =∠CBD ,∴∠CBD =∠ABD =∠E ,∴AB =AE ,在△ABD 和△AEF 中,AB AE E ABD BD EF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△AEF (SAS ),∴AD =AF ,∵点H 是DF 的中点,∴AH ⊥BE .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键. 2、(1)①(2)SAS(3)见解析(1)根据全等三角形的判定方法分析得出答案;(2)根据(1)直接填写即可;(3)利用SAS 进行证明.(1)解:∵AC EF ∥,∴∠A =∠F ,∵AC=EF ,∴当AB FD =时,可根据SAS 证明ABC FDE ∆≅∆;当BC DE =时,不能证明ABC FDE ∆≅∆,故答案为:①;(2)解:当AB FD =时,可根据SAS 证明ABC FDE ∆≅∆,故答案为:SAS ;(3)证明:在△ABC 和△FDE 中,AC EF A F AB FD =⎧⎪∠=∠⎨⎪=⎩, ∴ABC FDE ∆≅∆.【点睛】此题考查了添加条件证明两个三角形全等,正确掌握全等三角形的判定定理是解题的关键.3、(1)见解析;(2)105︒(1)根据平行线的性质可得A D ∠=∠,根据线段的和差关系可得AC DB =,进而根据SAS 即证明AEC DFB ≅;(2)根据三角形内角和定理以及补角的意义求得∠E ,进而根据(1)的结论即可求得∠F .【详解】(1)证明:AE DF ∥∴A D ∠=∠, AB CD =∴AB BC BC CD +=+即AC BD = 又AE DF =,∴AEC DFB ≅(2)解:40A ∠=︒,145ECD ∠=︒,18035ECA ECD ∴∠=︒-∠=︒180105E A ECA ∴∠=︒-∠-∠=︒AEC DFB ≅F E ∴∠=∠105=︒【点睛】本题考查了平行线的性质,三角形内角和定理,三角形全等的性质与判定,掌握全等三角形的性质与判定是解题的关键.4、25°【分析】直接利用等腰三角形的性质得出∠ABC =∠ACB =65°,进而利用三角形内角和定理得出答案.∵AB =AC ,∠A =50°,∴∠ABC =∠ACB =65°,∵CD ⊥BC 于点D ,∴∠BCD 的度数为:180°−90°−65°=25°.【点睛】此题主要考查了等腰三角形的性质,正确得出∠B 的度数是解题关键.5、(1)DF DC =(2)见解析(3)2AF EF AD -=【分析】(1)利用边相等和角相等,直接证明EDF BDC ∆∆≌,即可得到结论.(2)利用边相等和角相等,直接证明EDF BDC ∆∆≌,得到DF DC =和EF BC AC ==,最后通过边与边之间的关系,即可证明结论成立.(3)要证明2AF EF AD -=,先利用边相等和角相等,直接证明EDF BDC ∆∆≌,得到DF DC =和EF BC AC ==,最后通过边与边之间的关系,即可证明结论成立.【详解】(1)解:DF DC =90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=.(2)解:当点D 在线段AC 的延长线上时,如下图所示:90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=,EF BC AC ==,=2AF EF AD DF AC AD CD AD ∴+=++=+.(3)解:2AF EF AD -=,如下图所示:90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=,EF BC AC ==,()2AF EF AF AC AF DF AD AF DF AD AD ∴-=-=--=-+=.【点睛】本题主要是考查了三角形全等的判定和性质,熟练利用条件证明三角形全等,然后利用边相等以及边与边之间关系,即可证明结论成立,这是解决该题的关键.6、(1)证明见解析;(2)证明见解析;(3)113或53 【分析】(1)证明△AFD ≌△EAC ,根据全等三角形的性质得到DF =AC ,等量代换证明结论;(2)作FD ⊥AC 于D ,证明△FDG ≌△BCG ,得到DG =CG ,求出CE ,CB 的长,得到答案;(3)过F 作FD ⊥AG 的延长线交于点D ,根据全等三角形的性质得到CG =GD ,AD =CE =7,代入计算即可.【详解】(1)证明:∵FD ⊥AC ,∴∠FDA =90°,∴∠DFA +∠DAF =90°,同理,∠CAE +∠DAF =90°,∴∠DFA =∠CAE ,在△AFD 和△EAC 中,AFD EAC ADF ECA AF AE ∠∠⎧⎪∠∠⎨⎪⎩===, ∴△AFD ≌△EAC (AAS ),∴DF =AC ,∵AC =BC ,∴FD =BC ;(2)作FD ⊥AC 于D ,由(1)得,FD =AC =BC ,AD =CE ,在△FDG 和△BCG 中,90FDG BCG FGD BGCFD BC ∠∠︒⎧⎪∠∠⎨⎪⎩====, ∴△FDG ≌△BCG (AAS ),∴DG =CG =1,∴AD =2,∴CE=2,∵BC=AC=AG+CG=4,∴E点为BC中点;(3)当点E在CB的延长线上时,过F作FD⊥AG的延长线交于点D,BC=AC=4,CE=CB+BE=7,由(1)(2)知:△ADF≌△ECA,△GDF≌△GCB,∴CG=GD,AD=CE=7,∴CG=DG=1.5,∴AG=CG+AC=5.5,∴5.5111.53 AGCG==,同理,当点E在线段BC上时,AG= AC -CG+=2.5,∴2.551.53 AGCG==,故答案为:113或53.【点睛】本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.7、(1)证明见解析;(2)∠CDE =20°.【分析】(1)由“SAS ”可证△ABC ≌△DBE ;(2)由全等三角形的性质可得∠C =∠E ,由三角形的外角性质可求解.(1)证明:∵∠ABD =∠CBE ,∴∠ABD +∠DBC =∠CBE +∠DBC ,即:∠ABC =∠DBE ,在△ABC 和△DBE 中,BA BD ABC DBE BC BE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABC ≌△DBE (SAS );(2)解:由(1)可知:△ABC ≌△DBE ,∴∠C =∠E ,∵∠DFB =∠C +∠CDE ,∠DFB =∠E +∠CBE ,∴∠CDE =∠CBE ,∵∠ABD =∠CBE =20°,∴∠CDE =20°.【点睛】本题考查了全等三角形的判定和性质,三角形的外角性质,证明三角形全等是解题的关键.8、(1)证明见解析;(2)①补全图形见解析;②CMN △是等边三角形,证明见解析.【分析】(1)由等边三角形的性质可知60ACF BCE ∠=∠=︒,AC FC =,CB CE =.结合题意易得出ACE FCB ∠=∠.即可利用“SAS ”证明ACE FCB ≅,即得出AE BF =;(2)①根据题意补全图形即可;②由全等三角形的性质可知CAM CFN ∠=∠,AE BF =.再由题意点M ,N 分别是AE ,BF 的中点,即得出AM FN =.即可利用“SAS ”证明ACM FCN ≅,得出结论CM CN =,ACM FCN ∠=∠.最后根据ACM FCM FCN FCM ∠-∠=∠-∠,即得出60ACF MCN ∠=∠=︒,即可判定CMN △是等边三角形.(1)∵ACF 与BCE 都是等边三角形,∴60ACF BCE ∠=∠=︒,AC FC =,CB CE =,∴ACF ECF BCE ECF ∠+∠=∠+∠,即ACE FCB ∠=∠,在ACE 和FCB 中,∴AC FC ACE FCB CE CB =⎧⎪∠=∠⎨⎪=⎩, ∴()ACE FCB SAS ≅,∴AE BF =.(2)①画图如下:②CMN △是等边三角形.理由如下:∵ACE FCB ≅,∴CAM CFN ∠=∠,AE BF =.∵点M ,N 分别是AE ,BF 的中点,∴AM FN =,在ACM △和FCN △中,∵AC FC CAM CFN AM FN =⎧⎪∠=∠⎨⎪=⎩, ∴()ACM FCN SAS ≅,∴CM CN =,ACM FCN ∠=∠,∴ACM FCM FCN FCM ∠-∠=∠-∠,即60ACF MCN ∠=∠=︒,∴CMN △是等边三角形.【点睛】本题考查等边三角形的判定和性质,全等三角形的判定和性质,线段的中点.利用数形结合的思想是解答本题的关键.9、7cm【分析】由题意结合角平分线性质和全等三角形判定得出CBD EBD ≅,进而依据AED 的周长AE AD DE AE AD DC =++=++进行求解即可.【详解】解:∵8AB cm =,6BC cm =,2AE cm =,∴826,BE AB AE cm BE BC =-=-==,∵BD 是ABC 的角平分线,∴CBD EBD ∠=∠,在CBD 和EBD △中,BE BC CBD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩, ∴CBD EBD ≅,∴CD DE =,∵5AC AD DC cm =+=,∴AED 的周长257AE AD DE AE AD DC cm =++=++=+=.【点睛】本题考查全等三角形的判定与性质以及角平分线性质,熟练掌握利用全等三角形的判定与性质以及角平分线性质进行边的等量替换是解题的关键.10、85°【分析】由高的定义可得出∠ADB =∠ADC =90,在△ACD 中利用三角形内角和定理可求出∠ACB 的度数,结合CE 平分∠ACB 可求出∠ECB 的度数.由三角形外角的性质可求出∠AEC 的度数,【详解】解:∵AD 是BC 边上的高,∴∠ADB=∠ADC=90.在△ACD中,∠ACB=180°﹣∠ADC﹣∠CAD=180°﹣90°﹣20°=70°.∵CE平分∠ACB,∴∠ECB=1∠ACB=35°.2∵∠AEC是△BEC的外角,50B∠=︒,∴∠AEC=∠B+∠ECB=50°+35°=85°.答:∠AEC的度数是85°.【点睛】本题考查了三角形内角和定理、角平分线的定义以及三角形外角的性质,利用三角形内角和定理及角平分线的性质,求出∠ECB的度数是解题的关键.。
2021-2022学年度沪教版七年级数学第二学期第十四章三角形必考点解析练习题(无超纲)

沪教版七年级数学第二学期第十四章三角形必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列长度的三条线段能组成三角形的是( )A .3,4,7B .3,4,8C .3,4,5D .3,3,72、如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论:①30APO DCO ∠+∠=︒;②APO DCO ∠=∠;③POC △是等边三角形;④AB OA AP =+.其中正确的是( )A .①③④B .①②③C .②③④D .①②③④3、已知三角形的两边长分别为2cm 和3cm ,则第三边长可能是( )A .6cmB .5cmC .3cmD .1cm4、下列命题是真命题的是( )A .等腰三角形的角平分线、中线、高线互相重合B .一个三角形被截成两个三角形,每个三角形的内角和是90度C .有两个角是60°的三角形是等边三角形D .在ABC 中,2A B C ∠=∠=∠,则ABC 为直角三角形5、如图,若ABC 绕点A 按逆时针方向旋转40°后与11AB C △重合,则1AB B ∠=( ) .A .40°B .50°C .70°D .1006、下列叙述正确的是( )A .三角形的外角大于它的内角B .三角形的外角都比锐角大C .三角形的内角没有小于60°的D .三角形中可以有三个内角都是锐角7、如图,在ABC 中,5AB =,8BC =,60B ︒∠=,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,CD 的长为( )A .3B .4C .5D .68、如图,等边ABC 中,D 为AC 中点,点P 、Q 分别为AB 、AD 上的点,4BP AQ ==,3QD =,在BD 上有一动点E ,则PE QE +的最小值为( )A .7B .8C .10D .129、如图,ABC 和DEF 全等,且A D ∠=∠,AC 对应DE .若6AC =,5BC =,4AB =,则DF 的长为( )A .4B .5C .6D .无法确定10、有下列说法:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;②等腰三角形一腰上的高与底边的夹角与顶角互余;③等腰三角形顶角的平分线是它的对称轴;④等腰三角形两腰上的中线相等.其中正确的说法有( )个.A .1B .2C .3D .4第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,△ABC 中,∠B =20°,D 是BC 延长线上一点,且∠ACD =60°,则∠A 的度数是____________ 度.2、如图,在△ABC 中,CA =CB ,∠ACB =120°,E 为AB 上一点,∠DCE =∠DAE =60°,AD =2.4,BE =7,则DE =_____.3、如图,△ABC 中,AB 平分∠DAC ,AB ⊥BC ,垂足为B ,若∠ADC 与∠ACB 互补,BC =5,则CD 的长为_________.4、两角和它们的夹边分别相等的两个三角形全等(可以简写成 _____).5、如图,把两块大小相同的含45°的三角板ACF 和三角板CFB 如图所示摆放,点D 在边AC 上,点E 在边BC 上,且∠CFE =13°,∠CFD =32°,则∠DEC 的度数为_______.三、解答题(10小题,每小题5分,共计50分)1、如图,在Rt ACB △中,90ACB ∠=︒,CA CB =,点D 是ACB △内一点,连接CD ,过点C 作CE CD ⊥且CE CD =,连接AD ,BE .求证:AD BE =.2、下面是“作一个角的平分线”的尺规作图过程.已知:如图,钝角AOB ∠.求作:射线OC ,使AOC BOC ∠=∠.作法:如图,①在射线OA 上任取一点D ;②以点О为圆心,OD 长为半径作弧,交OB 于点E ;③分别以点D ,E 为圆心,大于12DE 长为半径作弧,在AOB ∠内,两弧相交于点C ;④作射线OC .则OC 为所求作的射线.完成下面的证明.证明:连接CD ,CE由作图步骤②可知OD =______.由作图步骤③可知CD =______.∵OC OC =,∴OCD OCE ≌△△. ∴AOC BOC ∠=∠(________)(填推理的依据).3、如图,在等边ABC 中,D 为BC 边上一点,连接AD ,将ACD △沿AD 翻折得到AED ,连接BE 并延长交AD 的延长线于点F ,连接CF .(1)若20CAD ∠=︒,求CBF ∠的度数;(2)若a CAD ∠=,求CBF ∠的大小;(3)猜想CF ,BF ,AF 之间的数量关系,并证明.4、如图,将一副直角三角板的直角顶点C 叠放在一起.(1)如图(1),若∠DCE =33°,则∠BCD = ,∠ACB = .(2)如图(1),猜想∠ACB 与∠DCE 的大小有何特殊关系?并说明理由.(3)如图(2),若是两个同样的直角三角板60°锐角的顶点A 重合在一起,则∠DAB 与∠CAE 的数量关系为 .5、已知,在△ABC 中,∠BAC =30°,点D 在射线BC 上,连接AD ,∠CAD =α,点D 关于直线AC 的对称点为E ,点E 关于直线AB 的对称点为F ,直线EF 分别交直线AC ,AB 于点M ,N ,连接AF ,AE ,CE .(1)如图1,点D 在线段BC 上.①根据题意补全图1;②∠AEF = (用含有α的代数式表示),∠AMF = °;③用等式表示线段MA ,ME ,MF 之间的数量关系,并证明.(2)点D 在线段BC 的延长线上,且∠CAD <60°,直接用等式表示线段MA ,ME ,MF 之间的数量关系,不证明.6、如图,ABC 为等边三角形,D 是BC 中点,60ADE ∠=︒,CE 是ABC 的外角ACF ∠的平分线. 求证:AD DE =.7、如图,在ABC 中,AD 平分BAC ∠,CE AD ⊥于点E .求证:ACE B ECD ∠=∠+∠.8、如图,点D ,E 在△ABC 的边BC 上,AB =AC ,AD =AE ,求证:BD =CE .9、如图,点B,F,C,E在一条直线上,AB=DE,∠B=∠E,BF=CE.求证:AC=DF.10、如图,将△ABC绕点A逆时针旋转得到△ADE,点D在BC上,已知∠B=70°,求∠CDE的大小.-参考答案-一、单选题1、C【分析】根据组成三角形的三边关系依次判断即可.【详解】A、 3,4,7中3+4=7,故不能组成三角形,与题意不符,选项错误.B、 3,4,8中3+4<8,故不能组成三角形,与题意不符,选项错误.C、 3,4,5中任意两边之和都大于第三边,任意两边之差都小于第三边,故能组成三角形,符合题意,选项正确.D、 3,3,7中3+3<7,故不能组成三角形,与题意不符,选项错误.故选:C.【点睛】本题考查了三角形的三边关系,在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边.2、A【分析】①利用等边对等角得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;④证明△OPA≌△CPE,则AO=CE,得AC=AE+CE=AO+AP.【详解】解:①如图1,连接OB,∵AB=AC,AD⊥BC,∴BD=CD,∠BAD=12∠BAC=12×120°=60°,∴OB=OC,∠ABC=90°﹣∠BAD=30°∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形,故③正确;④如图2,在AC上截取AE=PA,∵∠PAE =180°﹣∠BAC =60°,∴△APE 是等边三角形,∴∠PEA =∠APE =60°,PE =PA ,∴∠APO +∠OPE =60°,∵∠OPE +∠CPE =∠CPO =60°,∴∠APO =∠CPE ,∵OP =CP ,在△OPA 和△CPE 中,PA PE APO CPE OP CP =⎧⎪∠=∠⎨⎪=⎩, ∴△OPA ≌△CPE (SAS ),∴AO =CE ,∴AC =AE +CE =AO +AP ,∴AB =AO +AP ,故④正确;正确的结论有:①③④,故选:A .【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键.3、C【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.解:设第三边长为x cm ,根据三角形的三边关系可得:3-2<x <3+2,解得:1<x <5,只有C 选项在范围内.故选:C .【点睛】本题考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.4、C【分析】分别根据等腰三角形的性质、三角形的内角和定理、等边三角形的判定,直角三角形的判定即可判断.【详解】A.等腰三角形中顶角角平分线、底边上的中线和底边上的高线互相重合,即三线合一,故此选项错误;B.三角形的内角和为180°,故此选项错误;C.有两个角是60°,则第三个角为180606060︒-︒-︒=︒,所以三角形是等边三角形,故此选项正确;D.设C x ∠=,则2A B x ∠=∠=,故22180x x x ++=︒,解得36x =︒,所以72A B ∠=∠=︒,36C ∠=︒,此三角形不是直角三角形,故此选项错误.故选:C .【点睛】本题考查等腰三角形的性质,直角三角形的定义以及三角形内角和,掌握相关概念是解题的关键.5、C根据旋转的性质,可得140BAB ∠=︒ ,1AB AB = ,从而得到11ABB AB B ∠=∠,即可求解.【详解】解:∵ABC 绕点A 按逆时针方向旋转40°后与11AB C △重合,∴140BAB ∠=︒ ,1AB AB = , ∴()1111180702ABB AB B BAB ∠=∠=︒-∠=︒. 故选:C【点睛】本题主要考查了图形的旋转,等腰三角形的性质,熟练掌握图形旋转前后对应线段相等,对应角相等是解题的关键.6、D【分析】结合直角三角形,钝角三角形,锐角三角形的内角与外角的含义与大小逐一分析即可.【详解】解:三角形的外角不一定大于它的内角,锐角三角形的任何一个外角都大于内角,故A 不符合题意; 三角形的外角可以是锐角,不一定比锐角大,故B 不符合题意;三角形的内角可以小于60°,一个三角形的三个角可以为:20,70,90, 故C 不符合题意; 三角形中可以有三个内角都是锐角,这是个锐角三角形,故D 符合题意;故选D【点睛】本题考查的是三角形的的内角与外角的含义与大小,掌握“直角三角形,钝角三角形,锐角三角形的内角与外角”是解本题的关键.7、A【分析】先根据旋转的性质可得AB AD =,再根据等边三角形的判定与性质可得5BD AB ==,然后根据线段的和差即可得.【详解】由旋转的性质得:5AB AD ==,60B ∠=︒,ABD ∴是等边三角形,5BD AB ∴==,8BC =,853CD BC BD ∴=-=-=.故选:A .【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点,熟练掌握旋转的性质是解题关键.8、C【分析】作点Q 关于BD 的对称点Q ',连接PQ '交BD 于E ,连接QE ,此时PE EQ +的值最小,最小值PE PQ PE EQ PQ +=+'=',据此求解即可.【详解】解:如图,ABC ∆是等边三角形,BA BC ∴=,∵D 为AC 中点,∴BD AC ⊥,4AQ =,3QD =,7AD DC AQ QD ∴==+=,作点Q 关于BD 的对称点Q ',连接PQ '交BD 于E ,连接QE ,此时PE EQ +的值最小.最小值PE QE PE EQ PQ +=+'=',4AQ =,7AD DC ==,3QD DQ ∴='=,4CQ BP ∴'==,10AP AQ ∴='=,60A ∠=︒,APQ ∴∆'是等边三角形,10PQ PA ∴'==,PE QE ∴+的最小值为10.故选:C .【点睛】本题考查等边三角形的性质和判定,轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.9、A【分析】全等三角形对应边相等,对应角相等,根据题中信息得出对应关系即可.【详解】∵ABC和DEF全等,A D∠=∠,AC对应DE≅∴ABC DFE∴AB=DF=4故选:A.【点睛】本题考查了全等三角形的概念及性质,应注意①对应边、对应角是对两个三角形而言的,指两条边、两个角的关系,而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等,对应角的平分线相等,对应边上的中线相等,周长及面积相等③全等三角形有传递性.10、B【分析】根据轴对称的性质,轴对称图形的概念,等腰三角形的性质判断即可.【详解】解:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线,说法正确;②等腰三角形一腰上的高与底边的夹角与底角互余,原说法错误;③等腰三角形的顶角平分线在它的对称轴上,原说法错误;④等腰三角形两腰上的中线相等,说法正确.综上,正确的有①④,共2个,故选:B.【点睛】本题考查了轴对称的性质及等腰三角形的性质,掌握轴对称的性质,轴对称图形的概念,等腰三角形的性质是解题的关键.二、填空题1、40【分析】直接根据三角形外角的性质可得结果.【详解】解:∵∠B=20°,∠ACD=60°,∠ACD是△ABC的外角,∴∠ACD=∠B+∠A,∴602040∠=∠-∠=︒-︒=︒,A ACD B故答案为:40.【点睛】本题考查了三角形外角的性质,熟知三角形的一个外角等于与它不相邻的两个内角的和是解本题的关键2、4.6【分析】在AB上截取BF=AD,连接CF,通过证明△ADC≌△BFC,可得∠ACD=∠BCF,CD=CF,由“SAS”可得△DCE≌△FCE,可得DE=EF,即可求得结果.【详解】解:如图,在AB上截取BF=AD,连接CF,∵CA=CB,∠ACB=120°,∴∠CAB=∠CBA=30°,∵∠DAE=60°∴∠DAC=∠DAE﹣∠CAB=30°∴∠DAC=∠CBA,且AD=BF,AC=BC∴△ADC≌△BFC(SAS)∴∠ACD=∠BCF,CD=CF,∵∠ACB=∠ACE+∠ECF+∠BCF=∠ACE+∠ECF+∠ACD=∠DCE+∠ECF=120°∴∠ECF=60°=∠DCE,且CE=CE,DC=CF∴△DCE≌△FCE(SAS)∴DE=EF∴DE=BE﹣BF=BE﹣AD=7﹣2.4=4.6,故答案为4.6【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,添加恰当的辅助线构造全等三角形是本题的关键.3、10【分析】构造ABE≌,求得EB=BC,再通过等量代换、等角的补角相等求得∠E=∠CDE,△,再证得ABE ABC则CE=2BC=10.【详解】解:延长AD .和CB 交于点E .∵AB 平分∠DAC∴∠EAB =∠CAB又∵AB BC ⊥∴∠ABE =∠ABC又∵AB =AB∴ABE ABC ≌∴BC =EB =5,∠E =∠ACB ,180ADC CDE ∠+∠=︒又∵180ADC ACB ∠+∠=︒∴∠ACB =∠CDE∴∠E =∠CDE∴.CD =CE又∵CE =2BC =10∴CD =10故答案为:10.【点睛】 本题考查了全等三角形的性质和判定,等角的补角相等,能根据全等三角形的性质找到角与角之间的关系是解答此题的关键.4、角边角或【分析】根据全等三角形的判定定理得出即可.【详解】解答:解:两角和它们的夹边分别相等的两个三角形全等,简写成角边角或ASA , 故答案为:角边角或ASA .【点睛】本题考查了全等三角形的判定定理,掌握全等三角形的判定定理是解题的关键. 5、64︒【分析】作FH 垂直于FE ,交AC 于点H ,可证得()FAH FCE ASA ≅△△,由对应边、对应角相等可得出()HDF EDF SAS ≅△△,进而可求出58DEF ∠=︒,则64DEC CEF DEF ∠=∠-∠=︒.【详解】作FH 垂直于FE ,交AC 于点H ,∵90AFC EFH ∠=∠=︒又∵AFC AFH CFH ∠=∠+∠,HFE CFE CFH ∠=∠+∠∴13AFH CFE ∠=∠=︒∵45A FCE ∠=∠=︒,FA =CF∴()FAH FCE ASA ≅△△∴FH =FE∵321345DFE DFC EFC ∠=∠+∠=︒+︒=︒∵904545DFH HFE DFE ∠=∠-∠=︒-︒=︒∴DFE DFH ∠=∠又∵DF =DF∴()HDF EDF SAS ≅△△∴DHF DEF ∠=∠∵451358DHF A HFA ∠=∠+∠=︒+︒=︒∴58DEF ∠=︒∵180CFE CEF FCE ∠+∠+∠=︒∴1801801345122CEF CFE FCE ∠=︒-∠-∠=︒-︒-︒=︒∴1225864DEC CEF DEF ∠=∠-∠=︒-︒=︒故答案为:64︒.【点睛】本题考查了等腰三角形的性质,全等三角形的判定及其性质,作辅助线HF 垂直于FE 是解题的关键.三、解答题1、证明见解析.【分析】先根据角的和差可得ACD BCE ∠=∠,再根据三角形全等的判定定理证出ACD BCE ≅△△,然后根据全等三角形的性质即可得证.【详解】证明:90ACB ∠=︒,90ACD BCD ∴∠+∠=︒,CE CD ⊥,90BCE BCD ∠∴∠+=︒,ACD BCE ∠∠∴=,在ACD △和BCE 中,CA CB ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩, ()ACD BCE SAS ∴≅,AD BE ∴=.【点睛】本题考查了三角形全等的判定定理与性质等知识点,熟练掌握三角形全等的判定方法是解题关键.2、OE ; CE ;全等三角形的对应角相等【分析】根据圆的半径相等可得OD =OE ,CD =CE ,再利用SSS 可证明OCD OCE ≌△△,从而根据全等三角形的性质可得结论.【详解】证明:连接CD ,CE由作图步骤②可知OD =___OE ___.由作图步骤③可知CD =__CE ___.∵OC OC =,∴OCD OCE ≌△△. ∴AOC BOC ∠=∠(__全等三角形对应角相等__)故答案为:OE ; CE ;全等三角形的对应角相等【点睛】本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了全等三角形的判定和性质.3、(1)20°;(2)CBF α∠=;(3)AF = CF +BF ,理由见解析【分析】(1)由△ABC 是等边三角形,得到AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,∠EAD =∠CAD =20°,AC =AE ,则∠BAE =∠BAC -∠EAD -∠CAD =20°,AB =AE ,()1180=802ABE AEB BAE ==︒-︒∠∠∠,∠CBF =∠ABE -∠ABC =20°; (2)同(1)求解即可;(3)如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,先证明△AEF ≌△ACF 得到∠AFE =∠AFC ,然后证明∠AFE =∠AFC =60°,得到∠BFC =120°,即可证明F 、C 、G 三点共线,得到△AFG 是等边三角形,则AF =GF =CF +CG =CF +BF .【详解】解:(1)∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,∠EAD =∠CAD =20°,AC =AE ,∴∠BAE =∠BAC -∠EAD -∠CAD =20°,AB =AE , ∴()1180=802ABE AEB BAE ==︒-︒∠∠∠, ∴∠CBF =∠ABE -∠ABC =20°;(2)∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,EAD CAD α∠=∠=,AC =AE ,∴602BAE BAC EAD CAD α∠=∠-∠-∠=︒- ,AB =AE ,∴()1180=602ABE AEB BAE α==︒-︒+∠∠∠, ∴CBF ABE ABC α∠=∠-∠=;(3)AF = CF +BF ,理由如下:如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,∴AF =AG ,∠FAG =60°,∠ACG =∠ABF ,BF =CG在△AEF 和△ACF 中,=AE AC EAF CAF AF AF =⎧⎪∠∠⎨⎪=⎩, ∴△AEF ≌△ACF (SAS ),∴∠AFE =∠AFC ,∵∠CBF +∠BCF +∠BFD +∠CFD =180°,∠CAF +∠CFA +∠ACD +∠CFD =180°,∴∠BFD =∠ACD =60°,∴∠AFE =∠AFC =60°,∴∠BFC =120°,∴∠BAC +∠BFC =180°,∴∠ABF +∠ACF =180°,∴∠ACG +∠ACF =180°,∴F 、C 、G 三点共线,∴△AFG 是等边三角形,∴AF =GF =CF +CG =CF +BF .【点睛】本题主要考查了等边三角形的性质与判定,旋转的性质,折叠的性质,全等三角形的性质与判定,三角形内角和定理,熟知相关知识是解题的关键.4、(1)57°,147°;(2)∠ACB=180°-∠DCE,理由见解析;(3)∠DAB+∠CAE=120°【分析】(1)根据角的和差定义计算即可.(2)利用角的和差定义计算即可.(3)利用特殊三角板的性质,角的和差定义即可解决问题.【详解】解:(1)由题意,903357∠=︒-︒=︒;BCDACB∠=︒+︒=︒;9057147故答案为:57°,147°.(2)∠ACB=180°-∠DCE,理由如下:∵ ∠ACE=90°-∠DCE,∠BCD=90°-∠DCE,∴ ∠ACB=∠ACE+∠DCE+∠BCD=90°-∠DCE+∠DCE+90°-∠DCE=180°-∠DCE.(3)结论:∠DAB+∠CAE=120°.理由如下:∵∠DAB+∠CAE=∠DAE+∠CAE+∠BAC+∠CAE=∠DAC+∠EAB,又∵∠DAC=∠EAB=60°,∴∠DAB+∠CAE=60°+60°=120°.故答案为:∠DAB+∠CAE=120°.【点睛】本题考查三角形的内角和定理,角的和差定义等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.5、(1)①见解析;②60α︒-,60;③MF=MA+ME,证明见解析;(2)MF MA ME=-【分析】(1)①按照要求旋转作图即可;②由旋转和等腰三角形性质解出∠AEF;再由三角形外角定理求出∠AMF;③在FE上截取GF=ME,连接AG,证明△AFG≌△AEM且△AGM为等边三角形后即可证得MF =MA+ME;(2)根据题意画出图形,根据含30°的直角三角形的性质,即可得到结论.【详解】解:(1)①补全图形如下图:②∵∠CAE=∠DAC=α,∴∠BAE=30°+α∴∠FAE=2×(30°+α)∴∠AEF=()180-2+302α︒⨯︒=60°-α;∵∠AMF=∠CAE+∠AEF=α+60°-α=60°,故答案是:60°-α,60°;③MF=MA+ME.证明:在FE上截取GF=ME,连接AG.∵点D关于直线AC的对称点为E,∴△ADC ≌△AEC .∴∠CAE =∠CAD =α.∵∠BAC =30°,∴∠EAN =30°+α.又∵点E 关于直线AB 的对称点为F ,∴AB 垂直平分EF .∴AF =AE ,∠FAN =∠EAN =30°+α,∴∠F =∠AEF =()180230602αα︒-︒+=︒-.∴∠AMG =6060αα︒-+=︒.∵AF =AE ,∠F =∠AEF , GF =ME ,∴△AFG ≌△AEM .∴AG =AM .又∵∠AMG =60︒,∴△AGM 为等边三角形.∴MA =MG .∴MF =MG +GF =MA +ME .(2)MF MA ME =-,理由如下:如图1所示,∵点E 与点F 关于直线AB 对称,∴∠ANM =90°,NE =NF ,又∵∠NAM =30°,∴AM=2MN ,∴AM=2NE+2EM =MF+ME,∴MF=AM-ME;如图2所示,∵点E与点F关于直线AB对称,∴∠ANM=90°,NE=NF,∵∠NAM=30°,∴AM=2NM,∴AM=2MF+2NF=2MF+NE+NF=ME+MF,∴MF=MA-ME;综上所述:MF=MA-ME.【点睛】本题考查轴对称、三角形全等判定与性质、等边三角形判定与性质,掌握这些是本题关键.6、证明见解析.【分析】过D作DG∥AC交AB于G,由等边三角形的性质和平行线的性质得到∠BDG=∠BGD=60°,于是得到△BDG是等边三角形,再证明△AGD≌△DCE即可得到结论.【详解】证明:过D作DG∥AC交AB于G,∵△ABC是等边三角形,∴AB=AC,∠B=∠ACB=∠BAC=60°,又∵DG∥AC,∴∠BDG=∠BGD=60°,∴△BDG是等边三角形,∠AGD=180°−∠BGD=120°,∴DG=BD,∵点D为BC的中点,∴BD=CD,∴DG=CD,∵EC是△ABC外角的平分线,∴∠ACE =12(180°−∠ACB )=60°,∴∠BCE =∠ACB +∠ACE =120°=∠AGD ,∵AB =AC ,点D 为BC 的中点,∴∠ADB =∠ADC =90°,又∵∠BDG =60°,∠ADE =60°,∴∠ADG =∠EDC =30°,在△AGD 和△ECD 中,AGD ECD GD CDADG EDC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AGD ≌△ECD (ASA ).∴AD =DE .【点睛】本题是三角形综合题,主要考查了平行线的性质,全等三角形的性质与判定,等边三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.7、证明见解析.【分析】延长CE 交AB 于F ,求出∠AEC =∠AEF ,∠FAE =∠CAE ,根据ASA 证△FAE ≌△CAE ,推出∠ACE =∠AFC ,根据三角形外角性质得出∠AFC =∠B +∠ECD ,代入即可.【详解】证明:延长CE 交AB 于F ,∵CE⊥AD,∴∠AEC=∠AEF,∵AD平分∠BAC,∴∠FAE=∠CAE,在△FAE和△CAE中,∵FAE CAEAE AEAEF AEC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△FAE≌△CAE(ASA),∴∠ACE=∠AFC,∵∠AFC=∠B+∠ECD,∴∠ACE=∠B+∠ECD.【点睛】本题考查了全等三角形的性质和判定,三角形的外角性质等知识点,关键是作辅助线后求出∠AFC=∠ACE.8、见解析【分析】过A作AF⊥BC于F,根据等腰三角形的性质得出BF=CF,DF=EF,即可求出答案.【详解】证明:如图,过A作AF⊥BC于F,∵AB=AC,AD=AE,∴BF=CF,DF=EF,∴BF-DF=CF-EF,∴BD=CE.【点睛】本题考查了等腰三角形的性质的应用,注意:等腰三角形的底边上的高,底边上的中线,顶角的平分线互相重合.9、见解析【分析】先由BF=CE说明BC= EF.然后运用SAS证明△ABC≌△DEF,最后运用全等三角形的性质即可证明.【详解】证明:∵BF= CE,∴BC= EF.在△ABC和△DEF中,,,,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS ).∴AC =DF .【点睛】本题主要考查了全等三角形的判定与性质,正确证明△ABC ≌△DEF 是解答本题的关键.10、40︒【分析】先由旋转的性质证明,70,AB AD ADE B 再利用等边对等角证明70,ADB B 从而可得答案.【详解】 解: 把△ABC 绕点A 逆时针旋转得到△ADE ,∠B =70°,,70,AB AD ADE B 70,ADB B18040.CDE ADB ADE 【点睛】本题考查的是旋转的性质,等腰三角形的性质,掌握“旋转前后的对应角相等与等边对等角”是解本题的关键.。
2022年最新精品解析沪教版七年级数学第二学期第十四章三角形同步测评试卷(精选含答案)

沪教版七年级数学第二学期第十四章三角形同步测评考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、在平面直角坐标系xOy 中,点A (0,2),B (a ,0),C (m ,n )(0m >).若ABC 是等腰直角三角形,且AB BC =,当01a <<时,点C 的横坐标m 的取值范围是( )A .02m <<B .23m <<C .3m <D .3m >2、已知三角形的两边长分别为2cm 和3cm ,则第三边长可能是( )A .6cmB .5cmC .3cmD .1cm3、下列四个命题是真命题的有( )①同位角相等;②相等的角是对顶角;③直角三角形两个锐角互余;④三个内角相等的三角形是等边三角形.A .1个B .2个C .3个D .4个4、如图,ABC ≌DEF ,点B 、E 、C 、F 在同一直线上,若BC =7,EC =4,则CF 的长是( )A.2 B.3 C.4 D.75、有下列说法:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;②等腰三角形一腰上的高与底边的夹角与顶角互余;③等腰三角形顶角的平分线是它的对称轴;④等腰三角形两腰上的中线相等.其中正确的说法有()个.A.1 B.2 C.3 D.46、如图,在△ABC和△DEF中,∠A=∠D,AF=DC,添加下列条件中的一个仍无法证明△ABC≌△DEF 的是()A.BC=EF B.AB=DE C.∠B=∠E D.∠ACB=∠DFE7、下列说法错误的是()A.任意一个直角三角形都可以被分割成两个等腰三角形B.任意一个等腰三角形都可以被分割成两个等腰三角形C.任意一个直角三角形都可以被分割成两个直角三角形D.任意一个等腰三角形都可以被分割成两个直角三角形8、△BDE和△FGH是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC内.若BC =5,则五边形DECHF的周长为()A .8B .10C .11D .129、下列命题是真命题的是( )A .等腰三角形的角平分线、中线、高线互相重合B .一个三角形被截成两个三角形,每个三角形的内角和是90度C .有两个角是60°的三角形是等边三角形D .在ABC 中,2A B C ∠=∠=∠,则ABC 为直角三角形10、如图,将△OAB 绕点O 逆时针旋转80°得到△OCD ,若∠A 的度数为110°,∠D 的度数为40°,则∠AOD 的度数是( )A .50°B .60°C .40°D .30°第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,已知点A 是射线BE 上一点,过A 作CA BE ⊥交射线BF 于点C ,AD BF ⊥交射线BF 于点D ,给出下列结论:①1∠是B 的余角;②图中互余的角共有3对;③1∠的补角只有ACF ∠;④与ADB ∠互补的角共有3个,其中正确结论有______(把你认为正确的结论的序号都填上).2、如图,在△ABC 中,已知点D E F 、、分别为BC AD CE 、、的中点,若△ABC 的面积为24m ,则阴影部分的面积为 _________ 2cm3、如图,两根旗杆CA ,DB 相距20米,且CA ⊥AB ,DB ⊥AB ,某人从旗杆DB 的底部B 点沿BA 走向旗杆CA 底部A 点.一段时间后到达点M ,此时他分别仰望旗杆的顶点C 和D ,两次视线的夹角∠CMD =90°,且CM =DM .已知旗杆BD 的高为12米,该人的运动速度为每秒2米,则这个人从点B 到点M 所用时间是 _____秒.4、如图,在△ABC 中,点D 为BC 边延长线上一点,若∠ACD =75°,∠A =45°,则∠B 的度数为__________.5、如图,在△ABC 中,∠ACB =90°,点D 在AB 上,将△ABC 沿CD 折叠,点A 落在BC 边上的点A '处,若∠B =35°,则BDA '∠的度数为___________.三、解答题(10小题,每小题5分,共计50分)1、如图,AD 是ABC 的高,CE 是ADC 的角平分线.若BAD ECD ∠=∠,70B ∠=︒,求CAD ∠的度数.2、 “三等分角”是被称为几何三大难题的三个古希腊作图难题之一.如图1所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒PA ,PB 组成,两根棒在P 点相连并可绕点P 旋转,C 点是棒PA 上的一个固定点,点A ,O 可在棒PA ,PB 内的槽中滑动,且始终保持OA =OC =PC .∠AOB 为要三等分的任意角.则利用“三等分角仪”可以得到∠APB =13∠AOB .我们把“三等分角仪”抽象成如图2所示的图形,完成下面的证明.已知:如图2,点O ,C 分别在∠APB 的边PB ,PA 上,且OA =OC =PC .求证:∠APB =13∠AOB .3、如图,ABC 是等边三角形,D 点是BC 上一点,2BD CD =,DE AB ⊥于点E ,CE 交AD 于点P .求APE ∠的度数.4、命题:如图,已知,AC EF AC FE =∥,A D B F ,,,共线,(1),那么ABC FDE ∆≅∆.(1)从①AB FD =和②BC DE =两个条件中,选择一个填入横线,使得上述命题为真命题,你选择的条件为_______(填序号);(2)根据你选择的条件,判定ABC FDE ∆≅∆的方法是________;(3)根据你选择的条件,完成ABC FDE ∆≅∆的证明.5、如图1,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ,连接AC 和BD ,相交于点E ,连接BC .(1)求证DOB ≌AOC ;(2)求∠CEB 的大小;(3)如图2,OAB 固定不动,保持△OCD 的形状和大小不变,将OCD 绕点O 旋转(OAB 和OCD 不能重叠),求∠CEB 的大小.6、如图,点B ,F ,C ,E 在一条直线上,AB =DE ,∠B =∠E ,BF =CE .求证:AC =DF .7、如图,在ABC 中,AD 平分BAC ∠,CE AD ⊥于点E .求证:ACE B ECD ∠=∠+∠.8、如图,点A ,B ,C ,D 在一条直线上,AE DF ∥,AE DF =,AB CD =.(1)求证:AEC DFB ≅.(2)若40A ∠=︒,145ECD ∠=︒,求∠F 的度数.9、如图,AD 是ABC 的角平分线,DE AB ⊥于点E .(1)用尺规完成以下基本作图:过点D 作DF AC ⊥于点F ,连接EF 交AD 于点G .(不写作法,保留作图痕迹)(2)在(1)中所作的图形中,求证:AD EF ⊥.10、△ABC 中,AB =AC ,BD 平分∠ABC 交AC 于点D ,从点A 作AE ∥BC 交BD 的延长线于点E .(1)若∠BAC =40°,求∠E 的度数;(2)点F 是BE 上一点,且FE =BD .取DF 的中点H ,请问AH ⊥BE 吗?试说明理由.-参考答案-一、单选题1、B【分析】过点C 作CD x ⊥轴于D ,由“AAS ”可证AOB BDC ∆≅∆,可得2AO BD ==,BO CD n a ===,即可求解.【详解】解:如图,过点C 作CD x ⊥轴于D ,点(0,2)A ,2AO ∴=,ABC ∆是等腰直角三角形,且AB BC =,90ABC AOB BDC ∴∠=︒=∠=∠,90ABO CBD ABO BAO ∴∠+∠=︒=∠+∠,BAO CBD ∴∠=∠,在AOB ∆和BDC ∆中,AOB BDC BAO CBD AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AOB BDC AAS ∴∆≅∆,2AO BD ∴==,BO CD n a ===,01a ∴<<,2OD OB BD a m =+=+=,23m ∴<<,故选:B .【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质,解题的关键是画图及添加恰当辅助线构造全等三角形.2、C【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.【详解】解:设第三边长为x cm,根据三角形的三边关系可得:3-2<x<3+2,解得:1<x<5,只有C选项在范围内.故选:C.【点睛】本题考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.3、B【分析】利用平行线的性质、对顶角的定义、直角三角形的性质及等边三角形的性质分别判断后即可确定正确的选项.【详解】①两直线平行,同位角相等,故错误,是假命题;②相等的角是对顶角,错误,是假命题;③直角三角形两个锐角互余,正确,是真命题;④三个内角相等的三角形是等边三角形,正确,是真命题,综上所述真命题有2个,故选:B .【点睛】本题考查了命题真假的判断,要说明一个命题是正确的,需要根据命题的题设和已学的有关公理、定理进行说明、推理、证明,正确的命题叫做真命题,错误的命题叫做假命题.4、B【分析】根据全等三角形的性质可得BC EF =,根据CF EF EC =-即可求得答案.【详解】 解:ABC ≌DEF ,∴BC EF =点B 、E 、C 、F 在同一直线上,BC =7,EC =4,∴CF EF EC =-743BC EC -=-=故选B【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.5、B【分析】根据轴对称的性质,轴对称图形的概念,等腰三角形的性质判断即可.【详解】解:①轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线,说法正确;②等腰三角形一腰上的高与底边的夹角与底角互余,原说法错误;③等腰三角形的顶角平分线在它的对称轴上,原说法错误;④等腰三角形两腰上的中线相等,说法正确.综上,正确的有①④,共2个,故选:B.【点睛】本题考查了轴对称的性质及等腰三角形的性质,掌握轴对称的性质,轴对称图形的概念,等腰三角形的性质是解题的关键.6、A【分析】根据AF=DC求出AC=DF,再根据全等三角形的判定定理逐个判断即可.【详解】解:∵AF=DC,∴AF+FC=DC+FC,即AC=DF,A、BC=EF,AC=DF,∠A=∠D,不符合全等三角形的判定定理,不能推出△ABC≌△DEF,故本选项符合题意;B、AB=DE,∠A=∠D,AC=DF,符合全等三角形的判定定理SAS,能推出△ABC≌△DEF,故本选项不符合题意;C.∠B=∠E,∠A=∠D,AC=DF,符合全等三角形的判定定理AAS,能推出△ABC≌△DEF,故本选项不符合题意;D.∠ACB=∠DFE,AC=DF,∠A=∠D,符合全等三角形的判定定理ASA,能推出△ABC≌△DEF,故本选项不符合题意;故选:A.【点睛】本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.7、B【分析】根据等腰三角形和直角三角形的性质判断各选项即可得出答案.【详解】解:A、任意一个直角三角形一定能分成两个等腰三角形,本选项正确,不符合题意;B、任意一个等腰三角形不一定能分成两个等腰三角形,本选项错误,符合题意;C、任意一个直角三角形都可以被分割成两个直角三角形,本选项正确,不符合题意;D、任意一个等腰三角形都可以被分割成两个直角三角形,本选项正确,不符合题意;故选:B.【点睛】本题考查了等腰三角形和直角三角形的知识,解题的关键是能判断等腰三角形及直角三角形,可动手操作进行判断.8、B【分析】证明△AFH≌△CHG(AAS),得出AF=CH.由题意可知BE=FH,则得出五边形DECHF的周长=AB+BC,则可得出答案.【详解】解:∵△GFH为等边三角形,∴FH=GH,∠FHG=60°,∴∠AHF+∠GHC=120°,∵△ABC为等边三角形,∴AB=BC=AC=5,∠ACB=∠A=60°,∵∠AHF=180°-∠FHG-∠GHC=120°-∠GHC,∠HGC =180°-∠C -∠GHC =120°-∠GHC ,∴∠AHF =∠HGC ,在△AFH 和△CHG 中A C AHF HGC FH GH ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AFH ≌△CHG (AAS ),∴AF =CH .∵△BDE 和△FGH 是两个全等的等边三角形,∴BE =FH ,∴五边形DECHF 的周长=DE +CE +CH +FH +DF =BD +CE +AF +BE +DF ,=(BD +DF +AF )+(CE +BE ),=AB +BC =10.故选:B .【点睛】本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.9、C【分析】分别根据等腰三角形的性质、三角形的内角和定理、等边三角形的判定,直角三角形的判定即可判断.【详解】A.等腰三角形中顶角角平分线、底边上的中线和底边上的高线互相重合,即三线合一,故此选项错误;B.三角形的内角和为180°,故此选项错误;C.有两个角是60°,则第三个角为180606060︒-︒-︒=︒,所以三角形是等边三角形,故此选项正确;D.设C x ∠=,则2A B x ∠=∠=,故22180x x x ++=︒,解得36x =︒,所以72A B ∠=∠=︒,36C ∠=︒,此三角形不是直角三角形,故此选项错误.故选:C .【点睛】本题考查等腰三角形的性质,直角三角形的定义以及三角形内角和,掌握相关概念是解题的关键.10、A【分析】根据旋转的性质求解80,BOD AOC 110,C A 再利用三角形的内角和定理求解1801104030,COD 再利用角的和差关系可得答案.【详解】 解: 将△OAB 绕点O 逆时针旋转80°得到△OCD ,80,BOD AOC∠A 的度数为110°,∠D 的度数为40°,110,1801104030,C A COD 803050,AOD 故选A【点睛】本题考查的是三角形的内角和定理的应用,旋转的性质,掌握“旋转前后的对应角相等”是解本题的关键.二、填空题1、①④【分析】根据垂直定义可得∠BAC=90°,∠ADC=∠ADB=∠CAE=90°,结合三角形的内角和,然后再根据余角定义和补角定义逐一进行分析即可.【详解】⊥,解:CA BE190,B∴1∠是B的余角;故①符合题意;AD BF⊥,B BADCAD90,1+90,1,CAD互为余角,,B BAD互为余角,⊥,CA BE,CAD BAD互为余角,所以图中互余的角共有4对,故②不符合题意;ACF1180,∴1∠互补;∠与ACF∵∠1+∠DAC=90°,∠BAD+∠DAC=90°,∴∠1=∠BAD,∵∠BAD+∠DAE=180°,∴∠1+∠DAE=180°,∴∠1与∠DAE互补,故③不符合题意;⊥,AD BFCA BE⊥ADB ADC CAB CAE90,所以与ADB∠互补的角有,,,ADC CAB CAE共3个,故④符合题意;所以正确的结论有:①④故答案为:①④【点睛】本题考查的是垂直的定义,互余,互补的含义,三角形的内角和定理,掌握“互为余角的两个角之和为90,︒互为补角是两个角之和为180︒”是解本题的关键.2、1【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.【详解】解:∵点E是AD的中点,∴S△ABE=12S△ABD,S△ACE=12S△ADC,∴S△ABE+S△ACE=12S△ABC=12×4=2cm2,∴S△BCE=12S△ABC=12×4=2cm2,∵点F是CE的中点,∴S△BEF=12S△BCE=12×2=1cm2.故答案为:1.【点睛】本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.3、4【分析】先说明C DMB ∠=∠,再利用AAS 证明ACM BMD ≌,然后根据全等三角形的性质可得12AM BD ==米,再根据线段的和差求得BM 的长,最后利用时间=路程÷速度计算即可.【详解】解:∵90CMD ∠=︒,∴90CMA DMB +=︒∠∠,又∵90CAM ∠=︒,∴90CMA C ︒∠+∠=,∴C DMB ∠=∠,在Rt ACM 和Rt BMD △中,A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()Rt ACM Rt BMD AAS ≌,∴12AM BD ==米,20128BM =-=(米),∵该人的运动速度2m/s ,他到达点M 时,运动时间为824÷=s .故答案为:4.【点睛】本题主要考查了全等三角形的判定与性质,根据题意证得Rt ACM Rt BMD ≌是解答本题的关键. 4、30°【分析】根据三角形的外角的性质,即可求解.【详解】解:∵ACD A B ∠=∠+∠ ,∴B ACD A ∠=∠-∠ ,∵∠ACD =75°,∠A =45°,∴30B ∠=︒ .故答案为:30°【点睛】本题主要考查了三角形的外角性质,熟练掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.5、20°度【分析】先根据三角形内角和求出∠A ,利用翻折不变性得出55CA D A ∠'=∠=︒,再根据三角形外角的性质即可解决问题.【详解】解:90ACB ∠=︒,∠B =35°,180180903555A ACB B ∴∠=︒-∠-∠=︒-︒-︒=︒,CDA '△是由CDA 翻折得到,55CA D A ∴∠'=∠=︒,20CA D B BDA B ∠'=∠+∠'=∠+︒,553520BDA CA D B ''∴∠=∠-∠=︒-︒=︒.故答案为:20°.【点睛】本题考查三角形内角和定理和三角形外角的性质,翻折变换等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.三、解答题1、50︒【分析】AD 是ABC 的高,有90ADB ADC ∠=∠=︒;由70B ∠=︒知20BAD ∠=︒;CE 是ADC 的角平分线可得12ECD ACD ∠=∠;20BAD ECD ∠=∠=︒,40ACD ∠=︒;在ACD △中,904050CAD ∠=︒-︒=︒. 【详解】解:∵AD 是ABC 的高∴90ADB ADC ∠=∠=︒∵70B ∠=︒∴20BAD ∠=︒∵CE 是ADC 的角平分线 ∴12ECD ACD ∠=∠∵20BAD ECD ∠=∠=︒∴40ACD ∠=︒∴在ACD △中,904050CAD ∠=︒-︒=︒.【点睛】本题考查了角平分线.解题的关键在于正确表示各角度之间的数量关系.2、见解析【分析】由OA OC PC ==,得出,POC AOC 为等腰三角形,由外角的性质及等量代换得2CAO APB ∠=∠,再次利用外角的性质及等量代换得3AOB APB ∠=∠,即可证明.【详解】解:OA OC PC ==,,POC AOC ∴为等腰三角形,,APB COP ACO CAO ∴∠=∠∠=∠,由外角的性质得:2ACO APB COP APB ∠=∠+∠=∠,2CAO APB ∠=∠,再由外角的性质得:AOB APB CAO ∠=∠+∠,3AOB APB ∴∠=∠,13APB AOB ∴∠=∠. 【点睛】本题考查了等腰三角形、外角的性质、解题的关键是掌握外角的性质及等量代换的思想进行求解. 3、60APE ∠=︒【分析】由题意易得60ABC ACB ∠=∠=︒,AB AC BC ==,则有30BDE ∠=︒,然后可得BE CD =,进而可证BEC CDA ≌,则有BCE =∠∠CAD ,最后问题可求解.【详解】解:∵ABC 是等边三角形,∴60ABC ACB ∠=∠=︒,AB AC BC ==,∵DE AB ⊥,∴90DEB ∠=︒,∴30BDE ∠=︒,∴2BD BE =,∵2BD CD =,∴BE CD =,∴BEC CDA ≌(SAS ),∴BCE =∠∠CAD ,∵,60APE PAC ACP ACB DAC ACP ∠=∠+∠∠=∠+∠=︒,∴60APE ACB ∠=∠=︒.【点睛】本题主要考查等边三角形的性质、含30度直角三角形的性质及全等三角形的性质与判定,熟练掌握等边三角形的性质、含30度直角三角形的性质及全等三角形的性质与判定是解题的关键. 4、(1)①(2)SAS(3)见解析【分析】(1)根据全等三角形的判定方法分析得出答案;(2)根据(1)直接填写即可;(3)利用SAS 进行证明.(1)解:∵AC EF ∥,∴∠A =∠F ,∵AC=EF ,∴当AB FD =时,可根据SAS 证明ABC FDE ∆≅∆;当BC DE =时,不能证明ABC FDE ∆≅∆,故答案为:①;(2)解:当AB FD =时,可根据SAS 证明ABC FDE ∆≅∆,故答案为:SAS ;(3)证明:在△ABC 和△FDE 中,AC EF A F AB FD =⎧⎪∠=∠⎨⎪=⎩, ∴ABC FDE ∆≅∆.【点睛】此题考查了添加条件证明两个三角形全等,正确掌握全等三角形的判定定理是解题的关键.5、(1)见详解;(2)120°;(2)120°.【分析】(1)如图1,根据等边三角形的性质得到OD =OC =OA =OB ,∠COD =∠AOB =60°,则利用根据“SAS ”判断△AOC ≌△BOD ;(2)利用△AOC ≌△BOD 得到∠CAO =∠DBO ,然后根据三角形内角和可得到∠AEB =∠AOB =60°,即可求出答案;(3)如图2,与(1)的方法一样可证明△AOC ≌△BOD ;则∠CAO =∠DBO ,然后根据三角形内角和可求出∠AEB =∠AOB =60°,即可得到答案.【详解】(1)证明:如图1,∵△ODC 和△OAB 都是等边三角形,∴OD =OC =OA =OB ,∠COD =∠AOB =60°,∴∠BOD =∠AOC =120°,在△AOC 和△BOD 中OC OD AOC BOD OA OB =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD ;(2)解:∵△AOC ≌△BOD ,∴∠CAO =∠DBO ,∵∠1=∠2,∴∠AEB =∠AOB =60°,∴120CEB ∠=︒;(3)解:如图2,∵△ODC 和△OAB 都是等边三角形,∴OD =OC =OA =OB ,∠COD =∠AOB =60°,∴∠AOB +∠BOC =∠COD +∠BOC ,即∠AOC =∠BOD ,在△AOC 和△BOD 中OC OD AOC BOD OA OB =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD ;∴∠CAO =∠DBO ,∵∠1=∠2,∴∠AEB =∠AOB =60°,∴120CEB ∠=︒;即∠CEB 的大小不变.【点睛】本题考查了几何变换综合题:熟练掌握旋转的性质、等边三角形的性质和全等三角形的判定与性质;利用类比的方法解决(3)小题.6、见解析【分析】先由BF =CE 说明BC= EF .然后运用SAS 证明△ABC ≌△DEF ,最后运用全等三角形的性质即可证明.【详解】证明:∵BF= CE ,∴BC= EF .在△ABC 和△DEF 中,,,,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS ).∴AC =DF .【点睛】本题主要考查了全等三角形的判定与性质,正确证明△ABC ≌△DEF 是解答本题的关键.7、证明见解析.【分析】延长CE 交AB 于F ,求出∠AEC =∠AEF ,∠FAE =∠CAE ,根据ASA 证△FAE ≌△CAE ,推出∠ACE =∠AFC ,根据三角形外角性质得出∠AFC =∠B +∠ECD ,代入即可.【详解】证明:延长CE 交AB 于F ,∵CE ⊥AD ,∴∠AEC =∠AEF ,∵AD平分∠BAC,∴∠FAE=∠CAE,在△FAE和△CAE中,∵FAE CAEAE AEAEF AEC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△FAE≌△CAE(ASA),∴∠ACE=∠AFC,∵∠AFC=∠B+∠ECD,∴∠ACE=∠B+∠ECD.【点睛】本题考查了全等三角形的性质和判定,三角形的外角性质等知识点,关键是作辅助线后求出∠AFC=∠ACE.8、(1)见解析;(2)105︒【分析】(1)根据平行线的性质可得A D∠=∠,根据线段的和差关系可得AC DB=,进而根据SAS即证明AEC DFB≅;(2)根据三角形内角和定理以及补角的意义求得∠E,进而根据(1)的结论即可求得∠F.【详解】(1)证明:AE DF∥∴A D∠=∠,AB CD=∴AB BC BC CD+=+即AC BD=又AE DF =,∴AEC DFB ≅(2)解:40A ∠=︒,145ECD ∠=︒,18035ECA ECD ∴∠=︒-∠=︒180105E A ECA ∴∠=︒-∠-∠=︒AEC DFB ≅F E ∴∠=∠105=︒【点睛】本题考查了平行线的性质,三角形内角和定理,三角形全等的性质与判定,掌握全等三角形的性质与判定是解题的关键.9、(1)见解析;(2)见解析.【分析】(1)以点D 为圆心,适当长为半径,作弧,交AC 于两点,再分别以这两点为圆心,适当长为半径作弧,连接两条弧的交点所在的直线,该直线与AC 的交点即为点F ,连接EF 交AD 于点G ;(2)利用角平分线性质可得,DE DF EAD FAD =∠=∠,由此证明()EAD FAD AAS ≅,得到AE AF =,继而证明()EAG FAG SAS ≅,证得90AGE AGF ∠=∠=︒即可解题.【详解】解:(1)如图,点F 、G 即为所求作的点;⊥,(2)AD是ABC的角平分线,DE AB⊥,DF AC∴=∠=∠DE DF EAD FAD,=AD AD∴≅EAD FAD AAS()∴=AE AF∠=∠=EAD FAD AG AG,∴≅()EAG FAG SAS∴∠=∠AGE AGF∠+∠=︒AGE AGF180∴∠=∠=︒90AGE AGF∴⊥AD EF【点睛】本题考查角平分线的性质、全等三角形的判定与性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.10、(1)∠E=35°;(2)AH⊥BE.理由见解析.【分析】(1)根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD的度数,最后根据两直线平行,内错角相等求出;(2)由“SAS”可证△ABD≌△AEF,可得AD=AF,由等腰三角形的性质可求解.【详解】解:(1)∵AB=AC,∴∠ABC=∠ACB,∵∠BAC=40°,∴∠ABC =12(180°-∠BAC )=70°,∵BD 平分∠ABC ,∴∠CBD =12∠ABC =35°,∵AE ∥BC ,∴∠E =∠CBD =35°;(2)∵BD 平分∠ABC ,∠E =∠CBD ,∴∠CBD =∠ABD =∠E ,∴AB =AE ,在△ABD 和△AEF 中,AB AE E ABD BD EF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△AEF (SAS ),∴AD =AF ,∵点H 是DF 的中点,∴AH ⊥BE .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键.。
2022年强化训练沪教版七年级数学第二学期第十四章三角形专项攻克试题(含详细解析)

沪教版七年级数学第二学期第十四章三角形专项攻克考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,点A 、B 、C 、D 在一条直线上,点E 、F 在AD 两侧,BF CE ∥,BF CE =,添加下列条件不能判定ACE DBF ≌的是( )A .AE DF =B .AB CD =C .E F ∠=∠D .AE DF ∥2、下列说法错误的是( )A .任意一个直角三角形都可以被分割成两个等腰三角形B .任意一个等腰三角形都可以被分割成两个等腰三角形C .任意一个直角三角形都可以被分割成两个直角三角形D .任意一个等腰三角形都可以被分割成两个直角三角形3、如图,AD ∥BC ,∠C =30°,∠ADB :∠BDC =1:2,∠EAB =72°,以下四个说法:①∠CDF =30°;②∠ADB =50°;③∠ABD =22°;④∠CBN =108°其中正确说法的个数是( )A .1个B .2个C .3个D .4个4、已知三条线段的长分别是4,4,m ,若它们能构成三角形,则整数m 的最大值是( )A .10B .8C .7D .45、如图,等边ABC 中,D 为AC 中点,点P 、Q 分别为AB 、AD 上的点,4BP AQ ==,3QD =,在BD 上有一动点E ,则PE QE +的最小值为( )A .7B .8C .10D .126、如图,在ABC 中,AD 、AE 分别是边BC 上的中线与高,4AE =,CD 的长为5,则ABC 的面积为( )A .8B .10C .20D .407、如图点,,A B C 在同一条直线上,,CBE ADC 都是等边三角形,,AE BD 相交于点O ,且分别与,CD CE 交于点,M N ,连接,M N ,有如下结论:①DCB ACE ≅;②AM DN =;③CMN △为等边三角形;④60EOB ∠=︒.其中正确的结论个数是( )A .1个B .2个C .3个D .4个8、如图,BD 是ABC 的角平分线,∥DE BC ,交AB 于点E .若30A ∠=︒,50BDC ∠=︒,则BDE ∠的度数是( )A .10°B .20°C .30°D .50°9、如图,AD 是ABC 的角平分线,CE AD ⊥,垂足为F .若40CAB ∠=︒,50B ∠=︒,则BDE ∠的度数为( )A.35°B.40°C.45°D.50°10、在下列长度的四根木棒中,能与3cm,9cm的两根木棒首尾顺次相接钉成一个三角形的是()A.3cm B.6cm C.10cm D.12cm第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,点E,F分别为线段BC,DB上的动点,BE=DF.要使AE+AF最小值,若用作图方式确定E,F,则步骤是 _____.=,则BE 2、如图,在等边三角形ABC中,2AB=,BD是AC边的高线,延长BC至点E,使CE CD的长为__________.3、如图,上午9时,一艘船从小岛A 出发,以12海里的速度向正北方向航行,10时40分到达小岛B 处,若从灯塔C 处分别测得小岛A 、B 在南偏东34°、68°方向,则小岛B 处到灯塔C 的距离是______海里.4、如图,已知AB =3,AC =CD =1,∠D =∠BAC =90°,则△ACE 的面积是 _____.5、如图,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,BC =6,将△ABC 绕点C 顺时针旋转30°得到△A ′B ′C ,A 、B 分别与A ′、B ′对应,CA ′交AB 于点M ,则CM 的长为 ___.三、解答题(10小题,每小题5分,共计50分)1、直线l 经过点A ,ABC 在直线l 上方,AB AC =.(1)如图1,90BAC ∠=︒,过点B ,C 作直线l 的垂线,垂足分别为D 、E .求证:ABD CAE ≌(2)如图2,D ,A ,E 三点在直线l 上,若BAC BDA AEC α∠=∠=∠=(α为任意锐角或钝角),猜想线段DE 、BD 、CE 有何数量关系?并给出证明.(3)如图3,90BAC ∠=︒过点B 作直线l 上的垂线,垂足为F ,点D 是BF 延长线上的一个动点,连结AD ,作90DAE ∠=︒,使得AE AD =,连结DE ,CE .直线l 与CE 交于点G .求证:G 是CE 的中点.2、阅读填空,将三角尺(△MPN,∠MPN=90°)放置在△ABC上(点P在△ABC内),如图①所示,三角尺的两边PM、PN恰好经过点B和点C,我们来研究∠ABP与∠ACP是否存在某种数量关系.(1)特例探索:若∠A=50°,则∠PBC+∠PCB= 度,∠ABP+∠ACP= 度.(2)类比探索:∠ABP、∠ACP、∠A的关系是.(3)变式探索:如图②所示,改变三角尺的位置,使点P在△ABC外,三角尺的两边PM、PN仍恰好经过点B和点C,则∠ABP、∠ACP、∠A的关系是.3、如图,在△ABC中,AB=AC,M,N分别是AB,AC边上的点,并且MN∥BC.(1)△AMN是否是等腰三角形?说明理由;(2)点P是MN上的一点,并且BP平分∠ABC,CP平分∠ACB.①求证:△BPM是等腰三角形;②若△ABC的周长为a,BC=b(a>2b),求△AMN的周长(用含a,b的式子表示).4、如图,AD 是ABC 的角平分线,DE AB ⊥于点E .(1)用尺规完成以下基本作图:过点D 作DF AC ⊥于点F ,连接EF 交AD 于点G .(不写作法,保留作图痕迹)(2)在(1)中所作的图形中,求证:AD EF ⊥.5、已知,∠A =∠D ,BC 平分∠ABD ,求证:AC =DC .6、如图,在ABC 中,AD 平分BAC ∠,CE AD ⊥于点E .求证:ACE B ECD ∠=∠+∠.7、已知:如图,AD,BE相交于点O,AB⊥BE,DE⊥AD,垂足分别为B,D,OA=OE.求证:△ABO≌△EDO.8、已知:直线AB、CR被直线UV所截,直线UV交直线AB于点B,交直线CR于点D,∠ABU+∠CDV=180°.(1)如图1,求证:AB∥CD;(2)如图2,BE∥DF,∠MEB=∠ABE+5°,∠FDR=35°,求∠MEB的度数;(3)如图3,在(2)的条件下,点N在直线AB上,分别连接EN、ED,MG∥EN,连接ME,∠GME=∠GEM,∠EBD=2∠NEG,EB平分∠DEN,MH⊥UV于点H,若∠EDC=17∠CDB,求∠GMH的度数.9、如图,已知点B,F,C,E在同一直线上,AB∥DE,BF=CE,AB=ED,求证:∠A=∠D.10、如图,AD 是ABC 的高,CE 是ADC 的角平分线.若BAD ECD ∠=∠,70B ∠=︒,求CAD ∠的度数.-参考答案-一、单选题1、A【分析】根据题意,可得,BE CE FBD ECA =∠=∠,结合选项根据三角形全等的性质与判定逐项分析即可.【详解】 解:BF CE ∥∴FBD ECA ∠=∠ A. ,BE CE FBD ECA =∠=∠,AE DF =,不能根据SSA 证明三角形全等,故该选项符合题意;B. AB CD =AB BC BC CD ∴+=+AC BD ∴=,BE CE FBD ECA =∠=∠,∴ACE DBF ≌()SAS故能判定ACE DBF ≌,不符合题意; C. ,BE CE FBD ECA =∠=∠,E F ∠=∠,∴ACE DBF ≌()ASA ,故能判定ACE DBF ≌,不符合题意;D.AE DF ∥A D ∴∠=∠,BE CE FBD ECA =∠=∠∴ACE DBF ≌()AAS ,故能判定ACE DBF ≌,不符合题意;故选A【点睛】本题考查了平行线的性质,三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键.2、B【分析】根据等腰三角形和直角三角形的性质判断各选项即可得出答案.【详解】解:A 、任意一个直角三角形一定能分成两个等腰三角形,本选项正确,不符合题意;B 、任意一个等腰三角形不一定能分成两个等腰三角形,本选项错误,符合题意;C 、任意一个直角三角形都可以被分割成两个直角三角形,本选项正确,不符合题意;D 、任意一个等腰三角形都可以被分割成两个直角三角形,本选项正确,不符合题意;故选:B .本题考查了等腰三角形和直角三角形的知识,解题的关键是能判断等腰三角形及直角三角形,可动手操作进行判断.3、D【分析】根据AD∥BC,∠C=30°,利用内错角相等得出∠FDC=∠C=30°,可判断①正确;根据邻补角性质可求∠ADC=180°-∠FDC=180°-30°=150°,根据∠ADB:∠BDC=1:2,得出方程3∠ADB=150°,解方程可判断②正确;根据∠EAB=72°,可求邻补角∠DAN=180°-∠EAB=180°-72°=108°,利用三角形内角和可求∠ABD=180°-∠NAD-∠ADB=180°-108°-50°=22°可判断③正确,利用AD∥BC,同位角相等的∠CBN=∠DAN=108°可判断④正确即可.【详解】解:∵AD∥BC,∠C=30°,∴∠FDC=∠C=30°,故①正确;∴∠ADC=180°-∠FDC=180°-30°=150°,∵∠ADB:∠BDC=1:2,∴∠BDC=2∠ADB,∵∠ADC=∠ADB+∠BDC=∠ADB+2∠ADB=3∠ADB=150°,解得∠ADB=50°,故②正确∵∠EAB=72°,∴∠DAN=180°-∠EAB=180°-72°=108°,∴∠ABD=180°-∠NAD-∠ADB=180°-108°-50°=22°,故③正确∵AD∥BC,∴∠CBN=∠DAN=108°,故④正确其中正确说法的个数是4个.【点睛】本题考查平行线性质,角的倍分,邻补角性质,三角形内角和,一元一次方程,掌握平行线性质,邻补角性质,三角形内角和,一元一次方程地解题关键.4、C【分析】根据三角形三边关系列出不等式,根据不等式的解集求整数m的最大值.【详解】解:条线段的长分别是4,4,m,若它们能构成三角形,则m-<<+,即08<<4444m又m为整数,则整数m的最大值是7故选C【点睛】本题考查了求不等式的整数解,三角形三边关系,根据三角形的三边关系列出不等式是解题的关键.5、C【分析】+的值最小,最小值作点Q关于BD的对称点Q',连接PQ'交BD于E,连接QE,此时PE EQ+=+'=',据此求解即可.PE PQ PE EQ PQ【详解】解:如图,ABC ∆是等边三角形,BA BC ∴=,∵D 为AC 中点,∴BD AC ⊥,4AQ =,3QD =,7AD DC AQ QD ∴==+=,作点Q 关于BD 的对称点Q ',连接PQ '交BD 于E ,连接QE ,此时PE EQ +的值最小.最小值PE QE PE EQ PQ +=+'=',4AQ =,7AD DC ==,3QD DQ ∴='=,4CQ BP ∴'==,10AP AQ ∴='=,60A ∠=︒,APQ ∴∆'是等边三角形,10PQ PA ∴'==,PE QE ∴+的最小值为10.故选:C .【点睛】本题考查等边三角形的性质和判定,轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.6、C【分析】根据三角形中线的性质得出CB 的长为10,再用三角形面积公式计算即可.【详解】解:∵AD 是边BC 上的中线,CD 的长为5,∴CB =2CD =10, ABC 的面积为111042022BC AE ⨯=⨯⨯=, 故选:C .【点睛】本题考查了三角形中线的性质和面积公式,解题关键是明确中线的性质求出底边长.7、D【分析】由SAS 即可证明DCB ACE ∆≅∆,则①正确;有∠CAE =∠CDB ,然后证明△ACM ≌△DCN ,则②正确;由CM =CN ,∠MCN =60°,即可得到∆CMN 为等边三角形,则③正确;由AD∥CE ,则∠DAO =∠NEO =∠CBN ,由外角的性质60EOB OAC CBN ∠=∠+∠=︒,即可得到答案.【详解】解:∵△DAC 和△EBC 均是等边三角形,∴AC =CD ,BC =CE ,∠ACD =∠BCE =60°,∴∠ACD +∠DCE =∠BCE +∠DCE ,即∠ACE =∠BCD ,∠MCN =180°-∠ACD -∠BCE =60°,在△ACE 和△DCB 中,AC CD ACE BCD BC CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△DCB (SAS ),则①正确;∴AE =BD ,∠CAE =∠CDB ,在ACM 和△DCN 中,ACM DCN AC CD CAM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACM ≌△DCN (ASA ),∴CM =CN ,AM DN =;则②正确;∵∠MCN =60°,∴∆CMN 为等边三角形;则③正确;∵∠DAC =∠ECB =60°,∴AD∥CE ,∴∠DAO =∠NEO =∠CBN ,∴60EOB OAC CBN OAC DAO ∠=∠+∠=∠+∠=︒;则④正确;∴正确的结论由4个;故选D .【点睛】本题考查了等边三角形的性质与判定,全等三角形的判定与性质,平行线的性质与判定,综合性较强,但难度不是很大,准确识图找出全等三角形是解题的关键.8、B【分析】由外角的性质可得∠ABD=20°,由角平分线的性质可得∠DBC=20°,由平行线的性质即可求解.【详解】解:(1)∵∠A=30°,∠BDC=50°,∠BDC=∠A+∠ABD,∴∠ABD=∠BDC−∠A=50°−30°=20°,∵BD是△ABC的角平分线,∴∠DBC=∠ABD=20°,∵DE∥BC,∴∠EDB=∠DBC=20°,故选:B.【点睛】本题考查了平行线的性质,三角形外角的性质,角平分线的定义,灵活应用这些性质解决问题是解决本题的关键.9、B【分析】根据三角形的内角和求出∠ACB=90°,利用三角形全等,求出DC=DE,再利用外角求出答案.【详解】解:∵∠CAB=40°,∠B=50°,∴∠ACB=180°−40°−50°=90°,∵CE⊥AD,∴∠AFC=∠AFE=90°,∵AD是△ABC的角平分线,∴∠CAD=∠EAD=1×40°=20°,2又∵AF=AF,∴△ACF≌△AEF(ASA)∴AC=AE,∵AD=AD,∠CAD=∠EAD,∴△ACD≌△AED(SAS),∴DC=DE,∴∠DCE=∠DEC,∵∠ACE=90°−20°=70°,∴∠DCE=∠DEC=∠ACB−∠ACE=90°−70°=20°,∴∠BDE=∠DCE+∠DEC=20°+20°=40°,故选:B.【点睛】考查角平分线、全等三角形的判定和性质、三角形的内角和等知识,根据三角形的内角和求出相应各个角的度数是解决问题的关键.10、C【分析】设第三根木棒的长度为x cm,再确定三角形第三边的范围,再逐一分析各选项即可得到答案.【详解】解:设第三根木棒的长度为x cm,则x9393,x612,所以A,B,D不符合题意,C符合题意,故选C【点睛】本题考查的是三角形的三边的关系,掌握“利用三角形的三边关系确定第三边的范围”是解本题的关键.二、填空题∠=∠;②以点B为圆心、AD长为半径画弧,交BM于点P;③连接AP 1、①连接AD,作CBM ADB交BC于点E;④以点D为圆心、BE长为半径画弧,交DB于点F【分析】∠=∠;②以点B为圆心、AD长为半径画弧,交BM于点P;③连接AP 按照①连接AD,作CBM ADB交BC于点E;④以点D为圆心、BE长为半径画弧,交DB于点F的步骤作图即可得.【详解】∠=∠;解:步骤是①连接AD,作CBM ADB②以点B为圆心、AD长为半径画弧,交BM于点P;③连接AP交BC于点E;④以点D为圆心、BE长为半径画弧,交DB于点F;如图,点,E F即为所求.∠=∠;②以点B为圆心、AD长为半径画弧,交BM于点P;③故答案为:①连接AD,作CBM ADB连接AP交BC于点E;④以点D为圆心、BE长为半径画弧,交DB于点F.【点睛】本题考查了作一个角等于已知角、两点之间线段最短、作线段、全等三角形的判定与性质等知识点,熟练掌握尺规作图的方法是解题关键.2、3【分析】由等腰三角形三线合一的性质,得到AD =DC =1,由BE =BC +CE 不难求解.【详解】 解:三角形ABC 是等边三角形,∴BC =AC =2, 又 BD 是AC 边的高线,∴DC =112122AC =⨯=, CE ∴ CD ==1,213BE BC CE ∴=+=+=,故答案为:3.【点睛】本题考查了等边三角形的性质,掌握等腰三角形三线合一的性质是解本题的关键.3、20【分析】根据题干所给的角的度数,易证ABC 是等腰三角形,而AB 的长易求,即可根据等腰三角形的性质,得出BC 的值.【详解】解:据题意得,3468A DBC ∠=︒∠=︒,.∵DBC A C ∠=∠+∠,即6834C ︒=︒+∠,∴34A C ∠=∠=︒,∴AB BC =. 由题意可知这艘船行驶的时间为1005=603(小时). ∴512203AB =⨯=(海里),∴20BC =(海里).故答案为:20.【点睛】本题考查了三角形外角的性质,等腰三角形的判定和性质,方向角的问题,解题的关键是由已知得到三角形是等腰三角形,要学会把实际问题转化为数学问题,再用数学知识解决实际问题.4、32## 【分析】先根据三角形全等的判定定理证出ABC DEC ≅,再根据全等三角形的性质可得3AB DE ==,然后利用三角形的面积公式即可得.【详解】解:在ABC 和DEC 中,90ACB DCE AC DC BAC D ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩, ()ABC DEC ASA ∴≅,3AB DE ∴==,则ACE 的面积是11313222AC DE ⋅=⨯⨯=, 故答案为:32. 【点睛】本题考查了三角形全等的判定定理与性质,熟练掌握三角形全等的判定方法是解题关键. 5、6【分析】根据旋转的性质可得,30ACA '∠=︒,所以60BCM ∠=︒,由题意可得:60B ∠=︒,BCM 为等边三角形,即可求解.【详解】解:∵90ACB ∠=︒,30BAC ∠=︒,∴60B ∠=︒,由旋转的性质可得,30ACA '∠=︒,∴60BCM ACB ACM ∠=∠-∠=︒,∴BCM 为等边三角形,∴6CM BC ==,故答案为:6【点睛】此题考查了直角三角形的性质,旋转的性质以及等边三角形的判定与性质,解题的关键是灵活掌握相关基本性质进行求解.三、解答题1、(1)见解析;(2)猜想:DE BD CE =+,见解析;(3)见解析【分析】(1)先证明BDA AEC ∠=∠和ABD CAE ∠=∠,再根据AAS 证明ABD CAE ≌即可;(2)根据AAS 证明ABD CAE ≌得BD AE =,DA EC =,进一步可得出结论;(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,得出CM =EN ,证明CMG ENG ≌得CG EG =,从而可得结论.【详解】解:(1)证明:∵BD l ⊥,CE l ⊥,∴90BDA AEC ∠=∠=︒,∴90ABD DAB ∠+∠=︒∵90BAC ∠=︒,∴90CAE DAB ∠+∠=︒∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ABD CAE AAS ≌(2)猜想:DE BD CE =+,∵BDA BAC α∠=∠=∴180180ABD DAB BDA α∠+∠=︒-∠=︒-,180180CAE DAB BAC α∠+∠=︒-∠=︒-∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABD CAE AAS ≌,∴BD AE =,DA EC =,∴DE AE DA BD CE =+=+(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,∴AF CM =,AF EN =∴CM EN =,∵CM l ⊥,EN l ⊥,∴90CMG ENG ∠=∠=︒在CMG 与ENG 中CMG ENG CGM EGN CM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMG ENG AAS ≌,∴CG EG =,∴G 为CE 的中点.【点睛】本题考查了全等三角形的判定与性质、垂线的定义、角的互余关系,证得△ABD ≌△CAE是解决问题的关键.2、(1)90,40 ;(2)∠ABP+∠ACP+∠A=90°;(3)∠A+∠ACP-∠ABP=90°.【分析】△和ABC中的角的关系即可.(1)由三角形内角和为180°计算BPC(2)由(1)所得即可得出∠ABP、∠ACP、∠A的关系为∠ABP+∠ACP+∠A=90°.(3)由三角形外角的性质即可推出∠A+∠ACP-∠ABP=90°.【详解】△中(1)在BPC∵∠MPN=90°∴∠PBC+∠PCB=180°-∠MPN=180°-90°=90°在ABC中∵∠A+∠ABC+∠ACB=180°又∵∠ABC=∠PBC+∠ABP,∠ACB=∠ACP+∠BCP∴∠A+∠PBC+∠ABP +∠ACP+∠BCP=180°∵∠PBC+∠PCB=90°,∠A=50°∴∠ABP +∠ACP=180°-90°-50°=40°(2)由(1)问可知∠A+∠PBC+∠ABP +∠ACP+∠BCP=180°又∵∠PBC+∠PCB=90°∴∠A+∠ABP +∠ACP=180°-(∠PBC+∠PCB)=180°-90°=90°(3)如图所示,设PN与AB交于点H∵∠A+∠ACP=∠AHP又∵∠ABP+∠MPN=∠AHP∴∠A+∠ACP=∠ABP+∠MPN又∵∠MPN=90°∴∠A+∠ACP=90°+∠ABP∴∠A+∠ACP-∠ABP=90°.【点睛】本题考查了三角形的性质以及三角尺的角度计算问题,三角板的角度分别为90°,45°,45°;90°,60°,30°两种直角三角尺,三角形内角和是180°,三角形的一个外角等于与它不相邻的两个内角的和.3、(1)△AMN是是等腰三角形;理由见解析;(2)①证明见解析;②a﹣b.【分析】(1)由等腰三角形的性质得到∠ABC=∠ACB,由平行线的性质得到∠AMN=∠ABC,∠ANM=∠ACB,于是得到∠AMN=∠ANM,根据等角对等边即可证得结论;(2)①由角平分线的定义得到∠PBM=∠PBC,由平行线的性质得到∠MPB=∠PBC,于是得到∠PBM=∠MPB,根据等角对等边即可证得结论;②由①知MB=MP,同理可得:NC=NP,故△AMN的周长=AB+AC,再根据已知条件即可求出结果.(1)解:△AMN是是等腰三角形,理由如下:∵AB=AC,∴∠ABC=∠ACB,∵MN∥BC,∴∠AMN=∠ABC,∠ANM=∠ACB,∴∠AMN=∠ANM,∴AM=AN,∴△AMN是等腰三角形;(2)①证明:∵BP平分∠ABC,∴∠PBM=∠PBC,∵MN∥BC,∴∠MPB=∠PBC∴∠PBM=∠MPB,∴MB=MP,∴△BPM是等腰三角形;②由①知MB=MP,同理可得:NC=NP,∴△AMN的周长=AM+MP+NP+AN=AM+MB+NC+AN=AB+AC,∵△ABC的周长为a,BC=b,∴AB+AC+b=a,∴AB+AC=a﹣b∴△AMN的周长=a﹣b.【点睛】本题考查了等腰三角形的性质和判定,平行线的性质,列代数式,能够灵活应用这些性质是解决问题的关键.4、(1)见解析;(2)见解析.【分析】(1)以点D 为圆心,适当长为半径,作弧,交AC 于两点,再分别以这两点为圆心,适当长为半径作弧,连接两条弧的交点所在的直线,该直线与AC 的交点即为点F ,连接EF 交AD 于点G ;(2)利用角平分线性质可得,DE DF EAD FAD =∠=∠,由此证明()EAD FAD AAS ≅,得到AE AF =,继而证明()EAG FAG SAS ≅,证得90AGE AGF ∠=∠=︒即可解题.【详解】解:(1)如图,点F 、G 即为所求作的点;(2)AD 是ABC 的角平分线,DE AB ⊥,DF AC ⊥,,DE DF EAD FAD ∴=∠=∠AD AD =()EAD FAD AAS ∴≅AE AF ∴=,EAD FAD AG AG ∠=∠=()EAG FAG SAS ∴≅AGE AGF ∴∠=∠180AGE AGF∠+∠=︒90AGE AGF∴∠=∠=︒AD EF∴⊥【点睛】本题考查角平分线的性质、全等三角形的判定与性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.5、见解析【分析】证明△BAC≌△BDC即可得出结论.【详解】解:∵BC平分∠ABD,∴∠ABC=∠DBC,在△BAC和△BDC中A DABC DBCBC BC∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BAC≌△BDC,∴AC=DC.【点睛】本题考查角平分线的意义及全等三角形的判定与性质,解题关键是掌握角平分线的性质及全等三角形的判定与性质.6、证明见解析.【分析】延长CE交AB于F,求出∠AEC=∠AEF,∠FAE=∠CAE,根据ASA证△FAE≌△CAE,推出∠ACE=∠AFC,根据三角形外角性质得出∠AFC=∠B+∠ECD,代入即可.【详解】证明:延长CE交AB于F,∵CE⊥AD,∴∠AEC=∠AEF,∵AD平分∠BAC,∴∠FAE=∠CAE,在△FAE和△CAE中,∵FAE CAEAE AEAEF AEC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△FAE≌△CAE(ASA),∴∠ACE=∠AFC,∵∠AFC=∠B+∠ECD,∴∠ACE=∠B+∠ECD.【点睛】本题考查了全等三角形的性质和判定,三角形的外角性质等知识点,关键是作辅助线后求出∠AFC=∠ACE.7、见解析【分析】利用AAS 即可证明△ABO ≌△EDO .【详解】证明:∵AB ⊥BE ,DE ⊥AD ,∴∠B =∠D =90°.在△ABO 和△EDO 中,,B D AOB EOD OA OE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABO ≌△EDO .【点睛】本题考查了全等三角形的判定,熟练掌握三角形全等的判定方法是解题的关键.8、(1)见详解;(2)∠MEB =40°,(3)∠GMH =80°【分析】(1)根据等角的补角性质得出∠ABD =∠CDV ,根据同位角相等两直线平行可得AB ∥CD ;(2)根据AB ∥CD ;利用内错角相等得出∠ABD =∠RDB ,根据BE ∥DF ,得出∠EBD =∠FDB ,利用等量减等量差相等得出∠ABE =∠FDR ,根据∠FDR =35°,可得∠ABE =∠FDR =35°即可;(3)设ME 交AB 于S ,根据MG ∥EN ,得出∠NES =∠GMS =∠GES ,设∠NES =y °,可得∠NEG =∠NES +∠GES=2∠NES =2y °,根据∠EBD =2∠NEG ,得出∠EBD =4∠NES =4y °,根据∠EDC =17∠CDB ,设∠EDC =x °,得出∠CDB =7x °,根据AB ∥CD ,得出∠GBE +∠EBD +∠CDB =180°,可得35+4y +7x =180根据三角形内角和∠BDE =∠BDC -∠EDC =7x -x =6x ,∠BED =180°-∠EBD -∠EDB =180°-4y °-6x °,利用EB 平分∠DEN ,得出y °+40°=180°-4y °-6x °,解方程组7414565140x y x y +=⎧⎨+=⎩,解得1510x y =⎧⎨=⎩,可证ME ∥UV ,根据MH ⊥UV ,可求∠SMH =90°,∠SMG =∠NES =10°即可. 【详解】(1)证明:∵∠ABU+∠ABD=180°,∠ABU+∠CDV=180°.∴∠ABU=180°-∠ABD,∠CDV=180°-∠ABU,∴∠ABD=∠CDV,∴AB∥CD;(2)解:∵AB∥CD;∴∠ABD=∠RDB,∴∠ABE+∠EBD=∠FDB+∠FDR,∵BE∥DF,∴∠EBD=∠FDB,∴∠ABE=∠FDR,∵∠FDR=35°,∴∠ABE=∠FDR=35°,∴∠MEB=∠ABE+5°=35°+5°=40°,(3)解:设ME交AB于S,∵MG∥EN,∴∠NES=∠GMS=∠GES,设∠NES=y°,∵∠EBD=2∠NEG∴∠NEG=∠NES+∠GES=2∠NES=2y°,∴∠EBD=4∠NES=4y°,∵∠EDC=17∠CDB,设∠EDC=x°∴∠CDB=7x°,∵AB∥CD,∴∠ABD+∠CDB=180°,即∠GBE+∠EBD+∠CDB=180°,∴35+4y+7x=180,∵∠BDE=∠BDC-∠EDC=7x-x=6x,∴∠BED=180°-∠EBD-∠EDB=180°-4y°-6x°,∵EB平分∠DEN,∴∠NEB=∠BED,∵∠NEB=∠NES+∠SEB=y°+40°,∴y°+40°=180°-4y°-6x°,∴74145 65140x yx y+=⎧⎨+=⎩,解得1510xy=⎧⎨=⎩,∴∠EBD=4y°=40°=∠MEB,∴ME∥UV,∵MH⊥UV,∴MH⊥ME,∴∠SMH=90°,,∵∠SMG=∠NES=10°,∴∠GMH=90°-∠SMG=90°-10°=80°.【点睛】本题考查平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组,掌握平行线判定与性质,三角形内角和,垂直性质,角平分线定义,角的倍分,二元一次方程组是解题关键.9、见解析【分析】根据平行线的性质得出∠B =∠E ,进而利用SAS 证明ABC DEF ≅,利用全等三角形的性质解答即可.【详解】证明:FB CE =,FB CF CE CF ∴+=+,即BC EF =.//AB DE ,B E ∴∠=∠.在ABC 和DEF 中,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩, ()ABC DEF SAS ∴≅△△A D ∴∠=∠.【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证ABC DEF ≅是解题的关键.10、50︒【分析】AD 是ABC 的高,有90ADB ADC ∠=∠=︒;由70B ∠=︒知20BAD ∠=︒;CE 是ADC 的角平分线可得12ECD ACD ∠=∠;20BAD ECD ∠=∠=︒,40ACD ∠=︒;在ACD △中,904050CAD ∠=︒-︒=︒. 【详解】解:∵AD 是ABC 的高∴90ADB ADC ∠=∠=︒∵70B ∠=︒∴20BAD ∠=︒∵CE 是ADC 的角平分线 ∴12ECD ACD ∠=∠∵20BAD ECD ∠=∠=︒∴40ACD ∠=︒∴在ACD △中,904050CAD ∠=︒-︒=︒.【点睛】本题考查了角平分线.解题的关键在于正确表示各角度之间的数量关系.。
难点详解沪教版七年级数学第二学期第十四章三角形必考点解析试题(无超纲)

沪教版七年级数学第二学期第十四章三角形必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、已知三角形的两边长分别是3cm 和7cm ,则下列长度的线段中能作为第三边的是( )A .3cmB .4cmC .7cmD .10cm2、如图,点D 、E 分别在∠ABC 的边BA 、BC 上,DE ⊥AB ,过BA 上的点F (位于点D 上方)作FG ∥BC ,若∠AFG =42°,则∠DEB 的度数为( )A .42°B .48°C .52°D .58°3、如图,在ABC ∆中,BD 、CD 分别平分ABC ∠、ACB ∠,过点D 作直线平行于BC ,分别交AB 、AC 于点E 、F ,当A ∠大小变化时,线段EF 和BE CF +的大小关系是( )A .EF BE CF >+B .EF BE CF <+C .EF BE CF =+D .不能确定4、如图,在ABC 中,AD 是角平分线,且AD AC =,若60BAC ∠=︒,则B 的度数是( )A .45°B .50°C .52°D .58°5、如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是( )A .两点确定一条直线B .两点之间,线段最短C .三角形具有稳定性D .三角形的任意两边之和大于第三边6、若一个三角形的三个外角之比为3:4:5,则该三角形为( )A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形7、如图,在ABC 中,AB =AC ,D 是BC 的中点,∠B =35°,则∠BAD =( )A .110°B .70°C .55°D .35°8、如图,ABC ≌DEF ,点B 、E 、C 、F 在同一直线上,若BC =7,EC =4,则CF 的长是( )A .2B .3C .4D .79、以下列各组线段为边,能组成三角形的是( )A .3cm ,4cm ,5cmB .3cm ,3cm ,6cmC .5cm ,10cm ,4cmD .1cm ,2cm ,3cm10、如图,ABC DEC ≌△△,点E 在线段AB 上,75B ∠=︒,则ACD ∠的度数为( )A .20°B .25°C .30°D .40°第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、ABC 中,A ∠比B 大10°,50C ∠=︒,则A ∠=______.2、在等腰△ABC 中,∠A =40°,则∠B =_____°.3、如图,ABC 中,90A ∠=︒,点D 在AC 边上,∥DE BC ,若1145∠=︒,则B 的度数为_______.4、已知:如图,AB = DB .只需添加一个条件即可证明ABC DBC ≌△△.这个条件可以是______.(写出一个即可).5、若一个立体图形从正面看和从左面看都是等腰三角形,从上面看是带有圆心的圆,则这个立体图形是_____.三、解答题(10小题,每小题5分,共计50分)1、如图,点A ,B ,C ,D 在一条直线上,AB CD =,AE CF ∥,E F ∠=∠.求证:BE DF =.2、如图,AB =AD ,AC =AE ,BC =DE ,点E 在BC 上.(1)求证:∠EAC =∠BAD ;(2)若∠EAC =42°,求∠DEB 的度数.3、直线l 经过点A ,ABC 在直线l 上方,AB AC =.(1)如图1,90BAC ∠=︒,过点B ,C 作直线l 的垂线,垂足分别为D 、E .求证:ABD CAE ≌(2)如图2,D ,A ,E 三点在直线l 上,若BAC BDA AEC α∠=∠=∠=(α为任意锐角或钝角),猜想线段DE 、BD 、CE 有何数量关系?并给出证明.(3)如图3,90BAC ∠=︒过点B 作直线l 上的垂线,垂足为F ,点D 是BF 延长线上的一个动点,连结AD ,作90DAE ∠=︒,使得AE AD =,连结DE ,CE .直线l 与CE 交于点G .求证:G 是CE 的中点.4、如图,在等边三角形ABC 中,点P 为△ABC 内一点,连接AP ,BP ,CP ,将线段AP 绕点A 顺时针旋转60°得到'AP ,连接PP BP '', .(1)用等式表示BP ' 与CP 的数量关系,并证明;(2)当∠BPC =120°时,①直接写出P BP '∠ 的度数为 ;②若M 为BC 的中点,连接PM ,请用等式表示PM 与AP 的数量关系,并证明.5、如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段AB的端点都在格点上.要求以AB为边画一个等腰ABC,且使得点C为格点.请在下面的网格图中画出3种不同的等腰ABC.6、如图,AD,BC相交于点O,AO=DO.(1)如果只添加一个条件,使得△AOB≌△DOC,那么你添加的条件是(要求:不再添加辅助线,只需填一个答案即可);(2)根据已知及(1)中添加的一个条件,证明AB=DC.7、如图,CE⊥AB于点E,BF⊥AC于点F,BD=CD.(1)求证:△BDE≌△CDF;(2)求证:AE=AF.8、如图,在ABC 中,8AB cm =,6BC cm =,5AC cm =,BD 是ABC 的角平分线,点E 在AB 边上,2AE cm =.求AED 的周长.9、如图,点B ,F ,C ,E 在一条直线上,AB =DE ,∠B =∠E ,BF =CE .求证:AC =DF .10、已知:如图,点D 为BC 的中点,BAD CAD ∠=∠,求证:ABC 是等腰三角形.-参考答案-一、单选题1、C【分析】设三角形第三边的长为x cm ,再根据三角形的三边关系求出x 的取值范围,找出符合条件的x 的值即可.【详解】解:设三角形的第三边是xcm .则7-3<x <7+3.即4<x <10,四个选项中,只有选项C 符合题意,故选:C .【点睛】本题主要考查了三角形三边关系的应用.此类求三角形第三边的范围的题,实际上就是根据三角形三边关系定理列出不等式,然后解不等式即可.2、B【分析】根据两直线平行,同位角相等可得42B AFG ∠=∠=︒,再由垂直的性质及三角形内角和定理即可得.【详解】解:∵FG BC ∥,∴42B AFG ∠=∠=︒,∵DE AB ⊥,∴90BDE ∠=︒,∴18048DEB BDE B ∠=︒-∠-∠=︒,故选:B .【点睛】题目主要考查平行线及垂线的性质,三角形内角和定理等,理解题意,熟练运用平行线的性质是解题关键.3、C【分析】=,则由平行线的性质和角平分线的定义可得EBD EDB∠=∠,则ED BE=,同理可得DF FC =+,可得答案.EF BE CF【详解】EF BC,解://∴∠=∠,EDB DBCBD平分ABC∠,∴∠=∠,EBD DBCEDB EBD∴∠=∠,∴=,ED BE=,同理DF FCED DF BE FC∴+=+,=+.即EF BE CF故选:C【点睛】本题主要考查了等腰三角形的判定,平行线的性质,角平分线的定义,熟练掌握等腰三角形的判定定理,平行线的性质定理,角平分线的定义是解题的关键.4、A【分析】根据角平分线性质求出∠DCA,再根据等腰三角形的性质和三角形的内角和定理求解∠C和∠B即可.【详解】解:∵AD是角平分线,60BAC∠=︒,∴∠DCA=12BAC∠=30°,∵AD=AC,∴∠C=(180°-∠DCA)÷2=75°,∴∠B=180°-∠BAC-∠C=180°-60°-75°=45°,故选:A.【点睛】本题考查角平分线的性质、等腰三角形的性质、三角形的内角和定理,熟练掌握等腰三角形的性质是解答的关键.5、C【分析】根据三角形具有稳定性进行求解即可.【详解】解:工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是三角形具有稳定性,故选C.【点睛】本题主要考查了三角形的稳定性,熟知三角形具有稳定性是解题的关键.6、A【分析】根据三角形外角和为360°计算,求出内角的度数,判断即可.【详解】解:设三角形的三个外角的度数分别为3x、4x、5x,则3x+4x+5x=360°,解得,x=30°,∴三角形的三个外角的度数分别为90°、120°、150°,对应的三个内角的度数分别为90°、60°、30°,∴此三角形为直角三角形,故选:A.【点睛】本题考查的是三角形的外角和,掌握三角形外角和为360°是解题的关键.7、C【分析】根据等腰三角形三线合一的性质可得AD⊥BC,然后利用直角三角形两锐角互余的性质解答.【详解】解:∵AB=AC,D是BC的中点,∴AD⊥BC,∵∠B=35°,∴∠BAD=90°−35°=55°.故选:C.【点睛】本题主要考查了等腰三角形三线合一的性质,直角三角形两锐角互余的性质,是基础题,熟记性质是解题的关键.8、B【分析】根据全等三角形的性质可得BC EF =,根据CF EF EC =-即可求得答案.【详解】 解:ABC ≌DEF ,∴BC EF =点B 、E 、C 、F 在同一直线上,BC =7,EC =4,∴CF EF EC =-743BC EC -=-=故选B【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.9、A【分析】三角形的任意两条之和大于第三边,任意两边之差小于第三边,根据原理再分别计算每组线段当中较短的两条线段之和,再与最长的线段进行比较,若和大于最长的线段的长度,则三条线段能构成三角形,否则,不能构成三角形,从而可得答案.【详解】解:345, 所以以3cm ,4cm ,5cm 为边能构成三角形,故A 符合题意; 3+3=6, 所以以3cm ,3cm ,6cm 为边不能构成三角形,故B 不符合题意;4+510, 所以以5cm ,10cm ,4cm 为边不能构成三角形,故C 不符合题意; 1+2=3, 所以以1cm ,2cm ,3cm 为边不能构成三角形,故D 不符合题意;故选A【点睛】本题考查的是三角形的三边之间的关系,掌握“利用三角形三边之间的关系判定三条线段能否组成三角形”是解本题的关键.10、C【分析】根据全等三角形的性质可证得BC=CE ,∠ACB =∠DCE 即∠ACD =∠BCE ,根据等腰三角形的性质和三角形的内角和定理求解∠B =∠BEC 和∠BCE 即可.【详解】解:∵ABC DEC ≌△△,∴BC=CE ,∠ACB =∠DCE ,∴∠B =∠BEC ,∠ACD =∠BCE ,∵75B ∠=︒,∴∠ACD =∠BCE=180°-2×75°=30°,故选:C .【点睛】本题考查全等三角形的性质、等腰三角形的性质、三角形的内角和定理,熟练掌握全等三角形的性质和等腰三角形的性质是解答的关键.二、填空题1、70°【分析】根据三角形内角和定理可得130A B ∠+∠=︒,由题意A ∠比B ∠大10︒,可得10A B ∠-∠=︒,组成方程组求解即可.【详解】解:∵50C ∠=︒,∴130A B ∠+∠=︒,∵A ∠比B ∠大10︒,∴10A B ∠-∠=︒,∴13010A B A B ∠+∠=︒⎧⎨∠-∠=︒⎩, 解得:7060A B ∠=︒⎧⎨∠=︒⎩, 故答案为:70︒.【点睛】题目主要考查三角形内角和定理及二元一次方程组的应用,理解题意,列出代数式组成方程组是解题关键.2、40°或70°或100°【分析】本题要分两种情况讨论:当∠A =40°为顶角;当∠A =40°为底角时,则∠B 为底角时或顶角.然后求出∠B .【详解】分两种情况讨论:当∠A =40°为顶角时,18040702B ︒-︒∠==︒; 当∠A =40°为底角时,∠B 为底角时∠B =∠A =40°;∠B 为顶角时∠B =180°−∠A −∠C =180°−40°−40°=100°.故答案为:40°或70°或100°.【点睛】本题考查等腰三角形的性质,解题的关键是掌握等腰三角形的性质,分情况讨论问题.3、55︒【分析】先求出∠EDC =35°,然后根据平行线的性质得到∠C =∠EDC =35°,再由直角三角形两锐角互余即可求解.【详解】解:∵∠1=145°,∴∠EDC =35°,∵DE ∥BC ,∴∠C =∠EDC =35°,又∵∠A =90°,∴∠B =90°-∠C =55°,故答案为:55°.【点睛】本题主要考查了平行线的性质,直角三角形两锐角互余,求出∠C 的度数是解题的关键.4、AC =DC【分析】由题意可得,BC 为公共边,AB =DB ,即添加一组边对应相等,可证△ABC 与△DBC 全等.【详解】解:∵AB =DB ,BC =BC ,添加AC =DC ,∴在△ABC 与△DBC 中,AB DB BC BC AC DC =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△DBC (SSS ),故答案为:AC =DC .【点睛】本题考查了全等三角形的判定,灵活运用全等三角形的判定是本题的关键.5、圆锥【分析】根据立体图形视图、等腰三角形的性质分析,即可得到答案.【详解】根据题意,这个立体图形是圆锥故答案为:圆锥.【点睛】本题考查了等腰三角形、圆锥、立体图形视图的知识;解题的关键是熟练掌握立体图形视图的性质,从而完成求解.三、解答题1、见解析【分析】根据平行线的性质得出A FCD ∠=∠,运用“角角边”证明△AEB ≌△CFD 即可.【详解】证明:∵AE CF ∥,∴A FCD ∠=∠,在△AEB 和△CFD 中,E F A FCD AB CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△AEB≌△CFD,∴BE DF.【点睛】本题考查了全等三角形的判定与性质,解题关键是熟练运用全等三角形的判定定理进行证明.2、(1)见解析;(2)42°【分析】(1)利用边边边证得△ABC≌△ADE,可得∠BAC=∠DAE,即可求证;(2)根据等腰三角形的性质,可得∠AEC=∠C=69°,再由△ABC≌△ADE,可得∠AED=∠C=69°,即可求解.【详解】(1)证明:∵AB=AD,AC=AE,BC=DE,∴△ABC≌△ADE.∴∠BAC=∠DAE.∴∠BAC-∠BAE=∠DAE-∠BAE.即∠EAC=∠BAD;(2)解:∵AC=AE,∠EAC=42°,∴∠AEC=∠C=12×(180°-∠EAC)=12×(180°-42°)=69°.∵△ABC≌△ADE,∴∠AED=∠C=69°,∴∠DEB=180°-∠AED-∠C=180°-69°-69°=42°.【点睛】本题主要考查了全等三角形的判定和性质,等腰三角形的性质,熟练掌握全等三角形的判定和性质定理,等腰三角形的性质定理是解题的关键.3、(1)见解析;(2)猜想:DE BD CE =+,见解析;(3)见解析【分析】(1)先证明BDA AEC ∠=∠和ABD CAE ∠=∠,再根据AAS 证明ABD CAE ≌即可;(2)根据AAS 证明ABD CAE ≌得BD AE =,DA EC =,进一步可得出结论;(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,得出CM =EN ,证明CMG ENG ≌得CG EG =,从而可得结论.【详解】解:(1)证明:∵BD l ⊥,CE l ⊥,∴90BDA AEC ∠=∠=︒,∴90ABD DAB ∠+∠=︒∵90BAC ∠=︒,∴90CAE DAB ∠+∠=︒∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ABD CAE AAS ≌(2)猜想:DE BD CE =+,∵BDA BAC α∠=∠=∴180180ABD DAB BDA α∠+∠=︒-∠=︒-,180180CAE DAB BAC α∠+∠=︒-∠=︒-∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABD CAE AAS ≌,∴BD AE =,DA EC =,∴DE AE DA BD CE =+=+(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,∴AF CM =,AF EN =∴CM EN =,∵CM l ⊥,EN l ⊥,∴90CMG ENG ∠=∠=︒在CMG 与ENG 中CMG ENG CGM EGN CM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMG ENG AAS ≌,∴CG EG =,∴G 为CE 的中点.【点睛】本题考查了全等三角形的判定与性质、垂线的定义、角的互余关系,证得△ABD ≌△CAE 是解决问题的关键.4、(1)BP CP '=,理由见解析;(2)①60°;②PM =12AP ,见解析【分析】(1)根据等边三角形的性质,可得AB =AC ,∠BAC =60°,再由由旋转可知:60AP AP PAP ''=∠=︒,,从而得到BAP CAP '∠=∠,可证得ABP ACP '≌,即可求解 ; (2)①由∠BPC =120°,可得∠PBC +∠PCB =60°.根据等边三角形的性质,可得∠BAC =60°,从而得到∠ABC +∠ACB =120°,进而得到∠ABP +∠ACP =60°.再由ABP ACP '≌,可得ABP ACP '∠=∠ ,即可求解;②延长PM 到N ,使得NM =PM ,连接BN .可先证得△PCM ≌△NBM .从而得到CP =BN ,∠PCM =∠NBM .进而得到BN BP '= .根据①可得60P BP '∠︒=,可证得PNB PP B '≌,从而得到PN PP '= .再由PAP ' 为等边三角形,可得P P AP '= .从而得到PN AP = ,即可求解.【详解】解:(1)BP CP '= .理由如下:在等边三角形ABC 中,AB =AC ,∠BAC =60°,由旋转可知:60AP AP PAP ''=∠=︒,,∴PAP BAP BAC BAP '∠-∠=∠-∠即BAP CAP '∠=∠在ABP '△和△ACP 中AB AC BAP CAP AP AP =⎧⎪∠=''=∠⎨⎪⎩∴ABP ACP SAS '≌() .∴BP CP '= .(2)①∵∠BPC =120°,∴∠PBC +∠PCB =60°.∵在等边三角形ABC 中,∠BAC =60°,∴∠ABC +∠ACB =120°,∴∠ABP +∠ACP =60°.∵ABP ACP '≌ .∴ABP ACP '∠=∠ ,∴∠ABP +∠ABP '=60°.即60P BP '∠︒= ;②PM =12AP .理由如下:如图,延长PM 到N ,使得NM =PM ,连接BN .∵M 为BC 的中点,∴BM =CM .在△PCM 和△NBM 中PM NM PMC NMB CM BM =⎧⎪∠=∠⎨⎪=⎩∴△PCM ≌△NBM (SAS ).∴CP =BN ,∠PCM =∠NBM .∴BN BP '= .∵∠BPC =120°,∴∠PBC +∠PCB =60°.∴∠PBC +∠NBM =60°.即∠NBP =60°.∵∠ABC +∠ACB =120°,∴∠ABP +∠ACP =60°.∴∠ABP +∠ABP '=60°.即60P BP '∠︒= .∴P BP NBP '∠∠= .在△PNB 和P B P ' 中BN BP NBP P BP BP BP ''=⎧⎪∠=∠⎨⎪=⎩∴PNB PP B '≌ (SAS ).∴PN PP '= .∵60AP AP PAP ''=∠=︒,,∴PAP ' 为等边三角形,∴P P AP '= .∴PN AP = ,∴PM =12AP .【点睛】本题主要考查了等边三角形判定和性质,全等三角形的判定和性质,图形的旋转,熟练掌握等边三角形判定和性质定理,全等三角形的判定和性质定理,图形的旋转的性质是解题的关键.5、答案见解析【分析】 AB 为4个等边三角形组成的平行四边形的对角线,因此只要找到另一腰也4个等边三角形组成的平行四边形的对角线即可【详解】解:如图,……[答案不唯一]【点睛】本题考查等腰三角形的绘图,掌握等边三角形和等腰三角形性质即可.6、(1)OB =OC (或A D ∠=∠,或B C ∠=∠);(2)见解析【分析】(1)根据SAS 添加OB =OC 即可;(2)由(1)得△AOB ≌△DOC ,由全等三角形的性质可得结论.【详解】解:(1)添加的条件是:OB =OC (或A D ∠=∠,或B C ∠=∠)证明:在AOB ∆和DOC ∆中AO BO AOB COD BO CO =⎧⎪∠=∠⎨⎪=⎩所以,△AOB ≌△DOC(2)由(1)知,△AOB ≌△DOC所以,AB =DC .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解答本题的关键7、(1)见解析;(2)见解析【分析】(1)根据CE ⊥AB ,BF ⊥AC 就可以得出∠BED =∠CFD =90°,就可以由AAS 得出结论;(2)由(1)得DE =DF ,就可以得出BF =CE ,由AAS 就可以得出△AFB ≌△AEC 就可以得出结论.【详解】证明:(1)∵CE ⊥AB ,BF ⊥AC ,∴∠BED =∠CFD =90°,在△BED 和△CFD 中,BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△BED ≌△CFD (AAS );(2)∵△BED ≌△CFD ,∴DE =DF ,∴BD +DF =CD +DE ,∴BF =CE ,在△ABF 和△ACE 中,B C A A BF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABF ≌△ACE (AAS ),∴AE =AF .【点睛】本题考查了垂直的性质的运用,全等三角形的判定与性质的运用,等式的性质的运用,解答时证明三角形全等是关键.8、7cm【分析】由题意结合角平分线性质和全等三角形判定得出CBD EBD ≅,进而依据AED 的周长AE AD DE AE AD DC =++=++进行求解即可.【详解】解:∵8AB cm =,6BC cm =,2AE cm =,∴826,BE AB AE cm BE BC =-=-==,∵BD 是ABC 的角平分线,∴CBD EBD ∠=∠,在CBD 和EBD △中,BE BC CBD EBD BD BD =⎧⎪∠=∠⎨⎪=⎩, ∴CBD EBD ≅,∴CD DE =,∵5AC AD DC cm =+=,∴AED 的周长257AE AD DE AE AD DC cm =++=++=+=.【点睛】本题考查全等三角形的判定与性质以及角平分线性质,熟练掌握利用全等三角形的判定与性质以及角平分线性质进行边的等量替换是解题的关键.9、见解析【分析】先由BF =CE 说明BC= EF .然后运用SAS 证明△ABC ≌△DEF ,最后运用全等三角形的性质即可证明.【详解】证明:∵BF= CE ,∴BC= EF .在△ABC 和△DEF 中,,,,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS ).【点睛】本题主要考查了全等三角形的判定与性质,正确证明△ABC ≌△DEF 是解答本题的关键.10、证明见解析【分析】过点D 作DM AB ⊥,交AB 于点M ,过点D 做DN AC ⊥,交AC 于点N ,根据角平分线性质,得DM DN =;根据全等三角形的性质,通过证明ADM ADN △≌△,通过证明ADM ADN △≌△,得BM CN =,结合等腰三角形的性质,即可完成证明.【详解】如下图,过点D 作DM AB ⊥,交AB 于点M ,过点D 做DN AC ⊥,交AC 于点N∵BAD CAD ∠=∠∴DM DN =直角ADM △和直角ADN △中DM DN AD AD =⎧⎨=⎩∴ADM ADN △≌△∴AM AN =∵点D 为BC 的中点,直角BDM 和直角CDN △中DM DN BD CD =⎧⎨=⎩∴BDM CDN ≌∴BM CN =∵AB AM BM =+,AC AN CN =+∴AB AC =,即ABC 是等腰三角形.【点睛】本题考查了角平分线、三角形中线、全等三角形、等腰三角形的知识;解题的关键是熟练掌握角平分线、三角形中线,全等三角形的性质,从而完成求解.。
2022年最新沪教版七年级数学第二学期第十四章三角形章节训练试题(含详细解析)

沪教版七年级数学第二学期第十四章三角形章节训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,点A 、B 、C 、D 在一条直线上,点E 、F 在AD 两侧,BF CE ∥,BF CE =,添加下列条件不能判定ACE DBF ≌的是( )A .AE DF =B .AB CD =C .E F ∠=∠D .AE DF ∥2、如图,ABC ≌DEF ,点B 、E 、C 、F 在同一直线上,若BC =7,EC =4,则CF 的长是( )A .2B .3C .4D .73、如图,直线l 1∥l 2,被直线l 3、l 4所截,并且l 3⊥l 4,∠1=46°,则∠2等于( )A .56°B .34°C .44°D .46°4、如图,在ABC 中,5AB =,8BC =,60B ︒∠=,将ABC 绕点A 顺时针旋转得到ADE ,当点B 的对应点D 恰好落在BC 边上时,CD 的长为( )A .3B .4C .5D .65、如图,AB DF ∥,AC CE ⊥于点C ,BC 与DF 交于点E ,若20A ∠=︒,则CED ∠等于( )A .20°B .50°C .70°D .110°6、三根小木棒摆成一个三角形,其中两根木棒的长度分别是8cm 和5cm ,那么第三根小木棒的长度不可能是( )A .5cmB .8cmC .10cmD .13cm7、如图,点F ,C 在BE 上,AC =DF ,BF =EC ,AB =DE ,AC 与DF 相交于点G ,则与2∠DFE 相等的是( )A .∠A +∠DB .3∠BC .180°﹣∠FGCD .∠ACE +∠B8、如图,∠A =α,∠DBC =3∠DBA ,∠DCB =3∠DCA ,则∠BDC 的大小为( )A .3454a ︒+B .2603a ︒+C .3454a ︒-D .2603a ︒- 9、如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论:①30APO DCO ∠+∠=︒;②APO DCO ∠=∠;③POC △是等边三角形;④AB OA AP =+.其中正确的是( )A .①③④B .①②③C .②③④D .①②③④10、等腰三角形的一个顶角是80°,则它的底角是( ).A .40°B .50°C .60°D .70°第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,直线ED 把ABC 分成一个AED 和四边形BDEC ,ABC 的周长一定大于四边形BDEC 的周长,依据的原理是____________________________________.2、如图,在Rt△ABC 中,∠C =90°,两锐角的角平分线交于点P ,点E 、F 分别在边BC 、AC 上,且都不与点C 重合,若∠EPF =45°,连接EF ,当AC =6,BC =8,AB =10时,则△CEF 的周长为 _____.3、如图,AD ⊥BC ,∠1=∠B ,∠C=65°,∠BAC =__________4、如图,点A ,C 在直线l 上,AE AB ⊥且AE AB =,BC CD ⊥且BC CD =,过E ,B ,D 分别作EF l ⊥,BG l ⊥,DH l ⊥,若6EF =,3BG =,4DH =,则ABC 的面积是______.5、一个三角形的其中两个内角为88︒,32︒,则这个第三个内角的度数为______.三、解答题(10小题,每小题5分,共计50分)1、已知:如图,在△ABC 中,AB =3,AC =5.(1)直接写出BC 的取值范围是 .(2)若点D 是BC 边上的一点,∠BAC =85°,∠ADC =140°,∠BAD =∠B ,求∠C .2、已知,∠A =∠D ,BC 平分∠ABD ,求证:AC =DC .3、如图,在ABC 中,AD 是角平分线,54B ∠=︒,76C ∠=︒.(1)求BAD ∠的度数;(2)若DE AC ⊥,求EDC ∠的度数.4、在ABC 中,AB =AC ,点D 是直线BC 上一点(不与B 、C 重合),以AD 为一边在AD 的右侧作ADE ,使AD =AE ,∠DAE =∠BAC ,连接CE .(1)如图1,当点D 在线段BC 上,如果∠BAC =90°,则∠BCE = 度;(2)设BAC α∠=,BCE β∠=.①如图2,当点在线段BC 上移动,则α,β之间有怎样的数量关系?请说明理由;②当点在直线BC 上(线段BC 之外)移动,则α,β之间有怎样的数量关系?请直接写出你的结论.5、如图,在等腰△ABC 和等腰△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE 且C 、E 、D 三点共线,作AM ⊥CD 于M .若BD =5,DE =4,求CM .6、如图,灯塔B 在灯塔A 的正东方向,且75km AB =.灯塔C 在灯塔A 的北偏东20°方向,灯塔C 在灯塔B 的北偏西50°方向.(1)求ACB ∠的度数;(2)一轮船从B地出发向北偏西50°方向匀速行驶,5h后到达C地,求轮船的速度.7、已知∠POQ=120°,点A,B分别在OP,OQ上,OA<OB,连接AB,在AB上方作等边△ABC,点D 是BO延长线上一点,且AB=AD,连接AD(1)补全图形;(2)连接OC,求证:∠COP=∠COQ;(3)连接CD,CD交OP于点F,请你写出一个∠DAB的值,使CD=OB+OC一定成立,并证明8、如图是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点为格点,线段AB的端点都在格点上.要求以AB为边画一个等腰ABC,且使得点C为格点.请在下面的网格图中画出3种不同的等腰ABC.9、(1)我们把两个面积相等但不全等的三角形叫做“偏等积三角形”,如图1,ABC中,AC BC AB,P为AC上一点,当AP=_______时,ABP===7,9,10△与CBP是偏等积三角形;(2)如图2,四边形ABED 是一片绿色花园,ACB △、DCE 是等腰直角三角形,()90090∠=∠=︒<∠<︒ACB DCB BCE .①ACD △与BCE 是偏等积三角形吗?请说明理由;②已知60m,=BE ACD 的面积为22100m .如图3,计划修建一条经过点C 的笔直的小路CF ,F 在BE 边上,FC 的延长线经过AD 中点G .若小路每米造价600元,请计算修建小路的总造价.10、已知:如图,∠ABC =∠DCB ,∠1=∠2.求证AB =DC .-参考答案-一、单选题1、A【分析】根据题意,可得,BE CE FBD ECA =∠=∠,结合选项根据三角形全等的性质与判定逐项分析即可.【详解】 解:BF CE ∥∴FBD ECA ∠=∠ A. ,BE CE FBD ECA =∠=∠,AE DF =,不能根据SSA 证明三角形全等,故该选项符合题意;B. AB CD =AB BC BC CD ∴+=+AC BD ∴=,BE CE FBD ECA =∠=∠,∴ACE DBF ≌()SAS故能判定ACE DBF ≌,不符合题意; C. ,BE CE FBD ECA =∠=∠,E F ∠=∠,∴ACE DBF ≌()ASA ,故能判定ACE DBF ≌,不符合题意;D.AE DF ∥A D ∴∠=∠,BE CE FBD ECA =∠=∠∴ACE DBF ≌()AAS ,故能判定ACE DBF ≌,不符合题意;故选A【点睛】本题考查了平行线的性质,三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键.2、B【分析】根据全等三角形的性质可得BC EF =,根据CF EF EC =-即可求得答案.【详解】 解:ABC ≌DEF ,∴BC EF =点B、E、C、F在同一直线上,BC=7,EC=4,∴CF EF EC-=-==-743BC EC故选B【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.3、C【分析】依据l1∥l2,即可得到∠3=∠1=46°,再根据l3⊥l4,可得∠2=90°﹣46°=44°.【详解】解:如图:∵l1∥l2,∠1=46°,∴∠3=∠1=46°,又∵l3⊥l4,∴∠2=90°﹣46°=44°,故选:C.【点睛】本题考查了平行线性质以及三角形内角和,平行线的性质:两直线平行,同位角相等以及三角形内角和是180°.4、A【分析】先根据旋转的性质可得AB AD =,再根据等边三角形的判定与性质可得5BD AB ==,然后根据线段的和差即可得.【详解】由旋转的性质得:5AB AD ==,60B ∠=︒,ABD ∴是等边三角形,5BD AB ∴==,8BC =,853CD BC BD ∴=-=-=.故选:A .【点睛】本题考查了旋转的性质、等边三角形的判定与性质等知识点,熟练掌握旋转的性质是解题关键.5、C【分析】由AC CE ⊥与20A ∠=︒,即可求得ABC ∠的度数,又由AB DF ∥,根据两直线平行,同位角相等,即可求得CED ∠的度数.【详解】解:∵AC CE ⊥,∴90C ∠=︒,∵20A ∠=︒,∴70ABC ∠=︒,∵AB DF ∥,∴70CED ABC ∠=∠=︒.故选:C .【点睛】题目主要考查了平行线的性质与垂直的性质、三角形内角和定理,熟练掌握平行线的性质是解题关键.6、D【分析】设第三根木棒长为x 厘米,根据三角形的三边关系可得8﹣5<x <8+5,确定x 的范围即可得到答案.【详解】解:设第三根木棒长为x 厘米,由题意得:8﹣5<x <8+5,即3<x <13,故选:D .【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和>第三边,任意两边之差<第三边.7、C【详解】由题意根据等式的性质得出BC =EF ,进而利用SSS 证明△ABC 与△DEF 全等,利用全等三角形的性质得出∠ACB =∠DFE ,最后利用三角形内角和进行分析解答.【分析】解:∵BF =EC ,∴BF +FC =EC +FC ,∴BC =EF ,在△ABC 与△DEF 中,AC DF AB DE BC EF =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△DEF (SSS ),∴∠ACB =∠DFE ,∴2∠DFE =180°﹣∠FGC ,故选:C .【点睛】本题考查全等三角形的判定与性质,其中全等三角形的判定方法有:SSS ;SAS ;ASA ;AAS ;以及HL (直角三角形的判定方法).8、A【分析】根据题意设,ABD ACD βθ∠=∠=,根据三角形内角和公式定理βθ+,进而表示出α,进而根据三角形内角和定理根据()1803BDC βθ∠=︒-+即可求解【详解】解:∵∠A =α,∠DBC =3∠DBA ,∠DCB =3∠DCA ,设,ABD ACD βθ∠=∠=,∴3,3DBC DCB βθ∠=∠=180A ABC ACB ∠+∠+∠=︒即44180αβθ++=︒454αβθ∴+=︒-∴()1803BDC βθ∠=︒-+31803454544αα⎛⎫=︒-⨯︒-=︒+ ⎪⎝⎭故选A【点睛】本题考查了三角形内角和定理,掌握三角形内角和定理是解题的关键.9、A【分析】①利用等边对等角得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;④证明△OPA≌△CPE,则AO=CE,得AC=AE+CE=AO+AP.【详解】解:①如图1,连接OB,∵AB=AC,AD⊥BC,∴BD=CD,∠BAD=12∠BAC=12×120°=60°,∴OB=OC,∠ABC=90°﹣∠BAD=30°∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形,故③正确;④如图2,在AC上截取AE=PA,∵∠PAE=180°﹣∠BAC=60°,∴△APE是等边三角形,∴∠PEA=∠APE=60°,PE=PA,∴∠APO+∠OPE=60°,∵∠OPE+∠CPE=∠CPO=60°,∴∠APO=∠CPE,∵OP=CP,在△OPA 和△CPE 中,PA PE APO CPE OP CP =⎧⎪∠=∠⎨⎪=⎩, ∴△OPA ≌△CPE (SAS ),∴AO =CE ,∴AC =AE +CE =AO +AP ,∴AB =AO +AP ,故④正确;正确的结论有:①③④,故选:A .【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键.10、B【分析】依据三角形的内角和是180°以及等腰三角形的性质即可解答.【详解】解:(180°-80°)÷2=100°÷2=50°;答:底角为50°.故选:B .【点睛】本题主要考查三角形的内角和定理及等腰三角形的两个底角相等的特点.二、填空题1、三角形两边之和大于第三边【分析】表示出ABC 和四边形BDEC 的周长,再结合ADE 中的三边关系比较即可.【详解】解:ABC 的周长=AC AB BC AE AD CE CB BD ++=++++四边形BDEC 的周长=DE CE CB BD +++∵在ADE 中AE AD DE +>∴AE AD CE CB BD ++++>DE CE CB BD +++即ABC 的周长一定大于四边形BDEC 的周长,∴依据是:三角形两边之和大于第三边;故答案为三角形两边之和大于第三边【点睛】本题考查了三角形三边关系定理,关键是熟悉三角形两边之和大于第三边的知识点.2、4【分析】根据题意过点P 作PM ⊥BC 于M ,PN ⊥AC 于N ,PK ⊥AB 于K ,在EB 上取一点J ,使得MJ =FN ,连接PJ ,进而利用全等三角形的性质证明EF =EM +EN ,即可得出结论.【详解】解:如图,过点P 作PM ⊥BC 于M ,PN ⊥AC 于N ,PK ⊥AB 于K ,在EB 上取一点J ,使得MJ =FN ,连接PJ .∵BP 平分∠BC ,PA 平分∠CAB ,PM ⊥BC ,PN ⊥AC ,PK ⊥AB ,∴PM =PK ,PK =PN ,∴PM =PN ,∵∠C =∠PMC =∠PNC =90°,∴四边形PMCN 是矩形,∴四边形PMCN 是正方形,∴CM =PM ,∴∠MPN =90°,在△PMJ 和△PNF 中,90PM PN PMJ PNF MJ NF =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△PMJ ≌△PNF (SAS ),∴∠MPJ =∠FPN ,PJ =PF ,∴∠JPF =∠MPN =90°,∵∠EPF =45°,∴∠EPF =∠EPJ =45°,在△PEF 和△PEJ 中,PE PE EPF EPJ PF PJ =⎧⎪∠=∠⎨⎪=⎩, ∴△PEF ≌△PEJ (SAS ),∴EF =EJ ,∴EF =EM +FN ,∴△CEF 的周长=CE +EF +CF =CE +EM +CF +FN =2EM =2PM ,∵S △ABC =12•BC •AC =12(AC +BC +AB )•PM ,∴PM =2,∴△ECF 的周长为4,故答案为:4.【点睛】本题考查角平分线的性质定理,正方形的判定,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问.3、70°【分析】先根据AD ⊥BC 可知∠ADB =∠ADC =90°,再根据直角三角形的性质求出∠1与∠DAC 的度数,由∠BAC =∠1+∠DAC 即可得出结论.【详解】∵AD ⊥BC ,∴∠ADB =∠ADC =90°,∴∠DAC =90°﹣65°=25°,∠1=∠B =45°,∴∠BAC =∠1+∠DAC =45°+25°=70°.【点睛】本题考查的是三角形内角和定理,熟知三角形的内角和等于180°是解答此题的关键.4、15【分析】根据AAS 证明△EFA ≌△AGB ,△BGC ≌△CHD ,再根据全等三角形的性质以及三角形的面积公式求解即可.【详解】解:(1)∵EF ⊥FG ,BG ⊥FG ,∴∠EFA =∠AGB =90°,∴∠AEF +∠EAF =90°,又∵AE ⊥AB ,即∠EAB =90°,∴∠BAG +∠EAF =90°,∴∠AEF =∠BAG ,在△AEC 和△CDB 中,AEF BAG EFA AGB AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△EFA ≌△AGB (AAS );同理可证△BGC ≌△CHD (AAS ),∴AG =EF =6,CG =DH =4,∴S △ABC =12AC ⨯BG =12(AG +GC )⨯BG =12(6+4)⨯3=15.故答案为:15.【点睛】本题考查了三角形全等的性质和判定,解题的关键是灵活运用所学知识解决问题.5、60°【分析】依题意,利用三角形内角和为:180︒,即可;【详解】由题得:一个三角形的内角和为:180︒;又已知两个其中的内角为:88︒,32︒;︒-︒-︒=︒;∴ 第三个角为:180883260故填:60︒【点睛】本题主要考查三角形的内角和,关键在于熟练并运用基本的计算;三、解答题1、(1)2<BC<8;(2)25°【分析】(1)根据三角形三边关系解答即可;(2)根据三角形外角性质和三角形内角和解答即可.【详解】解:(1)∵AC-AB<BC<AC+AB,AB=3,AC=5.∴2<BC<8,故答案为:2<BC<8(2)∵∠ADC是△ABD的外角∴∠ADC=∠B+∠BAD=140︒∵∠B=∠BAD∴∠B =1140702⨯︒=︒∵∠B +∠BAC +∠C =180︒∴∠C =180︒﹣∠B ﹣∠BAC即∠C =180︒﹣70︒﹣85︒=25︒【点睛】本题考查了三角形第三边的取值范围,三角形内角和定理和三角形外角的性质,能根据三角形的外角的性质求出∠B 的度数是解此题的关键.2、见解析【分析】证明△BAC ≌△BDC 即可得出结论.【详解】解:∵BC 平分∠ABD ,∴∠ABC =∠DBC ,在△BAC 和△BDC 中A D ABC DBC BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△BAC ≌△BDC ,∴AC =DC .【点睛】本题考查角平分线的意义及全等三角形的判定与性质,解题关键是掌握角平分线的性质及全等三角形的判定与性质.3、(1)25BAD ∠=︒;(2)14EDC ∠=︒.【分析】(1)根据三角形内角和定理可求出50BAC ∠=︒,然后利用角平分线进行计算即可得;(2)根据垂直得出90AED ∠=︒,然后根据三角形内角和定理即可得.(1)解:∵54B ∠︒=,76C ∠︒=,∴180180547650BAC B C ∠=︒-∠-∠=︒-︒-︒=︒,∵AD 是角平分线, ∴1252BAD BAC ∠=∠=︒,∴25BAD ∠=︒;(2)∵DE AC ⊥,∴90AED ∠=︒,∴180180907614EDC AED C ∠=︒-∠-∠=︒-︒-︒=︒,∴14EDC ∠=︒.【点睛】题目主要考查三角形内角和定理,角平分线的计算等,熟练运用三角形内角和定理是解题关键.4、(1)90;(2)180αβ+=︒,见解析;②180αβ+=︒或αβ=【分析】(1)由等腰直角三角形的性质可得∠ABC =∠ACB =45°,由“SAS ”可证△BAD ≌△CAE ,可得∠ABC =∠ACE =45°,可求∠BCE 的度数;(2)①由“SAS ”可证△ABD ≌△ACE 得出∠ABD =∠ACE ,再用三角形的内角和即可得出结论;②分两种情况,由“SAS ”可证△ABD ≌△ACE 得出∠ABD =∠ACE ,再用三角形的内角和即可得出结论.【详解】解:(1)∵90BAC ∠=︒,∴90DAE BAC ∠=∠=︒,∵AB =AC ,AD =AE ,∴45B ACB ∠=∠=︒,45ADE AED ∠=∠=︒,∵DAE BAC ∠=∠,∴BAD CAE ∠=∠,在BAD 和CAE 中AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩ ∴BAD CAE ≅,∴45ACE B ∠=∠=︒,∴90BCE ACB ACE ∠=∠+∠=︒(2)αβ180+=︒或αβ=.理由:①∵BAC DAE ∠=∠,∴BAC DAC DAE DAC ∠-∠=∠-∠.即BAD CAE ∠=∠.在BAD 和CAE 中AB ACBAD CAE AD AE=⎧⎪∠=∠⎨⎪=⎩, ∴ABD ACE △≌△.∴B ACE ∠=∠.∴B ACB ACE ACB ∠+∠=∠+∠.∴B ACB β∠+∠=.∵180B ACB α+∠+∠=︒,∴180αβ+=︒.②如图:∵BAC DAE ∠=∠,∴BAC BAE DAE BAE ∠-∠=∠-∠.即BAD CAE ∠=∠.在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴ABD ACE △≌△.∴ABD ACE ∠=∠.∵+ABD ACB α∠=∠,ACE ACB β=∠-∠,ACE ABD βα∴=∠-∠+,αβ∴=.综上所述:点D 在直线BC 上移动,α+β=180°或α=β.【点睛】本题主要考查全等三角形的判定及性质,等腰三角形的性质和三角形内角和定理,掌握全等三角形的判定方法及性质是关键.5、CM =7.【分析】根据题意由“SAS ”可证△AEC ≌△ADB ,可得BD =CE ,由等腰三角形的性质可得DM =ME =2进行分析计算即可得出答案.【详解】解:∵∠BAC =∠DAE ,∴∠BAC ﹣∠BAE =∠DAE ﹣∠BAE ,∴∠BAD =∠CAE ,在△AEC 和△ADB 中,AE AD BAD CAE AC AB =⎧⎪∠=∠⎨⎪=⎩, ∴△AEC ≌△ADB (SAS ),又∵BD =5,∴CE =BD =5,∵AD =AE ,AM ⊥CD ,DE =4, ∴114222ME DE ==⨯=,∴CM=CE+EM=5+2=7.【点睛】本题考查全等三角形的判定和性质以及等腰三角形的性质,熟练掌握全等三角形的判定定理是解答本题的关键.6、(1)70°;(2)15km/h【分析】(1)根据题意得∠BAC=70°,∠ABC=40°,根据三角形的内角和定理即可求得∠ACB;(2)根据等腰三角形的判定可得BC=AB=75km,进而由速度=路程÷时间求解即可.【详解】解:(1)根据题意得∠BAC=70°,∠ABC=40°,∴∠ACB=180°-∠BAC-∠ABC=180°-70°-40°=70°;(2)∵∠BAC=∠ACB=70°,∴BC=AB=75km,∴轮船的速度为75÷5=15(km/h).【点睛】本题考查方位角、等腰三角形的判定、三角形的内角和定理,理解方位角,熟练掌握等腰三角形的等角对等边是解答的关键.7、(1)见解析;(2)见解析;(3)∠DAB=150°,见解析【分析】(1)依据题意作出相应图形即可;(2)在BQ上截取BE=AO,连接CE,由等边三角形的性质得,CA=CB,∠ACB=60°由同角的补角相等得∠CAO=∠CBE,由SAS证得△CAO和△CBE全等,即可得证;(3)由∠DAB=150°,DA=AB,得∠ADB=∠ABD=15°,由等边三角形性质,可得∠CAB=∠CBA=∠ACB=60°,故∠CAD =150°,由等边对等角得∠ADC =∠ACD =15°,由此∠DBC =∠DCB =75°,由等角对等边得DB =DC 再由∠POQ =120°,∠BDC =30°,得∠DFO =90°,等量代换即可得证.【详解】解:(1)如图所示:(2)证明如下:在BQ 上截取BE =AO ,连接CE ,∵△ABC 为等边三角形,∴CA =CB ,∠ACB =60°∵∠POQ =120°,∴∠CAO +∠CBO =180°∵∠CBO +∠CBE =180°,∴∠CAO =∠CBE ,在△CAO 和△CBE 中,CA CB CAO CBE AO BE =⎧⎪∠=∠⎨⎪=⎩, ∴△CAO ≌△CBE (SAS ),∴CO=CE,∠COA=∠CEB,∴∠COE=∠CEB,∴∠COP=∠COQ;(3)∠DAB=150°,如图:∵∠DAB=150°,DA=AB,∴∠ADB=∠ABD=15°∵△ABC为等边三角形,∴∠CAB=∠CBA=∠ACB=60°,∴∠CAD=150°,∵AD=AC,∴∠ADC=∠ACD=15°,∴∠DBC=∠DCB=75°,∴DB=DC,∵∠POQ=120°,∠BDC=30°,∴∠DFO=90°∵AD=AC,∴DF=FC∴DO=OC∵DB=DO+OB,∴DB=CO+OB,∴CD= OB + OC.【点睛】此题考查全等三角形的判定和性质、等腰三角形的判定和性质,等边三角形的判定和性质,以及添加辅助线构造全等三角形,掌握相应的判定和性质是解答此题的关键.8、答案见解析【分析】AB为4个等边三角形组成的平行四边形的对角线,因此只要找到另一腰也4个等边三角形组成的平行四边形的对角线即可【详解】解:如图,……[答案不唯一]【点睛】本题考查等腰三角形的绘图,掌握等边三角形和等腰三角形性质即可.9、(1)72;(2)①ACD△与BCE是偏等积三角形,理由见详解;②修建小路的总造价为42000元【分析】(1)当AP CP=时,则72AP=,证ABP CBPS S∆∆=,再证ABP∆与CBP∆不全等,即可得出结论;(2)①过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,证()ACM BCN AAS ∆∆≌,得AM BN =,则ACD BCE S S ∆∆=,再证ACD ∆与BCE ∆不全等,即可得出结论;②过点A 作//AN CD ,交CG 的延长线于N ,证得()AGN DGC AAS ∆∆≌,得到AN CD =,再证()ACN CBE SAS ∆∆≌,得ACN CBE ∠=∠,由余角的性质可证CF BE ⊥,然后由三角形面积和偏等积三角形的定义得12BCE S BE CF ∆=⋅,2100BCEACD S S ∆∆==,求出70()CF m =,即可求解. 【详解】解:(1)当72AP CP ==时,ABP ∆与CBP ∆是偏等积三角形,理由如下:设点B 到AC 的距离为h ,则12ABP S AP h ∆=⋅,12CBP S CP h ∆=⋅,ABP CBP S S ∆∆∴=,10AB =,7BC =,AB BC ∴≠,AP CP =、PB PB =,ABP ∴∆与CBP ∆不全等,ABP ∴∆与CBP ∆是偏等积三角形, 故答案为:72;(3)①ACD ∆与BCE ∆是偏等积三角形,理由如下:过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,如图3所示:则90AMC BNC ∠=∠=︒,ACB ∆、DCE ∆是等腰直角三角形,90ACB DCE ∴∠=∠=︒,AC BC =,CD CE =,3603609090180BCN ACD ACB DCE ∴∠+∠=︒-∠-∠=︒-︒-︒=︒,180ACM ACD ∠+∠=︒,ACM BCN ∴∠=∠,在∆ACM 和BCN ∆中,AMC BNC ACM BCN AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ACM BCN AAS ∴∆∆≌,AM BN ∴=,12ACD S CD AM ∆=⋅,12BCE S CE BN ∆=⋅, ACD BCE S S ∆∆∴=,180BCE ACD ∠+∠=︒,090BCE ︒<∠<︒,ACD BCE ∴∠≠∠,CD CE =,AC BC =,ACD ∴∆与BCE ∆不全等,ACD ∴∆与BCE ∆是偏等积三角形;②如图4,过点A 作//AN CD ,交CG 的延长线于N ,则N GCD ∠=∠, G 点为AD 的中点,AG GD ∴=,在AGN ∆和DGC ∆中,N GCD AGN DGC AG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()AGN DGC AAS ∴∆∆≌,AN CD ∴=,CD CE =,AN CE ∴=,//AN CD ,180CAN ACD ∴∠+∠=︒,90ACB DCE ∠=∠=︒,3609090180ACD BCE ∴∠+∠=︒-︒-︒=︒,BCE CAN ∴∠=∠,在ACN ∆和CBE ∆中,AN CE CAN BCE AC CB =⎧⎪∠=∠⎨⎪=⎩, ()ACN CBE SAS ∴∆∆≌,ACN CBE ∴∠=∠,1809090ACN BCF ∠+∠=︒-︒=︒,90CBE BCF ∴∠+∠=︒,90BFC ∴∠=︒,CF BE ∴⊥.由①得:ACD ∆与BCE ∆是偏等积三角形,12BCE S BE CF ∆∴=⋅,2100BCE ACD S S ∆∆==, 22210070()60BCE S CF m BE ∆⨯∴===, ∴修建小路CF 的总造价为:6007042000⨯=(元).【点睛】本题是四边形综合题目,考查了新定义“偏等积三角形”的定义、全等三角形的判定与性质、等腰直角三角形的性质、三角形面积等知识;本题综合性强,熟练掌握“偏等积三角形”的定义,证明ACM BCN ∆∆≌和ACN CBE ∆∆≌是解题的关键,属于中考常考题型.10、见解析【分析】由“ASA ”可证△ABO ≌△DCO ,可得结论.【详解】证明:如图,记,AC BD 的交点为,O∵∠ABC=∠DCB,∠1=∠2,又∵∠OBC=∠ABC−∠1,∠OCB=∠DCB−∠2,∴∠OBC=∠OCB,∴OB=OC,在△ABO和△DCO中,12OB OCAOB DOC∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABO≌△DCO(ASA),∴AB=DC.【点睛】本题考查了全等三角形的判定和性质,掌握全等三角形的判定定理是本题的关键.。
2022年必考点解析沪教版七年级数学第二学期第十四章三角形定向训练试卷(含答案详解)

沪教版七年级数学第二学期第十四章三角形定向训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,ABC 和DEF 全等,且A D ∠=∠,AC 对应DE .若6AC =,5BC =,4AB =,则DF 的长为( )A .4B .5C .6D .无法确定2、如果三角形一边上的中线等于这条边的一半,那么这个三角形一定是( ).A .锐角三角形B .直角三角形C .钝角三角形D .等腰三角形3、如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论:①30APO DCO ∠+∠=︒;②APO DCO ∠=∠;③POC △是等边三角形;④AB OA AP =+.其中正确的是( )A .①③④B .①②③C .②③④D .①②③④4、三角形的外角和是( )A .60°B .90°C .180°D .360°5、下列所给的各组线段,能组成三角形的是:( )A .2,11,13B .5,12,7C .5,5,11D .5,12,136、如图,工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是( )A .两点确定一条直线B .两点之间,线段最短C .三角形具有稳定性D .三角形的任意两边之和大于第三边7、根据下列已知条件,不能画出唯一ABC 的是( )A .60A ∠=︒,45B ∠=︒,4AB =B .30A ∠=︒,5AB =,3BC = C .60B ∠=︒,6AB =,10BC =D .90C ∠=︒,5AB =,3BC =8、如图,ABC 是等边三角形,点D 在AC 边上,40∠=︒DBC ,则ADB ∠的度数为( ).A.25°B.60°C.90°D.100°9、下列命题是真命题的是()A.等腰三角形的角平分线、中线、高线互相重合B.一个三角形被截成两个三角形,每个三角形的内角和是90度C.有两个角是60°的三角形是等边三角形D.在ABC中,2∠=∠=∠,则ABC为直角三角形A B C10、在△ABC中,∠A=50°,∠B、∠C的平分线交于O点,则∠BOC等于()A.65°B.80°C.115°D.50°第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,∠ACB=90°,AC=BC,AD⊥CD于点D,BE⊥CD于点E,有下面四个结论:①△CAD≌△BCE;② ∠ABE=∠BAD;③ AB=CD;④ CD=AD+DE.其中所有正确结论的序号是____________.2、在△ABC中,已知∠B是∠A的2倍,∠C比∠A大20°,则∠A=_____________.3、若一个立体图形从正面看和从左面看都是等腰三角形,从上面看是带有圆心的圆,则这个立体图形是_____.4、等腰三角形中,一条边长是2cm ,另一条边长是3cm ,这个等腰三角形的周长是________.5、如图,一把直尺的一边缘经过直角三角形ABC 的直角顶点C ,交斜AB 边于点D ;直尺的另一边缘分别交AB 、AC 于点E 、F ,若30B ∠=︒,50AEF ∠=︒,则DCB ∠=___________度.三、解答题(10小题,每小题5分,共计50分)1、如图,AD 为△ABC 的角平分线.(1)如图1,若BE ⊥AD 于点E ,交AC 于点F ,AB =4,AC =7.则CF = ;(2)如图2,CG ⊥AD 于点G ,连接BG ,若△ABG 的面积是6,求△ABC 的面积;(3)如图3,若∠B =2∠C ,AB =m ,AC =n ,则CD 的长为 .(用含m ,n 的式子表示)2、如图,在ABC 中,AD 是角平分线,54B ∠=︒,76C ∠=︒.(1)求BAD ∠的度数;(2)若DE AC ⊥,求EDC ∠的度数.3、如图,已知AB =AC ,AD =AE ,BD 和CE 相交于点O .求证:OB =OC .4、已知:如图,点D 为BC 的中点,BAD CAD ∠=∠,求证:ABC 是等腰三角形.5、阅读以下材料,并按要求完成相应的任务: 从正方形的一个顶点引出夹角为45︒的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:如下图1,在正方形ABCD 中,以A 为顶点的45EAF ︒∠=,AE 、AF 与BC 、CD 边分别交于E 、F 两点.易证得EF BE FD =+.大致证明思路:如图2,将ADF 绕点A 顺时针旋转90︒,得到ABH ,由180HBE ︒∠=可得H 、B 、E 三点共线,45HAE EAF ︒∠=∠=,进而可证明AEH AEF ≌,故EF BE DF =+.任务:如图3,在四边形ABCD 中,AB AD =,90B D ︒∠=∠=,120BAD ︒∠=,以A 为顶点的60EAF ︒∠=,AE 、AF 与BC 、CD 边分别交于E 、F 两点.请参照阅读材料中的解题方法,你认为结论EF BE DF =+是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.6、在ABC 中,AC BC =,90ACB ∠=︒,点D 是直线AC 上一动点,连接BD 并延长至点E ,使ED BD =.过点E 作EF AC ⊥于点F .(1)如图1,当点D 在线段AC 上(点D 不与点A 和点C 重合)时,此时DF 与DC 的数量关系是______.(2)如图2,当点D 在线段AC 的延长线上时,依题意补全图形,并证明:2AD AF EF =+.(3)当点D 在线段CA 的延长线上时,直接用等式表示线段AD ,AF ,EF 之间的数量关系是______.7、针对于等腰三角形三线合一的这条性质,老师带领同学们做了进一步的猜想和证明,提问:如果一个三角形中,一个角的平分线和它所对的边的中线重合,那么这个三角形是等腰三角形.已知:在△ABC中,AD平分∠CAB,交BC边于点D,且CD=BD,求证:AB=AC.以下是甲、乙两位同学的作法.甲:根据角平分线和中线的性质分别能得出一组角等和一组边等,再加一组公共边,可证△ACD≌△ABD,所以这个三角形为等腰三角形;乙:延长AD到E,使DE=AD,连接BE,可证△ACD≌△EBD,依据已知条件可推出AB=AC,所以这个三角形为等腰三角形(1)对于甲、乙两人的作法,下列判断正确的是();A.两人都正确B.甲正确,乙错误C.甲错误,乙正确(2)选择一种你认为正确的作法,并证明.8、如图1,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连接AC和BD,相交于点E,连接BC.(1)求证DOB ≌AOC ;(2)求∠CEB 的大小;(3)如图2,OAB 固定不动,保持△OCD 的形状和大小不变,将OCD 绕点O 旋转(OAB 和OCD 不能重叠),求∠CEB 的大小.9、如图,在ABC 中,AB BC =,120ABC ∠=︒,点D 在边AC 上,且线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,点F 是ED 与AB 的交点.(1)求证:AE CD =;(2)若40∠=︒DBC ,求BFE ∠的度数.10、已知,∠A =∠D ,BC 平分∠ABD ,求证:AC =DC .-参考答案-一、单选题1、A【分析】全等三角形对应边相等,对应角相等,根据题中信息得出对应关系即可.【详解】∵ABC和DEF全等,A D∠=∠,AC对应DE≅∴ABC DFE∴AB=DF=4故选:A.【点睛】本题考查了全等三角形的概念及性质,应注意①对应边、对应角是对两个三角形而言的,指两条边、两个角的关系,而对边、对角是指同一个三角形的边和角的位置关系②可以进一步推广到全等三角形对应边上的高相等,对应角的平分线相等,对应边上的中线相等,周长及面积相等③全等三角形有传递性.2、B【分析】根据题意画出图形,利用等腰三角形的性质及三角形内角和定理即可得到答案.【详解】如图,在△ABC中,CD是边AB上的中线∵AD=CD=BD∴∠A=∠DCA,∠B=∠DCB∵∠A+∠ACB+∠B=180°∴ ∠A+∠DCA+∠DCB+∠B=180即2∠A+2∠B=180°∴∠A+∠B=90°∴∠ACB=90°∴△ABC是直角三角形故选:B【点睛】本题考查了等腰三角形的性质及三角形内角和定理,熟练运用这两个知识是关键.3、A【分析】①利用等边对等角得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;④证明△OPA≌△CPE,则AO=CE,得AC=AE+CE=AO+AP.【详解】解:①如图1,连接OB,∵AB=AC,AD⊥BC,∴BD=CD,∠BAD=12∠BAC=12×120°=60°,∴OB=OC,∠ABC=90°﹣∠BAD=30°∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC 是等边三角形,故③正确;④如图2,在AC 上截取AE =PA ,∵∠PAE =180°﹣∠BAC =60°,∴△APE 是等边三角形,∴∠PEA =∠APE =60°,PE =PA ,∴∠APO +∠OPE =60°,∵∠OPE +∠CPE =∠CPO =60°,∴∠APO =∠CPE ,∵OP =CP ,在△OPA 和△CPE 中,PA PE APO CPE OP CP =⎧⎪∠=∠⎨⎪=⎩, ∴△OPA ≌△CPE (SAS ),∴AO =CE ,∴AC =AE +CE =AO +AP ,∴AB =AO +AP ,故④正确;正确的结论有:①③④,【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键.4、D【分析】根据三角形的内角和定理、邻补角的性质即可得.【详解】∠+∠=∠+∠=∠+∠=︒,解:如图,142536180∴∠+∠+∠+∠+∠+∠=︒,142536540又123180∠+∠+∠=︒,∴∠+∠+∠=︒-︒=︒,456540180360即三角形的外角和是360︒,故选:D.【点睛】本题考查了三角形的内角和定理、邻补角的性质,熟练掌握三角形的内角和定理是解题关键.5、D【分析】根据三角形三边关系定理,判断选择即可.∵2+11=13,∴A不符合题意;∵5+7=12,∴B不符合题意;∵5+5=10<11,∴C不符合题意;∵5+12=17>13,∴D符合题意;故选D.【点睛】本题考查了构成三角形的条件,熟练掌握三角形三边关系是解题的关键.6、C【分析】根据三角形具有稳定性进行求解即可.【详解】解:工人师傅在安装木制门框时,为防止变形,常常钉上两条斜拉的木条,这样做的数学依据是三角形具有稳定性,故选C.【点睛】本题主要考查了三角形的稳定性,熟知三角形具有稳定性是解题的关键.7、B【分析】根据三角形存在的条件去判断.【详解】∵60A ∠=︒,45B ∠=︒,4AB =,满足ASA 的要求,∴可以画出唯一的三角形,A 不符合题意;∵30A ∠=︒,5AB =,3BC =,∠A 不是AB ,BC 的夹角,∴可以画出多个三角形,B 符合题意;∵60B ∠=︒,6AB =,10BC =,满足SAS 的要求,∴可以画出唯一的三角形,C 不符合题意;∵90C ∠=︒,5AB =,3BC =,AB 最大,∴可以画出唯一的三角形,D 不符合题意;故选B .【点睛】本题考查了三角形的存在性,熟练掌握三角形全等的判定方法是解题的关键.8、D【分析】由等边三角形的性质及三角形外角定理即可求得结果.【详解】∵ABC 是等边三角形∴∠C =60°∴∠ADB =∠DBC +∠C =40°+60°=100°故选:D【点睛】本题考查了等边三角形的性质、三角形外角的性质,掌握这两个性质是关键.9、C【分析】分别根据等腰三角形的性质、三角形的内角和定理、等边三角形的判定,直角三角形的判定即可判断.【详解】A.等腰三角形中顶角角平分线、底边上的中线和底边上的高线互相重合,即三线合一,故此选项错误;B.三角形的内角和为180°,故此选项错误;C.有两个角是60°,则第三个角为180606060︒-︒-︒=︒,所以三角形是等边三角形,故此选项正确;D.设C x ∠=,则2A B x ∠=∠=,故22180x x x ++=︒,解得36x =︒,所以72A B ∠=∠=︒,36C ∠=︒,此三角形不是直角三角形,故此选项错误.故选:C .【点睛】本题考查等腰三角形的性质,直角三角形的定义以及三角形内角和,掌握相关概念是解题的关键.10、C【分析】根据题意画出图形,求出∠ABC +∠ACB =130°,根据角平分线的定义得到∠CBD =12∠ABC ,∠ECB =12∠ACB ,再根据三角形内角和定理和角的代换即可求解.【详解】解:如图,∵∠A =50°,∴∠ABC +∠ACB =180°-∠A =130°,∵BD 、CE 分别是∠ABC 、∠ACB 的平分线,∴∠CBD=12∠ABC,∠ECB=12∠ACB,∴∠BOC=180°-∠CBD-∠ECB=180°-(∠CBD+∠ECB)=180°- 12(∠ABC+∠ACB)=180°- 12×130°=115°.故选:C【点睛】本题考查了三角形内角和定理,角平分线的定义,熟知三角形内角和定理,并能根据角平分线的定义进行角的代换是解题关键.二、填空题1、①②④【分析】由∠ACB=90°,BE⊥CD,AD⊥CD,得到∠ACD+∠BCE=90°,∠ADC=∠CEB=90°,则∠ACD+∠CAD=90°,AD∥BE,即可判断②,即可利用AAS证明△CAD≌△BCE,即可判断①;则AD=CE,得到CD=CE+DE=AD+DE,即可判定④;由AB>AC>CD,得到AB≠CD,即可判断③.【详解】解:∵∠ACB=90°,BE⊥CD,AD⊥CD,∴∠ACD+∠BCE=90°,∠ADC=∠CEB=90°,∴∠ACD+∠CAD=90°,AD∥BE,∴∠CAD=∠BCE,∠ABE=∠BAD,故②正确;又∵AC=CB,∴△CAD≌△BCE(AAS),故①正确;∴AD=CE,∴CD=CE+DE=AD+DE,故④正确,∵AB>AC>CD,∴AB≠CD,故③错误;故答案为:①②④.【点睛】本题主要考查了全等三角形的性质与判定,平行线的性质与判定,熟知相关知识是解题的关键.2、40°【分析】根据已知得出∠B=2∠A,∠C=∠A+20°,代入∠A+∠B+∠C=180°得出方程∠A+2∠A+∠A+20°=180°,求出即可.【详解】解:∵∠B是∠A的2倍,∠C比∠A大20°,∴∠B=2∠A,∠C=∠A+20°,∵∠A+∠B+∠C=180°,∴∠A+2∠A+∠A+20°=180°,∴∠A=40°,故答案为:40°.【点睛】本题考查了三角形内角和定理的应用,注意:三角形的内角和等于180°,用了方程思想.3、圆锥【分析】根据立体图形视图、等腰三角形的性质分析,即可得到答案.【详解】根据题意,这个立体图形是圆锥故答案为:圆锥.【点睛】本题考查了等腰三角形、圆锥、立体图形视图的知识;解题的关键是熟练掌握立体图形视图的性质,从而完成求解.4、8cm或【分析】因为已知长度为2cm和3cm两边,没有明确是底边还是腰,所以有两种情况,需要分类讨论.【详解】解:①当2cm为底时,其它两边都为3cm,2cm、3cm、3cm可以构成三角形,周长为8cm;②当3cm为底时,其它两边都为2cm,2cm、2cm、3cm可以构成三角形,周长为7cm;故答案为:8cm或7cm.【点睛】本题考查了等腰三角形的性质和三角形的三边关系;已知没有明确腰和底边的题目一定要想到两种情况,解题的关键是利用分类进行讨论,还应验证各种情况是否能构成三角形进行解答,这点非常重要.5、20【分析】利用平行线的性质求出∠1,再利用三角形外角的性质求出∠DCB 即可.【详解】解:∵EF ∥CD ,∴150AEF ∠=∠=︒,∵∠1是△DCB 的外角,∴DCB ∠=∠1-∠B =50°-30°=20º,故答案为:20.【点睛】本题考查了平行线的性质,三角形外角的性质等知识,解题的关键是熟练掌握基本知识.三、解答题1、(1)3(2)12(3)2n n m- 【分析】(1)利用ASA 证明△AEF ≌△ABE ,得AE =AB =4,得出答案;(2)延长CG 、AB 交于点H ,设S △BGC =S △HGB =a ,用两种方法表示△ACH 的面积即可;(3)在AC 上取AN =AB ,可得CD =DN =n -m ,根据△ABD 和△ACD 的高相等,面积比等于底之比可求出CD 的长.(1)∵AD 是△ABC 的平分线,∴∠BAD =∠CAD ,∵BE ⊥AD ,∴∠BEA =∠FEA ,在△AEF 和△AEB 中,BAE FAE AE AEAEB AEF ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△AEF ≌△AEB (ASA ),∴AF =AB =4,∵AC =7∴CF =AC -AF =7-4=3,故答案为:3;(2)延长CG 、AB 交于点H ,如图,由(1)知AC =AH ,点G 为CH 的中点,设S △BGC =S △HGB =a ,根据△ACH 的面积可得:S △ABC +2a =2(6+a ),∴S △ABC =12;(3)在AC 上取AN =AB ,如图,∵AD 是△ABC 的平分线,∴∠NAD =∠BAD ,在△ADN 与△ADB 中,AN AB NAD BAD AD AD ⎧⎪∠∠⎨⎪⎩===, ∴△ADN ≌△ADB (SAS ),∴∠AND =∠B ,DN =BD ,∵∠B =2∠C ,∴∠AND =2∠C ,∴∠C =∠CDN ,∴CN =DN =AC -AB =n -m ,∴BD =DN =n -m ,根据△ABD 和△ACD 的高相等,面积比等于底之比可得:CD AC BD AB=, ∴CD n n m m=-, ∴2()n n m n CD n m m-==-, 故答案为:2n n m-. 【点睛】本题主要考查了全等三角形的判定与性质,角平分线的定义,三角形的面积等知识,利用角的轴对称性构造全等三角形是解题的关键.2、(1)25BAD ∠=︒;(2)14EDC ∠=︒.【分析】(1)根据三角形内角和定理可求出50BAC ∠=︒,然后利用角平分线进行计算即可得;(2)根据垂直得出90AED ∠=︒,然后根据三角形内角和定理即可得.(1)解:∵54B ∠︒=,76C ∠︒=,∴180180547650BAC B C ∠=︒-∠-∠=︒-︒-︒=︒,∵AD 是角平分线, ∴1252BAD BAC ∠=∠=︒,∴25BAD ∠=︒;(2)∵DE AC ⊥,∴90AED ∠=︒,∴180180907614EDC AED C ∠=︒-∠-∠=︒-︒-︒=︒,∴14EDC ∠=︒.【点睛】题目主要考查三角形内角和定理,角平分线的计算等,熟练运用三角形内角和定理是解题关键.3、见解析【分析】根据SAS 证明△AEC 与△ADB 全等,进而利用全等三角形的性质解答即可.【详解】证明:在△AEC 与△ADB 中,AB AC A A AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△AEC ≌△ADB (SAS ),∴∠ACE =∠ABD ,∵AB =AC ,∴∠ABC =∠ACB ,∴∠OBC =∠OCB ,∴OB =OC .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明△AEC ≌△ADB 是本题的关键.4、证明见解析【分析】过点D 作DM AB ⊥,交AB 于点M ,过点D 做DN AC ⊥,交AC 于点N ,根据角平分线性质,得DM DN =;根据全等三角形的性质,通过证明ADM ADN △≌△,通过证明ADM ADN △≌△,得BM CN =,结合等腰三角形的性质,即可完成证明.【详解】如下图,过点D 作DM AB ⊥,交AB 于点M ,过点D 做DN AC ⊥,交AC 于点N∵BAD CAD ∠=∠∴DM DN =直角ADM △和直角ADN △中DM DN AD AD=⎧⎨=⎩∴ADM ADN △≌△∴AM AN =∵点D 为BC 的中点,∴BD CD =直角BDM 和直角CDN △中DM DN BD CD=⎧⎨=⎩ ∴BDM CDN ≌∴BM CN =∵AB AM BM =+,AC AN CN =+∴AB AC =,即ABC 是等腰三角形.【点睛】本题考查了角平分线、三角形中线、全等三角形、等腰三角形的知识;解题的关键是熟练掌握角平分线、三角形中线,全等三角形的性质,从而完成求解.5、成立,证明见解析【分析】根据阅读材料将△ADF 旋转120°再证全等即可求得EF = BE +DF .【详解】解:成立.证明:将ADF ∆绕点A 顺时针旋转120︒,得到ABM ∆,ABM ADF ∴∆∆≌,90ABM D ︒=∠=∠,MAB FAD ∠=∠,AM AF =,MB DF =,180MBE ABM ABE ︒∠=∠+∠=∴,M 、B 、E 三点共线,60MAE MAB BAE FAD BAE BAD EAF ︒∠=∠+∠=∠+∠=∠-∠=.AM AF =,MAE FAE ∠=∠,AE AE =,()MAE FAE SAS ∴∆∆≌,EF ME MB BE DF BE ∴==+=+.【点睛】本题考查旋转中的三角形全等,读懂材料并运用所学的全等知识是本题关键.6、(1)DF DC =(2)见解析(3)2AF EF AD -=【分析】(1)利用边相等和角相等,直接证明EDF BDC ∆∆≌,即可得到结论.(2)利用边相等和角相等,直接证明EDF BDC ∆∆≌,得到DF DC =和EF BC AC ==,最后通过边与边之间的关系,即可证明结论成立.(3)要证明2AF EF AD -=,先利用边相等和角相等,直接证明EDF BDC ∆∆≌,得到DF DC =和EF BC AC ==,最后通过边与边之间的关系,即可证明结论成立.【详解】(1)解:DF DC =90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=.(2)解:当点D 在线段AC 的延长线上时,如下图所示:90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=,EF BC AC ==,=2AF EF AD DF AC AD CD AD ∴+=++=+.(3)解:2AF EF AD -=,如下图所示:90ACD ∠=︒,EF AC ⊥,90ACB EFD ∴∠=∠=︒,在EDF ∆和BDC ∆中,ACB EFD FDE BDC ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDF BDC AAS ∴∆∆≌,DF DC ∴=,EF BC AC ==,()2AF EF AF AC AF DF AD AF DF AD AD ∴-=-=--=-+=.【点睛】本题主要是考查了三角形全等的判定和性质,熟练利用条件证明三角形全等,然后利用边相等以及边与边之间关系,即可证明结论成立,这是解决该题的关键.7、(1)C ;(2)见解析【分析】(1)甲同学证明的两个三角形全等,没有边边角的判定,故错误,而乙的证明则正确,因此可作出判断;(2)按照乙的分析方法进行即可.【详解】(1)甲同学证明的两个三角形全等,边边角不能判定两个三角形全等,故错误,而乙的证明则正确,故选C ;(2)依据题意,延长AD 至E ,使DE =AD ,连接BE ,如图.∵D 为BC 中点.∴BD CD =.在△CAD 和△BED 中DE AD ADC EDB BD CD =⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BED (SAS ).∴DAC E ∠=∠,BE AC =∵AD 平分∠BAC ,∴BAD CAD ∠=∠∴DAB E ∠=∠∴BE AB =∴AB =AC∴△ABC 为等腰三角形【点睛】本题考查了全等三角形的判定与性质,等腰三角形的判定,关键是构造辅助线得到全等三角形.8、(1)见详解;(2)120°;(2)120°.【分析】(1)如图1,根据等边三角形的性质得到OD=OC=OA=OB,∠COD=∠AOB=60°,则利用根据“SAS”判断△AOC≌△BOD;(2)利用△AOC≌△BOD得到∠CAO=∠DBO,然后根据三角形内角和可得到∠AEB=∠AOB=60°,即可求出答案;(3)如图2,与(1)的方法一样可证明△AOC≌△BOD;则∠CAO=∠DBO,然后根据三角形内角和可求出∠AEB=∠AOB=60°,即可得到答案.【详解】(1)证明:如图1,∵△ODC 和△OAB 都是等边三角形,∴OD =OC =OA =OB ,∠COD =∠AOB =60°,∴∠BOD =∠AOC =120°,在△AOC 和△BOD 中OC OD AOC BOD OA OB =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD ;(2)解:∵△AOC ≌△BOD ,∴∠CAO =∠DBO ,∵∠1=∠2,∴∠AEB =∠AOB =60°,∴120CEB ∠=︒;(3)解:如图2,∵△ODC 和△OAB 都是等边三角形,∴OD =OC =OA =OB ,∠COD =∠AOB =60°,∴∠AOB +∠BOC =∠COD +∠BOC ,即∠AOC =∠BOD ,在△AOC 和△BOD 中OC OD AOC BOD OA OB =⎧⎪∠=∠⎨⎪=⎩∴△AOC ≌△BOD ;∴∠CAO =∠DBO ,∵∠1=∠2,∴∠AEB =∠AOB =60°,∴120CEB ∠=︒;即∠CEB 的大小不变.【点睛】本题考查了几何变换综合题:熟练掌握旋转的性质、等边三角形的性质和全等三角形的判定与性质;利用类比的方法解决(3)小题.9、(1)见解析;(2)110︒【分析】(1)由旋转的性质可得BD BE =,120EBD ∠=︒,再证明DBC ABE ∠=∠,结合,AB BC = 从而可得结论;(2)由ABE △≌CBD 可得40DBC ABE ∠==∠︒,再利用等腰三角形的性质求解30BED BDE ∠=∠=︒,再利用三角形的内角和定理可得答案.【详解】证明:(1)∵线段BD 绕着点B 按逆时针方向旋转120°能与BE 重合,∴BD BE =,120EBD ∠=︒,∵AB BC =,120ABC ∠=︒,∴120ABD DBC ABD ABE ∠+∠=∠+∠=︒,∴DBC ABE ∠=∠,∴ABE △≌CBD (S A S ),∴AE CD =.(2)解:由(1)知ABE △≌CBD∴ 40DBC ABE ∠==∠︒,BD BE =,120EBD ∠=︒, ∴()1180120302BED BDE ∠=∠=︒-︒=︒, ∴1801803040110BFE BED ABE ∠=︒-∠-∠=︒-︒-︒=︒.【点睛】本题考查的是全等三角形的判定与性质,旋转的性质,等腰三角形的性质,掌握“旋转前后的对应边相等,对应角相等”是解本题的关键.10、见解析【分析】证明△BAC ≌△BDC 即可得出结论.【详解】解:∵BC 平分∠ABD ,∴∠ABC =∠DBC ,在△BAC 和△BDC 中A D ABC DBC BC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△BAC ≌△BDC ,∴AC =DC .【点睛】本题考查角平分线的意义及全等三角形的判定与性质,解题关键是掌握角平分线的性质及全等三角形的判定与性质.。
沪教版七年级数学下册试题 第十四章 《三角形》单元测试卷(含答案)

第十四章《三角形》单元测试卷一、单选题(共18分)1.已知三角形的三边长分别为3,5,x,则x不可能是()A.3B.5C.7D.82.在△ABC和△FMN中,已知AB=6,BC=7,∠B=48°,MN=6,FN=7,∠N=48°,能证明△ABC≌△MNF的判定方式为()A.SAS B.AAS C.ASA D.SSA3.△ABC的三边分别是a,b,c,不能判定是等腰三角形的是()A.∠A:∠B:∠C=2:2:3B.a:b:c=2:2:3C.∠B=50°,∠C=80°D.2∠A=∠B+∠C4.下列说法中正确的是()A.两腰对应相等的两个等腰三角形全等B.两锐角对应相等的两个直角三角形全等C.面积相等的两个三角形全等D.斜边对应相等的两个等腰直角三角形全等5.若a、b是等腰三角形的两边长,且满足关系式(a−2)2+|b−5|=0,则这个三角形的周长是( )A.9cm B.12cm C.9cm或12cm D.15cm或6cm 6.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正△ABC 和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.一定成立的结论有().A.①②③B.①②④C.①②③④D.①②③⑤二、填空题(共24分)7.若三角形三个内角满足∠A=12∠B=13∠C,则∠C=______.8.已知a、b、c为三角形的三边,且则a2+b2+c2=ab+bc+ac,则三角形的形状是 _____.9.如图,在等边△ABC中AB=2,BD是AC边上的高,延长BC至点E,使CE=CD,则BE的长为 ___________.10.如图,将△ABC绕点A顺时针旋转40°得到△ADE,点B的对应点D恰好落在边BC上,则∠ADE=___________°.11.已知△ABC的三边长分别是4、5、8,△DEF的三边分别是4、2x−1、3y−1,若这两个三角形全等,则x+y=______.12.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线的垂线段BD、CE,若BD=5厘米,CE=8厘米,则DE的长为______.13.在等腰三角形ABC中,其中一内角为50°,腰AB的垂直平分线MN交AC所在的直线于点D,则∠DBC的度数为______.14.在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为18和21两个部分,则这个等腰三角形的底边长为______.15.如图,点E是△ABC的内角∠ABC和外角∠ACF的两条角平分线的交点,过点E作MN∥BC,交AB于点M,交AC于点N,若BM−CN=6,则线段MN的长度为____.16.如图,∠MON是一个钢架,∠MON=5°,为使钢架更牢固,需在其内部焊接一些钢管,如CD、DE、EF……若焊接的钢管的长度都与OC的长度相等,则最多能焊接___________根.17.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”,若等腰△ABC是“倍长三角形”,底边BC的长为5,则腰AB的长为___________.18.如图,过边长为2的等边△ABC的边AB上一点P,作PE⊥AC于点E,Q为BC 延长线上一点,当PA=CQ时,连接PQ交AC边于点D,则DE的长为______.三、解答题(共58分)19.(本题5分)如图,已知△ABC,∠ACB=85°,点E,F分别在AB,AC上,ED交AC于点G,交BC的延长线于点D,∠FEG=40°,∠CGD=45°.求证:EF ∥BC.20.(本题5分)如图,△ABC中,∠ABC=45°,两条高AD和BE交于H.求证:BH=AC.21.(本题7分)如图,在△ABC中,已知∠BAC=90°,AD⊥BC,AD与∠ABC的平分线交于点E,试说明△AEF是等腰三角形的理由.22.(本题7分)如图,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC,BF与CE相交于点M.(1)求证:EC=BF;(2)求证:EC⊥BF.23.(本题8分)如图,点E是等边△ABC外一点,点D是BC边上一点,AD=BE,∠CAD=∠CBE,连接ED,EC.(1)试说明△ADC与△BEC全等的理由;(2)试判断△DCE的形状,并说明理由.24.(本题8分)如图,已知等边△ABC和等边△CDE,P、Q分别为AD、BE的中点.(1)试判断△CPQ的形状并说明理由.(2)如果将等边△CDE绕点C旋转,在旋转过程中△CPQ的形状会改变吗?请你将图2中的图形补画完整并说明理由.25.(本题8分)已知:如图,△ABC、△CDE都是等边三角形,AD、BE相交于点O,点M、N分别是线段AD、BE的中点.(1)求∠DOE的度数;(2)试判断△MNC的形状,并说明理由.26.(本题10分)在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到如下图所示的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到如下图所示的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,不必证明;(3)当直线MN绕点C旋转到如图的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,不必证明.答案一、单选题1.D【分析】已知两边时,第三边的范围是大于两边的差,小于两边的和.这样就可以确定x 的范围,也就可以求出x 的不可能取得的值.【详解】解:∵3+5=8,5−3=2,∴2<x <8.故选:D .2.A【分析】根据全等三角形的判定方法并结合所给条件可得答案.【详解】解:∵AB =6,BC =7,∠B =48°,MN=6,FN =7,∠N =48°,∴AB =MN ,∠B =∠N ,BC =NF ,在△ABC 和△MNF 中,{AB =MN∠B =∠N BC =NF,∴△ABC ≌△MNF (SAS ).故选:A .3.D【分析】根据等腰三角形的判定,三角形内角和定理,进行计算逐一判断即可解答.【详解】解:A 、因为∠A:∠B:∠C =2:2:3,∠A +∠B +∠C =180°,所以∠A =∠B =180°×(22+2+3)=(3607)°,所以△ABC 是等腰三角形;B 、因为 a:b:c =2:2:3,所以设a =b =2x ,则有两边相等的△ABC 是等腰三角形;C 、因为 ∠A +∠B +∠C =180°,所以∠A =180°−∠B −∠C =180°−50°−80°=50°,则∠A =∠B ,所以△ABC 是等腰三角形;D 、因为2∠A =∠B +∠C ,∠A +∠B +∠C =180°,则∠A+2∠A=180°,那么∠A=60°,∠B+∠C=120°,不能判定是等腰三角形.故选:D.4.D【分析】根据全等三角形的判定方法和等腰三角形的性质判定即可.【详解】解:A、两腰对应相等的两个等腰三角形,只有两边对应相等,所以不一定全等,不合题意;B、两锐角对应相等的两个直角三角形,缺少对应的一对边相等,所以不一定全等,不合题意;C、面积相等的两个三角形形状不一定相同,则不一定全等,不合题意;D、斜边对应相等的两个等腰直角三角形,满足三个角及一条边对应相等,故全等,符合题意;故选:D.5.B【分析】利用非负性,求出a,b的值,分a是腰长和b是腰长,两种情况,讨论求解即可.【详解】解:∵(a−2)2+|b−5|=0,∴a−2=0,b−5=0,∴a=2,b=5;当a是腰长时:2+2<5,三边不能构成三角形,∴b为腰长,∴三角形的周长是:5+5+2=12cm;故选B.6.D【分析】①根据△ABC和△CDE是等边三角形可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≅△BCE,可推知AD=BE;②由△ACD≅△BCE得∠CBE=∠CAD和∠ACB=∠DCE=60°,AC=BC,得到△CQB ≅△CPA (ASA ),再根据∠PCQ =60°推出△PCQ 为等边三角形,又由∠PQC=∠DCE ,根据内错角相等,两直线平行,可知②正确;③同②得△ACP ≅△BCQ ,即可得出结论;④根据∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ,∠CDE=60°,可知∠DQE≠∠CDE ,可知④错误;⑤先根据全等三角形的性质可得∠DAC =∠EBC ,再根据∠AOB =∠DAC +∠BEC =∠EBC +∠BEC =∠ACB =60°,可知⑤正确.【详解】解:①∵△ABC 和△CDE 为等边三角形,∴AC =BC ,CD =CE ,∠BCA =∠DCE =60°,∴∠ACD =∠BCE ,在△ACD 和△BCE 中,{AC =BC∠ACD =∠BCE CD =CE,∴△ACD ≅△BCE (SAS ),∴AD =BE ,∠ADC =∠BEC ,①正确;②∠DCP=180°−2×60°=60°=∠ECQ ,在△CDP 和△CEQ 中,{∠ADC =∠BECCD =CE ∠DCP =∠ECQ,∴△CDP ≅△CEQ (ASA ).∴CP =CQ ,∴∠CPQ =∠CQP =60°,∴∠QPC =∠BCA ,∴PQ ∥AE ,②正确;③同②得:△ACP ≅△BCQ ,∴AP =BQ ,③正确;④∵DE >QE ,且DP =QE ,∴DE >DP ,④错误;⑤∵△ACD ≅△BCE ,∴∠DAC =∠EBC ,∴∠AOB =∠DAC +∠BEC =∠EBC +∠BEC =∠ACB =60°,⑤正确;故答案为:①②③⑤.二、填空题7.90°【分析】根据三角形内角和定理进行计算即可求解.【详解】解:∵∠A=12∠B=13∠C,∠A+∠B+∠C=180°∴13∠C+23∠C+∠C=180°解得:∠C=90°,故答案为:90°.8.等边三角形【分析】先把所给等式左右两边同时乘以2,然后利用完全平方公式得到(a−b)2 +(b−c)2+(c−a)2=0,由此求解即可.【详解】解:∵a2+b2+c2=ab+bc+ac,∴a2+b2+c2−ab−bc−ac=0,∴2a2+2b2+2c2−2ab−2bc−2ac=0,∴a2−2ab+b2+b2−2bc+c2+a2−2ac+c2=0,即(a−b)2+(b−c)2+(c−a)2=0,∴a﹣b=0,b﹣c=0,c﹣a=0,∴a=b=c,∴△ABC为等边三角形.故答案为:等边三角形.9.3【分析】由等边三角形的性质可得AC=BC=AB=2,根据BD是AC边上的高线,可得AD=CD,再由题中条件CE=CD,即可求得BE.【详解】解:∵△ABC是等边三角形,∴AC=BC=AB=2,∵BD是AC边上的高线,∴D为AC的中点,∴AD=CD=12AC,∵CE=CD,∴CE=12AC=1,∴BE=BC+CE=2+1=3.故答案为:3.10.70【详解】根据旋转的性质得到AD=AB,∠ADE=∠B,根据等腰三角形的性质得到∠ADB=∠B,求得∠ADE=∠ADB=70°.【解答】解:由旋转的性质可知,AD=AB,∠ADE=∠B,∴∠ADB=∠B,∵∠BAD=40°,∴∠ADE=∠ADB=∠B=12×(180°−40°)=70°,故答案为:70.11.6或132【分析】根据全等三角形的性质得到5=2x−1,8=3y−1,或8=2x−1,5=3y−1,分别求出x,y的值,代入计算即可.【详解】解:∵两个三角形全等,∴5=2x−1,8=3y−1,或8=2x−1,5=3y−1,∴{x=3y=3或{x=92y=2,∴x+y=3+3=6或x+y=92+2=132,故答案为:6或132.12.13厘米【分析】利用垂直的定义得到∠BDA=∠AEC,由平角的定义及同角的余角相等得到∠ABD=∠CAE,利用AAS证得△ABD≌△CAE,再由全等三角形对应边相等得到DB=AE=5,AD=CE=8,由DE=AD+AE即可求出DE长.【详解】解:∵BD⊥DE,CE⊥DE,∴∠BDA=∠BAC=∠AEC=90°,∴∠BAD +∠CAE =90°,∵∠BAD +∠ABD =90°,∴∠ABD =∠CAE ,在△ABD 和△CAE 中,{∠ADB =∠CEA ∠ABD =∠CAE AB =CA,∴△ABD ≌△CAE(AAS),∴DB =AE =5,CE =AD =8,则DE =AD +AE =8+5=13(厘米),故答案为:13厘米.13.15或30【分析】根据等腰三角形的一个内角为50°,分类讨论等腰三角形,①当等腰三角形角为:50,65,65;②当等腰三角形角为:50,50,80;再根据垂直平分线的性质,即可.【详解】∵等腰三角形ABC 中,其中一个内角为50°,∴①当AB =AC ,∠A =50°,如下图:∴∠CBA=65°,∵MN 垂直平分AB ,∴AD=BD ,∴∠BAD =∠DBA =50°,∴∠CBD=∠CBA −∠ABD =15°;②当BA =BC ,∠A =∠C =50°,如下图:∴∠ABC=80°,∵MN 垂直平分AB,∴AD =BD ,∴∠A =∠ABD =50°,∴∠CBD=80°−50°=30°,∴∠DBC 的度数为:15或者30.故答案为:15或者30.14.11或15【分析】根据题意画出图形,设等腰三角形的腰长为a ,底边为b ,根据中点定义得到AD 与DC 相等都等于腰长a 的一半,AC 边上的中线BD 将这个三角形的周长分为AB +AD 和BC +CD 两部分,分别表示出两部分,然后分AB +AD =18,BC +CD =21或AB +AD =21,BC +CD =18两种情况分别列出方程组,分别求出方程组的解即可得到a 与b 的两对值,根据三角形的两边之和大于第三边判定能否构成三角形,即可得到满足题意的等腰三角形的底边长.【详解】解:依题意可得:这一边上的中线为腰上的中线,画出图形如下:设这个等腰三角形的腰长为a ,底边长为b ,∵D 为AC 的中点,∴AD =DC =12AC =12a ,根据题意得:{a +12a =1812a +b =21或{a +12a =2112a +b =18,解得:{a =12b =15 或{a =14b =11.又∵三边长12、12、15和14、14、11均可以构成三角形,∴底边长为11或15.故答案为:11或15.15.6【分析】根据角平分线的定义得到∠MBE=∠CBE,根据平行线的性质得到∠MEB=∠CBE,等量代换得到∠MBE=∠MEB,求得BM=EM,同理,CN=EN,于是得到结论.【详解】∵BE平分∠ABC,∴∠MBE=∠CBE,∵MN∥BC,∴∠MEB=∠CBE,∴∠MBE=∠MEB,∴BM=EM,同理,CN=EN,∵BM−CN=9,∴MN=ME−EN=BM−CN=6,故答案为:6.16.17【分析】根据已知利用等腰三角形的性质及三角形外角的性质,找出图中存在的规律,根据规律及三角形的内角和定理求解.【详解】解:∵焊接的钢管的长度都与OC的长度相等,即OC=CD=DE=EF,∴∠CDO=∠MON=5°,即第一个等腰△OCD的底角是5°;∴∠DCE=∠DEC=10°,即第二个等腰△CDE的底角是10°;∴∠EDF=∠EFD=15°,即第三个等腰△DEF的底角是15°;……∴等腰三角形的底角度数是5的倍数,且最大的角为85°,∴最多能焊接85°÷5°=17(根),故答案为:17.17.10【分析】分两种情况讨论:①AB=AC=2BC;②BC=2AB=2AC,再利用三角形三边关系进行检验即可得到答案.【详解】解:∵△ABC是等腰三角形,∴AB=AC,∵△ABC是“倍长三角形”,BC=5,①当AB=AC=2BC时,AB=AC=10;②当BC=2AB=2AC时,AB=AC= 2.5,根据三角形三边关系,此时,A、B、C 不能构成三角形,不符合题意,所以,若等腰△ABC是“倍长三角形”,底边BC的长为5,则腰AB的长为10,故答案为:10.18.1【分析】过点P作PF∥BC交AC于点F,根据题意可证△APF是等边三角形,根据等腰三角形三线合一证明AE=FE,根据全等三角形判定定理可证△PFD≌△QCD,DF=DC,进而证明DE=1AC,计算求值即可.2【详解】过点P作PF∥BC交AC于点F,如图,∴∠APF=∠B=60°,∠A=60°,△APF是等边三角形,∴PF=PA,∵PE⊥AC,∴AE=FE;∵PA=CQ,∴PF=QC,∵PF∥BC,∴∠PFD=∠QCD,在△PFD和△QCD中,{PF=QC∠PFD=∠QCD∠PDF=∠QDC ∴△PFD≌△QCD,∴DF=DC;∴DF=12FC,EF=12AF,∵DF+EF=DE,FC+AF=AC,∴DE=12FC+12AF=12(FC+AF)=12AC,∵AC=2,DE=12AC=12×2=1故答案为:1三、解答题19.解:∵∠CGD=45°,∴∠EGF=∠CGD=45°,∵∠FEG=40°,∴∠AFE=∠EGF+∠FEG=45°+40°=85°,∵∠ACB=85°,∴∠AFE=∠ACB,∴EF∥BC.20.证明:由题意可得:∠ADB=∠ADC=∠BEC=90°∴∠HBD+∠BHD=∠HBD+∠C=90°∴∠BHD=∠C又∵∠ABD=45°∴AD=BD在△ADC和△BDH中{∠ADB=∠ADC∠BHD=∠CAD=BD∴△ADC≌△BDH(AAS)∴BH=AC21.解:∵BF平分∠ABC,∴∠ABF=∠DBF,又∵∠BAC=90°,AD⊥BC,∴∠AFE=90°−∠ABF,∠DEB=90°−∠DBF,∴∠AFE=∠DEB,又∵∠DEB=∠AEF,∴∠AEF=∠AFE,∴△AEF是等腰三角形.22.(1)证明:∵AE⊥AB,AF⊥AC,∴∠BAE=∠CAF=90°,∴∠BAE+∠BAC=∠CAF+∠BAC,即∠EAC=∠BAF,在△ABF和△AEC中,{AB=AE∠EAC=∠BAFAC=AF∴△ABF≌△AEC(SAS),∴EC=BF;(2)证明:设AB与CE交于点D,∵△ABF≌△AEC,∴∠AEC=∠ABF,∵AE⊥AB,∴∠BAE=90°,∴∠AEC+∠ADE=90°,∵∠ADE=∠BDM(对顶角相等),∴∠ABF+∠BDM=90°,在△BDM中,∠BMD=180°−∠ABF−∠BDM=180°−90°=90°,∴EC⊥BF.23.(1)∵△ABC是等边三角形,∴AC=BC,∠ACB=60°,在△ADC和△BEC中,{AC=BC∠CAD=∠CBE,AD=BE∴△ADC≌△BEC(SAS);(2)△DCE是等边三角形;理由如下:∵△ADC≌△BEC,∴∠ACD=∠BCE=60°,DC=EC,即△DCE是等腰三角形,∴△DCE是等边三角形.24.(1)如图1,△CPQ 是等边三角形.理由如下:∵△ABC 和△CDE 都是等边三角形,∴∠C =60°,AC =BC ,DC =EC ,∴AC ﹣DC =BC ﹣EC ,即AD =BE .∵P 、Q 分别为AD 、BE 的中点,∴PD =EQ ,∴CD +DP =CE +EQ ,即CP =CQ ,∴△CPQ 是等边三角形;(2)如果将等边△CDE 绕点C 旋转,在旋转过程中△CPQ 的形状不会改变.理由如下:如图2,∵△ABC 和△CDE 都是等边三角形,∴∠ACB =∠DCE =60°,AC =BC ,DC =EC ,∵∠ACD =∠DCE ﹣∠ACE ,∠BCE =∠ACB ﹣∠ACE ,∴∠ACD =∠BCE ,∴在△ACD 与△BCE 中,{AC =BC∠ACD =∠BCE DC =EC,∴△ACD ≌△BCE (SAS ),∴AD =BE ,∠CAD =∠CBE ,即∠CAP =∠CBQ .∵P 是AD 的中点,Q 是BE 的中点,∴AP =12AD ,BQ =12BE ,∴AP =BQ ,∴在△ACP 与△BCQ中,{AC =BC∠CAP =∠CBQ AP =BQ,∴△ACP ≌△BCQ (SAS ),∴PC =QC ,∠BCQ =∠ACP ,∵∠BCQ +∠ACQ =∠ACB =60°,∴∠ACP +∠ACQ =60°,∴∠PCQ =60°,∴△CPQ 是等边三角形.25.(1)解:∵△ABC 、△CDE 都是等边三角形,∴AC =BC ,CD =CE ,∠ACB =∠DCE =60°,∴∠ACB +∠BCD =∠DCE +∠BCD ,∴∠ACD =∠BCE ,在△ACD 和△BCE 中,{AC =BC∠ACD =∠BCE CD =CE ,∴△ACD ≌BCE (SAS ),∴∠ADC =∠BEC ,∵△DCE 是等边三角形,∴∠CED =∠CDE =60°,∴∠ADE +∠BED=∠ADC +∠CDE +∠BED=∠ADC +60°+∠BED =∠BEC +∠CED +60°=∠DEC +60°=60°+60°=120°,∴∠DOE =180°-(∠ADE +∠BED )=60°;(2)解:△MNC 是等边三角形,理由如下:由(1)得:△ACD ≌△BCE ,∴∠CAD =∠CBE ,AD =BE ,又∵点M 、N 分别是线段AD 、BE 的中点,∴AM =12AD ,BN =12BE ,∴AM =BN ,在△ACM 和△BCN 中,{AC =BC∠CAM =∠CBN AM =BN,∴△ACM ≌△BCN (SAS ),∴CM =CN ,∠ACM =∠BCN ,又∵∠ACB =60°,∴∠ACM +∠MCB =60°,∴∠BCN +∠MCB =60°,∴∠MCN =60°,∴△MNC 是等边三角形.26.(1)证明:①∵AD⊥MN ,BE ⊥MN ,∴∠ADC=∠BEC =90°,∵∠BCA=90°,∴∠ACD+∠BCE =90°,∠BCE +CBE =90°,∴∠ACD =∠CBE ,在△ADC 和△CEB 中,∵{∠ADC =∠CEB =90°∠ACD =∠CBE AC =BC,∴△ADC ≌△CEB (AAS );②∵△ADC ≌△CEB ,∴AD =CE ,BE =CD ,∴DE =DC +CE =BE +AD .(2)解:AD=BE +DE .∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠BEC =90°,∵∠ACB =90°,∴∠ACD +∠BCD =90°,∠BCD +∠CBE =90°,∴∠ACD =∠CBE ,在△ACD 和△CBE 中,∵{∠ADC =∠CEB∠ACD =∠CBEAC =BC ,∴△ACD ≌△CBE (AAS ),∴AD =CE ,BE =CD ,∴AD =CD +DE =BE +DE .(3)解:BE =AD +DE .∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠BEC =90°,∵∠ACB =90°,∴∠ACD +∠BCD =90°,∠BCD +∠CBE =90°,∴∠ACD =∠CBE ,在△ACD 和△CBE 中,∵{∠ADC =∠CEB∠ACD =∠CBEAC =BC ,∴△ACD ≌△CBE (AAS ),∴AD =CE ,BE =CD ,∴BE =CD =CE +DE =AD +DE .。
2022年强化训练沪教版七年级数学第二学期第十四章三角形定向练习试题(含答案及详细解析)

沪教版七年级数学第二学期第十四章三角形定向练习考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、BP是∠ABC的平分线,CP是∠ACB的邻补角的平分线,∠ABP=20°,∠ACP=50°,则∠P=()A.30°B.40°C.50°D.60°2、已知长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF 上的点B′处,得折痕EM,将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,则图中与∠B′ME互余的角有()A.2个B.3个C.4个D.5个3、如图点,,A B C 在同一条直线上,,CBE ADC 都是等边三角形,,AE BD 相交于点O ,且分别与,CD CE 交于点,M N ,连接,M N ,有如下结论:①DCB ACE ≅;②AM DN =;③CMN △为等边三角形;④60EOB ∠=︒.其中正确的结论个数是( )A .1个B .2个C .3个D .4个4、如图,等边ABC 中,D 为AC 中点,点P 、Q 分别为AB 、AD 上的点,4BP AQ ==,3QD =,在BD 上有一动点E ,则PE QE +的最小值为( )A .7B .8C .10D .125、如图,∠BAD =90°,AC 平分∠BAD ,CB =CD ,则∠B 与∠ADC 满足的数量关系为( )A .∠B =∠ADCB .2∠B =∠ADC C .∠B +∠ADC =180°D .∠B +∠ADC =90°6、如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论:①30APO DCO ∠+∠=︒;②APO DCO ∠=∠;③POC △是等边三角形;④AB OA AP =+.其中正确的是( )A .①③④B .①②③C .②③④D .①②③④7、下列三角形与下图全等的三角形是( )A .B .C .D .8、根据下列已知条件,不能画出唯一ABC 的是( )A .60A ∠=︒,45B ∠=︒,4AB =B .30A ∠=︒,5AB =,3BC = C .60B ∠=︒,6AB =,10BC =D .90C ∠=︒,5AB =,3BC =9、满足下列条件的两个三角形不一定全等的是( )A .周长相等的两个三角形B .有一腰和底边对应相等的两个等腰三角形C .三边都对应相等的两个三角形D .两条直角边对应相等的两个直角三角形10、三根小木棒摆成一个三角形,其中两根木棒的长度分别是8cm 和5cm ,那么第三根小木棒的长度不可能是( )A .5cmB .8cmC .10cmD .13cm第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,在Rt △ABC 中,∠ACB =90°,∠BAC =30°,BC =6,将△ABC 绕点C 顺时针旋转30°得到△A ′B ′C ,A 、B 分别与A ′、B ′对应,CA ′交AB 于点M ,则CM 的长为 ___.2、若2(3)|7|0a b -+-=,则以a 、b 为边长的等腰三角形的周长为________.3、如图,已知AB AD =,请添加一个条件,使得ABC ADC ≅△△,则添加的条件可以为___(只填写一个即可).4、在ABC 中,若50,A B C ∠=︒∠=∠,则B ∠=_______.5、如图,在ABC 中,BD 和CD 分别是ABC ∠和ACB ∠的平分线,EF 过点D ,且EF BC ∥,若3BE =,4CF =,则EF 的长为______.三、解答题(10小题,每小题5分,共计50分)1、如图,在等边△ABC 中,点P 是BC 边上一点,∠BAP =α(30°<α<60°),作点B 关于直线AP 的对称点D ,连接DC 并延长交直线AP 于点E ,连接BE .(1)依题意补全图形,并直接写出∠AEB 的度数;(2)用等式表示线段AE ,BE ,CE 之间的数量关系,并证明.分析:①涉及的知识要素:图形轴对称的性质;等边三角形的性质;全等三角形的判定与性质…… ②通过截长补短,利用60°角构造等边三角形,进而构造出全等三角形,从而达到转移边的目的. 请根据上述分析过程,完成解答过程.2、如图,在ABC 中,AD 平分BAC ∠,CE AD ⊥于点E .求证:ACE B ECD ∠=∠+∠.3、如图,已知点E 、C 在线段BF 上,BE CF =,AB DE ∥,ACB F ∠=∠.求证:ΔΔΔΔ≅ΔΔΔΔ.4、在四边形ABCD 中,AB BC ∥,点E 在直线AB 上,且DE CE =.(1)如图1,若90DEC A ∠=∠=︒,3BC =,2AD =,求AB 的长;(2)如图2,若DE 交BC 于点F ,DFC AEC ∠=∠,求证:BC AB AD =+.5、△ABC 中,AB =AC ,BD 平分∠ABC 交AC 于点D ,从点A 作AE ∥BC 交BD 的延长线于点E .(1)若∠BAC =40°,求∠E 的度数;(2)点F 是BE 上一点,且FE =BD .取DF 的中点H ,请问AH ⊥BE 吗?试说明理由.6、如图,点D 在AC 上,BC ,DE 交于点F ,BA BD =,BC BE =,ABD CBE ∠=∠.(1)求证:ABC DBE ≌;(2)若20ABD ∠=︒,求∠CDE 的度数.7、如图,将△ABC 绕点A 逆时针旋转得到△ADE ,点D 在BC 上,已知∠B =70°,求∠CDE 的大小.8、针对于等腰三角形三线合一的这条性质,老师带领同学们做了进一步的猜想和证明,提问:如果一个三角形中,一个角的平分线和它所对的边的中线重合,那么这个三角形是等腰三角形. 已知:在△ABC 中,AD 平分∠CAB ,交BC 边于点 D ,且CD =BD ,求证:AB =AC .以下是甲、乙两位同学的作法.甲:根据角平分线和中线的性质分别能得出一组角等和一组边等,再加一组公共边,可证△ACD ≌△ABD ,所以这个三角形为等腰三角形;乙:延长AD 到E ,使DE =AD ,连接BE ,可证△ACD ≌△EBD ,依据已知条件可推出AB =AC ,所以这个三角形为等腰三角形(1)对于甲、乙两人的作法,下列判断正确的是( );A .两人都正确B .甲正确,乙错误C .甲错误,乙正确(2)选择一种你认为正确的作法,并证明.9、如图,在等边ABC 中,D 为BC 边上一点,连接AD ,将ACD △沿AD 翻折得到AED ,连接BE 并延长交AD 的延长线于点F ,连接CF .(1)若20CAD ∠=︒,求CBF ∠的度数;(2)若a CAD ∠=,求CBF ∠的大小;(3)猜想CF ,BF ,AF 之间的数量关系,并证明.10、如图,点B ,F ,C ,E 在一条直线上,AB =DE ,∠B =∠E ,BF =CE .求证:AC =DF .-参考答案-一、单选题1、A【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和,可求出∠P的度数.【详解】∵BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,∴∠ABP=∠CBP=20°,∠ACP=∠MCP=50°,∵∠PCM是△BCP的外角,∴∠P=∠PCM−∠CBP=50°−20°=30°,故选:A.【点睛】本题考查三角形外角性质以及角平分线的定义,解题时注意:一个三角形的外角等于与它不相邻的两个内角的和.2、C【分析】先由翻折的性质得到∠AEN=∠A′EN,∠BEM=∠B′EM,从而可知∠NEM=12×180°=90°,然后根据余角的定义找出∠B′ME的余角即可.【详解】解:由翻折的性质可知:∠AEN=∠A′EN,∠BEM=∠B′EM.∠NEM=∠A′EN+∠B′EM=12∠AEA′+12∠B′EB=12×180°=90°.由翻折的性质可知:∠MB ′E =∠B =90°.由直角三角形两锐角互余可知:∠B ′ME 的一个余角是∠B ′EM .∵∠BEM =∠B ′EM ,∴∠BEM 也是∠B ′ME 的一个余角.∵∠NBF +∠B ′EM =90°,∴∠NEF =∠B ′ME .∴∠ANE 、∠A ′NE 是∠B ′ME 的余角.综上所述,∠B ′ME 的余角有∠ANE 、∠A ′NE 、∠B ′EM 、∠BEM .故选:C .【点睛】本题主要考查的是翻折的性质、余角的定义,掌握翻折的性质是解题的关键.3、D【分析】由SAS 即可证明DCB ACE ∆≅∆,则①正确;有∠CAE =∠CDB ,然后证明△ACM ≌△DCN ,则②正确;由CM =CN ,∠MCN =60°,即可得到∆CMN 为等边三角形,则③正确;由AD∥CE ,则∠DAO =∠NEO =∠CBN ,由外角的性质60EOB OAC CBN ∠=∠+∠=︒,即可得到答案.【详解】解:∵△DAC 和△EBC 均是等边三角形,∴AC =CD ,BC =CE ,∠ACD =∠BCE =60°,∴∠ACD +∠DCE =∠BCE +∠DCE ,即∠ACE =∠BCD ,∠MCN =180°-∠ACD -∠BCE =60°,在△ACE 和△DCB 中,AC CD ACE BCD BC CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△DCB (SAS ),则①正确;∴AE =BD ,∠CAE =∠CDB ,在ACM 和△DCN 中,ACM DCN AC CD CAM CDN ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△ACM ≌△DCN (ASA ),∴CM =CN ,AM DN =;则②正确;∵∠MCN =60°,∴∆CMN 为等边三角形;则③正确;∵∠DAC =∠ECB =60°,∴AD∥CE ,∴∠DAO =∠NEO =∠CBN ,∴60EOB OAC CBN OAC DAO ∠=∠+∠=∠+∠=︒;则④正确;∴正确的结论由4个;故选D .【点睛】本题考查了等边三角形的性质与判定,全等三角形的判定与性质,平行线的性质与判定,综合性较强,但难度不是很大,准确识图找出全等三角形是解题的关键.4、C【分析】作点Q 关于BD 的对称点Q ',连接PQ '交BD 于E ,连接QE ,此时PE EQ +的值最小,最小值PE PQ PE EQ PQ +=+'=',据此求解即可.【详解】解:如图,ABC ∆是等边三角形,BA BC ∴=,∵D 为AC 中点,∴BD AC ⊥,4AQ =,3QD =,7AD DC AQ QD ∴==+=,作点Q 关于BD 的对称点Q ',连接PQ '交BD 于E ,连接QE ,此时PE EQ +的值最小.最小值PE QE PE EQ PQ +=+'=',4AQ =,7AD DC ==,3QD DQ ∴='=,4CQ BP ∴'==,10AP AQ ∴='=,60A ∠=︒,APQ ∴∆'是等边三角形,10PQ PA ∴'==,PE QE ∴+的最小值为10.故选:C .【点睛】本题考查等边三角形的性质和判定,轴对称最短问题等知识,解题的关键是学会利用轴对称解决最短问题,属于中考常考题型.5、C【分析】由题意在射线AD 上截取AE =AB ,连接CE ,根据SAS 不难证得△ABC ≌△AEC ,从而得BC =EC ,∠B =∠AEC ,可求得CD =CE ,得∠CDE =∠CED ,证得∠B =∠CDE ,即可得出结果.【详解】解:在射线AD 上截取AE =AB ,连接CE ,如图所示:∵∠BAD =90°,AC 平分∠BAD ,∴∠BAC =∠EAC ,在△ABC 与△AEC 中,AC AC BAC EAC AB AE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABC ≌△AEC (SAS ),∴BC =EC ,∠B =∠AEC ,∵CB=CD,∴CD=CE,∴∠CDE=∠CED,∴∠B=∠CDE,∵∠ADC+∠CDE=180°,∴∠ADC+∠B=180°.故选:C.【点睛】本题主要考查全等三角形的判定与性质,解答的关键是作出适当的辅助线AE,CE.6、A【分析】①利用等边对等角得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;④证明△OPA≌△CPE,则AO=CE,得AC=AE+CE=AO+AP.【详解】解:①如图1,连接OB,∵AB=AC,AD⊥BC,∴BD=CD,∠BAD=12∠BAC=12×120°=60°,∴OB=OC,∠ABC=90°﹣∠BAD=30°∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC是等边三角形,故③正确;④如图2,在AC上截取AE=PA,∵∠PAE=180°﹣∠BAC=60°,∴△APE 是等边三角形,∴∠PEA =∠APE =60°,PE =PA ,∴∠APO +∠OPE =60°,∵∠OPE +∠CPE =∠CPO =60°,∴∠APO =∠CPE ,∵OP =CP ,在△OPA 和△CPE 中,PA PE APO CPE OP CP =⎧⎪∠=∠⎨⎪=⎩, ∴△OPA ≌△CPE (SAS ),∴AO =CE ,∴AC =AE +CE =AO +AP ,∴AB =AO +AP ,故④正确;正确的结论有:①③④,故选:A .【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键.7、C【分析】根据已知的三角形求第三个内角的度数,由全等三角形的判定定理即可得出答案.【详解】由题可知,第三个内角的度数为180514980︒-︒-︒=︒,A.只有两边,故不能判断三角形全等,故此选项错误;B.两边夹的角度数不相等,故两三角形不全等,故此选项错误;C.两边相等且夹角相等,故能判断两三角形全等,故此选项正确;D. 两边夹的角度数不相等,故两三角形不全等,故此选项错误.故选:C .【点睛】本题考查全等三角形的判定,掌握全等三角形的判定定理是解题的关键.8、B【分析】根据三角形存在的条件去判断.【详解】∵60A ∠=︒,45B ∠=︒,4AB =,满足ASA 的要求,∴可以画出唯一的三角形,A 不符合题意;∵30A ∠=︒,5AB =,3BC =,∠A 不是AB ,BC 的夹角,∴可以画出多个三角形,B 符合题意;∵60B ∠=︒,6AB =,10BC =,满足SAS 的要求,∴可以画出唯一的三角形,C 不符合题意;∵90C ∠=︒,5AB =,3BC =,AB 最大,∴可以画出唯一的三角形,D 不符合题意;故选B .【点睛】本题考查了三角形的存在性,熟练掌握三角形全等的判定方法是解题的关键.9、A【分析】根据全等三角形的判定方法求解即可.判定三角形全等的方法有:SSS,SAS对各选项进行一一判断即可.【详解】解:A、周长相等的两个三角形不一定全等,符合题意;B、有一腰和底边对应相等的两个等腰三角形根据三边对应相等判定定理可判定全等,不符合题意;C、三边都对应相等的两个三角形根据三边对应相等判定定理可判定全等,不符合题意;D、两条直角边对应相等的两个直角三角形根据SAS判定定理可判定全等,不符合题意.故选:A.【点睛】此题考查了全等三角形的判定方法,解题的关键是熟练掌握全等三角形的判定方法.判定三角形全等的方法有:SSS,SAS,AAS,ASA,HL(直角三角形).10、D【分析】设第三根木棒长为x厘米,根据三角形的三边关系可得8﹣5<x<8+5,确定x的范围即可得到答案.【详解】解:设第三根木棒长为x厘米,由题意得:8﹣5<x<8+5,即3<x<13,故选:D.【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和>第三边,任意两边之差<第三边.二、填空题1、6【分析】根据旋转的性质可得,30ACA '∠=︒,所以60BCM ∠=︒,由题意可得:60B ∠=︒,BCM 为等边三角形,即可求解.【详解】解:∵90ACB ∠=︒,30BAC ∠=︒,∴60B ∠=︒,由旋转的性质可得,30ACA '∠=︒,∴60BCM ACB ACM ∠=∠-∠=︒,∴BCM 为等边三角形,∴6CM BC ==,故答案为:6【点睛】此题考查了直角三角形的性质,旋转的性质以及等边三角形的判定与性质,解题的关键是灵活掌握相关基本性质进行求解.2、17【分析】先根据非负数的性质列式求出a 、b 的值,再分情况讨论求解即可.【详解】解:∵2(3)|7|0a b -+-=,∴30a -=,70b -=,解得:3a =,7b =,①若3a =是腰长,则底边为7,三角形的三边分别为3、3、7,∵337+<,∴3、3、7不能组成三角形;②若7b =是腰长,则底边为3,三角形的三边分别为7、7、3,能组成三角形,周长为:77317++=,∴以a 、b 为边长的等腰三角形的周长为17,故答案为:17.【点睛】本题考查了等腰三角形的性质,绝对值和平方的非负性,以及三角形的三边关系,难点在于要分类讨论求解.3、BAC DAC ∠=∠或CB CD =【分析】根据全等三角形的判定方法即可解决问题.【详解】解:由题意AB AD =,AC AC =,∴根据SAS ,可以添加BAC DAC ∠=∠,使得ABC ADC ∆≅∆,根据SSS ,可以添加CB CD =,使得ABC ADC ∆≅∆.故答案为:BAC DAC ∠=∠或CB CD =【点睛】本题主要考查了全等三角形的判定,熟练掌握全等三角形的判定方法——边角边、角边角、角角边、边边边是解题的关键.4、65°65度【分析】由三角形的内角和定理,得到180A B C ∠+∠+∠=︒,即可得到答案;【详解】解:在ABC 中,180A B C ∠+∠+∠=︒,∵50,A B C ∠=︒∠=∠,∴502180B ︒+∠=︒,∴65B ∠=︒;故答案为:65°.【点睛】本题考查了三角形的内角和定理,解题的关键是掌握三角形的内角和等于360°.5、7【分析】根据角平分线的定义和平行线的性质证明∠EBD =∠EDB ,∠FDC =∠FCD ,得到BE =DE ,CF =DF ,即可求解.【详解】解:∵EF∥BC ,∴∠EDB =∠DBC ,∠FDC =∠DCB ,又∵BD 和CD 分别是∠ABC 和∠ACB 的平分线,∴∠EBD =∠DBC ,∠FCD =∠DCB ,∴∠EBD =∠EDB ,∠FDC =∠FCD ,∴BE =DE ,CF =DF ,又∵BE =3,CF =4,∴EF =DE +DF =BE +CF =7.故答案为:7.【点睛】本题主要考查了平行线的性质,角平分的定义,等腰三角形的性质与判定,熟知相关知识是解题的关键.三、解答题1、(1)图见解析,∠AEB =60°;(2)AE =BE +CE ,证明见解析【分析】(1)依题意补全图形,如图所示:然后连接AD ,先求出60CAP α∠=︒-,然后根据轴对称的性质得到==PAD BAP α∠∠,AD =AB =AC ,∠AEC =∠AEB ,求出=260CAD α-︒∠,即可求出()1==180=1202ACD ADC CAD α︒-︒-∠∠∠,再由==120EAC AEC ACD α+︒-∠∠∠进行求解即可; (2)如图,在AE 上截取EG =BE ,连接BG .先证明△BGE 是等边三角形,得到BG =BE =EG ,∠GBE =60°. 再证明∠ABG =∠CBE ,即可证明△ABG ≌△CBE 得到AG =CE ,则AE =EG +AG =BE +CE .【详解】解:(1)依题意补全图形,如图所示:连接AD ,∵△ABC 是等边三角形,∴∠BAC =60°,AB =AC ,∵BAP α∠=,∴60CAP α∠=︒-,∵B 、D 关于AP 对称,∴==PAD BAP α∠∠,AD =AB =AC ,∠AEC =∠AEB ,∴()==60=260CAD PAD CAP ααα--︒--︒∠∠∠, ∴()1==180=1202ACD ADC CAD α︒-︒-∠∠∠,∴==120EAC AEC ACD α+︒-∠∠∠,∴60AEC ∠=︒∴∠AEB =60°.(2)AE =BE +CE .证明:如图,在AE 上截取EG =BE ,连接BG .∵∠AEB =60°,∴△BGE 是等边三角形,∴BG =BE =EG ,∠GBE =60°.∵△ABC 是等边三角形,∴AB =BC ,∠ABC =60°,∴∠ABG +∠GBC =∠GBC +∠CBE =60°,∴∠ABG =∠CBE .在△ABG 和△CBE 中,AB CB ABG CBE BG BE ⎧⎪∠∠⎨⎪⎩=,=,=, ∴△ABG ≌△CBE (SAS ),∴AG=CE,∴AE=EG+AG=BE+CE.【点睛】本题主要考查了全等三角形的性质,等边三角形的性质与判定,轴对称的性质,等腰三角形的性质与判定,三角形内角和定理,三角形外角的性质等等,熟知相关知识是解题的关键2、证明见解析.【分析】延长CE交AB于F,求出∠AEC=∠AEF,∠FAE=∠CAE,根据ASA证△FAE≌△CAE,推出∠ACE=∠AFC,根据三角形外角性质得出∠AFC=∠B+∠ECD,代入即可.【详解】证明:延长CE交AB于F,∵CE⊥AD,∴∠AEC=∠AEF,∵AD 平分∠BAC ,∴∠FAE =∠CAE ,在△FAE 和△CAE 中,∵FAE CAE AE AE AEF AEC ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴△FAE ≌△CAE (ASA ),∴∠ACE =∠AFC ,∵∠AFC =∠B +∠ECD ,∴∠ACE =∠B +∠ECD .【点睛】本题考查了全等三角形的性质和判定,三角形的外角性质等知识点,关键是作辅助线后求出∠AFC =∠ACE .3、见解析【分析】由平行线的性质可证明B DEF ∠=∠.再由BE CF =,可推出BC EF =.最后即可利用“ASA ”直接证明ABC DEF ≅.【详解】证明:AB DE ∥B DEF ∴∠=∠BE CF =BE EC CF EC ∴+=+,即BC EF =.∴在ABC和DEF中,B DEF BC EFACB F ∠=∠⎧⎪=⎨⎪∠=∠⎩()ABC DEF ASA∴≅.【点睛】本题考查三角形全等的判定,平行线的性质,线段的和与差.掌握三角形全等的判定条件是解答本题的关键.4、(1)5;(2)证明见解析【分析】(1)推出∠ADE=∠BEC,根据AAS证△AED≌△CEB,推出AE=BC,BE=AD,代入求出即可;(2)推出∠A=∠EBC,∠AED=∠BCE,根据AAS证△AED≌△BCE,推出AD=BE,AE=BC,即可得出结论.【详解】(1)解:∵∠DEC=∠A=90°,∴∠ADE+∠AED=90°,∠AED+∠BEC=90°,∴∠ADE=∠BEC,∵AD BC∥,∠A=90°,∴∠B+∠A=180°,∴∠B=∠A=90°,在△AED和△CEB中A BADE BECDE EC,∴△AED≌△BCE(AAS),∴AE=BC=3,BE=AD=2,∴AB=AE+BE=2+3=5.∥,(2)证明:∵AD BC∴∠A=∠EBC,∵∠DFC=∠AEC,∠DFC=∠BCE+∠DEC,∠AEC=∠AED+∠DEC,∴∠AED=∠BCE,在△AED和△BCE中AED BCEA EBC,DE EC∴△AED≌△BCE(AAS),∴AD=BE,AE=BC,∵BC=AE=AB+BE=AB+AD,即AB+AD=BC.【点睛】本题考查了三角形的外角的性质,全等三角形的性质和判定,平行线的性质等知识点的运用,掌握“利用AAS证明两个三角形全等”是解本题的关键.5、(1)∠E=35°;(2)AH⊥BE.理由见解析.【分析】(1)根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD的度数,最后根据两直线平行,内错角相等求出;(2)由“SAS”可证△ABD≌△AEF,可得AD=AF,由等腰三角形的性质可求解.【详解】解:(1)∵AB =AC ,∴∠ABC =∠ACB ,∵∠BAC =40°,∴∠ABC =12(180°-∠BAC )=70°,∵BD 平分∠ABC ,∴∠CBD =12∠ABC =35°,∵AE ∥BC ,∴∠E =∠CBD =35°;(2)∵BD 平分∠ABC ,∠E =∠CBD ,∴∠CBD =∠ABD =∠E ,∴AB =AE ,在△ABD 和△AEF 中,AB AE E ABD BD EF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△AEF (SAS ),∴AD =AF ,∵点H 是DF 的中点,∴AH ⊥BE .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键. 6、(1)证明见解析;(2)∠CDE =20°.【分析】(1)由“SAS ”可证△ABC ≌△DBE ;(2)由全等三角形的性质可得∠C =∠E ,由三角形的外角性质可求解.(1)证明:∵∠ABD =∠CBE ,∴∠ABD +∠DBC =∠CBE +∠DBC ,即:∠ABC =∠DBE ,在△ABC 和△DBE 中,BA BD ABC DBE BC BE =⎧⎪∠=∠⎨⎪=⎩, ∴△ABC ≌△DBE (SAS );(2)解:由(1)可知:△ABC ≌△DBE ,∴∠C =∠E ,∵∠DFB =∠C +∠CDE ,∠DFB =∠E +∠CBE ,∴∠CDE =∠CBE ,∵∠ABD =∠CBE =20°,∴∠CDE =20°.【点睛】本题考查了全等三角形的判定和性质,三角形的外角性质,证明三角形全等是解题的关键. 7、40【分析】先由旋转的性质证明,70,AB AD ADE B 再利用等边对等角证明70,ADB B 从而可得答案.【详解】 解: 把△ABC 绕点A 逆时针旋转得到△ADE ,∠B =70°,,70,AB AD ADE B 70,ADB B18040.CDE ADB ADE 【点睛】本题考查的是旋转的性质,等腰三角形的性质,掌握“旋转前后的对应角相等与等边对等角”是解本题的关键.8、(1)C ;(2)见解析【分析】(1)甲同学证明的两个三角形全等,没有边边角的判定,故错误,而乙的证明则正确,因此可作出判断;(2)按照乙的分析方法进行即可.【详解】(1)甲同学证明的两个三角形全等,边边角不能判定两个三角形全等,故错误,而乙的证明则正确,故选C ;(2)依据题意,延长AD 至E ,使DE =AD ,连接BE ,如图.∵D 为BC 中点.∴BD CD =.在△CAD 和△BED 中DE AD ADC EDB BD CD =⎧⎪∠=∠⎨⎪=⎩∴△CAD ≌△BED (SAS ).∴DAC E ∠=∠,BE AC =∵AD 平分∠BAC ,∴BAD CAD ∠=∠∴DAB E ∠=∠∴BE AB =∴AB =AC∴△ABC 为等腰三角形【点睛】本题考查了全等三角形的判定与性质,等腰三角形的判定,关键是构造辅助线得到全等三角形.9、(1)20°;(2)CBF α∠=;(3)AF = CF +BF ,理由见解析【分析】(1)由△ABC 是等边三角形,得到AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,∠EAD =∠CAD =20°,AC =AE ,则∠BAE =∠BAC -∠EAD -∠CAD =20°,AB =AE ,()1180=802ABE AEB BAE ==︒-︒∠∠∠,∠CBF =∠ABE -∠ABC =20°; (2)同(1)求解即可;(3)如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,先证明△AEF ≌△ACF 得到∠AFE =∠AFC ,然后证明∠AFE =∠AFC =60°,得到∠BFC =120°,即可证明F 、C 、G 三点共线,得到△AFG 是等边三角形,则AF =GF =CF +CG =CF +BF .【详解】解:(1)∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,∠EAD =∠CAD =20°,AC =AE ,∴∠BAE =∠BAC -∠EAD -∠CAD =20°,AB =AE , ∴()1180=802ABE AEB BAE ==︒-︒∠∠∠, ∴∠CBF =∠ABE -∠ABC =20°;(2)∵△ABC 是等边三角形,∴AB =AC ,∠BAC =∠ABC =60°,由折叠的性质可知,EAD CAD α∠=∠=,AC =AE ,∴602BAE BAC EAD CAD α∠=∠-∠-∠=︒- ,AB =AE , ∴()1180=602ABE AEB BAE α==︒-︒+∠∠∠, ∴CBF ABE ABC α∠=∠-∠=;(3)AF = CF +BF ,理由如下:如图所示,将△ABF 绕点A 逆时针旋转60°得到△ACG ,∴AF =AG ,∠FAG =60°,∠ACG =∠ABF ,BF =CG在△AEF 和△ACF 中,=AE AC EAF CAF AF AF =⎧⎪∠∠⎨⎪=⎩, ∴△AEF ≌△ACF (SAS ),∴∠AFE =∠AFC ,∵∠CBF +∠BCF +∠BFD +∠CFD =180°,∠CAF +∠CFA +∠ACD +∠CFD =180°,∴∠BFD =∠ACD =60°,∴∠AFE =∠AFC =60°,∴∠BFC =120°,∴∠BAC +∠BFC =180°,∴∠ABF +∠ACF =180°,∴∠ACG +∠ACF =180°,∴F 、C 、G 三点共线,∴△AFG 是等边三角形,∴AF =GF =CF +CG =CF +BF .【点睛】本题主要考查了等边三角形的性质与判定,旋转的性质,折叠的性质,全等三角形的性质与判定,三角形内角和定理,熟知相关知识是解题的关键.10、见解析【分析】先由BF =CE 说明BC= EF .然后运用SAS 证明△ABC ≌△DEF ,最后运用全等三角形的性质即可证明.【详解】证明:∵BF= CE ,∴BC= EF .在△ABC 和△DEF 中,,,,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (SAS ).∴AC =DF .【点睛】本题主要考查了全等三角形的判定与性质,正确证明△ABC ≌△DEF 是解答本题的关键.。
2022年精品解析沪教版七年级数学第二学期第十四章三角形必考点解析试卷(含答案解析)

沪教版七年级数学第二学期第十四章三角形必考点解析考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、我们称网格线的交点为格点.如图,在4×4的长方形网格中有两个格点A、B,连接AB,在网格中再找一个格点C,使得△ABC是等腰直角三角形,则满足条件的格点C的个数是()A.3 B.4 C.5 D.62、已知三条线段的长分别是4,4,m,若它们能构成三角形,则整数m的最大值是()A.10 B.8 C.7 D.4'',使点C的3、如图,ABC中,∠ACB=90°,∠ABC=40°.将ABC绕点B逆时针旋转得到A BC对应点C'恰好落在边AB上,则BA A∠'的度数是()A .50°B .70°C .110°D .120°4、满足下列条件的两个三角形不一定全等的是( )A .周长相等的两个三角形B .有一腰和底边对应相等的两个等腰三角形C .三边都对应相等的两个三角形D .两条直角边对应相等的两个直角三角形5、△BDE 和△FGH 是两个全等的等边三角形,将它们按如图的方式放置在等边三角形ABC 内.若BC =5,则五边形DECHF 的周长为( )A .8B .10C .11D .126、在下列长度的四根木棒中,能与3cm ,9cm 的两根木棒首尾顺次相接钉成一个三角形的是( )A .3cmB .6cmC .10cmD .12cm7、如图,等腰ABC 中,AB AC =,120BAC ∠=︒,AD DC ⊥于D ,点O 是线段AD 上一点,点P 是BA 延长线上一点,若OP OC =,则下列结论:①30APO DCO ∠+∠=︒;②APO DCO ∠=∠;③POC △是等边三角形;④AB OA AP =+.其中正确的是( )A .①③④B .①②③C .②③④D .①②③④8、已知等腰三角形有一个角为50°,则这个等腰三角形的底角度数是( ).A .65°B .65°或80°C .50°或80°D .50°或65°9、如图,点A 、B 、C 、D 在一条直线上,点E 、F 在AD 两侧,BF CE ∥,BF CE =,添加下列条件不能判定ACE DBF ≌的是( )A .AE DF =B .AB CD =C .E F ∠=∠D .AE DF ∥10、如图,ABC ≌DEF ,点B 、E 、C 、F 在同一直线上,若BC =7,EC =4,则CF 的长是( )A .2B .3C .4D .7第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、在新年联欢会上,老师设计了“你说我画”的游戏.游戏规则如下:甲同学需要根据乙同学提供的三个条件画出形状和大小都确定的三角形.已知乙同学说出的前两个条件是“4AB =,2BC =”.现仅存下列三个条件:①45A ∠=︒;②45B ∠=︒;③45C ∠=︒.为了甲同学画出形状和大小都确定的ABC ,乙同学可以选择的条件有: ______.(填写序号,写出所有正确答案)2、如图,1AP 为△ABC 的中线,2AP 为△1APC 的中线,3AP 为△2AP C 的中线,……按此规律,n AP 为△1n AP C -的中线.若△ABC 的面积为8,则△n AP C 的面积为_______________.3、△ABC 的高AD 所在直线与高BE 所在直线相交于点F 且DF =CD ,则∠ABC =______.4、如图,在Rt△ABC 中,∠C =90°,两锐角的角平分线交于点P ,点E 、F 分别在边BC 、AC 上,且都不与点C 重合,若∠EPF =45°,连接EF ,当AC =6,BC =8,AB =10时,则△CEF 的周长为 _____.5、如图,ABC 中,90A ∠=︒,点D 在AC 边上,∥DE BC ,若1145∠=︒,则B 的度数为_______.三、解答题(10小题,每小题5分,共计50分)1、如图,已知点B ,F ,C ,E 在同一直线上,AB ∥DE ,BF =CE ,AB =ED ,求证:∠A =∠D .2、如图,已知△ABC≌△DEB,点E在AB上,AC与BD交于点F,AB=6,BC=3,∠C=55°,∠D=25°.(1)求AE的长度;(2)求∠AED的度数.3、已知:在△ABC中,AD平分∠BAC,AE=AC.求证:AD∥CE.4、如图,在△ABC中,AB=AC,CD⊥AB于点D,∠A=50°,求∠BCD的度数.5、直线l 经过点A ,ABC 在直线l 上方,AB AC =.(1)如图1,90BAC ∠=︒,过点B ,C 作直线l 的垂线,垂足分别为D 、E .求证:ABD CAE ≌(2)如图2,D ,A ,E 三点在直线l 上,若BAC BDA AEC α∠=∠=∠=(α为任意锐角或钝角),猜想线段DE 、BD 、CE 有何数量关系?并给出证明.(3)如图3,90BAC ∠=︒过点B 作直线l 上的垂线,垂足为F ,点D 是BF 延长线上的一个动点,连结AD ,作90DAE ∠=︒,使得AE AD =,连结DE ,CE .直线l 与CE 交于点G .求证:G 是CE 的中点.6、如图,在等边三角形ABC 中,点D ,E 分别在边BC ,AC 上,且DE ∥AB ,过点E 作EF ⊥DE ,交BC 的延长线于点F .(1)求证:CE =CF ;(2)若CD =2,求DF 的长.7、已知:如图,点D 为BC 的中点,BAD CAD ∠=∠,求证:ABC 是等腰三角形.8、△ABC 中,AB =AC ,BD 平分∠ABC 交AC 于点D ,从点A 作AE ∥BC 交BD 的延长线于点E .(1)若∠BAC =40°,求∠E 的度数;(2)点F 是BE 上一点,且FE =BD .取DF 的中点H ,请问AH ⊥BE 吗?试说明理由.9、在等边ABC 中,D 、E 是BC 边上两动点(不与B ,C 重合)(1)如图1,,25AD AE BAD =∠=︒,求AEB ∠的度数;(2)点D 在点E 的左侧,且AD =AE ,点E 关于直线AC 的对称点为F ,连接AF ,DF .①依题意将图2补全;②求证:AD DF =.10、如图,在四边形ABCD 中,点E 在BC 上,连接DE 、AC 相交于点F ,∠BAE =∠CAD ,AB =AE ,AD =AC .(1)求证:∠DEC=∠BAE;(2)如图2,当∠BAE=∠CAD=30°,AD⊥AB时,延长DE、AB交于点G,请直接写出图中除△ABE、△ADC以外的等腰三角形.-参考答案-一、单选题1、A【分析】根据题意,结合图形,分两种情况讨论:①AB为等腰直角△ABC底边;②AB为等腰直角△ABC其中的一条腰.【详解】解:如图:分情况讨论:①AB为等腰直角△ABC底边时,符合条件的格点C点有0个;②AB为等腰直角△ABC其中的一条腰时,符合条件的格点C点有3个.故共有3个点,故选:A .【点睛】本题考查了等腰三角形的性质和判定;解答本题关键是根据题意,画出符合实际条件的图形,数形结合的思想是数学解题中很重要的解题思想.2、C【分析】根据三角形三边关系列出不等式,根据不等式的解集求整数m 的最大值.【详解】解:条线段的长分别是4,4,m ,若它们能构成三角形,则4444m -<<+,即08m <<又m 为整数,则整数m 的最大值是7故选C【点睛】本题考查了求不等式的整数解,三角形三边关系,根据三角形的三边关系列出不等式是解题的关键.3、B【分析】根据旋转可得40A BA ABC ∠'=∠=︒,A B AB '=,得70BAA ∠'=︒.【详解】解:90ACB ∠=︒,40ABC ∠=︒,90904050CAB ABC ∴∠=︒-∠=︒-︒=︒,将ABC ∆绕点B 逆时针旋转得到△A BC '',使点C 的对应点C '恰好落在边AB 上,40A BA ABC ∴∠'=∠=︒,A B AB '=,1(18040)702BAA BA A ∴∠'=∠'=⨯︒-︒=︒. 故选:B .【点睛】本题考查了旋转的性质,等腰三角形的性质,三角形内角和定理,解决本题的关键是掌握旋转的性质.4、A【分析】根据全等三角形的判定方法求解即可.判定三角形全等的方法有:SSS ,SAS 对各选项进行一一判断即可.【详解】解:A 、周长相等的两个三角形不一定全等,符合题意;B 、有一腰和底边对应相等的两个等腰三角形根据三边对应相等判定定理可判定全等,不符合题意;C 、三边都对应相等的两个三角形根据三边对应相等判定定理可判定全等,不符合题意;D 、两条直角边对应相等的两个直角三角形根据SAS 判定定理可判定全等,不符合题意.故选:A .【点睛】此题考查了全等三角形的判定方法,解题的关键是熟练掌握全等三角形的判定方法.判定三角形全等的方法有:SSS ,SAS ,AAS ,ASA ,HL(直角三角形).5、B【分析】证明△AFH ≌△CHG (AAS ),得出AF =CH .由题意可知BE =FH ,则得出五边形DECHF 的周长=AB +BC ,则可得出答案.【详解】解:∵△GFH 为等边三角形,∴FH =GH ,∠FHG =60°,∴∠AHF +∠GHC =120°,∵△ABC 为等边三角形,∴AB =BC =AC =5,∠ACB =∠A =60°,∵∠AHF =180°-∠FHG -∠GHC =120°-∠GHC ,∠HGC =180°-∠C -∠GHC =120°-∠GHC ,∴∠AHF =∠HGC ,在△AFH 和△CHG 中A C AHF HGC FH GH ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△AFH ≌△CHG (AAS ),∴AF =CH .∵△BDE 和△FGH 是两个全等的等边三角形,∴BE =FH ,∴五边形DECHF 的周长=DE +CE +CH +FH +DF =BD +CE +AF +BE +DF ,=(BD +DF +AF )+(CE +BE ),=AB +BC =10.故选:B .【点睛】本题考查了全等三角形的判定与性质,等边三角形的性质,熟练掌握全等三角形的判定方法是解题的关键.6、C【分析】设第三根木棒的长度为x cm,再确定三角形第三边的范围,再逐一分析各选项即可得到答案.【详解】解:设第三根木棒的长度为x cm,则9393,xx612,所以A,B,D不符合题意,C符合题意,故选C【点睛】本题考查的是三角形的三边的关系,掌握“利用三角形的三边关系确定第三边的范围”是解本题的关键.7、A【分析】①利用等边对等角得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;②因为点O是线段AD上一点,所以BO不一定是∠ABD的角平分线,可作判断;③证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形;④证明△OPA≌△CPE,则AO=CE,得AC=AE+CE=AO+AP.【详解】解:①如图1,连接OB,∵AB=AC,AD⊥BC,∴BD=CD,∠BAD=12∠BAC=12×120°=60°,∴OB=OC,∠ABC=90°﹣∠BAD=30°∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DCO=∠DBO,∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°,故①正确;②由①知:∠APO=∠ABO,∠DCO=∠DBO,∵点O是线段AD上一点,∴∠ABO与∠DBO不一定相等,则∠APO与∠DCO不一定相等,故②不正确;③∵∠APC+∠DCP+∠PBC=180°,∴∠APC+∠DCP=150°,∵∠APO+∠DCO=30°,∴∠OPC+∠OCP=120°,∴∠POC=180°﹣(∠OPC+∠OCP)=60°,∵OP=OC,∴△OPC 是等边三角形,故③正确;④如图2,在AC 上截取AE =PA ,∵∠PAE =180°﹣∠BAC =60°,∴△APE 是等边三角形,∴∠PEA =∠APE =60°,PE =PA ,∴∠APO +∠OPE =60°,∵∠OPE +∠CPE =∠CPO =60°,∴∠APO =∠CPE ,∵OP =CP ,在△OPA 和△CPE 中,PA PE APO CPE OP CP =⎧⎪∠=∠⎨⎪=⎩, ∴△OPA ≌△CPE (SAS ),∴AO =CE ,∴AC =AE +CE =AO +AP ,∴AB =AO +AP ,故④正确;正确的结论有:①③④,故选:A .【点睛】本题主要考查了全等三角形的判定与性质、等腰三角形的判定与性质、等边三角形的判定与性质等知识,正确作出辅助线是解决问题的关键.8、D【分析】50︒可以是底角,也可以是顶角,分情况讨论即可.【详解】当50︒角为底角时,底角就是50︒,当50︒角为等腰三角形的顶角时,底角为(18050)265︒-︒÷=︒,因此这个等腰三角形的底角为50︒或65︒.故选:D .【点睛】本题考查了等腰三角形的性质;若题目中没有明确顶角或底角的度数,做题时要注意分情况进行讨论,这是十分重要的,也是解答问题的关键.9、A【分析】根据题意,可得,BE CE FBD ECA =∠=∠,结合选项根据三角形全等的性质与判定逐项分析即可.【详解】 解:BF CE ∥∴FBD ECA ∠=∠ A. ,BE CE FBD ECA =∠=∠,AE DF =,不能根据SSA 证明三角形全等,故该选项符合题意;B. AB CD =AB BC BC CD ∴+=+AC BD ∴=,BE CE FBD ECA =∠=∠,∴ACE DBF ≌()SAS故能判定ACE DBF ≌,不符合题意; C. ,BE CE FBD ECA =∠=∠,E F ∠=∠,∴ACE DBF ≌()ASA ,故能判定ACE DBF ≌,不符合题意;D.AE DF ∥A D ∴∠=∠,BE CE FBD ECA =∠=∠∴ACE DBF ≌()AAS ,故能判定ACE DBF ≌,不符合题意;故选A【点睛】本题考查了平行线的性质,三角形全等的性质与判定,掌握三角形全等的性质与判定是解题的关键.10、B【分析】根据全等三角形的性质可得BC EF =,根据CF EF EC =-即可求得答案.【详解】 解:ABC ≌DEF ,∴BC EF =点B 、E 、C 、F 在同一直线上,BC =7,EC =4,∴CF EF EC =-743BC EC -=-=故选B【点睛】本题考查了全等三角形的性质,掌握全等三角形的性质是解题的关键.二、填空题1、②【分析】根据两边及其夹角对应相等的两个三角形全等,即可求解.【详解】解:①若选45A ∠=︒,是边边角,不能得到形状和大小都确定的ABC ;②若选45B ∠=︒,是边角边,能得到形状和大小都确定的ABC ;③若选45C ∠=︒,是边边角,不能得到形状和大小都确定的ABC ;所以乙同学可以选择的条件有②.故答案为:②【点睛】本题主要考查了全等三角形的判定,熟练掌握两边及其夹角对应相等的两个三角形全等是解题的关键.2、312n -【分析】根据三角形的中线性质,可得△1APC 的面积=182⨯,△2AP C 的面积=2182⨯,……,进而即可得到答案.【详解】由题意得:△1APC 的面积=182⨯,△2AP C 的面积=2182⨯,……,△n AP C 的面积=182n ⨯=312n -. 故答案是:312n -.【点睛】 本题主要考查三角形的中线的性质,掌握三角形的中线把三角形的面积平分,是解题的关键. 3、45°或135°【分析】根据题意,分两种情况讨论:①当ABC ∆为锐角三角形时;②当ABC ∆为钝角三角形时;作出相应图形,然后利用全等三角形的判定证明三角形全等,根据其性质及各角直角的等量关系即可得.【详解】解:①如图所示:当ABC ∆为锐角三角形时,∵AD BC ⊥,BE AC ⊥,∴90BDF ADC BEC ∠=∠=∠=︒,∴90C CBE ∠+∠=︒,90C CAD ∠+∠=︒,∴CBE CAD ∠=∠,在ΔΔΔΔ与ADC ∆中,CBE CAD BDF ADC DF CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴ΔΔΔΔ≅ΔΔΔΔ,∴BD AD =,∵90ADB ∠=︒,∴45ABC DAB ∠=∠=︒;②如图所示:当ABC ∆为钝角三角形时,∵AD BC ⊥,BE AC ⊥,∴90BDF ADC BEC ∠=∠=∠=︒,∴90C CAD ∠+∠=︒,90C CBE ∠+∠=︒,∴CBE CAD ∠=∠,∵DBF CBE ∠=∠,∴DBF CAD ∠=∠,在ΔΔΔΔ与ADC ∆中,DBF CAD BDF ADC DF CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴ΔΔΔΔ≅ΔΔΔΔ,∴BD AD =,∵90ADB ∠=︒,∴45ABD DAB ∠=∠=︒,18045135ABC ∠=︒-︒=︒,综合①②可得:ABC ∠为45︒或135︒,故答案为:45︒或135︒.【点睛】题目主要考查全等三角形的判定和性质,等腰三角形的性质,根据题意进行分类讨论,作出相应图形是解题关键.4、4【分析】根据题意过点P 作PM ⊥BC 于M ,PN ⊥AC 于N ,PK ⊥AB 于K ,在EB 上取一点J ,使得MJ =FN ,连接PJ ,进而利用全等三角形的性质证明EF =EM +EN ,即可得出结论.【详解】解:如图,过点P 作PM ⊥BC 于M ,PN ⊥AC 于N ,PK ⊥AB 于K ,在EB 上取一点J ,使得MJ =FN ,连接PJ .∵BP 平分∠BC ,PA 平分∠CAB ,PM ⊥BC ,PN ⊥AC ,PK ⊥AB ,∴PM =PK ,PK =PN ,∴PM =PN ,∵∠C =∠PMC =∠PNC =90°,∴四边形PMCN 是矩形,∴四边形PMCN 是正方形,∴CM =PM ,∴∠MPN =90°,在△PMJ 和△PNF 中,90PM PN PMJ PNF MJ NF =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△PMJ ≌△PNF (SAS ),∴∠MPJ =∠FPN ,PJ =PF ,∴∠JPF =∠MPN =90°,∵∠EPF =45°,∴∠EPF =∠EPJ =45°,在△PEF 和△PEJ 中,PE PE EPF EPJ PF PJ =⎧⎪∠=∠⎨⎪=⎩, ∴△PEF ≌△PEJ (SAS ),∴EF =EJ ,∴EF =EM +FN ,∴△CEF 的周长=CE +EF +CF =CE +EM +CF +FN =2EM =2PM ,∵S △ABC =12•BC •AC =12(AC +BC +AB )•PM ,∴PM =2,∴△ECF 的周长为4,故答案为:4.【点睛】本题考查角平分线的性质定理,正方形的判定,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问.5、55︒【分析】先求出∠EDC=35°,然后根据平行线的性质得到∠C=∠EDC=35°,再由直角三角形两锐角互余即可求解.【详解】解:∵∠1=145°,∴∠EDC=35°,∵DE∥BC,∴∠C=∠EDC=35°,又∵∠A=90°,∴∠B=90°-∠C=55°,故答案为:55°.【点睛】本题主要考查了平行线的性质,直角三角形两锐角互余,求出∠C的度数是解题的关键.三、解答题1、见解析【分析】≅,利用全等三角形的性质解答即根据平行线的性质得出∠B=∠E,进而利用SAS证明ABC DEF可.【详解】证明:FB CE =,FB CF CE CF ∴+=+,即BC EF =.//AB DE ,B E ∴∠=∠.在ABC 和DEF 中,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩, ()ABC DEF SAS ∴≅△△A D ∴∠=∠.【点睛】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证ABC DEF ≅是解题的关键.2、(1)3AE =;(2)80AED ∠=︒.【分析】(1)先根据全等三角形的性质可得3BE BC ==,再根据线段的和差即可得;(2)先根据全等三角形的性质可得55DBE C ∠=∠=︒,再根据三角形的外角性质即可得.【详解】解:(1)∵,3ABC DEB BC ≅=,∴3BE BC ==,∵6AB =,∴633AE AB BE =-=-=;(2)∵ABC DEB ≅△△,∴55DBE C ∠=∠=︒,∵25D ∠=︒,∴552580AED DBE D ∠=∠+∠=︒+︒=︒.【点睛】本题考查全等三角形的性质等知识点,熟练掌握全等三角形的对应角和对应边相等是解题关键.3、见解析.【分析】先根据角平分线的定义得到∠BAD =12∠BAC ,再根据等腰三角形的性质和三角形外角定理得到∠E =12∠BAC ,从而得到∠BAD =∠E ,即可证明AD ∥CE .【详解】解:∵AD 平分∠BAC ,∴∠BAD =12∠BAC ,∵AE =AC ,∴∠E =∠ACE ,∵∠E +∠ACE =∠BAC ,∴∠E =12∠BAC ,∴∠BAD =∠E ,∴AD ∥CE .【点睛】本题考查了角平分线的定义,等腰三角形的性质,平行线的判定,三角形外角定理,熟知相关定理并灵活应用是解题关键.4、25°【分析】直接利用等腰三角形的性质得出∠ABC =∠ACB =65°,进而利用三角形内角和定理得出答案.【详解】∵AB =AC ,∠A =50°,∴∠ABC =∠ACB =65°,∵CD ⊥BC 于点D ,∴∠BCD 的度数为:180°−90°−65°=25°.【点睛】此题主要考查了等腰三角形的性质,正确得出∠B 的度数是解题关键.5、(1)见解析;(2)猜想:DE BD CE =+,见解析;(3)见解析【分析】(1)先证明BDA AEC ∠=∠和ABD CAE ∠=∠,再根据AAS 证明ABD CAE ≌即可;(2)根据AAS 证明ABD CAE ≌得BD AE =,DA EC =,进一步可得出结论;(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,得出CM =EN ,证明CMG ENG ≌得CG EG =,从而可得结论.【详解】解:(1)证明:∵BD l ⊥,CE l ⊥,∴90BDA AEC ∠=∠=︒,∴90ABD DAB ∠+∠=︒∵90BAC ∠=︒,∴90CAE DAB ∠+∠=︒∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()ABD CAE AAS ≌(2)猜想:DE BD CE =+,∵BDA BAC α∠=∠=∴180180ABD DAB BDA α∠+∠=︒-∠=︒-,180180CAE DAB BAC α∠+∠=︒-∠=︒-∴ABD CAE ∠=∠,在ABD 与CAE 中BDA AEC ABD CAE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()ABD CAE AAS ≌,∴BD AE =,DA EC =,∴DE AE DA BD CE =+=+(3)分别过点C 、E 作CM l ⊥,EN l ⊥,同(1)可证ABF CAM ≌,ADF EAN ≌,∴AF CM =,AF EN =∴CM EN =,∵CM l ⊥,EN l ⊥,∴90CMG ENG ∠=∠=︒在CMG 与ENG 中CMG ENG CGM EGN CM EN ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CMG ENG AAS ≌,∴CG EG =,∴G 为CE 的中点.【点睛】本题考查了全等三角形的判定与性质、垂线的定义、角的互余关系,证得△ABD ≌△CAE 是解决问题的关键.6、(1)证明见解析;(2)4【分析】(1)根据等边三角形的性质和平行线的性质可证得∠EDC=∠ECD=∠DEC=60°,再根据直角定义和三角形的外角性质证得∠F=∠FEC=30°,利用等角对等边即可证得结论;(2)由等角对等边可知CE=DC=2,结合(1)中结论即可求解.(1)证明:∵△ABC是等边三角形,∴∠A=∠B=∠ACB=60°.∵DE∥AB,∴∠B=∠EDC=60°,∠A=∠CED=60°,∴∠EDC=∠ECD=∠DEC=60°,∵EF⊥ED,∴∠DEF=90°,∴∠F=30°∵∠F+∠FEC=∠ECD=60°,∴∠F=∠FEC=30°,∴CE=CF.(2)解:由(1)可知∠EDC=∠ECD=∠DEC=60°,∴CE=DC=2.又∵CE=CF,∴CF=2.∴DF=DC+CF=2+2=4.【点睛】本题考查等边三角形的性质、等腰三角形的判定、平行线的性质、三角形的外角性质、线段的和与差,熟练掌握相关知识的联系与运用是解答的关键.7、证明见解析【分析】过点D 作DM AB ⊥,交AB 于点M ,过点D 做DN AC ⊥,交AC 于点N ,根据角平分线性质,得DM DN =;根据全等三角形的性质,通过证明ADM ADN △≌△,通过证明ADM ADN △≌△,得BM CN =,结合等腰三角形的性质,即可完成证明.【详解】如下图,过点D 作DM AB ⊥,交AB 于点M ,过点D 做DN AC ⊥,交AC 于点N∵BAD CAD ∠=∠∴DM DN =直角ADM △和直角ADN △中DM DN AD AD=⎧⎨=⎩ ∴ADM ADN △≌△∴AM AN =∵点D 为BC 的中点,∴BD CD =直角BDM 和直角CDN △中DM DN BD CD=⎧⎨=⎩ ∴BDM CDN ≌∴BM CN =∵AB AM BM =+,AC AN CN =+∴AB AC =,即ABC 是等腰三角形.【点睛】本题考查了角平分线、三角形中线、全等三角形、等腰三角形的知识;解题的关键是熟练掌握角平分线、三角形中线,全等三角形的性质,从而完成求解.8、(1)∠E =35°;(2)AH ⊥BE .理由见解析.【分析】(1)根据等腰三角形两底角相等,已知顶角,可以求出底角,再根据角平分线的定义求出∠CBD 的度数,最后根据两直线平行,内错角相等求出;(2)由“SAS ”可证△ABD ≌△AEF ,可得AD =AF ,由等腰三角形的性质可求解.【详解】解:(1)∵AB =AC ,∴∠ABC =∠ACB ,∵∠BAC =40°,∴∠ABC =12(180°-∠BAC )=70°,∵BD 平分∠ABC ,∴∠CBD =12∠ABC =35°,∵AE ∥BC ,∴∠E =∠CBD =35°;(2)∵BD 平分∠ABC ,∠E =∠CBD ,∴∠CBD =∠ABD =∠E ,∴AB =AE ,在△ABD 和△AEF 中,AB AE E ABD BD EF =⎧⎪∠=∠⎨⎪=⎩, ∴△ABD ≌△AEF (SAS ),∴AD =AF ,∵点H 是DF 的中点,∴AH ⊥BE .【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,证明三角形全等是解题的关键.9、(1)85︒;(2)①作图见解析;②证明见解析【分析】(1)等边三角形ABC 中60BAC B C ∠=∠=∠=︒,由AD AE =知ADC AEB ∠=∠,ADC B BAD ∠=∠+∠,进而求出AEB ∠的值;(2)①作图见详解;②ADE B BAD ∠=∠+∠ ,AED C EAC ∠=∠+∠,BAD EAC ∠=∠,点E ,F 关于直线AC 对称,EAC FAC ∠=∠,AE AF AD ==,60FAC DAC BAD DAC ∠+∠=∠+∠=︒,ADF 为等边三角形,进而可得到AD DF =.【详解】解:(1)ABC 为等边三角形85ADC BAD B ∴∠=∠+∠=︒AD AE =85AEB ADC ∴∠=∠=︒.(2)①补全图形如图所示,②证明:ABC 为等边三角形60B C BAC ∴∠=∠=∠=︒AD AE =ADE AED ∴∠=∠ADE B BAD ∠=∠+∠ ,AED C EAC ∠=∠+∠BAD EAC ∴∠=∠点E ,F 关于直线AC 对称EAC FAC ∠=∠∴,AE AF =60FAC DAC BAD DAC ∴∠+∠=∠+∠=︒即60DAF=∠︒AD AF =ADF ∴为等边三角形AD AF ∴=.【点睛】本题考察了等边三角形的判定与性质,等腰三角形的性质,轴对称的性质.解题的关键在于角度的转化.10、(1)见解析;(2)△AEF 、△ADG 、△DCF 、△ECD【分析】(1)根据已知条件得到∠BAE =∠CAD ,根据全等三角形的性质得到∠AED =∠ABC ,根据等腰三角形的性质得到∠ABC =∠AEB ,于是得到结论;(2)根据等腰三角形的判定定理即可得到结论.【详解】证明:(1)如图1,∵∠BAE =∠CAD ,∴∠BAE +∠CAE =∠CAD +∠CAE ,即∠BAC =∠EAD ,在△AED 与△ABC 中,AB AE BAC EAD AD AC ⎧⎪∠∠⎨⎪⎩=== ∴△AED ≌△ABC ,∴∠AED =∠ABC ,∵∠BAE +∠ABC +∠AEB =180°,∠CED +∠AED +∠AEB =180°,∵AB =AE ,∴∠ABC =∠AEB ,∴∠BAE +2∠AEB =180°,∠CED +2∠AEB =180°,∴∠DEC =∠BAE ;(2)解:如图2,①∵∠BAE=∠CAD=30°,∴∠ABC=∠AEB=∠ACD=∠ADC=75°,由(1)得:∠AED=∠ABC=75°,∠DEC=∠BAE=30°,∵AD⊥AB,∴∠BAD=90°,∴∠CAE=30°,∴∠AFE=180°−30°−75°=75°,∴∠AEF=∠AFE,∴△AEF是等腰三角形,②∵∠BEG=∠DEC=30°,∠ABC=75°,∴∠G=45°,在Rt△AGD中,∠ADG=45°,∴△ADG是等腰直角三角形,③∠CDF=75°−45°=30°,∴∠DCF=∠DFC=75°,∴△DCF是等腰直角三角形;④∵∠CED=∠EDC=30°,∴△ECD是等腰三角形.【点睛】本题考查了全等三角形的判定与性质,等腰直角三角形的判定,等腰三角形的判定和性质,熟练掌握全等三角形的判定与性质是解题的关键.。
2021-2022学年基础强化沪教版七年级数学第二学期第十四章三角形月考试卷

沪教版七年级数学第二学期第十四章三角形月考考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、以下长度的三条线段,能组成三角形的是( )A .2,3,5B .4,4,8C .3,4.8,7D .3,5,92、已知,ABC ,DEF ,MNP △的相关数据如图所示,则下列选项正确的是( )A .ABC PNM ≌B .DEF PNM ≌C .PN EF =D .F A ∠=∠3、如图,ABN ≌ACM △,B 和C ∠是对应角,AB 和AC 是对应边,则下列结论中一定成立的是( )A .BAM MAN ∠=∠B .AM CN ==C.BAM ABM∠=∠D.AM AN4、已知等腰三角形两边的长分别为3和7,则此等腰三角形的周长为()A.10 B.15 C.17 D.195、等腰三角形的一个顶角是80°,则它的底角是().A.40°B.50°C.60°D.70°6、如图,等腰△ABC中,AB=AC,点D是BC边中点,则下列结论不正确...的是()A.∠B=∠C B.AD⊥BC C.∠BAD=∠CAD D.AB=2BC7、已知三角形的两边长分别为2cm和3cm,则第三边长可能是()A.6cm B.5cm C.3cm D.1cm8、如图,ABC的面积为18,AD平分∠BAC,且AD⊥BD于点D,则ADC的面积是()A.8 B.10 C.9 D.16∠的度数为()9、三个等边三角形的摆放位置如图所示,若12100∠+∠=°,则3A.80︒B.70︒C.45︒D.3010、如图,AC=BC,∠C=α,DE⊥AC于E,FD⊥AB于D,则∠EDF等于().αC.90°-αD.180°-2αA.αB.90°-12第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,两根旗杆CA,DB相距20米,且CA⊥AB,DB⊥AB,某人从旗杆DB的底部B点沿BA走向旗杆CA底部A点.一段时间后到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角∠CMD=90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为每秒2米,则这个人从点B到点M 所用时间是 _____秒.2、如图,在Rt△ABC中,∠C=90°,两锐角的角平分线交于点P,点E、F分别在边BC、AC上,且都不与点C重合,若∠EPF=45°,连接EF,当AC=6,BC=8,AB=10时,则△CEF的周长为_____.3、如图,在△ABC 中,已知点D E F 、、分别为BC AD CE 、、的中点,若△ABC 的面积为24m ,则阴影部分的面积为 _________ 2cm4、如图,1AP 为△ABC 的中线,2AP 为△1APC 的中线,3AP 为△2AP C 的中线,……按此规律,n AP 为△1n AP C 的中线.若△ABC 的面积为8,则△n AP C 的面积为_______________.5、如图,点C 是线段AB 的中点,DA EC ∥.请你只添加一个条件,使得DAC △≌ECB .(1)你添加的条件是______;(要求:不再添加辅助线,只需填一个答案即可)(2)依据所添条件,判定DAC △与ECB 全等的理由是______.三、解答题(10小题,每小题5分,共计50分)1、阅读填空,将三角尺(△MPN ,∠MPN =90°)放置在△ABC 上(点P 在△ABC 内),如图①所示,三角尺的两边PM 、PN 恰好经过点B 和点C ,我们来研究∠ABP 与∠ACP 是否存在某种数量关系.(1)特例探索:若∠A =50°,则∠PBC +∠PCB = 度,∠ABP +∠ACP = 度.(2)类比探索:∠ABP、∠ACP、∠A 的关系是 .(3)变式探索:如图②所示,改变三角尺的位置,使点P 在△ABC 外,三角尺的两边PM 、PN 仍恰好经过点B 和点C ,则∠ABP、∠ACP、∠A 的关系是 .2、如图,ABC 是等边三角形,D 点是BC 上一点,2BD CD =,DE AB ⊥于点E ,CE 交AD 于点P .求APE ∠的度数.3、ABC 中,CD 平分ACB ∠,点E 是BC 上一动点,连接AE 交CD 于点D .(1)如图1,若110ADC ∠=︒,AE 平分BAC ∠,则B 的度数为______;(2)如图2,若100ADC ∠=︒,53DCE ∠=︒,27B BAE ∠-∠=︒,则BAE ∠的度数为______;(3)如图3,在BC 的右侧过点C 作CF CD ⊥,交AE 延长线于点F ,且AC CF =,2B F ∠=∠.试判断AB 与CF 的位置关系,并证明你的结论.4、ACB △中,90C ∠=︒,以点A 为中心,分别将线段AB ,AC 逆时针旋转60︒得到线段AD ,AE ,连接DE ,延长DE 交CB 于点F .(1)如图1,若60A ∠=︒,CFE ∠的度数为________;(2)如图2,当3060A ︒<∠<︒吋,①依题意补全图2;②猜想CF 与AC 的数量关系,并加以证明.5、如图,AD ,BC 相交于点O ,AO =DO .(1)如果只添加一个条件,使得△AOB ≌△DOC ,那么你添加的条件是 (要求:不再添加辅助线,只需填一个答案即可);(2)根据已知及(1)中添加的一个条件,证明AB =DC .6、如图,在ABC 中,CD 是ACB ∠的平分线,点E 在边AC 上,且DE CE =.(Ⅰ)求证:∥DE BC ;(Ⅱ)若50A ∠=︒,60B ∠=︒,求BDC ∠的大小.7、在四边形ABCD 中,AB BC ∥,点E 在直线AB 上,且DE CE =.(1)如图1,若90DEC A ∠=∠=︒,3BC =,2AD =,求AB 的长;(2)如图2,若DE 交BC 于点F ,DFC AEC ∠=∠,求证:BC AB AD =+.8、如图,△ABC 中,AB =AC ,D 为BC 边的中点,AF ⊥AD ,垂足为A .求证:∠1=∠29、如图,CE ⊥AB 于点E ,BF ⊥AC 于点F ,BD =CD .(1)求证:△BDE ≌△CDF ;(2)求证:AE =AF .10、(1)我们把两个面积相等但不全等的三角形叫做“偏等积三角形”,如图1,ABC 中,7,9,10===AC BC AB ,P 为AC 上一点,当AP =_______时,ABP △与CBP 是偏等积三角形;(2)如图2,四边形ABED 是一片绿色花园,ACB △、DCE 是等腰直角三角形,()90090∠=∠=︒<∠<︒ACB DCB BCE .①ACD △与BCE 是偏等积三角形吗?请说明理由;②已知60m,=BE ACD 的面积为22100m .如图3,计划修建一条经过点C 的笔直的小路CF ,F 在BE 边上,FC 的延长线经过AD 中点G .若小路每米造价600元,请计算修建小路的总造价.-参考答案-一、单选题1、C【分析】由题意根据三角形的三条边必须满足:任意两边之和大于第三边,任意两边之差小于第三边进行分析即可.【详解】解:A 、2+3=5,不能组成三角形,不符合题意;B 、4+4=8,不能组成三角形,不符合题意;C 、3+4.8>7,能组成三角形,符合题意;D 、3+5<9,不能组成三角形,不符合题意.故选:C .【点睛】本题主要考查对三角形三边关系的理解应用.注意掌握判断是否可以构成三角形,只要判断两个较小的数的和大于最大的数即可.2、D【分析】根据三角形内角和定理分别求出三个三角形中未知角的度数,然后依据全等三角形的判定定理,从三个三角形中寻找条件证明全等,即可得出选项.【详解】解:180307080C ∠=︒-︒-︒=︒,180308070F ∠=︒-︒-︒=︒,在ABC ∆与ΔΔΔΔ中,C D B E AB EF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴ABC ∆≅ΔΔΔΔ,∴A F ∠=∠,A 、B 、C 三个选项均不能证明,故选:D .【点睛】题目主要考查三角形内角和定理、全等三角形的判定和性质,理解题意,熟练运用全等三角形的判定定理是解题关键.3、D【分析】根据全等三角形的性质求解即可.【详解】解:∵ABN ≌ACM △,B 和C ∠是对应角,AB 和AC 是对应边,∴BAN CAM ∠=∠,AM AN =,∴BAM CAN =∠∠,∴选项A 、B 、C 错误,D 正确,故选:D .【点睛】本题考查全等三角形的性质,熟练掌握全等三角形的性质是解答的关键.4、C【分析】等腰三角形两边的长为3和7,具体哪条是底边,哪条是腰没有明确说明,因此要分两种情况讨论.【详解】解:①当腰是3,底边是7时,3+3<7,不满足三角形的三边关系,因此舍去.②当底边是3,腰长是7时,3+7>7,能构成三角形,则其周长=3+7+7=17.故选:C.【点睛】本题考查了等腰三角形的性质和三角形的三边关系,解题时注意:若没有明确腰和底边,则一定要分类进行讨论,还应验证各种情况是否能构成三角形,这是解题的关键.5、B【分析】依据三角形的内角和是180°以及等腰三角形的性质即可解答.【详解】解:(180°-80°)÷2=100°÷2=50°;答:底角为50°.故选:B.【点睛】本题主要考查三角形的内角和定理及等腰三角形的两个底角相等的特点.6、D【分析】根据等腰三角形的等边对等角的性质及三线合一的性质判断.【详解】解:∵AB=AC,点D是BC边中点,∴∠B=∠C,AD⊥BC,∠BAD=∠CAD,故选:D.【点睛】此题考查了等腰三角形的性质:等边对等角,三线合一,熟记等腰三角形的性质是解题的关键.7、C【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.【详解】解:设第三边长为x cm,根据三角形的三边关系可得:3-2<x<3+2,解得:1<x<5,只有C选项在范围内.故选:C.【点睛】本题考查了三角形的三边关系,关键是掌握第三边的范围是:大于已知的两边的差,而小于两边的和.8、C【分析】延长BD交AC于点E,根据角平分线及垂直的性质可得:BAD EAD∠=∠,依据全等∠=∠,ADB ADE三角形的判定定理及性质可得:ABD AED=,再根据三角形的面积公式可得:≌,BD DEΔΔΔΔΔ,求解即可.ΔΔΔΔΔ=ΔΔΔΔΔ,ΔΔΔΔΔ=ΔΔΔΔΔ,得出ΔΔΔΔΔ=12【详解】解:如图,延长BD 交AC 于点E ,∵AD 平分BAE ∠,AD BD ⊥,∴BAD EAD ∠=∠,ADB ADE ∠=∠,在ABD 和AED 中,BAD EAD AD ADADB ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∴ABD AED ≌,∴BD DE =,∴ΔΔΔΔΔ=ΔΔΔΔΔ,ΔΔΔΔΔ=ΔΔΔΔΔ,∴ΔΔΔΔΔ=12ΔΔΔΔΔ=12×18=9,故选:C .【点睛】题目主要考查全等三角形的判定和性质,角平分线的定义等,熟练掌握基础知识,进行逻辑推理是解题关键.9、A【分析】利用三个平角的和减去中间三角形的内角和,再减去三个60︒的角即可.【详解】解:3180540⨯︒=︒,360180⨯︒=︒,540180180180∴︒-︒-︒=︒,123180∴∠+∠+∠=︒,12100∠+∠=︒,380∴∠=︒,故选:A .【点睛】本题主要考查了三角形的内角和定理,灵活运用三角形内角和定理成为解答本题的关键.10、B【分析】AC =BC ,∠C =α,DE ⊥AC 于E ,FD ⊥AB 于D ,有1802B A α︒-∠=∠=,90ADE A ∠=︒-∠,90EDF ADE ∠=︒-∠,即可求得角度. 【详解】 解:由题意知:1802B A α︒-∠=∠=,90ADF ∠=︒ 180909022ADE A αα︒-∠=︒-∠=︒-= 90902EDF ADE α∠=︒-∠=︒-故选B .【点睛】本题考查了等腰三角形的性质,几何图形中角度的计算.解题的关键在于确定各角度之间的数量关系.二、填空题1、4【分析】先说明C DMB ∠=∠,再利用AAS 证明ACM BMD ≌,然后根据全等三角形的性质可得12AM BD ==米,再根据线段的和差求得BM 的长,最后利用时间=路程÷速度计算即可.【详解】解:∵90CMD ∠=︒,∴90CMA DMB +=︒∠∠,又∵90CAM ∠=︒,∴90CMA C ︒∠+∠=,∴C DMB ∠=∠,在Rt ACM 和Rt BMD △中,A B C DMB CM MD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴()Rt ACM Rt BMD AAS ≌,∴12AM BD ==米,20128BM =-=(米),∵该人的运动速度2m/s ,他到达点M 时,运动时间为824÷=s .故答案为:4.【点睛】本题主要考查了全等三角形的判定与性质,根据题意证得Rt ACM Rt BMD ≌是解答本题的关键. 2、4【分析】根据题意过点P 作PM ⊥BC 于M ,PN ⊥AC 于N ,PK ⊥AB 于K ,在EB 上取一点J ,使得MJ =FN ,连接PJ ,进而利用全等三角形的性质证明EF =EM +EN ,即可得出结论.【详解】解:如图,过点P 作PM ⊥BC 于M ,PN ⊥AC 于N ,PK ⊥AB 于K ,在EB 上取一点J ,使得MJ =FN ,连接PJ .∵BP 平分∠BC ,PA 平分∠CAB ,PM ⊥BC ,PN ⊥AC ,PK ⊥AB ,∴PM =PK ,PK =PN ,∴PM =PN ,∵∠C =∠PMC =∠PNC =90°,∴四边形PMCN 是矩形,∴四边形PMCN 是正方形,∴CM =PM ,∴∠MPN =90°,在△PMJ 和△PNF 中,90PM PN PMJ PNF MJ NF =⎧⎪∠=∠=︒⎨⎪=⎩, ∴△PMJ ≌△PNF (SAS ),∴∠MPJ =∠FPN ,PJ =PF ,∴∠JPF =∠MPN =90°,∵∠EPF =45°,∴∠EPF =∠EPJ =45°,在△PEF 和△PEJ 中,PE PE EPF EPJ PF PJ =⎧⎪∠=∠⎨⎪=⎩, ∴△PEF ≌△PEJ (SAS ),∴EF =EJ ,∴EF =EM +FN ,∴△CEF 的周长=CE +EF +CF =CE +EM +CF +FN =2EM =2PM ,∵S △ABC =12•BC •AC =12(AC +BC +AB )•PM ,∴PM =2,∴△ECF 的周长为4,故答案为:4.【点睛】本题考查角平分线的性质定理,正方形的判定,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问.3、1【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.【详解】解:∵点E 是AD 的中点,∴S △ABE =12S △ABD ,S △ACE =12S △ADC ,∴S △ABE +S △ACE =12S △ABC =12×4=2cm 2,∴S △BCE =12S △ABC =12×4=2cm 2,∵点F 是CE 的中点,∴S △BEF =12S △BCE =12×2=1cm 2.故答案为:1.【点睛】本题考查了三角形的面积,主要利用了三角形的中线把三角形分成两个面积相等的三角形,原理为等底等高的三角形的面积相等.4、312n -【分析】根据三角形的中线性质,可得△1APC 的面积=182⨯,△2AP C 的面积=2182⨯,……,进而即可得到答案.【详解】由题意得:△1APC 的面积=182⨯,△2AP C 的面积=2182⨯,……,△n AP C 的面积=182n ⨯=312n -. 故答案是:312n -.【点睛】 本题主要考查三角形的中线的性质,掌握三角形的中线把三角形的面积平分,是解题的关键.5、AD =CE (或∠D =∠E 或∠ACD =∠B )(答案不唯一) SAS【分析】(1)由已知条件可得两个三角形有一组对应边相等,一组对应角相等,根据三角形全等的判定方法添加条件即可;(2)根据添加的条件,写出判断的理由即可.【详解】解:(1)添加的条件是:AD=CE(或∠D=∠E或∠ACD=∠B)故答案为:AD=CE(或∠D=∠E或∠ACD=∠B)(2)若添加:AD=CE∵点C是线段AB的中点,∴AC=BC∵DA EC∥∠=∠∴A BCE△≌ECB(SAS)∴DAC故答案为:SAS【点睛】本题主要考查了添加条件判断三角形全等,熟练掌握全等三角形的判断方法是解答本题的关键.三、解答题1、(1)90,40 ;(2)∠ABP+∠ACP+∠A=90°;(3)∠A+∠ACP-∠ABP=90°.【分析】△和ABC中的角的关系即可.(1)由三角形内角和为180°计算BPC(2)由(1)所得即可得出∠ABP、∠ACP、∠A的关系为∠ABP+∠ACP+∠A=90°.(3)由三角形外角的性质即可推出∠A+∠ACP-∠ABP=90°.【详解】△中(1)在BPC∵∠MPN=90°∴∠PBC+∠PCB=180°-∠MPN=180°-90°=90°在ABC中∵∠A+∠ABC+∠ACB=180°又∵∠ABC=∠PBC+∠ABP,∠ACB=∠ACP+∠BCP∴∠A+∠PBC+∠ABP +∠ACP+∠BCP=180°∵∠PBC+∠PCB=90°,∠A=50°∴∠ABP +∠ACP=180°-90°-50°=40°(2)由(1)问可知∠A+∠PBC+∠ABP +∠ACP+∠BCP=180°又∵∠PBC+∠PCB=90°∴∠A+∠ABP +∠ACP=180°-(∠PBC+∠PCB)=180°-90°=90°(3)如图所示,设PN与AB交于点H∵∠A+∠ACP=∠AHP又∵∠ABP+∠MPN=∠AHP∴∠A+∠ACP=∠ABP+∠MPN又∵∠MPN=90°∴∠A+∠ACP=90°+∠ABP∴∠A+∠ACP-∠ABP=90°.【点睛】本题考查了三角形的性质以及三角尺的角度计算问题,三角板的角度分别为90°,45°,45°;90°,60°,30°两种直角三角尺,三角形内角和是180°,三角形的一个外角等于与它不相邻的两个内角的和.2、60APE ∠=︒【分析】由题意易得60ABC ACB ∠=∠=︒,AB AC BC ==,则有30BDE ∠=︒,然后可得BE CD =,进而可证BEC CDA ≌,则有BCE =∠∠CAD ,最后问题可求解.【详解】解:∵ABC 是等边三角形,∴60ABC ACB ∠=∠=︒,AB AC BC ==,∵DE AB ⊥,∴90DEB ∠=︒,∴30BDE ∠=︒,∴2BD BE =,∵2BD CD =,∴BE CD =,∴BEC CDA ≌(SAS ),∴BCE =∠∠CAD ,∵,60APE PAC ACP ACB DAC ACP ∠=∠+∠∠=∠+∠=︒,∴60APE ACB ∠=∠=︒.【点睛】本题主要考查等边三角形的性质、含30度直角三角形的性质及全等三角形的性质与判定,熟练掌握等边三角形的性质、含30度直角三角形的性质及全等三角形的性质与判定是解题的关键.3、(1)40°;(2)10°;(3)AB ∥CF ,理由见解析【分析】(1)根据三角形的角和定理和角平分线的定义可求得∠BAC+∠ACB=140°即可求解;(2)根据三角形的外角性质求得∠B+∠BAE=47°即可求解;(3)延长AC到G,根据等腰三角形的性质和三角形的外角性质得到∠FCG=2∠F,再根据角平分线的定义和等角的余角相等得到∠BCF=2∠F,则有∠B=∠BCF,根据平行线在判定即可得出结论.【详解】解:(1)∵∠ADC=110°,∴∠DAC+∠DCA=180°-110°=70°,∵AE平分∠BAC,CD平分∠ACB,∴∠BAC=2∠DAC,∠ACB=2∠DCA,∴∠BAC+∠ACB=2(∠DAC+∠DCA)=140°,∴∠B=180°-(∠BAC+∠ACB)=180°-140°=40°,故答案为:40°;(2)∵∠ADC=∠DCE+∠DEC=100°,∠DCE=53°,∴∠DEC=100°-53°=47°,∴∠B+∠BAE=∠DEC=47°,∵∠B-∠BAE=27°,∴∠BAE=10°,故答案为:10°;(3)AB∥CF,理由为:如图,延长AC到G,∵AC=CF,∴∠F=∠FAC,∴∠FCG=∠F+∠FAC=2∠F,∵CF⊥CD,∴∠BCF+∠BCD=90°,∠FCG+∠ACD=90°,∵CD平分∠ACB,∴∠BCD=∠ACD,∴∠BCF=∠FCG=2∠F,∵∠B=2∠F,∴∠B=∠BCF,∴AB∥CF.【点睛】本题考查角平分线的定义、三角形的内角和定理、三角形的外角性质、等腰三角形的性质、等角的余角相等、平行线的判定,熟练掌握相关知识的联系与运用是解答的关键.4、(1)120°(2)①图形见解析;②AC=【分析】(1)根据60∠=︒进而判断出点E在边AB上,得出△ADE≌△ABC(SAS),进而得出A∠AED=∠ACB=90°最后用三角形的外角的性质即可得出结论;(2)①依题意补全图形即可;②先判断出△ADE≌△ABC(SAS),进而得出∠AEF=90°,即可判断出Rt△AEF≌Rt△ACF,进而求出∠CAF=1∠CAE=30°,即可得出结论.2(1)(1)如图1,在Rt△ABC中,∠B=30°,∴∠BAC=60°,由旋转知,∠CAE=60°=∠CAB,∴点E在边AB上,∵AD=AB,AE=AC,∴△ADE≌△ABC(SAS),∴∠AED=∠ACB=90°,∴∠CFE=∠B+∠BEF=30°+90°=120°,故答案为120°;(2)(2)①依题意补全图形如图2所示,②如图2,连接AF,∵∠BAD=∠CAE,∴∠EAD=∠CAB,∵AD=AB,AE=AC,∴△ADE≌△ABC(SAS),∴∠AED=∠C=90°,∴∠AEF=90°,∴Rt△AEF≌Rt△ACF(HL),∴∠EAF=∠CAF,∠CAE=30°,∴∠CAF=12AF,且AC2+CF2=AF2,在Rt△ACF中,CF=12∴AC=【点睛】此题是三角形综合题,主要考查了旋转的性质,全等三角形的判定和性质,三角形的外角的性质,含30度角的直角三角形的性质,勾股定理,判断出△ADE≌△ABC是解本题的关键.∠=∠);(2)见解析5、(1)OB=OC(或A D∠=∠,或B C【分析】(1)根据SAS 添加OB =OC 即可;(2)由(1)得△AOB ≌△DOC ,由全等三角形的性质可得结论.【详解】解:(1)添加的条件是:OB =OC (或A D ∠=∠,或B C ∠=∠)证明:在AOB ∆和DOC ∆中AO BO AOB COD BO CO =⎧⎪∠=∠⎨⎪=⎩所以,△AOB ≌△DOC(2)由(1)知,△AOB ≌△DOC所以,AB =DC .【点睛】本题主要考查了全等三角形的判定与性质,熟练掌握全等三角形的判定方法是解答本题的关键6、(Ⅰ)见解析;(Ⅱ)85︒【分析】(Ⅰ)由CD 是ACB ∠的平分线得出DCB DCE ∠=∠,由DE CE =得出CDE DCE ∠=∠从而得出DCB CDE ∠=,由平行线的判断即可得证;(Ⅱ)由三角形内角和求出70ACB ∠=︒,由角平分线得出35BCD ∠=︒,由三角形内角和求出BDC ∠即可得出答案.【详解】(Ⅰ)∵CD 是ACB ∠的平分线,∴DCB DCE ∠=∠,∵DE CE =,∴CDE DCE ∠=∠,∴DCB CDE ∠=,∴∥DE BC ;(Ⅱ)∵50A ∠=︒,60B ∠=︒,∴180506070ACB ∠=︒-︒-︒=︒, ∴1352BCD ACB ∠=∠=︒,∴18085BDC B BCD ∠=︒-∠-∠=︒.【点睛】本题考查平行线的判定以及三角形内角和定理,掌握相关知识是解题的关键7、(1)5;(2)证明见解析【分析】(1)推出∠ADE =∠BEC ,根据AAS 证△AED ≌△CEB ,推出AE =BC ,BE =AD ,代入求出即可;(2)推出∠A =∠EBC ,∠AED =∠BCE ,根据AAS 证△AED ≌△BCE ,推出AD =BE ,AE =BC ,即可得出结论.【详解】(1)解:∵∠DEC =∠A =90°,∴∠ADE +∠AED =90°,∠AED +∠BEC =90°,∴∠ADE =∠BEC ,∵AD BC ∥,∠A =90°,∴∠B +∠A =180°,∴∠B =∠A =90°,在△AED 和△CEB 中A BADE BEC,DE EC∴△AED≌△BCE(AAS),∴AE=BC=3,BE=AD=2,∴AB=AE+BE=2+3=5.∥,(2)证明:∵AD BC∴∠A=∠EBC,∵∠DFC=∠AEC,∠DFC=∠BCE+∠DEC,∠AEC=∠AED+∠DEC,∴∠AED=∠BCE,在△AED和△BCE中AED BCEA EBC,DE EC∴△AED≌△BCE(AAS),∴AD=BE,AE=BC,∵BC=AE=AB+BE=AB+AD,即AB+AD=BC.【点睛】本题考查了三角形的外角的性质,全等三角形的性质和判定,平行线的性质等知识点的运用,掌握“利用AAS证明两个三角形全等”是解本题的关键.8、见详解.【分析】根据等腰三角形三合一性质以及等边对等角性质得出AD ⊥BC ,∠B =∠C ,根据AF ⊥AD ,利用在同一平面内垂直同一直线的两直线平行得出AF∥BC ,利用平行线性质得出∠1=∠B ,∠2=∠C 即可.【详解】证明:∵△ABC 中,AB =AC ,D 为BC 边的中点,∴AD ⊥BC ,∠B =∠C ,∵AF ⊥AD ,∴AF∥BC ,∴∠1=∠B ,∠2=∠C ,∴∠1=∠2.【点睛】本题考查等腰三角形性质,平行线的判定与性质,掌握等腰三角形性质,平行线的判定与性质是解题关键.9、(1)见解析;(2)见解析【分析】(1)根据CE ⊥AB ,BF ⊥AC 就可以得出∠BED =∠CFD =90°,就可以由AAS 得出结论;(2)由(1)得DE =DF ,就可以得出BF =CE ,由AAS 就可以得出△AFB ≌△AEC 就可以得出结论.【详解】证明:(1)∵CE ⊥AB ,BF ⊥AC ,∴∠BED =∠CFD =90°,在△BED 和△CFD 中,BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△BED ≌△CFD (AAS );(2)∵△BED ≌△CFD ,∴DE =DF ,∴BD +DF =CD +DE ,∴BF =CE ,在△ABF 和△ACE 中,B C A A BF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABF ≌△ACE (AAS ),∴AE =AF .【点睛】本题考查了垂直的性质的运用,全等三角形的判定与性质的运用,等式的性质的运用,解答时证明三角形全等是关键.10、(1)72;(2)①ACD △与BCE 是偏等积三角形,理由见详解;②修建小路的总造价为42000元【分析】(1)当AP CP =时,则72AP =,证ABP CBP S S ∆∆=,再证ABP ∆与CBP ∆不全等,即可得出结论;(2)①过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,证()ACM BCN AAS ∆∆≌,得AM BN =,则ACD BCE S S ∆∆=,再证ACD ∆与BCE ∆不全等,即可得出结论;②过点A 作//AN CD ,交CG 的延长线于N ,证得()AGN DGC AAS ∆∆≌,得到AN CD =,再证()ACN CBE SAS ∆∆≌,得ACN CBE ∠=∠,由余角的性质可证CF BE ⊥,然后由三角形面积和偏等积三角形的定义得12BCE S BE CF ∆=⋅,2100BCEACD S S ∆∆==,求出70()CF m =,即可求解. 【详解】解:(1)当72AP CP ==时,ABP ∆与CBP ∆是偏等积三角形,理由如下:设点B 到AC 的距离为h ,则12ABP S AP h ∆=⋅,12CBP S CP h ∆=⋅,ABP CBP S S ∆∆∴=, 10AB =,7BC =,AB BC ∴≠,AP CP =、PB PB =,ABP ∴∆与CBP ∆不全等,ABP ∴∆与CBP ∆是偏等积三角形, 故答案为:72;(3)①ACD ∆与BCE ∆是偏等积三角形,理由如下:过A 作AM DC ⊥于M ,过B 作BN CE ⊥于N ,如图3所示:则90AMC BNC ∠=∠=︒,ACB ∆、DCE ∆是等腰直角三角形,90ACB DCE ∴∠=∠=︒,AC BC =,CD CE =,3603609090180BCN ACD ACB DCE ∴∠+∠=︒-∠-∠=︒-︒-︒=︒,180ACM ACD ∠+∠=︒,ACM BCN ∴∠=∠,在∆ACM 和BCN ∆中,ACM BCN AC BC ⎪∠=∠⎨⎪=⎩, ()ACM BCN AAS ∴∆∆≌,AM BN ∴=,12ACD S CD AM ∆=⋅,12BCE S CE BN ∆=⋅, ACD BCE S S ∆∆∴=,180BCE ACD ∠+∠=︒,090BCE ︒<∠<︒,ACD BCE ∴∠≠∠,CD CE =,AC BC =,ACD ∴∆与BCE ∆不全等,ACD ∴∆与BCE ∆是偏等积三角形;②如图4,过点A 作//AN CD ,交CG 的延长线于N ,则N GCD ∠=∠, G 点为AD 的中点,AG GD ∴=,在AGN ∆和DGC ∆中,AGN DGC AG DG ⎪∠=∠⎨⎪=⎩, ()AGN DGC AAS ∴∆∆≌,AN CD ∴=,CD CE =,AN CE ∴=,//AN CD ,180CAN ACD ∴∠+∠=︒,90ACB DCE ∠=∠=︒,3609090180ACD BCE ∴∠+∠=︒-︒-︒=︒,BCE CAN ∴∠=∠,在ACN ∆和CBE ∆中,AN CE CAN BCE AC CB =⎧⎪∠=∠⎨⎪=⎩, ()ACN CBE SAS ∴∆∆≌,ACN CBE ∴∠=∠,1809090ACN BCF ∠+∠=︒-︒=︒,90CBE BCF ∴∠+∠=︒,90BFC ∴∠=︒,CF BE ∴⊥.由①得:ACD ∆与BCE ∆是偏等积三角形,12BCE S BE CF ∆∴=⋅,2100BCE ACD S S ∆∆==, 22210070()60BCE S CF m BE ∆⨯∴===, ∴修建小路CF 的总造价为:6007042000⨯=(元).【点睛】本题是四边形综合题目,考查了新定义“偏等积三角形”的定义、全等三角形的判定与性质、等腰直角三角形的性质、三角形面积等知识;本题综合性强,熟练掌握“偏等积三角形”的定义,证明ACM BCN ∆∆≌和ACN CBE ∆∆≌是解题的关键,属于中考常考题型.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形
一、单选题
1.下列结论正确的是( )
A .面积相等的两个三角形全等
B .等边三角形都全等
C .底边和顶角对应相等的等腰三角形全等
D .两个等腰直角三角形全等
2.如图,△ABC△△DBE ,△DBC=150°,△ABD=40°,则△ABE 的度数是( )
A .70°
B .65°
C .60°
D .55°
3.如图,已知△ABC△△DEF ,若AC =22,CF =4,则CD 的长是( )
A .22
B .18
C .16
D .4
4.如图,点P 在BC 上,AB BC ⊥于点B ,DC BC ⊥于点C ,ABP DCP V V ≌,其中BP CD =,则下列结论中错误的是( )
A .A
B P
C = B .AP P
D = C .APB D ∠=∠ D .90A CPD ∠+∠=︒ 5.如图,已知AB =D
E ,△B =△DE
F ,下列条件中不能判定△ABC △△DEF 的是( )
A.△A=△D B.AC△DF
C.BE=CF D.AC=DF
6.下列各图中a、b、c为三角形的边长,则甲、乙、丙三个三角形和左侧△ABC全等的是()
A.甲和乙B.乙和丙C.甲和丙D.只有丙
7.下面是课本中“作一个角等于已知角”的尺规作图过程.已知:△AOB.求作:一个角,使它等于△AOB.作法:如图
(1)作射线O'A';
(2)以O为圆心,任意长为半径作弧,交OA于C,交OB于D;
(3)以O'为圆心,OC为半径作弧C'E',交O'A'于C';
(4)以C'为圆心,CD为半径作弧,交弧C'E'于D';
(5)过点D'作射线O'B'.
则△A'O'B'就是所求作的角.
请回答:该作图的依据是()
A .SSS
B .SAS
C .ASA
D .AAS
8.如图,在Rt AEB V 和Rt AFC V 中,BE 与AC 相交于点M ,与CF 相交于点D ,AB 与CF 相交于N ,90E F EAC FAB ︒∠=∠=∠=∠,.AE AF =给出下列结论:△B C ∠=∠;△CD=DN;△BE=CF ;△△ACN△△ABM .其中正确的结论是 ( )
A .△△△
B .△△△
C .△△△
D .△△△
9.小红用如图所示的方法测量小河的宽度.她利用适当的工具,使AB △BC ,
BO =OC ,CD △BC ,点A 、O 、D 在同一直线上,就能保证△ABO △△DCO ,从而可通过测量CD 的长度得知小河的宽度AB .在这个问题中,可作为证明△ABO △△DCO 的依据的是( )
A .SAS 或SSS
B .AAS 或SSS
C .ASA 或AAS
D .ASA 或SAS 10.程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q 在轨道槽AM 上运动,点P 既能在以A 为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN 上运动,图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:
△当△PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
△当△PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
△当△PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
△当△PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是( )
A .△△
B .△△
C .△△△
D .△△△△
二、填空题
11.如果ABC ADC △≌△,AB AD =,70B ∠=︒,3BC cm =,那么D ∠=___;DC =___cm .
12.一个三角形的三边为2、5、x ,另一个三角形的三边为y 、2、6,若这两个三角形全等,则x + y =________.
13.如图,AB△DC ,请你添加一个条件使得△ABD△△CDB ,可添条件是__________
14.王老师一块教学用的三角形玻璃不小心打破了,他想再到玻璃店划一块同样大小的三角形玻璃,为了方便他只要带第________块就可以.
三、解答题
15.如图所示,已知∆ACE△∆DBF ,AD=8,BC=3,
(1)求AC 的长.
(2)CE 与BF 平行吗?说明理由.
16.如图,把三角形纸片'A BC 沿D 折叠,点A '落在四边形BCDE 内部点A 处,
(1)写出图中一对全等的三角形,井写出它们的所有对应角.
(2)设AED ∠的度数为x ,ADE ∠的度数为y ,那么1,2∠∠的度数分别是多少(用含x 或y 的式子表示)?
(3)A ∠与12∠+∠之间有一种数量关系始终保持不变,请找出这个规律,井说明理由. 17.如图,有一个池塘,要到池塘两侧AB 的距离,可先在平地上取一个点C ,从C 不经过池塘可以到达点A 和B ,连接AC 并延长到点D ,使CD =CA ,连接BC 并延长到点E ,使
CE =CB ,连接DE ,那么量出DE 的长就是A ,B 的距离,为什么?
18.如图,在等腰△ABC 中,AB =AC ,CE 、BD 分别为△ACB 、△ABC 的角平分线,CE 、BD 相交于P .
(1)求证:CD =BE ;
(2)若△A =98°,求△BPC 的度数.
19.如图,在ABC ∆中,90C ∠=︒,4cm AC BC ==,点D 是斜边AB 的中点.点E 从点B 出发以1cm/s 的速度向点C 运动,点F 同时从点C 出发以一定的速度沿射线CA 方向运动,规定当点E 到终点C 时停止运动.设运动的时间为x 秒,连接DE 、DF .
(1)填空:ABC S ∆=______2cm ;
(2)当1x =且点F 运动的速度也是1cm/s 时,求证:DE DF =;
(3)若动点F 以3cm /s 的速度沿射线CA 方向运动,在点E 、点F 运动过程中,如果存
在某个时间x ,使得ADF ∆的面积是BDE ∆面积的两倍,请你求出时间x 的值。
