第11讲 数学建模竞赛题选讲(2)
2011全国数学建模竞赛B题附件2

全市路口节点标号路口所属区域1413359A 1.7说明:2403343A 2.13383.5351A 2.24381377.5A 1.75339376A 2.16335383A 2.57317362A 2.48334.5353.5A 2.49333342A 2.1坐标的长度单位为毫米10282325A 1.611247301A 2.612219316A 2.413225270A 2.214280292A 2.515290335A 2.116337328A 2.617415335A 2.518432371A 1.919418374A 1.820444394A 1.921251277A 1.422234271A 1.423225265A 2.424212290A 1.125227300A 1.626256301A 1.227250.5306A 0.828243328A 1.329246337A 1.430314367A 2.1路口的横坐标X 路口的纵坐标Y 发案率(次数)A列:是全市交通网络中路口节点的标号(序号)B列:路口节点的横坐标X,是在交通网络中的实际横坐标值C列:路口节点的纵坐标Y,是在交通网络中的实际纵坐标值D列:路口节点所属的区E列:各路口节点的发案率是每个路口平均每天的发生报警案件数量地图距离和实际距离的比例是1:100000,即1毫米对应100米31315351A 1.632326355A 1.5案发地P点的标号:32 33327350A 1.434328342.5A 1.735336339A 1.436336334A 1.137331335A0.138371330A 1.239371333A 1.440388.5330.5A 1.741411327.5A 1.442419344A 1.443411343A 1.744394346A 1.145342342A 1.446342348A 1.247325372A 1.648315374A 1.449342372A 1.250345382A 1.151348.5380.5A0.852351377A0.653348369A 1.454370363A0.955371353A156354374A0.557363382.5A0.858357387A 1.159351382A0.960369388A0.761335395A0.662381381A 1.2 63391375A 1.4 64392366A0.8 65395361A0.7 66398362A0.8 67401359A0.8 68405360A0.9 69410355A 1.1 70408350A0.9 71415351A 1.1 72418347A0.8 73422354A0.9 74418.5356A 1.1 75405.5364.5A0.8 76405368A 1.1 77409370A0.8 78417364A0.8 79420370A0.8 80424372A0.8 81438368A 1.4 82438.5373A 1.1 83434376A0.9 84438385A1 85440392A 1.2 86447392A 1.4 87448381A 1.1 88444.5383A0.9 89441385A 1.4 90440.5381.5A0.9 91445380A0.9 92444360A0.893140130B 1.6 94145118B 1.6 9516096B 1.6 96142.571B 2.1 9715070B 1.8 98186145B 1.6 9915873.5B 2.6 10012168B 2.6 101157145B 1.1 102158138.5B0.9 103159135B0.5 104133114B0.7 105137.5113B0.4 106144112B0.8 107139117B0.2 108144.5115B0.8 109151113B0.6 110151.5118B0.9 111150111B0.8 112158118B 1.1 113159109B0.8 114164108.5B0.4 115163105B0.7 11614999.5B 1.2 117143102B0.8 118137103B0.9 119131103B0.5 120130100B0.6 121127102B0.6 12212598B0.8 12312996B0.912413090B0.4 12512490B0.7 12613696B 1.1 12713690B0.8 12814296B0.8 12914896B0.7 13014291B0.6 13114791B0.7 13212871B 1.2 133136.576B0.8 13414279B 1.1 13514781B0.8 13615486B0.9 137148.574.5B 1.1 13814070B0.6 13914063B0.7 140137.563B0.8 14113859B0.4 14214363B 1.1 14315169B0.8 14415363B 1.1 14514360B0.7 14614357B0.6 14714351.5B0.8 14816065B 1.1 14916259B0.6 15014149B0.4 15114340B0.8 15215144B0.5 15315033B0.1 154164124B0.6155171125B0.7 156165.5139B 1.1 157181131B 1.4 158176141B 1.6 159170140B0.8 160168145B0.6 161166150B0.8 162176145B0.6 163180149B0.7 164183145B 1.1 165202131B 1.1 166137.5462C 2.6 167167399C 2.2 168376400C 1.4 169210390C 2.6 170263445C 2.2 171284409C 1.9 172278.5425C 2.2 173295382C2 174299444C 2.6 175362443C 2.2 176410408.5C 2.1 177395520C 2.2 178277496C 1.7 179235465C 2.2 180200466.5C 1.9 181167462C 2.4 182225443C 2.4 183400447C 1.2 184414422C 1.4 185424400C 1.2186411396C 1.4 187420401C0.8 188403404C 1.2 189376406C0.9 190380404C0.8 191377424C0.8 192374424C0.8 193370423C0.4 194368427.5C0.9 195374431C 1.2 196365448C 1.4 197356450C 1.4 198358459C 1.2 199354495C 1.1 200357513C 1.2 201359528C0.4 202347553C0.5 203261537.5C0.8 204270514C 1.4 205313511.5C0.4 206324511C0.8 207333511C0.7 208334497C0.8 209323497C0.7 210312498C 1.1 211317451C 1.1 212316448C0.8 213315.5444C0.7 214316434C0.9 215318412C 1.2 216291.5415C 1.4217284425C 1.4 218281421C 1.6 219299434C 1.4 220302451C 1.4 221305457C 1.2 222281458.5C 1.1 223274448C0.8 224273.5444C0.9 225267446C 1.1 226270440C0.9 227275422C 1.1 228276419C 1.2 229270415C0.8 230276405C 1.4 231288403C 1.4 232293.5392.5C 1.4 233296387C 1.1 234303386C 1.4 235298.5378C 1.6 236293376C 1.2 237296372C 1.7 238276352C1 239250350C 1.4 240247384C 1.2 241262399C 1.4 242269397C 1.2 243276402C 1.3 244282398.5C 1.2 245282386.5C 1.1 246273389C 1.2 247276361C 1.1248138.5378C0.8 249155396C 1.2 250163390C 1.5 251173364C 1.2 252183370C 1.2 253238382C0.7 254213412C0.8 255189413C 1.1 256210433C0.9 257201434C0.9 258150400C 1.2 259135395C 1.2 260143407C 1.1 261142414C0.8 262140430C 1.1 263121432C0.9 264109441C0.5 265138.5442C 1.2 266167442C 1.6 267168435C 1.4 268184440C 1.2 269194442C0.9 270200442C 1.4 271212443C 1.6 272220443C 1.7 273246444C 2.1 274246455C 1.4 275252458C 1.2 276257460.5C 1.5 277255.5466C 1.2 278249464C 1.1279247469C0.8 280254472C0.7 281251.5477C 1.1 282259478C0.8 283261470C0.4 284255494C 1.4 285240495C 1.4 286241514C0.8 287236514C0.7 288235496C0.7 289232487C0.8 290235.5486.5C0.8 291245474C 1.2 292225457.5C 1.4 293225451C 1.6 294219451C 1.4 295219462C 1.2 296228.5472C 1.6 297213481C 1.4 298211487C1 299208.5496C 1.2 300206507C0.8 301206515C 1.2 302200514C0.7 303200507C 1.2 304200497C 1.3 305200484C 1.4 306206466C 1.4 307194466C 1.4 308184463.5C 1.5 309184475C0.8310193.5475C0.7 311193484C0.9 312184484C0.6 313184496.5C0.8 314192.5496.5C0.7 315192507C0.9 316192514C0.8 317170516.5C0.6 318168507C 1.1 319167495.5C 1.4 320101343D 2.4 32191355D 1.7 32270377D 2.5 32346371D 2.4 32456424D 2.1 32520442D 2.2 32674326D 2.6 32776302D 2.1 32815240D 2.6 32928161D0.4 33034.5164.5D0.1 33130181D0.6 33227206D0.2 33342242D 1.4 33430246D 1.6 33531254D 1.1 33639254D 1.2 33750289D0.7 33872288D 1.1 33960246D0.7 34095299D 1.434181297D 1.6 34280287D 1.4 34367314D 1.7 34421330D 1.1 34536360D 1.2 34676344D0.8 34797339D 2.4 348103337D 1.2 349104341D 1.1 35097345D 1.6 35189345D0.8 35281344.5D0.8 35381350D0.4 35489350D0.7 35592.5351.5D 1.1 35688353D 1.4 35781.5353D0.9 35887359D 1.1 35984361D0.9 36076355D0.8 36158.5370D0.6 36234306D0.1 36338418.5D 1.4 36461425D 1.4 36557429D 1.6 36660433D 1.4 36785369D 1.9 368107.5362D 1.4 369131366.5D 1.2 370170342D 1.2 371174340D 1.5372232.5264E 2.4 373202223E 1.9 374241210E 2.4 375235197.5E 2.6 376228173E 2.6 377214164E 2.6 378278196E 2.6 379267168E 2.4 38090167E1 381123177.5E 1.1 382143153E 1.9 383192264E 2.6 384145285E 2.4 385133255E 2.4 38690198E 1.7 3872115E 1.1 3886068E0.8 3897084E0.2 39027149E 1.6 39162143E0.9 39258176E 1.4 39358160E0.6 39472163E0.7 39570176.5E0.7 39690178E0.8 397115168E0.6 398115177.5E0.8 399123168E0.7 400123164E0.6 401123155E0.7 402143164E0.9403144168E 1.2 404149177E0.9 405128178E0.9 406128188E 1.5 407164194E 1.7 408156177E0.8 409168177E 1.1 410156169E0.8 411167168E0.8 412172167E0.9 413167164E0.2 414160164E0.7 415163153.5E 1.2 416186168E 1.6 417269133E 1.6 418295112E 1.1 419302112E 1.4 420316141E 1.6 421278143E 1.7 422284173E 1.4 423257.5170E 1.9 424239198E0.4 425241198E0.3 426246199E0.6 427246.5202E0.4 428240202E0.4 429236201E 1.1 430231199E0.1 431232206.5E0.6 432239.5207.5E0.5 433242206E0.2434235209.5E0.4 435237.5212E0.1 436246208E0.4 437200194E 1.1 438170222E 1.6 43959189E0.8 44072189E0.9 44190187.5E0.6 44274198E0.7 44360196E0.4 44490211E 1.6 445151236E 1.4 446160244E 1.5 44790222E0.8 448129248E 1.7 449142265E 2.1 450152255.5E 1.1 451155258E0.6 452163258E0.8 453171258E 1.1 454171252.5E0.4 455171247E 1.2 456214235E 1.1 457244238E 1.1 458268237E 1.1 459259255E 1.1 460188261E 1.4 461184253E 1.2 462171263E 1.1 463171268E0.8 464163268E0.9465154268.5E0.7 466151275E0.4 467148274E 1.5 468162277.5E 1.5 469177281E0.7 470187284E 1.4 471155316E 1.6 472159292E 1.8 473125267E 1.8 474107285E 1.6 475382.5267F 2.4 476373250F 1.9 477330219F0.8 478400247F 2.3 479441442F 1.7 480417312F 1.5 481332246F 1.9 482321275F 1.7 483403140F 2.1 484420269F 2.4 485455335F 1.9 486295.5238F 1.4 487294244F 1.1 488316300F 1.5 489308257.5F 1.2 490327255F0.8 491316236F 1.4 492314230F0.9 493313223F0.6 494317215F0.2 495318.5222F0.3496320229F0.5 497326.5227.5F0.7 498325220F0.6 499323213F0.4 500329212F0.7 501332226F0.7 502334210.5F0.6 503346209F0.7 504342200F0.8 505356202F0.7 506358195F0.6 507345194F0.4 508348188F0.4 509357.5188F0.6 510359159F 1.1 511404161F 1.2 512403202F0.8 513379202F0.7 514386213F0.8 515373213F0.6 516363212F0.4 517362218F0.8 518354216.5F0.6 519348215F0.9 520349222F0.7 521353223F0.8 522371224F0.8 523371218.5F0.6 524375219F0.4 525388.5218F 1.1 526405213.5F0.8527389224.5F0.9 528388233F0.6 529353229.5F0.8 530334232F0.7 531336239F 1.1 532352247F 1.2 533353236F0.6 534362.5236F0.8 535370236F 1.1 536388237F 1.2 537395.5237.5F 1.4 538395233F 1.1 539408.5227F 1.5 540430237F 1.4 541450268F0.1 542394254F 1.4 543387250F0.9 544383250F 1.1 545369249.5F0.8 546367.5249F0.7 547362249F0.8 548350251F0.6 549348255F 1.4 550355265F 1.1 551367265F0.8 552367257.5F 1.2 553375258F 1.4 554376260F 1.1 555381260F 1.7 556378266F 1.4 557380270.5F 1.2558371284F 1.1 559356.5281F 1.4 560338297F 1.2 561372307F 1.4 562398308F 1.5 563392277F 1.1 564382.5276F0.9 565396270F 1.4 566411291F 1.2 567424297F0.8 568435319F0.9 569434307F0.7 570430295F 1.4 571441309F 1.2 572470342F0.2 573468432F 1.2 574455361F0.6 575453400F0.6 576425433F0.8 577462437F 1.4 578481457F0.6 579462447F 1.2 580440449F 1.4 581423448F1 582435507.5F0.4路线终点(节点)标号说明:17517824434536543946354955065973274789847935103411221126122512471142115715311614163817401742178118811883路线起点(节点)标号A列:全市交通网中连接两路口节点路线的起点标号B列:全市交通网中连接两路口节点路线的终点标号1979 2086 2122 22372 2213 2313 23383 2413 2425 2511 2627 2610 2712 2829 2815 2930 307 3048 3132 3134 3233 3334 338 349 3545 3635 3637 3616 3639 377 38393841 3940 402 4117 4192 4243 432 4372 443 4546 468 4655 4748 476 475 4861 4950 4953 5051 5152 5159 5256 5352 5354 5455 5463 553 5657 5758 5760 5745859 6062 6160 624 6285 6364 6465 6476 6566 6667 6676 6744 6768 6869 6875 6970 6971 691 702 7043 7172 7174 7273 7374 7318 741 7480 7576 7677 7778 77197879 7980 8018 8182 8283 8290 8384 8485 8520 8687 8688 8788 8792 8889 8891 8920 8984 8990 9091 9192 93104 94110 95116 95136 96137 96138 96142 9799 97143 98165 99148100132 100150 101102 102103 102156 10393 103154 104105 105106 105107 106111 106117 10794 10894 108107 108106 108109 109110 110112 111109 111113 112113 113114 113116 114115 114154 11595 115165 116117 116129 117118117128 118105 118119 118126 119120 120121 120123 121104 121122 122123 122125 123124 123126 124125 124127 125132 126127 126128 127130 127133 128129 128130 129131 130131 130134 131135 132133 133134 133140 134135 13496135136 135137 13699 13797 138139 139140 139142 140141 141146 142143 142145 143144 144145 144148 145146 146147 147149 147150 148149 149152 150151 150152 151152 152153 154155 155156 155157 156159 157158 157164 158159158162 158164 159160 160161 160162 161163 162163 163164 16498 165377 166265 166181 167250 167255 168189 170225 170227 171228 171216 171231 172219 173233 173232 173236 174213 174220 175197 175196 176184 176187 177582178210 178284 179291 179274 180305 180270 180306 180307 181308 182273 183184 183196 184185 185186 186168 187185 187186 188176 188186 189190 189192 19062 190191 191192 192193 194193 194175 195194 195188 195196 196197196198 198177 198199 199200 200201 201177 201202 203202 203204 204205 204178 205206 205210 206207 207200 207208 208199 209206 209208 210209 210211 211212 212213 213214 215214 215175 216215 216217 218217 218172 219214219174 220212 221211 221220 221222 222220 222178 222223 223224 224174 225223 225226 226224 226172 227172 227228 228218 229228 229230 230171 231232 232233 233234 234168 235234 23548 235173 236237 23730 237235 237238238239 23929 239240 240241 241242 242243 243230 243244 244231 245244 245232 245236 246241 246242 246245 246247 247237 247238 248369 248239 248249 249167 250251 250252 251252 252253 253240 253254 254169 255256 256257258249 258260 259258 259248 259260 261260 261262 262263 262267 263261 263264 265262 266181 266265 266267 267255 267268 268269 269270 270257 270271 271256 271272 271295 272182 273170 273241 274273 274275 275276 276170276277 277278 277283 278275 279278 279280 280277 280281 281282 282283 284282 285284 285281 286285 286204 286203 286287 287288 288285 289288 289290 290285 290291 291281 291279 292179 292293 293182 293274 294292 294293294272 295292 295296 296179 296290 297296 298289 298297 299298 299288 300299 300301 301287 302301 302303 303300 303304 304299 305304 306297 307269 308307 308268 308309 309310 309312 310307 310311 311305 312311 312313313314 314311 314304 315303 315314 315316 316302 317264 317203 317316 317318 318315 318319 319181 319313 320350 321356 321358 321368 322367 323363 324364 324365 326347 327343 329330 329331 331392 332330 333331 333334333339 334328 334335 335336 336333 336337 337338 337343 338339 338342 338327 339447 340341 341342 341327 343344 343326 344345 345346 345323 346326 346352 346360 347348 347320 348340 348349 349320 349371 350351 350355351352 351354 352353 353354 353357 354355 354356 355321 356357 356358 357358 357360 358359 359360 359367 360361 361362 361323 361322 361264 362332 363325 363324 364367 365364 365366 366369 367368 368349 368369 369370370371 37029 37128 37223 373431 373438 373456 374436 375424 375429 375430 376375 377416 377417 377376 378458 379423 380397 381399 381405 382402 382101 38293 383460 384467 384473 385449 385473 386442 386444 387388387390 388389 388391 388100 389330 389153 390391 390329 392393 392395 392439 393391 393394 394395 394380 395396 395440 396380 396398 396441 397398 398381 399400 399403 400401 400402 401382 402403 402414 403404 403410404405 404407 404408 405406 406407 407437 407438 408409 408410 409411 410411 411412 412413 412416 413414 414415 415101 415161 415416 416437 417418 417421 418419 419420 420421 420422 421379 422379 423376 423424 423378424425 424429 425426 425428 426427 427378 427428 427436 428429 428433 429431 429432 431434 432433 432434 432374 434435 435374 437373 438446 439440 439443 440441 440442 441386 442443 444445 444332 445446 446455 447444447448 448445 448385 449450 449467 450446 450451 451452 451465 452453 453454 453462 454455 454461 455456 456457 456372 457374 457458 457372 458459 458486 45914 45921 460461 460462 462463 463464 464452 465466 466467466468 468464 468469 469463 469470 470383 47024 471472 472468 472384 474447 474473 474471 474340 475555 475565 476545 477501 478542 478566 479577 479580 480568 482489 482559 484539 484570 485571 485572 485573 486487486491 487488 488482 488560 489487 489490 490481 490550 491481 491492 491530 492493 492496 493494 493495 494495 494499 495498 496495 496497 497498 497501 498499 498477 499500 500477 500502 501520 501530 502503 502504504505 505506 505513 506507 506509 507504 508507 508509 508510 509510 510511 511512 511483 512513 513514 514515 515516 516517 517518 517523 518505 518519 518521 519503 519520 520521 521522 521529 522523 522527 523524524515 524525 525514 525526 526512 527525 528527 528529 528536 528538 529530 530531 531481 531532 532533 532547 532548 533529 533534 534535 535536 536537 537538 537478 538539 539526 539540 539478 540541 540484 542543542565 543536 543544 544476 544555 545535 545546 546547 546552 547534 548549 548552 549481 549550 550551 550559 551552 551556 552553 553476 553554 554555 556554 556475 557475 557558 557564 558559 560549 56016 56056156138 561558 561562 562563 562480 563564 563565 565566 566567 567480 567569 568569 568574 569570 569571 570571 572541 572578 573578 574575 575576 576479 577573 577579 580579 580581 581576 581582 581183 582578交巡警平台编号交巡警平台位置标号说明:A11 A22 A33 A44 A55 A66 A77 A88 A99 A1010 A1111 A1212 A1313 A1414 A1515 A1616 A1717 A1818 A1919 A2020 B193 B294 B395 B496 B597 B698 B799 B8100 C1166 C2167 C3168 C4169 C5170 C6171 C7172 C8173 C9174 C10175 C11176 C12177 C13178 C14179 C15180 C16181 C17182 D1320 D2321 D3322A列:表示全市交巡警服务平台的名称编号B列:表示全市交巡警服务平台的位置标号。
2011年数学建模竞赛B题参考答案(只做了一半)

2011高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析,说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?题目A题城市表层土壤重金属污染分析摘要:本文研究的是某城区警车配置及巡逻方案的制定问题,建立了求解警车巡逻方案的模型,并在满足D1的条件下给出了巡逻效果最好的方案。
在设计整个区域配置最少巡逻车辆时,本文设计了算法1:先将道路离散化成近似均匀分布的节点,相邻两个节点之间的距离约等于一分钟巡逻路程。
数学建模简介2

罗钟瑞
张驹翔
王俊智
蔡少杰
王鸣涛
林瑶
黄维娜
林亦然
体育类省金奖 拓步体育旅游文化有限责任公司 09电信 09计科 林天飞 何陈文 09旅管 09财管 叶韩英 林丽婷 10电信 陈华津 10食科 林正方 10财管 10财管 许小青 陈巧炜
2013全国大学生创新创业计划训练项目
康跃体育旅游文化研究与企业开发利用 2013福建省大学生创新创业计划训练项目 小区智能监控系统的研制 基于时间序列与灰色拓扑的节假日火灾损失预测及综合治理
五、数学建模的实例
模型建立与求解
w(k) ~ 第k周(末)体重 c(k) ~第k周吸收热量
w(k 1) w(k ) c(k 1) w(k )
=1/8000(kg/kcal)
~ 代谢消耗系数(因人而异)
五、数学建模的实例
1)不运动情况的两阶段减肥计划
• 确定某甲的代谢消耗系数
赖晓燕
10财管 10食科 10农区 09土木
林莉莉 赖燕秋 陈志微 王世宇
11动医
林武涛
漳州市育松绞股蓝茶品加工厂
10国贸 10财管
林少郎 叶成群
10国贸 10财管 10计科 10广告
骆昊远 吴月 林燕凌 李鹏辉 乐圈传媒有限责任公司
09英语
邵瑛
09英语
周海燕
10机械 10财管
10食科 10工程
10食科 10电信 10电信 09土木
卢伟杰
石永杰
戴雪香
张凡凡
郑蓉芳
陈达隆 庄宇斌
刘芳伟
省优胜奖 农保生物农药有限公司 10食科 10电气 10财管 10食科 10土木 10农区 09土木 10国贸
数学建模竞赛命题过程及题目分析

油位探针
油位探测 装置
油位探针
油
β
3m
地平线垂直线
(a)无偏转倾斜的正截面图 (b)横向偏转倾斜后正截面图
结合评奖对本科组选作A, B题的分析
• 本科组全国14108队参赛,送全国1393份论文,其中A题877 份(63%),B题516份(37%),其比例基本代表全部参赛 队的情况.
• 获一等奖的210 队中A题133队,B题77队.
• A题获一等奖的队多数集中在重点高校:
北京17队(北航5、北大3、北邮3、清华2)
图3 储油罐截面示意图
油
注油口
位
出油管
探
针 油浮子
1.2m
1.2m
油 α
0.4m 2.05m (a) 小椭圆油罐cm正面示意图
水平线
1.78m
Байду номын сангаас
(b) 小椭圆油罐截面示意图
图4 小椭圆型油罐形状及尺寸示意图
附件1 实验数据
流水 C进油 D油位高
号
量/L 度/mm
采集时间
说明
2010-08-20 (1)罐体无变位进油,罐内
11
50 159.02
10:32:18 油量初值262L;
12
100 176.14
2010-08-20 (2)C列进油量是每次加入 10:33:18 50L油后的累加值
13
150 192.59
2010-08-20 (3)D列是原罐内初始油量加入 10:34:18 相应油量后油位高度值。
11 第11讲 函数模型及其应用

第11讲 函数模型及其应用1.几种常见的函数模型常用知识拓展“对勾”函数f (x )=x +ax(a >0)的性质(1)该函数在(-∞,-a ]和[a ,+∞)上单调递增,在[-a ,0)和(0,a ]上单调递减. (2)当x >0时,x =a 时取最小值2a ; 当x <0时,x =-a 时取最大值-2a .判断正误(正确的打“√”,错误的打“×”) (1)幂函数增长比一次函数增长更快.( )(2)在(0,+∞)内,随着x 的增大,y =a x (a >1)的增长速度会超过并远远大于y =x α(α>0)的增长速度.( )(3)指数型函数模型,一般用于解决变化较快,短时间内变化量较大的实际问题.( ) 答案:(1)× (2)√ (3)√下列函数中,随x 的增大,y 的增长速度最快的是( )A .y =1100e xB .y =100 ln xC .y =x 100D .y =100·2x答案:A生产一定数量商品的全部费用称为生产成本,某企业一个月生产某种商品x 万件时的生产成本为C (x )=12x 2+2x +20(万元).一万件售价是20万元,为获取更大利润,该企业一个月应生产该商品数量为( )A .36万件B .18万件C .22万件D .9万件 解析:选B.设利润为L (x ),则利润L (x )=20x -C (x )=-12(x -18)2+142,当x =18 时,L (x )有最大值.某城市客运公司确定客票价格的方法是:如果行程不超过100 km ,票价是0.5元/km ,如果超过100 km ,超过100 km 的部分按0.4元/km 定价,则客运票价y (元)与行驶千米数x (km)之间的函数关系式是________.解析:由题意可得y =⎩⎪⎨⎪⎧0.5x ,0<x ≤100,0.4x +10,x >100.答案:y =⎩⎪⎨⎪⎧0.5x ,0<x ≤100,0.4x +10,x >100(教材习题改编)某公司为了业务发展制定了一个激励销售人员的奖励方案,在销售额x 为8万元时,奖励1万元.销售额x 为64万元时,奖励4万元.若公司拟定的奖励模型为y =a log 4x +b .某业务员要得到8万元奖励,则他的销售额应为________万元.解析:依题意得⎩⎪⎨⎪⎧a log 48+b =1a log 464+b =4,即⎩⎪⎨⎪⎧32a +b =1,3a +b =4.解得a =2,b =-2. 所以y =2log 4x -2,当y =8时,即2log 4x -2=8. 解得x =1 024. 答案:1 024用函数图象刻画变化过程(师生共研)汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况.下列叙述中正确的是()A.消耗1升汽油,乙车最多可行驶5千米B.以相同速度行驶相同的路程,三辆汽车中,甲车消耗汽油量最多C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油D.某城市机动车最高限速80千米/小时,相同条件下,在该城市用丙车比用乙车更省油【解析】根据图象知消耗1升汽油,乙车最多行驶里程大于5千米,故选项A错;以相同速度行驶时,甲车燃油效率最高,因此以相同速度行驶相同路程时,甲车消耗汽油最少,故选项B错;甲车以80千米/小时的速度行驶时燃油效率为10千米/升,行驶1小时,里程为80千米,消耗8升汽油,故选项C错;最高限速80千米/小时,丙车的燃油效率比乙车高,因此相同条件下,在该市用丙车比用乙车更省油,故选项D对.【答案】 D判断函数图象与实际问题变化过程相吻合的方法(1)构建函数模型法:当根据题意易构建函数模型时,先建立函数模型,再结合模型选图象.(2)验证法:根据实际问题中两变量的变化快慢等特点,结合图象的变化趋势,验证是否吻合,从中排除不符合实际的情况,选择出符合实际情况的答案.已知正方形ABCD 的边长为4,动点P 从B 点开始沿折线BCDA 向A 点运动.设点P 运动的路程为x ,△ABP 的面积为S ,则函数S =f (x )的图象是( )解析:选D.依题意知当0≤x ≤4时,f (x )=2x ;当4<x ≤8时,f (x )=8;当8<x ≤12时,f (x )=24-2x ,观察四个选项知D 项符合要求.二次函数、分段函数、“对勾”函数模型(师生共研)小王大学毕业后,决定利用所学专业进行自主创业.经过市场调查,生产某小型电子产品需投入年固定成本为3万元,每生产x 万件,需另投入流动成本为W (x )万元,在年产量不足8万件时,W (x )=13x 2+x (万元).在年产量不小于8万件时,W (x )=6x +100x -38(万元).每件产品售价为5元.通过市场分析,小王生产的商品能当年全部售完.(1)写出年利润L (x )(万元)关于年产量x (万件)的函数解析式;(注:年利润=年销售收入-固定成本-流动成本)(2)年产量为多少万件时,小王在这一商品的生产中所获利润最大?最大利润是多少? 【解】 (1)因为每件商品售价为5元,则x 万件商品销售收入为5x 万元, 依题意得,当0<x <8时,L (x )=5x -⎝⎛⎭⎫13x 2+x -3=-13x 2+4x -3; 当x ≥8时,L (x )=5x -⎝⎛⎭⎫6x +100x -38-3=35-⎝⎛⎭⎫x +100x . 所以L (x )=⎩⎨⎧-13x 2+4x -3,0<x <8,35-⎝⎛⎭⎫x +100x ,x ≥8.(2)当0<x <8时,L (x )=-13(x -6)2+9.此时,当x =6时,L (x )取得最大值L (6)=9万元. 当x ≥8时,L (x )=35-⎝⎛⎭⎫x +100x ≤35-2 x ·100x =35-20=15,当且仅当x =100x时等号成立,即x =10时,L (x )取得最大值15万元.因为9<15,所以当年产量为10万件时,小王在这一商品的生产中所获利润最大,最大利润为15万元.解决实际应用问题的四大步骤(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型.(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型.(3)求模:求解数学模型,得出数学结论. (4)还原:将数学问题还原为实际问题. 以上过程用框图表示如下:[提醒] (1)构建函数模型时不要忘记考虑函数的定义域.(2)利用模型f (x )=ax +bx求解最值时,注意取得最值时等号成立的条件.1.某城市对一种售价为每件160元的商品征收附加税,税率为R %(即每销售100元征税R 元),若年销售量为(30-52R )万件,要使附加税不少于128万元,则R 的取值范围是( )A .[4,8]B .[6,10]C .[4%,8%]D .[6%,10%]解析:选A.根据题意,要使附加税不少于128万元, 需⎝⎛⎭⎫30-52R ×160×R %≥128, 整理得R 2-12R +32≤0,解得4≤R ≤8, 即R ∈[4,8].2.据气象中心观察和预测:发生于沿海M 地的台风一直向正南方向移动,其移动速度v (km/h)与时间t (h)的函数图象如图所示,过线段OC 上一点T (t ,0)作横轴的垂线l ,梯形OABC 在直线l 左侧部分的面积即为时间t (h)内台风所经过的路程s (km).(1)当t =4时,求s 的值;(2)将s 随t 变化的规律用数学关系式表示出来;(3)若N 城位于M 地正南方向,且距M 地650 km ,试判断这场台风是否会侵袭到N 城,如果会,在台风发生后多长时间它将侵袭到N 城?如果不会,请说明理由.解:(1)由图象可知,直线OA 的方程是v =3t ,直线BC 的方程是v =-2t +70. 当t =4时,v =12,所以s =12×4×12=24.(2)当0≤t ≤10时,s =12×t ×3t =32t 2;当10<t ≤20时,s =12×10×30+(t -10)×30=30t -150;当20<t ≤35时,s =150+300+12×(t -20)×(-2t +70+30)=-t 2+70t -550.综上可知,s 随t 变化的规律是 s =⎩⎪⎨⎪⎧32t 2,t ∈[0,10],30t -150,t ∈(10,20],-t 2+70t -550,t ∈(20,35].(3)当t ∈[0,10]时,s max =32×102=150<650,当t ∈(10,20]时,s max =30×20-150=450<650,当t ∈(20,35]时,令-t 2+70t -550=650,解得t =30或t =40(舍去),即在台风发生30小时后将侵袭到N 城.指数、对数函数模型(师生共研)(1)某公司为激励创新,计划逐年增加研发资金投入,若该公司2017年全年投入的研发资金为300万元,在此基础上,每年投入的研发资金比上一年增长10%,则该公司全年投入的研发资金开始超过600万元的年份是( )(参考数据:lg 1.1=0.041,lg 2=0.301) A .2023年 B .2024年 C .2025年D .2026年(2)里氏震级M的计算公式为:M=lg A-lg A0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅.假设在一次地震中,测震仪记录的最大振幅是1 000,此时标准地震的振幅为0.001,则此次地震的震级为________级;9级地震的最大振幅是5级地震最大振幅的________倍.【解析】(1)设从2017年后,第x年该公司全年投入的研发资金为y万元,则y=300×(1+10%)x,依题意得,300×(1+10%)x>600,即1.1x>2,两边取对数可得x>lg 2lg 1.1=0.3010.041≈7.3,则x≥8,即该公司全年投入的研发资金开始超过600万元的年份是2025年.故选C.(2)M=lg 1 000-lg 0.001=3-(-3)=6.设9级地震的最大振幅和5级地震的最大振幅分别为A1,A2,则9=lg A1-lg A0=lg A1 A0,则A1A0=109,5=lg A2-lg A0=lgA2A0,则A2A0=105,所以A1A2=104.即9级地震的最大振幅是5级地震最大振幅的10 000倍.【答案】(1)C(2)610 000指数型、对数型函数模型(1)在实际问题中,有关人口增长、银行利率、细胞分裂等增长率问题常用指数函数模型表示.通常可以表示为y=N(1+p)x(其中N为基础数,p为增长率,x为时间)的形式.解题时,往往用到对数运算,要注意与已知表格中给定的值对应求解.(2)有关对数型函数的应用题,一般都会给出函数解析式,要求根据实际情况求出函数解析式中的参数,或给出具体情境,从中提炼出数据,代入解析式求值,然后根据值回答其实际意义.候鸟每年都要随季节的变化而进行大规模地迁徙,研究某种鸟类的专家发现,该种鸟类的飞行速度v(单位:m/s)与其耗氧量Q之间的关系为:v=a+b log3Q10(其中a,b是实数).据统计,该种鸟类在静止的时候其耗氧量为30个单位,而其耗氧量为90个单位时,其飞行速度为1 m/s.(1)求出a,b的值;(2)若这种鸟类为赶路程,飞行的速度不能低于2 m/s ,则其耗氧量至少要多少个单位? 解:(1)由题意可知,当这种鸟类静止时,它的速度为0 m/s ,此时耗氧量为30个单位,故有a +b log 33010=0,即a +b =0;当耗氧量为90个单位时,速度为1 m/s , 故a +b log 39010=1,整理得a +2b =1.解方程组⎩⎪⎨⎪⎧a +b =0,a +2b =1,得⎩⎪⎨⎪⎧a =-1,b =1.(2)由(1)知,v =a +b log 3Q 10=-1+log 3Q10.所以要使飞行速度不低于2 m/s ,则有v ≥2,所以-1+log 3Q10≥2,即log 3Q 10≥3,解得Q10≥27,即Q ≥270.所以若这种鸟类为赶路程,飞行的速度不能低于2 m/s ,则其耗氧量至少要270个单位.数学建模——函数建模在实际问题中的妙用数学建模是对现实问题进行数学抽象,用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、构建模型,求解结论,验证结果并改进模型,最终解决实际问题.已知某公司生产某款手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设该公司一年内共生产该款手机x 万只并全部销售完,每万只的销售收入为R (x )万美元,且R (x )=⎩⎪⎨⎪⎧400-6x ,0<x ≤40,7 400x-40 000x 2,x >40.(1)写出年利润W (万美元)关于年产量x (万只)的函数解析式;(2)当年产量为多少万只时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.【解】 (1)当0<x ≤40时,W =xR (x )-(16x +40)=-6x 2+384x -40, 当x >40时,W =xR (x )-(16x +40)=-40 000x-16x +7 360.所以W =⎩⎪⎨⎪⎧-6x 2+384x -40,0<x ≤40,-40 000x -16x +7 360,x >40.(2)①当0<x ≤40时,W =-6(x -32)2+6 104, 所以W max =W (32)=6 104;②当x >40时,W =-40 000x -16x +7 360,由于40 000x+16x ≥240 000x×16x =1 600, 当且仅当40 000x =16x ,即x =50∈(40,+∞)时,取等号,所以W 取最大值为5 760.综合①②知,当x =32时,W 取最大值为6 104万美元.根据实际问题选择函数模型时应注意以下几点:(1)若能够根据实际问题作出满足题意的函数图象,可结合图象特征选择.(2)当研究的问题呈现先增长后减少的特点时,可以选用二次函数模型y =ax 2+bx +c (a ,b ,c 均为常数,a <0);当研究的问题呈现先减少后增长的特点时,可以选用二次函数模型y =ax 2+bx +c (a ,b ,c 均为常数,a >0).(3)对数函数(底数大于1时)增长越来越慢,而指数函数(底数大于1时)增长越来越快.某地西红柿上市后,通过市场调查,得到西红柿种植成本Q (单位:元/100 kg)与上市时间t (单位:天)的数据如下表:Q 与上市时间t 的变化关系:Q =at +b ,Q =at 2+bt +c ,Q =a ·b t ,Q =a ·log b t . 利用你选取的函数,求:(1)西红柿种植成本最低时的上市天数是________;(2)最低种植成本是________元/100 kg.解析:因为随着时间的增加,种植成本先减少后增加,而且当t =60和t =180时种植成本相等,再结合题中给出的四种函数关系可知,种植成本与上市时间的变化关系应该用二次函数Q =at 2+bt +c ,即Q =a (t -120)2+m 描述,将表中数据代入可得⎩⎪⎨⎪⎧a (60-120)2+m =116,a (100-120)2+m =84,解得⎩⎪⎨⎪⎧a =0.01,m =80,所以Q =0.01(t -120)2+80,故当上市天数为120时,种植成本取到最低值80元/100 kg. 答案:(1)120 (2)80[基础题组练]1.如图,在不规则图形ABCD 中,AB 和CD 是线段,AD 和BC 是圆弧,直线l ⊥AB 于E ,当l 从左至右移动(与线段AB 有公共点)时,把图形ABCD 分成两部分,设AE =x ,左侧部分面积为y ,则y 关于x 的大致图象为( )解析:选D.因为左侧部分面积为y ,随x 的变化而变化,最初面积增加得快,后来均匀增加,最后缓慢增加,只有D 选项适合.2.某市家庭煤气的使用量x (m 3)和煤气费f (x )(元)满足关系f (x )=⎩⎪⎨⎪⎧C ,0<x ≤A ,C +B (x -A ),x >A .已知某家庭今年前四个月的煤气费如下表:月份 一月份 二月份 三月份 四月份 用气量/m 3 4 5 25 35 煤气费/元4414193A .12.5元 B .12元 C .11.5元D .11元解析:选 A.由题意得C =4.将(25,14),(35,19)代入f (x )=4+B (x -A ),得⎩⎪⎨⎪⎧4+B (25-A )=14,4+B (35-A )=19,解得⎩⎪⎨⎪⎧A =5,B =12.所以f (x )=⎩⎪⎨⎪⎧4,0<x ≤5,4+12(x -5),x >5.故当x =22时,f (22)=12.5.故选A.3.成都市某物流公司为了配合“北改”项目顺利进行,决定把三环内的租用仓库搬迁到北三环外重新租地建设.已知仓库每月占用费y 1与仓库到车站的距离成反比,而每月车载货物的运费y 2与仓库到车站的距离成正比.据测算,如果在距离车站10千米处建仓库,这两项费用y 1,y 2分别是2万元和8万元,那么要使这两项费用之和最小,仓库应建在离车站( )A .5千米处B .4千米处C .3千米处D .2千米处解析:选A.设仓库应建在离车站x 千米处.因为仓库每月占用费y 1与仓库到车站的距离成反比,所以令反比例系数为m (m >0),则y 1=m x .当x =10时,y 1=m10=2,所以m =20.因为每月车载货物的运费y 2与仓库到车站的距离成正比,所以令正比例系数为n (n >0),则y 2=nx .当x =10时,y 2=10n =8,所以n =45.所以两项费用之和为y =y 1+y 2=20x +4x5≥220x ·4x5=8,当且仅当20x =4x5,即x =5时取等号.所以要使这两项费用之和最小,仓库应建在离车站5千米处.故选A.4.某工厂产生的废气经过过滤后排放,排放时污染物的含量不得超过1%.已知在过滤过程中废气中的污染物数量P (单位:毫克/升)与过滤时间t (单位:时)之间的函数关系为P =P 0e-kt(k ,P 0均为正的常数).如果在前5小时的过滤过程中污染物被排除了90%,那么排放前至少还需要过滤的时间是( )A.12小时 B.59小时 C .5小时D .10小时解析:选C.由题意,前5小时消除了90%的污染物.因为P =P 0e -kt ,所以(1-90%)P 0=P 0e -5k ,所以0.1=e -5k .设废气中污染物含量为1%所需过滤时间为t ,由1% P 0=P 0e -kt ,即0.01=e -kt ,得e -kt =(0.1)2=(e -5k )2=e -10k ,所以t =10,所以排放前至少还需过滤t -5=5(小时).故选C.5.(2019·河北武邑中学月考)已知某品牌商品靠广告宣传得到的收入R 与广告费A 之间满足关系R =a A (a 为常数且a >0),广告效应为D =a A -A .那么对于此商品,精明的商人为了取得最大的广告效应,投入的广告费应为________.(用常数a 表示)解析:由题意得D =a A -A =-⎝⎛⎭⎫A -a 22+a 24,且A ≥0,所以当A =a 2,即A =a24时,D 最大.答案:a 246.某人准备购置一块占地1 800平方米的矩形地块,中间建三个矩形温室大棚,大棚周围均是宽为1米的小路(如阴影部分所示),大棚占地面积为S 平方米,其中a ∶b =1∶2,若要使S 最大,则y =____________.解析:由题意可得xy =1 800,b =2a ,则y =a +b +3=3a +3,S =(x -2)a +(x -3)×b =(3x -8)a =(3x -8)×y -33=1 808-3x -83y =1 808-3x -83×1 800x =1 808-⎝⎛⎭⎫3x +4 800x ≤1 808-23x ×4 800x =1 808-240=1 568,当且仅当3x =4 800x,即x =40时取等号,所以当S 取得最大值时,y =1 80040=45.答案:457.声强级Y (单位:分贝)由公式Y =10lg ⎝⎛⎭⎫I10-12给出,其中I 为声强(单位:W/m 2).(1)平常人交谈时的声强约为10-6W/m 2,求其声强级;(2)一般常人能听到的最低声强级是0分贝,求能听到的最低声强为多少?解:(1)当声强为10-6W/m 2时,由公式Y =10lg ⎝ ⎛⎭⎪⎫I 10-12得Y =10lg ⎝ ⎛⎭⎪⎫10-610-12=10lg 106=60(分贝).(2)当Y =0时,由公式Y =10lg ⎝ ⎛⎭⎪⎫I 10-12得10lg ⎝ ⎛⎭⎪⎫I 10-12=0.所以I 10-12=1,即I =10-12W/m 2, 则最低声强为10-12W/m 2.8.“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v (单位:千克/年)是养殖密度x (单位:尾/立方米)的函数.当x 不超过4尾/立方米时,v 的值为2千克/年;当4<x ≤20时,v是x 的一次函数,当x 达到20尾/立方米时,因缺氧等原因,v 的值为0千克/年.(1)当0<x ≤20时,求函数v 关于x 的函数解析式;(2)当养殖密度x 为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.解:(1)由题意得当0<x ≤4时,v =2; 当4<x ≤20时,设v =ax +b , 显然v =ax +b 在(4,20]内是减函数,由已知得⎩⎪⎨⎪⎧20a +b =0,4a +b =2,解得⎩⎨⎧a =-18,b =52,所以v =-18x +52,故函数v =⎩⎪⎨⎪⎧2,0<x ≤4,-18x +52,4<x ≤20.(2)设年生长量为f (x )千克/立方米,依题意并由(1)可得f (x )=⎩⎪⎨⎪⎧2x ,0<x ≤4,-18x 2+52x ,4<x ≤20,当0<x ≤4时,f (x )为增函数,故f (x )max =f (4)=4×2=8;当4<x ≤20时,f (x )=-18x 2+52x =-18(x 2-20x )=-18(x -10)2+252,f (x )max =f (10)=12.5.所以当x =10时,f (x )的最大值为12.5.即当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值为12.5千克/立方米.[综合题组练]1.某位股民购进某支股票,在接下来的交易时间内,他的这支股票先经历了n 次涨停(每次上涨10%),又经历了n 次跌停(每次下跌10%),则该股民这支股票的盈亏情况(不考虑其他费用)为( )A .略有盈利B .略有亏损C .没有盈利也没有亏损D .无法判断盈亏情况解析:选B.设该股民购进这支股票的价格为a 元,则经历n 次涨停后的价格为a (1+10%)n=a ×1.1n 元,经历n 次跌停后的价格为a ×1.1n ×(1-10%)n =a ×1.1n ×0.9n =a ×(1.1×0.9)n=0.99n ·a <a ,故该股民这支股票略有亏损.2.(创新型)我们定义函数y =[x ]([x ]表示不大于x 的最大整数)为“下整函数”;定义y ={x }({x }表示不小于x 的最小整数)为“上整函数”;例如[4.3]=4,[5]=5;{4.3}=5,{5}=5.某停车场收费标准为每小时2元,即不超过1小时(包括1小时)收费2元,超过一小时,不超过2小时(包括2小时)收费4元,以此类推.若李刚停车时间为x 小时,则李刚应付费为(单位:元)( )A .2[x +1]B .2([x ]+1)C .2{x }D .{2x }解析:选C.如x =1时,应付费2元,此时2[x +1]=4,2([x ]+1)=4,排除A ,B ;当x =0.5时,付费为2元,此时{2x }=1,排除D ,故选C.3.一个容器装有细沙a cm 3,细沙从容器底下一个细微的小孔慢慢地匀速漏出,t min 后剩余的细沙量为y =a e-bt(cm 3),经过8 min 后发现容器内还有一半的沙子,则再经过________min ,容器中的沙子只有开始时的八分之一.解析:当t =0时,y =a ;当t =8时,y =a e -8b =12a ,故e -8b =12.当容器中的沙子只有开始时的八分之一时,即y =a e -bt =18a ,e -bt =18=(e -8b )3=e -24b ,则t =24,所以再经过16 min 容器中的沙子只有开始时的八分之一.答案:164.(应用型)一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x (x ∈N *)件.当x ≤20时,年销售总收入为(33x -x 2)万元;当x >20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y 万元,则y (万元)与x (件)的函数关系式为____________,该工厂的年产量为________件时,所得年利润最大(年利润=年销售总收入-年总投资).解析:当0<x ≤20时,y =(33x -x 2)-x -100=-x 2+32x -100;当x >20时,y =260-100-x =160-x .故y =⎩⎪⎨⎪⎧-x 2+32x -100,0<x ≤20,160-x ,x >20(x ∈N *).当0<x ≤20时,y =-x 2+32x -100=-(x -16)2+156,x =16时,y max =156.而当x >20时,160-x <140,故x =16时取得最大年利润.答案:y =⎩⎪⎨⎪⎧-x 2+32x -100,0<x ≤20,160-x ,x >20(x ∈N *) 165.某书商为提高某套丛书的销量,准备举办一场展销会.据市场调查,当每套丛书售价定为x 元时,销售量可达到(15-0.1x )万套.现出版社为配合该书商的活动,决定进行价格改革,将每套丛书的供货价格分成固定价格和浮动价格两部分,其中固定价格为30元,浮动价格(单位:元)与销售量(单位:万套)成反比,比例系数为10.假设不计其他成本,即销售每套丛书的利润=售价-供货价格.问:(1)每套丛书售价定为100元时,书商所获得的总利润是多少万元?(2)每套丛书售价定为多少元时,单套丛书的利润最大?解:(1)每套丛书售价定为100元时,销售量为15-0.1×100=5(万套),所以每套丛书的供货价格为30+105=32(元),故书商所获得的总利润为5×(100-32)=340(万元).(2)每套丛书售价定为x 元时,由⎩⎪⎨⎪⎧15-0.1x >0,x >0,得0<x <150.设单套丛书的利润为P 元,则P =x -(30+1015-0.1x )=x -100150-x -30,因为0<x <150,所以150-x >0,所以P =-[(150-x )+100150-x ]+120, 又(150-x )+100150-x≥2(150-x )·100150-x=2×10=20,当且仅当150-x =100150-x ,即x =140时等号成立,所以P max =-20+120=100.故每套丛书售价定为140元时,单套丛书的利润最大,为100元.6.(综合型)某厂有一个容量300吨的水塔,每天从早六点到晚十点供应生活和生产用水,已知该厂生活用水每小时10吨,生产用水总量W (吨)与时间t (单位:小时,规定早晨六点时t =0)的函数关系为W =100t ,水塔的进水量有10级,第一级每小时进水10吨,以后每提高一级,进水量增加10吨.若某天水塔原有水100吨,在供应同时打开进水管,问该天进水量应选择几级,既能保证该厂用水(即水塔中水不空),又不会使水溢出?解:设水塔进水量选择第n 级,在t 时刻水塔中的水容量y 等于水塔中的存水量100吨加进水量10nt 吨,减去生活用水10t 吨,再减去生产用水W =100t 吨,即y =100+10nt -10t -100t (0<t ≤16).若水塔中的水量既能保证该厂用水,又不会使水溢出,则一定有0<y ≤300,即0<100+10nt -10t -100t ≤300,所以-10t +10t +1<n ≤20t +10t +1对一切t ∈(0,16]恒成立.因为-10t +10t +1=-10⎝⎛⎭⎫1t -122+72≤72, 20t +10t +1=20⎝⎛⎭⎫1t +142-14≥194. 所以72<n ≤194,即n =4.即进水量应选择4级.。
2011年大学生数学建模竞赛B题参考答案

7
8Leabharlann 93031
32 0.0
33
34
35
36
45
46
47
48
11.4 13.4 17.7 17.2 11.7
5.1 12.7 21.9 26.9 28.6 22.7 24.2 24.3
再据以上表分析围堵方案:
C 区 30 → 5 — — 47 → —6— 48 → C 区 46 → 55 3 ← 2 8 → — 3 10 — — 3 45 → 34 → 35 → 9 → 3 6 (同 下 ) 16 — — → 36 → 37 39 15
1.2 重要关口平台调度 交通要道编号 12 14 16 21 22 23 24 28 29 30 38 48 62 被调度平台编号 12 16 9 14 10 13 11 15 7 8 2 5 4 距离(mm) 0.000 67.417 15.325 32.650 77.079 5.000 38.053 47.518 80.155 30.608 39.822 24.758 3.500 时间(min) 0.000 6.742 1.533 3.265 7.708 0.500 3.805 4.752 8.015 3.061 3.982 2.476 0.350
30574764884655321032334533493536164373639385614040173115ccf????????????????????????????????????????????????????????????????????????????????????????3
2011年全国大学生数学建模竞赛B题

2011高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写):B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):参赛队员(打印并签名):1.韩晓峰2.杨晓帆3.李弘倩指导教师或指导教师组负责人(打印并签名):日期:2011年9月11日赛区评阅编号(由赛区组委会评阅前进行编号):2011高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):赛区评阅记录(可供赛区评阅时使用):评阅人评分备注全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):交巡警服务平台的设置与调度摘要在(1)第一问中,我们根据附表1所给各路口坐标算出A图中每条路线的长度,然后通过floyd算法找出了两点之间的最短路程,得出矩阵D,通过使用matlab圈出各服务平台到周围路口小于3min(即3km)的点,再根据就近原则,将各路口划分到这个圈中离此路口最近的交巡警平台。
对于任意到交巡警平台路程大于3min(即3km)序号为28,29,38,39,61,92的五个路口,则采用就近原则人工划入距离其最近的交巡警平台辖区,这样就在保证出警时间基本都小于3min的条件下,划分出各警务平台合理的管辖范围。
对于(1)第二问中,我们采用指派模型,用lingo软件对20个巡警服务平台对17个城市出入口进行封锁的方法进行了优化,得到初步的调度方案。
2011高教社杯全国大学生数学建模竞赛题目 2

2011高教社杯全国大学生数学建模竞赛题目2011 全国数学建模大学生随着题荒的到来,很多数学建模题目的直接来源于众多老师的科研课题,至少华中数学建模竞赛的题目由我们这边命题时直接为正在研究且没有解决的科研问题,看来一方面锻炼学生建模能力的同时,又可以为“焦头难额”的老师们来自点新鲜的ideas,这些题目确实蛮好玩的。
A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土(0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析,说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?B题交巡警服务平台的设置与调度“有困难找警察”,是家喻户晓的一句流行语。
研究生数学建模竞赛优秀论文 (11)

针对问题二,本文基于菲涅尔-惠更斯理论,对 Fresnel 椭球进行建模,同 时得到 Fresnel 主反射区,从而简化能量在有限区域的无限次反射,并针对 Fresnel 主反射区的分析和计算,得到静区从诸墙面得到的反射信号的功率之 和与从信号源直接得到的微波功率之比γ的表达式,并验证了两种不同形状的
1.尖劈的高度: 尖劈需要一定的高度,是为了使波在尖劈之间能充分地来回反射,并使所有 反射波矢量由于相位相反或差别而抵消、以减小反射波分量。尖劈的高度最小值 应设计为最低频率处的一个波长。 2.尖顶角 2 的大小: 尖顶角 2 的大小决定了波在尖劈之间的反射次数,反射次数多,反射系数 就小,所以,要求高性能时, 2 就要小。反之,则可大一些。 3.底座高度: 如果底座高度太小,则一部分波得不到充分的衰减,影响吸收性能,且重心 在底座之外,对横向安装时的粘接强度带来影响,但也不宜太大,否则一则增加 重量,二则失去角锥的意义。一般取总高度的 1 ~ 1 为宜。
从国内外无回波暗室的发展情况来看,根据其测试频率可分为米波无回波暗 室和微波无回波暗室。[3]
1.2 吸波材料形状
1.2.1 吸波材料形状的选择 暗室用吸波材料的种类主要有平板和锥体两大结构类型。 1. 平板结构吸波材料 平板结构吸波材料主要有涂层型吸波材料和结构型吸波材料两大类。 (1)吸波涂层 吸波涂料层一般由吸波剂和粘结剂组成,其中具有特定电磁参数的吸波剂是
4
如图 1.1 和图 1.2 所示,矩形微波暗室能避免其他微波暗室的一些缺点,它 的通用性较好,微波暗室的两端均好使用。另外,有些实验必须在矩形微波暗室 中进行。例如,电磁兼容性实验,电子战中的一些电子设备的环境模拟实验,隐 身技术中雷达截面积测试的有关研究与发射机位置需要多元实验等。[2]
数学建模试题(带答案)大全

(14 分)
得分
四、(满分 10 分) 雨滴的速度 v 与空气密度 、粘滞系数 和重力加速度 g 有关,其中粘
滞系数的量纲[ ]= L1MT 1 1,用量纲分析方法给出速度 v 的表达式.
解:设 v , , , g 的关系为 f ( v , , , g ) =0.其量纲表达式为
[ v ]=LM0T-1,
学分 5 4 4
4
数据结构
3
5
应用统计
4
6
计算机模拟 3
7
计算机编程 2
8
预测理论
2
9
数学实验
3
所属类别 数学 数学 数学;运筹学
数学;计算机 数学;运筹学
计算机;运筹学 计算机 运筹学 运筹学;计算机
先修课要求
微积分;线性代 数 计算机编程 微积分;线性代 数 计算机编程
应用统计 微积分;线性代 数
由 U 0, U 0 可得到最优价格:
p1
p2
1
T
1
3T
p1 2b [a b(q0
)] 4
P2 2b [a b(q0 4 )]
前期销售量
T、(2 a
0
bp1
)dt
后期销售量
T
T /2 (a p2 )dt
总销售量
Q0
=
aT
bT 2
(
p1
p2 )
在销售量约束条件下 U 的最大值点为
~p1
a b
Q0 bT
T 8
,
P~2
a b
Q0 bT
T 8
7. (1)雨水淋遍全身, s 2(ab bc ac) 2*(1.5*0.5 0.5*0.2 1.5*0.2) 2.2m2
全国大学生数学建模竞赛历年试题
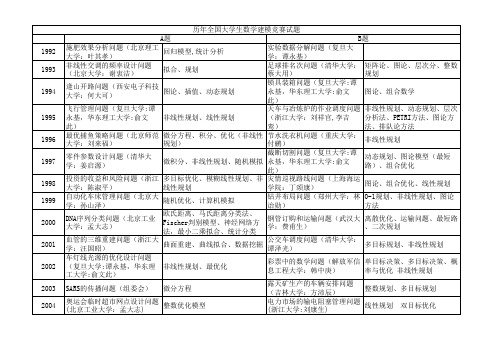
(浙江大学:刘祥官,李吉 分析法、PETRIБайду номын сангаас法、图论方
此)
鸾)
法、排队论方法
最优捕鱼策略问题(北京师范 大学:刘来福)
微分方程、积分、优化(非线性 规划)
节水洗衣机问题(重庆大学: 付鹂)
非线性规划
零件参数设计问题(清华大 学:姜启源)
截断切割问题(复旦大学:谭 微积分、非线性规划、随机模拟 永基,华东理工大学:俞文
微分方程
数码相机定位
非线性方程模型
制动器试验台的控制方法分析
DVD在线租赁问题(清华大学: 谢金星等)
GM
0-1规划 多目标规划
艾滋病疗法的评价及疗效的预
测(天大:边馥萍)
乘公交,看奥运(吉大:方沛
辰,国防科大:吴孟达)
高等教育学费标准探讨
(开放性题目)
眼科病床的合理安排
1999 2000 2001
拟合、规划
足球排名次问题(清华大学: 矩阵论、图论、层次分、整数
蔡大用)
规划
逢山开路问题(西安电子科技 大学:何大可)
图论、插值、动态规划
锁具装箱问题(复旦大学:谭 永基,华东理工大学:俞文 图论、组合数学 此)
飞行管理问题(复旦大学:谭
天车与冶炼炉的作业调度问题 非线性规划、动态规划、层次
永基,华东理工大学:俞文 非线性规划、线性规划
酒后开车问题(清华大学:姜 启源)
微分方程
雨量预报方法的评价问题(复 旦大学:谭永基)
模糊评价 插值
易拉罐形状和尺寸的最优设计
(北理工:叶其孝)
手机“套餐”优惠几何(信息
工程大学:韩中庚)
地面搜索
一笔画问题、数学规划模型
第十一届华为杯全国研究生数学建模竞赛D题—国家二等奖

(由组委会填写)第十一届华为杯全国研究生数学建模竞赛学校青岛科技大学参赛队号10426019队员姓名1.王玉江2.陈桂兵3.严春梅(由组委会填写)第十一届华为杯全国研究生数学建模竞赛题目人体营养健康角度的中国果蔬发展战略研究摘要:水果和蔬菜是重要的农产品,主要为人体提供矿物质、维生素、膳食纤维。
因此,预测我国果蔬的消费与生产趋势,科学地规划与调整我国果蔬的中长期的种植模式,具有重要的战略意义。
针对问题一,首先选取需要研究的主要水果、蔬菜品种,以其总计含量分别达到各自总产量的90%为约束条件,采用多目标规划(产量最多、营养含量最高、种类最少)筛选出主要的水果、蔬菜品种(水果10种、蔬菜8种,结果见表4、表5)。
随后,查询2002至2010年主要品种的产量,通过两种方法(损耗率、进出口差量)计算人均消费量,用灰色预测GM(1,1)和曲线拟合两种模型预测未来人均消费量,并分别检验拟合效果、进行误差分析,发现基于损耗率估计消费量灰色预测的效果较理想。
所以以苹果为例,综合考虑损耗率和进出口量利用灰色预测模型估计其2010至2020年的人均消费量(见表9、表12),拟合出曲线图(见图2、图6),分析其发展趋势。
针对问题二,首先依据10种营养成分在主要果蔬产品中含量的相似性,运用Spss 软件对10种营养成分进行Q型聚类降维得6大类营养成分(结果见表12),每类营养成分都筛选出一个营养成分作为代表分别是膳食纤维、维生素A、维生素C、维生素E、钙、锌。
采用正态分布中间型模型计算每种营养成分年均实际摄入量关于标准摄入量的隶属度,隶属度越接近1表明实际摄入量越趋近于标准量,以此评价2014年的营养年摄入水平。
用维生素A、C、E隶属度的乘积量化维生素这一大类营养元素趋于健康的程度,同样对钙锌采取相同的措施作为矿物质的量化值,关于时间作图可知2014至2019年中国居民的营养健康状况趋于好转,2019至2020年趋于恶化。
数学建模与竞赛案例选讲

数学建模与竞赛案例选讲数学建模和竞赛是现代数学教育中不可或缺的一部分。
数学建模是指利用数学方法,对实际问题进行分析、建模、求解和评价的过程。
竞赛则是通过比赛形式,来提高学生的数学能力和创造力。
本文将选取一些有代表性的数学建模和竞赛案例进行讲解。
一、数学建模案例1. 旅游路径规划旅游路径规划是一个非常有趣的建模问题。
假设一个人要参加某个国家的旅游,他想尽可能地游览这个国家的所有城市。
但是由于时间和费用有限,他不可能去到所有城市。
问题是,如何规划他的路线,使他在游览尽可能多的城市的同时,不会浪费太多时间和费用?这个问题可以建立一个旅游路径规划模型。
我们可以按照以下步骤进行:第一步,将这个国家的所有城市标注在地图上,并确定城市之间的距离。
第二步,制定一个有效的算法来求解最优路径。
一种常用的算法是旅行商问题(TSP)算法。
第三步,考虑一些现实因素的影响,如交通拥堵、天气等因素,将这些因素纳入到模型中。
通过这个建模过程,我们可以得到一个规划出的旅游路径,从而帮助人们更加有效地规划旅游行程。
2. 环境污染模拟现代化城市发展中,环境污染问题越来越受到关注。
环境污染模拟可以有效地评估城市中各种环境因素的影响。
我们可以按照以下步骤来建立环境污染模拟模型:第一步,建立一个三维城市地图。
这个城市地图可以包括建筑物、道路、污染源等信息。
第二步,将城市地图中的各种环境因素纳入到模型中,如空气污染、噪音污染等。
第三步,利用数学方法对各种环境因素进行模拟,发现环境污染的趋势和程度。
第四步,根据模拟结果,提出环境污染防治的措施。
通过这个建模过程,我们可以帮助城市规划师有效地评估和控制城市环境污染。
二、竞赛案例1. 国际数学奥林匹克竞赛(IMO)国际数学奥林匹克竞赛是世界上最具盛名的数学竞赛之一,每年分为两个阶段:初赛和决赛。
初赛是在各国内举行,本着公平、公正、公开的原则选拔出一定数量的佼佼者。
而决赛是在国际上举行,只有各国初赛的获胜者才能参加。
2011年全国大学生数学建模竞赛赛题预测(大全五篇)

2011年全国大学生数学建模竞赛赛题预测(大全五篇)第一篇:2011年全国大学生数学建模竞赛赛题预测2011年全国大学生数学建模竞赛赛题预测(一)2011年日本发生了核泄漏事故,对海洋生态造成了很大的影响。
据悉,近期日本核泄漏放射性物质已经到达中国海,所以预测污染物达到我国沿海的时间以及污染程度就显得很重要了!要求建立数学模型,预测污染物到达中国海的时间及污染程序,并建立仿图!本题点评:1、考擦数据的搜集能力;2、考察污染物海洋扩散模型;3、考察仿真热图;2011年全国大学生数学建模竞赛赛题预测(二)近年来,全球经济疲软,对我国的出口产生了很大影响,实现经济结构转型对我国显得迫切重要,寻找实现经济结构转型的引擎人群就显得迫切重要!问题:(1)请你建立“人群对经济结构转型影响模型”的评价体系;(2)请你选择一个角度,对中国大陆人群进行适当分类,建立不同人群对经济转型的影响模型;(提示:数据以中国统计年鉴最新的人口状况为基础建立模型)(3)利用你的评价体系评价你的模型(提示:总体目标:人群数越少越好,影响越大越好);考察点:1、搜索资料的能力(需要查找统计年鉴);2、模糊性问题通过假设精确化的能力;3、现学现卖的能力;4、数据建模的能力;第二篇:全国大学生数学建模竞赛历年赛题全国大学生数学建模竞赛历年赛题1992:A 施肥效果分析 B 实验数据分解1993:A 非线性交调的频率设计 B 足球队排名次 1994:A 逢山开路 B 锁具装箱1995:A 一个飞行管理问题 B 天车与冶炼炉的作业调度 1996:A 最优捕鱼策略 B 节水洗衣机 1997:A 零件参数 B 截断切割1998:A 投资的收益和风险 B 灾情巡视路线 1999:A 自动化车床管理 B 钻井布局 C 煤矸石堆积 D 钻井布局2000:A DNA序列分类 B 钢管购运 C 飞越北极 D 空洞探测2001:A 血管三维重建 B 公交车调度 C 基金使用 2002:A 车灯线光源 B 彩票中数学 D 赛程安排 2003:A SARS的传播 B 露天矿生产 D 抢渡长江 2004:A 奥运会临时超市网点设计 B 电力市场的输电阻塞管理 C 饮酒驾车 D 公务员招聘2005:A 长江水质的评价和预测 B DVD在线租赁C 雨量预报方法的评价D DVD在线租赁2006:A出版社的资源配置B 艾滋病疗法的评价及疗效的预测C 易拉罐形状和尺寸的最优设计D 煤矿瓦斯和煤尘的监测与控制 2007:A 中国人口增长预测 B 乘公交,看奥运C 手机“套餐”优惠几何D 体能测试时间安排 2008:A 数码相机定位 B 高等教育学费标准探讨C 地面搜索D NBA赛程的分析与评价2009:A 制动器试验台的控制方法分析 B 眼科病床的合理安排C 卫星和飞船的跟踪测控 D会议筹备 2010:A储油罐的变位识别与罐容表标定B 2010年上海世博会影响力的定量评估 C输油管的布置D对学生宿舍设计方案的评价2011: A 城市表层土壤重金属污染分析B 交巡警服务平台的设置与调度C 企业退休职工养老金制度的改革D 天然肠衣搭配问题2012: A 葡萄酒的评价B 太阳能小屋的设计C 脑卒中发病环境因素分析及干预D 机器人避障问题2013: A 车道被占用对城市道路通行能力的影响B 碎纸片的拼接复原C 古塔的变形D 公共自行车服务系统2014: A 嫦娥三号软着陆轨道设计与控制策略B 创意平板折叠桌C D 2015: A B C D 生猪养殖场的经营管理储药柜的设计太阳影子定位“互联网+”时代的出租车资源配置月上柳梢头众筹筑屋规划方案设计第三篇:全国大学生数学建模竞赛历年赛题全国大学生数学建模竞赛历年赛题1992A 施肥效果分析1992B 实验数据分解1993A 非线性交调的频率设计 1993B 足球队排名次1994A 逢山开路1994B 锁具装箱1995A 一个飞行管理问题 1995B 天车与冶炼炉的作业调度1996A 最优捕鱼策略1996B 节水洗衣机1997A 零件参数1997B 截断切割1998A 投资的收益和风险1998B 灾情巡视路线1999A 自动化车床管理1999B 钻井布局2000A DNA序列分类2000B 钢管购运2001A 血管三维重建2001B 公交车调度2002A 车灯线光源2002B 彩票中数学2003A SARS的传播2003B 露天矿生产2004A 奥运会临时超市网点设计2004B 电力市场的输电阻塞管理2005A 长江水质的评价和预测2005B DVD在线租赁2006A 出版社的资源配置2006B 艾滋病疗法的评价及疗效的预测2007A 中国人口增长预测2007B 乘公交,看奥运2008A 数码相机定位2008B 高等教育学费标准探讨2009A 制动器试验台的控制方法分析2009B 眼科病床的合理安排2010A 储油罐的变位识别与罐容表标定2010B2010年上海世博会影响力的定量评估38题/27与优化有关数学的实践与认识199601,199701,199801,199901,200001,200101 工程数学学报2002s1,200305(02),200307,200407,200507第四篇:2006全国大学生数学建模竞赛题目(A题)2006全国大学生数学建模竞赛题目-------A题:出版社的资源配置出版社的资源主要包括人力资源、生产资源、资金和管理资源等,它们都捆绑在书号上,经过各个部门的运作,形成成本(策划成本、编辑成本、生产成本、库存成本、销售成本、财务与管理成本等)和利润。
数学建模竞赛案例选讲省名师优质课赛课获奖课件市赛课一等奖课件

A(eii ei j )
cos(i i ) i sin(i i ) cos( j j ) i sin( j j ) cos i i sin i cos j i sin j
2 sin i i j j (sin i i j j i cos i i j j )
因为Δθi可正可负,为使各变量均非负,引入新变量:
1i , i2使i 1i i2
min
模型 化为
iijj
0时,1i 0时,1i
i2 i2
1j 1j
2j 2j
2ij 2ij
2ij 2ij
s.t.
1i i2 30 1i i2 30
1i i2
1i i2
30
1i , i2 , 0
模型求解
αij旳计算
model:
ij
arcsin( |
xi
8 xj
) |
sets:
plane/1..6/:x0,y0;
link(plane,plane):alpha,sin2;
endsets
@for(link(i,j)|i#ne#j:
sin2(i,j)=64/((x0(i)-x0(j))^2+(y0(i)-y0(j))^2);
ALPHA( 4, 2) ALPHA( 4, 3) ALPHA( 4, 4) ALPHA( 4, 5) ALPHA( 4, 6) ALPHA( 5, 1) ALPHA( 5, 2) ALPHA( 5, 3) ALPHA( 5, 4) ALPHA( 5, 5) ALPHA( 5, 6) ALPHA( 6, 1) ALPHA( 6, 2) ALPHA( 6, 3) ALPHA( 6, 4) ALPHA( 6, 5) ALPHA( 6, 6)
第十一届“华为杯”全国研究生数学建模竞赛E题获奖

曲春歌 李玉龙 于洋涛 梅钊 陆飞 罗俊文 焦同帅 赵航宇 樊世通 戴建星 贾冬雪 宗伟 潘一飞 高秋圆 邵玉龙 刘旭 马晓敏 文士发 张越 杜博闻 肖德华 夏季 钱浩然 胡燕双 王超超 朱利凯 韩泽文 许兆健 胡苇 顾福霖 车阳阳 杨若涵 李超 万炎杰 樊增智 徐国栋 陈明亮
北京邮电大学 中央财经大学 北京物资学院 中央民族大学 华北电力大学 天津大学 华北电力大学(保定) 华北电力大学(保定) 华北电力大学(保定) 大连理工大学 沈阳工业大学 沈阳工业大学 沈阳建筑大学 吉林大学 吉林大学 东北电力大学 哈尔滨工程大学 东北农业大学 复旦大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学
白玉凤 詹家煊 段衍林 吴畏 王俊豪 许家友 吕子遇 董金哲 林嘉麟 徐爱宝 俆田英 张金华 才晓旭 高健 邵雄 庄明振 刘伟红 张宁波 徐高伟 董礼 刘聪 刘凯 徐磊 苏淑娟 孙月梅 魏晖 陈鹏超 赵福壮 张潇予 张家竣 宋钰婷 陈小双 柳扬清 吴兵海 曾笮 范松丽 梁津垚
北京邮电大学 中央财经大学 北京物资学院 中央民族大学 华北电力大学 天津大学 华北电力大学(保定) 华北电力大学(保定) 华北电力大学(保定) 大连理工大学 沈阳工业大学 沈阳工业大学 沈阳建筑大学 吉林大学 吉林大学 东北电力大学 哈尔滨工程大学 东北农业大学 复旦大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 同济大学 上海交通大学 上海交通大学 上海交通大学 上海交通大学
张颖异 王亚楠 王伟 刘雪菲 李硕 冯家浩 赵慕铭 曾凡云 舒畅 毛笠 秦如 卓增泗 夏业超 王文韬 李腾达 王路洋 张雅涛 冯巍 李鲁阳 谢伟 唐丽英 杨凯 李帆 魏会芳 王丽 化 彬 张芳芳 刘其 王亚诚 鲁月乔 王庆阳 吕雪 李瑞雪 李华郁 王鹤林 姚建国 楼芝兰
数学建模历年竞赛试题

如何将这个调度问题抽象成一个明确、完整的数学模型,指出求解模型的方 法;根据实际问题的要求,如果要设计更好的调度方案,应如何采集运营数据。
在此基础上我们加入了每个病人可以传染他人的期限由于被严格隔离治愈死亡等并考虑在不同阶段社会条件下传染概率的变化然后先分析香港和广东的情况以获得比较合理的参数最后初步预测北京的疫情走势
目录
前言........................................................................................................................... - 0 目录........................................................................................................................... - 1 一、什么是数学模型............................................................................................... - 3 -
电力市场交易规则:............................................................................. - 25 输电阻塞管理原则:............................................................................. - 26 表 1 各机组出力方案(单位:兆瓦,记作 MW)............................. - 28 表 2 各线路的潮流值(各方案与表 1 相对应,单位:MW).......... - 29 表 3 各机组的段容量(单位:MW).................................................. - 30 表 4 各机组的段价(单位:元/兆瓦小时,记作元/MWh)..............- 30 表 5 各机组的爬坡速率(单位:MW/分钟).....................................- 30 表 6 各线路的潮流限值(单位:MW)和相对安全裕度.................. - 30 2008 年 B 题……高等教育学费标准探讨....................................................- 31 2008 年 D 题……NBA 赛程的分析与评价.................................................. - 32 2009 年 A 题……制动器试验台的控制方法分析....................................... - 33 2009 年 B 题……眼科病床的合理安排........................................................- 35 【附录】2008-07-13 到 2008-09-11 的病人信息................................. - 36 2009 年 D 题……会议筹备........................................................................... - 49 附表 1……10 家备选宾馆的有关数据................................................. - 49 附表 2……本届会议的代表回执中有关住房要求的信息(单位:人)- 50 附表 3……以往几届会议代表回执和与会情况.................................. - 50 附图(其中 500 等数字是两宾馆间距,单位为米)......................... - 51 二、为什么要学习数学..................................................... - 52 1、数学模型无处不在,我们的生活、工作、学习都离不开它............... - 52 例 1 买房贷款问题................................................................................. - 52 例 2 物体冷却过程的数学模型............................................................. - 53 2、是学好数学用好数学的必经之路........................................................... - 55 3、是数学教学改革的重要手段和有效路径............................................... - 56 4、数学建模竞赛所提唱的团队精神是现代大学生必须具备素质........... - 58 5、数学建模竞赛鼓励学生用跳跃式的、发散式的形象思维方法,这有利于 培养学生的创新意识。................................................................................. - 58 6、数学建模可以培养学生创新意识和创造精神....................................... - 59 -
2011年全国大学生数学数学建模竞赛参考答案

2003-2009全国大学生数学建模竞赛试题及参考答案2010-7-192005A题: 长江水质的评价和预测 (2)2005 A题评阅要点 (4)2005B题: DVD在线租赁 (6)2005 B题评阅要点 (8)2006A题:出版社的资源配置 (10)2006A题评阅要点 (11)2006B题: 艾滋病疗法的评价及疗效的预测 (14)2006 B题评阅要点 (15)2007A题:中国人口增长预测 (18)2007 A题评阅要点 (19)2007 B题:乘公交,看奥运 (22)2007 B题评阅要点 (23)2008A题数码相机定位 (26)2008 A题评阅要点 (28)2008B题高等教育学费标准探讨 (29)2008B题评阅要点 (30)2009 A题制动器试验台的控制方法分析 (31)2009 A题评阅要点 (34)2009B题眼科病床的合理安排 (38)2009 B题评阅要点 (40)2005A题: 长江水质的评价和预测水是人类赖以生存的资源,保护水资源就是保护我们自己,对于我国大江大河水资源的保护和治理应是重中之重。
专家们呼吁:“以人为本,建设文明和谐社会,改善人与自然的环境,减少污染。
”长江是我国第一、世界第三大河流,长江水质的污染程度日趋严重,已引起了相关政府部门和专家们的高度重视。
2004年10月,由全国政协与中国发展研究院联合组成“保护长江万里行”考察团,从长江上游宜宾到下游上海,对沿线21个重点城市做了实地考察,揭示了一幅长江污染的真实画面,其污染程度让人触目惊心。
为此,专家们提出“若不及时拯救,长江生态10年内将濒临崩溃”(附件1),并发出了“拿什么拯救癌变长江”的呼唤(附件2)。
附件3给出了长江沿线17个观测站(地区)近两年多主要水质指标的检测数据,以及干流上7个观测站近一年多的基本数据(站点距离、水流量和水流速)。
通常认为一个观测站(地区)的水质污染主要来自于本地区的排污和上游的污水。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xi ≥ 0, i = 1,2,L, n
四、模型求解
解法1 固定风险 水平,极大化净 收益——模型1
解法2 固定净收 益水平,极小化风 险损失——模型2
n
∑ max Q( x) = (ri − pi )xi i=0
min P ( x,α ) = α
s .t .
q
n
i
x
i
≤
α,
i = 1,2,L n
数学建模示例
(1998A)
——投资的收益和风险
建模示例——投资的收益和风险(1998A)
市场上有n种资产Si(i=1,2……n)可以选择, 现用数额为 M的相当大的资金作一个时期的投资. 这n种资产在这一时
期内购买Si的平均收益率为ri, 风险损失率为qi, 投资越分散, 总的风险越小, 总体风险可用投资的Si中最大的一个风险 来度量. 购买Si时要付交易费 (费率pi), 当购买额不超过给 定值ui时, 交易费按购买ui计算. 另外, 假定同期银行存款利 率是r0, 既无交易费又无风险(r0=5%). 已知n=4时相关数据
⎧min P ( x,α ) = α
⇔
⎨ ⎩
s
.t
.
qi xi ≤ α , i = 1,2,L n
简化后的模型——双目标线性规划模型
n
∑ max Q( x) = (ri − pi )xi i=0
min P ( x,α ) = α
s.t . qi xi ≤ α , i = 1,2,L n
n
∑ (1 + pi )xi = M
通常在分析 问题时,需要 取多组不同的
n
∑ max Q( x) = (ri − pi )xi i=0
s.t. qi xi ≤ a0M, i = 1,2,Ln
风险水平a0,观 察净收益的变
n
∑ (1 + pi )xi = M
化情况,以便
i=0
给出合理的风 险水平a0。
xi ≥ 0, i = 1,2,L, n
{ { }} 标
i=0
min P ( x ) = max qi xi i = 1,2,L , n
n
约 束
∑ (1 + pi )xi = M
i=0
条 件
xi ≥ 0, i = 1,2,L, n
4. 模型简化:
1) 简化总收益函数Q(x)
购买Si所付交易费是一个分段函数, 即交易费= pimax{ui, xi}; 而题目所给定的定值ui(单位:元)相对总投资M很小, piui更小,可 以忽略不计, 这样购买Si的净收益为(ri-pi)xi
模型3 权衡投资风险和预期净收益两方面, 对风险、 收益赋予权重s和1-s(s称为投资偏好系数)
注意这里决策 变量为x和a!
取多组不同的偏 好系数s,观察 风险和收益的变 化情况,以便给 出合理的偏好系 数s。
n
min sα − (1 − s)∑ (ri − pi )xi i=0
s.t . qi xi ≤ α , i = 1,2,L n
Si ri(%) qi (%) pi (%) ui (元) S11 11.8 31 5.1) 195 S12 9 5.5 5.7 320 S13 35 46 2.7 267 S14 9.4 5.3 4.5 328 S15 15 23 7.6 131
二、基本假设和符号规定
基本假设: 1. 投资数额M相当大, 为了便于计算,假设M=1; 2. 投资越分散,总的风险越小; 3. 总体风险用投资项目Si中最大的一个风险来度量; 4. n种资产Si之间是相互独立的; 5. 在投资的这一时期内, ri, pi, qi, r0为定值, 不受意外因素影响; 6. 净收益和总体风险只受 ri, pi, qi影响,不受其他因素干扰。
0 0.04 0.07 0.11 0.13
0 0 0 0 0 0 0 0 0
00 0.08 0.002 0.15 0.004 0.22 0.006
0 0.008 0 0.01 0 0.012 0 0.014 0 0.016 0 0.018 0 0.020 0 0.022 0 0.024 0 0.026
三、模型的建立与分析
1. 总体风险用所投资的Si中最大的一个风险来衡量,即 max{ qixi|i=1,2,…n}
2.购买Si所付交易费是一个分段函数, 即交易费= pimax{ui, xi};
3.要使净收益尽可能大,总体风险尽可能小, 这是一个多目标规
划模型:
n
∑ 目 max Q( x) = (ri xi − pi max{ui , xi })
符号规定: Si -------第i种投资项目,如股票,债券; ri, pi, qi ----分别为Si的平均收益率, 风险损失率, 交易费率; ui ---------Si的交易定额; r0 ---------同期银行利率; xi -------投资项目Si的资金; Q(x) ------总体收益函数; P(x)-------总体风险函数;
如取风险水平a0=0:0.001:0.1,可看出净收益的变 化情况如图。
0.3
1.00 0 0 0.66 0.08 0.13 0.33 0.16 0.27
0 0.24 0.40 0 0.32 0.53 0 0.40 0.58 0 0.48 0.51 0 0.56 0.43 0 0.64 0.35 0 0.72 0.27 0 0.80 0.19 0 0.88 0.11 0 0.96 0.03 0 0.99 0
4.在a=0.006附近有一个转折点,在这一点左边,风险增加很 少时,利润增长很快。在这一点右边,风险增加很大时,利润 增长很缓慢,所以对于风险和收益没有特殊偏好的投资者来 说,应该选择曲线的拐点作为最优投资组合。
返回
模型2 确定净收益水平下限b0,使每一项投资的净 收益不低于b0,并极小化风险,来得到最优投资组 合——把多目标问题转化为单目标问题
如下:
1) 试 给 设 计 一 种 投 资
Si ri(%) qi (%) pi (%) ui (元) 组合方案, 即用给定达到
S1 28 2.5 1 103 资金M, 有选择地购买若干
S2 21 1.5 2 198 种资产或存银行生息, 使
S3 23 5.5 4.5 S4 25 2.6 6.5
52 净收益尽可能大, 使总体 40 风险尽可能小.
0.25 0.2
0.15 0.1
0.05 0
0.02 0.04 0.06 0.08
0.1
a
a0=0.006<-----> a0=0.025
模型1结果分析:
1.风险大,收益也大。 2.当投资越分散时,投资者承担的风险越小,这与题意一致。 即:冒险的投资者会出现集中投资的情况,保守的投资者则尽 量分散投资。 3.曲线上的任一点都表示该风险水平的最大可能收益和该收益 要求的最小风险。对于不同风险的承受能力,选择该风险水平 下的最优投资组合。
n
n
∑ ∑ Q( x) = (ri xi − pi max{ui , xi }) ≈ (ri − pi )xi
i=0
i=0
2) 简化总体风险函数P(x):
{ } 令α = max qi xi i = 1,2,L, n ;则
min P ( x) = {max {qi xi i = 1,2,L , n}}
∑ (1 + pi )xi = M
i=0
xi ≥ 0, i = 1,2,L, n
解法3 权衡资产风险和预期净收益两方面, 对风险、收 益赋予权重s和1-s(s称为投资偏好系数)——模型3
模型1 确定风险水平a0,使每一项投资的风险损失 不超过a0*M,并极大化净收益,来得到最优投资组 合——把多目标问题转化为单目标问题
注意这里决策 变量为x和a!
同样在分析
问题时,取多 组不同的收益 水平下限b0,观 察风险的变化 情况,以便给 出合理的收益 水平下限b0。
min P ( x,α ) = α
s.t . qi xi ≤ α , i = 1,2,L n n ∑ (1 + pi )xi = M i=0 n ∑ (ri − pi )xi ≥ b0 i=0 xi ≥ 0, i = 1,2,L, n
n
∑ (1 + pi )xi = M
i=0
xi ≥ 0, i = 1,2,L, n
第三次小作业
针对前面的模型2或模型3,作类 似的分析,写一个不超过两页的 报告(要有数据支持)!
最后大作业
2003全国数学建模竞赛B题2)使就一般情况对以上问题进行讨论,并利用下表数据进 行计算:
Si ri(%) qi (%) pi (%) ui (元) S1 9.6 42 2.1 181 S2 18.5 54 3.2 407 S3 49.4 60 6.0 428 S4 23.9 42 1.5 549 S5 8.1 1.2 7.6 270 S6 14 39 3.4 397 S7 40.7 68 5.6 178 S8 31.2 33.4 3.1 220 S9 33.6 53.3 2.7 457 S10 36.8 40 2.9 248
