平行四边形判定专项练习题

合集下载

平行四边形的判定习题-含答案

解：猜想线段CD与线段AE的大小关系和位置关系是：平行且相等．
证明：∵CE∥AB，
∴∠DAO=∠ECO，
∵OA=OC，
∴△ADO≌△ECO，
∴AD=CE，
∴四边形ADCE是平行四边形，
∴CD AE．
6．如图，已知，▱ABCD中，AE=CF，M、N分别是DE、BF的中点．
求证：四边形MFNE是平行四边形．
证明：∵▱ABCD中，对角线AC交BD于点O，
∴OB=OD，
又∵四边形AODE是平行四边形，
∴AE∥OD且AE=OD，Fra bibliotek∴AE∥OB且AE=OB，
∴四边形ABOE是平行四边形，
同理可证，四边形DCOE也是平行四边形．
13．如图，已知四边形ABCD中，点E，F，G，H分别是AB、CD、AC、BD的中点，并且点E、F、G、H有在同一条直线上．
证明：如答图所示，
∵点O为平行四边形ABCD对角线AC，BD的交点，
∴OA=OC，OB=OD．
∵G，H分别为OA，OC的中点，
∴OG= OA，OH= OC，
∴OG=OH．
又∵AB∥CD，
∴∠1=∠2．
在△OEB和△OFD中，
∠1=∠2，OB=OD，∠3=∠4，
∴△OEB≌△OFD，
∴OE=OF．
∴四边形EHFG为平行四边形．
平行四边形的判定
1．如图所示，□AECF的对角线相交于点O，DB经过点O，分别与AE，CF交于B，D．求证：四边形ABCD是平行四边形．
2如图，已知，□ABCD中，AE=CF，M、N分别是DE、BF的中点．求证：四边形MFNE是平行四边形．
3如图，平行四边形ABCD，E、F两点在对角线BD上，且BE=DF，连接AE，EC，CF，FA．

(完整版)平行四边形练习题及答案(DOC)

20.1平行四边形的判断一、选择题1 ．四边形A BCD，从（ 1）AB∥CD；（ 2）AB=CD；（ 3）BC∥AD；（ 4） BC=AD这四个条件中任选两个，此中能使四边形ABCD是平行四边形的选法有（）A ．3种B．4种C．5种D．6种2．四边形的四条边长分别是a， b， c，d，此中 a，b 为一组对边边长， c，d?为另一组对边边长且知足a2+b2+c2+d2=2ab+2cd，则这个四边形是（）A ．随意四边形B．平行四边形C．对角线相等的四边形 D ．对角线垂直的四边形3．以下说法正确的选项是（）A．若一个四边形的一条对角线均分另一条对角线，则这个四边形是平行四边形B．对角线相互均分的四边形必定是平行四边形C．一组对边相等的四边形是平行四边形D．有两个角相等的四边形是平行四边形二、填空题4 ．在□ ABCD中，点 E， F 分别是线段A D， BC上的两动点，点 E 从点 A 向 D 运动，点F从 C?向 B 运动，点 E 的速度边形．m与点F 的速度n 知足 _______关系时，四边形BFDE为平行四5．如图 1 所示，平行四边形ABCD中， E， F 分别为AD，BC边上的一点，连结EF，若再增添一个条件_______，就能够推出BE=DF．图1图26 ．如图 2 所示， AO=OC，BD=16cm，则当 OB=_____cm时，四边形ABCD是平行四边形．三、解答题7．以下图，四边形 ABCD中，对角线 BD=4，一边长 AB=5，其他各边长用含有未知数 x 的代数式表示，且 AD⊥BD于点 D，BD⊥BC 于点 B．问：四边形 ABCD?是平行四边形吗？为什么？四、思虑题8．以下图，在□ABCD中， E，F 是对角线 AC上的两点，且 AF=CE，?则线段 DE?与 BF的长度相等吗？参照答案一、 1． B 点拨：可选择条件（1）（3）或（2）（ 4）或（ 1）（ 2）或（ 3）（4）．故有 4 种选法．2． B 点拨： a2+b 2+c2+d2=2ab+2cd 即（ a-b）2+（ c-d ）2=0，即（ a-b ）2=0 且（ c-d ）2=0．所以 a=b， c=d，即两组对边分别相等，所以四边形为平行四边形．3． B 点拨：娴熟掌握平行四边形的判断定理是解答这种题目的重点．二、 4．相等点拨：利用“一组对边平行且相等的四边形是平行四边形”来确立．5 ．AE=CF 点拨：此题答案不唯一，只需增添的条件能使四边形EBFD?是平行四边形即可．6． 8 点拨：依据对角线相互均分的四边形为平行四边形来进行鉴别．三、 7．解：以下图，四边形ABCD是平行四边形．原因以下：在 Rt△BCD中，依据勾股定理，得BC2+BD 2=DC 2，即（ x-5 ）2+42=（ x-3 ）2，解得 x=8．所以 AD=11-8=3， BC=x-5=3， DC=x-3=8-3=5 ，所以 AD=BC， AB=DC．所以四边形ABCD是平行四边形．点拨：此题主要告诉的是线段的长度，故只需说明AD=BC， AB=DC即可，此题也可在Rt△ABD中求 x 的值．四、 8．解：线段DE与BF 的长度相等；连结BD交AC于O点，连结DF， BE，以下图．在ABCD中， DO=OB， AO=OC，又因为 AF=EC，所以 AF-AO=CE-OC，即 OF=OE，所以四边形 DEBF是平行四边形，所以DE=BF．点拨：此题若用三角形全等，也能够解答，但过程复杂，学了平行四边形性质后，要学会应用．20.2矩形的判断一、选择题1．矩形拥有而一般平行四边形不拥有的性质是（）A．对角相等 B ．对边相等 C ．对角线相等 D ．对角线相互垂直2．以下表达中能判断四边形是矩形的个数是（）①对角线相互均分的四边形；②对角线相等的四边形；③对角线相等的平行四边形；④对角线相互均分且相等的四边形．A ． 1B． 2C． 3D． 43．以下命题中，正确的选项是（）A．有一个角是直角的四边形是矩形B．三个角是直角的多边形是矩形C．两条对角线相互垂直且相等的四边形是矩形 D ．有三个角是直角的四边形是矩形二、填空题4．如图 1 所示，矩形 ABCD中的两条对角线订交于点O，∠ AOD=120°， AB=4cm，则矩形的对角线的长为 _____．D E CF OA B图 1图 25．若四边形 ABCD的对角线 AC， BD相等，且相互均分于点 O，则四边形 ABCD?是_____ 形，若∠ AOB=60°，那么AB：AC=______．6．如图 2 所示，已知矩形ABCD周长为 24cm，对角线交于点O，OE⊥DC 于点 E，于点 F， OF-OE=2cm，则 AB=______， BC=______．三、解答题7．以下图，□ABCD的四个内角的均分线分别订交于E， F， G，H 两点，试说明四边形 EFGH是矩形．四、思虑题8．以下图，△ABC中， CE， CF分别均分∠ACB和它的邻补角∠ACD．AE⊥CE于 E，AF⊥CF 于F，直线EF分别交AB， AC于 M， N 两点，则四边形AECF是矩形吗？为何？参照答案一、 1． C点拨：A与B都是平行四边形的性质，而D是一般矩形与平行四边形都不具有的性质．2 ．B点拨：③是矩形的判断定理；④中对角线相互均分的四边形是平行四边形，对角线相等的平行四边形是矩形，故④能判断矩形，应选B．3． D 点拨：选项 D 是矩形的判断定理．二、 4． 8cm5．矩； 1： 2 点拨：利用对角线相互均分来判断此四边形是平行四边形，再依据对角线相等来判断此平行四边形是矩形．由矩形的对角线相等且相互均分，?可知△ AOB 是等腰三角形，又因为∠ AOB=60°，所以AB=AO=1AC．26 ． 8cm； 4cm三、 7．解：在□ABCD中，因为AD∥BC，所以∠ DAB+∠CBA=180°，又因为∠ HAB= 1∠DAB，∠ HBA=1∠CBA．22所以∠ HAB+∠HBA=90°，所以∠ H=90°．所以四边形EFGH是矩形．点拨：因为“两直线平行，同旁内角的均分线相互垂直”，所以很简单求出四边形EFGH 的四个角都是直角，从而求得四边形EFGH是矩形．四、 8．解：四边形AECF是矩形．原因：因为CE均分∠ ACB， ?CF?均分∠ ACD， ?所以∠ ACE=1∠ACB，∠ ACF=1∠ACD．所以∠ ECF=1（∠ ACB+∠ACD）=90°．222又因为 AE⊥CE，AF⊥CF， ?所以∠ AEC=∠AFC=90°，所以四边形AECF是矩形．点拨： ?此题是经过证四边形中三个角为直角得出结论．还能够经过证其为平行四边形，再证有一个角为直角得出结论．20.3菱形的判断一、选择题1．以下四边形中不必定为菱形的是（）A ．对角线相等的平行四边形B．每条对角线均分一组对角的四边形C．对角线相互垂直的平行四边形D．用两个全等的等边三角形拼成的四边形2．四个点 A， B， C，D 在同一平面内，从① AB∥CD；② AB=CD；③ AC⊥BD；④ AD=BC；5 个条件中任选三个，能使四边形ABCD是菱形的选法有（）．A ．1种B．2种C．3种D．4种3 ．菱形的周长为32cm，一个内角的度数是60°，则两条对角线的长分别是（）A．8cm和 4 3 cm B．4cm和83 cm C．8cm和83 cm D．4cm和43 cm二、填空题4．如图 1 所示，已知□ABCD，AC，BD订交于点O，?增添一个条件使平行四边形为菱形，增添的条件为 ________．（只写出切合要求的一个即可）图1图25．如图 2 所示， D， E，F 分别是△ ABC 的边 BC， CA，AB 上的点，且 DE∥AB，DF∥CA，要使四边形 AFDE是菱形，则要增添的条件是 ________．（只写出切合要求的一个即可）6 ．菱形 ABCD的周长为48cm，∠ BAD：∠ ABC=1：?2，?则 BD=?_____，?菱形的面积是______．7．在菱形ABCD中， AB=4， AB 边上的高DE垂直均分边AB，则 BD=_____，AC=_____．三、解答题8．以下图，在四边形ABCD中， AB∥CD， AB=CD=BC，四边形 ABCD是菱形吗？ ?说明理由．四、思虑题9．如图，矩形 ABCD的对角线订交于点 O，PD∥AC，PC∥BD， PD，PC订交于点 P，四边形 PCOD是菱形吗？试说明原因．参照答案一、 1． A点拨：此题用清除法作答．2． D 点拨：依据菱形的判断方法判断，注意不要漏解．3． C点拨：以下图，若∠ ABC=60°，则△ ABC为等边三角形，?所以 AC=AB=1×32=8（ cm）， AO=1AC=4cm．42因为 AC⊥BD，在 Rt△AOB中，由勾股定理，得OB=2222AB OA8 4 =43（cm ?），所以 BD=2OB=8 3 cm．二、 4． AB=BC 点拨：还可增添AC⊥BD 或∠ ABD=∠CBD等．5．点 D 在∠ BAC的均分线上（或 AE=AF）26． 12cm； 723 cm点拨：以下图，过 D 作 DE⊥AB 于 E，因为 AD∥BC， ?所以∠ BAD+∠ABC=180°．又因为∠ BAD：∠A BC=1：2，所以∠ BAD=60°，因为 AB=AD，所以△ ABD 是等边三角形，所以BD=AD=12cm．所以 AE=6cm．在 Rt△AED 中，由勾股定理，得 AE 2+ED 2=AD 2， 62+ED 2=12 2，所以 ED 2=108 ，所以 ED=6 3 cm，所以S菱形ABCD=12×63=72 3 （cm2）．7． 4；4 3点拨：以下图，因为DE垂直均分 AB，又因为 DA=AB，所以 DA=DB=4．所以△ ABD 是等边三角形，所以∠ BAD=60°，由已知可得AE=2．在 Rt△AED中，2222222?AE +DE=AD，即 2 +DE=4，所以 DE=12，所以 DE=2 3 ，因为1AC·BD=AB·DE，即1AC·4=4×2 3 ，所以AC=4 3 ．22三、 8．解：四边形ABCD是菱形，因为四边形ABCD中， AB∥CD，且AB=CD，所以四边形ABCD是平行四边形，又因为AB=BC，所以Y ABCD是菱形．点拨：依据已知条件，不难得出四边形ABCD为平行四边形，又AB=BC，即一组邻边相等，由菱形的定义能够鉴别该四边形为菱形．四、 9．解：四边形PCOD是菱形．原因以下：因为 PD∥OC，PC∥OD， ?所以四边形P COD是平行四边形．又因为四边形ABCD是矩形，所以OC=OD，所以平行四边形PCOD是菱形．20.4正方形的判断一、选择题1．以下命题正确的选项是（）A．两条对角线相互均分且相等的四边形是菱形B．两条对角线相互均分且垂直的四边形是矩形C．两条对角线相互垂直，均分且相等的四边形是正方形D．一组邻边相等的平行四边形是正方形2．矩形四条内角均分线能围成一个（）A．平行四边形B．矩形C．菱形 D ．正方形二、填空题3．已知点 D， E，F 分别是△ ABC 的边 AB， BC， CA的中点，连结 DE， EF， ?要使四边形ADEF是正方形，还需要增添条件_______．4．如图 1 所示，直线L 过正方形ABCD的极点 B，点 A， C 到直线 L?的距离分别是 1 和2，则正方形ABCD的边长是 _______．图1图2图35．如图 2 所示，四边形 ABCD是正方形，点 E 在 BC的延伸线上， BE=BD且 AB=2cm，则∠E的度数是 ______， BE 的长度为 ____．6．如图 3 所示，正方形 ABCD的边长为 4，E 为 BC上一点， BE=1，F?为 AB?上一点， AF=2，P 为 AC上一动点，则当 PF+PE取最小值时， PF+PE=______．三、解答题7．以下图，在 Rt△ABC中， CF为∠ ACB的均分线， FD⊥AC 于 D，FE⊥BC于点 E，试说明四边形 CDFE是正方形．BEF四、思虑题8．已知以下图，在正方形 ABCD中， E，F 分别是（1） AF 与 DE相等吗？为何？（2） AF 与 DE能否垂直？说明你的原因．C D A AB，BC边上的点，且 AE=BF，?请问：参照答案一、 1． C点拨：对角线相互均分的四边形是平行四边形，?对角线相互垂直的平行四边形是菱形，对角线相等的平行四边形是矩形，既是菱形又是矩形的四边形必定是正方形，应选 C．2． D 点拨：由题意画出图形后，利用“一组邻边相等的矩形是正方形”来判断．二、 3．△ ABC是等腰直角三角形且∠ BAC=90°点拨：还可增添△ ABC 是等腰三角形且四边形ADEF是矩形或∠ BAC=90°且四边形ADEF 是菱形等条件．4．5点拨：察看图形易得两直角三角形全等，由全等三角形的性质和勾股定理得正方形的边长为 2212=5．5． 67. 5°； 2 2 cm点拨：因为BD是正方形ABCD的对角线，所以∠ DBC=45°， AD=?AB=2cm．在 Rt△BAD中，由勾股定理得 AD 2+AB 2=BD 2，即 22+22=BD 2，所以 BD=2 2 cm，所以 BE=BD=2 2（ cm），又因为BE=BD，所以∠ E=∠EDB= 1（180°- 45°）=67. 5°．26．17点拨：以下图，作 F 对于AC的对称点G．连结EG交AC于P，则 PF+?PE=PG+PE=GE为最短．过 E 作 EH⊥AD．在 Rt△GHE中，HE=4，HG=AG-AH=AF-BE=1，所以 GE= 4212 = 17，?即 PF+PE= 17．三、 7．解：因为∠ FDC=∠FEC=∠BCD=90°，所以四边形CDFE是矩形，因为 CF?均分∠ ACB，FE⊥BC，FD⊥AC，所以FE=FD，所以矩形CDFE是正方形．点拨：此题先说明四边形是矩形，再求出有一组邻边相等，?还能够先说明其为菱形，再求其一个内角为90°．四、 8．解：（ 1）相等．原因：在△ ADE 与△ BAF 中， AD=AB，∠ DAE=∠ABF=90°， AE=BF，所以△ ADE≌△ BAF（ S． A． S．），所以 DE=AF．（ 2） AF 与 DE垂直．原因：如图，设DE与 AF 订交于点O．因为△ ADE≌△ BAF， ?所以∠ AED=∠BFA．又因为∠ BFA+∠EAF=90°，所以∠ AEO+∠EAO=90°，所以∠ EOA=90°，所以DE⊥AF．20.5等腰梯形的判断1 A C 一、选择题．以下结论中，正确的选项是（．等腰梯形的两个底角相等．一组对边平行的四边形是梯形）BD．两个底角相等的梯形是等腰梯形．两条腰相等的梯形是等腰梯形2．以下图，等腰梯形ABCD的对角线 AC，BD订交于点O，则图中全等三角形有（）A．2对B．3对C．4对D．5对3．课外活动课上， ?老师让同学们制作了一个对角线相互垂直的等腰梯形形状的风筝，其面积为450cm，则两条对角线所用的竹条长度之和起码为（）A． 30 2 cm B．30cm C．60cm D．60 2 cm二、填空题4．等腰梯形上底，下底和腰分别为 4，?10，?5，?则梯形的高为 _____，?对角线为 ______．5．一个等腰梯形的上底长为5cm，下底长为 12cm，一个底角为 60°，则它的腰长为____cm，周长为 ______cm．6．在四边形 ABCD中， AD∥BC，但 AD≠BC，若使它成为等腰梯形，则需要增添的条件是__________ （填一个正确的条件即可）．三、解答题7．以下图，AD是∠ BAC的均分线， DE∥AB， DE=AC，AD≠EC．求证： ?四边形 ADCE是等腰梯形．四、思虑题8．以下图，四边形ABCD中，有 AB=DC，∠ B=∠C，且AD<BC，四边形 ABCD是等腰梯形吗？为何？参照答案一、 1． D点拨：梯形的底角分为上底上的角和下底上的角，?所以在等腰梯形的性质和鉴别方法中一定重申同一底上的两个内角（?指上底上的两个内角或下底上的两个内角），不然就会出现错误，所以A， B 选项都不正确，而 C 选项中遗漏了限制条件此外一组对边不平行，若平行该四边形就形成了平行四边形了，所以应选D．2． B点拨：因为△ ABC≌△ DCB，△ BAD≌△ CDA，△ AOB≌△ DOC，所以共有 3 对全等的三角形．3． C点拨：设该等腰梯形对角线长为Lcm，因为两条对角线相互垂直，?所以梯形面积为122L =450，解得 L=30，所以所用竹条长度之和起码为2L=2× 30=60（cm）．二、 4． 4：65点拨：以下图，连结BD，过 A，D 分别作 AE⊥BC，DF⊥BC，垂足分别为E， F．易知△ BAE≌△ CDF，在四边形 AEFD为矩形，所以BE=CF=3， AD=EF=4．在 Rt△CDF 中， FC2+DF 2=CD 2，即 32+DF 2=52，所以 DF=4 ，在 Rt △BFD 中， BF2+DF 2=BD 2，即 72+42=BD 2，所以 BD=65 ．5． 7；31点拨：以下图，过点D作 DE∥AB 交 BC于 E．因为ABED是平行四边形．所以 BE=AD=5（cm）， AB=DE．又因为 AB=CD，所以 DE=?DC，又因为∠ C=60°，所以△ DEC 是等边三角形，所以 DE=DC=EC=7（ cm），所以周长为5+?12+7+7=31（cm）．6． AB=CD（或∠ A=∠D，或∠ B=∠C，或 AC=BD，或∠ A+∠C=180°，或∠B+∠D=180°）三、 7．证明：因为 AB∥ED，所以∠ BAD=∠ADE．又因为 AD是∠ BAC的均分线，所以∠ BAD=∠CAD，所以∠ CAD=∠ADE，所以 OA=OD．又因为AC=DE，所以 AC-OA=DE-OD即 OC=OE， ?所以∠ OCE=∠OEC，又因为∠ AOD=∠COE，所以∠ CAD=∠OCE．所以AD∥CE，而 AD≠CE，故四边形ADCE是梯形．又因为∠ CAD=∠ADE， AD=DA， AC=DE，所以△ DAC≌△ ADE，所以DC=?AE，所以四边形ADCE是等腰梯形．点拨：证明一个四边形是等腰梯形时，应先证其是梯形尔后再证两腰相等或同一底上的两个角相等．四、 8．解：四边形ABCD是等腰梯形．原因：延伸BA， CD，订交于点 E，以下图，由∠ B=∠C，可得EB=EC．又 AB=DC，所以 EB-AB=EC-DC，即 AE=DE，所以∠ EAD=∠EDA．因为∠ E+∠EAD+∠EDA=180°，∠ E+∠B+∠C=180°，所以∠ EAD=∠B．故 AD∥BC． ?又 AD<BC，所以四边形 ABCD是梯形．又 AB=DC，所以四边形 ABCD是等腰梯形．点拨：由题意可知，只需推出AD∥BC，再由AD<BC便可知四边形ABCD为梯形，再由AB=DC，即可求得此四边形是等腰梯形，由∠ B=∠C联想到延伸 BA，CD，即可获得等腰三角形，从而使 AD∥BC．华东师大版数学八年级（下）第 20 章平行四边形的判断测试（答卷时间： 90 分钟，全卷满分： 100 分）姓名得分 ____________一、认认真真选，沉稳应战！（每题 3 分，共 30 分）1. 正方形拥有菱形不必定拥有的性质是()（A ）对角线相互垂直（B）对角线相互均分（C）对角线相等（D）对角线均分一组对角2.如图 (1)，EF 过矩形 ABCD 对角线的交点 O，且分别交 AB 、CD 于 E、 F，那么暗影部分的面积是矩形ABCD 的面积的（）（A ）A 111（ D ）3A5（B ）（ C）1043D E FFEB C D HB C(1)(2)(3)3．在梯形ABCD 中， AD ∥ BC ，那么 A : B : C : D 能够等于（）（ A）4：5：6：3（B）6：5：4：3（C）6：4：5：3（D）3：4：5：64．如图 (2) ，平行四边形ABCD 中，DE ⊥ AB 于 E，DF⊥ BC 于 F，若Y ABCD的周长为48，DE ＝ 5， DF＝ 10，则Y ABCD的面积等于 ()（ A）87.5（B）80（C）75（D）72.55． A 、 B、 C、 D 在同一平面内，从① AB∥CD;② AB=CD;③ BC∥AD;④ BC=AD这四个条件中任选两个，能使四边形ABCD 是平行四边形的选法有（）（ A）3种（B）4种（C）5种（D）6种6．如图 (3) ，D、E、F分别是VABC各边的中点，AH 是高，假如 ED5cm ，那么 HF的长为（）（ A ） 5cm（B）6cm（C）4cm（D）不可以确立7.如图（ 4）：E 是边长为 1 的正方形 ABCD 的对角线 BD 上一点，且 BE ＝ BC， P 为 CE 上随意一点， PQ⊥BC 于点 Q， PR⊥ BE 于点 R，则 PQ＋PR 的值是（）2132（ A ）2（B）2（C）2（D）38．如图（ 5），在梯形ABCD 中， AD ∥ BC ， AB CD ， C 60 ，BD均分ABC ，假如这个梯形的周长为30，则AB的长（）（ A）4（ B）5（C）6（ D）7A DA DERPB C（ 5）B（4）Q C9．右图是一个利用四边形的不稳固性制作的菱形晾衣架．A B C 已知此中每个菱形的边长为20cm，墙上悬挂晾衣架的两个铁钉 A 、 B 之间的距离为20 3 cm，则∠1等于()1）（ A）90°（Ｂ） 60°（Ｃ） 45°（Ｄ） 30°10．某校数学课外活动研究小组，在老师的指引下进一步研究了完整平方公式．联合实数的性质发现以下规律：对于随意正数a、 b，都有 a+b ≥ 2ab 建立．某同学在做一个面积为3600cm2，对角线相互垂直的四边形风筝时，运用上述规律，求得用来做对角线用的竹条至少需要准备xcm．则 x 的值是（）(A) 1202(B) 602(C) 120(D) 60二、仔认真细填，记录自信！( 每题 2 分，共20 分)11．一个四边形四条边按序是a、b、c、d，且a2 b 2 c 2 d 22ac 2bd，则这个四边形是 _______________ ．12．在四边形ABCD中，对角线AC、BD交于点O，从（1）AB CD ；（2） AB∥CD ；（3）OA OC；（4）OB OD ；（5） AC ⊥ BD ；（6） AC 均分 BAD 这六个条件中，选用三个推出四边形ABCD是菱形．如（ 1）（ 2）（ 5）ABCD 是菱形，再写出切合要求的两个：ABCD 是菱形；ABCD 是菱形．13. 如图，已知直线l 把 Y ABCD 分红两部分，要使这两部分的面积相等，直线l 所在地点需知足的条件是____________________. （只需填上一个你以为适合的条件）lA DB C(第 13 题)(第 16 题)14.梯形的上底长为 6cm ，过上底的一极点引一腰的平行线，与下底订交，所构成的三角形周长为 21cm ，那么梯形的周长为_________ cm。

(完整版)平行四边形的性质判定练习题

第一部分平行四边形的性质练习题例题1、平行四边形得周长为50cm ，两邻边之差为5cm,求各边长。

变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形，∠BAC=90°,AB=3,AC=4,求AD 的长。

例题2.平行四边形ABCD 中，∠A-∠B=20°,求平行四边形各内角的度数。

变题3.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图，在平行四边形ABCD 中，∠BAC=34°, ∠ACB=26°，求∠DAC 与∠D 的度数。

例题3.如图，在平行四边形ABCD 中，CE ⊥AD,CF ⊥BA 交BA 的延长线于F ，∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。

变题5.如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

1、如图，四边形ABCD 是平行四边形，AB=6cm,BC=8cm ，∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________.3、平行四边形得周长为50cm ，两邻边之差为5cm,则长边是________ ，短边是__________.4、平行四边形ABCD 中，∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中，∠A+∠C=200°.则：∠A= _______，∠B= _________ .7、如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

平行四边形的判定练习题(含答案)

平行四边形的判定练习题(含答案)（1）因为AD∥BC，AB=CD，所以ABCD是平行四边形．（）（2）因为AB∥CD，AD=BC，所以ABCD是平行四边形．（）（3）因为AD∥BC，AD=BC，所以ABCD是平行四边形．（）（4）因为AB∥CD，AD∥BC，所以ABCD是平行四边形．（）（5）因为AB=CD，AD=BC，所以ABCD是平行四边形．（）（6）因为AD=CD，AB=AC，所以ABCD是平行四边形．（）5．已知AD∥BC，要使四边形ABCD为平行四边形，需要增加条件________．6．如图所示，∠1=∠2，∠3=∠4，问四边形ABCD是不是平行四边形．7．如图所示，在四边形ABCD中，AB=CD，BC=AD，E，F 为对角线AC上的点，且AE=CF，求证：BE=DF．8．如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．求证：CD=AF．9．如图所示，已知四边形ABCD是平行四边形，在AB 的延长线上截取BE=•AB，BF=BD，连接CE，DF，相交于点M．求证：CD=CM．10．如图所示，在四边形ABCD中，DC∥AB，以AD，AC为边作□ACED，延长DC•交EB于F，求证：EF=FB．知能点2 三角形的中位□线11．如图所示，已知E为□ABCD中DC边的延长线上的一点，且CE=DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF，求证：AB=2OF．12．如图所示，在ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF•交于点M，连接CF，DE交AD．于点N，求证：MN∥AD且MN=1213．如图所示，DE是△ABC的中位线，BC=8，则DE=_______．14．如图所示，在□ABCD中，对角线AC，BD交于点O，OE∥BC交CD•于E，•若OE=3cm，则AD的长为（）． A．3cm B．6cm C．9cm D．12cm 15．如图所示，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点，•则四边形EFGH是平行四边形吗？为什么？16．如图所示，在△ABC中，AC=6cm，BC=8cm，AB=10cm，D，E，F分别是AB，BC，CA的中点，求△DEF的面积．规律方法应用17．如图所示，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，•并分别找出AC和BC的中点M，N，如果测得MN=20m，那么A，B两点间的距离是多少？18．如图所示，在□ABCD中，AB=2AD，∠A=60°，E，F 分别为AB，CD的中点，EF=1cm，那么对角线BD的长度是多少？你是怎样得到的？19．如图所示，在△ABC中，E为AB的中点，CD平分∠ACB，AD⊥CD于点D．•（BC-AC）．试说明：（1）DE∥BC．（2）DE=12开放探索创新20．如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AD•于E，EF∥BC交AC于F，那么AE与CF相等吗？请验证你的结论．中考真题实战21．（长沙）如下左图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD•为平行四边形，则应添加的条件是________．（添加一个即可）22．（呼和浩特）如上右图所示，已知E，F，G，H是四边形ABCD各边的中点，•则S四边形EFGH ：S四边形ABCD的值是_________．23．（南京）已知如图19-1-55所示，在Y ABCD中，E，F分别是AB，CD的中点.求证：（1） △AFD≌△CEB．（2）四边形AECF是平行四边形．答案:1．C 2．C 3．D4．（1）× （2）× （3）∨ （4）∨ （5）∨ （6）×5．AD=BC或AB∥CD6．解：∵∠1=∠2，∴AD∥BC．又∵∠3=∠4，∴AB∥CD．∴四边形ABCD是平行四边形．7．证明：∵AB=CD，BC=AD，∴四边形ABCD是平行四边形．∴AB∥CD，∴∠BAE=∠DCF．又∵AE=CE，∴△ABE≌△CDF（SAS），∴BE=EF．8．证明：∵FC∥AB，∴∠DAC=∠ACF，∠ADF=∠DFC．又∵AE=CE，∴△ADE≌△CFE（AAS），∴DE=EF．∵AE=CE，∴四边形ADCF为平行四边形．∴CD=AF．9．证明：∵四边形ABCD是平行四边形．∴AB//DC．又∵BE=AB，∴BE//DC，∴四边形BDCE是平行四边形．∵DC∥BF，∴∠CDF=∠F．同理，∠BDM=∠DMC．∵BD=BF，∴∠BDF=∠F．∴∠CDF=∠CMD，∴CD=CM．10．证明：过点B作BG∥AD，交DC的延长线于G，连接EG．∵DC∥AB，∴ABGD是平行四边形，∴BG// AD．在□ACED中，AD//CE，∴CE//BG．∴四边形BCEG为平行四边形，∴EF=FB．11．证明：∵四边形ABCD是平行四边形，∴AB//CD，AD=BC．∵CE=CD，∴AB//CE，∴四边形ABEC为平行四边形．∴BF=FC，∴OF//1AB，即AB=2OF．212．证明：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC．又∵EF∥AB，∴EF∥CD．∴四边形ABEF，ECDF均为平行四边形．又∵M，N分别为Y ABEF和Y ECDF对角线的交点．∴M为AE的中点，N为DE的中点，即MN为△AED的中位线．∴MN∥AD且MN=12AD．13．4 14．B15．解：EFGH是平行四边形，连接AC，在△ABC中，∵EF是中位线，∴EF//12AC．同理，GH//12AC．∴EF//GH，∴四边形EFGH为平行四边形．16．解：∵EF，DE，DF是△ABC的中位线，∴EF=12AB，DE=12AC，DF=12BC．又∵AB=10cm，BC=8cm，AC=6cm，∴EF=5cm，DE=3cm，DF=4cm，而32+42=25=52，即DE2+DF2=EF2．∴△EDF为直角三角形．∴S△EDF =12DE·DF=12×3×4=6（cm2）．17．解：∵M，N分别是AC，BC的中点．∴MN是△ABC的中位线，∴MN=12AB．∴AB=2MN=2×20=40（m）．故A，B两点间的距离是40m．18．解：连接DE．∵四边形ABCD是平行四边形，∴AB//CD．∵DF=12CD，AE=12AB，∴DF//AE．∴四边形ADFE是平行四边形．∴EF=AD=1cm．∵AB=2AD，∴AB=2cm．∵AB=2AD，∴AB=2AE，∴AD=AE．∴∠1=∠4．∵∠A=60°，∠1+∠4+∠A=180°，∴∠1=∠A=∠4=60°．∴△ADE是等边三角形，∴DE=AE．∵AE=BE，∴DE=BE，∴∠2=∠3．∵∠1=∠2+∠3，∠1=60°，∴∠2=∠3=30°．∴∠ADB=∠3+∠4=90°．=cm）．19．解：延长AD交BC于F．（1）∵AD⊥CD，∴∠ADC=∠FDC=90°．∵CD平分∠ACB，∴∠ACD=∠FCD．在△ACD与△FCD中，∠ADC=∠FDC，DC=DC，∠ACD=∠FCD．∴△ACD≌△FCD，∴AC=FC，AD=DF．又∵E为AB的中点，∴DE∥BF，即DE∥BC．（2）由（1）知AC=FC，DE=12BF．∴DE=12（BC-FC）=12（BC-AC）．20．解：AE=CF．理由：过E作EG∥CF交BC于G，∴∠3=∠C．∵∠BAC=90°，AD⊥BC，∴∠ABC+∠C=90°，∠ABD+∠BAD=90°．∴∠C=∠BAD，∴∠3=∠BAD．又∵∠1=∠2，BE=BE，∴△ABE≌△GBE（AAS），∴AE=GE．∵EF∥BC，EG∥CF，∴四边形EGCF是平行四边形，∴GE=CF，∴AE=CF．21．答案不唯一，如AB=CD或AD∥BC．22．1223．解：（1）在□ABCD中，AD=CB，AB=CD，∠D=∠B．∵E，F分别为AB，CD的中点，∴DF=12CD，BE=12AB，∴DF=BE，∴△AFD≌△CEB．（2）在□ABCD中，AB=CD，AB∥CD．由（1）得BE=DF，∴AE=CE，∴四边形AECF是平行四边形．。

平行四边形判定专项练习30题

平行四边形的判定专项练习30题（有答案）求证：四边形ABCD 为平行四边形.I __ D ZX73 .已知四边形 ABCD 的对角线 AC 与BD 交于点0,现给出四个条件： ①0A=0C ;②AB=CD ;③/BAD= ZDCB ;④AD //BC •请你从中选择两个，推出四边形ABCD 为平行四边形，并写出你的推理过程.（1 ）从以上4个条件中任意选取 2个条件，能推出四边形 ABCD 是平行四边形的有（用序号表示） __________________ . （2 ）从（1 ）中选出一种情况，写出你的推理过程.4 .如图，已知：点 B 、E 、F 、D 在一条直线上，DF=BE , AE=CF .请从下列三个条件中选择一个合适的条件，添加到已知条件中，使四边形 ABCD 是平行四边形，并说明理由，供选择的三个条件（请从其中选择一个）：2 .如图，四边形 ABCD 中，/ BAC=90,AB=11 ABCD 是平行四边形.-x , BC=5 , CD=x - 5 , AD=x - 3, AC=4.AD //BC , ED //BF , AF=CE ，求证:①AB=DC :② BC=AD ;③/AED= /CFB .5 .如图，在？ ABCD中，AC交BD于点0,点E,点F分别是OA , OC的中点，请判断线段BE,7 .如图，已知BE丄AD , CF丄AD，且BE=CF .求证：(1 ) AD是△ABC的中线；(2)请连接BF、CE,试判断四边形BECF是何种特殊四边形，并说明理由.DF的位置关6.如图所示, 以△ABC的三边为边在BC的同侧分别作三个等边三角形厶ABD、ABCE、△XCF ,猜想: 四边形ADEFA8 .如图，矩形ABCD的两条对角线AC和BD相交于点O, E、F是BD上的两点，且/ AEB= /CFD .求证：四边形AECF是平行四边形.9 .如图：在四边形ABCD 中，AD //BC, AB=CD , E 是BC 上一点，DE=AB .10 .如图，已知AB //DC, E是BC的中点，AE , DC的延长线交于点F;(1 )求证：△ ABE 也£CE;11 .等边△ ABC 中，点D 在BC 上，点E 在AB 上，且CD=BE ，以AD 为边作等边△ ADF ，如图.求证：四边形 CDFE 是平行四边形.足为F ,连结DF . 求证：(1 )MBC 也△AF ; (2)四边形ADFE 是平行四边形.别从A 、C 同时出发，点 P 以2cm/秒的速度由A 向D 运动，点Q 以3cm/秒的速度由C 向B 运动.12 •如图，分别以 Rt △ABC 的直角边 AC 及斜边 AB 向外作等边△ ACD 、等边△ ABE .若/BAC=30,EF 丄 AB ，垂13 .已知：如图，在△ ABC 中，中线BE , CD 交于点O , F , G 分别是OB , OC 的中点.求证：四边形 DFGE 是平14 •如图所示：在四边形ABCD 中，AD //BC 、BC=18cm , CD=15cm , AD=10cm , AB=12cm ，动点P 、Q 分行四边形.实用标准文案(1 )几秒钟后，四边形ABQP为平行四边形？并求出此时四边形ABQP的周长PDCQ的周长.15 •求证：顺次连接四边形各边中点所得的四边形是平行四边形.16 .△ABC中，中线BE、CF相交于0 , M是BO的中点，N是CO的中点, 求证：四边形MNEF是平行四边形.17 .如图，AD=DB , AE=EC , FG //AB, AG //BC.(1 )证明：△ AGE ^/CFE;(2)说明四边形ABFG是平行四边形;(3)研究图中的线段DE, BF, FC之间有怎样的位置关系和数量关系.18 .如图，△ ABC和△ADE都是等边三角形，点D在BC边上，AB边上有一点F,且BF=DC，连接EF、EB.(1 )求证：△ ABE 也△CD ;19 .已知在△ ABC中，D、E分别是AB、AC的中点，点F在DE的延长线上，且EF=DE ,图中有几个平行四边形? 请说明你的理由.20 .如图，在△ ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F,连接BF. 求证：四边形AFBD是平行四边形.21 .如图：在四边形ABCD中，AD //BC, E是BC的中点，BC=2AD .找出图中所有的平行四边形，并选择一个22 •求证：两组对角分别相等的四边形是平行四边形.23 .已知：如图，A、B、C、D在同一条直线上，且AB=CD , AE //DF , AE=DF .求证：四边形 EBFC 是平行四边形.24 .如图，在△ ABC 中，D 是BC 边的中点，E 、F 分别在 AD 及其延长线上，CE//BF ,连接BE 、CF .形BFCE 是平行四边形吗？为什么?25 .已知点E 、F 、G 、H 分别为四边形 ABCD 四边的中点，试问四边形 EFGH 的形状并说明理由.26 .如图，已知四边形 ABCD 中AD=BC ，点A 、B 、E 在同一条直线上，且/ B= /EAD ，试说明四边形平行四边形.图中的四边ABCD 是28 .已知：△ ABC 的中线BD 、CE 交于点O , F 、G 分别是OB 、OC 的中点.求证：四边形 29 .如图，△ ACD 、MBE>ABCF 均为直线 BC 同侧的等边三角形.当 AB 丰AC 时，求证: 边形.30 .已知：在四边形 ABCD 中，AD //BC ,且 AB=DC=5 , AC=4 , BC=3 .求证：四边形ABCD 为平行四边形.ABCD 是平行四边形.DEFG 是平行四边形.四边形 ADFE 为平行四平行四边形的判定30题参考答案：1.TAD //BC,•••/DAE= ZBCF,TED //BF,•••/DEF= ZBFE,•••厶ED= ZCFB,又T AF=CE ,•••AE=CF ,在△ADE和ACBF中：T/DAE= ZBCF,ZAED= ZCFB,AE=CF ,.•.念DE 也zCBF (AAS ),•••AD=CB ,即：AD //CB , AD=CB ,•四边形ABCD是平行四边形，2.T/BAC=90° , AB=11 - x , BC=5 , AC=4 . •••(11 - x) 2+4 2=5 2,解得：x i =8 , X2=14 > 11 (舍去)，当x=8 时，BC=AD=5 , AB=CD=3 ,•四边形ABCD为平行四边形.3. (1 )解：能推出四边形ABCD是平行四边形的有①④、③④；故答案是：①④、③④；(2 )以①④为例进行证明.如图，在四边形ABCD中，OA=OC , AD //BC .证明：T AD //BC, •••/DAO= ZBCO .•••在△KOD 与△COB 中，r ZDA0-ZBC0{DA=0CZAOD-ZDOB (对顶角相等)•••ZAOD 也ZCOB (ASA ),•••AD=BC ,•••在四边形ABCD中，AD二BC, •四边形ABCD为平行四边形.4.选择①，VDF=BE , AE=CF, AB=CD ,•ZABE也/CDF ( sss),•ZABE= /CDF ,•••AB //CD,又TAB=CD ,•四边形ABCD是平行四边形.5. BE=DF , BE //DF因为ABCD是平行四边形，所以OA=OC , OB=OD ,因为E, F分别是OA, OC的中点，所以OE=OF ,36 •四边形ADEF是平行四边形.连接ED、EF,•••念BD 'ABCE'^ACF分别是等边三角形, •••AB=BD，BC=BE，/DBA= /EBC=60 °•••/DBE= /ABC ••••念BC 也QBE.同理可证厶ABC也/EEC,•••AB=EF , AC=DE .VAB=AD , AC=AF ,•••AD=EF , DE=AF .•••/BED= ZCFD .VZBDE= /CDF , BE=CF ,•••/BED也EFD .•••BD=CD .•••AD是EABC的中线.(2)四边形BECF是平行四边形,由(1)得：BD=CD , ED=FD .•四边形BECF是平行四边形8 •四边形ABCD是矩形•••AB //CD , AB=CD , •••/ABE= /CDF ,又v/AEB= ZCFD , /•ZABE也EDF ,•••BE=DF ,又•••四边形ABCD是矩形，•••OA=OC , OB=OD , •••OB - BE=OD - DF , •••OE=OF ,•四边形AECF是平行四边形9.TAD //BC, AB=CD , •四边形ABCD是等腰梯形，•••/B= ZC ,VDE=AB ,•••DE=CD ,•ZDEC= ZC ,•ZDEC= ZB ,•••AB //DE,•四边形ABED是平行四边形.10. (1 )证明：T AB //DC, •/= Z , ZFCE= ZEBA , •••E为BC中点，•••CE=BE, 所以BFDE是平行四边形，所以BE=DF , BE//DFT在ZABE 和AFCE 中，Z1= Z , ZFCE= ZEBA , CE=BE ,(2)四边形ABFC是平行四边形;理由：由(1 )知：AABE^△CE,•••EF=AE ,VCE=BE,•四边形ABFC是平行四边形11 •连接BF,•••念DF和AABC是等边三角形，/FAD=60 • /FAD -Z EAD= /CAB -ZEAD , •••/FAB= /CAD , 在AFAB和ADAC中；AF=AD彳ZFAB=ZCAD ,I AB=AC• △AB BAAC (SAS), •••BF=DC , ZABF= ZACD=60 VBE=CD ,•••BF=BE ,•ZBFE是等边三角形,•••ZACD BABE ( SAS),•••AD=CE=DF ,VEF=CD ,•四边形CDFE是平行四边形.5 D C12• (1 )vAABE为等边三角形，EF±AB ,•••EF 为ZBEA 的平分线，Z AEB=60 °,AE=AB , •••ZFEA=30。

八年级数学(下)第十八章《平行四边形的判定》同步练习(含答案)

八年级数学（下）第十八章《平行四边形的判定》同步练习（含答案）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．1．如图，DE是△ABC的中位线，且△ADE的周长为20，则△ABC的周长为A．30 B．40C．50 D．无法计算【答案】B2．如图，在四边形ABCD中，AB=CD，BC=AD，若∠D=120°，则∠C的度数为A．60°B．70°C．80°D．90°【答案】A【解析】∵AB=CD，BC=AD，∴四边形ABCD是平行四边形，∴AD∥BC，∴∠C+∠D=180°，∵∠D=120°，∴∠C=60°．故选A．3．四边形ABCD中，从∠A，∠B，∠C，∠D的度数之比中，能判定四边形ABCD是平行四边形的是A．1∶2∶3∶4 B．2∶3∶2∶3C．2∶2∶3∶3 D．1∶2∶2∶3【答案】B【解析】根据对角相等的四边形是平行四边形，A．1∶2∶3∶4，对角不相等，不能；B．2∶3∶2∶3，对角相等，能；C．2∶2∶3∶3，对角不相等，不能；D．1∶2∶2∶3，对角不相等，不能，故选B．4．依次连接任意四边形各边的中点，得到一个特殊图形，则这个图形一定是A．平行四边形B．矩形C．菱形D．梯形【答案】A【解析】如图，连接AC，∵四边形ABCD各边中点是E、F、G、H，∴HG∥AC，HG=12AC，EF∥AC，EF=12AC，∴EF=GH，EF∥GH，∴四边形EFGH是平行四边形．故选A．5．如图，在四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是A．AB∥CD，AD∥BC B．OA=OC，OB=ODC．AD=BC，AB∥CD D．AB=CD，AD=BC【答案】C6．如图，ABCD的对角线AC，BD相交于点O，E是AB中点，且AE+EO=4，则ABCD的周长为A．20 B．16 C．12 D．8【答案】B【解析】∵四边形ABCD是平行四边形，∴OA=OC，∵AE=EB，∴OE =12BC，∵AE+EO=4，∴2AE+2EO=8，∴AB+BC=8，∴平行四边形ABCD的周长=2×8=16，故选B．7．如图，在ABCD中，对角线AC，BD相交于点O，E，F是对角线AC上的两点，当E，F满足下列哪个条件时，四边形DEBF不一定是平行四边形A．AE=CF B．DE=BFC．∠ADE=∠CBF D．∠AED=∠CFB【答案】BD选项：∵∠AED=∠CFB，∴∠DEO=∠BFO ，∴DE∥BF，在△DOE和△BOF中，DOE BOF DEO BFO OD OB∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△DOE≌△BOF，∴DE=BF，∴四边形DEBF是平行四边形．故选项正确．故选B．8．如图，E，F分别是□ABCD的边AB，CD的中点，则图中平行四边形的个数共有A．2个B．3个C．4个D．5个【答案】C【解析】∵四边形ABCD是平行四边形，∴DC∥AB，DC=AB，∵E、F分别是边AB、CD的中点，∴DF=FC=12DC，AE=EB=12AB，∵DC=AB，∴DF=FC=AE=EB，∴四边形DFBE和CFAE都是平行四边形，∴DE∥FB，AF∥CE，∴四边形FHEG是平行四边形，故选C．二、填空题：请将答案填在题中横线上．9．如图，A、B两点被池塘隔开，在AB外选一点C，连接AC、BC，取AC、BC的中点D、E，量出DE=a，则AB=2a，它的根据是__________．【答案】三角形的中位线等于第三边的一半10．如图，在四边形ABCD中，AD∥BC，点E是BC边的中点，连接DE并延长，交AB的延长线于F点．已知AB=4，∠F=∠CDE，则BF的长为__________．【答案】4【解析】因为∠F=∠CDE，所以AB∥CD，因为AD∥BC，所以四边形ABCD是平行四边形，所以AB=CD，因为点E是BC边的中点，所以ED=EF，又因为∠F=∠CDE，∠DEC=∠FEB，所以△ECD≌△EBF，所以BF=CD，所以BF=AB，因为AB=4，所以BF=4，故答案为：4．11．如图，四边形ABCD中，AD∥BC，E是DC上一点，连接BE并延长交AD的延长线于点F，连接CF，BD，请你只添加一个条件：__________，使得四边形BDFC为平行四边形．【答案】DE=EC（答案不唯一）【解析】答案不唯一，比如：BD∥CF，构成两组对边分别平行的四边形是平行四边形；DF=BC，构成一组对边平行且相等的四边形是平行四边形；DE=EC，可以证明BE=EF，构成对角线相互平分的四边形是平行四边形，等等．故答案：DE=EC（答案不唯一）．12．如图，在平行四边形ABCD中，对角线交于点O，点E、F在直线AC上（不同于A、C），当E、F的位置满足__________的条件时，四边形DEBF是平行四边形．【答案】AE=CF（答案不唯一）三、解答题：解答应写出文字说明、证明过程或演算步骤．13．如图，已知D、E、F分别是△ABC各边的中点，求证：AE与DF互相平分．【解析】∵D、E、F分别是△ABC各边的中点，根据中位线定理知：DE∥AC，DE=AF，EF∥AB，EF=AD，∴四边形ADEF为平行四边形，故AE与DF互相平分．14．如图，ABCD中，E、F分别是AB、CD上的点，AE=CF，M、N分别是DE、BF的中点．求证：四边形ENFM是平行四边形．【解析】∵四边形ABCD是平行四边形，∴AB∥CD．∵AE=CF，∴FD=EB，∴四边形DEBF是平行四边形，∴DE∥FB，DE=FB．∵M、N分别是DE、BF的中点，∴EM=FN．∵DE∥FB，∴四边形MENF是平行四边形．15．如图，点M，N在线段AC上，AM=CN，AB∥CD，AB=CD．求证：∠1=∠2．16．如图1，平行四边形ABCD中，对角线BD、AC交于点O．将直线AC绕点O顺时针旋转分别交BC、AD于点E、F．（1）在旋转过程中，线段AF与CE的数量关系是__________．⊥，当旋转角至少为__________︒时，四边形ABEF是平行四边形，并证明（2）如图2，若AB AC此时的四边形是ABEF是平行四边形．【解析】（1）相等，理由如下：如图，在ABCD 中，AD ∥BC ，OA =OC ，∴∠1=∠2，在△AOF 和△COE 中，1234OA OC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AOF ≌△COE （ASA ）， ∴AF =CE ．（2）当旋转角为90︒时，90COE ∠=︒，如图，又∵AB ⊥AC ， ∴∠BAO =90°， ∠AOF =90°， ∴∠BAO =∠AOF ， ∴AB ∥EF ，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，即：AF ∥BE ， ∵AB ∥EF ，AF ∥BE ，∴四边形ABEF 是平行四边形．。

中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)

中考数学模拟题汇总《平行四边形的判定与证明》专项练习(附答案解析)一、综合题1．如图，在Rt△ABC中，∠ACB=90°，点D、E分别是AB、BC的中点，点F在AC的延长线上，∠FEC=∠B．（1）求证：DE=CF；（2）若AC=6cm，AB=10cm，求四边形DCFE的面积．2．已知△ABC内接于⊙O，AB是⊙O的直径，OD∥AC，AD＝OC.（1）求证：四边形OCAD是平行四边形；（2）若AD与⊙O相切，求∠B.3．已知：如图，点D在ΔABC的边AB上，CF//AB，DF交AC于E，EA=EC．（1）如图1，求证：CD=AF；（2）如图2，若AD=BD，请直接写出和ΔBDC面积相等的三角形．4．如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE=CF，DF=BE，且DF//BE，过点C作CG⊥AB交AB的延长线于点G．（1）求证：四边形ABCD是平行四边形；（2）若tan∠CAB=25，∠CBG=45°，BC=4√2，则▱ABCD的面积是．5．已知，如图，E、F是四边形ABCD的对角线AC上的两点，AF=CE，DF=BE，DF∥BE．（1）求证：△AFD≌△CEB；（2）四边形ABCD是平行四边形吗？请说明理由．6．如图，▱ABCD中，AC，BD相交于点O，E，F分别是OA，OC的中点.（1）求证：BE=DF；（2）设ACBD=k，当k为何值时，四边形DEBF是矩形？请说明理由.7．如图，在ΔABC中，点D、E、F分别在AB、AC、BC上，DE // BC，EF // AB．（1）求证：ΔADE∽ΔEFC；（2）如果AB=6，AD=4，求SΔADESΔEFC的值．8．如图，已知平行四边形ABCD，过A点作AM⊥BC于M，交BD于E，过C点作CN⊥AD于N，交BD于F，连接AF、CE．（1）求证：四边形AECF为平行四边形；（2）当AECF为菱形，M点为BC的中点时，求AB：AE的值．BC，9．如图，等边△ABC的边长是4,D、E分别为AB、AC的中点，延长BC至点F，使CF=12连接CD和EF .（1）求证：DE=CF；（2）求EF的长.10．如图，在四边形ABCD中，AB∥CD，且AB＝2CD，E，F分别是AB，BC的中点，EF与BD交于点H.（1）求证：四边形DEBC是平行四边形；（2）若BD＝9，求DH的长.11．已知锐角△ABC内接于⊙O，AD⊥BC于点D，连接AO．（1）如图1，求证：∠BAO＝∠CAD；（2）如图2，CE⊥AB于点E，交AD于点F，过点O作OH⊥BC于点H，求证：AF＝2OH；，BC＝2√15，求AC的长．（3）如图3，在（2）的条件下，若AF＝AO，tan∠BAO＝1312．如图，抛物线y=x2+bx+c与x轴交于点A(−1，0)，B(5，0)，与y轴交于点C.（1）求抛物线的解析式和顶点D的坐标.（2）连结AD，点E是对称轴与x轴的交点，过E作EF∥AD交抛物线于点F（F在E的右侧），过点F作FG∥x轴交ED于点H，交AD于点G，求HF的长.13．如图，CD是⊙O的直径，点A是⊙O外一点，AD与⊙O相切于点D，点B是⊙O上一点（点B不与点C，D重合），连接AO，AB，BC .（1）当BC与AO满足什么位置关系时，AB是⊙O的切线？请说明理由；（2）在（1）的条件下，当∠DAO=度时，四边形AOCB是平行四边形.（x＞0）的图象经过点A、B，点B的坐标为（2，2）．过点A作AC⊥x轴，垂足14．如图，已知函数y= kx为C，过点B作BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b的图象经过点A、D，与x轴的负半轴交于点EOD，求a、b的值；（1）若AC= 32（2）若BC∥AE，求BC的长．15．如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．（1）求证：△ABE≌△CDF；（2）若AC与BD交于点O，求证：AO=CO．16．如图.在一次数学研究性学习中，小华将两个全等的直角三角形纸片Rt△ABC和Rt△DEF拼在一起，使点A与点F重合，点C与点D重合（如图），其中∠ACB=∠DFE=90°，发现四边形ABDE是平行四边形.如图，小华继续将图中的纸片Rt△DEF沿AC方向平移，连结AE，BD，当点F与点C重合时停止平移.（1）请问：四边形ABDE是平行四边形吗？说明理由.cm时，请判断四边形ABDE的形（2）如图，若BC=EF=6cm，AC=DF=8cm，当AF=92状，并说明理由.参考答案与解析1．【答案】（1）证明：在△CDE 和△ECF 中，∵∠ACB=∠ECF=90°，点D 、E 是分别是AB 、BC 的中点．∴CD=BD=AD ，∴∠B=∠DCE ，∠CED=∠ECF=90°，又∵∠FEC=∠B ．．∠FEC=∠DCE ，又∵CE=EC ．∴△CDE ≌△ECF （ASA ），∴DE=CF ；（2）解：在Rt △ABC 中，∵∠ACB=90°，∴BC=√AB 2−AC 2=√102−62=8cm ， ∵点D 、E 分别是AB 、BC 的中点，∴DE ∥CF ，又DE=CF ， ∴四边形DCFE 是平行四边形，∴DE=12AC=12×6=3cm ，CE=12BC=12×8=4cm ， ∴S 四边形DCFE =DE ×CE=3×4=12cm ． 2．【答案】（1）证明：∵OA ＝OC ＝AD ， ∴∠OCA ＝∠OAC ，∠AOD ＝∠ADO ， ∵OD ∥AC ， ∴∠OAC ＝∠AOD ，∴180°﹣∠OCA ﹣∠OAC ＝180°﹣∠AOD ﹣∠ADO ，即∠AOC ＝∠OAD ， ∴OC ∥AD ， ∵OD ∥AC ，∴四边形OCAD 是平行四边形；（2）解：∵AD 与⊙O 相切，OA 是半径， ∴∠OAD ＝90°， ∵OA ＝OC ＝AD ， ∴∠AOD ＝∠ADO ＝45°，∵OD∥AC，∴∠OAC＝∠AOD＝45°，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠B＝45°.3．【答案】（1）证明：∵CF//AB∴∠DFC=∠ADF，∠DAC=∠ACF又∵EA=EC∴ΔADE≌ΔCFE(AAS)∴CF=AD又∵CF//AD∴四边形ADCF为平行四边形∴DC=AF（有一组对边平行且相等的四边形为平行四边形）（2）解：ΔADC，ΔADF，ΔCFD，ΔCFA∵AD=BD，∴SΔADC=SΔBDC (等底等高面积相等)∵四边形ADCF是平行四边形，∴SΔADC=SΔCDF=SΔADF=SΔACFF (等底等高面积相等) ．故与ΔBDC面积相等的三角形为：ΔADC，ΔADF，ΔCFD，ΔCFA．4．【答案】（1）证明：∵AE=CF，∴AE+EF=CF+EF，即AF=CE，∵DF//BE，∴∠DFA=∠BEC，∵DF=BE，∴ΔADF≅ΔCBE(SAS)，∴AD=CB，∠DAF=∠BCE，∴AD//CB，四边形ABCD是平行四边形（2）245．【答案】（1）证明：∵DF∥BE，∴∠DFA=∠BEC，在△ADF和△CBE中{DF=BE∠DFA=∠BECAF=CE，∴△AFD≌△CEB（SAS).（2）解：四边形ABCD是平行四边形，理由如下：∵△AFD≌△CEB，∴AD=CB，∠DAF=∠BCE，∴AD∥BC，∴四边形ABCD是平行四边形．6．【答案】（1）证明：如图，连接DE，BF，∵四边形ABCD是平行四边形，∴OA=OC，OB=OD，∵E，F分别是OA，OC的中点，∴OE=12OA=12OC=OF，∴四边形DEBF是平行四边形，∴BE=DF .（2）解：由（1）已证：四边形DEBF是平行四边形，要使平行四边形DEBF是矩形，则BD=EF，∵OE=12OA=12OC=OF，∴EF=OE+OF=12OA+12OC=OA=12AC，即AC=2EF，∴k=ACBD =2EFEF=2，故当k=2时，四边形DEBF是矩形. 7．【答案】（1）证明：∵DE//BC，EF//AB，∴∠A＝∠CEF，∠AED＝∠C，∴△ADE∽△EFC．（2）解：∵AB＝6，AD＝4，∴DB＝6－4＝2，∵DE//BC，EF//AB，∴四边形DBFE是平行四边形，∴EF＝DB=2，∵△ADE∽△EFC，SΔADE SΔEFC =(ADEF)2=(42)2=4．8．【答案】（1）证明∵四边形ABCD是平行四边形（已知），∴BC∥AD（平行四边形的对边相互平行）。

平行四边形的判定例题和练习题

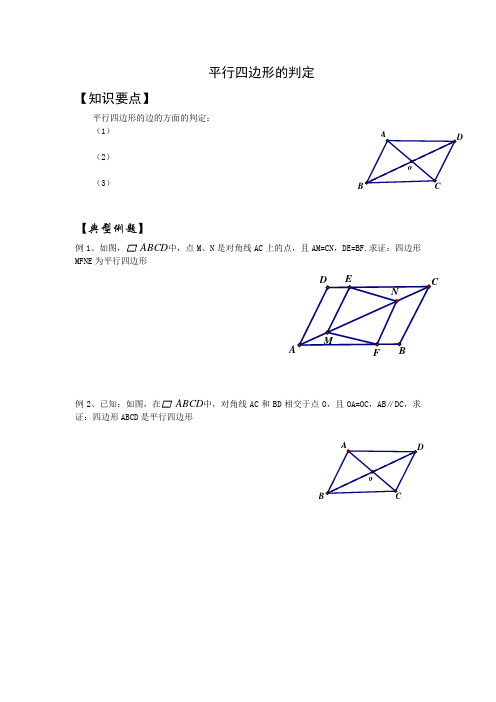
平行四边形的判定【知识要点】平行四边形的边的方面的判定：（1）（3）【典型例题】例1、如图，ABCD中，点M、N是对角线AC上的点，且AM=CN，DE=BF.求证：四边形MFNE为平行四边形例2、已知：如图，在ABCD中，对角线AC和BD相交于点O，且OA=OC，AB∥DC，求证：四边形ABCD是平行四边形CD【知识要点】平行四边形角的方面和对角线的方面的判定（1）由角方面的判定（2）由对角线方面的判定【经典例题】例1、如图所示，在平行四边形ABCD中，点E、F是对角线AC上两点，且AE=CF．求证四边形BEDF是平行四边形。

例2、已知，如图，AB、CD相交于点O，AC∥DB，AO=BO，E、F分别是OC、OD中点．连接AF、BE，求证：AF//BE.练习1、如图，在 ABCD 中，AE=CG ，求证：GF=HE 。

2、如图，AB//CD ，∠ABC=∠ADC ，AE=CF ，BE=DF ，求证：EF 与AC 互相平分。

3、已知：如图，在平行四边形ABCD 中，BE ⊥AC 于点E ，DF ⊥AC 于点F ，又M 、N 分别是DC 、AB 的中点。

求证：四边形EMFN 是平行四边形。

·A BCDEFHACNM4、已知：如图，分别以△ABC 的三边为边长在BC 边的同侧面作等边△ABD 、△BCE 、△ACF ，连结DE 、EF 。

求证：四边形ADEF 是平行四边形。

5、如图，△ABC 为等边三角形，D 、F 分别为CB 、BA 上的点，且CD=BF ，以AD为一边作等边△ADE 。

求证：（1）△ACD ≌△CBF ；（2）四边形CDEF 为平行四边形。

6、如图，以ABCD 的边AD 、BC 为一边向外作等边△ADE 和等边△BCF ，连结AC 、EF 求证：AC 和EF 互相平分EFCB。

平行四边形专项练习题

平行四边形专项练习题一．选择题（共12小题）1．在下列条件中，能够判定一个四边形是平行四边形的是（）A．一组对边平行，另一组对边相等B．一组对边相等，一组对角相等C．一组对边平行，一条对角线平分另一条对角线D．一组对边相等，一条对角线平分另一条对角线2．设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（）A．a＞b B．a=b C．a＜b D．b=a+180°3．如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（）A．4S1B．4S2C．4S2+S3D．3S1+4S34．在▱ABCD中，AB=3，BC=4，当▱ABCD的面积最大时，下列结论正确的有（）①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．A．①②③B．①②④C．②③④D．①③④5．如图，在▱ABCD中，AB=6，BC=8，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（）A．2 B．3 C．4 D．66．如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（）A．8 B．10 C．12 D．147．如图，在▱ABCD中，AB=12，AD=8，∠ABC的平分线交CD于点F，交AD的延长线于点E，CG⊥BE，垂足为G，若EF=2，则线段CG的长为（）A．B．4C．2D．8．如图，在▱ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（）A．AG平分∠DAB B．AD=DH C．DH=BC D．CH=DH9．如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B为（）A．66°B．104°C．114° D．124°10．如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO的周长是（）A．10 B．14 C．20 D．2211．四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD从中任选两个条件，能使四边形ABCD为平行四边形的选法有（）A．3种B．4种C．5种D．6种12．如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④D．④⑤二．填空题（共6小题）13．如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D1，折痕为EF，若∠BAE=55°，则∠D1AD=．14．如图，在▱ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是．15．如图所示，四边形ABCD的对角线相交于点O，若AB∥CD，请添加一个条件（写一个即可），使四边形ABCD是平行四边形．21．已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．22．如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．23．如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．（1）求证：四边形DEFG是平行四边形；（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．24．如图，▱ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N．（1）求证：四边形CMAN是平行四边形．（2）已知DE=4，FN=3，求BN的长．25．如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：（1）DE=BF；（2）四边形DEBF是平行四边形．26．如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF= BC，连接CD和EF．（1）求证：DE=CF；（2）求EF的长．参考答案与解析一．选择题1．【分析】根据平行四边形的判定方法以及全等三角形的判定方法一一判断即可．解：A、错误．这个四边形有可能是等腰梯形．B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．故选C．2．【分析】根据多边形的内角和定理与多边形外角的关系即可得出结论．解：∵四边形的内角和等于a，∴a=（4﹣2）•180°=360°．∵五边形的外角和等于b，∴b=360°，∴a=b．故选B．3．【分析】设等腰直角三角形的直角边为a，正方形边长为c，求出S2（用a、c表示），得出S1，S2，S3之间的关系，由此即可解决问题．解：设等腰直角三角形的直角边为a，正方形边长为c，则S2=（a+c）（a﹣c）=a2﹣c2，∴S2=S1﹣S3，∴S3=2S1﹣2S2，∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1．故选A．4．【分析】当▱ABCD的面积最大时，四边形ABCD为矩形，得出∠A=∠B=∠C=∠D=90°，AC=BD，根据勾股定理求出AC，即可得出结论．解：根据题意得：当▱ABCD的面积最大时，四边形ABCD为矩形，∴∠A=∠B=∠C=∠D=90°，AC=BD，∴AC==5，①正确，②正确，④正确；③不正确；故选：B．5．【分析】由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．解：∵四边形ABCD是平行四边形，∴AB∥CD，AD=BC=8，CD=AB=6，∴∠F=∠DCF，∵CF平分∠BCD，∴∠FCB=∠DCF，∴∠F=∠FCB，∴BF=BC=8，同理：DE=CD=6，∴AF=BF﹣AB=2，AE=AD﹣DE=2，∴AE+AF=4；故选：C．6．【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB，得出AF=AB=6，同理可证DE=DC=6，再由EF的长，即可求出BC的长．解：∵四边形ABCD是平行四边形，∴AD∥BC，DC=AB=6，AD=BC，∴∠AFB=∠FBC，∵BF平分∠ABC，∴∠ABF=∠FBC，则∠ABF=∠AFB，∴AF=AB=6，同理可证：DE=DC=6，∵EF=AF+DE﹣AD=2，即6+6﹣AD=2，解得：AD=10；故选：B．7．【分析】先由平行四边形的性质和角平分线的定义，判断出∠CBE=∠CFB=∠ABE=∠E，从而得到CF=BC=8，AE=AB=12，再用平行线分线段成比例定理求出BE，然后用等腰三角形的三线合一求出BG，最后用勾股定理即可．解：∵∠ABC的平分线交CD于点F，∴∠ABE=∠CBE，∵四边形ABCD是平行四边形，∴DC∥AB，∴∠CBE=∠CFB=∠ABE=∠E，∴CF=BC=AD=8，AE=AB=12，∵AD=8，∴DE=4，∵DC∥AB，∴，∴，∴EB=6，∵CF=CB，CG⊥BF，∴BG=BF=2，在Rt△BCG中，BC=8，BG=2，根据勾股定理得，CG===2，故选：C．8．【分析】根据作图过程可得得AG平分∠DAB，再根据角平分线的性质和平行四边形的性质可证明∠DAH=∠DHA，进而得到AD=DH，解：根据作图的方法可得AG平分∠DAB，∵AG平分∠DAB，∴∠DAH=∠BAH，∵CD∥AB，∴∠DHA=∠BAH，∴∠DAH=∠DHA，∴AD=DH，∴BC=DH，故选D．9．【分析】由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC，由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=∠1=22°，再由三角形内角和定理求出∠B即可．解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠ACD=∠BAC，由折叠的性质得：∠BAC=∠B′AC，∴∠BAC=∠ACD=∠B′AC=∠1=22°，∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°；故选：C．10．【分析】直接利用平行四边形的性质得出AO=CO，BO=DO，DC=AB=6，再利用已知求出AO+BO的长，进而得出答案．解：∵四边形ABCD是平行四边形，∴AO=CO，BO=DO，DC=AB=6，∵AC+BD=16，∴AO+BO=8，∴△ABO的周长是：14．故选：B．11．【分析】根据题目所给条件，利用平行四边形的判定方法分别进行分析即可．解：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；①③可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；①④可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；∴有4种可能使四边形ABCD为平行四边形．故选：B．12．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AB，从而判断出①不变；再根据三角形的周长的定义判断出②是变化的；确定出点P到MN 的距离不变，然后根据等底等高的三角形的面积相等确定出③不变；根据平行线间的距离相等判断出④不变；根据角的定义判断出⑤变化．解：∵点A，B为定点，点M，N分别为PA，PB的中点，∴MN是△PAB的中位线，∴MN=AB，即线段MN的长度不变，故①错误；PA、PB的长度随点P的移动而变化，所以，△PAB的周长会随点P的移动而变化，故②正确；∵MN的长度不变，点P到MN的距离等于l与AB的距离的一半，∴△PMN的面积不变，故③错误；直线MN，AB之间的距离不随点P的移动而变化，故④错误；∠APB的大小点P的移动而变化，故⑤正确．综上所述，会随点P的移动而变化的是②⑤．故选：B．二．填空题13．【分析】由平行四边形的性质和折叠的性质得出∠D1AE=∠BAD，得出∠D1AD=∠BAE=55°即可．解：∵四边形ABCD是平行四边形，∴∠BAD=∠C，由折叠的性质得：∠D1AE=∠C，∴∠D1AE=∠BAD，∴∠D1AD=∠BAE=55°；故答案为：55°．14．【分析】根据平行四边形性质得出AD∥CB，AB∥CD，推出∠DAB+∠CBA=180°，求出∠PAB+∠PBA=90°，在△APB中求出∠APB=90°，由勾股定理求出BP，证出AD=DP=5，BC=PC=5，得出DC=10=AB，即可求出答案．解：∵四边形ABCD是平行四边形，∴AD∥CB，AB∥CD，∴∠DAB+∠CBA=180°，又∵AP和BP分别平分∠DAB和∠CBA，∴∠PAB+∠PBA=（∠DAB+∠CBA）=90°，在△APB中，∠APB=180°﹣（∠PAB+∠PBA）=90°；∵AP平分∠DAB，∴∠DAP=∠PAB，∵AB∥CD，∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP是等腰三角形，∴AD=DP=5，同理：PC=CB=5，即AB=DC=DP+PC=10，在Rt△APB中，AB=10，AP=8，∴BP==6，∴△APB的周长=6+8+10=24；故答案为：24．15．【分析】根据平行四边形的定义或判定定理即可解答．解：可以添加：AD∥BC（答案不唯一）．故答案是：AD∥BC．16．【分析】结合题意，总结可知，每个图中三角形个数比图形的编号的4倍少3个三角形，即可得出结果．解：第①是1个三角形，1=4×1﹣3；第②是5个三角形，5=4×2﹣3；第③是9个三角形，9=4×3﹣3；∴第n个图形中共有三角形的个数是4n﹣3；故答案为：4n﹣3．17．【分析】连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，证明四边形DCMN 是平行四边形，得到DN=CM，根据直角三角形的性质得到CM=AB=3，等量代换即可．解：连接CM，∵M、N分别是AB、AC的中点，∴NM=CB，MN∥BC，又CD=BD，∴MN=CD，又MN∥BC，∴四边形DCMN是平行四边形，∴DN=CM，∵∠ACB=90°，M是AB的中点，∴CM=AB=3，∴DN=3，故答案为：3．18．【分析】首先证明四边形ADEF是平行四边形，根据三角形中位线定理求出DE、EF 即可解决问题．解：∵BD=AD，BE=EC，∴DE=AC=4cm，DE∥AC，∵CF=FA，CE=BE，∴EF=AB=3cm，EF∥AB，∴四边形ADEF是平行四边形，∴四边形ADEF的周长=2（DE+EF）=14cm．故答案为14．三．解答题19．【分析】（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAE=∠F，∠D=∠ECF，∵E是▱ABCD的边CD的中点，∴DE=CE，在△ADE和△FCE中，，∴△ADE≌△FCE（AAS）；（2）解：∵ADE≌△FCE，∴AE=EF=3，∵AB∥CD，∴∠AED=∠BAF=90°，在▱ABCD中，AD=BC=5，∴DE===4，∴CD=2DE=8．20．【分析】（1）由在▱ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．证明：（1）∵四边形ABCD是平行四边形，∴AB∥DF，∴∠ABE=∠FCE，∵E为BC中点，∴BE=CE，在△ABE与△FCE中，，∴△ABE≌△FCE（ASA），∴AB=FC；（2）∵AD=2AB，AB=FC=CD，∴AD=DF，∵△ABE≌△FCE，∴AE=EF，∴DE⊥AF．21．【分析】利用平行线的性质得出∠BAE=∠CFE，由AAS得出△ABE≌△FCE，得出对应边相等AE=EF，再利用平行四边形的判定得出即可．解：四边形ABFC是平行四边形；理由如下：∵AB∥CD，∴∠BAE=∠CFE，∵E是BC的中点，∴BE=CE，在△ABE和△FCE中，，∴△ABE≌△FCE（AAS）；∴AE=EF，又∵BE=CE∴四边形ABFC是平行四边形．22．【分析】（1）选取①②，利用ASA判定△BEO≌△DFO即可；（2）根据△BEO≌△DFO可得EO=FO，BO=DO，再根据等式的性质可得AO=CO，根据两条对角线互相平分的四边形是平行四边形可得结论．证明：（1）选取①②，∵在△BEO和△DFO中，∴△BEO≌△DFO（ASA）；（2）由（1）得：△BEO≌△DFO，∴EO=FO，BO=DO，∵AE=CF，∴AO=CO，∴四边形ABCD是平行四边形．23．【分析】（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC 且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF即可．解：（1）∵D、G分别是AB、AC的中点，∴DG∥BC，DG=BC，∵E、F分别是OB、OC的中点，∴EF∥BC，EF=BC，∴DG=EF，DG∥EF，∴四边形DEFG是平行四边形；（2）∵∠OBC和∠OCB互余，∴∠OBC+∠OCB=90°，∴∠BOC=90°，∵M为EF的中点，OM=3，∴EF=2OM=6．由（1）有四边形DEFG是平行四边形，∴DG=EF=6．24．【分析】（1）只要证明CM∥AN，AM∥CN即可．（2）先证明△DEM≌△BFN得BN=DM，再在RT△DEM中，利用勾股定理即可解决问题．（1）证明：∵四边形ABCD是平行四边形，∴CD∥AB，∵AM⊥BD，CN⊥BD，∴AM∥CN，∴CM∥AN，AM∥CN，∴四边形AMCN是平行四边形．（2）∵四边形AMCN是平行四边形，∴CM=AN，∵四边形ABCD是平行四边形，∴CD=AB，CD∥AB，∴DM=BN，∠MDE=∠NBF，在△MDE和△NBF中，，∴△MDE≌△NBF，∴ME=NF=3，在Rt△DME中，∵∠DEM=90°，DE=4，ME=3，∴DM===5，∴BN=DM=5．25．【分析】（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．证明：（1）∵四边形ABCD是平行四边形，∴AD∥CB，AD=CB，∴∠DAE=∠BCF，在△ADE和△CBF中，∴△ADE≌△CBF，∴DE=BF．（2）由（1），可得△ADE≌△CBF，∴∠ADE=∠CBF，∵∠DEF=∠DAE+∠ADE，∠BFE=∠BCF+∠CBF，∴∠DEF=∠BFE，∴DE∥BF，又∵DE=BF，∴四边形DEBF是平行四边形．26．【分析】（1）直接利用三角形中位线定理得出DE BC，进而得出DE=FC；（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长．（1）证明：∵D、E分别为AB、AC的中点，∴DE为△ABC的中位线，∴DE BC，∵延长BC至点F，使CF=BC，∴DE=FC；（2）解：∵DE FC，∴四边形DEFC是平行四边形，∴DC=EF，∵D为AB的中点，等边△ABC的边长是2，∴AD=BD=1，CD⊥AB，BC=2，∴DC=EF=．。

平行四边形的判定典型题

平行四边形的判定例题1：BD是平行四边形ABCD的对角线，点E、F在BD上，要使四边形AECF是平行四边形，还需要添加的一个条件是_________练习：1、如图，已知：E、F是平行四边形ABCD对角线AC 上的两点，并且AE=CF。

求证：四边形BFDE是平行四边形。

2.如图所示，在平行四边形ABCD中，P1、P2是对角线BD的三等分点，求证：•四边形AP1CP2是平行四边形．3、如图所示，在四边形ABCD中，M是BC中点，AM、BD互相平分于点O，那么请说明AM=DC 且AM∥DC例题2：（2013•镇江）如图，AB∥CD，AB=CD，点E、F在BC上，且BE=CF．（1）求证：△ABE≌△DCF；OMAB CD（2）试证明：以A 、F 、D 、E 为顶点的四边形是平行四边形．练习：1、11、如图，在□ABCD 中，已知两条对角线相交于点O ，E 、F 、G 、H 分别是AO 、BO 、CO 、DO 的中点，以图中的点为顶点，尽可能多地画出平行四边形2．（2012•惠城区模拟）如图，D 是AB 上的一点，DF 与AC 相交于E ，DE=EF ，CF∥BA．求证：四边形ADCF 是平行四边形．3、已知：如图所示，平行四边形ABCD 的对角线AC 、BD•相交于点O ，EF 经过点O 并且分别和AB 、CD 相交于点E 、F ，又知G 、H 分别为OA 、OC 的中点．求证：四边形EHFG 是平行四边形．例题3：、如图4.4-17，等边三角形ABC 的边长为a ，P 为△ABC 内一点，且PD ∥AB ，PE ∥BC ，PF ∥AC ，那么，PD+PE+PF 的值为一个定值.这个定值是多少?请你说出这个定值的来历.H GFE O A BCDHGFEO A BC DHGFE O ABCD HG FE O ABCD练习1：如图，平行四边形ABCD中，AF＝CH，DE＝BG。

求证：EG和HF互相平分。

平行四边形的性质与判定练习题

E D C OF B A一、选择题1、下面各条件中，能判定四边形是平行四边形的是〔〕A 、对角线互相垂直B 、对角线互相平分C 、一组对角相等D 、一组对边相等2、以下四个命题：①一组对边平行且相等的四边形；②两组对角分别相等的四边形；③对角线相等的四边形；④对角线互相平分的四边形。

其中能判定平行四边形的命题的个数为〔〕A 、1个B 、2个C 、3个D 、4个3、以下说法中错误的选项是〔〕A ．平行四边形的对角线互相平分B ．有两对邻角互补的四边形为平行四边形C ．对角线互相平分的四边形是平行四边形D ．一组对边平行，一组对角相等的四边形是平行四边形4、平行四边形的两条对角线及一边的长可依次取〔〕A 、6、6、6B 、6、4、3C 、6、4、6D 、3、4、55、以不共线三点为三个顶点作平行四边形，一共可作平行四边形的个数是〔〕A 、2个B 、3个C 、4个D 、5个6、四边形ABCD 的四个角∠A ∶∠B ∶∠C ∶∠D 满足以下哪一条件时，四边形ABCD 是平行四边形？〔〕A 、1∶2∶2∶1B 、2∶1∶1∶1C 、1∶2∶3∶4D 、2∶1∶2∶17、四边形ABCD 中，AD ∥BC ，要判定四边形ABCD 是平行四边形，还应满足〔〕A 、∠A ＋∠C ＝180°B 、∠B ＋∠D ＝180°C 、∠A ＋∠B ＝180°D 、∠A ＋∠D ＝180°8、根据以下条件，得不到平行四边形的是〔〕A 、AB ＝CD ，AD ＝BC B 、AB ∥CD ，AB ＝CD C 、AB ＝CD ，AD ∥BC D 、AB ∥CD ，AD ∥BC9、如图，在□ABCD 中，EF 过对角线的交点，假设AB ＝4，BC ＝7，OE ＝3，那么四边形EFDC 的周长是〔〕A 、14B 、11C 、10D 、179题图 10题图 11题图 12题图10、如图，线段a 、b 、c 的端点分别在直线l 1、l 2上，那么以下说法中正确的选项是〔〕A ．假设l 1∥l 2，那么a=bB ．假设l 1∥l 2，那么a=cC ．假设a∥b，那么a=bD ．假设l 1∥l 2，且a∥b，那么a=b11、如图，△ABC 中，AB=AC=15，D 在BC 边上，DE∥BA，DF∥CA，那么四边形AFDE 的周长是〔〕A .30B ． 25C ． 20D ．1512、如图，AB=CD ，BF=ED ，AE=CF ，由这些条件能得出图中互相平行的线段共有〔〕A ．1组 B ． 2组 C ． 3组 D ． 4组13、假设□ABCD 的周长为40cm ，ΔABC 的周长为27cm ，那么AC 的长是〔〕A 、13cmB 、3cmC 、7cmD 、14、平行四边形的对角线长分别是x 和y ，一边长为12，那么以下各组数据可能是x 与y 的值的是〔〕A 、8与14B 、10与14C 、18与20D 、10与3615、□ABCD 中,∠A:∠B=13：5，那么∠A 和∠B 的度数分别为〔〕A ．80° ，100°B ．130°，50°C ．160°，20°D ．60°，120°16、一个平行四边形的两条对角线把它分成的全等三角形的对数是( )A.2B.4 C17、E 、F 分别是□ABCD 的边AB 、DC 中点，DE 、BF 交AC 于M 、N ，那么( )⊥MD18、在□ABCD 中假设∠A ＞∠B ，那么∠A 的补角与∠B 的余角之和( )°°°19、从等腰三角形底边上任意一点分别作两腰的平行线与两腰所围成的平行四边形的周长等于三角形( )A B E C F DO A B D C20、平行四边形两条邻边的长分别是6厘米和4厘米，它们的夹角是60°，那么它的面积是( )A.123cm 2B.73cm 2C.63cm 2D.43cm 221、以下说法正确的有〔〕①平行四边形的对角线相等；②平行四边形的对边相等；③平行四边形的对角线互相垂直；④平行四边形的对角线互相平分；⑤两组对边分别相等的四边形是平行四边形；⑥一组对边平行而且另一组对边相等的四边形是平行四边形．A ．4个 B ． 3个 C ． 2个 D ． 1个22、平行四边形的一条对角线与一边垂直，且此对角线为另一边的一半，那么此平行四边形两邻角之比为( )∶∶3 C.1∶∶523、如图，□ABCD 和□EAFC 的顶点D 、E 、F 、B 在一条直线上，那么以下关系中一定正确的选项是( )A.DE ＞BFB.DE=BFC.DE ＜BFD.DE=EF=BF23题图 24题图 25题图24、如图，□ABCD 中，∠ABC=60°，AE∥BD，EF⊥BC 交BC 的延长线于点F ，DF=2，那么EF 的长为〔〕 A ．2 B ． 2 C ． 4 D ． 425、如图，∠BAC=120°，AD⊥AC，BD=CD ，那么以下结论正确的选项是〔〕A ． A D=ACB ． A B=AC C ． A B=2ACD ． A B=AC二、填空题1、□ABCD 中，∠B －∠A ＝40°，那么∠D ＝________.2、□ABCD 的周长是44cm ，AB 比AD 大2cm ，那么AB ＝________cm ，AD ＝________cm.3、平行四边形的两个相邻内角的平分线相交所成的角的度数是________.4、平行四边形的两条邻边的比为2∶1，周长为60cm ，那么这个四边形较短的边长为________.5、如右上图，在□ABCD 中，AE ⊥BC 于E ，AF ⊥CD 于F ，∠BAD ＝120°，BE ＝2，FD ＝3，那么∠EAF ＝________，□ABCD 的周长为________.6、假设平行四边形的两邻边的长分别为16和20，两长边间的距离为8，那么两短边间的距离为________．7、□ABCD 中，AB=6cm,BC=8cm ，∠B=70°,那么AD=__________,CD=__________, ∠D=__________,∠A=__________,∠C=__________.8、平行四边形周长为50cm ，两邻边之差为5cm,各边长为 . 9、如右图，平行四边形ABCD 的周长为30cm,它的对角线AC 和BD 相交于O,且△AOB 的周长比△BOC 的周长大5cm,那么AB=________，BC=________. 10、□ABCD 的对角线AC 和BD 相交于O,那么其中全等的三角形有________对.(1)由平行四边形的一个顶点在形内向两边引垂线，二垂线夹角为65°，那么这个平行四边形各内角的度数分别为________.(2)在□ABCD 中，∠A 的补角与∠B 的和等于210°，那么∠A=________,∠B=________.(3)在□ABCD 中，AB ∶BC=1∶2，∠D=30°，AE ⊥BC 于E ，AE=3cm,那么AB=________cm.这个平行四边形的周长是________cm.(4)平行四边形周长是40cm ，二邻边的比为3∶2，那么两邻边长分别是________.(5)在□ABCD 中，两邻边AB 、AD 的比是1∶2，M 是大边AD 的中点，那么∠BMC 的度数是________.(6)平行四边形的周长为50厘米，那么它两邻边之和是______cm ，每条对角线的长不能超过______cm.(7)□ABCD 中，周长为50厘米，AB=15cm ，∠A=30°，那么此平行四边形的面积为______cm 2.(8)□ABCD 的周长为50厘米，对角线交于O 点，△AOB 的周长比△BOC 的周长大5厘米，那么AB 、BC 的长分别是______、______.(9)有五条平行的直线，每相邻两条的距离相等，有一条直线和这组平行线相交成30°角，它介于相邻两条平行线之间的线段长是10厘米，那么这一组平行线最外面两条之间的距离是______厘米.(10)平行四边形周长为68厘米，被两条对角线分成两个不同的三角形的周长的和等于82厘米，两条对角线A BF CD EA BE CFDA BFOC DE的长度比为2∶1，那么两条对角线的长分别为______厘米，______厘米.11、等腰△ABC底边上任意一点D，AB=AC=5cm，过D作DE∥AC交AB于E，DF∥AB交AC于F，那么四边形AEDF的周长为．12、如图〔在下页〕，等边△ABC的边长为8，P是△ABC内一点，PD∥AC，PE∥AD，PF∥BC，点D，E，F分别在AB，BC，AC上，那么PD+PE+PF= ．第12题第13题第14题13、如图，在□ABCD中，E，F分别为AB，DC的中点，连接DE，EF，FB，那么图中共有个平行四边形．14、如图，在□ABCD中，E，F是对角线AC上的两点且AE=CF，在①BE=DF；②BE∥DF；③AB=DE；④四边形EBFD为平行四边形；⑤S△ADE=S△ABE；⑥AF=CE这些结论中正确的选项是．15、如图，梯形ABCD，AD∥BC，∠B+∠C=90°，EF=10，E，F分别是AD，BC的中点，那么BC﹣AD= ．第15题第16题第17题16、如图，六边形ABCDEF的每个内角都是120°，AB∥DE，BC∥EF，CD∥FA，且AB=4，BC=5，CD=6，DE=7，那么，六边形ABCDEF的周长是．17、如图，△ABC中，如果AB=30，BC=24，AC=27，DN∥GM∥AB，EG∥DF∥BC，FM∥EN∥AC，那么图中阴影局部的三个三角形周长之和为．18、如右图所示，木工师傅把曲尺的一边紧靠木板边缘，从曲尺的另一边上可以读出木板另一边缘的刻度，然后将曲尺移动到另一处〔紧靠木板边缘〕，如果两次读数一样，说明木板两个边缘平行，其中道理是 .三、解答题与证明题1、在□ABCD中，E、F分别在DC、AB上，且DE＝BF。

(完整版)平行四边形的判定练习及答案

诘你添加一个适当的条 A.1： 2 ：B.2 ： 2 ：C.2 ： 3 ：平行四边形的判定二、课中强化（10分钟训练）1•如图3,在匚ABCD 中，对角线F 满足F 列哪个条件时，四边形AC 、BD 相交于点0,E 、F 是对角线AC 上的两点，当E 、 DEBF 不一定是平行四边形（ A.AE=CFC.Z ADE=/CBFB.DE=BF D. / AED= / CFB 2•如图 4,AB\|DC, DC=EF=10 , DE=CF=8，则图中的平行四边形有由分别是 ___________________3.如图5,E 、F 是平行四边形ABCD 对角线BD 上的两点,'使四边形AECF 是平行四边形.4.如图6,AD=BC,要使四边形ABCD 是平行四边形，还需补充的一个条件是： __________三、课后巩固（30分钟训练）1 •以不在同一直线上的三个点为顶点作平行四边形最多能作（） A.4个 B.3个 C.2个 D.1个2. 下面给出了四边形ABCD 中/A 、/ B 、/ C 、/ D 的度数之比，其中能判定四边形ABCD 是平行四边形的是（）3. 九根火柴棒排成如右图形状，图中 __个平行四边形，你判断的根据是 __________________4. 已知四边形ABCD 的对角线AC 、BD 相交于点O,给出下列5个条件：①AB // CD ； OA=OC ; ③AB=CD :④/ BAD= / DCB ; ® AD // BC.（1）从以上5个条件中任意选取2个条件，能推出四边形ABCD 是平行四边形的有（用序图4图5 图6⑵对由以上5个条件中任意选取2个条件，不能推出四边形ABCD 是平行匹边形的，请选取一种情形举出反例说明 •5•若三条线段的长分别为平行四边形？20 cm,14 cm,16 cm,以其中两条为对角线，另一条为一边，是否可以画 6•如图，E 、F 是四边形ABCD 的对角线AC 上的两点，AF=CE , DF=BE , DF// BE.求证：(】)△AFD ©A CEB;(2)四边形ABCD 是平行四边形.17•如图，已知DC // AB ，且DC= —AB, E 为AB 的中点• 2⑴求证：△ AED EBC ;(2)观察图形，在不添加辅助线的情况下，除厶 EBC 夕卜，请再写出两个与厶AED 的面积相等的三角形(直接写出结果，不要求证明)： __________________________________8•如图，已知二1ABCD中DE丄AC,BF丄AC,证明四边形DEBF为平行四边形9•如图，已知■ ABCD中,E、F分别是AB、CD的中点•求证:(1) △ AFD ©A CEB;⑵四边形AECF是平行四边形•二、课中强化（10分钟训练）1懈析：当E、F满足AE=CF时，由平行四边形的对角线相等知OB=OD,OA=OC ,故OE=OF.可知四边形DEBF是平行四边形•当E、F满足/ ADE= / CBF 时，因为AD // BC,所以/ DAE= / BCF.又AD=BC，可证出厶ADE OA CBF，所以DE=BF，/ DEA= / BFC.故/ DEF= / BFE.因此DE// BF，可知四边形DEBF是平行四边形•类似地可说明D也可以•答案:B2•解析：因为ABWDC，根据一组对边平行且相等的四边形是平行四边形可判定四边形ABCD是平行四边形；DC=EF , DE=CF,根据两组对边分别相等的四边形是平行四边形可判定四边形CDEF是平行四边形•答案：四边形ABCD，四边形CDEF —组对边平行且相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形3•解析：根据平行四边形的定义和判定方法可填BE=DF ; Z BAE= / CDF^-答案：BE=DF或ZBAE=ZCDF等任何一个均可4•解析：根据平行四边形的判定定理，知可填（DAD// BC,② AB=CD,③ ZA+ZB=180。

(完整版)平行四边形的判定练习题(含答案)

(完整版)平行四边形的判定练习题(含答案)(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)平行四边形的判定练习题(含答案)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)平行四边形的判定练习题(含答案)(word版可编辑修改)的全部内容。

平行四边形的判定练习题含答案

平行四边形的判定及中位线知能点1 平行四边形的判定方法1．能够判定四边形ABCD是平行四边形的题设是（）．A．AB∥CD，AD=BC B．∠A=∠B，∠C=∠DC．AB=CD，AD=BC D．AB=AD，CB=CD2．具备下列条件的四边形中，不能确定是平行四边形的为（）．A．相邻的角互补 B．两组对角分别相等C．一组对边平行，另一组对边相等 D．对角线交点是两对角线中点3．如下左图所示，四边形ABCD的对角线AC和BD相交于点O，下列判断正确的是（）． A．若AO=OC，则ABCD是平行四边形;B．若AC=BD，则ABCD是平行四边形;C．若AO=BO，CO=DO，则ABCD是平行四边形;D．若AO=OC，BO=OD，则ABCD是平行四边形4．如上右图所示，对四边形ABCD是平行四边形的下列判断，正确的打“∨”，错误的打“×”．（1）因为AD∥BC，AB=CD，所以ABCD是平行四边形．（）（2）因为AB∥CD，AD=BC，所以ABCD是平行四边形．（）（3）因为AD∥BC，AD=BC，所以ABCD是平行四边形．（）（4）因为AB∥CD，AD∥BC，所以ABCD是平行四边形．（）（5）因为AB=CD，AD=BC，所以ABCD是平行四边形．（）（6）因为AD=CD，AB=AC，所以ABCD是平行四边形．（）5．已知AD∥BC，要使四边形ABCD为平行四边形，需要增加条件________．6．如图所示，∠1=∠2，∠3=∠4，问四边形ABCD是不是平行四边形．7．如图所示，在四边形ABCD中，AB=CD，BC=AD，E，F为对角线AC上的点，且AE=CF，求证：BE=DF．8．如图所示，D为△ABC的边AB上一点，DF交AC于点E，且AE=CE，FC∥AB．求证：CD=AF．9．如图所示，已知四边形ABCD是平行四边形，在AB的延长线上截取BE=•AB，BF=BD，连接CE，DF，相交于点M．求证：CD=CM．10．如图所示，在四边形ABCD中，DC∥AB，以AD，AC为边作□ACED，延长DC•交EB于F，求证：EF=FB．知能点2 三角形的中位□线11．如图所示，已知E为□ABCD中DC边的延长线上的一点，且CE=DC，连接AE，分别交BC，BD于点F，G，连接AC交BD于点O，连接OF，求证：AB=2OF．12．如图所示，在ABCD中，EF∥AB且交BC于点E，交AD于点F，连接AE，BF•交于点M，连接CF，DE交于点N，求证：MN∥AD且MN=12 AD．13．如图所示，DE是△ABC的中位线，BC=8，则DE=_______．14．如图所示，在□ABCD中，对角线AC，BD交于点O，OE∥BC交CD•于E，•若OE=3cm，则AD的长为（）．A．3cm B．6cm C．9cm D．12cm15．如图所示，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，AD的中点，•则四边形EFGH是平行四边形吗为什么16．如图所示，在△ABC中，AC=6cm，BC=8cm，AB=10cm，D，E，F分别是AB，BC，CA的中点，求△DEF的面积．规律方法应用17．如图所示，A，B两点被池塘隔开，在A，B外选一点C，连接AC和BC，•并分别找出AC和BC的中点M，N，如果测得MN=20m，那么A，B两点间的距离是多少18．如图所示，在□ABCD中，AB=2AD，∠A=60°，E，F分别为AB，CD的中点，EF=1cm，那么对角线BD的长度是多少你是怎样得到的19．如图所示，在△ABC中，E为AB的中点，CD平分∠ACB，AD⊥CD于点D．•试说明：（1）DE∥BC．（2）DE=12（BC-AC）．开放探索创新20．如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AD•于E，EF∥BC 交AC于F，那么AE与CF相等吗请验证你的结论．中考真题实战21．（长沙）如下左图所示，在四边形ABCD中，AB∥CD，要使四边形ABCD•为平行四边形，则应添加的条件是________．（添加一个即可）22．（呼和浩特）如上右图所示，已知E，F，G，H是四边形ABCD各边的中点，•则S四边形EFGH ：S四边形ABCD的值是_________．23．（南京）已知如图19-1-55所示，在Y ABCD中，E，F分别是AB，CD的中点.求证：（1） △AFD≌△CEB．（2）四边形AECF是平行四边形．答案:1．C 2．C 3．D4．（1）× （2）× （3）∨ （4）∨ （5）∨ （6）×5．AD=BC或AB∥CD6．解：∵∠1=∠2，∴AD∥BC．又∵∠3=∠4，∴AB∥CD．∴四边形ABCD是平行四边形．7．证明：∵AB=CD，BC=AD，∴四边形ABCD是平行四边形．∴AB∥CD，∴∠BAE=∠DCF．又∵AE=CE，∴△ABE≌△CDF（SAS），∴BE=EF．8．证明：∵FC∥AB，∴∠DAC=∠ACF，∠ADF=∠DFC．又∵AE=CE，∴△ADE≌△CFE（AAS），∴DE=EF．∵AE=CE，∴四边形ADCF为平行四边形．∴CD=AF．9．证明：∵四边形ABCD是平行四边形．∴AB//DC．又∵BE=AB，∴BE//DC，∴四边形BDCE是平行四边形．∵DC∥BF，∴∠CDF=∠F．同理，∠BDM=∠DMC．∵BD=BF，∴∠BDF=∠F．∴∠CDF=∠CMD，∴CD=CM．10．证明：过点B作BG∥AD，交DC的延长线于G，连接EG．∵DC∥AB，∴ABGD是平行四边形，∴BG// AD．在□ACED中，AD//CE，∴CE//BG．∴四边形BCEG为平行四边形，∴EF=FB．11．证明：∵四边形ABCD是平行四边形，∴AB//CD，AD=BC．∵CE=CD，∴AB//CE，∴四边形ABEC为平行四边形．∴BF=FC，∴OF//12AB，即AB=2OF．12．证明：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC．又∵EF∥AB，∴EF∥CD．∴四边形ABEF，ECDF均为平行四边形．又∵M，N分别为Y ABEF和Y ECDF对角线的交点．∴M为AE的中点，N为DE的中点，即MN为△AED的中位线．∴MN∥AD且MN=12 AD．13．4 14．B15．解：EFGH是平行四边形，连接AC，在△ABC中，∵EF是中位线，∴EF//12 AC．同理，GH//12 AC．∴EF//GH，∴四边形EFGH为平行四边形． 16．解：∵EF，DE，DF是△ABC的中位线，∴EF=12AB，DE=12AC，DF=12BC．又∵AB=10cm，BC=8cm，AC=6cm，∴EF=5cm，DE=3cm，DF=4cm，而32+42=25=52，即DE2+DF2=EF2．∴△EDF为直角三角形．∴S△EDF =12DE·DF=12×3×4=6（cm2）．17．解：∵M，N分别是AC，BC的中点．∴MN是△ABC的中位线，∴MN=12 AB．∴AB=2MN=2×20=40（m）．故A，B两点间的距离是40m．18．解：连接DE．∵四边形ABCD是平行四边形，∴AB//CD．∵DF=12CD，AE=12AB，∴DF//AE．∴四边形ADFE是平行四边形．∴EF=AD=1cm．∵AB=2AD，∴AB=2cm．∵AB=2AD，∴AB=2AE，∴AD=AE．∴∠1=∠4．∵∠A=60°，∠1+∠4+∠A=180°，∴∠1=∠A=∠4=60°．∴△ADE是等边三角形，∴DE=AE．∵AE=BE，∴DE=BE，∴∠2=∠3．∵∠1=∠2+∠3，∠1=60°，∴∠2=∠3=30°．∴∠ADB=∠3+∠4=90°．222221AB AD-=-3cm）．19．解：延长AD交BC于F．（1）∵AD⊥CD，∴∠ADC=∠FDC=90°．∵CD平分∠ACB，∴∠ACD=∠FCD．在△ACD与△FCD中，∠ADC=∠FDC，DC=DC，∠ACD=∠FCD．∴△ACD≌△FCD，∴AC=FC，AD=DF．又∵E为AB的中点，∴DE∥BF，即DE∥BC．（2）由（1）知AC=FC，DE=12 BF．∴DE=12（BC-FC）=12（BC-AC）．20．解：AE=CF．理由：过E作EG∥CF交BC于G，∴∠3=∠C．∵∠BAC=90°，AD⊥BC，∴∠ABC+∠C=90°，∠ABD+∠BAD=90°．∴∠C=∠BAD，∴∠3=∠BAD．又∵∠1=∠2，BE=BE，∴△ABE≌△GBE（AAS），∴AE=GE．∵EF∥BC，EG∥CF，∴四边形EGCF是平行四边形，∴GE=CF，∴AE=CF．21．答案不唯一，如AB=CD或AD∥BC．22．1 223．解：（1）在□ABCD中，AD=CB，AB=CD，∠D=∠B．∵E，F分别为AB，CD的中点，∴DF=12CD，BE=12AB，∴DF=BE，∴△AFD≌△CEB．（2）在□ABCD中，AB=CD，AB∥CD．由（1）得BE=DF，∴AE=CE，∴四边形AECF是平行四边形．。

平行四边形练习题40道

平行四边形40题一．选择题”1．下列给出的条件中，不能判定四边形ABCD是平行四边形的是（）A．AB∥CD，∠A＝∠C B．AB＝CD，∠B＝∠DC．AD＝BC，AD∥BC D．AB＝CD，AD＝BC2、下列条件中，能判定四边形ABCD为平行四边形的个数是（）①AB∥CD，AD＝BC；②AB＝CD，AD＝BC；③∠A＝∠B，∠C＝∠D；④AB＝AD，CB＝CDA．1个B．2个C．3个D．4个3、下列给出的条件中，不能判定四边形ABCD是平行四边形的是（）A．AB∥CD，∠A＝∠C B．AB＝CD，∠B＝∠DC．AD＝BC，AD∥BC D．AB＝CD，AD＝BC4．下面给出了四边形ABCD中∠A，∠B，∠C，∠D的度数之比，其中能判定四边形ABCD是平行四边形的是（）A．1：2：3：4B．2：2：3：3C．2；3：2：3D．2：3：3：25．如图，在四边形ABCD中，对角线AC，BD相交于点O，AB∥CD，添加下列条件不能使四边形ABCD 成为平行四边形的是（）A．AB＝CD B．OB＝ODC．∠BCD+∠ADC＝180°D．AD＝BC6．如图，E，F是四边形ABCD的对角线BD上的两点，AE∥CF，AB∥CD，BE＝DF，则下列结论①AE＝CF，②AD＝BC，③AD∥BC，④∠BCF＝∠DAE其中正确的个数为（）A．1个B．2个C．3个D．4个7．如图，两条平行线l1，l2被另外一组平行线l3，l4，l5所截，交点分别为A，B，C，D，E，F．则下列结论错误的是（）A．AB＝DE B．AD＝CF C．AB＝BC D．AC＝DF8．小峰不慎将一块平行四边形玻璃打碎成如图所示的四块，为了能在商店配到一块与原来相同的玻璃，他带了两块碎玻璃，其编号应该是（）A．①，②B．①，④C．③，④D．②，③9．如图，分别以Rt△ABC的直角边AC，斜边AB为边向外作等边三角形△ACD和△ABE，F为AB的中点，连接DF，EF，∠ACB＝90°，∠ABC＝30°．则以下4个结论：①AC⊥DF；②四边形BCDF为平行四边形；③DA+DF＝BE；④其中，正确的是（）A．只有①②B．只有①②③C．只有③④D．①②③④10．如图，E、F分别是平行四边形ABCD的边AD、BC上的点，且BE∥DF，AC分别交BE、DF于点G、H．下列结论：①四边形BFDE是平行四边形；②△AGE≌△CHF；③BG＝DH；④S△AGE：S△CDH＝GE：DH，其中正确的个数是（）A．1B．2个C．3个D．4个11．▱ABCD中，E、F分别在边AB和CD上，下列条件中，不能得出四边形AECF一定为平行四边形的是（）A．AE＝CF B．AF＝EC C．∠DAF＝∠BCE D．∠AFD＝∠CEB12．如图，E是▱ABCD边AD延长线上一点，连接BE，CE，BD，BE交CD于点F．添加以下条件，不能判定四边形BCED为平行四边形的是（）A．∠ABD＝∠DCE B．DF＝CF C．∠AEB＝∠BCD D．∠AEC＝∠CBD13．如图，两条宽度分别为1和2的方形纸条交叉放置，重叠部分为四边形ABCD，若AB+BC＝6，则四边形ABCD的面枳是（）A．4B．2C．8D．614．如图，在平行四边形ABCD中，AC与BD交于点M，点F在AD上，AF＝6cm，BF＝12cm，∠FBM ＝∠CBM，点E是BC的中点，若点P以1cm/秒的速度从点A出发，沿AD向点F运动：点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动，点P运动到F点时停止运动，点Q也同时停止运动，当点P运动（）秒时，以点P、Q、E、F为顶点的四边形是平行四边形．A．2B．3C．3或5D．4或515．如图，在△ABC中，点D，E，F分别是AB，BC，AC的中点，连接DE，EF，DF，则下列说法不正确的是（）A．S△DEF＝S△ABCB．△DEF≌△F AD≌△EDB≌△CFEC．四边形ADEF，四边形DBEF，四边形DECF都是平行四边形D．四边形ADEF的周长＝四边形DBEF的周长＝四边形DECF的周长二．填空题（共10小题）16．如图，在▱ABCD中，对角线AC、BD相交于点E，AC⊥BC．若AC＝4，AB＝5，则BD的长为．17．如图，两条宽度分别为2和4的纸条交叉放置，重叠部分为四边形ABCD，若AB•BC＝100，则四边形ABCD的面积是．18．如图所示，在▱ABCD中E，F分别在BC，AD上，若想使四边形AFCE为平行四边形，须添加一个条件，这个条件可以是，①AF＝CF；②AE＝CF；③∠BAE＝∠FCD；④∠BEA＝∠FCE．19．如图，在▱ABCD中，过对角线BD上一点P作EF∥BC，GH∥AB，则图中面积相等的平行四边形共有对．20．如图，在等边三角形ABC中，BC＝6cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，点F从点B出发沿射线BC以2cm/s的速度运动．如果点E、F同时出发，设运动时间为t（s）当t＝s时，以A、C、E、F为顶点四边形是平行四边形．21．如图，四边形ABCD中，AD∥BC，AD＝3，BC＝8，E是BC的中点，点P以每秒1个单位长度的速度从A点出发，沿AD向点D运动；点Q同时以每秒2个单位长度的速度从点C出发，沿CB向点B 运动，点P停止运动时，点Q也随之停止运动．当运动时间t＝秒时，以点P，Q，E，D为顶点的四边形是平行四边形．22．已知点A（1，0），B（4，0），C（0，2），在平面内找一点M使得以M、A、B、C为顶点的四边形为平行四边形，则点M的坐标为．23．已知点A（2，2），B（﹣2，0），C（3，﹣1），且以A，B，C，D为顶点的四边形是平行四边形，则点D的坐标为：．24．在平面直角坐标系xOy中，已知点A（1，1），B（﹣1，1），如果以A，B，C，O为顶点的四边形是平行四边形，那么满足条件的所有点C的坐标为．25．如图，分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE，F为AB的中点，DE，AB相交于点G，若∠BAC＝30°，下列结论：①EF⊥AC；②四边形ADFE为平行四边形；③AD ＝4AG；④△DBF≌△EF A．其中正确结论的序号是．三．解答题（共15小题）26．在▱ABCD中，E，F分别是AB，DC上的点，且AE＝CF，连接DE，BF，AF．（1）求证：四边形DEBF是平行四边形；（2）若AF平分∠DAB，AE＝3，DE＝4，BE＝5，求AF的长．27、如图，在△ABC中，∠ACB＝90°，D是BC的中点，DE⊥BC，CE∥AD．若AC＝2，CE＝4；（1）求证：四边形ACED是平行四边形．（2）求BC的长．28．如图，四边形ABCD中，AB∥CD，AC与BD相交于点O，AO＝CO．（1）求证：四边形ABCD是平行四边形；（2）若AC⊥BD，AB＝10，求BC的长．29、如图，在▱ABCD中，AF平分∠BAD交BC于点F，CE平分∠BCD交AD于点E．（1）若AD＝12，AB＝8，求CF的长；（2）连接BE和AF相交于点G，DF和CE相交于点H，求证：EF和GH互相平分．30．如图，以BC为底边的等腰△ABC，点D，E，G分别在BC，AB，AC上，且EG∥BC，DE∥AC，延长GE至点F，使得BE＝BF．（1）求证：四边形BDEF为平行四边形；（2）当∠C＝30°，时，求D，F两点间的距离．31．如图，在平行四边形ABCD中，∠BAD和∠DCB的平分线AE，CF分别交BC，AD于点E，F，点M，N分别是AE，CF的中点，连接FM，EN（1）求证：BE＝DF；（2）求证：四边形FMEN是平行四边形．32．如图，四边形ABCD的对角线AC、BD相交于点O，AO＝CO，EF过点O且与AD、BC分别相交于点E、F，OE＝OF（1）求证：四边形ABCD是平行四边形；（2）连接AF，若EF⊥AC，△ABF周长是15，求四边形ABCD的周长．33．如图，在▱ABCD中，O为AC的中点，EF过点O，分别交AD，CB的延长线于点E，F．（1）求证：四边形AFCE是平行四边形．（2）若AC平分∠BAE，AB＝6，AE＝8，求BF的长．34．如图，在平行四边形ABCD中，点F是AB的中点，连接DF并延长，交CB的延长线于点E，连接AE．（1）求证：四边形AEBD是平行四边形；（2）若BD＝BC＝5，CD＝6，求平行四边形AEBD的面积．35．如图，E、F是▱ABCD的对角线AC上的两点，且BE⊥AC，DF⊥AC，连接BE、ED、DF、FB．（1）求证：四边形BEDF为平行四边形；（2）若BE＝4，EF＝2，求BD的长．36、如图，在平行四边形ABCD中，点E、F别在BC，AD上，且BE＝DF．（1）如图①，求证：四边形AECF是平行四边形；（2）如图②，若∠BAC＝90°，且AB＝3．AC＝4，求平行四边形ABCD的周长．37．如图，在四边形ABCD中，AB∥CD，∠ABC＝∠ADC，DE垂直于对角线AC，垂足是E，连接BE．（1）求证：四边形ABCD是平行四边形；（2）若△ABE是等边三角形，四边形BCDE的面积等于2，求CE的长．38．如图，在△ABC中，∠BAC＝70°，∠ABC和∠ACB的角平分线交于D点，E、F、G、H分别是线段AB、AC、BD、CD的中点．（1）求∠BDC的度数；（2）证明：四边形EGHF为平行四边形．39．如图，在Rt△ABC中，∠B＝90°，AC＝60cm，∠A＝60°，点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D，E运动的时间是ts（0＜t≤15）．过点D作DF⊥BC 于点F，连接DE，EF．（1）求证：四边形AEFD是平行四边形；（2）当t为何值时，△DEF为直角三角形？请说明理由．40、【阅读材料】在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段中点坐标为（，）【运用】（1）已知O为▱ABCD的对角线AC与BD交点，点B的坐标为（4，3），则点D的坐标为（﹣1，1），则O的坐标为（，2）；（2）在直角坐标系中，有A（﹣1，2），B（3，1），C（1，4）三点，另有一点D与点A，B，C构成平行四边形的顶点，求点D的坐标．（提示：运用阅读材料完成）。

中考数学总复习《平行四边形的判定与性质》练习题及答案

中考数学总复习《平行四边形的判定与性质》练习题及答案班级:___________姓名：___________考号：_____________一、单选题1．如图在四边形ABCD中AB=CD，对角线AC、BD相交于点O，AE⊥BD于点E，CF⊥BD于点F，连接AF、CE，若DE=BF，则下列结论不一定正确的是（）A．CF=AE B．OE=OFC．△CDE为直角三角形D．四边形ABCD是平行四边形2．如图四边形ABCD中AB∥CD，∥B＝∥D点E为BC延长线上一点，连接AE，AE交CD于点H，∥DCE的平分线交AE于点G．若AB＝2AD＝10，点H为CD的中点，HE＝6，则AC的值为（）A．9B．√97C．10D．3 √103．如图在Rt∥ABC中∥ACB=90°，分别以AB、AC为腰向外作等腰直角三角形∥ABD和∥ACE，连结DE，CA的延长线交DE于点F,则与线段AF相等的是()A．AC B．AB C．BC D．AB4．如图在菱形ΑΒCD中∠Α=60∘，AD=8，F是ΑΒ的中点．过点F作FΕ⊥ΑD，垂足为Ε．将ΔΑΕF沿点Α到点Β的方向平移，得到ΔΑ′Ε′F ′．设Ρ、Ρ′分别是ΕF、Ε′F ′的中点，当点Α′与点Β重合时，四边形ΡΡ′CD的面积为（）A．28√3B．24√3C．32√3D．32√3−85．下列说法中错误的是()A．平行四边形的对角线互相平分B．对角线互相垂直的四边形是菱形C．菱形的对角线互相垂直D．对角线互相平分的四边形是平行四边形6．如图．若要使平行四边形ABCD成为菱形．则需要添加的条件是（）A．AB=CD B．AD=BC C．AB=BC D．AC=BD7．如图点A是直线l外一点，在l上取两点B，C，分别以A，C为圆心，BC，AB的长为半径作弧，两弧交于点D，分别连接AB，AD，CD，若∥ABC+∥ADC=120°，则∥A的度数是（）A．100°B．110°C．120°D．125°8．如图在∥ABC中AB＝AC＝10，BC＝12，点D是BC上一点，DE∥AC，DF∥AB，则∥BED与∥DFC的周长的和为（）A．34B．32C．22D．209．如图在平面直角坐标系中点A(1,5),B(4,1),C(m,−m),D(m−3,−m+4)，当四边形ABCD 的周长最小时，则m 的值为（）.A．√2B．32C．2D．310．如图分别在四边形ABCD的各边上取中点E，F，G，H，连接EG，在EG上取一点M，连接HM，过F作FN∥HM，交EG于N，将四边形ABCD中的四边形①和②移动后按图中方式摆放，得到四边形AHM′G′和AF′N′E，延长M′G′，N′F′相交于点K，得到四边形MM′KN′．下列说法中错误的是（）A．S四边形MM′KN′=S四边形ABCD B．HM=NFC．四边形MM′KN′是平行四边形D．∠K=∠AHM′11．如图,已知∥ABC与∥CDA关于点O成中心对称,过点O任作直线EF分别交AD,BC于点E,F,则下则结论:①点E和点F,点B和点D是关于中心O的对称点;②直线BD必经过点O;③四边形ABCD 是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤∥AOE与∥COF成中心对称.其中正确的个数为（）A．2B．3C．4D．512．如图P为平行四边形ABCD内一点，过点P分别作AB、AD的平行线交平行四边形于E、F、G、H四点，若S四边形AHPE＝3，S四边形PFCG＝5，则S∥PBD为（）A．0.5B．1C．1.5D．2二、填空题13．如图在平行四边形ABCD中点E，F分别在BC，AD上，请添加一个条件，使四边形AECF是平行四边形（只填一个即可）．14．如图在Rt△ABC中AC=2√3，BC=2，点P是斜边AB上任意一点，D是AC的中点，连接PD并延长，使DE=PD.以PE，PC为边构造平行四边形PCQE，则对角线PQ的最小值为.15．如图▱ABCD中∥BAD=120°，E、F分别在CD和BC的延长线上，AE∥BD，EF∥BC，EF=5√3，则AB的长是16．如图在∥ABC中∥ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD= 13BD，连接DM、DN、MN．若AB=6，则DN=．17．若AC＝10，BD＝8，那么当AO＝DO＝时，四边形ABCD是平行四边形。

(完整版)平行四边形专项练习题

平行四边形专项练习题一．选择题（共12小题）1．在下列条件中，能够判定一个四边形是平行四边形的是（）A．一组对边平行，另一组对边相等B．一组对边相等，一组对角相等C．一组对边平行，一条对角线平分另一条对角线D．一组对边相等，一条对角线平分另一条对角线2．设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（）A．a＞b B．a=b C．a＜b D．b=a+180°3．如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（）A．4S1B．4S2C．4S2+S3D．3S1+4S34．在▱ABCD中，AB=3，BC=4，当▱ABCD的面积最大时，下列结论正确的有（）①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．A．①②③B．①②④C．②③④D．①③④5．如图，在▱ABCD中，AB=6，BC=8，∠C的平分线交AD于E，交BA的延长线于F，则AE+AF的值等于（）A．2 B．3 C．4 D．66．如图，在▱ABCD中，BF平分∠ABC，交AD于点F，CE平分∠BCD，交AD于点E，AB=6，EF=2，则BC长为（）A．8 B．10 C．12 D．147．如图，在▱ABCD中，AB=12，AD=8，∠ABC的平分线交CD于点F，交AD的延长线于点E，CG⊥BE，垂足为G，若EF=2，则线段CG的长为（）A．B．4C．2D．8．如图，在▱ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（）A．AG平分∠DAB B．AD=DH C．DH=BC D．CH=DH 9．如图，将▱ABCD沿对角线AC折叠，使点B落在B′处，若∠1=∠2=44°，则∠B 为（）A．66°B．104°C．114°D．124°10．如图，▱ABCD的对角线AC、BD相交于点O，且AC+BD=16，CD=6，则△ABO 的周长是（）A．10 B．14 C．20 D．2211．四边形ABCD中，对角线AC、BD相交于点O，给出下列四个条件：①AD∥BC；②AD=BC；③OA=OC；④OB=OD从中任选两个条件，能使四边形ABCD为平行四边形的选法有（）A．3种 B．4种C．5种D．6种12．如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．其中会随点P的移动而变化的是（）A．②③B．②⑤C．①③④ D．④⑤二．填空题（共6小题）13．如图，把平行四边形ABCD折叠，使点C与点A重合，这时点D落在D1，折痕为EF，若∠BAE=55°，则∠D1AD=．14．如图，在▱ABCD中，P是CD边上一点，且AP和BP分别平分∠DAB和∠CBA，若AD=5，AP=8，则△APB的周长是．15．如图所示，四边形ABCD的对角线相交于点O，若AB∥CD，请添加一个条件（写一个即可），使四边形ABCD是平行四边形．16．如图，①是一个三角形，分别连接这个三角形三边中点得到图②，再连接图②中间小三角形三边的中点得到图③，按这样的方法进行下去，第n个图形中共有三角形的个数为．17．如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=BD，连接DM、DN、MN．若AB=6，则DN=．18．如图，在△ABC中，点D、E、F分别是边AB、BC、CA上的中点，且AB=6cm，AC=8cm，则四边形ADEF的周长等于cm．三．解答题（共8小题）19．如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F．（1）求证：△ADE≌△FCE．（2）若∠BAF=90°，BC=5，EF=3，求CD的长．20．如图，在▱ABCD中，E是BC的中点，连接AE并延长交DC的延长线于点F．（1）求证：AB=CF；（2）连接DE，若AD=2AB，求证：DE⊥AF．21．已知：如图，在四边形ABCD中，AB∥CD，E是BC的中点，直线AE交DC的延长线于点F．试判断四边形ABFC的形状，并证明你的结论．22．如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC 上（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．23．如图，点O是△ABC内一点，连结OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连结，得到四边形DEFG．（1）求证：四边形DEFG是平行四边形；（2）若M为EF的中点，OM=3，∠OBC和∠OCB互余，求DG的长度．24．如图，▱ABCD中，BD是它的一条对角线，过A、C两点作AE⊥BD，CF⊥BD，垂足分别为E、F，延长AE、CF分别交CD、AB于M、N．（1）求证：四边形CMAN是平行四边形．（2）已知DE=4，FN=3，求BN的长．25．如图，在▱ABCD中，点E，F在对角线AC上，且AE=CF．求证：（1）DE=BF；（2）四边形DEBF是平行四边形．26．如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=BC，连接CD和EF．（1）求证：DE=CF；（2）求EF的长．参考答案与解析一．选择题1．【分析】根据平行四边形的判定方法以及全等三角形的判定方法一一判断即可．解：A、错误．这个四边形有可能是等腰梯形．B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．故选C．2．【分析】根据多边形的内角和定理与多边形外角的关系即可得出结论．解：∵四边形的内角和等于a，∴a=（4﹣2）•180°=360°．∵五边形的外角和等于b，∴b=360°，∴a=b．故选B．3．【分析】设等腰直角三角形的直角边为a，正方形边长为c，求出S2（用a、c表示），得出S1，S2，S3之间的关系，由此即可解决问题．解：设等腰直角三角形的直角边为a，正方形边长为c，则S2=（a+c）（a﹣c）=a2﹣c2，∴S2=S1﹣S3，∴S3=2S1﹣2S2，∴平行四边形面积=2S1+2S2+S3=2S1+2S2+2S1﹣2S2=4S1．故选A．4．【分析】当▱ABCD的面积最大时，四边形ABCD为矩形，得出∠A=∠B=∠C=∠D=90°，AC=BD，根据勾股定理求出AC，即可得出结论．解：根据题意得：当▱ABCD的面积最大时，四边形ABCD为矩形，∴∠A=∠B=∠C=∠D=90°，AC=BD，∴AC==5，①正确，②正确，④正确；③不正确；故选：B．5．【分析】由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．解：∵四边形ABCD是平行四边形，∴AB∥CD，AD=BC=8，CD=AB=6，∴∠F=∠DCF，∵CF平分∠BCD，∴∠FCB=∠DCF，∴∠F=∠FCB，∴BF=BC=8，同理：DE=CD=6，∴AF=BF﹣AB=2，AE=AD﹣DE=2，∴AE+AF=4；故选：C．6．【分析】由平行四边形的性质和角平分线得出∠ABF=∠AFB，得出AF=AB=6，同理可证DE=DC=6，再由EF的长，即可求出BC的长．解：∵四边形ABCD是平行四边形，∴AD∥BC，DC=AB=6，AD=BC，∴∠AFB=∠FBC，∵BF平分∠ABC，∴∠ABF=∠FBC，则∠ABF=∠AFB，∴AF=AB=6，同理可证：DE=DC=6，∵EF=AF+DE﹣AD=2，即6+6﹣AD=2，解得：AD=10；故选：B．7．【分析】先由平行四边形的性质和角平分线的定义，判断出∠CBE=∠CFB=∠ABE=∠E，从而得到CF=BC=8，AE=AB=12，再用平行线分线段成比例定理求出BE，然后用等腰三角形的三线合一求出BG，最后用勾股定理即可．解：∵∠ABC的平分线交CD于点F，∴∠ABE=∠CBE，∵四边形ABCD是平行四边形，∴DC∥AB，∴∠CBE=∠CFB=∠ABE=∠E，∴CF=BC=AD=8，AE=AB=12，∵AD=8，∴DE=4，∵DC∥AB，∴，∴，∴EB=6，∵CF=CB，CG⊥BF，∴BG=BF=2，在Rt△BCG中，BC=8，BG=2，根据勾股定理得，CG===2，故选：C．8．【分析】根据作图过程可得得AG平分∠DAB，再根据角平分线的性质和平行四边形的性质可证明∠DAH=∠DHA，进而得到AD=DH，解：根据作图的方法可得AG平分∠DAB，∵AG平分∠DAB，∴∠DAH=∠BAH，∵CD∥AB，∴∠DHA=∠BAH，∴∠DAH=∠DHA，∴AD=DH，∴BC=DH，故选D．9．【分析】由平行四边形的性质和折叠的性质得出∠ACD=∠BAC=∠B′AC，由三角形的外角性质求出∠BAC=∠ACD=∠B′AC=∠1=22°，再由三角形内角和定理求出∠B 即可．解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠ACD=∠BAC，由折叠的性质得：∠BAC=∠B′AC，∴∠BAC=∠ACD=∠B′AC=∠1=22°，∴∠B=180°﹣∠2﹣∠BAC=180°﹣44°﹣22°=114°；故选：C．10．【分析】直接利用平行四边形的性质得出AO=CO，BO=DO，DC=AB=6，再利用已知求出AO+BO的长，进而得出答案．解：∵四边形ABCD是平行四边形，∴AO=CO，BO=DO，DC=AB=6，∵AC+BD=16，∴AO+BO=8，∴△ABO的周长是：14．故选：B．11．【分析】根据题目所给条件，利用平行四边形的判定方法分别进行分析即可．解：①②组合可根据一组对边平行且相等的四边形是平行四边形判定出四边形ABCD 为平行四边形；③④组合可根据对角线互相平分的四边形是平行四边形判定出四边形ABCD为平行四边形；①③可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；①④可证明△ADO≌△CBO，进而得到AD=CB，可利用一组对边平行且相等的四边形是平行四边形判定出四边形ABCD为平行四边形；∴有4种可能使四边形ABCD为平行四边形．故选：B．12．【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=AB，从而判断出①不变；再根据三角形的周长的定义判断出②是变化的；确定出点P到MN 的距离不变，然后根据等底等高的三角形的面积相等确定出③不变；根据平行线间的距离相等判断出④不变；根据角的定义判断出⑤变化．解：∵点A，B为定点，点M，N分别为PA，PB的中点，∴MN是△PAB的中位线，∴MN=AB，即线段MN的长度不变，故①错误；PA、PB的长度随点P的移动而变化，所以，△PAB的周长会随点P的移动而变化，故②正确；∵MN的长度不变，点P到MN的距离等于l与AB的距离的一半，∴△PMN的面积不变，故③错误；直线MN，AB之间的距离不随点P的移动而变化，故④错误；∠APB的大小点P的移动而变化，故⑤正确．综上所述，会随点P的移动而变化的是②⑤．故选：B．二．填空题13．【分析】由平行四边形的性质和折叠的性质得出∠D1AE=∠BAD，得出∠D1AD=∠BAE=55°即可．解：∵四边形ABCD是平行四边形，∴∠BAD=∠C，由折叠的性质得：∠D1AE=∠C，∴∠D1AE=∠BAD，∴∠D1AD=∠BAE=55°；故答案为：55°．14．【分析】根据平行四边形性质得出AD∥CB，AB∥CD，推出∠DAB+∠CBA=180°，求出∠PAB+∠PBA=90°，在△APB中求出∠APB=90°，由勾股定理求出BP，证出AD=DP=5，BC=PC=5，得出DC=10=AB，即可求出答案．解：∵四边形ABCD是平行四边形，∴AD∥CB，AB∥CD，∴∠DAB+∠CBA=180°，又∵AP和BP分别平分∠DAB和∠CBA，∴∠PAB+∠PBA=（∠DAB+∠CBA）=90°，在△APB中，∠APB=180°﹣（∠PAB+∠PBA）=90°；∵AP平分∠DAB，∴∠DAP=∠PAB，∵AB∥CD，∴∠PAB=∠DPA∴∠DAP=∠DPA∴△ADP是等腰三角形，∴AD=DP=5，同理：PC=CB=5，即AB=DC=DP+PC=10，在Rt△APB中，AB=10，AP=8，∴BP==6，∴△APB的周长=6+8+10=24；故答案为：24．15．【分析】根据平行四边形的定义或判定定理即可解答．解：可以添加：AD∥BC（答案不唯一）．故答案是：AD∥BC．16．【分析】结合题意，总结可知，每个图中三角形个数比图形的编号的4倍少3个三角形，即可得出结果．解：第①是1个三角形，1=4×1﹣3；第②是5个三角形，5=4×2﹣3；第③是9个三角形，9=4×3﹣3；∴第n个图形中共有三角形的个数是4n﹣3；故答案为：4n﹣3．17．【分析】连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，证明四边形DCMN是平行四边形，得到DN=CM，根据直角三角形的性质得到CM=AB=3，等量代换即可．解：连接CM，∵M、N分别是AB、AC的中点，∴NM=CB，MN∥BC，又CD=BD，∴MN=CD，又MN∥BC，∴四边形DCMN是平行四边形，∴DN=CM，∵∠ACB=90°，M是AB的中点，∴CM=AB=3，∴DN=3，故答案为：3．18．【分析】首先证明四边形ADEF是平行四边形，根据三角形中位线定理求出DE、EF即可解决问题．解：∵BD=AD，BE=EC，∴DE=AC=4cm，DE∥AC，∵CF=FA，CE=BE，∴EF=AB=3cm，EF∥AB，∴四边形ADEF是平行四边形，∴四边形ADEF的周长=2（DE+EF）=14cm．故答案为14．三．解答题19．【分析】（1）由平行四边形的性质得出AD∥BC，AB∥CD，证出∠DAE=∠F，∠D=∠ECF，由AAS证明△ADE≌△FCE即可；（2）由全等三角形的性质得出AE=EF=3，由平行线的性质证出∠AED=∠BAF=90°，由勾股定理求出DE，即可得出CD的长．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴∠DAE=∠F，∠D=∠ECF，∵E是▱ABCD的边CD的中点，∴DE=CE，在△ADE和△FCE中，，∴△ADE≌△FCE（AAS）；（2）解：∵ADE≌△FCE，∴AE=EF=3，∵AB∥CD，∴∠AED=∠BAF=90°，在▱ABCD中，AD=BC=5，∴DE===4，∴CD=2DE=8．20．【分析】（1）由在▱ABCD中，E是BC的中点，利用ASA，即可判定△ABE≌△FCE，继而证得结论；（2）由AD=2AB，AB=FC=CD，可得AD=DF，又由△ABE≌△FCE，可得AE=EF，然后利用三线合一，证得结论．证明：（1）∵四边形ABCD是平行四边形，∴AB∥DF，∴∠ABE=∠FCE，∵E为BC中点，∴BE=CE，在△ABE与△FCE中，，∴△ABE≌△FCE（ASA），∴AB=FC；（2）∵AD=2AB，AB=FC=CD，∴AD=DF，∵△ABE≌△FCE，∴AE=EF，∴DE⊥AF．21．【分析】利用平行线的性质得出∠BAE=∠CFE，由AAS得出△ABE≌△FCE，得出对应边相等AE=EF，再利用平行四边形的判定得出即可．解：四边形ABFC是平行四边形；理由如下：∵AB∥CD，∴∠BAE=∠CFE，∵E是BC的中点，∴BE=CE，在△ABE和△FCE中，，∴△ABE≌△FCE（AAS）；∴AE=EF，又∵BE=CE∴四边形ABFC是平行四边形．22．【分析】（1）选取①②，利用ASA判定△BEO≌△DFO即可；（2）根据△BEO≌△DFO可得EO=FO，BO=DO，再根据等式的性质可得AO=CO，根据两条对角线互相平分的四边形是平行四边形可得结论．证明：（1）选取①②，∵在△BEO和△DFO中，∴△BEO≌△DFO（ASA）；（2）由（1）得：△BEO≌△DFO，∴EO=FO，BO=DO，∵AE=CF，∴AO=CO，∴四边形ABCD是平行四边形．23．【分析】（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得EF∥BC且EF=BC，DG∥BC且DG=BC，从而得到DE=EF，DG∥EF，再利用一组对边平行且相等的四边形是平行四边形证明即可；（2）先判断出∠BOC=90°，再利用直角三角形斜边的中线等于斜边的一半，求出EF 即可．解：（1）∵D、G分别是AB、AC的中点，∴DG∥BC，DG=BC，∵E、F分别是OB、OC的中点，∴EF∥BC，EF=BC，∴DG=EF，DG∥EF，∴四边形DEFG是平行四边形；（2）∵∠OBC和∠OCB互余，∴∠OBC+∠OCB=90°，∴∠BOC=90°，∵M为EF的中点，OM=3，∴EF=2OM=6．由（1）有四边形DEFG是平行四边形，∴DG=EF=6．24．【分析】（1）只要证明CM∥AN，AM∥CN即可．（2）先证明△DEM≌△BFN得BN=DM，再在RT△DEM中，利用勾股定理即可解决问题．（1）证明：∵四边形ABCD是平行四边形，∴CD∥AB，∵AM⊥BD，CN⊥BD，∴AM∥CN，∴CM∥AN，AM∥CN，∴四边形AMCN是平行四边形．（2）∵四边形AMCN是平行四边形，∴CM=AN，∵四边形ABCD是平行四边形，∴CD=AB，CD∥AB，∴DM=BN，∠MDE=∠NBF，在△MDE和△NBF中，，∴△MDE≌△NBF，∴ME=NF=3，在Rt△DME中，∵∠DEM=90°，DE=4，ME=3，∴DM===5，∴BN=DM=5．25．【分析】（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．证明：（1）∵四边形ABCD是平行四边形，∴AD∥CB，AD=CB，∴∠DAE=∠BCF，在△ADE和△CBF中，∴△ADE≌△CBF，∴DE=BF．（2）由（1），可得△ADE≌△CBF，∴∠ADE=∠CBF，∵∠DEF=∠DAE+∠ADE，∠BFE=∠BCF+∠CBF，∴∠DEF=∠BFE，∴DE∥BF，又∵DE=BF，∴四边形DEBF是平行四边形．26．【分析】（1）直接利用三角形中位线定理得出DE BC，进而得出DE=FC；（2）利用平行四边形的判定与性质得出DC=EF，进而利用等边三角形的性质以及勾股定理得出EF的长．（1）证明：∵D、E分别为AB、AC的中点，∴DE为△ABC的中位线，∴DE BC，∵延长BC至点F，使CF=BC，∴DE=FC；（2）解：∵DE FC，∴四边形DEFC是平行四边形，∴DC=EF，∵D为AB的中点，等边△ABC的边长是2，∴AD=BD=1，CD⊥AB，BC=2，∴DC=EF=．。

平行四边形的性质判定练习题

1第一部分平行四边形的性质练习题例题1、平行四边形得周长为50cm ，两邻边之差为5cm,求各边长。

变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2：3，则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形，∠BAC=90°,AB=3,AC=4,求AD 的长。

例题2.平行四边形ABCD 中，∠A-∠B=20°,求平行四边形各内角的度数。

变题3.平行四边形ABCD 中，AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图，在平行四边形ABCD 中，∠BAC=34°, ∠ACB=26°，求∠DAC 与∠D 的度数。

例题3.如图，在平行四边形ABCD 中，CE ⊥AD,CF ⊥BA 交BA 的延长线于F ，∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。

变题5.如图，平行四边形ABCD 的周长为50，其中AB=15，∠ABC=60°，求平行四边形面积。

平行四边形性质及判定练习题及答案

平行四边形性质及判定练习题及答案1、已知平行四边形ABCD中，AE⊥BC，AF⊥CD，E，F分别是BC，CD的中点，则2、已知平行四边形ABCD中，AB=3cm，BC=5cm，对角线AC，BD相交于点O，则OA的取值范围是多少？3、已知平行四边形ABCD中，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，求AB的长。

4、下列哪些命题是正确的：（1）两组对边分别相等的四边形是平行四边形；（2）两组对角分别相等的四边形是平行四边形；（3）对角线互相平分的四边形是平行四边形；（4）一组对边平行且相等的四边形是平行四边形。

5、已知平行四边形ABCD中，AB=6，AC=4，E，D，F 分别是AB，BC，CA的中点，求四边形AEDF的周长。

6、已知平行四边形ABCD的对角线AC、BD相交于点O，下列哪个结论不正确：（A）DC∥AB；（B）OA=OC；（C）AD=BC；（D）DB平分∠ADC。

7、已知平行四边形ABCD中，AB=4，AD=2AB，CE平分∠BCD交AD边于点E，且AE=3，求BC的长。

8、已知平行四边形ABCD中，BD为对角线，E、F分别是AD、BD的中点，连接EF，若EF=3，则CD的长为多少？9、已知平行四边形ABCD中，对角线AC、BD相交于点O，点E是BC的中点，OE=3，求AB的长。

10、已知平行四边形ABCD中，AB=8，AD=5，E，F分别是AB，AD的中点，连接EF，求四边形CDEF的周长。

11、已知平行四边形ABCD中，AB=6，BC=8，对角线AC，BD相交于点O，OE=3，求AD的长。

12、已知平行四边形ABCD中，AB=5，BC=7，对角线AC，BD相交于点O，点E是BC的中点，求AE的长。

13、已知平行四边形ABCD中，AB=4，BC=6，BC边上的高AE=2，求DC边上的高AF的长度。

14、在平行四边形ABCD中，AB=2cm，BC=3cm，∠B、∠C的平分线分别交AD于F、E，求EF的长度。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

平行四边形的判定专项练习30题（有答案）1．如图，四边形ABCD中，AD∥BC，ED∥BF，AF=CE，求证：ABCD是平行四边形．2．如图，四边形ABCD中，∠BAC=90°，AB=11﹣x，BC=5，CD=x﹣5，AD=x﹣3，AC=4．求证：四边形ABCD为平行四边形．3．已知四边形ABCD的对角线AC与BD交于点O，现给出四个条件：①OA=OC；②AB=CD；③∠BAD=∠DCB；④AD∥BC．请你从中选择两个，推出四边形ABCD为平行四边形，并写出你的推理过程．（1）从以上4个条件中任意选取2个条件，能推出四边形ABCD是平行四边形的有（用序号表示）_________．（2）从（1）中选出一种情况，写出你的推理过程．4．如图，已知：点B、E、F、D在一条直线上，DF=BE，AE=CF．请从下列三个条件中选择一个合适的条件，添加到已知条件中，使四边形ABCD是平行四边形，并说明理由，供选择的三个条件（请从其中选择一个）：①AB=DC；②BC=AD；③∠AED=∠CFB．5．如图，在▱ABCD中，AC交BD于点O，点E，点F分别是OA，OC的中点，请判断线段BE，DF的位置关系和数量关系，并说明你的结论．6．如图所示，以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD、△BCE、△ACF，猜想：四边形ADEF是什么四边形，试证明你的结论．7．如图，已知BE⊥AD，CF⊥AD，且BE=CF．求证：（1）AD是△ABC的中线；（2）请连接BF、CE，试判断四边形BECF是何种特殊四边形，并说明理由．8．如图，矩形ABCD的两条对角线AC和BD相交于点O，E、F是BD上的两点，且∠AEB=∠CFD．求证：四边形AECF是平行四边形．9．如图：在四边形ABCD中，AD∥BC，AB=CD，E是BC上一点，DE=AB．求证：四边形ABED是平行四边形．10．如图，已知AB∥DC，E是BC的中点，AE，DC的延长线交于点F；（1）求证：△ABE≌△FCE；（2）连接AC，BF．则四边形ABFC是什么特殊的四边形？请说明理由．11．等边△ABC中，点D在BC上，点E在AB上，且CD=BE，以AD为边作等边△ADF，如图．求证：四边形CDFE是平行四边形．12．如图，分别以Rt△ABC的直角边AC和斜边AB向外作等边△ACD、等边△ABE．若∠BAC=30°，EF⊥AB，垂足为F，连结DF．求证：（1）△ABC≌△EAF；（2）四边形ADFE是平行四边形．13．已知：如图，在△ABC中，中线BE，CD交于点O，F，G分别是OB，OC的中点．求证：四边形DFGE是平行四边形．14．如图所示：在四边形ABCD中，AD∥BC、BC=18cm，CD=15cm，AD=10cm，AB=12cm，动点P、Q分别从A、C同时出发，点P以2cm/秒的速度由A向D运动，点Q以3cm/秒的速度由C向B运动．（1）几秒钟后，四边形ABQP为平行四边形？并求出此时四边形ABQP的周长（2）几秒钟后，四边形PDCQ为平行四边形？并求出此时四边形PDCQ的周长．15．求证：顺次连接四边形各边中点所得的四边形是平行四边形．16．△ABC中，中线BE、CF相交于O，M是BO的中点，N是CO的中点，求证：四边形MNEF是平行四边形．17．如图，AD=DB，AE=EC，FG∥AB，AG∥BC．（1）证明：△AGE≌△CFE；（2）说明四边形ABFG是平行四边形；（3）研究图中的线段DE，BF，FC之间有怎样的位置关系和数量关系．18．如图，△ABC和△ADE都是等边三角形，点D在BC边上，AB边上有一点F，且BF=DC，连接EF、EB．（1）求证：△ABE≌△ACD；（2）求证：四边形EFCD是平行四边形．19．已知在△ABC中，D、E分别是AB、AC的中点，点F在DE的延长线上，且EF=DE，图中有几个平行四边形？请说明你的理由．20．如图，在△ABC中，AD是中线，点E是AD的中点，过A点作BC的平行线交CE的延长线于点F，连接BF．求证：四边形AFBD是平行四边形．21．如图：在四边形ABCD中，AD∥BC，E是BC的中点，BC=2AD．找出图中所有的平行四边形，并选择一个说明它是平行四边形的理由．22．求证：两组对角分别相等的四边形是平行四边形．23．已知：如图，A、B、C、D在同一条直线上，且AB=CD，AE∥DF，AE=DF．求证：四边形EBFC是平行四边形．24．如图，在△ABC中，D是BC边的中点，E、F分别在AD和其延长线上，CE∥BF，连接BE、CF．图中的四边形BFCE是平行四边形吗？为什么？25．已知点E、F、G、H分别为四边形ABCD四边的中点，试问四边形EFGH的形状并说明理由．26．如图，已知四边形ABCD中AD=BC，点A、B、E在同一条直线上，且∠B=∠EAD，试说明四边形ABCD是平行四边形．27．如图，AD∥BC，ED∥BF，且AE=CF，求证：四边形ABCD是平行四边形．28．已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．29．如图，△ACD、△ABE、△BCF均为直线BC同侧的等边三角形．当AB≠AC时，求证：四边形ADFE为平行四边形．30．已知：在四边形ABCD中，AD∥BC，且AB=DC=5，AC=4，BC=3．求证：四边形ABCD为平行四边形．1．∵AD∥BC，∴∠DAE=∠BCF，∵ED∥BF，∴∠DEF=∠BFE，∴∠AED=∠CFB，又∵AF=CE，∴AE=CF，在△ADE和△CBF中：∵∠DAE=∠BCF，∠AED=∠CFB，AE=CF，∴△ADE≌△CBF（AAS），∴AD=CB，即：AD∥CB，AD=CB，∴四边形ABCD是平行四边形，2．∵∠BAC=90°，AB=11﹣x，BC=5，AC=4．∴（11﹣x）2+42=52，解得：x1=8，x2=14＞11（舍去），当x=8时，BC=AD=5，AB=CD=3，∴四边形ABCD为平行四边形．3．（1）解：能推出四边形ABCD是平行四边形的有①④、③④；故答案是：①④、③④；（2）以①④为例进行证明．如图，在四边形ABCD中，OA=OC，AD∥BC．证明：∵AD∥BC，∴∠DAO=∠BCO．∴在△AOD与△COB中，，∴△AOD≌△COB（ASA），∴AD=BC，∴在四边形ABCD中，AD BC，∴四边形ABCD为平行四边形．4．选择①，∵DF=BE，AE=CF，AB=CD，∴△ABE≌△CDF（sss），∴∠ABE=∠CDF，∴AB∥CD，又∵AB=CD，因为ABCD是平行四边形，所以OA=OC，OB=OD，因为E，F分别是OA，OC的中点，所以OE=OF，所以BFDE是平行四边形，所以BE=DF，BE∥DF 6．四边形ADEF是平行四边形．连接ED、EF，∵△ABD、△BCE、△ACF分别是等边三角形，∴AB=BD，BC=BE，∠DBA=∠EBC=60°．∴∠DBE=∠ABC．∴△ABC≌△DBE．同理可证△ABC≌△FEC，∴AB=EF，AC=DE．∵AB=AD，AC=AF，∴AD=EF，DE=AF．∴四边形ADEF是平行四边形7．（1）∵BE⊥AD，CF⊥AD，∴∠BED=∠CFD．∵∠BDE=∠CDF，BE=CF，∴△BED≌△CFD．∴BD=CD．∴AD是△ABC的中线．（2）四边形BECF是平行四边形，由（1）得：BD=CD，ED=FD．∴四边形BECF是平行四边形8．∵四边形ABCD是矩形∴AB∥CD，AB=CD，∴∠ABE=∠CDF，又∵∠AEB=∠CFD，∴△ABE≌△CDF，∴BE=DF，又∵四边形ABCD是矩形，∴OA=OC，OB=OD，∴OB﹣BE=OD﹣DF，∴OE=OF，∴四边形AECF是平行四边形9．∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∴∠B=∠C，∵DE=AB，∴DE=CD，∴∠DEC=∠C，∴∠DEC=∠B，∴AB∥DE，∴∠1=∠2，∠FCE=∠EBA，∵E为BC中点，∴CE=BE，∵在△ABE和△FCE中，∠1=∠2，∠FCE=∠EBA，CE=BE，∴△ABE≌△FCE；（2）四边形ABFC是平行四边形；理由：由（1）知：△ABE≌△FCE，∴EF=AE，∵CE=BE，∴四边形ABFC是平行四边形11．连接BF，∵△ADF和△ABC是等边三角形，∴AF=AD=DF，AB=AC=BC，∠ABC=∠ACD=∠CAB=∠FAD=60°，∴∠FAD﹣∠EAD=∠CAB﹣∠EAD，∴∠FAB=∠CAD，在△FAB和△DAC中，∴△FAB≌△DAC（SAS），∴BF=DC，∠ABF=∠ACD=60°，∵BE=CD，∴BF=BE，∴△BFE是等边三角形，∴EF=BE=CD，在△ACD和△CBE中∵，∴△ACD≌△CBE（SAS），∴AD=CE=DF，∵EF=CD，∴四边形CDFE是平行四边形．12．（1）∵△ABE为等边三角形，EF⊥AB，∴EF为∠BEA的平分线，∠AEB=60°，AE=AB，∴∠FEA=30°，又∠BAC=30°，∴∠FEA=∠BAC，在△ABC和△EAF中，，∴△ABC≌△EAF（AAS）；（2）∵∠BAC=30°，∠DAC=60°，∴∠DAB=90°，即DA⊥AB，∵EF⊥AB，∴AD∥EF，∵△ABC≌△EAF，∴EF=AC=AD，∴四边形ADFE是平行四边形13．在△ABC中，∵AD=BD，AE=CE，∴DE∥BC且DE=BC．在△OBC中，∵OF=FB，OG=GC，∴FG∥BC且FG=BC．∴DE∥FG，DE=FG．∴四边形DFGE为平行四边形14．（1）x秒后，四边形ABQP为平行四边形．则2x=18﹣3x，解得x=3.6．3.6秒钟后，四边形ABQP为平行四边形，此时四边形ABQP的周长是3.6×2×2+12×2=38.4cm．（2）y秒后，四边形PDCQ为平行四边形．10﹣2y=3y，解得y=2.2秒钟后，四边形PDCQ为平行四边形，此时四边形PDCQ的周长是3.6×2×2+15×2=43.2cm．15．：连接BD，∵E、F为AD，AB中点，∴FE BD．又∵G、H为BC，CD中点，∴GH BD，故GH FE．同理可证，EH FG．∴四边形FGHE是平行四边形16．∵BE，CF是△ABC的中线，∴EF∥BC且EF=BC，∵M是BO的中点，N是CO的中点，∴四边形MNEF是平行四边形．17．（1）证明：∵AG∥BC（已知）∴∠G=∠EFC（两直线平行，内错角相等）∵∠AEG=∠FEC（对顶角相等），又AE=EC（已知）∴△AGE≌△CFE（AAS）；（2）说明：∵FG∥AB，AG∥BC（已知）∴四边形ABFG是平行四边形（平行四边形的定义）；（3）解：线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE=BF=FC，理由：由（1）可知△AGE≌△CFE∴AG=FC，FE=EG（全等三角形的对应边相等），∴E是FG的中点，又∵AD=DB（已知）∴DE为三角形ABC的中位线，∴DE=BC，DE∥BC，即DE∥BF，DE∥FC，由（2）可知四边形ABFG是平行四边形∴AG=BF，∴BF=FC=BC，∴DE=BF=FC，即线段DE，BF，FC之间的位置关系是DE∥BF，DE∥FC，数量关系是DE=BF=FC．18．（1）∵△ABC和△ADE都是等边三角形，∴AE=AD，AB=AC，∠EAD=∠BAC=60°，∴∠EAD﹣∠BAD=∠BAC﹣∠BAD，即：∠EAB=∠DAC，∴△ABE≌△ACD（SAS）；（2）证明：∵△ABE≌△ACD，∴BE=DC，∠EBA=∠DCA，又∵BF=DC，∴BE=BF．∵△ABC是等边三角形，∴∠DCA=60°，∴△BEF为等边三角形．∴∠EFB=60°，EF=BF∵△ABC是等边三角形，∴∠ABC=60°，∴∠ABC=∠EFB，∴EF∥BC，即EF∥DC，∵EF=BF，BF=DC，19．平行四边形ADCF和平行四边形DBCF．理由：（1）∵D、E分别是AB、AC边的中点，∴DE∥BC ，．又∵EF=DE，∴DF=BC，∴四边形DBCF是平行四边形；（2）在四边形ADCF中，∵EF=DE，又∵E是AC边的中点，∴EA=EC，∴四边形ADCF是平行四边形20．∵E为AD中点，∴AE=DE，∵AF∥BC，∴∠AFE=∠DCE，在△AEF和△CED中∵，∴△AEF≌△CED（AAS），∴AF=DC，∵AD是△ABC的中线，∴BD=DC，∴AF=BD，即AF∥BD，AF=BD，故四边形AFBD是平行四边形21．图中有两个平行四边形：▱ABED、▱AECD．∵，∴AD=BE，∵AD∥BC，∴四边形ABED是平行四边形．22．已知：四边形ABCD，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形，证明：∵∠A=∠C，∠B=∠D，∠A+∠B+∠C+∠D=360°，∴2∠A+2∠B=360°，∴∠A+∠B=180°，∴AD∥BC，同理AB∥CD，∴四边形ABCD是平行四边形．23．∵AE∥DF，∴△ABE≌△DCF（SAS），∴EB=FC，∠ABE=∠DCF，∵∠ABE+∠EBC=180°，∠DCF+∠FCB=180°，∴∠EBC=∠FCB，∴BE∥FC，∵BE=FC，∴四边形EBFC是平行四边形24．∵CE∥BF，BD=CD，∴△BDF≌△CDE，∴BF=CE，∴四边形BFCE是平行四边形．25．四边形EFGH是平行四边形证明：连接AC、BD∵E、F、G、H分别为四边形ABCD四边的中点∴EH=BD，FG=BD，HG=AC，EF=AC ∴EH=FG，EF=HG∴四边形EFGH是平行四边形．26．∵∠B=∠EAD，∴AD∥BC，∵AD=BC，∴四边形ABCD是平行四边形．27．∵AD∥BC，∴∠EAD=∠FCB，又ED∥BF，∴∠FED=∠EFB，∠AED=180°﹣∠FED，∠CFB=180°﹣∠EFB，∴∠AED=∠CFB，又已知AE=CF，∴△AED≌△CFB，∴AD=BC，∴四边形ABCD是平行四边形．28．∵AD∥BC，∴∠EAD=∠FCB，又ED∥BF，∴∠FED=∠EFB，∠AED=180°﹣∠FED，∠CFB=180°﹣∠EFB，∴∠AED=∠CFB，又已知AE=CF，∴△AED≌△CFB，∴AD=BC，∴四边形ABCD是平行四边形．29．∵△ABE、△BCF为等边三角形，∴AB=BE=AE，BC=CF=FB，∠ABE=∠CBF=60°．∴∠FBE=∠CBA，在△FBE和△CBA中，，∴△FBE≌△CBA（SAS）．∴EF=AC．又∵△ADC为等边三角形，∴CD=AD=AC．∴EF=AD．同理可得AE=DF．∴四边形AEFD是平行四边形30．∵AB=5，AC=4，BC=3∴AB2=AC2+BC2∴∠BCA=90°∵AD∥BC∴∠DAC=∠BCA=90°∵DC=5，AC=4，∴AD2=DC2﹣AC2=9∴AD=BC=3∴四边形ABCD为平行四边形．。