最短路径问题同步练习题一
人教版八年级数学上册同步练习13.4 课题学习 最短路径问题(word版,含答案解析)

人教版八年级数学上册13.4 课题学习最短路径问题一、选择题(共16小题;共80分)1. 如图,直线是一条河,,是两个村庄.欲在上的某处修建一个水泵站,向,两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是A. B.C. D.2. 如图,四边形是直角梯形,,,点是腰上的一个动点,要使最小,则点应该满足A. B.C. D.3. 四边形中,,,在,上分别找一点,,使三角形周长最小时,则的度数为A. B. C. D.4. 如图,直线外存在不重合的两点,,在直线上求作一点,使得的长度最短,作法为:① 作点关于直线的对称点;②连接与直线相交于点,则点为所求作的点.在解决这个问题时没有运用到的知识或方法是A. 转化思想B. 三角形的两边之和大于第三边C. 两点之间,线段最短D. 三角形的一个外角大于与它不相邻的任意一个内角5. 如图,牧童在处放牛,其家在处,,到河岸的距离分别为和,且,若点到河岸的中点的距离为米,则牧童从处把牛牵到河边饮水再回家,最短距离是A. 米B. 米C. 米D. 米6. 如图,已知直线,且与之间的距离为,点到直线的距离为,点到直线的距离为,.试在直线上找一点,在直线上找一点,满足且的长度最短,则此时A. B. C. D.7. 如图,正的边长为,过点的直线,且与关于直线对称,为线段上一动点,则的最小值是A. B. C. D.8. 如图,在中,,,是的两条中线,是上一个动点,则下列线段的长度等于最小值的是A. B. C. D.9. 如图,在四边形中,,,在,上分别找一点,,使的周长最小,此时,A. B. C. D.10. 如图,,内有一定点,且,在上有一动点,上有一动点.若周长最小,则最小周长是A. B. C. D.11. 如图,四边形中,,,,分别是,上的点,当的周长最小时,的度数为A. B. C. D.12. 如图,在中,,,面积是,的垂直平分线分别交,边于,点.若点为边的中点,点为线段上一动点,则周长的最小值为A. B. C. D.13. 如图,在中,,,,为上一点,且,平分交于.若是上的动点,则的最小值等于A. B. C. D.14. 如图,圆柱形容器高为,底面周长为,在杯内壁离杯底的点处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿与蜂蜜相对的点处,则蚂蚁从外壁处到达内壁处的最短距离为A. C. D.15. 如图,点是内任意一点,且,点和点分别是射线和射线上的动点,当周长取最小值时,则的度数为A. B. C. D.16. 如图,,点是内任意一点,,点和点分别是射线和射线上的动点,若周长的最小值是,则的值是A. B. C. D.二、填空题(共5小题;共25分)17. 与的最小公倍数是.18. 如图,在中,是边的中点,过点作边的垂线,是上任意一点,且,,则的周长的最小值为.19. 如图,在中,,,的垂直平分线交于点,交于点,在直线上存在一点,使,,三点构成的的周长最小,则的周长最小值为.20. 已知,点在的内部,点是边上任意一点,点是边上任意一点,连接,,当的周长最小时,的度数为.21. 如图,是等腰直角三角形,,,为上的动点,则的最大值为.三、解答题(共3小题;共45分)22. 如图,已知直线及其同侧两点,,在直线上找一点,使得的长度最小.23. 如图,点,在的内部,为射线上的一个动点,为射线上的一个动点,求作点,,使得的长最短.作法:24. 如图,,两个小集镇在河流的同侧,分别到河的距离为千米,千米,且千米,现在要在河边建一自来水厂,向,两镇供水,铺设水管的费用为每千米万,请你在河流上选择水厂的位置,使铺设水管的费用最节省,并求出总费用是多少?答案第一部分1. D2. D 【解析】如图,作点关于的对称点,连接交于,连接.根据轴对称的性质,得,根据对顶角相等知,所以.3. C4. D5. B6. B7. A 【解析】如图所示.过点作的对称点,连接,与的延长线交于点 .此时,为最小值 .点在线段上,点在点处.的最小值为.8. B 【解析】如图连接,,,,,,,,,共线时,的值最小,最小值为的长度.9. D10. B【解析】设,则,作与相交于,并将延长一倍到,即,作与相交于,并将延长一倍到,即,连接与相交于,与相交于,再连接,,连接,,则即为周长最短的三角形,是的垂直平分线,;同理,是的垂直平分线,,的周长,,且,是等边三角形,,即在保持的条件下的最小周长为.11. D 【解析】作关于和的对称点,,连接,交于,交于,则即为的周长最小值.作延长线 .,...,,..12. C 【解析】连接.是等腰三角形,点是边的中点,,,解得,是线段的垂直平分线,点关于直线的对称点为点,的长为的最小值,13. D 【解析】如图,作点关于的对称点,连接交于,连接,此时的值最小,作于.,,,,,,,,,故选:D.14. D 【解析】如图:将杯子侧面展开,作关于的对称点,连接,则即为最短距离,.15. B【解析】分别作点关于,的对称点,,连接,分别交,于点,,如图所示:此时的周长取最小值.,,,,,,,.16. B第二部分17.18.19.【解析】如图,连接.,,的值最小时,的周长最小,垂直平分线段,,,的最小值为,的周长的最小值为.20.【解析】如图,过点作关于,的对称点,,连接,与,相交与点,,则此时的周长最小,为线段的长度;,,,,,,,,,,,解得:;故答案为:.21.第三部分22. 过点作直线的垂线,垂足为点,截取,连接,则与的交点就是点.23. 作点关于直线的对称点,作点关于直线的对称点交于,交于,则最短.24. 作关于的对称点,连接交于,点即为所求作的点,则可得:(千米),所以(千米),所以(千米),总费用为万元.。
人教版八年级数学上学期《最短路径问题》同步练习

人教版八年级数学上学期《最短路径问题》同步练习一.选择题1.如图,在△AOB中,∠OAB=∠AOB=15°,OB=8,OC平分∠AOB,点P在射线OC 上,点Q为边OA上一动点,则PA+PQ的最小值是()A.3B.4C.4 D.32.如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是()A.3 B.4 C.5 D.63.如图,为内一定点,、分别是射线、上一点,当周长最小时,,则A.40°B. 45°C. 50°D. 55°4.如图,在△ABC中,AB=AC,BC=4,面积是10.AB的垂直平分线ED分别交AC,AB 边于E、D两点,若点F为BC边的中点,点P为线段ED上一动点,则△PBF周长的最小值为()A.5 B.7 C.10 D.145.如图,直线表示一条河,点,表示两个村庄,想在直线上的某点处修建一个水泵站向,两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是A.B.C.D.6.已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点A1处,CA1与AB交于点N,且AN=AC,则∠A 的度数是()A.30°B.36°C.50°D.60°7.如图,中,垂直于点,且,上方有一动点满足,则点到,两点距离之和最小时,的度数为A.30° B. 45°C.65° D. 90°8.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为()A.(12,-4)B.(23,0)C.(43,0)D.(32,0)9.如图,等腰三角形ABC底边BC的长为4cm,面积为12cm2,腰AB的垂直平分线EF 交AB于点E,交AC于点F,若D为BC边上的中点,M为线段EF上一点,则△BDM 的周长最小值为()A.5cm B.6cm C.8cm D.10cm10.已知两点M(3,5),N(1,-1),点P是x轴上一动点,若使PM+PN最短,则点P的坐标应为()A.(12,-4)B.(23,0)C.(43,0)D.(32,0)11.如图,直线表示一条河,点,表示两个村庄,想在直线上的某点处修建一个水泵站向,两村庄供水.现有如图所示的四种铺设管道的方案(图中实线表示铺设的管道),则铺设的管道最短的是A.B.C.D.12.在平面直角坐标系中,A(3,0)、B(a,2)、C(0,m),D(n,0),且m2+n2=4,若E为CD中点.则AB+BE的最小值为()A.3 B.4 C.5 D.2二.填空题13.如图,,,是边的中点,是边上一动点,则的最小值是________.14.如图,已知∠AOB=30°,OC平分∠AOB,在OA上有一点M,OM=10cm,现要在OC、OA上分别找点Q、N,使QM+QN最小,则其最小值是.15.如图,若,为内一定点,上有一个点,上有一个点,当的周长取最小值时,则的度数是.16.如图,,四边形ABCD的顶点A在的内部,B,C两点在OM上(C在B,O之间),且,点D在ON上,若当CD⊥OM时,四边形ABCD的周长最小,则此时AD的长度是________.17.如图,锐角△ABC的边AC=6,△ABC的面积为15,AD平分∠BAC交BC于D,M,N 分别是AD和AB上的动点,则BM+MN的最小值是.、三.解答题18.如图,A、B在直线l的同侧,在直线l上求一点P,使△PAB的周长最小.19.请回答下列问题:如图,在单位长度为1 的正方形网格中,点A,B,C 都在格点上.①填空:的面积为;②画出关于直线L 对称的,其中点A,B,C 的对应点分别为A’,B’,C;③在直线L 上画出一个点P,使PA+PC 的值最小.20.如图,在平面直角坐标系中,点的坐标为.(1) 请在图中画出与关于轴对称的,并写出点 A 的坐标.(2) 请在图中的 y 轴上画出一点 p,使得的周长最短.21.在如图所示的平面直角坐标系中有下面各点:A(0,3),B(1,﹣2),C(3,﹣5),D(﹣3,﹣5),E(3,5),F(5,﹣3),G(4,0).(1)写出与点C关于坐标轴对称的点;(2)连接CE,则直线CE与y轴是什么关系(直接写出结论)?(3)若点P是x轴上的一个动点,连接PD,PF,当PD+PF的值最小时,在图中标出点P的位置,并直接写出P点的坐标.。
八年级数学上册13.4《课题学习最短路径问题》同步训练(含解析)

最短路径问题·一.选择题(共6小题);1.(2015•遵义)如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为;()A.50° B.60° C.70° D.80°2.(2015•黔南州)如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是;()A.转化思想B.三角形的两边之和大于第三边;C.两点之间,线段最短;D.三角形的一个外角大于与它不相邻的任意一个内角;3.(2015•同安区一模)如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD 上一动点,则线段EP+FP的长最短为();A.3 B.4 C.5 D.64.(2015•芜湖三模)如图,在矩形ABCD中,AB=9,BC=12,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为;()A.4 B.6 C.8 D.95.(2014•江西模拟)如图,在△ABC中,∠BAC=90°,AB⊥AC,AB=3,BC=5,EF垂直平分BC,点P为直线EF 上的任一点,则AP+BP的最小值是();A.4 B.5 C.6 D.76.(2014秋•监利县期末)如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC 边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为;()A.15° B.22.5°C.30° D.45°二.填空题(共6小题);7.(2015•攀枝花)如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为.;8.(2015•惠山区一模)如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为; .9.(2015春•沙坪坝区期末)如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE⊥OF,则△OEF周长的最小值是.;10.(2015•枣庄模拟)如图,在对角线长分别为12和16的菱形ABCD中,E、F分别是边AB、AD的中点,H 是对角线BD上的任意一点,则HE+HF的最小值是.;11.(2015•许昌一模)如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是.;12.(2015春•新泰市期末)如图,在平面直角坐标系中,点A、B的坐标分别为(﹣1,2)、(1,4),欲在x 轴上找一点P,使PA+PB最短,则点P的坐标为.;三.解答题(共4小题)13.(2014•清河区二模)已知直角坐标系中有两点A(﹣1,2)、B(5,4),要在x轴上找一点P,使得PA+PB 之和最小,求点P的坐标.;;14.(2014秋•嘉荫县期末)如图,小河CD边有两个村庄A村、B村,现要在河边建一自来水厂E为A村与B 村供水,自来水厂建在什么地方到A村、B村的距离和最小?请在下图中找出点E的位置.(保留作图痕迹,不写作法)(2014秋•沙河市校级期末)如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,15.且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为.16.(2015春•下城区期末)在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC 上的动点,连结AP,DP.(1)设BP=x,用含字母x的代数式分别表示线段AP,DP的长,并求当x=2的时候,AP+DP的值;(2)AP+DP是否存在最小值?若存在,求出其最小值.人教版八年级数学上册13.3.4《课题学习最短路径问题》同步训练习题(教师版)一.选择题(共6小题)1.(2015•遵义)如图,四边形ABCD中,∠C=50°,∠B=∠D=90°,E、F分别是BC、DC上的点,当△AEF的周长最小时,∠EAF的度数为()A.50° B.60° C.70° D.80°考点:轴对称-最短路线问题.分析:据要使△AEF的周长最小,即利用点的对称,使三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′E+∠A″=∠HAA′=50°,进而得出∠AEF+∠AFE=2(∠AA′E+∠A″),即可得出答案.解答:解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF 的周长最小值.作DA延长线AH,∵∠C=50°,∴∠DAB=130°,∴∠HAA′=50°,∴∠AA′E+∠A″=∠HAA′=50°,∵∠EA′A=∠EAA′,∠FAD=∠A″,∴∠EAA′+∠A″AF=50°,∴∠EAF=130°﹣50°=80°,故选:D.点评:本题考查的是轴对称﹣最短路线问题,涉及到平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出E,F的位置是解题关键.2.(2015•黔南州)如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是()A.转化思想B.三角形的两边之和大于第三边C.两点之间,线段最短D.三角形的一个外角大于与它不相邻的任意一个内角考点:轴对称-最短路线问题.分析:利用两点之间线段最短分析并验证即可即可.解答:解:∵点B和点B′关于直线l对称,且点C在l上,∴CB=CB′,又∵AB′交l与C,且两条直线相交只有一个交点,∴CB′+CA最短,即CA+CB的值最小,将轴对称最短路径问题利用线段的性质定理两点之间,线段最短,体现了转化思想,验证时利用三角形的两边之和大于第三边.故选D.点评:此题主要考查了轴对称最短路线问题,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合本节所学轴对称变换来解决,多数情况要作点关于某直线的对称点.3.(2015•同安区一模)如图,周长为16的菱形ABCD中,点E,F分别在AB,AD边上,AE=1,AF=3,P为BD 上一动点,则线段EP+FP的长最短为()A.3 B.4 C.5 D.6考点:轴对称-最短路线问题;菱形的性质.分析:在DC上截取DG=FD=AD﹣AF=4﹣3=1,连接EG,则EG与BD的交点就是P.EG的长就是EP+FP的最小值,据此即可求解.解答:解:在DC上截取DG=FD=AD﹣AF=4﹣3=1,连接EG,则EG与BD的交点就是P.∵AE=DG,且AE∥DG,∴四边形ADGE是平行四边形,∴EG=AD=4.故选B.点评:本题考查了轴对称,理解菱形的性质,对角线所在的直线是菱形的对称轴是关键.4.(2015•芜湖三模)如图,在矩形ABCD中,AB=9,BC=12,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为()A.4 B.6 C.8 D.9考点:轴对称-最短路线问题;矩形的性质.专题:探究型.分析:先作点E关于直线CD的对称点E′,连接AE′交CD于点F,再根据△CEF∽△BEA即可求出CF的长,进而得出DF的长.解答:解:作点E关于直线CD的对称点E′,连接AE′交CD于点F,∵在矩形ABCD中,AB=9,BC=12,点E是BC中点,∴BE=CE=CE′=6,∵AB⊥BC,CD⊥BC,∴CD∥AB,∴=,即=,解得CF=3,∴DF=CD﹣CF=9﹣3=6.故选B.点评:本题考查的是轴对称﹣最短路线问题及相似三角形的判定与性质,根据题意作出E点关于直线CD的对称点,再根据轴对称的性质求出CE′的长,利用相似三角形的对应边成比例即可得出结论.5.(2014•江西模拟)如图,在△ABC中,∠BAC=90°,AB⊥AC,AB=3,BC=5,EF垂直平分BC,点P为直线EF 上的任一点,则AP+BP的最小值是()A.4 B.5 C.6 D.7考点:轴对称-最短路线问题.分析:根据题意知点B关于直线EF的对称点为点C,故当点P与点D重合时,AP+BP的最小值,求出AC长度即可.解答:解:∵EF垂直平分BC,∴B、C关于EF对称,连接AC交EF于D,∴当P和C重合时,AP+BP的值最小,最小值等于AC的长,由勾股定理得:AC===4,故选A.点评:本题考查了勾股定理,轴对称﹣最短路线问题的应用,解此题的关键是找出P的位置.6.(2014秋•监利县期末)如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC 边上一点,若AE=2,当EF+CF取得最小值时,则∠ECF的度数为()A.15° B.22.5°C.30° D.45°考点:轴对称-最短路线问题;等边三角形的性质.分析:过E作EM∥BC,交AD于N,连接CM交AD于F,连接EF,推出M为AB中点,求出E和M关于AD对称,根据等边三角形性质求出∠ACM,即可求出答案.解答:解:过E作EM∥BC,交AD于N,∵AC=4,AE=2,∴EC=2=AE,∴AM=BM=2,∴AM=AE,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD对称,连接CM交AD于F,连接EF,则此时EF+CF的值最小,∵△ABC是等边三角形,∴∠ACB=60°,AC=BC,∵AM=BM,∴∠ECF=∠ACB=30°,故选C.点评:本题考查了轴对称﹣最短路线问题,等边三角形的性质,等腰三角形的性质,平行线分线段成比例定理等知识点的应用.二.填空题(共6小题)7.(2015•攀枝花)如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为.考点:轴对称-最短路线问题;等边三角形的性质.分析:作B关于AC的对称点B′,连接BB′、B′D,交AC于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D就是BE+ED的最小值,故E即为所求的点.解答:解:作B关于AC的对称点B′,连接BB′、B′D,交AC于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D就是BE+ED的最小值,∵B、B′关于AC的对称,∴AC、BB′互相垂直平分,∴四边形ABCB′是平行四边形,∵三角形ABC是边长为2,∵D为BC的中点,∴AD⊥BC,∴AD=,BD=CD=1,BB′=2AD=2,作B′G⊥BC的延长线于G,∴B′G=AD=,在Rt△B′BG中,BG===3,∴DG=BG﹣BD=3﹣1=2,在Rt△B′DG中,BD===.故BE+ED的最小值为.故答案为:.点评:本题考查的是最短路线问题,涉及的知识点有:轴对称的性质、等边三角形的性质、勾股定理等,有一定的综合性,但难易适中.8.(2015•惠山区一模)如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为 4 .考点:轴对称-最短路线问题.分析:因为EF=2,点G为EF的中点,根据直角三角形斜边上中线的性质得出DG=1,所以G是以D为圆心,以1为半径的圆弧上的点,作A关于BC的对称点A′,连接A′D,交BC于P,交以D为圆心,以1为半径的圆于G,此时PA+PG的值最小,最小值为A′G的长;根据勾股定理求得A′D=5,即可求得A′G=A′D﹣DG=5﹣1=4,从而得出PA+PG的最小值.解答:解:∵EF=2,点G为EF的中点,∴DG=1,∴G是以D为圆心,以1为半径的圆弧上的点,作A关于BC的对称点A′,连接A′D,交BC于P,交以D为圆心,以1为半径的圆于G,此时PA+PG的值最小,最小值为A′G的长;∵AB=2,AD=3,∴AA′=4,∴A′D=5,∴A′G=A′D﹣DG=5﹣1=4;∴PA+PG的最小值为4;故答案为4.点评:本题考查了轴对称﹣最短路线问题,判断出G点的位置是解题的关键.9.(2015春•沙坪坝区期末)如图,正方形ABCD中,AB=2,AC,BD交于点O.若E,F分别是边AB,BC上的动点,且OE⊥OF,则△OEF周长的最小值是2+.考点:轴对称-最短路线问题;正方形的性质.分析:根据正方形的对角线互相平分且相等可得AO=BO,∠AOB=90°,对角线平分一组对角可得∠OAE=∠OBF,再根据AE=BF,然后利用“SAS”证明△AOE和△BOF全等,根据全等三角形对应角相等可得∠AOE=∠BOF,可得∠EOF=90°,然后利用勾股定理列式计算即可得解.解答:解:在正方形ABCD中,AO=BO,∠AOB=90°,∠OAE=∠OBF=45°,∵点E、F的速度相等,∴AE=BF,在△AOE和△BOF中,,∴△AOE≌△BOF(SAS),∴∠AOE=∠BOF,∴∠AOE+∠BOE=90°,∴∠BOF+∠BOE=90°,∴∠EOF=90°,在Rt△BEF中,设AE=x,则BF=x,BE=2﹣x,EF===.∴当x=1时,EF有最小值为.∴OE=OF=1.∴△OEF周长的最小值=2+.故答案为:2.点评:本题考查了正方形的性质,全等三角形的判定与性质,同角的余角相等的性质,熟记正方形的性质,求出三角形全等的条件是解题的关键.10.(2015•枣庄模拟)如图,在对角线长分别为12和16的菱形ABCD中,E、F分别是边AB、AD的中点,H 是对角线BD上的任意一点,则HE+HF的最小值是10 .考点:轴对称-最短路线问题;菱形的性质.分析:要求HE+HF的最小值,HE、HF不能直接求,可考虑通过作辅助线转化HE、HF的值,从而找出其最小值求解.解答:解:如图:作EE′⊥BD交BC于E′,连接E′F,连接AC交BD于O.则E′F就是HE+HF的最小值,∵E、F分别是边AB、AD的中点,∴E′F AB,而由已知△AOB中可得AB====10,故HE+HF的最小值为10.故答案为:10.点评:考查菱形的性质和轴对称及平行四边形的判定等知识的综合应用.11.(2015•许昌一模)如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是(0,3).考点:轴对称-最短路线问题;坐标与图形性质.分析:根据轴对称做最短路线得出AE=B′E,进而得出B′O=C′O,即可得出△ABC的周长最小时C点坐标.解答:解:作B点关于y轴对称点B′点,连接AB′,交y轴于点C′,此时△A BC的周长最小,∵点A、B的坐标分别为(1,4)和(3,0),∴B′点坐标为:(﹣3,0),AE=4,则B′E=4,即B′E=AE,∵C′O∥AE,∴B′O=C′O=3,∴点C′的坐标是(0,3),此时△ABC的周长最小.故答案为(0,3).点评:此题主要考查了利用轴对称求最短路线以及平行线的性质,根据已知得出C点位置是解题关键.12.(2015春•新泰市期末)如图,在平面直角坐标系中,点A、B的坐标分别为(﹣1,2)、(1,4),欲在x 轴上找一点P,使PA+PB最短,则点P的坐标为(﹣,0).考点:轴对称-最短路线问题;坐标与图形性质.分析:先求出点A关于x轴的对称点A′的坐标,连接A′B,交x轴于P,则P即为所求的点,然后用待定系数法求出直线A′B的解析式,求出直线与x轴的交点即可.解答:解:∵点A(﹣1,2),∴点A关于x轴的对称点A′的坐标为(﹣1,﹣2),∵A′(﹣1,﹣2),B(1,4),设直线A′B的解析式为y=kx+b(k≠0),∴,解得,∴直线A′B的解析式为y=3x+1,当y=0时,x=﹣.∴P(﹣,0).故答案为(﹣,0).点评:本题考查的是轴对称﹣最短路线问题,待定系数法求一次函数的解析式,熟知“两点之间线段最短”是解答此题的关键.三.解答题(共4小题)13.(2014•清河区二模)已知直角坐标系中有两点A(﹣1,2)、B(5,4),要在x轴上找一点P,使得PA+PB 之和最小,求点P的坐标.考点:轴对称-最短路线问题;坐标与图形性质.分析:先求出点A关于x轴的对称点A′的坐标,连接A′B交x轴于P,此时PA+PB最小,用待定系数法求出直线A′B的解析式,然后求出直线与x轴的交点即可.解答:解:∵A(﹣1,2),∴点A关于x轴的对称点A′的坐标为(﹣1,﹣2),∵A′(﹣1,﹣2),B(5,4),设直线A′B的解析式为y=kx+b(k≠0),∴,解得,∴直线A′B的解析式为y=x﹣1,当y=0时,x=1.∴P(1,0).点评:本题考查的是轴对称﹣最短路线问题,熟知“两点之间线段最短”是解答此题的关键.14.(2014秋•嘉荫县期末)如图,小河CD边有两个村庄A村、B村,现要在河边建一自来水厂E为A村与B 村供水,自来水厂建在什么地方到A村、B村的距离和最小?请在下图中找出点E的位置.(保留作图痕迹,不写作法)考点:轴对称-最短路线问题;作图—应用与设计作图.分析:利用轴对称求最短路线的方法得出A点关于直线CD的对称点A′,再连接A′B交CD于点E,即可得出答案.解答:解:如图所示:点E即为所求.点评:此题主要考查了应用设计与作图以及轴对称求最短路径,得出A点对称点是解题关键.(2014秋•沙河市校级期末)如图,已知A,B两个村庄在河流CD的同侧,它们到河流的距离AC=10km,BD=30km,15.且CD=30km.现在要在河流CD上建立一个泵站P向村庄供水,铺设管道的费用为每千米2万元,要使所花费用最少,请确定泵站P的位置?(保留痕迹,不写作法)此时所花费用最少为100万元.考点:轴对称-最短路线问题.分析:根据已知得出作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点P到A、B两点的距离和最小,再利用构造直角三角形得出即可.解答:解:依题意,只要在直线l上找一点P,使点P到A、B两点的距离和最小.作点A关于直线l的对称点A′,连接A′B,则A′B与直线l的交点P到A、B两点的距离和最小,且PA+PB=PA′+PB=A′B.过点A′向BD作垂线,交BD的延长线于点E,在直角三角形A′BE 中,A′E=CD=30,BE=BD+DE=40,根据勾股定理可得:A′B=50(千米)即铺设水管长度的最小值为50千米.所以铺设水管所需费用的最小值为:50×2=100(万元).故答案为100万元.点评:此题主要考查了轴对称﹣最短路线问题和勾股定理的应用,解题关键是构建直角三角形.16.(2015春•下城区期末)在如图所示的方格中,点A,B,C,D都在格点上,且AB=BC=2CD=4,P是线段BC 上的动点,连结AP,DP.(1)设BP=x,用含字母x的代数式分别表示线段AP,DP的长,并求当x=2的时候,AP+DP的值;(2)AP+DP是否存在最小值?若存在,求出其最小值.考点:轴对称-最短路线问题.分析:(1)分别用x表示出BP、CD的长度,再根据勾股定理求出AP、DP的长即可;(2)作点A关于BC的对称点A′,连接A′D,再由对称的性质及勾股定理即可求解.解答:解:(1)由题意结合图形知:AB=4,BP=x,CP=4﹣x,CD=2,∴AP==,DP===;当x=2时,AP+DP=+=2+2;(2)存在.如图,作点A关于BC的对称点A′,连接A′D,∴A′E=4,DE=6,则A′D====,∴最小值为2.点评:本题主要考查的是最短线路问题及勾股定理,根据题意画出图形是解答此类题目的关键.。
最短路径问题同步练习题一

最短路径问题同步练习题一LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】课题学习 最短路径问题(一) 知识点:1.最短路径问题(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.2.运用轴对称解决距离最短问题运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同.3.利用平移确定最短路径选址 解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.同步练习:1.如图所示,点A ,B 分别是直线l 异侧的两个点,在l 上找一个点C ,使CA +CB 最短,这时点C 是直线l 与AB 的交点.2.如图所示,点A ,B分别是直线l 同侧的两个点,在l 上找一个点C ,使CA +CB 最短,3..在图中直线l 上找到一点M ,使它到A ,B 两点的距离和最小.4. 如图,小河边有两个村庄A ,B ,要在河边建一自来水厂向A 村与B 村供水.A B l(1)若要使厂部到A,B村的距离相等,则应选择在哪建厂?(2)若要使厂部到A,B两村的水管最短,应建在什么地方?5. 如图,从A地到B地经过一条小河(河岸平行),今欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从A地到B地的路程最短?6.(实际应用题)茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图a所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C 处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短?7.如图所示,A,B两点在直线l的两侧,在l上找一点C,使点C到点A、B的距离之差最大.参考答案:1.2.这时先作点B 关于直线l 的对称点B ′,则点C 是直线l 与AB ′的交点.为了证明点C 的位置即为所求,我们不妨在直线上另外任取一点C ′,连接AC ′,BC ′,B ′C ′,证明AC +CB <AC ′+C ′B .如下:证明:由作图可知,点B 和B ′关于直线l 对称,所以直线l 是线段BB ′的垂直平分线.因为点C 与C ′在直线l 上,所以BC =B ′C ,BC ′=B ′C ′.在△AB ′C ′中,AB ′<AC ′+B ′C ′,所以AC +B ′C <AC ′+B ′C ′,所以AC +BC <AC ′+C ′B .3. 解:如图所示:(1)作点B 关于直线l 的对称点B ′;(2)连接AB ′交直线l 于点M .(3)则点M 即为所求的点.4.解:(1)如图1,取线段AB 的中点G ,过中点G 画AB 的垂线,交EF 于P ,则P 到A ,B 的距离相等.也可分别以A 、B 为圆心,以大于12AB 为半径画弧,两弧交于两点,过这两点作直线,与EF 的交点P 即为所求.(2)如图2,画出点A 关于河岸EF 的对称点A ′,连接A ′B 交EF 于P ,则P 到A ,B 的距离和最短.5.解:(1)如图2,过点A作AC垂直于河岸,且使AC等于河宽.(2)连接BC与河岸的一边交于点N.(3)过点N作河岸的垂线交另一条河岸于点M.则MN为所建的桥的位置.6.解:如图b.(1)作C点关于OA的对称点C1,作D点关于OB的对称点D1,(2)连接C 1D1,分别交OA,OB于P,Q,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.7.解:如图所示,以直线l为对称轴,作点A关于直线l的对称点A′,A′B的连线交l于点C,则点C即为所求.理由:在直线l上任找一点C′(异于点C),连接CA,C′A,C′A′,C′B.因为点A,A′关于直线l对称,所以l为线段AA′的垂直平分线,则有CA=CA′,所以CA-CB=CA′-CB=A′B.又因为点C′在l上,所以C′A=C′A′.在△A′BC′中,C′A-C′B=C′A′-C′B<A′B,所以C′A′-C′B<CA-CB.点拨:根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题是常用的一种方法.。
初中数学八年级上册最短路径问题同步专项练习题含答案
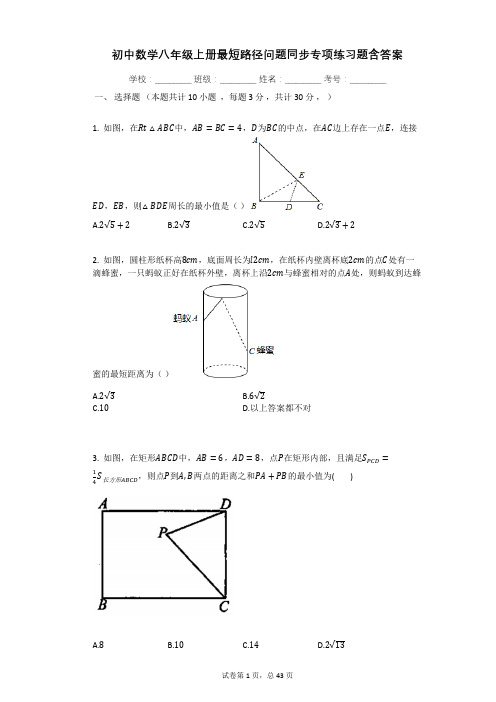
初中数学八年级上册最短路径问题同步专项练习题含答案学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(本题共计 10 小题,每题 3 分,共计30分,)1. 如图,在Rt△ABC中,AB=BC=4,D为BC的中点,在AC边上存在一点E,连接ED,EB,则△BDE周长的最小值是()A.2√5+2B.2√3C.2√5D.2√3+22. 如图,圆柱形纸杯高8cm,底面周长为l2cm,在纸杯内壁离杯底2cm的点C处有一滴蜂蜜,一只蚂蚁正好在纸杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为()A.2√3B.6√2C.10D.以上答案都不对3. 如图,在矩形ABCD中,AB=6,AD=8,点P在矩形内部,且满足S PCD=1 4S长方形ABCD,则点P到A,B两点的距离之和PA+PB的最小值为( )A.8B.10C.14D.2√134. 如图,直线l是一条河,P,Q是两个村庄.欲在l上的某处修建一个水泵站,向P,Q 两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是( )A. B.C. D.5. 如图,直线l是一条河,A、B两地相距10km,A、B两地到l的距离分别为8km、14km,欲在l上的某点M处修建一个水泵站,向A、B两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是()A. B.C. D.6. 如图所示,矩形ABCD中,BC=6,AB=4,点P是平面内的一个动点,点P运动过程中始终满足∠BPC=90∘,线段AP的最小值是( )A.1B.2C.3D.47. 如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )A.√2B.√3C.√5D.28. 如图,正方形ABCD的边长为8,M在DC上,且DM=2,N是AC上一动点,则DN+ MN的最小值为( )A.6B.8C.12D.109. 已知∠MON=40∘,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是()A.40∘B.100∘C.140∘D.50∘10. 如图,△ABC中,AC=BC=3,AB=2,将它沿AB翻折得到△ABD,点P、E、F 分别为线段AB、AD、DB上的动点,则PE+PF的最小值是()A. B. C. D.二、填空题(本题共计 10 小题,每题 3 分,共计30分,)11. 对于平面直角坐标系中的线段MN及点Q,给出如下定义:若点Q满足QM=QN,则称点Q为线段MN的“对称点”;当QM=QN=MN时,称点Q为线段MN的“完美对称点”.(1)如图1,点A坐标为(4,0),有点Q1(0,4),Q2(2,−4),Q3(1,√3),则线段OA的“对称点”是________.(填“Q1”"Q2"或 "Q3")(2)如图2,已知Q(2,2√3)为线段OA的“完美对称点”,D为线段OQ的中点,B为线段OA 的一个“对称点”,则BO+BD的最小值为________.12. 在矩形ABCD中,AB=20cm,BC=10cm,若在AC,AB上各取点M,N,使BM+NM最小,则BM+NM的最小值是________.AC,AB=8,E是AB上13. 如图,在Rt△ABC中,∠CAB=30∘,∠C=90∘.AD=14任意一点,F是AC上任意一点,则折线DEFB的最短长度为________.14. 小明在广场上散步,先向东走12m后,再向北又走了9m,现要以最短距离________m回到原地.15. 如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是________.16. 如图,矩形ABCD中,AB=3,BC=6,点E,F将对角线AC三等分,点P是矩形的边上的动点.则△PEF周长的最小值为________.17. 如图,△ABC中,∠ACB=45∘,边AB上一定点P,M、N分别是AC和BC边上的动点,当△PMN的周长最短时,∠MPN的度数是________.18. 一只蚂蚁从长为4cm、宽为3cm,高是12cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是________.19. 如图,在△ABC中,AC=4,AB=5,BC=6,⊙A的半径为2,点P是BC边上的动点,过点P作⊙A的一条切线PQ(其中点Q为切点),则线段PQ长度的最小值为________.20. 如图,∠AOB=45∘,点C在∠AOB内部,CD⊥OB于点D,CD=5,OD=13,点E、点F分别是射线OA、射线OB上的动点,那么FE+FC的最小值是________.三、解答题(本题共计 20 小题,每题 10 分,共计200分,)21. 如图所示,在△ABC中,∠ACB=90∘,AC=BC=2,D是BC的中点,E是AB上的一动点,且不与A,B重合,是否存在一个位置,使DE+CE的值最小?若不存在,说明理由;若存在,试求出最小值.22. 如图,要在河岸l修建一个水泵站P,分别向张庄、李庄送水,修在河岸l的什么地方:(1)使到张庄、李庄的距离相等.(2)使所用的水管最短?(请通过你所学的知识画出这个地点的位置,不必说明理由.请保留作图痕迹).23. 已知:如图所示(每个小正方形的边长为1),(1)求△ABC的面积,并求出它的AC边上高的长度;(2)在x轴上画出点P,使PA+PC最小,并求出该最小值.24. 一只蚂蚁从长为4cm,高时5cm的长方体纸箱的A点沿纸箱跑到B点,有不同的爬行路线.画出平面图示(相同类型画一个),并通过计算说明哪条线路最短,最短路线长多少?,高BC=12cm,P为BC的中点,求蚂25. 如图:有一个圆柱,底面圆的直径AB=16π蚁从A点爬到P点的最短距离.26. 如图,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是多少厘米?注:π取3.27. 如图,圆柱的高为12cm,底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离是多少cm?(π取3).28. 如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.(1)用含x的代数式表示AC+CE的长;并求AC+CE的最小值;(2)若x+y=12,x>0,y>0请仿照(1)中的规律,运用构图法求出代数式√x2+4+√y2+9的最小值.29. 如图,已知∠MON=30∘,在OM上有两点A、B分别到ON的距离为2cm和1cm,若在ON上找一点P使|PA−PB|的值最大,求P点到O点的距离.30. 从A村到B村要修一条路,中间隔着两条河,在河上需要架2座桥,桥与两岸垂直,桥架在什么地方,使A村到B村总路程最短?31. 如图,已知∠AOB=30∘,P为其内部一点,OP=3,M,N分别为OA,OB边上的一点,要使△PMN的周长最小,请给出确定点M,N位置的方法,并求出最小周长.32. 一只螳螂在松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的半径为10cm,A、B两点的距离为40cm.(其中π取3)(1)若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短距离.(要求画图)(2)螳螂得知又有一只虫子在点C处被松树油粘住不能动弹,这时螳螂还在A点,螳螂想吃掉虫子,求螳螂爬行的最短距离.(要求画图)(3)如果螳螂在点A处时,虫子在点E处不动,其中点E是CD的中点那么螳螂吃掉虫子的最短距离是多少cm?(要求画图)33.作图题:现要在形如△ABC的地面范围内建一中心医院,使医院到A,B两个居民小区的距离相等,并且到公路AB和AC的距离也相等,请确定这个中心医院的位置.(要求:保留作图痕迹,并用适当的文字说明作图方法)34. 在一条笔直公路上分布A,B,C,D,E五个工厂(各相邻工厂之间的距离均不相等),为方便这些工厂的员工,现要在公路上设一个汽车站,使各工厂到汽车站的距离之和最小.【简化分析】(1)假若由三个工厂A,B,C时,汽车站的位置有五种情形:①A厂门口,②AB之间,③B厂门口,④BC之间,⑤C厂门口.【分类讨论】①当车站设在A工厂门口时,则A厂到汽车站的距离为0,B厂到汽车站的距离为AB,C厂到汽车站的距离为AB+BC,所以各工厂到车站的距离之和为________②当车站设在A,B两工厂之间的P点时,则A厂到汽车站的距离为AP,B厂到汽车站的距离为BP,C厂到汽车站的距离为BP+BC,所以各工厂到车站的距离之和为_________③当车站设在B工厂门口,则各工厂到汽车站的距离之和为_________④当车站设在B,C两工厂之间的Q点时,则各工厂到汽车站的距离之和为_________⑤当车站设在C工厂门口,则各工厂到汽车站的距离之和为________【总结归纳】综上可知:汽车站设在________时,各工厂到汽车站的距离之和最小.【问题解决】 (2)当有A,B,C,D,E五个工厂时,汽车站设在哪里,才能使各工厂到汽车站的距离之和最小?请说明理由.35. 如图是平放在桌面上的长方体木块,其长为14cm,宽为10cm,高为20cm,点B是高CD的中点,一只蜘蛛要沿长方体木块的表面从A点爬到B点,请你求出蜘蛛爬行的最短路程是多少?36. (1)如图,已知:线段r和∠ACB=60∘,求作一⊙O,使它与∠ACB的两边相切,且圆的半径等于r;(不写作法,要求用直尺和圆规作图,保留作图痕迹)36.(2)如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,点C,使△ABC的周长最小.(不写作法,要求用直尺和圆规作图,保留作图痕迹)37. 如图,要在河边修建一个水泵站,分别向张村A和李村B送水,已知张村A、李村B 到河边的距离分别为2km和7km,且张、李二村庄相距13km.(1)水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置;(用尺规作图,保留作图痕迹,不写作法,不要求证明)(2)如果铺设水管的工程费用为每千米3000元,为使铺设水管费用最节省,请求出最节省的铺设水管的费用为多少元?38. 如图所示,一只昆虫要从正方体的一个顶点A爬到相距它最远的另一个顶点B,哪条路径最短?说明理由.39. 如图,C为线段BD上一动点,分别过点B,D作AB⊥BD,ED⊥BD,连结AC、EC.已知AB=5,DE=1,BD=8,设CD=x(1)用含x的代数式表示AC+CE的长;(2)试求AC+CE的最小值.40. 李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下三个问题,请你根据下列所给的重要条件分别求出蚂蚁需要爬行的最短路程的长.(1)如图1,正方体的棱长为5cm一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处;(2)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到C1处;(3)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且∠AOA1=120∘,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.参考答案与试题解析初中数学八年级上册最短路径问题同步专项练习题含答案一、选择题(本题共计 10 小题,每题 3 分,共计30分)1.【答案】A【考点】轴对称——最短路线问题【解析】求△BDE周长的最小值,就是要求DE+BE的最小值,根据勾股定理即可求得.【解答】解:过点B做BO⊥AC于点O,延长BO到B′,使OB′=OB,连接DB′,交AC于E,此时DB′=DE+EB′=DE+BE的值最小,连接CB′易证CB′⊥BC在RT△DCB′中,根据勾股定理可得DB′=√B′C2+CD2=√42+22=√20=2√5.故△BDE周长的最小值为2√5+2.故选:A.2.【答案】C【考点】平面展开-最短路径问题【解析】将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′C的长度即为所求.【解答】解:如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′C,则A′C即为最短距离,由题意可得出:A′D=6cm,CD=8cm,A′C=√A′D2+CD2=10(cm),故选:C.3.【答案】B【考点】路径最短问题【解析】此题暂无解析【解答】解:∵S PCD=14S长方形ABCD,设△PCD的CD边上的高为ℎ∴12CD⋅ℎ=14CD⋅AD,又AD=8,∴ℎ=4,∴动点P在与CD平行且与CD的距离为4的直线l上,如图,作D关于直线l的对称点A,连接AC,则AC的长就是所求的最短距离.在Rt△ADC中,CD=AB=6,AD=8∴AC=√AD2+CD2解得AC=10.故选B.4.【答案】D【考点】轴对称——最短路线问题利用对称的性质,通过等线段代换,将所求路线长转化为两定点之间的距离.【解答】解:作点P关于直线l的对称点P′,连结QP′交直线l于M.根据两点之间,线段最短,可知选项D铺设的管道,所需管道最短.故选D.5.【答案】B【考点】轴对称——最短路线问题【解析】作点A关于直线l的对称点,再把对称点与点B连接,根据轴对称确定最短路线问题,交点即为所求点M.【解答】解:根据轴对称确定最短路线问题,B选项图形方案符合.故选B.6.【答案】B【考点】路径最短问题【解析】要想求得点P的个数,由∠BPC=90∘可判断以BC为直径的圆与AD的交点个数即可.【解答】解:∵ 点P运动过程中始终满足∠BPC=90∘,∴ 点P在以BC为直径的半圆上,圆心为O,如下图所示,连接AO,AO与半圆的交点为P,此时AP距离最短.由题意知,AO=√AB2+OB2=√42+32=5,∴ AP=AO−OP=5−3=2,∴ 线段AP的最小值是2.7.【答案】C【考点】平面展开-最短路径问题【解析】本题考查了平面展开-最短路径问题,“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.【解答】解:将纸箱展开,如图所示,由勾股定理得:AB2=12+(1+1)2=5,∴ AB=√5.故选C.8.【答案】D【考点】轴对称——最短路线问题【解析】要使DN+MN最小,首先应分析点N的位置.根据正方形的性质:正方形的对角线互相垂直平分.知点D的对称点是点B,连接MB交AC于点N,此时DN+MN最小值即是BM的长.【解答】解:根据题意,连接BD,BM,则BM就是所求DN+MN的最小值,在Rt△BCM中,BC=8,CM=6根据勾股定理得:BM=√62+82=10,即DN+MN的最小值是10.故选D.9.【答案】B【考点】轴对称——最短路线问题【解析】AB+BP=P′P″,此时周长最小.根据轴对称的性质,可求出∠APB的度数.【解答】解:分别作点P关于OM、ON的对称点P′、P″,连接OP′、OP″、P′P″,P′P″交OM、ON 于点A、B,连接PA、PB,此时△PAB周长的最小值等于P′P″.由轴对称性质可得,OP′=OP″=OP,∠P′OA=∠POA,∠P″OB=∠POB,∴∠P′OP″=2∠MON=2×40∘=80∘,∴∠OP′P″=∠OP″P′=(180∘−80∘)÷2=50∘,又∵∠BPO=∠OP″B=50∘,∠APO=∠AP′O=50∘,∴∠APB=∠APO+∠BPO=100∘.故选B.10.【答案】C【考点】平面展开-最短路径问题【解析】首先证明四边四边形ABCD是菱形,得AD//BC,作出F关于AB的对称点M,再过M作ME′⊥AD,交AB于点P,此时PE′+PF最小,求出ME即可.【解答】解:作出F关于AB的对称点M,再过M作iM′⊥AD,交AB于点P,此时FE′+PF最小,此时PE′+PF=ME,过点A作AN⊥BC CH⊥AB于H,________△ABC沿AB翻折得到△ABDAC=AD BC=BD.AC=BCAC=AD=BC=BD四边形ADBC是菱形,.AD//BC∵AC=BCAE=1AB=1由勾股定理可得,CH=√32−12=2√2.12×AB×CH=12×BC×AN可得AN=4√23ME′=AN=4√2 3PE+PF最小为4√23故选:C.二、填空题(本题共计 10 小题,每题 3 分,共计30分)11.【答案】Q22.【考点】图形间的距离定义新图形路径最短问题坐标与图形性质【解析】(1)找到OA的垂直平分线即可找到对应的点.(2)利用“完美对称点”的特征,作出图象,从而确定最小值.【解答】解:(1)当点Q满足QO=QA时,Q为OA的“对称点”,∴ Q在线段OA的垂直平分线上,∵ A(4,0),∴ 线段OA的垂直平分线是直线x=2,∵Q2(2,−4),∴ 线段OA的“对称点”是Q2.故答案为:Q2.∵ Q(2,2√3)为线段OA的“完美对称点”,∴ QO=OA=QA,∴ △QOA是等边三角形,过点Q作QH⊥OA于H,则直线QH为线段AO的垂直平分线,如图:∵ B为线段OA的一个“对称点”,∴ BO=BA,∴ B是直线QH上的一点,显然,当Q、B重合时,BQ+BD有最小值,此时BQ+BD=BD,∵ Q(2,2√3),∴ OQ=√22+(2√3)2=4,∵ D为线段OQ的中点,∴ DQ=12OQ=12×4=2,∴ BD=2,∴ BQ+BD的最小值为2. 故答案为:2.12.【答案】16cm【考点】轴对称——最短路线问题【解析】过B点作BE⊥AC于O,使OE=OB,过E作EN⊥AB交AB于N点,交AC于M,此时BM+NM有最小值,EN就是所求的线段.【解答】解:过B点作BE⊥AC于O,使OE=OB,过E作EN⊥AB交AB于N点,交AC于M,此时BM+NM有最小值,EN就是所求的线段.∵AB=20cm,BC=10cm,∴AC=√AB2+BC2=10√5cm,∵12AB⋅BC=12AC⋅OB,∴OB=4√5cm,∴BE=8√5cm.∵△ABC∽△BEN,∴ENAB =BEAC,∴EN=AB⋅BEAC =√510√5=16cm.∴BM+NM的最小值为16cm,故答案为16cm.13.【答案】√67【考点】【解析】利用轴对称求最短路径的方法,重新构造直角三角形,进而利用勾股定理求出即可.【解答】解:作D 点关于AB 的对称点D′,B 点关于AC 的对称点B′,连接D′B′分别交AB 于点E ,AC 于点F ,作B′R ⊥AB ,过点D′作D′W ⊥B′R 于点W ,∵ ∠CAB =30∘,∠C =90∘.AD =14AC ,AB =8, ∴ BC =4,AC =4√3,则AD =√3,BB′=8,B′R =4√3,∴ DT =12AD =√32,AT =√AD 2−DT 2=32,BR =4, ∴ RW =√32,D′W =8−32−4=52, ∴ B′W =9√32,B′D′=√D′W 2+B′W 2=(52)+(9√32)=√67.故答案为:√67.14.【答案】15【考点】勾股定理路径最短问题 【解析】此题暂无解析【解答】解:设小明散步原地为O ,则先向东走12m 到达A 点后,再向北又走了9m 到达B 点,则要回到原地,最短行走距离为OB 的距离,根据勾股定理可得OB =√122+92=15m .15.【答案】√5【考点】平面展开-最短路径问题【解析】把此正方体的一面展开,然后在平面内,利用勾股定理求点A和B点间的线段长,即可得到蚂蚁爬行的最短距离.在直角三角形中,一条直角边长等于棱长,另一条直角边长等于两条棱长,利用勾股定理可求得.【解答】解:∵展开后由勾股定理得:AB2=12+(1+1)2=5,∴AB=√5.故答案为:√5.16.【答案】√5+√13【考点】轴对称——最短路线问题【解析】此题暂无解析【解答】解: ①P在AD上,如图所示:则作E点关于AD的对称点G,连接EG,FG交AD于点P′,则对AD上点P,PG=PE,则△PEF周长=PE+PF+EF=PG+PF+EF≥GF+EF,故当C△PEF最小时,PG+PF=GF,即P与P′重合,记GE交AD于点M,由AB=3,BC=6,四边形ABCD为矩形知:AC=√32+62=3√5,∵EF为三等分点,知AE=EF=13AC=√5,GM=ME=13CD=1,作FN⊥GE于N,则EN=1,FN=2,GF=√22+32=√13,C△PEF=GF+EF=√13+√5;②P在CD上,如图所示,则同理QF=FR=RH=2,EQ=1,当P与P′重合时,C△PEF最小,最小值为EF+EH=√5+√62+12=√5+√37>√13+√5,所以C△DEF最小值为√5+√13.故答案为:√5+√13.17.【答案】90∘【考点】轴对称——最短路线问题【解析】根据对称的性质,易求得∠C+∠EPF=180∘,由∠ACB=45∘,易求得∠D+∠G=45∘,继而求得答案.【解答】解:∵PD⊥AC,PG⊥BC,∴∠PEC=∠PFC=90∘,∴∠C+∠EPF=180∘,∵∠C=45∘,∴∠EPF=135∘,∵∠D+∠G+∠EPF=180∘,∴∠D+∠G=45∘,由对称可知:∠G=∠GPN,∠D=∠DPM,∴∠GPN+∠DPM=45∘,∴∠MPN=135∘−45∘=90∘,故答案为:90∘18.【答案】√193【考点】平面展开-最短路径问题【解析】先将图形展开,再根据两点之间线段最短,再由勾股定理求解即可.【解答】解:如图1:AB=√162+32=√265(cm),如图2:AB=√152+42=√241(cm),如图3:AB=√122+72=√193(cm),∴√265>√241>√193,∴它所行的最短路线的长是√193cm.故答案为:√193cm.19.【答案】√1114【考点】切线的性质勾股定理路径最短问题【解析】连接PA,AQ,由切线的性质得到∠AQP=90∘,由AQ=2是定值,要使PQ的长度最小,只有PA的值最小时才成立,进而确定出△PCA和△PBA是直角三角形,由勾股定理求出PC的长度,进而求出PA2,最后求勾股定理求解.【解答】解:连接PA,AQ,如下图.∵ PQ是⊙A的切线,∴ AQ⊥PQ,∴ ∠AQP=90∘.∵ AQ=2是定值,要使PQ的长度最小,∴ PA ⊥BC ,即PA 的值最小时才成立,∴ PQ 2=PA 2−AQ 2.由PA ⊥BC 可知,△PCA 和△PBA 是直角三角形,∵ AC =4,AB =5,BC =PC +PB =6,∴ PA 2=AC 2−PC 2,PA 2=AB 2−PB 2,∴ AC 2−PC 2=AB 2−PB 2,即42−PC 2=52−(6−PC )2,解得PC =94,∴ PA 2=42−(94)2, ∴ PQ =√PA 2−AQ 2=√16−8116−4=√11116=√1114, 即线段PQ 的最小值是√1114. 故答案为:√1114. 20.【答案】 9√2【考点】轴对称——最短路线问题【解析】如图,作点E 关于OD 的对称点E′,作射线OE′,作CE ″⊥OE′交OD 于F′,延长DC 交OA 于H ,作CM ⊥OA 于M .因为EF +CF =E′F +CF ,所以根据垂线段最短可知,当CE ″⊥OE′时,EF +CF 的值最小,最小值为CE ″,求出CE ″即可解决问题.【解答】如图,作点E 关于OD 的对称点E′,作射线OE′,作CE ″⊥OE′交OD 于F′,延长DC 交OA 于H ,作CM ⊥OA 于M .∵ EF +CF =E′F +CF ,∴ 根据垂线段最短可知,当CE ″⊥OE′时,EF +CF 的值最小,最小值为CE ″, ∵ ∠AOD =45∘,∠ADO =90∘,∴ ∠DOH =∠DHO =45∘,∴ OD =DH =13,∵ CD =5,∴ CH =8,∵ CM ⊥OA ,∴ ∠CMH =90∘,∠MCH =∠MHC =45∘,∴ CM =MH =4√2,∵ ∠AOE′=2∠AOD =90∘=∠OE ″C =∠CMO ,∴四边形CMOE″是矩形,∴OE″=CM=4√2,在Rt△OCD中,OC2=OD2+CD2=132+52=194,在Rt△OCE″中,CE″$= \sqrt{OC^{2} - OE"^{2}} = \sqrt{194 - 32} = 9\sqrt{2}$,∴EF+CF的值最小为9√2.三、解答题(本题共计 20 小题,每题 10 分,共计200分)21.【答案】解:如图所示:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC;连接DC′,交AB于E,连接CE,此时DE+CE=DE+EC′=DC′的值最小;连接BC′,由轴对称的性质得:∠C′BE=∠CBE=45∘,∴∠CBC′=90∘,∴BC′⊥BC,∠BCC′=∠BC′C=45∘,∴BC=BC′=2,∵D是BC边的中点,∴BD=1,根据勾股定理得:DC′=√BC′2+BD2=√22+12=√5;∴DE+CE的最小值为√5.【考点】轴对称——最短路线问题【解析】过点C作CO⊥AB于O,延长CO到C′,使OC′=OC;连接DC′,交AB于E,连接CE,此时DE+CE=DE+EC′=DC′的值最小;再根据勾股定理求出DC′即可.【解答】解:如图所示:过点C作CO⊥AB于O,延长CO到C′,使OC′=OC;连接DC′,交AB于E,连接CE,此时DE+CE=DE+EC′=DC′的值最小;连接BC′,由轴对称的性质得:∠C′BE=∠CBE=45∘,∴∠CBC′=90∘,∴BC′⊥BC,∠BCC′=∠BC′C=45∘,∴BC=BC′=2,∵D是BC边的中点,∴BD=1,根据勾股定理得:DC′=√BC′2+BD2=√22+12=√5;∴DE+CE的最小值为√5.22.【答案】解:(1)如图1,设河边为直线CD,∵到A,B两点的距离相等,∴可以作线段AB的垂直平分线,交河边CD于点P,则PA=PB,∴P点位置即为到张庄、李庄距离相等的点;(2)如图2,设河边为直线CD,点A关于直线CD的对称点为A′,连接A′B,交CD于点Q,则AQ=A′Q,∴A′B=AQ+BQ,∴此时到A、B两地的距离最短,∴Q点即为所求的位置.【考点】路径最短问题作图—应用与设计作图轴对称——最短路线问题线段垂直平分线的性质【解析】(1)可作线段AB的垂直平分线,与河边的交点即为所求的点;(2)找出A点关于河边的对称点A′,连接A′B交河边于点Q,则Q即为所求的点.【解答】解:(1)如图1,设河边为直线CD,∵到A,B两点的距离相等,∴可以作线段AB的垂直平分线,交河边CD于点P,则PA=PB,∴P点位置即为到张庄、李庄距离相等的点;(2)如图2,设河边为直线CD,点A关于直线CD的对称点为A′,连接A′B,交CD于点Q,则AQ=A′Q,∴A′B=AQ+BQ,∴此时到A、B两地的距离最短,∴Q点即为所求的位置.23.【答案】解:(1)△ABC的面积=3×4−12×1×2−12×2×3−12×2×4,=12−1−3−4,=12−8,=4,由勾股定理得,AC=√22+42=2√5,设AC边上高的长度为ℎ,则12×2√5ℎ=4,解得ℎ=4√55.所以,AC边上高的长度为4√55;(2)点P如图所示,由勾股定理得,PA+PC最小值=√62+42=2√15.【考点】轴对称——最短路线问题【解析】(1)利用三角形所在的矩形的面积减去四周三个直角三角形的面积列式求出△ABC的面积,再利用勾股定理列式求出AC,然后根据三角形的面积公式列式计算即可得解;(2)找出点A关于直线l的对称点A′,连接A′C,根据轴对称确定最短路线问题,A′C与直线l的交点即为所求的点P,最短距离为A′C的长度,再利用勾股定理列式计算即可得解.【解答】解:(1)△ABC的面积=3×4−12×1×2−12×2×3−12×2×4,=12−1−3−4,=12−8,=4,由勾股定理得,AC=√22+42=2√5,设AC边上高的长度为ℎ,则12×2√5ℎ=4,解得ℎ=4√55.所以,AC边上高的长度为4√55;(2)点P如图所示,由勾股定理得,PA+PC最小值=√62+42=2√15.24.【答案】解:如图1所示:AB=√(4+3)2+52=√74(cm),如图2所示:AB=√(5+3)2+42=√80(cm),∵√74<√80,∴蚂蚁按照图1这条路线爬行,路线最短,最短路线长为:√74cm.【考点】平面展开-最短路径问题【解析】利用展开图不同,分别结合勾股定理得出AB的长,进而求出答案.【解答】解:如图1所示:AB=√(4+3)2+52=√74(cm),如图2所示:AB=√(5+3)2+42=√80(cm),∵√74<√80,∴蚂蚁按照图1这条路线爬行,路线最短,最短路线长为:√74cm.25.【答案】解:已知如图:∵圆柱底面直径AB=16πcm、母线BC=12cm,P为BC的中点,∴圆柱底面圆的半径是8πcm,BP=6cm,∴AB=12×2×8π=8cm,在Rt△ABP中,AP=√AB2+BP2=10cm,∴蚂蚁从A点爬到P点的最短距离为10cm.【考点】平面展开-最短路径问题【解析】把圆柱的侧面展开,连接AP,利用勾股定理即可得出AP的长,即蚂蚁从A点爬到P点的最短距离.【解答】解:已知如图:∵圆柱底面直径AB=16πcm、母线BC=12cm,P为BC的中点,∴圆柱底面圆的半径是8πcm,BP=6cm,∴AB=12×2×8π=8cm,在Rt△ABP中,AP=√AB2+BP2=10cm,∴蚂蚁从A点爬到P点的最短距离为10cm.26.【答案】解:B为CE的中点.AB就是蚂蚁爬的最短路径.∵CE=2π⋅r=2×3×2=12厘米,∴CB=12÷2=6厘米.∵AC=8厘米,∴AB=√62+82=10厘米.蚂蚁要爬行的最短距离是10厘米.【考点】平面展开-最短路径问题【解析】圆柱展开为长方形,根据题意可知道点A和B在平面上的位置,根据两点之间线段最短可求出解.【解答】解:B为CE的中点.AB就是蚂蚁爬的最短路径.∵CE=2π⋅r=2×3×2=12厘米,∴CB=12÷2=6厘米.∴AB=√62+82=10厘米.蚂蚁要爬行的最短距离是10厘米.27.【答案】解:如图,将圆柱的侧面沿过A点的一条母线剪开,得到长方形ADFE,连接AB,则线段AB的长就是蚂蚁爬行的最短距离,其中C,B分别是AE,DF的中点.∵AD=12cm,DB=πr=3π=9cm(π取3),∴AB=√AD2+DB2=√122+92=15cm.故蚂蚁经过的最短距离为15cm.【考点】平面展开-最短路径问题【解析】先把圆柱的侧面展开得其侧面展开图,则A,B所在的长方形的长为圆柱的高12cm,宽为底面圆周长的一半为πr,蚂蚁经过的最短距离为连接A,B的线段长,由勾股定理求得AB的长.【解答】解:如图,将圆柱的侧面沿过A点的一条母线剪开,得到长方形ADFE,连接AB,则线段AB的长就是蚂蚁爬行的最短距离,其中C,B分别是AE,DF的中点.∵AD=12cm,DB=πr=3π=9cm(π取3),∴AB=√AD2+DB2=√122+92=15cm.故蚂蚁经过的最短距离为15cm.28.【答案】解:(1)∵CD=x,BD=8,∴CB=8−x,AC+CE=√52+(8−x)2+√x2+1,当A、C、E在同一直线上,AC+CE最小;当A、C、E在同一直线上时,延长AB,作EF⊥AB于点F,∵AB=5,DE=1,∴AF=6,∵∠ABD=90∘,∵∠BDE=∠BFE=90∘,∴四边形BFED是矩形,∴BD=EF=8,∴AE=√AF2+EF2=√62+82=10,;(2)如下图所示:作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,当BC=x,∵x+y=12,∴y=12−x,AE的长即为代数式√x2+4+√(12−x)2+9的最小值,过点A作AF // BD交ED的延长线于点F,得矩形ABDF,则AB=DF=2,AF=BD=12,所以AE=√AF2+EF2=√122+(3+2)2=13,即代数式√x2+4+√y2+9的最小值为13.【考点】轴对称——最短路线问题【解析】(1)根据勾股定理得出AC,CE的长进而得出用含x的代数式表示AC+CE的长;由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE>AE,故当A、C、E三点共线时,AC+CE的值最小,利用勾股定理求出即可;(2)由(1)的结果可作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,则AE的长即为代数式√x2+4+√y2+9的最小值,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值.【解答】解:(1)∵CD=x,BD=8,∴CB=8−x,AC+CE=√52+(8−x)2+√x2+1,当A、C、E在同一直线上,AC+CE最小;当A、C、E在同一直线上时,延长AB,作EF⊥AB于点F,∵AB=5,DE=1,∴AF=6,∵∠ABD=90∘,∴∠FBD=90∘,∵∠BDE=∠BFE=90∘,∴四边形BFED是矩形,∴BD=EF=8,∴AE=√AF2+EF2=√62+82=10,;(2)如下图所示:作BD=12,过点B作AB⊥BD,过点D作ED⊥BD,使AB=2,ED=3,连接AE交BD于点C,当BC=x,∵x+y=12,∴y=12−x,AE的长即为代数式√x2+4+√(12−x)2+9的最小值,过点A作AF // BD交ED的延长线于点F,得矩形ABDF,则AB=DF=2,AF=BD=12,所以AE=√AF2+EF2=√122+(3+2)2=13,即代数式√x2+4+√y2+9的最小值为13.29.【答案】解:因为A、B在OM上,要使|PA−PB|的值最大,P应在OM上,如果P不在OM上,则P、A、B构成三角形,根据三角形的三边关系,|PA−PB|<AB,所以,P是OM和ON的交点,即O点,所以P到O的距离为0.【考点】轴对称——最短路线问题【解析】根据三角形的三边关系,两边的差小于第三边,可以判定当P点在OM和ON的交点处|PA−PB|的值最大,从而求得P点到O点的距离.【解答】解:因为A、B在OM上,要使|PA−PB|的值最大,P应在OM上,如果P不在OM上,则P、A、B构成三角形,根据三角形的三边关系,|PA−PB|<AB,所以,P是OM和ON的交点,即O点,所以P到O的距离为0.30.【答案】解:把点A向下平移河②的宽度后得到A″,平移两条河的宽度后到点A′,连接A′B交于b于点P,作PQ⊥b,连接A″Q,交c于M,作MN⊥d于N,由于A″A′平行且等于PQ,AA′平行且等于MN,则四边形A″A′PQ是平行四边形,四边形AA′MN是平行四边形,有A′P=QA″,AN=A″M,由于A′B是点A′到点B的最短距离,所以在PQ、MN处建桥就是使得A村到B村总路程最短的桥的位置.【考点】轴对称——最短路线问题【解析】把点A向下平移河②的宽度后得到A″,平移两条河的宽度后到点A′,连接A′B交于b于点P,连接A″Q,交c于M,则点P、M就是所求的建桥的位置.【解答】解:把点A向下平移河②的宽度后得到A″,平移两条河的宽度后到点A′,连接A′B交于b于点P,作PQ⊥b,连接A″Q,交c于M,作MN⊥d于N,由于A″A′平行且等于PQ,AA′平行且等于MN,则四边形A″A′PQ是平行四边形,四边形AA′MN是平行四边形,有A′P=QA″,AN=A″M,由于A′B是点A′到点B的最短距离,所以在PQ、MN处建桥就是使得A村到B村总路程最短的桥的位置.31.【答案】解:作点P关于OA的对称点P1,点P关于OB的对称点P2,连结P1P2,与OA的交点即为点M,与OB的交点即为点N,△PMN的最小周长为:PM+MN+PN=P1M+MN+P2N=P1P2,。
人教版初中数学八年级上册《13.4 课题学习 最短路径问题》同步练习卷(含答案解析

人教新版八年级上学期《13.4 课题学习最短路径问题》同步练习卷一.选择题(共2小题)1.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是()A.15 km B.16 km C.17 km D.18 km2.如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB 上有一点R.若△PQR周长最小,则最小周长是()A.10B.15C.20D.30二.解答题(共18小题)3.如图,一个牧童在距离小河岸南400米的A处牧马,而他的家正位于牧马处A的东800米(BC=800米),南700米,(AC=700米)处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?4.为了探索代数式的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则,,则问题即转化成求AC+CE的最小值.(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得的最小值等于,此时x=;(2)请你根据上述的方法和结论,试构图求出代数式的最小值.5.如图,A、B两个小集镇在河流的同侧,分别到河岸L的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米2万元,请你在河岸L上选择水厂的位置M(作图并标注出来),使铺设水管的费用最节省,并求出总费用是多少?6.如图,要在街道旁修建一个牛奶站,向居民区A,B提供牛奶,牛奶站应建在什么地方,才能使A,B到它的距离之和最短?7.如图,铁路l的同侧有A、B两个工厂,要在路边建一个货物站C,使A、B 两厂到货物站C的距离之和最小,那么点C应该在l的哪里呢?画出你找的点C来.8.如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、BC,已知AB=5,DE=2,BD=12,设CD=x.(1)用含x的代数式表示AC+CE的长为.(2)请问点C在BD上什么位置时,AC+CE的值最小?为什么?并求出最小值.(3)根据(2)中规律和结论,请构图求出代数式的最小值.9.如图,在游艺室的水平地面上,沿着地面的AB边放一行球,参赛者从起点C 起步,跑向边AB任取一球,再折向D点跑去,将球放入D点的纸箱内便完成任务,完成任务的时间最短者获得胜利,如果邀请你参加,你将跑去选取什么位置上的球?为什么?10.如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.11.如图,在一条河的同岸有两个村庄A和B,两村要在河上合修一座便民桥,桥修在什么地方可以使桥到两村的距离之和最短?12.如图,直线l同侧有A、B两点,请利用直尺和圆规在直线l上求作一点P,使AP+BP值最小.(不写作法,保留作图痕迹)13.如图,已知A、B两点在直线l的同一侧,根据题意,尺规作图.(1)在(图1)直线l上找出一点P,使PA=PB.(2)在(图2)直线l上找出一点P,使PA+PB的值最小.(3)在(图3)直线l上找出一点P,使|PA﹣PB|的值最大.14.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.15.高速公路的同一侧有A,B两城镇,如图所示,它们到高速公路所在直线MN的距离分别为AA′=2km,BB′=4km,且A′B′=8km,要在高速公路上A′,B′之间建一个出口P,使A,B两城镇到P的距离之和最短,求这个最短距离.16.著名的“将军饮马”问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?17.如图,在旷野上,一个人骑着马从A到B,半路上他必须先到河岸l的P点去让马饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择饮马地点P、Q,才能使所走路程AP+PQ+QB为最短(假设河岸l、m 为直线).18.如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.19.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?20.解答题①已知:如图,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足.求:AD的长.②如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?人教新版八年级上学期《13.4 课题学习最短路径问题》同步练习卷参考答案与试题解析一.选择题(共2小题)1.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是()A.15 km B.16 km C.17 km D.18 km【分析】先作出点A关于小河MN的对称点A′,连接A′B,交河岸MN于点P,则A′B就是牧童要完成这件事情所走的最短路程.在Rt△A′DB中,利用勾股定理即可求解.【解答】解:如图,作出A点关于小河MN的对称点A′,连接A′B交MN于点P,则A′B就是牧童要完成这件事情所走的最短路程.在Rt△A′DB中,由勾股定理求得A′B===17km.则他要完成这件事情所走的最短路程是17km.故选:C.【点评】本题考查了轴对称﹣最短路线问题及两点之间线段最短的性质,并运用了勾股定理求解.2.如图,∠AOB=30°,∠AOB内有一定点P,且OP=10.在OA上有一点Q,OB 上有一点R.若△PQR周长最小,则最小周长是()A.10B.15C.20D.30【分析】先画出图形,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.再根据线段垂直平分线的性质得出△PQR=EF,再根据三角形各角之间的关系判断出△EOF的形状即可求解.【解答】解:设∠POA=θ,则∠POB=30°﹣θ,作PM⊥OA与OA相交于M,并将PM延长一倍到E,即ME=PM.作PN⊥OB与OB相交于N,并将PN延长一倍到F,即NF=PN.连接EF与OA相交于Q,与OB相交于R,再连接PQ,PR,则△PQR即为周长最短的三角形.∵OA是PE的垂直平分线,∴EQ=QP;同理,OB是PF的垂直平分线,∴FR=RP,∴△PQR的周长=EF.∵OE=OF=OP=10,且∠EOF=∠EOP+∠POF=2θ+2(30°﹣θ)=60°,∴△EOF是正三角形,∴EF=10,即在保持OP=10的条件下△PQR的最小周长为10.故选:A.【点评】本题考查的是最短距离问题,解答此类题目的关键根据轴对称的性质作出各点的对称点,即把求三角形周长的问题转化为求线段的长解答.二.解答题(共18小题)3.如图,一个牧童在距离小河岸南400米的A处牧马,而他的家正位于牧马处A的东800米(BC=800米),南700米,(AC=700米)处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?【分析】作出A点关于小河岸南的对称点A′,根据两点之间线段最短得出BA′的长即为牧童要走的最短路程,利用勾股定理解答即可.【解答】解:作A点关于小河岸南的对称点A′,连接BA′交河岸于点P,则PB+PA=PB+PA′=BA′最短.在△A′BC中,∠C=90°,BC=800,A′C=AA′+AC=400×2+700=1500,∴A′B==1700(米).故他要完成这件事情所走的最短路程是1700米.【点评】此题考查了轴对称﹣﹣最短路径问题在生活中的应用,要将轴对称的性质和勾股定理灵活应用,体现了数学在解决简单生活问题时的作用.4.为了探索代数式的最小值,小明巧妙的运用了“数形结合”思想.具体方法是这样的:如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=1,DE=5,BD=8,设BC=x.则,,则问题即转化成求AC+CE的最小值.(1)我们知道当A、C、E在同一直线上时,AC+CE的值最小,于是可求得的最小值等于10,此时x=;(2)请你根据上述的方法和结论,试构图求出代数式的最小值.【分析】(1)根据两点之间线段最短可知AC+CE的最小值就是线段AE的长度.过点E作EF∥BD,交AB的延长线于F点.在Rt△AEF中运用勾股定理计算求解.(2)由(1)的结果可作BD=12,过点A作AF∥BD,交DE的延长线于F点,使AB=2,ED=3,连接AE交BD于点C,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值就是代数式的最小值.【解答】解:(1)过点E作EF∥BD,交AB的延长线于F点,根据题意,四边形BDEF为矩形.AF=AB+BF=5+1=6,EF=BD=8.∴AE==10.即AC+CE的最小值是10.=10,∵EF∥BD,∴=,∴=,解得:x=.(2)过点A作AF∥BD,交DE的延长线于F点,根据题意,四边形ABDF为矩形.EF=AB+DE=2+3=5,AF=DB=12.∴AE==13.即AC+CE的最小值是13.【点评】本题主要考查了最短路线问题以及勾股定理应用,利用了数形结合的思想,通过构造直角三角形,利用勾股定理求解是解题关键.5.如图,A、B两个小集镇在河流的同侧,分别到河岸L的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米2万元,请你在河岸L上选择水厂的位置M(作图并标注出来),使铺设水管的费用最节省,并求出总费用是多少?【分析】此题的关键是确定点M的位置,需要首先作点A的对称点A′,连接点B和点A′,交l于点M,M即所求作的点.根据轴对称的性质,知:MA+MB=A′B.根据勾股定理即可求解.【解答】解:作A关于CD的对称点A′,连接A′B与CD,交点为M,点M即为所求作的点.则可得:DK=A′C=AC=10千米,∴BK=BD+DK=40千米,∴AM+BM=A′B==50千米,总费用为50×2=100万元.【点评】本题主要考查轴对称﹣最短路线问题的知识点,解答本题的关键是找出点M的位置,此题难度不大.6.如图,要在街道旁修建一个牛奶站,向居民区A,B提供牛奶,牛奶站应建在什么地方,才能使A,B到它的距离之和最短?【分析】作点A关于l的对出现A′,则MA=A′M,故此AM+BM=A′M+BM,然后依据两点之间线段最短的性质解答即可.【解答】解:作点A关于直线l的对称点A′,连接A′B交直线l于点M,则点M 即为所求点.【点评】本题主要考查的是轴对称﹣最短路径问题,熟练掌握相关知识是解题的关键.7.如图,铁路l的同侧有A、B两个工厂,要在路边建一个货物站C,使A、B 两厂到货物站C的距离之和最小,那么点C应该在l的哪里呢?画出你找的点C来.【分析】作点B关于直线l的对称点B′,连接AB′,交l于点C,则点C即为所求点.【解答】解:如图所示:点C即为所求点【点评】本题考查的是轴对称﹣最短路线问题,熟知两点之间线段最短是解答此题的关键.8.如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、BC,已知AB=5,DE=2,BD=12,设CD=x.(1)用含x的代数式表示AC+CE的长为+.(2)请问点C在BD上什么位置时,AC+CE的值最小?为什么?并求出最小值.(3)根据(2)中规律和结论,请构图求出代数式的最小值.【分析】(1)由于△ABC和△CDE都是直角三角形,故AC,CE可由勾股定理求得;(2)若点C不在AE的连线上,根据三角形中任意两边之和>第三边知,AC+CE >AE,故当A、C、E三点共线时,AC+CE的值最小;(3)由(1)(2)的结果可作BD=24,过点B作AB⊥BD,过点D作ED⊥BD,使AB=4,ED=3,连接AE交BD于点C,然后构造矩形AFDB,Rt△AFE,利用矩形的直角三角形的性质可求得AE的值就是代数式的最小值.【解答】解:(1)AC+CE=+.故答案是:+;(2)当点C是AE和BD交点时,AC+CE的值最小.∵AB∥ED,AB=5,DE=2,∴==,又∵BC+CD=BD=12,则BC=CD,CD=BC,∴CD+CD=12,解得:CD=.BC+BC=12,解得:BC=,CD=.故点C在BD上距离点B的距离为时,AC+CE的值最小;(3)如右图所示,过点B作AB⊥BD,过点D作ED⊥BD,使AB=4,ED=3,DB=24,连接AE交BD于点C,∵AE=AC+CE=,∴AE的长即为代数式的最小值.过点A作AF∥BD交ED的延长线于点F,得矩形ABDF,则AB=DF=4,AF=BD=24.所以AE===25,即AE的最小值是25.即代数式的最小值为25.【点评】本题主要考查最短路线问题,利用了数形结合的思想,可通过构造直角三角形,利用勾股定理求解.9.如图,在游艺室的水平地面上,沿着地面的AB边放一行球,参赛者从起点C 起步,跑向边AB任取一球,再折向D点跑去,将球放入D点的纸箱内便完成任务,完成任务的时间最短者获得胜利,如果邀请你参加,你将跑去选取什么位置上的球?为什么?【分析】可过点D作关于AB的对称点D′,连接CD′与AB交于点E,即为所求.【解答】解:如图,参赛者应向E点跑,因为AB所在直线是DD′的垂直平分线,所以ED=ED′,C,D′两点之间CE+ED′是最短的(两点之间线段最短),所以CE+ED是最短的.【点评】能够利用两点之间线段最短求解一些简单的实际问题.10.如图,在边长为1个单位长度的小正方形组成的网格中,请分别在边AB,AC上找到点E,F,使四边形PEFQ的周长最小.【分析】根据轴对称图形的作法得出对称点,进而解答即可.【解答】解:分别作P关于AB,Q关于AC的对称点P'Q',连接P'Q',交AB于E,交AC于F,则E,F即为所求.【点评】本题考查的是作图﹣轴对称变换,熟知轴对称的性质是解答此题的关键.11.如图,在一条河的同岸有两个村庄A和B,两村要在河上合修一座便民桥,桥修在什么地方可以使桥到两村的距离之和最短?【分析】如图作点A关于河岸的对称点C,连接BC交河岸于点P,点P就是桥的位置.【解答】解:如图作点A关于河岸的对称点C,连接BC交河岸于点P,点P就是桥的位置.理由:两点之间线段最短.【点评】本题考查轴对称﹣线段最短问题,两点之间线段最短等知识,解题的关键是利用对称找到点P(桥)的位置,属于中考常考题型.12.如图,直线l同侧有A、B两点,请利用直尺和圆规在直线l上求作一点P,使AP+BP值最小.(不写作法,保留作图痕迹)【分析】过A作直线l的垂线,在垂线上取点A′,使直线l是AA′的垂直平分线,连接BA′即可.【解答】解:作A点关于直线l的对称点A′,连接A′B交l于点P,则P点为所求.【点评】本题考查了轴对称﹣最短路线问题的应用,关键是正确画出图形,题型较好,难度适中.13.如图,已知A、B两点在直线l的同一侧,根据题意,尺规作图.(1)在(图1)直线l上找出一点P,使PA=PB.(2)在(图2)直线l上找出一点P,使PA+PB的值最小.(3)在(图3)直线l上找出一点P,使|PA﹣PB|的值最大.【分析】(1)连接AB,作线段AB的垂直平分线,交直线l于点P,则点P即为所求;(2)作A关于l的对称点A',连接BA′,线段BA′与l交于P,则P就是所求点.也可作B关于l的对称点B′;(3)过点A,B作直线AB与l交于P,则P就是所求点.【解答】解:(1)如图1所示:此时:PA=PB,如图所示:(2)此时:PA+PB最小;(3)如图所示:此时:|PA﹣PB|最大.【点评】本题考查了轴对称﹣最短路线问题的应用,关键是正确画出图形,题型较好,难度适中.14.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400米,BD=200米,CD=800米,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少.【分析】作点B关于河岸的对称点B′,连接AB′交CD于点P,过点B′作B′E⊥AC,垂足为E,由轴对称的性质和两点之间线段最短可知AB′的长度即为最短路程.【解答】解:作点B关于河岸的对称点B′,连接AB′交CD于点P,过点B′作B′E ⊥AC,垂足为E.由轴对称的性质可知:PB=PB′,DB′=DB.∴PA+PB=AP+PB′.由两点之间线段最短可知;当点A、P、B′在一条直线上时,PA+PB最短.在Rt△AEB′中,AB′===1000.【点评】本题主要考查的是轴对称的性质、勾股定理的应用,明确当点A、P、B′在一条直线上时PA+PB最短是解题的关键.15.高速公路的同一侧有A,B两城镇,如图所示,它们到高速公路所在直线MN的距离分别为AA′=2km,BB′=4km,且A′B′=8km,要在高速公路上A′,B′之间建一个出口P,使A,B两城镇到P的距离之和最短,求这个最短距离.【分析】根据题意画出图形,再利用轴对称求最短路径的方法得出P点位置,进而结合勾股定理得出即可.【解答】解:如图所示:作A点关于直线MN的对称点C,再连结CB,交直线MN于点P,则此时AP+PB最小,过点B作BD⊥CA延长线于点D,∵AA′=2km,BB′=4km,A′B′=8km,∴AC=4km,则CD=6km,在Rt△CDB中,CB==10(km),则AP+PB的最小值为:10km.【点评】此题主要考查了应用与设计作图,两点之间线段最短、勾股定理等知识,解题的关键是学会利用对称解决最短问题.16.著名的“将军饮马”问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?【分析】根据轴对称的性质作出B点与河面的对称点B′,连接AB′,AB′与河面的交点C即为所求.【解答】解:作B点与河面的对称点B′,连接AB′,可得到马喝水的地方C,如图所示,由对称的性质可知AB′=AC+BC,根据两点之间线段最短的性质可知,C点即为所求.【点评】本题考查的是最短路线问题,解答此题的关键是熟知两点之间线段最短.17.如图,在旷野上,一个人骑着马从A到B,半路上他必须先到河岸l的P点去让马饮水,然后再让马到河岸m的Q点再次饮水,最后到达B点,他应该如何选择饮马地点P、Q,才能使所走路程AP+PQ+QB为最短(假设河岸l、m 为直线).【分析】作出点A关于l的对称点A′,点B关于m的对称点B′,连接A′B′,交于l,m于点P,点Q,则AP,PQ,QB是他走的最短路线.【解答】解:如图,分别作A点关于直线l的对称点A′、B点关于直线m的对称点B′连接A′B′,分别交l于点P,交m于点Q,连接AP、BQ,所以路程AP+PQ+BQ最短.【点评】本题考查了轴对称的性质﹣最短路线问题,利用两点之间线段最短的性质求解是解本题的关键.18.如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.【分析】作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′依据两点之间线段最短可确定出点B、C的位置.【解答】解:作D关于OM的对称点D′,作A作关于ON的对称点A′,连接A′D′与OM,ON的交点就是C,B二点.此时AB+BC+CD=A′B+BC+CD′=A′D′为最短距离.【点评】此题考查了线路轴对称﹣最短的问题,利用轴对称的性质确定动点为何位置是解题的关键.19.如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?【分析】先作A关于MN的对称点,连接A′B,构建直角三角形,利用勾股定理即可得出答案.【解答】解:如图,作出A点关于MN的对称点A′,连接A′B交MN于点P,则A′B就是最短路线,在Rt△A′DB中,由勾股定理求得A′B===17km,答:他要完成这件事情所走的最短路程是17km.【点评】本题考查的是勾股定理和轴对称在实际生活中的运用,需要同学们联系实际,题目是一道比较典型的题目,难度适中.20.解答题①已知:如图,在△ABC中,∠CAB=120°,AB=4,AC=2,AD⊥BC,D是垂足.求:AD的长.②如图,一个牧童在小河的南4km的A处牧马,而他正位于他的小屋B的西8km北7km处,他想把他的马牵到小河边去饮水,然后回家.他要完成这件事情所走的最短路程是多少?【分析】①过C作CE⊥BE交BA的延长线于E,求出∠ACE=30°,求出AE,CE,根据三角形面积公式得出AB×CE=CB×AD,代入求出即可;②根据题意画出P点的位置,得出A、C关于小河对称,求出BO、CO,根据勾股定理求出BC,即可求出答案.【解答】①解:过C作CE⊥BA交BA的延长线于E,∵∠CAB=120°,∴∠CAE=60°,∴∠ACE=30°∵AC=2,∴AE=AC=1∵在Rt△ACE中,由勾股定理可得:CE2=AC2﹣AE2=3,∴CE=,在Rt△BCE中,由勾股定理可得:BC2=CE2+BE2=28,∴BC=∵AB×CE=CB×AD,∴×4×=××AD,∴AD=;②解:作A关于小河(EF)的对称点C,连接BC交EF于P,则此时AP+BP最小,过B作OB⊥AC于O,则BO=8,CA=4+4=8,CO=8+7=15,则PA+PB=PC+PB=BC==17(km),答:要完成这件事情所走的最短路程是17km.【点评】本题考查了勾股定理、轴对称﹣最短路线问题、含30度角的直角三角形的应用,解(1)的关键是得出关系式AB×CE=CB×AD和求出CB、CE的长,解(2)的关键是找出P点的位置.。
人教版八年级数学上册课题学习最短路径问题1同步练习题

13.4 课题学习最短路径问题基础巩固1.有两棵树位置如图,树脚分别为A,B.地上有一只昆虫沿A—B的路径在地面上爬行.小树顶D处一只小鸟想飞下来抓住小虫后,再飞到大树的树顶C处,问小鸟飞至AB之间何处时,飞行距离最短,在图中画出该点的位置.2.已知,如图所示,甲、乙、丙三个人做传球游戏,游戏规则如下:甲将球传给乙,乙将球立刻传给丙,然后丙又立刻将球传给甲.若甲站在∠AOB内的P点,乙站在OA上,丙站在OB 上,并且甲、乙、丙三人的传球速度相同.问乙和丙必须站在何处,才能使球从甲到乙、乙到丙、最后丙到甲这一轮所用的时间最少?3.如图所示,P,Q为△ABC边上的两个定点,在BC上求作一点R,使△PQR的周长最小.4.七年级(1)班同学做游戏,在活动区域边OP放了一些球(如图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?能力提升5.公园内两条小河MO,NO在O处汇合,两河形成的半岛上有一处景点P(如图所示).现计划在两条小河上各建一座小桥Q 和R,并在半岛上修三段小路,连通两座小桥与景点,这两座小桥应建在何处才能使修路费用最少?请说明理由.6.如图,牧童在A处放牛,其家在B处,A,B到河岸CD 的距离分别为AC,BD,且AC=BD,若A到河岸CD的中点的距离为500 m.(1)牧童从A处把牛牵到河边饮水后再回家,试问在何处饮水,所走路程最短?在图中作出该处,并说明理由;(2)最短路程是多少?参考答案1.解:如图,作D关于AB的对称点D′,连接CD′交AB 于点E,则点E就是所求的点.2.解:如图所示,(1)分别作点P关于OA,OB的对称点P1,P2;(2)连接P1P2,与OA,OB分别相交于点M,N.因为乙站在OA上,丙站在OB上,所以乙必须站在OA上的M 处,丙必须站在OB上的N处才能使传球所用时间最少.3.解:(1)作点P关于BC所在直线的对称点P′;(2)连接P′Q,交BC于点R,则点R就是所求作的点(如图所示).4.解:如图,作小明关于活动区域边线OP的对称点A′,连接AA′交OP于点B,则小明行走的路线是小明→B→A,即在B处捡球,才能最快拿到球跑到目的地A.5.解:如图,作P关于OM的对称点P′,作P关于ON的对称点P″,连接P′P″,分别交MO,NO于Q,R,连接PQ,PR,则P′Q=PQ,PR=P″R,则Q,R就是小桥所在的位置.理由:在OM上任取一个异于Q的点Q′,在ON上任取一个异于R的点R′,连接PQ′,P′Q′,Q′R′,P″R′,PR′,则PQ′=P′Q′,PR′=P″R′,且P′Q′+Q′R′+R′P″>P′Q+QR+RP″,所以△PQR的周长最小,故Q,R就是我们所求的小桥的位置.6.解:(1)作法:如图作点A关于CD的对称点A′;连接A′B交CD于点M.则点M即为所求的点.证明:在CD上任取一点M′,连接AM′,A′M′,BM′,AM,因为直线CD是A,A′的对称轴,M,M′在CD上,所以AM=A′M,AM′=A′M′,所以AM+BM=A′M+BM=A′B,在△A′M′B中,因为A′M′+BM′>A′B,所以AM′+BM′=A′M′+BM′>AM+BM,即AM+BM最小.(2)由(1)可得AM=A′M,A′C=AC=BD,所以△A′CM≌△BDM,即A′M=BM,CM=DM,所以M为CD的中点,且A′B=2AM,因为AM=500 m,所以A′B=AM+BM=2AM=1 000 m.即最短路程为1 000 m.关注数学的解题过程数学是一门非常严谨的科目,在平时的学习中,同学们应该养成积极思考、重视细节、严谨计算、活学活用的好习惯,这是学好数学的前提高效学习经验——注重解答过程中考状元XX在中考中仅仅丢掉了6分。
最短路径问题练习题

最短路径问题练习题最短路径问题是图论中的一个经典问题,主要研究在加权图中找到两个顶点之间的最短路径。
这个问题在实际生活中有广泛的应用,比如导航系统中的路线规划、网络中的数据传输等。
以下是一些关于最短路径问题的练习题,供同学们练习和思考。
练习题1:Dijkstra算法的应用给定一个包含6个顶点的图,顶点编号为1到6,边的权重如下所示:- 1-2: 7- 1-3: 9- 2-3: 14- 2-4: 10- 3-4: 15- 3-5: 6- 4-5: 11- 5-6: 2- 3-6: 20请使用Dijkstra算法找出从顶点1到顶点6的最短路径。
练习题2:Bellman-Ford算法的应用考虑一个包含5个顶点的图,顶点编号为A、B、C、D、E,边的权重如下所示:- A-B: 5- A-C: 3- B-C: 1- B-D: 2- C-E: 8使用Bellman-Ford算法计算从顶点A到顶点E的最短路径。
练习题3:Floyd-Warshall算法的应用给定一个包含4个顶点的图,顶点编号为1、2、3、4,边的权重如下所示:- 1-2: 4- 1-3: 5- 2-3: 3- 2-4: 7- 3-4: 2使用Floyd-Warshall算法计算所有顶点对之间的最短路径。
练习题4:有向图中的最短路径问题在一个有向图中,有5个顶点,编号为1到5,边的权重如下所示:- 1->2: 2- 1->3: 3- 2->3: 1- 2->4: 4- 3->4: 5- 3->5: 2- 4->5: 1找出从顶点1到顶点5的最短路径。
练习题5:负权重边的最短路径问题考虑一个包含4个顶点的图,顶点编号为1、2、3、4,边的权重如下所示:- 1-2: 10- 2-3: -3- 3-4: 1在这种情况下,使用Bellman-Ford算法找出从顶点1到顶点4的最短路径,并讨论负权重边对最短路径算法的影响。
八年级上《最短路径问题》同步练习含答案

八年级上《最短路径问题》同步练习含答案基础题知识点最短路径问题1.如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的值最小时,BP与HG的夹角(锐角)度数为________.2.已知,如图,在直线l的同侧有两点A,B.(1)在图1的直线上找一点P使PA+PB最短;(2)在图2的直线上找一点P,使PA-PB最长.3.如图均是由相同的小正方形组成的网格图,点A、B、C、D均落在格点上.请只用无刻度的直尺在格线CD上确定一点Q,使QA与QB的长度之和最小.4.如图,村庄A,B位于一条小河的两侧,若河岸a,b彼此平行,现在要建设一座与河岸垂直的桥CD,问桥址应如何选择,才能使A村到B村的路程最近?中档题5.如图,在△ABC中,AB=AC,AD平分∠CAB,N点是AB上的一定点,M是AD上一动点,要使MB+MN最小,请找点M的位置.6.如图,在△ABC的一边AB上有一点P.(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短?若能,请画出点M、N的位置,若不能,请说明理由;(2)若∠ACB=52°,在(1)的条件下,求出∠MPN的度数.7.如图,已知∠AOB,点P是∠AOB内部的一个定点,点E、F分别是OA、OB上的动点.(1)要使得△PEF的周长最小,试在图上确定点E、F的位置.(2)若OP=4,要使得△PEF的周长的最小值为4,则∠AOB=________.8.(兰州中考改编)如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△周长最小,求∠AMN+∠ANM的度数.综合题9.已知:如图,在∠POQ内部有两点M、N,∠MOP=∠NOQ.(1)画图并简要说明画法:在射线OP上取一点A,使点A到点M和点N的距离和最小;在射线OQ上取一点B,使点B到点M和点N的距离和最小;(2)直接写出AM+AN与BM+BN的大小关系.参考答案1.60° 2.(1)作点B关于直线l的对称点C,连接AC交直线l于点P,连接BP.点P即为所求.图略.(2)连接AB并延长,交直线l于点P.图略. 3.作B关于CD的对称点B′,连接AB′,交格线CD于Q,此时QA+QB=QA+QB′=AB′,根据两点之间线段最短,得此时QA+QB最小. 4.①过点A作AP⊥a,并在AP上向下截取AA′,使AA′的长等于河的宽度;②连接A′B交b于点D;③过点D作DE∥AA′交a 于点C;④连接AC.则CD即为桥的位置.图略. 5.连接NC与AD的交点为M点.点M即为所求.图略. 6.(1)①作出点P关于AC、BC的对称点D、G.②连接DG交AC、BC于点M、N.点M、N即为所求.(2)设PD交AC于E,PG交BC于F,∵PD⊥AC,PG⊥BC,∴∠PEC=∠PFC=90°.∴∠C+∠EPF=180°.∵∠C=52°,∴∠EPF=128°.∵∠D+∠G+∠EPF=180°,∴∠D+∠G=52°.由对称可知:∠G=∠GPN,∠D=∠DPM,∴∠GPN+∠DPM=52°.∴∠MPN=128°-52°=76°.7.(1)图略,作点P关于OA的对称点C,关于OB的对称点D,连接CD,交OA于E,OB于F.此时,△PEF的周长最小.(2)30°8.作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,连接AM,AN,则A′A″即为△AMN的周长最小值.作DA延长线AH.∵∠DAB=120°,∴∠HAA′=60°.∴∠AA′M+∠A″=∠HAA′=60°.∵∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,∴∠AMN+∠ANM=∠MA′A +∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°.9.(1)图略,点A,B即为所求.画法:①作点M关于射线OP的对称点M′;②连接M′N交OP于点A;③作点N关于射线OQ的对称点N′;④连接N′M交OQ于点B.(2)AM+AN=BM+BN.。
初中数学最短路径问题专练习题附答案

最短路径问题专练学校:___________姓名:___________班级:___________考号:___________一、单选题1.如图,点A ,B 的坐标分别为(2,0),(0,2)A B ,点C 为坐标平面内一点,1BC =,点M 为线段AC 的中点,连接OM ,则OM 的最大值为( )A1B 12C .1D .12【答案】B【解析】【分析】 如图所示,取AB 的中点N ,连接ON ,MN ,根据三角形的三边关系可知OM <ON+MN ,则当ON 与MN 共线时,OM= ON+MN 最大,再根据等腰直角三角形的性质以及三角形的中位线即可解答.【详解】解:如图所示,取AB 的中点N ,连接ON ,MN ,三角形的三边关系可知OM <ON+MN ,则当ON 与MN 共线时,OM= ON+MN 最大,∵(2,0),(0,2)A B ,则∵ABO 为等腰直角三角形,N 为AB 的中点,∵ON=12AB = 又∵M 为AC 的中点,∵MN 为∵ABC 的中位线,BC=1,则MN=1212BC =,12,∵OM 12【点睛】本题考查了等腰直角三角形的性质以及三角形中位线的性质,解题的关键是确定当ON与MN共线时,OM= ON+MN最大.2.如图,在∵ABC中,AB=2,∵ABC=60°,∵ACB=45°,D是BC的中点,直线l经过点D,AE∵l,BF∵l,垂足分别为E,F,则AE+BF的最大值为()B.C.D.A【答案】A【解析】【分析】把要求的最大值的两条线段经过平移后形成一条线段,然后再根据垂线段最短来进行计算即可.【详解】解:如图,过点C作CK∵l于点K,过点A作AH∵BC于点H,在Rt∵AHB中,∵BH =1,AH在Rt∵AHC 中,∵ACB =45°,∵AC=∵点D 为BC 中点,∵BD =CD ,在∵BFD 与∵CKD 中,90BFD CKD BDF CDK BD CD ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∵∵BFD∵∵CKD (AAS ),∵BF =CK ,延长AE ,过点C 作CN∵AE 于点N ,可得AE+BF =AE+CK =AE+EN =AN ,在Rt∵ACN 中,AN <AC ,当直线l∵AC,综上所述,AE+BF.故选:A .【点睛】本题主要考查了全等三角形的判定定理和性质定理及平移的性质,构建全等三角形是解答此题的关键.3.如图,在ABC 中,AB AC =,边AC 的垂直平分线MN 分别交AB ,AC 于点M ,N ,点D 是边BC 的中点,点P 是MN 上任意一点,连接PD ,PC ,若A α∠=,CPD β∠=,PCD 周长最小时,α,β之间的关系是( )A .αβ>B .αβ<C .αβ=D .90αβ=︒-【答案】C连接AP ,根据线段垂直垂直平分线的性质可知P A =PC ,PAC PCA ∠=∠.由PCD L DP PC CD =++,即得出PCD LDP PA CD =++,由此可知当A 、P 、D 在同一直线上时,PCD L 最小.再根据等腰三角形“三线合一”的性质可知AD 为BAC ∠的平分线,即1122PAC A α∠=∠=.最后根据三角形外角性质即得出PAC PCA β=∠+∠,由此即可判断αβ=.【详解】如图,连接AP ,∵直线MN 是线段AC 的垂直平分线,且P 在线段MN 上,∵P A =PC ,PAC PCA ∠=∠.∵PCD LDP PC CD =++, ∵PCDL DP PA CD =++. 由图可知CD 为定值,当A 、P 、D 在同一直线上时,DP PA +最小,即为AD 的长, ∵此时PCD L 最小.∵D 是边BC 的中点,AB =AC ,∵AD 为BAC ∠的平分线, ∵1122PAC A α∠=∠=. ∵CPD PAC PCA ∠=∠+∠,即PAC PCA β=∠+∠,∵αβ=.本题考查线段垂直垂直平分线的性质,等腰三角形的性质,角平分线的定义以及三角形外角性质.根据题意理解当A 、P 、D 在同一直线上时PCD L 最小是解题关键. 4.如图,在ABC 中,3AB =,4AC =,AB AC ⊥,EF 垂直平分BC ,点P 为直线EF 上一动点,则ABP △周长的最小值是( )A .6B .7C .8D .128【答案】B【解析】【分析】 根据题意知点B 关于直线EF 的对称点为点C ,故当点P 与点E 重合时,AP BP +的最小值,求出AC 长度即可得到结论.【详解】解:设AC 交EF 于点E ,连接CP ,EF 垂直平分BC ,B ∴、C 关于EF 对称,∵CP BP =,∵CP AP AC +≥∵BP AP AC +≥,∴当P 和E 重合时,AP BP +的值最小,最小值等于AC 的长,ABP ∴∆周长的最小值是437AC AB +=+=.故选:B .【点睛】题的关键是找出P的位置.5.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是()cmA B.13cm C.D.【答案】B【解析】【分析】将容器侧面展开,作A点关于EF的对称点A′,根据两点之间线段最短即可知A′B的长度即为最短距离.利用勾股定理求出A′B即可.【详解】如图:将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,∵A′D=5cm,A′E=AE=3,BD=12﹣3+A′E=12cm,∵A′B13cm.故选:B.【点睛】和勾股定理进行求解是解题的关键.6.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则MC+MD的最小值为()A.6B.8C.10D.12【答案】B【解析】【分析】连接AD,由于△ABC是等腰三角形,点D是BC边的中点,故AD∵BC,再根据三角形的面积公式求出AD的长,再再根据EF是线段AC的垂直平分线可知,点C关于直线EF的对称点为点A,故AD的长为CM+MD的最小值,由此即可得出结论.【详解】解:连接AD,∵∵ABC是等腰三角形,点D是BC边的中点,∵AD∵BC,∵S△ABC=12BC•AD=12×4×AD=16,解得AD=8,∵EF是线段AC的垂直平分线,∵点C关于直线EF的对称点为点A,∵AD的长为CM+MD的最小值,∵MC+MD的最小值为8.故选:B.【点睛】7.如图,在ABC 中,10AB AC BC ==,,60ABC S =△,AD BC ⊥于点D ,EF 垂直平分AB ,在EF 上确定一点P ,使PB PD +最小( )A .10B .11C .12D .13【答案】C【解析】【分析】 根据三角形的面积公式得到6AD =,由EF 垂直平分AB ,得到点A ,B 关于直线EF 对称,于是得到AD 的长度PB PD =+的最小值,即可得到结论.【详解】解:∵AB AC =,10BC =,60ABC S =△,AD BC ⊥, ∵1=602BC AD ⨯, ∵12AD =,∵EF 垂直平分AB ,∵点A ,B 关于直线EF 对称,∵EF 与AD 的交点即为P 的,此时PA PB =,AD 的长度PB PD =+的最小值, 即PB PD +的最小值为12,故选:C .【点睛】本题考查了轴对称﹣最短路线问题,线段的垂直平分线的性质,等腰三角形的性质,知道AD 的长度PB PD =+的最小值是解题的关键.分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则∵CDM周长的最小值为()A.6B.8C.10D.12【答案】C【解析】【分析】根据题意,点A,点C关于EF对称,连接AD,交EF于点M,则△CDM周长的最小值AD+DC,利用三角形面积公式计算AD即可.【详解】∵AC的垂直平分线EF分别交AC,AB边于E,F点,∵点A,点C关于EF对称,连接AD,交EF于点M,则△CDM周长的最小值是AD+DC,∵AB=AC,BC=4,△ABC的面积是16,点D为BC边的中点,∵AD∵BC,DC=2,11416 22BC AD AD=⨯⨯=,解得AD=8,∵△CDM周长的最小值为:AD+DC=8+2=10,故选C.【点睛】本题考查了线段的垂直平分线,等腰三角形的性质,将军饮马河原理,三角形的面积公式,熟练掌握等腰三角形的性质,将军饮马河原理是解题的关键.9.如图,菱形ABCD的边长为9,面积为P、E分别为线段BD、BC上的动点,则PE+PC的最小值为___.【答案】【解析】【分析】如图,连接AP,过点A作AH∵BC于H.说明P A=PC,再根据垂线段最短,解决问题即可.【详解】解:如图,连接AP,过点A作AH∵BC于H.∵四边形ABCD是菱形,∵A、C关于BD对称,∵P A=PC,∵PE+PC=AP+PE,∵AP+PE≥AH,∵S菱形ABCD=BC•AH,∵AH ,∵PE+PC∵PE+PC的最小值为故答案为:.垂线段最短解决最值问题,属于中考常考题型.三、解答题10.在平面直角坐标系xOy 中,点A 、B 分别在y 轴和x 轴上,已知点A (0,4).以AB 为直角边在AB 左侧作等腰直角△ABC ,∵CAB =90°.(1)当点B 在x 轴正半轴上,且AB =8时∵求AB 解析式;∵求C 点坐标;(2)当点B 在x 轴上运动时,连接OC ,求AC +OC 的最小值及此时B 点坐标.【答案】(1)∵4y =+;∵C (4,4--(2)(2,0)B【解析】【分析】(1)∵根据(0,4)A ,8AB =,推出OB B ,0),设直线AB 的解析式为4y kx =+,将A 、B 坐标代入即可求出AB 解析式;∵过点A 作x 轴的平行线,分别过点C 、B 作y 轴的平行线,交于G 、H .则AHB CGA ∆∆,所以4AG HB ==,CG AH ==C (4,4--; (2)由AGC BHA ∆≅∆可知4AG =,点C 在直线4x =-上运动,作点O 关于直线4x =-的对称点O ',所以AC OC AC O C '+=+,AC OC +的最小值为AO '的长度,此时2OB AH CG ===,即可求出B 坐标.(1)解:∵(0,4)A ,8AB =,OB ∴B ∴0),设直线AB 的解析式为4y kx =+,04∴=+,k =AB ∴解析式:4y x =+; ∵过点A 作x 轴的平行线,与分别过点C 、B 作y 轴的平行线交于G 、H .则AHB CGA ∆∆()AAS4AG HB ∴==,CG AH ==C ∴(4,4--;(2)由AGC BHA ∆≅∆可知4AG =,(B 在x 轴负半轴同理可说明)点C 在直线4x =-上运动,作点O 关于直线4x =-的对称点O ',4OC O C '∴==,448OO '=+=,AC OC AC O C '∴+=+.AC OC +的最小值为AO '=此时2OB AH CG ===,(2,0)B ∴.【点睛】 本题主要考查等腰直角三角形的性质、利用轴对称求最短线路.这里构造三角形全等找到点C的运动轨迹是关键.。
人教版数学八年级上册 13.4 最短路径问题 同步习题

13.4 最短路径问题同步习题一、选择题1.如图,点A,B在直线l的同侧,若要用尺规在直线l上确定一点P,使得AP+BP最短,则下列作图正确的是()A. B. C. D.2.如图,已知∠O ,点P 为其内一定点,分别在∠O 的两边上找点A 、B ,使△ PAB 周长最小的是()A. .B.C. D.3.如图,等边ΔABC的边长为8,AD是BC边上的中线,E是AD边上的动点,F是AB边上一点,若BF=4,当BE+EF取得最小值时,则∠EBC的度数为()A. 15∘B. 25∘C. 30∘D. 45∘4.如图,正ΔABC的边长为2,过点B的直线l⊥AB,且ΔABC与ΔA′B′C′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )A. 3B. 4C. 5D. 65.如图所示,在等边△ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在()A. △ABC的重心处B. AD的中点处C. A点处D. D点处6.如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是()A. 3B. 6C. 5D. 47.如图,已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,∠APB的度数是()A. 40°B. 100°C. 140°D. 50°8.如图,点P是∠AOB内任意一点,且∠AOB=40°,点M和点N分别是射线OA和射线OB上的动点,当△PMN 周长取最小值时,则∠MPN的度数为()A. 140°B. 100°C. 50°D. 40°9.如图,∠AOB=30º,∠AOB内有一定点P,且OP=10.在OA上有一动点Q,OB上有一动点R.若ΔPQR 周长最小,则最小周长是()A. 10 ∠ABD=∠ACEB. 10√2C. 20D. 20√210.如图,四边形ABCD中,∠BAD=120° , ∠B=∠D=90°,在BC、CD上分别找一点M、N,使ΔAMN周长最小时,则∠AMN+∠ANM的度数为()A. 130°B. 110°C. 120°D. 125°二、填空题11.如图,正方形ABCD的边长为3,点E在边AB上,且BE=1,若点P在对角线BD上移动,则PA+PE的最小值是________.12.如图,等边△ABC的边长为2,过点B的直线l⊥AB且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是________.13.在直角坐标系中,点A(-1,1),点B(3,2),P是x轴上的一点,则PA+PB的最小值是________ 。
八年级数学上册最短路径问题同步练习含解析

最短路径问题一、单选题(共10小题)1.如图所示,某工厂有三个住宅区,A,B,C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点在同一直线上),已知AB=300米,BC=600米.为了方便职工上下班,该厂的接送车打算在此路段只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在()A.点A B.点B C.AB之间 D.BC之间【答案】A【解析】此题为数学知识的应用,由题意设一个停靠点,为使所有的人步行到停靠点的路程之和最小,肯定要尽量缩短两地之间的里程,就用到两点间线段最短定理.【详解】解:①以点A为停靠点,则所有人的路程的和=15×300+10×900=13500(米),②以点B为停靠点,则所有人的路程的和=30×300+10×600=15000(米),③以点C为停靠点,则所有人的路程的和=30×900+15×600=36000(米),④当在AB之间停靠时,设停靠点到A的距离是m,则(0<m <300),则所有人的路程的和是:30m+15(300-m)+10(900-m)=13500+5m>13500,⑤当在BC之间停靠时,设停靠点到B的距离为n,则(0<n<600),则总路程为30(300+n)+15n+10(600—n)=15000+35n>13500.∴该停靠点的位置应设在点A;故选:A.【点睛】考查了比较线段的长短,此题为数学知识的应用,考查知识点为两点之间线段最短.2.已知村庄A和B分别在一条河的两岸,现要在河上造一座桥MN(假定河的两岸彼此平行,且桥与河岸互相垂直),下列示意图中,桥的建造位置能使从村庄A经桥过河到村庄B的路程最短的是()A.B.C.D.【答案】C【解析】如图作AI∥MN,且AI=MN,连接BI,由两点之间线段最短可知此时从A点到B点的距离最短,所以AM∥BN。
最短路径问题专题练习含答案

·P
O
N
4、在一条河的两岸有两个村庄,现在要在河上建一座小桥,桥的方向于河流垂 直,设河的宽度不变,试问:桥架在何处,才能使从 A 到 B 的距离最短?
·A
·B
参考答案
一、选择题 1、C
二、填空题 2、3
三、解答题 1、作图略,作法:作 P 关于 OM 的对称点 P’,作 P 关于 ON 的对称点 P”,连接 P’P”,分别交 MO,NO 于 Q,R 两点,连接 PQ,PR,则 P’Q=PQ,PR=P”R, 则 Q,R 就是小桥所在的位置 2、作图略,作法:作 BB’垂直于河岸 GH,使 BB’等于河宽,连接 AB’,与河 岸 EF 相交于点 P,作 PD⊥GH,交 GH 于点 D,则 PD//BB’且 PD=BB’。于是四 边形 PDBB’为平行四边形,故 PB’=BD。根据“两点之间线段最短”,知 AB’ 最短,即 AP+BD 最短。因此桥应该建在 PD 上就符合题意了
2、在边长为 2 的正三角形 ABC 中,E,F,G 分别为 AB,AC,BC 的中点,点 P 为线
段 EF 上一个动点,连接 BP,GP,则△BPG 的周长的最小值为( )
三、解答题 3、公园内两条小河 MO,NO 在 O 处汇合,两河形成的半岛上有一处景点 P,现计 划在两条小河上各建一座小桥 Q 和 R,并在半岛上修三段小路连通两座小桥与景 点,这两座小桥应建在何处才能使修路费用最少?
最短路径问题专题练习
一、选择题 1、如图,点 P 为∠AOB 内一点,分别作点 P 关于 OA,OB 的对称点 P1 ,P2 ,连接 P1 P2 ,
交 OA 于 M,交 OB 于 N,若 P1 P2 =6,则△PMN 的周长为( ) A、4 B、5 C、6 D、7
专题1.3 勾股定理之最短路径问题专项训练(30道)(举一反三)(北师大版)(解析版)

专题1.3 勾股定理之最短路径问题专项训练(30道)【北师大版】考卷信息:本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,涵盖了平面直角坐标系中的规律问题所有类型!一.选择题(共12小题)1.(2022春•五华区期末)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )A B.4cm C D.5cm【分析】正方体侧面展开为长方形,确定蚂蚁爬行的起点和终点,根据两点之间线段最短,根据勾股定理可求出最短路径长,【解答】解:如图,它运动的最短路程AB==cm).故选:C.2.(2022春•碑林区校级期末)如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC 上有一点D,且BC=10cm,DC=2cm.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.A.14B.12C.10D.8【分析】首先画出圆柱的侧面展开图,根据底面周长为12cm,求出AB的值;再在Rt△ABD中,根据勾股定理求出AD的长,AD即为所求.【解答】解:圆柱侧面展开图如图所示,∵圆柱的底面周长为12cm,∴AB=6cm.∵BD=8cm,在Rt△ABD中,AD2=AB2+BD2,∴AD10(cm),即蚂蚁从A点出发沿着圆柱体的表面爬行到点D的最短距离是10cm.故选:C.3.(2022春•洛阳期中)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm.在杯内离杯底4cm的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B C.12D.18【分析】将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,则先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,再利用勾股定理求A'C的长即可.【解答】解:如图所示,将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,故先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,根据两点之间线段最短,即可得到此时AF+CF最小,并且最小值为A'C的长度,如图所示,延长过C的母线,过A'作A'D垂直于此母线于D,由题意可知,A'D=18÷2=9(cm),CD=12﹣4+4=12(cm),由勾股定理得:A'C=15(cm),故蚂蚁到达蜂蜜的最短距离为15cm,故选:A.4.(2022秋•高州市期末)国庆节期间,茂名市一广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( )A B C D.5米【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.【解答】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,∵圆柱高3米,底面周长2米,∴AC2=22+1.52=6.25,∴AC=2.5,∴每根柱子所用彩灯带的最短长度为5m.故选:D.5.(2022秋•沈阳期末)如图,长方体的长为3,宽为2,高为4,点B离点C的距离为1,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是( )A B.5C D【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.【解答】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如图1:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=5;只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图2:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如图3:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=∵5∴蚂蚁爬行的最短距离是5.故选:B.6.(2022春•郾城区期末)如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )cm.A.B.C.120D.130【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【解答】解:如图所示,∵它的每一级的长宽高为20cm,宽30cm,长50cm,∴AB=cm).答:蚂蚁沿着台阶面爬行到点B的最短路程是,故选:B.7.(2022秋•揭阳校级月考)如图,一个棱长为3的正方体,把它分成3×3×3个小正方体,小正方体的棱长都是1.如果一只蚂蚁从点A爬到点B,那么估计A,B间的最短路程d的值为( )A.4B.5C.6D.7【分析】过B作BD⊥AC于D,根据勾股定理即可得到结论.【解答】解:过B作BD⊥AC于D,则AD=4,BD=3,∴A,B间的最短路程d=5,故选:B.8.(2022秋•牡丹区月考)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )(π取3)m.A.30B.28C.25D.22【分析】要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.【解答】解:其侧面展开图如图:作点C关于AB的对称点F,连接DF,∵中间可供滑行的部分的截面是半径为2.5m的半圆,∴BC=πR=2.5π≈7.5m,AB=CD=20m,∴CF=15m,在Rt△CDF中,DF==25(m),故他滑行的最短距离约为25m.故选:C.9.(2022春•靖西市期中)如图是放在地面上的一个长方体盒子,其中AB=7cm,BC=4cm,BF=6cm,点M在棱AB上,且AM=1cm,点N是FG的中点,一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为( )A.10cm B.C.D.【分析】利用平面展开图有2种情况,画出图形利用勾股定理求出MN的长即可.【解答】解:如图1中,MN=10(cm),如图2中,MN==10(cm),∴一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为10cm,故选:A.10.(2022秋•芝罘区期中)某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )A.8cm B.10cm C.12cm D.15cm【分析】画出三棱柱的侧面展开图,利用勾股定理求解即可.【解答】解:将三棱柱沿AA′展开,其展开图如图,则AA′=15(cm).故选:D.11.(2022秋•青岛期末)棱长分别为8cm,6cm的两个正方体如图放置,点A,B,E在同一直线上,顶点G在棱BC上,点P是棱E1F1的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P,它爬行的最短距离是( )A.+10)cm B.C D.+3)cm【分析】求出两种展开图PA的值,比较即可判断.【解答】解:如图,有两种展开方法:方法一:PA=,方法二:PA=..故选:C.12.(2022•广饶县一模)如图,长方体的底面边长分别为2厘米和4厘米,高为5厘米.若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )厘米.A.8B.10C.12D.13【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.【解答】解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12(cm),QA=5cm,∴PQ=13cm.故选:D.二.填空题(共8小题)13.(2022春•德城区期末)如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 25 cm.【分析】画出长方体的侧面展开图,根据勾股定理求出AB的长即可.【解答】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴BD=CD+BC=10+5=15(cm),AD=20cm,在直角三角形ABD中,根据勾股定理得:∴AB=25(cm);只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴BD=CD+BC=20+5=25(cm),AD=10cm,在直角三角形ABD中,根据勾股定理得:∴AB=cm);只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴AC=CD+AD=20+10=30(cm),在直角三角形ABC中,根据勾股定理得:∴AB==cm);∵25<∴蚂蚁爬行的最短距离是25cm.故答案为:25.14.(2022•潍城区一模)云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的,如图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图,该场地可以看作是从一个m,其边缘AB=CD=24m,点E在CD 长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为12π上,CE=4m,一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为.【分析】根据题意可得,AD=12,DE=CD﹣CE=24﹣4=20,线段AE即为滑行的最短路线长.在Rt△ADE中,根据勾股定理即可求出滑行的最短路线长.【解答】解:将半圆面展开可得:AD=12m,DE=DC﹣CE=20m,在Rt△ADE中,AE==m),即滑行的最短路线长为,故答案为:15.(2022春•仁怀市月考)如图,要在河边l上修建一个水泵站,分别向A村和B村送水,已知A村、B 村到河边的距离分别为2km和7km,且AB两村庄相距13km,则铺设水管的最短长度是 15 km.【分析】作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置;利用了轴对称的性质可得AP=A′P,在Rt△AEB中利用勾股定理可以算出AE的长,再在Rt△A′CB中利用勾股定理算出A′B的长,根据两点之间线段最短的性质即可求解.【解答】解:作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置,此时,(PA+PB)的值最小,即所铺设水管最短;过B点作l的垂线,过A′作l的平行线,设这两线交于点C,过A作AE⊥BC于E,则四边形AA′CE和四边形AMNE是矩形,∴EN=AM=2,EC=AA′=2+2=4,A′C=AE,在Rt△ABE中,依题意得:BE=BN﹣EN=7﹣2=5,AB=13,根据勾股定理可得:AE=12,在Rt△B A′C中,BC=BE+EC=5+4=9,A′C=12,根据勾股定理可得:A′B=15,∵PA=PA′,∴PA+PB=A′B=15(km),故答案为:15.16.(2022秋•锦江区校级期末)在一个长4米的长方形草地上,如图堆放着一根三棱柱的木块,它的侧棱长平行且大于场地宽AD,一只蚂蚁从点A处到C处需要走的最短路程是米.【分析】解答此题要将木块展开,然后根据两点之间线段最短解答.【解答】解:由题意可知,将木块展开,相当于是AB+等腰直角三角形的两腰,∴长为2+2﹣10(米);宽为4米.=故答案为:17.(2022秋•高新区校级期末)如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B【分析】可将教室的墙面ADEF与地面ABCD展开,连接P、B,根据两点之间线段最短,利用勾股定理求解即可.【解答】解:如图,过P作PG⊥BF于G,连接PB,∵AG=3米,AP=AB=5米,∴PG=4米,∴BG=8米,∴PB==故这只蚂蚁的最短行程应该是故答案为:18.(2022春•德州期中)如图,点A是正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B【分析】根据题意画出图形,过A作EA⊥CD于E,连接AB,则AB长为最短距离,求出OD=OC,∠DAC=90°,根据直角三角形斜边上中线性质求出AE=DE=EC=1,根据勾股定理求出即可.【解答】解:如图展开:过A作EA⊥CD于E,连接AB,则AB长为最短距离,∵四边形DFGC是正方形,DC=BC=2,∴OD=OC,∠DAC=90°,∴∠ADE=∠ECA=45°,∵AE⊥DC,∴DE=EC,∵∠DAC=90°,DC=1,∴AE=DE=EC=12在△AEB中,∠AEB=90°,BE=1+2=3,EA=1,由勾股定理得:AB19.(2022秋•中原区校级期末)如图,一个三棱柱盒子底面三边长分别为3cm,4cm,5cm,盒子高为9cm,一只蚂蚁想从盒底的点A沿盒子的表面爬行一周到盒顶的点B,蚂蚁要爬行的最短路程是 15 cm.【分析】将三棱柱侧面展开得出矩形,求出矩形对角线的长度即可.【解答】解:如图,右侧为三棱柱的侧面展开图,AA′=3+4+5=12cm,A′B=9cm,∠AA′B=90°,∴AB==15cm,故答案为:15.20.(2022秋•凤城市期中)如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm.在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处吃面包屑.则蚂蚁爬行的最短路线为 100 cm.【分析】作出A关于BC的对称点A′,连接A′G,与BC交于点Q,此时AQ+QG最短;A′G为直角△A′EG的斜边,根据勾股定理求解即可.【解答】解:如图所示作点A关于BC的对称点A′,连接A′G交BC与点Q,小虫沿着A→Q→G的路线爬行时路程最短.在直角△A′EG中,A′E=80cm,EG=60cm,∴AQ+QG=A′Q+QG=A′G=100cm.∴最短路线长为100cm.故答案为:100.三.解答题(共10小题)21.(2022春•宜城市期末)如图,某小区有两个喷泉A,B,两个喷泉的距离长为125m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为60m,BM的长为75m.(1)求供水点M到喷泉A,B需要铺设的管道总长;(2)求喷泉B到小路AC的最短距离.【分析】(1)根据勾股定理解答即可;(2)根据勾股定理的逆定理和垂线段解答即可.【解答】解:(1)在Rt△MNB中,BN==45(m),∴AN=AB﹣BN=125﹣45=80(m),在Rt△AMN中,AM100(m),∴供水点M到喷泉A,B需要铺设的管道总长=100+75=175(m);(2)∵AB=125m,AM=100m,BM=75m,∴AB2=BM2+AM2,∴△ABM是直角三角形,∴BM⊥AC,∴喷泉B到小路AC的最短距离是BM=75m.22.(2022秋•原阳县期末)如图,一个正方体木箱子右边连接一个正方形木板,甲蚂蚁从点A出发,沿a,b,d三个面走最短路径到点B;同时,乙蚂蚁以相同的速度从点B出发,沿d,c两个面走最短路径到点A.请你通过计算判断哪只蚂蚁先到达目的地?【分析】将正方体展开,根据两点之间线段最短,构造出直角三角形,进而求出最短路径的长.【解答】解析展开a,b,c与d在同一平面内,如图所示.由题意可知,甲蚂蚁走的路径为A1B,A1B=cm).乙蚂蚁走的路径为A2B,A2B==cm).所以A1B>A2B,故乙蚂蚁先到达目的地.23.(2022秋•江北区期末)在立方体纸盒的顶点A处有一只蚂蚁,在另一顶点E处有一粒糖,你能为这只蚂蚁设计一条最短路线,使它沿着立方体表面上的这一条路线爬行,最快捷吃到糖吗?以下提供三个方案:①A→B→C→E;②A→C→E;③A→D→E.(1)三种方案①、②、③中爬行路线最短的方案是 ③ ;最长的方案是 ① .(2)请根据数学知识说明理由.【分析】(1)根据“化曲面为平面”,且利用“两点之间线段最短”可知,爬行路线最短的方案是③;最长的方案是①;(2)分别求出三种方案蚂蚁爬行的路程,比较即可求解.【解答】解:(1)三种方案①、②、③中爬行路线最短的方案是③;最长的方案是①.故答案为:③;①;(2)爬行路线最短的方案是③;最长的方案是①.理由如下:‘’设立方体纸盒的棱长为a,则a>0.方案:①A→B→C→E蚂蚁爬行的路程为:AB+BC+CE=a+a+a=3a;方案;②A→C→E蚂蚁爬行的路程为:AC+CE=a+1)a;方案;③A→D→E.1)a<3a,∴爬行路线最短的方案是③;最长的方案是①.24.(2022秋•二道区期末)如图,已知线段BC是圆柱底面的直径,圆柱底面的周长为10,圆柱的高AB=12,在圆柱的侧面上,过点A、C两点嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 C ;(2)求该金属丝的长.【分析】(1)由平面图形的折叠及立体图形的表面展开图的特点解题;(2)要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.【解答】解:(1)因为圆柱的侧面展开面为长方形,AC展开应该是两线段,且有公共点C.故答案为:C;(2)如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为10,圆柱的高AB=12,∴该长度最短的金属丝的长为2AC==26.25.(2022秋•随县期末)如图1所示,长方形是由两个正方形拼成的,正方形的边长为a,对角线为b,长方形对角线为c.一只蚂蚁从A点爬行到C点.(1)求蚂蚁爬行的最短路线长(只能按箭头所示的三条路线走),并说明理由;(2)如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面(实线表示),则蚂蚁从A点到C点的最短路线长是多少?请在图2中画出路线图,若与图中的线段有交点,则要标明并说明交点的准确位置.(可测量猜想判断)【分析】(1)根据两点之间线段最短求解;(2)把正方体相邻的两个面展开成平面,连接A,C即是最短路线.【解答】解:(1)从A﹣B﹣C路线长:a+a+a=3a,从A﹣D﹣C路线长:a+a+a=3a,从A﹣E﹣C路线长:a+b.(3分)根据两点之间,线段最短.可得AD+DE>AE,即a+a>b,(6分)所以a+a+a>a+b,即3a>a+b(7分)(说明:只要写出理由“两点之间,线段最短”即给6分)故从A到C的最短路线长为a+b;(8分)(2)从A到C的最短路线长为C,(10分)图中的点M为线段EF的中点.(11分)位置如图.(13分)26.(2022秋•罗湖区期中)(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?【分析】(1)利用勾股定理直接求出木棒的最大长度即可.(2)将长方体展开,利用勾股定理解答即可;(3)将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解答】解:(1)由题意得:该长方体中能放入木棒的最大长度是:=13(cm).(2)分三种情况可得:AG=>AG>AG=,;(3)∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,∴A′D=5cm,BD=12﹣3+AE=12cm,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B=13(Cm).27.(2022秋•元宝区校级期中)一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,问:丝带共有多长?【分析】根据题意抽象出直角三角形,利用勾股定理求得彩色丝带的长即可.=150cm,答:丝带共有150cm.28.(2022秋•东明县期中)东明县是鲁西南的化工基地,有东明石化集团,洪业化工集团,玉皇化工集团等企业,化学工业越来越成为东明县经济的命脉,化工厂里我们会经常看到如图储存罐,根据需要,在圆柱形罐的外围要安装小梯子,如果油罐的底面半径为6米,高24米,梯子绕罐体半圆到达罐顶,则梯子至少要多长?【分析】把立体图形转化为平面图形,利用勾股定理即可解决问题.【解答】解:如图,根据题意,BC=24m,AB=1•2π•6≈18m,2在Rt△ABC中,AC30m,答:梯子至少要30m.29.(2022秋•福田区期末)如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则:(1)A′B,甲蚂蚁要吃到食物需爬行的路程长l1+1 cm;(2)乙蚂蚁要吃到食物需爬行的最短路程长l2(π取3);(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3≈1.4)【分析】(1)由∠A′O′B′=90°,可知△B′A′O′为等腰直角三角形,故此A′B′=′O ′,然后根据l1=A′B′+AA′求解即可;(2)先求得弧A′B′的长,然后根据勾股定理求得矩形AA′B′B的对角线的长度即可;(3 1.4代入从而可求得l1、l2的近似值,从而可作出判断.【解答】解:(1)∵∠A′O′B′=90°,O′A′=O′B′,∴A′B′=A′B′=′O′=∴l1=A′B′+AA′=1.故答案为:1.=6π=18.(2)A′B′=90°×2π×12360°将圆柱体的侧面展开得到如图1所示矩形AA′B′B.∵A′B′=18,∴A′B′=18.在Rt△ABB′中,AB′=故答案为:(3)∵l1=1≈12×1.4+1=17.8∴l21=316.84.∵l22=2=325,∴l21<l22.∴l1<l2.∴甲蚂蚁先到达食物处.30.(2022秋•安岳县期末)勾股定理是解决直角三角形很重要的数学定理.这个定理的证明的方法很多,也能解决许多数学问题.请按要求作答:(1)选择图1或图2中任一个图形来验证勾股定理;(2)利用勾股定理来解决下列问题:如图3,圆柱形玻璃杯高为12cm,底面周长为16cm,在杯外离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁且与蜂蜜C相对的点A处,点A离杯口3cm.则蚂蚁到达蜂蜜的最短距离为多少?【分析】(1)根据正方形的面积等于四个直角三角形的面积与正方形面积的即可得出结论;(2)蚂蚁实际上是在圆柱的半个侧面上爬行,如果将这半个侧面展开,根据:“两点之间,线段最短“,所求的最短路程就是这一个展开图AC的长.在R t△ABC中,AB=底面周长的一半=8cm,BC=12﹣3﹣3=6cm.,所以由勾股定理得:AC=10cm,所以蚂蚁爬行的最短路程为10cm.ab+c2,【解答】解:(1)若选图1,则由图形可知:(a+b)2=4×12整理得:a2+b2=c2;ab+(b﹣a)2=c2,若选图2,则由图形可知:4×12整理得:a2+b2=c2.(2)如图所示,∵在Rt△ABC中,AB=底面周长的一半=8cm,BC=12﹣3﹣3=6cm,∴由勾股定理得:AC=10cm,∴蚂蚁爬行的最短路程为10cm.。
课题学习最短路径问题 同步练习 人教版八年级数学上册

13.4课题学习最短路径问题同步优化(共25题)一、选择题(共15题)1.如图,在△ABC中,AB⊥AC,AB=3,BC=5,AC=4,EF为BC的垂直平分线,点P为直线EF上的任意一点,则△ABP周长的最小值是( )A.12B.6C.7D.82.如图,要在一条河上架一座桥MN(河的两岸互相平行,桥与河岸垂直),在如下四种方案中,使得E,F两地的路程最短的是( )A.B.C.D.3.如图,点P是直线a外一点,PB⊥a,A,B,C,D都在直线a上,下列线段中最短的是( )A.PA B.PB C.PC D.PD4.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如下四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是A.B.C.D.5.如图,在平面直角坐标系中,点A(−2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )A.(−2,0)B.(4,0)C.(2,0)D.(0,0)6.在如图所示的4×4的正方形网格中,有A,B两点,在直线a上求一点P,使PA+PB最小,则点P应选在( )A.C点B.D点C.E点D.F点7.A,B是两个居民小区,快递公司准备在公路l上选取的点P处建一个服务中心,使PA+PB最小.下面四种选址方案符合要求的是( )A.B.C.D.8.如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP的最小值的是( )A.AB B.DE C.BD D.AF9.如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点,若AE=2,则当EF+CF取得最小值时,∠ECF的度数为( )A.15∘B.22.5∘C.30∘D.45∘10.如图,点P是∠AOB内任意一点,且∠AOB=40∘,点M和点N分别是射线OA和射线OB上的动点,当△PMN的周长取最小值时,∠MPN的度数为( )A.140∘B.100∘C.50∘D.40∘11.如图所示,CD是△ABC的角平分线,△ABC的面积为12,BC的长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( )A.6B.4C.3D.212.如图,在四边形ABCD中,∠C=50∘,∠B=∠D=90∘,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )A.50∘B.60∘C.70∘D.80∘13.如图,在等边三角形ABC中,点E是AC边的中点,点P是△ABC的中线AD上一动点,且AD=6,则EP+CP的最小值是( )A.12B.9C.6D.314.如图,在△ABC中,AB=7,BC=5,AC的垂直平分线分别交AB,AC于点D,E,点F是DE上任意一点,则BF+CF的最小值是( )A.2B.12C.5D.715.如图,已知等边三角形ABC的边长为4,过点B的直线l⊥AB,△ABC与△AʹBCʹ关于直线l对称,D为BCʹ上一动点,则AD+CD的最小值为( )A.4√3B.6√2C.8D.4+2√3二、填空题(共5题)16.连接直线外一点与直线上各点的所有线段中,最短.17.如图,在△ABC中,∠ACB=90∘,AC=8,BC=6,AB=10.点E是AB上一动点,则CE的最小值为.18.两点之间的所有连线中,最短.19.如图,∠BAC=30∘,AB=2,点P是射线AC上一动点,则线段BP的最小值为.20.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短为.三、解答题(共5题)21.如图,点A,B在直线l的两侧,在直线l上求一点作P,使∣PA−PB∣的值最大.22.如图,点A,B在直线l的同侧,在直线l上求作一点P,使∣PB−PA∣的值最大.23.如图,∠AOB=30∘,点P为∠AOB内一点,OP=10,点M,N分别在OA,OB上,求△PMN周长的最小值.24.如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图).(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;(2)在DE上画出点P,使PB1+PC最小;(3)在DE上画出点Q,使QA+QC最小.25.如图,在Rt△ABC中,∠BAC=30∘,∠ACB=90∘,AC=3,E为AB的中点,在线段AC上找一点H,使得BH+EH的值最小,并求出该最小值.答案一、选择题(共15题)1. 【答案】C2. 【答案】B3. 【答案】B4. 【答案】D5. 【答案】C6. 【答案】A【解析】如图,点Aʹ是点A关于直线a的对称点,连接AʹB,则AʹB与直线a的交点即为点P,此时PA+PB最小,∵AʹB与直线a交于点C,∴点P应选在C点.7. 【答案】A【解析】根据题意得,在公路l上选取点P,使PA+PB最小,则选项A符合要求.8. 【答案】D【解析】如图,连接CP,由AD=CD,∠ADP=∠CDP=45∘,DP=DP,可得△ADP≌△CDP,∴AP=CP,∴AP+PE=CP+PE,∴当点E,P,C在同一条直线上时,AP+EP的最小值为CE的长,此时,由AB=CD,∠ABF=∠CDE,BF=DE,可得△ABF≌△CDE,∴AF=CE,∴AP+EP的最小值等于线段AF的长.9. 【答案】C【解析】如图,过E作EM∥BC,交AD于N,交AB于M,∵AC=4,AE=2,∴EC=2=AE,∵△ABC为等边三角形,∴∠ACB=∠BAC=60∘,∵EM∥BC,∴∠AEM=∠ACB=60∘,∴△AME为等边三角形,∴AM=AE=2,∵AB=4,∴BM=2=AM,∵AD是BC边上的中线,△ABC是等边三角形,∴AD⊥BC,∵EM∥BC,∴AD⊥EM,∵AM=AE,∴E和M关于AD所在直线对称,连接CM交AD于F,连接EF,则此时EF+CF的值最小,∵△ABC是等边三角形,AM=BM,∠ACB=30∘.∴∠ECF=1210. 【答案】B【解析】如图,分别作点P关于OA,OB的对称点P1,P2,连接P1P2,交OA于M,交OB于N,连接PM,PN,OP1,OP2,OP,易得OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O,MP=P1M,PN=P2N,则△PMN的周长的最小值=P1P2,易得∠P1OP2=2∠AOB=80∘,∴在等腰△OP1P2中,∠OP1P2+∠OP2P1=100∘,∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=100∘.11. 【答案】B【解析】如图,作点A关于CD的对称点H.∵CD是△ABC的角平分线,∴点H一定在BC上.过H作HF⊥AC与F,交CD于E,连接AE,此时AE+EF的值最小,AE+EF的最小值=HF.过A作AG⊥BC于G.∵△ABC的面积为12,BC的长为6,∴AG=4,∵CD垂直平分AH,∴AC=CH,∴S△ACH=12AC⋅HF=12CH⋅AC,∴HF=AG=4,∴AE+EF的最小值是4.12. 【答案】D【解析】如图,分别作点A关于直线BC和CD的对称点Aʹ,Aʺ,连接AʹAʺ,交BC于E,交CD 于F,则AʹAʺ的长即为△AEF周长的最小值.作DA的延长线AH,∵∠C=50∘,∠ABC=∠ADC=90∘,∴∠DAB=130∘,∴∠HAAʹ=50∘,∴∠AAʹE+∠Aʺ=∠HAAʹ=50∘,∵∠EAʹA=∠EAAʹ,∠AʺAF=∠Aʺ,∴∠EAAʹ+∠AʺAF=50∘,∴∠EAF=130∘−50∘=80∘.故选D.13. 【答案】C14. 【答案】D15. 【答案】C二、填空题(共5题)16. 【答案】垂线段17. 【答案】4.8【解析】作CF⊥AB于点F,当E与F重合时,CE最小,面积法可求CF=4.8.18. 【答案】线段19. 【答案】120. 【答案】10cm【解析】当CD与OA的交点为E,与OB的交点为F时,小蚂蚁爬行的路径最短.∵OA,OB分别是线段MC,MD的垂直平分线,∴ME=CE,MF=DF,∴小蚂蚁爬行的路径最短为CD=10cm.三、解答题(共5题)21. 【答案】作点A关于直线l的对称点Aʹ,连接AʹB并延长交直线l于点P.22. 【答案】连接BA并延长交直线l于点P23. 【答案】分别作点P关于OA,OB的对称点P1,P2,连接P1P2,交OA于点M,交OB于点N,连接PM,PN,此时,△PMN的周长最小,△PMN的周长=P1P2,∴P1P2=OP1=OP2=OP=10.24. 【答案】略.25. 【答案】作点E关于AC的对称点F,连接BF,交AC于点H,此时BH+EH最小,最小值为线段BF的长.易证△ABF≌△BAC,∴BF=AC=3,故BH+EH的最小值为3.。
2022-2023学年人教版八年级数学上册《13-4课题学习 最短路径问题》同步测试题(附答案)

2022-2023学年人教版八年级数学上册《13.4课题学习最短路径问题》同步测试题(附答案)一.选择题(共9小题,满分45分)1.如图,已知点D、E分别是等边三角形ABC中BC、AB边的中点,AD=6,点F是线段AD上的动点,则BF+EF的最小值为()A.3B.6C.9D.122.如图,在△ABC中,∠C=90°,AC=BC=2,D为AB上一动点,DE∥AC,DE=2,则AE+CE的最小值等于()A.4B.2C.3D.+23.如图,△ABC为等边三角形,边长为6,AD⊥BC,垂足为点D,点E和点F分别是线段AD和AB上的两个动点,连接CE,EF,则CE+EF的最小值为()A.B.3C.3D.24.如图,点M在等边△ABC的边BC上,BM=8,射线CD⊥BC,垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为()A.无法确定B.10C.13D.165.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,AB=5,AD平分∠CAB交BC 于D点,E、F分别是AD,AC上的动点,则CE+EF的最小值为()A.B.5C.3D.6.如图,∠AOB=30°,∠AOB内有一定点P,且OP=15,若在OA、OB上分别有动点M、N,则△PMN周长的最小值是()A.5B.15C.20D.307.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC,CD上分别找一点M,N,使△AMN的周长最小时,则∠ANM+∠AMN的度数为()A.80°B.90°C.100°D.130°8.如图,在△ABC中,AB的垂直平分线DE交BC于点D,垂足为E,M为DE上任意一点,BA=3,AC=4,BC=6,则△AMC周长的最小值为()A.7B.6C.9D.109.如图,在平面直角坐标系中,O为原点,点A,C,E的坐标分别为(0,4),(8,0),(8,2),点P,Q是OC边上的两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标为()A.(2,0)B.(3,0)C.(4,0)D.(5,0)二.填空题(共6小题,满分30分)10.在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N 分别是BD和BC边上的动点,则MN+MC的最小值是.11.如图,∠AOB=30°,点M、N分别是射线OA、OB上的动点,OP平分∠AOB,且OP=6,当△PMN的周长取最小值时,四边形PMON的面积为.12.如图,∠AOB=20°,点M,N分别是边OA,OB上的定点,点P,Q分别是边OB、OA上的动点,记∠MPQ=α,∠PQN=β,当MP+PQ+QN最小时,则β﹣α的值为.13.如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是.14.如图,长方形ABCD中,AB=4,BC=8,E为CD边的中点,点P、Q为BC边上两个动点,且PQ=2,当BP=时,四边形APQE的周长最小.15.如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q 分别在边OB、OA上,则MP+PQ+QN的最小值是.三.解答题(共5小题,满分45分)16.如图,在△ABC中,已知AB=AC,AB的垂直平分线交AB于点N,交AC于点M,连接MB.(1)若∠ABC=70°,则∠MBC的度数是度;(2)若AB=8cm,△MBC的周长是14cm.①求BC的长度;②若点P为直线MN上一点,请你直接写出△PBC周长的最小值.17.如图,在Rt△ABC中,∠BAC=30°,AB=2BC,E为AB边的中点,以BE为边作等边△BDE,连接AD,CD.(1)求证:△ADE≌△CDB;(2)若AC=3,在AC边上找一点H,使得BH+EH最小,并求出这个最小值.(并说明理由)18.如图,△ABC三个顶点的坐标分别为A(1,1)、B.(4,2)、C(3,4).(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为:A1,B1,C1;(2)若P为x轴上一点,则P A+PB的最小值为;(3)计算△ABC的面积.19.如图,已知∠ABC=∠ADC=90°,BC=CD,CA=CE.(1)求证:∠ACB=∠ACD;(2)过点E作ME∥AB,交AC的延长线于点M,过点M作MP⊥DC,交DC的延长线于点P.①连接PE,交AM于点N,证明AM垂直平分PE;②点O是直线AE上的动点,当MO+PO的值最小时,证明点O与点E重合.20.已知点D在△ABC外,∠BAC=90°,AB=AC,射线BD与△ABC的边AC交于点H,AE⊥BD,垂足为E,∠ABD=∠ACD.(1)如图1,求证:2DE+DC=BD;(2)如图2,已知∠ABE=25°,BE=4,点F在线段BC,且BE=BF,点M,N分别是射线BC、BD上的动点,在点M,N运动的过程中,请判断式子EM+MN+NF的值是否存在最小值,若存在,请直接写出这个最小值;若不存在,写出你的理由.参考答案一.选择题(共9小题,满分45分)1.解:连接CE交AD于点F,连接BF,∵△ABC是等边三角形,∴BF=CF,∴BF+EF=CF+EF=CE,此时BF+EF的值最小,最小值为CE,∵D、E分别是△ABC中BC、AB边的中点,∴AD=CE,∵AD=6,∴CE=6,∴BF+EF的最小值为6,故选:B.2.解:如图所示,过E作EF∥AB交CA的延长线于点F,作点A关于EF的对称点A',连接A'E和A'F,∴∠BAC=∠AFE=∠A'FE,AE=A'E,∴AE+CE=A'E+CE,由题可得,△ABC是等腰直角三角形,∴∠BAC=45°,∴∠A'FC=45°×2=90°,∵AF∥DE,EF∥AD,∴四边形ADEF是平行四边形,∴AF=DE=2,A'F=AF=2,当点C,点E,点A'在同一直线上时,AE+CE的最小值等于A'C的长,如图所示.此时,Rt△A'FC中,A'C=,∴AE+CE的最小值为,故选:B.3.解:过C作CF⊥AB交AD于E,则此时,CE+EF的值最小,且CE+EF的最小值=CF,∵△ABC为等边三角形,边长为6,∴BF=AB=6=3,∴CF=3,∴CE+EF的最小值为3,故选:C.4.解:∵△ABC是等边三角形,∴AC=BC,∠B=60°,作点M关于直线CD的对称点G,过G作GN⊥AB于N,交CD于P,则此时,MP+PN的值最小,∵∠B=60°,∠BNG=90°,∴∠G=30°,∵BN=9,∴BG=2BN=18,∴CM=CG=5,∴AC=BC=13,故选:C.5.解:在AB上取一点G,使AG=AF,∵∠CAD=∠BAD,AE=AE,∴△AEF≌△AEG(SAS),∴FE=EG,∴CE+EF=CE+EG,则最小值时CG垂直AB时,CG的长度,CG=.故选:D.6.解:作P关于OA的对称点D,作P关于OB的对称点E,连接DE交OA于M,交OB 于N,连接PM,PN,则此时△PMN的周长最小,连接OD,OE,∵P、D关于OA对称,∴OD=OP,PM=DM,同理OE=OP,PN=EN,∴OD=OE=OP=15,∵P、D关于OA对称,∴OA⊥PD,∴∠DOA=∠POA,同理∠POB=∠EOB,∴∠DOE=2∠AOB=2×30°=60°,∵OD=OE=15,∴△DOE是等边三角形,∴DE=15,即△PMN的周长是PM+MN+PN=DM+MN+EN=DE=15,故选:B.7.解:作A点关于CD的对称点F,作A点关于BC的对称点E,连接EF交CD于N,交BC于M,连接AM、AN,∵∠B=∠D=90°,∴AN=NF,AM=EM,∴△AMN的周长=AM+AN+MN=NF+MN+EM=EF,此时△AMN的周长有最小值,∵∠F AN=∠F,∠E=∠EAM,∴∠E+∠F=180°﹣∠BAD,∵∠BAD=130°,∴∠E+∠F=50°,∴∠BAM+∠F AN=50°,∴∠MAN=130°﹣50°=80°,∴∠ANM+∠AMN=180°﹣∠MAN=100°,故选:C.8.解:如图所示,连接BM,∵DE是AB的垂直平分线,∴AM=BM,∴AM+CM=BM+CM,当B,M,C在同一直线上时,AM+CM的最小值为BC的长,又∵AC=4,BC=6,∴△AMC周长的最小值=6+4=10,故选:D.9.解:如图,将点E(8,2)往左平移2个单位得到F(6,2),则EF=2=PQ,EF∥PQ,∴四边形EFPQ是平行四边形,∴FP=QE,作点F关于x轴的对称点F',连接PF',则PF'=PF,F'(6,﹣2),∴当点A、P、F在同一直线上上时,AP+PF'最小,即AP+EQ最小,∵A(0,4),F'(6,﹣2),∴直线AF'解析式:y=﹣x+4,∴P(4,0),故选:C.二.填空题(共6小题,满分30分)10.解:如图,在BA上截取BE=BN,连接CE.因为∠ABC的平分线交AC于点D,所以∠EBM=∠NBM,在△BME与△BMN中,,所以△BME≌△BMN,所以ME=MN.所以CM+MN=CM+ME≥CE.因为CM+MN有最小值.当CE是点C到直线AB的距离时,即C到直线AB的垂线段时,CE取最小值为,所以CM+MN的最小值是.故答案为.11.解:分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PC、PD.∵点P关于OA的对称点为C,关于OB的对称点为D,∴PM=CM,OP=OC,∠COA=∠POA;∵点P关于OB的对称点为D,∴PN=DN,OP=OD,∠DOB=∠POB,∴OC=OD=OP=6,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,∴△COD是等边三角形,∴CD=OC=OD=6.∵∠POC=∠POD,∴OP⊥CD,∴OQ=6×=3,∴PQ=6﹣3设MQ=x,则PM=CM=3﹣x,∴(3﹣x)2﹣x2=(6﹣3)2,解得x=6﹣9,∴MN=2MQ=12﹣18,∵S△PMN=MN×PQ,S△MON=MN×OQ,∴S四边形PMON=S△MON+S△PMN=MN×PQ+MN×OQ=MN×OP=×(12﹣18)×6=36﹣54.故答案为36﹣54.12.解:如图,作M关于OB的对称点M′,N关于OA的对称点N′,连接M′N′交OA于Q,交OB于P,则MP+PQ+QN最小,∴∠OPM=∠OPM′=∠NPQ,∠OQP=∠AQN′=∠AQN,∴∠QPN=(180°﹣α)=∠AOB+∠MQP=20°+(180°﹣β),∴180°﹣α=40°+(180°﹣β),∴β﹣α=40°,故答案为40°.13.解:如图1所示:作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ 的周长最小,∵AD=A′D=3,BE=BE′=1,∴AA′=6,AE′=4.∵DQ∥AE′,D是AA′的中点,∴DQ是△AA′E′的中位线,∴DQ=AE′=2;CQ=DC﹣DQ=3﹣2=1,∵BP∥AA′,∴=,即=,BP=,CP=BC﹣BP=3﹣=,S四边形AEPQ=S正方形ABCD﹣S△ADQ﹣S△PCQ﹣S BEP=9﹣AD•DQ﹣CQ•CP﹣BE•BP=9﹣×3×2﹣×1×﹣×1×=.故答案为:.14.解:如图,在AD上截取线段AF=PQ=2,作F点关于BC的对称点G,连接EG与BC交于一点即为Q点,过A点作FQ的平行线交BC于一点,即为P点,过G点作BC 的平行线交DC的延长线于H点.∵GH=DF=6,EH=2+4=6,∠H=90°,∴∠GEH=45°,∴∠CEQ=45°,设BP=x,则CQ=BC﹣BP﹣PQ=8﹣x﹣2=6﹣x,在△CQE中,∵∠QCE=90°,∠CEQ=45°,∴CQ=EC,∴6﹣x=2,解得x=4.故答案为4.15.解:作M关于OB的对称点M′,作N关于OA的对称点N′,连接M′N′,即为MP+PQ+QN的最小值.根据轴对称的定义可知:∠N′OQ=∠M′OB=30°,∠ONN′=60°,∴△ONN′为等边三角形,△OMM′为等边三角形,∴∠N′OM′=90°,∴在Rt△M′ON′中,M′N′==.故答案为.三.解答题(共5小题,满分45分)16.解:(1)∵AB=AC,∴∠C=∠ABC=70°,∴∠A=40°,∵AB的垂直平分线交AB于点N,∴MA=MB,∴∠MBA=∠A=40°,∴∠MBC=30°,故答案为:30;(2)①∵MN是AB的垂直平分线,∴AM=BM,∴△BCM的周长=BM+CM+BC=AM+MC+BC=AC+BC,∵AB=AC=8cm,△MBC的周长是14cm,∴BC=14﹣8=6(cm);②当P与M重合时,△PBC的周长最小.理由:∵PB+PC=P A+PC,P A+PC≥AC,∴当P与M重合时,P A+PC=AC,此时PB+PC最小值等于AC的长,∴△PBC的周长最小值=AC+BC=8+6=14(cm).17.(1)证明:在Rt△ABC中,∠BAC=30°,AB=2BC,E为AB边的中点,∴BC=EA,∠ABC=60°,∵△DEB为等边三角形,∴DB=DE,∠DEB=∠DBE=60°,∴∠DEA=120°,∠DBC=120°,∴∠DEA=∠DBC,在△ADE与△CDB中,,∴△ADE≌△CDB(SAS);(2)如图,作点E关于直线AC点E',连接BE'交AC于点H,则点H即为符合条件的点,由作图可知:EH=HE',AE'=AE,∠E'AC=∠BAC=30°,∠ABC=60°,∴∠EAE'=∠ABC=60°,∴△EAE'为等边三角形,∴EE'=EA=AE'=BC=AB,∵AB=BA,∴△ABE'≌△BAC(SAS);∴BE'=AC=3,∴BH+EH的最小值为3.18.解:(1)如图所示,△A1B1C1即为所求,由图知,A1的坐标为(﹣1,1)、B1的坐标为(﹣4,2)、C1的坐标为(﹣3,4);(2)如图所示:作出点A的对称点,连接A'B,则A'B与x轴的交点即是点P的位置,则P A+PB的最小值=A′B,∵A′B==3,∴P A+PB的最小值为3;(3)△ABC的面积=3×3﹣×3×1﹣×1×2﹣×2×3=,故答案为:(﹣1,1),(﹣4,2),(﹣3,4),3.19.证明:(1)∵∠ABC=∠ADC=90°,BC=CD,AC=AC,∴Rt△ABC≌Rt△ADC(HL),∴∠ACB=∠ACD;(2)①∵Rt△ABC≌Rt△ADC,∴∠BAC=∠CAD,∵CA=CE,∴∠CAE=∠CEA,∵∠EBA=90°,∴∠BEA=∠BAC=∠CAE=30°,∵PD⊥AE,MP⊥PD,∴AE∥MP,∴∠PMC=∠MAE=30°,∵ME∥AB,∴∠MEB=∠ABE=90°,∴∠MEA=90°+30°=120°,∵∠MAE=30°,∴∠EMA=30°,∵CP⊥MP,CE⊥ME,∠MCP=∠MCE=60°,∴△NEC≌△NPC(SAS),∴EN=PN,∴N是EP的中点,NC⊥PE,∴AM垂直平分PE;②延长PD、ME交于Q点,由①知,∠BEA=30°,∠MEB=90°,∴∠MEA=120°,∴∠DEQ=60°,∵PD⊥AE,∴∠EDQ=90°,∴∠EQD=30°,∵∠CPN=30°,∴∠EPD=∠DQE,∴PE=EQ,∴ME+PE=QE+ME≥MQ,此时ME+PE的值最小,∵点O是直线AE上的动点,∴当MO+PO的值最小时,E点与O点重合.20.(1)证明:如图1,作AF⊥CD于F,在△ABE和△ACF中,,∴△ABE≌△ACF(AAS),∴BE=CF,AE=AF,∵∠ABD=∠ACD,∠AHB=∠CHB,∴∠BDH=∠BAC=90°,∴∠AED=∠F=∠ADF=90°,∴四边形AEDF是矩形,∴矩形AEDF是正方形,∴DE=DF,∴BD=BE+DE=CF+DE=CD+DF+DE=CD+2DE;(2)如图2,作点E关于BC的对称点V,作点F关于BD的对称点R,连接RV,交BD于N,BC于M,∴EM=MV,NF=NR,∠RBN=∠CBD=∠ABC﹣∠ABD=20°,∠VBF=∠CBD=20°,BR=BF=BE=4,BV=BE=4,∴∠RBV=60°,∴△BRV是等边三角形,∴RV=BR=4,此时(EM+MN+NF)最小=MV+MN+RN=RV=4.。
人教版八年级上册数学课题学习最短路径问题同步训练

人教版八年级上册数学13.4 课题学习最短路径问题同步训练一、单选题1.如图,直线m表示一条河,点M、N表示两个村庄,计划在m上的某处修建一个水泵向两个村庄供水.在下面四种铺设管道的方案中,所需管道最短的方案是(图中实线表示铺设的管道)()A.B.C.D.2.如图,等边△ABC的边长为8,AD是BC边上的中线,E是AD边上的动点,F是AB 边上一点,若BF=4,当BE+EF取得最小值时,则△EBC的度数为()A.15°B.25°C.30°D.45°3.如图,直线1l,2l表示一条河的两岸,且1l∥2l.现要在这条河上建一座桥(桥与河的两岸相互垂直),使得从村庄P经桥过河到村庄Q的路程最短,应该选择路线()A.B.C .D .4.如图所示,有三条道路围成Rt ABC ∆,其中1000m BC =,一个人从B 处出发沿着BC 行走了700m ,到达D 处,AD 恰为CAB ∠的平分线,则此时这个人到AB 的最短距离为( )A .1000mB .700mC .300mD .1700m5.如图,∠AOB =60°,P 是∠AOB 角平分线上一点,PD ⊥AO ,垂足为D ,点M 是OP 的中点,且DM =4,如果点C 是射线OB 上一个动点,则PC 的最小值是( )A .8B .6C .4D .26.如图,在Rt ABC 中,90C ∠=︒,30A ∠=︒,7AB =,BD 是ABC 的角平分线,点P ,点N 分别是BD ,AC 边上的动点,点M 在BC 上,且1BM=,则PM PN +的最小值为( )A .3B .C .3.5D .7.如图,若△AOB=44°,P 为△AOB 内一定点,点M 在OA 上,点N 在OB 上,当△PMN的周长取最小值时,△MPN 的度数为( )A .82°B .84°C .88°D .92°8.如图,在△ABC 中,AB =AC =6cm ,AD ,CE 是△ABC 的两条中线,CE =4cm ,P 是AD 上的一个动点,则BP +EP 的最小值是( )A .3cmB .4cmC .6cmD .10cm二、填空题9.如图,已知ABC ,直线a AC ⊥于点D ,且AD CD =,点P 是直线a 上一动点,连接PB ,PC ,若5AB =,6AC =,3BC =,则PBC 周长的最小值是______.10.如图,在△ABC 中,AB =6,AC =9,EF 垂直平分线段BC ,P 是直线EF 上的任意一点,则△ABP 周长的最小值是______.11.如图,点P 是△AOB 内任意一点,OP =5cm ,点M 、N 分别是OB 、OA 边上的点,当△PMN 周长的最小值是5cm 时,则△AOB = ____________ .12.如图,等腰ABC的底边BC的长是6cm,面积是215cm,腰AB的垂直平分线MN+交AC于点N,垂足为M,若D为BC边上的一动点,P为MN上的一动点,求BP DP 的最小值_________.OP=,点M和点N分别是射线OA和射线OB 13.如图,点P是AOB∠内任意一点,3cm上的动点,30∠=︒,则PMN周长的最小值是______.AOB14.如图,正△ABC的边长为2,过点B的直线l△AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是_____.15.如图,将等边ABC折叠,使点B恰好落在AC边上的点D处,折痕为EF,O为折痕EF上的动点,若AD=2,AC=6,则OCD的周长最小值为______.16.如图,在四边形ABCD 中,AD △CD ,AB △BC ,△DAB =130°,点M ,N 分别是边BC ,CD 上两个动点,当△AMN 的周长最小时,△MAN 的度数为______.三、解答题17.如图,要在街道旁修建一个奶站,向居民区,A B 提供牛奶,牛奶站应建在什么地方,才能使,A B 到它的距离之和最短,作图并说明.18.如图,已知()3,4A ,()1,2B ,()5,1C .(1)作ABC 关于x 轴对称的111A B C △;(2)在x 轴上找一点P 使得PC PB +最小,画出点P 所在的位置;(3)求111A B C △的面积.19.如图,在平面直角坐标系中,ABC ∆在坐标系中A (1,1),B (4,2),C (3,4).(1)在图中画出ABC ∆关于x 轴的对称图形111A B C ∆,并分别写出对应点A 1、B 1、C 1的坐标. (2)求111A B C S ∆.(3)在y 轴上是否存在一点p ,使得AP +CP 最小,若存在,请在图中描出点P ,若不存在请说明理由.20.(1)唐朝诗人李顾的诗《古从军行》开头两句:“白日登山望烽火,黄昏饮马傍交河”,诗中隐含着一个有趣的数学问题:如图1所示,诗中大意是将军从山脚下的A 点出发,带着马走到河边P 点饮水后,再回到B 点宿营,请问将军怎样走才能使总路程最短?请你通过画图,在图中找出P 点,使PA PB +的值最小,不说明理由;(2)实践应用1,如图2,点P 为MON ∠内一点,请在射线OM 、ON 上分别找到两点A 、B ,使PAB △的周长最小,不说明理由;(3)实践应用2:如图3,在ABC 中,6AC =,8BC =,10AB =,90ACB ∠=︒,AD 平分BAC ∠,M 、N 分别是AD 、AC 边上的动点,求CM MN +的最小值.答案第1页,共1页 参考答案:1.D2.C3.C4.C5.C6.A7.D8.B9.810.1511.30°12.5cm13.314.415.1016.80°18. (3)519.(1) A 1(1,-1),B 1(4,-2)C 1(3,-4)(2)3.5(3)存在,20.(3)CM MN 的最小值为245。
13.4最短路径问题 同步练习人教新版八年级上册

2021-2022学年人教新版八年级上学期《13.4最短路径问题》同步练习一.选择题(共7小题)1.A,B,C三个车站在东西方向笔直的一条公路上,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在()A.在A的左侧B.在AB之间C.在BC之间D.B处2.如图,直线m表示一条河,M,N表示两个村庄,欲在m上的某处修建一个给水站,向两个村庄供水,现有如图所示的四种铺设管道的方案,图中实线表示铺设的管道,则所需管道最短的方案是()A.B.C.D.3.如图,在△ABC中,∠ACB=90°,以AC为底边在△ABC外作等腰△ACD,过点D作∠ADC 的平分线分别交AB,AC于点E,F.若AC=12,BC=5,△ABC的周长为30,点P是直线DE上的一个动点,则△PBC周长的最小值为()A.15 B.17 C.18 D.204.点A,B均在由边长为1的相同小正方形组成的网格的格点上,建立平面直角坐标系如图所示,若P是x轴上使得|PA−PB|的值最大的点,Q是y轴上使得QA+QB的值最小的点,则OP+OQ=( )A.72B.4 C.143D.55.如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点M为线段EF上一动点,则△CDM周长的最小值为()A.6 B.8 C.10 D.126.如图,∠AOB=30°,∠AOB内有一定点P,且OP=12,在OA上有一动点Q,OB上有一动点R.若△PQR周长最小,则最小周长是()A.6 B.12 C.16 D.207.如图,在直角坐标系中,点A、B的坐标分别为(1,5)和(4,0),点C是y轴上的一个动点,且A、B、C三点不再同一条直线上,当△ABC的周长最小时,点C的坐标是()A.(0,1)B.(0,2)C.(0,3)D.(0,4)二.填空题(共4小题)8.如图,在等边△ABC中,AB=6,N为线段AB上的任意一点,∠BAC的平分线交BC于点D,M是AD 上的动点,连结BM、MN,则BM+MN的最小值是________.9.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是米.10.如图,在锐角三角形ABC中,AB=4,△ABC的面积为8,BD平分∠ABC.若M、N分别是BD、BC上的动点,则CM+MN的最小值是.11.在平面直角坐标系中,已知A(1,1)B(2,3),C点在x轴上且BC﹣AC最大,则C点的坐标为.三.解答题(共3小题)12.如图,已知A,B在直线l的同侧,在直线l上求一点P,使PA+PB最小.13.河的两岸成平行线,A,B是位于河两岸的两个车间(如图),要在河上造一座桥,使桥垂直于河岸,并且使A,B间的路程最短确定桥的位置的方法是:作从A到河岸的垂线,分别交河岸PQ,MN于F,G.在AG上取AE=FG,连接EB,EB交MN于D.在D处作到对岸的垂线DC,垂足为C,那么DC就是造桥的位置.请说出桥造在CD位置时路程最短的理由,也就是(AC+CD+DB)最短的理由.14.请阅读下列材料:问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.小明的思路是:如图2所示,先作点A关于直线l的对称点A′,使点A′,B分别位于直线l的两侧,再连接A′B,根据“两点之间线段最短”可知A′B与直线l的交点P即为所求.请你参考小明同学的思路,探究并解决下列问题:(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP =1,AC=1,PD=2,直接写出AP+BP的值;(2)将(1)中的条件“AC=1”去掉,换成“BD=4﹣AC”,其它条件不变,直接写出此时AP+BP 的值;(3)请结合图形,求的最小值.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路径问题同步练习
题一
GE GROUP system office room 【GEIHUA16H-GEIHUA GEIHUA8Q8-
知识点:
1.最短路径问题
(1)求直线异侧的两点与直线上一点所连线段的和最小的问题,只要连接这两点,与直线的交点即为所求.
(2)求直线同侧的两点与直线上一点所连线段的和最小的问题,只要找到其中一个点关于这条直线的对称点,连接对称点与另一个点,则与该直线的交点即为所求.
2.运用轴对称解决距离最短问题
运用轴对称及两点之间线段最短的性质,将所求线段之和转化为一条线段的长,是解决距离之和最小问题的基本思路,不论题目如何变化,运用时要抓住直线同旁有两点,这两点到直线上某点的距离和最小这个核心,所有作法都相同.3.利用平移确定最短路径选址
解决连接河两岸的两个点的最短路径问题时,可以通过平移河岸的方法使河的宽度变为零,转化为求直线异侧的两点到直线上一点所连线段的和最小的问题.
同步练习:
1.如图所示,点A,B分别是直线l异侧的两个点,在l上找一个点C,使CA +CB最短,这时点C是直线l与AB的交点.
2.如图所示,点A ,B 分别是直线l 同侧的两个点,在l 上找一个点C ,使CA +CB 最短,
3..在图中直线l 上找到一点M ,使它到A ,B 两点的距离和最小.
4. 如图,小河边有两个村庄A ,B ,要在河边建一自来水厂向A 村与B 村供水.
(1)若要使厂部到A ,B 村的距离相等,则应选择在哪建厂?
(2)若要使厂部到A ,B 两村的水管最短,应建在什么地方?
5. 如图,从A 地到B 地经过一条小河(河岸平行),今欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从A 地到B 地的路程最短?
6.(实际应用题)茅坪民族中学八(2)班举行文艺晚会,桌子摆成如图a 所示两直排(图中的AO ,BO ),AO 桌面上摆满了橘子,OB 桌面上摆满了糖果,站在C 处的
学生小明先拿橘子再拿糖果,然后到
D 处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短? 7.如图所示,A ,B 两点在直线l 的两侧,在l 上找一点C ,使点C 到点A 、B 的距离之差最大.
参考答案:
1.
A B
l
2.这时先作点B关于直线l的对称点B′,则点C是直线l与AB′的交点.
为了证明点C的位置即为所求,我们不妨在直线上另外任取一点C′,连接AC′,BC′,B′C′,证明AC+CB<AC′+C′B.如下:
证明:由作图可知,点B和B′关于直线l对称,
所以直线l是线段BB′的垂直平分线.
因为点C与C′在直线l上,
所以BC=B′C,BC′=B′C′.
在△AB′C′中,AB′<AC′+B′C′,
所以AC+B′C<AC′+B′C′,
所以AC+BC<AC′+C′B.
3. 解:如图所示:(1)作点B关于直线l的对称点B′;
(2)连接AB′交直线l于点M.
(3)则点M即为所求的点.
4.解:(1)如图1,取线段AB的中点G,过中点G画AB的垂线,交EF于P,
则P到A,B的距离相等.也可分别以A、B为圆心,以大于1
2
AB为半径画弧,两弧
交于两点,过这两点作直线,与EF的交点P即为所求.
(2)如图2,画出点A关于河岸EF的对称点A′,连接A′B交EF于P,则P 到A,B的距离和最短.
5.解:(1)如图2,过点A作AC垂直于河岸,且使AC等于河宽.
(2)连接BC与河岸的一边交于点N.
(3)过点N作河岸的垂线交另一条河岸于点M.
则MN为所建的桥的位置.
6.解:如图b.
(1)作C点关于OA的对称点C1,作D点关于OB的对称点D1,(2)连接C1D1,分别交OA,OB于P,Q,那么小明沿C→P→Q→D的路线行走,所走的总路程最短.
7.解:如图所示,以直线l为对称轴,作点A关于直线l的对称点A′,A′B 的连线交l于点C,则点C即为所求.理由:在直线l上任找一点C′(异于点C),连接CA,C′A,C′A′,C′B.因为点A,A′关于直线l对称,所以l为线段AA′的垂直平分线,则有CA=CA′,所以CA-CB=CA′-CB=A′B.又因为点C′在l上,所以C′A=C′A′.在△A′BC′中,C′A-C′B=C′A′-C′B<A′B,所以C′A′-C′B<CA-CB.
点拨:根据轴对称的性质、利用三角形的三边关系,通过比较来说明最值问题
是常用的一种方法.。
