简单的旋转作图_习题精选
旋转作图题训练题

图1AO图2C 1A 1A【前言】从2013年旋转作图分值为7分,重要性加强了。
这个题的特点是:人人都能动手做,得满分的确不多。
变化是:加入了尺规作图的相关知识,这是课本上所没有的,要加强训练。
主要考什么:图形的平移、对称、旋转(三大变换)作图,加入点的轨迹,引入计算,常见考察弧长与扇形面积的问题,考察图形的变化规律问题。
确保本题满分条件:耐心(慢慢画)+细心(仔细看) 【2013元调】△ABC 为等边三角形,点O 是边AB 的延长线上一点(如图1),以点O 为中心,将△ABC 按顺时针方向旋转一定角度得到111A B C V(1)若旋转后的图形如图2所示,将111A B C V 以点O 为中心,按顺时针方向再次旋转同样的角度得到222A B C V ,在图2中用尺规作出222A B C V ,请保留作图痕迹,不要求写作法:(2)若将△ABC 按顺时针方向旋转到111A B C V 的旋转角度为α(0°<α<360°)且AC ∥11B C ,直接写出旋转角度α的值为_____________ 分析:(1)关键在于尺规作图得到同样的旋转角度 ①以O 为圆心,OA 为半径作圆;②以1A 为圆心,1AA 为半径作圆,交圆O 于点2A ,连接2OA ,从而得到了相同的旋转角,原因是△1AOA ≌△12A OA (SSS );③以O 为圆心,OB 为半径作圆,与2OA 的交点就是2B ;④分别以2B 、2A 为圆心,22A B 的长为半径作弧,二弧的交点就是2C (2)很容易得到答案60度,很容易漏掉240度得到111A B C V 后,构造中心对称,得到222A B C V 肯定也是符合条件的。
【2013四调】如图,在9×7的小正方形网格中,△ABC 的顶点A 、B 、C 在网格的格点上,将△ABC 向左平移3个单位,再向上平移3个单位得到△A′B′C′,将△ABC 按一定规律顺次旋转,第1次,将△ABC 绕点B 顺时针旋转90°得到△11A BC ,第2次,再将△11A BC 绕点1A 顺时针旋转90°得到△112A B C ,第3次,将△112A B C 绕点2C 顺时针旋转90°得到△222A B C ,第4次,将△222A B C 绕点2B 顺时针旋转90°得到△323A B C ,依次旋转下去。
第13课时 简单的旋转作图

简单的旋转作图练习题【典型例题】1、ABC 平移后,A 点移到A 1点,请作出平移后的图形,并将此图形绕点C 1逆时针旋转900,再作出所得图形。
2. 如图,将ΔABC 绕其顶点A 按逆时针方向旋转900,作出旋转后的图形. (不写作图步骤,要求线条清晰,表示清楚)3.△ABC 在方格纸中的位置如图所示,点A,B,C,O 都在格点上, (1)将△ABC 向右平移5个单位得到△A 1B 1C 1,请画出△A 1B 1C 1;(2)将△ABC 绕点O 顺时针旋转90度得到△A 2B 2C 2,请画出△A 2B 2C 2.4.如图,按要求画出图形.(1)将△ABC 向下平移五格后的△111A B C . (2)再画出△ABC 绕点O 旋转180º的△222A B C 。
ABCABC【巩固练习】1.如图1,若线段AB 是由线段CD 平移得到的,则线段AB 与CD 的关系是 且 . 2.小明把自己的左手手印和右手手印按在同一张白纸上,左手手印 (填能或不能) 通过平移与右手手印完全重合.3.正方形被其对角线分得的四个全等的等腰直角三角形, (填能或不能)通过平移完全重合在一起.4.在图形的平移、旋转、轴对称变换中,其相同的性质是 .5.如果甲图向上平移2个单位得到乙图,乙图向左平移2个单位得到丙图,丙图向下平移2个单位得到丁图,那么丁图 向 平移个单位可以得到甲图.6.边长为4cm 的正方形ABCD 绕它的顶点A 旋转180°,顶点B 所经过的路线长为 cm . 7.9点30分,时钟的时针和分针的夹角是 .8.如果图形b 可看作是图形a 经过平移得到的,也可看作是图形a 经过旋转得到的,试写出一个适合题意的图形a 为 (用图或用文字叙述均可).9.供行人穿越马路的“横道线”是画在马路面上的一系列互相 的白色线条.由其中一条白线,通过 可以得到其他白线. 10.如图3,P 是正△ABC 内的一点,若将△P AB 绕点A 逆时针旋转到△P ′AC ,则∠P AP ′的度数为________.二、选择题11.以下现象:① 直升机的螺旋桨的运动;② 打气筒打气时,活塞的运动;③ 钟摆的摆动;④ 传送带上,瓶装饮料的移动.其中属于平移的是( ) A .①② B .①③ C .②③ D .②④ 12.如果同一平面的两个图形通过平移,不论其起始位置如何,总能完全重合,则这两个图形是( ) A .两个点 B .两个半径相等的圆 C .两个点或两个半径相等的圆 D .两个全等的多边形 13.如下列所示的图形中,不能通过基本图形平移得到的是( )A .B . C. D.ABC · O P′PC BA图 714.将图2的图形按顺时针方向旋转90°后得到的图形是()15.下列所示的图形中,仅由图3通过平移得到的是()A.B.C.D.16.如图4,正△ODE可以看作由正△OAB绕点O逆时针依次旋转60°得到的,则旋转的次数是()A.3次B.4次C.5次D.6次17.如图5,△ABC由△A′B′C′绕O点旋转180°而得到,则下列结论不成立的是()A.点A与点A′是对应点B.BO=B′OC.∠ACB=∠C′A′B′D.AB∥A′B′18.将一图形绕着点O顺时针方向旋转70°后,再绕着点O逆时针方向旋转120°,这时如果要使图形回到原来的位置,需要将图形绕着点O什么方向旋转的角度是()A.顺时针方向50°B.逆时针方向50°C.顺时针方向190°D.逆时针方向190°三、解答题19.如图7是类似于日本“三菱”汽车的标志的图案,它可以看作是由什么“基本图案”通过怎样旋转得到的?每次旋转了多少度?20.用平移的知识分析如图9所示的两个图案的形成过程.21.如图10,△ABC 的∠BAC =120°,AB =AC ,∠DAE =60°,把△AEC 绕着点A 旋转到△AMB 的位置.(1)图中有哪些等角(请找出四组)?有哪些等线段? (2)图中有哪些全等三角形(请找出两组)?试说明理由.22. 如图1中的△ABC 是等腰直角三角形,BC 是斜边,P 为△ABC 内一点,将△ABP 绕点A 逆时针旋转后与△ABP /重合,如果AP=3,那么线段PP /的长等于多少?.23.如图,甲、乙两个单位分别位于一条封闭式街道的两旁,现准备合作修建一座过街天桥.问:(1)桥建在何处才能使由甲到乙的路线最短?(注:桥必须与街道垂直).(2)桥建在何处才能使甲、乙到桥的距离相等?24.如图,在1010⨯正方形网格中,每个小正方形的边长均为1个单位. (1)作ABC △关于点P 的对称图形A B C '''△。
旋转 典型例题(精品解析)

典型例题一例 如图,以点O 为旋转中心,将ABC ∆顺时针旋转45°,画出图形.分析 当旋转中心O 在图形之外时,O 是一个孤立的点,没有从O 出发的线段或射线作参照,就无法确定旋转的角度,因此,首先还须将O 与图形上的某点(或某些点)连结起来.解 如图,连结OA 、OB 、OC .将这三条线段绕O 点分别顺时针旋转45°,得C O B O A O '''、、,则C B A '''∆就是按题目要求得到的旋转后的图形.说明: 图形旋转后的效果有时不像平移那样直观,画图出现错误时可能不易发现,因此画图时要特别细心.典型例题二例 如图,正方形ABCD 中,E 是正方形内的一点,把AED ∆绕着点A 按逆时针旋转90°,画出旋转后的三角形,并回答:(1)图中有哪些等线段和等角?(2)哪两个三角形形状、大小都一样?分析 一个图形绕它的对称中心旋转一个角度后,图形中的每一点都绕旋转中心旋转了同样大小的角度.本例中可以发现AD 旋转90°后,刚好与AB 重合,于是将AE 旋转90°到E A '的位置,使︒='∠90E EA ,确定点E ',连E B ',则E AB '∆就是ADE ∆按要求旋转的三角形.(1)(2)中,根据图形旋转的特征,图形从一个位置旋转到另一个位置,形状和大小都没有改变,可确定相等的线段、相等的角以及形状相同的三角形.答案 (1)相等的线段有:E B DE E A AE CD BC AB AD '='====,,.相等的角有:E E E AB ADE E BA DAE '∠=∠'∠=∠'∠=∠,,.(2)ADE ∆与E AB '∆的形状和大小都一样.典型例题三例 如图,把一块砖ABCD 直立于地面上,然后将其轻轻推倒.在这个过程中,A 点保持不动,四边形ABCD 旋转到B C D A '''位置.(1)指出在这个过程中的旋转中心,并说出旋转的角度是多大?(2)指出图中的对应线段.分析(1)由于四边形B C D A '''是由四边形ADCB 旋转得到的,A 点保持不动,所以A 是旋转中心.又由于D A B ',,三点在一条直线上,且AB AD ⊥,所以旋转的角度是90°.(2)由于D C B A ,,,的对应点分别是D C B A ''',,,,所以不难找出图中的对应线段.答案 (1)A 是旋转中心,旋转的角度是90°.(2)CD BC AD AB ,,,的对应线段分别是D C C B D A B A '''''',,,.典型例题四例 (1)把长方形ABCD 绕着顶点A 逆时针旋转60°.如图.(2)把长方形ABCD 绕着长方形内一点P 逆时针旋转60°.解 (1)①AB 绕A 点逆时针旋转60°到B A '位置,.,60AB B A AB B ='︒='∠②连结AC ,作.,60AC C A AC C ='︒='∠③作.,60AD D A AD D ='︒='∠连结B C C D '''',,则四边形D C B A '''是四边形ABCD 逆时针旋转60°得到的图形.(2)①连结AP ,作︒='∠60PA A ,使.AP P A ='②用同样的方法作出D C B '''、、,连结A D D C C B B A ''''''''、、、.则四边形D C B A ''''是四边形ABCD 绕P 点逆时针旋转60°得到的图形.典型例题五例 画一个三角形,使通过这个三角形的旋转得到一个正六边形,指出这是一个什么三角形、旋转中心和每次旋转的角度、需要旋转多少次才能完成这个图形.分析 这个题目给了我们一个由三角形制作正多边形的方法.解 给出的三角形应该是正三角形,可以以它的任一个顶点为旋转中心,每次旋转60°,旋转六次便可完成这个图形.说明: 利用这个方法,可以画出任意边数的正多边形.请想一下,画正n 边形应该使用什么样的三角形?怎样旋转呢?典型例题六例 把8个同样大小的等腰梯形拼成如图所示的图形.(1)找出它的旋转中心.(2)当它旋转多少度后与自身重合.分析 (1)从图中可以看出,这八个等腰梯形的八个顶点H G F E D C B A ,,,,,,,恰好在同一个圆周上,该图形的旋转中心就是各顶点所在圆的圆心.因此只要把任意两腰延长,它们的延长线的交点就是旋转中心.(2)这八个等腰梯形将圆周八等分,因此,它只要旋转︒=︒458360后就能与自身重合. 答案 (1)任意延长任何梯形的两腰,这两腰延长线的交点就是旋转中心.(2)旋转的角度是45°.典型例题七例 找出下列图形中的旋转中心,旋转角以及旋转的“基本图案”。
画旋转练习题

画旋转练习题旋转是数学中的一种基本变换,也是美术创作中常用的技巧之一。
通过旋转,可以改变图形的方向和位置,创造出各种有趣的效果。
本文将介绍一些旋转练习题,帮助读者熟悉旋转变换,并提高绘画技巧。
1. 旋转练习题 - 画旋转平移图形在纸上画一个正方形,边长为10cm。
以正方形的中心点为旋转中心,逆时针旋转90度,并画出旋转后的图形。
解析:首先,确定旋转中心,在正方形的中心画一个小圆点。
然后,以这个中心点为基准逆时针旋转90度,并用铅笔画出旋转后的图形。
确保旋转后的正方形四个顶点与原来正方形的对应顶点连线相等,即边长为10cm。
2. 旋转练习题 - 画旋转图形画一个等边三角形,边长为8cm。
以三角形的顶点为旋转中心,顺时针旋转60度,并画出旋转后的图形。
解析:首先,画一个等边三角形,边长为8cm,注意保持三条边相等。
然后,在三角形的顶点处画一个小圆点作为旋转中心。
以这个中心点为基准顺时针旋转60度,并用铅笔画出旋转后的图形。
确保旋转后的三条边与原来等边三角形的对应边相等,即边长为8cm。
3. 旋转练习题 - 画旋转对称图形画一个心形图案,并以心形的中心为旋转中心,逆时针旋转180度,并画出旋转后的图形。
解析:首先,画一个心形图案,注意两个半圆的半径相等,两个半圆的圆心到心形的交点的距离也相等。
然后,在心形的中心处画一个小圆点作为旋转中心。
以这个中心点为基准逆时针旋转180度,并用铅笔画出旋转后的图形。
确保旋转后的图形与原来心形图案的对称轴重合。
通过以上三个练习题,读者可以熟悉和掌握旋转变换的基本操作和技巧。
在练习过程中,可以通过使用尺子和量角器来保证图形的准确性。
此外,还可以尝试使用不同的颜色和纸张来增加绘画作品的艺术感。
希望读者通过这些练习题,能够在绘画中灵活运用旋转变换,创造出更丰富多样的作品。
旋转练习题集锦(含答案)

旋转练习题集锦(含答案)一、作图题1、如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个和一点O,的顶点和点O均与小正方形的顶点重合.(1)在方格纸中,将△ABC向下平移5个单位长度得到,请画出;(2)在方格纸中,将△ABC绕点O旋转180°得到,请画出。
二、简答题2、如图,已知的三个顶点的坐标分别为、、.(1)请直接写出点关于轴对称的点的坐标;(2)将绕坐标原点逆时针旋转90°.画出图形,直接写出点的对应点的坐标;(3)请直接写出:以为顶点的平行四边形的第四个顶点的坐标.三、选择题3、如图所示,在平面直角坐标系中,点A、B的坐标分别为(2,0)和(2,0).月牙①绕点B顺时针旋转900得到月牙②,则点A的对应点A’的坐标为【】(A)(2,2)(B)(2,4)(C)(4,2) (D)(1,2)4、将图按顺时针方向旋转90°后得到的是( )5、在方格纸(每个小方格都是边长为1个单位长度的正方形)中,我们把每个小正方形的顶点称为格点,以格点为顶点的图形称为格点图形.如上图中的△ABC称为格点△ABC.现将图中△ABC绕点A顺时针旋转,并将其边长扩大为原来的2倍,则变形后点B的对应点所在的位置是()A.甲 B.乙C.丙 D.丁6、下图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合()A.60° B.90° C.120°D.180°7、在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是 ( )8、下面四个图案中,是旋转对称图形的是()A.B.C.D.9、下列运动是属于旋转的是( )A.电梯的上下运动 B.火车的运动C.钟表中分针的运动 D.升国旗时,国旗的徐徐运动10、如图所示,将其中的图甲变成图乙,可经过的变换是( )A.旋转、平移 B.平移、对称 C.旋转、对称 D.不能确定11、如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是()A.72° B.108° C.144° D.216°12、如图,D是等腰Rt△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD’的位置,则∠ADD’的度数是( )A.25° B.30° C.35°D.45°13、如图可以看作是一个等腰直角三角形旋转若干次而成的,则每次旋转的度数最小是( )A.90° B.60° C.45°D.30°14、如图,经过平移或旋转不可能将图甲变为图乙的是()15、下列图形中,既是中心对称图形,又是轴对称图形的是()A.菱形B.等边三角形 C.等腰三角形D.平行四边形16、如图所示,可由一个“基本图案”旋转l80°而形成的是()A B CD17、已知,将点A1(6,1)向左平移4个单位到达点A2的位置,再向上平移3个单位到达点A3的位置,△A1A2A3绕点A2逆时针方向旋转900,则旋转湖A3的坐标为()A.(-2,1) B.(1,1) C.(-1,1) D.(5,1)18、下图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,、、B在同一直线上,则∠CBD的度数()A.不能确定B.大于C.小于 D.等于四、计算题19、将一张透明的平行四边形胶片沿对角线剪开,得到图①中的两张三角形胶片和.将这两张三角形胶片的顶点与顶点重合,把绕点顺时针方向旋转,这时与相交于点.(1)当旋转至如图②位置,点,在同一直线上时,与的数量关系是.(2)当继续旋转至如图③位置时,(1)中的结论还成立吗?请说明理由.(3)在图③中,连接,探索与之间有怎样的位置关系,并证明.20、如图所示,左边方格纸中每个正方形的边长均为a,右边方格纸中每个正方形的边长均为b,将左边方格纸中的图形顺时针旋转90°,并按b:a的比例画在右边方格纸中.21、点B.C.E在同一直线上,点A.D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
简单的旋转作图 习题精选

3.4简单的旋转作图习题精选一1.如图,把绕O点逆时针旋转120°、240°,试一试画出的图形是怎样的图形.2.如图,画出长方形ABCD绕点C顺时针旋转120°所得到的图形.3.如图,画出绕点O顺时针旋转100°所得到的图形.4.如图,你能把圆O绕P点顺时针旋转90°吗?5.圈出图中的“基本图案”,说明这些美丽的图案都是怎样旋转得到的?6.图中的六边形中“基本图案”是怎样旋转而成下列图形的?7.把下面几个图形中左上角的图案绕着中心旋转90°,180°,270°,画出所得图案。
8.观察图,圈中其中的“基本图案”,说明它是怎样由“基本图案”旋转而成的.参考答案1.2.3.如下图4.如上图5.(1)一个花瓣顺时针旋转90°,180°,270°(2)螺旋桨的一半旋转180°(3)雪花顺时针旋转60°,120°,180°,240°,300°(4)一个猴子旋转180°(5)一个熊猫旋转90°,180°,270°(6)一只鸽子旋转180°画图:略.6.(1)(2)(3)中“基本图案”分别旋转60°,120°,180°,240°,300°(4)中“基本图案”旋转120°,240°.7.略.8.把“基本图案”顺时针旋转60°,120°,180°,240°,300°而成.二1.在图书、杂志、报纸、包装盒、广告单等处寻找几个旋转对称图形的实例.2.如图,非等腰三角板原在ABC的位置上,旋转后到了的位置上,请指出旋转中心、旋转角度和旋转方向.3.已知(如图),请画出以C点为旋转中心,旋转角为30°,(1)按顺时针方向旋转后的图形;(2)按逆时针方向旋转后的图形.4.下列各图形围绕自己的旋转中心最低需要旋转多少度之后,能够与它自身相重合?5.如图,下列各图形,不是旋转对称图形的是()6.如图,正方形ABCD,画出绕顶点C顺时针旋转90°后的图形.7.画一个三角形,使通过这个三角形的旋转得到一个正方形,指出这是一个什么三角形,旋转中心是什么,每次旋转的角度,需要旋转多少次才能完成这个图形.8.如图,以线段CD外的点A为旋转中心,按逆时针方向旋转120°,请画出图形.9.如图,已知点A、B,以A为旋转中心逆时针旋转30°,B点到达;继续旋转60°到;再继续旋转90°到;再继续旋转120°到.请画出多边形.10.图中给出的是一个数轴,以原点O为旋转中心,逆时针旋转90°.画图形,连同单位和标数一齐标注上.11.在图中,画出以O点为旋转中心,顺时针旋转90°后所得到的图形.12.画一个三角形,使通过这个三角形的旋转能得到一个正五边形,指出旋转中心、旋转的次数和每次旋转的角度.13.如图,已知平行四边形ABCD,画出以平行四边形对角线交点O为旋转中心顺时针旋转90°后所得到的图形.参考答案1.略.2.旋转中心是点A,旋转角度为30°,旋转方向为顺时针.3.见答图.4.(1)60°;(2)20°;(3)90°.5.D6.答图中的是旋转后的正方形.7.见答图.三角形为等腰直角三角形,直角顶点A为旋转中心,每次转90°,转4次.8.见答图.连结AC、AD,以A为旋转中心将A C、AD分别逆时针旋转120°,得,则即由CD旋转而成.9.见答图.10.见答图.这个由两个互相垂直的数轴所构成的图形叫做平面直角坐标系.它是一个很用的数学工具,在以后的数学学习中会经常用到.11.见答图.12.见答图.这个三角形是一个顶角为72°的等腰三角形,旋转中心为顶点A,旋转次数为5次,每次旋转的角度为360°÷5=72°.13.见答图(顺时针旋转两条对角线,使转过的角度为90°).。
八年级数学简单的旋转作图 同步练习1北师大版

简单的旋转作图 同步练习1一、选择题1.平面图形的旋转一般情况下改变图形的( ) A.位置 B.大小 C.形状 D.性质2.9点钟时,钟表的时针和分针之间的夹角是( )A.30°B.45°C.60°D.90°3.将平行四边形ABCD 旋转到平行四边形A ′B ′C ′D ′的位置,下列结论错误的是( ) A.AB =A ′B ′ B.AB ∥A ′B ′C.∠A =∠A ′D.△ABC ≌△A ′B ′C ′二、填空题4.钟表上的指针随时间的变化而移动,这可以看作是数学上的_______.5.菱形ABCD 绕点O 沿逆时针方向旋转到四边形D C B A '''',则四边形D C B A ''''是__________.6.△ABC 绕一点旋转到△A ′B ′C ′,则△ABC 和△A ′B ′C ′的关系是_______.7.钟表的时针经过20分钟,旋转了_______度.8.图形的旋转只改变图形的_______,而不改变图形的_______. 三、解答题9.下图中的两个正方形的边长相等,请你指出可以通过绕点O 旋转而相互得到的图形并说明旋转的角度.10.在图中,将大写字母H 绕它右上侧的顶点按逆时针方向旋转90°,请作出旋转后的图案.11.如图,菱形A ′B ′C ′D ′是菱形ABCD 绕点O 顺时针旋转90°后得到的,你能作出旋转前的图形吗?12.Rt △ABC ,绕它的锐角顶点A 分别逆时针旋转90°、180°和顺时针旋转90°,(1)试作出Rt△ABC旋转后的三角形;(2)将所得的所有三角形看成一个图形,你将得到怎样的图形?13.如图,将右面的扇形绕点O按顺时针方向旋转,分别作出旋转下列角度后的图形:(1)90°;(2)180°;(3)270°.你能发现将扇形旋转多少度后能与原图形重合吗?14.如图,分析图中的旋转现象,并仿照此图案设计一个图案.3.生活中的旋转4.简单的旋转作图一、1.A 2.D 3.B二、4.旋转 5.菱形 6.全等7.10 8.位置形状和大小三、9.△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,旋转的角度为90°10~14.略。
简单的旋转作图习题精选

习题精选
1.下图中的两个正方形的边长相等,请你指出可以通过绕点O旋转而相互得到的图形并说明旋转的角度.
2.在图中,将大写字母H绕它右上侧的顶点按逆时针方向旋转90°,请作出旋转后的图案.
3.如图,菱形A
1B
1
C
1
D
1
是菱形ABCD绕点O顺时针旋转90°后得到的,你
能作出旋转前的图形吗?
4.Rt△ABC,绕它的锐角顶点A分别逆时针旋转90°、180°和顺时针旋转90°,试作出Rt△ABC旋转后的三角形。
5.如图,将右面的扇形绕点O按顺时针方向旋转,分别作出旋转下列角度后的图形:
(1)90°;(2)180°;(3)270°.
你能发现将扇形旋转多少度后能与原图形重合吗?
参考答案:
1.△OAE和△OBF,△OEB和△OFC,△OAB和△OBC,旋转的角度为90°
2.图中黄色“H”即为旋转后的图案
3.下图中黄色菱形即为旋转前的
4.(1)图①中粉色三角形ΔAB
1C
1
即ΔABC逆时针旋转90º后的图形;图②
中蓝色三角形ΔAB
2C
2
即ΔABC逆时针旋转180º后的图形;图③中黄色三角形Δ
AB
3C
3
即ΔABC顺时针旋转90º后的图形
5.
旋转360º后与原图形重合。
初中数学旋转作图专题训练含答案

初中数学旋转作图专题训练含答案姓名:__________ 班级:__________考号:__________一、作图题(共20题)1、如图,在一个10×10的正方形DEFG网格中有一个△ABC。
①在网格中画出△ABC向下平移3个单位得到的△A1B1C1。
②在网格中画出△ABC绕C点逆时针方向旋转90°得到的△A2B2C。
③若以EF所在的直线为x轴,ED所在的直线为y轴建立直角坐标系,写出A1、A2两点的坐标。
2、如图,△ABC的顶点坐标分别为A(4,6),B(2,3),C(5,2)。
如果将△ABC 绕C点顺时针旋转90°,得到△A1B1 C。
(1)请在图中画出△A1B1 C;(2)请作出△A1B1C的外接圆(尺规作图,要求保留作图痕迹,不必写出作法);(3)在图中已画好的格点上,是否存在点D,使得=,请写出符合条件的所有D 点的坐标(C点除外)。
(原创)3、如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.ΔABO 的三个顶点A,B,O都在格点上.(1)画出ΔABO绕点O逆时针旋转900后得到的三角形Δ;(2)根据所画的图找出点和点的坐标.4、 ,如图,在由边长为的小正方形组成的方格纸中,有两个全等的三角形,即和.请你指出在方格纸内如何运用平移、旋转变换,将重合到上;5、已知△ABC在平面直角坐标系中的位置如图所示。
⑴分别写出图中点A和点C的坐标;⑵画出△ABC绕点A按逆时针方向旋转90°后的△AB′C′;⑶在⑵的条件下,求点C旋转到点C′所经过的路线长(结果保留π)6、如右图,在网格图中建立平面直角坐标系,的顶点坐标为、、.(1)若将向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的;顺时针方(2)画出绕C1向旋转900后得到的;(3)与是中心对称图形,请写出对称中心的坐标:;并计算的面积: .(4)在坐标轴上是否存在P点,使得△PAB与△CAB的面积相等,若有,则求出点P的坐标.7、在网格纸上按以下要求作图,不用写作法:(1)作出“小旗子”向右平移6格后的图案.(2)作出“小旗子”绕O 点按逆时针方向旋转90°后的图案.8、 如下图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点, △ABC 的顶点均在格点上.(1)画出将△ABC 向右平移2个单位后得到的△A 1B 1C 1,再画出将△A 1B 1C 1绕点B 1按逆时针方向旋转90°后所得到的△A 2B 1C 2;(2)求线段B 1C 1旋转到B 1C 2的过程中,点C 1所经过的路径长.9、 如图,在每个小正方形的边长均为1个单位长度的方格纸中,有一个△ABC 和一点O ,△ABC 的顶点与点O 均与小正方形的顶点重合.(1)在方格纸中,将△ABC 向下平移6个单位长度得到△A 1B 1C 1,请画△A 1B 1C 1. (2)在方格纸中,将△ABC 绕点O 旋转180°得到△A 2B 2C 2,请画△A 2B 2C 2.10、每个小方格都是边长为1个单位长度,正方形ABCD在坐标系中的位置如图所示.(1)画出正方形ABCD关于原点中心对称的图形;(2)画出正方形ABCD绕点D点顺时针方向旋转90°后的图形;(3)求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线.11、如图,在方格纸中每个小正方形的边长均为1个单位,△ABC的三个顶点都在小方格的顶点上.(1)在图中作出将△ABC向右平移5个单位后的图形△A1B1C1;(2)在图中作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A2B2 C.12、已知△ABC在平面直角坐标系中的位置如图所示.(1)分别写出图中点A和点C的坐标;(2)画出△ABC绕点C按顺时针方向旋转90°后的△A′B′C′;(3)求点A旋转到点A′所经过的路线长(结果保留π).13、在如图的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).(1)画出向下平移4个单位后的,并直接写出在平移过程中扫过的面积;(2)画出绕点顺时针旋转后的,并直接写出点旋转到所经过的路线长.14、如图,在平面直角坐标系中,和关于点成中心对称。
简单的旋转作图习题精选

简单的旋转作图习题精选一、知识要点1、旋转作图的三要素:(1)旋转中心:用点表示;(2)旋转方向:顺时针方向或逆时针方向;(3)旋转角度:用量角器度量,或通过画角等于已知角。
2、点的旋转做法:以旋转中心为圆心,旋转中心到待旋转点的距离为半径画圆,连接旋转中心到待旋转点的半径,过旋转中心按指定方向作另一半径(/),使与前一半径的夹角等于已知角,该半径交于圆上的点即为所求作。
依据:对应点与旋转中心的连线所成的角相等;对应点到旋转中心的距离相等。
3、图形的旋转可转化为点的旋转再连线。
二、典型例题与分析例1:将A点绕O点沿顺时针方向旋转60?。
【做法】:1、以点O为圆心,OA长为半径画圆;2.连接OA,用量角器或三角板(限特殊角)作出∠AOB,与圆周交于B点;学习目标:1、经历对具有旋转特征的图形进行观察、分析、画图和动手操作等过程,掌握画图技能,能够按要求作出简单图形旋转后的图形。
2、确定一个三角形旋转后的位置的条件,通过画图,进一步培养学生的动手操作能力。
3、在对具有旋转特征的图形进行观察、分析、画图过程中,进一步发展学生的审美观念。
重点、难点:重点:寻找旋转中心。
难点:按旋转角相等作图。
一、学前准备1、什么样的运动称为旋转?2、旋转有什么样的性质?3、每人准备一面小红旗,按课本P82引例操作,体验旋转的条件,同时在课本方格纸中作出图形。
第三章图形的平移与旋转4.简单的旋转作图一、学生起点分析学生已对轴对称、平移这两种简单的全等变换有了很好的认识,并对旋转有了初步的了解。
教材将旋转变换安排至此,目的是力求让学生从动态的角度观察图形、分析问题,为将来掌握“全等”知识奠定基础。
由于旋转与轴对称、平移都是全等变换,在特征上既存在共性又有特性;而学生已经掌握了轴对称、平移的特征,因此,探索、理解旋转区别于轴对称、平移的特征成了本节课学习的重要任务。
二、教学任务分析本节课的主要内容是通过实例进一步认识旋转变换,探索、理解旋转的特征,并应用旋转的特征作图、解决简单的图形问题。
旋转90°画图专项练习

旋转90°画图专项练习一、作图题1.如图,已知点A,B的坐标分别为(0,0)、(2,0),将△ABC绕C点按顺时针方向旋转90°得到△A1B1C.(1)画出△A1B1C;(2)A的对应点为A1,写出点A1的坐标;(3)求出B旋转到B1的路线长.2.如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).( 1 )将△ABC向下平移5个单位后得到△A1B1C1,请画出△A1B1C1;( 2 )将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2;( 3 )判断以O,A1,B为顶点的三角形的形状.(无须说明理由)3.如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(-4,1),B(-1,1),C(-1,3)请解答下列问题:①画出△ABC关于原点0的中心对称图形△A1B1C1并写出点C的对应点C1的坐标;②画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并直接写出点A2的坐标。
4.如图,△ABC的顶点都在方格线的交点(格点)上.(1)①将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.②将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.(2)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是.答案解析部分1.【答案】(1)解:△A 1B 1C 如图所示.(2)解:A 1(0,6)(3)解: BC =√12+32=√10,∴BB1⌢=nπr 180=90π×√10180=√102π.2.【答案】解:如图所示,△A 1B 1C 、△A 2B 2C 2即为所求三角形的形状为等腰直角三角形,OB=OA 1= √42+12=√17 ,A 1B= √52+32 = √34 , 即OB 2+OA 12=A 1B 2,所以三角形的形状为等腰直角三角形.3.【答案】解:C 1(1,-3)、A 1(-1,-4).4.【答案】(1)解:如图所示:△A′B′C′,△A″B″C″即为所求;(2)(2,﹣3).。
简单的旋转作图(共10张PPT)

(3)任意一对对应点与旋转中心的连线所成的角都
是旋转角,对应点到旋转中心的距离相等。
范例讲解
1.如图,△ABC绕点O旋转后,顶点 A的对应点为点D。试确定
顶点B的对应点的位置,以及 旋转后的三角形。
A
分析
D
1、“旋转”作图的步骤 :
如图,△ABC绕点O旋转后,顶点 A的对应点为点D。
转角. 在旋转过程中,确定一个三角形旋转后的位置,除需要此三角形原来的位置外,还需要什么条件?
根据旋转的性质知道:旋转角相等,(即作∠BOE=∠COF=∠AOD)
对应点到旋转中心的距离相等,则,OE=OB,OF=OC,
通过以上两个限制条件点E、F被确定。
4
解:
E
(1)连接OA,OD,OB,OC.
(2)如下图,分别以OB、OC为一边
2、能根据旋转作图步骤进行简单地旋转作图
一般作图题,在分析如何求 (2)经过旋转,图形上的每一点都绕旋转中心沿相
弄清旋转中心、方向和角度;
沿(作3)一分时定别的在,方射向线都和O角M要、度O分先N别上假作截出取设已经把所
求作的图形作出来,然后再 (1)经过旋转,图形的形状和大小不变;
沿一定的方向和角度分别作出
(2)分析所作图形: 找出构成图形的关键点; (3)旋转关键点: 沿一定的方向和角度分别作出
各关键点; (4)作出新图形: 顺次连接各关键点; (5)写出结论: 说明所作出的图形。
2、“旋转”作图的条件 :
(1)三角形原来的位置 (2)旋转中心 (3)旋转方向
(4)旋转角度
根据性质,确定如何操作 个方向转动一个角度,这样的图形运动称为旋
弄清旋转中心、方向和角度;
五年级下册旋转图练习题

五年级下册旋转图练习题旋转图是一种几何图形变换,它涉及到将图形绕某一点旋转一定的角度。
五年级下册的同学们可以通过以下练习题来加深对旋转图的理解。
1. 基础旋转练习题:- 题目:画出一个等边三角形ABC,然后绕点A顺时针旋转60°。
- 答案:首先确定点A的位置,然后画出等边三角形ABC。
接着,找到A点周围60°的位置,画出旋转后的三角形A'B'C',确保A'B'=AB,B'C'=BC,C'A'=AC。
2. 旋转角度计算题:- 题目:一个正方形的四个顶点分别是A、B、C和D。
如果将正方形绕点A顺时针旋转90°,求顶点B、C和D的新位置。
- 答案:旋转90°后,顶点B将移动到原顶点D的位置,顶点C将移动到原顶点B的位置,顶点D将移动到原顶点C的位置。
3. 旋转对称图形练习题:- 题目:在一张纸上画一个由四个相同的小正方形组成的大正方形,然后绕中心点旋转90°。
- 答案:首先画出由四个小正方形组成的大正方形。
然后确定中心点,绕该点顺时针旋转90°,画出旋转后的图形。
4. 旋转与图形变换练习题:- 题目:有一个由直线和曲线组成的图案,将其绕中心点旋转180°,观察图案的变化。
- 答案:画出图案,确定中心点,然后绕中心点旋转180°,观察旋转后的图案是否与原图案相同或有其他变化。
5. 旋转与实际应用题:- 题目:一个风车有四个叶片,如果风车绕中心轴旋转一周,叶片会经历几次旋转?- 答案:风车绕中心轴旋转一周,每个叶片都会经历一次360°的旋转。
6. 旋转与几何证明题:- 题目:证明一个正方形绕中心点旋转90°后,其四个顶点的连线仍然构成一个正方形。
- 答案:首先画出正方形和中心点,然后画出旋转后的图形。
通过测量和比较,可以证明旋转后的图形的四边长度相等,且相邻两边的夹角都是90°,因此仍然是一个正方形。
八年级数学简单的旋转作图 同步练习2北师大版

简单的旋转作图同步练习2
1.做一做
在图1中,将大写字母A绕着它右下侧的顶点按顺时针方向旋转90度,请作出旋转后的图案.
图1
2.将一个等腰直角三角形ABC(如图2∠A是直角)绕着它的一个顶点B逆时针方向旋转,分别作出旋转下列角度后的图形.
(1)45°(2)90°(3)135°(4)180°
图2
3.将下面的图案绕点O顺时针方向旋转90度,作出旋转后的图形.
图3
4.小华养了几条金鱼.每天放学回家,她都在鱼缸前欣赏鱼儿优雅的“泳姿”.今天数学课上老师讲了旋转作图的知识,并布置了一个作业:举生活中一个旋转的例子并作图.小华灵机一动,啊哈,有了!
(1)小鱼绕点O旋转180°,请做出小鱼旋转后的图形.
(2)如果小鱼绕点O旋转90°呢?
测验评价结果:_____________;对自己想说的一句话是:______________________. 参考答案
1.
2.
(1)
(2)
(3)
(4)
3.
4.(1)
(2)。
图形旋转画图训练
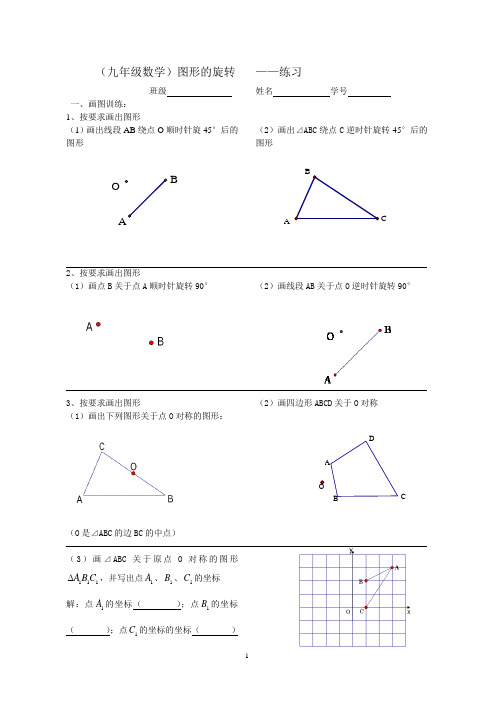
ODCB A(九年级数学)图形的旋转班级一、画图训练:1、按要求画出图形 (1)画出线段AB 绕点O 顺时针旋45°后的图形2、按要求画出图形(1)画点B 关于点A 顺时针旋转90°3、按要求画出图形(1)画出下列图形关于点O 对称的图形:(O 是⊿ABC 的边BC 的中点)(3)画⊿ABC 关于原点O 对称的图形111A B C ,并写出点1A 、1B 、1C 的坐标解:点1A 的坐标( );点1B 的坐标( );点1C 的坐标的坐标( )——练习姓名 学号(2)画出⊿ABC 绕点C 逆时针旋转45°后的图形(2)画线段AB 关于点O 逆时针旋转90°(2)画四边形ABCD 关于O 对称OB AC B AC BA 二、专题训练:1、按要求画出图形 (1)画出线段AB 绕点O 顺时针旋60°后的图形(2)画出⊿ABC 绕点C 逆时针旋转60°后的图形3、按要求画出图形(1)画出⊿ABC 绕点A 顺时针旋90°后的图形(2)画出⊿ABC 绕O 逆时针旋转90°后的图形2、如图,等边⊿ABC ,点P 是⊿ABC 内一点, (1)画出⊿APC 绕点A 顺时针旋转60°后的图形(2)若AP=4,PC=3,PB=5,求∠APC 的度数。
解:4、正方形ABCD ,E 、F 分别是边CD 和BC 上的点,连接EF ,若DE+BF=EF 求证:∠EAF=45° 证明:O BAC B A P C B AF ED C B A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.如图,非等腰三角板原在ABC的位置上,旋转后到了的位置上,请指出旋转中心、旋转角度和旋转方向.
3.已知(如图),请画出以C点为旋转中心,旋转角为30°,(1)按顺时针方向旋转后的图形;(2)按逆时针方向旋转后的图形.
4.下列各图形围绕自己的旋转中心最低需要旋转多少度之后,能够与它自身相重合?
5.如图,下列各图形,不是旋转对称图形的是()
6.如图,正方形ABCD,画出绕顶点C顺时针旋转90°后的图形.
7.画一个三角形,使通过这个三角形的旋转得到一个正方形,指出这是一个什么三角形,旋转中心是什么,每次旋转的角度,需要旋转多少次才能完成这个图形.
8.如图,以线段CD外的点A为旋转中心,按逆时针方向旋转120°,请画出图形.
9.如图,已知点A、B,以A为旋转中心逆时针旋转30°,B点到达;继续旋转60°到;再继续旋转90°到;再继续旋转120°到.请画出多边形.
10.图中给出的是一个数轴,以原点O为旋转中心,逆时针旋转90°.画图形,连同单位和标数一齐标注上.
11.在图中,画出以O点为旋转中心,顺时针旋转90°后所得到的图形.
12.画一个三角形,使通过这个三角形的旋转能得到一个正五边形,指出旋转中心、旋转的次数和每次旋转的角度.
13.如图,已知平行四边形ABCD,画出以平行四边形对角线交点O为旋转中心顺时针旋转90°后所得到的图形.
参考答案
1.略.
2.旋转中心是点A,旋转角度为30°,旋转方向为顺时针.
3.见答图.
4.(1)60°;(2)20°;(3)90°.
5.D
6.答图中的是旋转后的正方形.
7.见答图.三角形为等腰直角三角形,直角顶点A为旋转中心,每次转90°,转4次.
8.见答图.连结AC、AD,以A为旋转中心将A C、AD分别逆时针旋转120°,得,则即由CD旋转而成.
9.见答图.
10.见答图.这个由两个互相垂直的数轴所构成的图形叫做平面直角坐标系.它是一个很用的数学工具,在以后的数学学习中会经常用到.
11.见答图.
12.见答图.这个三角形是一个顶角为72°的等腰三角形,旋转中心为顶点A,旋转次数为5次,每次旋转的角度为360°÷5=72°.
13.见答图(顺时针旋转两条对角线,使转过的角度为90°).
解答题(二)
1.观察下列图形,哪个图形是由①图平移而得的?
2.如图,将线段AB沿水平方向向右平移2cm.
3.平行四边形ABCD经过若干次不同方向、不同距离的平移之后,能不能变成图中的位置?为什么?
4.模仿图画一个图形(可以改变图案样式).
5.如图,将按所示的方向和距离平移,得到,请画出.并写出所有的对应线段和对应角.
6.经过平移后得到,这时我们可以说与
是两个全等的三角形.请你说出全等三角形的一些特征.7.如图,平移正方形网格中的阴影图案,使AB移动到的位置.然后再移一次,向左平移6个单位.
8.如图,画出关于直线a的轴对称图形,再画出关于直线b的轴对称图形.指出和的位置关系.1.第④个图形是由①图平移而得到的.
2.分别过A、B向右作水平方向的线段,连结,就是平移后的线段(见答图).
3.不能.因为对应线段不平行,不满足平移的特征.
4.略.
5.见答图.过作且,过作且.连结就是平移后的三角形.对应线段为
,对应角为
6.全等三角形的对应边相等,对应角相等.
7.见答图.
8.见答图.与的位置关系是平移的关系.。
