振动和波习题课(2010级)
第14章振动和波(2010-2018)

新课标高考(2010-2018)全国理综卷物理试题分类解析:第14章机械振动和机械波江苏省特级教师戴儒京一、选择题1.(2011年)34.(1)(6分)一振动周期为T,振幅为A。
位于x=0点的波源从平衡位置沿y轴正方向开始做简谐运动,该波源产生的一维简谐横波沿x轴正向传播,波速为v,传播过程中无能量损失。
一段时间后,该振动传播到某质点P,关于质点P振动的说法正确的是(选对1个给3分,选对2个给4分,选对3个给6分,每选错1个扣3分,最低得分为0分)A. 振幅一定为AB. 周期一定为TC. 速度的最大值一定为vD. 开始振动的方向沿y轴向上或向下取决于它离波源的距离E.若P点离波源距离s=vT,则质点P的位移与波源相同【答案】ABE2.(2013年)34.【物理—选修3-4】(1)(6分)如图,a、b、c、d是均匀介质中x轴上的四个质点。
相邻两点的间距依次为2m、4m和6m一列简谐横波以2m/s的波速沿x轴正向传播,在t=0时刻到达质点a 处,质点a由平衡位置开始竖直向下运动,t=3s时a第一次到达最高点。
下列说法正确的是(填正确答案标号。
选对1个得3分,选对2个得4分,选对3个得6分。
每选错1个扣3分,最低得分为0分。
)A.在t=6s时刻波恰好传到质点d处B.在t=5s时刻质点c恰好到达最高点C.质点b开始振动后,其振动周期为4sD.在4s<t<6s的时间间隔内质点c向上运动E.当质点d向下运动时,质点b一定向上运动【解析】本题考查机械波的传播,波长、周期与波速的关系。
较容易。
波在6s内沿x正向传播的距离为m,因此t=6s时刻波传至d点。
选项A正确; 0时刻a处质点离开平衡位置向下振动,经3s第一次到达最高点。
因此有s,则波的周期T=4s。
波传至c点需要s=3s,此时c将向下运动,再过2s(半个周期)将经过平衡位置向上运动。
选项B错误CD正确;波长为m ,而b 、d 两点的距离为10m ,这两点不是反相点,运动方向不会总相反。
振动与波习题课

b
c
O
a
.
b
c X t
a 0
b
2
3 c 2
10.如图(a)为t=0时的波形曲线,经0.5s后波形变为(b) 求(1)波动方程 Y (a) (b) u
(2)P点的振动方程
解:O处的振动方程为 0.1
yo A cos(t )
由图得A=0.1 =/2 =4m
( 2k 1) 2 2 1 1 2 ( 2k 1) 4 r1 [ ] 2 ( 2k 1) 2 ( 2k 1)
Y
u=0.08m/s P . 0.02
X yo A cos(t ) -0.04 0.04 P点的振动方程 2 1 T u 0.08 令x=0.02 u 2 2 3 4 y P 0.04 cos(4t ) T 2 x y 0.04 cos[4 ( t ) ] 0.08 2
A A A 2 A1 A2 cos( 2 1 ) A1 sin 1 A2 sin 2 tg A1 cos 1 A2 cos 2 2 1 B.同方向不同频率:拍 拍频为:
A. 同方向同频率:
2 1 2 2
C.两个相互垂直同频率的振动:椭圆 D.两个相互垂直不同频率的振动:李萨如图 5.平面简谐波波动方程:
u 0.84m / s 取 /3
故得波动方程为
17 / 3
O a b
u
X
x y 0.1cos[7 ( t ) ]( m ) 0.84 3
13.题中图a表示一水平轻绳,左端D为振动器,右端 固定于B点。t0时刻振动器激起的简谐波传到O点。其 波形如图b所示。已知OB=2.4m,u=0.8m/s. 求:(1) 以为计时零点,写出O点的谐振动方程;(2)取O 点 为原点,写出向右传播的波动方程;(3)若B 处有 半波损失,写出反射波的波动方程(不计能量损失)。 2 D O 解:(1)由 B u 2 2 y(cm) 得 u 80 4 40 4
振动与波动习题课

(1) B处质元的振动动能减小 处质元的振动动能减小, 则其弹性势能必增大; 则其弹性势能必增大 错 答:质元的振动动能和弹 质元的振动动能和弹 性势能是同相位的 ,同 时增大,同时减少. 时增大,同时减少.
B
o
C
x
(2) A处质元回到平衡位置的过程中 它把自己的能量 处质元回到平衡位置的过程中,它把自己的能量 传给相邻的质元,其能量逐渐减小 其能量逐渐减小; 传给相邻的质元 其能量逐渐减小 错 在平衡位置质元的振动动能和弹性势能是最大, 答:在平衡位置质元的振动动能和弹性势能是最大,所 质元回到平衡位置的过程中能量应该逐渐增大 能量应该逐渐增大. 以A处质元回到平衡位置的过程中能量应该逐渐增大.
关于干涉条件的讨论
y1 = A1 cos( ω t + 10
y2 = A2 cos( ω t + 20
P点的合振动为 点的合振动为
2π r1
2π r2
λ
)
注意: 为正值! 注意:r1, r2为正值! P
r1
λ
)
S1 r2 S2
y = y1 + y2 = A cos( ω t + 0 )
2 1 2
波动学基础
教学要求
1 . 掌握平面简谐波波动方程的物理意义 掌握由质点 掌握平面简谐波波动方程的物理意义.掌握由质点 的谐振动方程或某时刻的简谐波波形曲线等已知条件建 立简谐波波动方程的方法. 立简谐波波动方程的方法 2 .理解波长,周期,频率,波速等概念的含意 并掌 理解波长, 理解波长 周期,频率,波速等概念的含意,并掌 握它们之间的关系. 握它们之间的关系 3 .理解波的干涉现象 掌握波的相干条件 能运用相位 理解波的干涉现象.掌握波的相干条件 理解波的干涉现象 掌握波的相干条件.能运用相位 差或波程差来确定相干波叠加后加强或减弱的条件. 差或波程差来确定相干波叠加后加强或减弱的条件 4 .理解驻波的特性及其形成条件 了解驻波与行波的 理解驻波的特性及其形成条件.了解驻波与行波的 理解驻波的特性及其形成条件 区别. 区别 5 .理解波的能量传播特征以及能流,能流密度等概念 理解波的能量传播特征以及能流, 理解波的能量传播特征以及能流 能流密度等概念. 6.掌握多普勒效应 6.掌握多普勒效应
振动和波习题课

振动和波习题课壹内容提要一. 振动1.简谐振动的定义:恢复力F=-kx微分方程d2x/d t2+ω2x=0运动方程x=A cos(ωt+ϕ0)弹簧振子ω=(k/m)1/2,单摆ω=(g/l)1/2,复摆ω=(mgh/J)1/2;2.描述谐振动的物理量:(1)固有量:固有频率ω,周期T,频率ν其关系为ω=2π/T=2πνν=1/T(2)非固有量,振幅A A=(x02+v02/ω2)1/2位相ϕϕ=ωt+ϕ0初位相ϕ0tanϕ0=-v0/(ω x0)(再结合另一三角函数定出ϕ0);3.旋转矢量法(略);4.谐振动能量:E k=E sin2(ωt+ϕ0)E p=E cos2(ωt+ϕ0)E=E k+ E p5.谐振动的合成:(1)同方向同频率两谐振动的合成A=[A12+A22+2A1A2cos(ϕ20-ϕ10)]1/2tgϕ0=(A1sinϕ10+A2sinϕ20)/(A1cosϕ10+A2cosϕ20) (再结合另一三角函数定出ϕ0)拍∆ω<<ω1拍频∆ν=|ν2-ν1| (2)相互垂直振动的合成ω1与ω2成简单整数比时成李萨如图形ω1=ω2时为椭圆方程:x2/A12+y2/A22- 2(x/A1)(y/A2)cos(ϕ20-ϕ10)=sin2(ϕ20-ϕ10) 二. 波动1.机械波的产生必须有波源及媒质,机械波的传播实质是相位(或振动状态)的传播;2.描述波的物理量:波长λ,频率ν,周期T,波速u其关系为T=1/ν=λ/u u=λ/T=λν3.平面简谐波的波动方程y=A cos(ωt-x/u+ϕ0)=A cos[2π(t/T-x/λ)+ϕ0]=A cos[(2π/λ)(x-ut)-ϕ0];4.平均能量密度w=ρA2ω2/2,能流密度(波的强度) I=w u=ρA2ω2u/25.惠更斯原理(略);6.波的叠加原理:独立性,叠加性;7.波的干涉(1)相干条件:频率相同,振动方向相同,位相差恒定。
10级大学物理复习题(第10章)

第10章 机械振动和波一、填空题易:1、质量为0.10kg 的物体,以振幅1cm 作简谐运动,其角频率为110s -,则物体的总能量为, 周期为 。
(4510J -⨯,0.628s )易:2、一平面简谐波的波动方程为y 0.01cos(20t 0.5x)ππ=-( SI 制),则它的振幅为 、角频率为 、周期为 、波速为 、波长为 。
(0.01m 、20π rad/s 、 0.1s 、 40m/s 、4m )易:3、一弹簧振子系统具有1.0J 的振动能量,0.10m 的振幅和1.0m/s 的最大速率,则弹簧的倔强系数为 ,振子的振动角频率为 。
(200N/m ,10rad/s )易:4、一横波的波动方程是y = 0.02cos2π(100t – 0.4X )( SI 制)则振幅是_________,波长是_ ,频率是 ,波的传播速度是 。
(0.02m ,2.5m ,100Hz ,250m.s -1)易:5、两个谐振动合成为一个简谐振动的条件是 。
(两个谐振动同方向、同频率)易:6、产生共振的条件是振动系统的固有频率与驱动力的频率 (填相同或不相同)。
(相同)易:7、干涉相长的条件是两列波的相位差为π的 (填奇数或偶数)倍。
(偶数)易:8、弹簧振子系统周期为T 。
现将弹簧截去一半,仍挂上原来的物体,作成一个新的弹簧振子,则其振动周期为 T 。
(T )易:9、作谐振动的小球,速度的最大值为,振幅为,则振动的周期为;加速度的最大值为。
(34π,2105.4-⨯)易:10、广播电台的发射频率为 。
则这种电磁波的波长为 。
(468.75m )易:11、已知平面简谐波的波动方程式为 则时,在X=0处相位为 ,在处相位为 。
(4.2s,4.199s)易:12、若弹簧振子作简谐振动的曲线如下图所示,则振幅;圆频率;初相。
(10m,1.2-s rad π,0)中:13、一简谐振动的运动方程为2x 0.03cos(10t )3ππ=+( SI 制),则频率ν为 、周期T 为 、振幅A 为 ,初相位ϕ为 。
(大学物理下册)2010习题2解答

作业8 波 动8-1 一个余弦横波以速度u 沿x 轴正方向传播,t 时刻波形曲线如图所示.试在图中画出A ,B ,C ,D ,E ,F ,G 各质点在该时刻的运动方向.并画出(t + T /4)时刻的波形曲线. 原题 20-18-2 地震波纵波和横波的速度分别为8000 m /s 和4450 m /s ,观测点测得这两种波到达的时间差=∆t 75.6 s ,则震中到观测点的距离 r = 7.58×105 m . 解: t u r u r ∆=-)()(12 )(2121u u u u t r -⋅∆==…= 7.58×105 m8-3 ⑴ 有一钢丝,长2.00 m ,质量20.0×103 kg ,拉紧后的张力是1000 N ,则此钢丝上横波的传播速率为 316 m /s .⑵ 钢棒中声速5200 m/s ,钢的密度=ρ7.8 g/cm 3,钢的弹性模量为 2.11×1011 (N/m 2).8-4 已知一波的波函数为 )6.0π10sin(105 2x t y -⨯=-⑴ 求波长,频率,波速及传播方向;⑵ 说明x = 0时波函数的意义.原题 20-3y8-5 一螺旋形长弹簧的一端系一频率为25 Hz 的波源,在弹簧上激起一连续的正弦纵波,弹簧中相邻的两个稀疏区之间的距离为24 cm .⑴ 试求该纵波的传播速度;⑵ 如果弹簧中质点的最大纵向位移为 0.30 cm ,而这个波沿x 轴的负向传播,设波源在 x = 0 处,而x = 0 处的质点在 t = 0 时恰好在平衡位置处,且向x 轴的正向运动,试写出该正弦波的波函数.解:⑴ νλ=u = 24 ×25 = 600 cm/s⑵ 波源处 ⎭⎬⎫>-===0sin 0cos 00ϕωυϕA A y 初相位 2π-=ϕ, 波源振动方程为 )π2cos(30.000ϕν+=t y )2ππ50cos(30.0-=t波沿x 轴的负向传播的波函数为])(cos[ϕω-+=u x t A y ]2π)600π(50cos[30.0-+=x t )]24π(252sin[30.0x t += 即,该正弦波的波函数为 )]24π(252sin[30.0x t y += (cm)8-6 波源作谐振动,周期为0.01s ,经平衡位置向正方向运动时,作为时间起点,若此振动以υ= 400 ms -1的速度沿直线传播,求:⑴ 距波源为8 m 处的振动方程和初相位;⑵ 距波源为9 m 和10 m 两点的相位差. 原题 20-58-7 一平面简谐波,沿x 轴正向传播,波速为4 m/s ,已知位于坐标原点处的波源的振动曲线如图(a)所示.⑴ 写出此波的波函数; ⑵ 在图(b)中画出t = 3 s 时刻的波形图(标明尺度)P317 13.16 解: ⑴ 由图知,A = 4 cm = 4 ×10-2 m , T = 4 s ∴ T π2=ω2π=,uT =λ= 4 × 4 = 16 m 原点处 A A y ==ϕcos 0 初相位 0=ϕ原点振动方程为 )cos(ϕω+=t A y t A ωcos =∴ 波函数为 )(cos u x t A y -=ω即 )]4(2cos[1042x t y -⨯=-π ⑵ 将t = 3 s 代入波函数,得波形曲线方程 )]43(2cos[1042x y -⨯=-π t = 3 s 时刻的波形图见图(b).8-8 一正弦式空气波沿直径为0.14 m 的圆柱形管道传播,波的平均强度为1.8⨯10-2 J/(sm 2),频率为300 Hz ,波速为300 m/s ,问波中的平均能量密度和最大能量密度各是多少?每两个相邻周相差为2π 的同相面之间的波段中包含有多少能量? 原题 20-78-9 频率为100 Hz ,传播速度为300 m /s 的平面简谐波,波线上两点振动的位相差为31π,则此两点距离为 0.5 m . 原题 20-11 解:νλu ==…= 3 m , x ∆=∆)π2(ϕ,))π2(λϕ∆=∆x =…= 0.5 m-题8-7图 -8-10 在弹性媒质中有一波动方程为)2ππ4cos(01.0--=x t y (SI )的平面波沿x 轴正向传播,若在x = 5.00处有一媒质分界面,且在分界面处相位突变 π,设反射后波的强度不变,试写出反射波的波函数.原题 20-108-11 一平面简谐波某时刻的波形图如图所示,此波以速率u 沿x 轴正向传播,振幅为A ,频率为v .⑴ 若以图中B 点为坐标原点,并以此时刻为 t = 0 时刻,写出此波的波函数; ⑵ 图中D 点为反射点,且为波节,若以D 点为坐标原点,并以此时刻为 t = 0 时刻,写出入射波的波函数和反射波的波函数;⑶ 写出合成波的波函数,并定出波节和波腹的位置坐标.P326 13.29解:⑴ B 点为坐标原点,t = 0 时刻, A A y -==ϕcos 0 ♉ 初相位 π=ϕ振动方程 )cos(ϕω+=t A y ♉ )ππ2cos(+=t A y B ν∴ 波函数为 ]π)(π2cos[+-=u x t A y ν⑵ D 点为坐标原点,t = 0 时刻,入射波: ⎭⎬⎫>'-=='=0sin 0cos 00ϕωυϕA A y ♉ 初相位 2π-='ϕ 反射波:∵D 点为波节,∴初相位 2ππ=+'=''ϕϕD 点振动方程 )2ππ2cos(-=t A y D ν入, )2ππ2cos(+=t A y D ν反∴波函数为 ]2π)(π2cos[--=u x t A y ν入, ]2π)(π2cos[++=x t A y ν反⑶ 合成波的波函数 )π2cos()2ππ2cos(2t x A y y y νν+=+=反入波节:由 π)21(2ππ2+=+k u x ν 得 νu k x ⋅=2 (k = 0, -1, -2, …) 波腹:由 π2ππ2k x =+ν 得 νu k x )412(-= (k = 0, -1, -2, …) 题8-11图8-12 入射波的波函数为)( π2cos 1λx T t A y +=,在x = 0处发生反射,反射点为自由端.⑴ 写出反射波的波函数;⑵ 写出驻波的波函数;⑶ 给出波节和波腹的位置. P327 13.30解:反射点为自由端,是波腹,无半波损失,⑴ 反射波的波函数为 )( π2cos 2λx T t A y -= ⑵ 驻波的波函数为 t Tx A y y y π2cos π2cos 221λ=+= ⑶ 当1π2cos =x λ,即ππ2 k x =λ时,得波腹的位置为 2λk x =,k = 0, 1, 2, … 当0π2cos =x λ,即2π)12(π2 +=k x λ时,得波节的位置为4)2( λ+=k x ,k = 0, 1, 2, …*8-13 一平面简谐波沿x 轴正向传播,振幅为A = 10 cm ,角频率π7=ω rad/s ,当t = 1.0 s 时,x = 10 cm 处a 质点的振动状态为0=a y ,0)d d (<a t y ;同时x = 20 cm 处b 质点的振动状态为0.5=b y cm ,0)d d (>b t y .设波长10>λcm ,求该波的波函数.P315 13.13解:当t = 1.0 s 时刻,a 质点 0cos ==a a A y ϕ,0sin )d d ( <-==a a a A t y ϕωυ,♉ 2ππ2+=k a ϕ ① b 质点 2cos A A y a b ==ϕ,0sin )d d ( >-==a b b A t y ϕωυ,♉ 3ππ2-'=k b ϕ a 、b 两点相位差 b a ϕϕϕ-=∆65π)(π2+'-=k ka 、b 两点间距λ<=-=∆10b a x x x ,∴π2<∆ϕ,则ϕ∆的取值可分两种情况 ⑴ 当0='-k k 时,b a ϕϕϕ-=∆65π=,♉λϕ2π=∆∆x ,则 )(2πϕλ∆∆=x = 24 (cm)∵波沿x 轴正向传播,可设波函数为)π2cos(0ϕλω+-=x t A y )24π2π7cos(100ϕ+-=x t 当t = 1.0 s ,x = 10 cm 时波函数的相位 a ϕϕ=+⨯-⨯01024π21.0π7 ② 由式①、②求得: 317ππ20-=k ϕ, 不妨取 k = 0,则 317π0-=ϕ 波函数为 )π31712ππ7cos(10--=x t y (cm) ⑵ 当1-='-k k 时,b a ϕϕϕ-=∆67π-= < 0,波将沿x 轴负向传播,故舍去.作业10 光的衍射10-1 如果单缝夫琅和费衍射的第一级暗纹发生在衍射角为︒=30θ的方位上,所用单色光波长为500=λnm ,则单缝宽度为: 1.0 μm .解: 暗纹公式 λθk a =sin10-2 在单缝夫琅和费衍射装置中,设中央明纹衍射角范围很小.若使单缝宽度a 变为原来的3/2,同时使入射单色光波长变为原来的3/4,则屏上单缝衍射条纹中央明纹的宽度2ρ将变为原来的 1/2 倍.解:由单缝衍射暗纹公式 λθk a =sin ,暗纹位置 θθsin tan f f x k ≈⋅=, ∴中央明半纹宽a f x λρ==1;若43λλ=',23a a =' 代入上式得 2ρρ=' 10-3 在单缝夫琅和费衍射中,设第一级暗纹的衍射角很小.若纳黄光(≈1λ589.3 nm )中央明纹宽度为4.00 mm ,则=2λ442 nm 的兰紫色光的中央明纹宽度为 3 mm. 解:单缝衍射中央明纹半宽度a f x λρ==1,∴2121λλρρ=,1122)(22ρλλρ== 3 mm 10-4 单缝夫琅和费衍射对应三级暗纹,单缝宽度所对应的波面可分为 6 个半波带.若缝宽缩小一半,原来第三级暗纹变为第 一级明 纹.(原题22-2)解:由单缝暗纹公式 263sin λλλθ⨯===k a ∴ 单缝面分为6个半波带.若缝宽缩小一半,单缝面分为3个半波带,所以原第三级暗纹为变第一级明纹. 10-5 波长分别为1λ和2λ的两束平面光波,通过单缝后形成衍射,1λ的第一极小和2λ的第二极小重合.问:⑴1λ与2λ之间关系如何?⑵ 图样中还有其他极小重合吗? 解:⑴ 由单缝极小条件 11sin λθ=a 222sin λθ=a而 21θθ= ∴ 212λλ=⑵ 由 111sin λθk a =与 222sin λθk a = ,如有其它级极小重合时,必有 21θθ= ,于是 2211λλk k = ,而212λλ=∴ 212k k = 即只要符合级数间的这个关系时,还有其它级次的极小还会重合.10-6 如图所示,用波长为546 nm 的单色平行光垂直照射单缝,缝后透镜的焦距为40.0 cm ,测得透镜后焦平面上衍射中央明纹宽度为1.50 mm ,求:⑴ 单缝的宽度;⑵ 若把此套实验装置浸入水中,保持透镜焦距不变,则衍射中央明条纹宽度将为多少?(水的折射率为1.33)原题22-1⑴ a = 2.912×10-4 m⑵ 中央明纹宽a f x λρ2221=== 1.13×10-3 m10-7 衍射光栅主极大公式λθk d =sin , ,3 ,2 ,1 ,0±±±=k .在k = 2的方向上第一条缝与第六条缝对应点发出的两条衍射光的光程差δ λ10 .解:光栅相邻缝对应点发出的衍射光在2=k 的方向上光程差为λ2,则1=N 与6=N 对应点发出的衍射光的光程差λλδ1052=⨯=.10-8 用波长为546.1 nm 的平行单色光垂直照射在一透射光栅上,在分光计上测得第一级光谱线的衍射角︒=30θ,则该光栅每一毫米上有 916 条刻痕.解:由光栅方程 λθk d =sin , 得 mm 91630sin 1条=︒==λd N 10-9 用一毫米内刻有500条刻痕的平面透射光栅观察钠光谱(3.589=λnm ),当光线垂直入射时,最多能看到第 3 级光谱.解:63102500101--⨯=⨯=d m ,光线垂直入射时,光栅衍射明纹条件λθk d =sin ∵1sin <θ, 得 39.3=<λd k ,取整数 3max =k 10-10 一束平行光垂直入射在平面透射光栅上,当光栅常数d /a = 3 时,k = 3, 6, 9级不出现.解:由光栅缺级条件()k a d k '=, ,3,2,1±±±='k 时, ,9,6,3±±±=k 级缺级当k '取1时,3=k ,∴a d 3=10-11 入射光波长一定时,当光线从垂直于光栅平面入射变为斜入射时,能观察到的光谱线最高级数max k 变大 (填“变小”或“变大”或“不变”).解:正入射光栅方程λθk d =sin ;斜入射光栅方程λθk i d '=+)sin (sin ,…,题10-6图∵︒<90θ,︒<≤︒900i ,∴1sin <θ,1sin 0<<i , ∴ m ax max k k >' 10-12 用波长范围为400~760 nm 的白光照射到衍射光栅上,其衍射光谱的第二级和第三级重叠,则第三级光谱被重叠部分的波长范围是 400 ~ 506.7 nm . 原题22-6 解:λλ''=k k ,2323λλ=,令 2λ= 760 nm ,得 3λ = 506.7 nm 10-13 从光源射出的光束垂直照射到衍射光栅上.若波长为3.6531=λnm 和2.4102=λnm 的两光线的最大值在︒=41θ处首次重合.问衍射光栅常数为何值? 解:由光栅方程公式有 dk d k 2211sin λλθ== ∴60.12.4103.6562112===λλk k 而1k 与 2k 必须是整数,又取尽量小的级数∴8,521==k k=︒⨯⨯==-41sin 103.6565sin 91θλk d 61000.5-⨯ m10-14 波长为500nm 的单色平行光垂直入射于光栅常数为3103-⨯=d mm 的光栅上,若光栅中的透光缝宽度3102-⨯=a mm ,问⑴ 哪些谱线缺级?⑵ 在光栅后面的整个衍射场中,能出现哪几条光谱线?解:⑴ 根据缺级条件 k ad k '=( ,3,2,1±±±='k )则光栅的第k 级谱线缺级(k 为整数) 本题 k k k a d k '='⨯⨯='=--2310210333 当 ='k 2、4、6….时k = 3、6、…则第±3、±6,…谱线缺级根据光栅方程 λθk d =sin , λθsin d k = , 令 2/πθ< 得 61050010103933=⨯⨯⨯=<---λdk ,再考虑到缺级. 只能出现 0、±1、±2、±4、±5共9条光谱线.10-15 一双缝,缝距 d = 0.40 mm ,两缝的宽度都是a = 0.080 mm ,用波长为480=λnm 的平行光垂直照射双缝,在双缝后放一焦距为f = 2.0 m 的透镜,求:⑴ 在透镜焦平面处的屏上,双缝干涉条纹的间距∆x ;⑵ 在单缝衍射中央亮纹范围内的双缝干涉亮纹数目.原题22-3⑴ ∆x = 2.4×10-3 m⑵ 在单缝衍射中央亮纹范围内有 9条 亮谱线:4 ,3 ,2 ,1 ,0±±±±级10-16 光学仪器的最小分辨角的大小[ C ](A) 与物镜直径成正比; (B) 与工作波长成反比(C) 取决于工作波长与物镜直径的比值;(D) 取决于物镜直径与工作波长的比值. 解:Dλϕ22.1δ= 10-17 人眼瞳孔随光强大小而变,平均孔径约为3.0 mm ,设感光波长为550 nm ,眼睛可分辨的角距离约为 1 分.解:取人眼孔径为3 mm ,入射光波长为550nm ,眼最小分辨角 122.1δ'≅= D λϕ10-18 在夜间人眼的瞳孔直径约为5.0 mm ,在可见光中人眼最敏感的波长为550 nm ,此时人眼的最小分辨角为 27.6 秒,有迎面驶来的汽车,两盏前灯相距1.30 m ,当汽车离人的距离为 9.69×103 m 时,人眼恰好可分辨这两盏灯.原题22-7 解: ==Dλϕ22.1δ; =∆∆=θx l 10-19 根据光学仪器分辨率的瑞利判据,要利用望远镜分辨遥远星系中的星体,可采用 增大透镜直径 或 用较短的波长 的方法.10-20 用一部照相机在距离地面20 km 的高空中拍摄地面上的物体,若要求它能分辨地面上相距为0.1m 的两点,问照相机镜头的直径至少要 13.4 cm .(设感光波长为550 nm )解:由 l s D ==λϕ22.1δ,得134.01.010*********.1 22.139=⨯⨯⨯⨯==-s l D λm = 13.4cm 10-21 以未知波长的X 射线掠入射于晶面间隔为10103-⨯=d m 的晶面上,测得第一级布喇格衍射角︒=51θ,则该X . 解:λϕk d =sin 2,k = 1,……10-22 一束波长范围为0.095 ~ 0.140 nm 的X 射线照射到某晶体上,入射方向与某一晶面夹角为︒30,此晶面间的间距为0.275 nm ,求这束X 射线中能在此晶面上产生强反射的波长的大小.原题22-8=λ0.1375 nm10-23 测量未知晶体晶格常数最有效的方法是X 射线衍射法.现用波长07126.0=λ nm (钼谱线)的X 射线照射到某未知晶体上,转动晶体,在三个相互正交的方位上各测得第2级布喇格衍射角分别为59561'''︒=ϕ、79132'''︒=ϕ、14943'''︒=ϕ,请分别求出这三个相互正交方位上的晶面间距.解:晶体的衍射满足布喇格方程 λϕk d =sin 2 ϕλsin 2k d = 已知 k = 2,︒=985.61ϕ、︒=319.32ϕ、︒=161.43ϕ解得:=1d 0.586 nm ,=2d 1.231 nm ,=3d 0.982 nm(该晶体为斜方晶系的无水芒硝)习题参考答案作业2 动量与角动量 功与能2-1 0.6 N·s ; 2 g 2-2 1.41 Ns2-3 M P '=2υ;=''F 30N ,=P 45W 2-4 5.30 × 1012 m 2-5 B A a b υυ= 2-6 0.45 m 2-7)(mr k ,)2(r k -2-8 )2(22k g m2-9 )6(R GMm ,)3(R GMm - 2-10 4.23×106 J , 151 s 2-11 31 J ,5.345 m /s2-12 22k ωq m E P =,222k ωp m E Q =222ωp m A x =,222ωq m A y -=作业4 气体动理论4-1 0.13 kg ,117升4-2 平衡状态,气体的准静态过程 4-3 1.53 × 104 Pa4-4 相同,不同,不同 4-5 kTpVN =4-6 10 : 3, 5 : 3, 1 : 1 4-7 略4-8 =∆E 41.55 J ,221007.2-⨯=∆K E 4-9 =∆T 0.481 K ,41000.2⨯=∆p Pa 4-10 R E 2,)5(2μE ,)π5(4μE4-11 υυυd )(d 100⎰⎰∞=='f NN N ,υυd )(100⎰∞=f P ,υυυυυυd )(d )(100100⎰⎰∞∞=f f4-12 D4-13 51035.1⨯=P Pa 4-14 n = 3.2×1017 m -3 ,=λ7.8 m ,=z 59.9 s -1 4-15 =⎪⎭⎫⎝⎛υ1kT m π2=, υυ1π41⋅=⎪⎭⎫ ⎝⎛ 4-16 )3(20υ=a ,=∆N 0.333 N ,=υ 1.220υ,=2υ 1.310υ作业6 狭义相对论基础6-1 93,10,0,2.5×10-7s 6-2 51033.3-⨯-s ,天津 6-3 3.61 m ,143369.33'︒=︒ 6-4 1.418×108 m /s = 0.473 c 6-5 12 m ,4 s6-6 =∆t 1.6 s ,='∆t 0.96 s 6-7 )(122c a υ-,)(122c mυ-,)1(22c ab mυ-6-8 cu cu l x -+=∆110,c u c u c l t -+=∆110,c =υ6-9 0.7×10-36-10 50.8%6-11 46-12 211k c -=υ 6-13 0.866 c ,0.866 c 6-14 2.94×105 eV 6-15 4.1×1066-16 m = 2.67m 0,=υ0.5c ,0031.2m m =' 6-17 c 115.0m ax =υ,=ke E 3.43×103eV ,==ke kp 1840E E 6.31×106eV作业8 波 动8-1 略 8-2 7.58×105 m 8-3 316, 2.11×10118-4 10.5m ,5Hz ,52.4m/s ,x 轴正方向x = 0处质元的振动方程 8-5 600 cm/s ,)]24π(252sin[30.0x t y +=(cm)8-6 2π9-=ϕ,2π=∆ϕ 8-7 )]4(2cos[1042x t y -⨯=-π,图略8-8 4106.0-⨯J/m 3,4102.1-⨯J/m 3;71024.9-⨯J 8-9 0.58-10 []2ππ4cos 01.0++=x t y 反 8-11 ]π)(π2cos[+-=x t A y ν]2π)(π2cos[--=x t A y ν入 ]2π)(π2cos[++=x t A y ν反波节:νu k x ⋅=2(k = 0, -1, -2, …),波腹:νu k x )412(-=(k = 0, -1, -2, …)8-12 )( π2cos 2λx T t A y -=,t Tx A y y y π2cos π2cos 221λ=+=波腹 2 λk x =,k = 0, 1, 2, …波节 4)2( λ+=k x ,k = 0, 1, 2, …8-13 )π31712ππ7cos(10--=x t y (cm)作业10 光的衍射10-1 1.0 10-2 1/2 10-3 310-4 6, 一级明10-5 212λλ=,1λ的第k 1极小和2λ的第k 2 = 2k 1极小重合. 10-6 a = 2.912×10-4m, =ρ2 1.13×10-3m 10-7 λ10 10-8 916 10-9 3 10-10 3 10-11 变大10-12 400 ~ 506.7 10-13 61000.5-⨯=d m10-14 第±3、±6,…谱线缺级,只出现 0,±1,±2,±4,±5共9条光谱线. 10-15 2.4 mm , 9条亮纹 10-16 C 10-17 110-18 27.6, 9.69×10310-19 增大透镜直径, 用较短的波长 10-20 13.410-21 111023.5-⨯ 10-22 =λ0.1375 nm10-23 =1d 0.586 nm ,=2d 1.231 nm ,=3d 0.982 nm。
大学物理振动和波习题课
12、一质点作简谐振动,周期为 T。质点由平衡
位置向X轴正方向运动时,由平衡位置到二分之一 最大位移这段路程所需要的时间为( )。
A T 4 B T 1 C 2 T 6 D T 8
解:令简谐振动为 xA si n t
则当 xA2 时, si n t0.5
Acos2(t 1) T2
Acos2T(t 13)
.
7.图中所示为两个简谐振动的振动曲线.若以余弦函数表 示这两个振动的合成结果,则合振动的方程为
xx1x2 0.04cos(t)
x (m)
0.08
O
-0.04
1
x1 t (s)
2 x2
.
8 如果在固定端 x0处反射的反射波方程式是
y2 Aco2stx
设反射波无能量损失,则入射波的方程式是( ) 形成的驻波的表达式是( )。
y1OAcos2vt y2OA cos2vt
形成的驻入 波射 为波 :方 程 y1Acos 2 t x
y y 1 y 2 A c 2 ot s2 x A c 2 ot s2 x
得:
S
wu
1 A22u
2
3.惠更斯原理和波的叠加原理
惠更斯原理:
波阵面上每一点都可以看作是发出球面子波的 新波源,这些子波的包络面就是下一时刻的波阵面。
波的叠加原理:
当几列波在介质中某点相遇时,该质点的
振动位移等于各列波单独传播时在该点引起位 移的矢量和。
.
4.波的干涉: 相干条件: 振动方向相同
频率相同
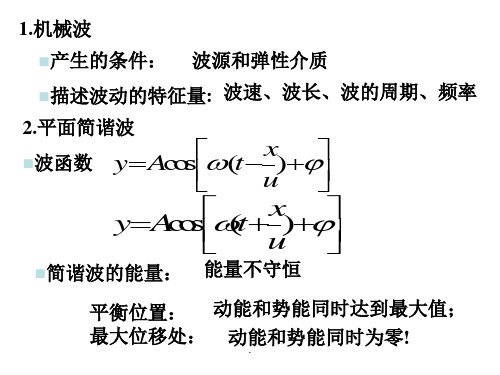
1.机械波
产生的条件: 波源和弹性介质
描述波动的特征量: 波速、波长、波的周期、频率
2.平面简谐波
波函数 yAcos(tux)
振动和波习题课

20000 5 2 S 1.6 10 J / m s 2 4 10000
10)入射波方程为y1=Acos2 (t/T+x/ ),在自由 端x=0处发生反射后形成驻波,设反射后波的强度 不变,则反射波方程为 ,在x=2/3处 质点合振动的振幅为 。
自由端:在反射点没有半波损失。
波动
1.理解机械波产生的条件;掌握描述平面简谐波 的各物理量及各量间的关系;掌握由已知质点 的简谐振动方程得出平面简谐波的波函数的方 法;能运用波形图线分析和解决问题。 2.理解波的能量传播特征及能流密度概念。 3.了解电磁波的性质。 4.理解惠更斯原理和波的叠加原理;掌握波的相 干条件。能运用相位差和波程差分析、确定相 干波叠加后振幅加强或减弱的条件。 5.理解驻波的概念及其形成条件,能确定波腹和 波节的位置。 6.能用多普勒频移公式计算。
振动练习
1)一弹簧振子作简谐振动,当其偏离平衡位置 的位移大小为振幅的1/4时,其动能为振动总能量的 [E ] (A)7/16
(B)9/16
(C)11/16
(D)13/16
(E)15/16
1 2 2 2 E k m A si n (t 0 ) 2 1 m 2 ( A2 x 2 ) 2
(D)1:1:2
1 1 1 弹簧的串并联: 串联时等效劲度系数 k k1 k 2
并联时等效劲度系数 k k1 k2
4)用余弦函数描述一简谐振动,速度V与时间t的 关系曲线如图所示,则振动初位相为[ A ] ( A) / 6 (B) /3 (C) /2 (D) 2/3 (E) 5/6
Байду номын сангаас振动
1.掌握描述简谐振动的各物理量,特别是相位, 及各物理量之间的关系。掌握位移-时间曲线, 掌握旋转矢量法。能根据给定的初始条件,写 出一维简谐振动的运动方程,并理解其物理意 义;能比较同频率的不同谐振动的相位差。 2.掌握简谐振动的动力学特征,能建立一维简谐 振动(弹簧振子、单摆、复摆等)的微分方程。 3.掌握同方向、同频率的两个简谐振动的合成规 律;了解拍和拍频;了解相互垂直、同频率的 两个简谐振动的合成情况。
振动与波动习题课

2.一简谐波沿X轴正方向传播,图中所示为
t =T /4 时的波形曲线。若振动以余弦函数
表示,且次提各点振动的初相取 到
之间的值,则:
(A)0点的初位相为 0= 0; (B)1点的初位相为 1= /2; (C)2点的初位相为 2= (D)3点的初位相为 3= /2;
频率为
(A)nS
(B)u uvRns
(C)uuvRnS ;
(D) u
u
vRnS
[B]
13.两列完全相同的平面简谐波相向而行 形成驻波。以下几种说法中为驻波所特有 的特征是: (A)有些质元总是静止不动; (B)迭加后各质点振动相位依次落后; (C)波节两侧的质元振动位相相反; (D)质元的振动能与势能之和不守恒。
(A) 1/2 ; (C) 1/3;
(B) 1/5; (D) 2/3.
[A]
13.两偏振片堆叠在一起,一束自然光垂 直入射其上时没有光线透过。当其中一偏 振片慢慢转动180 °时透射光强度发生的 变化为:
(A)光强单调增加; (B)光强先增加,后有减小至零; (C)光强先增加,后减小,再增加; (D)光强先增加,然后减小,再增加再 减小至零。
[B]
20.根据惠更斯-菲涅耳原理,若已知光在
某时刻的波阵面为 S,则 S 的前方某点 P 的光强度决定于波阵面 S 上所在面积元发 出的子波各自传到 P 点的
(A)振动振幅之和; (B)光强之和; (C)振动振幅之和的平方; (D)振动的相干叠加。
[D]
21.一束光是自然光和线偏振光的混合光, 让它垂直通过一偏振片。若以此入射光束 为轴旋转偏振片,测得透射光强度最大值 是最小值的 5 倍,那么入射光束中自然光 与线偏振光的光强比值为
振动和波习题课

习题:1. 下面关于声波的说法中正确的是 ( )A. 同一种声波在水中传播时的波长要比空气中传播时的波长要大B. 声波的传播速度与介质的种类及声源的振动频率有关C. 声波不论在什么介质中传播都是纵波D. 声波可以发生反射,也可以发生干涉和衍射2. 右图,两单摆的摆长相同,平衡时两球刚好接触,现将摆球A 向左拉开一小角度后释放,相碰后,两球分开各自做简谐振动。
以m A ,m B 分别代表A ,B 的质量,则: ( )A. 如果m A >m B ,下一次碰撞将发生在平衡位置的右侧。
B. 如果m A <m B ,下一次碰撞将发生在平衡位置的左侧。
C. 无论两球的质量之比是多少,下一次碰撞都不可能在平衡位置的右侧。
D. 无论两球的质量之比是多少,下一次碰撞都不可能在平衡位置的左侧。
3. 单摆的摆长为L ,最大摆角为θ(θ>5º),摆球的质量为m ,摆球由最大位移向平衡位置运动过程中:( ) A. 重力的冲量为gL m 2π B. 合力的冲量为gL m )cos 1(θπ-C. 合力的冲量为)cos 1(2θ-gL mD. 合力的冲量为gL m2π 4. 在波的传播方向上有M 、N 两个质点,相距3.0米。
(小于一个波长)右图为这两个质点的振动图象。
其中实线为M 质点的振动图象,虚线为N 质点的振动图象,则这列波的传播方向和传播速度可能为( )A. 向右传播,v =3米/秒B. 向右传播,v =1米/秒C. 向左传播,v =3米/秒D. 向左传播,v =1米/秒5. 水平弹簧振子的振动图线如图7所示,弹簧振子在1.0s 时的弹性势能是0.40J ,若振子的质量是0.20kg ,则振子在4.0s 时的速度大小是 ;方向是 ;加速度的大小是 。
6. 轻质线绳od的悬点与一单摆的悬点o´相靠近,且处于同一水平线上,如右图所示。
在悬线上穿着一个小球B,它可沿悬线滑动,将单摆的摆球A由偏角小于5º处释放,与此同时将B球由悬点o释放,当A第一次通过它的平衡位置时,正好与滑行中的B球相碰,求B球与悬线之间的摩擦力与B球所受重力之比。
振动与波习题课

6、简谐振动的合成: 简谐振动的合成: 同方向、同频率的简谐振动的合成: 同方向、同频率的简谐振动的合成:
v A2
ϕ2 ϕ ϕ1
v A
v A1
x1
x (t ) = x1 (t ) + x2 (t )
= A cos(ωt + ϕ )
o
合成结果仍为同频率的简谐运动
x2
x
x
A=
2 A12 + A2 + 2 A1 A2 cos( ϕ 2 − ϕ 1 )
2π (r2 − r1 ) = ±2kπ k = 0,1,2,3,.....
λ 相消干涉: 相消干涉:∆ϕ = (ϕ20 − ϕ10 ) − 2π (r2 − r1 ) = ±(2k + 1)π k = 0,1,2,3,..... λ
相位、相位差和初相位的求法: 相位、相位差和初相位的求法:
解析法和 常用方法为解析法 旋转矢量法。 常用方法为解析法和旋转矢量法。 1、由已知的初条件求初相位: 、由已知的初条件求初相位: 已知初位置的大小、正负以及初速度的正负。 ①已知初位置的大小、正负以及初速度的正负。 A [例1]已知某质点振动的初位置 y0 = 且v0 > 0 。 例 已知某质点振动的初位置 2 y = A cos( ω t + ϕ )
A1 sin ϕ 1 + A2 sin ϕ 2 ϕ = arctg A1 cos ϕ 1 + A2 cos ϕ 2
机械波: 二、机械波:
1、产生的条件:波源及弹性媒质。 产生的条件:波源及弹性媒质。 2、描述波的物理量: 、描述波的物理量: 波长: 波传播时, 在同一波线上两个相邻的相位差为2 波长 波传播时 在同一波线上两个相邻的相位差为 π 的 质元之间的距离 ( λ )。 周期:波前进一个波长的距离所需的时间( 周期:波前进一个波长的距离所需的时间(T )。 频率:单位时间内波动传播距离中所包含的完整波长的数目(ν)。 频率:单位时间内波动传播距离中所包含的完整波长的数目 。 波速: 波在介质中的传播速度为波速。( 。(u 波速 波在介质中的传播速度为波速。( ) 各物理量间的关系: 各物理量间的关系:
高中物理练习振动与波(习题含答案)

1.下列关于简谐振动和简谐波的说法,正确的是A.媒质中质点振动的周期一定和相应的波的周期相等B.媒质中质点振动的速度一定和相应的波的波速相等C.波的传播方向一定和媒质中质点振动的方向一致D.横波的波峰与波谷在振动方向上的距离一定是质点振幅的两倍2.做简谐振动的单摆摆长不变,若摆球质量增加为原来的4倍,摆球经过平衡位置时速度减小为原来的1/2,则单摆振动的A.频率、振幅都不变B.频率、振幅都改变C.频率不变、振幅改变D.频率改变、振幅不变3.家用洗衣机在正常脱水时较平稳,切断电源后,洗衣机的振动先是变得越来越剧烈,然后逐渐减弱。
对这一现象,下列说法正确的是A.正常脱水时,洗衣机脱水缸的运转频率比洗衣机的固有频率大B.正常脱水时,洗衣机脱水缸的运转频率比洗衣机的固有频率小C.正常脱水时,洗衣机脱水缸的运转频率等于洗衣机的固有频率D.当洗衣机的振动最剧烈时,脱水缸的运转频率恰好等于洗衣机的固有频率4.两个振动情况完全一样的波源S1、S2相距6m,它们在空间产生的干涉图样如图所示,图中实线表示振动加强的区域,虚线表示振动减弱的区域,下列说法正确的是A.两波源的振动频率一定相同B.虚线一定是波谷与波谷相遇处C.两列波的波长都为2mD.两列波的波长都为1m5.频率一定的声源在空气中向着静止的接收器匀速运动。
以u表示声源的速度,V表示声波的速度(u<V),v表示接收器接收到的频率。
若u增大,则A.v增大,V增大 B. v增大,V不变C. v不变,V增大D. v减少,V不变6.如图所示,沿x轴正方向传播的一列简谐横波在某时刻的波形图为一正弦曲线,其波速为200m/s,下列说法中正确的是A.图示时刻质点b的加速度将减小B.从图示时刻开始,经过0.01s,质点a通过的路程为0.4mC.若此波遇到另一列波并发生稳定干涉现象,则另一列波的频率为50HzD.若该波传播中遇到宽约4m的障碍物能发生明显的衍射现象7.一列沿x轴正方向传播的简谐横波,周期为0.50s。
振动和波10)

例题5.一质点在平衡位置O附近做简谐运动,从它经过平衡位置起开始计时,经0.13 s质点第一次通过M点,再经0.1 s第二次通过M点,则质点振动周期的可能值为多大?解析:将物理过程模型化,画出具体的图景如下图7-1-8所示.设质点从平衡位置O向右运动到M点,那么质点从O到M运动时间为0.13 s,再由M经最右端A返回M经历时间为0.1 s;如图7-1-9所示.另有一种可能就是M点在O点左方,如图7-1-10所示,质点由O点经最右方A点后向左经过O 点到达M点历时0.13 s,再由M向左经最左端A’点返回M历时0.1 s.根据以上分析,质点振动周期共存在两种可能性.如图7-1-9所示,可以看出O→M→A历时0.18 s,根据简谐运动的对称性,可得到T1=4×0.18 s=0.72 s.另一种可能如图7-1-10所示,由O→A→M历时t1=0.13 s,由M→A’历时t2=0.05s.设M→O 历时t,则4(t+t2)=t1+2t2+t,解得t=0.01 s,则T2=4(t+ t2)=0.24s所以周期的可能值为0.72 s和0.24 s.点评:(1)本题涉及的知识有:简谐运动周期、简谐运动的对称性.(2)本题的关健是:分析周期性,弄清物理图景,判断各种可能性.(3)解题方法:将物理过程模型化、分段分析、讨论.例题6.一列简谐横波在t1= 0时刻波形如下图所示,传播方向向左;当t2=0.7 s时,P点第二次出现波峰,Q点坐标是(-7,0),则以下判断中正确的是()A. t3=1.26 s末,Q点第一次出现波峰B. t4=0.9 s末, Q点第一次出现波峰C.质点Q位于波峰时,质点P处于波谷D. P,Q两质点运动方向始终相反解析:由波形图的物理意义知,t=0时,质点P正经平衡位置向波谷方向运动,经周期恰好第一次运动至波峰处,经周期恰好第二次出现波峰,所以=0.7 s,T=0.4 s.又由图知波长λ=4m,所以.离Q点最近的波峰距Q9 m,所以波峰第一次传至Q点历时,可见选项A错B对.又P、Q两点相距s PQ=10 m=2.5λ,为半波长的5倍,故P,Q两质点振动步调恰好相反,所以选项CD正确.点评:在波动过程中,在波的传播方向上,相距波长整数倍的质点的振动步调相同,相距半波长奇数倍的质点振动步调相反.这是一个重要的结论,必须熟记.另外,将质点振动的非匀速运动(变加速运动)问题转化为波形图的匀速运动问题,是本题解法中的一个突出技巧,也应理解并掌握.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
(C)
3 x2 A cos( t π ) 2
t π ) [B] (D)x2 A cos(
3. 一质点作简谐振动,其振动方程为 1 1 x = 0.24 cos( t ) (SI),试用旋转矢量法求出质 2 3 点由初始状态运动到x = -0.12 m,v < 0的状态所需 最短时间t. 2 结果: t / 0.667 ( s )
求出A后,再作旋转矢量图,由x0 、v0画出旋转矢 量的位置而求出初位相
9.同频同方向谐振动合成后仍然是同频率的简谐 A sin A sin 振动 x A cos( t ) tg
1 1 2
A1 cos 1 A 2 cos 2
2
A
2 A1
2 A2
2 A1 A2 cos
2
l 4 2 则=2 L =0 l 4
L
=
例1. 如图所示,质量为m的物体由劲度系数 为 k1 和 k2 的两个轻弹簧连接,在水平光滑导轨 上作微小振动,则系统的振动频率为
k1 m
提示:等效并联弹簧 k=k1+k2
1 k1 k2 结果 2π m
k2
例2.弹簧振子在光滑水平面上作简谐振动时, 弹性力在半个周期内所作的功为 (A)kA2. (B)
L kl ( k = 1,2,3,…), L ( 2k 1 )l / 2 ( k = 0, 1,2,…)
2L / l
4. 驻波表达式为 y A cos2x cos100t ,位于 x1= 3/8 m的质元P1与位于x2 = 5/8 m处的质元P2的 振动相位差为_________________
A1
A
X
与振幅大的分振动的初相相同 y
u
X
10. 描述波动的几个物理量 λ 0 1 2 3 4 56 (波长l;波的周期T;波速u) u
T
11、平面简谐波的波动方程的推导 将 t 理解为已知点振动了的时间,求出任一点
实际振动的时间,以此代替已知点振动方程中的t 就可得到任一点的振动方程,即为波动方程。 照抄已知点的振动方程,再将任一点振动超前 于或落后于已知点振动的位相补上,就得任一点 的振动方程,即为波动方程。(超前就“+”, 落后就 “ -” 。)
能形成驻波的两列波,其振幅相同,传播方 向相反,若已知其中一列波的波动方程为
y1 A cos( t +
2
l
2
x
4
)
则另一列波的波动方程必可设为
l 2 则=2 x l 4
若X=L处是波节
若X=L处是波腹
y 2 A cos( t-
x )
则=2
2 2
l
x 2 1
(2 k +1)
相邻两个波腹或相邻两个波节之间的 距离为半个波长。
20、半波损失 当波从波疏媒质垂直入射到波密媒质界 面上反射时,在反射点,入射波和反射波的 位相相反(即有半波损失), 形成波节。 当波从波密媒质垂直入射到波疏媒质界 面上反射时,在反射点,入射波和反射波的 位相相同(即无半波损失), 形成波腹。
1 2 kA .(C)(1/4)kA2. 2
[ D ] (D)0.
例3. 图中画出一向右传播的简谐波在t时刻的波形 图,BC为波密介质的反射面,波由P点反射,则反 射波在t时刻的波形图为 [ ]
y B P O -A x C
O -A
y
y
P (A)
x
O -A
P x
y
O -A (C) P
y
O
(B)
[B]
x
l
y
O
y
t+ t 时 13、x一定时的振动曲线 14. 速度的旋转矢量
t时刻
t
u
例:如图,画出该时刻 V~X之间 A 的关系图
V
y(v)
0 V 0
1 1
2
X
2
X
15.波形图上能量极值点 波形图上任意一点的动能与势能值时刻相等,在
平衡位置动能与势能同时达到最大,而在谷峰位 置动能与势能同时达到最小值(为零)。
满足相干条件外,还必须在同一直线上沿相反 方向传播,叠加后所形成的波叫驻波。
B. 求出驻波的表达式:
y 2 A cos( 2
( cos cos 2 cos cos 2 2 C. 位相:相邻两个波节之间的
l
x 1 ) cos( t 2 )
Y
能量极 小
X
能量极 大
能量极大
能量极 小
16、惠更斯原理:波阵面上的每一点,都是发射 子波的新波源,其后任意时刻,这些子波的包络 面就是新的波阵面。
17、相干条件:两波源应满足:振动方向相同,
频率相同,位相差恒定。
18、波的干涉 在P点引起的合振动的振幅为:
2 1 2 2
S2 S1
r2
p
2 ( 2 1 )+ ( r1 r2 ) A A A 2 A1 A2 cos l S1 r1 若波在两种不同介质中传播 l
时动能和势能相等。
用旋转矢量法解
6. 用余弦函数描述一谐振子的振动,若其速度--时间关系曲线如图所示,求振动的初相位。 v(m/s)
-0.5vm 0
由速度的旋转矢量图 得
6
-vm
t(s)
7. 在一轻弹簧下端悬挂m0 = 100g砝码时,弹簧伸 长8 cm.现在这根弹簧下端悬挂 m =250g的物体, 构成弹簧振子.将物体从平衡位置向下拉动4 cm, 并给以向上的21 cm/s的初速度(令这时t =0)选x 轴向下, 求振动方程的数值式.
解:k = m0g / l )
12.25 1 k/m s 7 s 1 0.25 21 2 2 2 2 2 A x0 v 0 / 4 ( ) cm 5 cm 7 4 cos = 0.64 rad
5
0.1 9.8 12.25 0.08
O x
O
X
x 0.05cos(7t 0.64) (SI)
8.一质点在x轴上作简谐振动,选取该质点向右 运动通过A点时作为计时起点( t = 0 ),经过2秒后 质点第一次经过B点,再经过2秒后质点第二次经 过B点,若已知该质点在A、B两点具有相同的速 x 率,且AB = 10 cm. 求 (1)质点的振动 A B v 方程; (2) 质点在A点处的速率. t= 4 s 解: t 2 - 2 2 ,
k 0, 1, 2,
( 必 在 1、 2 之 间)
A
A1
( 1) 2 k
A A1 A2
A2
振动加强; 此时有= 1= 2
A2
X
( 2) ( 2 k 1) k 0, 1, 2, A | A1 A2 | 振动减弱
y
y A cos[ 2(t
xL
) ] l 2
L P O
x
t1
L
l
k
k = 0, 1, 2, … [只写 t1 L /(l ) 也可以]
补充(二)13. 一平面简谐波沿Ox轴传播,波动 表达式为 y A cos[2(t x / l ) ],则x1 = L处介质 质点振动的初相是___________________;与x1处 质点振动状态相同的其它质点的位置是_________; 与x1处质点速度大小相同,但方向相反的其它各 质点的位置是___________.
0
# 逆时针旋 转为正角。
O
A
O
t A0
X
x
# 顺时针旋 转为负角。
A2
’
旋转矢量的端点在X轴上的投影点作简谐振动 1、2象限 v<0 ; 3、4象限 v>0
A1
O
A1
X O
A1
A2
O
振动2比振动1超前
X
X
A2
反相 同相
6.谐振动的动力学特征:f=-kx * 无阻尼自由振动的弹簧振子作简 谐振动,其固有圆频率为 = k m 7.简谐振动的能量 1 1 2 2 E mv 动能: k 2 势能: E p kx 简谐振动能量:
P (D)
-A
x
1. 一弹簧振子作简谐振动,振幅为A,周期为T, 其运动方程用余弦函数表示.若t = 0时, (1)振子在负的最大位移处,则初相为_____; -/2 (2) 振子在平衡位置向正方向运动,则初相为____ (3)振子在位移为A/2处,且向负方向运动,则初相 /3 . 为______ 2.两个质点各自作简谐振动,它们的振幅相同、 周期相同.第一个质点的振动方程为 x1 = Acos(t + ).当第一个质点从相对于其平衡 位置的正位移处回到平衡位置时,第二个质点正 在最大正位移处.则第二个质点的振动方程为 1 1 (A) x2 A cos( t π ) (B) x2 A cos( t π )
t ) 例:如图,已知P点的振动方程:yP Acos( y x
y A cos[ (t u ) ]
u
或 y A cos[ t
2
l
( x ) ]
p
O
X
x
12、t 时刻的波形图
y
O
u t
u
x 1 x2
•波线上两质点之间的位 X 相差 2 ( x x ) 1 2 2 1
)
