2019-2020学年河南省郑州市中牟县枫杨外国语学校九年级(下)第一次月考数学试卷
2019-2020学年郑州市枫杨外国语中学九年级(下)第一次月考化学试卷(含答案解析)

2019-2020学年郑州市枫杨外国语中学九年级(下)第一次月考化学试卷一、单选题(本大题共14小题,共14.0分)1.向酸碱溶液里滴加指示剂,改变颜色的是()A. 酸或碱B. 指示剂C. 溶液中的水D. 其他物质2.为减少“白色污染”,下列做法不正确的是()A. 焚烧废弃塑料B. 重复使用塑料袋C. 用布袋代替塑料袋D. 使用微生物降解塑料3.下列符号既表示一种元素,又表示一个原子,还表示一种物质的是()A. OB. O2C. FeD. H4.下列有关化学反应:BaCl2+H2SO4=BaSO4↓+2HCl的说法中,正确的是()A. 基本反应类型是置换反应B. 生成的BaSO4不溶于稀盐酸C. 反应中涉及到酸、碱、盐三类物质D. 反应后所得溶液能使酚酞溶液变成红色5.如图所示的“人工树叶”是一种模拟植物光合作用的装置,利用光能将水和二氧化碳转化为氧气和燃料丙醇(C3H8O)。
下列不属于“人工树叶”作用的是()A. 为人类提供食物B. 为人类提供能源C. 将光能转化为化学能D. 有利于减缓温室效应6.下列鉴别物质的方法中错误的是()A B C D待区分物质BaCO3 NaCl棉线涤纶酒精白醋食盐水稀盐酸鉴别方法加水点燃,闻气味闻气味滴加酚酞溶液A. AB. BC. CD. D7.分类是学习和研究化学的常用方法,下列分类中正确的是()A. 纯净物:冰水共存物、干冰B. 化合物:盐酸、小苏打C. 合成材料:合金、塑料D. 有机物:Na2CO3、CH3COOH8.下列离子在pH=1的溶液中能大量存在的是()A. CO32−B. HCO3−C. OH−D. Cl−9.现有Na2CO3、Fe、Ca(OH)2、H2SO4这四种物质两两之间能发生化学反应的有几组()A. 2组B. 3组C. 4组D. 5组10.下列图示操作正确的是()A. 闻气休气味B. 给液体加热C. 测定溶液的pHD. 取用锌粒11.下列做法对人体无害的是()A. 为了节约粮食,把霉变大米淘净后继续食用B. 用甲醛水溶液浸泡海产品,以达到保鲜目的C. 做馒头时加入适量的小苏打,使馒头松软可口D. 大多数维生素在人体内不能合成,每天需要大量摄取12.对如图所示实验的分析不正确的是()A. 甲:燃着的木条熄灭,说明气体X 一定是二氧化碳B. 乙:试管外壁发烫,说明生石灰与水的反应放出热量C. 丙:二极管发光,说明水果电池提供了电压D. 丁:穿旱冰鞋的小红用力推墙却向后运动,说明物体间力的作用是相互的 13.下表列出了除去物质中所含少量杂质的方法,其中错误的是( )物质 所含杂质 除去杂质的方法 ACO 2 CO 点燃混合气体 BNaCl 溶液 NaOH 加入适量的稀盐酸 CCu CuO 在纯氢气流中加热 D H 2 水蒸气 通过盛有浓硫酸的洗气瓶A. AB. BC. CD. D14. 下列各组物质的溶液,不另加试剂就不能鉴别出来的一是( )A. CuSO 4 NaOH KNO 3B. Na 2CO 3 HCl BaCl 2C. FeCl 3 AgNO 3 NaNO 3D. CaCl 2 K 2CO 3 NaCl二、填空题(本大题共5小题,共16.0分) 15. 燕麦片是家庭生活中常见的一种营养品.如表是某品牌燕麦片标签中的部分内容:每100g 含有的营养成分 糖类脂肪 蛋白质 钙 7.6g 7.8g 7.4g 201mg(1)在六大基本营养素中,除水之外,上表中没有列出的是______.(2)当老年人缺钙时,可能导致______.(3)小麦在种植过程中出现茎叶细小症状,同时有倒伏现象时,应施用复合肥,下列属于复合肥的是______(填序号).A.KClB.NH 4NO 3C.KNO 3.16.氨,或称氨气,是一种有刺激性气味,极易溶于水的气体。
郑州市2019-2020学年下学期第一次月考考试英语试题

号考郑州市2019-2020 学年下学期第一次月考考试题九年级英语考试时间:100 分钟,满分命题人:殷巍审题人:一、听力理解:(每小题 1 分,共20 分)第一节,听下面 5 段对话,每段对话后有一个小题, C 三个选项中选出最佳答案,每段对话读两遍。
()1.How was the weather now?A. Snowy.B. Rainy.)2.Who are they talking about?A. A teacher.B. A reporter. )3.What ' sNick 's b rliokteh?e rA. Quiet.B. Shy. )4.Who is learningFrench?A. Maria.B. Betty.)5.What is the man doing now?C. Mona.A .Giving a speech. B. Reading a book.120 分)陈爽从题中所给的 A 、B、C. Sunny.C. A singer.C. Outgoing.C. Listening to music. 第二节,听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳答案。
每段对话或独白读两遍。
听下面一段对话,回答第 6 至第7 两个小题()6.Where is Mr. Green now?A. At home. )7. What 's the man ' stelephone number?A.6603-6793. 听下面一段对话,回答第8至第9三个小题。
B. At the office.C.At a meeting.B.6603-6973.C.6603-7963.)8.What does the man want to buy?A. Bread and butter.B. Sugar and bread.)9. When will they play tennis?A. This afternoon.B. Tomorrow afternoon.C. Tomorrow morning. 听下面一段对话,回答第10 至第12 两个小题(C. Sugar and butter.)10.What do the two speakers need most? A.A watch. B. A map. C. A car.)11.Where are the two speakers?A.In a house.B. On a mountain.C. At the police station.)12.What ' s probably the relationship between the two speakers?A. Sister and brother.B. Teacher and student.C. Mother and son. 听下面一段对话,回答第13 至第15三个小题。
河南省郑州市东枫外国语学校(枫杨东校区)2019-2020学年九年级下学期月考化学试题(word无答案)

河南省郑州市东枫外国语学校(枫杨东校区)2019-2020学年九年级下学期月考化学试题一、单选题(★) 1 . 我国著名化学家侯德榜先生作出的重大贡献是()A.发明黑火药B.创造湿法冶金C.改进纯碱的生产D.发现了新元素(★) 2 . 下列关于糖类、蛋白质、油脂和维生素的说法正确的是()A.淀粉没有甜味,因此不属于糖B.维生素是人体不可缺少的营养物质C.葡萄糖不能转化为人体中的脂肪D.蛋白质中只含有碳、氢、氧三种元素(★) 3 . 关于固体氢氧化钠和浓硫酸的叙述,下列说法错误的是()A.都能在水溶液中解离出相同的离子面性质相似B.都有强烈的腐蚀性C.都需要密封保存D.溶于水时都放出大量的热,使溶液的温度升高(★) 4 . 有A、B、C三种溶液,A能使紫色石蕊试液变红,B能使无色酚酞试液变红,C遇紫色石蕊试液和无色酚酞试液均无变化,则三种溶液的pH由大到小的顺序是()A.A>C>B B.C>B>A C.B>A>C D.B>C>A(★★) 5 . 分类是学习和研究化学的常用方法。
下列分类中正确的是A.有机物:甲烷、乙醇、乙酸B.复合肥料:尿素、硝酸钾、磷酸氢二铵C.混合物:煤、石油、冰水共存物D.合成材料:合金、合成橡胶、合成纤维(★) 6 . 硒有防癌、抗癌作用。
如图为硒的原子结构示意图,下列说法不正确的是()A.图中x的值为8B.硒原子的质子数为34C.硒元素位于第四周期D.硒是人体必需微量元素(★) 7 . 下列实验方案中不可行的是A.用水区分氯化钙和碳酸钙B.用稀盐酸区分黄金和黄铜(含锌)C.用熟石灰区分氯化铵和硝酸铵D.用灼烧法区分羊毛线和腈纶线(★) 8 . 材料科学的发展对人类生活和社会进步会产生深远影响,下列有关表述错误的是()A.丝绸中的蚕丝属于人工合成纤维B.耐高温合金材料的开发加速了高性能航空发动机的研制进程C.废弃塑料制品的回收是对塑料材料的再利用D.玻璃钢是玻璃纤维与有机高分子合成材料制成的复合材料(★) 9 . 对于复分解反应,X+2NaOH═2Y+Cu(OH)2↓,下列分析中正确的是()A.X一定是CuCl2B.Y可能是H2OC.相对分子质量大小:X>Y D.Y可能是Na2SO4(★) 10 . 下列各组物质中,能发生复分解反应且反应前后溶液总质量变小的是()A.锌和稀硫酸B.氢氧化钠溶液和盐酸C.硫酸和氯化钡溶液D.氯化钾溶液和硫酸钠溶液(★★) 11 . 现有①Ba(NO 3 ) 2溶液、②KCl溶液、③K 2SO 4溶液、④CuSO 4溶液,不用其他试剂,可通过实验方法将它们一一鉴别开来,鉴别出来的先后顺序可能是( )A.①②③④B.①④③②C.④③②①D.④①③②(★) 12 . 甲化工厂排放的酸性污水和乙化工厂排放的污水,共含有以下6种离子中的各3种:K +、OH -、CO 32-、Ba 2+、H +、NO 3-,则乙化工厂排放的污水中所含有的3种离子是()A.K+、OH-、H+B.K+、OH-、CO32-C.Ba2+、OH-、NO3-D.OH-、K+、Ba2+(★★★★) 13 . 下列物质能在 pH=13 的无色溶液中大量共存的是()A.HCl、AgNO3、Na2CO3B.NaNO3、KNO3、NH4ClC.K2SO4、K2CO3、NaOH D.KMnO4、CuSO4、NaNO3(★★★★) 14 . 向一定质量的CaCl 2和HCl的混合溶液中逐滴加入溶质质量分数为10.6%的Na2CO 3溶液,实验过程中加入Na 2CO 3溶液的质量与产生沉淀或气体的质量关系如图所示。
郑州市2019-2020学年下学期第一次月考考试英语试题 - 副本

郑州市2019-2020学年下学期第一次月考考试题九年级英语 (考试时间: 100分钟,满分120分) 命题人:殷巍 审题人:陈爽 一、 听力理解:(每小题1分,共20分) 第一节,听下面5段对话,每段对话后有一个小题,从题中所给的A 、B 、C 三个选项中选出最佳答案,每段对话读两遍。
( )1.How was the weather now? A. Snowy. B. Rainy. C. Sunny. ( )2.Who are they talking about? A. A teacher. B. A reporter. C. A singer. ( )3.What’s Nick’s brother like? A. Quiet. B. Shy. C. Outgoing. ( )4.Who is learning French? A. Maria. B. Betty. C. Mona. ( )5.What is the man doing now? A . Giving a speech. B. Reading a book. C. Listening to music. 第二节,听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A 、B 、C 三个选项中选出最佳答案。
每段对话或独白读两遍。
听下面一段对话,回答第6至第7两个小题 ( )6.Where is Mr. Green now? A. At home. B. At the office. C.At a meeting. ( )7. What’s the man’s telephone number? A.6603-6793. B.6603-6973. C.6603-7963. 听下面一段对话,回答第8至第9三个小题。
( )8.What does the man want to buy? A. Bread and butter. B. Sugar and bread. C. Sugar and butter. ( )9. When will they play tennis? A. This afternoon. B. Tomorrow afternoon. C. Tomorrow morning. 听下面一段对话,回答第10至第12两个小题。
河南省郑州市枫杨2019-2020学年下期九年级第一次月考数学试卷及其解析

适当长度为半径作弧,分别交边 OA , OB 于点 D , E ;②分别以点 D , E 为圆心,大于 1 DE 的长为半径作 2
弧,两弧在 AOB 内交于点 F ;③作射线 OF ,交边 AC 于点 G .则点 G 的坐标为 ( )
A. (2, 4)
B. (5, 4)
C. (2, 4)
D. (3, 4)
x 1 1 x
1 x
17.(9 分)某公司的午餐采用自助餐的形式,并倡导员工“适度取餐,减少浪费”.该公司共有 10 个部门,且
各部门的人数相同,为了解午餐的浪费情况,从这 10 个部门中随机抽取了 A ,B 两个部门,进行了连续四周 (20
个工作日)的调查,得到这两个部门每天午餐浪费饭菜的重量,以下简称“每日餐余重量”(单位:千克),并
2019-2020 学年下期九年级第一次月考数学试卷
一.选择题(每题 3 分,共 30 分)
1.在 0.01,0, 5 , 1 这四个数中,最小的数是 (
)
5
A.0.01
B.0
C. 5
D. 1 5
2.地球的表面积约为 510000000km2 ,将 510000000 用科学记数法表示为 ( )
A. 0.51109
B. 5.1108
C. 5.1109
D. 51107
3.由 6 个大小相同的正方体搭成的几何体,被小颖拿掉 2 个后,得到如图 1 所示的几何体,图 2 是原几何体
的三视图.请你判断小颖拿掉的两个正方体原来放在 ( )
A.1 号的前后
B.2 号的前后
4.下列计算正确的是 ( )
到 ED ,连接 BE ,当 BD 3CD 时,请直接写出 BE 的长度.
2019-2020年初三第一次月考英语试卷及答案

2019-2020年初三第一次月考英语试卷及答案考生注意:请把答案写在答题卡上。
一、单项选择。
(共15个小题,每小题1分,满分15分)( )1.---Why don’t you listen to tapes to improve your listening skills? ---It’s _______ difficult for me ______ follow.A. to, tooB. too, toC. so, that D such, that( )2. ---How do you study for a test? ---________.A. At schoolB. In the libraryC. By reading the textbookD. For making word cards( )3. Our English teacher is so _________ with us that we all like her very much.A. crazyB. stupidC. unhappyD. patient( )4. I find _______ interesting to play with a dog.A. itB. thisC. himD. that( )5. Remember, my dear son. ________ careful you are, ________ mistakes you will make.A. The less, the moreB. The fewer, the moreC. The more, the lessD. The more, the fewer( )6. _______ nice day! Let’s go out to have a picnic.A. HowB. WhatC. How aD. What a( )7. ---Excuse me. Do you know these English words? ---Sorry, I don’t. But you can __________ in a dictionary.A. look it upB. look up itC. look them upD. look up them ( )8. ---Have they finished ________ the Water Festival? ---No, they haven’t.A. celebrateB. celebratedC. celebratingD. celebration ( )9. I don’t know ______ he will be back ______ the Dragon Boat Festival.A. whether, onB. if, inC. whether, inD. that, at( )10. She hardly ever speaks English because she is afraid ________ mistakes ________ grammar.A. to make, ofB. to make, onC. of making, atD. of making, in ( )11. The river is very deep. My mother warns me _________ in it.A. swimB. not to swimC. to swimD. not swim( )12. ---Could you tell me _____________? ---OK. Guiyang.A. where is Tom from?B. where Tom comes fromC. who is your pen palD. what is the boy doing( )13. ________ you meet, please say hello to him or her.A. WhoeverB. HoweverC. WhereverD. Whenever( )14. Annie keeps a diary every day. _________, she is good at writing.A. Because ofB. Instead ofC. As a resultD. So that( )15. I saw a _______ cat lying on the street when I went shopping yesterday afternoon.A. deathB. diedC. dieD. dead二、完形填空。
2019-2020学年河南省郑州市中牟县东枫杨外国语九年级(下)第一次月考(线上)语文试卷(有答案解析)

2019-2020学年河南省郑州市中牟县东枫杨外国语九年级(下)第一次月考(线上)语文试卷一、默写(本大题共1小题,共8.0分)1.古诗文默写。
______ ,山雨欲来风满楼。
(许浑《咸阳城东楼》)______ ,人道是,清光更多。
(辛弃疾《太常引•建康中秋夜为吕叔潜赋》)______ ,受上赏。
(《邹忌讽齐王纳谏》)《出师表》中一开篇就说明蜀国开国不顺的政治形势的一句是:______ 。
《曹刿论战》中体现曹刿注意细节的语句是______ ,______ 。
《临江仙•夜登小阁,忆洛中旧游》中作者以饱蘸着久历艰难和劫后余生的血泪的笔触,概括国家和个人的激剧变化的情况,写下的感慨深沉的句子是______ ,______ 。
二、现代文阅读(本大题共3小题,共31.0分)2.阅读下面的文章,完成各题。
占了命运的便宜①回乡过年,带小外甥去小店买花炮,回来路上听见有人喊他名字,我正要回头,却听小外甥压低声音说,快走。
我还没反应过来,他已经一溜烟跑回家了。
我转过头,看见一个和他年龄相仿的小男孩愣愣地站在远处,无所适从的样子。
②回到家里,小外甥说那是他同学,不过大家都不跟那小男孩玩。
小男孩有时撵着跟人家玩,有时候又会莫名其妙地骂人,甚至动手,下手还特别重,有次把一个男生的耳朵都打出血了。
③为什么会这样呢?小外甥的爸爸告诉我,小男孩没人管,妈妈几年前就没了,爸爸在外面打工,也不怎么回来,他跟着爷爷奶奶住。
④父子俩的话帮我拼凑出小男孩的处境:他打小没有父母照顾,家里经济条件较差。
他既孤单又暴躁,想靠近同学,又无法采取正确的方式,所以被孤立。
⑤我力劝小外甥对他好一点,还想买个礼物让小外甥送给他,小外甥统统不以为然。
我想这也非一人之力所能改变,就给他们老师写了一封信,让小外甥交给老师。
⑥倒不是因为我天性善良,更多的是不安全感使然。
这种不安全感包括两方面,一是我担心将来会在社会新闻里看到这个孩子。
⑦这些年新闻里的恶性事件,很多作案者都有着被伤害的童年,但人们往往拒绝倾听他们的童年故事。
河南省郑州枫杨外国语中学2019-2020学年下学期语文月考试卷%28无答案)(Word版)

2019-2020 年下期九年级语文测试卷(满分 120 分,考试时间 120 分钟)一、积累与运用(共 28 分)1.下列词语中加横线的字,每对读音都不同的一项是【】(2 分)A.踏实∕踏青奢靡∕风靡一时低声悄语∕悄然泪下B.孵化∕浮雕鞠躬∕笑容可掬风流倜傥∕丝绸之路C.角色∕角逐推磨∕磨杵成针烟熏火燎∕星火燎原D.旷野∕粗犷剽悍∕膘肥体壮踌躇满志∕铸就辉煌2.下列词语中没有错别字的一项是【】 (2 分)A.壁垒富饶易拉罐娇生惯养独竖一帜B.咋舌旌旗顶梁柱责无旁贷黯然失色C.静谧舵手蒸溜水花枝招展立竿见影D.提练翡翠满堂彩无动于衷别出心裁3.古诗文默写。
(共 8 分)(1)遥看是君家,。
(《十五从军征》)(2),愁云惨淡万里凝(《白雪歌送武判官归京》)(3)辛弃疾在《南乡子》中,侧面赞美孙权的句子是:“?”。
(4)边塞风光,独特壮观。
王维出使塞上,描绘了塞外“,”(《使至塞上》)的奇美壮丽风光:岑参歌咏白雪,再现了边地“,”(《白雪歌送武判官归京》)的雪压冬林景象。
4.名著阅读。
(任选一题作答)(4 分)(1)下面《水浒》中的两个回目都体现了“合作”精神, 请任选一个, 简要叙述其是怎样合作的。
①杨志押送金银担吴用智取生辰纲(第十六回)②梁山泊好汉劫法场白龙庙英雄小聚义 (第四十回)(2)《西游记》里孙悟空拥有一双“火眼金睛”, 很多妖魔鬼怪的把戏都被他识破,但他也有看走眼的时候。
比如在第八十六回“木母助威征怪物金公施法灭妖邪”中, 他就将豹子精抛出的假人头误认为是师父的, 好一番哭祭。
请简要概述孙悟空三次被骗的故事情节。
5.阅读下面材料, 按要求答题。
(共4分)在我国文学史上, 唐诗流传的数量最多, 影响最广。
这是什么原因呢?在唐之前, 也有《离骚》等优秀诗作, 但诗的语言过于文人化, 口语化程度不高, 能被完整记住、广为流传的名篇名句却不多。
唐代诗歌语言出现了一个巨大变化, 诗歌的平民化和口语化程度大大改善, 朗朗上口, 易记易背。
河南省郑州枫杨外国语中学2019-2020学年下期九年级第一次月考语文试卷(无答案)

2019-2020 九年级下学期第一次月考语文试卷一、积累与运用(共 28 分)1.下列词语中加点的字,每对读音都不同的一项是( )(2 分)A. 雇佣./佣.人隽.永/隽.逸曲.解/曲.高和寡鱼目混.珠/混.水摸鱼B. 诓.骗/眼眶.磅.礴/滂.沱复辟./开天辟.地矫.揉造作/骄.兵必败C. 旋.转/旋.风创.伤/创.始便.利/大腹便.便锐不可当./当.头棒喝D. 胚.胎/毛坯.遵循./咨询.驽.钝/剑拔弩.张险象迭.生/容貌昳.丽2.下列词语中没有错别字的一项是( )(2 分)A.婵联妥帖金刚钻白首起家毁家抒难B.部署栋粱峨眉山甘败下风山青水秀C.打蜡伎俩手动挡贻害无穷不落窠臼D.沉缅通缉陪小心触目伤怀骚首弄姿3.古诗文默写。
(9 分)(1)望西都,。
(张养浩《山坡羊·潼关怀古》(2)辛苦遭逢起一经, 。
(文天祥《过零丁洋》)(3) ,今日又南冠(夏完淳《别云间》)(4) ,半竿斜日旧关城。
(纳兰性德《浣溪沙》)(5) ,受上赏。
(《邹忌讽齐王纳谏》)(6)《出师表》中,诸葛亮给后主刘禅提了恳切的建议,其中劝谏刘禅赏罚要坚持统一标准的句子是:,。
(7)岑参《白雪歌送武判官归京》中,“,”一句,运用留白手法,描绘出诗人伫立在大雪中凝望友人离去的身影时的依依不舍之情。
4.名著阅读。
(4 分)(1)下面三句话是《水浒传》中和及时雨宋江有关的三个小故事,请先按照故事发生的先后顺序进行排序,然后简述相关故事情节。
①怒杀阎婆惜②私放晁天王③江州劫法场(2)鲁迅在《中国小说史略》中称《儒林外史①严贡生②周进5.在下面一段文字的横线处补写恰当的语句。
使整段文字语意完整、连贯(4 分)站在海边眺望远处驶来的船只时,我们总是先看到桅杆,再看到船体。
桅杆意味着事物的先兆。
“凡事预则立,不预则废。
”①?“预”其实就从懂得看“桅杆”中来。
善于看“桅杆”,就能把那些苗头性、倾向性的东西辨别出来,然后分析它的走向和演变,从中认识和把握矛盾运动的规律,从而看出信心和希望来。
2019-2020郑州外国语中学数学中考第一次模拟试卷(含答案)
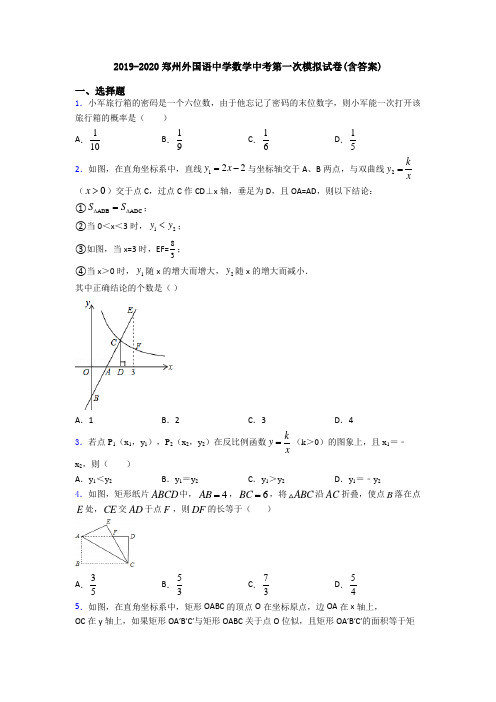
k x
( x 0 )交于点 C,过点 C 作 CD⊥x 轴,垂足为 D,且 OA=AD,则以下结论:
① SΔADB SΔADC ;
②当 0<x<3 时, y1 y2 ;
③如图,当 x=3 时,EF= 8 ; 3
④当 x>0 时, y1 随 x 的增大而增大, y2 随 x 的增大而减小.
其中正确结论的个数是( )
【详解】
解:∵四边形 ABMO 是圆内接四边形,∠BMO=120°,
∴∠BAO=60°,
∵∠AOB=90°,
∴AB 是⊙C 的直径, ∴∠ABO=90°-∠BAO=90°-60°=30°, ∵点 A 的坐标为(0,3), ∴OA=3, ∴AB=2OA=6, ∴⊙C 的半径长=3,故选:C 【点睛】 本题考查的是圆内接四边形的性质、圆周角定理及直角三角形的性质,熟知圆内接四边形 对角互补的性质是解答此题的关键.
x 的方程 x2=42+(6-x)2,解方程求出 x 即可. 【详解】
∵矩形 ABCD 沿对角线 AC 对折,使△ABC 落在△ACE 的位置, ∴AE=AB,∠E=∠B=90°, 又∵四边形 ABCD 为矩形, ∴AB=CD,
∴AE=DC, 而∠AFE=∠DFC, ∵在△AEF 与△CDF 中,
AFE=CFD
(1)求抛物线的解析式;
(2)点 D 是抛物线上一点,连接
BD、CD,满足 SDBC
3S 5
ABC ,求点 D 的坐标;
(3)点 E 在线段 AB 上(与 A、B 不重合),点 F 在线段 BC 上(与 B、C 不重合),是
否存在以 C、E、F 为顶点的三角形与△ABC 相似,若存在,请直接写出点 F 的坐标,若不
故选 A.
河南省郑州市2019-2020年下学期枫杨中学九年级语文2月份月考试卷(Word版、无答案)

2019-2020-2 九年级语文月考 1 试卷一、积累与运用(共 20 分)1.阅读下面文字,给加点的字注音,根据拼音写出汉字。
(3 分)异乡人这三个字,听起来音色苍凉;“他乡遇故知”,则是人生一快。
一个怯生生的船家女,偶尔在江上听到乡音,就不觉喜上眉梢,顾不得娇羞、和隔船的陌生男子搭讪:“君家何处住?妾住在横塘。
停船暂借问,或恐是同乡。
”辽阔的空间,悠miǎo(①)的时间,都不会使这种感情tuì(②)色:这就是乡土情结。
民族向心力的凝聚,并不取决于地理距离的远近。
我们第一代的华侨,含辛茹苦,寄籍外洋,生儿育女,却世代翘.(③)首神州,不忘桑梓之情,当祖国需要的时候,他们都做了慷慨的奉献。
2.根据下图,推测“杳”字的意思。
(2 分)(第 2 题图)3.古诗文默写。
(共 8 分)(1),山雨欲来风满楼。
(许浑《咸阳城东楼》)(2),人道是,清光更多。
(辛弃疾《太常引·建康中秋夜为吕叔潜赋》)(3),受上赏。
(《邹忌讽齐王纳谏》)(4)《出师表》中一开篇就说明蜀国开国不顺的政治形势的一句是:。
(5)《曹刿论战》中体现曹刿注意细节的语句是,。
(6)《临江仙·夜登小阁,忆洛中旧游》中作者以饱蘸着久历艰难和劫后余生的血泪的笔触,概括国家和个人的激剧变化的情况,写下的感慨深沉的句子是,。
4.综合性学习。
(7 分)为了弘扬传统文化、增强文化自信,黄海中学九(1)班决定开展以“会诗词•咏经典•信中国”为主题的语文实践活动,请你参与。
【会诗词】(2 分)在班级举行的赛诗会上,甲乙两位同学分别朗诵了一首词。
请你结合学过的古诗词知识,为这两首词选择正确的词牌名,将序号填在横线上。
A.卜算子B.浣溪沙C.如梦令D.相见欢乙:甲:【咏经典】(2 分)《经典咏流传》用现代的唱法和曲调来演绎传统经典,将诗词文化与电视媒介有机结合,兼顾诗词文化的意境悠远和表现形式的通俗易懂。
经典传唱人结合自身的音乐风格,将经典诗词转化为优美的歌曲,以现代人更喜闻乐见的方式,去学习诗词,“推动中华优秀传统文化创造性转化、创造性发展”,受到广大观众的一致好评。
河南省郑州市外国语中学2019-2020学年九年级下学期第一次月考数学试题

河南省郑州市外国语中学2019-2020学年九年级下学期第一次月考数学试题学校_________ 班级__________ 姓名__________ 学号__________一、单选题1. ﹣2020的倒数是()A.﹣2020B.﹣C.2020D.2. 某种冠状病毒的直径是120纳米,1纳米=米,则这种冠状病毒的直径是()厘米.A.B.C.D.3. 下列运算正确的是()A.2a+3a=5a2B.(﹣ab2)3=﹣a3b6C.a2?a3=a6D.(a+2b)2=a2+4b24. 下列倡导节约的图案中,是轴对称图形的是()A.B.C.D.5. 如图,Rt△ABC中,∠C=90°,∠B=30°,AC=.按以下步骤作图:①以A为圆心,以小于AC长为半径画弧,分别交AC、AB于点E、D;②分别以D、E为圆心,以大于DE长为半径画弧,两弧相交于点P;③连接AP交BC于点F.那么BF的长为()A.B.3 C.2 D.6. 某正方体的每个面上都有一个汉字,如图是它的一中展开图,那么在原正方体中,与点字所在面相对的面上的汉字是()A.青B.春C.梦D.想7. 某课外小组的同学们在社会实践活动中调查了20户家庭某月的用电量,如用电量(度)120 140 160 180 200户数 2 3 6 7 2A.7,6 B.7,3 C.180,160 D.180,1708. 中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x两,牛每头y两,根据题意可列方程组为()A.B.C.D.9. 如图,在平面直角坐标系中,若干个半径为3个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒3个单位长度,点在弧线上的速度为每秒π个单位长度,则2020秒时,点P的坐标是()A.(2020,0)B.(3030,0)C.( 3030,)D.(3030,﹣)10. 如图,在中,,,于点G,点D为BC 边上一动点,交射线CA于点E,作关于DE的轴对称图形得到,设CD的长为x,与重合部分的面积为y.下列图象中,能反映点D从点C向点B运动过程中,y与x的函数关系的是()A.B.C.D.二、填空题11. 计算:=_____.12. 如图,AB∥CD,∠B=75°,∠E=27°,则∠D的度数为_____.13. 已知不等式组有解但没有整数解,则a的取值范围为______.14. 如图,∠AOB=90°,∠B=30°,以点O为圆心,OA为半径作弧交AB于点C,交OB于点D,若OA=4,则阴影部分的面积为_____.15. 如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F 分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为_____.三、解答题16. 先化简,再求值:,其中x的值从不等式组中的整数解中选取.17. 为了扎实推进精准扶贫工作,某地出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:请根据图中信息回答下面的问题:(1)本次抽样调查了多少户贫困户?(2)抽查了多少户C类贫困户?并补全统计图;(3)若该地共有13000户贫困户,请估计至少得到4项帮扶措施的大约有多少户?(4)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用树状图或列表法求出恰好选中甲和丁的概率.18. 如图,AB为⊙O的直径,点C为AB上方的圆上一动点,过点C作⊙O的切线l,过点A作直线l的垂线AD,交⊙O于点D,连接OC,CD,BC,BD,且BD 与OC交于点E.(1)求证:△CDE≌△CBE;(2)若AB=6,填空:①当的长度是时,△OBE是等腰三角形;②当BC=时,四边形OADC为菱形.19. 如图是小米洗漱时的侧面示意图.洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小米身高160cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).(1)此时小米头部E点与地面DK相距多少?(2)若小米的头部E恰好在洗漱盆AB的中点O的正上方,她应向前或向后移动多少厘米?(sin80°≈0.98,cos80°≈0.18,≈1.41,结果精确到0.1)20. 如图,在直角坐标系中,已知点B(8,0),等边三角形OAB的顶点A在反比例函数y=的图象上.(1)求反比例函数的表达式;(2)把△OAB向右平移a个单位长度,对应得到△O′A′B′,当这个函数图象经过△O′A′B′一边的中点时,求a的值.21. 为了迎接疫情彻底结束后的购物高峰,某运动品牌专卖店准备购进甲、乙运动鞋价甲乙格进价(元/m m﹣20双)售价(元/240 160双)2400元购进乙种运动鞋的数量相同.(1)求m的值;(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且甲种运动鞋的数量不超过100双,问该专卖店共有几种进货方案?(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?22. 等腰直角三角形ABC和等腰直角三角形ADE中,∠BAC=∠DAE=90°,AB =4,AE=2,其中△ABC固定,△ADE绕点A作360°旋转,点F、M、N分别为线段BE、BC、CD的中点,连接MN、NF.问题提出:(1)如图1,当AD在线段AC上时,则∠MNF的度数为,线段MN和线段NF的数量关系为;深入讨论:(2)如图2,当AD不在线段AC上时,请求出∠MNF的度数及线段MN和线段NF的数量关系;拓展延伸:(3)如图3,△ADE持续旋转过程中,若CE与BD交点为P,则△BCP面积的最小值为.23. 如图1,在平面直角坐标系中,抛物线y=ax2+bx﹣3与直线y=x+3交于点A(m,0)和点B(2,n),与y轴交于点C.(1)求m,n的值及抛物线的解析式;(2)在图1中,把△AOC平移,始终保持点A的对应点P在抛物线上,点C,O 的对应点分别为M,N,连接OP,若点M恰好在直线y=x+3上,求线段OP的长度;(3)如图2,在抛物线上是否存在点Q(不与点C重合),使△QAB和△ABC的面积相等?若存在,直接写出点Q的坐标;若不存在,请说明理由.。
河南省郑州市外国语中学2019-2020学年九年级下学期开学考试英语试题

河南省郑州市外国语中学2019-2020学年九年级下学期开学考试英语试题学校_________ 班级__________ 姓名__________ 学号__________一、完成句子1. Complete the following sentences according to the Chinese meaning. 【小题1】Tom 现在正在超市对面的那间房子里下国际象棋。
Tom________ ________ ________in the house________ _________ the supermarket now.【小题2】到达营地后,我们搭帐篷、生火,然后开始准备饭菜。
After arriving at the campsite,we________ ________ ________ ________,________ ________ ________ and then started getting our meal ready. 【小题3】这家商店的产品以好的价格被出售。
The products in thestore________ ________ ________ _________ ________.【小题4】他拒绝了我的邀请,决定不参加这个活动,这让我非常失望。
He________ _________ ________ _________and________ _________ _________ _________ ________ __________ the activity. This made me very disappointed.【小题5】在过去的几周里,武汉的医生和病人缺少医疗用品。
The doctors and patients in Wuhan________ ________ __________ medical supplies in the past several weeks.【小题6】她吹灭了蜡烛,然后去睡觉了。
2019-2020学年河南省郑州市枫杨外国语中学九年级(下)第一次月考化学试卷

2019-2020学年河南省郑州市枫杨外国语中学九年级(下)第一次月考化学试卷一、解答题(共14小题,满分14分)1.(1分)溶液酸碱性酸性中性碱性指示剂变色红色橙色绿色小玉用一种茶花花瓣的酒精浸出液自制了酸碱指示剂,经实验得出其在不同酸碱性溶液中的显色情况如表。
日常生活的下列物质能使该自制酸碱指示剂显红色的是()溶液酸碱性酸性中性碱性指示剂变色红色橙色绿色A.石灰水B.矿泉水C.可乐D.食盐2.(1分)造成白色污染的物质是()A.废弃纸张B.废弃橡胶制品C.废弃塑料制品D.废旧金属3.(1分)下列物质的名称、化学式、俗称均一致的是()A.碳酸钙、CaCO3、生石灰B.碳酸钠、Na2CO3、苏打C.氢氧化钠、NaOH、纯碱D.氢氧化钙、CaO、熟石灰4.(1分)理解概念是化学学习的重要内容,下列说法正确的是()A.pH<7的降雨一定是酸雨B.中和反应一定是复分解反应C.能与酸反应产生气体的一定是碳酸盐D.盐中一定含有金属元素5.(1分)下列转化中,只有加入酸才能一步实现的是()A.CaCO3→CO2B.Zn→ZnSO4C.MgO→MgCl2D.Cu→CuCl26.(1分)下列物质所用的方法,错误的是()A.羊毛纤维和合成纤维﹣﹣点燃闻气味B.氢氧化钠和硝酸铵﹣﹣加水溶解C.用食盐水除去水壶中的水垢D.用食醋可以鉴别纯碱和食盐7.(1分)下列对物质的分类正确的是()A.有机物:葡萄糖、乙醇、乙酸B.微量元素:钙、铁、锌C.混合物:煤、石油、冰水共存物D.合成材料:合金、合成橡胶、合成纤维8.(1分)下列物质能在pH=13的溶液中大量共存的是()A.NO3﹣、Na+、SO42﹣、NH4+B.Fe3+、Na+、Cl﹣、OH﹣C.Ag+、Ca2+、NO3﹣、Cl﹣D.K+、Cl﹣、NO3﹣、Ba2+9.(1分)将Fe、CO2、NaOH、CuSO4、稀盐酸五种物质两两混合,在一定条件下能发生的化学反应有()A.4 个B.5 个C.6 个D.7 个10.(1分)如图示的操作正确的是()A.稀释浓硫酸B.移走蒸发皿C.测溶液的pH D.加热碳酸氢钠固体11.(1分)“民以食为天,食以安为先”,下列做法正确的是()A.用甲醛水溶液浸泡海产品,延长保质期B.为防止生长发育不良,大量补充锌元素C.用含碳酸氢钠的发酵粉焙制糕点D.用亚硝酸钠代替食盐腌制食物12.(1分)下列由于发生化学反应而使溶液质量变大的是()A.浓盐酸B.浓硫酸C.澄清石灰水D.氢氧化钠溶液13.(1分)除去如表物质中的少量杂质,所选用的试剂和操作方法都正确的是()选项物质杂质试剂和操作方法A FeCl3溶液(CuCl2)加入过量铁粉振荡、过滤B CO2 (HCl)将混合气体通过盛/有NaOH溶液的洗气瓶C K2CO3溶液(K2SO4)加入适量BaCO3粉末,充分反应后过滤D Fe2(SO4)3溶液(H2SO4)加入过量Fe2O3粉末,充分反应后过滤A.A B.B C.C D.D14.(1分)下列各组溶液,不外加试剂,通过下列试剂间两两互滴,就能鉴别出来的是()A.Na2CO3、HCl、BaCl2、NaClB.NaOH、FeCl3、HCl、HNO3C.KOH、KCl、稀HNO3、CuCl2D.NaOH、Ba(NO3)2、NaCl、MgSO4三、填空题(本题包括6个小题,每空1分,共21分)15.(3分)化学与生活密不可分(1)河南黄河大鲤鱼能够为人体补充的营养素主要为。
河南省郑州枫杨外国语中学2019-2020学年下期九年级第一次月考英语试卷(Word无答案)

2019—2020 学年下期第一次月考九年级英语试题卷注意:本试卷分试题卷和答题卡两部分。
考试时间 100 分钟,满分 120 分。
交卷时只交答题卡。
一、听力理解(20 小题,每小题1 分,共20 分)第一节听下面5 段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳答案。
每段对话读两遍。
( ) 1. Which festival does Mike like best?A. The Spring Festival.B. The Dragon Boat Festival.C. The Lantern Festival. ( ) 2. Who did Mary travel with?A. Her father.B. Her friend.C. Her mother.( ) 3. How does Tom go to work now?A. By car.B. By bike.C. By bus.( ) 4. When does the train leave?A. At 9:00.B. At 9:40.C. At 9:50.( ) 5. How much should the man pay if he stays in the hotel for two nights?A. 560 yuan.B. 280 yuan.C. 180 yuan.第二节听下面几段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C 三个选项中选出最佳答案。
每段对话或独白读两遍。
听下面一段对话,回答第6 至第7 两个小题。
( ) 6. Where does the man want to go?A. To the post office.B.To the museum.C. To the City Library. ( ) 7. How will the man probably go there?A. On foot.B. By taxi.C. By bus.听下面一段对话,回答第8 至第10 三个小题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年河南省郑州市中牟县枫杨外国语学校九年级(下)第一次月考数学试卷一、选择题(每题3分,共30分)1.(3分)在实数3.14,﹣π,,﹣中,倒数最小的数是()A.B.C.﹣πD.3.142.(3分)无锡的光伏技术不断进步,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占0.000 000 7mm2,这个数用科学记数法表示为()A.7×10﹣6mm2B.0.7×10﹣6mm2C.7×10﹣7mm2D.70×10﹣8mm23.(3分)下列计算错误的是()A.a•a2=a3 B.(3ab3)2=9a2b6C.(x2)3=x6D.2a2+3a2=5a44.(3分)不等式组的解集在数轴上表示正确的是()A.B.C.D.5.(3分)如图,∠BCD=95°,AB∥DE,则∠α与∠β满足()A.∠α+∠β=95°B.∠β﹣∠α=95°C.∠α+∠β=85°D.∠β﹣∠α=85°6.(3分)将一个圆柱和一个正三棱柱如图放置,则所构成的几何体的主视图是()A.B.C.D.7.(3分)为了解居民用电情况,小陈在小区内随机抽查了30户家庭的月用电量,结果如下表:月用电量/度4050608090100户数679521则这30户家庭的月用电量的众数和中位数分别是()A.60,60B.60,50C.50,60D.50,708.(3分)已知点A(1,y1),B(2,y2)在抛物线y=﹣(x+1)2+2上,则下列结论正确的是()A.2>y1>y2B.2>y2>y1C.y1>y2>2D.y2>y1>29.(3分)如图:已知菱形ABCD的顶点B(﹣2,0),且∠ABC=60°,点A在y轴的正半轴上.按以下步骤作图:①以点B为圆心,适当长度为半径作弧,分别交边AB、BC于点M、N;②分别以点M、N为圆心,大于MN的长为半径作弧,两弧在∠ABC内交于点P;③作射线BP,交菱形的对角线AC于点E,则点E的坐标为()A.(1,)B.(1,2)C.(,1)D.()10.(3分)如图,在等腰直角三角形ABC中,∠ACB=90°,AB=8cm,CH是AB边上的高,正方形DEFG的边DE在高CH上,F,G两点分别在AC,AH上.将正方形DEFG以每秒1cm的速度沿射线DB方向匀速运动,当点G与点B重合时停止运动.设运动时间为ts,正方形DEFG与△BHC重叠部分的面积为Scm2,则能反映S 与t的函数关系的图象()A.B.C.D.二.填空题(每题3分,共15分)11.(3分)计算﹣32﹣=.12.(3分)若关于x的方程(m﹣2)x2+2x+1=0有两个实数根,则m的取值是.13.(3分)一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,现随机从口袋里取出两张卡片,则两次摸出的卡片的数字之和等于5的概率.14.(3分)如图,在△ABC中,∠ABC=90°,∠ACB=30°,BC=2,BC是半圆O的直径,则图中阴影部分的面积为.15.(3分)如图,已知矩形ABCD中,AB=4,AD=m,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(s).已知m满足:在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,则所有这样的m的取值范围为.三、解答题(本大题共8个小题,满分75分)16.(8分)先化简,再求值:,其中x满足x2﹣x﹣1=0.17.(9分)《中国诗词大会》以“赏中华诗词,寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱,某中学为了解学校学生的诗词水平,从八、九年级各随机抽取了20名学生进行了测试,并将八、九年级测试成绩(百分制,单位:分)整理如下:收集数据八年级93 92 84 55 85 82 66 74 88 67 87 87 67 61 87 61 78 57 72 75九年级68 66 79 92 86 87 61 86 90 83 90 78 70 67 53 79 86 71 61 89整理数据按如下分数段整理数据,并补全表格:测试成绩x(分)50≤x<6060≤x<7070≤x<8080≤x<9090≤x≤100年级八24九15563说明:测试成绩x(分),其中x≥80为优秀,70≤x<80为良好,60≤x<70为合格,0≤x<60为不合格)分析数据补全下列表格中的统计量:年级平均数中位数众数八75.976.5九77.17986得出结论(1)在此次测试中,有位同学的成绩是78分,在他所在的年级属于中等偏上,则这位同学属于哪个年级?(2)若九年级有800名学生,估计九年级诗词水平达到优秀的学生有多少名?18.(9分)如图,在Rt△ABC中,∠B=90°,AB=6,CD平分∠ACB交AB于点D,点O在AC上,以CO为半径的圆经过点D,AE切⊙O于E.(1)求证:AD=AE.(2)填空:①当∠ACB=时,四边形ADOE是正方形;②当BC=时,四边形ADCE是菱形.19.(9分)如图,一次函数与反比例函数的图象交于点A(﹣4,﹣2)和B(a,4),直线AB交y轴于点C,连接QA、OB.(1)求反比例函数的解析式和点B的坐标:(2)根据图象回答,当x的取值在什么范围内时,一次函数的值大于反比例函数的值;(3)求△AOB的面积.20.(9分)如图所示,建筑物MN一侧有一斜坡AC,在斜坡坡脚A处测得建筑物顶部N的仰角为60°,当太阳光线与水平线夹角成45°时,建筑物MN的影子的一部分在水平地面上MA处,另一部分影子落在斜坡上AP处,已知点P的距水平地面AB的高度PD=5米,斜坡AC的坡度为(即tan∠P AD=),且M,A,D,B在同一条直线上.(测倾器的高度忽略不计,结果保留根号)(1)求此时建筑物MN落在斜坡上的影子AP的长;(2)求建筑物MN的高度.21.(10分)坚持农业农村优先发展,按照产业兴旺、生态宜居的总要求,统筹推进农村经济建设洛宁县某村出售特色水果(苹果).规定如下:品种购买数量低于50箱购买数量不低于50箱新红星原价销售以八折销售红富士原价销售以九折销售如果购买新红星40箱,红富士60箱,需付款4300元;如果购买新红星100箱,红富士35箱,需付款4950元(1)每箱新红星、红富士的单价各多少元?(2)某单位需要购置这两种苹果120箱,其中红富土的数量不少于新红星的一半,并且不超过60箱,如何购买付款最少?请说明理由;22.(10分)如图1,在△ABC中,AB=AC=2,∠BAC=120°,点D、E分别是AC、BC的中点,连接DE.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.探索发现:图1中,的值为;的值为.(2)拓展探完若将△CDE绕点C逆时针方向旋转一周,在旋转过程中的大小有无变化?请仅就图2的情形给出证明.(3)问题解决当△CDE旋转至A,D,E三点共线时,直接写出线段BE的长.23.(11分)如图,抛物线y=﹣x2+bx+c过点A(3,2),且与直线y=﹣x+交于B、C两点,点B的坐标为(4,m).(1)求抛物线的解析式;(2)点D为抛物线上位于直线BC上方的一点,过点D作DE⊥x轴交直线BC于点E,点P为对称轴上一动点,当线段DE的长度最大时,求PD+P A的最小值;(3)设点M为抛物线的顶点,在y轴上是否存在点Q,使∠AQM=45°?若存在,求点Q的坐标;若不存在,请说明理由.2019-2020学年河南省郑州市中牟县枫杨外国语学校九年级(下)第一次月考数学试卷参考答案与试题解析一、选择题(每题3分,共30分)1.【解答】解:在3.14,﹣π,,﹣中,倒数最小的数是两个负数中一个,所以先求两个负数的倒数:﹣π的倒数是﹣≈﹣0.3183,﹣的倒数是﹣≈﹣4472,所以﹣>﹣,故选:A.2.【解答】解:0.000 000 7=7×10﹣7,故选:C.3.【解答】解:A、a•a2=a3,正确,不合题意;B、(3ab3)2=9a2b6,正确,不合题意;C、(x2)3=x6,正确,不合题意;D、2a2+3a2=5a2,原式计算错误,符合题意;故选:D.4.【解答】解:解不等式x﹣1<1,得:x<2,解不等式x+1≥0,得:x≥﹣1,则不等式组的解集为﹣1≤x<2,故选:A.5.【解答】解:过C作CF∥AB,∵AB∥DE,∴AB∥CF∥DE,∴∠1=∠α,∠2=180°﹣∠β,∵∠BCD=95°,∴∠1+∠2=∠α+180°﹣∠β=95°,∴∠β﹣∠α=85°.故选:D.6.【解答】解:根据主视图的概念可知,从物体的正面看得到的视图是选项A.故选:A.7.【解答】解:这组数据的众数为60,中位数为=60,故选:A.8.【解答】解:当x=1时,y1=﹣(x+1)2+2=﹣(1+1)2+2=﹣2;当x=2时,y1=﹣(x+1)2+2=﹣(2+1)2+2=﹣7;所以2>y1>y2.故选:A.9.【解答】解:如图,作EH⊥BC于H.∵四边形ABC都是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∵B(﹣2,0),∴OB=2,OA=2,由作图可知:BE平分∠ABC,∴BE⊥AC,∴BE=OA=2,∴EH=,BH=EH=3,∴OH=1,∴E(1,),故选:A.10.【解答】解:由题意得:AH=BH=CH=4,FE=FG=GH=EH=2,(1)当0≤t≤2时,如图1,设EF交CH于点K,则S=S矩形EDHK=t×2=2t;(2)2<t≤4时,如图2,设EF与BC交于点M,DE于BC交于点N,S=S正方形DEFG﹣S△EMN=4﹣×[2﹣(4﹣t)]2=﹣(t﹣2)2+4;(3)4<t≤6时,如图3,设GF交BC于点L,S=S△BGL=×[2﹣(t﹣4)]2=(t﹣6)2;故选:B.二.填空题(每题3分,共15分)11.【解答】解:原式=﹣9﹣3=﹣12.故答案为:﹣12.12.【解答】解:由题意可知:△=4﹣4(m﹣2)≥0,∴m≤3,∵m﹣2≠0,∴m≠2,故答案为:m≤3且m≠213.【解答】解:根据题意画树状图如图:共有12种情况,两次摸出的卡片的数字之和等于5的有4种,∴两次摸出的卡片的数字之和等于5的概率为=,故答案为:.14.【解答】解:如图,连接OF.S阴=(S扇形OFC﹣S△OFC)+(S△ABC﹣S△OFC﹣S扇形OBF)=﹣•×+×2×﹣××﹣=﹣+﹣=+,故答案为:+.15.【解答】解:如图2中,当点P与A重合时,点E在BC的下方,点E到BC的距离为3.作EQ⊥BC于Q,EM⊥DC于M.则EQ=3,CE=DC=4,易证四边形EMCQ是矩形,∴CM=EQ=3,∠M=90°,∴EM===,∵∠DAC=∠EDM,∠ADC=∠M,∴△ADC∽△DME,=,∴=,∴AD=4,(当AD=4时,直线BC上方还有一个点满足条件,见图2)如图3中,当点P与A重合时,点E在BC的上方,点E到BC的距离为3.作EQ⊥BC于Q,延长QE交AD于M.则EQ=3,CE=DC=4在Rt△ECQ中,QC=DM==,由△DME∽△CDA,∴=,∴=,∴AD=,综上所述,在动点P从点D到点A的整个运动过程中,有且只有一个时刻t,使点E到直线BC的距离等于3,这样的m的取值范围≤m<4,故答案为:≤m<4.三、解答题(本大题共8个小题,满分75分)16.【解答】解:===,∵x2﹣x﹣1=0∴x2=x+1,∴原式==1.17.【解答】解:把八年级的测试成绩从小到大排列为:55,57,61,61,66,67,67,72,74,75,78,82,84,85,87,87,87,88,92,93.60≤x<70有5人;80≤x<90有7人;90≤x≤100有2人.故答案为:5;7;2;∵87出现的次数最多,故87是这组数据的众数.故答案为:87;得出结论(1)在此次测试中,有位同学的成绩是78分,在他所在的年级属于中等偏上,则这位同学属于八年级;(2)(人),若九年级有800名学生,估计九年级诗词水平达到优秀的学生有360名.18.【解答】(1)证明:∵CD平分∠ACB,∴∠ACD=∠DCB,∵OC=OD,∴∠ODC=∠OCD,∴∠ODC=∠DCB,∴OD∥BC,∵∠B=90°,∴∠ODA=90°,∵OD是半径,∴AD是圆的切线,∵AE切⊙O于E,∴AE=AD;(2)①当四边形ADOE是正方形时,∠AOD=45°,∵OD∥BC,∴∠AOD=∠ACB=45°,②当四边形ADCE是菱形,∴AD=CD=CE=AE,AC⊥DE,∴△CED是等边三角形,∴∠DCE=60°,∴∠DCA=30°,∴∠ACB=60°,∵AB=6,∴BC=AB.故答案为:45°;2.19.【解答】解:(1)设反比例函数的解析式为y=(k≠0),∵反比例函数图象经过点A(﹣4,﹣2),∴﹣2=,∴k=8,∴反比例函数的解析式为y=,∵B(a,4)在y=的图象上,∴4=,∴a=2,∴点B的坐标为B(2,4);(2)根据图象得,当x>2或﹣4<x<0时,一次函数的值大于反比例函数的值;(3)设直线AB的解析式为y=ax+b,∵A(﹣4,﹣2),B(2,4),∴,解得,∴直线AB的解析式为y=x+2,∴C(0,2),∴S△AOB=S△AOC+S△BOC=×2×4+=6.20.【解答】解:(1)如图,作PH⊥MN于H.则四边形PDMH是矩形.∵tan∠P AD==,PD=5,∴AD=15,P A==5(米),∴此时建筑物MN落在斜坡上的影子AP的长为5米.(2)∵∠NPH=45°,∠PHN=90°,∴∠PNH=∠NPH=45°,∴NH=PH,设NH=PH=x米,则MN=(x+5)米,AM=(x﹣15)米,在Rt△AMN中,∵tan60°=,∴MN=AM,∴x=5=(x﹣15)解得x=(10+25)(米),∴MN=x+5=(10+30)米.21.【解答】解:(1)设每箱新红星a元,每箱红富士b元,由题意可得:,解得,答:每箱新红星40元,每箱红富士50元;(2)设购置新红星x箱,则购置红富士(120﹣x)箱,所需的总费用为y元,由题意可得:,解得60≤x≤80,所以新红星箱数x的取值范围60≤x≤80,设购买付款费用为y元,则当60≤x≤70时,y=40×0.8x+50×0.9(120﹣x)=﹣13x+5400,∵k=﹣13<0,∴y随x的增大而减小,∴当x=70时,y的值最小,最小值为:y=﹣13×70+5400=4490;当70<x≤80时,y=40×0.8x+50(120﹣x)=﹣18x+6000,∵k=﹣18<0,∴y随x的增大而减小,∴当x=80时,y的值最小,最小值为:y=﹣18×80+6000=4560,∵4490<4560,∴购买新红星70箱,红富士50箱,费用最少,最少费用为4490元.22.【解答】解:(1)如图1,连接AE,∵AB=AC=2,点E分别是BC的中点,∴AE⊥BC,∴∠BEC=90°,∵AB=AC=2,∠BAC=120°,∴∠B=∠C=30°,在Rt△ABE中,AE=AB=1,根据勾股定理得,BE=∵点E是BC的中点,∴BC=2BE=2,∴==,∵点D是AC的中点,∴AD=CD=AC=1,∴==,故答案为:,;(2)无变化,理由:由(1)知,CD=1,CE=BE=,∴=,,∴=,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD∽△BCE,∴,(3)当点D在线段AE上时,如图2,过点C作CF⊥AE于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴DF=CD=,∴CF=DF=,在Rt△AFC中,AC=2,根据勾股定理得,AF==,∴AD=AF+DF=,由(2)知,,∴BE=AD=当点D在线段AE的延长线上时,如图3,过点C作CG⊥AD交AD的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴DG=CD=,∴CG=DG=,在Rt△ACG中,根据勾股定理得,AG=,∴AD=AG﹣DG=,由(2)知,,∴BE=AD=即:线段BE的长为或.23.【解答】解:(1)将点B的坐标为(4,m)代入y=﹣x+,m=﹣4+=﹣,∴B的坐标为(4,﹣),将A(3,2),B(4,﹣)代入y=﹣x2+bx+c,解得b=1,c=,∴抛物线的解析式y=;(2)设D(m,),则E(m,﹣m+),DE=()﹣(﹣m+)==﹣(m﹣2)2+2,∴当m=2时,DE有最大值为2,此时D(2,),作点A关于对称轴的对称点A',连接A'D,与对称轴交于点P.PD+P A=PD+P A'=A'D,此时PD+P A最小,∵A(3,2),∴A'(﹣1,2),A'D==,即PD+P A的最小值为;(3)作AH⊥对称轴于点H,连接AM、AQ、MQ、HA、HQ,∵抛物线的解析式y=,∴M(1,4),∵A(3,2),∴AH=MH=2,H(1,2)∵∠AQM=45°,∠AHM=90°,∴∠AQM=∠AHM,可知△AQM外接圆的圆心为H,∴QH=HA=HM=2设Q(0,t),则=2,t=2+或2﹣∴符合题意的点Q的坐标:Q1(0,2﹣)、Q2(0,2).。
