专题检测(八) 等差数列、等比数列
2020年高考数学(理)总复习:等差数列与等比数列(解析版)

2020年高考数学(理)总复习:等差数列与等比数列题型一等差、等比数列的基本运算【题型要点】方程思想在等差(比)数列的基本运算中的运用等差(比)数列的通项公式、求和公式中一共包含a1、d(或q)、n、an与Sn这五个量,如果已知其中的三个,就可以求其余的两个.其中a1和d(或q)是两个基本量,所以等差数列与等比数列的基本运算问题一般先设出这两个基本量,然后根据通项公式,求和公式构建这两者的方程组,通过解方程组求其值,这也是方程思想在数列问题中的体现.【例1】等比数列{an}的前n项和为Sn,已知a2a5=2a3,且a4与2a7的等差中项为54,则S5等于()A.29B.31C.33 D.36【例2】.an是公差不为0的等差数列,满足a24+a25=a26+a27,则该数列的前10项和S10等于()A.-10B.-5C.0D.5【例3】.已知递增数列{an}对任意n∈N*均满足an∈N*,aan=3n,记bn=a2•3n-1(n ∈N*),则数列{bn}的前n项和等于()A.2n+n B.2n+1-1C.3n+1-3n2D.3n+1-32题组训练一等差、等比数列的基本运算1.设等差数列{an}的前n项和为Sn,若a3+a5=4,S15=60则a20等于()A.4B.6C.10D.122.在等差数列{an}中,2(a1+a3+a5)+3(a8+a10)=36,则a6等于()A.8 B.6 C.4 D.33.已知等比数列{an}的前n项和为Sn,a1+a3=30,S4=120,设bn=1+log3an,那么数列{bn}的前15项和为()A.152 B.135 C.80 D.16题型二等差、等比数列的性质及应用【题型要点】(1)解决此类问题的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.(2)等差、等比数列的性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形.【例4】已知数列{an},{bn}满足bn=log2an,n∈N*,其中{bn}是等差数列,且a8•a2 008=14,则b1+b2+b3+…+b2 015等于()A.log22 015 B.2 015 C.-2 015 D.1 0082.各项均为正数的等比数列{an}的前n项和为Sn,若S4=10,S12=130,则S8等于()A.-30 B.40C.40或-30 D.40或-503.等比数列{an}的首项为32,公比为-12,前n项和为Sn,则当n∈N*时,Sn-1Sn 的最大值与最小值之和为()A.-23 B.-712C.14D.56题组训练二等差、等比数列的性质及应用1.在等比数列{an}中,a3,a15是方程x2-7x+12=0的两根,则a1a17a9的值为()A.23 B.4 C.±22 D.±42.设公差为d的等差数列{an}的前n项和为Sn,若a1=1,-217<d<-19,则当Sn 取最大值时n的值为________.3.若{an}是等差数列,首项a1>0,a2 016+a2 017>0,a2 016•a2 017<0,则使前n 项和Sn>0成立的最大正整数n是()A.2 016B.2 017 C.4 032 D.4 033题型三等差、等比数列的综合问题【题型要点】关于等差、等比数列的综合问题多属于两者运算的综合题以及相互之间的转化,关键是求出两个数列的基本量:首项和公差(或公比),灵活运用性质转化条件,简化运算,准确记忆相关的公式是解决此类问题的关键.【例3】已知等差数列{an}的公差为-1,且a2+a7+a12=-6.(1)求数列{an}的通项公式an与前n项和Sn;(2)将数列{an}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn,若存在m∈N*,使对任意n∈N*,总有Sn<Tm+λ恒成立,求实数λ的取值范围.题组训练三等差、等比数列的综合问题已知数列{an}中,a1=1,an•an+1=,记T2n为{an}的前2n项的和,bn=a2n+a2n -1,n∈N*.(1)判断数列{bn}是否为等比数列,并求出bn;(2)求T2n.题型四数列与其他知识的交汇【题型要点】数列在中学教材中既有相对独立性,又有较强的综合性,很多数列问题一般转化,特殊数列求解,一些题目常与函数、向量、三角函数、解析几何等知识交汇结合,考查数列的基本运算与应用.【例4】已知等差数列{an}的前n项和为Sn,若OB→=a1OA→+a2 016OC→,且A,B,C三点共线(该直线不过点O),则S2 016等于()A.1 007B.1 008C.2 015D.2 016题组训练四数列与其他知识的交汇1.在由正数组成的等比数列{an}中,若a3a4a5=3π,则sin(log3a1+log3a2+…+log3a7)的值为()A.12B.32C.1 D.-322.已知各项都为正数的等比数列{an}满足a7=a6+2a5,存在两项am,an使得am•an =4a1,则1m+4n的最小值为()A.32B.53C.256D.433.艾萨克•牛顿(1643年1月4日-1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f(x)的零点时给出一个数列xn满足xn+1=xn-′,我们把该数列称为牛顿数列.如果函数f(x)=ax2+bx+c(a>0)有两个零点1,2,数列xn为牛顿数列,设an=ln xn-2xn-1,已知a1=2,xn>2,则an的通项公式an=________.【专题训练】一、选择题1.等比数列{an}中,a4=2,a7=5,则数列{lg an}的前10项和等于()A.2B.lg 50C.10D.52.在正项等比数列{an}中,已知a3a5=64,则a1+a7的最小值为()A.64 B.32C.16 D.83.一个等比数列的前三项的积为2,最后三项的积为4,且所有项的积为64,则该数列的项数是()A.13 B.12C.11 D.104.在数列{an}中,若a1=2,且对任意正整数m,k,总有am+k=am+ak,则{an}的前n项和Sn等于()A.n(3n-1) +C.n(n+1) +5.记Sn为正项等比数列{an}的前n项和,若S12-S6S6-7•S6-S3S3-8=0,且正整数m,n满足a1ama2n=2a35,则1m+8n的最小值是()A.157B.95C.53D.756.数列an是以a为首项,b为公比的等比数列,数列bn满足bn=1+a1+a2+…+an(n =1,2,…),数列cn满足cn=2+b1+b2+…+bn(n=1,2,…),若cn为等比数列,则a+b 等于()A.2 B.3 C.5 D.6二、填空题7.数列{an}的通项an=n2•,其前n项和为Sn,则S30=________.8.已知数列{an}满足a1=2,且an=2nan-1an-1+n-1(n≥2,n∈N*),则an=________.9.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增一十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?()A.8日B.9日C.12日D.16日10.数列{logkan}是首项为4,公差为2的等差数列,其中k>0,且k≠1.设cn=anlg an,若{cn}中的每一项恒小于它后面的项,则实数k的取值范围为________.三、解答题11.已知数列an的前n项和为Sn,且Sn=2an-3n(n∈N*).(1)求a1,a2,a3的值;(2)是否存在常数λ,使得数列{an+λ}为等比数列?若存在,求出λ的值和通项公式an;若不存在,请说明理由.12.已知数列{an}的前n项和为Sn,且Sn-1=3(an-1),n∈N*.(1)求数列{an}的通项公式;(2)设数列{bn}满足an+1=an•bn,若bn≤t对于任意正整数n都成立,求实数t的取值范围.2020年高考数学(理)总复习:等差数列与等比数列题型一 等差、等比数列的基本运算 【题型要点】方程思想在等差(比)数列的基本运算中的运用等差(比)数列的通项公式、求和公式中一共包含a 1、d (或q )、n 、a n 与S n 这五个量,如果已知其中的三个,就可以求其余的两个.其中a 1和d (或q )是两个基本量,所以等差数列与等比数列的基本运算问题一般先设出这两个基本量,然后根据通项公式,求和公式构建这两者的方程组,通过解方程组求其值,这也是方程思想在数列问题中的体现.【例1】等比数列{a n }的前n 项和为S n ,已知a 2a 5=2a 3,且a 4与2a 7的等差中项为54,则S 5等于( )A .29B .31C .33D .36【解析】 法一:设等比数列{a n }的首项为a 1,公比为q ,由题意知⎩⎪⎨⎪⎧a 1qa 1q 4=2a 1q 2a 1q 3+2a 1q 6=2×54,解得⎩⎪⎨⎪⎧q =12a 1=16,所以S 5=a 1(1-q 5)1-q=31,故选B.法二:由a 2a 5=2a 3,得a 4=2.又a 4+2a 7=52,所以a 7=14,所以q =12,所以a 1=16,所以S 5=a 2(1-q 5)1-q=31,故选B.【答案】 B【例2】.{}a n 是公差不为0的等差数列,满足a 24+a 25=a 26+a 27,则该数列的前10项和S 10等于( )A .-10B .-5C .0D .5【解析】 由题意,得a 24-a 27=a 26-a 25,即()a 4-a 7()a 4+a 7=()a 6-a 5()a 6+a 5,即-3d ()a 4+a 7=d ()a 6+a 5,又因为d ≠0,所以a 4+a 7=a 6+a 5=0,则该数列的前10项和S 10=10(a 1+a 10)2=5()a 6+a 5=0.故选C.【答案】 C【例3】.已知递增数列{a n }对任意n ∈N *均满足a n ∈N *,aa n =3n ,记b n =a 2·3n -1(n ∈N *),则数列{b n }的前n 项和等于( )A .2n +nB .2n +1-1C.3n +1-3n 2D.3n +1-32【解析】 因为aa n =3n ,所以a 1≤3,若a 1=1,那么a 1=aa 1=3×1=3≠1矛盾,若a 1=2,那么a 2=aa 1=3×1=3成立,若a 1=3,那么a 3=aa 1=3×1=3=a 1矛盾,所以a 2=b 1=2,当aa an =3a n =a 3n ,所以b n =a 2·3n -1=a 3·2·3n -2=3a 2·3n -2=3b n -1,即b n b n -1=3,数列{b n }是首项为2,公比为3的等比数列,所以前n 项和为b 1(1-q n )1-q =3(1-33)1-3=3n +1-32,故选D.【答案】 D题组训练一 等差、等比数列的基本运算1.设等差数列{a n }的前n 项和为S n ,若a 3+a 5=4,S 15=60则a 20等于( ) A .4 B .6 C .10 D .12 【解析】 等差数列{a n }的前n 项和为S n , ∵a 3+a 5=4,S 15=60,∴⎩⎪⎨⎪⎧a 1+2d +a 1+4d =415a 1+15×142d =60, 解得a 1=12,d =12,∴a 20=a 1+19d =12+19×12=10.故选C.【答案】 C2.在等差数列{a n }中,2(a 1+a 3+a 5)+3(a 8+a 10)=36,则a 6等于( ) A .8 B .6 C .4D .3【解析】 由等差数列的性质可知,2(a 1+a 3+a 5)+3(a 8+a 10)=2×3a 3+3×2a 9=6(a 3+a 9)=6×2a 6=12a 6=36,∴a 6=3.故选D.【答案】 D3.已知等比数列{a n }的前n 项和为S n ,a 1+a 3=30,S 4=120,设b n =1+log 3a n ,那么数列{b n }的前15项和为( )A .152B .135C .80D .16【解析】 设等比数列{a n }的公比为q ,由a 1+a 3=30,a 2+a 4=S 4-(a 1+a 3)=90,所以公比q =a 2+a 4a 1+a 3=3,首项a 1=301+q 2=3,所以a n =3n ,b n =1+log 33n=1+n ,则数列{b n }是等差数列,前15项的和为15×(2+16)2=135,故选B. 【答案】 B题型二 等差、等比数列的性质及应用 【题型要点】(1)解决此类问题的关键是抓住项与项之间的关系及项的序号之间的关系,从这些特点入手选择恰当的性质进行求解.(2)等差、等比数列的性质是两种数列基本规律的深刻体现,是解决等差、等比数列问题既快捷又方便的工具,应有意识地去应用.但在应用性质时要注意性质的前提条件,有时需要进行适当变形.【例4】已知数列{a n },{b n }满足b n =log 2a n ,n ∈N *,其中{b n }是等差数列,且a 8·a 2 008=14,则b 1+b 2+b 3+…+b 2 015等于( ) A .log 22 015B .2 015C .-2 015D .1 008【解析】 ∵数列{a n },{b n }满足b n =log 2a n ,n ∈N *,其中{b n }是等差数列,∴数列{a n }是等比数列,由a 8·a 2 008=14,可得a 21 008=14,即a 1 008=12,∴a 1·a 2 015=a 2·a 2 014=…=a 1 007·a 1 009=a 21 008=14,∴b 1+b 2+b 3+…+b 2 015=log 2(a 1·a 2·…·a 2 015)=log 2201521⎪⎭⎫⎝⎛=-2 015.【答案】C2.各项均为正数的等比数列{a n }的前n 项和为S n ,若S 4=10,S 12=130,则S 8等于( ) A .-30 B .40 C .40或-30D .40或-50【解析】 ∵数列{a n }为等比数列且数列{a n }的前n 项和为S n ,∴S 4,S 8-S 4,S 12-S 8也构成等比数列.∴(S 8-S 4)2=S 4·(S 12-S 8),∵S 4=10,S 12=130,各项均为正数的等比数列{a n }, ∴(S 8-10)2=10·(130-S 8),∴S 8=40.故选B. 【答案】 B3.等比数列{a n }的首项为32,公比为-12,前n 项和为S n ,则当n ∈N *时,S n -1S n的最大值与最小值之和为( )A .-23B .-712C.14D.56【解析】 依题意得,S n =⎪⎭⎫ ⎝⎛--⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-21121123n=1-n⎪⎭⎫⎝⎛-21.当n 为奇数时,S n =1+12n 随着n 的增大而减小,1<S n =1+12n ≤S 1=32,S n-1S n 随着S n 的增大而增大,0<S n -1S n ≤56;当n 为偶数时,S n =1-12n 随着n 的增大而增大,34=S 2≤S n =1-12n <1,S n -1S n 随着S n 的增大而增大,-712≤S n -1S n <0.因此S n -1S n 的最大值与最小值分别为56、-712,其最大值与最小值之和为56-712=312=14,选C.【答案】 C题组训练二 等差、等比数列的性质及应用1.在等比数列{a n }中,a 3,a 15是方程x 2-7x +12=0的两根,则a 1a 17a 9的值为( )A .2 3B .4C .±2 2D .±4【解析】 ∵a 3,a 15是方程x 2-7x +12=0的两根,∴a 3a 15=12,a 3+a 15=7,∵{a n }为等比数列,又a 3,a 9,a 15同号,∴a 9>0,∴a 9=a 3a 15=23,∴a 1a 17a 9=a 29a 9=a 9=2 3.故选A.【答案】 A2.设公差为d 的等差数列{a n }的前n 项和为S n ,若a 1=1,-217<d <-19,则当S n 取最大值时n 的值为________.【解析】 因为等差数列{a n }的公差d 为负值,所以{a n }是递减数列.又a 1=1,所以由a n =a 1+(n -1)d >0得n <d -a 1d ,即n <1-1d ,因为-217<d <-19,所以192<1-1d <10,所以n ≤9,即当n ≤9时,a n >0,当n ≥10时,a n <0.所以当S n 取得最大值时n 的值为9.【答案】 93.若{a n }是等差数列,首项a 1>0,a 2 016+a 2 017>0,a 2 016·a 2 017<0,则使前n 项和S n>0成立的最大正整数n 是( )A .2 016B .2 017C .4 032D .4 033【解析】 因为a 1>0,a 2 016+a 2 017>0,a 2 016·a 2 017<0,所以d <0,a 2 016>0,a 2 017<0,所以S 4 032=4 032(a 1+a 4 032)2=4 032(a 2 016+a 2 017)2>0,S 4 033=4 033(a 1+a 4 033)2=4 033a 2017<0,所以使前n 项和S n >0成立的最大正整数n 是4 032,故选C.【答案】 C题型三 等差、等比数列的综合问题 【题型要点】关于等差、等比数列的综合问题多属于两者运算的综合题以及相互之间的转化,关键是求出两个数列的基本量:首项和公差(或公比),灵活运用性质转化条件,简化运算,准确记忆相关的公式是解决此类问题的关键.【例3】已知等差数列{a n }的公差为-1,且a 2+a 7+a 12=-6. (1)求数列{a n }的通项公式a n 与前n 项和S n ;(2)将数列{a n }的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{b n }的前3项,记{b n }的前n 项和为T n ,若存在m ∈N *,使对任意n ∈N *,总有S n <T m +λ恒成立,求实数λ的取值范围.【解析】 (1)由a 2+a 7+a 12=-6,得a 7=-2,∴a 1=4, ∴a n =5-n ,从而S n =n (9-n )2.(2)由题意知b 1=4,b 2=2,b 3=1,设等比数列{b n }的公比为q ,则q =b 2b 1=12,∴T m =2112114-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-m =8⎪⎭⎫ ⎝⎛-m )21(1, ∵m⎪⎭⎫⎝⎛21随m 增加而递减, ∴{T m }为递增数列,得4≤T m <8. 又S n =n (9-n )2=-12(n 2-9n )=-12⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫ ⎝⎛-481292n ,故(S n )max =S 4=S 5=10,若存在m ∈N *,使对任意n ∈N *总有S n <T m +λ, 则10<8+λ,得λ>2.即实数λ的取值范围为(2,+∞). 题组训练三 等差、等比数列的综合问题已知数列{a n }中,a 1=1,a n ·a n +1=n⎪⎭⎫ ⎝⎛21,记T 2n 为{a n }的前2n 项的和,b n =a 2n +a 2n -1,n ∈N *.(1)判断数列{b n }是否为等比数列,并求出b n ; (2)求T 2n .【解析】 (1)∵a n ·a n +1=n⎪⎭⎫⎝⎛21,∴a n +1·a n +2=121+⎪⎭⎫⎝⎛n ,∴a n +2a n =12,即a n +2=12a n .∵b n =a 2n +a 2n -1,∴b n +1b n =a 2n +2+a 2n +1a 2n +a 2n -1=12a 2n +12a 2n -1a 2n +a 2n -1=12所以{b n }是公比为12的等比数列.∵a 1=1,a 1·a 2=12,∴a 2=12⇒b 1=a 1+a 2=32.∴b n =32×121-⎪⎭⎫⎝⎛n =32n . (2)由(1)可知a n +2=12a n ,所以a 1,a 3,a 5,…是以a 1=1为首项,以12为公比的等比数列;a 2,a 4,a 6,…是以a 2=12为首项,以12为公比的等比数列. ∴T 2n =(a 1+a 3+…+a 2n -1)+(a 2+a 4+…+a 2n )=[]21121121211211-⎪⎭⎫ ⎝⎛-+-⎪⎭⎫⎝⎛-nn =3-32n .题型四 数列与其他知识的交汇 【题型要点】数列在中学教材中既有相对独立性,又有较强的综合性,很多数列问题一般转化,特殊数列求解,一些题目常与函数、向量、三角函数、解析几何等知识交汇结合,考查数列的基本运算与应用.【例4】 已知等差数列{a n }的前n 项和为S n ,若OB →=a 1OA →+a 2 016OC →,且A ,B ,C 三点共线(该直线不过点O ),则S 2 016等于( )A .1 007B .1 008C .2 015D .2 016 【解析】 ∵A 、B 、C 三点共线∴AB →=λAC →∴OB →-OA →=λ(OC →-OA →),OB →=(1-λ)OA →+λOC → 又∵OB →=a 1·OA →+a 2 016OC →,∴a 1=1-λ,a 2 016=λ ∴a 1+a 2 016=1∴S 2 016=2 016(a 1+a 2 016)2=1 008,∴选B.【答案】 B题组训练四 数列与其他知识的交汇1.在由正数组成的等比数列{a n }中,若a 3a 4a 5=3π,则sin(log 3a 1+log 3a 2+…+log 3a 7)的值为( )A.12B.32C .1D .-32【解析】 因为a 3a 4a 5=3π=a 34,所以a 4=3π3,即log 3a 1+log 3a 2+…+log 3a 7=log 3(a 1a 2…a 7)=log 3a 74=7log 33π3=7π3,所以sin(log 3a 1+log 3a 2+…+log 3a 7)=32. 【答案】 B2.已知各项都为正数的等比数列{a n }满足a 7=a 6+2a 5,存在两项a m ,a n 使得 a m ·a n =4a 1,则1m +4n的最小值为( )A.32B.53C.256D.43【解析】 由a 7=a 6+2a 5,得a 1q 6=a 1q 5+2a 1q 4,整理得q 2-q -2=0,解得q =2或q=-1(不合题意,舍去),又由a m ·a n =4a 1,得a m a n =16a 21,即a 212m+n -2=16a 21,即有m +n-2=4,亦即m +n =6,那么1m +4n =16(m +n )⎪⎭⎫⎝⎛+n m 41=16⎪⎪⎭⎫ ⎝⎛+⋅≥⎪⎭⎫ ⎝⎛++5426154m n n m m n n m =32,当且仅当4m n =n m ,即n =2m =4时取得最小值32.【答案】 A3.艾萨克·牛顿(1643年1月4日-1727年3月31日)英国皇家学会会长,英国著名物理学家,同时在数学上也有许多杰出贡献,牛顿用“作切线”的方法求函数f (x )的零点时给出一个数列{}x n 满足x n +1=x n -f (x n )f ′(x n ),我们把该数列称为牛顿数列.如果函数f (x )=ax 2+bx +c (a >0)有两个零点1,2,数列{}x n 为牛顿数列,设a n =ln x n -2x n -1,已知a 1=2,x n >2,则{}a n 的通项公式a n =________.【解析】 ∵ 函数f (x )=ax 2+bx +c (a >0)有两个零点1,2,∴⎩⎪⎨⎪⎧ a +b +c =0,4a +2b +c =0, 解得⎩⎪⎨⎪⎧c =2a ,b =-3a . ∴f (x )=ax 2-3ax +2a ,则f ′(x )=2ax -3a .则x n +1=x n -ax 2n -3ax n +2a 2ax n -3a =x n -x 2n -3x n +22x n -3=x 2n -22x n -3,∴x n +1-2x n +1-1=x 2n -22x n -3-2x 2n -22x n -3-1=x 2n -2-2(2x n -3)x 2n -2-(2x n -3)=212⎪⎪⎭⎫⎝⎛--n n x x , 则数列a n 是以2为公比的等比数列,又∵a 1=2 ,∴ 数列{}a n 是以2为首项,以2为公比的等比数列,则a n=2·2n-1=2n.【答案】2n【专题训练】一、选择题1.等比数列{a n}中,a4=2,a7=5,则数列{lg a n}的前10项和等于()A.2B.lg 50C.10D.5【解析】∵等比数列{a n}中,a4=2,a7=5,∴a1a10=a2a9=…=a4a7=10,∴数列{lg a n}的前10项和S=lg a1+lg a2+…+lg a10=lg a1a2…a10=lg 105=5,故选D【答案】 D2.在正项等比数列{a n}中,已知a3a5=64,则a1+a7的最小值为()A.64 B.32C.16 D.8【解析】在正项等比数列{a n}中,∵a3a5=64,∴a3a5=a1a7=64,∴a1+a7≥2a1a7=264=2×8=16,当且仅当a1=a7=8时取等号,∴a1+a7的最小值为16,故选C.【答案】 C3.一个等比数列的前三项的积为2,最后三项的积为4,且所有项的积为64,则该数列的项数是()A.13 B.12C.11 D.10【解析】设等比数列为{a n},其前n项积为T n,由已知得a1a2a3=2,a n a n-1a n-2=4,可得(a1a n)3=2×4,a1a n=2,∵T n=a1a2…a n,∴T2n=(a1a2…a n)2=(a1a n)(a2a n-1)…(a n a1)=(a1a n)n =2n=642=212,∴n=12.【答案】 B4.在数列{a n }中,若a 1=2,且对任意正整数m ,k ,总有a m +k =a m +a k ,则{a n }的前n 项和S n 等于( )A .n (3n -1)B.n (n +3)2C .n (n +1)D.n (3n +1)2【解析】 依题意得a n +1=a n +a 1,即有a n +1-a n =a 1=2,所以数列{a n }是以2为首项,2为公差的等差数列,a n =2+2(n -1)=2n ,S n =n (2+2n )2=n (n +1),选C.【答案】 C5.记S n 为正项等比数列{a n }的前n 项和,若S 12-S 6S 6-7·S 6-S 3S 3-8=0,且正整数m ,n满足a 1a m a 2n =2a 35,则1m +8n的最小值是( ) A.157 B.95 C.53D.75【解析】 ∵{a n }是等比数列,设{a n }的公比为q , ∴S 12-S 6S 6=q 6,S 6-S 3S 3=q 3,∴q 6-7q 3-8=0, 解得q =2(负值舍去).又a 1a m a 2n =2a 35,∴a 31·2m+2n -2=2(a 124)3=a 31213,∴m +2n =15,∴1m +8n =115⎪⎭⎫⎝⎛+n m 81(m +2n )=17+2n m +8m n 15≥17+22n m ×8m n 15=53,当且仅当2n m =8mn,即m =3,n =6时等号成立,∴1m +8n 的最小值是53,故选C. 【答案】 C6.数列{}a n 是以a 为首项,b 为公比的等比数列,数列{}b n 满足b n =1+a 1+a 2+…+a n (n =1,2,…),数列{}c n 满足c n =2+b 1+b 2+…+b n (n =1,2,…),若{}c n 为等比数列,则a +b 等于( )A. 2 B .3 C. 5D .6【解析】 由题意知,当b =1时,{c n }不是等比数列,所以b ≠1.由a n =ab n -1,则b n =1+a (1-b n )1-b =1+a 1-b -ab n 1-b ,得c n =2+nb a ⎪⎭⎫ ⎝⎛-+11-a 1-b ·b (1-b n )1-b =2-ab (1-b )2+1-b +a 1-b n +abn +1(1-b )2,要使{}c n为等比数列,必有⎩⎪⎨⎪⎧2-ab(1-b )2=0,1-b +a1-b =0,得⎩⎪⎨⎪⎧a =1,b =2,a +b =3,故选B.【答案】 B 二、填空题7.数列{a n }的通项a n =n 2·⎪⎭⎫ ⎝⎛-3sin 3cos22ππn n ,其前n 项和为S n ,则S 30=________. 【解析】 由题意可知,a n =n 2·cos 2n π3,若n =3k -2,则a n =(3k -2)2·⎪⎭⎫⎝⎛-21=-9k 2+12k -42(k ∈N *);若n =3k -1,则a n =(3k -1)2·⎪⎭⎫ ⎝⎛-21=-9k 2+6k -12(k ∈N *);若n =3k ,则a n =(3k )2·1=9k 2(k ∈N *),∴a 3k -2+a 3k -1+a 3k =9k -52,k ∈N *,∴S 30=9-52+90-522×10=470.【答案】 4708.已知数列{a n }满足a 1=2,且a n =2na n -1a n -1+n -1(n ≥2,n ∈N *),则a n =________.【解析】 由a n =2na n -1a n -1+n -1,得n a n =n -12a n -1+12,于是n a n -1=12⎪⎪⎭⎫ ⎝⎛---111n a n (n ≥2,n ∈N *). 又1a 1-1=-12,∴数列⎭⎬⎫⎩⎨⎧-1nan 是以-12为首项,12为公比的等比数列,故n a n -1=-12n ,∴a n =n ·2n2n -1(n ∈N *).【答案】 n ·2n2n -19.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增一十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?( )A .8日B .9日C .12日D .16日【解析】由题可知,良马每日行程a n 构成一个首项为103,公差13的等差数列,驽马每日行程b n 构成一个首项为97,公差为-0.5的等差数列,则a n =103+13(n -1)=13n +90,b n =97-0.5(n -1)=97.5-0.5n ,则数列{a n }与数列{b n }的前n 项和为1125×2=2250,又∵数列{a n }的前n 项和为n 2×(103+13n +90),数列{b n }的前n 项和为n 2×(97+97.5-0.5n ),n 2(103+3n +90)+n2(97+97.5-0.5n )=2250,整理得:25n 2+775n -9 000=0,即n 2+31n -360=0,解得:n =9或n =-40(舍),即九日相逢.故选B.【答案】B10.数列{log k a n }是首项为4,公差为2的等差数列,其中k >0,且k ≠1.设c n =a n lg a n ,若{c n }中的每一项恒小于它后面的项,则实数k 的取值范围为________.【解析】 由题意得log k a n =2n +2,则a n =k2n +2,∴a n +1a n =k 2(n +1)+2k2n +2=k 2,即数列{a n }是以k 4为首项,k 2为公比的等比数列,c n =a n lg a n =(2n +2)·k 2n +2lg k ,要使c n <c n +1对一切n ∈N *恒成立,即(n +1)lg k <(n +2)·k 2·lg k 对一切n ∈N *恒成立;当k >1时,lg k >0,n +1<(n +2)k 2对一切n ∈N *恒成立;当0<k <1时,lg k <0,n +1>(n +2)k 2对一切n ∈N *恒成立,只需k 2<⎪⎭⎫ ⎝⎛++21n n min .∵n +1n +2=1-1n +2单调递增,∴当n =1时,n +1n +2取得最小值,即⎪⎭⎫⎝⎛++21n n min =23,∴k 2<23,且0<k <1,∴0<k <63.综上,k ∈⎪⎪⎭⎫ ⎝⎛36,0∪(1,+∞).【答案】 ⎪⎪⎭⎫ ⎝⎛36,0∪(1,+∞) 三、解答题11.已知数列{}a n 的前n 项和为S n ,且S n =2a n -3n (n ∈N *).(1)求a 1,a 2,a 3的值;(2)是否存在常数λ,使得数列{a n +λ}为等比数列?若存在,求出λ的值和通项公式a n ;若不存在,请说明理由.【解】 (1)当n =1时,由S 1=2a 1-3×1,得a 1=3; 当n =2时,由S 2=2a 2-3×2,可得a 2=9; 当n =3时,由S 3=2a 3-3×3,得a 3=21.(2)令(a 2+λ)2=(a 1+λ)·(a 3+λ),即(9+λ)2=(3+λ)·(21+λ),解得λ=3. 由S n =2a n -3n 及S n +1=2a n +1-3(n +1),两式相减,得a n +1=2a n +3. 由以上结论得a n +1+3=(2a n +3)+3=2(a n +3),所以数列{a n +3}是首项为6,公比为2的等比数列,因此存在λ=3,使得数列{a n +3}为等比数列,所以a n +3=(a 1+3)×2n -1,a n =3(2n -1)(n ∈N *).12.已知数列{a n }的前n 项和为S n ,且S n -1=3(a n -1),n ∈N *.(1)求数列{a n }的通项公式;(2)设数列{b n }满足a n +1=⎪⎭⎫ ⎝⎛23a n ·b n ,若b n ≤t 对于任意正整数n 都成立,求实数t 的取值范围.【解】 (1)由已知得S n =3a n -2,令n =1,得a 1=1,又a n +1=S n +1-S n =3a n +1-3a n ⇒a n +1=32a n ,所以数列{a n }是以1为首项,32为公比的等比数列,所以a n =123-⎪⎭⎫ ⎝⎛n .(2)由a n +1=⎪⎭⎫⎝⎛23a n ·b n ,得b n =1a n log 32a n +1=(23)n -1log 32(32)n =n ·123-⎪⎭⎫ ⎝⎛n ,所以b n +1-b n =(n +1)·n ⎪⎭⎫ ⎝⎛32-n ·132-⎪⎭⎫ ⎝⎛n =2n -13n (2-n ),所以(b n )max =b 2=b 3=43,所以t ≥43.。
高考数学复习热点08 数列与不等式(原卷版)-2021年高考数学专练(新高考)

热点08 数列与不等式【命题趋势】在新高考卷的考点中,数列主要以两小和一大为主的考查形式,在小题中主要以等差数列和等比数列为主,大题中新高考比以往的考察有了很大的改变,以前是三角和数列在17题交替考查,现在作为主干知识必考内容,考察位置是17或18题,题型可以是多条件选择的开放式的题型。
由于三角函数与数列均属于解答题第一题或第二题的位置,考查的内容相对比较简单,这一部分属于必得分,对于小题部分,一般分布为一题简单题一道中等难度题目。
对于不等式内容新教材删除了线性规划和不等式选讲,新高考主要考察不等式性质和基本不等式。
基本不等式考察往往都是已基本不等式作为切入点形式出现,题目难度中等。
专题针对高考中数列、不等式等高频知识点,预测并改编一些题型,通过本专题的学习,能够彻底掌握数列,不等式。
请学生务必注意题目答案后面的名师点睛部分,这是对于本类题目的一个总结。
【满分技巧】1、等差、等比数列如果记住基本的通项公式以及求和公式和性质,基本上所有的等差、等比数列问题都可以解决。
2、数列求通项主要方法有:公式法、利用前n项和求通项、累加、累乘、构造等方法;这里要注意各个方法中递推关系的模型结构特点。
3、数列求和问题主要包含裂项求和,分组求和,绝对值求和,错位相减求和,掌握固定的求和方式即可快速得到答案;这里要注意各个方法中数列通项的结构模型;本专题有相应的题目供参考。
4、对于基本不等式类的题目应注意等号成立地条件和基本不等式的模型结构,对“1”的活用。
【考查题型】选择题、填空、解答题【常考知识】数列的概念、等差等比数列的概念和公式和性质、数列求通项的方法、数列求和的方法、不等式的性质、基本不等式【限时检测】(建议用时:90分钟)一、单选题1.(2020·云南省个旧市第一高级中学高三其他模拟(理))设等差数列的前项和为,且{}n a n n S ,则的值为( )1144S =378a a a ++A .11B .12C .13D .142.(2020年全国统一高考数学试卷(文科)(新课标Ⅰ))设是等比数列,且,{}n a 1231a a a ++=,则( )234+2a a a +=678a a a ++=A .12B .24C .30D .323.(2018·陆川中学高三其他模拟(理))等差数列的前项和为,且,.设{}n a n n S 10a >500S =,则当数列的前项和取得最大值时, 的值为( )()*12n n n n b a a a n N ++=∈{}nb n nT n A .23B .25C .23或24D .23或254.(2020·广西高三一模(理))已知数列,,则( )21131322n n n a a a --=++12a =()25log 1a +=A .B .C .D .263log 331-231log 315-363log 231-331log 215-5.(2020年浙江省高考数学试卷)已知等差数列{a n }的前n 项和S n ,公差d ≠0,.记b 1=S 2,11a d≤b n+1=S 2n+2–S 2n ,,下列等式不可能成立的是( )n *∈N A .2a 4=a 2+a 6B .2b 4=b 2+b 6C .D .2428a a a =2428b b b =6.(2020·江苏宝应中学高二期中)若a ,b 为正实数,且,则的最小值为( )1123a b +=3a b +A .2B .C .3D .4327.(2020·云南省个旧市第一高级中学高三其他模拟(理))已知数列的前项和为,且{}n a n n S ,,,则的通项公式为( )12n n S a n +=+-*n N ∈12a ={}n a A .B .C .D .121n n a -=-12n n a -=121n n a -=+2nn a =8.(2020·贵州高三其他模拟(理))已知是双曲线的半焦距,则的最c 2222:1(0,0)x y C a b a b -=>>a b c+大值是( )A BC D9.(2020·四川遂宁·高三零模(理))已知正项等比数列满足,,又为数{}n a 112a =2432a a a =+n S 列的前项和,则( ){}n a n 5S =A . 或B .312112312C .D .15610.(2020·河南焦作·高三一模(理))在等比数列中,,,则({}n a 11a =427a =352a a +=)A .45B .54C .99D .8111.(2020年全国统一高考数学试卷(理科)(新课标Ⅱ))数列中,,,若{}n a 12a =m n m n a a a +=,则( )155121022k k k a a a ++++++=- k =A .2B .3C .4D .512.(2020·江西高三二模(理))已知等比数列的首项,公比为,前项和为,则“{}n a 10a >q n n S”是“”的( )1q >3542S S S +>A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件13.(2020·浙江省东阳中学高三其他模拟)已知数列的前n 项和,则{}n a ()212,1n n S n a n a =≥=n a =( )A .B .C .D .()21n n +22(1)n +121n-121n -二、多选题14.(2020年新高考全国卷Ⅰ数学高考试题(山东))已知a >0,b >0,且a +b =1,则( )A .B .2212a b +≥122a b ->C .D 22log log 2a b +≥-+≤15.(2020·广东湛江·高三其他模拟)已知数列{a n }满足:0<a 1<1,.则下列说()14n n n a a ln a +-=-法正确的是( )A .数列{a n }先增后减B .数列{a n }为单调递增数列C .a n <3D .202052a >三、填空题16.(2020年浙江省高考数学试卷)我国古代数学家杨辉,朱世杰等研究过高阶等差数列的求和问题,如数列就是二阶等差数列,数列的前3项和是________.(1)2n n +⎧⎫⎨⎬⎩⎭(1)2n n +⎧⎫⎨⎬⎩⎭(N )n *∈17.(2020·广西高三一模(理))已知数列和满足,,,{}n a {}n b 12a =11b =1n n n a b b ++=.则=_______.114n n n a b a +++=20211008b a 18.(2020·山东济宁·高三其他模拟)已知,若不等式对140,0,1m n m n >>+=24m n x x a +≥-++已知的及任意实数恒成立,则实数最大值为_________.,m n x a 19.(2020·福建莆田·高三其他模拟)在△ABC 中,三边a ,b ,c 所对应的角分别是A ,B ,C ,已知a ,b ,c 成等比数列.若,数列满足,前n 项和为,sin sin sin B A C ={}n a 32|cos |2nn a nB =n S 2nS =__________.20.(2020·四川遂宁·高三零模(理))已知均为实数,函数在时取,a b 1()(2)2f x x x x =+>-x a =得最小值,曲线在点处的切线与直线_____2ln(1)y x =+()0,0y bx =a b +=四、解答题21.(2020·福建莆田·高三其他模拟)在①;②为等差数列,其中成131n n n a a a +=+1{}n a 236111,1,a a a +等比数列;③这三个条件中任选一个,补充到下面的问题中,然后解答2123111132n n na a a a -++++= 补充完整的题目.已知数列中,______.{}n a 11a =(1)求数列的通项公式;{}n a (2)设为数列的前项和,求证:.1,n n n n b a a T +={}n b n 13n T <注:如果选择多个条件分别解答,按第一个解答计分.22.(2020·安徽高三其他模拟(理))已知公比大于的等比数列满足,,1{}n a 2312a a +=416a =.2log n n b a =(1)求数列、的通项公式;{}n a {}n b (2)若数列的前项和为,求的前项和.{}n b n n S ()()*12n nnn a c n S -=∈N n n T 23.(2020年天津高考数学卷)已知为等差数列,为等比数列,{}n a {}n b .()()115435431,5,4a b a a a b b b ===-=-(Ⅰ)求和的通项公式;{}n a {}n b (Ⅱ)记的前项和为,求证:;{}n a n n S ()2*21n n n S S S n ++<∈N (Ⅲ)对任意的正整数,设求数列的前项和.n ()21132,,,.n nn n n n n a b n a a c a n b +-+⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数{}n c 2n 24.(2020年浙江省高考数学试卷)已知数列{a n },{b n },{c n }中,.1111121,,()nn n n n n n b a b c c a a c c n b +++====-=⋅∈*N (Ⅰ)若数列{b n }为等比数列,且公比,且,求q 与{a n }的通项公式;0q >1236b b b +=(Ⅱ)若数列{b n }为等差数列,且公差,证明:.0d >1211n c c c d +++<+*()n N ∈25.(2018·陆川中学高三其他模拟(理))已知数列为公差不为零的等差数列,且,{}n a 23a =1a 3a ,成等比数列.7a (1)求数列的通项公式;{}n a (2)若数列满足,记数列的前项和为,求证:.{}n b 110101n n n b a a +=+{}n b n n S 12n S <。
等差数列与等比数列专题辅导(小编推荐)

等差数列与等比数列专题辅导(小编推荐)第一篇:等差数列与等比数列专题辅导(小编推荐)等差数列与等比数列专题辅导(1)在等差数列{an}中, a7=9, a13=-2, 则a25=()A-22B-24C60D64(2)在等比数列{an}中, 存在正整数m, 有am=3,am+5=24, 则am+15=()A864B1176C1440D1536(3)已知等差数列{an}的公差为2,若a1,a3,a4成等比数列, 则a2=()A–4B–6C–8D–10(4)设数列{an}是等差数列,且a2=-6,a8=6,Sn是数列{an}的前n 项和,则()AS4>S3BS4=S2CS6(5)已知由正数组成的等比数列{an}中,公比q=2, a1·a2·a3·…·a30=245, 则a1·a4·a7·…·a28=5101520A 2B2C2D2(6)若{an}是等差数列,首项a1>0,a2003+a2004>0,a2003.a2004<0,则使前n项和Sn>0成立的最大自然数n是:()A.4005B.4006C.4007D.4008(7)在等比数列{an}中, a1<0, 若对正整数n都有anAq>1B0a1(3n-1)(8)设数列{an}的前n项和为Sn,Sn=(对于所有n≥1),且a4=54,则a1=__________.2(9)等差数列{an}的前m项和为30, 前2m项和为100, 则它的前3m项和为_________.(10)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数列, 且a1=2, 公和为5,那么a18的值为_______,这个数列的前21项和S21的值为.(11)已知等差数列{an}共2n+1项, 其中奇数项之和为290, 偶数项之和为261,求第n+1项及项数2n+1的值.(12)设{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110且a1,a2,a4成等比数列.(Ⅰ)证明a1=d;(Ⅱ)求公差d的值和数列{an}的通项公式.(13)已知等比数列{an}的各项都是正数, Sn=80, S2n=6560, 且在前n项中, 最大的项为54, 求n的值.(14)ΔOBC的三个顶点坐标分别为(0,0)、(1,0)、(0,2), 设P1为线段BC的中点,P2为线段CO的中点,P3为线段OP1的中点,对于每一个正整数n, Pn+3为线段PnPn+1的中点,令Pn的坐标为(xn,yn), an=(Ⅰ)求a1,a2,a3及an;(Ⅱ)证明yn+4=1-(Ⅲ)若记bn=y4n+41yn+yn+1+yn+2.2yn,n∈N*;4-y4n,n∈N*,证明{bn}是等比数列.答案:1-7 BDBDA BB8.29.21010.3, 5211.29, 1912.(2)d=2 an=2n13.n=414.(1)an=2(2)(3)证明略第二篇:等差数列与等比数列等差数列与等比数列⎧>0,递增数列⎪一、等差数列的定义:an+1-an=d(d:公差)(常数)⎨=0,常数列,⎪<0,递减数列⎩1.证明数列{an}为等差数列:(1)定义:an+1-an=d(常数)(2)等差中项:2an+1=an+an+2注:(1)不可用a2-a1=a3-a2=a4-a3=Λ=“常数”证(2)a1=⎨例1.(1)已知数列{an}为等差数列,求证:数列{an+an+1}为等差数列;变式:①已知数列{an}为等差数列,求证:数列{an+t}(t为常数)为等差数列;②已知数列{an}为等差数列,求证:数列{tan}(t为常数)为等差数列;③已知数列{an}、{bn}均为等差数列,求证:数列{an+bn}为等差数列(2)已知数列{an}的前n项和为Sn,且Sn=n2,求证:数列{an}为等差数列;变式:①已知数列{an}的前n项和为Sn,且Sn=n2+1,求:an②已知数列{an}的前n项和为Sn,且Sn=an2+bn,求:an ③已知数列{an}的前n项和为Sn,且Sn=an2+bn+c,求:an(3)已知数列{an}满足:a1=1,an+1=数列;(4)已知数列{an},a1=1,an+1=为等差数列(5)设数列{an}的前n项和为Sn,求证:数列{an}为等差数列的充要条件是{an}为等差数列⎧S1,n=1⎩Sn-Sn-1,n≥2an1,且bn=,求证:数列{bn}为等差an+1ann1an+,且bn=nan,求证:数列{bn}n+1n+1Sn=n(a1+an)22.证明数列{an}为单调数列:an+1-an=f(n)⎨⎧>0,递增数列递减数列⎩<0,注:(1)求数列{an}中an的极值也可采用此方法(2)已知数列{an}为等差数列ⅰ.若a1<0,d>0,则Sn有最小值;解法:①令an≤0{bn}②Snⅱ.若a1>0,d<0,则Sn有最大值;解法:①令an≥0②Sn例2.已知an=(11-2n)2n,求数列{an}的最大项例3.(1)已知等差数列{an}的前n项和为Sn,且an=10-2n,求Sn的最大值;(2)已知等差数列{an}的前n项和为Sn,且an=2n-13,求Sn的最小值;3.叠加法:已知a1=a,an+1-an=f(n),求an例4.(1)已知数列{an}为等差数列,首项为a1,公差为d,求an;(2)已知数列{an},a1=1,an+1=4.通项公式:an=a1+(n-1)d(1)an=am+(n-m)d(2)an是关于n的一次函数,且n的系数为公差d.例5.已知数列{an}为等差数列,a5=-3,a9=13,求an5.等差中项:若a、b、c成等差数列,则b=(1)若数列{an}为等差数列,则2an+1n+11an+,求an nna+c称为a、c的等差中项2=an+an+2;(2)若已知三个数成等差数列,且其和为定值,则可设这三个数为a-d、a、a+d;(3)若数列{an}为等差数列,且公差d≠0,则am+an=ap+aq⇔m+n=p+q(4)在有穷等差数列{an}中,与首尾两项距离相等的两项的和等于首尾两项的和.即:a1+an=a2+an-1=a3+an-2=Λ=ak+an-k+1例6.(1)已知:等差数列中连续三项的和为21,平方和为179,求这三项(2)在3与19之间插入3个数后成等差数列,求这三个数(3)已知:a、b、c成等差数列求证:①b+c、a+c、a+b成等差数列;②a(b+c)、b(a+c)、c(a+b)成等差数列;③a-bc、b-ac、c-ab 成等差数列(4)已知:a、b、c成等差数列,求证:2222111成等差数列 b+ca+ca+blg(a-c)、lg(a+c-2b)成等差(5)已知:成等差数列,求证:lg(a+c)、数列(6)若方程a(b-c)xb(c-a)x+c(a-b)=0有相等实根,求证:成等差111abc111abc数列例7.在等差数列{an}中,(1)若a5+a10=12,求S14;(2)若a8=m,求S15;(3)若a4+a6+a15+a17=50,求S20;(4)若a2+a4=18,a3+a5=32,求S6;(5)若a2+a5+a12+a15=36,求S16;(6)若a3+a4+a5+a6+a7=450,求a2+a8(7)若等差数列{an}的各项都是负数,且a32+a82+2a3⋅a8=9,则其前10项和S10= ____________(8)在等差数列{an}中,若a3+a15=a5+an,则n=_______6.数列{an}的前n项和Sn=注:(1)倒序法求和;(2)等差数列{an}的前n项和Sn是关于自然数n的二次函数,且n的系数为n(a1+an)n(n-1)n(n-1)=na1+d=nan-d 222d,2常数项为零,即:Sn=An2+Bn(当A=0时数列{an}为常数列);(3)①S2n-1=(2n-1)an(可以将项与和之间进行相互转化)。
28 高中数学等差等比数列证明专题训练

专题28高中数学等差等比数列证明专题训练【方法总结】1.等差数列的四个判定方法(1)定义法:a n +1-a n =d (常数)(n ∈N *)⇔{a n }是等差数列.(2)等差中项法:2a n +1=a n +a n +2(n ∈N *)⇔{a n }是等差数列.(3)通项公式法:a n =pn +q (p ,q 为常数,n ∈N *)⇔{a n }是等差数列.(4)前n 项和公式法:S n =An 2+Bn (A ,B 为常数,n ∈N *)⇔{a n }是等差数列.提醒:(1)定义法和等差中项法主要适合在解答题中使用,通项公式法和前n 项和公式法主要适合在选择题或填空题中使用.(2)若要判定一个数列不是等差数列,则只需判定存在连续三项不成等差数列即可.2.等比数列的四个判定方法(1)定义法:a n +1a n=q (q 是不为0的常数,n ∈N *)⇔{a n }是等比数列. (2)等比中项法:a 2n +1=a n ·a n +2(a n ·a n +1·a n +2≠0,n ∈N *)⇔{a n }是等比数列.(3)通项公式法:a n =cq n (c ,q 均是不为0的常数,n ∈N *)⇔{a n }是等比数列.(4)前n 项和公式法:S n =k ·q n -k (k 为常数且k ≠0,q ≠0,1),则{a n }是等比数列.提醒:(1)定义法和等比中项法主要适合在解答题中使用,通项公式法和前n 项和公式法主要适合在选择题或填空题中使用.(2)若要判定一个数列不是等比数列,则只需判定存在连续三项不成等比数列即可.【高考真题】1.(2022·全国甲理文) 记S n 为数列{a n }的前n 项和.已知2S n n+n =2a n +1. (1)证明:{a n }是等差数列;(2)若a 4,a 7,a 9成等比数列,求S n 的最小值.【题型突破】1.已知等差数列{a n }的前n 项和为S n ,且a 3=7,a 5+a 7=26.(1)求a n 及S n ;(2)令b n =S n n(n ∈N *),求证:数列{b n }为等差数列. 2.已知数列{a n }中,a 1=35,a n =2-1a n -1(n ≥2,n ∈N *),数列{b n }满足b n =1a n -1(n ∈N *). (1)求证:数列{b n }是等差数列;(2)求数列{a n }中的最大项和最小项,并说明理由.3.在数列{a n }中,a 1=4,na n +1-(n +1)a n =2n 2+2n .(1)求证:数列⎩⎨⎧⎭⎬⎫a n n 是等差数列;(2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n . 4.数列{a n }满足a 1=1,na n +1=(n +1)a n +n (n +1),n ∈N *.(1)求证:数列⎩⎨⎧⎭⎬⎫a n n 是等差数列; (2)设b n =3n ·a n ,求数列{b n }的前n 项和S n .5.若数列{a n }的前n 项和为S n ,且满足a n +2S n S n -1=0(n ≥2),a 1=12. (1)求证:⎩⎨⎧⎭⎬⎫1S n 成等差数列; (2)求数列{a n }的通项公式.6.已知数列{a n }的前n 项和为S n ,且2S n =3a n -3n +1+3(n ∈N *).(1)设b n =a n 3n ,求证:数列{b n }为等差数列,并求出数列{a n }的通项公式; (2)设c n =a n n -a n 3n ,T n =c 1+c 2+c 3+…+c n ,求T n . 7.(2021·全国乙)设S n 为数列{a n }的前n 项和,b n 为数列{S n }的前n 项积,已知2S n +1b n=2. (1)证明:数列{b n }是等差数列;(2)求{a n }的通项公式.8.(2014·全国Ⅰ)已知数列{a n }的前n 项和为S n ,a 1=1,a n ≠0,a n a n +1=λS n -1,其中λ为常数.(1)证明:a n +2-a n =λ;(2)是否存在λ,使得{a n }为等差数列?并说明理由.9.设数列{a n }的前n 项和为S n ,且满足a n -12S n -1=0(n ∈N *). (1)求数列{a n }的通项公式;(2)是否存在实数λ,使得数列{S n +(n +2n )λ}为等差数列?若存在,求出λ的值;若不存在,请说明理由.10.若数列{b n }对于任意的n ∈N *,都有b n +2-b n =d (常数),则称数列{b n }是公差为d 的准等差数列.如数列c n ,若c n =⎩⎪⎨⎪⎧4n -1,n 为奇数,4n +9,n 为偶数,则数列{c n }是公差为8的准等差数列.设数列{a n }满足a 1=a ,对于n ∈N *,都有a n +a n +1=2n .(1)求证:{a n }是准等差数列;(2)求{a n }的通项公式及前20项和S 20.11.已知数列{a n }的首项a 1>0,a n +1=3a n 2a n +1(n ∈N *),且a 1=23. (1)求证:⎩⎨⎧⎭⎬⎫1a n -1是等比数列,并求出{a n }的通项公式; (2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和T n .12.已知数列{a n }的前n 项和为S n ,n ∈N *,a 1=1,a 2=32,a 3=54,且当n ≥2时,4S n +2+5S n =8S n +1+S n - 1.(1)求a 4的值;(2)证明:⎩⎨⎧⎭⎬⎫a n +1-12a n 为等比数列. 13.已知数列{a n }的前n 项和S n 满足S n =2a n +(-1)n (n ∈N *).(1)求数列{a n }的前三项a 1,a 2,a 3;(2)求证:数列⎩⎨⎧⎭⎬⎫a n +23(-1)n 为等比数列,并求出{a n }的通项公式. 14.已知在正项数列{a n }中,a 1=2,点A n (a n ,a n +1)在双曲线y 2-x 2=1上,数列{b n }中,点(b n ,T n )在直线y =-12x +1上,其中T n 是数列{b n }的前n 项和. (1)求数列{a n }的通项公式;(2)求证:数列{b n }是等比数列.15.已知数列{a n }满足:a 1=1,a n +1=⎩⎪⎨⎪⎧a n +1,n 为奇数,2a n ,n 为偶数(n ∈N *),设b n =a 2n -1. (1)求b 2,b 3,并证明b n +1=2b n +2;(2)①证明:数列{b n +2}为等比数列;②若a 2k ,a 2k +1,9+a 2k +2成等比数列,求正整数k 的值.16.(2019·全国Ⅱ)已知数列{a n }和{b n }满足a 1=1,b 1=0,4a n +1=3a n -b n +4,4b n +1=3b n -a n -4.(1)证明:{a n +b n }是等比数列,{a n -b n }是等差数列;(2)求{a n }和{b n }的通项公式.17.(2018·全国Ⅰ)已知数列{a n }满足a 1=1,na n +1=2(n +1)a n ,设b n =a n n. (1)求b 1,b 2,b 3;(2)判断数列{b n }是否为等比数列,并说明理由;(3)求{a n }的通项公式.18.已知数列{a n }的前n 项和为S n ,a 1=1,a n >0,S 2n =a 2n +1-λS n +1,其中λ为常数.(1)证明:S n +1=2S n +λ;(2)是否存在实数λ,使得数列{a n }为等比数列,若存在,求出λ;若不存在,说明理由.19.设等差数列{a n }的前n 项和为S n ,a =(a 1,1),b =(1,a 10),若a·b =24,且S 11=143,数列{b n }的前n项和为T n ,且满足12n a -=λT n -(a 1-1)(n ∈N *).(1)求数列{a n }的通项公式及数列⎩⎨⎧⎭⎬⎫1a n a n +1的前n 项和M n ; (2)是否存在非零实数λ,使得数列{b n }为等比数列?并说明理由.20.已知数列{a n }满足a 1=1,a n +1=2a n +λ(λ为常数).(1)试探究数列{a n+λ}是不是等比数列,并求a n;(2)当λ=1时,求数列{n(a n+λ)}的前n项和T n.。
高中数学专题练习《数列、导数知识点》含详细解析

数列、导数知识点一、等差数列1.概念:如果一个数列从第2项起,每一项与它的前一项的差都等于同一个常数,那么这个数列就叫做等差数列,即a n+1-a n =d(n∈N *,d 为常数).2.等差中项:由三个数a,A,b 组成的等差数列可以看成是最简单的等差数列.这时,A 叫做a 与b 的等差中项,且2A=a+b.3.通项公式:等差数列{a n }的首项为a 1,公差为d,则其通项公式为a n =a 1+(n-1)d.4.前n 项和公式:S n =n (a 1+a n )2=na 1+n (n -1)2d(n∈N *).5.性质:(1)通项公式的推广:a n =a m +(n-m)d(m,n∈N *).(2)若m+n=p+q(m,n,p,q∈N *),则有a m +a n =a p +a q .(3)数列S m ,S 2m -S m ,S 3m -S 2m ,…也是等差数列.(4)数列{a n }是等差数列⇔S n =An 2+Bn(A,B 为常数).(5)在等差数列{a n }中,若a 1>0,d<0,则S n 存在最大值;若a 1<0,d>0,则S n 存在最小值.二、等比数列1.概念:如果一个数列从第2项起,每一项与它的前一项的比都等于同一个常数,那么这个数列叫做等比数列,即a n a n -1=q(n≥2,n∈N *,q 为非零常数).2.等比中项:如果在a 与b 中间插入一个数G,使a,G,b 成等比数列,那么G 叫做a 与b 的等比中项.此时,G 2=ab.3.通项公式:等比数列{a n }的首项为a 1,公比为q,则其通项公式为a n =a 1q n-1.4.前n 项和公式:S n ={na 1,q =1,a 1(1-q n )1-q=a 1-a n q 1-q,q ≠1.5.性质:(1)通项公式的推广:a n=a m q n-m(m,n∈N*).(2)若k+l=m+n(k,l,m,n∈N*),则有a k·a l=a m·a n.(3)当q≠-1或q=-1且n为奇数时,S n,S2n-S n,S3n-S2n,…仍成等比数列,其公比为q n.三、求一元函数的导数1.基本初等函数的导数公式基本初等函数导函数f(x)=c(c为常数) f'(x)=0f(x)=xα(α∈Q,且α≠0)f'(x)=αxα-1f(x)=sin x f'(x)=cos xf(x)=cos x f'(x)=-sin xf(x)=a x(a>0,且a≠1)f'(x)=a x ln af(x)=e x f'(x)=e xf(x)=log a x(a>0,且a≠1)f'(x)=1xlnaf(x)=ln x f'(x)=1x2.导数的四则运算法则已知两个函数f(x),g(x)的导数分别为f'(x),g'(x).若f'(x),g'(x)存在,则有:(1)[f(x)±g(x)]'=f'(x)±g'(x);(2)[f(x)g(x)]'=f'(x)g(x)+f(x)g'(x);(3)[f(x)g(x)]'=f'(x)g(x)-f(x)g'(x)[g(x)]2(g(x)≠0).3.简单复合函数的导数复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为y'x =y'u ·u'x .四、导数在研究函数中的应用 1.函数的单调性与导数一般地,函数f(x)的单调性与导函数f'(x)的正负之间具有如下的关系: 在某个区间(a,b)上,如果f'(x)>0,那么函数y=f(x)在区间(a,b)上单调递增; 在某个区间(a,b)上,如果f'(x)<0,那么函数y=f(x)在区间(a,b)上单调递减. 2.函数的极值与导数条件 f'(x 0)=0x 0附近的左侧f'(x)>0,右侧f'(x)<0x 0附近的左侧f'(x)<0,右侧f'(x)>0图象极值 f(x 0)为极大值 f(x 0)为极小值 极值点 x 0为极大值点x 0为极小值点3.函数的最大(小)值与导数(1)如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值, f(b)为函数的最大值;若函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值, f(b)为函数的最小值.(3)求函数y=f(x)在区间[a,b]上的最大值与最小值的步骤如下:①求函数y=f(x)在区间(a,b)上的极值;②将函数y=f(x)的各极值与端点处的函数值f(a), f(b)比较,其中最大的一个是最大值,最小的一个是最小值.。
等差数列与等比数列的应用综合练习题

等差数列与等比数列的应用综合练习题1. 定义和性质等差数列和等比数列是数学中常见的数列类型。
等差数列是指数列中任意两个相邻项之差相等的数列,而等比数列是指数列中任意两个相邻项之比相等的数列。
在等差数列中,我们使用首项a1和公差d来表示,公式为an = a1 + (n-1)d。
其中n为项数,an为第n项。
等差数列的求和公式为Sn = (n/2)(2a1 + (n-1)d),其中Sn表示前n项和。
在等比数列中,我们使用首项a1和公比r来表示,公式为an = a1 * r^(n-1)。
等比数列的求和公式为Sn = a1 * (1 - r^n) / (1 - r),当|r| < 1时成立。
2. 应用练习题(1) 某个等差数列的首项是3,公差是4,求第10项的值和前10项的和。
解析:根据等差数列的定义和性质,可以得到an = 3 + (10-1) * 4 = 39,Sn = (10/2)(2*3 + (10-1)*4) = 240。
结果:第10项的值是39,前10项的和是240。
(2) 某个等比数列的首项是2,公比是3,求第5项的值和前5项的和。
解析:根据等比数列的定义和性质,可以得到an = 2 * 3^(5-1) = 162,Sn = 2 * (1 - 3^5) / (1 - 3) = 242。
结果:第5项的值是162,前5项的和是242。
(3) 在等差数列和等比数列中,求和公式的推导过程。
解析:对于等差数列,我们可以通过列出前n项和Sn和Sn+1之间的关系,然后进行化简求解来得到求和公式。
具体推导过程如下:Sn = a1 + a2 + ... + anSn+1 = a1 + a2 + ... + an + an+1两式相减可得:Sn+1 - Sn = an+1根据等差数列的定义,an+1 = a1 + nd,代入上式可得:Sn+1 - Sn = a1 + nd化简得:Sn = n/2 * (2a1 + (n-1)d)对于等比数列,我们可以使用等比数列的通项公式和前n项和公式等进行推导。
等差数列与等比数列练习题

等差数列与等比数列练习题一、选择题1.对任意等比数列{}n a ,下列说法一定正确的是 A.139,,a a a 成等比数列 B.236,,a a a 成等比数列 C.248,,a a a 成等比数列 D.369,,a a a 成等比数列2.设等差数列{}n a 的公差为d ,若数列1{2}n a a为递减数列,则( )A .0d <B .0d >C .10a d <D .10a d >3.各项不为零的等差数列{n a }中,2a 3-27a +2a 11=0,数列{n b }是等比数列,且b 7=a 7, 则b 6b 8=( ).A .2B .4C .8D .164.设等差数列{}n a 的前n 项和为n S ,若7662a a +=,则9S 的值是( )A .18B .36C .54D .725.设n S 为等差数列{}n a 的前n 项和,若11a =,公差2d =,236n n S S +-=,则n =( )A . 5B . 6C . 7D .86.等差数列{}n a 的前n 项和为n S ,311a =,14217S =,则12a =( )A .18B .20C .21D .227.设n S 为公差不为零的等差数列{}n a 的前n 项和,若983S a =,则) A .15 B .17 C .19 D .218.已知等差数列{n a },62a =,则此数列的前11项的和11S =A .44B .33C .22D .119.等差数列{}n a 的公差0d ≠,120a =,且3a ,7a ,9a 成等比数列.n S 为{}n a 的前n 项和,则10S 的值为( )A .110-B .90-C .90D .11010.由3,11==d a 确定的等差数列{}n a ,当268=n a 时,序号n 等于( )A .80B .100C .90D .8811.设}{n a 是等差数列,}{n b 为等比数列,其公比q≠1, 且0>i b (i=1、2、3 …n)若11b a =,1111b a =则A .66b a =B .66b a >C .66b a <D .66b a >或 66b a <12.已知等差数列{a n }的公差d≠0,若a 5、a 9、a 15成等比数列,那么它的公比为A13.在等差数列{}n a 中,0>n a ,且408321=++++a a a a ,则54a a ⋅的最大值是( )A .5B .10C .25D .5014.已知数列}{n a 为等差数列,且21=a ,1332=+a a ,则=++654a a a ( )(A )45 (B )43 (C )42 (D )4015.已知等差数列{}n a 中,前10项的和等于前5项的和.若06=+a a m 则=m ( )A.10B.9C.8D.216.设等差数列{}n a 的前n 项和为n S ,若493=+a a ,则11S 等于(A )12 (B )18 (C )22 (D )4417.在等差数列}{n a 中,1352,10a a a =+=,则7a =( )A.5B.8C.10D.1418.设n S 为等差数列{}n a 的前n 项的和,20141-=a ,则2014S 的值为( )A 、-2013B 、-2014C 、2013D 、2014 19.已知等差数列{}n a 满足32=a ,171=-n a ,)2(≥n ,100=n S ,则n 的值为( ) A .10 B .9 C .8 D .1120.等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,A21.等差数列}{n a 的前n 项和为2811,30n S a a a ++=若,那么13S 值的是 ( )A .130B .65C .70D .以上都不对22.设数列{}n a 是等差数列,26,a =- 86a =,n s 是数列{}n a 的前n 项和,则( )A .54s s <B .54s s =C .56s s <D .56s s =23.已知递减的等差数列{}n a 满足2921a a =,则数列{}n a 的前n 项和n S 取最大值时,n =( )A .3B .4或5C .4D .5或624.等差数列{}n a 中,19,793==a a ,则5a 为( )A .13B .12C .11D .1025.等差数列{a n }中,a 2+a 6=8,a 3+a 4=3,那么它的公差是( ).A .4B .5C .6D .726.已知等差数列}{n a 的前n 项和S n 满足1021S S =,则下列结论正确的是( )A .数列{}n S 有最大值B .数列{}n S 有最小值C .150a =D .160a =27.设{}n a 是首项为1a ,公差为1-的等差数列,n S 为其前n 项和,若,,,421S S S 成等比数列,则1a =( )28.在数列{}n a 中,1a =1,12n n a a +-=,则51a 的值为( )A.99B.49C.102D. 10129.已知等差数列}{n a 的前n 项和为n S ,若5418a a -=,则=8S ( ) A.18 B.36 C.30.已知数列{}n a 中,,则101a 的值为 A .50 B .51 C .52 D .5331.若{a n }为等差数列,S n 为其前n 项和,若首项17a =,公差2d =-,则使S n 最大的序号n 为( )A .2B .3C .4D .532.等差数列{}n a 中,a 1=1,d=3,a n =298,则n 的值等于( ).A .98B . 100C .99D .101 33,)(1)1(*N n f ∈=,猜想()f n 的表达式为( )A C 34.等差数列}{n a 中, 384362=+=+a a a a ,, 那么它的公差是( )A.4B.5C.6D.735.已知等差数列{}n a 中,26a =,前7项和784S =,则6a 等于( )A.18B.20C.24D.3236.等比数列{a n }的各项均为正数,且a 5a 6+a 4a 7=18,则log 3a 1+log 3a 2+ +log 3a 10=( )A .12B .8C .10D .2+log 3537.已知等比数列{}n a ,且482,a a +=则62610(2)a a a a ++的值为( )A .4B .6C .8D .1038.已知{}n a 是等比数列,21,441==a a ,则公比q =( ) A 、21- B 、2- C 、2 D 、21 39.若正数a,b,c 成公差不为零的等差数列,则 ( )(A )lga lgb lgc ,, 成等差数列(B )lga lgb lgc ,, 成等比数列(C )2,2,2a b c 成等差数列(D )2,2,2a b c 成等比数列40.已知等比数列{}n a 中,1633a a +=,2532a a =,公比1q >,则38a a +=( )A .66B .132C .64D .12841.等比数列{}n a 中,37a =,前3项之和321S =,则公比q 的值为( )(A )1 (B (C )1或(D )1或42.在ABC ∆中,,,a b c 分别为,,A B C 的对边,若sin A 、sin B 、sin C 依次成等比数列,则( )A .,,a b c 依次成等差数列B .,,a b c 依次成等比数列C .,,a c b 依次成等差数列D .,,a c b 依次成等比数列43.若等比数列{}n a 的各项均为正数,且510119122a a a a e +=,则122l n l n l n a a a ++⋅⋅⋅+等于( ) A .50 B .25 C .75 D .10044.正项等比数列{}n a 的公比为2,若21016a a =,则9a 的值是A.8B.16C.32D.6445.设等比数列{}n a 中,前n 项和为n S ,已知7863==S S ,,则 =++987a a a ( )A 46.正项等比数列{}n a 的公比为2,若21016a a =,则9a 的值是A.8B.16C.32D.6447.已知等比数列{}n a 的前n 项和为S n ,( ) A .4n -1 B .4n-1 C .2n -1 D .2n-148.已知等比数列{}n a 中,各项都是正数,成等差数列,( )A49.已知{}n a 是首项为1的等比数列,n s 是{}n a 的前n 项和,且639s s =,的前5项和为( )A5 B5 C50.在等比数列}{n a 中, ,8,1641=-=a a 则=7a ( ) A.4- B.4± C .2- D .2±51.若等比数列{}n a 的前n 项和为n S ,且314S =,12a =,则4a =( )A .16B .16或-16C .-54D .16或-5452.公比为2的等比数列{n a } 的各项都是正数,且 3a 11a =16,则5a =( ) A .1 B .2 C .4 D .853.数列{a n }是各项均为正数的等比数列,{b n }是等差数列,且a 6=b 7,则有A .a 3+a 9<b 4+b 10B .a 3+a 9≥b 4+b 10C .a 3+a 9≠b 4+b 10D .a 3+a 9与b 4+b 10的大小不确定 54.设等比数列{}n a 的公比2=q , 前n 项和为n S ,则) A .2 B .4 CD 55.等比数列{}n a 的首项11a =-,前n 项和为,n S则公比q 等于 ( )A.2 D .-2 56.各项不为零的等差数列{}n a 中,02211273=+-a a a ,数列{}n b 是等比数列,且77a b =,则=86b b ( )A 、2B 、4C 、8D 、16 57.若等比数列{}n a 满足153a a a =,则3a =( )(A )1 (B )1- (C )0或1 (D )1-或158.已知数列{}n a 是公比为2的等比数列,若416a =,则1a = ( )A .1B .2C .3D .459.在等比数列{}n a 中,若2n n a =,则7a 与9a 的等比中项为( )A .8aB .8a -C .8a ±D .前3个选项都不对60n 为( ) A .3 B .4 C .5 D .661.已知等比数列{n a }.等,则5cos a =( )A62.在等比数列{}n a 中,若,则=⋅82a a ( )A .-3B . 3C .-9D .963.已知{}n a 是等比数列,,则公比q =( ) A.2- C .2 D64.等比数列{}n a 的前n 项和为n S ,若1233a a a ++=,4566a a a ++=,则12S =( )A .15B .30C .45D .6065.数列{}n a 的首项为1,数列{}n b 为等比数列且,若10112b b ⋅=,则21a =( )A.20B.512C.1013D.102466.已知等比数列{}n a 中,74=a ,216=a ,则8a 的值 ( )A.35B.63C.321D. 321±67.在ABC ∆中的内角,,A B C 所对的边分别为,,a b c ,若60B ∠=,,a b c 且成等比数列,则ABC ∆的形状为A. 直角三角形B. 等腰三角形C. 等边三角形D. 不确定68.如果-1,a ,b ,c ,-9成等比数列,那么( ) A .b =3,ac =9 B .b =-3,ac =9C .b =3,ac =-9D .b =-3,ac =-969.设首项为l 的等比数列{}n a 的前n 项和为n S ,则 ( ) A.21n n S a =- B.32n n S a =-C.43n n S a =-D.32n n S a =-70.设{a n }是由正数组成的等比数列,S n 为其前n 项和.已知a 2·a 4=1,S 3=7,则S 5=( )71.在等比数列{}n a 中,418a a =,则公比q 的值为(A )2 (B )3 (C )4 (D )872.等比数列}{n a 中,如果585,25a a ==则2a 等于( )C.5D.173.[2014·北京西城区期末]设f(n)=2+24+27+210+…+23n +10(n ∈N *),则f(n)等于( )n -n +1-1) n +3-n +4-1)二、双选题(题型注释)三、综合题(题型注释)四、填空题 74.数列{}n a 是等差数列,若1351,3,5a a a +++构成公比为q 的等比数列,则q =________.75.(2013•重庆)已知{a n }是等差数列,a 1=1,公差d≠0,S n 为其前n 项和,若a 1,a 2,a 5成等比数列,则S 8= _________ .等差数列与等比数列练习题参考答案1.D【解析】试题分析:因为数列{}n a 为等比数列,设其公比为q ,则()22852391116a a a q a q a q a⋅=⋅⋅⋅=⋅= 所以,369,,a a a 一定成等比数列,故选D.考点:1、等比数列的概念与通项公式;2、等比中项.2.C【解析】 试题分析:因为{}n a 是等差数列,则2(1)1111(1)22a a a a n d n n a a n d +-=+-∴=,又由于1{2}n a a 为递减数列,所以 C.考点:1.等差数列的概念;2.递减数列.3.D【解析】试题分析:由等差数列的性质可知,,27113a a a =+由2a 3-27a +2a 11=0,可得,47=a 又b 7=a 7,47=b ,由等比数列的性质,可得.162786==b b b 故选D. 考点:等差数列、等比数列的性质.4.C .【解析】试题分析:设等差数列{}n a 的首项为1a ,公差为d ,则由7662a a +=,得d a d a 66)5(211++=+, 即641=+d a ,即65=a ;则. 考点:等差数列.5.D .【解析】试题分析:由题意得:12-=n a n ,∴22136362321368n n n n S S a a n n n +++-=⇒+=⇒+++=⇒=. 考点:等差数列的通项公式.6.B【解析】 选B . 考点:1.等差数列的求和公式;2.等差数列的性质.7.A【解析】 试题分析:由等差数列的性质知959S a =,15815S a =,所以选A . 考点:等差数列的性质,等差数列的前n 项和.8.C【解析】 试题分析:由等差数列的前n 项和公式,得 C. 考点:1、等差数列的前n 项和公式;2、等差数列的性质.9.D【解析】试题分析:d d a a 220213+=+=,d d a a 620617+=+=,d d a a 820819+=+=,由9327a a a ⋅=,()()()d d d 8202206202+⋅+=+∴,整理得022=+d d ,2-=∴d 或0=d(舍去), D. 考点:等差数列的通项公式和前n 项和公式.10.C【解析】试题分析:根据题意可知,32n a n =-,令32268n -=,解得90n =,故选C. 考点:等差数列.11.B 【解析】试题分析:由题可知,61111112a b b a a =+=+,因为公比q≠1, 且0>i b (i=1、2、3 …n),,即666622b a b a >⇒>。
等差等比数列练习题(含答案)以及基础知识点

由题意可得
解得
∵等差数列 的各项为正,∴
∴∴Biblioteka 22(I):是以 为首项,2为公比的等比数列。
即
(II)证法一:
①
②
②-①,得
即
④-③,得
即
是等差数列。
19、有四个数,其中前三个数成等比数列,其积为216,后三个数成等差数列,其和为36,求这四个数。
20、已知 为等比数列, ,求 的通项式。
21、数列 的前 项和记为
(Ⅰ)求 的通项公式;
(Ⅱ)等差数列 的各项为正,其前 项和为 ,且 ,又 成等比数列,求
22、已知数列 满足
(I)求数列 的通项公式;
(A) (B) (C) (D)不确定
4、互不相等的三个正数 成等差数列, 是a,b的等比中项, 是b,c的等比中项,那么 , , 三个数()
(A)成等差数列不成等比数列(B)成等比数列不成等差数列
(C)既成等差数列又成等比数列(D)既不成等差数列,又不成等比数列
5、已知数列 的前 项和为 , ,则此数列的通项公式为()
2°.若 是公差为q的等比数列, 组成公差为qn的等比数列.(注意:当q=-1,n为偶数时这个结论不成立)
⑤若 是等比数列,
则顺次n项的乘积: 组成公比这 的等比数列.
⑥若 是公差为d的等差数列,
1°.若n为奇数,则 而S奇、S偶指所有奇数项、所有偶数项的和);
2°.若n为偶数,则
(二)学习要点:
1.学习等差、等比数列,首先要正确理解与运用基本公式,注意①公差d≠0的等差数列的通项公式是项n的一次函数an=an+b;②公差d≠0的等差数列的前n项和公式项数n的没有常数项的二次函数Sn=an2+bn;③公比q≠1的等比数列的前n项公式可以写成“Sn=a(1-qn)的形式;诸如上述这些理解对学习是很有帮助的.
【专题训练】数列(等差、等比) 知识点总结及题型归纳

基本量法求数列的通项公式11.复习 等差数列(1)定义: 如果一个数列从第2项起,每一项与它的前一项的差等于同一个常.数.,那么这个数列就叫等差数列, 1(2)n n a a d n --=≥d a a n n =1--d a a n n =2-1--(由定义,累加法推得通项公式)…… d a a =12-(2)通项公式1(1)n a a n d =+-(3)性质: 在等差数列{}n a 中,若m ,n ,p ,q N +∈且m n p q +=+,则m n p q a a a a +=+;(4)前项和公式d n n na a a n S n n 2)1(2)(11-+=+=等比数列(1)定义 : 如果一个数列从第二项起....,每一项与它的前一项的比等于同一个常数..,那么这个数列就叫做等比数列,1n a +:(0)n a q q =≠ (2)通项公式11-⋅=n n q a a(3)性质:在等比数列{}n a 中,q p n m a a a a q p n m ⋅=⋅+=+,则若),,,(*∈N q p n m 其中(4)前项和公式)1(11)1()1(111≠⎪⎩⎪⎨⎧--=--==q q qa a qq a q na S n nn例1(2015年全国卷I ) n S 为数列{}n a 的前n 项和.已知20,243n n n n a a a S >+=+,(1)求{}n a 的通项公式:变式1:(湖北省武汉部分重点中学2020届高三起点考试)已知数列{a n }是等比数列,S n 为数列{a n }的前n 项和,且a 3=3,S 3=9 (1)求数列{a n }的通项公式;变式2:已知等差数列{}n a 的公差0d ≠,其前n 项和为n S ,若2822a a +=,且4712,,a a a 成等比数列.(1)求数列{}n a 的通项公式;例2已知数列{a n }的前n 项和为S n ,且2n n S a n =-.(1) 证明数列{1n a +}是等比数列,并求数列{}n a 的通项公式;变式1:(湖北省黄冈中学2019届高三数学模拟试题1)已知各项均为正数的等比数列{a n }的前n 项和为S n ,a 1=14,a 3+a 5=564.(1)求数列{a n }的通项公式;变式3:已知数列{}n a ,{}n b ,其中1,511-==b a ,且满足)3(2111---=n n n b a a ,)3(2111----=n n n b a b ,2*,≥∈n N n .(1)求证:数列{}n n b a -为等比数列,并求数列{a n }、{b n }的通项公式;例3 .已知等差数列{a n }的公差为2,前n 项和为S n ,且S 1,S 2,S 4成等比数列.(1)求数列{a n }的通项公式; 变式(浙江省名校联盟2020届高三第一次联考试题)已知等比数列{}n a 的公比1q >,且13542a a a ++=,39a +是1a ,5a 的等差中项.数列{}n b的通项公式nn b =Νn *∈.(1)求数列{}n a 的通项公式;数列(等差、等比)知识点清单一、数列的概念1.数列定义:按一定次序排列的一列数叫做数列;数列中的每个数都叫这个数列的项。
数列等差数列与等比数列练习题

数列等差数列与等比数列练习题数列是数学中基础而重要的概念之一,同时也是数学的应用领域中常见的数学模型之一。
其中,等差数列和等比数列是数列中最基础的两种常见类型。
本文将为大家提供一些关于等差数列和等比数列的练习题,以巩固和提高大家对数列的理解和运用能力。
【练习题一】1. 若等差数列的首项是3,公差是4,求第n项的表达式。
解析:由题意,首项是3,公差是4。
所以等差数列的通项公式可以表示为an = a1 + (n-1)d,其中a1为首项,d为公差,n为项数。
代入已知条件,可得an = 3 + (n-1)4。
2. 若等差数列的第7项是18,公差是2,求首项和第n项的和。
解析:由题意,第7项是18,公差是2。
所以等差数列的通项公式为an = a1 + (n-1)d,其中a1为首项,d为公差,n为项数。
代入已知条件,可得18 = a1 + (7-1)2。
解方程得a1 = 5。
首项和第n项的和可以表示为Sn = (n/2) * (a1 + an),其中n为项数,a1为首项,an为第n项。
代入已知条件,得Sn = (n/2) * (5 + 5 + (n-1)*2)。
【练习题二】1. 若等比数列的首项是2,公比是3,求第n项的表达式。
解析:由题意,首项是2,公比是3。
所以等比数列的通项公式可以表示为an = a1 * r^(n-1),其中a1为首项,r为公比,n为项数。
代入已知条件,可得an = 2 * 3^(n-1)。
2. 若等比数列的第4项是16,公比是2,求首项和第n项的和。
解析:由题意,第4项是16,公比是2。
所以等比数列的通项公式为an = a1 * r^(n-1),其中a1为首项,r为公比,n为项数。
代入已知条件,可得16 = a1 * 2^(4-1)。
解方程得a1 = 2。
首项和第n项的和可以表示为Sn = a1 * (1 - r^n) / (1 - r),其中n为项数,a1为首项,r为公比。
代入已知条件,得Sn = 2 * (1 - 2^n) / (1 - 2)。
新高考数学二轮专题复习高频考点强化训练8(附解析)

强化训练8 等差数列与等比数列——小题备考一、单项选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一个是符合题目要求的)1.[2022·山东威海三模]等差数列{a n }的前n 项和为S n ,若a 3=4,S 9=18,则公差d =( )A .1B .-1C .2D .-22.[2022·湖南常德一模]设S n 为等比数列{a n }的前n 项和,若a 4=4,S 3=S 2+2,则a 1=( )A .12B .1C .2D .23.[2022·湖南岳阳一模]已知等差数列{a n }满足a 2=4,a 3+a 5=4(a 4-1),则数列{a n }的前5项和为( )A .10B .15C .20D .304.[2022·湖南师大附中二模]设等比数列{a n }的首项为a 1,公比为q ,则“a 1<0,且0<q <1”是“对于任意N *都有a n +1>a n ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.[2022·辽宁鞍山二模]设等差数列{a n },{b n }的前n 项和分别是S n ,T n ,若S n T n=2n 3n +7,则 a 3b 3 =( ) A .1 B .511C .2217D .386.已知a 1=1,a n =n (a n +1-a n )(n ∈N +),则数列{a n }的通项公式是a n =( )A .2n -1B .(n +1n)n +1 C .n 2 D .n7.[2022·河北邯郸一模]“中国剩余定理”又称“孙子定理”,可见于中国南北朝时期的数学著作《孙子算经》卷下第十六题的“物不知数”问题,原文如下:今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二.问物几何?现有一个相关的问题:将1到2 022这2 022个自然数中被3除余2且被5除余4的数按照从小到大的顺序排成一列,构成一个数列,则该数列的项数为( )A .132B .133C .134D .1358.[2022·北京北大附中三模]已知数列{a n }满足a 1a 2a 3…a n =n 2,其中n =1,2,3,…,则数列{a n }( )A .有最大项,有最小项B .有最大项,无最小项C .无最大项,有最小项D .无最大项,无最小项二、多项选择题(本大题共4小题,每小题5分,共20分,在每小题给出的四个选项中,有多个符合题目要求,全部选对得5分,部分选对得2分,选错或多选得0分)9.在数列{a n }中,a 1=1,数列⎩⎨⎧⎭⎬⎫1a n +1 是公比为2的等比数列,设S n 为{a n }的前n 项和,则( )A .a n =12n -1B .a n =12n +12C .数列{a n }为递减数列D .S 3>7810.[2022·湖南永州三模]已知等差数列{a n }是递减数列,S n 为其前n 项和,且S 7=S 8,则( )A .d >0B .a 8=0C .S 15>0D .S 7、S 8均为S n 的最大值11.[2022·山东枣庄三模]给出构造数列的一种方法:在数列的每相邻两项之间插入此两项的和,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列.现自1,1起进行构造,第1次得到数列1,2,1,第2次得到数列1,3,2,3,1,…,第n (n ∈N *)次得到数列1,x 1,x 2,…,x k ,1,记a n =1+x 1+x 2+…+x k +1,数列{a n }的前n 项和为S n ,则( )A.a 4=81B .a n =3a n -1-1C .a n =3n +1D .S n =12 ×3n +1+n -3212.[2022·河北沧州二模]已知数列{a n }满足a 1=1,a n +2=(-1)n +1(a n -n )+n ,记{a n }的前n 项和为S n ,则( )A .a 48+a 50=100B .a 50-a 46=4C .S 48=600D .S 49=601三、填空题(本题共4小题,每小题5分,共20分)13.[2022·辽宁丹东一模]在等差数列{a n }中,已知a 1+2a 7=15,则a 2+a 8=________.14.[2022·广东潮州二模]记S n 为等比数列{a n }的前n 项和.若a 1=1,S 3=34,则a 4=________.15.[2022·山东泰安二模]已知数列{a n }是公差大于0的等差数列,a 1=2,且a 3+2,a 4,a 6-4成等比数列,则a 10=________.16.[2022·河北唐山二模]已知数列{a n }满足a 1=a 5=0,|a n +1-a n |=2,则{a n }前5项和的最大值为________.强化训练8 等差数列与等比数列1.解析:由题可知⎩⎪⎨⎪⎧a1+2d =49a1+9×82·d =18 ⇒⎩⎨⎧a1=6d =-1 . 答案:B2.解析:由已知a3=S3-S2=2,q =a4a3 =42 =2,所以a1=a3q2 =222 =12 .答案:A3.解析:等差数列{an}中,2a4=a3+a5=4(a4-1),解得a4=2,于是得公差d =a4-a24-2=-1,a1=5, 所以数列{an}的前5项和为S5=5a1+5(5-1)2d =15. 答案:B4.解析:若a1<0,且0<q<1,则an +1-an =a1qn -a1qn -1=a1qn -1(q -1)>0,所以an +1>an ,反之,若an +1>an ,则an +1-an =a1qn -a1qn -1=a1qn -1(q -1)>0, 所以a1<0,且0<q<1或a1>0,且q>1,所以“a1<0,且0<q<1”是“对于任意N*,都有an +1>an”的充分不必要条件. 答案:A5.解析:因为等差数列{an},{bn}的前n 项和分别是Sn ,Tn ,所以a3b3 =a1+a52b1+b52 =5(a1+a5)25(b1+b5)2=S5T5 =1015+7=511 . 答案:B6.解析:由an =n (an +1-an ),得(n +1)an =nan +1,即an +1an =n +1n ,则an an -1 =n n -1 ,an -1an -2 =n -1n -2 ,an -2an -3 =n -2n -3,…,a2a1 =21 ,n≥2, 由累乘法可得an a1 =n ,所以an =n ,n≥2,又a1=1,符合上式,所以an =n.答案:D7.解析:因为由1到2 022这2 022个自然数中被3除余2且被5除余4的数按照从小到大的顺序所构成的数列是一个首项为14,公差为15的等差数列{an},所以该数列的通项公式为an =14+15(n -1)=15n -1.令an =15n -1≤2 022, 解得n≤134,即该数列的项数为134.答案:C8.解析:依题意,因为a1a2a3…an =n2,其中n =1,2,3,…,当n =1时,a1=12=1,当n≥2时,a1a2a3…an -1=(n -1)2,a1a2a3…an =n2,两式相除有an =n2(n -1)2 =(1+1n -1)2,n≥2,易得an 随着n 的增大而减小,故an≤a2=4,且an>1=a1,故最小项为a1=1,最大项为a2=4.答案:A9.解析:因为a1=1,数列⎩⎨⎧⎭⎬⎫1an +1 是公比为2的等比数列,所以1an +1=2·2n -1=2n ,所以an =12n -1,故A 正确,B 错误; 因为y =2x -1,(x≥1)是单调增函数,故y =12x -1,(x≥1)是单调减函数,故数列{an}是减数列,故C 正确;S3=a1+a2+a3=1+13 +17 >78 ,故D 正确.答案:ACD10.解析:因为等差数列{an}是递减数列,所以an +1-an<0,所以d<0,故A 错误;因为S7=S8,所以a8=S8-S7=0,故B 正确;因为S15=15(a1+a15)2=15a8=0,故C 错误; 因为由题意得,⎩⎨⎧a7>0a8=0a9<0,所以S7=S8≥Sn (n ∈N*),故D 正确. 答案:BD11.解析:由题意得:a1=4,a2=10=3×4-2,a3=28=3×10-2,a4=82=3×28-2,所以有an =3an -1-2,因此选项AB 不正确;an =3an -1-2⇒an -1=3(an -1-1),所以数列{an -1}是以a1-1=3为首项,3为公比的等比数列,因此有an -1=3·3n -1=3n ⇒an =3n +1,因此选项C 正确;Sn =3(1-3n )1-3+n =12 ×3n +1+n -32 ,所以选项D 正确. 答案:CD12.解析:因为a1=1,an +2=(-1)n +1(an -n )+n ,所以当n 为奇数时,an +2=an =a1=1;当n 为偶数时,an +an +2=2n.所以a48+a50=96,选项A 错误;又因为a46+a48=92,所以a50-a46=4,选项B 正确;S48=a1+a3+a5+…+a47+[(a2+a4)+(a6+a8)+…+(a46+a48)]=24×1+2×(2+6+…+46)=24+2×(2+46)×122=600,故C 正确; S49=S48+a49=600+1=601,选项D 正确.答案:BCD13.解析:由题意在等差数列{an}中,设公差为d ,则a1+2a7=3a1+12d =3a5=15,所以a5=5,于是a2+a8=2a5=10.答案:1014.解析:设等比数列{an}的公比为q ,由已知S3=a1+a1q +a1q2=1+q +q2=34 ,即q2+q +14 =0,解得q =-12 ,所以a4=1·(-12 )3=-18 .答案:-1815.解析:设公差为d ,则a 24 =(a3+2)(a6-4),即(2+3d )2=(2+2d +2)(2+5d -4),化简得d2+4d -12=0,解得d =2或d =-6,又d>0,故d =2,则a10=a1+9d =20.答案:2016.解析:∵a1=a5=0,|an +1-an|=2,∴|a2-a1|=|a2|=2,∵求an 前5项和的最大值,∴取a2=2,∵|an +1-an|=2,∴|a3-a2|=|a3-2|=2.∵求an 前5项和的最大值,∴取a3=4,∵|a4-a3|=|a4-4|=2①|a5-a4|=|0-a4|=|a4|=2②结合①和②,∴a4=2时前5项和可有最大值.∴{an}前5项和的最大值为:0+2+4+2+0=8.答案:8。
高中数学《等差数列、等比数列》专题练习题(含答案解析)

高中数学《等差数列、等比数列》专题练习题(含答案解析)一、选择题1.(2017·全国卷Ⅰ)记S n 为等差数列{a n }的前n 项和.若a 4+a 5=24,S 6=48,则{a n }的公差为( )A .1B .2C .4D .8 C [设{a n }的公差为d ,则由⎩⎪⎨⎪⎧a 4+a 5=24,S 6=48,得⎩⎪⎨⎪⎧a 1+3d a 1+4d24,6a 1+6×52d =48,解得d =4.故选C .]2.设公比为q (q >0)的等比数列{}a n 的前n 项和为S n ,若S 2=3a 2+2,S 4=3a 4+2,则a 1等于( )A .-2B .-1C .12D .23B [S 4-S 2=a 3+a 4=3a 4-3a 2 ,即3a 2+a 3-2a 4=0,即3a 2+a 2q -2a 2q 2=0 ,即2q 2-q -3=0,解得q =-1 (舍)或q =32,当q =32时,代入S 2=3a 2+2,得a 1+a 1q =3a 1q +2,解得a 1=-1,故选B .]3.(2018·莆田市3月质量检测)等比数列{a n }的前n 项和为S n ,已知S 2=a 1+2a 3,a 4=1,则S 4=( )A .78B .158C .14D .15D [由S 2=a 1+2a 3,得a 1+a 2=a 1+2a 3,即a 2=2a 3,又{a n }为等比数列,所以公比q =a 3a 2=12,又a 4=a 1q 3=a 18=1,所以a 1=8.S 4=a 11-q 41-q=8×⎝ ⎛⎭⎪⎫1-1161-12=15.故选D .]4.设等差数列{a n }的前n 项和为S n ,且a 1>0,a 3+a 10>0,a 6a 7<0,则满足S n >0的最大自然数n 的值为( )A .6B .7C .12D .13C [∵a 1>0,a 6a 7<0,∴a 6>0,a 7<0,等差数列的公差小于零,又a 3+a 10=a 1+a 12>0,a 1+a 13=2a 7<0,∴S 12>0,S 13<0,∴满足S n >0的最大自然数n 的值为12.]5.(2018·衡水模拟)设等比数列{a n }的前n 项和为S n ,若S m -1=5,S m =-11,S m+1=21,则m 等于( )A .3B .4C .5D .6C [在等比数列中,因为S m -1=5,S m =-11,S m +1=21,所以a m =S m -S m -1=-11-5=-16,a m +1=S m +1-S m =32.则公比q =a m +1a m=32-16=-2,因为S m =-11, 所以a 1[12m ]1+2=-11,①又a m +1=a 1(-2)m =32,② 两式联立解得m =5,a 1=-1.] 6.等差数列{a n }中,a na 2n是一个与n 无关的常数,则该常数的可能值的集合为( )A .{1}B .⎩⎨⎧⎭⎬⎫1,12C .⎩⎨⎧⎭⎬⎫12D .⎩⎨⎧⎭⎬⎫0,12,1B [a na 2n =a 1n -1da 12n -1d =a 1-d +nda 1-d +2nd,若a 1=d ,则a na 2n =12;若a 1≠0,d =0,则a n a 2n =1.∵a 1=d ≠0,∴a na 2n ≠0,∴该常数的可能值的集合为⎩⎨⎧⎭⎬⎫1,12.] 7.已知等比数列{a n }中,a 2a 10=6a 6,等差数列{b n }中,b 4+b 6=a 6,则数列{b n }的前9项和为( )A .9B .27C .54D .72B [根据等比数列的基本性质有a 2a 10=a 26=6a 6,a 6=6,所以b 4+b 6=a 6=6,所以S 9=9b 1+b 92=9b 4+b 62=27.]8.(2018·安阳模拟)正项等比数列{a n }中,a 2=8,16a 24=a 1a 5,则数列{a n }的前n 项积T n 中的最大值为( )A .T 3B .T 4C .T 5D .T 6A [设正项等比数列{a n }的公比为q (q >0),则16a 24=a 1a 5=a 2a 4=8a 4,a 4=12,q 2=a 4a 2=116,又q >0,则q =14,a n =a 2q n -2=8×⎝ ⎛⎭⎪⎫14n -2=27-2n ,则T n =a 1a 2…a n =25+3+…+(7-2n )=2n (6-n ),当n =3时,n (6-n )取得最大值9,此时T n 最大,即(T n )max =T 3,故选A .]二、填空题9.已知公差不为0的等差数列{a n }满足a 1,a 3,a 4成等比数列,S n 为数列{a n }的前n 项和,则S 3-S 2S 5-S 3的值为________.2 [根据等比中项有a 23=a 1·a 4,即(a 1+2d )2=a 1(a 1+3d ),化简得a 1=-4d ,S 3-S 2S 5-S 3=a 3a 4+a 5=a 1+2d 2a 1+7d =-2d -d=2.] 10.已知数列{a n }满足a 1=-40,且na n +1-(n +1)a n =2n 2+2n ,则a n 取最小值时n 的值为________.10或11 [由na n +1-(n +1)a n =2n 2+2n =2n (n +1),两边同时除以n (n +1),得a n +1n +1-a nn =2,所以数列⎩⎨⎧⎭⎬⎫a n n 是首项为-40、公差为2的等差数列,所以a nn =-40+(n -1)×2=2n -42,所以a n=2n 2-42n ,对于二次函数f (x )=2x 2-42x ,在x =-b2a=--424=10.5时,f (x )取得最小值,因为n 取正整数,且10和11到10.5的距离相等,所以n 取10或11时,a n 取最小值.]11.已知正项等差数列{a n }的前n 项和为S n ,S 10=40,则a 3·a 8的最大值为________. 16 [S 10=10a 1+a 102=40⇒a 1+a 10=a 3+a 8=8,a 3·a 8≤⎝ ⎛⎭⎪⎫a 3+a 822=⎝ ⎛⎭⎪⎫822=16, 当且仅当a 3=a 8=4时“=”成立.]12.已知函数{a n }满足a n +1+1=a n +12a n +3,且a 1=1,则数列⎩⎨⎧⎭⎬⎫2a n +1的前20项和为________.780 [由a n +1+1=a n +12a n +3得2a n +3a n +1=1a n +1+1,即1a n +1+1-1a n +1=2,∴数列⎩⎨⎧⎭⎬⎫1a n +1是以12为首项,2为公差的等差数列,则1a n +1=2n -32,∴数列⎩⎨⎧⎭⎬⎫2a n +1是以1为首项,4为公差的等差数列,其前20项的和为20+10×19×4=780.]三、解答题13.(2018·德阳二诊)已知数列{a n }满足a 1=1,a n +1=2a n +1 . (1)求证:数列{a n +1}为等比数列;(2)求数列⎩⎨⎧⎭⎬⎫2n a n a n +1的前n 项和T n . [解] (1)∵a n +1=2a n +1,∴a n +1+1=2(a n +1). 又a 1=1,∴a 1+1=2≠0,a n +1≠0.∴{a n +1}是以2为首项,2为公比的等比数列. (2)由(1)知a n =2n -1, ∴2na n a n +1=2n2n -12n +1-1=12n -1-12n +1-1,∴T n =12-1-122-1+122-1-123-1+…+12n -1-12n +1-1=1-12n +1-1.14.已知数列{}a n 的前n 项和为S n ,且S n =2a n -3n (n ∈N *). (1)求a 1,a 2,a 3的值;(2)是否存在常数λ,使得数列{a n +λ}为等比数列?若存在,求出λ的值和通项公式a n ;若不存在,请说明理由.[解] (1)当n =1时,由S 1=2a 1-3×1,得a 1=3; 当n =2时,由S 2=2a 2-3×2,可得a 2=9; 当n =3时,由S 3=2a 3-3×3,得a 3=21. (2)令(a 2+λ)2=(a 1+λ)·(a 3+λ), 即(9+λ)2=(3+λ)·(21+λ),解得λ=3. 由S n =2a n -3n 及S n +1=2a n +1-3(n +1), 两式相减,得a n +1=2a n +3.由以上结论得a n +1+3=(2a n +3)+3=2(a n +3), 所以数列{a n +3}是首项为6,公比为2的等比数列, 因此存在λ=3,使得数列{a n +3}为等比数列,所以a n+3=(a1+3)×2n-1,a n=3(2n-1)(n∈N*).。
2023年新高考数学创新题型微专题08 数列专题(新定义)(解析版)

专题08 数列专题(新定义)一、单选题1.(2023春·甘肃张掖·高二高台县第一中学校考阶段练习)对于正项数列{}n a 中,定义:12323nn a a a na G n+++⋅⋅⋅+=为数列{}n a 的“匀称值”已知数列{}n a 的“匀称值”为2n G n =+,则该数列中的10a =( ) A .83B .125 C .94D .2110【答案】D【分析】确定()123223n n nG n n a a a na =+=+++⋅⋅⋅+,取10n =和9n =带入式子,相减得到答案. 【详解】123232nn a a a na G n n+++⋅⋅⋅+==+,即()123223n n nG n n a a a na =+=+++⋅⋅⋅+,故()12310231010102a a a a +++⋅⋅⋅+=⨯+;()1239239992a a a a +++⋅⋅⋅+=⨯+; 两式相减得101021a =,所以102110a =. 故选:D2.(2023春·浙江·高三开学考试)对任意正整数对(,)h k ,定义函数(,)f h k 如下:(1,)1f j =,()()()()11,,,i f i j j i f i j i ++=−≤,则( )A .(1,)1f j j +=B .1(,)2C i j f i j −=C .()21(,)21jji j f i j j =⎡⎤⋅=⋅−⎣⎦∑D .[]11(,)22jn nj i j f i j n ==⋅=+−∑∑【答案】C【分析】根据新定义得(1,)(,)1f i j j if i j i +−=+,令i j =即可判断A ,根据()()()()()()2,3,4,123,,,1,22,33,4f j f j f j j j j f j f j f j −−−===累乘可判断B ,利用二项式定理求得12C C C 21nnnnn+++=−,结合()211(,)21jji jji i j f i j j C j ==⎡⎤⋅==−⎣⎦∑∑判断C ,[]()111(,)21j n nj j i j j f i j ===⋅=−∑∑∑,结合等比数列的前n 项和公式判断D. 【详解】()()()()()()1,11,,,,1f i j j ii f i j j i f i j f i j i +−++=−∴=+,令i j =,则(1,)0(,)f j j f j j +=,(1,)0f j j ∴+=,A 错误;(2,)1(3,)2(4,)3,,,(1,)2(2,)3(3,)4f j j f j j f j j f j f j f j −−−===,(,)1,(1,)f i j j i f j i−+= 累乘得:(,)(1)(2)(3)(1)1C (1,)2345ij f i j j j j j i f j i j−−−−+==⨯⨯⨯⨯⨯,1(1,)1,(,)C ,()ij f j f i j i j j=∴=≤,令1i =,则B 错误; 因为()01211C C C C nnn n n n +=++++,所以12C C C 21n nn n n +++=−,()211(,)C 21jji jj i i jf i j j j ==⎡⎤⋅==−⎣⎦∑∑,则C 正确;[]()11112(12)(,)212212n jnnjn j i j j f i j n n +===−⋅=−=−=−−−∑∑∑,则D 错误. 故选:C .3.(2023春·安徽·高二合肥市第八中学校联考开学考试)定义:对于数列{}n a ,如果存在一个常数()*N T T ∈,使得对任意的正整数0n n ≥恒有n T n a a +=,则称数列{}n a 是从第0n 项起的周期为T 的周期数列.已知周期数列{}n b 满足:11b =,23b =,12n n n b b b −−=−(3n ≥),则2023b =( ) A .1− B .3− C .2− D .1【答案】D【分析】写出周期数列{}n b 的前几项,发现周期为6,进而求得2023b 的值. 【详解】写出周期数列{}n b 的前几项:1,3,2,1−,3−,2−,1,3,2,1−,3−,2−,1,…, 发现周期数列{}n b 是周期为6的周期数列, ∴20233376111b b b ⨯+===. 故选:D .4.(2023秋·福建南平·高二统考期末)若数列{}n a 的前n 项和为n S ,nn S b n=,则称数列{}n b 是数列{}n a 的“均值数列”.已知数列{}n b 是数列{}n a 的“均值数列”且n bn =,设数列⎧⎫的前n 项和为n T ,若()2132n m m T −<对*n ∈N 恒成立,则实数m 的取值范围为( ) A .[]1,2−B .()1,2-C .()(),12,−∞−⋃+∞D .(][),12,−∞−⋃+∞【答案】B【分析】由新定义求得n S ,然后由1n n n a S S −=−求得n a ,从而可求得n T (裂项相消法)后得n T 的最小值,解相应不等式可得结论. 【详解】由题意nS n n=,即2n S n =, ∴2n ≥时,221(1)21n n n a S S n n n −=−=−−=−,又111a S ==,∴*n ∈N 时,21n a n =−,==2n n T +=+=, 易知1{}2是递增数列,∴1{}2的最小值是12(1n =时取得), 由题意21(3)2m m −<,解得12m −<<.故选:B .5.(2023秋·山西长治·高三校联考阶段练习)对于一个n 项数列()*1212:,,,,1,n k k A a a a S a a a k n k =+++≤≤∈N ,记A 的“Cesaro 平均值”为()121+++n S S S n,若数列121010,,,a a a 的“Cesaro 平均值”为2022,数列121010,,,,x a a a 的“Cesaro 平均值”为2046,则x =( )A .24B .26C .1036D .1541【答案】B【分析】先求出121010S S S +++的值,再根据Cesaro 平均值的求法列出等式,即可求出x 的值.【详解】因为数列121010,,,a a a 的“Cesaro 平均值”为12101020221010S S S +++=,所以12101020221010S S S +++=⨯. 因为121010,,,,x a a a 的“Cesaro 平均值”为()()()12101020461011x x S x S x S +++++++=,所以10112022101020461011x +⨯=,所以20202046x +=,解得26x =,故选:B.6.(2023春·湖北咸宁·高二校考开学考试)等比数列{}n a 中1512a =,公比12q =−,用12Π⋅⋅⋅⋅⋅⋅=n n a a a 表示它的前n 项之积,则1Π,2Π,…,n ∏中最大的是( ) A .11Π B .10Π C .9Π D .8Π【答案】C【分析】根据题意分析,n n a ∏的符号,结合前n 项之积的性质运算求解.【详解】∵110,02a q >=−<,则当n 为奇数时,0n a >,当n 为偶数时,0n a <,∴当()43N n k k *=−∈或()4N n k k *=∈时,0n ∏>,当()42N n k k *=−∈或()41N n k k *=−∈时,0n ∏<,由题意可得:115122n n a −⎛⎫=− ⎪⎝⎭,令1151212n n a −⎛⎫=≥ ⎪⎝⎭,解得10n ≤,若n ∏取到最大,则3k =,9n =,即{}n ∏中最大的是9Π. 故选:C.7.(2022秋·北京·高二北京二中校考期末)如果数列{}n a 满足211n n n na a k a a +++−=(k 为常数),那么数列{}n a 叫做等比差数列,k 叫做公比差.下列四个结论中所有正确结论的序号是( ) ①若数列{}n a 满足12n na n a +=,则该数列是等比差数列;②数列{}2nn ⋅是等比差数列;③所有的等比数列都是等比差数列; ④存在等差数列是等比差数列. A .①②③ B .①③④ C .①②④ D .②③④【答案】B【分析】根据比等差数列的定义211n n n na a k a a +++−=(k 为常数),逐一判断①②③④是否是等比差数列即可可得到答案.【详解】①数列{}n a 满足12n na n a +=,则2112(1)22n n n na a n n a a +++−=+−=,满足等比差数列的定义,故①正确; ②数列{2}n n ⋅,+212111(2)2(1)2(1)22n n n n n nn n a a a a n n n n +++++−=+⋅+⋅−+⋅⋅ 2(2)2(1)22(1)(1)n n n n n n n ⋅+⋅−+⋅==−⋅+⋅+,不满足等比差数列的定义,故②错误; ③设等比数列的公比为q ,则2110n n n na a a a q q +++−==−,满足等比差数列,故③正确; ④设等差数列的公差为d , 则22112()n n n n n n n n n n a a a a a d a d d a d a a a d +++−++−=−=++, 故当0d=时,满足2110n n n na a a a +++−=,故存在等差数列是等比差数列,即④正确;故答案为:①③④ 故选:B.8.(2019秋·北京·高三101中学校考阶段练习)定义在()(),00,∞−+∞U 上的函数()f x ,如果对于任意给定的等比数列{}n a ,(){}n f a 仍是等比数列,则称()f x 为“保等比数列函数”.现有定义在()(),00,∞−+∞U 上的如下函数:①()2f x x =;②()2xf x =;③()1f x x=;④()ln f x x =,其中是“保等比数列函数”的序号为( ) A .①② B .③④ C .①③ D .②④【答案】C【分析】根据新定义,结合等比数列性质221n n n a a a ++=,一一加以判断,即可得到结论.通过积的乘方,即可判断①;通过指数的幂的运算,即可判断②;通过积的运算即可判断③;由对数的运算法则,即可判断④.【详解】设{}n a 是等比数列,由等比数列性质知221n n n a a a ++=,对于①,()()()()222222211n n n n n n a a f a f a a f a ++++===,即(){}n f a 仍是等比数列,故正确;对于②,()()()22122212222n n n n n a a a a a n n n f a f a f a ++++++==≠=,即(){}n f a 不是等比数列,故不正确; 对于③,()()()221221111n n n n n n f a f a f a a a a ++++=⋅==,即(){}n f a 是等比数列,故正确;对于④,()()()()222211ln ln ln n n n n n n f a f a a a a f a ++++=≠=, 即(){}n f a 不是等比数列,故不正确; 故选:C .9.(2023秋·吉林·高二吉林一中校考期末)若数列{}n a 满足1120n na a +−=,则称{}n a 为“必会数列”,已知正项数列{}n a 为“必会数列”,若453a a +=,则23a a +=( ). A .19B .1C .6D .12【答案】D【分析】根据数列新定义可得数列{}n a 是以12q =为公比的等比数列,利用等比数列通项公式,即可求得答案.【详解】由题意数列{}n a 满足1120n n a a +−=,可得112n n a a +=, 故正项数列{}n a 是以12q =为公比的等比数列, 则2322532341()()3,124a a a a a a a a q +===+∴=++,故选:D10.(2022秋·陕西渭南·高二统考期末)设{}n a 是无穷数列,若存在正整数k ,使得对任意的n *∈N ,均有n k n a a +>,则称{}n a 是间隔递增数列,k 是{}n a 的间隔数.若{}n b 是间隔递增数列,则数列{}n b 的通项不可能...是( )A .92n b n n=−B .31n n b =+C .113n nb =−D .()2nn b n =−−【答案】D【分析】根据间隔递增数列的定义求解即可. 【详解】对于A :()()9922n k n b n k n b n k n ++−=−++−,化简得:()920n n kb k n b n k +⎡⎤=+>⎢⎥+−⎢⎥⎣⎦,存在正整数k ,使得对任意的n *∈N ,0n n k b b +>−恒成立,所以{}n b 是间隔递增数列;对于B :()3131313n k n k nk n n b b ++=+−−−−=, 因为k 为正整数且n *∈N ,所以()3130k n−>,所以0n n k b b +>−,所以{}n b 是间隔递增数列; 对于C :11111113333n k n k n nn k b b ++⎪−⎛⎫=−−+=− ⎝⎭, 因为k 为正整数且n *∈N ,所以111033n k ⎛⎫−> ⎪⎝⎭,所以0n n k b b +>−,所以{}n b 是间隔递增数列; 对于D :()()()22n knn k n b n k n b ++−=−+−+−()()()22n kn n k ⎡⎤=−−+−⎣⎦,当k ∈正奇数,n *∈N 时,()()20kn n k −+−>,()2n−的正负由n 的奇偶性决定,此时0n n k b b +>−不恒成立,不符合间隔递增数列的定义;当k ∈正偶数,n *∈N 时,()()20kn n k −+−<,()2n−的正负由n 的奇偶性决定,此时0n n k b b +>−不恒成立,不符合间隔递增数列的定义; 故选:D.11.(2023·全国·高三专题练习)对于数列{}n a ,若存在正整数()2k k ≥,使得1k k a a −<,1k k a a +<,则称k a 是数列{}n a 的“谷值”,k 是数列{}n a 的“谷值点”.在数列{}n a 中,若98n a n n=+−,则数列{}n a 的“谷值点”为( ) A .2 B .7C .2,7D .2,5,7【答案】C【分析】先求出12a =,232a =,32a =,474a =,565a =,612a =,727a =,898a =,再得到7n ≥,N n ∈,980n n+−>,结合数列的单调性以及谷值点的定义即可得求解.【详解】因为98n a n n=+−, 所以12a =,232a =,32a =,474a =,565a =,612a =,727a =,898a =,当7n ≥,N n ∈,980n n+−>,所以9988n a n n n n =+−=+−,因为函数98y x x=+−在[)7,+∞上单调递增, 所以7n ≥时,数列98n a n n=+−为单调递增数列, 所以21a a <,23a a <,76a a <,78a a <, 所以数列{}n a 的“谷值点”为2,7. 故选:C.12.(2023·全国·高二专题练习)若数列{}n a 满足121n n a a +=−,则称{}n a 为“对奇数列”.已知正项数列{}1n b +为“对奇数列”,且12b =,则n b =( ) A .123n −⨯ B .12n − C .12n + D .2n【答案】D【分析】根据题意可得()11211n n b b ++=+−,进而可得{}n b 为等比数列,再求得通项公式即可.【详解】由题意得()11211n n b b ++=+−,所以12n n b b +=,又12b =,所以{}n b 是首项为2,公比为2的等比数列,所以1222n nn b −=⨯=.故选:D .13.(2022春·辽宁葫芦岛·高二校联考阶段练习)设()n a Ω表示落在区间[],n n a 内的偶数个数.在等比数列{}n a n −中,14a=,211a =,则()4a Ω=( )A .21B .20C .41D .40【答案】C【分析】设{}n a n −的公比为q ,根据1a 和2a 求出q ,从而得n a 和4a ,再根据()n a Ω的定义可求出结果. 【详解】设{}n a n −的公比为q ,则2121123141a q a −−===−−, 所以111(1)(41)33n n n n a n a q−−−=−⋅=−⋅=,则3n n a n =+,所以445438a =+=.所以落在区间[]4,85内的偶数共有41个,故()441a Ω=. 故选:C14.(2023春·湖北·高三黄冈中学校联考开学考试)对于数列{}n a ,定义11222−=+++n n n A a a a 为数列{}n a 的“加权和”,已知某数列{}n a 的“加权和”12n n A n +=⋅,记数列{}+n a pn 的前n 项和为n T ,若5≤n T T 对任意的N n *∈恒成立,则实数p 的取值范围为( )A .127,53⎡⎤−−⎢⎥⎣⎦B .167,73⎡⎤−−⎢⎥⎣⎦C .512,25⎡⎤−−⎢⎥⎣⎦D .169,74⎡⎤−−⎢⎥⎣⎦【答案】A【分析】根据n A 与n a 的关系求出n a ,再根据等差数列的求和公式求出n T ,将5≤n T T 化为216(5)06+⎛⎫−+≤ ⎪+⎝⎭n n p n 对任意的n N *∈恒成立,分类讨论n 可求出结果.【详解】由1112222n n n n A a a a n −+=+++=⋅,∴2n ≥时,212122(1)2n n n a a a n −−+++=−⋅,∴1122(1)2−+⋅=⋅−−⋅n n n n a n n ,∴22n a n =+,1n =时,14a =也成立,∴22n a n =+,∴数列{}+n a pn 的前n 项和为:12(12)n n T a a a p n =+++++++2(422)(1)(1)3222++++=+⋅=++⋅n n n n n n p n n p ,∵5≤n T T 对任意的n N *∈恒成立,∴225(1)56353522+⨯++⋅≤=+⨯+⨯n n n n p T p , 即225335(1)5(51)022p pn n n n −+−⨯++−⨯⨯+≤, 即22225335(5)(5)022p pn n n n −+−⨯+−+−≤, 即5(5)(53)0222pn p p n n −+++++≤, 即(6)(5)(8)02p n n n +−++≤, 即216(5)06+⎛⎫−+≤ ⎪+⎝⎭n n p n 对任意的n N *∈恒成立,当14n ≤≤时,2164266+−≤=+++n p n n 对任意的n N *∈恒成立, 因为4412226465n +≥+=++,∴125−≤p ,所以125p ≥−,当5n =时,216(5)06n n p n +⎛⎫−+= ⎪+⎝⎭恒成立,R p ∈,当6n ≥时,2164266+−≥=+++n p n n 对任意的n N *∈恒成立, 因为447226663n +≤+=++,∴73−≥p ,所以73p ≤−,综上可得:实数p 的取值范围为127,53⎡⎤−−⎢⎥⎣⎦.故选:A .15.(2023·全国·高三专题练习)若数列{}n b 满足:若()*,m n b b m n ∈=N ,则11m n b b ++=,则称数列{}n b 为“等同数列”.已知数列{}n a 满足55a =,且()1+=−n n n a n a a ,若“等同数列”{}n b 的前n 项和为n S ,且114b a b ==,22b a =,510S a =,则2022S =( )A .4711B .4712C .4714D .4718【答案】D【分析】先对已知关系式变形,求出数列{}n a 的通项公式,再利用“等同数列”的定义与已知条件得{}n b 是周期数列,即可得2022S . 【详解】由()1+=−n n n a n a a 得11n n a a n n+=+,则1251125n n n a a aa n n n −−=====−−, 故n a n =,所以111b a ==,222b a ==,411b a ==, 所以41b b =,所以522b b ==1010S a ==,所以3121210b ++++=,解得34b =,同理得634b b ==, 741b b ==,852b b ==,…,故数列{}n b 是以3为周期的数列,所以()202267431246744718S S ⨯==++⨯=, 故选:D .16.(2022·全国·高三专题练习)设数列{}n a ,若存在常数t ,对任意小的正数s ,总存在正整数0n ,当0n n ≥时,n a t s −<,则数列{}n a 为收敛数列.下列关于收敛数列说法正确的是( ) A .若等比数列{}n a 是收敛数列,则公比()0,1q ∈ B .等差数列不可能是收敛数列C .设公差不为0的等差数列{}n a 的前n 项和为()0n n S S ≠,则数列1n S ⎧⎫⎨⎬⎩⎭一定是收敛数列D .设数列{}n a 的前n 项和为n S ,满足11a =,11n n S a +=+,则数列{}n a 是收敛数列 【答案】C【分析】根据题中定义,结合特殊的等差数列和等比数列、数列的周期性、等差数列前n 项和公式逐一判断即可.【详解】当数列为常数列(不为零),因此该数列是等差数列又是等比数列,显然该数列是收敛数列,因此选项AB 不正确;选项C :设等差数列{}n a 的公差为()d d ≠0,所以1111(1)2n S na n n d =+−,当0d ≠时,当n →+∞时,10nS →, 所以数列1n S ⎧⎫⎨⎬⎩⎭一定是收敛数列,因此本选项正确;选项D :因为11a =,11n n S a +=+,所以可得21a =,当2,N n n *≥∈时,由1111n n n n S a S a +−=+⇒=+,两式相减,得11n n n a a a +−=−,所以345670,1,1,0,1a a a a a ==−=−==,所以该数列的周期为6,该数列不可能是收敛数列,因此本选项说法不正确, 故选:C【点睛】关键点睛:利用数列的周期性、常数列的性质是解题的关键.17.(2022春·安徽亳州·高三蒙城县第六中学校联考开学考试)设数列{}m A :1a ,2a ,…,()2m a m ≥,若存在公比为q 的等比数列{}1m B +:1b ,2b ,…,1m b +,使得1k k k b a b +<<,其中1k =,2,…,m ,则称数列{}1m B +为数列{}m A 的“等比分割数列”.若数列{}10A 的通项公式为()21,2,,10nn a n ==,其“等比分割数列”{}11B 的首项为1,则数列{}11B 的公比q 的取值范围是( ) A .()9102,2 B .()10112,2C .()1092,2D .()11102,2【答案】C【分析】由题意可得,()121,2,3,,10n n n qq n −<<=L ,从而可得2q >且()121,2,3,,10n n q n −<=L ,可得122nn q −<<,再根据指数函数的单调性求出12nn −的最小值即可【详解】由题意可得,()121,2,3,,10n n n qq n −<<=L ,所以2q >,且()121,2,3,,10n n qn −<=L ,当1n =时,12<成立;当2n =,3,…,10时,应有12nn q −<成立, 因为2x y =在R 上单调递增,所以111122nn n −−+=随着n 的增大而减小,故1092q <,综上,q 的取值范围是()1092,2. 故选:C.18.(2022春·江苏无锡·高二江苏省江阴市第一中学校考开学考试)若数列{an }满足21321111222n n a a a a a a −−<−<<−<……,则称数列{an }为“半差递增”数列.已知“半差递增”数列{cn }的前n项和Sn 满足*221()n n S c t n N +=−∈,则实数t 的取值范围是( )A .1(,)2−∞B .(-∞,1)C .1(,)2+∞D .(1, +∞)【答案】A【分析】根据*221()n n S c t n N +=−∈,利用递推公式求得数列{}n c 的通项公式.再根据新定义的意义,代入解不等式即可求得实数t 的取值范围.【详解】因为*221()n n S c t n N +=−∈所以当2n ≥时, 11221n n S c t −−+=−两式相减可得1220n n n c c c −+−=,即123n n c c −=,所以数列{}n c 是以公比23q =的等比数列 当1n =时,1213t c −=所以121233n n t c −−⎛⎫=⋅ ⎪⎝⎭,则1221121221221223363183n n n n n t t t c c −−−−−−−⎛⎫⎛⎫⎛⎫−=⋅−⋅=⋅ ⎪⎪⎪⎝⎭⎝⎭⎝⎭11112121212212233233183nn n n n t t t c c −−+−−−⎛⎫⎛⎫⎛⎫−=⋅−⋅=⋅ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭由“差半递增”数列的定义可知21212212183183n n t t −−−−⎛⎫⎛⎫⋅<⋅ ⎪ ⎪⎝⎭⎝⎭化简可得()221213t t −<−⨯解不等式可得12t <即实数t 的取值范围为1,2⎛⎫−∞ ⎪⎝⎭故选:A.19.(2022·浙江·高二学业考试)通过以下操作得到一系列数列:第1次,在2,3之间插入2与3的积6,得到数列2,6,3;第2次,在2,6,3每两个相邻数之间插入它们的积,得到数列2,12,6,18,3;类似地,第3次操作后,得到数列:2,24,12,72,6,108,18,54,3.按上述这样操作11次后,得到的数列记为{}n a ,则1025a 的值是( ) A .6 B .12 C .18 D .108【答案】A【分析】设数列经过第n 次拓展后的项数为n b ,因为数列每一次拓展是在原数列的相邻两项中增加一项,则经过第1n +次拓展后增加的项数为1n b −,从而可得1121n n n n b b b b +=+−=−,从而可求出21nn b =+,从而可知经过11次拓展后在2与6之间增加的数为1021−,由此可得出经过11次拓展后6所在的位置,即可得出答案.【详解】解:设数列经过第n 次拓展后的项数为n b ,因为数列每一次拓展是在原数列的相邻两项中增加一项,则经过第1n +次拓展后增加的项数为1n b −, 所以1121n n n n b b b b +=+−=−, 即()1121n n b b +−=−,即1121n n b b +−=−, 所以数列{}1−n b 是以12b =为首项,2为公比的等比数列,是以12nn b −=,所以21n n b =+,则经过11次拓展后在2与6之间增加的数为1021−,所以经过11次拓展后6所在的位置为第10102111211025−++=+=, 所以10256a =. 故选:A.二、多选题20.(2022秋·安徽阜阳·高三安徽省临泉第一中学校联考阶段练习)若数列{}n a 满足:对任意正整数{}1,n n n a a +−为递减数列,则称数列{}n a 为“差递减数列”.给出下列数列{}()*N n a n ∈,其中是“差递减数列”的有( ) A .2n n a = B .2n a n =C .n aD .ln n a n =【答案】CD【分析】利用差递减数列的定义及函数的单调性即可求解.【详解】对A ,若2n n a =,则11222n n nn n a a ++−=−=,由函数2n y =在()0,∞+上单调递增,所以{}1n n a a +−为递增数列,故A 错误;对B ,若2n a n =,则221(1)21n n a a n n n +−=+−=+,由函数21y n =+在()0,∞+上单调递增,所以{}1n n a a +−为递增数列,故B 错误;对C ,若n a =1n n a a +−==y =()0,∞+上单调递减,所以{}1n n a a +−为递减数列,故C 正确;对D ,若ln n a n =,则()111ln 1ln ln ln 1n n n a a n n n ++⎛⎫−=+−==+ ⎪⎝⎭,由函数1ln 1y n ⎛⎫=+ ⎪⎝⎭在()0,∞+上单调递减,所以{}1n n a a +−为递减数列,故D 正确. 故选:CD .21.(2023春·江西新余·高二新余市第一中学校考阶段练习)若数列{}n a 满足:,A B ∃∈R ,0AB ≠,使得对于*n ∀∈N ,都有21n n n a Aa Ba ++=+,则称{}n a 具有“三项相关性”,下列说法正确的有( ). A .若数列{}n a 是等差数列,则{}n a 具有“三项相关性” B .若数列{}n a 是等比数列,则{}n a 具有“三项相关性” C .若数列{}n a 是周期数列,则{}n a 具有“三项相关性”D .若数列{}n a 具有正项“三项相关性”,且正数A ,B 满足1A B +=,12a a B +=,数列{}n b 的通项公式为n n b B =,{}n a 与{}n b 的前n 项和分别为n S ,n T ,则对*n ∀∈N ,n n S T <恒成立【答案】ABD【分析】根据题目给出的“三项相关性”的定义,逐项验证即可.【详解】若{}n a 为等差数列,则有211n n n n a a a a +++−=−,212n n n a a a ++=−,A 正确;若数列{}n a 是等比数列,则21n n a qa ++=,1n n a qa +=,(0q ≠),即()211n n n a q a qa ++=−+,易知1q ≠,显然成立,1q =时,21n n n a a a ++==,取12A B ==,有211122n n n a a a ++=+,也成立,所以B 正确; 对周期数列:0,0,1,0,0,1,⋅⋅⋅,所以1n =时,100A B =⨯+⨯,显然不成立,所以C 错误; 对D ,()211n n n a B a Ba ++=−+,即()211n n n n a a B a a ++++=+,12a a B += ∴121n n n n a a B BB −+++=⋅=,1B >,易知()211n n n n n a a B a a a ++++=+>,即n n b a >,*N n ∈,故n n S T <,D 正确; 故选:ABD22.(2023春·广东惠州·高三校考阶段练习)斐波那契数列又称黄金分割数列,因数学家列昂纳多·斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”.斐波那契数列用递推的方式可如下定义:用n a 表示斐波那契数列的第n 项,则数列{}n a 满足:121a a ==,21n n n a a a ++=+,记121ni n i a a a a ==++⋅⋅⋅+∑,则下列结论正确的是( )A .数列{}n a 是递增数列B .()2123n n n a a a n −+=+≥C .20222202220231i i a a a ==⋅∑D .2021202311i i a a ==−∑【答案】BCD【分析】由数列的递推公式可判断A,B ;利用累加法计算可判断选项C,D.【详解】对A ,由21n n n a a a ++=+知,{}n a 的前10项依次为:1,1,2,3,5,8,13,21,34,55, 其中,第一二项相等,不满足递增性,故A 错误;对B ,根据递推公式12n n n a a a −−=+,得()21213n n n n n n n a a a a a a a n −−−++=++=+≥,故B 正确;对C ,2121a a a =⋅,()222312321a a a a a a a a =⋅−=⋅−⋅,()233423432a a a a a a a a =⋅−=⋅−⋅,……,()220222022202320212022202320222021a a a a a a a a =⋅−=⋅−⋅,∴22212202220222023a a aa a ++⋅⋅⋅=⋅,即20222202220231i i a a a ==⋅∑,故C 正确;对D ,由递推式,得321a a a −=,432a a a −=,…,202320222021a a a −=, 累加得324320232022122021a a a a a a a a a −+−+⋅⋅⋅+−=++⋅⋅⋅+, ∴20232122021a a a a a −=++⋅⋅⋅+, ∴1220212023220231a a a a a a ++⋅⋅⋅+=−=−, 即2021202311i i a a ==−∑,故D 正确;故选:BCD .23.(2023秋·河北邯郸·高二统考期末)若{}n a 不是等比数列,但{}n a 中存在互不相同的三项可以构成等比数列,则称{}n a 是局部等比数列.下列数列中是局部等比数列的是( ) A .(){}28n−+ B .137n ⎧⎫⎨⎬+⎩⎭C .17122n n +⎧⎫−⎨⎬⎩⎭D .{}225n +【答案】ABD【分析】对于ABD ,直接取特定项验证即可;对于C ,定义法可证为等比数列后即可判断.【详解】对于A :若()28nn a =−+,则16a =,212a =,424a =,由212624=⨯,得1a ,2a ,4a 成等比数列,因为(){}28n−+不是等比数列,所以(){}28n−+是局部等比数列.故A 正确;对于B :若137n a n =+,则1110a =,11140a =,511160a =,由21114010160⎛⎫=⨯ ⎪⎝⎭,得1a ,11a ,51a 成等比数列,因为137n ⎧⎫⎨⎬+⎩⎭不是等比数列,所以137n ⎧⎫⎨⎬+⎩⎭是局部等比数列. 故B 正确;对于C :若117113222n n n n a ++=−=,则112n n a a +=,则{}n a 是等比数列,所以17122n n +⎧⎫−⎨⎬⎩⎭不是局部等比数列. 故C 错误;对于D :若225n a n =+,则550a =,15250a =,351250a =,由250125050250=,得5a ,15a ,35a 成等比数列,因为{}225n +不是等比数列,所以{}225n +是局部等比数列. 故D 正确.故选:ABD.24.(2023春·安徽蚌埠·高二蚌埠二中校考阶段练习)已知数列{}n a 是各项均为正数且公比不等于1的等比数列()*N n ∈,对于函数()f x ,若数列(){}ln n f a 为等差数列,则称函数()f x 为“保比差数列函数”,则定义在()0,∞+上的如下函数中是“保比差数列函数”的有( ) A .()1f x x=为“保比差数列函数” B .()2f x x =为“保比差数列函数”C .()e xf x =为“保比差数列函数” D .()f x =“保比差数列函数”【答案】ABD【分析】设数列{}n a 的公比为()1q q ≠,利用保比差数列函数的定义,结合等差数列的定义逐项验证即可. 【详解】设数列{}n a 的公比为()1q q ≠, 选项A :()1ln lnn nf a a =, 所以()()11111ln ln lnln ln ln n n n n n n af a f a q a a a +++−=−==−是常数, 所以数列(){}ln n f a 为等差数列,A 满足题意;选项B :()2ln ln n n f a a =,所以()()22221112ln ln ln ln ln ln 2ln n n n n nna f a f a aa q q a +++−=−===是常数,所以数列(){}ln n f a 为等差数列,B 满足题意;选项C :()ln ln e n an n f a a ==,所以()()11ln ln n n n n f a f a a a ++−=−不是常数, 所以数列(){}ln n f a 不为等差数列,C 不满足题意; 选项D :()ln n f a =所以()()11ln ln ln 2n n f a f a q +−==是常数,所以数列(){}ln n f a 为等差数列,D 满足题意; 故选:ABD25.(2022秋·福建福州·高二校联考期末)在数列{}n a 中,若221(2,,n n a a p n n p *−−=≥∈N 为常数),则称{}n a 为“平方等差数列”.下列对“平方等差数列”的判断,其中正确的为( )A .{}(2)n−是平方等差数列B .若{}n a 是平方等差数列,则{}2n a 是等差数列C .若{}n a 是平方等差数列,则{}(,,,n ka b k b k b *+∈N 为常数)也是平方等差数列D .若{}n a 是平方等差数列,则{}(,,,kn b a k b k b *+∈N 为常数)也是平方等差数列【答案】BD【分析】根据等差数列的定义,结合平方等差数列的定义逐一判断即可. 【详解】对于A ,当n 为奇数时,则()1n −为偶数,所以()()()11122223?2n n n n n −−−−−−=−+=−,当n 为偶数时,则()1n −为奇数,所以()()()11122223?2n n n n n −−−−−−=+=,即{}(2)n−不符合平方等差数列的定义,故错误;对于B ,若{}n a 是平方等差数列,则221(2,,n n a a p n n p *−−=≥∈N 为常数),即{}2n a 是首项为21a ,公差为p 的等差数列,故正确;对于C ,若{}n a 是平方等差数列,则221(2,,n n a a p n n p *−−=≥∈N 为常数), 则()()()()222221112n n n n n n ka b ka b k a a kb a a −−−+−+=−+−,即()())222112n n n n ka b ka b k p kb a a −−+−+=+−,当{}n a 为等差数列时,1n n a a d −−=,则{}n ka b +为平方等差数列, 当{}n a 不为等差数列时,则{}n ka b +不为平方等差数列,故错误;对于D ,因为{}n a 是平方等差数列,所以()()222222121111+++++−−=−==−=kn kn kn kn kn k n a a a a a a p ,把以上的等式相加,得()()()()()222222121111+++++−−+−+⋯+−=kn kn kn kn k n k n a a a a a a kp , 22(1)k n kn a a kp +∴−=,则()221kn b k n ba a kp +++−=,即数列{}knb a +是平方等差数列,故正确; 故选:BD26.(2023秋·山西吕梁·高二统考期末)定义:在数列的每相邻两项之间插入此两项的积,形成新的数列,这样的操作叫作该数列的一次“美好成长”.将数列1,4进行“美好成长”,第一次得到数列1,4,4;第二次得到数列1,4,4,16,4,L ,设第n 次“美好成长”后得到的数列为121,,,,,4k x x x L ,并记()412log 14n k a x x x =⨯⨯⨯⨯⨯L ,则( )A .25a =B .131n n a a +=−C .21nk =+D .数列{}n na 的前n 项和为()()13213218n n n n +−+++【答案】ABD【分析】对A :由题意直接运算判断;对B :根据第1n +次“美好成长”与第n 次“美好成长”的关系分析运算;对C :根据题意分析可得:()1121n n b b ++=+,利用构造法结合等比数列分析运算;对D :由131n n a a +=−,利用构造法结合等比数列可得312n n a +=,利用裂项相消结合分组求和运算求解.【详解】对A :()()25144244log 144log 42,log 144164log 45a a =⨯⨯===⨯⨯⨯⨯==,A 正确;对B :由题意可知:()()()(){}()()212141211241214log 1414log 1414k n k k k x x x a x x x x x x x x x x +⎡⎤⨯⨯⨯⨯⨯⎡⎤=⨯⨯⨯⨯⨯⨯⨯⨯=⨯⨯⨯⨯⨯⨯⎢⎥⎣⎦⨯⎢⎥⎣⎦()()312441214log 3log 141314k k n x x x x x x a ⨯⨯⨯⨯⨯==⨯⨯⨯⨯⨯−=−,故131n n a a +=−,B 正确;对C :设第n 次“美好成长”后共插入n b 项,即n k b =,共有1n b +个间隔,且11b =, 则第1n +次“美好成长”后再插入1n b +项,则()1121n n n n b b b b +=++=+, 可得()1121n n b b ++=+,且1120b +=≠,故数列{}1n b +是以首项为2,公比为2的等比数列, 则11222n n n b −+=⨯=,故21n n k b ==−,C 错误;对D :∵131n n a a +=−,则111322n n a a +⎛⎫−=− ⎪⎝⎭,且113022a −=≠, 故数列12n a ⎧⎫−⎨⎬⎩⎭是以首项为32,公比为3的等比数列,则11333222n n n a −−=⨯=,即312n n a +=,设()()()1313232332222n n n n n n n n nna An B A n B An A B +=+⋅−++⋅+=−−−⋅+=⨯+⎡⎤⎣⎦,则122320A A B ⎧−=⎪⎨⎪−−=⎩,解得1438A B ⎧=−⎪⎪⎨⎪=⎪⎩,故1321233882n n n n n nna +−−=⋅−⋅+, 设数列{}n na 的前n 项和为n S , 则22311211133212122333333888888222n n n n n n n S a a na +⎡−−−−−⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=⨯−⨯+⨯−⨯++⋅−⋅++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦L L L()()1113122321322388218n n n n n n n n ++⎛⎫+ −++⎪−⎝⎭=−⋅++=, 即数列{}n na 的前n 项和为()()13213218n n n n +−+++,D 正确.故选:ABD. 【点睛】结论点睛:(1)构造法:()()110,1n n n n a ka m km k a a λλ++=+≠≠⇔+=+;(2)裂项构造:()()()11n n n kn b q An B q A n B q ++⋅=+⋅−++⋅⎡⎤⎣⎦.27.(2023春·安徽·高二合肥市第八中学校联考开学考试)在数学课堂上,教师引导学生构造新数列:在数列的每相邻两项之间插入此两项的和,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列,将数列1,2进行构造,第1次得到数列1,3,2;第2次得到数列1,4,3,5,2;…;第()*N n n ∈次得到数列1,1x ,2x ,3x ,…,k x ,2.记1212n k a x x x =+++⋅⋅⋅++,数列{}n a 的前n 项和为n S ,则( ) A .342a = B .133n n a a +=− C .()2332n a n n =+ D .()133234n n S n +=+− 【答案】ABD【分析】根据数列的构造方法先写出前面几次数列的结果,寻找规律,再进行推理运算即可. 【详解】解:由题意可知,第1次得到数列1,3,2,此时1k =, 第2次得到数列1,4,3,5,2,此时3k =,第3次得到数列1,5,4,7,3,8,5,7,2,此时7k =,第4次得到数列1,6,5,9,4,11,7,10,3,11,8,13,5,12,7,9,2,此时15k =,第n 次得到数列1,1x ,2x ,3x ,L ,k x ,2,此时21n k =−, 由此可得133a =+,2339a =++,33392742a =+++=,故A 正确; 43392781a =++++,…,()112331333333333132n n nna +−+=++++⋅⋅⋅+=+=−,故C 错误; 由1332n n a ++=,可得2133332n n n a a +++==−,故B 正确;由()()()23411129131313333333232221324n n n n n n n S a a a n ++−=++⋅⋅⋅+=+++⋅⋅⋅++=⨯+=+−−,故D 正确.故选:ABD .三、填空题28.(2022春·上海长宁·高二上海市延安中学校考期中)对于数列{}n a ,若存在正整数m ,使得对任意正整数n ,都有n m n a a q +=(其中q 为非零常数),则称数列{}n a 是以m 为周期,以q 为周期公比的“类周期性等比数列”.若“类周期性等比数列”的前4项为1,1,2,3,周期为4,周期公比为3,则数列{}n a 前21项的和为__. 【答案】1090【分析】确定43n n a a +=,数列{}n a 从第二项起连续四项成等比数列,利用等比数列公式计算得到答案. 【详解】43n n a a +=,故513a a q ==,由题意得数列{}n a 从第二项起连续四项成等比数列, 234512339,3a a a a q +++=+++==,则数列{}n a 前21项的和为()5523451913()(1)11090113a a a a q a q ⨯−+++−+=+=−−. 故答案为:109029.(2022秋·福建泉州·高二统考期末)对于数列{}n a ,记:()()()()()()()1212311112n n n n n n n n n a a +++∆∆∆=∆=∆=∆∆,,,…,()()()111k k n n k n−+−∆∆=∆(其中*n ∈N ),并称数列(){}k n ∆为数列{}n a 的k 阶商分数列.特殊地,当(){}kn ∆为非零常数数列时,称数列{}n a 是k 阶等比数列.已知数列{}n a 是2阶等比数列,且20123220482a a a ===,,,若n m n a a −=,则m =___________. 【答案】23【分析】根据给定的定义,计算(1)(1)12,∆∆,进而求出数列(1){}n ∆的公比及通项,再借助累乘法求出数列{}n a 的通项即可推理计算作答.【详解】由数列{}n a 是2阶等比数列,得(2)(0)nq q ∆=≠,即(1)(2)1(1)n nnq +∆∆==∆, 且(1)(1)10(1)932212(1)12112,2,2a a q a a ∆∆==∆====∆,即数列(1){}n ∆是首项为102,公比为12的等比数列, 则有(1)10111112()()22n n n −−∆=⨯=,即1111()2n n n a a −+=,当2n ≥时, 22320109121(10)(9)(12)3221121111112()()()()()22222nn n n n n n aa a a a a a a −+−−−−+−+−++−−=⋅⋅⋅⋅=⨯⨯⨯⨯==,而12a =满足上式,因此22320212n n n a −+⎛⎫= ⎪⎝⎭,由n m n a a −=得:222320()23()202211()()22nn m n m n −+−−−+=,即222320()23()20n n m n m n −+=−−−+,整理得(2)23(2)m n m n m −=−,又n 为小于m 的任意正整数,所以23m =. 故答案为:23【点睛】关键点睛:涉及数列新定义问题,关键是正确理解给出的定义,由给定的数列结合新定义探求数列的相关性质,并进行合理的计算、分析、推理等方法综合解决.30.(2023·河南郑州·统考一模)“外观数列”是一类有趣的数列,该数列由正整数构成,后一项是前一项的“外观描述”.例如:取第一项为1,将其外观描述为“1个1”,则第二项为11;将描述为“2个1”,则第三项为21;将21描述为“1个2,1个1”,则第四项为1211;将1211描述为“1个1,1个2,2个1”,则第五项为111221,…,这样每次从左到右将连续的相同数字合并起来描述,给定首项即可依次推出数列后面的项.则对于外观数列{}n a ,下列说法正确的有______. ①若13a =,则从4a 开始出现数字2;②若1a k =(1k =,2,3,…,9),则()*n a n ∈N 的最后一个数字均为k ;③{}n a 不可能为等差数列或等比数列; ④若1123a =,则()*n a n ∈N 均不包含数字4.【答案】②④【分析】对①,由外观数列定义列举判断; 对②,由外观数列定义判断; 对③,取反例,如122a =;对④,由反证法,结合外观数列定义判断.【详解】对①,12343,13,1113,3113a a a a ====,①错;对②,由外观数列的定义,每次都是从左到右描述,故一开始的k (1k =,2,3,…,9)始终在最右边,即最后一个数字,②对; 对③,取122a =,则2322a a ===,此时既为等差数列,也为等比数列,③错;对④,1234123,111213,31121113,1321123113a a a a ====,设数列()*,5k a k k N ∈≥首次出现数字4,则1k a −必出现了4个连续的相同数字m (1m =,2,3,…,9),而2k a −的描述必包含“1个m ,1个m ”,与1k a −的描述矛盾,故()*n a n ∈N 均不包含数字4,④对.故选:②④31.(2023秋·内蒙古阿拉善盟·高三阿拉善盟第一中学校考期末)设数列{}n a 的前n 项和为n S ,对任意n *∈N 都有1n n a a t ++=(t 为常数),则称该数列为“t 数列”,若数列{}n a 为“2数列”,且11a =−,则2023S =______. 【答案】2021【分析】利用并项求和即可.【详解】根据题意得到:2320222402532a a a a a a ++=+===,所以()()()202312345202220232101112021S a a a a a a a =+++++++=⨯−=.故答案为:2021.32.(2023秋·宁夏吴忠·高二吴忠中学校考期末)定义n 个正数12,,,n p p p ⋯的“均倒数”为12nnp p p ++⋅⋅⋅+,若各项均为正数的数列{}n a 的前n 项的“均倒数”为121n +,则2023a 的值为______ 【答案】8091【分析】利用“均倒数”的概念求出(21)n S n n =+,再利用递推关系求出41n a n =−,再代入值即可. 【详解】由已知可得数列{}n a 的前n 项的“均倒数”为 121,21n n n n a a a S n ==++⋯++可得(21)n S n n =+,则2n …时, 21[2(1)1](1)231n S n n n n −=−+−=−+141n n n a S S n −∴=−=−,当1n =时,113a S ==,满足41n a n =−, 202341,4202318091n a n a ∴=−=⨯−=.故答案为: 8091 .33.(2023秋·安徽淮北·高二淮北一中校考期末)对给定的数列{}()0n n a a ≠,记1n n na b a +=,则称数列{}n b 为数列{}n a 的一阶商数列;记1n n nb c b +=,则称数列{}n c 为数列{}n a 的二阶商数列;以此类推,可得数列{}n a 的P 阶商数列()P *∈N ,已知数列{}n a 的二阶商数列的各项均为e ,且121,1a a ==,则10a =___________.【答案】36e【分析】由题意可得1e n n n b c b +==,从而得1e n n b −=,即11e n n naa −+=,由累乘法即可求得10a 的值. 【详解】解:由数列{}n a 的二阶商数列的各项均为e ,可知1e n n nb c b +==, 而2111a b a ==, 故数列{}n b 是以1为首项,e 为公比的等比数列,即1e n n b −=,即11e ,n n na n a −*+=∈N , 即283102412391,e,e ,,e a a a a a a a a ====. 所以()18828128363102421011239··11e e ?·e e =e=e a a a a a a a a a a +⋅+++=⋅⋅⋅=⋅⋅⋅=,故3610e a =.故答案为:36e34.(2022秋·上海·高二期中)定义:对于任意数列{}n a ,假如存在一个常数a 使得对任意的正整数n 都有n a a <,且lim n n a a →+∞=,则称a 为数列{}n a 的“上渐近值”.已知数列{}n a 有12,a a a p ==(p 为常数,且0p >),它的前n 项和为n S ,并且满足()12n n n a a S −=,令2112n n n n n S S p S S ++++=+,记数列{}122n p p p n +++−的“上渐近值”为k ,则100coskπ的值为 _____. 【答案】12−##-0.5【分析】先根据n S 求解数列{}n a 的通项公式,得出等差数列后,利用等差数列求和方法求出n S ,代入n p 得出n p 的表达式,最后即可得出上渐近值. 【详解】解:当1n =时,()1111102a a S a ⨯−===,当2n ≥时,()()()1111122n n n n n n a a n a a a S S −−−−−=−=−,得到112n n n a a n −−=−, 根据累乘法:()212332123421n n n n a a n p n n n −−−=⨯⨯⨯⨯⨯⨯=−−−−;满足n=1情况, 故而数列{}n a 是首项为0,公差为p 的等差数列,()12n n n pS −∴=,21122112222n n n n n S S n n p S S n n n n +++++⎛⎫∴=+=+=+− ⎪++⎝⎭, 122n p p p n ∴+++−=111111111221232435112n n n n n n ⎛⎫+−+−+−++−+−− ⎪−++⎝⎭11121212n n ⎛⎫=+−− ⎪++⎝⎭()()46312n n n +=−++,()()()1246li 231m l 32im n n n n p p p n n n →+∞→+∞⎛⎫+∴+++−=−= ⎪ ⎪++⎝⎭, 3k ∴=,10010021coscos cos 332k πππ⎛⎫∴==−=− ⎪⎝⎭. 故答案为:12−35.(2023·高二课时练习)定义:各项均不为零的数列{}n a 中,所有满足10i i a a +⋅<的正整数i 的个数称为这个数列{}n a 的变号数.已知数列{}n b 的前n 项和26n S n n a =−+(n *∈N ,5a ≠),令41n na b =−(n *∈N ),若数列{}n a 的变号数为2,则实数a 的取值范围是___________. 【答案】()(),59,−∞+∞。
高中数学等差数列、等比数列,典型例题、常见考题、基础测试、考试模拟,全部附答案
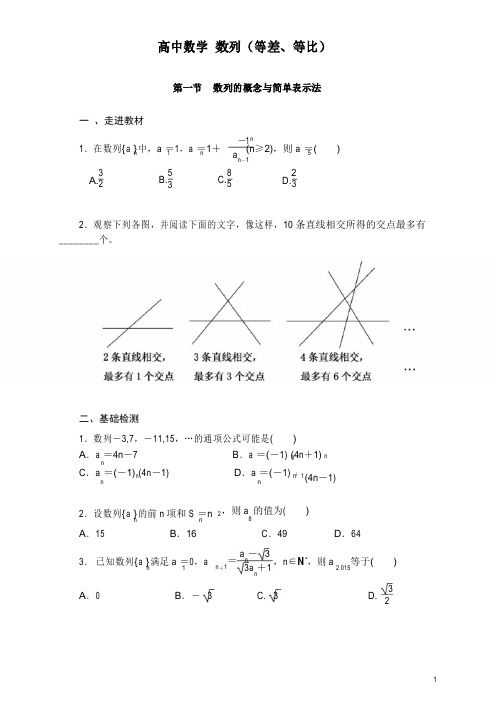
高中数学数列(等差、等比)第一节数列的概念与简单表示法一、走进教材-11.在数列{a}中,a=1,a=1+(n≥2),则a=( )an-13A. B.53 C.82D.2.观察下列各图,并阅读下面的文字,像这样,10条直线相交所得的交点最多有________个。
二、基础检测1.数列-3,7,-11,15,…的通项公式可能是()A.a=4n-7B.a=(-1)(4n+1)nnC.a=(-1)(4n-1)D.a=(-1)+n n(4n-1)2.设数列{a}的前n项和S=nn n 2,则a的值为()8A.15B.16C.49D.643.已知数列{a}满足a=0,an1n+1=a-3n3a+1n,n∈N,则a等于( )2015A.0B.-3 C.3 D.3 2nn1n5 253nn n1*4.已知数列{a}的前n项和S=nn n 2+1,则a=________。
n5.已知数列{a}满足a=1,a=3a+2,则a=________。
n1n+1n n考点一考点精讲由数列的前几项求数列的通项公式【典例1】根据数列的前几项,写出下列各数列的一个通项公式。
(1)-1,7,-13,19,…;(2)0.8,0.88,0.888,…;115132961(3),,-,,-,,…。
【变式训练】(1)已知数列的前4项为2,0,2,0,则依此归纳该数列的通项不可能是( )A.a=(-1)-nnπC.a=2sinn +12,n为奇数B.a =0,n为偶数D.a=cos(n-1)π+1248163264n1n 2n(2)3 5 7 9 a +b已知数列 , , , , ,…,根据前三项给出的规律,则实2 4 6 a -b 10数对(a ,b )可能是()A .(19,3)B .(19,-3)C. ,D. ,-考点二由 a 与 S 的关系求通项公式 nn【典例 2】 (1). 已知数列{a }的前 n 项和为 S ,且 a =1,a =S +1,其中 n ∈nn1n +1nN ,则数列{a }的通项公式是 a =________。
等差数列与等比数列专题

等差数列与等比数列专题等差数列与等比数列专题一、选择题(本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一个选项是符合题目要求的) 1.公比不为1等比数列{}n a 的前n 项和为n S ,且1233,,a a a --成等差数列.若11=a ,则4S =A .20-B .0C .7D .402.已知数列{}n a 为等比数列,且5642a a a =?,设等差数列{}n b 的前n 项和为n S ,若552b a =,则9S =A .36B .32C .24D .223.已知等比数列{}n a 的公比2q =,且42a ,6a ,48成等差数列,则{}n a 的前8项和( )A .127B .255C .511D .10234.(2015福建高考真题)若,a b 是函数()()20,0f x x px q p q =-+>> 的两个不同的零点,且,,2a b -这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则p q + 的值等于() A .6 B .7 C .8 D .95.已知数列{a n }为等比数列,S n 是它的前n 项和.若a 2·a 3=2a 1,且a 4与2a 7的等差中项为54,则S 5=A. 35B. 33C. 31D. 29 6.已知()f x 是定义在R 上的不恒为零的函数,且对于任意实数,a b R ∈满足**(2)(2)()()(),(2)2,(),()2n n n n n f f f a b af b bf a f a n N b n N n ?=+==∈=∈ 考察下列结论:①(0)(1)f f =;②()f x 为偶函数;③数列{}n a 为等比数列;④数列{}n b 为等差数列。
其中正确的结论是( )A .①②③B .②③④C .①②④D .①③④7.已知等差数列{}n a 的前n 项和为n S , 918S =-,1352S =-,{}n b 为等比数列,且55b a =,77b a =,则15b 的值为()A .64B .128C .-64D .-1288.设{}n a 是由正数组成的等差数列,{}n b 是由正数组成的等比数列,且11a b =,20032003a b =,则必有()A.10021002a b >B.10021002a b =C.10021002a b ≥D.10021002a b ≤9.已知等差数列{}n a 的公差为2,若134,,a a a 成等比数列,则1a = ()A.4-B.6-C.8-D.10-10.已知n S ,n T 分别是首项为1的等差数列{n a }和首项为1的等比数列{n b }的前n 项和,且满足43S =6S ,93T =86T ,则1n nS b 的最小值为() A.1 B.12 C.23 D.4911.已知数列{}n a 是等差数列,{}n b 是正项等比数列,且189,n n b b a b +≠=,则()A.313810a a b b +>+B.313810a a b b +<+C.313810a a b b +≥+D.313810a a b b +≤+ 12.已知{}n a 是首项为1的等比数列,且1234,2,a a a 成等差数列,则数列1{}na 的前5项的和为() A.31 B.32 C.3116 D.3132二、填空题(本大题共4小题,每小题5分,共20分)13.等比数列{}n a 的前n 项和为n S,且321,2,4a a a 成等差数列。
等差数列与等比数列的求和题

等差数列与等比数列的求和题数列是数学中的重要概念,是由一系列数按照特定规律排列而成的。
在数列中,等差数列和等比数列是最常见的两种形式。
等差数列是指数列中相邻两项之差相等的数列,而等比数列是指数列中相邻两项之比相等的数列。
求和题则是要求计算数列的前n项和。
一、等差数列的求和公式对于等差数列a1, a2, a3, ... , an,其公差为d,则数列的前n项和Sn可以通过以下公式来计算:Sn = (n/2)(a1 + an)或者Sn = (n/2)[2a1 + (n-1)d]其中,a1代表数列的首项,an代表数列的第n项,n代表数列的项数。
二、等比数列的求和公式对于等比数列a1, a2, a3, ... , an,其公比为r(不等于1),则数列的前n项和Sn可以通过以下公式来计算:当r=1时,Sn = na1当r不等于1时,Sn = a1 * (1 - r^n) / (1 - r)三、等差数列求和题示例下面通过一个简单的例子来演示等差数列的求和过程。
例题:计算等差数列1,3,5,7,9的前10项和Sn。
解析:首先,我们可以观察出这个等差数列的首项a1=1,公差d=2。
然后,根据等差数列的求和公式Sn = (n/2)(a1 + an),带入相应的值进行计算。
Sn = (10/2)(1 + 19) = 5 * 20 = 100所以,等差数列1,3,5,7,9的前10项和为100。
四、等比数列求和题示例下面通过一个简单的例子来演示等比数列的求和过程。
例题:计算等比数列2,4,8,16,32的前5项和Sn。
解析:首先,我们可以观察出这个等比数列的首项a1=2,公比r=2。
然后,根据等比数列的求和公式Sn = a1 * (1 - r^n) / (1 - r),带入相应的值进行计算。
Sn = 2 * (1 - 2^5) / (1 - 2) = 2 * (1 - 32) / (-1) = (2/(-1)) * (-31) = -2 * 31 = -62所以,等比数列2,4,8,16,32的前5项和为-62。
等差数列与等比数列的求和问题综合练习题

等差数列与等比数列的求和问题综合练习题数列是数学中常见的一个概念,它包含了一系列按照某种规律排列的数字。
在数列中,等差数列和等比数列是两种常见的类型,它们之间存在着不同的求和方法。
本文将通过综合练习题的方式,详细探讨等差数列与等比数列的求和问题。
一、等差数列求和等差数列是指数列中相邻两项之间的差值保持恒定的数列。
首先,我们来看一个等差数列求和的例子。
例题1:已知等差数列的首项a1为3,公差d为4,求前10项的和S10。
解题思路:利用等差数列通项公式an = a1 + (n-1)d,其中an代表数列的第n 项。
首先计算出第10项的值a10 = a1 + (10-1)d = 3 + (10-1)4 = 3 + 9*4 = 3 + 36 = 39。
其次计算出前10项的和S10 = (a1 + a10) * n / 2 = (3 + 39) * 10 / 2= 42 * 10 / 2 = 210。
答案:前10项的和S10为210。
二、等比数列求和等比数列是指数列中相邻两项之间的比值保持恒定的数列。
下面我们来看一个等比数列求和的例子。
例题2:已知等比数列的首项a1为3,公比q为2,求前5项的和S5。
解题思路:利用等比数列通项公式an = a1 * q^(n-1),其中an代表数列的第n 项。
首先计算出第5项的值a5 = a1 * q^(5-1) = 3 * 2^(5-1) = 3 * 2^4 = 3 * 16 = 48。
其次计算出前5项的和S5 = a1 * (1 - q^n) / (1 - q) = 3 * (1 - 2^5) / (1 - 2) = 3 * (1 - 32) / (1 - 2) = 3 * (-31) / (-1) = 93。
答案:前5项的和S5为93。
三、综合练习题接下来,我将给出一些综合训练题,涵盖了等差数列与等比数列的求和问题。
请你根据题意,独立思考并计算出答案。
练习题1:已知等差数列的首项a1为2,公差d为3,求前20项的和S20。
等差数列等比数列综合经典例题

以下是等差数列和等比数列的经典例题:
等差数列求和问题:已知一个等差数列的首项为a1,公差为d,第n项为an,求前n项和Sn。
解法:根据等差数列的通项公式an = a1 + (n-1)d,得到Sn = (a1+an)n/2 = n(a1+an)/2 = n(a1+a1+(n-1)d)/2。
将其化简可得Sn = n(a1+an)/2 = n(a1+a1+(n-1)d)/2 = (n/2)(a1+an) = (n/2)(a1+a1+(n-1)d),其中a1和an可以根据公式计算出来,从而求得Sn。
等比数列求和问题:已知一个等比数列的首项为a1,公比为q,第n项为an,求前n项和Sn。
解法:根据等比数列的通项公式an = a1q^(n-1),得到Sn = a1(1-q^n)/(1-q)。
将其化简可得Sn = a1*(1-q^n)/(1-q) = a1*(1-q)*(1+q+q^2+...+q^(n-1))/(1-q)。
由于1+q+q^2+...+q^(n-1)是一个等比数列的前n项和,因此可以用等比数列求和公式S=q^n-1/(q-1)求出,将其代入上式,就可以得到Sn的表达式。
这些例题是等差数列和等比数列求和问题中比较经典的例子,掌握了这些例题的解法,就能够比较顺利地解决一类问题。
在实际应用中,还会有更加复杂的情况,需要根据具体的条件设计相应的求和方法。
高考数学复习考点题型专题讲解8 等差数列与等比数列

高考数学复习考点题型专题讲解专题8 等差数列与等比数列高考定位 1.等差、等比数列的基本运算和性质的考查是高考热点,经常以小题形式出现;2.数列的通项也是高考热点,难度中档以下.1.(2022·全国乙卷)已知等比数列{a n }的前3项和为168,a 2-a 5=42,则a 6=( ) A.14 B.12 C.6 D.3 答案 D解析 法一 设等比数列{a n }的首项为a 1,公比为q , 由题意可得⎩⎨⎧S 3=168,a 2-a 5=42,即⎩⎨⎧a 1(1+q +q 2)=168,a 1q (1-q 3)=42,解得⎩⎨⎧a 1=96,q =12,所以a 6=a 1q 5=3,故选D.法二 设等比数列{a n }的首项为a 1,公比为q , 由题意可得⎩⎨⎧S 3=168,a 2-a 5=42,即⎩⎨⎧a 1(1-q 3)1-q =168,a 1q (1-q 3)=42,解得⎩⎨⎧a 1=96,q =12,所以a 6=a 1q 5=3,故选D.2.(2021·全国甲卷)记S n 为等比数列{a n }的前n 项和.若S 2=4,S 4=6,则S 6=( ) A.7 B.8 C.9 D.10 答案 A解析 法一 因为S 2=4,S 4=6,且易知公比q ≠±1,所以由等比数列的前n 项和公式,得⎩⎪⎨⎪⎧S 2=a 1(1-q 2)1-q =a 1(1+q )=4,S 4=a 1(1-q 4)1-q =a 1(1+q )(1+q 2)=6,两式相除,得q 2=12,所以⎩⎨⎧a 1=4(2-2),q =22或⎩⎨⎧a 1=4(2+2),q =-22,所以S 6=a 1(1-q 6)1-q=7.故选A.法二 易知S 2,S 4-S 2,S 6-S 4构成等比数列,由等比中项得S 2(S 6-S 4)=(S 4-S 2)2,即4(S 6-6)=22,所以S 6=7.故选A.3.(2022·新高考Ⅱ卷)图1是中国古代建筑中的举架结构,AA ′,BB ′,CC ′,DD ′是桁,相邻桁的水平距离称为步,垂直距离称为举,图2是某古代建筑屋顶截面的示意图,其中DD 1,CC 1,BB 1,AA 1是举,OD 1,DC 1,CB 1,BA 1是相等的步,相邻桁的举步之比分别为DD 1OD 1=0.5,CC 1DC 1=k 1,BB 1CB 1=k 2,AA 1BA 1=k 3.已知k 1,k 2,k 3成公差为0.1的等差数列,且直线OA 的斜率为0.725,则k 3等于( )A.0.75B.0.8C.0.85D.0.9答案 D解析设OD1=DC1=CB1=BA1=1,则CC1=k1,BB1=k2,AA1=k3,依题意,有k3-0.2=k1,k3-0.1=k2,且DD1+CC1+BB1+AA1OD1+DC1+CB1+BA1=0.725,所以0.5+3k3-0.34=0.725,故k3=0.9.4.(2021·全国甲卷)已知数列{a n}的各项为正数,记S n为{a n}的前n项和,从下面①②③中选取两个作为条件,证明另外一个成立.①数列{a n}是等差数列;②数列{S n}是等差数列;③a2=3a1.注:若选择不同的组合分别解答,则按第一个解答计分.解①③⇒②.已知{a n}是等差数列,a2=3a1.设数列{a n}的公差为d,则a2=3a1=a1+d,得d=2a1,所以S n=na1+n(n-1)2d=n2a1.因为数列{a n }的各项均为正数, 所以S n =n a 1,所以S n +1-S n =(n +1)a 1-n a 1=a 1(常数),所以数列{S n }是等差数列. ①②⇒③.已知{a n }是等差数列,{S n }是等差数列. 设数列{a n }的公差为d , 则S n =na 1+n (n -1)2d=12n 2d +⎝⎛⎭⎪⎫a 1-d 2n .因为数列{S n }是等差数列,所以数列{S n }的通项公式是关于n 的一次函数, 则a 1-d2=0,即d =2a 1, 所以a 2=a 1+d =3a 1. ②③⇒①.已知数列{S n }是等差数列,a 2=3a 1, 所以S 1=a 1,S 2=a 1+a 2=4a 1. 设数列{S n }的公差为d ,d >0, 则S 2-S 1=4a 1-a 1=d ,得a 1=d 2, 所以S n =S 1+(n -1)d =nd , 所以S n =n 2d 2,所以n ≥2时,a n =S n -S n -1=n 2d 2-(n -1)2d 2=2d 2n -d 2, 对n =1也适合,所以a n =2d 2n -d 2,所以a n +1-a n =2d 2(n +1)-d 2-(2d 2n -d 2)=2d 2(常数), 所以数列{a n }是等差数列.热点一 等差数列、等比数列的基本公式1.等差数列的通项公式:a n =a 1+(n -1)d ;2.等比数列的通项公式:a n =a 1·q n -1.3.等差数列的求和公式:S n =n (a 1+a n )2=na 1+n (n -1)2d ;4.等比数列的求和公式:S n =⎩⎨⎧a 1(1-q n )1-q =a 1-a n q1-q ,q ≠1,na 1,q =1.例 1 (1)已知等比数列{a n }的各项均为正数,且3a 12,a 34,a 2成等差数列,则a 20+a 19a 18+a 17等于( ) A.9 B.6 C.3 D.1(2)(2022·全国乙卷)记S n 为等差数列{a n }的前n 项和.若2S 3=3S 2+6,则公差d =________.(3)已知{a n }是递减的等比数列,且a 2=2,a 1+a 3=5,则{a n }的通项公式为________;a 1a 2+a 2a 3+…+a n a n +1(n ∈N *)=________. 答案 (1)A (2)2(3)a n =⎝ ⎛⎭⎪⎫12n -3(n ∈N *) 323×⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫14n解析 (1)设公比为q ,由3a 12,a 34,a 2成等差数列, 可得3a 12+a 2=a 32,所以3a 12+a 1q =a 1q 22,则q 2-2q -3=0,解得q =-1(舍去)或q =3.所以a 20+a 19a 18+a 17=a 18q 2+a 17q 2a 18+a 17=q 2=9.(2)由2S 3=3S 2+6,可得2(a 1+a 2+a 3)=3(a 1+a 2)+6, 化简得2a 3=a 1+a 2+6, 即2(a 1+2d )=2a 1+d +6, 解得d =2.(3)设等比数列{a n }的公比为q , 由a 2=2,a 1+a 3=5, 得2q+2q =5, 解得q =12或q =2,又{a n }是递减的等比数列, 所以q =12,所以a n =a 2×⎝ ⎛⎭⎪⎫12n -2=12n -3,所以a n a n +1=12n -3·12n -2=122n -5,则a 1a 2+a 2a 3+…+a n a n +1是首项为8, 公比为14的等比数列的前n 项和,故a 1a 2+a 2a 3+…+a n a n +1=8×⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫14n1-14=323×⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫14n.规律方法 等差数列、等比数列的基本量问题的求解策略 (1)抓住基本量:首项a 1、公差d 或公比q .(2)熟悉一些结构特征,如前n 项和为S n =an 2+bn (a ,b 是常数)形式的数列为等差数列,通项公式为a n =p ·q n -1(p ,q ≠0)形式的数列为等比数列.训练1 (1)(2022·潍坊三模)已知等差数列{a n }的前n 项和为S n ,若S 7-S 6=24,a 3=8,则数列{a n }的公差d =( ) A.2 B.4 C.6 D.8(2)已知等比数列{a n }的前n 项和为S n ,a 1+a 3=30,S 4=90,设b n =log 2⎝ ⎛⎭⎪⎫13a n ,则数列{b n }的前15项和为( ) A.16 B.80 C.120 D.150(3)(2022·成都诊断)程大位是我国明代伟大的数学家,在他所著的《算法统宗》中有一道“竹筒容米”题:家有九节竹一茎,为因盛米不均平;下头三节三升九,上梢四节贮三升;惟有中间二节竹,要将米数次第盛;若是先生能算法,教君只算到天明.用你所学的数学知识求得中间二节的容积和为( ) A.2.1升 B.2.6升 C.2.7升 D.2.9升 答案 (1)B (2)C (3)A解析 (1)设等差数列{a n }的首项为a 1, 公差为d ,则a n =a 1+(n -1)d , 而a 7=S 7-S 6=24,又a 3=8,∴a 7-a 3=a 1+6d -(a 1+2d )=4d =16, 解得d =4,故选B.(2)设等比数列{a n }的公比为q ,则S 4=a 1+a 2+a 3+a 4=(a 1+a 3)(1+q )=90, 又a 1+a 3=a 1(1+q 2)=30, 解得a 1=6,q =2, 所以a n =a 1q n -1=3·2n , 所以b n =log 2⎝ ⎛⎭⎪⎫13a n =n ,则{b n }为等差数列, 所以数列{b n }的前15项和T 15=15(b 1+b 15)2=15×(1+15)2=120.故选C.(3)设从下到上每节竹容积构成数列{a n },易知{a n }为等差数列, 设其公差为d ,则a 1+a 2+a 3=3.9,a 6+a 7+a 8+a 9=3,即(a 1+a 3)×32=3.9,(a 6+a 9)×42=3,所以a 1+a 3=2.6,a 6+a 9=1.5, 即2a 1+2d =2.6,2a 1+13d =1.5, 解得a 1=1.4,d =-0.1, 所以a 4=1.1,a 5=1, 所以a 4+a 5=2.1.故选A.热点二 等差数列、等比数列的性质1.通项性质:若m +n =p +q =2k (m ,n ,p ,q ,k ∈N *),则对于等差数列,有a m +a n =a p +a q =2a k ,对于等比数列,有a m a n =a p a q =a 2k .2.前n 项和的性质(m ,n ∈N *):对于等差数列有S m ,S 2m -S m ,S 3m -S 2m ,…成等差数列;对于等比数列有S m ,S 2m -S m ,S 3m -S 2m ,…成等比数列(q =-1且m 为偶数情况除外).例2 (1)在各项均为正数的等比数列{a n }中,a 3=2-2,a 5=2+1,则a 1a 5+2a 2a 6+a 3a 7=( ) A.1 B.9C.52+7D.32+9(2)(2022·徐州二模)设等比数列{a n }的前n 项和为S n ,若S 6S 3=3,则S 9S 6=( ) A.2 B.73C.83D.3(3)(2022·金华模拟)设S n 为等差数列{a n }的前n 项和,a 6+a 7=1,则S 12=________;若a 7<0,则使得不等式S n <0成立的最小整数n =________. 答案 (1)B (2)B (3)6 13 解析 (1)由等比数列的性质可得:a 1a 5+2a 2a 6+a 3a 7=a 23+2a 3a 5+a 25=(a 3+a 5)2=(2-2+2+1)2=9,故选B. (2)因为等比数列{a n }的前n 项和为S n ,S 6S 3=3,即S 6=3S 3, 则S 3,S 6-S 3,S 9-S 6成等比数列, 即S 6-S 3S 3=S 9-S 6S 6-S 3, 故4S 3=S 9-S 6,故S 9=7S 3,故S 9S 6=73.(3)根据题意,{a n }为等差数列, 若a 6+a 7=1,则S 12=(a 1+a 12)×122=(a 6+a 7)×122=6,若a 7<0,则S 13=(a 1+a 13)×132=13a 7<0,则使不等式S n <0成立的最小整数n =13. 规律方法 等差、等比数列性质问题的求解策略(1)抓住项与项之间的关系及项与序号之间的关系,从这些特点入手选择恰当的性质进行求解.(2)数列是一种特殊的函数,具有函数的一些性质,如单调性、周期性等,可利用函数的性质解题.训练2 (1)(2022·长沙三模)在等比数列{a n}中,a7,a11是方程x2+5x+2=0的两根,则a3a9a15a5a13的值为( )A.-2+22B.- 2C.2D.-2或 2(2)(2022·聊城检测)设S n是等差数列{a n}的前n项和,若S4S8=25,则S8S16=( )A.514B.726C.35 D.25(3)已知各项均为正数的等比数列{a n},a6,3a5,a7成等差数列,若{a n}中存在两项a m,a n ,使得4a1为其等比中项,则1m+4n的最小值为( )A.4B.9C.23 D.32答案(1)B (2)A (3)D解析(1)在等比数列{a n}中,a7,a11是方程x2+5x+2=0的两根,则a7+a11=-5,a7·a11=2,∴a9=-2,则a3a9a15a5a13=a39a29=a9=- 2.(2)因为数列{a n}为等差数列,所以S4,S8-S4,S12-S8,S16-S12成等差数列.因为S 4S 8=25,所以设S 4=2k ,S 8=5k ,k ≠0, 则S 8-S 4=3k ,可知S 12-S 8=4k ,S 16-S 12=5k , 所以S 12=9k ,S 16=14k , 所以S 8S 16=5k 14k =514.(3)因为a 6,3a 5,a 7成等差数列, 所以2×3a 5=a 6+a 7.又{a n }是各项均为正数的等比数列, 设其首项为a 1,公比为q , 所以6a 1q 4=a 1q 5+a 1q 6, 所以q 2+q -6=0,解得q =2或q =-3(舍去), 又4a 1为a m ,a n 的等比中项, 所以(4a 1)2=a m ·a n ,所以16a 21=a 1·2m -1·a 1·2n -1=a 21·2m +n -2=24×a 21,所以m +n -2=4,即m +n =6,所以1m +4n =16(m +n )·⎝ ⎛⎭⎪⎫1m +4n =16⎝ ⎛⎭⎪⎫1+4m n +n m +4≥16⎝ ⎛⎭⎪⎫5+24mn ·n m =32, 当且仅当4m n =nm,即m =2,n =4时,等号成立,所以1m+4n的最小值为32.故选D.热点三等差数列、等比数列的判断与证明证明数列为等差(比)数列一般使用定义法.例3(2021·全国乙卷)设S n为数列{a n}的前n项和,b n为数列{S n}的前n项积,已知2Sn +1bn=2.(1)证明:数列{b n}是等差数列;(2)求{a n}的通项公式.(1)证明因为b n是数列{S n}的前n项积,所以n≥2时,S n=bnbn-1,代入2Sn+1bn=2可得,2b n-1bn+1bn=2,整理可得2b n-1+1=2b n,即b n-b n-1=12(n≥2).又2S 1+1b 1=3b 1=2,所以b 1=32, 故{b n }是以32为首项,12为公差的等差数列.(2)解 由(1)可知,b n =32+12(n -1)=n +22,则2S n +2n +2=2,所以S n =n +2n +1, 当n =1时,a 1=S 1=32,当n ≥2时,a n =S n -S n -1=n +2n +1-n +1n =-1n (n +1). 故a n=⎩⎪⎨⎪⎧32,n =1,-1n (n +1),n ≥2.易错提醒a n +1=a n q 和a 2n =a n -1a n +1(n ≥2)都是数列为等比数列的必要不充分条件,判定时还要看各项是否为零.训练3 已知数列{a n }的前n 项和为S n ,a 2=6,S n =12a n +1+1.(1)证明:数列{S n -1}为等比数列,并求出S n ;(2)求数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 的前n 项和T n .(1)证明 由S n =12a n +1+1,得S n =12(S n +1-S n )+1,即S n +1-1=3(S n -1),又a 2=6,∴S 1=2a 2+1=4,S 1-1=3≠0,∴数列{S n -1}是首项为3,公比为3的等比数列,即S n -1=3n , ∴S n =3n +1.(2)解 由(1)可得:S n =12a n +1+1=3n +1,∴a n +1=2×3n , ∴a n =2×3n -1(n ≥2), 又a 1=4≠2×31-1=2, ∴a n =⎩⎨⎧4,n =1,2×3n -1,n ≥2, ∴1a n=⎩⎪⎨⎪⎧14,n =1,12×3n -1,n ≥2,∴当n ≥2时,T n =1a 1+1a 2+1a 3+…+1a n =14+12×13⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫13n -11-13=12-14×3n -1,当n =1时T 1=14也符合上式,综上,T n =12-14×3n -1.一、基本技能练1.已知等比数列{a n }满足a 1=2,a 3a 5=4a 26,则a 3的值为( ) A.1 B.2C.1或-1D.2答案 A解析 由题意得a 3a 5=a 24=4a 26,又在等比数列中偶数项同号, ∴a 4=2a 6,∴q 2=12,∴a 3=a 1q 2=1,故选A.2.设数列{a n }是等差数列,S n 是数列{a n }的前n 项和,a 3+a 5=10,S 5=15,则S 6=( ) A.18 B.24 C.30 D.36 答案 B解析 由等差数列的性质知a 4=a 3+a 52=5,而S 5=a 1+a 52×5=5a 3=15,则a 3=3,等差数列{a n }的公差d =a 4-a 3=2, 所以a 1=a 3-2d =-1,则S 6=6a 1+6×(6-1)2·d =-6+30=24.3.北京天坛的圜丘坛为古代祭天的场所,分上、中、下三层.上层中心有一块圆形石板(称为天心石),环绕天心石砌9块扇面形石板构成第一环,向外每环依次增加9块.下一层的第一环比上一层的最后一环多9块.向外每环依次也增加9块.已知每层环数相同,且下层比中层多729块,则三层共有扇面形石板(不含天心石)( )A.3 699块B.3 474块C.3 402块D.3 339块答案 C解析设每一层有n环,由题意可知,从内到外每环之间构成公差为d=9,首项为a1=9的等差数列.由等差数列的性质知S n,S2n-S n,S3n-S2n成等差数列,且(S3n-S2n)-(S2n-S n)=n2d,则9n2=729,解得n=9,则三层共有扇面形石板S3n=S27=27×9+27×262×9=3 402(块).4.若等差数列{a n}的前n项和为S n,则“S2 022>0,S2 023<0”是“a1 011a1 012<0”的( )A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件答案 B解析因为S2 022>0,S2 023<0,所以(a1+a2 022)×2 0222>0,(a1+a2 023)×2 0232<0,即a1+a2 022=a1 011+a1 012>0,a1+a2 023=2a1 012<0,所以a1 011>0,a1 012<0,且a1 011>|a1 012|,所以a1 011a1 012<0,充分性成立;而当a1 011a1 012<0时,a1 011>0,a1 012<0或a1 011<0,a1 012>0,则S2 022>0,S2 023<0不一定成立.故“S2 022>0,S2 023<0”可以推出“a1 011a1 012<0”,但“a1 011a1 012<0”不能推出“S2 022>0,S2 023<0”,所以“S2 022>0,S2 023<0”是“a1 011a1 012<0”的充分不必要条件.故选B.5.(多选)已知等比数列{a n}的公比为q,且a5=1,则下列选项正确的是( )A.a3+a7≥2B.a4+a6≥2C.a7-2a6+1≥0D.a3-2a4-1≥0答案AC解析因为等比数列{a n}的公比为q,且a5=1,所以a3=1q2,a4=1q,a6=q,a7=q2,因为a3+a7=1q2+q2≥2,当且仅当q2=1时等号成立,故A正确;因为a4+a6=1q+q,当q<0时式子为负数,故B错误;因为a7-2a6+1=q2-2q+1=(q-1)2≥0,故C正确;因为a3-2a4-1=1q2-2q-1=⎝⎛⎭⎪⎫1q-12-2,则a3-2a4-1≥0不成立,故D错误.6.(多选)(2022·张家口质检)已知数列{a n}的前n项和为S n,下列说法正确的是( )A.若S n=n2+1,则{a n}是等差数列B.若S n=3n-1,则{a n}是等比数列C.若{a n }是等差数列,则S 9=9a 5D.若{a n }是等比数列,且a 1>0,q >0,则S 1·S 3>S 22 答案 BC解析 若S n =n 2+1,当n ≥2时,a n =2n -1,a 1=2不满足a n =2n -1, 故A 错误;若S n =3n -1,当n ≥2时,a n =S n -S n -1=2·3n -1, 由于a 1=S 1=31-1=2, 满足a n =2·3n -1,所以{a n }是等比数列,故B 正确; 若{a n }是等差数列,则S 9=9(a 1+a 9)2=9a 5,故C 正确;当q =1时,S 1·S 3-S 22=a 21(1+q +q 2)-a 21(1+q )2=-a 21q <0,故D 错误, 综上,选BC.7.写出一个公差为2,且前3项和小于第3项的等差数列a n =________. 答案 2n -4(n ∈N *)(答案不唯一) 解析 依题意得⎩⎨⎧a 1+a 2+a 3<a 3,d =2,解得a 1<-1,不妨令a 1=-2,∴a n =2n -4.8.(2022·菏泽模拟)已知数列{a n }的前n 项和是S n ,且S n =2a n -1,若a n ∈(0,2 022),则称项a n 为“和谐项”,则数列{a n }的所有“和谐项”的和为________. 答案 2 047解析当n≥2时,a n=S n-S n-1=2a n-1-(2a n-1-1)=2a n-2a n-1,∴a n=2a n-1,又由a1=S1=2a1-1,得a1=1,∴{a n}是公比为2,首项为1的等比数列,∴a n=2n-1,由a n=2n-1<2 022,得n-1≤10,即n≤11,∴所求和为S11=1-2111-2=2 047.9.已知数列{a n}满足a1=1,(a n+a n+1-1)2=4a n a n-1,且a n+1>a n(n∈N*),则数列{a n}的通项公式a n=________.答案n2解析因为a1=1,a n+1>a n≥a1>0,所以a n+1>a n.由(a n+a n+1-1)2=4a n a n+1得a n+1+a n-1=2a n a n+1,所以(a n+1-a n)2=1,所以a n+1-a n=1,所以数列{a n}是首项为1,公差为1的等差数列,所以a n=n,即a n=n2.10.(2022·福州模拟)已知数列{a n}是各项均为正数的等比数列,S n为数列{a n}的前n项和,若S2+a2=S3-3,则a4+3a2的最小值为________.答案18解析由S2+a2=S3-3得a2=S3-S2-3=a3-3,所以a 1q =a 1q 2-3⇒a 1=3q 2-q>0⇒q >1,所以a 4+3a 2=a 1q 3+3a 1q =3(q 3+3q )q 2-q =3(q 2+3)q -1=3×(q -1)2+2(q -1)+4q -1=3⎣⎢⎡⎦⎥⎤(q -1)+4q -1+6 ≥3×2(q -1)·4q -1+6=18,当且仅当q -1=4q -1, 即q =3时等号成立,故a 4+3a 2的最小值为18. 11.设等比数列{a n }满足a 1+a 2=4,a 3-a 1=8. (1)求{a n }的通项公式;(2)记S n 为数列{log 3a n }的前n 项和.若S m +S m +1=S m +3(m ∈N *),求m . 解 (1)设{a n }的公比为q ,则a n =a 1qn -1.由已知得⎩⎨⎧a 1+a 1q =4,a 1q 2-a 1=8,解得⎩⎨⎧a 1=1,q =3.所以{a n }的通项公式为a n =3n -1(n ∈N *). (2)由(1)知log 3a n =n -1, 故S n =n (n -1)2(n ∈N *).由S m +S m +1=S m +3,得m (m -1)+(m +1)m =(m +3)(m +2), 即m 2-5m -6=0.解得m =-1(舍去)或m =6.12.(2022·新高考Ⅱ卷)已知{a n }是等差数列,{b n }是公比为2的等比数列,且a 2-b 2=a3-b3=b4-a4.(1)证明:a1=b1;(2)求集合{k|b k=a m+a1,1≤m≤500}中元素的个数.(1)证明设等差数列{a n}的公差为d,由a2-b2=a3-b3得a1+d-2b1=a1+2d-4b1,即d=2b1,由a2-b2=b4-a4得a1+d-2b1=8b1-(a1+3d),即a1=5b1-2d,将d=2b1代入,得a1=5b1-2×2b1=b1,即a1=b1.(2)解由(1)知a n=a1+(n-1)d=a1+(n-1)×2b1=(2n-1)a1,b n=b1·2n-1,由b k=a m+a1,得b1·2k-1=(2m-1)a1+a1,由a1=b1≠0得2k-1=2m,由题知1≤m≤500,所以2≤2m≤1 000,所以k=2,3,4,…,10,共9个数,即集合{k|b k=a m+a1,1≤m≤500}={2,3,4,…,10}中元素的个数为9.二、创新拓展练13.(多选)(2022·济南质检)在等比数列{a n}中,公比为q,其前n项积为T n,并且满足a 1>1,a99·a100-1>0,a99-1a100-1<0,下列结论中正确的是( )A.0<q<1B.a99·a101-1<0C.T100的值是T n中最大的D.使T n>1成立的最大自然数n值等于198 答案ABD解析对于A,∵a99·a100-1>0,∴a 21·q 197>1,∴(a 1·q 98)2·q >1. ∵a 1>1,∴q >0. 又∵a 99-1a 100-1<0, ∴a 99>1,且a 100<1, ∴0<q <1,故A 正确;对于B ,∵a 2100=a 99·a 101,a 100<1, ∴0<a 99·a 101<1,即a 99·a 101-1<0,故B 正确; 对于C ,由于T 100=T 99·a 100, 而0<a 100<1,故有T 100<T 99,故C 错误;对于D ,T 198=a 1·a 2·…·a 198=(a 1·a 198)(a 2·a 197)·…·(a 99·a 100)=(a 99·a 100)99>1,T 199=a 1·a 2·…·a 199=(a 1·a 199)·(a 2·a 198)…(a 99·a 101)·a 100=(a 100)100<1,故D 正确. 故选ABD.14.(多选)(2022·石家庄模拟)已知数列{a n }满足a 1=10,a 5=2,且a n +2-2a n +1+a n =0(n ∈N *),则下列结论正确的是( ) A.a n =12-2nB.|a 1|+|a 2|+|a 3|+…+|a n |=⎩⎨⎧30,n ≤5,n 2+5,n >5C.|a n |的最小值为0D.当且仅当n =5时,a 1+a 2+a 3+…+a n 取得最大值30 答案 AC解析 由a n +2-2a n +1+a n =0, 可得a n +2-a n +1=a n +1-a n ,所以数列{a n }是等差数列,设公差为d , 因为a 1=10,a 5=2, 所以d =a 5-a 15-1=-2,所以a n =10-2(n -1)=12-2n , 故A 正确;当n =6时,a n =0,所以当n ≤5时,a n >0, 当n >5时,a n ≤0,所以当n ≤5时,|a 1|+|a 2|+|a 3|+…+|a n |=a 1+a 2+a 3+…+a n =n (10+12-2n )2=11n -n 2.当n >5时,|a 1|+|a 2|+|a 3|+…+|a n | =a 1+a 2+…+a 5-a 6-…-a n=-(a 1+a 2+a 3+…+a n )+2(a 1+a 2+…+a 5) =-S n +2S 5 =-(11n -n 2)+60 =n 2-11n +60,所以|a 1|+|a 2|+|a 3|+…+|a n |=⎩⎨⎧11n -n 2,n ≤5,n 2-11n +60,n >5,故B 错误;|a n |=|12-2n |,当n =6时,|a n |取得最小值为0,故C 正确; 当n =5或n =6时,a 1+a 2+a 3+…+a n 取最大值30,故D 错误.15.(多选)已知S n 是数列{a n }的前n 项和,且a 1=a 2=1,a n =a n -1+2a n -2(n ≥3),则下列结论正确的是( ) A.数列{a n +1+a n }为等比数列 B.数列{a n +1-2a n }为等比数列 C.a n =2n +1+(-1)n3D.S 20=23(410-1)答案 ABD解析 因为a n =a n -1+2a n -2(n ≥3), 所以a n +a n -1=2a n -1+2a n -2 =2(a n -1+a n -2), 又a 1+a 2=2≠0,所以{a n +a n +1}是等比数列,A 正确;同理a n -2a n -1=a n -1+2a n -2-2a n -1=-a n -1+2a n -2=-(a n -1-2a n -2),而a 2-2a 1=-1, 所以{a n +1-2a n }是等比数列,B 正确; 若a n =2n +1+(-1)n3,则a 2=23+(-1)23=3,但a 2=1≠3,C 错误;由A 知{a n +a n +1}是等比数列,且公比为2,因此数列a 1+a 2,a 3+a 4,a 5+a 6,…仍然是等比数列,公比为4,其前10项和为T 10, 则S 20=T 10=2(1-410)1-4=23(410-1),故D 正确.16.(多选)(2022·泰州调研)若正整数m ,n 只有1为公约数,则称m ,n 互质,对于正整数k ,φ(k )是不大于k 的正整数中与k 互质的数的个数,函数φ(k )以其首名研究者欧拉命名,称为欧拉函数,例如:φ(2)=1,φ(3)=2,φ(6)=2,φ(8)=4.已知欧拉函数是积性函数,即如果m ,n 互质,那么φ(mn )=φ(m )φ(n ),例如:φ(6)=φ(2)φ(3),则( ) A.φ(5)=φ(8)B.数列{φ(2n )}是等比数列C.数列{φ(6n )}不是递增数列D.数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1φ(6n )的前n 项和小于35 答案 ABD解析 ∵φ(5)=4,φ(8)=4, ∴φ(5)=φ(8),A 对.∵φ(2n )=2n -1,∴{φ(2n )}是等比数列,B 对.∵φ(6n )=2·6n -1,∴{φ(6n )}一定是单调递增数列,故C 错.φ(6n )=2·6n -1,⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1φ(6n)的前n 项和S n =12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫16n1-16=35⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫16n<35,D 对,选ABD. 17.已知数列{a n }的前n 项和为S n ,a 1=12,S n +1·(2-S n )=1.(1)求证:⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1S n -1是等差数列; (2)求数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 中最接近2 023的数.(1)证明1S 1-1=1a 1-1=-2.由S n +1·(2-S n )=1,得S n +1=12-S n. 因为1S n +1-1-1S n -1=112-S n-1-1S n -1=2-S n S n -1-1S n -1=-1,所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1S n -1是以-2为首项,-1为公差的等差数列.(2)解 由(1)得1S n -1=-2+(n -1)×(-1)=-(n +1),即S n =nn +1,则a n =S n -S n -1=nn +1-n -1n =1n (n +1)(n ≥2),当n =1时,a 1=12满足上式,所以a n =1n (n +1)(n ∈N *),则1a n=n (n +1).由f (x )=x (x +1)=⎝⎛⎭⎪⎫x +122-14在(0,+∞)上单调递增, 当n =44时,1a 44=44×45=1 980;当n =45时,1a 45=45×46=2 070.所以数列⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫1a n 中最接近2 023的数是1 980.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题检测(八) 等差数列、等比数列A 组——“6+3+3”考点落实练一、选择题1.(2019·成都高三摸底考试)已知等差数列{a n }的前n 项和为S n ,且a 4=52,S 10=15,则a 7=( )A.12 B .1 C.32D .2解析:选A法一:设等差数列{a n}的公差为d ,则由题设得⎩⎨⎧a 4=a 1+3d =52,S 10=10a 1+10×92d =15,解得⎩⎨⎧a 1=92,d =-23,所以a 7=a 1+6d =92+6×⎝⎛⎭⎫-23=12.故选A. 法二:因为S 10=10(a 1+a 10)2=15,所以a 1+a 10=3,又a 4+a 7=a 1+a 10,a 4=52,所以52+a 7=3,解得a 7=12.故选A. 2.(2019·福州市质量检测)已知数列{a n }中,a 3=2,a 7=1.若数列⎩⎨⎧⎭⎬⎫1a n 为等差数列,则a 9=( )A.12 B .54C.45D .-45解析:选C 因为数列⎩⎨⎧⎭⎬⎫1a n 为等差数列,a 3=2,a 7=1,所以数列⎩⎨⎧⎭⎬⎫1a n 的公差d =1a 7-1a 37-3=1-127-3=18,所以1a 9=1a 7+(9-7)×18=54,所以a 9=45.故选C.3.等比数列{a n }的各项均为正实数,其前n 项和为S n .若a 3=4,a 2a 6=64,则S 5=( ) A .32 B .31 C .64D .63解析:选B 法一:设首项为a 1,公比为q ,因为a n >0,所以q >0,由条件得⎩⎪⎨⎪⎧a 1·q 2=4,a 1q ·a 1q 5=64,解得⎩⎪⎨⎪⎧a 1=1,q =2,所以S 5=31.故选B.法二:设首项为a 1,公比为q ,因为a n >0,所以q >0,由a 2a 6=a 24=64,a 3=4,得q =2,a 1=1,所以S 5=31.故选B.4.若等差数列{a n }的前n 项和为S n ,若S 6>S 7>S 5,则满足S n S n +1<0的正整数n 的值为( ) A .10 B .11 C .12D .13解析:选C 由S 6>S 7>S 5,得S 7=S 6+a 7<S 6,S 7=S 5+a 6+a 7>S 5,所以a 7<0,a 6+a 7>0,所以S 13=13(a 1+a 13)2=13a 7<0,S 12=12(a 1+a 12)2=6(a 6+a 7)>0,所以S 12S 13<0,即满足S n S n +1<0的正整数n 的值为12.故选C.5.(2019·江西临川期末)已知正项等比数列{a n }满足a 5·a 6·a 7=1,且f (x )=⎩⎪⎨⎪⎧x ln x ,x ≥1,ln xx ,0<x <1,若f (a 1)+f (a 2)+…+f (a 10)=a 1,则a 1的值为( )A. e B .e C .2eD .1+e解析:选B 由题知正项等比数列{a n }满足a 5·a 6·a 7=1,则a 6=1,所以a 2·a 10=a 3·a 9=a 4·a 8=a 5·a 7=1,当x >1时,f (x )+f ⎝⎛⎭⎫1x =x ln x +ln 1x 1x=0, 当x =1时,f (1)=0,所以f (a 1)+f (a 2)+…+f (a 10)=f (a 1)+[f (a 2)+f (a 10)]+[f (a 3)+f (a 9)]+[f (a 4)+f (a 8)]+[f (a 5)+f (a 7)]+f (a 6)=f (a 1)+f (a 6)=a 1可化为f (a 1)=a 1.当a 1>1时,f (a 1)=a 1ln a 1=a 1,解得a 1=e ; 当a 1<1时,f (a 1)=ln a 1a 1=a 1,无解.故选B.6.(2019·石家庄市模拟(一))已知数列{a n }的前n 项和为S n ,且S n +1+S n =n 2-19n2(n ∈N *),若a 10<a 11,则S n 取最小值时n 的值为( )A .9B .10C .11D .12解析:选B ∵S n +1+S n =n 2-19n2,①∴a 2+2a 1=-9,又n ≥2时,S n +S n -1=(n -1)2-19(n -1)2,②①-②得:a n +1+a n =n -10, ∴a 4+a 3=-7,a 6+a 5=-5,a 8+a 7=-3,a 10+a 9=-1,a 12+a 11=1, ∴n ≥11且n 为奇数时,a n +1+a n >0,S 2+a 1>S 4+a 1>…>S 10+a 1,S 10+a 1<S 12+a 1<S 14+a 1<…,即S 2>S 4>…>S 10,S 10<S 12<S 14<….∵a 3+a 2=-8,a 5+a 4=-6,a 7+a 6=-4,a 9+a 8=-2,a 11+a 10=0,a 13+a 12=2,∴n ≥12且n 为偶数时,a n +1+a n >0,S 3-a 1>S 5-a 1>…>S 9-a 1=S 11-a 1,S 11-a 1<S 13-a 1<S 15-a 1<…,即S 3>S 5>…>S 9=S 11,S 11<S 13<S 15<….又a 11+a 10=0,a 10<a 11,∴a 11>0,∴S 11-S 10=a 11>0,∴S 11>S 10,∴S n 取得最小值时的n =10.故选B.二、填空题7.(2019·长春市质量监测(二))等差数列{a n }中,S n 是它的前n 项和,a 2+a 3=10,S 6=54,则该数列的公差d 为________.解析:法一:由题意,知⎩⎪⎨⎪⎧a 1+d +a 1+2d =10,6a 1+6×52d =54, 解得⎩⎪⎨⎪⎧a 1=-1,d =4.法二:∵S 6=(a 1+a 6)·62=(a 3+a 4)·62=54,∴a 3+a 4=18.∵a 2+a 3=10,∴a 4-a 2=18-10=8=2d ,∴d =4.答案:48.设公比为q (q >0)的等比数列{a n }的前n 项和为S n .若S 2=3a 2+2,S 4=3a 4+2,则a 1=________.解析:由S 2=3a 2+2,S 4=3a 4+2, 得a 3+a 4=3a 4-3a 2,即q +q 2=3q 2-3, 解得q =-1(舍去)或q =32,将q =32代入S 2=3a 2+2中,得a 1+32a 1=3×32a 1+2,解得a 1=-1. 答案:-19.(2019·山西太原期中改编)已知集合P ={x |x =2n ,n ∈N *},Q ={x |x =2n -1,n ∈N *},将P ∪Q 的所有元素从小到大依次排列构成一个数列{a n },记S n 为数列{a n }的前n 项和,则a 29=________,使得S n <1 000成立的n 的最大值为________.解析:数列{a n }的前n 项依次为1,2,3,22,5,7,23,….利用列举法可得,当n =35时,P ∪Q 的所有元素从小到大依次排列,构成一个数列{a n }, 所以数列{a n }的前35项分别为1,3,5,7,9,11,13,15,17,19,21,23,25,…,57,59,2,4,8,16,32,故a 29=49.S 35=30+30(30-1)2×2+2(25-1)2-1=302+26-2=962<1 000.当n =36时,P ∪Q 中的所有元素从小到大依次排列,构成一个数列{a n },所以数列{a n }的前36项分别为1,3,5,7,9,11,13,15,17,19,21,23,25,…,59,61,2,4,8,16,32,S 36=31+31(31-1)2×2+2(25-1)2-1=961+62=1 023>1 000.所以n 的最大值为35. 答案:49 35 三、解答题10.(2019·北京高考)设{a n }是等差数列,a 1=-10,且a 2+10,a 3+8,a 4+6成等比数列.(1)求{a n }的通项公式;(2)记{a n }的前n 项和为S n ,求S n 的最小值. 解:(1)设{a n }的公差为d .因为a 1=-10,所以a2=-10+d,a3=-10+2d,a4=-10+3d.因为a2+10,a3+8,a4+6成等比数列,所以(a3+8)2=(a2+10)(a4+6).所以(-2+2d)2=d(-4+3d).解得d=2.所以a n=a1+(n-1)d=2n-12.(2)由(1)知,a n=2n-12.则当n≥7时,a n>0;当n≤6时,a n≤0.所以S n的最小值为S5=S6=-30.11.已知数列{a n}的前n项和为S n,且S n=2a n-3n(n∈N*).(1)求a1,a2,a3的值;(2)设b n=a n+3,证明:数列{b n}为等比数列,并求通项公式a n.解:(1)因为数列{a n}的前n项和为S n,且S n=2a n-3n(n∈N*).所以n=1时,由a1=S1=2a1-3×1,解得a1=3,n=2时,由S2=2a2-3×2,得a2=9,n=3时,由S3=2a3-3×3,得a3=21.(2)因为S n=2a n-3n,所以S n+1=2a n+1-3(n+1),两式相减,得a n+1=2a n+3,①把b n=a n+3及b n+1=a n+1+3,代入①式,得b n+1=2b n(n∈N*),且b1=6,所以数列{b n}是以6为首项,2为公比的等比数列,所以b n=6×2n-1,所以a n=b n-3=6×2n-1-3=3(2n-1).12.(2019·武汉调研)已知等差数列{a n}前三项的和为-9,前三项的积为-15.(1)求等差数列{a n}的通项公式;(2)若{a n}为递增数列,求数列{|a n|}的前n项和S n.解:(1)设公差为d,则依题意得a2=-3,则a1=-3-d,a3=-3+d,∴(-3-d )(-3)(-3+d )=-15,得d 2=4,d =±2, ∴a n =-2n +1或a n =2n -7.(2)由题意得a n =2n -7,所以|a n |=⎩⎪⎨⎪⎧7-2n ,n ≤3,2n -7,n ≥4,①n ≤3时,S n =-(a 1+a 2+…+a n )=5+(7-2n )2n =6n -n 2;②n ≥4时,S n =-a 1-a 2-a 3+a 4+…+a n =-2(a 1+a 2+a 3)+(a 1+a 2+…+a n )=18-6n +n 2.综上,数列{|a n |}的前n 项和S n =⎩⎪⎨⎪⎧-n 2+6n ,n ≤3,n 2-6n +18,n ≥4.B 组——大题专攻强化练1.(2019·湖南省湘东六校联考)已知数列{a n }满足a n +1-3a n =3n (n ∈N *)且a 1=1. (1)设b n =a n3n -1,证明:数列{b n }为等差数列;(2)设c n =na n,求数列{c n }的前n 项和S n .解:(1)证明:由已知得a n +1=3a n +3n,得b n +1=a n +13n =3a n +3n 3n =a n3n -1+1=b n +1,所以b n +1-b n =1,又a 1=1,所以b 1=1, 所以数列{b n }是首项为1,公差为1的等差数列. (2)由(1)知,b n =a n 3n -1=n ,所以a n =n ·3n -1,c n =13n -1,所以S n =1×⎝⎛⎭⎫1-13n 1-13=32⎝⎛⎭⎫1-13n =32-12·3n -1.2.(2019·昆明检测)已知数列{a n }是等比数列,公比q <1,前n 项和为S n ,若a 2=2,S 3=7.(1)求{a n }的通项公式;(2)设m ∈Z ,若S n <m 恒成立,求m 的最小值.解:(1)由a 2=2,S 3=7得⎩⎪⎨⎪⎧a 1q =2,a 1+a 1q +a 1q 2=7,解得⎩⎪⎨⎪⎧a 1=4,q =12或⎩⎪⎨⎪⎧a 1=1,q =2(舍去).所以a n =4·⎝⎛⎭⎫12n -1=⎝⎛⎭⎫12n -3.(2)由(1)可知,S n =a 1(1-q n)1-q =4⎝⎛⎭⎫1-12n 1-12=8⎝⎛⎭⎫1-12n <8. 因为a n >0,所以S n 单调递增.又S 3=7,所以当n ≥4时,S n ∈(7,8). 又S n <m 恒成立,m ∈Z ,所以m 的最小值为8.3.(2019·广州市综合检测(一))已知{a n }是等差数列,且lg a 1=0,lg a 4=1. (1)求数列{a n }的通项公式;(2)若a 1,a k ,a 6是等比数列{b n }的前3项,求k 的值及数列{a n +b n }的前n 项和. 解:(1)因为lg a 1=0,lg a 4=1,所以a 1=1,a 4=10. 设等差数列{a n }的公差为d , 则d =a 4-a 14-1=3.所以a n =a 1+3(n -1)=3n -2. (2)由(1)知a 1=1,a 6=16,因为a 1,a k ,a 6是等比数列{b n }的前3项, 所以a 2k =a 1a 6=16. 又a n =3n -2>0, 所以a k =4. 因为a k =3k -2, 所以3k -2=4,得k =2. 设等比数列{b n }的公比为q ,所以q =b 2b 1=a 2a 1=3×2-21=4.所以b n =4n -1.所以a n +b n =3n -2+4n -1.所以数列{a n +b n }的前n 项和为S n =n (3n -1)2+1-4n 1-4=32n 2-12n +13(4n -1).4.已知数列{a n }是等差数列,满足a 2=5,a 4=13,数列{b n }的前n 项和是T n ,且T n+b n =3.(1)求数列{a n }及数列{b n }的通项公式; (2)设c n =a n ·b n ,求数列{c n }中的最大项. 解:(1)设等差数列{a n }的首项为a 1,公差为d ,由题意,得⎩⎪⎨⎪⎧a 1+d =5,a 1+3d =13,解得⎩⎪⎨⎪⎧a 1=1,d =4,所以a n =4n -3.又T n +b n =3,所以T n +1+b n +1=3, 两式相减得,2b n +1-b n =0, 所以b n +1=12b n .当n =1时,T 1+b 1=3,即b 1+b 1=3,所以b 1=32.所以数列{b n }为等比数列,且首项是32,公比是12,所以b n =32×⎝⎛⎭⎫12n -1=32n .(2)因为c n =a n ·b n =3(4n -3)2n ,所以c n +1=3(4n +1)2n +1,所以c n +1-c n =3(4n +1)2n +1-3(4n -3)2n =3(7-4n )2n +1.所以当n =1时,c 2-c 1>0; 当n ≥2时,c n +1-c n <0,所以c1<c2>c3>c4>…,所以(c n)max=c2=154.。
