函数对矩阵求偏导公式

合集下载

矩阵的求导

矩阵的求导矩阵的求导是数学中的一个重要概念，它在计算机科学、物理学、经济学等领域都有广泛的应用。

矩阵求导的过程可以用来求解函数的梯度、计算机算法中的参数更新等。

本文将介绍矩阵求导的基本概念和常见方法，以及它们的应用。

我们需要明确什么是矩阵求导。

矩阵求导是指对给定的矩阵函数，计算其对矩阵自变量的导数。

矩阵求导的结果也是一个矩阵，它的每个元素都是函数对自变量的偏导数。

矩阵求导的过程可以通过链式法则和分部积法则等方法进行推导和计算。

在矩阵求导中，最常见的是对矩阵的每个元素进行求导，即所谓的元素级求导。

元素级求导是指对矩阵中的每个元素，分别对自变量求导。

这种求导方法适用于矩阵中每个元素都是独立变量的情况，比如矩阵中的每个元素都是一个标量变量。

在元素级求导中，可以使用求导规则中的加法、减法、乘法、除法等规则来计算每个元素的导数。

除了元素级求导，还有一种常见的矩阵求导方法是矩阵级求导。

矩阵级求导是指对整个矩阵作为一个整体，对自变量求导。

这种求导方法适用于矩阵中的每个元素都是函数的情况，比如矩阵中的每个元素都是一个函数。

在矩阵级求导中，可以使用矩阵的迹、行列式等运算来计算整个矩阵的导数。

在实际应用中，矩阵求导常常用于求解函数的梯度。

函数的梯度是函数在某一点的变化率，它是一个向量，其方向指向函数在该点变化最快的方向，其模表示函数在该点变化的速率。

函数的梯度在优化算法中有着广泛的应用，比如在机器学习中的梯度下降算法中，通过计算损失函数对模型参数的梯度，来更新模型参数以优化模型的性能。

矩阵求导在深度学习中也有着重要的应用。

深度学习中的神经网络通常由多个层组成，每个层都包含大量的参数，通过对参数进行求导，可以计算模型的梯度，并根据梯度进行参数的更新。

矩阵求导在深度学习中可以用来计算损失函数对模型参数的梯度，从而进行反向传播算法，实现模型的训练过程。

除了梯度计算，矩阵求导还可以用于解决约束优化问题。

约束优化问题是指在满足一定约束条件下，求解目标函数的最优解。

矩阵求导

1. 矩阵Y对标量x求导：相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导：注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)T3. 行向量Y T对列向量X求导：注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：dX T/dX = Id(AX)T/dX = A T4. 列向量Y对行向量X T求导：转化为行向量Y T对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX T = (dY T/dX)T5. 向量积对列向量X求导运算法则：注意与标量求导有点不同。

d(UV T)/dX = (dU/dX)V T + U(dV T/dX)d(U T V)/dX = (dU T/dX)V + (dV T/dX)U重要结论：d(X T A)/dX = (dX T/dX)A + (dA/dX)X T = IA + 0X T = Ad(AX)/dX T = (d(X T A T)/dX)T = (A T)T = Ad(X T AX)/dX = (dX T/dX)AX + (d(AX)T/dX)X = AX + A T X6. 矩阵Y对列向量X求导：将Y对X的每一个分量求偏导，构成一个超向量。

注意该向量的每一个元素都是一个矩阵。

7. 矩阵积对列向量求导法则：d(uV)/dX = (du/dX)V + u(dV/dX)d(UV)/dX = (dU/dX)V + U(dV/dX)重要结论：d(X T A)/dX = (dX T/dX)A + X T(dA/dX) = IA + X T0 = A8. 标量y对矩阵X的导数：类似标量y对列向量X的导数，把y对每个X的元素求偏导，不用转置。

偏导数计算公式

偏导数计算公式关于偏导数，我们可以从算法的角度进行简单的介绍。

偏导数计算公式也就是算法的表示。

偏导数可以用来指定一个变量对函数的变化率（斜率），表达式写作：$\frac{\partial y}{\partial x}$其中，y是函数，x是自变量。

如果函数的变量是w，那么表示式为：$\frac{\partial y}{\partial w}$偏导数是一种数学工具，用于衡量特定函数对特定变量的变化率。

有时，我们也称其为斜率，这种数学工具最常用于做梯度下降法，也就是minimization或优化问题。

偏导数的计算可以使用直接的微分法，也可以使用高级的数学工具，如极限法或泰勒展开。

通常，许多复杂函数的计算需要极限或泰勒展开法。

直接微分法（Direct Differentiation Method）是最常用的偏导数计算算法。

它可以获得一个复杂函数的解析解（Analytical Solution），类似于除微分几何中的画曲线，采用该法可以计算出复杂函数的偏导数。

示例：给定一个函数 y = x^2。

直接微分法求偏导数：$\frac{\partial y}{\partial x} = 2x$从这个例子可以看出，直接微分法就是根据偏导数的计算公式，通过求导的方式求得偏导数的结果。

此外，还可以使用极限法（Limit Method）和泰勒展开法（Tailor Series Expansion Method）来求取偏导数。

极限法是一种数学工具，用于计算有限的函数的极限或相似的表达式。

而泰勒展开法可以用于给定函数的一阶偏导及其多次级导数，其表示式：$\frac{\partial^n f(x)}{\partial x^n} = \sum_{k=0}^n\frac{f^{(k)}(x_0)}{k!}\binom{n}{k} (x-x_0)^k$其中，k为自变量x的取值，n为$f^{(k)}(x_0)$阶数，x为自变量x的新取值，$x_0$表示自变量x初始取值。

矩阵求导的一些公式

.在网上看到有人贴了如下求导公式：Y = A * X --> DY/DX = A'Y = X * A --> DY/DX = AY = A' * X * B --> DY/DX = A * B'Y = A' * X' * B --> DY/DX = B * A'于是把以前学过的矩阵求导部分整理一下：1. 矩阵Y对标量x求导：相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导：注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'3. 行向量Y'对列向量X求导：注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导：转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则：注意与标量求导有点不同。

d(UV')/dX = (dU/dX)V' + U(dV'/dX)d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'重要结论：d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = A.d(AX)/dX' = (d(X'A')/dX)' = (A')' = Ad(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X6. 矩阵Y对列向量X求导：将Y对X的每一个分量求偏导，构成一个超向量。

矩阵求导公式

转载]矩阵求导公式【转】(2011-11-15 11:03:34)转载▼标签：转载原文地址：矩阵求导公式【转】作者：三寅今天推导公式，发现居然有对矩阵的求导，狂汗--完全不会。

不过还好网上有人总结了。

吼吼，赶紧搬过来收藏备份。

基本公式：Y = A * X --> DY/DX = A'Y = X * A --> DY/DX = AY = A' * X * B --> DY/DX = A * B'Y = A' * X' * B --> DY/DX = B * A'1. 矩阵Y对标量x求导：相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导：注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'3. 行向量Y'对列向量X求导：注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导：转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则：注意与标量求导有点不同。

d(UV')/dX = (dU/dX)V' + U(dV'/dX)d(U'V)/dX = (dU'/dX)V + (dV'/dX)U'重要结论：d(X'A)/dX = (dX'/dX)A + (dA/dX)X' = IA + 0X' = Ad(AX)/dX' = (d(X'A')/dX)' = (A')' = Ad(X'AX)/dX = (dX'/dX)AX + (d(AX)'/dX)X = AX + A'X6. 矩阵Y对列向量X求导：将Y对X的每一个分量求偏导，构成一个超向量。

矩阵求导定义

矩阵求导定义矩阵求导定义矩阵求导是一种非常有用的数学工具，它可以帮助人们在各种数学问题中更加快速和方便地解决问题。

矩阵求导的定义可以简单地表示为：对于一个矩阵函数f(x)，其导数矩阵df(x)/dx可以表示为：df(x)/dx = lim(h→0) [f(x+h)-f(x)]/h其中，x表示一个行向量，h表示一个标量，df(x)/dx是一个矩阵，f(x+h)和f(x)都是和x大小相同的矩阵。

矩阵求导的基本规则在矩阵求导的过程中，有一些基本规则需要遵守，这些规则包括：①线性性：若f(x)和g(x)是两个矩阵函数，a和b分别为标量，则有：d[a*f(x)+b*g(x)]/dx = a*df(x)/dx + b*dg(x)/dx②乘法规则：若f(x)和g(x)是两个矩阵函数，则有：d[f(x)*g(x)]/dx = df(x)/dx*g(x) + f(x)*dg(x)/dx③转置规则：若f(x)是一个矩阵函数，则有：d[f(x)']/dx = (df(x)/dx)'④逆矩阵规则：若f(x)是一个可逆的矩阵函数，则有：d[f(x)^-1]/dx = -f(x)^-1*(df(x)/dx)*f(x)^-1应用实例矩阵求导可以在各种数学问题中得到应用，以下是一些实例：1、矩阵优化问题：矩阵求导可以在矩阵优化问题中得到广泛应用，例如，在机器学习模型的训练过程中，使用梯度下降算法优化损失函数，需要对损失函数求导得到梯度。

2、协方差矩阵的求导：在数据分析领域中，协方差矩阵常常被用来描述不同变量之间的关系。

矩阵求导可以在计算协方差矩阵的导数时得到应用。

3、矩阵微积分学：矩阵微积分学是一门关于矩阵导数和积分的学科，矩阵求导是其中非常重要的一部分。

结语矩阵求导是一个非常有用的数学工具，它可以帮助人们在各种数学问题中更加快速和方便地解决问题。

在应用矩阵求导的过程中，需要遵守基本规则，同时还需要理解它的应用实例。

矩阵求导(本质、原理与推导)详解

矩阵求导(本质、原理与推导)详解1.引言矩阵求导是数学分析中重要的一部分，广泛应用于机器学习、数据挖掘和优化问题中。

本文将介绍矩阵求导的本质、原理以及推导过程，为读者提供一个比较全面的了解。

2.矩阵的本质及相关概念在矩阵求导前，我们需要先了解矩阵的本质及相关概念。

矩阵是一个按照规律排列的方阵，其中每个元素通常是实数或者复数。

以$n$行$m$列的矩阵$A$为例，可以表示为：$$A=\begin{bmatrix}a_{1,1}&a_{1,2}&\cdots&a_{1,m}\\a_{2,1}&a_{2,2}&\cdots&a_{2,m}\\\vdots&\vdots&\ddots&\vdots\\a_{n,1}&a_{n,2}&\cdots&a_{n,m}\\\end{bmatrix}$$其中$a_{i,j}$表示矩阵$A$中第$i$行第$j$列的元素。

矩阵还有一些相关的概念，如矩阵的转置、逆矩阵、伴随矩阵等等，这里不一一赘述。

3.标量函数对向量、矩阵的导数在开始矩阵求导之前，我们需要先了解标量函数对向量或矩阵的导数。

设矩阵$A$是一个$m\times n$的矩阵，$x$是一个$n \times1$的向量，函数$f(x)$将$x$映射为一个标量。

我们定义$f(x)$对$x$的导数为：$$\frac{\partial f(x)}{\partial x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}&\frac{\partial f(x)}{\partial x_2}&\cdots&\frac{\partial f(x)}{\partial x_n}\end{bmatrix}$$其中每一项$\frac{\partial f(x)}{\partial x_i}$表示$f(x)$对$x_i$的偏导数。

向量、矩阵偏导数(机器学习、深度学习基础)

矩阵的导数运算1. 矩阵Y=F(x )对标量x 求导相当于每个元素求导数 111122212212()()()()()()()()()n n m m mn df x df x df x dx dx dx df x df x df x d dx dx dx dx df x df x df x dxdx dx ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦Y 2. 标量y 对列向量x 求导注意与上面不同，这次括号内是求偏导，对m×1向量求导后还是m×1向量 12()m f x f dy x y f d f x ∂⎡⎤⎢⎥∂⎢⎥∂⎢⎥⎢⎥∂=→=⎢⎥⎢⎥⎢⎥∂⎢⎥⎢⎥∂⎣⎦x x3. 行向量y T 对列向量x 求导注意1×n 向量对m×1向量求导后是m×n 矩阵。

将y 的每一列对x 求偏导，将各列构成一个矩阵。

121111222212()()()()()()()()()n n T n mm m f x f x f x x x x f x f x f x d x x x d f x f x f x x x x ∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥∂⎢∂∂⎥⎢⎥∂∂∂=⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦y x 重要结论： ()TT Td d d d ==x I x Ax A x4. 列向量y 对行向量x T 求导转化为行向量y T 对列向量x 的导数，然后转置。

注意m×1向量对1×n 向量求导结果为m×n 矩阵。

121111222212()()()()()()()()()Tm T m T T m nn n f x f x f x x x x f x f x f x d d x x x d d f x f x f x x x x ∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥∂⎢∂∂⎥⎛⎫⎢⎥∂∂∂== ⎪⎢⎥⎝⎭⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦y y x x 重要结论： ()T Td d d d ==x I x Ax A x5. 向量积对列向量x 求导运算法则注意与标量求导有点不同。

矩阵微积分

在网上看到有人贴了如下求导公式：Y = A * X --> DY/DX = A'Y = X * A --> DY/DX = AY = A' * X * B --> DY/DX = A * B'Y = A' * X' * B --> DY/DX = B * A'于是把以前学过的矩阵求导部分整理一下：1. 矩阵Y对标量x求导：相当于每个元素求导数后转置一下，注意M×N矩阵求导后变成N×M了Y = [y(ij)] --> dY/dx = [dy(ji)/dx]2. 标量y对列向量X求导：注意与上面不同，这次括号内是求偏导，不转置，对N×1向量求导后还是N×1向量y = f(x1,x2,..,xn) --> dy/dX = (Dy/Dx1,Dy/Dx2,..,Dy/Dxn)'3. 行向量Y'对列向量X求导：注意1×M向量对N×1向量求导后是N×M矩阵。

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导：转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则：注意与标量求导有点不同。

矩阵方程求导

矩阵方程求导矩阵方程是一种常用的求解数学问题的方法，它可以帮助我们求解复杂的数学模型。

本文主要讨论如何求解矩阵方程的导数，以及矩阵方程求导的一些重要原理。

1.阵方程求导的基础知识在求解矩阵方程的导数之前，我们需要了解一些基础知识，包括：（1）关于矩阵的定义：一个K×L的矩阵是一个拥有K行和L列的矩阵，元素Aij表示第i行第j列的元素。

（2）关于矩阵的运算：矩阵的运算是指矩阵的加减乘除以及幂次运算等。

（3）关于矩阵的逆：矩阵的逆是一个K×K的矩阵，此矩阵的元素和原来的矩阵相乘后得到单位矩阵。

（4）关于矩阵的转置：矩阵的转置就是把原矩阵的行变成列，列变成行，所以比如原来Aij变成Aji后。

2.阵方程求导的基本原理矩阵方程求导的基本原理是通过使用链式法则，利用矩阵求导的性质来求得每个变量的偏导数。

首先，需要将矩阵方程化为一个通用的一元函数，然后使用微积分的链式法则来求导，最后将其根据矩阵中的变量进行分解，也就是求出每个变量偏导数。

这里需要了解到，矩阵的偏导数是指在矩阵中某一元素的变化让函数值发生变化时，此元素对函数值变化的影响程度。

简言之，就是矩阵偏导数反应了函数中变量对函数值变化的影响程度。

3.阵求导的一些特殊情况除了矩阵的偏导数的求解外，在求解矩阵的导数过程中还有一些特殊情况，它们如下列出：（1）如果函数是一个非矩阵函数，那么它的矩阵导数就是零矩阵。

（2）如果矩阵是一个对称矩阵，那么它的导数将是一个只有对称元素的对称矩阵。

（3）如果函数是一个向量函数，那么它的矩阵导数就是一个与向量函数的大小相同的矩阵。

（4）如果函数是一个多项式，那么它的矩阵导数就是一个与多项式的阶数相同的矩阵。

（5）如果函数是一个向量函数，那么它的矩阵导数就是一个向量乘以它的函数矩阵所得到的矩阵。

4.论本文介绍了矩阵方程求导的基础知识，基本原理以及一些特殊情况，也就是如何正确地运用链式法则和矩阵的求导性质来求得矩阵方程的导数。

矩阵范数和矩阵求导

矩阵范数和矩阵求导今天发现两篇宝藏⽂章，关于矩阵范数和矩阵求导的，转载收藏⼀下。

感谢⼤佬们的分享！{抱拳}矩阵范数转载⾃：今天看了半天强化学习，看得很不开⼼。

因为⼀直处于懵圈状态。

于是乎不想看了，稍微总结⼀下矩阵范数的求解来放松⼀下⾝⼼吧~这⾥总结的矩阵范数主要是F 范数、1范数、2范数、核范数以及全变分TV 范数与1、2的搭配1、F 范数概念：矩阵各个元素平⽅和开根，概念上⾮常像向量的L2范数导数：求导的⽅法则是将其展开来，⼀般情况下我们不会直接求原始的范数||A||F ，因为很⿇烦，即使是在损失函数中也是⽤F 范数的平⽅项来简化运算，⽽常见的损失函数⼀般是，此时对X 求导，则需要将内部的Y-X 展开来，所以对中X 求导即为 2、1范数概念：║A ║1 = max{ ∑|ai1|, ∑|ai2| ,…… ,∑|ain| } (列和范数，A 每⼀列元素绝对值之和的最⼤值)　(其中∑|ai1|第⼀列元素绝对值的和∑|ai1|=|a11|+|a21|+…+|an1|,其余类似)；矩阵的1范数和向量的1范数雷同，不能直接求解，只能分情况讨论求导：常规的L1范数的求导是在损失函数中作为正则项出现，即，这⾥前半部分求导是，后半部分则需要分情况讨论，最终结果为为3、2范数概念：指的是A 最⼤的奇异值或者半正定矩阵A*A 最⼤特征值开根求导：对于问题存在近似解4、TV 范数概念：全变分范数，其实就是对矩阵乘上⼀个⼀阶的差分矩阵，乘完还是个矩阵，所以要⼀般要结合前边的1范数或者2范数再对其进⾏约束求解5、核范数概念：即矩阵奇异值的和求解：对于存在近似解表⽰这⾥, . , 和分别是<script type="math/tex" id="MathJax-Element-1851">M</script>的左奇异向量、右奇异向量和奇异值（markdown 模式下可以⽤latex 写东西真的太⽅便了= =⾄于各个范数的效果，实质上1范数和2范数在矩阵分解上效果差得不多，基本上2范数能分离出的⾼频成分1范数能更快的分离出来，在⼀维层⾯上也容易想想，1范数相⽐2范数能够更快的收敛（直指坐标中⼼），核范数效果对低频成分的提取也⽐TV_1/TV_2范数的效果要好很多。

常用矩阵导数公式

常⽤矩阵导数公式1 矩阵$Y=f(x)$对标量x求导矩阵Y是⼀个$m\times n$的矩阵，对标量x求导，相当于矩阵中每个元素对x求导\[\frac{dY}{dx}=\begin{bmatrix}\dfrac{df_{11}(x)}{dx} & \ldots & \dfrac{df_{1n}(x)}{dx} \\ \vdots & \ddots &\vdots \\ \dfrac{df_{m1}(x)}{dx} & \ldots & \dfrac{df_{mn}(x)}{dx} \end{bmatrix}\]2 标量y=f(x)对矩阵X求导注意与上⾯不同，这次括号内是求偏导，$X$是是⼀个$m\times n$的矩阵，函数$y=f(x)$对矩阵$X$中的每个元素求偏导，对$m\times n$矩阵求导后还是$m\times n$矩阵\[\frac{dy}{dX} = \begin{bmatrix}\dfrac{\partial f}{\partial x_{11}} & \ldots & \dfrac{\partial f}{\partial x_{1n}}\\ \vdots & \ddots & \vdots\\\dfrac{\partial f}{\partial x_{m1}} & \ldots & \dfrac{\partial f}{\partial x_{mn}}\end{bmatrix}\]3 函数矩阵Y对矩阵X求导矩阵$Y=F(x)$对每⼀个$X$的元素求导，构成⼀个超级矩阵\[F(x)=\begin{bmatrix}f_{11}(x) & \ldots & f_{1n}(x)\\ \vdots & \ddots &\vdots \\ f_{m1}(x) & \ldots & f_{mn}(x) \end{bmatrix}\]\[X=\begin{bmatrix}x_{11} & \ldots & x_{1s}\\ \vdots & \ddots &\vdots \\ x_{r1} & \ldots & x_{rs}\end{bmatrix}\]\[\frac{dF}{dX} = \begin{bmatrix}\dfrac{\partial F}{\partial x_{11}} & \ldots & \dfrac{\partial F}{\partial x_{1s}}\\ \vdots & \ddots & \vdots\\\dfrac{\partial F}{\partial x_{r1}} & \ldots & \dfrac{\partial F}{\partial x_{rs}}\end{bmatrix}\]其中\[\frac{\partial F}{\partial x_{ij}} = \begin{bmatrix}\dfrac{\partial f_{11}}{\partial x_{ij}} & \ldots & \dfrac{\partial f_{1n}}{\partial x_{ij}}\\ \vdots & \ddots & \vdots \\\dfrac{\partial f_{m1}}{\partial x_{ij}} & \ldots & \dfrac{\partial f_{mn}}{\partial x_{ij}}\end{bmatrix}\]4 向量导数若$m\times 1$向量函数$y=[y_1,y_2,…,y_m]^T$,其中，$y_1,y_2,…,y_m$是向量的标量函数。

向量、矩阵偏导数(机器学习、深度学习基础)

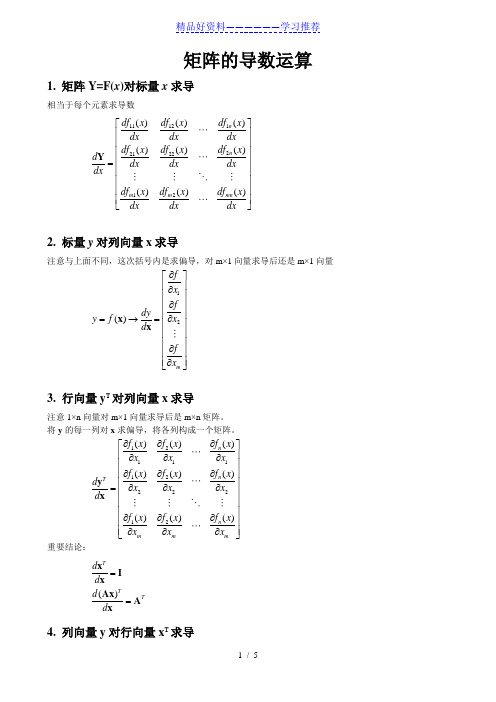
矩阵的导数运算1. 矩阵Y=F(x )对标量x 求导相当于每个元素求导数111122212212()()()()()()()()()n n m m mn df x df x df x dx dx dx df x df x df x d dx dx dx dx df x df x df x dxdx dx ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦Y2. 标量y 对列向量x 求导注意与上面不同，这次括号内是求偏导，对m×1向量求导后还是m×1向量12()m f x f dy x y f d f x ∂⎡⎤⎢⎥∂⎢⎥∂⎢⎥⎢⎥∂=→=⎢⎥⎢⎥⎢⎥∂⎢⎥⎢⎥∂⎣⎦x x3. 行向量y T 对列向量x 求导注意1×n 向量对m×1向量求导后是m×n 矩阵。

将y 的每一列对x 求偏导，将各列构成一个矩阵。

121111222212()()()()()()()()()n n Tn mmm f x f x f x xx x f x f x f x d x x x d f x f x f x x x x ∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥∂⎢∂∂⎥⎢⎥∂∂∂=⎢⎥⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦yx重要结论：()TTTd d d d ==x I xAx A x4. 列向量y 对行向量x T 求导转化为行向量y T 对列向量x 的导数，然后转置。

注意m×1向量对1×n 向量求导结果为m×n 矩阵。

121111222212()()()()()()()()()Tm Tm T T m nnn f x f x f x xx x f x f x f x d d x x x d d f x f x f x x x x ∂∂∂⎡⎤⎢⎥∂∂∂⎢⎥∂⎢∂∂⎥⎛⎫⎢⎥∂∂∂== ⎪⎢⎥⎝⎭⎢⎥⎢⎥∂∂∂⎢⎥⎢⎥∂∂∂⎣⎦y y x x重要结论：()TTd d d d ==xI x Ax A x5. 向量积对列向量x 求导运算法则注意与标量求导有点不同。

矩阵转置乘积求偏导的运算

矩阵转置乘积求偏导的运算说到矩阵转置乘积求偏导这事儿，哎呀，很多同学一听到这个，就感觉要被数学这座大山压垮了。

别急，慢慢来，放轻松。

其实这东西嘛，听起来挺复杂，但说白了，就是矩阵和它的转置之间的一点小互动，没什么大不了的。

你想啊，矩阵转置就好像是你拿了一面镜子，看着自己的一模一样，然而，你的每一个动作、每一个细节都反射在镜子里。

矩阵乘积也是个差不多的道理。

两者结合起来，等于一个特别精妙的组合。

关键是求偏导的时候，弄清楚这两个对象之间的关系，搞明白了，哎，什么都不难！不过啊，偏导这个东西，表面上看，似乎就是给你一个公式，要求你对某个元素求导，结果你就直接算出来。

但是，嘿，你要是不仔细，那矩阵的那些奇奇怪怪的规则和行列的排列组合一下子就能让你蒙圈。

你有没有想过，矩阵本身就是个“合成怪”，它其实就是好多行和列的“孩子们”聚在一起。

想象一下，你家的孩子们一起组队，结果他们乱成一团。

可你呢，不知道该怎么给他们“分配任务”——就是要找出最合适的方式，去分析它们之间的“亲密关系”。

矩阵转置乘积求偏导这事儿其实就像一场小小的“亲子游戏”。

你得先理解“爸爸”和“妈妈”分别是谁，“转置”和“乘积”在这场游戏里扮演的角色是什么。

每个元素的偏导，就相当于是“爸爸”和“妈妈”之间的互动。

你算出来的偏导，其实就是那对父母在这场合作中各自的“功劳”。

当你把转置和乘积两个操作放在一起，哎呀，数学的美感就出来了。

整个过程看似复杂，实际是一层一层的拼图，拆开一看，原来是这么简单。

还有一点特别有意思，就是你算偏导时，常常会碰到矩阵运算的那些小技巧。

比如啊，转置运算往往跟乘积的顺序不太一样。

想想，如果你把两个矩阵按顺序相乘，然后再做转置，那就得小心了。

因为它和先做转置再乘这两种操作的顺序可完全不同，搞不好顺序不对，整个结果就乱了套。

就像你给人做个煎蛋，结果先打蛋再炒菜，可能弄得一团糟，打蛋是为了让菜更好吃，可顺序错了，根本吃不到好味道。

矩阵求导的定义

矩阵求导的定义
矩阵求导是指对一个矩阵函数进行求导的操作。

在矩阵求导中，我们将矩阵视为一个整体，而不是将其看作是一组数值的集合。

矩阵求导的定义如下：
设 $F$ 是一个从 $n$ 维实向量空间 $V$ 到 $m$ 维实向量空
间 $W$ 的映射，$F(x)$ 是其对应的矩阵函数。

如果存在一个 $m times n$ 的矩阵 $A$，使得对于所有的 $x in V$，有
$$
lim_{|h| to 0} frac{|F(x+h)-F(x)-Ah|}{|h|} = 0
$$
则称 $F$ 在 $x$ 处可导，且其导数为 $A$，记作 $F'(x)=A$。

其中，$| cdot |$ 表示向量的模，即 $| x | = sqrt{x_1^2 + x_2^2 + cdots + x_n^2}$。

需要注意的是，矩阵求导与标量求导有很大的不同。

在标量求导中，导数表示的是函数的斜率，而在矩阵求导中，导数表示的是函数在某个点的线性近似。

此外，矩阵求导也与矩阵微积分密切相关，可以应用于机器学习、优化等领域。

- 1 -。

h矩阵求导的一些公式

将Y的每一列对X求偏导，将各列构成一个矩阵。

重要结论：dX'/dX = Id(AX)'/dX = A'4. 列向量Y对行向量X’求导：转化为行向量Y’对列向量X的导数，然后转置。

注意M×1向量对1×N向量求导结果为M×N矩阵。

dY/dX' = (dY'/dX)'5. 向量积对列向量X求导运算法则：注意与标量求导有点不同。

矩阵求导法则范文

矩阵求导法则范文矩阵求导是微积分中的一个重要概念，它在许多数学和工程问题中都有应用。

矩阵求导法则是指用于计算矩阵求导的一系列规则和定理，这些法则包括向量对向量的求导法则、矩阵对标量的求导法则、矩阵对矩阵的求导法则等。

下面将详细介绍这些法则。

1.向量对向量的求导法则：假设有一个向量函数u关于向量x的导数。

那么，u关于x的导数是一个由偏导数所构成的矩阵，其中矩阵的第(i,j)个元素表示u的第i个分量关于x的第j个分量的偏导数。

这个矩阵被称为Jacobian矩阵。

2.矩阵对标量的求导法则：假设有一个矩阵A和一个标量x。

那么，A对x的导数是一个和矩阵A大小相同的矩阵，其中每个元素都等于x对A相应元素的偏导数。

3.矩阵对矩阵的求导法则：(a)矩阵对矩阵相加或相减的导数等于它们分别对应元素的导数之和或之差。

(b)矩阵对矩阵乘法的导数等于矩阵对应元素的导数之和。

(c)矩阵对矩阵的转置的导数等于该矩阵对应元素的导数的转置。

4.标量对矩阵的求导法则：(a)标量对矩阵的和或差的导数等于标量对应元素的导数之和或之差。

(b)标量对矩阵的乘积的导数等于标量与矩阵的转置的乘积。

5.矩阵的逆的导数：假设矩阵A可逆，那么A的逆对A的导数等于负的A逆与A的导数的乘积。

6.逆矩阵导数的链式法则：假设矩阵A是一个可逆的函数，B是一个可微分的函数，那么(A的逆乘以A)对B的导数等于(A的逆对A的导数)乘以B对A的导数。

7.矩阵行列式的微分法：假设矩阵A是一个可微分的函数，那么矩阵A的行列式对A的导数等于矩阵A的行列式乘以A的逆的转置。

以上是矩阵求导法则的一些基本规则和定理，它们在矩阵微积分中起着重要的作用。

矩阵求导法则不仅在数学领域被广泛应用，而且在机器学习、统计学和信号处理等领域也有重要的应用。

通过应用这些法则，我们可以更方便地求解矩阵函数的导数，从而解决各种数学和工程问题。