2017年江苏高考附加题及答案

合集下载

江苏2017高考语文试题及答案

2017年普通高等学校招生全国统一考试（江苏卷）语文I一、语言文字运用（15分）1．在下面一段话的空缺处依次填入词语，最恰当的一组是（3分）刺绣画艺术，就是以绘画为稿本，以针黹、缣帛为绣材的艺术再创作。

在其传承与发展过程中，无数绣娘以的工匠精神，创作出令人的作品。

它们或如摄影写实，或如油画般立体，或姿态婀娜，或设色古雅，可谓争奇斗艳，。

A．精益求精耳目一新美不胜收B．励精求治刮目相看美不胜收C．精益求精刮目相看数不胜数D．励精求治耳目一新数不胜数2．下列语句中，没有使用比喻手法的一项是（3分）A．“一带一路”是我国推动经济全球化而提出的一项互利共赢的倡议，它已成为推动全球经济转型升级、走出衰退困境的新引擎。

B．气象部门预计，随着暖湿气流增强，我省明天会迎来一场及时雨，空气中污染物浓度将快速下降，人们的舒适度会大幅度提升。

C．一种突如其来的网络病毒洪水猛兽般地袭击全球，导致150多个国家受灾，我国也有近3万家机构的计算机受到影响。

D．我国企业在参与发展中国家的基础设施建设过程中，主动强化环保意识，积极承担社会责任，带动了东道主在观念上弯道超车。

3．下列对联中，适合悬挂在杜甫草堂的一组是（3分）①为闻庐岳多真隐别有天地非人间②十年幕府悲秦月一卷唐诗补蜀风③狂到世人皆欲杀醉来天子不能呼④秋天一鹄先生骨春水群鸥野老心A．①③B．①④C．②③D．②④4．在下面一段文字横线处填入语句，衔接最恰当的一项是（3分）一个人在创作和欣赏时所表现的趣味，大半由资禀性情、身世经历和传统习尚三个因素决定。

，，。

这三层功夫就是通常所谓的学问修养，而纯正的趣味必定是学问修养的结果。

①它们的影响有好有坏②我们应该根据固有的资禀性情而加以磨砺陶冶③接收多方的传统习尚而融会贯通④这三者都是很自然地套在一个人的身上的⑤不易也不必完全摆脱⑥扩充身世经历而加以细心体验A．②③⑥④①⑤B．②⑥③④⑤①C．④①⑤②⑥③D．④⑤①②③⑥5．下列诗句中，与右图漫画的情境最吻合的一项是（3分）A．小梅香里黄莺啭，垂柳阴中白马嘶。

2017年江苏省语文高考试卷及答案(含附加题)

2017年普通高等学校招生统一考试(江苏卷)语文I试题一、语言文字运用（15分）1．在下面一段话的空缺处依次填入词语，最恰当的一组是：（A）（3分）刺绣画艺术，就是以绘画为稿本，以针黹、缣帛为绣材的艺术再创作。

在其传承与发展过程中，无数绣娘以的工匠精神，创作出令人的作品。

它们或如摄影般写实，或如油画般立体，或姿态婀娜，或设色古雅，可谓争奇斗艳，。

A、精益求精，耳目一新，美不胜收B、励精求治，刮目相看，美不胜收C、精益求精，刮目相看，数不胜数D、励精求治耳目一新数不胜数2．下列语句中，没有使用比喻手法的一项是：（B）（3分）A、“一带一路”是我国为推动经济全球化而提出的一项互利共赢的倡议，它已成为推动全球经济转型升级、走出衰退困境的新引擎。

B、气象部门预计，随着暖湿气流增强，我省明天会迎来一场及时雨，空气中污染物浓度将快速下降，人们的舒适度会大幅度提升。

C、一种突如其来的网络病毒洪水猛兽般地袭击全球，导致150多个国家受灾，我国也有近3万家机构的计算机受到影响。

D、我国企业在参与发展中国家的基础设施建设过程中，主动强化环保意识，积极承担社会责任，带动了东道国在观念上弯道超车。

3．下列对联中，适合悬挂在杜甫草堂的一组是：（D）（3分）①为闻庐岳多真隐别有天地非人间②十年幕府悲秦月一卷唐诗补蜀风③狂到世人皆欲杀醉来天子不能呼④秋天一鹄先生骨春水群鸥野老心A、①③B、①④C、②③D、②④4．在下面一段文字横线处填入语句，衔接最恰当的一项是：（C ）（3分）一个人在创作和欣赏时所表现的趣味，大半由资禀性情、身世经历和传统习尚三个因素决定。

，，。

这三层功夫就是通常所谓的学问修养，而纯正的趣味必定是学问修养的结果。

①它们的影响有好有坏②我们应该根据固有的资禀性情而加以磨砺陶冶③接收多方的传统习尚而融会贯通④这三者都是很自然地套在一个人的身上的⑤不易也不必完全摆脱⑥扩充身世经历而加以细心地体验A、②③⑥④①⑤B、②⑥③④⑤①C、④①⑤②⑥③D、④⑤①②③⑥5．下列诗句中，与右图漫画的情境最吻合的一项是：（D）（3分）A、小梅香里黄莺啭，垂柳阴中白马嘶。

江苏高考语文附加题

一、阅读文言文材料，完成19～21题。

(10分)19．用斜线“/”给下面画线的文言文断句。

（限6处）（6分）阳明子曰，求圣人之学而弗成者殆以志之弗立欤天下之人志轮而轮焉志裘而裘焉志巫医而巫医焉志其事而弗成者，吾未之见也。

轮、裘、巫医遍天下，求圣人之学者间数百年而弗一二见，为其事之难欤？亦其志之难欤？弗志其事而能有成者，吾亦未之见也。

（节选自《王阳明全集》行知录之三）求圣人之学而弗成者/殆以志之弗立欤/天下之人/志轮而轮焉/志裘而裘焉/志巫医而巫医焉/志其事而弗成者20．王阳明是中国哪个朝代最著名的思想家、哲学家、文学家和军事家？是什么学说的集大成者？（2分）明代，陆王心学（心学）21．作者认为怎数百年难有成就圣人之学的原因是什么？请用自己的话回答。

求学之路艰难，树立求学的志向更难（2分）二、名著阅读题（15分）22．下面对有关名著名篇的说明，不正确．．．的两项是（5分）A．《边城》中的人物勤劳善良，纯朴可爱。

老船夫忠于职守，对过河人分文不收。

船总顺顺常常体恤穷苦人，老船夫死后，他资助并组织安排料理丧事。

表现出仁厚、纯朴的民俗、乡风。

B．《哈姆莱特》中安排剑术高超的雷欧提斯与哈姆莱特比剑，让雷欧提斯偷偷换上利剑，并且准备好毒酒庆祝哈姆莱特胜利，双管齐下，确保杀死哈姆莱特，这是戏剧矛盾冲突的高潮。

C．《红楼梦》第二十七回黛玉去怡红院访宝玉，因晴雯不开门，而闷闷不乐。

又看见宝玉送宝钗出来，触动了寄人篱下的凄凉心境，于是因满地落花勾起无限伤春愁思，感花伤己，含泪葬花。

D．《家》中的觉民性格温和稳健，不爱参加社会活动。

但作为五四新思潮唤醒的年轻一代，也向往民主自由，当祖父为他包办婚姻时，他毅然离家出走，和琴成为小说中唯一一对胜利者。

E．《凤凰涅槃》中凤凰自焚前，它们回旋低昂起舞，共同歌唱。

凡鸟应声而和，鞭挞了现实中的丑恶和庸俗的同时，进一步赞美凤凰自焚的悲壮和辉煌。

C．应是袭人不开门。

E．凡鸟讥讽和嘲弄，反衬了凤凰的沉痛和壮美。

2017年江苏数学高考试卷含答案和解析

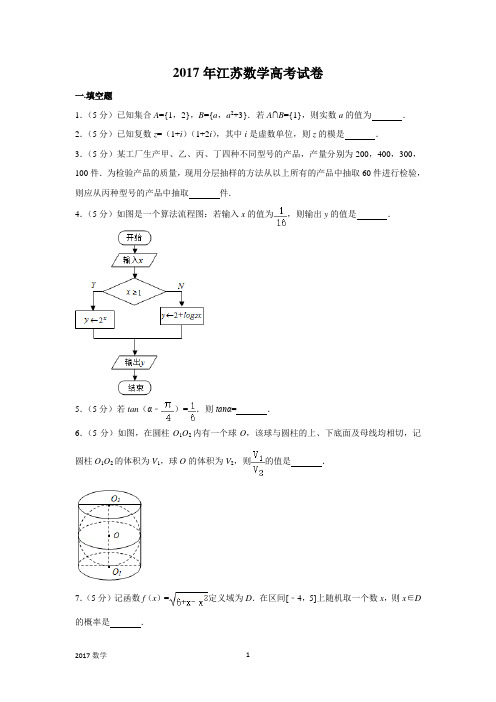
2017年江苏数学高考试卷一.填空题1．（5分）已知集合A={1，2}，B={a，a2+3}．若A∩B={1}，则实数a的值为．2．（5分）已知复数z=（1+i）（1+2i），其中i是虚数单位，则z的模是．3．（5分）某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取件．4．（5分）如图是一个算法流程图：若输入x的值为，则输出y的值是．5．（5分）若tan（α﹣）=．则tanα=．6．（5分）如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．7．（5分）记函数f（x）=定义域为D．在区间[﹣4，5]上随机取一个数x，则x∈D 的概率是．8．（5分）在平面直角坐标系xOy中，双曲线﹣y2=1的右准线与它的两条渐近线分别交于点P，Q，其焦点是F1，F2，则四边形F1PF2Q的面积是．9．（5分）等比数列{a n}的各项均为实数，其前n项为S n，已知S3=，S6=，则a8=．10．（5分）某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是．11．（5分）已知函数f（x）=x3﹣2x+e x﹣，其中e是自然对数的底数．若f（a﹣1）+f（2a2）≤0．则实数a的取值范围是．12．（5分）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且ta nα=7，与的夹角为45°．若=m+n（m，n∈R），则m+n=．13．（5分）在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2=50上．若≤20，则点P的横坐标的取值范围是．14．（5分）设f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）=，其中集合D={x|x=，n∈N*}，则方程f（x）﹣lgx=0的解的个数是．二.解答题15．（14分）如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．16．（14分）已知向量=（cosx，sinx），=（3，﹣），x∈[0，π]．（1）若∥，求x的值；（2）记f（x）=，求f（x）的最大值和最小值以及对应的x的值．17．（14分）如图，在平面直角坐标系xOy中，椭圆E：=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为，两准线之间的距离为8．点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2．（1）求椭圆E的标准方程；（2）若直线l1，l2的交点Q在椭圆E上，求点P的坐标．18．（16分）如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．19．（16分）对于给定的正整数k，若数列{a n}满足：a n﹣k+a n﹣k+1+…+a n﹣1+a n+1+…a n+k﹣+a n+k=2ka n对任意正整数n（n＞k）总成立，则称数列{a n}是“P（k）数列”．1（1）证明：等差数列{a n}是“P（3）数列”；（2）若数列{a n}既是“P（2）数列”，又是“P（3）数列”，证明：{a n}是等差数列．20．（16分）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．二.非选择题，附加题（21-24选做题）【选修4-1：几何证明选讲】（本小题满分0分）21．如图，AB为半圆O的直径，直线PC切半圆O于点C，AP⊥PC，P为垂足．求证：（1）∠P AC=∠CAB；（2）AC2 =AP•AB．[选修4-2：矩阵与变换]22．已知矩阵A=，B=．（1）求AB；（2）若曲线C1：=1在矩阵AB对应的变换作用下得到另一曲线C2，求C2的方程．[选修4-4：坐标系与参数方程]23．在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），曲线C的参数方程为（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．［选修4-5：不等式选讲］24．已知a，b，c，d为实数，且a2+b2=4，c2+d2=16，证明ac+bd≤8．【必做题】25．如图，在平行六面体ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1=，∠BAD=120°．（1）求异面直线A1B与AC1所成角的余弦值；（2）求二面角B﹣A1D﹣A的正弦值．26．已知一个口袋有m个白球，n个黑球（m，n∈N*，n≥2），这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…，m+n的抽屉内，其中第k次取出的球放入编号为k的抽屉（k=1，2，3，…，m+n）．1 2 3 …m+n（1）试求编号为2的抽屉内放的是黑球的概率p；（2）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数，E（X）是X的数学期望，证明E（X）＜．2017年江苏高考数学参考答案与试题解析一.填空题1．（5分）（2017•江苏）已知集合A={1，2}，B={a，a2+3}．若A∩B={1}，则实数a的值为1．【分析】利用交集定义直接求解．【解答】解：∵集合A={1，2}，B={a，a2+3}．A∩B={1}，∴a=1或a2+3=1，解得a=1．故答案为：1．【点评】本题考查实数值的求法，是基础题，解题时要认真审题，注意交集定义及性质的合理运用．2．（5分）（2017•江苏）已知复数z=（1+i）（1+2i），其中i是虚数单位，则z的模是．【分析】利用复数的运算法则、模的计算公式即可得出．【解答】解：复数z=（1+i）（1+2i）=1﹣2+3i=﹣1+3i，∴|z|==．故答案为：．【点评】本题考查了复数的运算法则、模的计算公式，考查了推理能力与计算能力，属于基础题．3．（5分）（2017•江苏）某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取18件．【分析】由题意先求出抽样比例即为，再由此比例计算出应从丙种型号的产品中抽取的数目．【解答】解：产品总数为200+400+300+100=1000件，而抽取60辆进行检验，抽样比例为=，则应从丙种型号的产品中抽取300×=18件，故答案为：18【点评】本题的考点是分层抽样．分层抽样即要抽样时保证样本的结构和总体的结构保持一致，按照一定的比例，即样本容量和总体容量的比值，在各层中进行抽取．4．（5分）（2017•江苏）如图是一个算法流程图：若输入x的值为，则输出y的值是﹣2．【分析】直接模拟程序即得结论．【解答】解：初始值x=，不满足x≥1，所以y=2+log2=2﹣=﹣2，故答案为：﹣2．【点评】本题考查程序框图，模拟程序是解决此类问题的常用方法，注意解题方法的积累，属于基础题．5．（5分）（2017•江苏）若tan（α﹣）=．则tanα=．【分析】直接根据两角差的正切公式计算即可【解答】解：∵tan（α﹣）===∴6tanα﹣6=tanα+1，解得tanα=，故答案为：．【点评】本题考查了两角差的正切公式，属于基础题6．（5分）（2017•江苏）如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．【分析】设出球的半径，求出圆柱的体积以及球的体积即可得到结果．【解答】解：设球的半径为R，则球的体积为：R3，圆柱的体积为：πR2•2R=2πR3．则==．故答案为：．【点评】本题考查球的体积以及圆柱的体积的求法，考查空间想象能力以及计算能力．7．（5分）（2017•江苏）记函数f（x）=定义域为D．在区间[﹣4，5]上随机取一个数x，则x∈D的概率是．【分析】求出函数的定义域，结合几何概型的概率公式进行计算即可．【解答】解：由6+x﹣x2≥0得x2﹣x﹣6≤0，得﹣2≤x≤3，则D=[﹣2，3]，则在区间[﹣4，5]上随机取一个数x，则x∈D的概率P==，故答案为：【点评】本题主要考查几何概型的概率公式的计算，结合函数的定义域求出D，以及利用几何概型的概率公式是解决本题的关键．8．（5分）（2017•江苏）在平面直角坐标系xOy中，双曲线﹣y2=1的右准线与它的两条渐近线分别交于点P，Q，其焦点是F1，F2，则四边形F1PF2Q的面积是．【分析】求出双曲线的准线方程和渐近线方程，得到P，Q坐标，求出焦点坐标，然后求解四边形的面积．【解答】解：双曲线﹣y2=1的右准线：x=，双曲线渐近线方程为：y=x，所以P（，），Q（，﹣），F1（﹣2，0）．F2（2，0）．则四边形F1PF2Q的面积是：=2．故答案为：2．【点评】本题考查双曲线的简单性质的应用，考查计算能力．9．（5分）（2017•江苏）等比数列{a n}的各项均为实数，其前n项为S n，已知S3=，S6=，则a8=32．【分析】设等比数列{a n}的公比为q≠1，S3=，S6=，可得=，=，联立解出即可得出．【解答】解：设等比数列{a n}的公比为q≠1，∵S3=，S6=，∴=，=，解得a1=，q=2．则a8==32．故答案为：32．【点评】本题考查了等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．10．（5分）（2017•江苏）某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是30．【分析】由题意可得：一年的总运费与总存储费用之和=+4x，利用基本不等式的性质即可得出．【解答】解：由题意可得：一年的总运费与总存储费用之和=+4x≥4×2×=240（万元）．当且仅当x=30时取等号．故答案为：30．【点评】本题考查了基本不等式的性质及其应用，考查了推理能力与计算能力，属于基础题．11．（5分）（2017•江苏）已知函数f（x）=x3﹣2x+e x﹣，其中e是自然对数的底数．若f （a﹣1）+f（2a2）≤0．则实数a的取值范围是[﹣1，]．【分析】求出f（x）的导数，由基本不等式和二次函数的性质，可得f（x）在R上递增；再由奇偶性的定义，可得f（x）为奇函数，原不等式即为2a2≤1﹣a，运用二次不等式的解法即可得到所求范围．【解答】解：函数f（x）=x3﹣2x+e x﹣的导数为：f′（x）=3x2﹣2+e x+≥﹣2+2=0，可得f（x）在R上递增；又f（﹣x）+f（x）=（﹣x）3+2x+e﹣x﹣e x+x3﹣2x+e x﹣=0，可得f（x）为奇函数，则f（a﹣1）+f（2a2）≤0，即有f（2a2）≤﹣f（a﹣1）=f（1﹣a），即有2a2≤1﹣a，解得﹣1≤a≤，故答案为：[﹣1，]．【点评】本题考查函数的单调性和奇偶性的判断和应用，注意运用导数和定义法，考查转化思想的运用和二次不等式的解法，考查运算能力，属于中档题．12．（5分）（2017•江苏）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且ta nα=7，与的夹角为45°．若=m+n（m，n∈R），则m+n=3．【分析】如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．可得cosα=，sinα=．C．可得cos（α+45°）=．sin（α+45°）=．B．利用=m+n（m，n∈R），即可得出．【解答】解：如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．∴cosα=，sinα=．∴C．cos（α+45°）=（cosα﹣sinα）=．sin（α+45°）=（sinα+cosα）=．∴B．∵=m+n（m，n∈R），∴=m﹣n，=0+n，解得n=，m=．则m+n=3．故答案为：3．【点评】本题考查了向量坐标运算性质、和差公式，考查了推理能力与计算能力，属于中档题．13．（5分）（2017•江苏）在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2=50上．若≤20，则点P的横坐标的取值范围是[﹣5，1]．【分析】根据题意，设P（x0，y0），由数量积的坐标计算公式化简变形可得2x0+y0+5≤0，分析可得其表示表示直线2x+y+5≤0以及直线下方的区域，联立直线与圆的方程可得交点的横坐标，结合图形分析可得答案．【解答】解：根据题意，设P（x0，y0），则有x02+y02=50，=（﹣12﹣x0，﹣y0）•（﹣x0，6﹣y0）=（12+x0）x0﹣y0（6﹣y0）=12x0+6y+x02+y02≤20，化为：12x0+6y0+30≤0，即2x0+y0+5≤0，表示直线2x+y+5≤0以及直线下方的区域，联立，解可得x0=﹣5或x0=1，结合图形分析可得：点P的横坐标x0的取值范围是[﹣5，1]，故答案为：[﹣5，1]．【点评】本题考查数量积的运算以及直线与圆的位置关系，关键是利用数量积化简变形得到关于x0、y0的关系式．14．（5分）（2017•江苏）设f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f （x）=，其中集合D={x|x=，n∈N*}，则方程f（x）﹣lgx=0的解的个数是8．【分析】由已知中f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）=，其中集合D={x|x=，n∈N*}，分析f（x）的图象与y=lgx图象交点的个数，进而可得答案．【解答】解：∵在区间[0，1）上，f（x）=，第一段函数上的点的横纵坐标均为有理数，又f（x）是定义在R上且周期为1的函数，∴在区间[1，2）上，f（x）=，此时f（x）的图象与y=lgx有且只有一个交点；同理：区间[2，3）上，f（x）的图象与y=lgx有且只有一个交点；区间[3，4）上，f（x）的图象与y=lgx有且只有一个交点；区间[4，5）上，f（x）的图象与y=lgx有且只有一个交点；区间[5，6）上，f（x）的图象与y=lgx有且只有一个交点；区间[6，7）上，f（x）的图象与y=lgx有且只有一个交点；区间[7，8）上，f（x）的图象与y=lgx有且只有一个交点；区间[8，9）上，f（x）的图象与y=lgx有且只有一个交点；在区间[9，+∞）上，f（x）的图象与y=lgx无交点；故f（x）的图象与y=lgx有8个交点；即方程f（x）﹣lgx=0的解的个数是8，故答案为：8【点评】本题考查的知识点是根的存在性及根的个数判断，函数的图象和性质，转化思想，难度中档．二.解答题15．（14分）（2017•江苏）如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【分析】（1）利用AB∥EF及线面平行判定定理可得结论；（2）通过取线段CD上点G，连结FG、EG使得FG∥BC，则EG∥AC，利用线面垂直的性质定理可知FG⊥AD，结合线面垂直的判定定理可知AD⊥平面EFG，从而可得结论．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF⊊平面ABC，AB⊆平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，所以FG⊥BC，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．【点评】本题考查线面平行及线线垂直的判定，考查空间想象能力，考查转化思想，涉及线面平行判定定理，线面垂直的性质及判定定理，注意解题方法的积累，属于中档题．16．（14分）（2017•江苏）已知向量=（cosx，sinx），=（3，﹣），x∈[0，π]．（1）若∥，求x的值；（2）记f（x）=，求f（x）的最大值和最小值以及对应的x的值．【分析】（1）根据向量的平行即可得到tanx=﹣，问题得以解决，（2）根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出【解答】解：（1）∵=（cosx，sinx），=（3，﹣），∥，∴﹣cosx=3sinx，∴tanx=﹣，∵x∈[0，π]，∴x=，（2）f（x）==3cosx﹣sinx=2（cosx﹣sinx）=2cos（x+），∵x∈[0，π]，∴x+∈[，]，∴﹣1≤cos（x+）≤，当x=0时，f（x）有最大值，最大值3，当x=时，f（x）有最小值，最大值﹣2．【点评】本题考查了向量的平行和向量的数量积以及三角函数的化简和三角函数的性质，属于基础题17．（14分）（2017•江苏）如图，在平面直角坐标系xOy中，椭圆E：=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为，两准线之间的距离为8．点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2．（1）求椭圆E的标准方程；（2）若直线l1，l2的交点Q在椭圆E上，求点P的坐标．【分析】（1）由椭圆的离心率公式求得a=2c，由椭圆的准线方程x=±，则2×=8，即可求得a和c的值，则b2=a2﹣c2=3，即可求得椭圆方程；（2）设P点坐标，分别求得直线PF2的斜率及直线PF1的斜率，则即可求得l2及l1的斜率及方程，联立求得Q点坐标，由Q在椭圆方程，求得y02=x02﹣1，联立即可求得P点坐标；【解答】解：（1）由题意可知：椭圆的离心率e==，则a=2c，①椭圆的准线方程x=±，由2×=8，②由①②解得：a=2，c=1，则b2=a2﹣c2=3，∴椭圆的标准方程：；（2）设P（x0，y0），则直线PF2的斜率=，则直线l2的斜率k2=﹣，直线l2的方程y=﹣（x﹣1），直线PF1的斜率=，则直线l2的斜率k2=﹣，直线l2的方程y=﹣（x+1），联立，解得：，则Q（﹣x0，），由Q在椭圆上，则y0=，则y02=x02﹣1，则，解得：，则，又P在第一象限，所以P的坐标为：P（，）．【点评】本题考查椭圆的标准方程，直线与椭圆的位置关系，考查直线的斜率公式，考查数形结合思想，考查计算能力，属于中档题．18．（16分）（2017•江苏）如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．【分析】（1）设玻璃棒在CC1上的点为M，玻璃棒与水面的交点为N，过N作NP∥MC，交AC于点P，推导出CC1⊥平面ABCD，CC1⊥AC，NP⊥AC，求出MC=30cm，推导出△ANP∽△AMC，由此能出玻璃棒l没入水中部分的长度．（2）设玻璃棒在GG1上的点为M，玻璃棒与水面的交点为N，过点N作NP⊥EG，交EG 于点P，过点E作EQ⊥E1G1，交E1G1于点Q，推导出EE1G1G为等腰梯形，求出E1Q=24cm，E1E=40cm，由正弦定理求出sin∠GEM=，由此能求出玻璃棒l没入水中部分的长度．【解答】解：（1）设玻璃棒在CC1上的点为M，玻璃棒与水面的交点为N，在平面ACM中，过N作NP∥MC，交AC于点P，∵ABCD﹣A1B1C1D1为正四棱柱，∴CC1⊥平面ABCD，又∵AC⊂平面ABCD，∴CC1⊥AC，∴NP⊥AC，∴NP=12cm，且AM2=AC2+MC2，解得MC=30cm，∵NP∥MC，∴△ANP∽△AMC，∴=，，得AN=16cm．∴玻璃棒l没入水中部分的长度为16cm．（2）设玻璃棒在GG1上的点为M，玻璃棒与水面的交点为N，在平面E1EGG1中，过点N作NP⊥EG，交EG于点P，过点E作EQ⊥E1G1，交E1G1于点Q，∵EFGH﹣E1F1G1H1为正四棱台，∴EE1=GG1，EG∥E1G1，EG≠E1G1，∴EE1G1G为等腰梯形，画出平面E1EGG1的平面图，∵E1G1=62cm，EG=14cm，EQ=32cm，NP=12cm，∴E1Q=24cm，由勾股定理得：E1E=40cm，∴sin∠EE1G1=，sin∠EGM=sin∠EE1G1=，cos，根据正弦定理得：=，∴sin，cos，∴sin∠GEM=sin（∠EGM+∠EMG）=sin∠EGMcos∠EMG+cos∠EGMsin∠EMG=，∴EN===20cm．∴玻璃棒l没入水中部分的长度为20cm．【点评】本题考查玻璃棒l没入水中部分的长度的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．19．（16分）（2017•江苏）对于给定的正整数k，若数列{a n}满足：a n﹣k+a n﹣k+1+…+a n﹣+a n+1+…a n+k﹣1+a n+k=2ka n对任意正整数n（n＞k）总成立，则称数列{a n}是“P（k）数列”．1（1）证明：等差数列{a n}是“P（3）数列”；（2）若数列{a n}既是“P（2）数列”，又是“P（3）数列”，证明：{a n}是等差数列．【分析】（1）由题意可知根据等差数列的性质，a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3=（a n﹣3+a n+3）+（a n﹣2+a n+2）+（a n﹣1+a n+1）═2×3a n，根据“P（k）数列”的定义，可得数列{a n}是“P（3）数列”；（2）由“P（k）数列”的定义，则a n﹣2+a n﹣1+a n+1+a n+2=4a n，a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3=6a n，变形整理即可求得2a n=a n﹣1+a n+1，即可证明数列{a n}是等差数列．【解答】解：（1）证明：设等差数列{a n}首项为a1，公差为d，则a n=a1+（n﹣1）d，则a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3，=（a n﹣3+a n+3）+（a n﹣2+a n+2）+（a n﹣1+a n+1），=2a n+2a n+2a n，=2×3a n，∴等差数列{a n}是“P（3）数列”；（2）证明：由数列{a n}是“P（2）数列”则a n﹣2+a n﹣1+a n+1+a n+2=4a n，①数列{a n}是“P（3）数列”a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3=6a n，②由①可知：a n﹣3+a n﹣2+a n+a n+1=4a n﹣1，③a n﹣1+a n+a n+2+a n+3=4a n+1，④由②﹣（③+④）：﹣2a n=6a n﹣4a n﹣1﹣4a n+1，整理得：2a n=a n﹣1+a n+1，∴数列{a n}是等差数列．【点评】本题考查等差数列的性质，考查数列的新定义的性质，考查数列的运算，考查转化思想，属于中档题．20．（16分）（2017•江苏）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．【分析】（1）通过对f（x）=x3+ax2+bx+1求导可知g（x）=f′（x）=3x2+2ax+b，进而再求导可知g′（x）=6x+2a，通过令g′（x）=0进而可知f′（x）的极小值点为x=﹣，从而f（﹣）=0，整理可知b=+（a＞0），结合f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值可知f′（x）=0有两个不等的实根，进而可知a＞3．（2）通过（1）构造函数h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），结合a＞3可知h（a）＞0，从而可得结论；（3）通过（1）可知f′（x）的极小值为f′（﹣）=b﹣，利用韦达定理及完全平方关系可知y=f（x）的两个极值之和为﹣+2，进而问题转化为解不等式b﹣+﹣+2=﹣≥﹣，因式分解即得结论．【解答】（1）解：因为f（x）=x3+ax2+bx+1，所以g（x）=f′（x）=3x2+2ax+b，g′（x）=6x+2a，令g′（x）=0，解得x=﹣．由于当x＞﹣时g′（x）＞0，g（x）=f′（x）单调递增；当x＜﹣时g′（x）＜0，g（x）=f′（x）单调递减；所以f′（x）的极小值点为x=﹣，由于导函数f′（x）的极值点是原函数f（x）的零点，所以f（﹣）=0，即﹣+﹣+1=0，所以b=+（a＞0）．因为f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，所以f′（x）=3x2+2ax+b=0有两个不等的实根，所以4a2﹣12b＞0，即a2﹣+＞0，解得a＞3，所以b=+（a＞3）．（2）证明：由（1）可知h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），由于a＞3，所以h（a）＞0，即b2＞3a；（3）解：由（1）可知f′（x）的极小值为f′（﹣）=b﹣，设x1，x2是y=f（x）的两个极值点，则x1+x2=，x1x2=，所以f（x1）+f（x2）=++a（+）+b（x1+x2）+2=（x1+x2）[（x1+x2）2﹣3x1x2]+a[（x1+x2）2﹣2x1x2]+b（x1+x2）+2=﹣+2，又因为f（x），f′（x）这两个函数的所有极值之和不小于﹣，所以b﹣+﹣+2=﹣≥﹣，因为a＞3，所以2a3﹣63a﹣54≤0，所以2a（a2﹣36）+9（a﹣6）≤0，所以（a﹣6）（2a2+12a+9）≤0，由于a＞3时2a2+12a+9＞0，所以a﹣6≤0，解得a≤6，所以a的取值范围是（3，6]．【点评】本题考查利用导数研究函数的单调性、极值，考查运算求解能力，考查转化思想，注意解题方法的积累，属于难题．二.非选择题，附加题（21-24选做题）【选修4-1：几何证明选讲】（本小题满分0分）21．（2017•江苏）如图，AB为半圆O的直径，直线PC切半圆O于点C，AP⊥PC，P为垂足．求证：（1）∠P AC=∠CAB；（2）AC2 =AP•AB．【分析】（1）利用弦切角定理可得：∠ACP=∠ABC．利用圆的性质可得∠ACB=90°．再利用三角形内角和定理即可证明．（2）由（1）可得：△APC∽△ACB，即可证明．【解答】证明：（1）∵直线PC切半圆O于点C，∴∠ACP=∠ABC．∵AB为半圆O的直径，∴∠ACB=90°．∵AP⊥PC，∴∠APC=90°．∴∠P AC=90°﹣∠ACP，∠CAB=90°﹣∠ABC，∴∠P AC=∠CAB．（2）由（1）可得：△APC∽△ACB，∴=．∴AC2 =AP•AB．【点评】本题考查了弦切角定理、圆的性质、三角形内角和定理、三角形相似的判定与性质定理，考查了推理能力与计算能力，属于中档题．[选修4-2：矩阵与变换]22．（2017•江苏）已知矩阵A=，B=．（1）求AB；（2）若曲线C1：=1在矩阵AB对应的变换作用下得到另一曲线C2，求C2的方程．【分析】（1）按矩阵乘法规律计算；（2）求出变换前后的坐标变换规律，代入曲线C1的方程化简即可．【解答】解：（1）AB==，（2）设点P（x，y）为曲线C1的任意一点，点P在矩阵AB的变换下得到点P′（x0，y0），则=，即x0=2y，y0=x，∴x=y0，y=，∴，即x02+y02=8，∴曲线C2的方程为x2+y2=8．【点评】本题考查了矩阵乘法与矩阵变换，属于中档题．[选修4-4：坐标系与参数方程]23．（2017•江苏）在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），曲线C的参数方程为（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．【分析】求出直线l的直角坐标方程，代入距离公式化简得出距离d关于参数s的函数，从而得出最短距离．【解答】解：直线l的直角坐标方程为x﹣2y+8=0，∴P到直线l的距离d==，∴当s=时，d取得最小值=．【点评】本题考查了参数方程的应用，属于基础题．［选修4-5：不等式选讲］24．（2017•江苏）已知a，b，c，d为实数，且a2+b2=4，c2+d2=16，证明ac+bd≤8．【分析】a2+b2=4，c2+d2=16，令a=2cosα，b=2sinα，c=4cosβ，d=4sinβ．代入ac+bd化简，利用三角函数的单调性即可证明．【解答】证明：∵a2+b2=4，c2+d2=16，令a=2cosα，b=2sinα，c=4cosβ，d=4sinβ．∴ac+bd=8（cosαcosβ+sinαsinβ）=8cos（α﹣β）≤8．当且仅当cos（α﹣β）=1时取等号．因此ac+bd≤8．【点评】本题考查了对和差公式、三角函数的单调性、不等式的性质，考查了推理能力与计算能力，属于中档题．【必做题】25．（2017•江苏）如图，在平行六面体ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1=，∠BAD=120°．（1）求异面直线A1B与AC1所成角的余弦值；（2）求二面角B﹣A1D﹣A的正弦值．【分析】在平面ABCD内，过A作Ax⊥AD，由AA1⊥平面ABCD，可得AA1⊥Ax，AA1⊥AD，以A为坐标原点，分别以Ax、AD、AA1所在直线为x、y、z轴建立空间直角坐标系．结合已知求出A，B，C，D，A1，C1的坐标，进一步求出，，，的坐标．（1）直接利用两法向量所成角的余弦值可得异面直线A1B与AC1所成角的余弦值；（2）求出平面BA1D与平面A1AD的一个法向量，再由两法向量所成角的余弦值求得二面角B﹣A1D﹣A的余弦值，进一步得到正弦值．【解答】解：在平面ABCD内，过A作Ax⊥AD，∵AA1⊥平面ABCD，AD、Ax⊂平面ABCD，∴AA1⊥Ax，AA1⊥AD，以A为坐标原点，分别以Ax、AD、AA1所在直线为x、y、z轴建立空间直角坐标系．∵AB=AD=2，AA1=，∠BAD=120°，∴A（0，0，0），B（），C（，1，0），D（0，2，0），A1（0，0，），C1（）．=（），=（），，．（1）∵cos＜＞==．∴异面直线A1B与AC1所成角的余弦值为；（2）设平面BA1D的一个法向量为，由，得，取x=，得；取平面A1AD的一个法向量为．∴cos＜＞==．∴二面角B﹣A1D﹣A的正弦值为，则二面角B﹣A1D﹣A的正弦值为．【点评】本题考查异面直线所成的角与二面角，训练了利用空间向量求空间角，是中档题．26．（2017•江苏）已知一个口袋有m个白球，n个黑球（m，n∈N*，n≥2），这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…，m+n 的抽屉内，其中第k次取出的球放入编号为k的抽屉（k=1，2，3，…，m+n）．1 2 3 …m+n（1）试求编号为2的抽屉内放的是黑球的概率p；（2）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数，E（X）是X的数学期望，证明E（X）＜．【分析】（1）设事件A i表示编号为i的抽屉里放的是黑球，则p=p（A2）=P（A2|A1）P（A1）+P（A2|）P（），由此能求出编号为2的抽屉内放的是黑球的概率．（2）X的所有可能取值为，…，，P（x=）=，k=n，n+1，n+2，…，n+m，从而E（X）=（）=，由此能证明E（X）＜．【解答】解：（1）设事件A i表示编号为i的抽屉里放的是黑球，则p=p（A2）=P（A2|A1）P（A1）+P（A2|）P（）===．证明：（2）∵X的所有可能取值为，…，，P（x=）=，k=n，n+1，n+2，…，n+m，∴E（X）=（）==＜==•（）==，∴E（X）＜．【点评】本题考查概率的求法，考查离散型随机变量的分布列、数学期望等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．。

2017年高考数学江苏卷(附参考答案及详解)

""!0平面 "$&'#且 "$'"''$#""!'槡(#.$"''!$#;! $!%求异面直线 "!$ 与"&! 所成角的余弦值* $$%求二面角 $5"!'5" 的正弦值!
第 $$ 题图
#"
参考答案与详细解析
"#!$ 年普通高等学校招生全国统一考试江苏卷
$$%若直线:!#:$ 的交点 - 在椭圆A 上#求点 * 的坐标!
!9!$本小题满分 !& 分%对于给定的正整数?#若数列!0%"满足 &0%)? 10%)?1! 1 ' 10%)! 10%1! 1 ' 10%1?)! 10%1? '$?0%#对任意正整数 %$%$?%总成立 #则称数列 !0% "是 -*$?%数列 .! $!%证明 &等差数列 !0% "是 -*$(%数列 .* $$%若数列 !0% "既是 -* $$%数列 .#又是 -* $(%数列 .# 证明 &!0% "是等差数列 !
写在题中横线上
!!已知集合 "'!!#$"#$'!0#0$1("!若 "%$'!!"#则实数0 的
值为!!!!!
$!已知复数.'$!10%$!1$0%#其中0是虚数单位#则. 的模是!!
!!!
(!某工厂生产甲,乙,丙,丁四种不同型号的产品#产量分别为 $###

2017江苏语文高考附加题

2017江苏语文高考附加题自主命题的江苏高考语文试题都会有一些附加题在卷尾,那么江苏卷附加题是什么题型?考核了什么内容和知识点?下面是店铺为大家推荐的2017江苏语文高考试题，仅供大家参考!2017江苏语文高考试题附加题一、阅读材料,完成20～22题。

(10分)20.用斜线“/”给下面画线的文言文断句。

(限6处)(6分)胡子厚与予论诗曰：“人有恒言曰，唐以诗取士，故诗盛;今代以经义选举，故诗衰。

”此论非也。

诗之盛衰系于人之才与学不因上之所取也汉以射策取士而苏李之诗班马之赋出焉此岂系于上乎?屈原之《骚》，争光日月，楚岂以骚取人耶?况唐人所取五言八韵之律，今所传省题诗，多不工。

今传世者，非省题诗也。

(选自杨慎《升庵诗话》)21.文中的“班马”指的是▲ 和司马迁，他们分别著述了“前四史”中的《▲ 》和《史记》。

(2分)22.简要概括作者反驳胡子厚的理由。

(2分)二、名著阅读题(15分)23.下列对有关名著的说明，不正确的两项是(5分)A.在《三国演义》中，“独行千里报主之志坚，义释华容酬恩之谊重”称赞的是关羽，他所报答的“主”指的是刘备，他“义释”的人是曹操。

B.赵伯韬、杜竹斋在吴公馆的亭子里密议合伙做“多头”的事情，尚仲礼也认定这其中有利可图，并积极大胆地促成这桩买卖，最终大赚了一笔钱财。

C.《哈姆莱特》中，哈姆莱特从家庭的变故看到宫墙外的社会问题，产生了强烈的责任感，他意识到自己的责任不是单纯地复仇，而是要重整乾坤，消灭一切罪恶。

D.《茶馆》中的常四爷乐于助人，富于正义感，当王利发正愁要关城门还没买菜时，是他送来了咸菜和鸡;第三幕中他还为松二爷化缘买棺材。

E.《欧也妮·葛朗台》中，葛朗台抢女儿的梳妆匣，太太气得昏死过去，他怕太太气坏身体，马上放弃了梳妆匣，足见吝啬的葛朗台对太太尚有一丝温情。

24.简答题(10分)(1)《红楼梦》七十八回中，宝玉撰诔文祭晴雯，黛玉建议将“红绡帐里，公子情深”改为“茜纱窗下，公子多情”，小说中哪些情节最能表现晴雯和宝玉之间的“情深”?当宝玉改为“茜纱窗下，我本无缘;黄土陇中，卿何薄命”后，黛玉为何“陡然变色”?(6分)(2)《呐喊》中，夏瑜对牢头红眼睛阿义说“这大清的天下是我们大家的”，劝其造反，却遭来阿义的拳头，事后众人也认为夏瑜“疯了”。

(完整版)2017年江苏省高考数学试卷

精心整理2017年江苏省高考数学试卷一.填空题1．（5分）已知集合A={1，2}，B={a，a2+3}．若A∩B={1}，则实数a 的值为．2．（5分）已知复数z=（1+i）（1+2i），其中i是虚数单位，则z的模是．3．（5分）某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取件．4．（5分）如图是一个算法流程图：若输入x的值为，则输出y的值是．5．（5分）若tan（α﹣）=．则tanα=．6．（5分）如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．7．（5分）记函数f（x）=定义域为D．在区间[﹣4，5]上随机取一个数x，则x∈D的概率是．8．（5分）在平面直角坐标系xOy中，双曲线﹣y2=1的右准线与它的两条渐近线分别交于点P，Q，其焦点是F1，F2，则四边形F1PF2Q的面积是．9．（5分）等比数列{a n}的各项均为实数，其前n项为S n，已知S3=，S6=，则a8=．10．（5分）某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是．11．（5分）已知函数f（x）=x3﹣2x+e x﹣，其中e是自然对数的底数．若f（a﹣1）+f（2a2）≤0．则实数a的取值范围是．12．（5分）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且tanα=7，与的夹角为45°．若=m+n（m，n∈R），则m+n=．13．（5分）在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2=50上．若≤20，则点P的横坐标的取值范围是．14．（5分）设f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）=，其中集合D={x|x=，n∈N*}，则方程f（x）﹣lgx=0的解的个数是．二.解答题15．（14分）如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F （E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．16．（14分）已知向量=（cosx，sinx），=（3，﹣），x∈[0，π]．（1）若∥，求x的值；（2）记f（x）=，求f（x）的最大值和最小值以及对应的x的值．17．（14分）如图，在平面直角坐标系xOy中，椭圆E：=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为，两准线之间的距离为8．点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2．（1）求椭圆E的标准方程；（2）若直线l1，l2的交点Q在椭圆E上，求点P的坐标．18．（16分）如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．19．（16分）对于给定的正整数k，若数列{a n}满足：a n﹣k+a n﹣k+1+…+a n﹣1+a n+1+…+a n+k﹣1+a n+k=2ka n对任意正整数n（n＞k）总成立，则称数列{a n}是“P（k）数列”．（1）证明：等差数列{a n}是“P（3）数列”；（2）若数列{a n}既是“P（2）数列”，又是“P（3）数列”，证明：{a n}是等差数列．20．（16分）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f （x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．二.非选择题，附加题（21-24选做题）【选修4-1：几何证明选讲】（本小题满分0分）21．如图，AB为半圆O的直径，直线PC切半圆O于点C，AP⊥PC，P为垂足．求证：（1）∠PAC=∠CAB；（2）AC2=AP?AB．[选修4-2：矩阵与变换]22．已知矩阵A=，B=．（1）求AB；（2）若曲线C1：=1在矩阵AB对应的变换作用下得到另一曲线C2，求C2的方程．[选修4-4：坐标系与参数方程]23．在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），曲线C的参数方程为（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．［选修4-5：不等式选讲］24．已知a，b，c，d为实数，且a2+b2=4，c2+d2=16，证明ac+bd≤8．【必做题】25．如图，在平行六面体ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1=，∠BAD=120°．（1）求异面直线A1B与AC1所成角的余弦值；（2）求二面角B﹣A1D﹣A的正弦值．26．已知一个口袋有m个白球，n个黑球（m，n∈N*，n≥2），这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…，m+n的抽屉内，其中第k次取出的球放入编号为k的抽屉（k=1，2，3，…，m+n）．123…m+n（1）试求编号为2的抽屉内放的是黑球的概率p；（2）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数，E（X）是X的数学期望，证明E （X）＜．2017年江苏省高考数学试卷参考答案与试题解析一.填空题1．（5分）（2017?江苏）已知集合A={1，2}，B={a，a2+3}．若A∩B={1}，则实数a的值为1．【考点】1E：交集及其运算．【分析】利用交集定义直接求解．【解答】解：∵集合A={1，2}，B={a，a2+3}．A∩B={1}，∴a=1或a2+3=1，解得a=1．故答案为：1．2．（5分）（2017?江苏）已知复数z=（1+i）（1+2i），其中i是虚数单位，则z的模是．【考点】A5：复数代数形式的乘除运算．【分析】利用复数的运算法则、模的计算公式即可得出．【解答】解：复数z=（1+i）（1+2i）=1﹣2+3i=﹣1+3i，∴|z|==．故答案为：．3．（5分）（2017?江苏）某工厂生产甲、乙、丙、丁四种不同型号的产品，产量分别为200，400，300，100件．为检验产品的质量，现用分层抽样的方法从以上所有的产品中抽取60件进行检验，则应从丙种型号的产品中抽取18件．【考点】B3：分层抽样方法．【分析】由题意先求出抽样比例即为，再由此比例计算出应从丙种型号的产品中抽取的数目．【解答】解：产品总数为200+400+300+100=1000件，而抽取60辆进行检验，抽样比例为=，则应从丙种型号的产品中抽取300×=18件，故答案为：184．（5分）（2017?江苏）如图是一个算法流程图：若输入x的值为，则输出y的值是﹣2．【考点】EF：程序框图．【分析】直接模拟程序即得结论．【解答】解：初始值x=，不满足x≥1，所以y=2+log2=2﹣=﹣2，故答案为：﹣2．5．（5分）（2017?江苏）若tan（α﹣）=．则tanα=．【考点】GR：两角和与差的正切函数．【分析】直接根据两角差的正切公式计算即可【解答】解：∵tan（α﹣）===∴6tanα﹣6=tanα+1，解得tanα=，故答案为：．6．（5分）（2017?江苏）如图，在圆柱O1O2内有一个球O，该球与圆柱的上、下底面及母线均相切，记圆柱O1O2的体积为V1，球O的体积为V2，则的值是．【考点】L5：旋转体（圆柱、圆锥、圆台）；LF：棱柱、棱锥、棱台的体积；LG：球的体积和表面积．【分析】设出球的半径，求出圆柱的体积以及球的体积即可得到结果．【解答】解：设球的半径为R，则球的体积为：R3，圆柱的体积为：πR2?2R=2πR3．则==．故答案为：．7．（5分）（2017?江苏）记函数f（x）=定义域为D．在区间[﹣4，5]上随机取一个数x，则x∈D的概率是．【考点】CF：几何概型．【分析】求出函数的定义域，结合几何概型的概率公式进行计算即可．【解答】解：由6+x﹣x2≥0得x2﹣x﹣6≤0，得﹣2≤x≤3，则D=[﹣2，3]，则在区间[﹣4，5]上随机取一个数x，则x∈D的概率P==，故答案为：8．（5分）（2017?江苏）在平面直角坐标系xOy中，双曲线﹣y2=1的右准线与它的两条渐近线分别交于点P，Q，其焦点是F1，F2，则四边形F1PF2Q的面积是．【考点】KC：双曲线的简单性质．【分析】求出双曲线的准线方程和渐近线方程，得到P，Q坐标，求出焦点坐标，然后求解四边形的面积．【解答】解：双曲线﹣y2=1的右准线：x=，双曲线渐近线方程为：y=x，所以P（，），Q（，﹣），F1（﹣2，0）．F2（2，0）．则四边形F1PF2Q的面积是：=2．故答案为：2．9．（5分）（2017?江苏）等比数列{a n}的各项均为实数，其前n项为S n，已知S3=，S6=，则a8= 32．【考点】88：等比数列的通项公式．【分析】设等比数列{a n}的公比为q≠1，S3=，S6=，可得=，=，联立解出即可得出．【解答】解：设等比数列{a n}的公比为q≠1，∵S3=，S6=，∴=，=，解得a1=，q=2．则a8==32．故答案为：32．10．（5分）（2017?江苏）某公司一年购买某种货物600吨，每次购买x吨，运费为6万元/次，一年的总存储费用为4x万元．要使一年的总运费与总存储费用之和最小，则x的值是30．【考点】7F：基本不等式．【分析】由题意可得：一年的总运费与总存储费用之和=+4x，利用基本不等式的性质即可得出．【解答】解：由题意可得：一年的总运费与总存储费用之和=+4x≥4×2×=240（万元）．当且仅当x=30时取等号．故答案为：30．11．（5分）（2017?江苏）已知函数f（x）=x3﹣2x+e x﹣，其中e是自然对数的底数．若f（a﹣1）+f（2a2）≤0．则实数a的取值范围是[﹣1，]．【考点】6B：利用导数研究函数的单调性．【分析】求出f（x）的导数，由基本不等式和二次函数的性质，可得f（x）在R上递增；再由奇偶性的定义，可得f（x）为奇函数，原不等式即为2a2≤1﹣a，运用二次不等式的解法即可得到所求范围．【解答】解：函数f（x）=x3﹣2x+e x﹣的导数为：f′（x）=3x2﹣2+e x+≥﹣2+2=0，可得f（x）在R上递增；又f（﹣x）+f（x）=（﹣x）3+2x+e﹣x﹣e x+x3﹣2x+e x﹣=0，可得f（x）为奇函数，则f（a﹣1）+f（2a2）≤0，即有f（2a2）≤﹣f（a﹣1）=f（1﹣a），即有2a2≤1﹣a，解得﹣1≤a≤，故答案为：[﹣1，]．12．（5分）（2017?江苏）如图，在同一个平面内，向量，，的模分别为1，1，，与的夹角为α，且tanα=7，与的夹角为45°．若=m+n（m，n∈R），则m+n=3．【考点】9R：平面向量数量积的运算．【分析】如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．可得cosα=，sinα=．C．可得cos（α+45°）=．sin（α+45°）=．B．利用=m+n （m，n∈R），即可得出．【解答】解：如图所示，建立直角坐标系．A（1，0）．由与的夹角为α，且tanα=7．∴cosα=，sinα=．∴C．cos（α+45°）=（cosα﹣sinα）=．sin（α+45°）=（sinα+cosα）=．∴B∵=m+n（m，n∈R），∴=m﹣n，=0+n，解得n=，m=．则m+n=3．故答案为：3．13．（5分）（2017?江苏）在平面直角坐标系xOy中，A（﹣12，0），B（0，6），点P在圆O：x2+y2=50上．若≤20，则点P的横坐标的取值范围是[﹣5，1]．【考点】9R：平面向量数量积的运算；7B：二元一次不等式（组）与平面区域．【分析】根据题意，设P（x0，y0），由数量积的坐标计算公式化简变形可得2x0+y0+5≤0，分析可得其表示表示直线2x+y+5≤0以及直线下方的区域，联立直线与圆的方程可得交点的横坐标，结合图形分析可得答案．【解答】解：根据题意，设P（x0，y0），则有x02+y02=50，=（﹣12﹣x0，﹣y0）?（﹣x0，6﹣y0）=（12+x0）x0﹣y0（6﹣y0）=12x0+6y+x02+y02≤20，化为：12x0﹣6y0+30≤0，即2x0﹣y0+5≤0，表示直线2x+y+5≤0以及直线下方的区域，联立，解可得x0=﹣5或x0=1，结合图形分析可得：点P的横坐标x0的取值范围是[﹣5，1]，故答案为：[﹣5，1]．14．（5分）（2017?江苏）设f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）=，其中集合D={x|x=，n∈N*}，则方程f（x）﹣lgx=0的解的个数是8．【考点】54：根的存在性及根的个数判断．【分析】由已知中f（x）是定义在R上且周期为1的函数，在区间[0，1）上，f（x）=，其中集合D={x|x=，n∈N*}，分析f（x）的图象与y=lgx图象交点的个数，进而可得答案．【解答】解：∵在区间[0，1）上，f（x）=，第一段函数上的点的横纵坐标均为有理数，又f（x）是定义在R上且周期为1的函数，∴在区间[1，2）上，f（x）=，此时f（x）的图象与y=lgx有且只有一个交点；同理：区间[2，3）上，f（x）的图象与y=lgx有且只有一个交点；区间[3，4）上，f（x）的图象与y=lgx有且只有一个交点；区间[4，5）上，f（x）的图象与y=lgx有且只有一个交点；区间[5，6）上，f（x）的图象与y=lgx有且只有一个交点；区间[6，7）上，f（x）的图象与y=lgx有且只有一个交点；区间[7，8）上，f（x）的图象与y=lgx有且只有一个交点；区间[8，9）上，f（x）的图象与y=lgx有且只有一个交点；在区间[9，+∞）上，f（x）的图象与y=lgx无交点；故f（x）的图象与y=lgx有8个交点；即方程f（x）﹣lgx=0的解的个数是8，故答案为：8二.解答题15．（14分）（2017?江苏）如图，在三棱锥A﹣BCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，点E、F（E与A、D不重合）分别在棱AD，BD上，且EF⊥AD．求证：（1）EF∥平面ABC；（2）AD⊥AC．【考点】LS：直线与平面平行的判定；LO：空间中直线与直线之间的位置关系．【分析】（1）利用AB∥EF及线面平行判定定理可得结论；（2）通过取线段CD上点G，连结FG、EG使得FG∥BC，则EG∥AC，利用线面垂直的性质定理可知FG⊥AD，结合线面垂直的判定定理可知AD⊥平面EFG，从而可得结论．【解答】证明：（1）因为AB⊥AD，EF⊥AD，且A、B、E、F四点共面，所以AB∥EF，又因为EF?平面ABC，AB?平面ABC，所以由线面平行判定定理可知：EF∥平面ABC；（2）在线段CD上取点G，连结FG、EG使得FG∥BC，则EG∥AC，因为BC⊥BD，所以FG∥BC，又因为平面ABD⊥平面BCD，所以FG⊥平面ABD，所以FG⊥AD，又因为AD⊥EF，且EF∩FG=F，所以AD⊥平面EFG，所以AD⊥EG，故AD⊥AC．16．（14分）（2017?江苏）已知向量=（cosx，sinx），=（3，﹣），x∈[0，π]．（1）若∥，求x的值；（2）记f（x）=，求f（x）的最大值和最小值以及对应的x的值．【考点】GL：三角函数中的恒等变换应用；9R：平面向量数量积的运算．【分析】（1）根据向量的平行即可得到tanx=﹣，问题得以解决，（2）根据向量的数量积和两角和余弦公式和余弦函数的性质即可求出【解答】解：（1）∵=（cosx，sinx），=（3，﹣），∥，∴﹣cosx=3sinx，∴tanx=﹣，∵x∈[0，π]，∴x=，（2）f（x）==3cosx﹣sinx=2（cosx﹣sinx）=2cos（x+），∵x∈[0，π]，∴x+∈[，]，∴﹣1≤cos（x+）≤，当x=0时，f（x）有最大值，最大值3，当x=时，f（x）有最小值，最大值﹣2．17．（14分）（2017?江苏）如图，在平面直角坐标系xOy中，椭圆E：=1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为，两准线之间的距离为8．点P在椭圆E上，且位于第一象限，过点F1作直线PF1的垂线l1，过点F2作直线PF2的垂线l2．（1）求椭圆E的标准方程；（2）若直线l1，l2的交点Q在椭圆E上，求点P的坐标．【考点】KL：直线与椭圆的位置关系．【分析】（1）由椭圆的离心率公式求得a=2c，由椭圆的准线方程x=±，则2×=8，即可求得a和c的值，则b2=a2﹣c2=3，即可求得椭圆方程；（2）设P点坐标，分别求得直线PF2的斜率及直线PF1的斜率，则即可求得l2及l1的斜率及方程，联立求得Q点坐标，由Q在椭圆方程，求得y02=x02﹣1，联立即可求得P点坐标；方法二：设P（m，n），当m≠1时，=，=，求得直线l 1及l1的方程，联立求得Q点坐标，根据对称性可得=±n2，联立椭圆方程，即可求得P点坐标．【解答】解：（1）由题意可知：椭圆的离心率e==，则a=2c，①椭圆的准线方程x=±，由2×=8，②由①②解得：a=2，c=1，则b2=a2﹣c2=3，∴椭圆的标准方程：；（2）方法一：设P（x 0，y0），则直线PF2的斜率=，则直线l2的斜率k2=﹣，直线l2的方程y=﹣（x﹣1），直线PF 1的斜率=，则直线l2的斜率k1=﹣，直线l1的方程y=﹣（x+1），联立，解得：，则Q（﹣x0，），由P，Q在椭圆上，P，Q的横坐标互为相反数，纵坐标应相等，则y0=，∴y02=x02﹣1，则，解得：，则，又P在第一象限，所以P的坐标为：P（，）．方法二：设P（m，n），由P在第一象限，则m＞0，n＞0，当m=1时，不存在，解得：Q与F 1重合，不满足题意，当m≠1时，=，=，由l 1⊥PF1，l2⊥PF2，则=﹣，=﹣，直线l1的方程y=﹣（x+1），①直线l2的方程y=﹣（x﹣1），②联立解得：x=﹣m，则Q（﹣m，），由Q在椭圆方程，由对称性可得：=±n2，即m2﹣n2=1，或m2+n2=1，由P（m，n），在椭圆方程，，解得：，或，无解，又P在第一象限，所以P的坐标为：P（，）．18．（16分）（2017?江苏）如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm．现有一根玻璃棒l，其长度为40cm．（容器厚度、玻璃棒粗细均忽略不计）（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度；（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度．【考点】LF：棱柱、棱锥、棱台的体积．【分析】（1）设玻璃棒在CC1上的点为M，玻璃棒与水面的交点为N，过N作NP∥MC，交AC 于点P，推导出CC1⊥平面ABCD，CC1⊥AC，NP⊥AC，求出MC=30cm，推导出△ANP∽△AMC，由此能出玻璃棒l没入水中部分的长度．（2）设玻璃棒在GG1上的点为M，玻璃棒与水面的交点为N，过点N作NP⊥EG，交EG于点P，过点E作EQ⊥E1G1，交E1G1于点Q，推导出EE1G1G为等腰梯形，求出E1Q=24cm，E1E=40cm，由正弦定理求出sin∠GEM=，由此能求出玻璃棒l没入水中部分的长度．【解答】解：（1）设玻璃棒在CC1上的点为M，玻璃棒与水面的交点为N，在平面ACM中，过N作NP∥MC，交AC于点P，∵ABCD﹣A1B1C1D1为正四棱柱，∴CC1⊥平面ABCD，又∵AC?平面ABCD，∴CC1⊥AC，∴NP⊥AC，∴NP=12cm，且AM2=AC2+MC2，解得MC=30cm，∵NP∥MC，∴△ANP∽△AMC，∴=，，得AN=16cm．∴玻璃棒l没入水中部分的长度为16cm．（2）设玻璃棒在GG1上的点为M，玻璃棒与水面的交点为N，在平面E1EGG1中，过点N作NP⊥EG，交EG于点P，过点E作EQ⊥E1G1，交E1G1于点Q，∵EFGH﹣E1F1G1H1为正四棱台，∴EE1=GG1，EG∥E1G1，EG≠E1G1，∴EE1G1G为等腰梯形，画出平面E1EGG1的平面图，∵E1G1=62cm，EG=14cm，EQ=32cm，NP=12cm，∴E1Q=24cm，由勾股定理得：E1E=40cm，∴sin∠EE1G1=，sin∠EGM=sin∠EE1G1=，cos，根据正弦定理得：=，∴sin，cos，∴sin∠GEM=sin（∠EGM+∠EMG）=sin∠EGMcos∠EMG+cos∠EGMsin∠EMG=，∴EN===20cm．∴玻璃棒l没入水中部分的长度为20cm．19．（16分）（2017?江苏）对于给定的正整数k，若数列{a n}满足：a n﹣k+a n﹣k+1+…+a n﹣1+a n+1+…+a n+k +a n+k=2ka n对任意正整数n（n＞k）总成立，则称数列{a n}是“P（k）数列”．﹣1（1）证明：等差数列{a n}是“P（3）数列”；（2）若数列{a n}既是“P（2）数列”，又是“P（3）数列”，证明：{a n}是等差数列．【考点】8B：数列的应用．【分析】（1）由题意可知根据等差数列的性质，a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3=（a n﹣3+a n+3）+（a n﹣2+a n+2）+（a n+a n+1）═2×3a n，根据“P（k）数列”的定义，可得数列{a n}是“P（3）数列”；﹣1（2）由“P（k）数列”的定义，则a n﹣2+a n﹣1+a n+1+a n+2=4a n，a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3=6a n，变形整理即可求得2a n=a n﹣1+a n+1，即可证明数列{a n}是等差数列．【解答】解：（1）证明：设等差数列{a n}首项为a1，公差为d，则a n=a1+（n﹣1）d，则a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3，=（a n﹣3+a n+3）+（a n﹣2+a n+2）+（a n﹣1+a n+1），=2a n+2a n+2a n，=2×3a n，∴等差数列{a n}是“P（3）数列”；（2）证明：由数列{a n}是“P（2）数列”则a n﹣2+a n﹣1+a n+1+a n+2=4a n，①数列{a n}是“P（3）数列”a n﹣3+a n﹣2+a n﹣1+a n+1+a n+2+a n+3=6a n，②由①可知：a n﹣3+a n﹣2+a n+a n+1=4a n﹣1，③a n﹣1+a n+a n+2+a n+3=4a n+1，④由②﹣（③+④）：﹣2a n=6a n﹣4a n﹣1﹣4a n+1，整理得：2a n=a n﹣1+a n+1，∴数列{a n}是等差数列．20．（16分）（2017?江苏）已知函数f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，且导函数f′（x）的极值点是f（x）的零点．（极值点是指函数取极值时对应的自变量的值）（1）求b关于a的函数关系式，并写出定义域；（2）证明：b2＞3a；（3）若f（x），f′（x）这两个函数的所有极值之和不小于﹣，求a的取值范围．【考点】6D：利用导数研究函数的极值．【分析】（1）通过对f（x）=x3+ax2+bx+1求导可知g（x）=f′（x）=3x2+2ax+b，进而再求导可知g′（x）=6x+2a，通过令g′（x）=0进而可知f′（x）的极小值点为x=﹣，从而f（﹣）=0，整理可知b=+（a＞0），结合f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值可知f′（x）=0有两个不等的实根，进而可知a＞3．（2）通过（1）构造函数h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），结合a＞3可知h（a）＞0，从而可得结论；（3）通过（1）可知f′（x）的极小值为f′（﹣）=b﹣，利用韦达定理及完全平方关系可知y=f （x）的两个极值之和为﹣+2，进而问题转化为解不等式b﹣+﹣+2=﹣≥﹣，因式分解即得结论．【解答】（1）解：因为f（x）=x3+ax2+bx+1，所以g（x）=f′（x）=3x2+2ax+b，g′（x）=6x+2a，令g′（x）=0，解得x=﹣．由于当x＞﹣时g′（x）＞0，g（x）=f′（x）单调递增；当x＜﹣时g′（x）＜0，g（x）=f′（x）单调递减；所以f′（x）的极小值点为x=﹣，由于导函数f′（x）的极值点是原函数f（x）的零点，所以f（﹣）=0，即﹣+﹣+1=0，所以b=+（a＞0）．因为f（x）=x3+ax2+bx+1（a＞0，b∈R）有极值，所以f′（x）=3x2+2ax+b=0有两个不等的实根，所以4a2﹣12b＞0，即a2﹣+＞0，解得a＞3，所以b=+（a＞3）．（2）证明：由（1）可知h（a）=b2﹣3a=﹣+=（4a3﹣27）（a3﹣27），由于a＞3，所以h（a）＞0，即b2＞3a；（3）解：由（1）可知f′（x）的极小值为f′（﹣）=b﹣，设x1，x2是y=f（x）的两个极值点，则x1+x2=，x1x2=，所以f（x1）+f（x2）=++a（+）+b（x1+x2）+2=（x1+x2）[（x1+x2）2﹣3x1x2]+a[（x1+x2）2﹣2x1x2]+b（x1+x2）+2=﹣+2，又因为f（x），f′（x）这两个函数的所有极值之和不小于﹣，所以b﹣+﹣+2=﹣≥﹣，因为a＞3，所以2a3﹣63a﹣54≤0，所以2a（a2﹣36）+9（a﹣6）≤0，所以（a﹣6）（2a2+12a+9）≤0，由于a＞3时2a2+12a+9＞0，所以a﹣6≤0，解得a≤6，所以a的取值范围是（3，6]．二.非选择题，附加题（21-24选做题）【选修4-1：几何证明选讲】（本小题满分0分）21．（2017?江苏）如图，AB为半圆O的直径，直线PC切半圆O于点C，AP⊥PC，P为垂足．求证：（1）∠PAC=∠CAB；（2）AC2=AP?AB．【考点】NC：与圆有关的比例线段．【分析】（1）利用弦切角定理可得：∠ACP=∠ABC．利用圆的性质可得∠ACB=90°．再利用三角形内角和定理即可证明．（2）由（1）可得：△APC∽△ACB，即可证明．【解答】证明：（1）∵直线PC切半圆O于点C，∴∠ACP=∠ABC．∵AB为半圆O的直径，∴∠ACB=90°．∵AP⊥PC，∴∠APC=90°．∴∠PAC=90°﹣∠ACP，∠CAB=90°﹣∠ABC，∴∠PAC=∠CAB．（2）由（1）可得：△APC∽△ACB，∴=．∴AC2=AP?AB．[选修4-2：矩阵与变换]22．（2017?江苏）已知矩阵A=，B=．（1）求AB；（2）若曲线C1：=1在矩阵AB对应的变换作用下得到另一曲线C2，求C2的方程．【考点】OE：矩阵与矩阵的乘法的意义．【分析】（1）按矩阵乘法规律计算；（2）求出变换前后的坐标变换规律，代入曲线C1的方程化简即可．【解答】解：（1）AB==，（2）设点P（x，y）为曲线C1的任意一点，点P在矩阵AB的变换下得到点P′（x0，y0），则=，即x0=2y，y0=x，∴x=y0，y=，∴，即x02+y02=8，∴曲线C2的方程为x2+y2=8．[选修4-4：坐标系与参数方程]23．（2017?江苏）在平面直角坐标系xOy中，已知直线l的参数方程为（t为参数），曲线C的参数方程为（s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．【考点】QH：参数方程化成普通方程．【分析】求出直线l的直角坐标方程，代入距离公式化简得出距离d关于参数s的函数，从而得出最短距离．【解答】解：直线l的直角坐标方程为x﹣2y+8=0，∴P到直线l的距离d==，∴当s=时，d取得最小值=．［选修4-5：不等式选讲］24．（2017?江苏）已知a，b，c，d为实数，且a2+b2=4，c2+d2=16，证明ac+bd≤8．【考点】7F：基本不等式；R6：不等式的证明．【分析】a2+b2=4，c2+d2=16，令a=2cosα，b=2sinα，c=4cosβ，d=4sinβ．代入ac+bd化简，利用三角函数的单调性即可证明．另解：由柯西不等式可得：（ac+bd）2≤（a2+b2）（c2+d2），即可得出．【解答】证明：∵a2+b2=4，c2+d2=16，令a=2cosα，b=2sinα，c=4cosβ，d=4sinβ．∴ac+bd=8（cosαcosβ+sinαsinβ）=8cos（α﹣β）≤8．当且仅当cos（α﹣β）=1时取等号．因此ac+bd≤8．另解：由柯西不等式可得：（ac+bd）2≤（a2+b2）（c2+d2）=4×16=64，当且仅当时取等号．∴﹣8≤ac+bd≤8．【必做题】25．（2017?江苏）如图，在平行六面体ABCD﹣A1B1C1D1中，AA1⊥平面ABCD，且AB=AD=2，AA1=，∠BAD=120°．（1）求异面直线A1B与AC1所成角的余弦值；（2）求二面角B﹣A1D﹣A的正弦值．【考点】MT：二面角的平面角及求法；LM：异面直线及其所成的角．【分析】在平面ABCD内，过A作Ax⊥AD，由AA1⊥平面ABCD，可得AA1⊥Ax，AA1⊥AD，以A为坐标原点，分别以Ax、AD、AA1所在直线为x、y、z轴建立空间直角坐标系．结合已知求出A，B，C，D，A1，C1的坐标，进一步求出，，，的坐标．（1）直接利用两法向量所成角的余弦值可得异面直线A1B与AC1所成角的余弦值；（2）求出平面BA1D与平面A1AD的一个法向量，再由两法向量所成角的余弦值求得二面角B﹣A1D﹣A的余弦值，进一步得到正弦值．【解答】解：在平面ABCD内，过A作Ax⊥AD，∵AA1⊥平面ABCD，AD、Ax?平面ABCD，∴AA1⊥Ax，AA1⊥AD，以A为坐标原点，分别以Ax、AD、AA1所在直线为x、y、z轴建立空间直角坐标系．∵AB=AD=2，AA1=，∠BAD=120°，∴A（0，0，0），B（），C（，1，0），D（0，2，0），A1（0，0，），C1（）．=（），=（），，．（1）∵cos＜＞==．∴异面直线A1B与AC1所成角的余弦值为；（2）设平面BA1D的一个法向量为，由，得，取x=，得；取平面A1AD的一个法向量为．∴cos＜＞==．∴二面角B﹣A1D﹣A的正弦值为，则二面角B﹣A1D﹣A的正弦值为．26．（2017?江苏）已知一个口袋有m个白球，n个黑球（m，n∈N*，n≥2），这些球除颜色外全部相同．现将口袋中的球随机的逐个取出，并放入如图所示的编号为1，2，3，…，m+n的抽屉内，其中第k次取出的球放入编号为k的抽屉（k=1，2，3，…，m+n）．123…m+n（1）试求编号为2的抽屉内放的是黑球的概率p；（2）随机变量x表示最后一个取出的黑球所在抽屉编号的倒数，E（X）是X的数学期望，证明E （X）＜．【考点】CH：离散型随机变量的期望与方差．【分析】（1）设事件A i表示编号为i的抽屉里放的是黑球，则p=p（A2）=P（A2|A1）P（A1）+P （A2|）P（），由此能求出编号为2的抽屉内放的是黑球的概率．（2）X的所有可能取值为，…，，P（x=）=，k=n，n+1，n+2，…，n+m，从而E（X）=（）=，由此能证明E（X）＜．【解答】解：（1）设事件A i表示编号为i的抽屉里放的是黑球，则p=p（A 2）=P（A2|A1）P（A1）+P（A2|）P（）===．证明：（2）∵X的所有可能取值为，…，，P（x=）=，k=n，n+1，n+2，…，n+m，∴E（X）=（）==＜==?（）==，∴E（X）＜．参与本试卷答题和审题的老师有：zlzhan；沂蒙松；whgcn；cst；qiss；maths；双曲线；danbo7801；豫汝王世崇；铭灏2016；zhczcb；sxs123（排名不分先后）菁优网2017年6月11日。

2017年江苏高考附加题及答案

语文Ⅱ卷(附加题)一、阅读材料，完成21～23题。

(10分)宋政和间官局编书，诸臣之文，独《临川集》得预其列。

靖康之祸，官书散失。

私集竟无完善之本，弗如欧集、曾集、老苏大苏集之盛行于时也。

公绝类之英，间气所生。

同时文人，虽或意见素异，尚且推崇公文，口许心服，每极其至。

而后来卑陋之士不满其相业因并废其文此公生平所谓流俗胡于公死后而犹然也？(节选自吴澄《临川王文公集>业序》)21．用斜线“/”给上面文言文中的画线部分断句。

(限4处)(4分)22．文中的老苏、大苏是指__________、__________。

(2分)23．根据材料，概括王安石《临川集》在不同时期的命运。

(4分)二、名著阅读题(15分)24．下列对有关名著的说明，不正确的两项是：(5分)A．《三国演义》中，曹操青梅煮酒，品评天下人物，认为当世只有自己和刘备可称英雄，刘备听后大喜，于是有了夺取天下的雄心。

B．《边城》里，第一个端午，翠翠在河边等爷爷，突然一阵害怕：“假若爷爷死了？”后来，爷爷在雷雨的夜里死去。

死亡的阴影让小说笼上一层淡淡的忧伤。

C．《子夜》前三章用吴老太爷之死把军、政、工、商、学等各界人物聚拢到一处，为小说全景式反映中国社会面貌、剖析中国社会性质奠定了基础。

D．《哈姆莱特》中，克劳狄斯送哈姆莱特赴英国，实际是要借刀杀人，后来哈姆莱特识破了克劳狄斯的奸计，撕毁了给英王的国书，才得以脱险。

E．《老人与海》中，圣地亚哥捕鱼时体会到大马林鱼仿佛也是他的朋友和兄弟，不过为了渔夫的尊严必须杀死它。

这一矛盾具有扣人心弦的张力。

25．简答题(10分)⑴《红楼梦》第四十五回“金兰契互剖金兰语，风雨夕闷制风雨词”中，黛玉对宝钗说：“我最是个多心的人，只当你心里藏奸……往日竟是我错了，实在误到如今。

”请说明黛玉对宝钗的认识发生变化的原因。

(6分)⑵《阿Q正传》中，未庄谣传革命党个个白盔白甲，“穿着崇正皇帝的素”；《祝福》里，鲁四老爷一见“我”就大骂其新党，但“他所骂的还是康有为”。

江苏高考语文近五年附加题(含答案)

第一套（2010年）一、阅读材料，完成19～21题。

(10分)19．用斜线“／”给下面画线的文言文断句。

(限6处)(6分)欧阳修尝慨《七略》四部，目存书亡，以谓其人之不幸，盖伤文章之不足恃也……然读《史》《汉》之书，而察徐广、裴驷、服虔、应劭诸家之注释，其间不得迁固之意者，十常四五焉。

以专门之攻习犹未达古人之精微况泛览所及爱憎由己耶夫不传者有部目空存之慨其传者，又有推求失旨之病，与爱憎不齐之数。

(节选自《文史通义》) 20．“四部”是我国古代图书的分类名称，通常指哪四类?(2分)答：21．《文史通义》作者是清代的哪位学者?(2分)答：二、名著阅读题(15分)22．下列有关名著的说明，不正确的两项是(5分)A．《阿Q正传》中，阿Q为了革命，用砖砸开了静修庵，砸了庵里“皇帝万岁万万岁”的龙牌，并顺手拿走了观音娘娘座前的宣德炉。

B．《女神•湘累》中，屈原在洞庭湖上说：“我效法造化底精神，我自由创造，自由地表现我自己。

”作者借此表现了五四个性解放精神。

C．在《边城》的结尾部分，傩送出走了，白塔倾圮了，老船夫也死了，老马兵觉得自己却成了翠翠“这孤雏的唯一靠山唯一信托人”。

D．《哈姆莱特》中所写的哈姆莱特、雷欧提斯和小福丁布拉斯三人复仇的举动，既是为了各自故去的父亲，也是为了争得骑士荣誉。

E．《红楼梦》中贾宝玉梦游太虚幻境所见判词：“子系中山狼，得志便猖狂。

金闺花柳质，一载赴黄粱。

”其中暗示了迎春的悲惨命运。

23．简答题(10分)(1)《老人与海》中，圣地亚哥说：“一个人可以被毁灭，但不能给打败。

”结合人物形象，说说你对这句话的理解。

(4分)答：(2)《三国演义》“官渡之战”中“许攸投奔曹操”这一情节，表现了曹操什么样的性格特征? (6分)答：三、材料概括分析题(15分)在健康的城市化进程中，城市不能以剥夺农村为手段采发展自己。

因为城市并不必然代表先进，农村更不意味着落后。

工业区边界的推进和农田的退缩并非天然正当的。

2017江苏高考语文试卷(含附加题)及解答

2017年普通高等学校招生全国统一考试（江苏卷）语文一、语言文字运用（15分）1．在下面一段话的空缺处依次填入词语，最恰当的一组是（3分）( )刺绣画艺术，就是以绘画为稿本，以针黹、缣帛为绣材的艺术再创作。

在其传承与发展过程中，无数绣娘以的工匠精神，创作出令人的作品。

它们或如摄影写实，或如油画般立体，或姿态婀娜，或设色古雅，可谓争奇斗艳，。

A．精益求精耳目一新美不胜收B．励精求治刮目相看美不胜收C．精益求精刮目相看数不胜数D．励精求治耳目一新数不胜数2．下列语句中，没有使用比喻手法的一项是（3分）( )A．“一带一路”是我国推动经济全球化而提出的一项互利共赢的倡议，它已成为推动全球经济转型升级、走出衰退困境的新引擎。

B．气象部门预计，随着暖湿气流增强，我省明天会迎来一场及时雨，空气中污染物浓度将快速下降，人们的舒适度会大幅度提升。

C．一种突如其来的网络病毒洪水猛兽般地袭击全球，导致150多个国家受灾，我国也有近3万家机构的计算机受到影响。

D．我国企业在参与发展中国家的基础设施建设过程中，主动强化环保意识，积极承担社会责任，带动了东道主在观念上弯道超车。

3．下列对联中，适合悬挂在杜甫草堂的一组是（3分）( )①为闻庐岳多真隐别有天地非人间②十年幕府悲秦月一卷唐诗补蜀风③狂到世人皆欲杀醉来天子不能呼④秋天一鹄先生骨春水群鸥野老心A．①③B．①④C．②③D．②④4．在下面一段文字横线处填入语句，衔接最恰当的一项是（3分）( )一个人在创作和欣赏时所表现的趣味，大半由资禀性情、身世经历和传统习尚三个因素决定。

，，。

这三层功夫就是通常所谓的学问修养，而纯正的趣味必定是学问修养的结果。

①它们的影响有好有坏②我们应该根据固有的资禀性情而加以磨砺陶冶③接收多方的传统习尚而融会贯通④这三者都是很自然地套在一个人的身上的⑤不易也不必完全摆脱⑥扩充身世经历而加以细心体验A．②③⑥④①⑤B．②⑥③④⑤①C．④①⑤②⑥③D．④⑤①②③⑥5．下列诗句中，与右图漫画的情境最吻合的一项是（3分）( )A．小梅香里黄莺啭，垂柳阴中白马嘶。

江苏省近三年(2015年-2017年)语文高考试题(含附加)及答案

2015年普通高等学校招生统一考试语文I试题一、语言文字运用〔15分〕1.在下面一段话空缺处依次填入词语，最恰当的一组是〔3分〕书是整个人类的记忆。

没有书，也许历史还在混沌未开的蒙昧中____▲_____。

读书，让绵延的时光穿越我们的身体，让几千年来 ____▲_____ 的智慧在我们每一个人的血液里汩汩流淌。

读书，不仅需要____▲_____的精神，还需要懂得快慢精粗之分。

A.徘徊积聚宵衣旰食B.徘徊积淀废寝忘食C.踟蹰积淀宵衣旰食D.踟蹰积聚废寝忘食2.以下各句中，没有语病．．．．的一项是〔3分〕A.英国政府计划从今年9月开始，推行4到5岁幼童将接受语文和算术能力的“基准测验”，此政策遭到了教师工会的强烈反对。

B.一种观念只有被人们普遍接受、理解和掌握并转化为整个社会的群体意识，才能成为人们自觉遵守和奉行的准则。

C.批评或许有对有错，甚至偏激，但只要出于善意，没有违犯法律法规，没有损害公序良俗，我们就应该以包容的心态对待。

D.今年5月9 日是俄罗斯卫国战争胜利70周年，有近30个国家和国际组织的领导人参加了在莫斯科红场举行的阅兵式。

3.以下诗句中，没有．．使用比拟手法的一项是〔3分〕A.东风便试新刀尺，万叶千花一手裁。

B.浮萍破处见山影，小艇归时闻草声。

C.有情芍药含春泪，无力蔷薇卧晓枝。

D.唯有南风旧相识，偷开门户又翻书。

4.在下面一段文字横线处填入语句，衔接最恰当的一项是〔3分〕自宋元至明清，清明节除了要祭扫家墓，还要在门楣、窗户上插上柳条。

____▲_____，____▲_____。

____▲_____，____▲_____，____▲_____，____▲_____。

①到达人丁兴旺、身体健康的目的②于是在郊游踏青时③它便成了人类文化中生命力的象征④人们企盼将这种生命力转移到自家门庭和家庭成员身上⑤不会忘记顺便折一些柳条回来⑥由于柳树最先送来春的消息并且具有旺盛的生殖力A.⑥③④①②⑤B.②⑤①④⑥③C.②④⑥③①⑤D.⑥④②⑤③①5.以下对“中国文化遗产”标志理解不恰当．．．的一项是〔3分〕A.标志整体呈圆形，既表达民族团结、和谐包容的文化内涵，也表达文化遗产保护的理念。

2017江苏高考语文附加题答案_2017江苏高考语文试题（2）

2017江苏高考语文附加题答案_2017江苏高考语文试题(2)五、现代文阅读(一)(20分)阅读下面的作品，完成13 ~16题。

一个圣诞节的回忆[美]杜鲁门·卡波特请设想一下二十多年前一个十一月的早晨，一个白发剪得短短的妇人站在窗口，大声说：“这是做水果蛋糕的好天气!巴迪，去把我们的车推来，我们要烤三十个水果蛋糕呢。

”那时我七岁，她六十光景，我们是很远的表亲。

从我记事起，我俩就住在一起。

她叫我“巴迪”，为了纪念她以前最好的朋友。

那个巴迪早死了，当时她自己还是个孩子。

她现在仍是个孩子。

我们把童车推进山核桃树丛。

童车是我出生时买的，快散了，轮子摇来摆去，像醉鬼的腿。

奎尼是我们养的一条小狗，她挺过了一场瘟疫和两次响尾蛇的噬咬，现在一路小跑跟在小车旁。

三个小时后我们回到厨房，把拉回家的满满一车风吹自落的山核桃的壳剥去。

欢快的裂壳声像是微弱的雷鸣，核桃肉散发着甜美的香气。

奎尼求我们给她点尝尝，我的朋友时不时偷偷给她一点，但我俩是绝对不可以吃的，“这些山核桃还不见得够做三十个水果蛋糕呢。

”明月高照，小车空了，碗满满的。

第二天，我最喜欢的事开始了：大采购。

樱桃，柑橘，香草，葡萄干，威士忌，大量的面粉和黄油……嗬，简直要一匹小马才能把车拉回家。

我们没钱，但每年总能用尽各种办法，筹到一笔水果蛋糕基金：卖破烂，卖摘来的一桶桶黑莓、一罐罐自制的果酱、苹果冻，为葬礼和婚礼采集鲜花。

黑驴子加足了煤和柴火，烧得像一直发光的南瓜。

打蛋器旋转着，调羹在一碗碗黄油和糖里搅动，香蕉让空气变得甜甜的，姜又增加了香味。

厨房里浓香扑鼻，弥漫到整幢屋子。

四天后，大功告成，三十只蛋糕放在窗台、搁板上晾着。

蛋糕给谁呢?朋友呗。

不一定是邻近的，大半倒是只见过一次，甚至素未谋面的，我们喜欢的朋友。

例如罗斯福总统，一年来镇上两次的小个子磨刀人，帕克(班车司机，他每天在尘土飞扬中嗖地一声驶过时和我们互相挥手招呼)。

是不是因为我的朋友太害羞了，才把这些陌生人当作真正的朋友?我想是的。

高考语文第五部分附加题专题一文言文阅读的断句、简答1高考体验高三全册语文

(节选自司马迁《史记·平准书》)
12/10/2021
解析：本题考查根据句式的对应关系和特殊虚词断句的能力。断句时先通读画线部分疏通大意。从中不难看出“贵诈力”与 “贱仁义”相对，“先”与“后”相对，“富者”与“贫者”相对，“国强”与“弱国”相对，这些词语领起的句子构成四组对比句。答案：天下争于战国/贵诈力而贱仁义/先富有而后推让/故庶人之富者或累巨万/而贫者或不厌糟糠/有国强者或并群小以臣诸侯/而弱国或绝祀而灭世
12/10/2021
(节选自严允肇《〈今世说〉序》)
12/10/2021
7．用斜线“/”给上面文言文中的画线部分断句。(限 5 处) 解析：本题考查文言语段的断句能力。文言文断句的基础在于对通篇文章的领会。首先，通读这篇短文，大致了解整个故事。然后抓住标志词，先断开比较明显的地方。标志词多为虚词，画线句中的两个“者”后面要断开，虚词“因”“以”“其”前面要断开。点断之后，再翻译一遍看能不能读通，最后确定点断处。答案：凡一言一行之可纪述者/靡不旁搜广辑/因文析类/以成一家言/其大要采诸序记杂文之行世者/而不敢妄缀一词
12/10/2021
五、(2013·高考江苏卷)阅读材料，完成 14～16 题。 14．用斜线“/”给下面文言文中的画线部分断句。(限 6 处)
齐桓公用管仲之谋，通轻重之权，徼山海之业，以朝诸侯，用区区之齐显成霸名。魏用李克，尽地力，为强君。自是之后，天下争于战国贵诈力而贱仁义先富有而后推让故庶人之富者或累巨万而贫者或不厌糟糠有国强者或并群小以臣诸侯而弱国或绝祀而灭世。以至于秦，卒并海内。
12/10/2021
2．文中的老苏、大苏是指________、________。解析：苏洵、苏轼、苏辙同列“唐宋八大家”，世称“三苏”。苏洵被称为“老苏”，苏轼(苏东坡)被称为“大苏”，苏辙被称为“小苏”。“三苏”均以文章显名于世，特别是号称全能大家的苏轼，文章堪称天下一绝，留下许多传世之作。答案：苏洵苏轼

2017江苏语文高考试卷附加题

2017江苏语文高考试卷附加题2017江苏语文高考试卷附加题高考,作为选拔人才的高规格的考试。

江苏采用的自主命题试题是有附加题的，那么江苏高考语文试题附加题的考核内容是怎样的?下面是店铺为大家推荐的2017江苏语文高考试卷附加题，仅供大家参考!2017江苏语文高考试卷附加题一一、阅读材料，完成20—22题。

(10分)东坡《志林》云：“白乐天尝为王涯所谗，贬江州司马。

甘露之祸，乐天有诗云当君自首同归日是我青山独往时不知者以乐天为幸之乐天岂幸人之祸者哉盖悲之也。

予读白集有《咏史》一篇，注云：九年十一月作。

其词曰：“秦磨利刃斩李斯，齐烧沸鼎烹郦其，可怜黄绮入商洛，闲卧白云歌紫芝，彼为菹醢机上尽。

此作鸾凰天外飞，去者逍遥来者死，乃知祸福非天为。

”正为甘露事而作，其悲之之意可见矣。

(选自《容斋随笔》)20.用斜线“/”给上面文言文中的画线部分断句。

(限5处)(5分)乐天有诗云当君自首同归日是我青山独往时不知者以乐天为幸之乐天岂幸人之祸者哉盖悲之也。

21.请指出白居易积极倡导什么运动?他的文学主张是什么?(2分)22.根据文意，说说白居易对甘露之变的情感、态度(3分)二、名著阅读题(15分)23.下列对有关名著的说明，不正确的两项是( )(5分)A. 樊城被曹操包围，诸葛亮劝刘备到襄阳躲避。

刘备不忍心丢下百姓，派人告诉他们，愿意跟随的就派船接到对岸。

百姓扶老携幼，哭声不断。

刘备伤心至极，想投江自杀，被人阻止了。

B.吴荪甫雄心勃勃，总想扩大自己的事业。

他和几个朋友组建了益中信托公司，以较低的价格收购了几个小厂，并准备加以扩充。

他希望自己生产的灯泡、肥皂等日用品将来能销往乡村。

C.侄子夏尔来葛朗台家中做客，葛朗台对夏尔冷若冰霜。

隔天他从报上得知弟弟已经破产自杀了，且将夏尔托付给自己。

他对弟弟的死讯，无动于衷，却将夏尔视为累赘。

D.沈从文的小说中多有对湘西民俗的展现：青年男女月夜对歌，表达爱慕之情，展现了当地的婚恋习俗;清明节时年轻小伙子赛龙舟，表现了湘西的生活习俗;崇拜“傩神”，表现了湘西人的宗教习俗。

2017年江苏高考数学(带附加题)

求证：（1）∠PAC=∠CAB; （2）AC2 =AP·AB。
B.[选修 4-2：矩阵与变换]（本小题满分 10 分）已知矩阵 A= (1) 求 AB; 若曲线 C1; ，B= .
x 2 y2 =1 在矩阵 AB 对应的变换作用下得到另一曲线 C2 ，求 C2 的方程. 8 2
6
高中学习交流群：9854211
23. （本小题满分 10）已知一个口袋有 m 个白球，n 个黑球（m,n N
2
,n 2）,这些球除颜色外全部相同。现将口袋中的球随
机的逐个取出，并放入如图所示的编号为 1,2,3，……，m+n 的抽屉内，其中第 k 次取球放入编号为 k 的抽屉（k=1,2,3，……，m+n）.
（1）试求编号为 2 的抽屉内放的是黑球的概率 p; （ 2 ）随机变量 x 表示最后一个取出的黑球所在抽屉编号的倒数， E(x) 是 x 的数学期望，证明
19.（本小题满分 16 分）对于给定的正整数 k,若数列 lanl 满足 an k an k 1 ... an 1 an 1 ... an k 1 an k 2k an =2kan 对任意正整数 n(n> k) 总成立，则称数列 lanl 是“P(k)数列”. (1)证明：等差数列 lanl 是“P(3)数列”；
注意事项考生在答题前请认真阅读本注意事项及各题答题要求 1. 本试卷共 2 页，均为非选择题（第 21 题 ~ 第 23 题）。本卷满分为 40 分，考试时间为 30 分钟。考试结束后，请将本试卷和答题卡一并交回。 2. 答题前，请务必将自己的姓名、准考证号用 0.5 毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。 3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。 4.作答试题，必须用 0.5 毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。 5.如需改动，须用 2B 铅笔绘、写清楚，线条、符号等须加黑、加粗

江苏高考附加题综合测试七

综合测试七
一、阅读材料，完成1～3题。 1．海明威的著名小说《老人与海》虽然手法是写实的，但人们普遍认为其有象征意义。请说说小说中的大海、鲨鱼、梦中的狮子分别象征什么。答：_________________________________________________________________ _____________________________________________________________________ 答案小说中的大海和鲨鱼象征着神秘的命运和不可预知的世界，梦中的狮子象征
6．简述老街“像是文章里被引用的典故”在文中的含意。
答：__________________________________________________________________ ____________________________________________________________________ 答案老街被郑重保护起来的，刻意地进行复古的修饰，以让窄窄的它承载浩繁
答案相传周公客人来访时，“一沐三握发，一饭三吐哺”。意思是，洗一次
澡，三次停下来，握着散乱的头发出来接待客人；吃一次饭，三次吐掉嘴里残留的饭，赶忙迎接客人。 3．请概括这段文字所反映出的李白写这封信的主要目的。答：__________________________________________________________________ _____________________________________________________________________ 答案渴望得到韩荆州的赏识和举荐，以便施展才华。
生活，原本是一个快速后退的过程，又有什么是可以挽留的？

2017江苏高考语文试卷附加题_江苏语文测试题

2017江苏高考语文试卷附加题_江苏语文测试题岁月如梭，时间经不起等待，要抓紧时间高考复习，不可浪费一分一秒。

加油，祝高考成功!下面是爱汇网小编为大家整理的2017江苏高考语文试卷附加题,供大家阅读!江苏语文测试题第Ⅰ卷阅读题甲必考题一、现代文阅读(9分，每小题3分)阅读下面的文字，完成1～3题。

神话“是人类心理在最基层水平上的象征和形象的表现”，西方神话学理论认为，神话中最早出现的是创世神话，这是神话发展的第一个阶段。

这个时期人尚未完全意识到自己的存在，自我意识刚刚萌芽，与客观世界混沌为一的动物意识还占着上风，主宰着人类。

英雄神话的产生是神话发展的第二个阶段，“在英雄神话中，世界作为宇宙的中心，而人则处于世界的中心”。

可以看出，有些西方神话学理论对于神话的分类，主要不是根据神话的内容，而是根据神话所体现的人类意识和精神的成长历程，也就是根据神话所蕴含的哲学观念。

这种植根于以希腊神话为代表的西方神话和历史文化土壤中的西方神话理论，未必适用于中国神话。

产生于自然崇拜观念基础上的希腊神话，其新神、旧神之间不但界限清楚，而且由于自然崇拜观念的统一性，具有一个内在统一的普遍的神系以及处于神系统治地位的主神。

具有内在统一性和系统性的神话便于容纳和展示系统的东西，所以，人类意识和精神的发展能够在其中比较清晰地反映出来。

正因为如此，希腊神话在被哲学家、思想家批判、扬弃之后，才能被希腊哲学吸收，成为希腊精神的原型。

与希腊神话不同，主要是产生于祖先崇拜观念基础上的中国神话，不但新神、旧神之间的界限不清楚，而且由于祖先崇拜所崇拜的对象不同，所以始终没有形成一个内在统一的普遍的神系以及处于核心地位上的主神。

中华民族形成和发展的历史道路与古希腊根本不同。

夏、商、周三个王朝的前身分别是以原始氏族血缘关系为基础的夏部族、商部族和周部族。

他们各自生息、发展于一隅，后来才先后入主中原，成为天下的共主。

地位虽然变了，但是，在统治阶级内部仍然保持着原先的那种血缘亲族关系。

历届高考数学附加题(江苏卷)及答案解析

历届高考数学附加题（江苏卷）（2018.江苏）21.【选做题】本题包括A ,B ,C ,D 四小题,请选定其中两小题并作答．．．．．．．．．．．,若多做,则按作答的前两小题评分、解答时应写出文字说明、证明过程或演算步骤。

A .[选修4—1：几何证明选讲](本小题满分10分)如图,圆O 的半径为2,AB 为圆O 的直径,P 为AB 延长线上一点,过点P 作圆O 的切线,切点为C ,若PC =,求BC 的长.B .[选修4—2：矩阵与变换](本小题满分10分) 已知矩阵2312A ⎡⎤=⎢⎥⎦⎣(I)求A 的逆矩阵1A -；(Ⅱ)若点P 在矩阵A 对应的变换作用下得到点'31P （，）,求点P 的坐标。

C .[选修4—4：坐标系与参数方程](本小题满分10分) 在极坐标系中,直线l 的方程为26psin πθ-=（）,曲线C 的方程为4p cos θ=,求直线被曲线C 截得的弦长.D .[选修4-5：不等式选讲](本小题满分10分)若x y z ，，为实数,且226x y z ++=,求222x y z ++的最小值.（2018.江苏）【必做题】第22题、第23题,每题10分,共计20分.解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分)如图,在正三棱柱111ABC A B C -中,12AB AA ==,点P Q ，分别为11,A B BC 的中点.(I)求异面直线BP 与1AC 所成角的余弦值； (Ⅱ)求直线1CC ,与平面1AQC 所成角的正弦值.（2018.江苏）23.(本小题满分10分) 设*N n ∈,对1,2,…,n 的一个排列12n i i i ,如果当s t <时,有s t i i >,则称s t i i （，）是排列12n i i i 的一个逆序,排列12n i i i 的所有逆序的总个数称为其逆序数.例如：对1,2,3的一个排列231,只有两个逆序()()2,13,1，,则排列231的逆序数为2.记n f k （）为1,2,n ,的所有排列中逆序数为k 的全部排列的个数。