第3章 离散点绘制平面曲线-
离散点插值方法、等值线的绘制及平滑技巧

离散点插值方法、等值线的绘制及平滑技巧2008-06-10 22:45由于等值线图看起来非常直观、形象,因此在天气预报、气候预测分析等方面用得非常多,已成为预报员不可缺少的工具之一。
如各等压面层的位势高度图、高空环流、温度及降水分布图等等。
目前也有一些非常好的微机用绘图软件,如SUFER、GRADS 等。
这些软件一般都只有DOS 版,在流行的WINDOWS平台上,虽然可以调用,但不能使用鼠标操作,故不如使用在WINDOWS 环境中开发的软件方便。
因此,许多希望在自己开发的应用程序中能方便地显示及打印各类等值线图的人,都想知道绘制等值线图的原理方法。
如何用格点资料绘制等值线图在文献〔1〕中已有介绍,而离散点(如气象台站) 的资料必须通过插值才能绘制等值线图。
插值的方法有几种,比如三角网插值,它是将相邻的三个点连成一个个三角形,然后用文献〔1〕介绍的追踪法或其它方法在三角形边上进行插值。
此方法的优点是需要插的值少,插值算法简单,数据处理量少。
缺点是三角网的生成随意性很大,任意四个点可生成二组不同的三角形,不同的三角网插值得出的等值线也不可能完全相同。
若人为固定三角网,当有资料缺测时,就不得不重新调整三角网,因此程序的通用性不高。
目前比较流行的是通用性好的网格化方法。
1 离散点网格化理论上,离散点网格化可采用局部曲面拟合方法,用多元回归方法建立V ( X , Y) = a + bX + c Y或二次方程V ( X , Y) = a + bX + c Y + dX2 + eY2 + f X Y所谓局部,是指采用拟合点周围一定范围的部分离散点进行拟合。
这种做法虽然在许多情况下效果不错,但通常总是有些地方与实际情况有较大出入。
因此根据人工绘制等值线时的直接内插方式,采用以下几个步骤。
111 定点(1) 根据离散点的分布范围确定整个网格的范围及网格距,网格距不宜过大或过细。
(2) 确定每个离散点属于哪一个网格,也即每个网格包含哪些离散点。
绘制曲线的基本方法

P3 P2
P4
两种连接法
Pn
2.样条曲线表达式的推导
P1
设有一离散点列Pi,(i=1,2,….,n)。我们 可以用上述方法每经过相邻的三点作 一条抛物线,则由n个点最多总共可以 作出(n-2)条抛物线。见图。
P3 P2 P4 Pn P1
在第二种连接方式的(n-2)条抛物线 中,第i条抛物线的方程应为:
2 i 1
t i 1 ) Pi 3
(0ti,ti+11)
一般来说,两段曲线 Si 和 Si+1 在其 重叠区间是不可能完全自然重合的。 见图 Pi+1 (t)
Pi+1(t) S i (ti ) Pi Pi+1 Pi+2 Pi+3 S i+1(t i+1)
但是,整个点列必须是只能用一条曲 线连接起来的。为了做到这一点,在 两条曲线的共同区间内,必须想法让 它们按照一定的规则结合组成一条曲 线。有效的办法就是 加权合成。 所谓的加权合成,就是用权函数来分 配原曲线在形成的合成曲线中各自所 占的比例。
所以椭圆的绘图程序可写成:
void ellipse(x0, y0, a, b, dt) int x0, y0, a, b, dt; { int x, y, n, i; float t1, t=0.0; t1=dt*0.01745; n=360/dt; moveto(x0+a, y0); for(i=1; i<n; i++) { t=t+t1; x=x0+a*cos(t); y=y0+b*sin(t); lineto(x, y); } lineto(x0+a, y0); }
2 3 1 n n+1 n-1 0 n-2
离散点拟合曲线,Bezier,B样条

a0 b0
a1t b1t
a2t 2 b2t 2
(0 t 1)
§2 贝塞尔曲线
P(t) A0 A1t A2t 2 (0 t 1)
设上述抛物曲线满足下列条件: P1
⑴ t = 0时,抛物线经过P0,
并与P0 P1相切。
⑵ t = 1时,抛物线经过P2
,并与P1 P2相切。
P0
P2
( )
描述的曲线,即曲线的方程已知。 这类曲线的绘制方法:以足够小的步长取曲线上足够多
的点,然后利用曲线方程求出这些点的坐标,最后用直线 连接相邻的点即可绘出曲线。
曲线的绘制精度取决于曲线上取点的密度,密度越大, 精度就越高,曲线就越光滑。
➢ 不规则曲线(拟合曲线):指已 知平面一些离散点的坐标,但曲线方 程未知,需要人为设计曲线方程对这 些点进行拟合形成的曲线。
小。 即:曲线方程是对所有已
知点的“逼近”。 典型例子:地层孔隙度-
深度变化曲线。 “点点通过”式也称为插
1000-
总孔隙度 (%)
2000-
深 度 /m
3000-
密度
(g/cm3 )
(g/cm3 )
值曲线,“平均通过”式也称
为逼近曲线。
4000§1 概述
三、曲线的方程分类
一般可分为直角坐标方程和参数方程两类。 例如:对于圆心坐标为(x0 , y0),半径为 r 的圆, 其直角坐标方程为:
P
(t
)
x(t y(t
) )
a0 b0
a1 b1
t
a2 b2
t
2
§1 概述
四、曲线段的光滑连接
当平面上已知数据点较多时,针对所有点拟合曲线方程 有时非常困难,或者得到的曲线方程非常复杂、不实用。
python离散点拟合曲线

python离散点拟合曲线离散点拟合曲线是一种常用的数据处理方法,能够将散点数据点转化为一条平滑的曲线,以便更好地理解和分析数据趋势。
在Python中,有多种方法可以实现离散点拟合曲线,本文将介绍两种常用的方法,分别是多项式拟合和样条插值。
1. 多项式拟合多项式拟合是一种基于最小二乘法的拟合方法,可以通过一条低阶多项式来逼近一组离散的数据点。
在Python中,可以使用numpy库中的polyfit()函数进行多项式拟合。
下面是一个示例代码:```import numpy as npimport matplotlib.pyplot as plt# 定义离散数据点x = np.array([1, 2, 3, 4, 5])y = np.array([2.3, 4.5, 6.7, 8.9, 11.2])# 进行二次多项式拟合coefficients = np.polyfit(x, y, 2)polynomial = np.poly1d(coefficients)# 生成拟合曲线上的点x_fit = np.linspace(x[0], x[-1], 100)y_fit = polynomial(x_fit)# 绘制原始数据点和拟合曲线plt.scatter(x, y, label='Data Points')plt.plot(x_fit, y_fit, label='Polynomial Fit')# 添加图例和标题plt.legend()plt.title('Polynomial Fit')# 显示图形plt.show()```2. 样条插值样条插值是一种基于插值原理的拟合方法,它利用多段低阶多项式来逼近离散数据点。
在Python中,可以使用scipy库中的interp1d()函数进行样条插值。
下面是一个示例代码:```import numpy as npimport matplotlib.pyplot as pltfrom scipy.interpolate import interp1d# 定义离散数据点x = np.array([1, 2, 3, 4, 5])y = np.array([2.3, 4.5, 6.7, 8.9, 11.2])# 进行样条插值f = interp1d(x, y, kind='cubic')# 生成拟合曲线上的点x_fit = np.linspace(x[0], x[-1], 100)y_fit = f(x_fit)# 绘制原始数据点和拟合曲线plt.scatter(x, y, label='Data Points')plt.plot(x_fit, y_fit, label='Spline Interpolation') # 添加图例和标题plt.legend()plt.title('Spline Interpolation')# 显示图形plt.show()```通过以上示例代码,我们可以分别实现多项式拟合和样条插值,并绘制出对应的拟合曲线。
第03章06节平面曲线的曲率
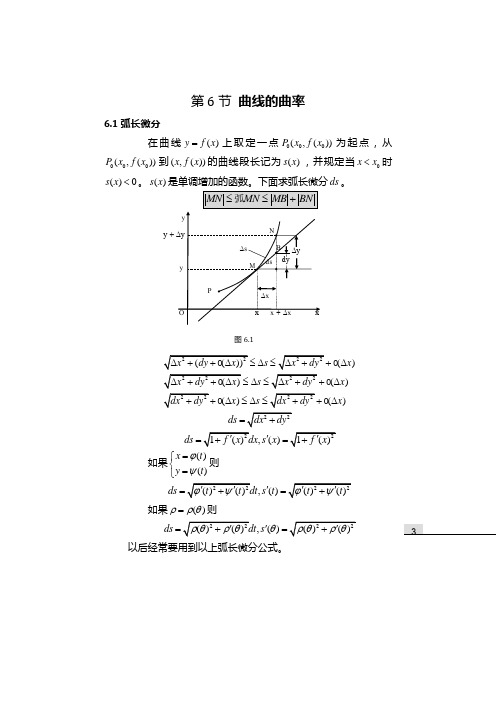
第6节 曲线的曲率6.1弧长微分在曲线()y f x =上取定一点000(,())P x f x 为起点,从000(,())P x f x 到(,())x f x 的曲线段长记为()s x ,并规定当0x x <时()0s x <。
()s x 是单调增加的函数。
下面求弧长微分ds 。
()()()()s x s x x s x ≤∆≤∆≤∆≤∆∆≤∆≤∆ds =,()ds s x '== 如果()()xt y t ϕψ=⎧⎨=⎩则,()ds s t '==如果()ρρθ=则,()ds s θ'==以后经常要用到以上弧长微分公式。
图6.1y +离 散数 学6.2曲线的曲率这节讨论曲线的曲率,也就是曲线的弯曲程度。
设曲线()y f x =在()00,()x f x 的切线0L 与x 轴正向的夹角为0θ,在()00,()x x f x x +∆+∆的切线x L ∆与x 轴正向的夹角为x θ∆。
经过x ∆,切线的夹角变化了0x θθθ∆∆=-设()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的长为s ∆。
容易想见,()00,()x f x 和()00,()x x f x x +∆+∆之间曲线的曲率(弯曲程度)与θ∆成正比,与s ∆成反比,平均曲率()k x sθ∆∆=∆ 让0x ∆→求极限,就得到曲线()y f x =在()00,()x f x 的曲率(弯曲程度)000()lim ()limx x d k x k x s dsθθ∆→∆→∆=∆==∆ 下面我们求出d dsθ从而得到求曲率的计算公式。
用x 作参数 ()()s s x x θθ=⎧⎨=⎩()()2222tan ()1()cos 1tan ()1()()()1()f x d f x dx d f x dx f x d f x dxd f x dx f x θθθθθθθ'=''=''+='''+=''='+第1章集 合322()1()d f x d ds dxdxds f x θθ''=='⎡⎤+⎣⎦003220()()1()f x k x f x ''='⎡⎤+⎣⎦例子:求半径为r 的圆上一点的曲率。
用c语言实现离散点拟合曲线

用c语言实现离散点拟合曲线离散点拟合曲线是一种利用已知数据点来推断未知数据点的方法。
在计算机科学领域,离散点拟合曲线通常是一个重要的问题,因为它可以帮助我们在数据可视化,数据分析和数据预测中更好地理解数据的变化。
在C语言中实现离散点拟合曲线有多种方法,下面介绍其中一种通用的方法,即使用最小二乘法。
最小二乘法是一种对数据进行拟合的方法,它基于最小化数据点和曲线之间的距离来查找最符合数据的函数。
下面是C语言实现离散点拟合曲线的步骤:1. 收集数据点,包括x和y的坐标。
2. 创建一个公式来表示拟合曲线(例如,直线,二次曲线等等)。
3. 对于每个数据点,计算该点在拟合曲线上的值,并计算该值与实际值之间的距离。
4. 最小化所有距离的平方和。
这就是所谓的最小二乘法。
5. 可以使用数值计算库(例如GNU Scientific Library)来解决最小二乘法问题,或手动实现。
下面是一个使用C语言手动实现最小二乘法来拟合一条直线的示例代码:```c#include <stdio.h>#include <stdlib.h>#define MAX_POINTS 50int main() {int num_points;double x[MAX_POINTS], y[MAX_POINTS], sum_x = 0.0, sum_y = 0.0, sum_xx = 0.0, sum_xy = 0.0;double a, b;printf("Enter the number of data points: ");scanf("%d", &num_points);if (num_points > MAX_POINTS) {printf("Too many data points, exiting...\n");exit(1);}for (int i = 0; i < num_points; i++) {printf("Enter point %d (x, y): ", i+1);scanf("%lf %lf", &x[i], &y[i]);sum_x += x[i];sum_y += y[i];sum_xx += x[i] * x[i];sum_xy += x[i] * y[i];}a = (num_points * sum_xy - sum_x * sum_y) / (num_points * sum_xx - sum_x * sum_x);b = (sum_y - a * sum_x) / num_points;printf("\nThe linear equation that best fits the given data:\n"); printf("y = %.2lfx + %.2lf\n", a, b);return 0;}```在上述示例代码中,我们首先使用`scanf()`函数获取数据点的数量和每个数据点的x和y坐标。
离散点拟合曲线

离散点拟合曲线离散点拟合曲线是一种用于对一组无序数据点进行估计和预测的数学方法。
它可以将这些离散的数据点拟合成一个连续的曲线或函数,从而使我们能够更好地理解和分析数据。
离散点拟合曲线的应用非常广泛,包括经济学、医学、物理学、地球科学等领域。
它可以用于预测未来的趋势或现象,或者用于解释已有的数据集。
离散点拟合曲线的拟合方法主要有两种,分别是最小二乘法和最小二次曲线拟合。
最小二乘法是一种用于在线性回归中寻找最佳拟合直线的方法,而最小二次曲线拟合则是将数据点拟合成一个二次曲线。
下面我们将详细介绍这两种方法以及它们的优缺点。
一、最小二乘法最小二乘法是一种常见的拟合方法,它的基本思想是将拟合曲线与数据点之间的误差最小化。
这种方法利用了一个称为残差平方和(RSS)的指标来衡量模型的质量。
残差平方和是指每个数据点与拟合曲线之间的距离的平方之和。
最小二乘法的目标是使这个距离最小,从而获得最佳的拟合曲线。
利用最小二乘法可以拟合各种类型的曲线,包括线性、指数、对数、多项式等。
最小二乘法的优点是:1、它是一种强大的统计工具,可以处理许多类型的曲线。
2、它能够有效地解决噪声和误差的问题,从而提高数据的准确性。
3、它易于实现和使用。
1、它假设数据点之间的误差符合正态分布,而这种假设在实际应用中可能不成立。
2、最小二乘法对离群值敏感,因为在这种情况下,残差平方和会被放大,从而影响拟合曲线的准确性。
二、最小二次曲线拟合1、它能够更精确地描述非线性趋势的数据。
2、它对离群值的敏感度较低,因为曲线更能够适应数据点的变化。
但是,最小二次曲线拟合也存在一些缺点:1、它仅适用于拟合二次函数,因此在处理其他类型的曲线时可能不太灵活。
2、它需要更多的计算量和时间,因为计算二次函数需要更多的参数。
需要注意的是,无论是最小二乘法还是最小二次曲线拟合,都需要考虑到拟合曲线的精度和辨识度是否够高。
因此在实践中,我们需要经过多次试验和调整来确定最佳的拟合曲线。
离散点拟合曲线算法

离散点拟合曲线算法一、概述离散点拟合曲线算法是一种通过给定的离散数据点来拟合出一条连续的曲线的方法。
这种算法在实际应用中非常常见,比如在图像处理、机器学习、数据分析等领域都有广泛的应用。
二、常见的离散点拟合曲线算法1. 多项式拟合多项式拟合是最简单和最常用的拟合方法之一。
它通过给定的数据点,构造一个多项式函数来逼近真实曲线。
通常情况下,多项式函数为n次多项式,其中n为给定数据点数减1。
多项式函数可以表示为:f(x) = a0 + a1*x + a2*x^2 + ... + an*x^n其中a0, a1, ..., an是待求解的系数。
2. 最小二乘法拟合最小二乘法是另一种常见的离散点拟合方法。
它通过最小化误差平方和来得到一个最优解。
误差平方和可以表示为:S = Σ(yi - f(xi))^2其中yi是给定数据点中第i个点的y坐标,f(xi)是x坐标为xi时多项式函数f(x)的值。
3. 样条插值样条插值是一种基于分段多项式函数的拟合方法。
它将曲线分成若干个小段,每个小段内部使用一个低次数的多项式函数来拟合数据点。
这种方法可以得到非常平滑的曲线,但是对于数据点较少或者分布不均匀的情况下可能会出现过拟合的问题。
三、如何选择合适的离散点拟合曲线算法在实际应用中,我们需要根据具体情况选择合适的离散点拟合曲线算法。
以下是一些选择算法的建议:1. 数据量较少且分布均匀时,可以使用多项式拟合。
2. 数据量较大或者存在一定噪声时,可以使用最小二乘法拟合。
3. 需要得到平滑曲线时,可以使用样条插值。
4. 如果需要同时考虑多个因素来进行拟合,则可以使用多元回归分析。
四、常见问题及解决方案1. 过拟合问题过拟合是指模型在训练集上表现很好,但在测试集上表现很差的情况。
解决过拟合问题有以下几种方法:a. 增加训练数据量;b. 减小模型复杂度;c. 正则化。
2. 数据量不足问题如果数据量不足,可能会导致拟合曲线的精度不高。
解决这个问题的方法是增加数据量或者使用更加复杂的模型。
多个点生成平滑函数曲线

多个点生成平滑函数曲线在数据分析和可视化中,经常需要将一组离散的点拟合成一条平滑的曲线。
这通常可以通过插值(Interpolation)或曲线拟合(Curve Fitting)来实现。
下面是一些常用的方法:多项式插值:多项式插值是一种通过多项式函数来逼近离散数据点的方法。
常见的插值算法包括拉格朗日插值、牛顿插值和分段插值等。
样条插值:样条插值是一种数学方法,用于通过一组离散点生成一条平滑曲线。
这种方法通常使用分段多项式函数,并且在连接点处保持一定的连续性(如C0连续、C1连续、C2连续等)。
常用的样条插值包括三次样条插值。
最小二乘法拟合:最小二乘法是一种常用的数学优化技术,用于寻找一组参数,使得某个模型(如线性模型、多项式模型等)与给定数据之间的残差平方和最小。
通过最小二乘法,可以将一组点拟合成一条平滑曲线。
贝塞尔曲线和B样条曲线:贝塞尔曲线和B样条曲线是计算机图形学中常用的参数曲线,它们能够生成平滑且易于控制的曲线。
这些曲线由一组控制点定义,并通过特定的数学公式计算得到。
高斯过程回归:高斯过程回归是一种非参数贝叶斯方法,用于回归问题。
它不仅能够提供预测值,还能给出预测的不确定性。
高斯过程回归可以生成平滑的曲线,并且对于非线性关系也能处理得很好。
局部加权散点图平滑(LOESS/LOWESS):LOESS(局部加权回归散点图平滑)是一种非参数回归方法,它结合了多元线性回归和局部加权平滑的概念。
LOESS能够在每个点的邻域内拟合一个多项式回归模型,并且根据距离远近给每个邻点赋予不同的权重。
核密度估计与核平滑:核密度估计是一种用于估计随机变量概率密度函数的方法。
在曲线拟合的上下文中,核平滑可以用来估计离散点集上的连续函数。
这种方法通常涉及选择一个核函数(如高斯核),并通过卷积来平滑数据点。
选择哪种方法取决于你的具体需求,比如数据的性质(是否线性、是否有噪声等)、所需的平滑程度以及计算复杂度等因素。
在实际应用中,可能需要尝试不同的方法,以找到最适合你数据的平滑曲线生成技术。
离散点插值方法、等值线的绘制及平滑技巧

离散点插值方法、等值线的绘制及平滑技巧离散点插值方法、等值线的绘制及平滑技巧2008-06-10 22:45由于等值线图看起来非常直观、形象,因此在天气预报、气候预测分析等方面用得非常多,已成为预报员不可缺少的工具之一。
如各等压面层的位势高度图、高空环流、温度及降水分布图等等。
目前也有一些非常好的微机用绘图软件,如SUFER、GRADS 等。
这些软件一般都只有DOS 版,在流行的WINDOWS平台上,虽然可以调用,但不能使用鼠标操作,故不如使用在WINDOWS 环境中开发的软件方便。
因此,许多希望在自己开发的应用程序中能方便地显示及打印各类等值线图的人,都想知道绘制等值线图的原理方法。
如何用格点资料绘制等值线图在文献〔1〕中已有介绍,而离散点(如气象台站) 的资料必须通过插值才能绘制等值线图。
插值的方法有几种,比如三角网插值,它是将相邻的三个点连成一个个三角形,然后用文献〔1〕介绍的追踪法或其它方法在三角形边上进行插值。
此方法的优点是需要插的值少,插值算法简单,数据处理量少。
缺点是三角网的生成随意性很大,任意四个点可生成二组不同的三角形,不同的三角网插值得出的等值线也不可能完全相同。
若人为固定三角网,当有资料缺测时,就不得不重新调整三角网,因此程序的通用性不高。
目前比较流行的是通用性好的网格化方法。
1 离散点网格化理论上,离散点网格化可采用局部曲面拟合方法,用多元回归方法建立V ( X , Y) = a + bX + c Y或二次方程V ( X , Y) = a + bX + c Y + dX2 + eY2 + f X Y所谓局部,是指采用拟合点周围一定范围的部分离散点进行拟合。
这种做法虽然在许多情况下效果不错,但通常总是有些地方与实际情况有较大出入。
因此根据人工绘制等值线时的直接内插方式,采用以下几个步骤。
111 定点(1) 根据离散点的分布范围确定整个网格的范围及网格距,网格距不宜过大或过细。
离散点拟合曲线

§1 概述 §2 贝塞尔(Bezier) 曲线 §3 B样条曲线 §4 抛物线调配曲线 §5 三次参数样条曲线
本章小结
§1 概述
一、规则曲线与不规则曲线
平面曲线一般分 规则和不规则曲线两类。 ? 规则曲线 是指可以用一个方程
y ? f (x) 或 f (x, y) ? 0
[ p(t) ? x(t), y(t)] ? ? t ? ?
? ? ? (? )
描述的曲线,即 曲线的方程已知 。 这类曲线的绘制方法:以足够小的步长取曲线上足够
多的点,然后利用曲线方程求出这些点的坐标,最后用直 线连接相邻的点即可绘出曲线。
曲线的绘制精度取决于曲线上取点的密度,密度越大, 精度就越高,曲线就越光滑。
拟合方法不同 → 曲线拟合方程不同 → 绘制的曲线形 状也不同。
但是,一旦拟合方法确定并得到相应的曲线拟合方程, 不规则曲线也就变成了规则曲线。
本章的内容就是介绍: 如何根据离散点的坐标,利用 拟合方法建立曲线拟合方程,绘制不规则曲线 。
§1 概述
二、不规则曲线(拟合曲线)的分类
在用拟合方法建立曲线拟合方程时,通常把不规则曲 线分为两类:
§1 概述
2. “平均通过 ”式
当已知数据点有一定误差时, 所 拟合的曲线不通过所有已知点 ,曲线 代表的是这些数据点的 变化趋势 。
要求 :设计的曲线方程与
所有已知点的“距离”总和最
10 20 30 40 2.0 2.2 2.4
小。
即:曲线方程是对所有已 知点的“逼近”。
典型例子:地层孔隙度- 深度变化曲线。
其中
P
(t)
?
? ???
x (t ) y(t)
用c语言实现离散点拟合曲线

用c语言实现离散点拟合曲线标题:用C语言实现离散点拟合曲线介绍:在数据分析和模式识别的领域中,离散点拟合曲线是一个关键概念。
通过使用C语言,我们可以实现一个离散点拟合曲线的算法,以将离散的数据点拟合成平滑的曲线。
在本文中,我们将深入探讨离散点拟合曲线的背景知识、使用C语言实现的步骤以及一些应用实例。
通过阅读本文,您将能够更全面、深刻和灵活地理解离散点拟合曲线的概念和实现方法。
1. 离散点拟合曲线的概述离散点拟合曲线是一种通过离散的数据点来拟合一个连续的曲线的方法。
该方法可以用于对实验数据、传感器测量值等进行模型拟合,以便更好地理解和解释数据。
离散点拟合曲线通常使用不同的拟合函数,比如多项式函数、高斯函数等。
在深入了解如何用C语言实现离散点拟合之前,我们需要先对拟合函数和拟合精度等概念有一个基本的了解。
2. 使用C语言实现离散点拟合曲线的步骤在C语言中,我们可以使用一些数学库函数来实现离散点拟合曲线算法。
以下是一个基本的步骤:2.1 数据预处理在开始拟合之前,我们需要对原始的离散数据进行预处理。
这包括去除异常值、数据平滑处理等,以保证数据的可靠性和准确性。
2.2 选择拟合函数根据数据的特性和问题的需求,我们需要选择合适的拟合函数。
例如,可以选择多项式拟合函数、指数函数、对数函数等。
拟合函数的选择应根据实际情况进行权衡。
2.3 拟合曲线参数估计通过调整拟合函数的参数,我们可以使拟合曲线与离散数据点的误差最小化。
这一步骤通常使用最小二乘法等数学方法来进行拟合参数的估计。
2.4 曲线生成与优化根据估计得到的参数,我们可以生成离散点拟合曲线,并进一步对曲线进行优化以提高拟合精度。
这可以通过迭代算法、数值优化方法等来实现。
3. 应用实例离散点拟合曲线在实际应用中有广泛的用途。
以下是一些应用实例:3.1 数据分析和预测通过对历史数据的离散点拟合,我们可以对未来趋势和发展进行预测。
这在金融、市场调研等领域中具有重要意义。
离散点拟合曲线,Bezier,B样条

§1 概述
二、不规则曲线(拟合曲线)的分类
在用拟合方法建立曲线拟合方程时,通常把不规则曲 线分为两类: 1. “点点通过”式 当已知离散点的位置较精确时, 拟合的曲线通过所有的已知点。 曲线方程确定后 → 规则曲线 → 以足够小的步长获取 相邻离散点之间若干个数据点(插值点)的坐标,并用直 线连接它们。 当步长极小时,所绘出的直线连线在视觉上便是一条 光滑的曲线。 求相邻离散点之间若干数据点的问题称为插值问题。
P(t ) A0 A1t A2t
2
(0 t 1)
二次B样条曲线参数方程的矩阵形式为:
二次B样条曲线参数方程的矩阵形式:
P (t ) [t 2 1 2 t 1] 1 2 2 2 1 1 1 P0 0 P1 0 P2
P2
两条曲线段在连接点P3处,并非光滑,需对该点进行 光滑处理。在光滑处理时,达到什么标准为“光滑”呢? 给出2个一般标准:
P1
P3
P2
P1
P3
P4
P5
§1 概述
1. C 1连续 在连接点 pj 处,若两曲线段的切线斜率相等(相同 的切线),或者说一阶导数连续,即 pj 称两曲线段在连接点 pj 处的光滑连接达到C 1连续。 2. C 2连续 在连接点 pj 处,不仅两曲线段的切线斜率相同,而 且切线斜率的变化率也相同,即 p( ) p( ) 及 pj( ) pj( ) j j
§1 概述
2. “平均通过”式 当已知数据点有一定误差时,所 拟合的曲线不通过所有已知点,曲线 代表的是这些数据点的变化趋势。 要求:设计的曲线方程与 所有已知点的“距离”总和最 小。 即:曲线方程是对所有已 知点的“逼近”。 典型例子:地层孔隙度- 深度变化曲线。 “点点通过”式也称为插 值曲线,“平均通过”式也称 为逼近曲线。
第32讲 绘制(散点绘制)

第32讲绘制(散点绘制)散点绘制是一种用于可视化数据的方法,通过在坐标系中绘制离散的数据点来展示它们的分布和关系。
本文档将介绍如何进行散点绘制以及如何解读散点图。
散点绘制的步骤散点绘制通常需要以下几个步骤:1. 准备数据:首先,你需要选择要绘制的数据,并准备好它们的数值。
这些数据可以是一组相关的数据,比如两个变量之间的关系,或者是一组独立的数据,比如样本的分布。
2. 创建坐标系:在绘制散点图之前,你需要创建一个合适的坐标系。
坐标系通常由两个轴组成,分别代表数据的两个维度。
例如,x轴可以表示一个变量的取值,y轴可以表示另一个变量的取值。
3. 绘制数据点:一旦坐标系准备好,你可以开始绘制数据点了。
根据数据的具体取值,在坐标系中标出每一个数据点。
你可以使用不同的符号或颜色来表示不同的数据点,以区分它们的属性或类别。
4. 添加标签和标题:为了增加图表的可读性,你可以在数据点附近添加标签,以显示数据的具体值。
此外,还可以添加一个标题,说明图表的主题或目的。
散点图的解读散点图可以提供以下信息:- 数据的分布:通过观察散点图中的点的分布情况,你可以了解数据的分布模式。
例如,如果数据点趋向于聚集在一起,可能表示存在某种相关性或趋势。
- 变量之间的关系:散点图可以显示两个变量之间的关系。
如果数据点呈现出一种特定的形态,比如线性、曲线或聚集,那么可以得出这两个变量之间存在一种关联关系。
- 异常值的检测:通过观察散点图,你可以发现是否存在异常值。
异常值是与其他数据点明显不同的值,可能是由于测量错误或异常情况引起的。
总结散点绘制是一种用于展示数据分布和变量关系的方法。
通过遵循准备数据、创建坐标系、绘制数据点以及添加标签和标题的步骤,你可以轻松地绘制散点图。
通过解读散点图,你可以获得关于数据的分布、变量关系和异常值的有用信息。
> 注意:本文档提供了散点绘制的基本概念和步骤,但在实际应用中可能需要根据具体情况进行调整和进一步的学习。
第3章 离散点绘制平面曲线解读

(g/cm3 )
2.0 2.2 2.4 密度
(g/cm3 )
3000-
4000-
三、曲线的方程分类
一般可分为直角坐标方程和参数方程两类。 例如:对于圆心坐标为(x0 , y0),半径为 r 的圆, 其直角坐标方程为: (x - x0)2 + (y - y0)2 = r2 参数方程为: x = x0 + r cos(t) y = y0 + r sin(t) (0≤t≤2π)
2. “平均通过”式 当已知数据点有一定误差时,所 拟合的曲线不通过所有已知点,曲线 代表的是这些数据点的变化趋势。 要求:设计的曲线方程与 所有已知点的“距离”总和最 小。 即:曲线方程是对所有已 知点的“逼近”。 典型例子:地层孔隙度- 深度变化曲线。 “点点通过”式也称为插 值曲线,“平均通过”式也称 为逼近曲线。
P(t ) A0 A1t A2t
2
(0 t 1)
a0 a1 a2 x (t ) 其中 P (t ) y (t ) , A0 b , A2 b b , A1 1 2 0
四、曲线段的光滑连接
当平面上已知数据点较多时,针对所有点拟合曲线方 程有时非常困难,或者得到的曲线方程非常复杂、不实用。 可分别针对部分点进行分段拟合,分段拟合得到的曲 线段会涉及到曲线段的连接问题。 例如:若已知3个平面离散点,用1条抛物线段对其拟 合;若有5个点,可用2条抛物线段进行分段拟合。
不规则曲线(拟合曲线):指已 知平面一些离散点的坐标,但曲线方 程未知,需要人为设计曲线方程对这 些点进行拟合形成的曲线。
第3章 离散点绘制平面曲线

( )
描述的曲线,即曲线的方程已知。 绘制方法:以足够小的步长取曲线上足够多的点,然 后利用曲线方程求出这些点的坐标,最后用直线连接相邻 的点即可绘出曲线。 曲线的绘制精度取决于曲线上取点的密度,密度越大, 精度就越高,曲线就越光滑。
二、不规则曲线(拟合曲线)的分类
在用拟合方法建立曲线拟合方程时,通常把不规则曲 线分为两类: 1. “点点通过”式 当已知离散点的位置较精确时, 拟合的曲线通过所有的已知点。 曲线方程确定后 → 规则曲线 → 以足够小的步长获取 相邻离散点之间若干个数据点(插值点)的坐标,并用直 线连接它们。 当步长极小时,所绘出的直线连线在视觉上便是一条 光滑的曲线。 求相邻离散点之间若干数据点的问题称为插值问题。
P0
P1
P2 n等份
dt =1.0/n a0=x0 a1=2*(x1-x0) a2=x0-2*x1+x2
(将参数 t 的区间[0 , 1] n等份)
x(t ) a0 a1t a2t
2
100
b0=y0 2 y(t ) b0 b1t b2t b1=2*(y1-y0) b2=y0-2*y1+y2 call movea(x0 , y0) do 100 k=1 , n t =k*dt t2 =t*t x=a0+a1*t+a2*t2 绘制Bezier 曲线 y=b0+b1*t+b2*t2 call linea(x , y) continue end
2. “平均通过”式 当已知数据点有一定误差时,所 拟合的曲线不通过所有已知点,曲线 代表的是这些数据点的变化趋势。 要求:设计的曲线方程与 所有已知点的“距离”总和最 小。 即:曲线方程是对所有已 知点的“逼近”。 典型例子:地层孔隙度- 深度变化曲线。 “点点通过”式也称为插 值曲线,“平均通过”式也称 为逼近曲线。
绘制平面曲线.

立方參數曲線
從解析幾何的觀點來說,若要用多項式來定義連續且平滑的曲 線,則最少必須用立方多項式。立方參數曲線的定義如下:
P(t) (x(t), y(t)) x(t) a3xt 3 a2xt 2 a1xt a0x y(t) a3yt 3 a2 yt 2 a1yt a0 y
2
1
b (u,v) a
conic sections (二次錐線): ax2 bxy cy2 2dx 2ey f 0
然而,隱函式並不適合用來繪製其所代表的曲線。原因在於 我們必須求出滿足方程式 f(x, y) = 0 的解,在多半的情形下, 方程式的解並不容易算出來。
參數曲線
對任意的參數式 P(t) = (x(t), y(t)) ,下列的演算法用 n 條線段 來繪製 P(t) 介於參數區間 [a, b] 的圖形。
dt = (b – a) / n; glBegin(GL_LINE_STRIP); for (t = a; t <= b; t += dt)
glVertex2f (x(t), y(t)); glEnd();
*/
HermiteCurve(point P0, point P1, point P2, int n) {
float dt, t2, t3, f1, f2, f3, f4; point PT0, PT1;
dt = 1.0/n; // t runs from 0 to 1. PT0.x = P2.x - P0.x; PT0.y = P2.y - P0.y; PT1.x = P1.x – P2.x; PT1.y = P1.y – P2.y; glBegin(GL_LINE_STRIP);
????????????????????????????3????????????????t32102301022103321033221203333232131030303i10010033036133113336333131t31pppptttptpptppptppppptpttptptptbptbptbpbptbtpiicompositebeziercurve使用bezier曲線來定義字型的外框decasteljausalgorithmor0iif0bwhere111?1nitttbtbttbnininini???証明
用c语言实现离散点拟合曲线

用c语言实现离散点拟合曲线离散点拟合曲线是指通过一组离散的数据点,找到一条最符合这些数据点的曲线。
在实际应用中,离散点拟合曲线常用于数据分析、图像处理、机器学习等领域。
本文将介绍如何用C语言实现离散点拟合曲线。
我们需要明确离散点拟合曲线的数学模型。
常用的模型包括线性模型、多项式模型、指数模型、对数模型等。
在本文中,我们将以多项式模型为例进行讲解。
多项式模型是指通过多项式函数来拟合数据点。
多项式函数的一般形式为:y = a0 + a1*x + a2*x^2 + ... + an*x^n其中,y为因变量,x为自变量,a0、a1、a2、...、an为多项式系数,n为多项式次数。
接下来,我们需要确定多项式的次数。
一般来说,多项式次数越高,拟合效果越好,但也容易出现过拟合的情况。
因此,我们需要通过交叉验证等方法来确定最优的多项式次数。
在确定多项式次数后,我们需要求解多项式系数。
求解多项式系数的方法有很多种,比如最小二乘法、牛顿插值法、拉格朗日插值法等。
在本文中,我们将以最小二乘法为例进行讲解。
最小二乘法是指通过最小化误差平方和来求解多项式系数。
误差平方和的一般形式为:S = Σ(yi - f(xi))^2其中,yi为实际值,f(xi)为拟合值。
通过对S求导,可以得到多项式系数的解析解。
具体实现过程可以参考以下代码:```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define MAXN 1000double x[MAXN], y[MAXN];double a[MAXN];int n, m;void input(){printf("请输入数据点个数n:");scanf("%d", &n);printf("请输入多项式次数m:"); scanf("%d", &m);printf("请输入数据点:\n");for (int i = 0; i < n; i++) {scanf("%lf%lf", &x[i], &y[i]);}}void solve(){double A[MAXN][MAXN], B[MAXN]; for (int i = 0; i <= m; i++) {for (int j = 0; j <= m; j++) {A[i][j] = 0;for (int k = 0; k < n; k++) {A[i][j] += pow(x[k], i+j);}}B[i] = 0;for (int k = 0; k < n; k++) {B[i] += y[k] * pow(x[k], i);}}for (int i = 0; i <= m; i++) {for (int j = i+1; j <= m; j++) { double t = A[j][i] / A[i][i]; for (int k = i; k <= m; k++) { A[j][k] -= t * A[i][k];}B[j] -= t * B[i];}}for (int i = m; i >= 0; i--) {for (int j = i+1; j <= m; j++) { B[i] -= A[i][j] * a[j];}a[i] = B[i] / A[i][i];}}void output(){printf("拟合多项式为:\n"); for (int i = m; i >= 0; i--) {printf("%+.2lf*x^%d", a[i], i); }printf("\n");}int main(){input();solve();output();return 0;}```以上代码实现了最小二乘法求解多项式系数的过程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P3
P2
P3
P4
P5
两条曲线段在连接点P3处,并非光滑,需对该点进行 光滑处理。在光滑处理时,达到什么标准为“光滑”呢? 给出2个一般标准:
P1
P1
§1 概述
1. C 1连续 在连接点 pj 处,若两曲线段的切线斜率相等(相同 的切线),或者说一阶导数连续,即 pj 称两曲线段在连接点 pj 处的光滑连接达到C 1连续。 2. C 2连续 在连接点 pj 处,不仅两曲线段的切线斜率相同,而 且切线斜率的变化率也相同,即
其中
x (t ) P (t ) y (t )
,
a0 A0 b 0
a 0 a1t a 2 t 2 x (t ) p(t ) 2 y ( t ) b 0 b1 t b 2 t
p j
()
p j
()
p j
( )
及 称两曲线段在连接点 pj 处的光滑连接达到C 2连续。 显然C 2连续比C 1连续要求更高,曲线的连接更光滑。 另外还有更高的连续标准,但对一般绘图,曲线段的 连接满足C 1或C 2连续,其光滑已足够。
。
p j
( )
p j
()
p j
因此,该抛物线段的参数矢量方程为:
P ( t ) P0 2 ( P1 P0 ) t ( P0 2 P1 P2 ) t
2
(0 t 1)
或用矩阵形式表示:
P (t ) [t
2
t
1 1] 2 1
2 2 0
1 P0 0 P1 0 P2
第三章 离散点绘制平面曲线
§1 概述 §2 贝塞尔(Bezier)曲线 §3 B样条曲线 §4 抛物线调配曲线 §5 三次参数样条曲线 本章小结
§1 概述
一、规则曲线与不规则曲线
平面曲线一般分规则和不规则曲线两类。 规则曲线是指可以用一个方程 y f ( x) 或 f ( x, y ) 0
p ( t ) [ x ( t ), y ( t )] t
( )
描述的曲线,即曲线的方程已知。 这类曲线的绘制方法:以足够小的步长取曲线上足够 多的点,然后利用曲线方程求出这些点的坐标,最后用直 线连接相邻的点即可绘出曲线。 曲线的绘制精度取决于曲线上取点的密度,密度越大, 精度就越高,曲线就越光滑。
10 20 30 40 1000总孔隙度 (%) 2000深 度 /m
( g/cm
3
2.0 2.2 2.4 密度
( g/cm
3
)
)
3000-
4000-
§1 概述
三、曲线的方程分类
一般可分为直角坐标方程和参数方程两类。 例如:对于圆心坐标为(x0 , y0),半径为 r 的圆, 其直角坐标方程为: (x - x0)2 + (y - y0)2 = r2 参数方程为: x = x0 + r cos(t) y = y0 + r sin(t) (0≤t≤2π)
P0
P2
③曲线落在特征多边形的凸包之内,它比特征多边 形更趋于光滑。 ④贝塞尔曲线属于“平均通过”式曲线。
§2 贝塞尔曲线
§3 B样条曲线
B样条曲线是在Bezier 曲线基础上发展起来的一类曲 线,它克服了Bezier 曲线整体控制性所带来的不便,最常 用的是二次和三次B样条曲线。 一、二次B样条曲线 1. 参数方程 已知三个平面离散点P0、P1、P2,由这三点可以定义 二次抛物线段,其参数矢量方程形式为:
可以用低次Bezier 曲线进行分段拟合(常使用二次和三 次Bezier 曲线);需要对连接点进行光滑处理(C 1连续、 C 2连续),已有CG方面的论文研究了此问题。
地质绘图中常采用低次Bezier 曲线的分段拟合。
§2 贝塞尔曲线
二、二次Bezier 曲线的程序设计思路 已知:平面上 3 个离散点P0、P1、P2的坐标( x0 , y0 )、 ( x1 , y1 )、( x2 , y2)。 二次Bezier 曲线参数方程的分量形式:
i i (ni)
,C n
i ! ( n i )!
其分量形式为:
x (t ) y (t )
B
i0 n
n
i ,n
(t ) x i
( 0 t 1)
B
i0
i ,n
(t ) yi
§2 贝塞尔曲线
实际应用中,对多个离散点(如:7个离散点)绘制 Bezier 曲线时: 可以用高次Bezier 曲线进行绘制(如:7个离散点使用 六次Bezier 曲线);
其中
a 0 x 0 a1 2( x1 x 0 ) a x 2 x x 0 1 2 2
绘制方法:将参数 t 的区间[0 , 1]划分为 n 等份,依 次取t = 1/n , 2/n , 3/n , … ,利用曲线参数方程计算对应的 各点坐标,并用直线段依次连接各点。 在已知三个平面离散点时,可绘制二次Bezier曲线; 若有n+1个平面离散点时,则可绘制n次Bezier曲线。
x (t ) a 0 a1t a 2t 2 2 y ( t ) b 0 b1 t b 2 t
( 0 t 1)
b0 y 0 b1 2 ( y 1 y 0 ) b y 2 y y 0 1 2 2
其中
a 0 x 0 a1 2( x1 x 0 ) a x 2 x x 0 1 2 2
该方程描述的曲线称为二次贝塞尔曲线。 其分量形式为:
§2 贝塞尔曲线
x (t ) a 0 a1t a 2t 2 2 y ( t ) b 0 b1 t b 2 t
( 0 t 1)
b0 y 0 b1 2 ( y 1 y 0 ) b y 2 y y 0 1 2 2
编程思路:将参数 t 的区间[0 , 1]划分为 n 等份,依 次取t = 1/n , 2/n , 3/n , … ,利用方程计算对应各点的坐标, 并用直线段依次连接各点。
§2 贝塞尔曲线
三、Bezier 曲线的特点
①曲线通过始点和终点,并与特征多边形首末两边相 切于始点和终点,中间点将曲线拉向自己。 P1 ②平面离散点控制曲线的形状,改 变一个离散点的坐标,曲线的形状将随 之改变(点对曲线具有整体控制性)。
2. Bezier 曲线的参数方程 已知三个平面离散点P0、P1、P2,那么由这三点可以 定义二次抛物线段,其参数矢量方程可表示为:
P ( t ) A 0 A1 t A 2 t
2
( 0 t 1)
, a1 A1 b 1 , a2 A2 b 2
P2
P ( 0 ) A 0 P0
P ( 0 ) A 1 P0 P1的斜率
P ( 1 ) A 0 A 1 A 2 P2
P (1 ) A1 2 A 2 P1 P 2的斜率
经过推导(详见教材P58),可求出A0、A1、A2:
§2 贝塞尔曲线
A 0 P0 A 1 2 ( P1 P 0 ) A P 2P P 0 1 2 2
不规则曲线(拟合曲线):指已 知平面一些离散点的坐标,但曲线方 程未知,需要人为设计曲线方程对这 些点进行拟合形成的曲线。 对于这类曲线的绘制,首先要找出一种合理的拟合方 法来设计曲线方程。 拟合方法包括:贝塞尔曲线法、B样条曲线法、抛物 线调配曲线法、三次参数样条曲线法,最小二乘法等。 拟合方法不同 → 曲线拟合方程不同 → 绘制的曲线形 状也不同。 但是,一旦拟合方法确定并得到相应的曲线拟合方程, 不规则曲线也就变成了规则曲线。 本章的内容就是介绍:如何根据离散点的坐标,利用 拟合方法建立曲线拟合方程,绘制不规则曲线。
设
x (t ) P (t ) y (t )
,
a0 A0 b 0
,
上述参数方程可写为:
P ( t ) A 0 A1 t A 2 t
2
0 t 1
②
方程②称为曲线的参数矢量方程。 在构建曲线方程时,通常采用方程②的矢量形式;在 绘制曲线时,通常采用方程①的分量形式。
x (t ) a 0 P (t ) y (t ) b 0 a1 a2 2 t t b b 1 2
§1 概述
四、曲线段的光滑连接
当平面上已知数据点较多时,针对所有点拟合曲线方 程有时非常困难,或者得到的曲线方程非常复杂、不实用。 可分别针对部分点进行分段拟合,分段拟合得到的曲 线段会涉及到曲线段的连接问题。 例如:若已知3个平面离散点,用1条抛物线段对其拟 合;若有5个点,可用2条抛物线段进行分段拟合。
()
§2 贝塞尔曲线
一、Bezier 曲线 1. 特征多边形 特征多边形是用直线段依次 连接平面上离散点所形成的折线 多边形。它反映了所要设计曲线 P0 的大致轮廓。
P1 P2 P5 P3 P4
可以设计一个光滑的曲线段去逼近这个特征多边形。 贝塞尔曲线就属于这类曲线。 该曲线由法国汽车工程师Bezier首先提出,最初用于 汽车零件外形的设计。目前广泛应用于与计算机绘图相关 的各个领域。
P ( t ) A 0 A1 t A 2 t
2
( 0 t 1)
二次B样条曲线参数方程的矩阵形式为:
二次B样条曲线参数方程的矩阵形式:
P (t ) [t
2
t
Hale Waihona Puke 1 2 1] 1 2 2 2 1 1
