n维向量,线性相关性
将系数矩阵A分裂成列向量 A (1 , 2 , , n ) ,
则方程组改写为 x11 x2 2 xn n ,
线性方程组 Ax 解的问题， 等价于常数列 被 A 的列向量组线性表示的问题.
11
定理3.3 n维向量 可由n维向量组 α1，α2， ，αs 线性表示 n元线性方程组 x1α1 x2 α2 xs αs β 有解 矩阵 A (α1 ,α2 , ,αs )与矩阵 A (α1 ,α2 ,,αs , β) 的秩相等. 由此可知： （1）n维向量 β 可由n维向量组 α1，α2， ，αs 唯一线 性表示 r ( A) r ( A) s； （2）n维向量 β 可由n维向量组 α1，α2， ，αs 线性表 示且表示法不唯一 r ( A) r ( A) s ； （3）n维向量 β 不能由n维向量组 α1，α2， ，αs 线性 表示 r ( A) r ( A) .
由定义3.4 不难验证向量组的等价关系具有下列性质： 设(A)，(B)，(C)均为n维向量组，则 反身性 任一维向量组(A) (A). 对称性 若(A) (B)，则(B) (A). 传递性 若(A) (B) ,(B) (C) 则(A) (C).
16
设向量组 β1 , β 2 ,, βt 可由向量组 α1，α2， ，αs 线性表示为 k1 j k2 j β j k 1j α 1 k 2j α 2 k sj α s α1，α 2， ，α s k sj ( j 1,2,, t ) 将上述线性表示式写成矩阵形式：
14
1 2 0 3 1 2 0 3 0 - 1 1 - 2 0 1 -1 2 , 0 0 a -1 0 0 1 -1 b 0 0 0 - 1 a - 2 0 b - 2
(1) b 2 时， 不能由1 , 2 , 3 线性表出；
6 31 2 2 - 5 3 ,
1 ( 3 1 2 2 - 5 3 ) (1,2,3) . 6
5
定义3.2 数域F上所有n维向量组成的集合
F n {(a1 , a2 ,, an )T a1 , a2 ,, an F}
连同其上定义的加法和数量乘法，称为数域F上的n n 维向量空间(vector space). 特别， R 表示实数域R 上的n维向量空间. 以后，若无特别说明，涉及的向 量均为 R n 中的向量.
定理3.5 （1）若矩阵A经有限次初等行（列）变换 化成矩阵B，则矩阵A与B的行（列）向量组等价. （2）若矩阵A经有限次初等行（列）变换化成矩阵 B，则矩阵B的列（行）向量与矩阵A的列（行）向 量间有相同的线性关系，即矩阵的初等行（列）变 换不改变矩阵的列（行）向量间的线性关系.
19
证明 设矩阵A经有限次初等行变换化成矩阵B，则 存在可逆矩阵P使 PA B ，所以矩阵A与B的行向量 组等价且
则 (a1 b1 , a2 b2 ,, an bn )，
k (ka1 , ka2 ,, kan ) .
3
向量的线性运算满足以下八条运算律：
(1) +=+ (2) +(+)=(+)+ (3) +0= (4) +(-)= 0 (5) (k+l)=k+l (6) k(+)=k+k (7) (kl)=k(l) (8) 1=
8
例如, =(2,-1,1), 1=(1,0,0), 2=(0,1,0), 3=(0,0,1),
因为 = 21-2+3 ,
即 是 1,2,3 的线性组合,
或者说 可由1,2,3 线性表示.
☎ ☎
零向量能被任何向量组1 ,, s 线性表示:
o 01 0 s .
定理3.4 向量组 β1 , β 2 ,, βt 可由向量组 α1，α2， ，αs 线性表示的充要条件是 r ( A) r ( A, B) ，其中
A α1，α2， ，αs , B β1 , β2 ,, βt
18
推论3.4 设矩阵 A α1，α2， ，αs , B β1 , β2 ,, βt ，那么 （1）向量组 β1 , β 2 ,, βt 与向量组 α1，α2， ，αs 等价的 充要条件是 r ( A) r ( B) r ( A, B) . （2）若向量组 β1 , β2 ,, βt 可由向量组α1，α2， ，αs 线性 表示，则 r ( B) r ( A) . （3）r ( AB) min{r ( A), r ( B)} ，特别，当矩阵A可逆时， r ( AB) r ( B)
其中, , 都是n维向量, k, l 为实数.
4
除了上述八条运算规则，显然还有以下性质：
(1' ) 0 o, ko o(其 0 为 零 , k为 意 ) ; 中 数 任 数
(2' ) 若k o, 则 k 0, 或 o ; 故 或
kα O k 0或α O
☎
任意一个 n 维向量 ( a1 , a 2 , , a n ) 都能被向量
组 1 , 2 , , n 线性表示:
a1 1 a2 2 an n .
10
x1 b1 x2 b2 对线性方程组 Ax , x , , x b n n
(3' ) 向量方程 x 有唯一解x - . 移项规则
例1 设 3(1 - ) 2( 2 ) 5( 3 ) ， 其中 1 (2,5,1) , 2 (10,1,5) , 3 (4,1,-1) , 求 .
解 31 - 3 2 2 2 5 3 5 ,
则上式可写成: B AK （K叫该线性表示的系数矩阵）
17
一般地，若矩阵 A, B, C 具有关系 A BC ，则矩阵A 的列向量组可由矩阵B的列向量组线性表示，C为这 一表示的系数矩阵；而矩阵A的行向量组可由矩阵C 的行向量组线性表示，B为这一表示的系数矩阵. 特别，若矩阵C可逆，则矩阵A的列向量组与矩阵 B的列向量组等价；若矩阵B可逆，则矩阵A的行向量 组与矩阵C的行向量组等价. 上述讨论表明： 向量组 β1 , β 2 ,, βt 可由向量组 α1，α2， ，αs线性表示 的充要条件是矩阵方程 AX B 有解 X K (kij ) st 其中 A α1，α2， ，αs , B β1 , β2 ,, βt
练习：
P123
习题三
6
§3.3
7
一、线性组合、线性表示
定义3.3 给定 n 维向量 1 ,, s 和 , 若存在 s 个数
k1 ,, ks ，使 k11 ks s ，则称 是向量 组 1 ,, s 的一个线性组合，或称 能被向量组 1 ,, s 线性表示(线性表出)。
k1 k1 k1 k2 k2 k2 A O PA B O k k k n n n
13
例2
设向量组 1 (1, 4, 0, 2) ， 2 ( 2, 7, 1, 3) ，
T T
T
3 ( 0, 1, - 1, a) ， (3, 10, b, 4)T ，问：a, b 满
足什么条件时,
(1) 可由 1 , 2 , 3 线性表出，且表示法唯一；
12
1 1 2 2 例1 设 1 0 , 2 2 , 3 1 , 5 , 1 1 0 4
能否由1 , 2 , 3 线性表示?
(2) b 2 且a 1 时， 可由1 , 2 , 3 唯一表出；
(3) b 2 且a 1 时， 可由1 , 2 , 3 线性表出；
但表示法不唯一: β (3 - 2t )α1 tα2 (-2 t )α3 , (t R)
15
现在讨论两个向量组之间的线性表示问题.
向量组 1 , , s 01 1 j 0 s .
9
称 1 (1 , 0 , , 0) , 2 (0 , 1 , , 0) , , n (0 , 0 , , 1) 为n维基本单位向量组。
定义 3.4 如果向量组(Ⅰ) 1 ,, s 中每个向量
均可由向量组(Ⅱ) 1 ,, t 线性表出，则称向量组 (Ⅰ)可由向量组(Ⅱ)线性表出； 若两向量组 1 ,, s 与 1 ,, t 可以互相线性 表出,则称它们等价，记为{α1，α2， ，αs } {β1 , β2 ,, βt }
§3.2
1
定义3.1 n 个数组成的有序数组 (a1 , a2 ,, an ) 称为
一个 n 维向量。
a1 , a2 ,, an 称为向量 的分量或坐标。
行向量
(a1 , a2 ,, an )
a1 a2 a n
列向量
或 (a1 , a2 ,, an )T
2
一般用希腊字母 , , 等表示 n 维向量。
分量全部为零的向量称为零向量，记为 o 。 向量可视为特殊的矩阵, 因此, 向量的相等、加减法、 数乘等概念完全与矩阵相同.
31,2 n维向量及其运算 向量组的线性相关性
,
，如果存在一
m
组数k1，k2， , km， 使得
k11 k22 kmm
则称向量
可以由向量组1
,
，
2
,
的线性表示，
m
或称向量是向量组1,2, ,m的线性组合.
任意一个n维向量a都能由n维单位坐标向量组
e1,e2,…,en线性表示.
a (a1,a2, ,an )T , e1 (1,0, ,0)T ,
则存在一组数k1, ki1, ki1, km , 满足
i k11 ki1 i1 ki1 i1 kmm
即存在不全为0的数k1, ki1, 1，ki1, km ,
使得k11 ki1 i1 (1)i ki1 i1 kmm 0
二、线性相关性
定义3 给定向量组A :1,2 ,,m ,如果存在不
向量组的等价具有性质： 1. 自反性 任一向量组与其自身等价. 2. 对称性 若向量组(I)与(II)等价，则向
量组(II)也与(I)等价. 3. 传递性 若向量组(I)与(II)等价，向量
组(II)与(III)等价，则向量组(I)与(III)等 价.
如果 1,2 ,
,
中有一个向量
m
（不妨设 i）能用其余向量线性表示，
又有m个n维行向量
a11 a21
a12 a22
a1n a2n
A ai1
ai2
ain
am1 am2 amn
向量组 , , …， 称为矩阵A的行向量组．
反之，由有限个同维的向量所组成的向量组 可以构成一个矩阵.
m个n维列向量所组成的向量组1,2 , ,m ,
构成一个n m矩阵
e2 (0,1, ,0)T , ,en (0,0, ,1)T
(完整版)n维向量及其线性相关剖析
0 0
- 11 14
1 1 - 1 - 6
0 0 1 9
-111 142 93
线性代数
17
练习 判断向量 b1 (4, 3, -1,11) 与 b2 (4, 3,0,11) 是否为
向量组 a1 (1, 2, -1,5), a2 (2, -1,1,1) 的线性组合. 若是,
即线性方程组
有解.
x11 x2 2 xm m b
线性代数
14
6
3
2
例1
向 量
9
能
否
由
向
量
组1
3,2
5,
6
6
4
3
6 9
线 性 表 示 。
15
设
向
量可
由
向
量
组1，
2，
线
3
性
表
示
为
：
x11 x22 x33
3 x1 3 x1
2x2 5x2
6x3 9x3
6 9
线性代数
1
本讲内容：
1、n 维向量及其线性运算 2、向量组的线性组合 3、向量组的线性相关性
线性代数
2
一、n维向量的概念：
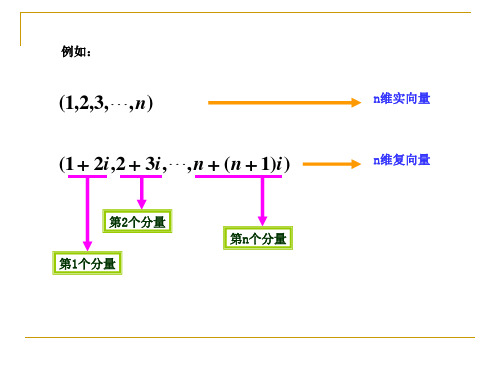
定义1 n 个 有 次 序 的 数a1, a2 , , an 所 组 成 的 数 组 称 为n维向量，这n个数称为该向量的n个分量， 第i个 数ai称 为 第i个 分 量.
分量全为实数的向量称为实向量，
线性代数
7
n 维向量的实际意义
确定飞机的状态，需
要以下6个参数：
机身的仰角 机翼的转角
(-
)
2
2
(- )
机身的水平转角 (0 2 )
n维向量组a1a2a3a4线性相关
n维向量组a1a2a3a4线性相关线性相关，指的是两个或多个变量之间存在着一定程度上的相关性。
只要任意两个变量间有任何线性关系，它们就被认为是线性相关的。
维向量组a1a2a3a4之间存在线性相关性，那么关于它们的内容有：1. 维向量组a1a2a3a4可以表示为m维空间里的n个线性方程，即a1、a2、a3、a4都可以表示为：$x_1c_1 + x_2c_2 + x_3c_3 + x_4c_4 = 0$ 。
2. a1a2a3a4之间的线性关系可以表示为：一个变量值的变化会改变其他变量的值，或者说某一变量的变化会引起其他变量的变化。
3. 根据a1a2a3a4的线性相关性，在满足一定约束条件时，可以求出4个变量之间的相对关系。
4. a1a2a3a4之间的线性相关性包括两个方面：一是它们本身存在线性关系，二是它们之间存在线性关系。
5. 维向量组a1a2a3a4之间的线性相关性可以通过线性回归分析等方法来进行评估和确定。
6. 定量分析维向量组a1a2a3a4之间的线性相关性，可以通过Kendall系数法，Spearman等秩相关系数等方法来测定。
7. 维向量组a1a2a3a4之间的线性相关性可以用多元线性回归模型进行预测和分析，来验证其定量分析结果。
8. 利用维向量组a1a2a3a4之间的线性相关性可以分析多个指标之间的关系，从而实现建模和预测。
9. 如果维向量组a1a2a3a4之间的线性关系很强，那么可以用回归模型来表示，从而可以实现估算变量值，也可以给出变量的可信区间。
10. 利用维向量组a1a2a3a4之间的线性关系可以计算特征向量的投影，可以解决多维特征间相关性的研究问题，使特征维度减少，数据表达更加简洁。
06高数—— 向量组的线性相关性知识点速记
向量组的线性相关性1、n 维向量由n 个数组成的有序数组()12,,,n a a a 称作一个n 维向量，记作()12,,,n a a a α= ，其中i a 称作α的第i 个坐标。
设()12,,,n a a a α= ，()12,,,n b b b β= ，当()1,2,,i i a i n b == 时，称α与β相等，记作αβ=。
称()12,,,n a a a α= 为n 维列向量，αT 为n 维行向量。
分量全为0的向量称为零向量。
向量()12,,,n a a a α= 的各分量的相反数所组成的向量，称为α的负向量，记作α-，即()12,,n a a a α=---- 。
向量加法定义：()1122,,,n n a b a b a b αβ+=+++ ；向量减法定义：()()1122,,,n n a b a b a b αβαβ-=+-=--- 。
向量α与数乘积定义；k 为任意实数，则()12,,,n k k k k αααα= n 维向量的加法和数乘运算满足下面性质（设α、β、γ表示n 维向量，k 、l 表示数量）。
（1）αββα+=+；（2）()()αβγαβγ++=++；（3）0αα+=；（4）()0αα+-=；（5）()k k k αβαβ+=+；（6）()k l k l ααα+=+。
2、向量的线性表示设12,,,s ααα ，β均为n 维向量，若存在一组数12,,,s k k k ，使得1122k k αβα=+++ s s k α，则称向量β是向量组12,,,s ααα 的一个线性组合，也称向量β可由向量组12,,,s ααα 线性表示。
3、向量组的线性相关性对于m 个n 维向量12,,,m ααα ，若存在不全为零的数12,,,m k k k ，使得11220m m k k k ααα+++= ，则称这m 个向量线性相关；否则，称它们线性无关。
通过线性相关和线性无关的定义可推出：（1）单独一个0向量，线性相关；高 数向量组的线性相关性知识点速记（2）含有0向量的向量组，线性相关；（3）单独一个非0向量，线性无关；（4）由n 个标准单位向量()11,0,0,,0=ε ，()20,1,0,,0=ε ，…，()0,,0,1n =ε 组成的向量组，线性无关。
第1节 n维向量及其线性相关性(全)
第四章向量及向量空间§1 n维向量及其线性相关性§2 向量组的秩§3 线性方程组解的结构§4 向量空间§1 n维向量及其线性相关性●n维向量●线性相关性定义1 n 个有次序的数所组成的数组称为n 维向量，这n 个数称为该向量的n 个分量，第i 个数称为第i 个分量。
,,,12n a a a i a ◆分量全为实数的向量称为实向量◆分量为复数的向量称为复向量本书中除特别指明者外，一般只讨论实向量◆n 维向量写成一行的称为行向量◆n 维向量写成一列的称为列向量(),,,n a a a 1212 n a a a ⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭◆实数域R 上全体n 维向量组成的集合称为n 维实向量空间记为R n说明：◎行向量和列向量总被看作是两个不同的向量。
◎所讨论的向量在没有指明是行向量还是列向量时，都当作列向量。
◎通常情况下，列向量用黑色小写字母a ,b ,α,β等表示，行向量则用a ,b ,αT ,βT 表示。
◎行向量和列向量也分别称为行矩阵和列矩阵，并规定都按矩阵的运算规则进行运算。
◎若干个同维数的列向量(行向量)所组成的集合称为向量组。
11121314342122232431323334a a a a A a a a a a a a a ⎛⎫ ⎪= ⎪ ⎪⎝⎭()1234,,,αααα=123T T T βββ⎛⎫ ⎪= ⎪⎪⎝⎭结论：含有限个向量的有序向量组与矩阵一一对应．有限向量组例如定义2 设a∈R n, k i∈R, (i=1, 2, …, m)，则向量ik1a1 + k2a2 + … + k m a m称为向量组a, a2, …, a m在实数域R上的一个线性组合。
1k1, k2, …, k m 称为这个线性组合的系数．定义：若记b= k1a1 + k2a2 + … + k m a m, a2, …, a m线性表示。
则称向量b 可由向量组a1b 可由向量组a1, a2, …, a m线性表示方程组xa1 + x2a2 + … + x m a m = b有解1例：设()123100,,010001E e e e ⎛⎫ ⎪== ⎪ ⎪⎝⎭100203170001⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭123237e e e =++237b ⎛⎫ ⎪= ⎪ ⎪⎝⎭那么线性组合的系数e 1, e 2, e 3的线性组合一般地，对于任意的n 维向量b ，必有1231000010000100001n b b b b ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=+++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭123n b b b b b ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭n 阶单位矩阵E n 的列向量叫做n 维单位坐标向量．1231000010000100001n b b b b ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪=+++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭123n b b b b b ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭1000010000100001n E ⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭例零向量是任何一组向量的线性组合.例向量组a 1, a 2, …, a s 中的任一向量a j (1≤j ≤s )都是此向量组a 1,a 2, …, a s 的线性组合。
n维向量,线性相关性
分量全部为零的向量称为零向量，记为 o 。 向量可视为特殊的矩阵, 因此, 向量的相等、加减法、 数乘等概念完全与矩阵相同.
设 (a1 , a2 ,, an )， (b1 , b2 ,, bn ),
则 (a1 b1 , a2 b2 ,, an bn )，
k (ka1 , ka2 ,, kan ) .
3
向量的线性运算满足以下八条运算律：
(1) +=+ (2) +(+)=(+)+ (3) +0= (4) +(-)= 0 (5) (k+l)=k+l (6) k(+)=k+k (7) (kl)=k(l) (8) 1=
练习：
7
一、线性组合、线性表示
定义3.3 给定 n 维向量 1 ,, s 和 , 若存在 s 个数
k1 ,, ks ，使 k11 ks s ，则称 是向量 组 1 ,, s 的一个线性组合，或称 能被向量组 1 ,, s 线性表示(线性表出)。
12
1 1 2 2 例1 设 1 0 , 2 2 , 3 1 , 5 , 1 1 0 4
能否由1 , 2 , 3 线性表示?
(3' ) 向量方程 x 有唯一解x - . 移项规则
例1 设 3(1 - ) 2( 2 ) 5( 3 ) ， 其中 1 (2,5,1) , 2 (10,1,5) , 3 (4,1,-1) , 求 .
解 31 - 3 2 2 2 5 3 5 ,
则上式可写成: B AK （K叫该线性表示的系数矩阵）
n维向量及向量组的线性相关性
类,似 矩 A 地 阵 (a i)jm n 又 m 个 有 n 维行
a 11 a 21
a 12 a 22
a 1n a2n
T 1
T 2
A ai1
ai2
a in
T i
a m 1 a m 2 a mn
T m
向量组
T 1
,
T 2
,
…，
T m
称为矩阵A的行向量组．
反之，由有限个向量所组成的向量组可以构 成一个矩阵.
1 (a1, a2, a3, a4, a5)T , 2 (b1,b2,b3,b4,b5)T , 3 (c1, c2, c3, c4, c5)T 也线性无关.
定 理 5 若 n维 向 量 组 1, 2 ,..., s线 性 无 关 ,
则 在 每 个 向 量 中 添 加 m个 分 量 ,得 到 的
2
，
3
3
1
，
2
4
1
0
1
1
1
0
1
例5 试证向量组1, 2 ,
,
中
s
任
意
一
向
量
i (i 1, 2,..., s)可以由向量组线性表出。
例6
已
知
是
1，
2
,
...,
的
t
线
性
组
合
，
且
每一个i
(i
1,
2,...,
t)又是
1,
2 , ...,
的线性
s
组
合
，
证
明
也
是
1
,
2
,
...,
3.1 n维向量及其线性相关性
, an )T.
1. 行向量和列向量总被看作是两个不同的向量.
2. 当未说明是行向量还是列向量时, 都当作列向量.
公共基础课部 线性代数 2014秋季
定义3.2 设 = (a1, a2,, an) Fn , = (b1, b2,, bn) Fn, F , F为数域 (1) = 当且仅当 ai=bi ， i=1,2,,n (2) 向量加法（ 与 之和 ） : + = (a1+b1, a2+b2,, an+bn) (3) 向量数乘（数量乘法，数 与 之乘积）: = (a1,a2,,an)
n 维实向量 n 维复向量
第n个分量
第1个分量
公共基础课部
线性代数
2014秋季
n 维向量写成一行, 称为行向量, 也就是行矩阵, 如
(a1 , a2 , , an );
n 维向量写成一列, 称为列向量, 也就是列矩阵, 如
a1 a β 2 (a1 , a2 , an
, αm (m 2) 线性相关,
, km , 使得
则存在一组不全为零的数 k , k ,
k1α k2α
不妨设 k 0, 则
kmαm 0,
k3 km k2 α α α3 αm , k1 k1 k1 可见向量 α1 是其余向量的线性组合.
公共基础课部 线性代数 2014秋季
, αm 构成 n m 矩阵:
A [α1 α 2
m 个 n 维行向量 β , β ,
T 1 T 2 T m
α m ];
, β 构成 m n 矩阵:
β1T T β2 B . T βm
n维向量的线性相关性
例如 对向量α=(1, 1, 0), β=(2, 1, 1), γ=(1, 0, 1),
β=α+γ, β是α, γ的线性组合.
在n维向量空间中，设
1,0,,0, 0,1,,0, , 0,0,,1,
1
2
则对任何一个n维向量
(a ,a ,,na )
12
n
都有 a11 a2 2 an n .
证 用反证法，利用性质2即得。
4．若向量组i=(ai1, ai2,…, ain), i=1, 2, …, m, 线
性相关， 则去掉最后r个分量(1≤r<n)后，所得 到的向量组： βi=(ai1, ai2,…, ain-r) , i=1, 2, …, m 也线性相关.
证 由 α1, α2, …, αm 线性相关，故存在着
a ,a ,,a i 1,2,,n
i
i1 i2
in
线性相关的充分必要条件为
a a a
11
21
n1
a a a
D
12
22
n2
0.
a a a
1n
2n
nn
向量组的线性相关与线性无关的性质
1．含有零向量的向量组必线性相关.
证 不失一般性，设所给的m个向量为
0, ,, .
1
2
m
从而存在不全为零的数1,0,…,0，使得
解 设 k k k 0,
11
22
33
即 系数行列式
k 1
2k 2
k 3
0
2k
1
k
2
3k 3
0
2k 1
k 2
k 3
0
1 2 1
不能用克莱
n维向量组的线性相关性
即 b=(2, -1, 1)是向量组a1，a2 ，a3的线性组合，也就是说b可由 a1，a2 ，a3线性表示.
下页
7.1 线性组合与线性表示
定义1 给定n维向量b，a1，a2， ，am，如果存在一组数
定义1 给定n维向量b，a1，a2， ，am，如果存在一组数
k1，k2， ，km，使
b=k1a1+k2a2+ + kmam， 则称向量b是向量组a1，a2 ， ，am的线性组合，或称b可由向量 组a1，a2 ， ，am线性表示.
例1．设 a1=(1, 0, 0)，a2=(0, 1, 0)，a3=(0, 0, 1)， b=(2, -1, 1)， 则b=(2, -1, 1)是向量组a1，a2 ，a3的线性组合.
例3．零向量是任何一组向量的线性组合.
这是因为 o=0a1+ 0a2+ + 0 am . 例4．向量组a1，a2 ， ，am中的任一向量ai(1im)都是
此向量组的线性组合.
这是因为 ai=0a1+ + 1ai + + 0 am .
下页
例5．线性方程组的向量表示(向量方程)
a11x1 + a12x2 + + a1nxn = b1
k1，k2， ，kn，使
k1a1+k2a2+ + knan=o 成立 .
由向量的运算性质可得
k1a1+k2a2+ +kn an=o，即
a11 a21
an1 0