中考数学三视图专项训练

合集下载

2019-2020届初三中考复习三视图综合题专项练习(含答案解析)教学提纲

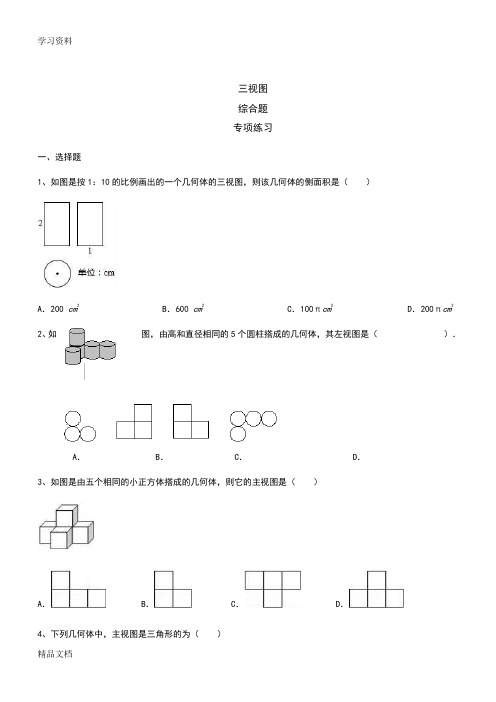
三视图综合题专项练习一、选择题1、如图是按1：10的比例画出的一个几何体的三视图，则该几何体的侧面积是（）A．200 cm2 B．600 cm2 C．100πcm2 D．200πcm2 2、如图，由高和直径相同的5个圆柱搭成的几何体，其左视图是（）．A． B． C． D．3、如图是由五个相同的小正方体搭成的几何体，则它的主视图是（）A． B． C． D．4、下列几何体中，主视图是三角形的为（）A． B． C． D．5、观察下列几何体，主视图、左视图和俯视图都是矩形的是（）A． B． C． D．6、如图是某几何体的三视图及相关数据，则判断正确的是（）A．a＞c B．b＞c C．4a2+b2=c2 D．a2+b2=c27、如图是由一些相同的小正方体搭成的几何体的三视图，搭成这个几何体的小正方体个数是( ) A．2个B．3个C．4个D．6个8、如图所示的几何体的俯视图是（）9、如图是一个由5个相同的正方体组成的立体图形，它的三视图是（）A． B．C． D．10、已知某几何体的三视图如图所示，则该几何体的体积为（）A． B． C． D．二、填空题11、如图是由两个长方体组合而成的一个立体图形的三视图，根据图中所标尺寸(单位：cm)，计算出这个立体图形的表面积是________cm2.12、如图，方桌正上方的灯泡(看作一个点)发出的光线照射方桌后，在地面上形成阴影(正方形)示意图，已知方桌边长1.2 m，桌面离地面1.2 m，灯泡离地面3.6 m，则地面上阴影部分的面积为________．13、如图是由几个相同的小立方块组成的三视图，小立方块的个数是 .14、长方体的主视图与俯视图如图297，则这个长方体的体积是________．图29715、三棱柱的三视图如图6226，在△EFG中，EF＝8 cm，EG＝12 cm，∠EGF＝30°，则AB的长为____________cm.16、.图11-1是三个直立于水平面上的形状完全相同的几何体（下底面为圆面，单位：cm）．将它们拼成如图11-2的新几何体，则该新几何体的体积为_______________cm3．（计算结果保留）17、一位美术老师在课堂上进行立体模型素描教学时，把14个棱长为1分米的正方体摆在课桌上成如图6形式，然后他把露出的表面都涂上不同的颜色，则被他涂上颜色部分的面积为______.18、一个长方体的主视图和左视图如图所示(单位：cm)，则其俯视图的面积是_______________.19、如图，分别是由若干个完全相同的小正方体组成的一个物体的主视图和俯视图，则组成这个物体的小正方体的个数是个．20、如图所示是用小立方块搭成的几何体的主视图、俯视图，它最少需要___________个小立方块，最多需要_____________个小立方块．三、简答题21、一个零件的主视图、左视图、俯视图如图所示（尺寸单位：厘米），（1）这个零件是什么几何体？（2）求这个零件的表面积、体积（结果保留π）22、某几何体的主视图、左视图和俯视图分别如图，试求该几何体的体积.23、由6个相同的小立方块搭成的几何体如图所示，请画出从三个方向看所得到的形状图．24、如图，下列是一个机器零件的毛坯，请将这个机器零件的三视图补充完整．25、已知图为一几何体从不同方向看的图形：（1）写出这个几何体的名称；（2）任意画出这个几何体的一种表面展开图；（3）若长方形的高为10厘米，三角形的边长为4厘米，求这个几何体的侧面积．26、画图：（1）画出圆锥的三视图．已知∠AOB，用直尺和圆规作∠A′O′B′=∠AOB（要求：不写作法，保留作图痕迹）27、如图是一个几何体的二视图（左图为正视图，右图为俯视图），求该几何体的体积（л取3.14）．28、由一些大小相同的小正方体组成的简单几何体的主视图和俯视图（如图11）. （1）请你画出这个几何体的一种左视图；（2分）（2）若组成这个几何体的小正方体的块数为n，请你写出n的所有可能值.（4分）29、如图是一个由若干个棱长相等的正方体构成的几何体的三视图。

(完整)初中数学三视图专题试题及答案1,推荐文档

面右图由 7 个立方体叠成的几何体，从正前方观察，可画出的平面图形是
（
）
A
B
C
D
4、下面是空心圆柱在指定方向上的视图，正确的是…（）
(A)
(B)
(C)
(D)
5、画出下面实物的三视图：
参考答案：课前小测：
72
1、短 2、
35
第二十九章投影与视图 29．2 三视图
64
3、 4、矩形，圆 5、空心圆柱
A．O B． 6 C．快 D．乐三、综合训练：
1．小明从正面观察下图所示的两个物体，看到的是（）
正面
A
B
C
D
ห้องสมุดไป่ตู้
2、右图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用
的小立方块的个数是（）
A5个 B6个
C7个
D8个
主主主主主主
主主主
主主主
3、如果用□表示 1 个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么下
第二十九章投影与视图
29．2 三视图一、课前小测： 1、身高相同的甲、乙两人分别距同一路灯 2 米、3 米，路灯亮时，甲的影子比乙的影子
（填“长”或“短”） 2、小刚和小明在太阳光下行走，小刚身高 1.75 米，他的影长为 2.0m，小刚比小明矮
5cm，此刻小明的影长是________m. 3、墙壁Ｄ处有一盏灯（如图），小明站在Ａ处测得他的影长与身长相等都
15
二、基础训练： 1、(1)球，圆柱体；（2）实线，虚线；（3）圆锥，正四棱锥，倒放的正三棱柱等；（4）
圆锥；（5）俯视图，正视图，左视图；（6）12. 2、A；3、C 4、B 5、B 三、综合训练： 1、C 2、D 3、B；4、A；5、题图：

中考数学专题复习《视图、投影与尺规作图》专项检测题 ( 含答案)

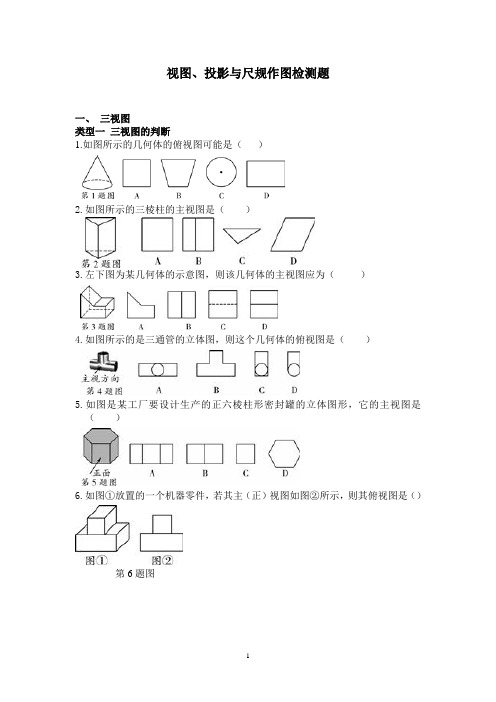
视图、投影与尺规作图检测题一、三视图类型一三视图的判断1.如图所示的几何体的俯视图可能是（）2.如图所示的三棱柱的主视图是（）3.左下图为某几何体的示意图，则该几何体的主视图应为（）4.如图所示的是三通管的立体图，则这个几何体的俯视图是（）5.如图是某工厂要设计生产的正六棱柱形密封罐的立体图形，它的主视图是（）6.如图①放置的一个机器零件，若其主（正）视图如图②所示，则其俯视图是（）第6题图7.如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）8.如图，几何体上半部为正三棱柱，下半部为圆柱，其俯视图是（）9.下列几何体中，正视图是矩形的是( )10.如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中有三个的某一种视图都是同一种几何图形，则另一个几何体是( )11.一个几何体由大小相同的小立方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是（）类型二由三视图还原几何体及相关计算1.一个几何体的三视图如图所示，这个几何体是（）A. 棱柱B. 圆柱C. 圆锥D. 球第1题图第2题图2.如图，一个简单几何体的三视图的主视图与左视图都为正三角形，其俯视图为正方形，则这个几何体是( )A. 四棱锥B. 正方体C. 四棱柱D. 三棱锥3.下面是一个几何体的三视图，则这个几何体的形状是（）第3题图A. 圆柱B. 圆锥C. 圆台D. 三棱柱4.一个几何体的三视图如图所示，那么这个几何体是（）第4题图5.小颖同学到学校领来n盒粉笔，整齐地摞在讲桌上，其三视图如图所示，则n 的值是（）第5题图A. 6B. 7C. 8D. 96.某超市货架上摆放着某品牌红烧牛肉方便面，如图是它们的三视图，则货架上的红烧牛肉方便面至少有( )第6题图A. 8B. 9C. 10D. 117.由若干个边长为1 cm的正方体堆积成一个几何体，它的三视图如图，则这个几何体的表面积是( )A. 15 2cmcm D. 24 2cm C. 21 2cm B. 18 2第7题图第8题图8.某商品的外包装盒的三视图如图所示，则这个包装盒的体积是（）A. 200π3cmcm B. 500π3C. 1000π3cmcm D. 2000π3命题点2 投影1.下面是一天中四个不同时刻两座建筑物的影子，将它们按时间先后顺序排列正确的是（）A. （3）（1）（4）（2）B. （3）（2）（1）（4）C. （3）（4）（1）（2）D. （2）（4）（1）（3）命题点3 立体图形的展开与折叠1.在市委、市府的领导下，全市人民齐心协力，将广安成功地创建为“全国文明城市”，为此小红特制作了一个正方体玩具，其展开图如图所示，原正方体与“文”字所在的面相对的面上标的字应是( )A. 全B. 明C. 城D. 国第1题图2.下列四个图形是正方体的平面展开图的是（）3.把如图中的三棱柱展开，所得到的展开图是（）第3题图第4题图4.如图，透明的圆柱形容器（容器厚度忽略不计）的高为12 cm ，底面周长为10 cm ，在容器内壁离容器底部3 cm 的点B 处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿3cm 的点A 处，则蚂蚁吃到饭粒需爬行的最短路径是( )A. 13 cmB. 261 cmC. 61 cmD. 234 cm命题点4 尺规作图1.如图，在△ABC 中，∠C =90°，∠B =30以A 为圆心，任意长为半径画弧分别交AB 、AC 于点M 和N ，再分别以M 、N 为圆心，大于21MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ，则下列说法中正确的个数是（） ①AD 是∠BAC 的平分线；②∠ADC =60°；③点D 在AB 的中垂线上； ④S △DAC ：S △ABC =1∶3.A. 1B. 2C. 3D. 4第1题图2.如图所示，已知线段AB .（1）用尺规作图的方法作出线段AB 的垂直平分线l （保留作图痕迹，不要求写出作法）；（2）在（1）中所作的直线l 上任意取两点M 、N （线段AB 的上方）,连接AM 、AN 、BM 、BN ，求证：∠MAN =∠MBN .第2题图参考答案命题点1三视图类型一三视图的判断1. C【解析】圆锥的主视图、左视图和俯视图分别为等腰三角形、等腰三角形和带圆心的圆．2. B 【解析】主视图是从几何体正面看得到的图形，该几何体从正面看，是两个具有公共边的长方形组成的图形，只有选项B符合题意．3. A【解析】从前往后看，可得到本题的主视图为五边形．4. A【解析】俯视图指的是从上向下看到的平面图形．圆柱体的俯视图是长方形，圆应该在长方形的中间．5. A【解析】A选项是主视图，B选项是左视图，C选项不是这个正六棱柱形密封罐的视图，D选项是俯视图．6. D【解析】长方体的俯视图是一个长方形，从上面看共有三列，所以这个组合体的俯视图是D.7. B【解析】俯视图即从上面看物体所得的平面图形．观察图形可得，从上往下看，该几何体的小正方体共有三行三列，第一行第二列有1个，第二行每列1个，第三行第一列1个，因此B选项正确．8. C【解析】俯视图是由上往下观察几何体所得到的图形．几何体上半部为正三棱柱，下半部为圆柱，所以其俯视图由圆和其内接等边三角形组成，故选C.9. B×××10. C视图都是圆，故选C.11. D【解析】从正面看共三列，第一列有三个小正方形，第二列有两个小正方形，第三列有三个小正方形，故选D.类型二由三视图还原几何体及相关计算1. B【解析】本题的几何体是常见几何体，从正面看到的是一个矩形，从左面看到的是一个矩形，从上面看到的是一个圆，所以这个几何体为圆柱．2. A【解析】由底面是有对角线的正方形，侧面是正三角形可以推断出它是四棱锥．3. B【解析】选项名称三视图(主视图，左视图，俯视图)正误A圆柱矩形，矩形，圆×B圆锥等腰三角形，等腰三角形，带圆心的圆√C圆台等腰梯形，等腰梯形，无圆心的同心圆×D三棱柱矩形，矩形，三角形×4. C【解析】选项逐项分析正误A 圆锥的主视图和左视图是等腰三角形，俯视图为带圆心的圆×B 这个几何体由圆锥和圆柱两部分构成，因此俯视图应该为带圆心的圆×C 主视图为中间有一条竖线的矩形，左视图为矩形，俯视图为三角形√D主视图、左视图、俯视图均为三角形×5. B【解析】由主视图可得这些粉盒共有3层，由俯视图可得最底层有4盒，由主视图和左视图可得第二层有2盒，第三层有1盒，共有7盒．6. B【解析】由三视图得第一层有4碗，第二层最少有3碗，第三层最少有2碗，所以至少有9碗．7. B【解析】由几何体的三视图得几何体如解图所示，这个几何体是由4个边长为1 cm的小正方体组成，且重叠部分的面积正好为一个小正方体的表面积，则这个几何体的表面积为6×3＝18 cm2.第7题解图8. B【解析】由三视图可知该几何体是圆柱，且底面圆半径r＝5 cm，高h ＝20 cm，所以v＝πr2h＝π×52×20＝500πcm3.命题点2投影C【解析】从太阳“东升西落”入手．太阳光在物体上的投影随时间而变化，投影的方向是先朝西，再逐渐转向朝东，且影长的变化经历：长→短→长(中午时刻的影长最短)，因此(3)表示的时刻最早，(2)表示的时刻最晚；由于地球绕着太阳运转，物体的投影应从西边开始顺时针向东旋转，所以(4)表示的时间比(1)表示的时间早．故按时间顺序应排列为(3)→(4)→(1)→(2)．命题点3立体图形的展开与折叠1. C【解析】正方体的表面展开图，相对的面之间一定相隔一个正方形，“全”与“明”是相对面；“国”与“市”是相对面；“文”与“城”是相对面．2. B【解析】选项逐项分析正误A折叠后有两个面重合，缺少一个底面×B可以折叠成一个正方体√C 是“凹”字格，故不能折叠成一个正方体×D 是“田”字格，故不能折叠成一个正方体×3. B【解析】根据“两个全等的三角形，在侧面三个长方形的两侧，这样的图形围成的是三棱柱”把图中的三棱柱展开，所得到的展开图是B.4. A【解析】将圆柱沿A所在的高剪开，展平如解图所示．则MM′＝NN′＝10，作A关于MM′的对称点A′，连接A′B，则线段A′B即蚂蚁走的最短路径．过B作BD⊥A′N于D，则BD＝NE＝5，A′D＝MN＋A′M－BE＝12＋3－3＝12，在Rt△A′BD中，由勾股定理得A′B＝A′D2＋BD2＝13.第4题解图命题点4尺规作图1. D【解析】由尺规作图的作法可知，AD是∠BAC的平分线，∴①正确；∵∠BAC＝60°，AD又是∠BAC的平分线，则∠CAD＝30°，又∵∠C＝90°，则∠ADC＝60°，∴②正确；∵∠DAB＝30°，∠B＝30°，则AD＝BD，所以点D在AB的中垂线上，∴③正确；设BD＝AD＝a，因为∠CAD＝30°，∠C＝90°，则CD＝a2，根据勾股定理得：AC＝3a2，∴S△ADC＝3a28；BC＝3a2，S△ABC＝33a28，则S△DAC ：S△ABC＝3a28：33a28＝1∶3，∴④正确；正确的共有4个．2. (1)解：如解图：第2题解图①………………………………………………………………………(5分)【作法提示】分别以A、B两点为圆心，以大于12AB为半径画弧，与两弧分别有两个交点，两点确定的直线即为线段AB的垂直平分线l.(2)证明：如解图②，∵直线l是线段AB的垂直平分线，∴MA＝MB，∴∠MAB＝∠MBA，……………………(6分)同理：∠NAB＝∠NBA，∴∠MAB－∠NAB＝∠MBA－∠NBA，……………………(8分) 即：∠MAN＝∠MBN. ……………………(9分)第2题解图②。

2023年九年级人教版数学中考复习考点专练：几何体的三视图原卷版

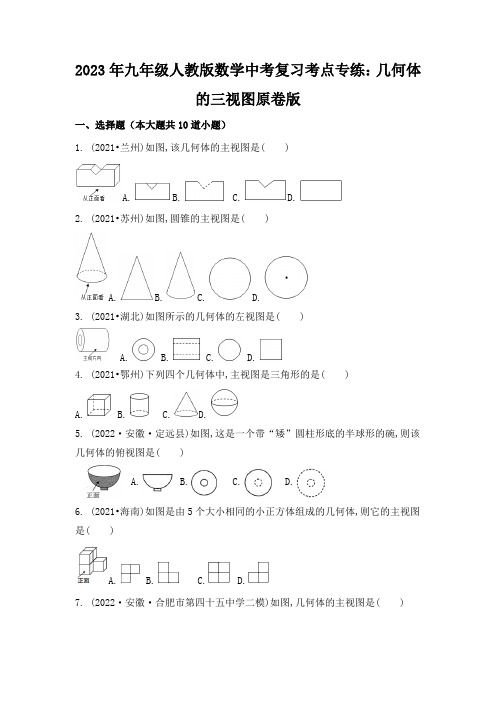
2023年九年级人教版数学中考复习考点专练：几何体的三视图原卷版一、选择题（本大题共10道小题）1. (2021•兰州)如图,该几何体的主视图是( )A. B. C. D.2. (2021•苏州)如图,圆锥的主视图是( )A. B. C. D.3. (2021•湖北)如图所示的几何体的左视图是( )A. B. C. D.4. (2021•鄂州)下列四个几何体中,主视图是三角形的是( )A. B. C. D.5. (2022·安徽·定远县)如图,这是一个带“矮”圆柱形底的半球形的碗,则该几何体的俯视图是( )A. B. C. D.6. (2021•海南)如图是由5个大小相同的小正方体组成的几何体,则它的主视图是( )A. B. C. D.7. (2022·安徽·合肥市第四十五中学二模)如图,几何体的主视图是( )A. B. C. D.8. (2021•朝阳)如图所示的几何体是由6个大小相同的小立方块搭成的,它的左视图是( )A. B. C. D.9. (2022·河北邯郸)如图,一个圆柱体在正方体上沿虚线从左向右平移,平移过程中不变的是( )A.主视图B.左视图C.俯视图D.主视图和俯视图10. (2021•河南)如图所示,几何体由7个小正方体搭成,将图中标甲、乙、丙的三个小正方体中的一个拿走,得到的新几何体与原来几何体的三视图一样,那么应该拿走( )A.甲B.乙C.丙D.都不行二、填空题（本大题共6道小题）11. (2021•房山区二模)如图是某几何体的三视图,该几何体是.12. (2022·河北保定)一个几何体的三视图如图所示,则这个几何体是_____;它的侧面积是_____cm2.13. (2022·安徽定远县)已知一个几何体的三视图如图,则该几何体的体积为____cm314. (2022·云南模拟)如图是一个几何体的三视图,则该几何体的体积为.15. (2022·胶州模拟)已知某几何体的三视图如图所示,则该几何体的体积为.16. (2021•云南)如图图形是某几何体的三视图(其中主视图也称正视图,左视图也称侧视图).已知主视图和左视图是两个全等的矩形.若主视图的相邻两边长分别为2和3,俯视图是直径等于2的圆,则这个几何体的体积为.三、解答题（本大题共6道小题）17. (2022·安徽定远县)一几何体的三视图如右所示,求该几何体的体积.18. (2022·安徽淮南·模拟预测)如图,一个几何体的三视图分别是两个矩形,一个扇形,求这个几何体表面积的大小(结果保留π).19. (2022七上·东港期中)如图是由小正方体搭成的一个几何体从上面着到的形状图,小正方形中的数字表示在该位置的小正方体的个数,请你画出它从正面和从左面看到的形状图.20. (2022·河北唐山)第24届冬奥会吉祥物“冰墩墩”收获无数“迷弟”“迷妹”而一“墩”难求;为了满足需求,其中一间正规授权生产厂通过技术改造来提高产能,两次技术改造后,由日产量2000个扩大到日产量2420个.(1)求这两次技术改造日产量的平均增长率;(2)这生产厂家还设计了三视图如图所示的“冰墩墩”盲盒,(单位:cm),请计算此类盲盒的表面积.21. (2022·安徽·定远县育才学校一模)如图所示,一幢楼房AB背后有台阶CD,台阶每层高0.2米,且AC=17.2米,设太阳光线与水平地面的夹角为α,当α=60°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶MN上晒太阳.(1)求楼房的高度约为多少米?(结果精确到0.1米)(2)过了一会儿,当α=45°时,小猫还能不能晒到太阳?请说明理由.(参考数据:1.732)22. (2021七上·和平期中)用棱长都为5cm的小立方块搭成几何体,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.(1)请你分别画出从正面和从左面看到的这个几何体的形状图;(2)若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加大小相同的小立方块,以搭成一个大正方体,至少还需要个小立方块;(3)①图中的几何体的表面积(包括与桌面接触的部分)为cm2;②若新搭一个几何体,且满足如下三个条件:图中从上面看到的几何体的形状图不变,小立方块的总数不变,从上面看到的小正方形中的数字可以改变,则新搭几何体的表面积(包括与桌面接触的部分)最小值和最大值分别为cm2, cm2.。

中考数学每日一练：由三视图判断几何体练习题及答案_2020年单选题版

中考数学每日一练：由三视图判断几何体练习题及答案_2020年单选题版答案答案答案2020年中考数学：图形的变换_投影与视图_由三视图判断几何体练习题~~第1题~~(2017荆门.中考真卷) 已知：如图，是由若干个大小相同的小正方体所搭成的几何体的三视图，则搭成这个几何体的小正方体的个数是（）A . 6个B . 7个C . 8个D . 9个考点：由三视图判断几何体;~~第2题~~(2020遵化.中考模拟) 由若干个完全相同的小正方体组成一个立体图形，它的左视图和俯视图如图所示，则小正方体的个数不可能是（）A . 5B . 6C . 7D . 8考点：由三视图判断几何体;~~第3题~~(2020温岭.中考模拟) 如图，是某个几何体从不同方向看到的形状图（视图），这个几何体的表面能展开成下面的哪个平面图形？（） A . B . C . D .考点：由三视图判断几何体;~~第4题~~(2020迁安.中考模拟) 下图是某圆锥的主视图和左视图，该圆锥的全面积是（）答案答案答案答案答案A . 36π B . 24π C . 20π D . 15π考点：勾股定理;圆锥的计算;由三视图判断几何体;~~第5题~~(2019荆州.中考模拟) 如图，是从不同的方向看一个物体得到的平面图形，该物体的形状是（）A . 圆锥B . 圆柱C . 三棱锥D . 三棱柱考点：由三视图判断几何体;~~第6题~~(2017平谷.中考模拟) 如图是某几何体从不同角度看到的图形，这个几何体是（）A . 圆锥B . 圆柱C . 正三棱柱D . 三棱锥考点：由三视图判断几何体;~~第7题~~(2019通州.中考模拟) 如图是某个几何体的三视图，该几何体是（）A . 圆锥B . 四棱锥C . 圆柱D . 四棱柱考点：由三视图判断几何体;~~第8题~~(2018青海.中考真卷) 由一些相同的小立方块搭成的几何体的三视图如图所示，则搭成该几何体的小立方块有（）A . 3块B . 4块C . 6块D . 9块考点：由三视图判断几何体;~~第9题~~(2019呼和浩特.中考真卷) 如图是一个几何体的三视图，其中主视图与左视图完全一样，则这个几何体的表面积是（）答案答案 A . B . C . D .考点：几何体的表面积;由三视图判断几何体;~~第10题~~(2019阜新.中考真卷) 如图所示的主视图和俯视图对应的几何体(阴影所示为右)是（）A .B .C .D .考点：由三视图判断几何体;2020年中考数学：图形的变换_投影与视图_由三视图判断几何体练习题答案1.答案：B2.答案：A3.答案：A4.答案：A5.答案：A6.答案：A7.答案：B8.答案：B9.答案：B10.答案：C。

中考数学真题《三视图与展开图》专项测试卷(附答案)

中考数学真题《三视图与展开图》专项测试卷(附答案) 学校:___________班级：___________姓名：___________考号：___________一．选择题（共9小题）1．（2024•顺义区二模）在下列几何体中主视图为三角形的是()A．B．C．D．2．（2024•大兴区二模）如图是某个几何体的展开图该几何体是()A．圆柱B．三棱锥C．三棱柱D．圆锥3．（2024•丰台区二模）榫卯(sǔnmǎo)是中国古代建筑家具及其它器械的主要结构方式是我国工艺文化精神的传承凸出部分叫榫凹进部分叫卯．如图是某个部件“榫”的实物图它的主视图是()A．B．C．D．4．（2024•海淀区二模）如图是一张长方形纸片用其围成一个几何体的侧面这个几何体可能是()A．圆柱B．圆锥C．球D．三棱锥5．（2024•朝阳区二模）如图是某个几何体的展开图该几何体是()A．圆柱B．圆锥C．三棱柱D．正方体6．（2024•石景山区二模）如图是某几何体的展开图该几何体是()A．三棱柱B．三棱锥C．四棱锥D．圆柱7．（2024•北京二模）下列几何体中主视图为三角形的是()A．B．C．D．8．（2024•西城区二模）如图是某几何体的三视图该几何体是()A．圆柱B．圆锥C．三棱柱D．长方体9．（2024•门头沟区二模）某几何体的展开图是由大小形状相等的两个正方形四个长宽不等的矩形组成则，该几何体是()A．正方体B．长方体C．四棱锥D．三棱柱10.（2024房山二模）右图是某几何体的展开图该几何体是（A）圆柱（B）长方体（C）圆锥（D）三棱柱参考答案与试题解析一．选择题（共9小题）1．（2024•顺义区二模）在下列几何体中主视图为三角形的是()A．B．C．D．【答案】D【考点】简单几何体的三视图【分析】根据主视图的定义判断即可．【解答】解：A．该几何体的主视图是矩形故本选项不合题意B．该几何体的主视图是一行两个矩形故本选项不合题意C．该几何体的主视图是正方形故本选项不合题意D．该几何体的主视图是等腰三角形故本选项符合题意故选：D．2．（2024•大兴区二模）如图是某个几何体的展开图该几何体是()A．圆柱B．三棱锥C．三棱柱D．圆锥【答案】D【考点】几何体的展开图【分析】根据展开图是一个扇形与圆知该几何体是圆锥．【解答】解：几何体的展开图是扇形与圆可知该几何体是圆锥故选：D．3．（2024•丰台区二模）榫卯(sǔnmǎo)是中国古代建筑家具及其它器械的主要结构方式是我国工艺文化精神的传承凸出部分叫榫凹进部分叫卯．如图是某个部件“榫”的实物图它的主视图是()A．B．C．D．【答案】D【考点】简单几何体的三视图【分析】从正面看到的平面图形是主视图根据主视图的含义可得答案．【解答】解：如图所示的几何体的主视图如下：．故选：D．4．（2024•海淀区二模）如图是一张长方形纸片用其围成一个几何体的侧面这个几何体可能是()A．圆柱B．圆锥C．球D．三棱锥【答案】A【考点】展开图折叠成几何体【分析】根据圆柱的侧面展开图是矩形解答即可．【解答】解：如图是一张长方形纸片用其围成一个几何体的侧面这个几何体可能是圆柱故选项A符合题意．故选：A．5．（2024•朝阳区二模）如图是某个几何体的展开图该几何体是()A．圆柱B．圆锥C．三棱柱D．正方体【答案】A【考点】几何体的展开图【分析】侧面为长方形底面为2个圆形故原几何体为圆柱．【解答】解：观察图形可知该几何体是圆柱．故选：A．6．（2024•石景山区二模）如图是某几何体的展开图该几何体是()A．三棱柱B．三棱锥C．四棱锥D．圆柱【答案】A【考点】几何体的展开图【分析】根据三棱柱的展开图解答．【解答】解：由图可知该几何体的两个底面是正三角形且有3个侧面侧面都是矩形故这个几何体是三棱柱．故选：A．7．（2024•北京二模）下列几何体中主视图为三角形的是()A．B．C．D．【答案】A【考点】简单几何体的三视图【分析】主视图是从找到从正面看所得到的图形注意要把所看到的棱都表示到图中．【解答】解：A圆锥的主视图是等腰三角形故此选项符合题意B三棱柱的主视图是一个矩形矩形内部有一个纵向的实线故此选项不符合题意C球的主视图是一个圆故此选项不符合题意D圆柱的主视图是一个矩形故此选项不符合题意．故选：A．8．（2024•西城区二模）如图是某几何体的三视图该几何体是()A．圆柱B．圆锥C．三棱柱D．长方体【答案】B【考点】由三视图判断几何体【分析】根据几何体的主视图和左视图是全等的等腰三角形可判断该几何体是锥体再根据府视图的形状可判断锥体底面的形状即可得出答案．【解答】解：因为主视图和左视图是全等的等腰三角形所以该几何体是锥体又因为府视图是含有圆心的圆所以该几何体是圆锥．故选：B．9．（2024•门头沟区二模）某几何体的展开图是由大小形状相等的两个正方形四个长宽不等的矩形组成则，该几何体是()A．正方体B．长方体C．四棱锥D．三棱柱【答案】B【考点】几何体的展开图【分析】根据常见几何体的展开图解答即可．【解答】解：A．正方体的展开图由大小形状相等的六个正方形组成故本选项不符合题意B．当长方体的两个底面是正方形时它的展开图是由大小形状相等的两个正方形四个长宽不等的矩形组成故本选项符合题意C．四棱锥的展开图是由一个四边形和四个三角形组成故本选项不符合题意D．三棱柱的展开图是两个三角形和三个矩形组成故本选项不符合题意．故选：B．10.（2024房山二模）右图是某几何体的展开图该几何体是（A）圆柱（B）长方体（C）圆锥（D）三棱柱【答案】A。

精品九年级数学中考专题三视图综合练习题

）
4. 如图是一些大小相同的小正方形组成的几何体，其主视图如图所示，则其俯视图是（
）
5. 如图，圆锥的侧面积恰好等于其底面积的 2 倍，则该圆锥侧面展开图所对应扇形圆心角的度数为（ 0 0 0 0 A. 60 B. 90 C. 120 D. 180 6. 如图，是由相同小正方形组成的立体图形，它的左视图是（）
3
解直角三角形
1.已知为锐角，则 m=sin +cos 的值（ A.m>1 B.m=1 C.m<1 ） D. m 1
2.如图， ⊙O 是 △ ABC 的外接圆， AD 是 ⊙O 的直径，若 ⊙O 的半径为是（） A．
3 ， AC 2 ，则 sin B 的值 2
2Байду номын сангаас3
B．
3 2
22.如图都是由边长为 1 的正方体叠成的图形。例如第（1）个图形的表面积为 6 个平方单位，第（2）个图形的表面积为 18 个平方单位，第（3）个图形的表面积是 36 个平方单位。依此规律，则第（5）个图形的表面积是__________个平方单位。
三、计算题：
23.由一些大小相同的小正方体组成的几何体的主视图和俯视图。（1）请你画出这个几何体的一种左视图；（2）若组成这个几何体的小正方形的块数 n，请你写出 n 的所有可能值。
6. 在直角三角形 ABC 中，∠C=900,∠A=300,E 为 AB 上一点，且 AE:EB=4:1,EF AC 于 F,连接 FB,则 tan ∠CFB 的值等于（）
α
二、填空题：
7.已知角的终边上一点 P(x,2)，且 sin = 2 ，则 x＝_____
3
8.已知角的终边经过点 P(- 3 ,1)，则 tan(180 - )＝____

中考三视图练习题

中考三视图练习题一、选择题1. 下列哪个选项是正确的主视图？A. 左视图B. 俯视图C. 右视图D. 仰视图2. 三视图包括哪三个视图？A. 俯视图、左视图、右视图B. 主视图、俯视图、左视图C. 仰视图、俯视图、左视图D. 仰视图、右视图、左视图3. 观察一个物体时，哪个视图可以提供物体的宽度信息？A. 主视图B. 俯视图C. 左视图D. 仰视图4. 下列哪个选项是正确的俯视图？A. 显示物体的顶面形状B. 显示物体的侧面形状C. 显示物体的正面形状D. 显示物体的底面形状5. 当物体的主视图和左视图都相同，且都是矩形时，该物体可能是：A. 立方体B. 圆柱体C. 长方体D. 球体二、填空题6. 在三视图中，______视图显示物体的正面形状。

7. 当物体的主视图和俯视图都是圆形时，该物体可能是______。

8. 一个物体的三视图可以提供物体的______、______和______三个方向的信息。

9. 俯视图通常显示物体的______面形状。

10. 如果一个物体的主视图和左视图都是正方形，那么该物体可能是______。

三、判断题11. 一个物体的主视图和左视图可能完全不同。

（）12. 三视图中的任何一个视图都不能单独表示物体的全部信息。

（）13. 俯视图可以提供物体的高度信息。

（）14. 物体的三视图是相互独立的，没有联系。

（）15. 一个物体的三视图可以完全相同的情况是不存在的。

（）四、简答题16. 请简述三视图在工程制图中的应用意义。

17. 描述如何通过三视图来确定一个物体的形状。

五、绘图题18. 根据以下描述，绘制一个物体的三视图：- 主视图：一个矩形，长为10cm，宽为5cm。

- 俯视图：一个矩形，长为8cm，宽为6cm。

- 左视图：一个矩形，长为10cm，宽为8cm。

19. 假设你面前有一个立方体，其边长为4cm，请绘制其三视图。

六、综合应用题20. 你是一名工程师，需要根据客户提供的三视图来制作一个零件。

初三年级数学下册期中三视图测试题(含答案解析)

2019 初三年级数学下册期中三视图测试题(含答案分析 )2019 初三年级数学下册期中三视图测试题(含答案分析 )一、选择题（每题 3 分，共 30 分）1.平行投影中的光芒是（）A. 平行的B.聚成一点的C.不平行的D.向四周八方发散的2.小明在操场上练习双杠时，在练习的过程中他发此刻地上双杠的两横杠的影子（）A. 订交B.平行C.垂直D.没法确立3.以以下图中是在太阳光下形成的影子的是（）D4.两个不同样长度的物体在同一时辰同一地点的太阳光下获得的投影是（）Ａ.相等 B.长的较长 C.短的较长 D.不可以确立5.小明从正面察看以以下图的两个物体，看到的是（）6. (2019?x 疆中考 )以下几何体中，主视图同样的是（）A. ①②B.①③C.①④D.②④7.假如用□表示 1 个立方体，用表示 2 个立方体叠加，用■表示 3 个立方体叠加，如图由7 个立方体叠成的几何体，从正前面察看，可画出的平面图形是（）8.以以下图是一根电线杆在一天中不同样时辰的影长图，则按一天中时间先后次序摆列，正确的选项是（）A. ①②③④B.④①③②C.④②③①D.④③②①9.(2019?湖北黄冈中考 )已知一个正棱柱的俯视图和左视图以以下图，则其主视图为（）10.以以下图是由一些同样的小正方体构成的几何体的三视图，则构成这个几何体的小正方体的个数是（）A.4B.5C.6D.7二、填空题（每题 3 分，共 24 分）11.小军夜晚到广场去玩，他发现有两人的影子一个向东，一个向西，于是他必然的说：“广场上的大灯泡必然位于两人”.12.墙壁 D 处有一盏灯（如图），小明站在Ａ处测得他的影长与身高相等，都为 1.6 m，小明向墙壁走了 1 m 抵达 B 处，发现影子恰好落在 A 点，则灯泡与地面的距离 CD＝ .13．以以下图是由几个同样的小立方块构成的几何体的三视图，小立方块的个数是.14．以以下图是某几何体的三视图，则该几何体的体积是.15．把棱长为 1 米的 7 个同样正方体摆成以以下图的图形，今后把表面涂上颜色，那么涂色的面积为??_____平方米 .16.如图是一个正六棱柱的主视图和左视图，则图中的a＝_____ .17.由个同样的小正方体堆成的几何体，其视图以以下图，则的最大值是 _______ .18．如图，在以下几何体中，它们各自的三视图（主视图、左视图、俯视图）都同样的是_______.（把全部符合条件的都写上）三、解答题（共66 分）19.（ 5 分）如图，小赵和路人在路灯下行走，试确立图中路灯灯泡的地点，并画出小赵在灯光下的影子.20．（5 分）以以下图为一机器部件的三视图.（1）请写出符合这个机器部件形状的几何体的名称.（2）若俯视图中三角形为正三角形，那么请依据图中所标的尺寸，计算这个几何体的表面积（单位：cm2 ）.21．（6 分）由若干个同样的小立方体搭成的一个几何体的主视图和俯视图以以下图，俯视图的方格中的字母和数字表示该地点上小立方体的个数，求x ，y 的值．22．（6 分）由几个小立方体叠成的几何体的主视图和左视图以以下图，求构成几何体的小立方体个数的最大值与最小值，并画出相应的俯视图.23.（10 分）如图是由同样的 5 个小正方体构成的几何体，请画出它的三种视图，若每个小正方体的棱长为a，试求出该几何体的表面积.24.（12 分）如图，某同学想丈量旗杆的高度，他在某一时刻测得 1 米长的竹竿竖直搁置时影长 1.5 米，在同一时辰测量旗杆的影长时，因旗杆凑近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为21 米，留在墙上的影高为 2 米，求旗杆的高度.25.（10 分）（ 1）如图，假如你的地点在点 A ，你能看到高大的建筑物N 吗？为何？（2）假如两楼之间相距20 m，两楼的高各为10 m 和 30 m，则当你最少与M 楼相距多少米时，才能看到后边的N 楼？26.（12 分）一透明的敞口正方体容器ABCD- A′ B′ C′装有D′一些液体，棱AB 素来在水平桌面上，容器底部的倾斜角为α（∠ CBE=α，如图①所示） .研究如图①，液面恰好过棱CD，并与棱 BB′交于点 Q，此时液体的形状为直三棱柱，其三视图及尺寸如图②所示 .解决问题：（1）CQ 与 BE 的地点关系是，BQ的长是dm；（2）求液体的体积；（参照算法：直棱柱体积V 液 =底面积S△ BCQ×高 AB ）（3）求α的度数 .（注： sin 49 ＝°cos 41 ＝°，tan 37 ＝°）拓展在图①的基础上，以棱 AB 为轴将容器向左或向右旋转，但不可以使液体溢出，③或④是其正面表示 .若液面与棱 C′C 或 CB 交于点 P， PC=x dm ，BQ=y dm. 分就③和④求 y 与 x 的函数关系式，并写出相的α的范.其 ,任何一学科都离不开死硬背,关是有技巧, “死”今后会“活用”。

中考数学三视图专项训练新完整版

中考数学三视图专项训练新HEN system office room [HEN 16H-HENS2AHENS8Q8-HENH1688]A. B. C. D.L 如图所示的是某几何体的三视图，则该几何体的形状是（图1A.长方体 B,三棱柱 C.圆锥 D.正方体2 .下面的三视图所对应的物体是（）3 .如图是一个立体图形的正视图、左视图和俯视图，那么这个立体图形是（）A.圆锥B.三棱锥C.四棱锥D.五棱锥2. （2015湖南岳阳笫2题3分）有一种圆柱体茶叶筒如图所示，则它的主视图是4.如图是一彳卜立方及组成的几何体，请你画出这个几何体的三种视图.觇图6.下图中所示的几何体的主视图是10. ）11 4个相同何不呼万I 块搭成的＞!师如形中工®今4斗正形都标4?倒住.若面上的颜色都一样，那么不可能是这一个正方体的展肝图的是（一.选择J 1.A.，第产绿B.是（正方L 何/i）7.如图1所示痴八伸砒两楣视图是（ 9.图2中几何体的主视图是（,图2AB红红B C B.图2D黄所示,红红绿 T7三儿彳下舔〃师刀k,4个红 C绿黄 D4. （2015 ♦湖北省武汉市，第7题3分）如图，是由一个圆柱体和7卷?体组成的儿何体，其主视图是（）（）5、（2015 •湖北省孝感市，第1题4分）如图是一个几何体的三视陶石则我个儿何体是A.正方体B.长方体C.三棱柱D.三棱锥6.（2015?山东莱芜，第6题3分）右图所示的儿何体是由一些小立方块搭成的，则这个儿何体的俯视图是（）A. B. C. D.7.（2015 •湖南省益阳市，第4题5分）一个几何体的三视图如图所示，则这个儿何体是（）A.三棱锥B. 三棱柱C. 圆柱D. 长方体8.（2015?江苏南昌，第4题3分）如图是将正方体切去一个角后形成的几何体，则该几何体的左视图为（）9.（2015?甘肃武威,第5题3分）如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）10. （2015?广东广州，第6题3分）如图是一个几何体的三视图，则该儿何体的展开C. D.图可以是（）11. （2015?四川南充,第3题3分）如图是某工厂要设计生产的正六棱柱形密封罐的立体图形，它的主视图是（12. （2015?四川资阳，第2题3分）如图1是一个圆台，它的主视图是14. （2015?浙江宇波，第5题4分）如图是由五个相同的小立方块搭成的几何体,则它的俯视图是【】15. （2015?四川省内江市，第3题，3分）如图，几何体上半部为正三棱柱，下半部为圆柱，其俯视图是（B.C □□13. （2015?浙江丽水，第3题3分）由4个相同小立方体搭成)聋近#向DA16. （2015?四川省宜宾市，第2题，3分）如图，立体图形的左视图是（A ）19. （2015?四川凉山州，第2题4分）如图是由四个相同小正方体摆成的立体图形,它的俯视图是（）第2题3分）如图1是由四个大小相同的正方体组成的几何体，那么它的主视图是（正面图1（月）（5）（C ）23. （2015 ♦贵州六盘水，第5题3分）下列说法不正确的是（）17. （2015?浙江省绍兴市, 第3题，4分）有6个相同的立方体搭成的几何体如图（月）(5) (C) (D)A. D.21. (2015 •深圳，第5题分）下列主视图正确的是（）22. (2015 •南宁,所示，则它的主视图是18. （2015?四川成都,第2题3分）如图所示的三棱柱的主视图是20. （2015?四川眉山，第4题3分）下列四个图形中是正方体的平面展开图的是A.圆锥的俯视图是圆B.对角线互相垂直平分的四边形是菱形C.任意一个等腰三角形是钝角三角形D.周长相等的正方形、长方形、圆，这三个几何图形中，圆面积最大24.（2015 •河南，第2题3分）如图所示的几何体的俯视图是（）25.（犯士隈化,为2题 0左下将是一些完全小同中、正才体搭成的儿麻体的烈喻。

人教版九年级下册数学第二十九章第2节《三视图》训练题 (36)(含答案解析)

20．观察如图所示的几何体，从左面看到的图形是（）
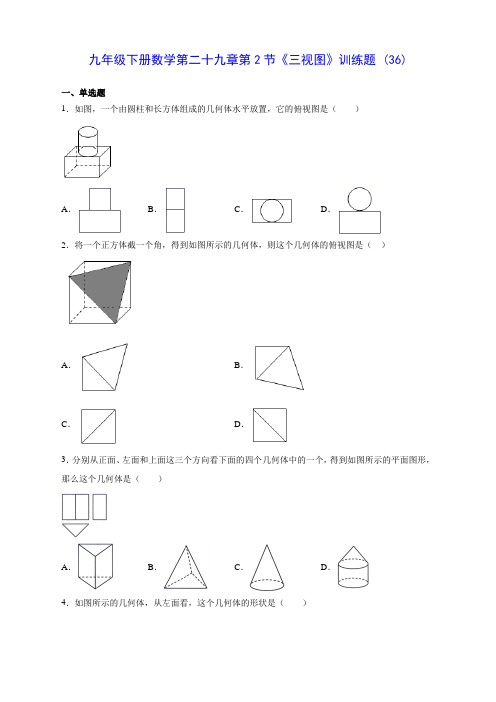
A． B． C． D．
21．如图，该立体图形的左视图是（由5个相同的小正方体组成的立体图形，它的主视图是（）
A． B． C． D．
23．某物体的展开图如图所示，它的左视图为（）
A． B． C． D．
24．如图的几何体是由四个大小相同的正方体组成的，它的主视图是()
两个底面是两个全等的直角三角形，
故选D．
本题考查的是利用三视图判断几何体的形状，同时考查简单几何体的表面积的计算，掌握以上知识是解题的关键．
10．B
【解析】
利用主视图以及俯视图即可得出该几何体是三棱柱，进而得出答案.
解：根据三视图可得这个几何体的名称是三棱柱；
故选：B.
此题考查简单几何体的三视图，正确掌握各几何体的三视图的图形是解题的关键.
根据左视图的画法解答即可．
A.不是三视图，故本选项错误；
B.是左视图，故本选项正确；
C.是主视图，故本选项错误；
D.是俯视图，故本选项错误.
故选：B．
本题考查了由三视图判断几何体，解题的关键是根据左视图的画法判断．
27．（1）C；（2）4
【解析】
（1）本题根据展开图可直接得出答案．
（2）本题根据体积等于底面积乘高求解即可．
11．C
【解析】
根据俯视图的定义和空间想象，得出图形即可．
解：俯视图从左到右分别是2，1，1个正方形，并且第一行有三个正方形．
故选C．
此题考查了简单组合体的俯视图，关键是对几何体的三种视图的空间想象能力．
12．A
【解析】
根据从上边看得到的图形是俯视图，可得答案．
从上边看如图，
，
故选：A．

中考复习之三视图(含答案)

中考复习之三视图1、如图是由一些相同的小正方体搭成的立体图形的三视图,则搭成该立体图形的小正方体的个数是.2、在一仓库里堆放着若干相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有A. 箱B. 箱C. 箱D. 箱3、如图所示是由若干个完全相同的小正方体搭成的几何体的主视图和俯视图，则这个几何体可能是由____________________个小正方体搭成的．4、一个几何体是由许多规格相同的小正方体堆积而成的，其主视图、左视图如图所示，要摆成这样的图形，至少需用块小正方体，最多需用块小正方体．5、如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是__ __(结果保留π).6、已知某几何体的三视图如图所示，其中俯视图为正六边形，则该几何体的所有侧面积之和为．7、如图所示是某种型号的正六角螺母毛坯的三视图，则它的侧面积为cm2．8、如图是一个底面直径为，母线长也为的圆锥，是母线上的一点，，从点沿圆锥侧面到点的最短路径长是．9、如图是一个正六棱柱的主视图和左视图,则图中a的值为.10、图1是一个每条棱长均相等的三棱锥,图2是它的主视图、左视图与俯视图.若边AB的长度为a,则在这三种视图的所有线段中,长度为a的线段有()A.12条B.9条C.5条D.4条11、一个几何体的三视图如图所示,则这个几何体的表面积是 .12、如图所示的礼盒上下底面为全等的正六边形，其主视图与左视图均由矩形构成，主视图中大矩形边长如图所示，左视图中包含两个全等的矩形．如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（结果保留整数）．13、如图是一个长方体的表面展开图，其中四边形ABCD是正方形，根据图中标注的数据可求得原长方体的体积是 cm314、如图是由两个长方体组合而成的一个立体图形的从三个不同方向看到的形状图，根据图中所标尺寸(单位：mm)，计算出这个立体图形的表面积是__________mm2.15、三棱柱的三视图如图所示，已知△EFG中，EF＝8cm，EG＝12cm，∠EFG＝45°．则AB的长为cm．16、如图是某几何体的三视图，根据图中数据，求得该几何体的表面积为．17．如图，一个几何体的三视图分别是两个矩形、一个扇形，则这个几何体表面积的大小为．18、如图是一个几何体的主视图与俯视图,根据图中数据(单位:mm),求该几何体的体积(π取值3.14).19、如图1是一种包装盒的表面展开图,将它围起来可得到一个几何体的模型.(1)请说出这个几何体模型的最确切的名称是________.(2)如图2是根据 a,h的取值画出的几何体的主视图和俯视图(图中的粗实线表示的正方形(中间一条虚线)和粗实线表示的三角形),请在网格中画出该几何体的左视图.(3)在(2)的条件下,已知h=20 cm,求该几何体的表面积.20、如图所示，在平整的地面上，有若干个完全相同的棱长为10cm的正方体堆成的一个几何体．（1）这个几何体由个正方体组成．（2）如果在这个几何体的表面（露出的部分）喷上黄色的漆，则在所有的正方体中，有_________个正方体只有一个面是黄色，有个正方体只有两个面是黄色，有个正方体只有三个面是黄色．（3）求这个几何体喷漆的面积．21、某几何体的三视图如图所示，已知在△EFG中，FG＝18cm，EG＝12cm，∠EGF＝30°；在矩形ABCD中，AD＝16cm．（1）请根据三视图说明这个几何体的形状．（2）请你求出AB的长；（3）求出该几何体的体积．。

部编数学九年级下册专题09三视图(重难点突破)(解析版)_new含答案

专题09 三视图理解三视图的概念，掌握三视图之间的位置与数量关系，能熟练画出简单几何体重点的三视图能用一个物体的三视图来描述这个物体，并能应用三视图的知识解决一些实际问难点题易错画物体的三视图时用线易出现错误一、物体的三视图三视图中的各视图，分别从不同方面表示物体的形状，三者合起来能够较全面地反映物体的形状，单独一个视图难以全面地反映物体的形状，在实际生活中常用三视图描述物体的形状．【例1】关于如图所示的几何体的三视图，下列说法正确的是（）A．主视图和俯视图都是矩形B．俯视图和左视图都是矩形C．主视图和左视图都是矩形D．只有主视图是矩形【答案】C【详解】解：依据圆柱体放置的方位来说，主视图和左视图都是矩形，俯视图是一个圆．故选：C．【例2】图中几何体的三视图是（）A．B．C．D．【答案】C【详解】由几何体可知，该几何体的三视图为故选C二、根据三视图确定几何体1.由三视图想象立体图时，要先分别根据主视图、俯视图和左视图想象立体图的前面、上面和左侧面，然后再综合起来考虑整体图形．2.从实线和虚线想象几何体看得见和看不见的部分的轮廓线．【例1】如图是一个立体图形的正视图、左视图和俯视图，那么这个立体图形是（）A．圆锥B．三棱锥C．四棱锥D．五棱锥【答案】C【详解】解：根据三视图可以想象出该物体由四条棱组成，底面是正方形，此只有四棱柱的三视图与题目中的图形相符，故选：C．【例2】在下面的几个选项中，可以把左边的图形作为该几何体的三视图的是（）A．B．C．D．【答案】C【详解】解：由主视图和左视图可知该几何体的正面与左侧面都是矩形，所以A 不符合题意；再由主视图中矩形的内部有两条虚线，可知B 不符合题意；根据俯视图，可知该几何体的上面不是梯形，而是一个任意的四边形，所以D 不符合题意．符合题意的是C ．故选：C ．三、由视图确定几何体的表面积和体积某些立体图可沿其中一些线剪开成一个平面展开图，在实际生产中，常将立体图、三视图和平面展开图相结合进行相关运算．【例1】一个几何体的三视图如图所示，则这个几何体的表面积是（）A ．18pB ．20pC ．16pD ．14p【答案】A 【详解】解：依题意知这个几何体是圆锥和圆柱的组合体，圆锥的底面半径422=¸=，母线长为3，圆柱的底面半径422=¸=，高为2，则这个几何体的表面积是223222264818p p p p p p p ´´+´+´´´=++=．故选：A ．【例2】某圆锥的三视图如图所示，由图中数据可知，该圆锥的体积为（）A ．312cm p B ．320cm p C ．332cm p D ．348cm p 【答案】A 【详解】观察三视图得：圆锥的底面半径为()623cm ¸=，高为4cm ，即圆锥的体积为()223113412cm 33r h p p p =´´=，故选：A ．一、单选题1．下面四个几何体中，俯视图是三角形的是（）．A ．B ．C ．D ．【答案】D 【详解】解：A 的俯视图是四边形，B 的俯视图是圆及圆心，C 的俯视图是圆，D 的俯视图是三角形，A 、故选项错误，不符合题意；B 、故选项错误，不符合题意；C 、故选项错误，不符合题意；D 、故选项正确，符合题意．故选：D ．2．用四个相同的小正方体搭几何体，要求每个几何体从正面看、从左面看、从上面看得到的图形中，至少有两种图形的形状是相同的，下列四种摆放方式中，不符合要求的是（）．A ．B ．C ．D ．【答案】D 【详解】选项主视图左视图俯视图ABCD只有选项D的三视图两两都不相同，故选D.3．如图试一个几何体的三视图，则这个几何体的形状是（）A．圆柱B．圆锥C．球D．三棱锥【答案】B【详解】由于主视图和左视图为三角形可得此几何体为锥体，由俯视图为圆形可得为圆锥．故选：B．4．如图是一个立方体的三视图，这个立方体由一些相同大小的小正方体组成，这些相同的小正方体的个数是（）A．4B．5C．6D．7【答案】D【详解】根据题意，在俯视图上标注各个位置的个数为：所以一共有：1+2+2+1+1=7（个）故选D．5．由5个完全相同的小长方体搭成的几何体的主视图和左视图如图所示，则这个几何体的俯视图是（）A．B．C．D．【答案】A【详解】解：结合主视图、左视图可知俯视图中右上角有2层,其余1层.故选:A.6．长方体的主视图与俯视图如图1所示，则这个长方体的体积是（）．A．52B．32C．24D．9【答案】C【详解】由主视图可知，这个长方体的长和高分别为4和3，由俯视图可知，这个长方体的长和宽分别为4和2，因此这个长方体的长、宽、高分别为4、2、3，因此这个长方体的体积为4×2×3=24平方单位，故选C二、填空题7．如图，棱长为5cm的正方体，无论从哪一个面看，都有三个穿透的边长为1cm的正方形孔（阴影部分），则这个几何体的表面积（含孔内各面）是_______cm2．【答案】252【详解】解：由正方体的6个外表面的面积为5×5×6﹣1×1×3×6＝132（cm2），9个内孔的内壁的面积为1×1×4×4×9﹣1×1×2×6＝120（cm2），因此这个有孔的正方体的表面积（含孔内各面）为132+120＝252（cm2），故答案为：252．8．如图所示的是从不同方向观察一个圆柱体得到的形状图，由图中数据计算此圆柱体的侧面积为________（结果保留π）【答案】6π【详解】解：∵圆柱的底面直径为2，高为3，∴侧面积= 2•π×3=6π．．故答案为：6π．三、解答题9．请你在下边的方格中画出如图所示几何体的三视图．【答案】见解析【详解】解：如图所示：10．已知一个模型的三视图如图所示(单位：m)．(1)请描述这个模型的形状；(2)若制作这个模型的木料密度为360 kg/m3，则这个模型的质量是多少？(3)如果用油漆漆这个模型，每千克油漆可以漆4 m2，那么需要多少千克油漆？【答案】（1）详见解析；（2）43380kg；（3）41.625kg．【详解】解：(1)此模型由两个长方体组成：上面的是小长方体，下面的是大长方体．(2)模型的体积＝3×6×6＋2.5×2.5×2＝120.5(m3)，模型的质量＝120.5×360＝43380(kg)．(3)模型的表面积＝2×2.5×2.5＋2×2×2.5＋2×6×3＋2×3×6＋2×6×6＝166.5(m2)，需要油漆：166.5÷4＝41.625(kg)．一、单选题1．下列几何体中，同一个几何体从正面看和从上面看不同的是（）A．正方体B．球C．棱柱D．圆柱【答案】C【详解】解：A：正方体从正面看和从上面看均为正方形，故选项A不符合题意；B：球从正面看和从上面看均为圆，故选项B不符合题意；C：棱柱从正面看为长方形，从下面看为三角形，故选项C符合题意；D ：圆柱从正面看和从上面看均为长方形，故选项D 不符合题意；故选：C ．2．如图，分别是从上面、正面、左面看某立体图形得到的平面图形，则该立体图形是下列的（）A ．长方体B ．圆柱C ．三棱锥D ．三棱柱【答案】D 【详解】根据三视图的意义，该立体图形是三棱柱．故选：D ．3．一个几何体由若干个大小相同的小正方体组成，从上面和左面观察这个几何体如图所示，则搭建这个几何体的小正方体的个数最多是（）A ．8个B ．10个C ．12个D ．13个【答案】D 【详解】解：由题意得：如图此时，小正方体的个数最多：3332213++++=；故选：D ．4．图2是图1中长方体的三视图，用S 表示面积，223,,S x x S x x =+=+主左则S =俯（）A ．232x x ++B ．221x x ++C ．243x x ++D ．224x x+【答案】C 【详解】解：∵()233S x x x x =+=+主，()21S x x x x =+=+左，∴俯视图的长为()3x + ，宽为()1x +，∴()()23143S x x x x =++=++俯．故选：C5．如图是一个几何体的三视图，根据图中所示数据计算这个几何体的侧面积是（）A ．212πcmB ．215πcmC ．224πcmD ．230πcm【答案】B 【详解】解：由三视图可知，原几何体为圆锥，∵5l ==∴26ππ515πcm 2S r l =××=´´=侧故选：B ．6．从某个方向观察一个正六棱柱，可看到如图所示的图形，其中四边形ABCD 为矩形，E F 、分别是AB DC 、的中点．若86AD AB ==，，则这个正六棱柱的侧面积为( )A ．B ．96C ．144D ．【答案】D 【详解】解：如图，正六边形的边长为AG BG 、，过点G 作GE AB ^∴GE 垂直平分AB ，由正六边形的性质可知，11203032AGB A B AE AB Ð=°Ð=Ð=°==，，，∴ cos30AE AG ===°正六棱柱的侧面积668AG AD =´=´=故选：D ．二、填空题7．某款不倒翁如图①所示，其主视图如图②所示，PA ，PB 分别与¼AMB所在圆相切于点A ，B ．若该圆半径是10cm ，36P Ð=°，则¼AMB 的长是______（结果保留p ）．【答案】12πcm ##12π厘米【详解】解：如图，设¼AMB所在的圆的圆心为O ，连接AO ，BO ，∵PA ，PB 分别与¼AMB所在圆相切于点A ，B ．∴AO PA ^，BO AB ^，∴90OAP OBP Ð=Ð=°，∵36P Ð=°，∴144AOB Ð=°，∴优弧AMB 对应的圆心角为360144216°-°=°，∴优弧AMB 的长是：216π1012π180´=，故答案为：12πcm ．8．如图为一个用正方体积木搭成的几何体的三视图，俯视图中方格上的数字表示该位置上积木累积的个数．若保证正视图和左视图成立，则+++a b c d 的最大值为 _____．【答案】13【详解】解：由正视图第1列和左视图第1列可知a 最大为3，由正视图第2列和左视图第2列可知b 最大为3，由正视图第3列和左视图第1列和第2列可知c 最大为4，d 最大为3；所以+++a b c d 的最大值为：+++=334313故答案为：13三、解答题9．如图是一个几何体的展开图．(1)写出该几何体的名称______；(2)用一个平面去截该几何体，截面形状可能是______（填序号）；①三角形；②四边形；③五边形；④六边形(3)根据图中标注的长度，求该几何体的表面积和体积．【答案】(1)长方体(2)①②③④(3)222m ；36m 【详解】（1）解：根据几何体的展开图共有6个面，且各面有正方形及长方形，∴此几何体为长方体，故答案为：长方体；（2）∵长方体有六个面，∴用平面去截长方体时最多与六个面相交得六边形，最少与三个面相交得三角形，∴用一个平面去截长方体，截面的形状可能是三角形、四边形、五边形、六边形，故答案为：①②③④；（3）231232221222(m )S =´´+´´+´´=，所以表面积是222m ；33216(m )V =´´=，所以体积是36m ．10．用棱长为2cm 的若干小正方体按如所示的规律在地面上搭建若干个几何体．图中每个几何体自上而下分别叫第一层、第二层，L ，第n 层（n 为正整数)（1）搭建第④个几何体的小立方体的个数为．（2）分别求出第②、③个几何体的所有露出部分（不含底面）的面积．（3）为了美观，若将几何体的露出部分都涂上油漆（不含底面），已知喷涂21cm 需要油漆0.2克，求喷涂第20个几何体，共需要多少克油漆？【答案】（1）30；（2）第②个几何体露出部分（不含底面）面积为264cm ，第③个几何体露出部分（不含底面）面积为2132cm ；（3）992克．【详解】（1）搭建第①个几何体的小立方体的个数为1，搭建第②个几何体的小立方体的个数为21412+=+，搭建第③个几何体的小立方体的个数为22149123++=++，归纳类推得：搭建第④个几何体的小立方体的个数为22212341491630+++=+++=，故答案为：30；（2）第②个几何体的三视图如下：由题意，每个小正方形的面积为2224()cm ´=，则第②个几何体的所有露出部分（不含底面）面积为()232324464()cm ´+´+´=；第③个几何体的三视图如下：则第③个几何体的所有露出部分（不含底面）面积为()2626294132()cm ´+´+´=；（3）第20个几何体从第1层到第20层小立方体的个数依次为221,2,,20L ，则第20个几何体的所有露出部分（不含底面）面积为()()2221220212202044960()cm éù´++++´++++´=ëûL L ，因此，共需要油漆的克数为49600.2992´=（克），答：共需要992克油漆．。

初中数学三视图练习题

初中数学三视图练习题初中数学三视图练习题数学是一门重要的学科，它不仅培养了我们的逻辑思维能力，还帮助我们解决实际生活中的问题。

在初中数学中，三视图是一个重要的概念，它能够帮助我们理解和描述三维物体的形状。

在本文中，我将介绍一些初中数学三视图练习题，并探讨其解题方法。

第一题：一个长方体的三视图如下图所示，请你画出这个长方体的展开图。

这道题要求我们根据给定的三视图来画出长方体的展开图。

展开图是将一个三维物体展开成一个平面图形，以便我们更好地理解其形状。

要解决这道题，我们可以先观察三视图，找出它们之间的关系。

在这个例子中，我们可以发现，底视图和正视图是一样的，而侧视图则是将底视图旋转了90度。

因此，我们可以根据这个关系来画出长方体的展开图。

第二题：一个正方体的三视图如下图所示，请你计算这个正方体的表面积和体积。

这道题要求我们根据给定的三视图来计算正方体的表面积和体积。

表面积是指正方体的所有面的总面积，而体积则是指正方体的内部空间的大小。

要解决这道题，我们可以先观察三视图，找出它们之间的关系。

在这个例子中，我们可以发现，正视图和侧视图是一样的，而顶视图则是将正视图旋转了90度。

因此，我们可以根据这个关系来计算正方体的表面积和体积。

在计算表面积时，我们可以将正方体分解成六个面，然后计算每个面的面积，最后将它们相加。

在计算体积时，我们可以利用正方体的边长来计算，即体积等于边长的立方。

通过解决这些练习题，我们可以加深对三视图的理解，并提高解决实际问题的能力。

三视图是一个重要的数学概念，它不仅在数学中有着广泛的应用，还在许多其他领域中起着重要作用，如工程、建筑等。

因此，我们应该认真学习和掌握三视图的相关知识。

总结起来，初中数学三视图练习题是一个有趣且具有挑战性的练习，它能够帮助我们提高数学思维能力和解决实际问题的能力。

通过反复练习和探索，我们可以更好地理解和应用三视图的知识。

希望大家能够喜欢并享受这个过程，并在学习中取得好成绩！。

中考数学专题复习题：直棱柱的三视图

中考数学专题复习题：直棱柱的三视图一、单项选择题（共10小题）1．如图所示三棱柱的主视图是（）2．如图所示的几何体的俯视图是（）3．如图所示的几何体，其左视图是（）4．如图所示的主视图对应的几何体是（）5．下列选项中，不是如图所示的几何体的主视图、左视图、俯视图之一的是（）6．如图所示的几何体的主视图是（）7．如图，是由6个相同的正方体组成的立体图形，它的俯视图是（）8．一个几何体如图所示，则该几何体的三视图正确的是（）9．如图，该几何体的左视图是（）10．如图所示的正六棱柱的主视图是（）二、填空题（共4小题）11．如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②，关于平移前后几何体的三视图，主视图______, 左视图______, 俯视图______.(均选填“相同”或“不相同”)12．请将六棱柱的三视图名称填在相应的横线上．（1）____________；（2）__________；（3）__________．13．分别观察下列几何体，其中主视图、左视图和俯视图完全相同的是________．圆锥圆柱三棱柱正方体14．三棱柱的三视图如下图所示，已知在△EFG中，EF＝8cm，EG＝12cm，∠EFG＝45°.则AB的长为________cm.三、解答题（共5小题）15．画出如图所示几何体的三视图．16．请画出如图所示的正五棱柱的三视图．17．画出下面立体图形的三视图．18．两个四棱柱的底面均为等腰梯形，它们的俯视图分别如图所示，画出它们的主视图和左视图．19．如图1是由两个长方体所组成的立体图形，图2中的长方体是图1中的两个长方体的另一种摆放形式，图①②③是从不同的方向看图1所得的平面图形．（1）填空：图①是________视图，图②是________视图，图③是________视图；（2）请根据各图中所给的信息(单位：cm)，计算出图1中上面的小长方体的体积．。

三视图习题50道(含答案)

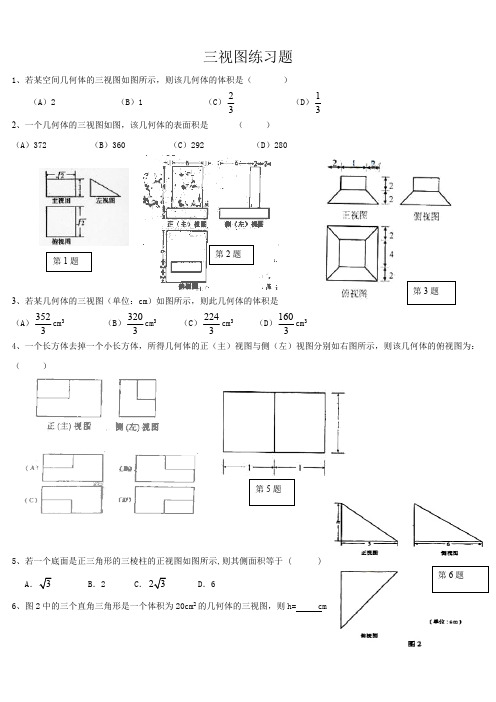
三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为（）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

初中三视图试题及答案

初中三视图试题及答案
1. 题目：观察下列物体的正视图和侧视图，画出其俯视图。

答案：根据正视图和侧视图，我们可以确定物体的俯视图是一个圆形。

2. 题目：给出一个物体的三视图，判断该物体的形状。

答案：该物体是一个长方体。

3. 题目：如果一个物体的正视图和俯视图都是矩形，而侧视图是一个
三角形，那么这个物体是什么形状？
答案：这个物体是一个三角柱。

4. 题目：观察下列物体的三视图，计算其体积。

答案：物体的体积为长×宽×高，具体数值根据三视图中给出的尺
寸计算得出。

5. 题目：根据下列物体的三视图，判断其表面积。

答案：物体的表面积为各面面积之和，具体数值根据三视图中给出
的尺寸计算得出。

6. 题目：如果一个物体的正视图是一个正方形，侧视图是一个矩形，
俯视图是一个圆形，那么这个物体是什么形状？
答案：这个物体是一个圆柱。

7. 题目：观察下列物体的三视图，判断其是否为对称图形。

答案：该物体是对称图形，因为它的三视图在对称轴两侧是相同的。

8. 题目：给出一个物体的三视图，计算其棱长总和。

答案：物体的棱长总和为各棱长度之和，具体数值根据三视图中给出的尺寸计算得出。

9. 题目：如果一个物体的三视图都是相同的圆形，那么这个物体是什么形状？
答案：这个物体是一个球体。

10. 题目：观察下列物体的三视图，判断其是否为多面体。

答案：该物体是一个多面体，因为它的三视图显示了多个平面的交线。

中考数学真题《几何图形初步与三视图、相交线与平行线》专项测试卷(附答案)

中考数学真题《几何图形初步与三视图相交线与平行线》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________（84题）一、单选题1．（2023·湖北鄂州·统考中考真题）下列立体图形中主视图是圆的是（）A．B．C．D．2．（2023·湖北鄂州·统考中考真题）如图，直线AB CD GE EF∠的BGE⊥于点E．若60∠=︒，则EFD度数是（）A．60︒B．30︒C．40︒D．70︒3．（2023·吉林长春·统考中考真题）下图是一个多面体的表面展开图每个面都标注了数字．若多面体的底面是面③，则多面体的上面是（）A．面③B．面③C．面③D．面③∠的角平分线根据作图痕迹下列结论4．（2023·吉林长春·统考中考真题）如图，用直尺和圆规作MAN不一定正确的是（）A ．AD AE =B ．AD DF =C ．DF EF =D ．AF DE ⊥5．（2023·甘肃兰州·统考中考真题）如图，直线AB 与CD 相交于点O ，则BOD ∠=（）A ．40︒B ．50︒C ．55︒D ．60︒6．（2023·山东东营·统考中考真题）如图，AB CD ∥ 点E 在线段BC 上（不与点B C 重合）连接DE 若40D ∠=︒ 60BED ∠=︒，则B ∠=（）A ．10︒B ．20︒C ．40︒D ．60︒7．（2023·内蒙古·统考中考真题）几个大小相同的小正方体搭成几何体的俯视图如图所示图中小正方形中数字表示对应位置小正方体的个数该几何体的主视图是（）A ．B ．C ．D ．8．（2023·内蒙古·统考中考真题）如图，直线a b 直线l 与直线,a b 分别相交于点,A B 点C 在直线b 上且CA CB =．若132∠=︒，则2∠的度数为（）A ．32︒B ．58︒C ．74︒D ．75︒9．（2023·全国·统考中考真题）图③是2023年6月11日吉林市全程马拉松男子组颁奖现场．图③是领奖台的示意图，则此领奖台的主视图是（）A．B．C．D．10．（2023·黑龙江绥化·统考中考真题）将一副三角板按下图所示摆放在一组平行线内125∠=︒230∠=︒，∠的度数为（）则3A．55︒B．65︒C．70︒D．75︒11．（2023·黑龙江绥化·统考中考真题）如图是一个正方体被切去一角，则其左视图是（）A．B．C．D．12．（2023·黑龙江齐齐哈尔·统考中考真题）如图，若几何体是由六个棱长为1的正方体组合而成的，则该几何体左视图的面积是（）A ．2B ．3C ．4D ．513．（2023·黑龙江齐齐哈尔·统考中考真题）如图，直线12l l ∥ 分别与直线l 交于点A B 把一块含30︒角的三角尺按如图所示的位置摆放若145∠=︒，则2∠的度数是（）A ．135︒B ．105︒C ．95︒D ．75︒14．（2023·河南·统考中考真题）如图，直线AB CD 相交于点O 若180∠=︒ 230∠=︒，则AOE ∠的度数为（）A ．30︒B ．50︒C ．60︒D ．80︒15．（2023·河南·统考中考真题）北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一具有极高的历史价值文化价值．如图所示关于它的三视图下列说法正确的是（）A ．主视图与左视图相同B ．主视图与俯视图相同C ．左视图与俯视图相同D ．三种视图都相同16．（2023·黑龙江·统考中考真题）一个几何体由若干大小相同的小正方体组成它的俯视图和左视图如图所示那么组成该几何体所需小正方体的个数最少为（）A ．4B ．5C ．6D ．717．（2023·湖北·统考中考真题）如图是一个立体图形的三视图该立体图形是（）A ．三棱柱B ．圆柱C ．三棱锥D ．圆锥18．（2023·湖南张家界·统考中考真题）如图是由5个完全相同的小正方体组成的立体图形其主视图是（）A ．B ．C ．D ．19．（2023·辽宁大连·统考中考真题）如图，直线,45,20AB CD ABE D ∠=∠=︒︒∥，则E ∠的度数为（）A ．20︒B ．25︒C ．30︒D ．35︒20．（2023·辽宁大连·统考中考真题）如图所示的几何体中主视图是（）A．B．C．D．21．（2023·广东·统考中考真题）如图，街道AB与CD平行拐角137ABC∠=︒，则拐角BCD∠=（）A．43︒B．53︒C．107︒D．137︒∠=︒，则22．（2023·山东·统考中考真题）一把直尺和一个含30︒角的直角三角板按如图方式放置若120∠=（）2A．30︒B．40︒C．50︒D．60︒23．（2023·山东·统考中考真题）如图所示的几何体是由5个大小相同的小正方体组成的它的主视图是（）A．B．C．D．24．（2023·山东·统考中考真题）如图，,a b 是直尺的两边 a b 把三角板的直角顶点放在直尺的b 边上若135∠=︒，则2∠的度数是（）A ．65︒B ．55︒C ．45︒D ．35︒25．（2023·山东·统考中考真题）一个几何体的三视图如下，则这个几何体的表面积是（）A ．39πB ．45πC ．48πD ．54π26．（2023·福建·统考中考真题）下图是由一个长方体和一个圆柱组成的几何体它的俯视图是（）A ．B ．C ．D ．27．（2023·湖北荆州·统考中考真题）观察如图所示的几何体下列关于其三视图的说法正确的是（）A ．主视图既是中心对称图形又是轴对称图形B ．左视图既是中心对称图形又是轴对称图形C ．俯视图既是中心对称图形又是轴对称图形D ．主视图左视图俯视图都是中心对称图形28．（2023·湖北荆州·统考中考真题）如图所示的“箭头”图形中 AB CD ∥ 80B D ∠=∠= 47E F ∠=∠=，则图中G ∠的度数是（）A ．80B ．76C ．66D ．5629．（2023·山东聊城·统考中考真题）如图，分别过ABC 的顶点A B 作AD BE ．若25CAD ∠=︒ 80EBC ∠=︒，则ACB ∠的度数为（）A ．65︒B ．75︒C ．85︒D ．95︒30．（2023·山东聊城·统考中考真题）如图所示几何体的主视图是（）A ．B ．C ．D ．31．（2023·四川·统考中考真题）某几何体是由四个大小相同的小立方块拼成其俯视图如图所示图中数字表示该位置上的小立方块个数，则这个几何体的左视图是（）A ．B ．C ．D ．32．（2023·广西·统考中考真题）如图，一条公路两次转弯后又回到与原来相同的方向如果130A ∠=︒ 那么B ∠的度数是（）A ．160︒B ．150︒C ．140︒D ．130︒33．（2023·湖南·统考中考真题）如图，直线,a b 被直线c 所截已知,150a b ︒∠=∥，则2∠的大小为（）A ．40︒B ．50︒C ．70︒D ．130︒34．（2023·湖北黄冈·统考中考真题）如图，Rt ABC △的直角顶点A 在直线a 上斜边BC 在直线b 上若155a b ∠=︒，，则2∠=（）A．55︒B．45︒C．35︒D．25︒35．（2023·湖北黄冈·统考中考真题）下列几何体中三视图都是圆的是（）A．长方体B．图柱C．圆锥D．球36．（2023·湖南郴州·统考中考真题）下列几何体中各自的三视图完全一样的是（）A．B．C．D．37．（2023·湖北宜昌·统考中考真题）“争创全国文明典范城市让文明成为宜昌人民的内在气质和城市的亮丽名片”．如图，是一个正方体的平面展开图把展开图折叠成正方体后“城”字对面的字是（）．A．文B．明C．典D．范38．（2023·湖北宜昌·统考中考真题）如图，小颖按如下方式操作直尺和含30︒角的三角尺依次画出了直线a b c．如果170∠，则2=︒∠的度数为（）．A．110︒B．70︒C．40︒D．30︒39．（2023·湖北武汉·统考中考真题）如图是由4个相同的小正方体组成的几何体它的左视图是（）A．B．C．D．40．（2023·湖北十堰·统考中考真题）下列几何体中三视图的三个视图完全相同的几何体是（）A．B．C．D．41．（2023·四川内江·统考中考真题）如图是由5个完全相同的小正方体堆成的物体其主视图是（）A．B．C．D．42．（2023·山东滨州·统考中考真题）如图所示摆放的水杯其俯视图为（）A ．B ．C ．D ．43．（2023·湖北随州·统考中考真题）如图是一个放在水平桌面上的圆柱体该几何体的三视图中完全相同的是（）A ．主视图和俯视图B ．左视图和俯视图C ．主视图和左视图D ．三个视图均相同44．（2023·湖北随州·统考中考真题）如图，直线12l l ∥ 直线l 与1l 2l 相交若图中160∠=︒，则2∠为（）A ．30︒B ．60︒C ．120︒D ．150︒45．（2023·天津·统考中考真题）如图是一个由6个相同的正方体组成的立体图形它的主视图是（）A．B．C．D．46．（2023·山东枣庄·统考中考真题）榫卯是古代中国建筑家具及其它器械的主要结构方式是我国工艺文化精神的传奇凸出部分叫榫凹进部分叫卯下图是某个部件“卯”的实物图它的主视图是（）A．B．C．D．47．（2023·山东临沂·统考中考真题）下图是我国某一古建筑的主视图最符合视图特点的建筑物的图片是（）A．B．C．D．∠的度数是（）48．（2023·山东临沂·统考中考真题）下图中用量角器测得ABCA．50︒B．80︒C．130︒D．150︒49．（2023·湖南永州·统考中考真题）下列几何体中其三视图的主视图和左视图都为三角形的是（）A．B．C．D．50．（2023·江苏苏州·统考中考真题）今天是父亲节小东同学准备送给父亲一个小礼物．已知礼物外包装的主视图如图所示，则该礼物的外包装不可能．．．是（）A．长方体B．正方体C．圆柱D．三棱锥51．（2023·湖南·统考中考真题）作为中国非物质文化遗产之一的紫砂壶成型工艺特别造型式样丰富陶器色泽古朴典雅从一个方面鲜明地反映了中华民族造型审美意识．如图是一把做工精湛的紫砂壶“景舟石瓢” 下面四幅图是从左面看到的图形的是（）A．B．C．D．52．（2023·山东烟台·统考中考真题）如图，对正方体进行两次切割得到如图③所示的几何体，则图③几何体的俯视图为（）A ．B ．C ．D ．53．（2023·湖南岳阳·统考中考真题）已知AB CD 点E 在直线AB 上点,F G 在直线CD 上 EG EF ⊥于点,40E AEF ∠=︒，则EGF ∠的度数是（）A ．40︒B ．45︒C ．50︒D ．60︒54．（2023·湖南岳阳·统考中考真题）下列几何体的主视图是圆的是（）A ．B ．C ．D ．55．（2023·江苏扬州·统考中考真题）下列图形中是棱锥的侧面展开图的是（）A ．B ．C ．D ． 56．（2023·四川乐山·统考中考真题）下面几何体中是圆柱的是（）A ．B ．C ．D ．57．（2023·浙江绍兴·统考中考真题）由8个相同的立方体搭成的几何体如图所示，则它的主视图是（）A ．B ．C ．D ．58．（2023·浙江台州·统考中考真题）如图是由5个相同的正方体搭成的立体图形其主视图是（）．A ．B ．C ．D ．59．（2023·浙江温州·统考中考真题）截面为扇环的几何体与长方体组成的摆件如图所示它的主视图是（）A ．B ．C ．D ．60．（2023·湖南怀化·统考中考真题）如图，平移直线AB 至CD 直线AB CD 被直线EF 所截 160∠=︒，则2∠的度数为（）A ．30︒B ．60︒C ．100︒D ．120︒61．（2023·江西·统考中考真题）如图，平面镜MN 放置在水平地面CD 上墙面PD CD ⊥于点D 一束光线AO 照射到镜面MN 上反射光线为OB 点B 在PD 上若35AOC ∠=︒，则OBD ∠的度数为（）A．35︒B．45︒C．55︒D．65︒62．（2023·云南·统考中考真题）某班同学用几个几何体组合成一个装饰品美化校园．其中一个几何体的三视图（其中主视图也称正视图左视图也称侧视图）如图所示这个几何体是（）A．球B．圆柱C．长方体D．圆锥63．（2023·浙江宁波·统考中考真题）如图所示的几何体是由一个圆柱和一个长方体组成的它的主视图是()A．B．C．D．64．（2023·四川眉山·统考中考真题）由相同的小正方体搭成的立体图形的部分视图如图所示，则搭成该立体图形的小正方体的最少个数为（）A．6B．9C．10D．1465．（2023·四川眉山·统考中考真题）如图，ABC 中 ,40=∠=︒AB AC A ，则ACD ∠的度数为（）A ．70︒B ．100︒C ．110︒D ．140︒66．（2023·江苏连云港·统考中考真题）下列水平放置的几何体中主视图是圆形的是（）A ．B ．C ．D ．67．（2023·四川遂宁·统考中考真题）生活中一些常见的物体可以抽象成立体图形以下立体图形中三视图形状相同的可能是（）A ．正方体B ．圆锥C ．圆柱D ．四棱锥68．（2023·四川广安·统考中考真题）如图，由5个大小相同的小正方体搭成的几何体它的俯视图是（）A ．B ．C．D．69．（2023·浙江金华·统考中考真题）某物体如图所示其俯视图是（）A．B．C．D．70．（2023·浙江嘉兴·统考中考真题）如图的几何体由3个同样大小的正方体搭成它的俯视图是（）A．B．C．D．71．（2023·安徽·统考中考真题）某几何体的三视图如图所示，则该几何体为（）A．B．C．D．72．（2023·浙江·统考中考真题）如图，箭头所指的是某陶艺工作室用于垫放陶器的5块相同的耐火砖搭成的几何体它的主视图是（）A．B．C．D．73．（2023·四川凉山·统考中考真题）光线在不同介质中的传播速度是不同的因此光线从水中射向空气时∠=︒∠=︒，要发生折射．由于折射率相同所以在水中平行的光线在空气中也是平行的．如图，145,2120∠+∠=（）则34A．165︒B．155︒C．105︒D．90︒74．（2023·四川凉山·统考中考真题）如图是由4个相同的小立方体堆成的几何体的俯视图小正方形中的数字表示该位置小立方体的个数，则这个几何体的主视图是（）A．B．C．D．75．（2023·重庆·统考中考真题）如图，直线a b被直线c所截若a b163∠=︒，则2∠的度数为( )．A ．27︒B ．53︒C ．63︒D ．117︒76．（2023·重庆·统考中考真题）四个大小相同的正方体搭成的几何体如图所示从正面看到的视图是（）A ．B ．C ．D ．77．（2023·四川泸州·统考中考真题）一个立体图形的三视图如图所示，则该立体图形是（）A ．圆柱B ．圆锥C ．长方体D ．三棱柱78．（2023·四川泸州·统考中考真题）如图，AB CD ∥ 若55D ∠=︒，则1∠的度数为（）A ．125︒B ．135︒C ．145︒D ．155︒79．（2023·四川自贡·统考中考真题）如图，某人沿路线A B C D →→→行走 AB 与CD 方向相同 1128∠=︒，则2∠=（）A ．52︒B ．118︒C ．128︒D ．138︒80．（2023·四川自贡·统考中考真题）如图中六棱柱的左视图是（）A ．B ．C ．D ．二填空题81．（2023·全国·统考中考真题）如图，在ABC 中 AB AC = 分别以点B 和点C 为圆心大于12BC 的长为半径作弧两孤交于点D 作直线AD 交BC 于点E ．若=110BAC ∠︒，则BAE ∠的大小为__________度．82．（2023·内蒙古通辽·统考中考真题）将一副三角尺如图所示放置其中AB DE ∥，则CDF ∠=___________度．83．（2023·山东烟台·统考中考真题）一杆古秤在称物时的状态如图所示已知1102∠=︒，则2∠的度数为_____．∠=︒，则③2的度数为84．（2023·浙江台州·统考中考真题）用一张等宽的纸条折成如图所示的图案若120________．参考答案一单选题1．（2023·湖北鄂州·统考中考真题）下列立体图形中主视图是圆的是（）A．B．C．D．【答案】D【分析】分别得出棱柱圆柱圆锥球体的主视图得出结论．【详解】解：棱柱的主视图是矩形（中间只有一条线段）不符合题意圆柱的主视图是矩形不符合题意圆锥的主视图是等腰三角形不符合题意球体的主视图是圆符合题意故选：D．【点睛】本题考查了三视图的知识主视图是从物体的正面看得到的视图．2．（2023·湖北鄂州·统考中考真题）如图，直线AB CD GE EF∠的⊥于点E．若60∠=︒，则EFDBGE度数是（）A ．60︒B ．30︒C ．40︒D ．70︒【答案】B 【分析】延长GE 与DC 交于点M 根据平行线的性质求出FME ∠的度数再直角三角形的两锐角互余即可求出EFD ∠．【详解】解：延长GE 与DC 交于点M③AB CD 60BGE ∠=︒③60FME BGE ∠∠==︒③GE EF ⊥③906030EFD ∠=︒-︒=︒故选：B ．【点睛】本题考查平行线的性质和直角三角形的性质正确作出辅助线和正确利用平行线的性质是解题的关键．3．（2023·吉林长春·统考中考真题）下图是一个多面体的表面展开图每个面都标注了数字．若多面体的底面是面③，则多面体的上面是（）A ．面③B ．面③C ．面③D ．面③【答案】C 【分析】根据底面与多面体的上面是相对面，则形状相等间隔1个长方形且没有公共顶点即可求解．【详解】解：依题意多面体的底面是面③，则多面体的上面是面③故选：C ．【点睛】本题考查了长方体的表面展开图熟练掌握基本几何体的展开图是解题的关键．4．（2023·吉林长春·统考中考真题）如图，用直尺和圆规作MAN ∠的角平分线根据作图痕迹下列结论不一定正确的是（）A ．AD AE =B ．AD DF =C ．DF EF =D ．AF DE ⊥【答案】B【分析】根据作图可得,AD AE DF EF == 进而逐项分析判断即可求解．【详解】解：根据作图可得,AD AE DF EF == 故A C 正确③,A F 在DE 的垂直平分线上③AF DE ⊥ 故D 选项正确而DF EF =不一定成立故C 选项错误故选：B ．【点睛】本题考查了作角平分线垂直平分线的判定熟练掌握基本作图是解题的关键．5．（2023·甘肃兰州·统考中考真题）如图，直线AB 与CD 相交于点O ，则BOD ∠=（）A ．40︒B ．50︒C ．55︒D ．60︒【答案】B【分析】利用对顶角相等得到BOD AOC ∠=∠ 即可求解．【详解】解：读取量角器可知：50AOC ∠=︒③50BOD AOC ∠=∠=︒故选：B ．【点睛】本题考查了对顶角相等量角器读数是基础题．6．（2023·山东东营·统考中考真题）如图，AB CD ∥ 点E 在线段BC 上（不与点B C 重合）连接DE 若40D ∠=︒ 60BED ∠=︒，则B ∠=（）A ．10︒B ．20︒C ．40︒D ．60︒【答案】B 【分析】根据三角形的外角的性质求得20C ∠=︒ 根据平行线的性质即可求解．【详解】解：③40D ∠=︒ 60BED ∠=︒③20C BED D ∠=∠-∠=︒③AB CD ∥③B ∠=20C ∠=︒故选：B ．【点睛】本题考查了三角形的外角的性质平行线的性质熟练掌握以上知识是解题的关键． 7．（2023·内蒙古·统考中考真题）几个大小相同的小正方体搭成几何体的俯视图如图所示图中小正方形中数字表示对应位置小正方体的个数该几何体的主视图是（）A ．B ．C ．D ．【答案】D【分析】根据各层小正方体的个数然后得出三视图中主视图的形状即可得出答案．【详解】解：根据俯视图可知这个几何体中：主视图有三列：左边一列1个中间一列2个右边一列2个所以该几何体的主视图是故选：D ．【点睛】此题主要考查了学生对三视图掌握程度和灵活运用能力同时也体现了对空间想象能力方面的考查熟练掌握三视图的判断方法是解题关键．8．（2023·内蒙古·统考中考真题）如图，直线a b 直线l 与直线,a b 分别相交于点,A B 点C 在直线b 上且CA CB =．若132∠=︒，则2∠的度数为（）A ．32︒B ．58︒C ．74︒D ．75︒【答案】C 【分析】由CA CB = 132∠=︒ 可得1801742CBA CAB ︒-∠∠=∠==︒ 由a b 可得2CBA ∠=∠ 进而可得2∠的度数．【详解】解：③CA CB = 132∠=︒ ③1801742CBA CAB ︒-∠∠=∠==︒ ③a b ③274CBA ∠=∠=︒故选：C ．【点睛】本题考查了等边对等角三角形的内角和定理平行线的性质．解题的关键在于明确角度之间的数量关系．9．（2023·全国·统考中考真题）图③是2023年6月11日吉林市全程马拉松男子组颁奖现场．图③是领奖台的示意图，则此领奖台的主视图是（）A ．B ．C ．D ．【答案】A 【分析】主视图是从几何体正面观察到的视图．【详解】解：领奖台从正面看是由三个矩形组成的．三个矩形右边最低中间最高故选：A．【点睛】本题考查主视图掌握三视图的特征是解题关键．10．（2023·黑龙江绥化·统考中考真题）将一副三角板按下图所示摆放在一组平行线内125∠=︒230∠=︒，∠的度数为（）则3A．55︒B．65︒C．70︒D．75︒【答案】C【分析】根据两直线平行内错角相等即可求解．∠+︒=∠+︒【详解】解：依题意190345③125∠=︒∠=︒③370故选：C．【点睛】本题考查了平行线的性质熟练掌握两直线平行内错角相等是解题的关键．11．（2023·黑龙江绥化·统考中考真题）如图是一个正方体被切去一角，则其左视图是（）A．B．C．D．【答案】B【分析】根据左视图的意义判断即可．【详解】根据题意该几何体的左视图为：故选：B ．【点睛】本题考查了三视图的画法熟练掌握三视图的空间意义是解题的关键．12．（2023·黑龙江齐齐哈尔·统考中考真题）如图，若几何体是由六个棱长为1的正方体组合而成的，则该几何体左视图的面积是（）A ．2B ．3C ．4D ．5【答案】C 【分析】首先确定该几何体左视图的小正方形数量然后求解面积即可．【详解】解：该几何体左视图分上下两层其中下层有3个小正方形上层中间有1个正方形共计4个小正方形③小正方体的棱长为1③该几何体左视图的面积为4故选：C ．【点睛】本题考查简单组合体的三视图理解左视图即为从左边看到的图形是解题关键．13．（2023·黑龙江齐齐哈尔·统考中考真题）如图，直线12l l ∥ 分别与直线l 交于点A B 把一块含30︒角的三角尺按如图所示的位置摆放若145∠=︒，则2∠的度数是（）A ．135︒B ．105︒C ．95︒D ．75︒【答案】B 【分析】依据12l l ∥ 即可得到1345∠=∠=︒ 再根据430∠=︒ 即可得出荅案．【详解】解：如图，12l l ∥1345∴∠=∠=︒又430∠=︒2180341804530105∴∠=︒-∠-∠=︒-︒-︒=︒故选：B ．【点睛】此题主要考查了平行线的性质解本题的关键是熟记平行线的性质：两直线平行同位角相等． 14．（2023·河南·统考中考真题）如图，直线AB CD 相交于点O 若180∠=︒ 230∠=︒，则AOE ∠的度数为（）A ．30︒B ．50︒C ．60︒D ．80︒【答案】B 【分析】根据对顶角相等可得180AOD ∠=∠=︒ 再根据角的和差关系可得答案．【详解】解：③180∠=︒③180AOD ∠=∠=︒③230∠=︒③2803050AOE AOD ∠=∠-∠=︒-︒=︒故选：B.【点睛】本题主要考查了对顶角的性质解题的关键是掌握对顶角相等．15．（2023·河南·统考中考真题）北宋时期的汝官窑天蓝釉刻花鹅颈瓶是河南博物院九大镇院之宝之一具有极高的历史价值文化价值．如图所示关于它的三视图下列说法正确的是（）A．主视图与左视图相同B．主视图与俯视图相同C．左视图与俯视图相同D．三种视图都相同【答案】A【分析】直接利用已知几何体分别得出三视图进而分析得出答案．【详解】解：这个花鹅颈瓶的主视图与左视图相同俯视图与主视图和左视图不相同．故选：A．【点睛】此题主要考查了简单几何体的三视图掌握三视图的概念是解题关键．16．（2023·黑龙江·统考中考真题）一个几何体由若干大小相同的小正方体组成它的俯视图和左视图如图所示那么组成该几何体所需小正方体的个数最少为（）A．4B．5C．6D．7【答案】B【分析】在“俯视打地基”的前提下结合左视图知俯视图上一行三个小正方体的上方（第2层）至少还有1个正方体据此可得答案.【详解】解：由俯视图与左视图知该几何体所需小正方体个数最少分布情况如下图所示：所以组成该几何体所需小正方体的个数最少为5故选：B．【点睛】本题主要考查由三视图判断几何体解题的关键是掌握口诀“俯视打地基主视疯狂盖左视拆违章”．17．（2023·湖北·统考中考真题）如图是一个立体图形的三视图该立体图形是（）A．三棱柱B．圆柱C．三棱锥D．圆锥【答案】D【分析】根据主视图和左视图确定是柱体锥体球体再由俯视图确定具体形状．【详解】解：由主视图和左视图为三角形判断出是锥体根据俯视图是圆可判断出这个几何体应该是圆锥．故选：D．【点睛】本题考查了由物体的三种视图确定几何体的形状考查了学生的思考能力和对几何体三种视图的空间想象能力和综合能力．18．（2023·湖南张家界·统考中考真题）如图是由5个完全相同的小正方体组成的立体图形其主视图是（）A．B．C．D．【答案】D【分析】根据从正面看得到的图形是主视图可得答案．【详解】解：其主视图有2列从左到右依次有3 1个正方形图形如下：故选：D ．【点睛】本题考查了简单组合体的三视图掌握从正面看到的图形是主视图是解题关键．19．（2023·辽宁大连·统考中考真题）如图，直线,45,20AB CD ABE D ∠=∠=︒︒∥，则E ∠的度数为（）A ．20︒B ．25︒C ．30︒D ．35︒【答案】B【分析】先根据平行线的性质可得45ABE BCD ∠∠==︒ 再根据三角形的外角性质即可得．【详解】解：,45AB CD ABE ∠=︒∥45ABE BCD ∴=∠=∠︒20D ∠=︒25BCD D E ∠-∠==∴∠︒故选：B ．【点睛】本题考查了平行线的性质三角形的外角性质熟练掌握平行线的性质是解题关键．20．（2023·辽宁大连·统考中考真题）如图所示的几何体中主视图是（）A ．B ．C ．D ．【答案】B【分析】根据主视图是从正面看得到的图形解答即可．【详解】解：从正面看看到的是故选：B ．【点睛】本题考查了三视图的知识属于简单题熟知主视图是从物体的正面看得到的视图是解题的关键．21．（2023·广东·统考中考真题）如图，街道AB 与CD 平行拐角137ABC ∠=︒，则拐角BCD ∠=（）A ．43︒B ．53︒C ．107︒D ．137︒【答案】D 【分析】根据平行线的性质可进行求解．【详解】解：③AB CD 137ABC ∠=︒③137BCD ABC ∠=∠=︒故选：D ．【点睛】本题主要考查平行线的性质熟练掌握平行线的性质是解题的关键．22．（2023·山东·统考中考真题）一把直尺和一个含30︒角的直角三角板按如图方式放置若120∠=︒，则2∠=（）A ．30︒B ．40︒C ．50︒D ．60︒【答案】B 【分析】根据平行线的性质得出3120∠=∠=︒ 进而260340．【详解】由图知 3120∠=∠=︒③2603602040 故选：B.【点睛】本题考查平行线的性质特殊角直角三角形由图形的位置关系推出角之间的数量关系是解题的关键．23．（2023·山东·统考中考真题）如图所示的几何体是由5个大小相同的小正方体组成的它的主视图是（）A ．B ．C ．D ．【答案】A 【分析】根据主视图是从正面看到的图形进行求解即可．【详解】解：从正面看该几何体有三列第一列有2层第二和第三列都只有一层如图所示：故选：A ．【点睛】本题主要考查了简单几何组合体的三视图熟知三视图的定义是解题的关键．24．（2023·山东·统考中考真题）如图，,a b 是直尺的两边 a b 把三角板的直角顶点放在直尺的b 边上若135∠=︒，则2∠的度数是（）A ．65︒B ．55︒C ．45︒D ．35︒【答案】B【分析】根据平行线的性质及平角可进行求解．【详解】解：如图：③a b 135∠=︒③135,2ACD BCE ∠=∠=︒∠=∠③180BCE ACB ACD ∠+∠+∠=︒ 90ACB ∠=︒③1809035552BCE ∠=︒-︒-︒=︒=∠故选：B ．【点睛】本题主要考查平行线的性质熟练掌握平行线的性质是解题的关键．25．（2023·山东·统考中考真题）一个几何体的三视图如下，则这个几何体的表面积是（）A ．39πB ．45πC ．48πD ．54π【答案】B【分析】先根据三视图还原出几何体再利用圆锥的侧面积公式和圆柱的侧面积公式计算即可．【详解】根据三视图可知该几何体上面是底面直径为6 母线为4的圆锥下面是底面直径为6 高为4的圆柱该几何体的表面积为：211π646π4π612π24π9π45π22S ⎛⎫=⨯⨯⨯+⨯+⨯⨯=++= ⎪⎝⎭．故选：B ．【点睛】本题主要考查了简单几何体的三视图以及圆锥的侧面积公式和圆柱的侧面积公式根据三视图还原出几何体是解决问题的关键．26．（2023·福建·统考中考真题）下图是由一个长方体和一个圆柱组成的几何体它的俯视图是（）A ．B ．C ．D ．【答案】D【分析】根据从上面看得到的图形是俯视图即可解答．【详解】解：从上面看下边是一个矩形矩形的上边是一个圆故选：D ．【点睛】本题考查了简单组合体的三视图掌握从上面看得到的图形是俯视图是解答本题的关键． 27．（2023·湖北荆州·统考中考真题）观察如图所示的几何体下列关于其三视图的说法正确的是（）A ．主视图既是中心对称图形又是轴对称图形B ．左视图既是中心对称图形又是轴对称图形C ．俯视图既是中心对称图形又是轴对称图形D ．主视图左视图俯视图都是中心对称图形【答案】C【分析】先判断该几何体的三视图再根据轴对称和中心对称图形定义逐项判断三视图即可求出答案.【详解】解：A 选项：主视图是上下两个等腰三角形不是中心对称图形是轴对称图形故不符合题意 B 选项：左视图是上下两个等腰三角形不是中心对称图形是轴对称图形故不符合题意 C 选项：俯视图是圆（带圆心）既是中心对称图形又是轴对称图形故符合题意D 选项：由A 和B 选项可知主视图和左视图都不是中心对称图形故不符合题意.故选：C.【点睛】本题考查了简单几何体的三视图轴对称图形和中心对称图形解题的关键在于掌握轴对称和中心对称的定义. 如果一个平面图形沿着一条直线折叠后直线两旁的部分能够互相重合那么这个图形叫做轴对称图形中心对称是指把一个图形绕着某一点旋转180︒ 如果它能够与另一个图形重合那么就说这两个图形关于这个点对称或中心对称.28．（2023·湖北荆州·统考中考真题）如图所示的“箭头”图形中 AB CD ∥ 80B D ∠=∠= 47E F ∠=∠=，则图中G ∠的度数是（）A ．80B ．76C ．66D ．56【答案】C 【分析】延长AB 交EG 于点M 延长CD 交GF 于点N 过点G 作AB 的平行线GH 根据平行线的性质。

三视图练习题

三视图练习题在我们学习几何的过程中，三视图可是一个非常重要的知识点。

它就像是一个神奇的魔法，能够让我们通过不同角度的观察，了解一个物体的形状和结构。

今天，咱们就一起来做做三视图的练习题，好好地练练手！先来看看什么是三视图。

三视图，简单来说，就是从三个不同的方向去观察一个物体，然后把看到的形状分别画出来。

这三个方向通常是正视图（也叫主视图）、侧视图（分为左视图和右视图）和俯视图。

比如说，有一个长方体，它的长、宽、高分别是 5 厘米、3 厘米、2 厘米。

那正视图看到的就是一个长 5 厘米、高 2 厘米的长方形；左视图呢，是一个宽 3 厘米、高 2 厘米的长方形；俯视图则是一个长 5 厘米、宽 3 厘米的长方形。

咱们来做一道练习题。

有一个圆柱体，底面半径是 2 厘米，高是 5厘米。

那它的正视图是什么样的？答案就是一个长 4 厘米（因为直径是 4 厘米）、高 5 厘米的长方形。

俯视图呢，是一个半径为 2 厘米的圆。

左视图和正视图是一样的。

再看这道题，有一个圆锥，底面半径 3 厘米，高 4 厘米。

正视图是一个底边为 6 厘米（直径），高 4 厘米的等腰三角形。

俯视图是一个半径为 3 厘米的圆。

左视图也是一个底边为 6 厘米，高 4 厘米的等腰三角形。

做三视图练习题的时候，有几个要点要注意。

首先，一定要看清楚题目中给出的物体的尺寸和形状，别粗心大意。

其次，要想象自己站在不同的角度去看这个物体，在脑海里形成清晰的图像。

还有，画图的时候，线条要画直，比例要正确，尺寸标注要清晰。

下面咱们来做几道稍微有点难度的练习题。

有一个组合体，是由一个长方体和一个圆柱体组成的。

长方体的长、宽、高分别是 5 厘米、4 厘米、3 厘米，圆柱体的底面直径是 2 厘米，高是 4 厘米，放在长方体的上面，并且圆柱体的底面圆心和长方体上面的中心重合。

那这道题的正视图怎么画呢？先画一个长 5 厘米、高 3 厘米的长方形，这是长方体部分。

然后在长方形的上面中间位置，画一个直径 2厘米、高 4 厘米的长方形，这是圆柱体部分。

初三数学三视图练习题

初三数学三视图练习题三视图是指一个物体在不同视角下的投影图，包括俯视图、前视图和左视图。

通过练习解题，可以帮助初三学生提高对三视图的理解和解题能力。

下面是一些初三数学三视图练习题。

练习题一：有一块长方体，其长度、宽度和高度分别为9cm、4cm和6cm。

请画出该长方体的俯视图、前视图和左视图。

解答：俯视图：描绘长方体的俯视图时，应该将长方体放置在一个透明的正交坐标系内，使得长方体的底面与坐标系的平面重合，然后根据长方体的尺寸，在坐标系内描绘长方体的底面。

在本题中，长方体的底面尺寸为9cm×4cm，所以在坐标系内描绘一个9cm×4cm的矩形。

前视图：描绘长方体的前视图时，应该将长方体放置在坐标系的正交平面内，使长方体的前面与坐标系的平面重合。

然后根据长方体的尺寸，在坐标系内描绘长方体的前面。

在本题中，长方体的尺寸为9cm×4cm×6cm，所以在坐标系内描绘一个9cm×6cm的矩形。

左视图：描绘长方体的左视图时，应该将长方体放置在坐标系的正交平面内，使长方体的左面与坐标系的平面重合。

然后根据长方体的尺寸，在坐标系内描绘长方体的左面。

在本题中，长方体的尺寸为4cm×6cm，所以在坐标系内描绘一个4cm×6cm的矩形。

练习题二：有一块正方体，边长为5cm。

请画出该正方体的俯视图、前视图和左视图。

解答：俯视图：根据正方体的定义，正方体的底面是一个边长为5cm的正方形。

因此，在坐标系内描绘一个边长为5cm的正方形。

前视图：由于正方体的所有面都是相等的正方形，所以正方体的前视图和俯视图是相同的。

因此，在坐标系内描绘一个边长为5cm的正方形。

左视图：由于正方体的所有面都是相等的正方形，所以正方体的左视图和俯视图是相同的。

因此，在坐标系内描绘一个边长为5cm的正方形。

通过练习解题，我们可以更好地理解和掌握三视图的绘制方法。

希望以上练习题对你的数学学习有所帮助。

中考数学三视图专项训练

2019-2020届初三 中考复习 三视图 综合题 专项练习(含答案解析)教学提纲

(完整)初中数学三视图专题试题及答案1,推荐文档

中考数学专题复习《视图、投影与尺规作图》专项检测题 ( 含答案)

2023年九年级人教版数学中考复习考点专练：几何体的三视图原卷版

中考数学每日一练：由三视图判断几何体练习题及答案_2020年单选题版

中考数学真题《三视图与展开图》专项测试卷(附答案)

精品 九年级数学 中考专题 三视图 综合练习题

中考三视图练习题

初三年级数学下册期中三视图测试题(含答案解析)

中考数学三视图专项训练新完整版

人教版九年级下册数学第二十九章第2节《三视图》训练题 (36)(含答案解析)

中考复习之三视图(含答案)

部编数学九年级下册专题09三视图(重难点突破)(解析版)_new含答案

初中数学三视图练习题

中考数学专题复习题：直棱柱的三视图

三视图习题50道(含答案)

初中三视图试题及答案

中考数学真题《几何图形初步与三视图、相交线与平行线》专项测试卷(附答案)

三视图练习题

初三数学三视图练习题

2019-2020届初三中考复习三视图综合题专项练习(含答案解析)教学提纲

精品九年级数学中考专题三视图综合练习题