三视图专题练习(一).

新人教版七年级几何图形初步练习专题(一)---三视图、展开图专题

三视图、展开图专题【题型一】从不同方向看几何体1、如图所示的立体图形从上面看到的图形是（）2、从左面看图中四个几何体，得到的图形是四边形的几何体共有（） A. 1个 B. 2个 C. 3个 D. 4个3、从不同方向看一只茶壶，如图，下列选项中从上往下看的效果图是（）。

4、从三个不同方向看一个几何体，得到的平面图形如图所示，则这个几何体是（）。

A. 圆柱B. 三棱锥C. 球D. 圆锥5、由四个相同的小正方体搭建了一个积木，它的左视图和主视图均如图所示，则这堆积木不可能是（）6、由7个大小相同的正方体搭成的几何体如图所示，则关于它的视图说法正确的是（）A ．从正面看面积最大B ．从左面看面积最大C ．从上面看面积最大D ．三个视图的面积一样大AB CD从左面看从上面看从正面看ABC D7、5个棱长为1的正方体组成图所示的几何体．（1）该几何体的体积是（立方单位），表面积是（平方单位）. （2）画出从正面看和从左面看到的平面图形.8、如图，这个图形从正面看是__________，从左面看是__________，从上面看是__________．【题型二】正方体的展开与折叠1、如图是一个长方体包装盒，则它的平面展开图是（）A ．B ．C ．D ．2、下列四张正方形硬纸片，剪去阴影部分后，如果沿虚线折叠，可以围成一个封闭的长方形包装盒的是（）A ．B ．C ．D ．3、把如图中的三棱柱展开，所得到的展开图是（）A ．B ．C ．D ．4、下列四个图形中，是三棱柱的平面展开图的是（）A ．B ．C ．D ．5、小明为了鼓励芦山地震灾区的学生早日走出阴影，好好学习，制作了一个正方体礼盒（如1 2 3x y图）．礼盒每个面上各有一个字，连起来组成“芦山学子加油”，其中“芦”的对面是“学”，“加”的对面是“油”，则它的平面展开图可能是（）．A. B. C. D6、一个正方体的平面展开图如图所示，将它折成正方体后，与汉字“岳”相对的面上的汉字是（） A ．建 B ．设C ．和D ．谐7、如图是一个正方体展开图，把展开图折叠成正方体后，“你”字一面相对面上的字是（）A ．我B ．中C ．国D ．梦月8、一个正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（）9、下面四个图形中，经过折叠能围成如图所示的几何图形的是【】10、若要使图中平面展开图按折叠成正方体后，相对面上两个数之和为6，x=_ ___， y=______.A。

三视图练习题

29.2 三视图一、选择题（共15小题；共75分）1. 下列物体的主视图、俯视图和左视图不全是圆的是 ( )A. 橄榄球B. 兵乓球C. 篮球D. 排球2. 如图，几何体的俯视图是A. B.C. D.3. 长方体的主视图与左视图如图所示（单位：cm），则其俯视图的面积是A. 12 cm2B. 8 cm2C. 6 cm2D. 4 cm24. 如图所示，几何体的俯视图是A. B.C. D.5. 如图是有几个相同的小正方体组成的一个几何体．它的左视图是A. B.C. D.6. 如图是由八个相同小正方体组成的几何体，则其主视图是A. B.C. D.7. 桌面上放着1个长方体和1个圆柱体，按下图所示的方式摆放在一起，其左视图是A. B. 与原题图不一样C. D.8. 下列几何体中，有一个几何体的俯视图的形状与其它三个不一样，这个几何体是 ( )A. B.C. D.9. 图中三视图所对应的直观图是A. B.C. D.10. 如图是常用的一种圆顶螺杆，它的俯视图正确的是A. B.C. D.11. 如图的几何体的三视图是A. B.C. D.12. 如图是由一些相同的小正方体搭成的几何体的三视图，则构成这个几何体的小正方体的个数为A. 4个B. 5个C. 6个D. 7个13. 一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是A. B.C. D.14. 一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为．A. 6B. 8C. 12D. 2415. 如图所示是某几何体的三视图，根据图中数据，求得该几何体的体积为A. 60πB. 70πC. 90πD. 160π二、填空题（共6小题；共30分）16. 一个几何体的主视图、俯视图和左视图都是大小相同的圆，则这个几何体是．17. 如图，在一次数学活动课上，张明用17个边长为1的小正方体搭成了一个几何体，然后他请王亮用其他同样的小正方体在旁边再搭一个几何体，使王亮所搭几何体恰好可以和张明所搭的几何体拼成一个大长方体（不改变张明所搭几何体的形状），那么王亮至少还需要个小正方体，王亮所搭几何体表面积为．18. 如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是．19. 由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数可能是．20. 用八个同样大小的小立方体粘成一个大立方体如图 1，得到的几何体的三视图如图 2 所示，若小明从八个小立方体中取走若干个，剩余小立方体保持原位置不动，并使得到的新几何体的三视图仍是图 2，则他取出的小立方体最多可以是个．21. 在桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，设组成这个几何体的小正方体的个数为n，则n的最小值为．三、解答题（共2小题；共26分）22. 如图所示的几何体是由12块棱长为1 cm的正方体堆积而成的．请求出它的表面积．23. 如图，四边形ABCD，将其绕CD所在直线旋转一周得到一个几何体，请画出这个几何体的从正面、左面、上面看到的形状图．答案第一部分1. A2. D3. A4. C5. B6. C7. C8. A9. C 10. B11. C 12. A 13. D 14. B 15. B第二部分16. 球体17. 19；4818. 619. 4或5或6或720. 421. 5第三部分22. (1) 由题意，得S=8×12×2+5×12×2+7×12×2=40．所以它的表面积为40 cm2．23. (1) 如图所示．。

通用技术三视图专题练习(一).docx

三视图专题练习（一）
1.根据立体图，补全俯视图和左视图所缺的线条。

（2008年会考）
2、请据题图所示形体，1时出主视图，补全左视图的缺漏线条。

3.根据立体图，补齐俯视图和左视图
主视
4.根据立体图，画出俯视图、补齐俯视图和左视图
5.根据立体图，补全俯视图和左视图屮所缺漏的图线。

6 •根据立体图，补全俯视图和左视图屮所缺漏的图线（2008年10月高考题）
第21题图
7.根据轴测图补慚三视图屮所缺的线条。

9•下图是小锤的止等轴侧图，请补全俯视图，并闹出它的左视图。

8.根据题图所不形体，画出主视图。

补全俯视图的缺漏线条。

10.根据立体图，曲出主视图和左视图
O O
11、根据立体图补全三视图屮所缺®图线（2009予9申丙彎®
第21题图
12、根据立体图补全三视图屮所缺的图线（2009年3月高考题）
13.根据立体模型补向视图屮所缺的线。

三视图习题50道(含答案)

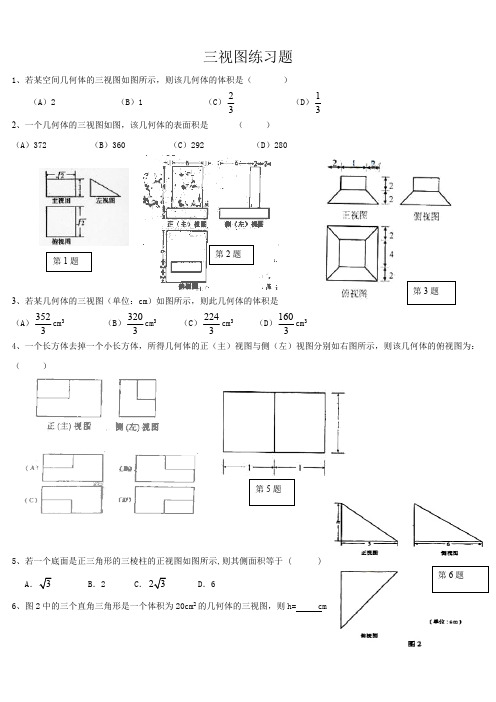
三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为（）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

高三专项训练：三视图练习题(一)

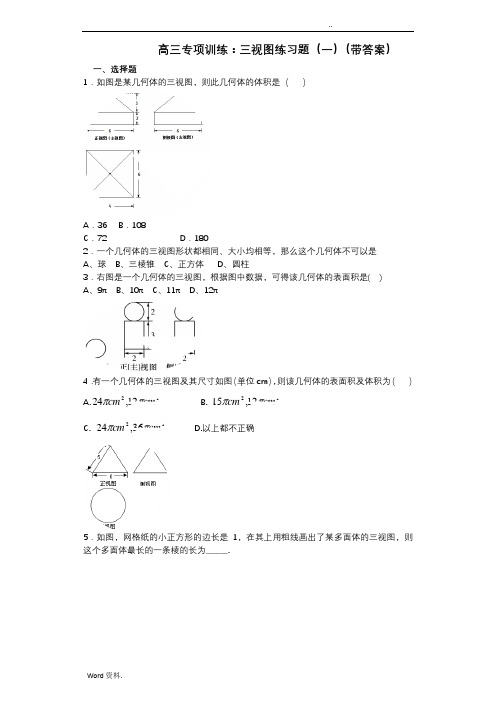
高三专项训练：三视图练习题（一）（带答案）一、选择题1．如图是某几何体的三视图，则此几何体的体积是（）A ．36B ．108C ．72D ．1802．一个几何体的三视图形状都相同、大小均相等，那么这个几何体不可以是A 、球B 、三棱锥C 、正方体D 、圆柱3．右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是( )A 、9πB 、10πC 、11πD 、12π4．有一个几何体的三视图及其尺寸如图（单位cm ），则该几何体的表面积及体积为（）A.3212,24cm cm ππB. 3212,15cm cm ππC. 3236,24cm cm ππD.以上都不正确5．如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.A． B． CD ．36．一空间几何体的三视图如图所示，则该几何体的体积为.A. B. C D. [7．若某空间几何体的三视图如图所示，则该几何体的体积是A ．13 B ．23C ．1D ．28．右图是某几何体的三视图，则该几何体的体积为（）A ．Ｂ．Ｃ．Ｄ．1362942π+3618π+9122π+9182π+正视图俯视图9．已知一个几何体的三视图如图所示，则该几何体外接球的表面积为（）A ．43π B ． 163π C ．1912π D ． 193π 10．某几何体的正视图如图所示，则该几何体的俯视图不可能的是11．已知某个几何体的三视图如图（主视图中的弧线是半圆），根据图中标出的尺寸(单位：cm)，可得这个几何体的体积是( )cm 3.A ．π+8B ．328π+C ．π+12D ．3212π+侧视图主视俯视第8题图俯视图侧视图正视图12．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（）（A ）243cm （B ）223cm （C ）28cm （D ）24cm13．下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．6πB ．7πC ．8πD ．9π14．如右图所示，一个空间几何体的正视图和侧视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的表面积为（）A ．π3B ．π2C ．π23 D ．π4 15．如图是一个几何体的三视图，若它的体积是33，则图中正视图所标a=（）A ．1B 3C 3D ．316．已知某几何体的三视图如图所示（单位：cm ），其中正视图、侧视图都是等腰直角三角形，则这个几何体的体积是（）A ．338cmB ．3316cm C ．33216cm D ． 3332cm17．一个几何体的三视图如右图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．B ．C ．D ．18．若某空间几何体的三视图如图所示，则该几何体的体积是（）A.13 B. 23C. 1D. 2 俯视图侧视图正视图22119．某物体是空心的几何体，其三视图均为右图，则其体积为（）A 、8B 、43π C 、483π+ D 、483π- π12π34π3π312正视图侧视图俯视图正视第9题22 4 2侧视图 22俯视20．如图，水平放置的三棱柱ABC-A 1B 1C 1中，侧棱AA 1⊥平面A 1B 1C 1，其正视图是边长为a 的正方形．俯视图是边长为a 的正三角形，则该三棱柱的侧视图的面积为A ．a 2B ．a 2C a 2D 221．右图是一个几何体的三视图（侧视图中的弧线是半圆），则该几何体的表面积是（）A ．20＋3π B ．24＋3π C ．20＋4π D ．24＋4π22．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为A ．12πB ．π34C ．3πD ．π312．23.如右图为一个几何体的三视图，其中俯视图为正三角形，A 1B 1=2，AA 1=4，则该几何体的表面积为（）12正视图侧视图俯视图 AC A 11正视图侧视图俯视图24．图１是设某几何体的三视图，则该几何体的体积为（）A．942π+Ｂ．3618π+Ｃ．9122π+Ｄ．9182π+、25．已知某几何体的三视图如图所示，根据图中标注的尺寸（单位cm）可得该几何体的体积是（）A．313cm B．323cmC．343cm D．383cm26．小红拿着一物体的三视图(如图所示)给小明看，并让小明猜想这个物件的形状是A. 长方形 B. 圆柱 C. 立方体 D. 圆锥27．一个几何体的三视图如图所示，则这个几何体的体积为（）正视图侧视图俯视图332正视图俯视图图1AB ．12C ．32 D1+28．一个空间几何体的三视图如图（1）所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积和表面积分别为（）A 、64，48+B 、32，48+ C 、643，32+D 、332，48+29．若某多面体的三视图（单位: cm ）如图所示,则此多面体的体积是（） A ．21cm 3 B ．32cm 3 C ．65cm 3 D ．87cm 3正视图俯视图图（1）侧（左）视图 1111130．一个空间几何体的正视图、侧视图均是长为2、高为3的矩形，俯视图是直径为2的圆(如右图），则这个几何体的表面积为A ．12π+B ．7πC ． π8D ．π2031．（一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B.C.D. 32．已知几何体其三视图（如图），若图中圆半径为1，等腰三角形腰为3，则该几何体表面积为（） A ．6π B ．5π C．4π D．3π2π+4π+2π4π+正视侧视俯视俯视..A ．2，23B ．22，2D ．2，434．如图，有一个几何体的正视图与侧视图都是底为6cm ，腰为5cm 的等腰三角形，俯视图是直径为6cm 的圆，则该几何体的体积为 ( )A ．12πcm 3B ．24πcm 3C ．36πcm 3D ．48πcm 335 （A ）348cm （B ）324cm （C ）332cm （D ）328cm36．如图，直三棱柱的侧棱长和底面边长均为2，正视图和俯视图如图所示，则其侧视图的面积为（）A ．4B ．3C ．32D ．237．某四面体的三视图如下图所示，则该四面体的四个面中，直角三角形的面积和是_______.二、填空题正视图左视图俯视图正视图侧视图俯视图第6题 ·38．一个几何体的三视图如右图所示,主视图与俯视图都是一边长为3cm 的矩形,左视图是一个边长为2cm 的等边三角形,则这个几何体的体积为________．39．如图所示是一个几何体的三视图（单位：cm ），主视图和左视图是底边长为4cm ，腰长为22的等腰三角形，俯视图是边长为4的正方形，则这个几何体的表面积是-__________40．某几何体的三视图如图所示，则该几何体的体积的最大值为 .41．一正多面体其三视图如图所示，该正多面体的体积为___________.主视图左视图俯视图3主视图俯视图侧视图42．若某几何体的三视图（单位：cm ）如右图所示，则该几何体的体积为 cm 2．43．已知某几何体的三视图如图所示,其中侧视图是等腰直角三角形,正视图是直角三角形,俯视图ABCD 是直角梯形,则此几何体的体积为；44．某四面体的三视图如上图所示，该四面体四个面的面积中最大的是1正视图俯视图左视图45．一个几何体的三视图如右图所示（单位：），则该几何体的体积为__________46．一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是_____．47．如图，一个简单空间几何体的三视图其主视图与左视图都是边长为的正三角形,其俯视图轮廓为正方形，则其体积是_________.48．某几何体的三视图如图所示，则它的体积是___________俯视图m 3m 249．设某几何体的三视图如图所示，则该几何体表面积是50．一个几何体的三视图如右图所示，正视图是一个边长为2的正三角形，侧视图是一个等腰直角三角形，则该几何体的体积为．三视图练习题（一）参考答案1．B【解析】此几何体是一个组合体，下面是一个正四棱柱上面是一个四棱锥．其体积为166********V =⨯⨯+⨯⨯⨯=．2．D【解析】圆的正视图（主视图）、侧视图（左视图）和俯视图均为圆；三棱锥的正视图（主视图）、侧视图（左视图）和俯视图可以为全等的三角形；正方体的正视图（主视图）、侧视图（左视图）和俯视图均为正方形；圆柱的正视图（主视图）、侧视图（左视图）为矩形，俯视图为圆。

三视图练习题及答案

三视图练习题及答案三视图是工程设计、制图等领域中常用的表达方式之一，它能够以三个不同的视角展示一个物体的外观和内部结构，帮助人们更好地理解和分析物体的形状和构造。

为了提高对三视图的理解和应用能力，下面将给出一些三视图练习题及答案，希望对读者有所帮助。

1. 请根据给出的三视图，画出物体的立体图。

答案：根据三视图，我们可以确定物体的形状和尺寸，然后利用透视法将其转化为立体图。

在绘制过程中，需要注意比例和透视关系，以保证立体图的准确性。

2. 给出一个物体的立体图，请根据立体图绘制出相应的三视图。

答案：在绘制三视图时，我们需要观察立体图中的各个面，然后根据其相对位置和大小来绘制对应的正视图、俯视图和侧视图。

在绘制过程中，需要注意比例和尺寸的准确性，以确保三视图能够准确地表达立体图的形状和结构。

3. 请根据给出的三视图，判断物体的形状是什么？答案：通过观察三视图中的线条和面，我们可以判断物体的形状。

例如，如果正视图中的线条是直的，侧视图中的线条是弯曲的，那么物体可能是一个圆柱体。

通过观察三视图中的特征，我们可以逐步推断出物体的形状。

4. 给出一个物体的形状，请根据形状绘制出相应的三视图。

答案：在绘制三视图时，我们需要观察物体的形状和结构，然后根据其特征来绘制对应的正视图、俯视图和侧视图。

在绘制过程中，需要注意线条的粗细和长度，以确保三视图能够准确地表达物体的形状和结构。

通过以上的练习题和答案，我们可以提高对三视图的理解和应用能力。

练习三视图不仅可以帮助我们更好地理解和分析物体的形状和结构，还可以提高我们的制图能力和空间想象力。

在实际工程设计和制图中，三视图是非常重要的表达方式，掌握好三视图的绘制和解读技巧对于工程师和设计师来说是非常必要的。

总之，通过不断地练习和应用，我们可以提高对三视图的掌握程度，为工程设计和制图提供更准确、更有效的表达方式。

希望以上的练习题和答案能够对读者有所帮助，进一步提高对三视图的理解和应用能力。

三视图练习题含答案

23正视图侧视图2俯视图 2第3题三视图练习题（一）1.某几何体的三视图如图所示，则它的体积是（）A.283π-B.83π-C.π28-D.23π2.某四棱锥的三视图如图所示，该四棱锥的表面积是（）A ．32 B.16+162 C.48 D.16322+3.如图，某几何体的正视图（主视图），侧视图（左视图）和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体的体积为（） A ．43 B ．4C ．23 D ．24.如图是某几何体的三视图，则该几何体的体积为（）A ．942π+ Ｂ．3618π+Ｃ．9122π+Ｄ．9182π+5.一个空间几何体的三视图如图所示，则该几何体的表面积为（） A. 48 B.32+817C.48+817D.806.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是（）A.35233cmB.32033cmC.22433cmD.16033cm7．若某空间几何体的三视图如图所示，则该几何体的体积是（）A.2B.1C.23D.138.某几何体的三视图如图所示，则该几何体的体积为（） A.π816+ B.π88+ C.π1616+ D.π168+9. 某四棱台的三视图如图所示，则该四棱台的体积是（） A.4 B.314 C.316D.610. 某三棱锥的三视图如图所示,已知该三视图中正视图和俯视图均为边长为2的正三角形,侧视图为如图所示的直角三角形,则该三棱锥的体积为（）A ．1B ．3C ．4D ．511．一个几何体的三视图如图所示,则这个几何体的体积为（）332正视图侧视图俯视图第4题第5题第7题第1题第2题第8题第9题第6 题A ．(8)36π+B ．(82)36π+C ．(6)36π+D ．(92)36π+12.某几何体的底面为正方形,其三视图如图所示,则该几何体的体积等于( )A ．1B ．2C ．3D ．413.某几何体的三视图如图所示，则其体积为______.14.若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积等于______3cm . 15.某几何体的三视图如图所示，则该几何体的体积是______.16.已知某三棱锥的三视图（单位：cm ）如图所示，则该三棱锥的体积是 17.一个空间几何体的三视图如图所示,则这个空间几何体的体积是. 18.如图所示,一个三棱锥的三视图是三个直角三角形,则该三棱锥外接球的表面积为19.若某空间几何体的三视图如下图所示,则该几何体的表面积是_______________.20．一个正方体的内切球与它的外接球的体积比是（）．A ．1∶33B ．1∶22C ．1∶383 D ．1∶4221.已知球面上A 、B 、C 三点的截面和球心的距离都是球半径的一半，且AB ＝BC ＝CA ＝2，则球表面积是( )A.π964 B. π38 C. π4 D. π91622. P 、A 、B 、C 是球O 面上的四点，且PA 、PB 、PC 的两两垂直，PA=PB=PC=9，则球心O 到截面ABC 的距离为23.半径为5的球被一个平面所截，截面面积为16π，则球心到截面的距离为（） A.4 B.3 C.2.5 D.224.表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________. 25.答案1.A2.B3.C4.D5.C6.B7.B8.A9.B 10.A 11.A 12.A 13.3π14.24 15.1616-π 16.1 17.67π18.29π 19. 20+82 20.A 21.A 22.233第10题3122正视图侧视图俯视图第11题 211俯视图侧视图正视图13第12题第17题24 3正视图侧视图俯视图第18题第15题第14题第13题第16题第19题23.B 24. 2 25. ︒90 26.3500π27.π6 28.π29 29.72 30. 3629+3226-31.2500π 32.π1200。

三视图练习题

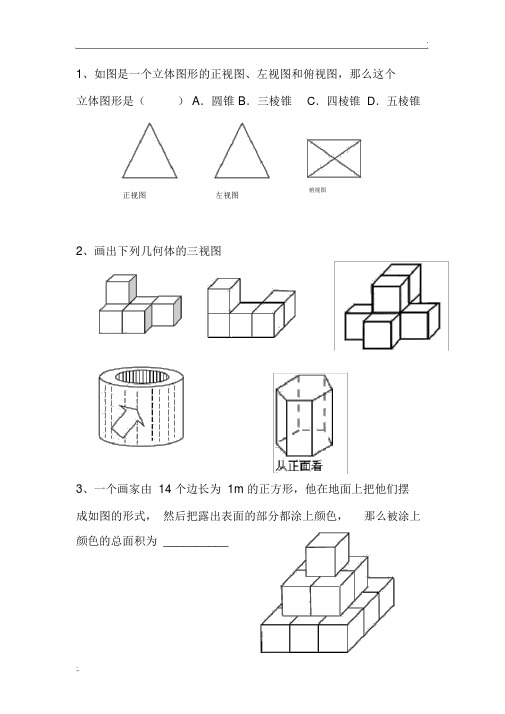
.1、如图是一个立体图形的正视图、左视图和俯视图，那么这个立体图形是（） A．圆锥 B．三棱锥C．四棱锥 D．五棱锥俯视图正视图左视图2、画出下列几何体的三视图3、一个画家由 14 个边长为 1m 的正方形，他在地面上把他们摆成如图的形式，然后把露出表面的部分都涂上颜色，那么被涂上颜色的总面积为 __________例题：某几何体的俯视图，请图出它的主视图和左视图21134、下图是由一些相同的小正方形构成的几何体的三视图，这些相同的小正方形的个数是 ( )5、下图是由一些相同的小正方形构成的几何体的三视图，这些相同的小正方形的个数是()主视图左视图俯视7、下图是由一些相同的小正方形构成的几何体的三视图，这些相同的小正方形的个数是()主视图左视图俯视图8、下图是由一些相同的小正方形构成的几何体的三视图，这些相同的小正方形的个数是()主（正）视图左视图俯视图8、如图 7 是由几个小立方块所搭成的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，则这个几何体的左视图为（）3 11 2图7A．B．C．D．9、下列左图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方块的个数，则该几何体的主视图为（）342112A B CD10、如图，分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图，则组成这个几何体的小正方体的个数是（）11、由一些完全相同的小正方体的搭成的几何体的主视图和俯视图如图所示，则组成这个几何体的小正方体的个数可能是______．12、桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体可以由个这样的正方体组成。

13、（2013?黑龙江）由若干个相同的小正方体搭成的一个几何体的主视图和俯视图如图所示，则组成这个几何体的小正方体的个数有（）个14、（2011?牡丹江）由一些大小相同的小正方体搭成的几何体的主视图与左视图如图所示，则搭成这个几何体的小正方体的个数最少为（）A、3 B、4 C、5D、615、由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示，则搭成这个几何体的小正方体的个数最多为（）A．3 个B．4 个C．5 个D．不能确定16、如图，分别是由若干个完全相同的小正方体组成的一个几何体的主视图和俯视图，则组成这个几何体的小正方体的个数是（）主视图俯视图17、如图所示，是由些相同的小正方体搭成的两层几何体的主视图和左视图，那么搭成这个几何体的小正方体的个数最少有（）个A、4B、5C、6D、7主视图左视图18、（2013?齐齐哈尔）如图所示是由若干个完全相同的小正方体搭成的几何体的主视图和俯视图．则这个几何体可能是由个正方体搭成的．19、由一些完全相同的小正方体搭成的几何体的主视图和左视图图所如示，则组成这个几何体的小正方体的个数可能是20、如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图，若组成这个几何体的小正方体的块数为n，则 n 的所有可能的值之和为。

三视图练习题（含答案）

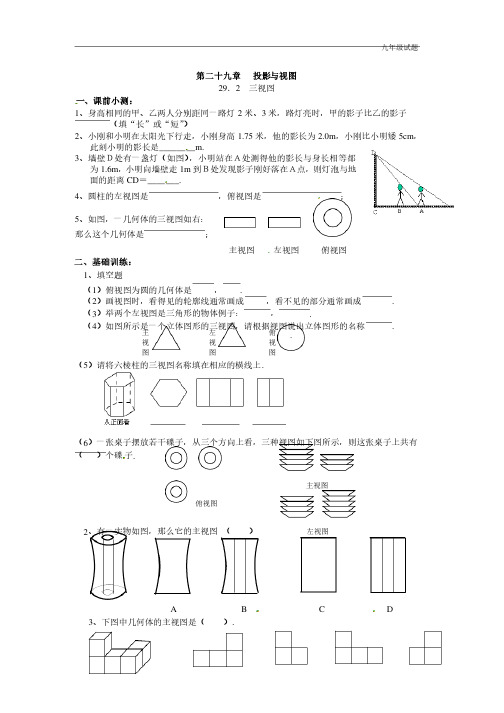
第二十九章投影与视图29．2 三视图一、课前小测：1、身高相同的甲、乙两人分别距同一路灯2米、3米，路灯亮时，甲的影子比乙的影子（填“长”或“短”）2、小刚和小明在太阳光下行走，小刚身高1.75米，他的影长为2.0m ，小刚比小明矮5cm ，此刻小明的影长是________m.3、墙壁Ｄ处有一盏灯（如图），小明站在Ａ处测得他的影长与身长相等都为1.6m ，小明向墙壁走1m 到Ｂ处发现影子刚好落在Ａ点，到Ｂ处发现影子刚好落在Ａ点，则灯泡与地则灯泡与地面的距离CD ＝_______.4、圆柱的左视图是，俯视图是；5、如图，一几何体的三视图如右：那么这个几何体是；主视图左视图俯视图二、基础训练：1、填空题（1）俯视图为圆的几何体是，.（2）画视图时，看得见的轮廓线通常画成，看不见的部分通常画成. （3）举两个左视图是三角形的物体例子：，.（4）如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称.（5）请将六棱柱的三视图名称填在相应的横线上.（6）一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有（）个碟子.2、有一实物如图，那么它的主视图（）AB C D 3、下图中几何体的主视图是（）. 俯视图主视图左视图主视图左视图俯视图俯视图主（正）视图左视图(A) (B) (C ) (D)4、若干桶方便面摆放在桌子上，实物图片左边所给的是它的三视图，则这一堆方便面共有（有（）（A ）5桶（B ） 6桶（C ）9桶（D ）12桶5、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示，如图是一个正方体的表面展开图，若图中“2”在正方体的前面，则这个正方体的后面是方体的前面，则这个正方体的后面是 ( ) ( )A ．OB O B．． 6C 6 C．快．快．快D D D．乐．乐．乐三、综合训练：1．小明从正面观察下图所示的两个物体，看到的是（．小明从正面观察下图所示的两个物体，看到的是（）2、右图是由一些完全相同的小立方块搭成的几何体的三种视图，那么搭成这个几何体所用的小立方块的个数是（的小立方块的个数是（）A 5个B 6个C 7个D 8个3、如果用□表示1个立方体，用表示两个立方体叠加，用■表示三个立方体叠加，那么下面右图由7个立方体叠成的几何体，从正前方观察，可画出的平面图形是（）4、下面是空心圆柱在指定方向上的视图，正确的是…（、下面是空心圆柱在指定方向上的视图，正确的是…（）B AC D正面 A B C D (A) (B) (C) (D)5、画出下面实物的三视图：实物的三视图：第二十九章投影与视图29．2 三视图三视图参考答案：考答案：课前小测：课前小测：1、短、短2、35723、15644、矩形，圆、矩形，圆5、空心圆柱、空心圆柱二、基础训练：二、基础训练：1、(1)球，圆柱体；（2）实线，虚线；（3）圆锥，正四棱锥，倒放的正三棱柱等；（4）圆锥；（5）俯视图，正视图，左视图；（6）12.2、A ；3、C4、B5、B三、综合训练：三、综合训练：1、C2、D3、B ；4、A ；5、题图：图：主视图左视图俯视图。

三视图习题50道(含答案)

三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为（）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

三视图习题50道(含答案)

三视图练习题1、若某空间几何体的三视图如图所示，则该几何体的体积是（）（A）2（B）1（C）23（D）132、一个几何体的三视图如图，该几何体的表面积是（）（A）372 （B）360 （C）292 （D）2803、若某几何体的三视图（单位：cm）如图所示，则此几何体的体积是（A）3523cm3（B）3203cm3 （C）2243cm3（D）1603cm34、一个长方体去掉一个小长方体，所得几何体的正（主）视图与侧（左）视图分别如右图所示，则该几何体的俯视图为：（）5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )AB．2 C．．66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图，则h= cm第2题第5题7、一个几何体的三视图如图所示，则这个几何体的体积为。

8、如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为______.9、如图1，△ ABC 为正三角形，AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图（也称主视图）是（）10、一空间几何体的三视图如图所示,则该几何体的体积为( ).A.2π+B. 4π+C. 2π+D. 4π11、上图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（）A ．B ．C ．D ．9π10π11π12π第7题侧(左)视图正(主)视图俯视图俯视图正(主)视图侧(左)视图12、一个棱锥的三视图如图，则该棱锥的全面积（单位：c 2m ）为（）（A ）（B ）（C ）（D ）13、若某几何体的三视图（单位：cm ）如图所示，则此几何体的体积是 3cm ．14、设某几何体的三视图如上图所示。

CAD三视图练习题

投影与三视图练习题1.填空题（1）俯视图为圆的几何体是_______，______。

（2）画视图时，看得见的轮廓线通常画成_______，看不见的部分通常画成_______。

（3）举两个左视图是三角形的物体例子：________，_______。

（4）如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______。

请将六棱柱的三视图名称填在相应的横线上.（6）、如图所示是一个立体图形的三视图，请根据视图说出立体图形的名称_______。

（7）、一张桌子摆放若干碟子，从三个方向上看，三种视图如下图所示，则这张桌子上共有________个碟子。

（8）、某几何体的三种视图分别如下图所示，那么这个几何体可能是_____。

（9）人在观察目标时，从眼睛到目标的叫做视线。

所在的位置叫做视点，有公共的两条所成的角叫做视角。

视线不能到达的区域叫做。

（10）物体在光线的照射下，在某个内形成的影子叫做，这时光线叫做，投影所在的叫做投影面。

由的投射线所形成的投影叫做平行投影。

由的投射线所形成的投影叫做中心投影。

（11）在平行投影中，如果投射线垂直于投影面，那么这种投影就称为正投影。

（12）物体的三视图是物体在三个不同方向的。

上的正投影就是主视图，水平面上的正投影就是，上的正投影就是左视图。

2.选择题（1）圆柱对应的主视图是（）。

（A）（B）（C）（D）（2）某几何体的三种视图分别如下图所示，那么这个几何体可能是（）。

（A）长方体（B）圆柱（C）圆锥（D）球（3）下面是空心圆柱在指定方向上的视图，正确的是…（）(4)一个四棱柱的俯视图如右图所示，则这个四棱柱的主视图和左视图可能是（）（5）主视图、左视图、俯视图都是圆的几何体是（）。

（A）圆锥（B）圆柱（C）球（D）空心圆柱（6）在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（）A、小明的影子比小强的影子长B、小明的影子比小强的影子短C、小明和小强的影子一样长D、无法判断谁的影子长3、解答题（1）根据要求画出下列立体图形的视图。

组合体三视图练习题

组合体三视图练习题一、选择题（每题2分，共20分）1. 组合体三视图包括主视图、左视图和哪个视图？A. 俯视图B. 仰视图C. 侧视图D. 底视图2. 在组合体三视图中，主视图通常表示物体的哪个面？A. 正面B. 侧面C. 顶面D. 底面3. 以下哪个不是三视图的画法规则？A. 长对正B. 高平齐C. 宽相等D. 角度一致4. 组合体三视图中，如果一个视图上的线条与另一个视图上的线条不相交，这些线条表示的是？A. 同一条线B. 不同的线C. 相互平行的线D. 相互垂直的线5. 在组合体三视图中，如果一个物体的俯视图和左视图的尺寸相同，那么这个物体可能是？A. 立方体B. 圆柱体C. 圆锥体D. 球体6. 组合体三视图中，若主视图和俯视图的尺寸不同，但左视图与主视图尺寸相同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体7. 在组合体三视图中，若主视图和左视图的尺寸相同，但俯视图的尺寸不同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体8. 组合体三视图中，若主视图和左视图的尺寸不同，但俯视图与主视图尺寸相同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体9. 在组合体三视图中，若俯视图和左视图的尺寸相同，但主视图的尺寸不同，该物体可能是？A. 长方体B. 正方体C. 圆柱体D. 圆锥体10. 组合体三视图中，若俯视图是一个圆形，左视图和主视图是两个相同的矩形，该物体可能是？A. 长方体B. 圆柱体C. 圆锥体D. 球体二、填空题（每题2分，共20分）11. 组合体三视图中，______视图通常用来表示物体的顶面或底面。

12. 在组合体三视图中，______视图通常用来表示物体的侧面。

13. 组合体三视图中，______视图通常用来表示物体的正面。

14. 组合体三视图的画法规则包括______、______和______。

15. 如果一个物体的三视图都是圆形，那么这个物体可能是______。

高中三视图试题及答案

高中三视图试题及答案一、选择题（每题2分，共10分）1. 在三视图中，主视图、左视图和俯视图分别表示物体的哪个面？A. 正面、侧面、上面B. 侧面、正面、上面C. 正面、上面、侧面D. 上面、侧面、正面2. 以下哪个选项不是三视图的组成部分？A. 主视图B. 左视图C. 右视图D. 俯视图3. 根据三视图的规则，物体的长、宽、高分别在哪个视图中表示？A. 主视图、俯视图、左视图B. 俯视图、主视图、左视图C. 左视图、主视图、俯视图D. 主视图、左视图、俯视图4. 如果一个物体的主视图和俯视图都是圆形，那么这个物体可能是：A. 圆柱体B. 圆锥体C. 球体D. 立方体5. 在绘制三视图时，如果一个物体的左视图和主视图相同，那么这个物体可能是：A. 正方体B. 长方体C. 圆柱体D. 圆锥体二、填空题（每空1分，共10分）6. 三视图包括______、______和______。

7. 物体的三视图应该按照______、______、______的顺序排列。

8. 在三视图中，______视图可以反映物体的高度和长度。

9. 如果一个物体的主视图是一个矩形，左视图是一个圆形，那么这个物体可能是______。

10. 在绘制三视图时，需要考虑物体的______、______和______。

三、简答题（每题5分，共10分）11. 简述三视图的定义及其重要性。

12. 描述如何根据一个物体的主视图和俯视图推断其形状。

四、绘图题（每题5分，共10分）13. 根据以下描述绘制一个物体的三视图：- 主视图：一个正方形- 左视图：一个矩形，宽度为正方形的边长的一半- 俯视图：一个圆形，直径等于正方形的边长14. 根据以下三视图，描述物体的形状：- 主视图：一个圆形- 左视图：一个矩形- 俯视图：一个圆形答案：一、选择题1. A2. C3. D4. C5. A二、填空题6. 主视图、左视图、俯视图7. 主视图、左视图、俯视图8. 左视图9. 圆柱体10. 长度、宽度、高度三、简答题11. 三视图是工程图学中用来描述物体形状的三个基本视图，包括主视图、左视图和俯视图。

职高三视图练习题大全

职高三视图练习题大全第一部分：数学视图练习题目一：数与代数1. 分解因式：(x^2 + 3x + 2)2. 化简代数表达式：(2a + 5b) - (3a - 2b)3. 解方程：2x - 3 = 74. 求根：x^2 - 4x + 4 = 05. 求直线的斜率：已知直线上两点A(2, 3)和B(-1, 5)，求直线AB的斜率。

题目二：图形与空间几何1. 计算图形的面积：已知正方形边长为3cm，计算其面积。

2. 求圆的周长：已知圆的半径为5cm，求圆的周长。

3. 判断图形：判断以下各图形中哪些是四边形，哪些是多边形：矩形、正方形、圆、三角形。

4. 定理应用：使用勾股定理计算直角三角形的斜边长度。

5. 空间几何体的体积：已知长方体的长、宽、高分别为5cm、3cm、8cm，求长方体的体积。

题目三：函数与统计1. 函数求值：已知函数f(x) = 2x + 3，求f(5)的值。

2. 函数图像：绘制函数y = x^2的图像。

3. 平均数计算：计算以下一组数据的平均数：{1, 4, 3, 2, 5}。

4. 统计分析：给出以下一组数据的最大值、最小值和中位数：{9, 5, 2, 8, 4, 6}。

5. 概率计算：有一副扑克牌，从中随机抽取一张牌，计算抽到红心的概率。

第二部分：英语视图练习题目四：阅读理解阅读以下短文，回答相关问题。

Once upon a time, there was a little boy named Jack who loved adventures. One day, he found a treasure map in his grandfather's attic. The map led to a hidden treasure located on a desert island.Excited, Jack packed his bags and set off on a journey to find the treasure. He followed the map carefully, crossing oceans and climbing mountains. Finally, he arrived at the desert island.However, the island was not what Jack had expected. It was full of dangerous animals and thick jungles. Jack knew he had to be smart to survive and find the treasure. He used his skills and knowledge to build a shelter, find food, and avoid the wild animals.Months passed, and Jack finally discovered the location of the treasure. It was buried deep underground. With great effort, he dug it up and found a box full of gold and precious gems.Jack returned home a rich and wise young man. He used his treasure to help others and went on more exciting adventures.1. What did Jack find in his grandfather's attic?2. Where did the treasure map lead to?3. What did Jack encounter on the desert island?4. How did Jack manage to survive on the island?5. What did Jack do with his treasure?题目五：语法与词汇从给出的选项中选择合适的单词或词组填空。

三视图练习题六年级

三视图练习题六年级在学习图学的过程中，三视图是一个非常重要的概念。

通过观察物体的正视图、侧视图和俯视图，我们可以更好地理解和描述物体的形状和结构。

本文将为六年级的学生提供一些三视图练习题，帮助他们加深对三视图的理解和运用。

练习题一：绘制三视图请你根据下面的描述，用适当比例绘制物体的三视图。

物体描述：这个物体是一个立方体，所有的边长都相等。

正视图上，你能看到正方形的轮廓，左上角有一个小正方形，表示开放的一面。

侧视图上，你能看到一个竖直方向的线段，表示物体的高度。

俯视图上，你能看到一个水平方向的线段，表示物体的宽度。

练习题二：识别物体下面是三个物体的正视图、侧视图和俯视图，请你根据给出的视图，识别物体的形状并写下对应的名称。

正视图：（图片描述）侧视图：（图片描述）（图片描述）练习题三：推测三视图下面是一个物体的正视图和侧视图，请你根据这两个视图，推测物体的俯视图，并画出来。

正视图：（图片描述）侧视图：（图片描述）练习题四：绘制三视图（进阶）请你使用适当比例，根据下面的描述绘制物体的三视图。

物体描述：这个物体是一个长方体，长边是短边的2倍。

正视图上，你能看到一个长方形的轮廓，短边朝向左侧。

侧视图上，你能看到一个竖直方向的线段，表示物体的高度。

俯视图上，你能看到一个水平方向的线段，表示物体的宽度。

练习题五：识别物体（进阶）下面是三个物体的三视图，请你根据给出的视图，识别物体的形状并写下对应的名称。

（图片描述）侧视图：（图片描述）俯视图：（图片描述）练习题六：推测三视图（进阶）下面是一个物体的正视图和俯视图，请你根据这两个视图，推测物体的侧视图，并画出来。

正视图：（图片描述）俯视图：（图片描述）以上是六年级的三视图练习题，希望对你们的学习有所帮助。

通过练习，相信你们能够更加熟练地观察和绘制物体的三视图，提高对图学的理解和运用能力。

加油！。