半导体物理与器件实验报告
半导体元器件检测实习报告

半导体元器件检测实习报告一、实习目的与要求本次实习旨在让我们了解和掌握半导体元器件的基本知识,学会使用常见的检测仪器和工具,提高我们对半导体元器件的识别和检测能力。
实习要求我们能够识别常用的半导体元器件,如二极管、三极管、场效应晶体管等,并能够熟练地使用万用表、示波器等检测工具进行检测。
二、实习内容与过程1. 半导体元器件的知识学习在实习开始阶段,我们首先学习了半导体元器件的基本知识。
半导体元器件是电子电路中不可或缺的部分,它们具有导电性能介于导体和绝缘体之间的特性。
我们了解了半导体的掺杂性、热敏性和光敏性等主要特性,以及常用的半导体材料锗和硅的性质。
2. 半导体元器件的识别我们学习了如何识别常用的半导体元器件。
以二极管为例,我们学会了通过观察其外观、引脚分布、标记等特征来识别不同类型的二极管,如整流二极管、稳压二极管等。
同时,我们还学会了如何识别三极管、场效应晶体管等元器件。
3. 检测工具的使用在实习过程中,我们学习了如何使用万用表、示波器等检测工具。
以万用表为例,我们学会了如何测量电阻、电容、电压等参数,并学会了如何根据测量结果判断元器件的好坏。
此外,我们还学会了如何使用示波器观察信号波形,判断元器件的工作状态。
4. 半导体元器件的检测实践在掌握了相关知识后,我们进行了实际的检测操作。
我们分组进行了二极管、三极管、场效应晶体管等元器件的检测练习,通过测量其电阻、电流等参数,判断元器件的好坏。
在检测过程中,我们学会了如何避免测量误差,提高了检测能力。
三、实习收获与体会通过本次实习,我对半导体元器件的基本知识有了更深入的了解,能够熟练地使用万用表、示波器等检测工具,提高了我对半导体元器件的识别和检测能力。
同时,实习过程中的实践操作,使我对电子电路的组成和原理有了更直观的认识。
实习让我认识到,半导体元器件的检测不仅需要理论知识的支持,还需要实际操作的技巧。
在今后的学习和工作中,我将继续努力提高自己的实践能力,为更好地理解和应用半导体元器件打下坚实的基础。
半导体物理实验报告1
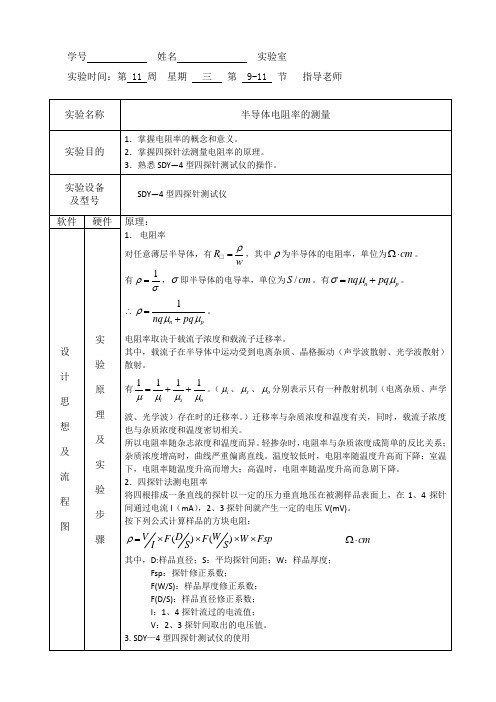
学号 姓名 实验室 实验时间:第 11 周 星期 三 第 9-11 节 指导老师 实验名称半导体电阻率的测量实验目的1.掌握电阻率的概念和意义。
2.掌握四探针法测量电阻率的原理。
3.熟悉SDY —4型四探针测试仪的操作。
实验设备 及型号 SDY —4型四探针测试仪软件硬件 原理:1. 电阻率对任意薄层半导体,有R wρ=□,其中ρ为半导体的电阻率,单位为cm Ω⋅。
有1ρσ=,σ即半导体的电导率,单位为/S cm 。
有n p nq pq σμμ=+。
∴1n pnq pq ρμμ=+。
电阻率取决于载流子浓度和载流子迁移率。
其中,载流子在半导体中运动受到电离杂质、晶格振动(声学波散射、光学波散射)散射。
有1111isoμμμμ=++。
(i μ、s μ、o μ分别表示只有一种散射机制(电离杂质、声学波、光学波)存在时的迁移率。
)迁移率与杂质浓度和温度有关,同时,载流子浓度也与杂质浓度和温度密切相关。
所以电阻率随杂志浓度和温度而异。
轻掺杂时,电阻率与杂质浓度成简单的反比关系;杂质浓度增高时,曲线严重偏离直线。
温度较低时,电阻率随温度升高而下降;室温下,电阻率随温度升高而增大;高温时,电阻率随温度升高而急剧下降。
2.四探针法测电阻率将四根排成一条直线的探针以一定的压力垂直地压在被测样品表面上,在1、4探针间通过电流I (mA ),2、3探针间就产生一定的电压V(mV)。
按下列公式计算样品的方块电阻:()()V W D F F W Fsp I S S ρ=⨯⨯⨯⨯ cm Ω⋅其中,D:样品直径;S :平均探针间距;W :样品厚度; Fsp :探针修正系数;F(W/S):样品厚度修正系数; F(D/S):样品直径修正系数; I :1、4探针流过的电流值; V :2、3探针间取出的电压值。
3. SDY —4型四探针测试仪的使用设计思想及流程图实 验原 理及 实 验 步骤源代码及注释实验步骤面板介绍:K7:电流换向按键K6:测量/电流方式选择按键(开机时自动在电流位)K5:/Rρ□测量选择按键(开机时自动设置在R□)K4、K3、K2、K1:测量电流量程选择按键W1:电流粗调电位器W2:电流细调电位器L:主机数字及状态显示器实验内容及步骤:1.开启主机电源,预热5分钟。
半导体实习报告(共5篇)-

半导体实习报告(共5篇)第1篇: 半导体实习报告实习报告1.实习目的:根据学院对专科生要求, 我在深圳意法半导体制造(深圳)有限公司, 为期十个月的实习。
毕业实习的目的是:接触实际, 了解社会, 增强社会主义事业心, 责任感, 巩固所学理论, 获取专业实际知识, 培养初步的工作能力, 具体如下:培养从事工作的专业技能, 了解日常事物和工作流程, 学会工作的方法, 理解所学专业的意义。
培养艰苦奋斗的精神和社会注意责任感, 形成热爱专业, 热爱劳动的良好品质。
预演和准备就业, 找出自身状况和社会实际所需的差距, 并在以后的实践期间及时补充和改正, 为求职和正式工作做好从分的知识和能力储备。
2.实习时间:我于2012年7月初到2013年4月底, 为期十个月的实践学习3.实习单位:3-1.单位地址和规模:实习单位位于深圳市龙岗宝龙社区高科大道12号, 意法半导体制造(深圳)有限公司, 公司是一个子公司, 现拥有在职员工**** 柴荣 1于人, 多条生产线, 拥有产能70亿只/年的生产能力。
3-2.实习期间在单位主要职务:在实习期间, 协助工程师处理一些质量和工艺流程方面的问题, 以及提高产品的成品率。
3-2.实习单位的历史和发展:意法半导体制造(深圳)有限公司于2005年9月在深圳市正式注册成立, 由意法半导体公司全资公司意法半导体(中国)投资有限公司出资成立, 公司的成立是为了深圳市龙岗区开发建设集成电路封装测试项目, 字公司成立以来到现在, 已经拥有5000余名员工, 8条生产线, 年产能70亿只/年, 涉及十几种产品, 主要是封装测试稳压管。
3-3.实习单位.部门.职位:我在意法半导体制造(深圳)有限公司, TO220部门从事工程师助理, 主要协助工程师解决产品质量问题和工艺流程。
提高产品的成品率以及其他方面的一些实验和跟踪一些项目。
4.实习过程:2012年7月2日, 我正式在深圳意法半导体制造(深圳)有限公司, 开始了为期十个月的实习之旅, 刚来的时候, 有7天的培训, 初步了解公司的运作方式, 重点强调了安全方面的培训, 早晨8:30分开始上班, 到晚上5:30分下班, 一个星期工作40小时, 海港开**** 柴荣2始培训玩的时候, 我被分到了M/D工位做工程师助理, 接触和了解了很多工艺流程方面的知识, 以及一定的管理方法。
半导体实验报告

半导体物理实验报告
班级:
学号:
姓名:
实验一 MOS结构C—V特性测试一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
当栅压在形成反型层之前迅速突变时,高频C-V特性将发生怎样的变化?
实验二霍尔效应测量载流子浓度实验一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
如何通过洛仑兹力方向和输出霍尔电压的正负来判断半导体样品的极性?
实验三霍尔效应测量载流子迁移率实验一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
思考样品尺寸参数误差会给霍尔效应测试实验带来怎样的误差?
实验四太阳能电池光伏效应实验
实验四太阳能电池光伏效应实验一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
为什么要把PN结串联起来用作太阳能电池?串联数目多少是由那些因素决定?。
半导体物理与器件实验报告..

课程实习报告HUNAN UNIVERSITY题目:半导体物理与器件学生姓名:周强强学生学号:20100820225专业班级:通信二班完成日期:2012.12.22运行结果截图:2.2 函数(),cos(2/)Vx t x t πλω=-也是经典波动方程的解。
令03x λ≤≤,请在同一坐标中绘出x 的函数(),Vx t 在不同情况下的图形。
(1)0;(2)0.25;(3)0.5;(4)0.75;(5)t t t t t ωωπωπωπωπ=====。
3.27根据式(3.79),绘制出0.2()0.2F E E eV -≤-≤范围内,不同温度条件下的费米-狄拉克概率函数:()200,()300,()400a T K b T K c T K ===。
4.3 画出a ()硅,b ()锗,c ()砷化镓在温度范围200600K T K ≤≤内的本征载流子浓度曲线(采用对数坐标)。
4.46 已知锗的掺杂浓度为153a =310cm N -⨯,d =0N 。
画出费米能级相对于本征费米能级的位置随温度变化200600)K T K ≤≤(的曲线。
5.20硅中有效状态密度为 193/2c 2.810()300T N =⨯ 193/21..0410()300TN ν=⨯ 设迁移率为 3/2n =1350300T μ-⎛⎫⎪⎝⎭3/2=480300T ρμ-⎛⎫⎪⎝⎭设禁带宽带为g =1.12V E e ,且不随温度变化。
画出200600K T K ≤≤范围内,本征电导率随绝对温度T 变化的关系曲线。
6.34 n 型硅样品的掺杂浓度为16310dN cm -=,产生的过剩载流子的浓度为()1443()10exp /10p x x cm δ--=-。
在140410x ≤≤⨯范围内,绘出Fi FpE E -随x 变化的函数。
7.4均匀掺杂的GaAspn 结,其掺杂浓度为183163510,510a d N cm N cm --=⨯=⨯。
半导体物理实验报告..

电子科技大学半导体物理实验报告姓名:艾合麦提江学号:2010033040008班级:固电四班实验一 半导体电学特性测试测量半导体霍尔系数具有十分重要的意义。
根据霍尔系数的符号可以判断材料的导电类型;根据霍尔系数及其与温度的关系,可以计算载流子的浓度,以及载流子浓度同温度的关系,由此可确定材料的禁带宽度和杂质电离能;通过霍尔系数和电阻率的联合测量.能够确定我流子的迁移约 用微分霍尔效应法可测纵向载流子浓度分布;测量低温霍尔效应可以确定杂质补偿度。
霍尔效应是半导体磁敏器件的物理基础。
1980年发现的量子霍尔效应对科技进步具有重大意义。
早期测量霍尔系数采用矩形薄片样品.以及“桥式”样品。
1958年范德堡提出对任意形状样品电阻率和霍尔系数的测量方法,这是一种有实际意义的重要方法,目前已被广泛采用。
本实验的目的使学生更深入地理解霍尔效应的原理,掌握霍尔系数、电导率和迁移率的测试方法,确定样品的导电类型。
一、实 验 原 理如图,一矩形半导体薄片,当沿其x 方向通有均匀电流I ,沿Z 方向加有均匀磁感应强度的磁场时,则在y 方向上产生电势差。
这种想象叫霍尔效应。
所生电势差用V H 表示,成为霍尔电压,其相应的电场称为霍尔电场E y 。
实验表明,在弱磁场下,E y 同J (电流密度)和B 成正比E y =R H JB(1)式中R H 为比例系数,称为霍尔系数。
在不同的温度范围,R H 有不同的表达式。
在本征电离完全可以忽略的杂质电离区,且主要只有一种载流子的情况,当不考虑载流子速度的统计分布时,对空穴浓度为p 的P 型样品0pq1R H >=(2) 式中q 为电子电量。
对电子浓度为n 的N 型样品0nq1R H <-=(3)当考虑载流子速度的统计分布时,式(2)、(3)应分别修改为nq 1R pq 1R nH H p H H ⎪⎪⎭⎫ ⎝⎛μμ-=⎪⎪⎭⎫ ⎝⎛μμ=(4)式中μH 为霍尔迁移率。
半导体实习报告4篇

半导体实习报告4篇为期第三个月的实习结束了,我在这三个月的实习中学到了很多在课堂上根本就学不到的知识,受益非浅。
现在我就对这个月的实习做一个工作小结。
实习是每一个大学毕业生必须拥有的一段经历,他使我们在实践中了解社会,让我们学到了很多在课堂上根本就学不到的知识,也打开了视野,长了见识,为我们以后进一步走向社会打下坚实的基础。
实习使我开拓了视野,实习是我们把学到的理论知识应用在实践中的一次尝试。
实习时把自己所学的理论知识用于实践,让理论知识更好的与实践相结合,在这结合的时候就是我们学以致用的时候,并且是我们扩展自己充实自己的时候。
实习期间,我利用此次难得的机会,努力工作,严格要求自己,遇到不懂的问题就虚心地向师傅们请教,搞清原理,找到方法,然后再总结经验,让自己能很快融入到工作中去,更好更快的完成任务。
同时我也利用其他时间参考一些书籍、搜索一些材料来完善自己对策划管理工作的认识,这也让我收获颇多,让我在应对工作方面更加得心应手。
矽格公司是在1997年经历千辛万苦独立出来自主经营的公司,已经有十三多年的发展历史,以成为集研制、生产、销售、技术培训于一体,拥有高精度电脑控制机械加工中心等全套加工设备的大型专业包装设备制造厂。
目前主要生产驱动类集成ic与光电鼠标等,产品包括:自动和半自动轮转循环,机械有d/b 与w/b,这些机械都是日本、美国高科技的技术。
具有高精度、高效率、先进的自动模切机、dbing机、wbing机等。
该半导体厂的组织机构设置很简练。
主要是总经理——副总经理——主管管理各个部门。
由于矽格公司的设备很先进,在生产线上不会像往常的工厂那样满布工人,主要是某三五个人负责工作流程。
这对我了解该工厂的生产流程提供了方便。
该厂生产的ic依据季节可以算得上的需求稳定,是属于定单供货型的生产。
由于产品的质量要求和技术含量要求都很高,因此,生产周期也比较长,单次产品需求的数量也不大。
同时,每台产品的价格非常昂贵,在万元以上。
半导体实验报告

半导体物理实验报告
班级:
学号:
姓名:
实验一 MOS结构C—V特性测试一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
当栅压在形成反型层之前迅速突变时,高频C-V特性将发生怎样的变化?
实验二霍尔效应测量载流子浓度实验一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
如何通过洛仑兹力方向和输出霍尔电压的正负来判断半导体样品的极性?
实验三霍尔效应测量载流子迁移率实验一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
思考样品尺寸参数误差会给霍尔效应测试实验带来怎样的误差?
实验四太阳能电池光伏效应实验
实验四太阳能电池光伏效应实验一、实验目的
二、实验器材
三、实验说明
四、实验内容和步骤
五、实验结果整理
六、实验心得体会
七、回答思考题
为什么要把PN结串联起来用作太阳能电池?串联数目多少是由那些因素决定?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程实习报告HUNAN UNIVERSITY题目:半导体物理与器件学生姓名:周强强学生学号:20100820225专业班级:通信二班完成日期:2012.12.22运行结果截图:2.2 函数(),cos(2/)Vx t x t πλω=-也是经典波动方程的解。
令03x λ≤≤,请在同一坐标中绘出x 的函数(),Vx t 在不同情况下的图形。
(1)0;(2)0.25;(3)0.5;(4)0.75;(5)t t t t t ωωπωπωπωπ=====。
3.27根据式(3.79),绘制出0.2()0.2F E E eV -≤-≤范围内,不同温度条件下的费米-狄拉克概率函数:()200,()300,()400a T K b T K c T K ===。
4.3 画出a ()硅,b ()锗,c ()砷化镓在温度范围200600K T K ≤≤内的本征载流子浓度曲线(采用对数坐标)。
4.46 已知锗的掺杂浓度为153a =310cm N -⨯,d =0N 。
画出费米能级相对于本征费米能级的位置随温度变化200600)K T K ≤≤(的曲线。
5.20硅中有效状态密度为 193/2c 2.810()300T N =⨯ 193/21..0410()300TN ν=⨯ 设迁移率为 3/2n =1350300T μ-⎛⎫⎪⎝⎭3/2=480300T ρμ-⎛⎫⎪⎝⎭设禁带宽带为g =1.12V E e ,且不随温度变化。
画出200600K T K ≤≤范围内,本征电导率随绝对温度T 变化的关系曲线。
6.34 n 型硅样品的掺杂浓度为16310dN cm -=,产生的过剩载流子的浓度为()1443()10exp /10p x x cm δ--=-。
在140410x ≤≤⨯范围内,绘出Fi FpE E -随x 变化的函数。
7.4均匀掺杂的GaAspn 结,其掺杂浓度为183163510,510a d N cm N cm --=⨯=⨯。
画出200500K T K ≤≤温度区间内,内建电势差随温度变化的曲线。
8.3 300T K =,理想硅pn 结的少子寿命分别为670010,10n p s s ττ--==。
N 区的掺杂浓度为16310d N cm -=。
绘制出当a N 的范围是151831010a N cm -≤≤时,空间电荷区内空穴电流占总电流的比例随a N 变化的曲线图(采用对数坐标)。
9.10 金与掺杂浓度为16310d N cm -=的n 型硅基础形成肖特基二极管。
简要说明肖特基势垒降低现象。
()a 绘出肖特基势垒降低值φ∇与反偏电压在050R V V ≤≤时的图形;()b 绘出()()/0sT R sT R J V J V =与反偏电压在050R V V ≤≤时的图形。
实验源代码(基于mathematica7.0):2.2V1=Cos[ 2 π x / λ - 0];V2=Cos[ 2 π x / λ - 0.5 π];V3=Cos[ 2 π x / λ - π];V4=Cos[ 2 π x / λ - 1.5 π];V5=Cos[ 2 π x / λ - 2 π];λ =1;Plot [{V1,V2,V3,V4,V5},{x,0,3}, PlotStyle→{RGBColor[1,0,1], RGBColor[1,0.5,0],RGBColor[1,0,0.5],RGBColor[0,1,0],RGBColor[0,0,1]},AxesLabel→{"(/λ)","V(x,t)"}]3.27F1 = 1/(1+Exp[ x/(k * 200)]);F2 = 1/(1+Exp[ x/(k * 300)]);F3 = 1/(1+Exp[ x/(k * 400)]);k=0.0000861;Plot [{F1,F2,F3},{x,-0.2,0.2},PlotStyle→{RGBColor[1,0,0],RGBColor[0,1,0],RGBColor[0,0,1]},AxesLabel→{"(E-E)"," "}]F4.3(*设x=1000/T*)Si =Sqrt[2.8 * 1.04 * 1038* (1000/ x /300 )^3 * Exp[-1.12/(0.0000861*1000/x)]];Ge =Sqrt[1.04 * 6 * 1037* (1000 /x /300 )^3 * Exp[-0.66/(0.0000861* 1000 /x)]];GaAs =Sqrt[4.7 * 7 * 1035* (1000 /x /300 )^3 * Exp[-1.42/(0.0000861* 1000/ x)]];LogLogPlot[{Si,Ge,GaAs},{x,10/6,5},PlotStyle→{RGBColor[1,0,0],RGBColor[0,1,0],RGBColor[0,0,1]},AxesLabel→{"(1000/T)","本征载流子浓度Ni"}]4.46Nc=1.04 * 1019;Nv=6 * 1019;Eg=0.66;k =8.62 *10-5;Na=1015;Nd=0;ni =N c N vT3003ExpE gk T;p0=(Na-Nd)/2+N a N d22n i2;f=k * T * Log[p0/ni];Plot[f,{T,200,600}, AxesLabel->{"T",""}]5.20Nc=2.8 * 1019 (T/300)3/2 ;Nv= 1.04 * 1019 (T/300)3/2 ; μn=1350 (T/300)-3/2 ;μp = 480 (T/300)-3/2 ;ni =N c N v ExpE gk T;k=8.62 * 10-5;Eg=1.12;n=ni;p=ni;e=1.6 *10-19;σ=e*(μn * n + μp * p);Plot[σ,{T,200,600}, AxesLabel->{"T","σ"}] 6.34δp[x] = 1014 Exp[-x/10-4];Nd=1016;ni=1.5 * 1010;n0= Nd;p0=Subscript[n, i]2/n;kT=0.0259;f=kT * Log[(p0+ δp[x])/ni];Plot[f,{x,0,4 * 10-4}, AxesLabel ->{"x", "EFi -EFp"}]7.4Nd=5*1016;Na=5 *1018;Nc=4.7 * 1017;Nv=7*1018;k = 1.38 *10-23;e = 1.6 * 10-19;Eg=1.42;ni =N c N vT3003ExpE g0.0259300T;V bi =(k * T)/e Log[(N a N d )/Subscript[n, i]2]; Plot[V bi ,{T,200,500 }, AxesLabel->{"T","V bi "}] 8.3τn0=10-6;τp0=10-7;N d =1016; D n =25; b=10;f=(1/N dbp0)/(1/N dbp0+1/N aD nn0);LogLogPlot[f,{N a ,1015,1018}, PlotStyle →{RGBColor[0,1,0]}, AxesLabel->{"N a ",""}]9.10aφm=5.1; χ=4.01;N c =2.8*1019;N d =1016;εs=11.7 * 8.85 *10-14;e=1.6 * 10-19;φB0=φm-χ;φn=0.0259 Log[N c /N d ]; V bi =φB0-φn;x n =2sV bi V ReN d;E 1=(e * N d )/εs* x n ;∆φ=e E 14s;Plot[∆φ,{V R ,0,50},AxesLabel->{"V R ","∆φ"}]9.10bφm=5.1; χ=4.01;N c =2.8*1019;N d =1016;εs=11.7 * 8.85 *10-14;e=1.6 * 10-19;φB0=φm-χ;φn=0.0259 Log[N c /N d ]; V bi =φB0-φn;x n =2sV bi V ReN d;E 1=(e * N d )/εs* x n ;∆φ=e E 14s;x n1=2sV bi eN d;E 2=(e * N d )/εs* x n1;∆φ1=e E 24s;k=1.38 * 10-23; T = 300;f=Exp[(e*∆φ)/(k*T)]/Exp[(e*∆φ1)/(k*T)]Plot[f,{V R ,0,50},AxesLabel->{"V R ","J sT (V R )/J sT (V R =0)"}]。
