matlab环境下无标度网络生成程序
无标度网络模型构造

课题:无标度网络模型构造姓名赵训学号201026811130班级实验班1001一、源起无标度网络(或称无尺度网络)的概念是随着对复杂网络的研究而出现的。
“网络”其实就是数学中图论研究的图,由一群顶点以及它们之间所连的边构成。
在网络理论中则换一套说法,用“节点”代替“顶点”,用“连结”代替“边”。
复杂网络的概念,是用来描述由大量节点以及这些节点之间错综复杂的联系所构成的网络。
这样的网络会出现在简单网络中没有的特殊拓扑特性。
自二十世纪60年代开始,对复杂网络的研究主要集中在随机网络上。
随机网络,又称随机图,是指通过随机过程制造出的复杂网络。
最典型的随机网络是保罗·埃尔德什和阿尔弗雷德·雷尼提出的ER模型。
ER模型是基于一种“自然”的构造方法:假设有个节点,并假设每对节点之间相连的可能性都是常数。
这样构造出的网络就是ER模型网络。
科学家们最初使用这种模型来解释现实生活中的网络。
ER模型随机网络有一个重要特性,就是虽然节点之间的连接是随机形成的,但最后产生的网络的度分布是高度平等的。
度分布是指节点的度的分布情况。
在网络中,每个节点都与另外某些节点相连,这种连接的数目叫做这个节点的度。
在网络中随机抽取一个节点,它的度是多少呢?这个概率分布就称为节点的度分布。
在一般的随机网络(如ER模型)中,大部分的节点的度都集中在某个特殊值附近,成钟形的泊松分布规律(见下图)。
偏离这个特定值的概率呈指数性下降,远大于或远小于这个值的可能都是微乎其微的,就如一座城市中成年居民的身高大致的分布一样。
然而在1998年,Albert-László Barab ási、Réka Albert等人合作进行一项描绘万维网的研究时,发现通过超链接与网页、文件所构成的万维网网络并不是如一般的随机网络一样,有着均匀的度分布。
他们发现,万维网是由少数高连接性的页面串联起来的。
绝大多数(超过80%)的网页只有不超过4个超链接,但极少数页面(不到总页面数的万分之一)却拥有极多的链接,超过1000个,有一份文件甚至与超过200万个其他页面相连。
如何使用MATLAB进行网络分析与建模

如何使用MATLAB进行网络分析与建模网络分析与建模是数据科学领域中的重要研究方法之一,它涉及到了计算机科学、数学、统计学等多个学科领域。
而在现代信息爆炸的时代,网络数据的规模和复杂性不断增加,对于分析和建模工具的要求也越来越高。
MATLAB作为一个强大的数学计算软件,提供了丰富的功能和工具,可以帮助我们进行网络分析与建模。
本文将介绍如何使用MATLAB进行网络分析与建模。
第一部分:网络分析基础网络分析是研究网络结构、功能和演化规律的一种方法。
在网络分析中,我们通常需要描述网络的拓扑结构、节点与边的关系、节点的属性等信息。
而MATLAB提供了一些常用的工具和函数,可以方便地进行网络分析。
首先,我们需要将网络数据导入到MATLAB中。
MATLAB支持导入各种格式的网络数据,如邻接矩阵、边列表、节点属性等。
使用MATLAB的数据导入和读取函数,我们可以将网络数据转换成MATLAB中的矩阵或表格,方便后续的分析和建模。
其次,我们可以使用MATLAB提供的函数和工具来计算网络的基本属性,如网络的度分布、聚类系数、平均路径长度等。
这些属性可以帮助我们了解网络的结构和功能,并进行比较和分类。
MATLAB还提供了可视化工具,可以直观地展示网络的拓扑结构和属性分布。
第二部分:网络建模与预测网络建模是研究网络演化和行为规律的关键内容。
借助MATLAB的数学建模和机器学习工具,我们可以构建各种网络模型,并使用这些模型来预测网络的演化和行为。
常用的网络建模方法包括随机网络模型、小世界网络模型、无标度网络模型等。
我们可以使用MATLAB的随机数生成函数和图论工具,生成各种类型的网络模型,并进行参数调节和性能评估。
此外,MATLAB还提供了机器学习和深度学习工具箱,可以用于网络模型的训练和预测。
网络预测是网络分析与建模的重要应用之一。
通过分析网络的演化规律和行为模式,我们可以预测网络的未来走向和趋势。
MATLAB提供了一些预测模型和函数,如时间序列分析、回归分析、神经网络等。
在Matlab中实现神经网络的方法与实例

在Matlab中实现神经网络的方法与实例神经网络是一种模拟人类大脑神经系统的计算模型,它能够通过学习数据的模式和关联性来解决各种问题。
在计算机科学和人工智能领域,神经网络被广泛应用于图像识别、自然语言处理、预测等任务。
而Matlab作为一种功能强大的科学计算软件,提供了一套完善的工具箱,可以方便地实现神经网络的建模和训练。
本文将介绍在Matlab中实现神经网络的方法与实例。
首先,我们会简要介绍神经网络的基本原理和结构,然后详细讲解在Matlab中如何创建并训练神经网络模型,最后通过几个实例展示神经网络在不同领域的应用。
一、神经网络的原理和结构神经网络模型由神经元和它们之间的连接构成。
每个神经元接收输入信号,并通过权重和偏置进行加权计算,然后使用激活函数对结果进行非线性变换。
这样,神经网络就能够模拟复杂的非线性关系。
常见的神经网络结构包括前馈神经网络(Feedforward Neural Network)和循环神经网络(Recurrent Neural Network)。
前馈神经网络是最基本的结构,信号只能向前传递,输出不对网络进行反馈;而循环神经网络具有反馈连接,可以对自身的输出进行再处理,适用于序列数据的建模。
神经网络的训练是通过最小化损失函数来优化模型的参数。
常用的训练算法包括梯度下降法和反向传播算法。
其中,梯度下降法通过计算损失函数对参数的梯度来更新参数;反向传播算法是梯度下降法在神经网络中的具体应用,通过反向计算梯度来更新网络的权重和偏置。
二、在Matlab中创建神经网络模型在Matlab中,可以通过Neural Network Toolbox来创建和训练神经网络模型。
首先,我们需要定义神经网络的结构,包括输入层、隐藏层和输出层的神经元数量,以及每个神经元之间的连接权重。
例如,我们可以创建一个三层的前馈神经网络模型:```matlabnet = feedforwardnet([10 8]);```其中,`[10 8]`表示隐藏层的神经元数量分别为10和8。
无标度网络matlab建模

复杂系统无标度网络研究与建模XXX南京信息工程大学XXXX系,南京 210044摘要:21世纪是复杂性的世界,基于还原论的世界观与方法论已经无法满足当前人们对作为一个整体系统的自然界和人类社会的认识和研究,利用系统科学的方法对科学重新审视已近变为迫切的需要。
现实生活中众多复杂网络都具有无标度性,这种无标度网络的增长性和择优连接性很好的解释了富者越富的“马太效应”。
对无标度网络的深入研究,让人们深刻的认识到其在Internet、地震网、病毒传播和社会财富分布网中的理论与现实意义。
本文通过对复杂网络中的无标度网络的分析与研究,介绍了无标度网络区别于一般随机网络的特性与现实意义,并利用了Matlab生成了一个无标度网络。
关键词:无标度网络,幂律特性,模型建立1 引言任何一种网络都可以看作是由一些节点按某种方式连接在一起而构成的一个系统,曾经关于网络结构的研究常常着眼于包含几十个到几百个节点的网络,而近几年关于复杂网络的研究中则常常可以见上万个节点的网络,网络规模尺度上的改变也促使网络分析方法做相应的改变,而复杂网络是近年来随着网络规模、理论和计算机技术的飞速发展而出现的一个新的研究方向。
它的出现不仅顺应了现代科技的发展趋势,而且反映了在以信息科学为支柱的新世纪中,各学科理论及应用交叉、渗透和融合的发展趋势[1]。
复杂系统主要研究其个体之间相互作用所产生的系统的整体性质与行为“复杂系统的复杂性体现在系统的整体性质与行为往往不是系统各个个体的状态的简单综合”因此,复杂系统的研究不能采用还原论的方法,而要从整体上进行研究。
在对复杂系统的研究中,美国物理学家Barabasi和Albert通过对万维网的研究,发现万维网中网页连接的度分布服从幂律分布,而万维网中少数网页(Hub点)具有非常大的连接,大多数网页的连接数甚小Barabasi等把度分布为幂律分布(Power law)的复杂网络称为无标度网络(scale-free net)[2]。
MATLAB矩阵生成无向网络图

MATLAB矩阵⽣成⽆向⽹络图 寝室有⼀个是做⽹络的,需要把矩阵变为⽹络图使其形象⼀点,所以我在这⾥就写了这样⼀个函数。
功能是将邻接矩阵或关联矩阵变为⽹络图,不过我这⾥只能转换为⽆向图,有向图的箭头我还需要在研究⼀下,似乎有annotation函数可以调⽤。
1 %函数名netplot2 %使⽤⽅法输⼊请help netplot3 %⽆返回值%函数只能处理⽆向图4 %作者:tiandsp5 %最后修改:2012.12.266 function netplot(A,flag)7 %调⽤⽅法输⼊netplot(A,flag),⽆返回值8 %A为邻接矩阵或关联矩阵9 %flag=1时处理邻接矩阵10 %flag=2时处理关联矩阵11 %函数只能处理⽆向图12if flag==1 %邻接矩阵表⽰⽆向图13 ND_netplot(A);14return;15 end1617if flag==2 %关联矩阵表⽰⽆向图18 [m n]=size(A); %关联矩阵变邻接矩阵19 W=zeros(m,m);20for i=1:n21 a=find(A(:,i)~=0);22 W(a(1),a(2))=1;23 W(a(2),a(1))=1;24 end25 ND_netplot(W);26return;27 end2829 function ND_netplot(A)30 [n n]=size(A);31 w=floor(sqrt(n));32 h=floor(n/w);33 x=[];34 y=[];35for i=1:h %使产⽣的随机点有其范围,使显⽰分布的更⼴36for j=1:w37 x=[x 10*rand(1)+(j-1)*10];38 y=[y 10*rand(1)+(i-1)*10];39 end40 end41 ed=n-h*w;42for i=1:ed43 x=[x 10*rand(1)+(i-1)*10];44 y=[y 10*rand(1)+h*10];45 end46 plot(x,y,'r*');4748 title('⽹络拓扑图');49for i=1:n50for j=i:n51if A(i,j)~=052 c=num2str(A(i,j)); %将A中的权值转化为字符型53 text((x(i)+x(j))/2,(y(i)+y(j))/2,c,'Fontsize',10); %显⽰边的权值54 line([x(i) x(j)],[y(i) y(j)]); %连线55 end56 text(x(i),y(i),num2str(i),'Fontsize',14,'color','r'); %显⽰点的序号57 hold on;58 end59 end60 end6162 end调⽤⽅法⾥⾯都写了,我就不多说了。
如何使用MATLAB创建一个最简单的程序

如何使用MATLAB创建一个最简单的程序使用MATLAB创建一个最简单的程序可以按照以下步骤进行:
例如,你可以使用disp函数在命令窗口中打印消息:
```
disp('Hello, World!');
```
或者,你可以使用fprintf函数在命令窗口中输出格式化的文本:```
fprintf('The sum of 2 and 3 is %d\n', 2+3);
```
这里,%d是一个格式化占位符,它将被替换为一个整数值。
4.运行程序。
在MATLAB命令窗口中,输入脚本文件名(不带.m扩展名),并按下回车键即可运行程序。
例如,如果你的脚本文件名为hello_world,你可以在命令窗口中输入:
```
hello_world
```
这将执行你所编写的MATLAB程序,并在命令窗口中显示输出结果。
以上是创建最简单的MATLAB程序的基本步骤。
此外,MATLAB还提供了一系列丰富的功能和工具箱,可以用于进行数值计算、绘图和数据分析等。
你可以在程序中使用这些功能来实现更复杂的任务。
Matlab与复杂网络理论的交叉研究与应用

Matlab与复杂网络理论的交叉研究与应用引言近年来,随着互联网的迅猛发展和数据科学的兴起,复杂网络理论作为解析网络结构与功能的一种新兴方法得到了广泛关注。
而Matlab作为一种强大的数值计算和可视化分析工具,正逐渐被应用于复杂网络理论的研究与实践中。
本文将探讨Matlab与复杂网络理论的交叉研究与应用,并通过几个具体的案例来展示其在不同领域中的广泛应用。
复杂网络理论简介复杂网络理论研究的是由大量节点和边构成的复杂网络的结构和性质。
复杂网络可以用于描述各种复杂系统,如社交网络、蛋白质相互作用网络、脑神经网络等。
通过复杂网络理论的研究,我们可以揭示网络的拓扑结构、节点之间的相互关系以及网络的功能等重要信息。
Matlab在复杂网络理论研究中的应用1. 复杂网络模型的构建与分析Matlab提供了丰富的工具箱和函数,可以方便地构建各种复杂网络模型,并对网络的拓扑结构进行分析。
例如,通过使用Matlab中的Graph对象和相关函数,我们可以构建随机网络模型、无标度网络模型、小世界网络模型等,并计算网络的度分布、聚集系数、平均最短路径长度等网络指标。
这些指标可以帮助我们理解网络的特性和行为。
2. 复杂网络的动力学模拟与分析复杂网络的动力学模拟是复杂网络理论中的重要问题之一。
Matlab提供了优秀的数值求解和模拟工具,可以方便地对复杂网络的动力学进行模拟与分析。
例如,我们可以使用Matlab中的差分方程求解器和常微分方程求解器,对复杂网络的节点动态行为进行模拟,从而研究网络的同步、稳定性和干扰传播等动力学行为。
3. 复杂网络的可视化与图形分析Matlab具有强大的数据可视化和图形分析功能,可以帮助我们直观地理解和分析复杂网络。
通过Matlab的图形绘制函数和工具箱,我们可以将网络的拓扑结构和节点属性以图形的形式展示出来,从而帮助我们观察网络的模式、结构分布规律以及节点的重要性等。
同时,Matlab还提供了基于图的分析工具,如最大连通子图、最短路径查找等,便于我们对复杂网络进行进一步的分析。
利用Matlab进行神经科学研究和大脑连接分析

利用Matlab进行神经科学研究和大脑连接分析引言:神经科学是一门研究大脑和神经系统的学科,它试图理解神经元如何工作以及它们之间的连接方式。
近年来,随着计算机和数据分析技术的快速发展,研究人员开始借助计算机编程和数据处理工具进行神经科学研究,并获得了许多重要的发现。
在这篇文章中,我们将重点讨论利用Matlab进行神经科学研究和大脑连接分析的方法和技术。
一、Matlab在神经科学中的应用Matlab是一种流行的科学计算和数据分析软件,它提供了丰富的工具和函数,方便研究人员进行各种科学实验和数据分析。
在神经科学研究中,Matlab被广泛应用于数据处理、模型建立和可视化等方面。
1. 数据处理神经科学研究中经常需要处理大量的数据,包括脑电图(EEG)、功能磁共振成像(fMRI)和神经元活动记录等。
Matlab提供了丰富的数据处理函数和工具箱,方便研究人员处理和分析这些数据。
例如,可以使用Matlab对脑电图数据进行预处理,包括信号滤波、通道去噪和伪迹去除等,以提取有用的信息。
2. 模型建立神经科学研究中常常需要建立数学模型来描述和解释神经系统的工作原理。
Matlab提供了强大的数学建模和仿真功能,可以方便地构建和调整神经网络模型、神经元活动模型等。
研究人员可以使用Matlab进行模型参数估计、模拟实验和模型验证,以帮助理解大脑的工作机制。
3. 可视化Matlab提供了丰富的绘图和可视化函数,可以用于展示和呈现神经科学研究的结果。
研究人员可以使用Matlab绘制脑电图图谱、大脑活动热力图、神经网络拓扑图等,以便更直观地展示研究结果。
二、大脑连接分析大脑是一个复杂的网络系统,其中包含数以亿计的神经元和神经元之间的连接。
大脑连接分析旨在揭示不同脑区之间的连接方式,以及这些连接对大脑功能和疾病的影响。
利用Matlab进行大脑连接分析主要包括以下几个方面。
1. 脑电图和功能磁共振成像数据的预处理脑电图和功能磁共振成像是常用的大脑连接分析技术。
matlab编写程序

mathematics Basic Matrix Operations>> a=[1 2 3 4 5]生成矩阵;>> b=a+2矩阵加上数字>> plot(b)画三点图>> grid on生成网格>> bar(b)生成条状图>> xlabel('sample#') 给X轴加标注>> ylabel('pound') 给Y轴加标注>> title('bar plot')加标题>> plot(b,'*')用*表示点>> axis([0 10 10 20 0 20])各个轴的范围>> A = [1 2 0; 2 5 -1; 4 10 -1]>> B=A'转置>> C=A*B矩阵相乘>> C=A.*B数组相乘>> X=inv(A)逆>> I=inv(A)*A单位矩阵>> eig(A)特征值>> svd(A) the singular value decomposition. 奇异值分解>> p = round(poly(A))生成特征多项式的系数>> roots(p) 特征多项式的根,即矩阵的特征值>> q = conv(p,p) 向量的卷积>> r = conv(p,q) 再向量的卷积>> plot(r)>> who 变量列表 >> whos 变量的详细列表>> sqrt(-1);>> sqrt(2) 开方Matrix Manipulation>> A = magic(3) 生成魔方矩阵graphics2-D PlotsLine Plot of a Chirp(线状图)>> doc plot 在帮助中查看plot更多的信息>> x=0:0.05:5;>> y=sin(x.^2);>> plot(x,y);>> plot(x,y,'o');>> xlabel('Time')>> ylabel('Amplitude')Bar Plot of a Bell Shaped Curve(条状图)>> x = -2.9:0.2:2.9;>> bar(x,exp(-x.*x));函数中包括了计算,plot直接完成Stairstep Plot of a Sine Wave(阶梯图)>> x=0:0.25:10;>> stairs(x,sin(x));Errorbar Plot>> x=-2:0.1:2;>> y=erf(x);>> y=erf(x);e = rand(size(x))/10>> errorbar(x,y,e);Polar Plot>> t=0:0.01:2*pi;>> polar(t,abs(sin(2*t).*cos(2*t))); abs绝对值Stem Plot>> x = 0:0.1:4;>> y = sin(x.^2).*exp(-x);>> stem(x,y)Scatter Plot>> load count.dat>> scatter(count(:,1),count(:,2),'r*')>> xlabel('Number of Cars on Street A');>> ylabel('Number of Cars on Street B');更多plot的类型可以在命令行输入doc praph2d查看3-D PlotsMesh Plot of Peaks>> z=peaks(25);peaks is a function of two variables, obtained by translating and scaling Gaussian distributions, which is useful for demonstrating mesh, surf, pcolor, contour, and so on.>> mesh(z);>> meshc(z);带有轮廓线>> colormap(hsv);对mesh的图象使用不同的色彩,如gray, hot, bone. EtcSurface Plot of Peaks>> z=peaks(25);>> surf(z); 3-D shaded surface plot>> surfc(z);带有轮廓线>> colormap jet;同>> colormap(jet); 对mesh的图象使用不同的色彩Surface Plot (with Shading) of Peaks>> z=peaks(25);>> surfl(z); Surface plot with colormap-based lighting>> shading interp; Set color shading properties>> colormap(pink);Contour Plot of Peaks>> z=peaks(25);>> contour(z,16) 轮廓线>> colormap(hsv)Quiver (Quiver or velocity plot)>> x = -2:.2:2;>> y = -1:.2:1;>> [xx,yy] = meshgrid(x,y);>> zz = xx.*exp(-xx.^2-yy.^2);>> [px,py] = gradient(zz,.2,.2);>> quiver(x,y,px,py,2);Slice(Volumetric slice plot)>> [x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2);>> v = x.*exp(-x.^2-y.^2-z.^2);>> xslice = [-1.2,.8,2];>> yslice = 2;>> zslice = [-2,0];>> [x,y,z] = meshgrid(-2:.2:2,-2:.25:2,-2:.16:2); >> slice(x,y,z,v,xslice,yslice,zslice)>> colormap hsvProgramming Manipulating Multidimensional Arrays Creating Multi-Dimensional ArraysThe CAT function is a useful tool for building multidimensional arrays. B = cat(DIM,A1,A2,...) builds a multidimensional array by concatenating A1, A2 ... along the dimension DIM.Calls to CAT can be nested.>> B = cat( 3, [2 8; 0 5], [1 3; 7 9], [2 3; 4 6]); B(:,:,1) =2 80 5B(:,:,2) =1 37 9B(:,:,3) =2 34 6>> A = cat(3,[9 2; 6 5], [7 1; 8 4]);>> B = cat(3,[3 5; 0 1], [5 6; 2 1]);>> C = cat(4,A,B,cat(3,[1 2; 3 4], [4 3; 2 1])); C(:,:,1,1) =9 26 5C(:,:,2,1) =7 18 4C(:,:,1,2) =3 50 1C(:,:,2,2) =5 62 1C(:,:,1,3) =1 23 4C(:,:,2,3) =4 32 1>> A = cat(2,[9 2; 6 5], [7 1; 8 4]);>> B = cat(2,[3 5; 0 1], [5 6; 2 1]);>> C = cat(4,A,B,cat(2,[1 2; 3 4], [4 3; 2 1]))C(:,:,1,1) =9 2 7 16 5 8 4C(:,:,1,2) =3 5 5 60 1 2 1C(:,:,1,3) =1 2 4 33 4 2 1>> C = cat(2,A,B,cat(2,[1 2; 3 4], [4 3; 2 1]))C =9 2 7 1 3 5 5 6 1 2 4 3;6 5 8 4 0 1 2 1 3 4 2 1>> C = cat(1,A,B,cat(2,[1 2; 3 4], [4 3; 2 1]))C =9 2 7 1 6 5 8 4 3 5 5 60 1 2 11 2 4 3 3 4 2 1 Finding the Dimensions >>SzA = size(A)>>DimsA = ndims(A)>>SzC = size(C)>>DimsC = ndims(C) Accessing Elements>> K = C(:,:,1,[1 3])K(:,:,1,1) =9 26 5K(:,:,1,2) =1 23 4Manipulating Multi-Dimensional Arrays>> A = rand(3,3,2);>> B = permute(A, [2 1 3]);>> C = permute(A, [3 2 1]);Selecting 2D Matrices From Multi-Dimensional Arrays >> A = cat( 3, [1 2 3; 9 8 7; 4 6 5], [0 3 2; 8 8 4;5 3 5], ...[6 4 7; 6 8 5; 5 4 3]);>>% The EIG function is applied to each of the horizontal 'slices' of A.for i = 1:3eig(squeeze(A(i,:,:)))end>> x1 = -2*pi:pi/10:0;>> x2 = 2*pi:pi/10:4*pi;>> x3 = 0:pi/10:2*pi;>> [x1,x2,x3] = ndgrid(x1,x2,x3);>> z = x1 + exp(cos(2*x2.^2)) + sin(x3.^3);>> slice(z,[5 10 15], 10, [5 12]);>> axis tight;Structures% Draw a visualization of a structure.>> strucdem_helper(1)>> = 'John Doe';>> patient.billing = 127.00;>> patient.test = [79 75 73; 180 178 177.5; 172 170 169]; >> patientpatient =name: 'John Doe'billing: 127test: [3x3 double]>> patient(2).name = 'Ann Lane';>> patient(2).billing = 28.50;>> patient(2).test = [68 70 68; 118 118 119; 172 170 169];% Update the visualization.>> strucdem_helper(2);>> fnames1 = fieldnames(patient)>> patient2 = rmfield(patient,'test');>> fnames2 = fieldnames(patient2)fnames1 ='name''billing''test'fnames2 ='name''billing'>> A = struct( 'data', {[3 4 7; 8 0 1], [9 3 2; 7 6 5]}, ... 'nest', {...struct( 'testnum', 'Test 1', ... 'xdata', [4 2 8], 'ydata', [7 1 6]), ... struct( 'testnum', 'Test 2', ... 'xdata', [3 4 2], 'ydata', [5 0 9])}) % Update the visualization.>> strucdem_helper(3)聚类分析K(C)均值算法:x=[-7.82 -4.58 -3.97;-6.68 3.16 2.17;4.36 -2.19 2.09;6.72 0.88 2.80;...] -8.64 3.06 3.5;-6.87 0.57 -5.45;4.47 -2.62 5.76;6.73 -2.01 4.18;... -7.71 2.34 -6.33;-6.91 -0.49 -5.68;6.18 2.81 5.82;6.72 -0.93 -4.04;... -6.25 -0.26 0.56;-6.94 -1.22 1.13;8.09 0.20 2.25;6.81 0.17 -4.15;... -5.19 4.24 4.04;-6.38 -1.74 1.43;4.08 1.3 5.33;6.27 0.93 -2.78];[idx,ctrs]=kmeans(x,3)如何编写求K-均值聚类算法的Matlab程序在聚类分析中,K-均值聚类算法(k-means algorithm)是无监督分类中的一种基本方法,其也称为C-均值算法,其基本思想是:通过迭代的方法,逐次更新各聚类中心的值,直至得到最好的聚类结果。
基于Matlab的无标度网络仿真

1 无 标 度 网 络 的概 念 及 基 本 性 质
19 9 9年 , b r、e n AletJ o g和 B rb s 现 WWW 网页 的度分 布不 是 通 常 认 为 的 P i o aa d 发 os n分 布 , s 而是 重 尾特 征 的幂律分 布 , 而且 WWW 基 本 上是 由少数 具有 大量 超链 接 的网页 串连起 来 的 , 大部 分 网页 的链接 很少 , 绝 他
无 标度 网络模 型涉及 概率论 、 算机 编程 和 图像 处 理等 内容 , 于 数 学模 型课 程 来 说是 一 个 较好 的案 例 。 计 对 本文基 于 Malb软件 实现 无标 度 网络模 型算法 , 利用 P jk 软件做 出无 标度 网络 的 图像 , 冀 能对 参加 大 t a 并 ae 希 学生数 学建模培 训 的学生 有所启 迪 。
李 光 正 , 龙 余 , 传桂 翟 左
( 苏财经 职 业技术 学 院 基 础部 , 苏淮安 2 3 0 ) 江 江 2 0 3
摘 要 : 文 章基 于 Malb软件 实现无 标 度 网络 模 型算 法 , t a 并利 用 P jk软件 做 出无标 度 网络 a e 的图像 , 为培 养学 生的数 学建模 能 力提 供 了一 个较好 的案例 。
19 9 9年 B rb s 和 Alet 出 S ae re 无标 度 ) aa di br提 c1—fe ( 网络 模 型 。与 古 典模 型 相 比 , 两种 网络 模 型较 好 地 ] 这
解释 了一些 实际 网络 ( 因特 网和 演员合 作 网等 ) 自组 织形 成 机制 。进 一 步 的实证 研 究 发 现 , 如 的 大量 的实 际 网
维普资讯
第2 l卷 第 3期
matlab课程论文—无尺度网络的实现与可视化

可以用 graph_plot 函数可视化 scale_free 函数生成的邻接矩阵。例如在 matlab 输入: graph_plot(scale_free(50)),可以得到一个可视化的有 50 个节点的无尺度网络。
这个图上从 0°到 360°按照逆时针排列着 50 个节点, 每个节点上的数字代表着节点的 度,这些连线代表着节点之间的边。从图上可以大致看出比较靠前的节点的度比较大,而后 来新加入的节点度稍微小一些, 而且图上大部分的节点度都比较小, 而很少数的节点则拥有
fori = 1: m0 for j = 1:m0 if (j ~= i) %去除每个点自身形成的? adjacent_matrix(i,j) =1; %建立初始邻接矩阵,3个节点构成完全图 end end end node_degree = zeros(1,m0+1); temp = sum(adjacent_matrix); %初始化点的度 %求每个节点的度
很大的度,复合二八定律。 下面这张图是 100 个节点的无尺度网络可视化结果。 由于节点比较多, 看起来没有那么 舒适,但是还是可以看到度分布的二八定律。
4 分析与思考
无尺度网络还有一个特点就是“富者越富” ,因为新节点发出的边的选择是优先选择度 比较大的点。从可视化结果就可看出,度比较大的点基本都分布在第一象限,也就是最初选 定的初始节点和比较早加进去的点。 这也是因为网络中最开始出现的节点在最初几步新加入 节点时有较大的概率被新加的节点选中作为邻居。 而由于比较早的节点有较大的几率在每一 步被选中, 因而他们的度相比于后加入的节点会比较大, 在后续节点加入过程中更容易被选 中。有如滚雪球般,最初的节点度比较大,容易被选中。容易被选中就导致度更大,最后导 致了度分布为幂率分布。 当然还有一些值得思考的问题, 例如后加入的节点有没有可能因为某个关系而突然取得 领先优势, 在网络中成为度最大的节点?或者在最开始每个节点的度都一样的时候, 度最大 的节点时如何逐渐脱颖而出的?
matlab点生成函数

matlab点生成函数在MATLAB中,你可以使用一些内置的函数来生成点或创建矢量。
以下是一些常用的MATLAB 点生成函数:1.linspace 函数:•用于在两个给定的值之间生成等间隔的点。
•语法:linspace(start, end, n),其中start是起始值,end是结束值,n是生成的点的数量。
x = linspace(0, 1, 100); % 在0 到1 之间生成100 个等间隔的点2.logspace 函数:•用于在对数刻度上生成等间隔的点。
•语法:logspace(start, end, n),其中start和end是对数刻度上的起始和结束幂次,n是生成的点的数量。
x = logspace(-2, 2, 100); % 在对数刻度上生成100 个等间隔的点3.colon 运算符:•用于创建等间隔的点或矢量。
•语法:start:step:end,其中start是起始值,step是步长,end是结束值。
x = 0:0.01:1; % 在0 到1 之间生成步长为0.01 的点4.zeros 函数:•用于创建包含零的矢量或矩阵。
•语法:zeros(m, n),其中m和n是矩阵的行数和列数。
x = zeros(1, 100); % 创建一个包含100 个零的行向量5.ones 函数:•用于创建包含全为一的矢量或矩阵。
•语法:ones(m, n),其中m和n是矩阵的行数和列数。
x = ones(1, 100); % 创建一个包含100 个一的行向量这些函数可以根据你的具体需求生成不同类型的点或矢量。
根据任务的不同,选择合适的函数以满足你的需求。
模糊神经和模糊聚类的MATLAB实现

模糊神经和模糊聚类的MATLAB实现模糊神经网络(Fuzzy Neural Networks)是一种结合了模糊逻辑和神经网络的方法,用于处理不确定性和模糊性问题。
它具有模糊逻辑的灵活性和神经网络的学习和优化能力。
在MATLAB中,可以使用Fuzzy Logic Toolbox来实现模糊神经网络。
下面将介绍如何使用MATLAB实现模糊神经网络。
首先,我们需要定义输入和输出的模糊集合。
可以使用Fuzzy Logic Toolbox提供的各种方法来定义模糊集合的隶属函数,例如使用trimf定义三角隶属函数或者使用gaussmf定义高斯隶属函数。
```input1 = trimf(inputRange, [a1, b1, c1]);input2 = gaussmf(inputRange, [mean, sigma]);output = trapmf(outputRange, [d1, e1, f1, g1]);```接下来,可以使用FIS Editor界面来创建和训练模糊神经网络。
在MATLAB命令窗口中输入fuzzy命令即可打开FIS Editor界面。
在FIS Editor界面中,可以添加输入和输出变量,并设置它们的隶属函数。
然后,可以添加规则来定义输入与输出之间的关系。
规则的形式可以使用自然语言或者模糊规则表达式(Fuzzy Rule Expression)。
训练模糊神经网络可以使用基于模糊神经网络的系统识别方法。
在MATLAB中,可以使用anfis函数来进行自适应网络训练。
anfis函数可以根据训练数据自动调整隶属函数参数和规则权重,以优化模糊神经网络的性能。
```fis = anfis(trainingData);```使用trainfis命令可以将训练好的模糊神经网络应用于新的数据。
trainfis命令将输入数据映射到输出模糊集中,并使用模糊推理进行预测。
输出结果是一个模糊集,可以使用defuzz命令对其进行模糊化。
matlab里边net函数的用法

Matlab是一种常用的科学计算软件,它提供了丰富的函数和工具箱,用于进行数据处理、图像处理、数值计算等各种科学计算任务。
其中,net函数是Matlab中的一个重要函数,它可以用来构建和训练神经网络模型,是进行机器学习和深度学习任务的重要工具之一。
在本文中,我们将重点介绍Matlab中net函数的用法,包括如何创建神经网络模型、如何进行训练和预测,以及如何对模型进行评估和优化。
希望通过本文的介绍,读者能够更加深入地了解Matlab中net 函数的用法,从而能够更加熟练地使用这一强大的工具进行科学计算和研究。
一、net函数的基本用法在Matlab中,我们可以使用net函数来创建一个神经网络模型。
我们需要定义网络的结构,包括输入层的神经元数目、隐藏层的神经元数目、输出层的神经元数目等。
我们可以使用net函数来创建一个空白的神经网络模型,如下所示:net = newff(minmax(input),[10 1], {'tansig' 'purelin'}, 'tr本人nlm', 'learngdm', 'mse');在上面的代码中,我们首先使用newff函数来创建一个空白的神经网络模型。
其中,minmax(input)表示输入数据的范围,[10 1]表示隐藏层和输出层的神经元数目,{'tansig' 'purelin'}表示隐藏层和输出层的激活函数,'tr本人nlm'表示训练函数,'learngdm'表示学习函数,'mse'表示性能函数。
二、net函数的训练与预测在创建好神经网络模型之后,我们需要对模型进行训练,以便使其能够对输入数据进行预测。
在Matlab中,我们可以使用tr本人n函数来对神经网络模型进行训练,如下所示:net = tr本人n(net,input,target);在上面的代码中,我们使用tr本人n函数对神经网络模型net进行训练,其中input表示训练数据的输入,target表示训练数据的输出。
如何利用Matlab进行网络分析与优化

如何利用Matlab进行网络分析与优化引言:在当今信息时代,网络技术的发展已经成为人们生活和工作的重要组成部分。
因此,网络的分析与优化,尤其是对于大规模网络的分析与优化,成为了重要的研究领域。
Matlab作为一种强大的科学计算软件,在网络分析与优化中扮演着重要的角色。
本文将围绕如何利用Matlab进行网络分析与优化展开探讨。
一、网络分析在网络分析中,我们可以利用Matlab进行网络的建模与分析。
首先,我们需要将网络表示为一个图,其中节点表示网络中的实体,边表示节点间的连接关系。
利用Matlab的图论工具包,我们可以方便地进行网络的可视化、统计特性的计算以及网络模型的构建。
1.1 网络可视化Matlab的图论工具包提供了各种绘制网络图的函数和工具,让我们能够直观地展示网络的拓扑结构。
通过对网络进行可视化,我们可以更好地理解网络的结构和特性,并有助于后续的分析与优化工作。
1.2 统计特性计算网络的统计特性是了解网络行为和性质的重要指标。
在Matlab中,我们可以利用图论工具包计算网络的度分布、聚类系数、路径长度等统计特性。
这些特性可以帮助我们深入了解网络的性质,为后续的优化工作提供基础。
1.3 网络模型构建为了更好地理解和分析网络,我们可以利用Matlab构建各种经典的网络模型,如随机网络、小世界网络和无标度网络等。
通过这些模型,我们可以模拟真实网络中的一些特性,从而更深入地研究网络的结构和行为。
二、网络优化网络优化旨在改善网络的性能和效率,使得网络能够更好地满足用户和应用的需求。
在网络优化中,我们可以利用Matlab进行网络流量优化、资源分配优化以及拓扑结构优化等方面的工作。
2.1 网络流量优化网络流量优化是指通过合理的路由和调度策略,使得网络中的数据能够以最优的方式传输,从而提高网络的传输效率和吞吐量。
在Matlab中,我们可以利用线性规划、整数规划和最优化算法等进行网络流量的优化设计,从而改善网络的性能和效果。
模糊pid控制matlab程序

模糊pid控制matlab程序
模糊PID控制是一种结合模糊控制和PID控制的方法,它可以
在控制系统中应对非线性和不确定性。
在MATLAB中,实现模糊PID
控制可以分为以下几个步骤:
1. 定义模糊系统,首先,需要使用MATLAB中的Fuzzy Logic Toolbox来定义模糊系统。
可以使用fuzzy函数来创建一个模糊系
统对象,并定义输入、输出和隶属函数等参数。
2. 设计模糊控制器,接下来,需要设计模糊控制器。
可以使用fisedit函数来打开模糊逻辑编辑器,通过编辑器来定义模糊控制
器的输入、输出和规则等。
3. 整合PID控制器,在MATLAB中,可以使用pid函数来创建
一个PID控制器对象。
然后,将模糊控制器和PID控制器整合在一起,可以通过串联、并联或级联的方式来实现模糊PID控制。
4. 闭环控制,最后,将设计好的模糊PID控制器应用于闭环控
制系统中。
可以使用sim函数来进行仿真,观察系统的响应和性能。
需要注意的是,模糊PID控制的设计涉及到模糊集合的定义、隶属函数的选择、规则的设置等,需要根据具体的控制对象和要求来进行调整和优化。
同时,对于PID控制器的参数调节也需要谨慎处理,可以使用MATLAB中的工具箱来进行参数整定和性能分析。
总的来说,实现模糊PID控制的MATLAB程序需要综合运用模糊逻辑工具箱和控制系统工具箱,通过适当的建模和调节来实现模糊PID控制器的设计和应用。
使用matlab工具箱创建神经网络模型
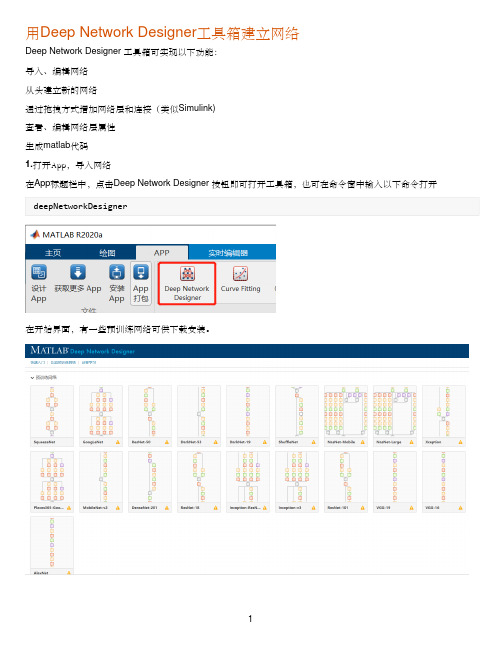
用Deep Network Designer工具箱建立网络Deep Network Designer 工具箱可实现以下功能:导入、编辑网络从头建立新的网络通过拖拽方式增加网络层和连接(类似Simulink)查看、编辑网络层属性生成matlab代码1.打开App,导入网络在App标题栏中,点击Deep Network Designer 按钮即可打开工具箱,也可在命令窗中输入以下命令打开在开始界面,有一些预训练网络可供下载安装。
一般通过新建或从工作区导入的方式创建网络2.增加/编辑网络层App提供了常用的网络层模块,可通过拖拽的方式添加,软件自带的层模块有:输入层(图片/序列输入)、卷积和全连接层(二维/三维卷积)、池化层、序列层(lstm、gru、NLP处理)、激活函数(relu、elu、tanh等)、归一化等工具(BN、dropout)、目标检测、输出层。
另外,可以通过命令行自己建立新的层,并添加到网络中。
在工作区中点击每个层,可以查看修改层属性参数,也可选中各层进行复制、剪切、删除等操作。
3.分析网络点击Analyze按钮可以检查分析网络,检查网络结构是否有问题,分析各层的可学习参数数量,errors为0时,网络可用于训练。
4.使用Deep Network Designer进行训练首先在Data 栏中,点击Import Data 按钮导入训练集,然后在Training栏中,进行网络训练。
App中可对训练集进行数据增强,可设置训练参数。
5.网络导出也可将建好的网络导出到matlab工作区,通过 trainNetwork 命令进行训练。
也可先在App中训练完毕,将训练好的网络导出到工作区,这样导出的网络包含已学习的权重参数。
基于LabVIEW的BA无标度网络演化模拟软件

基于LabVIEW的BA无标度网络演化模拟软件周茜;陈佳莹;刘海洋;王玫宝;吕孟轩;刘松;刘歌群【摘要】BA无标度网络模型可对自然界和人类社会中大多数的网络演化特征进行描述.然而目前还没有一种可以描述BA无标度网络增长特性和优先连接特性的演化模拟软件.针对软件的缺失,设计了基于LabVIEW与Matlab的BA无标度网络演化模拟软件.利用LabVIEW构建人机界面和实现动态演化,并以Matlab计算邻接矩阵、节点度和连接概率等数据.最终实现每点击一次增长按钮,就会增加一个节点的BA无标度网络演化的动态显示.该软件有利于学习和理解BA无标度网络模型.通过BA无标度网络演化示例进行结果验证表明,软件不仅能够演示网络演化过程,还可动态计算邻接矩阵、节点度和连边概率.【期刊名称】《电子科技》【年(卷),期】2016(029)007【总页数】3页(P58-60)【关键词】LabVIEW;Matlab;BA无标度网络【作者】周茜;陈佳莹;刘海洋;王玫宝;吕孟轩;刘松;刘歌群【作者单位】上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093;上海理工大学光电信息与计算机工程学院,上海200093【正文语种】中文【中图分类】TN941.4当今是网络化的世界,各种网络种类繁多。
而这些网络又具有共同的特性:大部分节点只有少数几个连接,而某些节点却拥有与其他节点的大量连接。
表现在度分布上就是有幂律分布[1],即p(k)~k-γ。
有大量连接的节点称为“集散节点”,由于包含集散节点的这类网络的节点的度没有明显的特征长度,故称为无标度网络[1]。
而无标度网络中的经典模型为Barabási和Albert提出的BA模型[2-3]。
WS以及NW小世界网络的生成(MATLAB)

WS以及NW⼩世界⽹络的⽣成(MATLAB)WS⼩世界⽹络⽣成算法,⼀般⼩世界⽹络⽣成算法速度慢,节点度分布与数学推导不符,在⽹络仿真中造成不便,这⾥针对实际⽹络动⼒学仿真过程撰写了WS⼩世界⽹络的MATLAB⽣成算法,并考虑了矩阵化,具有较⾼的速度。
以下是対应的代码:% The simulation of WS-smallworld network% the algorithm of WS-smallworld's generation has been improved in speed,% and tend to be easily understood% writen by winter-my-dream@% Example:% N = 100; %network size (number of nodes)% m = 6; %2*m is the average edges of each nodes% p = 0.1; %rewiring probability% matrix = small_world_WS_new(N,m,p);function matrix = small_world_WS_new(N,m,p)rng('default')rng('shuffle')matrix=zeros(N,N);% generate regular networkfor i=m+1:N-mmatrix(i,i-m:i+m)=1;endfor i=1:mmatrix(i,1:i+m)=1;endfor i=N-m+1:Nmatrix(i,i-m:N)=1;endfor i=1:mmatrix(i,N-m+i:N)=1;matrix(N-m+i:N,i)=1;end% rewiring the networkfor i = 1:N% then rewiring the edges with the probability of p[series1,series2] = range_sort(N,m,i);index0 = series1(rand(2*m,1)>1-p);if(~isempty(index0))matrix(i,index0) = 0;matrix(i,series2(randperm(length(series2),length(index0))))=1;endendmatrix = matrix -diag(diag(matrix));endfunction [series1,series2] = range_sort(N,m,i)% select the index of nodes in row i for rewiringif(i-m>0 && i+m<=N)series1 = i-m:i+m;series2 = setdiff(1:N,series1);elseif(i-m<=0)series1 = [1:i+m,N-m+i:N];series2 = setdiff(1:N,series1);elseseries1 = [1:m-N+i,i-m:N];series2 = setdiff(1:N,series1);end% Without considering the connection of diagonal elementsseries1(series1==i) = [];end参考⽂献:Watts D J, Strogatz S H. Collective dynamics of ‘small-world’networks[J]. nature, 1998, 393(6684): 440-442.NW⼩世界⽹络的⽣成⽅法相对简单,我这⾥附加对应代码:% 基于Matlab 的⼩世界⽹络仿真% 经过矩阵化修改后,⽣成速度已经⼤⼤加快function matrix = small_world_NW(N,m,p)% N=50;m=3;p=0.1;% matrix=sparse([]);matrix = zeros(N,N);for i=m+1:N- mmatrix(i,i- m:i+m)=1;endfor i=1:mmatrix(i,1:i+m)=1;endfor i=N- m+1:Nmatrix(i,i- m:N)=1;endfor i=1:mmatrix(i,N- m+i:N)=1;matrix(N- m+i:N,i)=1;end% Random add edgekk=(rand(N,N)<p);matrix = logical(matrix + kk);matrix = matrix -diag(diag(matrix));对应⽣成⽹络的测试图的代码:clear,clc,close all% load A.txtN=10;m=2;p=0.1;% A= small_world_WS_new(N,m,p);A = small_world_NW(N, m, p);t=linspace(0,2*pi,N+1);x=sin(t);y=cos(t);figureset(gcf,'color','w')plot(x,y,'o','markerfacecolor','k'),hold onfor i=1:Nfor j=1:Nif (A(i,j)==1)fp1=plot([x(i),x(j)],[y(i),y(j)],'r-'); hold on set(fp1,'linesmoothing','on')endendendaxis([-1.05,1.05,-1.05,1.05])axis squareaxis offsum(sum(A))。
