计算机系统结构第二章第一部分
系统结构讲义-2

码元分配:从树根开始,对每个中间结点的左右2个分支边各赋予
一位代码“0”和“1”(“0”在哪一侧不限)。读出从根结点到任一片树叶 的路径上依次出现的代码位就排成了这个事件(即指令)的完整编码。 由于频度高的事件较晚被合并,它的编码位数也就较少,符合Huffman压 缩原则。
上面所说的频度值就是各事件实际出现次数的百分比, 它是理论出现概率的近似值。 例:假设一台模型计算机共有7种不同的操作码,已 知各种操作码在程序中出现的概率如下表,利用Huffman 编码法进行操作码编码。 指令 概率 I1 0.45 I2 0.30 I3 0.15 I4 0.05 I5 0.03 I6 0.01 I7 0.01
第二章 指令系统
2.3 指令格式的优化设计
指令格式的优化是指如何用最短的二进制位数表示指令的操作码信息和 地址码信息,使指令的平均字长最短,同时便于译码。
指令的组成 操作码 地址码
1) 指令的操作种类。 2) 所用操作数数据 类型。
1) 操作数地址。 2) 地址附加信息。 3) 寻址方式。
指令格式的优化设计目标: 1) 使程序中指令的平均字长最短,节省程序的存储空间。 2) 指令格式要规整,减少硬件译码的复杂程度。
1632和64位固定32位指令时钟频率随技术发展而变化随技术发展而变化寄存器堆824个通用寄存器32192个分离的整数和浮点寄存器堆指令系统规模和类型约300条多于48种指令类型大都基于寄存器寻址方式约12种包含间接变址寻址35种只有取存寻址存储器高速缓存设计较早使用合一高速缓存有些使用分离高速缓存大多数使用分离的数据和指令高速缓存cpi及平均cpi120个周期平均4个简单操作1个周期平均约15个cpu控制大多数用微程序控制有些使用硬连线控制大多数用硬连线控制没有控制存储器代表性商品化处理器intelx86vax8600ibm390mc68040intelpentiumamd486和cyrix686sunultrasparcmipsr10000powerpc604hppa8000digitalalpha21164混合混合ciscriscciscrisc体系结构体系结构pentiumpropentiumpro处理器的处理器的ciscriscciscrisc体系结构体系结构分分基于基于riscrisc核心核心dbab将将x86x86代码转化为代码转化为riscrisc指令指令
第2章计算机系统的组成

2.2 计算机硬件系统
算
输 入 设 备 备 设 出
输
1.1 计算机硬件
2. 2. 1
微型计算机的硬件组成
微型计算机硬件系统由主机和常用外围设备两大部分 组成。 组成。 主机由中央处理器(CPU)和内存储器 和内存储器(ROM,RAM)组 主机由中央处理器 和内存储器 组 用来执行程序、处理数据, 成,用来执行程序、处理数据,主机芯片都安装在一 块电路板上,这块电路板称为主机板(主板)。 )。为了 块电路板上,这块电路板称为主机板(主板)。为了 与外围设备连接, 与外围设备连,在主机板上还安装有若干个接口插 槽,可以在这些插槽上插入不同外围设备连接的接口 用来连接不同的外部设备。 卡,用来连接不同的外部设备。 主机与外围设备之间信息通过两种接口传输。 主机与外围设备之间信息通过两种接口传输。一种是 串行接口,如鼠标;一种是并行接口,如打印机。 串行接口,如鼠标;一种是并行接口,如打印机。
常用的总线结构有: 常用的总线结构有: (1)ISA总线 ) 总线 (2)MCA总线 ) 总线 (3)EISA总线 ) 总线 (4)VESA总线 ) 总线 (5)PCI总线 ) 总线
2. 2. 2
微型计算机的常见外设
微型计算机常用外围设备有显示器、键盘、 微型计算机常用外围设备有显示器 、 键盘 、 鼠标器 及外存储器。外存中常用的有硬磁盘(硬盘) 及外存储器 。 外存中常用的有硬磁盘 ( 硬盘 ) 、 软 磁盘(软盘)和光盘。 磁盘 ( 软盘 ) 和光盘 。 如果需要还可以根据用户的 要求配置打印机、绘图仪、投影仪; 要求配置打印机 、 绘图仪 、 投影仪 ; 同时为了联网 还可以配置调制解调器等通信设备。 ,还可以配置调制解调器等通信设备。 微机用键盘按照按键个数多少可分为84键 微机用键盘按照按键个数多少可分为 键、101键、 键 104键等几种,目前广泛使用的是 键等几种, 键等几种 目前广泛使用的是101键、104键标准 键 键标准 键盘。这两种键盘一般可分为四个区域: 键盘 。 这两种键盘一般可分为四个区域 : 主键盘区 功能键区、编辑键区、小键盘区(数字键区) 、功能键区、编辑键区、小键盘区(数字键区)。
【精品】计算机

7.在浮点加法运算中,完整的操作步骤是对阶。尾数相加、结果规格化、舍入、溢出检查。
8.定点运算器中一般包括ALU、寄存器、对路选择器、移位器和数据通路。
9.ALU的基本逻辑结构是快速进位加法器,它比行波进位加法器优越,具有先行进位逻辑,不仅可以实现高速运算,还能完成逻辑运算。
10.浮点运算器由阶码运算器和尾数运算器组成,它们都是定点运算器,尾数运算器要求能进行加、减、乘、除运算。
18.一条机器指令由一段微指令构成的微程序来解释执行;微指令可由一系列微命令组成。
19.控制部件通过控制线向执行部件发出各种控制命令,通常把这种控制命令叫做微命令。而执行部件接受此控制命令后进行的操作叫做微操作。
20.一条微指令可划分为微命令字段和控制字段;微指令的基本格式可分为水平型和垂直型。
12.虚拟存储器管理的基本方法有页式、段式和段页式三种。
13.在虚拟存储器中,一般采用全相联地址映像方法和LRU更新策略。
14.虚拟存储器中,程序正在执行时,由操作系统完成地址映像。
15.在磁表面存储器中,调频制(FM)记录方式目前主要用于单密度磁盘存储器,改进调频制(MFM)记录方式主要用于双密度磁盘存储器,而在磁带存储器中一般采用调相制(PE)和成组编码(GCR)记录方式。
21.由于数据通路之间的结构关系,微操作可分为相容性和相斥性两种;
在同一微周期中不可能同时出现的微命令,称之为互斥的微命令。
在同一微周期中可以同时出现的微命令,称之为相容的微命令。
22.在微指令的字段编码中,操作控制字段的分段必须遵循的原则包括:
把互斥性的微命令分在同一段内。
一般每个小段要留出一个状态0,表示不操作。
1.-1的补码定点整数表示时为1...1,用定点小数表示时为1...0。
计算机组成与系统结构课后答案免费版全(清华大学出版社 袁春风主编)

计算机组成与系统结构课后答案免费版全(清华大学出版社袁春风主编)计算机组成与系统结构课后答案免费版全(清华大学出版社-袁春风主编)第一章练习答案5.若有两个基准测试程序p1和p2在机器m1和m2上运行,假定m1和m2的价格分别是5000元和8000元,下表给出了p1和p2在m1和m2上所花的时间和指令条数。
程序p1p2m1指令条数200×106300×103执行时间(ms)100003指令条数150×106420×103m2执行时间(ms)50006请回答下列问题:(1)对于p1,哪台机器的速度快?快多少?对于p2呢?(2)在m1上执行p1和p2的速度分别是多少mips?在m2上的执行速度又各是多少?从执行速度让我们看看,对于P2,哪台机器速度快?多快?(3)假设M1和M2的时钟频率分别为800 MHz和1.2 GHz,则P1在M1和M2上执行时的平均时钟周期期数cpi各是多少?(4)如果某个用户需要大量使用程序p1,并且该用户主要关心系统的响应时间而不是吞吐率,那么,当用户需要购买大量机器时,他应该选择M1还是M2?为什么?(注意:在性价比方面)(5)如果另一个用户也需要购买大量机器,但用户同样使用P1和P2,那么主要的问题是响应时间间,那么,应该选择m1还是m2?为什么?参考答案:(1)对于p1,m2比m1快一倍;对于p2,m1比m2快一倍。
(2)对于M1,P1的速度为200m/10=20mips;P2为300K/0.003=100mips。
对于m2,p1的速度为:150m/5=30mips;p2为420k/0.006=70mips。
就执行速度而言,对于P2,因为100/70=1.43倍,M1比m2快0.43倍。
(3)在M1上执行P1时的平均时钟周期数CPI为:10×800m/(200×106)=40在m2上执行p1时的平均时钟周期数cpi为:5×1.2g/(150×106)=40。
第二章 计算机控制系统的组成
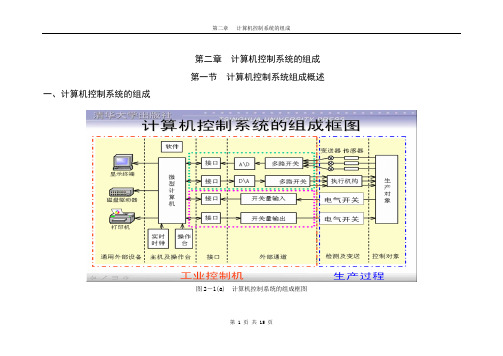
第二章 计算机控制系统的组成第 1 页 共 15 页第二章 计算机控制系统的组成 第一节 计算机控制系统组成概述一、计算机控制系统的组成图2-1(a) 计算机控制系统的组成框图如图2-1(a)所示,计算机控制系统主要由工业控制机和生产过程两大部分组成。
工业控制机是指按生产过程控制的特点和要求而设计的计算机,它包括硬件和软件两部分;生产过程包括被控对象、测量变送、执行机构、电气开关等装置,这些装置有各种类型的标准产品,在设计计算机控制系统时根据需要进行合理选型。
二、工业控制机工业控制机是指按生产过程控制的特点和要求而设计的计算机,它包括硬件和软件两部分。
1、工业控制机的硬件组成图2-1(b)工业控制机的硬件组成原理图工业控制机的硬件包括主机板、内部总线和外部总线、人机接口、磁盘系统、通信接口、输入输出通道。
(1)主机板:CPU、RAM、ROM等。
作用:进行数值计算、逻辑判断、数据处理。
(2)内部总线和外部总线内部总线:工业控制机内部各组成部分进行信息传送的公共通道,它是一组信号线的集合。
常用内部总线有IBM PC、PCI总线和STD总线。
外部总线:工业控制机与其它计算机和智能设备进行信息传递的公共通道。
RS—232C、USB和IEEE—488通信总线。
(3)人—机接口:键盘、显示器、打印机。
(4)磁盘系统:软盘和硬盘。
(5)通信接口: 工业控制机和其它计算机或智能外设通信的接口。
常用RS—232C、USB和IEEE—488接口。
(6)系统支持功能①监控定时器(看门狗-Watchdog) ②电源掉电检测③保护重要数据的后备存贮器体 ④实时日历时钟(7) 输入输出通道工业控制机和生产过程之间设置的信号传递和变换的连接通道。
它包括模拟量输入(AI)通道、模拟量输出(AO)通道、数字量(或开关量)输入(DI)通道、数字量(或开关量)输出(DO)通道。
它的作用有两个:其一、是将生产过程的信号变换成主机能够接受和识别的代码;其二、是将主机输出的控制命令和数据,经变换后作为执行机构或电气开关的控制信号。
计算机体系结构知识点

第一章计算机体系结构得基本概念1 计算机系统结构得经典定义程序员所瞧到得计算机属性,即概念性结构与功能特性。
2 透明性在计算机技术中,把这种本来存在得事物或属性,但从某种角度瞧又好像不存在得概念称为透明性。
3 系列机由同一厂家生产得具有相同系统结构、但具有不同组成与实现得一系列不同型号得计算机。
4 常见得计算机系统结构分类法有两种:Flynn 分类法、冯氏分类法Flynn 分类法把计算机系统得结构分为4 类:单指令流单数据流(SISD)单指令流多数据流(SIMD)多指令流单数据流(MISD)多指令流多数据流(MIMD)5 改进后程序得总执行时间系统加速比为改进前与改进后总执行时间之比6CPI(Cycles Per Instruction ):每条指令执行得平均时钟周期数CPI = 执行程序所需得时钟周期数/IC7 存储程序原理得基本点:指令驱动8冯•诺依曼结构得主要特点1 以运算器为中心。
2 在存储器中,指令与数据同等对待。
指令与数据一样可以进行运算,即由指令组成得程序就是可以修改得。
3 存储器就是按地址访问、按顺序线性编址得一维结构,每个单元得位数就是固定得。
4 指令得执行就是顺序得5 指令由操作码与地址码组成。
6 指令与数据均以二进制编码表示,采用二进制运算。
9 软件得可移植性一个软件可以不经修改或者只需少量修改就可以由一台计算机移植到另一台计算机上正确地运行。
差别只就是执行时间得不同。
我们称这两台计算机就是软件兼容得。
实现可移植性得常用方法:采用系列机、模拟与仿真、统一高级语言。
软件兼容:向上(下)兼容:按某档机器编制得程序,不加修改就能运行于比它高(低)档得机器。
向前(后)兼容:按某个时期投入市场得某种型号机器编制得程序,不加修改地就能运行于在它之前(后)投入市场得机器。
向后兼容就是系列机得根本特征。
兼容机:由不同公司厂家生产得具有相同系统结构得计算机。
10 并行性:计算机系统在同一时刻或者同一时间间隔内进行多种运算或操作。
系统结构复习

中国地质大学(武汉)计算机学院吴湘宁计算机体系结构习题及答案第一章基础知识1.名词解释翻译解释模拟仿真透明性程序访问局部性[答案]略2. 一个经解释实现的计算机可以按功能划分为四级. 每一级为了执行一条指令需要下一级的N条指令. 若执行第一级的一条指令需要的时间为K ns, 那么执行第二、三、四级的一条指令各需要多少时间?3. 计算机系统按功能划分层次结构的好处主要体现在哪些方面?[答案] (1) 有利于理解软件, 硬件和固件在系统中的地位和作用;(2) 有利于理解各种语言的实质和实现途径;(3) 有利于推动计算机系统结构的发展;(4) 有利于理解计算机系统结构的定义.4. 什么是透明性? 对计算机系统结构, 下列哪些是透明的? 哪些是不透明的?1) 存储器的模m交叉存取; 2) 浮点数据表示; 3) I/O系统是采用通道方式还是I/O处理机方式; 4) 阵列运算部件; 5) 数据总线宽度; 6) 通道是采用结合型的还是独立型的; 7) 访问方式保护; 8) 程序性中断; 9) 串行、重叠还是流水控制方式; 10) 堆栈指令; 11) 存储器的最小编址单位; 12) Cache存储器.[答案] 一种本来是存在的事务或属性, 但从某种角度看却好像不存在, 称为透明性.对计算机系统结构来说透明的是: 1), 4), 5), 6), 9), 12)对计算机系统结构来说不透明的是:2), 3), 7), 8), 10), 11)5. 什么是计算机体系结构? 什么是计算机组成? 什么是计算机实现? 并说明三者的关系和相互影响?[答案] 计算机系统结构是计算机系统的软, 硬件分界面, 是机器语言程序员或是编译程序员所需了解的计算机属性;计算机组成是计算机系统结构的逻辑事项;计算机实现是计算机组成的物理实现.三者的关系和互相影响为:(1) 具有相同系统结构的计算机可以采用不同的组成;(2)(2) 一种计算机组成可以采用多种不同的计算机实现;(3) 计算机组成、计算机实现对计算机系统结构有着很大的影响;(4) 计算机系统结构的设计不应限制计算机组成和实现技术,应能用于高档机,也可用于低挡机;(5) 在不同时期, 计算机系统结构,、组成和实现所包含的内容会有所变化,三者之间的界线常常很模糊.6. 从机器(汇编)语言程序员角度看, 以下哪些是透明的?1) 指令地址存储器; 2) 指令缓冲器; 3) 时标发生器; 4) 条件码寄存器; 5) 乘法器; 6) 主存地址寄存器; 7) 磁盘外设; 8) 先行进位链; 10) 通用寄存器; 11) 中断字寄存器.[答案] 对机器(汇编)语言程序员来说透明的有: 2), 3), 5), 6), 8), 9)对机器(汇编)语言程序员来说不透明的有: 1), 4), 7), 10), 11)7. 假设在一台40 MHz处理机上运行200 000条指令的目标代码, 程序主要由四种类型的指令所组成. 根据程序跟踪实验结果, 各类指令的混合比和每类指令的CPI值如表1.9所示.(1) 试计算在单处理机上执行上述该程序时的平均CPI;(2) 根据(1)所得到的CPI, 计算相应的MIPS速率及程序的执行时间.[答案] (1) 2.24 CPI (2) 17.86 MPIS; 0.0112 s8. 某工作站采用时钟频率为15 MHz、处理速率为10 MIPS的处理机来执行一个程序,假定每次存储器存取为1周期延迟, 试问:(1) 此计算机的有效CPI是多少?(2) 假定将处理机的时钟频率提高到30 MHz, 但存储器子系统速率不变, 这样, 每次存储器存取需要两个时钟周期. 如果30%的指令每条只需要一次存储存取, 而另外5%的指令每条需要两次存储存取, 还假定已知混合程序的指令数不变, 并与原工作站兼容, 试求改进后的处理机性能.[答案] (1) 1.5 CPI; (2) 15.8 MPIS9.什么是并行性?它分为哪两种类型?开发计算机系统并行性的主要技术途径有哪三个?沿这些途径分别发展出什么类型的计算机?[答案]略10.实现软件移植的途径有哪些?[答案]略11.什么是Flynn分类法,按照Flynn分类法可将计算机系统分为哪几类?[答案]略第二章指令系统1. 名词解释数据类型、数据表示、规格化浮点数、Huffman编码、扩展编码、RISC[答案]略2. 某模型机有8条指令I1~I8, 它们的使用频度分别为0.3, 0.3, 0.2, 0.1, 0.05, 0.02, 0.02, 0.01.(1) 试分别用Huffman编码和平均码长最短的等长扩展码(限定为两种码长)对其操作码进行编码.(2) 分别计算Huffman编码和等长扩展码编码的平均长度.[答案] (1) 操作码的Huffman编码和2-4等长扩展码编码如下表1所示.(2) Huffman编码的平均长度为2.38位; 等长扩展码编码的平均码长为2.8位.3. 某模型机有10条指令I1~I10, 它们的使用频度分别为0.3, 0.24, 0.16, 0.12, 0.07, 0.04, 0.03,0.02, 0.01, 0.01.(1) 计算机采用等长操作码表示时的信息冗余量.(2) 要求操作码平均码长最短, 试设计操作码的编码, 并计算所设计操作码的平均长度. (3) 设计2-5扩展操作码编码,并计算平均码长.(4) 设计2-4(2/8)等长扩展码编码,并计算平均码长. [答案] (1) 采用等长操作码表示时的信息冗余量为33.5%. (2) 操作码的Huffman编码如表2所示, 此种编码的平均长度为2.7位.(3) 操作码的2-5扩展码编码如表2所示, 此种编码的平均长度为2.9位.(4) 操作码的2-4(2/4)等长扩展码编码如表2所示, 此种编码的平均长度为2.92位.4. 何谓指令格式的优化? 操作码和地址码的优化一般采用哪些方法?[答案] 指令格式的优化是指通过采用多种不同的寻址方式, 地址制, 地址形式和地址码长度以及多种指令字长, 并将它们与可变长操作码的优化表示相结合, 就可以构成冗余度尽可能少的指令字. 操作码的优化采用扩展操作码编码法. 地址码优化有以下四种方法:(1) 在指令中采用不同的寻址方式;(2)(2) 在指令中采用多地址制;(3) 同一种地址制还可以采用多种地址形式和长度, 也可以考虑利用空白处来存放直接操作数或常数等;(4) 在以上措施的基础上, 还可以进一步考虑采用多种指令字长度的指令.5. 若某机设计有如下指令格式的指令:三地址指令12种, 一地址指令254种, 设计指令的长度为16位, 每个地址码字段的位数均为4位. 若操作码的编码采用扩展操作码, 问二地址指令最多可以设计多少种? [答案] 二地址指令最多可以设计48种.6. 一台模型机共有九条指令I1~I9, 各指令的使用频度分别为0.3,0.2,0.2,0.1,0.08,0.6,0.03, 0.02, 0.01. 该模型机有8位和16位两种指令字长. 8位字长指令为寄存器----寄存器(R--R)二地址类型, 16位字长指令为寄存器----存储器(R--M)二地址变址寻址类型.(1) 试设计有两种码长的扩展操作码, 使其平均码长最短, 并计算此种编码的平均码长. (2) 在(1)的基础上, 该机允许使用多少个可编址的通用寄存器?(3) 若采用通用寄存器作为变址寄存器, 试设计该机的两种指令格式, 并标出各字段的位数.(4) 计算变址寻址的偏移地址范围.[答案] (1) 操作码的2-5扩展码编码如表3所示, 此种编码的平均长度位2.9位.2) 在(1)的基础上, 该机允许使用8个可编址的通用寄存器.(3) 该机的两种指令格式及各字段的位数如下:R-R型: 操作码OP (2位) | 源寄存器RS (3位) | 目的寄存器Rd (3位)R-M型: 操作码OP (5位) | 源寄存器RS (3位) | 变址寄存器RX (3位) | 偏移地址 (5位)(4) 变址寻址的偏移地址范围为-16~+15.7. 简述CISC的特点.[答案] CISC的特点如下:(1) 庞大的指令系统;(2) 采用了可变长度的指令格式;(3) 指令使用的寻址方式繁多;(4) CISC指令系统中包括一些用于特殊用途的指令, 各种指令的使用频度相当悬殊.8. 从指令格式, 寻址方式以及平均CPI三个方面, 比较经典CISC和纯RISC体系结构.[答案] 略9.简述RISC设计的一般原则。
02325计算机系统结构复习资料

第一章计算机系统结构的基本概念从处理数据的角度看,并行级别有位串字串,位并字串,位片串字并,全并行。
位串字串和位并字串基本上构成了SIMD。
位片串字并的例子有:相联处理机STARAN,MPP。
全并行的例子有:阵列处理机ILLIACIV。
从加工信息的角度看,并行级别有存储器操作并行,处理器操作步骤并行,处理器操作并行,指令、任务、作业并行。
存储器操作并行是指可以在一个存储周期内并行读出多个CPU字的,采用单体多字、多体单字或多体多字的交叉访问主存系统,进而采用按内容访问方式,位片串字并或全并行方式,在一个主存周期内实现对存储器中大量字的高速并行操作。
例子有并行存储器系统,以相联存储器为核心构成的相联处理机。
处理器操作步骤并行是指在并行性概念中引入时间因素,让多个处理过程在时间上错开,轮流重复地执行使用同一套设备的各个部分,加快硬件周转来赢得速度。
例子有流水线处理机。
处理器操作并行是指一个指令部件同时控制多个处理单元,实现一条指令对多个数据的操作。
擅长对向量、数组进行处理。
例子有阵列处理机。
指令、任务、作业并行是指多个独立的处理机分别执行各自的指令、任务、作业。
例子有多处理机,计算机网络,分布处理系统。
并行性的开发途径有时间重叠(Time Interl eaving ),资源重复(Resou rceReplication),资源共享(ResourceSharing)。
时间重叠是指在并行性概念中引入时间因素,让多个处理过程在时间上错开,轮流重复地执行使用同一套设备的各个部分,加快硬件周转来赢得速度。
例子有流水线处理机。
资源重复是指一个指令部件同时控制多个处理单元,实现一条指令对多个数据的操作。
例子有阵列处理机,相联处理机。
资源共享是指用软件方法让多个用户按一定时间顺序轮流使用同一套资源以提高资源的利用率,从而提高系统性能。
例子有多处理机,计算机网络,分布处理系统。
SISD:一个指令部件控制一个操作部件,实现一条指令对一个数据的操作。
计算机系统结构年串讲及汇总第一部分

第一章计算机系统结构的基本概念1. 从使用语言的角度可以将系统看成是按功能划分的多个机器级组成的层次结构;由高到低分别为:1应用语言机器级 2高级语言机器级 3汇编语言机器级 4操作系统机器级 5传统机器语言机器级 6微程序机器级;2. 应用程序语言经应用程序包的翻译成高级语言程序;3. 高级语言程序经编译程序的翻译成汇编语言程序;4.汇编语言程序经汇编程序的翻译成机器语言程序;5.在操作系统机器级,一般用机器语言程序解释作业控制语句;6.传统机器语言机器级,是用微指令程序来解释机器指令;7.微指令由硬件直接执行;8. 在计算机系统结构的层次结构中,机器被定义为能存储和执行相应语言程序的算法和数据结构的集合体;9.透明指的是客观存在的事物或属性从某个角度看不到,它带来的好处是简化某级的设计,带来的不利是无法控制10.翻译:先用转换程序将高一级机器级上的程序整个地变换成底一级机器级上行将的程序,然后在低一级机器级上实现的技术11.解释:在低级机器级上用它的一串语句或指令来仿真高级机器级上的一条语句或指令的功能,通过高级机器语言程序中的每条语句或指令逐条解释来实现的技术;12硬件取舍原则:1应考虑在现有硬器件主要是逻辑器件和存储器件条件下,系统要有高的性能价格比;2要考虑到准备采用和可能采用的组成技术,使它尽可能不要过多或不合理地限制各种组成、实现技术的采用;3不能仅从“硬”的角度考虑如何便于应用组成技术的成果和便于发挥器件技术的进展,还应从“软”的角度把如何为编译和操作系统的实现以及为高级语言程序的设计提供更多更好的硬件支持放在首位;13. 计算机系统的设计思路:1由上往下2由下往上3由中间开始14. 软件的可移植性:指的是软件不修改或只经少量修改就可由一台机器搬到另一台机器上运行,同一软件可应用于不同的环境;15. 实现欠件移植的几个基本技术:1统一高级语言 2采用系列机 3模拟与仿真16. 为什么没有对各种应用真正通用的语言1不同的用途要求语言的语法、语义结构不同;2人们对语言的基本结构看法不一;3即使同一种高级语言在不同厂家的机器上也不能完全通用;4受习惯势力阻挠,人们不愿意抛弃惯用的语言;17 模拟:用机器语言程序解释实现软件移植的方法称为模拟;需经二重解释,速度低,实时性差模拟灵活,可实现不同系统间的软件移植,系统差异太大时效率速度急剧下降18 仿真:用微程序直接解释另一种机器指令系统的方法称为仿真;速度上损失小,但不灵活,只在差别不大的机器上使用,两种机器差别太大时,就很难仿真19 模拟与仿真的区别:仿真是用微程序解释,其解释程序存入在控制存储器中;而模拟是用机器语言程序来解释,其解释程序存放在主存中;20 并行性:把解题中具有可以同时进行运算或操作的特性;并行性包括1同时性和2并发性同时性:指两个或多个事件在同一时刻发生并发性:指两个或多个事件在同一时间间隔内发生21开发并行性途径:1时间重叠 2资源重复 3资源共享时间重叠:让多个处理过程在时间上相互错开,轮流重叠地使用同一套硬件设备的各个部分,加快硬件周围来赢得速度;资源重复:通过得利设置硬件资源来提高可靠性或性能;资源共享:用软件方法让多个用户按一定时间顺序轮流使用同一套资源来提高其利用率,相应也就提高了系统的性能;第二章数据表示与指令系统1.数据表示:指的是能由机器硬件直接识别昨引用的数据类型;2.数据结构反映了应用中要用的各种数据元素或信息单元之间的结构关系; 数据表示是数据结构的组成元素;3.数据结构和数据表示是软、硬件的交界面;数据表示的确定实质是软、硬件的取舍;4.高级数据表示:1自定义数据表示 2微量数组数据表示 3堆栈数据表示5.标志符数据表示:将数据类型和数据本身直接联系到一起;合存于同一存储单元中6.标志符数据表示的优点:1简化了指令系统和程序设计2简化了编译程序3便于实现一至性校验4能由硬件自动变换数据类型5支持了数据库系统的实现与数据类型无关的要求6为软件调试和应用软件开发提供了支持7.标志符数据表示可能带来的问题:1每个数据字因增设标志符,会增加程序所占的主存空间2采用标志符会降低指令的执行速度8.规模机器的特征:(1)有高速寄存器组成的硬件堆栈,并附加控制电路让它与主存中的堆栈区在逻辑上构成整体,使堆栈的访问速度是寄存器,容量是主存的(2)有丰富的堆栈操作指令且功能很强,直接可对堆栈中的数据进行各种去处和处理(3)有力地支持高级语言程序的编译(4)有力地支持子程序的嵌套和递归调用9.引入数据表示的原则:(1)看系统的效率有否提高,即是否减少了实现时间的存储空间(2)看引入这种数据表示后,其通用性和利用率是否高10.浮点数尾数的下溢处理方法:1截值法 2舍入法 3恒置1法 4查表舍入法11.寻址方式:指的是指令按什么方式寻长或访问到所需的操作数或信息;12.寻址方式在指令中的两种指明方式:1 占有操作码中的某些位 2在地址码部分专门设置寻址方式位字段指明13.逻辑地址是程序员编程用的地址;物理地址是程序在主存中的实际地址;14.静态再定位:在目的程序装入主存时,由装入程序用软件方法把目的程序的逻辑地址变换成物理地址15.动态再定位:在执行每条指令时才形成访存物理地址的方法16.指令由操作码和地址码两部分构成;操作码指明操作种类和所用操作数的数据类型;地址码包括操作数的地址、地址的附加信息、寻址方式等;17.指令格式的优化:指的是如何用最短的倍数来表示指令的操作信息和地址信息,使程序中指令的平均字长最短;18.操作码的优化表示,主要是为了缩短指令字长,减少程序总位数及增加指令字能表示的操作信息和地址信息;19.哈夫曼压缩概念的基本思想:当各种事件发生的概率不均等时,采用优化技术对发生概率最高的事件用最短的位数时间来表示处理,而对出现概率较低的,允许用较长的位数时间来表示处理,这样,就会导致表示处理的平均时间的缩短;20.操作码的表示方式通常有下列三种:1固定长度编码法 2哈夫曼编码法 3扩展操作码编码法21.指令系统的设计、发展和改进上的两种不同方向:1CISC 2RISC22.CISC:进一步增强原有指令的功能以及设置更为复杂的新指令取代原先由软子程序完成的功能,实现软件功能的硬化;23.CISC复杂指令系统计算机的优化实现:1 面各目标程序的优化2 面向高级语言的优化3 面向操作系统的优化24.面向目标程序的优化1 对存贮器语言程序及其执行情况进行统计各种指令和指令串的使用频度来加以分析和改进;静态使用频度:对程序中统计出的指令及指令串使用频度着眼于减少目标程序所占用的储存空间动态使用频度:在目标程序执行过程中对指令和指令串统计出的频度着眼于减少目标程序的执行时间2 增设强功能复合指令来取代原先是由常用宏指令或子程序实现的功能,用微程序解释实现;25.面向高级语言优化实现改进尽可能缩短高级语言和机器语言的语义差距,支持高级语言编译,缩短编译程序长度和编译时间1 通过对源程序中各种高级语言语句的使用频度进行统计来分析改进;2 如果面向编译,优化代码生成来改进;3 设法改进指令系统,使它与各种语言间的语义差距都有同等的缩小;4 让机器具有分别面向各种高级语言的多种指令系统、各种系统结构;5 发展高级语言计算机或称高级语言机器26.面向操作系统的优化1 对常用指令和指令串的使用频度进行统计分析来改进;改进指令系统2 考虑如何增设专用于操作系统的新指令;改进指令系统3 把操作系统中频繁使用的对速度影响大的某些软件子程序硬化或固化,改为直接用硬件或微程序解释实现;4 发展让操作系统由专门的处理机来执行的功能分布处理系统结构;27.CISC存在的问题:1 指令系统庞大,一般在200条指令以上;许多指令功能异常复杂;2 由于许多指令的繁杂,执行速度很低;3 指令系统庞大,故高级语言编译程序选择目标指令的范围大太,难以优化生成高效机器语言程序,编译程序也太长太复杂;4 由于指令系统庞大,各种指令的使用频度都不会太高,具差别很大,其中相当一部分指令的利用率很低;28.设计RISC的原则:1 只选择那些使用频度很高的指令,再增加少量其他功能的指令,使之一般不超过100条2 减少指令系统寻址方式各类,一般不超过两种,并让全部指令都是相同的长度;3 让所有指令都在一个机器周期内完成4 扩大通用寄存器数,尽量减少访存;仅存store、取load指令访存,其他指使一律对寄存器操作;5 大多数年指令都用硬联控制实现,少数指令用微程序实现;6 精简指令和优化设计编译程序,简单有效地支持高级语言的实现;29.设计RISC结构用的基本技术:1 按RISC一般原则设计2 逻辑实现用硬联和微程序结合3 用重叠寄存器窗口4 指令用流水和延迟转移5 优化设计编译系统30.采用RISC技术带来的好处:1 简化指令系统设计,适合VLSI实现2 提高机器的执行速度和效率3 设计成本,提高了系统的可靠性4 可直接支持高级语言的实现31.RISC的不足:1 由于指令少,一条CISC指令能完成的某些功能需要多条RISC指令才能完成,加重了汇编各方程序设计的负担,增加了机器语言程序的长度,占用在座空间多,加大了指令的信息流量;2 对浮点去处执行的虚拟存储器的支持虽有很大加强,但仍显不足;3 RISC机器的编译程序比CISC的难写;第三章总线、中断与输入输出系统1.输入输出系统包括输入输出设备、设备控制器及与输入输出操作有关的软硬件2.I/O系统设计主要考虑解决好CPU、主存和I/O设备在速度上的巨大差距;3.输入输出系统发展经历了三个阶段:1程序控制I/O 2直接存储器访问 3I/O处理机方式a.通道 b.外围处理机方式4.总线类型:按信息传送方向分:1单向传输 2双向传输按用法分:1专用 2非专用相关介绍及优缺点见P635.非专用总线总线控制方式:集中式控制:总线控制机构基本上集中在一起; 分布式控制:总线控制逻辑分散在各个部件中 P646.集中式总线控制:1串行链接控制 2定时查询方式 3独立查询方式P647.集中式串行链接式的总线分配过程:1.部件发总线请求;2.总线不忙时,总线控制器返回总线响应总线可用信号;3.没发总线请求信号的部件传送总线响应信号,发的部件截留响应信号;4.截留后,发总线忙状态,撤销请求,开始占用总线;5.传送结束撤销总线忙;6.总线不忙后,撤销总线响应;8.优点: 1.选择算法简单,控制线线数少; 2.部件增加容易,可扩充性好; 3.容易通过重复设置提高可靠性;9.缺点: 1.对“总线可用”线及其有关电路的失效敏感; 2.优先级是线连固定,不灵活; 3.限制了总线的分配速度;10.集中定时查询方式的总线分配过程:1.部件发总线请求;2.总线不忙时,总线控制器的查询计数器开始计数;3.定时查询各部件;4.部件接收计数值,并判断,若与部件号一致,则发总线忙,撤销请求,并占用总线;5.总线控制器收到总线忙,停止计数,停止查询;6.传送结束撤销总线忙;11.优点: 1.优先次序可用程序控制,灵活性强; 2.可靠性高;12.缺点: 1.总线线数较多; 2.部件数受限于定时查询线线数; 3.控制较为复杂; 4.总线分配的速度不能提高;13.集中式独立请求方式的总线分配过程:1.部件发总线请求;2.总线不忙时,按某种算法,发一个总线响应;3.被响应部件发总线忙状态,撤销请求,开始占用总线;4.传送结束,撤销总线忙;5.总线不忙后,撤销总线响应;14.优点:1.总线分配速度快; 2.可用选定的方式确定响应的部件; 3.能方便的隔离失效部件的请求;15.缺点:1.控制线数量过大; 2.总线控制器要复杂的多;16.总线的传送方式分为:1同步通信 2异步通信17.同步通信:两个部件之间的信息传送是通过定宽定距的系统时标进行同步的受同步时钟的控制18.同步通信的优点:信息传送速率高,受总线的长度影响小;19.同步通信的缺点:但会因时钟在总线上的时滞而造成同步误差, 且时钟线上的干扰信号易引起误同步;20.异步通信:用于I/O总线,连接不同速度的I/O设备;又可分为a.单向控制和b.双向请求/回答控制两种1单向控制:指的是通信过程只由目的或源部件中的一个单一控制;单向控制又有源控制和目的控制两种;优点:简单,高速;缺点:未能保证下一数据传送之前让所有数据线和控制线的电平信号恢复成初始状态,从而可能造成错误;2请求/回答双向控制:由源和目共同控制;特点:增加了信号总线来回传送的次数,使控制硬件变得复杂,但它能适应各种不同速度的I/O设备,保证数据传送的正确性,有较高的数据传送率;21.数据宽度:是I/O设备取得I/O总线使用权后在一次I/O总线分配期间内,所传送数据的总量;22.数据通路宽度:数据总线的位数,是数据传送的物理宽度;即一个时钟周期所传送的信息量,它直接取决于数据总线的线数;23.总线的线数越多,成本越高、干扰越大、可靠性越低、占用的空间也越大,当然传送速度和流量也越高;为此,越是长的总线,其线数就应尽可能减少;24.减少线数的方法:1同一根线多个功能复用; 2并/串—串/并转换 3编码25.中断源:引起中断的各种事件; 中断请求:中断源向中断系统发出请求中断的申请; 中断响应:允许中断请求中断CPU现行程序的运行,转去对该请求进行预处理,包括保存好断点现场,调出有关处理该中断的中断处理程序,准备运行;26.中断分类的目的:中断源数量很多,若形成单独入口,硬件复杂,代价大,故进行分类,把性质相近的中断源归为一类;同一类中断共用一个中断入口地址,再由软件形成实际入口地址;27.中断的分类:1机器校验中断第一级:设备故障,电源故障,主存出错;2管理程序调用访管中断第二级:访管指令;3程序性中断第二级:溢出,除数为零,数据格式错;4外部中断第三级:定时器,外部信号;5输入/输出中断第四级:I/O请求;6重新启动中断第五级:启动另一个程序;28.中断分级的目的:解决多个中断请求同时发生时的响应次序问题;29.分级原则: 1同一类的优先次序由软件管理一般情况下,同类同级,不同类不同级2不同类的中断根据中断的轻重缓急分成不同的级别;30.中断嵌套原则: 1禁止同级或低级中断; 2允许高级中断;31.中断响应次序和处理次序中断响应次序用排队器硬件实现,次序是由高到低定死的,但可以根据需要用软件改变实际的中断处理完次序简称中断处理次序;中断级屏蔽位的作用:决定某级中断请求能否进入排队器只要能进入,还是按上面讲的优先级次序由高到底响应中断中断响应次序由硬件定死;而处理次序由中断屏蔽位决定;32.中断系统的功能包括:中断请求的保存与清除,确定优先级,保护断点,保护现场,中断源分析,中断处理,中断返回等;33.中断系统的软、硬件功能分配实质是中断处理程序软件和中断响应硬件的功能分配;34.中断系统的软件与硬件的功能分配主要考虑如下两个因素:1中断响应时间 2灵活性;35.通道的功能:1接受CPU的输入输出操作指令,按指令要求控制外设接受指令2从主存读取通道程序,并执行即向设备控制器发送各种指令执行程序3组织和控制数据在内存与外设之间的传送操作传送数据4读取外设的状态信息,形成整个通道的状态信息,提供给CPU或保存在主存中通道状态5向CPU发出输入输出操作中断请求中断请求36.通道的工作过程:1用户在目态中安排广义I/O指令;包括访管指令和参数2当目态程序执行到访管指令后,产生访管中断;3CPU响应中断,第一次访管态,运行管态程序;4管理程序编制通道程序;根据参数:设备号、主存地址、信息长度等通道程序放在主存中,由通道执行5执行“启动I/O”指令:选择通道,校验第一条通道指令格式,选择设备并启动通道及设备;6通道启动后,<1>CPU退出管态,运行目态程序;<2>通道与设备开始传送数据;7通道传送结束后,向CPU发I/O中断;8CPU 响应中断,第二次转管态,对刚才的通道作“善后”处理;9返回目态,运行目态程序;37. 通道的种类:(1) 字节多路通道:适用于大量的像光电机等字符类低速设备;数据宽度:单字节多设备交叉(2) 数组多路通道:适合于连接多台像磁盘等调整设备;数据宽度:定长块多设备交叉(3) 选择通道:适合于优先级高的磁盘等调整设备,让它独占通道,只执行一台通道程序;数据宽度:可变长块独占38. 通道流量:通道在数据传送期内,单位时间内传送的字节数字节传输速率;它能达到的最大流量称通道极限流量;重要参数: TS : 选择一次设备的时间; TD :传送一个字节的时间; K :定长块的字节长度; N :传送的全部字节个数;39. 通道极限流量:字节多路通道:f max ·byte = 1/TS+TD 每选择一台设备,只传送一字节 数组多路通道:f max ·block = K/TS+K ·TD= 1/TS/K+TD 每选择一台设备,传送定长K 字节 选择通道: f max ·select = N/TS+N ·TD= 1/TS/N+TD显然,若通道的TS 、TD 一定, 且N>K 时,字节多路方式工作时所能达到的极限流量最小,数组多路方式工作的居中, 选择方式工作的最大;40. 如果通道上所挂p 设备都被启动,则设备对通道要求的的实际最大流量分别为:字节多路通道应为该通道所接各设备的字节传送速率之和, 即而对于其他两种类型的通道应为所接各设备的字节传送速率中之最大的那个, 即41. 保证第j 号通道上所挂的设备在满负荷的最坏情况下都不丢失信息的条件: 设备最大流量 <= 极限流量 ∑=⋅⋅=j p i j i j byte f f 1。
计算机系统结构(第2版(课后习题答案

word 文档下载后可自由复制编辑你计算机系统结构清华第 2 版习题解答word 文档下载后可自由复制编辑1 目录1.1 第一章(P33)1.7-1.9 (透明性概念),1.12-1.18 (Amdahl定律),1.19、1.21 、1.24 (CPI/MIPS)1.2 第二章(P124)2.3 、2.5 、2.6 (浮点数性能),2.13 、2.15 (指令编码)1.3 第三章(P202)3.3 (存储层次性能), 3.5 (并行主存系统),3.15-3.15 加 1 题(堆栈模拟),3.19 中(3)(4)(6)(8)问(地址映象/ 替换算法-- 实存状况图)word 文档下载后可自由复制编辑1.4 第四章(P250)4.5 (中断屏蔽字表/中断过程示意图),4.8 (通道流量计算/通道时间图)1.5 第五章(P343)5.9 (流水线性能/ 时空图),5.15 (2种调度算法)1.6 第六章(P391)6.6 (向量流水时间计算),6.10 (Amdahl定律/MFLOPS)1.7 第七章(P446)7.3 、7.29(互连函数计算),7.6-7.14 (互连网性质),7.4 、7.5 、7.26(多级网寻径算法),word 文档下载后可自由复制编辑7.27 (寻径/ 选播算法)1.8 第八章(P498)8.12 ( SISD/SIMD 算法)1.9 第九章(P562)9.18 ( SISD/多功能部件/SIMD/MIMD 算法)(注:每章可选1-2 个主要知识点,每个知识点可只选 1 题。
有下划线者为推荐的主要知识点。
)word 文档 下载后可自由复制编辑2 例 , 习题2.1 第一章 (P33)例 1.1,p10假设将某系统的某一部件的处理速度加快到 10倍 ,但该部件的原处理时间仅为整个运行时间的40%,则采用加快措施后能使整个系统的性能提高多少?解:由题意可知: Fe=0.4, Se=10,根据 Amdahl 定律S n To T n1 (1Fe )S n 1 10.6 0.4100.64 Fe Se 1.56word 文档 下载后可自由复制编辑例 1.2,p10采用哪种实现技术来求浮点数平方根 FPSQR 的操作对系统的性能影响较大。
(完整word版)计算机与网络技术基础(00894)

计算机网络技术与基础(00894)一、基础部分(一)第一章计算机基础知识●电子计算机的发展阶段,以构成计算机的电子器件来分为:1 第一代电子计算机。
用电子管.1946年第一台电子计算机。
2 第二代电子计算机的特点是用晶体管。
3 第三代电子计算机的主要特点是以中、小规模集成电路。
4 第四代电子计算机的主要特点是用大规模集成电路(LSI)和超大规模集成电路(VLSI)●目前计算机的发展方向:①巨型化;②微型化;③网络化;④智能化。
●计算机的性能特点:1 运算速度快;2 计算精度高;3 存储功能强;4 具有逻辑判断能力;5 具有自动运行能力。
与其它计算工具最本质的区别。
●计算机的应用领域:1、科学计算。
2、数据处理。
3、过程控制。
过程控制是指实时采集、检测数据,并进行处理和判定,按最佳值进行调节的过程。
4、计算机辅助设计及辅助教学。
5、人工智能●计算机采用二进制的原因:1 物理上容易实现2 不易出错,可靠性好3 易于进行逻辑运算●计算机的分类:原理:电子数字式计算机、电子模拟式计算机、混合式计算机用途:通用机和专用机规模:巨型机大中型机小型机和微型机●数制计算:2、8、16转变为10进制(分别乘以2、8、16的位数)10转变为2、8、16 (分别除2、8、16) 8转变为2 (4 2 1) 16___2 (8 4 2 1) 8____16 (先变成二进制)●位权:对于多位数,处在某一位上的1所表示的数值的大小,称为该位的位权。
例如,十进制第2位的位权为10第3位上的位权为100,而二进制数的第2位上的位权为2,第3位上的位权为4。
一般情况下,对于N进制数,整数部分,第i位上的位权是N i-1,而小数部分,第j位上的位权为N—j●二进制数算术运算:加法:0+0=0 0+1=1+0=1(进位) 减法:0-0=1-1=0 1-0=1 0-1=1(借位)乘法:0*0=0 0*1=1*0=0 1*1=1除法:0/1=0 1/1=1●会做练习册和辅导书上的计算题。
计算机系统结构 复习要点

计算机系统结构:第一章基本概念填空题、选择题复习:1、从使用语言角度,系统按功能划分层次结构由低到高分别为:微程序机器M0、传统机器M1、操作系统机器M2、汇编语言机器M3、高级语言机器M4、应用语言机器M5.2、计算机系统的设计思路:“从中间开始”设计的“中间”是指层次结构中的软硬件交界面,目前多数在传统机器语言机器级与操作系统机器级之间。
3、翻译与解释的区别与联系:区别:翻译是整个程序转换,解释是低级机器的一串语句仿真高级机器的一条语句;联系:都是高级机器程序在低级机器上执行的必须步骤。
4、模拟与仿真的区别:模拟:用机器语言解释实现软件移植的方法,解释的语言存在主存中;仿真用微程序解释,存储在控制存储器中。
5、解决好软件的可移植性方法有统一高级语言、采用系列机、模拟与仿真。
6、系列机必须保证向后兼容,力争向上兼容。
7、非用户片也称通用片,其功能是由器件厂生产时定死的,器件的用户只能用,不能改;现场片,用户根据需要改变器件内部功能;用户片是专门按用户的要求生产高集成度VLSI器件,完全按用户的要求设计的用户片称为全用户片。
一般同一系列内各档机器可分别用通用片、现场片或用户片实现。
8、计算机应用可归纳为向上升级的4类:数据处理、信息处理、知识处理、智能处理。
9、并行性开发的途径有:时间重叠、资源重复和资源共享。
10、并行性是指:同一时刻或同一时间间隔内完成两种或两种以上性质相同或不同的工作,并行性包含同时性和并发性二重含义。
11、科学计算中的重大挑战性课题往往要求计算机系统能有1TFLOPS的计算能力、1TBYTE 的主存容量、1TBYTE/S的I/O带宽。
12、并行处理计算机的结构:流水线计算机——时间重叠,阵列处理机——资源重复,多处理机——资源共享。
13、多机系统分多处理机系统和多计算机系统,多处理机系统:多台处理机组成的单一系统,多计算机系统:多台独立的计算机组成的系统。
14、多机系统的耦合度可以分为最低耦合、松散耦合和紧密耦合。
计算机体系结构各章简答题及答案

计算机体系结构各章简答题及答案第⼀章计算机体系结构的基本概念1. 什么是计算机系统的多级层次结构?2. 硬件和软件在什么意义上是等效的在什么意义上是不等效的?3. 经典计算机系统结构的实质是什么?4. 语⾔实现的两种基本技术是什么?5. 对于通⽤寄存器型机器来说,机器语⾔程序设计者所看到的计算机的属性主要有哪些?6. 什么是软件兼容软件兼容有⼏种其中哪⼀种是软件兼容的根本特征?7. 什么是系列机它的出现较好地解决了什么⽭盾?8. 对计算机发展⾮常关键的实现技术有哪些?9. 实现软件移植的主要途径有哪些?10. 试以系列机为例,说明计算机系统结构、计算机组成和计算机实现三者之间的关系。
11. 存储程序计算机在系统结构上的主要特点是什么?12. 从系统结构的发展情况看,新型系统结构的设计主要从哪两⽅⾯着⼿?13. 软件技术两个最重要的发展趋势是什么?14. 计算机系统设计⼈员的技术挑战主要来⾃哪⼏个⽅⾯?15. ⼀种计算机系统结构的⽣命周期是怎样的?16. 商品的标价(价格)由哪些因素构成?17. 对计算机系统成本产⽣影响的主要因素有哪些?18. ⽤户CPU时间由哪三个因素决定?19. ⽬前常⽤的测试程序分为哪五类?20. 什么叫测试程序组件在评价计算机系统设计时最常见的测试程序组件是哪个?21. SPEC2000测试程序组件中包括哪⼏个测试程序组件?22. 测试基于Microsoft公司的Windows系列操作系统平台的最常⽤测试组件有哪些?23. 常⽤的专门的性能指标测试程序有哪些?24. 计算机系统结构设计和分析中最经常使⽤的三条基本原则是什么25. 根据Amdahl定律,系统加速⽐由哪两个因素决定?26. 从执⾏程序的⾓度看,并⾏性等级从低到⾼可分为哪⼏级?27. 从处理数据的⾓度,并⾏性等级从低到⾼可以分为哪⼏级?28. 计算机系统中提⾼并⾏性的技术途径有哪三种?29. 多机系统的耦合度可以分为哪⼏类?30. 单机系统和多机系统中,都是按哪三种技术途径分别发展为哪三类多处理机?31. 三种类型的多处理机(同构型多处理机、异构型多处理机、分布处理系统)的主要区别是什么1. 什么是计算机系统的多级层次结构从计算机语⾔的⾓度,把计算机系统按功能划分成以下多级层次结构:2. 硬件和软件在什么意义上是等效的在什么意义上是不等效的硬件和软件在功能实现上是等效的,即⼀种功能可以由软件实现,也可以由硬件实现。
计算机系统结构第二章(习题解答)

计算机系统结构第⼆章(习题解答)1. 数据类型、数据表⽰和数据结构之间是什么关系?在设计⼀个计算机系统时,确定数据表⽰的原则主要有哪⼏个?答:略2. 假设有A 和B 两种不同类型的处理机,A 处理机中的数据不带标志位,其指令字长和数据字长均为32位。
B 处理机的数据带有标志位,每个数据的字长增加⾄36位,其中有4位是标志符,它的指令条数由最多256条减少⾄不到64条。
如果每执⾏⼀条指令平均要访问两个操作数,每个存放在存储器中的操作数平均要被访问8次。
对于⼀个由1000条指令组成的程序,分别计算这个程序在A 处理机和B 处理机中所占⽤的存储空间⼤⼩(包括指令和数据),从中得到什么启发?答:我们可以计算出数据的总数量:∵程序有1000条指令组成,且每条指令平均要访问两个操作数∴程序访问的数据总数为:1000×2=2000个∵每个数据平均访问8次∴程序访问的不同数据个数为:2000÷8=250对于A 处理机,所⽤的存储空间的⼤⼩为:bit4000032250321000MemMemMemdataninstructio A=?+?=+=对于B 处理机,指令字长由32位变为了30位(条数由256减少到64),这样,所⽤的存储空间的⼤⼩为:bit3900036250301000MemMemMemdataninstructio B=?+?=+=由此我们可以看出,由于数据的平均访问次数要⼤于指令,所以,采⽤带标志符的数据表⽰不会增加总的存储空间⼤⼩。
3. 对于⼀个字长为64位的存储器,访问这个存储器的地址按字节编址。
假设存放在这个存储器中的数据中有20%是独⽴的字节数据(指与这个字节数据相邻的不是⼀个字节数据),有30%是独⽴的16位数据,有20%是独⽴的32位数据,另外30%是独⽴的64位数据;并且规定只能从⼀个存储字的起始位置开始存放数据。
⑴计算这种存储器的存储空间利⽤率。
⑵给出提⾼存储空间利⽤率的⽅法,画出新⽅法的逻辑框图,并计算这种⽅法的存储空间利⽤率。
02325计算机系统结构复习资料全

第一章计算机系统结构的基本概念从处理数据的角度看,并行级别有位串字串,位并字串,位片串字并,全并行。
位串字串和位并字串基本上构成了SIMD。
位片串字并的例子有:相联处理机STARAN,MPP。
全并行的例子有:阵列处理机ILLIAC IV。
从加工信息的角度看,并行级别有存储器操作并行,处理器操作步骤并行,处理器操作并行,指令、任务、作业并行。
存储器操作并行是指可以在一个存储周期内并行读出多个CPU字的,采用单体多字、多体单字或多体多字的交叉访问主存系统,进而采用按内容访问方式,位片串字并或全并行方式,在一个主存周期内实现对存储器中大量字的高速并行操作。
例子有并行存储器系统,以相联存储器为核心构成的相联处理机。
处理器操作步骤并行是指在并行性概念中引入时间因素,让多个处理过程在时间上错开,轮流重复地执行使用同一套设备的各个部分,加快硬件周转来赢得速度。
例子有流水线处理机。
处理器操作并行是指一个指令部件同时控制多个处理单元,实现一条指令对多个数据的操作。
擅长对向量、数组进行处理。
例子有阵列处理机。
指令、任务、作业并行是指多个独立的处理机分别执行各自的指令、任务、作业。
例子有多处理机,计算机网络,分布处理系统。
并行性的开发途径有时间重叠(TimeInterleaving),资源重复(Resource Replication),资源共享(Resource Sharing)。
时间重叠是指在并行性概念中引入时间因素,让多个处理过程在时间上错开,轮流重复地执行使用同一套设备的各个部分,加快硬件周转来赢得速度。
例子有流水线处理机。
资源重复是指一个指令部件同时控制多个处理单元,实现一条指令对多个数据的操作。
例子有阵列处理机,相联处理机。
资源共享是指用软件方法让多个用户按一定时间顺序轮流使用同一套资源以提高资源的利用率,从而提高系统性能。
例子有多处理机,计算机网络,分布处理系统。
SISD:一个指令部件控制一个操作部件,实现一条指令对一个数据的操作。
《计算机组成原理》

Intel 8086: 16位
Intel 80386,80486, pentium:32位
精品ppt
13
1计算机的组成
1.1中央处理器 1.2存储体系 1.3主板主要部件 1.4系统总线 1.5输入设备 1.6输出设备
精品ppt
14
中央处理器( CPU )
包含运算器和控制器
能够高速地进行算术运算和逻辑运算 负责对输入信息进行各种处理的部件 一台计算机中有多个处理器,它们各有其不
精品ppt
25
指令和指令系统基本概念
计算机指令系统的“兼容性”问题
由于每种类型的CPU都有自己的指令系统, 因此,某一类计算机的可执行程序代码未必 能在其他计算机上运行。
同一公司的CPU产品通常“向下兼容”—— 新型号的处理器在旧型号处理器指令系统基 础上进行扩充。
精品ppt
26
指令执行过程
(1)CPU的控制器从存储器读取一条指令并放 入指令寄存器。
(2)指令寄存器中的指令经过译码,决定该 指令应该进行何种操作、操作数在哪里。
(3)根据操作数的位置从存储器取得操作数。
……→
精品ppt
27
指令执行过程
(4)运算器按照指令操作码的要求,对 操作数完成规定的运算处理,并根据运 算结果修改或设置处理器的一些状态标 志。
精品ppt
18
中央处理器( CPU )
超标量结构
为了加快CPU中指令的处理速度,CPU在执 行当前指令的同时,可以使用指令预取部件 提前向主存或快存去取出一些准备要执行的 指令。CPU采取“流水线”式的工作方式和 结构,实现了“超标量结构”。
精品ppt
19
中央处理器
并行处理和多处理器系统
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章指令系统∙指令系统是计算机系统结构的主要组成部分∙指令系统是软件与硬件分界面的一个主要标志∙指令系统软件与硬件之间互相沟通的桥梁∙指令系统与软件之间的语义差距越来越大2.1 数据表示2.2 寻址技术2.3 指令格式的优化设计2.4 指令系统的功能设计2.5 RISC指令系统2.1 数据表示∙新的研究成果,如浮点数基值的选择∙新的数据表示方法,如自定义数据表示2.1.1 数据表示与数据类型2.1.2 浮点数的设计方法2.1.3 自定义数据表示2.1.1 数据表示与数据类型∙数据的类型:文件、图、表、树、阵列、队列、链表、栈、向量、串、实数、整数、布尔数、字符∙数据表示的定义:数据表示研究的是计算机硬件能够直接识别,可以被指令系统直接调用的那些数据类型。
例如:定点、逻辑、浮点、十进制、字符、字符串、堆栈和向量∙确定哪些数据类型用数据表示实现,是软件与硬件的取舍问题∙确定数据表示的原则:一是缩短程序的运行时间,二是减少CPU与主存储器之间的通信量,三是这种数据表示的通用性和利用率。
例2.1:实现A=A+B,A和B均为200×200的矩阵。
分析向量指令的作用解:如果在没有向量数据表示的计算机系统上实现,一般需要6条指令,其中有4条指令要循环4万次。
因此,CPU与主存储器之间的通信量:取指令2+4×40,000条,读或写数据3×40,000个,共要访问主存储器7×40,000次以上如果有向量数据表示,只需要一条指令减少访问主存(取指令)次数:4×40,000次缩短程序执行时间一倍以上N m m er =⋅∙ 数据表示在不断扩大,如字符串、向量、堆栈、图、表 ∙ 用软件和硬件相结合的方法实现新的数据表示例如:用字节编址和字节运算指令来支持字符串数据表示 用变址寻址方式来支持向量数据表示2.1.2 浮点数的设计方法1、浮点数的表示方式∙ 一个浮点数N 可以用如下方式表示: 需要有6个参数来定义。
两个数值:m :尾数的值,包括尾数的码制(原码或补码)和数制(小数或整数) e :阶码的值,移码(偏码、增码、译码、余码等)或补码,整数 两个基值:r m :尾数的基值,2进制、4进制、8进制、16进制和10进制等 r e :阶码的基值,通常为2 两个字长:p :尾数长度,当r m =16时,每4个二进制位表示一位尾数 q :阶码长度,阶码部分的二进制位数 p 和q 均不包括符号位 ∙ 浮点数的存储式注:m f 为尾数的符号位,e f 为阶码的符号位,e 为阶码的值,m 为尾数的值。
2、浮点数的表数范围∙ 尾数为原码 尾数用原码、纯小数,阶码用移码、整数时,规格化浮点数N 的表数范围:---⋅≤≤-⋅-111r r N r r m mp m m q e qe r r () ∙ 尾数为补码尾数用补码表示时,正数区间的表数范围与尾数采用原码时完全相同,而负数区间的表数范围为:q e qe r r r N r r r m m p m m ----≤≤-+⋅-11() ∙ 浮点数在数轴上的分布情况min max min max例2.2:设p =23,q =7,r m =r e =2,尾数用原码、纯小数表示,阶码用移码、整数表示,求规格化浮点数N 的表数范围。
解:规格化浮点数N 的表数范围是:1227722321122-≤≤-⋅--N () 即:-129231272122≤≤-⋅-N () 例2.3:尾数用补码、纯小数表示,阶码用移码、整数表示,p =6,q =6,r m =16,r e =2,求规格化浮点数N 的表数范围。
解: 规格化浮点数N 在正数区间的表数范围是:-656631611616≤≤-⋅-N ()在负数区间的表数范围是:63664161616116-≤≤-+⋅--N ()3、浮点数的表数精度(误差)∙ 产生误差的根本原因是浮点数的不连续性 ∙ 误差产生的直接原因有两个:一是两个浮点数都在浮点集内,而运算结果却可能不在这个浮点集内, 二是数据从十进制转化为2、4、8、16进制,产生误差。
∙ 规格化尾数的表数精度为:δ(,)()r p p m m r =--11 最后1个有效位的可信度为一半, 当r m =2时,有:δ(,)()222121p p p ==⋅---4、浮点数的表数效率∙ 浮点数是一种冗余数制(Redundat Number System)∙ 浮点数的表数效率定义为:η==⋅⋅-⋅⋅+⋅⋅⋅-可表示的规格化浮点数的个数全部浮点数个数2121221()r r r r r m m e m e p q p q 简化表示:η()r r r m m m=-1当尾数基值为2时,浮点数的表数效率为:η()221250%=-= ∙ 浮点数的表数效率随r m 增大当尾数基值r m =16时,浮点数的表数效率为:η()1616194%=-= 尾数基值r m =16与r m =2相比,浮点数的表数效率提高了:T ==ηη()().1621875倍4、浮点数尾数基值的选择∙ 在表示浮点数的6个参数中,只有尾数基值r m 、尾数长度p 和阶码长度q 与表数范围、表数精度和表数效率有关∙ 在字长确定的情况下,如何选择尾数基值r m ,使表数范围最大、表数精度和表数效率最高;假设有两种表示方式F1和F2,它们二进制字长相同,尾数都用原码或补码、小数表示,阶码都用移码、整数表示,阶码的基均为2,尾数的基不同。
浮点数表示方式F1:尾数基值r m1=2,尾数长度p1,阶码长度q1, 二进制字长:L1=p1+q1+2。
浮点数表示方式F2:尾数基值r m2=2k ,尾数长度p2,阶码长度q2, 二进制字长:L2=k p2+q2+2。
由F1与F2的二进制字长相同,即L1=L2,得:p1+q1=k p2+q2 (2.1)∙ 字长和表数范围确定时,尾数基值r m 与表数精度的关系F1的表数范围是:q N 1212||max =, F2的表数范围是:|max |()N q k 2222=,F1与F2的表数范围相同,得到:q q k 1222=⋅ 两边取以2为底的对数,得到:q1=q2+log 2 k (2.2) 把(2.2)式代入(2.1)式,得到:p1=k p2-log 2 k (2.3) F1的表数精度是:δ111122=⋅-p(2.4)把(2.3)代入(2.4)得到:δ112122=⋅-+kp k logF2的表数精度是:δ212122=⋅⋅-k p ()取F2与F1表数精度的比值:T k k ==--δδ2112log(2.5)只有k =1(尾数基值r m =2)或k =2(尾数基值r m =4)时,比值T =1。
结论1:在字长和表数范围一定时,尾数基值r m 取2或4,浮点数具有最高的表数精度。
∙ 字长和表数精度一定,尾数基值r m 与表数范围的关系 由F1与F2的表数精度相同得到:1221221112⋅=⋅--p p k () 即: p1=kp2-k +1 (2.6) 把(2.6)代入(2.1)得到:q1=q2+k -1 (2.7)F1的表数范围:q q k q k 121212222222==+--⋅F2的表数范围:q q k k222222()=⋅假设表数范围F2大于F1,则阶码的最大值F2大于F1:q q k k k k 22112222⋅>⋅--> 即这个不等式在正整数定义域内没有解,即不存在比F1的表数范围更大的浮点数表示方式只有k =1(尾数基值r m =2)或k =2(尾数基值r m =4)时,F2阶码的最大值等于F1阶码的最大值。
结论2:在字长和表数精度一定时,尾数基值r m 取2或4,浮点数具有最大的表数范围。
推论1:在字长确定之后,尾数基值r m 取2或4,浮点数具有最大的表数范围和最高的表数精度。
例2.4:IBM 370系列计算机的短浮点数表示方式,尾数基值r m =16,尾数字长为16进制6位,阶码基值r m =2,阶码字长6位,尾数用原码、小数表示,阶码用移码、整数表示。
求表数范围和表数精度,并尾数基址r m =2的浮点数表示方式进行比较。
解: 表数精度为:δ==⋅---121626121()表数范围是:N max ==62256162若尾数基值r m =2,则有:1222121⋅=---()p解得p =21,则q =32-21-2=9,它的表数范围是:N max ==9251222推论2:浮点数的尾数基值r m 取2,并采用隐藏位表数方法是最佳的浮点数表示方式。
这种浮点数表示方式能做到表数范围最大、表数误差最小、表数效率最高。
目前,IBM 公司的IBM360、370、4300系列机等,尾数基值r m =16。
Burroughs 公司的B6700、B7700等大型机,尾数基值r m =8。
DEC 公司的PDP-11、VAX-11和Alpha 等小型机,CDC 公司的CDC6600、CYBER70等大型机,Intel 公司的x86系列机等均采用尾数基值r m =2。
5、浮点数格式的设计定义浮点数表示方式的6个参数的确定原则: ∙ 尾数:多数机器采用原码、小数表示采用原码制表示:加减法比补码表示复杂,乘除法比补码简单 表示非常直观。
采用小数表示能简化运算,特别是乘除法运算。
∙ 阶码:一般机器都采用整数、移码表示采用移码表示的主要原因是:浮点0与机器0一致。
阶码进行加减运算时,移码的加减法运算要比补码复杂 ∙ 尾数的基值r m 选择2, ∙ 阶码的基值r e 取2,浮点数格式设计的关键问题是:在表数范围和表数精度给定的情况下,如何确定最短的尾数字长p 和阶码字长q例2.5:要求设计一种浮点数格式,其表数范围不小于1037,正、负数对称,表数精度不低于10-16。
解:根据表数范围的要求:q2137210-> 解这个不等式:q >+=log(log /log )log .3710212695 取阶码字长q =7根据表数精度的要求,得到:12211610⋅--<-(P )解这个不等式:p >-=-log log .16102532由于浮点数字长通常是8的倍数,因此取尾数字长p =55 所设计浮点数的格式如下:所设计浮点数的主要参数如下: 最大尾数值:()()11255-=---p r m绝对值最小的尾数值:112r m =最大阶码:q r e -=-=1211277 最小阶码:-=-=-q r e 72128 最大正数:7215555127381112212217010--⋅=-⋅-⋅⨯----==(pqr r m e m r )()().;最小正数:--⋅=⋅⨯--==72129391122214710r r m e mqr .; 最大负数:---⋅=-⋅⨯--=-=-7212939112214710r r m e mqr .; 最小负数:7215555127381112212217010---⋅--⋅-⋅⨯----=-=-(pqr r me m r )()().; 表数精度:δ=⋅⋅==⨯------=112222781015515517r r m m p ()().;浮点零:浮点零与机器零相同,64位全为0; 表数效率:采用隐藏位,表数效率η=100%;6、浮点数的舍入处理∙ 浮点数要进行舍入处理的原因是:十进制实数转化为浮点数时,有效位长度超过给定的尾数字长。
