spss_大数据正态分布检验方法及意义要点
SPSS统计分析1:正态分布检验.

正态分布检验一、正态检验的必要性[1]当对样本是否服从正态分布存在疑虑时,应先进行正态检验;如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时,不必进行正态检验。
当然,在正态分布存疑的情况下,也就不能采用基于正态分布前提的参数检验方法,而应采用非参数检验。
二、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
Q-Q图为佳,效率较高。
以上两种方法以3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
三、计算法1、峰度(Kurtosis)和偏度(Skewness)(1)概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。
这个统计量需要与正态分布相比较,峰度为0表示该总体数据分布与正态分布的陡缓程度相同;峰度大于0表示该总体数据分布与正态分布相比较为陡峭,为尖顶峰;峰度小于0表示该总体数据分布与正态分布相比较为平坦,为平顶峰。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
峰度的具体计算公式为:注:SD就是标准差σ。
峰度原始定义不减3,在SPSS中为分析方便减3后与0作比较。
偏度与峰度类似,它也是描述数据分布形态的统计量,其描述的是某总体取值分布的对称性。
这个统计量同样需要与正态分布相比较,偏度为0表示其数据分布形态与正态分布的偏斜程度相同;偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏,即有一条长尾巴拖在右边,数据右端有较多的极端值;偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏,即有一条长尾拖在左边,数据左端有较多的极端值。
SPSS统计分析1:正态分布检验

正态分布检验一、正态检验的必要性[1]当对样本是否服从正态分布存在疑虑时,应先进行正态检验;如果有充分的理论依据或根据以往积累的信息可以确认总体服从正态分布时,不必进行正态检验。
当然,在正态分布存疑的情况下,也就不能采用基于正态分布前提的参数检验方法,而应采用非参数检验。
二、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
三、计算法1、峰度(Kurtosis)和偏度(Skewness)(1)概念解释峰度是描述总体中所有取值分布形态陡缓程度的统计量。
这个统计量需要与正态分布相比较,峰度为0表示该总体数据分布与正态分布的陡缓程度相同;峰度大于0表示该总体数据分布与正态分布相比较为陡峭,为尖顶峰;峰度小于0表示该总体数据分布与正态分布相比较为平坦,为平顶峰。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
峰度的具体计算公式为:注:SD就是标准差σ。
峰度原始定义不减3,在SPSS中为分析方便减3后与0作比较。
偏度与峰度类似,它也是描述数据分布形态的统计量,其描述的是某总体取值分布的对称性。
这个统计量同样需要与正态分布相比较,偏度为0表示其数据分布形态与正态分布的偏斜程度相同;偏度大于0表示其数据分布形态与正态分布相比为正偏或右偏,即有一条长尾巴拖在右边,数据右端有较多的极端值;偏度小于0表示其数据分布形态与正态分布相比为负偏或左偏,即有一条长尾拖在左边,数据左端有较多的极端值。
spss判断是否符合正态分布
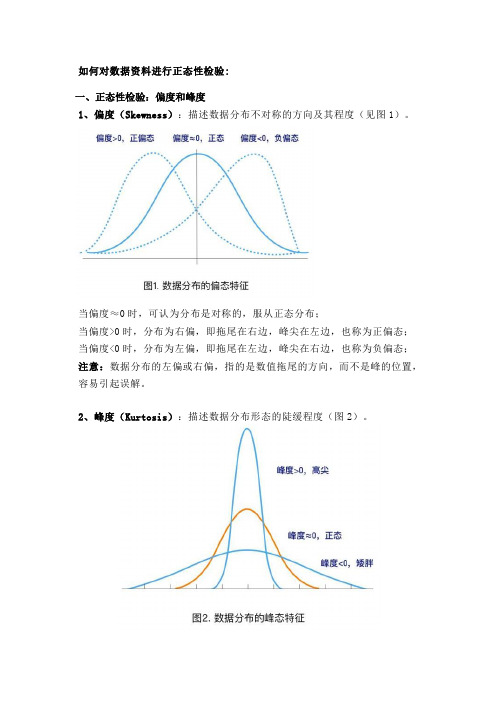
如何对数据资料进行正态性检验:一、正态性检验:偏度和峰度1、偏度(Skewness):描述数据分布不对称的方向及其程度(见图1)。
当偏度≈0时,可认为分布是对称的,服从正态分布;当偏度>0时,分布为右偏,即拖尾在右边,峰尖在左边,也称为正偏态;当偏度<0时,分布为左偏,即拖尾在左边,峰尖在右边,也称为负偏态;注意:数据分布的左偏或右偏,指的是数值拖尾的方向,而不是峰的位置,容易引起误解。
2、峰度(Kurtosis):描述数据分布形态的陡缓程度(图2)。
当峰度≈0时,可认为分布的峰态合适,服从正态分布(不胖不瘦);当峰度>0时,分布的峰态陡峭(高尖);当峰度<0时,分布的峰态平缓(矮胖);利用偏度和峰度进行正态性检验时,可以同时计算其相应的Z评分(Z-score),即:偏度Z-score=偏度值/标准误,峰度Z-score=峰度值/标准误。
在α=0.05的检验水平下,若Z-score在±1.96之间,则可认为资料服从正态分布。
了解偏度和峰度这两个统计量的含义很重要,在对数据进行正态转换时,需要将其作为参考,选择合适的转换方法。
3、SPSS操作方法以分析某人群BMI的分布特征为例。
(1) 方法一选择Analyze → Descriptive Statistics → Frequencies将BMI选入Variable(s)框中→点击Statistics →在Distribution框中勾选Skewness和Kurtosis(2) 方法二选择Analyze → Descriptive Statistics → Descriptives将BMI选入Variable(s)框中→点击Options →在Distribution框中勾选Skewness和Kurtosis4、结果解读在结果输出的Descriptives部分,对变量BMI进行了基本的统计描述,同时给出了其分布的偏度值0.194(标准误0.181),Z-score = 0.194/0.181 = 1.072,峰度值0.373(标准误0.360),Z-score = 0.373/0.360 = 1.036。
spss_数据正态分布检验方法及意义

spss 数据正态分布检验方法及意义判读要观察某一属性的一组数据是否符合正态分布,可以有两种方法(目前我知道这两种,并且这两种方法只是直观观察,不是定量的正态分布检验):1:在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。
具体如下:Analyze-----Descriptive S tatistics-----Frequencies,打开频数统计对话框,在Statistics里可以选择获得各种描述性的统计量,如:均值、方差、分位数、峰度、标准差等各种描述性统计量。
在Charts里可以选择显示的图形类型,其中Histograms选项为柱状图也就是我们说的直方图,同时可以选择是否绘制该组数据的正态曲线(With nor ma curve),这样我们可以直观观察该组数据是否大致符合正态分布。
如下图:从上图中可以看出,该组数据基本符合正态分布。
2:正态分布的Q-Q图:在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。
具体步骤如下:Analyze-----Descriptive Statistics-----Explore打开对话框,选择Plots选项,选择Normality plots with tests选项,可以绘制该组数据的q-q 图。
图的横坐标为改变量的观测值,纵坐标为分位数。
若该组数据服从正态分布,则图中的点应该靠近图中直线。
纵坐标为分位数,是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置,n为样本容量。
若该数组服从正态分布则其q-q图应该与理论的q-q图(也就是图中的直线)基本符合。
对于理论的标准正态分布,其q-q图为y=x直线。
非标准正态分布的斜率为样本标准差,截距为样本均值。
如下图:如何在spss中进行正态分布检验1(转)(2009-07-22 11:11:57)标签:杂谈一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
spss正态分布检验方法

spss正态分布检验方法SPSS正态分布检验方法。
SPSS(Statistical Package for the Social Sciences)是一款广泛应用于统计分析领域的软件,它提供了丰富的统计分析工具和功能,其中包括对数据正态分布进行检验的方法。
正态分布检验是统计学中常用的一种方法,用于检验数据是否符合正态分布。
本文将介绍在SPSS软件中如何进行正态分布检验,并对其结果进行解释。
在SPSS中,进行正态分布检验需要借助于数据分布的直方图和正态Q-Q图。
首先,我们需要导入待检验的数据,并打开“分析”菜单下的“描述统计”选项。
在弹出的对话框中选择“统计”选项,并勾选“正态分布曲线”和“Q-Q图”选项,然后点击“确定”按钮进行分析。
分析完成后,我们会得到数据的直方图和正态Q-Q图。
直方图可以直观地展示数据的分布情况,而正态Q-Q图则可以用来检验数据是否符合正态分布。
在正态Q-Q图中,数据点如果分布在一条直线附近,则表明数据符合正态分布;反之,如果数据点偏离直线较远,则表明数据不符合正态分布。
通过观察直方图和正态Q-Q图,我们可以初步判断数据是否符合正态分布。
但为了更加准确地进行判断,我们还可以借助于SPSS提供的正态性检验方法。
在SPSS中,可以使用Shapiro-Wilk检验、Kolmogorov-Smirnov检验或者Anderson-Darling检验来检验数据的正态性。
这些方法都可以帮助我们对数据的正态分布进行更加严谨的检验。
在进行正态性检验时,我们需要注意以下几点。
首先,对于Shapiro-Wilk检验和Kolmogorov-Smirnov检验,如果显著性水平小于0.05,则可以拒绝原假设,即数据不符合正态分布;反之,如果显著性水平大于0.05,则接受原假设,即数据符合正态分布。
而对于Anderson-Darling检验,我们需要关注统计量的大小和临界值的比较,如果统计量小于临界值,则可以认为数据符合正态分布。
spss-数据正态分布检验方法及意义要点

spss 数据正态分布检验方法及意义判读要观察某一属性的一组数据是否符合正态分布,可以有两种方法(目前我知道这两种,并且这两种方法只是直观观察,不是定量的正态分布检验):1:在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。
具体如下:Analyze-----Descriptive S tatistics-----Frequencies,打开频数统计对话框,在Statistics里可以选择获得各种描述性的统计量,如:均值、方差、分位数、峰度、标准差等各种描述性统计量。
在Charts里可以选择显示的图形类型,其中Histograms选项为柱状图也就是我们说的直方图,同时可以选择是否绘制该组数据的正态曲线(With norma curve),这样我们可以直观观察该组数据是否大致符合正态分布。
如下图:从上图中可以看出,该组数据基本符合正态分布。
2:正态分布的Q-Q图:在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。
具体步骤如下:Analyze-----Descriptive Statistics-----Explore打开对话框,选择Plots选项,选择Normality plots with tests选项,可以绘制该组数据的q-q 图。
图的横坐标为改变量的观测值,纵坐标为分位数。
若该组数据服从正态分布,则图中的点应该靠近图中直线。
纵坐标为分位数,是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置,n为样本容量。
若该数组服从正态分布则其q-q图应该与理论的q-q图(也就是图中的直线)基本符合。
对于理论的标准正态分布,其q-q图为y=x直线。
非标准正态分布的斜率为样本标准差,截距为样本均值。
如下图:如何在spss中进行正态分布检验1(转)(2009-07-22 11:11:57)标签:杂谈一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
利用SPSS检验数据是否符合正态分布

利用SPSS检验数据是否符合正态分布(2011-04-24 06:30:42)正态分布也叫常态分布,在我们后面说的很多东西都需要数据呈正态分布。
下面的图就是正态分布曲线,中间隆起,对称向两边下降。
下面我们来看一组数据,并检验“期初平均分” 数据是否呈正态分布(此数据已在SPSS里输入好)在SPSS里执行“分析—>描述统计—>频数统计表”(菜单见下图,英文版的可以找到相应位置),然后弹出左边的对话框,变量选择左边的“期初平均分”,再点下面的“图表”按钮,弹出图中右边的对话框,选择“直方图”,并选中“包括正态曲线”设置完后点“确定”,就后会出来一系列结果,包括2个表格和一个图,我们先来看看最下面的图,见下图,上图中横坐标为期初平均分,纵坐标为分数出现的频数。
从图中可以看出根据直方图绘出的曲线是很像正态分布曲线。
如何证明这些数据符合正态分布呢,光看曲线还不够,还需要检验:检验方法一:看偏度系数和峰度系数我们把SPSS结果最上面的一个表格拿出来看看(见下图):偏度系数Skewness=-0.333;峰度系数Kurtosis=0.886;两个系数都小于1,可认为近似于正态分布。
检验方法二:单个样本K-S检验在SPSS里执行“分析—>非参数检验—>单个样本K-S检验,弹出对话框,检验变量选择“期初平均分”,检验分布选择“正态分布”,然后点“确定”。
检验结果为:从结果可以看出,K-S检验中,Z值为0.493,P值(sig 2-tailed)=0.968>0.05,因此数据呈近似正态分布检验方法三:Q-Q图检验在SPSS里执行“图表—>Q-Q图”,弹出对话框,见下图:变量选择“期初平均分”,检验分布选择“正态”,其他选择默认,然后点“确定”,最后可以得到Q-Q图检验结果,结果很多,我们只需要看最后一个图,见下图。
QQ Plot 中,各点近似围绕着直线,说明数据呈近似正态分布。
SPSS数据正态性检验解析

SPSS数据正态性检验解析正态性检验是数据分析中的一个关键步骤,它通常用于检查一个数据集是否符合正态分布。
如果数据集符合正态分布,则可以使用更广泛的统计方法。
SPSS软件是一个广泛使用的统计分析工具,它提供了一系列的正态性检验方法,用于帮助用户评估他们的数据是否符合正态分布。
本文将介绍如何使用SPSS进行正态性检验。
正态性检验数据的正态性是指数据集在正态分布上的贴合程度。
在正态分布中,数据的均值、中位数和众数相等,数据分散程度由标准差来度量。
正态分布在自然界中非常普遍,例如,身高、体重和智力得分通常符合正态分布。
正态性检验是用于检查一个数据集是否符合正态分布的一种方法。
如果数据集的分布不是正态分布,则在分析数据时需要采取更多的措施。
一些因素导致数据不符合正态分布,例如较小的样本量、抽样偏差、异常值等。
正态性检验的目的是确定一个分布是否足够接近正态分布,以使得正态性假设在数据分析中得到保证。
正态性假设是很重要的,在大多数情况下,如果数据是接近正态分布,则可以使用更广泛的统计方法。
如果数据不符合正态分布,则需要使用非参数方法。
SPSS中的正态性检验SPSS提供了一系列正态性检验方法,用于分析数据集的正态性。
以下将分别介绍这些方法:1.直方图与正态概率图检验直方图可以通过展示数据集的频率分布来检查正态性。
用户可以通过观察直方图形状是否类似于正态分布来评估正态性。
此外,正态概率图也可以用来评估正态性。
正态概率图绘制了每个观测值在正态分布上的位置,并将这些观测值与理论正态分布进行比较。
2.基于统计值的正态性检验SPSS中的一些统计测试可以用于定量检测正态性。
例如,Shapiro-Wilk检验是一种基于统计值的正态性检验方法。
这种测试计算数据的W值,如果W值不显著,则数据符合正态分布。
其他常用的基于统计值的正态性检验方法包括Kolmogorov-Smirnov检验和Anderson-Darling检验。
3.用Q-Q图检验正态性Q-Q图是评估一个数据集是否为正态分布的一种图形方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
spss 数据正态分布检验方法及意义判读要观察某一属性的一组数据是否符合正态分布,可以有两种方法(目前我知道这两种,并且这两种方法只是直观观察,不是定量的正态分布检验):1:在spss里的基本统计分析功能里的频数统计功能里有对某个变量各个观测值的频数直方图中可以选择绘制正态曲线。
具体如下:Analyze-----Descriptive S tatistics-----Frequencies,打开频数统计对话框,在Statistics里可以选择获得各种描述性的统计量,如:均值、方差、分位数、峰度、标准差等各种描述性统计量。
在Charts里可以选择显示的图形类型,其中Histograms选项为柱状图也就是我们说的直方图,同时可以选择是否绘制该组数据的正态曲线(With nor ma curve),这样我们可以直观观察该组数据是否大致符合正态分布。
如下图:从上图中可以看出,该组数据基本符合正态分布。
2:正态分布的Q-Q图:在spss里的基本统计分析功能里的探索性分析里面可以通过观察数据的q-q图来判断数据是否服从正态分布。
具体步骤如下:Analyze-----Descriptive Statistics-----Explore打开对话框,选择Plots选项,选择Normality plots with tests选项,可以绘制该组数据的q-q 图。
图的横坐标为改变量的观测值,纵坐标为分位数。
若该组数据服从正态分布,则图中的点应该靠近图中直线。
纵坐标为分位数,是根据分布函数公式F(x)=i/n+1得出的.i为把一组数从小到大排序后第i个数据的位置,n为样本容量。
若该数组服从正态分布则其q-q图应该与理论的q-q图(也就是图中的直线)基本符合。
对于理论的标准正态分布,其q-q图为y=x直线。
非标准正态分布的斜率为样本标准差,截距为样本均值。
如下图:如何在spss中进行正态分布检验1(转)(2009-07-22 11:11:57)标签:杂谈一、图示法1、P-P图以样本的累计频率作为横坐标,以安装正态分布计算的相应累计概率作为纵坐标,把样本值表现为直角坐标系中的散点。
如果资料服从整体分布,则样本点应围绕第一象限的对角线分布。
2、Q-Q图以样本的分位数作为横坐标,以按照正态分布计算的相应分位点作为纵坐标,把样本表现为指教坐标系的散点。
如果资料服从正态分布,则样本点应该呈一条围绕第一象限对角线的直线。
以上两种方法以Q-Q图为佳,效率较高。
3、直方图判断方法:是否以钟形分布,同时可以选择输出正态性曲线。
4、箱式图判断方法:观测离群值和中位数。
5、茎叶图类似与直方图,但实质不同。
二、计算法1、偏度系数(Skewness)和峰度系数(Kurtosis)计算公式:g1表示偏度,g2表示峰度,通过计算g1和g2及其标准误σg1及σg2然后作U检验。
两种检验同时得出U<U0.05=1.96,即p>0.05的结论时,才可以认为该组资料服从正态分布。
由公式可见,部分文献中所说的“偏度和峰度都接近0……可以认为……近似服从正态分布”并不严谨。
2、非参数检验方法非参数检验方法包括Kolmogorov-Smirnov检验(D检验)和Shapiro- Wilk(W检验)。
SAS中规定:当样本含量n≤2000时,结果以Shapiro –Wilk(W检验)为准,当样本含量n >2000时,结果以Kolmogorov –Smirnov(D检验)为准。
SPSS中则这样规定:(1)如果指定的是非整数权重,则在加权样本大小位于3和50之间时,计算Shapiro-Wilk统计量。
对于无权重或整数权重,在加权样本大小位于3和5000之间时,计算该统计量。
由此可见,部分SPSS教材里面关于“Shapiro –Wilk适用于样本量3-50之间的数据”的说法是在是理解片面,误人子弟。
(2)单样本Kolmogorov-Smirnov 检验可用于检验变量(例如income)是否为正态分布。
对于此两种检验,如果P值大于0.05,表明资料服从正态分布。
三、SPSS操作示例SPSS中有很多操作可以进行正态检验,在此只介绍最主要和最全面最方便的操作:1、工具栏--分析—描述性统计—探索性2、选择要分析的变量,选入因变量框内,然后点选图表,设置输出茎叶图和直方图,选择输出正态性检验图表,注意显示(Display)要选择双项(Both)。
3、Output结果(1)Descriptives:描述中有峰度系数和偏度系数,根据上述判断标准,数据不符合正态分布。
S k=0,K u=0时,分布呈正态,Sk>0时,分布呈正偏态,Sk<0时,分布呈负偏态,时,Ku>0曲线比较陡峭,Ku<0时曲线比较平坦。
由此可判断本数据分布为正偏态(朝左偏),较陡峭。
(2)Tests of Normality:D检验和W检验均显示数据不服从正态分布,当然在此,数据样本量为1000,应以W检验为准。
(3)直方图直方图验证了上述检验结果。
(4)此外还有茎叶图、P-P图、Q-Q图、箱式图等输出结果,不再赘述。
结果同样验证数据不符合正态分布。
spss 判断两组数据的相关性(已使用)(2009-07-22 13:07:34)标签:杂谈两组体重数据:先要为数据分组2.0 3000.02.0 3700.02.0 2900.02.0 3200.02.0 2950.02.0 3100.02.0 700.02.0 3200.02.0 2500.02.0 3650.02.0 4600.0 2.0 2700.0 2.0 2500.0 2.0 3150.0 2.0 3500.0 2.0 3800.0 2.0 2800.0 2.0 2400.0 2.0 3600.0 2.0 3200.0 2.0 1770.0 2.0 1450.0 2.0 1700.0 2.0 3250.0 2.0 2700.0 2.0 3000.0 2.0 2250.0 2.0 2150.0 2.0 2450.0 2.0 1600.0 2.0 3100.0 2.0 4050.0 2.0 4250.0 2.0 2900.0 2.0 3250.0 2.0 3750.0 2.0 3500.0 2.0 4100.0 2.0 3100.0 2.0 2400.0 2.0 3250.0 2.0 2600.0 2.0 3100.0 2.0 3400.0 1.0 2400.0 1.0 2100.0 1.0 3000.01.0 4000.01.0 2200.01.0 1400.01.0 3000.01.0 3200.01.0 3600.01.0 2850.01.0 2850.01.0 3300.01.0 3500.01.0 3900.01.0 3250.01.0 3800.01.0 2800.01.0 3500.01.0 2650.01.0 2350.01.0 1400.01.0 2900.01.0 2550.01.0 2850.01.0 3300.01.0 2250.01.0 2500.0使用命令: spss的t检验:菜单Analyze->Compare Means->Independent-Samples T Test运行结果:经方差齐性检验: F= 0.393 P=0.532,即两方差齐。
(因为p大于0.05)所以选用 t检验的第一行方差齐情况下的t检验的结果:就是选用方差假设奇的结果所以,t=0.644 , p=0.522, 没有显著性差异。
(因为p < 0.05表示差异有显著性)。
均值相差:113.30159解释:使用compare means里的independent smaples T test,检验结果里的 Levene\'s Test for Equality of Variances就是对方差齐性的检验,如果P值大于0.05则认为是方差齐,统计量为F= S1^2/S^2 ~ F(n1-1,n2-1) ,显著水平一般为0.05,0.01,原假设H0:方差相等。
方差分析(Anaylsis of Variance, ANOVA)要求各组方差整齐,不过一般认为,如果各组人数相若,就算未能通过方差整齐检验,问题也不大。
One-Way ANOVA对话方块中,点击Options…(选项…)按扭,勾Homogeneity-of-variance即可。
它会产生Levene、Cochran C、Bartlett-Box F等检验值及其显著性水平P值,若P值<于0.05,便拒绝方差整齐的假设。
顺带一提,Cochran和Bartlett检定对非正态性相当敏感,若出现「拒绝方差整齐」的检测结果,或因这原因而做成。
Statistics菜单->Compare Means->Independent-samples T Test..再看看结果中p值的大小是否<.05,若然即达显著水平。
SPSS学习笔记描述样本数据一般的,一组数据拿出来,需要先有一个整体认识。
除了我们平时最常用的集中趋势外,还需要一些离散趋势的数据。
这方面EXCEL就能一次性的给全了数据,但对于SPSS,就需要用多个工具了,感觉上表格方面不如EXCEL好用。
个人感觉,通过描述需要了解整体数据的集中趋势和离散趋势,再借用各种图观察数据的分布形态。
对于SPSS提供的OLAP cubes(在线分析处理表),Case Summary(观察值摘要分析表),Descriptives (描述统计)不太常用,反喜欢用Frequencies(频率分析),Basic Table(基本报表),Crosstabs(列联表)这三个,另外再配合其它图来观察。
这个可以根据个人喜好来选择。
一.使用频率分析(Frequencies)观察数值的分布。
频率分布图与分析数据结合起来,可以更清楚的看到数据分布的整体情况。
以自带文件Trends chapter 13.sav为例,选择Analyze->Descriptive Statistics->Frequencies,把hstarts选入Variables,取消在Display Frequency table前的勾,在Chart里面histogram,在Statistics选项中如图1图1分别选好均数(Mean),中位数(Median),众数(Mode),总数(Sum),标准差(Std. deviation),方差(Variance),范围(range),最小值(Minimum),最大值(Maximum),偏度系数(Skewness),峰度系数(Kutosis),按Continue返回,再按OK,出现结果如图2图2表中,中位数与平均数接近,与众数相差不大,分布良好。
