[课程]Eviews时间序列分析实例
ARMA模型的eviews的建立--时间序列分析实验指导
时间序列分析实验指导42-2-450100150200250统计与应用数学学院前言随着计算机技术的飞跃发展以及应用软件的普及,对高等院校的实验教学提出了越来越高的要求。
为实现教育思想与教学理念的不断更新,在教学中必须注重对大学生动手能力的培训和创新思维的培养,注重学生知识、能力、素质的综合协调发展。
为此,我们组织统计与应用数学学院的部分教师编写了系列实验教学指导书。
这套实验教学指导书具有以下特点:①理论与实践相结合,书中的大量经济案例紧密联系我国的经济发展实际,有利于提高学生分析问题解决问题的能力。
②理论教学与应用软件相结合,我们根据不同的课程分别介绍了SPSS、SAS、MATLAB、EVIEWS等软件的使用方法,有利于提高学生建立数学模型并能正确求解的能力。
这套实验教学指导书在编写的过程中始终得到安徽财经大学教务处、实验室管理处以及统计与应用数学学院的关心、帮助和大力支持,对此我们表示衷心的感谢!限于我们的水平,欢迎各方面对教材存在的错误和不当之处予以批评指正。
统计与数学模型分析实验中心 2007年2月目录实验一 EVIEWS中时间序列相关函数操作···························- 1 - 实验二确定性时间序列建模方法 ····································- 8 - 实验三时间序列随机性和平稳性检验 ···························· - 18 - 实验四时间序列季节性、可逆性检验 ···························· - 21 - 实验五 ARMA模型的建立、识别、检验···························· - 27 - 实验六 ARMA模型的诊断性检验····································· - 30 - 实验七 ARMA模型的预测·············································· - 31 - 实验八复习ARMA建模过程·········································· - 33 - 实验九时间序列非平稳性检验 ····································· - 35 -实验一 EVIEWS中时间序列相关函数操作【实验目的】熟悉Eviews的操作:菜单方式,命令方式;练习并掌握与时间序列分析相关的函数操作。
EVIEWS时间序列实验指导(上机操作说明)

⒉在工作文件窗口中选取所要删除或更名的变量,点击工作文件窗口菜单栏中的Objects/Delete selected…(Rename selected…),即可删除(更名)变量
进行预测:打开对应的方程窗口,点forecast按纽,将出现对话框,修改对话框 sample range for forecast中的时间期限的截止日期为预测期.
相对误差的计算公式为:(实际值-预测值)/实际值
二、单参数和双参数指数平滑法进行预测的操作练习
2、某地区1996~2003年的人口数据如表1.2,运用二次指数平滑法预测该镇2004年底的人口数(单位:人)。
掌握确定性时间序列建立模型的几种常用方法。
【实验内容】
一、多项式模型和加权最小二乘法的建立;
二、单参数和双参数指数平滑法进行预测的操作练习;
三、二次曲线和对数曲线趋势模型建立及预测;
【实验步骤】
一、多项式模型和加权最小二乘法的建立;
1、我国1974—1994年的发电量资料列于表中,已知1995年的发电量为10077.26亿千瓦小时,试以表1.1中的资料为样本:
建立系列方程:smpl 1974 1994
ls y c t
ls y c t t^2
ls y c t t^2 t^3
通过拟合优度和外推检验的结果发现一元三次多项式模型效果最好。
首先生成权数序列:genr m=sqr(0.6^(21-t))
加权最小二乘法的命令方式:ls(w=m) y c t
普通最小二乘法命令方式:ls y c t
步骤:(1)打开该文件。
Eviews 应用实例

指数平滑对话框中包含五个部分的选项:平滑方法 (Smoothing Method)、平滑系数(Smoothing Method)、平滑系数(Smoothing Parameters)、平滑后生成序列的名称(Smoothed Parameters)、平滑后生成序列的名称(Smoothed Series)、预测样本范围(Estimation Sample)和季节变动 Series)、预测样本范围(Estimation Sample)和季节变动 周期(Cycle 周期(Cycle for Seasonal)。 Seasonal)。 对话框左上部分的平滑方法(Smoothing Method)包括: 对话框左上部分的平滑方法(Smoothing Method)包括: Single 一次指数平滑 Double 二次指数平滑 Holt-Winters- Holt-Winters-No seasonal Holt-Winters无 Holt-Winters无 季节模型 Holt-Winters- Holt-Winters-Additive Holt-Winters季节 Holt-Winters季节 迭加模型 Holt-Winters- Holt-Winters-Multiplicative Holt-Winters季 Holt-Winters季 节乘积模型 平滑系数(Smoothing Parameters)包括Alpha,Beta, 平滑系数(Smoothing Parameters)包括Alpha,Beta, Gamma。平滑系数可由系统自动给定,也可以由用户指定。 Gamma。平滑系数可由系统自动给定,也可以由用户指定。 缺省状态是由系统自动给定。如果用户需要指定,只需在对应 参数的位置填入指定的数值。
出于预测的考虑,有时系统给定的系数不是很 理想,用户需要自己指定平滑系数值。平滑系数取 什么值比较合适呢?一般来说,如果序列变化比较 平缓,平滑系数值应该比较小,比如小于0.l;如果 平缓,平滑系数值应该比较小,比如小于0.l;如果 序列变化比较剧烈,平滑系数值可以取得大一些, 如0.3~0.5。若平滑系数值大于0.5才能跟上序列 0.3~0.5。若平滑系数值大于0.5才能跟上序列 的变化,表明序列有很强的趋势,不能采用一次指 数平滑进行预测。 [例1 [例1]某企业食盐销售量预测。现在拥有最近 连续30个月份的历史资料(见表l 连续30个月份的历史资料(见表l),试预测下一 月份销售量。
时间序列 eviews操作

1.打开EVIEWS新建一个工作文件,步骤如下:
出现如下对话框,选择数据频率为季度,开始日期为1989年1季度,结束日期为2004年4季度,即为工作文件的范围区间。
点击ok生成工作文件
2.若要改变工作文件的范围区间,双击Range,出现如下对话框
3.利用命令series 生成时间序列gdp
点击Edit+/-改变数据的编辑状态,打开EXCEL文件将数据复制粘贴到数据区域,查看数据序列的折线图,步骤如下:
结果:
从图中可看出时间序列有明显的季节波动。
4.对gdp序列进行描述统计分析:
5.对原GDP数据进行季节调整,调整后时间序列存为GDP_SA
6.做出折线图:
由图知序列受季节影响程度变小。
7.进行单位根检验,结果如下:
计算自相关函数和偏相关函数如下:
9.利用方程建立ARMA(3,3)模型
10.建立组,包括gdp gdp_sa dgdp
建组后展示如下:
11.将建组后的收据以EXCEL格式输出:
点击ok即可。
如何用eviews分析时间序列课程

如何用eviews分析时间序列课程时间序列分析是一种常用的数据分析方法,通过对一系列时间上连续测量的数据进行观察、描述和分析,可以发现其中的规律和趋势,从而预测未来的发展走势。
Eviews是一种专业的时间序列分析软件,具有强大的数据处理和统计分析功能。
本文将介绍如何使用Eviews进行时间序列分析。
首先,打开Eviews软件,并导入需要分析的时间序列数据。
在Eviews的工作区中,选择“File”菜单下的“Open”选项,然后选择需要导入的数据文件,点击“Open”按钮导入数据。
导入数据后,可以在Eviews的对象浏览器中看到导入的数据对象。
接下来,对时间序列数据进行初步的观察和描述分析。
在对象浏览器中,选择需要分析的数据对象,右键点击并选择“Open as Group”选项,将数据对象打开为一个分析组。
然后,在Eviews的对象浏览器中,选择分析组,在右侧窗口中可以看到该组中包含的所有时间序列数据。
可以通过列出每个时间序列的统计概要、绘制时间序列图、查看自相关和偏自相关等方式对数据进行初步的观察和描述分析。
接下来,进行时间序列模型的构建和估计。
在Eviews的操作菜单中,选择“Quick”菜单下的“Estimate Equation”选项,打开方程估计窗口。
在方程估计窗口中,选择需要构建的时间序列模型类型,如AR、MA、ARMA等。
然后,在“Dependent Variable”栏目中选择需要分析的时间序列数据,将其作为因变量。
在“Independent Variables”栏目中选择需要作为自变量的时间序列数据,可以根据需求选择多个自变量。
点击“OK”按钮,Eviews将根据所选择的时间序列模型类型和数据进行模型的估计。
估计完成后,可以查看估计结果。
在方程估计窗口中,可以看到估计结果的统计指标、系数估计值、显著性水平等信息。
可以根据需要查看和分析各个系数的显著性水平、置信区间等信息,判断模型的有效性和可靠性。
Eviews案例解析
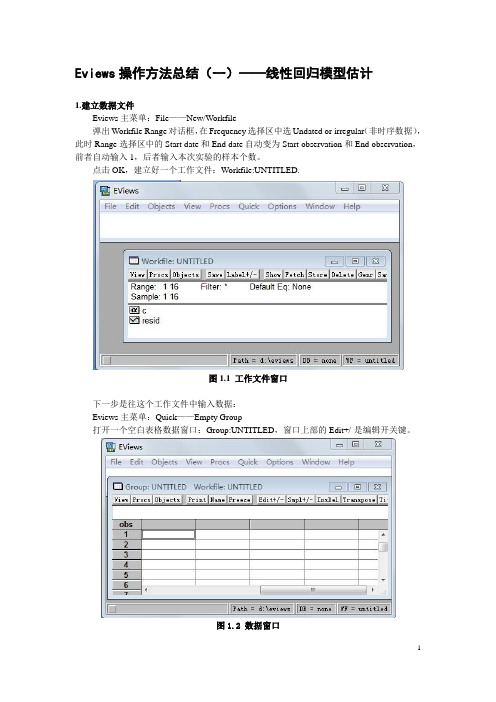
Eviews操作方法总结(一)——线性回归模型估计1.建立数据文件Eviews主菜单:File——New/Workfile弹出Workfile Range对话框,在Frequency选择区中选Undated or irregular(非时序数据),此时Range选择区中的Start date和End date自动变为Start observation和End observation,前者自动输入1,后者输入本次实验的样本个数。
点击OK,建立好一个工作文件:Workfile:UNTITLED.图1.1 工作文件窗口下一步是往这个工作文件中输入数据:Eviews主菜单:Quick——Empty Group打开一个空白表格数据窗口:Group:UNTITLED,窗口上部的Edit+/-是编辑开关键。
图1.2 数据窗口数据表的一行表示一个样本,一列代表一个变量,一般把被解释变量(如Y)放在第一列。
例子:图1.3 数据编辑状态2.画散点图Eviews主菜单:Quick——Graph/Scatter弹出Series List对话框,要求输入画图所用的变量名,对3.1以上版本,应先输入解释变量名,后输入被解释变量名,中间用空格隔开。
图1.4 作图变量输入窗口点OK,得散点图:图1.5 散点图3.OLS(普通最小二乘法)估计,以及线性回归模型的建立与检验Eviews主菜单:Quick——Estimate Equation弹出Equation Specification(方程设定)对话框,依次输入被解释变量Y,系数C(实际的方程中应该包括截距项和斜率项,而软件默认该变量的输出结果为截距项),解释变量X,中间用空格隔开。
在Estimation Setting(估计设定)选择框中,Method框选择LS-Least Squares(NLS and ARMA),Sample框默认为1 16(即样本个数)。
图1.6 方程设定窗口点OK,得方程的估计结果输出表:图1.7 估计结果输出表窗口对应的回归表达式:y i=−0.762928+0.40428x i(-0.624856)(12.11266)R2=0.91289, S.E.=2.036319 上式还可以从图1.7的V iew——Presentation得到:图1.8 回归方程窗口按Stats键可以还原回图1.7的估计结果输出表,按Estimate键可以随时改变估计模型的数学形式、样本范围和估计方法。
eviews时间序列分析

方差分解
❖ 利用VAR模型,还可以进行方差分解研究模 型的动态特征。其主要思想是,把系统中每 个内生变量(m)的波动按其成因分解为与 各方程新息相关联的m个组成部分,从而了 解各新息对模型内生变量的相对重要性。
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。21. 11.1821.11.18Thursday, November 18, 2021
❖ 例3 下面以1949 ~2001年中国人口时间序列 数据(case42)为例介绍: (1)时间序列图; (2)求 中国人口序列的相关图和偏相关图,识别模 型形式; (3)估计时间序列模型; (4)样本外预 测。
❖ 1、画时间序列图
❖ 点击View键,选择Graph/Line功能
❖ 从人口序列y的变化特征看,这是一个非平 稳序列。
yt c t yt1 j yt j t j 1
❖ PP检验
❖ 例1:661天的深证成指(SZ)序列见case37。
❖ 初步选择①ADF检验,②对原序列sz,做单 位根检验,③检验式中不包括趋势项,但包 括截距项。
❖ 因为常数项没有显著性。从检验式中去掉截 距项,继续迸行单位根检验。
第三节 模型的预测
❖ 比如用估计的模型Dyt = 0. 0547 + 0. 6171 Dy t- 1+ vt预测2001年的中国总人口,在窗口 中点击forecast键,弹出对话窗口。在S. E. (optional)选择区填入yfse,把Forecast sample (预测样本区间)改为2001 ~2001,预 测方法(Method)选静态预测(Static)
❖ 输出结果由两部分组成。左半部分是序列的
用EVIEWS处理时间序列分析

应用时间序列分析实验手册目录目录 (2)第二章时间序列的预处理 (3)一、平稳性检验 (3)二、纯随机性检验 (9)第三章平稳时间序列建模实验教程 (10)一、模型识别 (10)二、模型参数估计(如何判断拟合的模型以及结果写法) (14)三、模型的显著性检验 (17)四、模型优化 (18)第四章非平稳时间序列的确定性分析 (19)一、趋势分析 (19)二、季节效应分析 (34)三、综合分析 (38)第五章非平稳序列的随机分析 (44)一、差分法提取确定性信息 (44)二、ARIMA模型 (57)三、季节模型 (62)第二章时间序列的预处理一、平稳性检验时序图检验和自相关图检验(一)时序图检验根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界、无明显趋势及周期特征例2.1检验1964年——1999年中国纱年产量序列的平稳性1.在Eviews软件中打开案例数据图1:打开外来数据图2:打开数据文件夹中案例数据文件夹中数据文件中序列的名称可以在打开的时候输入,或者在打开的数据中输入图3:打开过程中给序列命名图4:打开数据2.绘制时序图可以如下图所示选择序列然后点Quick选择Scatter或者XYline;绘制好后可以双击图片对其进行修饰,如颜色、线条、点等图1:绘制散点图图2:年份和产出的散点图图3:年份和产出的散点图(二)自相关图检验 例2.3导入数据,方式同上;在Quick 菜单下选择自相关图,对Qiwen 原列进行分析;可以看出自相关系数始终在零周围波动,判定该序列为平稳时间序列。
图1:序列的相关分析图2:输入序列名称图2:选择相关分析的对象图3:序列的相关分析结果:1. 可以看出自相关系数始终在零周围波动,判定该序列为平稳时间序列2.看Q统计量的P值:该统计量的原假设为X的1期,2期……k期的自相关系数均等于0,备择假设为自相关系数中至少有一个不等于0,因此如图知,该P值都>5%的显著性水平,所以接受原假设,即序列是纯随机序列,即白噪声序列(因为序列值之间彼此之间没有任何关联,所以说过去的行为对将来的发展没有丝毫影响,因此为纯随机序列,即白噪声序列.) 有的题目平稳性描述可以模仿书本33页最后一段.(三)平稳性检验还可以用:单位根检验:ADF,PP检验等;非参数检验:游程检验图1:序列的单位根检验表示不包含截距项图2:单位根检验的方法选择图3:ADF检验的结果:如图,单位根统计量ADF=-0.016384都大于EVIEWS给出的显著性水平1%-10%的ADF临界值,所以接受原假设,该序列是非平稳的。
精选EVIEWS面板数据分析操作教程及实例krn

格兰杰因果检验(因果检验的前提是变量协整)。Eviews好像没有在POOL窗口中提供Granger causality test,如果想对面板数据中的某些合成序列做因果检验的话,不妨先导出相关序列到一个组中(POOL窗口中的Proc/Make Group),再来试试
因果分析
2.099652(0.044)*
Panel rho-Statistic
-3.415758(0.0012)*
Panel PP-Statistic
-5.991403(0.0000)*
Panel ADF-Statistic
-7.835311(0.0000)*
H0: = 1 H1 :(i = )< 1
录入 数据软件操作(EVIEW6.0)方式一 File/New/ Workfile Workfile structure type : Dated-regular frequency Start date 1935 End date 1954 OK Objects/New Object : Type of Object pool OKCross Section Identifiers:_GM _CH _GE _WE _USView/Spreadsheet View:i? m? k? 方式二(方式是否正确,有待考证)File/New/ Workfile Workfile structure type : Balanced Panel Start date 1935 End date 1954 Number of cross 1 OKCross Section Identifiers:_GM _CH _GE _WE _USView/Spreadsheet View:i? m? k?
用EVIEWS处理时间序列分析

应用时间序列分析实验手册AHA12GAGGAGAGGAFFFFAFAF目录目录 (2)第二章时间序列的预处理 (3)一、平稳性检验 (3)二、纯随机性检验 (9)第三章平稳时间序列建模实验教程 (10)一、模型识别 (10)二、模型参数估计(如何判断拟合的模型以及结果写法) (13)三、模型的显著性检验 (17)四、模型优化 (18)第四章非平稳时间序列的确定性分析 (19)一、趋势分析 (19)二、季节效应分析 (34)三、综合分析 (38)第五章非平稳序列的随机分析 (44)一、差分法提取确定性信息 (44)AHA12GAGGAGAGGAFFFFAFAF二、ARIMA模型 (58)三、季节模型 (62)AHA12GAGGAGAGGAFFFFAFAF第二章时间序列的预处理一、平稳性检验时序图检验和自相关图检验(一)时序图检验根据平稳时间序列均值、方差为常数的性质,平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动,而且波动的范围有界、无明显趋势及周期特征例2.1检验1964年——1999年中国纱年产量序列的平稳性1.在Eviews软件中打开案例数据图1:打开外来数据AHA12GAGGAGAGGAFFFFAFAF图2:打开数据文件夹中案例数据文件夹中数据文件中序列的名称可以在打开的时候输入,或者在打开的数据中输入图3:打开过程中给序列命名AHA12GAGGAGAGGAFFFFAFAF图4:打开数据2.绘制时序图可以如下图所示选择序列然后点Quick选择Scatter或者XYline;绘制好后可以双击图片对其进行修饰,如颜色、线条、点等AHA12GAGGAGAGGAFFFFAFAFAHA12GAGGAGAGGAFFFFAFAFAHA12GAGGAGAGGAFFFFAFAF图1:绘制散点图图2:年份和产出的散点图 010020030040050060019601970198019902000YEAR O U T P U T图3:年份和产出的散点图(二)自相关图检验例2.3导入数据,方式同上;在Quick菜单下选择自相关图,对Qiwen原列进行分析;可以看出自相关系数始终在零周围波动,判定该序列为平稳时间序列。
数模之Eviews教程时间序列ARIMA模型

图形表示出:该序列具有相同的均值,但从样本自相关图看,虽然自相关系数缓慢下降到0,但随着时间的推移,则在0附近波动且呈发散趋势。 样本自相关系数显示:r1=0.48,落在了区间[-0.4497, 0.4497]之外,因此在5%的显著性水平上拒绝1的真值为0的假设。 该随机游走序列是非平稳的。
可以看出:k>0时,rk的值确实落在了该区间内,因此可以接受 k(k>0)为0的假设。同样地,从QLB统计量的计算值看,滞后17期的计算值为26.38,未超过5%显著性水平的临界值27.58,因此,可以接受所有的自相关系数k(k>0)都为0的假设。因此,该随机过程是一个平稳过程。
序列Random2是由一随机游走过程 Xt=Xt-1+t生成的一随机游走时间序列样本。其中,第0项取值为0, t是由Random1表示的白噪声。
随机时间序列的计量经济学模型
时间序列的平稳性及其检验随机时间序列分析模型协整分析与误差修正模型
§9.1 时间序列的平稳性及其检验
一、问题的引出:非平稳变量与经典回归模型二、时间序列数据的平稳性三、平稳性的图示判断四、平稳性的单位根检验五、单整、趋势平稳与差分平稳随机过程
一、问题的引出:非平稳变量与经典回归模型
进行回归,如果确实发现=1,就说随机变量Xt有一个单位根。
一般地:
检验一个时间序列Xt的平稳性,可通过检验带有截距项的一阶自回归模型: Xt=+Xt-1+t (*)中的参数是否小于1。
或者:检验其等价形式: Xt=+Xt-1+t (**)中的参数是否小于0 。
(*)式可变形成差分形式: Xt=(-1)Xt-1+ t =Xt-1+ t (**)检验(*)式是否存在单位根=1,也可通过(**)式判断是否有 =0。
利用eviews实现时间序列的平稳性检验与协整检验以及GARCH模型

在对时间序列Y、X1进行回归分析时需要考虑Y与X1之间是否存在某种切实的关系,所以需要进行协整检验。
1.1利用eviews创建时间序列Y、X1 :打开eviews软件点击file-new-workfile,见对话框又三块空白处workfile structure type处又三项选择,分别是非时间序列unstructured/undate,时间序列dated-regular frequency,和不明英语balance panel。
选择时间序列dated-regular frequency。
在date specification中选择年度,半年度或者季度等,和起始时间。
右下角为工作间取名字和页数。
点击ok。
在所创建的workfile中点击object-new object,选择series,以及填写名字如Y,点击OK。
将数据填写入内。
1.2对序列Y进行平稳性检验:此时应对序列数据取对数,取对数的好处在于可将间距很大的数据转换为间距较小的数据。
具体做法是在workfile y的窗口中点击Genr,输入logy=log(y),则生成y的对数序列logy。
再对logy序列进行平稳性检验。
点击view-United root test,test type选择ADF检验,滞后阶数中lag length选择SIC 检验,点击ok得结果如下:Null Hypothesis: LOGY has a unit rootExogenous: ConstantLag Length: 0 (Automatic based on SIC, MAXLAG=1)t-Statistic Prob.*Augmented Dickey-Fuller teststatistic -2.75094601716637 0.0995139988900359Test critical values: 1% level -4.297072756022265% level -3.2126963902622510% level -2.74767611540013当检验值Augmented Dickey-Fuller test statistic的绝对值大于临界值绝对值时,序列为平稳序列。
Eviews时间序列分析实例.

Eviews时间序列分析实例时间序列是市场预测中经常涉及的一类数据形式,本书第七章对它进行了比较详细的介绍。
通过第七章的学习,读者了解了什么是时间序列,并接触到有关时间序列分析方法的原理和一些分析实例。
本节的主要内容是说明如何使用Eviews软件进行分析。
一、指数平滑法实例所谓指数平滑实际就是对历史数据的加权平均。
它可以用于任何一种没有明显函数规律,但确实存在某种前后关联的时间序列的短期预测。
由于其他很多分析方法都不具有这种特点,指数平滑法在时间序列预测中仍然占据着相当重要的位置。
(-)一次指数平滑一次指数平滑又称单指数平滑。
它最突出的优点是方法非常简单,甚至只要样本末期的平滑值,就可以得到预测结果。
一次指数平滑的特点是:能够跟踪数据变化。
这一特点所有指数都具有。
预测过程中添加最新的样本数据后,新数据应取代老数据的地位,老数据会逐渐居于次要的地位,直至被淘汰。
这样,预测值总是反映最新的数据结构。
一次指数平滑有局限性。
第一,预测值不能反映趋势变动、季节波动等有规律的变动;第二,这种方法多适用于短期预测,而不适合作中长期的预测;第三,由于预测值是历史数据的均值,因此与实际序列的变化相比有滞后现象。
指数平滑预测是否理想,很大程度上取决于平滑系数。
Eviews提供两种确定指数平滑系数的方法:自动给定和人工确定。
选择自动给定,系统将按照预测误差平方和最小原则自动确定系数。
如果系数接近1,说明该序列近似纯随机序列,这时最新的观测值就是最理想的预测值。
出于预测的考虑,有时系统给定的系数不是很理想,用户需要自己指定平滑系数值。
平滑系数取什么值比较合适呢?一般来说,如果序列变化比较平缓,平滑系数值应该比较小,比如小于0.l;如果序列变化比较剧烈,平滑系数值可以取得大一些,如0.3~0.5。
若平滑系数值大于0.5才能跟上序列的变化,表明序列有很强的趋势,不能采用一次指数平滑进行预测。
[例1]某企业食盐销售量预测。
现在拥有最近连续30个月份的历史资料(见表l),试预测下一月份销售量。
EVIEWS时间序列实验指导(上机操作说明)

EVIEWS时间序列实验指导(上机操作说明)时间序列分析实验指导42-2-450100150200250NRND数学与统计学院目录实验一 EVIEWS中时间序列相关函数操作···························- 1 - 实验二确定性时间序列建模方法 ····································- 8 - 实验三时间序列随机性和平稳性检验 ···························· - 18 - 实验四时间序列季节性、可逆性检验 ···························· - 21 - 实验五 ARMA模型的建立、识别、检验···························· - 27 - 实验六 ARMA模型的诊断性检验····································· - 30 - 实验七 ARMA模型的预测·············································· - 31 - 实验八复习ARMA建模过程·········································· - 34 - 实验九时间序列非平稳性检验 ····································· - 37 -实验一 EVIEWS中时间序列相关函数操作【实验目的】熟悉Eviews的操作:菜单方式,命令方式;练习并掌握与时间序列分析相关的函数操作。
Eviews作时间序列分析的一个实例

Eviews作时间序列分析的⼀个实例时间序列分析是作时间序列数据预测的⼀个重要部分,由于此次实验室竞赛也⽤到了时间序列分析,就在此说⼀下平稳性分析以及⾮平稳处理的⽅法:1.判断平稳性1.1平稳性的定义(1)严平稳严平稳是⼀种条件⽐较苛刻的平稳性定义,它认为只有当序列所有的统计特性都不会随着时间的推移⽽发⽣变化时,该序列才能被认为平稳。
满⾜如下条件的序列称为严平稳序列:(2)宽平稳宽平稳是使⽤序列的特征统计量来定义的⼀种平稳性。
它认为序列的统计性质主要由它的低阶矩决定,所以只要保证序列低阶矩平稳(⼆阶),就能保证序列的主要性质近似稳定。
满⾜如下条件的序列称为宽平稳序列: 1.2平稳性检验的⽅法 (1)时序图检验: 根据平稳时间序列均值、⽅差为常数的性质,平稳序列的时序图应该显⽰出该序列始终在⼀个常数值附近随机波动,⽽且波动的范围有界、⽆明显趋势及周期特征 (2)⾃相关图检验: 平稳序列通常具有短期相关性。
该性质⽤⾃相关系数来描述就是随着延迟期数的增加,平稳序列的⾃相关系数会很快地衰减向零。
2.时序分析实例 下⾯以国际原油2011年⾄2017年每天国际原油的价格作为时间序列数据进⾏分析2.1时序图检验⾸先需要作出时序图,通过时序图作出⼀个基本的判断。
⽤Eviews作出的时序图如下: 从图中可以看出,该时间序列不是平稳的,接着再⽤⾃相关图进⼀步检验。
2.2⾃相关图检验 作出的⾃相关图如下: ⾃相关系数也并不是很快衰减到0,⽽且图中的prob数值都是⼩于0.05的,更加证实了该序列是⾮平稳的。
接下来对该序列进⾏差分运算(即后项减去前项),差分后的序列的时序图如下: 其⾃相关系数图如下: 此时,可以看出,差分后的序列是平稳的。
Eviews多元时间序列分析案例研究

Eviews多元时间序列分析案例研究介绍本文档旨在通过一个案例研究,展示如何使用Eviews进行多元时间序列分析。
我们将使用Eviews进行数据准备、模型建立以及结果分析。
数据准备首先,我们需要准备用于分析的多元时间序列数据。
数据应包含多个相关变量,以便我们能够观察它们之间的相互影响。
在Eviews中,我们可以导入外部数据或使用内部示例数据。
通过导入外部数据,我们可以使用来自其他来源的实际数据进行分析。
此外,Eviews还提供了一些内置的示例数据集,这些数据集可用于研究和实践分析技术。
模型建立在数据准备完成后,我们可以开始建立多元时间序列的模型。
Eviews提供了各种统计方法和模型选项,可用于分析时间序列数据。
常见的多元时间序列模型包括VAR(向量自回归)模型、VARMA(向量自回归移动平均)模型以及VARX(包含外生变量的向量自回归)模型等。
我们可以根据数据特点和研究目的选择合适的模型,并进行参数估计和模型诊断。
结果分析完成模型估计后,我们可以对结果进行分析和解释。
Eviews提供了丰富的结果输出和图表展示功能,可以直观地展示模型的性质和统计显著性。
我们可以分析模型的系数、残差、拟合优度、滞后阶数选择等指标,评估模型的拟合程度和显著性。
此外,Eviews还支持进行模型对比和冲击响应分析,以更深入地理解多元时间序列数据的动态性质。
总结本文档简要介绍了如何使用Eviews进行多元时间序列分析。
我们从数据准备开始,使用Eviews进行模型建立和结果分析。
通过合理运用Eviews的功能,我们可以有效地研究和理解多元时间序列数据。
请注意,本文档仅为案例研究的简要介绍,具体的步骤和分析方法还需要根据具体情况进行调整和深入研究。
EViews统计分析在计量经济学中的应用--第6章-时间序列模型

1
在图6.9中,有两个选 择:一是针对何种数 据生成相关图,主要 分为原变量(level)、 一阶差分变量(1st difference)及二阶 差分变量(2st difference),这里 选择level;二是确定 相关图的滞后期 (Lags to include), 这里选择36。
15
自相关、偏自相关图
图6.26 图示对话框
2021/2/4
1
30
自相关函K”按钮, 可得自相关 函数和偏自 相关函数, 如图6.27 所示。
图6.27 对数二阶差分自相关函数
2021/2/4
1
31
自相关函数和偏自相关函数
对数二阶差分序列自相关和偏自相关函数,如图 6.27所示,由两部分组成,左半部分为自相关 (Autocorrelation)与偏自相关(Partial Correlation)分析图,右半部分为自相关系数 (AC)、偏自相关系数(PAC)、Q统计量(QStat)与相伴概率(Prob)。由图6.27可知,自 相关和偏自相关函数的峰值同为滞后1期,自相关 函数1阶截尾,偏自相关函数2阶截尾,可初步判 定p=1,2,q=1,即可能适合的模型有 ARMA(2,1),ARMA(1,1),AR(1),AR(2), MA(1)。
2021/2/4
如图6.15所示,单位根检验选项有四个选择 区域: Test type(检验方法):包括6种检验方法, 主要为ADF检验、DF检验、PP检验、KPSS 检验、ERSPO检验及NP检验,系统默认选择 ADF检验; Test for unit in(所检验的序列),有三种 可供选择: ◆Level:表示对水平序列进行单位根检验; ◆1st difference:表示对序列的一阶差分 序列进行单位根检验; ◆2nd difference:表示对序列的二阶差分 序列进行单位根检验;
时间序列分析应用实例(使用Eviews软件实现)

时间序列分析应⽤实例(使⽤Eviews软件实现)引⾔某公司的苹果来货量数据是以时间先后为顺序记录的⼀组数据,从计量经济学的⾓度来分类就是⼀组时间序列数据。
为了提⾼苹果来货量预测的准确度以及预测结果的可信度,下⾯运⽤Eviews软件包(即Econometrics Views 计量经济学软件包)并结合计量经济学的理论知识,选取2017年1⽉⾄2019年4⽉的苹果来货量⽉度数据(事前对原始数据进⾏处理,把数值单位从吨转换为万吨)为样本数据,⽤⼀个时间序列模型来拟合上述样本数据,然后利⽤建⽴好的模型预测苹果未来⼏个⽉的来货量情况,并对预测结果进⾏分析。
1 平稳性检验1.1 初步检验设来货量时间序列为Qt,⾸先观察Qt的折线图,如图1所⽰:图1 Qt的折线图从图1可知,苹果来货量的⽉度数据总体呈下降趋势,并存在季节性因素,进⽽通过序列原⽔平的⾃相关系数图进⼀步探讨序列的平稳性,结果如图2所⽰:图2 Qt的⾃相关系数图从图2可以看到,所有的⾃相关系数(Autocorrelation)均落在2倍标准差之内(垂⽴的两道虚线表⽰2倍标准差),初步判定序列Qt是平稳的。
下⾯运⽤ADF单位根检验法证明序列的平稳性。
1.2 ADF单位根检验假设序列Qt的特征⽅程存在多个特征根,那么序列平稳的条件为所有特征根λi的绝对值均⼩于1,即所有特征根都在单位圆内。
构造该ADF 检验的原假设H0:存在i,使得λi>1,备择假设H1:λ1, λ2, … , λp<1,运⽤Eviews软件对序列Qt的原⽔平进⾏带常数项(Intercept)的ADF检验,采⽤SC准则⾃动选择滞后阶数,检验结果如图3所⽰:图3 ADF检验根据图3的检验结果可知,t统计量(t-Statistic)的伴随概率p为0.00,在显著性⽔平α=0.05下,因此我们有理由拒绝原假设(p<α),说明序列Qt是平稳的。
2 模型识别从图2可知,序列Qt的⾃相关系数(Autocorrelation)和偏⾃相关系数(Partial correlation)均在阶数1处突然衰减为在零附近⼩值波动,因此我们初步选择AR(1)、ARMA(1,1)这两个模型拟合样本数据3 模型参数估计3.1 AR(1)模型的拟合与参数估计设AR(1)模型为:Qt=C + Φ*Qt-1 +εt,其中C为常数项,Φ为待估计的Qt滞后⼀阶的系数,εt为服从均值为零、⽅差为常数正态分布的正态分布(即⽩噪声序列),下⾯运⽤Eviews软件对AR(1)模型的参数采⽤最⼩⼆乘估计法(⽆偏估计)进⾏参数估计,模型估计结果如图4所⽰:图4 AR(1)模型拟合结果根据图4的参数估计结果来看,在显著性⽔平α=0.05下,常数项显著不为零,⽽参数Φ的显著性估计结果并不是太好,另外AR(1)模型的特征⽅程的根(Inverted AR Roots)为-0.16,印证了序列Qt是平稳的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[课程]Eviews时间序列分析实例Eviews时间序列分析实例时间序列是市场预测中经常涉及的一类数据形式,本书第七章对它进行了比较详细的介绍。
通过第七章的学习,读者了解了什么是时间序列,并接触到有关时间序列分析方法的原理和一些分析实例。
本节的主要内容是说明如何使用Eviews软件进行分析。
一、指数平滑法实例所谓指数平滑实际就是对历史数据的加权平均。
它可以用于任何一种没有明显函数规律,但确实存在某种前后关联的时间序列的短期预测。
由于其他很多分析方法都不具有这种特点,指数平滑法在时间序列预测中仍然占据着相当重要的位置。
(,)一次指数平滑一次指数平滑又称单指数平滑。
它最突出的优点是方法非常简单,甚至只要样本末期的平滑值,就可以得到预测结果。
一次指数平滑的特点是:能够跟踪数据变化。
这一特点所有指数都具有。
预测过程中添加最新的样本数据后,新数据应取代老数据的地位,老数据会逐渐居于次要的地位,直至被淘汰。
这样,预测值总是反映最新的数据结构。
一次指数平滑有局限性。
第一,预测值不能反映趋势变动、季节波动等有规律的变动;第二,这种方法多适用于短期预测,而不适合作中长期的预测;第三,由于预测值是历史数据的均值,因此与实际序列的变化相比有滞后现象。
指数平滑预测是否理想,很大程度上取决于平滑系数。
Eviews提供两种确定指数平滑系数的方法:自动给定和人工确定。
选择自动给定,系统将按照预测误差平方和最小原则自动确定系数。
如果系数接近1,说明该序列近似纯随机序列,这时最新的观测值就是最理想的预测值。
出于预测的考虑,有时系统给定的系数不是很理想,用户需要自己指定平滑系数值。
平滑系数取什么值比较合适呢,一般来说,如果序列变化比较平缓,平滑系数值应该比较小,比如小于0.l;如果序列变化比较剧烈,平滑系数值可以取得大一些,如0.3,0.5。
若平滑系数值大于0.5才能跟上序列的变化,表明序列有很强的趋势,不能采用一次指数平滑进行预测。
〔例1〕某企业食盐销售量预测。
现在拥有最近连续30个月份的历史资料(见表l),试预测下一月份销售量。
表1 某企业食盐销售量单位:吨解:使用Eviews对数据进行分析,第一步是建立工作文件和录入数据。
有关操作在本章第一节中已经阐明,这里不再赘述。
假设已经建立工作文件,并生成了一个样本期为l,30的序列,命名为SALES。
序列SALES中包含例1中需要分析的数据。
第二步,绘制序列图形。
在序列对象窗口中,点击View?Line Graph。
屏幕显示图1所示图形。
图1 某企业近30个月的销售量动态图从图1中可以看出,这个企业近30个月的销售量并不存在明显的趋势,并且没有明显的季节趋势。
因此,从直观上判断可以采用一次指数平滑法对企业下个月的销售量进行预测。
第三步,扩大样本期。
本例要求对下一个月的销售量进行预测,而工作文件的样本期是1,30,在Eviews中要求先更改样本期。
更改样本期的操作在本章第一节已经讲过,这里将样本期改为l,31。
第四步,进行指数平滑。
指数平滑的菜单操作方法有两种:一是在主工作文件窗口打开的情况下,点击主窗口的Quick?Series Statistics?Exponential Smoothing;二是在序列对象窗口中点击Procs?Exponential Smoothing。
点击后屏幕出现如图2所示的指数平滑对话框。
指数平滑对话框中包含五个部分的选项:平滑方法(Smoothing Method)、平滑系数(Smoothing Parameters)、平滑后生成序列的名称(Smoothed Series)、预测样本范围(Estimation Sample)和季节变动周期(Cycle for Seasonal)。
对话框左上部分的平滑方法(Smoothing Method)包括:Single 一次指数平滑Double 二次指数平滑Holt,Winters,No seasonal Holt,Winters无季节模型Holt,Winters,Additive Holt,Winters季节迭加模型Holt,Winters,Multiplicative Holt,Winters季节乘积模型平滑系数(Smoothing Parameters)包括Alpha,Beta,Gamma。
平滑系数可由系统自动给定,也可以由用户指定。
缺省状态是由系统自动给定。
如果用户需要指定,只需在对应参数的位置填入指定的数值。
本例中,分别指定Alpha的值为0.3和0.5。
当指定平滑系数为0.3时,预测的残差平方和为137.2978;当平滑系数为0.5时,预测的残差平方和为165.0685。
因此这里选择平滑系数为0.3时的预测结果。
根据一次指数平滑方法的预测,该企业下个月的销售量应为29.2吨。
图2 指数平滑对话框(二)二次指数平滑二次指数平滑又称双重指数平滑。
相对于一次指数平滑,二次指数平滑可以预测有一定线性趋势的序列,其预测期也长一些。
[例2]某公司1990,2001年的实际销售额如表2所示。
请根据此资料预测2002年和2003年企业销售额。
表2 某公司销售额单位:万元解:第一步,建立工作文件,样本期为1990,2001的年度数据。
在新建立的工作文件中,生成一个名为SALES的新序列。
打开SALES序列对话框,将表2中的数据录入。
第二步,绘制序列图形。
从图中可以看到,该企业的销售额存在明显的增长趋势(见图3)。
序列的波动并不是很剧烈。
由此判断,使用二次指数平滑法进行预测比较合适。
第三步,扩大样本期。
由于本例需要预测下两年的销售额,因此将工作文件的样本期更改为1990,2003年。
图3 某企业1990,2001年销售额变动情况第四步,指数平滑。
根据前例中的方法,用户可以进入如图2的指数平滑对话框。
本例中,选择二次指数平滑的方法,并让系统自动确定系数。
结果如表3所示。
原序列SALES中共有12个观测值,即1990,2001年的企业销售额。
在进行二次指数平滑时,系统根据这12个数值自动确定了最优的平滑系数α,0.244。
此时,对序列进行二次指数平滑预测的残差平方和为101.3594,均方根误差为2.906306。
在Eviews给出指数平滑结果统计表(见表3)时,并没有直接给出对2002年和2003年销售额的预测值。
这两个数值保存在系统生成的平滑序列SALESSM中,用户只需打开该序列就可以看到二次指数平滑方法预测的结果。
结果显示,该企业在2002年和2003年的销售额,分别预计为56(6万元和59(4万元。
表3 二次指数平滑结果如果将二次指数平滑的预测结果和原观测值共同显示在同一张图上,可以使用户看起来更清楚。
首先在工作文件菜单中同时选中两个序列SALES和SALESSM,方法是先点击一个序列,之后按住键盘上的Shift键再点击另外一个序列。
然后点击工作文件菜单工具栏中的Show,在弹出的对话框中点击OK。
此时,系统将弹出一个类似序列对象窗口的群窗口(见图4),窗口中以Excel表格的形式同时显示出SALES和SALESSM。
最后点击该窗口上方的View?Graph?Line(见图5)。
图4 群对象窗口图5 实际销售额与平滑值序列对比图二、趋势延伸法实例时间序列的趋势即序列随时间变化的基本规律和特点。
对于存在趋势的序列,通常可以选取适当的模型进行分析和预测。
(,)直线趋势直线趋势模型是一种最常用,也是最成熟的方法。
模型的基本结构为:Yt,a,bt式中,a,b是模型的参数。
这种模型的结构比较简单,估计方法非常成熟,是很多其他趋势模型估计的基础。
下面结合实例说明如何使用该软件进行直线趋势模型的预测。
[例3]设某市1992,2002年市场鸡蛋销售量如表4所示。
试预测2003年该市鸡蛋销售量。
表4 某市鸡蛋销售量单位:万千克解:第一步,建立一个新的工作文档,文档的样本期为1992,2002年。
生成序列SALES,录入表4中的销售量观测值。
第二步,打开SALES序列对象窗口,点击View?Line Graph,绘制序列散点图(见图6)。
图6 序列散点图Eviews中没有直接绘制散点图的菜单选项。
当需要绘制散点图时,首先需要绘制连线图(Line Graph)。
屏幕显示图形对象窗口后,用鼠标左键双击图形的任意位置,或者点击右键,然后在弹出的菜单中选择Options。
此时,系统将弹出图形属性对话框。
图形属性对话框中的选项很多。
用户在这里可以方便地更改图形的类型(Graph Type)、图形的属性(Graph Attitude)、线形图格式见(Line Graph)、条形图格式(Bar Graph)等。
这里,将图形的类型选择为线形图(Line Graph),再在线形图格式中选择仅有标示(Symba1s Only)。
点击OK。
从散点图上可以看出,该序列基本呈现出一种直线增长的趋势,因而宜采用直线趋势延伸的方法进行预测。
第三步,生成时间变量T。
在进行模型参数的估计时通常要用到最小二乘的方法,其中,观测值就是因变量,序列T就是自变量。
生成一个新序列的方法有很多,可以通过菜单操作,也可以直接在主窗口中输入命令行实现。
有关菜单操作的方法在本章第一节中已经说明,这里采用命令行的形式生成序列T。
Eviews生成序列的命令为data,用户只需在主窗口中输入命令:data T。
对于序列T,用户可以在打开的对象窗口中为它赋值,比如赋值1,2,3,…如果用户需要直接生成含有值的序列T,也可以利用函数生成序列,在主窗口中输入命令行(见图7)。
图7 T序列生成命令和取值情况节略genr T=,trend系统自动生成序列T,并从0开始计数,它的取值依次为0,l,2,3,…第四步,模型估计。
在Eviews中最小二乘回归的命令是LS,它的基本书写格式为:LS 因变量 C 自变量其中,C代表模型中的常数项,对于没有常数项的模型可以不写。
本例中,使用下面的命令进行回归: LS SALES C T(见表5)。
表5 最小二乘回归结果根据表5的结果,得到如下模型:sale,31.227,2.391×T第五步,进行预测。
根据上述模型结果,可以很容易地给出2003年鸡蛋销售量的预测结果。
将T,11代入上述模型,计算结果表明该企业2003年的鸡蛋销售额为57.5万元。
(二)曲线趋势经济序列中有很多呈现出曲线变化的趋势。
直线趋势的估计比较简单,曲线趋势的估计则更为常用。
指数曲线、二次曲线、三次曲线和龚拍兹曲线是在市场经济序列中常见的模型,它们的估计也大同小异,这里就以指数曲线为例介绍如何使用Eviews进行模型的估计。
〔例4〕某市近9年灯具商品销售量资料如表6所示。
试预测2002年的销售量。
解:第一步,建立一个新的工作文档,文档的样本期为1993,2001年。
